
 В 4 классе во втором полугодии, все также изучают математику, предмет этот важный и основной в процессе обучения. Это значит что есть только один способ "победить" его, - начать его изучать, понимать и решать! Только в этом случае он не будет доставлять вам проблем. Если же у вас по каким-либо причинам возникают недопонимания по математике, то тут уж без подсказки и нашей помощи не обойтись. Собственно такую помощь мы и хотели вам предложить в этой статье.
В 4 классе во втором полугодии, все также изучают математику, предмет этот важный и основной в процессе обучения. Это значит что есть только один способ "победить" его, - начать его изучать, понимать и решать! Только в этом случае он не будет доставлять вам проблем. Если же у вас по каким-либо причинам возникают недопонимания по математике, то тут уж без подсказки и нашей помощи не обойтись. Собственно такую помощь мы и хотели вам предложить в этой статье.
Здесь можно будет найти ответы, так называемые среди школьников ГДЗ к учебнику математики за 4 класс, 2 части по программе "Перспективная начальная школа" автора Чекина. Мы бы вам рекомендовали использовать эти ответы не для списывания, а именно для самоконтроля, то есть для сверки и не более. Это будет более правильно и вам полезнее.
Пару слов о том, как пользоваться материалом для проверки. Перелистывайте вкладки-странички, чтобы найти нужную вам страницу с ответами. После смотрим нужное вам упражнение, вот и все!
Ответы к части 2 учебника математики за 4 класс, Чекин:
Что же, хватит вам объяснять, сейчас вы все поймете и без нас... Если же нет, то задавайте свои вопросы в комментариях, мы ответим на них!
Стр. 7
-
Ответы к странице учебника 7. Деление на однозначное число столбиком
1. Выполни деление числа 59 на число 7 столбиком. Будет ли число 56 наибольшим числом, которое делится нацело на число 7 и не превосходит число 59?
— 59 |7
56 |8
3 — ост.
Да, 56 : 7 = 8 и не превосходит 59.2. Запиши в порядке возрастания все числа, при делении каждого из которых на число 7 в неполном частном получается число 8.
57 : 7 = 8 (ост. 1)
58 : 7 = 8 (ост. 2)
59 : 7 = 8 (ост. 3)
60 : 7 = 8 (ост. 4)
61 : 7 = 8 (ост. 5)
62 : 7 = 8 (ост. 6)3. Какой наибольший остаток может получиться при делении на число 7? Найди наибольшее число, которое при делении на число 7 даёт в неполном частном однозначное число.
Остаток не может быть больше или равен делителю. Следовательно, если делитель 7, то наибольший остаток 6.
Наибольшее однозначное число в неполном частном — это 9. Наибольший остаток при делении на 7 — это 6. Тогда: 7 • 9 + 6 = 69 — наибольшее число, которое при делении на 7 даёт однозначное неполное частное.4. Рассмотри следующие записи деления:
69 : 7 = 9 (ост. 6) 699 : 7 = 99 (ост. 6)
70 : 7 = 10 700 : 7 = 100
Можно ли сказать, что число 70 — это наименьшее число, которое в результате деления на число 7 даёт двузначное число? Почему?
Почему 699 — это наибольшее число, которое в результате деления на число 7 даёт двузначное число?Можно, поскольку предыдущее число 69, как видно из записи, при делении на 7 даёт в результате деления однозначное число.
Потому, что последующее число 700, как видно из записи, при делении на 7 даёт в результате деления трёхзначное число.5. Выполни деление столбиком на число 7 каждого из следующих чисел: 63, 77, 210, 357, 693. Назови те случаи, в которых сначала вычисляется число десятков, а потом число единиц искомого результата. Какое наименьшее число десятков должно быть в делимом, чтобы при делении на число 7 полученный результат содержал разряд десятков?
_63 |7 _77 |7
63 |9 7 |11
0 _7
7
0
_210 |7 _357 |7
21 |30 35 |51
0 _ 7
7
0
_693 |7
63 |99
_ 63
63
0
77 : 7 = 11 — один десяток
210 : 7 = 30 — три десятка
357 : 7 = 51- пять десятков
693 : 7 = 99 — девять десятков
Наименьшее число десятков, как видно из первых двух примеров деления столбиком, должно быть семь. 8
-
Ответы к странице учебника 8
6. Назови старший разряд в числе 699. Какое наименьшее число сотен должно быть в делимом, чтобы при делении на число 7 полученный результат содержал разряд сотен?
Сколько сотен в числе 699? Сколько цифр, считая слева направо, нужно отделить дугой сверху в записи числа 699, чтобы показать число сотен в этом числе? Сравни число сотен в числе 699 с делителем — числом 7.
Если разделить число 699 на число 7, то будет ли полученное неполное частное иметь разряд сотен? Почему?Старший разряд в числе 699 — разряд сотен. В делимом должно быть 7 сотен — это наименьшее число сотен.
В числе 699 6 сотен. Нужно отделить дугой одну цифру — цифру 6. Число сотен в числе 699 — 6, оно меньше делителя 7.
Не будет, поскольку число сотен 6 меньше делителя 7 и результат деления начинается с разряда десятков.7. В числе 699 имеется 69 десятков. Отдели в записи числа 699, считая слева направо, дугой сверху такое количество цифр, которое покажет имеющееся число десятков.
Будет ли это число больше делителя, которым является число 7? Раздели 69 десятков на число 7 с остатком. Сколько десятков будет в неполном частном? Сколько десятков мы разделили полностью на 7 равных частей и сколько десятков ещё осталось?
После деления десятков числа 699 на число 7 осталось ещё 6 десятков, а также 9 единиц исходного числа, то есть 69 единиц. Выполни деление оставшегося числа единиц на число 7.
Какую цифру нужно записать в разряд единиц неполного частного и сколько единиц ещё остаётся в остатке?
Сделай запись деления с остатком числа 699 на число 7 столбиком.699 — имеющееся число десятков 69.
Число десятков 69 больше делителя 7. 69 : 7 = 9 (ост. 6). В неполном частном 9 десятков. Полностью на 7 равных частей мы разделили 63 десятка (7 • 9 = 63) и осталось ещё 6 десятков (69 — 63 = 9).
69 : 7 = 9 (ост. 6).
В разряд единиц неполного частного надо записать 9 и останется ещё 6 единиц в остатке.
— 699 |7
63 |99
_ 69
63
6 — ост. 9
-
Ответы к странице учебника 9
8. Рассмотри запись деления с остатком числа 715 на число 8 столбиком и определи, во сколько этапов выполнено это деление. Делимое на первом этапе деления 71 десяток. Назовём его ПЕРВЫМ ПРОМЕЖУТОЧНЫМ ДЕЛИМЫМ. Какое неполное частное и какой остаток получаются на первом этапе?
Делимое на втором этапе — 75 единиц. Это ВТОРОЕ ПРОМЕЖУТОЧНОЕ ДЕЛИМОЕ. Как оно получено? Какое неполное частное и какой остаток получаются на втором этапе? Назови окончательный результат деления с остатком.
— 715 |8
64 |89
_ 75
72
3 — остатокДеление проходит в 2 этапа. На первом этапе получается неполное частное 8 десятков и остаток 7 десятков.
На втором этапе деления к остатку 7 десятков приписали оставшееся число из разряда единиц — получили 75. При делении на втором этапе неполное частное равно 9 единиц, а остаток — 3 единицы. Окончательный результат — частное 89, остаток — 3.9. Выполни деление с остатком столбиком числа 653 на число 9 в два этапа, показав первое неполное делимое с помощью дуги. Сколько промежуточных делимых у тебя получилось?
_653 |9
63 |72
_ 23
18
5 — ост.
Получилось 2 промежуточных делимых: 65 десятков и 23 единицы.10. Выполни деление с остатком столбиком числа 957 на число 4 в три этапа показав первое промежуточное делимое с помощью знака ?.
— 957 |4
8 |238
_ 15
12
_ 37
32
5 — ост.
Первое промежуточное делимое 9 сотен, второе — 15 десятков, третье — 37 единиц.11. Выполни деление с остатком столбиком для следующих пар чисел: 359 и 6, 423 и 8, 856 и 3, 995 и 4, показав первое промежуточное делимое.
— 359 |6 — 423|8
30 |59 40 |52
_ 59 _ 23
54 16
5 — ост. 7 — ост.
— 856 |3 — 995|4
6 |285 8 |248
_ 25 _ 19
24 16
_ 16 _ 35
15 32
1 — ост. 3 — ост.12. Какое неполное частное получается в тех случаях, когда делимое меньше делителя? Выполни деление с остатком в строчку числа 3 на число 7.
Неполное частное равно 0, а остаток равен делимому.
3 : 7 = 0 (ост. 3) 10
-
Ответы к странице учебника 10
13. Рассмотри запись деления числа 283 на число 7 столбиком.
— 283 |7
28 |40
_ 3
0
3 — остаток
Назови второе промежуточное делимое. Сравни его с делителем. Какую цифру в таком случае пишут в неполном частном?Второе промежуточное делимое — 3 единицы. Это делимое меньше делителя: 3 < 7. В таком случае в неполном частном пишут цифру 0.
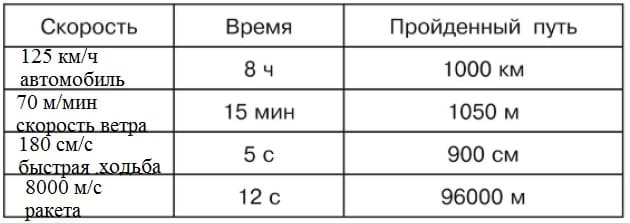
14. Выполни деление столбиком для следующих пар чисел.
382 и 6 564 и 9 797 и 7 898 и 9— 382 |6 — 564 |9
36 |63 54 |62
_ 22 _ 24
18 18
4 — ост. 6 — ост.
— 797 |7 — 898 |9
7 |113 81 |99
_ 9 _ 88
7 81
_ 27 7 — ост.
21
6 — ост.15. Реши задачу. Вычисли и запиши ответ.
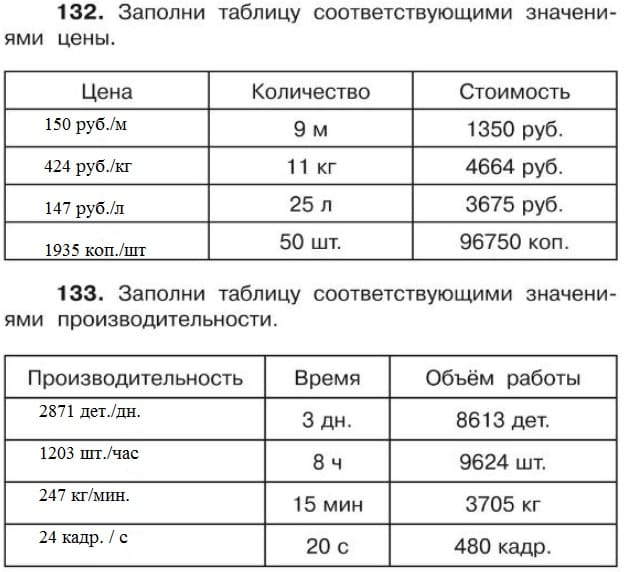
В одном рулоне было 351 м ткани, что в 3 раза больше, чем в другом.
Сколько метров ткани в двух этих рулонах?1) 351 : 3 = 117 (м) — во втором рулоне
2) 351 + 117 = 468 (м)
Ответ: в двух рулонах 468 м ткани.16. Вычисли периметр прямоугольника, у которого длина одной стороны 438 см, а длина другой стороны в 6 раз меньше.
1) 438 : 6 = 73 (см) — ширина
2) (438 + 73) • 2 = 1022 (см)
Ответ: периметр 1022 см.17. Вычисли площадь прямоугольника, у которого длина одной стороны 455 мм, что в 7 раз больше длины другой стороны.
1) 455 : 7 = 65 (см) — ширина
2) 455 • 65 = 29575 (кв.см)
Ответ: площадь 29575 кв.см.18. Вычисли площадь треугольника, если она в 9 раз меньше, чем площадь квадрата с длиной стороны 12 см.
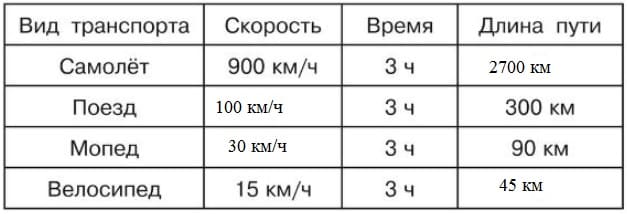
1) 12 • 12 = 144 (кв.см) — площадь квадрата
2) 144 : 9 = 16 (кв.см) — площадь треугольника
Ответ: площадь 16 кв.см. 11
-
Ответы к странице учебника 11 Число цифр в записи неполного частного
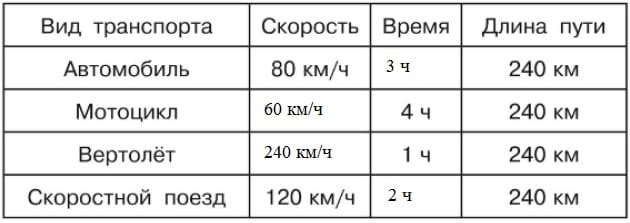
19. Если при делении одного числа на другое первое промежуточное 28 сотен, то какой разряд будет старшим в неполном частном?
Сотни.
Назови все разряды неполного частного. Сколько цифр будет в записи этого неполного частного?
Сотни, десятки, единицы. Будет три цифры.
20. Из данных случаев деления выпиши только те, в которых первое промежуточное делимое выражает число десятков.
487 : 8 =
254 : 6 =
83 : 7 =
94 : 6 =
В неполном частном будет во всех случаях по 2 цифры.21. В каждой записи деления столбиком определи старший разряд неполного частного
569/7 - десятки
862/6 - сотни
1458/5 - сотни
9253/8 - тысячи
51/4 - десятки
569I 7
I ..
862I 6
I ...
1458I 5
I ...
9253I 8
I ....
51I 4
I .. 12
-
Ответы к странице учебника 12
22. Какая цифра пропущена в числе *57, если известно, что при делении этого числа на число 9 получается трехзначное неполное частное?
Это может быть только цифра 9.
23. Какая цифра пропущена в записи четырехзначного числа *561, если при делении этого числа на 2 получается трехзначное неполное частное? Раздели найденное четырехзначное число на число 2.
Это цифра 1, то есть число 1561
-1561I 2
14 I 780 (остаток 1)
-16
16
024. Запиши пять трехзначных чисел, каждое из которых при делении на число 7 дает трехзначное неполное частное.
1055
955
855
1255
115625. Запиши пять трехзначных чисел, каждое из которых при делении на число 7 дает двухзначное неполное частное.
655
451
355
255
15526. Может ли при делении трехзначного числа на однозначное получиться однозначное неполное частное?
Нет, так как в любое трехзначное нельзя взять даже один раз из однозначного.
27. Запиши пять четырехзначных чисел, каждое из которых при делении на число 23 дает трехзначное неполное частное.
2488
2588
2688
3088
408828. Запиши пять четырехзначных чисел, каждое из которых при делении на число 23 дает двузначное неполное частное
2211
2011
1911
1511
111129. Может ли при делении четырехзначного числа на двухзначное получиться однозначное неполное частное? А четырехзначное неполное частное? Почему?
При делении на 2-значное 4-pначного получиться однозначное не может. Так как в 2-значном нет даже одного 4-значного.
Четырехзначное тоже не может получиться, так как числа с одинаковыми разрядами не больше одно другого даже в 10 раз, а четырехзначное число подразумевает разницу в 1000 раз. 13
-
Ответы к странице учебника 13
30. Предлагается найти методом подбора наибольшее число, которое при умножении на число 23 дает в результате число, не превосходящее число 117. Искомым числом будет число 5. Такое число можно считать неполным частным.
-117I 23
115 I5 (остаток 2)
2Решение:
Для его нахождения достаточно умножать последовательно число 23 на числа 1, 2, 3, 4, … до тех пор, пока не получится число, которое больше, чем число 117. В этом случае процесс умножения нужно прекратить, а в качестве ответа взять число, на которое умножали число 23 не в последнем, а в предпоследнем случае. При этом умножение в тех случаях, когда результат будет заведомо меньше числа 117, можно и не проводить. К таким случаям явно относятся случаи умножения на числа 1, 2 и 3. После того как будет найдено интересующее нас число (число 5), нужно очень обстоятельно поработать со второй частью задания.
Именно эта часть несет основную смысловую нагрузку. Отвечая на поставленные вопросы, учащиеся должны для себя четко уяснить, что описанным выше способом они искали не просто наибольшее число, которое при умножении на число 23 дает в результате число, не превосходящее число 117, а по существу искали неполное частное при делении числа 117 на число 23. Таким образом, учащиеся познакомились с одним из способов подбора однозначного неполного частного, который можно применять при выполнении
деления столбиком.31. Делаем вычисление столбиком.
-67I 17
51I 3 (остаток 16)
16
189:21=9, - В этом делении частное полное, без остатка. (не записываем!!!)
-79I 15
75I 5 (остаток 4)
4
-365I 44
352I 8 (остаток 13)
13
-58I 11
55I 5 (остаток 3)
332. Рассмотрим умножение.
17*2=34
17*4=68
17*6=102
17*8=136При умножении числа 17 последовательно на четные однозначные числа впервые получается число, которое больше числа 89, в случае, когда число 17 умножают на число 6. После этого нужно умножить число 17 на предшествующее число (5) и сравнить полученный результат (85) с делимым (89). Так как этот результат меньше, чем делимое (85 < 89), то искомым неполным частным будет число 5.Если бы он оказался больше, чем делимое, то искомым неполным частным было бы число
4.
-89I 17
85I 5 (остаток 4)
433. Находим неполное частное при делении 110 на 18
-110I 18
108I 6 (остаток 2)
2 14
-
Ответы к странице учебника 14
34.
При решении данной задачи эти рассуждения выглядят так:
первый раз при заполнении таблицы слева направо число, которое больше числа 79, встречается как значение произведения 16•6 (96 > 79). Это означает, что на роль искомого неполного частного может претендовать либо число 4, либо число 5. Осуществим проверку для числа 4, вычисляя предполагаемый остаток (79 – 64 = 15). Так как полученный остаток (15) оказался меньше делителя (16), то число 4 и является искомым неполным частным. Если бы этот предполагаемый остаток был бы больше или равен делителю, то в качестве искомого неполного частного нужно было бы взять число 5, так как число 4 на эту роль не подходило бы в силу нарушения правила, связывающего остаток и делитель.n 2 4 6 8 16*n 32 64 96 128 -79I 16
64I 4 (остаток 15)
15.35. Проверяем сколько раз можно вычесть 16 из 79
-79
16
-63
16
-47
16
- 31
16
1536. Выполняем деление столиком
-98I 17
85I 5 (остаток 13)
13
-156I 47
141 I3 (остаток 15)
15
-253I 51
204I 4 (остаток 49)
49
-347I 72
288 I 4 (остаток 59)
5937. Решаем задачу. Какое наибольшее число наборов по 12 тарелок можно составить из 155 тарелок?
-155I 12
144I 12 (остаток 11)
11
Ответ: 12 наборов по 12 тарелок можно составить из 155 тарелок. 15
-
Ответы к странице учебника 15
38. Выполни деление.
-2536I 5
25 I507 (остаток 1)
-36
35
1Ответы на вопросы:
Выделить дугой первые две цифры в записи делимого и рассмотреть соответствующее двузначное число. Так как первое промежуточное делимое выражает число сотен(25 сотен), то запись неполного частного будет состоять из трех цифр. Нужно найти результат деления первого промежуточного делимого (25) на делитель (5) и записать соответствующую этому результату цифру (5) в старший разряд искомого неполного частного. Если не в последнем промежуточном делении остаток получился равным 0, то его записывать не нужно (в данном примере имеет место именно такая ситуация).Запись следующего промежуточного делимого получается с помощью приписывания к записи остатка, полученного на предыдущем этапе деления (если он не равен 0), первой из оставшихся незадействованных цифр делимого. Если остаток равен 0, то записывают только соответствующую цифру делимого.
Следующую цифру в записи неполного частного определяет результат деления соответствующего промежуточного делимого на делитель. Если промежуточное делимое меньше делителя, то в неполном частном на соответствующем месте нужно писать цифру 0. Процесс деления нужно заканчивать тогда, когда будет выполнено деление последнего промежуточного делимого.Остаток, который получается при делении последнего промежуточного делимого на делитель, и будет являться окончательным остатком.39.
Переписываем в тетрадm деление столбиком 3579 на 17.
16
-
Ответы к странице учебника 16
40. Является продолжением предыдущего задания. По существу эти два задания должны рассматриваться как одно, но по чисто технической причине, связанной с расположением текста задания на разных сторонах листа учебника, оно разбито на два отдельных задания. Иначе учащимся было бы трудно с ним работать.
Итак, в задании 40 учащимся предлагается система вопросов, которая аналогична системе вопросов из задания 38, но теперь речь идет о случае деления с остатком столбиком на двузначное число. При этом соответствующая запись деления дана учащимся в готовом виде, и она уже перенесена ими в тетрадь. Что касается ответов на поставленные вопросы, то они должны практически полностью повторять ответы, сформулированные при выполнении задания 38. Выделить дугой первые две цифры в записи делимого и рассмотреть соответствующее двузначное число. Так как первое промежуточное делимое выражает число сотен (35 сотен), то запись неполного частного будет состоять из трех цифр. Нужно найти результат деления первого промежуточного делимого (35) на делитель (17) и записать соответствующую этому результату цифру (2) в старший разряд искомого неполного частного. Запись каждого следующего промежуточного делимого получается с помощью приписывания к записи остатка, полученного на предыдущем этапе деления (если он не равен 0) первой из оставшихся незадействованных цифр делимого. Если остаток равен 0, то записывают только соответствующую цифру делимого.Каждую следующую цифру в записи неполного частного определяет результат деления соответствующего промежуточного делимого на делитель.
Если промежуточное делимое меньше делителя, то в неполном частном на соответствующем месте нужно писать цифру 0. Процесс деления нужно заканчивать тогда, когда будет выполнено деление последнего промежуточного делимого. Остаток, который получается при делении последнего промежуточного делимого на делитель, и будет являться окончательным остатком.
41. Учащимся предлагается сформулировать алгоритм деления столбиком, ответив на вопросы и опираясь на пример. Данный пример был подобран таким образом, чтобы обратить внимание учащихся на промежуточные этапы деления, в которых появляется число 0 либо в качестве остатка (второй этап), либо в качестве промежуточного неполного частного (третий этап). Особое внимание к таким ситуациям продиктовано тем, что именно там, где должно появиться число 0 в процессе деления, учащиеся и совершают наибольшее число ошибок.
17
-
Ответы к странице учебника 17
42. Делим столбиком.
-24368I 6
24 I 4061 (остаток 2)
-36
36
-8
6
2
-56928I 15
45 I 3728 (остаток 8)
-119
105
-42
30
128
120
8
-87693I 3
6 I 29231 (остаток 0)
-27
27
-6
6
-9
9
-3
3
0
-36429I 24
24 I 1517 (остаток 21)
-124
120
-42
24
-189
168
21
-386592I 8
32 I 48324
-66
64
-25
24
-19
16
-32
32
0
-169834I 31
155 I 5478 (остаток 16)
-148
124
-243
217
-264
248
1643. Решаем задачу. В двух рулонах было 864 м пленки. Сколько пленки было в каждом рулоне, если в одном в 7 раз больше, чем в другом?
1)
-864I 8
8 I 18 (м) - в одном рулоне.
-64
64
0
2) 864 - 18 = 846 (м) - во втором рулоне.
Ответ: 18 метров пленки в одном рулоне и 846 метров во втором. 18
-
Ответы к странице учебника 18
44. Сравниваем две записи.
Записи различаются подробностью их записи. Первая из записей является полной, а вторая – сокращенной. При этом обязательно нужно обратить внимание учащихся на тот факт, что сокращается в записи этап, в котором требуется разделить меньшее число (27) на большее число (28), что приводит к появлению 0 в записи неполного частного.
45. Предлагается распознать сокращенные формы записи. Сделать это учащиеся могут, проанализировав каждый этап деления в каждой записи: если на каком-то этапе нужно делить
меньшее число на большее (в записи неполного частного появляется цифра 0), а процедура вычисления остатка с помощью вычитания в этом случае отсутствует, то это и означает, что использован
сокращенный вариант записи.Все записи сокращенные. Переписываем их в полные.
-5320I 17
51 I 312
-22
17
-50
34
-16
0
16
-5150I 17
51 I302
-50
34
-16
0
16
-5260I 17
51 I309
-160
153
-7
0
7 19
-
Ответы к странице учебника 19
46. Деление.
-2435I 8
24 I 304 (остаток 3)
- 35
32
-3
0
347. Делим. Будет 3 цифры.
-962I 3
9 I320 (остаток 2)
-6
6
-2
0
248. Делим.
Вначале сокращенно
-4925I 16
48 I 307 (остаток 13)
- 125
112
13Полная запись
-4925I 16
48 I 307 (остаток 13)
- 125
112
-13
0
1349. Точками показано количество цифр для НЕПОЛНЫХ частных.
-2135I 7
21 I 305
- 35
35
0
-2175I 7
21 I*** (остаток 5); ***-310
- 7
7
-5
0
5
-6045I 15
60 I 403
- 45
45
0
-6155I 15
60 I*** (остаток 10); ***-403
- 55
45
1050. Восстанавливаем цифры.
-36752I 24
24 I 3531 (остаток 12)
-127
120
-75
72
-32
24
12 20
-
Ответы к странице учебника 20
51. Смотрим рисунок.

52. Восстанавливаем запись деления столбиком.
-361286I 7
35 I 51612
- 11
7
-42
42
- 8
7
-16
16
0
-25687I 43
215 I 597 (остаток 16)
- 418
387
-317
301
16
-892347I 23
69 I 38797 (остаток 16);
-202
184
-183
161
-224
207
-177
161
1653. Устно сделай прикидку.
145 на 6 - частное 2 цифры
145 на 21 - частное 2 цифры
896 на 5 - частное 3 цифры
4568 на 15 - частное 3 цифры.
-145I 6
12 I 24 (остаток 1)
- 25
24
1
-145I 12
12 I 12 (остаток 1)
- 25
24
1
-896I 5
5 I 179 (остаток 1)
-39
35
-46
45
1
-4568I 15
45 I 304 (остаток 8)
- 68
60
854. Реши задачу. В зрительном зале учащиеся расставили 625 стульев по 25 стульев в ряд. Сколько рядов получилось?
-625I 25
50 I 26
-125
125
0
Ответ: 26 рядов по 25 стульев получилось в зале.54.
Так как первая цифра в записи неполного частного по условию равна 4, а делитель равен числу 9, то наименьшее первое промежуточное делимое определяется достаточно легко: оно получается в результате умножения этих чисел и равно числу 36 (4•9 = 36).
Если взять промежуточное делимое меньше, чем 36, то первая цифра в записи неполного частного уже не будет равна 4 (она будет либо 3, либо 2, либо 1).
Далее нужно определить верхнюю границу для первого неполного делимого. Сделать это можно следующим образом. Можно сначала найти наименьшее число, которое при делении на число 9 дает в результате число 5. Это будет число 45 (5•9 = 45).
Следовательно, искомое первое промежуточное делимое должно быть меньше этого числа, т. е. самое большое может быть равно числу 44.
Выполнив деление столбиком числа 449 на число 9, учащиеся смогут убедиться в том, что если первое промежуточное делимое равно 44, то первая цифра в записи неполного частного при делении на число 9 равна 4. 21
-
Ответы к странице учебника 21
56. Неполное частное может быть либо пятизначным, либо четырехзначным числом,
Примеры.
-21357I 7
21 I 3051
- 35
35
-7
7
0
-700000I 7
7 I 10000
057. Неполное частное может быть либо четырехзначным, либо трехзначным числом.
Примеры.
-36429I 24
24 I 1517 (остаток 21)
-124
120
-42
24
-189
168
21
-12024I 24
120 I 501
- 24
24
058. Сформулируй задачу.
Из цеха на склад готовой продукции в первый день привезли 2850 изделий, а во второй 3645 изделий. При этом все их расфасовали в коробки по 15 штук. Сколько коробок получилось?(2850+3645):15
+2850
3645
6495
-6495I 15
60 I 433
-49
45
-45
45
0
Ответ: 433 коробки получилось.59. Найди число, которое при делении на число 17 дает в неполном частном число 3002, а остаток 8.
Для этого они сначала должны умножить неполное частное (3002) на делитель (17), а потом к полученному результату прибавить остаток (8). В итоге должно получиться число 51 042.
После этого учащиеся должны разделить это число на число 17, используя сокращенную форму записи. При этом не следует забывать, что результат этого деления им уже известен, что существенно упрощает осуществление всей процедуры деления.х3002
17
51034
51034 + 8 = 51042
-51042 |17
51 |3002
_42
34
860. На территории лесопарка всадили 2569 саженцев ели, что в 12 раз больше, чем саженцев лиственницы. Сколько всего саженцев этих деревьев высадили в лесопарке?
-2568I 12
24 I 214 (саж.) - лиственницы
-16
12
-48
48
0
2568+214=2782 (саж.) высадили в лесопарке
Ответ: 2782 саженца всего высадили в лесопарке.61. Сформулируйте задачу, решением которой будет являться следующее уравнение. x * 14 = 4228 ...
В магазин привезли 4228 кг крупы в мешках по 14 кг. Сколько мешков крупы привезли?
x * 14 = 4228
х = 4228 : 14
х = 302
-4228I 14
42 I 302
- 28
28
0
Ответ: 302 мешка привезли в магазин. 22
-
Ответы к странице учебника 22 Сложение и вычитание величин
62. Из данных величин составь и запиши все возможные суммы и разности значений.
2536 кг + 89763 кг = 92299
89763 кг - 2536 кг = 84227
56934 дм + 74689 м = 56934 дм + 746890 дм = 803824 дм
74689 м - 56934 дм = 746890 дм - 56934 дм = 17755 дм
74689 м = 746890 дм
2 ч + 3265с = 3600 с + 3265 с = 6865 с
2 ч - 3265 с = 3600 с - 3265 с = 335 с
2 ч = 3600 с
324 куб. дм + 659 куб .м = 324 куб. дм + 659000 куб. дм = 659324 куб. дм
659 куб. м - 324 куб. дм = 659000 куб. дм - 324 куб. дм = 658676 куб. дм
659 куб. м = 659000 куб. дм63. Какие из величин можно сложить с площадью 5 кв. м?
Можно сложить: 7 кв. см и 17 кв. дм
64. Какие из величин можно вычесть из объема 350 л?
350 л = 350 куб. дм.
Можно вычесть: 150 куб. дм 450 куб. см65. С одного поля собрали 50 т зерна, с другого - на 20 ц меньше, чем с первого, а с третьего - на 45 ц больше, чем со второго. Сколько центнеров зерна собрали с этих трех полей?
1 поле - 50 т I
2 поле - на 20 ц меньше, чем с 1 поля > ?
3 поле - на 45 ц больше, чем со 2 поля I
1 т = 10 ц
1) 500 - 20 = 480 (кг) - зерна собрали со второго поля.
2) 480 + 45 = 525 (кг) - зерна собрали с 3 поля.
3) 500 + 525 + 480 = 1505 (кг) - собрали всего зерна.
Ответ: 1505 кг собрали всего зерна.Обратная задача.
С трех полей собрали 1505 ц зерна , при этом со второго поля собрали на 20 ц меньше, чем с первого, а с третьего - на 45 ц больше, чем со второго. Сколько центнеров зерна собрали с первого поля?
1 поле - ? I
2 поле - на 20 ц меньше, чем с 1 поля > 1505 кг
3 поле - на 45 ц больше, чем со 2 поля I
1 т = 10 ц
1) 45 - 20 = 25 (кг) - на столько больше собрали зерна с третьего поля, чем с первого.
2) 1505 + 20 - 25 = 1500 (кг) - столько зерна собрали с 3 полей, если бы они все были бы такими как 1 поле.
3) 1500 : 3 = 500 (кг) - собрали с 1 поля.
Ответ: 500 кг собрали с 1 поля. 23
-
Ответы к странице учебника 23
66. Сформулируй задачу с выражением.
46500 кв. м - (21300 кв. м + 15600 кв. м)При починке крыши в цехе площадью 46500 кв. м в 1 день перекрыли 21300 кв. м, а во второй день 15600кв.м. Сколько кв. м крыши осталось перекрыть?
46500 кв. м - (21300 кв. м + 15600 кв. м)=46500-36900=9600 (кв. м) осталось перекрыть
Ответ: 9600 кв. м крыши осталось перекрыть.67.
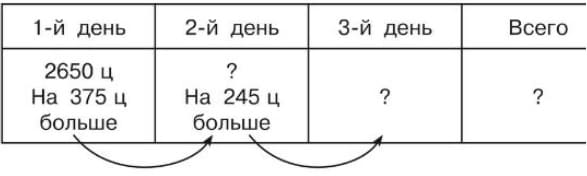
При сборе урожая в первый день собрали 2650 ц зерна, что на 375 ц больше, чем во второй день. Во второй день собрали на 245 ц больше, чем в третий. Сколько всего зерна собрали.
1) 2650 + 375 = 3025 (ц) зерна собрали во 2 день
2) 3025 + 245 = 3270 (ц) зерна собрали в 3 день.
3) 2650 + 3025 + 3270 = 8945 (ц) зерна собрали всего.
Ответ: 8945 ц зерна собрали всего.68.
Учащимся предлагается выбрать из данных величин ту, которая меньше величины 3 ч на 240 с. Для этого нужно сначала вычислить искомую величину, уменьшив 3 ч на 240 с. В итоге должна получиться величина 176 мин (3 ч – 240 с = 80 мин – 4 мин = 176 мин), которая и определяет нужный выбор.
3 ч – 240 с = 80 мин – 4 мин = 176 мин
Ответ: 176 мин.69.
Аналогично предыдущему заданию. Отличие состоит лишь в том, что в качестве данной величины рассматривается масса, а искомая величина вычисляется с помощью сложения.
2 т + 500 кг = 2 000 кг + 500 кг = 2 500 кг = 2 т 5 ц
Ответ: 2 т 5 ц.70. Относится к заданиям повышенной сложности. Для ответа на поставленный вопрос учащиеся должны обратить внимание на тот факт, что молоко в одном бидоне выражается с помощью объема (3 л), а в другом – с помощью массы (3 кг). На практике молоко измеряют и в единицах объема, и в единицах массы, но складывать в этом случае указанные величины нельзя, так как они являются разнородными и «общую» величину в результате они дать не могут. Поэтому данную задачу, сформулированную в таком виде, решить нельзя, если только не принять в качестве ответа такое утверждение: «В двух бидонах 3 л молока и еще 3 кг молока». Но такой ответ нас устроить не может, так как он просто повторяет условие задачи.
24
-
Ответы к странице учебника 24
71. Запиши произведения в виде суммы.
25 м * 3 = 25 м + 25 м + 25 м = 75 м
56 кг * 4 = 56 кг + 56 кг + 56 кг + 56 кг = 224 кг
24 ч * 7 = 24 ч + 24 ч +24 ч + 24 ч + 24 ч + 24 ч + 24 ч = 168 ч
58 кв. м * 2 = 58 кв.м + 58 кв. м = 116 кв. м72. Увеличиваем в 3 раза
25 кв.м*3=75 кв. м
125 кв. м * 3 = 375 кв. м
48 кг*3=144 кг
14л*3=42 л
12ч*3=36ч
65р*3=195рУвеличиваем в 5 раз
25 кв.м*5=125 кв. м
125 кв. м * 5 = 625 кв. м
48 кг*5=240 кг
14л*5=70 л
12ч*5=60ч
65р*5=325р
Если увеличить в 3 раза, а потом в 5, то всего увеличим в 15 раз.73.
Задача может быть сформулирована следующим образом: «В 1 неделе 7 суток, а в 1 сутках 24 часа. Сколько часов длится 1 неделя?» Чтобы записать решение этой задачи, нужно воспользоваться либо суммой 24 ч + 24 ч + 24 ч +24 ч + 24 ч + 24 ч + 24 ч, либо произведением 24 ч•7.
Решение:
24*7=168 часов длится 1 неделя.
или
24 ч + 24 ч + 24 ч +24 ч + 24 ч + 24 ч + 24 ч = 168 ч
Ответ: 168 часов длится 1 неделя.
Продолжительность недели больше продолжительности суток в 7 раз. Продолжительность суток больше продолжительности часа в 24 раза. Продолжительность недели больше продолжительности часа в 168 раз. 25
-
Ответы к странице учебника 25
74. Обозначь длину данного отрезка буквой а. Как можно записать длину отрезка, который в 3 раза длиннее данного? Запиши длину второго отрезка с помощью суммы и с помощью произведения.
Решение:
(а + а + а)
а • 375. Измерить и сравнить.
Решение:
6 см : 2 см = в 3 (раза)
Сопоставляем этот факт с приведенными в задании обозначениями длин отрезков (а и 3а) и отвечаем на вопрос: какая длина должна получиться, если число 3 умножить на длину 2 см? Приходим к выводу, что длина должна получиться 6 см.76.
Записываем произведения в виде суммы. Составляем равенства:
5 • 18 см = 18 см • 5;
4 • 38 дм = 38 дм • 4;
3 • 23 мм = 23 мм • 377.
2 л • 8 и 8 • 2 л.
Два оставшихся произведения решением этой задачи быть не могут (так как они не отвечают данным задачи), хотя при вычислении их значений также получается величина 16 л. 26
-
Ответы к странице учебника 26
78. На сколько равных частей нужно разделить отрезок, чтобы одна часть была в 4 раза короче всего отрезка?
Например, если длину отрезка 8 см разделить на 4 равные части, то одна такая часть (2 см) будет в 4 раза меньше, чем длина всего отрезка.
79. Даны величины. На какое число надо разделить, чтобы уменьшить в 2 раза? В 4 раза?
В 2 раза:
8 см : 2 = 4см
24 ч : 2 = 12ч
40 кг : 2 = 20 кг
16 кв.м : 2 = 8 кв.м
32 куб.дм : 2 = 16 куб.м.В 4 раза:
8 см : 4 = 21 см
24 ч : 4 = 8 ч
40 кг : 4 = 10 кг
16 кв.м : 4 = 4 кв.м
32 куб.дм : 4 = 8 куб.м.80. Уменьши вместимость 24 л на следующее количество раз 2, 3, 4, 6, 8, 12.
В 2 раза:
24л:2=12л
В 3 раза:
24л:3=8л
В 4 раза:
24л:4=8л
В 6 раза:
24л:6=4л
В 8 раза:
24л:8=3л
В 12 раза:
24л:12=2л81. Торт массой 1 кг разделили на 8 равных частей. Сколько граммов в каждой части?
Решение:
1кг=1000г
1000:8=125 (г) - весит каждая часть торта.
Ответ: 125 грамм весит каждая часть торта.82. Выполни вычисление столбиком.
-891I 9
81 I99
-81
81
0
-84I 6
6 I14
-24
24
0
-75I 5
5 I15
-25
25
0
-147I 7
14 I21
-7
7
0 27
-
Ответы к странице учебника 27
83. Вычисли.
-891I 9
81 I 99
-81
81
0
810 : 9 + 81 : 9 = 90 + 9 = 99
Если сразу вычислять значение этого выражения, то получится, что его можно преобразовать к частному 891 км : 9, значение которого было уже вычислено (99 км). С другой стороны, применение правила деления суммы на число предполагает следующую возможность: (810 км+81 км) : 9 = 810 км : 9 + 81 км : 9 = 90 км + 9 км = 99 км. Таким образом, получается одна и та же величина.84. На автозаправочную станцию привезли 2350 л бензина, что в 5 раз больше, чем дизельного топлива. Сколько всего литров горючего привезли?
1)
-2350I 5
20 I470
-35
35
0
2) 2350 + 470 = 2820 (л) - топлива всего привезли на заправочную станцию.
Ответ: 2820 литров топлива всего привезли на заправочную станцию.85. Сначала торт массой 1 кг 200 г разрезали на 4 равные части, а потом каждую такую часть разрезали еще пополам. На сколько равных частей в итоге разрезали торт? Сколько граммов в одной части?
Решение:
В итоге торт разрезали на 8 равных частей.
1 кг 200 г = 1200 г
1200 : 8 = 150 г
Ответ: 150 г в каждой части.86.
Учащимся нужно сначала понять, что ни 1 м, ни 10 дм, ни 100 см нельзя нацело разделить на 8 равных частей. Единственно возможным вариантом представления данной длины в известных им единицах остается выражение ее в миллиметрах. В этом случае получается 1 000 мм, а число 1 000 делится нацело на число 8 (1 000 : 8 = 125). Это и означает, что данную длину 1 м нужно было выразить в миллиметрах (1 м = 1 000 мм). Заключительный вопрос задания направлен на формирование у учащихся понимания того факта, что соотношение 1 м = 1 000 мм означает, что 1 мм составляет тысячную долю от 1 м.
1 м = 1000 мм
1 000 : 8 = 125 (мм)
Тысячную долю.87.
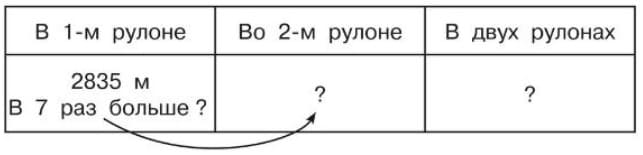
Формулируем задачу.В магазин привезли 2 рулона пленки. В 1 было 2835 метров пленки, а во втором в 7 раз больше. Сколько всего метров пленки привезли?
Решение:
1) 2835*7=19845 (м) - пленки во 2 рулоне.
2) 2835+19845=22680 (м) - пленки всего
Ответ: 22680 метров пленки всего. 28
-
Ответы к странице учебника 28
88. Напиши, какую долю составляет закрашенная часть полоски от всей полоски. Сделай это для каждой из 3 полосок.
Для верхней это треть, для средней это половина, для нижней это четверть.
Чтобы получить половину надо разделить на 2. Чтобы найти треть надо разделить на 3. Чтобы четвертую часть на 4. Для десятой части на 10, а для 100 на 100.89. Делим квадрат.
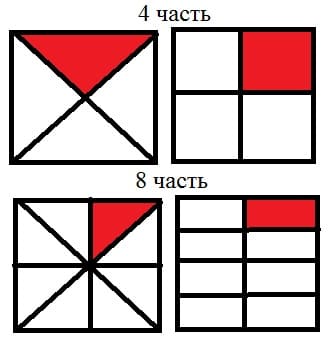
Например, проведя диагонали квадрата, либо проведя «средние линии», т. е. отрезки, соединяющие середины противоположных сторон. Для вычисления площади одной такой части (а такая часть может быть названа четвертью, либо одной четвертой частью) нужно выполнить деление площади квадрата (16 кв. см) на число 4. Для выполнения последней части задания учащиеся должны продолжить процесс деления на равные части, разделив каждую из полученных частей пополам. Сделать это учащиеся могут разными способами, но наиболее очевидным, на наш взгляд, является способ, в котором проводятся и диагонали, и «средние линии». Для вычисления площади одной восьмой части можно разделить площадь всего квадрата на число 8, но можно разделить пополам площадь одной четвертой части, которая была вычислена ранее.
4 часть
16 : 4 = 4 (см. кв) площадь 4 части квадрата.
8 часть
16 : 8 = 2 (см. кв) площадь 8 части квадрата.90. Туристам надо преодолеть расстояние 75 км. В первый день они преодолели треть Намеченного пути. Какое расстояние туристы преодолели за 1 день?
75 : 3 = 25 (км) - преодолели за 1 день.
Ответ: 25 км преодолели за 1 день. 29
-
Ответы к странице учебника 29
91. Во сколько раз надо увеличить треть, чтобы получить всю величину?
В 3 раза.
Вычисли длину отрезка, если треть 5 см.
5 * 3 = 15 (см) - длина всего отрезка.
Ответ: 15 см длина всего отрезка.92. Праздничный торт разделили на 8 равных частей. Одна часть имеет массу 125 г. Какая масса всего торта?
8 * 125 = 1000 (г) - масса всего торта.
Ответ: 1000 г масса всего торта.93. В первое хранилище привезли 300 т картофеля, что составило четверть всего собранного в хозяйстве урожая. Во второе хранилище привезли треть всего собранного картофеля. Сколько тонн картофеля привезли во второе хранилище.
1) 300 * 4 = 1200 (т) - собрали всего картофеля.
2) 1200 : 3 = 400 (т) - привезли во второе хранилище.
Ответ: 400 т привезли во второе хранилище.94. За первый день бригада дорожных рабочих отремонтировала 200 кв. м дорожного полотна, что составило одну пятую часть всего запланированного объема работы. Сколько квадратных метров дорожного полотна осталось осталось отремонтировать бригаде?
Решение:
1) 200 * 5 = 1000 (кв. м.) - всего надо было отремонтировать.
2) 1000 - 200 = 800 (кв.м.) - осталось отремонтировать.
Ответ: 800 кв.м. осталось отремонтировать.95. Сколько стоит батон колбасы, если его пятая часть стоит 32 рубля?
Решение:
5 * 32 = 160 (р) - стоит батон колбасы.
Ответ: 160 рублей стоит батон колбасы.96. На сколько минут треть часа больше, чем четверть часа? (на 5 минут)
60 : 20 - 60 : 4 = 20 - 15 = 5 (мин.)
Ответ: на 5 минут.Во сколько раз половина часа больше четверти часа? (в 2 раза)
(60 : 2) : (60 : 4) = 30 : 15 = 2 (раза)
Ответ: в 2 раза. 30
-
Ответы к странице учебника 30
97. Вычисли, чему равняются две трети от 60 кг и три четверти от 60 кг.
Две трети:
60 : 3 = 20 - 1 часть
20 * 2 = 40 - это две трети от 60Три четверти:
60 : 4 = 15
15 * 3 = 45 - это три четверти от 6098. Рассмотри диаграмму и назови какую часть от площади всего круга составляет площадь закрашенной части, если круг разделен на одинаковые доли.
На диаграмме закрашена одна четвертая часть или две восьмых, что по площади одно и тоже.
28 : 4 = 7 (уч.) - это отличники
Ответ: 7 отличников в классе.99. Чему равны три седьмых некоторой длины, если ее одна седьмая часть равна 25 м?
25 * 3 = 75 - это будет три седьмых.
100. Вычисли три седьмых от каждой из величин.
49т : 7 * 3 = 21 т
147 л : 7 * 3 = 63 л
294 кв. м : 7 * 3 = 126 кв. м
301 куб см : 7 * 3 = 129 куб см. 31
-
Ответы к странице учебника 31
101. Туристам нужно было пройти расстояние 40 км. За день они смогли пройти три четверти этого пути. Сколько осталось пройти?
1) 40 : 4 * 3 = 10 * 3 = 30 (км) - они прошли
2) 40 - 30 = 10 (км) - осталось пройти
Ответ: 10 км осталось пройти туристам.102. В магазин привезли 70 кг яблок. Две седьмых всех яблок продали. Сколько кг яблок в итоге продали?
Решение:
1) 70 : 7 = 10 (кг) - это одна седьмая часть всех яблок.
2) 10 * 2 = 20 (кг) - продали.
В одно выражение:
70:7*2=20 (кг) яблок продали.
Ответ: 20 кг яблок продали.103. Найди от массы 120 кг части. две трети, три четверти, четыре пятых, четыре шестых, пять восьмых
две трети - 120 : 3 * 2 = 40 * 2 = 80 кг
три четверти - 120 : 4 * 3 = 30 * 3 = 90 кг
четыре пятых - 120 : 5 * 4 = 24 * 4 = 96 кг
четыре шестых - 120 : 6 * 4 = 20 * 4 = 80 кг
пять восьмых - 120 : 8 * 5 = 15 * 5 = 75 кгСреди найденных одинаковые части четыре шестых и две трети. Вначале мы взяли меньшее количество частей, но за счет их большего общего количества получили тот же результат. Это все равно как взяли бы меньшее количество частей, но сразу большей массы. Здесь главное соблюсти пропорции.
Точно такой же принцип используется для диаграммы ниже.104. Задача.
Если туристы каждый день преодолевали одно и то же расстояние и за неделю преодолели 175 км, то за 1 день они преодолевали по 25 км (175 км : 7 = 25 км), т. е. одну седьмую всего расстояния. Тогда за 3 дня они преодолели 75 км (25 км•3 = 75 км), что составляет три седьмых всего расстояния.
Решение:
1) 175 км : 7 = 25 (км) - туристы проходили каждый день.
2) 25 км • 3 = 75 (км) - туристы прошли за 3 дня.
Ответ: 75 км туристы прошли за 3 дня. 32
-
Ответы к странице учебника 32
105. По плану три четверти всех собранных яблок заложили на зимнее хранение. Сколько кг яблок собрали всего, если на зимнее хранение заложили 270 кг?
1) 270 кг : 3 = 90 (кг)
2) 90 кг • 4 = 360 (кг)
Ответ: 360 кг яблок собрали.
Решение можно записать и в виде одного выражения:
270 кг : 3 • 4 = 360 (кг)
Ответ: 360 кг яблок собрали.106. Найди одну седьмую, если четыре седьмых составляют 156 метров.
156 : 4 = 39 (м) - это одна седьмая
Во сколько раз вся длина больше, чем одна седьмая часть этой длины?
В 7 раз.
Чему равна вся длина.
39 * 7 = 273 (м) - вся длина провода.
Найди длину провода, если четыре седьмых равны 176 метрам.
176 : 4 * 7 = 308 (м) - длина всего провода.
33
-
Ответы к странице учебника 33
107. Чему равна вся величина, если две пятых от этой величины равны 100?
100 : 2 * 5 = 250 вся величина
Две пятых 80?
80 : 2 * 5 = 200 вся величина
Две пятых 60?
60 : 2 * 5 = 150 вся величина
108. Чему равна вся величина, если 24 л составляют две трети этой величины?
24 : 2 * 3 = 36 вся величина
Три четверти?
24 : 3 * 4 = 32 вся величина
Четыре пятых?
24 : 4 * 5 = 30 вся величина
109. Три пятых участка занимает фруктовый сад. Какова площадь всего участка, если площадь сада 6 соток?
6 : 3 * 5 = 2 * 5 = 10 (сот) - площадь всего сада.
Ответ: 10 соток площадь всего сада.110. Две пятых площади одного земельного участка равны четырем десятым площади другого участка и составляют 8 соток.
Вычисли площадь каждого участка. Сравни полученные результаты. Объясни почему площади равны.8 : 2 * 5 = 20 это две пятых
8 : 4 * 10 = 20 это четыре десятых
Как видно из выражений, эти доли равны. Смотрим на диаграмму.
111. Две третьих вместимости одного бака воды равны 54 л. Выполни разностное сравнение вместимостей этих баков.
54 : 2 * 3 = 27 * 3 = 81 (л) - емкость первого бака
54 : 3 * 4 = 18 * 4 = 72 (л) - емкость второго бака
81 - 72 = 9 (л) - на столько первый бак больше второго.
Ответ: на 9 литров первый бак больше второго. 34
-
Ответы к странице учебника 34
112. Выполняем сравнение.
48 кг 68 кг = 6 раз
5 т = 50 ц
50 ц : 2 ц = 25 раз
96 м : 6 м =16 раз
1 ч = 60 мин
60 : 3 = 20 раз
91 л : 7 л =13 раз
1 р = 100 коп
100 : 1 = 100 разВ какой паре одна величина больше другой в 25 раз?
В качестве пары величин, в которой одна величина отличается от другой в 25 раз, должна быть названа пара, состоящая из 5 т и 2 ц. По результатам выполненных делений можно установить, какую долю меньшая величина составляет от большей величины. Так, 2 ц составляют 25-ю долю от 5 т.
113. Сформулируй задачу, для решения которой нужно разделить длину пройденного пути 250 км на затраченное для этого время 5 ч.
Автомобиль за 5 часов проехал 250 км. С какой скоростью двигался автомобиль, если известно, что на протяжении всего пути его скорость была одинаковой?
250 : 5 = 50 (км/ч) была скорость автомобиля.
Скорость можно выразить в м/с, км/с , м/ч и т.д.
То есть скорость это всегда расстояние деленное на время.114. Цена получается когда общую стоимость делим на количество товара. Заполняем таблицу.
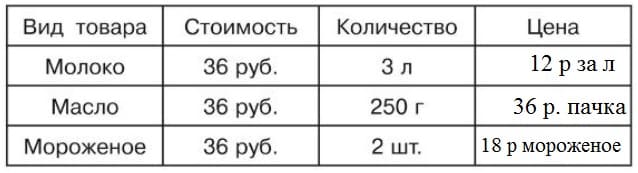
Цена в р/кв. м может быть применена для линолеума, ковров, ткани.
35
-
Ответы к странице учебника 35
115. Общая площадь полей засеянных в фермерском хозяйстве, равна 50 га. Весь урожай, собранный с полей, составляет 1750 ц. Вычисли урожайность пшеницы в данном хозяйстве в ц/га.
1750 : 50 = 35 (ц/га) - урожайность пшеницы.
Ответ: 35 ц/га.
Поделили массу урожая на площадь на которой он собран.116. Сформулируй задачу, в которой требуется найти производительность токаря за час работы, если его производительность оставалась постоянной в течение всей смены 8 - часового смены.
За смену в 8 часов токарь изготовил 240 деталей. Какая у него была производительность?
240 : 8 = 30 (дет/ч) - производительность токаря.
Ответ: 30 дет/ч.117. Приведи 3 примера единиц производительности. Какую величину на какую надо разделить, чтобы получить производительность?
Примеры:
л/час , деталей/в минуту, тонн/в сутки
Для получения производительности надо взять единицу того, что производят и разделить на время118.
На основе анализа единицы этой величины (чел./кв. км) учащиеся должны прийти к выводу, что для получения этой величины нужно число всех жителей данного региона разделить на площадь этого региона.
119.
Итак, если разделить массу некоторого объекта на его объем, то получается величина, которая показывает массу единицы объема. В международной системе единиц единицей такой величины является кг/куб. м, но можно использовать и другие единицы, например г/куб. см.
120.
Предлагается сформулировать задачу, в ответе которой получается величина 8 км/с. Так как искомая величина, судя по ее единице, является скоростью, то нужно сначала установить, какой объект может двигаться с такой скоростью. Для многих учащихся уже хорошо известно, что с такой скоростью могут двигаться космические аппараты (ракета-носитель, космический корабль, спутник). Других транспортных средств, передвигающихся с такой большой скоростью, мы назвать не сможем.
Формулировка и задача.
Ракета после старта за 10 секунд пролетела 80 км. С какой средней скоростью она двигалась?
80:10=8 (км/с) - скорость ракеты
Ответ: 8 км/с. 36
-
Ответы к странице учебника 36
121. Выполни сложение столбиком
+56987 м
32478 м
89465 м
+25683 л
74317 л
100000 л
-45862I 60
420 I764 минуты и 22 секунды
-386
360
-262
240
22
то есть с остатком, значит переводим минуты в секунды 356*60=21360 сек.
+45862 с
21360 с
67222 с
+689247 кг
124563 кг
813810 кг
переводим дм в см 56874 дм = 568740 см
+162256 см
568740 см
730996 см
переводим кв. м в кв. дм. 321 кв. м = 32100 кв. дм.
+32100 кв.м
36248 кв.м
68348 кв.м122. Выполняем вычитание.
- 65489 м
56897 м
8592 м
-453218 л
96587 л
356631 л
245 ч = 14700 мин
-14700 мин
10256 мин
4444 мин
-458967 т
324567 т
134400 т
36285 см = 362850 мм
- 362850 мм
324567 мм
38283 мм
5 кв. м = 5000 кв. см
-50000 кв.см
39875 кв.см
10125 кв.см123. Выполняем умножение.
х 45687
5
288435 (км)
х 6274
23
+18822
12548
144302 (с)
х 23187
8
185496 (кг)
х 47689
4
190756 (куб.дм)
х 1236
39
+ 11124
3708
48204 (л)
х 6354
16
+38124
6354
101664 (кв.м)124. Выполняем умножение.
х 58672
7
410704 (мм)
х 6543
15
+32715
6543
98145 (ч)
х 42357
6
254142 (ц)
х 75863
3
227589 (куб. см)
х 3598
34
+10156
10794
122332 (л)
х 3698
27
+25886
7396
99846 (кв.см)125. Выполняем деление.
-24579I 9
18 I2731 (см)
-65
63
-27
27
- 9
9
0
-693432I 18
54 I38524 (кв. м)
-153
144
-94
90
- 43
36
- 72
72
0
-968735I 5
5 I193747 (кг)
-46
45
-18
15
- 37
35
- 23
20
-35
35
0
-968732I 4
8 I242183 (кг)
-16
16
- 8
8
- 7
4
- 33
32
-12
12
0
-631275I 15
60 I42085 (куб. м)
-31
30
- 127
120
- 75
75
0
-475233I 11
44 I43203 (с)
-35
33
- 22
22
- 33
33
0126. Найди треть.
-456312I 3
3 I 152104
-15
15
- 6
6
- 3
3
-12
12
0
-73245I 3
6 I 24415
-13
12
-12
12
- 4
3
-15
15
0
-891243I 3
6 I 297081
-29
27
-21
21
- 24
24
-3
3
0
-231963I 3
21 I 77321
-21
21
-9
9
- 6
6
-3
3
0 37
-
Ответы к странице учебника 37
127. Найти всю величину по 4 части.
х 86973
4
347892
х 56387
4
2255487
х 891243
4
3564972
х 231963
4
927852128. Найди три четвертых каждой из величин
16256 : 4 * 3 = 12192
41872 : 4 * 3 = 31404
82456 : 4 * 3 = 61842
26752 : 4 * 3 = 20064129. Найти всю величину по части (пять седьмых)
43245 : 5 * 7 = 60543
23675 : 5 * 7 = 33145
16895 : 5 * 7 = 23653
23485 : 5 * 7 = 32879130. Выполняем сравнение.
46530 : 15 = 3102 (раз)
57024 : 27 = 2112 (раз)
896375 : 25 = 35855 (раз)131. Заполняем таблицу.
38
-
Ответы к странице учебника 38
132 и 133. Смотрите таблицы.
134. При покраске стены площадью 30 кв. м строители израсходовали 2 кг 700 г краски. Вычисли расход краски на единицу площади.
Решение:
2 кг 700 г = 2700 г
1) 2700 : 30 = 90 (г/кв. м) - расход краски.
Ответ: 90 г/кв. м расход краски.Обратные задачи:
1) На 1 метр расходовали 90 г/кв.м краски и израсходовали 2700 г. Сколько метров покрасили?
2700 : 90 = 30 (кв. м)
Ответ: 30 кв. м покрасили.
2) На 1 метр расходовали 90 г/кв.м краски и покрасили 30 кв.м. Сколько краски израсходовали?
90 * 30 = 2700 (г)
Ответ: 2700 г краски израсходовали.
Строители уложились в норму 950 г/кв.мКомментарий писать не нужно: ...аж в 10 раз выше норма, видимо чтобы можно было попилить денег на госзаказах!
39
-
Ответы к странице учебника 39
135.
Выигрывает соревнование тот спортсмен, который за это время преодолеет самое большое расстояние. Если во всех традиционных соревнованиях по бегу постоянной характеристикой является длина дистанции, а победитель определяется по наименьшему времени, затраченному на преодоление этой дистанции, то в «суточном беге» постоянной характеристикой является время движения, а победитель определяется по наибольшей длине пройденного пути. На самом деле оба указанных типа соревнований по бегу можно описать с помощью одной общей характеристики – и в том, и в другом случае победителем является тот спортсмен, у которого средняя скорость передвижения была больше, чем у других. Другими словами, при одинаковом времени движения большее расстояние преодолеет тот объект, у которого
средняя скорость движения больше. Именно на этот факт и нужно обратить внимание учащихся при выполнении данного задания.Что касается вычисления средней скорости участника соревнования по «суточному бегу», то она легко вычисляется с помощью деления всего пройденного пути (120 км) на затраченное время (24 ч). В итоге получается 5 км/ч.
120 : 24 = 5 (км/ч) - средняя скорость участника соревнования по «суточному бегу».
Ответ: 5 км/ч.136. Так как средняя скорость движения на каждой части пути была своя (80 км/ч и 75 км/ч), то время оказывается одинаковым (2 ч). Анализ этой ситуации показывает, что если время движения не изменяется, то с увеличением (уменьшением) скорости увеличивается (уменьшается) пройденный путь. Этот факт характеризует прямую зависимость пройденного пути от скорости при постоянном времени, но пока мы еще ничего не говорим о пропорциональном характере этой зависимости.
160 : 80 = 2 (ч)
150 : 75 = 2 (ч)
Время не изменилось.137. Смотрим таблицу.
Если объединить указанные выше две характеристики (характеристику прямой зависимости и характеристику пропорциональной зависимости), то мы получим характеристику прямой пропорциональной зависимости, которая звучит следующим образом: при постоянном времени движения увеличение (уменьшение) скорости движения в некоторое число раз приводит к увеличению (уменьшению) пройденного пути в это же число раз.
40
-
Ответы к странице учебника 40
138. За первый час автомобиль проехал 60 км, а за второй час пути - 120 км. Во сколько раз увеличились средняя скорость автомобиля и пройденный путь за второй час?
Если время движения не изменяется, но путь за то же самое врем увеличился в два раза, то с увеличением (уменьшением) пути увеличивается (уменьшается) и скорость.
120 : 60 = 2 (раза)
Ответ: в 2 раза увеличились средняя скорость автомобиля и пройденный путь за второй час.139. Дачнику, чтобы добраться от города до дачного поселка, нужно сначала 45 мин ехать на автобусе, а потом 45 мин идти пешком. Какое расстояние преодолевает дачник, если средняя скорость автобуса в 15 раз больше средней скорости пешехода, а пешком дачнику нужно преодолеть 3 км?
1) 3 * 15 = 45 (км) - дачник преодолевает на автобусе.
2) 45 + 3 = 48 (км) - дачник преодолевает всего.
Ответ: 48 км.140.
При выполнении задания 140 учащиеся получают возможность подвести своеобразный итог установленным выше фактам. Этот итог должен быть представлен в виде получения соответствующей формулы, в которой пройденный путь (s) выражен через скорость (v) и время (t) : s = v•t. Анализируя эту формулу с точки зрения влияния изменения одного множителя на значение произведения (при постоянном другом множителе), учащиеся еще раз имеют возможность убедиться в справедливости правила, характеризующего зависимость пройденного пути от скорости при постоянном времени, которое они установили эмпирически.
41
-
Ответы к странице учебника 41
141. См таблицу.
Отмеченный тип зависимости может быть выражен в следующей формулировке: при постоянной длине пройденного пути увеличение скорости в некоторое число раз (в 2 раза) приводит к уменьшению времени в это же число раз (также в 2 раза).
142. Расстояние между населенными пунктами на велосипеде можно преодолеть за 2 ч. Во сколько раз автомобиль должен ехать быстрее, чтобы преодолеть это расстояние за 30 мин.
Решение:
Соотношение времени будет пропорционально соотношению пройденного пути. То есть если мы хотим преодолеть тоже самое расстояние быстрее во сколько то раз, то во столько же раз надо двигаться быстрее. Получается что 2 часа это 120 мин, а
120 : 30 = 4 (раза) - во столько раз машина должна ехать быстрее, чтобы проехать тоже самое расстояние, что и велосипедист.
Ответ: в 4 раза. 42
-
Ответы к странице учебника 42
143. Первый км дистанции пловец проплыл за 20 мин, а второй - за 40 мин. Во сколько раз увеличилось время, затраченное пловцом на втором километре, по сравнению со временем, затраченным на первом километре? Во сколько раз уменьшилась скорость?
Решение:
При постоянной длине пройденного пути увеличение времени в некоторое число раз (в 2 раза) приводит к уменьшению скорости в это же число раз (также в 2 раза).
144. Запиши формулу, в которой скорость V выражается через пройденный путь S и время T.
Итог должен быть представлен в виде получения соответствующей формулы, в которой скорость (v) выражена через пройденный путь (s) и время (t):
v = s : t
Если делитель увеличить в 3 раза, а делимое не менять, то частное станет меньше в 3 раза.
120 : 20 = 6
120 : 60 = 20
Если время увеличилось в 3 раза, то скорость уменьшилась в 3 раза.
180 : 2 = 90 (км/ч) скорость
180 : 6 = 30 (км/ч) скорость
Чтобы путь был пройден в 4 раза быстрее, необходимо чтобы скорость была в 4 раза выше.
240 : 8 = 30 (км/ч)
240 : 2 = 120 (км/ч)145. Расстояние 160 км автобус преодолел за время на 2 ч больше, чем автомобиль. С какой скоростью он двигался, если его скорость была в 2 раза ниже, чем у автомобиля?
Так как скорость автобуса в два раза ниже и он ехал на 2 часа больше, то половина времени будет равна 2 часа, а все время два раза по 2.
1) 2 + 2 = 4 (ч) - ехал автобус.
2) 160 : 4 = 40 (км/ч) - скорость автобуса.
Ответ: 40 км/ч. 43
-
Ответы к странице учебника 43
146. См таблицу
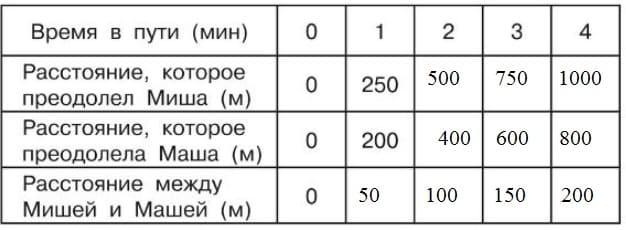
Миш потратил 4 минуты на весь путь. Маша за это время проехала 800 метров. Когда Миша проехал 1 км, то обогнал Машу на 200 метров. Расстояние между Машей и Мишей каждую минуту увеличивалось на 50 метров.
250 м/мин - 200м/мин = 50 м/ мин 44
-
Ответы к странице учебника 44
147.
Если Маша получит фору 200 метров, то через 1 километр Миша и Маша сравняются, то есть Миша догонит Машу.
148. От одной автостанции по одному и тому же маршруту с интервалом в 1 ч отправились сначала автобус, затем легковое такси. Средняя скорость автобуса - 60 км/ч, а такси - 80 км/ч. Через сколько часов такси догонит автобус?
1) 80 - 60 =20 (км/ч) - скорость сближения автобуса и такси.
2) 60 : 20 =3 (ч) - надо чтобы такси догнала автобус.
Ответ: 3 ч надо чтобы такси догнала автобус.149. Когда спортсмен из команды 4А класса на последнем этапе принял эстафетную палочку от своего товарища, его соперник из команды 4Б класса был впереди на 15 м. Участник из команды 4Б бежит со скоростью 5 м/с, а его соперник - 6 м/с. Через сколько сек второй догонит первого? Сможет ли победить 4А, если длина последнего этапа 90 метров?
Решение:
1) 6 - 5 = 1 (м/с) - скорость сближения соперников из 4А и 4Б
2) 15 : 1 = 15 (с) - надо чтобы участник из 4А догнал участника из 4Б
3) 90 : 5 =18 (с) - надо чтобы добежать участнику из 4А до финиша.
Ответ: участник из 4А догонит участника из 4 Б за 15 секунд, при этом команда из 4 А победит.150. Используя следующее правило, вычисли скорость изменения расстояния между каждой парой автомобилей, движущихся в одном направлении, если скорости, если скорости этих автомобилей постоянны и равны соответственно 80км/ч, 20м/с и 1000м/мин.
Надо привести все величины к одной единице измерения. Как перевести скорость из м/с (м/ мин) в км/час:
20 м/с - значит 20 м за 1 секунду. В часе 3600 секунд . Значит за час
20 * 3600 = 72000 метров/час.
в 1 км -1000 метров
72000 : 1000 = 72 км/час1000 м/мин - значит 1000 за 1 минуту. В часе 60 минут. Значит за час
1000 * 60= 60 000 метров за час
в 1 км - 1000 м
60000 : 1000 = 60 км/час
Теперь можно сравнивать.Записываем:
20 м/с = 20 * 3600 : 1000 =72 км/час
1000 м/мин = 1000 * 60 : 1000 = 60 км/час
1 и 2 автомобиль
Скорость первого больше, чем скорость второго.
В одном направлении он будет удалятся от второго со скоростью
80 - 72 = 8 (км/час)
1 и 3 автомобиль
Скорость первого больше, чем скорость третьего.
В одном направлении он будет удаляться со скоростью
80 - 60 = 20 (км/час)
2 и 3 автомобиль
Скорость второго больше, чем скорость третьего.
В одном направлении он будет удаляться со скоростью
72 - 60 = 12 (км/час) 45
-
Ответы к странице учебника 45
151. От одной пристани одновременно вниз по течению реки отплыл катер и плот. На каком расстоянии они окажутся друг от друга через 2 часа движения, если скорость катера в стоячей воде 20 км/ч?
Решение:
1) 20 * 2 = 40 (км) - расстояние между катером и плотом через 2 часа.
Ответ: 40 км.
Скорость плота знать не надо, так как у катера будет дополнительно точно такая же скорость.152. Сформулируем задачу.
Из одной точки отправления по одному маршруту выехали автомобиль и мотоцикл. У мотоцикла была скорость 50 км/ч, а у автомобиля - 70 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
1) 70 - 50 = 20 (км/ч) - скорость отдаления.
2) 20 * 2 = 40 (км) - расстояние между мотоциклом и автомобилем через 2 часа.
Ответ: 40 км. 46
-
Ответы к странице учебника 46
153. Два поезда двигались в противоположных направлениях. После их встречи прошел 1 ч, в течении которого первый поезд двигался с скорость 80 км/ч, а второй - 70 км/ч. На каком расстоянии находятся эти поезда?
1) 80 + 70 = 150 (км/ч) скорость изменения расстояния.
2) 150 * 1 = 150 (км) расстояние будет между поездами через 1 час.
3) 150 * 2 = 300 (км) расстояние будет между поездами через 2 часа.
Ответ: 150 км расстояние будет между поездами через 1 час, 300 км через - 2 часа.154. Два поезда расстояние между которыми 300 км, двигались навстречу друг другу. Через сколько часов произойдет встреча этих поездов, если первый поезд двигается с постоянной скоростью 80 км/ч, а второй - 70 км/ч? Какое расстояние будет через 3 часа после встречи?
Решение:
1) 80 + 70 = 150 (км/ч) - скорость сближения.
2) 300 : 150 = 2 (ч) - через столько поезда встретятся.
3) 150 * 3 = 450 (км) - расстояние через 3 часа после встречи.
Ответ: 2 часа, 450 км.155. Сформулируй задачу...
Навстречу двигались автобус и автомобиль, расстояние между которыми 280 км. Через сколько часов произойдет встреча этих транспортных средств, если автомобиль двигается с постоянной скоростью 80 км/ч, а автобус - 60 км/ч.
Решение:
1) 80 + 60 = 140 (км/ч) - скорость сближения.
2) 280 : 140 = 2 (ч) - через столько автобус и машина встретятся.
Ответ: через 2 часа. 47
-
Ответы к странице учебника 47
156. От одной пристани одновременно вниз по течению отплыл плот, а вверх по течению - катер. На каком расстоянии они окажутся через 2 часа друг от друга, если скорость катера в стоячей воде 20 км/ч?
Для решения надо знать скорость плота или скорость реки.
Нельзя узнать даже скорость катера против течения, так как на нее будет влиять скорость течения, которую мы не знаем.
Если скорость течения 2 км/ч, то получается:
1) 20 - 2 = 18 (км/ч) - скорость катера против течения.
2) 18 + 2 = 20 (км/ч) - скорость удаления.
3) 20 * 2 = 40 (км) - расстояние между катером и плотом через 2 часа.
Ответ: 40 км.157.
От одной станции в противоположных направлениях отправились два поезда, только первый поезд двигался со скоростью 50 км/ч, а второй – со скоростью 70 км/ч, причем второй поезд выехал на 1 ч позже.
Какое расстояние будет между поездами через 2 ч после того, как начал движение второй поезд?»Решая такую задачу, учащиеся, прежде всего, должны обратить внимание на тот факт, что к моменту, когда начал движение второй поезд, первый уже был в движении 1 ч и проехал за это время 50 км (50 км/ч•1 ч = 50 км). За 2 ч совместного движения расстояние между поездами увеличилось еще на 240 км (50 км/ч + 70 км/ч = 120 км/ч и 120 км/ч•2 ч = 240 км).Таким образом, искомое расстояние между поездами будет равно 290 км (50 км + 240 км = 290 км).
Решение:
1) 50 * 1 = 50 (км) - прошел 1 поезд, когда выехал второй.
2) 50 + 70 = 120 (км/ч) - скорость удаления.
3) 120 * 2 + 50 = 290 (км) - будет расстояние между поездами.
Ответ: 290 км. 48
-
Ответы к странице учебника 48
158.
При выполнении задания учащиеся получают возможность с помощью данных схем закрепить знания о характере процесса движения в одном и том же направлении при одновременном начале этого движения. Различие заключается в том, как изначально расположены эти объекты.
На схеме (а) речь идет о движении из одного пункта. При таком движении один объект постоянно будет удаляться от другого.
На схеме (б) речь идет о движении из разных пунктов при условии, что скорость второго объекта («догоняющего») больше, чем скорость первого объекта («убегающего»). При таком движении расстояние между объектами сначала будет сокращаться (до тех пор, пока второй объект не догонит первый), а потом будет увеличиваться (второй объект начнет удаляться от первого).
На схеме (в) речь идет о движении из разных пунктов при условии, что скорость второго объекта меньше скорости первого объекта. В этом случае первый объект будет еще дальше удаляться от второго.
Если говорить о схематической иллюстрации предложенной задачи, то для нее будет подходить схема (б). Нас интересует время, когда пассажирский поезд догонит товарный. Чтобы его вычислить, нужно сначала узнать скорость изменения расстояния между поездами. Она будет равна 20 км/ч (80 км/ч – 60 км/ч = 20 км/ч), а потом вычислить время, за которое исходное расстояние между поездами (80 км) будет «ликвидировано» (80 км : 20 км/ч = 4 ч).
1) 80 км/ч – 60 км/ч = 20 км/ч
2) 80 км : 20 км/ч = 4 ч
Ответ: 4 часа.Что касается ответа на дополнительное требование, то его получить достаточно просто. Это расстояние будет равно 40 км (20 км/ч•2 ч = 40 км). Полезно предложить учащимся проиллюстрировать с помощью одной из данных схем задачу, которая определяется этим новым требованием (скорости поездов остаются теми же самыми). Для этого они должны выбрать схему (а).
20 км/ч • 2 ч = 40 км
49
-
Ответы к странице учебника 49
159.
Задание 159 аналогично предыдущему заданию, только в нем речь идет о движении объектов в противоположных направлениях. При анализе данных схем обязательно нужно обратить внимание на то, что схемы (а) и (в) описывают процесс движения, в котором происходит постоянное удаление одного объекта от другого, а схема (б) – процесс, в котором сначала объекты сближаются (до момента их встречи), а потом начинают удаляться друг от друга.
Для иллюстрации данной задачи учащиеся должны выбрать схему (а). С ее помощью они без особого труда должны решить предложенную задачу. Для этого сначала они должны найти скорость изменения расстояния между поездами (60 км/ч + 80 км/ч = 140 км/ч), а потом вычислить, каким будет это расстояние через 3 ч, если движение они начали из одного пункта (140 км/ч•3 ч = 420 км).
1) 60 км/ч + 80 км/ч = 140 км/ч
2) 140 км/ч • 3 ч = 420 км
Ответ: 420 км. 50
-
Ответы к странице учебника 50
160. Задание 160 является логическим продолжением задания 159. Их обязательно нужно рассматривать как общее задание. Разбиение на два задания было продиктовано лишь техническими причинами (текст одного задания не должен располагаться на двух сторонах одного и того же листа учебника). Что касается решения задачи из предыдущего задания, то мы его уже привели выше. А для ответа на требование из данного задания нужно лишь вычислить время, за которое при скорости 140 км/ч расстояние между поездами станет равным 280 км. Это время равно 2 ч (280 км : 140 км/ч = 2 ч).
Решение:
1) 60 + 80 = 140 (км/ч) - скорость удаления.
2) 280 : 140 = 2 (ч) - столько надо поездам, чтобы удалиться на расстояние 280 км.
Ответ: 2 часа.161. Так как скорость одного объекта известна (40 км/ч) и известна скорость изменения расстояния между объектами (60 км/ч), то скорость второго объекта можно найти, только однозначного ответа не получится.
Решение:
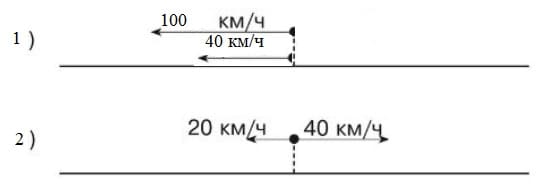
1) Если движение осуществляется в одном и том же направлении, то разность скоростей этих объектов должна равняться 60 км/ч. Следовательно, скорость второго объекта будет равна 100 км/ч.
100 км/ч – 40 км/ч = 60 км/ч
2) Если же объекты движутся в противоположных направлениях, то сумма скоростей этих объектов должна равняться 60 км/ч. Следовательно, скорость второго объекта равна 20 км/ч.
40 км/ч + 20 км/ч = 60 км/ч
162. Предлагается сформулировать задачу по каждой из предложенных схем движения. При формулировке задач прежде всего учащиеся должны определиться с выбором транспортных средств так, чтобы данные скорости соответствовали этим транспортным средствам. Только потом формулировать условие, в котором будет идти речь о движении из одного пункта с данными скоростями, и требование, в котором будет идти речь либо о расстоянии, либо о времени, которые определяются скоростью изменения расстояния между объектами.
Формулируем задачи.
1) От одной станции в разных направлениях отправились два поезда, один со скоростью 20 км/ч, второй - 40 км/ч. На каком расстоянии они будут друг от друга через 1 час.
2) От одной станции в разных направлениях отправились два поезда, один со скоростью 60 км/ч, второй - 40 км/ч. На каком расстоянии они будут друг от друга через 1 час.
3) От одной станции в разных направлениях отправились два поезда, один со скоростью 100 км/ч, второй - 40 км/ч. На каком расстоянии они будут друг от друга через 1 час. 51
-
Ответы к странице учебника 51
163. Деление столбиком.
-625I 9
54 I 69
-85
81
4 (остаток)
-597I 12
48 I 49
-117
108
9 (остаток)
-894I 3
6 I298
-29
27
- 24
24
0
-238I 25
225I 9
13 (остаток)
-3457I 8
32 I 432
-25
24
- 17
16
1 (остаток)
-8346I 15
75 I 556
-84
75
- 96
90
6 (остаток)
-5273I 4
4 I 1318
-12
12
- 7
4
- 33
32
1 (остаток)
-2468I 32
224 I 77
-228
224
4 (остаток)164. Покупатель в магазине истратил денег в 4 раза больше, чем на рынке. Сколько всего денег истратил покупатель, если в магазине он истратил на 1563 рубля больше, чем на рынке?
Решение:
Получается что на рынке покупатель истратил 1 часть, а в магазине 4 таких части. Если принять х за потраченные деньги на рынке, то можно составить уравнение, при условии, что четыре пятых всех денег были потрачены в магазине, то есть х+1563 это четыре пятых от всей суммы, которая равна 5 частям потраченным на рыке, если добавить к ней одну часть. То есть 5х - это все деньги. Получается.
1) 5х = х + х + 1563
1563 = 5х - 2х
1563 = 3х
х = 521 (р) - потратил покупатель на рынке.
2) 521 + 1563 = 2084 (р) - покупатель потратил в магазине.
3) 2084 + 521 = 2605 (р) - всего потратил покупатель.
Ответ: 2605 рублей всего потратил покупатель.165. Сформулируй задачу на движение в одном направлении, используя следующую схему. Реши сформулированную задачу. Вычисли и запиши ответ.
Из двух населенных пунктов в одном направлении одновременно выехали две машины. У одной была скорость 70 км/ч, а у второй 80 км/ч. Через сколько расстояние между машинами увеличится на 30 км?
Решение:
1) 80-70=10 (км/ч) - скорость удаления.
2) 30:10=3 (ч) - через столько расстояние между машинами увеличится на 30 км.
Ответ: через 3 ч.166. Сформулируй задачу на движение в противоположных направлениях, используя следующую схему. Реши сформулированную задачу. Вычисли и запиши ответ.
Из двух населенных пунктов навстречу друг другу, выехали две машины. У одной была скорость 60 км/ч, а у второй 50 км/ч. Через сколько расстояние между машинами уменьшится на 220 км, при условии, что они все еще не встретились?
Решение:
1) 60 + 50 = 110 (км/ч) - скорость сближения.
2) 220 : 2 = 2 (ч) - через столько времени расстояние между машинами уменьшится на 220 км.
Ответ: через 2 ч. 52
-
Ответы к странице учебника 52
167. Прочитай две задачи...
а) Автобус первые четыре часа ехал со скоростью 40 км/ч, а следующие четыре часа со скоростью в 2 раза больше. Во сколько раз расстояние пройденное автобусом за вторые четыре часа, больше расстояния, пройденного за первые четыре часа?
б) Токарь первые 4 часа работал с производительностью 40 дет./ч...
Отличие от предыдущего задания состоит лишь в том, что в данном задании речь идет об уменьшении объема произведенной продукции, а в предыдущем задании речь шла об увеличении произведенной продукции. Однако это не означает, что характер зависимости изменился: и в первом, и во втором случае зависимость остается прямой пропорциональной.
Решение:
а)
1) 40 * 4 = 160 (км) - автобус проехал за первые 4 часа.
2) 40 * 2 = 80 (км/ч) - скорость автобуса во вторые 4 часа.
3) 80 * 4 = 320 (км) - автобус проехал за вторые 4 часа.
4) 320 : 160 = 2 (раза) расстояние во вторые 4 часа больше расстояния большего в первые 4 часа.
Ответ: в 2 раза.
б)
1) 40 * 4 = 160 (дет.) - токарь выточил в первые 4 часа.
2) 40 * 2 =80 (дет./ч) - точил вторые 4 часа.
3) 80 * 4 = 320 (дет.) - токарь выточил за вторые 4 часа.
4) 320 : 160 = 2 (раза) - во столько больше токарь выточил во вторые 4 часа, чем в первые 4 часа.
Ответ: в 2 раза.168.
Если время работы одинаковое, то увеличение (уменьшение) производительности в некоторое число раз приводит к увеличению (уменьшению) объема выполненной работы в это же число раз.
1) 120 : 8 = 15 (дет/ч) - должна быть производительность при 8 часов дне и изготовлении 120 деталей за день.
2) 120 * 3 = 360 (дет) - при увеличенном объеме деталей за день в 3 раза.
3) 360 : 8 = 45 (д/ч) - должна быть производительность при 8 часов дне и изготовлении 360 деталей за день.
4) 45 : 15 = в 3 (раза) - должна быть выше производительность.169.
Если время работы одинаковое, то увеличение (уменьшение) производительности в некоторое число раз приводит к увеличению (уменьшению) объема выполненной работы в это же число раз.
1) 40 * 8 = 320 (дет.) - сделают при производительность 40 дет/ ч и при 8 часов рабочем дне.
2) 40 : 4 =10 (дет./ч) - будут делать при снижении производительности в 4 раза.
3) 10 * 8 = 80 (дет.) - сделают при производительность 10 дет/ ч и при 8 часов рабочем дне.
4) 320 : 80 = 4 (раз) - во столько раз снизится объем выпускаемой продукции. 53
-
Ответы к странице учебника 53
170. См таблицу.
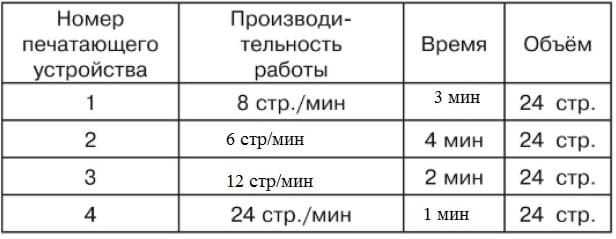
Производительность 3 устройства 2 раза выше, чем 2.
Время работы при печати того же количества страниц для 2 устройства в 2 раза меньше, чем для устройства 3.
При увеличении производительности в 2 раза время работы уменьшается в 2 раза, если объем выполненной работы остается одним и тем же. Для соответствующих величин другой пары печатающих устройств имеет место та же самая обратная пропорциональная зависимость, только коэффициент пропорциональности равен не числу 2, а числу 3.
171.
Для выполнения задания нужно применить установленное выше правило, связывающее производительность и время при постоянном объеме работы. Но перед этим учащиеся должны выполнить кратное сравнение данных промежутков времени (12 ч и 360 мин). Сделать это будет совсем легко, если выразить второй временной промежуток в часах (360 мин = 6 ч). Тогда новое время в 2 раза меньше старого (12 ч : 6 ч = 2 (раза)).
360 мин = 6 ч
12 ч : 6 ч = 2 (раза)
Это означает, что новая производительность должна быть в 2 раза больше старой, т. е. производительность должна увеличиться в 2 раза. 54
-
Ответы к странице учебника 54
172.
Время строительства уменьшилось в два раза. При этом производительность увеличилась в 2 раза. Правило верное.
173. Одна бригада овощеводов собирает урожай с поля площадью 12 га за 6 рабочих дней. Во сколько раз больше производительность второй бригады, если она выполняет эту работу за 3 дня?
1) 12 : 6 = 2 (га/день) - производительность первой бригады.
2) 12 : 3 = 4 (га/день) - производительность второй бригады.
3) 4 : 2 = 2 (раза) - производительность второй бригады выше, чем первой.
Ответ: в 2 раза.174. Во сколько раз уменьшится врем производства фабрикой данного объема продукции, если производительность на фабрике возрастет в 2 раза? Проверить на примере выпуска 240 плиток, если фабрика работает с производительность 5 плиток в минуту.
Учащимся предлагается сначала сделать вывод о том, как изменится время по выполнению данного объема работы при увеличении производительности в 2 раза и проверить его на конкретном примере. После этого они должны сформулировать соответствующее правило, которое отличается от правила из задания 172 тем, что меняется направление зависимости между величинами (в данном случае время зависит от производительности).
Решение:
1) 240 : 5 = 48 (мин) - потребуется фабрике, чтобы произвести 240 плиток, с производительность 5 плиток в минуту.
2) 5 * 2 = 10 (пл./мин) - производительность выше в два раза.
3) 240 : 10 = 24 (мин) - потребуется фабрике, чтобы произвести 240 плиток, с производительность 10 плиток в минуту.
4) 48 : 24 = 2 (раза) - потребуется меньше времени.
Ответ: в 2 раза меньше времени потребуется. 55
-
Ответы к странице учебника 55
175. Два токаря выполняют одинаковую работу. Один работает с производительностью 5 дет./ч, а второй 6 - дет./ч. Сколько деталей они делают за 1 ч?
Решение:
1) 6 + 5 = 11 (дет.) - сделают токари за 1 час
Ответ: (дет.) сделают токари за 1 час.
Совместная производительность находится путем сложения производительности каждого из рабочих.176. Один контролер проверяет за 8 часовой рабочий день 96 деталей, а другой работает с производительностью 10 дет/ч. Сколько деталей проверят оба контроллера за 1 час, если производительность первого не изменится в течении рабочего дня?
1) 96 : 8 = 12 (дет/ч) - производительность одного из контролеров.
2) 10 + 12 = 22 (дет/ч) - производительность двух контролеров.
Ответ: 22 дет/ч производительность двух контроллеров.177. На складе в течение 8 часового рабочего дня каждый час должны привозить 20 магнитофонов, а увозить в течение дня 150 магнитофонов.
Через сколько рабочих дней в таком режиме число магнитофонов на складе увеличится до 1000 штук?Решение:
1) 8 * 20 = 160 (маг./день) - появляется на складе.
2) 16 - 150 = 10 (маг./день) - увеличение магнитофонов на складе за день.
3) 1000 : 10 = 100 (дн.) - на складе будет 1000 магнитофонов.
Ответ: через 100 дней. 56
-
Ответы к странице учебника 56
178. Предприятие каждый день сбрасывает в очистные сооружения 80 куб. м. грязной воды. Производительность очистных сооружений 3 куб. м/ч. Имеется еще один бассейн накопитель вместимостью 320 куб. м. который заполнен наполовину. Сколько дней в таком режиме может проработать станция очистки, если очистные сооружения и предприятие работают круглосуточно?
Сначала учащиеся должны найти «исходные» производительности за сутки. Они будут равны 80 куб. м/сут. и 72 куб. м/сут.(3 куб. м/ч•24 ч = 72 куб. м). После этого следует вычислить «итоговую» производительность: 80 куб. м/сут. – 72 куб. м/сут. = 8 куб. м/сут., а также найти вместимость половины бассейна: 320 куб. м : 2 = 160 куб. м. После этого уже можно вычислять искомое время: 160 куб. м : 8 куб. м/сут. = 20 сут.
Решение:
1) 3 * 24 = 72 (куб.м) - производительность очистных за сутки.
2) 80 - 72 = 8 (куб.м.) - воды остается каждые сутки в бассейне.
3) 320 : 2 = 160 (куб.м.) - в бассейне свободны.
4) 160 : 8 = 20 (сут.) - будет заполняться оставшаяся часть бассейна.
Ответ: 20 суток проработает предприятие в таком режиме.179.
Приведем пример такой задачи: «Первая бригада за 5 ч работы обрабатывает 135 деталей. Если эту же работу вместе с первой бригадой будет выполнять и вторая бригада, то за 3 ч они смогут обработать 150 деталей. С какой производительностью в этом случае будет работать вторая бригада, если производительность первой бригады не будет меняться?» При решении такой задачи учащиеся должны воспользоваться правилом, в котором «итоговая» производительность выражается в виде суммы «исходных» производительностей. Только искомой в этом равенстве является одна из «исходных» производительностей, поэтому она находится с помощью действия вычитания. Приведем запись решения сформулированной задачи с вычислением ее ответа:
1) 135 дет : 5 ч = 27 дет./ч;
2)150 дет. : 3 ч = 50 дет./ч;
3) 50 дет./ч – 27 дет./ч = 23 дет./ч.
Ответ: 23 дет./ч. с такой производительностью должна работать вторая бригада.180. При совместной работе две типографии могут отпечатать тираж журнала 20000 экземпляров за 4 рабочих дня. С какой производительностью в этом случае работает вторая типография, если первая работает с производительностью 3000 экз./день?
Решение:
1) (20000 - 4 * 3000) : 4 = 2000 (экз./ день) производительность второй типографии.
Ответ: 2000 экземпляров в день. 57
-
Ответы к странице учебника 57
181.
Учащимся сначала предлагается по имеющимся данным составить перечень бригад, которые вместе за 1 год смогут построить 12 зданий. Для выполнения этой части задания учащиеся должны воспользоваться правилом о сложении «индивидуальных» производительностей. Для получения «итоговой» производительности в 12 зд./год нужно сложить производительности 1-й, 2-й и 3-й бригад.
После этого учащиеся должны найти для каждой из выбранных бригад число месяцев, которое нужно соответствующей бригаде для строительства 1 здания. Так как производительность бригад остается постоянной, то время и объем выполненной работы связаны прямой пропорциональной зависимостью. Поэтому на основании известной производительности бригады (например, для 1-й бригады это 4 зд./год) можно легко вычислить время строительства 1 здания этой бригадой. Оно будет во столько же раз меньше 1 года (12 месяцев), во сколько объем работы при строительстве 1 здания меньше, чем объем работы при строительстве 4 таких зданий (12 мес. : 4 = 3 мес.).
Аналогично вычисляем интересующее нас время для двух других бригад.
Ответы:
Чтобы построить 12 зданий за год, надо пригласить 2 и 3 бригаду.
12 мес. : 4 = 3 мес. - время строительства 1 здания 1-й бригадой
12 мес. : 6 = 2 мес. - время строительства 1 здания 2-й бригадой
12 мес. : 6 = 2 мес. - время строительства 1 здания 3-й бригадой
12 мес. : 3 = 4 мес. - время строительства 1 здания 4-й бригадой
Для строительства 12 зданий для каждой бригады надо:
12 : 4 = 3 (года) - нужно 1-й бригаде, чтобы построить 12 зданий
12 : 6 = 2 (года) - нужно 2-й бригаде, чтобы построить 12 зданий
12 : 6 = 2 (года) - нужно 3-й бригаде, чтобы построить 12 зданий
12 : 3 = 4 (года) - нужно 4-й бригаде, чтобы построить 12 зданий182.
Учащимся сначала предлагается решить задачу на нахождение времени совместной работы. Сделать это они могут следующим образом:
1) 48 : 6 = 8 (сот./дн.) - производительность одной бригады
2) 48 : 3 = 16 (сот./дн.) - производительность другой бригады
3) 8 + 16 = 24 (сот./дн.) - совместная производительность.
4) 48 : 24 = 2 (дн.) - надо на уборку урожая двумя бригадами.
Ответ: 2 дня собрали бы весь урожай две бригады.После этого учащимся предлагается проверить, измениться ли ответ задачи, если все данные задачи сохранить, кроме одного, а одно изменить (площадь участка 48 соток нужно заменить на 24 сотки или на 18 соток). Итогом проверки должен стать вывод о том, что искомое время не изменяется. Это объясняется тем, что искомое время связано не с объемом выполненной работы, а с индивидуальным временем выполнения этого объема работы каждой бригадой.
183.
«Так как все коровы поедают корма с одинаковой скоростью, то две коровы съедят весь запас кормов за то же время, за которое одна корова съест половину этого запаса. Но половину запаса кормов одна корова съест за 3 дня, так как весь запас кормов одна корова съедает за 6 дней (6 дн. : 2 = 3 дн.)». Пусть речь идет о трех коровах. Рассуждая аналогично, приходим к выводу, что «искомое время равно времени, за которое одна корова съедает третью часть всех кормов, т. е. за 2 дня (6 дн. : 3 = 2 дн.)».Пусть речь идет о шести коровах. Рассуждая аналогично, приходим к выводу, «что искомое время равно времени, за которое одна корова съедает шестую часть всех кормов, т. е. за 1 день (6 дн. : 6 = 1 дн.)»
6 : 2 = 3 (дн.) - за столько дней 1 корова съедает половину запаса кормов, вторая съедает столько же, значит за 3 дня 2 коровы съедят весь запас.
6 : 3 = 2 (дн.) - 3 коровы съедят весь запас
6 : 6 = 1 (дн.) - 6 коров съедят весь запас 58
-
Ответы к странице учебника 58
184. Предлагается решить задачу, в которой искомое время работы можно найти, разделив объем работы на соответствующую производительность. Что же касается нахождения этой производительности, то для этого учащиеся должны воспользоваться тем правилом, о котором речь шла в примечании к заданию 180.Решение выглядит следующим образом.
Решение:
1) 48 : 8 ч = 6 (ап./ч) - производительность двух контролеров.
2) 48 : 12 = 4 (ап./ч) - производительность первого контролера.
3) 6 – 4 = 2 (ап./ч) -производительность второго контролера.
4) 48 : 2 = 24 (ч.) - потребуется второму контролеру на ту же работу.
Ответ: 24 часа.185.
Приведем пример такой задачи: «Первая бригада за 9 дней работы может выпустить 36 т продукции. Вторая бригада этот же объем продукции может выпустить за 18 дней. Сколько дней потребуется этим двум бригадам для выпуска этой же продукции, если они будут работать совместно и с той же производительностью?»
186.
Итак, если 2 бригады работают с одинаковой производительностью, то для выполнения всей работы им нужно столько же времени, как для выполнения половины всей работы одной бригадой (вторую половину работы выполняет вторая бригада). Но для выполнения половины всей работы одной бригаде нужно в 2 раза меньше времени, чем на выполнение всей работы. Поэтому время совместной работы двух бригад будет также в 2 раза меньше, чем время работы одной бригады.
187.
В задании 187 учащимся предлагается устно решить задачу на нахождение времени работы одного землекопа. Для ее решения нужны не столько знания зависимости между величинами, описывающими процесс работы, сколько внимательное прочтение и анализ условия задачи. Если 5 землекопов за 5 дней могут вырыть 5 км траншеи, то это означает, что 1 землекоп за эти же 5 дней может вырыть 1 км траншеи (производительность всех землекопов по условию задачи одинаковая). Поэтому ответом данной задачи будет 5 дней, а не 1 день, как может подумать ученик, который отнесется к анализу задачи поверхностно.
59
-
Ответы к странице учебника 59
188.
В задании 188 учащимся предлагается решить задачу «на совместную работу» двух бригад проходчиков. При этом условие данной задачи они могут проиллюстрировать с помощью схемы движения навстречу друг другу двух объектов из разных пунктов. Решается такая задача в два действия:
1) 2 + 3 = 5 (м/дн.) - столько метров проходят в день.
2) 1 000 : 5 = 200 (дн.) - через 200 рабочих дней бригады встретятся при соединении двух частей тоннеля.
Ответ: через 200 рабочих дней.189.
В задании 189 учащимся предлагается сформулировать и решить задачу по данной краткой записи.
Приведем пример такой задачи: «За 8 ч работы в 1-м цехе выпустили 2 568 м ткани. Сколько метров ткани за это же время выпустили во 2-м цехе, если производительность во 2-м цехе на 10 м/ч больше, чем в 1-м?»
1) 2 568 : 8 = 321 (м/ч) - производительность в час в 1 цехе
2) 321 + 10 = 331 (м/ч) - производительность в час во 2 цехе
3) 331 • 8 = 2 648 (м) - выпустят ткани во 2 цехе за 8 часов.
Ответ: 2648 м выпустят ткани во 2 цехе за 8 часов.Но можно предложить и более рациональный путь решения:
1) 10 •8 = 80 (м) - на столько больше выпустят во 2 цехе, чем в 1.
2) 2 568 + 80 = 2648 (м) - выпустят ткани во 2 цехе за 8 часов.
Ответ: 2648 м выпустят ткани во 2 цехе за 8 часов.190.
-3724I 6
36 I620
-12
12
4 (остаток)
-3618I 18
36 I201
-18
18
0
-4912I 7
49 I701
-12
7
5 (остаток)
-5273I 17
51 I310
-17
17
3 (остаток)
-2504I 5
25 I500
4 (остаток)
-7609I 19
76 I400
9 (остаток) 60
-
Ответы к странице учебника 60
191. За 3 часа с конвейера сошло 48 автомобилей. Сколько автомобилей сойдет с конвейера за 12 часов работы с той же производительностью.
Предлагается решить задачу «на нахождение четвертого пропорционального» двумя способами: вычисляя и не вычисляя производительность. При этом второй вариант решения они не могут использовать в том случае, когда число выпущенных автомобилей равно 160.
Решение:
1 способ.
1) 48 : 3 = 16 (ав./ч) - производительность конвейера.
2) 16 * 12 = 192 (ав.) - выпустят за 12 часов.
Ответ: 192 автомобиля.
2 способ
1) 12 : 3 = 4 (раза) - в 12 часах по 3.
2) 48 * 4 = 192 (ав.) - выпустят за 12 часов.
Ответ: 192 автомобиля.
Для того чтобы выпустить 160 автомобилей:
1) 48 : 3 = 16 (ав./ч) - производительность конвейера.
2) 160 : 16 = 10 (ч) - надо будет конвейеру для выпуска 160 машин.
Ответ: 10 часов.
1 вариант помог с решением этого вопроса.192. При совместной работе мастер и его ученики за 2 ч могут обработать 24 детали. За какое время при сохранении той же производительности сможет обработать эти 24 детали один ученик, если производительности мастера в 3 раза выше.
Предлагается решить задачу «на совместную работу», в которой вычисление производительности ученика представляет собой задачу «на сумму и частное». Для вычисления производительности ученика учащиеся могут воспользоваться предложенной схемой, в которой вся полоска изображает «совместную» производительность мастера и ученика, равную 12 дет./ч (24 дет. : 2 ч = 12 дет./ч). Одна часть этой полоски изображает производительность ученика, которая равна 3 дет./ч (1 + 3 = 4 (части), 12 дет./ч : 4 = 3 дет./ч).
Решение:
1) 24 : 2 = 12 (д./ч) - производительность мастера и ученика.
2) 12 : 4 = 3 (д./ч) - производительность ученика.
3) 24 : 3 = 8 (ч) - надо ученику, чтобы сделать 24 детали.
Ответ: 8 часов. 61
-
Ответы к странице учебника 61
193. При совместной работе мастер и его ученики за 2 ч могут обработать 24 детали. За какое время при сохранении той же производительности сможет обработать эти 24 детали один ученик, если производительности мастера на 6 д./час выше ученика?
Предлагается решить задачу «на совместную работу», в которой вычисление производительности ученика представляет собой задачу «на сумму и разность». Для вычисления производительности ученика учащиеся могут воспользоваться предложенной схемой, в которой вся полоска изображает совместную производительность мастера и ученика, равную 12 дет./ч (24 дет. : 2 ч = 12 дет./ч). Половина незакрашенной части этой полоски изображает производительность ученика, которая равна 3 дет./ч (12 дет./ч – 6 дет./ч = 6 дет./ч, 6 дет./ч : 2 = 3 дет./ч).
Решение:
1) 24 : 2 = 12 (д./ч) - производительность мастера и ученика.
2) (12 - 6) : 2 = 3(д./ч) - производительность ученика.
3) 24 : 3 = 8 (ч) - надо ученику, чтобы обработать 24 детали.
Ответ: 8 часов.194.
Предлагается решить задачу «на движение», которая по своей математической сути является задачей «на две разности».
Решение:
1) 10 – 7 = 3 (ч) - на столько часов меньше в пути были туристы во 2 день.
2) 12 : 3 = 4 (км/ч) - скорость туристов.
3) 10 + 7 = 17 (ч) - всего часов шли туристы.
4) 4 •17 = 68 (км) - прошли туристы за 2 дня.
Ответ: 68 км.195.
1 3 4 2
а) (25241+37889)*12:(69581-69577)=189390
1)
+ 25241
37889
63130
2)
- 69581
69577
4
3)
х 63130
12
+ 12626
63130
757560
4)
-757560I 4
4 I189390
-35
32
-37
36
-15
12
-36
36
0
1 3 4 2
б) (35472+27792):12*(78953-78929)=126528
1)
+ 35472
27792
63264
2)
- 78953
78929
24
3)
-63264I 12
60 I 5272
-32
24
-86
84
-24
24
0
4)
х5272
24
+21088
10544
126528 62
-
Ответы к странице учебника 62
196.
а) Автобус первые 4 часа ехал со скоростью 40 км/ч, а в следующие четыре часа со скоростью в 2 раза больше. Во сколько раз больше путь преодолел автобус за вторые четыре часа по сравнению с первыми.
Решение:
1) 40 * 4 = 160 (км) - проехал автобус за первые 4 часа.
2) 40 * 2 = 80 (км/ч) - скорость автобус за вторые 4 часа.
3) 80 * 4 = 320 (км) - проехал автобус за вторые 4 часа.
4) 320 : 160 =2 (р.) - больше проехал автобус за вторые 4 часа, чем за первые.
Ответ: в 2 раза больше.б) Токарь первые четыре часа работал с производительностью 40 дет/ч, а следующие четыре часа с производительностью в 2 раза больше. Во сколько раз больше деталей обработал токарь за вторую половину 8 часового дня, чем за первую?
1) 40 * 4 = 160 (дет) - токарь обработал за первые 4 часа.
2) 40 * 2 = 80 (дет) - токарь обработал за вторые 4 часа.
3) 80 * 4 = 320 (дет) - токарь обработал за вторые 4 часа.
4) 320 : 160 = 2 (р.) - больше токарь обработал за вторые 4 часа, чем за первые.
Ответ: в 2 раза больше токарь обработал за вторые 4 часа, чем за первые.При выполнении задания учащиеся получают возможность еще раз убедиться в существовании полной аналогии в зависимости соответствующих величин при описании трех процессов – процесса движения, процесса работы и процесса купли-продажи. Для решения трех предложенных задач можно использовать одно и то же числовое выражение, которое выглядит следующим образом: (40•2•4) : (40•4). Так как в этом выражении делимое в 2 раза больше, чем делитель, то значение этого выражения равно числу 2. Именно в 2 раза стоимость второй покупки будет больше, чем стоимость первой. Другими словами, мы еще раз предложили учащимся убедиться в том, что при увеличении цены в несколько раз стоимость увеличивается в это же число раз (если, конечно, количество остается постоянным).
197.
В задании 197 учащимся предлагается ответить на вопрос, как должна измениться цена товара, чтобы стоимость той же самой покупки увеличилась в 3 раза. На основании факта существования прямой пропорциональной зависимости между этими величинами (и здесь можно опираться на принцип аналогии) учащиеся должны прийти к выводу, что цена должна также увеличиться в 3 раза.
198. Как должна измениться стоимость покупки, если цена товара уменьшиться в 4 раза, а количество останется тем же самым?
На основании факта существования прямой пропорциональной зависимости между величинами учащиеся должны прийти к выводу, что стоимость должна также уменьшится в 4 раза.
63
-
Ответы к странице учебника 63
199. Смотрим таблицу.
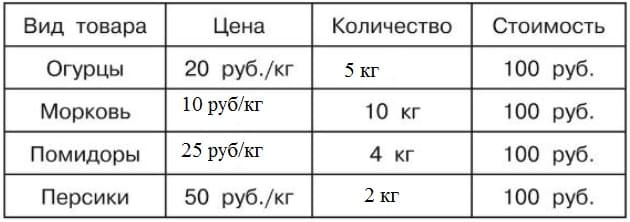
При увеличении цены в 2 раза количество товара уменьшается в 2 раза, если стоимость покупки остается одной и той же. Для соответствующих величин другой пары товаров имеет место та же самая обратная пропорциональная зависимость с тем же самым коэффициентом пропорциональности.
200.
В задании 200 не только предлагается учащимся познакомиться с формулировкой правила, в котором выражена обратная пропорциональная зависимость между ценой и количеством при постоянной стоимости, но и еще раз убедиться в его справедливости на конкретном примере.
64
-
Ответы к странице учебника 64
201.
В задании 201 предлагается решить задачу с использованием правила из предыдущего задания. Для этого они сначала должны выполнить кратное сравнение количества огурцов, купленных по одной цене и по другой цене (напоминаем, что стоимость покупок остается одной и той же). В результате у них получится, что во втором случае они купили огурцов в 5 раз больше (15 кг : 3 кг = 5 (раз)). После этого можно обратиться к правилу и сделать вывод о том, что цена огурцов уменьшилась в 5 раз.
Решение:
15 : 3 = 5 (раз)
Ответ: в 5 раз цена огурцов летом ниже, чем зимой.202.
В задании 202 предлагается решить еще одну задачу с использованием правила из задания 200. Отличие состоит лишь в том, что теперь нужно начать с выполнения кратного сравнения цен. Результат этого сравнения равен числу 2 (30 руб./кг : 15 руб./кг = 2 (раза)).Следовательно, помидоров можно на эти же деньги купить в 2 раза меньше, чем огурцов, т. е. 10 кг (20 кг : 2 = 10 кг). Данную задачу можно было бы решить и по другому, вычислив в первом действии стоимость покупки (15 руб./кг•20 кг = 300 руб.), а во втором – количество купленных помидоров (300 руб. : 30 руб./кг = 10 кг), но при таком способе решения мы никак не используем сформулированное выше правило, что с методической точки зрения будет не совсем правильно.
Решение:
1) 30 : 15 = 2 (раза) - во столько раз помидоры дороже огурцов.
2) 20 : 2=10 (кг) - помидоров можно купить за те же деньги.
Ответ: 10 кг помидоров.203.
Учащимся предлагается сформулировать и решить задачу по данной краткой записи. Приведем пример такой задачи:
За 4 кг кур заплатили 300 руб. Купленная рыба по цене оказалась в 2 раза дороже, чем куры. Сколько килограммов рыбы купили, если за нее заплатили столько же, сколько и за кур?
При решении этой задачи можно опираться на нахождение цены каждого вида товара и тогда решение задачи будет состоять из трех действий:
1) 300 : 4 = 75 (руб./кг) - стоит курица.
2) 75 • 2 = 150 (руб./кг) - стоит рыба.
3) 300 : 150 = 2 (кг) - рыбы купили
Ответ: 2 кг в рыбы купили.Если же воспользоваться правилом из задания 200, то решение данной задачи будет состоять из одного действия:
1) 4 кг : 2 = 2 (кг) в рыбы купили.
Ответ: 2 кг в рыбы купили.204.
В задании 204 учащимся предлагается сформулировать правило, которое будет отличаться от правила из задания 200 только тем, что количество и цена в нем меняются ролями – цена становится исходной независимой величиной, а количество зависит от цены. Все остальные составляющие правила не изменяются.
65
-
Ответы к странице учебника 65
205.
Учащиеся познакомятся с понятием «цена набора товаров» на примере набора, состоящего из 1 кг ягод и 1 кг сахарного песка. Для этого учащиеся сначала должны найти стоимость каждого из этих видов товара. После этого можно с помощью сложения найти стоимость набора товаров, который состоит из 1 кг ягод и 1 кг сахарного песка. Теперь можно находить количество таких наборов, которые можно купить на 120 руб.
Решение:
1) 120 : 3 = 40 (руб.) - стоимость ягод
2) 120 : 6 = 20 (руб.) - стоимость сахара.
3) 40 + 20 = 60 (руб.) - эта стоимость определяет цену данного набора товаров (60 руб./наб.) сахар + ягоды.
4) 120 : 60 = 2 (наб.) - ягоды + сахар.
Ответ: 2 набора можно купить на 120 рублей.206.
При выполнении задания 206 учащиеся имеют возможность поупражняться в вычислении цены набора товаров, которая будет складываться из стоимости каждого вида товара, входящего в этот набор. Сначала нужно вычислить эти стоимости. Так, стоимость 1 книги равна 103 руб. (2575 руб. : 25 = 103 руб.), стоимость 1 ручки – 10 руб. (250 руб. : 25 = 10 руб.) и стоимость 1 тетради – 20 руб. (500 руб. : 25 = 20 руб.).После этого можно находить стоимость 1 набора, состоящего из 1 книги, 1 ручки и 1 тетради. Она будет равна 133 руб. (103 руб. + 10 руб. + 20 руб. = 133 руб.). Это означает, что цена интересующего нас набора равна 133 руб./наб.
Решение:
1) 2575 : 25 = 103 (руб.) - стоимость книги.
2) 250 : 25 = 10 (руб.) - стоимость ручки.
3) 500 : 25 = 20 (руб.) - стоимость тетради.
4) 103 + 10 + 20 = 133 (руб.) - стоимость набора.
Ответ: 133 рубля.207.
При выполнении задания 207 учащиеся получают возможность продемонстрировать свое умение формировать набор заданной цены по известным ценам отдельных товаров. Для этого они сначала должны определить, какой должна быть цена искомого набора. В данном случае цена равняется 160 руб./наб. (800 руб. : 5 наб. = 160 руб./наб.). После этого можно составлять набор по данным ценам, которые указаны в таблице. Например, это может быть набор, состоящий из 1 альбома и 4 фломастеров, или из 4 коробок карандашей и 3 фломастеров. Можно предложить и другие варианты. Главное, чтобы суммарная стоимость всех товаров из набора составляла 160 руб.
800 руб. : 5 наб. = 160 руб./наб.
1 альбом + 4 фломастера
4 кор. карандашей + 3 фломаст. 66
-
Ответы к странице учебника 66
208. За 15 одинаковых коробок конфет заплатили 765 рублей. Сколько стоят 20 таких же коробок конфет? Как нужно изменить данные в формулировке этой задачи, чтобы ее можно было решить, не вычисляя стоимость 1 коробки?
Решение:
1) 765 : 15 = 51 (руб.) - стоит одна коробка конфет
2) 51 * 20 = 1020 (руб.) - стоят 20 таких же коробок конфет.
Ответ: 1020 рублей.
Учащимся предлагается творческое задание, связанное с изменением данных в формулировке задачи таким образом, чтобы новую задачу можно было решить, не вычисляя цены. Для выполнения творческого задания учащиеся сначала должны вспомнить правило, которое связывает стоимость покупки и количество купленного товара при постоянной цене, а уже потом выбрать такое количество коробок при второй покупке, чтобы можно было выполнить кратное сравнение этого количества с количеством коробок при первой покупке. Например, можно 20 коробок заменить на 30 коробок или на 45 коробок. Таких вариантов может быть сколько угодно.209. Стоимость 1 кг конфет, 1 кг печенья и 1 кг сушек 330 руб. Определи цену конфет, печенья и сушек, если за 1 кг конфет и 1 кг печенья нужно было заплатить 200 руб., а за 1 кг печенья и 1 кг сушек 210 руб.
Решение:
1) 330 - 210 =120 (р.) - стоит 1 кг сушек.
2) 330 - 200 =130 (р.) - стоит 1 кг сушек.
3) 330 - 120 - 130 =80 (р.) - стоит 1 кг конфет.
Ответ: 80 р. стоит 1 кг конфет, 120 р стоит 1 кг сушек, 130 р стоит кг печенья.210.
В задании 210 предлагается решить задачу на нахождение стоимости по известной цене и количеству, которое предварительно нужно вычислить. Для вычисления количества купленной ткани учащиеся должны найти количество ткани, которое требуется для пошива 12 костюмов, если на 1 костюм расходуется 3 м ткани. Это количество равно 36 м (3 м•12 = 36 м). После этого можно находить и стоимость всей покупки. Она равна 12 600 руб.
(350 руб./м • 36 м = 12 600 руб.).Решение:
1) 3 - 12 = 36 (м) - ткани надо для пошива 12 костюмов.
2) 350 * 36 =12600 (р.) - стоимость всей покупки.
Ответ: 12600 рублей.211. Цена проката велосипеда 120 руб./ч, лодки - 80 руб./ч. На какое время можно взять напрокат вместе велосипед и лодку, заплатив 600 руб.?
Задание 211 относится к заданиям повышенной сложности. Причиной тому является тот факт, что ранее учащимся еще не предлагались для решения задачи такого типа. Однако это совсем не означает, что учащиеся не подготовлены к выполнению этого задания и доля их самостоятельного участия в его выполнении должна быть сведена к минимуму. Скорее, наоборот, имеет смысл предоставить учащимся максимум самостоятельности в поиске решения предложенной задачи, так как они (без помощи учителя или при минимальном его участии) могут и должны увидеть то, что эта задача полностью аналогична хорошо известным им задачам на движение в противоположных направлениях (когда требуется найти время преодоления заданного расстояния) или задачам на совместную работу (когда требуется найти время выполнения заданного объема работы). Рассуждая по аналогии, учащиеся сначала смогут найти общую цену проката лодки и велосипеда (80 руб./ч + 120 руб./ч = 200 руб./ч), а потом вычислить искомое время (600 руб. : 200 руб./ч = 3 ч).При выполнении второго действия от учащихся потребуется умение делить на число 200. Выполнение такого деления может быть осуществлено разными способами. Здесь можно использовать правило деления на произведение, можно подобрать значение частного с опорой на связь между умножением и делением, а можно воспользоваться кратным вычитанием. Выбор способа остается за учащимися. В качестве дополнения к этому заданию можно предложить учащимся самим сформулировать несколько задач, при решении которых необходимо выполнить сложение цен.
Решение:
1) 80 + 120 = 200 (р/ч) - стоит прокат лодки и велосипеда.
2) 600 : 200 = 3 (ч) - на столько можно взять в прокат одновременно лодку и велосипед.
Ответ: на 3 часа. 67
-
Ответы к странице учебника 67
212.
-2721I 3
27 I 907
-21
21
0
-3852I 7
35 I 550
-35
35
2 (остаток)
-4021I 13
39 I 309
-121
117
4
-5754I 25
50 I 230
-75
75
4 (остаток)213. В задании 213 учащимся предлагается решить задачу «на движение в противоположных направлениях», основной структурной составляющей которой является задача «на сумму и разность». При этом необходимую сумму скоростей предварительно нужно вычислить. Она оказывается равной 140 км/ч (280 км : 2 ч = 140 км/ч). Разность же этих скоростей известна по условию. Она равна 20 км/ч. После такой предварительной работы остается решить
стандартную задачу «на сумму и разность». Учащиеся могут использовать любой из известных им способов решения таких задач. Например, они могут сначала найти удвоенную меньшую скорость:
140 км/ч – 20 км/ч = 120 км/ч. А потом и саму меньшую скорость: 120 км/ч : 2 = 60 км/ч. Тогда большая скорость будет равна 80 км/ч (60 км/ч + 20 км/ч = 80 км/ч).Решение:
1) 20 * 2 = 40 (км) - на столько прошел больше один из поездов.
2) 280 - 40 = 240 (км) - прошли бы поезда, если бы двигались с одинаковой скоростью.
3) 240 : 4 = 60 (км/ч) - скорость одного из поездов.
4) 60 + 20 = 80 (км/ч) - скорость второго поезда.
Ответ: 60 и 80 км/ч скорости поездов.214. Теплоход и катер отправились одновременно от одной пристани в одном направлении. Через 3 ч катер обогнал теплоход на 75 км. С какой скоростью двигался теплоход, если катер двигался со скоростью 45 км/ч?
В задании 214 предлагается решить задачу «на движение в одном и том же направлении», в которой требуется найти скорость более медленного транспортного средства по известной скорости другого транспортного средства и по вычисляемой скорости изменения расстояния между этими транспортными средствами. Анализируя формулировку задачи, не составляет особого труда заметить, что по имеющимся данным можно вычислить скорость изменения расстояния между катером и теплоходом. Она равна 25 км/ч (75 км : 3 ч = 25 км/ч). Так как скорость изменения расстояния между транспортными средствами при движении в одном и том же направлении равна разности скоростей этих транспортных средств, то при вычитании ее из большей индивидуальной скорости получится меньшая индивидуальная скорость (45 км/ч – 25 км/ч = 20 км/ч).
Решение:
1) 75 : 3 = 25 (км/ч) - на столько больше скорость у катера.
2) 45 - 25 = 20 (км/ч) - скорость теплохода.
Ответ: 20 км/ч.215.
В задании 215 учащимся предлагается начертить прямоугольник, периметр которого известен, а длина одной стороны на 4 см больше, чем длина другой стороны. Это задание геометрического характера фактически является арифметической задачей «на сумму и разность», если не учитывать сам процесс построения прямоугольника, а говорить только о вычислении длин этого прямоугольника. Дело в том, что разность длин соседних сторон известна по условию (она равна 4 см), а сумму этих длин можно легко вычислить, разделив периметр пополам. Эта сумма будет равна 90 мм (180 мм : 2 = 90 мм). Для осуществления дальнейших вычислений нужно привести указанные длины к одной единице, а именно: выразить 4 см в миллиметрах. После этого можно применять хорошо известный способ решения задач «на сумму и разность»: 90 мм – 40 мм = 50 мм, 50 мм : 2 = 25 мм, 90 мм – 25 мм = 65 мм. Таким образом, стороны имеют длины соответственно 65 мм и 25 мм. Остается только начертить прямоугольник с такими сторонами.
180 : 2 = 90 (мм) - сумма длин двух сторон
4 см = 40 мм
90 – 40 = 50 (мм)
50 : 2 = 25 (мм) - длина 1 стороны
90 – 25 = 65 (мм) - длина 2 стороны
Ответ: стороны прямоугольника 65 мм и 25 мм.
Чертим этот прямоугольник.216.
В задании 216 учащимся предлагается начертить прямоугольник, периметр которого известен, а длина одной стороны в 3 раза больше, чем длина другой стороны. Это задание геометрического характера фактически является арифметической задачей «на сумму и частное», если не учитывать сам процесс построения прямоугольника, а говорить только о вычислении длин этого прямоугольника. Дело в том, что результат кратного сравнения длин соседних сторон известен по условию (длина одной стороны в 3 раза больше, чем длина другой), а сумму этих длин можно легко вычислить, разделив периметр пополам. Эта сумма будет равна 100 мм (200 мм : 2 = 100 мм). После этого можно применить хорошо известный способ решения задач «на сумму и частное»: 1 ч. + 3 ч. = 4 ч., 100 мм : 4 = 25 мм, 25 мм•3 = 75 мм. Таким образом, стороны имеют длины соответственно 25 мм и 75 мм. Остается только начертить прямоугольник с такими сторонами.
200 : 2 = 100 (мм) - сумма длин двух сторон
1 + 3 = 4 (ч.)
100 : 4 = 25 (мм)
25 • 3 = 75 (мм)
Ответ: стороны имеют длины соответственно 25 мм и 75 мм.
Чертим прямоугольник с такими сторонами.217.
В задании 217 предлагается решить задачу на использование правила нахождения цены набора товаров. При этом нам известна стоимость набора (гвоздики в упаковке). Она составляет 100 руб. Если из этой стоимости вычесть стоимость 1 упаковки, т. е. 25 руб., то останется стоимость 5 гвоздик. Так как эта стоимость равна 75 руб.(100 руб. – 25 руб. = 75 руб.), то стоимость одной гвоздики равна 15 руб. (75 руб. : 5 = 15 руб.). Следовательно, гвоздики продаются по цене 15 руб./шт.
Решение:
1)100 - 25=75 (р) - стоят гвоздики без упаковки.
2) 75 : 5=15 (р) - стоит 1 гвоздика.
Ответ: 15 рублей. 68
-
Ответы к странице учебника 68
218.
-25I 8
24 I3 (неполное частное)
1 (остаток)
До точки число - 3
Если при выполнении деления в результате получилось целое число, то оно и будет неполным частным, а остаток в этом случае равен 0.219.
При выполнении задания 219 учащиеся имеют возможность познакомиться с сокращенным способом вычитания из данного числа одного и того же числа несколько раз. При этом процедуру многократного вычитания одного и того же числа мы связываем с выполнением деления с остатком.
220.
В задании 220 предлагается найти неполное частное, выполняя кратные вычитания делителя из делимого. При этом остаток в результате такого кратного вычитания также вычисляется.
-153I 21
147 I7 (неполное частное)
6 (остаток)221.
В задании 221 учащимся сначала предлагается найти с помощью калькулятора неполное частное при делении числа 45 689 на число 17. О том, как это можно сделать, было сказано в задании 218. После этого предлагается выполнить деление столбиком указанных чисел. При условии, что неполное частное уже найдено, его можно записать на соответствующем месте и использовать при выполнении всех промежуточных этапов деления в алгоритме деления столбиком.
2687 - неполное частное.
_45689 |17
34 |2687
_116
102
_148
136
_129
119
10 69
-
Ответы к странице учебника 69
222.
При выполнении задания 222 учащиеся имеют возможность поупражняться в выполнении деления столбиком с помощью калькулятора. При этом они могут использовать как способ из задания 218,так и способ из задания 220. В помощь учащимся мы предлагаем формулировку правила по нахождению остатка.
Неполное частное: 15807, 5699, 2841
223.
Выполняя задание 223, учащиеся фактически упражняются в нахождении неполного частного при делении каждого из данных чисел на число 47.
Неполные частные: 549, 8063, 2743, 7827
224.
Сначала данное число нужно уменьшить на величину остатка, а уже потом полученное число можно уменьшать (или увеличивать) на величину делителя любое число раз. Это означает, что сначала нужно найти интересующий нас остаток. Как это сделать, учащиеся
уже знают (см. правило из задания 222). Остаток в данном случае равен 36. Тогда искомое число равно 387 885 (387 921 – 36 = 387921).Другие два числа могут быть такими:
387 790 (387 885 – 95 = 387790)
и 387 695 (387 790 – 95 = 387 695).225.
Задание 225 относится к заданиям повышенной сложности. Для того чтобы его выполнить, учащиеся прежде всего должны понять, что сначала данное число нужно увеличить на значение разности между делителем и остатком, а уже потом это полученное
число можно уменьшать (или увеличивать) на величину делителя любое число раз. Это означает, что сначала нужно найти интересующий нас остаток. Как это сделать, учащиеся уже знают. Остаток в данном случае равен 2. Тогда искомое число равно 258 400 (258 317 + (85 – 2) = 258 400).Другие два числа могут быть такими:
258 485 (258 400 + 85 = 258 485) и
258 570 (258 485 + 85 = 258 570).226.
Считаем на калькуляторе. Порядок действий: вначале в скобках, потом по порядку слева направо.
70
-
Ответы к странице учебника 70
227.
В задании 227 мы предлагаем учащимся познакомиться с тем, в каком смысле употребляются союзы «и» и «или». При этом мы знакомим их не с обыденным смыслом этих союзов, а с математическим, но на примере ситуации из повседневной жизни.
228.
При выполнении задания 228 учащиеся получают возможность продемонстрировать то, как они понимают смысл союзов «и» и «или» на основе их сопоставления. Следует обратить внимание на то, что все числа из первого столбика обязательно должны входить во второй столбик. При этом во втором столбике записаны и другие числа (35 471 и 8 946), которые не входили в первый столбик, так как эти числа удовлетворяют только одному из двух данных условий: число 35 471 – пятизначное, но не является четным; число 8 946 – не пятизначное, но четное.
Решение:
В первый столбик они должны записать числа 25 698, 54 718 и 23 564 (четные и пятизначные),
а во второй – числа 25 698, 35 471, 8 946, 54 718 и 23 564 (четные или пятизначные).229.
При выполнении задания 229 учащиеся познакомятся с понятием двойного неравенства, которое представляет собой соединение двух соответствующих неравенств в одно двойное неравенство с помощью союза «и».
568897<568935< 569241
230.
В задании 230 учащимся предлагается самим составить двойное неравенство с данным знаком и данными числами.
896353<896354< 896355
71
-
Ответы к странице учебника 71
231.
Задание 231 относится к заданиям повышенной сложности. В нем учащимся предлагается самостоятельно сформулировать условие, которое учитывает все возможные случаи получения числа 0 при умножении двух чисел. Сложность этого задания заключается в том, что в этом условии нужно учесть сразу три случая:
1) первый множитель равен 0, а второй – не равен 0;
2) второй множитель равен 0, а первый – не равен 0;
3) оба множителя равны 0
Все эти три случая легко объединить с помощью союза «или».Именно такой логический смысл и заключает в себе этот союз. Таким образом, искомое условие может быть сформулировано следующим
образом: «Значение произведения двух множителей равно 0,если первый множитель равен 0 или второй множитель равен 0 (хотя бы один из двух множителей равен 0)».232. На квадратном листе бумаге надо начертить круг. Можно ли это сделать если радиус 5 см, а ширина листа 10 см, больше 10 см?
Если ширина бумаги 10 см, а круг 5 см, то границы круга будут заканчиваться вместе с границами листа бумаги. Начертить можно, но круг только только впишется в размер листа. Здесь можно условно сказать, что он вписался или не вписался. Также как рассуждать о том, к чему относится 0, к положительной или отрицательной величине. Если размер листа (ширина, высота более 10 см), то круг легко впишется.
233.
В задании 233 предлагается выписать все натуральные числа, которые удовлетворяют данному «нестрогому» неравенству (фактически речь идет о решении данного неравенства в натуральных числах). Этими числами будут все натуральные числа от 1 до 12 включительно. На число 12 следует обратить особое внимание.
Ответ:
1,2,3,4,5,6,7,8,9,10,11,12
234.
В задании 234 предлагается выписать пять натуральных чисел, которые удовлетворяют данному «нестрогому» неравенству. Говорить о выписывании всех таких чисел (см. предыдущее задание) в данном случае не имеет смысла, так как таких чисел бесконечно много. Особое внимание и в этом задании нужно обратить на число 12. Это число также удовлетворяет данному неравенству.
Ответ:
12, 14, 20, 25, 1000
72
-
Ответы к странице учебника 72
235. Дачнику до железнодорожной платформы от которой отправляется электричка надо идти 2 км, с какой скоростью надо идти дачнику, чтобы успеть на электричку через полчаса.
Решение:
1) 2 + 2 = 4 (км/ч) не менее того должна быть скорость дачника.
Ответ: v ? 4 (км/ч).236. Выписываем натуральные числа.
Ответ:
а) 1,2,3,4,56,7,8,9
б) 4,5,6,7,8,9,10,11,12
в) 1,2,3,4,5,6,7,8,9,10
г) 3,4,5,6,7, 8, 9, 10, 11, 12, 13
д) 1,2,3,4,5,6,7,8,9
е) 4,5,6,7, 8, 9, 10, 11, 12, 13237.
В задании 237 предлагается выписать те утверждения, в которых союз «или» можно заменить на союз «и», не нарушая истинности этого утверждения. Сделать это можно только в тех случаях, когда две части утверждения, соединенные союзом «или», могут выполняться одновременно. Таким свойством обладают утверждения под № 3, 4 и 5.
73
-
Ответы к странице учебника 73
238.
При выполнении задания 238 учащиеся познакомятся с логической конструкцией, о которой речь шла выше. Особенность такой конструкции заключается в том, что она строится с помощью логической связки «если …, то…» или с помощью других равнозначных логических связок («когда …, тогда …», «из того, что …, следует …» и т. п.). При этом истинность первого утверждения обеспечивает истинность второго. В данном задании мы предлагаем познакомиться с логическим смыслом такой конструкции на примере описания реальной ситуации. Так как Миша уверен, что Маша должна выполнить свое обязательство, то это означает, что первое условие им выполнено, т. е. Миша получил «пять» за контрольную работу по математике. Нарушить свое обещание Маша может только в одном случае, если Миша получит «пять» за контрольную работу, а она не подарит ему набор наклеек о футболе. Если же Миша не получит «пять» за контрольную работу, то любое поведение Маши не нарушит их договоренности (даже если она подарит Мише обещанный набор).
239.
Решением задания 239 должно стать следующее утверждение:
Если у прямоугольника все стороны равны, то этот прямоугольник является квадратом.
240.
В задании 240 учащимся предлагается завершить построение следующих утверждений так, чтобы они получились верными. Приведем пример решения этого задания:
а) если запись числа оканчивается на четную цифру, то это число является четным;
б) если в треугольнике есть прямой угол, то этот треугольник является прямоугольным;
в) если первую фигуру можно разместить внутри второй, то площадь первой фигуры меньше, чем площадь второй фигуры;
г) Если сложить два нечетных числа, то в результате получится четное число;
д) если длины сторон двух квадратов равны, то периметры этих квадратов равны;
е) если хотя бы один из множителей равен 0, то значение произведения равно 0.Для выполнения этого задания учащиеся должны не только знать, как правильно построить утверждение с логической связкой «если …, то …», но и хорошо помнить перечисленные факты из ранее изученного материала.
74
-
Ответы к странице учебника 74
241.
При выполнении задания 241 учащиеся познакомятся со смыслом логической связки «не только …, но и …» на конкретном примере описания реальной ситуации. Для проведения логического анализа этой ситуации имеет смысл предложить учащимся рассмотреть отдельно ее составляющие. Во-первых, сравнить по смыслу данное утверждение со следующим утверждением: «Миша всегда очень радуется только тогда, когда сам получает «пятерки», которое несет другой смысл не только с позиции логики, но и с нравственных позиций, на что обязательно нужно обратить внимание учащихся. Во-вторых, в исходной формулировке не исключается тот факт, что Миша радуется своим успехам в учебе, но присутствует и другое: он радуется успехам в учебе и своих одноклассников.
242. При покупке фотоальбом и книги заплатили 180 рублей. Фотоальбом дешевле книги на 20 рублей. Сколько стоит один фотоальбом?
В формулировке задания 242 присутствует логическая связка, о которой речь идет в формулировке темы урока. Учащиеся должны научиться правильно истолковывать утверждения такого типа. Обязательно нужно обратить внимание учащихся, что в первой части этого утверждения («Запиши решение данной задачи не только по действиям»), хотя и содержится частица «не», заключена все же позитивная информация. Это означает, что вариант решения по действиям нужно записывать. Но нужно записывать и другой вариант решения – в виде одного выражения. К такой ситуации приводит наличие слова «только». Если его исключить, то получится следующая формулировка: «Запиши решение данной задачи не по действиям, а с помощью одного выражения». В такой формулировке вариант решения по действиям записывать не нужно.
Решение по действиям:
1) 180 - 20 =160 (р.) - стоят 2 фотоальбома.
2) 160 : 2 = 80 (р.) - стоит один фотоальбом.
Ответ: 80 рублей.Одним выражением:
(180 - 20) : 2 = 80 (р.)
Ответ: 80 рублей стоит один фотоальбом.243.
При выполнении задания 243 учащимся предлагается продемонстрировать то, как они поняли смысл употребления изучаемой логической связки. Для этого они должны выписать все числа (из данных чисел), в записи которых есть цифра 3 и которые являются нечетными. Таких чисел три:
7583, 53381, 3333.
244. задании 244 предлагается дополнить данные предложения так, чтобы получились верные утверждения. Приведем возможный вариант решения этого задания:
а) треугольник бывает не только равнобедренным, но и разносторонним;
б) натуральные числа бывают не только четными, но и нечетными;
в) единицей вместимости является не только литр, но и кубический сантиметр;
г) длину можно измерять не только с помощью линейки, но и с помощью рулетки;
д) величину можно не только умножать на натуральное число, но и делить на натуральное число.Эти же утверждения можно переформулировать с помощью союза «и», сохранив их смысл:
а) треугольник бывает равнобедренным и разносторонним;
б) натуральные числа бывают четными и нечетными;
в) единицей вместимости является литр и кубический сантиметр;
г) длину можно измерять с помощью линейки и с помощью рулетки;
д) величину можно умножать на натуральное число и делить на натуральное число. 75
-
Ответы к странице учебника 75
245.
Для правильного выполнения задания 245 учащиеся должны истолковать предложенную характеристику искомого числа, как логическую конструкцию, состоящую из трех частей и соединенную союзами «и». В свою очередь, это должно быть истолковано следующим образом: каждое из указанных трех условий должно быть выполнено для искомого числа. Если мы будем рассматривать шестизначные числа, которые меньше, чем число 100 010, то их будет всего десять: 100 009, 100 008, 100 007, …, 100 001 и 100 000. Среди них только последнее число является «круглым». Это число 100 000. Оно и будет искомым.
Ответ:
100 000.
246.
Задание 246 внешне похоже на предыдущее задание: в нем также нужно найти числа, которые удовлетворяют данной характеристике (данному характеристическому свойству). Принципиальное отличие состоит в том, что отдельные условия этого характеристического свойства связывает союз «или», а не союз «и», как это было в предыдущем задании. Логический смысл союза «или» говорит о том, что искомое число должно удовлетворять хотя бы одному из указанных требований: быть круглым двузначным или быть двузначным, которое меньше 15. Перечислим все такие числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, 14, 13, 12, 11. Из всех этих чисел есть одно, которое удовлетворяет сразу двум данным требованиям. Это число 10. Оно и круглое двузначное, и двузначное, которое меньше 15. Но соединительный смысл союза «или» допускает такую возможность. Поэтому число 10 также входит в список искомых чисел.
Ответ:
10, 20, 30, 40, 50, 60, 70, 80, 90, 14, 13, 12, 11.
247.
При выполнении задания 247 учащиеся столкнуться с характеристическим свойством геометрических фигур, которое с логической точки зрения состоит из двух частей, соединенных союзом «или». При этом каждая из указанных частей, в свою очередь, состоит из двух частей, соединенных союзом «и». Это означает, что сначала учащиеся могут отобрать те фигуры, которые удовлетворяют первой «половине» всего характеристического свойства, т. е. речь идет о фигурах, которые являются треугольниками и в них есть прямой угол. Фактически речь идет о прямоугольных треугольниках. После этого они должны к выбранным фигурам добавить те фигуры, которые удовлетворяют второй «половине» всего характеристического свойства, т. е. добавить четырехугольники, у которых есть прямой угол (добавить прямоугольную трапецию). Таким образом, невыбранными останутся три фигуры: остроугольный и тупоугольный треугольники (в них нет прямого угла) и пятиугольник с прямым углом (он не является ни треугольником, ни четырехугольником).
Ответ:
76
-
Ответы к странице учебника 76
248.
В задании 248 предлагается выбрать из данных верные утверждения и доказать это. Приведем соответствующие доказательства для каждого из данных утверждений:
а) утверждение верно, так как все треугольники делятся на три типа – остроугольные, прямоугольные и тупоугольные, и в каждом таком треугольнике обязательно есть острый угол (полная индукция);
б) утверждение неверно, так как, например, в остроугольном треугольнике не может быть прямого угла по определению;
в) утверждение верно, так как оно фактически является определением прямоугольного треугольника;
г) утверждение неверно, так как, например, в прямоугольном треугольнике есть прямой угол, но он не является остроугольным;
д) утверждение неверно, так как, например, в прямоугольнике все углы прямые, а он является четырехугольником;
е) утверждение неверно, так как прямоугольная трапеция является четырехугольником, имеющим прямой угол, но она не является прямоугольником;
ж) утверждение верно, так как оно фактически является определением прямоугольника.249.
В задании 249 предлагается логическая задача, для решения которой достаточно внимательно проанализировать предложенную ситуацию. Так, ответ на первый вопрос будет отрицательным, так
как по условию один из двух мальчиков (Витя или Сережа) обязан сидеть с Колей, а это означает, что вместе они сидеть не могут (все парты двухместные).
Ответом на второй вопрос будет формулировка условия, при котором Витя и Сережа могут сидеть вместе. Этим условием будет отсутствие Коли на уроке.
Ответ на последнюю часть задания будет положительным, так как условие «Петя сидит вместе с Сережей» не противоречит исходному условию о том, что Коля всегда сидит с Витей или с Сережей, так как остается возможность его выполнить.Ответ:
нужно Колю посадить с Витей, что и является ответом на самый последний вопрос задания.
250. Задание 250 относится к заданиям повышенной сложности. Это связано с тем, что такого типа задания еще не предлагали учащимся, хотя мы не исключаем, что с ними учащиеся встречались при знакомстве с другими учебниками или учебными пособиями. Прежде всего, учащимся нужно четко разъяснить правило кодирования цифр, которое сформулировано в самом задании. После этого можно предложить учащимся разгадать первый или второй ребус на выбор.
1) Если начинать с первого ребуса, то сначала нужно обратить внимание на разряд десятков. Указанную ситуацию можно реализовать только в том случае, когда буква «Р» обозначает цифру «0». После этого можно расшифровать и другие цифры. Например, буква «И» может обозначать цифру «1», тогда буква «А» обозначает цифру «2». После этого можно перейти к расшифровке буквы «Т». Она может обозначать цифру «3», тогда буква «Ы» обозначает цифру «6».
Остается буква «Д», которая может обозначать любую из оставшихся пяти «свободных» цифр: 4, 5, 7, 8, 9.
Ответ:
+301
301
46022) Для расшифровки второго ребуса достаточно заметить, что в нем записано вычитание однозначного числа из четырехзначного при условии, что в результате получается трехзначное число, записанное тремя одинаковыми цифрами. Такая ситуация возможна лишь тогда, когда записан следующий случай вычитания:
1000 – 1 = 999. Это и есть расшифровка данного ребуса.
Ответ:
-1000
1
9993) Расшифровка третьего ребуса представляет собой гораздо более сложную задачу. Для ее решения учащиеся сначала должны обратить внимание на разряд десятков тысяч (буква «К» обозначает цифру «1»), а потом на разряд единиц и разряд единиц тысяч. Зашифрованные в этих разрядах цифры могут быть найдены простым перебором, начиная с разряда единиц. Такой перебор показывает, что буква «Л» обозначает цифру «3», а буква «С» – цифру «6». После этого можно расшифровать буквы в разряде десятков: буква «О» обозначает, например, цифру «4», а буква «У» – цифру «2». Наконец, переходим к разряду сотен: буква «Т» может обозначать цифру «5», а буква «А» – цифру «0».
Ответ:
+6543
6523
13066 77
-
Ответы к странице учебника 77
251. Вычисли.
1 3 2
(236589+348967)-361215:45=577529
1)
236589
+348967
585556
2)
-361215I 45
360 I 8027
-121
90
-315
315
0
3)
-585556
8027
577529
1 2 4 3
(452369-450864)*16-23418:18= 22779
1)
452369
-450864
1505
2)
х 1505
16
+9030
1505
24080
3)
-23418I 18
18 I 1301
-54
54
-18
18
0
4)
-24080
1301
22779252. Площадь первого земельного участка 2538 кв. м, что на 315 кв. м меньше, чем площадь второго участка, и в 3 раза больше, чем площадь третьего. Чему равна площадь всех трех участков?
Решение:
1) 2538 + 315 = 2835 (кв.м) - площадь второго участка.
2) 2538 : 3 = 846 (кв. м) - площадь третьего участка.
3) 2538 + 2835 + 846 = 6219 (кв.м) - площадь трех участков.
Ответ: 6219 кв.метров.253. Начерти прямоугольник, у которого одна сторона в 4 раза больше и на 75 мм больше, чем другая.
Решение:
Необходимо вычислить стороны. Мы знаем, что если одна сторона больше в 4 раза и на 75 мм, то одна часть из 4 этой стороны, которая равна второй стороне прямоугольника, будет 3 часть от 75 мм. То есть...
75 : 3 = 25 (мм) - одна сторона прямоугольника
25 * 4 = 100 (мм) - вторая сторона прямоугольника.
Чертим прямоугольник со сторонами 25 и 100 мм.254. При выполнении задания 254 учащиеся имеют возможность поупражняться в вычислении площади квадрата по известной длине стороны этого квадрата и в выполнении кратного сравнения найденных площадей квадратов. Подводя итог выполнения этого задания, можно обратить внимание учащихся на тот факт, что увеличение стороны квадрата в 3 раза приводит к увеличению площади в 9 раз (3•3 = 9).
Решение:
Нам не важно какая длина стороны квадрата. Важно понимать, что каждая из сторон увеличилась в 3 раза. Это увеличение сторон мы и учитываем.
3 * 3 = 9 (раз)
Ответ: в 9 раз увеличится площадь квадрата при увеличении его стороны в 3 раза.255. Длины сторон прямоугольника 2 см и 112 см, второго - 21 см и 21 см. Вычисли периметр и площадь каждого прямоугольника. У какого из прямоугольников периметр больше? Площадь какого больше?
В задании 255 мы хотим напомнить учащимся о том, что между периметром и площадью нет ни прямой, ни обратной зависимости. При увеличении периметра прямоугольника площадь может как увеличиваться (что очевидно), так и уменьшаться (что не так очевидно, но что и должны подтвердить учащиеся, выполняя данное задание). Для этого они могут построить два прямоугольника: один с длинами сторон 9 см и 2 см, а другой – 6 см и 4 см. Периметр первого прямоугольника больше, чем второго, а площадь – меньше.
Решение:
1) 2 * 112 = 224 (кв.см) - площадь первого прямоугольника.
2) (2 + 112) * 2 = 228 (см) - периметр первого прямоугольника.
3) 21 * 21 = 441 (кв.см) - площадь второго прямоугольника.
4) (21 + 21) * 2 = 84 (см) - периметр второго прямоугольника.
Ответ: у первого прямоугольника площадь меньше, но периметр больше.256.
Задание 256 относится к заданиям повышенной сложности. Для его выполнения можно воспользоваться идеей, с помощью которой было выполнено предыдущее задание. Если одну сторону прямоугольника делать большой по длине, а другую очень маленькой, то можно достичь как угодно большого периметра (он будет приблизительно равен удвоенной длине большей стороны) и как угодно маленькой площади (она может быть близка к 0 за счет достаточно маленькой длины второй стороны). Если воспользоваться этой идеей, то искомый прямоугольник должен иметь приблизительно следующие размеры: длина большей стороны чуть меньше 500 м, а длина меньшей стороны очень близка к нулю и отличается от нуля на столько, на сколько длина большей стороны отличается от 500 м.
Примечание. Только для учителя мы даем более точную информацию о размере искомого прямоугольника. Эти размеры должны быть приблизительно такими: 49 999,99 998 см и 0,00002 см.257.
-853 I 7
7 I121
-15
14
-13
7
6 (остаток)
-527 I 12
48 I43
-47
36
11 (остаток)
-654 I 8
64 I81
-14
8
6 (остаток)
-327 I 32
32 I 10
7 (остаток)
-2783I 5
25 I 556
-28
25
-33
30
3 (остаток)
-2851 I 29
261 I 98
-241
232
9 (остаток) 78
-
Ответы к странице учебника 78
258. При выполнении задания 258 учащиеся познакомятся с таким понятием, как поверхность куба, которая состоит из шести квадратов. Суммарная площадь этих квадратов (граней этого куба) представляет собой площадь поверхности куба. Для нахождения объема куба с ребром 2 см учащиеся должны мысленно (или с помощью рисунка) разбить этот куб на кубы с ребром 1 см. Таких «единичных» кубов будет 8, и объем каждого из них равен 1 куб. см. Поэтому объем данного куба равен 8 куб. см.
Решение:
2 * 2 * 2 = 8 (см. куб)
Ответ: объем куба с длиной грани 2 см 8 куб.см.259. Сколько краски потребуется для покраски модели куба, если длина ребра куба равна 50 см, а расход краски составляет 100 г на 1 кв. м?
Вычислим площадь поверхности куба и узнаем какой расход будет у краски.
Решение:
1) 50 * 50 * 6 = 15000 (кв.см) - площадь поверхности куба.
2) 10000 : 100 = 100 (кв.см) - можно покрасить 1 г краски.
3) 15000 : 100 = 150 (г) - краски надо на куб.
Ответ: 150 г краски надо на куб.260. Мастеру нужно сделать открытый аквариум в форме куба вместимостью 1000 л. Для этого он взял 5 квадратных листов стекла сто стороной 1 м. Получится ли у него аквариум заданной вместимости?
Вычисляем объем исходя из того, что 1 литр это 10 см * 10см * 10см = 1 куб.дм = 1000 куб.см , а 1 м = 100 см.
Решение:
1) 100 * 100 * 100 = 1000000 (куб.см) - объем аквариума.
2) 1000000 : 1000 = 1000 (куб.дм) - объем аквариума.
Ответ: объем аквариума будет ровно 1000 литров.261.
Задание 261 относится к заданиям повышенной сложности. Для выполнения этого задания учащимся нужно привлечь все свое «геометрическое воображение», хотя в некоторые моменты они могут опираться и на имеющуюся иллюстрацию.
Приведем правильные ответы на все вопросы данного задания:
1) раскрашенными оказались 54 «маленькие» грани (9•6 = 54);
2) нераскрашенным оказался только 1 «маленький» кубик, который был расположен в центре «большого» кубика;
3) раскрашена только одна грань у 6 «маленьких» кубиков, которые были расположены в центре каждой грани «большого» кубика;
4) раскрашены две грани у 12 «маленьких» кубиков, которые были расположены между «угловыми» кубиками;
5) раскрашены три грани у 8 «маленьких» кубиков, которые были расположены в углах «большого» кубика.
Таким образом, мы описали тип раскрашивания для всех 27 «маленьких» кубиков (1 + 6 + 12 + 8 = 27). 79
-
Ответы к странице учебника 79
262.
Для выполнения задания нужно найти число ребер куба. Это число равно 12.
263.
Задание 263 относится к заданиям повышенной сложности. Его можно считать продолжением задания 261. Отличие состоит в том, что теперь речь пойдет о ребрах «маленьких» кубиков, а в задании 261 речь шла о гранях этих кубиков.
Приведем правильные ответы на все предложенные вопросы:
1) ни одно ребро не раскрашено у 7 «маленьких» кубиков, которые были расположены либо в центре «большого» кубика (1), либо в центре каждой грани «большого кубика (6);
2) одно ребро раскрашены у 12 «маленьких» кубиков, которые были расположены между угловыми кубиками;
3) три ребра раскрашены у 8 «маленьких» кубиков, которые были расположены в углах «большого» кубика.
Таким образом, мы описали все 27 «маленьких» кубиков (7 + 12 + 8 = 27). Это доказывает, что других типов раскрашивания ребер у «маленьких» кубиков не существует.Примечание. Подводя итог выполнения заданий 261 и 263,было бы желательно вместе с учащимися проверить полученные результаты практически, построив и раскрасив соответствующие модели. Но такая работа требует от учителя серьезной под-
готовки в технологическом плане, а также достаточно большого времени при ее проведении. По этой причине мы и говорим об этом виде работы только в рекомендательном плане. 80
-
Ответы к странице учебника 80
264.
При выполнении задания 264 учащиеся на примере глобуса Земли имеют возможность повторить то, что им известно о линиях на глобусе (на поверхности шара), которые называются меридианами и параллелями, а также получить первые представления о сечении шара плоскостью. При этом важно знать, что все меридианы – это окружности одного и того же радиуса, совпадающего с радиусом шара, а параллели – это окружности разных радиусов, которые измеряются в пределах от 0 до радиуса шара. Если параллель имеет радиус, равный радиусу шара, то эта параллель называется экватором. В сечении шара плоскостью, проходящей через центр, получается круг.
265.
В задании 265 описан путь по глобусу, который возможен только в том случае, когда движение начинается из точки, называемой полюсом. Таких точек на глобусе две: Северный и Южный полюс. Траектория описанного в этом задании перемещения по глобусу напоминает треугольник, только стороны этого «треугольника» будут образованы не отрезками, а дугами.
266.
Задание 266 является логическим продолжением предыдущего задания. Если перенести путешествие белого медведя с поверхности земли на глобус, то мы столкнемся с ситуацией, описанной в задании 265 (передвижение строго на юг и строго на север можно осуществить только по меридианам, а строго на восток – только по параллелям). Так как белый медведь оказался в той же точке, из которой он начал свой путь, то этой точкой является Северный полюс. Южный полюс не подходит, так как первый этап движения был осуществлен в направлении на юг, а из Южного полюса на юг двигаться нельзя.
Примечание. Задачу можно усложнить, заменив вопрос задачи другим: «Какого цвета был медведь?» На первый взгляд с таким вопросом задача превращается в неуместную шутку, и никакого решения иметь не может. Если провести рассуждения, как и при решении задания 266, то мы получим, что медведь первоначально находился на Северном полюсе, и это означает, что он белого цвета, т. е. цвет медведя мы смогли вычислить.267.
При выполнении задания 267 учащиеся еще раз смогут обратить внимание на тот факт, что круг – это плоская фигура, а шар – это объемная фигура. Кроме этого, они узнают о том, какой отрезок называется радиусом шара.
81
-
Ответы к странице учебника 81
268.
При выполнении задания 268 учащиеся познакомятся с числами, которые называются «треугольными» (но сам этот термин мы не сообщаем учащимся). Происхождение такого названия вполне понятно из приведенной иллюстрации. Нахождение других «треугольных» чисел (кроме данного числа 6) учащиеся должны осуществить опытным путем с помощью построения фигур, аналогичных изображенной на рисунке. Нетрудно догадаться, что если убрать ряд из трех кругов, то оставшаяся фигура также будет напоминать по форме равносторонний треугольник. Это означает, что число 3 также будет относиться к «треугольным» числам. К изображенной на рисунке фигуре можно добавить ряд из 4 кругов и снова получить фигуру, которая будет напоминать равносторонний треугольник.
Следовательно, число 10 относится к «треугольным» числам (этот факт используется в учебниках Н.Б. Истоминой при изображении десятка в виде треугольника). Вообще, если сложить все натуральные числа от числа 1 до некоторого числа n, то в результате получится «треугольное» число (1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10, 1 + 2 + 3 + 4 + 5 = 15 и т. д.).
Примечание. Без особого труда можно вывести и формулу «треугольных» чисел. Для этого достаточно знать формулу суммы членов арифметической прогрессии. Тогда получается, что 1 + 2 + … + n = (n•(n + 1))/2. Правая часть этого равенства и есть формула «треугольных» чисел. Но эти сведения мы сообщаем только учителю. Для учащихся их пока рассматривать рано, хотя для особо подготовленных учащихся можно предложить поработать и с приведенной выше формулой. Указанные фигуры, которые по форме напоминают треугольник, можно строить не только из кругов, но и из шаров. Так, из 15 шаров можно построить фигуру, которая по форме напоминает равносторонний треугольник. Этот факт используется в такой игре с шарами, как бильярд. В следующем задании мы предлагаем учащимся поработать с конструкциями, построенными из одинаковых шаров.269.
В задании 269 учащимся предлагается рассмотреть конструкции, которые построены из одинаковых шаров, а по форме напоминают правильную треугольную пирамиду. Такие конструкции можно построить следующим образом: сначала взять несколько подряд идущих (начиная с 1 шара) «треугольных» конструкций, построенных из шаров. Например, конструкцию из 1 шара (ее также принято считать треугольной), конструкцию из 3 шаров, конструкцию из 6 шаров и т. д., а потом на самый большой «треугольник» разместить предшествующий, на него – ему предшествующий и дойти до конструкции из 1 шара, которая и будет завершать построение этой «пирамиды». Если следовать этому правилу, то изображенную на рисунке «пирамиду» можно дополнить еще одним треугольным слоем, состоящем из 6 шаров. Тогда получится «пирамида», состоящая из 10 шаров.
Примечание. Возможное число шаров для построения такой «пирамиды» получается как результат сложения подряд идущих треугольных чисел, начиная с числа 1 (1 + 3 = 4, 1 + 3 + 6 = 10, 1 + 3 + 6 + 10 = 20, 1 + 3 + 6 + 10 + 15 = 35 и т. д.). Однако учащимся об этой закономерности пока говорить еще рано, но для учителя эти знания не будут лишними. 82
-
Ответы к странице учебника 82
270. Смотрим рисунок
Миша не сможет измерить объем квадрата, так как эта фигура плоская.
271.
В задании 271 учащимся не только предлагается на данной иллюстрации указать объемные фигуры, но и обратить внимание на те фигуры, поверхность которых состоит из многоугольников. Таким образом, мы подводим учащихся к понятию «многогранник». Указанный термин мы не вводим в активный словарь учащихся, но получить некоторые сведения о многогранниках учащиеся могут из словаря учебника (части 2, с. 123). Куб относится к многогранникам и у него 6 граней. Он также относится к призмам и прямоугольным параллелепипедам как их частный случай.
Примечание. Наличие 6 граней у куба является основанием для другого его названия, которое имеет греческое происхождение. Куб называют еще гексаэдром, т. е. шестигранником.Решение:
Объемные фигуры: 1,3,6,8,9
Многогранники: 8,9
Куб относится к многогранникам, не относится к призмам и является частным случаем прямоугольного параллелепипеда. 83
-
Ответы к странице учебника 83
272.
В задании 272 учащимся предлагается сначала распознать фигуры, имеющие форму многогранника. К таким фигурам относятся третья фигура (имеет форму призмы) и пятая фигура (имеет форму усеченной пирамиды). Оставшиеся фигуры не имеют форму многогранника. Они имеют форму цилиндра (первая фигура), шара (вторая фигура) и усеченного конуса (четвертая фигура), т. е. форму некоторых фигур вращения, к детальному рассмотрению которых мы перейдем в следующем задании. При выполнении же данного задания учащимся можно предложить назвать реальные предметы, которые по форме напоминают каждую из перечисленных фигур.
273.
При выполнении задания 273 учащиеся получают возможность познакомиться с тремя основными фигурами (телами) вращения – шаром, цилиндром и конусом. Более подробные сведения об этих фигурах учащиеся могут получить из словаря.
Ответы:
Если вращать, то увидим:
прямоугольник вокруг стороны - цилиндр;
прямоугольник вокруг катета - две пирамиды соединенных у основания.274.
В задании 274 учащимся предлагается найти радиус шара, если известна длина ребра куба, в который этот шар вписан. Понятно, что никакого определения вписанной фигуры мы не даем учащимся, но из тех сведений, которые сообщаются учащимся, нетрудно сделать вывод, что диаметр шара имеет длину, равную длине ребра куба (4 см). Следовательно, радиус шара равен 2 см (4 см : 2 = 2 см).
Решение:
4 : 2 = 2 (см) радиус шара.
Ответ: 2 см. 84
-
Ответы к странице учебника 84
275.
При выполнении задания 275 учащиеся познакомятся со способом измерения площади фигуры (прямоугольного треугольника) с помощью палетки, когда палетка разбивает фигуру как на «полные» единичные квадраты, так и на «половинки» единичных квадратов. О том, как найти число, с помощью которого можно выразить площадь данной фигуры, было рассказано выше в общих рекомендациях к данной теме. В рассмотренном случае мы имеем возможность «точно» измерить площадь треугольника, что можно подтвердить соответствующими вычислениями его площади без проведения измерения с помощью палетки.
Ответы:
6 клеток палетки полностью находятся в площади треугольника, площадь равна 6 клеткам, то есть 6 кв.см.
4 клетки палетки частично находятся в площади треугольника, 2 клетки по половине составляют 1 целую клетку. Площадь этих клеток 4 раза по пол клетки, то есть 2 кв.см.
В итоге площадь треугольника 6+2=8 (кв.см)
Проверяем с помощью вычисления
4*4:2=16:2=8 (кв.см) площадь треугольника. Все верно. 85
-
Ответы к странице учебника 85
276.
В задании 276 учащимся предлагается самостоятельно осуществить процедуру измерения по той схеме, с которой познакомились при выполнении предыдущего задания.
Решение:
26 клеток целых, то есть 26 кв.см.
4 клетки палетки частично находятся в площади четырехугольника, 2 клетки по половине составляют 1 целую клетку. Площадь этих клеток 4 раза по пол клетки, то есть 2 кв.см.
26 + 2 = 28 (кв.см)
Ответ: 28 кв.см площадь четырехугольника.277.
Чтобы измерить с помощью палетки площадь фигуры из задания 277, учащиеся сначала должны убедиться в том, что верхний ряд разбиения этой фигуры состоит из «половинок» единичных квадратов. Когда квадрат разбивался на половинки с помощью диагонали, такой проверки не требовалось. А теперь ситуация изменилась: без дополнительных измерений мы не знаем, будут ли полученные прямоугольники «половинками» единичного квадрата.
Решение:
10 клеток целых, то есть 10 кв.см.
10 клеток по половине составляют 5 целых клеток. Площадь этих клеток 5 кв.см.
10+5=15 (кв.см) - площадь четырехугольника.
Ответ: 15 кв.см. 86
-
Ответы к странице учебника 86
278.
В результате выполнения задания 278 учащиеся познакомятся со способом измерения (приближенного) площади произвольной фигуры (которая по форме напоминает «лужу») с помощью палетки. Вся процедура подробно описана в задании, а также в общих рекомендациях к данной теме. Поэтому нам остается только сформулировать правило, к выводу которого должны прийти учащиеся самостоятельно. Это правило формулируется так: «Площадь фигуры в данных единицах площади приближенно равна числу, которое получается в результате сложения числа клеток палетки, полностью расположенных в границе данной фигуры, и половине числа клеток, которые лишь частично расположены в пределах границы данной фигуры».
Решение:
4 клетки палетки полностью находятся в площади фигуры, то есть 4 кв.см.
Подбираем части клетки: из 12 частей клетки можно получить примерно 6 целых клеток, то есть 6 кв.см.
4 + 6 = 10 (кв.см) - площадь всей фигуры.
Ответ: 10 кв.см.
Правило основано на том предположении, что произвольность измеряемой фигуры обеспечивает для каждой «неполной» клеточки наличие другой «неполной» клеточки, которые вместе дают такую же площадь, как и 1 «полная» клеточка. Практика измерения показывает, что это предположение, как правило, хорошо работает. 87
-
Ответы к странице учебника 87
279.При выполнении задания 279 учащиеся имеют возможность поупражняться в теоретическом применении правила, которое было сформулировано при выполнении предыдущего задания.
Решение:
15 полных клеток это 15 кв.см.
12 неполных это 6 полных, то есть 6 кв.см.
15+6=21 (кв.см) - площадь фигуры.
Ответ: 21 кв.см.280.
При выполнении задания 280 учащиеся имеют возможность поупражняться в практическом применении правила, которое было сформулировано при выполнении задания 278.
Напишите нам сколько полных и неполных клеток у вас получилось и мы решим эту задачу.
281.
В задании 281 мы знакомим учащихся с тем, как надо поступать в ситуации, когда число «неполных» клеточек является нечетным числом. Как мы уже говорили ранее, это число нужно заменить ближайшим четным числом. Таких чисел будет два: одно предшествует данному нечетному числу, а другое за ним следует.
Ответ:
Если руководствоваться правилом выше, то должно было получиться 12+4, если не учитывать одну неполную клетку, то есть
12+4=16 (кв.см).
Миша решил правильно.
Однако если учитывать неполную клетку и округлять до большего значения, то получится
12+5=17 (кв.см), что тоже будет правильно.
Это будет вопросом принятия условной точности и принятия условных правил, а не отражением фактического значения. Что в данном случае допустимо.282.
При выполнении задания 282 учащиеся получают возможность поупражняться в практическом применении правила, о котором речь шла в предыдущем задании.
Напишите нам сколько полных и неполных клеток у вас получилось и мы решим эту задачу.
88
-
Ответы к странице учебника 88
283.
В задании 283 учащимся предлагается найти площадь данных фигур с помощью палетки. При этом для каждого из двух данных прямоугольников мы предлагаем сравнить результат нахождения площади с помощью палетки с результатом вычисления площади
на основе измерения длин сторон этого прямоугольника.Решение:
2 прямоугольника.
Напишите нам сколько полных и неполных клеток у вас получилось и мы решим эту задачу (укажите страницу и задание).
284.
Задание 284 относится к заданиям повышенной сложности. В нем учащимся предлагается найти вместимость бака, имеющего форму куба с ребром 2 дм. Так как мы не знакомили учащихся с формулой вычисления объема куба, то учащиеся должны найти
«обходной» путь решения этого задания. Один из таких путей заключается в умении «мысленно разбить» данный куб на «единичные» кубы с ребром 1 дм. Так как данный куб можно «разбить» на 8 «единичных» кубов, то искомый объем равен 8 куб. дм или 8 л.Решение:
2 * 2 * 2 = 8 (куб. дм) объем бака.
1 куб. дм =1 л, то есть объем бака 8 литров.
2 * 2 = 4 (кв. дм) - площадь одной стенки бака
2 * 5 = 10 (куб. дм) - площадь всех стенок бака, если у него нет верхней крышки.
Ответ: 4 кв. дм площадь одной стенки бака и 10 куб. дм площадь всех стенок бака, если у него нет верхней крышки. 89
-
Ответы к странице учебника 89
285.
В задании 285 учащимся сначала предлагается найти объем воды, которая помещается в бассейне прямоугольной формы данных размеров. Другими словами, учащимся нужно найти вместимость этого бассейна. Сделать это они смогут тем же способом, которым мы пользовались при выполнении предыдущего задания. Для этого воду, заполняющую весь бассейн, нужно «мысленно разбить» на «единичные» кубы с ребром 1 м. Таких кубов получится 15. Это означает, что искомый объем равен 15 куб. м. Во второй части задания учащимся предлагается вычислить площадь дна и стенок бассейна. Все они имеют форму прямоугольников, размеры которых нам известны. Дно бассейна имеет площадь 15 кв. м (5 м • 3 м = 15 кв. м), каждая из «длинных» стенок имеет площадь 5кв. м (5 м • 1 м = 5 кв. м), а каждая из «коротких» стенок имеет площадь 3 кв. м (3 м • 1 м = 3 кв. м).
Решение:
5 * 3 * 1 = 15 (куб. м.) - объем бассейна
5 * 1 * 2 + 3 * 1 * 2 + 5 * 3 = 10 + 6 + 15 = 31 (кв. м) - такую площадь плитки надо для того, чтобы выложить бассейн.
Ответ: 15 куб. м. объем бассейна и 31 кв. м плитки надо для того, чтобы выложить бассейн.286. В задании 286 предлагается построить 5 различных многоугольников, каждый из которых имеет площадь 12 кв. см. Для этого они должны воспользоваться «клетчатой основой» тетрадного листа.
Решение:
Так как площадь 1 кв. см имеет фигура, состоящая из 4 клеток (этот факт устанавливается с помощью соответствующих вычислений), то искомые фигуры должны состоять из 48 клеток. Остается такие фигуры построить.
287. В задании 287 мы еще раз возвращаем учащихся к вопросу нахождения объема куба по известной длине ребра этого куба. Используя метод «разбиения» куба на «единичные» кубы, можно установить, что в данном кубе содержится 125 «единичных» кубов с ребром 1 дм (5 слоев по 25 «единичных» кубов). Следовательно, вместимость аквариума равна 125 куб. дм или 125 л. Поэтому для заполнения этого аквариума требуется 25 пятилитровых банок (125 л : 5 л = 25 (б.)).
Решение:
1) 5 * 5 * 5 = 125 (куб. дм) - объем куба.
2) 125 : 5 = 25 (б.) - надо чтобы заполнить куб.
Ответ: 25 банок надо. 90
-
Ответы к странице учебника 90. Поупражняемся в вычислениях и повторим пройденное
288. Проверь, правильно ли выполнены данные вычисления.
+572847 _876324
365195 795651
938042 80673
? 3624 — 76250 |24
35 72 |3177
+18120 _ 42
10872 24
126840 _ 185
168
_ 170
168
2 — ост.289. Реши задачу. Вычисли и запиши ответ.
Из двух населённых пунктов навстречу друг другу с интервалом в 2 ч выехали сначала автобус, а потом легковой автомобиль. Автобус за каждый час проезжал 60 км, а автомобиль — 80 км. Найди расстояние между населёнными пунктами, если до встречи с автомобилем автобус был в пути 4 ч.1) 60 • 4 = 240 (км) — проехал автобус
2) 80 • (4 — 2) =160 (км) — проехал автомобиль
3) 240 + 160 = 400 (км) —расстояние между пунктами
Ответ: 400 км.290. Начерти два квадрата так, чтобы площадь одного была в 9 раз больше, чем площадь другого, а в сумме их площади составляли 1000 кв. мм.
1) 9 + 1 = 10 (частей) — всего
2) 1000 : 10 = 100 (кв. мм) = 1 (кв. см) — одна часть
3) 1 • 9 = 9 (кв. см) — площадь одного квадрата
4) 1 • 1 = 1 (кв. см) — площадь второго квадрата
291. Начерти два таких квадрата, чтобы площадь одного была на 800 кв. мм больше, чем площадь другого, а в сумме их площади составляли 1000 кв. мм.
Можно ли было для иллюстрации решения данного задания воспользоваться квадратами, полученными при выполнении предыдущего задания?1) 1000 — 800 = 200 (кв. мм) — поровну
2) 200 : 2 = 100 (кв. мм) = 1 (кв. см) — площадь одного квадрата
3) 800 + 100 = 900 (кв. мм) = 9 (кв. см) — площадь второго квадрата
Воспользоваться рисунком можно. 91
-
Ответы к странице учебника 91
292. Сравни значения следующих выражений и запиши полученный результат в виде двойного неравенства со знаком <.
25113 : 3 + 36985 : 5
(568972 — 559423) • 14 : 7
256897 + 3564 • 25 : 1025113 : 3 + 36985 : 5 = 8371 + 7397 = 15768
(568972 — 559423) • 14 : 7 = 9549 • 14 : 7 = 133686 : 7 = 19098
256897 + 3564 • 25 : 10 = 72847 =256897 + 89100 : 10 = 256897 + 8910 = 265807
15768 < 19098 < 265807293. Кубик нужно раскрасить так, чтобы любые соседние грани были разного цвета, а любые противоположные — одного и того же. Сколько различных красок для этого потребуется?
У кубика 6 граней, из них противоположных пар 6 : 2 = 3 штуки. Потребуется 3 краски.
294. Начерти прямоугольник, периметр которого равен 210 мм, а длина одной стороны составляет одну шестую часть другой стороны.
Вычисли площадь этого прямоугольника.1) 210 : 2 = 105 (мм) — сумма двух сторон
2) 6 + 1 = 7 (частей) — всего
3) 105 : 7 = 15 (мм) — длина одной стороны
4) 15 • 6 = 90 (мм) — длина второй стороны
5) 15 • 90 = 1350 (кв. мм) — площадь
295. Длина одной стороны прямоугольника равна 2 см, что составляет одну третью часть длины другой стороны. Вычисли периметр и площадь этого прямоугольника.
Начерти этот прямоугольник.1) 2 • 3 : 1 = 6 (см) — вторая сторона
2) (2 + 6) • 2 = 16 (см) — периметр
3) 2 • 6 = 12 (кв. см) — площадь296. Длина одной стороны прямоугольника равна 8 см, а длина другой стороны составляет три четверти длины первой. Вычисли периметр и площадь этого прямоугольника.
1) 8 : 4 • 3 = 6 (см) — длина второй стороны
2) (8 + 6) • 2 = 28 (см) — периметр
3) 8 • 6 = 48 (кв. см) — площадь297. Длина одной стороны прямоугольника равна 6 см, что составляет две третьих длины другой стороны. Вычисли периметр и площадь этого прямоугольника.
1) 6 : 2 • 3 = 9 (см) — длина другой стороны
2) (6 + 9) • 2 = 30 (см) — периметр
3) 6 • 9 = 54 (кв. см) — площадь 92
-
Ответы к странице учебника 92. Уравнение. Корень уравнения
298. Среди данных записей найди и выпиши уравнения.
х + 25 = 245 х • 3 = 81 х > 25 х — 27При подстановке в какое из выписанных уравнений вместо х числа 27 получается верное равенство? Число 27 — КОРЕНЬ этого уравнения.
х + 25 = 245 х • 3 = 81
27 • 3 = 81
81 = 81299. Найди корни следующих уравнений, используя соответствующие свойства сложения и умножения.
х + 25689 = 25689 + 37541
х + 25689 = 37541 + 25689
х = 37541
х + (6534 + 241) = (4173 + 6534) + 241
х + (6534 + 241) = 4173 + (6534 + 241)
х = 4173
6598 • х = 2379 • 6598
6598 • х = 6598 • 2379
х = 2379
х • (25 • 37) = (42 • 25) • 37
х • (25 • 37) = 42 • (25 • 37)
х = 42300. Из данных уравнений составь пары так, чтобы уравнения в паре имели один и тот же корень.
х + 25698 = 356 + 25698 х — 217 = 356 — 217
х — 356 = 217 х — 25698 = 356
х — 217 = 356 х — 356 = 25698х + 25698 = 356 + 25698 х — 217 = 356 — 217
х = 356 х = 356
х — 356 = 217 х — 217 = 356
х = 217 + 356 х = 356 + 217
х = 573 х = 573
х — 25698 = 356 х — 356 = 25698
х = 356 + 25698 х = 25698 + 356
х = 26054 х = 26054301. Если уменьшить каждую часть верного равенства на одно и то же число, то каким будет полученное равенство: верным или неверным?
Подтверди свой вывод на примере равенства 25 + 75 = 100.
Методом подбора определи корень уравнения х + 75 = 100.
На какое число нужно уменьшить каждую часть данного уравнения, чтобы в левой части осталось только неизвестное х? Какое выражение в этом случае будет находиться в правой части?
Будет ли значение этого выражения корнем исходного уравнения?Полученное равенство будет верным:
25 + 75 = 100
25 + 75 — 25 = 100 — 25
75 = 75
х + 75 = 100
х = 25
Нужно уменьшить на 75:
х + 75 — 75 = 100 — 75
х = 100 — 75
х = 25
100 — 75 — значение этого выражения является корнем уравнения. 93
-
Ответы к странице учебника 93
302. Найди корень каждого из данных уравнений, уменьшив каждую часть уравнения на такое число, чтобы в левой части осталось только неизвестное х.
х + 256 = 958 х + 427 = 15698х + 256 = 958
х + 256 — 256 = 958 — 256
х = 702
х + 427 = 15698
х + 427 — 427 = 15698 — 427
х = 15271303. Если увеличить каждую часть верного равенства на одно и тоже число, то каким будет полученное равенство: верным или неверным?
Подтверди свой вывод на примере равенства 100 — 85 = 15.
Методом подбора определи корень уравнения.
х — 85 = 15
На какое число нужно увеличить каждую часть данного уравнения, чтобы в левой части осталось только неизвестное х? Какое выражение в этом случае будет находиться в правой части?
Будет ли значение этого выражения корнем исходного уравнения?Полученное равенство будет верным:
100 — 85 = 15
100 — 85 + 85 = 15 + 85
100 = 100
х — 85 = 15
х = 100
Нужно увеличить на 85:
х — 85 + 85 = 15 + 85
х = 15 + 85
х = 100
15 + 85 — значение этого выражения является корнем уравнения.304. Найди корень каждого из данных уравнений, увеличив каждую часть уравнения на такое число, чтобы в левой части осталось только неизвестное х.
х — 256 = 358 х — 427 = 198
х — 217 = 356 х — 8567 = 39912х — 256 = 358
х — 256 + 256 = 358 + 256
х = 614
х — 217 = 356
х — 217 + 217 = 356 + 217
х = 573
х — 427 = 198
х — 427 + 427 = 198 + 427
х = 625
х — 8567 = 39912
х — 8567 + 8567 = 39912 + 8567
х = 48479 94
-
Ответы к странице учебника 94 Учимся решать задачи с помощью уравнений
305. Для того чтобы решить следующую задачу с помощью уравнения, ответь сначала на вопросы и выполни соответствующие указания.
При покупке футбольного и волейбольного мячей заплатили 250 руб. Футбольный мяч на 30 руб. дороже волейбольного. Сколько стоит волейбольный мяч?
Что является искомым в этой задаче? Обозначь искомое через х и сделай соответствующую запись.
Что известно о стоимости футбольного мяча? Как можно записать стоимость футбольного мяча в виде буквенного выражения? Сделай соответствующую запись и пояснения к ней.
Как можно записать стоимость футбольного и волейбольного мячей в виде одного буквенного выражения? Сделай соответствующую запись и пояснения к ней.
Что известно из условия задачи о стоимости футбольного и волейбольного мячей? Составь уравнение, в одной части которого будет записана стоимость футбольного и волейбольного мячей в виде буквенного выражения, а в другой — в виде данного числа.
Если у тебя получилось следующее уравнение:
х + (х + 30) = 250,
то все указания были выполнены верно и тебе удалось правильно решить задачу с помощью уравнения.Искомое — цена волейбольного мяча. х — стоимость волейбольного мяча.
Известно, что футбольный мяч на 30 руб. дороже волейбольного. х + 30 — стоимость футбольного мяча.
х + (х + 30) — стоимость волейбольного и футбольного мячей.
По условию задачи стоимость мячей 250 руб. х + (х + 30) = 250.
х = 110 (руб.) — стоимость волейбольного мяча.306. Составь уравнение к следующей задаче.
За ласты и маску для подводного плавания заплатили 350 руб. Ласты на 30 руб. дороже маски. Сколько стоят ласты?х — стоимость маски
х + 30 — стоимость ласт
х + (х + 30) = 350
х = 160 (руб.) — стоимость маски
160 + 30 = 190 (руб.) — стоимость ласт
Ответ: ласты стоят 190 руб. 95
-
Ответы к странице учебника 95
307. Пасека находится на другом берегу реки от дома. Весь путь от дома до пасеки через мост составляет 1 км.
Сколько метров нужно пройти от дома до моста, если это расстояние на 100 м больше, чем расстояние от моста до пасеки?
С помощью какого из следующих уравнений можно решить данную задачу?
х + (х + 100) = 1000 (х + 100) + х = 1000 х + (х — 100) = 1000х — расстояние от дома до моста.
х — 100 — расстояние от моста до пасеки.
х + (х — 100) = 1000 — с помощью этого уравнения.
х = 550 (м)308. Сформулируй задачу, которую можно решить с помощью следующего уравнения:
х + (х + 80) = 280.
Методом подбора найди корень этого уравнения.
Запиши ответ сформулированной задачи.Купили краски и альбом за 280 руб. Краски дороже альбома на 80 руб. Сколько стоит альбом?
х — стоимость альбома
х + 80 — стоимость красок
х + (х + 80) = 280
х = 100 (руб.) — стоимость альбома
Ответ: альбом стоит 100 руб.309. Составь два уравнения (одно — с неизвестным делителем, а другое — с неизвестным множителем), с помощью каждого из которых можно решить следующую задачу.
Для школьной библиотеки закупили 45 одинаковых хрестоматий, заплатив за них 2250 руб. Какова цена одной хрестоматии?
Найди корень каждого из составленных уравнений.
Запиши ответ задачи.
Сформулируй две обратные задачи. Для каждой из них составь уравнение, с помощью которого можно решить эту задачу. Найди корень каждого уравнения. Запиши ответ каждой задачи.2250 : х = 45 х • 45 = 2250
х = 2250 : 45 х = 2250 : 45
х = 50 х = 50
Ответ: цена хрестоматии 50 руб.
Для школы купили 45 хрестоматий по 50 руб. за каждую. Сколько всего стоили хрестоматии?
50 • 45 = х
х = 2250
Ответ: стоимость хрестоматий 2250 руб.
Для школы купили хрестоматии на 2250 руб. Каждая хрестоматия стоила 50 руб. Сколько всего хрестоматий купили?
50 • х = 2250
х = 2250 : 50
х = 45
Ответ: купили 45 хрестоматий. 96
-
Ответы к странице учебника 96. Поупражняемся в вычислениях и повторим пройденное
310. Найди корни данных уравнений.
х — 256873 = 482369 х + 156897 = 689324
234651 + х = 852134 756981 — х = 325647
х : 28 = 35687 х • 18 = 51372
15 • х = 12645 21288 : х = 12
Все вычисления выполни столбиком.х — 256873 = 482369
х = 482369 + 256873
+482369
256873
739242
х = 739242
234651 + х = 852134
х = 852134 — 234651
_852134
234651
617483
х = 617483
х + 156897 = 689324
х = 689324 — 156897
_689324
156897
532427
х = 532427
756981 — х = 325647
х = 756981 — 325647
_756981
325647
431334
х = 431334
х : 28 = 35687
х = 35687 • 28
? 35687
28
+285496
71374
999236
х = 999236
х • 18 = 51372
х = 51372 : 18
— 51372|18
36 |2854
_153
144
_97
90
_72
72
0
х = 2854
15 • х = 12645
х = 12645 : 15
— 12645|15
120 |843
_64
60
_45
45
0
х = 843
21228 : х = 12
х = 21228 : 12
— 21228 |12
12 |1769
_92
84
_82
72
_108
108
0
х = 1769311. Реши задачу. Вычисли и запиши ответ.
От одной пристани одновременно в противоположных направлениях отплыли теплоход и катер. Через 2 ч пути расстояние между ними было 120 км.
С какой средней скоростью плыл теплоход, если его скорость была в 2 раза меньше, чем скорость катера?1) 120 : 2 = 60 (км/ч) — скорость удаления
2) 1 + 2 = 3 (части) — всего
3) 60 : 3 = 20 (км/ч) — скорость теплохода
Ответ: скорость теплохода 20 км/ч.312. Составь уравнение, с помощью которого можно решить следующую задачу.
Периметр равнобедренного треугольника равен 190 мм, а основание его имеет длину 20 мм. Найди длину боковой стороны.
Методом подбора найди корень составленного уравнения.х — длина боковой стороны треугольника
х + х + 20 = 190
х = 85 (мм)
Ответ: длина боковой стороны 85 мм.313. Реши задачу. Вычисли и запиши ответ.
Трёхлитровая банка с соком стоит 63 руб.
Какова цена сока, если закупочная цена пустой банки 3 руб./шт.?
Запиши выражение, которое является решением этой задачи.(63 — 3) : 3 = 20 (руб./л)
Ответ: цена сока 20 руб./л. 97
-
Ответы к странице учебника 97. Разные задачи
314. Миша и Маша играли в настольную игру, по правилам которой нужно считать число очков, выпадающих сразу на двух игральных кубиках. Сначала они заметили, что 12 очков выпадает очень редко, а 7 очков очень часто. Чтобы объяснить этот факт, они решили составить таблицу, в которой были бы учтены все возможные суммы очков, выпадающих на двух кубиках, и указано значение каждой такой суммы.
Такая таблица приведена ниже. Заверши её заполнение в тетради самостоятельно.
Сколько раз в заполненной таблице встречается число 12?Очки 1-го кубика 1 2 3 4 5 6 Очки 2-го кубика 1 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5 6 7 8 9 10 5 6 7 8 9 10 11 6 7 8 9 10 11 12 Число 12 встречается один раз.
98
-
Ответы к странице учебника 98
315. Сколько раз в таблице из задания 314 встречается число 7?
Какое число (или какие числа) встречается среди значений этой таблицы наменьшее число раз? А наибольшее число раз? Объясняет ли этот факт наблюдение, которое сделали Маши и Миша?
Для каждого возможного числа из таблицы определи, сколько раз оно встречается среди значений таблицы.
Если для выигрыша Мише нужно, чтобы при очередном бросании двух кубиков выпало 9 очков, а Маше — чтобы выпало 8 очков, то кто из них имеет больше шансов выиграть?Число 7 встречается 6 раз.
Числа 2 и 12 встречаются наименьшее число раз. Число 7 — наибольшее число раз. Да, объясняет.
Числа 2 и 12 — 1 раз, числа 3 и 11 — 2 раза, числа 4 и 10 — 3 раза, числа 5 и 9 — 4 раза, числа 6 и 8 — 5 раз, число 7 — 6 раз.
Маша, поскольку число 8 встречается больше раз, чем число 9.316. Опытным путём установи, сколько раз каждое возможное число очков на игральном кубике выпадает при проведении 30 бросаний кубика.
Какой вывод можно сделать по результатам этого опыта?
Проверь свой вывод дома: проведи 90 бросаний и подсчитай, число повторений для каждого возможного случая выпадения очков на кубике.Возможное число очков на кубике 1 2 3 4 5 6
Количество повторений 6 5 4 5 6 4
Количество повторений возможных чисел примерно одинаково, поскольку каждое возможное число встречается на кубике по одному разу.317. Предложи соседу по парте провести «математическое» соревнование: один должен составить и записать как можно больше сумм из двух однозначных слагаемых, значениие которых равно числу 11, а другой сделать то же самое, но для числа 12. Какое бы задание ты оставил(ла) для себя?
Какое из этих двух заданий гарантирует победу в соревновании, если записать все возможные варианты сумм?9 + 2 = 11 9 + 3 = 12
8 + 3 = 11 8 + 4 = 12
7 + 4 = 11 7 + 5 = 12
6 + 5 = 11 6 + 6 = 12
5 + 6 = 11 5 + 7 = 12
4 + 7 = 11 4 + 8 = 12
3 + 8 = 11 3 + 9 = 12
2 + 9 = 11
Задание с числом 11 — это задание гарантирует победу, поскольку для числа 12 есть лишь один вариант записи 6 + 6 = 12 99
-
Ответы к странице учебника 99
318. Если в классе 9 мальчиков и 18 девочек, а учитель может выбрать на одинаковых условиях любого ученика для ответа у доски, то во сколько раз больше шансов у девочки оказаться у доски, чем у мальчика?
18 : 9 = 2 (раза) — больше девочек
Следовательно, шансов оказаться у доски у девочки соответственно в 2 раза больше.319. В закрытом барабане находятся шары с номерами по порядку от 1 до 99. Из барабана наугад вынимается один шар. Одинаков ли шанс вынуть шар с чётным номером или с нечётным номером? Почему?
Шанс вынуть шар с нечётным номером больше, поскольку шаров с нечётными номерами 50 штук, а с чётными — 49 штук.
320. Какой результат в таблице сложения однозначных натуральных чисел встречается чаще: 9 или 10?
10
321. Какой результат в таблице умножения однозначных натуральных чисел встречается чаще: 12 или 16?
12
322. Какой результат в таблице сложения однозначных натуральных чисел встречается чаще: чётный или нечётный?
А в таблице умножения однозначных натуральных чисел?
Выпиши один столбик таблицы умножения только с чётными результатами.И в таблице сложения и в таблице умножения чаще встречаются чётные числа.
При умножении любого числа на чётное число получается чётное число. Следовательно, только чётные результаты будут при умножении на 2, 4, 6, 8.
1 • 4 = 4
2 • 4 = 8
3 • 4 = 12
4 • 4 = 16
5 • 4 = 20
6 • 4 = 24
7 • 4 = 28
8 • 4 = 32
9 • 4 = 36
10 • 4 = 40 100
-
Ответы к странице учебника 100. Натуральные числа и число 0 (повторение)
323. Назови самое маленькое натуральное число. Является ли число 0 натуральным?
Существует ли самое большое натуральное число? Как это можно доказать?
Какое самое большое натуральное число ты можешь назвать? Сколько «значным» является это число?Самое маленькое натуральное число — 1. 0 — не натуральное число.
Не существует. Всегда можно назвать число, следующее за предыдущим и большее на 1.
9999999. Это семизначное число.324. Запиши самое маленькое и самое большое из пятизначных натуральных чисел. Сколько всего существует пятизначных натуральных чисел? Как это число можно вычислить?
10000 и 99999. Всего пятизначных чисел 90000: 99999 — 10000 + 1 = 90000.
325. Следующие числа запиши в порядке возрастания.
23654 687369 96542 142578 6873623654, 68736, 96542, 142578, 687369
326. Следующие числа запиши в порядке убывания.
389621 125369 96547 857931 84635857931, 389621, 125369, 96547, 84635
327. Назови натуральное число, которое находится между числами 458963 и 458961. Запиши ответ с помощью верного двойного неравенства.
458961 < 458962 < 458963
328. Запиши все возможные числа с помощью перестановки цифр в записи числа 123. Сколько таких чисел у тебя получилось? Какое из этих чисел будет самым большим? Каких чисел среди них больше: чётных или нечётных?
123, 132, 231, 213, 312, 321
Получилось 6 таких чисел. Самое большое — 321. Среди них больше нечётных чисел, так как в записи числа 123 две нечётные цифры (1 и 3) и одна чётная (2). 101
-
Ответы к странице учебника 101
329. Определи, чётным или нечётным будет значение каждого из следующих выражений, не вычисляя этих значений.
(256897 + 23569) — (24563 + 57864)
(65342 + 75891) • (87562 + 56483)В первом выражении получается разность чётного и нечётного числа — это число нечётное.
Во втором выражении получается произведение нечётных чисел — это число нечётное.330. Найди натуральное число, которое делится нацело на числа 2, 3 и 5.
Это число 30: 30 : 2 = 15, 30 : 3 = 10, 30 : 5 = 6.
331. Найди натуральное число, которое при делении на 2, 3 и 5 даёт в остатке число 1.
Это число 31: 31 : 2 = 15 (ост. 1), 31 : 3 = 10 (ост. 1), 31 : 5 = 6 (ост. 1).
332. Значение какого из следующих выражений нельзя вычислить? Почему?
а) (253471 +325834) + (378964 — 378964)
б) (253471 +325834) — (378964 — 378964)
в) (253471 +325834) • (378964 — 378964)
г) (253471 +325834) : (378964 — 378964)
Значение какого из оставшихся выражений легко можно вычислить устно? Запиши это выражение и его значение.Выражение г) нельзя вычислить — получается частное с делителем 0, а на 0 делить нельзя. Легко вычислить выражение в) — при умножении на 0 всегда будет 0 в произведении.
333. Найди натуральное число, которое является пятизначным и в котром число единиц в каждом следующем разряде на 2 больше, чем в предыдущем.
Сколько таких чисел существует?
Запиши эти числа.86420, 97531. Таких чисел существует два — начинаем с разряда единиц прибавлять 2 и получать число в следующем разряде. При числе 2 в разряде единиц получим число 108642 — оно не подходит по условию задания.
334. Составь и запиши выражение, которое содержит все четыре действия и значение котрого равно 1000.
800 + 2000 : 20 • 3 — 100 = 1000
102
-
Ответы к странице учебника 102. Алгоритмы вычисления столбиком (повторение)
335. Выполни сложение столбиком для чисел 654381 и 165827.
Изменится ли значение суммы, если поменять местами слагаемые?
Сделай проверку правильности выполнения сложения столбиком, используя переместительное свойство сложения.
Что должно получиться в результате, если из значения суммы вычесть одно из слагаемых?
Сделай проверку правильности выполнения сложения с помощью вычитания.+654381 +165827
165827 654381
820208 820208
Не изменится.
Другое слагаемое.
_820208 _820208
654381 165827
165827 654381336. Выполни вычитание столбиком для чисел 654381 и 165827.
Что должно получиться в результате, если из уменьшаемого вычесть значение разности?
Сделай проверку правильности выполнения вычитания с помощью вычитания.
Что должно получиться в результате, если к значению разности прибавить вычитаемое?
Сделай проверку правильности выполнения вычитания с помощью сложения._654381
165827
488554
Вычитаемое.
_654381
488554
165827
Уменьшаемое.
+165827
488554
654381337. Выполни умножение столбиком для чисел 381 и 27.
Изменится ли значение произведения, если поменять местами множители?
Сделай проверку правильности выполнения умножения столбиком, используя переместительное свойство умножения.
Что должно получиться в результате, если значение произведения разделить на один из множителей?
Сделай проверку правильности выполнения умножения с помощью деления.? 381
27
+2667
762
10287
Не изменится.
? 27
381
27
+216
81
10287
Другой множитель.
_10287 |27
81 |381
_218
216
_27
27
0 103
-
Ответы к странице учебника 103
338. Выполни деление столбиком числа 25844 на число 14.
Что должно получиться в результате, если делимое разделить на значение частного?
Сделай проверку правильности выполнения деления с помощью деления.
Что должно получиться в результате, если значение частного умножить на делитель?
Сделай проверку правильности выполнения деления с помощью умножения._25844 |14
14 |1846
_118
112
_64
56
_84
84
0
Делитель.
_25844 |1846
1846 |14
_7384
7384
0
Делимое.
? 1846
14
+ 7384
1846
25844339. Вычисли значение каждого из следующих выражений. Все вычисления выполни столбиком.
45368 — 25689 + 135897 — 96734
1268 • 39 : 13 • 25
25687 • 3 — 123456 : 3 + 89635
(368957 + 243651) — (890653 -546321)
(256537 — 254149) • (895364 — 895315)
(456872 — (626356 — 170124)) • 18 : (100000 — 99991)45368 – 25689 + 135897 – 96734 = 58842
1268 • 39 : 13 • 25 = 95100
25687 • 3 — 123456 : 3 + 89635 = 125544
(368957 + 243651) — (890653 — 546321) = 268276
(256537 — 254149) • (895364 — 895315) = 117012
(456872 — (626356 — 170124)) • 18 : (100000 — 99991) = 1280340. Выполни деление столбиком числа 51034 на число 17, используя сокращённую форму записи.
Сделай проверку правильности выполнения деления с помощью умножения._51034|17
51 |3002
_34
34
0
? 3002
17
+21014
3002
51034341. Составь задание на вычитание столбиком и предложи соседу по парте решить его.
Выполни вычитание столбиком для чисел 654321 и 456132.
_654321
456132
198189 104
-
Ответы к странице учебника 104. Действия с величинами (повторение)
342. Из данных величин составь и запиши все возможные суммы, значения которых имеет смысл вычислять.
25634 м 145 л 240 ч 564 кв. м 54 куб. м
563 кг 347 мин 135 дм 5 га 250 ц
Вычисли значения составленных сумм.25634 м + 135 дм = 25634 м + 1350 м = 26984 м
54 куб. м — 145 л = 54000 л — 145 л = 53855 л
240 ч — 347 мин = 14400 мин — 347 мин = 14053 мин
5 га — 564 кв. м = 50000 кв. м — 564 кв. м = 49436 кв. м
563 кг + 250 ц = 563 кг + 25000 кг = 25563 кг343. Из данных величин составь и запиши все возможные разности, значения которых имеет смысл вычислять.
25634 м 145 л 240 ч 564 кв. м 54 куб. м
563 кг 347 мин 135 дм 5 га 250 ц
Вычисли значения составленных разностей.25634 м — 135 дм = 25634 м — 1350 м = 24284 м
145 л + 54 куб. м = 145 л + 54000 л = 54145 л
240 ч + 347 мин = 14400 мин + 347 мин = 14747 мин
564 кв. м + 5 га = 564 кв. м + 50000 кв. м = 50564 кв. м
250 ц — 563 кг = 25000 кг — 563 кг = 24437 кг344. Каждую из данных величин увеличь в 2 раза, а потом ещё в 5 раз.
568 см 145 руб. 350 куб. см 60 т 30 с
Во сколько раз в итоге увеличилась каждая величина?568 см • 2 = 1136 см, 1136 см • 5 = 5680 см
145 руб. • 2 = 290 руб., 290 руб. • 5 = 1450 руб.
350 куб. см • 2 = 700 куб. см, 700 куб. см • 5 = 3500 куб. см
60 т • 2 = 120 т, 120 т • 5 = 600 т
30 с • 2 = 60 с, 60 с • 5 = 300 с
В итоге величины увеличились в 10 раз.345. Каждую из данных величин уменьши сначала в 2 раза, а потом ещё в 5 раз.
2350 ц 3840 м 5320 руб. 2990 л
Во сколько раз в итоге уменьшилась каждая величина?2350 ц : 2 = 1175 ц, 1175 ц : 5 = 235 ц
3840 м : 2 = 1920 м, 1920 м : 5 = 384 м
5320 руб. : 2 = 2660 руб., 2660 руб. : 5 = 532 руб.
2990 л : 2 = 1495 л, 1495 л : 5 = 299 л
В итоге величины уменьшились в 10 раз. 105
-
Ответы к странице учебника 105
346. Выполни разностное сравнение следующих величин.
60 км/ч и 20 м/с 90 дет./ч и 2 дет./мин 50 руб./кг и 4500 руб./ц20 м/с = 72000 м/ч = 72 км/ч
72 км/ч — 60 км/ч = 12 км/ч
2 дет./мин = 120 дет./ч
120 дет./ч — 90 дет./ч = 30 дет./ч
50 руб./кг = 5000 руб./ц
5000 руб./ц — 4500 руб./ц = 500 руб./ц347. Выполни кратное сравнение следующих величин.
180 км/ч и 5 м/с 15 стр./мин и 1 стр./с 60 руб./ц и 300 руб./т5 м/с = 18000 м/ч = 18 км/ч
180 км/ч : 18 км/ч = 10 (раз)
1 стр./с = 6 стр./мин
60 стр./мин : 15 стр./мин = 4 (раза)
60 руб./ц = 600 руб./т
600 руб./т : 300 руб./т = 2 (раза)348. Каждую из данных величин уменьши в 9 раз.
63918 м 321642 л 851499 кв. м 514341 куб. см63918 м : 9 = 7102 м
321642 л : 9 = 35738 л
851499 кв. м : 9 = 94611 кв. м
514341 куб. см : 9 = 57149 куб. см349. Вычисли три одиннадцатых каждой из данных величин.
534622 дм 277211 кг 612337 л534622 дм : 11 • 3 = 145806 дм
277211 кг : 11 • 3 = 75603 кг
612337 л : 11 • 3 = 167001 л350. Вычисли величину, если известно, чему равняется четыре седьмых этой величины.
68924 см 254232 г 489084 руб.68924 см : 4 • 7 = 120617 см
254232 г : 4 • 7 = 444906 г
489084 руб. : 4 • 7 = 855897 руб.351. Известно, что 12 м электрического провода имеют массу 360 г. Что можно узнать, если разделить массу 360 г на длину 12 м? Выполни это деление. Вычисли массу 20 м такого электропровода.
360 : 12 = 30 (г/м) — масса 1 м провода
30 • 20 = 600 (г) — масса 20 м электропровода
Ответ: 600 г.352. Выполни кратное сравнение следующих пар величин.
10 м и 200 см 15 мин и 3 ч 2000 кг и 60 ц10 м = 1000 см
1000 см : 200 см = 5 (раз)
3 ч = 180 мин
180 мин : 15 мин = 12 (раз)
2000 кг = 20 ц
60 ц : 20 ц = 3 (раза) 106
-
Ответы к странице учебника 106. Как мы научились решать задачи (повторение)
353. Запиши решение данной задачи в виде одного выражения.
Продолжительность полёта самолёта по расписанию 240 мин. Полёт над тайгой занял 1 ч 25 мин, а над тундрой на 45 мин больше, чем над тайгой. Сколько ещё минут осталось до посадки самолёта?
Реши задачу. Вычисли и запиши ответ.1 ч 25 мин = 85 мин
240 — (85 + 85 + 45) = 25 (мин)
Ответ: осталось 25 мин.354. Построй схему к данной задаче.
Два автобуса одновременно выехали навстречу друг другу из двух населённых пунктов, расстояние между которыми 220 км. Встретились эти автобусы через 2 ч. Найди среднюю скорость второго автобуса, если средняя скорость первого 60 км/ч.
Реши задачу. Вычисли и запиши ответ.
На каком расстоянии от каждого населённого пункта произошла встреча двух автобусов?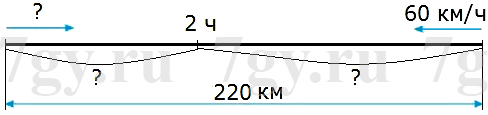
1) 220 : 2 = 110 (км/ч) — скорость сближения автобусов
2) 110 — 60 = 50 (км/ч) — скорость второго автобуса
3) 60 • 2 = 120 (км)
4) 50 • 2 = 100 (км)
Ответ: скорость второго автобуса 50 км/ч, расстояние от населённых пунктов 120 км и 100 км.355. Реши задачу. Вычисли и запиши ответ.
Из аэропорта с интервалом в 1 ч по одному и тому же маршруту вылетели два самолёта. Средняя скорость первого самолёта 900 км/ч, а расстояние, которое он должен преодолеть, — 1800 км. С какой средней скоростью летел второй самолёт, если он приземлился на 40 мин позже, чем первый?
Если ты затрудняешся в нахождении времени полёта второго самолёта, то можешь предположить, что первый самолёт вылетел в 9.00. После этого легко определить время приземления первого самолёта, а потом время вылета и время приземления второго.1 ч = 60 мин
1) 1800 : 900 = 2 (ч) = 120 (мин) — летел первый самолёт
2) 120 — 60 + 40 = 100 (мин) — летел второй самолёт
3) 1800 : 100 = 18 (км/мин) = 1080 (км/ч)
Ответ: скорость второго самолёта 1080 км/ч. 107
-
Ответы к странице учебника 107
356. Реши задачу. Вычисли и запиши ответ.
Нужно упаковать 360 банок сока в одинаковые коробки. Для упаковки 96 банок потребовалось 16 коробок. Сколько ещё таких коробок нужно взять, чтобы упаковать оставшиеся банки?1) 96 : 16 = 6 (б./к.) — в одной коробке
2) 360 : 6 = 60 (к.) — нужно всего
3) 60 — 16 = 44 (к.)
Ответ: нужно 44 коробки.357. За 5 кг яблок и 5 кг абрикосов заплатили 600 руб. Абрикосы в 2 раза дороже яблок. Сколько килограммов абрикосов можно купить на 240 руб.?
Построй схему, с помощью которой можно определить цену абрикосов и цену яблок.
Реши задачу. Вычисли и запиши ответ.
1) 2 + 1 = 3 (ч.) — всего
2) 600 : 3 = 200 (руб.) — стоимость яблок
3) 200 • 2 = 400 (руб.) — стоимость абрикосов
4) 400 : 5 = 80 (руб.) — цена абрикосов
5) 240 : 80 = 3 (кг)
Ответ: можно купить 3 кг абрикосов.358. Реши задачу. Вычисли и запиши ответ.
От одной пристани одновременно в противоположных направлениях отплыли два катера. Средняя скорость одного на 10 км/ч больше, чем другого. Через 2 ч расстояние между катерами равнялось 140 км. С какой скоростью двигался каждый катер?1) 140 : 2 = 70 (км/ч) — скорость удаления
2) 70 — 10 = 60 (км/ч) — равная скорость
3) 60 : 2 = 30 (км/ч) — скорость одного катера
4) 30 + 10 = 40 (км/ч) — скорость другого катера
Ответ: скорости катеров 30 км/ч и 40 км/ч.359. Моторная лодка в стоячей воде может развивать максимальную скорость 40 км/ч. Если эта же лодка плывёт вниз по течению реки, то её максимальная скорость равняется 43 км/ч, а если вверх по течению, то — 37 км/ч. Объясни, почему это происходит? Чему в этом случае равняется скорость течения реки? Как можно вычислить скорость течения реки, если известны только скорость движения моторной лодки по течению и скорость движения против течения реки?
Течение реки имеет свою скорость, которая подгоняет лодку вниз по течению и тормозит её вверх по течению.
Скорость течения реки:
43 — 40 = 3 (км/ч)
40 — 37 = 3 (км/ч)
(43 — 37) : 2 = 6 : 2 = 3 (км/ч) — если известны только скорости лодки вниз и вверх по течению 108
-
Ответы к странице учебника 108
360. Реши задачу. Вычисли и запиши ответ.
На изготовление одного свитера вязальщица расходует 600 г шерсти. Сколько таких свитеров может изготовить вязальщица из шерсти, закупленной на 6000 руб. по цене 2000 руб./кг?1) 6000 : 2000 = 3 (кг) = 3000 (г) — шерсти всего купили
2) 3000 : 600 = 5 (с.)
Ответ: можно изготовить 5 свитеров.361. Реши задачу. Вычисли и запиши ответ.
На старом оборудовании пекарня выпускала за 8-часовую смену 1200 батонов хлеба. На новом оборудовании производительность пекарни увеличилась в 2 раза. Сколько батонов хлеба за смену стала выпускать пекарня на новом оборудовании?Поскольку продолжительность смены не изменилась, а увеличилась производительность оборудования в 2 раза, то и выход готовой продукции увеличился в 2 раза.
1200 • 2 = 2400 (шт.)
Ответ: 2400 батонов хлеба.362. Реши задачу. Вычисли и запиши ответ.
На мебельной фабрике двое рабочих за 3 ч совместной работы обработали 150 одинаковых панелей. Первый рабочий за 5 ч работы может обработать 135 таких панелей. С какой производительностью работает второй рабочий, если их производительность в течение рабочего дня не изменяется?1) 150 : 3 = 50 (д./ч) — совместная производительность
2) 135 : 5 = 27 (д./ч) — производительность первого рабочего
3) 50 — 27 = 23 (д./ч)
Ответ: производительность второго рабочего 23 д./ч.363. Дополни следующие задачи недостающими данными из географического атласа.
а. На сколько квадратных километров площадь Ладожского озера больше, чем площадь Онежского озера?
б. На сколько метров высота над уровнем моря вершины Эльбрус больше, чем вершины Казбек?
Реши дополненные задачи. Вычисли и запиши ответ каждой задачи.
Для каждой задачи сформулируй обратную задачу и реши её.а. Площадь Ладожского озера 17870 кв. км, а Онежского озера — 9720 кв. км.
17870 — 9720 = 8150 (кв. км)
Ответ: на 8150 кв. км
Площадь Ладожского озера 17870 кв. км, а Онежского на 8150 кв. км меньше. Какова площадь Онежского озера?
17870 — 8150 = 9720 (кв. км)
Ответ: площадь Онежского озера 9720 кв. км.
б. Высота вершины Эльбрус 5642 м над уровнем моря, а высота вершины Казбек — 5033 м.
5642 — 5033 = 609 (м)
Ответ: на 609 м.
Высота вершины Эльбрус 5642 м над уровнем моря, а высота вершины Казбек на 609 м меньше. Какова высота вершины Казбек?
5642 — 609 = 5033 (м)
Ответ: высота вершины Казбек 5033 м. 109
-
Ответы к странице учебника 109. Геометрические фигуры и их свойства (повторение)
364. Начерти прямоугольник с длиной сторон 8 см и 6 см. Построй диагональ в этом прямоугольнике. Измерь длину этой диагонали.
На какие два треугольника разбит построенный прямоугольник? Вычисли периметр любого из треугольников.
Вычисли площадь прямоугольника и площадь одного прямоугольного треугольника.
Измерь площадь этого треугольника с помощью палетки, заменяя каждые два неполных квадрата на один полный квдрат. Сравни результат, полученный вычислением, с результатом измерения с помощью палетки.
Диагональ 10 см.
На два одинаковых прямоугольных треугольника.
Периметр треугольника: 6 + 8 + 10 = (24 см).
Площадь прямоугольника: 6 • 8 = 48 (кв. см).
Площадь треугольника: 48 : 2 = 24 (кв. см).
Площадь измерением палеткой 24 кв. см.365. Начерти окружность радиусом 3 см. Проведи диаметр этой окружности и обозначь концы диаметра буквами А и В. Начерти ещё две окружности того же радиуса, что и первая окружность, но с центрами соответственно в точках А и В. Отметь точки пересечения этих окружностей с первой окружностью и обозначь эти точки буквами М, Е, К и Т. Охарактеризуй многоугольник, вершины которого находятся в шести обозначенных буквами точках.
Полученный шестиугольник имеет равные стороны, так как каждая сторона — это радиус окружности.366. Построй равносторонний треугольник с длиной стороны 4 см. Разбей его на 4 одинаковых равносторонних треугольника.
367. Начерти отрезок длиной 5 см. С помощью циркуля и линейки раздели его на 4 равные части.
Начертим две окружности из каждого конца отрезка радиусом чуть больше половины длины отрезка («на глаз»). Точки пересечния этих окружностей между собой соединим отрезком. Этот отрезок проходит перпендикулярно исходному отрезку, точка их пересечения и будет серединой исходного отрезка. Аналогично поступаем для двух половин исходного отрезка и делим их на две равные части — в итоге получаем четыре равных отрезка. 110
-
Ответы к странице учебника 110
368. Используя клетчатую основу листа в тетради, начерти два отрезка, которые пересекаются под прямым углом.
369. Построй остроугольный треугольник, у которого одна из сторон имеет длину 10 см.
370. Построй тупоугольный треугольник, у которого одна из сторон имеет длину 10 см.
371. Построй прямоугольный треугольник, у которого одна из сторон имеет длину 10 см.
372. Построй треугольник, у которого одна сторона имеет длину 8 см, а высота, проведённая к этой стороне, имеет длину 4 см.
373. Что общего у всех данных треугольников? К какому виду треугольников относится каждый из них?
Чем является бoльшая сторона каждого треугольника для соответствующей окружности?
Начерти прямоугольный треугольник, у которого бoльшая сторона имеет длину 4 см.
Все эти треугольники вписаны внутрь окружности. Каждый из них является прямоугольным треугольником.
Бoльшая сторона каждого треугольника является диаметром соответствующей окружности. 111
-
Ответы к странице учебника 111. Буквенные выражения и уравнения (повторение)
374. Вычисли значения указанных в таблице выражений при заданных значениях переменной ?. Запиши эти значения в таблицу в тетради.
? 72 345 2781 12549
? + 658 730 1003 3439 13207
78963 — ? 78891 78618 76182 66414
? • 25 1800 8625 69525 313725
? : 3 24 115 927 4183375. Для каждого многоугольника составь буквенное выражение, с помощью которого можно вычислить периметр этого многоугольника, если указанными буквами обозначены длины соответствующих сторон многоугольников.
Периметр прямоугольника: 2 • (? + b).
Периметр ромба: 4 • ?.
Периметр трапеции: 2 • c + b + ?. 112
-
Ответы к странице учебника 112
376. Что получится в результате сложения некоторого числа ? с числом 0?
Запиши это свойство сложения с помощью соответствующего равенства.Получится число ?.
? + 0 = ?377. Что получится, если из некоторого числа ? вычесть число 0?
Что получится, если из некоторого числа ? вычесть это же число?
Запиши эти свойства вычитания с помощью соответствующих равенств.Получится число ?.
Получится число 0.
? — 0 = ?
? — ? = 0378. Что получится, если некоторое число ? умножить на число 0?
Что получится, если некоторое число ? умножить на число 1?
Запиши эти свойства умножения с помощью соответствующих равенств.Получится число 0.
Получится число ?.
? • 0 = 0
? • 1 = ?379. Что получится, если число 0 разделить на некоторое натуральное число ??
Запиши это свойство деления с помощью соответствующего равенства.
Обязательно укажи, что число ? в этом равенстве не может равняться 0!Получится число 0.
0 : ? = 0, ? ? 0380. Что получится, если некоторое число ? разделить на число 1?
Что получится, если некоторое натуральное число ? разделить на это же число ??
Запиши эти свойства деления с помощью соответствующих равенств.Получится число ?.
Получится число 1.
? : 1 = ?
? : ? = 1 113
-
Ответы к странице учебника 113
381. Найди корни следующих уравнений.
х + 25689 = 365148 462351 — х = 42365
х — 45361 = 75892 х • 15 = 42825
81954 : х = 18 х : 37 = 3652х + 25689 = 365148 462351 — х = 42365
х = 365148 — 25689 х = 462351 — 42365
х = 339459 х = 419986
х — 45361 = 75892 х • 15 = 42825
х = 75892 + 45361 х = 42825 : 15
х = 121253 х = 2855
81954 : х = 18 х : 37 = 3652
х = 81954 : 18 х = 3652 • 37
х = 4553 х = 135124382. Составь уравнение, корнем которого является неизвестное число, удовлетворяющее следующему условию: если к неизвестному числу прибавить число 38, а полученный результат разделить на 25, то в итоге получится 8.
(х + 38) : 25 = 8
383. Запиши, какое выражение является делимым в следующем уравнении:
(х + 38) : 25 = 8.
Можно ли по данному уравнению найти, чему должно быть равно делимое? Вычисли это число и составь новое уравнение с тем же самым неизвестным.
Найди корень составленного уравнения и проверь, будет ли это число являться корнем исходного уравнения.Делимым является выражение х + 38.
Можно:
(х + 38) : 25 = 8
(х + 38) = 8 • 25
х + 38 = 200
Новое уравнение:
х + 38 = 200
х = 200 — 38
х = 162
Проверка:
(162 + 38) : 25 = 8
200 : 25 = 8
8 = 8
Следовательно, х = 162 — корень исходного уравнения.384. Проверь, корнем какого из данных уравнений является число 237.
х + 53896 = 54123 82581 + х = 82918
х — 235689 = 125682 536982 — х = 536650
х • 36 = 7956 99 • х = 23661
х : 13 = 21 237237 : х = 1001х + 53896 = 54123 82581 + х = 82918
х = 54123 — 53896 х = 82948 — 82581
х = 227 х = 367
х — 235689 = 125682 536982 — х = 536650
х = 125682 + 235689 х = 536982 — 536650
х = 361371 х = 332
х • 36 = 7956 99 • х = 23661
х = 7956 : 36 х = 23661 : 99
х = 221 х = 239
х : 13 = 21 237237 : х = 1001
х = 21 • 13 х = 237237 : 1001
х = 273 х = 237
Число 237 является корнем уравнения 237237 : х = 1001.385. Составь три разных уравнения, корнем каждого из которых является число 725.
6525 : х = 9 5 • х = 3625 125 + х = 850
х = 6525 : 9 х = 3625 : 5 х = 850 — 125
х = 725 х = 725 х = 725 114
-
Ответы к странице учебника 114. Учимся находить последовательности
386. Миша вырезал 33 одинаковых круга и стал составлять из них фигуры в форме равностороннего треугольника (вырежи и ты 15 таких кругов, они тебе пригодятся).
Составляя первую фигуру, Миша взял 1 круг и ещё 2 круга.
Составляя вторую фигуру, он взял столько кругов, сколько для первой фигуры и ещё 3 круга.
Составляя третью фигуру, он взял столько кругов, сколько для второй фигуры и ещё 4 круга.
Сколько кругов потребовалось Мише для составления первой, второй и третьей фигур? Запиши последовательно эти три числа.
Миша не стал составлять четвёртую фигуру. Он знал, что для неё у него не хватит 1 круга.
Сколько кругов потребуется Мише для составления следующей фигуры?
Если не можешь ответить на вопрос, то сначала построй четвёртую фигуру из третьей.
Миша, составляя фигуры в форме равностороннего треугольника из одинаковых кругов, понял правило, по которому можно сосчитать число кругов, необходимых для составления любой следующей фигуры.
Получилась очень интересная последовательность, состоящая из сумм чисел: (1 + 2), (1 + 2 + 3), (1 + 2 + 3 + 4), (1 + 2 + 3 + 4 + 5), (1 + 2 + 3 + 4 + 5 + 6)…
Можешь воспользоваться открытием Миши и найти шестое и седьмое числа этой последовательности.Для составления первой, второй и третьей фигур потребовалось: 3, 6, 10 кругов.
Для составления следующей фигуры Мише понадобится 15 кругов.
(1 + 2 + 3 + 4 + 5 + 6 + 7) = 28 — шестое число последовательности
(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8) = 36 — седьмое число последовательности 115
-
Ответы к странице учебника 115
387. Числа 5, 10, 25 являются первыми тремя числами некоторой последовательности. Проверь, с помощью какого из трёх данных правил получается каждое следующее число этой последовательности:
а) увеличением предыдущего числа на 5;
б) увеличением предыдущего числа в 2 раза;
в) увеличением предыдущего числа в 3 раза и уменьшением полученного результата на 5.
Вычисли четвёртое число этой последовательности.Правило в).
25 • 3 — 5 = 75 — 5 = 70388. Числа 1, 3, 5 являются первыми по порядку тремя натуральными числами, которые не делятся на 2. Вычисли и запиши четвёртое, пятое и шестое числа этой последовательности.
Проверь правильность вычисления. Эти числа не должны делиться на 2.
Запиши в столбик суммы первого и шестого, второго и пятого, третьего и четвёртого чисел этой последовательности. Найди значение каждой суммы. Проверь правильность вычисления. Значения сумм должны быть равны.
А чему равно значение суммы всех трёх полученных в результате чисел?
Докажи, что полученное число является значением суммы шести первых чисел этой последовательности.Правило: увеличение предыдущего числа на 2.
5 + 2 = 7, 7 + 2 = 9, 9 + 2 = 11
7 : 2 = 3 (ост. 1), 9 : 2 = 4 (ост. 1), 11 : 2 = 5 (ост. 1)
1 + 11 = 12
3 + 9 = 12
5 + 7 = 12
Значения сумм равны между собой и равны 12.
12 + 12 + 12 = 36
1 + 3 + 5 + 7 + 9 + 11 = 36 116
-
Ответы к странице учебника 116
389.
В процессе выполнения задания 389 учащиеся смогут не только внимательно познакомиться с построчной формой записи очень важного и полезного для повседневной жизни алгоритма, но и самостоятельно построить построчную запись аналогичного алгоритма:
1. Подойти к началу перехода и остановиться.
2. Дождаться разрешающего переход сигнала светофора (должен загореться «зеленый человечек»).
3. Перейти улицу.390.
Задание 390 относится к заданиям повышенной сложности. Основной целью задания является знакомство учащихся с такой формой записи алгоритма, которую принято называть блок-схемой.
При этом важно обратить внимание учащихся на то, какие геометрические фигуры используются для построения блок-схемы и что обозначает каждый блок.
Если учащиеся правильно поняли алгоритм, записанный с помощью блок-схемы, то они без особого труда смогут сделать построчную запись этого алгоритма. Далее они должны сформулировать построчно алгоритм вычисления периметра прямоугольника, который основан на другом правиле.
1. Узнать (измерить, вычислить) длину и ширину прямоугольника.
2. Длину прямоугольника умножить на 2.
3. Ширину прямоугольника умножить на 2.
4. Получить периметр прямоугольника как результат сложения величин, вычисленных в пунктах 1 и 2.В заключительной части задания учащиеся получают возможность поупражняться в переходе от построчной записи алгоритма к записи в виде блок-схемы. При этом они должны ориентироваться на имеющуюся в задании блок-схему, внеся в нее соответствующие изменения.
117
-
Ответы к странице учебника 117
391.
Поупражняемся в составлении алгоритма вычисления периметра квадрата, используя две формы записи. Построчная запись в этом случае будет выглядеть так:
1. Узнать (измерить, вычислить) длину стороны квадрата.
2. Длину стороны квадрата умножить на 4.
3. Получить периметр квадрата как результат умножения из пункта 2.По этой построчной записи можно без особого труда составить соответствующую блок-схему, добавив пункты начало и конец.
392.
Задание 392 аналогично предыдущему заданию. Отличие состоит лишь в том, что в этом задании речь идет не о квадрате, а о равностороннем треугольнике. Учащимся хорошо известна формула, с помощью которой можно вычислить периметр равностороннего треугольника. Эта формула отличается от соответствующей формулы для квадрата лишь заменой множителя 4 на множитель 3. Именно это изменение и должно быть внесено в алгоритм, построенный при выполнении предыдущего задания (это нужно сделать и для построчной записи и для записи алгоритма в виде блок-схемы).
118
-
Ответы к странице учебника 118
393.
В процессе выполнения задания 393 учащиеся познакомятся с возможностью представлять количественную структуру данного множества с помощью круговой диаграммы. В качестве примера им предлагается рассмотреть множество учеников класса (в классе 24 ученика), которое структурировано по одному из указанных признаков. Другими словами, по каждому из указанных признаков в данном множестве выделяется определенное подмножество (нам известна численность этого подмножества). Используя эти данные, можно вычислить ту долю, которую в количественном смысле подмножество составляет от всего множества. Так, для учеников, занимающихся в изостудии, эта доля будет восьмой; для посещающих секцию гимнастики – шестой; для занимающихся бальными танцами – двенадцатой; для поющих в хоре – третьей.
После этого учащимся следует проанализировать представленные круговые диаграммы на предмет того, какую долю составляет закрашенная часть (сектор) от всего круга. Сделанные на окружностях деления позволяют установить, что на первой диаграмме выделена третья доля, на второй – шестая доля, на третьей – восьмая доля, на четвертой – двенадцатая доля.
Теперь можно без особого труда установить соответствие между рассмотренными ранее подмножествами и диаграммами: первая диаграмма иллюстрирует долю учащихся, поющих в хоре, вторая – долю учащихся, посещающих секцию гимнастики, третья – долю учащихся, занимающихся в изостудии, четвертая – долю учащихся, занимающихся бальными танцами.
394.
Задание 394 относится к заданиям повышенной сложности. В нем предлагается познакомиться с одним из способов построения диаграммы, иллюстрирующей девятую долю. Так как способа простыми построениями разделить окружность (круг) на 9 равных частей не существует, а сделать это «на глаз» также совсем непросто, то мы предлагаем использовать для решения этой задачи наши знания о движении часовой стрелки по круглому циферблату.
Сначала учащиеся должны уяснить, что полный оборот часовая стрелка делает за 12 часов, т. е. за 720 минут. Девятую долю от этой величины составляет промежуток в 80 минут (720 мин : 9 = 80 мин) или в 1 час 20 минут. Теперь остается понять, какой сектор описывает часовая стрелка за 1 час 20 минут (этот сектор и будет составлять девятую долю от всего круга).
Хорошо известно, что часовая стрелка описывает сектор между двумя минутными делениями на циферблате за 12 минут (60 мин : 5 = 12 мин), поэтому за 1 час 20 минут часовая стрелка проходит путь приблизительно такой же (на самом деле несколько меньше), что и минутная стрелка за 7 минут (точнее следовало бы взять для минутной стрелки промежуток в 6 минут 40 секунд, но для решения данной задачи нас вполне устраивает промежуток в 7 минут). После таких рассуждений не составляет труда установить, что из двух данных диаграмм девятую долю иллюстрирует вторая диаграмма, так как именно на ней и показан сектор, который описывает минутная стрелка приблизительно за 7 минут (или, если быть точным, описывает часовая стрелка за 1 час 20 минут).
Стр. 119-122 Вопросы для повторения
Стр. 123-125 Словарь
Стр. 126-128 ПриложениеНу и все, далее у школьников каникулы. Желаем хорошо отдохнуть и ждем вас в следующем учебном году!


