ГДЗ к учебнику математики за 4 класс, 1 часть Рудницкой (Начальная школа 21 века)

: Категория: ГДЗ по математике за 4 класс

Последний класс начальной школы, - 4 класс. В нем как и в предыдущих классах все также изучают математику, разве что она становится чуть сложнее и разнообразнее. В 4 классе по математике по программе "Начальная школа 21 век" в проходят темы и встречаются задачи на скорость сближения и удаления, задачи связанные с вычислениями площади, задания связанные с объемными многоугольниками.
Все это довольно просто, но видимо не для всех... Так вот, для кого подобные задачи будут вызывать затруднения очень кстати придется наша страничка. Ведь здесь можно будет найти ГДЗ, то есть готовые домашние задания для учебника по математике за 4 класс "Начальная школа 21 века". Теперь же пару слов о том, как смотреть наши задания и переходим к ответам.

Найти нужный вам ответ весьма просто. Для этого необходимо выбрать нужную страничку и кликнуть по ней. Откроется страница, где и можно будет посмотреть ответы.

Ответы для учебника по математике за 4 класс, 1 часть, автора Рудницкая (Начальная школа 21 века)

Теперь же сами ответы.

Ответы для учебника по математике за 4 класс, 1 часть, автора Рудницкая (Начальная школа 21 века)

Теперь же сами ответы.

Страница 4

УЗНАЁМ НОВОЕ
Десятичная система счисления

1. Прочитайте числа. В какой из записей цифра 5 обозначает число сотен, в какой — число десятков, в какой? — число единиц?

В числе 594 цифра 5 стоит в разряде сотен и обозначает 5 сотен.
В числе 451 цифра 5 стоит в разряде десятков и обозначает 5 десятков.
В числе 275 цифра 5 стоит в разряде единиц и обозначает 5 единиц.

Что обозначает каждая из цифр в записи числа: 555, 333, 888?

555 - пять сотен пять десятков пять единиц.
333 - три сотни три десятка три единицы.
888 - восемь сотен восемь десятков восемь единиц.

5

Страница 5

Одна и та же цифра в записи числа может обозначать и число единиц, и число десятков, и число сотен в зависимости от того, в каком разряде она стоит. Число, которое обозначает эта цифра, от разряда к разряду (от единиц к сотням) увеличивается в 10 раз. Поэтому систему записи чисел, которой мы пользуемся, называют десятичной системой счисления.

2. Что обозначает каждая цифра в записи числа:
67, - шесть десятков семь единиц.
290, - две сотни девять десятков ноль единиц.
666, - шесть сотен шесть десятков шесть единиц.
400, - 4 сотни ноль десятков ноль единиц.
101? - одна сотня ноль десятков одна единица.

3. Запишите цифрами число, в котором:
четыре сотни, - 400
четыре десятка, - 40
восемь единиц; - 8
девять сотен, - 900
пять единиц; - 5
девять сотен, - 500
пять десятков. - 50

В числе 836 содержится 8 сотен (8 · 100), 3 десятка (3 · 10) и 6 единиц. Его можно записать в виде суммы:
836 = 8 · 100 + 3 · 10 + 6.
Каждое слагаемое суммы называют разрядным слагаемым; число 836 представлено в виде суммы разрядных слагаемых.

4. Запишите в виде суммы разрядных слагаемых каждое из чисел: 327, 638, 418, 999, 207, 270, 620.

3*100+2*10+7=327
6*100+30*10+8=638
4*100+1*10+8=418
9*100+9*10+9=999
2*100+7=207
2*100+7*10=270
6*100+2*10=620

5. Числа представлены в виде суммы разрядных слагаемых. Какие это числа?

6 · 100 + 9 · 10 + 2 = 692
1 · 10 + 8 = 18
1 · 100 + 3 · 10 = 130
7 · 100 + 5 = 705

Проверьте себя: найдите ответы среди чисел 705, 130, 18, 692.

6

Страница 6

6. Запишите все возможные трёхзначные числа, используя цифры 8, 0 и 5 так, чтобы в записи каждого числа:

1) цифры не повторялись;

508
580
805
850

2) цифры повторялись.

500
505
508
550
555
558
580
585
588

800
805
808
850
855
858
880
885
888

7*. Приведите примеры двузначных чисел, в которых число единиц в 2 раза меньше числа десятков.

84
63

Кроме десятичной системы счисления часто используют римскую систему записи чисел. Например, римские цифры можно увидеть на циферблатах часов, на старинных зданиях; римскими цифрами иногда записывают номер главы в книге, век. При записи чисел римскими цифрами используются семь цифр.

8. Проследите, какое число обозначает каждая из семи римских цифр.

I 1
V 5
X 10
L 50
C 100
D 500
M 1 000

9.
1) Проанализируйте записи чисел от 2 до 20 римскими цифрами. Попробуйте сформулировать правила записи чисел.
II 2
VI 6
IX 9
III 3
VII 7
XI 11
IV 4
VIII 8
XII 12

К более высоким разрядам, если они переходят от одного к другому, вначале начинает прибавляться самый низкий разряд I, затем разряд V, затем X и т.д.. При этом у римских чисел есть особенность, перед переходом одного разряда к другому, есть число предшествующее разряду. Перед ним ставится разряд и I. Например IX.

7

Страница 7

XIII 13
XVI 16
XIX 19
XIV 14
XVII 17
XX 20
XV 15
XVIII 18

2) Запишите римскими цифрами числа: 25, 30, 48, 51, 120, 600.

XXV - 25
XXXXVIII - 48
LI - 51
CXX - 120
DC - 600

10. В каком году построен замок? 1514

Какое время показывают часы? 3 часа 23 минуты

11. Вычислите устно.

25 + 6 = 31              40 · 6 = 240                80 : 2 = 40
130 – 20 = 110        120 : 30 = 40              15 · 4 = 60
12 · 4 = 48               681 – 600 = 681         230 + 70 = 300
51 : 17 = 3                64 + 36 = 28             100 – 75 = 25

12. Чем похожи и чем различаются выражения

48 : 6 + 26 · 2 и (48 : 6 + 26) · 2?

Похожи числами в выражении, отличаются порядком операций.

Выполните вычисления.

48 : 6 + 26 · 2 = 8 + 52 =60
(48 : 6 + 26) · 2 = 32 * 2 = 64

8

Страница 8

13. Запишите выражения и вычислите их значения.

Из числа 760 вычесть частное чисел 60 и 4.

760 - 60 : 4 = 760 - 15 = 745

Произведение чисел 17 и 5 уменьшить на 38.

17*5 - 38 = 85 - 38 = 47

Частное чисел 52 и 4 увеличить в 5 раз.

52 : 4 * 5 = 13 * 5 = 65

Сумму чисел 120 и 60 уменьшить в 90 раз.

(120 + 60) : 90 = 180 : 90 = 2

14. Вычислите.

750 – 560 = 190       96 : 8 = 12          45 · 9 = 405
144 + 38 = 182        640 : 20 = 32       129 · 5 = 645
375 – 29 = 346        990 : 30 = 33       16 · 24 = 384
546 + 128 = 674      72 : 6 = 12         46 · 15 = 690
105 : 15 = 7            840 : 210 = 4        432 : 108 = 4

15. Вычислите значение выражения:
1) 38 · х, если х = 10, 8, 5;

38 * 10 = 380
38 * 8 = 304
38 * 5 = 190

2) 409 + у, если у = 302, 501, 511;

409 + 302 = 711
409 + 501 = 910
409 + 511 = 920

3) а – 199, если а = 200, 800, 1 000;

200 - 199 = 1
800 - 199 = 601
1000 - 199 = 801

4) n : 7, если n = 140, 280, 980.

140 : 7 = 20
280 : 7 = 40
980 : 7 = 140

16. В бочке было 85 л воды. Сколько воды долили в бочку, если в ней стало 192 л?

192 - 85 = 107 (л.) воды было в бочке.
Ответ: 107 литров.

17. Ученик купил по одинаковой цене 9 тетрадей в линейку и 5 тетрадей в клетку. Каких тетрадей ученик купил больше и на сколько? За какие тетради он заплатил больше денег?

9 - 5 = 4 (т.) больше было куплено тетрадей в линейку, чем в клетку.
Ответ: на 4 тетради больше куплено в линейку, чем в клетку. Так как цена каждой тетради одинаковая, то за тетради в линейку он заплатил больше.

18. Ученик купил по одинаковой цене тетради в клетку и в линейку. Тетрадей в линейку он купил на 4 больше, чем в клетку, и поэтому заплатил за них на 12 р. больше. Какова цена тетради?

12 : 4 = 3 (р) цена тетради.
Ответ: 3 рубля.

9

Страница 9

19. Ученик купил по одинаковой цене 9 тетрадей в линейку и 5 тетрадей в клетку. За тетради в линейку он заплатил на 12 р. больше. Сколько стоили тетради в линейку? Сколько стоили тетради в клетку?

1) 9 - 5 = 4 (т.) в линейку больше, чем в клетку.
2) 12 : 4 = 3 (р.) стоила тетрадь.
3) 5 * 3 = 15 (р.) стоили тетради в клетку.
4) 15 + 12 = 27 (р.) стоили тетради в линейку.
Ответ: 15 рублей стоили тетради в клетку и 27 рублей в линейку.

20. Купили 4 м ткани за 320 р. Какова цена 1 м ткани? Какова стоимость 7 м этой ткани?

1) 320 : 4 = 80 (р.) стоит метр ткани.
2) 80 * 7 = 560 (р) стоит 7 метров ткани.
Ответ: 560 рублей.

21. В трёх одинаковых ящиках 48 кг слив. Сколько слив в шести таких же ящиках? Решите задачу двумя способами.

1 способ

1) 48 : 3 = 16 (кг) слив в каждом ящике.
2) 16 * 6 = 96 (кг) слив в 6 ящиках.
Ответ: 96 килограмм.

2 способ

1) 6 : 3 = 2 (р.) больше слив в 6 ящиках, чем в 3.
2) 48 * 2 = 96 (кг) слив в 6 ящиках.
Ответ: 96 килограмм.

22. Кепка стоит 126 р., перчатки на 67 р. дороже, чем кепка, а футболка стоит столько, сколько кепка и перчатки вместе. Какова цена футболки?

1) 126 + 67 = 193 (р.) стоят перчатки.
2) 126 + 193 = 219 (р.) стоит футболка.
Ответ: 219 рублей стоит футболка.

23. Для кабинета географии купили 5 глобусов по а р. и 7 карт по х р. Составьте выражение для вычисления стоимости покупки. Вычислите цену одного глобуса и одной карты, если стоимость всех купленных глобусов 900 р., а карт — 861 р.

а * 5 + х * 7 - выражение.
а * 5 = 900
а = 900 : 5
а = 180 р.

х * 7 = 861
х = 861 : 7
х = 123

24. Ломаная линия длиной 90 см состоит из шести одинаковых по длине звеньев. Чему равна длина трёх звеньев этой ломаной? Найдите решение задачи двумя способами.

1 способ

1) 90 : 6 = 15 (см) длина одного звена.
2) 15 * 3 = 45 (см) длин трех звеньев.
Ответ: 45 см.

2 способ

1) 6 : 3 = 2 (раза) во столько 3 звена короче 6 звеньев.
2) 90 : 2 = 45 (см) длин трех звеньев.
Ответ: 45 см.

10

Страница 10

25. Начертите окружность, длина радиуса которой 5 см. Отметьте точку A на этой окружности. Постройте квадрат ABXM так, чтобы все его вершины лежали на этой окружности.

Смотри рисунок.

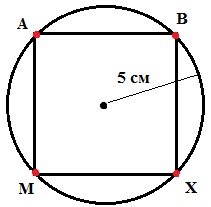
26*. Площадь квадратной клумбы увеличили в 4 раза, сохранив её форму. Выскажите предположение о том, во сколько раз увеличили длину стороны этой клумбы. Проверьте своё предположение, выполнив от руки рисунок.

Сторона увеличится в 2 раза. Смотри рисунок.

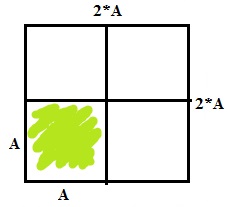
27. Найдите и назовите пару отрезков, симметричных относительно оси ON.

Симметричны: AB и CD.

28. Почему лучи AB и CD не являются симметричными относительно оси ON?

Потому что начало одного и второго луча не совпадает!

29. Вырежьте из бумаги квадрат с длиной стороны 5 см. Разрежьте его по диагонали. Сложите из полученных частей треугольник.

Смотри рисунок.

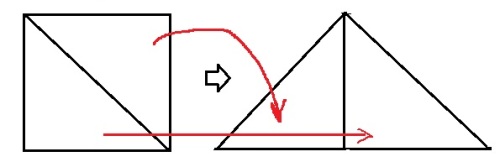
11

Страница 11

30. Верно ли утверждение?

Поясните свой ответ на примерах.

1) Число 250 делится не только на числа 2 и 5, но и на произведение этих чисел.

Да, верно! 5*2=10 250:10=25

2) Число 24 делится не только на числа 8 и 2, но и на их произведение.

Нет, неверно! 8*2=16 24:16=1 (остаток 8)

3) Если при пересечении диагоналей четырёхугольника образуются прямые углы, то этот четырёхугольник является квадратом.

Да, верно!

4) Если в прямоугольнике провести прямую через середины противоположных сторон, то противоположные вершины прямоугольника будут симметричными относительно этой прямой.

Да, верно!

31. Вова решает задачу: «В прямоугольнике с длинами сторон 3 см и 4 см проведена диагональ длиной 5 см. Вычислите периметр каждого из получившихся треугольников».
Для решения задачи Вова сделал рисунок. Затем он составил план решения:
«Прямоугольник разделился на два одинаковых треугольника. Поэтому я сначала найду периметр прямоугольника, а затем разделю его на 2». В чём ошибка в рассуждении Вовы?

В том, что Вова не учитывает диагональ прямоугольника, то есть гипотенузу треугольника!

12

Страница 12

32. В таблице представлены данные об электротоварах, проданных в магазине в первом квартале года. Ответьте на вопросы, используя данные таблицы.
Сколько утюгов продано в каждом месяце? 54 в январе, 48 в феврале, 60 в марте.
Сколько чайников продано в феврале; в марте? в феврале 65, в марте 28
В какие месяцы продано более 20 холодильников? в феврале и марте
Верно ли, что наибольшее число холодильников продано в феврале? нет, наибольшее количество холодильников продано в марте
Сколько чайников продано за три месяца? 70+65+28=163 чайника
Сколько указанных электротоваров продал магазин в марте? 60+28+24=112 электротоваров.
Подсчитайте число проданных в январе утюгов и чайников. 54 + 70 = 124 утюгов и чайников продано в январе
На сколько больше продано в январе чайников, чем утюгов? 70 - 5 4 = 16 на столько больше продано чайников в январе, чем утюгов.
В каком месяце магазин продал наименьшее число чайников? Наименьшее количество чайников продано в марте.

33*. Имеется линейка длиной 20 см. Длина крышки стола больше длины линейки в 5 раз, а её ширина больше трёхкратной длины линейки на 13 см. Вычислите длину и ширину крышки стола.

1) 20 * 5 = 100 (см) длина крышки стола.
2) 20*3+13=73 (см) ширина крышки стола.
Ответ: 100 см длина и 73 см ширина крышки стола.

13

Страница 13

УЗНАЁМ НОВОЕ

Чтение и запись многозначных чисел

1. Как вы думаете, почему число на флажке у Зайца называют трёхзначным, у Волка — шестизначным, а у Белки — девятизначным? Поясните свой ответ.

У каждого зверя число называется по числу разрядов!

В записи трёхзначного числа 328 цифры образуют три разряда — единицы, десятки, сотни. Старшим (высшим) разрядом является разряд сотен. Эти три разряда объединяют вместе и называют классом единиц. В числе 328 цифра 3 обозначает три сотни (триста), цифра 2 — два десятка (двадцать), цифра 8 — восемь единиц. Число 328 читают так: триста двадцать восемь. Число 625 347 — шестизначное. Первые три цифры справа образуют класс единиц, а сле- (продолжение на след. странице)

14

Страница 14

Следующие три цифры — класс тысяч. В классе тысяч три разряда, которые называют так: единицы тысяч, десятки тысяч, сотни тысяч. В числе 625 347 цифра 6 обозначает шесть сотен (шестьсот) тысяч, цифра 2 — два десятка (двадцать) тысяч, цифра 5 — пять тысяч. Всего в этом числе 625 тысяч 347 единиц. Поэтому число 625 347 читают так: шестьсот двадцать пять тысяч триста сорок семь (слово «единиц» не произносят).

Число 126 281 539 — девятизначное.

Первые три цифры справа образуют класс единиц, следующие три цифры — класс тысяч, а последние три цифры — класс миллионов. В классе миллионов три разряда, которые называют так: единицы миллионов, десятки миллионов, сотни миллионов. Десять единиц любого разряда в любом классе образуют единицу следующего разряда. 10 тысяч образуют единицу следующего разряда — десяток тысяч, 10 десятков тысяч — сотню тысяч, 10 сотен тысяч — миллион, 10? миллионов — десяток миллионов, 10 десятков миллионов — сотню миллионов.

15

Страница 15

Попробуйте прочитать число, используя таблицу.

Проверьте себя: сто двадцать шесть миллионов двести восемьдесят одна тысяча пятьсот тридцать девять.

2. Что обозначает каждая цифра в записи чисел?

Прочитайте каждое число. Сравните свой ответ с текстом на странице 16

Шестьсот пять
Одна тысяча.
Тридцать девять тысяч восемнадцать
Сто тридцать девять тысяч восемнадцать.
Один миллион.
Сорок шесть миллионов пятьсот тридцать тысяч девятьсот шестьдесят.

16

Страница 16

Чтобы прочитать многозначное число, его запись разбивают справа налево на классы по три разряда в каждом (в последнем слева классе может отсутствовать один или два разряда). Затем называют число единиц каждого класса, начиная с самого старшего разряда. Пример. Прочитаем число 3 000 624. Разобьём запись справа налево на классы по три разряда. Называем число единиц каждого класса и добавляем его название (название класса единиц не произносим). Во всех разрядах класса тысяч — нули, поэтому его название не произносят. Число 3 000 624 читается так: три миллиона шестьсот двадцать четыре.

3. Прочитайте предложения.

1) Масса Земли меньше массы Солнца в 329 000 раз.
2) Самая высокая горная вершина на Земле? — Джомолунгма. Её высота 8 848 м над уровнем моря.
3) Глубина Тихого океана в Марианской впадине достигает 11 022 м.

4. Прочитайте числа, написанные на билетах.

Слева направо:

Сто сорок две тысячи семьдесят пять тысяч восемьдесят три.
Сорок тысяч триста десять.
Сто девятнадцать миллионов шестьсот семьдесят тысяч сто девяносто.

17

Страница 17

5. Прочитайте числа:

1) 2 000, 5 830, 5 083, 5 308, 9 999;

две тысячи, пять тысяч восемьсот тридцать, пять тысяч восемьдесят три, пять тысяч триста восемь, девять тысяч девятьсот девяносто девять.

2) 16 835, 28 036, 80 007, 91 003, 31 030, 30 900;

Шестнадцать тысяч восемьсот тридцать пять, двадцать восемь тысяч тридцать шесть, восемьдесят тысяч семь, девяносто одна тысяча три, тридцать тысяч девятьсот.

3) 969 384, 703 856, 255 000, 100 100, 999 999, 203 050;

девятьсот шестьдесят девять тысяч триста восемьдесят четыре, семьсот три тысячи восемьсот пятьдесят шесть, двести пятьдесят пять тысяч, сто тысяч сто, девять сот девяносто девять тысяч девять сот девяносто девять, двести три тысячи пятьдесят.

4) 1 000 000, 2 000 000, 5 360 036, 25 635 007.

Один миллион, два миллиона, пять миллионов триста шестьдесят тысяч тридцать шесть, двадцать пять миллионов шестьсот тридцать пять тысяч семь.

6. Сколько цифр в каждом из классов в записях чисел?

3 625 - 5 разрядов.
26 806 - 5 разрядов.
309 958 - 6 разрядов.
7 012 - 4 разряда.
40 091 - 5 разрядов.
900 064 - 6 разрядов.

При записи многозначного числа нужно следить за тем, чтобы в разрядах каждого класса (кроме, может быть, первого слева) было три цифры. Если в каком-нибудь классе отсутствуют единицы того или иного разряда, то в? этих разрядах пишут нули. Пример. Запишем цифрами число сто семьдесят тысяч восемьдесят. В классе тысяч пишем 170, в классе единиц — 080. Получится запись: 170 080.

7. Запишите числа:

двести восемьдесят три тысячи сорок девять; 283 049
девять миллионов четыре тысячи триста; 9 004 300
семьсот тысяч два; 700 002
тридцать шесть миллионов сто семьдесят тысяч; 36 170 000
один миллион сто один. 1 000 101

Проверьте себя: сравните свои записи с записями этих чисел на следующей странице.

18

Страница 18

283 049, 9 004 300, 700 002, 36 170 000, 1 000 101

Все верно!

8*. Запишите по шесть четырёхзначных чисел, используя цифры 5, 3, 4, 0.

В записи каждого числа:
1) цифры могут повторяться;

3045
5405
3450
4355
5503

2) цифры не должны повторяться.

3045
3405
3450
4305
4350

9. Назовите общие свойства чисел:

1 111, 5 555, 3 333, 8 888.

Во всех числах у всех разрядов одинаковые значения чисел. Также все они делятся на 1 111 без остатка.

10. Назовите по порядку числа:

1) от 9 000 до 9 007;

девять тысяч,
девять тысяч один,
девять тысяч два,
девять тысяч три,
девять тысяч четыре,
девять тысяч пять,
девять тысяч шесть,
девять тысяч семь.

2) от 99 998 до 100 005.

девяносто девять тысяч девятьсот девяносто восемь,
девяносто девять тысяч девятьсот девяносто девять,
сто тысяч,
сто тысяч один,
сто тысяч два,
сто тысяч три,
сто тысяч четыре,
сто тысяч пять.

11. Запишите три числа, которые при счёте следуют за числом 3 997, и три числа, которые предшествуют ему.

3994
3995
3996
3997
3998
3999
4000

12. К какому числу надо прибавить 1, чтобы получилось число:

1) 100 000;

99 999 + 1 = 100 000

2) миллион?

999 999 + 1 = 1 000 000

13. Из какого четырёхзначного числа надо вычесть 1, чтобы получилось трёхзначное число?

10 000

14. Используя цифры от 1 до 9, запишите какое-нибудь трёхзначное число. Поменяйте в нём местами цифры в разрядах единиц и сотен. Запишите получившееся число. Какое число больше и на сколько?

119
191

191 больше 119 на 191 - 119 = 72

19

Страница 19

15. Какому числу равна сумма чисел?

30 000 и 5 000              30 000 + 5 000 = 35 000
6 020 и 100                   6 020 + 100 = 6 120
30 000 и 500                 30 000 + 500 = 30 500
100 800 и 2 000            100 800 + 2000 = 102 800
30 000 и 50                   30 000 + 50 = 30 050
76 400 и 30                    76 400 + 30 = 76 430
30 000 и 5                     30 000 + 5 = 30 005
1 000 000 и 900 000     1 000 000 + 900 000 = 1 900 000

16. Вычислите устно.

3 600 – 600 = 3 000
1 275 – 1 000 – 200 – 70 = 5
28 000 – 20 000 = 8 000
1 999 – 999 = 1 000

17. Выразите в километрах и метрах:

124 568 м, 124 км 568 м
70 031 м, 70 км 31 м
504 040 м. 504 км 40 м

Выразите в метрах:

72 км 275 м, 72 275 м
8 км 64 м, 8064 м
10 км 740 м. 10 740м

18. Запишите в виде суммы разрядных слагаемых числа:

12 164,    12 000 + 100 + 60 + 4 = 12 164
798 053,   700 000 + 90 000 + 8 000 + 50 + 3 = 798 053
80 070,     80 000 + 70 = 80 070
70 190,    70 000 +100 + 90 = 70 190
606 060. 600 000 + 6 000 + 60 = 606 060

19. Выполните действия в выражениях и сравните результаты.

1)
730 – 170 + 290 = 850
730 – (170 + 290) = 270

2)
(630 + 270 : 9) : 2 = 330
(630 + 270) : 9 : 2 = 50

20. Проверьте, верны ли равенства и неравенства.

706 + 43 = 749 верно        270 · 2 : 10 > 54 неверно
769 – 45 = 724 верно       880 : 44 · 10 > 100 верно
45 + 432 = 477 верно        488 – 135 < 353 неверно

20

Страница 20

21. Найдите значения выражений.

1 2 4 5 3
15 · 18 : 9 + 361 – 954 : 3 = 73

*15
18
+120
15_
270

2) 270:9=30

- 954|3
9    | 318
   -5
    3
    -24
     24
       0

4) 30+361=391
5) 391-318=73

2 1 4 5 3
64 · (8 + 2) – 549 + 36 · 9 = 415

1) 8 + 2 = 10
2) 64 * 10 = 640

*36
9
+54
27
324

4) 640 - 549 = 91
5) 91 + 324 = 415

22. Выполните деление с остатком и сделайте проверку.

327 : 5 = 65 (остаток 2)

-327|5
30 |65
-27
25
2 (остаток)

Проверка.

*65
5
325

325+2=327

800 : 24 = 33 (остаток 8)

-800|24
72   |33
-80
   72
     8   (остаток)

Проверка.

*24
33
+72
72
792

792 + 8 = 800

129 : 4 = 32 (остаток 1)

-129|4
12   |32
    -9
     8
      1 (остаток)

Проверка.

32 * 4 = 128

128 + 1 = 129

465 : 23 = 20 (остаток 5)

-465|23
46 |20
5 (остаток)

Проверка.

23*20=460

460 + 5 = 465

391 : 33 = 11 (остаток 28)

-391|33
33 |11
   -61
    33
    28

Проверка.

*33
11
+ 33
33
363

363 + 28 = 391

23. Проверьте равенство и сделайте вывод (верно, неверно).

527 : 63 = 8 (ост. 23)

Проверка

63 * 8 = 504
504 + 23 = 527

132 : 54 = 2 (ост. 24)

Проверка

54 * 2 = 108
108 + 24 = 132

24. При переработке 696 кг нефти керосин составил третью часть этой массы. Сколько килограммов керосина получилось?

696 : 3 = 232 (кг) керосина получилось.
Ответ: 232 кг.

25. Мальчик купил 7 одинаковых карандашей, а девочка купила 11 таких же карандашей и заплатила на 12 р. больше. Сколько стоит один карандаш? Сколько заплатила за свою покупку девочка и сколько заплатил мальчик?

1) 11 - 7 = 4 (кар.) на столько больше купила девочка.
2) 12 : 4 = 3 (р.) стоил карандаш.
3) 3 * 7 = 21 (р.) заплатил мальчик.
4) 3 * 11 = 33 (р.) заплатила девочка.
Ответ: 3 рубля стоит карандаш, мальчик заплатил за свои 21 рублей, а девочка 33.

21

Страница 21

26. Ученикам сначала купили 64 тетради, а затем ещё 40 тетрадей. Все тетради им раздали поровну. Сколько тетрадей получил каждый ученик, если в классе было 12 девочек и 14 мальчиков?

1) 64 + 40 = 104 (тет.) купили всего.
2) 12 + 14 = 26 (уч.) было всего.
3) 104 : 26 = 4 (тет.) получил каждый ученик.
Ответ: 4 тетради.

27. Составьте задачу, решением которой является выражение, записанное Зайцем. Решите эту задачу, если:

Из ящика с морковью взяли 4 кг моркови. Сколько кг осталось в ящике?

1) x = 20;

20 - 4 = 16 (кг) осталось моркови в ящике.
Ответ: 16 кг.

2) x = 15.

15 - 4 = 11 (кг) осталось моркови в ящике.
Ответ: 11 кг.

28. Цена пачки печенья 68 р., а плитки шоколада 75 р. Какова стоимость покупки, если купили a пачек печенья и две шоколадки?

а * 58 + 2 * 75 = а * 58 + 150

22

Страница 22

29. Постройте:

1) прямоугольник со сторонами 4 см и 6 см;
2) квадрат со стороной 1 дм.

Самостоятельно.

30. Сколько треугольников на каждом рисунке?

На 1 - 5.
На 2 - 4.

31*. Как можно вычислить площадь каждой фигуры? Сделайте необходимые измерения и выполните вычисления.

Смотри рисунок.

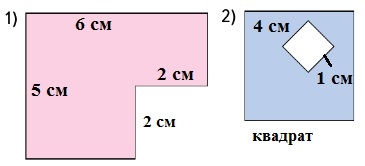
1 фигура.

5 * 6 - 2 * 2 = 30 - 4 = 26 (см2) площадь фигуры.
Ответ: 26 см2.

2 фигура.

4 * 4 - 1 * 1 = 16 - 1 = 15 (см2) площадь фигуры.
Ответ: 15 см2.

32. Вычислите устно.

10 р. – 9 р. 50 к. = 50 к
6 р. – 20 к. = 5 р 80 к.
75 к. + 25 к. = 1 р
1 р. 50 к. + 60 к. = 2 р 10 к
7 р. 80 к. + 7 р. 20 к. = 15 р.
1 р. 50 к. · 2 = 3 р
30 р. – 90 к. = 29 р 10 к
164 р. : 4 = 41 р.
12 р. 60 к. : 3 = 4 р 20 к

23

Страница 23

33*. Клоун жонглирует шестью одинаковыми по виду кольцами. Одно из колец легче каждого из остальных, одинаковых по массе. Как найти это кольцо, выполнив только два взвешивания колец на чашечных весах без гирь?

1) Вначале поделить все кольца пополам и положить на весы. 3 кольца с более легким будут весить меньше. Выбираем их.
2) Далее из 3 оставшихся кладем любые два на весы. Если весы уравновешены, значит третье кольцо самое легкое. Если какое-то кольцо из 2 легче другого, то именно оно самое легкое.

34. Подсчитайте стоимость покупки по чеку.

13+142+54+36+124+1=155+90+125=370 р.

У покупателя есть дисконтная карта на право получения скидки в размере одной десятой части стоимости купленного товара. На какую сумму он получит скидку?

370 :10 = 37 р.

Сколько денег заплатит покупатель за свою покупку с учётом скидки?

370 - 37 = 333 рубля.

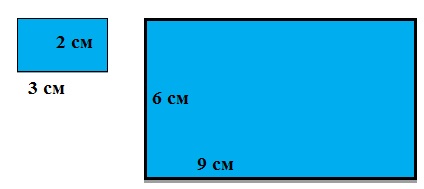
35. Увеличьте размеры данного прямоугольника в 3 раза. Постройте прямоугольник с новыми размерами.

Данный прямоугольник имеет размеры 2 на 3 см.

2 * 3 = 6 см и 3 * 3 = 9 см.

Строим прямоугольник с размерами 6 на 9 см.

24

Страница 24

УЗНАЁМ НОВОЕ

Сравнение многозначных чисел

1. Вспомните способ поразрядного сравнения чисел. Какое из чисел больше: 416 или 316, 275 или 245, 367 или 360?

416 >316,
275 >245,
367 > 360

Поясните свои ответы.

Сравниваем вначале более старшие разряды, если они равны переходим к более младшим и так далее, пока один из них не будет больше или меньше. По нему и определяем отношения чисел.

Число 591 больше числа 568, так как сотен в них поровну, а десятков в числе 591 больше, чем в числе 568.

2. Сравните числа. 361 и 613 90 652 и 91 003 2 976 и 2 859 26 578 и 26 758 1 999 и 2 000 194 057 и 194 107 4 503 и 4 518 68 341 и 6 843

361 < 613
90 652 <91 003
2 976 > 2 859
26 578 < 26 758
1 999 < 2 000
194 057 < 194 107
4 503 < 4 518
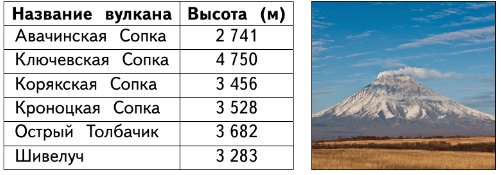
68 341 > 6 843

3. В таблице перечислены крупнейшие вулканы Камчатки и их высоты. Назовите высоту каждого из вулканов. Какой вулкан самый высокий? Назовите вулканы в порядке уменьшения их высот.

Ключевская сопка, Острый Толбачек, Кроноцкая сопка, Корякская сопка, Шивелуч, Авачинская сопка

25

Страница 25

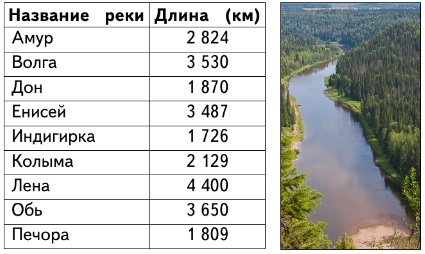
4. В таблице указаны названия и длины крупнейших рек России. Какая из них имеет наибольшую длину и какая — наименьшую?

Наибольшую: Лена.
Наименьшую: Индигирка.

Назовите реки в порядке увеличения их длин.

Индигирка, Печора, Дон, Колыма, Амур, Енисей, Волга, Обь, Лена

5. Прочитайте неравенства. Какие из них верные?

6 140 > 6 240 неверное
1 967 > 10 967 неверное
2 001 > 1 002 верное
90 603 < 90 613 верное
777 < 7 777 верное
5 200 < 42 000 верное

6. Назовите самое большое шестизначное число;

999 999

самое маленькое семизначное число.

1 000 000

7. Назовите самое большое четырёхзначное число, в записи которого все цифры различны.

9 876

Назовите самое маленькое пятизначное число, записанное различными цифрами.

10 234

8. Верно ли неравенство?

* 306 > 1 036 - да верно
47 91* < 4 800 - нет неверно

26

Страница 26

9. Запишите цифрами числа, встречающиеся в предложениях.

1) Самое глубокое место в Атлантическом океане — впадина Милуоки; её глубина — девять тысяч двести девятнадцать метров.

9 219

2) Самый большой остров в Европе — Великобритания; его площадь составляет примерно двести тридцать тысяч квадратных километров.

230 000

3) Первый искусственный спутник Земли был запущен в тысяча девятьсот пятьдесят седьмом году.

1957

10. Вычислите устно.

15 · 4 = 60 1 250 – 50 = 1200 609 + 1 = 610
150 · 4 = 600 6 084 + 200 = 6 284 690 – 1 = 689

11. Выразите время: в минутах:

6 ч, 6 * 60 = 360 мин.
1 ч 12 мин, 60 + 12 = 72 мин.
120 с, 120 : 60 = 2 мин.
720 с; 720 :60 = 12 мин.

в часах:

360 мин, 360 :60 = 6 ч.
5 суток; 5 * 24 = 120 ч.

в секундах:

3 мин, 3 * 60 = 180 с.
4 мин 40 c, 4 * 60 + 40 = 280 с.
9 мин 9 c. 9 * 60 + 9 = 549 с.

12. Разделите c остатком:

968 на 5,

- 968|5
5    |193
-46
45
   -18
    15
      0 (остаток 3)

100 на 16.

-100|16
96 |6
4 (остаток)

13. При делении 100 на неизвестное число частное равно 7, а остаток — 2. Расскажите, как найти неизвестное число. Какое это число?

Вычитаем из 100 2 и делим на 7.

1) 100-2=98
2) 98:7=14
Ответ: неизвестное равно 14

14. Увеличьте на 4 сотни каждое из чисел:

12 058 + 400 = 12 458
100 000 + 400 = 100 400
9 030 + 400 = 9 430

15. Уменьшите на 5 тысяч каждое из чисел:

855 000 - 5 000 = 850 000
305 100 - 5 000 = 300 100
4 995 000 - 5 000 = 4 990 000

27

Страница 27

16. Какие числа написаны на перевёрнутых карточках?

+ 279 = 801

801 - 279 = 522. Ответ: 522

... · 42 = 168

168 : 42 = 4 Ответ: 4

17. Купили банан массой 250 г. Масса кожуры составляет две пятых этой массы. Вычислите массу съедобной части банана.

1) 250 : 5 * 2=100 (г) масса кожуры.
2) 250 - 100 = 150 (г) масса съедобной части банана.
Ответ: 150 г.

18. В бочке было 250 л воды. На полив грядок из неё взяли четыре пятых всей воды. На сколько литров уменьшилось количество воды в бочке?

1) 250 : 5 * 4=200 (л) ушло на полив.
Ответ: 200 л.

28

Страница 28

19. Как называется каждая из этих фигур? Начертите в тетради такую же таблицу. Расставьте в клетках таблицы знаки +. Название каждой фигуры должно соответствовать её номеру.

Номер фигуры	Треугольник	Круг	Четырехугольник	Пятиугольник
1	+
2		+
3				+
4	+
5			+
6			+
7		+
8			+

20. Какое свойство не является общим для чисел

3 045,
4 125,
3 095,
8 005?

1) Все числа четырёхзначные.
2) Все числа больше числа 3 000.
3) Запись каждого числа оканчивается цифрой 5.
4) В каждом числе в разряде сотен стоит цифра 0. (не является общим)

29

Страница 29

21. Каждому из четвероклассников предложили назвать месяц, в котором он родился. Прочитайте результаты опроса.
Саша: май
Валя: февраль
Маша: июль
Коля: апрель
Юра: май
Федя: июль
Оля: январь
Петя: август
Катя: май
Таня: август
Света: июнь
Даша: сентябрь
Аня: январь
Толя: июль
Серёжа: сентябрь
Ася: декабрь
Дима: февраль
Юля: сентябрь

Составьте и заполните таблицу по образцу!

Ответьте на вопросы, используя данные таблицы.

Сколько детей отмечают свой день рождения:
в апреле; - 1
в сентябре; - 3
в июле? - 3

Кто родился:

зимой; Оля, Аня, Дима, Валя, Ася.
весной; Саша, Юра, Катя, Коля.
летом; Маша, Света, Федя, Петя, Таня, Толя.
осенью? Сережа, Даша, Юля.

В каком месяце родилось:

больше всего учеников; июль
меньше всего учеников? июнь
Сколько девочек отмечают свой день рождения в сентябре? - 2
Кто из мальчиков родился в июле? - Федя и Толя.

Соберите такие же сведения о своих друзьях. Составьте похожую таблицу. Ответьте на вопросы.

30

Страница 30

Родился ли кто-нибудь из твоих друзей: зимой; весной; в марте; в октябре? Сколько человек родилось: в мае; в ноябре?

22. Выполните необходимые измерения. Сравните стороны четырёхугольника. Какие стороны равны? Можно ли назвать этот четырёх угольник прямоугольником? Вычислите периметр четырёхугольника двумя способами.

Смотрите рисунок.

Равны противоположные стороны.

Это не прямоугольник.

1 способ.

3+3+4+4=6*8=14 (см) периметр четырехугольника.
Ответ: 14 см.

2 способ

(3+4)*2= 7 * 2 = 14 (см) периметр четырехугольника.
Ответ: 14 см.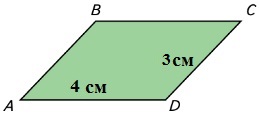

23. В словах пропущены гласные буквы. Какие это слова?

Запишите их правильно. Тргльнк, трзк, всмндцть, рвнств, квдрт.

Треугольник, отрезок, восемнадцать, равенство, квадрат

24*. В ёлочной гирлянде лампочек всех цветов поровну, и они чередуются так: жёлтая, красная, зелёная, синяя. Сколько лампочек в гирлянде, если красных лампочек 15?

15 * 4 = 60 (л) в гирлянде.
Ответ: 60 лампочек.

25. Прямоугольник с длинами сторон 10 cм и 5 см разрезали на два одинаковых квадрата. Найдите периметр каждого квадрата. Петя записал такое решение:

1) (10 + 5) · 2 = 30 (см);
2) 30 : 2 = 15 (см).
Ответ: 15 cм. Согласны ли вы с Петей? Ответ обоснуйте.

Нет не правильно, так как Петя не учел смежную сторону квадратов, по которой они соединяются.

31

Страница 31

УЗНАЁМ НОВОЕ

Сложение многозначных чисел

1. Вспомните способ письменного сложения трёхзначных чисел. Выполните сложение чисел 528 и 165 и объясните свои действия.

+528
165
713

2. Используя способ поразрядного сложения, объясните, как каждый из учеников вычислил сумму многозначных чисел.

Белка складывала числа и у нее не было переполнения разрядов.
У лисы было переполнение разряда единиц, сотен и тысяч, а значит она добавила плюсом значения в десятки, тысячи и сотни тысяч.
У ежа было переполнение разряда единиц, сотен, а значит она добавила плюсом значения в десятки и тысячи.
У зайца было переполнение разряда десятков и сотен, а значит она добавила плюсом значения в сотни и тысячи.

3. Найдите сумму чисел.

+68305
9286
77591

+12869
673
13542

+ 18000
6375
24375

+ 260387
1480
261867

+306250
18998
325248

+458207
207954
666161

32

Страница 32

4. Верно ли высказывание: «Если одно из двух слагаемых равно нулю, то сумма равна другому слагаемому»?

Да, верно!

В математике это свойство сложения в обобщённом виде записывают так. При любом значении а верны равенства

а + 0 = а,
0 + а = а.

5. Вычислите устно значение выражения:

1) 3 685 + a, если a = 0; 3685+0=3685
2) a + 5 001, если a = 0; 0 +5001=5001
3) a + 0, если a = 16 000. 16000+0=16000

6. Выполните действия.
2 3 1
70 616 + 19 796 + 217 · 3 = 91 063

*217
3
651

+70616
19796
90412

+90412
651
91063

3 4 1 5 2
56 380 + 325 478 + 130 · 6 + 714 : 7 = 382 740

*130
6
780

-714|7
7 |102
   -14
    14
      0

+325478
56380
381858

+381858
780
382638

+382638
102
382740

7. Подставьте вместо звёздочки число 70 000. Запишите полученное выражение и вычислите его значение.

3 507 + (70 000 + 9) = 3507 + 70009 = 73516
(3 507 + 70 000) + 9 = 73 507 + 9 = 73516

Зная значение первого выражения, можно ли назвать значение второго выражения, не выполняя вычислений?

Да, можно, так как для данного выражения действует сочетательное правило.

Составьте выражения, подставляя вместо звёздочки число: 16 504, 89. Найдите значения выражений.

3 507 + (16 504 + 9) = 3 507 + 16 513 = 2020
(3 507 + 16 504) + 9 = 20 011 + 9 = 2020

3 507 + (89 + 9) = 3 507 + 98 = 3 605
(3 507 + 89) + 9 = 3 596 + 9 = 3 605

8. Увеличьте на 264 308 каждое из чисел: 80 945, 12 007, 503 965.

+264308
80945
345253

+264308
12007
276315

+264308
503965
668273

9. Вулкан Везувий на Апеннинах расположен на высоте 1 277 м над уровнем моря. Вулкан Этна в Сицилии на 2 063 м выше Везувия. Чему равна высота вулкана Этна над уровнем моря?

2063+1277=3340 (м) высота вулкана Этна над уровнем моря.

+2063
1277
3340

Ответ: 3340 м.

33

Страница 33

10. В хозяйстве вырастили 15 467 штук рассады помидоров, рассады огурцов вырастили на 10 023 штуки больше, чем рассады помидоров, и рассады капусты — на 9 786 штук больше, чем рассады помидоров. Сколько рассады вырастили?

1) 15467+10023=25490 (шт.) рассады огурцов.

+15467
10023
25490

2) 15467 + 9786 = 25253 (шт.) рассады капусты.

+15467
9786
25253

3) 25490+25253=50743 (шт.) рассады капусты и огурцов.

+25490
25253
50743

4) 50743 + 15467 = 66 210 (шт.) рассады всего высадили.

+50743
15467
66210

Ответ: 66 210 штук рассады всего высадили.

11. После того как из кассы выдали 128 509 р., в кассе осталось 14 902 р. Сколько денег было в кассе?

128509+14902=143411 (р.) было в кассе.

+128509
14902
143411

Ответ: 143 411 рублей было в кассе.

12. В саду собрали 1 500 кг яблок, а груш — на 967 кг больше. Сколько килограммов груш собрали? Измените вопрос задачи так, чтобы она решалась в два действия. Решите новую задачу.

Сколько всего килограммов фруктов собрали?

1) 1500+967=2467 (кг) собрали груш.

+1500
967
2467

2) 2467 + 1500 = 3967 (кг.) фруктов собрали.

+2467
1500
3967

Ответ: 3967 кг.

13. Куликовская битва произошла в 1380 году, а Бородинское сражение — 432 года спустя. В каком году произошло Бородинское сражение?

1380+432=1812 (г.) произошло Бородинское сражение.

+1380
432
1812

Ответ: в 1812 г.

14.

1) Сложите значения длины 367 м и 687 м. Выразите результат в километрах и метрах.

367+687=1054 м = 1 км 54 м

+687
367
1054

2) Сложите 23 м 9 дм 8 см и 53 см.

23 м 9 дм 8 см = 23098 см

23098+53=23151 см = 23 м 15 дм 1 см

+23098
53
23151

3) Чему равна сумма 12 кг 581 г и 13 419 г?

12 кг 581 г 12 581 г

12 581 + 13 419 = 26000 г = 26 кг

+12581
13419
26000

15. Поле имеет форму прямоугольника. Его длина равна 850 м, а ширина 625 м. Каков периметр поля?

(850+625)*2=1475*2=2950 (м) периметр поля.

1)
+850
625
1475

16. Какое из чисел больше?

3 678 < 12 540
997 054 > 874
309 091 > 4 444
1 000 000 < 10 000 000

34

Страница 34

17. Какое из чисел меньше?

6 050 > 605
1 000 < 10 000
815 007 > 8 150
101 010 > 10 100

18. Сравните значения величин.

2 006 м = 2 км 6 м
9 м > 90 cм
3 000 cм > 3 м
15 ч 20 мин < 16 ч 40 мин
7 мин 45 c = 465 c
12 ч < 725 мин

19. В 9 ч 25 мин от автостанции отошёл автобус. Через 35 мин он сделал первую остановку, на которой простоял 2 мин. Затем автобус отправился дальше и через 18 мин сделал вторую остановку. Вычислите время прибытия автобуса на вторую остановку.

1) 9 ч 25 м + 35 м = 10 (ч) автобус сделал первую остановку.
2) 10 ч + 2 м = 10 ч 2 мин во столько автобус поехал дальше.
3) 10 ч 2 мин + 18 мин = 10 ч 20 мин во столько автобус прибыл на вторую остановку.
Ответ: 10 ч 20 мин.

20. Сравните тексты задач. Чем они похожи и чем различаются?

1) Из автобуса вышли 9 человек, и в нём осталось в n раз больше человек, чем вышло. Сколько человек осталось в автобусе?
2) Из автобуса вышли n человек, и в нём осталось в 3 раза больше человек, чем вышло. Сколько человек осталось в автобусе?

Составьте выражения для решения задач. Решите эти задачи при n, равном 3.

Для первой 9*n

9*3=27 (чел.) осталось в автобусе.

Ответ: 27 человек.

Для второй n*3

3*3=9 (чел.) осталось в автобусе.
Ответ: 9 человек.

21. Вычислите устно.

400 – 50 =350        9 · 8 =72                (270 + 90) : 6 = 60
400 : 20 = 20           90 · 8 = 720          (950 – 150) : 400 = 2
400 : 200 = 2           80 · 9 = 720          640 : 8 + 620 = 700

35

Страница 35

22. Представьте числа в виде суммы разрядных слагаемых.

1) 12 305 = 10 000 + 2 000 + 300 + 5
2) 1 300 254 = 1 000 000 + 300 000 + 200 +50 + 4

23. Числа представлены в виде суммы разрядных слагаемых. Назовите эти числа и за пишите их.

1) 2 000 000 + 800 000 + 5 000 + 7 = 2 850 000
2) 60 000 + 4 000 + 800 + 60 + 3 = 64 863

24. Назовите следующие 10 чисел последовательности: 1 375, 1 380, 1 385, … .

1 390, 1 395, 1 400, 1 405, 1 410, 1 415, 1 420, 1 425, 1 430, 1 435

25. Чему равна сумма?

218 000 + 507 = 218 507 50 000 + 86 = 50 086
999 000 + 413 = 999 413 11 000 + 10 = 11 010

26*. Сколько квадратных керамических плиток площадью 1 дм2 нужно для облицовки части стены площадью 1 м2?

10*10=100 (пл.) площадью 1 дм2 надо для облицовки 1 м2
Ответ: 100 плиток

27. Выразите в метрах, дециметрах и сантиметрах:

642 cм = 6 м 4 дм 2 см
604 cм = 6 м 4 см
39 дм 2 cм = 3 м 9 дм 2 см
510 cм = 5 м 1 дм
700 cм = 7 м
47 дм 6 cм = 4 м 7 дм 6 см

28. Длина прямоугольной площадки 18 м, а ширина 9 м. Сколько шагов надо сделать, чтобы её обойти, если длина шага 75 cм?

9м = 900 см

1) 900 : 75 = 12 (ш.) надо сделать чтобы пройти вдоль ширины.
2) 18:9=2 (раза) больше шагов надо сделать вдоль длины.
3) 12*2=24 (ш.) надо сделать вдоль длины.
4) (24+12)*2= 72 (ш.) надо сделать вдоль периметра площадки.
Ответ: 72 шага.

36

Страница 36

29. Купили 5 м синей тесьмы и 7 м такой же красной тесьмы. Сколько стоит каждый кусок тесьмы, если всего заплатили 360 р.?

1) 5+7=12 (м) тесьмы купили.
2) 360 :12 = 30 (р.) стоит метр тесьмы.
3) 30*5=150 (р.) стоит синяя тесьма.
4) 30*7=210 (р) стоит красная тесьма.
Ответ: 150 р. синяя и 210 р красная.

30. В двух кусках 8 м ленты. Один кусок стоит 150 р., а другой — 90 р. Сколько метров ленты в каждом куске?

1) 150+90=240 (р) стоит 8 метров ленты.
2) 240:8=30 (р.) стоит метр ленты.
3) 150:30=5 (м) в одном куске.
4) 90:30=3 (м) во втором куске.
Ответ: 5 м и 3 м.

31. Мастер за 1 ч изготавливает 48 деталей, а его ученик — 22 детали. За какое время, работая вместе, они изготовят 280 деталей?

1) 48+22=70 (д.) изготавливают за час мастер и ученик.
2) 280 : 70 =4 (ч.) надо чтобы мастер и ученик изготовили 280 деталей.
Ответ: 4 часа.

32*. Килограмм одних конфет стоит 250 р., а других — 125 р. Какова стоимость 200 г и 500 г этих конфет по указанным ценам?

1) 1000:200=5 (ч.) от килограмма в 200 граммах.
2) 1000:500=2 (ч) от килограмма в 500 граммах.
3) 250:5=50 (р.) стоят 200 гр. конфет по 250 р за кг.
4) 125:2=62 р 50 к стоят 500 гр конфет по 125 р за кг.
Ответ: 50 (р.) стоят 200 гр. конфет по 250 р за кг и 62 р 50 к стоят 500 гр конфет по 125 р за кг.

33. У Миши 45 р. Девятую часть этих денег он потратил на покупку ластика, а на остальные деньги купил 4 тетради. Какова цена ластика? Какова цена тетради?

1) 45:9=5 (р.) стоит ластик.
2) 45-5=40 (р.) потратила на тетради.
3) 40:4=10 (р.) стоит тетрадь.
Ответ: 5 р стоит ластик и 10 р тетрадь.

34. На покупку 6 тетрадей Маша истратила треть своих денег. Сколько тетрадей она могла бы купить на все деньги?

6*3=18 (т.) могла бы купить Маша.
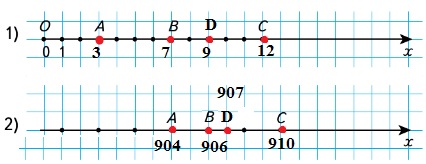
Ответ: 18 тетрадей.

35. На числовом луче отмечены точки A, B и C. Какие числа соответствуют этим точкам?

1) A = 3, B = 7, C=12.
2) A = 1242, B = 1246, C=1248.

37

Страница 37

36. Начертите часть числового луча и отметьте на нём точки, которым соответствуют числа:

1) 4, 7, 9, 12;
2) 904, 906, 907, 910.

Смотрите рисунок.

37. Постройте прямоугольный треугольник, в котором длины сторон, образующих прямой угол, равны 4 cм и 3 cм. Измерьте длину третьей стороны треугольника и вычислите его периметр.

Строим прямоугольник со сторонами 4 и 3 см.

(4+3)*2=7*2=14 (см) периметр прямоугольника.
Ответ: 14 см

Строим треугольник со сторонами 4 и 3 см. При этом если угол будет прямой, то измерив гипотенузу треугольника вы увидите, что она равна 5 см.

4+3+5=7+5=12 (см) периметр треугольника.
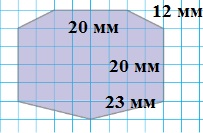
Ответ: 12 см.

38. Постройте в тетради такую фигуру. Охарактеризуйте её (название, число вершин, число сторон). Измерьте длину каждой стороны в миллиметрах.

Семиугольник, 7 вершин, 7 сторон.

Смотрите рисунок.

39. Переведите предложения с математического языка, записав их словами.

100 : (20 + 5) = 4

Частное ста и суммы двадцати и пяти равно четырем.

48 + 14 > 520 : 10

Сумма сорока восьми и четырнадцати больше частного пятьсот двадцати и десяти.

40. Не выполняя указанных вычислений, оцените результат каждого действия: он больше или меньше числа 500?

493 + 16 >500        210 · 3 >500        950 – 400 > 500
700 – 296 <500        951 : 3 < 500        105 · 4 <500
64 + 336 <500        800 : 2 <500        600 : 30<500

38

Страница 38

УЗНАЁМ НОВОЕ

41. Для 150 туристов нужно купить одноразовые стаканчики. Стаканчики продаются упаковками, в каждой 20 штук. Сколько упаковок придётся закупить?

Выберите верный ответ: 5, 6, 7, 8.

Надо будет купить 6 упаковок.

42. Катя и Петя увидели сидящую на ветке птицу. Катя утверждает, что это дрозд, а Петя — что это дятел.

Могут ли быть верными оба утверждения? Нет.
Если верно одно из них, то каким является другое? Ложным.
Могут ли оба утверждения быть неверными? Могут.
Поясните свои ответы.

43*. Не выполняя деление, докажите, что частное чисел 952 и 7, если оно существует, не может оканчиваться цифрой 8. Постройте своё рассуждение на предположении, что частное этих чисел оканчивается цифрой 8.

Если частное чисел 952 и 7 оканчивалось бы цифрой 8, то зная, что 8*7=56, надо чтобы число которое делят на 7 оканчивалось на 6. В нашем случае это не так!

44. Определите, верно ли заключение.

1) Все звери — млекопитающие. Волк — зверь. Значит, волк — млекопитающее. Да, верное!
2) Все отличники, которые учатся в 4 классе, занимаются в математическом кружке. Четвероклассник Юра тоже занимается в этом кружке. Значит, Юра — отличник. Нет, неверно!
3) Любой прямоугольник имеет только две оси симметрии. Квадрат является прямоугольником. Значит, у квадрата тоже только две оси симметрии.
Нет, неверно!

39

Страница 39

УЗНАЁМ НОВОЕ
Вычитание многозначных чисел

1. Вспомните способ письменного вычитания трёхзначных чисел. Выполните вычитание чисел 815 и 637 и объясните свои действия.

-815
637
178

2. Используя способ поразрядного вычитания, объясните, как каждый из учеников вычислил разность многозначных чисел.

Лисе пришлось занять единицу из разряда десятков.
Белке пришлось занять единицу из разряда десятков и десятков тысяч.
Ежу пришлось занять единицы из десятков, сотен, тысяч, десятков тысяч.

3. Выполните вычитание и проверьте результаты с помощью калькулятора.

7 589 – 6 680 = 909                100 000 – 99 991 = 9
89 320 – 80 567 = 8753         58 903 – 9 =58894
2 654 – 709 = 1945               407 502 – 34 = 407468

4. Вычислите значение выражения:

1) 10 204 – a, если a = 964, 1 050, 9 204, 10 000;

10204-964=9240
10204-1050=9 154
10204-9204=1000
10204-10000=204

2) b – 697, если b = 1 000, 2 030, 192 697

1000-697=303
2030-697=1333
192697-697=192000

40

Страница 40

5. Запишите какое-нибудь четырёхзначное число без использования 0 и не повторяя цифр в его записи. Переставьте в нём цифры в разрядах:

1234

1) сотен и единиц;

1432

2) единиц тысяч и десятков.

3412

Запишите получившееся в каждом случае число и сравните его с первоначальным. Какое из этих двух чисел больше и на сколько?

1234<1423 больше на 189
1432<3412 больше на 1980

1) Найдите разность чисел 8 081 и 7 808.

-8081
7808
273

2) Уменьшаемое — 10 000, вычитаемое — 6 000. Чему равна разность?

10000-6000=4000

3) Разность двух чисел равна 3 520. Одно из чисел — 854. Чему равно другое число?

3520+854=4374

4) К какому числу надо прибавить 3 742, чтобы получить 8 651?

-8651
3742
4909

5) Какое число надо вычесть из 1 907, чтобы разность была равна 374?

-1904
374
1530

7. Если к задуманному числу прибавить 504, то получится 1 408. Какое число задумано?

1408+504=1912

8. Вычислите значения выражений.

8 065 + 35 124 – 2 637 = 43189 - 2637= 40552
900 100 – 80 400 + 504 = 819700 +504 = 820204
100 000 – (248 730 – 199 006) = 100 000 - 49724 = 50 276
(5 + 77 896) – (89 107 – 82 164) = 77901 - 6943 = 70958
3 500 – 184 – (71 203 – 69 350) = 3500-184-1853=1463
9 004 – 687 + 13 + 12 501 = 8317 + 12514 = 20831

41

Страница 41

9. Найдите устно значения выражений.

(7 356 + 506) – 506 = 7356
(10 863 – 9 524) + 9 524 = 10 863

10. Составьте выражение:
1) из числа 80 000, знака минус и разности чисел 5 308 и 906;
2) из суммы чисел 2 396 и 814, знака минус и произведения чисел 36 и 9.

Найдите значения составленного выражения.

80000-(5308-906) = 80000-4402=75598
(2396+814)-(36+9) = 3210-45=3165

11. Площадь поверхности Ладожского озера равна семнадцати тысячам семистам квадратным километрам. Это на триста пятьдесят три тысячи триста квадратных километров меньше площади Каспийского моря. Вычислите площадь Каспийского моря.

17700+353300=371000 (км2) площадь Каспийского моря.
Ответ: 371000 км2.

12. С одного участка собрали 120 кг 500 г земляники, а с другого — на 17 кг 800 г меньше. Сколько всего земляники собрали? Составьте выражение и найдите его значение.

120 кг 500 г = 120 500 г
17 кг 800 г = 17 800 г

120 500 + (120 500 - 17 800) = 223 200 (г.) земляники собрали.

Ответ: 223 200 г или 223 кг 200 г.

13. В магазине было 2 000 тетрадей в клетку и 4 000 тетрадей в линейку. Сколько всего тетрадей осталось в магазине, если продали 1 350 тетрадей в клетку и 2 968 тетрадей в линейку?

1) 1350+2968=4318 (тет.) всего продали.
2) 2000+4000=6000 (тет.) всего было.
3) 6000-4318= 2682 (тет.) осталось.
Ответ: 2682 тетради.

14*. Сумма трёх чисел равна 3 217. Первое слагаемое — наименьшее трёхзначное число, второе слагаемое — наибольшее двузначное число. Найдите каждое из трёх слагаемых.

100 - наименьшее трехзначное.
99 - наибольшее трехзначное.

1) 100+99=199 второе и третье слагаемое.
2) 3217-199=3018 первое слагаемое.
Ответ: слагаемые: 3018, 100, 99.

42

Страница 42

15. Вычислите устно.

24 · 2 =48        490 – 1 489        64 + 16 = 80
40 : 40 =1        230 · 3 690            900 – 400 =5 00
360 : 60 =6       17 · 10 =170        9 · 80 = 720
180 : 90 = 2      800 : 100 = 8        60 · 5 = 300

16. Запишите цифрами числа:
двести шесть тысяч восемь; 206 008
пятьсот тысяч шестьдесят; 500 060
тридцать тысяч один; 13 001
девятьсот тысяч. 900 000

17. Запишите наибольшее семизначное число, в записи которого все цифры различные.

9876543

18. Сравните выражения, не вычисляя их значения.

324 + 68 = 68 + 324
409 + 48 > 409 – 48
1 020 – 68 > 1 020 – 72
960 : 2 > 960 : 3
15 · 8 < 15 · 12
1 000 : 25 > 800 : 25

19. Вычислите.

84 : 7 =12        64 : 4 = 18        78 : 3 = 26        300 : 60 = 5
80 : 5 = 16       96 : 8 = 12        98 : 7 = 14        120 : 40 = 3
56 : 4 = 9         54 : 3 = 18        70 : 5 = 14        770 : 11 = 70

20. Найдите число, которое:

1) в 4 раза меньше суммы чисел 22 и 14;

(22+14):4=9

2) в 5 раз меньше разности чисел 87 и 42;

(87-42):5=45:5=9

3) в 3 раза меньше частного 24 и 4.

24:4:3=2

43

Страница 43

21. Что означает цифра 3 в записях чисел 13, 234, 1 369, 38 210?

13 - единицы
234 - десятки
1 369 - сотни
38 210 - десятки тысяч

22. Во сколько раз увеличится число 842, если к нему справа приписать нуль?

в 10 раз

На сколько оно увеличится?

8420-842=7578

на 7578

23. Вычислите неизвестные числа в равенствах.

507 + 207= 714

(714-507=207)

1 000 – 904= 96

(1000-96=904)

24. Выполните умножение.

124 · 6 = 744 24 · 19 = 456 240 · 4 = 960 98 · 7 = 686
208 · 4 = 832 35 · 28 = 980 16 · 16 = 256 85 · 9 = 765

25. Спортсмен сделал 50 выстрелов по мишеням. Три пятых числа пуль попали в цель. Сколько раз спортсмен промахнулся?

1) 50:5*3=30 (раз) попал в мишень спортсмен.
2) 50-30=20 (раз) промахнулся.
Ответ: 20 раз.

26. За 6 ч рабочий изготавливает 60 деталей. За сколько часов он изготовит 40 таких же деталей, работая в том же темпе? Рассмотрите два способа решения задачи и поясните каждое действие.

Способ 1

6 ч = 360 мин

1) 360:60=6 (мин) столько надо времени на изготовление одной детали.

2) 6 · 40 = 240 (мин) столько надо времени на 40 деталей.

240 мин = 4 ч

Ответ: 4 ч.

Способ 2

1) 60 : 6 = 10 (дет.) делает за 1 час.
2) 40 : 10 = 4 (ч) времени уйдет на 40 деталей.

Ответ: 4 ч.

27. Из 2 кг муки выпекают 3 кг хлеба. Сколько килограммов хлеба выпекут:
из 8 кг муки;
из 16 кг муки; из 40 кг муки?

1) 8:2=4 (р.) больше выпекут хлеба из 8 кг муки, чем из 2
2) 16:2=8 (р.) больше выпекут хлеба из 16 кг муки, чем из 2
3) 3*4=12 (кг) хлеба выпекут из 8 кг муки.
4) 3*8=24 (кг) хлеба выпекут из 16 кг муки.
Ответ: 12 кг хлеба из 8 кг муки и 24 кг из 16.

44

Страница 44

28. За 5 кг картофеля заплатили 75 р. Сколько картофеля можно купить на 45 р.?

1) 75:5=15 (р.) стоит 1 кг картофеля.
2) 45:15=3 (кг) можно купить на 45 р.
Ответ: 3 кг.

9. В столовую в первую неделю привезли 4 одинаковых мешка крупы, а во вторую — 5 таких же мешков крупы. Всего за две недели привезли 540 кг крупы. Сколько килограммов крупы привозили каждую неделю?

1) 4+5=9 (м) привезли за 2 недели.
2) 540:9=60 (кг) в одном мешке.
3) 60*4=240 (кг) привезли в первую неделю.
4) 60*5=300 (кг) привезли во вторую неделю.
Ответ: 240 кг в первую неделю и 300 во вторую.

30. В столовую за две недели привезли 9 одинаковых мешков крупы. В первую неделю привезли 240 кг крупы, а во вторую — 300 кг крупы. Сколько мешков крупы привезли в первую неделю?

1) 240+300=540 (кг) привезли крупы за 2 недели.
2) 540:9=60 (кг) было в 1 мешке.
3) 240:60=4 (м) привезли в первую неделю.
4) 300:60=5 (м) привезли во вторую неделю.
Ответ: 4 мешка в первую и 5 во вторую.

31. Таня вышла из дома и пошла в школу. Через некоторое время из этого дома вышел Митя и пошёл в школу по той же дороге. Дети пришли в школу одновременно. Кто из них шёл быстрее?

Митя шел быстрее.

32. Из города Дмитров в Москву одновременно выехали машины «Газель» и «Волга». «Волга» ехала медленнее, чем «Газель». Какая машина раньше прибыла в Москву?

Газель приехала первой.

33. Найдите закономерность в записи чисел 340, 390, 440, … и назовите следующие три числа.

490, 540, 590

34*. На подносе стоят 12 стаканов с тремя напитками, которые чередуются так: какао, сок, молоко, какао, ... . Дети выпили весь сок, но не пили какао и молоко. Определите число пустых стаканов. Сколько осталось стаканов с какао и молоком?

Пустых стаканов 3. 9 стаканов осталось с какао и молоком.

45

Страница 45

35. Яблоки продаются по цене 75 р. за килограмм, а виноград — по цене 90 р. за килограмм. Запишите на математическом языке:

1) стоимость 3 кг яблок и 2 кг винограда равна 405 р.;

75*3+90*2=405

2) 2 кг яблок дороже 1 кг винограда на 60 р.;

75*2-90=60

3) если купить по 1 кг яблок и винограда, то нужно заплатить 165 р.

75+90=165

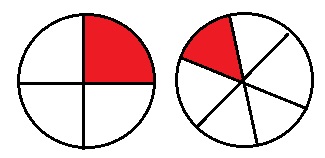
36. Начертите два одинаковых круга любого радиуса. Разделите один круг на 4 равные части, а другой — на 6 равных частей. Закрасьте по одной части каждого круга. Какая часть больше — четвёртая или шестая?

Одна четвертая больше. Смотри рисунок.

37. Сколько треугольников на каждом рисунке?

В 1 случае: 11 треугольников.
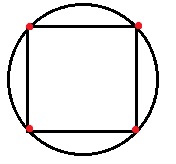
Во 2 случае: 13 треугольников.

38. Начертите квадрат. Объясните, как можно начертить окружность, проходящую через все вершины квадрата.

Надо чтобы квадрат был вписан в окружность. Смотри рисунок.

39. Не выполняя указанного действия, определите, каким будет старший разряд суммы 5 267 + 3 928. Проверьте свой ответ: выполните вычисления.

Старший разряд будет тысячи.

+5267
3928
9195

46

Страница 46

40. Постройте прямой угол с помощью угольника.

Строим прямой угол.

41. Постройте четырёхугольник, у которого:

а) два противоположных угла прямые;
б) только два соседних угла прямые.

Строим такие прямоугольники.

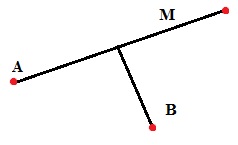
42. Проведите прямую AM. Отметьте точку B вне прямой AM. Проведите через точку B прямую, которая образует прямой угол с прямой AM.

Смотри рисунок.

43. У Даши 1 500 р. Ей нужно купить два фена разных моделей. Цены на фены в разных отделах торгового центра указаны в таблице. В каком случае стоимость покупки будет наименьшей?

В 3 случае

Сколько денег останется у Даши в этом случае?

1) 585+586=1171 (р) будет стоить покупка.
2) 1500-1171=329 (р) останется.
Ответ: 329 р.

44. Для ограждения прямоугольного участка привезли металлические щиты длиной 3 м каждый. Ширина участка 36 м, а длина — 120 м. Сколько щитов привезли для ограждения

1) (36+120)*2=156*2=312 (м) периметр участка.
2) 312:3=104 (щит.) привезли для ограждения.
Ответ: 104 щита.

47

Страница 47

УЗНАЁМ НОВОЕ

Построение прямоугольников

1. Постройте в тетради прямоугольник с длинами сторон 3 cм и 4 cм. Объясните, как вы выполняли построение. Как Волк и Заяц построили прямоугольник с такими же длинами сторон на классной доске? Какие инструменты они использовали?

Использовали угольник. Вначале провели направляющие для сторон, под прямым углом, потом отмерили стороны и завершили построение замыканием контура.

48

Страница 48

2. Постройте прямоугольник с длинами сторон 4 cм 5 мм и 3 cм так, как это делали Волк и Заяц.

Использовали угольник. Вначале провели направляющие для сторон, под прямым углом, потом отмерили стороны (4 cм 5 мм и 3 cм) и завершили построение замыканием контура.

3. Прямоугольный участок земли имеет размеры 120 м и 96 м. Постройте план этого участка на листе бумаги, если одному сантиметру на плане соответствуют 8 м на местности.

Откладываем 14 см, это будет соизмеримо со стороной в 120 м и откладываем 12 см, то будет соизмеримо со стороной в 96 м.

4. Как Волк и Заяц построили квадрат?

Заяц построил прямой угол, затем отложил размер по горизонтали. Волк же от отмеренного размера зайцем отложил размер по вертикали, такого же размера как и заяц по горизонтали.

5. Постройте квадрат с длиной стороны 5 cм так, как это делали Волк и Заяц.

Строим квадрат.

49

Страница 49

6. Предложите способ построения квадрата, используя умение делить окружность на 4 равные части.

Можно в окружности провести два диаметра, перпендикулярно друг другу. Они поделят окружность на 4 равные части, при этом расстояние между точками касания радиусов окружности будут все равны. Если из эти точки соединить, то получится квадрат.

7. Предложите план построения квадрата, периметр которого равен 14 cм. Начертите этот квадрат.

Вначале необходимо узнать какой длины будет сторона квадрата. Для этого 14 см :4 = 3 см 5 мм.

Далее строим квадрат так, как ранее. То есть проводим две направляющих перпендикулярно друг другу. По ним откладываем длину сторон квадрата. Замыкаем квадрат еще двумя такими же сторонами зеркально относительно тех, что уже есть.

8. Начертите прямоугольник, ширина которого 4 см, а периметр равен 24 cм.

Находим вторую сторону.

1) 24-(4*2)=16 (см) длина двух других сторон.
2) 16:6=8 (см) длина второй стороны.
Чертим прямоугольник со сторонами 4 и 8 см.

9. Рассмотрите таблицу и ответьте на вопросы.

Чему равна сумма чисел в каждой строке, в каждом столбце?

100+200+300=600
400+500+600=1500
1100+1200+1300=3600

Чему равна сумма чисел по диагоналям?

100+500+1300=1900
1100+500+300=1900

Какие три числа из этой таблицы надо сложить, чтобы получить 1 000?

500+200+300=1000 или 100+300+600=1000

Разность каких двух чисел из этой таблицы равна 1 000?

1300-300=1000 или 1200-200=1000 или 1100-100=1000

Найдите все варианты ответов.

10. Вычислите устно.

420 + 80 =500    480 : 20 240        1 000 : 10 =100
290 – 50 = 240    560 : 7 = 80        10 · 100 = 1000
20 · 5 = 100        20 · 30 = 600       452 · 1 = 452
14 · 2 = 28        70 · 5 = 350           0 : 958 = 0

50

Страница 50

11. Сравните числа.

220 445 > 219 445 302 007 < 320 070
190 006 > 19 006 800 050 > 800 005

12. Назовите результаты действий.

85 450 – 400 = 85 050 199 999 + 1 = 200 000
70 000 – 30 000 = 40 000 900 000 – 1 = 899 999

13. К какому числу надо прибавить 1, чтобы получить число: 200 000; 1 000 000; 450 000?

199 999 + 1 = 200 000
999 999 + 1 = 1 000 000
449 999 + 1 = 450 000

14. Если из задуманного числа вычесть 3 058, то получится число, равное вычитаемому. Какое число задумано?

3058+3058=6116

15. Найдите значения выражений.

3 685 + 200 481 + 958 = 204166+958=205124
101 030 – 98 104 – 56 = 2870
100 000 – (586 + 49 503) = 49 911
7 510 + (301 296 – 4 098) = 304708

16. Назовите все значения выражения 18 : x, если x равен 1, 2, 3, 6, 9, 18.

18:1=18
18:2=9
18:3=6
18:6=3
18:9=2
18:18=1

17. Вычислите.

6 + 12 : 3 – 1 = 9            904 + 80 = 984
56 : 7 · 3 : 4 = 6              625 : 125 = 5
48 : 6 + 36 : 9 = 12           832 : 208 = 4
(6 + 12) : (3 – 1) = 9        450 : 150 = 3
16 : (15 – 11) = 16                425 – 20 = 405

18. Выразите в секундах:
1 мин 20 c = 80 с
12 мин = 720 с
3 мин 10 = 190 с

51

Страница 51

19. Капитан пиратской шхуны отпустил команду на берег, но приказал пиратам собраться на шхуне в 9 ч. Одни пираты пришли в 9 ч вечера, а другие в 9 ч утра следующих суток. Почему пираты не поняли капитана? Как должен был звучать его приказ?

Не поняли потому, что часы тогда были стрелочные, а стрелка дважды за сутки проходит часовую отметку в 9 часов. Надо было уточнить время суток.

20. В коридоре, длина которого 5 м и ширина 2 м, пол выложили квадратными плитками. Сколько плиток потребовалось, если площадь одной плитки 1 дм2?

10 м2 = 10*100=1000 дм2

1) 5*2=10 (м2) плитки положили.
2) 1000 : 10 = 100 (шт.) плиток положили.
Ответ: 100 штук.

21. Катя сложила из палочек прямоугольник, длина которого 25 cм, а ширина — 10 cм. Сколько палочек использовала Катя, если длина одной палочки 50 мм?

1) (25+10)*2=35*2=70 (см) периметр прямоугольника.
2) 700:50=14 (пал.) надо для того, чтобы выложить прямоугольник.
Ответ: 14 палочек.

22. В 4 коробки разложили карандаши, по 12 штук в каждую. Сколько коробок потребуется, если эти же карандаши разложить по 24 штуки?

1) 24:12=2 (раза) меньше коробок надо будет.
2) 4:2=2 (кор.) надо будет
Ответ: 2 коробки.

23. На фарфоровой фабрике за смену изготовили 396 тарелок. Их разложили в коробки по 18 штук. На складе оставили 15 коробок, а остальные отправили в магазин. Сколько коробок с тарелками отправили в магазин? Сколько тарелок в этих коробках?

1) 396:18=22 (кор.) было всего.
2) 22-15=7 (кор.) отправили в магазин.
3) 7*18=126 (тар.) в 7 коробках.
Ответ: отправили 7 коробок в которых 126 тарелок.

24. На книжной ярмарке в первый день продали 8 700 книг. Это на 1 800 книг больше, чем продали во второй день. Всего за три дня продали 24 500 книг. Сколько книг продали в третий день?

1) 8700-1800=6 900 (кн.) продали во второй день.
2) 6900+8700=14 600 (кн.) продали за 1 и 2 день.
3) 24 500 - 14 600 = 9 900 (кн.) продали в 3 день.
Ответ: 9 900 книг.

52

Страница 52

25. В трёх шкафах 2 640 книг. В первом и втором шкафах 1 710 книг, а во втором и третьем — 1 820 книг. Сколько книг в каждом шкафу?

1) 2640-1710=930 (кн.) в 3 шкафу.
2) 1820-930=890 (кн.) во 2 шкафу.
3) 1710-890=820 (кн.) в первом шкафу.
Ответ: в 1 820 книг, во втором 890, в третьем 930.

26*. Для варки варенья из чёрной смородины на 2 кг ягод берут 3 кг сахара. На варенье израсходовали 12 кг сахара. Сколько килограммов ягод потребовалось?

1) 12:3=4 (р.) по 2 кг. взяли ягод.
2) 2*4=8 (кг) ягод взяли.
Ответ: 8 кг.

27. Для праздника ученики сделали одну гирлянду из красных шариков и три такие же гирлянды из синих шариков. Всего они взяли 48 шариков. Сколько синих и сколько красных шариков взяли ученики?

1) 48:4=12 (ш.) в каждой гирлянде.
2) 48-12=36 (ш.) было синих.
Ответ: 12 шариков красных и 36 синих.

28*. Перед праздником в классе развесили 48 синих и красных шариков, причём синих было в 3 раза больше, чем красных. Сколько синих и сколько красных шариков развесили?

1) 48:4=12 (ш.) в каждой гирлянде.
2) 48-12=36 (ш.) было синих.
Ответ: 12 шариков красных и 36 синих.

29. В разное время от автовокзала в аэропорт отъехали такси и автобус. Такси двигалось быстрее автобуса, но в аэропорт они прибыли одновременно. Какая машина раньше отправилась от автовокзала?

Автобус выехал раньше.

30. Расстояние от дома до кинотеатра Юра прошёл за 12 мин, а Женя — за 18 мин. Кто из мальчиков шёл быстрее?

Юра шел быстрее.

53

Страница 53

31*. Длина стороны квадрата выражается целым числом сантиметров. Дима вычислил площадь этого квадрата и получил число, запись которого оканчивается цифрой 3. Можно ли утверждать, даже не зная длину стороны квадрата, что Дима ошибся при вычислении?

Да, можно утверждать, что Дима ошибся, так как при умножении числа самого на себя с учетом, что оно целое, нет результата оканчивающегося на 3.

32. В магазин привезли 24 ящика красных яблок и 32 ящика жёлтых яблок. В каждом ящике 15 кг яблок. На сколько килограммов жёлтых яблок привезли больше, чем красных? Дима записал такое решение:

1) 32 – 24 = 8 (ящ.); - вначале Дима нашел разницу между ящиками желтых и красных яблок.
2) 15 · 8 = 120 (кг). - затем умножил на количество кг в каждом ящике.

Ответ: на 120 кг. Поясните каждое действие.

33. Полкилограмма сыра стоит 170 р. По какой цене продаётся сыр?

1) 1000:500=2 (р) по пол килограмма в 1 килограмме сыра.
2) 170*2=340 (р.) за кг продается сыр

Сколько надо заплатить за полтора килограмма сыра?

1) 1500:500=3 (р) по пол килограмма в 1,5 килограммах сыра.
2) 170*3=510 (р.) надо заплатить за 1,5 кг

За два с половиной килограмма сыра?

1) 2500:500=5 (р) по пол килограмма в 2,5 килограммах сыра.
2) 170*5=850 (р.) надо заплатить за 2,5 кг

34. Прочитайте ряд чисел: 12 567, 56 712, 65 217, 25 178, 76 521. Верны ли высказывания?

В ряду пять чисел. Да, верно
Число 65 217 — наибольшее в ряду. Нет неверно.
Все числа записаны одними и теми же цифрами. Нет неверно
Предпоследнее число в ряду — 56 712. Нет, неверно
В записи числа 65 217 старшим разрядом является разряд десятков тысяч. Да, верно

54

Страница 54

УЗНАЁМ НОВОЕ

Скорость 1.

Волк и Заяц соревновались в беге. Рассмотрите таблицу и ответьте на вопросы.

1) Какова длина дистанции? 150 метров
2) За какое время пробежал эту дистанцию Волк и за какое время — Заяц? Волк 15 секунд, заяц - 10 с.

Вычислите, сколько метров за одну секунду пробегал каждый из спортсменов. Кто из них бежал быстрее? Поясните свой ответ. Быстроту движения характеризует величина, которая называется скорость.

150:15=10 (м/с) с такой скоростью бежал волк.
150:10=15 (м/с) с такой скоростью бежал заяц.

Скорость показывает, какое расстояние преодолевается за единицу времени (секунду, минуту, час).

55

Страница 55

2. Волк и Заяц набрали из колодца воды и пошли домой.

Рассмотрите таблицу. Как узнать, кто шёл с большей скоростью — Волк или Заяц?

Объяснение написано ниже.

Сравните свой ответ с текстом.

Волк за 1 мин прошёл 10 м (120 : 12), значит, он шёл со скоростью 10 м в минуту. Заяц за 1 мин прошёл 15 м (150 : 10), значит, он шёл со скоростью 15 м в минуту. За 1 мин Волк прошёл 10 м, а Заяц — 15 м. Значит, Заяц шёл с большей скоростью, чем Волк.

Наиболее часто скорость движения измеряют в? следующих единицах: километр в час (км/ч), метр в минуту (м/мин), метр в секунду (м/с).

56

Страница 56

3. Прибор, которым измеряют скорость, называется спидометром. Его устанавливают на многих транспортных средствах (автомобилях, автобусах, самолётах и др.). Рассмотрите рисунок. С какой скоростью едет автомобиль?

Автомобиль едет со скоростью 110 км/ч.

4. Прочитайте значение скорости.

6 м/с - шесть метров в секунду
50 м/с - пятьдесят метров в секунду
12 м/мин - 12 метров в минуту
280 км/ч - двести восемьдесят километров в час
36 км/мин - тридцать шесть километров в минуту
2 cм/мин - два сантиметра в минуту
160 м/ч - сто шестьдесят километров в минуту
13 км/с - тринадцать километров в секунду.

5. Какое расстояние преодолевается за единицу времени в каждом случае?

Мышь убегает от кота со скоростью 3 м/с. три метра в секунду
Лыжник идёт по лыжне со скоростью 12 км/ч. двенадцать километров в час
Караван верблюдов движется по пустыне со скоростью 80 км/день. восемьдесят километров в день
Собака бежит со скоростью 310 м/мин. триста десять метров в минуту
Ракета летит со скоростью 13 км/с. тринадцать километров в секунду.

6. За 3 ч поезд прошёл 240 км. С какой скоростью шёл поезд?

240:3=80 (км/ч) шел поезд.
Ответ: 80 км/ч

7. Плот проплыл 20 км за 5 ч. Какова скорость движения плота?

20:5=4 (км/ч) скорость плота.
Ответ: 4 км/ч

57

Страница 57

8. За 5 c орёл пролетел 150 м. Найдите скорость полёта орла.

150:5=30 (м/с) скорость орла.
Ответ: 30 м/с

9. Лошадь пробежала 406 м за 2 мин. Вычислите скорость движения лошади.

406:2=103 (м/мин) скорость лошади.
Ответ: 103 м/мин

10. Миша идёт со скоростью 6 км/ч, а Катя бежит со скоростью 12 км/ч. Во сколько раз Катя двигается быстрее?

12:6=2 (р.) Катя бежит быстрее, чем Миша идет.
Ответ: в 2 раза.

11. Скорость товарного поезда 58 км/ч, а скорость пассажирского поезда на 12 км/ч больше. С какой скоростью идёт пассажирский поезд?

58+12=70 (км/ч) скорость пассажирского поезда.
Ответ: 70 км/ч

12. Начертите на листе бумаги прямоугольник с длинами сторон 2 cм 3 мм и 9 cм 7 мм и квадрат с длиной стороны 1 дм 2 cм 5 мм. Вырежьте эти фигуры.

Чертим и вырезаем!

13. Выполните действия и сравните значения выражений.

3 · 8 – 20 : 4 > (3 · 8 – 20) : 4

3 · 8 – 20 : 4 = 24 - 5 = 19
(3 · 8 – 20) : 4 = 4 : 4 = 1

73 – 17 + 29 > 73 – (17 + 29)

73-17+29=85
73-(17+29)=27

48 + 36 + 14 = 48 + (36 + 14)

48 + 36 + 14 = 98
48 + (36 + 14) = 98

12 : 6 · 2 > 12 : (6 · 2)

12 : 6 · 2 = 4
12 : (6 · 2) = 1

14. Вычислите.

11 111 – 3 939 + 2 121 = 9293
86 009 – 6 009 + 3 030 303 = 3110303
1 928 – 630 : 126 · 156 = 1928 - 780 = 1148
12 · 15 + 2 000 : 100 + 87 654 = 180 + 20 + 87 654 = 87854

58

Страница 58

15. Продолжите ряд чисел:

1) 2 000, 2 500, 3 000, 3 500 до числа 8 000;

3500, 4000, 4500, 5000, 5500, 6000, 6500, 7000, 7500, 8000

2) 8 160, 8 140, 8 120, 8 100 до числа 8 000.

8100, 8080, 8060, 8040, 8020, 8000

16. Какие числа закрыты карточками?

426 : 2 = 213

8 · 36 = 288

17. В корзине лежат x красных и y жёлтых яблок. Известно, что жёлтых яблок меньше, чем красных. Запишите выражение, которое показывает, на сколько красных яблок больше, чем жёлтых. Подставьте вместо x число 15, а вместо y — число 9 и вычислите значение этого выражения.

Выражение:
х - у =

15 - 9 = 6 (яб.) красных меньше, чем желтых.
Ответ: на 6 яблок.

18. С первого участка собрали 28 мешков картофеля, а со второго — 23 таких же мешка. Со второго участка собрали на 250 кг картофеля меньше, чем с первого. Сколько килограммов картофеля собрали с каждого участка?

1) 28 - 23 = 5 (меш.) на столько больше собрали с первого участка, чем с первого.
2) 250 : 5 = 50 (кг) в мешке.
3) 28 * 50 = 1400 (кг) собрали с первого участка.
4) 23 * 50 = 1150 (кг) собрали со второго участка.
Ответ: 1400 кг собрали с первого и 1150 кг собрали со второго участка.

19*. Две бригады рабочих посадили 220 яблонь. Первая бригада сажала в день 40 яблонь, вторая — 50 яблонь. Вторая бригада начала работу на один день позже первой. Сколько яблонь посадила каждая бригада?

1) 220 - 40 = 180 (яб.) посадили бригады работая вместе.
2) 40 + 50 = 90 (яб.) садили каждый день бригады.
3) 180 : 90 = 2 (д.) работали бригады вместе.
4) 2 * 50 = 100 (яб.) посадила вторая бригада.
5) 40+2*40=120 (яб.) посадили первая бригада.
Ответ: 120 яблонь посадила первая и 100 яблонь вторая.

20. В первый магазин привезли 135 кг печенья в 9 коробках, а во второй магазин привезли печенье в 7 таких же коробках. На сколько килограммов печенья меньше привезли во второй магазин, чем в первый?

1) 135 : 9 = 15 (кг) печенья в одной коробке.
2) 15 * 7 = 105 (кг) печенья привезли во второй магазин.
3) 135 - 105 = 30 (кг) на столько больше привезли в первый магазин, чем во второй.
Ответ: на 30 кг.

59

Страница 59

21. Рукопись в 60 страниц Ирина, работая одна, может напечатать за 10 ч, а Ольга — за 15 ч. За сколько часов напечатают эту рукопись Ирина и Ольга, если начнут работу одновременно?

1) 60:10=6 (стр/ч) производительность Ирины.
2) 60:15=4 (стр/ч) производительность Ольги.
3) 6+4=10 (стр/ч) общая производительность Ирины и Ольги.
4) 60:10=6 (ч.) надо будет чтобы напечатать рукопись вдвоем.
Ответ: 6 часов.

22*. Работая в поле до обеда, тракторист проехал на тракторе 70 км, а после обеда на 15 км меньше. Сколько топлива израсходовал тракторист за весь день, если на 1 км пути он расходовал 200 г топлива?

1) 70-15=55 (км) тракторист проехал после обеда.
2) 70+55=125 (км) проехал тракторист всего.
3) 125*200=25000 (г) израсходовал тракторист за день.
Ответ: 25000 г или 25 кг.

23. Отдыхающий приехал в санаторий утром 28 августа, а выехал обратно вечером 20 сентября. Сколько дней он провёл в санатории?

В августе полных 3 дня + в сентябре полных 20 дней = 23 дня.

24*. Площадь одного квадрата 1 дм2, а другого — 1 м2. Во сколько раз площадь первого квадрата меньше площади второго?

1 м2 = 100 дм2, то есть 100:1=100 (раз)
Ответ: в 100 раз.

25. Сколько прямоугольников на рисунке?

1) 6 прямоугольников.
2) 8 прямоугольников.

60

Страница 60

Дюйм — старинная единица длины. Это слово в переводе с голландского языка буквально означает «большой палец». По международным соглашениям дюйм принят равным примерно 25 мм.

Выразите в сантиметрах длину:
4 дюйма;

4*25=100 мм = 10 см

8 дюймов;

8 * 25 = 200 мм = 20 см

20 дюймов.

20 * 25 = 500 мм = 50 см

26*. Длина стороны квадрата ABCD равна 16 cм. Середины его сторон соединены отрезками так, что они образовали другой квадрат. Предложите способ вычисления площади этого квадрата.

1) Можно посчитать площадь квадрата и разделить пополам, так как каждая из четвертинок квадрата как раз делится пополам.

27*. Диагонали четырёхугольника ABCD, пересекаясь под прямым углом, делятся пополам. Длины диагоналей равны 6 cм и 8 cм. Как вычислить площадь четырёхугольника ABCD?

Можно вначале вычислить площадь мнимого прямоугольника, в который как бы будет вписан ромб ABCD, а затем поделить его площадь пополам. При этом площадь прямоугольника можно вычислить по диагоналям в ромбе, так как его стороны будут равны и паралельны.

1) 6*8=48 (см2) площадь прямоугольника.
2) 48:2=24 (см2) площадь ABCD.
Ответ: 24 см2

61

Страница 61

УЗНАЁМ НОВОЕ

Задачи на движение

1. Заяц пошёл в гости к Волку. За 2 ч он прошёл 6 км. С какой скоростью шёл Заяц?

6:2=3 (км/ч) шел заяц

Для того чтобы найти скорость, нужно знать путь и время движения. Обычно скорость обозначают буквой v, путь — буквой s, а время — буквой t.

Чтобы найти скорость, надо пройденный путь разделить на время движения.

v = s:t

Из данных выражений выберите то, которое является решением задачи: 6 + 2, 6 – 2, 6 : 2, 6 · 2. Запишите решение и выполните вычисление. Проверьте себя Решение: s = 6 км v = s : t t = 2 ч v = 6 : 2 = 3 (км/ч) v = ? Ответ: 3 км/ч.

2. На соревнованиях спортсмен проплыл 50 м за 25 c. С какой скоростью плыл спортсмен?

50 : 25 = 2 (м/с) с такой скоростью плыл спортсмен.
Ответ: 2 м/с.

62

Страница 62

3. За 15 мин машина проехала 30 км. Вычислите скорость машины.

1) 30 : 15 = 2 (км/мин) скорость машины.
2) 2*60=120 (км/ч) скорость машины.
Ответ: 2 км/мин или 120 км/ч.

4. От лыжной базы до озера 36 км. В 10 ч утра с базы вышел лыжник и направился к озеру. В 13 ч он был на месте. Определите скорость движения лыжника.

1) 13-10=3 (ч) шел лыжник.
2) 36:3=12 (км/ч) скорость лыжника.
Ответ: 12 км/ч

5. За полчаса лыжник прошёл 6 км. С какой скоростью шёл лыжник?

6*2=12 (км/ч) шел лыжник
Ответ: 12 км/ч скорость лыжника.

6. Заяц шёл к Волку 2 ч со скоростью 3 км/ч. Какой путь прошёл Заяц?

2 * 3 = 6 (км) прошел заяц.
Ответ: 6 км.

v = 3 км/ч
t = 2 ч
s = ?

Чтобы найти пройденный путь, надо скорость умножить на время движения.

s = v·t

Из данных выражений выберите то, которое является решением задачи: 3 + 2, 3 – 2, 3 · 2.

Запишите решение и выполните вычисление. Проверьте себя

Решение: s = v · t s = 3 · 2 = 6 (км)
Ответ: 6 км.

63

Страница 63

7. Поезд шёл 12 ч со скоростью 56 км/ч. Какой путь прошёл поезд?

56 * 12 = 672 (км) прошел поезд.
Ответ: 672 км.

8. Сколько метров пролетела муха со скоростью 5 м/с за полминуты?

5*30=150 (м) пролетела муха за полминуты.
Ответ: 150 метров.

9. Дачник отъехал от дома на автомобиле со скоростью 60 км/ч и через полчаса приехал на дачу. На каком расстоянии от дома находится дача?

60 : 2 = 30 (км) расстояние до дачи.
Ответ: 30 км.

10. Туристы 2 ч плыли на катере со скоростью 23 км/ч и 3 ч ехали в автобусе со скоростью 55 км/ч. Сколько километров туристы прошли на катере и проехали на автобусе?

1) 23 * 2 = 46 (км) проплыли на катере.
2) 55 * 3 = 165 (км) ехали на автобусе.
3) 46+165=211 (км) прошли и проехали.
Ответ: 211 км.

11. Заяц прошёл 6 км со скоростью 3 км/ч. Сколько часов он был в пути?

s = 6 км
v = 3 км/ч
t = ?

Чтобы найти время движения, надо пройденный путь разделить на скорость.

t = s :v

Из данных выражений выберите то, которое является решением задачи: 6 + 3, 6 – 3, 6 : 3, 6 · 3.

Запишите решение и выполните вычисление.

6 : 3 = 2 (ч) заяц был в пути.
Ответ: 2 часа.

64

Страница 64

Проверьте себя

Решение:
t = s : v t = 6 : 3 = 2 (ч)
Ответ: 2 ч.

12. Вертолёт поднялся в воздух и пролетел 900 км со скоростью 300 км/ч. Сколько времени вертолёт был в полёте?

900 : 300 = 3 (ч) летел вертолет.
Ответ: 3 часа.

13. Плот проплыл 630 м со скоростью 90 м/мин. Вычислите время движения плота.

630 : 90 = 7 (м) плыл плот.
Ответ: 7 минут

14. Поезд вышел из Москвы в Санкт-Петербург в 23 ч 50 мин. В какое время поезд прибыл к месту назначения, если он шёл со скоростью 90 км/ч? Для упрощения вычислений расстояние между этими городами считайте равным 630 км.

1) 630:90=7 (ч) шел поезд.
2) 23 ч 50 м + 7 ч = 6 ч 50 мин прибыл поезд.
Ответ: 6 ч 50 мин.

15. Пара лошадей в упряжке пробежала 60 км со скоростью 30 км/ч. Сколько часов бежали лошади?

60 : 30 = 2 (ч) бежали лошади.
Ответ: 2 часа.

16. Туристы плыли по озеру на лодке со скоростью 6 км/ч и были в пути 5 ч. Обратно они возвращались на катере, который шёл со скоростью 15 км/ч. Сколько времени туристы затратили на обратный путь?

1) 6 * 5 = 30 (км) проплыли на лодке.
2) 30 :15 = 2 (ч) затратили на обратный путь.
Ответ: 2 часа.

17. Поезд прошёл 5 ч со скоростью 62 км/ч. После этого ему осталось пройти до места назначения расстояние в 2 раза больше того, что он прошёл. Сколько километров составляет весь путь этого поезда?

1) 5 * 62 = 310 (км) прошел поезд.
2) 310 * 2 = 620 (км) осталось пройти.
3) 310 + 620 = 930 (км) весь путь поезда.
Ответ: 930 км.

65

Страница 65

18. Поезд прошёл 432 км за 9 ч. На сколько километров в час машинист должен увеличить скорость поезда, чтобы пройти то же расстояние за 6 ч?

1) 432 : 9 = 48 (км/ч) была скорость поезда.
2) 432 : 6 = 72 (км/ч) с такой скоростью должен ехать поезд, чтобы проехать путь за 6 часов.
3) 72 - 48 = 24 (км/ч) на столько надо увеличить скорость.
Ответ: на 24 км/ч

19*. Мотоциклист был в пути 6 ч. После этого ему осталось проехать ещё 144 км. С какой скоростью ехал мотоциклист, если всего он должен проехать 432 км?

1) 432-144=288 (км) проехал мотоциклист.
2) 288:6=48 (км/ч) была скорость мотоциклиста.
Ответ: 48 км/ч.

20. Велосипедист ехал 3 ч со скоростью 18 км/ч. Обратно он поехал другой дорогой, которая была длиннее первой на 9 км, но и скорость велосипедиста на обратном пути была на 3 км/ч больше. Сколько времени велосипедист затратил на обратную дорогу?

1) 18 *3 = 54 (км) проехал в одну сторону.
2) 54 + 9 = 63 (км) обратный путь.
3) 18 + 3 = 21 (км/ч) скорость на обратном пути.
4) 63 : 21 = 3 (ч) ехал обратно.
Ответ: 3 часа.

21. Вычислите устно.

20 · 5 =100            290 – 20 = 270        28 + 4 = 32        360 + 40 = 400
490 : 7 = 70            975 – 70 = 905        30 – 6 = 24        56 + 7 = 63
100 · 10 = 1000    444 – 44 = 400        7 · 80 = 560        408 : 4 =    102

66

Страница 66

22. Выполните деление.

928 : 4 = 232     468 : 9 = 52          256 : 16 = 16
305 : 5 = 61       540 : 45 = 12       552 : 24 = 23
258 : 3 = 86       512 : 64 = 8       121 : 11 = 11
920 : 20 = 46       480 : 40 = 12       574 : 82 = 7

23. Найдите частное подбором.

900 : 300 = 3 630 : 105 = 6 888 : 444 = 2
420 : 105 = 4 812 : 116 = 7 625 : 125 = 5

24. Разделите с остатком.

158 : 7 = 22 (ост. 4)

-158|7
154| 22
4

527 : 28 = 18 (ост. 6)

-527|28
28 |18
-24
18
6

904 : 68 = 13 (ост. 20)

-904 |68
68 |13
-224
204
20

605 : 8 = 75 (ост. 5)

-605|8
56 |75
-45
40
5

675 : 31 = 21 (ост. 24)

-675|31
62 |21
-55
31
24

396 : 89 = 4 (ост. 40)

-396|89
356 |4
40

25. На весах лежат 4 одинаковых по массе апельсина. Весы показывают 800 г. Если один апельсин заменить грейпфрутом, то весы покажут 1 100 г. Какова масса грейпфрута?

1) 800 : 4 = 200 (г) весит апельсин.
2) 800 - 200 = 600 (г) весят 3 апельсина.
3) 1100 - 600 = 500 (г) весит грейпфрут.
Ответ: 500 г.

26. На весы положили 3 одинаковые по массе дыни. Одну из дынь заменили арбузом, который вдвое тяжелее дыни. Весы показали 16 кг. Какова масса дыни?

1) 16:2=8 (кг) масса арбуза.
2) 8:2=4 (кг) масса дыни.
Ответ: 4 кг.

27. Нарисуйте:

1) 8 фишек и закрасьте две из них;
2) 9 фишек и закрасьте три из них. Какая часть всех фишек закрашена в каждом случае?

Смотри рисунок.

28. Запишите пять различных двузначных чисел так, чтобы ни одна цифра в записях этих чисел не повторялась.

12, 34, 56, 78, 90

67

Страница 67

29. Не выполняя указанных вычислений, определите, какой цифрой оканчивается произведение. 23 · 75 · 36 · 129

Оканчивается 0.

30*. Покупатель просит продавца взвесить ему 4 кг винограда. Сможет ли продавец это сделать, используя чашечные весы и гири массой 5 кг и 3 кг?

Да. Алгоритм такой:
1) На одной стороне виноград, на другой гиря 5 кг.
2) Меняем гирю на 3 кг и уравновешиваем весы, отложив 2 кг винограда в сторону.
3) Снова ставим гирю на 5 кг и уравновешиваем докладывая виноград на весы, рядом с имеющимся.

Когда чаши уравновесятся, снимаем тот виноград что доложили и прикладываем к нему ранее отложенный. Там и будет 4 кг.

31. Начертите на листе бумаги квадрат с длиной стороны 10 cм. Вырежьте его и разрежьте по диагоналям. Сложите из четырёх полученных частей два квадрата.

Смотрите рисунок.

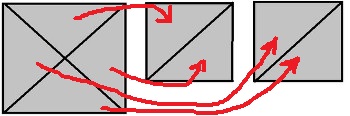
32. Начертите луч. Отметьте от его начала один за другим четыре отрезка, длина каждого из которых равна 2 cм 5 мм.

Чертим лучи и отмечаем точки. В итоге последняя точка будет на расстоянии 10 см от начала отсчета.

33*. Как достроить полукруг до целого круга? Составьте план и выполните построение.

1) Необходимо замерить диаметр и поделить его пополам, то есть получим радиус.
2) После этого откладываем с одной стороны по прямой радиус и находим центр окружности.
3) Из центра окружности проводим полуокружность с выбранным раствором радиуса на незаконченной половине.

34. Рассмотрите чертёж. Проверьте с помощью угольника, является ли угол A прямым.

Да, является. В 1 и во 2 случае.

68

Страница 68

35*. Вырежьте из бумаги квадрат площадью 81 cм2. Объясните, как вы будете действовать.

Вначале надо узнать сторону квадрата. Для этого надо подобрать такие числа, которые при умножении друг на друга дают результат 81 см2.

Это 9*9=81. В итоге строим квадрат со сторонами 9 см и вырезаем его из бумаги.

36. Начертите три разных отрезка, длина каждого из которых больше 5 cм и меньше 6 cм. Укажите длину каждого из отрезков.

Чертим отрезки:

5 см 3 мм,
5 см 5 мм,
5 см 7 мм.

37. Петя, Митя, Серёжа, Аня и Коля живут на одной улице.

Кто из них живёт в одной и той же квартире? Петя и Коля
В одном ли доме живут Аня и Митя? Да, в одном.
В одной ли квартире живут Аня и Петя? В разных, но с одинаковым номером.
Назовите номер дома и квартиры Коли. д 18, кв 12
Кто из детей живёт в доме 18? Петя и Коля
У кого из детей квартира с номером 18? Митя и Сережа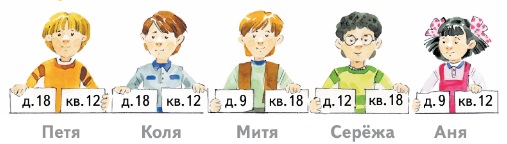

38. Выберите правило, с помощью которого составлен ряд чисел: 4, 8, 12, 20, 32, 52, 84.

1) Каждое следующее число на 4 больше предыдущего.
2) Каждое следующее число в 2 раза больше предыдущего.
3) Каждое следующее число, начиная с третьего, равно сумме двух предыдущих чисел. (это верное правило)

69

Страница 69

УЗНАЁМ НОВОЕ

Координатный угол

1. Волк и Заяц купили билеты на футбольный матч.

В каком ряду и на каком месте будет сидеть каждый из них? волк ряд 2 место 5, заяц ряд 4 место 6
Между кем из зрителей сядет Заяц и между кем — Волк? Волк между лисой и львом. Заяц между белкой и ежиком.

Назовите соседей Зайца и соседей Волка. У волка лиса и лев, у зайца белка и ежик.

Назовите, в каком ряду и на каком месте сидят Удав, Мартышка, Жираф.

Удав 1 ряд 2 место. Мартышка 1 ряд, 3 место. Жираф 3 ряд 6 место.

Для того чтобы точно описать расположение какого-нибудь предмета, его обозначают точкой и указывают координаты точки на координат-

70

Страница 70

ной сетке. Сетку строят так. Выбирают точку О (начало координат) и из неё проводят под прямым углом два числовых луча Ox и Oy. Эти лучи называются осями и образуют координатный угол. Положение любой точки определяется двумя числами: первое указывается по горизонтальной оси Ox, а второе — по вертикальной оси Oy. Например, расположение точки A можно описать парой чисел (2, 4). Числа 2 и 4 называют координатами точки А. Координаты точки записывают так: А (2, 4). Опишите парами чисел расположение остальных отмеченных точек.

M (0,6)
D (0,3)
B (4,7)
X (5,5)
K (3,0)
C (6,1)
Y (8,8)
E (9,0)

71

Страница 71

2. Назовите пары чисел, соответствующих вершинам каждой фигуры.

А (2,7)
B (2,3)
С (6,3)
D (6,7)

M (1,0)
K (4,7)
E (7,4)

3. Какое слово зашифровано на рисунке, если буквы читать в том порядке, в котором следуют пары чисел?

(3, 6); У
(5, 0); М
(1, 4); Н
(6, 5); И
(0, 2); Ц
(4, 3). А

УМНИЦА

4. Выполните действия.

420 – 5 · (36 + 9) + 632 : 8 = 116           9 345 + 100 755 = 110100
532 : 4 + 6 · (42 – 8) – 237 = 102          10 845 – 2 699 = 8146
512 384 – 95 326 = 417058                         4 028 + 172 = 4200

72

Страница 72

5. Вычислите устно.

7 600 + 400 = 8000           20 075 + 25 = 20 100
7 600 – 400 = 7200           20 075 – 25 = 20 050
7 600 + 600 = 8200           20 075 – 75 = 20 000
7 600 – 600 = 7000           20 075 – 20 000 = 75

6. На сколько наименьшее четырёхзначное число меньше наибольшего четырёхзначного числа?

9999 - 1000 = 8 999

На 8 999.

7. Составьте выражения и найдите их значения.

1) Разность чисел 948 и 36 разделить на 8.

(948-36) : 8 = 114

2) Сумму чисел 135 и 108 увеличить в 4 раза.

(135+108) * 4 = 972

8. Расстояние между двумя пристанями 864 км. Теплоход проплыл это расстояние со скоростью 27 км/ч. Сколько времени теплоход затратил на весь путь?

864:27=32 (ч) плыл теплоход.

- 864|27
81 |32
-54
54
0

Ответ: 32 часа.

9. В параде участвовали 500 спортсменов. Двадцать человек ехали впереди на велосипедах, а остальные двигались колоннами по 24 человека. Сколько было колонн спортсменов?

1) 500-20=480 (ч) было в колоннах.
2) 480:24=20 (кол) было.
Ответ: 20 колонн.

10. Уменьшите на 7 десятков тысяч каждое число:

989 705 - 70 = 989635
97 509 - 70 = 97439
100 000 - 70 = 99930
70 025 - 70 = 69955

11. Увеличьте на 8 десятков тысяч каждое число:

635 + 80 = 715
1 287 + 80 = 1367
98 451 + 80 = 98531
538 104 + 80 = 538184

12. На шоссе чистили снег три бригады. Первая бригада очистила 5 км 600 м, вторая — на 1 км 170 м больше, чем первая, а третья — на 1 км 900 м меньше, чем вторая. Какой длины шоссе очистили три бригады?

1) 5600+1170=6770 (м) очистила вторая бригада.
2) 6770-1900=4870 (м) очистила третья.
3) 5600+6770+4870 = 17240 (м) почистили три бригады.
Ответ: 17 240 м

73

Страница 73

13. В первый день в газетном киоске продали газеты на сумму 128 р. 60 к., а во второй день — на 42 р. 40 к. больше. На какую сумму продали газеты в киоске за два дня?

1) 12860+4240=17100 (к.) продали газет на такую сумму во второй день.
2) 12860+17100=29960 (к.) на такую сумму продали газет за два дня. 299 р 60 к.

Ответ: 299 р 60 к.

14. Отец может вскопать одну грядку за 15 мин, а сын ту же грядку — за 20 мин. Верно ли, что если они будут работать вместе, то им потребуется: больше 15 мин;
меньше 15 мин? верно

15. На ели сидели 8 ворон и 5 сорок. Улетели 6 птиц. Можно ли утверждать, что на ели осталась хотя бы одна:
1) ворона; Да, можно
2) сорока? Нет, нельзя

16. Начертите отрезок любой длины и попробуйте разделить его на две равные части с помощью циркуля, используя метод проб.

Пробуем подобрать раствор циркуля так, чтобы точка на отрезке с разных сторон сходилась.

17. Рассмотрите чертёж. Точки А и B лежат на окружности с центром в точке О. Отрезок AB, проходящий через точку О, называют диаметром окружности. Как называются отрезки OA и OB?

Радиусы.

Измерьте длину радиуса окружности и длину её диаметра. Во сколько раз длина диаметра больше длины радиуса?

В два раза.

74

Страница 74

18. Рассмотрите таблицу.

Какая планета самая большая; Юпитер
самая маленькая? Меркурий
Какие планеты меньше Земли; Меркурий, Венера, Марс
больше Земли? Юпитер, Сатурн, Уран, Нептун.

Назовите планеты Солнечной системы в порядке увеличения их диаметров.

Меркурий, Марс, Венера, Земля, Нептун, Уран, Сатурн, Юпитер

19. Пете 18 лет. Катя на t лет моложе Пети. Запишите выражение для вычисления возраста Кати.

18 - t

Выполните вычисление при t, равном 3.

18-3=15 (лет) Кате
Ответ: 15 лет.

20. Начертите окружность с центром в точке O. Проведите диаметр AB. Отметьте на окружности точки M и K. Постройте треугольники AMB и AKB. Убедитесь, используя угольник, что эти треугольники имеют прямые углы.

Смотри рисунок.

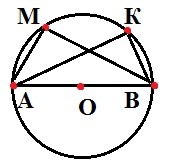
21. Какая часть круга закрашена каждым цветом?

1 вариант.

Синим - половина.
Красным - четверть.
Зеленым - одна восьмая.
Коричневым - одна восьмая.

2 вариант

Зеленым - четверть.
Желтым - три четвертых.

75

Страница 75

УЗНАЁМ НОВОЕ

Графики. Диаграммы. Таблицы

1. Каждый год в день рождения Волка Заяц измеряет его рост в сантиметрах и делает отметки. Используя полученные данные, Заяц изобразил в виде графика, как увеличивался рост Волка.

Рассмотрите график и ответьте на вопросы. Что обозначают числа по осям Ox и Oy?

Ox - возраст
Oy - рост

Какого роста был Волк, когда ему исполнилось:

1 год; - 20 см
3 года; - 50 см
5 лет? - 70 см

Вырос ли Волк за последний год?

Нет!

Сколько лет было Волку, когда его рост был равен:

40 cм; - 2 года
50 cм; - 3 года
70 cм; - 5 лет
75 cм? - 6 лет

На сколько сантиметров вырос

Волк:

1) с 1 года до 3 лет; на 30 см.
2) с 3 лет до 7 лет? на 25 см.

За какой год Волк вырос больше всего?

за 5 год.

76

Страница 76

2. Волк и Заяц соревновались в беге на 500 м. Через 70 c после старта Волк устал и сошёл с дистанции. Рассмотрите график, на котором показано, как бежали Волк и Заяц, и ответьте на вопросы.

Сколько секунд бежал Заяц и сколько — Волк? заяц 80, а волк 70 секунд
Сколько метров Волк не добежал до финиша? 500-300=200 метров
За сколько секунд пробежал 300 м Волк и за сколько — Заяц? заяц за 20 секунд, волк за 70 секунд
Какое расстояние пробежал за первые 10 c Волк и какое — Заяц? Волк 100 метров, заяц 150 метров

3. Волк и Заяц собрали данные об увлечениях четвероклассников своей школы. Результаты они записали в таблицу и передали её Медведю. Объясните, как Волк и Заяц составили таблицу

Всего 3 столбика и 6 строк с увлечениями плюс шапка.

77

Страница 77

Полученные данные Медведь представил в виде столбчатой диаграммы. Рассмотрите диаграмму и ответьте на вопросы.

Что обозначают зелёные и красные столбики на диаграмме? Зеленые полоски данные по 4 А классу, а красные по 4 Б.
В каком классе больше учеников увлекаются:
театром; в 4Б 25 учеников
спортом; в 4А 15 учеников
чтением; в 4А 25 учеников
танцами? в 4Б 20 учеников.

В каком классе нет ни одного ученика, который увлекался бы рисованием? в 4Б
Сколько учеников увлекаются музыкой в каждом классе? в 4А 5 учеников, в 4Б тоже 5.

78

Страница 78

4. На круговой диаграмме показано, какую часть всех животных, живущих в доме, занимает каждый из видов. Ответьте на вопросы.

Кого больше:
рыбок или птиц; рыбок больше, чем птиц
черепах или птиц; птиц больше, чем птиц
рыбок или собак? рыбок больше, чем собак

Какую часть всех животных занимают
кошки; одну четвертую
собаки; одну четвертую
кошки и собаки; половину
все остальные животные, кроме кошек и собак? половину

Каких животных
больше всего; рыбок
меньше всего? черепах

5. Начертите отрезок длиной 1 дм 2 cм. Выделите цветом его третью часть.

Чертим отрезок отмеряем и выделяем цветом 4 см.

6. Выполните действия.
875 : 35 · 5 = 125 28 750 + 1 250 = 30000
3 · (991 – 661) : 45 = 22 888 + 999 = 1887

7. Выполните вычисления.

37 024 + 22 465 = 59489 78 879 – 45 307 = 33572
44 307 + 55 572 = 99879 58 956 – 20 343 = 38613

8. Вычислите.

72 : 24 + 38 = 3+38=41                             100 + 25 · 4 =100+100=200
360 – 120 · (192 – 189) = 0                       108 – 31 · 2 = 46
18 · 4 + 81 : 27 = 72 + 3 = 75                    15 · 12 : 3 = 60

Сложите значения всех выражений. Сумма должна быть равна числу 422.

41+200+0+46+75+60 = 422

79

Страница 79

9. Вычислите значение выражения 2 · y – x, если:

1) x = 580, y = 450;

2*450-580=900-580=320

2) x = 91, y = 168.

2*91-168=182-168=14

10. Чему равно значение выражения b – 256 : 4, если:

1) b = 1 000;

1000-256:4=1000-64=936

2) b = 2 563?

2563-256:4=2563-64=2499

11. Длина куска ткани 75 м. Продали четыре пятых части куска. Сколько метров ткани осталось? Решите задачу двумя способами.

1 способ

1) 75:5=15 (м) в одном куске ткани.
2) 15*4=60 (м) ткани продали.
3) 75-60=15 (м) ткани осталось
Ответ: 15 метров.

2 способ

1) 75:5=15 (м) в одном куске ткани.
2) 5-4=1 (ч) ткани осталось.
3) 1*15=15 (м) осталось.
Ответ: 15 метров.

12. Зонт стоит a рублей, а плащ — в 5 раз дороже. Какова цена плаща? Запишите выражение и найдите его значение при a, равном 120.

а*5

120*5=600 (р) стоит плащ.
Ответ: 600 рублей.

13. Мальчик принёс из леса орехи. Половину всех орехов он отдал сестре, а половину оставшихся орехов — брату. После этого у него осталось 4 ореха. Сколько орехов принёс мальчик?

1) 4+4=8 (ор.) отдал сестре.
2) 8+8=16 (ор.) принес из леса.
Ответ: 16 орехов.

14. Из 69 л молока получается 3 кг масла. Сколько килограммов масла получится из 92 л молока?

1) 69:3=23 (л) молока надо на 1 кг масла.
2) 92:23=4 (кг) масла получится из 92 литров молока.
Ответ: 92 литра.

15. На складе было 330 ящиков с керамическими плитками. Когда со склада увезли часть ящиков, распределив их поровну на 12 машинах, осталось ещё 126 ящиков. Сколько ящиков с плитками погрузили на каждую машину?

1) 330-126=204 (ящ.) увезли
2) 204:12=17 (ящ.) погрузили в каждую машину.
Ответ: 17 ящиков.

16*. На тарелке лежат 4 пирожка с капустой и 7 пирожков с грибами. Взяли наугад 5 пирожков. Какое наибольшее число пирожков с капустой могло остаться на тарелке?

Могло остаться 4 пирожка с капустой.

Замените число 5 числом 6 и решите новую задачу.

Могло остаться 4 пирожка с капустой.

80

Страница 80

УЗНАЁМ НОВОЕ

Переместительные свойства сложения и умножения

1. Почему Заяц, не выполняя вычислений дважды, назвал сумму? Каким свойством сложения он пользовался?

Воспользовался переместительным свойством.

Проверьте это свойство для чисел: 2 875 и 40 287.

+40287
2875
43162

или

+2875
40287
43162

Сформулируйте переместительное свойство сложения. Сравните свою формулировку с приведённой в учебнике на странице 81.

При перестановке слагаемых сумма не меняется.

81

Страница 81

При перестановке слагаемых значение их суммы не изменяется. В математике переместительное свойство сложения записывают в обобщённом виде, используя буквы. Для любых чисел а и b верно равенство а + b = b + а.

2. Используя переместительное свойство сложения, запишите выражения, равные данным.

80 126 + 984 = 984 + 80 126 527 + х = х + 527 m + n = n+m

59 + 13 679 = 13679 +59 а + 8 000 = 8000 + а 9 · а + b = b + 9 · а

3. Обладает ли умножение переместительным свойством?

Да!

Приведите примеры. Сформулируйте это свойство. Сравните свою формулировку с приведённой в учебнике.

7*3=3*7=63
5+6=6+5=30

4. Используя буквы а и b, попробуйте записать переместительное свойство умножения в обобщённом виде.

а · b = b · а

Сравните свою запись с записью в учебнике. При перестановке множителей значение их произведения не изменяется. Для любых чисел а и b верно равенство а · b = b · а.

5. Используя переместительное свойство умножения, запишите выражения, равные данным.

5 · 120 = 120 * 5 12 · х = x * 12 y · х = y * x
60 · 7 = 7 * 60 р · 8 = 8 * p (х + 6) · a = a * (х + 6)

82

Страница 82

6. Не выполняя вычислений, объясните, почему верны равенства.

269 + 1 050 = 1 050 + 269
460 + 380 = 380 + 460
124 · 5 = 5 · 124
13 · 16 = 16 · 13

Потому что можно применить переместительное свойство сложения и умножения.

7. Используя равенство 936 + 1 504 = 2 440, вычислите значение выражения: 367 + (1 504 + 936).

367+2440=2807

8. Используя равенство 13 · 15 = 195, найдите значение выражения 4 · (15 · 13).

4*195=780

9*. Не выполняя вычислений, определите, верно ли равенство (15 + 20) · 7 = 7 · (20 + 15). Ответ поясните.

Да верно. Используется перестановочное свойство для суммы и произведения.

10. Назовите координаты вершин четырёхугольника. Как называется четырёхугольник ABCD?

1 вариант

А(2,3), B(2,7), С(6,7), D(6,3)

2 вариант

А(2,2), B(6,7), С(6,8), D(2,8)

83

Страница 83

11. Как называется каждый из многоугольников? Назовите все его вершины и стороны.

1) Четырехугольник
2) Пятиугольник
3) Треугольник.

12. Не выполняя вычисления, определите, сколько цифр в частном 375 : 5.

2 цифры

13. Какое число надо прибавить к каждому из чисел 3 000, 2 500, 8 800, 9 000, 9 997, 5 000, чтобы получилось 10 000?

3000+7000=10000
2500+7500=10000
8800+1200=10000
9000+1000=10000
9997+3=10000
5000+5000=10000

Умение решать сложные математические задачи приобретается не сразу. Здесь вам помогут упорство, труд, вера в свои силы и знания. Только тогда вы добьётесь успеха. В истории можно найти много примеров, подтверждающих это. Вот один из них. Французский школьник Симеон Дени Пуассон, который жил около 200 лет назад, математику не любил и успехами в изучении этой науки не отличался. Но однажды учитель предложил ему решить следующую задачу

84

Страница 84

Задача 1. Имеется восьмиведёрная бочка воды. Как отлить из неё ровно половину воды, пользуясь только бочками вместимостью три и пять вёдер?

1) Из 8 ведерной переливаем в 3 ведерную, а из 3 ведерной в 5 ведерную.
2) Потом снова из 8 ведерной выливаем в трехведерную и там остается 2 ведра, а во остальных бочках по 3.
3) Из трехведерной выливаем воду в 5 ведерную до полной,
4) Получается 2 ведра в 8 ведерной, полная 5 ведерная и 3 ведерная с одним ведром.
5) Выливаем 1 ведро из 3 ведерной.
6) Выливаем из 5 ведерной воду в 3 ведерную.
7) Остается 2 ведра в 8 ведерной, 2 ведра в 5 ведерной и полная трехведерная.
8) Переливаем из 5 ведерной в 8 ведерную и там будет 4 литра.

Симеон долго бился над решением этой задачи. И всё же решил! С этого времени изучение математики стало делом его жизни — он стал знаменитым учёным. Попытайтесь самостоятельно решить задачу Пуассона. У вас достаточно знаний для этого. Надо только проявить смекалку и находчивость. А если задача всё же не получается, решите похожую, но более простую, а к задаче Пуассона вернётесь позже.

Задача 2. Имеется восьмиведёрная бочка воды. Как отлить из неё ровно половину воды, пользуясь только бочками вместимостью одно ведро и пять вёдер?

1) Из 8 ведерной выливаем в 5 ведерную.
2) Из 5 ведерной выливаем в 1 ведерную, в ней остается 4 ведра. Это и есть половина!

85

Страница 85

14*. Четырёхзначное число, записанное четырьмя одинаковыми цифрами, увеличили на 10 000 и получили пятизначное число, записанное теми же цифрами. Найдите эти числа.

1 111+ 10 000=11 111

15. Какое время показывают часы? слева 1 час 25 минут, посредине 10 часов 50 минут, справа 11 часов 45 минут
Какое время они показывали полтора часа назад? 12 часов 55 минут, 9 часов 20 минут, 10 часов 15 минут
Какое время покажут часы через четверть часа? 1 час 40 минут, 11 часов 5 минут, 12 часов 00 минут

16. В каком году было построено каждое здание?

Здесь встают вопросы:

1) MCMLIX какой это год?

м - 1000 с-100 L-50 x-10 I-1

Получается, что у здания MCMLIX 1959 год постройки.

2) MCDVI какой это год?

M=1000
C=100
D=500
V=5
I=1

MCDVI= 1000+(500-100)+5+1=1000+400+6=1406 год постройки

17. Машина проехала по асфальту 5 ч со скоростью 70 км/ч и по грунтовой дороге 3 ч со скоростью 40 км/ч. Какое расстояние проехала машина?

1) 70*5=350 (км) машина проехала по асфальту.
2) 40*3=120 (км) по грунтовой дороге.
3) 350+120=470 (км) проехала машина всего.
Ответ: 470 км

18. За 2 ч велосипедист проехал 18 км. Сколько километров он проедет за 3 ч c той же скоростью?

1) 18:2=9 (км/ч) скорость велосипедиста.
2) 3*9=27 (км) проедет велосипедист за 3 часа.
Ответ: 27 километров.

86

Страница 86

19. От пристани до посёлка 120 км. Из посёлка к пристани выехал автобус со скоростью 48 км/ч. На каком расстоянии от посёлка будет находиться автобус через 2 ч? Сколько километров ему останется проехать до пристани?

1) 48*2=96 (км) проедет автобус за 2 часа.
2) 120-96=24 (км) останется проехать до пристани.
Ответ: 96 км проедет автобус за 2 часа от поселка и 24 км останется до пристани.

20. Муравей ползёт по соломинке длиной 28 cм. Он прополз четверть длины соломинки и остановился. Сколько сантиметров ему осталось проползти до другого конца соломинки?

1) 28:4=7 (см) прополз муравей.
2) 28-7=21 (см) осталось проползти.
Ответ: 21 см

21. На соревнованиях по стрельбе спортсмен сделал 20 выстрелов. Промахи составили четверть числа выстрелов. Сколько раз спортсмен попал в цель?

1) 20:4=5 (р.) промахнулся.
2) 20-5=15 (р.) попал.
Ответ: 15 раз.

22. Мастерская переплела 360 книг, переплетая ежедневно 30 книг. Сколько книг она переплетёт за тот же срок, если будет переплетать ежедневно по 40 книг?

1) 360 : 30 = 12 (дн.) переплетала по 30 книг в день.
2) 40*12=480 (кн.) переплела бы за тот же срок, но по 40 книг в день.
Ответ: 480 книг.

23. В магазин привезли 12 одинаковых ящиков слив. За день продали 69 кг слив, после чего осталось 27 кг слив. Сколько килограммов слив было в каждом ящике?

1) 69+27=96 (кг) слив было всего.
2) 96:12=8 (кг) было в каждом ящике.
Ответ: 8 кг.

87

Страница 87

24*. В коробке лежат 10 красных и 15 жёлтых бусин. Из неё наугад взяли 12 бусин.

Обязательно ли среди взятых бусин окажется хотя бы одна бусина:
1) красного цвета; Нет, не обязательно!
2) жёлтого цвета? Да, обязательно!

25. У Кати, Тани и Ани билеты в кинотеатр на места под номерами 24, 25 и 26. Кто на каком месте может сидеть? Рассмотрите все варианты.

Катя -24, Таня - 25, Аня - 26
Катя -24, Аня - 25, Таня - 26
Таня -24, Катя - 25, Аня - 26
Таня -24, Аня - 25, Катя - 26
Аня -24, Таня - 25, Катя - 26
Аня -24, Катя - 25, Таня - 26

26. Какие числа написаны на перевёрнутых карточках?

923 + 3 086 = 4 009
12201 + 891 = 13 092
18315 – 6 203 = 12 112
83000 – 947 = 82 053

27. Во сколько раз a больше b, если a = 60, b = 30?

60:30=2 раза

Во сколько раз x меньше y, если y = 280, x = 10?

280 : 10 = 28 раз

28. Какая последовательность цифр является записью числа пятьсот четыре тысячи сто шестнадцать?

504 160
540 116
540 160
504 116 - вот эта!

29. В записи какого числа нет трёх одинаковых цифр?

660 536
30 805 - в этом
586 565
702 717

30. В записях каких чисел есть все три цифры: 4, 1 и 9?

84 091 - здесь
38 900
69 432
14 005
91 754 - здесь

Есть ли среди чисел: пятизначное число; да все они пятизначные

семизначное число? - нет нету.

88

Страница 88

УЗНАЁМ НОВОЕ

(400 + 80) + 20

400 + (80 + 20)

Сочетательные свойства сложения и умножения

1. Одинаковые ли результаты получат Волк и Заяц, когда выполнят вычисления?

Да

Можно ли ответить на этот вопрос без вычислений?

Да

Обоснуйте свой ответ.

2. Вспомните и сформулируйте сочетательное свойство сложения. Как можно к сумме двух чисел прибавить третье число? Сравните свою формулировку с приведённой в учебнике. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.

89

Страница 89

В математике сочетательное свойство сложения записывают в обобщённом виде, используя буквы латинского алфавита. Для любых чисел а, b и с верно равенство (а + b) + с = а + (b + с).

3. Используя сочетательное свойство сложения, запишите выражение, равное данному.

(265 + 405) + 2 603 = 265 + (405 + 2 603)
(12 + х) + 96 = 12 + (х + 96)
472 + (38 + 691) = (472 + 38) + 691
(54 + 158) + а = 54 + (158 + а)

4. Не переставляя слагаемые, вычислите значение выражения 189 + 11 + 9 двумя способами.

189 + 11 + 9 = 200 +9 = 209
189 + 11 + 9 = 189 +20 = 209

5. Группируя слагаемые удобным способом, вычислите сумму.

3 608 + 402 + 9 054 + 46 = 4 010 + 10 100 = 14 110
2 000 + 315 + 685 = 2000 + 1000 = 3000

6. Обладает ли умножение сочетательным свойством? Сформулируйте это свойство. Сравните свою формулировку с приведённой в учебнике.

См. объяснение ниже.

7. Используя буквы а, b и с, запишите сочетательное свойство умножения в обобщённом виде. Сравните свою запись с записью в учебнике. Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел. Для любых чисел а, b и с верно равенство (а · b) · с = а · (b · с).

90

Страница 90

8. Используя сочетательное свойство умножения, запишите выражения, равные данным.

(12 · 4) · 5 = 12 · (4 · 5) (8 · х) · 3 = 8 · (х · 3)
25 · (8 · 3) = (25 · 8) · 3 (100 · 7) · m = 100 · (7 · m)

9. Не переставляя множители, вычислите значение выражения 8 · 7 · 10 двумя способами.

8 · 7 · 10 = 56 * 10 = 560
8 · 7 · 10 = 8 *70 = 560

10. Группируя множители удобным способом, вычислите произведение.

9 · 15 · 2 = 9 * 30 = 270
50 · 4 · 3 = 200 * 3 = 600

11. Сравните значения выражений, не выполняя указанных вычислений. Поясните свои ответы.

(248 + 622) + 1 927 = 248 + (622 + 1 927)
(700 + 300) + 50 > 700 + (290 + 50)
(10 · 8) · 7 > 10 · (8 · 5)
(20 · 3) · 9 = 20 · (3 · 9)

12. Используя равенство 518 + 409 = 927, вычислите значение выражения (320 + 518) + 409.

320 + 927 = 1247

13. Выполните действия, используя сочетательное свойство сложения.

(77 + 19) + 51 = 77 + 70 = 147
18 + (32 + 7) = 50 + 7 = 57
(623 + 1 200) + 800 = 623 + 2000 = 2623
327 + (33 + 589) = 360 + 589 = 949

14. Выполните действия, используя сочетательное свойство умножения.

(4 · 5) · 2 = 4 * 10 =40
(14 · 12) · 5 = 14 * 60 = 840
(10 · 10) · 7 = 10 * 70 = 700
(8 · 4) · 25 = 8 * 1000 = 800

91

Страница 91

15. Используя равенство 9 · 5 = 45, найдите значение выражения (11 · 9) · 5.

11*45=495

16. За месяц в магазине продали 5 ящиков чая. В каждом ящике было 8 коробок, а в каждой коробке 16 пачек чая. Сколько пачек чая продали в магазине? Решите задачу двумя способами.

1 способ

1) 5 * 8 = 40 (кор.) было с чаем
2) 40 * 16 = 640 (пач.) было чая.
Ответ: 640 пачек

2 способ

1) 8 * 16 = 128 (пач.) в одной коробке.
2) 128 * 5 = 640 (пач.) было всего.
Ответ: 640 пачек.

17. Выполните вычисления и сделайте проверку двумя способами: перестановкой чисел и вычитанием:

1) 13 206 + 98 = 13304

Проверка:
98+13206=13304 или 13304 -13206=98

2) 7 561 + 101 017 = 108578

Проверка:
101017+7561=108578
108578-101017=7561

18. Какие числа должны быть записаны в пустых клетках таблицы?

а-1	а	а+1
799 999	800 000	800 001
4 999	5 000	5 001
20 000	20 001	20 002

92

Страница 92

19. Выполните вычисления и сделайте проверку двумя способами: перестановкой чисел и делением:

1) 15 · 18= 270

Проверка: 18 * 15 = 270 или 270 : 15 = 18

2) 4 · 204 = 816

Проверка: 204 * 4 = 816 или 816 : 4 = 204

20. Петя и Вася стоят на левом берегу реки. Петя прыгнул в воду и переплыл реку 3 раза, а Вася, прыгнув вслед за ним, переплыл реку 6 раз. На каком берегу окажется каждый из мальчиков?

Петя окажется на противоположном тому, на котором он стоял. Вася будет на том же берегу, на котором стоял.

21. Дима нашёл в лесу 120 опят. Это в 3 раза меньше числа опят, найденных Колей. Вместе мальчики нашли 160 опят. Сколько опят нашёл Коля? Имеет ли задача решение?

Нет, не имеет, так как 3 * 120 = 360 это больше того, сколько нашли мальчики вместе

Что нужно изменить в тексте задачи, чтобы она имела решение?

Надо убрать условие о том, сколько мальчики нашли опят вместе, так как это можно вычислить!

120 * 3 = 360 (оп.) нашел Коля
Ответ: 360 опят.

22. Легковая машина едет со скоростью 2 км/мин, а грузовая — со скоростью 1 км/мин. Какое расстояние проедет каждая из машин за 35 мин?

1) 2*35=70 (км) проедет легковая машина.
2) 1 * 35 = 35 (км) проедет грузовая машина.
Ответ: 70 км легковая и 35 км грузовая.

23. Туристы проехали несколько километров в автобусе, а дальше шли пешком 5 ч со скоростью 4 км/ч. Сколько километров туристы проехали в автобусе, если весь путь составил 189 км?

1) 4*5=20 (км) туристы прошли пешком.
2) 189-20=169 (км) туристы проехали на автобусе.
Ответ: 169 км.

93

Страница 93

УЗНАЁМ НОВОЕ

План и масштаб

1. На пря мо уголь ной грядке Маша решила по сеять морковь и редис . На каждый квадратный метр грядки расходуется один пакетик семян. Сколько пакетиков семян каждой овощной культуры нужно Маше?

1) 1*2=2 (м2) под посадку моркови, то есть 2 пакетика.
2) 1*3=3 (м2) под посадку редиса, то есть 3 пакетика редиса.
Ответ: надо 2 пакета моркови и 3 пакета редиса.

Рассмотри те рисунок и вы пол ни те необходимые расчёты. На листе бумаги Маша на чертила план своей грядки. Во сколько раз все размеры на плане меньше соответствующих размеров грядки?

В 100 раз.

Отрезок на местности, равный ширине грядки, Маша изобразила на плане отрезком длиной 1 см, то есть уменьшила его в 100 раз (1 м = 100 cм). Так же в 100 раз она уменьшила и остальные размеры грядки.

94

Страница 94

На практике часто приходится изображать план квартиры, земельного участка, улицы. В этих случаях на плане действительные размеры уменьшают в одно и то же число раз. Маша выполнила план грядки в масштабе один к ста. Записывают это так:

Масштаб 1 : 100.

Эта запись означает, что 1 см на плане соответствует 100 cм на местности. Первое число масштаба всегда относится к длине на плане. Начертите в тетради план грядки, как у Маши. Поставьте на нём размеры в метрах и укажите масштаб плана.

2. Объясните, что означает масштаб.
1 : 10 - размеры в 10 раз меньше, чем размеры в реальности
1 : 1 000 - размеры в 1000 раз меньше, чем размеры в реальности
1 : 5 - размеры в 5 раз меньше, чем размеры в реальности
1 : 2 000 000 - размеры в 2 000 000 раз меньше, чем размеры в реальности

3. Запишите масштаб плана, если 1 cм на плане соответствует в действительности:

10 000 cм; 1 : 10 000
50 см; 1 : 50
10 м; 1 : 1000
1 км. 1 : 100 000

4. Измерьте длину ключа, изображённого на рисунке. Какую длину имеет ключ, если рисунок выполнен в масштабе 1 : 2?

Ключ 5 см, то есть его реальная длина должна быть 5*2=10 см

Начертите отрезок, длина которого соответствует действительной длине ключа.

Чертим отрезок 10 см.

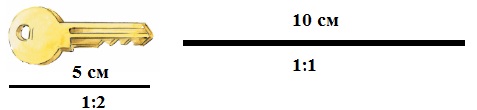
95

Страница 95

5. Чертёж треугольной клумбы сделан в масштабе 1 : 100. Дли на каждой её стороны на плане равна 4 cм. Чему равна длина каждой стороны клумбы в действительности?

4*100=400 см = 4 м

6. Определите масштаб плана детской площадки, выполнив необходимые измерения и вычисления.

Сторона площадки на плане 5 см, то есть масштаб 1:4

Так как 20 : 5 = 4

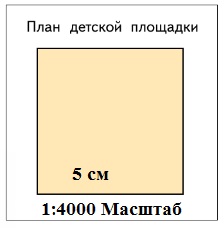
7. Из мерьте длину гусеницы на рисунке. Чему равна длина этой гусеницы в природе, если её размеры на рисунке увеличены в 2 раза?

8 см длина гусеницы, значит с масштабом 2:1 она на самом деле 8 : 2 = 4 см

Говорят, что рисунок гусеницы сделан в масштабе 2 : 1. Объясни те, что означает этот масштаб

Масштаб говорит о том, что гусеница увеличена в два раза по сравнению со своим реальным размером.

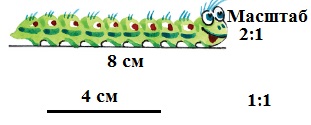
96

Страница 96

Масштаб 2 : 1 означает, что 2 см на рисунке (плане) соответствует 1 см в действительности, то есть все размеры на рисунке (плане) в 2 раза больше, чем в действительности.

8. Что означает масштаб?
10 : 1 Масштаб 10 : 1 означает, что все размеры на рисунке (плане) в 10 раз больше, чем в действительности.
3 : 1 Масштаб 3 : 1 означает, что все размеры на рисунке (плане) в 3 раза больше, чем в действительности.
5 : 1 Масштаб 5 : 1 означает, что все размеры на рисунке (плане) в 5 раз больше, чем в действительности.
4 : 1 Масштаб 4 : 1 означает, что все размеры на рисунке (плане) в 4 раза больше, чем в действительности.

9. Запишите масштаб плана, если 1 см на плане соответствует в действительности:

5 мм; 2 : 1
10 мм. 1 : 1

10. Измерьте длину радиуса колёсика часов, изображённого на рисунке в масштабе 10 : 1. Вычислите на стоящую длину радиуса этого колёсика.

4 см на плане, то есть 4 мм на само деле.

11. Определите масштаб рисунка, если на нём каждому отрезку длиной 3 cм соответствует в действительности отрезок длиной 3 мм.

10 : 1

12. Начертите план в масштабе 1 : 100:

а) своей класс ной комнаты;

б) одной из комнат своей квартиры.

Измеряем размер и делим его на 100, тогда у нас получится план в масштабе 1 : 100.

97

Страница 97

13. Даны скорости: 6 км/ч, 24 км/ч, 850 км/ч, 70 км/ч, 13 км/ч. Какая из них может быть скоростью:

1) пешехода; 6 км/ч
2) велосипедиста; 13 км/ч
3) поезда; 70 км/ч
4) самолёта? 850 км/ч

14. Какими деньгами Петя может расплатиться без сдачи за покупку трёх вещей?

25 + 15 + 85 = 125 (р.) - покупка.

Можно дать 100 +10 + 10 + 5 = 125

15. В треугольнике ABC стороны AB и AC равны и имеют длину по 28 мм. Чему равна длина стороны BC, если периметр треугольника равен 72 мм?

1) 28 * 2 = 56 (мм) длина сторон AB и AC.
2) 72 - 56 = 16 (мм) длина BC.
Ответ: 16 мм.

16. Какая фигура нарушает признак, по которому отобраны остальные фигуры?

В 4 фигуре 2 диагонали, а во всех предыдущих 1 диагональ и одно сечение делящее фигуру пополам.

98

Страница 98

17. Вычислите неизвестное число.

50 505 – 45 556 = 4 949
768 : 6 = 128

18*. Трое мальчиков родились в одном и том же году. Дни своего рождения они отмечают 6 мая, 3 сентября и 1 июня. Петя родился 1 июня. Он старше Толи, но моложе Алёши. Назовите дни рождения Толи и Алёши.

Петя родился 1 июня.
Толя родился 3 сентября.
Алеша родился 6 мая.

19. Вычислите значения выражений.

(43 · 14 – 602 : 301) : 50 = (602 - 2) : 50= 600 : 50 = 12
2 700 – 700 : 50 = 2700 - 14 = 2 686
(55 + 45) · 7 : 35 + 35 = 700 : 35 + 35 = 55
500 + 500 : 25 = 500 + 20 = 520

20. Запишите каждое из предложений в виде равенства или неравенства. Определите, верное оно или неверное.

1) Сумма чисел 2 768 и 604 больше числа 3 000.

2768+604>3000 верное

2) Разность чисел 30 087 и 29 672 равна числу 315.

30087-29672 = 315 неверное так как 30087-29672 = 415

3) Если 965 разделить на 5, то получится 193.

965 : 5 = 193 верное

4) Если 203 умножить на 4, то получится 802.

203 * 4 = 802 неверное так как 203*4 = 812

5) Число 1 260 меньше произведения чисел 18 и 55.

1260 < 18 *55 неверное, так как 18 * 55 = 990

21. На занятиях кружка юных экологов одна пятая часа была посвящена рассказу об уходе за черепахами, ещё три пятых часа занял показ фильма о природе, а затем полчаса ребята рассказывали о своей работе. Сколько времени продолжалось занятие кружка?

1) 60:5=12 (мин.) - посвящена рассказу об уходе за черепахами.
2) 60 * 3 : 5 = 180 : 5 = 36 (мин) фильм о природе.
3) 12 + 36 + 30 = 78 (мин) продолжалось занятие кружка

99

Страница 99

22. Рассмотрите график зависимости массы Юры от его возраста. Какой была масса Юры:

в 2 года; 10 кг
5 лет; 15 кг
7 лет; 20 кг
9 лет? 35 кг

На сколько килограммов его масса увеличилась:

за 3 года (от 2 до 5 лет); на 5 кг (15 - 10 = 5)
за 2 года (от 7 до 9 лет)? на 15 кг (35-20=15)

Во сколько лет его масса стала равной:

25 кг; в 8 лет
45 кг? в 14 лет

За сколько лет масса Юры увеличилась от 25 кг до 40 кг? за 2 года с 8 до 10 лет.

23. Проведите окружность радиусом 2 см 5 мм и разделите её на 6 равных частей. Постройте круговую диаграмму, используя информацию:

шестая часть учащихся четвёртых классов поехала в цирк (закрасьте эту часть круга жёлтым цветом),
две шестых — в кино (закрасьте зелёным цветом) и три шестых — в кукольный театр (закрасьте синим цветом).

Смотри рисунок.

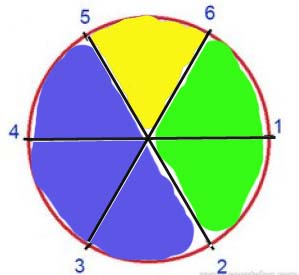
100

Страница 100

УЗНАЁМ НОВОЕ

Многогранник

1. Рассмотрите фигуры.

Из каких многоугольников состоит поверхность каждой из них?

Слева из прямоугольников, по центру из треугольников, справа из прямоугольников.

Фигура, поверхность которой состоит из многоугольников, называется многогранником. Каждый из многоугольников называют гранью многогранника. Стороны многоугольников называют рёбрами многогранника, а вершины многоугольников? — вершинами многогранника. Сколько у каждого изображённого многогранника:

1) вершин; слева 6 вершин, по центру 4 вершины, справа 6 вершин
2) рёбер; слева 12 ребер, по центру 6 ребер, справа 12 ребер
3) граней? слева 6 граней, по центру 4 грани, справа 6 граней

Какие из уже известных вам фигур можно назвать многогранниками?

Пирамида, параллелепипед.

2. Из данных предметов выберите и назовите те, которые по форме похожи на многогранник.

Коробка с карандашами, коробка с печеньем.

101

Страница 101

3. Назовите каждую вершину, ребро и грань многогранника. Какие рёбра и грани невидимы?

Вершины: A, B, C, D, E, M, K, P
Грани: ABCD, EMKP, ABEM, DCKP
Ребра: AD, BC, AB, DC, EM, KP, EK, MP

4. Рассмотрите модель куба.

Сколько у него рёбер, граней, вершин? ребер -12, граней - 6, вершин - 8
Какую форму имеет каждая грань куба? квадрат
Сколько рёбер выходит из каждой вершины? 3 ребра

Объясните, почему куб является многогранником.

Так как его поверхность состоит из многоугольников.

5*. Как попасть из вершины A в вершину K куба, двигаясь по его рёбрам? Укажите несколько вариантов.

1 вариант: A-D-P-K
2 вариант: A-E-P-K
3 вариант: A-D-C-K

6. Найдите среди окружающих вас предметов те, которые имеют форму разных многогранников.

Коробки, аквариум, кубики - пирамиды.

102

Страница 102

7. Используя палочки и пластилин, сделайте модели многогранников.

Делаем пирамиды как на рисунке в учебнике.

8. Вычислите устно.

2 500 + 60 + 8 = 2 568           12 · 4 = 48               100 : 25 = 4
7 + 100 + 1 000 = 1 107        100 · 5 = 500            18 : 3 = 6
9 600 + 400 = 10 000            6 · 40 = 240            180 : 3 = 60
3 000 + 9 000 = 12 000        11 · 9 = 99                180 : 30 = 6
1 000 : 100 =10                    84 : 42 = 2                1800 : 30 = 60

9. Не вычисляя, сравните значения выражений.

230 + 280 < 250 + 280
640 – 130 > 600 – 130
405 – 25 > 405 – 65
125 + 274 = 274 + 125

10. Вычислите.

1 3 2
(327 392 – 326 528) + 160 · 5 = 864+900=1764

1)
-327 392
326 528
864

2) 160*5=900

3)
+900
864
1764

1 3 2
(204 293 – 203 321) + 58 : 2 = 1001

1)
-204293
203321
972

2)
-58| 2
4 |29
-18
18
0

+972
29
1001

1 3 2
324 : 2 + 243 : 27 = 171

1) 324 : 2 = 162

-243|27
243| 9
0

3) 162+9=171

1 2 3
(25 + 125) : 5 · 8 = 240

1) 25+125=150

2) 150 : 5 = 30

3) 30 * 8 = 240

11*. Отцу и сыну вместе 60 лет. Сын моложе отца в 4 раза. Каков возраст отца и возраст сына?

1) 4+1=5 (частей) в 60 годах из них 4 части относятся к возрасту отца, а одна к возрасту сына..
2) 60:5=12 (лет) сыну.
3) 60 - 12= 48 (лет) отцу
Ответ: 48 лет отцу и 12 лет сыну.

103

Страница 103

12*. Миша утверждает, что если сумма двух чисел делится на 5, то и каждое слагаемое делится на 5. Докажите, что Миша неправ. Приведите примеры.

Пример
14 + 1 = 15
15 :5 = 3

Однако 1 : 5 и 14 : 1 не делится так, чтобы получались натуральные числа.

13.
1) Уменьшите:

15 кг 700 г на 8 кг 250 г;

15700-8250=7 450 г или 7 кг 450 г

24 cм 5 мм на 19 cм 9 мм.

245 - 199 = 46 мм

2) Найдите разность 120 р. 40 к. и 56 р. 56 к.

12040 - 5656= 6384 к = 63 р 84 к

3) Найдите сумму 124 м 36 cм и 45 м 8 cм.

12436 + 458 = 12894 см = 128 м 94 см

14. Выразите время: в минутах:

2 ч 16 мин, = 2*60+16=136 мин.
8 ч 1 мин, = 8*60+1=481 мин.
10 ч; 10*60=600 мин

в секундах:
9 мин, = 9 * 60 = 540 с
6 мин, = 6 * 60 = 360 с
3 мин 58 c, = 3 * 60 + 58 = 238 с
4 мин 1 c; = 4 * 60 + 1 = 241 с

в сутках:
72 ч, = 72 : 24 = 3 сут.
144 ч, = 144 : 24 = 6 сут.
192 ч, = 192 : 24 = 8 сут.
120 ч. = 120 :24 = 5 суток

15. Неизвестное число увеличили на 3 562 и получили 14 017. Найдите неизвестное число.

14017 - 3562 = 10455
Ответ: 10 455

16. Если из 170 200 вычесть задуманное число, то получится 2 345. Какое число задумано?

170200 - 2345 = 167855
Ответ: 167 855

17. К какому числу надо прибавить разность чисел 1 903 и 618, чтобы получить 8 040?

8040 - (1903-618) = 6755
Ответ: 6755

18. В таблице представлены значения выражений при заданных значениях входящих в них букв.

смотри продолжение на следующей странице.

104

Страница 104

При каких значениях а и b значение выражения а · b:

равно 400; а = 100, b = 4
равно 1 000; а = 200, b = 5
меньше 400? а = 0, b = 36 и а = 50, b = 1

При каких значениях а и b значение выражения а : b:

равно 40; а = 200, b = 5
меньше 50; а = 100, b = 4 и а = 0, b = 36 и а = 50, b = 1
больше 25? а = 200, b = 5 и а = 50, b = 1

Назовите значения а и b, при которых значения выражений а · b и а : b равны. а = 0, b = 36 и а = 50, b = 1

19*. На аллее лип в 3 раза больше, чем тополей. Всего лип и тополей 24.

Сколько лип и сколько тополей на аллее?

Решите задачу способом подбора, предполагая, что тополей может быть 1, 2, 3, … .

Составьте таблицу.

Тополей	Лип	Всего
1	3	4
2	6	8
3	9	12
4	12	16
5	15	20
6	18	24

или как в карточке рекомендуемой в учебнике

Тополя	1	2	3	4	5	6
Липы	3	6	9	12	15	18
Всего	4	8	12	16	17	24

Ответ: 6 тополей и 18 лип.

20*. Килограмм шоколадных конфет стоит 280 р. Сколько рублей надо заплатить за 250 г этих конфет?

1) 1000 : 250 = 4 (р.) меньше в 250 г чем в 1000 г.
2) 280 : 4 = 70 (р.) стоит 250 г конфет.
Ответ: 70 рублей.

21*. Составьте таблицу для выражений
х + y и х – y, если х = 2 036, 12 800, 3 000, 850, а y = 936, 2 800, 50, 850.

х+y	х-y	x	y
2972	1100	2036	936
15600	10000	12800	2800
3050	2950	3000	50
1700	0	850	850

Выполните вычисления и заполните таблицу. При каких значениях х и y выражение х – y равно нулю? x= 850 и y =850
При каких значениях х и y выражение х + y принимает наибольшее значение? x= 12800 и y =2800
При каких значениях х и y выражение х – y принимает наименьшее значение? x= 850 и y =850

105

Страница 105

УЗНАЁМ НОВОЕ

Распределительные свойства умножения

1. Как ученики выполнили умножение суммы на число? Вспомните и сформулируйте правило умножения суммы на число. Сравните свою формулировку с приведённой в учебнике. Чтобы сумму двух чисел умножить на какое-нибудь число, можно каждое из них умножить на это число и результаты сложить.

Это свойство называют распределительным свойством умножения относительно сложения. В математике это свойство в обобщённом виде записывают так. Для любых чисел а, b и с верно равенство (а + b) · с = а · с + b · с.

106

Страница 106

2. Используя распределительное свойство умножения относительно сложения, запишите выражения, равные данным.

(112 + 44) · 3 = 112 * 3 + 44 * 3 = 336 + 132 = 468
(7 + 4) · 132 = 7 * 132 + 4 * 132 = 924 + 528 = 1452
(16 + 18) · 25 = 16 *25 + 18 * 25 = 400 + 450 = 850
(36 + 24) · 9 = 36 * 9 + 24 * 9 = 324 + 216 = 540

3. Найдите значение выражения двумя способами:

1) (50 + 19) · 2;

1 способ

(50 + 19) · 2 = 69 * 2 = 138 - менее удобно

2 способ

(50 + 19) · 2 = 50 * 2 + 19 * 2 = 100 + 38 = 138

2) (72 + 28) · 7.

1 способ

(72 + 28) · 7 = 100 * 7 = 700

2 способ

(72 + 28) · 7 = 72 * 7 + 28 * 7 = 504 + 196 = 700 - менее удобно

В каком примере при вычислении пользоваться распределительным свойством неудобно?

4. Проанализируйте записи.
Как выполнял вычисления Слон? не использовал распределительное свойство
Как Мышка умножала разность чисел 90 и 25 на число 4? использовала распределительное свойство

Сравните результаты вычислений Слона и Мышки. Чей способ вычисления лучше? Мышки
Почему? Легче считать.

107

Страница 107

Попробуйте сформулировать свойство умножения разности на число. Сравните свою формулировку с данной в учебнике.

Чтобы разность умножить на какое-нибудь число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.

Это свойство называют распределительным свойством умножения относительно вычитания.

5. Выполните вычисления.
(42 – 15) · 2 = 42*2-15*2=84-30=54
(31 – 8) · 5 = 31*5-8*5=155-40=115

6. Используя распределительное свойство умножения относительно вычитания, запишите выражения, равные данным.

(135 – 84) · 3 = 135 * 3 - 84 * 3          = 405 - 252 = 153
(60 – 15) · 12 = 60 * 12 - 15 * 12        = 720 - 180 = 540
(90 – 43) · 10 = 90 * 10 - 43 * 10        = 900 - 430 = 470
(164 – 97) · 9 = 164 * 9 - 97 * 9           = 1476 - 873 = 603

7. Применяя распределительное свойство умножения относительно вычитания, найдите значения выражений.

(30 – 5) · 6 = 30 * 6 - 5 * 6 = 180 -30 =150
(200 – 106) · 5 = 200 * 5 - 106 * 5 =1000 - 530 = 470
(65 – 56) · 10 = 65 *10 - 56 *10 = 650 - 560 =90
(300 – 299) · 0 = 300 * 0 - 299 * 0 = 0

Сделайте вывод. Попробуйте сформулировать и записать распределительное свойство умножения относительно вычитания в обобщённом виде с помощью букв а, b и с. Сравните свою формулировку с записью в учебнике. Для любых чисел а, b и с, кроме тех случаев, когда а < b, верно равенство (а – b) · с = а · с – b · с.

108

Страница 108

8. Выполните действия, используя распределительное свойство умножения относительно вычитания.

(400 – 20) · 2 = 400 * 2 - 20 * 2 = 800 - 40 = 760
(25 – 9) · 4 = 25 * 4 - 9 * 4 = 100 - 36 = 64
(80 – 1) · 5 = 80 * 5 - 5 = 400 - 5 = 395
(20 – 1) · 7 = 20 * 7 - 1 * 7 = 140 - 7 = 133

9. Выполните вычисления устно, применяя, где это удобно, распределительное свойство умножения.

(60 + 1) · 7 = 60 * 7 + 1 * 7 = 420 + 7 = 427
(67 – 17) · 4 = 50 * 4 = 200
(17 – 13) · 5 = 4 * 5 = 20
(30 – 2) · 5 = 30 * 5 - 2 * 5 = 150 - 10 = 140

10. Выполните умножение устно.

42 · 4 = 168
69 · 4 = 276
92 · 3 = 276
51 · 6 = 306
75 · 4 = 290
48 · 5 = 240

11. Назовите невидимые рёбра и грани многогранника.

Для 1 варианта

KBC, ABCD, CKD

Для 2 варианта

BKC KCD BCDEA

12. Вычислите устно.

27 · 3 = 81
700 : 35 = 20
35 600 : 100 · 0 = 0
111 · 6 = 666
78 : 6 = 13
57 : 57 = 1
5 · 120 = 600
24 · (3 · 10) = 720
57 : 19 = 3
98 : 14 = 7
90 : (5 · 2) = 9
570 : 57 = 10

109

Страница 109

13. Чему равна разность произведений

40 · 4 и 14 · 6?

40 · 4 - 14 · 6 = 160 - 84 = 76

14. Найдите сумму частных

420 : 6 и 700 : 5.

420 : 6 + 700 : 5 = 80 + 140 = 220

15. Выполните действия.

5 730 + 70 787 + 59 724 = 76517 + 59724 = 136241
183 018 – 10 056 – 2 088 = 172962 - 2088 = 170874
10 091 – 9 842 + 67 991 = 249 + 67 991 = 68240
40 009 + 52 700 – 4 176 = 92709 - 4176 = 88533

16. Запишите выражение: из числа 800 вычесть частное c и 12. Вычислите значение выражения, если:

1) c = 480;

800 - 480 : 12 = 800 - 40 = 760

2) c = 960.

800 - 960 :12 = 800 - 80 = 720

17. В шести одинаковых ящиках 72 кг винограда. Сколько таких ящиков потребуется для упаковки 90 кг винограда?

1) 72 : 6 = 12 (кг) винограда в 1 ящике.
2) 90 : 12 = 7 остаток 5, то есть округляем до ближайшего большего, до 8. (ящ.)
Ответ: 8 ящиков

18. Оля обшила тесьмой 2 одинаковых носовых платка, а Нина — 4 таких же платка. Оля истратила на 1 м тесьмы меньше, чем Нина. Сколько метров тесьмы истратила каждая из девочек?

1) 4 : 2 = 2 (р.) больше надо Нине, чем Оле тесьмы.
2) 1 * 2 = 2 (м.) потратила Нина.
Ответ: 2 метра Нина и 1 метр Оля.

19. Группа туристов плыла 2 ч на плоту, преодолевая каждый час 4 км, а затем шла пешком 3 ч, проходя каждый час 6 км. Найдите длину всего маршрута туристов.

1) 4 * 2 = 8 (км) проплыла на плоту.
2) 6 * 3 = 18 (км) шли пешком.
3) 8 + 18 = 26 (км) преодолели туристы.
Ответ: 26 км.

20*. Купили 48 конфет и раздали поровну пятерым детям. Верно ли, что осталось 4 конфеты?

48 : 5 = 9 остаток 3

Нет не верно, осталось 3 конфеты.

110

Страница 110

21. На рисунке изображён план двухкомнатной квартиры в масштабе 1 : 100. Вычислите действительные размеры гостиной и спальни.

Гостиная на плане 3 х 5 см, то есть 3*100 = =300 см = 3 метра 5*100 = 500 см = 5 метров - 3 х 5 метров
Спальня 3 х 3 см, то есть 3 * 100 = 300 см = 3 метра - 3 х 3 метра

22. Участнику телевизионной викторины Волкову был задан вопрос: «В каком году был запущен первый искусственный спутник Земли» и даны четыре варианта ответа. Волков затруднился с ответом и попросил помощи у зала. Компьютер обобщил полученные из зала ответы. На экране появилась диаграмма:
Какой вариант ответа надо выбрать Волкову, чтобы выиграть? - 1957 год

111

Страница 111

23*. В двух корзинах грибов поровну. Сколько грибов надо переложить из одной корзины в другую, чтобы во второй стало на 4 гриба больше?

2 гриба

24. Длина оконного стекла 22 дм, а ширина составляет половину длины. Чему равна площадь стекла? Чему равна площадь пяти таких же стёкол?

1) 22:2=11 (дм) ширина стекла.
2) 22*11=242 (дм2) площадь стекла.
3) 242*5=1210 (дм2) площадь 5 стекол.

Ответ: 242 дм2 площадь одного стекла и 1210 дм2 площадь пяти стекол.

25. Площадь прямоугольника равна 36 м2, ширина — 4 м. Постройте этот прямоугольник в масштабе 1 : 100.

1) 36:9=9 (м) длина прямоугольника.

Строим прямоугольник с длинами сторон 9 и 4 см, это и будет масштаб 1 : 100.

26. Назовите многоугольники, которые имеют:

общий угол С; - треугольник BCD, параллелограмм BCDE, параллелограмм ACDM.
общую сторону BD. - треугольник BCD и треугольник BDE

27. Автомат расфасовывает в пачки готовые пельмени массой по 14 г каждый. В одну пачку входит 350 г пельменей. Сколько штук пельменей в каждой пачке? Сколько штук пельменей в 40 пачках?

1) 350:14=25 (пел.) в каждой пачке.
2) 25*40=1000 (пел.) в 40 пачках.
Ответ: 25 пельменей в пачке и 1000 в 40 пачках.

28*. За какое время можно пройти 1 км, двигаясь со скоростью 6 км/ч?

60:6=10 (мин) столько надо времени, чтобы пройти 1 км двигаясь со скоростью 6 км/ч
Ответ: 10 минут

29. Выразите скорость 120 км/ч в километрах в минуту.

120:60=2 (км/мин)
Ответ: 120 км/ч=2 км/мин

112

Страница 112

УЗНАЁМ НОВОЕ

Умножение на 1 000, 10 000, …

1. Как умножать число:

1) на 10; взять число 10 раз, но так как у нас десятичная система исчисления, то в конце просто добавиться 0.
2) на 100? взять число 100 раз, но так как у нас десятичная система исчисления, то в конце просто добавиться два 0.

Приведите примеры.

2. Рассуждая так же, как при умножении чисел на 10 и на 100, попробуйте сформулировать правило умножения на 1 000, 10 000, ... и найдите произведения чисел.

1 000 и 5             5*1000=5 000
10 000 и 9          9*10000=90 000
100 000 и 6        6*100000=600 000
8 и 1 000             8*1000=8 000
3 и 10 000         3*10000=30 000
7 и 100 000         7*100000=700 000
20 и 1 000         20*1000=20 000
40 и 10 000         40*10000=400 000
2 и 1 000 000     2*1000000=2 000 000

3. Выполните умножение.

24 · 1 000 = 24 000 154 · 100 000 = 154 000 000 50 · 100 · 20 = 1000 * 100 = 100 000
48 · 10 000 = 480 000 13 · 1 000 000 = 13 000 000 10 · 40 · 1 000 = 400 * 1 000 = 400 000

4. Вычислите значения выражения 15 · a, если a =

100, 15*100 = 1 500
1 000, 15 * 1000 = 15 000
10 000. 15* 10 000 = 150 000

5. В магазине бытовой техники кофеварки и чайники продаются по цене 1 000 р. За месяц продали 15 кофеварок и 23 чайника. Сколько денег выручил магазин за продажу этих товаров?

1) 15+23=38 (тов.) продали.
2) 38*1000=38 000 (р) выручил магазин.
Ответ: 38 000 рублей.

6. Какая единица длины в 1 000 раз больше метра? километр

Выразите в метрах:

6 км, 6*1000=6 000
11 км, 11 * 1000 = 11 000 м
125 км, 125 * 1000 =125 000 м
5 км 300 м, 5 * 1000 + 300 = 5 300 м
42 км 50 м. 42 * 1000 + 50 = 42 000 + 50 = 42 050 м

113

Страница 113

7. Какая единица массы в 1 000 раз больше грамма? килограмм

Выразите в граммах:

8 кг, 8 * 1000 = 8 000 г
12 кг, 12 * 1000 = 12 000 г
150 кг, 150 * 1000 = 150 000 г
3 кг 200 г, 3 * 1000 + 200 = 3 200 г
20 кг 7 г. 20* 1000 + 7 = 20 007 г

8. После того как самолёт пролетел 3 ч со скоростью 1 000 км/ч, до аэродрома ему осталось лететь 787 км. Какова длина маршрута самолёта?

1) 3*1000=3000 (км) пролетел самолет.
2) 3000 + 787 = 3 787 (км) длина маршрута.
Ответ: 3 787 км.

9. Найдите значения выражений.

100 000 · 9 – (3 828 + 14 963) = 900 000 - 18 791= 881 209
756 : 108 · 1 000 000 – 6 995 308 = 7 * 1000 000 - 6 995 308 = 7 000 000 - 6 995 308 = 4 692
358 · 10 000 – (970 : 10) · 1 000 = 3 580 000 - 97*1000 = 3 580 000 - 97 000 = 3 483 000
1 039 · 10 + 1 039 · 100 + 1 039 · 1 000 = 10 390 + 103 900 + 1 039 000 = 1 153 290

10. Каждое из чисел 25, 609, 5 050 увеличьте:

1) в десять тысяч раз; 25 *10 000 = 250 000, 609*10 000= 6 090 000, 5050*10 000 = 50 500 000
2) в сто тысяч раз. 25 *100 000 = 2 500 000, 609*100 000= 60 900 000, 5050*100 000 = 500 500 000

11. В киноцентре на Красной Пресне в Москве установлен гигантский экран. Его длина равна 23 м, а ширина — 10 м. Вычислите площадь этого экрана.

23*10=230 (м2) площадь экрана.
Ответ: 230 м2

12. Верно ли, что в одном километре содержится:

миллион миллиметров; да, верно
сто метров; нет, неверно
десять тысяч дециметров; да, верно
сто тысяч сантиметров? да, верно

114

Страница 114

13. Найдите сумму чисел:

6 458 и 872,

+6458
872
7330

5 245 и 3 270,

+5245
3270
8515

35 700 и 16 300.

+35700
16300
52000

14. Вычислите разность чисел:

70 635 и 8 240,

-70635
8240
62395

2 514 и 1 664,

- 2514
1664
850

9 531 и 1 230.

- 9531
1230
8301

15. Составьте выражение:

1) из произведения чисел 7 и 8, знака «минус» и частного чисел 36 и 6;

7*8-36:6=54-4=50

2) из разности чисел 126 и 87, знака «плюс» и числа 208;

(126-87) + 208 = 39 +208 = 247

3) из трёх слагаемых, каждое из которых является произведением чисел 6 и 4;

6*4+6*4+6*4= 24+24+24=72

4) из произведения числа 6 и разности чисел 12 и 8, знака «плюс» и частного 18 и суммы чисел 4 и 5.

6*(12-8)+18:(4+5)=6*4+18:9=24+2=26

16. Разделите с остатком:

827 на 9,

-827|9
81 |91
- 17
9
8 (остаток)

300 на 8,

-300|8
24 |37
- 60
56
4 (остаток)

348 на 13,

-348|13
26 |26
- 88
78
10 (остаток)

504 на 25

-504|25
50 |20
4 (остаток)

17. Найдите значение второго выражения, используя значение первого.

а)
25 · 4 = 100
250 · 4 = 1 000

б)
13 · 5 = 65
130 · 5 = 650

в)
32 · 3 = 96
320 · 3 = 960

18. Сравните значение величин.

1)
5 кг 250 г < 6 кг
4 108 г < 5 кг
12 кг 470 г > 10 кг
220 651 г > 220 561 г

2)
5 км > 500 м
240 см > 2 м
60 дм = 600 см
3 м < 300 дм

115

Страница 115

19. Даша за 3 дня прочитала 48 страниц книги. Сколько страниц она прочитает за 6 дней, если будет читать по столько же страниц в день, как и раньше? Решите задачу двумя способами.

1 способ

1) 48:3=16 (стр.) читала Даша в день.
2) 16 * 6 = 96 (стр.) прочитает за 6 дней.
Ответ: 96 страниц.

2 способ

1) 6:3=2 (р.) больше 6 дней, чем 3.
2) 48*2=96 (стр.) прочитает за 6 дней.
Ответ: 96 страниц.

20. Назовите рёбра многогранника, которые:

1) выходят из вершины A; AD, AB, AE
2) выходят из вершины K. KE, KD, KP

Назовите видимые и невидимые рёбра.

Видимые: AD, AB, DC, BC, AE, BM, CP, EM, MP
Невидимые: EK, KD, KP

Какие грани видны на рисунке и какие не видны?

Видимые: ADCB ABME BCPM

Невидимые: ADKE DKPC EKPM

21. Составьте три задачи, используя данные таблицы, и решите их.

1 задача

Купили 3 метра ткани по 320 рублей за метр, при этом расплатились купюрой в 1000 рублей. Сколько было получено сдачи?

1) 3*320=960 (р.) стоит ткань
2) 1000-960=40 (р.) было сдачи.
Ответ: 40 рублей.

2 задача

Купили ткань по 150 рублей за метр, при этом расплатились купюрой в 500 рублей и получили сдачу 50 рублей. Сколько было куплено ткани?

1) 500-50=450 (р.) заплатили за ткань.
2) 450:150=3 (м) ткани купили.
Ответ: 3 метра.

3 задача

Купили 2 метра ткани по 80 рублей за метр, при этом получили сдачи 40 рублей. Сколько заплатили в кассу?

1) 80*2=160 (р.) стоила ткань.
2) 60+40=200 (р.) заплатили в кассу.
Ответ: 200 рублей.

22. Расстояние между двумя посёлками автобус проезжает за 4 ч со скоростью 40 км/ч. С какой скоростью должен ехать автобус, чтобы проехать это расстояние за 2 ч?

Решите задачу двумя способами.

1 способ

1) 40*4 = 160 (км) между поселками.
2) 160:2 = 80 (км/ч) должен ехать автобус.
Ответ: 80 км/ч

2 способ

1) 4:2 = 2 (р.) больше по времени 4 часа, чем 2.
2) 40*2 = 80 (км/ч) должна быть скорость автобуса.
Ответ: 80 км/ч

116

Страница 116

УЗНАЁМ НОВОЕ

23. Автомобиль проехал 32 км за 30 мин. Сколько километров за это же время проедет мотоцикл, если его скорость составляет три четверти скорости автомобиля?

1) 60:30=2 (р) больше проедет за час.
2) 32*2=64 (км/ч) скорость машины.
3) 64 : 4 * 3 = 48 (км/ч) скорость мотоциклиста.
4) 48:2=24 (км) проедет мотоциклист.
Ответ: 24 километра.

24. Какие прямые линии не являются осями симметрии фигур?

первая слева картинка - 2 линия
вторая слева картинка - 2 линия
третья слева картинка - 1 линия
4 слева картинка - 1 линия

25. Перечертите фигуры в тетрадь и постройте симметричные им фигуры.

см. рисунок.

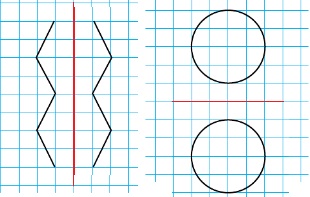
26. Начертите круг с длиной радиуса 3 cм 4 мм. Проведите пять его осей симметрии.

Чертим круг и проводим пять линий через его центр.

27. Из всех млекопитающих самым быстрым животным считается гепард. На коротких дистанциях он может развить скорость 120 км/ч. Выразите эту скорость в километрах в минуту.

120:60=2 (км/мин) скорость гепарда.
Ответ: 2 км/мин

117

Страница 117

УЗНАЁМ НОВОЕ

Прямоугольный параллелепипед. Куб

1. Предметы, изображённые на рисунке, имеют форму многогранника. Каждый такой многогранник называют прямоугольным параллелепипедом. Есть ли в вашей классной комнате предметы или их части, имеющие форму прямоугольного параллелепипеда? Назовите их.

Пенал, тумба, аквариум.

2. Произнесите несколько раз слово «параллелепипед», запишите его два раза в тетради и запомните, как оно пишется.

Самостоятельно.

3. Рассмотрите моде ль прямоугольного параллелепипеда и ответь те на вопросы.

Сколько граней имеет прямоугольный параллелепипед? 6
Какую форму имеет каждая его грань? прямоугольник
Почему такой параллелепипед называют прямоугольным? потому что грани и ребра между собой находятся под прямыми углами
Сколько вершин и сколько рёбер у прямоугольного параллелепипеда? 8 вершин и 12 ребер
Есть ли у него равные грани, рёбра? да, противолежащие

Покажите их.

Сколько рёбер выходит из каждой его вершины? 3

118

Страница 118

4. Возьмите модель куба. Объясните, почему куб является прямоугольным параллелепипедом.

Потому что у куба ребра и грани расположены под прямым углом друг относительно друга.

5. Рассмотрите чертёж прямоугольного параллелепипеда. Назовите рёбра, которые выходят из вершины А,

AE, AD, AB

из вершины К.

KD, KP, KE

Назовите каждое видимое и каждое невидимое ребро.

Видимые: EA AD AB DC BC BM EM MP

Невидимые: EK KD KP

Какие грани видны на рисунке и какие не видны?

Видны: ABCD, BCPM, ABME

Не видны: ADKE, DCPK, EKPM

Назовите пары равных рёбер, граней.

AB - DC - KP - EM
AD - BC - EK - MP

6. Найдите площадь поверхности (площадь всех граней) куба, длина ребра которого равна:

а) 8 cм;

1) 8*8=64 (см2) площадь 1 грани.
2) 64 * 6 = 384 (см2) площадь всех граней куба

б) 5 дм;

1) 5*5=25 (дм2) площадь 1 грани.
2) 25 * 6 = 150 (дм2) площадь всех граней куба

в) 4 м.

1) 4*4=16 (м2) площадь 1 грани.
2) 16 * 6 = 96 (м2) площадь всех граней куба

119

Страница 119

7. Из проволоки сделан каркас куба. Сколько проволоки пошло на его изготовление?

12 * 2 = 24 (дм) проволоки пошло на каркас.

8*. Назовите длину каждого ребра прямоугольного параллелепипеда. Вычислите:

2 см: OP TS DC AB
3 см: OA TD SC PB
4 см: AD OT PS BC

а) площадь каждой грани;

6 см2 TSCD OPBA
8 см2 ABCD OPST
12 см2 OTDA PSCB

б) площадь всех граней прямоугольного параллелепипеда.

6+6+8+8+12+12=12+16+24=52 (cм2) площадь всех граней

9. Запишите цифрами числа:

триста две тысячи шесть; 302 006
пятьсот двадцать тысяч; 520 000
четыреста восемьдесят тысяч пятьдесят; 480 050
два миллиона семьдесят тысяч десять. 2 070 010

120

Страница 120

10. Спортсмен сделал 50 выстрелов по мишени. Промахи составили десятую часть всех выстрелов. Сколько раз спортсмен попал в цель?

1) 50:10=5 (выс.) было мимо.
2) 50-5=45 (выс.) попал.
Ответ: 45 выстрелов.

11. Вычислите устно.

450 · 2 =900        700 – 1 =699                    250 + 250 = 500
630 : 3 = 210        12 · 100 = 1 200            9 000 – 5 000 = 4 000
270 : 90 = 3            500 : 100 = 5                6 000 + 4 000 =10 000
3 250 · 1 =3250     925 + 175 = 1 100        16 240 : 1 = 16 240

12. За всю игру баскетболист 12 раз забросил мяч в корзину соперника. Попадания составили восьмую часть всех произведённых бросков мяча в эту корзину. Сколько бросков было сделано?

12 * 8 = 96 (брос.) сделал спортсмен.
Ответ: 96 бросков.

13. Сравните значения выражений, не выполняя указанных вычислений. Обоснуйте свои ответы.

8 000 – 1 500 > 8 000 – 2 500
3 650 – 380 < 4 650 – 380
560 : 28 < 560 : 14
145 · 9 > 145 · 7

14. Сколько лет составляют:

5 веков; 100* 5 = 500 лет
13 веков; 13 * 100= 1 300 лет
18 веков; 18 * 100 = 1 800 лет
25 веков? 25 * 100 = 2 500 лет

15. Рассмотрите схему линий московского метро.

121

Страница 121

Как проехать: от станции «Севастопольская» до станции «Курская»;

1. По серой ветке доехать до коричневой кольцевой, а потом против часовой стрелки до "Курской".

Севастопольская - Нахимовский проспект - Нагорная - Нагатинская - Тульская - Добрынинская - Павелецкая - Таганская - Курская (9 станций, меньше станций)

2. По серой ветке доехать до синей ветки, а потом до "Курской".

Севастопольская - Нахимовский проспект - Нагорная - Нагатинская - Тульская - Добрынинская - Полянка - Боровицкая - Театральная - Курская (10 станций)

от станции «Алтуфьево» до станции «Парк культуры»?

1. По серой ветке доехать до коричневой кольцевой, а потом против часовой стрелки до "Парка культуры".

Альтуфьево - Бибирево - Отрадное - Владыкино - Новослабодская - Белорусская - Краснопресненская - Киевская - Парк культуры (9 станций)

2. По серой ветки доехать до красной ветки, а потом до "Парка культуры".

Альтуфьево - Бибирево - Отрадное - Владыкино - Новослабодская - Цветной бульвар - Тверская - Боровицкая - Парк культуры (9 станций)

Укажите разные маршруты, называя промежуточные станции.

На каком из маршрутов меньше всего промежуточных станций?

122

Страница 122

УЗНАЁМ НОВОЕ

Тонна. Центнер

1. На складе перед отправкой в магазины пшеничную муку развесили по килограмму в 1 000 пакетов, а ржаную — по килограмму в 100 пакетов.

Сколько килограммов муки каждого сорта отправили в магазины?

Тысяча килограммов составляет одну тонну. Сто килограммов составляет один центнер. Тонна и центнер — единицы массы. Их обозначают так: тонна — т, центнер — ц.

1 т = 1 000 кг
1 ц = 100 кг

2. Верно ли, что 1 т содержит 10 ц? Да, верно!

3. Выразите: в килограммах:

3 т, 3 * 1000 = 3000 кг
6 т, 6 * 1000 = 6000 кг
14 т, 14 *1000 = 14 000 кг
6 ц, 6 * 100 = 600 кг
8 ц, 8 * 100 = 800 кг
15 ц; 15 * 100 = 1 500 кг

в центнерах:

5 т, 5 * 10 = 50 ц
12 т, 12 * 10 = 120 ц
20 т. 20 * 100 = 200 ц

Во сколько раз 15 т больше 5 ц? 15 *10 = 150 ц 150 : 5 = 30 раз
На сколько 15 т больше 5 ц? 15 *10 = 150 ц 150 - 5 = 145 ц
На сколько 160 кг меньше 2 ц? 2 * 100= 200 кг, 200-160=40 кг
На сколько 4 т больше 4 ц? 4 * 10 =40 ц, 40 - 4 = 36 ц
На сколько 500 г меньше 4 кг? 4 * 1000 = 4 000, 4000 - 500 = 3 500 г

5. На базе было 30 т капусты. На следующий день привезли ещё две трети этого количества. На сколько тонн увеличилась масса капусты на базе?

1) 30 :3*2=20 (т) - привезли на второй день.
Ответ: на 20 тонн.

123

Страница 123

6. На двух тракторных прицепах привезли песок, по 5 т на каждом прицепе. Сколько всего килограммов песка привезли?

1) 5 * 1000 = 5000 (кг) было в каждом прицепе.
2) 5000 + 5000 = 10 000 (кг) привезли.
Ответ: 10 000 кг.

7. На трёх грузовых машинах привезли картофель, по 3 т на каждой машине. Сколько всего центнеров картофеля привезли?

1) 3 * 10 = 30 (ц) было на каждой машине.
2) 30 * 3 = 90 (ц) всего привезли.
Ответ: 90 центнеров

8. На складе было 4 т сахара. В один магазин отправили 1 265 кг сахара, во второй — на 375 кг больше. Сколько килограммов сахара осталось на складе?

1) 4 * 1000 = 4000 (кг) сахара было на складе.
2) 1265+375=1640 (кг) сахара отправила во второй магазин.
3) 4000 - 1640 - 1265 = 1095 (кг) осталось на складе.
Ответ: 1095 кг

9. Составьте задачу и решите её.

Со склада отгрузили два грузовика картофеля. В одном было 35 центнеров, а во втором 4280 кг. Сколько осталось на складе картофеля, если изначально там было 10 тонн?

1) 35*100=3500 (кг) - картофеля было в одном из грузовиков.
2) 3500 + 4280 = 7 780 (кг) - картофеля увезли на грузовиках.
3) 10*1000 = 10 000 (кг) картофеля было на складе.
4) 10 000 - 7 780 = 2 220 (кг) - осталось на складе.
Ответ: 2 220 кг осталось на складе.

10.

1) Запишите наибольшее шестизначное число и три следующих за ним при счёте числа.

999 999, 1 000 000, 1 000 001, 1 000 002

2) Запишите наименьшее семизначное число и три предшествующих ему при счёте числа.

10 000 000, 9 999 999, 9 999 998, 9 999 997

3) Прочитайте число 1 010 000. Один миллион десять тысяч.

Вычтите из него число 1 и запишите результат.

1 010 000 - 1 = 1 009 999

124

Страница 124

11. Какие числа нужно записать в пустых клетках таблицы?

a-100	a	a+1000
5900	6000	7000
5100	5200	6200
6040	6140	7140

12. Выполните вычисления.

6 234 – 5 734 = 500 10 000 – 3 280 + 40 857 = 47577
128 060 – 8 179 = 119 881 91 919 + 191 – 7 314 = 84 796

13. Найдите значение выражения:

1) x · 42 + y · 107, если x = 14, y = 8;

14 * 42 + 8 * 107 = 588 + 856 = 1444

2) a · m + x, если a = 60, m = 9, x = 360.

60*9+360 = 540 + 360 = 900

14. Проверьте равенство, не выполняя вычислений.

64 · 7 + 1 692 = 64 · 8 + 1 692

Не верно! так как 64 · 8 больше 64 · 7.

15. Выполните действия.

96 : 6 = 16                            52 · 6 = 312                   350 : 14 = 25
88 : 8 =11                             248 · 3 = 744                (354 – 127) · 100 = 22 700
452 : 3 = 150 (2 ост.)          315 : 9 =35                    (398 + 176) · 1 000 = 574 000
125 · 8 = 1000                    288 : 60 = 4 (48 ост.)     (1 000 – 408) · 10 000 = 5 920 000

16. Запишите числа в порядке уменьшения:

13 954 380, 13 954 270, 1 522 448, 1 385 361.

17. Из 3 м ткани получается 2 одинаковых по длине полотенца. Сколько таких полотенец получится из 6 м этой ткани?

Решите задачу двумя способами. Каким способом быстрее получается результат?

1 способ

3 м=300 см, 6 м = 600 м

1) 300 : 2 = 150 (см) длина одного полотенца.
2) 600 : 150 = 4 (пол.) получится из 6 м ткани.
Ответ: 4 полотенца.

2 способ

1) 6:3=2 (р.) кусок 6 метров ткани больше куска 3 метров.
2) 2 * 2 = 4 (пол.) получится из 6 м ткани.
Ответ: 4 полотенца.

125

Страница 125

18. Три швеи сшили по несколько одинаковых наволочек, израсходовав вместе 48 м ткани. Первая швея сшила 6 наволочек, вторая — 10 наволочек, третья — 8 наволочек. Сколько метров ткани израсходовала каждая швея?

1) 6 + 10 + 8 = 24 (нав.) - сшили швеи.
2) 48 : 24=2 (м) - идет на одну наволочку.
3) 6 * 2 = 12 (м) - израсходовала 1 швея.
4) 10 * 2 = 20 (м) - израсходовала 2 швея.
5) 8 * 2 = 16 (м) - израсходовала 3 швея.
Ответ: 12 м израсходовала 1 швея, 20 метров израсходовала 2 швея, 16 метров израсходовала 3 швея.

19. Назовите координаты центра каждой из окружностей.
синей: 4:4
красной: 7:4

20. По течению реки катер прошёл 150 км за 5 ч. Против течения его скорость была на 12 км/ч меньше, чем по течению. Какое расстояние катер прошёл против течения за 3 ч?

1) 150:5=30 (км/ч) скорость катера по течению.
2) 30-12=18 (км/ч) была скорость против течения.
3) 18*3=54 (км) прошел катер против течения за 3 часа.
Ответ: 54 км.

21. Изобразите в тетради такие многогранники. Как называется каждый из них?

слева куб, справа прямоугольный параллелепипед

126

Страница 126

22. Составьте три задачи, используя данные таблицы, и решите их.

1 задача

Мотоциклист ехал 5 часов со скоростью 24 км/ч, какое расстояние он проехал?

24*5=120 (км) проехал мотоциклист.
Ответ: 120 км.

2 задача

Автомобиль проехал 120 км со скоростью 60 км/ч. Сколько часов ехал автомобиль?

120:60=2 (ч.) ехал автомобиль.
Ответ: 2 часа.

3 задача

Автобус за 5 часов проехал 180 км. Какая была средняя скорость автобуса за это время?

180:5=36 (км/ч) средняя скорость автобуса.
Ответ: 36 км/ч.

23. Рассмотрите многогранник.

Назовите невидимые рёбра:

нижней грани; AB BC

задней грани. KB BC

Какие грани видимые и какие невидимые?

Видимые: KO MK EO ME MA ED OC AD DC

Невидимые: KB BC AB

Решите старинную задачу. Марфа купила красных и чёрных ниток. Красных — 2 катушки, а чёрных — на 1 катушку больше. За катушку красных ниток она заплатила 3 р. 50 к., а за катушку чёрных ниток — на 50 к. меньше. Какие нитки обошлись Марфе дороже и на сколько?

3 р 50к = 350 к

1) 350*2=700 (к) стоили красные нитки.
2) 350-50=300 (к) стоила катушка черных ниток.
3) 300*3=900 (к) стоили 3 катушки черных ниток.
4) 900-700=200 (к) на 2 рубля дороже обошлись черные нитки.
Ответ: на 2 рубля дороже обошлись черные нитки.

127

Страница 127

24. Вычислите площадь четырёхугольника ABCD, если ширина прямоугольника ABCE равна 2 см, а длина — 4 cм. Известно, что площадь треугольника CED равна 6 cм2.

1) 2*4=8 (см2) площадь прямоугольника.
2) 8+6=14 (см2) площадь ABCD.
Ответ: 14 см2

25*. На этикетке товара часто можно увидеть слова «нетто» и «брутто». Нетто — это масса товара без упаковки, а брутто — масса товара с упаковкой. На этикетке банки с огурцами написано: брутто 1 050 г, нетто 900 г. Когда все огурцы съели, мама вымыла банку и положила в неё 650 г томатной пасты. Как теперь должна была бы выглядеть надпись на этикетке?

1) 1050-900=150 (г.) весит банка.
2) 150+650=800 (г) брутто.

Значит надо записать так:

брутто 800 г, нетто 650 г.

26. За каждое прямое попадание мяча в корзину баскетболисту засчитали 2 очка. При каждом прямом броске Петрова и Васильева мяч попадал в корзину. Судья записал Петрову 24 очка, а Васильеву — 36. На сколько меньше попаданий было у Петрова, чем у Васильева?

1) 24:2=12 (бр.) в цель было у Петрова.
2) 36:2=18 (бр.) в цель было у Васильева.
3) 18-12=6 (бр.) на меньше попал в кольцо Петров, чем Васильев.
Ответ: 6 бросков.

27. Вырежьте из прозрачной или неплотной бумаги два треугольника и наложите их один на другой так, чтобы их общей частью был:

1) пятиугольник;
2) шестиугольник.

Смотри рисунок

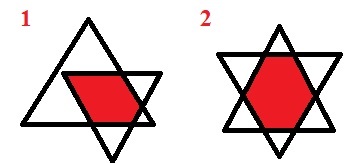
128

Страница 128

28. Начертите в тетради такой прямоугольник. Разделите построенный прямоугольник отрезком на два равных прямоугольника.

Сколькими способами это можно сделать? 2 способа
Вычислите периметр каждого прямоугольника.

1 вариант 6 см * 1 см

(6+1)*2=7*2=14 см
Ответ: 14 см

2 вариант 2 см * 3 см

(2+3)*26*2=12 см
Ответ: 12 см

Сколько решений имеет задача?

2 решения.

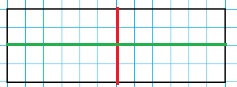
29. В питомник для посадки привезли 480 ягодных кустарников. На круговой диаграмме показано, какую часть числа всех кустов занимает каждый из видов этих кустарников. Подсчитайте число кустов

смородины, - 1 / 2                        480 :2=240 (кустов)
малины, - 1/4                                480:4=120 (кустов)
крыжовника и голубики, 1/4       480:4=120 (кустов)

используя диаграмму.

30. В кинотеатре на дневной сеанс было продано 300 билетов. Непроданной осталась шестая часть всех билетов. Сколько мест в зале?

1) 300:5=60 (м.) это одна часть из 6
2) 60*6=360 (м.) в зале.
Ответ: 360 мест.

129

Страница 129

УЗНАЁМ НОВОЕ

Задачи на движение в противоположных направлениях

1. В каких случаях машины двигаются в одном направлении и в каких — в противоположных направлениях?

Проверьте себя.

Возьмите две фишки: пусть они изображают машины, которые двигаются так, как показано на схемах. Повторите движения машин, используя взятые фишки.

2. Из палатки вышли два туриста и пошли в противоположных направлениях. Один турист двигался со скоростью 6 км/ч и через 3 ч дошёл до озера, а другой двигался со скоростью 4 км/ч и за то же время дошёл до водопада.

Продолжение на след странице...

130

Страница 130

Рассмотрите рисунок. Покажите с помощью моделей, как двигались туристы. Ответьте на вопросы.

На какое расстояние от палатки удалился каждый турист за 1 ч? Слева на 6 км, а справа на 4 км.

Какое расстояние стало между туристами через 1 ч после начала движения? 6+4=10 км

На какое расстояние от палатки удалился каждый турист за 2 ч? 6*2=12 км слева и 4 * 2 = 8 км справа.

Какое расстояние стало между туристами через 2 ч после начала движения? 12 + 8 = 20 км

На какое расстояние от палатки удалился каждый турист за 3 ч? 6 * 3 = 18 км слева и 4 * 3 = 12 км справа

Какое расстояние стало между туристами через 3 ч после начала движения? 18 + 12 = 30 км

Рассмотрите два способа вычисления расстояния от озера до водопада. Объясните, что означает каждая запись.

Способ 1

1) 6 · 3 = 18 (км);
2) 4 · 3 = 12 (км);
3) 18 + 12 = 30 (км).

Способ 2

1) С какой скоростью туристы удаляются друг от друга каждый час? (Какова скорость удаления туристов друг от друга?)

6 + 4 = 10 (км/ч)

131

Страница 131

2) На какое расстояние туристы удалятся друг от друга за 3 ч?

(Каково расстояние от озера до водопада?)

10 · 3 = 30 (км)

Какой способ вычисления вам нравится больше?

Объясните свой выбор.

3. В 8 ч утра Антон и Олег вышли из дома. Антон пошёл на почту со скоростью 100 м/мин, а Олег — в поликлинику со скоростью 85 м/мин. Какое расстояние будет между ними через 5 мин? Решите задачу двумя способами.

1 способ

1) 100+85=185 (м) на столько удалялись Антон от Олега каждую минуту.
2) 185*5=925 (м) будет расстояние между Антоном и Олегом через 5 минут.
Ответ: 925 метров.

2 способ

1) 100*5=500 (м) пройдет Антон за 5 минут.
2) 85*5=425 (м) пройдет Олег за 5 минут.
Ответ: 925 метров.

4. Составьте задачу по схеме. Ответьте на вопросы. Объясните способ вычисления.

Из двух населенных пунктов Лесное и Дубки расположенных между собой на расстоянии 75 км, вышли два пешехода в разных направлениях. Какое расстояние будет между ними через 3 часа?

1) На сколько километров за 3 ч удалился от села Лесное пешеход, который шёл со скоростью 5 км/ч?

5 * 3 = 15 км

132

Страница 132

2) На сколько километров за 3 ч удалился от села Дубки пешеход, который шёл со скоростью 6 км/ч?

6 * 3 = 18 км

3) Какое расстояние будет между пешеходами через 3 ч?

Запишите решение задачи. Прочитайте план решения задачи другим способом. (1 способ, 2 способ ниже)

1) 5*3=15 (км) пройдет пешеход из Лесного за 3 часа.
2) 6*3=18 (км) пройдет пешеход из Дубков за 3 часа.
3) 15+18=33 (км) удалятся пешеходы друг от друга за 3 часа.
4) 33+75=108 (км) будет расстояние между пешеходами через 3 часа.
Ответ: 108 км

1) На сколько километров удалились бы пешеходы друг от друга за 1 ч, если бы они начали движение из одной точки?

5+6=11 км

2) На сколько километров удалятся пешеходы друг от друга за 3 ч?

(5+6)*3=33 км

3) Какое расстояние будет между ними через 3 ч?

Запишите решение задачи. (2 способ решения задачи)

1) 5+6=11 (км) удаляются пешеходы друг от друга каждый час.
3) 11*3=33 (км) удалятся пешеходы друг от друга за 3 часа.
4) 33+75=108 (км) будет расстояние между пешеходами через 3 часа.
Ответ: 108 км

5. Найдите устно значения выражений. Каким свойством умножения вы пользовались?

286 · 82 + 286 · 18 = 286*100=28 600
348 · 67 + 33 · 348 = 348*100= 34 800

6. Выполните вычисления, используя известные вам свойства умножения.

468 · 2 · 5 = 468*10= 4 680 5 · 19 · 20 = 19 * 100=1900 25 · 34 · 4 = 34 * 100 = 3400

7. За карандаш и тетрадь нужно заплатить 20 р. Если купить ту же тетрадь и два карандаша, то покупка будет стоить 23 р. Какова цена карандаша? Сколько стоит тетрадь?

1) 23-20=3 (р.) стоит карандаш.
2) 20-3=17 (р.) стоит тетрадь.
Ответ: 3 рубля стоит карандаш и 17 рублей стоит тетрадь.

8. Увеличьте на 3 десятка каждое из чисел:

1 330 + 30 = 1360
10 470 + 30 = 10 500
2 048 + 30 = 2078
2 408 + 30 = 2438

133

Страница 133

9. В таблице указаны примерные расстояния между планетами Солнечной системы и Солнцем. Прочитайте данные таблицы. Ответьте на вопросы, используя данные таблицы.

Какая из планет наиболее удалена от Солнца? Нептун
Какая из планет находится ближе всех к Солнцу? Меркурий
Какая из планет находится ближе к Солнцу:

Сатурн или Марс, Марс
Земля или Венера, Венера
Меркурий или Юпитер? Меркурий

10. Вычислите устно.

560 : 7 =80 320 : 8 = 40 1 319 + 1 = 1320 16 · 10 = 160
280 : 4 =70 320 : 80 =40 2 760 – 1 =2759 720 : 10 = 72

11. Каждое из чисел 48, 104, 116 представьте в виде суммы двух равных слагаемых.

40 + 8 = 48
100 + 4 = 104
100 +10 + 6 = 116

12*. Каждое из чисел 49, 107, 115 представьте в виде суммы двух слагаемых, разность которых равна 3.

23 + 26 = 49
52 + 55 = 107
56 + 59 = 115

134

Страница 134

13. Выполните действия.

820 – 5 · 12 = 820 - 60 = 720
13 · 11 + 77 · 11 = 143 + 847 = 990
(630 + 270 : 9) : 2 = 660 : 2 = 330
465 102 + 559 – 10 299 = 455362
240 : 3 + 150 · 3 = 80 + 450 = 530
3 · 120 – 200 : 5 = 360 - 40 = 320
730 – (170 + 290) = 730-460 = 270
1 010 101 – (782 + 18 927) = 1 010 101 - 19709 = 990392

14. Сравните значения величин.

9 км 720 м > 972 м
8 420 ц > 84 т 2 ц
180 мин > 2 ч 50 мин
4 520 cм < 45 м 2 дм
12 т 250 кг < 12 350 кг
360 кг 820 г > 36 820 г

15. Сравните числа попарно. Составьте высказывания о числах и сделайте записи с помощью знаков > и <.

709 < 2870
709 < 12 600
2870 < 12600

403 000>34000
403 000>43000
403 000>3 040
43 000 > 34 000
43 000 > 3 040
34 000> 3 040

16. Из 120 м ткани сшили 30 одинаковых костюмов. Сколько таких костюмов можно сшить из 180 м ткани?

1) 120 :30 = 4 (м) такни ушло на 1 костюм.
2) 180 : 4 = 45 (к.) можно сшить из 180 м ткани.
Ответ: 45 костюмов

135

Страница 135

17. Вырежьте 4 такие фигуры и сложите из них квадрат.

Смотри рисунок

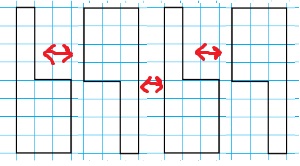
18. Вырежьте из бумаги квадрат. Разрежьте его по диагоналям. Сложите из четырёх полученных частей два квадрата.

Смотри рисунок

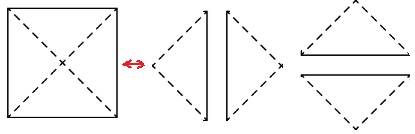
19. В магазине было продано 840 кг яблок, груш, слив и винограда. Используя диаграмму, вычислите массу каждого вида продукции.

840 : 4 = 210 (кг) слив было продано.
540:4=210 (кг) яблок было продано.
840:8=105 (кг) винограда было продано.
840:8*3=315 (кг) груш было продано.

Во сколько раз слив продали больше, чем винограда?

210 : 105 = 2 (р.) больше продали слив, чем винограда.

На сколько килограммов больше продали груш, чем яблок?

315 - 210 = 105 (кг) на столько больше продали груш, чем яблок.

136

Страница 136

20. Многоугольник имеет 12 вершин. Как он называется?

Двенадцатиугольник.

Начертите этот многоугольник.

Чертим многоугольник у которого 12 вершин.

21*. Измените с помощью скобок порядок выполнения действий так, чтобы равенства были верными.

(630 + 270) : 90 : 2 = 5
3 · (12 – 20 : 4) = 21

22*. Одинаковые значки заменяют в записях одинаковые числа. Что должно быть вместо вопросительного знака?

Смотри рисунок.

23. Какие фигуры являются многогранниками?

2 и 3

24. Животные изображены в масштабе 1 : 100.
Какой длины в действительности крокодил?

Крокодил 6 см, то есть 6*100 = 600 см = 6 м

Какой высоты жираф?

Жираф 4 см, то есть 4*100 = 400 см = 4 м

137

Страница 137

25*. Одинаковые фигуры заменяют в записях одинаковые числа. Что должно быть вместо вопросительного знака?

В первом варианте квадрат. Во втором, - ромб минус круг.

26. В каких случаях завяжется узел, если потянуть за концы верёвочки? Проверьте свой ответ, используя верёвочку.

На желтой и на красной веревке.

27. Найдите на Кольцевой линии метро (схема на с. 121) станцию «Белорусская», а на жёлтой линии — станцию «Третьяковская». Укажите несколько маршрутов проезда от «Белорусской» до «Третьяковской». Называйте промежуточные станции.

28. Самое большое дерево в мире — секвойя-дендрон (мамонтово дерево) — растёт в Калифорнии (США). Его масса равна 2 145 000 кг, а высота — 8 300 см. Выразите массу этого дерева в тоннах, а высоту в метрах.

2 145 тонн и 83 метра

138

Страница 138

УЗНАЁМ НОВОЕ

Пирамида

Одним из семи чудес света по праву считается пирамида Хеопса, построенная в Древнем Египте в первой половине 3-го тысячелетия до н. э. В те времена она была самым высоким сооружением в мире: изначальная высота пирамиды равна 146 м 60 cм, сторона квадратного основания — около 230 м. Пирамида Хеопса сложена более чем из 2 млн 300 тыс. каменных блоков общей массой свыше 6 млн т. В сооружении великой пирамиды и ведущей к ней дороги участвовали 100 тыс. человек. Форма пирамиды часто используется и в современном строительстве. Например,

139

Страница 139

В виде пирамид оформляются крыши башен, кафе, беседок, дачных домов. Форму пирамиды имеют некоторые предметы быта.

1. Возьмите модель пирамиды и рассмотрите её поверхность. Объясните, почему пирамида является многогранником.

2. Рассмотрите чертёж пирамиды. Назовите её основание, боковые грани, рёбра, вершину. У любой пирамиды боковые грани — треугольники, а основание — многоугольник. Название пирамиды зависит от формы основания. Если основание — треугольник, то пирамиду называют треугольной, если основание — четырёхугольник, то четырёхугольной, и так далее.

3. В чём отличие пирамиды от прямоугольного параллелепипеда?

140

Страница 140

4. Используя палочки и пластилин, сделайте модель пирамиды.

Какой фигурой является основание пирамиды? В первом случае пятиугольник, во втором шестиугольник
Как называется пирамида? Пятиугольная и шестиугольная.

5. В таблице приведены данные о пяти самых больших по площади странах мира. Найдите эти страны на карте мира.

Ищем страны на карте.

141

Страница 141

Ответьте на вопросы, используя данные таблицы.

Какая из этих стран имеет самую большую и какая — самую маленькую площадь? Россия самую большую и Бразилия самую маленькую
На сколько квадратных километров площадь России больше площади Канады? 17125191 - 9 984670 = 7 140 521 км2
Какую площадь имеет Китай? 9 598 962 км2
На сколько площадь Китая больше площади США? 9 598 962 - 9 519 431 = 79 531 км2

6. Проверьте результаты действий. Есть ли в вычислениях ошибки?

1 400 м – 967 м = 433 м
3 км – 305 м = 2 км 595 м (верно 2 км 695 м)
5 т – 3 т 178 кг = 822 кг (верно 1 т 822 кг)
25 ц 30 кг + 5 ц 70 кг = 31 ц

7. Цена рамы составляет шестую часть цены картины. Рама стоит 150 р. Какова стоимость картины в раме?

150 * 7 = 1050 (р.) цена картины.
Ответ: 1050 рублей.

8*. Расставьте скобки так, чтобы стало верным равенство.

1) 240 : ( 6 · 5 – 20) = 24
2) (480 – 200) : 4 · 5 = 350

9. Понаблюдайте, как изменяются числа в выражениях. Запишите ещё по три выражения в каждом столбце и выполните вычисления.

100 + 10 · 1 = 110        260 – (10 + 10) = 240
100 + 20 · 2 = 140        360 – (20 + 20) = 400
100 + 30 · 3 = 130        460 – (30 + 30) = 400
100 + 40 · 4 = 260        560 – (40 + 40) = 480

142

Страница 142

10. Вычислите и проверьте умножение делением, а деление умножением.

954 : 9 = 106         Проверка 106 * 9 = 954
920 : 4 = 230         Проверка 230 * 4 = 920
864 : 12 = 72         Проверка 72 * 12 = 864
205 · 3 = 615        Проверка 615 : 3 = 205

11. Охарактеризуйте фигуру (название, число звеньев, число вершин).

ломанная с 5 звеньями с 6 вершинами
ломанная с 4 звеньями с 5 вершинами

12. Вырежьте прямоугольник с длинами сторон 8 cм и 4 cм. Отрежьте от прямоугольника полоску шириной 1 cм. Вычислите площадь оставшейся части.

Сколько решений имеет задача?

Два решения, так как полоску можно отрезать вдоль длины и вдоль ширины.

Обсудите с соседом по парте варианты выполнения задания. Пусть каждый из вас выберет свой вариант и выполнит работу. Затем проверьте работу друг друга.

1) 8*4=32 (см2) площадь прямоугольника.
2) 1*8=8 (см2) площадь полоски если ее отрезать по длине.
3) 32 - 8 = 24 (см2) площадь прямоугольника с отрезанной полоской по длине.
Ответ: 24 см2

13. Какая единица не является единицей массы:

грамм,
тонна,
метр, не является единицей массы.
центнер?

Какая единица не является единицей скорости:

км/ч,
м/с,
м/мин,
км, не является единицей скорости
cм/с?

14. Выразите скорость:

180 м/мин в метрах в секунду; 180:60=3 (м/с)
4 м/с в метрах в минуту; 4 * 60 = 240 (м/мин)
5 км/мин в километрах в час. 5 * 60 = 300 (км/час)

143

Страница 143

УЗНАЁМ НОВОЕ

Задачи на движение в противоположных направлениях (встречное движение)

1. Из двух посёлков одновременно вышли навстречу друг другу Миша и Петя и встретились через 15 мин. Миша прошёл до встречи 900 м, а Петя — 870 м.

Рассмотрите схему движения мальчиков.

Чем отличается этот вид движения от тех, которые вы рассматривали на предыдущих уроках?

Ответьте на вопросы.

Сколько времени до встречи был в пути Миша и сколько — Петя? 15 минут тот и другой
С какой скоростью шёл Миша? 900:15= 60 (м/мин)
С какой скоростью шёл Петя? 870 : 15 = 58 (м/мин)
Какое расстояние между посёлками? 900+870=1770 (м)

2. Из двух сёл выехали одновременно навстречу друг другу два мотоциклиста и встретились через 2 ч. Один ехал со скоростью 60 км/ч, а другой — со скоростью 75 км/ч. Вычислите расстояние между сёлами.

Смотрим решения на следующей странице

144

Страница 144

Рассмотрите решение Пети и Кати.

Петя

1) 60 · 2 = 120 (км);
2) 75 · 2 = 150 (км);
3) 120 + 150 = 270 (км).

Катя

1) 60 + 75 = 135 (км/ч);
2) 135 · 2 = 270 (км).

Сформулируйте вопросы к каждому способу решения.

Вопросы можно взять из текста далее.

Проверьте, есть ли ваш вопрос к первому действию Кати среди следующих вариантов.

а) На сколько километров за каждый час мотоциклисты приближались друг к другу? 135 км
б) На сколько километров каждый час уменьшалось расстояние между мотоциклистами? 135 км
в) Какова скорость сближения мотоциклистов? 135 км/ч

3. В 8 ч утра от двух пристаней отправились навстречу один другому два теплохода и встретились в 11 ч того же дня. Расстояние между пристанями 210 км. Скорость одного теплохода 34 км/ч. С какой скоростью шёл другой теплоход? Рассмотрите схему движения теплоходов и ответьте на вопросы.

Продолжение на следующей странице

145

Страница 145

Сколько часов до встречи был в пути каждый теплоход? 11 - 8 = 3 часа
Сколько километров до встречи прошёл теплоход, скорость которого 34 км/ч? 34 * 3 = 102 км
Сколько километров до встречи прошёл другой теплоход? 210-102=108 км
С какой скоростью шёл другой теплоход? 108 : 3 = 36 (км/ч)

Запишите решение задачи.

1) 11 - 8 = 3 (ч.) плыли теплоходы.
2) 34 * 3 = 102 (км) проплыл один теплоход.
3) 210 - 102 = 108 (км) проплыл второй теплоход.
4) 108 : 3 = 36 (км/ч) скорость второго теплохода.
Ответ: 36 км/ч.

4. От двух вокзалов, расстояние между которыми 720 км, вышли одновременно навстречу один другому два поезда. Скорость одного поезда 50 км/ч, а другого — 40 км/ч. Через сколько часов они встретятся?

Рассмотрите схему движения поездов.

Проверьте, верно ли Петя решил эту задачу: сначала он вычислил скорость сближения поездов и получил 90 км/ч, а затем вычислил время, через которое произойдёт встреча, и у него получилось 8 ч.

Да, верно!

146

Страница 146

5. Вычислите устно.

275 · 0 = 0        (931 – 120) · 0 = 0        960 : 10 · 0 = 0
1 · 300 = 300    (315 + 85) · 1 = 400      200 · 0 · 5 = 0
4 603 – 0 =        0 · 587 · 1 + 0 = 0         28 650 + 0 = 28 650

6. Прочитайте числа:

20 057, двадцать тысяч пятьдесят семь
13 837, тринадцать тысяч восемьсот тридцать семь
90 909, девяносто тысяч девятьсот девять
32 323, тридцать две тысячи триста двадцать три
500 880, пятьсот тысяч восемьсот восемьдесят
1 002 615, один миллион две тысячи шестьсот пятнадцать
77 777 777, семьдесят семь миллионов семьсот семьдесят сем тысяч семьсот семьдесят семь
400 004. четыреста тысяч четыре

Запишите эти числа в порядке уменьшения, начиная с самого большого.

77 777 777, 1 002 615, 500 880, 400 004, 90 909, 32 323, 20 057, 13 837

7. Уменьшите на 4 сотни каждое из чисел:

80 523 - 400 = 80 123
12 400 - 400 = 12 000
1 000 - 400 = 600

Запишите полученные числа в порядке возрастания.

600, 12 000, 80 123

8. Вычислите значение выражения x · y, если:

1) x = 50, y = 20;

50*20=1000

2) x = 15, y = 8;

15 * 8 = 120

3) x = 7, y = 120;

7 * 120 = 840

4) x = 250, y = 4.

250* 4 = 1000

9. Запишите выражения для определения площади каждого из участков. Выполните вычисления, подставляя вместо x число 20, а вместо y — число 32.

1) х*35. 20 * 35 = 700 м2
2) 30 * y. 30 * 32 = 960 м2

147

Страница 147

10. Выполните вычисления.

3 4 1 5 2
5 000 – 3 681 + 48 · 5 – (9 180 – 8 810) = 1189

1) 48*5=240

- 9180
8810
370

3)
-5000
3681
1319

4)
1319+240=1559

5)
1559-370=1189

Проверьте себя: значение выражения должно быть равно 1 189.

11. Выполните действия.

26 · 9 = 234 927 : 3 = 309 300 : 150 = 3 125 · 5 = 650
18 · 15 = 270 616 : 11 = 56 870 : 435 = 2 230 · 4 = 920

12. На гранях игрального кубика нанесено от 1 до 6 очков. Катя бросала кубик 26 раз. Вот какие результаты получились:

1, 6, 4, 3, 5, 4, 5, 1, 2, 1, 2, 5, 4, 6, 3, 4, 6, 4, 5, 6, 2, 2, 3, 2, 1, 4.

Представьте эту информацию в виде таблицы с помощью следующих обозначений: — выпало 1 раз, — выпало 5 раз.

Заполнив таблицу, ответьте на вопросы.

Выпало очков	Подсчеты	Сколько раз выпало
1	////	4
2	/////	5
3	///	3
4	//////	6
5	////	4
6	////	4

Сколько раз выпадало по 3 очка? 3 раза
Какое число очков выпадало чаще всех остальных? 4
Сколько очков выпало наименьшее число раз? 3

Повторите действия Кати.

Запишите получившиеся результаты и занесите их в таблицу. Сравните. На основании своих результатов создаем свою аналогичную таблицу.

148

Страница 148

13. В магазине было 3 рулона ткани, по 60 м в каждом. Продали пятую часть всей ткани. Сколько метров ткани осталось?

1) 60*3=180 (м) ткани было.
2) 180 : 5 = 36 (м) ткани продали.
3) 180 - 36 = 144 (м) ткани осталось.
Ответ: 144 м.

14. Ёлочные шары разложили в 5 коробок по 9 штук. Колокольчиков было вдвое больше, чем шаров. Их разложили поровну в 6 коробок. Сколько колокольчиков положили в каждую из этих коробок?

1) 9 * 5 = 45 (ш.) было.
2) 45 * 2 = 90 (кол.) было.
3) 90 : 6 = 15 (кол.) было в каждой коробке.
Ответ: 15 колокольчиков.

15. Багаж авиапассажира состоит из чемодана массой 10 кг 250 г, сумки массой 6 кг 130 г и портфеля. Чему равна масса портфеля, если масса всего груза 20 кг?

1) 10 250 + 6 130 = 16 380 (г) масса чемодана и сумки.
2) 20 000 - 16 380 = 3 620 (г) масса портфеля.
Ответ: 3 620 г или 3 кг 620 г.

16. Докажите, что прямая AB не является осью симметрии семиугольника.

Не все вершины семиугольника находятся на одинаковом расстоянии от прямой AB.

Скажем с левого верхнего угла до прямой 2 клетки, а с левого нижнего 1. Хотя для симметрии должно быть одно и тоже количество.

149

Страница 149

17. Назовите два четырёхугольника, у которых общей является:

1) вершина A;

ABOM ABCD

2) сторона MO;

ABOM MOCD

3) сторона CD?

BCDA OCDM

18*. Лена приложила два равных квадрата с длиной стороны 3 cм один к другому так, что получился прямоугольник. Чтобы найти периметр этого прямоугольника, она вычислила периметр одного квадрата и умножила его на 2. Получилось 24 cм. Не ошиблась ли Лена в нахождении периметра прямоугольника?

Ошиблась, так как учла два раза сторону квадрата, которая не является периметром прямоугольника.

(3+3)*2+3*2=12+6=18 (см) периметр прямоугольника.
Ответ: 18 см периметр прямоугольника.

19. Масса бублика 80 г. Масса ватрушки на 40 г больше массы бублика. Какова масса пяти ватрушек?

1) 80 + 40 = 120 (г) масса ватрушки
2) 120 * 5 = 600 (г) масса 5 ватрушек.

20. В магазине в большие пакеты отвешивают по 750 г риса, а в маленькие — на 250 г риса меньше. Сколько риса в 10 маленьких пакетах?

1) 750 - 250 = 500 (г) риса в маленьких пакетах.
2) 500 * 5 = 2500 (г) риса в 5 маленьких пакетах.

150

Страница 150

21. Катер двигался по прямой между двумя пристанями по озеру Байкал. На рисунке изображён график движения катера.

В какое время катер отошёл от пристани? 11 часов

Вычислите, с какой скоростью он шёл. Он шел со скоростью 30 км/ч. Для этого берем разницу во времени в 1 час и вычисляем разницу в км.

30 - 0 = 30 (км/ч)

На каком расстоянии от пристани катер был:

в 13 ч; 60 км
в 14 ч; 90 км
в 11 ч 30 мин; 15 км
в 13 ч 30 мин? 75 км

В какое время катер находился от пристани на расстоянии:

30 км; в 12 часов
45 км; в 12 - 30
105 км? в 14 - 30

151

Страница 151

УЗНАЁМ НОВОЕ

Умножение многозначного числа на однозначное число

1. Вспомните и расскажите, как умножить 127 на 4. Объясните, как выполнено умножение.

2. Выполните умножение.

126 · 4

*126
4
504

596 · 4

*596
4
2384

205 · 9

*205
9
1845

480 · 9

*480
9
4320

675 · 9

*675
9
6075

706 · 8

*706
8
5648

608 · 5

*608
5
3040

903 · 8

*903
8
7224

284 · 5

*284
5
1420

404 · 7

*404
7
2828

290 · 7

* 290
7
2030

560 · 8

*560
8
4480

338 · 7

*338
7
2366

208 · 4

*208
4
832

210 · 4

*210
4
840

408 · 2

* 408
2
816

Проверьте результаты с помощью калькулятора.

3. Верно ли высказывание «Если один из множителей равен 1, то произведение равно другому множителю»? Да, верно!

Приведите примеры. В математике это свойство умножения в обобщённом виде записывают так. При любом значении а верны равенства а · 1 = а, 1 · а = а.

Примеры:

10*1=10
25*1=25

152

Страница 152

Аналогично сформулируйте высказывание об умножении любого числа на число 0 и сделайте запись. Сравните свою запись с записью в учебнике. При любом значении а верны равенства а · 0 = 0, 0 · а = 0.

4. Какими числами надо заполнить таблицу?

x	1	385	1	0	999
y	250	1	1	1264	0
x*y	250	385	1	0	0

5. На двух складах было 6 080 кг угля. Когда с первого склада отгрузили 820 кг угля, а со второго — в 4 раза больше, то на втором складе угля не осталось.

Сколько угля осталось на первом складе?

1) 820 * 4 = 3280 (кг) отгрузили со второго склада.
2) 3280 + 820 = 4100 (кг) всего отгрузили угля.
3) 6080 - 4100 = 1980 (кг) осталось угля на 1 складе.
Ответ: 1980 кг осталось на 1 складе.

Проверьте себя: получится ли число 6 080, если сложить количество угля, хранившегося на первом и втором складах?

Проверка:

1980+820+3280=6080 (кг) угля было всего!

6. Вычислите устно.

500 · 4 = 2000 400 · 6 = 2400 200 · 30 = 6000 100 · 100 = 10 000
800 · 5 = 4000 70 · 80 = 5600 40 · 500 = 2000 2 000 · 7 = 14 000

7. Найдите значение выражения 630 · x + 125 · y, если:

1) x = 3, y = 5;

630 * 3 + 125 * 5 = 1890 + 125 = 2 015

2) x = 4, y = 4;

630 * 4 + 125 * 4 = 755 * 4 = 3 020

3) x = 5, y = 3;

630 * 5 + 125 * 3 = 3525

4) x = 0, y = 1.

630 * 0 + 125 * 1 = 125

153

Страница 153

8. В вагон погрузили 10 больших и 7 маленьких ящиков. В маленьком ящике помещается 2 532 детали, а в большом ящике таких деталей в 3 раза больше. Сколько всего деталей погрузили в вагон?

1) 2532 * 7 = 17 724 (дет.) было в маленьких ящиках.
2) 2532 * 3 = 7596 (дет.) в 1 большом ящике.
3) 7596 *10 = 75 960 (дет.) в больших ящиках.
4) 75 960 + 17 724 = 93 684 (дет.) погрузили в вагон.
Ответ: 93 684 детали.

9. Выполните умножение.

1 258 · 7 = 8806

*1258
7
8806

5 072 · 4 = 20 288

*5072
4
20288

60 005 · 3 = 180 015

* 60005
3
180015

12 587 · 6 = 75 522

* 12587
6
75522

1 364 · 2 = 2 728

* 1364
2
2728

110 084 · 4 = 440 336

* 110084
4
440336

41 005 · 3 = 123 015

* 41005
3
123015

973 · 5 = 4 865

*973
5
4865

40 003 · 8 = 320 024

*40003
8
320024

10. Выполните действия.

1 4 2 3
8 · 24 372 – (12 143 + 11 778) · 7 = 27 529

*24372
8
194976

+ 12143
11778
23921

*23921
7
167447

- 194976
167447
27529

2 1 3 5 4
100 · (11 372 – 10 599) · 6 + 19 060 · 4 = 54 040

-11372
10599
773

773*100=77 300

*77300
6
463800

*19060
4
76240

+463800
76240
54040

1 2 5 3 4
(24 375 – 3 979) · 8 + 90 · 10 : 5 = 16348

-24375
3979
20396

*20396
8
163168

90*10=900

900:5=180

+16168
180
16348

1 2 5 3 6 4
180 : 12 · 1 000 – 906 : 3 + 3 007 · 2 = 20 712

-180|12
12 | 15
-60
60
0

15*1000=15 000

-906|3
9     |302
    -6
     6
     0

3007 * 2 = 6 014

15000 - 302 = 14 698

14698 + 6 014 = 20 712

11. Турист пролетел 3 ч на самолёте Ту-154 со скоростью 950 км/ч и 2 ч на самолёте Ан-24 со скоростью 650 км/ч. Сколько всего километров пролетел турист?

1) 950*2=1900 (км) пролетел турист на самолете Ту-154.
2) 650 * 2 = 1300 (км) пролетел турист на самолете Ан - 24.
3) 1900 + 1300 = 3100 (км) всего пролетел турист.
Ответ: 3100 км.

12. Выполните умножение.

1 700 · 8 = 13600

*1700
8
13600

12 100 · 4 = 48 400

* 12100
4
48400

345 090 · 5 = 1 725 450

* 345090
5
1725450

4 050 · 5 = 20250

*4050
5
20250

25 040 · 7

*25040
7
175270

810 000 · 9 = 7 290 000

* 810000
9
7 290 000

20 300 · 6 = 121 800

*20 300
6
121 800

303 800 · 2

*303800
2
607600

1 000 200 · 5 = 5 001 000

44 500 · 3

*44500
3
133500

180 400 · 8

*180400
8
1443200

2 120 000 · 4 = 8 480 000

13. На двух базах было 45 т арбузов. Когда с первой базы вывезли 8 т 200 кг арбузов, а со второй — в 4 раза больше, то на второй базе арбузов не осталось. Сколько арбузов осталось на первой базе и сколько их было на второй базе?

1) 8200*4=32800 (кг) вывезли арбузов со второй базы.
2) 32800+8200= 41000 (кг) арбузов вывезли всего.
3) 45000-41000=4000 (кг) осталось на первой базе.
Ответ: 4 т осталось на первой базе и 32800 кг было на второй.

154

Страница 154

14. Длина каждой стороны девятиугольника равна 12 дм 8 см. Вычислите его периметр.

128*9=1152 (см) периметр девятиугольника.
Ответ: 1152 см

15. Из двух городов выехали две машины одновременно навстречу одна другой и встретились через 4 ч. Какое расстояние между городами, если скорости машин 75 км/ч и 82 км/ч?

1) 75+82=157 (км/ч) скорость сближения.
2) 157*4=628 (км) расстояние между городами.
Ответ: 628 км.

16. На овощном складе было 128 т 970 кг картофеля и моркови. В 8 магазинов отвезли по 3 265 кг картофеля и по 2 735 кг моркови. Сколько этих овощей осталось на складе? Решите задачу двумя способами.

1 способ

1) 8 * 3265 = 26120 (кг) отвезли картофеля.
2) 8 * 2735 = 21 880 (кг) отвезли моркови.
3) 21880+26120=48000 (кг) всего овощей забрали со склада.
4) 128970-48000=80970 (кг) осталось на складе.

Ответ: 80790 кг или 80 т 970 кг овощей осталось на складе.

2 способ

1) 3265+2735=6000 (кг) овощей отвезли в каждый магазин.
2) 6000 * 8 = 48000 (кг) всего овощей забрали со склада.
3) 128970-48000=80970 (кг) осталось на складе.

Ответ: 80790 кг или 80 т 970 кг овощей осталось на складе.

17. Для подарков купили 8 кг шоколадных конфет по цене 324 р. 50 к. за килограмм и столько же пряников по 96 р. за килограмм. Какова стоимость покупки? Решите задачу двумя способами.

1 способ

1) 32450*8=259600 (коп.) стоили конфеты
2) 9600*8=76800 (коп.) стоили пряники
3) 76800+259600=336400 (коп.) стоила покупка.
Ответ: 3364 рубля

2 способ

1) 32450+9600=42050 (коп.) стоил 1 кг конфет и 1 кг пряников.
2) 42050*8=336400 (коп.) стоила покупка.
Ответ: 3364 рубля

18. С аэродрома одновременно поднялись в воздух два самолёта и полетели в противоположных направлениях. Скорость каждого самолёта 850 км/ч. На каком расстоянии будут самолёты один от другого через 3 ч полёта?

1) 850+850=1700 (км/ч) скорость удаления.
3) 1700*3=5100 (км) расстояние будет между самолетами, через 3 часа.
Ответ: 5100 км.

155

Страница 155

19. Сравните значения массы.

18 ц 20 кг > 1 т 82 ц
400 т 560 кг < 401 т
125 кг 60 г < 125 кг 600 г
32 кг 156 г > 31 кг 900 г

20. Вычислите устно.

36 + 22 = 58                        97 – 45 = 52                    83 · 10 = 830
360 + 220 = 580                970 – 450 = 520                83 · 100 = 8 300
3 600 + 2 200 = 5 800        9 700 – 4 500 = 5 200        83 · 1 000 = 83 000

21*. На заборе сидят на некотором расстоянии друг от друга три птицы: сорока, ворона и галка. Расстояние между сорокой и вороной 20 м, а между вороной и галкой — 12 м. Какое расстояние между сорокой и галкой? Найдите два решения этой задачи.

1 вариант

20+12=32 (м) расстояние между сорокой и галкой
Ответ: 32 метра

2 вариант

20 - 12 = 8 (м) расстояние между сорокой и галкой
Ответ: 32 метра

22. Катер проходил расстояние между двумя пристанями за 3 ч со скоростью 20 км/ч. Катер заменили теплоходом, скорость которого 30 км/ч. За какое время теплоход проходит расстояние между этими пристанями? Сколько времени экономят пассажиры?

1) 30*2=60 (км) расстояние между пристанями.
2) 60 :30 = 2 (ч) надо теплоходу чтобы проплыть маршрут.
3) 3-2=1 (ч) экономят пассажиры.
Ответ: 2 часа надо теплоходу и 1 час экономят пассажиры.

23. Из одного города в другой, расстояние между которыми 300 км, выехали автобус и машина. Водитель автобуса проехал четвёртую часть пути, а водитель машины — шестую часть пути. Кому из них осталось ехать меньшее расстояние?

Меньше осталось ехать водителю автобуса, так как 1/4 > 1/6

156

Страница 156

24. Подставьте в каждое неравенство вместо x число 285. Верно или неверно каждое из неравенств при этом значении x?

1 000 – x < 700, 1000 - 285 < 700 - неверно!

650 + x > 936, 650 + 285 > 936 - неверно!

25. На одном станке можно изготовить 25 деталей за минуту, а на другом — 30 деталей за минуту. За сколько времени на каждом из станков можно изготовить 750 деталей?

1) 750:25=30 (мин.) надо для того, чтобы изготовить 750 деталей на 1 станке.
2) 750:30= 25 (мин.) надо для того, чтобы изготовить 750 деталей на 2 станке.
Ответ: 30 минут и 25 минут надо соответственно потратить на каждом станке, чтобы изготовить 750 деталей.

26*. Одно и то же число одинаковых деталей можно сделать на одном станке за 7 мин, а на другом — за 10 мин. Сколько деталей за одну минуту можно сделать на втором станке, если на первом за минуту можно сделать 40 деталей?

1) 7*40=280 (дет.) сделают на 1 станке.
2) 280:10=28 (дет.) сделают на 2 станке за минуту.
Ответ: 28 деталей.

27. За 3 ч катер на подводных крыльях проплыл 240 км. Идущий вслед за ним обычный катер проплыл 80 км за 4 ч. Во сколько раз скорость катера на подводных крыльях больше?

1) 240:3=80 (км/ч) скорость катера на подводных крыльях.
2) 80:4=20 (км/ч) скорость обычного катера.
3) 80:20=4 (р.) больше скорость катера на подводных крыльях, чем обычного.
Ответ: в 4 раза.

28. Достаточно ли купить 15 м ткани, чтобы сшить шторы на 3 окна, если на каждое окно нужно две полосы этой ткани длиной 2 м 60 cм каждая? Выделите условие и вопрос задачи. Решите задачу.

1) 260*2=520 (см) ткани нужно на каждое окно.
2) 1500:3=500 (см) получается ткани на каждое окно при длине ткани в 15 метров.
500 < 520, то есть ткани не хватит.

29. Изобразите ломаную такой же длины, но состоящую из трёх одинаковых звеньев.

Смотри рисунок.

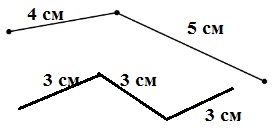
157

Страница 157

30. Из двух сёл одновременно навстречу друг другу выехали два мотоциклиста. Скорость одно го мотоцикла равна 65 км/ч, а другого — 70? км/ч. Через час расстояние между ними стало 8 км 500 м. Какое расстояние между сёлами?

1) 65+70=135 (км/ч) скорость сближения, и столько 135 км они проехали за час.
2) 8500+13500=22000 (м) или 22 км было расстояние между селами.
Ответ: 22 км.

31. У какого из многоугольников все вершины лежат на окружности?

1) в первом случае у треугольника.
2) во втором тоже у треугольника.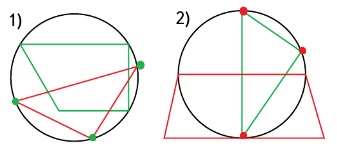

32. В саду собрали 444 кг яблок сорта «богатырь» и 348 кг яблок сорта «мелба». Все собранные яблоки разложили по сортам в ящики по 12 кг. Сколько потребовалось ящиков? Решите задачу другим способом при условии, что в ящики можно класть яблоки разных сортов.

1 способ

1) 444:12=37 (ящ.) надо для сорта "богатырь".
2) 348:12=29 (ящ.) надо для сорта "мелба".
3) 37+29=66 (ящ.) надо для всех яблок.
Ответ: 66 ящиков

2 способ

1) 444+348 = 792 (кг) всего яблок.
2) 792 : 12 = 66 (ящ.) всего надо под яблоки.
Ответ: 66 ящиков.

33. Вычислите периметр двадцатиугольника, длина каждой стороны которого равна 3 cм 5 мм. Выразите результат в сантиметрах.

35*20=700 (мм) или 70 см длина периметра двадцатиугольника.
Ответ: 70 см периметр двадцатиугольника.

158

Страница 158

34. Начертите отрезок АВ в масштабе 5 : 1.

AB = 2 см, то есть 5:1 это 2*5 = 10 см, надо начертить этот отрезок.

35. О человеке, который медленно идёт, обычно говорят: «Ползёт как черепаха». Самая крупная из известных черепах — кожистая черепаха (длина тела — до 2 м, масса — до 600 кг) — живёт в тропических морях. В воде она способна развить скорость 35 км/ч.

Сколько километров проплывёт черепаха за 12 мин? 12 минут — это пятая часть часа.

35:5=7 (км) проплывет черепаха.
Ответ: 7 км.

36*. На мельнице при обмолоте проса получается крупа, которую называют пшеном. Отходы при этом составляют пятую часть массы проса. Сколько мешков пшена получится из тонны проса, если в каждый мешок будут насыпать 50 кг пшена?

1) 1000 : 5 = 200 (кг) отходов.
2) 1000 - 200 = 800 (кг) получится пшена.
3) 800:50=16 (м.) получится пшена.
Ответ: 16 мешков.

37*. Из аэропорта в 7 ч утра вылетели в противоположных направлениях два самолёта. Скорость одного самолёта 950 км/ч, а другого — 850 км/ч. Какое расстояние будет между ними через 30 мин после вылета?

1) 950+850=1800 (км/ч) скорость удаления и это расстояние, которое образовывается между самолетами за каждый час.
2) 1800:2=900 (км) будет между самолетами через 30 минут.
Ответ: 900 км.

38. Как быстрее всего доехать на метро (см. схему на с. 121) от станции «Дмитровская» до станции «Автозаводская»? Опишите словами этот маршрут.

По серой ветке метро доехать до Тверской. Пересесть на зеленую ветку и доехать до Автозаводской.