Не важно являетесь ли вы гуманитарием или человеком, который хочет связать свою жизнь с техникой и естественными науками, основы математики показано знать всем. Ведь базовые принципы математики пригождаются каждодневно каждому и повсеместно.
Собственно руководствуясь этой мыслью и принципом и настало время поговорить об одном из возможным учебных пособий, об ответах к рабочей тетради по математике 5 класс, часть 2, Ерина к учебнику Виленкина. 2 часть этой тетради будет востребована в 5 классе во второй половине учебного года. И в нашей статье речь пойдет об ответах, как говорят школьники о ГДЗ по этой самой рабочей тетради, которая создана по материалам учебника. Ну что же, весьма кратко но четко мы обозначили свои позиции о предмете математика, о том зачем создана наша статья, а значит самое время переходить уже к нашим ответам.
Ответы приведены во вкладках.
ГДЗ ответы к рабочей тетради по математике 5 класс, часть 2, Ерина к учебнику Виленкина
Выбирайте ту самую вкладку, которая соответствует актуальной информации по изучаемой вами информации и кликайте на нее.
Окружность и круг 1
-
Окружность и круг. Номер №1
Постройте окружность с центром в точке A и радиусом, длина которого равна 1,5 см. Постройте еще две окружности с тем же радиусом и центром в точках B и C.
Решение
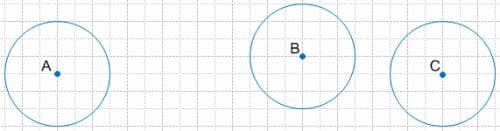
2
-
Номер №2
Постройте окружность с центром в точке K, проходящую через точку M. Проведите радиус этой окружности. Чему равен радиус?
Решение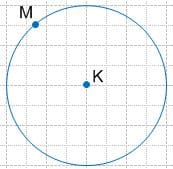
r = KM = 2 (см) − радиус окружности;
d = 2 * KM = 2 * 2 = 4 (см) − диаметр окружности.
Ответ: 2 см − радиус; 4 см − диаметр. 3
-
Номер №3
Проведите диаметр окружности и измерьте его.
Решение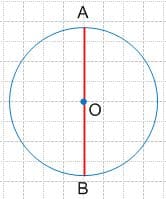
d = AB = 3 см 7 мм − диаметр окружности O
Ответ: 3 см 7 мм 4
-
Номер №4
Проведите три радиуса окружности с центром в точке A и три диаметра окружности с центром в точке B.
Решение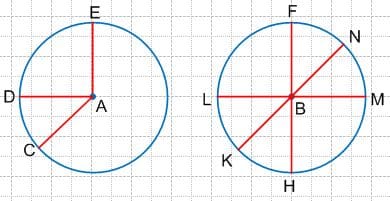
Радиусы: AE, AD, AC.
Диаметры: LM, KN, FH. 5
-
Номер №5
Отметьте:
а) красным цветом 5 точек, лежащих на окружности O;
б) синим цветом 5 точек, не лежащих на окружности O.
Решение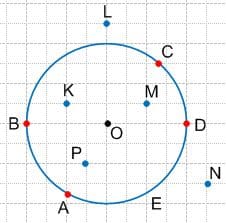
а) точки A, B, C, D, E − лежат на окружности O.
б) точки K, L, M, N, P − не лежат на окружности O. 6
-
Номер №6
Радиус окружности равен 3 см. Точка A лежит на окружности. Чему равно расстояние от точки A до центра окружности − точки O?
Ответ: _.
Внутри круга отмечена точка B, а вне круга − точка C. Измерьте расстояние от этих точек до центра окружности и результаты измерений занесите в таблицу.
Отметьте еще несколько точек вне и внутри круга, измерьте расстояние от каждой из них до центра окружности и результаты измерений занесите в таблицу.
Сделайте вывод:
Если точка лежит на окружности, то расстояние от нее до центра окружности равно _. Если точка лежит внутри круга, то расстояние от нее до центра окружности _ радиуса окружности. Если точка лежит вне круга, то расстояние от нее до центра окружности _ радиуса окружности.
Решение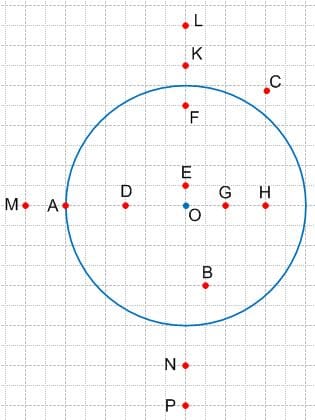
AO = 3 смТочка вне круга Точка внутри круга
Точка Расстояние до точки 0 в мм Точка Расстояние до точки 0 в мм C 35 B 20 K 35 D 15 L 45 E 5 M 40 F 25 N 40 G 10 P 50 H 20 Если точка лежит на окружности, то расстояние от нее до центра окружности равно радиусу. Если точка лежит внутри круга, то расстояние от нее до центра окружности меньше радиуса окружности. Если точка лежит вне круга, то расстояние от нее до центра окружности больше радиуса окружности.
7
-
Номер №7
Начертите одну окружность с центром в точке A, другую с центром в точке B так, чтобы:
а) эти окружности пересеклись;
б) не имели общих точек.
Решение а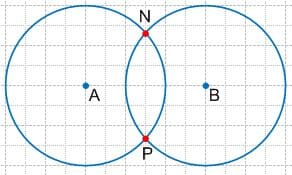
Точки N и P − точки пересечения окружностей A и B.
Решение б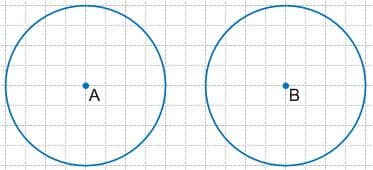
8
-
Номер №8
Закрасьте $\frac{1}{2}$ круга синим цветом, $\frac{1}{6}$ часть − красным цветом, $\frac{1}{3}$ часть − желтым цветом.
Решение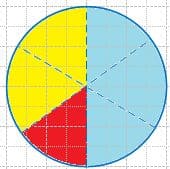
9
-
Номер №9
Решите устно задачу.
На трех полках 96 книг. Когда с одной полки сняли 6 книг, а с другой 12 книг, то на каждой полке осталось книг поровну. Сколько книг осталось на каждой полке?
Решение
1) 6 + 12 = 18 (книг) − сняли всего;
2) 96 − 18 = 78 (книг) − осталось;
3) 78 : 3 = (60 + 18) : 3 = 60 : 3 + 18 : 3 = 20 + 6 = 26 (книг) − осталось на каждой полке.
Ответ: 26 книг 10
-
Номер №10
Решите задачи, составив уравнения.
а) Когда неизвестное число разделили на 11 и результат увеличили в 5 раз, получили 110. Найдите неизвестное число.
б) Если разделить неизвестное число на 5 и прибавить 25, получится 40. Найдите неизвестное число.
в) Если умножить неизвестное число на 5 и разделить на 2, получится 50. Найдите неизвестное число.
Решение а
Пусть x − неизвестное число, тогда:
x : 11 * 5 = 110
x : 11 = 110 : 5 = (100 + 10) : 5 = 100 : 5 + 10 : 5 = 20 + 2
x : 11 = 22
x = 22 * 11 = 22 * (10 + 1) = 22 * 10 + 22 * 1 = 220 + 22
x = 242 − неизвестное число
Ответ: 242
Решение б
Пусть x − неизвестное число, тогда:
x : 5 + 25 = 40
x : 5 = 40 − 25
x : 5 = 15
x = 15 * 5 = (10 + 5) * 5 = 10 * 5 + 5 * 5 = 50 + 25
x = 75 − неизвестное число
Ответ: 75
Решение в
Пусть x − неизвестное число, тогда:
x * 5 : 2 = 50
x * 5 = 50 * 2
x * 5 = 100
x = 100 : 5
x = 20 − неизвестное число
Ответ: 20 Доли 1
-
Номер №1
Закрасьте $\frac{1}{8}$ часть круга зеленым цветом, $\frac{3}{8}$ части − красным цветом, $\frac{1}{4}$ − синим цветом.
Какая часть не закрашена?
Какая часть закрашена?
Решение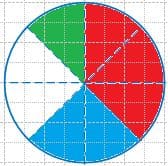
$\frac{6}{8} = \frac{3}{4}$ − круга закрашена;
$\frac{2}{8} = \frac{1}{4}$ − круга не закрашена. 2
-
Номер №2
Закрасьте в каждой фигуре часть, соответствующую указанной дроби.
а)
б)
Решение а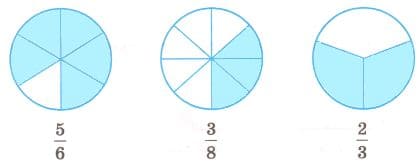
Решение б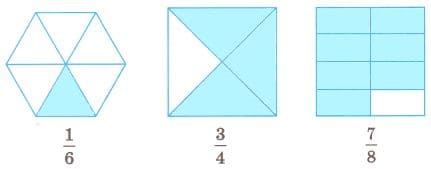
3
-
Номер №3
Запишите, какая часть каждой фигуры закрашена.
а)
б)
Решение а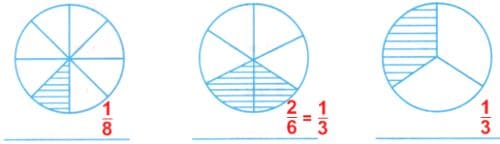
Решение б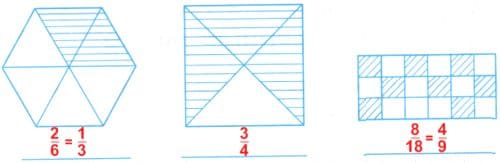
4
-
Номер №4
Закрасьте $\frac{1}{6}$ часть каждой фигуры.
Решение
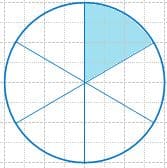
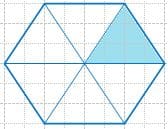
5
-
Номер №5
Постройте отрезок, длина которого составляет указанную часть отрезка AB.
Решение а
$\frac{3}{8}$
Решение б
$\frac{7}{8}$
Решение в
$\frac{1}{4}$
Решение г
$\frac{1}{2}$ 6
-
Номер №6
Допишите равенства.
а)
1 см = $\frac{1}{10}$ дм
1 ц = _ т
1 г = _ т
1 коп. = _ руб.
б)
5 ц = _ т
38 м = _ км
8 мм = _ см
5 мин = _ час
Решение а
1 см = $\frac{1}{10}$ дм
1 ц = $\frac{1}{10}$ т
1 г = $\frac{1}{1000000}$ т
1 коп. = $\frac{1}{100}$ руб.
Решение б
5 ц = $\frac{5}{10}$ т
38 м = $\frac{38}{1000}$ км
8 мм = $\frac{8}{10}$ см
5 мин = $\frac{5}{60}$ час 7
-
Номер №7
Заполните пропуски.
а)
$\frac{3}{10}$ м = 30 см
$\frac{3}{5}$ м = _
$\frac{1}{2}$ м = _
$\frac{3}{4}$ м = _
б)
$\frac{1}{2}$ т = _ кг
$\frac{3}{4}$ кг = _ г
$\frac{1}{4}$ т = _ ц
$\frac{3}{4}$ ц = _ кг
в)
$\frac{1}{8}$ суток = _ час
$\frac{1}{3}$ час = _ мин
$\frac{1}{4}$ мин = _ сек
$\frac{3}{4}$ час = _ мин
г)
$\frac{1}{4}$ рубля = _ коп
$\frac{3}{4}$ рубля = _ коп
$\frac{2}{5}$ рубля = _ коп
$\frac{7}{10}$ рубля = _ коп
Решение а
1 м = 100 см,
тогда:
$\frac{3}{10}$ м = (100 : 10) * 3 = 10 * 3 = 30 см
$\frac{3}{5}$ м = (100 : 5) = 20 * 3 = 60 см
$\frac{1}{2}$ м = (100 : 2) * 1 = 50 * 1 = 50 см
$\frac{3}{4}$ м = (100 : 4) * 3 = 25 * 3 = 75 см
Решение б
1 т = 1000 кг;
1 кг = 1000 г;
1 т = 10 ц;
1 ц = 100 кг,
тогда:
$\frac{1}{2}$ т = (1000 : 2) * 1 = 500 * 1 = 500 кг
$\frac{3}{4}$ кг = (1000 : 4) * 3 = 250 * 3 = 750 г
$\frac{1}{4}$ т = (10 : 4) * 1 = 2,5 * 1 = 2,5 ц
$\frac{3}{4}$ ц = (100 : 4) * 3 = 25 * 3 = 75 кг
Решение в
1 сутки = 24 час;
1 ч = 60 мин;
1 мин = 60 сек,
тогда:
$\frac{1}{8}$ суток = (24 : 8) * 1 = 3 * 1 = 3 час
$\frac{1}{3}$ час = (60 : 3) * 1 = 20 * 1 = 20 мин
$\frac{1}{4}$ мин = (60 : 4) * 1 = 15 * 1 = 15 сек
$\frac{3}{4}$ час = (60 : 4) * 3 = 15 * 3 = 45 мин
Решение г
1 рубль = 100 коп,
тогда:
$\frac{1}{4}$ рубля = (100 : 4) * 1 = 25 * 1 = 25 коп
$\frac{3}{4}$ рубля = (100 : 4) * 3 = 25 * 3 = 75 коп
$\frac{2}{5}$ рубля = (100 : 5) * 2 = 20 * 2 = 40 коп
$\frac{7}{10}$ рубля = (100 : 10) * 7 = 10 * 7 = 70 коп 8
-
Номер №8
Решите задачи.
а) Кедр может расти до 1000 лет, а грецкий орех − $\frac{3}{5}$ этого числа лет. Сколько лет может расти грецкий орех?
б) Куриное яйцо весит обыкновенно 60 г. На скорлупу приходится $\frac{1}{6}$ этого веса, на белок − $\frac{1}{2}$ веса, а остальное − желток. Сколько весит каждая часть яйца?
в) При помоле на белую муку отходит в отруби $\frac{2}{5}$ массы зерна. Сколько килограммов отрубей и сколько килограммов белой муки получится при помоле 1 т зерна?
Решение а
1000 : 5 * 3 = 200 * 3 = 600 (лет) − может расти грецкий орех.
Ответ: 600 лет
Решение б
1) 60 : 6 * 1 = 10 * 1 = 10 (г) − весит скорлупа;
2) 60 : 2 * 1 = 30 * 1 = 30 (г) − весит белок;
3) 60 − (10 + 30) = 60 − 40 = 20 (г) − весит желток.
Ответ: 10 г − скорлупа; 30 г − белок; 20 г − желток.
Решение в
1 т = 1000 кг
1) 1000 : 5 * 2 = 200 * 2 = 400 (кг) − отрубей получится;
2) 1000 − 400 = 600 (кг) − муки получится.
Ответ: 400 кг отрубей и 600 кг муки 9
-
Номер №9
Вычислите.
а)
$ \begin{array}{rl} 24000 : 80 & \\ *7 & \\ :5 & \\ +80 & \end{array} $
б)
$ \begin{array}{rl} 19000 + 11000 & \\ :600 & \\ *80 & \\ +600 & \end{array} $
в)
$ \begin{array}{rl} 63000 - 45000 & \\ :600 & \\ *320 & \\ +400 & \end{array} $
г)
$ \begin{array}{rl} 40000 - 22900 & \\ :900 & \\ *140 & \\ +520 & \end{array} $
д)
$ \begin{array}{rl} 4800 : 80 & \\ :3 & \\ *20 & \\ -131 & \end{array} $
е)
$ \begin{array}{rl} 15000 : 6 & \\ *4 & \\ :5 & \\ *7 & \end{array} $
Решение а
$ \begin{array}{r|l} 24000 : 80 & 300\\ *7 & 2100\\ :5 & 420\\ +80 & 500 \end{array} $
Ответ: 500
Решение б
$ \begin{array}{r|l} 19000 + 11000 & 30000\\ :600 & 50\\ *80 & 400\\ +600 & 1000 \end{array} $
Ответ: 1000
Решение в
$ \begin{array}{r|l} 63000 - 45000 & 18000\\ :600 & 30\\ *320 & 9600\\ +400 & 10000 \end{array} $
Ответ: 10000
Решение г
$ \begin{array}{r|l} 40000 - 22900 & 17100\\ :900 & 19\\ *140 & 2660\\ +520 & 3180 \end{array} $
Ответ: 3180
Решение д
$ \begin{array}{rl} 4800 : 80 & 60\\ :3 & 20\\ *20 & 400\\ -131 & 269 \end{array} $
Ответ: 269
Решение е
$ \begin{array}{rl} 15000 : 6 & 2500\\ *4 & 10000\\ :5 & 2000\\ *7 & 14000 \end{array} $
Ответ: 14000 Сравнение дробей 1
-
Сравнение дробей. Номер №1
Под каждой парой рисунков напишите две дроби, сравните их. Запишите результаты сравнений с помощью знаков < или >.
а)
б)
в)
г)
Решение а
$\frac{5}{8} > \frac{3}{8}$
Решение б
$\frac{3}{5} < \frac{4}{6}$
Решение в
$\frac{4}{6} < \frac{5}{6}$
Решение г
$\frac{5}{12} < \frac{10}{18}$ 2
-
Номер №2
Сравните дроби.
а) $\frac{2}{3} ☐ \frac{1}{3}$
б) $\frac{3}{7} ☐ \frac{5}{7}$
в) $\frac{1}{2} ☐ \frac{3}{6}$
г) $\frac{7}{10} ☐ \frac{9}{10}$
д) $\frac{5}{100} ☐ \frac{3}{100}$
е) $\frac{4}{8} ☐ \frac{3}{6}$
Решение а
$\frac{2}{3} > \frac{1}{3}$
Решение б
$\frac{3}{7} < \frac{5}{7}$
Решение в
$\frac{1}{2} = \frac{3}{6}$
Решение г
$\frac{7}{10} < \frac{9}{10}$
Решение д
$\frac{5}{100} > \frac{3}{100}$
Решение е
$\frac{4}{8} = \frac{3}{6}$ 3
-
Номер №3
Запишите дроби.
а) пять восьмых _
б) две трети _
в) девять десятых _
г) семь тридцатых _
д) одна десятая _
е) одна сотая _
Решение а
пять восьмых $\frac{5}{8}$
Решение б
две трети $\frac{2}{3}$
Решение в
девять десятых $\frac{9}{10}$
Решение г
семь тридцатых $\frac{7}{30}$
Решение д
одна десятая $\frac{1}{10}$
Решение е
одна сотая $\frac{1}{100}$ 4
-
Номер №4
Запишите дроби со знаменателем 10, являющиеся координатами точек, расположенных на луче между точками x и y.
Решение
$\frac{2}{10}, \frac{3}{10}, \frac{4}{10}, \frac{5}{10}, \frac{6}{10}, \frac{7}{10}, \frac{8}{10}$ 5
-
Номер №5
Закрасьте часть каждой фигуры, соответствующую данной дроби, и сравните результаты.
а)
б)
в)
г)
д)
е)
Решение а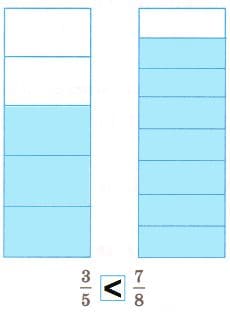
Решение б
Решение в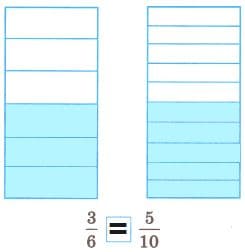
Решение г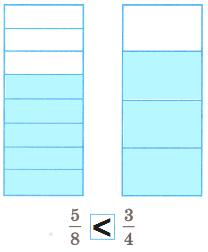
Решение д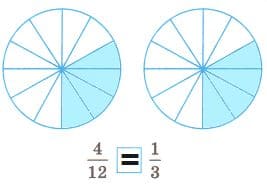
Решение е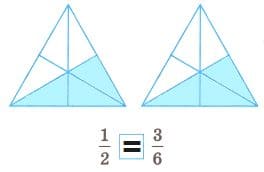
6
-
Номер №6
Пользуясь координатным лучом, сравните дроби.
а) $\frac{3}{8} ☐ \frac{6}{8}$
б) $\frac{5}{8} ☐ \frac{2}{8}$
в) $\frac{5}{8} ☐ \frac{1}{8}$
г) $\frac{7}{8} ☐ \frac{8}{8}$
Решение а
$\frac{3}{8} < \frac{6}{8}$
Решение б
$\frac{5}{8} > \frac{2}{8}$
Решение в
$\frac{5}{8} > \frac{1}{8}$
Решение г
$\frac{7}{8} < \frac{8}{8}$
Номер №7
Решите задачи.
а) Какую часть от 20 копеек составляют 10 копеек?
б) Какую часть квадрата в 16 клеток составляют 4 клетки?
в) Какую часть часа составляют 30 минут?
г) Какую часть часа составляют 15 минут?
Решение а
$10 : 20 = \frac{10}{20} = \frac{1}{2}$ − часть от 20 копеек составляют 10 копеек.
Ответ: $\frac{1}{2}$ часть
Решение б
$4 : 16 = \frac{4}{16} = \frac{1}{4}$ − часть квадрата в 16 клеток составляют 4 клетки.
Ответ: $\frac{1}{4}$ часть
Решение в
1 ч = 60 мин
$30 : 60 = \frac{30}{60} = \frac{1}{2}$ − часть часа составляют 30 минут.
Ответ: $\frac{1}{2}$ часть
Решение г
1 ч = 60 мин
$15 : 60 = \frac{15}{60} = \frac{1}{4}$ − часть часа составляют 15 минут.
Ответ: $\frac{1}{4}$ часть Правильные и неправильные дроби 1
-
25. Правильные и неправильные дроби. Номер №1
Заполните пропуски.
а) Дробь, в которой числитель меньше знаменателя, называют _ дробью.
б) Дробь называют неправильной дробью, если ее числитель _ или _ знаменателю.
в) Правильная дробь всегда _ неправильной дроби.
г) Правильная дробь _ единицы.
д) Неправильная дробь _ единицы.
Решение
а) Дробь, в которой числитель меньше знаменателя, называют правильной дробью.
б) Дробь называют неправильной дробью, если ее числитель больше или равен знаменателю.
в) Правильная дробь всегда меньше неправильной дроби.
г) Правильная дробь меньше единицы.
д) Неправильная дробь равна или больше единицы. 2
-
Номер №2
Выпишите из данных дробей:
$\frac{1}{100}; \frac{17}{8}; \frac{5}{2}; \frac{2}{3}; \frac{6}{6}; \frac{13}{17}; \frac{9}{1}; \frac{3}{40}$.
а) правильные дроби: _
б) неправильные дроби: _
Решение
а) правильные дроби: $\frac{1}{100}, \frac{2}{3}, \frac{13}{17}, \frac{3}{40}$.
б) неправильные дроби: $\frac{17}{8}, \frac{5}{2}, \frac{6}{6}, \frac{9}{1}$. 3
-
Номер №3
Придумайте и запишите 6 правильных и 6 неправильных дробей.
а) правильные дроби: _
б) неправильные дроби: _
Решение
а) правильные дроби: $\frac{1}{2}, \frac{3}{4}, \frac{5}{8}, \frac{12}{13}, \frac{27}{29}, \frac{99}{100}$.
б) неправильные дроби: $\frac{2}{2}, \frac{3}{2}, \frac{13}{10}, \frac{22}{22}, \frac{30}{29}, \frac{100}{50}.$ 4
-
Номер №4
Обведите правильные записи.
а) $\frac{7}{9} < 1$
б) $\frac{7}{10} > \frac{10}{7}$
в) $\frac{16}{15} > 1$
г) $\frac{5}{5} = 1$
д) $\frac{1}{7} = \frac{7}{1}$
е) $\frac{5}{8} < 1$
ж) $\frac{2}{2} = \frac{3}{3}$
з) $1 < \frac{7}{5}$
и) $1 > \frac{7}{5}$
Решение
а) $\frac{7}{9} < 1$
б) $\frac{7}{10} > \frac{10}{7}$
в) $\frac{16}{15} > 1$
г) $\frac{5}{5} = 1$
д) $\frac{1}{7} = \frac{7}{1}$
е) $\frac{5}{8} < 1$
ж) $\frac{2}{2} = \frac{3}{3}$
з) $1 < \frac{7}{5}$
и) $1 > \frac{7}{5}$ 5
-
Номер №5
Выпишите те дроби, которые больше 1.
$\frac{8}{9}, \frac{1}{7}, \frac{18}{3}, \frac{6}{6}, \frac{5}{4}, \frac{17}{30}, \frac{9}{8}, \frac{101}{100}$.
Решение
$\frac{18}{3} > 1$
$\frac{5}{4} > 1$
$\frac{9}{8} > 1$
$\frac{101}{100} > 1$
Ответ: $\frac{18}{3}, \frac{5}{4}, \frac{9}{8}, \frac{101}{100}$. 6
-
Номер №6
Придумайте и запишите 5 дробей, у которых:
а) числитель в 6 раз больше знаменателя _
б) числитель в 6 раз меньше знаменателя _
Решение а
Пусть знаменатели 5 дробей будут равны:
1, 2, 3, 4, 5, тогда их числители будут равны:
1 * 6 = 6
2 * 6 = 12
3 * 6 = 18
4 * 6 = 24
5 * 6 = 30
Ответ: $\frac{6}{1}, \frac{12}{2}, \frac{18}{3}, \frac{24}{4}, \frac{30}{5}$.
Решение б
Пусть числители 5 дробей будут равны:
1, 2, 3, 4, 5, тогда их знаменатели будут равны:
1 * 6 = 6
2 * 6 = 12
3 * 6 = 18
4 * 6 = 24
5 * 6 = 30
Ответ: $\frac{1}{6}, \frac{2}{12}, \frac{3}{18}, \frac{4}{24}, \frac{5}{30}$. 7
-
Номер №7
Сколько в единице:
пятых долей? _
сотых долей? _
шестых долей? _
тринадцатых долей? _
Решение
$1 = \frac{5}{5}$
$1 = \frac{100}{100}$
$1 = \frac{6}{6}$
$1 = \frac{13}{13}$
Ответ:
В единице
пятых долей: 5
сотых долей: 100
шестых долей: 6
тринадцатых долей: 13 8
-
Номер №8
Запишите на луче координаты всех точек, являющиеся дробями со знаменателем 6. Выпишите отдельно правильные и неправильные дроби.
Правильные дроби: _
Неправильные дроби: _
Решение
Правильные дроби: $\frac{1}{6}, \frac{2}{6}, \frac{3}{6}, \frac{4}{6}, \frac{5}{6}$.
Неправильные дроби: $\frac{6}{6}, \frac{7}{6}, \frac{8}{6}, \frac{9}{6}, \frac{10}{6}, \frac{11}{6}, \frac{12}{6}, \frac{13}{6}, \frac{14}{6}$. 9
-
Номер №9
Решите задачи.
а) В стопе 500 листов бумаги. Сколько листов в четверти стопы?
б) В стаде 800 голов рогатого скота. Из них $\frac{1}{10}$ − козы, $\frac{1}{4}$ − коровы, а остальные овцы. Сколько овец в стаде?
Решение а
500 : 4 = 125 (листов) − в четверти стопы.
Ответ: 125 листов
Решение б
1) 800 : 10 * 1 = 80 * 1 = 80 (коз) − в стаде;
2) 800 : 4 * 1 = 200 * 1 = 200 (коров) − в стаде;
3) 800 − (80 + 200) = 800 − 280 = 520 (овец) − в стаде.
Ответ: 520 овец 10
-
Номер №10
Вычислите:
а)
$ \begin{array}{rl} 4\;м\;500\;мм & \\ :3 & \\ +650\;мм & \\ *12 & \end{array} $
б)
$ \begin{array}{rl} 4\;м\;8\;дм & \\ *5 & \\ :12\;мм & \\ *6 & \end{array} $
в)
$ \begin{array}{rl} 9\;ц\;60\;кг & \\ :8 & \\ +80\;кг & \\ *25 & \end{array} $
г)
$ \begin{array}{rl} 3\;км\;500\;м & \\ :50 & \\ *8 & \\ +40\;м & \end{array} $
д)
$ \begin{array}{rl} 4\;т\;500\;кг & \\ :900 & \\ +995\;кг & \\ :25 & \end{array} $
е)
$ \begin{array}{rl} 2\;м\;50\;см & \\ :5 & \\ *8 & \\ -1\;м\;60\;см & \end{array} $
Решение а
1) 4 м 500 мм : 3 = 4 м 5 дм : 3 = 45 дм : 3 = 15 дм = 1 м 5 дм
2) 1 м 5 дм + 650 мм = 1 м 50 см + 65 см = 1 м 115 см = 2 м 15 см = 2 м 1 дм 5 см
3) 2 м 1 дм 5 см * 12 = 215 см * 12 = (200 + 10 + 5) см * 12 = 2400 см + 120 см + 60 см = 2520 см + 60 см = 2580 см = 25 м 8 дм
$ \begin{array}{r|l} 4\;м\;500\;мм & \\ :3 & 1\;м\;5\;дм\\ +650\;мм & 2\;м\;1\;дм\;5\;см\\ *12 & 25\;м\;8\;дм \end{array} $
Ответ: 25 м 8 дм
Решение б
1) 4 м 8 дм * 5 = 48 дм * 5 = 240 дм = 24 м
2) 24 м : 12 = 2 м
3) 2 м * 6 = 12 м
$ \begin{array}{r|l} 4\;м\;8\;дм & \\ *5 & 24\;м\\ :12\;мм & 2\;м\\ *6 & 12\;м \end{array} $
Ответ: 12 м
Решение в
1) 9 ц 60 кг : 8 = 960 кг : 8 = 120 кг = 1 ц 20 кг
2) 1 ц 20 кг + 80 кг = 1 ц 100 кг = 2 ц
3) 2 ц * 25 = 50 ц = 5 т
$ \begin{array}{r|l} 9\;ц\;60\;кг & \\ :8 & 1\;ц\;20\;кг\\ +80\;кг & 2\;ц\\ *25 & 5\;т \end{array} $
Ответ: 5 т
Решение г
1) 3 км 500 м : 50 = 3500 м : 50 = 70 м
2) 70 м * 8 = 560 м
3) 560 м + 40 м = 600 м
$ \begin{array}{r|l} 3\;км\;500\;м & \\ :50 & 70\;м\\ *8 & 560\;м\\ +40\;м & 600\;м \end{array} $
Ответ: 600 м
Решение д
1) 4 т 500 кг : 900 = 4500 кг : 900 = 5 кг
2) 5 кг + 995 кг = 1000 кг = 1 т
3) 1 т : 25 = 1000 кг : 25 = 40 кг
$ \begin{array}{r|l} 4\;т\;500\;кг & \\ :900 & 5\;кг\\ +995\;кг & 1\;т\\ :25 & 40\;кг \end{array} $
Ответ: 40 кг
Решение е
1) 2 м 50 см : 5 = 250 см : 5 = 50 см = 5 дм
2) 5 дм * 8 = 40 дм = 4 м
3) 4 м − 1 м 60 см = 40 дм − 16 дм = 24 дм = 2 м 4 дм
$ \begin{array}{r|l} 2\;м\;50\;см & \\ :5 & 5\;дм\\ *8 & 4\;м\\ -1\;м\;60\;см & 2\;м\;4\;дм \end{array} $
Ответ: 2 м 4 дм 11
-
Номер №11
Сколько кубических сантиметров в одной сотой кубического метра?
Решение
1 $м^3$ = 1000000 $cм^3$
$\frac{1}{100} м^3 = (1000000 : 100) cм^3 = 10000 cм^3$
Ответ: 10000 $cм^3$ в одной сотой кубического метра 12
-
Номер №12
Сколько метров в половине километра?
Решение
1 км = 1000 м
$\frac{1}{2}$ км = (1000 : 2) м = 500 м
Ответ: 500 метров в половине километра. 13
-
Номер №13
Почтовый голубь пролетает в час 92 км. Сколько он пролетит за $\frac{3}{4}$ часа?
Решение
92 : 4 * 3 = 23 * 3 = 69 (км) − пролетит почтовый голубь за $\frac{3}{4}$ часа.
Ответ: 69 км 14
-
Номер №14
Велосипедист проехал 12 км, что составляет $\frac{1}{4}$ намеченного маршрута. Сколько километров должен был проехать велосипедист?
Решение
12 * 4 = 48 (км) − должен был проехать велосипедист.
Ответ: 48 км 15
-
Номер №15
$\frac{1}{3}$ отрезка прямой равна 2 см. Сколько сантиметров во всем отрезке?
Решение
2 * 3 = 6 (см) − во всем отрезке.
Ответ: 6 см 16
-
Номер №16
При каких натуральных значениях a:
а) будут правильными дроби $\frac{5}{a}$ и $\frac{a}{11}$ _
б) будут неправильными дроби $\frac{a}{13}$ и $\frac{14}{a}$ _
в) будут правильными дроби $\frac{8}{a}$ и $\frac{a}{12}$ _
г) будут неправильными дроби $\frac{12}{a}$ и $\frac{a}{8}$ _
Решение а
дроби $\frac{5}{a}$ и $\frac{a}{11}$ будут правильными
при a = 6; 7; 8; 9; 10.
Решение б
дроби $\frac{a}{13}$ и $\frac{14}{a}$ будут неправильными
при a = 13; 14.
Решение в
дроби $\frac{8}{a}$ и $\frac{a}{12}$ будут правильными
при a = 9; 10; 11.
Решение г
дроби $\frac{12}{a}$ и $\frac{a}{8}$ будут неправильными
при a = 8; 9; 10; 11; 12. 17
-
Номер №17
При каких натуральных значениях a выполняется неравенство:
а) $\frac{1}{2} < \frac{a}{10} < 1$
б) $\frac{1}{3} < \frac{a}{6} < 1$
в) $\frac{1}{6} < \frac{a}{24} < \frac{1}{3}$
г) $\frac{1}{4} < \frac{a}{16} < \frac{1}{2}$
Решение а
$\frac{1}{2} < \frac{a}{10} < 1$
$\frac{5}{10} < \frac{a}{10} < 1$, значит неравенство выполняется
при a = 6; 7; 8; 9.
Решение б
$\frac{1}{3} < \frac{a}{6} < 1$
$\frac{2}{6} < \frac{a}{6} < 1$, значит неравенство выполняется
при a = 3; 4; 5.
Решение в
$\frac{1}{6} < \frac{a}{24} < \frac{1}{3}$
$\frac{4}{24} < \frac{a}{24} < \frac{8}{24}$, значит неравенство выполняется
при a = 5; 6; 7.
Решение г
$\frac{1}{4} < \frac{a}{16} < \frac{1}{2}$
$\frac{4}{16} < \frac{a}{16} < \frac{8}{16}$, значит неравенство выполняется
при a = 5; 6; 7. Сложение и вычитание дробей 1
-
26. Сложение и вычитание дробей с одинаковыми знаменателями . Номер №1
Вставьте пропущенные слова так, чтобы получились верные высказывания.
а) Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их _, а _ оставить тот же.
б) Чтобы из данной дроби вычесть дробь с тем же знаменателем, нужно из _ первой дроби вычесть _ второй дроби, а _ оставить тот же.
Решение
а) Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
б) Чтобы из данной дроби вычесть дробь с тем же знаменателем, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же. 2
-
Номер №2
Запишите недостающие числа.
а) $\frac{5}{7} + \frac{1}{7} = \frac{}{7}$
б) $\frac{3}{8} + \frac{2}{8} = \frac{}{8}$
в) $\frac{4}{11} + \frac{5}{11} = \frac{}{11}$
г) $\frac{5}{6} - \frac{3}{6} = \frac{}{6}$
д) $\frac{3}{4} - \frac{2}{4} = \frac{}{4}$
е) $\frac{5}{10} - \frac{5}{10} = ...$
ж) $\frac{2}{3} + \frac{1}{3} = ...$
з) $\frac{8}{13} - \frac{5}{13} = \frac{}{13}$
и) $\frac{9}{9} - \frac{1}{9} = \frac{}{9}$
Решение а
$\frac{5}{7} + \frac{1}{7} = \frac{6}{7}$
Решение б
$\frac{3}{8} + \frac{2}{8} = \frac{5}{8}$
Решение в
$\frac{4}{11} + \frac{5}{11} = \frac{9}{11}$
Решение г
$\frac{5}{6} - \frac{3}{6} = \frac{2}{6}$
Решение д
$\frac{3}{4} - \frac{2}{4} = \frac{1}{4}$
Решение е
$\frac{5}{10} - \frac{5}{10} = 0$
Решение ж
$\frac{2}{3} + \frac{1}{3} = \frac{3}{3} = 1$
Решение з
$\frac{8}{13} - \frac{5}{13} = \frac{3}{13}$
Решение и
$\frac{9}{9} - \frac{1}{9} = \frac{8}{9}$ 3
-
Номер №3
Запишите результат действий.
а) $\frac{3}{5} + \frac{2}{5} =$
б) $\frac{8}{10} - \frac{3}{10} =$
в) $\frac{31}{100} + \frac{31}{100} =$
г) $\frac{29}{30} - \frac{29}{30} =$
д) $\frac{3}{7} + \frac{4}{7} =$
е) $\frac{8}{11} + \frac{2}{11} =$
ж) $\frac{18}{49} - \frac{11}{49} =$
з) $\frac{3}{4} - \frac{2}{4} =$
и) $\frac{8}{8} - \frac{3}{8} =$
Решение а
$\frac{3}{5} + \frac{2}{5} = \frac{5}{5} = 1$
Решение б
$\frac{8}{10} - \frac{3}{10} = \frac{5}{10}$
Решение в
$\frac{31}{100} + \frac{31}{100} = \frac{62}{100}$
Решение г
$\frac{29}{30} - \frac{29}{30} = 0$
Решение д
$\frac{3}{7} + \frac{4}{7} = \frac{7}{7} = 1$
Решение е
$\frac{8}{11} + \frac{2}{11} = \frac{10}{11}$
Решение ж
$\frac{18}{49} - \frac{11}{49} = \frac{7}{49}$
Решение з
$\frac{3}{4} - \frac{2}{4} = \frac{1}{4}$
Решение и
$\frac{8}{8} - \frac{3}{8} = \frac{5}{8}$ 4
-
Номер №4
Сложите дроби.
а) $\frac{2}{17} + \frac{3}{17} + \frac{9}{17} =$
б) $\frac{1}{5} + \frac{3}{5} + \frac{1}{5} =$
в) $\frac{3}{4} + \frac{5}{11} + \frac{6}{11} + \frac{1}{4} =$
г) $\frac{3}{16} + \frac{7}{16} + \frac{5}{16} =$
д) $\frac{7}{10} + \frac{1}{10} + \frac{1}{10} =$
е) $\frac{14}{15} + \frac{3}{2} + \frac{16}{15} + \frac{1}{2} =$
Решение а
$\frac{2}{17} + \frac{3}{17} + \frac{9}{17} = \frac{5}{17} + \frac{9}{17} = \frac{14}{17}$
Решение б
$\frac{1}{5} + \frac{3}{5} + \frac{1}{5} = \frac{4}{5} + \frac{1}{5} = \frac{5}{5} =1$
Решение в
$\frac{3}{4} + \frac{5}{11} + \frac{6}{11} + \frac{1}{4} = (\frac{3}{4} + \frac{1}{4}) + (\frac{5}{11} + \frac{6}{11}) = \frac{4}{4} + \frac{11}{11} = 1 + 1 = 2$
Решение г
$\frac{3}{16} + \frac{7}{16} + \frac{5}{16} = \frac{10}{16} + \frac{5}{16} = \frac{15}{16}$
Решение д
$\frac{7}{10} + \frac{1}{10} + \frac{1}{10} = \frac{8}{10} + \frac{1}{10} = \frac{9}{10}$
Решение е
$\frac{14}{15} + \frac{3}{2} + \frac{16}{15} + \frac{1}{2} = (\frac{14}{15} + \frac{16}{15}) + (\frac{3}{2} + \frac{1}{2}) = \frac{30}{15} + \frac{4}{2} = 2 + 2 = 4$ 5
-
Номер №5
Закончите решения уравнений.
а)
$x + \frac{3}{17} = \frac{14}{17}$
$x = \frac{14}{17} ... \frac{3}{17}$
x =
б)
$\frac{4}{11} + y = \frac{5}{11}$
$y = \frac{5}{11} ... \frac{4}{11}$
y =
в)
$a - \frac{3}{8} = \frac{2}{8}$
$a = \frac{2}{8} ... \frac{3}{8}$
a =
г)
$\frac{5}{13} - b = \frac{2}{13}$
$b = \frac{5}{13} ... \frac{2}{13}$
b =
д)
$c + \frac{8}{15} = \frac{12}{15}$
c =
c =
е)
$\frac{11}{43} - x = \frac{3}{43}$
x =
x =
Решение а
$x + \frac{3}{17} = \frac{14}{17}$
$x = \frac{14}{17} - \frac{3}{17}$
$x = \frac{11}{17}$
Ответ: $x = \frac{11}{17}$
Решение б
$\frac{4}{11} + y = \frac{5}{11}$
$y = \frac{5}{11} - \frac{4}{11}$
$y = \frac{1}{11}$
Ответ: $y = \frac{1}{11}$
Решение в
$a - \frac{3}{8} = \frac{2}{8}$
$a = \frac{2}{8} + \frac{3}{8}$
$a = \frac{5}{8}$
Ответ: $a = \frac{5}{8}$
Решение г
$\frac{5}{13} - b = \frac{2}{13}$
$b = \frac{5}{13} - \frac{2}{13}$
$b = \frac{3}{13}$
Ответ: $b = \frac{3}{13}$
Решение д
$c + \frac{8}{15} = \frac{12}{15}$
$c = \frac{12}{15} - \frac{8}{15}$
$c = \frac{4}{15}$
Ответ: $c = \frac{4}{15}$
Решение е
$\frac{11}{43} - x = \frac{3}{43}$
$x = \frac{11}{43} - \frac{3}{43}$
$x = \frac{8}{43}$
Ответ: $x = \frac{8}{43}$ 6
-
Номер №6
Заполните таблицы.Первое слагаемое Второе слагаемое Сумма $\frac{1}{2}$ $\frac{1}{2}$ 1 $\frac{1}{3}$ 1 $\frac{3}{5}$ 1 $\frac{9}{13}$ 1 Первое слагаемое Второе слагаемое Сумма $\frac{}{14}$ $\frac{}{14}$ 1 $\frac{}{19}$ $\frac{}{19}$ 1 $\frac{}{21}$ $\frac{7}{}$ 1 $\frac{8}{}$ $\frac{16}{}$ 1
Решение
Заполните таблицы.Первое слагаемое Второе слагаемое Сумма $\frac{1}{2}$ $\frac{1}{2}$ 1 $\frac{1}{3}$ $\frac{2}{3}$ 1 $\frac{2}{5}$ $\frac{3}{5}$ 1 $\frac{9}{13}$ $\frac{4}{13}$ 1 Первое слагаемое Второе слагаемое Сумма $\frac{1}{14}$ $\frac{13}{14}$ 1 $\frac{2}{19}$ $\frac{17}{19}$ 1 $\frac{14}{21}$ $\frac{7}{21}$ 1 $\frac{8}{24}$ $\frac{16}{24}$ 1 7
-
Номер №7
Решите задачи.
а) Два поезда идут навстречу друг другу. Один прошел две пятых всего пути, а другой − половину. Сколько километров осталось им идти до встречи, если между ними было 200 км?
б) Руда содержит железо в количестве три пятых от ее массы. Сколько железа можно получить из 1 тонны руды?
в) Одна треть отреза равна 4 см. Сколько сантиметров во всем отрезе?
г) Один самолет пролетает в одну пятую часа 90 км, а другой в одну десятую часа 60 км. На сколько километров один самолет пролетает в час больше другого?
Решение а
1) 200 : 5 * 2 = 40 * 2 = 80 (км) − прошел первый поезд;
2) 200 : 2 = 100 (км) − прошел второй поезд;
3) 200 − (80 + 100) = 200 − 180 = 20 (км) − осталось идти поездам до встречи.
Ответ: 20 км
Решение б
1 т = 10 ц
10 : 5 * 3 = 2 * 3 = 6 (ц) − железа можно получить из 1 тонны.
Ответ: 6 ц
Решение в
4 * 3 = 12 (см) − во всем отрезе.
Ответ: 12 см
Решение г
1) 90 * 5 = 450 (км) − в час пролетает первый самолет;
2) 60 * 10 = 600 (км) − в час пролетает второй самолет;
3) 600 − 450 = 150 (км) − на столько больше в час пролетает второй самолет, чем первый.
Ответ: на 150 км 8
-
Номер №8
Выполните действия.
а) $\frac{107}{111} - \frac{75}{111} - \frac{12}{111}$
б) $\frac{132}{163} - \frac{17}{163} - \frac{75}{163}$
в) $\frac{62}{103} - \frac{37}{103} - \frac{15}{103}$
г) $\frac{100}{187} - \frac{43}{187} - \frac{37}{187}$
Решение а
$\frac{107}{111} - \frac{75}{111} - \frac{12}{111} = \frac{107}{111} - (\frac{75}{111} + \frac{12}{111}) = \frac{107}{111} - \frac{87}{111} = \frac{20}{111}$
Решение б
$\frac{132}{163} - \frac{17}{163} - \frac{75}{163} = \frac{132}{163} - (\frac{17}{163} + \frac{75}{163}) = \frac{132}{163} - \frac{92}{163} = \frac{40}{163}$
Решение в
$\frac{62}{103} - \frac{37}{103} - \frac{15}{103} = \frac{62}{103} - (\frac{37}{103} + \frac{15}{103}) = \frac{62}{103} - \frac{52}{103} = \frac{10}{103}$
Решение г
$\frac{100}{187} - \frac{43}{187} - \frac{37}{187} = \frac{100}{187} - (\frac{43}{187} + \frac{37}{187}) = \frac{100}{187} - \frac{80}{187} = \frac{20}{187}$ 9
-
Номер №9
Выполните действия.
а) $\frac{17}{179} + \frac{167}{179} - \frac{77}{179} - \frac{67}{179}$
б) $\frac{102}{109} + \frac{18}{109} - \frac{39}{109} - \frac{51}{109}$
в) $\frac{19}{131} + \frac{129}{131} - \frac{49}{131} - \frac{39}{131}$
г) $\frac{61}{153} + \frac{109}{153} - \frac{68}{153} - \frac{2}{153}$
Решение а
$\frac{17}{179} + \frac{167}{179} - \frac{77}{179} - \frac{67}{179} = \frac{17}{179} + (\frac{167}{179} - \frac{77}{179}) - \frac{67}{179} = \frac{17}{179} + \frac{90}{179} - \frac{67}{179} = \frac{107}{179} - \frac{67}{179} = \frac{40}{179}$
Решение б
$\frac{102}{109} + \frac{18}{109} - \frac{39}{109} - \frac{51}{109} = (\frac{102}{109} + \frac{18}{109}) - (\frac{39}{109} + \frac{51}{109}) = \frac{120}{109} - \frac{90}{109} = \frac{30}{109}$
Решение в
$\frac{19}{131} + \frac{129}{131} - \frac{49}{131} - \frac{39}{131} = \frac{19}{131} + (\frac{129}{131} - \frac{49}{131}) - \frac{39}{131} = \frac{19}{131} + \frac{80}{131} - \frac{39}{131} = \frac{99}{131} - \frac{39}{131} = \frac{60}{131}$
Решение г
$\frac{61}{153} + \frac{109}{153} - \frac{68}{153} - \frac{2}{153} = (\frac{61}{153} + \frac{109}{153}) - (\frac{68}{153} + \frac{2}{153}) = \frac{170}{153} - \frac{70}{153} = \frac{100}{153}$ 10
-
Номер №10
Выполните действия.
а) $(\frac{31}{47} - \frac{6}{47}) - (\frac{11}{47} - \frac{6}{47})$
б) $(\frac{29}{53} - \frac{9}{53}) - (\frac{21}{53} - \frac{9}{53})$
в) $\frac{17}{27} - (\frac{2}{27} + (\frac{9}{27} - \frac{4}{27}))$
г) $\frac{18}{29} - (\frac{3}{29} + (\frac{16}{29} - \frac{11}{29}))$
Решение а
$(\frac{31}{47} - \frac{6}{47}) - (\frac{11}{47} - \frac{6}{47}) = \frac{25}{47} - \frac{5}{47} = \frac{20}{47}$
Решение б
$(\frac{29}{53} - \frac{9}{53}) - (\frac{21}{53} - \frac{9}{53}) = \frac{20}{53} - \frac{12}{53} = \frac{8}{53}$
Решение в
$\frac{17}{27} - (\frac{2}{27} + (\frac{9}{27} - \frac{4}{27})) = \frac{17}{27} - (\frac{2}{27} + \frac{5}{27}) = \frac{17}{27} - \frac{7}{27} = \frac{10}{27}$
Решение г
$\frac{18}{29} - (\frac{3}{29} + (\frac{16}{29} - \frac{11}{29})) = \frac{18}{29} - (\frac{3}{29} + \frac{5}{29}) = \frac{18}{29} - \frac{8}{29} = \frac{10}{29}$ 11
-
Номер №11
Решите уравнения.
а) $\frac{53}{71} - (\frac{65}{71} - x) = \frac{14}{71}$
б) $(x - \frac{11}{53}) - \frac{3}{53} = \frac{17}{53}$
в) $\frac{37}{41} - (\frac{25}{41} + (\frac{17}{41} - x)) = \frac{2}{41}$
г) $\frac{4}{19} + (\frac{11}{19} - (x - \frac{1}{19})) = \frac{3}{19}$
Решение а
$\frac{53}{71} - (\frac{65}{71} - x) = \frac{14}{71}$
$\frac{65}{71} - x = \frac{53}{71} - \frac{14}{71}$
$\frac{65}{71} - x = \frac{39}{71}$
$x = \frac{65}{71} - \frac{39}{71}$
$x = \frac{26}{71}$
Ответ: $x = \frac{26}{71}$
Решение б
$(x - \frac{11}{53}) - \frac{3}{53} = \frac{17}{53}$
$x - \frac{11}{53} = \frac{17}{53} + \frac{3}{53}$
$x - \frac{11}{53} = \frac{20}{53}$
$x = \frac{20}{53} + \frac{11}{53}$
$x = \frac{31}{53}$
Ответ: $x = \frac{31}{53}$
Решение в
$\frac{37}{41} - (\frac{25}{41} + (\frac{17}{41} - x)) = \frac{2}{41}$
$\frac{25}{41} + (\frac{17}{41} - x) = \frac{37}{41} - \frac{2}{41}$
$\frac{25}{41} + (\frac{17}{41} - x) = \frac{35}{41}$
$\frac{17}{41} - x = \frac{35}{41} - \frac{25}{41}$
$\frac{17}{41} - x = \frac{10}{41}$
$x = \frac{17}{41} - \frac{10}{41}$
$x = \frac{7}{41}$
Ответ: $x = \frac{7}{41}$
Решение г
$\frac{4}{19} + (\frac{11}{19} - (x - \frac{1}{19})) = \frac{3}{19}$
в тетради опечатка, чтобы уравнение возможно было решить, оно должно выглядеть так:
$\frac{4}{19} - (\frac{11}{19} - (x - \frac{1}{19})) = \frac{3}{19}$
$\frac{11}{19} - (x - \frac{1}{19}) = \frac{4}{19} - \frac{3}{19}$
$\frac{11}{19} - (x - \frac{1}{19}) = \frac{1}{19}$
$x - \frac{1}{19} = \frac{11}{19} - \frac{1}{19}$
$x - \frac{1}{19} = \frac{10}{19}$
$x = \frac{10}{19} + \frac{1}{19}$
$x = \frac{11}{19}$
Ответ: $x = \frac{11}{19}$ 12
-
Номер №12
Решите задачи.
а) За 2 часа водой заполняется $\frac{5}{19}$ бассейна, а выливается за то же время $\frac{2}{19}$ бассейна. На какую часть изменится уровень воды в бассейне через 6 часов?
б) Максим прочитал $\frac{7}{13}$ книги и еще 8 страниц, после чего Максиму осталось прочитать $\frac{2}{13}$ книги. Сколько страниц в книге?
Решение а
1) $\frac{5}{19} - \frac{2}{19} = \frac{3}{19}$ (бассейна) − наполняется за 2 часа;
2) 6 : 2 = 3 (раза) − больше наполнится бассейн за 6 часов;
3) $3 * \frac{3}{19} = \frac{3}{19} + \frac{3}{19} + \frac{3}{19} = \frac{9}{19}$ (бассейна) − наполнится за 6 часов.
Ответ: $\frac{9}{19}$ бассейна
Решение б
Вся книга равна 1, тогда:
1) $1 - (\frac{7}{13} + \frac{2}{13}) = \frac{13}{13} - \frac{9}{13} = \frac{4}{13}$ (книги) − составляют 8 страниц;
2) 8 : 4 = 2 (страницы) − составляют $\frac{1}{13}$ книги;
3) 2 * 13 = 26 (страниц) − всего в книге.
Ответ: 26 страниц Деление и дроби 1
-
27. Деление и дроби. Номер №1
Каждую дробь запишите в виде отношения. Если возможно, упростите результаты.
Образец: $\frac{10}{5} = 10 : 5 = 2$.
а) $\frac{1}{3} =$
б) $\frac{24}{6} =$
в) $\frac{10}{7} =$
г) $\frac{32}{8} =$
д) $\frac{3}{8} =$
е) $\frac{11}{1} =$
Решение а
$\frac{1}{3} = 1 : 3$
Решение б
$\frac{24}{6} = 24 : 6 = 4$
Решение в
$\frac{10}{7} = 10 : 7$
Решение г
$\frac{32}{8} = 32 : 8 = 4$
Решение д
$\frac{3}{8} = 3 : 8$
Решение е
$\frac{11}{1} = 11 : 1 = 11$ 2
-
Номер №2
Представьте каждое частное в виде дроби.
Образец: $7 : 9 = \frac{7}{9}$
а) 3 : 5 =
б) 1 : 10 =
в) 15 : 7 =
г) 84 : 10 =
д) 30 : 4 =
е) 9 : 1 =
Решение а
$3 : 5 = \frac{3}{5}$
Решение б
$1 : 10 = \frac{1}{10}$
Решение в
$15 : 7 = \frac{15}{7}$
Решение г
$84 : 10 = \frac{84}{10}$
Решение д
$30 : 4 = \frac{30}{4}$
Решение е
$9 : 1 = \frac{9}{1}$ 3
-
Номер №3
Заполните таблицу.Делимое Делитель Частное Дробь Числитель дроби Знаменатель дроби 5 11 5:11 $\frac{5}{11}$ 5 11 19 40 3:13 7 10 18 25
Решение
Заполните таблицу.Делимое Делитель Частное Дробь Числитель дроби Знаменатель дроби 5 11 5:11 $\frac{5}{11}$ 5 11 19 40 19 : 40 $\frac{19}{40}$ 19 40 3 13 3:13 $\frac{3}{13}$ 3 13 7 10 7 : 10 $\frac{7}{10}$ 7 10 18 25 18 : 25 $\frac{18}{25}$ 18 25 4
-
Номер №4
Отметьте на координатном луче точку, соответствующую числу 1.
Решение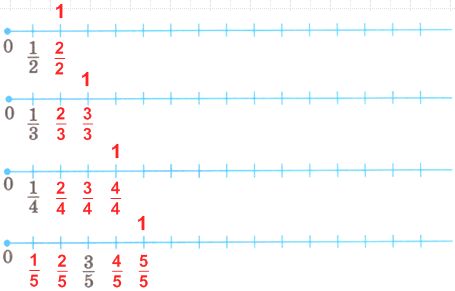
5
-
Номер №5
Запишите 8 в виде дроби со знаменателем:
а) 2
б) 3
в) 4
г) 5
д) 10
е) 100
Решение а
2 − знаменатель дроби;
2 * 8 = 16 − числитель дроби.
Ответ: $\frac{16}{2}$
Решение б
3 − знаменатель дроби;
3 * 8 = 24 − числитель дроби.
Ответ: $\frac{24}{3}$
Решение в
4 − знаменатель дроби;
4 * 8 = 32 − числитель дроби.
Ответ: $\frac{32}{4}$
Решение г
5 − знаменатель дроби;
5 * 8 = 40 − числитель дроби.
Ответ: $\frac{40}{5}$
Решение д
10 − знаменатель дроби;
10 * 8 = 80 − числитель дроби.
Ответ: $\frac{80}{10}$
Решение е
100 − знаменатель дроби;
100 * 8 = 800 − числитель дроби.
Ответ: $\frac{800}{100}$ 6
-
Номер №6
Заполните пропуски.
а) $\frac{3}{5}$ км = _ м
б) $\frac{1}{2}$ т = _ ц
в) $\frac{1}{4}$ руб. = _ коп
г) $\frac{7}{10}$ т = _ кг
д) $\frac{1}{8}$ кг = _ г
е) $\frac{5}{8}$ суток = _ час
Решение а
1 км = 1000 м
1000 м : 5 * 3 = 200 * 3 = 600 м
Ответ: $\frac{3}{5}$ км = 600 м
Решение б
1 т = 10 ц
10 ц : 2 * 1 = 5 * 1 = 5 ц
Ответ: $\frac{1}{2}$ т = 5 ц
Решение в
1 руб. = 100 коп
100 коп. : 4 * 1 = 25 * 1 = 25 коп
Ответ: $\frac{1}{4}$ руб. = 25 коп
Решение г
1 т = 1000 кг
1000 кг : 10 * 7 = 100 * 7 = 700 кг
Ответ: $\frac{7}{10}$ т = 700 кг
Решение д
1 кг = 1000 г
1000 г : 8 = 125 * 1 = 125 г
Ответ: $\frac{1}{8}$ кг = 125 г
Решение е
1 сут. = 24 час
24 час : 8 * 5 = 3 * 5 = 15 час
Ответ: $\frac{5}{8}$ суток = 15 час 7
-
Номер №7
Решите задачи.
а) В школе 600 учащихся. Одна пятая этого числа − отличники. Сколько в школе отличников?
б) В одной деревне 160 детей. Из них: $\frac{1}{8}$ − в яслях, $\frac{1}{5}$ − в детском саду, $\frac{1}{4}$ − дома, а остальные посещают школу. Сколько детей посещают школу?
в) В саду 168 деревьев. $\frac{3}{7}$ этих деревьев − яблони, $\frac{1}{3}$ всех деревьев − груши, а остальные вишни. Сколько было вишен?
Решение а
600 : 5 * 1 = 120 (отличников) − в школе.
Ответ: 120 отличников
Решение б
1) 160 : 8 * 1 = 20 (детей) − в яслях;
2) 160 : 5 * 1 = 32 (ребенка) − в детском саду;
3) 160 : 4 * 1 = 40 (детей) − дома;
4) 160 − (20 + 32 + 40) = 160 − 92 = 68 (детей) − посещают школу.
Ответ: 68 детей
Решение в
1) 168 : 7 * 3 = 24 * 3 = 72 (яблони) − растут в саду;
2) 168 : 3 * 1 = 56 (груш) − растет в саду;
3) 168 − (72 + 56) = 168 − 128 = 40 (вишен) − растет в саду.
Ответ: 40 вишен 8
-
Номер №8
Сложите $\frac{1}{4}$ числа 60 с $\frac{1}{8}$ числа 72.
Решение
60 : 4 + 72 : 8 = 15 + 9 = 24
Ответ: 24 9
-
Номер №9
Вычтите $\frac{3}{4}$ числа 84 из $\frac{7}{8}$ числа 96.
Решение
96 : 8 * 7 − 84 : 4 * 3 = 12 * 7 − 21 * 3 = 84 − 63 = 21
Ответ: 21 10
-
Номер №10
Заполните таблицу.a 9 100 7 1 5 b 8 10 3 0 5 3a 12a
Решение
при a = 9 и b = 8:
3a + 4b = 3 * 9 + 4 * 8 = 27 + 32 = 59
12a − 7b = 12 * 9 − 7 * 8 = 108 − 56 = 52
при a = 100 и b = 10:
3a + 4b = 3 * 100 + 4 * 10 = 300 + 40 = 340
12a − 7b = 12 * 100 − 7 * 10 = 1200 − 70 = 1130
при a = 7 и b = 3:
3a + 4b = 3 * 7 + 4 * 3 = 21 + 12 = 33
12a − 7b = 12 * 7 − 7 * 3 = 84 − 21 = 63
при a = 1 и b = 0:
3a + 4b = 3 * 1 + 4 * 0 = 3 + 0 = 3
12a − 7b = 12 * 1 − 7 * 0 = 12 − 0 = 12
при a = 5 и b = 5:
3a + 4b = 3 * 5 + 4 * 5 = 15 + 20 = 35
12a − 7b = 12 * 5 − 7 * 5 = 60 − 35 = 25
Ответ:a 9 100 7 1 5 b 8 10 3 0 5 3a 59 340 33 3 35 12a 52 1130 63 12 25 11
-
Номер №11
Вычислите:
а)
$ \begin{array}{rl} 96000 : 3200 & \\ *27 & \\ +90 & \\ :6 & \end{array} $
б)
$ \begin{array}{rl} 19000 + 11000 & \\ :600 & \\ *19 & \\ +50 & \end{array} $
в)
$ \begin{array}{rl} 1000 - 550 & \\ :9 & \\ :2 & \\ *3 & \end{array} $
Решение а
1) 96000 : 3200 = 960 : 32 = 30
2) 30 * 27 = 30 * (20 + 7) = 30 * 20 + 30 * 7 = 600 + 210 = 810
3) 810 + 90 = 900
4) 900 : 6 = (600 + 300) : 6 = 600 : 6 + 300 : 6 = 100 + 50 = 150
$ \begin{array}{r|l} 96000 : 3200 & 30\\ *27 & 810\\ +90 & 900\\ :6 & 150 \end{array} $
Ответ: 150
Решение б
1) 19000 + 11000 = 30000
2) 30000 : 600 = 300 : 6 = 50
3) 50 * 19 = 50 * (20 − 1) = 50 * 20 − 50 * 1 = 1000 − 50 = 950
4) 950 + 50 = 1000
$ \begin{array}{r|l} 19000 + 11000 & 30000\\ :600 & 50\\ *19 & 950\\ +50 & 1000 \end{array} $
Ответ: 1000
Решение в
1) 1000 − 550 = 450
2) 450 : 9 = 50
3) 50 : 2 = 25
4) 25 * 3 = (20 + 5) * 3 = 20 * 3 + 5 * 3 = 60 + 15 = 75
$ \begin{array}{r|l} 1000 - 550 & 450\\ :9 & 50\\ :2 & 25\\ *3 & 75 \end{array} $
Ответ: 75 12
-
Номер №12
Решите задачи.
а) Из 9 м ткани сшили 14 полотенец. Сколько метров ткани затратили на одно полотенце?
б) 7 кг варенья разлили в 13 банок. Сколько килограммов варенья в одной банке?
в) Дедушка разлили 11 кг меда в 7 больших банок и 6 кг меда в 7 маленьких банок. На сколько килограммов меда больше в большой банке, чем в маленькой?
г) Максим пробегает 90 м за 12 сек., а Ваня за это же время − 78 м. На сколько скорость Максима больше скорости Вани?
Решение а
$9 : 14 = \frac{9}{14}$ (м) − ткани затратили на одно полотенце.
Ответ: $\frac{9}{14}$ м
Решение б
$7 : 13 = \frac{3}{13}$ (кг) − варенья в одной банке.
Ответ: $\frac{7}{13}$ кг
Решение в
1) $11 : 7 = \frac{11}{7}$ (кг) − меда в одной большой банке;
2) $6 : 7 = \frac{6}{7}$ (кг) − меда в одной маленькой банке;
3) $\frac{11}{7} - \frac{6}{7} = \frac{5}{7}$ − на столько килограммов меда больше в большой банке, чем в маленькой.
Ответ: на $\frac{5}{7}$ кг
Решение г
1) $90 : 12 = \frac{90}{12}$ (м/с) − скорость Максима;
2) $78 : 12 = \frac{78}{12}$ (м/с) − скорость Вани;
3) $\frac{90}{12} - \frac{78}{12} = \frac{12}{12} = 1$ (м/с) − на столько скорость Максима больше скорости Вани.
Ответ: на 1 м/с Смешанные числа 1
-
28. Смешанные числа. Номер №1
Заполните таблицу.Смешанное число Целая часть Дробная часть $3\frac{2}{5}$ 3 $\frac{2}{5}$ 5 $\frac{3}{4}$ 8 $\frac{10}{23}$
РешениеСмешанное число Целая часть Дробная часть $3\frac{2}{5}$ 3 $\frac{2}{5}$ $2\frac{1}{7}$ 2 $\frac{1}{7}$ $5\frac{3}{4}$ 5 $\frac{3}{4}$ $8\frac{10}{23}$ 8 $\frac{10}{23}$ 2
-
Номер №2
Запишите в виде смешанного числа суммы.
а) $3 + \frac{4}{5} =$
б) $\frac{8}{9} + 2 =$
в) $30 + \frac{7}{8} =$
г) $3 + 6 + \frac{2}{3} =$
д) $4 + \frac{2}{7} + 3 =$
е) $31 + \frac{5}{5} + \frac{2}{9} =$
Решение а
$3 + \frac{4}{5} = 3\frac{4}{5}$
Решение б
$\frac{8}{9} + 2 = 2\frac{8}{9}$
Решение в
$30 + \frac{7}{8} = 30\frac{7}{8}$
Решение г
$3 + 6 + \frac{2}{3} = (3 + 6) + \frac{2}{3} = 9 + \frac{2}{3} = 9\frac{2}{3}$
Решение д
$4 + \frac{2}{7} + 3 = (4 + 3) + \frac{2}{7} = 7 + \frac{2}{7} = 7\frac{2}{7}$
Решение е
$31 + \frac{5}{5} + \frac{2}{9} = 31 + 1 + \frac{2}{9} = (31 + 1) + \frac{2}{9} = 32 + \frac{2}{9} = 32\frac{2}{9}$ 3
-
Номер №3
Представьте неправильные дроби в виде смешанных чисел.
а) $\frac{5}{4} = 1\frac{1}{4}$
б) $\frac{20}{7} = 2\frac{}{7}$
в) $\frac{38}{6} = 6\frac{}{6}$
г) $\frac{13}{7} = 1\frac{}{7}$
д) $\frac{30}{4} = 7\frac{}{4}$
е) $\frac{48}{5} = 9\frac{}{5}$
ж) $\frac{19}{3} =$
з) $\frac{58}{5} =$
и) $\frac{203}{10} =$
Решение а
$\frac{5}{4} = 1\frac{1}{4}$
Решение б
$\frac{20}{7} = 2\frac{6}{7}$
Решение в
$\frac{38}{6} = 6\frac{2}{6}$
Решение г
$\frac{13}{7} = 1\frac{6}{7}$
Решение д
$\frac{30}{4} = 7\frac{2}{4}$
Решение е
$\frac{48}{5} = 9\frac{3}{5}$
Решение ж
$\frac{19}{3} = 6\frac{1}{3}$
Решение з
$\frac{58}{5} = 11\frac{3}{5}$
Решение и
$\frac{203}{10} = 20\frac{3}{10}$ 4
-
Номер №4
Представьте смешанные числа в виде неправильных дробей.
а) $1\frac{2}{3} = \frac{5}{3}$
б) $4\frac{3}{7} = \frac{}{7}$
в) $8\frac{1}{9} = \frac{73}{}$
г) $10\frac{2}{11} = \frac{}{11}$
д) $3\frac{1}{100} = \frac{}{100}$
е) $7\frac{3}{5} = \frac{38}{}$
ж) $6\frac{1}{9} =$
з) $20\frac{3}{17} =$
и) $4\frac{2}{9} =$
к) $5\frac{1}{13} =$
л) $10\frac{3}{11} =$
м) $9\frac{8}{9} =$
Решение а
$1\frac{2}{3} = \frac{1 * 3 + 2}{3} = \frac{3 + 2}{3} = \frac{5}{3}$
Решение б
$4\frac{3}{7} = \frac{4 * 7 + 3}{7} = \frac{28 + 3}{7} = \frac{31}{7}$
Решение в
$8\frac{1}{9} = \frac{8 * 9 + 1}{9} = \frac{72 + 1}{9} = \frac{73}{9}$
Решение г
$10\frac{2}{11} = \frac{10 * 11 + 2}{11} = \frac{110 + 2}{11} = \frac{112}{11}$
Решение д
$3\frac{1}{100} = \frac{3 * 100 + 1}{100} = \frac{300 + 1}{100} = \frac{301}{100}$
Решение е
$7\frac{3}{5} = \frac{7 * 5 + 3}{5} = \frac{35 + 3}{5} = \frac{38}{5}$
Решение ж
$6\frac{1}{9} = \frac{6 * 9 + 1}{9} = \frac{54 + 1}{9} = \frac{55}{9}$
Решение з
$20\frac{3}{17} = \frac{20 * 17 + 3}{17} = \frac{340 + 3}{17} = \frac{343}{17}$
Решение и
$4\frac{2}{9} = \frac{4 * 9 + 2}{9} = \frac{36 + 2}{9} = \frac{38}{9}$
Решение к
$5\frac{1}{13} = \frac{5 * 13 + 1}{13} = \frac{65 + 1}{13} = \frac{66}{13}$
Решение л
$10\frac{3}{11} = \frac{10 * 11 + 3}{11} = \frac{110 + 3}{11} = \frac{113}{11}$
Решение м
$9\frac{8}{9} = \frac{9 * 9 + 8}{9} = \frac{81 + 8}{9} = \frac{89}{9}$ 5
-
Номер №5
Выполните действия.
а) $\frac{13}{19} + \frac{6}{19} =$
б) $\frac{8}{21} + \frac{3}{21} + \frac{5}{21} =$
в) $\frac{36}{100} - \frac{14}{100} =$
г) $\frac{48}{50} - \frac{14}{50} =$
д) $\frac{3}{11} + \frac{7}{11} =$
е) $\frac{18}{23} - \frac{9}{23} =$
ж) $\frac{36}{48} + \frac{7}{48} - \frac{1}{48} =$
з) $\frac{35}{100} - \frac{9}{100} + \frac{1}{100} =$
и) $\frac{17}{41} + \frac{14}{41} - \frac{8}{41} =$
Решение а
$\frac{13}{19} + \frac{6}{19} = \frac{19}{19} = 1$
Решение б
$\frac{8}{21} + \frac{3}{21} + \frac{5}{21} = \frac{11}{21} + \frac{5}{21} = \frac{16}{21}$
Решение в
$\frac{36}{100} - \frac{14}{100} = \frac{22}{100}$
Решение г
$\frac{48}{50} - \frac{14}{50} = \frac{34}{50}$
Решение д
$\frac{3}{11} + \frac{7}{11} = \frac{10}{11}$
Решение е
$\frac{18}{23} - \frac{9}{23} = \frac{9}{23}$
Решение ж
$\frac{36}{48} + \frac{7}{48} - \frac{1}{48} = \frac{43}{48} - \frac{1}{48} = \frac{42}{48}$
Решение з
$\frac{35}{100} - \frac{9}{100} + \frac{1}{100} = \frac{26}{100} + \frac{1}{100} = \frac{27}{100}$
Решение и
$\frac{17}{41} + \frac{14}{41} - \frac{8}{41} = \frac{31}{41} - \frac{8}{41} = \frac{23}{41}$ 6
-
Номер №6
Решите задачи.
а) Жираф достигает высоты 27 дм. Выразите эту высоту в метрах.
б) Размах крыльев у кондора 275 см. Выразите его в метрах.
в) Тигры достигают 290 см в длину. Выразите эту величину в метрах.
г) Кит достигает в весе 50000 кг. Сколько тонн весит кит?
Решение а
1 м = 10 дм
27 дм = $\frac{27}{10}$ м = $2\frac{7}{10}$ м − достигает высота жирафа.
Ответ: $2\frac{7}{10}$ м
Решение б
1 м = 100 см
275 см = $\frac{275}{100}$ м = $2\frac{75}{100}$ м − размах крыльев у кондора.
Ответ: $2\frac{75}{100}$ м
Решение в
1 м = 100 см
290 см = $\frac{290}{100}$ м = $2\frac{90}{100}$ м − достигает длина тигра.
Ответ: $2\frac{90}{100}$ м
Решение г
1 т = 1000 кг
50000 кг = $\frac{50000}{1000}$ т = 50 т − достигает в весе кит.
Ответ: 50 т Сложение и вычитание смешанных чисел 1
-
29. Сложение и вычитание смешанных чисел. Номер №1
Представьте натуральные числа в виде смешанных по образцу:
$7 = 6\frac{5}{5}$
а) $8 = 7\frac{}{6}$
б) $9 = 8\frac{}{4}$
в) $14 = 13\frac{}{10}$
г) $9 = 8\frac{}{5}$
д) $6 = ...\frac{3}{3}$
е) $12 = ...\frac{7}{7}$
ж) $15 = ...\frac{8}{8}$
з) $24 = ...\frac{11}{11}$
и) $3 = 2\frac{4}{}$
к) $9 = 8\frac{7}{}$
л) $28 = 27\frac{10}{}$
м) $40 = 39\frac{21}{}$
Решение а
$8 = 7\frac{6}{6}$
Решение б
$9 = 8\frac{4}{4}$
Решение в
$14 = 13\frac{10}{10}$
Решение г
$9 = 8\frac{5}{5}$
Решение д
$6 = 5\frac{3}{3}$
Решение е
$12 = 11\frac{7}{7}$
Решение ж
$15 = 14\frac{8}{8}$
Решение з
$24 = 23\frac{11}{11}$
Решение и
$3 = 2\frac{4}{4}$
Решение к
$9 = 8\frac{7}{7}$
Решение л
$28 = 27\frac{10}{10}$
Решение м
$40 = 39\frac{21}{21}$ 2
-
Номер №2
Преобразуйте смешанные числа по образцу: $3\frac{1}{9} = 2\frac{10}{9}$
а) $7\frac{2}{3} = 6\frac{}{3}$
б) $15\frac{7}{9} = 14\frac{}{9}$
в) $12\frac{5}{8} = 11\frac{}{8}$
г) $1\frac{6}{10} = \frac{}{10}$
д) $11\frac{2}{7} = 10\frac{}{}$
е) $16\frac{1}{5} = 15\frac{}{}$
ж) $3\frac{6}{7} = 2\frac{}{}$
з) $2\frac{8}{9} = 1\frac{}{}$
и) $1\frac{1}{7} =$
к) $1\frac{3}{5} =$
л) $1\frac{4}{9} =$
м) $1\frac{9}{100} =$
Решение а
$7\frac{2}{3} = 6\frac{2 + 3}{3} = 6\frac{5}{3}$
Решение б
$15\frac{7}{9} = 14\frac{7 + 9}{9} = 14\frac{16}{9}$
Решение в
$12\frac{5}{8} = 11\frac{5 + 8}{8} = 11\frac{13}{8}$
Решение г
$1\frac{6}{10} = \frac{6 + 10}{10} = \frac{16}{10}$
Решение д
$11\frac{2}{7} = 10\frac{2 + 7}{7} = 10\frac{9}{7}$
Решение е
$16\frac{1}{5} = 15\frac{1 + 5}{5} = 15\frac{6}{5}$
Решение ж
$3\frac{6}{7} = 2\frac{}{} = 2\frac{6 + 7}{7} = 2\frac{13}{7}$
Решение з
$2\frac{8}{9} = 1\frac{8 + 9}{9} = 1\frac{17}{9}$
Решение и
$1\frac{1}{7} = \frac{1 + 7}{7} = \frac{8}{7}$
Решение к
$1\frac{3}{5} = \frac{3 + 5}{5} = \frac{8}{5}$
Решение л
$1\frac{4}{9} = \frac{4 + 9}{9} = \frac{13}{9}$
Решение м
$1\frac{9}{100} = \frac{9 + 100}{100} = \frac{109}{100}$ 3
-
Номер №3
Выполните действия.
а) $7\frac{1}{2} + 4 = (7 + 4) + \frac{1}{2} = 11\frac{1}{2}$
б) $7\frac{1}{2} - 4 = (7 - 4) + \frac{1}{2} = 3\frac{1}{2}$
в) $13\frac{3}{7} + 5 =$
г) $2\frac{8}{9} + 19 =$
д) $37\frac{5}{9} - 9 =$
е) $4\frac{13}{15} - 4 =$
ж) $15\frac{1}{10} - 8 =$
з) $34\frac{5}{11} + 9 =$
Решение а
$7\frac{1}{2} + 4 = (7 + 4) + \frac{1}{2} = 11\frac{1}{2}$
Решение б
$7\frac{1}{2} - 4 = (7 - 4) + \frac{1}{2} = 3\frac{1}{2}$
Решение в
$13\frac{3}{7} + 5 = (13 + 5) + \frac{3}{7} = 18\frac{3}{7}$
Решение г
$2\frac{8}{9} + 19 = (2 + 19) + \frac{8}{9} = 21\frac{8}{9}$
Решение д
$37\frac{5}{9} - 9 = (37 - 9) + \frac{5}{9} = 28\frac{5}{9}$
Решение е
$4\frac{13}{15} - 4 = (4 - 4) + \frac{13}{15} = \frac{13}{15}$
Решение ж
$15\frac{1}{10} - 8 = (15 - 8) + \frac{1}{10} = 7\frac{1}{10}$
Решение з
$34\frac{5}{11} + 9 = (34 + 9) + \frac{5}{11} = 43\frac{5}{11}$ 4
-
Номер №4
Выполните сложение.
а) $3\frac{3}{5} + \frac{1}{5} = 3 + \frac{3}{5} + \frac{1}{5} = 3 + (\frac{3}{5} + \frac{1}{5}) = 3\frac{4}{5}$
б) $4\frac{3}{7} + 2\frac{4}{7} = 6\frac{7}{7} = 6 + 1 = 7$
в) $3\frac{5}{6} + \frac{1}{6} =$
г) $15\frac{3}{8} + 4\frac{2}{8} =$
д) $\frac{7}{11} + 3\frac{2}{11} =$
е) $9\frac{3}{10} + 4\frac{1}{10} =$
ж) $17\frac{5}{12} + 1\frac{7}{12} =$
з) $\frac{1}{9} + 9\frac{8}{9} =$
Решение а
$3\frac{3}{5} + \frac{1}{5} = 3 + \frac{3}{5} + \frac{1}{5} = 3 + (\frac{3}{5} + \frac{1}{5}) = 3\frac{4}{5}$
Решение б
$4\frac{3}{7} + 2\frac{4}{7} = 6\frac{7}{7} = 6 + 1 = 7$
Решение в
$3\frac{5}{6} + \frac{1}{6} = 3 + \frac{5}{6} + \frac{1}{6} = 3 + (\frac{5}{6} + \frac{1}{6}) = 3\frac{6}{6} = 4$
Решение г
$15\frac{3}{8} + 4\frac{2}{8} = (15 + 4) + (\frac{3}{8} + \frac{2}{8}) = 19\frac{5}{8}$
Решение д
$\frac{7}{11} + 3\frac{2}{11} = 3 + \frac{7}{11} + \frac{2}{11} = 3 + (\frac{7}{11} + \frac{2}{11}) = 3\frac{9}{11}$
Решение е
$9\frac{3}{10} + 4\frac{1}{10} = (9 + 4) + (\frac{3}{10} + \frac{1}{10}) = 13\frac{4}{10}$
Решение ж
$17\frac{5}{12} + 1\frac{7}{12} = (17 + 1) + (\frac{5}{12} + \frac{7}{12}) = 18\frac{12}{12} = 19$
Решение з
$\frac{1}{9} + 9\frac{8}{9} = 9 + \frac{1}{9} + \frac{8}{9} = 9 + (\frac{1}{9} + \frac{8}{9}) = 9\frac{9}{9} = 10$ 5
-
Номер №5
Выполните вычитание.
а) $5\frac{3}{7} - 2\frac{2}{7} = (5 - 2) + (\frac{3}{7} - \frac{2}{7}) = 3\frac{1}{7}$
б) $15\frac{3}{100} - 3 = (15 - 3) + \frac{3}{100} = 12\frac{3}{100}$
в) $14\frac{3}{11} - \frac{3}{11} =$
г) $7\frac{2}{13} - 7 =$
д) $11\frac{1}{2} - 11\frac{1}{2} =$
е) $18\frac{4}{9} - 9\frac{3}{9} =$
ж) $10\frac{3}{7} - \frac{1}{7} =$
з) $16\frac{3}{10} - 16\frac{1}{10} =$
Решение а
$5\frac{3}{7} - 2\frac{2}{7} = (5 - 2) + (\frac{3}{7} - \frac{2}{7}) = 3\frac{1}{7}$
Решение б
$15\frac{3}{100} - 3 = (15 - 3) + \frac{3}{100} = 12\frac{3}{100}$
Решение в
$14\frac{3}{11} - \frac{3}{11} = 14 + (\frac{3}{11} - \frac{3}{11}) = 14$
Решение г
$7\frac{2}{13} - 7 = (7 - 7) + \frac{2}{13} = \frac{2}{13}$
Решение д
$11\frac{1}{2} - 11\frac{1}{2} = (11 - 11) + (\frac{1}{2} - \frac{1}{2}) = 0$
Решение е
$18\frac{4}{9} - 9\frac{3}{9} = (18 - 9) + (\frac{4}{9} - \frac{3}{9}) = 9\frac{1}{9}$
Решение ж
$10\frac{3}{7} - \frac{1}{7} = 10 + (\frac{3}{7} - \frac{1}{7}) = 10\frac{2}{7}$
Решение з
$16\frac{3}{10} - 16\frac{1}{10} = (16 - 16) + (\frac{3}{10} - \frac{1}{10}) = \frac{2}{10}$ 6
-
Номер №6
Выполните вычитание.
а) $3 - \frac{1}{4} = 2\frac{4}{4} - \frac{1}{4} = 2\frac{3}{4}$
б) $2 - \frac{1}{3} =$
в) $5 - \frac{3}{4} =$
г) $10 - \frac{2}{9} =$
д) $11 - \frac{11}{100} =$
е) $5 - \frac{2}{7} =$
ж) $13 - \frac{7}{10} =$
з) $1 - \frac{2}{5} =$
Решение а
$3 - \frac{1}{4} = 2\frac{4}{4} - \frac{1}{4} = 2\frac{3}{4}$
Решение б
$2 - \frac{1}{3} = 1\frac{3}{3} - \frac{1}{3} = 1\frac{2}{3}$
Решение в
$5 - \frac{3}{4} = 4\frac{4}{4} - \frac{3}{4} = 4\frac{1}{4}$
Решение г
$10 - \frac{2}{9} = 9\frac{9}{9} - \frac{2}{9} = 9\frac{7}{9}$
Решение д
$11 - \frac{11}{100} = 10\frac{100}{100} - \frac{11}{100} = 10\frac{89}{100}$
Решение е
$5 - \frac{2}{7} = 4\frac{7}{7} - \frac{2}{7} = 4\frac{5}{7}$
Решение ж
$13 - \frac{7}{10} = 12\frac{10}{10} - \frac{7}{10} = 12\frac{3}{10}$
Решение з
$1 - \frac{2}{5} = \frac{5}{5} - \frac{2}{5} = \frac{3}{5}$ 7
-
Номер №7
Выполните вычитание.
а) $9 - 2\frac{1}{5} = 8\frac{5}{5} - 2\frac{1}{5} = 6\frac{4}{5}$
б) $3 - \frac{1}{3} =$
в) $7 - \frac{3}{4} =$
г) $6 - 5\frac{5}{6} =$
д) $7 - 3\frac{7}{9} =$
е) $7 - 5\frac{4}{10} =$
ж) $1 - \frac{20}{30} =$
з) $1 - \frac{2}{7} =$
Решение а
$9 - 2\frac{1}{5} = 8\frac{5}{5} - 2\frac{1}{5} = 6\frac{4}{5}$
Решение б
$3 - \frac{1}{3} = 2\frac{3}{3} - \frac{1}{3} = 2\frac{2}{3}$
Решение в
$7 - \frac{3}{4} = 6\frac{4}{4} - \frac{3}{4} = 6\frac{1}{4}$
Решение г
$6 - 5\frac{5}{6} = 5\frac{6}{6} - 5\frac{5}{6} = \frac{1}{6}$
Решение д
$7 - 3\frac{7}{9} = 6\frac{9}{9} - 3\frac{7}{9} = 3\frac{2}{9}$
Решение е
$7 - 5\frac{4}{10} = 6\frac{10}{10} - 5\frac{4}{10} = 1\frac{6}{10}$
Решение ж
$1 - \frac{20}{30} = \frac{30}{30} - \frac{20}{30} = \frac{10}{30}$
Решение з
$1 - \frac{2}{7} = \frac{7}{7} - \frac{2}{7} = \frac{5}{7}$ 8
-
Номер №8
Закончите записи.
а) $5\frac{4}{7} + 8\frac{3}{7} = 13\frac{7}{7} =$
б) $6\frac{2}{9} + 2\frac{8}{9} = 8\frac{10}{9} = 8 + 1\frac{1}{9} =$
в) $5\frac{7}{8} + 2\frac{3}{8} = 7 +$
г) $6\frac{8}{9} + \frac{4}{9} = 6 +$
д) $8\frac{6}{10} - 3\frac{7}{10} = 7\frac{16}{10} - 3\frac{7}{10} = 4 +$
е) $5\frac{8}{10} - 2\frac{9}{10} = 4\frac{18}{10} - 2\frac{9}{10} =$
ж) $7\frac{5}{8} + 3\frac{4}{8} =$
з) $9\frac{3}{14} - 7\frac{5}{14} =$
и) $2\frac{2}{5} + 3\frac{3}{5} =$
к) $4\frac{3}{7} - 2\frac{3}{7} =$
Решение а
$5\frac{4}{7} + 8\frac{3}{7} = 13\frac{7}{7} = 13 + 1 = 14$
Решение б
$6\frac{2}{9} + 2\frac{8}{9} = 8\frac{10}{9} = 8 + 1\frac{1}{9} = 9\frac{1}{9}$
Решение в
$5\frac{7}{8} + 2\frac{3}{8} = 7 + \frac{10}{8} = 7 + 1\frac{2}{8} = 8\frac{2}{8}$
Решение г
$6\frac{8}{9} + \frac{4}{9} = 6 + \frac{12}{9} = 6 + 1\frac{3}{9} = 7\frac{3}{9}$
Решение д
$8\frac{6}{10} - 3\frac{7}{10} = 7\frac{16}{10} - 3\frac{7}{10} = 4\frac{9}{10}$
Решение е
$5\frac{8}{10} - 2\frac{9}{10} = 4\frac{18}{10} - 2\frac{9}{10} = 2\frac{9}{10}$
Решение ж
$7\frac{5}{8} + 3\frac{4}{8} = 10 + \frac{9}{8} = 10 + 1\frac{1}{8} = 11\frac{1}{8}$
Решение з
$9\frac{3}{14} - 7\frac{5}{14} = 8\frac{17}{14} - 7\frac{5}{14} = 1\frac{12}{14}$
Решение и
$2\frac{2}{5} + 3\frac{3}{5} = 5 + \frac{5}{5} = 5 + 1 = 6$
Решение к
$4\frac{3}{7} - 2\frac{3}{7} = 2 + 0 = 2$ 9
-
Номер №9
Решите уравнения.
а) $1\frac{2}{7} + x = 2$
x =
б) $y + 3\frac{2}{5} = 6\frac{3}{5}$
y =
в) $3\frac{3}{10} - x = 2\frac{7}{10}$
x =
г) $y - 7\frac{2}{10} = 1\frac{7}{10}$
y =
Решение а
$1\frac{2}{7} + x = 2$
$x = 2 - 1\frac{2}{7}$
$x = 1\frac{7}{7} - 1\frac{2}{7}$
$x = \frac{5}{7}$
Ответ: $x = \frac{5}{7}$
Решение б
$y + 3\frac{2}{5} = 6\frac{3}{5}$
$y = 6\frac{3}{5} - 3\frac{2}{5}$
$y = 3\frac{1}{5}$
Ответ: $y = 3\frac{1}{5}$
Решение в
$3\frac{3}{10} - x = 2\frac{7}{10}$
$x = 3\frac{3}{10} - 2\frac{7}{10}$
$x = 2\frac{13}{10} - 2\frac{7}{10}$
$x = \frac{6}{10}$
Ответ: $x = \frac{6}{10}$
Решение г
$y - 7\frac{2}{10} = 1\frac{7}{10}$
$y = 1\frac{7}{10} + 7\frac{2}{10}$
$y = 8\frac{9}{10}$
Ответ: $y = 8\frac{9}{10}$ 10
-
Номер №10
Решите задачи.
а) Один литр подсолнечного масла имеет массу 920 г. Какова масса $\frac{1}{4}$ литра подсолнечного масла?
б) Мотоциклист проехал 26 км, что составляет $\frac{1}{4}$ часть намеченного маршрута. Сколько километров должен был проехать мотоциклист?
Решение а
920 : 4 = (800 + 120) : 4 = 800 : 4 + 120 : 4 = 200 + 30 = 230 (г) − масса $\frac{1}{4}$ литра подсолнечного масла.
Ответ: 230 г
Решение б
26 * 4 = (20 + 6) * 4 = 20 * 4 + 6 * 4 = 80 + 24 = 104 (км) − должен был проехать мотоциклист.
Ответ: 104 км 11
-
Номер №11
Вычислите:
а)
$ \begin{array}{rl} 354 + 126 & \\ :3 & \\ +50 & \\ :7 & \\ :2 & \end{array} $
б)
$ \begin{array}{rl} 320 : 40 & \\ *12 & \\ +204 & \\ :75 & \end{array} $
в)
$ \begin{array}{rl} 386 + 214 & \\ :8 & \\ -45 & \\ *7 & \\ :5 & \end{array} $
г)
$ \begin{array}{rl} 800 : 25 & \\ *20 & \\ -410 & \\ :10 & \\ *5 & \end{array} $
д)
$ \begin{array}{rl} 441 + 209 & \\ -160 & \\ :7 & \\ *5 & \\ :35 & \\ *7 & \end{array} $
е)
$ \begin{array}{rl} 900 : 150 & \\ *90 & \\ +260 & \\ :16 & \end{array} $
Решение а
1) 354 + 126 = 480
2) 480 : 3 = (300 + 180) : 3 = 300 : 3 + 180 : 3 = 100 + 60 = 160
3) 160 + 50 = 210
4) 210 : 7 = 30
5) 30 : 2 = 15
$ \begin{array}{r|l} 354 + 126 & 480\\ :3 & 160\\ +50 & 210\\ :7 & 30\\ :2 & 15 \end{array} $
Ответ: 15
Решение б
1) 320 : 40 = 32 : 4 = 8
2) 8 * 12 = 8 * (10 + 2) = 8 * 10 + 8 * 2 = 80 + 16 = 96
3) 96 + 204 = 300
4) 300 : 75 = 4
$ \begin{array}{r|l} 320 : 40 & 8\\ *12 & 96\\ +204 & 300\\ :75 & 4 \end{array} $
Ответ: 4
Решение в
1) 386 + 214 = 600
2) 600 : 8 = 75
3) 75 − 45 = 30
4) 30 * 7 = 210
5) 210 : 5 = (200 + 10) : 5 = 200 : 5 + 10 : 5 = 40 + 2 = 42
$ \begin{array}{r|l} 386 + 214 & 600\\ :8 & 75\\ -45 & 30\\ *7 & 210\\ :5 & 42 \end{array} $
Ответ: 42
Решение г
1) 800 : 25 = 32
2) 32 * 20 = 640
3) 640 − 410 = 230
4) 230 : 10 = 23
5) 23 * 5 = (20 + 3) * 5 = 20 * 5 + 3 * 5 = 100 + 15 = 115
$ \begin{array}{r|l} 800 : 25 & 32\\ *20 & 640\\ -410 & 230\\ :10 & 23\\ *5 & 115 \end{array} $
Ответ: 115
Решение д
1) 441 + 209 = 650
2) 650 − 160 = 490
3) 490 : 7 = 70
4) 70 * 5 = 350
5) 350 : 35 = 10
6) 10 * 7 = 70
$ \begin{array}{r|l} 441 + 209 & 650\\ -160 & 490\\ :7 & 70\\ *5 & 350\\ :35 & 10\\ *7 & 70 \end{array} $
Ответ: 70
Решение е
1) 900 : 150 = 6
2) 6 * 90 = 540
3) 540 + 260 = 800
4) 800 : 16 = 50
$ \begin{array}{rl} 900 : 150 & 6\\ *90 & 540\\ +260 & 800\\ :16 & 50 \end{array} $
Ответ: 50 12
-
Номер №12
Решите уравнения.
а) $30 - x = 4\frac{11}{23}$
б) $(x - \frac{17}{29}) + \frac{11}{29} = 2\frac{9}{29}$
в) $52 - x = 19\frac{13}{37}$
г) $(7\frac{36}{37} - x) + 6\frac{8}{37} = 9\frac{1}{37}$
Решение а
$30 - x = 4\frac{11}{23}$
$x = 30 - 4\frac{11}{23}$
$x = 29\frac{23}{23} - 4\frac{11}{23}$
$x = 25\frac{12}{23}$
Ответ: $x = 25\frac{12}{23}$
Решение б
$(x - \frac{17}{29}) + \frac{11}{29} = 2\frac{9}{29}$
$x - \frac{17}{29} = 2\frac{9}{29} - \frac{11}{29}$
$x - \frac{17}{29} = 1\frac{38}{29} - \frac{11}{29}$
$x - \frac{17}{29} = 1\frac{27}{29}$
$x = 1\frac{27}{29} + \frac{17}{29}$
$x = 1\frac{44}{29}$
$x = 2\frac{15}{29}$
Ответ: $x = 2\frac{15}{29}$
Решение в
$52 - x = 19\frac{13}{37}$
$x = 52 - 19\frac{13}{37}$
$x = 51\frac{37}{37} - 19\frac{13}{37}$
$x = 32\frac{24}{37}$
Ответ: $x = 32\frac{24}{37}$
Решение г
$(7\frac{36}{37} - x) + 6\frac{8}{37} = 9\frac{1}{37}$
$7\frac{36}{37} - x = 9\frac{1}{37} - 6\frac{8}{37}$
$7\frac{36}{37} - x = 8\frac{38}{37} - 6\frac{8}{37}$
$7\frac{36}{37} - x = 2\frac{30}{37}$
$x = 7\frac{36}{37} - 2\frac{30}{37}$
$x = 5\frac{6}{37}$
Ответ: $x = 5\frac{6}{37}$ 13
-
Номер №13
Решите уравнения.
а) $(x - 6\frac{3}{19}) - 3\frac{11}{19} = 2\frac{9}{19}$
б) $(x + 12\frac{7}{13}) - 4\frac{9}{13} = 12\frac{5}{13}$
в) $7\frac{15}{23} - (5\frac{15}{23} - x) = \frac{7}{23}$
г) $19\frac{1}{17} - 8\frac{6}{17} - x = 5\frac{1}{17} + 3\frac{16}{17}$
Решение а
$(x - 6\frac{3}{19}) - 3\frac{11}{19} = 2\frac{9}{19}$
$x - 6\frac{3}{19} = 2\frac{9}{19} + 3\frac{11}{19}$
$x - 6\frac{3}{19} = 5\frac{20}{19}$
$x - 6\frac{3}{19} = 6\frac{1}{19}$
$x = 6\frac{1}{19} + 6\frac{3}{19}$
$x = 12\frac{4}{19}$
Ответ: $x = 12\frac{4}{19}$
Решение б
$(x + 12\frac{7}{13}) - 4\frac{9}{13} = 12\frac{5}{13}$
$x + 12\frac{7}{13} = 12\frac{5}{13} + 4\frac{9}{13}$
$x + 12\frac{7}{13} = 16\frac{14}{13}$
$x = 16\frac{14}{13} - 12\frac{7}{13}$
$x = 4\frac{7}{13}$
Ответ: $x = 4\frac{7}{13}$
Решение в
$7\frac{15}{23} - (5\frac{15}{23} - x) = \frac{7}{23}$
$5\frac{15}{23} - x = 7\frac{15}{23} - \frac{7}{23}$
$5\frac{15}{23} - x = 7\frac{8}{23}$
$x = 5\frac{15}{23} - 7\frac{8}{23}$
решить нельзя
Решение г
$19\frac{1}{17} - 8\frac{6}{17} - x = 5\frac{1}{17} + 3\frac{16}{17}$
$18\frac{18}{17} - 8\frac{6}{17} - x = 8\frac{17}{17}$
$10\frac{12}{17} - x = 9$
$x = 10\frac{12}{17} - 9$
$x = 1\frac{12}{17}$
Ответ: $x = 1\frac{12}{17}$ 14
-
Номер №14
Найдите число x, если при делении числа x на 9 получилось:
а) $5\frac{7}{9}$
б) $8\frac{5}{9}$
Решение а
$x : 9 = 5\frac{7}{9}$
$\frac{x}{9} = \frac{52}{9}$
x = 52
Ответ: x = 52
Решение б
$x : 9 = 8\frac{5}{9}$
$\frac{x}{9} = \frac{77}{9}$
x = 77
Ответ: x = 77 15
-
Номер №15
Найдите число, если оно больше:
а) своей половины на $8\frac{1}{3}$
б) своей четверти на $\frac{5}{11}$
Решение а
Целое число состоит из двух половин. Так как число больше своей половины на половину, значит $8\frac{1}{3}$ − половина числа.
Тогда:
$8\frac{1}{3} + 8\frac{1}{3} = 16\frac{2}{3}$ − искомое число.
Ответ: $16\frac{2}{3}$
Решение б
Целое число состоит из четырех четвертей. Так как число больше своей четверти на $\frac{5}{11}$, значит $\frac{5}{11}$ − три четверти числа.
Тогда:
$\frac{5}{11} = \frac{15}{33}$ − три четверти числа;
$\frac{15}{33} = \frac{5}{33} + \frac{5}{33} + \frac{5}{33}$ − значит одна четверть числа равна $\frac{5}{33}$;
$\frac{15}{33} + \frac{5}{33} = \frac{20}{33}$ − искомое число.
Ответ: $\frac{20}{33}$ 16
-
Номер №16
Решите задачи.
а) Туристам необходимо пройти 42 км. В первый день они прошли $12\frac{6}{25}$ км, во второй день − $15\frac{11}{25}$ км. Сколько километров им осталось пройти?
б) В одном ящике $16\frac{3}{8}$ кг яблок, а во втором ящике − на $3\frac{7}{8}$ кг больше. Сколько килограммов яблок в двух ящиках?
в) Десять ребят разделили между собой поровну шоколадки. И каждому досталось по $1\frac{2}{5}$ плитки. Сколько шоколадок разделили ребята?
Решение а
1) $12\frac{6}{25} + 15\frac{11}{25} = 27\frac{17}{25}$ (км) − прошли туристы за первые 2 дня;
2) $42 - 27\frac{17}{25} = 41\frac{25}{25} - 27\frac{17}{25} = 14\frac{8}{25}$ (км) − осталось пройти туристам.
Ответ: $14\frac{8}{25}$ км
Решение б
1) $16\frac{3}{8} + 3\frac{7}{8} = 19\frac{10}{8} = 20\frac{2}{8}$ (кг) − яблок во втором ящике;
2) $16\frac{3}{8} + 20\frac{2}{8} = 36\frac{5}{8}$ (кг) − яблок в двух ящиках.
Ответ: $36\frac{5}{8}$ кг
Решение в
1) $1\frac{2}{5} = \frac{7}{5}$ (плитки) − шоколада досталось каждому из десяти мальчиков;
2) 10 : 5 * 7 = 2 * 7 = 14 (плиток) − шоколада разделили ребята.
Ответ: 14 плиток Десятичная запись дробных чисел 1
-
30. Десятичная запись дробных чисел. Номер №1
Запишите каждую из дробей так, чтобы в числителе было столько цифр, сколько нулей в знаменателе.
а) $\frac{7}{1000} = \frac{007}{1000}$
б) $\frac{5}{100} = \frac{05}{100}$
в) $\frac{13}{10000} =$
г) $\frac{3}{10000} =$
д) $\frac{79}{100000} =$
е) $\frac{11}{1000} =$
ж) $\frac{1}{100} =$
з) $\frac{31}{10000} =$
и) $\frac{48}{100000} =$
Решение а
$\frac{7}{1000} = \frac{007}{1000}$
Решение б
$\frac{5}{100} = \frac{05}{100}$
Решение в
$\frac{13}{10000} = \frac{0013}{10000}$
Решение г
$\frac{3}{10000} = \frac{0003}{10000}$
Решение д
$\frac{79}{100000} = \frac{00079}{100000}$
Решение е
$\frac{11}{1000} = \frac{011}{1000}$
Решение ж
$\frac{1}{100} = \frac{01}{100}$
Решение з
$\frac{31}{10000} = \frac{0031}{10000}$
Решение и
$\frac{48}{100000} = \frac{00048}{100000}$ 2
-
Номер №2
Представьте дробные числа в виде десятичных дробей.
а) $7\frac{3}{10} = 7,3$
б) $1\frac{5}{100} =$
в) $4\frac{13}{100} =$
г) $56\frac{324}{1000} =$
д) $\frac{7}{10} = 0,$
е) $\frac{5}{100} = 0,$
ж) $50\frac{7}{100} =$
з) $\frac{58}{100} =$
и) $\frac{17}{1000} =$
Решение а
$7\frac{3}{10} = 7,3$
Решение б
$1\frac{5}{100} = 1,05$
Решение в
$4\frac{13}{100} = 4,13$
Решение г
$56\frac{324}{1000} = 56,324$
Решение д
$\frac{7}{10} = 0,7$
Решение е
$\frac{5}{100} = 0,05$
Решение ж
$50\frac{7}{100} = 50,07$
Решение з
$\frac{58}{100} = 0,58$
Решение и
$\frac{17}{1000} = 0,017$ 3
-
Номер №3
Запишите десятичные дроби в виде обыкновенны дробей или смешанных чисел.
а) 7,3 =
б) 92,04 =
в) 8,23 =
г) 0,005 =
д) 0,0342 =
е) 5,340 =
ж) 100,0001 =
з) 0,20202 =
и) 9,84 =
к) 3,004 =
л) 0,54 =
м) 0,001 =
Решение а
$7,3 = 7\frac{3}{10}$
Решение б
$92,04 = 92\frac{4}{100}$
Решение в
$8,23 = 8\frac{23}{100}$
Решение г
$0,005 = \frac{5}{1000}$
Решение д
$0,0342 = \frac{342}{10000}$
Решение е
$5,340 = 5\frac{340}{1000}$
Решение ж
$100,0001 = 100\frac{1}{10000}$
Решение з
$0,20202 = \frac{20202}{100000}$
Решение и
$9,84 = 9\frac{84}{100}$
Решение к
$3,004 = 3\frac{4}{1000}$
Решение л
$0,54 = \frac{54}{100}$
Решение м
$0,001 = \frac{1}{1000}$ 4
-
Номер №4
Решите задачи с помощью уравнения.
а) Через 13 лет отец будет втрое старше сына. Сколько лет теперь отцу, если сыну 7 лет?
б) Половина веса сома больше четверти его веса на 1 кг. Сколько весит сом?
в) В трех цехах 87 рабочих. В первом на 17 человек больше, чем во втором, а во втором в три раза больше, чем в третьем. Сколько рабочих в каждом цехе?
г) Стакан втрое, а чашка вдвое дешевле сахарницы. За стакан, чашку и сахарницу заплатили 121 руб. 11 коп. Сколько стоит сахарница?
Решение а
Пусть x (лет) − отцу теперь, тогда:
x + 13 (лет) − будет отцу через 13 лет;
7 + 13 (лет) − будет сыну через 13 лет.
Так как, через 13 лет отец будет втрое старше сына, можно составить уравнение:
x + 13 = 3(7 + 13)
x + 13 = 3 * 20
x + 13 = 60
x = 60 − 13
x = 47 (лет) − отцу теперь.
Ответ: 47 лет
Решение б
Пусть x (кг) − четверть веса сома, тогда:
2x (кг) − половина четверти сома.
Так как, половина веса сома больше четверти его веса на 1 кг, можно составить уравнение:
2x − x = 1
x = 1 (кг) − четверть веса сома, тогда:
1 * 4 = 4 (кг) − весит сом.
Ответ: 4 кг
Решение в
Пусть x (рабочих) − в третьем цехе, тогда:
3x (рабочих) − во втором цехе;
3x + 17 (рабочих) − в первом цехе.
Так как, в трех цехах 87 рабочих, можно составить уравнение:
x + 3x + 3x + 17 = 87
7x = 87 − 17
7x = 70
x = 70 : 7
x = 10 (рабочих) − в третьем цехе, тогда:
3x = 3 * 10 = 30 (рабочих) − во втором цехе;
3x + 17 = 3 * 10 + 17 = 30 + 17 = 47 (рабочих) − в первом цехе.
Ответ: 47, 30 и 10 рабочих.
Решение г
Пусть 6x (руб) − стоит сахарница, тогда:
$\frac{6}{3}x = 2x$ (руб.) − стоит стакан;
$\frac{6}{2}x = 3x$ (руб.) − стоит чашка.
Так как, за стакан, чашку и сахарницу заплатили 121 руб. 11 коп. (12111 коп), можно составить уравнение:
6x + 2x + 3x = 12111
11x = 12111
x = 12111 : 11 = (11000 + 1100 + 11) : 11 = 11000 : 11 + 1100 : 11 + 11 : 11 = 1000 + 100 + 1
x = 1101 (коп) = 11 руб. 1 коп., тогда:
6x = 6 * 1101 = 6606 = 66 руб. 6 коп. − стоит сахарница.
Ответ: 66 руб. 6 коп. 5
-
Номер №5
Выполните действия.
а) $4\frac{3}{10} + 2\frac{7}{10} + 3\frac{9}{10} =$
б) $30\frac{1}{6} - \frac{2}{6} - \frac{4}{6} =$
в) $(7\frac{2}{5} + \frac{3}{5}) * 100 =$
г) $(18\frac{4}{9} - \frac{4}{9}) : 6 =$
Решение а
$4\frac{3}{10} + 2\frac{7}{10} + 3\frac{9}{10} = 6\frac{10}{10} + 3\frac{9}{10} = 7 + 3\frac{9}{10} = 10\frac{9}{10}$
Решение б
$30\frac{1}{6} - \frac{2}{6} - \frac{4}{6} = 29\frac{7}{6} - \frac{2}{6} - \frac{4}{6} = 29\frac{5}{6} - \frac{4}{6} = 29\frac{1}{6}$
Решение в
$(7\frac{2}{5} + \frac{3}{5}) * 100 = 7\frac{5}{5} * 100 = 8 * 100 = 8$
Решение г
$(18\frac{4}{9} - \frac{4}{9}) : 6 = 18 : 6 = 3$ 6
-
Номер №6
Сравните значения выражений: $x^3 - y$ и 3x − y при заданных значениях букв.
Если x = 0, y = 0, то _
Если x = 1, y = 1, то _
Если x = 2, y = 2, то _
Если x = 4, y = 5, то _
Решение
Если x = 0, y = 0, то:
$x^3 - y = 0^3 - 0 = 0$
3x − y = 3 * 0 − 0 = 0
0 = 0, значит:
$x^2 - y = 3x - y$
Если x = 1, y = 1, то:
$x^2 - y = 1^3 - 1 = 1 - 1 = 0$
3x − y = 3 * 1 − 1 = 3 − 1 = 2
0 < 2, значит:
$x^2 - y < 3x - y$
Если x = 2, y = 2, то:
$x^2 - y = 2^3 - 2 = 8 - 2 = 6$
3x − y = 3 * 2 − 2 = 6 − 2 = 4
6 > 4, значит:
$x^2 - y > 3x - y$
Если x = 4, y = 5, то:
$x^2 - y = 4^3 - 5 = 64 - 5 = 59$
3x − y = 3 * 4 − 5 = 12 − 5 = 7
59 > 7, значит:
$x^2 - y > 3x - y$ Сравнение десятичных дробей 1
-
31. Сравнение десятичных дробей. Номер №1
Закончите предложения.
а) Если в записи десятичной дроби справа приписать один или несколько нулей, то получится дробь, _ данной дроби.
б) Если в записи десятичной дроби отбросить справа один или несколько нулей, то получится дробь, _ данной дроби.
Решение
а) Если в записи десятичной дроби справа приписать один или несколько нулей, то получится дробь, равная данной дроби.
б) Если в записи десятичной дроби отбросить справа один или несколько нулей, то получится дробь, равная данной дроби. 2
-
Номер №2
Запишите дробь, равную данной дроби:
а) имеющую две цифры после запятой.
18,700 =
5,0900 =
0,070 =
4,18000 =
0,96000 =
13,0800 =
167,87000 =
0,010000 =
8,37000 =
б) имеющую четыре цифры после запятой:
2,70 =
13,01 =
0,080 =
7,56 =
0,003 =
2,405 =
6,3 =
97,01 =
100,034 =
Решение а
18,700 = 18,70
5,0900 = 5,09
0,070 = 0,07
4,18000 = 4,18
0,96000 = 0,96
13,0800 = 13,08
167,87000 = 167,87
0,010000 = 0,01
8,37000 = 8,37
Решение б
2,70 = 2,7000
13,01 = 13,0100
0,080 = 0,0800
7,56 = 7,5600
0,003 = 0,0030
2,405 = 2,4050
6,3 = 6,3000
97,01 = 97,0100
100,034 = 100,0340 3
-
Номер №3
Сравните десятичные дроби, используя знаки: >, =, <.
а) 7,8 _ 7,7
б) 8,13 _ 8,7
в) 16,34 _ 12,3
г) 5,1786 _ 5,178600
д) 2,0100 _ 2,010
е) 0,458 _ 0,459
Решение а
7,8 > 7,7
Решение б
8,13 < 8,7
Решение в
16,34 > 12,3
Решение г
5,1786 = 5,178600
Решение д
2,0100 = 2,010
Решение е
0,458 < 0,459 4
-
Номер №4
Запишите четыре решения неравенства.
а) 1 < x < 1,8
б) 3 < x < 3,7
в) 5,1 < x < 5,8
г) 5,03 < x < 5,04
Решение а
1 < x < 1,8
x = 1,1; 1,2; 1,3; 1,4.
Решение б
3 < x < 3,7
x = 3,1; 3,2; 3,3; 3,4.
Решение в
5,1 < x < 5,8
x = 5,2; 5,3; 5,4; 5,5.
Решение г
5,03 < x < 5,04
5,030 < x < 5,040
x = 5,031; 5,032; 5,033; 5,034. 5
-
Номер №5
Выполните действия.
а) $\frac{1}{7} + \frac{6}{7} =$
б) $\frac{3}{5} + 4\frac{2}{5} =$
в) $9 - \frac{1}{6} =$
г) $7 + 13\frac{3}{11} =$
д) $9 - 1\frac{1}{2} =$
е) $3\frac{3}{4} - 2 =$
ж) $1\frac{1}{100} - \frac{9}{100} =$
з) $\frac{7}{10} + 5\frac{4}{10} =$
Решение а
$\frac{1}{7} + \frac{6}{7} = \frac{7}{7} = 1$
Решение б
$\frac{3}{5} + 4\frac{2}{5} = 4\frac{5}{5} = 5$
Решение в
$9 - \frac{1}{6} = 8\frac{6}{6} - \frac{1}{6} = 8\frac{5}{6}$
Решение г
$7 + 13\frac{3}{11} = 20\frac{3}{11}$
Решение д
$9 - 1\frac{1}{2} = 8\frac{2}{2} - 1\frac{1}{2} = 7\frac{1}{2}$
Решение е
$3\frac{3}{4} - 2 = 1\frac{3}{4}$
Решение ж
$1\frac{1}{100} - \frac{9}{100} = \frac{101}{100} - \frac{9}{100} = \frac{92}{100}$
Решение з
$\frac{7}{10} + 5\frac{4}{10} = 5\frac{11}{10} = 6\frac{1}{10}$ 6
-
Номер №6
Заполните пропуски.
а) 7,8 м = _ см
б) 37,5 м = _ см
в) 19,3 м = _ дм
г) 46 мм = _ дм
д) 87 мм = _ см
е) 42,345 м = _ км
ж) 73 мин = _ час
з) 4 час 20 мин = _ мин
Решение а
1 м = 100 см
7,8 м = 7,80 м = 780 см
Решение б
1 м = 100 см
37,5 м = 37,50 м = 3750 см
Решение в
1 м = 10 дм
19,3 м = 193 дм
Решение г
1 дм = 100 мм
46 мм = $\frac{46}{100}$ дм = 0,46 дм
Решение д
1 см = 10 мм
87 мм = $\frac{87}{10}$ см = $8\frac{7}{10}$ см = 8,7 см
Решение е
1 км = 1000 м
42,345 м = $\frac{42345}{1000000}$ км = 0,042345 км
Решение ж
1 час = 60 мин
73 мин = $\frac{73}{60}$ час = $1\frac{13}{60}$ час
Решение з
4 час 20 мин = (4 * 60 + 20) мин = (240 + 20) мин = 260 мин 7
-
Номер №7
Начертите три окружности с центром в точке A и разными радиусами.
Решение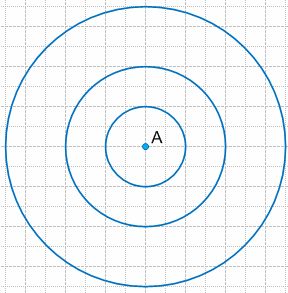
8
-
Номер №8
Начертите квадрат площадью 9 $см^2$ и три разных прямоугольника площадью.
Решение
9 $см^2$ = 3 см * 3 см, значит сторона квадрата равна 3 см.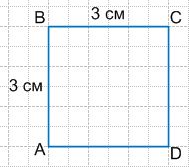
24 $см^2$ = 2 см * 12 см, значит стороны первого прямоугольника будут равны 2 см и 12 см
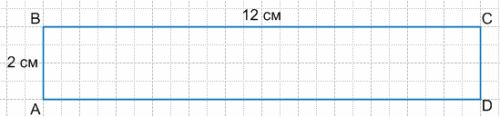24 $см^2$ = 3 см * 8 см, значит стороны второго прямоугольника будут равны 3 см и 8 см
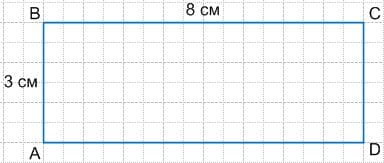24 $см^2$ = 4 см * 6 см, значит стороны третьего прямоугольника будут равны 4 см и 6 см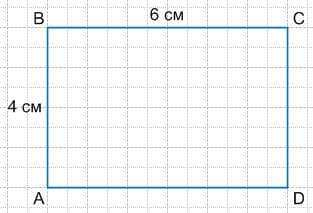
9
-
Номер №9
Решите задачу.
Два туриста выехали навстречу друг другу один после другого через 3 часа. Через сколько часов после отъезда первого они встретятся, если первый проезжал 10 км в час, а второй − 12 км в час и если расстояние между ними 140 км?
Решение
1) 10 * 3 = 30 (км) − проехал первый турист до выезда второго;
2) 140 − 30 = 110 (км) − было между туристами во время выезда второго туриста;
3) 10 + 12 = 22 (км/ч) − скорость сближения туристов;
4) 110 : 22 = 5 (ч) − прошло до встречи туристов, после выезда второго туриста;
5) 5 + 3 = 8 (ч) − прошло до встречи туристов, после выезда первого туриста.
Ответ: 8 ч Сложение и вычитание десятичных дробей 1
-
32. Сложение и вычитание десятичных дробей. Номер №1
Сравните дроби.
а) 3,741 _ 3,739
б) 18,99 _ 20
в) 50,07 _ 49
г) 5,7 _ 6,6
д) 14 _ 7,8
е) 9,2 _ 9,201
ж) 47,001 _ 47,0001
з) 1,2 _ 1,201
Решение а
3,741 > 3,739
Решение б
18,99 < 20
Решение в
50,07 > 49
Решение г
5,7 < 6,6
Решение д
14 > 7,8
Решение е
9,2 < 9,201
Решение ж
47,001 > 47,0001
Решение з
1,2 < 1,201 2
-
Номер №2
Выполните сложение.
а)
+9,04
1,69
б)
+2,900
4,271
в)
+4,916
0,700г)
+13,475
14,596
д)
+3,48
14,37
е)
+11,309
0,18
ж)
+37,879
2,7
з)
+ 5,3
0,4976
Решение а
+ 9,04
1,69
10,73
Решение б
+2,900
4,271
7,171
Решение в
+4,916
0,700
5,616
Решение г
+13,475
14,596
28,071
Решение д
+3,48
14,37
17,85
Решение е
+11,309
0,18
11,489
Решение ж
+37,879
2,7
40,579
Решение з
+ 5,3
0,4976
5,7976 3
-
Номер №3
Выполните вычитание.
а)
-7,66
1,54
б)
-8,05
1,69в)
-1,316
0,800
г)
-10,834
6,959д)
-8,900
4,382
е)
-5,3
3,2ж)
-13,975
9,898з)
-28,104
9,204
Решение а
-7,66
1,54
6,12
Решение б
-8,05
1,69
6,36
Решение в
-1,316
0,800
0,516
Решение г
-10,834
6,959
3,875
Решение д
-8,900
4,382
4,518
Решение е
-5,3
3,2
2,1
Решение ж
-13,975
9,898
4,077
Решение з
-28,104
9,204
18,900 4
-
Номер №4
Выполните действия.
а)
-6,4
0,597б)
-6,07
4,9в)
-9,41
7,089г)
+39,498
3,7д)
-52,03
5,294е)
-53,001
9,2972ж)
+11,461
8,0698з)
+17,209
2,91
Решение а
-6,4
0,5976
5,8024
Решение б
-6,07
4,9
1,1
Решение в
+ 9,41
7,089
16,499
Решение г
+39,498
3,7
43,198
Решение д
-52,03
5,294
57,324
Решение е
-53,001
9,2972
43,7038
Решение ж
+11,461
8,0698
19,5308
Решение з
+17,209
2,91
20,119 5
-
Номер №5
Выполнив указанные действия устно, запишите результаты.
а) 7,25 − 0,99 =
б) 9,34 + 4,98 =
в) 146,2 + 99,9 =
г) 49,9 − 47,81 =
д) 9,99 + 0,01 =
е) 11 − 6,8 =
ж) 0,13 + 0,87 =
з) 51,84 − 0,84 =
Решение а
7,25 − 0,99 = 6,26
Решение б
9,34 + 4,98 = 14,32
Решение в
146,2 + 99,9 = 246,1
Решение г
49,9 − 47,81 = 2,09
Решение д
9,99 + 0,01 = 10
Решение е
11 − 6,8 = 4,2
Решение ж
0,13 + 0,87 = 1
Решение з
51,84 − 0,84 = 51 6
-
Номер №6
Упростите выражения.
а) 3,7a + 4,3a =
б) 16,5b − 7,5b =
в) 18x − 0,7x =
г) 13,9y + 7,2y =
д) 0,4a + 0,5a + 0,1a =
е) 8,6b − 3,2b − 5,4b =
ж) 2x − 1,5x − 0,3x =
з) 5y + 0,7x + 1,8x =
Решение а
3,7a + 4,3a = 8a
Решение б
16,5b − 7,5b = 9b
Решение в
18x − 0,7x = 17,3x
Решение г
13,9y + 7,2y = 21,1y
Решение д
0,4a + 0,5a + 0,1a = (0,4a + 0,1a) + 0,5a = 0,5a + 0,5a = 1a = a
Решение е
8,6b − 3,2b − 5,4b = 8,6b − (3,2b + 5,4b) = 8,6b − 8,6b = 0
Решение ж
2x − 1,5x − 0,3x = 0,5x − 0,3x = 0,2x
Решение з
5y + 0,7x + 1,8x = 5y + 2,5x 7
-
Номер №7
Вставьте пропущенные цифры.
а)
+3,....8
..,78..
9,999
б)
+19,....5
..,32..
22,481в)
+..,..86
3,......
9,084г)
+..8,..7..
..,8..7
9,254д)
+1..,....3
9,99..
11,004
Решение а+3,....8
..,78..
9,999Найдем количество тысячных во втором слагаемом:
9 − 8 = 1
Получим:+3,....8
..,781
9,999Найдем количество сотых в первом слагаемом:
9 − 8 = 1
Получим:+3,.18
..,781
9,999Найдем количество десятых в первом слагаемом:
9 − 7 = 2
Получим:+3,218
..,781
9,999Найдем количество единиц во втором слагаемом:
9 − 3 = 6
Ответ:
+3,218
6,781
9,999
Решение б+19,....5
..,32..
22,481Найдем количество тысячных во втором слагаемом:
11 − 5 = 6
Получим:+19,...5
..,326
22,481Найдем количество сотых в первом слагаемом:
8 − 2 = 6, но так как количество тысячных в сумме равно 11, то убираем одну сотую:
6 − 1 = 5
Получим:+19,.55
..,326
22,481Найдем количество десятых в первом слагаемом:
4 − 3 = 1
Получим:+19,155
..,326
22,481Найдем количество единиц во втором слагаемом:
22 − 19 = 3
Ответ:
+19,155
3,326
22,481
Решение в+..,..86
3,......
9,084Найдем количество тысячных во втором слагаемом:
14 − 6 = 8
Получим:+..,..86
3,...8
9,084Найдем количество сотых во втором слагаемом:
8 − 8 = 0, но так как количество тысячных в сумме равно 14, то убираем одну сотую:
10 − 1 = 9
Получим:+..,..86
3,.98
9,084Найдем количество десятых в первом и втором слагаемом.
Так как в сумме стоит 0, значит в сумме количество десятых должно быть равно 10. Но так как количество сотых в сумме равно 18, то убираем одну десятую. Значит в сумме количество десятых должно быть равно 9. Пусть в первом слагаемом будет 4 десятых, тогда во втором 5 десятых.
Получим:+..,486
3,598
9,084Найдем количество единиц в первом слагаемом:
9 − 3 = 6, но так как количество десятых в сумме равно 10, то убираем одну единицу:
6 − 1 = 5
Ответ:+5,486
3,598
9,084
Решение г+..8,..7..
..,8..7
9,254Найдем количество тысячных в первом слагаемом:
14 − 7 = 7
Получим:+..8,.77
..,8..7
9,254Найдем количество сотых во втором слагаемом:
15 − 7 = 8, но так как количество тысячных в сумме равно 14, то убираем одну сотую:
8 − 1 = 7
Получим:+..8,.77
..,877
9,254Найдем количество десятых в первом слагаемом:
12 − 8 = 4, но так как количество сотых в сумме равно 15, то убираем одну десятую:
4 − 1 = 3
Получим:+..8,377
..,877
9,254Найдем количество единиц во втором слагаемом:
9 − 8 = 1, но так как количество десятых в сумме равно 12, то убираем одну единицу:
1 − 1 = 0
Получим:+..8,377
0,877
9,254Найдем количество десятков в первом слагаемом. Так как в сумме нет десятков, значит ни в одном из слагаемых не может быть десятков. Следовательно количество десятков в первом слагаемом равно 0.
Ответ:+8,377
0,877
9,254
Решение д+1..,....3
9,99..
11,004Так как в первом слагаемом точно 10 единиц, а во втором 9 единиц, то сумма единиц не может быть равна 11. Поэтому скорее всего в тетради опечатка и правильный пример должен выглядеть так:
+1..,....3
9,99..
21,004Найдем количество тысячных во втором слагаемом:
4 − 3 = 1
Получим:+1..,....3
9,991
21,004Найдем количество сотых в первом слагаемом:
10 − 9 = 1
Получим:+1..,..13
9,991
21,004Найдем количество десятых в первом слагаемом:
10 − 9 = 1, но так как количество сотых в сумме равно 10, то убираем одну десятую:
1 − 1 = 0
Получим:+1..,013
9,991
21,004Найдем количество единиц в первом слагаемом:
11 − 9 = 2, но так как количество десятых в сумме равно 10, то убираем одну единицу:
2 − 1 = 0
Ответ:+11,013
9,991
21,004 8
-
Номер №8
Заполните таблицы.
а)+ 0,6 5,13 12,4 7,8 10,6 1,33
б)+ 4,35 17,55 22,7 9,05 50,65 17 Решение а
Вторая строка+7,8
0,6
8,4
+7,80
5,13
12,93
+7,8
12,4
20,2
Третья строка
+10,6
0,6
11,2
+10,60
5,13
15,73
+10,6
12,4
23,0
Четвертая строка
+1,33
0,60
1,93
+1,33
5,13
6,46
+1,33
12,40
13,73
Ответ:+ 0,6 5,13 12,4 7,8 8,4 12,93 20,2 10,6 11,2 15,73 23 1,33 1,93 6,46 13,73
Решение б
Найдем второе слагаемое во второй строке в первом столбике:-17,55
4,35
13,2Получим:
+ 4,35 13,2 17,55 22,7 9,05 50,65 17
Найдем первое слагаемое в первой стоке в третьей столбце:-50,65
9,05
41,60
Получим:+ 4,35 41,6 13,2 17,55 22,7 9,05 50,65 17
Найдем сумму во второй строке в третьем столбце:+13,2
41,6
54,8
Получим:+ 4,35 41,6 13,2 17,55 54,8 22,7 9,05 50,65 17
Найдем первое слагаемое в первой строке в четвертом столбце:-22,7
13,2
9,5+ 4,35 41,6 9,5 13,2 17,55 54,8 22,7 9,05 50,65 17
Найдем второе слагаемое в четвертой строке в первом столбце:-17,0
9,5
7,5Получим:
+ 4,35 41,6 9,5 13,2 17,55 54,8 22,7 9,05 50,65 7,5 17
Найдем сумму в третьей строке во втором столбце:+4,35
9,05
13,40Получим:
+ 4,35 41,6 9,5 13,2 17,55 54,8 22,7 9,05 13,4 50,65 7,5 17
Найдем сумму в третьей строке в четвертом столбце:
+9,50
9,05
18,55Получим:
+ 4,35 41,6 9,5 13,2 17,55 54,8 22,7 9,05 13,4 50,65 18,55 7,5 17
Найдем сумму в четвертой строке во втором столбце:+4,35
7,50
11,85Получим:
+ 4,35 41,6 9,5 13,2 17,55 54,8 22,7 9,05 13,4 50,65 18,55 7,5 11,85 17
Найдем сумму в четвертой строке в третьем столбце:+41,6
7,5
49,1
Ответ:+ 4,35 41,6 9,5 13,2 17,55 54,8 22,7 9,05 13,4 50,65 18,55 7,5 11,85 49,1 17 9
-
Номер №9
Решите задачи.
а) Бак, длина которого 2 метра, ширина 15 дм и высота 1 метр, наполнен доверху водой. Сколько литров воды налито в этот бак?
б) Прямоугольный участок земли размерами 100 метров и 25 метров огорожен изгородью. На сколько меньше по длине понадобится изгороди для огораживания квадратного участка такой же площади?
в) Два поезда вышли одновременно навстречу друг другу из двух городов, расстояние между которыми 480 км. Один поезд проходит в $\frac{1}{5}$ часа 10 км, а другой в $\frac{1}{7}$ часа − 10 км. Через сколько часов поезда встретятся?
г) 12 мужских костюмов и 10 пальто стоят 19600 рублей. Пальто стоит на 200 рублей дороже костюма. Сколько стоит пальто и сколько стоит костюм в отдельности?
Решение а
2 м = 20 дм
1 м = 10 дм
20 * 15 * 10 = 300 * 10 = 3000 $(дм^3)$ = 3000 (л) − воды налито в этот бак.
Ответ: 3000 литров
Решение б
1) 100 * 25 = 2500 $(м^2)$ − площадь участка;
2) 2500 = 50 * 50, значит 50 (м) − длина стороны квадратного участка;
3) 2 * (100 + 25) = 2 * 125 = 250 (м) − периметр прямоугольного участка;
4) 4 * 50 = 200 (м) − периметр квадратного участка;
5) 250 − 200 = 50 (м) − на столько меньше по длине понадобится изгороди для огораживания квадратного участка.
Ответ: на 50 метров
Решение в
1) 10 * 5 = 50 (км/ч) − скорость первого поезда;
2) 10 * 7 = 70 (км/ч) − скорость второго поезда;
3) 50 + 70 = 120 (км/ч) − скорость сближения поездов;
4) 480 : 120 = 48 : 12 = 4 (ч) − пройдет до встречи поездов.
Ответ: через 4 часа
Решение г
Пусть x (руб.) − стоит костюм, тогда:
x + 200 (руб.) − стоит пальто;
12x (руб.) − стоят 12 костюмов;
10(x + 200) (руб.) − стоят 10 пальто.Так как, 12 мужских костюмов и 10 пальто стоят 19600 рублей, можно составить уравнение:
12x + 10(x + 200) = 19600
12x + 10x + 2000 = 19600
22x = 19600 − 2000
22x = 17600
x = 17600 : 22
x = 800 (руб.) − стоит костюм, тогда:
x + 200 = 800 + 200 = 1000 (руб.) − стоит пальто.
Ответ: 800 рублей стоит костюм, 1000 рублей стоит пальто.
Вычисления:
-17600|22
176 |800
-0
0
-0
0
0 10
-
Номер №10
Выполните действия.
а) 42,56 − 17,798 + 20,7
б) (3,07 + 4,78) − 2,09
в) 34,978 − 21,4059 + 764,3
г) 30,06 − (7,085 + 8,02)
Решение а
42,56 − 17,798 + 20,7 = 24,762 + 20,7 = 45,462
1)
42,56 − 17,798 = 24,762-42,560
17,798
24,7622)
24,762 + 20,7 = 45,462+24,762
20,700
45,462
Решение б
(3,07 + 4,78) − 2,09 = 7,85 − 2,09 = 5,76
1)
3,07 + 4,78 = 7,85+3,07
4,78
7,852)
7,85 − 2,09 = 5,76-7,85
2,09
5,76
Решение в
34,978 − 21,4059 + 764,3 = 13,5721 + 764,3 = 777,8721
1)
34,978 − 21,4059 = 13,5721-34,9780
21,4059
13,5721
2)
13,5721 + 764,3 = 777,8721+13,5721
764,3000
777,8721
Решение г
30,06 − (7,085 + 8,02) = 30,06 − 15,105 = 14,955
1)
7,085 + 8,02 = 15,105+7,085
8,020
15,105
2)
30,06 − 15,105 = 14,955-30,060
15,105
14,955 11
-
Номер №11
Выполните действия.
а) 7234 − 72,34 + 7,234
б) 562,01 − 5,6201 + 56,201
в) 1200 + 0,012 − 1,2
г) 7260,43 − 726,043 + 7,26043
Решение а
7234 − 72,34 + 7,234 = 7161,66 + 7,234 = 7168,894
1)
7234 − 72,34 = 7161,66-7234,00
72,34
7161,662)
7161,66 + 7,234 = 7168,894+7161,660
7,234
7168,894
Решение б
562,01 − 5,6201 + 56,201 = 556,3899 + 56,201 = 612,5909
1)
562,01 − 5,6201 = 556,3899-556,3899
5,6201
556,38992)
556,3899 + 56,201 = 612,5909+556,3899
56,201
612,5909
Решение в
1200 + 0,012 − 1,2 = 1200,012 − 1,2 = 1198,812
1)
1200 + 0,012 = 1200,012+1200,000
0,012
1200,0122)
1200,012 − 1,2 = 1198,812-1200,012
1,200
1198,812
Решение г
7260,43 − 726,043 + 7,26043 = 6534,387 + 7,26043 = 6541,64743
1)
7260,43 − 726,043 = 6534,387-7260,430
726,043
6534,3872)
6534,387 + 7,26043 = 6541,64743+6534,38700
7,26043
6541,64743 12
-
Номер №12
Решите уравнения.
а) 35 − x = 24,675
б) 70,8 − (x − 8,93) = 54,2
в) 4,86x + 19,4x + 0,54x = 2020
г) (43,2 − x) − 5,09 = 14,2
Решение а
35 − x = 24,675
x = 35 − 24,675
x = 10,325
Ответ: x = 10,325
Вычисления:
-35,000
24,675
10,325
Решение б
70,8 − (x − 8,93) = 54,2
x − 8,93 = 70,8 − 54,2
x − 8,93 = 16,6
x = 16,6 + 8,93
x = 25,53
Ответ: x = 25,53
Вычисления:
-70,8
54,2
16,6
+16,60
8,93
25,53
Решение в
4,86x + 19,4x + 0,54x = 2020
24,26x + 0,54x = 2020
24,8x = 2020
x = 2020 : 24,8
x = 20200 : 248
$x = \frac{20200}{248} = \frac{2525}{31} = 81\frac{14}{31}$
Ответ: $x = 81\frac{14}{31}$
Вычисления:
+4,86
19,40
24,26
+24,26
0,54
24,80
Решение г
(43,2 − x) − 5,09 = 14,2
43,2 − x = 14,2 + 5,09
43,2 − x = 19,29
x = 43,2 − 19,29
x = 23,91
Ответ: x = 23,91
Вычисления:
+14,20
5,09
19,29
-43,20
19,29
23,91 13
-
Номер №13
Замените все звездочки одной и той же цифрой так, чтобы оба неравенства были верными.
а) 0,*4 > 0,4* и 0,*7 < 0,7*
б) 0,*6 < 0,6* и 0,*3 > 0,3*
Решение а
0,*4 > 0,4* и 0,*7 < 0,7*
0,54 > 0,45 и 0,57 < 0,75
0,64 > 0,46 и 0,67 < 0,76
Ответ: * = 5; 6.
Решение б
0,*6 < 0,6* и 0,*3 > 0,3*
0,46 < 0,64 и 0,43 > 0,34
0,56 < 0,65 и 0,53 > 0,35
Ответ: * = 4; 5. Приближенные значения чисел
-
33. Приближенные значения чисел. Округления чисел. Номер №1
Заполните пропуски, чтобы высказывания были верными.
а) Если a < x < b, то a называют приближенным значением x с _ , а b _ приближенным значением x с _ .
б) Если первая отброшенная или замененная нулями цифра равна 5, 6, 7, 8 или 9, то стоящую перед ней цифру _ на 1.
в) Если число округляют до какого−нибудь разряда, то все следующие за этим разрядом цифры заменяют _, а если они стоят после запятой, то их _ .
г) Если первая отброшенная или замененная нулем цифра − 0, 1, 2, 3 или 4, то цифру, стоящую перед ней, _ .
Решение
а) Если a < x < b, то a называют приближенным значением x с недостатком , а b называют приближенным значением x с избытком.
б) Если первая отброшенная или замененная нулями цифра равна 5, 6, 7, 8 или 9, то стоящую перед ней цифру увеличивают на 1.
в) Если число округляют до какого−нибудь разряда, то все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают.
г) Если первая отброшенная или замененная нулем цифра − 0, 1, 2, 3 или 4, то цифру, стоящую перед ней, не меняют. 2
-
Номер №2
Округлите число до десятых.
а) 8,174 ≈
б) 0,32 ≈
в) 0,2829 ≈
г) 4,1046 ≈
д) 17,5624 ≈
е) 1,6439 ≈
ж) 10,8957 ≈
з) 23,2541 ≈
Решение а
8,174 ≈ 8,2
Решение б
0,32 ≈ 0,3
Решение в
0,2829 ≈ 0,3
Решение г
4,1046 ≈ 4,1
Решение д
17,5624 ≈ 17,6
Решение е
1,6439 ≈ 1,6
Решение ж
10,8957 ≈ 10,9
Решение з
23,2541 ≈ 23,3 3
-
Номер №3
Округлите число до сотых.
а) 2,1873 ≈ _
б) 127,314 ≈ _
в) 103,1309 ≈ _
г) 121,3476 ≈ _
д) 0,0291 ≈ _
е) 0,9219 ≈ _
ж) 1023,1829 ≈ _
з) 8,3754 ≈ _
Решение а
2,1873 ≈ 2,19
Решение б
127,314 ≈ 127,31
Решение в
103,1309 ≈ 103,13
Решение г
121,3476 ≈ 121,35
Решение д
0,0291 ≈ 0,03
Решение е
0,9219 ≈ 0,92
Решение ж
1023,1829 ≈ 1023,18
Решение з
8,3754 ≈ 8,38 4
-
Номер №4
Округлите число до тысячных.
а) 2,34516 ≈ _
б) 0,2172 ≈ _
в) 7,15671 ≈ _
г) 9,008521 ≈ _
д) 132,78503 ≈ _
е) 13,011624 ≈ _
ж) 5,324831 ≈ _
з) 7,020701 ≈ _
Решение а
2,34516 ≈ 2,345
Решение б
0,2172 ≈ 0,217
Решение в
7,15671 ≈ 7,157
Решение г
9,008521 ≈ 9,009
Решение д
132,78503 ≈ 132,785
Решение е
13,011624 ≈ 13,012
Решение ж
5,324831 ≈ 5,325
Решение з
7,020701 ≈ 7,021 5
-
Номер №5
Округлите число до десятков.
а) 48276 ≈ _
б) 58307 ≈ _
в) 78413 ≈ _
г) 385125 ≈ _
д) 142482 ≈ _
е) 874550 ≈ _
Решение а
48276 ≈ 48280
Решение б
58307 ≈ 58310
Решение в
78413 ≈ 78410
Решение г
385125 ≈ 385130
Решение д
142482 ≈ 142480
Решение е
874550 ≈ 874550 6
-
Номер №6
Округлите число до сотен.
а) 48276 ≈ _
б) 58307 ≈ _
в) 78413 ≈ _
г) 394192 ≈ _
д) 1485356 ≈ _
е) 645901 ≈ _
Решение а
48276 ≈ 48300
Решение б
58307 ≈ 58300
Решение в
78413 ≈ 78400
Решение г
394192 ≈ 394200
Решение д
1485356 ≈ 1485400
Решение е
645901 ≈ 645900 7
-
Номер №7
Округлите число до тысяч.
а) 147423 ≈ _
б) 281502 ≈ _
в) 1934913 ≈ _
г) 938403 ≈ _
д) 844721 ≈ _
е) 3290649 ≈ _
Решение а
147423 ≈ 147000
Решение б
281502 ≈ 282000
Решение в
1934913 ≈ 1935000
Решение г
938403 ≈ 938000
Решение д
844721 ≈ 845000
Решение е
3290649 ≈ 3291000 8
-
Номер №8
Укажите два последовательных натуральных числа, между которыми заключено число. Ответ запишите в виде двойного неравенства.
а) 6,8
б) 4,39
в) 3,57
Решение а
6 < 6,8 < 7
Решение б
4 < 4,39 < 5
Решение в
3 < 3,57 < 4 9
-
Номер №9
Решите задачи.
а) Хозяйка купила 5,25 кг риса, 1,5 кг сахара, 3,71 кг гречки. Сколько килограммов продуктов купила хозяйка? Ответ округлите до десятых.
б) Автомобиль проехал в первый день 163,5 км, во второй − 207,75 км, в третий − 398,89 км. Найдите длину всего маршрута и округлите результат до целых.
Решение а
5,25 + 1,5 + 3,71 = 6,75 + 3,71 = 10,46 ≈ 10,5 (кг) − продуктов купила хозяйка.
Ответ: 10,5 кг
Вычисления:
+5,25
1,50
6,75
+6,75
3,71
10,46
Решение б
163,5 + 207,75 + 398,89 = 371,25 + 398,89 = 770,14 ≈ 770 (км) − длина всего маршрута.
Ответ: 770 км
Вычисления:
+163,50
207,75
371,25
+371,25
398,89
770,14 10
-
Номер №10
Решите уравнения.
а) x + 4,95 = 5
б) 1,358 + y = 4,903
в) a − 8,98 = 9,09
г) 10,356 − b = 8,099
Решение а
x + 4,95 = 5
x = 5 − 4,95
x = 0,05
Ответ: x = 0,05
Вычисления:
-5,00
4,95
0,05
Решение б
1,358 + y = 4,903
y = 4,903 − 1,358
y = 3,545
Ответ: y = 3,545
Вычисления:
-4,903
1,358
3,545
Решение в
a − 8,98 = 9,09
a = 9,09 + 8,98
a = 18,07
Ответ: a = 18,07
Вычисления:
+9,09
8,98
18,07
Решение г
10,356 − b = 8,099
b = 10,356 − 8,099
b = 2,257
Ответ: b = 2,257
Вычисления:
-10,356
8,099
2,257 Умножение десятичных дробей 1
-
34. Умножение десятичных дробей. Номер №1
Заполните пропуски так, чтобы высказывания были верными.
а) Чтобы умножить десятичную дробь на натуральное число, надо:
1) умножить ее на это число, не обращая внимания на _;
2) в полученном произведении отделить запятой столько цифр, сколько их отделено запятой в _ .
б) Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби перенести запятую на столько цифр _ , сколько _ в множителе после единицы.
Решение
а) Чтобы умножить десятичную дробь на натуральное число, надо:
1) умножить ее на это число, не обращая внимания на запятую;
2) в полученном произведении отделить запятой столько цифр, сколько их отделено запятой в десятичной дроби.
б) Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей в множителе после единицы. 2
-
Номер №2
Закончите запись умножения чисел, поставив в ответе запятые.
Решение а
*1.679
6
10.074
Решение б
*16.625
4
66.500
Решение в*62.04
7
434.28
Решение г
*723.1
5
3615.5
Решение д
*0.48
37
336
144
17.76
Решение е
* 4.8
37
+336
144
177.6
Решение ж
*0.048
37
+336
144
1.776
Решение з
*0.0048
37
+336
144
0.1776 3
-
Номер №3
Выполните умножение.
а)
*6,34
9
б)
*8,362
3
в)
*41,56
7
г)
*1,396
9
д)
*0,037
18
е)
*0,0067
19ж)
*3,28
24
з)
*741,3
59
Решение а
*6.34
9
57.06
Решение б
*8.362
3
25.086
Решение в
*41.56
7
290.92
Решение г
*1.396
9
12.564
Решение д
*0.037
18
296
37
0.666
Решение е
*0.0067
19
603
67
0.1273
Решение ж
*3.28
24
1312
656
78.72
Решение з
*741.3
59
+66717
37065
43736.7 4
-
Номер №4
Выполните умножение.
а) 37,96 * 10
б) 0,39 * 100
в) 5,358 * 10
г) 140,548 * 100
д) 0,0001 * 1000
е) 3,4598 * 10000
Решение а
37,96 * 10 = 379,6
Решение б
0,39 * 100 = 39
Решение в
5,358 * 10 = 53,58
Решение г
140,548 * 100 = 14054,8
Решение д
0,0001 * 1000 = 0,1
Решение е
3,4598 * 10000 = 34598 5
-
Номер №5
Заполните таблицы.
а)х 10 100 1000 7,48 0,19 4,5 б)
х 10 100 1000 5,6 560 83,4 0,89 890
Решение а
Вторая строка
7,48 * 10 = 74,8
7,48 * 100 = 748
7,48 * 1000 = 7480
Третья строка
0,19 * 10 = 1,9
0,19 * 100 = 19
0,19 * 1000 = 190
Четвертая строка
4,5 * 10 = 45
4,5 * 100 = 450
4,5 * 1000 = 4500
Ответ:х 100 100 1000 7,48 74,8 748 7480 0,19 1,9 19 190 4,5 45 450 4500 Решение б
Найдем множитель в первой строке во втором столбце:
560 : 5,6 = 5600 : 56 = 100
Получим:х 100 10 5,6 560 83,4 0,89 890 Найдем множитель в первой строке в четвертом столбце:
890 : 0,89 = 89000 : 89 = 1000
Получим:х 100 10 1000 5,6 560 83,4 0,89 890
Найдем множитель в третьей строке в первом столбце:
83,4 : 10 = 8,34
Получим:х 100 10 1000 5,6 560 8,34 83,4 0,89 890
Тогда:
Вторая строка
5,6 * 10 = 56
5,6 * 1000 = 5600
Третья строка
8,34 * 100 = 834
8,34 * 1000 = 8340
Четвертая строка
0,89 * 100 = 89
0,89 * 10 = 8,9
Ответ:х 100 10 1000 5,6 560 56 5600 8,34 834 83,4 8340 0,89 89 8,9 890 6
-
Номер №6
Вставьте в окошки числа, чтобы получились верные равенства.
а) 708,3 : ☐ = 7,083
б) 5634,95 : ☐ = 5,63495
в) 970 : ☐ = 9,7
г) 2811,01 : ☐ = 2,81101
д) 589,3 : ☐ = 0,05893
е) 642,8 : ☐ = 0,06428
Решение а
708,3 : 100 = 7,083
Решение б
5634,95 : 1000 = 5,63495
Решение в
970 : 100 = 9,7
Решение г
2811,01 : 1000 = 2,81101
Решение д
589,3 : 10000 = 0,05893
Решение е
642,8 : 10000 = 0,06428 7
-
Номер №7
Выполните умножение.
а)
*8000,2
8б)
*800,02
80
в)
*80,002
800
г)
*8,0002
800
д)
*0,036
5
е)
*0,36
50
Решение а
*8000,2
8
64001,6
Решение б
* 800,02
80
64001,60
Решение в
* 80,002
800
64001,600
Решение г
* 8,0002
800
6400,1600
Решение д
* 0,036
5
0,180
Решение е
* 0,36
50
18,00 8
-
Номер №8
Решите задачи.
а) Сумма двух чисел равна разности между 56,6 и 17,4; одно из этих чисел 25,39. Найдите другое число.
б) Одна чугунная отливка имеет массу 24,9 кг, другая на 9,75 кг тяжелее первой, а третья на 1,9 кг легче второй. Какова масса всех трех отливок?
Решение а
1) 56,6 − 17,4 = 39,2 − сумма двух чисел;
2) 39,2 − 25,39 = 13,81 − второе число.
Ответ: 13,81
Вычисления:
1)
-56,6
17,4
39,22)
-39,20
25,39
13,81
Решение б
1) 24,9 + 9,75 = 34,65 (кг) − масса второй отливки;
2) 34,65 − 1,9 = 32,75 (кг) − масса третьей отливки;
3) 24,9 + 34,65 + 32,75 = 59,55 + 32,75 = 92,3 (кг) − масса всех трех отливок.
Ответ: 92,3 кг
Вычисления:
1)
+24,90
9,75
34,652)
-34,65
1,90
32,753)
+24,90
34,65
59,55
+59,55
32,75
92,30 Деление десятичных дробей 1
-
35. Деление десятичных дробей на натуральные числа. Номер №1
Заполните пропуски, чтобы получились верные высказывания.
а) Чтобы разделить десятичную дробь на натуральное число, надо:
1) разделить дробь на это число, не обращая внимание на _ ;
2) поставить в частном запятую, когда кончится _ .
б) Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби перенести запятую на столько цифр _, сколько _ стоит после единицы в _ .
Решение
а) Чтобы разделить десятичную дробь на натуральное число, надо:
1) разделить дробь на это число, не обращая внимание на запятую ;
2) поставить в частном запятую, когда кончится деление целой части.
б) Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби перенести запятую на столько цифр влево, сколько нулей стоит после единицы в делителе. 2
-
Номер №2
Закончите выполнение деления.
Решение а
-16.1|7
14 |2.3
-21
21
0
Решение б
-2.87|14
28 |0.205
-7
0
-70
70
0
Решение в
-11.284|14
112 |0.205
-8
0
-84
84
0
Решение г
-225.68|28
224 |8.06
-16
0
-168
168
0 3
-
Номер №3
Выполните деление.
а) 42,5 : 10
б) 148,56 : 100
в) 10,001 : 100
г) 3794,51 : 1000
д) 8,49 : 100
е) 0,7 : 10
ж) 9,467 : 100
з) 298,7 : 100
Решение а
42,5 : 10 = 4,25
Решение б
148,56 : 100 = 1,4856
Решение в
10,001 : 100 = 0,10001
Решение г
3794,51 : 1000 = 3,79451
Решение д
8,49 : 100 = 0,0849
Решение е
0,7 : 10 = 0,07
Решение ж
9,467 : 100 = 0,09467
Решение з
298,7 : 100 = 2,987 4
-
Номер №4
Представьте обыкновенную дробь в виде десятичной.
Решение а
$\frac{7}{25} = 0,28$-7|25
0|0.28
-70
50
-200
200
0
Решение б
$\frac{3}{8} = 0,375$-3|8
0|0.375
-30
24
-60
56
-40
40
0
Решение в
$\frac{8}{125} = 0,064$-8|125
0|0,064
-800
750
-500
500
0
Решение г
$\frac{9}{32} = 0,28125$-9|32
0|0.28125
-90
64
-260
256
-40
32
-80
64
-160
160
0 5
-
Номер №5
Запишите порядок действий и найдите значение выражения.
а)
б)
Решение а
1) 0,38 + 0,12 = 0,5
2) 0,5 * 0,8 = 0,4
3) 4,08 : 4 = 1,02
4) 1,02 * 5 = 5,1
5) 0,4 + 5,1 = 5,5
Ответ: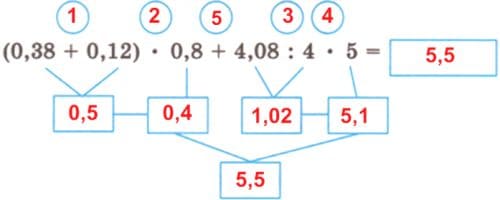
Решение б
1) 20 * 0,8 = 16
2) 16 : 10 = 1,6
3) 1,6 + 0,5 = 2,1
4) 2,1 : 7 = 0,3
5) 5,4 : 9 = 0,6
6) 0,6 * 2 = 1,2
7) 0,3 + 1,2 = 1,5
Ответ: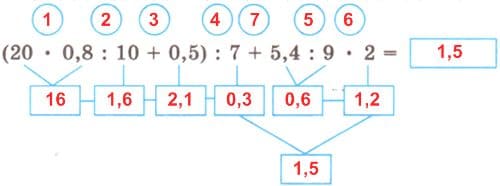
6
-
Номер №6
Решите задачи.
а) По линиям метро за 12 лет перевезено 12,18 млрд пассажиров. Сколько пассажиров в среднем было перевезено за год?
б) Чему равна длина прямоугольника, если площадь его равна 5,202 $м^2$, а ширина равна 3 м?
в) Масса 24 столовых ложек и 36 чайных − 3,3 кг, а масса 36 столовых ложек и 36 чайных − 4,5 кг. Какова масса столовой и масса чайной ложки?
г) Поезд за 1 час 20 минут проезжает 80 км. Сколько километров проедет он в сутки при 10 остановках, каждая из которых по 7,5 минуты?
Решение а
12,18 : 12 = 1,015 (млрд пассажиров) − в среднем было перевезено за год.
Ответ: 1,015 млрд пассажиров
Вычисления:
-12.18|12
12 |1,015
-1
0
-18
12
-60
60
0
Решение б
5,202 : 3 = 1,734 (м) − длина прямоугольника.
Ответ: 1,734 м
Вычисления:
-5.202|3
3 |1,734
-22
21
-10
9
-12
12
0
Решение в
1) 36 − 24 = 12 (столовых) − ложек больше во втором наборе, чем в первом;
2) 4,5 − 3,3 = 1,2 (кг) − на столько второй набор тяжелее первого, значит это масса двенадцати столовых ложек;
3) 1,2 : 12 = 0,1 (кг) − масса одной столовой ложки;
4) 24 * 0,1 = 2,4 (кг) − масса 24 столовых ложек;
5) 3,3 − 2,4 = 0,9 (кг) − масса 36 чайных ложек;
6) 0,9 : 36 = 0,025 (кг) − масса одной чайной ложки.
Ответ: 0,9 кг и 0,025 кг
Вычисления:
-0.9|36
0 |0.025
-90
72
-180
180
0
Решение г
1 ч 20 мин = 80 мин
1 сут. = 24 ч = 1440 мин
1) 80 : 80 = 1 (км/мин) − скорость поезда;
2) 7,5 * 10 = 75 (мин) − общая длительность остановок;
3) 1440 − 75 = 1365 (мин) − поезд будет в движении;
4) 1365 * 1 = 1365 (км) − проедет поезд за сутки.
Ответ: 1365 км Умножение десятичных дробей 1
-
36. Умножение десятичных дробей. Номер №1
Заполните пропуски так, чтобы высказывания были верными.
Чтобы перемножить две десятичные дроби, надо:
1) выполнить умножение, не обращая внимания на _ ;
2) отделить запятой столько цифр справа, сколько их стоит после запятой в _ .
Решение
Чтобы перемножить две десятичные дроби, надо:
1) выполнить умножение, не обращая внимания на запятые;
2) отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях. 2
-
Номер №2
Закончите запись умножения чисел, поставив в ответе запятые.
а)
б)
в)
г)
д)
е)
Решение а
*82.35
0.07
5.7645
Решение б
*16.625
0.8
13.3000
Решение в
*723.1
0.006
4.3386
Решение г
*2.4
0.37
168
72
0.888
Решение д
* 0.329
0.24
+1316
658
0.07896
Решение е
* 0.48
0.37
+336
144
0.1776 3
-
Номер №3
Выполните умножение.
а)
*5,96
2,8
б)
*4,53
0,26
в)
*0,378
57,5
г)
*0,0423
37,5
д)
*2,427
0,34
е)
*4,079
0,35
ж)
*437,8
2,7
з)
*541,08
0,341
Решение а
*5.96
2.8
+4768
1192
16.688
Решение б
* 4.53
0.26
+2718
906
1.1778
Решение в
*0.378
57.5
+1890
2646
1890
21.7350
Решение г
*0.0423
37.5
2115
2961
1269
1.58625
Решение д
*2.427
0.34
+9708
Решение е
*4.079
0.35
+20395
12237
1.42765
Решение ж
*437.8
2.7
+30646
8756
1182.06
Решение з
* 541.08
0.341
+ 54108
216432
162324
184.50828 4
-
Номер №4
Решите уравнения.
а) x : 9,6 = 17,38
б) y : 0,052 = 3,451
в) a − 0,961 = 9,51
г) b + 13,001 = 17
д) 10 − x = 8,341
е) 17,345 + y = 20,991
ж) x : 0,5 = 9,756
з) y : 2,43 = 45,9
Решение а
x : 9,6 = 17,38
x = 17,38 * 9,6
x = 166,848
Ответ: x = 166,848
Вычисления:
*17.38
9.6
+10428
15642
166.848
Решение б
y : 0,052 = 3,451
y = 3,451 * 0,052
y = 0,179452
Ответ: y = 0,179452
Вычисления:
* 3.451
0.052
+6902
17255
0.179452
Решение в
a − 0,961 = 9,51
a = 9,51 + 0,961
a = 10,471
Ответ: a = 10,471
Вычисления:
+9,510
0,961
10,471
Решение г
b + 13,001 = 17
b = 17 − 13,001
b = 3,999
Ответ: b = 3,999
Вычисления:
-17,000
13,001
3,999
Решение д
10 − x = 8,341
x = 10 − 8,341
x = 1,659
Ответ: x = 1,659
Вычисления:
-10,000
8,341
1,659
Решение е
17,345 + y = 20,991
y = 20,991 − 17,345
y = 3,646
Ответ: y = 3,646
Вычисления:
-20,991
17,345
3,646
Решение ж
x : 0,5 = 9,756
x = 9,756 * 0,5
x = 4,878
Ответ: x = 4,878
Вычисления:
*9.756
0.5
4.8780
Решение з
y : 2,43 = 45,9
y = 45,9 * 2,43
y = 111,537
Ответ: y = 111,537
Вычисления:
*45.9
2.43
+ 1377
1836
918
111.537 5
-
Номер №5
Решите задачи.
а) Одна из смежных сторон прямоугольника равна 6,8 см, а другая − в 3,5 раза больше. Чему равна площадь этого прямоугольника?
б) Два парохода вышли одновременно из двух портов навстречу друг другу. Скорость первого 25,5 км/ч, а второго − 19,7 км/ч. Они встретились через 3,75 часа. Чему равно расстояние между портами?
в) Доску перепилили на две части так, что длина одной из них была 3,45 м, длина другой − в 1,7 раза больше. Найдите первоначальную длину доски.
г) Найдите объем прямоугольного параллелепипеда, размеры которого указаны на рисунке (в метрах).
Решение а
1) 6,8 * 3,5 = 23,8 (см) − сторона другой стороны прямоугольника;
2) 6,8 * 23,8 = 161,84 ($см^2$) − площадь прямоугольника.
Ответ: 161,84 $см^2$
Вычисления:
1)
*6.8
3.5
+340
204
136
161.84
2)
* 6.8
23.8
+544
204
136
161.84
Решение б
1) 25,5 + 19,7 = 45,2 (км/ч) − скорость сближения пароходов;
2) 45,2 * 3,75 = 169,5 (км) − расстояние между портами.
Ответ: 169,5 км
Вычисления:
1)
+25,5
19,7
45,2
2)
*45.2
3.75
+2260
3164
1356
169.500
Решение в
1) 3,45 * 1,7 = 5,865 (см) − длина другой части;
2) 3,45 + 5,865 = 9,315 (см) − первоначальная длина доски.
Ответ: 9,315 см
Вычисления:
1)
* 3.45
1.7
+2415
345
5.865
2)
+3,450
5,865
9,315
Решение г
7,8 * 3,4 * 2,3 = 26,52 * 2,3 = 60,996 $(м^3)$ − объем прямоугольного параллелепипеда.
Ответ: 60,996 $м^3$
Вычисления:
* 7.8
3.4
+312
234
26.52
* 26.52
2.3
+7956
5304
60.996 Деление на десятичную дробь 1
-
37. Деление на десятичную дробь. Номер №1
Заполните пропуски так, чтобы высказывания были верными.
Чтобы разделить число на десятичную дробь, надо:
1) в делимом перенести запятую вправо на столько цифр, сколько их после запятой в _ ;
2) после этого выполнить деление на _ число.
Решение
Чтобы разделить число на десятичную дробь, надо:
1) в делимом перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
2) после этого выполнить деление на целое число. 2
-
Номер №2
Найдите частное и выполните проверку.
а) 5,32 : 2,8 = 53,2 : 28
Проверка:
_
б) 30,45 : 8,7 = 304,5 : 87
Проверка
_
в) 28,602 : 0,09 = 2860,2 : 9
Проверка
_
Решение а
5,32 : 2,8 = 53,2 : 28 = 1,9
-53.2|28
28 |1.9
-252
252
0
Проверка:
1,9 * 2,8 = 5,32* 1.9
2.8
+152
38
5.32
Решение б
30,45 : 8,7 = 304,5 : 87 = 3,5-304.5|8.7
261 |3.5
-435
435
0
Проверка:
3,5 * 8,7 = 30,45* 3.5
8.7
+245
280
30.45
Решение в
28,602 : 0,09 = 2860,2 : 9 = 317,8-2860.2|9
27 |317.8
-16
9
-70
63
- 72
72
0
Проверка:
317,8 * 0,09
*317.8
0.09
28.602 3
-
Номер №3
Выполните деление:
а) 27,88 : 4,1 = 278,8 : 41
б) 1,6157 : 0,302
в) 54,0784 : 0,73
г) 2548,61 : 4,3
д) 509,722 : 4,3
е) 161,57 : 5,35
Решение а
27,88 : 4,1 = 278,8 : 41 = 6,8-278.8|41
246 |6.8
-328
328
0
Решение б
1,6157 : 0,302 = 1615,7 : 302 = 5,35-1615.7|302
1510 |5.35
-1057
906
-1510
1510
0
Решение в
54,0784 : 0,73 = 5407,84 : 73 = 74,08-5407.84|73
511 |5.35
-297
292
-58
0
-584
584
0
Решение г
2548,61 : 4,3 = 25486,1 : 43 = 592,7-25486.1|43
215 |592.7
-398
387
-116
86
-301
301
0
Решение д
509,722 : 4,3 = 5097,22 : 43 = 118,54
-5097.22|43
43 |118.54
-79
43
-367
344
-232
215
-172
172
0
Решение е
161,57 : 5,35 = 16157 : 535 = 30,2-16157|535
1605 |30.2
-107
0
-1070
1070
0 4
-
Номер №4
Решите уравнения.
а) 6,04 * x = 3231,4
б) 32,314 : y = 5,35
в) a * 7,1 = 216,55
г) 7,7418 : x = 2,07
Решение а
6,04 * x = 3231,4
x = 3231,4 : 6,04
x = 323140 : 604
x = 535
Ответ: x = 535
Вычисления:-323140|604
3020 |535
-2114
1812
-3020
3020
0
Решение б
32,314 : y = 5,35
y = 32,314 : 5,35
y = 32314 : 535
y = 60,4
Ответ: y = 60,4
Вычисления:-32314|535
3210 |60.4
-214
0
-2140
2140
0
Решение в
a * 7,1 = 216,55
a = 216,55 : 7,1
a = 2165,5 : 71
a = 30,5
Ответ: a = 30,5
Вычисления:-2165.5|71
213 |30.5
-35
0
-355
355
0
Решение г
7,7418 : x = 2,07
x = 7,7418 : 2,07
x = 774,18 : 207
x = 3,74
Ответ: x = 3,74
Вычисления:-774.18|207
621 |3.74
-1531
1449
-828
828
0 5
-
Номер №5
а) Как изменится частное 7,8 : 0,13, если к делимому прибавить 0,39?
б) Какую часть площади полной поверхности куба с ребром 0,15 м составляет площадь полной поверхности куба с ребром 0,075 м?
в) Два парохода вышли одновременно из одного порта и идут в одном направлении. Первый в каждые 1,5 часа проходит 25,5 км, а второй − 19,5 км. Через сколько времени первый пароход обгонит второй на 16 км?
г) Расстояние от A до B равно 450 км. В 8 часов утра выехали одновременно из A почтовый, а из B товарный поезд и идут друг другу навстречу. Товарный поезд проходит весь путь за 18 часов, а почтовый вдвое быстрее. Когда они встретятся?
Решение а
1) 7,8 : 0,13 = 780 : 13 = 60 − первоначальное частное;
2) 7,8 + 0,39 = 8,19 − увеличенное делимое;
3) 8,19 : 0,13 = 819 : 13 = 63 − увеличенное частное;
4) 63 − 60 = 3 − на столько увеличилось частное.
Ответ: частное увеличится на 3
Вычисления:
1)-780|13
78 |60
-0
0
0
2)
+7.80
0.39
8.19
3)-819|13
78 |63
-39
39
0
Решение б
1) $6 * 0,15^2 = 6 * 0,0225 = 0,135 (м^2)$ − площадь полной поверхности куба с ребром 0,15 м;
2) $6 * 0,075^2 = 6 * 0,005625 = 0,03375 (м^2)$ − площадь полной поверхности куба с ребром 0,075 м;
3) $0,03375 : 0,135 = 33,75 : 135 = 0,25 = \frac{25}{100} = \frac{1}{4}$ − часть площади полной поверхности куба с ребром 0,15 м составляет площадь полной поверхности куба с ребром 0,075 м.
Ответ: $\frac{1}{4}$ часть
Вычисления:
1)* 0.15
0.15
+75
15
0.0225
*0.0225
6
0.1350
2)* 0.075
0.075
+ 375
525
0.005625
* 0.005625
6
0.033750
3)-33.75|135
270 |0.25
-675
675
0
Решение в
1) 25,5 : 1,5 = 255 : 15 = 17 (км/ч) − скорость первого парохода;
2) 19,5 : 1,5 = 195 : 15 = 13 (км/ч) − скорость второго парохода;
3) 17 − 13 = 4 (км/ч) − скорость удаления пароходов;
4) 16 : 4 = 4 (ч) − потребуется первому пароходу, чтобы обогнать второй пароход на 16 км.
Ответ: через 4 часа
Вычисления:
1)- 255|15
15 |17
-105
105
0
2)-195|15
15 |13
-45
45
0
Решение г
1) 450 : 18 = 25 (км/ч) − скорость товарного поезда;
2) 25 * 2 = 50 (км/ч) − скорость почтового поезда;
3) 25 + 50 = 75 (км/ч) − скорость сближения поездов;
4) 450 : 75 = 6 (ч) − пройдет до встречи поездов;
5) 8 + 6 = 14 (ч) − время встречи поездов.
Ответ: в 14 часов
Вычисления:
1)-450|18
36 |25
-90
90
0 6
-
Номер №6
Выполните деление.
а) 34,781 : 0,1
б) 9,345 : 0,01
в) 0,0958 : 0,001
г) 1,04 : 0,0001
д) 0,507 : 0,01
е) 0,005 : 0,001
ж) 3,856 : 0,0001
з) 357,2 : 0,01
Решение а
34,781 : 0,1 = 347,81 : 1 = 347,81
Решение б
9,345 : 0,01 = 934,5 : 1 = 934,5
Решение в
0,0958 : 0,001 = 95,8 : 1 = 95,8
Решение г
1,04 : 0,0001 = 10400 : 1 = 10400
Решение д
0,507 : 0,01 = 50,7 : 1 = 50,7
Решение е
0,005 : 0,001 = 5 : 1 = 5
Решение ж
3,856 : 0,0001 = 38560 : 1 = 38560
Решение з
357,2 : 0,01 = 35720 : 1 = 35720 7
-
Номер №7
Найди значение выражения.
а) $3,44 + (0,9 : 0,45)^2 - 2,4 * 0,6$
б) $(0,7 : 0,35)^2 - 4,3 * 0,7 + 2,56$
в) $(2,84 + 0,02 : 0,125)^2 - 4,3 * 0,17 + 0,658$
г) $(0,035 * (2,408 - (0,065 : 0,325)^3) + 1,916)^2$
Решение а
$3,44 + (0,9 : 0,45)^2 - 2,4 * 0,6 = 6$
1) $0,9 : 0,45 = 90 : 45 = 2$
2) $2^2 = 4$
3) 2,4 * 0,6 = 1,44
4) 3,44 + 4 = 7,44
5) 7,44 − 1,44 = 6
Вычисления:
3)*2.4
0.6
1.44
Решение б
$(0,7 : 0,35)^2 - 4,3 * 0,7 + 2,56 = 3,55$
1) 0,7 : 0,35 = 70 : 35 = 2
2) $2^2 = 4$
3) 4,3 * 0,7 = 3,01
4) 4 − 3,01 = 0,99
5) 0,99 + 2,56 = 3,55
Вычисления:
3)*4.3
0.7
3.01
Решение в
$(2,84 + 0,02 : 0,125)^2 - 4,3 * 0,17 + 0,658 = $
1) 0,02 : 0,125 = 20 : 125 = 0,16
2) 2,84 + 0,16 = 3
3) $3^2 = 9$
4) 4,3 * 0,17 = 0,731
5) 9 − 0,731 = 8,269
6) 8,269 + 0,658 = 8,927
Вычисления:
1)-20 |125
0 |0.16
-200
125
-750
750
0
2)
+2,84
0,16
3,00
4)* 4.3
0.17
+301
43
0.731
5)
-9,000
0,731
8,2696)
+8,269
0,658
8,927
Решение г
$(0,035 * (2,408 - (0,065 : 0,325)^3) + 1,916)^2 = 4$1) 0,065 : 0,325 = 65 : 325 = 0,2
2) $0,2^3 = 0,008$
3) 2,408 − 0,008 = 2,4
4) 0,035 * 2,4 = 0,084
5) 0,084 + 1,916 = 2
6) $2^2 = 4$
Вычисления:
1)-65 |325
0 |0.2
-650
650
0
4)*0.035
2.4
+140
70
0.0840
5)
+0,084
1,916
2,000 8
-
Номер №8
Решите уравнения.
а) (0,35 − x) * 0,46 = 0,092
б) (x − 0,08) * 0,37 = 0,148
в) (1,77 − 0,3x) : 0,36 = 4,5
г) (2,61 − 4x) : 0,03 + 4,6 = 90
Решение а
(0,35 − x) * 0,46 = 0,092
0,35 − x = 0,092 : 0,46
0,35 − x = 9,2 : 46
0,35 − x = 0,2
x = 0,35 − 0,2
x = 0,15
Ответ: x = 0,15
Вычисления:-9.2|46
92 |0.2
0
Решение б
(x − 0,08) * 0,37 = 0,148
x − 0,08 = 0,148 : 0,37
x − 0,08 = 14,8 : 37
x − 0,08 = 0,4
x = 0,4 + 0,08
x = 0,48
Ответ: x = 0,48
Вычисления:-14.8|37
148 |0.4
0
Решение в
(1,77 − 0,3x) : 0,36 = 4,5
1,77 − 0,3x = 4,5 * 0,36
1,77 − 0,3x = 1,62
0,3x = 1,77 − 1,62
0,3x = 0,15
x = 0,15 : 0,3
x = 1,5 : 3
x = 0,5
Ответ: x = 0,5
Вычисления:* 4.5
0.36
+270
135
1.620
Решение г
(2,61 − 4x) : 0,03 + 4,6 = 90
(2,61 − 4x) : 0,03 = 90 − 4,6
(2,61 − 4x) : 0,03 = 85,4
2,61 − 4x = 85,4 * 0,03
2,61 − 4x = 2,562
4x = 2,61 − 2,562
4x = 0,048
x = 0,048 : 4
x = 0,012
Ответ: x = 0,012
Вычисления:* 85.4
0.03
2.562
-2,610
2,562
0,048 Среднее арифметическое 1
-
38. Среднее арифметическое. Номер №1
Заполните пропуски так, чтобы получилось верное высказывание. Средним арифметическим нескольких чисел называют частное от деления _ этих чисел на _ слагаемых.
Решение
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых. 2
-
Номер №2
Найдите среднее арифметическое чисел.
а) 5,8 и 3,6
б) 3,5; 9,3; 8,5
в) 16,5; 18,5; 14,4; 17,6
г) 9,12; 8,14; 7,78; 8,94
Решение а
(5,8 + 3,6) : 2 = 9,4 : 2 = 4,7
Вычисления:- 9.4|2
8 |4.7
-14
14
0
Решение б
(3,5 + 9,3 + 8,5) : 3 = (12 + 9,3) : 3 = 21,3 : 3 = 7,1
Вычисления:-21.3|3
21 |7.1
-3
3
0
Решение в
(16,5 + 18,5 + 14,4 + 17,6) : 4 = (35 + 32) : 4 = 67 : 4 = 16,75
Вычисления:-67|4
4 |16.75
-27
24
-30
28
-20
20
0
Решение г
(9,12 + 8,14 + 7,78 + 8,94) : 4 = (16,9 + 17,08) : 4 = 33,98 : 4 = 8,495
Вычисления:-33.98| 4
32 |8.495
-19
16
-38
36
-20
20
0 3
-
Номер №3
На сореdнованиях по фигурному катанию две фигуристки получили (по шестибальной шкале) оценки судей, представлеyные в таблице.Номер фигуристки Номер судьи 1 2 3 4 5 6 7 8 9 1 4,8 5,6 4,9 5,3 4,8 4,9 4,9 4,7 4,7 2 5,1 4,2 5,3 4,9 5,2 5,1 5 5,1 5
Которая из фигуристок выступила лучше?
Решение
1) $(4,8 + 5,6 + 4,9 + 5,3 + 4,8 + 4,9 + 4,9 + 4,7 + 4,7) : 9 = (2 * 4,8 + 3 * 4,9 + 2 * 4,7 + 5,6 + 5,3) : 9 = (9,6 + 14,7 + 9,4 + 10,9) : 9 = (24,3 + 20,3) : 9 = 44,6 : 9 = 446 : 90 = \frac{446}{90} = 4\frac{86}{90}$ − средняя оценка первой фигуристки;
2) $(5,1 + 4,2 + 5,3 + 4,9 + 5,2 + 5,1 + 5 + 5,1 + 5) : 9 = (3 * 5,1 + 2 * 5 + 4,2 + 4,9 + 5,2 + 5,3) : 9 = (15,3 + 10 + 9,1 + 10,5) : 9 = (25,3 + 19,6) : 9 = 44,9 : 9 = 449 : 90 = \frac{449}{90} = 4\frac{89}{90}$ − средняя оценка второй фигуристки;
3) $4\frac{86}{90} < 4\frac{89}{90}$ − значит вторая фигуристка выступила лучше.
Ответ: вторая фигуристка 4
-
Номер №4
Среднее арифметическое двух чисел равно 7,86. Одно из этих чисел 5,9. Найдите второе число.
Решение
1) 7,86 * 2 = 15,72 − сумма двух чисел;
2) 15,72 − 5,9 = 9,82 − второе число.
Ответ: 9,82
Вычисления:
1)*7.86
2
15.72
2)
-15,72
5,90
9,82 5
-
Номер №5
Одно из двух чисел в 4 раза больше другого, а их среднее арифметическое равно 57,98. Найдите эти числа.
Решение
Пусть х − меньшее число, тогда:
4x − большее число.Так как, среднее арифметическое чисел равно 57,98, можно составить уравнение:
(x + 4x) : 2 = 57,98
5x : 2 = 57,98
5x = 57,98 * 2
5x = 115,96
x = 115,96 : 5
x = 23,192 − меньшее число, тогда:
4x = 4 * 23,192 = 92,768 − большее число.
Ответ: 23,192 и 92,768
Вычисления:-115.96|5
10 |23.192
-15
15
-9
5
-46
45
-10
10
0*23.192
4
92.768 6
-
Номер №6
Вычислите.
а)
$ \begin{array}{rl} 3,6 : 9 & \\ *0,4 & \\ +1,24 & \\ *5 & \\ :3,5 & \end{array} $
б)
$ \begin{array}{rl} 8,4 & \\ +2,6 & \\ :5,5 & \\ *7,5 & \end{array} $
в)
$ \begin{array}{rl} 1,44 & \\ *5 & \\ -2,2 & \\ :2,5 & \end{array} $
Решение а
$ \begin{array}{r|l} 3,6 : 9 & 0,4\\ *0,4 & 0,16\\ +1,24 & 1,4\\ *5 & 7\\ :3,5 & 2 \end{array} $
Ответ: 2
Решение б
$ \begin{array}{r|l} 8,4 & \\ +2,6 & 11\\ :5,5 & 2\\ *7,5 & 15 \end{array} $
Ответ: 15
Решение в
$ \begin{array}{r|l} 1,44 & \\ *5 & 7,2\\ -2,2 & 5\\ :2,5 & 2 \end{array} $
Ответ: 2 7
-
Номер №7
Заполните таблицу.a 0,32 0,46 2,82 0,053 0,111 7,84 b 33,2 188,2 3256,1 28,4 6,6 117 1000 * a 320 b : 10 3,32 1000 * a + b : 10 323,32
Решениеa 0,32 0,46 2,82 0,053 0,111 7,84 b 33,2 188,2 3256,1 28,4 6,6 117 1000 * a 320 460 2820 53 111 7840 b : 10 3,32 18,82 325,61 2,84 0,66 11,7 1000 * a + b : 10 323,32 478,82 3145,61 55,84 111,66 7851,7 Микрокалькулятор 1
-
39. Микрокалькулятор. Номер №1
С помощью микрокалькулятора выполните действия.
а) 804359 + 149876
б) 3246835 − 986359
в) 3124 * 186
г) 6570 : 125
Решение а
804359 + 149876 = 954235
Решение б
3246835 − 986359 = 2260476
Решение в
3124 * 186 = 581064
Решение г
6570 : 125 = 52,56 2
-
Номер №2
Выполните действия письменно, а затем проверьте результат с помощью микрокалькулятора.
а)
+37,9782
13,0217
б)
-6,3775
1,49893
в)
*9,17
1,89
Решение а
+37,9782
13,0217
50,9999
Решение б
-6,3775
1,49893
4,87857
Решение в* 9.17
1.89
8253
7336
917
17.3313 3
-
Номер №3
С помощью микрокалькулятора проверьте, верны ли равенства.
а) 16,4 : 0,4 + 9 * 0,8 = 40
б) 0,4 * 0,96 : 8 + 0,052 = 0,1
в) 1,5 : 6 * 8 : 5 + 5,8 − 3,9 = 2,3
г) 800 * 0,34 : 0,8 : 1,7 * 0,4 = 90
Решение а
16,4 : 0,4 + 9 * 0,8 = 40
41 + 7,2 = 40
48,2 = 40 − не верно
Решение б
0,4 * 0,96 : 8 + 0,052 = 0,1
0,4 * 0,96 : 8 + 0,052 = 0,1
0,384 : 8 + 0,052 = 0,1
0,048 + 0,052 = 0,1
0,1 = 0,1 − верно
Решение в
1,5 : 6 * 8 : 5 + 5,8 − 3,9 = 2,3
0,25 * 8 : 5 + 1,9 = 2,3
2 : 5 + 1,9 = 2,3
0,4 + 1,9 = 2,3
2,3 = 2,3 − верно
Решение г
800 * 0,34 : 0,8 : 1,7 * 0,4 = 90
272 : 0,8 : 1,7 * 0,4 = 90
340 : 1,7 * 0,4 = 90
200 * 0,4 = 90
80 = 90 − не верно 4
-
Номер №4
Найдите с помощью калькулятора значения выражений.
а) 84,7 * 1,995 − 35,3396
б) (95,862 + 35,109) * 4,22
в) 142,88 : 0,125 + 0,8989
г) (26006 − 22458) * 5,06
Решение а
84,7 * 1,995 − 35,3396 = 168,9765 − 35,3396 = 133,6369
Решение б
(95,862 + 35,109) * 4,22 = 130,971 * 4,22 = 552,69762
Решение в
142,88 : 0,125 + 0,8989 = 1143,04 + 0,8989 = 1143,9389
Решение г
(26006 − 22458) * 5,06 = 3548 * 5,06 = 17952,88 5
-
Номер №5
По формуле V = abc найдите с помощью микрокалькулятора объем прямоугольного параллелепипеда, если a = 28,56, b = 23,48, c = 37,59.
Ответ округлите до тысячных.
Решение
V = abc = 28,56 * 23,48 * 37,59 = 670,5888 * 37,59 = 25207,432992 ≈ 25207,433 − объем прямоугольного параллелепипеда.
Ответ: 25207,433 Проценты 1
-
40. Проценты. Номер №1
Заполните пропуски так, чтобы получились верные высказывания.
а) Процентом называют _ часть.
б) Чтобы десятичную дробь обратить в проценты, нужно ее _ на 100.
в) Чтобы перевести проценты в десятичную дробь, нужно _ число процентов на 100.
Решение
а) Процентом называют сотую часть.
б) Чтобы десятичную дробь обратить в проценты, нужно ее умножить на 100.
в) Чтобы перевести проценты в десятичную дробь, нужно разделить число процентов на 100. 2
-
Номер №2
Запишите числа в виде десятичной дроби.
а) 7%
б) 85%
в) 15,6%
г) 3,8%
д) 148%
е) 0,7%
Решение а
7% = 7% : 100% = 0,07
Решение б
85% = 85% : 100% = 0,85
Решение в
15,6% = 15,6% : 100% = 0,156
Решение г
3,8% = 3,8% : 100% = 0,038
Решение д
148% = 148% : 100% = 1,48
Решение е
0,7% = 0,7% : 100% = 0,007 3
-
Номер №3
Запишите десятичные дроби в процентах.
а) 0,74
б) 0,37
в) 0,498
г) 3,25
д) 45,641
е) 0,16
Решение а
0,74 = 0,74 * 100% = 74%
Решение б
0,37 = 0,37 * 100% = 37%
Решение в
0,498 = 0,498 * 100% = 49,8%
Решение г
3,25 = 3,25 * 100% = 325%
Решение д
45,641 = 45,641 * 100% = 4564,1%
Решение е
0,16 = 0,16 * 100% = 16% 4
-
Номер №4
Запишите числа в виде десятичной дроби, а затем в виде процентов.
а) $\frac{1}{4}$
б) $\frac{1}{2}$
в) $6\frac{3}{4}$
г) $3\frac{1}{20}$
Решение а
$\frac{1}{4} = 0,25 = 25$%
Решение б
$\frac{1}{2} = 0,5 = 50$%
Решение в
$6\frac{3}{4} = 6,75 = 675$%
Решение г
$3\frac{1}{20} = 3,05 = 305$% 5
-
Номер №5
Заполните таблицу.Проценты 1% 3% 75% 100% 110% 1020% Десятичная дробь 0,01 0,03 Дробь $\frac{1}{100}$ $\frac{3}{100}$
РешениеПроценты 1% 3% 75% 100% 110% 1020% Десятичная дробь 0,01 0,03 0,75 1 1,1 10,2 Дробь $\frac{1}{100}$ $\frac{3}{100}$ $\frac{75}{100}$ $\frac{100}{100}$ $1\frac{10}{100}$ $10\frac{20}{100}$ 6
-
Номер №6
Закрасьте 50% площади каждой фигуры.
Решение
50%$ = 0,5 = \frac{1}{2}$ фигуры, значит надо закрасить половину каждой фигуры.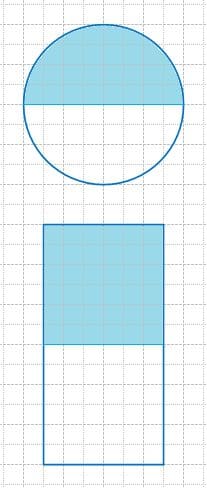
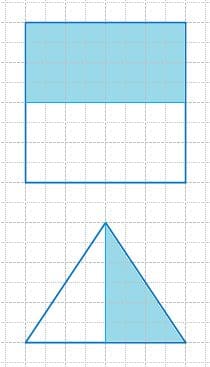
7
-
Номер №7
Закрасьте 25% площади каждой фигуры.
Решение
25%$ = 0,25 = \frac{1}{4}$ фигуры, значит надо закрасить четверть каждой фигуры.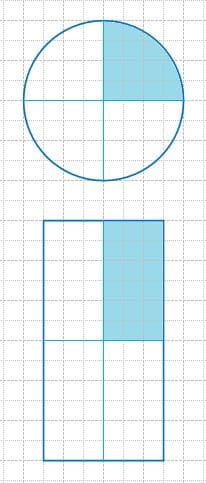
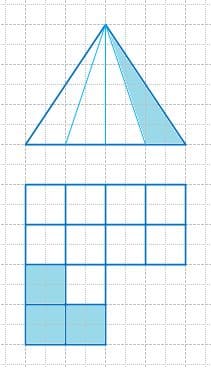
8
-
Номер №8
Сколько процентов площади прямоугольника составляет закрашенная часть?
Решение
Первый прямоугольник
1) 4 * 5 = 20 (клеток) − в прямоугольнике всего;
2) 4 * 2 = 8 (клеток) − закрашено;
3) $\frac{8}{20} = 0,4 = 40$% − площади прямоугольника составляет закрашенная часть.Второй прямоугольник
1) 10 * 10 = 100 (клеток) − в прямоугольнике всего;
2) 2 * 3 = 6 (клеток) − закрашено;
3) $\frac{6}{100} = 0,06 = 6$% − площади прямоугольника составляет закрашенная часть.
Ответ: 1) 40%; 2) 6%. 9
-
Номер №9
Найдите.
а) 3% от 80.
б) 5% от 4
в) 12% от 60
г) 60% от 90
Решение а
1) Найдем, чему равен 1% от 80:
80 : 100 = 0,8
2) Найдем, чему равны 3% от 80:
0,8 * 3 = 2,4
Ответ: 2,4
Решение б
1) Найдем, чему равен 1% от 4:
4 : 100 = 0,04
2) Найдем, чему равны 5% от 4:
0,04 * 5 = 0,2
Ответ: 0,2
Решение в
1) Найдем, чему равен 1% от 60:
60 : 100 = 0,6
2) Найдем, чему равны 12% от 60:
0,6 * 12 = 7,2
Ответ: 7,2
Решение г
1) Найдем, чему равен 1% от 90:
90 : 100 = 0,9
2) Найдем, чему равны 60% от 90:
0,9 * 60 = 54
Ответ: 54 10
-
Номер №10
Решите задачи.
а) При помощи ржи получают 75% муки. Сколько килограммов муки получится при помоле 1560 кг ржи?
б) Участок земли имеет прямоугольную форму, его длина равна 1,5 км, а ширина составляет 0,6 длины. Лес составляет 30% всей площади. Определите в гектарах площадь, занятую лесом.
Решение а
75% = 0,75
1560 * 0,75 = 1170 (кг) − муки получится при помоле 1560 кг ржи.
Ответ: 1170 кг
Вычисления: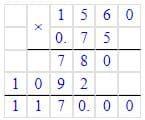
Решение б
30% = 0,3
1) 1,5 * 0,6 = 0,9 (км) − ширина участка;
2) 1,5 * 0,9 = 1,35 $(км^2)$ − площадь участка;
3) 1,35 * 0,3 = 0,405 $(км^2)$ = 40,5 (га) − занято лесом.
Ответ: 40,5 га
Вычисления:
1)
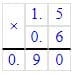2)
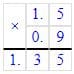3)
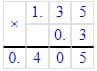
11
-
Номер №11
Закончите запись.
а) если 20% − это 6 р., то 100% − это _ р.
б) если 10% − это 14 р., то 100% − это _ р.
в) если 5% − это 100 р., то 100% − это _ р.
г) если 50% − это 3 р., то 100% − это _ р.
д) если 25% − это 1 р., то 100% − это _ р.
е) если 75% − это 60 р., то 100% − это _ р.
Решение а
(100 : 20) * 6 = 5 * 6 = 30 (р.)
Ответ: если 20% − это 6 р., то 100% − это 30 р.
Решение б
(100 : 10) * 14 = 10 * 14 = 140 (р.)
Ответ: если 10% − это 14 р., то 100% − это 140 р.
Решение в
(100 : 5) * 100 = 20 * 100 = 2000 (р.)
Ответ: если 5% − это 100 р., то 100% − это 2000 р.
Решение г
(100 : 50) * 3 = 2 * 3 = 6 (р.)
Ответ: если 50% − это 3 р., то 100% − это 6 р.
Решение д
(100 : 25) * 1 = 4 * 1 = 4 (р.)
Ответ: если 25% − это 1 р., то 100% − это 4 р.
Решение е
(100 : 75) * 60 = (100 * 60) : 75 = 6000 : 75 = 80 (р.)
Ответ: если 75% − это 60 р., то 100% − это 80 р. 12
-
Номер №12
Машина в первый день проехала 750 км, что составило 30% всего пути. Какой путь предстояло проехать машине?
Решение
Найдем, сколько километров составляет 1% пути:
750 : 30 = 75 : 3 = 25 (км)
Найдем, сколько километров составляет 100% пути, то есть каков весь путь:
25 * 100 = 2500 (км)
Ответ: 2500 км 13
-
Номер №13
Площадь земельного участка 1500 $м^2$. Кусты смородины занимают 450 $м^2$. Какой процент участка занимают кусты смородины?
Решение
Найдем, какую часть площади земельного участка занимает смородина:
450 : 1500 = 0,3- 450|1500
0 |0.3
-4500
4500
0
Выразим полученную дробь в процентах:
0,3 * 100% = 30%
Ответ: 30% 14
-
Номер №14
Найдите число, если:
а) 1% этого числа равен 700
б) 7% этого числа равны 9,8
в) 350% этого числа равны 7
г) 1% этого числа равен $5\frac{1}{2}$
д) $\frac{1}{8}$% этого числа равна 1,25
е) 25% этого числа равны 4% от 25
Решение а
700 * 100 = 70000 − искомое число.
Ответ: 70000
Решение б
1) 9,8 : 7 = 1,4 − составляет 1% от числа;
2) 1,4 * 100 = 140 − искомое число.
Ответ: 140
Решение в
1) 7 : 350 = 0,02 − составляет 1% от числа;
2) 0,02 * 100 = 2 − искомое число.
Ответ: 2
Вычисления:-7 |350
0 | 0.02
-70
0
-700
700
0
Решение г
$5\frac{1}{2} * 100 = 5,5 * 100 = 550$ − искомое число.
Ответ: 550
Решение д
1) $1,25 : \frac{1}{8} = 1,25 : 0,125 = 10$ − составляет 1% от числа;
2) 10 * 100 = 1000 − искомое число.
Ответ: 1000
Вычисления:-1 |8
0 |0.125
-10
8
-20
16
-40
40
0
Решение е
4% = 0,04
1) 25 * 0,04 = 1 − составляет 4% от 25;
2) 1 : 25 = 0,04 − составляет 1% от числа;
3) 0,04 * 100 = 4 − искомое число.
Ответ: 4
Вычисления:- 1 |25
0 |0.04
-10
0
-100
100
0 15
-
Номер №15
Сколько процентов от числа составляет:
а) число 23,4 от 46,8
б) число 30 от 0,3
в) число $4\frac{1}{8}$ от $8\frac{1}{4}$
г) число 119 от 700
Решение а
23,4 : 46,8 * 100% = 0,5 * 100% = 50%
Решение б
30 : 0,3 * 100% = 100 * 100% = 10000%
Решение в
$4\frac{1}{8} : 8\frac{1}{4} * 100$% = 4,125 : 8,25 * 100% = 0,5 * 100% = 50%
Решение г
119 : 700 * 100% = (119 * 100%): 700 = 11900% : 700 = 119% : 7 = 17% 16
-
Номер №16
Решите задачи.
а) Рыбак поймал 18 лещей, что составляет 36% всего улова. Сколько всего рыб поймал рыбак?
б) Из 80 г семян взошло 64 г. Найдите процент всхожести семян.
в) Молоко содержит 8% сливок. Сколько потребуется молока, чтобы получить 16,8 кг сливок?
г) За день Егор выкопал 9 ведер картошки вместо 12. Сколько процентов плана осталось не выполнено?
д) В библиотеке 4300 книг. И них 40% в твердом переплете, в мягком переплете − 115% от книг в твердом переплете, остальные − в электронном виде. Сколько книг в электронном виде в библиотеке?
е) После 10−процентного и 15−процентного снижения цен стоимость куртки составила 3060 рублей. Сколько стоила куртка первоначально?
Решение а
1) 18 : 36 = 0,5 (леща) − составляет 1% всего улова;
2) 0,5 * 100% = 50 (рыб) − всего поймал рыбак.
Ответ: 50 рыб
Решение б
64 : 80 * 100% = 0,8 * 100% = 80% − составила всхожесть семян.
Ответ: 80%
Решение в
1) 16,8 : 8 = 2,1 (кг) − молока составляет 1%;
2) 2,1 * 100 = 210 (кг) − молока потребуется, чтобы получить 16,8 кг сливок.
Ответ: 210 кг
Решение г
1) 9 : 12 * 100% = (9 * 100%) : 12 = 900% : 12 = 75% − плана выполнил Егор;
2) 100% − 75% = 25% − плана осталось не выполнено.
Ответ: 25%
Решение д
40% = 0,4
115% = 1,15
1) 4300 * 0,4 = 1720 (книг) − в твердом переплете;
2) 1720 * 1,15 = 1978 (книг) − в мягком переплете;
3) 4300 − (1720 + 1978) = 4300 − 3698 = 602 (книги) − в электронном виде.
Ответ: 602 книги
Вычисления:
1)
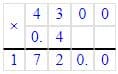2)
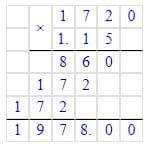3)
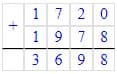
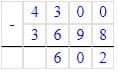
Решение е
1) 100% − 15% = 85% − составляет 3060 рублей;
2) 3060 : 85 * 100 = 36 * 100 = 3600 (рублей) − стоила куртка после первого снижения цены;
3) 100% − 10% = 90% − составляет 3600 рублей;
4) 3600 : 90 * 100 = 400 * 100 = 4000 (рублей) − стоила куртка первоначально.
Ответ: 4000 рублей
Вычисления:-3060|85
255 |36
-510
510
0 Угол. Прямой и развернутый 1
-
41. Угол. Прямой и развернутый угол. Чертежный треугольник. Номер №1
Заполните пропуски так, чтобы высказывания были верными.
а) Углом называют фигуру, образованную двумя _ , выходящими из _ точки.
б) Лучи, образующие угол, называют _, а точку из которой они выходят, _ угла.
в) Два дополнительных друг другу луча образуют _ угол. Стороны этого угла вместе составляют _ .
г) Прямым углом называют _ развернутого угла.
Решение
а) Углом называют фигуру, образованную двумя лучами, выходящими из одной точки.
б) Лучи, образующие угол, называют сторонами, а точку из которой они выходят, вершиной угла.
в) Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию.
г) Прямым углом называют половину развернутого угла. 2
-
Номер №2
Запишите названия углов, изображенных на рисунках.
Решение
а) ABC
б) CDF
в) KMN
г) POE 3
-
Номер №3
Найдите на рисунке прямые углы.
Прямые углы _
Решение
Прямые углы ABC, LTC. 4
-
Номер №4
Начертите развернутый угол со стороной OA. Обозначьте его.
Решение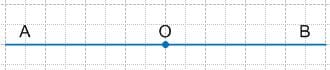
∠AOB 5
-
Номер №5
Постройте с помощью чертежного треугольника прямой угол со стороной BC. Сколько таких улов можно построить?
Решение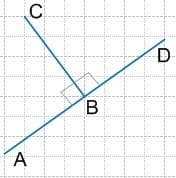
Можно провести два прямых угла со стороной BC. Это углы: ABC и CBD 6
-
Номер №6
Какие из углов имеют общую сторону?
Углы Стороны
Решение
Углы Стороны
∠CKP и ∠BKP KP
∠CKP и ∠CKB CK
∠CKB и ∠BKP BK 7
-
Номер №7
Запишите называния каждого угла:
а) треугольника
б) прямоугольника
в) пятиугольника
Решение а
∠ABC, ∠ACB, ∠BAC.
Решение б
∠AMP, ∠MPK, ∠PKA, ∠KAM.
Решение в
∠FTO, ∠TOB, ∠OBC, ∠BCF, ∠CFT. 8
-
Номер №8
С помощью чертежного треугольника постройте прямоугольник со сторонами 5 см и 3 см.
Заполните пропуски.
Площадь прямоугольника равна _ $см^2$;
периметр прямоугольника равен _ см.
Решение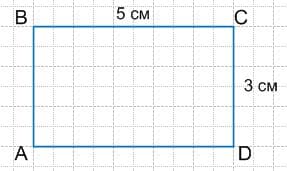
1) 5 * 3 = 15 $(см^2)$ − площадь прямоугольника;
2) 2 * (5 + 3) = 2 * 8 = 16 (см) − периметр прямоугольника.
Ответ:
Площадь прямоугольника равна 15 $см^2$;
периметр прямоугольника равен 16 см. Измерение углов 1
-
42. Измерение углов. Транспортир. Номер №1
Заполните пропуски так, чтобы высказывания были верными.
а) Градусом называют _ долю развернутого угла.
б) Развернутый угол равен _ градусам, прямой угол равен _ градусам.
в) Если угол меньше 90°, то его называют _ углом.
г) Если угол больше 90°, но меньше 180°, то его называют _ углом.
Решение
а) Градусом называют $\frac{1}{180}$ долю развернутого угла.
б) Развернутый угол равен 180 градусам, прямой угол равен 90 градусам.
в) Если угол меньше 90°, то его называют острым углом.
г) Если угол больше 90°, но меньше 180°, то его называют тупым углом. 2
-
Номер №2
Измерьте углы и запишите их величины.
Решение
∠BAC = 50°
∠FOK = 50°
∠PLT = 90°
∠MKP = 30° 3
-
Номер №3
Постройте с помощью транспортира углы с общей стороной OK, равные 45°, 70°, 90°, 145°, 180°.
Решение
∠KOB = 45°
∠KOC = 70°
∠KOD = 90°
∠KOE = 145°
∠KOF = 180° 4
-
Номер №4
Измерьте ∠AOC. Проведите луч OM, который делит этот угол пополам. Обозначьте образовавшиеся углы и измерьте их.
Решение
∠AOC = 120°
∠AOB = 60°
∠BOC = 60° 5
-
Номер №5
Измерьте величину данного угла. Дополните его до развернутого и вычислите величину угла, дополняющего даннный угол до развернутого.
∠ABC =
∠TPF =
Решение а
∠ABC = 110°
∠ABD = 180° − так как развернутый
∠СBD = ∠ABD − ∠ABC = 180° − 110° = 70°
Решение б
∠TPF = 50°
∠TPK = 180° − так как развернутый
∠FPK = ∠TPK − ∠TPF = 180° − 50° = 130° 6
-
Номер №6
Проведите лучи OM и OF так, чтобы ∠POM был равен 90°, а ∠FOM − 120°, и луч OA так, чтобы ∠POA был равен 90°, а ∠AOF − 60°.
Решение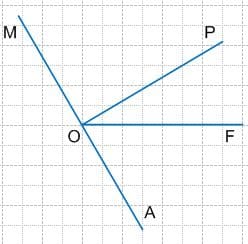
7
-
Номер №7
Пользуясь транспортиром, постройте ∠ABC, равный 140°.
Решение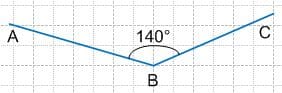
Круговые диаграммы 1
-
43. Круговые диаграммы. Номер №1
На круговой диаграмме показано распределение цветов, которые выращивают на садовом участке. Используй диаграмму, определите верные утверждения и подчеркните их.
а) Больше всего места отведено под розы.
б) Пионы занимают столько же места, сколько и ромашки.
в) Астры и гладиолусы занимают половину участка.
г) Под пионы отведено больше места, чем под астры.
Решение
а) Больше всего места отведено под розы.
б) Пионы занимают столько же места, сколько и ромашки.
в) Астры и гладиолусы занимают половину участка.
г) Под пионы отведено больше места, чем под астры. 2
-
Номер №2
На круговой диаграмме показано наличие книг в фонде некоторой библиотеки. Пользуясь диаграммой, заполните пропуски.
а) Большую часть фонда занимает _ .
б) Учебная и педагогическая литература занимает _ %.
в) Энциклопедий и словарей столько же, сколько _ .
г) Меньше всего в библиотеке _ .
д) Половину фонда библиотеки составляет общественно−политическая и _ .
Решение
а) Большую часть фонда занимает художественная и детская литература.
б) Учебная и педагогическая литература занимает 25 %.
в) Энциклопедий и словарей столько же, сколько общественно−политической литературы.
г) Меньше всего в библиотеке научно−технической литературы.
д) Половину фонда библиотеки составляет общественно−политическая и художественная и детская литература. 3
-
Номер №3
В саду $\frac{1}{3}$ всех деревьев − яблони, $\frac{1}{6}$ − груши, а остальные − вишневые деревья. Постройте круговую диаграмму, показывающую распределение деревьев в саду.
Решение
Вся окружность 360°, тогда:
1) 360° : 3 = 120° на диаграмме будут занимать яблоки;
2) 360° : 6 = 60° на диаграмме будут занимать груши;
3) 360° − (120° + 60°) = 360° − 180° = 180° на диаграмме будут занимать вишневые деревья.
Ответ: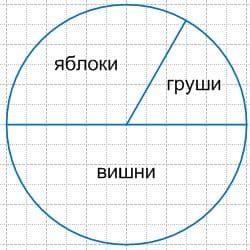
4
-
Номер №4
Пшеница при размоле дает 80% муки. Остальное − отруби. Покажите на круговой диаграмме распределение муки и отрубей при размоле пшеницы.
Решение
1) 100% − 80% = 20% − отрубей дает при размоле пшеница;
80% = 0,8
20% = 0,2
2) 360° * 0,8 = 288° − будет занимать на диаграмме мука;
3) 360° * 0,2 = 72° − будут занимать на диаграмме отруби.
Ответ: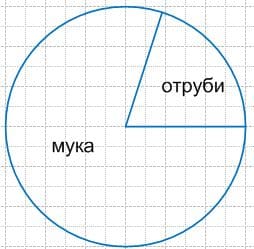
5
-
Номер №5
На теплоходе находились 25% мужчин, 55% женщин, остальные − дети. Постройте круговую диаграмму, показывающую состав пассажиров на теплоходе.
Решение
1) 100% − (25% + 55%) = 100% − 80% = 20% − на теплоходе составляли дети;
25% = 0,25
55% = 0,55
20% = 0,2
2) 360° * 0,25 = 90° − будут занимать на диаграмме мужчины;
3) 360° * 0,55 = 198° − будут занимать на диаграмме женщины;
4) 360° * 0,2 = 72° − будут занимать на диаграмме дети.
Ответ:
6
-
Номер №6
Вставьте пропущенные числа.
а) Число _ составляет 25% от числа 90.
б) Число 45 составляет _ % от числа 90.
в) Число 60 составляет 10% от числа _ .
Решение а
25% = 0,25
90 * 0,25 = 22,5
Ответ: Число 22,5 составляет 25% от числа 90.
Решение б
1) 45 : 90 = 0,5
2) 0,5 * 100% = 50%
Ответ: Число 45 составляет 50% от числа 90.
Решение в
1) 60 : 10 = 6 − составляет 1%;
2) 6 * 100 = 600
Ответ: Число 60 составляет 10% от числа 600. 7
-
Номер №7
Сравните величины, используя знаки >, < или =.
а) 40% от 10 _ 10% от 40
б) 20% от 60 _ 60% от 20
в) 50% от 48 _ 48% от 50
г) 70% от 20 _ 20% от 70
Решение а
1) 10 * 0,4 = 4 − составляет 40% от 10;
2) 40 * 0,1 = 4 − составляет 10% от 40.
4 = 4, значит:
40% от 10 = 10% от 40
Решение б
1) 60 * 0,2 = 12 − составляет 20% от 60;
2) 20 * 0,6 = 12 − составляет 60% от 20.
12 = 12, значит:
20% от 60 = 60% от 20
Решение в
1) 0,5 * 48 = 24 − составляет 50% от 48;
2) 0,48 * 50 = 24 − составляет 48% от 50.
24 = 24, значит:
50% от 48 = 48% от 50
Решение г
1) 0,7 * 20 = 14 − составляет 70% от 20;
2) 0,2 * 70 = 14 − составляет 20% от 70.
14 = 14, значит:
70% от 20 = 20% от 70 Понятие множества 1
-
44. Понятие множества. Номер №1
Запишите с помощью перечисления, используя фигурные скобки или знак ∅, множество:
а) двузначных чисел, оканчивающихся цифрой 7 _
б) двузначных чисел, оканчивающихся цифрой 6 _
в) двузначных чисел, делящихся на 9 _
г) правильных дробей со знаменателем 10 _
д) натуральных чисел, кратных 3 и меньших 20 _
е) вершин шестиугольника ABCDEF _
ж) сторон шестиугольника ABCDEF _
з) натуральных чисел, находящихся между числами 100 и 101
Решение
а) двузначных чисел, оканчивающихся цифрой 7 {17, 27, 37, 47, 57, 67, 77, 87, 97}
б) двузначных чисел, оканчивающихся цифрой 6 {16, 26, 36, 46, 56, 66, 76, 86, 96}
в) двузначных чисел, делящихся на 9 {18, 27, 36, 45, 54, 63, 72, 81, 90, 99}
г) правильных дробей со знаменателем 10 {$\frac{1}{10}, \frac{2}{10}, \frac{3}{10}, \frac{4}{10}, \frac{5}{10}, \frac{6}{10}, \frac{7}{10}, \frac{8}{10}, \frac{9}{10}$}
д) натуральных чисел, кратных 3 и меньших 20 {3, 6, 9, 12, 15, 18}
е) вершин шестиугольника ABCDEF {A, B, C, D, E, F}
ж) сторон шестиугольника ABCDEF {AB, BC, CD, DE, EF, AF}
з) натуральных чисел, находящихся между числами 100 и 101 ∅ 2
-
Номер №2
Задайте множество цифр, с помощью которых записывается число:
а) 4365
б) 4363
в) 5555555
г) 10100100010000
Решение а
{4, 3, 6, 5}
Решение б
{4, 3, 6}
Решение в
{5}
Решение г
{0, 1} 3
-
Номер №3
Множество A состоит из всех трехзначных чисел, которые можно составить из цифр 7, 8, 0 так, чтобы цифры не повторялись. Сколько элементов содержит множество A?
Решение
A = {780, 708, 870, 807}
Ответ: множество A содержит четыре элемента 4
-
Номер №4
Задайте множество B описанием.
а) B = {2, 4, 6, 8}
б) B = {11, 22, 33, 44, 55, 66, 77, 88, 99}
в) B = {$\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}$}
Решение а
B = {2, 4, 6, 8}
Множество B состоит из множества четных однозначных натуральных чисел.
Решение б
B = {11, 22, 33, 44, 55, 66, 77, 88, 99}
Множество B состоит из множества двузначных натуральных чисел, в которых количество единиц и десятков равно.
Решение в
B = {$\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}$}
Множество B состоит из множества правильных дробей со знаменателем 5. 5
-
Номер №5
Определите, по какому признаку составлено множество чисел:
а) A = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
б) B = {13, 26, 39, 52, 65, 78, 91}
в) C = {14, 24, 34, 44, 54, 64, 74, 84, 94}
г) D = {2, 4, 8, 16, 32, 64}
Решение а
A = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
Множество A состоит из множества натуральных чисел, кратных 3 и меньше 31.
Решение б
B = {13, 26, 39, 52, 65, 78, 91}
Множество B состоит из множества двузначных натуральных чисел, кратных 13.
Решение в
C = {14, 24, 34, 44, 54, 64, 74, 84, 94}
Множество C состоит из множества двузначных натуральных чисел, оканчивающихся на 4.
Решение г
D = {2, 4, 8, 16, 32, 64}
Множество D состоит из множества четных натуральных чисел меньших 100, в котором каждое последующее число больше предыдущего в 2 раза. 6
-
Номер №6
Запишите с помощью фигурных скобок или знака ∅ множества A, B, C, D, если:
а) A − множество обыкновенных несократимых дробей с однозначным знаменателем, заключенных между числами $\frac{1}{9}$ и $\frac{1}{2}$
б) B − множество десятичных дробей с одним знаком после запятой, больших $\frac{1}{4}$ и меньших 1
в) C − множество трехзначных чисел, в записи которых используются лишь цифры 3, 5 и 0
г) D − множество букв M, которые использовались для записи слова "букварь"
Решение а
$\frac{1}{9} = \frac{2}{18}$
$\frac{1}{2} = \frac{9}{18}$
$\frac{2}{18}$ < {$\frac{3}{18}, \frac{4}{18}, \frac{5}{18}, \frac{6}{18}, \frac{7}{18}, \frac{8}{18}$} < $\frac{9}{18}$
$\frac{3}{18} = \frac{1}{6}$
$\frac{4}{18} = \frac{2}{9}$
$\frac{6}{18} = \frac{1}{3}$
$\frac{8}{18} = \frac{4}{9}$,
тогда:
A = {$\frac{1}{6}, \frac{2}{9}, \frac{1}{3}, \frac{4}{9}$}
Решение б
$\frac{1}{4} = 0,25$
B = {0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9}
Решение в
C = {333, 335, 330, 355, 300, 350, 305, 303, 353, 555, 553, 550, 533, 500, 530, 503, 505, 535}
Решение г
D = ∅ 7
-
Номер №7
Пусть A − множество двузначных чисел, B − множество трехзначных чисел.
Запишите, используя знак ∈, какое из чисел 59, 621, 18, 4127 принадлежит множеству A, а какое − множеству B.
Решение
59 ∈ A
621 ∈ B
18 ∈ A
4127 ∉ A
4127 ∉ B 8
-
Номер №8
A − множество двузначных чисел, делящихся на 9. Запишите множество A с помощью фигурных скобок. С помощью знаков ∈ и ∉ запишите, какие из чисел 9, 17, 27, 41, 45, 54 принадлежат множеству A и какие ему не принадлежат.
Решение
A = {18, 27, 36, 45, 54, 63, 72, 81, 90, 99}
9 ∉ A
17 ∉ A
27 ∈ A
41 ∉ A
45 ∈ A
54 ∈ A 9
-
Номер №9
Вычислите:
а) 6364 − 6364 : (880 : 20 + 42)
б) $548316 : (41 - 38)^3$
Решение а
6364 − 6364 : (880 : 20 + 42) = 6290
1) 880 : 20 = 88 : 2 = 44
2) 44 + 42 = 86
3) 6364 : 86 = 74
4) 6364 − 74 = 6290
Вычисления:-6364|86
602 |74
-344
344
0
Решение б
$548316 : (41 - 38)^3 = 20308$
1) 41 − 38 = 3
2) $3^3 = 3 * 3 * 3 = 27$
3) 548316 : 27 = 20308
Вычисления:-548316|27
54 |20308
-8
0
-83
81
-21
0
-216
216
0 10
-
Номер №10
Решите задачу. Известно, что A больше B в 6 раз, а B меньше C в 2 раза. Какое из чисел больше A или C? Во сколько раз?
Решение
Пусть B = x, тогда:
A = 6x
C = 2x
6x > 2x
6x : 2x = 3 − значит A больше C в 3 раза.
Ответ: A больше C в 3 раза. Общая часть множеств 1
-
45. Общая часть множеств. Объединение множеств. Номер №1
Даны множества:
A = {6, 8, 14, 17, 25, 30}, B = {6, 25}, C = {14, 25, 30}, D = {25}, E = {6, 17}.
С помощью знака включения (⊂) запишите, в каком отношении находятся эти множества между собой.
Решение
B ⊂ A
C ⊂ A
D ⊂ A
E ⊂ A
D ⊂ B
D ⊂ C 2
-
Номер №2
Пусть A − множество однозначных натуральных чисел. Составьте с помощью перечисления элементов подмножество множества A, в котором все элементы:
а) четные числа
б) нечетные числа
в) числа, кратные 3
Решение
A = {1, 2, 3, 4, 5, 6, 7, 8, 9}Подмножества множества A:
а) {2, 4, 6, 8}
б) {1, 3, 5, 7, 9}
в) {3, 6, 9} 3
-
Номер №3
Пусть B − множество натуральных чисел кратных 5. Составьте с помощью перечисления элементов подмножество множества B, которое состоит из:
а) чисел, меньших 65
б) четных чисел, меньших 65
в) нечетных чисел, меньших 65
Решение
Подмножества множества B:
а) {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60}
б) {10, 20, 30, 40, 50, 60}
в) {5, 15, 25, 35, 45, 55} 3*
-
Номер №3*
Из некоторого множества P составили все его подмножества:
∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}.
Запишите множество P.
Решение
P = {a, b, с} 4
-
Номер №4
Даны множества: A = {1, 2, 7}, B = {1, 2, 7, 10}, C = {4, 10}.
Найдите:
а) A U B
б) A U C
в) B U C
г) A ∩ B
д) A ∩ C
е) C ∩ B
Решение а
A U B = {1, 2, 7, 10}
Решение б
A U C = {1, 2, 4, 7, 10}
Решение в
B U C = {1, 2, 4, 7, 10}
Решение г
A ∩ B = {1, 2, 7}
Решение д
A ∩ C = ∅
Решение е
C ∩ B = {10} 5
-
Номер №5
Даны множества: M = {a, b, c}, K = {x, y}, P = {b, c, x}.
Найдите:
а) M U K
б) K U P
в) M U P
г) M ∩ K
д) K ∩ P
е) M ∩ P
Решение а
M U K = {a, b, c, x, y}
Решение б
K U P = {b, c, x, y}
Решение в
M U P = {a, b, c, x}
Решение г
M ∩ K = ∅
Решение д
K ∩ P = {x}
Решение е
M ∩ P = {b, c} 6
-
Номер №6
Какое из двух множеств является подмножеством другого:
а) B или A U B
б) B или A ∩ B
Решение а
Множество B является подмножеством A U B.
Решение б
Множество A ∩ B является подмножеством множества B. 6*
-
Номер №6*
Пусть A − множество двузначных чисел, оканчивающихся нулем, а B − множество двузначных чисел, кратных 5. Выпишите эти числа.
_
Найдите:
а) A U B. Решение: A U B = { _ }
б) A ∩ B. Решение: A ∩ B = { _ }
Решение
A = {10, 20, 30, 40, 50, 60, 70, 80, 90}
B = {10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95}
A U B = {10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95}
A ∩ B = {10, 20, 30, 40, 50, 60, 70, 80, 90} 7
-
Номер №7
A и B − некоторые множества. Воспользовавшись рисунком, закончите равенства:
(A ∩ B) U A =
(A U B) ∩ A =
Решение а
(A ∩ B) U A = A
Решение б
(A U B) ∩ A = A 8
-
Номер №8
Расположите 5 элементов в двух множествах так, чтобы в каждом из них было по 4 элемента.
Решение
A = {a, b, с, d}
B = {b, с, d, e}
A U B = {a, b, с, d, e}
9
-
Номер №9
В классе 13 мальчиков. И них 9 человек занимаются волейболом и 8 − баскетболом, и нет таких, кто не занимался хотя бы одним из этих видов спорта. Сколько мальчиков занимаются и тем и другим?
Решение
(9 + 8) − 13 = 17 − 13 = 4 (мальчика) − занимаются и тем и другим.
Ответ: 4 мальчика 10
-
Номер №10
Из 70 туристов, приехавших в Москву, 34 хотят посетить Малый театр, 30 − Художественный театр, 16 хотят посетить оба театра, остальные в театр ходить не хотят. Сколько человек не собираются идти в театр?
Решение
1) (34 + 30) − 16 = 64 − 16 = 48 (туристов) − собираются идти как минимум в один театр;
2) 70 − 48 = 22 (туриста) − не собираются идти в театр.
Ответ: 22 туриста 11
-
Номер №11
Множества A и B содержат соответственно 6 и 8 элементов, а множество A ∩ B − 5 элементов. Сколько элементов в множестве A U B?
Решение
Так как множество A ∩ B содержит 5 элементов, значит из элементов множеств A и B можно составить 5 пар одинаковых элементов, тогда:
(6 + 8) − 5 = 14 − 5 = 9 (элементов) − в множестве A U B.
Ответ: 9 элементов 12
-
Номер №12
Установите соответствие между каждым рисунком и символьным обозначением подмножества, пересечения и объединения множеств.
1) A U B
2) A ⊂ B
3) A ∩ B
4) B ⊂ A
Решение
1 2 3 4
в б а г 13
-
Номер №13
Вычислите.
а) 45 * 58 + 34 * 45 + 8 * 45 − 134000 : (67 * 78 − 68 * 67)
б) $((9^3 - 7^2) : 8 + 15)^2$
Решение а
45 * 58 + 34 * 45 + 8 * 45 − 134000 : (67 * 78 − 68 * 67) = 45 * (58 + 34 + 8) − 134000 : (67 * (78 − 68)) = 45 * (92 + 8) − 134000 : (67 * 10) = 45 * 100 − 134000 : 670 = 4500 − 200 = 4300
Решение б
$((9^3 - 7^2) : 8 + 15)^2 = ((729 - 49) : 8 + 15)^2 = (680 : 8 + 15)^2 = (85 + 15)^2 = 100^2 = 10000$ 14
-
Номер №14
Решите задачу.
Три фермера закупили для посева 1836 кг ржи. Второму фермеру нужно в 3 раза меньше ржи, чем первому, а третьему − в 4 раза меньше, чем второму. Сколько килограммов ржи нужно каждому фермеру?
Решение
Пусть x (кг) − ржи нужно третьему фермеру, тогда:
4x (кг) − ржи нужно второму фермеру;
3 * 4x = 12x (кг) − ржи нужно первому фермеру.
Так как, три фермера закупили для посева 1836 кг ржи, можно составить уравнение:
x + 4x + 12x = 1836
17x = 1836
x = 1836 : 17
x = 108 (кг) − ржи нужно третьему фермеру, тогда:
4x = 4 * 108 = 432 (кг) − ржи нужно второму фермеру;
12x = 12 * 108 = 1296 (кг) − ржи нужно первому фермеру.
Ответ: 1296 кг − первому; 432 кг − второму; 108 кг − третьему.
Вычисления:-1836|17
17 |108
-13
0
-136
136
0
*108
4
432
* 108
12
+ 216
108
1296 Верно или неверно 1
-
46. Верно или неверно. Номер №1
Выберите верные утверждения.
а) При умножении десятичной дроби на 1000 запятая переносится влево на три знака.
б) При делении десятичной дроби на 10 запятая переносится влево на один знак.
в) При умножении на 0,04 число уменьшается.
г) Три с половиной метра равны 350 сантиметрам.
Решение
а) неверно, так как при умножении десятичной дроби на 1000 запятая переносится вправо на три знака.
б) верно
в) верно
г) верно
Ответ: б, в, г. 2
-
Номер №2
Выберите верные утверждения.
а) При делении на 0,01 число увеличивается.
б) Четыре с половиной дециметра равны 450 миллиметрам.
в) При делении десятичной дроби на 1000 запятая переносится вправо на три знака.
г) При умножении десятичной дроби на 100 запятая переносится вправо на три знака.
Решение
а) верно
б) верно
в) неверно, так как при делении десятичной дроби на 1000 запятая переносится влево на три знака.
г) неверно, так как при умножении десятичной дроби на 100 запятая переносится вправо на два знака.
Ответ: а, б. 3
-
Номер №3
Выберите верные утверждения.
а) При умножении на 0,5 натуральное число увеличивается вдвое.
б) Произведение десятичных дробей может быть меньше единицы.
в) Среднее арифметическое нескольких чисел может быть меньше одного из них.
г) Найти процент от числа можно умножением этого числа на дробь, соответствующую данному проценту.
Решение
а) неверно, так как при умножении на 0,5 натуральное число уменьшается вдвое.
б) верно
в) верно
г) верно
Ответ: б, в, г. 4
-
Номер №4
Укажите верные утверждения.
а) Если десятичная дробь больше 0,01, то она больше 0,001.
б) Если десятичная дробь оканчивается цифрой 9, то при любом округлении она увеличивается.
в) Равные десятичные дроби могут иметь разное количество знаков после запятой.
г) Сумма двух десятичных дробей не может быть числом натуральным.
Решение
а) верно
б) верно
в) верно, так как к любой дроби можно приписать бесконечное количество нулей. Например: 0,1 = 0,10000
г) неверно, так как например 0,8 + 0,2 = 1 − число натуральное
Ответ: а, б, в. 5
-
Номер №5
Укажите верные утверждения.
а) Сумма двух неправильных дробей может быть смешанным числом.
б) Разность двух правильных дробей может быть смешанным числом.
в) Сумма двух смешанных чисел может быть натуральным числом.
г) Две дроби с разными числителями и знаменателями могут быть равными.
Решение
а) верно
б) неверно, так как любая правильная дробь меньше единицы, значит и их разность будет меньше единицы.
в) верно
г) верно
Ответ: а, в, г. 6
-
Номер №6
Укажите верные утверждения.
а) Разность неправильной дроби и единицы − правильная дробь.
б) Сумма натурального числа и неправильной дроби может быть натуральным числом.
в) При увеличении знаменателя дробь увеличивается.
г) Ноль может быть знаменателем дроби.
Решение
а) неверно, так как если неправильная дробь больше или равна двум, то разность неправильной дроби и единицы будет больше единицы, а значит не будет правильной дробью.
б) верно
в) неверно, так как при увеличении знаменателя дробь уменьшается.
г) неверно, так как на ноль делить нельзя.
Ответ: б 7
-
Номер №7
Укажите верные утверждения.
а) Если площади двух прямоугольников равны, то их периметры также равны.
б) Существует такое значение a, при котором верно равенство a : a = a.
в) Прямоугольники с равными площадями равны.
г) Делимое равно произведению делителя и частного.
Решение
а) неверно, так как например у прямоугольника со сторонами 3 и 8 и прямоугольника со сторонами 4 и 6 равные площади, но разные периметры.
б) верно, так как при a = 1 верно равенство a : a = a.
в) неверно, так как например у прямоугольника со сторонами 3 и 8 и прямоугольника со сторонами 4 и 6 равные площади, но прямоугольники не равны.
г) верно
Ответ: б, г. 8
-
Номер №8
Укажите верные утверждения.
а) Площадь прямоугольника равна произведению длин его сторон.
б) На нуль делить нельзя.
в) Если произведение равно нулю, то все множители равны нулю.
г) В примере, не содержащем скобок, сложение выполняется раньше умножения.
Решение
а) верно
б) верно
г) неверно, так как если произведение равно нулю, то хотя бы один из множителей равен нулю.
д) неверно, так как в примере, не содержащем скобок, сложение выполняется позже умножения. 9
-
Номер №9
Укажите верные утверждения.
а) При любых значениях a, b и c верно равенство (a − b) * c = a * (b − c)
б) Существует значение a, при котором a * a = a.
в) При любых значениях a, b и c верно равенство a * (b + c) = ab + ac.
г) Прямоугольники с равными периметрами равны.
Решение
а) неверно, при любых значениях a, b и c верно равенство (a − b) * c = ac − bc
б) верно, при a = 0 и при a = 1
в) верно
г) неверно, так например, периметр прямоугольника равен 40 см, тогда его длина и ширина могут быть следующими: 18 и 2, 16 и 4, 12 и 8 и т.д.
Ответ: б, в. 10
-
Номер №10
Укажите верные утверждения.
а) Сумма градусных мер двух острых углов меньше 90°.
б) Если все углы треугольника тупые, то его называют тупоугольным.
в) Половина тупого угла − острый угол.
г) Углом называется фигура, образованная двумя лучами.
Решение
а) неверно, так как например сумма градусных мер двух острых углов 50° и 60° больше 90°.
б) неверно, так как не существует треугольника со всеми тупыми углами.
в) верно
г) верно, если у этих лучей общая вершина
Ответ: в, г. 11
-
Номер №11
Укажите верные утверждения.
а) Половина развернутого угла − прямой угол.
б) Угол, который меньше развернутого, − тупой.
в) Угол, который больше острого угла, − прямой.
г) Ноль меньше любого натурального числа.
Решение
а) верно
б) неверно, так острые углы тоже меньше развернутого.
в) неверно, так как помимо прямого угла, больше острого угла может быть и острый угол, и тупой угол и развернутый угол.
г) верно
Ответ: а, г. 12
-
Номер №12
Укажите верные утверждения.
а) Сумма уменьшаемого и разности равна вычитаемому.
б) Чтобы произведение двух чисел умножить на третье число, нужно каждое из двух чисел умножить на третье число.
в) Сумма вычитаемого и разности равна уменьшаемому.
г) Частное двух натуральных чисел всегда является натуральным числом.
Решение
а) неверно, так как разность уменьшаемого и разности равна вычитаемому.
б) неверно
в) верно
г) неверно, так как например частное натуральных чисел 5 и 2, равно 2,5.
Ответ: в 13
-
Номер №13
Решите задачу.
Если для экскурсии будут поданы три прогулочных катера, то для 18 человек не хватит места. Если же будут поданы четыре таких катера, то останется 12 свободных мест. Сколько было экскурсантов?
Решение
1) 18 + 12 = 30 (экскурсантов) − вмещает один катер;
2) 30 * 4 = 120 (экскурсантов) − может вместить четыре катера;
3) 120 − 12 = 108 (экскурсантов) − было всего.
Ответ: 108 экскурсантов 14
-
Номер №14
Решите уравнения.
а) x : 18 = 16 (ост.17)
б) 863 : x = 26 (ост.5)
Решение а
x : 18 = 16 (ост.17)
x = 18 * 16 + 17
x = 288 + 17
x = 305
Ответ: 305
Вычисления:*18
16
108
18
288
Решение б
863 : x = 26 (ост.5)
x = (863 − 5) : 26
x = 858 : 26
x = 33
Ответ: 33
Вычисления:- 858|26
78 |33
-78
78
0
