 Задания на нахождение площади треугольника встречаются в основном среди задач с кратким ответом и не требуют подробного решения. Опять же, есть и задачи супер-простые, есть и довольно сложные.
Задания на нахождение площади треугольника встречаются в основном среди задач с кратким ответом и не требуют подробного решения. Опять же, есть и задачи супер-простые, есть и довольно сложные.
Вспомним, что площадь треугольника можно найти несколькими способами.
1) S = 1/2 ahа, где а - сторона, hа - высота к этой стороне. Высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону. В прямоугольном треугольнике катеты являются высотами друг к другу.
2) S = 1/2 ab sinγ , a и b - стороны, γ - угол между ними.
Эти формулы будут у вас в справочных материалах на ОГЭ. Но есть такие, которых в справочнике не будет, а через них решать подобные задания проще и быстрее. Поэтому, повторите тему о подобии треугольников (признаки подобия; площади подобных треугольников относятся как квадраты их соответственных сторон). Еще нужно вспомнить, что если треугольники имеют общую вершину, а их основания лежат на одной прямой, то отношение их площадей равно отношению их оснований.
Открытый банк заданий ФИПИ располагает следующими заданиями, которые могут попасться вам на реальном экзамене в этом году.
Реальные задания по геометрии из банка ФИПИ
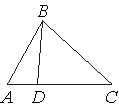
На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
Решение:
Для вычисления площади треугольника существует несколько формул. Ни для одной из них у нас не хватает данных. Значит недостающие данные надо получить.
1 способ
Посмотрим, что общее есть у треугольников ABC и BCD:
1. Сторона BC
2. Угол BCD.
Воспользуемся формулой "через две стороны и угол между ними".
Площадь треугольника ABC равняется половине произведения сторон на синус угла между ними:
SABC=1/2*AC*BC*sinC
Так как АС = АD + DС, то
SABC=1/2*(AD+DC)*BC*sinC, поэтому
BC*sinC=$\frac{S_{ABC}}{\displaystyle\frac12\ast(AD+DC)}=\frac{20}{{\displaystyle\frac12}\ast(3+7)}=4$
Выразим площадь треугольника BCD через sinC:
SBCD=1/2*DC*BC*sinC
Подставляем значение BC*sinC, полученное ранее, и значение DC, известное из условия:
SBCD=1/2*7*4
SBCD=14
Ответ: 14
2 способ
Площадь треугольника равна половине произведения основания на высоту, следовательно, можно найти высоту треугольника ABC:
SАВС=1/2 АС*h
а так как АС = АD + DС, то
SАВС=1/2 (АD + DС)*h
$h=\frac{2S_{АВС}}{АD+DС}=\frac{2\ast20}{3+7}=4$
Треугольник BCD имеет такую же высоту, что и треугольник ABC, значит,
SВСD=1/2 DС*h = 1/2 * 7 * 4 = 14
Ответ: 14
3 способ (самый короткий)
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 3 + 7 = 10
SВСD = 20 * 7 / 10 = 14
Ответ: 14
4F1471

На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10. Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 6 + 10 = 16
SВСD = 48 * 10 / 16 = 30
Ответ: 30
214ED6

На стороне AC треугольника ABC отмечена точка D так, что AD=4, DC=8. Площадь треугольника ABC равна 36. Найдите площадь треугольника BCD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 4 + 8 = 12
SВСD = 36 * 8 / 12 = 24
Ответ: 24
E88B4B

На стороне AC треугольника ABC отмечена точка D так, что AD=2, DC=7. Площадь треугольника ABC равна 27. Найдите площадь треугольника BCD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 2 + 7 = 9
SВСD = 27 * 7 / 9 = 21
Ответ: 21
972236

На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=9. Площадь треугольника ABC равна 56. Найдите площадь треугольника BCD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 5 + 9 = 14
SВСD = 56 * 9 / 14 = 36
Ответ: 36
BC4593

На стороне AC треугольника ABC отмечена точка D так, что AD=4, DC=7. Площадь треугольника ABC равна 55. Найдите площадь треугольника ABD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 4 + 7 = 11
SВСD = 55 * 7 / 11 = 35
Ответ: 35
258E9A

На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=10. Площадь треугольника ABC равна 39. Найдите площадь треугольника ABD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 3 + 10 = 13
SВСD = 39 * 10 / 13 = 30
Ответ: 30
4065B0

На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=8. Площадь треугольника ABC равна 42. Найдите площадь треугольника ABD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 6 + 8 = 14
SВСD = 42 * 8 / 14 = 24
Ответ: 24
B4CAE7

На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7. Площадь треугольника ABC равна 60. Найдите площадь треугольника ABD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 5 + 7 = 12
SВСD = 60 * 7 / 12 = 35
Ответ: 35
F63DA7

На стороне AC треугольника ABC отмечена точка D так, что AD=2, DC=13. Площадь треугольника ABC равна 75. Найдите площадь треугольника ABD.
Решение:
Треугольники ABC и BCD имеют общую вершину B, а их основания лежат на одной прямой, следовательно, отношение их площадей равно отношению их оснований:
SВСD /SАВС = DC/АС, тогда
SВСD = SАВС * DC / АС
АС = 2 + 13 = 15
SВСD = 75 * 13 / 15 = 65
Ответ: 65
0D7C95
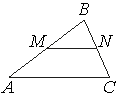
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=18, MN=8. Площадь треугольника ABC равна 81. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$\frac{S_{MNB}}{S_{ABC}}=\left(\frac{MN}{AC}\right)^2$ , ⇒
$S_{MNB}=\left(\frac{MN}{AC}\right)^2\ast S_{ABC}$
SMNB = (8/18)2 * 81 = 64 * 81 /324 = 16
Ответ: 16
8EBCEB

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=21, MN=14. Площадь треугольника ABC равна 27. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$\frac{S_{MNB}}{S_{ABC}}=\left(\frac{MN}{AC}\right)^2$ , поэтому
$S_{MNB}=\left(\frac{MN}{AC}\right)^2\ast S_{ABC}$
SMNB = (14/21)2 * 27 = 12
Ответ: 12
DABB4F

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=24, MN=18. Площадь треугольника ABC равна 48. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$\frac{S_{MNB}}{S_{ABC}}=\left(\frac{MN}{AC}\right)^2$ , поэтому
$S_{MNB}=\left(\frac{MN}{AC}\right)^2\ast S_{ABC}$
SMNB = (18/24)2 * 48 = 27
Ответ: 27
F8DE6C

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=27, MN=18. Площадь треугольника ABC равна 63. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$\frac{S_{MNB}}{S_{ABC}}=\left(\frac{MN}{AC}\right)^2$ , поэтому
$S_{MNB}=\left(\frac{MN}{AC}\right)^2\ast S_{ABC}$
SMNB = (18/27)2 * 63 = 28
Ответ: 28
BB979E

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=30, MN=12. Площадь треугольника ABC равна 25. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$\frac{S_{MNB}}{S_{ABC}}=\left(\frac{MN}{AC}\right)^2$ , поэтому
$S_{MNB}=\left(\frac{MN}{AC}\right)^2\ast S_{ABC}$
SMNB = (12/30)2 * 25 = 4
Ответ: 4
4CC815

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=16, MN=12. Площадь треугольника ABC равна 80. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$\frac{S_{MNB}}{S_{ABC}}=\left(\frac{MN}{AC}\right)^2$ , поэтому
$S_{MNB}=\left(\frac{MN}{AC}\right)^2\ast S_{ABC}$
SMNB = (12/16)2 * 80 = 45
Ответ: 45
9ACF8B

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=27. Площадь треугольника ABC равна 96. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$\frac{S_{MNB}}{S_{ABC}}=\left(\frac{MN}{AC}\right)^2$ , поэтому
$S_{MNB}=\left(\frac{MN}{AC}\right)^2\ast S_{ABC}$
SMNB = (27/36)2 * 96 = 54
Ответ: 54
9C5C4D

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=48, MN=40. Площадь треугольника ABC равна 72. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$\frac{S_{MNB}}{S_{ABC}}=\left(\frac{MN}{AC}\right)^2$ , поэтому
$S_{MNB}=\left(\frac{MN}{AC}\right)^2\ast S_{ABC}$
SMNB = (40/48)2 * 72 = 50
Ответ: 50
51F110

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=44, MN=24. Площадь треугольника ABC равна 121. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$\frac{S_{MNB}}{S_{ABC}}=\left(\frac{MN}{AC}\right)^2$ , поэтому
$S_{MNB}=\left(\frac{MN}{AC}\right)^2\ast S_{ABC}$
SMNB = (24/44)2 * 121 = 36
Ответ: 36
A1451C

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=28. Площадь треугольника ABC равна 162. Найдите площадь треугольника MBN.
Решение:
Рассмотрим треугольники ABC и MBN, углы BMN и BAC равны как соответственные при параллельных прямых, угол B — общий, следовательно, эти треугольники подобны. Площади подобных треугольников относятся как квадраты их соответственных сторон:
$\frac{S_{MNB}}{S_{ABC}}=\left(\frac{MN}{AC}\right)^2$ , поэтому
$S_{MNB}=\left(\frac{MN}{AC}\right)^2\ast S_{ABC}$
SMNB = (28/36)2 * 162 = 98
Ответ: 98
22636E
Два катета прямоугольного треугольника равны 6 и 7. Найдите площадь этого треугольника.
Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 6 * 7 = 21
Ответ: 21
F594AC
Два катета прямоугольного треугольника равны 9 и 6. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 9 * 6 = 27
Ответ: 27
0DA313
Два катета прямоугольного треугольника равны 4 и 11. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 4 * 11 = 22
Ответ: 22
1E12D2
Два катета прямоугольного треугольника равны 14 и 5. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 14 * 5 = 35
Ответ: 35
201E89
Два катета прямоугольного треугольника равны 6 и 13. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 6 * 13 = 39
Ответ: 39
9C5CE2
Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 4 * 9 = 18
Ответ: 18
916443
Два катета прямоугольного треугольника равны 11 и 6. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 11 * 6 = 33
Ответ: 33
1276A8
Два катета прямоугольного треугольника равны 4 и 10. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 4 * 10 = 20
Ответ: 20
F6B402
Два катета прямоугольного треугольника равны 13 и 4. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 13 * 4 = 26
Ответ: 26
5F6CB3
Два катета прямоугольного треугольника равны 7 и 12. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 7 * 12 = 42
Ответ: 42
C10B89
Два катета прямоугольного треугольника равны 12 и 5. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 12 * 5 = 30
Ответ: 30
160CE6
Два катета прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.

Решение:
Площадь прямоугольного треугольника равна половине произведения катетов.
S = 1/2 * 18 * 7 = 63
Ответ: 63
5E7907
Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 31. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 14 *31 = 217
Ответ: 217
8582E2
Сторона треугольника равна 24, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 24 * 19 = 228
Ответ: 228
43135F
Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 17. Найдите площадь этого треугольника.

Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 18 * 17 = 153
Ответ: 153
33F315
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.

Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 16 * 19 = 152
Ответ: 152
7A4858
Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 23. Найдите площадь этого треугольника.

Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 14 * 23 = 161
Ответ: 161
CB2956
Сторона треугольника равна 29, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника.

Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 29 * 12 = 174
Ответ: 174
8993A6
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 27. Найдите площадь этого треугольника.

Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 16 * 27 = 216
Ответ: 216
DC9E1D
Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.

Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 12 * 33 = 198
Ответ: 198
22C21A
Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 22. Найдите площадь этого треугольника.

Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 18 * 22 = 198
Ответ: 198
B45622
Сторона треугольника равна 8, а высота, проведённая к этой стороне, равна 31. Найдите площадь этого треугольника.

Решение:
Площадь треугольника равна половине произведения стороны треугольника на высоту, проведенную к этой стороне:
S = 1/2 аh = 1/2 * 8 * 31 = 124
Ответ: 124
C15599
Периметр треугольника равен 50, одна из сторон равна 20, а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 50/2 * 4 = 100
Длина одной из сторон - лишние данные, игнорируем их.
Ответ: 100
099B7F

Периметр треугольника равен 48, одна из сторон равна 18, а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 48/2 * 3 = 72
Длина одной из сторон - лишние данные, игнорируем их.
Ответ: 72
691110

Периметр треугольника равен 71, одна из сторон равна 21, а радиус вписанной в него окружности равен 6. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 71/2 * 6 = 213
Длина одной из сторон - лишние данные, игнорируем их.
Ответ: 213
F93971

Периметр треугольника равен 56, одна из сторон равна 19, а радиус вписанной в него окружности равен 5. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 56/2 * 5 = 140
Длина одной из сторон - лишние данные, игнорируем их.
Ответ: 140
2E895A

Периметр треугольника равен 110, одна из сторон равна 38, а радиус вписанной в него окружности равен 10. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 110/2 * 10 = 550
Длина одной из сторон - лишние данные, игнорируем их.
Ответ: 550
A70D9B

Периметр треугольника равен 120, одна из сторон равна 40, а радиус вписанной в него окружности равен 7. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 120/2 * 7 = 420
Длина одной из сторон - лишние данные, игнорируем их.
Ответ: 420
569EAC

Периметр треугольника равен 140, одна из сторон равна 56, а радиус вписанной в него окружности равен 9. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 140/2 * 9 = 630
Длина одной из сторон - лишние данные, игнорируем их.
Ответ: 630
17E9C9

Периметр треугольника равен 60, одна из сторон равна 12, а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 60/2 * 3 = 90
Длина одной из сторон - лишние данные, игнорируем их.
Ответ: 90
B0D10B

Периметр треугольника равен 33, одна из сторон равна 7, а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 33/2 * 2 = 33
Длина одной из сторон - лишние данные, игнорируем их.
Ответ: 33
65845E

Периметр треугольника равен 54, одна из сторон равна 15, а радиус вписанной в него окружности равен 1. Найдите площадь этого треугольника.
Решение:
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:
S = pr = 54/2 * 1 = 27
Длина одной из сторон - лишние данные, игнорируем их.
Ответ: 27
239EF1
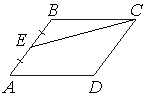
Площадь параллелограмма ABCD равна 68. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 68/2 = 34
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 34 = 17
Ответ: 17
795F61

Площадь параллелограмма ABCD равна 44. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 44/2 = 22
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 22 = 11
Ответ: 11
1ABE2A

Площадь параллелограмма ABCD равна 84. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 84/2 = 42
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 42 = 21
Ответ: 21
A6BEE2

Площадь параллелограмма ABCD равна 196. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 196/2 = 98
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 98 = 49
Ответ: 49
ADA977

Площадь параллелограмма ABCD равна 112. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 112/2 = 56
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 56 = 28
Ответ: 28
4DB6C1

Площадь параллелограмма ABCD равна 104. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 104/2 = 52
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 52 = 26
Ответ: 26
CDB192

Площадь параллелограмма ABCD равна 148. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 148/2 = 74
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 74 = 37
Ответ: 37
E2BFC0

Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 140/2 = 70
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 70 = 35
Ответ: 35
20E710

Площадь параллелограмма ABCD равна 136. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABС = 136/2 = 68
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SEBC = 1/2 SABC = 1/2 * 68 = 34
Ответ: 34
2373D8


