Следующие задачи на эту тему предлагает открытый банк заданий ФИПИ к ОГЭ по математике (раздел геометрия). Любое из них может вам попасться на ОГЭ в этом году. Задания включают в себя алгоритмы связанные с окружностью, с ее радиусной мерой и зависимость углов вписанных в нее. Так скажем надо будет знать, что угол в вершине угла образованный внутри окружности равен половине ее радиусной мере, если мерить от концов прямых, которые ее касаются. Также в задачах активно применяется обобщенная теорема синусов, это то, что вам в обязательном порядке надо повторить.
Следующие задачи на эту тему предлагает открытый банк заданий ФИПИ к ОГЭ по математике (раздел геометрия). Любое из них может вам попасться на ОГЭ в этом году. Задания включают в себя алгоритмы связанные с окружностью, с ее радиусной мерой и зависимость углов вписанных в нее. Так скажем надо будет знать, что угол в вершине угла образованный внутри окружности равен половине ее радиусной мере, если мерить от концов прямых, которые ее касаются. Также в задачах активно применяется обобщенная теорема синусов, это то, что вам в обязательном порядке надо повторить.
Реальные задания по геометрии из банка ФИПИ
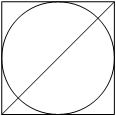
Радиус вписанной в квадрат окружности равен 2√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти. Запишем равенство используя теорему Пифагора
х=2√((2√2)2+(2√2)2)=2√(4*2+4*2)=8
Ответ: 8
7E4CCF

Радиус вписанной в квадрат окружности равен 4√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти. Запишем равенство используя теорему Пифагора
х=2√((4√2)2+(4√2)2)=2√(16*2+16*2)=2*8=16
Ответ: 16
C84B98

Радиус вписанной в квадрат окружности равен 6√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти. Запишем равенство используя теорему Пифагора
х=2√((6√2)2+(6√2)2)=2√(36*2+36*2)=2*12=24
Ответ: 24
40FF58

Радиус вписанной в квадрат окружности равен 8√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти. Запишем равенство используя теорему Пифагора
х=2√((8√2)2+(8√2)2)=2√(64*2+64*2)=2*16=32
Ответ: 32
4E821A

Радиус вписанной в квадрат окружности равен 10√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти. Запишем равенство используя теорему Пифагора
х=2√((10√2)2+(10√2)2)=2√(100*2+100*2)=2*20=40
Ответ: 40
E12730

Радиус вписанной в квадрат окружности равен 14√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти. Запишем равенство используя теорему Пифагора
х=2√((14√2)2+(14√2)2)=2√(196*2+196*2)=2*28=56
Ответ: 56
17DF0C

Радиус вписанной в квадрат окружности равен 16√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти. Запишем равенство используя теорему Пифагора
х=2√((16√2)2+(16√2)2)=2√(256*2+256*2)=2*32=64
Ответ: 64
E4E4A6

Радиус вписанной в квадрат окружности равен 18√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти. Запишем равенство используя теорему Пифагора
х=2√((18√2)2+(18√2)2)=2√(324*2+324*2)=2*36=72
Ответ: 72
D173D1

Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти. Запишем равенство используя теорему Пифагора
х=2√((22√2)2+(22√2)2)=2√(484*2+484*2)=2*44=88
Ответ: 88
4DCFDB

Радиус вписанной в квадрат окружности равен 24√2. Найдите диагональ этого квадрата.
Решение:
Если провести радиус перпендикулярно к любой стороне, то получим прямоугольный треугольник, в котором можно найти гипотенузу. Причем эта гипотенузе будет равна половине диагонали, которую нам надо найти. Запишем равенство используя теорему Пифагора
х=2√((24√2)2+(24√2)2)=2√(576*2+576*2)=2*48=96
Ответ: 96
7B13AD
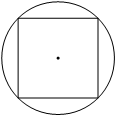
Радиус окружности, описанной около квадрата, равен 4√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны используя теорему Пифагора. Записываем.
$\left(2\ast4\surd2\right)^2=2x^2\\x^2=\frac{\left(2\ast4\surd2\right)^2}2\\x=\sqrt{\frac{\left(2\ast4\surd2\right)^2}2}\\х=\frac{2\ast4\surd2}{\sqrt2}=8$
Ответ: 8
CF5BF1

Радиус окружности, описанной около квадрата, равен 16√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны используя теорему Пифагора. Записываем.
$\left(2\ast16\surd2\right)^2=2x^2\\x^2=\frac{\left(2\ast16\surd2\right)^2}2\\x=\sqrt{\frac{\left(2\ast16\surd2\right)^2}2}\\х=\frac{2\ast16\surd2}{\sqrt2}=32$
Ответ: 32
CD5252

Радиус окружности, описанной около квадрата, равен 14√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны используя теорему Пифагора. Записываем.
$\left(2\ast14\surd2\right)^2=2x^2\\x^2=\frac{\left(2\ast14\surd2\right)^2}2\\x=\sqrt{\frac{\left(2\ast14\surd2\right)^2}2}\\х=\frac{2\ast14\surd2}{\sqrt2}=28$
Ответ: 28
B927DB

Радиус окружности, описанной около квадрата, равен 26√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны используя теорему Пифагора. Записываем.
$\left(2\ast26\surd2\right)^2=2x^2\\x^2=\frac{\left(2\ast26\surd2\right)^2}2\\x=\sqrt{\frac{\left(2\ast26\surd2\right)^2}2}\\х=\frac{2\ast26\surd2}{\sqrt2}=52$
Ответ: 52
32A97B

Радиус окружности, описанной около квадрата, равен 34√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны используя теорему Пифагора. Записываем.
$\left(2\ast34\surd2\right)^2=2x^2\\x^2=\frac{\left(2\ast34\surd2\right)^2}2\\x=\sqrt{\frac{\left(2\ast34\surd2\right)^2}2}\\х=\frac{2\ast34\surd2}{\sqrt2}=68$
Ответ: 68
20ED7A

Радиус окружности, описанной около квадрата, равен 28√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны используя теорему Пифагора. Записываем.
$\left(2\ast28\surd2\right)^2=2x^2\\x^2=\frac{\left(2\ast28\surd2\right)^2}2\\x=\sqrt{\frac{\left(2\ast28\surd2\right)^2}2}\\х=\frac{2\ast28\surd2}{\sqrt2}=56$
Ответ: 56
F27430

Радиус окружности, описанной около квадрата, равен 18√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны используя теорему Пифагора. Записываем.
$\left(2\ast18\surd2\right)^2=2x^2\\x^2=\frac{\left(2\ast18\surd2\right)^2}2\\x=\sqrt{\frac{\left(2\ast18\surd2\right)^2}2}\\х=\frac{2\ast18\surd2}{\sqrt2}=36$
Ответ: 36
B07B04

Радиус окружности, описанной около квадрата, равен 22√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны используя теорему Пифагора. Записываем.
$\left(2\ast22\surd2\right)^2=2x^2\\x^2=\frac{\left(2\ast22\surd2\right)^2}2\\x=\sqrt{\frac{\left(2\ast22\surd2\right)^2}2}\\х=\frac{2\ast22\surd2}{\sqrt2}=44$
Ответ: 44
C0C526

Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны используя теорему Пифагора. Записываем.
$\left(2\ast36\surd2\right)^2=2x^2\\x^2=\frac{\left(2\ast36\surd2\right)^2}2\\x=\sqrt{\frac{\left(2\ast36\surd2\right)^2}2}\\х=\frac{2\ast36\surd2}{\sqrt2}=72$
Ответ: 72
466413

Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Решение:
Радиус окружности равен половине диаметра. В данном случае диаметром является диагональ квадрата. А значит исходя из того, что диагональ в квадрате образует два прямоугольных треугольника можно ее найти стороны используя теорему Пифагора. Записываем.
$\left(2\ast32\surd2\right)^2=2x^2\\x^2=\frac{\left(2\ast32\surd2\right)^2}2\\x=\sqrt{\frac{\left(2\ast32\surd2\right)^2}2}\\х=\frac{2\ast32\surd2}{\sqrt2}=64$
Ответ: 64
FA41B7
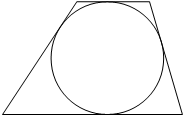
Радиус окружности, вписанной в трапецию, равен 16. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*16=32
Ответ: 32
D00494

Радиус окружности, вписанной в трапецию, равен 18. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*18=36
Ответ: 36
BC46E4

Радиус окружности, вписанной в трапецию, равен 34. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*34=68
Ответ: 68
FE4FCD

Радиус окружности, вписанной в трапецию, равен 26. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*26=52
Ответ: 52
E5AF5A

Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*48=96
Ответ: 96
7C5CEF

Радиус окружности, вписанной в трапецию, равен 42. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*16=42
Ответ: 84
F45C93

Радиус окружности, вписанной в трапецию, равен 36. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*36=72
Ответ: 72
6623F6

Радиус окружности, вписанной в трапецию, равен 38. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*38=76
Ответ: 76
4B2B64

Радиус окружности, вписанной в трапецию, равен 24. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*24=48
Ответ: 48
4A4F32

Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*32=64
Ответ: 64
4CC220
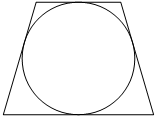
Радиус окружности, вписанной в равнобедренную трапецию, равен 12. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*12=24
Ответ: 24
1314AB

Радиус окружности, вписанной в равнобедренную трапецию, равен 14. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*14=28
Ответ: 28
897F1A

Радиус окружности, вписанной в равнобедренную трапецию, равен 30. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*30=60
Ответ: 60
03DDD9

Радиус окружности, вписанной в равнобедренную трапецию, равен 22. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*22=44
Ответ: 44
60F5F8

Радиус окружности, вписанной в равнобедренную трапецию, равен 44. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*44=88
Ответ: 88
5B197F

Радиус окружности, вписанной в равнобедренную трапецию, равен 38. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*38=76
Ответ: 76
B8967A

Радиус окружности, вписанной в равнобедренную трапецию, равен 32. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*32=64
Ответ: 64
B1F719

Радиус окружности, вписанной в равнобедренную трапецию, равен 34. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*34=68
Ответ: 68
F794FE

Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*20=40
Ответ: 40
82E915

Радиус окружности, вписанной в равнобедренную трапецию, равен 28. Найдите высоту этой трапеции.
Решение:
Ответ: Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*28=56
Ответ: 56
788577
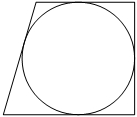
Радиус окружности, вписанной в прямоугольную трапецию, равен 10. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*10=20
Ответ: 20
1AE9FC

Радиус окружности, вписанной в прямоугольную трапецию, равен 12. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*12=24
Ответ: 24
301A24

Радиус окружности, вписанной в прямоугольную трапецию, равен 28. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*28=56
Ответ: 56
81B7DF

Радиус окружности, вписанной в прямоугольную трапецию, равен 20. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*20=40
Ответ: 40
B404D2

Радиус окружности, вписанной в прямоугольную трапецию, равен 42. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*42=84
Ответ: 84
654235

Радиус окружности, вписанной в прямоугольную трапецию, равен 36. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*36=72
Ответ: 72
2231C2

Радиус окружности, вписанной в прямоугольную трапецию, равен 30. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*30=60
Ответ: 60
74C85E

Радиус окружности, вписанной в прямоугольную трапецию, равен 32. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*32=64
Ответ: 64
7CF9EB

Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*18=36
Ответ: 36
D5823B

Радиус окружности, вписанной в прямоугольную трапецию, равен 26. Найдите высоту этой трапеции.
Решение:
Собственно из рисунка видно, что диаметр окружности равен высоте окружности, особенно это становится очевидным, если высоту провести перпендикулярно основаниям через центр окружности. То есть получается высота равна два радиуса
2*26=52
Ответ: 52
288717
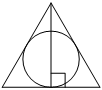
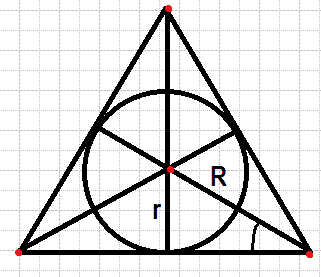
Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
E41C75Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r
5*3=15
Ответ: 15

Радиус окружности, вписанной в равносторонний треугольник, равен 7. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r
7*3=21
Ответ: 21
A73120

Радиус окружности, вписанной в равносторонний треугольник, равен 8. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r
8*3=24
Ответ: 24
55F2B4

Радиус окружности, вписанной в равносторонний треугольник, равен 15. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r
3*15=45
Ответ: 45
25FB46

Радиус окружности, вписанной в равносторонний треугольник, равен 18. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r
3*18=54
Ответ: 54
07E18E

Радиус окружности, вписанной в равносторонний треугольник, равен 4. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r
4*3=12
Ответ: 12
490AD4

Радиус окружности, вписанной в равносторонний треугольник, равен 9. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r
9*3=27
Ответ: 27
209F1B

Радиус окружности, вписанной в равносторонний треугольник, равен 11. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r
11*3=33
Ответ: 33
907529

Радиус окружности, вписанной в равносторонний треугольник, равен 12. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r
12*3=36
Ответ: 36
A44A54

Радиус окружности, вписанной в равносторонний треугольник, равен 14. Найдите высоту этого треугольника.
Решение:
Проведем еще две высоты в равностороннем треугольнике. Причем высоты являются биссектрисами и медианами. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=2r+r=3r
14*3=42
Ответ: 42
A3A364
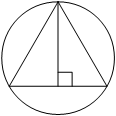
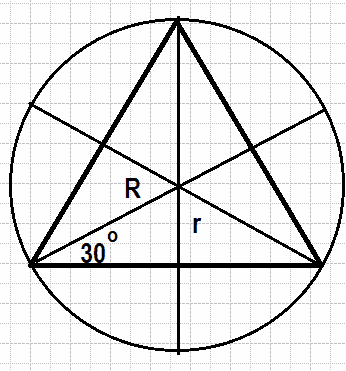
Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R
6*1.5=9
Ответ: 9
6606B6

Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R
10*1.5=15
Ответ: 15
711898

Радиус окружности, описанной около равностороннего треугольника, равен 8. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R
8*1.5=12
Ответ: 12
29E0BA

Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R
16*1.5=24
Ответ: 24
23E335

Радиус окружности, описанной около равностороннего треугольника, равен 18. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R
18*1.5=27
Ответ: 27
8CA0CF

Радиус окружности, описанной около равностороннего треугольника, равен 4. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R
4*1.5=6
Ответ: 6
40E6BC

Радиус окружности, описанной около равностороннего треугольника, равен 20. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R
20*1.5=30
Ответ: 30
59CE06

Радиус окружности, описанной около равностороннего треугольника, равен 2. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R
2*1.5=3
Ответ: 3
FCF728

Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R
12*1.5=18
Ответ: 18
F7AB41

Радиус окружности, описанной около равностороннего треугольника, равен 14. Найдите высоту этого треугольника.
Решение:
Проведем еще две прямые в равностороннем треугольнике. Причем на прямой часть ее будет высотой, а одновременно биссектрисой и медианой. В итоге получим 6 прямоугольных треугольников, у которых есть угол в 30 градусов, а значит R =2r, то есть вся высота H=1.5R
14*1.5=21
Ответ: 21
6B0A52
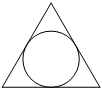
Радиус окружности, вписанной в равносторонний треугольник, равен 2√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4\left(2\surd3\right)^2=\left(2\surd3\right)^2+x^2\\x^2=\;3\left(2\surd3\right)^2\\х^2=3\ast4\ast3\\х=sqrt{36}\\х=6$
6*2=12
Ответ: 12
D07B18

Радиус окружности, вписанной в равносторонний треугольник, равен 3√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4\left(3\surd3\right)^2=\left(3\surd3\right)^2+x^2\\x^2=\;3\left(3\surd3\right)^2\\х^2=3\ast9\ast3\\х=sqrt{81}\\х=9$
9*2=18
Ответ: 18
AB32B8

Радиус окружности, вписанной в равносторонний треугольник, равен 4√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4\left(4\surd3\right)^2=\left(4\surd3\right)^2+x^2\\x^2=\;3\left(4\surd3\right)^2\\х^2=3\ast16\ast3\\х=\sqrt{144}\\х=12$
12*2=24
Ответ: 24
C03CA1

Радиус окружности, вписанной в равносторонний треугольник, равен 5√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4\left(5\surd3\right)^2=\left(5\surd3\right)^2+x^2\\x^2=\;3\left(5\surd3\right)^2\\х^2=3\ast25\ast3\\х=\sqrt{225}\\х=15$
15*2=30
Ответ: 30
7F1E51

Радиус окружности, вписанной в равносторонний треугольник, равен 6√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4\left(6\surd3\right)^2=\left(6\surd3\right)^2+x^2\\x^2=\;3\left(6\surd3\right)^2\\х^2=3\ast36\ast3\\х=\sqrt{324}\\х=18$
18*2=36
Ответ: 36
047CDE

Радиус окружности, вписанной в равносторонний треугольник, равен 7√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4\left(7\surd3\right)^2=\left(7\surd3\right)^2+x^2\\x^2=\;3\left(7\surd3\right)^2\\х^2=3\ast49\ast3\\х=\sqrt{441}\\х=21$
21*2=12
Ответ: 42
CAC621

Радиус окружности, вписанной в равносторонний треугольник, равен 8√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4\left(8\surd3\right)^2=\left(8\surd3\right)^2+x^2\\x^2=\;3\left(8\surd3\right)^2\\х^2=3\ast64\ast3\\х=\sqrt{576}\\х=24$
24*2=48
Ответ: 48
41D84A

Радиус окружности, вписанной в равносторонний треугольник, равен 9√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4\left(9\surd3\right)^2=\left(9\surd3\right)^2+x^2\\x^2=\;3\left(9\surd3\right)^2\\х^2=3\ast81\ast3\\х=\sqrt{729}\\х=27$
27*2=54
Ответ: 54
6D0284

Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4\left(10\surd3\right)^2=\left(10\surd3\right)^2+x^2\\x^2=\;3\left(10\surd3\right)^2\\х^2=3\ast100\ast3\\х=\sqrt{900}\\х=30$
30*2=60
Ответ: 60
F99836

Радиус окружности, вписанной в равносторонний треугольник, равен 11√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$4\left(11\surd3\right)^2=\left(11\surd3\right)^2+x^2\\x^2=\;3\left(11\surd3\right)^2\\х^2=3\ast121\ast3\\х=\sqrt{1089}\\х=33$
33*2=66
Ответ: 66
79607C
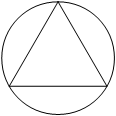
Решение:
Радиус окружности, описанной около равностороннего треугольника, равен 2√3. Найдите длину стороны этого треугольника.
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$\left(2\surd3\right)^2=\left(\frac{2\surd3}2\right)^2+x^2\\x^2=\;4{\surd3}^2-\surd3^2\\х^2=3\sqrt3^2\\х=\sqrt{3\ast3}\\х=3$
3*2=6
Ответ: 6
4F011

Радиус окружности, описанной около равностороннего треугольника, равен 3√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$\left(3\surd3\right)^2=\left(\frac{3\surd3}2\right)^2+x^2\\x^2=\;\frac{4\left(3\surd3\right)^2}4-\frac{\left(3\surd3\right)}4^2\\х^2=\frac{3\left(3\surd3\right)^2}4\\х=\sqrt{\frac{3\ast9\ast3}4}\\х=\sqrt{\frac{81}4}=\frac92=4.5$
4.5*2=9
Ответ: 9
DDDC3E

Радиус окружности, описанной около равностороннего треугольника, равен 4√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$\left(4\surd3\right)^2=\left(\frac{4\surd3}2\right)^2+x^2\\x^2=\;\frac{4\left(4\surd3\right)^2}4-\frac{\left(4\surd3\right)}4^2\\х^2=\frac{3\left(4\surd3\right)^2}4\\х=\sqrt{\frac{3\ast16\ast3}4}\\х=\sqrt{\frac{144}4}=\frac{12}2=6$
6*2=12
Ответ: 12
4864D6

Радиус окружности, описанной около равностороннего треугольника, равен 5√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$\left(5\surd3\right)^2=\left(\frac{5\surd3}2\right)^2+x^2\\x^2=\;\frac{4\left(5\surd3\right)^2}4-\frac{\left(5\surd3\right)}4^2\\х^2=\frac{3\left(5\surd3\right)^2}4\\х=\sqrt{\frac{3\ast25\ast3}4}\\х=\sqrt{\frac{225}4}=\frac{15}2=7.5$
7.5*2=15
Ответ: 15
297C02

Радиус окружности, описанной около равностороннего треугольника, равен 6√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$\left(6\surd3\right)^2=\left(\frac{6\surd3}2\right)^2+x^2\\x^2=\;\frac{4\left(6\surd3\right)^2}4-\frac{\left(6\surd3\right)}4^2\\х^2=\frac{3\left(6\surd3\right)^2}4\\х=\sqrt{\frac{3\ast36\ast3}4}\\х=\sqrt{\frac{324}4}=\frac{18}2=9$
9*2=18
Ответ: 18
8E90C6

Радиус окружности, описанной около равностороннего треугольника, равен 7√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$\left(7\surd3\right)^2=\left(\frac{7\surd3}2\right)^2+x^2\\x^2=\;\frac{4\left(7\surd3\right)^2}4-\frac{\left(7\surd3\right)}4^2\\х^2=\frac{3\left(7\surd3\right)^2}4\\х=\sqrt{\frac{3\ast49\ast3}4}\\х=\sqrt{\frac{441}4}=\frac{21}2=10.5$
10.5*2=21
Ответ: 21
48D77B

Радиус окружности, описанной около равностороннего треугольника, равен 8√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$\left(8\surd3\right)^2=\left(\frac{8\surd3}2\right)^2+x^2\\x^2=\;\frac{4\left(8\surd3\right)^2}4-\frac{\left(8\surd3\right)}4^2\\х^2=\frac{3\left(8\surd3\right)^2}4\\х=\sqrt{\frac{3\ast64\ast3}4}\\х=\sqrt{\frac{576}4}=\frac{24}2=12$
12*2=24
Ответ: 24
426C70

Радиус окружности, описанной около равностороннего треугольника, равен 9√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$\left(9\surd3\right)^2=\left(\frac{9\surd3}2\right)^2+x^2\\x^2=\;\frac{4\left(9\surd3\right)^2}4-\frac{\left(9\surd3\right)}4^2\\х^2=\frac{3\left(9\surd3\right)^2}4\\х=\sqrt{\frac{3\ast81\ast3}4}\\х=\sqrt{\frac{729}4}=\frac{27}2=13.5$
13.5*2=26
Ответ: 26
71EE14

Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$\left(10\surd3\right)^2=\left(\frac{10\surd3}2\right)^2+x^2\\x^2=\;\frac{4\left(10\surd3\right)^2}4-\frac{\left(10\surd3\right)}4^2\\х^2=\frac{3\left(10\surd3\right)^2}4\\х=\sqrt{\frac{3\ast100\ast3}4}\\х=\sqrt{\frac{900}4}=\frac{30}2=15$
15*2=30
Ответ: 30
E566FC

Радиус окружности, описанной около равностороннего треугольника, равен 11√3. Найдите длину стороны этого треугольника.
Решение:
Проведем еще две прямые (биссектрисы, медианы, высоты) в равностороннем треугольнике. Получим 6 прямоугольных равных треугольников, в который один угол равен 30 градусов, а значит равен половине гипотенузы. Используя теорему Пифагора можем вычислить второй катет этого треугольника и умножить на два, тем самым получив сторону треугольника.
$\left(11\surd3\right)^2=\left(\frac{11\surd3}2\right)^2+x^2\\x^2=\;\frac{4\left(11\surd3\right)^2}4-\frac{\left(11\surd3\right)}4^2\\х^2=\frac{3\left(11\surd3\right)^2}4\\х=\sqrt{\frac{3\ast121\ast3}4}\\х=\sqrt{\frac{1089}4}=\frac{33}2=16.5$
16.5*2=33
Ответ: 33
07781B
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 25. Найдите AC, если BC=48.
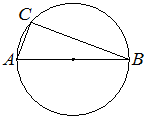
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем AC и подставляем значения.
$\left(2\frac{AB}2\right)^2=AC^2+CB^2\\AC^2=4\left(\frac{AB}2\right)^2-CB^2\\AC=\sqrt{4\left(\frac{AB}2\right)^2-CB^2}\\AC=\sqrt{4\ast25^2-48^2}\\AC=\sqrt{4\ast625-2304}=\sqrt{196}=14$
Ответ: 14
CABA26
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20. Найдите BC, если AC=32.
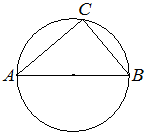
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем BC и подставляем значения.
$\left(2\frac{AB}2\right)^2=AC^2+CB^2\\CB^2=4\left(\frac{AB}2\right)^2-AC^2\\CB=\sqrt{4\left(\frac{AB}2\right)^2-AC^2}\\CB=\sqrt{4\ast20^2-32^2}\\CB=\sqrt{4\ast400-1024}=\sqrt{1600-1024}=24$
Ответ: 24
E7C22E
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 13. Найдите AC, если BC=24.

Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем AC и подставляем значения.
$\left(2\frac{AB}2\right)^2=AC^2+CB^2\\AC^2=4\left(\frac{AB}2\right)^2-CB^2\\AC=\sqrt{4\left(\frac{AB}2\right)^2-CB^2}\\AC=\sqrt{4\ast13^2-24^2}\\AC=\sqrt{4\ast169-576}=\sqrt{676-576}=10$
Ответ: 10
4045A6
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 17. Найдите AC, если BC=30.

Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем AC и подставляем значения.
$\left(2\frac{AB}2\right)^2=AC^2+CB^2\\AC^2=4\left(\frac{AB}2\right)^2-CB^2\\AC=\sqrt{4\left(\frac{AB}2\right)^2-CB^2}\\AC=\sqrt{4\ast17^2-30^2}\\AC=\sqrt{4\ast289-900}=\sqrt{256}=16$
Ответ: 16
1845C2
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.

Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем BC и подставляем значения.
$\left(2\frac{AB}2\right)^2=AC^2+CB^2\\CB^2=4\left(\frac{AB}2\right)^2-AC^2\\CB=\sqrt{4\left(\frac{AB}2\right)^2-AC^2}\\CB=\sqrt{4\ast10^2-16^2}\\CB=\sqrt{4\ast100-256}=\sqrt{400-256}=12$
Ответ: 12
C8A9ED

Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем BC и подставляем значения.
$\left(2\frac{AB}2\right)^2=AC^2+CB^2\\CB^2=4\left(\frac{AB}2\right)^2-AC^2\\CB=\sqrt{4\left(\frac{AB}2\right)^2-AC^2}\\CB=\sqrt{4\ast15^2-24^2}\\CB=\sqrt{4\ast225-576}=\sqrt{324}=18$
Ответ: 18
EF5960
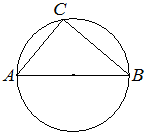
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 14,5. Найдите AC, если BC=21.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем AC и подставляем значения.
$\left(2\frac{AB}2\right)^2=AC^2+CB^2\\AC^2=4\left(\frac{AB}2\right)^2-CB^2\\AC=\sqrt{4\left(\frac{AB}2\right)^2-CB^2}\\AC=\sqrt{4\ast14.5^2-12^2}\\AC=\sqrt{4\ast210.25-900}=\sqrt{841-441}=20$
Ответ: 20
6D03EB

Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20,5. Найдите BC, если AC=9.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем BC и подставляем значения.
$\left(2\frac{AB}2\right)^2=AC^2+CB^2\\CB^2=4\left(\frac{AB}2\right)^2-AC^2\\CB=\sqrt{4\left(\frac{AB}2\right)^2-AC^2}\\CB=\sqrt{4\ast20.5^2-9^2}\\CB=\sqrt{4\ast420.25-81}=\sqrt{1600}=40$
Ответ: 40
E7626A

Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 8,5. Найдите BC, если AC=8.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем BC и подставляем значения.
$\left(2\frac{AB}2\right)^2=AC^2+CB^2\\CB^2=4\left(\frac{AB}2\right)^2-AC^2\\CB=\sqrt{4\left(\frac{AB}2\right)^2-AC^2}\\CB=\sqrt{4\ast8.5^2-8^2}\\CB=\sqrt{4\ast72.25-64}=\sqrt{225}=15$
Ответ: 15
748A0C

Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 6,5. Найдите AC, если BC=12.
Решение:
Угол ACB – вписан в окружность. Величина вписанного угла в два раза меньше градусной меры дуги, на которую он опирается. Градусная мера круга 360 °. Дуга AB – половина круга, значит ее градусная мера 360/2 = 180 °. Угол ACB опирается на дугу AB, значит угол ACB = (дуга AB) / 2 = 180 / 2 = 90 °. Теперь используя теорему Пифагора выражаем AC и подставляем значения.
$\left(2\frac{AB}2\right)^2=AC^2+CB^2\\AC^2=4\left(\frac{AB}2\right)^2-CB^2\\AC=\sqrt{4\left(\frac{AB}2\right)^2-CB^2}\\AC=\sqrt{4\ast6.5^2-12^2}\\AC=\sqrt{4\ast42.25-900}=\sqrt{169-144}=5$
Ответ: 5
7B6202
Задания с развернутым ответом
Углы B и C треугольника ABC равны соответственно 71° и 79°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 8.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)
Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
6AFB28
Углы B и C треугольника ABC равны соответственно 73° и 77°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 9.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)
Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
A4813D
Углы B и C треугольника ABC равны соответственно 61° и 89°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 10.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)
Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
64DBE8
Углы B и C треугольника ABC равны соответственно 63° и 87°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 11.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)
Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
DC2396
Углы B и C треугольника ABC равны соответственно 62° и 88°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 12.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)
Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
FC2D84
Углы B и C треугольника ABC равны соответственно 64° и 86°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 13.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)
Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
18FAEE
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)
Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
AE3B14
Углы B и C треугольника ABC равны соответственно 66° и 84°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)
Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
E5A864
Углы B и C треугольника ABC равны соответственно 67° и 83°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 16.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)
Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
CF7752
Углы B и C треугольника ABC равны соответственно 72° и 78°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 17.
Решение:
По обобщенной теореме синусов 2 радиуса равны катет поделенный на синус угла против него. В нашем случае известны два угла и неизвестен как раз угол напротив катета, который и предстоит узнать. Угол можно вычислить из условия того, что в треугольнике сумма всех углов равна 180 градусов. Получаем:
2R=BC/sinA
BC=2*R*sinA
BC=2*R*sin(180-∠B-∠C)
Подставляем значения и находим BC
BC=2*8*sin(180°-71°-79°)=16*sin30°=16*1/2=8
Ответ: 8
CF802A