Если вы в здравом уме, то невозможно оспорить факт того, что математика одна из популярных, основных и весьма нужных школьных наук. Математические знания дают нам возможность анализировать и вычислять не только какие-либо мнимые и возможные ситуации, которые приведены в заданиях, но и часто помогают решать по-настоящему жизненные вопросы.
 Что относительно настоящей статьи, то она расскажет об ответах, о так называемых ГДЗ, то есть готовых домашних заданиях для рабочей тетради по математике за 5 класс, 2 часть авторов Мерзляк, Полонский, Якир. Вторая часть рабочей тетради как и следует из размышлений, будет актуальна для школьников во второй половине учебного года.
 Теперь после всех этих измышлений пришло время перейти уже непосредственно к ответам. 

Что насчет ответов, то их можно будет посмотреть далее

ГДЗ ответы по математике за 5 класс рабочая тетрадь, 2 часть авторов Мерзляк, Полонский, Якир

Вы можете выбрать задание и кликнуть по вкладке. Перед вами откроется материал с ответами.

 Если вы в здравом уме, то невозможно оспорить факт того, что математика одна из популярных, основных и весьма нужных школьных наук. Математические знания дают нам возможность анализировать и вычислять не только какие-либо мнимые и возможные ситуации, которые приведены в заданиях, но и часто помогают решать по-настоящему жизненные вопросы.
 Что относительно настоящей статьи, то она расскажет об ответах, о так называемых ГДЗ, то есть готовых домашних заданиях для рабочей тетради по математике за 5 класс, 2 часть авторов Мерзляк, Полонский, Якир. Вторая часть рабочей тетради как и следует из размышлений, будет актуальна для школьников во второй половине учебного года.
 Теперь после всех этих измышлений пришло время перейти уже непосредственно к ответам. 

Что насчет ответов, то их можно будет посмотреть далее

ГДЗ ответы по математике за 5 класс рабочая тетрадь, 2 часть авторов Мерзляк, Полонский, Якир

Вы можете выбрать задание и кликнуть по вкладке. Перед вами откроется материал с ответами.

Номер 306

Понятие обыкновенной дроби. Номер №306

Заполните пропуски.
1) Записи вида 1/6 , 1/12 , 3/5 , 14/19 называют _
2) Обыкновенные дроби записывают с помощью двух _ и _ дроби.
3) Число, записанное над чертой дроби, называют _ дроби, а число записанное под чертой, − _ дроби.
4) Знаменатель дроби показывает, на сколько _ нечто целое, а числитель − _ взяли.

Решение
1) Записи вида 1/6 , 1/12 , 3/5 , 14/19 называют дробями.
2) Обыкновенные дроби записывают с помощью двух натуральных чисел и черты дроби.
3) Число, записанное над чертой дроби, называют числителем дроби, а число записанное под чертой, − знаменателем дроби.
4) Знаменатель дроби показывает, на сколько равных частей нечто целое, а числитель − сколько таких частей взяли.

307

Номер №307

Запишите как читается дробь.
1) 1/6 − _
2) 3/9 − _

Решение 1
1/6 − одна шестая

Решение 2
3/9 − три девятых

308

Номер №308

Запишите в виде дроби число:
1) три седьмых;
2) восемь девятых;
3) девять четырнадцатых;
4) двадцать три сорок вторых;
5) пять десятых;
6) тридцать четыре сотых.
Ответ: 1) ☐; 2) ☐; 3) ☐; 4) ☐; 5) ☐; 6) ☐.

Решение 1
3 7 − три седьмых

Решение 2
8 9 − восемь девятых

Решение 3
9/14 − девять четырнадцатых

Решение 4
23/42 − двадцать три сорок вторых

Решение 5
5/10 − пять десятых

Решение 6
34/100 − тридцать четыре сотых

309

Номер №309

Запишите дробью, какая часть фигур закрашена.


Решение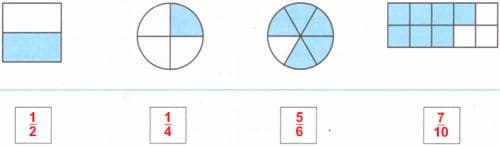

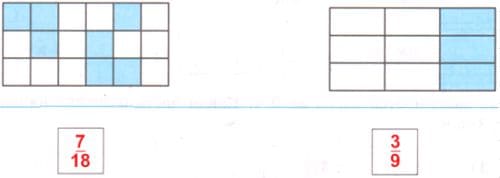
310

Номер №310

Заштрихуйте соответствующую дроби часть фигуры.

Решение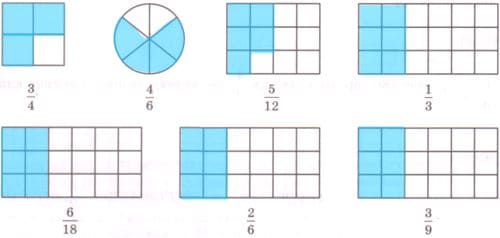

311

Номер №311
Начертите квадрат со стороной 5 см, разделите его на 25 равных частей. Закрасьте квадрат так, чтобы 9/25 квадрата было синим, а 12/25 квадрата − красным. Какая часть квадрата осталась незакрашенной?

Решение

4/25 квадрата осталась незакрашенной.

312

Номер №312

Заполните пропуски.
1 мм = 1 10 см
1 см = ☐ дм
1 дм = ☐ м
1 см = ☐ м
1 м = ☐ км
1 г = ☐ кг
1 кг = ☐ ц
1 кг = ☐ т
1 ц = ☐ т
1 к. = ☐ р.
1 с = ☐ мин
1 мин = ☐ ч
1 с = ☐ ч
1 ч = ☐ сут
1 а = ☐ га

Решение
1 мм = 1 10 см, так как 1 см = 10 мм;
1 см = 1 10 дм, так как 1 дм = 10 см;
1 дм = 1 10 м, так как 1 м = 10 дм;
1 см = 1 100 м, так как 1 м = 100 см;
1 м = 1 1000 км, так как 1 км = 1000 м;
1 г = 1 1000 кг, так как 1 кг = 1000 г;
1 кг = 1 100 ц, так как 1 ц = 100 кг;
1 кг = 1 1000 т, так как 1 т = 1000 кг;
1 ц = 1 10 т, так как 1 т = 10 ц;
1 к. = 1 100 р., так как 1 р. = 100 к.;
1 с = 1 60 мин, так как 1 мин = 1 с;
1 мин = 1 60 ч, так как 1 ч = 60 мин;
1 с = 1 3600 ч, так как 1 ч = 3600 с;
1 ч = 1 24 сут., так как 1 сут. = 24 ч;
1 а = 1 100 га, так как 1 га = 100 а.

313

Номер №313

Бассейн заполняется водой за 9 ч. Какая часть бассейна наполняется:
1) за 1 ч;
2) 2 ч;
3) 5 ч?

Решение 1
1 9 бассейна наполняется за 1 час.

Решение 2
2 9 бассейна наполняется за 2 часа.

Решение 3
5 9 бассейна наполняется за 5 часов.

314

Номер №314

В классе 34 учащихся, из них 15 − девочки. Какую часть учащихся класса составляют девочки?

Решение
15 34 учащихся класса составляют девочки.

315

Номер №315

В саду растет 180 деревьев, из них 4 9 составляют вишни. Сколько вишен растет в саду?
Решение.
1) (деревьев) − составляют 1 9 всех деревьев.
Ответ:

Решение
1) 180 : 9 = 20 (деревьев) − составляют 1 9 всех деревьев;
2) 20 * 4 = 80 (вишен) − растет в саду.
Ответ: 80 вишен

316

Номер №316

Белый медведь живет в среднем 32 года что составляет 4/5 средней продолжительности жизни льва. Сколько лет живет лев?
Решение.
1) (лет) − составляют 1/5 средней продолжительности жизни льва.
Ответ:

Решение
1) 32 : 4 = 8 (лет) − составляют 1 5 средней продолжительности жизни льва;
2) 8 * 5 = 40 (лет) − живет лев.
Ответ: 40 лет

317

Номер №317

Заполните пропуски.
1)
4 10 м = 40 см;
1 2 м = _ см;
1 4 м = _ см;
2 5 м = _ см;
6 25 м = _ см.
2)
1 5 кг = _ г;
17 100 кг = _ г;
8 125 кг = _ г;
9 100 ц = _ кг;
23 50 ц = _ кг.
3)
49 60 ч = _ мин;
1 3 ч = _ мин;
7 12 ч = _ мин;
8 15 мин = _ с;
19 30 мин = _ с.
4)
1 2 р. = _ к.;
3 4 р. = _ к.;
7 10 р. = _ к.;
4 25 р. = _ к.;
79 100 р. = _ к.

Решение 1
4 10 м = 40 см, так как 100 : 10 * 4 = 10 * 4 = 40;
1 2 м = 50 см, так как 100 : 2 * 1 = 50 * 1 = 50;
1 4 м = 25 см, так как 100 : 4 * 1 = 25 * 1 = 25;
2 5 м = 40 см, так как 100 : 5 * 2 = 20 * 2 = 40;
6 25 м = 24 см, так как 100 : 25 * 6 = 4 * 6 = 24.

Решение 2
1 5 кг = 200 г, так как 1000 : 5 * 1 = 200 * 1 = 200 г;
17 100 кг = 170 г, так как 1000 : 100 * 17 = 10 * 17 = 170 г;
8 125 кг = 64 г, так как 1000 : 125 * 8 = 8 * 8 = 64 г;
9 100 ц = 9 кг, так как 100 : 100 * 9 = 1 * 9 = 9;
23 50 ц = 46 кг, так как 100 : 50 * 23 = 2 * 23 = 46.

Решение 3
49 60 ч = 49 мин, так как 60 : 60 * 49 = 1 * 49 = 49;
1 3 ч = 20 мин, так как 60 : 3 * 1 = 20 * 1 = 20;
7 12 ч = 35 мин, так как 60 : 12 * 7 = 5 * 7 = 35;
8 15 мин = 32 с, так как 60 : 15 * 8 = 4 * 8 = 32;
19 30 мин = 38 с, так как 60 : 30 * 19 = 2 * 19 = 38.

Решение 4
1 2 р. = 50 к., так как 100 : 2 * 1 = 50 * 1 = 50;
3 4 р. = 75 к., так как 100 : 4 * 3 = 25 * 3 = 75;
7 10 р. = 70 к., так как 100 : 10 * 7 = 10 * 7 = 70;
4 25 р. = 16 к., так как 100 : 25 * 4 = 4 * 4 = 16;
79 100 р. = 79 к., так как 100 : 100 * 79 = 1 * 79 = 79.

318

Номер №318

Отрезок на рисунке изображает 1 км. Начертите отрезки, соответствующие 1/3 км, 5/6 км, 3/4 км.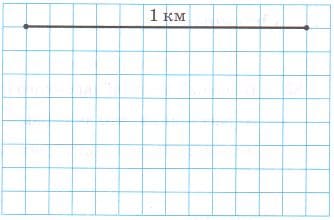

Решение
Отрезок 1 км состоит из 12 клеток, тогда:
12 : 3 * 1 = 4 * 1 = 4 (клетки) − будет в отрезке 1/3 км;
12 : 6 * 5 = 2 * 5 = 10 (клеток) − будет в отрезке 5/6 км;
12 : 4 * 3 = 3 * 3 = 9 (клеток) − будет в отрезке 3/4 км.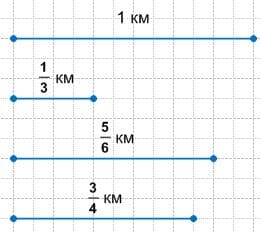

319

Номер №319

Сколько градусов составляют:
1) 7/15 величины прямого угла;
2) 19/36 величины развернутого угла?

Решение 1
90° : 15 * 7 = 6 * 7 = 42° − составляют 7/15 величины прямого угла.
Ответ: 42°

Решение 2
180° : 36 * 19 = 5 * 19 = 95° − составляют 9/36 величины развернутого угла.
Ответ: 95°

320

Номер №320

Три мальчика собрали 144 гриба. Один из них собрал 5/16 всех грибов, а другой − 6/11 остальных грибов. Сколько грибов собрал третий мальчик?

Решение
1) 144 : 16 = 9 * 5 = 45 (грибов) − собрал один мальчик;
2) 144 − 45 = 99 (грибов) − собрали вместе второй и третий мальчики;
3) 99 : 11 * 6 = 9 * 6 = 54 (гриба) − собрал второй мальчик;
4) 99 − 54 = 45 (грибов) − собрал третий мальчик.
Ответ: 45 грибов

321

Номер №321

В первый день байдарочного похода турист проплыл 56 км, во второй день − 6/7 того расстояния, что за первый, а в третий − 13/16 того, что во второй. Сколько всего километров проплыл турист за три дня?

Решение
1) 56 : 7 * 6 = 8 * 6 = 48 (км) − проплыл турист во второй день;
2) 48 : 16 * 13 = 3 * 13 = 39 (км) − проплыл турист в третий день;
3) 56 + 48 + 39 = 104 + 39 = 143 (км) − проплыл турист за три дня.
Ответ: 143 км

322

Номер №322

Одно из слагаемых равно 252, и оно составляет 21/32 суммы. Найдите второе слагаемое.

Решение
1) 252 : 21 * 32 = 12 * 32 = 384 − сумма;
2) 384 − 252 = 132 − второе слагаемое.
Ответ: 132

Вычисления:
1)

 252| 21
-21  |12
-  41
   41
     0

2)

*12
  32
+24
36
384

 

323

Номер №323

В семье четыре сына. У каждого есть одна сестра. Сколько всего детей в семье?

Решение
В семье всего одна дочь, которая одновременно является сестрой каждому из сыновей, тогда:
4 + 1 = 5 (детей) − всего в семье.
Ответ: 5 детей

324

Номер №324

Карета, запряженная тройкой коней, проехала 60 км. Сколько километров проскакал каждый конь?

Решение
Каждый конь проскакал 60 км, так как скакали они вместе в одной упряжке.
Ответ: 60 км

325

Номер №325

Найдите:
1) два в квадрате;
2) три в квадрате;
3) угол в квадрате.

Решение 1
2² = 2 ∗ 2 = 4
Ответ: 4

Решение 2
3² = 3 ∗ 3 = 9
Ответ: 9

Решение 3

ABCD − квадрат. Каждый угол в квадрате равен 90°.
Ответ: 90°

326

Сравнение дробей. Номер №326

Заполните пропуски.
1) Если числитель дроби равен знаменателю, то дробь равна _
2) Дробь a b (a и b − натуральные числа) называют правильной, если a ☐ b.
3) Дробь a b (a и b − натуральные числа) называют неправильной, если a ☐ b или a ☐ b.
4) 9/14 − _ дробь, поскольку 9 ☐ 14.
5) 7/5 − _ дробь, поскольку 7 ☐ 5.
6) 16/16 − _ дробь, поскольку 16 ☐ 16.

Решение
1) Если числитель дроби равен знаменателю, то дробь равна 1.
2) Дробь a b (a и b − натуральные числа) называют правильной, если a < b.
3) Дробь a b (a и b − натуральные числа) называют неправильной, если a > b или a = b.
4) 9/14 − правильная дробь дробь, поскольку 9 < 14.
5) 7/5 − неправильная дробь дробь, поскольку 7 > 5.
6) 16/16 − неправильная дробь дробь, поскольку 16 = 16.

327

Номер №327

Выпишите из дробей 1/20 , 16/9 , 7/2 , 14/23 , 10/10 , 5/32 , 11/2:
1) правильные дроби;
2) неправильные дроби.

Решение
1)
правильные дроби:
1/20, так как 1 < 20;
14/23, так как 14 < 23;
5/32, так как 5 < 32.
2)
неправильные дроби:
16/9, так как 16 > 9;
7/2, так как 7 > 2;
10/10, так как 10 = 10;
11/2, так как 11 > 2.

328

Номер №328

Придумайте и запишите:
1) 5 правильных дробей;
2) 5 неправильных дробей.

Решение
1)
правильные дроби:
1/2, 3/7, 11/13, 4/5, 2/3.
2)
неправильные дроби:
3/2, 7/7, 15/13, 7/5, 3/3.

329

Номер №329

Запишите все правильные дроби со знаменателем 9.

Решение
1/9, 2/9, 3/9, 4/9, 5/9, 6/9, 7/9, 8/9.

330

Номер №330

Запишите все неправильные дроби с числителем 9.

Решение
9/1, 9/2, 9/3, 9/4, 9/5, 9/6, 9/7, 9/8, 9/9.

331

Номер №331

Две одинаковые полоски разделили на 7 равных частей. Закрасьте 4/7 одной полоски и 6/7 другой. Сравните полученные дроби: 4/7 ☐ 6/7.
Сформулируйте правило сравнения дробей с одинаковыми знаменателями:
из двух дробей с одинаковыми знаменателями больше та, у которой _

Решение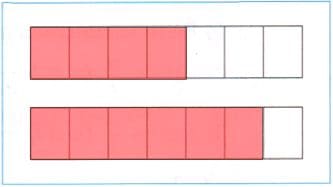

4/7 < 6/7
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

332

Номер №332

Две одинаковые полоски разделили на части. Одну полоску разделили на 7 равных частей, а другую − на 5 равных частей. Закрасьте 3/7 первой полоски и 3/5 второй. Сравните полученные дроби: 3/7 ☐ 3/5.
Сформулируйте правило сравнения дробей с одинаковыми числителями:
из двух дробей с одинаковыми числителями больше та, у которой _

Решение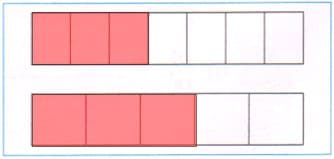

3/7 < 3/5
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

333

Номер №333

Заполните пропуски.
1) Все правильные дроби меньше _, а неправильные − _ или равны _.
2) Каждая неправильная дробь _ любой правильной дроби, а каждая правильная дробь меньше _.
3) На координатном луче из двух дробей большая дробь расположена _ меньшей.

Решение
1) Все правильные дроби меньше 1, а неправильные − больше 1 или равны 1.
2) Каждая неправильная дробь больше любой правильной дроби, а каждая правильная дробь меньше любой неправильной.
3) На координатном луче из двух дробей большая дробь расположена правее меньшей.

334

Номер №334

Обведите верные утверждения.
1) 2/3 < 1
2) 14/13 > 1
3) 12/13 > 13/12
4) 2/2 = 1
5) 1 < 18/20
6) 19/19 = 99/99
7) 25/27 > 3/2
8) 57/94 < 5/4

Решение
1) 2/3 < 1, верно, так как любая правильная дробь меньше 1.
2) 14/13 > 1, верно, так как любая дробь у которой числитель больше знаменателя больше 1.
3) 12/13 > 13/12, неверно, так как любая правильная дробь меньше любой неправильной дроби.
4) 2/2 = 1, верно, так как 2 : 2 = 1.
5) 1 < 18/20, неверно, так как любая правильная дробь меньше 1.
6) 19/19 = 99/99, верно, так как 19 : 19 = 1 и 99 : 99 = 1.
7) 25/27 > 3/2, неверно, так как любая правильная дробь меньше любой неправильной.
8) 57/94 < 5/4, верно, так как любая правильная дробь меньше любой неправильной.

335

Номер №335

Сравните числа.
1) 5/11 ☐ 9/11
2) 17/25 ☐ 14/25
3) 9/40 ☐ 9/37
4) 24/51 ☐ 24/53
5) 7/12 ☐ 1
6) 13/10 ☐ 1
7) 7/7 ☐ 18/18
8) 8/7 ☐ 41/44

Решение 1
5/11 < 9/11

Решение 2
17/25 > 14/25

Решение 3
9/40 < 9/37

Решение 4
24/51 > 24/53

Решение 5
7/12 < 1

Решение 6
13/10 > 1

Решение 7
7/7 = 18/18

Решение 8
8/7 > 41/44

336

Номер №336

Какие из дробей 10 11 , 16 4 , 18 17 , 24 24 , 205 207 , 310 303 , 39 40 больше 1?

Решение
16/4 > 1
18/17 > 1
310/303 > 1

337

Номер №337

Расположите дроби 5 29 , 7 29 , 4 29 , 25 29 , 17 29 , 13 29 в порядке убывания.
Ответ: 25 29 ,

Решение
25 > 17 > 13 > 7 > 5 > 4, значит:
25/29 < 17/29 < 13/29 < 7/29 < 5/29 < 4/29
Ответ: 25/29, 17/29, 13/29, 7/29 , 5/29, 4/29.

338

Номер №338

Отметьте на координатном луче все числа, являющиеся дробями со знаменателем 5, расположенные между числами 0 и 3. Какие из отмеченных чисел являются правильными дробями, а какие − неправильными?

Ответ:
1) правильные дроби:
2) неправильные дроби;

Решение

Ответ:
1) правильные дроби:
1/5 , 2/5 , 3/5 , 4/5.
2) неправильные дроби:
5/5, 6/5, 7/5, 8/5 , 9/5, 10/5 , 11/5, 12/5, 13/5, 14/5, 15/5.

339

Номер №339

Найдите все натуральные значения x, при которых дробь x 8 будет правильной.

Решение
Дробь будет правильной, если числитель будет меньше знаменателя, значит:
x может быть равен: 1, 2, 3, 4, 5, 6, 7.

340

Номер №340

Найдите все натуральные значения x, при которых дробь 11 x будет неправильной.

Решение
Дробь будет неправильной, если числитель будет больше или равна знаменателю, значит:
x может быть равен: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.

341

Номер №341

1) Впишите в пустые клетки цифры так, чтобы образовалась правильная дробь.
2 ☐ 4/ 205 , 382/ 3 ☐ 2 , 2 ☐ 8/ 20 ☐ , ☐ ☐ /☐ 101.
2) Впишите в пустые клетки цифры так, чтобы образовалась неправильная дробь.
5 ☐ 3 /593 , 411 /4 ☐ 1 , 615 /6 ☐ 7 , ☐ 90/ 99 ☐ , ☐ ☐ /☐ 999.

Решение 1
204/205 , 382/392 , 208/209 , 100/101.

Решение 2
593/593 , 411/401 , 615/607 , 990/990 , 999/999.

342

Номер №342

Постройте и обозначьте отрезок, длина которого составляет:
1) 9/8 длины отрезка AB;
2) 10/8 длины отрезка AB;
3) 7/4 длины отрезка AB;
4) 3/2 длины отрезка AB.

Решение 1
Отрезок AB состоит из 8 клеток, тогда:
8 : 8 * 9 = 1 * 9 = 9 (клеток) − будет составлять отрезок равный 9/8 длины отрезка AB.

Решение 2
Отрезок AB состоит из 8 клеток, тогда:
8 : 8 * 10 = 1 * 10 = 10 (клеток) − будет составлять отрезок равный 10/8 длины отрезка AB.

Решение 3
Отрезок AB состоит из 8 клеток, тогда:
8 : 4 * 7 = 2 * 7 = 14 (клеток) − будет составлять отрезок равный 7/4 длины отрезка AB.

Решение 4
Отрезок AB состоит из 8 клеток, тогда:
8 : 2 * 3 = 4 * 3 = 12 (клеток) − будет составлять отрезок равный 3/2 длины отрезка AB.

343

Номер №343

Саша планировал прочитать за день 42 страницы книги, а прочитал 7 6 запланированного. Сколько страниц прочитал Саша?

Решение
42 : 6 * 7 = 7 * 7 = 49 (страниц) − прочитал Саша.
Ответ: 49 страниц

344

Номер №344

Найдите все натуральные значения x, при которых выполняется неравенство:
1) x/15 < 7/15;
2) 10/x > 10/9.

Решение 1
x/15 < 7/15
6/15 < 7/15
5/15 < 7/15
4/15 < 7/15
3/15 < 7/15
2/15 < 7/15
1/15 < 7/15
Ответ: 1, 2, 3, 4, 5, 6.

Решение 2
10/x > 10/9
10/8 > 10/9
10/7 > 10/9
10/6 > 10/9
10/5 > 10/9
10/4 > 10/9
10/3 > 10/9
10/2 > 10/9
10/1 > 10/9
Ответ: 1, 2, 3, 4, 5, 6, 7, 8.

345

Номер №345

Используя цифры 1, 4, 5, 7 и черту дроби, запишите все возможные правильные дроби.
Ответ: 1,

Решение
Ответ: 1/4 , 1/5 , 1/7 , 4/5 , 4/7 , 5/7.

346

Номер №346

Найдите все натуральные значения m, при которых дробь 4 m + 5 17 будет правильной.
Ответ: m =

Решение
Дробь будет правильной если числитель будет меньше знаменателя.
4m + 5 = 17
4m = 17 − 5
4m = 12
m = 12 : 4
m = 3, значит дробь будет правильной при m < 3.
Ответ: m = 1; 2.

347

Номер №347

Найдите все натуральные значения a, при которых дробь 10 a будет неправильной, а дробь 7 a − правильной.

Решение
Дробь 10 a будет неправильной при a ≤ 10.
Дробь 7 a будет правильной при a > 7.
Тогда при 7 < a ≤ 10 дробь 10 a будет неправильной, а дробь 7 a − правильной.
Ответ: a = 8; 9; 10.

348

Номер №348

Натуральные числа a, b, c и d такие, что a < b, b < c и c < d. Сравните дроби.
1) a/b ☐ b/a
2) c/a ☐ b/d
3) b/a ☐ c/d
4) a/d ☐ c/b

Решение 1
a/b − правильная дробь, так как a < b;
b/a − неправильная дробь, так как a < b, значит:
a/b < b/a, так как любая неправильная дробь больше любой правильной дроби.

Решение 2
c/a − неправильная дробь, так как a < b и b < c, значит a < c.
b/d − правильная дробь, так как b < c и c < d, значит b < d, значит:
c/a > b d, так как любая неправильная дробь больше любой правильной дроби.

Решение 3
b/a − неправильная дробь, так как a < b.
c/d − правильная дробь, так как c < d, значит:
b/a > c d, так как любая неправильная дробь больше любой правильной дроби.

Решение 4
a/d − правильная дробь, так как a < b, b < c и c < d, значит a < d.
c/b − неправильная дробь, так как b < c, значит:
a/d < c/b, так как любая неправильная дробь больше любой правильной дроби.

349

Номер №349

Заполните пропуски.
1) Чтобы сложить две дроби с одинаковыми знаменателями, нужно _, а знаменатель _.
2) В буквенном виде правило сложения дробей с одинаковыми знаменателями записывают так: _
3) Чтобы вычесть дроби с одинаковыми знаменателями, нужно из _ вычесть _, а _
4) В буквенном виде правило вычитания дробей с одинаковыми знаменателями записывают так: _

Решение
1) Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
2) В буквенном виде правило сложения дробей с одинаковыми знаменателями записывают так: a/c + b/c = (a + b)/ c.
3) Чтобы вычесть дроби с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
4) В буквенном виде правило вычитания дробей с одинаковыми знаменателями записывают так: a/c − b/c = (a − b)/ c.

350

Номер №350

Выполните действия.
1) 6/13 + 5/13 =
2) 32/45 − 14/45 =
3) 13/44 + 18/44 − 15/44 =
4) 72/95 − 26/95 + 38/95 =

Решение 1
6/13 + 5/13 = 6 + 5/13 = 11/13

Решение 2
32/45 − 14/45 = 32 − 14/45 = 18/45

Решение 3
13/44 + 18/44 − 15/44 = 13 + 18 − 15/44 = 31 − 15/44 = 16/44

Решение 4
72/95 − 26/95 + 38/95 = 46 + 38/95 = 84/95

351

Номер №351

В первый день туристы прошли 4/15 всего пути, а во второй − 6/15 пути. Какую часть пути прошли туристы за два дня?

Решение
4/15 + 6/15 = 4 + 6/15 = 10/15 (пути) − прошли туристы за два дня.
Ответ: 10/15 пути

352

Номер №352

Решите уравнение.
1) x + 12/23 = 20/23
2) 31/37 − x = 16/37
3) x − 11/17 = 3/17

Решение 1
x + 12/23 = 20/23
x = 20/23 − 12/23
x = 20 − 12/23
x = 8/23
Ответ: x = 8 23

Решение 2
31/37 − x = 16/37
x = 31/37 − 16/37
x = 31 − 16/37
x = 15/37
Ответ: x = 15/37

Решение 3
x − 11/17 = 3/17
x = 3/17 + 11/17
x = 3 + 11/17
x = 14/17
Ответ: x = 14/17

353

Номер №353

Решите уравнение.
1) ( 12/47 + x ) − 18/47 = 28/47
2) ( x − 19/32 ) + 15/32 = 17/32

Решение 1
(12/47 + x ) − 18/47 = 28/47
12/47 + x = 28/47 + 18/47
12/47 + x = 46/47
x = 46/47 − 12/47
x = 34/47
Ответ: x = 34/47

Решение 2
( x − 19/32) + 15/32 = 17/32
x − 19/32 = 17/32 − 15/32
x − 19/32 = 2/32
x = 2/32 + 19/32
x = 21/32
Ответ: x = 21/32

354

Номер №354

Магазин продал 180 кг апельсинов. В первый день было продано 13/36 всех апельсинов, а во второй − 19/36 всех апельсинов. Сколько килограммов апельсинов было продано за два дня?

Решение
1) 13/36 + 19/36 = 13 + 19/36 = 3/36 − всех апельсинов было продано за два дня;
2) 180 : 36 * 32 = 5 * 32 = 160 (кг) − апельсинов было продано за два дня.
Ответ: 160 кг апельсинов

355

Номер №355

Общая масса Пети и Коли равна 55 кг, Коли и Саши − 57 кг, Пети и Саши − 62 кг. Какова масса каждого мальчика?
Решение.
Удвоенная масса всех мальчиков равна
Ответ:

Решение
Удвоенная масса всех мальчиков равна:
55 + 57 + 62 = 112 + 62 = 174 (кг), тогда:
1) 174 : 2 = 87 (кг) − общая масса всех мальчиков;
2) 87 − 55 = 32 (кг) − масса Саши;
3) 57 − 32 = 25 (кг) − масса Коли;
4) 55 − 25 = 30 (кг) − масса Пети.
Ответ: 32 кг масса Саши; 25 кг масса Коли; 30 кг масса Пети.

356

Номер №356

Применяя знаки арифметических действий и скобки, запишите:
1) с помощью семи цифр 7 выражение, значение которого равно 700;
2) с помощью восьми цифр 2 выражение, значение которого равно 200;
3) с помощью десяти цифр 6 выражение, значение которого равно 600;
4) с помощью десяти цифр 9 выражение, значение которого равно 1000.
Ответ:
1/) 777 − 77 + 7 − 7;
2) _;
3) _;
4) _.

Решение 1
777 − 77 + 7 − 7 = (777 − 77) + (7 − 7) = 700 + 0 = 700

Решение 2
222 − 2 * 22 + 22 = 222 − 44 + 22 = (222 + 22) − 44 = 244 − 44 = 200

Решение 3
666 + 6 * (66 − 66) − 66 = 666 + 6 * 0 − 66 = 666 − 66 = 600

Решение 4
9 : 9 + 999 + 9 * (99 − 99) = 1 + 999 + 9 * 0 = 1000 + 0 = 1000

357

Номер №357

Заполните пропуски.
1) Черту дроби можно рассматривать как знак действия _
2) Результат деления двух натуральных чисел может быть _ числом или _ числом..
3) Любое натуральное число можно записать в виде _

Решение
1) Черту дроби можно рассматривать как знак действия деления.
2) Результат деления двух натуральных чисел может быть натуральным числом или дробным числом..
3) Любое натуральное число можно записать в виде дроби с любым знаменателем.

358

Номер №358

Запишите частное в виде дроби.
1) 3 : 4 = ☐
2) 1 : 7 = ☐
3) 12 : 29 = ☐
4) 18 : 6 = ☐

Решение 1
3 : 4 = 3 4

Решение 2
1 : 7 = 1 7

Решение 3
12 : 29 = 12 29

Решение 4
18 : 6 = 18 6

Номер №359

Запишите дробь в виде частного.
1) 1/9 = ☐
2) 8/11 = ☐
3) 5/3 = ☐
4) 20/4 = ☐

Решение 1
1/9 = 1 : 9

Решение 2
8/11 = 8 : 11

Решение 3
5/3 = 5 : 3

Решение 4
20/4 = 20 : 4

360

Номер №360

Заполните таблицу.

Делимое	Делитель	Частное	Дробь	Числитель дроби	Знаменатель дроби
7	13	7:13
15	22
		14:9
			5/24
1					8
				6	29

Решение

Делимое	Делитель	Частное	Дробь	Числитель дроби	Знаменатель дроби
7	13	7:13	7/13	7	13
15	22	15:22	15/22	15	22
14	9	14:9	14/9	14	9
5	24	5:24	5/24	5	24
1	8	1:8	1/8	1	8
6	29	6:29	6/29	6	29

 

361

Номер №361

Какому натуральному числу равна дробь?
1) 35/7 = ☐
2) 8/2 = ☐
3) 84/14 = ☐

Решение 1
35/7 = 35 : 7 = 5

Решение 2
8 2 = 8 : 2 = 4

Решение 3
84/14 = 84 : 14 = 6

362

Номер №362

Запишите число 7 в виде дроби с указанным знаменателем.
1) 7 = 1
2) 7 = 5
3) 7 = 12

Решение 1
7 = x/1
7 = x : 1
x = 7 * 1
x = 7
Ответ: 7 = 7/1

Решение 2
7 = x/5
7 = x : 5
x = 7 * 5
x = 35
Ответ: 7 = 35/5

Решение 3
7 = x/12
7 = x : 12
x = 12 * 7
x = 84
Ответ: 7 = 84/12

363

Номер №363

Дополните записи.
1) 36 = 1
2) 24 = 2
3) 20 = 5
4) 9 = 8
5) 100 = 3
6) 50 = 100

Решение 1
36 = x/1
36 = x : 1
x = 1 * 36
x = 36
Ответ: 36 = 36/1

Решение 2
24 = x/2
24 = x : 2
x = 2 * 24
x = 48
Ответ: 24 = 48/2

Решение 3
20 = x/5
20 = x : 5
x = 5 * 20
x = 100
Ответ: 20 = 100 5

Решение 4
9 = x/8
9 = x : 8
x = 8 * 9
x = 72
Ответ: 9 = 72/8

Решение 5
100 = x/3
100 = x : 3
x = 3 * 100
x = 300
Ответ: 100 = 300/3

Решение 6
50 = x/100
50 = x : 100
x = 100 * 50
x = 5000
Ответ: 50 = 5000/100

364

Номер №364

Решите уравнение.
1) x − 5/3 = 7;
2) 84/9 − y = 21;
x − 5 =

Решение 1
x − 5/3 = 7
x − 5 = 7 * 3
x − 5 = 21
x = 21 + 5
x = 26
Ответ: x = 26

Решение 2
84/9 − y = 21
9 − y = 84 : 21
9 − y = 4
y = 9 − 4
y = 5
Ответ: y = 5

365

Номер №365

Заполните пропуски.
1) Число 3 4 9 называют _ числом, в этом числе число 3 называют _ числа, а дробь 4 9 − его _
2) Дробная часть смешанного числа − это _ дробь.
3) Любую _ дробь, у которой числитель нацело не делится на _, можно представить в виде смешанного числа.
4) Чтобы неправильную дробь, числитель которой нацело _ на знаменатель, преобразовать в смешанное число, надо _ разделить на _; полученное неполное частное записать как _ смешанного числа, а _ как числитель его _
5) Чтобы смешанное число преобразовать в неправильную дробь, надо _ умножить на _ и к полученному произведению прибавить _; эту сумму записать как _ неправильной дроби, а в ее _ записать знаменатель дробной части смешанного числа.
6) Чтобы сложить два смешанных числа, надо _
7) Чтобы найти разность двух смешанных чисел, надо из _ вычесть соответственно _

Решение
1) Число 3 4 9 называют смешанным числом, в этом числе число 3 называют целой частью смешанного числа, а дробь 4 9 − его дробной частью.
2) Дробная часть смешанного числа − это правильная дробь.
3) Любую неправильную дробь, у которой числитель нацело не делится на знаменатель, можно представить в виде смешанного числа.
4) Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток как числитель его дробной части.
5) Чтобы смешанное число преобразовать в неправильную дробь, надо целую часть умножить на знаменатель дробной части и к полученному произведению прибавить числитель; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
6) Чтобы сложить два смешанных числа, надо отдельно сложить их целые и дробные части.
7) Чтобы найти разность двух смешанных чисел, надо из целой и дробной частей уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

366

Номер №366

Заполните таблицу.

Смешанное число	Целая часть	Дробная часть
1 1/3
4 2/9
	6	3/5
	12	29/39

Решение

Смешанное число	Целая часть	Дробная часть
1 1/3	1	1/3
4 2/9	4	2/9
6 3/5	6	3/5
12 29/39	12	29/39

367

Номер №367

Проверьте, верно ли выделены целая и дробная части числа. Если задание выполнено неверно, приведите справа верное решение.
1) 9/5 = 1 4/5
2) 17/4 = 3 1/4
3) 31/7 = 3 4/7
4) 42/10 = 3 12/10
5) 36/9 = 3 9/9
6) 69/24 = 2 21/24

Решение
1) 9/5 = 1 4/5, верно, так как 9 : 5 = 1 (остаток 4);
2) 17/4 = 3 1/4, неверно, так как 17 : 4 = 4 (остаток 1), значит 17/4 = 4 1/4;
3) 31/7 = 3 4/7, неверно, так как 31 : 7 = 4 (остаток 3), значит 31/7 = 4 3/7;
4) 42/10 = 3 12/10, неверно, так как 42 : 10 = 4 (остаток 2) и дробная часть смешанного числа должна быть правильной дробью, значит 42/10 = 4 2/10;
5) 36/9 = 3 9/9, неверно, так как 36 : 9 = 4 и дробная часть смешанного числа должна быть правильной дробью, значит 36/9 = 4;
6) 69/24 = 2 21/24, верно, так как 69 : 24 = 2 (остаток 21).

368

Номер №368

Запишите число в виде неправильной дроби.
1) 2 3/8 =
2) 3 7/12 =
3) 1 1/8 =
4) 5 16/100 =

Решение 1
2 3/8 = 2 ∗ 8 + 3/8 = 16 + 3/8 = 19/8

Решение 2
3 7/12 = 3 ∗ 12 + 7/12 = 36 + 7/12 = 43/12

Решение 3
1 1/8 = 1 ∗ 8 + 1/8 = 8 + 1/8 = 9/8

Решение 4
5 16/100 = 5 ∗ 100 + 16/100 = 500 + 16/100 = 516/100

369

Номер №369

Выполните действия.
1) 4 6/23 + 2 13/23 =
2) 12 19/28 − 5 11/28 =
3) 6 + 7/16 =
4) 7/15 + 8/15 =
5) 23/26 + 12/26 =

Решение 1
4 6/23 + 2 13/23 = (4 + 2) + (6/23 + 13/23) = 6 + 6 + 13/23 = 6 + 19/23 = 6 19/23

Решение 2
12 19/28 − 5 11/28 = (12 − 5) + (19/28 − 11/28) = 7 + 19 − 11/28 = 7 + 8/28 = 7 8/28

Решение 3
6 + 7/16 = 6 7/16

Решение 4
7/15 + 8/15 = 7 + 8/15 = 15/15 = 1

Решение 5
23/26 + 12/26 = 23 + 12/26 = 35/26 = 1 9/26

370

Номер №370

Заполните пропуски.
1) 3/7 + _ = 1
2) 16/39 + _ = 1
3) 19/9 − _ = 1
4) 17/3 − _ = 1

Решение 1
3/7 + x = 1
3/7 + x = 7/7
x = 7/7 − 3/7
x = 4/7
Ответ: 3/7 + 4/7 = 1

Решение 2
16/39 + x = 1
16/39 + x = 39/39
x = 39/39 − 16/39
x = 23/39
Ответ: 16/39 + 23/39 = 1

Решение 3
19/9 − x = 1
19/9 − x = 9/9
x = 19/9 − 9/9
x = 10/9 = 1 1/9
Ответ: 19/9 − 1 1/9 = 1

Решение 4
17/3 − x = 1
17/3 − x = 3/3
x = 17/3 − 3 3
x = 14/3 = 4 2/3
Ответ: 17/3 − 4 2/3 = 1

371

Номер №371

Представьте натуральное число в виде дробного числа по образцу: 4 = 3 4 4.
1) 7 = 6 _/5
2) 10 = 9 _/10
3) 12 = 11 ^11/
4) 32 = 31 ^8/
5) 5 = ☐ 7/7
6) 18 = ☐ 9/9

Решение 1
7 = 6 5/5

Решение 2
10 = 9 10/10

Решение 3
12 = 11 11/11

Решение 4
32 = 31 8/8

Решение 5
5 = 4 7/7

Решение 6
18 = 17 9/9

372

Номер №372

Представьте смешанное число по образцу: 5 2/7 = 4 9/7.
1) 2 1/2 = 1  _/2
2) 14 5/12 = 13  _/12
3) 1 5/8 = /8
4) 9 4/17 = 8 −
5) 16 3/5 = ☐
6) 8 11/19 = ☐

Решение 1
2 1/2 = 1 (1 + 2)/2 = 1 3/2

Решение 2
14 5/12 = 13 (5 + 12)/12 = 13 17/12

Решение 3
1 5/8 = (5 + 8)/8 = 13/8

Решение 4
9 4/17 = 8 (4 + 17)/17 = 8 21/17

Решение 5
16 3/5 = 15 (3+5)/5 = 15 8/5

Решение 6
8 11/19 = 7 (11 + 19)/19 = 7 30/19

373

Номер №373

Расшифруйте название геометрической фигуры.

Р 1 − 12/19 =
О 1 − 25/29 =
У 2 − 5/8 =
Ь 7 − 9/16 =
Н 6 − 1 3/5 =
И 4 − 2 1 5 =
Т 5 3/8 − 2 5/8 =
К 9 10/17 − 4 15/17 =
Е 4 19/29 − 2 23/29 =
Л 16 11/17 − 10 15/17 =
Г 2 7/18 − 1 11/18 =


Решение

Р 1 − 12 19 = 19 19 − 12 19 = 7/19
О 1 − 25 29 = 29 29 − 25 29 = 4/29
У 2 − 5 8 = 1 8 8 − 5 8 = 1 + ( 8 8 − 5 8 ) = 1 3/8
Ь 7 − 9 16 = 6 16 16 − 9 16 = 6 + ( 16 16 − 9 16 ) = 6 7/16
Н 6 − 1 3 5 = 5 5 5 − 1 3 5 = ( 5 − 1 ) + ( 5 5 − 3 5 ) = 4 2/5
И 4 − 2 1 5 = 3 5 5 − 2 1 5 = ( 3 − 2 ) + ( 5 5 − 1 5 ) = 1 4/5
Т 5 3 8 − 2 5 8 = 4 11 8 − 2 5 8 = ( 4 − 2 ) + ( 11 8 − 5 8 ) = 2 6/8
К 9 10 17 − 4 15 17 = 8 27 17 − 4 15 17 = ( 8 − 4 ) + ( 27 17 − 15 17 ) = 4 12/17
Е 4 19 29 − 2 23 29 = 3 48 29 − 2 23 29 = ( 3 − 2 ) + ( 48 29 − 23 29 ) = 1 25/29
Л 16 11 17 − 10 15 17 = 15 28 17 − 10 15 17 = ( 15 − 10 ) + ( 28 17 − 15 17 ) = 5 13/17
Г 2 7 18 − 1 11 18 = 1 25 18 − 1 11 18 = ( 1 − 1 ) + ( 25 18 − 11 18 ) = 14/18

2 6/8	7/19	1 25/29	1 3/8	14/18	4/29	5 13/17	6 7/16	4 2/5	1 4/5	4 12/17
Т	Р	Е	У	Г	О	Л	Ь	Н	И	К

374

Номер №374

Заполните цепочку вычислений.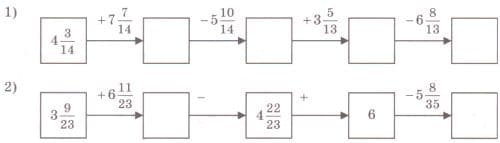

Решение 1
4 3/14 + 7 7/14 = (4 + 7) + (3/14 + 7/14) = 11 + 10/14 = 11 10/14
11 10/14 − 5 10/14 = (11 − 5) + (10/14 − 10/14 ) = 6 + 0 = 6
6 + 3 5/13 = (6 + 3) + 5/13 = 9 + 5/13 = 9 5/13
9 5/13 − 6 8/13 = 8 18/13 − 6 8/13 = (8 − 6) + (18/13 − 8/13) = 2 + 10/13 = 2 10/13
Ответ:

Решение 2
3 9/23 + 6 11/23 = (3 + 6) + (9/23 + 11/23 ) = 9 + 20/23 = 9 20/23
9 20/23 − 4 22/23 = 8 43/23 − 4 22/23 = (8 − 4) + (43/23 − 22/23 ) = 4 + 21/23 = 4 21/23
6 − 4 22/23 = 5 23/23 − 4 22/23 = 1 1/23
6 − 5 8/35 = 5 35/35 − 5 8/35 = (5 − 5) + ( 35/35 − 8 /5) = 0 + 27/35 = 27/35
Ответ:

375

Номер №375

Решите уравнение.
1) 8/11 + x = 1 1/11;
2) x − 4 8/25 = 2 17/25;
3) 10 − x = 5 6/13.

Решение 1
8/11 + x = 1 1/11
x = 1 1/11 − 8/11
x = 12/11 − 8/11
x = 4/11
Ответ: x = 4 11

Решение 2
x − 4 8/25 = 2 17/25
x = 2 17/25 + 4 8/25
x = (2 + 4) + (17/25 + 8/25)
x = 6 + 25/25
x = 6 + 1
x = 7
Ответ: 7

Решение 3
10 − x = 5 6/13
x = 10 − 5 6/13
x = 9 13/13 − 5 6/13
x = (9 − 5) + (13/13 − 6/13)
x = 4 + 7/13
x = 4 7/13
Ответ: x = 4 7/13

376

Номер №376

Какое наибольшее натуральное значение m удовлетворяет неравенству m < 74/9?

Решение
m < 74/9
74/9 = 8 2/9
m < 8 2/9
8 < 8 2/9
Ответ: m = 8 − наибольшее натуральное значение

377

Номер №377

Какое наименьшее натуральное значение m удовлетворяет неравенству m > 58/11?

Решение
m > 58/11
58/11 = 5 3/11
m > 5 3/11
6 > 5 3/11
Ответ: m = 6 − наименьшее натуральное значение

378

Номер №378

Найдите все натуральные значения x, при которых верно двойное неравенство.
1) 2 1/4 < x/4 < 3 3/4;
2) 2 2/9 < 20/x < 6 2/3.

Решение 1
2 1/4 < x/4 < 3 3/4
2 1/4 = 2 ∗ 4 + 1/4 = 8 + 1/4 = 9/4
3 3/4 = 3 ∗ 4 + 3/4 = 12 + 3/4 = 15/4
тогда:
9/4 < x/4 < 15/4
9 < x < 15
x = 10; 11; 12; 13; 14.
Ответ: 10; 11; 12; 13; 14.

Решение 2
2 2/9 < 20 x < 6 2/3
2 2/9 = 2 ∗ 9 + 2/9 = 18 + 2/9 = 20/9
6 2/3 = 6 ∗ 3 + 2/3 = 18 + 2/3 = 20/3
тогда:
20/9 < 20/x < 20/3
так как, чем знаменатель больше, тем дробь меньше, значит:
3 < x < 9
x = 4; 5; 6; 7; 8.
Ответ: 4; 5; 6; 7; 8.

379

Номер №379

Решите уравнение.
1) (2 9/59 − a) − 16/59 = 1 5/59;
2) 3 4/9 − (x − 1 7/9) = 2 2/9;
3) 10 6/10 − (7 3/10 − y) = 4 9/10;
4) 17 18/35 − (n + 4 23/35) = 9 12/35.

Решение 1
(2 9/59 − a) − 16/59 = 1 5/59
2 9/59 − a = 1 5/59 + 16 59
2 9/59 − a = 1 21/59
a = 2 9/59 − 1 21/59
a = 1 68/59 − 1 21/59
a = 47/59
Ответ: a = 47/59

Решение 2
3 4/9 − ( x − 1 7/9 ) = 2 2/9
x − 1 7/9 = 3 4/9 − 2 2/9
x − 1 7/9 = 1 2/9
x = 1 2/9 + 1 7/9
x = 2 9/9
x = 3
Ответ: x = 3

Решение 3
10 6/10 − ( 7 3/10 − y ) = 4 9/10
7 3/10 − y = 10 6/10 − 4 9/10
7 3/10 − y = 9 16/10 − 4 9/10
7 3/10 − y = 5 7/10
y = 7 3/10 − 5 7/10
y = 6 13/10 − 5 7/10
y = 1 6/10
Ответ: y = 1 6/10

Решение 4
17 18/35 − (n + 4 23/35) = 9 12/35
n + 4 23/35 = 17 18/35 − 9 12/35
n + 4 23/35 = 8 6/35
n = 8 6/35 − 4 23/35
n = 7 41/35 − 4 23/35
n = 3 18/35
Ответ: n = 3 18/35

380

Номер №380

Четверо друзей собрались съесть торт. Один хотел взять 6/25 торта, второй − 7/25, третий − 8/25, а четвертый − 9/25. Могли ли они так поделить торт?

Решение
Весь торт равен 1, тогда:
1) 6/25 + 7/25 + 8/25 + 9/25 = 6 + 7 + 8 + 9/25 = 30/25 = 1 5/25
2) 1 < 1 5/25 − значит друзья не могли так поделить торт, так как при такой дележке торта бы не хватило.
Ответ: нет, не могли.

381

Номер №381

Найдите все натуральные значения a, при которых верно неравенство.
1) 24/a > 3;
2) 12/a > a.

Решение 1
24/a > 3
24/a > 24/8
так как, чем знаменатель дроби больше, тем дробь меньше, значит:
a < 8
a = 1; 2; 3; 4; 5; 6; 7.

Решение 2
12/a > a
12 > a²
a = 1; 2; 3.

382

Номер №382

Впишите в квадратики цифры так, чтобы получились верные неравенства.
1) 2 6/9 < 2 ☐ 9 < 2 ☐ 9 < 3 < ☐ ☐ 3 < ☐ ☐ 3 < 4
2) 8 2/7 > ☐ 4/7 > 6 6/7 > ☐ 4/5 > 6 ☐ 5 > 6 2/5

Решение 1
2 6/9 < 2 7/9 < 2 8/9 < 3 < 3 1/3 < 3 2/3 < 4

Решение 2
8 2/7 > 7 4/7 > 6 6/7 > 6 4/5 > 6 3/5 > 6 2/5

383

Номер №383

Заполните пропуски.
1) Десятичную форму записи числа применяют к дробям, знаменатели которых равны _, _, _, _ и т.д.
2) В записи десятичной дроби целую часть числа от дробной отделяет _
3) Целая часть правильной дроби равна _
4) Запись дробной части десятичной дроби содержит столько цифр, сколько _ в записи _ соответствующей _ дроби.
5) В записи десятичной дроби после запятой идет разряд _, далее разряд _, затем разряд _ и т.д.
6) При чтении десятичной дроби сначала называют ее _ часть, добавляя слово " _ ", а затем называют _ часть, добавляя название последнего разряда.

Решение
1) Десятичную форму записи числа применяют к дробям, знаменатели которых равны 10, 100, 1000, 10000 и т.д.
2) В записи десятичной дроби целую часть числа от дробной отделяет запятой.
3) Целая часть правильной дроби равна 0.
4) Запись дробной части десятичной дроби содержит столько цифр, сколько нулей в записи знаменателя соответствующей обыкновенной дроби.
5) В записи десятичной дроби после запятой идет разряд десятых, далее разряд сотых, затем разряд тысячных и т.д.
6) При чтении десятичной дроби сначала называют ее целую часть, добавляя слово "целых", а затем называют дробную часть, добавляя название последнего разряда.

384

Номер №384

Заполните таблицу.

Решение

Десятичная дробь	Количество цифр после запятой	Обыкновенная дробь
0,28	2	28/100
0,196	3	196/1000
0,08	2	8/100
0,0054	4	54/10000
0,7802	4	7802/10000
0,000003	6	3/1000000

385

Номер №385

Запишите числа, приведенные в таблице, в виде десятичной дроби.

Решение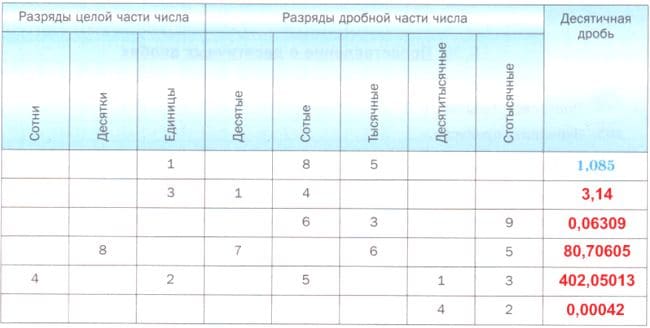

386

Номер №386

Запишите данное число в виде десятичной дроби.
1) 7/10 =
2) 43/100 =
3) 389/1000 =
4) 2 3/10 =
5) 12 58/100 =
6) 6/100 =
7) 4/1000 =
8) 8 62/1000 =
9) 1 1/10000 =

Решение 1
7/10 = 0,7

Решение 2
43/100 = 0,43

Решение 3
389/1000 = 0,389

Решение 4
2 3/10 = 2,3

Решение 5
12 58/100 = 12,58

Решение 6
6/100 = 0,06

Решение 7
4/1000 = 0,004

Решение 8
8 62/1000 = 8,062

Решение 9
1 1 10000 = 1 , 0001

387

Номер №387

Выделите целую и дробную части числа и запишите данное число в виде десятичной дроби.
1) 32/10 = 3 2/10 =
2) 764/100 =
3) 2538/1000 =
4) 4242/100 =
5) 9005/1000 =
6) 123456/10000 =

Решение 1
32/10 = 3 2/10 = 3,2

Решение 2
764/100 = 7 64/100 = 7,64

Решение 3
2538/1000 = 2 538/1000 = 2,538

Решение 4
4242/100 = 42 42/100 = 42,42

Решение 5
9005/1000 = 9 5/1000 = 9,005

Решение 6
123456/10000 = 12 3456/10000 = 12,3456

388

Номер №388

Запишите число в виде обыкновенной дроби или смешанного числа.
1) 1,6 =
2) 0,2 =
3) 0,73 =
4) 2,25 =
5) 4,018 =
6) 0,00006 =

Решение 1
1,6 = 1 6/10

Решение 2
0,2 = 2/10

Решение 3
0,73 = 73/100

Решение 4
2,25 = 2 25/100

Решение 5
4,018 = 4 18/1000

Решение 6
0,00006 = 6/100000

389

Номер №389

Запишите в виде десятичной дроби число, в котором:
1) четыре единицы, шесть десятых, две сотых;
2) шесть десятков, одна единица, одна сотая, шесть тысячных;
3) восемь десятых, семь сотых, пять десятитысячных.

Решение 1
4,62 − четыре целых шестьдесят две сотых

Решение 2
61,016 − шестьдесят одна целая, шестнадцать тысячных

Решение 3
0,8705 − ноль целых восемь тысяч семьсот пять десятитысячных

390

Номер №390

Выразите в дециметрах и запишите в виде десятичной дроби.
1) 26 см = 26/10 дм = 2 6/10 дм = 2,6 дм
2) 2 см =
3) 549 см =
4) 4 см 5 мм =

Решение 1
26 см = 26/10 дм = 2 6/10 дм = 2,6 дм

Решение 2
2 см = 2/10 дм = 0,2 дм

Решение 3
549 см = 549 10 дм = 54 9 10 дм = 54,9 дм

Решение 4
4 см 5 мм = 45 мм = 45/100 дм = 0,45 дм

391

Номер №391

Выразите в метрах и запишите в виде десятичной дроби.
1) 35 см = 35/100 м = 0,35 м
2) 3 см =
3) 6 дм 8 см =
4) 47 дм 4 см =

Решение 1
35 см = 35/100 м = 0,35 м

Решение 2
3 см = 3/100 м = 0,03 м

Решение 3
6 дм 8 см = 68 см = 68 100 м = 0,68 м

Решение 4
47 дм 4 см = 474 см = 474/100 м = 4 74/100 м = 4,74 м

392

Номер №392

Выразите в килограммах и запишите в виде десятичной дроби.
1) 2584 г = 2584/1000 кг = 2 584/1000 кг = 2,584 кг
2) 285 г =
3) 72 г =
4) 8 г =
5) 9 кг 35 г =
6) 10 кг 4 г =

Решение 1
2584 г = 2584/1000 кг = 2 584/1000 кг = 2,584 кг

Решение 2
285 г = 285/1000 кг = 0,285 кг

Решение 3
72 г = 72/1000 кг = 0,072 кг

Решение 4
8 г = 8/1000 кг = 0,008 кг

Решение 5
9 кг 35 г = 9035 г = 9035/1000 кг = 9 35/1000 кг = 9,035 кг

Решение 6
10 кг 4 г = 10004 г = 10004/1000 кг = 10 4/1000 кг = 10,004 кг

393

Номер №393

Найдите координаты точек, изображенных на рисунке.

Ответ: A(), B(), _

Решение
A(0,1); B(0,4); C(0,7); D(0,9); E(1,1); F(1,4); M(1,6); N(1,7); P(1,9); K(2,2).

394

Номер №394

Запишите в виде десятичной дроби частное.
1) 36 : 10 = 36/10 = 3 6/10 = 3,6
2) 48 : 100 =
3) 7 : 10 =
4) 546 : 100 =
5) 68 : 1000 =
6) 2975 : 1000 =

Решение 1
36 : 10 = 36/10 = 3 6/10 = 3,6

Решение 2
48 : 100 = 48/100 = 0,48

Решение 3
7 : 10 = 7/10 = 0,7

Решение 4
546 : 100 = 546/100 = 5 46/100 = 5,46

Решение 5
68 : 1000 = 68/1000 = 0,068

Решение 6
2975 : 1000 = 2975/1000 = 2 975/1000 = 2,975

395

Номер №395

Заполните пропуски.
1) Из двух десятичных дробей с неравными целыми частями больше та, у которой _
2) Если к десятичной дроби справа приписать любое количество _, то получится дробь, _
3) Значение десятичной дроби, оканчивающейся нулями, _, если последние нули в ее записи _
4) Чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания _ уравнять количество цифр в _ после чего сравнить полученные дроби поразрядно.

Решение
1) Из двух десятичных дробей с неравными целыми частями больше та, у которой целая часть больше.
2) Если к десятичной дроби справа приписать любое количество нулей, то получится дробь, равная данной.
3) Значение десятичной дроби, оканчивающейся нулями, не изменится, если последние нули в ее записи отбросить.
4) Чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях после чего сравнить полученные дроби поразрядно.

396

Номер №396

Упростите десятичную дробь.
1) 3,600 = _
2) 10,2060 = _
3) 0,780 = _

Решение 1
3,600 = 3,6

Решение 2
10,2060 = 10,206

Решение 3
0,780 = 0,78

397

Номер №397

Уравняйте количество цифр после запятой в данных дробях.
1) 4,28 = _
2) 12,1 = _
3) 0,328 = _
4) 1,2 = _

Решение
1) 4,28 = 4,280
2) 12,1 = 12,100
3) 0,328 = 0,328
4) 1,2 = 1,200

398

Номер №398

Запишите десятичную дробь, равную данной и имеющую три цифры после запятой.
1) 1,60 = _
2) 12,1 = _
3) 4,0800 = _
4) 0,3 = _
5) 0,300000 = _
6) 4 = _
7) 0,01000 = _
8) 20,02 = _

Решение 1
1,60 = 1,600

Решение 2
12,1 = 12,100

Решение 3
4,0800 = 4,080

Решение 4
0,3 = 0,300

Решение 5
0,300000 = 0,300

Решение 6
4 = 4,000

Решение 7
0,01000 = 0,010

Решение 8
20,02 = 20,020

399

Номер №399

Сравните числа.
1) 8,4 ☐ 9,2
2) 19,1 ☐ 16,5
3) 10,6 ☐ 10,4
4) 13,29 ☐ 13,21
5) 5,4 ☐ 5,42
6) 2,58 ☐ 2,396
7) 0,4 ☐ 0,09
8) 0,1 ☐ 0,076
9) 19,687 ☐ 19,7

Решение 1
8,4 < 9,2

Решение 2
19,1 > 16,5

Решение 3
10,6 > 10,4

Решение 4
13,29 > 13,21

Решение 5
5,4 < 5,42, так как 5,40 < 5,42

Решение 6
2,58 > 2,396, так как 2,580 > 2,396

Решение 7
0,4 > 0,09, так как 0,40 > 0,09

Решение 8
0,1 > 0,076, так как 0,100 > 0,076

Решение 9
19,687 < 19,7, так как 19,687 < 19,700

400

Номер №400

Запишите в порядке возрастания числа:
8,5; 8,7; 8,42; 8,04; 8,2; 8,514.

Решение
8,5 = 8,500
8,7 = 8,700
8,42 = 8,420
8,04 = 8,040
8,2 = 8,200
8,040 < 8,200 < 8,420 < 8,500 < 8,514 < 8,700, значит:
8,04 < 8,2 < 8,42 < 8,5 < 8,514 < 8,7
Ответ: 8,04; 8,2; 8,42; 8,5; 8,514; 8,7.

401

Номер №401

Запишите в пустую клетку цифру так, чтобы образовалось верное неравенство.
1) 1,☐1 < 1,02
2) 5,614 > 5,6☐7
3) 3,4☐5 > 3,492
4) 0,886 < 0,☐0987
5) 6☐,787 < 60,7☐6
6) 12,☐8☐ > 12,988

Решение 1
1,01 < 1,02

Решение 2
5,614 > 5,607

Решение 3
3,495 > 3,492

Решение 4
0,886 < 0,90987

Решение 5
60,787 < 60,796

Решение 6
12,989 > 12,988

402

Номер №402

Найдите все натуральные значения x, при которых верно двойное неравенство:
1) 6,67 < x < 9,003;
2) 13,45 < x < 18.

Решение 1
6,67 < x < 9,003
6,670 < 7,000 < 9,003
6,670 < 8,000 < 9,003
6,670 < 9,000 < 9,003
Ответ: x = 7; 8; 9.

Решение 2
13,45 < x < 18
13,45 < 14,00 < 18,00
13,45 < 15,00 < 18,00
13,45 < 16,00 < 18,00
13,45 < 17,00 < 18,00
Ответ: x = 14; 15; 16; 17.

403

Номер №403

Между какими соседними числами натурального ряда находится число:
1) 8,99;
2) 1,736?
Ответ запишите в виде двойного неравенства.

Решение 1
8,00 < 8,99 < 9,00
Ответ: 8 < 8,99 < 9

Решение 2
1,000 < 1,736 < 2,000
Ответ: 1 < 1,736 < 2

404

Номер №404

Запишите, какую цифру можно поставить вместо звездочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи).
1) 7,48 < 7,4*
2) 4,13 > 4,*8
3) 6,1 > 6,*7
4) 9,67 > 9,*3
5) 17,52 < 1*,71
6) 0,0*2 > 0,053

Решение 1
7,48 < 7,4*
7,48 < 7,49
Ответ: 9

Решение 2
4,13 > 4,*8
4,13 > 4,08
Ответ: 0

Решение 3
6,1 > 6,*7
6,1 > 6,07
Ответ: 0

Решение 4
9,67 > 9,*3
9,67 > 9,03
9,67 > 9,13
9,67 > 9,23
9,67 > 9,33
9,67 > 9,43
9,67 > 9,53
9,67 > 9,63
Ответ: 0; 1; 2; 3; 4; 5; 6.

Решение 5
17,52 < 1*,71
17,52 < 17,71
17,52 < 18,71
17,52 < 19,71
Ответ: 7; 8; 9.

Решение 6
0,0*2 > 0,053
0,062 > 0,053
0,072 > 0,053
0,082 > 0,053
0,092 > 0,053
Ответ: 6; 7; 8; 9.

405

Номер №405

Запишите наибольшую десятичную дробь:
1) с одной цифрой после запятой, меньшую 1;
2) с двумя цифрами после запятой. меньшую 3;
3) с пятью цифрами после запятой, меньшую 1.

Решение 1
0,9 < 1
Ответ: 0,9

Решение 2
2,99 < 3
Ответ: 2,99

Решение 3
0,99999 < 1
Ответ: 0,99999 < 1

406

Номер №406

Запишите наименьшую десятичную дробь:
1) с одной цифрой после запятой, большую 2;
2) с двумя цифрами после запятой, большую 1;
3) с тремя цифрами после запятой, большую 5.

Решение 1
2 < 2,1
Ответ: 2,1

Решение 2
1 < 1,01
Ответ: 1,01

Решение 3
5 < 5,001
Ответ: 5,001

407

Номер №407

Запишите три числа, каждое из которых:
1) больше 2,6 и меньше 2,8;
2) больше 4,48 и меньше 4,49.

Решение 1
2,6 < 2,65 < 2,8
2,6 < 2,7 < 2,8
2,6 < 2,75 < 2,8
Ответ: 2,65; 2,7; 2,75.

Решение 2
4,48 < 4,481 < 4,49
4,48 < 4,482 < 4,49
4,48 < 4,483 < 4,49
Ответ: 4,481; 4,482; 4,483.

408

Номер №408

Найдите все цифры, которые можно поставить вместо звездочек, чтобы образовалось верное неравенство (в правой и левой частях неравенства звездочкой обозначена одна и та же цифра).
1) 0,*4 > 0,6*
2) 4,5* < 4,*8
3) 0,*7 < 0,7*
4) 0,*7 > 0,7*

Решение 1
0,*4 > 0,6*
0,74 > 0,67
0,84 > 0,68
0,94 > 0,69
Ответ: 7; 8; 9.

Решение 2
4,5* < 4,*8
4,55 < 4,58
4,56 < 4,68
4,57 < 4,78
4,58 < 4,88
4,59 < 4,98
Ответ: 5; 6; 7; 8; 9.

Решение 3
0,*7 < 0,7*
0,07 < 0,70
0,17 < 0,71
0,27 < 0,72
0,37 < 0,73
0,47 < 0,74
0,57 < 0,75
0,67 < 0,76
Ответ: 0; 1; 2; 3; 4; 5; 6.

Решение 4
0,*7 > 0,7*
0,87 > 0,78
0,97 > 0,79
Ответ: 8; 9.

409

Номер №409

Заполните пропуски.
1) Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т.д., надо все следующие за этим разрядом цифры _. Если при этом первая из отбрасываемых цифр равна 0, 1, 2, 3, или 4, то последняя из оставшихся цифр _; если же первая из отбрасываемых цифр равна _, то последняя из оставшихся цифр _
2) При округлении натуральных чисел до какого−либо разряда вместо всех следующих за ним цифр младших разрядов пишут _. При этом если первая из цифр, следовавших за этим разрядом, была равной _, то цифра в данном разряде _; если же первая из цифр, следовавших за этим разрядом, была равной _, то цифра в данном разряде _

Решение
1) Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т.д., надо все следующие за этим разрядом цифры отбросить. Если при этом первая из отбрасываемых цифр равна 0, 1, 2, 3, или 4, то последняя из оставшихся цифр не изменяется; если же первая из отбрасываемых цифр равна 5, 6, 7, 8, 9, то последняя из оставшихся цифр увеличивается на единицу.
2) При округлении натуральных чисел до какого−либо разряда вместо всех следующих за ним цифр младших разрядов пишут нули. При этом если первая из цифр, следовавших за этим разрядом, была равной 0, 1, 2, 3, 4, то цифра в данном разряде не изменяется; если же первая из цифр, следовавших за этим разрядом, была равной 5, 6, 7, 8, 9, то цифра в данном разряде увеличивается на единицу.

410

Номер №410

1) Округлите число до десятых;
5,92 ≈ ☐;
4,381 ≈ ☐;
0,4894 ≈ ☐;
5,617 ≈ ☐.
2) Округлите число до сотых:
12,605 ≈ ☐;
6,726 ≈ ☐;
0,3246 ≈ ☐;
82,2018 ≈ ☐.
3) Округлите число до целых:
19,26 ≈ ☐;
24,58 ≈ ☐;
2,098 ≈ ☐;
8,37 ≈ ☐.
4) Округлите число до тысячных:
0,6371 ≈ ☐;
3,4093 ≈ ☐;
5,55555 ≈ ☐;
1,47672 ≈ ☐.

Решение 1
5,92 ≈ 5,9;
4,381 ≈ 4,4;
0,4894 ≈ 0,5;
5,617 ≈ 5,6.

Решение 2
12,605 ≈ 12,61;
6,726 ≈ 6,73;
0,3246 ≈ 0,32;
82,2018 ≈ 82,20.

Решение 3
19,26 ≈ 19;
24,58 ≈ 25;
2,098 ≈ 2;
8,37 ≈ 8.

Решение 4
0,6371 ≈ 0,637;
3,4093 ≈ 3,409;
5,55555 ≈ 5,556;
1,47672 ≈ 1,477.

411

Номер №411

Впишите в пустую клетку такую цифру, чтобы запись была верной.
1) 4,☐4 ≈ 4,6;
2) 32,688 ≈ 32,6☐;
3) 84,7☐6 ≈ 84,71;
4) 12,5125 ≈ 12,51☐.

Решение 1
4,64 ≈ 4,6

Решение 2
32,688 ≈ 32,69

Решение 3
84,706 ≈ 84,71

Решение 4
12,5125 ≈ 12,513.

412

Номер №412

1) Округлите число до сотен:
451 ≈ ☐;
609 ≈ ☐;
5780 ≈ ☐;
93837 ≈ ☐.
2) Округлите число до тысяч:
1326 ≈ ☐;
68912 ≈ ☐;
5555 ≈ ☐;
96804 ≈ ☐.
3) Округлите число до наивысшего разряда данного числа:
763 ≈ ☐;
3451 ≈ ☐;
28446 ≈ ☐;
873028 ≈ ☐;
6139800 ≈ ☐;
462650768 ≈ ☐.

Решение 1
451 ≈ 500;
609 ≈ 600;
5780 ≈ 5800;
93837 ≈ 93800.

Решение 2
1326 ≈ 1000;
68912 ≈ 69000;
5555 ≈ 6000;
96804 ≈ 97000.

Решение 3
763 ≈ 800;
3451 ≈ 3000;
28446 ≈ 30000;
873028 ≈ 900000;
6139800 ≈ 6000000;
462650768 ≈ 500000000.

413

Номер №413

Найдите все цифры, которые можно поставить вместо звездочки, чтобы округление было выполнено верно.
1) 3,2* ≈ 3,2;
2) 64,*7 ≈ 65;
3) 0,78*9 = 0,79;
4) 234*,87 ≈ 2340.

Решение 1
3,2* ≈ 3,2
3,20 ≈ 3,2
3,21 ≈ 3,2
3,22 ≈ 3,2
3,23 ≈ 3,2
3,24 ≈ 3,2
Ответ: 0; 1; 2; 3; 4.

Решение 2
64,*7 ≈ 65
64,57 ≈ 65
64,67 ≈ 65
64,77 ≈ 65
64,87 ≈ 65
64,97 ≈ 65
Ответ: 5; 6; 7; 8; 9.

Решение 3
0,78*9 = 0,79
0,7859 = 0,79
0,7869 = 0,79
0,7879 = 0,79
0,7889 = 0,79
0,7899 = 0,79
Ответ: 5; 6; 7; 8; 9.

Решение 4
234*,87 ≈ 2340
2340,87 ≈ 2340
2341,87 ≈ 2340
2342,87 ≈ 2340
2343,87 ≈ 2340
2344,87 ≈ 2340
Ответ: 0; 1; 2; 3; 4.

414

Номер №414

1) Запишите в метрах, предварительное округлив до сотен сантиметров:
359 см ≈ ☐ см ≈ ☐ м;
4254 см ≈ ☐ см = ☐ м;
4392 см ≈ ☐ см = ☐ м;
20046 см ≈ ☐ см = ☐ м.
2) Запишите в сантиметрах, предварительно округлив до десятков миллиметров:
785 мм ≈ ☐ мм = ☐ см;
62 мм ≈ ☐ мм = ☐ см;
67314 мм ≈ ☐ мм = ☐ см;
4936 мм ≈ ☐ мм = ☐ см.
3) Запишите в килограммах, предварительно округлив до тысяч граммов:
6482 г ≈ ☐ г = ☐ кг;
735 г ≈ ☐ г = ☐ кг;
1298 г ≈ ☐ г = ☐ кг;
48538 г ≈ ☐ г = ☐ кг.

Решение 1
359 см ≈ 400 см ≈ 4 м;
4254 см ≈ 4300 см = 43 м;
4392 см ≈ 4400 см = 44 м;
20046 см ≈ 20000 см = 200 м.

Решение 2
785 мм ≈ 790 мм = 79 см;
62 мм ≈ 60 мм = 6 см;
67314 мм ≈ 67310 мм = 6731 см;
4936 мм ≈ 4940 мм = 494 см.

Решение 3
6482 г ≈ 6000 г = 6 кг;
735 г ≈ 1000 г = 1 кг;
1298 г ≈ 1000 г = 1 кг;
48538 г ≈ 49000 г = 49 кг.

415

Номер №415

Некоторое число округлили до сотен и получили 32600. Укажите наименьшее и наибольшее числа, при округлении которых до сотен будет получено данное число.

Решение
32550 ≈ 32600
32649 ≈ 32600
Ответ:
32550 − наименьшее число;
32649 − наибольшее число.

416

Номер №416

Заполните пропуски.
А. Чтобы сложить две десятичные дроби, надо:
1) уравнять в _ количество цифр _
2) записать слагаемые _ так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом _
3) сложить полученные числа так, как складывают _
4) поставить в полученной сумме _ под _ в слагаемых.
Б. Чтобы из одной десятичной дроби вычесть другую, надо:
1) _ и вычитаемом _ после запятой;
2) записать _ под _ так, чтобы каждый разряд _ оказался под соответствующим _
3) произвести вычитание так, как вычитают _;
4) поставить в полученной _ под _ в уменьшаемом и _

Решение
А. Чтобы сложить две десятичные дроби, надо:
1) уравнять в слагаемых количество цифр после запятой.
2) записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого.
3) сложить полученные числа так, как складывают натуральные числа.
4) поставить в полученной сумме запятую под запятыми в слагаемых.
Б. Чтобы из одной десятичной дроби вычесть другую, надо:
1) уравнять в уменьшаемом и вычитаемом количество цифр после запятой;
2) записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого.
3) произвести вычитание так, как вычитают натуральные числа;
4) поставить в полученной разности запятую под запятыми в уменьшаемом и вычитаемом.

417

Номер №417

Выполните действия.
1)
+ 5,8
    6,7
2)
+ 6,4
   2,85
3)
+ 12
    3,9
4)
+ 12,822
    34,51
5)
- 28,44
  18,58
6)
- 17,5
   8,36
7)
- 10
    3,82
8)
- 5,4
  2,573

Решение 1
+ 5,8
   6,7
   12,5

Решение 2
+ 6,40
   2,85
   9,25

Решение 3
+ 12,0
    3,9
    15,9

Решение 4
+ 12,822
    34,510
    47,332

Решение 5
- 28,44
  18,58
    9,86

Решение 6
- 17,50 8,36 9,14

Решение 7
- 10,00 3,82 6,18

Решение 8
- 5,400
  2,573
  2,827

418

Номер №418

Вычислите.
1) 0,8 + 0,2 =
2) 0,88 + 0,02 =
3) 0,888 + 0,002 =
4) 0,8888 + 0,0002 =
5) 0,88 + 0,2 =
6) 0,888 + 0,02 =
7) 0,88 + 0,12 =
8) 0,888 + 0,012 =

Решение 1
0,8 + 0,2 = 1

+ 0,8
   0,2
   1,0

Решение 2
0,88 + 0,02 = 0,9

+ 0,88
   0,02
   0,90

Решение 3
0,888 + 0,002 = 0,89

+ 0,888
   0,002
   0,890

Решение 4
0,8888 + 0,0002 = 0,889

+ 0,8888
   0,0002
   0,8890

Решение 5
0,88 + 0,2 = 1,08

+ 0,88
   0,20
   1,08

Решение 6
0,888 + 0,02 = 0,908

+ 0,888
   0,020
   0,908

Решение 7
0,88 + 0,12 = 1

+ 0,88
   0,12
   1,00

Решение 8
0,888 + 0,012 = 0,9

+ 0,888
   0,012
   0,900

419

Номер №419

В пустые кружки впишите разность числа 1 и указанных чисел.

Решение
1 − 0,1 = 0,9

- 1,0
  0,1
  0,9

1 − 0,06 = 0,94

- 1,00
  0,06
  0,94

1 − 0,32 = 0,68

- 1,00
  0,32
  0,68

1 − 0,16 = 0,84

- 1,00
  0,16
  0,84

1 − 0,01 = 0,99

- 1,00
  0,01
  0,99

1 − 0,001 = 0,999

- 1,000
  0,001
  0,999

1 − 0,035 = 0,965

- 1,000
  0,035
  0,965

1 − 0,4 = 0,6

- 1,0
  0,4
  0,6
Ответ: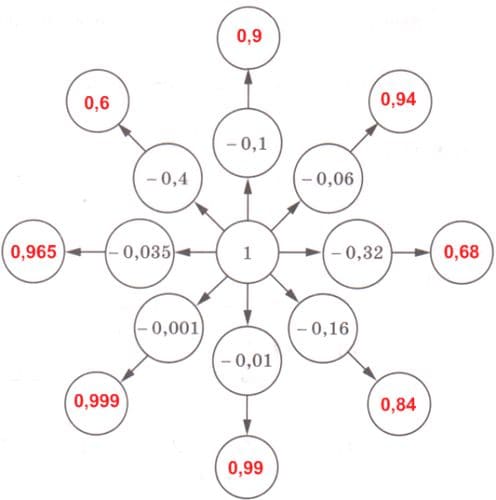

420

Номер №420

Выполните действия.
1) 4,5 + 16,691 =
2) 7,54 + 3,4 =
3) 18,35 + 38,016 =
4) 86,58 + 5,825 =
5) 83,24 + 42,76 =
6) 14,02 − 10,739 =
7) 7,004 − 5,3245 =
8) 12,5 − 8,005 =
9) 262,5 − 41,54 =
10) 16 − 0,568 =

Решение 1
4,5 + 16,691 = 21,191

+ 4,500
   16,691
   21,191

Решение 2
7,54 + 3,4 = 10,94

+ 7,54
   3,40
  10,94

Решение 3
18,35 + 38,016 = 56,366

+ 18,350
    38,016
    56,366

Решение 4
86,58 + 5,825 = 92,405

+ 86,580
     5,825
    92,405

Решение 5
83,24 + 42,76 = 126

+ 83,24
   42,76
  126,00

Решение 6
14,02 − 10,739 = 3,281

- 14,020
  10,739
    3,281

Решение 7
7,004 − 5,3245 = 1,6795

- 7,0040
  5,3245
  1,6795

Решение 8
12,5 − 8,005 = 4,495

- 12,500
    8,005
    4,495

Решение 9
262,5 − 41,54 = 220,96

- 262,50
    41,54
  220,96

Решение 10
16 − 0,568 = 15,432

- 16,000
     0,568
   15,432

421

Номер №421

Решите уравнение:
1) x + 2,34 = 6;
2) 40,18 − x = 6,291;
3) 5,62 + x = 12,2;
4) x − 26,64 = 13,36.

Решение 1
x + 2,34 = 6
x = 6 − 2,34
x = 3,66
Ответ: x = 3,66

Вычисления:
- 6,00
   2,34
   3,66

Решение 2
40,18 − x = 6,291
x = 40,18 − 6,291
x = 33,889
Ответ: x = 33,889

Вычисления:

- 40,180
    6,291
  33,889

Решение 3
5,62 + x = 12,2
x = 12,2 − 5,62
x = 6,58
Ответ: x = 6,58

Вычисления:

- 12,20
    5,62
    6,58

Решение 4
x − 26,64 = 13,36
x = 13,36 + 26,64
x = 40
Ответ: 40

Вычисления:

- 13,36
  26,64
  40,00

422

Номер №422

Заполните таблицу.

Слагаемое 1,3 0,6 0,12 4,35
Слагаемое 7 2,5 1,8 8,1
Сумма 8 6,55 19 20

Решение
1 столбец:
1,3 + 7 = 8,3

+ 1,3
    7,0
    8,3

2 столбец:
8 − 0,6 = 7,4

- 8,0
  0,6
  7,4

3 столбец:
6,55 − 2,5 = 4,05

- 6,55
   2,5
  4,05

4 столбец:
0,12 + 1,8 = 1,92

+ 0,12
    1,80
    1,92

5 столбец:
19 − 8,1 = 10,9

- 19,0
    8,1
  10,9

6 столбец:
20 − 4,35 = 15,65

- 20,00
    4,35
  15,65
Ответ:

Слагаемое	1,3	0,6	4,05	0,12	10,9	4,35
Слагаемое	7	7,4	2,5	1,8	8,1	15,65
Сумма	8,3	8	6,55	1,92	19	20

 

423

Номер №423

Заполните таблицу.

Уменьшаемое 4,5 10 5,35 1,226
Вычитаемое 0,15 1,23 7,2
Разность 3,47 1,3 0,126

Решение
1 столбец:
4,5 − 0,15 = 4,35

-  4,50
   0,15
   4,35

2 столбец:
3,47 + 1,23 = 4,7

+ 3,47
   1,23
   4,70

3 столбец:
10 − 7,2 = 2,8

- 10,0
    7,2
    2,8

4 столбец:
5,35 − 1,3 = 4,05

- 5,35
   1,30
   4,05

5 столбец:
1,226 − 0,126 = 1,1

- 1,226
  0,126
  1,100
Ответ:

Уменьшаемое	4,5	4,7	10	5,35	1,226
Вычитаемое	0,15	1,23	7,2	4,05	1,1
Разность	4,35	3,47	2,8	1,3	0,126

 

424

Номер №424

Заполните таблицу.

Собственная скорость катера Скорость течения реки Скорость катера по течению Скорость катера против течения
12 км/ч 1,5 км/ч
20 км/ч 22 км/ч
24 км/ч 20 км/ч
0,8 км/ч 18 км/ч
2,5 км/ч 16 км/ч

Решение
1 строка:
12 + 1,5 = 13,5 км/ч − скорость катера по течению;

+ 12,0
     1,5
    13,5

12 − 1,5 = 10,5 км/ч − скорость катера против течения.

- 12,0
    1,5
   10,5

2 строка:
22 − 20 = 2 (км/ч) − скорость течения реки;
20 − 2 = 18 (км/ч) − скорость катера против течения.

3 строка:
24 − 20 = 4 (км/ч) − скорость течения реки;
24 + 4 = 28 (км/ч) − скорость катера по течению.

4 строка:
18 − 0,8 = 17,2 (км/ч) − собственная скорость катера;

- 18,0
   0,8
  17,2

17,2 − 0,8 = 16,4 (км/ч) − скорость катера против течения.

- 17,2
    0,8
   16,4

5 строка:
16 + 2,5 = 18,5 (км/ч) − собственная скорость катера;

+ 16,0
     2,5
    18,5

18,5 + 2,5 = 21 (км/ч) − скорость катера по течению реки.

+ 18,5
     2,5
   21,0
Ответ:

Собственная скорость катера	Скорость течения реки	Скорость катера по течению	Скорость катера против течения
12 км/ч	1,5 км/ч	13,5 км/ч	10,5 км/ч
12 км/ч	1,5 км/ч	13,5 км/ч	10,5 км/ч
20 км/ч	2 км/ч	22 км/ч	18 км/ч
24 км/ч	4 км/ч	28 км/ч	20 км/ч
17,2 км/ч	0,8 км/ч	18 км/ч	16,4 км/ч
18,5 км/ч	2,5 км/ч	21 км/ч	16 км/ч

 

425

Номер №425

Заполните цепочку вычислений.

Решение
2 ячейка:
0,84 + 0,22 = 1,06

+ 0,84
   0,22
   1,06

3 ячейка:
6,4 − 4 = 2,4

-  6,4
   4,0
   2,4

2 стрелка:
2,4 − 1,06 = 1,34

- 2,40
  1,06
  1,34

 

5 ячейка:
6,2 − 1,2 = 5

- 6,2
  1,2
  5,0

4 ячейка:
5 + 1,4 = 6,4

+ 5,0
   1,4
   6,4

Ответ:

426

Номер №426

В первый день туристы прошли 5,4 км, что на 1,7 км больше, чем во второй день, и на 2,1 км меньше, чем в третий. Сколько километров прошли туристы за три дня?

Решение
1) 5,4 − 1,7 = 3,7 (км) − прошли туристы во второй день;
2) 5,4 + 2,1 = 7,5 (км) − прошли туристы в третий день;
3) 5,4 + 3,7 + 7,5 = 9,1 + 7,5 = 16,6 (км) − прошли туристы за три дня.
Ответ: 16,6 км

Вычисления:
1)
- 5,4
  1,7
  3,7
2)
+ 5,4
   2,1
   7,5
3)
+ 5,4
   3,7
   9,1

+ 9,1
    7,5
  16,6

427

Номер №427

Запишите последовательность из шести чисел, если:
1) первое число равно 2,4, а в каждое следующее на 0,4 больше предыдущего: 2,4; 2,8; _
2) первое число равно 6, а каждое следующее на 0,2 меньше предыдущего: _

Решение 1
1) 2,4 + 0,4 = 2,8 − второе число;
2) 2,8 + 0,4 = 3,2 − третье число;
3) 3,2 + 0,4 = 3,6 − четвертое число;
4) 3,6 + 0,4 = 4 − пятое число;
5) 4 + 0,4 = 4,4 − шестое число.
Ответ: 2,4; 2,8; 3,2; 3,6; 4; 4,4.

Вычисления:
1)
+ 2,4
   0,4
   2,8
2)
+ 2,8
   0,4
   3,2
3)
+ 3,2
   0,4
   3,6
4)
+ 3,6
   0,4
   4,0
5)
+ 4,0
   0,4
   4,4

Решение 2
1) 6 − 0,2 = 5,8 − второе число;
2) 5,8 − 0,2 = 5,6 − третье число;
3) 5,6 − 0,2 = 5,4 − четвертое число;
4) 5,4 − 0,2 = 5,2 − пятое число;
5) 5,2 − 0,2 = 5,0 − шестое число.
Ответ: 6; 5,8; 5,6; 5,4; 5,2; 5.

Вычисления:
1)
- 6,0
  0,2
  5,8
2)
- 5,8
  0,2
  5,6
3)
- 5,6
  0,2
  5,4
4)
- 5,4
  0,2
  5,2
5)
- 5,2
  0,2
  5,0

428

Номер №428

Запишите три следующих числа последовательности:
1) 0; 0,7; 1,4; _
2) 12; 10,5; 9; _

Решение 1
0,7 − 0 = 0,7
1,4 − 0,7 = 0,7, значит в последовательности каждое последующее число на 0,7 больше предыдущего, тогда:
1,4 + 0,7 = 2,1 − четвертое число;
2,1 + 0,7 = 2,8 − пятое число;
2,8 + 0,7 = 3,5 − шестое число.
Ответ: 0; 0,7; 1,4; 2,1; 2,8; 3,5.

Вычисления:
- 1,4
  0,7
  0,7

+ 1,4
   0,7
   2,1

+ 2,1
   0,7
   2,8

+ 2,8
   0,7
   3,5

Решение 2
12 − 10,5 = 1,5
10,5 − 9 = 1,5, значит в последовательности каждое последующее число на 1,5 меньше предыдущего, тогда:
9 − 1,5 = 7,5 − четвертое число;
7,5 − 1,5 = 6 − пятое число;
6 − 1,5 = 4,5 − шестое число.
Ответ: 12; 10,5; 9; 7,5; 6; 4,5.

Вычисления:
- 12,0
    1,5
  10,5

- 10,5
    1,5
    9,0

- 9,0
   1,5
   7,5

- 7,5
  1,5
  6,0

- 6,0
  1,5
  4,5

429

Номер №429

Решите уравнение.
1) (2,34 + x) − 8,5 = 4,73;
2) (x − 20,8) + 12,17 = 22,2;
3) (64,2 − a) − 1,28 = 3,242;
4) 5,05 − (y − 0,76) = 2,075.

Решение 1
(2,34 + x) − 8,5 = 4,73
2,34 + x = 4,73 + 8,5
2,34 + x = 13,23
x = 13,23 − 2,34
x = 10,89
Ответ: x = 10,89

Вычисления:
+ 4,73
   8,50
  13,23

- 13,23
    2,34
  10,89

Решение 2
(x − 20,8) + 12,17 = 22,2
x − 20,8 = 22,2 − 12,17
x − 20,8 = 10,03
x = 10,03 + 20,8
x = 30,83
Ответ: x = 30,83

Вычисления:
- 22,20
  12,17
  10,03

+ 10,03
   20,80
   30,83

Решение 3
(64,2 − a) − 1,28 = 3,242
64,2 − a = 3,242 + 1,28
64,2 − a = 4,522
a = 64,2 − 4,522
a = 59,678
Ответ: a = 59,678

Вычисления:
+ 3,242
   1,280
   4,522

- 64,200
    4,522
  59,678

Решение 4
5,05 − (y − 0,76) = 2,075
y − 0,76 = 5,05 − 2,075
y − 0,76 = 2,975
y = 2,975 + 0,76
y = 3,735
Ответ: y = 3,735

Вычисления:
- 5,050
  2,075
  2,975

+ 2,975
   0,760
   3,735

430

Номер №430

Выполните сложение, выбирая удобный порядок вычислений.
1) (3,25 + 0,419) + 6,75 =
2) (7,26 + 26,8) + 73,2 =
3) 4,56 + 0,333 + 0,44 + 0,067 =
4) 0,631 + 0,308 + 1,369 + 0,692 =

Решение 1
(3,25 + 0,419) + 6,75 = (3,25 + 6,75) + 0,419 = 10 + 0,419 = 10,419

Решение 2
(7,26 + 26,8) + 73,2 = 7,26 + (26,8 + 73,2) = 7,26 + 100 = 107,26

Решение 3
4,56 + 0,333 + 0,44 + 0,067 = (4,56 + 0,44) + (0,333 + 0,067) = 5 + 0,4 = 5,4

Решение 4
0,631 + 0,308 + 1,369 + 0,692 = (0,631 + 1,369) + (0,308 + 0,692) = 2 + 1 = 3

431

Номер №431

Впишите в пустые клетки цифры так, чтобы сложение (вычитание) было выполнено верно.
1)
+ 2,☐6☐
  ☐,3☐
     4,025
2)
+ ☐☐,7☐
        0,☐2☐
    20,103
3)
- ☐3,☐3☐
    6,8☐
   2☐,294

Решение 1
Уравняем количество цифр после запятой:
+ 2,☐6☐
   ☐,3☐0
   4,025

Найдем количество тысячных в первом слагаемом:
5 − 0 = 5
получим:
+ 2,☐65
  ☐,3☐0
   4,025

Найдем количество сотых во втором слагаемом:
12 − 6 = 6
получим:
+ 2,☐65
  ☐,360
   4,025

Найдем количество десятых в первом слагаемом:
10 − 3 = 7, но так как количество сотых в сумме получилось 12, значит вычтем еще одну десятую:
7 − 1 = 6
получим:
+ 2,665
  ☐,360
   4,025

Найдем количество единиц во втором слагаемом:
4 − 2 = 2, , но так как количество десятых в сумме получилось 10, значит вычтем еще одну единицу:
2 − 1 = 1
получим:
+ 2,665
   1,360
   4,025

Ответ:
+ 2,665
   1,36
   4,025

Решение 2
Уравняем количество цифр после запятой:
+ ☐☐,7☐0
       0,☐2☐
     20,103
Найдем количество тысячных во втором слагаемом:
3 − 0 = 3

получим:
+ ☐☐,7☐0
       0,☐23
     20,103
Найдем количество сотых в первом слагаемом:
10 − 2 = 8

получим:
+ ☐☐,780
       0,☐23
     20,103

Найдем количество десятых во втором слагаемом:
11 − 7 = 4, но так как количество сотых в сумме получилось 10, значит вычтем еще одну десятую:
4 − 1 = 3
получим:
+ ☐☐,780
       0,323
     20,103
Найдем количество единиц в первом слагаемом:
10 − 0 = 10, но так как количество десятых в сумме получилось 11, то вычтем еще одну единицу:
10 − 1 = 9
получим:
+ ☐9,780
     0,323
   20,103

Найдем количество десятков в первом слагаемом:
2 − 0 = 2, но так количество единиц в сумме получилось 10, значит вычтем еще один десяток:
2 − 1 = 1

получим:
+ 19,780
     0,323
   20,103

Ответ:
+ 19,78
    0,323
   20,103

Решение 3
Уравняем количество цифр после запятой:
- ☐3,☐3☐
    6,8☐0
 2☐,294

Найдем количество тысячных в уменьшаемом:
4 + 0 = 4
получим:
- ☐3,☐34
    6,8☐0
  2☐,294

Найдем количество сотых в вычитаемом:
13 − 9 = 4
получим:

- ☐3,☐34
    6,840
 2☐,294

Найдем количество десятых в уменьшаемом:
2 + 8 = 10, но так как мы занимали одну десятую для вычитания сотых, то прибавим еще одну десятую:
10 + 1 = 11
получим:
- ☐3,134
    6,840
  2☐,294

Найдем количество единиц в разности:
13 − 6 = 7, но так как мы занимали одну единицу для вычитания десятых, то вычтем еще одну единицу:
7 − 1 = 6
получим:

- ☐3,134
     6,840
   26,294
Найдем количество десятков в уменьшаемом:
2 + 0 = 2, но так как мы занимали одни десяток для вычитания единиц, то прибавим еще один десяток:
2 + 1 = 3
получим:
- 33,134
    6,840
  26,294
Ответ:
- 33,134
   6,84
 26,294

432

Номер №432

Заполните пропуски.
1) Если одно из слагаемых увеличить на 1,6, а другое − на 2,8, то сумма _
2) Если одно из слагаемых увеличить на 8,4, а другое уменьшить на 7,25, то сумма _
3) Если одно из слагаемых увеличить на 0,32, а другое уменьшить на 0,48, то сумма _
4) Если вычитаемое уменьшить на 19,378, то разность _
5) Если уменьшаемое уменьшить на 284,15, то разность _
6) Если уменьшаемое увеличить на 0,8, а вычитаемое − на 0,5, то разность _
7) Если уменьшаемое уменьшить на 1,9, а вычитаемое − на 0,4, то разность _
8) Если уменьшаемое увеличить на 6,4, а вычитаемое уменьшить на 2,6, то разность _
9) Если уменьшаемое уменьшить на 5,2, а вычитаемое увеличить на 6,1, то разность _
10) Если уменьшаемое увеличить на 9,8, а вычитаемое − на 9,8, то разность _

Решение 1
+ 1,6
   2,8
   4,4
Если одно из слагаемых увеличить на 1,6, а другое − на 2,8, то сумма увеличится на 4,4.

Решение 2
- 8,40
  7,25
  1,15
Если одно из слагаемых увеличить на 8,4, а другое уменьшить на 7,25, то сумма увеличится на 1,15.

Решение 3
- 0,48
  0,32
  0,16
Если одно из слагаемых увеличить на 0,32, а другое уменьшить на 0,48, то сумма уменьшится на 0,16.

Решение 4
Если вычитаемое уменьшить на 19,378, то разность увеличится на 19,378.

Решение 5
Если уменьшаемое уменьшить на 284,15, то разность уменьшится на 284,15.

Решение 6
- 0,8
  0,5
  0,3
Если уменьшаемое увеличить на 0,8, а вычитаемое − на 0,5, то разность увеличится на 0,3.

Решение 7
- 1,9
  0,4
  1,5
Если уменьшаемое уменьшить на 1,9, а вычитаемое − на 0,4, то разность уменьшится на 1,5.

Решение 8
+ 6,4
   2,6
   9,0
Если уменьшаемое увеличить на 6,4, а вычитаемое уменьшить на 2,6, то разность увеличится на 9.

Решение 9
+ 5,2
   6,1
  11,3
Если уменьшаемое уменьшить на 5,2, а вычитаемое увеличить на 6,1, то разность уменьшится на 11,3.

Решение 10
- 9,8
  9,8
  0,0
Если уменьшаемое увеличить на 9,8, а вычитаемое − на 9,8, то разность не изменится.

433

Номер №433

Вычислите, записав данные величины в дециметрах.
1) 6,29 дм − 14 см = 6,29 дм − 1,4 дм =
2) 3,2 дм + 8 см =
3) 28 дм − 146 см =
4) 4 м 6 дм 5 см − 27 см 4 мм =

Решение 1
6,29 дм − 14 см = 6,29 дм − 1,4 дм = 4,89

- 6,29
  1,40
  4,89

Решение 2
3,2 дм + 8 см = 3,2 дм + 0,8 дм = 4 дм

+ 3,2
   0,8
   4,0

Решение 3
28 дм − 146 см = 28 дм − 14,6 дм = 13,4 дм

- 28,0
  14,6
  13,4

Решение 4
4 м 6 дм 5 см − 27 см 4 мм = 46,5 дм − 2,74 дм = 43,76 дм

- 46,50
   2,74
  43,76

434

Номер №434

Вычислите, записав данные величины в центнерах.
1) 4 ц − 318 кг =
2) 28 ц 7 кг + 63 кг =
3) 3,48 т + 572 кг =
4) 3 т 2 ц 1 кг − 1 т 10 кг =

Решение 1
4 ц − 318 кг = 4 ц − 3,18 ц = 0,82 ц

- 4,00
  3,18
  0,82

Решение 2
28 ц 7 кг + 63 кг = 28,07 ц + 0,63 ц = 28,7 ц

+ 28,07
     0,63
    28,7

Решение 3
3,48 т + 572 кг = 34,8 ц + 5,72 ц = 40,52 ц

+ 34,80
     5,72
   40,52

Решение 4
3 т 2 ц 1 кг − 1 т 10 кг = 32,01 ц − 10,1 ц = 21,91 ц

- 32,01
  10,1
  21,91

435

Номер №435

Найдите значение выражения, выбирая удобный порядок вычислений.
1) (3,79 + 5,18) − 2,18 = (5,18 − 2,18) + =
2) (76,4 + 9,724) − 19,4 =
3) 0,957 − (0,357 + 0,064) = ( − ) − =
4) 12,92 − (4,898 + 3,92) =

Решение 1
(3,79 + 5,18) − 2,18 = (5,18 − 2,18) + 3,79 = 3 + 3,79 = 6,79

Решение 2
(76,4 + 9,724) − 19,4 = (76,4 − 19,4) + 9,724 = 57 + 9,724 = 66,724

Решение 3
0,957 − (0,357 + 0,064) = (0,957 − 0,357) − 0,064 = 0,6 − 0,064 = 0,536

Решение 4
12,92 − (4,898 + 3,92) = (12,92 − 3,92) − 4,898 = 9 − 4,898 = 4,102

436

Номер №436

Заполните пропуски.
А. Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби _ соответственно на _ и т.д. цифры.
Б. Если запятую перенести влево на 1, 2, 3 и т.д. цифры, то дробь _ соответственно _ и т.д. раз.
В. Чтобы перемножить две десятичные дроби, надо:
1) умножить их как _, не обращая внимания на _
2) в полученном произведении _ столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Г. Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т.д., надо в этой дроби _ соответственно _ и т.д. цифры.

Решение
А. Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби перенести запятую вправо соответственно на 1, 2, 3 и т.д. цифры.
Б. Если запятую перенести влево на 1, 2, 3 и т.д. цифры, то дробь уменьшится соответственно в 10, 100, 1000 и т.д. раз.
В. Чтобы перемножить две десятичные дроби, надо:
1) умножить их как натуральные числа, не обращая внимания на запятые;
2) в полученном произведении оделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Г. Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т.д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т.д. цифры.

437

Номер №437

Найдите произведение.
1) 3,74 * 10 = ☐
2) 3,74 * 100 = ☐
3) 3,74 * 1000 = ☐
4) 3,74 * 10000 = ☐
5) 3,74 * 0,1 = ☐
6) 3,74 * 0,001 = ☐

Решение 1
3,74 * 10 = 37,4

Решение 2
3,74 * 100 = 374

Решение 3
3,74 * 1000 = 3740

Решение 4
3,74 * 10000 = 37400

Решение 5
3,74 * 0,1 = 0,374

Решение 6
3,74 * 0,001 = 0,00374

438

Номер №438

В пустые кружки впишите произведение числа 100 и указанных чисел.

Решение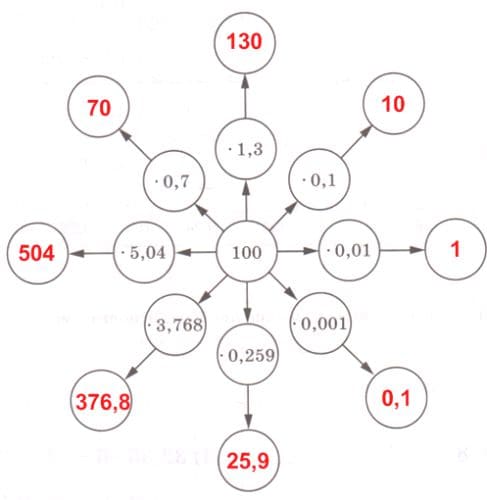

439

Номер №439

Выполните умножение.
1) 6,9 * 10 = ☐
2) 23,864 * 10 = ☐
3) 0,04 * 100 = ☐
4) 5,7 * 1000 = ☐
5) 0,19 * 10000 = ☐
6) 2,4 * 0,1 = ☐
7) 98 * 0,1 = ☐
8) 3,3 * 0,01 = ☐
9) 129,4 * 0,01 = ☐
10) 76,5 * 0,0001 = ☐

Решение 1
6,9 * 10 = 69

Решение 2
23,864 * 10 = 238,64

Решение 3
0,04 * 100 = 4

Решение 4
5,7 * 1000 = 5700

Решение 5
0,19 * 10000 = 1900

Решение 6
2,4 * 0,1 = 0,24

Решение 7
98 * 0,1 = 9,8

Решение 8
3,3 * 0,01 = 0,033

Решение 9
129,4 * 0,01 = 1,294

Решение 10
76,5 * 0,0001 = 0,00765

440

Номер №440

Впишите в прямоугольники числа так, чтобы получились верные равенства.
1) 0,29 * ☐ = 2,9
2) 3,8 * ☐ = 0,38
3) 240 * ☐ = 0,24
4) 532,6 * ☐ = 532600
5) 4000 * ☐ = 4
6) 0,05 * ☐ = 500

Решение 1
0,29 * 10 = 2,9

Решение 2
3,8 * 0,1 = 0,38

Решение 3
240 * 0,001 = 0,24

Решение 4
532,6 * 1000 = 532600

Решение 5
4000 * 0,001 = 4

Решение 6
0,05 * 10000 = 500

441

Номер №441

Известно, что 234 * 56 = 13104. Поставьте в правой части равенства запятую чтобы умножение было выполнено верно.
1) 2,34 * 56 = 131,04
2) 23,4 * 5,6 = 13104
3) 23,4 * 0,56 = 13104
4) 2,34 * 5,6 = 13104
5) 0,234 * 5,6 = 13104
6) 0,234 * 0,56 = 13104

Решение 1
2,34 * 56 = 131,04

Решение 2
23,4 * 5,6 = 131,04

Решение 3
23,4 * 0,56 = 13,104

Решение 4
2,34 * 5,6 = 13,104

Решение 6
0,234 * 5,6 = 1,3104

Решение 7
0,234 * 0,56 = 0,13104

442

Номер №442

Расшифруйте слово.

А 0,2 * 3 =
П 0,4 * 0,6 =
И 1,6 * 2 =
Р 4,2 * 0,3 =
Т 0,07 * 0,8 =
С 0,009 * 0,05 =
Н 2,5 * 4 =
О 0,5 * 0,6 =

0,056	1,26	0,6	10	0,00045	0,24	0,3	1,26	0,056	3,2	1,26

Расшифрованное слово − название прибора, используемого _

Решение
А 0,2 * 3 = 0,6
П 0,4 * 0,6 = 0,24
И 1,6 * 2 = 3,2
Р 4,2 * 0,3 = 1,26
Т 0,07 * 0,8 = 0,056
С 0,009 * 0,05 = 0,00045
Н 2,5 * 4 = 10
О 0,5 * 0,6 = 0,3

0,056	1,26	0,6	10	0,00045	0,24	0,3	1,26	0,056	3,2	1,26
Т	Р	А	Н	С	П	О	Р	Т	И	Р

Расшифрованное слово − название прибора, используемого при измерении углов.

443

Номер №443

Выполните умножение.
1) 4,2 * 3,8 =
× 4,2
   3,8

2) 8,5 * 2,4 =

× 8,5
   2,4
3) 0,96 * 1,6 =

× 0,96
    1,6

4) 32,35 * 6 =
× 32,35
     6
5) 2,64 * 0,18 =

× 2,64
   0,18

6) 0,375 * 1,24 =

× 0,375
    1,24

Решение 1
4,2 * 3,8 = 15,96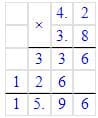

Решение 2
8,5 * 2,4 = 20,4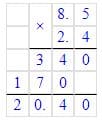

Решение 3
0,96 * 1,6 = 1,536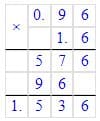

Решение 4
32,35 * 6 = 194,1

Решение 5
2,64 * 0,18 = 0,4752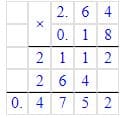

Решение 6
0,375 * 1,24 = 0,465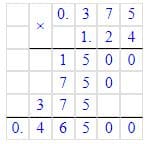

444

Номер №444

Вычислите.
1) 0 , 2 2 = ☐
2) 0 , 3 3 = ☐
3) 1 , 2 2 = ☐

Решение 1
0 , 2 2 = 0 , 04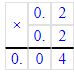

Решение 2
0 , 3 3 = 0 , 027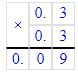

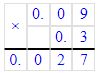
Решение 3
1 , 2 2 = 1 , 44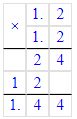

445

Номер №445

Найдите значение выражения.
1) (8,76 + 3,64) * (9,6 − 5,82) =
2) 0,25 * (12,8 * 1,5 − 7,98) =

Решение 1
(8,76 + 3,64) * (9,6 − 5,82) = 12,4 * 3,78 = 46,872
1)

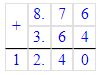
2)

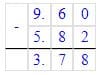
3)

Решение 2
0,25 * (12,8 * 1,5 − 7,98) = 0,25 * (19,2 − 7,98) = 0,25 * 11,22 = 2,805
1)

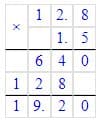
2)

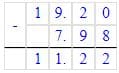
3)

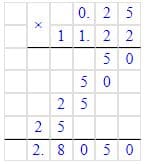
446

Номер №446

Автомобиль преодолевает расстояние между двумя городами со скоростью 62,5 км/ч за 3,6 ч. Какое расстояние между этими городами?

Решение
62,5 * 3,6 = 225 (км) − расстояние между городами.
Ответ: 225 км

Вычисления: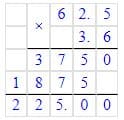

447

Номер №447

Вычислите значение выражения, выбирая удобный порядок вычислений.
1) 0,4 * 29 * 2,5 = (0,4 * 2,5) * 29 =
2) 0,2 * 43,9 * 0,5 =
3) 0,04 * 18,7 * 50 =
4) 12,5 * 7,29 * 0,08 =

Решение 1
0,4 * 29 * 2,5 = (0,4 * 2,5) * 29 = 1 * 29 = 29

Решение 2
0,2 * 43,9 * 0,5 = (0,2 * 0,5) * 43,9 = 0,1 * 43,9 = 4,39

Решение 3
0,04 * 18,7 * 50 = (0,04 * 50) * 18,7 = 2 * 18,7 = 37,4

Решение 4
12,5 * 7,29 * 0,08 = (12,5 * 0,08) * 7,29 = 1 * 7,29 = 7,29

448

Номер №448

Упростите выражение.
1) 0,2a * 0,3 = ☐
2) 0,7 * 0,06m = ☐
3) 0,4a * 9b = ☐
4) 0,5x * 0,3y * 4z = ☐

Решение 1
0,2a * 0,3 = (0,2 * 0,3)a = 0,06a

Решение 2
0,7 * 0,06m = (0,7 * 0,06)m = 0,042m

Решение 3
0,4a * 9b = (0,4 * 9)ab = 3,6ab

Решение 4
0,5x * 0,3y * 4z = (0,5 * 0,3 * 4)xyz = (0,3 * 2)xyz = 0,6xyz

449

Номер №449

Проверьте, верно ли выполнено упрощение выражения. Если задание выполнено неверно, приведите справа верное решение.
1) 0,3a + 1,2a = 1,5a
2) 0,15b + 0,9b = 0,24b
3) 3x − 0,3x = 0,27x
4) m − 0,16m = 0,74m
5) 0,2a + 0,7a + 0,9a = 0,18a
6) 9,7c − 1,3c + 2,6 = 11c

Решение 1
0,3a + 1,2a = (0,3 + 1,2)a = 1,5a
Ответ: верно

Вычисления:
+ 0,3
   1,2
   1,5

Решение 2
0,15b + 0,9b = (0,15 + 0,9)b = 1,05b
Ответ: неверно

Вычисления:

+ 0,15
   0,90
   1,05

Решение 3
3x − 0,3x = (3 − 0,3)x = 2,7x
Ответ: неверно

Вычисления:
- 3,0
  0,3
  2,7

Решение 4
m − 0,16m = (1 − 0,16)m = 0,84m
Ответ: неверно

Вычисления:
- 1,00
  0,16
  0,84

Решение 5
0,2a + 0,7a + 0,9a = (0,2 + 0,7 + 0,9)a = 1,8a
Ответ: неверно

Вычисления:
  0,2
+0,7
  0,9
  1,8

Решение 6
9,7c − 1,3c + 2,6 = (9,7 − 1,3)c + 2,6 = 8,4c + 2,6
Ответ: неверно

Вычисления:

- 9,7
  1,3
  8,4

450

Номер №450

Вычислите значение выражения, используя распределительное свойство умножения.
1) 4,28 * 7,4 + 4,28 * 2,6 = 4,28 * ( + ) =
2) 71,6 * 38,4 − 71,5 * 38,4 =
3) 9,18 * 123,5 − 9,18 * 122,5 =
4) 5,6 * 0,68 + 5,6 * 0,19 − 5,6 * 0,85 =

Решение 1
4,28 * 7,4 + 4,28 * 2,6 = 4,28 * (7,4 + 2,6) = 4,28 * 10 = 42,8

Решение 2
71,6 * 38,4 − 71,5 * 38,4 = 38,4 * (71,6 − 71,5) = 38,4 * 0,1 = 3,84

Решение 3
9,18 * 123,5 − 9,18 * 122,5 = 9,18 * (123,5 − 122,5) = 9,18 * 1 = 9,18

Решение 4
5,6 * 0,68 + 5,6 * 0,19 − 5,6 * 0,85 = 5,6 * (0,68 + 0,19 − 0,85) = 5,6 * (0,87 − 0,85) = 5,6 * 0,02 = 0,112

451

Номер №451

Упростите выражения и найдите его значение.
1) 0,5a * 20b, если a = 3, b = 5,4;
0,5a * 20b = (0,5 * 20)ab =
2) 0,25m * 0,4n, если m = 1,6, n = 0,5;
3) 6x * 0,5y, если x = 0,33, y = 1000;
4) 0,8c * 12,5d, если c = 0,42, d = 0,1.

Решение 1
0,5a * 20b = (0,5 * 20)ab = 10ab
если a = 3, b = 5,4, то:
10 * 3 * 5,4 = (10 * 5,4) * 3 = 54 * 3 = 162

Решение 2
0,25m * 0,4n = (0,25 * 0,4)mn = 0,1mn
если m = 1,6, n = 0,5, то:
0,1 * 1,6 * 0,5 = 0,16 * 0,5 = 0,08

Решение 3
6x * 0,5y = (6 * 0,5)xy = 3xy
если x = 0,33, y = 1000, то:
3 * 0,33 * 1000 = 3 * 330 = 990

Решение 4
0,8c * 12,5d = (0,8 * 12,5)cd = 10cd
если c = 0,42, d = 0,1, то:
10 * 0,42 * 0,1 = 4,2 * 0,1 = 0,42

452

Номер №452

Выполните вычисления по схеме и запишите выражение,

1) (7 − 1,8) * 0,4 =

Решение 1
1) 7 − 1,8 = 5,2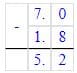

2) 5,2 * 0,4 = 2,08

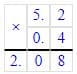
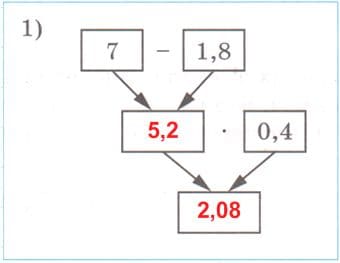
(7 − 1,8) * 0,4 = 5,2 * 0,4 = 2,08

Решение 2
1) 0,3 * 0,6 = 0,18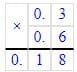

2) 2 − 0,18 = 1,82

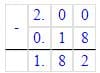
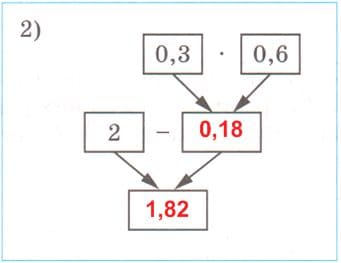
2 − (0,3 * 0,6) = 2 − 0,18 = 1,82

Решение 3
1) 4,25 + 1,55 = 5,8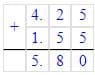

2) 9,8 − 4,8 = 5

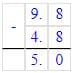
3) 5,8 * 5 = 29

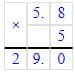
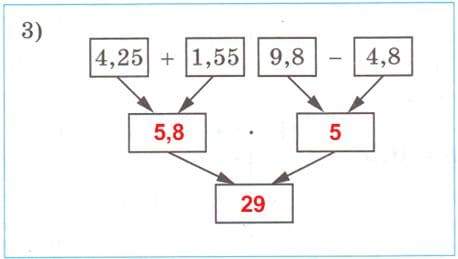
(4,25 + 1,55) * (9,8 − 4,8) = 5,8 * 5 = 29

453

Номер №453

Из одного порта в другой одновременно вышли теплоход и катер. Скорость теплохода равна 28,8 км/ч, а скорость катера − 32,3 км/ч. Какое расстояние будет между ними через 3,8 ч после начала движения?

Решение
1) 32,3 − 28,8 = 3,5 (км/ч) − скорость удаления катера от теплохода;
2) 3,5 * 3,8 = 13,3 (км) − будет между катером и теплоходом через 3,8 ч после начала движения.
Ответ: 13,3 км

Вычисления:
1)

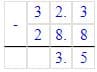
2)

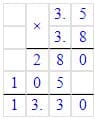
454

Номер №454

Из одного города в противоположных направлениях выехали одновременно два автомобиля. Скорость одного из них равна 83,5 км/ч, что на 7,8 км/ч больше скорости другого. Какое расстояние будет между ними через 4,5 ч после начала движения?

Решение
1) 83,5 − 7,8 = 75,7 (км/ч) − скорость второго автомобиля;
2) 83,5 + 75,7 = 159,2 (км/ч) − скорость удаления автомобилей;
3) 159,2 * 4,5 = 716,4 (км) − будет между автомобилями через 4,5 ч.
Ответ: 716,4 км

Вычисления:
1)

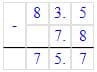
2)

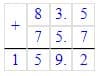
3)

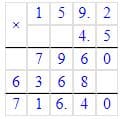
455

Номер №455

Из двух сел одновременно навстречу друг другу отправились велосипедист и пешеход. Пешеход двигался со скоростью 3,2 км/ч, что в 3,5 раза меньше, чем скорость велосипедиста. Найдите расстояние между селами, если велосипедист и пешеход встретились через 1,5 ч после начала движения.

Решение
1) 3,2 * 3,5 = 11,2 (км/ч) − скорость велосипедиста;
2) 3,2 + 11,2 = 14,4 (км/ч) − скорость сближения пешехода и велосипедиста;
3) 14,4 * 1,5 = 21,6 (км) − расстояние между селами.
Ответ: 21,6 км

Вычисления:
1)

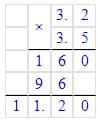
2)

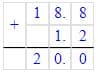
3)

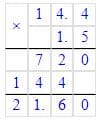
456

Номер №456

Лодка плыла 1,6 ч по течению реки и 2,4 ч против течения. Какой путь преодолела лодка за все время движения, если скорость течения равна 1,2 км/ч, а собственная скорость лодки составляет 18,8 км/ч?

Решение
1) 18,8 + 1,2 = 20 (км/ч) − скорость лодки по течению;
2) 18,8 − 1,2 = 17,6 (км/ч) − скорость лодки против течения;
3) 20 * 1,6 = 32 (км) − проплыла лодка по течению;
4) 17,6 * 2,4 = 42,24 (км) − проплыла лодка против течения;
5) 32 + 42,24 = 74,24 (км) − преодолела лодка за все время движения.
Ответ: 74,24 км

Вычисления:
1)

2)

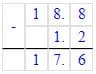
3)

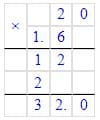
4)

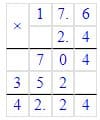
5)

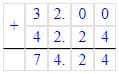
457

Номер №457

На какое число надо умножить 0,23, чтобы получить:
1) 23;
2) 23000;
3) 0,023;
4) 0,000023?

Решение 1
0,23 * 100 = 23
Ответ: на 100

Решение 2
0,23 * 100000 = 23000
Ответ: на 100000

Решение 3
0,23 * 0,1 = 0,000023
Ответ: на 0,1

Решение 4
0,23 * 0,0001 = 0,023
Ответ: на 0,0001

458

Номер №458

Куб и прямоугольный параллелепипед с измерениями 1,2 дм, 0,6 дм и 0,3 дм имеют равные объемы. Найдите длину ребра куба.

Решение
V = abc = 1,2 * 0,6 * 0,3 = 0,72 * 0,3 = 0,216 ( д м 3 ) − объем прямоугольного параллелепипеда;
V = a 3 − объем квадрата, тогда:
0 , 216 = a 3
0 , 6 3 = a 3
a = 0,6 (дм) − длина ребра куба.
Ответ: 0,6 дм

Вычисления: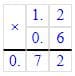

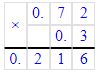
459

Номер №459

Заполните пропуски.
1) Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби _ соответственно на _ и т.д. цифры.
2) Если делимое и делитель увеличить одновременно в 10, 100, 1000 и т.д. раз, то частное _
3) Чтобы разделить десятичную дробь на десятичную, надо:
а) перенести в _ и в _ на столько цифр, сколько их содержится _;
б) выполнить деление на _
4) Если делимое меньше делителя, то целая часть частного равна _

Решение
1) Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т.д. цифры.
2) Если делимое и делитель увеличить одновременно в 10, 100, 1000 и т.д. раз, то частное не изменится.
3) Чтобы разделить десятичную дробь на десятичную, надо:
а) перенести в делимом и в делители запятые вправо на столько цифр, сколько их содержится после запятой в делителе;
б) выполнить деление на натуральное число.
4) Если делимое меньше делителя, то целая часть частного равна 0.

460

Номер №460

Выполните деление.
1) 2,7 : 3 = ☐
2) 0,48 : 6 = ☐
3) 4,5 : 5 = ☐
4) 0,036 : 12 = ☐
5) 5 : 2 = ☐
6) 8,48 : 4 = ☐
7) 0,9 : 2 = ☐
8) 14 : 4 = ☐
9) 17 : 2 = ☐

Решение 1
2,7 : 3 = 0,9

Решение 2
0,48 : 6 = 0,08

Решение 3
4,5 : 5 = 0,9

Решение 4
0,036 : 12 = 0,003

Решение 5
5 : 2 = 2,5

Решение 6
8,48 : 4 = 2,12

Решение 7
0,9 : 2 = 0,45

Решение 8
14 : 4 = 3,5

Решение 9
17 : 2 = 8,5

461

Номер №461

Найдите частное.
1) 184 : 10 = ☐
2) 184 : 100 = ☐
3) 184 : 1000 = ☐
4) 184 : 10000 = ☐
5) 6,3 : 10 = ☐
6) 6,3 : 100 = ☐
7) 6,3 : 1000 = ☐
8) 6,3 : 10000 = ☐

Решение 1
184 : 10 = 18,4

Решение 2
184 : 100 = 1,84

Решение 3
184 : 1000 = 0,184

Решение 4
184 : 10000 = 0,0184

Решение 5
6,3 : 10 = 0,63

Решение 6
6,3 : 100 = 0,063

Решение 7
6,3 : 1000 = 0,0063

Решение 8
6,3 : 10000 = 0,00063

462

Номер №462

Выполните деление:
1) 8,61 : 7 =

8,61|7 

2) 170 : 8 =

170|8

3) 82,8 : 36 =

82,8|36

4) 7,68 : 24 =

7,68|24

5) 32,24 : 52 =

32,24|52

6) 11,424 : 48 =

11,424|48

7) 64,32 : 16 =

64,32|16

8) 35 : 14 =

35|14

9) 3 : 12 =

3|12

10) 12 : 96 =

12|96

Решение 1
8,61 : 7 = 1,23

   8,61|7
-  7    |1,23
 - 16
   14 
    -21
     21
       0
  

Решение 2
170 : 8 = 21,25

  170|8
- 16  |21,25
   -10
      8
     -20
      16
      - 40
        40
          0

Решение 3
82,8 : 36 = 2,3

-82,8|36
 72   |2.3
-108
 108
    0

Решение 4
7,68 : 24 = 0,32

- 7.68|24
  72   |0.32
-  48
   48
     0

Решение 5
32,24 : 52 = 0,62

- 32.24|52
  312   |0.62
-  104
   104
      0

Решение 6
11,424 : 48 = 0,238

-11.424|48
 96      |0.238
 182
 144
  -384
   384
      0

Решение 7
64,32 : 16 = 4,02

-64.32|16
 64    |4.02
   -30
    24
    -60
     60
       0

Решение 8
35 : 14 = 2,5

-35|14
 28|2.5
  -70
   70
     0

Решение 9
3 : 12 = 0,25

-3 |12
 0 |0.25
 30
 24
-  60
   60
     0

Решение 10
12 : 96 = 0,125

-12|96
 0  |0.125
-120
 96
- 240
  192
   -480
    480
       0

463

Номер №463

Решите уравнение.
1) 12 * x = 88,8;
2) 1,326 : x = 13.

Решение 1
12 * x = 88,8
x = 88,8 : 12
x = 7,4
Ответ: 7,4

Вычисления:

  -88.8|12
   84   |7.4
   -48
    48
      0

Решение 2
1,326 : x = 13
x = 1,326 : 13
x = 0,102
Ответ: 0,102

Вычисления:

 -1.326|13
  13    |0.102
     -2
      0
    - 26
      26
        0

464

Номер №464

С какой скоростью двигался автомобиль, если за 5 ч он проехал 382 км?

Решение
382 : 5 = 76,4 (км/ч) − скорость движения автомобиля.
Ответ: 76,4 км/ч

Вычисления:

-382|5
 35  |76.4
  -32
   30
   -20
    20
     0

465

Номер №465

Расшифруйте название прибора, применяемого в морском деле для измерения углов.

Е 2,4 : 0,8 =
Т 0,36 : 0,6 =
Н 0,063 : 0,03 =
С 0,015 * 0,5 =
А 4,8 : 0,12 =
К 0,3618 : 0,018 =

0,03	3	20,1	0,03	0,6	40	2,1	0,6

Решение
Е 2,4 : 0,8 = 3
Т 0,36 : 0,6 = 0,6
Н 0,063 : 0,03 = 2,1
С 0,015 : 0,5 = 0,03
А 4,8 : 0,12 = 40
К 0,3618 : 0,018 = 20,1

0,03	3	20,1	0,03	0,6	40	2,1	0,6
C	Е	К	С	Т	А	Н	Т

Вычисления:
Е

-24|8
 24|3
   0
Т

-3.6|6
 36 |0.6
   0

Н

-6.3|3
 6   |2.1
  -3
   3
   0

С

-0.15|5
 15   |0.03
   0

А

-480|12
 48  |40
  - 0
    0
    0

К

-361.8|18
 36     |20.1
   -1
    0
   -18
    18
      0

466

Номер №466

Вычислите.
1) 2,88 : 1,6 = 28,8 : 16 =
2) 10,08 : 0,28 =
3) 72 : 0,225 =
4) 5,508 : 1,8 =
5) 7,67 : 0,0065 =
6) 3 : 0,075 =

Решение 1
2,88 : 1,6 = 28,8 : 16 = 1,8

-28,8|16
 16   |1.8
-128
 128
    0

Решение 2
10,08 : 0,28 = 1008 : 28 = 36

-1008 |28
 84    |36
-168
 168
    0

Решение 3
72 : 0,225 = 72000 : 225 = 320

-72000|225
 675    |320
  -450
   450
      0

Решение 4
5,508 : 1,8 = 55,08 : 18 = 3,06

-55.08|225
 54     |3.06
  -10
     0
  -108
   108
       0

Решение 5
7,67 : 0,0065 = 76700 : 65 = 1180

-76700|65
 65      |1180
-117
   65
  -520
   520
   -  0
      0
      0

Решение 6
3 : 0,075 = 3000 : 75 = 40

-3000|75
 300  |40
     -0
      0
      0

 

467

Номер №467

Найдите значение выражения.
1) (44,66 : 2,2 − 5,74) * 2,5 + 3,6 =
2) (5,37 : 1,5 + 0,62) : 0,56 − 0,39 =

Решение 1
(44,66 : 2,2 − 5,74) * 2,5 + 3,6 = (20,3 − 5,74) * 2,5 + 3,6 = 14,56 * 2,5 + 3,6 = 36,4 + 3,6 = 40
1)

-446.6|22
 44     |20.3
   - 6
     0
    -66
     66
       0

2)

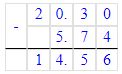
3)

4)

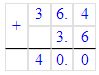
Решение 2
(5,37 : 1,5 + 0,62) : 0,56 − 0,39 = (3,58 + 0,62) : 0,56 − 0,39 = 4,2 : 0,56 − 0,39 = 7,5 − 0,39 = 7,11
1)

-53.7|15
 45   |3.58
  -87
   75
  -120
   120
      0

2)

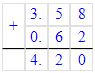
3)

-420|56
 392|7.5
 -280
  280
     0

4)

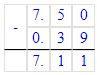
468

Номер №468

Выполните деление.
1) 48,1 : 0,1 = ☐
2) 7 : 0,1 = ☐
3) 12 : 0,01 = ☐
4) 3 : 0,001 = ☐
5) 2,389 : 0,01 = ☐
6) 1,2 : 0,0001 = ☐

Решение 1
48,1 : 0,1 = 481 : 1 = 481

Решение 2
7 : 0,1 = 70 : 1 = 70

Решение 3
12 : 0,01 = 1200 : 1 = 1200

Решение 4
3 : 0,001 = 3000 : 1 = 3000

Решение 5
2,389 : 0,01 = 238,9 : 1 = 238,9

Решение 6
1,2 : 0,0001 = 12000 : 1 = 12000

469

Номер №469

В первый день турист прошел 0,4 маршрута, длина которого составляет 28 км. Сколько километров прошел турист в первый день?
Решение.
0,4 =
1) _ (км) − составляют 1 10 маршрута.
Ответ:

Решение
0 , 4 = 4 10
1) 28 : 10 = 2,8 (км) − составляют 1 10 маршрута.
2) 2,8 * 4 = 11,2 (км) − прошел турист в первый день.
Ответ: 11,2 км

Вычисления: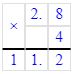

470

Номер №470

Маша собрала 4,2 кг яблок, что составляет 0,7 количества яблок, собранных Катей. Сколько килограммов яблок собрала Катя?
Решение.
0,7 =
1) _ (кг) − составляют 1/10 яблок, собранных Катей.
Ответ:

Решение
0,7 = 7/10
1) 4,2 : 7 = 0,6 (кг) − составляют 1/10 яблок, собранных Катей.
2) 0,6 * 10 = 6 (кг) − яблок собрала Катя.
Ответ: 6 кг

471

Номер №471

За первую неделю было отремонтировано 2,56 км дороги, что составляет 0,32 протяженности всей дороги, которую требовалось отремонтировать. Сколько километров дороги требовалось отремонтировать?

Решение
0 , 32 = 32 100
1) 2,56 : 32 = 0,08 (км) − составляют 1/100 дороги;
2) 0,08 * 100 = 8 (км) − дороги требовалось отремонтировать.
Ответ: 8 км

Вычисления:

-2,56|32
 256 |0.08
     0

472

Номер №472

Преобразуйте в десятичную дробь:
1) 1 5;
2) 1 4;
3) 3 8;
4) 11 20;
5) 14 25;
6) 57 40.

Решение 1
1/ 5 = ^{1 ∗ 2}/_{5 ∗ 2} = 2/10 = 0 , 2

Решение 2
1/ 4 = ^{1 ∗ 25}/_{4 ∗ 25} = 25/ 100 = 0 , 25

Решение 3
3/ 8 = ^{3 ∗ 125}/_{8 ∗ 125} = 375/ 1000 = 0 , 375

Решение 4
11/ 20 = ^{11 ∗ 5}/_{20 ∗ 5} = 55 100 = 0 , 55

Решение 5
14 25 = ^{14 ∗ 4}/_{25 ∗ 4} = 56 100 = 0 , 56

Решение 6
57/40 = 1 17/40 = 1 ^{17 ∗ 25}/_{40 ∗ 25} = 1 ⁴²⁵/₁₀₀₀ = 1,425

473

Номер №473

Решите уравнение.
1) 7,429x + 9,571x = 4,25;
2) 28x − x = 0,729;
3) 1,5x − 0,78x = 1,8;
4) 3,6y + 2,8y = 22,4.

Решение 1
7,429x + 9,571x = 4,25
17x = 4,25
x = 4,25 : 17
x = 0,25
Ответ: 0,25

Вычисления:
+ 7,429
   9,571
  17,000

-4,25|17
 34  |0,25
  -85
   85
     0

Решение 2
28x − x = 0,729
27x = 0,729
x = 0,729 : 27
x = 0,027
Ответ: 0,027

Вычисления:

-0,729|27
 54    |0.027
-189
 189
    0

Решение 3
1,5x − 0,78x = 1,8
0,72x = 1,8
x = 1,8 : 0,72
x = 2,5
Ответ: 2,5

Вычисления:
- 1,50
  0,78
  0,72

-180|72
 144|2.5
  -360
   360
       0


Решение 4
3,6y + 2,8y = 22,4
6,4y = 22,4
y = 22,4 : 6,4
y = 3,5
Ответ: 3,5

Вычисления:

+ 3,6
   2,8
   6,4

-224|64
 192 |3.5
 -320
  320
     0

474

Номер №474

Выполните вычисления по схеме и запишите соответствующее выражение.

Решение 1
1) 3,76 + 3,44 = 7,2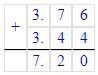

2) 7,2 : 0,18 = 40

-720|18
 72  |40
   -0
    0
    0

3) 40 − 15,82 = 24,18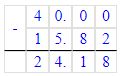

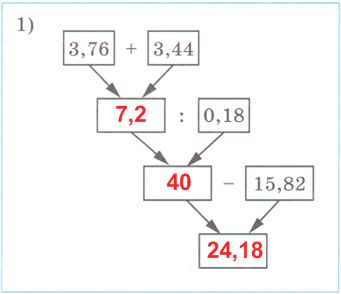
(3,76 + 3,44) : 0,18 − 15,82 = 24,18

Решение 2
1) 3,8 * 3,5 = 13,3

2) 7,35 : 0,75 = 9,8

-735|75
 675|9.8
-600
 600
    0

3) 13,3 − 9,8 = 3,5

4) 3,5 : 1,4 = 2,5

-35|14
 28|2.8
 -70
  70
   0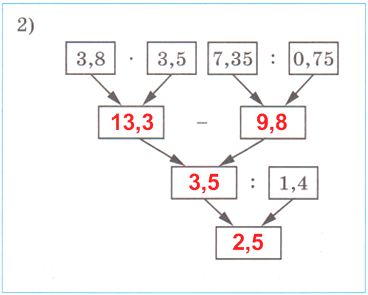

(3,8 * 3,5 − 7,35 : 0,75) : 1,4 = 2,5

475

Номер №475

Решите уравнение.
1) (2,4 + x) * 18 = 61,2;
2) (6,3 − x) * 15 = 3,3;
3) (5,12 + x) * 0,14 = 8,4;
4) (x − 4,7) * 3,4 = 12,92;
5) 2,472 : (30 − y) = 0,12;
6) 12,7 − 4,5x = 8,29;
7) 7x + 5x + 0,28 = 8,92;
8) 17x − 2x − 2,35 = 4,1;
9) 24 * (3x − 5,2) = 0,12;
10) 7,98 : (2x + 0,18) = 19.

Решение 1
(2,4 + x) * 18 = 61,2
2,4 + x = 61,2 : 18
2,4 + x = 3,4
x = 3,4 − 2,4
x = 1
Ответ: 1

Вычисления:

-61.2|18
 54   |3.4
 -72
  72
    0

Решение 2
(6,3 − x) * 15 = 3,3
6,3 − x = 3,3 : 15
6,3 − x = 0,22
x = 6,3 − 0,22
x = 6,08
Ответ: 1

Вычисления:

-3,3|15
 30 |0.22
  -30
   30
    0

- 6,30
  0,22
  6,08

Решение 3
(5,12 + x) * 0,14 = 8,4
5,12 + x = 8,4 : 0,14
5,12 + x = 60
x = 60 − 5,12
x = 54,88
Ответ: 54,88

Вычисления:

-840|14
 84  |60
   -0
    0
    0

- 60,00
    5,12
   54,88

Решение 4
(x − 4,7) * 3,4 = 12,92
x − 4,7 = 12,92 : 3,4
x − 4,7 = 3,8
x = 3,8 + 4,7
x = 8,5
Ответ: 8,5

Вычисления:

-129.2|34
 102   |3.8
   -272
    272
       0

+ 3,8
   4,7
   8,5

Решение 5
2,472 : (30 − y) = 0,12
30 − y = 2,472 : 0,12
30 − y = 20,6
y = 30 − 20,6
y = 9,4
Ответ: 9,4

Вычисления:

- 30,0
  20,6
    9,4

Решение 6
12,7 − 4,5x = 8,29
4,5x = 12,7 − 8,29
4,5x = 4,41
x = 4,41 : 4,5
x = 0,98
Ответ: 0,98

Вычисления:

- 12,70
    8,29
    4,41

-44,1|45
 405 |0.98
-360
 360
    0 


Решение 7
7x + 5x + 0,28 = 8,92
12x = 8,92 − 0,28
12x = 8,64
x = 8,64 : 12
x = 0,72
Ответ: 0,72

Вычисления:
- 8,92
  0,28
  8,64

-8,64|12
 84   |0.72
  -24
   24
     0


Решение 8
17x − 2x − 2,35 = 4,1
15x = 4,1 + 2,35
15x = 6,45
x = 6,45 : 15
x = 0,43
Ответ: 0,43

Вычисления:
+ 4,10
   2,35
   6,45

-6.45|15
 60   |0.43
 -45
  45
    0


Решение 9
24 * (3x − 5,2) = 0,12
3x − 5,2 = 0,12 : 24
3x − 5,2 = 0,005
3x = 0,005 + 5,2
3x = 5,205
x = 5,205 : 3
x = 1,735
Ответ: 1,735

Вычисления:

-0.12|24
 0     |0.005
-120
 120
    0

+ 0,005
   5,200
   5,205

-5.205|3
 3      |1.735
-22
 21
  -10
     9
    -15
     15
       0


Решение 10
7,98 : (2x + 0,18) = 19
2x + 0,18 = 7,98 : 19
2x + 0,18 = 0,42
2x = 0,42 − 0,18
2x = 0,24
x = 0,24 : 2
x = 0,12
Ответ: 0,12

Вычисления:

-7.98|19
 76   |0.42
  -38
   38
     0

- 0,42
  0,18
  0,24

 

-0.24|2
 2     |0.12
  -4
   4
   0

476

Номер №476

Длина прямоугольника равна 56 см, а его ширина составляет 0,45 длины. Вычислите периметр прямоугольника.

Решение
0 , 45 = 45 100
1) 56 : 100 = 0,56 (см) − составляет 1 10 длины прямоугольника;
2) 0,56 * 45 = 25,2 (см) − ширина прямоугольника;
3) (56 + 25,2) * 2 = 81,2 * 2 = 162,4 (см) − периметр прямоугольника.
Ответ: 162,4 см

Вычисления:
2)

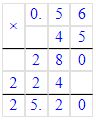
3)

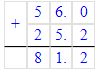
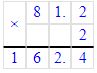
477

Номер №477

Площадь прямоугольника равна площади квадрата со стороной 1,8 см. Одна из сторон прямоугольника равна 1,2 см. Вычислите периметр прямоугольника.

Решение
1) 1,8 * 1,8 = 3,24 ( с м 2 ) − площадь квадрата, равная площади прямоугольника;
2) 3,24 : 1,2 = 2,7 (см) − вторая сторона прямоугольника;
3) (1,2 + 2,7) * 2 = 3,9 * 2 = 7,8 (см) − периметр прямоугольника.
Ответ: 7,8 см

Вычисления:
1)

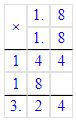
2)

-32.4|12
 24   |2.7
 -84
  84
    0

3)

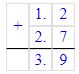
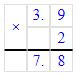
478

Номер №478

От двух станций, расстояние между которыми равно 206,4 км, отправились одновременно навстречу друг другу два поезда, которые встретились через 1,5 ч после начала движения. Один из поездов шел со скоростью 62,4 км/ч. Найдите скорость другого поезда.

Решение
1) 206,4 : 1,5 = 137,6 (км/ч) − скорость сближения поездов;
2) 137,6 − 62,4 = 75,2 (км/ч) − скорость второго поезда.
Ответ: 75,2 км/ч

Вычисления:
1)

-2064|15
 15   |137.6
  -56
   45
  -114
   105
    -90
     90
      0

2)
- 137.6
   62.4
   75.2

479

Номер №479

Из села на станцию вышел пешеход. Когда он отошел от села на 7,56 км, следом за ним выехал велосипедист со скоростью 10,5 км/ч. За какое время велосипедист догонит пешехода, если скорость пешехода в 2,5 раза меньше скорости велосипедиста?
Решение.
1) _ (км/ч) − скорость пешехода.
2) _ (км) − на столько уменьшается расстояние между ними каждый час.
Ответ:

Решение
1) 10,5 : 2,5 = 4,2 (км/ч) − скорость пешехода;
2) 10,5 − 4,2 = 6,3 (км) − на столько уменьшается расстояние между ними каждый час;
3) 7,56 : 6,3 = 1,2 (ч) − время, через которое велосипедист догонит пешехода.
Ответ: через 1,2 ч

Вычисления:
1)
-105|25
 100|4,2
  -50
   50
    0


2)
- 10,5
    4,2
    6,3

3)
-75.6|63
 63   |1.2
-126
 126
     0

480

Номер №480

За 3 ч лодка проплыла 51,6 км против течения реки. Какое расстояние проплывет лодка по течению реки за 4,5 ч, если скорость течения равна 1,4 км/ч?

Решение
1) 51,6 : 3 = 17,2 (км/ч) − скорость лодки против течения;
2) 17,2 + 1,4 = 18,6 (км/ч) − собственная скорость лодки;
3) 18,6 + 1,4 = 20 (км/ч) − скорость лодки по течению;
4) 4,5 * 20 = 90 (км) − проплывет лодка по течению реки за 4,5 ч.
Ответ: 90 км

Вычисления:
1)
- 51,6|3
  3     |17,2
 -21
  21
   -6
    6
    0
2)

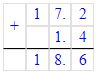
3)

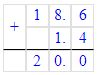
4)

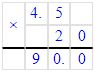
481

Номер №481

Моторная лодка проплыла 85,5 км по течению реки и 46,2 км против течения. Сколько времени было потрачено на весь путь, если собственная скорость лодки равна 32,5 км/ч, а ее скорость по течению составляет 34,2 км/ч?

Решение
1) 34,2 − 32,5 = 1,7 (км/ч) − скорость течения реки;
2) 32,5 − 1,7 = 30,8 (км/ч) − скорость лодки против течения;
3) 85,5 : 34,2 = 2,5 (ч) − время движения лодки по течению;
4) 46,2 : 30,8 = 1,5 (ч) − время движения лодки против течения;
5) 2,5 + 1,5 = 4 (ч) − было потрачено не весь путь.
Ответ: 4 ч

Вычисления:
1)
- 34,2
  32,5
   1,7
2)
- 32,5
    1,7
  30,8
3)

-855|342
 684|2.5
-1710
 1710
      0

4)

-462|308
 308|1.5
-1540
 1540
      0

5)
+ 2,5
   1,5
   4,0

482

Номер №482

Одно из слагаемых равно 3,24, что составляет 0,72 суммы. Найдите второе слагаемое.

Решение
1) 3,24 : 0,72 = 4,5 − сумма;
2) 4,5 − 3,24 = 1,26 − второе слагаемое.
Ответ: 1,26

Вычисления:
1)
-324 |72
 288 |4,5
 -360
  360
     0


2)
- 4,50
  3,24
  1,26

483

Номер №483

Заполните пропуски в цепочке вычислений.

Решение
1 пропуск:
7,6 − 5,7 = 1,9

- 7,6
  5,7
  1,9

2 пропуск:
7,6 : 2 = 3,8

-7,6 |2
 6    |3,8
-16
 16
   0

3 пропуск:
2 − 1,2 = 0,8

- 2,0
  1,2
  0,8

4 пропуск:
0,36 : 1,2 = 0,3

-3,6|12
 36 |0,3
   0

Ответ:

484

Номер №484

Заполните пропуски в цепочке вычислений, если:
1) x = 0,7;
2) x = 2,1.


Решение 1
1 пропуск:
0,7 − 0,3 = 0,4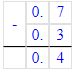

2 пропуск:
0,4 * 4 = 1,6 < 2, тогда: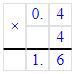

3 пропуск:
1,6 + 0,8 = 2,4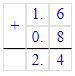

4 пропуск:
2,4 : 0,3 = 8

24:3=8

Ответ:

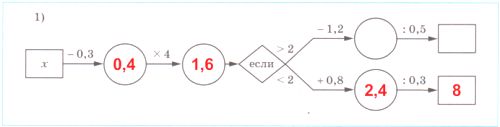
Решение 2
1 пропуск:
2,1 − 0,3 = 1,8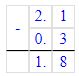

2 пропуск:
1,8 * 4 = 7,2 > 2, тогда: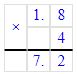

3 пропуск:
7,2 − 1,2 = 6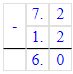

4 пропуск:
6 : 0,5 = 12

Ответ:

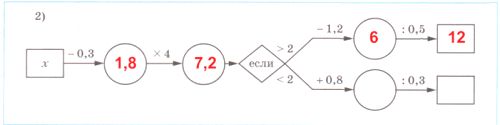
485

Номер №485

Найдите число, 0,26 которого равны 0,65 от числа 60.

Решение
Пусть x − неизвестное число, тогда:
0,26x = 0,65 * 60
0,26x = 39
x = 39 : 0,26
x = 150
Ответ: 150 − искомое число

Вычисления: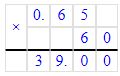

-3900|26
 26    |150
-130
 130
     -0
      0
      0

486

Номер №486

Когда автомобиль проехал 0,35, а затем еще 0,2 всего пути, то оказалось, что он проехал на 16,5 км больше, чем половина намеченного пути. Какой путь должен был проехать автомобиль?
Решение.
1) (0,35 + 0,2) − = всего пути составляют 16,5 км.
Ответ:

Решение
1) (0,35 + 0,2) − 0,5 = 0,55 − 0,5 = 0,05 − всего пути составляют 16,5 км;
2) 16,5 : 0,05 = 1650 : 5 = 330 (км) − должен был проехать автомобиль.
Ответ: 330 км

Вычисления:

-1650|5
 15    |330
  -15
   15
    -0
     0
     0

487

Номер №487

Катер проплыл 148,5 км между двумя пристанями по течению реки за 9 ч, а против течения − за 11 ч. Найдите скорость течения реки.

Решение
1) 148,5 : 9 = 16,5 (км/ч) − скорость катера по течению;
2) 148,5 : 11 = 13,5 (км/ч) − скорость катера против течения;
3) 16,5 − 13,5 = 3 (км/ч) − удвоенная скорость течения реки;
4) 3 : 2 = 1,5 (км/ч) − скорость течения реки.
Ответ: 1,5 км/ч

Вычисления:
1)

-148,5|9
 9       |16.5
-58
 54
  -45
   45
     0

2)

-148,5|11
 11     |13.5
 -38
  33
  -55
   55
     0

3)
- 16,5
  13,5
    3,0
4)

-3|2
 2|1.5
-10
 10
   0

488

Номер №488

Если в некотором числе перенести запятую влево на две цифры, то оно уменьшится на 118,8. Найдите это число.
Решение.
Пусть полученное число равно x. Поскольку полученное число в _ раз меньше числа, которое надо найти, то искомое число равно _. Так как полученное число на 118,8 меньше искомого, то составляем уравнение.

Решение
Пусть полученное число равно x. Поскольку полученное число в 100 раз меньше числа, которое надо найти, то искомое число равно 100x. Так как полученное число на 118,8 меньше искомого, то составляем уравнение.
100x − x = 118,8
99x = 118,8
x = 118,8 : 99
x = 1,2 − полученное число, тогда:
100x = 100 * 1,2 = 120 − искомое число.
Ответ: 120

Вычисления:

-118.8|99
 99    |1.2
-198
 198
    0

 

489

Номер №489

За тетрадь и две ручки надо заплатить 96 р., а за тетрадь и пять таких ручек − 204 р. Сколько стоит одна ручка?

Решение
Так как во второй покупке купили на три ручки больше, то:
1) 204 − 96 = 108 (р.) − стоят три ручки;
2) 108 : 3 = 36 (р.) − стоит одна ручка.
Ответ: 36 рублей

Вычисления:
1)
- 204
    96
  108

2)

-108|3
  9   |36
 -18
  18
    0

490

Номер №490

Известно, что 4 шоколадки и пирожное стоят 73 р., а одна шоколадка и 4 пирожных − 52 р. Найдите цену одного пирожного.

Решение
Обозначим цену одной шоколадки буквой Ш, а цену одного пирожного буквой П, тогда:
(4Ш + П) + (Ш + 4П) = 73 + 52
5Ш + 5П = 125
5(Ш + П) = 125
Ш + П = 125 : 5
Ш + П = 25 (р.) − стоят 1 шоколадка и 1 пирожное.
По условию:
Ш + 4П − (Ш + П) = 52 − 25
Ш + 4П − Ш − П = 27
3П = 27
П = 27 : 3
П = 9 (р.) − цена одного пирожного.
Ответ: 9 рублей

491

Среднее значение величины. Номер №491

Заполните пропуски.
1) Средним арифметическим нескольких чисел называют _
2) Среднее арифметическое чисел 7 и 11 равно (☐ + ☐) : ☐ = ☐.
3) Среднее арифметическое чисел 4; 6; 9; 10; 12 равно (_) _ = _

Решение
1) Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на количество слагаемых.
2) Среднее арифметическое чисел 7 и 11 равно (7 + 11) : 2 = 9.
3) Среднее арифметическое чисел 4; 6; 9; 10; 12 равно (4 + 6 + 9 + 10 + 12) : 5 = 8,2

492

Номер №492

Найдите среднее арифметическое чисел.
1) 2,6; 4,3 и 5,1;
2) 3,4; 3,8; 4,4; 4,9 и 5,2.

Решение 1
(2,6 + 4,3 + 5,1) : 3 = 12 : 3 = 4
Ответ: 4 − среднее арифметическое

Вычисления:

  2,6
+4,3
  5,1
 12,0

Решение 2
(3,4 + 3,8 + 4,4 + 4,9 + 5,2) : 5 = 21,7 : 5 = 4,34
Ответ: 4,34 − среднее арифметическое

Вычисления:
  3,4
  3,8
+4,4
  4,9
  5,2
 21,7

 -21,7|5
  20   |4,34
  -17
   17
   -20
    20
      0

493

Номер №493

Автомобиль ехал 3 ч со скоростью 60 км/ч и 2 ч со скоростью 55 км/ч. Найдите среднюю скорость движения автомобиля на всем пути.
Решение.
1) _ (км) − составляют весь путь.
2) _ (ч) − составляют все время движения автомобиля.
3)
Ответ:

Решение
1) 60 * 3 + 55 * 2 = 180 + 110 = 290 (км) − составляют весь путь;
2) 3 + 5 = 5 (ч) − составляют все время движения;
3) 290 : 5 = 58 (км/ч) − средняя скорость движения автомобиля на всем пути.
Ответ: 58 км/ч

494

Номер №494

Среднее арифметическое чисел 6,4 и x равно 6,8. Найдите число x.

Решение
(6,4 + x) : 2 = 6,8
6,4 + x = 6,8 * 2
6,4 + x = 13,6
x = 13,6 − 6,4
x = 7,2
Ответ: 7,2 − искомое число

Вычисления:
× 6.8
   2
  13.6

- 13,6
    6,4
    7,2

495

Номер №495

Вася купил 2,5 кг печенья одного вида по 72 р. за килограмм и еще 1,5 кг печенья другого вида. Средняя цена купленного печенья составила 84 р. Сколько стоил килограмм печенья второго вида?
Решение.
1) _ (кг) − печенья купил Вася.
2) _ (р.) − стоила вся покупка.
Ответ:

Решение
1) 2,5 + 1,5 = 4 (кг) − печенья купил Вася.
2) 84 * 4 = 336 (р.) − стоила вся покупка.
3) 72 * 2,5 = 180 (р.) − заплатили за печенье первого вида;
4) 336 − 180 = 156 (р.) − заплатили за печенье второго вида;
5) 156 : 1,5 = 104 (р.) − стоил килограмм печенья второго вида.
Ответ: 104 рубля

Вычисления:
1)
+ 2,5
   1,5
   4,0
2)
× 84
     4
  336
3)
× 75
   2.5
  375
150
187.5

4)
- 336
  180
  156
5)

-1560|15
 15    |104
   -6
    0
  - 60
    60
      0

496

Номер №496

Среднее арифметическое четырех чисел равно 3,2, а среднее арифметическое пяти других чисел − 4,1. Найдите среднее арифметическое этих девяти чисел.

Решение
1) 3,2 * 4 = 12,8 − сумма четырех чисел;
2) 4,1 * 5 = 20,5 − сумма пяти чисел;
3) 12,8 + 20,5 = 33,3 − сумма девяти чисел;
4) 33,3 : 9 = 3,7 − среднее арифметическое девяти чисел.
Ответ: 3,7

Вычисления:
1)
× 3.2
      4
   12.8
2)
× 4.1
      5
   20.5
3)
+ 12,8
   20,5
   33,3
4)
-33,3|9
 27   |3,7
 -63
  63
   0

497

Номер №497

Заполните пропуски.
1) Процентом называют _
2) Чтобы найти 1% величины, надо ее значение _
3) 100% некоторой величины − это _
4) Чтобы проценты представить десятичной дробью или натуральным числом, надо _, стоящее перед знаком %, _
5) Чтобы представить десятичную дробь или натуральное число в процентах, надо это число _ и к результату приписать _

Решение
1) Процентом называют сотую часть величины.
2) Чтобы найти 1% величины, надо ее значение разделить на 100.
3) 100% некоторой величины − это вся эта величина.
4) Чтобы проценты представить десятичной дробью или натуральным числом, надо число, стоящее перед знаком %, разделить на 100.
5) Чтобы представить десятичную дробь или натуральное число в процентах, надо это число умножить на 100 и к результату приписать %.

498

Номер №498

Один процент от числа:
1) 600 равен _
2) 40 равен _
3) 7 равен _
4) 0,8 равен _

Решение 1
600 : 100 = 6 − составляет 1% от числа 600
Ответ: 6

Решение 2
40 : 100 = 0,4 − составляет 1% от числа 40
Ответ: 0,4

Решение 3
7 : 100 = 0,07 − составляет 1% от числа 7
Ответ: 0,07

Решение 4
0,8 : 100 = 0,008 − составляет 1% от числа 0,8
Ответ: 0,008

499

Номер №499

Шесть процентов от числа:
1) 100 равны _
2) 300 равны _
3) 4000 равны _
4) 80 равны _
5) 12 равны _
6) 5 равны _

Решение 1
100 : 100 * 6 = 1 * 6 = 6 − составляет 6% от числа 100
Ответ: 6

Решение 2
300 : 100 * 6 = 3 * 6 = 18 − составляет 6% от числа 300
Ответ: 18

Решение 3
4000 : 100 * 6 = 40 * 6 = 240 − составляет 6% от числа 4000
Ответ: 240

Решение 4
80 : 100 * 6 = 0,8 * 6 = 4,8 − составляет 6% от числа 80
Ответ: 4,8

Решение 5
12 : 100 * 6 = 0,12 * 6 = 0,72 − составляет 6% от числа 12
Ответ: 0,72

Решение 6
5 : 100 * 6 = 0,05 * 6 = 0,3 − составляет 6% от числа 5
Ответ: 0,3

500

Номер №500

Запишите в виде десятичной дроби.
1) 1% = ☐
2) 9% = ☐
3) 60% = ☐
4) 120% = ☐
5) 300% = ☐
6) 2,5% = ☐

Решение 1
1% = 1 : 100 = 0,01

Решение 2
9% = 9 : 100 = 0,09

Решение 3
60% = 60 : 100 = 0,6

Решение 4
120% = 120 : 100 = 1,2

Решение 5
300% = 300 : 100 = 3

Решение 6
2,5% = 2,5 : 100 = 0,025

501

Номер №501

Запишите в процентах.
1) 0,39 = ☐%
2) 0,06 = ☐%
3) 0,6 = ☐%
4) 1,7 = ☐%
5) 9 = ☐%
6) 0,846 = ☐%

Решение 1
0,39 = 0,39 * 100 = 39%

Решение 2
0,06 = 0,06 * 100 = 6%

Решение 3
0,6 = 0,6 * 100 = 60%

Решение 4
1,7 = 1,7 * 100 = 170%

Решение 5
9 = 9 * 100 = 900%

Решение 6
0,846 = 0,846 * 100 = 84,6%

502

Номер №502

Запишите в виде обыкновенной дроби.
1) 50% = ☐
2) 25% = ☐
3) 75% = ☐
4) 10% = ☐
5) 20% = ☐
6) 60% = ☐

Решение 1
50% = 50/100 = 1/2

Решение 2
25% = 25/100 = 1/4

Решение 3
75% = 75/100 = 3/4

Решение 4
10% = 10/100 = 1/10

Решение 5
20% = 20/100 = 1/5

Решение 6
60% = 60/100 = 3/5

503

Номер №503

Закрасьте 50% площади каждой фигуры.

Решение
50% = 50 100 = 1 2 − значит надо закрасить половину площади фигуры.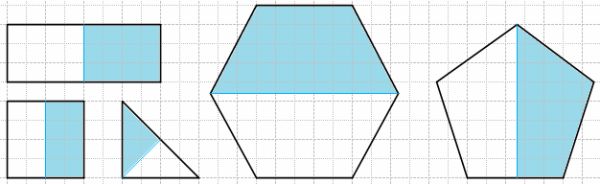

504

Номер №504

Закрасьте 25% площади каждой фигуры.

Решение
25% = 25 100 = 1 4 − значит надо закрасить четвертую часть площади фигуры.

505

Номер №505

Площадь поля составляет 240 га. Пшеницей засеяли 35% поля. Сколько гектаров засеяли пшеницей?
Решение.
1) _ (га) − составляют 1% площади поля.
Ответ:

Решение
1) 240 : 100 = 2,4 (га) − составляют 1% площади поля.
2) 2,4 * 35 = 84 (га) − засеяли пшеницей.
Ответ: 84 га

Вычисления:
× 2.4
    35
+120
  72
  84.0

506

Номер №506

Сплав содержит 7% цинка. Сколько килограммов цинка содержится в 130 кг сплава?

Решение
1) 130 : 100 = 1,3 (кг) − составляют 1% содержания цинка;
2) 1,3 * 7 = 9,1 (кг) − цинка содержится в 130 кг сплава.
Ответ: 9,1 кг

Вычисления:
× 1.3
      7
    9.1

507

Номер №507

В саду растет 400 деревьев. Из них 52% составляют вишни, а остальное − яблони. Сколько яблонь растет в саду?
Решение.
1) _ (%) всех деревьев составляют яблони.
Ответ:

Решение
1) 100% − 52% = 48% − всех деревьев составляют яблони;
2) 400 : 100 = 4 (дерева) − составляют 1% всех деревьев сада;
3) 4 * 48 = 192 (яблони) − растет в саду.
Ответ: 192 яблони

Вычисления:
× 48
     4
  192

508

Номер №508

В магазин завезли 1600 кг овощей. Из них 32% составляли огурцы, 26% − помидоры, а остальное − капуста. Сколько килограммов капусты завезли в магазин?
Решение
1) _ (%) всех овощей составляли огурцы и помидоры.
Ответ:

Решение
1) 32 + 26 = 58% − всех овощей составляли огурцы и помидоры;
2) 100% − 58% = 42% − всех овощей составляет капуста;
3) 1600 : 100 = 16 (кг) − составляет 1% всех овощей;
4) 16 * 42 = 672 (кг) − капусты завезли в магазин.
Ответ: 672 кг

Вычисления:
× 16
   42
   32
 64
 672

509

Номер №509

В автопарке 250 автомобилей, из них 70% составляют грузовые автомобили, а легковые составляют 36% от количества грузовых. Сколько в автопарке легковых автомобилей?

Решение
1) 250 : 100 = 2,5 (автомобиля) − составляют 1% всех автомобилей;
2) 2,5 * 70 = 175 (грузовых) − автомобилей в автопарке;
3) 175 : 100 = 1,75 (автомобиля) − составляют 1% грузовых автомобилей;
4) 1,75 * 36 = 63 (легковых) − автомобилей в автопарке.
Ответ: 63 легковых автомобиля

Вычисления:
2)

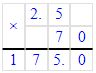
4)

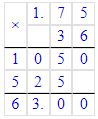
510

Номер №510

Вкладчик положил в банк 26000 р. под 8% годовых. Какая сумма будет на его счете через год?

Решение
1) 26000 : 100 = 260 (р.) − составляют 1% от всего вклада;
2) 260 * 8 = 2080 (р.) − составят начисленные проценты;
3) 26000 + 2080 = 28080 (р.) − будет на его счете через год.
Ответ: 28080 рублей

Вычисления:
2)

3)

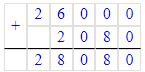
511

Номер №511

За четыре дня турист проехал 420 км. В первый день он проехал 35% всего пути, во второй − 5 7 того, что в первый день, в третий − 120% того, что во второй. Сколько километров проехал турист в четвертый день?

Решение
1) 420 : 100 = 4,2 (км) − составляют 1% всего пути;
2) 4,2 * 35 = 147 (км) − проехал турист в первый день;
3) 147 : 7 * 5 = 21 * 5 = 105 (км) − проехал турист во второй день;
4) 105 : 100 = 1,05 (км) − составляют 1% пути пройденного во второй день;
5) 1,05 * 120 = 126 (км) − проехал турист в третий день;
6) 420 − (147 + 105 + 126) = 420 − 378 = 42 (км) − проехал турист в четвертый день.
Ответ: 42 км

Вычисления:
2)

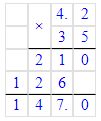
5)

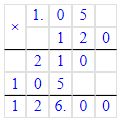
6)
  147
+105
  126
  378

- 420
  378
    42

512

Номер №512

Заполните таблицу.

1% числа	Данное число
8
2
3,8
9,25

 

Решение

1% числа	Данное число
8	8*100=800
2	2*100=200
3,8	3,8*100=380
9,25	9,25*100=925

 

513

Номер №513

Найдите число, если:

1) 4% этого числа равны 32
2) 13% этого числа равны 2,6
3) 32% этого числа равны 0,96

Решение
1) 32 : 4 * 100 = 8 * 100 = 800
2) 2,6 : 13 * 100 = (2,6 * 10) : 13 * 10 = 26 : 13 * 10 = 2 * 10 = 20
3) 0,96 : 32 * 100 = (0,96 * 100) : 32 = 96 : 32 = 3

Ответ:

1) 4% этого числа равны 32	800
2) 13% этого числа равны 2,6	20
3) 32% этого числа равны 0,96	3

 

514

Номер №514

Закончите предложение.
1) Если 50% составляют 18 кг, то 100% − ☐ кг.
2) Если 10% составляют 24 кг, то 100% − ☐ кг.
3) Если 25% составляют 6 кг, то 100% − ☐ кг.
4) Если 20% составляют 5 кг, то 100% − ☐ кг.

Решение 1
(100% : 50%) * 18 = 2 * 18 = 36
Ответ:
Если 50% составляют 18 кг, то 100% − 36 кг.

Решение 2
(100% : 10%) * 24 = 10 * 24 = 240
Ответ:
Если 10% составляют 24 кг, то 100% − 240 кг.

Решение 3
(100% : 25%) * 6 = 4 * 6 = 24
Ответ:
Если 25% составляют 6 кг, то 100% − 24 кг.

Решение 4
(100% : 20%) * 5 = 5 * 5 = 25
Ответ:
Если 20% составляют 5 кг, то 100% − 25 кг.

515

Номер №515

За неделю отремонтировали 24 км дороги, что составляет 30% всей дороги. Какова длина дороги, которую надо отремонтировать?
Решение.
1) _ (км) − составляют 1% дороги.
Ответ:

Решение
1) 24 : 30 = 0,8 (км) − составляют 1% дороги.
2) 0,8 * 100 = 80 (км) − длина дороги.
Ответ: 80 км

Вычисления:
-24|30
 0  |0,8
-240
 240
    0

516

Номер №516

Руда содержит 70% железа. Сколько надо взять руды, чтобы получить 84 т железа?

Решение
1) 84 : 70 = 1,2 (т) − составляет 1% железа;
2) 1,2 * 100 = 120 (т) − руды надо взять.
Ответ: 120 т

Вычисления:
-84|70
 70|1,2
-140
 140
    0

517

Номер №517

Масса сушеных яблок составляет 16% массы свежих яблок. Сколько килограммов свежих яблок надо взять, чтобы получить 36 кг сушеных?

Решение
1/) 36 : 16 = 2,25 (кг) − составляет 1% свежих яблок;
2) 2,25 * 100 = 225 (кг) − свежих яблок надо взять.
Ответ: 225 кг

Вычисления:
-36|16
 32 |2,25
 -40
  32
  -80
   80
     0

518

Номер №518

За день рабочий изготовил 44 детали, что составляет 110% количества деталей, которые он должен был сделать по плану. Сколько деталей надо было сделать по плану?

Решение
1) 44 : 110 = 0,4 (детали) − составляет 1% деталей, которые нужно было сделать по плану;
2) 0,4 * 100 = 40 (деталей) − надо было сделать по плану.
Ответ: 40 деталей

Вычисления:
-44|110
 0  |0,4
-440
 400
  -400
   400
      0

519

Номер №519

Петя потратил 52% своих денег на покупку новой книги, 40% денег − на конфеты, после чего у него осталось 28 р. Сколько денег было у Пети сначала?
Решение.
1) _ (%) всех денег потратил Петя на покупку книг и конфет.
2) _ (%) составляют 28 р.
Ответ:

Решение
1) 52% + 40% = 92% − всех денег потратил Петя на покупку книг и конфет.
2) 100% − 92% = 8% − составляют 28 рублей;
3) 28 : 8 = 3,5 (р.) − составляют 1% всех денег;
4) 3,5 * 100 = 350 (р.) − было у Пети сначала.
Ответ: 350 рублей

Вычисления:
-28|8
 24 |3,5
- 40
  40
    0

520

Номер №520

Градусная мера угла A равна 140°. Градусная мера угла B составляет 65% градусной меры угла A и 70% градусной меры угла C. Найдите градусные меры углов B и C.

Решение
1) 140° : 100 = 1,4° − составляет 1% угла A;
2) 1,4° * 65 = 91° − градусная мера угла B;
3) 91° : 70 = 1,3° − составляет 1% угла C;
4) 1,3° * 100 = 130° − градусная мера угла C.
Ответ: ∠B = 91°, ∠C = 130°.

Вычисления:
2)
× 1.4
     65
     70
   84
   91.0  

3)

-91|70
 70|1,3
 -210
  210
     0

520

Номер №521

В парке растут дубы и клены. причем дубов растет на 30 деревьев больше, чем кленов. Клены составляют 38% всех деревьев. Сколько деревьев растет в парке?
Решение.
1) _ (%) всех деревьев составляют дубы.
2) _ (%) − на столько процентов дубов больше, чем кленов.
Ответ:

Решение
1) 100% − 38% = 62% − всех деревьев составляют дубы.
2) 62% − 38% = 24% − на столько процентов дубов больше, чем кленов;
3) 30 : 24 = 1,25 (дерева) − составляет 1% всех деревьев в парке;
4) 1,25 * 100 = 125 (деревьев) − всего растет в парке.
Ответ: 125 деревьев

Вычисления:
-30|24
 24|1,25
 -60
  48
  -120
   120
      0

522

Номер №522

Магазин продал за три дня партию яблок, причем в первый день было продано 45% всех яблок, во второй − 60% оставшегося, а в третий − остальные 660 кг. Сколько всего килограммов яблок было продано за три дня?

Решение
1) 100% − 45% = 55% − яблок осталось после первого дня;
2) 55 : 100 = 0,55% − составляют 1% оставшихся яблок;
3) 0,55 * 60 = 33% − яблок продали во второй день;
4) 100% − (45% + 33%) = 100% − 78% = 22% − яблок продали в третий день;
5) 660 : 22% = 30 (кг) − яблок составляют 1% всех яблок, проданных за 3 дня;
6) 30 * 100 = 3000 (кг) − яблок было продано за 3 дня.
Ответ: 3000 кг

Вычисления
3)

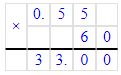
5)
- 660|22
  66  |30
    -0
     0
     0

523

Номер №523

Яблони составляют 40% всех деревьев сада, вишни − 80% количества яблонь, а остальные деревья в саду − груши, и их 21 дерево. Сколько всего деревьев в саду?

Решение
1) 40 : 100 = 0,4% − составляет 1% яблонь;
2) 0,4 * 80 = 32% − всех деревьев сада составляют вишни;
3) 100% − (40% + 32%) = 100% − 72% = 28% − всех деревьев сада составляют груши;
4) 21 : 28 = 0,75 (дерева) − составляет 1% всех деревьев сада;
5) 0,75 * 100 = 75 (деревьев) − всего в саду.
Ответ: 75 деревьев

Вычисления:
-21 |28
 0   |0,75
-210
 196
 -140
  140
     0

524

Номер №524

В магазин завезли 15 двухколесных и трехколесных велосипедов. У всех велосипедов вместе было 40 колес. Сколько велосипедов каждого вида завезли в магазин?

Решение
Допустим, что все привезенные велосипеды были двухколесными, тогда:
1) 15 * 2 = 30 (колес) − было бы всего на пятнадцати велосипедах;
2) 40 − 30 = 10 (колес) − осталось лишних, поэтому если добавить эти колеса по одному к каждому двухколесному велосипеду, получим, что привезли 10 трехколесных велосипеда;
3) 15 − 10 = 5 (двухколесных) − велосипеда привезли.
Ответ: 5 двухколесных и 10 трехколесных велосипеда.

525

Номер №525

Решите кроссворд.

По горизонтали:
3. Прямоугольный ... .
5. Сотая часть величины.
9. Единица измерения углов.
10. Единица измерения массы.
11. Единица измерения площади.
12. Сумма сторон многоугольника.
14. Четырехугольник с прямыми углами.

По вертикали:
1. Результат деления.
2. Единица измерения времени.
4. Знак арифметического действия.
6. При делении числа 13 на 5 число 3 − ... .
7. Геометрическая фигура.
8. Единица измерения длины.
13. Одна из частей прямой, на которые прямую разбивает лежащая на ней точка.

Решение
По горизонтали:
3. параллелепипед
5. процент
9. градус
10. центнер
11. гектар
12. периметр
14. прямоугольник
По вертикали:
1. частное
2. секунда
4. плюс
6. остаток
7. треугольник
8. дециметр
13. луч