Начальные классы школы позади. Теперь у наших школьников будет все несколько сложнее, это касается и такого школьного предмета как математика. Одним из распространенных и принятых для обучения школьников учебником является учебник авторов Виленкин, Жохов, Чесноков. Издание 37-е. 2019 год.  В этом учебнике (5 класс 2 часть) собраны несколько более сложные задания, чем были ранее, ведь здесь придется решать не только логические задачи и задачи с вычислениями, но еще и упражнения связанные с частями, то есть с дробями. Теперь эти понятия останутся с ваши не то что до 11 класса, а на всю жизнь!
 Кроме того, в учебнике будут приведены и задания связанные с геометрией, то есть будут заложены основы этого предмета, для изучения в старших классах.

 ...страница нашего сайта как раз и будет посвящена ответам, так называемым ГДЗ для учебника 5 класса, авторы: Бунимович Е. А., Дорофеев Г. В., Суворова С. Б. Конечно, все задания вы должны делать в первую очередь сами, но если по какой-то причине это не удалось, а времени уже на то чтобы подумать нет, то и выбора уже нет... Кроме того, эта страничка подойдет для того, чтобы провести самопроверку. Для того чтобы проверить задания, вам достаточно выбрать интересующее вас из формы ниже и посмотреть ответ.

Ответы по заданиям для учебника математики 5 класс учебник Виленкин, Жохов, Чесноков 

 Выбирайте нужную страницу и смотрите ответы.

 Начальные классы школы позади. Теперь у наших школьников будет все несколько сложнее, это касается и такого школьного предмета как математика. Одним из распространенных и принятых для обучения школьников учебником является учебник авторов Виленкин, Жохов, Чесноков. Издание 37-е. 2019 год.  В этом учебнике (5 класс 2 часть) собраны несколько более сложные задания, чем были ранее, ведь здесь придется решать не только логические задачи и задачи с вычислениями, но еще и упражнения связанные с частями, то есть с дробями. Теперь эти понятия останутся с ваши не то что до 11 класса, а на всю жизнь!
 Кроме того, в учебнике будут приведены и задания связанные с геометрией, то есть будут заложены основы этого предмета, для изучения в старших классах.

 ...страница нашего сайта как раз и будет посвящена ответам, так называемым ГДЗ для учебника 5 класса, авторы: Бунимович Е. А., Дорофеев Г. В., Суворова С. Б. Конечно, все задания вы должны делать в первую очередь сами, но если по какой-то причине это не удалось, а времени уже на то чтобы подумать нет, то и выбора уже нет... Кроме того, эта страничка подойдет для того, чтобы провести самопроверку. Для того чтобы проверить задания, вам достаточно выбрать интересующее вас из формы ниже и посмотреть ответ.

Ответы по заданиям для учебника математики 5 класс учебник Виленкин, Жохов, Чесноков 

 Выбирайте нужную страницу и смотрите ответы.

Страницы 7 8 9 10 11 12

Параграф 5. Обыкновенные дроби

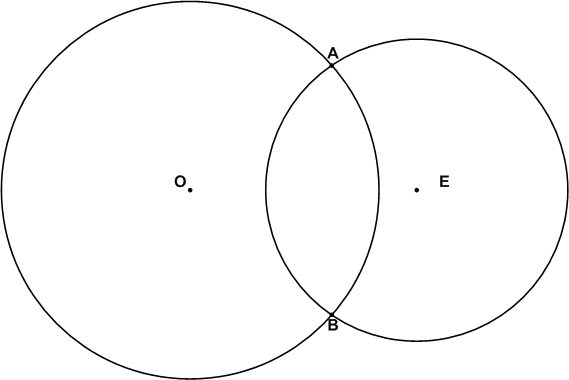
Ответы к пункту 22. Окружность и круг, стр. 7

Задание 1

Какие из точек, отмеченных на рисунке 97:
а) лежат на окружности;
б) лежат внутри круга;
в) не лежат на окружности;
г) лежат вне круга?

Решение

а) В, D.

б) А, О, E.

в) А О, Е, С, F.

г) С, F.

Задание 2

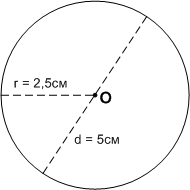
Отметьте в тетради точку О. Постройте окружность с центром в этой точке. Измерьте радиус окружности. Чему равен её диаметр?

Задание 3

Начертите окружность и отметьте на ней три точки А, В и С. Назовите дуги, на которые эти точки делят окружность.

Решение

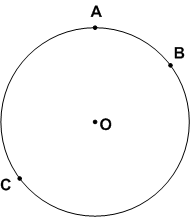
Точки A, В, С делят окружность на дуги АС, АВ, СВ.

Задание 4

Изобразите круг, радиус которого 3 см. Отметьте точку А внутри круга и точку В вне круга. Измерьте расстояние от центра круга до точки А и до точки В. Сравните эти расстояния с радиусом круга. Соедините точки А и В отрезком. Пересекается ли он с окружностью?

Решение

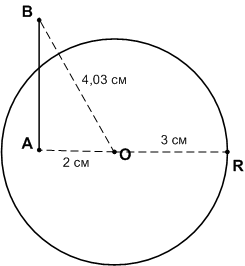
ОА = 2 см < ОR = 3 см; ОВ = 4,03 см > ОR = 3 см.
Отрезок АВ пересекается с окружностью.

Задание 5

Начертите окружность с центром в точке О и радиусом 3 см 5 мм. Проведите прямую, которая пересекает окружность в точках М и К. На каком расстоянии от центра окружности находятся эти точки?

Решение

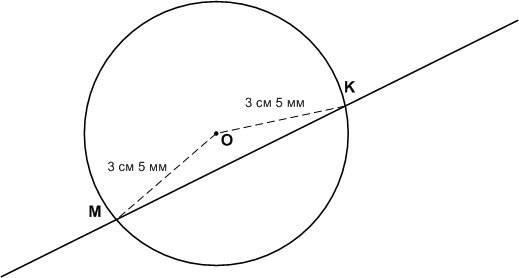
ОМ = OK = 3 см 5 мм.

Задание 6

Начертите отрезок CD, равный 5 см. Проведите окружность с центром С и радиусом 3 см, а также другую окружность с центром D и радиусом 4 см. Обозначьте точки пересечения окружностей буквами А и В. Чему равны длины отрезков АС, СВ, DA и BD?

Решение

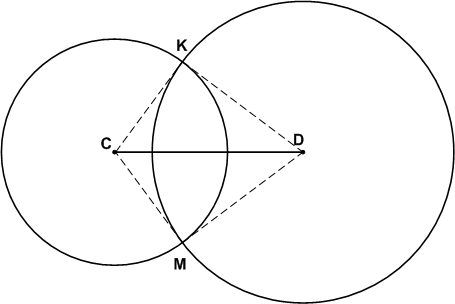
СK = СM = 3 см, DK = DM = 4 см.

Задание 7

Начертите отрезок MP, равный 6 см. Найдите две точки А и В, которые находились бы на расстоянии 4 см от точки М и 5 см от точки Р.

 

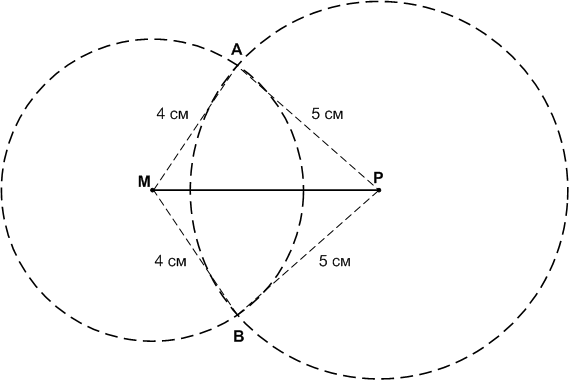
Задание 8

Автомобиль приближается к городу, по улицам которого разрешается ехать со скоростью не более чем 60 км/ч. В кабине автомобиля установлен спидометр − прибор, показывающий скорость движения. Посмотрите на спидометр (рис. 98). Нарушит ли шофёр правила уличного движения, если не снизит скорость? На сколько и в какую сторону передвинется стрелка, когда скорость снизится до 50 км/ч? Каким будет показание спидометра, когда автомобиль остановится?

Решение

На рисунке спидометр показывает скорость 90 км/ч. Значит, если шофёр не снизит скорость, то нарушит правила дорожного движения. При снижении скорости до 50 км/ч, стрелка спидометра передвинется влево на 4 деления. При остановке автомобиля спидометр покажет скорость 0 км/ч.

Задание 9

На рисунке 99 изображена шкала прибора, показывающего, сколько литров бензина осталось в баке автомобиля. Сколько литров бензина сейчас в баке? На сколько делений и в какую сторону передвинется стрелка прибора, если:
а) в бензобак нальют ещё 20 л бензина;
б) при движении будет израсходовано 30 л бензина?

Решение

а) В баке 40 л бензина. Если влить еще 20 л бензина, то стрелка передвинется на 6 делений вправо и покажет 60 л.

б) В баке 40 л бензина. Eсли будет израсходовано 30 л бензина, то стрелка передвинется на 9 делений влево и покажет 10 л.

Задание 10

Какое время показывают часы на рисунке 96? Какое время будут показывать часы, если минутную стрелку передвинуть:
а) назад на 3 больших деления;
б) вперёд на 20 малых делений?

Решение

а) На часах 3 ч 30 мин. Если минутную стрелку передвинуть назад на 3 больших деления, то часы покажут 3 ч 15 мин.

б) На часах 3 ч 30 мин. Если минутную стрелку передвинуть вперёд на 20 маленьких делений, то часы покажут 3 ч 50 мин.

Задание 11

Вычислите устно:

Решение

a) 360, 240, 3, 90.

б) 4, 100, 240, 4.

в) 250, 25, 1000, 700.

г) 70, 140, 350, 7.

д) 400, 8, 1000, 840.

Задание 12

Миллион уменьшили в 100 раз и результат уменьшили на тысячу. Сколько получили?

Решение

1000000 : 100 − 1000 = 10000 − 1000 = 9000.

Задание 13

Укажите координаты точек А, B, С и D, если М(10) (рис. 100). Сравните координаты точек В и С; С и D.

Решение

Одна клетка на рисунке соответствует 2 единицам.
Следовательно координаты других точек: В(6), С(17), A(24), D(28); 6 < 17, 17 < 28.

Задание 14

Сколько сантиметров:
а) в четверти метра;
б) в десятой доле дециметра;
в) в десятой доле метра;
г) в двадцать пятой доле метра?

Решение

a) 1 м = 100 см, 1 дм = 10 cм:
100 см : 4 = 25 см

б) 1 м = 100 см, 1 дм = 10 cм:
100 см : 10 = 10 см

в) 1 м = 100 см, 1 дм = 10 cм:
10 см : 10 = 1

г) 1 м = 100 см, 1 дм = 10 cм:
100 см : 25 = 4 см.

Задание 15

Сколько килограммов:
а) в десятой доле центнера;
б) в сотой доле тонны;
в) в двадцатой доле центнера;
г) в двадцатой доле тонны?

Решение

а) 1 ц = 100 кг, 1 т = 1000 кг:
100 кг : 10 = 10 кг

б) 1 ц = 100 кг, 1 т = 1000 кг:
1000 кг : 100 = 10 кг

в) 1 ц = 100 кг, 1 т = 1000 кг:
100 кг : 20 = 5 кг

г) 1 ц = 100 кг, 1 т = 1000 кг:
1000 кг : 20 = 50 кг

Задание 16

Представьте себе, что один куб с ребром 1 дм разрезали на кубики с ребром 1 см и из этих маленьких кубиков сложили башню, поставив их один на другой. Второй куб с ребром 1 дм разрезали на кубики с ребром 1 мм и из этих кубиков так же сложили башню. Какая из этих башен выше? Во сколько раз?

Решение

Объем куба с ребром 1 дм − V = 1 дм³ = 1000 см³ = 1000000 мм³.
Высота башни из кубиков с ребром 1 см равна 1 * 1000 = 1000 см = 10000 мм, а высота башни из кубиков с ребром 1 мм равна 1 * 1000000 = 1000000 мм.
Поэтому вторая башня выше первой в 1000000 : 10000 = 100 раз.

Задание 17

Проверьте, справедливы ли равенства:
1³ + 2³ = ( 1 + 2 )² ;
1³ + 2³ + 3³ = ( 1 + 2 + 3 )² ;
1³ + 2³ + 3³ + 4³ = ( 1 + 2 + 3 + 4 )² .
Попробуйте рассказать, какова в этих равенствах зависимость между квадратами и кубами чисел. Проверьте, выполняется ли это свойство для пяти, шести чисел.

Решение

1³ + 2³ = 1 + 8 = 9 ,
( 1 + 2 )² = 3² = 9 ;

1³ + 2³ + 3³ = 1 + 8 + 27 = 36 ,
( 1 + 2 + 3 )² = 6² = 36 ;

1³ + 2³ + 3³ + 4³ = 1 + 8 + 27 + 64 = 100 ,
( 1 + 2 + 3 + 4 )² = 10² = 100

Сумма кубов n первых натуральных чисел равна квадрату суммы этих чисел.

1³ + 2³ + 3³ + 4³ + 5³= 1 + 8 + 27 + 64 + 125 = 225 ,
( 1 + 2 + 3 + 4 + 5)² = 15² = 225

1³ + 2³ + 3³ + 4³ + 5³ + 6³= 1 + 8 + 27 + 64 + 125 + 216 = 441 ,
( 1 + 2 + 3 + 4 + 5 + 6 )² = 21² = 441

Задание 18

Найдите объём и площадь наружной поверхности бака без крышки, изображённого на рисунке 101. Сколько понадобится краски, чтобы покрасить этот бак снаружи и изнутри, если на покраску 1 дм² нужно 2 г краски? Сколько литров бензина можно влить в этот бак?

Решение

V бака = 80 * 90 * 70 = 504000 (см³ ).
S наружн.поверхности = 90 * 70 + 2 * ( 80 * 90 + 80 * 70 ) = 6300 + 2 * 12800 = 31900 (см² )
31900 * 2 : 100 * 2 = 1276 (г) краски потребуется  на покраску бака.
504000 : 1000 = 504 (л) - бензина можно влить в бак

Задание 19

Сторона одного куба 9 см, а другого 5 см; На сколько объём первого куба больше объёма второго? На сколько площадь поверхности первого куба больше площади поверхности второго?

Решение

1) 9³ − 5³ = 729 − 125 = 604 (см³ ) - на столько объем первого куба больше объёма второго куба.
2) ( 9² − 5² ) = 6 * 56 = 336 (см² ) - на столько площадь поверхности первого куба больше.

Задание 20

Найдите площадь фигуры, изображённой на рисунке 102. Площадь одной клетки 25 мм².

Решение

1) 7 + 2 * 5 = 17 (клеток) - в фигуре
2) 17 * 25 = 425 (мм²) - площадь фигуры
Ответ: 425 мм².

Задание 21

На одной чашке весов стоит банка с вареньем, а на другой − гиря в 1 кг. Весы находятся в равновесии. Сколько граммов варенья находится в банке, если пустая банка легче варенья в 4 раза?

Решение от

Пусть пустая банка весит х г, тогда варенье весит 4х г.
Общая масса банки с вареньем равна (х + 4х) г.
Составим и решим уравнение:
х + 4х = 1000
5x = 1000
х = 1000 : 5
х = 200 (г) - весит пустая банка
4 * 200 = 800 (г) - весит варенье
Ответ: 800 г  варенья находится в банке.

Задание 22

Решите задачу:
1) На крыше дома сидели голуби. Когда к ним прилетели ещё 15 голубей, а 18 голубей улетели, то на крыше оказалось 16 голубей. Сколько голубей сидело на крыше первоначально?
2) Когда от товарного состава отцепили 6 вагонов, а прицепили к нему 19 вагонов, в нём стало 50 вагонов. Сколько вагонов было в составе первоначально?

Решение задач

1) Пусть на крыше сидели х голубей, тогда на ней стало (х + 15 − 18) голубей.
Составим и решим уравнение:
х + 15 − 18 = 16
х = 16 + 3
х = 19 (г.)
Ответ: 19 голубей сидело на крыше первоначально.

2) Пусть в составе было х вагонов, тогда в составе стало (z − 6 + 19) вагонов.
Составим и решим уравнение:
z − 6 + 19 = 50
z = 50 − 13
z = 37 (в.)
Ответ: 37 вагонов было в составе первоначально.

!Задание 23

Выполните действия:
1) (1 445 561 : 3587 − 208) * 356 − 3580;
2) (1 420 288 : 4672 + 259) * 234 − 1742.

Решение

1) (1445561 : 3587 − 208) * 356 + 3580 = (403 − 208) * 356 + 3580 = 69420 − 3580 = 65840

2) (1420288 : 4672 + 259) * 234 − 1742 = (304 + 259) * 234 − 1742 = 131742 − 1742 = 130000

Задание 24

Начертите круг с центром А и радиусом 2 см. Отметьте две точки:
а) лежащие на окружности;
б) лежащие внутри круга;
в) лежащие вне круга.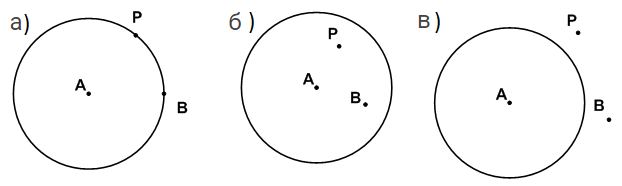

Страница 12

Задание 25

Отметьте две точки А и В так, чтобы АВ = 3 см. С помощью циркуля постройте ещё три точки С, D и Е, которые находились бы от точки А на расстоянии 3 см.

Задание 26

Отметьте две точки К и Р так, чтобы КР = 6 см. Постройте окружность с центром К и радиусом 5 см и окружность с центром Р и радиусом 4 см. Пересекаются ли эти окружности?

Решение

Окружности пересекаются в точках А и B.

Задание 27

Отметьте точки О и Е так, чтобы ОЕ = 8 см. Постройте окружность с центром О и радиусом 2 см и окружность с центром Е и радиусом 4 см. Пересекаются ли эти окружности?

Решение

Окружности не пересекаются.

Задание 28

В старину часто пользовались солнечными часами, они известны более 3000 лет. В солнечных часах время определяется по положению тени от наклонного стержня на циферблате (циферблат и стержень располагали так, чтобы в полдень тень от стержня была направлена на отметку 12 ч). подумайте, что общего у солнечных часов (рис. 103) с современными, в чём их достоинства и недостатки.

Решение

Солнечные и современные часы показывают время, их достоинство в том, что они не требуют энергии для своей работы, а недостаток в том, что они не показывают время ночью и ими неудобно пользоваться.

Задание 29

Решите уравнение:
а) (х − 152) * 59 = 6018;
б) 975 * (у − 361) = 14 625;
в) (30 142 + z) : 876 = 49;
г) 51 815 : (р − 975) = 1205;
д) 13х + 15x − 24 = 60;
е) 18у − 7у − 10 = 12.

Решение

а) (х − 152) * 59 = 6018
x − 152 = 6018 : 59
x = 102 + 152
х = 254
Ответ: 254.

б) 975 * (у − 361) = 14625
у − 361 = 14625 : 975
у = 15 + 361
у = 376
Ответ: 376.

в) (30142 + z) : 876 = 49
30142 + z = 49 * 876
z = 42924 − 30142
z = 12782
Ответ: 12782.

г) 51815 : (р − 975) = 1205
р − 975 = 51815 : 1205
р = 43 + 975
р = 1018
Ответ: 1018.

д) 13х + 15x − 24 = 60
28х = 60 + 24
х = 84 : 28
х = 3
Ответ: 3.

е) 18у − 7у − 10 = 12
11у = 12 + 10
у = 22 : 11
у = 2
Ответ: 2.

Задание 30

Выполните деление с остатком числа 987654 на 391.

Решение

_987654 |391   
  782       |2525
_2056
  1955
  _1015
      782
    _2334
      1955
        379
987654 = 2525 * 391 + 379.

Задание 31

Найдите объём фигуры, изображённой на рисунке 12. Объём каждого кубика 1 см³.

Решение

а) 2 * 2 * 5 = 20 (см³ )
Ответ: объем фигуры 20 см³ .

б) 10 * 10 * 10 = 1000 (см³ )
Ответ: объем фигуры 1000 см³ .

в) 10 * 10 * 5 = 500 (см³)
Ответ: объем фигуры 500 см³ .

Задание 32

Масса 1 л бензина 650 г. В бензобак автомобиля входит 95 л бензина. Какова масса бензина в полном баке этой автомашины?

Решение

95 * 650 = 61750 (г)  -  масса бензина в бензобаке.
61750 г = 61 кг 750 г
Ответ: 61 кг 750 г.

Задание 33

По формуле а = bq + r найдите число а, если делитель b равен 81, неполное частное q равно 561 и остаток r равен 23.

Решение

Если b = 81, q = 561, r = 23;
a = bq + r = 81 * 561 + 23 = 45441 + 23 = 45464.

!Задание 34

Найдите значение выражения:
а) 507 * 664 − 296 085;
б) 485 979 + 691 * 308;
в) 12³ + 5³ * 4 ;
г) ( 10³ + 8³ ) : 18 .

Решение

а) 507 * 664 − 296085 = 336648 − 296085 = 40563

б) 485979 + 691 * 308 = 485979 + 212828 = 698807

в) 12³ + 5³ * 4 = 144 * 12 + 125 * 4 = 1728 + 500 = 2228

г) ( 10³ + 8³ ) : 8 = ( 1000 + 512 ) : 18 = 1512 : 18 = 84

13 14 15 16 17 18 19 20

Ответы к пункту 23. Доли. Обыкновенные дроби, стр. 13

Задание 35

Начертите в тетради квадрат со стороной в 6 клеток. Разделите его на три доли. Начертите отдельно треть квадрата.

Задание 36

Разделите тремя способами квадрат со стороной 4 см на 4 доли. Начертите четверть квадрата, половину квадрата.

Задание 37

Какая часть фигуры закрашена (рис. 109)?

Решение

а) закрашена 1/7 часть отрезка 

б) закрашена 1/3 часть квадрата 

в) закрашена 1/4 часть круга 

г) закрашена 1/2 часть треугольника 

д) закрашено 2/5 части прямоугольника 

е) закрашено 2/5 части круга 

ж) закрашено 1/3 части треугольника 

з) закрашено 5/6 части прямоугольника 

и) закрашено 4/10 части квадрата 

к) закрашено 5/5 частей круга 

л) закрашена 1/2 часть квадрата 

м) закрашено 3/5 части прямоугольника 

н) закрашено 7/8 частей круга 

o) закрашено 8/100 частей квадрата

Задание 38

Как называется:
а) одна сотая доля метра;
б) одна тысячная доля тонны;
в) одна двадцать четвёртая доля суток;
г) одна шестидесятая доля часа;
д) одна миллионная доля квадратного метра;
е) одна миллионная доля кубического метра?

Решение

a) 1 см

б) 1 кг

в) 1 ч

г) 1 мин

д) 1 мм

е) 1 см³

Задание 39

Прочитайте записи: 1/7 отрезка, 1/100 кг, 1/12 суток, 1/3 дороги, 1/4 дыни, 1/2 яблока.

Решение

Одна седьмая часть отрезка, одна сотая часть килограмма, одна двенадцатая часть суток, одна третья часть дороги, одна четвёртая часть дыни, одна вторая часть яблока.

Задание 40

Купили кусок ткани длиной 2 м 50 см и из 1/5 куска сшили платье для куклы. Сколько сантиметров ткани ушло на это платье?

Решение

250 * $\frac15$ = 50 (см) -  ткани ушло на платье.
Ответ: 50 см.

 

Задание 41

Купили дыню массой 2 кг 400 г. Ване отрезали 1/5 дыни, а Маше − 1/6 дыни. Чему равна масса каждого отрезанного куска? Сколько граммов дыни осталось?

Решение

1) 2400 * $\frac15$ = 480 (г) -  дыни отрезали Ване. 
2) 2400 * $\frac16$ = 400 (г) -  дыни отрезали Маше.
3) 2400 − (480 + 400) = 2400 − 880 = 1520 (г) - дыни осталось.
Ответ: 480 г, 400 г, 1520 г.

Задание 42

Петя готовил уроки 1 ч 40 мин. На математику он потратил 1/5 этого времени, а на историю − 1/4 оставшегося времени. Сколько минут Петя готовил уроки по математике и сколько по истории?

Решение

 
1) 100 * $\frac15$ = 20 (мин) - потратил Петя на математику.
2) (100 − 20) * $\frac14$ = 80 * 1/4 = 20 (мин) - потратил Петя на историю.
Ответ: по 20 минут.

Задание 43

Начертите квадрат со стороной 6 клеток. Разделите его на 3 доли и закрасьте 2/3 квадрата. Какая часть квадрата осталась незакрашенной?

Решение

Не закрашенной осталась 1/3 часть квадрата.

Задание 44

Начертите отрезок длиной 8 см. Отметьте цветным карандашом 5/8 отрезка. Какая часть отрезка осталась неотмеченной?

Решение

Не отмеченными остались 3/8.

Задание 45

Прочитайте дроби: 2/7 , 3/4 , 9/10 , 6/12 , 3/1000 , 5/247 , 7/90000 .
Назовите числитель и знаменатель каждой дроби.

Решение

2/7 − две седьмых,
3/4 − три четвертых,
9/10 − девять десятых,
6/12 − шесть двенадцатых,
3/1000 − три тысячных,
5/247 − пять двести сорок седьмых,
7/90000 − семь девяносто тысячных.
Числитель вверху, знаменатель внизу.

Задание 46

Запишите в виде обыкновенной дроби:
а) три шестых;
б) одна треть;
в) половина;
г) три четверти;
д) семь десятых;
е) одиннадцать сотых;
ж) одиннадцать сорок восьмых.

Решение

а) $\frac36$

б) $\frac13$

в) $\frac12$

д) $\frac34$

е) $\frac{11}{100}$

ж) $\frac{11}{48}$

Задание 47

Дорога от Фабричного до Ильинского равна 8 км (рис. 110). Лена прошла по этой дороге 3 км. Какую часть дороги она прошла?

Решение

Длина всей дороги равна 8 км.
Поэтому 1 км составляет 1/8 всей дороги, а 3 км - 3/8 дороги.
Значит, Лена прошла 3/8 дороги.

Задание 48

В январе 31 день, а в году 365 дней. Какую часть года составляет январь? апрель? февраль?

Решение

Один день − $\frac{1}{365}$ часть года.

В январе 31 день,поэтом у он составляет $\frac{31}{365}$ года.

В апреле 30 дней − $\frac{30}{365}$ года.

В феврале 28 дней − $\frac{28}{365}$ года.

Задание 49

В январе 1995 года с 1 января по 10 января были зимние каникулы, 15, 22 и 29 января были воскресными днями, а остальные − учебными. Какую часть января составили свободные от учёбы дни? Какую часть составили учебные дни?

Решение от

В январе 31 день, поэтому 1 день составляет $\frac{1}{31}$ часть января.

Свободным от учебы в январе были 13 дней, что составляет $\frac{13}{31}$ часть месяца.

Учебных дней в январе было 31 − 13 = 18, что составляет − $\frac{18}{31}$ часть месяца.

Задание 50

Площадь поля 16 км². Пшеницей засеяли 11 км², рожью − 5 км². Какая часть поля засеяна пшеницей и какая рожью?

Решение

По условию 1 км² составляет 1/16 часть поля, следовательно пшеницей засеяно 11/16 поля, а рожью 5/16 поля.

Задание 51

Дорога от Фабричного до Отдыха составляет 3/4 дороги от Фабричного до Ильинского. Чему равно расстояние от Фабричного до Отдыха, если от Фабричного до Ильинского 8 км?

Решение

Разделим всю дорогу на 4 доли (рис. 111).
Тогда длина одной доли дороги равна 8 : 4, то есть 2 км.
А длина 3/4 дороги, то есть трёх таких долей, равна 2 * 3, то есть 6 км.
Значит, от Фабричного до Отдыха 6 км.

Задание 52

Длина дороги 20 км. Заасфальтировали 2/5 дороги. Сколько километров дороги заасфальтировали? Сколько осталось заасфальтировать?

Решение

Длина одной пятой дороги равна 20 : 5 = 4 км, следовательно 2/5 дороги составляют 2 * 4 = 8 км, и осталось заасфальтировать 20 − 8 = 12 км.

Задание 53. На базу в Антарктиду доставили 22 собаки. Из 5/11 всех собак составили упряжку, на которой отправились в поход. Сколько собак не вошло в упряжку?

Решение

1) 22 : 11 * 5 = 10 (с.) -  вошли в упряжку.
2) 22 − 10 = 12 (с.) - не вошло в упряжку.
Ответ: 12 собак не вошло в упряжку.

Задание 54. Купили 5 кг 600 г сахара и израсходовали на варенье 7/8 всего сахара. Сколько сахара пошло на варенье? Сколько сахара осталось?

Решение

1) 5600 : 8 * 7 = 4900 (г) - израсходовали на варенье.
4900 г = 4 кг 900 г
2) 5600 − 4900 = 700 (г) - сахара осталось.
Ответ: 4900 г сахара израсходовали на варенье, 700 г осталось.

Задание 55

Сколько молока в бидоне, если 1/5 этого молока составляет 13 л?

Решение

Всего в бидоне в пять раз больше, то есть
13 * 5 = 65 (л)  молока.

Задание 56

Дорога от Фабричного до Кратова равна 5 км, что составляет 5/8 дороги от Фабричного до Ильинского. Найдите расстояние от Фабричного до Ильинского.

Решение

Так как пять восьмых дороги составляют 5 км, то одыа восьмая этой дороги равна 5 : 5, то есть 1 км. А тогда вся дорога в 8 раз длиннее, чем 1 км, то есть имеет длину 1 * 8, или 8 км.
Итак, от Фабричного до Ильинского 8 км.

 

Задание 57

Человек прошёл 2/3 дороги. Какова длина всей дороги, если он прошёл 4 км?

Решение

4 : 2 * 3 = 6 (км)
Ответ: длина всей дороги 6 км.

Задание 58

Велосипедист проехал 2/9 дороги. Какова длина дороги, если он проехал 40 км?

Решение

Из условий задачи следует что 2/9 пути равны 40 км, значит 1/9 пути равна 40 : 2 = 20 км, а длина всего пути 20 * 9 = 180 км.

40 : 2 9 = 180 (км)
Ответ: длина дороги 180 км.

Задание 59

Миша исписал 10 страниц тетради, что составляет 5/6 всей тетради. Сколько страниц в тетради?

Решение

Из условий задачи следует что 5/6 тетради составляют 10 страниц, значит 1/6 тетради составляют 10 : 5 = 2 страницы, а всего в тетради 2 * 6 = 12 страниц.

10 : 5 * 6 = 12 (стр.)
Ответ? в тетради 12 страниц.

Задание 60

В куске материи 96 м. Для детского сада взяли 3/8 этого куска, а для детских яслей 5/12 куска. Для кого взяли больше материи − для детского сада или для яслей? На сколько метров?

Решение

1) 96 : 8 * 3 = 12 * 3 = 36 (м) - материи взяли для детского сада. 
2) 96 : 12 * 5 = 8 * 5 = 40 (м) - материи для яслей.
3) 40 − 36 = 4 (м) - материи больше взяли для яслей.
Ответ: на 4 м материи больше взяли для яслей.

Задание 61

Вычислите устно:

Решение

a) 810, 9, 450, 600.

б) 10, 300, 550, 11.

в) 630, 9, 360, 500.

г) 8, 1000, 5, 600.

Задание 62

Десятую часть миллиона уменьшили на 10 000 и результат уменьшили в тысячу раз. Сколько получили?

Решение

(1000000 : 10 − 10000) : 1000 = (100000 − 10000) : 1000 = 90000 : 1000 = 90.

Задание 63. Имеется круг, диаметр которого 10 см. Найдутся ли две точки этого круга, расстояние между которыми: 5 см; 1 см; 10 см; 12 см? Ответьте на те же вопросы для окружности радиусом 5 см.

Решение

Максимальное расстояние между точками круга не превышает длину диаметра этого круга, следовательно у круга с диаметром 10 см есть точки, между которыми 5 см, 1 см, 10 см, но не существует точек между которыми расстояние 12 см. Круг радиусом 5 см это то же самое, что и круг диаметром 10 см.

Задание 64

Приведите примеры предметов, имеющих форму окружности; круга; дуги окружности; полукруга.

Решение

Окружность: обруч, кольцо.
Круг: тарелка, крышка, колесо.
Дуга окружности: лезвие серпа; ободок; подкова.
Полукруг: арбузная долька, полумесяц.

Задание 65

Поставьте вместо многоточия необходимые слова: ««Отрезок называется диаметром, если он ... и он ...»

Решение

Отрезок называется диаметром, если он соединяет 2 точки окружности и он проходит через ее центр.

Задание 66

Сколько минут:
а) в трети часа;
б) в четверти часа;
в) в половине часа;
г) в десятой доле часа;
д) в двенадцатой доле часа;
е) в шестой доле половины часа?

Решение

а) $\frac13$ ч = 60 : 3 = 20 мин

б) $\frac14$ ч = 60 : 4 = 15 мин

в) $\frac12$ ч = 60 : 2 = 30 мин

г) $\frac1{10}$ ч = 60 : 10 = 6 мин

д) $\frac1{12}$ ч = 60 : 12 = 5 мин

е) $\frac16$ от $\frac12$ ч = 30 : 6 = 5 мин

Задание 67

Сколько секунд:
а) в 5 минутах;
б) в четверти часа;
в) в одном часе;
г) в четверти минуты;
д) в трети минуты;
е) в половине минуты?

Решение

a) 5 мин = 5 * 60 = 300 с

б) $\frac14$ ч = 60 * 60 : 4 = 900 с

в) 1 ч = 60 * 60 = 3600 с

г) $\frac14$ мин = 60 : 4 = 15 с

д) $\frac13$ мин = 60 : 3 = 20 с

е) $\frac12$ мин = 60 : 2 = 30 с

 

Задание 68

Сколько в действительности времени, если часы, отражённые в зеркале (рис. 113), показывают 9 ч; 8 ч; 6 ч 15 мин; 10 ч 40 мин? Когда часы и их отражение покажут одинаковое время?

Решение

Показания часов в зеркале и их показания в действительности симметричны относительно вертикальной оси проходящей через цифры 6 и 12. Поэтому 9 ч в зеркале − 3 ч в действительности, 8 ч − 4 ч, 6 ч 15 мин − 5 ч 45 мин, 10 ч 40 мин − 1 ч 20 мин. Одинаковое время на часах будет когда минутная и часовая стрелки находятся одновременно на вертикальной оси, то есть в 12 ч и 6 ч.

Задание 69. Отметьте точки А и В так, что АВ = 5 см. Проведите окружности одинакового радиуса с центрами А и B так, чтобы они:
а) пересекались в двух точках;
б) не имели общих точек.

Задание 70

Начертите отрезок АВ = 6 см. Найдите точки, которые удалены от А и от В на 6 см.

Решение

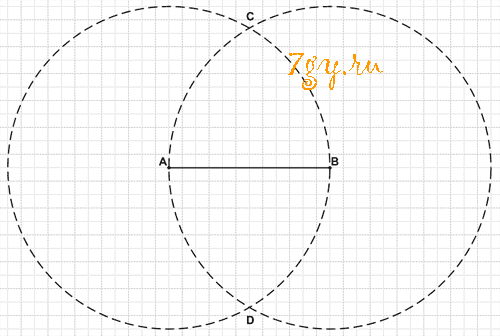
Точки C и D удалены от А и от В на 6 см.

Задание 71. Начертите окружность с центром в точке О и радиусом 2 см 6 мм (рис. 114). Отметьте такую точку К, чтобы ОК = 4 см. Найдите с помощью циркуля на окружности точки, удалённые от точки К на 3 см.

Решение

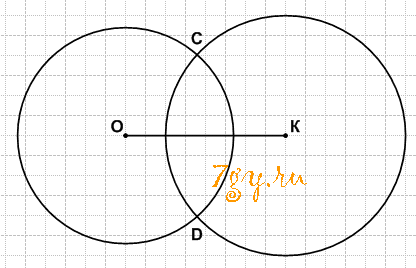
Точки С и D удалены от точки K на 3 см.

Задание 72

 

Бетонный блок имеет длину 12 дм, ширину 8 дм и высоту 5 дм. Из таких блоков сложили стену длиной 240 дм, шириной 24 дм и высотой 30 дм. Сколько блоков потребовалось для этого?

Решение

1) 12 * 8 * 5 = 480 (дм³) - объем одного блока.
2) 240 * 24 − 30 = 172800 (дм³) - объем стены.
3) 172 800 : 480 = 360 (б.) - потребовалось
Ответ: на строительство стены потребовалось 360 блоков.

Задание 73

На книжную полку ставят 6 разных книг. Сколькими способами эти книги можно разместить на полке?

Решение

6! = 1 * 2 * 3 * 4 * 5 * 6 = 720 (способами)

Задание 74

Решите задачу:
1) В двух спортивных секциях поровну участников. Если в каждую из них войдут ещё по 2 участника, то всего в них будет 36 человек. Сколько человек занимается в каждой секции?
2) В трёх классах поровну учащихся. Если в каждый класс добавить ещё по 3 учащихся, то всего в них будет 129 учащихся. Сколько человек учится в каждом классе?

Решение

1) Пусть в каждой секции занимается х человек, тогда после пополнения всего будут
заниматься 2 * (х + 2) человека.
Составим и решим уравнение:
2(х + 2) = 36
х + 2 = 36 : 2 = 18
х = 18 − 2
х = 16 (ч.)
Ответ: по 16 человек занимается в каждой секции.

2) Пусть в каждом классе х учащихся, тогда в каждом классе станет (x + 3) учащихся.
Общее число учащихся будет 3 * (х + 3) человека.
Составим и решим уравнение:
3 * (х + 3) = 129
у + 3 = 129 : 3 = 43
у = 43 − 3
у = 40 (уч.)
Ответ: по 40 учащихся в каждом классе.

!Задание 75

Выполните действия:
1) 90 720 : (207 : 23 * 840);
2) 22 624 : 56 * (816 : 8);
3) 14 700 : 21 : 7 * 49;
4) 140 : 10 : (49 : 7) : (10 : 5).

Решение

1) 90720 : (207 : 23 * 840) = 90720 : (9 * 840) = 90720 : 7560 = 12

2) 22624 : 56 * (816 : 8) = 404 * 102 = 41208

3) 14700 : 21 : 7 − 49 = 700 : 7 − 49 = 100 * 49 = 4900

4) 140 : 10 : (49 : 7) : (10 : 5) = 14 : 7 : 2 = 2 : 2 = 1

Задание 76. Начертите круг радиусом 2 см и закрасьте 3/4 круга.

Задание 77

Из трёхлитрового бидона с молоком взяли 2 л молока. Какую часть всего молока взяли?

Решение

1 л молока составляет 1/3 часть бидона, следовательно всего взяли 2/3 молока.

Задание 78

Площадь квадрата 16 см². Найдите, чему равна площадь:
а) 3/4 квадрата;
б) половины квадрата.

Решение

a) 16:4*3 = 4*3 = 12 (см²)

б) 16:2 = 8 (см²)

Задание 79

На огороде собрали 42 кг огурцов и 5/7 всех огурцов засолили. Сколько килограммов огурцов засолили?

Решение

1/7 часть огурцов равна 42 : 7 = 6 кг, значит засолили 5 * 6 = 30 кг огурцов.

42 : 7 * 5 = 30 (кг) - огурцов засолили.
Ответ: 30 кг огурцов.

 

Задание 80

Мастерская получила 700 м шёлка. Из 2/7 полученной ткани сшили блузки, а из 2/5 полученной ткани сшили платья. Сколько метров шёлка осталось?

Решение

1) 700 : 7 * 2 = 100 * 2 = 200 (м) - ткани пошло на блузки,
2) 700 : 5 * 2 = 140 * 2 = 280 (м) - ткани пошло на платья.
3) 700 − (200 + 280) = 700 − 480 = 220 (м) - ткани осталось.
Ответ: 220 м шёлка осталось.

Задание 81

До перерыва шахматисты играли 4/5 всего времени партии. Сколько времени продолжалась партия, если до перерыва шахматисты играли 2 ч?

Решение

1) 120 м : 4 = 30 мин - 1/5 часть времени партии.
2) 30 * 5 = 150 мин = 2 ч 30 мин продолжалась партия.
Ответ: партия продолжалась 2 ч 30 мин.

Задание 882

До обеда выгрузили 7/10 зерна, находившегося в товарном вагоне. Сколько тонн зерна было в вагоне, если выгрузили 42 т?

Решение

42 : 7 * 10 = 60 (т) - зерна было в вагоне.
Ответ: 6 т.

Задание 83

Постройте круг радиусом 5 см. Проведите в нём диаметр АВ. Отметьте на окружности точку М и соедините её с точками А и В. Измерьте: диаметр АВ, отрезок АМ, отрезок MB. Какой из этих отрезков самый длинный?

Решение

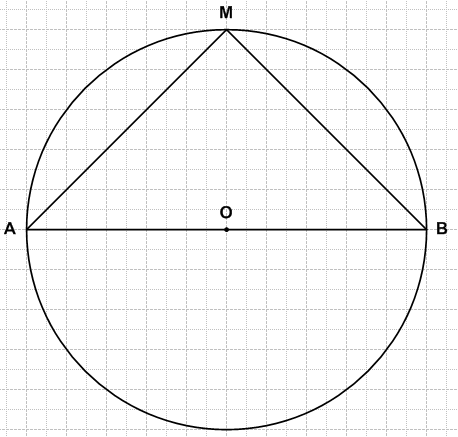
AB = 10 см − самый длинный
AM = MB = 7 см 7 мм

Задание 84

Какую часть 1 м³ составляет 1 см³? Какую часть 1 м² составляет 1 см²?

Решение

1) $1{\operatorname м}^3=1000000{\operatorname с}{\operatorname м}^3,1{\operatorname с}{\operatorname м}^3=\frac1{1000000}{\operatorname м}^3$
2) $1{\operatorname м}^2=10000{\operatorname с}{\operatorname м}^2,1{\operatorname с}{\operatorname м}^2=\frac1{10000}{\operatorname м}^2$

Задание 85

Найдите значение выражения:
а) 87619 + 57994 : 271 − 15975 : 75;
б) 532 * 109 − 48016 + 13631 : 43.
Для выражения а) составьте программу и схему вычисления.

Решение

а) 1) Делим 57994 на 271;
2) Делим 15975 на 75;
3) 87619 + результат 1 действия;
4) Результат 3 действия − результат 2 действия.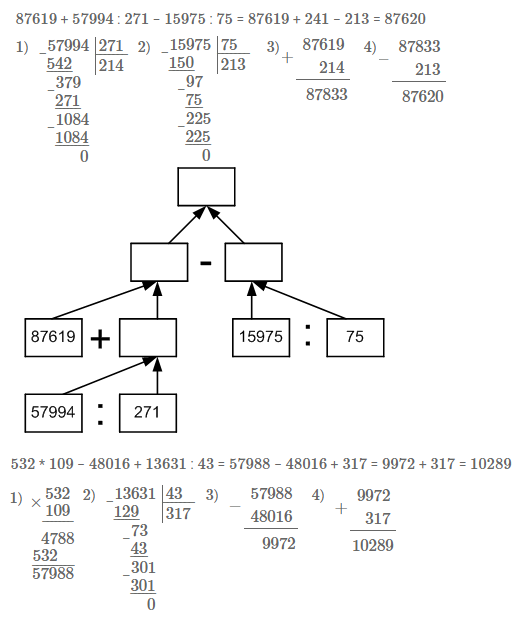

Задание 86

Разгадайте кроссворд, помещённый на форзаце в конце учебника.

Решение

По горизонтали:
1. Двести. 3. Вершок. 8. Секунда. 9. Деление. 10. Уравнение. 14. Дециметр.
По вертикали:
2. Игрек. 4. Штрих. 5. Баррель. 6. Фунт. 7. Единица. 11. Мера. 12. Литр. 13. Промилле.

Задание 87

Иван Иванович отправился из дому на рыбную ловлю. Три часа он ехал поездом со скоростью 75 км/ч. Потом а ч он шёл пешком со скоростью 5 км/ч, наконец, 2 ч плыл на лодке по озеру со скоростью v км/ч. Какой путь проделал Иван Иванович от вокзала до места рыбалки? Найдите значение получившегося выражения, если:
а) а = 3, v = 6;
б) а = 4, v = 10.

Решение

а) Составим и упростим выражение 3 * 75 + а * 5 + 2 * v = 225 + 5а + 2v (км)
При а = 3 и v = 6
225 + 5а + 2v = 225 + 5 * 3 + 2 * 6 = 225 + 15 + 12 = 252 (км)

б) Составим и упростим выражение 3 * 75 + а * 5 + 2 * v = 225 + 5а + 2v (км)
При а = 4 и v = 10
225 + 5а + 2v = 225 + 5 * 4 + 2 * 10 = 225 + 20 + 20 = 265 (км)

Задание 88

Мотоциклист и велосипедист едут навстречу друг другу. Через сколько часов они встретятся, если расстояние между ними 272 км, скорость велосипедиста 12 км/ч, а скорость мотоциклиста 56 км/ч?

Решение

272 : (12 + 56) = 272 : 68 = 4 (ч)
Ответ: мотоциклист и велосипедист встретятся через 4 часа.

Задание 89

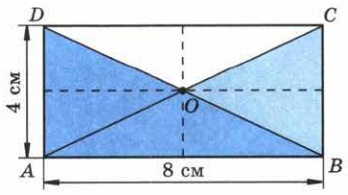
По рисунку 115 найдите площади треугольников ABC, ACD, ABO и ВСО.

Решение

S ABCD = AB * AD = 8 * 4 = 32 см²;
S ABC = S ABCD : 2 = 30 : 2 = 16 см²;
S ACD = S ABC = 16 см²,
S ABO = S ABCD : 4 = 32 : 4 = 8 см²,
S ВСО = S ABCD : 4 = 32 : 4 = 8 см².

Задание 90

У продавца 80 кг яблок. Первый покупатель приобрёл 10 кг яблок, а остальные а покупателей − по 6 кг каждый. Сколько яблок осталось у продавца? Какие значения может принимать а?

Решение

У продавца осталось 80 − (10 + 6 * а) = 70 − 6а (кг) яблок.
В полученном выражении а может принимать натуральные значения от 0 до 11.

21 22 23 24 25 26

Ответы к пункту 24. Сравнение дробей, стр. 21

Задание № 91

Объясните с помощью рисунка, почему
а) 1/3 = 4/12; б) 3/4=9/12

Решение

а) На рисунке квадрат поделён на 3 и на 12 частей, а закрашенная площадь у них одинакова, значит
1 = 4
3   12

На рисунке квадрат поделён на 4 и на 12 частей, а закрашенная площадь у них одинакова, значит
3 = 9
4  12

Задание № 92

Начертите в тетради отрезок длиной в 18 клеток. С помощью этого отрезка объясните, почему: а) 2/9 = 4/18; б) 5/6=15/18.

Решение

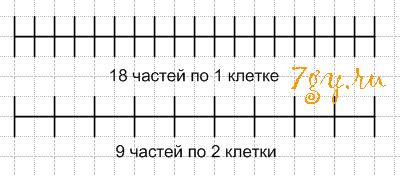
а) Отрезок АВ можно разбить на 18 частей по 1 клетке или на 9 частей по 2 клетки, тогда:
4 части по 1 клетки равны 2 частям по 2 клеткам, то есть
2 = 4
9   18


б) Отрезок АВ можно разбить на 18 частей по 1 клетке или на б частей по 3 клетки, тогда:
15 частей по 1 клетки равны 5 частям по 3 клеткам, то есть
5 = 15
6   18

Задание № 93

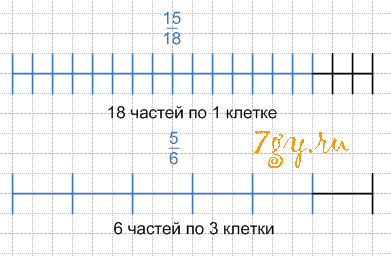
Единичный отрезок равен 12 клеткам. Отметьте на координатном луче точки
A(5/6) и B(10/12). Объясните результат.

Решение

Отрезок можно поделить на 12 частей по одной клетке или на б частей по 2 клетки.
Из рисунка видно, что 5 частей по 2 клетки равняется 10 частям пр 1 клетки.

Задание № 94

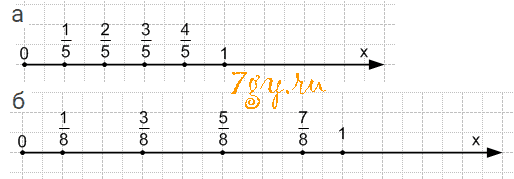
Отметьте на координатном луче точки, координаты которых равны:
а) 1/5,2/5,3/5,4/5;
б) 1/8,3/8,5/8,7/8.

Ответ

Задание № 95

Единичный отрезок равен длине 6 клеток тетради. Отметьте на координатном луче точки с координатами 1/2;1/3;1/6;2/3. Какая из этих точек левее всех расположена на луче, а какая правее всех?

Решение

Левее всего расположена точка 1/6.
Правее всего расположена точка 2/3.

Задание № 96

Расставьте в порядке возрастания дроби:7/12; 1/12; 5/12; 9/12; 11/12; 4/12.
Расставьте эти дроби в порядке убывания.

Решение

1) 1  4    5   7   9  11
   12 12 12 12 12 12
2) 11  9   7   5   4   1
    12 12 12 12 12 12

Задание № 97

Замените звёздочку знаком < или > в записях

Решение

3 > 7
10 10

5 > 1
8 8

9 < 13
16 16

5 > 3
7 7

Задание № 98

Какая из дробей больше

Решение

4 > 2
5    5

3 < 13
19  19

  23  > 21
1000  1000

 87 > 78
100  100

Задание № 99

Какая из точек лежит левее на координатном луче:
а) A(3/7) или B(5/7);
б) M(11/13) или N(9/13)?

Решение

а) Так как 3/7 < 5/7 , то точка А лежит левее точки B.
б) Так как 9/13 < 11/13 то точка N лежит левее точки M.

Задание № 100

Вычислите устно

Решение

a) 60, 300, 480, 6, 90.
б) 150, 200, 5, 350, 7.
в) 45, 90, 75, 3, 270.
г) 180, 250, 50, 400, 16.
д) 160, 680, 480, 8, 1000.

Задание № 101

Прочитайте дроби...Назовите числитель и знаменатель.

Решение

1
5 − одна пятая, 1 − числитель, 5 − знаменатель;
1
8 − одна восьмая 1 − числитель, 8 − знаменатель;
10
11 − десять одиннадцатых 10 − числитель, 11 − знаменатель;
12
23 − двенадцать двадцать третьих 12 − числитель, 23 − знаменатель;
20
57 − двадцать пятьдесят седьмых 20 − числитель, 57 − знаменатель;
1
61 − одна шестьдесят первая 1 − числитель, 61 − знаменатель;
11
90 − одиннадцать девяностых 11 − числитель, 90 − знаменатель;
17
100 − семнадцать сотых 17 − числитель, 100 − знаменатель;
111
120 − сто одиннадцать сто двадцатых 111 − числитель, 120 − знаменатель;
100
277 − сто двести семьдесят седьмых 100 − числитель, 277 − знаменатель;
15
582 − пятнадцать пятьсот восемьдесят вторых 15 − числитель, 582 − знаменатель.

 

Задание № 102

На координатном луче отмечены следующие точки: A ( 2/8 ) ; B ( 1/7 ) ; C ( 1/4 ) ; D ( 2/14 ) ; E ( 5/20 ) ; K ( 10/70 ) . Есть ли среди них совпадающие?

Решение

Так как 2/8 = 1/4 = 5/20 и 1/7 = 2/14 = 10/70 , то совпадают точки:
A (2/8) , C (1/4) , E (5/20) и
B (1/7) , D (2/14) , K (10/70).

Задание № 103

Какую часть на рисунке 120 составляет:
а) треугольник АВО от четырёхугольника АВСО;
б) треугольник АВО от четырёхугольника ABCD;
в) четырёхугольник АВСО от четырёхугольника ABCD;
г) четырёхугольник АВСО от шестиугольника ABCDEK?

Решение

а) Треугольник ABO составляет
1
2 часть от четырехугольника АВСО
б)
треугольник ABO составляет
1
3 часть от четырехугольника ABCD
в) четырехугольник АВСО составляет
2
3 от четырехугольника ABCD
г) четырехугольник АВСО составляет
2
6 от шестиугольника ABCDEK

Задание № 104

Попробуйте найти самый короткий путь по поверхности куба от точки А к точке В (рис. 121).
Сколько таких путей можно указать?

Решение

Для нахождения кратчайшего пути можно сделать развертку куба.

На развертке указаны 4 самых коротких пути.

Задание № 105

Выполните деление с остатком:
а) 5 на 2;
б) 100 на 30;
в) 29 на 9;
г) 100 на 11.

Решение

a) 5 = 2 * 2 + 1
б) 100 = 30 * 3 + 10
в) 29 = 9 * 3 + 2
г) 100 = 11 * 9 + 1

Задание № 106

Какую долю составляют: а) сутки от года; б) сутки от недели; в) дециметр от метра; г) 1 см³ от литра? Подумайте, почему 1 см³ называют ещё и миллилитром (1 мл).

Решение

a)  1 год = 365 суток, 1 сутки = 1/365 года
б) 1 неделя = 7 суток, 1 сутки = 1/7 недели
в) 1 м = 10 дм, 1 дм = 1/10 метра
г) 1 л = 1000 см³ , 1 см³ = 1/1000 л
1 см³ называют миллилитром (1 мл),
потому что 1000 см³ = 1 дм³ , а 1 дм³ = 1 л.

Задание № 107

Объём кувшина 5 л. В него налили а л воды. Какая часть объёма кувшина занята водой? Дайте ответ при а = 1; 2; 3; 4.

Решение

Водой занята а/5 часть кувшина.
При а = 1 , а/5 = 1/5
при а = 2 , а/5 = 2/5
при а = 3 , а/5 = 3/5
при а = 4 , а/5 = 4/5

Задание № 108

Решение

Какую часть периметра квадрата составляет длина одной стороны? длина трёх сторон?

Если длина стороны квадрата а, то его периметр Р = 4а, а сумма длин трёх сторон 3а.
Следовательно, длина одной стороны составляет 1/4 периметра, а длина трёх сторон составляет 3/4 периметра.

Задание № 109

Продолжительность урока 45 мин. На решение задачи ушло 7 мин. Какая часть урока ушла на решение задачи?

Решение

1 минута составляет 1/45 часть урока, значит 7 минут составляют 7/45 урока.

Задание № 110

От доски длиной 9 м отпилили 4 м. Какую часть доски отпилили?

Решение

1 метр составляет 1/9 часть доски, значит 4 метра составляют 4/9 часть доски.

Задание № 111

Андрей гулял 2 ч. В хоккей он играл 4/5 этого времени. Сколько времени Андрей играл в хоккей?

Решение

1/5 от 2 ч составляет 120 : 5 = 24 мин, а 4/5 от 2 ч составляют 24 * 4 = 96 мин = 1 ч 36 мин.

Задание № 112

Около дома стояло 7 машин. Из них 2 были серыми, а остальные − синими. Какую часть всех машин составляли синие машины?

Решение

1 машина составляет 1/7 часть от числа всех машин, количество синих машин равно 7 − 2 = 5, что составляет 5/7 от общего числа машин.

Задание № 113

В аквариум напили 6 л воды, заполнив 6/7 его объёма. Сколько литров воды вмещает аквариум?

Решение

Так как 6 литров составляют 6 частей аквариума, то одна часть аквариума равна 1 литру, а всего аквариум вмещает 1 * 7 = 7 (л) воды.

 

Задание № 114

Можно ли из прямоугольного листа фанеры длиной 6 дм и шириной 4 дм вырезать круг радиусом:
а) 3 дм;
б) 2 дм;
в) 1 дм?

Решение

а) Если радиус круга 3 дм, то его диаметр 2r = 2 * 3 = 6 дм.
Так как 6 дм > 4 дм, то из прямоугольного листа фанеры размерами 6 дм х 4 дм круг радиуса 3 дм вырезать нельзя.
б) При r = 2 дм => d = 2r = 4 дм, 4 дм < 4 дм < 6 − круг можно вырезать.
в) При r = 1 дм => d = 2r = 2 дм, 2 дм < 4 дм < 6 дм − круг можно вырезать.

Задание № 115

Выполните действия:
1) 229 372 : 286 * 506;
2) 282 370 : 302 : 85;
3) 195 840 : (32 * 18);
4) 538 * (301 608 : 426).

Решение

1) 229372 : 286 * 506 = 802 * 506 = 405812
2) 282370 : 302 : 85 = 935 : 85 = 11
3) 195840 : (32 * 18) = 195840 : 576 = 340
4) 538 * (301608 : 426) = 538 * 708 = 380904

Задание № 116

Примите за единичный отрезок длину 10 клеток тетради и отметьте на координатном луче числа: 1/10,2/10,3/10,4/10,5/10,6/10,7/10,8/10,9/10.

Решение

Задание № 117

Поставьте вместо звёздочек знаки < или > так, чтобы получилось верное неравенство:
а) 5/9 * 8/9;
б) 14/105 * 13/105;
в) 0 * 14/15;
г) 67430087 * 67430093.

Решение

а) $\frac59<\frac89$
б) $\frac{14}{105}>\frac{13}{105}$
в) $0<\frac{14}{15}$
г) 67430087 < 67430093

Задание № 118

Какую часть недели составляют:
а) пять суток;
б) шесть суток?

Решение

1 сутки = 1/7 недели
5 суток = 5/7 недели
6 суток = 6/7 недели

Задание № 119

Масса тыквы 2 кг 800 г. Найдите массу:
а) 1/4 тыквы;
б) 3/4 тыквы;
в) 2/7 тыквы;
г) 5/7 тыквы.

Решение

a) 2800 : 4 = 700 г
б) 2800 : 4 * 3 = 700 * 3 = 2100 г = 2 кг 100 г
в) 2800 : 7 * 2 = 400 * 2 = 800 г
г) 2800 : 7 * 5 = 400 * 5 = 2000 г = 2 кг

Задание № 120

Дом занимает 1/15 всего садового участка. Найдите площадь участка, если площадь земли под домом 40 м².

Решение

S = 40 * 15 = 600 (м²)

Задание № 121

Два мотоциклиста едут навстречу друг другу. Скорость одного мотоциклиста 62 км/ч, а скорость другого 54 км/ч. Через сколько часов мотоциклисты встретятся, если сейчас между ними 348 км?

Решение

348 : (62 + 54) = 348 : 116 = 3 (ч)
Ответ: через 3 часа встретятся мотоциклисты.

Задание № 122

Масса пачки печенья 125 г, а масса пачки сухарей 380 г. Что тяжелее:
а) 9 пачек печенья или 4 пачки сухарей;
б) 22 пачки печенья или 7 пачек сухарей?

Решение

4 * 380 = 1520 г > 9 * 125 = 1125 г
22 * 125 = 2750 г > 7 * 380 = 2660 г

Задание № 123

В литровой банке помещается 910 г пшена или 780 г гороха. Какая масса меньше:
а) 3 банок пшена или 4 банок гороха;
б) 7 банок пшена или 8 банок гороха?

Решение

3 * 910 = 2730 г < 4 * 780 = 3120 г
8 * 780 = 6240 г < 7 * 910 = 6370 г

Задание № 124

От куска проволоки длиной а м в первый раз отрезали b м, а во второй раз − с м. Какой смысл имеют следующие выражения:
а) b + с;
б) a − (b + с);
в) a − b;
г) a − b − с?
Какие из этих выражений принимают одинаковые значения при любых значениях букв а, b, с?
Проверьте ваш ответ при а = 45, b = 7 и с = 12.

Решение

b + с соответствует общей длине отрезанной проволоки
a − (b + с) соответствует длине оставшейся проволоки
a − b соответствует длине проволоки, оставшейся после отрезания
a − b − с = a − (b + с) соответствует общей длине отрезанной проволоки.
При а = 45, b = 7, с = 12;
a − (b + с) = 45 − (7 + 12) = 45 − 19 = 26,
a − b − с = 45 − 7 − 12 = 38 − 12 = 26.

27 28 29 30

Ответы к пункту 25. Правильные и неправильные дроби, стр. 27

Задание № 125

Длина отрезка АВ равна 8 см. Начертите отрезок, длина которого равна:
а) 3/4 длины отрезка АВ;
б) 5/4 длины отрезка АВ.

Решение

а)

б)

Задание № 126

Отметьте на луче точки с координатами: 1/4;2/4;3/4;4/4;5/4;6/4;7/4;8/4.
За единичный отрезок примите длину 12 клеток тетради.

Решение

Задание № 127

Напишите:
а) все правильные дроби со знаменателем 6;
б) все неправильные дроби с числителем 5.

Решение

а) $\frac16,\frac26,\frac36,\frac46,\frac56$

б) $\frac51,\frac52,\frac53,\frac54,\frac55$

Задание № 128

При каких значениях а дробь:
а) a/10 будет правильной;
б) 16/a будет неправильной?

Решение

При а = 1, 2, 3, 4, 5, 6, 7, 8, 9 дробь a/10 является правильной
При а = 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16 дробь 16/a является неправильной.

Задание № 129

Машина за 6 мин может вырыть канаву длиной в 1 м.
Какой длины канаву выроет машина за 1 мин; 5 мин; 7 мин; 11 мин?

Решение

Задание № 130

Одним килограммом краски можно покрасить 5 м² поверхности.
Сколько понадобится краски, чтобы покрасить 3 м²; 6 м²; 13 м² поверхности?

Решение

Задание № 131

Бригада строителей построила ферму за 48 дней. По плану требовалось 5/4 этого времени. Сколько дней отводилось на постройку фермы по плану?

Решение

48 : 4 * 5 = 12 * 5 = 60 (д.)
Ответ: 60 дней отводилось на постройку фермы по плану.

Задание № 132

Токарь за 3 ч выточил на токарном станке 135 деталей, выполнив 3/5 дневной нормы. Сколько деталей он должен был выточить за рабочий день (8 часов) по норме? Сколько деталей он выточит за рабочий день, если будет работать с той же производительностью?

Решение

1) 135 : 3 * 5 = 45 * 5 = 225 (д.) - дневная норма токаря
2) 135 : 3 = 45 (д.) - вытачивает токарь за 1 ч
3) 45 * 8 = 360 (д.) - сделает токарь за 8 ч
Ответ: 360 деталей.

Задание № 133

Токарь выточил на токарном станке 135 деталей, выполнив 27/20 дневной нормы. Какова его дневная норма?

Решение

135 : 27 * 20 = 5 * 20 = 100 (д)
Ответ: 100 деталей - дневная норма токаря.

Задание № 134

Концерт юных музыкантов вместо запланированных 3 ч продолжался 13/10 этого времени, так как зрители просили повторить некоторые понравившиеся выступления. Сколько времени продолжался концерт? Сколько минут продолжались выступления на бис?

Решение

1) 3 * 60 : 10 * 13 = 18 * 13 = 234 (мин) - продолжался концерт
234 (мин) = 3 ч 54 мин
2) 3 ч 54 мин - 3 ч = 54 мин - продолжалось выступление на бис
Ответ: 3 ч 54 мин, 54 мин.

Задание № 135

Вычислите устно:
а) 400 : 25
* 5
+ 40
: 12
+ 190
?
б) 700 - 20
: 4
* 2
: 17
+ 480
?
в) 420 : 14
* 6
+ 120
: 25
* 8
?
г) 320 + 240
: 80
* 50
- 60
: 29
?

Решение

а) 16, 80, 120, 10, 200.
б) 680, 170, 340, 20, 500.
в) 30, 180, 300, 12, 96.
г) 560, 7, 350, 290, 10.

Задание № 136

Сколько минут в часе? Какую часть часа составляет 1 мин; 7 мин; 15 мин?

Решение

1 ч = 60 мин, 1 мин = 1/60 ч, 7 мин = 7/60 ч, 15 мин = 15/60 ч.

Задание № 137

Во сколько раз центнер больше килограмма? Какую часть центнера составляет килограмм? На сколько центнер больше килограмма?

Решение

1 ц = 100 кг,
100 кг : 1 кг = 100,
1 кг = 1/100 ц,
1 ц − 1 кг = 100 кг − 1 кг = 99 кг.

Задание № 138

Сколько минут:
в 1/10 ч;в 1/4 ч;в 1/3 ч;в 2/5 ч;в 3/4 ч?

Решение

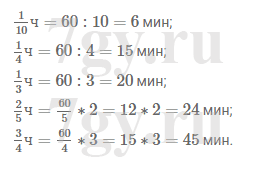
Задание № 139

Сложите 2/5 числа 40 и 2/3 числа 60.
Из 5/6 числа 72 вычтите 2/9 числа 81.

Решение

Задание № 140

Половина числа равна 18. Найдите это число. Треть числа равна 27. Найдите это число. Три четверти числа равны 60. Найдите это число.

Решение

18 * 2 = 36
27 * 3 = 81
60 : 3 * 4 = 80

Задание № 141

Какая часть четырёхугольника ABCD (рис. 125) закрашена? Какая часть осталась незакрашенной?

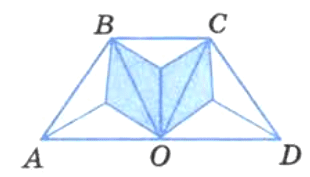
Решение

Закрашено 4/9 четырехугольника ABCD, осталось не закрашено 5/9 четырехугольника.

Задание № 142

Выразите в граммах:
а) 3 кг 400 г;
б) 2 кг 30 г;
в) 15 кг.

Решение

a) 3 кг 400 г = 3400 г
б) 2 кг 30 г = 2030 г
в) 15 кг = 15000 г

Задание № 143

Расположите в порядке возрастания дроби:4/11;2/11;10/11;9/11;8/11;7/11.
Расположите эти же дроби в порядке убывания.

Решение

В порядке возрастания: $\frac2{11}<\frac4{11}<\frac7{11}<\frac8{11}<\frac9{11}<\frac{10}{11}$
В порядке убывания: $1\frac{10}{11}>\frac9{11}>\frac8{11}>\frac7{11}>\frac4{11}>\frac2{11}$

 

Задание № 144

Назовите четыре дроби, которые меньше, чем 1/1000000.

Решение

$\frac1{1100000}<\frac1{1010000}<\frac1{1001000}<\frac1{1000100}<\frac1{1000000}$

Задание № 145

Назовите 5 дробей, которые больше, чем 1/9.

Решение

$\frac69>\frac59>\frac49>\frac39>\frac29>\frac19$

Задание № 146

Начертите квадрат со стороной 4 см. Покажите на чертеже: 6/16 квадрата, 3/8 квадрата. Найдите площади этих частей квадрата и объясните полученный результат.

Решение

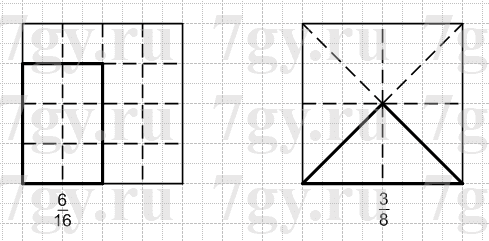
$S_{квадрата}=4\ast4=16\;(см^2)$
$16\ast6:16=6\;(см^2)$ - площадь 6/16 квадрата;
$16\ast3:8=6\;(см^2)$ - площадь 3/8 квадрата.

Задание № 147

В первый день бригада собрала 5 т 400 кг картофеля, а во второй − на 1 т 200 кг меньше, чем в первый. В третий день бригада собрала в 2 раза больше картофеля, чем во второй. Сколько картофеля собрано бригадой за эти три дня?

Решение

1) 5 т 400 кг − 1 т 200 кг = 5400 кг − 1200 кг = 4200 кг картофеля собрала бригада во второй день
2) 2 * 4200 = 8400 (кг) - картофеля собрала бригада в третий день
3) 5400 + 4200 + 8400 = 18000 (кг) = 18 (т) - картофеля собрала бригади за 3 дня
Ответ: 18 т картофеля.

Задание № 148

Составьте задачу по уравнению:
а) (у + 6) − 2 = 15;
б) 2(a − 5) = 24;
в) 3(25 + b) + 15 = 135.

Решение

а) У Вити было на 6 рублей больше чем у Пети. Сколько рублей было у Пети, если у Вити, истратившего 2 рубля осталось 15 рублей.
Пусть у Пети было y рублей, тогда у Пети было у + 6 рублей.
Составим уравнение:
(у + 6) − 2 = 15
у + 4 = 15
y = 15 − 4 = 11 (р.) - было у Пети

б) Скорость первого велосипедиста на 5 км/ч меньше скорости второго велосипедиста. Найдите скорость второго велосипедиста, если первый велосипедист за 2 часа проехал 24 км.
Пусть скорость второго велосипедиста равна а км/ч, тогда скорость первого велосипедиста равна (а − 5) км/ч.
Составим уравнение:
2(a − 5) = 24
2a − 10 = 24
2a = 24 + 10 = 34
a = 34 : 2 = 17 (км/ч) - скорость второго велосипедиста

в) Расстояние между селом и городом равно 135 км. Найдите скорость мотоцикла, если известно, что автомобиль, выехавший из села со скоростью на 25 км/ч больше скорости мотоцикла, через три часа не доехал до города 15 км.
Пусть скорость мотоцикла равна b км/ч, тогда скорость автомобиля равна (25 + b) км/ч.
Составим уравнение:
3(25 + b) + 15 = 135
75 + b + 15 = 135
b = 135 − 75 − 15 = 45 (км/ч) - скорость мотоцикла

Задание № 149

В первом вагоне ехали а человек, а во втором − b человек. На остановке из первого вагона вышли с человек, а из второго − d человек. Какой смысл имеют следующие выражения:
a + b; с + d; (a + b) − (с + d);
a − с; b − d; (a − с) + (b − d)?
Объясните, почему
(a + b) − (c + d) = (a − c) + (b − d) при а > с, b > d.
Проверьте это равенство при а = 45, b = 39, с = 14, d = 12.
Используя полученное равенство, вычислите значение выражения:
а) (548 + 897) − (148 + 227);
б) (391 + 199) − (181 + 79).

Решение

a + b − число пассажиров в первом и втором вагонах,
с + d − общее число вышедших пассажиров,
(a + b) − (с + d) − число оставшихся пассажиров в первом и втором вагонах,
a − с − число пассажиров оставшихся в первом вагоне,
b − d − число пассажиров оставшихся во втором вагоне;
(a − с) + (b − d) = a − c + b − d = (a + b) − (с + d).
Если a = 45, b = 39, с = 14, d = 12,
(a + b) − (с + d) = (45 + 39) − (14 + 12) = 84 − 26 = 58;
(a − c) + (b − d) = (45 − 14) + (39 − 12) = 31 + 27 = 58.

а) (548 + 897) − (148 + 227) = (548 − 148) + (897 − 227) = 400 + 670 = 1070
б) (391 + 199) − (181 + + 79) = (391 − 181) + (199 − 79) = 210 + 120 = 330

Задание № 150

Придумайте пять дробей, у которых числитель на 3 меньше знаменателя. Запишите пять дробей, у которых числитель в 3 раза больше знаменателя.

Решение

$\frac47,\frac58,\frac69,\frac7{10},\frac8{11}$
$\frac62,\frac93,\frac{12}4,\frac{15}5,\frac{18}6$

Задание № 151

При каких значениях х дробь 8/х будет неправильной?

Решение

При х от 1 до 8 дробь 8/х будет неправильной.

Задание № 152

Фермер наметил собрать с поля 12 т овощей, а собрал 7/6 этого количества. Сколько тонн овощей собрал фермер?

Решение

12 : 6 * 7 = 2 * 7 = 14 (т)
Ответ: 14 т овощей собрал фермер.

Задание № 153

Турист прошёл за первый день 18 км, что составляет 6/5 пути, который он должен пройти во второй день. Сколько километров должен пройти турист за эти два дня?

Решение

1) 18 : 6 * 5 = 3 * 5 = 15 (км) - должен пройти турист за второй день
2) 18 + 15 = 33 (км) - должен пройти турист за два дня
Ответ: 33 км.

Задание № 154

Из Санкт−Петербурга в Москву вышел товарный поезд со скоростью 48 км/ч, а через час после этого из Москвы в Санкт−Петербург вышел скорый поезд со скоростью 82 км/ч. Найдите расстояние между поездами:
а) через 1 ч после выхода скорого поезда;
б) через 3 ч после выхода товарного поезда;
в) через 5 ч после выхода скорого поезда.
Расстояние от Москвы до Санкт−Петербурга 650 км.

Решение

a) 650 − (48 * 1 + (82 + 48 * 1) = 650 − (48 + 130) = 650 − 178 = 472 км
б) 650 − (48 * 3 + 82 * 2) = 650 − (144 + 164) = 650 − 308 = 342 км
в) 48 * 6 + 82 * 5 − 650 = 288 + 410 − 650 = 698 − 650 = 48 км

Задание № 155

Найдите значение выражения:
а) 8060 * 45 − 45 150 : 75 * 105;
б) (2 254 175 + 94 447) : 414 − 1329;
в) (12³−9³):(12−9);
г) (6²+3²)².

Решение

а) 8060 * 45 − 45 150 : 75 * 105 = 362700 − 602 * 105 = 362700 − 63210 = 299490

б) (2254175 + 94447) : 414 − 1329 = 2348622 : 414 − 1329 = 5673 − 1329 = 4344

в) $(12^3-9^3):(12-9)=(144\ast12-81\ast9):3=999:3=333$

г) $(6^2+3^2)^2=(36+9)^2=452=2025$

31 32 33 34 35 36 37 38

Ответы к пункту 26. Сложение и вычитание дробей с одинаковыми знаменателями, стр. 31

Задание № 156

Из помидоров массой 5/16 кг и огурцов массой 9/16 кг сделали салат. Какова масса салата?

Решение

$\frac5{16}+\frac9{16}=\frac{5+9}{16}=\frac{14}{16}$ (кг)
Ответ: масса салата $\frac{14}{16}$ кг.

Задание № 157

Масса станка равна 73/100 т, а масса его упаковки 23/100 т. Найдите массу станка вместе с упаковкой.

Решение

 73   + 23 = 96 (т)
100   100   100
Ответ: 96 т.
           100

Задание № 158

В первый день картофель посадили на 2/7 участка, а во второй день − на 3/7 участка. Какая часть участка была засажена картофелем за эти два дня?

Решение

2 + 3 = 5 (уч.)
7    7    7
Ответ: 5 участка засадили за два дня
            7

Задание № 159

Одна бригада получила 7/10 т гвоздей, а вторая − на 3/10 т меньше. Сколько гвоздей получила вторая бригада?

Решение

  7 - 3 = 4 (т)
10  10  10
Ответ: 4 т гвоздей получила вторая бригада.
           10

Задание № 160

За два дня засеяли 10/11 поля. В первый день засеяли 4/11 поля. Какую часть поля засеяли во второй день?

Решение

$\frac{10}{11}-\frac4{11}=\frac{10-4}{11}=\frac6{11}$
Ответ: $\frac6{11}$ поля засеяли во второй день.

Задание № 161

Цистерна на 3/5 наполнена бензином. 1/5 цистерны перелили в бочку. Какая часть цистерны осталась заполненной бензином?

Решение

$\frac35-\frac15=\frac{3-1}5=\frac25$
Ответ: $\frac25$ цистерны осталась заполненной бензином.

 

Задание № 162 с ответами

Выполните действие:

а) $\frac47+\frac27=\frac{4+2}7=\frac67$
б) $\frac19+\frac69=\frac{1+6}9=\frac79$
в) $\frac{13}{19}+\frac5{19}=\frac{13+5}{19}=\frac{18}{19}$
г) $\frac{13}{100}+\frac{26}{100}=\frac{13+26}{100}=\frac{39}{100}$
д) $\frac79-\frac29=\frac{7-2}9=\frac59$
е) $\frac45-\frac35=\frac{4-3}5=\frac15$
ж) $\frac{13}{17}-\frac4{17}=\frac{13-4}{17}=\frac9{17}$
з) $\frac{37}{100}-\frac{16}{100}=\frac{37-16}{100}=\frac{21}{100}$

Задание № 163

Найдите значение выражения:
а) 4/11+a, если а=1/11,3/11,5/11;
б) b−1/10, если b=7/10,5/10,3/10;
в) 3/14+6/14+c, если c=1/14,2/14;
г) 12/17−3/17−d, если d=4/17,5/17.

Решение

Задание № 164

Из 11 теплиц овощеводческого хозяйства 4 засажены помидорами, а 2 − огурцами. Какая часть теплиц занята огурцами и помидорами? Решите задачу двумя способами.

Решение

1 способ.
Помидорами и огурцами занято 4 + 2 = 6 теплиц, что составляет 6/11 всех теплиц.
2 способ.
Помидорами занято 4/11 теплиц, огурцами − 2/11 теплиц.
Всего помидорами и огурцами занято
4 + 2 = 6 (т.)
11 11   11
Ответ: 6 теплиц.
           11

Задание № 165

Для посадки леса выделили участок площадью 300 га. Ель высадили на 3/10 участка, а сосну − на 4/10 участка. Сколько гектаров занято елью и сосной вместе?

Решение

1) 3 + 4 = 7 (уч.) - занято елью и сосной
  10   10   10
2) 300 : 10 * 7 = 30 * 7 = 210 (га)
Ответ: 210 га занято елью и сосной.

Задание № 166

Бригада решила изготовить 175 изделий сверх плана. В первый день она изготовила 9/25 этого количества, во второй день − 13/25 этого количества. Сколько изделий изготовила бригада за эти два дня? Сколько изделий ей осталось изготовить?

Решение

1) 9 + 13 = 22 (ч) - от всех деталей изготовила бригада за 2 дня
    25   25   25
2) 175 : 25 * 22 = 7 * 22 = 154 (д.) - изготовила бригада за 2 дня
3) 175 − 154 = 21 (д.) - осталось изготовить
Ответ: 154 детали, 21 деталь.

Задание № 167

Картофелем засажено 11/17 поля овощеводческого хозяйства. Огурцами засеяно на 1/17 поля больше, чем морковью, и на 8/17 поля меньше, чем картофелем. Какая часть поля засеяна огурцами и какая морковью? Какая часть поля занята картофелем, огурцами и морковью вместе?

Решение

1) 11 - 8 = 3 (части) - засеяна огурцами
    17  17  17
2)  3 - 1 = 2 (части) - засеяно морковью
    17 17  17
3) 11 + 3 + 2 = 16 (части) - засеяно картофелем, огурцами и морковью засеяно
    17   17  17   17
Ответ: 3/17, 2/17, 16/17.

Задание № 168

Выполните действия:

а) $\frac{18}{19}-\frac7{19}+\frac3{19}=\frac{18-7+3}{19}=\frac{14}{19}$

б) $\frac27+\frac47-\frac57=\frac{2+4-5}7=\frac17$

в) $\frac9{11}-\frac3{11}-\frac2{11}=\frac{9-3-2}{11}=\frac4{11}$

г) $\frac5{12}+\frac3{12}+\frac3{12}=\frac{5+3+3}{12}=\frac{11}{12}$

д) $\frac{11}{15}-(\frac3{15}+\frac7{15})=\frac{11}{15}-\frac{3+7}{15}=\frac{11}{15}-\frac{10}{15}=\frac1{15}$

е) $\frac{13}{16}-(\frac{13}{16}-\frac3{16})=\frac{13}{16}-\frac{13-3}{16}=\frac{13}{16}-\frac{10}{16}=\frac3{16}$

Задание № 169 с ответами

Решите уравнение:

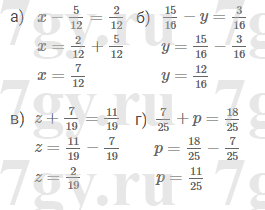
Задание № 170

В палатке было 2 ц 70 кг фруктов. Яблоки составляли 5/9 всех фруктов, а груши − 1/9 всех фруктов. На сколько масса яблок больше массы груш? Решите задачу двумя способами.

Решение

1 способ.
2 ц 70 кг = 270 кг
1) 270 : 9 * 5 = 150 (кг) - масса яблок
2) 270 : 9 = 30 (кг) - масса груш
3) 150 − 30 = 120 (кг) - яблок больше чем груш.
Ответ: на 120 кг.

2 способ.
Яблок больше, чем груш на
5 - 1 = 4 (ч.) - на столько яблок больше, чем груш
9 9 9
270 : 9 * 4 = 120 (кг) - на столько яблок больше, чем груш
Ответ: на 120 кг.

Задание № 171

В первый день турист прошёл 5/14 всего пути, а во второй день − 7/14 всего пути. Известно, что за эти два дня турист прошёл 36 км. Сколько километров составляет весь путь туриста?

Решение

1) 5 + 7 = 12 (ч) пути прошли туристы за 2 дня
   14  14   14
2) 36 : 12 * 14 = 42 (км) - весь путь
Ответ: 42 км.

Задание № 172

Первый рассказ занимал 5/13 книги, а второй рассказ − 2/13 книги. Известно, что первый рассказ занимал на 12 страниц больше, чем второй. Сколько страниц во всей книге?

Решение

1) 5 - 2 = 3 (ч.) - книги составляет 12 страниц
   13  13 13
2) 12 : 3 * 13 = 52 (стр.) - вся книга
Ответ: 52 страницы.

Задание № 173

Воспользовавшись равенством 4/25+12/25=16/25, найдите значения выражений и решите уравнения:

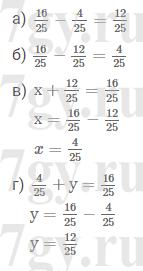
Задание № 174

Вычислите устно:
а) 24 - 9
* 8
+ 12
- 17
: 9
?
б) 57 - 49
* 7
+ 14
- 28
: 7
?
в) 66 - 59
* 7
+ 17
- 38
: 4
?
г) 42 - 33
* 6
+ 27
- 9
: 8
?
д) 72 - 67
* 6
+ 24
- 20
: 17
?

Ответы

a) 5, 40, 52, 45, 5.
б) 9, 54, 81, 72, 9.
в) 8, 56, 70, 42, 6.
г) 5, 30, 54, 34, 2.
д) 7, 49, 66, 28, 7.

Задание № 175

На экскурсию отправляются 260 человек. Сколько нужно заказать автобусов, если в каждом автобусе должно быть не более 30 пассажиров?

Решение

260 : 30 = 8 (ост.20)
Ответ: нужно заказать не менее 9 автобусов.

Задание № 176

Начертите отрезок. Затем начертите отрезок, длина которого равна:
а) 1/3 длины данного отрезка;
б) 3/4 длины данного отрезка;
в) 5/5 длины данного отрезка;
г) 7/5 длины данного отрезка.

Решение

а) 

б)

в)

г)

Задание № 177

Найдите координаты точек A, B, С, D, Е, М, К (рис. 128) и сравните эти координаты с 1.

Решение

$A(\frac3{10}),B(\frac{13}{10}),{\operatorname С}(\frac5{10}),D(\frac9{10}),{\operatorname Е}(2),{\operatorname М}(1),{\operatorname К}(\frac{17}{10})$
$\frac3{10}<\frac5{10}<\frac9{10}<1<\frac{13}{10}<\frac{17}{10}<2$

Задание № 178

Вычислите периметр и площадь треугольника ABC (рис. 129).

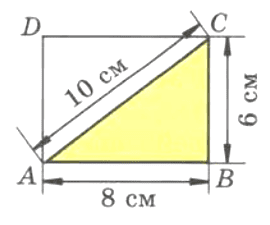
Решение

$P_{ABC}=10+8+6=24\;(см)$
$S_{ABC}=8\ast6:2=24\;(см^2)$

 

Задание № 179

Сравните:
а) 1/5 ц и 1/5 т;
б) 1/5 ц и
1/50 т;
в) 1/100 га и 1/10 а;
г) 1/10 л и 20 см3;
д) 1/4 кг и 250 г.

Решение

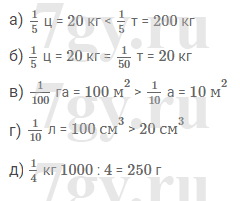
Задание № 180

Верно ли, что:
а) 157/289 меньше 289/157;
б) 12/11 больше 751/751?

Решение

$\frac{157}{289}<1<\frac{289}{157}$
$\frac{12}{11}>1=\frac{751}{751}$

Задание № 181

Найдите все значения х, при которых дробь x/15 будет правильной а дробь 8/х − неправильной.

Решение

При х = 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14 − дробь x/15 будет правильной,
а при х = 1; 2; 3; 4; 5; 6; 7; 8 − дробь 8/х будет неправильной.

Задание № 182

Назовите 3 правильные дроби, числитель которых больше, чем 100. Назовите 3 неправильные дроби, знаменатель которых больше, чем 200.

Решение

$\frac{150}{200},\frac{300}{400},\frac{412}{715}$ − правильные дроби, у которых числитель больше 100;
$\frac{220}{210},\frac{700}{350},\frac{635}{228}$ − неправильные дроби, у которых знаменатель больше 200.

Задание № 183

Сравните:
а) 7/15 и 13/15;
б) 8/3 и 5/3;
в) 1 и 4/9;
г) 9/4 и 1;
д) 5/3 и 0;
е) 1/1000000 и 0.

Решение

а) 7/15 < 13/15;
б) 8/3 > 5/3;
в) 1 > 4/9;
г) 9/4 > 1;
д) 5/3 > 0;
е) 1/1000000 > 0.

Задание № 184

Длина прямоугольного параллелепипеда 8 м, ширина 6 м и высота 12 м. Найдите сумму площадей наибольшей и наименьшей граней этого параллелепипеда.

Решение

8 * 12 = 96 (м²) - площадь наибольшей грани
8 * 6 = 48 (м²) - площадь наименьшей грани
96 + 48 = 144 (м²) - сумма площадей

Задание № 185

Для изготовления 750 м вискозной ткани требуется 10 кг целлюлозы. Из 1 м3 древесины можно получить 200 кг целлюлозы. Сколько метров вискозной ткани можно получить из 20 м³ древесины?

Решение

200 * 20 : 10 * 750 = 400 * 750 = 300000 (м)
Ответ: 300000 м вискозной ткани можно получить из 20 м³ древесины.

Задание № 186

Кодовый замок имеет шесть кнопок. Чтобы его открыть, нужно нажать кнопки в определённой последовательности (набрать код). Сколько существует вариантов кода для этого замка?

Решение

Если каждую кнопку можно нажать только один раз, то первую выбираем из 6 кнопок, вторую - из 5, третью - из 4, четвёртую - из 3, пятую - из двух, шестая -1 кнопка.
6*5*4*3*2*1=720 (способов)
Ответ: существует 720 вариантов кода для этого замка.

Задание № 187

Решите уравнение:
а) (х − 111) * 59 = 11 918;
б) 975(y − 615) = 12 675;
в) (30 901 − а) : 605 = 51;
г) 39 765 : (b − 893) = 1205.

Решение

a) (x − 111) * 59 = 11918
x − 111 = 11918 : 59 = 202
x = 202 + 111
x = 313

б) 975 * (y − 615) = 12675
у − 615 = 12675 : 975 = 13
у = 13 + 615
у = 628

в) (30901 − a) : 605 = 51
30901 − a = 51 * 605 = 30901
a = 30901 − 30855
a = 46

г) 39765 : (b − 893) = 1205
b − 893 = 39765 : 1205 = 33
b = 33 + 893
b = 926

Задание № 188

Решите задачу:
1) Из 30 высаженных семян взошли 23. Какая часть высаженных семян взошла?
2) На пруду плавали 40 лебедей. Из них 30 были белыми. Какую часть всех лебедей составляли белые лебеди?

Решение

1) Взошло 23/32 всех семян.
2) Белые лебеди составляли 30/40=3/4

Задание № 189

Найдите значение выражения:
1) 76 * (3569 + 2795) − (24 078 + 30 785);
2) (43 512 − 43 006) * 805 − (48 987 + 297 305).

Решение

1) 76 * (3569 + 2795) − (24078 + 30785) = 76 − 6364 − 54863 = 483664 − 54863 = 428801
2) (43512 − 43006) * 805 − (48987 + 297305) = 506 * 805 − 346 292 = 407330 − 346292 = 61038

 

Задание № 190

За первый час было расчищено от снега 5/17 всей дороги, а за второй час 9/17 всей дороги. Какая часть дороги была расчищена от снега за эти два часа? На какую часть дороги было расчищено меньше в первый час, чем во второй?

Решение

1) 5 + 9 = 14 (части) расчищено за 2 часа
   17  17   17
2) 9 - 5 = 4 (ч.) - на столько расчищено меньше в первый час
   17 17  17
Ответ: 14/17, на 4/17.

Задание № 191

На платье для первой куклы было израсходовано 6/25 м ткани, а на платье для второй куклы 9/25 м ткани. Сколько ткани было израсходовано на оба платья? На сколько больше ткани было израсходовано на платье второй куклы, чем на платье первой куклы?

Решение

1) 6 + 9 = 15 (т.) израсходовано на оба платья
   25   25   25
2) 9 - 6 = 3 (т.) на столько больше пошло на платье второй куклы
    25 25 25
Ответ: на 3/25 ткани.

Задание № 192 с ответами

Выполните действия:

а) $\frac2{11}+\frac5{11}=\frac{2+5}{11}=\frac7{11}$

б) $\frac18+\frac48=\frac{1+4}8=\frac58$

в) $\frac6{15}-\frac4{15}=\frac{6-4}{15}=\frac2{15}$

г) $\frac{11}{25}-\frac3{25}=\frac{11-3}{25}=\frac8{25}$

д) $\frac39+\frac29-\frac49=\frac{3+2-4}9=\frac19$

е) $\frac5{18}+\frac{12}{18}-\frac9{18}=\frac{5+12-9}{18}=\frac8{18}$

ж) $\frac{12}{19}-\frac1{19}-\frac5{19}=\frac{12-1-5}{19}=\frac6{19}$

з) $\frac{25}{23}-\frac{10}{23}+\frac3{23}=\frac{25-10+3}{23}=\frac{18}{23}$

Задание № 193

Решите уравнение:
а) $\frac{17}{20}-x=\frac{14}{20}-\frac3{20}$
б) $\frac8{15}-\frac7{15}+y=\frac{14}{15}$

Решение

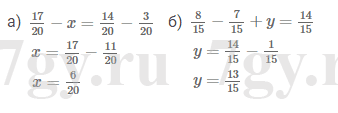
Задание № 194

Геологи прошли маршрут длиной 75 км. В первый день они прошли 3/25 всего маршрута, а во второй − 4/25 всего маршрута. Какой путь прошли геологи за эти два дня?

Решение

1) 3 + 4 = 7 (м.) прошли за 2 дня
   25   25  25
2) 75 : 25 * 7 = 3 * 7 = 21 (км) - путь за 2 дня
Ответ: 21 км.

Задание № 195

От деревни Никольское до города 24 км. Дорога лесом составляет 5/12 пути, а остальная часть проходит полем. Сколько километров дороги проходит полем?

Решение

1) 1 − 5 = 7 (п.) - дорога полем
    12 12   12
2) 24 : 12 * 7 = 14 (км) - проходит полем
Ответ: 14 км.

Задание № 196

Из 12 дней зимних каникул Лена была 7 дней у бабушки. Какую часть каникул Лена была у бабушки?

Решение

Лена была у бабушки 7/12 своих каникул.

Задание № 197

Из сливок получили 18 кг масла, что составляет 1/5 массы сливок. Сколько было взято сливок?

Решение

18 * 5 : 1 = 90 (кг)
Ответ: 90 кг сливок было взято.

Задание № 198

Автомашина за 3 дня прошла 980 км. За первые 2 дня она прошла 725 км. Сколько прошла автомашина в каждый из этих дней, если во второй день она прошла больше, чем в третий день, на 123 км?

Решение

1) 980 − 725 = 255 (км) - проехала автомашина за третий день
2) 255 + 123 = 378 (км) - проехала автомашина во второй день
3) 725 − 378 = 347 (км) - проехала автомашина в первый день
Ответ: 347 км, 378 км, 255 км.

Задание № 199

Турист проехал 378 км. Поездом он ехал 4 ч, а на мотоцикле 3 ч. С какой скоростью турист ехал на мотоцикле, если поезд шёл со скоростью 60 км/ч?

Решение

1) 60 * 4 = 240 (км) - проехал на поезде
2) 378 - 240 = 138 (км) - проехал на мотоцикле
3) 138 : 3 = 46 (км/ч) - ехал на мотоцикле
Ответ: 48 км/ч.

Задание № 200

Выполните действия:
а) 2035303998 + 63008007665;
б) 23268841675 + 6777888.

Решение

а)
+2035303998
63008007665
65043311663
б)
+23268841675
          6777888
  23275619563

Задание № 201

Четвёртый лишний. В каждом ряду три числа обладают общим свойством, а одно число этим свойством не обладает. Укажите, что это за свойство и какое число лишнее.

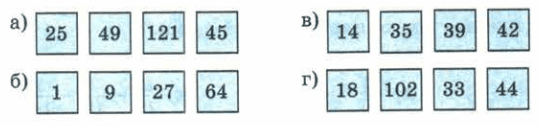
Решение

a) Числа 25 = 52, 49 = 72, 121 = 112 − квадраты натуральных чисел, а число 45 не является квадратом натурального числа, поэтому оно лишнее.
б) Числа 1 = 13, 27 = 33, 64 = 43 − кубы натуральных чисел, а число 9 не является кубом натурального числа, и оно лишнее.
в) Числа 14, 35, 42 кратны 7, а число 39 не кратно 7, поэтому оно лишнее.
г) Числа 18, 102, 33 кратны 3, а число 44 не кратно 3, поэтому оно лишнее.

39 40 41 42 43 44

Ответы к пункту 27. Деление и дроби, стр. 39

Задание № 202

Запишите в виде дроби частные:
2 : 5; 1 : 10; 15 : 8; 7 : 1; 20 : 4; 77 : 10.

Решение

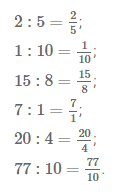
Задание № 203

Запишите каждую из дробей 299/23,527/31 в виде частного и найдите его значение.

Решение

$\frac{299}{23}=299:23=13$
$\frac{527}{31}=527:31=17$

Задание № 204 с ответами

Заполните пустые клетки таблицы:

Задание № 205

За неделю израсходовано 3 кг сахара. Сколько килограммов сахара в среднем расходовали за один день?

Решение

3 : 7 = 3 (кг)
7 
Ответ: 3/7 кг сахара в среднем расходовали за один день.

Задание № 206

Изделие на конвейере за 5 мин продвигается на 4 м. Найдите скорость движения конвейера.

Решение

4 : 5 = 4 (м/мин) = 400 см : 5 мин = 80 см/мин
5
Ответ: 80 см/мин.

Задание № 207

Из 4 м ткани сшили 7 юбок. Сколько ткани пошло на каждую юбку?

Решение

4 : 7=4 (м)
7
Ответ: 4/7 м ткани пошло на каждую юбку.

Задание № 208

Верёвку длиной в 7 м разрезали на 12 равных кусков. Найдите длину каждого куска.

Решение

 7 : 12 = 7 (м)
12
Ответ: 7/12 м - длина каждого куска.

Задание № 209

Решите уравнение:

а) $\frac x9=13$
б) $\frac{132}k=11$
в) $\frac m{12}=28$
г) $\frac{528}y=66$
д) $\frac{n-11}{16}=7$

Решение уравнений

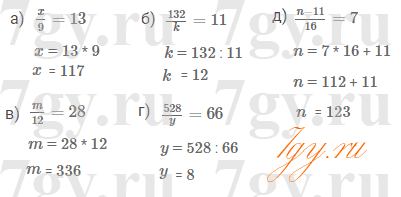
Задание № 210

Найдите значение выражения, применяя свойство деления суммы на число:
а) (48 + 80) : 16;
б) (3393 + 999) : 3;
в) 405 : 27 + 135 : 27;
г) 2926 : 19 + 874 : 19.

Решение

a) (48 + 80) : 16 = 48 : 16 + 80 : 16 = 3 + 5 = 8
б) (3393 + 999) : 3 = 3393 : 3 + 999 : 3 = 1131 + 333 = 1464
в) 405 : 27 + 135 : 27 = (405 + 135) : 27 − 540 : 27 = 20
г) 2926 : 19 + 874 : 19 = (2926 + 874) : 19 = 3800 : 19 = 200

Задание № 211

Расскажите, как на координатном луче отметить точки:
$A(\frac18),B(\frac38),C(\frac44),D(\frac{11}8),E(\frac2{16})$

Решение

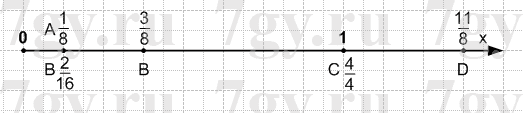
Первым шагом необходимо выбрать единичный отрезок. Для удобства лучше выбрать отрезок, который является наименьшим общим кратным знаменателей указанных координат (в данном номере лучше выбрать за единичный отрезок 16 клеток тетради).
Для того чтобы узнать где на координатном луче поставить точку необходимо количество клеток, взятых за единичный отрезок, умножить на числитель координаты точки и поделить на знаменатель координаты точки. Получившийся результат будет показывать сколько клеток от начала координат Вам нужно отсчитать, чтобы поставить точку.
Например для точки A(1/8): 16 * 1 : 8 = 2 клетки тетради необходимо отсчитать вправо от начала координат, чтобы поставить точку А.

Задание № 212

Вычислите устно:
а) 55 - 47
* 9
- 34
: 19
* 24
?
б)
75 - 66
* 9
- 27
+ 18
: 18
?
в) 84 - 78
* 8
+ 12
: 5
* 30
?
г) 91 : 13
* 80
+ 240
- 500
: 15
?
д) 98 : 14
* 70
+ 210
: 35
* 15
?

Ответы

a) 8, 72, 38, 2, 48.
б) 7, 560, 800, 300, 20.
в) 9, 81, 54, 72, 4.
г) 7, 490, 700, 20, 300.
д) б, 48, 60, 12, 360.

Задание № 213

Представьте числа 64, 144, 1000 в виде суммы их половин, четвертей и восьмых по образцу:

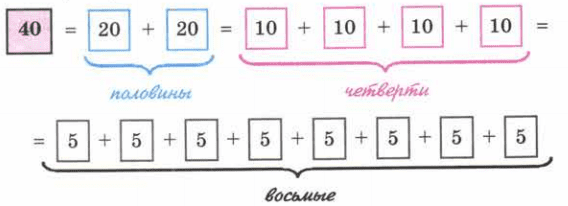
Решение

64 = 32 + 32 = 16 + 16 + 16 + 16 = 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8;
144 = 72 + 72 = 36 + 36 + 36 + 36 = 18 + 18 + 18 + 18 + 18 + 18 + 18 + 18;
1000 = 500 + 500 = 250 + 250 + 250 + 250 = 125 + 125 + 125 + 125 + 125 + 125 + 125 + 125.

Задание № 214

Сколько получится, если:
а) удвоить половину числа а;
б) утроить треть числа х?

Решение

а) $2\ast\frac a2=\frac a2+\frac a2=a$
б) $3\ast\frac{\operatorname х}3=\frac{\operatorname х}3+\frac{\operatorname х}3+\frac{\operatorname х}3=x$

 

Задание № 215

Восстановите цепочку вычислений:

Решение

a) 1 кг → 250 г → 400 г → 1200 с → 6.
б) 1 ч → 4 мин → 10 мин → 30 с → 6.

Задание № 216

Массы монет выпуска 1961 г. в 1 к., 2 к., 3 к. и 5 к. были равны соответственно 1 г, 2 г, 3 г и 5 г. Какую часть массы пятикопеечной монеты составляет масса каждой из остальных монет? Какую часть массы трёхкопеечной монеты составляет масса каждой из остальных монет?

Монета в 1 коп. составляет 1/5 от массы монеты в 5 коп.
Монета в 2 коп. − 2/5 от массы монеты в 5 коп.
Монета в 3 коп. − 3/5 от массы монеты в 5 коп.
Монета в 1 коп. составляет 1/3 от массы монеты в 3 коп.
Монета в 2 коп. − 2/3 от массы монеты в 3 коп.
Монета в 5 коп. 5/3 от массы монеты в 3 коп.

Задание № 217

За одно сокращение сердце человека выталкивает 150 см³ крови. Сколько крови перекачивает сердце человека за 1 мин, за 1 ч при пульсе 60 (пульс − число сокращений сердца за 1 мин)?

Решение

1) 150 * 60 = 9000 (см³)  - крови перекачает сердце за 1 мин
9000 см³ = 9 л
2) 9000 * 60 = 540000 (см³) = 540 (л) - крови перекачает сердце за 1 час
Ответ: 9 л, 540 л.

Задание № 218 с ответами

Выполните действия:

а) $\frac8{25}+\frac7{25}+\frac9{25}=\frac{8+7+9}{25}=\frac{24}{25}$

б) $\frac{13}{15}-(\frac8{15}+\frac4{15})=\frac{13-(8+4)}{15}=\frac1{15}$

в) $(\frac{17}{100}+\frac{27}{100})-(\frac8{100}+\frac3{100})=\frac{17+27}{100}-\frac{8+3}{100}=\frac{44}{100}-\frac{11}{100}=\frac{44-11}{100}=\frac{33}{100}$

г) $(\frac{19}{23}-\frac8{23})+(\frac{16}{23}-\frac{11}{23})=\frac{19-8}{23}+\frac{16-11}{23}=\frac{11}{23}+\frac5{23}=\frac{11+5}{23}=\frac{16}{23}$

Задание № 219

Сколько:
а) граммов в 1/2 кг; в 3/4 кг; в 7/20 кг;
б) минут в 1/2 ч; в 3/4 ч; в 5/6 ч;
в) квадратных метров в 1/2 га; в 1/4 га; в 3/4 га;
г) кубических сантиметров в 1/2м3, в 1/5м3, в 2/5м3?

Решение

Задание № 220

В классе 40 человек. Из них 13 человек ещё не научились плавать. Какая часть учащихся класса умеет плавать?

Решение

40 − 13 = 27 (ч.) - умеют плавать
Это 27 от числа всех учащихся.
       40
Ответ: 27.
            40

Задание № 221

Кусок джинсовой ткани разрезали на равные части. Из 3 частей сшили брюки, а из 7 остальных частей − куртки. Какую часть материи израсходовали на брюки и какую на куртки?

Решение

3 + 7 = 10 (частей) составляет весь кусок
 3 куска израсходовали на брюки
10
 7 куска - на куртки
10

Задание № 222

К полднику в детском саду на четырёхместный стол поставили сок, молоко, какао и компот. Сколькими способами четверо детей могут выбрать себе один из напитков?

Решение

Четверо детей могли выбрать напитки 1 * 2 * 3 * 4 = 24 способами.

Задание № 223

По формуле а = bq + r найдите:
а) а, если b = 19, q = 64 и r = 18;
б) b, если а = 567, q = 37 и r = 12;
в) q, если а = 361, b = 25 и r = 11.

Решение

а) при b = 19, q = 64, r = 18;
a = bq + r = 19 • 64 + 18 = 1216 − 1 − 18 = 1234.
б) при a = 567, q = 37, r = 12;
b = (a − r) : q = (567 − 12) : 37 = 555 : 37 = 14.
в) при а = 361, b = 25, r = 11;
q = (a − r) : b = (361 − 11) : 25 = 350 : 25 = 14.

Задание № 224

Решите задачу:
1) Время движения подводной лодки на поверхности воды в 20 раз меньше, чем время движения под водой. Сколько времени подводная лодка находилась под водой, если это время на 57 ч больше, чем время движения на поверхности воды?
2) Подводная лодка прошла под водой путь, в 17 раз больший, чем путь на поверхности воды. Сколько километров прошла лодка под водой, если на поверхности воды она прошла на 320 км меньше, чем под водой?

Решение

1) Время движения на поверхности примем за 1 часть, тогда под водой - 20 частей. Разница между этими частями составляет 57 часов.
1) 57 : 19 = 3 (ч) - лодка находилась на поверхности
2) 3 * 20 = 60 (ч) - лодка находилась под водой
Ответ: 60 ч.

2) Путь на поверхности примем за 1 часть, тогда под водой - 17 частей. Разница между частями составит 320 км.
2) 320 : 16 = 20 (км) - лодка прошла на поверхности воды, а под водой она прошла
17 * 20 = 340 (км) - лодка прошла под водой
Ответ: 360 км.

Решение с помощью уравнений

1) Пусть подводная лодка двигалась на поверхности воды х ч, тогда под водой она находилась 20x ч.
Под водой лодка находилась на (20х − х) ч больше, чем на поверхности.
Составим и решим уравнение:
20х − x = 57
x = 57 : 19
х = 3 (ч)- лодка находилась на поверхности
20 : 3 = 60 (ч) - лодка находилась под водой
Ответ: 60 ч.

2) Пусть подводная лодка прошла на поверхности воды у км , тогда под водой она прошла 17у км.
Под водой лодка прошла на (17у − у) км больше, чем но поверхности.
Составим и решим уравнение:
17у − у = 320
у = 320 : 16
у = 20 (км) - лодка прошла на поверхности воды, а под водой она прошла
17 * 20 = 340 (км) - лодка прошла под водой
Ответ: 360 км.

Задание № 225

Выполните деление с остатком:
1) 2738 на 125;
2) 3049 на 134.

Решение

_2738 |125
  250   |21
  _238
    125
    113
 
_3049 |134
  268   |22
  _369
    268
    101

Задание № 226

В углах квадратной площадки установлены одинаковые столбы с четырьмя изоляторами для крепления проводов (рис. 130). Надо протянуть по два провода от столба А к столбу С и от столба В к столбу D так, чтобы провода не касались друг друга. Найдите несколько способов, как это можно сделать.

Ответ

Задание № 227

Запишите в виде дроби частное:
а) 4 : 7;
б) 8 : 11;
в) 1 : 6;
г) 9 : 1.

Решение

а) $4:7=\frac47$
б) $8:11=\frac8{11}$
в) $1:6=\frac16$
г) $9:1=\frac91$

Задание № 228

Запишите дробь в виде частного:
а) 5/9;
б) 18/13;
в) 11/6;
г) 139/100.

Решение

а) $\frac59=5:9$
б) $\frac{18}{13}=18:13$
в) $\frac{11}6=11:6$
г) $\frac{139}{100}=139:100$

 

Задание № 229

7 м проволоки разрезали на 8 равных кусков. Сколько метров проволоки в одном куске?

Решение

7 : 8 = 7 (м) проволоки
           8
Ответ: 7 м проволоки в одном куске.
            8

Задание № 230

4 кг варенья разложили в 5 банок поровну. Сколько килограммов варенья в каждой банке?

Решение

4 : 5 = 4 (кг)
           5
Ответ: 4 кг варенья в каждой банке.
            5

Задание № 231

Две тракторные бригады вспахали вместе 762 га поля. Первая бригада работала 8 дней и вспахивала за день 48 га. Сколько гектаров поля вспахивала за день вторая бригада, если она работала 9 дней? Какая бригада вспахала больше и на сколько?

Решение

1) 8 * 48 = 384 (га) - вспахала первая бригада
2) 762 − 384 = 378 (га) - вспахала вторая бригада
3) 378 : 9 = 42 (га) - вспахивала за день вторая бригада
384 − 378 = 6 (га) - больше вспахала первая бригада, чем вторая.
Ответ: 42 га, на 6 га.

Задание № 232

Расстояние между двумя станциями 784 км. С этих станций одновременно навстречу друг другу вышли два поезда. Они встретились через 8 ч. Найдите скорость каждого поезда, если скорость первого на 10 км/ч больше скорости второго.

Решение

1) 10 * 8 = 80 (км) - на столько обгонит один поезд
2) 784 - 80 = 704 (км) - прошли бы оба поезда с одинаковой скоростью
3) 704 : 2 = 352 (км) - пройдет первый поезд
4) 352 : 8 = 44 (км/ч) - скорость первого поезда
5) 44 + 10 = 54 (км/ч) - скорость второго поезда
Ответ: 44 км/ч, 54 км/ч.

Решение с помощью уравнения

Пусть скорость второго поезда х км/ч, тогда скорость первого поезда (х + 10) км/ч.
Скорость сближения поездов равна (х + х + 10) км/ч, они встретились через 784 : (х + х + 10) ч.
Составим и решим уравнение:
784 : (х + х + 10) = 8
2х + 10 = 784 : 8
х = (98 − 10) : 2
х = 44 (км/ч) − скорость второго поезда
44 + 10 = 54 (км/ч) - скорость первого поезда
Ответ: 44 км/ч, 54 км/ч.

Задание № 233

Выполните деление с остатком:
а) 874 267 на 301;
б) 765 420 на 523.

Решение

а) 874 267 : 301 = 2904 (ост.163)
Проверка: 301 * 2904 + 163 = 874267
б) 765 420 : 523 = 1463 (ост.271)
Проверка: 532 * 1463 + 271 = 765420

Задание № 234

Найдите делимое, если делитель равен 78, неполное частное 96 и остаток 17.

Решение

78 * 96 + 17 = 7488 + 17 = 7505

45 46 47 48 49 50

Ответы к пункту 28. Смешанные числа. Страница 45

Задание № 235

Представьте число в виде суммы его целой и дробной частей:

а) $3\frac45=3+\frac45$
б) $8\frac7{10}=8+\frac7{10}$
в) $25\frac{15}{17}=25+\frac{15}{17}$
г) $\frac{11}{14}=0+\frac{11}{14}$

Задание № 236 с ответами

Запишите в виде смешанного числа сумму:

а) $4+\frac3{17}=4\frac3{17}$
б) $18+\frac{27}{100}=18\frac{27}{100}$

Задание № 237

Выделите целую часть из дробей:
5/4;18/7;69/14;83/25;98/11;37/10;503/100;2073/1000;9/3;18/6;77/77;77/7.

Решение

Задание № 238

Запишите в виде смешанного числа частные:
7 : 3; 15 : 4; 20 : 7; 87 : 10; 247 : 23; 377 : 18; 249 : 100.

Решение

Задание № 239

Примите за единичный отрезок длину 6 клеток тетради и отметьте на координатном луче точки с координатами: 3 1/3; 2 5/6; 2 2/3; 1 1/2.

Решение

Задание № 240

За неделю семья израсходовала 8 кг картофеля. Сколько килограммов картофеля расходовали в среднем в один день?

Решение

$8:7=\frac87=1\frac17$ (кг)
Ответ: $1\frac17$ кг картофеля.

Задание № 241

Турист прошёл 25 км за 4 ч. Найдите его скорость.

Решение

$25:4=\frac{25}4=6\frac14$ (км/ч)
Ответ: $6\frac14$км/ч скорость туриста.

Задание № 242

Ученик решил 12 уравнений за 40 мин. Сколько минут в среднем он решал каждое уравнение? Сколько секунд он потратил на решение каждого уравнения?

Решение

$40:12=\frac{40}{12}=3\frac4{12}$ (мин) потратил в среднем на решение каждого уравнения
60 : 12 * 40 = 200 (с) он потратил на решение каждого уравнения
Ответ: $3\frac4{12}$ мин, 200 секунд.

 

Задание № 243

Запишите в виде неправильной дроби числа:
а) 3 1/2; 5 2/3; 4 3/7; 2 9/10;
б) 2; 4; 5; 27 со знаменателями 7 и 11.

Решение

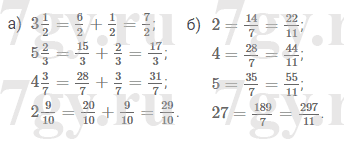
Задание № 244

Выразите:
а) в часах: 1 ч 31 мин, 5 ч 19 мин, 34 мин, 1 сутки 9 ч 16 мин;
б) в километрах: 2 км 260 м, 15 км 876 м.

Решение

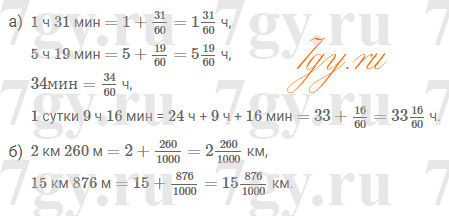
Задание № 245

Площадь фигуры равна 2 3/4 см². Выразите площадь фигуры в виде неправильной дроби. Скольким квадратным миллиметрам равна эта площадь?

Решение

$S=2\frac34=\frac84+\frac34=\frac{11}4{\operatorname с}{\operatorname м}^2=100\ast11:4=1100:4=275{\operatorname м}{\operatorname м}^2$

Задание № 246

У Винни−Пуха несколько банок, вмещающих по 1/2 кг мёда. Сколько ему понадобится таких банок, чтобы разлить в них 6 1/2 кг мёда?

Решение

$6\frac12=\frac{12}2+\frac12=\frac{13}2$
Ответ: Винни−Пуху понадобится 13 банок.

Задание № 247

Бревно, длина которого 9 2/3 м, распилили на части, по 1/3 м в каждой. Сколько получилось таких частей?

Решение

$9\frac23=\frac{27}3+\frac23=\frac{29}3$
Ответ: получится 29 частей.

Задание № 248

Вычислите устно:
а) 53 - 46
* 7
+ 31
- 45
: 7
?
б) 63 - 57
* 6
+ 34
- 30
: 8
?
в) 81 - 73
* 8
+ 26
- 58
: 8
?
г) 520 + 280
: 20
* 5
: 25
* 125
?
д) 600 - 120
: 4
* 2
: 5
* 20
?

Ответы

a) 7, 49, 80, 35, 5.
б) 800, 40, 200, 8, 1000.
в) б, 36, 70, 40, 5.
г) 480, 120, 240, 48, 960.
д) 8, 64, 90, 32, 4.

Задание № 249

Представьте числа 2, 1, 1/2 в виде суммы их половин, четвертей и восьмых по образцу:

Решение

$2=1+1=\frac12+\frac12+\frac12+\frac12=\frac14+\frac14+\frac14+\frac14+\frac14+\frac14+\frac14+\frac14$
$1=\frac12+\frac12=\frac14+\frac14+\frac14+\frac14=\frac18+\frac18+\frac18+\frac18+\frac18+\frac18+\frac18+\frac18$
$\frac12=\frac14+\frac14=\frac18+\frac18+\frac18+\frac18=\frac1{16}+\frac1{16}+\frac1{16}+\frac1{16}+\frac1{16}+\frac1{16}+\frac1{16}+\frac1{16}$

 

Задание № 250

Восстановите цепочку вычислений:

Решение

Задание № 251

Какую часть длины отрезка АВ составляет длина каждого отрезка на рисунке 133?

Решение

Задание № 252

Как изменится правильная дробь и как изменится неправильная дробь, если у каждой из них поменять местами числитель и знаменатель?

Ответ

У правильной дроби числитель меньше знаменателя, и если их поменять местами, числитель новой дроби будет больше её знаменателя, и дробь станет больше 1, то есть она станет неправильной. Если числитель неправильной дроби равен её знаменателю, то их замена друг на друга ничего не изменит. Если же числитель неправильной дроби больше её знаменателя, то перемена превратит дробь в правильную дробь, то есть она станет меньше 1.

Задание № 253

Подумайте, сколько полушек в алтыне. Сколько грошей в пятаке?
Как гривенник можно разменять на алтыны и гроши?
Сколько сдачи с пятиалтынного надо получить при покупке стоимостью в гривенник и три гроша?
Сколько пятаков в четвертаке?
Почему 25 к. называли четвертаком, а 50 к. − полтинником?

Ответы

12 полушек в алтыне;
1 пятак = 10 грошей;
1 гривенник = 10 копеек = 3 алтына + 2 гроша = ;
1 пятиалтынный = 15 копеек = 1 гривенник + 3 гроша = 1 алтын + 1 грош;
1 четвертак = 25 копеек = 1/4 (четвертая часть) рубля;
1 полтинник = 50 копеек = 1/2 (половина) рубля.

Задание № 254

Запишите в виде дроби частные 7 : 4, 21 : 11, 2 : 1 и в виде частного дроби 19/41,11/6,5/5,28/7.

Решение

Задание № 255

Длина прямоугольника 8 см, а ширина 3 см. Чему равна 1/6 площади прямоугольника?

Решение

8 * 3 : 6 = 24 : 6 = 4 (см)

Задание № 256

Купили 2 кг 100 г крупы и высыпали её в три банки. В первую банку крупы вошло в 3 раза больше, чем во вторую, а в третью банку насыпали 500 г крупы. Сколько крупы насыпали в первую и сколько во вторую банки?

Решение

Пусть во вторую банку вошло х г крупы,тогда в первую банку вошло 3х г крупы.
Всего в три банки насыпали (3х + х + 500) г крупы.
Составим и решим уравнение:
3х + х + 500 = 2100
4х = 2100 − 500
х = 1600 : 4 = 400 (г) крупы насыпали во вторую банку, а в первую банку насыпали
3 * 400 = 1200 (г) крупы насыпали в первую банку
Ответ: 1200 г, 400 г.

Задание № 257

Два автобуса вышли в разное время навстречу друг другу из двух городов, расстояние между которыми 480 км. Скорость первого автобуса 52 км/ч, а скорость второго 42 км/ч. Пройдя 312 км, первый автобус встретился со вторым. На сколько часов первый автобус вышел раньше второго?

Решение

1) 312 : 52 = 6 (ч) - ехал первый автобус
          168
2) (480 − 312) : 42 = 4 (ч) - ехал второй автобус
3) 6 − 4 = 2 (ч) - на столько раньше вышел первый автобус
Ответ: на 2 часа.

Задание № 258

Решите уравнение:
1) (327x − 5295) : 57 = 389;
2) (27x + 11) * 315 = 11970.

Решение

1)
(327x − 5295) : 57 = 389
(327x − 5295) = 389 * 57 = 22173
327x = 22173 + 5295 = 27468
x = 27468 : 327 = 84
2)
(27x + 11) * 315 = 11970
27x + 11 = 11970 : 315 = 38
27x = 38 − 11 = 27
x = 1

Задание № 259

Найдите значение выражения:
1) 10 351 − (12 617 : 31 + 208 * 43);
2) 35 * 309 + 11 638 : 23 − 9321.

Решение

1) 10351 − (12617 : 31 + 208 * 43) = 10351 − (407 + 8944) = 10351 − 9351 = 1000
2) 35 * 309 + 11638 : 23 − 9321 = 10815 + 506 − 9321 = 11321 − 9321 = 2000

Задание № 260

Выделите целую часть числа:
а) 31/8;
б) 43/10;
в) 78/17;
г) 917/11.

Решение

а) $\frac{31}8=3\frac78$
б) $\frac{43}{10}=4\frac3{10}$
в) $\frac{78}{17}=4\frac{10}{17}$
г) $\frac{917}{11}=83\frac4{11}$

Задание № 261

Запишите в виде неправильной дроби числа:
а) 7, 9 и 10 со знаменателем 4;
б) 2, 3 и 8 со знаменателем 5.

Решение

а) $7=\frac{28}4,9=\frac{36}4,10=\frac{40}4$
б) $2=\frac{10}5,3=\frac{15}5,8=\frac{40}5$

 

Задание № 262

Запишите в виде неправильной дроби: 7 1/8; 3 4/5; 1 7/10; 9 14/15; 5 3/16.

Решение

Задание № 263

В первой канистре было в 5 раз больше бензина, чем во второй. Весь бензин из этих канистр вылили в пустой бензобак автомашины. Если в этот бак долить ещё 7 л бензина, то он окажется полным. Сколько литров бензина было в каждой канистре, если ёмкость бензобака 55 л?

Решение

Пусть во второй канистре было х л бензина, тогда в первой канистре было 5х л.
Составим и реши уравнение:
х + 5х + 7 = 55
6х = 55 − 7 = 48
х = 48 : 6
х = 8 (л) было во второй канистре
5х = 5 * 8
5х = 40 (л) было в первой канистре
Ответ: 8 л, 40 л.

Задание № 264

С аэродрома вылетел вертолёт со скоростью 210 км/ч. Через 2 ч с этого же аэродрома вылетел вслед за вертолётом самолёт, который через 3 ч после своего вылета перегнал вертолёт на 840 км. Найдите скорость самолёта.

Решение

1) 2 + 3 = 5 (ч) - летел вертолет
2) 210 * 5 = 1050 (км) - пролетел вертолет за 5 ч
3) 1050 + 840 = 1890 (км) - пролетел самолет за 3 ч
4) 1890 : 3 = 630 (км/ч) - скорость самолета
Ответ: 630 км/ч.

Задание № 265

Составьте программу вычисления выражения:
883 336 : 218 + 2967 * 305 и найдите его значение.

Решение

883336 |÷| 218 |M+| 2967 |Х| 305 |M+| |MR|
883336 : 218 + 2967 * 305 = 4052 + 904935 = 908987

51 52 53 54 55 56 57

Ответы к пункту 29. Сложение и вычитание смешанных чисел, страница 51

Задание № 266

В одной коробке 2 3/8 кг конфет, а в другой коробке 2 1/8 кг. Сколько килограммов конфет в этих двух коробках?

Решение

$2\frac38+2\frac18=2+2+\frac38+\frac18=4\frac48$ (кг)
Ответ: $4\frac48$ кг конфет в двух коробках.

Задание № 267

Чему равна длина белой ленты, если длина красной ленты 3 3/5 м, а белая лента на 2 1/5 короче красной?

Решение

$3\frac35-2\frac15=3-2+\frac35-\frac15=1\frac25$ (м)
Ответ:$1\frac25$ м.

Задание № 268 с ответами

Выполните действия:

а) $5+2\frac38=7\frac38$

б) $10\frac34-7=3\frac34$

в) $4\frac16+10=14\frac16$

г) $12\frac8{15}-12=\frac8{15}$

д) $4\frac19+3\frac49=7\frac59$

е) $7\frac57-4\frac37=3\frac27$

ж) $3\frac8{11}+5\frac2{11}=8\frac{10}{11}$

з) $9\frac7{12}-7\frac6{12}=2\frac1{12}$

и) $4\frac35+2\frac45=6\frac75=7\frac25$

к) $8\frac9{13}+7\frac{12}{13}=15\frac{21}{13}=16\frac8{13}$

л) $5\frac35-1\frac45=4\frac85-1\frac45=3\frac45$

м) $4\frac5{11}-2\frac8{11}=3\frac{16}{11}-2\frac8{11}=1\frac8{11}$

н) $4-\frac59=3\frac99-\frac59=3\frac49$

о) $8-\frac7{12}=7\frac{12}{12}-\frac7{12}=7\frac5{12}$

п) $5-3\frac38=4\frac88-3\frac38=\frac58$

р) $4-3\frac59=3\frac99-3\frac59=\frac49$

Задание № 269

Найдите значение выражения:

а) $4\frac7{12}-1\frac5{12}+2\frac{11}{12}=(4-1+2)+(\frac7{12}-\frac5{12}+\frac{11}{12})=5+\frac{13}{12}=5\frac{13}{12}=6\frac1{12}$

б) $6\frac{14}{15}-3\frac2{15}-1\frac7{15}=(6-3-1)+(\frac{14}{15}-\frac2{15}-\frac7{15})=2+\frac5{15}=2\frac5{15}$с

Задание № 270

На базу привезли яблоки на двух грузовиках. На первом было 4 3/10
т яблок, а на втором − на 1 1/10 т меньше. Сколько тонн яблок привезли на базу? Выразите ответы в центнерах.

Решение

$4\frac3{10}+(4\frac3{10}-1\frac1{10})=\frac{43}{10}+3\frac2{10}=7\frac5{10}$ (т)
10 : 10 * 75 = 75 (ц)
Ответ: $7\frac5{10}$ т, 75 ц.

Задание № 271

Два шахматиста сыграли две партии: первая партия продолжалась 1 1/4 ч, а вторая − на 3/4 ч больше. Сколько часов продолжалась игра? Выразите продолжительность игры в минутах.

Решение

1) $1\frac14+\frac34=1\frac44=2$ (ч) - продолжалась вторая партия
2) $1\frac14+2=3\frac14$ (ч) - продолжалась игра
3) 60 * 3 + 60 : 4 = 180 + 15 = 195 (мин) - продолжалась игра
Ответ: $3\frac14$ч, 195 мин.

Задание № 272

Вычислите устно:
а) 8² : 4
+56
:18
*25
−61
?
б) 3³ * 2
:6
*7
+7
+230
?
в) 10² * 3
:150
*48
+44
:7
?
г) 4³ : 8
*9
+19
:13
*120
?
д) 5² * 8
:40
*60
−120
:30
?

Ответы

a) 64, 16, 72, 4, 100, 39.
б) 27, 54, 9, 63, 70, 300.
в) 100, 300, 2, 96, 140, 20.
г) 64, 8, 72, 91, 7, 840.
д) 25, 200, 5, 300, 180, 6.

 

Задание № 273

Восстановите цепочку вычислений:

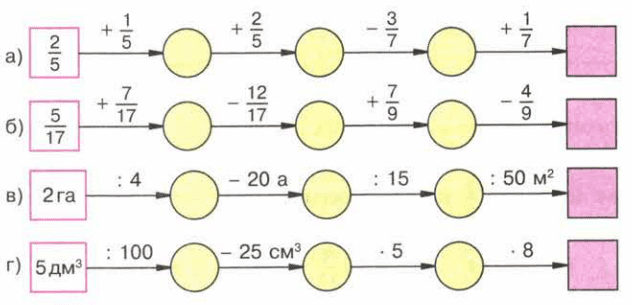
Решение

Задание № 274

Каковы координаты точек, отмеченных на рисунке 136? Чему равно расстояние (в единичных отрезках) между точками:
О и Е, О и К, О и С, D и С, А и Е, М и Е? Сравните координаты точек С и D, С и Е, М и К, N и А, А и В.

Решение

$0(0),D(\frac25),{\operatorname С}(\frac35),E(1),{\operatorname А}(\frac85),K(2),{\operatorname М}(\frac{13}5),N(\frac{14}5),B(\frac{16}5)$
$OE=1,OK=2,OC=\frac35,DC=\frac15,AE=\frac35,ME=\frac85$
$\frac25<\frac35;\frac35<1;2<\frac{13}5;\frac85<\frac{14}5;\frac85<\frac{16}5$

Задание № 275

Между какими натуральными числами на координатном луче расположены смешанные числа: 1 5/7, 3 1/10, 15 2/9, 1200 1/100?

Решение

$1<1\frac57<2$
$3<3\frac1{10}<4$
$15<15\frac29<16$
$1200<1200\frac1{100}<1201$

Задание № 276

При каких значениях а частное 12 : а будет:
а) натуральным числом;
б) неправильной дробью;
в) правильной дробью?
Ответьте на те же вопросы для частного а : 6.

Ответы

а) 12 : a: при а равном 1; 2; 3; 4; 6; 12;
a : 6: при а кратным 6.
б)12 : a: при а равном 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12;
a : 6: при а > 6.
в) 12 : a: при натуральном а > 12;
a : 6: при a < 6 частное.

Задание № 277

Составьте задачу по уравнению:
а) $x+\frac29=\frac79$
б) $y-\frac57=\frac17$
в) $3\frac58-z=2$

Решение

а) Тракторист за день вспахал 7/9 поля, причем после обеда он вспахал 2/9 поля. Какую часть поля вспахал тракторист до обеда.
Пусть до обеда тракторист вспахал х поля
$x+\frac29=\frac79$
$x=\frac79-\frac29$
$x=\frac59$
Ответ: $\frac59$ поля вспахал тракторист до обеда.

б) За день семья выкопала 5/7 огорода картофеля и им осталось выкопать еще 1/7 часть. Какая часть огорода была не выкопанной на начало дня?
Решение:
Пусть на начало дня было не выкопано y огорода, тогда:
$y-\frac57=\frac17$
$y=\frac17+\frac57$
$y=\frac67$
Ответ: $\frac67$ огорода было не выкопано.

в) В магазине было 3 5/8 мешка сахара. Сколько мешков сахара было продано, если на конец дня осталось два мешка.
Пусть продали z мешков, тогда:
$3\frac58-z=2$
$z=3\frac58-2$
$z=1\frac58$
Ответ: $1\frac58$ мешка сахара было продано.

 

Задание № 278

По рисунку 137 составьте уравнение и решите его.

Решение

а) $\frac7{11}+{\operatorname х}=\frac{10}{11}$
$x=\frac{10}{11}-\frac7{11}$
$x=\frac3{11}$

б) $x+\frac7{10}=1\frac2{10}$
$x=1\frac2{10}-\frac7{10}$
$x=\frac{12}{10}-\frac7{10}$
$x=\frac5{10}$

Задание № 279

В старинных книгах можно встретить такие названия дробей: 1/2 − пол, полтина; 1/5 − пятина; 1/7 − седьмина; 1/10 − десятина.
Подумайте, как появились следующие названия: 1/4 − четь; 1/8 − полчети; 1/16 − полполчёти; 1/32 − полполполчети (малая четь).
Дробь 1/3 называли «треть».
Попробуйте догадаться, как называли дроби: 1/6, 1/12, 1/24.
Подумайте, почему смешанные числа называли:
1 1/2 − полвтора; 2 1/2 − полтретья; 3 1/2 − полчётверта; 4 1/2 − полпяты; 5 1/2 − полшесты и т. д.
Сохранился ли такой способ чтения в наше время?

Решение

В наше время такой способ чтения не сохранился.

Задание № 280

Из дробей 49/5; 11/3; 19/12; 48/16; 355/100; 817/121; 3407/1000 выделите целую часть, а смешанные числа 1 2/3; 5 4/11; 7 13/17; 9 45/51; 8 9/1000; 6 13/1000 запишите в виде неправильных дробей.

Решение

Задание № 281

Выполните действия:

а) $\frac6{19}-\frac3{19}+\frac{15}{19}=\frac{6-3+15}{19}=\frac{18}{19}$
б) $\frac{19}{21}-\frac{17}{21}+\frac9{21}=\frac{19-17+9}{21}=\frac{11}{21}$
в) $\frac{25}{32}-\frac6{32}+\frac{19}{32}=\frac{25-6+19}{32}=\frac{38}{32}=1\frac6{32}$

Задание № 282

Лесник прошёл 3 км и 4 ч ехал на лошади. С какой скоростью он ехал на лошади, если весь путь равен 34 км?

Решение

1) 34 − 3 = 31 (км) - проехал лесник на лошади
2) $31:4=\frac{31}4=7\frac34$ (км/ч) - скорость, с которой он ехал на лошади
Ответ: $7\frac34$ км/ч.

Задание № 283

Пошёл дождь. Под водосточную трубу поставили пустую бочку. В неё вливалось каждую минуту 8 л воды, а через щель в бочке выливалось 3 л воды в минуту.
Сколько литров воды будет в бочке через 1 мин; 2 мин; 3 мин?
Успеет ли бочка наполниться, если её объём 400 л, а дождь шёл 1 ч 10 мин?

Решение

Через t мин в бочке будет (8 − 3)t = 5t (л) воды
Через 1 мин в бочке будет 5 * 1 = 5 (л)
через 2 мин: 5 * 2 = 10 (л)
через 3 мин: 5 * 3 = 15 (л)
За 1 ч 10 мин = 70 мин в бочке будет 5 * 70 = 350 л, что меньше 400 л, значит бочка не успеет наполниться водой.
Ответ: 5 л, 10 л, 15 л. Не успеет.

Задание № 284

Легковой автомобиль движется со скоростью 70 км/ч, а грузовой − со скоростью 40 км/ч. Сейчас легковой автомобиль находится сзади грузовика на расстоянии 60 км. Оба автомобиля движутся в одном направлении. Какое расстояние будет между ними через 1 ч, через 2 ч, через 3 ч?

Решение

Через t ч между автомобилями будет расстояние
60 − (70 − 40)t = 60 − 30t (км)
через 1 ч: 60 − 30 * 1 = 30 (км)
через 2 ч: 60 − 30 * 2 = 60 − 60 = 0 (км) легковой автомобиль догонит грузовой
через 3 ч: 30 * 3 − 60 = 90 − 60 = 30 (км) легковой автомобиль обгонит грузовой
Ответ: 30 км, 0 км, 30 км.

Задание № 285

Решите задачу:
1) В третьем классе 35 учеников. Из них 5/7 умеют играть в шахматы. Сколько ребят в этом классе ещё не научились играть в шахматы?
2) В бригаде 15 человек. Из них 2/5 владеют только одной специальностью, а остальные − двумя. Сколько человек в бригаде владеют двумя специальностями?

Решение

1) 1) 35 : 7 * 5 = 25 (р.) - умеют играть в шахматы
2) 35 − 25 = 10 (р.) - не умеют играть в шахматы
Ответ: 10 ребят.

2) 1) 15 : 5 * 2 = 6 (ч.) - владеют одной специальностью
2) 15 − 6 = 9 (ч.) - владеют двумя специальностями
Ответ: 9 человек.

Задание № 286

Найдите значение выражения:
1) (38 * 35 − 35) : 259;
2) (43 * 21 + 1671) : 429.

Решение

1) (38 * 35 − 35) : 259 = (1330 − 35) : 259 = 1295 : 259 = 5
2) (43 * 21 + 1671) : 429 = (903 + 1671) : 429 = 2574 : 429 = 6

Задание № 287 с ответами

Выполните действия:

а) $3+8\frac5{12}=11\frac5{12}$

б) $10\frac67-3=7\frac67$

в) $4\frac2{13}+5\frac7{13}=9\frac9{13}$

г) $8\frac7{12}-4\frac2{12}=4\frac5{12}$

д) $4\frac8{11}+5\frac7{11}=9\frac{15}{11}=10\frac4{11}$

е) $7\frac59-2\frac89=6\frac{14}9-2\frac89=4\frac69$

ж) $7-\frac38=6\frac88-\frac38=6\frac58$

з) $10-3\frac7{15}=9\frac{15}{15}-3\frac7{15}=6\frac8{15}$

Задание № 288

Длина прямоугольника 1 4/20 м, а ширина на 3/20 м меньше длины. Найдите периметр прямоугольника.

Решение

1) $1\frac4{20}-\frac3{20}=1\frac1{20}$ (м) - ширина прямоугольника
2) $1\frac4{20}+1\frac4{20}+1\frac1{20}+1\frac1{20}=4\frac{10}{20}$ (м) - периметр
Ответ: $4\frac{10}{20}$ м.

Задание № 289

В один из дней зимних каникул мальчик 2 3/5 ч катался на лыжах, а на коньках на 1 4/5 ч меньше. Сколько всего времени он катался на лыжах и коньках?

Решение

1) $2\frac35-1\frac45=1\frac85-1\frac45=\frac45$ (ч) мальчик катался на коньках
2) $2\frac35+\frac45=2\frac75=3\frac25$ (ч) мальчик катался на лыжах и коньках
Ответ: $3\frac25$ ч.

Задание № 290

Верёвку длиной 256 м разрезали на две части, одна из которых в 7 раз длиннее второй. На сколько метров одна часть верёвки длиннее второй?

Решение

Пусть х − длина короткой части, тогда длина длинной части 7х.
x + 7x (м) - длина веревки
256 (м) - длина веревки
Составляем уравнение:
x + 7x = 256
1x + 7x = 256
(1+7) x = 256
8 x = 256
x = 256 : 8
х = 32 (м) - длина короткой части
32*7=224(м) - длина длинной части
224 - 32 = 192 (м)
Ответ: одна часть на 192 м длиннее второй.

Задание № 291

В археологических раскопках древнего города участвовали две экспедиции. В первой было в три раза больше сотрудников, чем во второй. Когда во вторую экспедицию прибыли ещё 18 человек, то в двух экспедициях вместе стало 66 сотрудников. Сколько стало сотрудников во второй экспедиции?

Решение

Пусть во второй экспедиции было х человек, тогда 3х человек было в первой экспедиции.
Всего в обеих экспедициях было (3х + х) человек.
Составим уравнение:
3х + (х + 18) = 66
4х = 66 − 18 = 48
х = 48 : 4
х = 12
Значит, 12 сотрудников было во второй экспедиции
12 + 18 = 30 (с.) - стало во второй экспедиции
Ответ: 30 сотрудников.

Задание 292

В куске 112 м материи. Из 11/16 куска сшили детские костюмы. Сколько метров материи осталось?

Решение

1) 112 : 16 * 11 = 7 * 11 = 77 (м) - пошло на костюмы, 
2) 112 − 77 = 35 (м) материи осталось.
Ответ: 35 м.

Задание 293

Площадь прямоугольника 616 м², а его длина 28 м. Найдите площадь такого квадрата, у которого периметр равен периметру прямоугольника.

Решение

b = 616 : 28 = 22 (м) - ширина прямоугольника
Р = 2 * (а + b) = 2 * (28 + 22) = 2 * 50 = 100 (м) - периметр прямоугольника
Так как периметр квадрата также равен 100 м, то
Р : 4 = 100 : 4 = 25 (м) - длина его стороны
S = 25² = 625 (м²) - площадь квадрата
Ответ: 625 м².

Задание 294

Выполните действия:
а) (936 : 24 + 32 * 14) : 487;
б) (43 * 56 + 43 * 44) : 215 − 15.

Решение

а) (936 : 24 + 32 − 14) : 487 = (39 + 448) : 487 = 487 : 487 = 1

б) (43 * 56 + 43 * 44) : 215 − 15 = (2408 + 1892) : 215 − 15 = 4300 : 215 − 15 = 20 − 15 = 5

58-59 Задания для самопроверки

Задания для самопроверки, страница 58-59

№1

11/15

№2

35000 * 2/7 = 1000 (р.) - стоимость покупки
Ответ: 1000 рублей.

№3

240 * 8/3 = 1920 : 3 = 640 (кг) - картофеля было в магазине первоначально
Ответ: 640 кг картофеля.

№4

в) 2/3
г) 4/7

№5

а) 7
в) 1
г) 4

№6

г) 4 4/7

№7

А 3
Б 2
В 4
Г 3

№8

1 и 4

№9

3_7/10 – 1_3/10 = 2_4/10 = 2_2/5 (т) - гречки привезли в магазин
Ответ: 2_2/5 т.

№10

1) 24_3/10 – 9_5/10 = 24 – 9 + 3/10 – 5/10 = 15 + 3/10 – 5/10 = 14 + 13/10 – 5/10 = 14_8/10 (т) - яблок поступило на склад
2) 14_8/10 + 24_3/10 = 38_11/10 = 39_1/10 = 39,1 т = 391 (ц) - фруктов привезли на склад
Ответ: 391 ц фруктов.

61 62 63 64 65 66

Параграф 6. Десятичные дроби

Сложение и вычитание десятичных дробей

Пункт 30. Десятичная запись дробных чисел, страница 61

Задание 295

Запишите в виде десятичной дроби:
2 4/10 ; 4 9/10 ; 24 25/100 ; 98 3/100 ; 1 1/100 ; 1 1/10 ; 4 333/1000 ; 8 45/1000 ; 75 8/10000 ; 9 565/10000.

Решение

2_4/10 = 2,4
4_9/10 = 4,9
24_25/100 = 24,25
98_3/100 = 98,03
1_1/100 = 1,01
1_1/10 = 1,1
4_333/1000 = 4,333
8_45/1000 = 8,045
75_8/10000 = 75,0008
9_565/10000 = 9,0565

Задание 296

Прочитайте десятичные дроби:
а) 2,7; 11,4; 401,1; 666,6; 0,8; 9,9; 99,9; 909,9;
б) 5,64; 21,87; 381,77; 54,60; 2,80; 0,55; 0,09; 0,77;
в) 1,579; 12,882; 326,703; 145,008; 21,094; 0,049; 0,001;
г) 203,6; 20,36; 0,02036; 0,20506; 0,010101.

Решение

а) 2,7 − две целых семь десятых
11,4 − одиннадцать целых четыре десятых
401,1 − четыреста одна целая одна десятая
666,6 − шестьсот шестьдесят шесть целых шесть десятых
0,8 − ноль целых восемь десятых
9,9 − девять целых девять десятых
99,9 − девяносто девять целых девять десятых
909,9 − девятьсот девять целых девять десятых

б) 5,64 − пять целых шестьдесят четыре сотых
21,87 − двадцать одна целая восемьдесят семь сотых
381,77 − триста восемьдесят одна целая семьдесят семь сотых
54,60 − пятьдесят четыре целых шестьдесят сотых
2,80 − две целых восемьдесят сотых
0,55 − ноль целых пятьдесят пять сотых
0,09 − ноль целых девять сотых
0,77 − ноль целых семьдесят семь сотых

в) 1,579 − одна целая пятьсот семьдесят девять тысячных
12,882 − двенадцать целых восемьсот восемьдесят две тысячных
326,703 − триста двадцать шесть целых семьсот три тысячных
145,008 − сто сорок пять целых восемь тысячных
21,094 − двадцать одна целая девяносто четыре тысячных
0,049 − ноль целых сорок девять тысячных
0,001 − ноль целых одна тысячная

г) 203,6 − двести три целых шесть десятых
20,36 − двадцать целых тридцать шесть сотых
0,02036 − ноль целых две тысячи тридцать шесть стотысячных
0,20506 − ноль целых двадцать тысяч пятьсот шесть стотысячных
0,010101 − ноль целых десять тысяч сто одна миллионная

Задание 297

Запишите в виде десятичных дробей числа:
а) 7 целых 8 десятых; 5 целых 45 сотых; 0 целых 59 сотых; 78 целых 1 сотая; 4 целых 601 тысячная; 76 целых 32 тысячных;
б) 6 целых 6 тысячных; 0 целых 2 сотых; 9 целых 3 тысячных; 785 целых 5 тысячных; 33 целых 8 десятитысячных.

Решение

а) 7,8; 5,45; 0,59; 78,01; 4,601; 76,032.

б) 6,006; 0,02; 9,003; 785,005; 33,0008.

Задание 298

Запишите в виде дроби или смешанного числа:
2,7; 31,4; 567,39; 6,005; 42,78; 0,64; 0,60; 0,07; 0,99.

Решение

2,7 = 2_7/10
31,4 = 31_4/10
567,39 = 567_39/100
6,005 = 6_5/1000
42,78 = 42_78/100
0,64 = 64/100
0,60 = 60/100
0,07 = 7/100
0,99 = 99/100

Задание 299

Выразите:
а) в дециметрах: 5 дм 6 см; 3 дм 1 см; 9 см;
б) в центнерах: 24 ц 6 кг; 72 кг; 30 ц 65 кг;
в) в килограммах: 6 кг 339 г; 5 кг 58 г; 6 т 14 кг 8 г;
г) в тоннах и килограммах: 1,785 т; 24,300 т; 4,076 т; 5,050 т;
д) в метрах и сантиметрах: 3,78 м; 2,09 м;
е) в квадратных метрах и квадратных дециметрах 3,15 м² ; 4,08 м².

Решение

а) 5 дм 6 см = 5,6 дм
3 дм 1 см = 3,1 дм
9 см = 0,9 дм

б) 24 ц 6 кг = 24,06 ц
72 кг = 0,72 ц
30 ц 65 кг = 30,65 ц

в) 6 кг 339 г = 6,339 кг
5 кг 58 г = 5,058 кг
6 т 14 кг 8 г = 6014,008 кг

г) 1,785 т = 1 т 785 кг
24,300 т = 24 т 300 кг
4,076 т = 4 т 76 кг
5,050 т = 5 т 50 кг

д) 3,78 м = 3 м 78 см
2,09 м = 2 м 9 см

е) 3,15 м² = 3 м² 215 дм²
4,08 м² = 4 м² 8 дм²

Задание 300

Запишите в виде десятичных дробей частные:
182 : 10;
5405 : 100;
631 : 10 000;
74 : 1000;
849 : 1000;
3 : 100 000.

Решение

182 : 10 = 18,2
5405 : 100 = 54,05
631 : 10000 = 0,0631
74 : 1000 = 0,074
849 : 1000 = 0,849
3 : 100 000 = 0,00003

Задание 301

Начертите отрезки: АВ = 1,3 см; CD = 2,1 см; MP = 0,8 см.

Решение

Задание 302

Вычислите устно:
а) 6² + 24
: 12
* 20
+ 60
: 32
?
б) 2³ * 9
− 34
+ 18
: 14
* 25
?
в) 6 м 20 см : 31
+ 30 с м
* 4
− 1 м 60 см
?
г) 2 к г 50 г : 5
+ 190 г
* 8
− 3 кг 300 г
?

Решение

а) 36, З0, 5, 100, 160, 5.

б) 8, 72, 38, 56, 4, 100.

в) 20 см, 50 см, 2 м, 40 см.

г) 410 г, 600 г, 4800 г, 1 кг 500 г.

Задание 303

Назовите целую и дробную части числа:
а) 3 5/7;
б) 2 8/15;
в) 17;
г) 1 3/10;
д) 16/19.

Решение

а) 3_5/7: 3 − целая часть, 5 7 − дробная часть.

б) 2_8/15: 2 − целая часть, 8 15 − дробная часть.

в) 17: 17 − целая часть, 0 − дробная часть.

г) 1_3/10: 1 − целая часть, 3 10 − дробная часть.

д) 16/19: 0 − целая часть, 16 19 − дробная часть.

Задание 304

Сравните числа: 23, 2300, 023, 230, 00023.

Решение

00023 = 023 = 23 < 230 < 2300.

Задание 305

Замените дробью или смешанным числом частные: 9 : 2; 5 : 11; 8 : 10; 15 : 10.

Решение

9 : 2 = 9/2 = 4_1/2
5 : 11 = 5/11
8 : 10 = 8/10
15 : 10 = 15/10 = 1_5/10

Задание 306

Укажите координаты точек А, В, С, D (рис. 138). Каково расстояние в единичных отрезках между точками:
О и С, О и D, А и В, С и D?

Решение

А (90/10) , В (1 7/10) , С (3/10) , D (1 4/10).
ОС = 3/10 , ОD = 1 4/10 , АВ = 8/10 , СD = 1 1/10.

Задание 307

Какое число записывается:
а) единицей с четырьмя последующими нулями;
б) единицей с шестью последующими нулями;
в) единицей с семью последующими нулями?

Решение

а) 10000 − десять тысяч

б) 1000000 − один миллион

в) 10000000 − десять миллионов

Задание 308

Определите координаты точек, отмеченных на рисунке 139. Назовите эти координаты в порядке убывания. Назовите два числа, которые больше любой из этих координат.

Решение

О (О) , А (3/6) , Е (1) , P (7/6) , B (10/6) , М (2) , D (14/6).
Два числа: 3, 4.

Задание 309

Выполните действия:
а) 2 4/9 + 3 3/9 − 1 1/9 + 1 2/9;
б) 8 6/7 − 5 5/7 + 3 3/7 + 1 2/7.

Решение

а) $2\frac49+3\frac39-1\frac19+1\frac29=2+3-1+1+\frac49+\frac39-\frac19+\frac29=5+\frac89=\frac{55}9=5\frac89$

б) $8\frac67-5\frac57+3\frac37+1\frac27=8-5+3+1+\frac67-\frac57+\frac37+\frac27=7+\frac67=7\frac67$

Задание 310

Запишите все числа, у которых целая часть 2, а знаменатель дробной части 6.

Решение

$2\frac16;2\frac26;2\frac36;2\frac46;2\frac56$

Задание 311

Из чисел 3/2 ; 27/10 ; 39/4 ; 177/20 ; 801/100 выделите целую часть, а числа 1 1/2 ; 2 7/10 ; 12 3/4 ; 8 7/20 ; 9 1/10 запишите в виде неправильной дроби.

Решение

3/2 = 1_1/2
27/10 = 2_7/10
39/4 = 9_3/4
177/20 = 8_17/20
801/100 = 8_1/100

1_1/2 = 3/2
2_7/10 = 27/10
12_3/4 = 51/4
8_7/20 = 167/20
9_1/10 = 91/10

Задание 312

Сравните:
а) 4 3/5 и 4 1/5;
б) 7 2/9 и 6 8/9;
в) 9 3/7 и 68/7;
г) 2 3/4 м и 265 см.

Решение

а) 4_3/5 > 4 1/5

б) 7_2/9 > 6 8/9

в) 9_3/7 = 66/7 < 68/7

г) 2_3/4 м = 275 см > 265 см.

Задание 313

На рисунке 140 показан план квартала города. Ширина каждого дома 25 м, длина 50 м, ширина дорог 25 м. Расскажите, как ближайшим путём пройти от точки А до входа в школу; на почту; в ателье; в дом № 9. Как бы вы объяснили дорогу от дома № 5 до дома № 11; до дома № 6?

Решение

Чтобы пройти от дома № 5 до дома № 11 нужно при выходе из дома № 5 повернуть налево и идти все время прямо. После дома № 15 необходимо повернуть налево и идти снова прямо до дома № 11.

Чтобы пройти от дома № 5 до дома № 9 нужно при выходе из дома № 5 повернуть налево и завернуть еще раз налево, тем самым обогнув угол дома № 5 и идти прямо мимо ателье до дома № 9.

Задание 314

Длина прямоугольного параллелепипеда 14 см, ширина 8 см и высота 7 см. Найдите высоту другого прямоугольного параллелепипеда, если его длина 28 см, ширина 7 см, а объём равен объёму первого параллелепипеда.

Решение

1) 14 * 8 * 7 = 112 * 7 = 784 (см³) - объем первого параллелепипеда
2) 784 : (28 − 7) = 784 : 196 = 4 (см) - высота параллелепипеда, объём которого равен объёму первого
Ответ: 4 см.

Задание 315

Решите задачу:
1) Масса арбуза и трёх одинаковых дынь 10 кг. Дыня в 2 раза легче арбуза. Какова масса арбуза?
2) Масса тыквы и трёх одинаковых кабачков 20 кг. Тыква в 2 раза тяжелее кабачка. Какова масса тыквы?
3) За три прыжка кенгуру преодолел расстояние 20 м 70 см. Первые два прыжка оказались одинаковыми, а третий − на 1 м 20 см длиннее. Какова длина второго прыжка кенгуру?
4) Расстояние до норы в 6 м заяц преодолел в четыре прыжка. Первые три прыжка оказались одинаковыми, а последний на 40 см короче остальных. Найдите длину второго прыжка зайца.

Решение

1) Пусть х − масса дыни, тогда масса арбуза 2х кг.
Масса арбуза и трёх одинаковых дынь равна (3х + 2х) кг.
Составим уравнение:
3х + 2х = 10
5х = 10
х = 10 : 5
х = 2
Значит, масса дыни равна 2 кг, а масса арбуза
2х = 2 * 2 = 4 (кг)
Ответ: 4 кг.

2) Пусть у − масса кабачка, тогда масса тыквы 2у кг.
Масса тыквы и трёх одинаковых кабачков равна (3у + 2у) кг.
Составим уравнение:
3y + 2у = 20
5y = 20
у = 20 : 5
у = 4
Значит, масса кабачка 4 кг, а масса тыквы
2у = 2 * 4 = 8 (кг)
Ответ: 8 кг.

3) 20 м 70 см = 2070 см
1 м 20 см = 120 см
Пусть длина первого прыжка равна z см, длина второго z, а длина третьего прыжка (z + 120) см.
Сумма длин всех прыжков кенгуру равна (2z + z + 120) см.
Составим уравнение:
z + z + (z + 120) = 2070
3z = 1950
z = 1950 : 3
z = 650
Значит, длина второго прыжка 650 см.
Ответ: 650 см.

4) Пусть длина каждого из первых трех прыжков равна х см, тогда длина четвёртого прыжка будет (x − 40) см.
Сумма длин четырёх прыжков (3x + x − 40) см.
Составим уравнение:
3х + х − 40 = 600
4х = 600 + 40
4х = 640
х = 640 : 4
х = 160 
Значит, длина второго прыжка 160 см.
Ответ: 160 см.

Задание 316

Решите уравнение:
1) х : 16 = 4759 + 1441;
2) у : 27 = 2467 − 1867;
3) 13 600 : z = 3876 − 3851;
4) (2865 + k) * 125 = 542875.

Решение

1) x : 16 = 4759 + 1441
x : 16 = 6200
x = 6200 * 16
х = 99200

2) у : 27 = 2467 − 1867
у : 27 = 600
у = 600 * 27
у = 16200

3) 13600 : z = 3876 − 3851
13600 : z = 25
z = 13600 : 25
z = 544

4) (2865 + k) − 125 = 542875
2865 + k = 542875 : 125
2865 + k = 4343
k = 4343 − 2865
k = 1478

Задание 317

Запишите в виде десятичной дроби числа:
а) 3 7/10 ; 6 3/10 ; 11 11/100 ; 9 27/100 ; 7 9/100 ; 10 1/100 ; 1 547/1000 ; 13 23/1000;
б) 124 4/1000 ; 8 12/10000 ; 18 103/100000 ; 160 1/10000 ; 3/10 ; 7/100 ; 1/10000.

Решение

а) 3_7/10 = 3,7
6_3/10 = 6,3
11_11/100 = 11,11
9_27/100 = 9,27
7_9/100 = 7,09
10_1/100 = 10,01
1_547/1000 = 1,547
13_23/1000 = 13,023

б) 124_4/1000 = 124,004
8_12/10000 = 18,0012
18_103/100000 = 18,00103
160_1/10000 = 160,0001
3/10 = 0,3
7/100 = 0,07
1/10000 = 0,0001

Задание 318

Сравните:
а) 11 4/9 и 12 1/9;
б) 8 2/3 и 25/3;
в) 6 17/25 и 6 16/25.

Решение

а) 11_4/9 < 12 1/9

б) 8_2/3 = 26/3 > 25/3

в) 6_17/25 > 6 16/25

Задание 319

Выразите:
а) в километрах: 8 км 907 м; 35 м; 250 м; 1 м;
б) в центнерах и килограммах: 4,2 ц; 7,33 ц; 0,24 ц; 0,05 ц.

Решение

а) 8 км 907 м = 8,907 км
35 м = 0,035 км
250 м = 0,250 км
1 м = 0,001 км

б) 4,2 ц = 4 ц 20 кг
7,33 ц = 7 ц 33 кг
0,24 ц = 24 кг
0,05 ц = 5 кг

Задание 320

Из двух пунктов, расстояние между которыми 7 км 500 м, одновременно в одном направлении вышел пешеход со скоростью 6 км/ч и выехал автобус. Определите скорость автобуса, если он догнал пешехода через 15 мин.

Решение

6 км/ч = 6 км/ч * 1000 м : 60 мин = 100 м/мин.
(7500 + 100 * 15) : 15 = 7500 : 15 + 100 = 500 + 100 = 600 (м/мин) - скорость автобуса
600 м/мин = 36 км/ч
Ответ: 36 км/ч.

Задание 321

С трёх лугов собрали 197 ц сена. С первого и второго лугов собрали поровну, а с третьего − на 11 ц больше, чем с первого. Сколько сена собрали с каждого луга?

Решение

Пусть с первого и второго лугов собрали х ц сена, тогда с третьего луга собрали (х + 11) ц сена.
Всего с трёх лугов собрали (2х + х + 11) ц сена.
Составим уравнение:
2х + х + 11 = 197
3х = 197 − 11
3х = 186
х = 186 : 3
х = 62
Значит, 62 ц собрали с первого и второго лугов
62 + 11 = 73 (ц) - сена собрали с третьего луга
Ответ: 73 ц сена.

Задание 322

Выполните действия:
а) ((22 962 : 534 + 9936 : 48) : 25 + 37) * 43;
б) 38 * 203 + 75 * (514 − 476) + (15 + 23) * 22.

Решение

а) ((22 962 : 534 + 9936 : 48) : 25 + 37) * 43 = ((43 + 207) : 25 + 37) * 43 = (10 + 37) • 43 = 2021

б) 38 − 203 + 75 * (514 − 476) + (15 + 23) − 22 = 7714 + 75 − 38 + 38 − 22 = 7714 + 2850 + 836 = 11400

67 68 69 70 71 72

Пункт 31. Ответы к теме Сравнение десятичных дробей, страница 67

Задание 323

Напишите десятичную дробь:
а) с четырьмя знаками после запятой, равную 0,87;
б) с пятью знаками после запятой, равную 0,541;
в) с тремя знаками после запятой, равную 35;
г) с двумя знаками после запятой, равную 8,40000.

Решение

а) 0,87 = 0,8700

б) 0,54 = 0,54100

в) 35 = 35,000

г) 8,40000 = 8,40

Задание 324

Приписав справа нули, уравняйте число знаков после запятой в десятичных дробях: 1,8; 13,54 и 0,789.

Решение

11,800; 13,540; 0,789.

Задание 325

Запишите короче дроби: 2,5000; 3,02000; 20,010.

Решение

2,5000 = 2,5; 3,02000 = 3,02; 20,010 = 20,01.

Задание 326

Сравните числа:
85,09 и 67,99;
55,7 и 55,7000;
0,5 и 0,724;
0,908 и 0,918;
7,6431 и 7,6429;
0,0025 и 0,00247.

Решение

85,09 > 67,99;
55,7 = 55,7000;
0,5 < 0,724;
0,908 < 0,918;
7,6431 > 7,6429;
0,0025 > 0,00247.

Задание 327

Расставьте в порядке возрастания числа: 3,456; 3,465; 8,149; 8,079; 0,453.
А числа 0,0082; 0,037; 0,0044; 0,08; 0,0091 расставьте в порядке убывания.

Решение

0,453 < 3,456 < 3,465 < 8,079 < 8,149;
0,08 > 0,037 > 0,0091 > 0,0082 > 0,0044.

Задание 328

Примите за единичный отрезок длину десяти клеток тетради и отметьте на координатном луче точки
А(0,1), В(0,5), С(0,9), D(1,2), E(1,7).

Решение

Задание 329

Какая из точек лежит левее на координатном луче:
а) А(1,2) или В(1,7);
б) С(0,31) или D(0,35);
в) E(3,3) или K(3,25)?

Решение

а) А(1,2) левее В(1,7)

б) С(0,31) левее D(0,35)

в) K(3,25) левее E(3,3)

Задание 330

Какая из точек лежит правее на координатном луче:
а) A(2,8) или В(2,4);
б) С(0,45) или D(0,49);
в) E(7,85) или K(7,9)?

Решение

а) A(2,8) правее В(2,4)

б) D(0,49) правее C(0,45)

в) K(7,9) правее E(7,85)

Задание 331

Замените звёздочки знаками < или > так, чтобы получилось верное неравенство:
21 * 18,75; 8,006 * 9,0001; 7,2 * 7,2005; 4,009 * 3,999.

Решение

21 > 18,75;
8,006 < 9,0001;
7,2 < 7,2005;
4,09 > 3,999.

Задание 332

Какие цифры можно поставить вместо звёздочки, чтобы получилось верное неравенство:
а) 2,1 > 2,01;
б) 1,34 < 1,3?

Решение

а) 2,*1 > 2,01 => * > 0

6) 1,34 < 1,3* => * > 4

Задание 333

Между какими соседними натуральными числами находится дробь:
а) 2,7;
б) 12,21;
в) 3,343;
г) 9,111?

Решение

а) 2 < 2,7 < 3

б) 12 < 12,21 < 13

в) 3 < 3,343 < 4

г) 9 < 9,111 < 10

Задание 334

Найдите какое−нибудь значение х, при котором верно неравенство:
а) 1,41 < х < 4,75;
б) 0,1 < х < 0,2;
в) 2,7 < х < 2,8;
г) 2,99 < х < 3;
д) 7 < х < 7,01;
е) 0,12 < х < 0,13.

Решение

а) 1,41 < 1,43 < 4,75

б) 0,1 < 0,15 < 0,2

в) 2,7 < 2,75 < 2,8

г) 2,99 < 2,999 < 3

д) 7 < 7,005 < 7,01

e) 0,12 < 0,125 < 0,13

Задание 335

Сравните величины:
а) 98,52 м и 65,39 м;
б) 149,63 кг и 150,08 кг;
в) 3,55°С и 3,61°С;
г) 6,781 ч и 6,718 ч;
д) 0,605 т и 691,3 кг;
е) 4,572 км и 4671,3 м;
ж) 3,835 га и 383,7 а;
з) 7,521 л и 7538 с м 3.
Можно ли сравнить 3,5 кг и 8,12 м?
Приведите несколько примеров величин, которые нельзя сравнивать.

Решение

а) 98,52 м > 65,39 м

б) 149,63 кг< 150,08 кг

в) 3,55°С < 3,61°С

г) 6,781 ч > 6,718 ч

д) 0,605 т = 605 кг < 691,3 кг

е) 4,572 км = 4572 м < 4671,3 м

ж) 3,835 га = 383,5 а < 383,7 а

з) 7,521 л = 7521 см³ < 7538 см³

Нельзя сравнивать величины, выражающие различные физические величины,
например кг и м, ° и м, скорость и время.

Задание 336

Вычислите устно:
а) 9² : 27
* 32
+ 14
: 10
− 11
?
б) 5³ * 8
: 20
− 49
* 80
: 5
?
в) 1 ч 20 мин : 4
− 15 мин
: 10
+ 7 с
?
г) 2 га 10 а : 7
+ 15 а
: 500
− 9 м²
?

Решение

а) 81, 3, 96, 110, 11, 0.

б) 125, 1000, 50, 1, 80, 16.

в) 20 мин, 5 мин, 3 с, 10 с.

г) 30 а, 45 а, 9 м², 0.

Задание 337

Восстановите цепочку вычислений:

при а = 6/17 ; 15/17 ; 9/17 ; 1.

Решение

6/17 → 4/17 → 13/17 → 16/17 → 12/17;
15/17 → 13/17 → 22/17 → 17/17 → 16/17;
9/17 → 7/17 → 16/17 → 19/17 → 15/17;
1 = 17/17 → 15/17 → 24/17 → 19/17 → 18/17.

Задание 338

Можно ли сказать, сколько цифр после запятой в записи десятичной дроби, если её название заканчивается словом:
а) сотых;
б) десятитысячных;
в) десятых;
г) миллионных?

Решение

а) две

б) четыре

в) одна

г) шесть

Задание 339

Какую часть килограмма составляют: 1 г; 10 г; 100 г; 300 г?

Решение

1 г = 1/1000 = 0,001 кг;
10 г = 10/1000 = 0,01 кг;
100 г = 100/1000 = 0,1 кг;
300 г = 300/1000 = 0,3 кг.

Задание 340

Найдите число, если 1/10 его равна: 20; 15; 3; 1.

Решение

20 * 10 = 200
15 * 10 = 150
3 * 10 = 30
1 * 10 = 10

Задание 341

Используя рисунок 142, попробуйте догадаться, какое число стоит вместо звездочки:
а) 1/2 = */10;
б) 1/5 = */10;
в) */5 = 6/10;
г) 2/5 = 4/*.

Решение

а) 1/2 = 5/10

б) 1/5 = 2/10

в) 3/5 = 6/10

г) 2/5 = 4/10.

Задание 342

Все шесть граней куба − квадраты. Подумайте, какие из фигур, изображённых на рисунке 143, являются развёрткой поверхности куба.

Решение

Развёртки − в) и г) .

Задание 343

Выразите в тоннах и килограммах:
а) 3,236 т;
б) 11,800 т;
в) 0,006 т;
г) 7,001т;
д) 8,009 т;
е) 10,001 т.

Решение

а) 3,236 т = 3 т 236 кг

б) 11,800 т = 11 т 800 кг

в) 0,006 т = 6 кг

г) 7,001 т = 7 т 1 кг

д) 8,009 т = 8 т 9 кг

е) 10,001 т = 10 т 1 кг

Задание 344

Выразите:
а) в миллионах: 8 984 000; 91,78 млрд;
б) в тысячах: 1306; 8,065 млн; 17,8 млрд.

Решение

а) 8984000 = 8,984 млн.
91,78 млрд = 91780 млн

б) 1306 = 1,306 тыс.
8,065 млн. = 8065 тыс.
17,8 млрд. = 17800000 тыс.

 

Задание 345

Запишите в виде десятичных дробей частные:
7206 : 100;
61 : 1000;
7 : 100;
1849 : 1000.

Решение

7206 : 100 = 72,06
61 : 1000 = 0,061
7 : 100 = 0,07
1849 : 1000 = 1,849

Задание 346

Решите задачу:
а) Теплоход идёт вниз по реке. Какова скорость движения теплохода, если скорость течения реки 4 км/ч, а собственная скорость теплохода (скорость в стоячей воде) равна 21 км/ч?
б) Моторная лодка идёт вверх по реке. Какова скорость движения лодки, если скорость течения 3 км/ч, а собственная скорость лодки 14 км/ч?

Решение

1) 21 + 4 = 25 (км/ч) - скорость теплохода

2) 14 − 3 = 11 (км/ч) - скорость лодки

Задание 347

Разложите по разрядам числа: 5089; 6 781 802; 8000; 98000560.

Решение

5089 = 5000 + 80 + 9
6781802 = 6000000 + 700000 + 80000 + 1000 + 800 + 2
8000 = 8000 + 0
98000560 = 90000000 + 8000000 + 500 + 60

Задание 348

Выполните действие:
а) 9/14 + 3/14;
б) 21/50 + 29/50;
в) 2 + 4/17;
г) 17 + 9/13;
д) 6 2/3 − 1 1/3;
е) 18 5/11 − 7 1/11;
ж) 4 − 3/5;
з) 15 − 6/7;
и) 3 1/5 − 1 3/5;
к) 2 4/9 − 1 7/9;
л) 1 5/7 + 6/7;
м) 5 8/13 + 4 7/13.

Решение

а) $\frac9{14}+\frac3{14}=\frac{9+3}{14}=\frac{12}{14}$

б) $\frac{21}{50}+\frac{29}{50}=\frac{21+29}{50}=\frac{50}{50}=1$

в) $2+\frac4{17}=2\frac4{17}$

г) $17+\frac9{13}=17\frac9{13}$

д) $6\frac23-1\frac13=6-1+\frac23-\frac13=5+\frac13=5\frac13$

е) $18\frac5{11}-7\frac1{11}=18-7+\frac5{11}-\frac1{11}=11+\frac4{11}=11\frac4{11}$

ж) $4-\frac35=3+\frac55-\frac35=3\frac25$

з )$15-\frac67=14+\frac77-\frac67=14\frac17$

и) $3\frac15-1\frac35=2\frac65-1\frac35=2-1+\frac65-\frac35=1\frac35$

к) $2\frac49-1\frac79=1\frac{13}9-1\frac79=1-1+\frac{13}9-\frac79=\frac69$

л) $1\frac57+\frac67=1\frac{11}7=2\frac47$

м) $5\frac8{13}+4\frac7{13}=5+4+\frac8{13}+\frac7{13}=9\frac{15}{13}=10\frac2{13}$

Задание 349

Решите задачу:
1) Co станции вышел товарный поезд со скоростью 50 км/ч. Через 3 ч с той же станции вслед за ним вышел электропоезд со скоростью 80 км/ч. Через сколько часов после своего выхода электропоезд догонит товарный поезд?
2) Самолёт вылетел с аэродрома со скоростью 500 км/ч. Через 2 ч с этого же аэродрома в том же направлении вылетел другой самолёт со скоростью 700 км/ч. Через сколько часов после вылета второй самолёт догонит первый?

Решение

1)
1) 50 * 3 = 150 (км) - проехал товарный поезд за 3 ч
2) 80 − 50 = 30 (км/ч) скорость электропоезда
3) 150 : 30 = 5 (ч) - время, через которое электропоезд догонит товарный поезд
Ответ: через 5 ч.

2) 500 − 2 : (700 − 500) = 1000 : 200 = 5 (ч) - время, через которое второй самолет догонит первый.
Ответ: через 5 ч.

Задание 350

Сравните числа:
а) 3,573 и 3,581;
б) 8,605 и 8,59;
в) 7,299 и 7,3;
г) 6,504 и 6,505;
д) 3,29 и 3,3;
е) 4,85 и 0,1.

Решение

а) 3,573 < 3,581

6) 8,605 > 8,59

в) 7,299 < 7,3

г) 6,504 < 6,505

д) 3,29 < 3,3

е) 4,85 > 0,1

Задание 351

Напишите все цифры, которые можно поставить вместо звёздочки, чтобы получилось верное неравенство:
а) 0,3 > 0,13;
б) 0,1 < 0,18;
в) 5,64 > 5,8;
г) 3,51 < 3,1;
д) 12,4 > 12,53;
е) 0,001 < 0,01.

Решение

а) 2; 3; 4; 5; 6; 7; 8; 9.

б) 0; 1; 2; 3; 4; 5; 6; 7.

в) 0; 1; 2; 3; 4; 5.

г) 6; 7; 8; 9.

д) 5; 6; 7; 8; 9.

е) 1; 2; 3; 4; 5; 6; 7; 8; 9.

Задание 352

Напишите число, меньшее 0,000001.

Решение

0,0000005 < 0,000001.

Задание 353

Примите за единичный отрезок длину десяти клеток тетради и отметьте на координатном луче точки:
А(0,7), В(1,2), С(1,8).

Решение

Задание 354

Разложите по разрядам 49008 и 67813742.

Решение

49008 = 40000 + 9000 + 8;
67813742 = 60000000 + 7000000 + 800000 + 10000 + 3000 + 700 + 40 + 2.

Задание 355

Выполните действия:
а) 11 2/7 + 4 3/7 − 6 4/7;
б) 26 7/19 − 13 4/19 + 5 2/19;
в) 44 2/9 + 8 5/9 − 7/9;
г) 5 7/10 + 3 9/10 + 1 3/10;
д) 3 17/100 − 2 13/100 − 1;
е) 8 − 4 31/100 − 2 57/100.

Решение

а) $11\frac27+4\frac37-6\frac47=11+4-6+\frac27+\frac37-\frac47=9+\frac17=9\frac17$

б) $26\frac7{19}-13\frac4{19}+5\frac2{19}=26-13+5+\frac7{19}-\frac4{19}+\frac2{19}=18+\frac5{19}=18\frac5{19}$

в) $44\frac29+8\frac59-\frac79=44+8+\frac29+\frac59-\frac79=52+0=52$

г) $5\frac7{10}+3\frac9{10}+1\frac3{10}=5+3+1+\frac7{10}+\frac9{10}+\frac3{10}=9+\frac{19}{10}=9+1\frac9{10}=9+1+\frac9{10}=10\frac9{10}$

д) $3\frac{17}{100}-2\frac{13}{100}-1=3-2-1+\frac{17}{100}-\frac{13}{100}=0+\frac4{100}=\frac4{100}$

е)$8-4\frac{31}{100}-2\frac{57}{100}=8-4-2-\frac{31}{100}-\frac{57}{100}=7-4-2+\frac{100}{100}-\frac{31}{100}-\frac{57}{100}=1+\frac{12}{100}=1\frac{12}{100}$

Задание 356

Два поезда вышли в разное время навстречу друг другу из двух городов, расстояние между которыми 782 км. Скорость первого поезда 52 км/ч, а второго 61 км/ч. Пройдя 416 км, первый поезд встретился со вторым. На сколько один из поездов вышел раньше другого?

Решение

1) 416 : 52 = 8 (ч) - находился в пути первый поезд до встречи
2) (782 − 416) : 61 = 366 : 61 = 6  (ч) - находился в пути второй поезд до встречи
3) 8 − 6 = на 2 (ч) - раньше вышел первый поезд, чем второй.
Ответ: на 2 ч.

Задание 357

С одной и той же станции в одно и то же время вышли в противоположных направлениях два поезда. Скорость одного поезда 50 км/ч, а скорость другого 85 км/ч. Через какое время расстояние между ними будет равно 540 км?

Решение

540 : (85 + 50) = 540 : 135 = 4 (ч) - время, через котое расстояние между ними будет равно 540 км
Ответ: через 4 ч.

Задание 358

Чтобы добраться из города до села, я проехал 5 ч на поезде, 2 ч на автобусе и 3 ч прошёл пешком. Скорость автобуса была 35 км/ч, скорость поезда вдвое больше скорости автобуса, а пешком я шёл со скоростью, на 65 км/ч меньшей, чем скорость поезда. Какой путь я проделал от города до села?

Решение

1) 2 * 35 = 70 (км/ч) - скорость поезда
2) 70 − 65 = 5 (км/ч) - скорость пешком
3) 70 * 5 + 35 * 2 + 5 * 3 = 350 + 70 + 15 = 435 (км) - путь от города до села
Ответ: 435 км.

Задание 359

Поле в 1260 га засеяли озимой пшеницей вместо яровой и собрали по 28 ц зерна с гектара. Урожайность яровой пшеницы была 18 ц с гектара. Какую прибавку зерна получили со всей площади?

Решение

(28 − 18) * 1260 = 10 * 1260 = 12600 (ц) - прибавка зерна со всей площади
Ответ: 12600 ц.

Задание 360

Решите уравнение:
а) 14х − (8х + 3х) = 1512;
б) 11у − (5у − 3у) = 8136.

Решение

а) 14х − (8x + 3x) = 1512
14x − 11x = 1512
3x = 1512
x = 1512 : 3
х = 504

б) 11у − (5у − 3у) = 8136
11y − 2y = 8136
9x = 8136
y = 8136 : 9
у = 904

73 74 75 76 77 78 79 80

Пункт 32. Ответы к теме Сложение и вычитание десятичных дробей, страница 73

Задание 361

На пальто израсходовали 3,2 м ткани, а на костюм − 2,63 м. Сколько ткани израсходовали на пальто и костюм вместе? Решите задачу сложением десятичных дробей и путём перехода к сантиметрам.

Решение

1способ
3,2 + 2,63 = 5,83 (м) - ткани было израсходовано на пальто и костюм
Ответ: 5,83 м.
2 способ
3 м 20 см + 2 м 63 см = 320 см + 263 см = 583 см = 5 м 83 см - ткани было израсходовано на пальто и костюм
Ответ: 5 м 83 см.

Задание 362

Масса автомобиля «Нива» 11,5 ц, а масса автомобиля «Волга» 14,2 ц. На сколько масса «Волги» больше массы «Нивы»? Решите задачу с помощью десятичных дробей и переводом данных в килограммы.

Решение

14,2 − 11,5 = на 2,7 (ц) - масса «Волги» больше массы «Нивы»
14 ц 20 кг − 11 ц 50 кг = 1420 кг − 1150 кг = 270 кг = 2 ц 70 кг
Ответ: на 2,7 ц или  2 ц 70 кг.

Задание 363

Выполните сложение:
а) 0,769 + 42,389;
б) 5,8 + 22,191;
в) 95,381 + 3,219;
г) 8,9021 + 0,68;
д) 2,7 + 1,35 + 0,8;
е) 13,75 + 8,2 + 0,115.

Решение

а) 
+ 0.769
 42.389
 43.158

б)
+ 5.8
 22.191
 27.991

в)
+ 95.381
     3.219
   98.6

г)
+ 8.9021
   0.68    
   9.5821

д)
+ 2.7
   1.35
   0.8  
   4.85

е)
+ 13.75
     8.2
     0.115
   22.065

Задание 364

Выполните вычитание
а) 9,4 − 7,3;
б) 16,78 − 5,48;
в) 7,79 − 3,79;
г) 11,1 − 2,8;
д) 88,252 − 4,69;
е) 6,6 − 5,99.

Решение

а) 
- 9.4
  7.3
  2.1

б)
- 16.78
    5.48
  11.3

в)
- 7.79
  3.79
  4

г)
- 11.1
    2.8
    8.3

д)
- 88.252
    4.69  
  83.562

е)
- 6.6
  5.99
  0.61

Задание 365

С одного участка собрали 95,37 т зерна, а с другого − на 16,8 т больше. Сколько тонн зерна собрали с двух участков?

Решение

 95,37 + (95,37 + 16,8) = 95,37 + 112,17 = 307,54 (т) - собрали с двух участков
Ответ: 307,54 т.

Задание 366

Один тракторист вспахал 13,8 га земли, что оказалось на 4,7 га меньше, чем вспахал второй тракторист. Сколько гектаров земли вспахали оба тракториста вместе?

Решение

 13,8 + (13,8 + 4,7) = 13,8 + 18,5 = 32,3 (га) - вспахали оба тракториста
Ответ: 32,3 га.

Задание 367

От куска провода длиной 30 м отрезали 4,75 м. Сколько метров провода осталось в куске?

Решение

 30 − 4,75 = 25,25 (м) - провода осталось в куске
Ответ: 25,25 м.

Задание 368

Груз, поднимаемый вертолётом, легче вертолёта на 4,72 т. Какова масса вертолёта вместе с грузом, если масса груза 1,24 т?

Решение

(4,72 + 1,24) + 1,24 = 5,96 + 1,24 = 7,2 т - масса вертолёта вместе с грузом
Ответ: 7,2 т.

Задание 369

Выполните действие:
а) 7,8 + 6,9;
б) 129 + 9,72;
в) 8,1 − 5,46;
г) 96,3 − 0,081;
д) 24,2 + 0,867;
е) 830 − 0,0097;
ж) 0,02 − 0,0156;
з) 0,003 − 0,00089;
и) 1 − 0,999;
к) 425 − 2,647;
л) 83 − 82,877;
м) 37,2 − 0,03.

Решение

а) 
+ 7.8
   6.9
 14.7

б)
+ 129
       9.72
   138.72

в)
- 8.1
  5.46
  2.64

г)
- 96.3
    0.081
  96.219

д)
+ 24.2
     0.867
   25.067

е)
- 830
      0.0097
  829.9903

ж)
- 0.02
  0.0156
  0.0044

з)
- 0.003
  0.00089
  0.00211

и)
- 1
  0.999
  0.001

к)
- 425
      2.647
  422.353

л)
- 83
  82.877
    0.123

м)
- 37.2
    0.03
  37.17

Задание 370

Собственная скорость катера (скорость в стоячей воде) равна 21,6 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость катера по течению и против течения.

Решение

1)  21,6 + 4,7 = 3 (км/ч) - корость катера по течению реки
2) 21,6 − 4,7 = 16,9 (км/ч) - скорость катера против течения
Ответ: 3 км/ч, 16,9 км/ч

Задание 371

Скорость теплохода по течению равна 37,6 км/ч. Найдите собственную скорость теплохода и его скорость против течения, если скорость течения реки 3,9 км/ч.

Решение

1) 37,6 − 3,9 = 33,7 (км/ч) - собственная скорость теплохода
2) 33,7 − 3,9 = 29,8 (км/ч) - скорость теплохода против течения
Ответ: 33,7 км/ч, 29,8 км/ч.

Задание 372

Скорость велосипедиста 15 км/ч, а скорость пешехода на 9,7 км/ч меньше. На сколько уменьшится расстояние между ними за 1 ч, если они движутся навстречу друг другу? На сколько увеличивается расстояние между ними за 1 ч, если они движутся из одной точки в противоположные стороны?

Решение

1) 15 − 9,7 = 5,3 (км/ч) - скорость пешехода
2) 15 + 5,3 = 20,3 (км/ч) - скорость сближения и скорость удаления
Значит, расстояние между ними за 1 час уменьшится на 20,3 км,  если они движутся навстречу друг другу, и увеличится на 20,3 км, если они движутся из одной точки в противоположные стороны.
Ответ:  на 20,3 км.

Задание 373

Расстояние между городами 156 км. Из них навстречу друг другу выехали два велосипедиста. Один проезжает в час 13,6 км, а второй − 10,4 км. Через сколько часов они встретятся?

Решение

(13,6 + 10,4) = 24 (км/ч) - скорость сближения велосипедистов
$156:24=\frac{156}{24}=6\frac12$ (ч) - время, через которое они встретятся
Ответ: через $6\frac12$ ч.

Задание 374

Верёвку разрезали на пять кусков. Первый кусок больше второго на 4,2 м, но меньше третьего на 2,3 м. Четвёртый кусок больше пятого на 3,7 м, но меньше третьего на 1,3 м. Какова длина веревки, если длина четвёртого куска 7,8 м?

Решение

1) 7,8 + 1,3 = 9,1 (м) - длина третьего куска
2) 7,8 − 3,7 = 4,1 (м) - длина пятого куска
3) 9,1 − 2,3 = 6,8 (м) - длина первого куска
4) 6,8 − 4,2 = 2,6 (м) - длина второго куска
5) 6,8 + 2,6 + 9,1 + 7,8 + 4,1 = 30,4 (м) -  длина верёвки
Ответ: 30,4 м.

Задание 375

Найдите периметр треугольника ABC, если АВ = 2,8 см, ВС больше АВ на 0,8 см, но меньше АС на 1,1 см.

Решение

ВС = 2,8 + 0,8 = 3,6 см
АС = 3,6 + 1,1 = см
РАВС = 2,8 + 3,6 + 4,7 = 6,4 + 4,7 = 11,1 см

Задание 376

Используя буквы х и у, запишите переместительное свойство сложения и проверьте его, если х = 7,3, а у = 29.
Используя буквы a, b и с, запишите сочетательное свойство сложения и проверьте его при а = 2,3; b = 4,2 и с = 3,7.

Решение

x + у = у + x,
при x = 7,3, у = 29
х + у = 7,3 + 29 = 36,3;
y + x = 29 + 7,3 = 36,3.
Выражение верно.

(a + b) + с = a + (b + с),
при a = 2,3; b = 4,2; c = 3,7
(a + b) + с = (2,3 + 4,2) + 3,7 = 6,5 + 3,7 = 10,2;
a + (b + с) = 2,3 + (4,2 + 3,7) = 2,3 + 7,9 = 10,2.
Выражение верно.

Задание 377

Используя буквы a, b и с, запишите свойство вычитания числа из суммы и свойство вычитания суммы из числа.
Проверьте эти свойства при a = 13,2; b = 4,8 и с = 2,7.

Решение

(a + b) − с = a + (b − с),
при a = 13,2; b = 4,8; с = 2,7:
(a + b ) − c = (13,2 + 4,8) − 2,7 = 18 − 2,7 = 15,3;
a + (b − с) = 13,2 + (4,8 − 2,7) = 13,2 + 2,1 = 15,3.

a − (b + с) = a − b − c,
при а = 13,2; b = 4,8; c = 2,7:
a − (b + c) = 13,2 − (4,8 + 2,7) = 13,2 − 7,5 = 5,7;
a − b − c = 13,2 − 4,8 − 2,7 = 8,4 − 2,7 = 5,7.

Задание 378

Используя свойства сложения и вычитания, вычислите самым удобным способом значение выражения:
а) 2,31 + (7,65 + 8,69);
б) 0,387 + (0,613 + 3,142);
в) (7,891 + 3,9) + (6,1 + 2,109);
г) 14,537 − (2,237 + 5,9);
д) (24,302 + 17,879) − 1,302;
е) (25,243 + 17,77)− 2,77.

Решение

а) 2,31 + (7,65 + 8,69) = (2,31 + 8,69) + 7,65 = 11 + 7,65 = 18,65

6) 0,387 + (0,613 + 3,142) = (0,387 + 0,613) + 3,142 = 1 + 3,142 = 4,142

в) (7,891 + 3,9) + (6,1 + 2,109) = (7,891 + 2,109) + (3,9 + 6,1) = 10 + 10 = 20

г) 14,537 − (2,237 + 5,9) = (14,537 − 2,237) − 5,9 = 12,3 − 5,9 = 6,4

д) (24,302 + 17,879) − 1,302 = (24,302 − 1,302) + 17,879 = 23 + 17,879 = 40,879

e) (25,243 + 17,77) − 2,77 = 25,243 + (17,77 − 2,77) = 25,243 + 15 = 40,243

Задание 379

Выполните действия:
а) 9,83 − 1,76 − 3,28 + 0,11;
б) 12,371 − 8,93 + 1,212;
в) 14,87 − (5,82 − 3,27);
г) 14 − (3,96 + 7,85).

Решение

а) 9,83 − 1,76 − 3,28 + 0,11 = (9,83 + 0,11) − (1,76 + 3,28) = 9,94 − 5,04 = 4,9

б) 12,371 − 8,93 + 1,212 = 3,441 + 1,212 = 4,653

в) 14,87 − (5,82 − 3,27) = 14,87 − 2,55 = 12,32

г) 14 − (3,96 + 7,85) = 14 − 11,81 = 2,19

Задание 380

Сколько единиц в каждом разряде числа: 32,547; 2,6034?

Решение

Число 32,547:
в разряде десятков 3 единицы, в разряде единиц − 2, в разряде десятых − 5,
в разряде сотых − 4, в разряде тысячных − 7. Число 2,6034:
в разряде единиц − 2, в разряде десятых − 6, в разряде сотых − 0,
в разряде тысячных − З, в разряде десятитысячных − 4.

Задание 381

==

Решение

а) 24, 578
   20 + 4 + 0,5 = 0,07 + 0, 008 = 24, 578

б) 0,520001
    0,5 + 0,02 + 0,000001 = 0,520001

Задание 382

Разложите по разрядам число:
а) 24,578;
б) 0,520001.

Решение

а) 24,578 = 20 + 4 + 0,5 + 0,07 + 0,008

б) 0,520001 = 0,5 + 0,02 + 0,000001

Задание 383

Запишите десятичную дробь, в которой:
а) 15 целых, 3 десятых, 7 сотых и 9 тысячных;
б) 0 целых, 3 десятых, 0 сотых и 4 тысячных.

Решение

а) 15,379

б) 0,304

Задание 384

Выразите длину отрезка АВ = 5 м 7 дм 6 см 2 мм:
а) в метрах;
б) в дециметрах;
в) в сантиметрах;
г) в миллиметрах.
Выразите длину отрезка СМ в метрах, дециметрах, сантиметрах и миллиметрах, если СМ = 4,573 м.

Решение

а) 5 м 7 дм 6 см 2 мм = 5 м + 0,7 м +0,06 м + 0,002 м = 5,762 м

б) 5 м 7 дм 6 см 2 мм = 50 дм + 7 дм + 0,6 дм + 0,02 дм = 57,62 дм

в) 5 м 7 дм 6 см 2 мм = 500 см + 70 см + 6 см + 0,2 см = 576,2 см

г) 5 м 7 дм 6 см 2 мм = 5000 мм + 700 мм + 60 мм + 2 мм = 5762 мм

СМ = 4,573 м = 45,73 дм = 457,3 см = 4573 мм

 

Задание 385

Найдите координаты точек А, В, С, D и К (рис. 146).

Решение

A(5,3), B(5,8), С(6,2), D(6,6), K(6,8).

Задание 386

Зная, что 11,87 − 7,39 = 4,48, найдите значение выражения или решите уравнение:
а) 7,39 + 4,48;
6) 11,87 − 4,48;
в) х − 7,39 = 4,48;
г) 7,39 + у = 11,87;
д) 4,48 + z = 11,87;
е) 11,87 − р = 7,39.

Решение

а) 7,39 + 4,48 = 11,87

б) 11,87 − 4,48 = 7,39

в) х − 7,39 = 4,48
х = 4,48 + 7,39
х = 11,38

г) 7,39 + у = 11,87
у = 11,87 − 7,39
у = 4,48

д) 4,48 + z = 11,87
z = 11,87 − 4,48
z = 7,39

е) 11,87 − р = 7,39
р = 11,87 − 7,39
р = 4,48

Задание 387

Прочитайте показания термометров (рис. 147). Сколько градусов будет показывать каждый из них, если его столбик:
а) поднимется на 4 малых деления; на 2 больших деления; на 0,5°С; на 1,3 °С;
б) опустится на 7 малых делений; на одно большое деление; на 0,3°С; на 1,4 °С?

Решение

Термометр 1 показывает температуру 36,7°С, термометр 2 − 36,1°С, термометр 3 − 37,1°С, термометр 4 − 39,8°С.

а) Если температура поднимется на 4 малых деления, то термометры покажут:
1 − 37,1°С, 2 − 3б,5°С, 3 − 37,5°C, 4 − 40,2°C;
если температура поднимется на 2 больших деления, то термометры покажут:
1 − 38,7°С, 2 − 38,1°С, 3 − 39,1°С, 4 − 41,8°С;
если температура поднимется на 0,5°С, то термометры покажут:
1 − 37,2°С, 2 − 36,6°С, 3 − 37,б°С, 4 − 40,3°С,
если температура поднимется на 1,3°С, то термометры покажут:
1 − 38°С, 2 − 37,4°С, 3 − 38,4°С, 4 − 41,1°С.

б) Если температура опустится на 7 малых делений, то термометры покажут:
1 − 36°С, 2 − 35,4°С, 3 − 3б,4°С, 4 − 39,1°С;
если температура опустится на 1 большое деление, то термометры покажут:
1 − 35,7°С, 2 − 35,1°С, 3 − 36,1°С, 4 − 38,8°С;
если температура опустится на 0,3°С, то термометры покажут:
1 − 36,4°С, 2 − 35,8°С, 3 − −3б,8°С, 4 − 39,5°С;
если температура опустится на 1,4°С, то термометры покажут:
1 − 35,3°С, 2 − 34,7°С, 3 − 35,7°С, 4 − 38,4°С.

Задание 388

Решите уравнение:
а) z + 3,8 = 8;
б) у − 6,5 = 12;
в) 13,5 − х = 1,8;
г) 15,4 + k = 15,4;
д) 2,8 + l + 3,7 = 12,5;
е) (5,6 − r) + 3,8 = 4,4.

Решение

а) z + 3,8 = 8
z = 8 − 3,8
z = 4,2

б) у − 6,5 = 12
у = 12 + 6,5
у = 18,5

в) 13,5 − x − 1,8
х = 13,5 − 1,8
х = 11,7

г) 15,4 + k = 15,4
k = 15,4 − 15,4
k = 0

д) 2,8 + z + 3,7 = 12,5
z = 12,5 − 6,5
z = 6

е) (5,6 − r) + 3,8 = 4,4
r = 5,6 − 0,6
r = 5

Задание 389

Вычислите устно:
а) 60 - 36
* 3
: 4
+ 27
: 3
?
б) 55 + 25
: 5
+ 7
* 3
+ 31
?
в) 75 : 25
* 15
: 9
* 12
+ 240
?
г) 15 * 6
- 39
: 17
* 18
+ 46
?
д) 45 + 30
: 15
* 20
- 34
: 11
?

Решение

а) 24, 72, 18, 45, 15.

б) 80, 16, 23, 69, 100.

в) 3, 45, 5, 60, 300.

г) 90, 51, 3, 54, 100.

д) 75, 5, 100, 66, 6.

Задание 390

Восстановите цепочку вычислений

при х = 6/11 , 14/11 , 4/11 , 3/11 , 1 7/11.

Решение

6/11 → 9/11 → 10/11 → 3/11 → 1 6/11 → 3_6/11;
14/11 → 17/11 → 18/11 → 1 → 7/10;
4/11 → 7/11 → 8/11 → 1/11 → 1_4/11 → 3_4/11;
3/11 → 6/11 → 7/11 → 0 → 1_3/11 → 3_3/11;
1_7/11 → 1_10/11 → 2 → 1_4/11 → 4/11 → 3_6/11.

Задание 391

Назовите какое−либо число, расположенное на координатном луче:
а) между числами 0,1 и 0,2;
б) между 0,02 и 0,03;
в) левее 0,001, но правее 0.

Решение

а) 0,1 < 0,15 < 0,2

6) 0,02 < 0,025 < 0,3

в) 0 < 0,0005 < 0,001

Задание 392

Какую часть квадратного метра составляет:
а) 1 дм²;
б) 1 см²;
в) 10 дм²;
г) 100 см²?

Решение

а) 1 дм² = 1/100 = 0,0001 м²

б) 1 см² = 1/10000 = 0,0001 м²

в) 10 дм² = 10/100 = 0,01 м²

г) 100 см² = 100/10000 = 0,01 м²

Задание 393

Стороны треугольника 3/7 м, 4/7 м, 5/7 м. Найдите его периметр.

Решение

Р ∆ = 3/7 + 4/7 + 5/7 = 7/7 + 5/7 = 1 5/7 м.

Задание 394

Найдите число, если 3/10 его равны: 30; 15; 6.

Решение

30 : 3 * 10 = 10 * 10 = 100
15 : 3 * 10 = 5 * 10 = 50
6 : 3 * 10 = 2 * 10 = 20

Задание 395

Какая часть периода хоккейного матча сыграна, если с начала матча прошло: 5 мин; 10 мин; 15 мин; 1 мин 20 с; 20 с? (Период продолжается 20 мин.)

Решение

5 : 20 = 5/20
10 : 20 = 10/20
15 : 20 = 15/20
(60 + 20) : (20 * 60) = 80/1200
20 : (20 * 60) = 20/1200

Задание 396

Сколько Буратино заплатил за арбуз, который стоил 20 сольдо и ещё пол−арбуза?

Решение

Половина арбуза стоит 20 сольдо, поэтому арбуз стоит в 2 раза больше
20 * 2 = 40 (с.)
Ответ: 40 сольдо.

Задание 397

Сравните числа:
а) 12,567 и 125,67;
б) 7,399 и 7,4.

Решение

а) 12,567 < 125,67

б) 7,399 < 7,4

Задание 398

Между какими двумя соседними натуральными числами находится число:
а) 5,1;
б) 6,32;
в) 9,999;
г) 25,257?

Решение

а) 5 < 5,1 < 6

б) 6 < 6,32 < 7

в) 9 < 9,999 < 10

г) 25 < 25,257 < 26

Задание 399

Расставьте в порядке убывания числа:
0,915; 2,314; 0,9078; 2,316; 2,31; 10,45.

Решение

0,9078 < 0,915 < 2,31 < 2,314 < 2,316 < 10,45.

Задание 400

Расставьте в порядке возрастания величины: 8,09 км; 8165,3 м; 8154257 мм; 815376 см.

Решение

8,09 км = 8090 м
8154257 мм = 8154,257 м
815 376 см = 8153,76 м
8090 м = 8,09 км < 8153,76 м = 815376 см < 8154,257 м = 8154257 мм

Задание 401

Решите уравнение:
а) 3/5 + х = 4/5;
б) у − 2/7 = 6/7;
в) 11/25 − k = 7/25;
г) d + 2/9 = 1/9 + 7/9.

Решение

а) 3/5 + х = 4/5
x = 4/5 − 3/5
х = 1/5

б) у − 2/7 = 6/7
y = 6/7 + 2/7
у = 8/7
у = 1_1/7

в) 11/25 − k = 7/25
k = 11/25 − 7/25
k = 4/25

г) d + 2/9 = 1/9 + 7 9
d = 8/9 − 2/9
d = 6/9

Задание 402

Выразите:
а) в метрах: 17 м 8 см; 8 м 17 см; 4 см; 15 дм;
б) в тоннах: 3 т 8 ц 67 кг; 1244 кг; 710 кг.

Решение

а) 17 м 8 см = 17,08 м
8 м 17 см = 8
4 см = 0,04 м
15 дм = 1,5 м

б) 3 т 8 ц 67 = 3,867 т
1244 кг = 1,244 т
710 кг = 0,71 т

Задание 403

Решите задачу:
1) На машину погрузили 7 одинаковых мешков с мукой и 12 одинаковых мешков с крупой. Масса мешка с мукой в 2 раза больше массы мешка с крупой. Найдите массу мешка с мукой и мешка с крупой, если всего на машину погрузили 780 кг.
2) Масса индюка меньше массы овцы в 3 раза, а масса трёх таких овец больше массы пяти индюков на 60 кг. Какова масса одного индюка и какова масса одной овцы?

Решение

1) Пусть масса мешка с крупой х кг, тогда масса мешка с мукой 2х кг.
Всего на машину погрузили (7 * 2х + 12х) кг.
Составим уравнение:
7 * 2х + 12x = 780
24x = 780
х = 780 : 26
х = 30
Значит, масса мешка с крупой равна 30 кг
2 * 30 = 60 (кг) - масса мешка с мукой
Ответ: 60 кг, 30 кг.

2) Пусть у − масса индюка, тогда масса овцы 3у кг.
Разница в массе 3 овец и 5 индюков равна (3 * 3у − 5у) кг.
Составим уравнение:
3 * 3у − 5у = 60
4у = 60
у = 60 : 4
у = 15
Значит, масса индюка 15 кг
3 * 15 = 45 (кг) - масса овцы
Ответ: 15 кг, 45 кг.

Задание 404

Разгадайте чайнворд, помещённый на форзаце в конце учебника.

Решение

Гектар. 2. Разряд. 3. Длина. 4. Акр. 5.Разложение. 6. Единица. 7. Ар. 8. Радиус.
Сорок. 10. Карат. 11. Тонна. 12. Аршин. 13. Неделя. 14. Ярд. 15. Делимое.

Задание 405

Выполните сложение:
а) 395,486 + 4,58;
б) 7,6 + 908,67;
в) 0,54 + 24,1789;
г) 1,9679 + 269,0121;
д) 23,84 + 0,267;
е) 0,01237 + 0,0009876.

Решение

а) 
+ 395.486
       4.58  
   400.066

б)
+  7.6
908.67
916.27

в)
+ 0.54
 24.1789
 24.7189

г)
+  1.9679
269.0121
270.98

д)
+ 23.84
    0.267
  24.107

е)
+ 0.01237
   0.0009876
   0.0133576

Задание 406

Выполните вычитание:
а) 0,59 − 0,27;
б) 6,05 − 2,87;
в) 3,1 − 0,09;
г) 18,01 − 2,9
д) 15 − 1,12;
е) 3 − 0,07;
ж) 7,45 − 4,45;
з) 206,48 − 90,507;
и) 0,067 − 0,00389.

Решение

а)
- 0.59
  0.27
  0.32

б)
- 6.05
  2.87
  3.18

в)
- 3.1
  0.09
  3.01

г)
- 18.01
    2.9 
  15.11

д)
- 15
    1.12
  13.88

е)
- 3
  0.07
  2.93

ж)
- 7.45
  4.45
  3

з)
- 206.48
    90.507
  115.973

и)
- 0.067
  0.00389
  0.06311

Задание 407

Одна из сторон треугольника 83,6 см, вторая на 14,8 см длиннее первой, а третья на 8,6 см длиннее второй. Найдите периметр треугольника.

Решение

1) 83,6 + 14,8 = 98,4 (см) - длина второй стороны треугольника
2)  98,4 + 8,6 = 107 (см) - длина третьей стороны
3) Р∆ = 83,6 + 98,4 + 107 = 289 см = 2 м 89 см - периметр треугольника
Ответ: 2 м 89 см.

Задание 408

Трубу длиной 9,35 м разрезали на две части. Длина одной части 2,89 м. На сколько метров вторая часть длиннее первой?

Решение

1) 9,35 − 2,89 = 6,46 (м) - длина второй части 
2) 6,46 − 2,89 = 3,57 (м) -  на столько больше длина второй части трубы, чем длина первой части.
Ответ: на 3,57 м.

Задание 409

Воздушный шар состоит из оболочки, гондолы для пассажиров и газовой горелки для нагрева воздуха внутри оболочки. Масса гондолы 0,24 т, и она меньше массы оболочки на 0,32 т, но больше массы газовой горелки на 0,15 т. Какова масса воздушного шара?

Решение

 1) 0,24 + 0,32 = 0,56 (т) - масса оболочки шара
 2) 0,24 − 0,15 = 0,09 (т) - масса газовой горелки
3) 0,24 + 0,56 + 0,09 = 0,89 (т) - масса воздушного шара
Ответ: 0,89 т.

Задание 410

Автомашина в первый час прошла 48,3 км, во второй час − на 15,8 км меньше, чем в первый, а в третий час − на 24,3 км меньше, чем за первые два часа вместе. Какой путь прошла автомашина за эти три часа?

Решение

1) 48,3 − 15,8 = 32,5 (км) - прошла автомашина во второй час
2) (48,3 + 32,5) − 24,3 = 80,8 − 24,3 − 56,5 (км) - прошла автомашина в третий час
3) 48,3 + 32,5 + 56,5 = 80,8 + 56,5 = 137,3 (км) - прошла автомашина за три часа
Ответ: 137,3 км.

Задание 411

Собственная скорость теплохода 40,5 км/ч, а скорость течения 5,8 км/ч. Найдите скорость теплохода по течению и против течения.

Решение

1) 40,5 + 5,8 = 46,3 (км/ч) - скорость теплохода по течению 
2) 40,5 − 5,8 = 34,7 (км/ч) - скорость против течения 
Ответ: 46,3 км/ч, 34,7 км/ч.

Задание 412

Скорость катера по течению 23,7 км/ч. Найдите собственную скорость катера и его скорость против течения, если скорость течения 3,8 км/ч.

Решение

1) 23,7 − 3,8 = 19,9 (км/ч) - собственная скорость катера
2) 19,9 − 3,8 = 16,1 (км/ч) - скорость катера против течения

Задание 413

Выполните действия:
а) 73,12 − (5,34 + 13,12);
б) 101,3 + (84,7 + 1,11);
в) (47,28 − 34,98) + (55,02 + 34,98);
г) (46,83 + 15,77) − (6,83 − 5,77).

Решение

а) 73,12 − (5,34 + 13,12) = (73,12 − 13,12) − 5,34 = 60 − 5,34 = 54,66

б) 101,3 + (84,7 + 1,11) = (101,3 + 84,7) + 1,11 = 186 + 1,11 = 187,11

в) (47,28 − 34,98) + (55,02 + 34,98) = (47,28 + 55,02) + (34,98 − 34,98) = 102,3

г) (46,83 + 15,77) − (6,83 − 5,77) = (46,83 − 6,83) + (15,77 + 5,77) = 40 + 21,54 = 61,54

Задание 414

Разложите по разрядам числа: 41,87; 0,6098; 13,5401.

Решение

41,87 = 40 + 1 + 0,8 + 0,07
0,6098 = 0,6 + 0,009 + 0,0008
13,5401 = 10 + 3 + 0,5 + 0,04 + 0,0001

Задание 415

Запишите десятичную дробь, в которой:
а) 21 целая, 2 десятых, 8 сотых;
б) 0 целых, 0 десятых, 3 сотых, 5 тысячных.

Решение

а) 21,28

б) 0,035

Задание 416

Выразите длину отрезка AВ в метрах, дециметрах, сантиметрах и миллиметрах, если АВ = 8,906 м.

Решение

8,906 м = 89,06 дм = 890,6 см = 8906 мм.

Задание 417

Отметьте на координатном луче числа: 0,25; 0,5; 0,9; 0,37; 0,73; 1,24. За единичный отрезок примите 1 дм.

Решение

Задание 418

Решите уравнение:
а) (х − 18,2) + 3,8 = 15,6;
б) 34,2 − (17,9 − у) = 22;
в) 16,5 − (t + 3,4) = 4,9;
г) r + 16,23 − 15,8 = 7,1.

Решение

а) (х − 18,2) + 3,8 = 15,6
x − 18,2 = 15,6 − 3,8
x = 11,8 + 18,2
х = 30

б) 34,2 − (17,9 − у) = 22
17,9 − у = 34,2 − 22
у = 17,9 − 12,2
у = 5,7

в) 16,5 − (t + 3,4) = 4,9
t + 3,4 = 16,5 − 4,9
t = 11,6 − 3,4
t = 8,2

г) r + 16,23 − 15,8 = 7,1
r + 0,53 = 7,1
r = 7,1 − 0,53
r = 6,57

Задание 419

Объём прямоугольного параллелепипеда 84 см³. Этот параллелепипед разделили на две части. Найдите объём каждой части, если:
а) объём одной части в 6 раз больше объёма другой;
б) объём одной части на 40 см³ больше объёма другой.

Решение

а) Пусть х − объём меньшей части параллелепипеда, тогда 6х − объем большей части.
Сумма этих объёмов равна (х + 6х) см³.
Составим уравнение:
х + 6х = 84
х = 84 : 7
х = 12
Значит, 12 см³ − объём меньшей части
6 * 12 = 72 (см³) - объем большей части
Ответ: 12 см³ , 72 см³.

б) Пусть у − объём одной части, тогда (у + 40) − объём другой.
Сумма этих объёмов равна (у + у + 40) см³.
Составим уравнение:
у + (у + 40) = 84
2у = 84 − 40 = 44
у = 44 : 2
у = 22
Значит, 22 см³ − объём одной части
22 + 40 = 62 (см³) - объем другой части
Ответ: 22 см³ , 62 см³.

81 82 83 84 85 86 87

Пункт 33. Приближенные значения чисел. Округление чисел. Страница 81

Задание 420

Между какими соседними натуральными числами расположена каждая из дробей: 6,78; 83,74; 126,2? К какому из этих чисел дробь ближе?

Решение

6 < 6,78 < 7;
дробь 6,78 расположена ближе к числу 7; 83 < 83,74 < 84;
дробь 83,74 расположена ближе к числу 84; 126 < 126,2 < 127;
дробь 126,2 расположена ближе к числу 126.

Задание 421

Длина прямоугольника х см, а его ширина у см. Укажите приближённые значения с недостатком и с избытком для периметра и для площади этого прямоугольника, если:
а) 7 < х < 8, 3 < у < 4;
б) 20 < х < 25, 16 < у < 18.

Решение

а) P = 2(a + b), S = ab, где а − длина, b − ширина прямоугольника:
при 7 < x < 8, 3 < y < 4,
то 2 * (7 + 3) < Р < 2 * (8 + 4) => 20 < Р < 24;
7 * 3 < S < 8 * 4 => 21 < S < 32.

б) P = 2(a + b), S = ab, где а − длина, b − ширина прямоугольника:
при 20 < х < 25, 16 < у < 18,
то 2 * (20 + 16) < Р < 2 * (25 + 18) => 72 < Р < 86,
20 * 16 < 5 < 25 * 18 => 320 < S < 450.

Задание 422

Округлите до единиц дроби:
7,265; 11,638; 0,23; 8,5; 300,499; 6,5108; 0,8.

Решение

7,265 ≈ 7
11,638 ≈ 12
0,23 ≈ 0
8,5 ≈ 9
300,499 ≈ 300
6,5108 ≈ 7
0,8 ≈ 1

Задание 423

Старинная русская мера массы пуд равна 16,38 кг. Округлите это значение до целых, до десятых. Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков, до сотен. Старинная русская мера длины сажень равна 2,13 м. Округлите это значение до целых, до десятых.

Решение

1 пуд = 16,38 кг ≈ 16 кг, 16,38 кг ≈ 16,4 кг;
1 верста = 1067 м ≈ 1070 м; 1067 м ≈ 1100 м;
1 сажень = 2,13 м ≈ 2 м, 2,13 м ≈ 2,1 м.

Задание 424

Округлите дроби:
а) 2,781; 3,1423; 203,962; 80,46 до десятых;
б) 0,07268; 1,35506; 10,081; 76,544; 4,455 до сотых;
в) 167,1; 2085,04; 444,4; 300,7; 137 до десятков.

Решение

а) 2,781 ≈ 2,8
3,1423 ≈ 3,1
203,962 ≈ 204,0
80,46 ≈ 80,5

б) 0,07268 ≈ 0,07
1,35506 ≈ 1,36
10,081 ≈ 10,08
76,544 ≈ 76,54
4,455 ≈ 4,46

в) 167,1 ≈ 170
2085,04 ≈ 2090
444,4 ≈ 440
300,7 ≈ 300
137 ≈ 140

Задание 425

Одна деталь имеет массу 13,26 кг, вторая − 14,43 кг, третья − 1,66 кг, а четвёртая − 15,875 кг. Найдите общую массу этих четырёх деталей и округлите результат до десятых долей килограмма. Сравните ответ с результатом, полученным, если сначала округлить данные задачи до десятых долей, а потом её решить.

Решение

Общая масса деталей равна 13,26 + 14,43 + 1,66 + 15,875 = 45,225 (кг)
45,225 кг ≈ 45,2 кг
13,26 кг ≈ 13,3 кг;
14,43 кг ≈ 14,4 кг;
1,66 кг ≈ 1,7 кг;
15,875 кг ≈ 15,9;
13,3 + 14,4 + 1,7 + 15,9 = 45,3 (кг)
видно, что результат округления суммы не равен сумме округлённых слагаемых.

Задание 426

Трасса лыжных гонок состоит из 4 участков. Первый участок имеет длину 4,35 км, второй − 5,75 км, третий − 6,95 км и четвёртый − 2,8 км. Найдите длину всей трассы и округлите ответ:
а) до десятых долей километра;
б) до целых километров.

Решение

а)  4,35 + 5,75 + 6,95 + 2,8 = 19,85 (км) - длина всей трассы
     19,85 км ≈ 19,9 км
Ответ: 19,9 км.

б)  4,35 + 5,75 + 6,95 + 2,8 = 19,85 (км) - длина всей трассы
    19,85 км ≈  20 км
Ответ: 20 км.

Задание 427

Найдите периметр четырёхугольника ABCD, если АВ = 6,2 дм, CD больше АВ на 3,14 дм, но меньше ВС на 2,31 дм; AD больше ВС на 1,2 дм. Ответ округлите:
а) до десятых долей дециметра;
б) до целых дециметров.

Решение

а) CD = 6,2 + 3,14 = 9,34 (дм)
ВС = 9,34 + 2,31 = 11,65 (дм)
AD = 11,65 + 1,2 = 12,85 (дм)
PABCD = 6,2 + 9,34 + 11,65 + 12,85 = 40,04 (дм)
40,04 дм ≈ 40,0 дм.

б) CD = 6,2 + 3,14 = 9,34 (дм)
ВС = 9,34 + 2,31 = 11,65 (дм)
AD = 11,65 + 1,2 = 12,85 (дм)
PABCD = 6,2 + 9,34 + 11,65 + 12,85 = 40,04 (дм)
40,04 дм ≈ 40 дм.

Задание 428

Вычислите устно:
а)6² + 2²
+ 50
: 15
* 20
− 25
?
б) 3³ + 5²
: 13
* 25
+ 150
: 125
?
в) 4³ − 3²
: 11
* 40
− 75
: 25
?
г) 2³ + 9²
+ 21
: 11
* 18
: 45
?

Решение

а) 36 + 4 = 40, 90, 6, 120, 95.

б) 27 + 25 = 52, 4, 100, 250, 2.

в) 64 − 9 = 55, 5, 200, 125.

г) 8 + 81 = 89, 110, 10, 180, 4.

Задание 429

Восстановите цепочку вычислений:

Решение

а) 2 → 2,8 → 2,3 → 3,3 → 4 → 3,9

б) 1 → 1 3/7 → 1 2/7 → 2 → 1 2/3 → 2/3

Задание 430

На координатном луче число х расположено между числами а и b. Определите, к какому из чисел ближе х, если:
а) а = 2,3, b = 2,7, х = 2,6;
б) а = 1,34, b = 1,35, х = 1,342;
в) а = 5,6, b = 5,7, х = 5,65.

Решение

а) x расположено ближе к числу b:
х − а = 2,6 − 2,3 = 0,3 > b − х − 2,7 − 2,6 = 0,1

б) х расположено ближе к числу а:
х − а = 1,342 − 1,34 = 0,002 < b − х = 1,35 − 1,342 = 0,008

в) х расположено на одинаковом расстоянии от чисел а и b:
х − а = 5,65 − 5,6 = 0,05 = b − х = 5,7 − 5,65 = 0,05

Задание 431

К числу 76890 приписали справа нуль, два нуля, три нуля. Во сколько раз увеличилось число? Прочитайте каждое из получившихся чисел.

Решение

Число увеличилось в 10 раз;
768900 − семьсот шестьдесят восемь тысяч девятьсот. Число увеличилось в 100 раз;
7689000 − семь миллионов шестьсот восемьдесят девять тысяч. Число увеличилось в 1000 раз;
76890000 − семьдесят шесть миллионов восемьсот девяносто тысяч.

Задание 432

В числе 89452200 зачеркнули два последних нуля. Во сколько раз уменьшилось число?

Решение

Число уменьшилось в 100 раз.

Задание 433

Укажите два числа, которые на координатном луче расположены между числами:
а) 2,1 и 2,2;
б) 0,8 и 0,9;
в) 0 и 0,02;
г) 3,1 и 3,11.

Решение

а) 2,1 < 2,15 < 2,17 < 2,2

б) 0,8 < 0,85 < 0,89 < 0,9

в) 0 < 0,015 < 0,018 < 0,02

г) 3,1 < 3,101 < 3,102 < 3,11

Задание 434

Шахматная доска состоит из 8 рядов по 8 клеток в каждом из них. Какую часть доски составляет:
а) один ряд клеток;
в) одна клетка;
б) 3 ряда клеток;
г) 7 клеток?
Шахматный конь может двигаться на две клетки по вертикали или горизонтали и на одну клетку в сторону. Подумайте, может ли конь переместиться из клетки А шахматной доски в клетку В.

Решение

а) Всего на шахматной доске 8 * 8 = 64 клетки:
1 ряд клеток = 8 клеткам = 8/64 = 1/8 шахматной доски.

б) Всего на шахматной доске 8 * 8 = 64 клетки:
3 ряда клеток = 24 клеткам = 24/64 = 3/8 шахматной доски.

в) Всего на шахматной доске 8 * 8 = 64 клетки:
1 клетка = 1/64 доски.

г) Всего на шахматной доске 8 * 8 = 64 клетки:
7 клеток = 7/64 шахматной доски.

Да, шахматный конь может переместиться из клетки А в клетку В.

Задание 435

Какую часть кубического метра составляет:
а) 1 л;
б) 10 дм³;
в) 100 л;
г) 100 см³?

Решение

а) 1л = 1/1000 = 0,01 м³

б) 10 д м 3 = 10/1000 = 0,01 м³

в) 100 л = 100/1000 = 0,01 м³

г) 100 см³ = 100/1000000 = 0,0001 м³

Задание 436

Найдите число, которое:
а) на 1 3/11 больше 3 7/11;
б) на 8/17 меньше 1.

Решение

а) $3\frac7{11}+1\frac3{11}=3+1+\frac7{11}+\frac3{11}=4\frac{10}{11}$

б) $1-\frac8{17}=\frac{17}{17}-\frac8{17}=\frac9{17}$

Задание 437

Используя рисунок 150, найдите число а:

Решение

а) a = 0,1 + 0,1 + 0,1 + 0,1 + 0,1 = 0,5

б) a = 0,04 + 0,04 + 0,04 = 0,12

Задание 438

Согласны ли вы с утверждением: «Если участки огорожены заборами одинаковой длины, то площади этих участков равны»? Подтвердите своё мнение примерами.

Решение

Это утверждение неверно. Например, прямоугольный участок длиной 6 м и шириной 12 м имеет
Р = 2 * (6 + 12) = 36 м;
S = 6 * 12 = 72 м², но квадратный участок со стороной 9 м имеет такой же
Р = 4 * 9 = 36 м, но S = 9 * 9 = 81 м².

Задание 439

Скорость течения реки 60 м/мин. Продвигается ли лодка, в каком направлении и с какой скоростью, если её собственная скорость:
а) 90 м/мин направлена по течению;
б) 90 м/мин направлена против течения;
в) 60 м/мин направлена по течению;
г) 60 м/мин направлена против течения?

Решение

а) 60 + 90 = 150 (м/мин) - скорость лодки по течению реки
Ответ: лодка движется по течению со скоростью 150 м/мин.

б) 90 − 60 = 30 (м/мин) - скорость лодки против течения реки
Ответ: лодка движется против течения со скоростью 30 м/мин

в) 60 + 60 = 120 (м/мин) - скорость лодки по течению реки
Ответ: лодка движется по течению со скоростью 120 м/мин

г) 60 − 60 = 0 (м/мин) - скорость лодки против течения, то есть лодка не двигается.
Ответ: лодка не движется.

Задание 440

Запишите 4 числа, первое из которых 4,612, а каждое следующее на 2,154 больше предыдущего.

Решение

4,612 + 2,154 = 6,766
6,766 + 2,154 = 8,92
8,92 + 2,154 = 11,074
Ответ: 4,612; 6,766; 8,92; 11,074

Задание 441

Найдите значение выражения 84 − а и выражения а + 6,546,
если a = 30,4; 2,454; 83,998.

Решение

при a = 30,4
84 − a = 84 − 30,4 = 53,6;
a + 6,546 = 30,4 + 6,546 = 36,946;

при a = 2,454
84 − a = 84 − 2,454 = 81,546;
a + 6,546 = 2,454 + 6,546 = 9;

при a = 83,998
84 − a = 84 − 83,998 = 0,002;
a + 6,546 = 83,998 + 6,546 = 90,544.

Задание 442

Представьте произведение 2,75 * 3 в виде суммы и найдите его значение.

Решение

2,75 * 3 = 2,75 + 2,75 + 2,75 = 5,5 + 2,75 = 8,25.

Задание 443

Выполните действия:
а) 68,7 − (44 + 0,375);
б) 90,4 + 65,4 − 90,8;
в) 504 − 47,9 + (58,7 − 49);
г) 17,654 − (37 − 22,9) + 0,345.

Решение

а) 68,7 − (44 + 0,375) = 68,7 − 44,375 = 24,325

б) 90,4 + 65,4 − 90,8 = 155,8 − 90,8 = 65

в) 504 − 47,9 + (58,7 − 49) = 456,1 − 9,7 = 465,8

г) 17,654 − (37 − 22,9) + 0,345 = 17,654 − 14,1 + 0,345 = 3,554 + 0,345 = 3,899

Задание 444

Вместо звёздочки поставьте знак >, = или < так, чтобы получилось верное равенство или неравенство:
а) 0,483 * 0,479;
б) 4,781 * 4,79;
в) 95,3 * 95,300;
г) 0,045 * 0,0045.

Решение

а) 0,483 > 0,479

б) 4,781 < 4,79

в) 95,3 = 95,300

г) 0,045 > 0,0045

Задание 445

Собственная скорость лодки 4,5 км/ч, скорость течения 2,5 км/ч. Найдите скорость лодки при движении по течению и против течения. Какой путь пройдёт лодка по течению за 4 ч и какой путь она пройдёт против течения за 3 ч?

Решение

1) 4,5 + 2,5 = 7 (км/ч) - скорость лодки по течению
2) 4,5 − 2,5 = 2 (км/ч) - скорость лодки против течения
3) 7 * 4 = 28 (км) - пройдет лодка за 4 часа по течению
4) 2 * 3 = 6 (км) - пройдет лодка за 3 ч против течения
Ответ: 28 км, 6 км.

Задание 446

Решите задачу:
1) В школу завезли 24 т угля. За зиму израсходовали 7/8 привезённого угля. Сколько тонн угля осталось?
2) Маляры израсходовали 5/6 купленной краски для ремонта школы. Сколько краски осталось, если купили её 300 кг?

Решение

1) 1 − 7/8 = 1/8 привезённого угля осталась
   24 : 8 = 3 (т) - осталось
Ответ: 3 т.

2) 1 − 5/6 = 1/6 купленной краски осталось
    300 : 6 = 50 (кг) - осталось
Ответ: 50 кг.

Задание 447

Округлите дроби:
а) 1,69; 1,198; 37,444; 37,5444; 802,3022 до целых;
б) 0,3691; 0,8218; 0,9702; 81,3501 до десятых.

Решение

а) 1,69 ≈ 2
1,198 ≈ 1
37,44 ≈ 37
37,5444 ≈ 38
802,3022 ≈ 802

б) 0,3691 ≈ 0,4
0,8218 ≈ 0,8
0,9702 ≈ 1,0
81,3501 ≈ 81,4

Задание 448

Для каждого из чисел найдите натуральные приближённые значения с недостатком и с избытком:
3,97; 21,609; 10,394; 1,057.

Решение

3 < 3,97 < 4
21 < 21,609 < 22
10 < 10,394 < 11
1 < 1,057 < 2

Задание 449

==

Решение

                    76,3681  36,4545  194,0817  97,5983
до дес-ков     80             40           190          100
до един.         76             36            194         98
до десятых    76,4          36,5        194,1       97,6
до сотых        76,37       36,45       194,08     97,60
до тыс-ных    76,368     36,455     194,082   97,598

Задание 450

Запишите число, которое:
а) меньше миллиона в 10 раз; на 10;
б) больше миллиона в 10 раз; на 10;
в) больше числа 709 в 100 раз; в 1000 раз;
г) меньше числа 623 100 000 в 10 раз; в 1000 раз; в 100 000 раз.

Решение

а) 100000, 999990.

б) 10000000, 1000010.

в) 70900, 709000.

г) 62310000, 623100, 6231.

Задание 451

Найдите значение выражения:
а) 8000 * 60000;
б) 1700 * 800000;
в) 250000 * 600 * 40;
г) 19000 * 20000 * 50.

Решение

а) 8000 * 60000 = 480000000

б) 1700 * 800000 = 1360000000

в) 250000 * 600 * 40 = 10000000 * 600 = 6000000000

г) 19000 * 20000 * 50 = 19000 * 1000000 = 19000000000

Задание 452

Собственная скорость теплохода 21,6 км/ч. Скорость течения 4,9 км/ч. Найдите скорость теплохода по течению и против течения.

Решение

1) 21,6 + 4,9 = 26,5 (км/ч) - скорость теплохода по течению
2) 21,6 − 4,9 = 16,7 (км/ч) - скорость теплохода против течения
Ответ: 26,5 км/ч, 16,7 км/ч.

Задание 453

Теплоход шёл по озеру 3 ч со скоростью 27 км/ч, а потом 4 ч по реке, впадающей в это озеро. Найдите весь путь, который прошёл теплоход за эти 7 ч, если скорость течения реки 3 км/ч.

Решение

1)  27 * 7 = 81 (км) - теплоход прошёл по озеру
2) (27 − 3) * 4 = 96 (км) - теплоход прошёл по реке против течения
3) 81 + 96 = 177 (км)- всего прошел теплоход
Ответ: 177 км.

Задание 454

В сокровищнице Кощея Бессмертного 32 000 ларцов, в каждом ларце 210 одинаковых по массе слитков золота и серебра. Какова масса запасов золота и серебра у Кощея, если масса десятка слитков 900 г?

Решение

(32000 * 210) : 100 * 900 = 672000 * 900 = 604800000 (г) - масса запасов золота и серебра
604800000 г = 604,8 т
Ответ: 604,8 т.

Задание 455

Поставьте вместо звёздочек пропущенные цифры:
а) + 6*3*785
         3*4*82
        *9367**
б) + 37*743*
        4*4*2*5
        *106*93

Решение

а) + 6631785
   304982
       6936767

б) + 3757438
4349255
       8106693

88 Задания для самопроверки

Страница 88. Задания для самопроверки

№1

г)

№2

Точка А

№3

А 3
Б 4
В 1
Г 2

№4

20 м – 3,25 м = 16,75 (м) - ленты осталось в куске
Ответ: 16,75 м.

№5

у + 5,2 = 20
у = 20 – 5,2
у = 14,8

№6

1) 4,8 + 4,7 = 9,5 (км/ч) - скорость сближения
2) 9,5 * 1 = 9,5 (км) - пройдут пешеходы за 1 ч
3) 12 – 9,5 = 2,5 (км) - расстояние между ними через час пути
Ответ: 2,5 км.

№7

7,6 см – 2,8 см = 4,8 (см) - сторона АС
РΔАВС = АВ + ВС + АС = 7,6 + 5,5 + 4,8 = 17,9 (см)
Ответ: 17,9 см.

№8

234, 1

№9

1) 25,3 – 3,8 = 21,5 (км/ч) - скорость катера против течения реки
Ответ: 21,5 км/ч

№10

1) 15,4 – 11,4 = 4 (км/ч) - скорость течения реки
Ответ: 4 км/ч.

90 91 92 93 94

Параграф 7. Умножение и деление десятичных дробей
Пункт 34. Умножение десятичных дробей на натуральные числа.

Задание 456

Представьте произведение в виде суммы и найдите его значение:
а) 8,75 * 4;
б) 2,3 * 5.

Решение

а) 8,75 * 4 = 8,75 + 8,75 + 8,75 + 8,75 = 17,5 + 17,5 = 35

б) 2,3 * 5 = 2,3 + 2,3 + 2,3 + 2,3 + 2,3 = 11,5

Задание 457

Найдите значение выражения:
а) 8,9 * 6;
б) 3,75 * 12;
в) 0,075 * 24;
г) 10,45 * 42;
д) 137,64 * 35;
е) 25,85 * 98;
ж) 4,55 * 6 * 7;
з) 12,344 * 15 * 16;
и) (2,8 + 5,3) * 12;
к) (8,7 − 4,3) * 15;
л) (6,31 + 2,59) * 25;
м) (7,329 − 2,079) * 14.

Решение

а) 8,9 * 6 = 53,4

б) 3,75 * 12 = 45

в) 0,075 * 24 = 1,8

г) 10,45 * 42 = 438,9

д) 137,64 * 35 = 4817,4

е) 25,85 * 98 = 2533,3

ж) 4,55 * 6 * 7 = 27,3 * 7 = 191,1

з) 12,34415 * 16 = 185,16 * 16 = 2962,56

и) (2,8 + 5,3) * 12 = 8,1 * 12 = 97,2

к) (8,7 − 4,3) * 15 = 4,4 * 15 = 66

л) (6,31 + 2,59) * 25 = 8,9 * 25 = 222,5

м) (7,329 − 2,079) * 14 = 5,25 * 14 = 73,5

Задание 458

Запишите сумму в виде произведения и выполните умножение:
а) 3,69 + 3,69 + 3,69 + 3,69 + 3,69;
б) 18,04 + 18,04 + 18,04 + 18,04 + 18,04 + 18,04.

Решение

а) 3,69 + 3,69 + 3,69 + 3,69 + 3,69 = 5 * 3,69 = 18,45

б) 18,04 + 18,04 + 18,04 + 18,04 + 18,04 + 18,04 = 6 * 18,04 = 108,24

Задание 459

Все стороны шестиугольника имеют одинаковую длину 9,76 см. Найдите периметр шестиугольника.

Решение

 Р = 6 * 9,76 = 58,56 (см) - периметр шестиугольника
Ответ: 58,56 см.

Задание 460

Масса одного электромотора равна 57,85 кг. Найдите массу 9 таких электромоторов.

Решение

9 * 57,85 = 520,65 (кг) - масса девяти электромоторов
Ответ: 520,65 кг.

Задание 461

Выполните умножение:
а) 6,42 * 10; 0,17 * 10; 3,8 * 10; 0,1 * 10; 0,01 * 10;
б) 6,387 * 100; 20,35 * 100; 0,006 * 100; 0,75 * 100; 0,1 * 100; 0,01 * 100;
в) 45,48 * 1000; 7,8 * 1000; 0,00081 * 1000; 0,006 * 10000; 0,102 * 10000.

Решение

а) 6,42 * 10 = 64,2
0,17 * 10 = 1,7
3,8 * 10 = 38
0,1 * 10 = 1
0,01 * 10 = 0,1

б) 6,387 * 100 = 638,7
20,35 * 100 = 2035
0,006 * 100 = 0,6
0,75 * 100 = 75 0,1 * 100 = 10
0,01 * 100 = 1

в) 45,48 * 1000 = 45480
7,8 * 1000 = 7800
0,00081 * 1000 = 0,81
0,006 * 10 000 = 60
0,102 * 10000 = 1020

Задание 462

Запишите цифрами числа:
4,4 тыс.; 87,4 тыс.; 764,3 тыс.; 8,9 млн; 67,56 млн; 0,956 млн; 1,1 млрд; 0,27 млрд.

Решение

4,4 тыс = 44 * 1000 = 4400
87,4 тыс = 87,4 * 1000 = 87400
764,3 тыс 764,3 * 1000 = 764300
8,9 млн 8,9 * 1000000 = 8 900 000
67,56 млн = 67,56 * 1000000 = 67560000
0,956 млн = 0,956 * 1000000 = = 956000
1,1 млрд 1,1 * 1000000000 = 1100000000
0,27 млрд 0,27 * 1000000000 = 270000000

Задание 463

Автомашина прошла 3 ч со скоростью 48,4 км/ч и 5 ч со скоростью 56,6 км/ч. Какой путь прошла автомашина за всё это время?

Решение

48,4 * 3 + 56,6 * 5 = 145,2 + 283 = 428,2 (км) - прошла автомашина
Ответ: 428,2 км.

Задание 464

Пятачок съел 3 баночки мёда, по 0,65 кг в каждой, а Винни−Пух − 10 горшочков мёда, по 0,84 кг в каждом. Сколько мёда они съели? На сколько больше мёда съел Винни−Пух, чем Пятачок?

Решение

1)  3 * 0,65 + 10 * 0,84 = 1,95 + 8,4 = 10,35 (кг) - меда Винни−Пух и Пятачок съели вместе
2) 8,4 − 1,95 = 6,45 (кг) - на столько меда больше  съел Винни−Пух, чем Пятачок.
Ответ: 10,35 кг, на 6,45 кг.

Задание 465

Для сборки прибора первого вида требуется 1,4 ч, а для сборки прибора второго вида − на 0,6 ч меньше. Сколько всего времени потребуется для сборки 3 приборов первого вида и 5 приборов второго вида?

Решение

 3 * 1,4 + 5 * (1,4 − 0,6) = 4,2 + 4 = 8,2 (ч) - потребуется для сборки 3 приборов первого вида и 5 приборов второго вида
Ответ: 8,2 ч.

Задание 466

Найдите значение выражения:
а) 61,3х, если х = 8; 42; 100;
б) 100а + b, если а = 3,214 и b = 7,5;
в) 14с + 6d, если с = 2,3 и d = 3,7;
г) 5,2m + 3,7m − 4,1m, если m = 5; 10; 15; 120.

Решение

а) При х = 8,
61,3x = 61,3 * 8 = 490,4.
При х = 42,
61,3x = 61,3 * 42 = 2574,6.
При х = 100,
61,3x = 61,3 * 100 = 6130.

б) При а = 3,214 и b = 7,5,
100а + b = 100 * 3,214 + 7,5 = 321,4 + 7,5 = 328,9.

в) При с = 2,3 и d = 3,7,
14с + 6d = 14 * 2,3 + 6 * 3,7 = 32,2 + 22,2 = 54,4.

г) 5,2m + 3,7m − 4,1m = 8,9m − 4,1m = 4,8m;
При m = 5,
4,8 * 5 = 24.
При m = 10.
4,8 * 10 = 48;
При m = 15,
4,8 * 15 = 72.
При m = 120,
4,8 * 120 = 576.

Задание 467

Вычислите устно:
а)7² − 5
* 3
: 4
+ 12
: 2
?
б) 10² − 4²
: 4
+ 27
: 3
* 5
?
в) 9² + 3²
: 6
+ 30
* 2
: 15
?
г) 4³ − 14
: 25
* 17
+ 41
: 15
?

Решение

а) 49 − 25 = 24, 72, 18, 30, 15.

б) 100 − 16 = 84, 21, 48, 16, 80.

в) 81 + 9 = 90, 15, 45, 90.

г) 64 − 14 = 50, 2, 34, 75, 5.

Задание 468

Найдите значение выражения:
а) 2,7 − 0,6;
б) 3,5 + 2,3;
в) 5,8 − 1,9;
г) 0,69 + 0;
д) 3,6 + 0,8;
е) 7,1 − 0;
ж) 4,9 + 6,3;
з) 0,84 − 0,22.

Решение

а) 2,7 − 0,6 = 2,1

б) 3,5 + 2,3 = 5,8

в) 5,8 − 1,9 = 3,9

г) 0,69 + 0 = 0,69

д) 3,6 + 0,8 = 4,4

e) 7,1 − 0 = 7,1

ж) 4,9 + 6,3 = 11,2

з) 0,84 − 0,22 = 0,62

Задание 469

Вычислите:
а) 0,29 + 0,35;
б) 0,67 − 0,48;
в) 0,74 − 0,2;
г) 0,57 + 0,3;
д) 1,36 + 2,0;
е) 2,45 − 1,3;

Решение

а) 0,29 + 0,35 = 0,64

6) 0,67 − 0,48 = 0,19

в) 0,74 − 0,2 = 0,54

г) 0,57 + 0,3 = 0,87

д) 1,36 + 2,0 = 3,36

e) 2,45 − 1,3 = 1,15

ж) 3 + 0,24 = 3,24

з) 2 − 0,6 = 1,4

Задание 470

Восстановите цепочку вычислений

если х = 0,8; 1,3; 1,8; 2,3.

Решение

0,8 → 0,5 → 1,2 → 0,2 → 2,3 → 1,7;
1,3 → 1 → 1,7 → 0,7 → 2,8 → 2,2;
2,3 → 2 → 2,7 → 1,7 → 0,8 → 1,9.

Задание 471

Какую цифру (одну и ту же) можно подставить вместо звёздочки, чтобы было верно:
а) 2,3 = 2,3;
б) 3,5 > 2,8;
в) 0,7 < 0,3;
г) 0,75 < 0,86?

Решение

а) 3

б) любую цифру

в) 0; 1; 2

г) любую цифру

Задание 472

Отметьте на координатном луче точки с координатами: 0,2 ; 0,5 ; 0,8 ; 1,4 ; 1/2 ; 1/5 ; 2/5 ; 4/2 ; 1 2/5.

Решение

Задание 473

Во сколько раз лестница на девятый этаж длиннее лестницы на третий этаж этого дома?

Решение

Между 1 и 3 этажом − 2 пролёта, а между 1 и 9 − восемь, значит лестница на 9 этаж в 8 : 2 = 4 раза длиннее.

Задание 474

Найдите пропущенное число:

Решение

а) 7,1 − среднее число равно сумме крайних чисел.

б) 0,5 − среднее число равно разности крайних чисел.

Задание 475

Округлите:
а) 2,789; 0,8321; 247,356 до десятых;
б) 32 028,7; 16 513,5; 811,9 до тысяч.

Решение

а) 2,789 ≈ 2,8;
0,8321 ≈ 0,8;
247,356 ≈ 247,4.

б) 32028,7 ≈ 32000;
16513,5 ≈ 17000;
811,9 ≈ 1000.

Задание 476

Выполните действия:
а) 1243,5 + (279,48 + 105,24);
б) 28,348 − (12,652 − 0,7);
в) 542,3 + (600 − 541,3);
г) (38,45 − 27,35) − 8,45.

Решение

а) 1243,5 + (279,48 + 105,24) = 1243,5 + 384,72 = 1628,22

б) 28,348 − (12,652 − 0,7) = 28,348 − 11,952 = 16,396

в) 542,3 + (600 − 541,3) = 600 + (542,3 − 541,3) = 600 + 1 = 601

г) (38,45 − 27,35) − 8,45 = 38,45 − 8,45 − 27,35 = 30 − 27,35 = 2,65

Задание 477

Решите уравнение:
а) х + 2,8 = 3,72 + 0,38;
б) 4,1 + у − 20,3 − 4,9;
в) z − 6,8 = 8,7 + 6,4;
г) 10 − v + 4,3 = 10,7.

Решение

а) x + 2,8 − 3,72 + 0,38
x = 4,1 − 2,8
х = 1,3

6) 4,1 + у = 20,3 − 4,9
у = 20,3 − 4,9 − 4,1
у = 11,3

в) z − 6,8 = 8,7 + 6,4
z − 15,1 + 6,8
z = 21,9

г) 10 − v + 4,3 = 10,7
v = 14,3 − 10,7
v = 3,6

Задание 478

С одной станции в противоположных направлениях вышли два поезда в одно и то же время. Скорость одного поезда 65 км/ч, а скорость другого на а км/ч больше. Какое расстояние будет между поездами через 3 ч? Составьте выражение для решения задачи и найдите его значение при а = 10; 25; 40.

Решение

Скорость второго поезда равна (65 + а) км/ч.
Скорость удаления поездов друг от друга 65 + (а + 65) = 130 + а км/ч.
Через 3 ч между поездами будет (130 + а) * 3 км.
При а = 10, (130 + a) = 3 * (130 + 10) = 3 * 140 = 420 (км)
При а = 25, (130 + а) = (130 + 25) = 155 * 3 = 465 (км)
При а = 40, (130 + а) * 3 = (130 + 40) * 3 = 170 * 3 = 510 (км)

Задание 479

Решите задачу:
1) Скорость дельфина в 2 раза больше скорости акулы. Скорость акулы на 25 км/ч меньше скорости дельфина. Какова скорость каждого животного?
2) Масса петуха меньше массы индюка в 5 раз, а масса индюка на 8 кг больше массы петуха. Какова масса каждой птицы?

Решение

1) Пусть скорость акулы х км/ч, тогда скорость дельфина 2х км/ч.
Скорость дельфина больше скорости акулы на (2х − х) км/ч.
Составим уравнение:
2х − х = 25
х = 25
Значит, 25 км/ч − скорость акулы
2 * 25 = 50 (км/ч) - скорость дельфина
Ответ: 25 км/ч, 50 км/ч.

2) Пусть у − масса петуха, тогда масса индюка 5у.
Масса петуха меньше массы индюка на (5у − у) кг.
Составим уравнение:
5у − у = 8
4у = 8
y = 8 : 4
у = 2 
Значит, 2 кг − масса петуха
5 * 2 = 10 (кг) - масса индюка
Ответ: 2 кг, 10 кг.

Задание 480

Решите уравнение:
1) 5,5 + х − 23,5 = 8,75;
2) 6,2 − у − 1,8 = 4,39.

Решение

1) 5,5 + x − 23,5 = 8,75
x = 8,75 + 23,5 − 5,5
х = 26,75

2) 6,2 − у − 1,8 = 4,39
у = 4,4 − 4,39
у = 0,01

Задание 481

Найдите значение выражения:
а) 84,25 * 3;
б) 0,255 * 28;
в) 0,125 * 312;
г) 6,75 * 144;
д) (4,8 + 3,5) * 15;
е) (18,6 − 9,1) * 32.

Решение

а) 84,25 * 3 = 252,75

б) 0,255 * 25 = 6,375

в) 0,125 * 312 = 39

г) 6,75 * 144 = 972

д) (4,8 + 3,5) *15 = 8,3 * 15 = 124,5

e) (18,6 − 9,1) * 32 = 9,5 * 32 = 304

Задание 482

Найдите периметр восьмиугольника, если каждая его сторона имеет длину 3,75 см.

Решение

8 * 3,75 = 30 (см) - периметр восьмиугольника 
Ответ: 30 см.

Задание 483

Каждый ящик с яблоками имеет массу 30,25 кг. Найдите массу 76 таких ящиков.

Решение

 76 * 30,25 = 2299 (кг) - масса 76 ящиков с яблоками
Ответ: 2299 кг.

Задание 484

Найдите значение произведения:
а) 4,55 * 10;
б) 18,3 * 10;
в) 0,235 * 10;
г) 8,354 * 100;
д) 2,3 * 100;
е) 0,048 * 100;
ж) 3,8457 * 1000;
з) 0,0358 * 1000;
и) 0,003 * 1000.

Решение

а) 4,55 * 10 = 45,5

б) 18,3 * 10 = 183

в) 0,235 * 10 = 2,35

г) 8,354 * 100 = 835,4

д) 2,3 * 100 = 230

e) 0,048 * 100 = 4,8

ж) 3,8457 * 1000 = 3845,7

з) 0,0358 * 1000 = 35,8

и) 0,003 * 1000 = 3

Задание 485

Найдите значение выражения:
а) 15,2x + 1,73у, если х = 8 и у = 6; х = 10 и у= 100;
б) 16,52а + 18,1b, если а = 85 и b = 10.

Решение

а) При x = 8 и у = 6:
15,2х + 1,73у = 15,2 * 8 + 1,73 * б = 121,6 + 10,38 = 131,98;

При х = 10 и у = 100:
15,2x + 1,73y = 15,2 * 10 + 1,73 * 100 = 152 + 173 = 325.

б) При а = 85 и b = 10:
16,52а + 18,1b = 16,52 * 85 + 18,1 * 10 = 1404,2 + 181 = 1585,2

Задание 486

Никита проехал 3 ч на автобусе и 4 ч на поезде. На сколько километров больше Никита проехал на поезде, чем на автобусе, если скорость автобуса была 40,6 км/ч, а скорость поезда − 55,2 км/ч?

Решение

 55,2 * 4 − 40,6 * 3 = 220,8 − 121,8 = 99 (км) - на столько  Никита проехал на поезде больше, чем на автобусе
Ответ: на 99 км.

Задание 487

На автомобиль погрузили 6 ящиков, по 0,25 т каждый, и 3 контейнера, по 0,44 т каждый. Какова масса всего этого груза?

Решение

6 * 0,25 + 3 * 0,44 = 1,5 + 1,32 = 2,82 (т) - масса всего груза 
Ответ: 2,82 т.

Задание 788

Велосипедист проехал за час 12 км.
Какое расстояние он проедет с той же скоростью: за 4 ч; за 1/4 ч; за 3/4 ч?

Решение

За 4 ч велосипедист проедет 12 * 4 = 48 км,
за 1/4 ч − 12 : 4 = 3 км,
за 3/4 ч − 12 : 4 * 3 = 3 * 3 = 9 км.

Задание 489

Масса пирога 1600 г. Какова масса 3 таких пирогов? 1/8 пирога? 3/8 пирога?

Решение

Масса 3 пирогов 3 * 1600 = 4800 г,
масса 1/8 пирога − 1600 : 8 = 200 г,
масса 3/8 пирога − 1600 : 8 * 3 = 200 * 3 = 600 г.

Задание 490

Вместо звёздочек поставьте пропущенные цифры:
а)
× 4*3
    2*
  *83
  ***
 *****

б)
× 318
      **
  **90
 *54
*****

Решение

а)
  × 483
       21
     483
   966 
10143

б)
 × 318
      35
  1590
  954  
11130

95 96 97 98 99 100 101

Пункт 35. Деление десятичных дробей на натуральные числа. Со страницы 95

Задание 491

Выполните деление:
а) 20,7 : 9 = 2,3;
б) 243,2 : 8 = 30,4;
в) 88,298 : 7 = 12,614;
г) 772,8 : 12 = 64,4;
д) 93,15 : 23 = 4,05;
е) 0,644 : 92 = 0,007;
ж) 1 : 80 = 0,0125;
з) 0,909 : 45 = 0,0202;
и) 3 : 32 = 0,09375;
к) 0,01242 : 69 = 0,00018;
л) 1,016 : 8 = 0,127;
м) 7,368 : 24 = 0,307.

Решение

а)
_20,7 |9   
  18    |2,3
  _27
    27
      0

б)
_243,2 |8     
  24      |30,4
  _32
    32
      0

в)
_88,298 |7          
  7          |12,614
_18
  14
  _42
    42
    _9
      7
    _28
      28
        0

г)
_772,8 |12   
  72      |64,4
_52
  48
  _48
    48
      0

д)
_93,15 |23   
  92      |4,05
  _115
    115
        0

е)
_0,644 |92     
     644 |0,007
         0

ж)
_1 |80       
  0 |0,0125
_10
    0
_100
    80
  _200
    160
    _400
      400
          0

з)
_0,909 |45       
     90   |0,0202
      _90
        90
          0 

и)
_3 |32         
  0 |0,09375
_30
    0
_300
  288
_120
    96
  _240
    224
   _160
     160
         0

к)
_0,01242 |69        
         69   |0,00018
      _552
        552
            0

л)
_1,016 |8        
     8     |0,127
   _21
     16
     _56
       56
         0

м)
_7,368 |24     
  72      |0,307
  _168
    168
        0

Задание 492

В самолёт для полярной экспедиции загрузили 3 трактора, массой 1,2 т каждый, и 7 аэросаней. Масса всех аэросаней на 2 т больше массы тракторов. Какова масса одних аэросаней?

Решение

 (3 * 1,2 + 2) : 7 = 5,6 : 7 = 0,8 (т) - масса одних аэросаней
Ответ: 0,8 т.

Задание 493

Стороны одного прямоугольника 12 см и 6,6 см. Площадь второго прямоугольника в 11 раз меньше площади первого. Найдите ширину второго прямоугольника, если его длина 8 см.

Решение

12 * 6,6 : 11 : 8 = 79,2 : 11 = 7,2 : 8 = 0,9 (см) - ширина второго прямоугольника
Ответ: 0,9 см.

Задание 494

Турист должен был пройти за два дня 25,2 км. В первый день он прошёл 3 7 пути. Сколько километров прошёл турист во второй день?

Решение

1) 25,2 : 7 * 3 = 3,6 * 3 = 10,8 (км) - прошел турист в первый день
2) 25,2 − 10,8 = 14,4 (км) - прошел турист во второй день
Ответ: 14,4 км.

Задание 495

Собрали 36,9 т клубники. На консервный завод отправили 7/9 собранной клубники, а остальную клубнику передали для продажи населению. Сколько тонн клубники было продано населению?

Решение

1) 36,9 : 9 * 7 = 4,1 * 7 = 28,7 (т) - клубники отправили на консервный завод
2) 36,9 − 28,7 = 8,2 (т) - клубники продали населению
Ответ: 8,2 т.

Задание 496

Для посева было приготовлено 25,2 т семян. В первый день на посев израсходовали 4/9 всех семян, а во второй − 4/7 остатка. Сколько семян осталось после двух дней посева?

Решение

1)  25,2 : 9 * 4 = 2,8 * 4 = 11,2 (т) -  семян израсходовали в первый день
2) (25,2 − 11,2) : 7 * 4 = 14 : 7 * 4 = 8 (т) -  семян израсходовали во второй день
3)  25,2 − (11,2 + 8) = 25,2 − 19,2 = 6 (т) - семян осталось после двух дней посева
Ответ: 6 т.

Задание 497

На соревнованиях по бегу Вася пробежал дистанцию за 1,2 мин, что составило 5/6 времени, затраченного Колей на эту же дистанцию. За какое время Коля пробежал дистанцию?

Решение

1,2 : 5 * 6 = 0,24 * 6 = 1,44 (мин) - время, за которое Коля пробежал дистанцию
Ответ: за 1,44 мин.

Задание 498

Электрифицировано 16,1 км железной дороги, что составляет 7/9 всей дороги между двумя станциями. Какова длина дороги между этими станциями?

Решение

16,1 : 7 * 9 = 2,3 * 9 = 20,7 (км) - длина дороги между двумя станциями
Ответ: 20,7 км.

Задание 499

Решите уравнение:
а) 4х − х = 8,7;
б) 3y + 5у = 9,6;
в) а + а + 8,154 = 32;
г) 7k − 4k − 55,2 = 63,12.

Решение

а) 4x − x = 8,7
3x = 8,7
x = 8,7 : 3
х = 2,9

б) 3y + 5y = 9,6
8x = 9,6
y = 9,6 : 8
у = 1,2

в) a + a + 8,154 = 32
2a = 32 − 8,154 = 23,846
a = 23,846 : 2
а = 11,923

г) 7k − 4k − 55,2 = 63,12
3k = 63,12 + 55,2 = 118,32
k = 118,32 : 3
k = 39,44

Задание 500

В двух корзинах 16,8 кг помидоров. Масса помидоров в одной корзине в 2 раза больше, чем в другой. Сколько килограммов помидоров в каждой корзине?

Решение

Пусть в одной корзине х кг помидоров, тогда в другой корзине 2х кг.
Составим уравнение:
х + 2х = 16,8
3х = 16,8
х = 16,8 : 3
х = 5,6
Значит, 5,6 кг в одной корзине
2 * 5,6 = 11,2 (кг) - помидоровв другой
Ответ: 5,6 кг, 11,2 кг.

Задание 501

Площадь первого поля в 5 раз больше площади второго. Чему равна площадь каждого поля, если площадь второго на 23,2 га меньше площади первого?

Решение

Пусть у − площадь второго поля, тогда площадь первого поля 5y га.
Составим уравнение:
(5y − у) = 23,2
4у = 23,2
у = 23,2 : 4
у = 5,8
Значит, 5,8 га − площадь второго поля
5 * 5,8 = 29 (га) - площадь первого поля
Ответ: 5,8 га, 29 га.

Задание 502

Для приготовления компота составили смесь из 8 частей (по массе) сухих яблок, 4 частей урюка и 3 частей изюма. Сколько килограммов каждого из сухофруктов понадобилось для 2,7 кг такой смеси?

Решение

Пусть х − масса одной части, тогда:
8x + 4x + 3х = 2,7
x = 2,7 : 15
х = 0,18 (кг)
Следовательно для приготовления 2,7 кг смеси понадобилось:
8 * 0,18 = 1,44 (кг) - яблок
4 * 0,18 = 0,72 (кг) - урюка
3 * 0,18 = 0,54 (кг) - изюма.
Ответ: 1,44 кг, 0,72 кг, 0,54 кг.

Задание 503

В двух мешках 1,28 ц муки. В первом мешке на 0,12 ц муки больше, чем во втором. Сколько центнеров муки в каждом мешке?

Решение

Пусть во втором мешке х ц муки,
тогда в первом мешке (х + 12) ц муки.
Составим уравнение:
х + (х + 0,12) = 1,28
х = (1,28 − 0,12) : 2
х = 0,58
Значит, 0,58 ц во втором мешке
0,58 + 0,12 = 0,7 (ц) -  муки в первом мешке
Ответ: 0,58 ц, 0,7 ц.

Задание 504

В двух корзинах 18,6 кг яблок. В первой корзине яблок на 2,4 кг меньше, чем во второй. Сколько килограммов яблок в каждой корзине?

Решение

Пусть в первой корзине х кг яблок, тогда во второй корзине (x + 2,4) кг яблок.
Составим уравнение:
х + (х + 2,4) = 18,6
х = (18,6 − 2,4) : 2
х = 8,1
Значит, 8,1 кг в первой корзине
8,1 + 2,4 = 10,5 (кг) -  яблок во второй корзине
Ответ: 8,1 кг, 10,5 кг.

Задание 505

Представьте в виде десятичной дроби:
3/4 ; 5/8 ; 7/4 ; 83/25 ; 5 1/2 ; 70 3/75 ; 4 21/84.

Решение

3/4 = 0,75
5/8 = 0,625
7/4 = 1,75
83/25 = 3,32
5 1/2 = 5,5
70 3/75 = 70,04
4 21/84 = 4,25

Задание 506

Чтобы собрать 100 г мёда, пчела доставляет в улей 16 тыс. нош нектара. Какова масса одной ноши нектара?

Решение

100 : 16000 = 0,00625 (г) - масса одной ноши нектара пчелы
Ответ: 0,00625 г.

Задание 507

В пузырьке 30 г лекарства− Найдите массу одной капли лекарства, если в пузырьке 1500 капель.

Решение

 30 : 1500 = 0,02 (г) - масса одной капли лекарства
Ответ: 0,02 г.

Задание 508

Представьте обыкновенную дробь в виде десятичной и выполните действия:
а) 2/3 + 0 , 8;
б) 1,34 − 4/25;
в) 2/3 : 15;
г) 9/60 * (0,6 + 3,4);
д) (2/5 + 0,7) : 11;
е) (7/4 − 0,25) * 27.

Решение

а) 2/3 + 0,8 = 0,75 + 0,8 = 1,55

б) 1,34 − 4/25 = 1,34 − 0,16 = 1,18

в) 2/3 : 15 = 0,6 : 15 = 0,04

г) 9/60 * (0,6 + 3,4) = 0,15 * 4 = 0,6

д) (2/5 + 0,7 ) : 11 = (0,4 + 0,7) : 11 = 1,1 : 11 = 0,1

е) (7/4 − 0,25 ) * 27 = (1,75 − 0,25 ) * 25 = 1,5 * 27 = 40,5

Задание 509

Решите уравнение:
а) (х − 5,46) * 2 = 9;
б) (у + 0,5) : 2 = 1,57.

Решение

а) (x − 5,46) * 2 = 9
x = 9 : 2 + 5,46
х = 9,96

б) (y + 0,5) : 2 = 1,57
у = 1,57 * 2 − 0,5
у = 2,64

Задание 510

Найдите значение выражения:
а) 91,8 : (10,56 − 1,56) + 0,704;
б) (61,5 − 5,16) : 30 + 5,05;
в) 66,24 − 16,24 : (3,7 + 4,3);
г) 28,6 + 11,4 : (6,595 + 3,405);
д) 15,3 − 4 : 9 + 3,2;
е) (4,3 + 2,4 : 8) * 3;
ж) 280,8 : 12 − 0,3 * 24;
з) (17,6 * 13 − 41,6) : 12.

Решение

а) 91,8 : (10,56 − 1,56) + 0,704 = 91,8 : 9 + 0,704 = 10,2 + 0,704 = 10,904

б) (61,5 − 5,16) : 30 + 5,05 = 56,34 : 30 + 5,05 = 1,878 + 5,05 = 6,928

в) 66,24 − 16,24 : (3,7 + 4,3) = 66,24 − 16,24 : 8 = 66,24 − 2,03 = 64,21

г) 28,6 + 11,4 : (6,595 + 3,405) = 28,6 + 11,4 : 10 = 28,6 + 1,14 = 29,74

д) 15,3 − 4 : 9 + 3,2 = 61,2 : 9 + 3,2 = 6,8 + 3,2 = 10

е) (4,3 + 2,4 : 8) * 3 = (4,4 + 0,3) * 3 = 4,7 * 3 = 14,1

ж) 280,8 : 12 − 0,3 * 24 = 23,4 − 7,2 = 16,2

з) (17,6 * 13 − 41,6) : 12 = (228,8 − 41,6) : 12 = 187,2 : 12 = 15,6

Задание 511

Вычислите устно:
а)
2,5 − 1,6;
3,2 − 1,4;
0,47 − 0,27;
0,64 − 0,15;
0,71 − 0,28;
б)
1,8 + 2,5;
2,7 + 1,6;
0,63 + 0,17;
0,38 + 0,29;
0,55 + 0,45;
в)
3,4 − 0,2;
2,6 − 0,05;
4,52 − 1,2;
4 − 0,8;
1 − 0,45;
г)
5 + 0,35;
3,7 + 0,24;
0,46 + 1,8;
0,57 + 3;
1,64 + 0,36.

Решение

а) 2,5 − 1,6 = 0,9
3,2 − 1,4 = 1,8
0,47 − 0,27 = 0,2
0,64 − 0,15 = 0,49
0,71 − 0,28 = 0,43

б) 1,8 + 2,5 = 4,3
2,7 + 1,6 = 4,3
0,63 + 0,17 = 0,8
0,38 + 0,29 = 0,67
0,55 + 0,45 = 1

в) 3,4 − 0,2 = 3,2
2,6 − 0,05 = 2,55
4,52 − 1,2 = 3,32
4 − 0,8 = 3,2
1 − 0,45 = 0,55

г) 5 + 0,35 = 5,35
3,7 + 0,24 = 3,94
0,46 + 1,8 = 2,26
0,57 + 3 = 3,57
1,64 + 0,36 = 2

Задание 512

Выполните умножение:
а) 0,3 * 2;
б) 0,8 * 3;
в) 1,2 * 2;
г) 2,3 * 3;
д) 0,21 * 4;
е) 1,6 * 5;
ж) 3,7 * 10;
з) 0,09 * 6;
и) 0,18 * 5;
к) 0,87 * 0.

Решение

а) 0,3 * 2 = 0,6

б) 0,8 * 3 = 2,4

в) 1,2 * 2 = 2,4

г) 2,3 * 3 = 6,9

д) 0,21 * 4 = 0,84

е) 1,6 * 5 = 8

ж) 3,7 * 10 = 37

з) 0,09 * 6 = 0,54

и) 0,18 * 5 = 0,9

к) 0,87 * 0 = 0

Задание 513

Догадайтесь, каковы корни уравнения:
а) 2,9x = 2,9;
б) 5,25x = 0;
в) 3,7x = 37;
г) x² = x;
д) a³ = a;
е) m² = m³.

Решение

а) 2,9x = 2,9
x = 1

6) 5,25x = 0
x = 0

в) 3,7x = 37
x = 10

г) х² = х
x = 1

д) a³ = a
a = 1

е) m² = m³
m = 1

Задание 514

Как изменится значение выражения 2,5а, если а:
увеличить на 1? увеличить на 2? увеличить в 2 раза?

Решение

Значение выражения 2,5а увеличится на 2,5:
2,5(a + 1) − 2,5a = 2,5a + 2,5 − 2,5a = 2,5.
Значение выражения 2,5a увеличится на 5:
2,5(a + 2) = 2,5a + 5 − 2,5a = 5;
Значение выражения 2,5a увеличится в 2 раза:
(2,5 * 2a) : 2,5a = 2.

Задание 515

Расскажите, как на координатном луче отметить число: 1/4 ; 3/4 ; 0,25 ; 0,5 ; 0,75.
Подумайте, какие из данных чисел равны.
Какой дроби со знаменателем 4 равны 0,5?
Сложите: 3/4 и 0,25; 1/4 и 0,15.

Решение

2/5 = 0,5
3/4 + 0,25 = 0,75 + 0,25 = 1
1/4 + 0,15 = 0,25 + 0,15 = 0,4.

Задание 516

Подумайте, по какому правилу составлен ряд чисел, и запишите ещё два числа этого ряда:
а) 1,2; 1,8; 2,4; 3; ...
б) 9,6; 8,9; 8,2; 7,5; ...
в) 0,9; 1,8; 3,6; 7,2; ...
г) 1,2; 0,7; 2,2; 1,4; 3,2; 2,1; ...

Решение

а) Каждое последующее число больше предыдущего на 0,6: 1,2; 1,8; 2,4; 3; 3,6; 4,2...

б) Каждое последующее число меньше предыдущего на 0,7: 9,6; 8,9; 8,2; 7,5; 6,8; 6,1...

в) Каждое последующее число больше предыдущего в 2 раза: 0,9; 1,8; 3,6; 7,2; 14,4; 28,8...

г) Каждое последующее число, стоящее на нечетном месте, больше предыдущего числа, стоящего на нечетном месте на 1; каждое число, стоящее на четном месте, больше предыдущего числа, стоящего на четном месте, на 0,7: 1,2; 0,7; 2,2; 1,4; 3,2; 2,1; 4,2; 2,8...

Задание 517

Выполните действия:
а) (37,8 − 19,1) * 4;
б) (14,23 + 13,97) * 31;
в) (64,37 + 33,21 − 21,56) * 14;
г) (33,56 − 18,29) * (13,2 + 24,9 − 38,1).

Решение

а) (37,8 − 19,1) * 4 = 74,8

б) (14,23 + 13,97) * 31 = 28,2 * 31 = 874,2

в) (64,37 + 33,21 − 21,56) * 14 = 76,02 * 14 = 1064,28

г) (33,56 − 18,29) * (13,2 + 24,9 − 38,1) = 15,27 − 0 = 0

Задание 518

Увеличьте каждое из чисел:
а) 3,705; 62,8; 0,5 в 10 раз;
б) 2,3578; 0,0068; 0,3 в 100 раз.

Решение

а) 3,705 * 10 = 37,05
62,8 * 10 = 628
0,5 * 10 = 5

б) 2,3578 * 100 = 235,78
0,0068 * 100 = 0,68
0,3 * 100 = 30

Задание 519

Округлите число 82719,364:
а) до единиц;
б) до сотен;
в) до десятых;
г) до сотых;
д) до тысяч.

Решение

а) 82719,364 ≈ 82719

б) 82 719,364 ≈ 82700

в) 82719,364 ≈ 82719,4

г) 82 719,364 ≈ 82719,36

д) 82719,364 ≈ 83000

Задание 520

Выполните действие:
а) 3 1/12 + 4 7/12;
б) 4 3/7 − 1 2/7;
в) 8 3/5 − 2/5;
г) 4/9 + 7 1/9.

Решение

а) $3\frac1{12}+4\frac7{12}=3+4+\frac1{12}+\frac7{12}=7\frac8{12}$

б) $4\frac37-1\frac27=4-1+\frac37-\frac27=3\frac17$

в) $8\frac35-\frac25=8\frac15$

г) $\frac49+7\frac19=7\frac59$

Задание 521

Сравните:
а) 2/11 + 7/11 и 4/11 + 6/11;
б) 8/13 − 3/13 и 9/13 − 4/13.

Решение

а) $\frac2{11}+\frac7{11}=\frac9{11}<\frac4{11}+\frac6{11}=\frac{10}{11}$

б) $\frac8{13}-\frac3{13}=\frac5{13}=\frac9{13}-\frac4{13}=\frac5{13}$

Задание 522

Коля, Петя, Женя и Сеня взвесились на весах. Получились результаты: 37,7 кг; 42,5 кг; 39,2 кг; 40,8 кг. Найдите массу каждого мальчика, если известно, что Коля тяжелее Сени и легче Пети, а Женя легче Сени.

Решение

В порядке возрастания веса мальчики располагаются так:
Женя − 37,7 кг, Сеня − 39,2 кг, Коля − 40,8 кг и Петя − 42,5 кг.

Задание 523

Упростите выражение и найдите его значение:
а) 23,9 − 18,55 − m, если m = 1,64;
б) 16,4 + k + 3,8, если k = 2,7.

Решение

а) 23,9 − 18,55 − m = 5,35 − m;
при m = 1,64
5,35 − m = 5,35 − 1,64 = 3,71.

б) 16,4 + k + 3,8 = 20,2 + k;
при k = 2,7
20,2 + k = 20,2 + 2,7 = 22,9.

Задание 524

Решите уравнение:
а) 16,1 − (х − 3,8) = 11,3;
б) 25,34 − (2,7 + у) = 15,34.

Решение

а) 16,1 − (x − 3,8) = 11,3
x − 3,8 = 16,1 − 11,3 = 4,8
x = 4,8 + 3,8
х = 8,6

б) 25,34 − (2,7 + y) = 15,34
2,7 + y = 25,34 − 15,34 = 10
y = 10 − 2,7
у = 7,3

Задание 525

Найдите значение выражения:
1) (1070 − 104040 : 2312) * 74 + 6489;
2) (38529 + 205 * 87) : 427 − 119.

Решение

1) (1070 − 104040 : 2312) * 74 + 6489 = (1070 − 45) * 74 + 6489 = 1025 * 74 + 6489 = 75850 + 6489 = 82339

2) (38529 + 205 * 87) : 427 − 119 = (38529 + 17835) : 427 − 119 = 56364 : 427 − 119 = 132 − 119 = 13

Задание 526

Выполните деление:
а) 53,5 : 5;
б) 1,75 : 7;
в) 0,48 : 6;
г) 13,2 : 24;
д) 0,7 : 25;
е) 7,9 : 316;
ж) 543,4 : 143;
з) 40,005 : 127;
и) 9,607 : 10;
к) 14,706 : 1000;
л) 0,0142 : 100;
м) 0,75 : 10000.

Решение

а) 53,5 : 5 = 10,7

б) 1,75 : 7 = 0,25

в) 0,48 : 6 = 0,08

г) 13,2 : 24 = 0,55

д) 0,7 : 25 = 0,028

e) 7,9 : 316 = 0,025

ж) 543,4 : 143 = 3,8

з) 40,005 : 127 = 0,315

и) 9,607 : 10 = 0,9607

к) 14,706 : 1000 = 0,014706

л) 0,0142 : 100 = 0,000142

м) 0,75 : 10 000 = 0,000075

Задание 527

Автомашина шла по шоссе 3 ч со скоростью 65,8 км/ч, а затем 5 ч она шла по грунтовой дороге. С какой скоростью она шла по грунтовой дороге, если весь её путь равен 324,9 км?

Решение

 (324,9 − 65,8 * 3) : 5 = 127,5 : 5 = 25,5 (км/ч) - скорость машины по грунтовой дороге
Овет: 25,5 км/ч.

Задание 528

На складе было 180,4 т угля. Для отопления школ отпущено 3/11 этого угля. Сколько тонн угля осталось на складе?

Решение

1) 180,4 : 11 * 3 = 16,4 * 3 = 49,2  (т) -  угля было отпущено на отопление
2) 180,4 − 49,2 = 131,2 (т ) - угля осталось на складе
Ответ: 131,2 т.

Задание 529

Вспахали 5/7 поля. Найдите площадь этого поля, если вспахали 32,5 га.

Решение

 32,5 : 5 * 7 = 6,5 * 7 = 45,5 (га) - площадь всего поля равна
Ответ: 45,5 га.

Задание 530

Решите уравнение:
а) 15x = 0,15;
б) 3,08 : у = 4;
в) 3a + 8a = 1,87;
г) 72 − 3z = 5,12;
д) 2t + 5t + 3,18 = 25,3;
е) 8p − 2p − 14,21 = 75,19;
ж) 295,1 : (n − 3) = 13;
з) 34 * (m + 1,2) = 61,2;
и) 15 * (k − 0,2) = 21.

Решение

а) 15x = 0,15
x = 0,15 : 15
х = 0,01

б) 3,08 : у = 4
у = 3,08 : 4
у = 0,77

в) 3a + 8a = 1,87
a = 1,87 : 11
а = 0,17

г) 72 − 3z = 5,12
z = 5,12 : 4
z = 1,28

д) 2t + 5t + 3,18 = 25,3
t = (25,3 − 3,18) : 7
t = 3,16

е) 8p − 2p − 14,21 = 75,19
p = (75,19 + 14,21) : 6
p = 14,9

ж) 295,1 : (n − 3) = 13
n = 295,1 : 13 + 3
n = 25,7

з) 34 * (m + 1,2) = 61,2
m = 61,2 : 34 − 1,2
m = 0,6

и) 15 * (k − 0,2) = 21
k = 21 : 15 + 0,2
k = 1,6

Задание 531

Найдите значение выражения:
а) 0,24 : 4 + 15,3 : 5 + 12,4 : 8 + 0,15 : 30;
б) (1,24 + 3,56) : 16;
в) 2,28 + 3,72 : 12;
г) 3,6 + 2,4 : (11,7 − 3,7).

Решение

а) 0,25 : 4 + 15,3 : 5 + 12,4 : 8 + 0,15 : 30 = 0,0625 + 3,06 + 1,55 + 0,005 = 4,6775

б) (1,24 + 3,56) : 16 = 4,8 : 16 = 0,3

в) 2,28 + 3,72 : 12 = 2,28 + 0,31 = 2,59

г) 3,6 + 2,4 : (11,7−3,7) = 3,6 + 2,4 : 8 = 3,6 + 0,3 = 3,9

Задание 532

С трёх лугов собрали 19,7 т сена. С первого и второго лугов собрали сена поровну, а с третьего собрали на 1,1 т больше, чем с каждого из первых двух. Сколько сена собрали с каждого луга?

Решение

Пусть с каждого из первых двух лугов собрали х т сена,
тогда с третьего луга собрали (х + 1,1) т сена.
Составим уравнение:
х + х + (х + 1,1) = 19,7
х = (19,7 − 1,1) : 3
х = 6,2
Значит, 6,2 т сена собрали с первого и столько же со второго луга.
х + 1,1 = 7,3 (т) - собрали с третьего луга
Ответ: 6,2 т, 6,2 т, 7,3 т.

Задание 533

Магазин за 3 дня продал 1240,8 кг сахара. В первый день было продано 543 кг, во второй − в 2 раза больше, чем в третий. Сколько килограммов сахара продано в третий день?

Решение

Пусть в третий день продали х кг сахара,
тогда во второй день продали 2х кг.
Составим уравнение:
543 + 2х + х = 1240,8
х = (1240,8 − 543) : 3
х = 232,6
Значит, 232,6 кг сахара было продано в третий день.
Ответ: 232,6 кг.

Задание 534

Машина прошла первый участок пути за 3 ч, а второй участок − за 2 ч. Длина обоих участков вместе 267 км. С какой скоростью шла машина на каждом участке, если скорость на втором участке была на 8,5 км/ч больше, чем на первом?

Решение

Пусть скорость машины на первом участке была х км/ч,
тогда на втором участке (х + 8,5) км/ч.
Составим уравнение:
3х + 2 * (х + 8,5) = 267
3х + 2х + 17 = 267
х = (267 − 17) : 5
х = 50
Значит, 50 км/ч − скорость машины на первом участке
50 + 8,5 = 58,5 (км/ч) - её скорость на втором участке
Ответ: 50 км/ч, 58,5 км/ч.

Задание 535

Обратите в десятичные дроби: 9/20 ; 7/40 ; 11/400 ; 21/168 ; 35/280 ; 47/367.

Решение

9/20 = 45/100 = 0,45
7/40 = 175/1000 = 0,175
11/400 = 275/10000 = 0,0275
21/168 = 1/8 = 125/1000 = 0,125
35/280 = 1/8 = 125/1000 = 0,125
47/376 = 1/8 = 125/1000 = 0,125

Задание 536

Постройте фигуру, равную фигуре, изображённой на рисунке 151.

Решение

Площадь данной фигуры 28 клеток, значит равновеликой может быть например любая фигура из 28 клеток.

Задание 537

Из города выехал велосипедист со скоростью 13,4 км/ч. Через 2 ч вслед за ним выехал другой велосипедист, скорость которого 17,4 км/ч. Через сколько часов после своего выезда второй велосипедист догонит первого?

Решение

(13,4 * 2) : (17,4 − 13,4) = 26,8 : 4 = 6,7 (ч) - через столько после своего выезда второй велосипедист догонит первого
Ответ: через 6,7 ч.

Задание 538

Катер, двигаясь против течения, за 6 ч прошёл 177,6 км. Найдите собственную скорость катера, если скорость течения равна 2,8 км/ч.

Решение

 177,6 : 6 + 2,8 = 29,6 + 2,8 = 32,4 (км/ч) - собственная скорость катера
Ответ: 32,4 км/ч.

Задание 539

Кран, который подаёт в минуту 30 л воды, за 5 мин наполнил ванну. Потом кран закрыли и открыли сливное отверстие, через которое вся вода вылилась за 6 мин. Сколько литров воды выливалось за 1 мин?

Решение

1) 30 * 5 = 150 (л) -  воды налилось в ванну
2) 150 : 6 = 25 (л) -  воды выливалось за 1 минуту
Ответ: 25 л.

Задание 540

Решите уравнение:
а) 26 * (х + 427) = 15756;
б) 101 * (351 + у) = 65549;
в) 22 374 : (k − 125) = 1243;
г) 38 007 : (4223 − t) = 9.

Решение

а) 26 * (х + 427) = 15 756
x = 15 756 : 26 − 427
х = 606 − 427
х = 179

б) 101 * (351 + у) = 65549
у = 65549 : 101 − 351
у = 649 − 351
у = 298

в) 22 374 : (k − 125) = 1243
k = 22374 : 1243 + 125
k = 18 + 125
k = 143

г) 38007 : (4223 − t) = 9
t = 4223 − 38007 : 9
t = 4223 − 4223
t = 0

102 103 104 105 106 107 108 109

Пункт 36. Умножение десятичных дробей. Со страницы 102

Задание 541

Найдите площадь прямоугольника со сторонами 12,5 дм и 6,2 дм. Решите эту же задачу, переводя дециметры в сантиметры.

Решение

 12,5 * 6,2 = 77,5 (дм²) - площадь прямоугольника
или переводя в см²:
125 * 62 = 7750 (см²) - - площадь прямоугольника
Ответ: 77,5 дм², 7750 см².

Задание 542

Выполните умножение:
а) 354,2 * 0,1;
б) 248,34 * 0,1;
в) 3788,2 * 0,001;
г) 2,8 * 0,1;
д) 4,5 * 0,01;
е) 0,08 * 0,1;
ж) 54 * 0,001;
з) 37 * 0,0001;
и) 0,01 * 0,0001.

Решение

а) 354,2 * 0,1 = 35,42

б) 248,34 * 0,1 = 24,834

в) 3788,2 * 0,001 = 3,7882

г) 2,8 * 0,1 = 0,28

д) 4,5 * 0,01 = 0,045

е) 0,08 * 0,1 = 0,008

ж) 54 * 0,001 = 0,054

з) 37 * 0,0001 = 0,0037

и) 0,01 * 0,0001 = 0,000001

Задание 543

Длина пола 6,35 м, а его ширина 4,82 м. Чему равна площадь пола? Ответ округлите до десятых долей квадратного метра.

Решение

 6,35 * 4,82 = 30,607 (м²)  - площадь поля
30,607 м² ≈ 30,6 м²
Ответ: 30,6 м².

Задание 544

При посеве редиса расходуют 0,55 кг семян на один ар. Сколько килограммов семян редиса потребуется для посева на участке площадью 4 а; 0,1 а; 2,3 а; 1,5 а; 0,8 а; 1 га?

Решение

Для посева на площади х а потребуется 0,55х кг семян:
4 а − 0,55 * 4 = 2,2 кг;
0,1 а − 0,55 * 0,1 = 0,055 кг;
2,3 а − 0,55 * 2,3 = 1,265 кг;
1,5 а − 0,55 * 1,5 = 0,825 кг;
0,8 а − 0,55 * 0,8 = 0,44 кг;
1 га − 0,55 * 100 = 55 кг.

Задание 545

Скорость поезда 85 км/ч. Сколько километров пройдёт поезд
за 5 ч; за 0,1 ч; за 3,8 ч; за 1,5 ч; за 0,4 ч?

Решение

За x ч поезд пройдёт
за 5 ч: 85 * 5 = 425 км;
за 0,1 ч: 85 * 0,1 = 85 км;
за 2,8 ч: 85 * 2,8 = 238 км;
за 1,5 ч: 85 * 1,5 = 127,5 км;
0,4 ч = 85 * 0,4 = 34 км.

Задание 546

Масса 1 см³ железа равна 7,9 г. Найдите массу железной детали объёмом 3 см³ ; 0,1 см³ ; 4,9 см³ ; 0,5 см³.

Решение

Масса детали объёмом х см³ равна 7,9х кг:
3 см³: 7,9 * 3 = 23,7 г,
0,1 см³: 7,9 * 0,1 = 0,79 г,
4,9 см³: 7,9 * 4,9 = 38,71 г,
0,5 см³: 7,9 * 0,5 = 3,95 г.

Задание 547

Верёвку разрезали на две части. Длина одной части 5,4 м, а другая часть в 2,5 раза больше. Найдите первоначальную длину всей верёвки.

Решение

5,4 + (2,5 * 5,4) = 5,4 + 13,5 = 18,9 (м) - первоначальная длина веревки
Ответ: 18,9 м.

Задание 548

Выполните умножение:
а) 6,25 * 4,8;
б) 85,8 * 3,2;
в) 74 * 4,9;
г) 12,6 * 7,8;
д) 0,8 * 0,92;
е) 2,5 * 0,37;
ж) 3,43 * 0,12;
з) 0,25 * 0,48;
и) 1,15 * 0,07;
к) 6,023 * 5,6;
л) 8,4 * 18,478;
м) 2,749 * 0,48.

Решение

а) 6,25 * 4,8 = 30
б) 85,8 * 3,2 = 274,56
в) 74 * 4,9 = 362,6
г) 12,6 * 7,8 = 98,28
д) 0,8 * 0,92 = 0,736
е) 2,5 * 0,37 = 0,925
ж) 3,43 * 0,12 = 0,4116
з) 0,25 * 0,48 = 0,12
и) 1,15 * 0,07 = 0,0805
к) 6,023 * 5,6 = 33,7288
л) 8,4 * 18,478 = 155,2152
м) 2,749 * 0,48 = 1,31952

Задание 549

Запишите выражение:
а) произведение суммы чисел а и 3,1 и числа b;
б) сумма произведения чисел 4,1 и х и числа 8,65;
в) разность произведений чисел 7,8 и m и чисел 0,45 и n;
г) произведение суммы чисел a и b разности чисел c и d.

Решение

а) (а + 3,1) * b

б) 4,1 * х + 8,65

в) 7,8 * m − 0,45 − n

г) (a + b) * (c − d)

Задание 550

Прочитайте выражение:
а) (а + 9,7) * (b − 3,61);
б) 6,5mт − 7,6n;
в) 0,8x + 0,9у;
г) (m − n)(р + k).

Решение

а) произведение суммы чисел а и 9,7 и разности чисел b и 3,61

б) разность произведения чисел 6,5 и m и произведения чисел 7,6 и n

в) сумма произведения чисел 0,8 и х и произведения чисел 0,9 и у

г) произведение разности чисел m и n суммы чисел р и k

Задание 551

Увеличьте в 2,8 раза число 3,8; 0,705; 100; 9,2.

Решение

3,8 * 2,8 = 10,64;
0,705 * 2,8 = 1,974;
100 * 2,8 = 280;
9,2 * 2,8 = 25,76.

Задание 552

Придумайте задачу, которая решалась бы умножением:
а) 3,4 на 1,5;
б) 3,4 на 0,9.

Решение

а) Скорость пешехода 3,4 км/ч. Какое расстояние пройдет пешеход за 1,5 ч?
3,4 * 1,5 = 5,1 (км) - пройдет пешеход.
Ответ: 5,1 км.

б) В 3,4 кг смеси 0,9 массы занимает вода. Найдите массу воды.
3,4 * 0,9 = 3,06 (кг) - масса воды.
Ответ: 3,06 кг.

Задание 553

Запишите с помощью букв а, b, с сочетательное и переместительное свойства умножения и проверьте их при
a = 3,5; b = 0,4 и с = 0,6.
Используя эти свойства, упростите выражение:
а) 4 * 1,7y * 0,25;
б) 0,5 * 3,58m * 0,2.

Решение

Сочетательное свойство умножения: (a − b) * c = a * (b * с).
Переместительное свойство умножения: a * b = b * a.
При a = 3,5, b = 0,4, с = 0,6;
(a * b) * c = (3,5 * 0,4) * 0,6 = 1,4 * 0,6 = 0,84;
a * (b * c) = 3,5 * (0,4 * 0,6) = 3,5 * 0,24 = 0,84.

а) 4 * 1,7y * 0,25 = 4 * 0,25 * 1,7у = 1 * 1,7y = 1,7у

б) 0,5 * 3,58m * 0,2 = 0,5 * 0,2 * 3,58m = 0,1 * 3,58m = 0,358m

Задание 554

Найдите значение произведения:
а) 2,5 * 1,035 * 4;
б) 7,5 * 79,6 * 0,4;
в) 3 * 0,13 * 0,5 * 2;
г) 1,2 * 7,09 * 5 * 10.

Решение

а) 2,5 * 1,035 * 4 = 2,5 * 4 * 1,035 = 10 * 1,035 = 10,35

б) 7,5 * 79,6 * 0,4 = 7,5 * 0,4 * 79,6 = 3 * 79,6 = 238,8

в) 3 * 0,13 * 0,5 * 2 = 3 * 0,13 * (0,5 * 2) = 0,39 * 1 = 0,39

г) 1,2 * 7,09 * 5 * 10 = 1,2 * 5 * (7,09 * 10) = 6 * 70,9 = 425,4

Задание 555

Запишите с помощью букв a, b, c распределительное свойство умножения относительно сложения и относительно вычитания. Проверьте эти свойства при a = 6,2, b = 3,8, с = 0,2.
Используя эти свойства, найдите значение выражения:
а) 57,48 * 0,9093 + 42,52 * 0,9093;
б) 6,395 * 835,67 + 6,395 * 164,33;
в) 104,76 * 378,91 − 94,76 * 378,91;
г) 0,78 * 496,6 − 396,6 * 0,78.

Решение

Распределительное свойство умножения относительно сложения:
(a + b) * c = a * c + b * c.
Распределительное свойство умножения относительно вычитания:
(a − b) * с = a * c − b * c.
При a = 6,2, b = 3,8, c = 0,2;
(a + b) * с = (6,2 + 3,8) * 0,2 = 10 * 0,2 = 2;
a * с + b * c = 6,2 * 0,2 + 3,8 * 0,2 = 1,24 + 0,76 = 2;
(a − b) * c = (6,2 − 3,8) * 0,2 = 2,4 * 0,2 = 0,48;
a * c − b * c = 6,2 * 0,2 − 3,8 * 0,2 = 1,24 * 0,76 = 0,48.

а) 57,48 * 0,9093 + 42,52 * 0,9093 = (57,48 + 42,52) * 0,9093 = 100 * 0,9093 = 90,93

б) 6,395 * 835,67 + 6,395 * 164,33 = (835,67 + 164,33) * 6,395 = 1000 * 6,395 = 6395

в) 104,76 * 378,91 − 94,76 * 378,91 = (104,76 − 94,76) * 378,91 = 10 * 378,91 = 3789,1

г) 0,78 * 496,6 − 396,6 * 0,78 = (496,6 − 396,6) * 0,78 = 100 * 0,78 = 78

Задание 556

Упростите выражение:
а) 1,2x + 3,8x − 2,7x;
б) 4,5y − 2,3у + 1,6у;
в) 0,72m − 0,24m − 0,46m;
г) 8,3k − 4,3k + 1,6k.

Решение

а) 1,2x + 3,8х − 2,7x = 5х − 2,7х = 2,3х

б) 4,5y − 2,3у + 1,6у = 2,2у + 1,6у = 3,8у

в) 0,72m − 0,24m − 0,4бm = 0,72m − (0,24m + 0,46m) = 0,72m − 0,7m = 0,02m

г) 8,3k − 4,3k + 1,6k = 4k + 1,6k = 5,6k

Задание 557

Найдите значение выражения:
а) 9,8x + 23,7 + 6,2x + 55,1 при х = 8,2 и при x = 0,7;
б) (5,1а + 1,38) − 3,4а при а = 0,6 и при а = 1,8;
в) 44,2b − (15,7b + 23,45) при b = 0,9 и при b = 1,7;
г) 0,056m + 0,044m − 0,037 при m = 3,7 и при m = 0,37;
д) 3,45n − 3,44n + 0,024 при n = 7,6 и при n = 0,6.

Решение

а) 9,8x + 23,7 + 6,2x + 55,1 = 9,8x + 6,2x + (23,7 + 55,1) = 16x + 78,8
При x = 8,2
16x + 78,8 = 16 * 8,2 + 78,8 = 131,2 + 78,8 = 210
При х = 0,7
16x + 78,8 = 16 * 0,7 + 78,8 = 11,2 + 78,8 = 90

б) (5,1а + 1,38) − 3,4а = 5,1а − 3,4а + 1,38 = 1,7а − 1,38
При а = 0,6
1,7а + 1,38 = 1,7 * 0,6 + 1,38 = 1,02 + 1,38 = 2,4
При а = 1,8
1,7а + 1,38 = 1,7 * 1,8 + 1,38 = 3,06 + 1,38 = 4,44

в) 44,2b − (15,7b + 23,45) = 44,2b − 15,7b − 23,45 = 28,5b − 23,45
При b = 0,9
28,5b − 23,45 = 28,5 * 0,9 − 23,45 = 25,65 − 23,45 = 2,2
При b = 1,7
28,5b − 23,45 = 28,5 * 1,7 − 23,45 = 48,45 − 23,45 = 25

г) 0,056m + 0,044m − 0,037 = 0,1m − 0,037
При m = 3,7
0,1m − 0,037 = 0,1 * 3,7 − 0,037 = 0,37 − 0,037 = 0,333
При m = 0,37
0,1m − 0,037 = 0,1 * 0,37 − 0,037 = 0,037 − 0,037 = 0

д) 3,45n − 3,44n + 0,024 = 0,01n + 0,024
При n = 7,6
0,01n + 0,024 = 0,01 * 7,6 + 0,024 = 0,76 + 0,024 = 0,1
При n = 0,6
0,01n + 0,024 = 0,01 * 0,6 + 0,024 = 0,006 + 0,024 = 0,03

Задание 558

Найдите значение выражения
а) (6 − 4,94) * 2,5 − 2,35;
б) 0,18 * (8,2 + 3,75) − 1,051;
в) 67,45 − 7,45 * (3,8 + 4,2);
г) 28,6 + 11,4 * (6,595 + 3,405);
д) 20,4 * 6,5 + 3,8 * 18;
е) 7,2 * 3,6 − 4,8 * 5,4.

Решение

а) (6 − 4,94) * 2,5 − 2,35 = 1,06 * 2,5 − 2,35 = 2,65 − 2,35 = 0,3

б) 0,18 * (8,2 + 3,75) − 1,051 = 0,18 * 11,95 − 1,051 = 2,151 − 1,051 = 1,1

в) 67,45 − 7,45 * (3,8 + 4,2) = 67,45 − 7,45 * 8 = 67,45 − 59,6 = 7,85

г) 28,6 + 11,4 * (6,595 + 3,405) = 28,6 + 11,4 * 10 = 28,6 + 114 = 142,6

д) 20,4 * 6,5 + 3,8 * 18 = 132,6 + 68,4 = 201

e) 7,2 * 3,6 − 4,8 * 5,4 = 25,92 − 25,92 = 0

Задание 559

Найдите сумму площадей стен комнаты, длина которой 6,4 м, ширина 3,5 м и высота 2,69 м. Найдите объём комнаты. Ответы округлите до десятых.

Решение

S = а * (a b + b c + а с)
2 * (6,4 * 2,69 + 3,5 * 2,69 ) = 2 * 2,69 * (6,4 + 3,5) = 5,38 * 9,9 = 53,262 (м²) - сумма площадей стен комнаты
53,262 м² ≈ 53,3 м²
V = а b с
6,4 * 3,5 * 2,69 = 22,4 * 2,69 = 60,256 (м³) - объем комнаты
60,256 м³ ≈ 60,3 м³
Ответ: 53,3 м², 60,3 м³.

Задание 560

Высота прямоугольного параллелепипеда больше его ширины в полтора раза и меньше длины тоже в полтора раза. Найдите объём параллелепипеда, если его ширина 0,4 дм.

Решение

1) 1,5 * 0,4 = 0,6 (дм) - высота параллелепипеда
2) 1,5 * 0,6 = 0,9 (дм) - длина параллелепипеда
3) V = a b c = 0,9 * 0,4 * 0,6 = 0,36 * 0,6 = 0,216 (дм³) - объем параллелепипеда
Ответ: 0,216 дм³.

Задание 561

Скорость движения Земли вокруг Солнца 29,8 км/с, а скорость Марса на 5,7 км/с меньше. Какой путь пройдёт каждая из планет за 3 с; за 4,5 с; за 16,8 с; за 1 мин?

Решение

29,8 − 5,7 = 24,1 (км/с) - скорость движения Марса
29,8 * 3 = 89,4 (км) - пройдёт  Земля за 3 с
24,1 * 3 = 72,3 (км) - пройдёт  Марс за 3 с
29,8 * 4,5 = 134,1 (км) - пройдёт  Земля за 4,5 с
24,1 * 4,5 = 108,45 (км) - пройдёт  марс за 4,5 с
29,8 * 16,8 = 500,64 (км) - пройдёт  Земля за 16,8 с
24,1 * 16,8 = 404,88 (км) - пройдёт  Марс за 16,8 с
29,8 * 60 = 1788 (км) - пройдёт  Земля за 1мин
24,1 * 60 = 1446 (км) - пройдёт  Марс за 1мин

Задание 562

Площадь одного поля 207,5 га, а площадь второго на 17 га больше. Сколько пшеницы собрали с обоих полей, если с каждого гектара первого поля собирали 32,4 ц, ас каждого гектара второго − 28,6 ц? Ответ округлите до целых.

Решение

207,5 * 32,4 + (207,5 + 17) * 28,6 = 6723 + 6420,7 = 13 143,7 (ц) - пшеницы было собрано с обоих полей
13 143,7 ц ≈ 13 144 ц
Ответ: 13 144 ц.

Задание 563

Два пешехода вышли одновременно навстречу друг другу и встретились через 2,5 ч. Скорость первого пешехода равна 4,2 км/ч, а скорость второго 5,2 км/ч. Какое расстояние было между пешеходами в начале движения?

Решение

(4,2 + 5,2) * 2,5 = 9,4 * 2,5 = 23,5 (км) - расстояние между пешеходами в начале движения
Ответ: 23,5 км.

Задание 564

Найдите значение выражения:
а) 0,32; 0,33; 0,12; 0,13; 0,23; 0,22;
б) 0,42 + 0,52; 0,62 − 0,2; 2,32 − 3,19; 1,83 + 2,68.

Решение

а) 0,32 = 0,3 * 0,3 = 0,09
0,33 = 0,3 * 0,3 * 0,3 = 0,09 * 0,3 = 0,027
0,12 = 0,1 * 0,1 = 0,01
0,13 = 0,1 * 0,1 * 0,1 = 0,01 * 0,1 = 0,001
0,23 = 0,2 * 0,2 * 0,2 = 0,04 * 0,2 = 0,008
0,22 = 0,2 * 0,2 = 0,04

б) 0,42 + 0,52 = 0,4 * 0,4 + 0,5 * 0,5 = 0,16 + 0,25 = 0,41
0,62 − 0,2 = 0,6 * 0,6 − 0,2 = 0,36 − 0,2 = 0,16
2,32 − 3,19 = 2,3 * 2,3 − 3,19 = 5,29 − 3,19 = 2,1
1,83 + 2,68 = 1,8 * 1,8 * 1,8 + 2,68 = 5,832 + 2,68 = 8,512

Задание 565

Вычислите устно:
а)
0,3 * 3 = 0,9;
0,7 * 5 = 3,5;
0,06 * 4 = 0,24;
8 * 0,04 = 0,32;
0,55 * 0 = 0.
б)
0,26 − 0,02 = 0,24;
0,34 + 0,6 = 0,94;
1 − 0,8 = 0,2;
0,74 + 0,26 = 1;
3 − 0,44 = 2,56.
в)
0,125 * 8 = 1;
0,04 * 5 = 0,2;
0,25 * 4 = 1;
1,5 * 6 = 9;
0,18 * 5 = 0,9;
г)
2,7 * 10 = 27;
0,1 * 3 = 0,3;
0,691 * 100 = 69,1;
15 * 0,01 = 0,15;
3,8 * 1000 = 3800.

Решение

а) 0,3 * 3 = 0,9
0,7 * 5 = 3,5
0,06 * 4 = 0,24
8 * 0,04 = 0,32
0,55 * 0 = 0

б) 0,26 − 0,02 = 0,24
0,34 + 0,6 = 0,94
1 − 0,8 = 0,2
0,74 + 0,26 = 1
3 − 0,44 = 2,56

в) 0,125 * 8 = 1
0,04 * 5 = 0,2
0,25 * 4 = 1
1,5 * 6 = 9
0,18 * 5 = 0,9

г) 2,7 * 10 = 27
0,1 * 3 = 0,3
0,691 * 100 = 69,1
15 * 0,01 = 0,15
3,8 * 1000 = 3800

Задание 566

Найдите:
0,8 числа 90; 0,2 числа 40; 1,3 числа 20; 0,5 числа 180.

Решение

90 * 0,8 = 72
40 * 0,2 = 8
20 * 1,3 = 26
180 * 0,5 = 90

Задание 567

Выполните деление:
а) 55,5 : 5;
б) 5,55 : 5;
в) 4 : 5;
г) 3/5;
д) 1,2/2;
е) 2,7/3;
ж) 0,64 : 4;
з) 0,28 : 7;
и) 46,2 : 10;
к) 3,8/10;
л) 23 : 100;
м) 19,2 : 1000.

Решение

а) 55,5 : 5 = 11,1
б) 5,55 : 5 = 1,11
в) 4 : 5 = 0,8
г) 3/5 = 0,6
д) 1,2/2 = 0,6
е) 2,7/3 = 0,9
ж) 0,64 : 4 = 0,16
з) 0,28 : 7 = 0,04
и) 46,2 : 10 = 4,62
к) 3,8/10 = 0,38
л) 23 : 100 = 0,23
м) 19,2 : 1000 = 0,0192

Задание 568

Вычислите площадь прямоугольника, если его стороны равны:
а) 3,5 см и 4 см;
б) 1,8 дм и 5 дм;
в) 8 м и 1,25 м.

Решение

а) S = 3,5 * 4 = 14 см²

б) S = 1,8 * 5 = 9 дм²

в) S = 8 * 1,25 = 10 м²

Задание 569

Какую цифру (одну и ту же) можно подставить вместо звёздочки, чтобы было верно:
а) 0,5* = 0,5;
б) 0,3 > 0,5;
в) 6,81 < 6,82*?

Решение

а) 5

б) 6; 7; 8; 9.

в) 0; 1; 2.

Задание 570

Попробуйте объяснить, почему приписывание нуля справа к натуральному числу увеличивает его значение в 10 раз, а приписывание нуля к десятичной дроби не меняет её значения.

Решение

При приписывании нуля справа к натуральному числу его значение увеличивается на 10, так как числа смещаются по разрядам в сторону увеличения, а при том же самом действии с десятичной дробью числа не смещаются по разрядам.

Задание 571

Разделите:
а) 42,6; 3,85 и 7 на 10;
б) 586,1; 80,3 и 90 на 100.

Решение

а) 42,6 : 10 = 4,26
3,85 : 10 = 0,385
7 : 10 = 0,7

б) 586,1 : 100 = 5,861
80,3 : 100 = 0,803
90 : 100 = 0,9

Задание 572

Выполните деление:
а) 61,699 : 158;
б) 46,002 : 164;
в) 1,31313 : 13;
г) 1,717 : 17.

Решение

а) 61,699 : 158 = 0,3905

б) 46,002 : 164 = 0,2805

в) 1,31313 : 13 = 0,10101

г) 1,717 : 17 = 0,101

Задание 573

Чтобы собрать 100 г мёда, пчела посещает 1 млн цветков. Сколько граммов мёда собирает пчела с одного цветка?

Решение

 100 : 1000 000 = 0,0001 (г) - меда пчела собирает с одного цветка
Ответ: 0,0001 г.

Задание 574

Катер, собственная скорость которого 14,8 км/ч, шёл 3 ч по течению и 4 ч против течения. Какой путь проделал катер за всё это время, если скорость течения 2,3 км/ч?

Решение

(14,8 + 2,3) * 3 + (14,8 − 2,3) * 4 = 17,1 * 3 + 12,5 * 4 = 51,3 + 50 = 101,3 (км) - прошел катер
Ответ: 101,3 км.

Задание 575

На рисунке 152 попугаи, мартышки и удавы. Сосчитайте их, считая всех подряд по порядку: первый попугай, первый удав, второй попугай, первая мартышка, третий попугай и т. д. Если не удастся сосчитать с первого раза, возвращайтесь к этому заданию несколько раз.

Решение

7 попугаев, 5 удавов, 6 мартышек.

Задание 576

Два теплохода движутся навстречу друг другу. Сейчас между ними 185,5 км. Первый теплоход имеет собственную скорость 24,5 км/ч и движется по течению, а второй теплоход имеет собственную скорость 28,5 км/ч и движется против течения. Через сколько часов они встретятся, если скорость течения 2,5 км/ч?

Решение

1) (24,5 + 2,5) + (28,5 − 2,5) = 24,5 + 28,5 = 53 (км/ч) - скорость сближения теплоходов
2) 185,5 : 53 = 3,5 (ч) - через столько они встретятся
Ответ: через 3,5 ч.

Задание 577

Лодка шла по течению со скоростью 12,6 км/ч, а против течения − со скоростью 8,8 км/ч. Найдите скорость течения, зная, что собственная скорость лодки не изменялась.

Решение

Пусть х − скорость течения, тогда собственная скорость лодки, с одной стороны, равна (12,6 − х) км/ч, а с другой стороны, (8,8 + х) км/ч.
Составим уравнение:
12,6 − x = 8,8 + х
x = (12,6 − 8,8) : 2
х = 1,9 
Значит, 1,9 км/ч- скорость течения
Ответ: 1,9 км/ч.

Задание 578

Две лодки, собственная скорость каждой из которых 12,5 км/ч, движутся по реке навстречу одна другой. Через сколько часов они встретятся, если сейчас расстояние между ними 80 км, а скорость течения 2,5 км/ч?
Решите ту же задачу, если скорость течения 3 км/ч. Какое условие в задаче лишнее?

Решение

1) (12,5 + 2,5) + (12,5 − 2,5) = 12,5 + 12,5 + (2,5 − 2,5) = 25 (км/ч) - скорость сближения лодок
2) 80 : 25 = 3,2 (ч) - через столько времени встретятся лодки.
3) (12,5 + 3) + (12,5 − 3) = 12,5 + 12,5 + (3 − 3) = 25 (км/ч) - скорость сближения лодок при скорости течения 3 км/ч
Следовательно, время встречи определяется только собственными скоростями лодок, а скорость течения не влияет на конечный результат.

Задание 579

Запишите в миллионах числа:
13000000; 3700000; 24250000; 243760000.
Запишите в тысячах числа:
320000; 75000; 15700; 365240; 1875900; 17 млн; 6 млрд 524 млн.

Решение

13000000 = 13 млн
3700000 = 3,7 млн
24250000 = 24,25 млн
243760000 = 243,76 млн
320000 = 320 тыс.
75000 = 75 тыс.
700 = 15,7 тыс.
365240 = 365,24 тыс.
1875900 = 1875,9 тыс.
17 млн = 17000 тыс.
6 млрд 524 млн = 6524000 тыс.

Задание 580

Найдите значение выражения:
1) (37,8 * 4 − 111,96) : 12;
2) (87,38 : 17 + 7,36) * 21.

Решение

1) (37,8 * 4 − 111,96) : 12 = (151,2 − 111,96) : 12 = 39,24 : 12 = 3,27

2) (87,38 : 17 + 7,36) * 21 = (5,14 + 7,36) * 21 = 12,5 * 21 = 262,5

Задание 581

Решите задачу:
1) Сумма двух чисел 15,9. Одно число на 3,7 больше другого. Найдите эти числа.
2) Сумма двух чисел 19,8. Одно из них на 5,4 меньше другого. Найдите эти числа.

Решение

1) Составим уравнение:
х + (х + 3,7) = 15,9 
х = (15,9 − 3,7) : 2
х = 6,1 − одно число
6,1 + 3,7 = 9,8 - другое число
Ответ: 6,1 и  9,8.

2) Составим уравнение:
у + (у + 5,4) = 19,8
y = (19,8 − 5,4) : 2
у = 7,2 − одно число
7,2 + 5,4 = 12,6 - другое число
Ответ: 7,2 и 12,6.

Задание 582

Найдите значение произведения:
а) 48,5 * 0,1; 83,75 * 0,1; 5,76 * 0,1; 27 * 0,1;
б) 435,7 * 0,01; 4,2 * 0,01; 82,1 * 0,01; 82 * 0,01; 0,01 * 0,01;
в) 56,2 * 0,001; 0,3 * 0,001; 427,5 * 0,0001; 365 * 0,0001.

Решение

а) 48,5 * 0,1 = 4,85
83,75 * 0,1 = 8,375
5,76 * 0,1 = 0,576
27 * 0,1 = 2,7

б) 435,7 * 0,01 = 4,357
4,2 * 0,01 = 0,042
82,1 * 0,01 = 0,821
82 * 0,01 = 0,82
0,01 * 0,01 = 0,0001

в) 56,2 * 0,001 = 0,0562
0,3 * 0,001 = 0,0003
427,5 * 0,0001 = 0,04275
365 * 0,0001 = 0,0365

Задание 583

Выполните умножение:
а) 0,2 * 0,3;
б) 0,25 * 0,4;
в) 2,87 * 5,6;
г) 1,4 * 4,76;
д) 0,85 * 4,07;
е) 5,497 * 0,42;
ж) 8,5 * 1,04;
з) 0,25 * 0,0008;
и) 125 * 1,6;
к) 3,14 * 500;
л) 630 * 0,544;
м) 3,12 * 0,012.

Решение

а) 0,2 * 0,3 = 0,06

б) 0,25 * 0,4 = 0,1

в) 2,87 * 5,6 = 16,072

г) 1,4 * 4,76 = 6,664

д) 0,85 * 4,07 = 3,4595

e) 5,497 * 0,42 = 2,30874

ж )8,5 * 1,04 = 8,84

з) 0,25 * 0,0008 = 0,0002

и) 125 * 1,6 = 200

к) 3,14 * 500 = 1570

л) 630 * 0,544 = 342,72

м) 3,12 * 0,012 = 0,03744

Задание 584

Длина школьного коридора 30,24 м, а ширина 5,12 м. Найдите его площадь в квадратных метрах. Ответ округлите до сотых.

Решение

30,24 * 5,12 = 154,8288 (м²)  - площадь школьного коридора
154,8288 м² ≈ 154,83 м²
Ответ: 154,83 м².

Задание 585

Скорость планеты Меркурий при движении вокруг Солнца 47,8 км/с, а скорость планеты Венера на 12,8 км/с меньше.
Какой путь пройдёт каждая планета за 5 с; за 12,5 с; за 20,9 с?

Решение

1) 47,8 − 12,8 = 35 (км/с) - скорость движения Венеры вокруг Солнца
За 5 с при движении вокруг Солнца Меркурий пройдет путь 47,8 * 5 = 239 км,
а Венера − 35 * 5 = 175 км;
за 12,5 с Меркурий: 47,8 * 12,5 = 597,5 км,
а Венера − 35 * 12,5 = 437,5 км;
за 20,9 с Меркурий: 47,8 * 20,9 = 999,02 км,
а Венера − 35 * 20,9 = 731,5 км.

Задание 586

От Заречной до Мухино я шёл 0,8 ч со скоростью 5,5 км/ч, а от Мухино до Каменки ехал на велосипеде 1,4 ч со скоростью 12,5 км/ч. На сколько километров Мухино дальше от Каменки, чем от Заречной?

Решение

(12,5 * 1,4) − (5,50,8) = 17,5 − 4,4 = 13,1 (км) - на столько Мухино дальше от Каменки, чем от Заречной.
Ответ: на 13,1 км.

Задание 587

Скорый поезд догонит товарный через 21 мин. Найдите расстояние между ними, если скорость товарного поезда 1,2 км/мин, а скорого 1,5 км/мин.

Решение

 (1,5 − 1,2) * 21 = 0,3 * 21 = 6,3 (км) - расстояние между поездами
Ответ: 6,3 км.

Задание 588

Длина прямоугольного параллелепипеда равна а см, ширина b см и высота с см. Найдите объем, площадь поверхности и сумму длин всех рёбер этого параллелепипеда, если:
а) а = 5,9, b = 4, с = 12;
б) а = 14,1, b = 8, с = 2,5;
в) а = 0,67, b = 0,85, с = 2,52;
г) а = 2,07, b = 0,95, с = 4,24.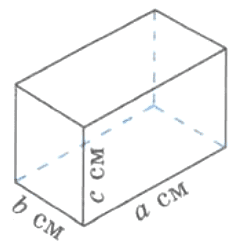

Решение

а) V = abc; S = 2 * (ab + ac + bc); L = 4 * (а + b + с):
при а = 5,9, b = 4, с = 12;
V = 5,9 * 4 * 12 = 5,9 * 48 = 283,2 см³;
S = 2 * ( 5,9 * 4 + 5,9 * 12 + 4 * 12 ) = 2 * ( 23,6 + 70,8 + 48 ) = 2 * 142,4 = 284,8 см²;
L = 4 * (5,9 + 4 + 12) = 4 * 21,9 = 87,6 см.

б) V = abc; S = 2 * (ab + ac + bc); L = 4 * (а + b + с):
при а = 14,1, b = 8, с = 2,5;
V = 14,1 * 8 * 2,5 = 14,1 * 20 = 282 с м³;
S = 2 * (14,1 * 8 + 14,1 * 2,5 + 8 * 2,5) = 2 * (112,8 + 35,25 + 20) = 2 * 168,05 = 336,1 см²;
L = 4 * (14,1 + 8 + 2,5) = 4 * 24,6 = 98,4 см.

в) V = abc; S = 2 * (ab + ac + bc); L = 4 * (а + b + с):
при а = 0,67, b = 0,85, с = 2,52;
V = 0 , 67 * 0,85 * 2,52 = 0,67 * 2,142 = 1,43514 см³;
S = 2 * (0,67 * 0,85 + 0,67 * 2,52 + 0,85 * 2,52) = 2 * 4,3999 = 8,7998 см²;
L = 4 * (0,67 + 0,85 + 2,52) = 4 * 4,04 = 16,16 см.

г) V = abc; S = 2 * (ab + ac + bc); L = 4 * (а + b + с):
при а = 2,07, b = 0,95, с = 4,24;
V = 2,07 * 0,95 * 4,24 = 2,07 * 4,028 = 8,33796 см³;
S = 2 * (2,07 * 0,95 + 2,07 * 4,24 + 0,95 * 4,24) = 29,5426 см²;
L = 4 * (2,07 + 0,95 + 4,24) = 4 * 7,26 = 29,04 см.

Задание 589

Одновременно из села в город выехали два автомобиля. Скорость первого равна 40 км/ч, а второго − в 1,5 больше. Каким будет расстояние между автомобилями через 2,5 ч?

Решение

 (40 * 1,5 − 40) * 2,5 = (60 − 40) * 2,5 = 20 * 2,5 = 50 (км) - будет между ними через 2,5 ч
Ответ: 50 км.

Задание 590

Упростите:
а) 8,3а + 1,7а;
б) 71,4b − 70,2b;
в) 2,5с + 1,2 + 3,6с + 5;
г) 8,8 − 9,7d − 2,5d − 3,7.

Решение

а) 8,3а + 1,7а = 10а

б) 71,4b − 70,2b = 1,2b

в) 2,5с + 1,2 + 3,6с + 5 = (2,5 + 3,6)с + (1,2 + 5) = 6,1с + 6,2

г) 8,8 − 9,7d − 2,5d − 3,7 = 8,8 − 3,7 − (9,7 + 2,5)d = 5,1 − 12,2d

Задание 591

Найдите значение выражения:
а) 0,7542x + 0,2458x − 20,9, если х = 220;
б) 66,6y − 44,4у + 8,11, если у = 10.

Решение

а) 0,7542x + 0,2458x − 20,9 = x − 20,9
При x = 220
x − 20,9 = 220 − 20,9 = 199,1

б) 66,6у − 44,4y + 8,11 = 22,2y + 8,11
При у = 10,22
2y + 8,11 = 22,2 * 10 + 8,11 = 222 + 8,11 = 230,11

Задание 592

Решите уравнение:
а) 45,7х + 0,3x − 2,4 = 89,6;
б) 80,1у − 10,1y + 4,7 = 81,7.

Решение

а) 45,7x + 0,3x − 2,4 = 89,6
46x = 89,6 + 2,4
x = 92 : 46
х = 2

б) 80,1y − 10,1y + 4,7 = 81,7
70y = 81,7 − 4,7 = 77
y = 77 : 70
у = 1,1

Задание 593

Найдите значение выражения:
а) 0,32 * 10;
б) 0,23 * 100;
в) 0,12 + 0,13;
г) 42 * 0,13;
д) 2,52 * 1000;
е) 0,62 + 0,82 − 0,23.

Решение

а) 0,32 * 10 = 0,3 * 0,3 * 10 = 0,09 * 10 = 0,9

б) 0,23 * 100 = 0,2 * 0,2 * 0,2 * 100 = 0,008 * 100 = 0,8

в) 0,12 + 0,13 = 0,1 * 0,1 + 0,1 * 0,1 * 0,1 = 0,01 + 0,001 = 0,011

г) 42 * 0,13 = 4 * 4 * 0,1 * 0,1 * 0,1 = 16 * 0,001 = 0,016

д) 2,52 * 1000 = 2,5 * 2,5 * 1000 = 6,25 * 1000 = 6250

е) 0,62 + 0,82 − 0,23 = 0,6 * 0,6 + 0,8 * 0,8 − 0,2 * 0,2 * 0,2 = 0,36 + 0,64 − 0,008 = 1 − 0,008 = 0,992

110 111 112 113 114 115 116

Пункт 37. Деление на десятичную дробь. Со страницы 110

Задание 594

Найдите частное и выполните проверку умножением:
а) 0,8 : 0,5;
б) 3,51 : 2,7;
в) 14,335 : 0,61.

Решение

а) 0,8 : 0,5 = 8 : 5 = 1,6
0,5 * 1,6 = 0,8

б) 3,51 : 2,7 = 35,1 : 27 = 1,3
2,7 * 1,3 = 3,51

в) 14,335 : 0,61 = 1433,5 : 61 = 23,5
0,61 * 23,5 = 14,335

Задание 595

Найдите частное и выполните проверку делением:
а) 0,096 : 0,12;
б) 0,126 : 0,9;
в) 42,105 : 3,5.

Решение

а) 0,096 : 0,12 = 9,6 : 12 = 0,8
0,096 : 0,8 = 0,96 : 8 = 0,12

б) 0,126 : 0,9 = 1,26 : 9 = 0,14
0,126 : 0,14 = 12,6 : 14 = 0,9

в) 42,105 : 3,5 = 421,05 : 35 = 12,03
42,105 : 12,03 = 4210,5 : 1203 = 3,5

Задание 596

Выполните деление:
а) 7,56 : 0,6;
б) 0,161 : 0,7;
в) 0,468 : 0,09;
г) 0,00261 : 0,03;
д) 0,824 : 0,8;
е) 10,5 : 3,5;
ж) 6,944 : 3,2;
з) 0,0456 : 3,8;
и) 0,182 : 1,3;
к) 131,67 : 5,7;
л) 189,54 : 0,78;
м) 636 : 0,12;
н) 14,976 : 0,72;
о) 168,392 : 5,6;
п) 24,576 : 4,8;
р) 16,51 : 1,27;
с) 46,08 : 0,384;
т) 22,256 : 20,8.

Решение

а) 7,56 : 0,6 = 75,6 : 6 = 12,6

б) 0,161 : 0,7 = 1,61 : 7 = 0,23

в) 0,468 : 0,09 = 46,8 : 9 = 5,2

г) 0,00261 : 0,03 = 0,261 : 3 = 0,087

д) 0,824 : 0,8 = 8,24 : 8 = 1,03

e) 10,5 : 3,5 = 105 : 35 = 3

ж) 6,944 : 3,2 = 69,44 : 32 = 2,17

з) 0,0456 : 3,8 = 0,456 : 38 = 0,012

и) 0,182 : 1,3 = 1,82 : 13 = 0,14

к) 131,67 : 5,7 = 1316,7 : 57 = 23,1

л) 189,54 : : 0,78 = 18 954 : 78 = 243

м) 636 : 0,12 = 63600 : 12 = 5300

н) 14,976 : 0,72 = 1497,6 : 72 = 20,8

о) 168,392 : 5,6 = 1683,92 : 56 = 30,07

п) 24,576 : 4,8 = 245,76 : 48 = 5,12

р) 16,51 : 1,27 = 1651 : 127 = 13

с) 46,08 : 0,384 = 46080 : 384 = 120

т) 22,256 : 20,8 = 222,56 : 208 = 1,07

Задание 597

Запишите выражения:
а) частное от деления суммы а и 2,6 на разность b и 8,5;
б) сумму частного х и 3,7 и частного 3,1 и y.

Решение

а) (a + 2,6) : (b − 8,5)

б) x : 3,7 + 3,1 : y

Задание 598

Прочитайте выражение:
а) m : 12,8 − n : 4,9;
б) (х + 0,7) : (у + 3,4);
в) (а : b) * (8 : с).

Решение

а) разность частного от деления m на 12,8 и частного от деления n на 4,9

б) частное от деления суммы х и 0,7 на сумму у и 3,4

в) произведение частного от деления а на b и частного от деления 8 на с

Задание 599

Шаг человека равен 0,8 м. Сколько шагов надо ему сделать, чтобы пройти расстояние 100 м?

Решение

100 : 0,8 = 1000 : 8 = 125 (ш.) - надо сделать человеку, чтобы пройти 100 м.
Ответ: 125 шагов.

Задание 600

Алёша проехал на поезде 162,5 км за 2,6 ч. С какой скоростью шёл поезд?

Решение

162,5 : 2,6 = 1625 : 26 = 62,5 (км/ч) - скорость поезда.
Ответ: 62,5 км/ч.

Задание 601

Найдите массу 1 см³ льда, если масса 3,5 см³ льда равна 3,08 г.

Решение

3,08 : 3,5 = 30,8 : 35 = 0,88 (г) - масса 1 см³ льда
Ответ: 0,88 г.

Задание 602

Верёвку разрезали на две части. Длина одной части 3,25 м, а длина другой части в 1,3 раза меньше первой. Какова была длина верёвки?

Решение

3,254 + 3,25 : 1,3 = 3,25 + 32,5 : 13 = 3,25 + 2,5 = 5,75 (м) - длина веревки
Ответ: 5,75 м.

Задание 603

В первый пакет вошло 6,72 кг муки, что в 2,4 раза больше, чем во второй пакет. Сколько килограммов муки вошло в оба пакета?

Решение

6,72 + 6,72 : 2,4 = 6,72 + 67,2 : 24 = 6,724 + 2,8 = 9,52 (кг) - муки вошло в оба пакета
Ответ: 9,52 кг.

Задание 604

На приготовление уроков Боря затратил в 3,5 раза меньше времени, чем на прогулку. Сколько времени ушло у Бори на прогулку и на приготовление уроков, если прогулка заняла 2,8 ч?

Решение

 2,8 + 2,8 : 3,5 = 2,84 + 28 : 35 = 2,84 + 0,8 = 3,6 (ч) - ушло на прогулку и приготовление уроков у Бори
Ответ: 3,6 ч.

Задание 605

За 2,4 ч мальчик прошёл 7,2 км. Сколько километров он пройдёт с той же скоростью за 1,6 ч?
Придумайте задачи с теми же числами в условии и в ответе:
а) про стоимость и количество товара;
б) про площадь поля и урожай;
в) про время работы и количество выпущенной продукции.

Решение

7,2 : 2,4 • 1,6 = 72 : 24 • 1,6 = 3 • 1,6 = 4,8 (км) - пройдет за 1,6 ч
Ответ:  4,8 км.

Задание 606

Алюминиевый шар, объём которого 50 см³, имеет массу 135 г. Чему равна масса стального шара того же объёма, если масса 1 см³ алюминия на 5,2 г меньше массы 1 см³ стали?

Решение

1) 135 : 504 + 5,2 = 2,7 + 5,2 = 7,9 (г) - масса 1 см³ стали
2) 50 * 7,9 = 395 (г) - масса стального шара объемом 50 см³
Ответ: 395 г.

Задание 607

Питательный раствор для подкормки растений поступает в теплицу по двум трубам. Первая была открыта 0,6 ч, а вторая 0,4 ч. В результате поступило 3,32 л раствора. Сколько питательного раствора подаётся за 1 ч по второй трубе, если по первой поступает 3,6 л раствора за 1 ч?

Решение

1)  3,6 * 0,6 = 2,16 (л) - раствора поступило через первую трубу за 0,6 ч
2)  3,32 − 2,16 = 1,16 (л) - раствора поступило через вторую трубу за 0,4 ч 
3) 1,16 : 0,4 = 11,6 : 4 = 2,9 (л) - раствора поступает за 1 ч через вторую трубу
Ответ: 2,9 л.

Задание 608

Выполните деление:
а) 4,9 : 0,1; 7,54 : 0,1; 0,8939 : 0,1; 0,8 : 01;
б) 5,453 : 0,01; 25,43 : 0,01; 0,84 : 0,01; 0,006 : 0,001; 4 : 0,01;
в) 0,00081 : 0,001; 7,8 : 0,001; 0,0001 : 0,001; 4 : 0,001; 0,0102 : 0,001.

Решение

а) 4,9 : 0,1 = 49
7,54 : 0,1 = 75,4
0,8939 : 0,1 = 8,939
0,8 : 0,1 = 8

б) 5,453 : 0,01 = 545,3
25,43 : 0,01 = 2543
0,84 : 0,01 = 84
0,006 : 0,001 = 6
4 : 0,01 = 400

в) 0,00081 : 0,001 = 0,81
7,8 : : 0,001 = 7800
0,0001 : 0,001 = 0,1
4 : 0,001 = 4000
0,0102 : 0,001 = 10,2

Задание 609

На сколько килограммов масса 1 м³ пробки меньше массы 1 м³ воды, если масса 1 см³ воды равна 1 г, а масса 1 см³ пробки равна 0,22 г?

Решение

 (1 − 0,22) * 1000000 = 0,78 * 1000000 = 780000 г = 780 (кг) - на столько масса 1 м³ воды больше массы 1 м³ пробки
Ответ: на 780 кг.

Задание 610

Решите уравнение:
а) 10 − 2,4x = 3,16;
б) (у + 26,1) * 2,3 = 70,84;
в) (z − 1,2) : 0,6 = 21,1;
г) 3,5m + m = 9,9;
д) 4,2p − р = 5,12;
е) 8,2t − 4,4t = 38,38;
ж) (10,49 − s) : 4,02 = 0,805;
з) 9k − 8,67k = 0,6699.

Решение

а) 10 − 2,4x = 3,16
x = (10 − 3,16) : 2,4x
х = 2,85

б) (y + 26,1) * 2,3 = 70,84
у = 70,84 : 2,3 − 26,1
у = 4,7

в) (z − 1,2) : 0,6 = 21,1
z = 21,1 − 0,6 + 1,2
z = 13,86

г) 3,5m + m = 9,9
m = 9,9 : 4,5
m = 2,2

д) 4,2p − p = 5,12
p = 5,12 : 3,2
p = 1,6

e) 8,2t − 4,4t = 38,38
t = 38,38 : 3,8
t = 10,1

ж) (10,49 − s) : 4,02 = 0,805
s = 10,49 − 0,805 * 4,02
s = 7,2539

з) 9k − 8,67k = 0,6699
k = 0,6699 : 0,33
k = 2,03

Задание 611

В двух цистернах было 119,88 т бензина. В первой цистерне бензина было больше, чем во второй, в 1,7 раза. Сколько бензина было в каждой цистерне?

Решение

Пусть во второй цистерне было х т бензина,
тогда в первой цистерне было 1,7х т бензина.
Составим уравнение:
х + 1,7х = 119,88
х = 119,88 : 2,7
х = 44,4
Значит, 44,4 т было во второй цистерне
1,7 * 44,4 = 75,48 (т) -  бензина было  в первой цистерне
Ответ: 44,4 т и 75,48 т.

Задание 612

С трёх участков собрали 87,36 т капусты. При этом с первого участка собрали в 1,4 раза больше, а со второго в 1,8 раза больше, чем с третьего участка. Сколько тонн капусты собрали с каждого участка?

Решение

Пусть с третьего участка собрали х т капусты,
тогда с первого участка собрали 4х т, а со второго 1,8х т.
Составим уравнение:
1,4x + 1,8x + х = = 87,36
х = 87,36 : 4,2
х = 20,8
Значит, 20,8 т собрали с третьего участка,
1,4 * 20,8 = 29,12 (т) - собрали с первого участка
1,8 * 20,8 = 37,44 (т) - капусты собрали со второго участка
Ответ: 20,8 т, 29,12 т, 37,44 т.

Задание 613

Кенгуру ниже жирафа в 2,4 раза, а жираф выше кенгуру на 2,52 м. Какова высота жирафа и какова высота кенгуру?

Решение

Пусть х − высота кенгуру,
тогда высота жирафа − 2,4x м.
Составим уравнение:
2,4х − х = 2,52
х = 2,52 : 1,4
х = 1,8
Значит, 1,8 м − высота кенгуру,
2,4 * 1,8 = 4,32 (м) - высота жирафа
Ответ: 1,8 м, 4,32 м.

Задание 614

Два пешехода находились на расстоянии 4,6 км друг от друга. Они пошли навстречу друг другу и встретились через 0,8 ч. Найдите скорость каждого пешехода, если скорость одного из них в 1,3 раза больше скорости другого.

Решение

Пусть х − скорость одного пешехода,
тогда 1,3x − скорость другого.
Скорость сближения пешеходов равна (х + 1,3x) км/ч, и они встретились через 4,6 : (x + 1,3x) ч.
Составим уравнение:
4,6 : (х + 1,3х) = 0,8
2,3х = 4,6 : 0,8
х = 5,75 : 2,3
х = 2,5
Значит, 2,5 км/ч − скорость одного пешехода
1,3 * 2,5 = 3,25 (км/ч) - скорость другого
Ответ: 2,5 км/ч, 3,25 км/ч.

Задание 615

Выполните действия:
а) (130,2 − 30,8) : 2,8 − 21,84;
б) 8,16 : (1,32 + 3,48) − 0,345;
в) 3,712 : (7 − 3,8) + 1,3 * (2,74 + 0,66);
г) (3,4 : 1,7 + 0,57 : 1,9) * 4,9 + 0,0825 : 2,75;
д) (4,44 : 3,7 − 0,56 : 2,8) : 0,25 − 0,8;
е) 10,79 : 8,3 * 0,7 − 0,46 * 3,15 : 6,9.

Решение

а) (130,2 − 30,8) : 2,8 − 21,84 = 99,4 : 2,8 − 21,84 = 35,5 − 21,84 = 13,66

б) 8,16 : (1,32 + 3,48) − 0,345 = 8,16 : 4,8 − 0,345 = 1,7 − 0,345 = 1,355

в) 3,712 : (7 − 3,8) + 1,3 * (2,74 + 0,66) = 3,712 : 3,2 + 1,3 * 3,4 = 1,16 + 4,42 = 5,58

г) (3,4 : 1,7 + 0,57 : 1,9)4,9 + 0,0825 : 2,75 = (2 + 0,3)4,9 + 0,03 = 11,27 + + 0,03 = 11,3

д) (4,44 : 3,7 − 0,56 : 2,8) : 0,25 − 0,8 = (1,2 − 0,2) : 0,25 − 0,8 = 1 : 0,25 − 0,8 = 4 − 0,8 = 3,2

е) 10,79 : 8,3 * 0,7 − 0,46 * 3,15 : 6,9 = 1,3 * 0,7 − 1,449 : 6,9 = 0,91 − 0,21 = 0,7

Задание 616

Представьте обыкновенную дробь в виде десятичной и найдите значение выражения:
а) 3/4 : 0 , 2;
б) (4,75 − 2 1/8) : 0,8;
в) (1 − 0,532) : 13/20;
г) 12,375 : ( 3/4 + 0,75).

Решение

а) $\frac34:0,2=0,75:0,2=3,75$

б) $(4,75-2\frac18):0,8=(4,75-2,125):0,8=2,625:0,8=3,28125$

в) $(1-0,532):\frac{13}{20}=0,468:0,65=0,72$

г) $12,375:(\frac34+0,75)=12,375:1,5=8,25$

Задание 617

Вычислите устно:
а)
25,5 : 5;
1,5 : 3;
4,7 : 10;
0,48 : 4;
0,9 : 100;
б)
9 * 0,2;
1 * 0,1;
16 * 0,01;
24 * 0,3;
0,5 * 26;
в)
0,3 : 2;
2 : 5;
17,17 : 17;
25,5 : 25;
0,8 : 16;
г)
6,7 − 2,3;
6 − 0,02;
3,08 + 0,2;
2,54 + 0,06;
8,2 − 2,2.

Решение

а) 25,5 : 5 = 5,1
1,5 : 3 = 0,5
4,7 : 10 = 0,47
0,48 : 4 = 0,12
0,9 : 100 = 0,009

б) 9 * 0,2 = 1,8
1 * 0,1 = 0,1
16 * 0,01 = 0,16
24 * 0,3 = 7,2
0,5 * 26 = 13

в) 0,3 : 2 = 0,15
2 : 5 = 0,4
17,17 : 17 = 1,01
25,5 : 25 = 1,02
0,8 : 16 = 0,05

г) 6,7 − 2,3 = 4,4
6 − 0,02 = 5,98
3,08 + 0,2 = 3,28
2,54 + 0,06 = 2,6
8,2 − 2,2 = 6

Задание 618

Найдите произведение:
а) 0,1 * 0,1;
6) 1,3 * 1,4;
в) 0,3 * 0,4;
г) 0,4 * 0,4;
д) 0,06 * 0,8;
е) 0,01 * 100;
ж) 0,7 * 0,001;
з) 100 * 0,09;
и) 0,3 * 0,3 * 0,3.

Решение

а) 0,1 * 0,1 = 0,01

б) 1,3 * 1,4 = 1,82

в) 0,3 * 0,4 = 0,12

г) 0,4 * 0,4 = 0,16

д) 0,06 * 0,8 = 0,048

e) 0,01 * 100 = 1

ж) 0,7 * 0,001 = 0,0007

з) 100 * 0,09 = 9

и) 0,3 * 0,3 * 0,3 = 0,09 * 0,3 = 0,027

Задание 619

Найдите:
0,4 числа 30;
0,5 числа 18;
0,1 числа 6,5;
2,5 числа 40;
0,12 числа 100;
0,01 числа 1000.

Решение

30 * 0,4 = 12
18 * 0,5 = 9
6,5 * 0,1 = 0,65
40 * 2,5 = 100
100 * 0,12 = 12
1000 * 0,01 = 10

Задание 620

Каково значение выражения 5683,25а при а = 10; 0,1; 0,01; 100; 0,001; 1000; 0,00001?

Решение

При а = 10
5683,25а = 5683,25 * 10 = 56832,5
При а = 0,1
5683,25а = 5683,25 * 0,1 = 568,325
При а = 0,01
5683,25а = 5683,25 * 0,01 = 56,8325
При а = 100
5683,25а = 5683,25 * 100 = 568325
При а = 0,001
5683,25а = 5683,25 * 0,001 = 5,68325
При а = 1000
5683,25а = 5683,25 * 1000 = 5 683 250
При а = 0,00001
5683,25а = 5683,25 * 0,00001 = 0,0568325

Задание 621

Подумайте, какие из чисел могут быть точными, какие − приближёнными:
а) в классе 32 ученика;
б) расстояние от Москвы до Киева 900 км;
в) у параллелепипеда 12 рёбер;
г) длина стола 1,3 м;
д) население Москвы 8 млн человек;
е) в пакете 0,5 кг муки;
ж) площадь острова Куба 105 000 к м 2;
з) в школьной библиотеке 10 000 книг;
и) одна пядь равна 4 вершкам, а вершок равен 4,45 см (вершок − длина фаланги указательного пальца).

Решение

а) точная величина

б) приближенная величина

в) точная величина

г) приближенная величина

д) приближенная величина

е) приближенная величина

ж) приближенная величина

з) точная величина

и) приближенная величина

Задание 622

Найдите три решения неравенства:
а) 1,2 < х < 1,6;
б) 2,1 < х < 2,3;
в) 0,001 < х < 0,002;
г) 0,01 < х < 0,011.

Решение

а) 1,2 < x < 1,6
при х = 1,38; 1,5; 1,59.

б) 2,1 < x < 2,3
при х = 2,15; 2,18; 2,2.

в) 0,001 < х < 0,002
при х = 0,0015; 0,0018; 0,0019.

г) 0,01 < х < 0,011
при х = 0,0101; 0,0102; 0,0103.

Задание 623

Сравните, не вычисляя, значения выражений:
а) 24 * 0,15 и (24 * 15) : 100;
б) 0,084 * 0,5 и (84 * 5) : 10000.
Объясните полученный ответ.

Решение

а) 24 * 0,15 = (24 * 15) : 100 = 24 * (15 : 100)

б) 0,084 * 0,5 = (84 * 5) : 10000 = (84 * 5) : (1000 * 10) = (84 : 1000) * (5 : 10)

Задание 624

Округлите числа:

Решение

82,257 3,645 9,0819 12,5961
до единиц 82 3 9 12
до десятых 82,3 3,6 9,1 12,6
до сотых 82,26 3,65 9,08 12,60

Задание 625

Выполните деление:
а) 22,7 : 10; 23,3 : 10; 3,14 : 10; 9,6 : 10;
б) 304 : 100; 42,5 : 100; 2,5 : 100; 0,9 : 100; 0,03 : 100;
в) 143,4 : 12; 1,488 : 124; 0,3417 : 34; 159,8 : 235; 65,32 : 568.

Решение

а) 22,7 : 10 = 2,27
23,3 : 10 = 2,33
3,14 : 10 = 0,314
9,6 : 10 = 0,96

б) 304 : 100 = 3,04
42,5 : 100 = 0,425
2,5 : 100 = 0,025
0,9 : 100 = 0,009
0,03 : 100 = 0,0003

в) 143,4 : 12 = 11,95
1,488 : 124 = 0,012
0,3417 : 34 = 0,01005
159,8 : 235 = 0,68
65,32 : 568 = 0,115

Задание 626

Велосипедист выехал из села со скоростью 12 км/ч. Через 2 ч в противоположном направлении из того же села выехал другой велосипедист, причём скорость второго в 1,25 раза больше скорости первого. Какое расстояние будет между ними через 3,3 ч после выезда второго велосипедиста?

Решение

12 * 2 + (12 + 12 * 1,25) * 3,3 = 24 + 27 * 3,3 = 24 + 89,1 = 113,1 (км) - будет между ними через 2 ч после выезда второго велосипедиста
Ответ: 113,1 км.

Задание 627

Собственная скорость лодки 8,5 км/ч, а скорость течения 1,3 км/ч. Какое расстояние пройдёт лодка по течению за 3,5 ч? Какое расстояние пройдёт лодка против течения за 5,6 ч?

Решение

1) 8,5 + 1,3 = 9,8 (км/ч) - скорость лодки по течению
2)  8,5 − 1,3 = 7,2 (км/ч) - скорость лодки против течения
3)  9,8 * 3,5 = 34,3 (км) - лодка пройдёт за 3,5 ч по течению
4) 7,2 * 5,6 = 40,32 (км) - лодка пройдёт за 5,6 ч против течения
Ответ: 34,3 км, 40,32 км.

Задание 628

Завод изготовил 3,75 тыс. деталей и продал их по цене 950 р. за штуку. Расходы завода на изготовление одной детали составили 637,5 р. Найдите прибыль, полученную заводом от продажи этих деталей.

Решение

 (950 − 637,5) * 3750 = 312,5 * 3750 = 1171875 (р.) - прибыль завода
Ответ: 1171875 рублей.

Задание 629

Ширина прямоугольного параллелепипеда 7,2 см, что составляет 3/4 длины и 5/4 высоты. Найдите объём этого параллелепипеда и округлите ответ до целых.

Решение

1) 7,2 : 3 * 4 = 2,4 * 4 = 9,6 (см) - длина прямоугольного параллелепипеда
2)  7,2 : 5 * 4 = 1,44 * 4 = 5,76 (см) - высота параллелепипеда
3) 9,6 * 7,2 * 5,76 = 398,1312 (см³)  - объем параллелепипеда
398,1312 см³ ≈ 398 см³
Ответ: 398 см³.

Задание 630

Папа Карло пообещал каждый день давать Пьеро по 4 сольдо, а Буратино в первый день 1 сольдо, а в каждый следующий день на 1 сольдо больше, если он будет вести себя хорошо. Буратино обиделся: он решил, что, как бы ни старался, никогда не сможет получить в сумме столько же сольдо, сколько Пьеро. Подумайте, прав ли Буратино.

Решение

За 7 дней хорошего поведения Буратино получит:
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 сольдо, а Пьеро за это время также получит 7 * 4 = 28 сольдо, следовательно за неделю хорошего поведения Буратино получит такую же сумму, что и Пьеро.

Записываем:

1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 (с.) получит Буратино за 7 дней хорошего поведения
7 * 4 = 28 (с.) - получит Пьер за 7 дней
Ответ: за неделю хорошего поведения Буратино получит такую же сумму, что и Пьеро.

Задание 631

На 3 шкафа и 9 книжных полок пошло 231 м досок, причём на шкаф идёт в 4 раза больше материала, чем на полку. Сколько метров досок идёт на шкаф и сколько − на полку?

Решение

Пусть на полку затрачивается х м материала,
тогда на шкаф 4х м материала.
На 3 шкафа и 9 полок пошло (3 * 4х + 9х) м материала.
Составим уравнение:
3 * 4х + 9х = 231
12х + 9х = 231
х = 231 : 21
х = 11
Значит, 11 м затрачивается на полку
4 * 11= 44 (м) - на шкаф
Ответ: 11 м, 44 м.

Задание 632

Решите задачу:
1) Первое число равно 6,3 и составляет 3/7 второго числа. Третье число составляет 2/3 второго. Найдите второе и третье числа.
2) Первое число 8,1. Второе число составляет 5/9 от первого числа и 3/4 от третьего числа. Найдите второе и третье числа.

Решение

1) 6,3 : 3 * 7 = 2,1 * 7 = 14,7 - второе число
   14,7 : 3 * 2 = 4,9 * 2 = 9,8 - третье число
Ответ: 14,7 и 9,8.

2) 8,1 : 9 * 5 = 0,9 * 5 = 4,5 - второе число
    4,5 : 3 * 4 = 1,5 * 4 = 6  - третье число
Ответ: 4,5 и 6.

Задание 633

Найдите значение выражения:
1) (7 − 5,38) * 2,5;
2) (8 − 6,46) * 1,5.

Решение

1) (7 − 5,38) * 2,5 = 1,62 * 2,5 = 4,05

2) (8 − 6,46) * 1,5 = 1,54 * 1,5 = 2,31

Задание 634

Найдите значение частного:
а) 17,01 : 6,3;
б) 1,598 : 4,7;
в) 39,156 : 7,8;
г) 1,4245 : 3,5;
д) 193,2 : 8,4;
е) 0,045 : 0,18;
ж) 0,02976 : 0,024;
з) 11,59 : 3,05;
и) 74,256 : 18,2.

Решение

а) 17,01 : 6,3 = 170,1 : 63 = 2,7

б) 1,598 : 4,7 = 15,98 : 47 = 0,34

в) 39,156 : 7,8 = 391,56 : 78 = 5,02

г) 1,4245 : 3,5 = 14,245 : 35 = 0,407

д) 193,2 : 8,4 = 1932 : 84 = 23

е)0,045 : 0,18 = 4,5 : 18 = 0,25

ж)0,02976 : 0,024 = 29,76 : 24 = 1,24

з)11,59 : 3,05 = 1159 : 305 = 3,8

и)74,256 : 18,2 = 742,56 : 182 = 4,08

Задание 635

Путь от дома до школы равен 1,1 км. Девочка проходит этот путь за 0,25 ч. С какой скоростью идёт девочка?

Решение

1,1 : 0,25 = 110 : 25 = 4,4 (км/ч) - скорость девочки
Ответ: 4,4 км/ч.

Задание 636

В двухкомнатной квартире площадь одной комнаты 20,64 м 2, а площадь другой комнаты в 2,4 раза меньше. Найдите площадь этих двух комнат вместе.

Решение

 20,64 + 20,64 : 2,4 = 20,64 + 8,6 = 29,24 (м²) - площадь обеих комнат квартиры
Ответ: 29,24 м².

Задание 637

Двигатель за 7,5 ч расходует 111 л горючего. Сколько литров горючего израсходует двигатель за 1,8 ч?

Решение

 111 : 75 * 1,8 = 14,8 * 1,8 = 26,64 (л) - горючего  двигатель израсходует за 1,8 ч
Ответ: 26,64 л.

Задание 638

Металлическая деталь объёмом в 3,5 дм³ имеет массу 27,3 кг. Другая деталь из этого же металла имеет массу 10,92 кг. Каков объём второй детали?

Решение

1) 27,3 : 3,5 = 273 : 35 = 7,8 (кг) - масса 1 дм³ детали
2)  10,92 : 7,8 = 109,2 : 78 = 1,4 (дм³) - объем второй детали
Ответ: 1,4 дм³.

Задание 639

В цистерну через две трубы налили 2,28 т бензина. Через первую трубу поступало 3,6 т бензина в час, и она была открыта 0,4 ч. Через вторую трубу поступало за час на 0,8 т бензина меньше, чем через первую. Сколько времени была открыта вторая труба?

Решение

1)  3,6 − 0,8 = 2,8 (т) - бензина поступало через вторую трубу за 1 ч
2) (2,28 − 3,6 * 0,4) : 2,8 = (2,28 − 1,44) : 2,8 = 0,84 : 2,8 = 0,3 (ч) - была открыта вторая труба
Ответ: 0,3 ч.

Задание 640

Решите уравнение:
а) 2,136 : (1,9 − x) = 7,12;
б) 4,2 * (0,8 + у) = 8,82;
в) 0,2t + 1,7t − 0,54 = 0,22;
г) 5,6z − 2z − 0,7z + 2,65 = 7.

Решение

а) 2,136 : (1,9 − x) = 7,12
1,9 − x = 2,136 : 7,12 = 1,9
x = 1,9 − 0,3
х = 1,6

б) 4,2 * (0,8 + y) = 8,82
0,8 + y = 8,82 : 4,2 = 2,1
y = 2,1 − 0,8
у = 1,3

в) 0,2t + 1,7t − 0,54 = 0,22
1,9t = 0,22 + 0,54 = 0,76
t = 0,76 : 1,9
t = 0,4

г) 5,6z − 2z − 0,7z + 2,65 = 7
2,9z= 7 − 2,65 = 4,35
z = 4,35 : 2,9
z = 1,5

Задание 641

Товар массой в 13,3 т распределили на три автомашины. На первую автомашину погрузили в 1,3 раза больше, а на вторую − в 1,5 раза больше, чем на третью автомашину. Сколько тонн товара погрузили на каждую автомашину?

Решение

Пусть на третью машину погрузили х т,
тогда на первую машину погрузили 1,3х т груза, а на вторую 1,5x т.
Составим уравнение:
1,3х + 1,5х + х = 13,3
3,8х = 13,3
х = 13,3 : 3,8
х = 3,5
Значит, 3,5 т погрузили на третью машину, 
1,3 * 3,5 = 4,55 (т) - погрузили на первую 
1,5 * 3,5 = 5,25 (т) -  груза погрузили на вторую
Ответ: 4,55 т, 5,25 т, 3,5 т.

Задание 642

Два пешехода вышли одновременно из одного места в противоположных направлениях. Через 0,8 ч расстояние между ними стало равным 6,8 км. Скорость одного пешехода была в 1,5 раза больше скорости другого. Найдите скорость каждого пешехода.

Решение

Пусть х − скорость первого пешехода,
тогда 1,5у − скорость второго пешехода.
Составим уравнение:
(х + 1,5x) * 0,8 = 6,8
2,5у = 6,8 : 0,8
2,5у  = 8,5
х = 8,5 : 2,5
х = 3,4
Значит, 3,4 км/ч − скорость первого пешехода
1,5 * 3,4 = 5,1 (км/ч) - скорость второго пешехода
Ответ: 3,4 км/ч, 5,1 км/ч.

Задание 643

Выполните действия:
а) (21,2544 : 0,9 + 1,02 * 3,2) : 5,6;
б) 4,36 : (3,15 + 2,3) + (0,792 − 0,78) * 350;
в) (3,91 : 2,3 * 5,4 − 4,03) * 2,4;
г) 6,93 : (0,028 + 0,36 * 4,2) − 3,5.

Решение

а) (21,2544 : 0,9 + 1,02 * 3,2) : 5,6 = (23,616 + 3,264) : 5,6 = 26,88 : 5,6 = 4,8

б) 4,36 : (3,15 + 2,3) + (0,792 − 0,78) * 350 = 4,36 : 5,45 + 0,012 * 350 = 0,8 + 4,2 = 5

в) (3,91 : 2,3 − 5,4 − 4,03) * 2,4 = (1,7 − 5,4 − 4,03) * 2,4 = (9,18 − 4,03) * 2,4 = 5,15 * 2,4 = 12,36

г) 6,93 : (0,028 + 0,36 * 4,2) − 3,5 = 6,93 : (0,028 + 1,512) − 3,5 = 6,93 : 1,54 − 3,5 = 4,5 − 3,5 = 1

Задание 644

В школу пришёл врач и принёс для прививки 0,25 кг сыворотки. Скольким ребятам он может сделать уколы, если для каждого укола нужно 0,002 кг сыворотки?

Решение

0,25 : 0,002 = 250 : 2 = 125 (ук.) - можно сделать
Ответ: 125 уколов.

Задание 645

В магазин завезли 2,8 т пряников. До обеда было продано 5/7 этих пряников. Сколько тонн пряников осталось ещё продать?

Решение

1) 2,8 : 7 * 5 = 0,4 * 5 = 2 (т) -  пряников продали до обеда,
2) 2,8 − 2 = 0,8 (т) - осталось продать
Ответ: 0,8 т пряников.

Задание 646

От куска ткани отрезали 5,6 м. Сколько метров ткани было в куске, если отрезали 2/7 этого куска?

Решение

 5,6 : 2 * 7 = 2,8 * 7 = 19,6 (м) - было в куске
Ответ: 19,6 м.

117 118 119 120 121 122

Пункт 38. Среднее арифметическое, со страницы 117

Задание 647

Найдите среднее арифметическое чисел 2 и 10. Изобразите на координатном луче число 2, число 10 и их среднее арифметическое. Сделайте вывод.

Решение

(10 + 2) : 2 = 6
Среднее арифметическое чисел на координатном луче будет являться серединой отрезка построенного между данными числами.

Задание 648

Найдите среднее арифметическое чисел:
а) 70,6 и 71,3;
б) 0,1; 0,2 и 0,3;
в) 1,11; 1,12; 1,19 и 1,48;
г) 7,381; 5,004; 6,118; 8,019; 7,815 и 5,863.

Решение

а) (70,6 + 71,3) : 2 = 141,9 : 2 = 70,95

б) (0,1 + 0,2 + 0,3) : 3 = 0,6 : 3 = 0,2

в) (1,11 + 1,12 + 1,19 + 1,48) : 4 = 4,9 : 4 = 1,225

г) (7,381 + 5,004 + 6,118 + 8,019 + 7,815 + 5,863) : 6 = 6,7

Задание 649

На рисунке 153 АВ = ВС, где А(8,9) и В(9,5). Найдите координату точки С. Чему равно среднее арифметическое координат точек А и С?

Решение

Координата точки С(9,5 + (9,5 − 8,9)) = С(9,5 + 0,6) = С(10,1).
Среднее арифметическое координат точек А и С равно (8,9 + 10,1) : 2 = 19 : 2 = 9,5 − это координата точки В.

Задание 650

Четыре поля имеют площадь по 200 га каждое. На первом поле собрали 7220 ц пшеницы, на втором − 7560 ц пшеницы, на третьем − 7090 ц пшеницы и на четвёртом − 7130 ц пшеницы. Определите урожайность пшеницы на каждом поле и найдите среднюю урожайность.

Решение

1) 7220 : 200 = 36,1 (ц/га) - урожайность пшеницы на первом поле:
2) 7560 : 200 = 37,8 (ц/га) - на втором поле
3) 7090 : 200 = 35,45 (ц/га) -  на третьем поле
4) 7130 : 200 = 35,65 (ц/га) - на четвёртом поле
5) (36,1 + 37,8 + 35,45 + 35,65) : 4 = 145 : 4 = 36,25 (ц/га) - средняя урожайность пшеницы
Ответ: 36,25 ц/га.

Задание 651

С поля площадью 87 га сняли урожай 10450 ц картофеля, а с поля площадью 113 га собрали 14980 ц картофеля. Найдите среднюю урожайность картофеля на этих полях.

Решение

(10450 + 14980) : (87 + 113) = 25430 : 200 = 127,15 (ц/га) - средняя урожайность картофеля
Ответ: 127,15 ц/га.

Задание 652

==

Решение

(10 + 9 + 12 + 8 + 9 + 11 + 15 + 10 + 12 + 14) : 10 = 110 : 10 =  11^о - средняя температура
Ответ: 11^о.

Задание 653

=

Решение

Время  8.00-11.00 11.00-14.00 14.00-17.00 17.00-20.00
t, ^oC       9                 12                 13                     10

(9 + 12 + 13 + 10) : 4 = 44 : 4 = 11^о - средняя температура
Ответ: 11^о.

Задание 654

Найдите среднее арифметическое чисел 84,32; 84,47; 84,56 и 84,68 и округлите его до десятых.

Решение

(84,32 + 84,47 + 84,56 + 84,68) : 4 = 338,03 : 4 = 84,5075 ≈ 84,5.

Задание 655

Участница соревнований по фигурному катанию на коньках получила оценки 5,3; 4,8; 5,4; 5,0; 5,3; 5,4; 5,3; 5,2; 5,1. Найдите среднюю оценку этой участницы.

Решение

 (5,3 + 4,8 + 5,4 + 5,0 + 5,3 + 5,4 + 5,3 + 5,2 + 5,1) : 9 = 5,2 - средняя оценка
Ответ: 5,2.

Задание 656

Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч по грунтовой дороге со скоростью 45 км/ч, наконец, 0,3 ч по просёлочной дороге со скоростью 30 км/ч. Найдите среднюю скорость движения автомобиля на всём пути.

Решение

(90 * 3,2 + 45 * 1,5 + 30 * 0,3) : (3,2 + 1,5 + 0,3) = (288 + 67,5 + 9) : 5 = 364,5 : 5 = 72,9 (км/ч) - средняя скорость автомобиля
Ответ: 72,9 км/ч.

Задание 657

Поезд шёл 4 ч со скоростью 70 км/ч и 3 ч со скоростью 84 км/ч. Найдите среднюю скорость поезда на пройденном за это время пути.

Решение

(4 * 70 + 4 * 2,25)/2 = 76 (км/ч) - средняя скорость поезда
Ответ: 76 км/ч.

Задание 658

Среднее арифметическое двух чисел равно 3,1. Одно число равно 3,8. Найдите второе число.
Сумма чисел = (Среднее арифметическое) * (количество чисел)

Решение

с = (a + b) : 2 => a = 2c − b:
при а = 3,8, с = 3,1;
a = 2c − b = 2 * 3,1 − 3,8 = 6,2 − 3,8 = 2,4.

Задание 659

Среднее арифметическое шести чисел равно 3,5, а среднее арифметическое четырёх других чисел − 2,25. Найдите среднее арифметическое этих десяти чисел.

Решение

 (6 * 3,5 + 4 * 2,25) : 2 = 3 - среднее арифметическое 10 чисел
Ответ: 3.

Задание 660

На первом участке пути поезд шёл 2 ч со скоростью 60 км/ч, а на втором он шёл 3 ч. С какой скоростью шёл поезд на втором участке, если его средняя скорость на двух участках была равна 51 км/ч?

Решение

Пусть скорость поезда на втором участке равна х,
тогда его средняя скорость равна
(60 * 2 + х * 3) : (2 + 3) км/ч.
Составим уравнение:
(60 * 2 + х * 3) : (2 + 3) = 51
120 + 3х = 51 * 5
х = (255 − 120) : 3
х = 45
Значит,  скорость поезда на втором участке 45 км/ч.
Ответ: 45 км/ч.

Задание 661

Скорость катера по течению 18,6 км/ч, а против течения 14,2 км/ч. Найдите собственную скорость катера и скорость течения.

Решение

Пусть скорость течения − x км/ч,
тогда скорость катера по течению (18,6 − x) км/ч,
а против течения (14,2 + x) км/ч.
Составим уравнение:
(18,6 − x) = (14,2 + x)
x = (18,6 − 14,2) : 2
х = 2,2
Значит, 2,2 км/ч − скорость течения
18,6 − 2,2 = 16,4 (км/ч) - собственная скорость катера
Ответ: 16,4 км/ч, 2,2 км/ч.

Задание 662

Одно число больше другого в 1,5 раза, среднее арифметическое этих двух чисел равно 30. Найдите эти числа.

Решение

Пусть одно число − х, тогда другое число − 1,5x.
Среднее арифметическое этих чисел равно (х + 1,5x) : 2.
Составим уравнение:
(x + 1,5x) : 2 = 30
2,5x = 30 * 2
x = 60 : 2,5
х = 24 − одно число
1,5 * 24 = 36 - другое число
Ответ: 24 и 36.

Задание 663

Вычислите устно:
а)
0,14 + 0,06;
2 − 0,7;
100 * 0,012;
0,42 : 7;
б)
3,18 − 1,08;
2,06 + 1,04;
5,4 * 0,1;
4,08 : 4;
в)
5,7 + 0,13;
2,85 − 1,5;
0,8 * 0,5;
0,5 : 2;
г)
0,4²;
0,3²;
0,05²;
0,01³.

Решение

а) 0,14 + 0,06 = 0,2
2 − 0,7 = 1,3
100 * 0,012 = 1,2
0,42 : 7 = 0,06

б) 3,18 − 1,08 = 2,1
2,06 + 1,04 = 3,1
5,4 * 0,1 = 0,54
4,08 : 4 = 1,02

в) 5,7 + 0,13 = 5,83
2,85 − 1,5 = 1,35
0,8 * 0,5 = 0,4
0,5 : 2 = 0,25

г) 0,4² = 0 , 16
0,3² = 0 , 09
0,05² = 0 , 0025
0,01³ = 0 , 000001

Задание 664

Выполните деление:
а) 40: 0,4;
б) 0,8 : 0,2;
в) 20 : 0,5;
г) 100 : 0,1;
д) 1000 : 0,01;
е) 6 : 0,3;
ж) 0,18 : 0,6;
з) 0,1 : 0,01;
и) 1 : 0,5.

Решение

а) 40 : 0,4 = 400 : 4 = 100

б) 0,8 : 0,2 = 8 : 2 = 4

в) 20 : 0,5 = 200 : 5 = 40

г) 100 : 0,1 = 1000

д) 1000 : 0,01 = 100000

e) 6 : 0,3 = 60 : 3 = 20

ж) 0,18 : 0,6 = 1,8 : 6 = 0,3

з) 0,1 : 0,01 = 10

и) 1 : 0,5 = 10 : 5 = 2

Задание 665

В летний лагерь детей отправляли на 6 одинаковых автобусах. В автобусах оказалось 29, 41, 28, 22, 27 и 33 человека. Можно ли было отъезжающих разместить в автобусах поровну?

Решение

29 + 41 + 28 + 22 + 27 + 33 = 180 (д.) - привезли всего
Так как 180 : 6 = 30, то следовательно, отъезжающих можно разместить на 6 автобусах по 30 человек в каждом.

Задание 666

Вы знаете, что:
0,1 = 1/10 0,125 = 1/8 0,25 = 1/4 0,2 = 1/5 0,5 = 1/2
Поэтому умножить число на 0,5 означает найти половину числа, умножить на 0,125 означает найти восьмую часть числа и т.д.
Подумайте как проще найти значение выражения:
а) 400 * 0,1;
б) 20 * 0,2;
в) 84 * 0,25;
г) 16 * 0,125;
д) 68 * 0,5.

Решение

а) 400 * 0,1 = 400 : 10 = 40

б) 20 * 0,2 = 20 : 10 • 2 = 4

в) 84 * 0,25 = 84 : 4 = 21

г) 16 * 0,125 = 16 : 8 = 2

д) 68 * 0,5 = 68 : 2 = 34

Задание 667

Может ли произведение двух чисел оказаться меньше одного из множителей? Меньше обоих множителей? Может ли частное оказаться больше делимого? Приведите примеры.

Решение

Произведение меньше одного из множителей: 0,1 * 10 = 1.
Произведение меньше каждого из множителей: 0,1 * 0,5 = 0,05.
Частное больше делимого: 1 : 0,1 = 10.

Задание 668

Мальчик решил определить длину моста через реку. Он заметил, что расстояние между двумя столбиками, на которых крепятся перила, равно двум шагам, а столбиков всего 30. Какова длина моста, если один шаг мальчика 0,4 м?

Решение

Между 30 столбиками находятся 29 промежутков, поэтому длина всего моста равна

2 * 0,4 * 29 = 0,8 * 29 = 23,2 (м) - длина моста
Ответ: 23,2 м.

Задание 669

Выполните деление:
а) 0,432 : 0,24;
б) 0,8625 : 0,375;
в) 1,872 : 2,34;
г) 0,481 : 0,037;
д) 41,48 : 34;
е) 127,2 : 159.

Решение

а) 0,432 : 0,24 = 43,2 : 24 = 1,8

б) 0,8625 : 0,375 = 862,5 : 375 = 2,3

в) 1,872 : 2,34 = 187,2 : 234 = 0,8

г) 0,481 : 0,037 = 481 : 37 = 13

д) 41,48 : 34 = 1,22

e) 127,2 : 159 = 0,8

Задание 670

Решите уравнение:
а) 3,5x − 2,3x + 3,8 = 4,28;
б) 4,7y − (2,5y + 12,4) = 1,9;
в) (8,3 − k) * 4,7 = 5,64;
г) (9,2 − m) * 3,2 = 16.

Решение

а) 3,5x − 2,3x + 3,8 = 4,28
1,2x = 4,28 − 3,8
x = 0,48 : 1,2
х = 0,4

б) 4,7у − (2,5y + 12,4) = 1,9
2,2y = 1,9 + 12,4
у = 14,3 : 2,2
у = 6,5

в) (8,3 − k) * 4,7 − 5,64
8,3 − k = 5,64 : 4,7
k = 8,3 − 1,2
k = 7,1

г) (9,2 − m) * 3,2 = 16
9,2 − m = 16 : 3,2
m = 9,2 − 5
m = 4,2

Задание 671

Школьная географическая площадка занимает 36 м². Это составляет 0,1 всего пришкольного участка. Найдите площадь пришкольного участка.

Решение

 36 : 0,1 = 360 (м²) - площадь пришкольного участка
Ответ: 360 м².

Задание 672

В 12 ч скорый поезд догнал пассажирский, а в 18 ч был уже впереди его на 120 км. Какое расстояние между поездами было в 10 ч, если скорость пассажирского поезда 70 км/ч? Какое данное в условии задачи лишнее?

Решение

1) 120 : (18 − 12) = 120 : 6 = 20 (км/ч) - скорость удаления скорого поезда от пассажирского
2) 20 * (12 − 10) = 20 * 2 = 40 (км) -  было в 10 ч между поездами
Ответ: 40 км.
Лишнее данное − значение скорости пассажирского поезда.

Задание 673

Длина стороны основания пирамиды Хеопса 230 м. Туристы, осматривая пирамиду, идут со скоростью 0,32 м/с. Успеют ли туристы за час обойти вокруг пирамиды?

Решение

Так как у пирамиды четыре стороны, то на обход пирамиды туристам потребуется
230 * 4 : 0,32 = 920 : 0,32 = 2875 с < 3600 с = 1 ч, то есть туристы успеют обойти вокруг пирамиды за 1 ч.

Задание 674

Заполните таблицу:

Решение

Задание 675

Вычислите:
1) (7 − 5,38) * 2,5;
2) (8 − 6,46) * 1,5.

Решение

1) (7 − 5,38) * 2,5 = 1,62 * 2,5 = 4,05

2) (8 − 6,46) * 1,5 = 1,54 * 1,5 = 2,31

Задание 676

В двоичной системе счисления при записи числа используют всего две цифры: 0 и 1. Число «один» записывается, как обычно, 1, но число «два» составляет уже единицу второго разряда и поэтому записывается так: 102 «одна двойка и нуль единиц* (цифра 2, находящаяся внизу в конце записи числа, означает, что число записано в двоичной системе). Число «три» изображается: 112 «одна двойка и одна единица». Число «четыре» представляет собой единицу следующего, третьего разряда и поэтому записывается так: 1002 «одна четвёрка, нуль двоек и нуль единиц». Таким образом, если в записи числа цифру 1 передвинуть влево на один разряд, то её значение увеличивается вдвое (а не в десять раз, как в нашей десятичной системе). Сравните представление числа, запись которого состоит из четырёх цифр 1, в виде суммы разрядных единиц в десятичной и двоичной системах:
1111 = 1 * 1000 + 1 * 100 + 1 * 10 + 1 = 1 * 10³ + 1 * 10² + 1 * 10 + 1;
1111 2 = 1 * 8 + 1 * 4 + 1 * 2 + 1 = 1 * 2³ + 1 * 2² + 1 * 2 + 1 = 15.

Решение

10 2 = 1 * 2 = 2;
100 2 = 1 * 2² = 4;
101 2 = 1 * 2² + 1 = 5;
110 2 = 1 * 2² + 1 * 2 = 6;
1110 2 = 1 * 2³ + 1 * 2² + 1 * 2 = 14;
1 = 1 2 , 2 = 10 2 , 3 = 11 2 , 4 = 100 2 , 5 = 101 2 , 6 = 110 2 , 7 = 111 2 , 8 = 1000 2 , 9 = 1001 2 , 10 = 1010 2 , 11 = 1011 2 , 12 = 1100 2 , 13 = 1101 2 , 14 = 1110 2 , 15 = 1111 2

Задание 677

Найдите среднее арифметическое чисел:
а) 32,15; 31,28; 29,16; 34,54 и округлите ответ до сотых;
б) 3,234; 3,452; 4,185; 2,892 и округлите ответ до тысячных.

Решение

а) (32,15 + 31,28 + 29,16 + 34,54) : 4 = 127,13 : 4 = 31,7825 ≈ 31,78

б) (3,234 + 3,452 + 4,185 + 2,892) : 4 = 13,763 : 4 = 3,44075 ≈ 3,441

Задание 678

Измерьте длину десяти своих шагов и найдите среднюю длину

Решение

(51 + 52 + 59 + 50 + 49 + 50 + 51 + 52 + 50 + 50) : 10 = 54 : 10 = 50,4 см.

Задание 679

Автомашина шла 3 ч со скоростью 53,5 км/ч, 2 ч со скоростью 62,3 км/ч и 4 ч со скоростью 48,2 км/ч. Найдите среднюю скорость движения автомашины на всём пути.

Решение

Средняя скорость движения автомашины
(53,5 * 3 + 62,3 * 2 + 48,2 * 4) : (3 + 2 + 4) = (160,5 + 124,6 + 192,8) : 9 = 477,9 : 9 = 53,1 км/ч.

Задание 680

Турист шёл 3,8 ч со скоростью 1,2 м/с, а затем 2,2 ч со скоростью 0,9 м/с. Какова средняя скорость движения туриста на всём пути?

Решение

(1,2 * 3,8 * 3600 + 0,9 * 0,2 * 3600) : (3,8 + 2,2) = (16416 + 7128) : 6 = 23544 : 6 = 3924 (м/ч)  - средняя скорость движения туриста
3924 м/ч = 3,924 км/ч
Ответ: 3,924 км/ч.

Задание 681

Среднее арифметическое двух чисел 4,6. Одно число 5,4. Найдите другое число.

Решение

Пусть х - неизвестное число.
Составим уравнение
(х + 5,4) : 2 = 4,6
х = 4,6 * 2 − 5,4
х = 3,8
Ответ: 3,8.

Задание 682

Среднее арифметическое двух чисел 4,4. Найдите эти числа, если одно из них на 1,4 больше другого.

Решение

Пусть 1 число - х, тогда второе (х + 1,4)
Составим уравнение:
(х + (х + 1,4)) : 2 = 4,4
2х + 1,4 = 4,4 * 2 
x = (8,8 − 1,4) : 2
х = 3,7
Значит, 3,7 − одно число
3,7 + 1,4 = 5,1 - другое число
Ответ: 3,7 и 5,1.

Задание 683

Среднее арифметическое трёх чисел 6. Найдите эти числа, если первое число в 2,5 раза больше, а второе в 1,5 раза больше третьего.

Решение

Пусть третье число равно х,
тогда первое число равно 2,5х,
а второе число равно 1,5x.
Составим уравнение:
(2,5х + 1,5х + х) : 3 = 6
5х = 6 * 3 
х = 18 : 5
х = 3,6 − третье число,
2,5 * 3,6 = 9 − первое число,
1,5 * 3,6 = 5,4 − второе число.
Ответ: 9; 5,4; 3,6 .

Задание 684

За 7 ч тракторист вспахал 4,9 га. С какой скоростью двигался трактор, если ширина полосы, вспахиваемая плугами, равна 1,75 м?

Решение

    4,9 га = 49000 м²
1) 49000 : 1,75 = 28000 (м)  - длина полосы, вспаханная трактористом
    28000 м = 28 км
2)  28 : 7 = 4 (км/ч) -  скорость движения трактора
Ответ: 4 км/ч.

Задание 685

Для приготовления салата из зелёного лука берут 150 г зелёного лука и 30 г сметаны. Сколько сметаны потребуется повару, чтобы приготовить салат из 27 кг зелёного лука?

Решение

 (27000 : 150) * 30 = 180 * 30 = 5400 (г) -  сметаны потребуется для приготовления салата.
5400 г = 5,4 кг
Ответ: 5,4 кг сметаны.

Задание 686

Каждый год растительный мир даёт 117 млрд т прироста массы. Каждые 3 т этой массы дают столько же энергии, сколько 1 т нефти. Сколько тонн нефти может заменить прирост массы растений за 4 года?

Решение

За 4 года прирост массы растений составит
117 млрд. т * 4 = 468 млрд.т, что заменяет 468 млрд.т : 3 = 156 млрд.т нефти.

Задание 687

Найдите значение выражения:
а) 3,4x + 5,7x + 6,6x − 4,7x при x = 3,6; 0,8; 10;
б) 3,8m − (2,8m + 0,7m) при m = 2,4; 8,57;
в) 16,75y − (4,75y + 10,8) при у = 0,9; 3,01.

Решение

а) 3,4x + 5,7x + 6,6x − 4,7x = (3,4x + 6,6х) + (5,7x − 4,7x) = 10х + x = 11x
При x = 3,6
11x = 11 * 3,6 = 39,6
При x = 0,8
11х = 11 * 0,8 = 8,8
При x = 10
11х = 11 * 10 = 110

б) 3,8m − (2,8m + 0,7m) = 3,8m − 2,8m − 0,7m = m − 0,7m = 0,3m
При m = 2,4
0,3m = 0,3 * 2,4 = 0,72
При m = 8,57
0,3m = 0,3 * 8,57 = 2,571

в) 16,75y − (4,75y + 10,8) = 16,75y − 4,75y − 10,8 = 12y − 10,8
При у = 0,9
12у − 10,8 = 12 * 0,9 − 10,8 = 10,8 − 10,8 = 0
При у = 3,01
12y − 10,8 − 12 * 3,01 − 10,8 = 36,12 − 10,8 − 25,32

Задание 688

Выполните действия:
а) 42,165 − 22,165 : (0,61 + 3,42);
б) 243,08 + 256,32 : (28 − 25,5).

Решение

а) 42,165 − 22,165 : (0,61 + 3,42) = 42,165 − 22,165 : 4,03 = 42,165 − 5,5 = 36,665

б) 243,08 + 256,32 : (28−25,5) = 243,08 + 256,32 : 2,5 = 243,08 + 102,528 = 345,608

123-124 Задания для самопроверки

Страницы 123-124 Задания для самопроверки

№1

Р = 5 * а
5 * 4,44 = 22,2 (см) - периметр пятиугольника
Ответ: 22,2 см

№2

А 3
Б 4
В 1
Г 3

№3

1; 3; 2; 5, 4

№4

1) 60 * 1,5 = 90 (км) - автомобиль проехал со скорость 60 км/ч
2) 75, 2 * 3 = 225,6 (км) - автомобиль проехал со скоростью 75,2 км/ч
3) 90 + 225,6 = 315,6 (км) - проехал автомобиль
Ответ: 315,6 км.

№5

1) 1 – 5/8 = 8/8 – 5/8 = 3/8 -  часть дороги которую необходимо отремонтировать
2) 49,6 * 3/8 = 49,6 * 0,375 = 18,6 (км) - осталось отремонтировать
Ответ: 18,6 км.

№6

175,5 : 2,5 = 70,2 (км/ч) - скорость поезда
Ответ: 70,2 (км/ч

№7

63, 705 : 0,01 = 6370,5

№8

а) 5х – х = 88,6
4х = 88,6
х = 88,6 : 4
х = 22,15

б) n + n – 2,7 = 42,34
2n – 2,7 = 42,34
2n = 42,34 + 2,7
2n = 45,04
n = 45,04 : 2
n = 22,52

в) (26,7 – х) * 0,5 = 8,35
26,7 – х = 8,35 : 0,5
26,7 – х = 16,7
х = 26,7 – 16,7
х = 10

г) 2,4у – 20 = 4,24
2,4у = 4,24 + 20
2,4у = 24,24
у = 24,24 : 2,4
у = 10,1

Ответ: А 3, Б 1, В 2, Г 4.

№9

S = a * b
7,2 * 5 = 36 (см²) - площадь одного прямоугольника
36 : 6 = 6 (см²) - площадь второго прямоугольника
6 = 1,5 * b
b = 6 : 1,5 =4 (см) - длина второго прямоугольника
Ответ: 4 см

№10

1 кг = 1000 г
1) 4500 : 3 = 1500 (г) - сахара
2) 1500 * 2 = 3000 (г) - ягод
3000 г = 3 кг
1500 г = 1,5 кг
Ответ: 1,5 кг сахара.

126 - 156

Параграф 8. Инструменты для вычислений и измерений

Пункт 39. Микрокалькулятор

Задание 689

Прочитайте показание на индикаторе (рис. 157):

Решение

Две тысячи пятьсот четыре целых одна тысяча семьсот тридцать четыре десятитысячных.

Задание 690

Введите в микрокалькулятор числа:
20 000; 45 897; 3,9045; 0,000761.

После введения каждого числа не забывайте сбрасывать предыдущее число.

Задание 691

Выполните с помощью микрокалькулятора действия:
а)
39,614 + 89,213;
560,98 + 1039,71;
0,0876 + 0,0876;
0,0876 + 0,91469;
24714395 + 39623008;
б)
98,542 − 67,413;
714,932 − 521,081;
0,09854 − 0,05421;
76539086 − 22612007;
в)
24,15 * 39,52;
1,987 * 2,608;
0,5637 * 0,451;
0,0567 * 2,371;
г)
18,324169 : 3,427;
621,83538 : 24,501;
673074,72 : 941,1.

Решение

а) 39,614 + 89,213 = 128,827
560,98 + 1039,71 = 1600,69
0,0876 + 0,0876 = 0,1752
0,0876 + 0,91469 = 1,00229
24174395 + 39623008 = 63797403

б) 98,542 − 67,413 = 31,129
714,932 − 521,081 = 193,851
0,09854 − 0,05421 = 0,04433
76539086 − 22612007 = 53927079

в) 24,15 * 39,52 = 954,408
1,987 * 2,608 = 5,182096
0,5637 * 0,451 = 0,2542287
0,0567 * 2,371 = 0,1333257

г) 18,324169 : 3,427 = 5,347
621,83538 : 24,501 = 25,38
673074,72 : 941,1 = 715,2

Задание 692

Выполните письменно, а потом проверьте ответ с помощью микрокалькулятора:
а) 45,614 + 20,542;
б) 510,78 − 248,81;
в) 76,2 * 2,45;
г) 821,1 : 34,5.

Решение

а) + 45.614
       20.542
       66.156

б) - 510.78
      248.81
      261.97

в) × 76,2
       2,45
      3810
    3048
  1524     
 186,690

г) 821,1 : 34,5 = 8211 : 345
_8211 |345
  690   |23,8
_1311
  1035
  _2760
    2760
          0

Задание 693

С помощью микрокалькулятора найдите значение выражения:
а) 412,89 + 306,24 − 678,59;
б) 8,508 + 9,439 − 2,524;
в) 0,769 * 5,142 * 3,71;
г) 9,725 * 1,06 : 3,89;
д) 24,78 * 51,8 + 248,713;
е) 871,017 : 5,05 − 11,376;
ж) (280,65 + 317,25) * 4,24;
з) (953,54 − 396,41): 75,8 * 4,12.

Решение

а) 412,89 + 306,24 − 678,59 = 719,13 − 678,59 = 40,54

б) 8,508 + 9,439 − 2,524 = 17,947 − 2,524 = 15,423

в) 0,769 * 5,142 * 3,71 = 3,954198 * 3,71 = 14,67007458

г) 9,725 * 1,06 : 3,89 = 10,3085 : 3,89 = 2,65

д) 24,78 * 51,8 + 248,713 = 1283,604 + 248,713 = 1532,317

e) 871,017 : 5,05 − 11,376 = 161,786 − 11,376 = 150,410

ж) (280,65 + 317,25) * 4,24 = 597,9 * 4,24 = 2535,096

з) (953,54 − 396,41) : 75,8 * 4,12 = 557,13 : 75,8 * 4,12 = 7,35 * 4,12 = 30,282

Задание 694

Вычислите устно:
а) 7 + 0,2
: 9
* 3
+ 0,6
?
б) 10,9 - 1
: 3
+ 2,7
: 4
?
в) 6 - 2,4
: 6
+ 0,4
: 2
?
г) 40 * 0,4
: 10
+ 0,5
: 7
?

Решение

а) 7,9, 0,8, 2,4, 3.

б) 9,9, 3,3, 6, 1,5.

в) 3,6, 0,6, 1, 0,5.

г) 16, 1,6, 2,1, 0,3.

Задание 695

Выполните деление:
а) 2/5;
6) 1/20;

в) 1/25;
г) 1/4;
д) 18/10;
е) 1 : 2 = 0,5;
ж) 3 : 15 = 0,2;
з) 5 : 0,2 = 25;
и) 1 : 0,01 = 100;
к) 0,8 : 0,04 = 20;
л) 1 : 0,25 = 4;
м) 1 : 1,25 = 0,8.

Решение

а)
_2 |5   
  0 |0,4
_20
  20
    0

б)
_1 |20   
  0 |0.05
_10
    0
_100
  100
      0

в)
_1 |25    
  0 |0.04
_10
    0
_100
  100
      0

г)
_1 |4     
  0 |0.25
_10
    8
  _20
    20
      0

д)
_18 |10  
  10 |1.8
  _80
    80
      0

е)
_1 |2   
  0 |0,5
_10
  10
    0

ж) 
_3 |15
  0 |0,2
_30
  30
    2

з) 5 : 0,2 = 50 : 2 =25

и) 1 : 0,01 = 100 : 1 = 100

к) 0,8 : 0,04 = 80 : 4 = 20

л) 1 : 0,25 = 100 : 25 = 4

м) 1 : 1,25 = 100 : 125 = 0,8
_100 |125
      0 |0,8
_1000
  1000
        0

Задание 696

Найдите:
а) 0,01 числа 50;
б) 0,07 числа 300;
в) 0,6 числа 40;
г) 0,25 числа 36.

Решение

а) 50 * 0,01 = 0,5

б) 300 * 0,07 = 21

в) 40 * 0,6 = 24

г) 36 * 0,25 = 9

Задание 697

Каким одним действием можно:
а) уменьшить число в 10 раз; в 100 раз?
б) увеличить число в 100 раз; в 1000 раз?
Приведите примеры.

Решение

а) при делении на 10, 100

б) при умножении на 100, 1000

Задание 698

На первом участке пути автомобиль двигался 3 ч со скоростью 40 км/ч, а на втором − 1 ч со скоростью 60 км/ч. Какова средняя скорость автомобиля на всём пути?

Решение

Средняя скорость движения автомобиля равна (40 * 3 + 60 * 1) : (3 + 1) = (120 + 60) : 4 = 180 : 4 = 45 км/ч.

Задание 699

Составьте задачу по числовому выражению:
а) (2,6 + 2,8) : 2;
б) (3,8 + 3,7 + 3,6) : 3.

Решение

а) Турист до обеда шел со скоростью 2,6 км/ч, а после обеда 2,8 км/ч. С какой средней скоростью прошел маршрут турист?

(2,6 + 2,8) : 2 = 5,4 : 2 = 2,7 (км/ч) - средняя скорость туриста.
Ответ: 2,7 км/ч.

б) Три грибника собирали грибы. Первый собрал 3,8 кг, второй 3,7 кг, а третий 3,6 кг. Сколько грибов будет у каждого грибника, если они решили что разделят все собранные грибы поровну?

(3,8 + 3,7 + 3,6) : 3 = 11,1 : 3 = 3,7 (кг) - грибов будет у каждого грибника.
Ответ: 3,7 кг.

Задание 700

Найдите четвёртое число в последовательности:
а) 2; 4; 16; ?;
б) 3; 9; 81;?;
в) 6; 3; 1,5; ?;
г) 0,1; 0,5; 2,5; ?.

Решение

а) Каждое следующее число равно квадрату предыдущего: 2; 4; 16; 256.

б) Каждое следующее число равно квадрату предыдущего: 3; 9; 81; 6561.

в) Каждое следующее число равно половине предыдущего: 6; 3; 1,5; 0,75.

г) Каждое следующее число в 5 раз больше предыдущего: 0,1; 0,5; 2,5; 12,5.

Задание 701

Найдите среднее арифметическое чисел:
а) 81,242; 65,312; 412,54; 94,376;
б) 71,3; 25,7; 39,8; 12,9; 56,4.

Решение

а) (81,242 + 65,312 + 412,54 + 94,376) : 4 = 653,47 : 4 = 163,3675

б) (71,3 + 25,7 + 39,8 + 12,9 + 56,4) : 5 = 206,1 : 5 = 41,22

Задание 702

Теплоход прошёл 70 км по реке за 2 ч и 90 км по озеру за 3 ч. С какой средней скоростью прошёл теплоход весь путь?

Решение

Теплоход прошёл весь путь со средней скоростью (70 + 90) : (2 + 3) = 160 : 5 = 32 км/ч.

Задание 703

Овощевод−опытник снял с одного куста помидоров 12 плодов по 250 г, 10 плодов по 330 г и 8 плодов по 210 г. Найдите среднюю массу одного помидора.

Решение

(250 * 12 + 330 * 10 + 210 * 8) : (12 + 10 + 8) = (3000 + 3300 + 1680) : 30 = 7980 : 30 = 266 (г) - средняя масса одного помидора
Ответ: 266 г.

Задание 704

Среднее арифметическое четырёх чисел 6,7. Первое равно 2, второе в 1,2 раза больше первого, а третье меньше четвёртого в 1,5 раза. Найдите третье и четвёртое числа.

Решение

Пусть третье число равно x.
Составим уравнение:
(2 + (1,2 * 2) + 1,5x + х) : 4 = 6,7
4,4 + 2,5х = 6,7 * 4
х = (26,8 − 4,4) : 2,5
х = 8,96 − третье число,
1,5 * 8,96 = 13,44 − четвёртое число.
Ответ: 8,96 и 13,44.

Задание 705

Пассажирский поезд прошёл путь от одной станции до другой со средней скоростью 67 км/ч. Вначале он шёл 4 ч со скоростью 59,5 км/ч, а затем увеличил скорость и прибыл на вторую станцию через 3 ч. Найдите скорость поезда на втором участке пути.

Решение

Пусть х − скорость поезда на втором участке пути,
тогда средняя скорость поезда на всем пути равна
(59,5 * 4 + х * 3) : (4 + 3) км/ч.
Составим уравнение:
(59,5 * 4 + х * 3) : (4 + 3) 
                      469
238 + 3х = 67 * 7 
х = (469 − 238) : 3
х = 231 : 3
х = 77
Значит,  скорость поезда на втором участке пути 77 км/ч.
Ответ: 77 км/ч.

Задание 706

Серёжа стал на велосипеде догонять Наташу, идущую пешком, когда между ними было 600 м, и догнал её через 4 мин. Найдите скорость, с которой шла Наташа, если её скорость в 4 раза меньше скорости Серёжи.

Решение

Пусть х м/мин − скорость Наташи,
тогда скорость Сережи 4х м/мин.
Составим уравнение:
600 : (4х − х) = 4
3х = 600 : 4 
х = 150 : 3
х = 50
Значит, скорость Наташи 50 м/мин.
Ответ: 50 м/мин.

Задание 707

С двух грядок, общая площадь которых 40,5 м², получили 137,7 кг моркови. Сколько килограммов моркови собрали с каждой грядки, если площадь одной из них на 4,5 м² меньше, чем площадь другой, а урожайность одинакова?

Решение

Пусть площадь одной грядки − х м²,
тогда (х + 4,5) м² − площадь другой грядки.
Составим уравнение:
х + х + 4,5 = 40,5
2х = 40,5 − 4,5 − 36
х = 36 : 2
х = 18
Значит, 18 м² − площадь одной грядки,
18х + 4,5 = 22,5 (м²) − площадь другой грядки.
137,7 : 40,5 = 3,4 (кг/м²) - урожайность моркови
18 * 3,4 = 61,2 (кг) - моркови получили с первой грядки
22,5 * 3,4 = 76,5 (кг) - моркови получили со второй грядки
Ответ: 61,2 кг,  76,5 кг.

Задание 708

Запишите в виде равенства предложение:
а) 5n на 8,11 больше n;
б) утроенное а на 5,18 больше а;
в) разность m и 9,11 в 4 раза меньше их суммы.

Решение

а) 5n − n = 8,11

б) 3а − а = 5,18

в) (m + 9,11) : (m − 9,11) = 4

Задание 709

С помощью микрокалькулятора вычислите значение выражения:
а) 78,627 + 3,081;
б) 735,24 − 261,87;
в) 41,65 * 85,38;
г) 62,14 : 9,241;
д) 508,3 + 891,4 : 35,4;
е) 92,5 * 11,6 − 429,15.

Решение

а) 78,627 + 3,081 = 81,708

б) 735,24 − 261,87 = 473,37

в) 41,65 − 85,38 = 3556,077

г) 62,14 : 9,241 = 6,7243804

д) 508,3 + 891,4 : 35,4 = 508,3 + 25,181 = 533,481

e) 92,5 * 11,6 − 429,15 = 1073 − 429,15 = 643,85

Задание 710

Найдите с помощью микрокалькулятора объём прямоугольного параллелепипеда по формуле V = abc, если:
a = 2,81 дм; b = 1,76 дм; с = 4,9 дм; ответ округлите до сотых.

Решение

При a = 2,81 дм, b = 1,76 дм и с = 4,9 дм:
V = a b с = 2,81 * 1,76 * 4,9 = 24,23344 (дм³)
24,23344 дм³ ≈ 24,23 дм³.
Ответ: 24,23 дм³.

Задание 711

Два поезда одновременно вышли навстречу друг другу из двух городов, расстояние между которыми 495 км. Через 3 ч они встретились. Какова скорость каждого поезда, если известно, что скорость одного из них на 5 км/ч больше скорости другого?

Решение

Пусть х км/ч скорость одного поезда,
тогда (х + 5) км/ч скорость другого поезда.
Скорость сближения поездов равна (х + х + 5) км/ч,
поезда встретились через 495 : (х + х + 5) ч.
Составим уравнение:
495 : (х + х + 5) = 3
2х + 5 = 495 : 3
х = (165 − 5) : 2
х = 80
Значит, 80 км/ч − скорость одного поезда равна
80 + 5 = 85 (км/ч) - скорость другого поезда
Ответ: 80 км/ч и 85 км/ч.

Задание 712

Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков, расстояние между которыми 76 км. Через 2 ч они встретились. Какова скорость каждого велосипедиста, если известно, что скорость одного из них в 1,5 раза больше скорости другого?

Решение

Пусть х − скорость одного велосипедиста,
тогда 1,5x − скорость другого велосипедиста.
Велосипедисты встретились через 76 : (x + 1,5x) ч.
Составим уравнение:
76 : (у + 1,5y) = 2
2,5у = 76 : 2
у = 38 : 2,5
у = 15,2
Значит, 15,2 км/ч − скорость одного велосипедиста
1,5 * 15,2 = 22,8 (км/ч) - скорость другого велосипедиста
Ответ: 15,2 км/ч, 22,8 км/ч.

Задание 713

Выполните действия и проверьте ответ с помощью микрокалькулятора:
((4 : 0,128 + 14 628,25) : 1,011 * 0,00008 + 6,84) : 12,5.

Решение

((4 : 0,128 + 14628,25) : 1,011 * 0,00008 + 6,84) : 12,5 = (14500 − 0,00008 + 6,84) : 12,5 = 8 : 12,5 = 0,64.

 

Пункт 40. Проценты

Задание 714

Запишите в виде десятичной дроби:
1%; 6%; 45%; 123%; 2,5%; 0,4%.

Решение

1% = 1 * 0,01 = 0,01
6% = 6 * 0,01 = 0,06
45% = 45 * 0,01 = 0,45
123% = 123 * 0,01 = 1,23
2,5% = 2,5 * 0,01 = 0,025
0,4% = 0,4 * 0,01 = 0,004

Задание 715

Запишите в процентах десятичные дроби: 0,87; 0,07; 1,45; 0,035; 2,672; 0,907.

Решение

0,87 = 0,87 * 100% = 87%
0,07 = 0,07 * 100% = 7%
1,45 * 100% = 145%
0,035 * 100% = 3,5%
2,672 = 2,672 * 100% = 267,2%
0,907 = 0,907 * 100% = 90,7%

Задание 716

Запишите обыкновенные дроби 1/2 ; 1/4 ; 3/4 ; 2/5 ; 17/50 в виде десятичных, а потом в виде процентов.

Решение

1/2 = 0,5 = 0,5 * 100% = 50%
1/4 = 0,25 = 0,25 * 100% = 25%
3/4 = 0,75 = 0,75 * 100% = 75%
2/5 = 0,4 = 0,4 * 100% = 40%
17/50 = 0,34 = 0,34 * 100% = 34%

Задание 717

Заполните таблицу:

Решение

Задание 718

В школьной библиотеке 7000 книг. Маша прочитала одну сотую всех этих книг. Сколько библиотечных книг прочитала Маша?
Серёжа прочитал 1% всех книг школьной библиотеки. Сравните число библиотечных книг, прочитанных Машей и Серёжей.

Решение

1/100 это и есть 1%, значит Маша и Миша прочитали одинаковое количество книг.
Проверим:
1) 7000 * 0,01 = 70 (к.) - прочитала Маша
2) 7000 : 100 * 1 = 70 (к.) - прочитал Серёжа
Ответ: по 70 книг прочитали Маша, Серёжа.

Задание 719

В палатку завезли 850 кг огурцов. Первый покупатель взял для соления 1% всех огурцов, а второй − 3% всех огурцов. Сколько килограммов огурцов купил каждый из них?

Решение

850 - 100%
    ? - 1%
1) 850 : 100 * 1 = 8,5 (кг) - огурцов купил первый покупатель
850 - 100%
    ? - 3%
2) 850 : 100 * 3 = 8,5 * 3 = 25,5 (кг) - огурцов купил второй покупатель
Ответ: 8,5 кг и 25,5 кг.

Именно таким способом разобрано решение задач на проценты в учебнике Виленкина. Но можно их решить другим способом - переводя проценты в десятичную дробь. Ваш учитель может потребовать от вас решение обеими способами, поэтому, на примере данной задачи раберем и второй. 

    1 % = 0,01
1) 850 * 0,01 = 8,5 (кг) - огурцов купил первый покупатель
    3% = 0,03
2) 850 * 0,03 = 8,5 * 3 = 25,5 (кг) - огурцов купил второй покупатель
Ответ: 8,5 кг и 25,5 кг.

Напишите нам в комментариях, каким способом решаете задачи на проценты вы: находя сначала 1% делением на 100 или через перевод процентов в дроби?

Задание 720

На поле, площадь которого 620 га, работали хлопкоуборочные машины. За сутки они убрали 15% всего поля. Сколько гектаров хлопка убрали за сутки?

Решение

620 га - 100%
       ? - 15%
620 : 100 * 15 = 93 (га) - хлопка убрали за сутки
Ответ: 93 га.

Задание 721

Бригаде поручили отремонтировать участок дороги длиной 760 м. Сколько метров дороги бригада отремонтирует, когда выполнит: 30% задания; 50% задания; 10% задания?

Решение

1) 760 : 100 = 7,6 (м) - 1%
2) 7,6 * 30 = 228 (м) - дороги отремонтируют, когда выполнят 30% задания
3) 7,6 * 50 = 380 (м) - дороги отремонтируют, когда выполнят 50% задания
4) 7,6 * 10 = 76  (м) - дороги отремонтируют, когда выполнят 10% задания
Ответ: 228 м, 380 м, 76 м. 

Задание 722

Предприятие изготовило за квартал 500 насосов, из которых 60% имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?

Решение

500 : 100 * 60 = 5 • 60 = 300 (н.) - высшей категории качества изготовило предприятие.
Ответ: 300 насосов.

Задание 723

В плодовом саду собирали яблоки. За день было собрано 4840 кг. 25% собранных яблок отправили в магазин, а остальные − на склад. Сколько килограммов яблок отправили на склад?

Решение

1) 100% − 25% = 75% собранных яблок отправили на склад,
2) 4840 : 100 * 75 = 48,4 * 75 = 3630 (кг) - яблок отправили на склад
Ответ: 3630 кг.

Задание 724

Себестоимость изготовления одной детали равна 650 р. Внедрение новой технологии позволило снизить себестоимость детали на 2%. Какова стала себестоимость такой детали?

Решение

1) 100% − 2% = 98% от прежней себестоимости составила новая себестоимость детали,
2) 650 : 100 * 98 = 6,5 * 98 = 637 (р.) - стала себестоимость детали
Ответ: 637 рублей.

Задание 725

Поле на рисунке 158 разбито на 100 долей. Закрашенная на рисунке часть засеяна горохом. Найдите площадь всего поля, если горохом засеяно 24,8 га.

Решение

Горохом засеяно 8% всего поля, что соответствует 24,8 га.
24,8 : 8 * 100 = 3,1 * 100 = 310 (га) - площадь всего поля
Ответ: 310 га.

Задание 726

Сколько человек было в кино, если 1% всех зрителей составляет 7 человек?

Решение

7 : 0,01 = 7 * 100 = 700 (ч.) - было в кино
Ответ: 700 человек.

Задание 727

Мотоциклист за день проехал некоторое расстояние. 1% пути он ехал по просёлочной дороге, что составило 3,2 км. Какое расстояние проехал мотоциклист за день?

Решение

3,2 : 0,01 = 3,2 * 100 = 320 (км) - проехал мотоциклист за день
Ответ: 320 км.

Задание 728

Двор разбит на 100 равных частей. Часть площади двора, закрашенная на рисунке 159, отведена под стоянку машин. Найдите площадь двора, если стоянка занимает 146,4 м².

Решение

Стоянка машин занимает 4% от площади двора, что соответствует 146,4 м².
146,4 : 4 * 100 = 36,6 * 100 = 3660 (м²) - площадь двора
Ответ: 3660 м².

Задание 729

Ученик прочитал 138 страниц, что составляет 23% числа всех страниц в книге. Сколько страниц в книге?

Решение

138 : 23 * 100 = 6 * 100 = 600 (с.) - в книге
Ответ: 600 страниц.

Задание 730

Масса медвежонка составляет 15% массы белого медведя. Найдите массу белого медведя, если масса медвежонка 120 кг.

Решение

120 : 15 * 100 = 8 * 100 = 800 (кг) - масса белого медведя
Ответ: 800 кг.

Задание 731

Сливочное мороженое содержит 14% сахара. На приготовление мороженого израсходовали 35 кг сахара. Сколько сделали порций мороженого, если в каждой порции 100 г?

Решение

1) 35 : 14 * 100 = 2,5 * 100 = 250 кг - мороженого получили из 35 кг сахара 
250 кг = 250000 (г)
2) 250000 : 100 = 2500 (п.) - мороженого получили
Ответ: 2500 порций.

Задание 732

Применяя интенсивную технологию, бригада изготовила сверх плана 250 деталей, перевыполнив тем самым план на 5% . Сколько деталей изготовила бригада?

Решение

1) 250 : 5 * 100 = 50 * 100 = 5000 (д.) - должна была изготовить бригада по плану
2) 5000 + 250 = 5250 (д.) - всего изготовила бригада
Ответ: 5250 деталей.

Задание 733

В школе 700 учащихся. Среди них 357 мальчиков. Сколько процентов учащихся этой школы составляют мальчики?

Решение

357 : 700 = 0,51 часть всех учащихся составляют мальчики
0,51 = 51%
Ответ: 51%.

Задание 734

Фрекен Бок испекла 80 пирожков, и Карлсон тут же съел 10 пирожков. Сколько процентов всех пирожков съел Карлсон?

Решение

10 : 80 = 0,125 часть всех пирожков съел Карлсон
0,125 = 12,5%
Ответ: 12,5%.

Задание 735

В механическом цехе установлено 350 станков, из которых 35 находятся в ремонте. Сколько процентов станков находятся в действующем состоянии?

Решение

1) 350 − 35 = 315 (с.) - находится в действующем состоянии
2) 315 : 350 = 0,9 всех станков находится в действующем состоянии
0,9 = 90%
Ответ: 90%.

Задание 736

При плане 35 деталей в день рабочий сделал 42 детали. На сколько процентов он выполнил норму? На сколько процентов он перевыполнил норму?

Решение

1) 42 : 35 = 1,2 часть всего плана выполнил рабочий
    1,2 = 120%
2) 120% − 100% = 20% - на столько рабочий перевыполнил норму
Ответ: на 20%.

Задание 737

Сколько процентов соли содержит раствор, приготовленный из 35 г соли и 165 г воды?

Решение

1) 35 + 165 = 200 (г) - масса раствора
2) 35 : 200 = 0,175 всего раствора занимает соль
0,175 = 17,5%
Ответ: 17,5%.

Задание 738

В 4−А классе 40 учеников. С задачей справились 32 ученика. В 4−Б классе 35 учеников, а с задачей справились 28 учеников. Какой класс лучше справился с задачей?

Решение

1) 32 : 40 = 0,8 от всех учеников справились  с задачей в 4А
     0,8 = 80%
2) 28 : 35 = 0,8 от всех учеников справились с задачей в 4Б
    0,8 = 80%
Ответ: оба класса одинаково хорошо справились с задачей.

Задание 739

Найдите 0,3 числа:
а) 150;
б) 600;
в) 100;
г) 5.

Решение

а) 150 * 0,3 = 45

б) 600 * 0,3 = 180

в) 100 * 0,3 = 30

г) 5 * 0,3 = 1,5

Задание 740

Вычислите устно:
а) 1,45 + 0,15
* 4
+ 0,8
: 0,8
?
б) 9,8 - 5,9
: 1,3
+ 1,8
* 2
?
в) 30 * 0,01
+ 2,4
: 0,9
: 0,1
?
г) 0,2 * 50
: 2,5
+ 0,8
* 5
?
д) 8 * 0,2
: 0,8
- 0,6
* 5
?

Решение

а) 1,6, 6,4, 7,2, 9.

б) 3,9, 3, 4,8, 9,6.

в) 0,3, 2,7, 3, 30.

г) 10, 4, 4,8, 24.

д) 1,6, 2, 1,4, 7.

Задание 741

Представьте в виде десятичной дроби 3 1/2 ; 1 1/4 ; 2 1/5 ; 7 1/20 ; 9 1/25.

Решение

3 1/2 = 3,5
1 1/4 = 1,25
2 1/5 = 2,2
7 1/20 = 7,05
9 1/25 = 9,04

Задание 742

Восстановите цепочки вычислений и попробуйте объяснить, почему они приводят к одному ответу:

Решение

50 → 0,5 → 0,1 → 1
50 → 0,5 → 0,1 → 1
Деление производится на обратное умножению число.

Задание 743

Собственная скорость катера 18 км/ч. Отметьте её на координатном луче. Вычислите и отметьте на этом луче скорости катера против течения и по течению, если скорость течения 1,5 км/ч. Используя чертёж, подумайте:
а) как найти собственную скорость катера, если известны его скорости по течению и против течения;
б) как найти скорость катера против течения, если известны скорость течения и скорость катера по течению;
в) на сколько скорость катера по течению больше его скорости против течения?

Решение

а) При известных скоростях катера по течению и против собственная скорость катера равна среднему арифметическому этих скоростей.

б) При известной скорости катера по течению и скорости течения скорость против течения равна разности скорости по течению и удвоенной скорости течения.

в) Скорость катера по течению больше скорости против течения на величину удвоенной скорости течения.

Задание 744

Попробуйте представить правило нахождения среднего арифметического нескольких чисел и средней скорости в виде последовательности команд по схемам:...

Решение

Чтобы найти среднее арифметическое нескольких чисел, нужно:
1) найти сумму этих чисел;
2) найти число этих чисел;
3) разделить сумму чисел на их число.
Чтобы найти среднюю скорость, нужно:
1) найти пройденный путь;
2) найти общее время движения;
3) разделить пройденный путь на время движения.

Задание 745

Найдите значение выражения:
а) 2,0928 + 47,9072 : (7 − 0,195);
б) 100,5876 − 88,5856 : (6,0811 + 8,4889);
в) 687,8 + (88,0802 − 85,3712) : 0,045.
Проверьте ответ с помощью микрокалькулятора.

Решение

а) 2,0928 + 47,9072 : (7 − 0,195) = 2,0928 + 47,9072 : 6,805 = 2,0928 + 7,04 = 9,1328

б) 100,5876 − 88,5856 : (6,0811 + 8,4889) = 100,5876 − 88,5856 : 14,57 = 100,5867 − 6,08 = 94,5076

в) 687,8 + (88,0802 − 85,3712) : 0,045 = 687,8 + 2,709 : 0,045 = 687,8 + 60,2 = 748

Задание 746

Автобус шёл 3 ч по шоссе, 1,5 ч по грунтовой дороге и 0,5 ч по просёлочной дороге. Известно, что скорость автобуса по грунтовой дороге была в 2 раза больше скорости по просёлочной дороге, а скорость по шоссе в 3,5 раза больше скорости по просёлочной дороге. Найдите скорость движения автобуса по просёлочной дороге, если средняя скорость автобуса на всём пути 33,6 км/ч.

Решение

Пусть скорость автобуса по проселочной дороге − х км/ч ,
тогда его скорость по грунтовой дороге − 2х км/ч,
а скорость автобуса по шоссе − 3,5х км/ч.
Средняя скорость автобуса на всем маршруте равна:
(3,5х − 3 + 2x1,5 + х − 0,5) : (3 + 1,5 + 0,5) км/ч.
Составим уравнение:
(3,5х − 3 + 2x1,5 + х − 0,5) : (3 + 1,5 + 0,5) = 33,6
10,5х + 3х + 0,5х = 33,6 − 5 
14х = 168
х = 168 : 14
х = 12
Значит, скорость движения автобуса по просёлочной дороге 12 км/ч.
Ответ: 12 км/ч.

Задание 747

Марина сварила варенье, истратив 5/8 имевшегося у неё сахара. Сколько сахара осталось у Марины, если на варенье она израсходовала 0,8 кг сахара?

Решение

1) 0,8 : 5 * 8 = 0,16 * 8 = 1,28 (кг) - сахара было у Марины всего
2) 1,28 − 0,8 = 0,48 (кг) - сахараосталось
Ответ: 0,48 кг.

Задание 748

В куске было 112,2 м материи. В первый раз отрезали 3/17 куска, а во второй раз 7/17 куска. Сколько метров материи было отрезано за оба раза?

Решение

1) 3/17 + 7/17 = 10/17 куска материи было отрезано за оба раза
2) 112,2 : 17 * 10 = 6,6 * 10 = 66 (м) - материи было отрезано за оба раза
Ответ: 66 м.

Задание 749

Выполните действия:
1) (3,1 * 5,3 − 14,39) : 1,7 + 0,8;
2) (21,98 − 4,2 * 4,6) : 1,9 + 0,6.

Решение

1) (3,1 * 5,3 − 14,39) : 1,7 + 0,8 = (16,43 − 14,39) : 1,7 + 0,8 = 2,04 : 1,7 + 0,8 = 1,2 + 0,8 = 2

2) (21,98 − 4,2 * 4,6) : 1,9 + 0,6 = (21,98 − 19,32) : 1,9 + 0,6 = 2,66 : 1,9 + 0,6 = 1,4 + 0,6 = 2

Задание 750

Решите задачу:
1) Первое число в 2,4 раза больше третьего, а второе число на 0,6 больше третьего числа. Найдите эти три числа, если их среднее арифметическое равно 2,4.
2) Второе число на 0,8 больше первого, а третье число в 3,2 раза больше первого. Найдите эти три числа, если их среднее арифметическое равно 4,6.

Решение

1) Пусть у − третье число равно,
тогда первое число − 2,4y,
а второе: у + 0,6.
Среднее арифметическое этих чисел равно (2,4y + у + 0,6 + у) : 3.
Составим уравнение:
(2,4y + у + 0,6 + у) : 3 = 2,4
4,4y + 0,6 = 2,4 * 3
y = (7,2 − 0,6) : 4,4y
у = 1,5 − третье число,
2,4 − 1,5 = 3,6 − первое число,
1,5 + 0,6 = 2,1 − второе число.
Ответ: 3,6; 2,1; 1,5.

2) Пусть х − первое число, тогда второе число − х + 0,8, третье − 3,2х.
Среднее арифметическое этих чисел равно (х + x + 0,8 + 3,2x) : 3.
Составим уравнение:
(х + х + 0,8 + 3,2Х) : 3 = 4,6
5,2х + 0,8 = 4,6 * 3
x = (13,8 − 0,8) : 5,2
x = 2,5 − первое число,
2,5 + 0,8 = 3,3 − второе число,
3,2 * 2,5 = 8 − третье число.
Ответ: 2,5; 3,3; 8.

Задание 751

Запишите в виде процентов десятичные дроби 6,51; 2,3; 0,095.

Решение

6,51 = 6,51 * 100% = 651%
2,3 = 2,3 * 100% = 230%
0,095 = 0,095 * 100% = 9,5%

Задание 752

Запишите в виде десятичной дроби
42%; 8%; 7,25%; 568%.

Решение

42% = 42 * 0,01 = 0,42
8% = 8 * 0,01 = 0,08
7,25% = 7,25 * 0,01 = 0,0725
568% = 568 * 0,01 = 5,68

Задание 753

Слесарь и его ученик изготовили 1200 деталей. Ученик сделал 30%. всех деталей. Сколько деталей сделал ученик?

Решение

30% = 0,3
1200 * 0,3 = 360 (д.) - сделал ученик
Ответ: 360 деталей

Задание 754

На водопой пригнали 220 лошадей и жеребят. Жеребята составляли 15% всего табуна. Сколько жеребят было в табуне?

Решение

15% = 0,15
220 * 0,15 = 33 (ж.) - было в табуне
Ответ: 33 жеребёнка.

Задание 755

Геологи проделали путь длиной 2450 км. 10% пути они пролетели на самолёте, 60% пути проплыли в лодках, а остальную часть прошли пешком. Сколько километров геологи прошли пешком?

Решение

1) 100% − (10% + 60%) = 100% − 70% = 30% пути прошли геологи пешком
30% = 0,3
2) 2450 * 0,3 = 735 (км) - прошли геологи пешком
Ответ: 735 км.

Задание 756

Из молока получается 10% творога. Сколько творога получится из 32,8 кг молока? Из 58,7 кг молока?

Решение

10% = 0,1
В 32,8 кг молока 10% творога
1) 32,8 * 0,1 = 3,28 (кг) - творога получится из 32,8 кг молока
В 58,7 кг молока 10% творога
2) 58,7 * 0,01 * 10 = 0,587 * 10 = 5,87 (кг) - творога получится из 58,7 кг молока
Ответ: 3,28 кг, 5,87 кг.

Задание 757

Площадь одной комнаты 12 м², и она составляет 25% площади всей квартиры. Найдите площадь всей квартиры.

Решение

25% составляет 12 м²
25% = 0,25
12 : 0,25 = 48 (м²) - площадь всей квартиры
Ответ: 48 м².

Задание 758

Автотурист проехал в первый день 120 км, что составляет 15% всего намеченного пути. Какой длины намеченный путь?

Решение

15% составляет 120 км
15% = 0,15
120 : 0,15 = 800 (км) - длина намеченного пути 
Ответ: 800 км.

Задание 759

Засеяли 24% поля. Осталось засеять 45,6 га этого поля. Найдите площадь всего поля.

Решение

1) 100% − 24% = 76% поля осталось засеять
    76% составляет 45,6 га.
    76% = 0,76
2) 45,6 : 0,76 = 60 (га)  - площадь всего поля

Задание 760

Из пшеницы получается 80% муки. Сколько смололи пшеницы, если получили 2,4 т муки? Сколько муки получится из 2,5 т пшеницы?

Решение

80% = 0,8
2,4 т составляют 80%
1)  2,4 : 0,8 = 3 (т) - пшеницы смололи при получении 2,4 т муки
80% от 2,5 т
2) 2,5 * 0,8 = 2  (т) - муки получится из 2,5 т пшеницы
Ответ: 3 т, 2 т.

Задание 761

Масса сушёных яблок составляет 16% массы свежих яблок. Сколько надо взять свежих яблок, чтобы получить 4 т сушёных? Сколько сушёных яблок получится из 4,5 т свежих яблок?

Решение

16% = 0,16
4 т  составляют 16%
1)  4 : 0,16 = 25 (т) -  свежих яблок надо взять для получения 4 т сушёных яблок
16% от 4,5 т 
2) 4,5 * 0,16 = 0,72 (т) сушеных яблок получится из 4,5 т свежих яблок

Задание 762

Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелые арбузы?

Решение

16 : 200 = 0,08 всех арбузов оказались незрелыми
0,08 = 8%
Ответ: 8%.

Задание 763

В классе 17 мальчиков, а девочек на 6 больше. Сколько процентов класса составляют девочки и сколько процентов класса составляют мальчики?

Решение

1) 17 + 6 = 23 (уч.) - девочек в классе
2) 17 + 23 = 40 (уч.) - всего в классе
3)  23/40 = 0,575 от всех учеников в классе составляют девочки
     0,575 = 57,5%
4) 100% − 57,5% = 42,5% - мальчики
Ответ: 57,5%, 42,5%.

Задание 764

В санатории отдыхали мужчины и женщины. Мужчины составляли 40% всех отдыхающих. Какой процент всех отдыхающих составляли женщины?

Решение

100% − 40% = 60% всех отдыхающих составляли женщины
Ответ: 60%.

Задание 765

Выполните действия:
а) (3,8 * 1,75 : 0,95 − 1,02) : 2,3 + 0,4;
б) (11,28 + 3,4 : 0,85 * 1,55) : 4,6 − 0,8.

Решение

а) (3,8 * 1,75 : 0,95 − 1,02) : 2,3 + 0,4 = (7 − 1,02) : 2,3 + 0,4 = 2,6 + 0,4 = 3

б) (11,28 + 3,4 : 0,85 * 1,55) : 4,6 − 0,8 = (11,28 + 6,2) : 4,6 − 0,8 = 3,8 − 0,8 = 3

 

Пункт 41. Угол. Прямой и развернутый угол. Чертежный треугольник

Задание 766

Назовите углы, изображённые на рисунке 168. Запишите их обозначения.

Решение

∠ABC, ∠EFK, ∠PTS, ∠XVZ, ∠LDH, ∠MON.

Задание 767

Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость?

Решение

Шесть углов: ∠АОВ, ∠AOC, ∠AOD, ∠BOC, ∠BOD, ∠COD.
Лучи делят плоскость на 4 части.

Задание 768

Укажите, какие точки на рисунке 169 лежат внутри угла КОМ. Какие точки лежат вне этого угла? Какие точки лежат на стороне ОК, a какие − на стороне ОМ?

Решение

Внутри угла КОМ лежат точки А и D. Вне угла лежат точки В и С.
На стороне ОК лежит точка Р. На стороне ОМ лежат точки N и Е.

Задание 769

Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.

Решение

Луч ОТ делит ∠MOD = ∠MOT + ∠TOD.

Задание 770

Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин − на угол ВОС, а ещё за 15 мин − на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).

Решение

∠AOB = ∠BOC, ∠COD < ∠BOC, ∠AOC > ∠AOB, ∠AOC > ∠COD.

Задание 771

Изобразите с помощью чертёжного треугольника 4 прямых угла в разных положениях.

Решение

Задание 772

С помощью чертёжного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.

Решение

∠CDE и ∠FBL − прямые.

Задание 773

Укажите прямые углы в классной комнате.

Решение

Углы столов, углы стен и потолка и др.

Задание 774

Начертите прямоугольник со сторонами 6 см и 4 см и квадрат со стороной 7 см.

Решение

Задание 775

С помощью чертёжного треугольника начертите две прямые, которые при пересечении образуют прямые углы. На сколько частей они делят плоскость? Сколько развёрнутых углов на чертеже?

Решение

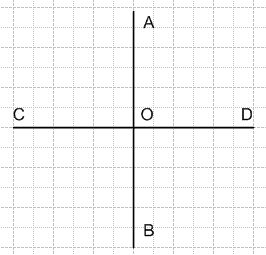
Четыре прямых угла ∠AOD, ∠AOC, ∠DOB, ∠BOC делят плоскость на четыре части.
Развёрнутые углы − ∠AOB и ∠DOC.

Задание 776

Начертите круг с центром О и радиусом 4,5 см. Разделите круг на четыре доли и закрасьте 3/4 круга.

Решение

Задание 777

Вычислите устно:
а) 8,1 - 0,9
: 8
* 0,2
+ 0,22
?
б) 0,62 - 0,4
: 0,2
+ 3,4
* 2
?
в) 4,8 : 6
* 5
* 0,4
: 0,8
?
г) 7 : 100
+ 0,33
* 50
- 0,9
?
д) 1,25 : 5
+ 1,2
* 0,3
?

Решение

а) 7,2, 0,9, 0,18, 0,4.

б) 0,22, 1,1, 4,5, 9.

в) 0,8, 4, 1,6, 2.

г) 0,07, 0,4, 20, 19,1.

д) 2,5, 0,5, 1,7, 0,51.

Задание 778

Уменьшится или увеличится число, если его:
а) умножить на 2,5; 0,7; 0,01; 1,001;
б) разделить на 2,5; 0,7; 0,01; 1,001?

Решение

а) При умножении на 2,5 и 1,001 исходное число увеличится, а при умножении на 0,7; 0,01 исходное число уменьшится.

б) При делении на 2,5 и 1,001 частное меньше делимого, а при делении на 0,7; 0,01 частное больше делимого.

Задание 779

Расскажите, как найти 7% числа а. Найдите:
а) 8% от 400;
б) 30% от 20;
в) 10% от 46;
г) 25% от 28;
д) 20% от 5.

Решение

а) 400 : 100 * 8 = 32

б) 20 : 100 * 30 = 6

в) 46 : 100 * 10 = 4,6

г) 28 : 100 * 25 = 7

д) 5 : 100 * 20 = 1

Задание 780

Найдите число, если 5% этого числа равны:
20; 40; 100; 0,1; 0,6; 1,5.

Решение

20 : 5 * 100 = 400
40 : 5 * 100 = 800
100 : 5 * 100 = 2000
0,1 : 5 * 100 = 2
0,6 : 5 * 100 = 12
1,5 : 5 * 100 = 30

Задание 781

Составьте задачу по числовому выражению:
а) 0,09 * 200;
б) 208 * 0,4;
в) 130 * 0,1 + 80 * 0,1.

Решение

а) В 200 грамм раствора содержится 9% твердого вещества. Сколько грамм твердого вещества содержится в растворе?

0,09 * 200 = 18 (г) - твердого вещества в растворе
Ответ: 18 г.

б) Поле площадью 208 га на 40% засеяно пшеницей. Сколько га пшеницы засеяно?

208 * 0,4 = 83,2 (га) - занимает пшеница
Ответ: 83,2 га.

в) У Пети было 130 рублей, а у Васи 80 рублей. Сколько рублей потратили вмести мальчики в магазине, если каждый из них потратил 10% от имеющихся у них денег?

130 * 0,1 + 80 * 0,1 = 13 + 8 = 21 (р.) - потратили вместе мальчики
Ответ: 21 рубль.

Задание 782

Сколько процентов от 400 составляет число
200; 100; 4; 40; 80; 400; 600?

Решение

(200 : 400) * 100% = 50%
(100 : 400) * 100% = 25%
(4 : 400) * 100% = 1%
(40 : 400) * 100% = 10%
(80 : 400) * 100% = 20%
(400 : 400) * 100% = 100%
(600 : 400) * 100% = 150%

Задание 783

Найдите пропущенное число:
а)         б)
2 5 3    2 3 5
1 3 6    1 2 1
2 3 ?    4 2 ?

Решение

а) Число − 5. Правило: сумма чисел в строке равна 10.

б) Число − 1. Правило: сумма чисел в столбце равна 7.

Задание 784

Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овёс − 8%, пшеница − 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?

Решение

2 * 8 = 16% поля занимает гречиха
Ответ: 16%.

Задание 785

За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?

Решение

100% - 40% = 60 % - тетрадей осталось у Пети
30 т. составляют 60%
60% = 0,6
30 : 0,6  = 50 (т.) - осталось у Пети
Ответ: 50 тетрадей.

Задание 786

Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?

Решение

1) 6 + 34 = 40 (кг) - масса сплава
2) 34 : 40 = 0,85 сплава составляет медь
0,85 = 85%
Ответ: 85%.

Задание 787

Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.

Решение

Пусть x − высота башен Московского Кремля равна,
тогда высота Александрийского, маяка − 1,7x м,
высота здания Московского университета − (1,7x + 119) м.
Александрийский маяк выше башен Кремля на (1,7x − х) м.
Составим уравнение:
(1,7x − х) = 49
x = 49 : 0,7
х = 70
Значит, высота башен Кремля 70 м,
1,7 * 70 = 119 (м) - высота Александрийского маяка
119 + 119 = 238 (м) - высота здания Московского университета
Ответ: 70 м, 119 м, 238 м.

Задание 788

Найдите с помощью микрокалькулятора:
а) 4,5% от 168;
б) 147,6% от 2500;
в) 28,3% от 569,8;
г) 0,09% от 456800.

Решение

а) 168 : 100 * 4,5 = 1,68 * 4,5 = 7,56

б) 2500 : 100 * 147,6 = 25 * 147,6 = 3690

в) 569,8 : 100 * 28,3 = 5,698 * 28,3 = 161,2534

г) 456800 : 100 * 0,09 = 4568 * 0,09 = 411,12

Задание 789

Решите задачу:
1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день − 35% огорода. Сколько аров осталось ещё вскопать?
2) У Серёжи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него ещё осталось?

Решение

1)
30% + 35% = 65% огорода вскопали всего
100% − 65% = 35% огорода осталось вскопать
6,4 : 100 * 35 = 2,24 (а) - осталось вскопать
Ответ: 2,24 а.

2)
35% + 40% = 75% времени потратил Сережа
100% − 75% = 25% свободного времени у него осталось
4,8 : 100 * 25 = 1,2 (ч) - свободного времени
Ответ: 1,2 ч.

Задание 790

Выполните действия:
1) ((23,79 : 7,8 − 6,8 : 17) * 3,04 − 2,04) * 0,85;
2) (3,42 : 0,57 * 9,5 − 6,6) : ((4,8 − 1,6) * (3,1 + 0,05)).

Решение

1) ((23,79 : 7,8 − 6,8 : 17) * 3,04 − 2,04) * 0,85 = (8,056 − 2,04) * 0,85 = 6,016 * 0,85 = 5,1136

2) (3,42 : 0,57 * 9,5 − 6,6) : ((4,8 − 1,6) * (3,1 + 0,05) = (57 − 6,6) : 10,08 = 50,4 : 10,08 = 5

Задание 791

Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.

Решение

Задание 792

Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК?
Какая точка лежит внутри угла АМВ, но вне угла АМК? Какие точки лежат на сторонах угла АМК?

Решение

Внутри ∠AMK лежат точки X и Е.
Точки У и Т лежат внутри ∠AMB, но вне ∠AMК.
Точка N лежит на стороне ∠АМК.

Задание 793

Найдите с помощью чертёжного треугольника прямые углы на рисунке 173.

Решение

∠PNS и ∠МОА.

Задание 794

Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.

Решение

P = 4 * 43 = 172 мм 17,2 см;
S = 43 * 43 = 1849 мм² = 18,49 см².

Задание 795

Найдите значение выражения:
а) 14,791 : а + 160,961 : b, если а = 100, b = 10;
б) 361,62с + 1848 : d, если с = 100, d =100.

Решение

а) При а = 100 и b = 10
14,791 : а + 160,961 : b = 14,791 : 100 + 160,961 : 10 = 0,14791 + 16,0961 = 16,24401

б) При с = 100 и d = 100
361,62с + 1848 : d = 361,62 * 100 + 1848 : 100 = 36162 + 18,48 = 36180,48

Задание 796

Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные − во второй. Сколько деталей изготовил рабочий во второй день?

Решение

100% − 60% = 40% деталей изготовил рабочий во второй день
450 : 100 * 40 = 180 (д.) - изготовил рабочий во второй день
Ответ: 180 деталей.

Задание 797

В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?

Решение

1) 8000 + 2000 = 10000 (к.) - стало через год
2) 10000 : 8000 * 100% = 125% - книг стало в библиотеке
3) 125% − 100% = 25% - на столько увеличилось количество книг
Ответ: на 25%.

Задание 798

Грузовики в первый день проехали 24% намеченного пути, во второй день − 46% пути, а в третий − остальные 450 км. Сколько километров проехали эти грузовики?

Решение

1)100% − (24% + 46%) = 100% − 70% = 30% всего пути проехали грузовики в третий день
450 км составляет 30%
30% = 0,3
2) 450 : 0,3 = 1500 (км) - проехали грузовики
Ответ: 1500 км.

Задание 799

Найдите, сколько составляют:
а) 1% от тонны;
б) 1% от литра;
в) 5% от 7 т;
г) 6% от 80 км.

Решение

а) 1 т = 1000 кг, 1000 кг : 100 = 10 кг.

б) 1 л = 1000 с м 3 , 1000 с м 3 : 100 = 10 с м 3.

в) 7 т = 7000 кг, 7000 кг : 100 * 5 = 350 кг.

г) 80 км = 80000 м, 80000 м : 100 * 6 = 4800 м.

Задание 800

Масса детёныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детёнышем их масса равна 0,9 т?

Решение

Пусть х − масса детёныша, тогда 9у − масса взрослого моржа.
Составим уравнение:
у + 9у = 900
у = 90 : 10
y = 90
Значит, масса детёныша 90 кг
9 * 90 = 810 (кг) - масса взрослого моржа
Ответ: 810 кг.

Задание 801

Во время манёвров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?

Решение

Пусть солдат во втором отряде было х,
тогда в первом отряде было 6х солдат.
Составим уравнение:
х + 6х = 200 * (1 − 0,3)
7х = 140
х = 140 : 7
х = 20
Значит, 20 солдат было во втором отряде
6 * 20 = 120 (с.) - было в первом отряде
Ответ: 120 солдат.

 

Пункт 42. Измерение углов. Транспортир

Задание 802

По рисунку 178 определите градусные меры углов:
а) AKD, АКБ, AKF;
б) BKF, ВКЕ, ВКС, BKD;
в) DKC, DKE, DKF, СКЕ, CKF и EKF.

Решение

а) ∠AKD = 45°, ∠AKE = 110°, ∠AKF = 155°.

б) ∠BKF = 25°, ∠BKE = 70°, ∠BKE = 120°, ∠BKD = 135°.

в) ∠DKC = 60° − 45° = 15°, ∠DKE = 110° − 45° = 65°, ∠DKF = 155° − 45° = 110°, ∠CKE = 110° − 60° = 50°, ∠CKF = 155°− 60° = 95°, ∠EKF = 155° − 110° = 45°.

Задание 803

Начертите луч ОА. С помощью транспортира по одну сторону от луча ОА постройте:
∠AOB = 45°, ∠AOC = 30°, ∠AOD = 135°, ∠AOE = 90°.

Решение

∠AOB = 45°, ∠AOC = 30°, ∠AOD = 135°, ∠AOE = 90°.

Задание 804

Измерьте углы, изображённые на рисунке 179, и запишите результаты измерений.

Решение

LDEF = 75°, ∠PSK = 135°, ∠NOM = 112°, ∠ABC = 50°.

Задание 805

Луч ОС лежит внутри угла АОВ, причём ∠AOC = 37°, ∠BOC = 19°. Чему равен угол АОВ?

Решение

∠AOB = ∠АОС + ∠BOC = 37° + 19° = 56°.

Задание 806

Какую часть развёрнутого угла составляют углы в 30°; 45°; 60°?
Какую долю прямого угла составляют углы в 30°; 15°; 60°; 75°?

Решение

30 ° = 30 : 180 = 1/6
45 ° = 45 : 180 = 1/4
60 ° = 60 : 180 = 1/3

30 ° = 30 : 90 = 1/3
15 ° = 15 : 90 = 1/6
60 ° = 60 : 90 = 2/3
75 ° = 75 : 90 = 5/6

Задание 807

Сколько градусов содержит угол, если он составляет:
а) 1/2 развёрнутого угла;
б) 1/3 развёрнутого угла;
в) 5/6 прямого угла;
г) 3/5 прямого угла;
д) 0,1 прямого угла;
е) 0,2 развёрнутого угла?

Решение

а) 1/2 * 180 ° = 180 ° : 2 = 90 °

6) 1/3 * 180 ° = 180 ° : 3 = 60 °

в) 5/6 * 90 ° = 90 ° : 6 * 5 = 75 °

г) 3/5 * 90 ° = 90 ° * 3 : 5 = 54 °

д) 0,1 * 90° = 9°

e) 0,2 * 180° = 36°

Задание 808

Сколько градусов содержит угол, если он составляет:
а) 20% от 360°;
б) 25% от 60°;
в) 45% развёрнутого угла;
г) 80% прямого угла?

Решение

а) 360° : 100 * 2 = 72°

б) 60° : 100 * 25 = 15°

в) 180° : 100 * 45 = 81°

г) 90° : 100 * 80 = 72°

Задание 809

Какой угол образуют часовая и минутная стрелки часов:
а) в 3 ч;
б) в 5 ч;
в) в 10 ч;
г) в 11 ч;
д) в 2 ч 30 мин;
е) в 5 ч 30 мин?

Решение

а) в 3 ч − угол 90°

б) в 5 ч − угол 180° : 6 * 5 = 150°

в) в 10 ч − угол 180° : 6 * 2 = 60°

г) в 11 ч − угол 180° : 6 = 30°

д) в 2 ч 20 мин − угол 120° − 70° = 50°

е) в 5 ч 30 мин − угол 180° − 165° = 15°

Задание 810

Постройте с помощью транспортира угол 70° и проведите луч, который делит угол пополам.
Такой луч называется биссектрисой угла.

Решение

Задание 811

С помощью транспортира проведите луч, который делит пополам прямой угол.

Решение

Задание 812

Постройте угол АОВ в 120° и разделите его на 3 равных угла.

Решение

Задание 813

Какие из углов острые и какие тупые, если ∠A = 67°; ∠B = 175°; ∠C = 92°; ∠D = 3°?

Решение

Острые углы: ∠A = 67°, ∠D = 3°.
Тупые углы: ∠B = 175°, ∠C = 92°.

Задание 814

С помощью чертёжного треугольника найдите на рисунке 180 острые, прямые и тупые углы. С помощью транспортира найдите их градусную меру.

Решение

Острые углы: ∠BAC = 20°, ∠CAD = 70°, ∠PKM = 20°, ∠PKN = 38°, ∠MKN = 58°, ∠XOE = 55°.
Прямой угол: ∠BAD = 90°.
Тупой угол: ∠EOV = 25°.
Развернутый угол ∠XOV = 180°.

Задание 815

Начертите круг радиусом 3 см. Обозначьте его центр буквой О. Проведите через точку О прямую АВ. С помощью транспортира разделите развёрнутые углы AОВ с обеих сторон прямой на 3 равных угла. На сколько равных частей разделился круг?

Решение

Круг разделен на 6 равных частей.

Задание 816

Угол АОВ развёрнутый, а ОС − луч. Найдите градусные меры углов АОС и СОВ, если:
а) градусная мера угла АОС втрое больше, чем градусная мера угла СОВ;
б) градусная мера угла АОС на 60° больше градусной меры угла СОВ;
в) градусная мера угла АОС в 4 раза меньше, чем градусная мера угла СОВ.

Решение

а) Пусть ∠COB = x°, тогда ∠AOC = 3x°.
Сумма ∠COB + ∠AOC = ∠AOB = (x + 3х)°.
Составим уравнение:
х + 3х = 180
х = 180 : 4
х = 45°
∠COB = 45°, ∠AОС = 3 * 45 = 135°.

б) Пусть ∠COB = х°, тогда ∠AOC = (x + 60)°.
Сумма ∠COB + ∠AOC = ∠AOB = (х + x + 60)°.
Составим уравнение:
x + х + 30 = 180
x = (180 − 60) : 2
х = 60°
∠COB = 60°, ∠AOC = 60 + 60 = 120°.

в) Пусть ∠AOC = х°, тогда ∠COB = 4х°.
Сумма ∠COB + ∠AOC = ∠AOB = (х + 4x)°.
Составим уравнение:
х + 4х = 180
x = 180 : 5°
x = 36°
∠AOC = 36°, ∠COB = 4 * 36 = 144°.

Задание 817

Внутри прямого угла АОВ проведён луч ОС. Найдите градусные меры углов АОС и СОВ, если:
а) угол АОС в 5 раз больше угла СОВ;
б) разность градусных мер углов СОВ и АОС равна 46°;
в) угол АОС в 4 раза меньше угла СОВ.

Решение

а) Пусть ∠COB = x°, тогда ∠AOC = 5х°.
Сумма ∠COB + ∠AOC = ∠AOB = (х + 5х) градусов.
Составим уравнение:
х + 5x = 90
х = 90 : 6
х = 15°
∠COB = 15°, LAOC = 5 * 15 = 75°.

б) Пусть ∠COB = x°, тогда ∠AOC = (90 − x)°.
Сумма ∠COB + ∠AOC = ∠AОВ = (x − (90 − x)°.
Составим уравнение:
х − (90 − х) = 46
х + х − 90 = 46
х = (46 + 90) : 2
х = 68°
∠COB = 68°, ∠AOC = 90 − 68 = 22°.

в) Пусть ∠AOC = х°, тогда ∠СОВ = 4х°.
Сумма ∠COB + ∠AOC = ∠AOB = (x + 4x)°.
Составим уравнение:
x + 4х = 90
x − 90 : 5
х = 18°
∠AOC = 18°, ∠COB = 4 * 18° = 72°.

Задание 818

Чему равна градусная мера каждого угла прямоугольника? Чему равна сумма этих градусных мер? Чему равна сумма градусных мер углов каждого из треугольников ABC и CDA (рис. 181)?

Решение

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
∠AВС + ∠BCD + ∠CDA + ∠DAB = 90° + 90° + 90° + 90° = 360°
∠ABC + ∠ВСА + ∠CAB = 180°
∠ACD + ∠CDA + ∠DAC = 180°

Задание 819

Измерьте каждый угол треугольника ACD, изображённого на рисунке 182, Найдите сумму градусных мер этих углов.

Решение

∠CAD = 110°, ∠ADC = 35°, ∠ACD = 35°
∠CAD + ∠ADC + ∠ACD = 110° + 35° + 35° = 180°

Задание 820

Начертите какой−нибудь треугольник и измерьте каждый его угол.
Проверьте, что сумма градусных мер углов треугольника равна 180°.
Запомните это свойство углов треугольника.

Решение

∠BAD + ∠ABD + ∠BDA = 90° + 45° + 45° = 180°

Задание 821

В треугольнике один из углов равен 75°, а другой − 80°. Чему равен третий угол этого треугольника?

Решение

180° − (75° + 80°) = 180° − 155° = 25°

Задание 822

В треугольнике ABC градусная мера угла ABC равна 40°, а градусная мера угла CAB в 3 раза больше. Найдите градусную меру угла АСВ.

Решение

∠АСВ = 180° − (∠ABC + ∠CAB) = 180° − (40° + 3 * 40°) = 180° − 160 = 20°

Задание 823

Вычислите устно:
а) 2,8 + 0,70
: 5
* 90
-3,5
?
б) 6 - 1,2
: 8
* 9
+ 1,9
?
в) 8,7 : 3
+ 2,6
- 1,5
* 0,6
?
г) 0,4 * 5
- 0,01
+ 0,28
: 0,15
?
д) 14 : 70
* 1,5
+ 3,7
* 0,25
?

Решение

а) 3,5, 0,7, 63, 59,5.

б) 4,8, 0,6, 5,4, 7,3.

в) 2,9, 5,5, 4, 2,4.

г) 2, 0,02, 0,3, 2.

д) 0,2, 0,3, 4, 1.

Задание 824

Назовите каждый из углов, изображённых на рисунке 183, а и б. Найдите среди этих углов прямые и развёрнутые углы.

Решение

Углы: ∠АСЕ, ∠МКР, ∠BOD, ∠FHL, ∠ВОМ,
∠МОА, ∠АОК, ∠КОВ, ∠МОК, ∠АОВ, ∠ВСЕ, ∠DCN, ∠DCP, ∠NCP, ∠РСЕ, ∠NCE.
Прямые углы: ∠АСЕ, ∠FHP.
Развернутые углы: ∠МКР, ∠МОК, ∠AOB, ∠DCE.

Задание 825

Найдите 5%, 15%, 25%, 45% числа 360. Попробуйте предложить разные способы решения этой задачи.

Решение

360 : 100 * 5 = 360 : 20 = 18
360 : 100 * 15 = 18 * 3 = 54
360 : 100 * 25 = 360 : 4 = 90
360 : 100 * 45 = 18 * 9 =162

Задание 826

5% некоторого числа равны 11. Найдите 15%, 20%, 35%, 50%, 100% этого числа.

Решение

Число равно 11 : 5 = 100 = 220
220 : 100 * 15 = 33
220 : 100 * 20 = 44
220 : 100 * 35 = 77
220 : 100 * 50 = 110
220 : 100 * 100 = 220

Задание 827

В зале кинотеатра 600 зрителей.
а) Сколько человек составляют 1%, 5%, 10%, 40% всех зрителей?
б) Сколько процентов зрителей составляют 12 человек, 90 человек, 300 человек?

Решение

а) 600 : 100 * 1 = 6
600 : 100 * 5 = 30
600 : 100 * 10 = 60
600 : 100 * 40 = 240

б) (12 : 600) * 100% = 2%
(90 : 600) * 100% = 15%
(300 : 600) * 100% = 50%

Задание 828

а) Число 60 увеличили на 15. На сколько процентов увеличилось число?
б) Число 75 уменьшили на 15. На сколько процентов уменьшилось число?
в) Некоторое число увеличили в 2 раза. На сколько процентов увеличилось число?
г) Некоторое число уменьшили в 2 раза. На сколько процентов уменьшилось число?

Решение

а) 60 + 15 = 75
(75 : 60) * 100% = 125%
125% − 100% = 25%

б) 75 − 15 − 60
(60 : 75) * 100% = 80%
100% − 80% = 20%

в) 2х : х * 100% = 200
200% − 100% = 100%

г) 0,5х : х * 100% = 50
100% − 50% = 50%

Задание 829

Найдите пропущенные числа:

Решение

а) Число: 0,8/3,6.
Правило: числитель каждой следующей дроби на 0,1 меньше числителя предыдущей дроби, а знаменатель каждой следующей дроби на 0,8 больше знаменателя предыдущей дроби.

б) Число: 0,05/0,15.
Правило: числитель и знаменатель каждой дроби через одну в 4 раза меньше числителя и знаменателя предыдущей дроби через одну.

Задание 830

Стреляя в тире, Дима в 76% случаев попал в мишень. Сколько промахов допустил Дима, если всего он произвёл 50 выстрелов?

Решение

1) 100% − 76% = 24% случаев Дима не попал в мишень
2) 50 : 100 * 24 = 12 (п.) - совершил Дима
Ответ: 12 промахов.

Задание 831

За три дня в магазине продано 1280 кг яблок. В первый день продали 25% всех яблок, а во второй день − 45% всех яблок. Сколько килограммов яблок продали в третий день? Решите задачу двумя способами. Какой из этих способов проще?

Решение

1 способ.
    25% = 0,25
1) 1280 * 0,25 = 320 (кг) - яблок продано в первый день
    45% = 0,45
2) 1280 * 0,45 = 576 (кг) - яблок продано во второй день
3) 1280 − (320 + 576) = 1280 − 896 = 384 (кг) - яблок продано в третий день
Ответ: 384 кг.

2 способ.
1) 100% − (25% + 45%) = 100% − 70% = 30% всех яблок продано в третий день
2) 1280 : 100 * 30 = 384 (кг) - яблок  продано в третий день
Ответ: 384 кг.

Второй способ решения проще первого.

Задание 832

Объясните смысл предложения:
а) «Из молока получается 25% сливок»;
б) «В свёкле содержится 20% сахара».

Решение

а) Это означает, что из х л молока получается 0,25x л сливок.

б) Это означает, что из х кг свёклы получается 0,2х кг сахара.

Задание 833

При перегонке нефти получается 30% керосина. Сколько керосина можно получить из 12 т; из 28 т; из 36,5 т нефти?

Решение

30% = 0,3
1) 12 * 0,3 = 3,6 (т) - керосина получается из 12 т нефти
2) 28 * 0,3 = 8,4 (т) - керосина получается из 28 т нефти
3) 36,5 * 0,3 = 10,95  (т) - керосина получается из 36,5 т нефти
Ответ: 3,6 т, 8,4 т, 10,95  т.

Задание 834

Решите задачу:
1) Площадь поля 560 га. В первый день засеяли 3/7 поля, а остальное − во второй день.
Сколько гектаров засеяли во второй день?
2) Площадь поля 450 га. Овсом засеяли 2/5 поля, а пшеницей − остальную часть.
Сколько гектаров засеяли пшеницей?

Решение

1) 1 − 3/7 = 4/7 всего поля  засеяли во второй день,
     560 * 4/7 = 80 * 4 = 320 (га) -  асеяли во второй день
Ответ: 320 га.

2) 1 − 2/5 = 3/5 поля засеяли пшеницей
    450 * 3/5 = 90 * 3 = 270 (га) - засеяли пшеницей
Ответ: 270 га.

Задание 835

Начертите два угла − в 60° и в 100° − с общей вершиной так, чтобы они имели общую сторону и лежали по разные стороны от неё. Найдите градусную меру угла, образованного двумя другими сторонами этих углов.

Решение

∠AOB = 60°, ∠AOC = 100°, ∠BOC = 100° + 60° = 160°.

Задание 836

Начертите произвольный четырёхугольник ABCD, измерьте транспортиром его углы и сложите результаты измерений.

Решение

∠DAB = 90°, ∠CDA = 90°, ∠ABC = 90°, ∠BCD = 90°;
∠DAB + ∠CDA + ∠ABC + ∠BCD = 90° + 90° + 90° + 90° = 360°.

Задание 837

Начертите произвольный четырёхугольник ABCD и проведите прямые АС и BD. Измерьте транспортиром углы АОВ, ВОС, COD и DOA, где О − точка пересечения прямых АС и BD. Какие из этих углов имеют одинаковую градусную меру? Сумма градусных мер каких углов равна 180°?

Решение

∠COD = 90°,
∠BOC = 90°,
∠AOB = 90°,
∠AOD = 90°,
∠AOB = ∠COD, ∠BOC = ∠AOD;
∠AOB + ∠BOC = ∠BOC + ∠COD = ∠COD + ∠DOA = ∠AOD + ∠AOB = 180°.

Задание 838

Найдите градусные меры углов треугольника MNKy если угол М меньше угла N на 40° и больше угла К на 10°.

Решение

Пусть градусная мера ∠M равна х, тогда ∠N = (х + 40)°, а ∠К = (х − 10)°.
Составим уравнение:
x + x + 40 + x − 10 = 180
3x + 30 = 180
х = (180 − 30) : 3
х = 50°.
∠M = 50°, ∠N = 50 + 40 = 90°, ∠K = 50 − 10 = 40°.

Задание 839

Найдите градусные меры углов треугольника CDE, если угол С вдвое больше угла D и втрое меньше угла Е.

Решение

Пусть ∠D = х°, тогда ∠C = 2х°, a ∠E = 3 * 2х°.
Составим уравнение:
х + 2х + 3 * 2х = 180
х = 180 : 9
х = 20°.
∠D = 20°, ∠C = 2 * 20 = 40°, ∠E = 3 * 40 = 120°.

Задание 840

В механическом цехе установлено 400 станков. В первую смену работало 380 станков, а во вторую − 350 станков. Какой процент станков работал в первую смену и какой во вторую?

Решение

1)   (380 : 400) * 100% = 95% всех станков работало в первую смену,
2)   (350 : 400) * 100% = 87,5% всех станков работало во вторую смену
Ответ:  95%, 87,5%.

Задание 841

Никелевая руда содержит 1,3% никеля. Сколько тонн никеля получится из 24 860 т руды? Сколько тонн этой руды надо переработать, чтобы добыть 2405 т никеля?

Решение

    1,3% = 0,013
    1,3% от 24 860 т
1)   24860 * 0,013 = 323,18 (т) - никеля получится из 24860 т руды
    2405 т составляют 1,3%
2)  2405 : 0,013 = 185 000 (т) руды надо переработать для добычи 2405 т никеля
Ответ: 323,18 т, 185 000 т.

Задание 842

Магнитный железняк содержит 70% чистого железа. Сколько тонн чистого железа содержится в 4,6 т магнитного железняка?

Решение

70% от  4,6 т
70% = 0,7
4,6 * 0,7 = 3,22 (т) - чистого железа содержится в 4,6 т магнитного железняка 
Ответ: 3,22 т.

Задание 843

Из чайного листа после сушки получается 4,2% чая. Сколько получится чая из 225 кг чайного листа?

Решение

4,2% от 225 кг
4,2% = 0,042
225 * 0,042 = 9,45 (кг) - чая получится из 225 кг чайного листа.
Ответ: 9,45 кг.

Задание 844

Привезли 500 т руды с содержанием меди 6,5% и 700 т руды с содержанием меди 4,5%. Из какой руды получится больше меди?

Решение

1)  500 : 100 * 6,5 = 32,5 (т) - меди получится из 500 т руды, содержащей 6,5% меди
2) 700 : 100 * 4,5 = 31,5 (т) - меди получится из 700 т руды, содержащейся 4,5% меди
Ответ:  из первой руды получится больше меди.

Второй способ оформления задачи:

6,5% от 500 т
6,5% = 0,065
1)  500 * 0,065 = 32,5 (т) - меди получится из 500 т руды, содержащей 6,5% меди
4,5% от 700 т
4,5% = 0,045
2) 700 * 0,045 = 31,5 (т) - меди получится из 700 т руды, содержащейся 4,5% меди
Ответ:  из первой руды получится больше меди.

Задание 845

С помощью микрокалькулятора найдите значение выражения:
а) 284,3 * 159,6 + 51 189,1 : 32,1 − 651,2 * 34,8;
б) 376,64 : 4,4 : 3,2 + 0,479 * 0,37 * 44,5.

Решение

а) 284,3 * 159,6 + 51189,1 : 32,1 − 651,2 • 34,8 = 45374,28 + 1594,676 − 22661,76 = 24307,196

б) 376,64 : 4,4 : 3,2 + 0,479 • 0,37 • 44,5 = 26,75 + 7,886735 = 34,636735

 

Пункт 43. Круговые диаграммы

Задание 846

Известно, что 3 8 массы льняного семени составляет масло. Постройте круговую диаграмму содержания масла в льняном семени.

Решение

360° * 3 : 8 = 45 * 3 = 135°

Задание 847

Вода занимает 0,7 всей поверхности земного шара. Постройте круговую диаграмму распределения воды и суши на земной поверхности.

Решение

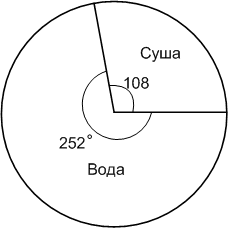
360° * 0,7 = 252° на диаграмме будет занимать вода;
360° − 252° = 108° на диаграмме будет занимать суша.

Задание 848

Врачи рекомендуют дневную норму питания распределить на 4 приёма: утренний завтрак − 25%, второй завтрак − 15%, обед − 45% и ужин − 15%. Постройте круговую диаграмму распределения дневной нормы питания.

Решение

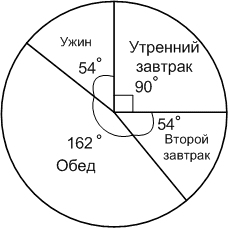
360° * 0,25 = 90° на диаграмме будет занимать сектор утреннего завтрака;
360° * 0,15 = 54° сектор второго завтрака;
360° * 0,45 = 162° сектор обеда;
360° * 0,15 = 54° сектор ужина.

Задание 849

Постройте круговую диаграмму площадей частей света Земли, предварительно заполнив таблицу (используйте микрокалькулятор):

Решение

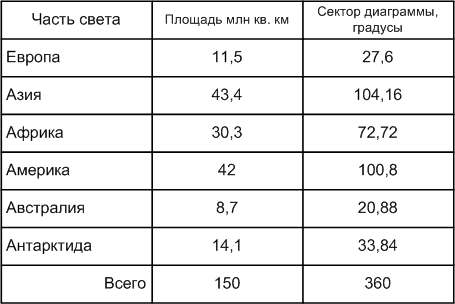
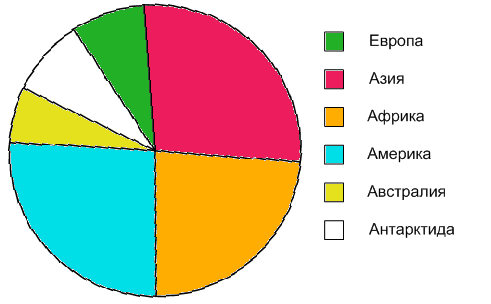
Задание 850

Вычислите устно:
а) 1 - 0,2
* 10
: 40
+ 3,8
?
б) 4,9 + 1,4
: 3
+ 3,9
: 12
?
в) 0,4 * 20
: 0,2
: 100
+ 2,6
?
г) 63 : 90
+ 0,5
* 4
- 0,9
?
д) 15 : 2,5
+ 2,1
: 2,7
- 0,6
?

Решение

а) 0,8, 8, 0,2, 4.

б) 6,3, 2,1, б, 0,5.

в) 8, 40, 0,4, 3;

г) 0,7, 1,2, 4,8, 3,9.

д) 6, 8,1, 3, 2,4.

Задание 851

Найдите:
а) 50% от 6 т; 1 ч; 1 дм; 90°;
б) 10% от 1 кг; 2000 р.; 1 а; 1 л; 180°.

Решение

а) 6 т * 50 : 100 = 3 т;
1 ч * 50 : 100 = 0,5 ч = 30 мин;
1 дм * 50 : 100 = 5 см;
90° * 50 : 100 = 45°.

б) 1 кг * 10 : 100 = 1000 г *10 : 100 = 100 г;
2000 p. * 10 : 100 = 200 p.;
1 a * 10 : 100 = 100 м² * 10 : 100 = 10 м²;
1 л * 10 : 100 = 1000 см³ * 10 : 100 = 100 см³;
180° * 10 : 100 = 18°.

Задание 852

Сколько процентов составляют:
а) 8 кг от 1 ц;
б) 15 с от 1 мин;
в) 35 см от 1 м;
г) 100 л от 1 м³?

Решение

а) 1 ц = 100 кг, (8 : 100) * 100% = 8%

б) 1 мин = 60 с, (15 : 60) * 100% = 25%

в) 1 м = 100 см, (35 : 100) * 100% = 35%

г) 1 м³ = 1000 л, (100 : 1000) * 100% = 10%

Задание 853

Найдите число, если:
а) 1% этого числа равен 1; 6; 0,7; 1,8;
б) 10% этого числа равны 0,3; 1; 15; 2,4;
в) 25% этого числа равны 2; 10; 25; 0,5; 1,2.

Решение

а) Если 1% числа равен х, то число равно х : 100 * 100 = 100х:
при х = 1 => 100 * 1 = 100;
при х = 6 => 100 * 6 = 600;
при х = 0,7 => 100 * 0,7 = 70;
при х = 1,8 => 100 * 1,8 = 180.

б) Если 10% числа равны х, то число равно х : 10 * 100 = 10х:
при х = 0,3 => 10 * 0,3 = 3;
при х = 1 => 10 * 1 = 10;
при х = 15 => 10 * 15 = 150;
при х = 2,4 => 10 * 2,4 = 2,4.

в) Если 25% числа равно х, то число равно х : 100 * 25 = 4х:
при х = 2 => 4 * 2 = 8;
при х = 10 => 4 * 10 = 40;
при х = 25 => 4 * 25 = 100;
при х = 0,5 => 4 * 0,5 = 2;
при х = 1,2 => 4 * 1,2 = 4,8.

Задание 854

Вычислите градусную меру угла АОВ, используя рисунок 186.

Решение

а) ∠AOB = 180° − 65° = 115°

б) ∠AOB = 90° − 20° = 70°

в) ∠AOB = 180° − (60° + 50°) = 180° − 110° = 70°

г) ∠BOD = 180° − 140° = 40°;
∠COA = 180° − 120° = 60°;
∠AOB = 180° − (40° + 60°) = 180° − 100° = 80°.

Задание 855

ABCD − прямоугольник, ∠ACB = 30° (рис. 187). Найдите градусную меру углов: ACD, ВАС, CAD.

Решение

∠ACD = 90° − 30° = 60°;
∠ВАС = 180° − (90° + 30°) = 180° − 120° = 60°,
∠CAD = 90° − 60° = 30°.

Задание 856

Начертите угол ABC, равный 120°. На стороне ВА отложите отрезок ВМ, равный 3 см, а на стороне ВС − отрезок BN, равный 4 см. Соедините отрезком точки М и N. Измерьте стороны и углы получившегося треугольника и найдите периметр и сумму градусных мер углов этого треугольника.

Решение

ВM = 3 см, BN = 4 см, MN = 6 см,
PMBN = 3 + 4 + б = 13 см;
∠MBN = 120°, ∠BMN = 35°, ∠BNM = 25°,
∠MBN + ∠BMN + ∠BNM = 120° + 35°+ 25° = 180°.

Задание 857

В треугольнике ABC ∠A = 50°, a ∠B = 30°. Вычислите градусную меру угла С.

Решение

∠C = 180° − (50° + 30°) = 180° − 80° = 100°.

Задание 858

Молоко даёт 25% сливок, сливки дают 20% масла. Сколько масла получится из молока, надоенного за 15 дней от 360 коров, если каждая корова в среднем даёт 15 кг молока в день?

Решение

Получится 15 * 15 * 360 : 100 * 25 : 100 * 20 = 4050 кг масла.

Задание 859

Постройте круговую диаграмму распределения суши на Земле по следующим данным:

Решение

Задание 860

В классе 36 учеников. По математике за четверть отметку «5» имеют 8 человек, отметку «4» − 12 человек, а остальные − отметку «3». Постройте круговую диаграмму.

Решение

8 : 36 * 360° = 80° сектор отличников на диаграмме;
12 : 36 * 360° = 120° сектор ударников на диаграмме;
36 − (8 + 12) = 36 − 20 = 16 учеников получили отметку «3»,
16 : 36 * 360° = 160° сектор троечников на диаграмме.

Задание 861

Экипаж экскаватора работал 480 мин. Из них основная работа заняла 330 мин, вспомогательная работа − 90 мин, простой по техническим причинам − 30 мин и подготовительные работы − 30 мин. Постройте круговую диаграмму распределения рабочего времени этого экипажа.

Решение

330 мин : 480 мин * 360° = 247,5° сектор основной работы на диаграмме;
90 мин : 480 мин * 360° = 67,5° сектор вспомогательной работы на диаграмме;
30 мин : 480 мин * 360° = 22,5° сектор простоя по техническим причинам на диаграмме;
30 мин : 480 мин * 360° = 22,5° сектор подготовительных работ на диаграмме.

Задание 862

Велосипедист стал догонять пешехода, когда между ними было 2,1 км, и догнал его через 0,25 ч. Найдите скорость велосипедиста и скорость пешехода, если скорость пешехода была в 3,4 раза меньше скорости велосипедиста.

Решение

Пусть х − скорость пешехода, тогда скорость велосипедиста 3,4х км/ч.
Составим уравнение:
2,1 : (3,4х − х) = 0,25
2,4x = 2,1 : 0,25
х = 8,4 : 2,4 = 3,5 км/ч − скорость пешехода, а скорость велосипедиста равна 3,4 * 3,5 = 11,9 км/ч.

Задание 863

Сколько градусов содержит угол между часовой и минутной стрелками часов:
а) в 9 ч;
б) в 6 ч;
в) в 2 ч;
г) в 8 ч?

Решение

а) 90°

б) 180°

в) 180° : 3 = 60°

г) 180° : 3 * 2 = 120°

157-158 Задания для самопроверки

Страницы 157-158 Задания для самопроверки

№1

В) квадратный дециметр

№2

а) 1/2 = 0,5 = 50%
б) 1/4 = 0,25 = 25%
в) 3/20 = 0,15 = 15%
г) 2/5 = 0,4 = 40%

№3

1) 64360 : 100 = 643,6 (кг) картофеля 1%
2) 25 * 643,6 = 16090 (кг) картофеля отправили в магазин
Ответ: 16090 кг картофеля.

№4

1% - 70 тыс. чел.
100% - х тыс. чел.
х = (100 * 70)/1 = 7000 (тыс.) - человек ежедневно перевозит московское метро
Ответ: 7000 тыс. человек

№5

1) 6700 : 100 = 67 (р.) - стоимость 1% куртки
2) 67 * 5 = 335 (р.) - стоимость 5% куртки
3) 6700 – 335 = 6365 (р.) - стоит куртка
Ответ: 6365 рублей.

№6

10% - 78 км
100% - х км
х = (100 * 78)/10 = 780 (км) - длина пути
Ответ: 780 км

№7

100% - 800 д.
х% - 384 д.
х = (100 * 384)/800 = 48% - плана было сделано
Ответ: 48% плана.

№8

1) 90 – 75 = 15 (х.) - на столько больше продал магазин
75х – 100%
15х – х%
х = (15 * 100)/75 = 20% - от плана составляют проданные холодильники
Ответ: 20%.

№9

1) 60 + 140 = 200 (г) - вес раствора
200 г – 100%
60 г – х%
х = (60 * 100)/200 = 30% - соли содержит раствор
Ответ: 30% соли.

№10

Углеводы

160 - 171

Параграф 9. Множества
Пункт 44.  Понятие множества. Со страницы 160

Задание 864

Приведите примеры, в которых вместо слова множество применяют слова команда, бригада, коллекция, набор.

Команда футболистов, бригада слесарей, коллекция марок, набор конфет.

Задание 865

Запишите с помощью фигурных скобок множество:
а) предметов, которые изучаются в 5-м классе;
б) различных букв в слове математика;
в) четных однозначных чисел;
г) нечетных однозначных чисел.

а) {математика, литература, русский язык, биология, история, обществознание, технология, география, физкультура, ОПД, информатика}
б) {м,а,т,е,и,к}
в) {2,4,6,8}
г) {1,3,5,7}

Задание 866

а) дни недели
б) 12 месяцев

Задание 867

{11, 12, 13, 14}
{11, 12}

Задание 868

а) {1, 2, 3, 4, 5, 6, 7, 8, 9}
б) {13, 23, 33, 43, 53, 63, 73, 83, 93}
в) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
г) { 0 }
д) {1, 2, 3, 4, 5, 6, 7, 8}

Задание 869

{19, 99}

Задание 870

{28, 25, 82, 58, 52}

Задание 871

{371, 317, 713, 731, 137, 173}

Задание 872

{111, 112, 121, 211, 212, 221, 222}

Задание 873

А = {январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь}
В = {мизинец, безымянный, средний, указательный, большой}
D = { 0 }
С = {1 коп; 5 коп., 10 коп., 50 коп.}

Задание 874

К = {Марс, Земля}
К = {Меркурий, Венера, Марс, Юпитер, Сатурн, Уран, Нептун}

Задание 875

М = {24, 338, 900, 2}
Е = {75,725, 255, 5}

Задание 876

А = {724, 532, 531, 222, 725, 839}
В = {532, 222, 42, 1022}

Задание 877

М = {январь; март; май, июль, август, октябрь, декабрь}
Р = {апрель, июнь, сентябрь, ноябрь}
Февраль не входит не в одно из этих множеств.

Задание 878

Назовем тропинки «тр1», «тр2», «тр3».
Если подняться по одной тропинке, спуститься можно лишь по двум другим, и так как всего тропинок 3, то маршрутов:
2 * 3 = 6 (маршрутов)
Маршруты:
1) «тр1», «тр2»
2) «тр1», «тр3»
3) «тр2», «тр3»
4) «тр2», «тр1»
5) «тр3», «тр1»
6) «тр3», «тр2»

Задание 879

3 * 4 = 12 способами

Задание 880

а) 612228 + (53007 – 52275 : 615) = 665150
1)                      2)              3)
_52275 |615      _53007    +612228
  4920   |85                85        52922
  _3075                52922      665150
    3075
          0
б) 343 * (324378 : 54 – 4862) + 777 = 393512
1)                           2)         3)
_324378 |54          _6007   x1145
  324       |6007        4862      343
      _378                  1145    3435
        378                            4580
            0                          3435    
4)                                     392735
+392735
        777
  393512

Задание 881

а) (0,87m – 0,66m) * 10 : 2 : 3 = 0
_0,87
  0,66
  0,21
0,21m * 10 : 2 : 3 = 0
0,21m * 5 = 0 * 3
0,21m * 5 = 0
0,21m = 0 : 5
0,21m = 0
m = 0
б) 10 * (1,37k – 0,12k) : 5 : 8 = 0
_1,37
  0,12
  1,25
10 * 1,25k : 5 : 8 = 0
10 * 1,25k : 5 = 8 * 0
10 * 1,25k : 5 = 0
10 * 1,25k = 0 * 5
10 * 1,25k = 0
1,25k = 0 : 10
1,25k = 0
k =0 : 1,25
k = 0

Задание 882

Пусть х мужчин ехало в трамвае,
тогда женщин (3х) .
После остановки мужчин стало (х – 2 + 4),
а женщин после остановки (3х – 7 + 1).
Составим уравнение
х – 2 + 4 + 3х – 7 + 1 = 36
4х = 36 + 2 – 4 + 7 – 1
4х = 40
х = 40 : 4
х = 10
Значит, 10 мужчин ехало в трамвае
3х = 3 * 10 = 30 (ж.) - было в трамвае до остановки
Ответ: 30 женщин.

Задание 883

ФИО: Иванов Николай Сергеевич
Адрес: г. Урал, ул. Советская, д.31, кв.14
Код     тариф      показ счетч.     Расход     тариф    Сумма к
плат.   зона      текущ. предыд.   факт.       (руб.)      опл. (руб.)
1 день (Т1)       7293      6543      750            4,18        3135
_7293     х 4,18
  6543           750
    750       2090
               2926     
              3135,00

Задание 884

Аня Оля Ася Юля

Задание 885

{ABD,ACB,ACD,ABC,AOD,AOB,BOC,COD}

Задание 886

а) {2, 4, 9, 5, 7, 11}
б) {3, 8, 5, 10, 6}

Задание 887

А = {98, 99, 100, 101, 102, 103, 104}
97 ∉ А
100 ∈ А
106 ∈ А

Задание 888

а) В = {1, 2, 3, 4, 5}
б) {22}
в) 0

Задание 889

К = {98, 99, 100, 101, 102, 103}
80 ∉ К
90 ∉ К
100 ∈ К
110 ∉ К

Задание 890

A, B, C, D, AB, BA, CD, DC, CB, CA, DA, DB, AC, AD, BC, BD

Задание 891

Задача
1) 1360 + 3950 = 5310 (р.) стоимость одного детского костюма и взрослого костюма
  1360
+3950
  5310
2) 42480 : 5310 = 8 (к.) детских и взрослых было продано
Ответ: 8 костюмов было продано.

Задание 892

а) 48 * 96 + 39 * 403 = 4608 + 15717 = 20325
1)       2)           3)
  х 48   х 403    +15717
     96       39        4608
   288   3627      20325
432    1209  
4608  15717

б) 53578 : 89 – 27268 : 68 = 602 – 401 = 201
1)                      2)
_53578 |89       _27268 |68  
  534     |602       272     | 401
    _178                   _68
      178                     68
         0                        0
3)
_602
  401
  201

Задание 893

Задача
1) 28 + 21 = 49 (д.) посадят за 1 день оба класса
  28
+21
  49
2) 441 : 49 = 9 (дн.) ученики закончат посадку деревьев
Ответ: за 9 дней ученики закончат посадку деревьев.

Задание 894

13,2 + 421,68 : (40,3 – 31,9) = 13,2 + 421,68 : 8,4 = 13,2 + 50,2 = 63,4
1)            2)                     3)
_40,3    _ 4216,8 |84     +13,2
  31,9       420      |50,2     50,2
    8,4         _168               63,4
                    168
                        0

Задание 895

а) {k,y,c,p}
б) {a,b,x,m}
в) {a,b,x,m,k,y,c,p}
г) 0
д) 0
е) {c,p}
ж) {m,b,y}
з) {a,k,x}

Задание 896

а) А – треугольники
В – фигура синего цвета
А ⋂ В = 0
б) А – четырехугольники
В – фигуры красного цвета
А ⋂ В = у
в) А – круг
В – зеленого цвета
А ⋂ В = 0
г) А – четырехугольники
В – фигуры зеленого цвета
А ⋂ В = а, х
д) А – треугольники
В – четырехугольники
С – все фигуры
А ⊂ В
В ⊂ С

Задание 897

24 : А = {24, 12, 8, 6, 4, 2,1}
36 : В = {36, 12, 9, 6, 4, 3, 2, 1}
А ⋂ В = 12, 6, 4, 2, 1
А ⋂ В = 12

Задание 898

А – все числа двузначные делятся на 6
А = {12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96}
В – все двузначные числа, которые делятся на 15
В = {15, 30, 45, 60, 75, 90}
А ⋂ В = {30, 60, 90}
Наименьшее число в общей части 30
30 делится и на 6 и на 15

Задание 899

В – множество городов регионов РФ
А – множество столиц России
С – множество сел России

Задание 900

А – множество имен существительных в рус. яз.
В – множество всех рус. слов
С – множество глаголов

Задание 902

а) АВ = 3 см
СВ = 5 см
б) АВ = 4,5 см
∠ВАС = 40°

Задание 903

а) 2_1/7 + (3_5/7 – 2_4/7) = 2_1/7 + (3 – 2 + 5/7 – 4/7) = 2_1/7 + 1_1/7 = 2 + 1 + 1/7 + 1/7 = 3_2/7
б) 6_2/5 – (4_4/5 – 4/5) = 6_2/5 – 4 = 6 – 4 + 2/5 = 2_2/5

Задание 904

Задача
1) 50% + 30% + 18% = 98% семейный бюджет без учета стипендии сына
2) 100% - 98% = 2% семейного бюджета составляет стипендия сына
3) 1350 : 2 * 100 = 67500 (р.) - семейный бюджет без стипендии сына
4) 67500 + 1350 = 68850 (р.) - получила семья Астаховых в 2013 году в месяц
Ответ: 68850 р.

Задание 905

Задача 1.
Пусть х задуманное число.
Составим уравнение:
(х + 5) * 9 + х – 25 = 200
9х + 45 + х – 25 = 200
10х + 45 – 25 = 200
10х + 20 = 200
10х = 200 – 20
10х = 180
х = 180 : 10
х = 18
Значит,  задуманное число 18
Ответ: 18.

Задача 2.
Пусть х задуманное число.
Составим уравнение:
(х – 3) * 6 – х + 48 = 90
6х – 18 – х + 48 = 90
6х – х – 18 + 48 = 90
5х – 18 + 48 = 90
5х – 18 = 90 – 48
5х – 18 = 42
5х = 18 + 42
5х = 60
х = 60 : 5
х = 12
Значит,  задуманное число 12.
Ответ: 12.

Задание 906

7 + 6 = 13
76

Задание 907

74
7 + 4 = 11
7 – 4 = 3

Задание 908

х + у + z = 18
x = y
2x + z = 18
x – 3 = z
2x+ x – 3 = 18
3x – 3 = 18
3x = 18 + 3
3x = 21
x = 21 : 3
x = 7
z = x – 3
z = 4
7 + 7 + 4 = 18

Задание 909

а) А = {5, 10, 15, 20, 25}
В = {15, 20, 25, 30, 35}
А ⋂ В = {15, 20, 25}
б) А – множество делителей числа 20
А = {1, 2, 4, 5, 10}
В – множество делителей числа 30
В = {1, 2, 3, 5, 6, 10}
А ⋂ В = {1, 2, 5, 10}

Задание 910

А = {7, 8, 9, 10}
С = {9, 10, 11, 12, 13}
А ⋂ С = {9, 10}
А ⋃ С = {7, 8, 9, 10, 11, 12, 13}

Задание 911

а) Правильные дроби 1/2, 2/3, 2/5
б) Неправильные дроби 4/3, 5/2, 7/7

Задание 912

Задача
1) 150 : 100 * 80 = 1,5 * 80 = 120 (кг) - уменьшилась масса вишни
2) 150 – 120 = 30 (кг) - получилось вишен после сушки
Ответ: 30 кг вишен.

Задание 913

Задача
1) 40000 : 100 * 17 = 6800 (р.) - рабочий заработал больше в августе на 17%
2) 40000 + 6800 = 46800 (р.) - заработал рабочий за август
+40000
    6800
  46800
Ответ: 46800 р. .

Задание 914

а) верно
б) неверно
в) неверно
г) неверно

Задание 915

а) 651 + 208 = 809 неверно
  651
+208
  859

б) 715 – 69 = 646 верно
_715
    69
  646

в) 347 * 6 = 857 неверно
х 347
      6
2082

г) 426 : 3 = 142 верно
_426 |3    
  3     |142
_12
  12
    _6
      6
      0

Задание 916

1 ∈ Р верно
1 ∉ Р неверно
13 ∉ Р верно
7 ∈ Р верно

Задание 917

«год состоит из 7 суток» - неверно
«месяц состоит из 7 суток» - неверно
«неделя состоит из 7 суток» - верно

Задание 918

а) 125 < 202верно
б) 307 > 406 неверно
в) 3048 < 3049 верно
г) 26786 > 9989 верно

Задание 919

а) 3, 4, 5, 6, 7, 8
б) 176, 177, 178, 179, 180, 181, 182

Задание 920

✓ «овца питается травой» - верно
✓ «собака питается травой» - неверно
✓ «лев питается травой» - неверно
✓ «корова питается травой» - верно
✓ «лошадь питается травой» - верно

Задание 921

y < 7, y = 0,3, 4, 10, 7
0 < 7верно
3 < 7 верно
4 < 7 верно
10 < 7 неверно
7 < 7 неверно

Задание 922

х – 3 = 8
х = 3, 5, 11, 16
3 – 3 = 8 неверно
5 – 3 = 8 неверно
11 – 3 = 8 верно
16 – 3 = 8 неверно

Задание 923

«Река Дон впадает в Черное море» - неверно
«Река Волга впадает в Черное море» - неверно
«Река Дунай впадает в Черное море» - верно
«Река Кубань впадает в Черное море» - неверно
«Река Днепр впадает в Черное море» - верно

Задание 924

а) х = 5941 * 198
х = 1176318
   х 5941
        198
    47528
+53469
  5941    
1176318

б) х = 37920 : 12
х = 3160

_37920 |12    
  36       |3160
  _19
    12
    _72
      72
        0

Задание 925

а) а < (30000 – 17008) : 64

_30000   _12992 |64  
  17008     128     |204
  12992       _192
                     192
                         0
a = 204 неверно
а = 130 верно

б) a > 12 * 497 + 17 * 326

  х 497   х 326   +5964
      12        17     5542
    994    2282   11506
+497    +326  
  5964    5542

а = 11507 верно
а = 2071 неверно

Задание 926

а) (338 * а + 985 * b) - расход воды в сентябре
(347 * а + 999 * b) - расход воды в октябре
(358 * а + 1011 * b) - расход воды в ноябре
(371 * а + 1019 * b) - расход воды в декабре

б) тариф на холодную воду – 21 р.
тариф на горячую воду – 96 р.
1) 338 * 21 + 985 * 96 = 101658 (р.) - за расход воды в сентябре

  х 338    х 985    +94560
       21        96         7098
     338     5910    101658
+ 676   +8865  
   7098   94560

2) 347 * 21 + 999 * 96 = 103191 (р.) - за расход воды в октябре

  х 347    х 999   +95904
       21         96       7287
     347     5994   103191
+ 694   +8991  
   7287   95904

3) 358 * 21 + 1011 * 96 = 97056 (р.) - за расход воды в ноябре

  х 358   х 1011   +97056
       21         96       7518
     358     6066   104574
 +716   +9099  
   7518   97056

4) 371 * 21 + 1019 * 96 = 105615 (р.) за расход воды в декабре

  х 371   х 1019   +97824
       21          96       7791
     371      6114   105615
  +742   +9171   
    7791   97824

Задание 927

а) 18408 : (268 * 75 – 19746) + 959 = 18408 : (20100 – 19746) + 959 = 18408 : 354 + 959 = 1011
1)          2)               3)
х 268     _20100     _18408 |354
     75       19746       1770   |52
 1340           354         _708
1876                             708
20100                               0

4)
+959
    52
 1011

б) (86 * 217 + 275116) : 859 + 279569 = (18662 + 275116) : 859 + 279569 = 293778 : 859 + 279569 = 279911
1)             2)                 3)
  х 217       +275116     _293778 |859
       86           18662       2577     |342
   1302         293778       _3607
 1736                                3436
 18662                              _1718
                                           1718
                                                 0
4)
+279569
        324
  279911

Задание 928

1-ю фигуру мы можем раскрасить в 4 цвета, 2-ю фигуру - в 3, 3-ю - в 2 цвета.
4 * 3 * 2 = 12 * 2 = 24 (с.)
Ответ: 24 способа.

Задание 929

а) 507 < 781
б) 307 < 3007
в) 444 > 1
г) 35 = 35
д) 2000 > 0
е) 0 < 376

Задание 930

а) нет
б) да
в) нет
г) да

Задание 931

а) 3кг 500г = 35х0г
    х = 0
    3 кг 500г = 3500г

б) 4 км 250м = 4250м

в) 3ч 45мин = 225мин
    3ч = 3 * 60 = 180мин
     180мин + 45мин = 225мин

г) 6350г = 6кг 350г

д) 402см = 4м 2см

е) 100с = 1мин 40с
    100 – 60 = 40с

Задание 932

«Город Москва находится в России» - верно
«Город Киев находится в России» - неверно
«Город Берлин находится в России» - неверно
«Город Санкт – Петербург находится в России» - верно
«Город Париж находится в России» - неверно
«Город Севастополь находится в России» - верно

Задание 933

а) х < 206 * 504 – 208 * 401

  х 206      х 208    _103824
     504         401        83408
  + 824       +208        20416
1030        832    
103824    83408

х < 20416
x = 2; 20310 – верно
х = 20417, 324071 – неверно

б) у < 12322 : 61 – 3328 : 32

_12322 |61        _3328 |32     _202
  122     |202        32     |104     104
   _122                _128                98
     122                  128
         0                      0
у < 98
y = 89, 15 – верно
у = 99, 123 – неверно

Задание 934

а) m = 1701 * 52 – 69093

 х 1701    _88452
        52      69093
    3402      19359
+8505  
  88452

m = 19359 – верно
m = 19349 – неверно
m = 18351 – неверно

б) m = 61001 – 6902 : 17

_6902 |17      _61001
  68     |406          406
   _102             60595
102
         0
m = 60595 – верно
m = 60594, 135498 – неверно

172-173 Задания для самопроверки

Страницы 172-173 Задания для самопроверки

№1

8, 9, 0
n1 = 2 (т.к. 0 не может быть 1-ой цифрой)
n2 = 3
n3 = 3
N = 2 * 3 * 3 = 18

№2

б, в, д

№3

В

№4

1)

№5

А 1
Б 4
В 3

№6

б)

№7

в)

№8

1)

№9

Совпадает 12 букв: А; В; Е; К; М; Н; О; Р; С; Т; У; Х.
Автомобильный номер содержит 3 буквы
12³ = 1728
12 * 11 * 10 = 1320 комбинаций букв не повторяется

№10

У Вовы нет книг. Верно высказывание «меньше 1000 книг»

175-188 Итоговое повторение

Итоговое повторение, стр. 175

Задание 935

Приведите примеры:
а) натуральных чисел;
б) обыкновенных дробей;
в) чисел, не являющихся натуральными;
г) десятичных дробей.

Решение

а) 1; 2; 100; 10000.

б) 1/2 ; 1/3 ; 5/20 ; 10/100.

в) 0 ; 1/3 ; 1,5 ; 0,001.

г) 5,2; 18,5; 100,01; 0,0001.

Задание 936

Среди следующих чисел укажите натуральные:
18 ; 1/2 ; 1 ; 0 , 6 ; 0 ; 105 ; 12 , 4.

Решение

18; 1; 105 − натуральные числа.

Задание 937

Пятизначное число оканчивается цифрой 6. В этом числе переставили две последние цифры, но оно не изменилось. Какая цифра стояла в числе перед цифрой 6?

Решение

6.

Задание 938

На сколько изменится семизначное число, оканчивающееся на 40, если эти две цифры поменять местами?

Решение

***40 − ***04 = 36.

Задание 939

Верно ли, что если цифры, из которых составлено шестизначное число, записать в обратном порядке, то получится опять шестизначное число?

Решение

Нет, если шестизначное число оканчивается на 0.

Задание 940

В каком порядке выполняются действия в выражении без скобок, если в нём встречаются только сложение и деление?

Решение

Сначала деления − слева направо, а затем сложения − слева направо.

Задание 941

Вычислите устно:
а) 10 : 4
- 1,3
* 0,4
+ 0,32
?
б) 4 - 3,4
* 1,4
+ 0,06
: 1,8
?
в) 3 : 300
+ 0,37
: 1,9
* 8
?
г) 70 : 20
: 10
* 4
+ 1,04
?
д) 9,8 : 7
* 3
- 0,3
+ 2,1
?
е) 49 : 70
+ 9,8
: 5
: 0,3
?
ж) 3,9 + 2,7
: 11
* 13
?
з) 4,6 + 2,2
- 30,5
* 0,1
?

Решение

а) 2,5, 1,2, 0,48, 0,8.

б) 0,6, 0,84, 0,9, 0,5.

в) 0,01, 0,38, 0,2, 1,6.

г) 3,5, 0,35, 1,4, 2,44.

д) 1,4, 4,2, 3,9, 6.

e) 0,7, 10,5, 2,1, 7.

ж) 6,6, 0,6, 7,8, 5,05.

з) 6,8, 34, 3,5, 0,35.

Задание 942

Выполните действия:
1) 5555 + (82320 : 84 − 693) * 66;
2) 32087 − 87 * (67 + 62524 : 308);
3) 467915 + 137865 : (31353 − 48 * 609);
4) 51003 − (4968 + 709 * 52) + 203;
5) 612228 + (53007 − 52275 : 615);
6) 343 * (324378 : 54 − 4862) + 777;
7) 18408 : (268 * 75 − 19746) + 959;
8) (86 * 217 + 275116) : 859 + 279569.

Решение

1) 5555 + (82 320 : 84 − 693) * 66 = 5555 + (980 − 693) * 66 = 5555 + 287 * 66 = 555 + 18 942 = 24497

2) 32087 − 87 * (67 + 62524 : 308) = 32087 − 87 * (67 + 203) = 32087 − 87 * 270 = 32087 − 23490 = 8597

3) 467915 + 137865 : (31353 − 48 * 609) = 467915 + 137865 : (31353 − 29232) = 467915 + 137865 : 2121 = 467915 + 65 = 467980

4) 51003 − (4968 + 709 − 52) + 203 = 51003 − (4968 + 36 868) + 203 = 51003 − 41836 + 203 = 9167 + 203 = 9370

5) 612228 + (53007 − 52275 : 615) = 612228 + (53007 − 85) − 612228 + 52922 = 665150

6) 343 * (324378 : 54 − 4862) + 777 = 343 * (6007 − 4862) + 777 = 343 * 1145 + 777 = 392735 + 777 = 393512

7) 18408 : (268 * 75 − 19746) + 959 = 18408 : (20100 − 19746) + 959 = 18408 : 354 + 959 = 52 + 959 = 1011

8) (86 * 217 + 275116) : 859 + 279569 = (18662 + 275116) : 859 + 279569 = 293778 : 859 + 279569 = 342 + 279569 = 279911

Задание 943

Сформулируйте и запишите с помощью букв:
а) свойства сложения чисел;
б) свойства вычитания чисел;
в) свойства умножения чисел.
Приведите примеры, когда использование свойств арифметических действий упрощает вычисления.

Решение

а) a + b = b + a; (a + b) + c = a + (b + c)

б) a − (b + c) = a − b − c, a − (b − c) = a − b + c

в) a − b = b − а; (аb)с = а(bс); (а + b)c = ac + bc; (a − b)c = ac − bc

Задание 944

При каком условии:
а) сумма двух чисел равна одному из них;
б) разность равна уменьшаемому, нулю;
в) произведение равно одному из множителей, нулю;
г) частное равно делимому, нулю, единице?
Как найти делимое, если известны делитель, неполное частное и остаток?

Решение

а) если второе число равно 0

б) если вычитаемое равно 0, уменьшаемое равно вычитаемому

в) если второй множитель равен 1;
если хотя бы один из множителей равен 0.

г) Если делитель равен 1.
Если делимое равно 0, а делитель не равен 0.
Если делимое равно делителю, кроме случая, когда они оба равны 0.

Задание 945

Выполните деление с остатком:
а) 27450 на 89;
б) 30394 на 307.

Решение

а) 27450 = 89 * 308 + 38

б) 30394 = 307 * 99 + 1

Задание 946

При делении числа с на 12 получили в частном 7 и в остатке 5. Чему будут равны частное и остаток при делении числа с на 7?

Решение

Так как 5 < 7, то в остатке также будет 5, а неполное частное будет равно 12.

Задание 947

Найдите значение выражения:
а) 85 + 203x + 102x + 91, если х = 76; 201;
б) 79у − (23у − 15у), если у = 15; 309.

Решение

а) 85 + 203x + 102x + 9 = 305x + 176
При x = 76
305 * 76 + 176 = 23356
При x = 201
305 * 201 + 176 = 61481

б) 79y − (23y − 15y) = 79y − 23y + 15y = 71y
При у = 15
71 * 15 = 1065
При у = 309
71 * 309 = 21939

Задание 948

Какая дробь называется правильной; неправильной? Как представить в виде неправильной дроби число 2 1/7 ; 4?
Как выделить целую часть числа 19/6?

Решение

Правильной называется дробь у которой числитель меньше знаменателя.
Неправильной называется дробь у которой числитель больше или равен знаменателю.
$2\frac17=2+\frac17=\frac{14}7+\frac17=\frac{15}7$
$4=\frac41$
$\frac{19}6=\frac{6\ast3}6+\frac16=3\frac16$

Задание 949

Запишите в виде неправильной дроби число:
а) 3 12/13;
б) 203 11/15;
в) 4 11/12;
г) 704 9/14.

Решение

а) $3\frac{12}{13}=\frac{39}{13}+\frac{12}{13}=\frac{51}{13}$

б) $203\frac{11}{15}=\frac{3045}{15}+\frac{11}{15}$

в) $4\frac{11}{12}=\frac{48}{12}+\frac{11}{12}=\frac{59}{12}$

г) $704\frac9{14}=\frac{9856}{14}+\frac9{14}=\frac{9865}{14}$

Задание 950

Выполните действия:
а) 4 3/8 − ( 3 5/7 − 1 5/7 ) + 1 5/8;
б) 12 7/12 − 4 5/12 − ( 20 3/4 − 19 3/4 ).

Решение

а) $4\frac38-(3\frac57-1\frac57)+1\frac58=4\frac38-2+1\frac58=6-2=4$

б) $12\frac7{12}-4\frac5{12}-(20\frac34-19\frac34)=8\frac2{12}-1=7\frac2{12}$

Задание 951

В коробку положили 15 конфет «Маска», 20 конфет «Ромашка» и 40 ирисок. Какую часть всех конфет составляют конфеты каждого сорта?

Решение

15 + 20 + 40 = 75 (к.) - было всего
масок 15/75,
ромашек 20/75,
а ирисок 40/75.

Задание 952

Сколькими способами 4 пассажира могут разместиться в четырёхместном купе поезда?

Решение

4! = 1 * 2 * 3 * 4 = 24 (с.)
Ответ: 24 способами.

Задание 953

Мастерская за месяц должна сшить 38 костюмов. В первую неделю было сшито 7 костюмов, во вторую − 11 костюмов. Какую часть всех костюмов осталось сшить?

Решение

За первую неделю сшили 7/38,
за вторую неделю 11/38,
за первые две недели сшили 7/38 + 11/38 = 18/38,
тогда осталось сшить 1 − 18/38 = 38/38 − 18/38 = 20/38.

Задание 954

За месяц завод должен отгрузить 42 вагона продукции. В первую неделю отгрузили 12 вагонов, во вторую неделю − 8 вагонов. Какую часть всех вагонов осталось отгрузить заводу?

Решение

В первую неделю отгрузили 12/42, во вторую 8/42,
1 − 12/42 = 42/42 − 12/42 − 8/42 = 22/42 -  часть всех вагонов осталось отгрузить
Ответ: 22/42 часть всех вагонов.

Задание 955

Длина одной стороны четырёхугольника составляет 3/11 его периметра, длина другой 4/11 периметра, а сумма длин этих сторон равна 28 см. Найдите периметр четырёхугольника.

Решение

1) 3/11 + 4/11 = 7/11 - составляет длина первой и второй сторон вместе
2) 28 : 7 * 11 = 44 (см) - периметр
Ответ: 44 см.

Задание 956

Число лет сына составляет 2/11 числа лет отца, а число лет дочери 5/11 числа лет отца. Сколько лет отцу, если сыну и дочери вместе 28 лет?

Решение

1) 2/11 + 5/11 = 7/11 числа лет отца сыну и дочери вместе,
2) 28 : 7 * 11 = 44 (года) - отцу.
Ответ: 44 года.

Задание 957

В палатку привезли 1260 кг картофеля. В первый день было продано 2 3 всего картофеля, во второй день 5/7 г остатка. Сколько килограммов картофеля осталось после двух дней продажи?

Решение

1) 1 − 2/3 = 1/3 всего картофеля осталось после первого дня
2)  1260 * 1/ 3 = 1260 : 3 = 420 (кг) - картофеля осталось после первого дня
3)  1 − 5/7 = 2/7 - картофеля осталось после второго дня
4) 420 * 2/7 = 420 : 7 * 2 = 120 (кг) - картофеля осталось после двух дней продажи
Ответ: 120 кг.

Задание 958

Приняв за единичный отрезок длину 10 клеток тетради, отметьте на луче точки, координаты которых равны:
а) 0 ; 1 ; 0,3 ; 3/5 ; 0,6 ; 1 2/5 ; 1,2;
б) 0 ; 1 ; 0,2 ; 4/5 ; 0,8 ; 1 3/5 ; 1,4.

Решение

Задание 959

Назовите какое−нибудь значение координаты точки С, лежащей на координатном луче между точками А и В, если:
а) А(2) и В(5);
б) А(2) и В(3);
в) А(2,8) и В(3,5);
г) А(2,9) и В(3);
д) А(4/5) и В(1).

Решение

а) C(3,2)

б) С(2,8)

в) С(3)

г) C(2,99)

д) C(0,85)

Задание 960

Как на координатном луче расположены точки А(х) и В(у), если:
а) х > у;
б) х = у;
в) х < у?

Решение

а) А правее В

б) А и В одна и та же точка

в) А левее В

Задание 961

Как сравнить:
а) четырёхзначное и пятизначное натуральные числа;
б) два шестизначных числа, первое из которых начинается цифрой 7, а второе − цифрой 5;
в) натуральное число и 0;
г) обыкновенные дроби с одинаковыми знаменателями;
д) десятичные дроби с разными целыми частями;
е) десятичные дроби с одинаковыми целыми частями?

Решение

а) Пятизначное всегда больше четырехзначного

б) То число, которое начинается на 7 всегда больше того, что начинается на 5

в) Натуральное число всегда больше, чем 0.

г) Из двух обыкновенных дробей с одинаковыми знаменателями больше то, у которого больше числитель

д) Из двух десятичных дробей с разными целыми частями больше то, у которой больше целая часть.

е) Из двух десятичных дробей с одинаковыми целыми частями больше та, у которой больше дробная часть.

Задание 962

Сравните числа:
а) 4357 и 986;
б) 7615 и 7613;
в) 0,75 и 1,000;
г) 12,815 и 2,819;
д) 1,2 и 1 3/5;
е) 3/4 и 7/8;
ж) 1 3/5 и 1 1/2;
з) 1 4/5 и 9/10;
и) 5/8 и 1/2.

Решение

а) 4357 > 986

б) 7615 > 7613

в) 0,75 < 1,000

г) 12,815 > 2,819

д) 1,2 < 1 3/5

е) 3/4 = 6/8 < 7/8

ж) 1 3/5 = 1,6 > 1 1/2 = 1,5

з) 1 4/5 = 1,8 < 9/10 = 1,9

и) 5/8 > 1/2 = 4/8

Задание 963

Приведите примеры округления:
а) натурального числа до тысячи;
б) десятичной дроби до единиц;
в) десятичной дроби до сотых.

Решение

а) 1900 ≈ 2000; 23100 ≈ 23000.

б) 0,6 ≈ 1; 0,01 ≈ 0.

в) 0,052 ≈ 0,05; 10,602 ≈ 10,60.

Задание 964

Как найти среднее арифметическое нескольких чисел? Как найти среднюю скорость?

Решение

Для нахождения среднего арифметического нескольких чисел нужно сумму этих чисел разделить на количество этих чисел. Средняя скорость равна частному от деления пройденного пути на время.

Задание 965

Вычислите устно:
а) 6 : 1,2
- 5
* 0,97
+ 3,15
?
б) 9 : 1,5
- 5
* 0,25
+ 6
?
в) 3 * 1,6
-1,2
: 12
+ 1,2
?
г) 0,6 * 6
+ 1,2
: 40
* 50
?
д) 30 * 3
- 4,8
: 0,7
* 0,01
?
е) 2 * 1,9
- 2,2
: 0,8
: 0,1
?
ж) 7 - 0,7
: 0,9
* 0,02
+ 0,66
?
з) 1,5 * 6
: 5
* 2
+ 2,4
?

Решение

а) 5, 0, 0, 3,15.

б) 6, 1, 0,25, 6,25.

в) 4,8, 3,6, З, 4,2.

г) 3,6, 4,8, 0,12, 6.

д) 9, 4,2, 6, 0,06.

е)3,8, 1,6, 2, 20.

ж) 6,3, 7, 0,14, 0,8.

з) 9, 1,8, 3,6, 6.

Задание 966

На рисунке 188 изображена шкала расстояний от города А до города B. Каждое деление шкалы соответствует расстоянию 20 км. Точками M, N, P отмечены расстояния, которые прошла автомашина через каждый час, двигаясь из города А в город В.
Определите:
а) чему равно расстояние от города А до города В;
б) какое расстояние прошла автомашина за первые два часа; за вторые два часа;
в) на каком расстоянии от города В была автомашина через 2 ч после выхода из города А;
г) какое расстояние прошла автомашина за 3 ч;
д) с какой средней скоростью шла автомашина в первые 2 ч; во вторые 2 ч.

Решение

а) 360 км

б) 180 км; 180 км.

в) 180 км

г) 300 км

д) 180 : 2 = 90 км/ч; 180 : 2 = 90 км/ч.

Задание 967

Какую дробь называют десятичной? Приведите примеры таких дробей и назовите по порядку первые четыре разряда, стоящие в десятичной дроби справа от запятой. Изменится ли десятичная дробь, если к ней справа приписать один или несколько нулей? Как представить обыкновенную дробь в виде десятичной? Приведите пример.

Решение

Десятичная дробью называют дробь, знаменатель которой кратен 10, например: 0,5; 1,1; 100,255;
При приписывании нулей справа от запятой в конец дроби, дробь не меняется:
1/10 = 0,1 ;
5 5/1000 = 5,005.

Задание 968

По какому правилу выполняется:
а) сложение (вычитание) обыкновенных дробей с одинаковыми знаменателями;
б) сложение (вычитание) десятичных дробей;
в) умножение десятичных дробей;
г) умножение десятичной дроби на 10, 100, 1000 и т. д.;
д) деление десятичной дроби на натуральное число;
е) деление числа на десятичную дробь;
ж) умножение десятичной дроби на 0,1; 0,01; 0,001 и т. д.;
з) деление десятичной дроби на 10, 100, 1000 и т. д.;
и) деление десятичной дроби на 0,1; 0,01; 0,001 и т. д.?

Решение

а) Числители складываются (вычитаются), а знаменатель остается тем же.

б) Как натуральные числа, с учётом запятой.

в) Дроби умножаются как натуральные числа, с учётом запятой.

г) Запятая сдвигается вправо на 1; 2; 3 знака и т. д.

д) Дробь делится на число, только в частном запятая сдвигается влево на число знаков после запятой в делимом.

е) Число делится на дробь, только в частном запятая сдвигается вправо на число знаков после запятой в делителе.

ж) В дроби запятая сдвигается влево на 1; 2; 3 знака и т. д.

з) В дроби запятая сдвигается влево на 1; 2; 3 знака и т. д.

и) В дроби запятая сдвигается вправо на 1; 2; 3 знака и т. д.

Задание 969

Найдите значение выражения:
а) 427 051 : 839 − 390 912 : 768 + 252 000 : 1260 + 249 249 : 249;
б) 917 580 : (194 + 25 * 37) − 386;
в) (23,79 : 7,8 − 6,8 : 17) * 3,04 − 2,04 * 0,85;
г) (15,36 − 4,36 * (20,74 : 6,8 − 7,6 : 19)) * 0,25;
д) ((3,2 + 0,32) : 0,1 − (50 − 7,2) * 0,1) * 100;
е) ((4,3 − 1,08) : 0,1 + (40 − 8,4) * 0,1) * 100.

Решение

а) 427051 : 839 − 390912 : 768 + 252000 : 1260 + 249249 : 249 = 509 − 509 + 200 + 1001 = 1201

б) 917580 : (194 + 25 * 37) − 386 = 917580 : (194 + + 925) − 386 = 917580 : 1119 − 386 = 820 − 386 = 434

в) (23,79 : 7,8 − 6,8 : 17) * 3,04 − 2,04 * 0,85 = (3,05 − 0,4) * 3,04 − 1,734 = 2,65 * 3,04 − 1,734 = 8,056 − 1,734 = 6,322

г) (15,36 − 4,36 * (20,74 : 6,8 − 7,6 : 191)) * 0,25 = (15,36 − 4,36 * (3,05 − 0,4) * 0,25 = (15,36 − 4,36 * 2,65) * 0,25 = (15,36 − 11,55) * 0,25 = 3,806 * 0,25 = 0,9515

д) ((3,2 + 0,32) : 0,1 − (50 − 7,2) * 0,1) * 100 = (3,52 : 0,1 − 42,8 * 0,1) * 100 = (35,2 − 4,28) * 100 = 30,92 * 100 = 3092

e) ((4,3 − 1,08) : 0,1 + (40 − 8,4) * 0,1) * 100 = (3,22 : 0,1 + 31,6 * 0,1) * 100 = (32,2 + 3,16) * 100 = 35,36 * 100 = 3536

Задание 970

Найдите значение выражения:
а) 8 * (1,4x + 13,6y) + 13 * (0,8x − 0,6у) при х = 1; у = 1;
б) 3 * (2,9р − 1,9m) + 2 * (2,3р + 0,7m) при р = 0,1; m = 0.

Решение

а) 8 * (1,4x + 13,6y) + 13 * (0,8x − 0,6y) = 8 * 1,4x + 8 * 13,6у + 13 * 0,8х − 13 * 0,6y =
= 11,2x + 10,4x + 108,8y − 7,8y = 21,6x + 101y;
при x = 1, у = 1 => 21,6 * 1 + 101 * 1 = 21,6 + 101 = 122,6.

б) 3 * (2,9р − 1,9m) + 2 * (2,3р + 0,7m) = 3 * 2,9р − 3 * 1,9m + 2 * 2,3р + 2 * 0,7m = 8,7р − 5,7m + 4,6р + 1,4m = 13,3р − 4,3m;
при р = 0,1, m = 0 => 13,3 * 0,1 − 4,3 * 0 = 1,33.

Задание 971

Надо было перевезти 51 т зерна. Зерно перевозили в машине с двумя прицепами. Сколько сделали поездок, если в кузов машины входило 4,8 т зерна, а в каждый из прицепов − 2,7 т?

Решение

1) 4,8 + 2,7 * 2 = 4,8 + 5,4 = 10,2 (т) - может перевезти машина с двумя прицепами за один раз
2) 51 : 10,2 = 5 (поездок) - потребуется для перевозки 51 т зерна
Ответ: 5 поездок.

Задание 972

За первые 14 рабочих дней завод изготовил 560 стиральных машин, а затем стал изготавливать в день на 5 машин больше. Сколько машин выпустил завод за 20 рабочих дней?

Решение

1) 560 : 14 = 40 (м.)  - в день изготавливал завод сначала
2) 20 − 14 = 6 (д.) - завод работал с повышенной производительностью
3) 40 + 5 = 45 (м.) - стал изготавливать завод в день
4) 45 * 6 = 270 (м.) - изготовил завод за последние 6 дней
4) 560 + 270 = 830 (м.) - изготовил завод за 20 дней
Ответ: 830 машин.

Задание 973

Отцу 40 лет, сыну 5 лет. Во сколько раз отец будет старше сына через 2 года? На сколько лет отец старше сына сейчас и на сколько лет будет старше через 2 года?

Решение

1) 40 − 5 = на 35 (лет) - отец старше сына сейчас
2)  40 + 2 = 42 (г.) будет отцу через 2 года,
3) 5 + 2 = 7 (лет) - будет сыну
4) 42 : 7 = в 6 (раз) - отец будет старше сына
Ответ: в 6 раз.

Задание 974

В классе 7 человек хорошо умеют плавать. Сколькими способами из них можно составить команду из трёх человек для участия в школьных соревнованиях?

Решение

7 * 6 * 5 = 210 (с.) - можно составить команду
Ответ: 210 способами.

Задание 975

По какому правилу находится
а) неизвестное слагаемое;
б) неизвестное уменьшаемое;
в) неизвестное вычитаемое;
г) неизвестный множитель;
д) неизвестное делимое;
е) неизвестный делитель?

Решение

а) из суммы вычитается известные слагаемые

б) к разности прибавляется вычитаемое

в) из уменьшаемого вычитается разность

г) произведение делится на известный множитель

д) делитель умножается на частное

е) делимое делится на частное

Задание 976

Решите уравнение:
а) 22x + х − 10 = 59;
б) 14у − 2у + 76 = 100;
в) (7а − 2а) * 8 = 80;
г) (15b + b) : 4 = 3;
д) (0,87m − 0,66m) * 10 : 2 : 3 = 0;
е) 10 * (1,37k − 0,12k) : 5 : 8 = 0.

Решение

а) 22z + x − 10 = 59
23x = 59 + 10
x = 69 : 23
х = 3

б) 14y − 2y + 76 = 100
12y = 100 − 76
у = 24 : 12
у = 2

в) (7a − 2a) * 8 = 80
5a = 80 : 8 
a = 10 : 5
а = 2

г) (15b + b) : 4 = 3
16b = 3 * 4 
16b =  12
b = 12 : 16
b = 0,75

д) (0,87m − 0,66m) * 10 : 2 : 3 = 0
0,87m − 0,66m = 0
(0,87 − 0,66) * m = 0
m = 0

е)10 * (1,37k − 0,12k) : 5 : 8 = 0
1,37k − 0,12k = 0
(1,37 − 0,12) * k = 0
k = 0

Задание 977

В одном пакете 3 яблока и 10 слив, а в другом − 3 яблока и 15 слив. Какова масса одного яблока и какова масса одной сливы, если масса первого пакета 0,5 кг, а масса второго 0,6 кг?

Решение

1) 15 - 10 = 5 (с.) - на столько больше слив во втором пакете
2) 0,6 − 0,5 = 0,1 (кг) - масса пяти слив
3) 0,1 : 5 = 0,02 (кг) - масса одной сливы
4) 0,5 − 0,02 * 10 = 0,3 (кг) - весят 3 яблока
5) 0,3 : 3 = 0,1 (кг) - весит одно яблоко
Ответ: 0,1 кг и  0,02 кг.

Задание 978

Масса деревянного бруска объёмом 4 дм³ равна 2,8 кг. На сколько килограммов масса стального бруска такого же объёма больше, если известно, что масса стального бруска объёмом 3 дм³ равна 23,4 кг?

Решение

1) 23,4 : 3 = 7,8 (кг) - масса 1 дм³ стали
2) 7,8 * 4 = 31,2 (кг) - весят 4 дм³ стали
3) 31,2 − 2,8 = 28,4 (кг) - на столько 4 дм³ стали тяжелее 4 д м 3 дерева
Ответ: на 28,4 кг.

Задание 979

Масса слонихи вместе со слонёнком равна 7,2 т. Какую массу имеет слонёнок, если он легче слонихи в 5 раз?

Решение

Пусть масса слоненка х,
тогда масса слонихи 5х.
Составим уравнение:
х + 5х = 7,2
6х = 7,2
х = 7,2 : 6
х = 1,2
Значит, 1,2 т весит слоненок
Ответ: 1,2 т.

Задание 980

Саша спросил Сеню: «Сколько тебе лет?» Сеня ответил: «Если число моих лет увеличить в 3 раза, а потом уменьшить на 17, то получится 16 лет». Сколько лет Сене?

Решение

Пусть Сене х лет
Составим уравнение:
3х − 17 = 16
3х = 33
х = 11
Значит, Сене 11 лет.
Ответ: 11 лет.

Задание 981

Если число лет Кати увеличить на 11 и полученный результат уменьшить в 6 раз, то будет 4. Сколько лет Кате?

Решение

Пусть Кате х лет
Составим уравнение:
(х + 11) : 6 = 4
х + 11 = 4 * 6
х = 24 − 11
х = 13
Значит, Кате 13 лет.
Ответ: 13 лет.

Задание 982

Один раз в год наступают сутки, когда день на 40 мин длиннее ночи. Сколько времени длится ночь в эти сутки?

Решение

Пусть ночь длится х мин,
тогда день длится х + 40 мин,
60 * 24 = 1440 (мин) - всего в сутках.
Составим уравнение:
х + (х + 40) = 1440
2х = 1440 − 40
х = 1400 : 2
х = 700
Значит, 700 минут длится ночь
700 мин = 11 ч 40 мин.
Ответ: 11 ч 40 мин.

Задание 983

На чтение девочка потратила в 3 раза меньше времени, чем на прогулку. Сколько времени заняла прогулка, если она продолжалась на 40 мин больше, чем чтение?

Решение

Пусть прогулка у девочки длилась х минут,
тогда чтение (х : 3) мин.
Составим уравнение:
х − х : 3 = 40
2х = 40 * 3
х = 120 : 2
х = 60
Значит, 60 минут длилась прогулка.
60 мин = 1 час.
Ответ: 1 час.

Задание 984

Что называется процентом? Как найти один процент числа? Как найти несколько процентов числа?

Решение

Процентом называется одна сотая часть. Чтобы найти 1% от числа, нужно число разделить на 100.
Чтобы найти 5 процентов от числа, нужно число разделить на 100 и умножить на 5.

Задание 985

На складе было 3,2 т риса. 80% всего риса отправили в магазин и палатку, причём в магазин отправили на 1,28 т больше, чем в палатку. Сколько риса отправили в палатку?

Решение

Пусть в палатку отправили х т,
тогда в магазин х + 1,28 т,
а всего в палатку и магазин 3,2 : 100 * 80 = 2,56 т.
Составим уравнение:
х + (х + 1,28) = 2,56
2х = 2,56 − 1,28
х = 1,28 : 2
х = 0,64
Значит, 0,64 т отправили в палатку.
Ответ: 0,64 т.

Задание 986

На дровяном складе продали в первый день 17% всех дров, во второй день − 18%, а в третий − лишь 5% всех дров. После этого на складе осталось 6000 м³ дров. Сколько кубических метров дров было на складе и сколько продали в первый день?

Решение

1) 100 − (17 + 18 + 5) = 60% (д.) осталось на складе
2) 6000 : 60 * 100 = 10000 (м³) - дров было на складе
3) 10000 : 100 * 17 = 1700 (м³) - дров продали в первый день
Ответ: 10000 м³ и 1700 м³.

Задание 987

Какие отрезки, лучи и прямые на рисунке 189 пересекаются? Какие из этих фигур пересекают окружность?

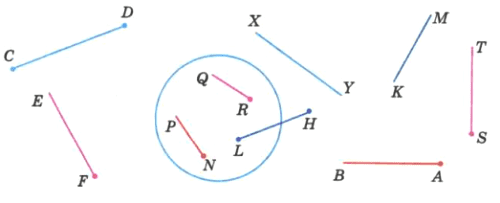
Решение

Пересекаются: FE и NP, FE и RQ, XY и KM, XY и LH, XY и AB, ST и KM, AB и KM, KM и NР, NP и RQ.
Окружность пересекают: NP, RQ, LH, AB, KM.

Задание 988

Выполните рисунки:
а) начертите отрезок и отметьте точку, лежащую на отрезке, и точку, не лежащую на нём;
б) начертите прямую и отметьте на ней точку М; ответьте, как называются части, на которые точка М делит прямую;
в) начертите отрезок и луч так, чтобы они не пересекались; чтобы отрезок лежал на луче; чтобы отрезок и луч имели одну общую точку;
г) начертите угол и прямую так, чтобы прямая пересекала только одну сторону угла.

Решение

а)


б) Точка М делит прямую на два луча.


в)

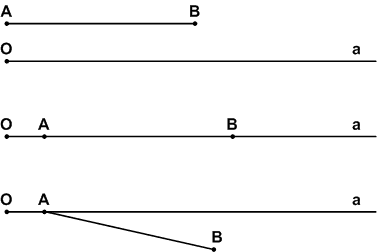
г) 

Задание 989

Можно ли сравнить:
а) два отрезка, зная их длины;
б) два угла, зная их градусные меры?

Решение

а) Из двух отрезков больше тот, у которого больше длина.

б) Из двух углов больше тот, у которого больше градусная мера.

Задание 990

На луче РК взята точка М так, что РМ = 5 см. Сколько отрезков длиной 3 см можно отложить на луче от точки М? Сколько отрезков длиной 7 см можно отложить на луче от точки М?

Решение

Отрезки длиной 3 см можно отложить влево 1, а вправо любое количество;
длиной 7 см − влево ни одного, а вправо любое количество.

Задание 991

На прямой отмечены точки А, В, С и D (рис. 190) так, что АВ = CD. Поставьте вместо звёздочки знак или = так, чтобы для длин отрезков получилось верное равенство или неравенство:
а) ВА * DC;
б) АС * СВ;
в) АС * BD;
г) AD* ВС.

Решение

а) ВА = DC

б) АС > СВ

в) АС = BD

г) AD > ВС

Задание 992

На отрезке MN отмечены две точки С и D так, что точка С лежит между точками N и D. Найдите длину отрезка MNy если DC = 2 см, DN = 6 см, МС = 5 см.

Решение

MN = MD + DC + CN = (MC − DC) + DC + DN − DC = MC + DN − DC = 6 + 5 − 2 = 9 см.

Задание 993

Стороны многоугольника ABCDE равны: АВ = 6,4 см, ВС = 5 см, CD = 6,3 см, DE = 5,8 см и АЕ = 3 см. Найдите периметр этого многоугольника. Как называется такой многоугольник? Что такое периметр многоугольника?

Решение

PABCDE = AB + BC + CD + DE + AE = 6,4 + 5 + 6,3 + 5,8 + 3 = 26,5 см.
ABCDE − пятиугольник.

Задание 994

С помощью какого инструмента можно найти:
а) длину отрезка;
б) градусную меру угла?
В каких единицах измеряются эти величины?

Решение

а) с помощью линейки

б) с помощью транспортира

Длина измеряется в миллиметрах, сантиметрах, дециметрах, метрах и километрах.
Углы измеряется в градусах.

Задание 995

Начертите острый угол ВСЕ и тупой угол DAK и определите их градусные меры. Начертите прямой угол Р и развёрнутый угол М. Какова градусная мера прямого угла? развёрнутого угла? Какую часть развёрнутого угла составляет угол в 1°?

Решение

∠ВСЕ = 45° < 90° − острый угол, 90° < ∠DAK = 135° < 180° − тупой угол,
∠P = 90° − прямой угол, ∠M = 180° − развернутый угол.
Угол в 1° составляет 1/180 часть развернутого угла.

Задание 996

Начертите угол МОК в 160°. Проведите луч ОВ так, чтобы он разделил угол МОК пополам. Как называется такой луч?

Решение

Луч ОB называется биссектрисой угла МОК.

Задание 997

Начертите четырёхугольник ABCD, у которого ∠A = 40°, ∠B = 140°, ∠C = 50°. Измерьте величину угла D.

Решение

Величина угла ∠D = 130°.

Задание 998

Угол АОВ на рисунке 191 разделён на 5 равных углов. Назовите углы, которые составляют 3/5 угла АОВ. Найдите величину угла СОР, если угол АОВ равен 100°.

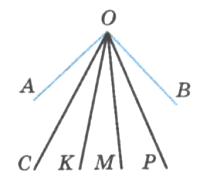
Решение

∠ AOM =∠ COP =∠ KOB = 3/5 ∠ AOB;
∠ COP = 100 * 3/5 = 60 °.

Задание 999

На рисунке 192 угол АОС равен углу DOB. Докажите, что угол АО В равен углу COD.

Решение

∠AOB + ∠DOB = ∠AOD;
∠COD + ∠AOC = ∠AOD;
∠AOB = ∠AOD − ∠DOB;
∠COD = ∠AOD − ∠AOC.
Так как ∠DOB = ∠AOC => ∠AOB = ∠COD.

Задание 1000

Прямые АВ и CD (рис. 193) пересекаются в точке О. Докажите, что углы АОС и BOD равны.

Решение

∠AOB = ∠COD = 180°;
∠COD = ∠AOC + ∠AOD;
∠AOB = ∠AOD + ∠BOD;
∠AOD + ∠AOC = ∠AOD+ ∠BOD;
∠AOC = ∠BOD + ∠AOD − ∠AOD;
∠AOC = ∠BOD.

Задание 1001

Не пользуясь транспортиром, определите угол между стрелками часов на рисунке 194.

Решение

а) 30° * 2 = 60°

б) 5 * 30° = 150°

в) 1,5 * 30° = 45°

г) 3,5 * 3° = 10,5°

д) 4,5 * 30° = 135°

Задание 1002

Вычислите устно:
а) 0,5 * 4
: 0,1
- 0,8
: 30
?
б) 2 - 0,6
* 0,3
: 6
+ 0,23
?
в) 7,2 : 0,1
: 7,2
* 0,36
+ 0,7
?
г) 7,5 * 10
: 50
: 5
* 0,4
?
д) 57 * 0,1
: 3
+ 4,4
: 0,9
?
ж) 0,82 - 0,4
: 0,6
* 5
- 2,5
?
з) 4,4 : 11
: 0,1
* 0,25
: 20
?
е) 0,25 * 2
* 0,6
+ 3,7
: 10
?

Решение

а) 2, 20, 19,2, 0,64.

б) 1,4, 4,2, 0,7, 0,93.

в) 7,2, 10, 3,6, 4,3.

г) 75, 1,5, 0,3, 0,12.

д) 5,7, 1,9, 6,3, 7.

e) 0,42, 0,7, 3,5, 1.

ж) 0,4, 4, 1, 0,05.

з) 0,5, 0,3, 4, 0,4.

Задание 1003

Паша пустился догонять Борю, когда тот отбежал от него на 360 м, и догнал через 9 мин. С какой скоростью бежал Паша, если скорость Бори была 0,2 км/мин?

Решение

Пусть х - скорость Паши,
тогда он догонял Борю со скоростью х − 0,2 , это скорость сближения.
Составим уравнение:
(х − 0,2) * 9 = 0,36
х − 0,2 = 0,04
х = 0,240
Значит, скорость Паши 0,240 км/мин.
Ответ: 0,240 км/мин.

Задание 1004

Серёжа стал догонять Колю, когда тот находился от него на расстоянии 840 м, и догнал через 6 мин. Найдите скорость Коли, если его скорость была в 2 раза меньше скорости Серёжи.

Решение

Пусть х − скорость Коли,
тогда 2х − скорость Сережи.
Составим уравнение:
(2х − х) * 6 = 840
х = 840 : 6
х = 140
Значит, скорость Коли 140 м/мин.
Ответ: 140 м/мин.

Задание 1005

Из двух пунктов одновременно навстречу друг другу вышли грузовая и легковая машины. Скорость грузовой автомашины в 2 раза меньше скорости легковой. Найдите скорость каждой автомашины, если известно, что расстояние между пунктами 480 км и машины встретились через 4 ч.

Решение

Пусть скорость грузовой машины − х,
тогда скорость легковой − 2x.
Составим уравнение:
(х + 2x) * 4 = 480
3х = 480 : 4 = 120
х = 120 : 3
х = 40 
Значит, 40 км/ч − скорость грузовой машины,
40 * 2 = 80 (км/ч) - скорость легковой машины
Ответ: 40 км/ч и 80 км/ч.

Задание 1006

Два поезда вышли навстречу друг другу одновременно из двух городов, расстояние между которыми 592 км. Через 4 ч они встретились. Какова скорость каждого поезда, если известно, что скорость одного из них на 8 км/ч больше скорости другого?

Решение

Пусть х − скорость первого поезда,
тогда х + 5 − скорость второго поезда.
Составим уравнение:
х * 3 + (х + 5) * 3 = 495
3х + 3х = 495 − 15
х = 480 : 6
х = 80
Значит, 80 км/ч − скорость первого поезда,
80 + 5 = 85 (км/ч) − скорость второго поезда.
Ответ: 80 км/ч и 85 км/ч.

Задание 1007

Из города А в город В выехал велосипедист. Через 3 ч после его выезда навстречу ему из города В выехал мотоциклист со скоростью 42 км/ч. Через 2 ч после выезда мотоциклиста они встретились. Найдите скорость велосипедиста, если расстояние между городами А и В равно 144 км.

Решение

Пусть х − скорость велосипедиста,
он ехал 3 + 2 = 5 часов.
Составим уравнение:
5х = 144 − 2 * 42 = 144 − 84 = 60
х = 60 : 5
х = 12
Значит, скорость велосипедиста 12 км/ч.
Ответ: 12 км/ч.

Задание 1008

Из одного и того же пункта одновременно в противоположных направлениях вышли два пешехода. Через 3 ч расстояние между ними стало 21 км. Найдите скорость второго пешехода, если скорость первого 4 км/ч.

Решение

Пусть х − скорость второго пешехода,
тогда скорость удаления пешеходов x + 4 км/ч.
Составим уравнение:
(х + 4) * 3 = 21
х + 4 = 7
х = 7 − 4
х = 3
Значит, скорость второго пешехода 3 км/ч.
Ответ: 3 км/ч.

Задание 1009

Из одной и той же точки шоссе в противоположных направлениях выехали два велосипедиста, один со скоростью 12 км/ч, а другой со скоростью 14 км/ч. Первый велосипедист выехал на час раньше второго. Через сколько времени после выезда первого велосипедиста расстояние между велосипедистами будет равно 64 км?

Решение

Пусть первый велосипедист ехал х часов,
тогда второй ехал х − 1 ч.
Составим уравнение:
12x − 14(х − 1) = 64
12x + 14x − 14 = 64
26х = 64 + 14 = 78
x = 78 : 26
х = 3
Значит, 3 часа ехал первый велосипедист.
Ответ: 3 часа.

Задание 1010

Скорость течения 2,2 км/ч. Собственная скорость катера 15,3 км/ч. Какой путь прошёл катер, если по течению он шёл 3 ч, а против течения 4 ч?

Решение

 (15,3 + 2,2) * 3 + (15,3 − 2,2) * 4 = 104,9 (км) - прошел катер
Ответ: 104,9 км

Задание 1011

Теплоход прошёл по течению 145 км за 5 ч. Сколько времени ему потребовалось на обратный путь, если скорость течения 4,5 км/ч?

Решение

1) 145 : 6 = 29 (км/ч) - скорость теплохода по течению
2)  29 − 2 * 4,5 = 20 (км/ч) - скорость против течения
3)  145 : 20 = 7,25 (ч) -  затратил теплоход на обратный путь
7,25 ч = 7 ч 15 мин. 
Ответ: 7 ч 15 мин.

Задание 1012

Назовите известные вам единицы измерения длины, площади, объёма.

Решение

Длина: метр, сантиметр, миллиметр;
Площадь: га, акр, сотка;
Объем: литр, декалитр, кубический метр.

Задание 1013

Сколько аров в гектаре? квадратных метров в аре? квадратных сантиметров в квадратном дециметре? квадратных сантиметров в квадратном метре?

Решение

1 га = 100 а, 1 а = 100 м², 1 дм² = 100 см², 1 м² = 10000 см².

Задание 1014

Какую часть квадратного сантиметра составляет квадратный миллиметр? Какую часть квадратного метра составляет квадратный сантиметр? Какую часть гектара составляет квадратный метр? Какую часть квадратного километра составляет гектар?

Решение

1 мм² = 0,01 см², 1 см² = 0,0001 м², 1 м² = 0,0001 га, 1 га = 0,01 км².

Задание 1015

Выразите:
а) в метрах: 6 дм, 23 см, 29 дм, 129 см, 2 м 3 дм;
б) в квадратных метрах: 3 дм², 27 дм², 288 дм²;
в) в часах: 11 мин, 35 мин, 73 мин, 1 ч 24 мин;
г) в тоннах: 4 кг, 15 кг, 240 кг, 1250 кг.

Решение

а) 6 дм = 0,6 м
23 см = 0,23 м
29 дм = 2,9 м
129 см = 1,29 м
2 м 3 дм = 2,3 м

б) 3 д м² = 0,03 м²
27 дм² = 0,27 м²
288 дм² = 2,88 м²

в) 11 мин = 11/60 ч
35 мин = 35/60 ч
73 мин = 1 13/60 ч
1 ч 24 мин = 1 24/60 ч

г) 4 кг = 0,004 т
15 кг = 0,015 т
240 кг = 0,24 т
1250 кг = 1,25 т

Задание 1016

Самый длинный день в Москве длится 1057 мин. Выразите в часах продолжительность этого дня. Какова продолжительность самой короткой ночи?

Решение

1057 мин 17 * 30 + 37 мин = 17 ч 37 мин;
24 ч − 17 ч 37 мин = 6 ч 23 мин. - продолжительность самой короткой ночи
Ответ: 6 ч 23 мин.

Задание 1017

Как найти:
а) площадь прямоугольника;
б) площадь квадрата;
в) объём прямоугольного параллелепипеда;
г) объём куба?
Запишите эти правила в виде формул.

Решение

а) S = ab, где а и b − длины его сторон.

б) S = а², где а − длина его стороны.

в) V = аbс, где а, b, с − длины его ребер.

г) V = а³, где а длина ребра куба.

Задание 1018

Сколько кубических сантиметров в кубическом дециметре? Сколько кубических дециметров в кубическом метре? Чему равен литр? Какую долю кубического дециметра составляет кубический сантиметр? Какую долю кубического метра составляет кубический сантиметр?

Решение

1 дм³ = 1000 см³; 1 м³ = 1000 дм³; 1 л = 1 дм³; 1 см³ = 0,001 дм³; 1 с м³ = 0,000001 м³.

Задание 1019

Из скольких прямоугольников состоит поверхность прямоугольного параллелепипеда? Сколько граней, рёбер, вершин имеет прямоугольный параллелепипед? Какой прямоугольный параллелепипед называют кубом? Из каких фигур состоит поверхность куба? Каковы рёбра куба?

Решение

Из 6 прямоугольников; 6 граней, 12 ребер, 8 вершин.
Кубом называется прямоугольный параллелепипед, у которого все ребра равны.
Поверхность куба состоит из 6 квадратов. Все ребра куба равны между собой.

Задание 1020

Как формулируется:
а) свойство площадей равных фигур;
б) свойство площадей фигуры и её частей;
в) свойство объёмов равных фигур;
г) свойство объёмов фигуры и её частей?

Решение

а) площади равных фигур равны

б) площадь фигуры равна сумме площадей ее частей

в) объемы равных фигур равны

г) объем фигуры равен сумме объемов ее частей

Задание 1021

Найдите площадь прямоугольника, стороны которого равны 24,6 см и 18,5 см. Выразите площадь в квадратных дециметрах.

Решение

S = ab = 24,6 * 18,5 = 455,1 см² = 4,551 дм².

Задание 1022

а) Найдите объём прямоугольного параллелепипеда с измерениями 28,2 см, 30 см и 25,5 см и выразите его в кубических дециметрах.
б) Найдите объём куба с ребром 8 дм и выразите его в кубических метрах.

Решение

а) V = abc = 28,2 * 30 * 25,5 = 21573 см³ = 21,573 дм³

б) V = а³ = 83 = 256 дм³ = 0,256 м³

Задание 1023

Два прямоугольника имеют одну и ту же площадь. Длина первого прямоугольника равна 0,6 м, а ширина − 4 дм. Чему равна длина второго прямоугольника, если его ширина 30 см? Найдите и сравните периметры этих прямоугольников.

Решение

0,6 м = 60 см, 4 дм = 40 см;
S = 60 * 40 = 2400 см²,
a = S : b = 2400 : 30 = 80 см.
P 1 = 2 * (60 + 40) = 2 * 100 = 200 см;
P 2 = 2 * (80 + 30) = 2 * 110 = 220 см.
P 2 > P 1.

Задание 1024

Периметр прямоугольника 0,36 м. Его длина в 2 раза больше ширины. Чему равна площадь прямоугольника?

Решение

Пусть ширина прямоугольника равна х,
тогда его длина равна 2х.
Составим уравнение:
(х + 2х) * 2 = 0,36
3х = 0,36 : 2 = 0,18
х = 0,18 : 3
х = 0,06
Значит, 0,06 м − ширина прямоугольника,
0,06 − 2 = 0,12 (м) − длина прямоугольника.
S = a b = 0,06 * 0,12 = 0,0072 м² - площадь
0,0072 м² = 72 см²
Ответ: 72 см².

Задание 1025

Найдите площадь поверхности и объём прямоугольного параллелепипеда, длина которого равна 12 см, ширина − 7,5 см, а высота − 10 см.

Решение

S = 2 ( a b + а с + b c ) = 2 * (12 * 7,5 + 12 * 10 + 10 * 7,5 ) = 570 (см²) - площадь поверхности
V = a b c = 12 * 10 * 7,5 = 900 (см³) - объем
Ответ: 570 см², 900 см³.

Задание 1026

Ширина прямоугольного параллелепипеда равна а см, длина на 5 см больше ширины, а высота равна 4 см. Составьте выражение для нахождения объёма параллелепипеда.

Решение

V = a * (a + 5) * 4 = 4a * (a + 5).

Задание 1027

Из деревянного бруска, длина которого 8 см, ширина 0,6 дм и высота 4 см, вырезали куб с ребром 0,04 м. Чему равен объём оставшейся части бруска?

Решение

0,6 дм = 6 см; 0,04 м = 4 см.
1)  43 = 64 (см³) - объем куба
2) V = abc = 8 * 6 * 4 = 192 (см³)- объем бруска
3) 192 − 64 = 128 (см³) - объем оставшейся части
Ответ: 128 см³.

Задание 1028

Какой объём занимает вода, налитая в мензурку (рис. 195)? Числа на шкале мензурки означают кубические сантиметры (миллилитры).

Решение

Налито 250 см³ воды.

Задание 1029

Какие из квадратов на рисунке 196 равны?

Решение

Равны между собой внешний квадрат верхнего
рисунка и внешний квадрат нижнего, внутренний квадрат верхнего и внутренний нижнего рисунка.

Задание 1030

Среди фигур, обозначенных буквами, найдите равные фигуры (рис. 197).

Решение

C = K, A = P = M = X, F = B.

Задание 1031

На рисунке 198 изображён куб. Назовите рёбра верхней и нижней граней, переднюю грань, вершины правой грани, равные рёбра.

Решение

Ребра верхней грани: АВ, ВР, РК, КА.
Ребра нижней грани: CD, DN, NM, МС.
Передняя грань ВРМС.
Вершины правой грани: А, В, С, D.
Все рёбра куба равны между собой.

Задание 1032

Пятиугольное поле ABCDM, план которого изображён на рисунке 199, разбито на четыре части отрезками АС и ВМ. Назовите эти части и найдите площадь поля, если площади треугольных частей равны 50 тыс. м², 60 тыс. м², 170 тыс. м², а четырёхугольной − 380 тыс. м².

Решение

Поле разбито на части: АВР, СРВ, АРМ, CDMP.
Площадь равна сумме площадей частей поля
S = 50 + 60 + 170 + 380 = 660 тыс. м².

Задание 1033

Дополните каждый треугольник, изображённый на рисунке 200, до прямоугольника и найдите площади треугольников.

Решение

S DEK = S DMEP * 2 + S PENK : 2 = 3 * 2 : 2 + 6 * 3 : 2 = 12 (см).
S ABC = S ABCF : 2 = 5 * 4 : 2 = 10 (см²).

Задание 1034

Каким свойством обладают точки окружности? Какой отрезок называют радиусом окружности? Диаметром окружности? Начертите окружность и проведите три радиуса этой окружности и её диаметр.

Решение

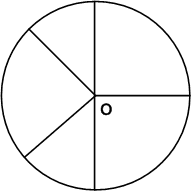
Точки окружности равноудалены от центра окружности.
Радиус − отрезок, один конец которого находится в центре окружности, а другой лежит на ней.
Диаметр − отрезок проходящий через центр окружности, оба конца которого лежат на ней.

Задание 1035

Начертите окружность и проведите два её радиуса, образующие прямой угол.

Решение

Задание 1036

Начертите окружность с центром О и радиусом 4,7 см. Постройте два отрезка АВ и АС длиной 3 см так, чтобы точки А, В и С лежали на окружности.

Решение

Задание 1037

Запишите все трёхзначные числа, для записи которых используются только цифры 3 и 0.

Решение

300, 330, 303, 333.

Задание 1038

Выполните действия:
а) (246535 − 85897) : 1306;
б) 157464 : (14904 : 23);
в) 1600731 : (5163 − 356);
г) 515453 : (261 924 : 156);
д) (97548 + 69432) : (16400 − 15388);
е) 1067154 : 4807 − 189 + 707 * 390.

Решение

а) (246535 − 85897) : 1306 = 160638 : 1306 = 123

б) 157464 : (14904 : 23) = 157464 : 648 = 243

в) 1600731 : (5163 − 356) = 1600731 : 4807 = 333

г) 515453 : (261924 : 156) = 515453 : 1679 = 307

д) (97548 + 69 432) : (16400 − 15388) = 166980 : 1012 = 165

е)1067154 : 4807 − 189 + 707 * 390 = 222 − 189 + 275730 = 275763

Задание 1039

Составьте выражение и найдите его значение:
а) сумму 369 и 471 разделите на разность 872 и 842;
б) произведение чисел 38 и 48 разделите на сумму 39 и 57.

Решение

а) (369 + 471) : (872 − 842) = 840 : 30 = 28

б) (38 * 48) : (39 + 57) = 1824 : 96 = 19

Задание 1040

Решите уравнение:
а) 13x + 12x + 15 = 240;
б) (14x − 2х) : 17 = 312.

Решение

а) 13x + 12x + 15 = 240
25x = 225
x = 225 : 25
х = 9

б) (14x − 2x) : 17 = 312
12x = 312 * 17 = 5304
x = 5304 : 12
х = 442

Задание 1041

Верно ли неравенство 398 + 24 * 87 < 3100?

Решение

Да, верно: 398 + 24 * 87 = 398 + 2088 = 2486 < 3100.

Задание 1042

Подсчитайте, сколько печатных знаков:
а) на странице, если в ней 40 строк, а в строке 58 знаков (основной шрифт);
б) в строке, если на странице 48 строк, а всего на странице 3360 знаков (петит).

Решение

а) 40 * 58 = 2320 знаков

б) 3360 : 48 = 70 знаков

Задание 1043

Выделите целую часть числа:
а) 347/15;
б) 3271/32;
в) 437/24;
г) 4389/43.

Решение

а) $\frac{347}{15}=23\frac2{15}$

б) $\frac{3271}{32}=102\frac7{32}$

в) $\frac{437}{24}=18\frac5{24}$

г) $\frac{4389}{43}=102\frac3{43}$

Задание 1044

Выполните действия:
а) 7 3/17 + 8 5/17 − 1 6/17;
б) 5 7/10 − ( 4 3/10 − 2 1/10 );
в) 10 7/15 − 3 1/15 + 4 4/15;
г) 9 9/11 − ( 3 2/11 − 2 3/11 ).

Решение

а) $7\frac3{17}+8\frac5{17}-1\frac6{17}=7+8-1+\frac{3+5-6}{17}=14+\frac2{17}=14\frac2{17}$

б) $5\frac7{10}-(4\frac3{10}-2\frac1{10})=5\frac7{10}-2\frac2{10}=3\frac5{10}$

в) $10\frac7{15}-3\frac1{15}+4\frac4{15}=10-3+4+\frac{7-1+4}{15}=11+\frac{10}{15}=11\frac{10}{15}$

г) $9\frac9{11}-(3\frac2{11}-2\frac3{11})=9\frac9{11}-\frac{10}{11}=8\frac{10}{11}$

Задание 1045

Из 15 гусей белыми были 7, а остальные − серыми. Какую часть всех гусей составляли серые гуси?

Решение

15 − 7 = 8 (г.) - серых
Ответ: 8/15 от общего количества гусей.

Задание 1046

Из 18 верблюдов в караване 5 были одногорбыми, а остальные − двугорбыми. Какую часть всех верблюдов каравана составляли двугорбые верблюды?

Решение

18 − 5 = 13 (в.) - двугорбых
Ответ: 13/18.

Задание 1047

Площадь кухни 8 м², что составляет 1/5 площади всей квартиры. Какова площадь квартиры?

Решение

 8 : 1 * 5 = 40 (м²) - площадь всей квартиры
Ответ: 40 м².

Задание 1048

Выразите в метрах и дециметрах: 3 3/10 м ; 1 1/2 м ; 3 2/5 м.

Решение

3 3/10 м = 3 м 3 дм;
1 1/2 м = 1 м 5 дм;
3 2/5 м = 3 м 4 дм.

Задание 1049

Выразите в минутах: 1/5 ч; 3/4 ч; 2 1/2 ч; 5 2/3 ч.

Решение

1/5 ч 60 : 5 = 12 мин;
3/4 ч = 60 : 4 * 3 = 45 мин;
2 1/2 ч = 2 * 60 + 60 : 2 * 1 = 150 мин;
5 2/3 ч = 5 * 60 + 60 : 3 * 2 = 340 мин.

Задание 1050

В одни из суток года продолжительность ночи на 20 мин меньше продолжительности дня. Сколько времени длится день в эти сутки?

Решение

Пусть х − продолжительность дня,
тогда х − 40 − продолжительность ночи.
Составим уравнение:
х + (х − 40) = 24 * 60
2х = 1440 + 40
х = 1480 : 2
х = 740
Значит, продолжительность дня 740 мин.
740 мин = 12 ч 20 мин.

Задание 1051

Начертите координатный луч, приняв за единичный отрезок длину 10 клеток тетради.
Отметьте на этом луче точки: А (0) , В (0,3) , С (0,6) , D (1 1/2) , E (1,2) , М (1) , N (0,2) , K (4/5) , Р (0,8) , T (1 3/5).

Решение

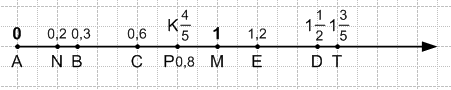
Задание 1052

Сравните числа:
а) 3 001 257 и 3 010 256;
б) 2,57 и 1,837;
в) 0,0005 и 0,003;
г) 0,94 и 0,495;
д) 1 8/17 и 2 1/17;
е) 12/25 и 9/25.

Решение

а) 3 001 257 < 3 010 256

б) 2,57 > 1,837

в) 0,0005 < 0,003

г) 0,94 > 0,495

д) 1 8/17 < 2 1/17

е)12/25 > 9/25

Задание 1053

Из деревни вышел пешеход, а через 2 ч вслед за ним выехал велосипедист. Скорость велосипедиста 10 км/ч, а скорость пешехода 5 км/ч. Через сколько времени после своего выезда велосипедист догонит пешехода?

Решение

Пусть х часов ехал велосипедист,
тогда пешеход шел х + 2 часа:
Составим уравнение:
(х + 2) * 5 = х * 10
5х + 10 = 10x
5х = 10
х = 2
Ответ: через 2 часа.

Задание 1054

Расстояние между двумя поездами, идущими навстречу друг другу, равно 8500 км. Через сколько часов поезда встретятся, если они будут идти без остановок: один со скоростью 80 км/ч, другой − 90 км/ч?

Решение

1) v = 80 + 90 = 170 (км/ч) - скорость сближения двух поездов
2) 8500 : 170 = 50 (ч) - через столько времени встретятся поезда.
Ответ: через 50 часов.

Задание 1055

С одной станции одновременно в противоположных направлениях вышли два поезда. Скорость одного из них 54 км/ч, а скорость другого на 18 км/ч больше. Через сколько часов расстояние между ними будет равно 504 км?

Решение

1) 54 + 54 + 18 = 126 (км/ч) - скорость удаления поездов
2) 504 : 126 = 4 (ч) - через столько времени между поездами будет 504 км
Ответ: через 4 часа.

Задание 1056

Теплоход шёл 2,5 ч по течению реки и 3,2 ч против течения. Какой общий путь прошёл теплоход, если его собственная скорость 22 км/ч, а скорость течения 3 км/ч?

Решение

1) 22 + 3 = 25 (км/ч) - скорость теплохода по течению
2)  22 − 3 = 19 (км/ч) - скорость против течения 
3)  2,5 * 25 + 3,2 * 19 = 123,3 (км) - прошел теплоход
Ответ: 123,3 км.

Задание 1057

Выполните действия:
а) (5124 − 4267) * 23 − 5200 : 325;
б) (13 412 + 124 956) : 46 − 73 * 36;
в) 3,42 : 0,57 * (9,5 − 1,1) : ((4,8 − 1,6) * (3,1 + 0,05));
г) (6,9 − 5,52 : 0,69 * 0,85) * ((5 − 0,125) : (3,7 + 0,05));
д) 1,7 * (3,9658 + 16,0142) − 8,591 : (7,1 − 5,68);
е) 14,1414 : (89,413 − 75,413) + 0,808 * (0,9163 + 0,0837).

Решение

а) (5124 − 4267) * 23 − 5200 : 325 = 857 * 23 − 16 = 19695

б) (13412 + 124956) : 46 − 73 • 36 = 138 368 : 46 − 2628 = 380

в) 3,42 : 0,57 * (9,5 − 1,1) : ((4,8 − 1,6) * (3,1 + 0,05) = 6 * 8,4 : (3,2 * 3,15) = 50,4 : 10,08 = 5

г) (6,9 − 5,52 : 0,69 * 0,85) * ((5 − 0,125) : (3,7 + 0,05)) = (6,9 − 8 * 0,85) * (4,875 : 3,75) = 0,1 * 1,3 = 0,13

д) 1,7 * (3,9658 + 16,0142) − 8,591 : (7,1 − 5,68) = 1,7 * 19,98 − 8,591 : 1,42 = 33,966 − 6,05 = 27,916

е)14,1414 : (89,413 − 75,413) + 0,808 * (0,9163 + 0,0837) = 14,1414 : 14 + 0,808 * 1 = 1,8181

Задание 1058

Упростите выражение:
а) 5а + 12,4 + 2,6 + 3,14 + 1,4а + 0,4а + 2,4;
б) 13,4 + 6 + 5,6 + 8,2b + 7,28 + 1,7b + 2,3.

Решение

а) 5a + 12,4 + 2,6 + 3,14 + 1,4a + 0,4a + 2,4 = 6,8a + 20,54

б) 13,4 + 6 + 5,6 + 8,2b + 7,28 + 1,7b + 2,3 = 9,9b + 34,58

Задание 1059

Найдите значение выражения:
а) 19,1у + 121,4 + 0,9у при у = 48,5;
б) 5,6m + 8,4m + 186,4 при m = 35,5.

Решение

а) 19,1y + 121,4 + 0,9y = 20y + 121,4
при y = 48,5 => 20 * 48,5 + 121,4 = 970 + 121,4 = 1091,4

б) 5,6m + 8,4m + 186,4 = 14m + 186,4
при m = 35,5 => 14 * 35,5 + 186,4 = 497 + 186,4 = 683,4

Задание 1060

В пяти маленьких и двух больших коробках 54 цветных карандаша, а в трёх маленьких и двух больших коробках 42 карандаша. Сколько карандашей в одной маленькой и сколько в одной большой коробке?

Решение

Из условий задачи следует, что 2 маленькие коробки содержат
1) 54 − 42 = 12 (к.) - содержат 2 маленькие коробки
2) 12 : 2 = 6 (к.) - содержит 1 маленькая коробка
3) (42 − 6 * 3) : 2 = (42 − 18) : 2 = 12 (к.) - содержит одна большая коробка
Ответ: 6 и 12 карандашей.

Задание 1061

Длина прямоугольника в 5 раз больше его ширины. Найдите стороны прямоугольника, если его периметр 1212 см.

Решение

Пусть х − ширина прямоугольника,
тогда 5х − его длина.
Составим уравнение:
2 * (х + 5х) = 1212
6х = 1212 : 2 = 606
х = 606 : 6
х = 101
Значит, ширина прямоугольника 101 см,
5 * 101 = 505 (см) - длина прямоугольника 
Ответ: 101 см, 505 см.

Задание 1062

В одной бочке было в 3 раза больше бензина, чем в другой. Когда в первую налили ещё 46 л, а во вторую 18 л, то в двух бочках стало 184 л бензина. Сколько литров бензина было в каждой бочке первоначально?

Решение

Пусть х − количество бензина в первой бочке,
тогда 3х − количество бензина во второй бочке.
Составим уравнение:
(3x + 46) + (х + 18) = 184
4х = 184 − 46 − 18 = 120
х = 120 : 4
х = 30
Значит, объем первой бочки 30 л,
3 * 30 = 90 (л) − объем второй бочки.
Ответ: 30 л, 90 л.

Задание 1063

Площадь земли, засеянной пшеницей, в 6 раз больше площади, засеянной ячменём, а площадь, засеянная рожью, в 3 раза меньше площади, засеянной пшеницей. Сколько гектаров земли засеяно каждой культурой, если рожью засеяно на 120 га больше, чем ячменём?

Решение

Пусть засеяно ячменем − х,
тогда засеяно пшеницей − 6x,
а засеяно рожью − 6х : 3 = 2х.
Составим уравнение:
2х − х = 120
х = 120
Значит, 120 га засеяно ячменём,
2 * 120  = 240 (га) − засеяно рожью,
6 * 120 = 720 (га) − засеяно пшеницей.
Ответ: 120 га, 240 га, 720 га.

Задание 1064

В зрительном зале кинотеатра 16 рядов, и в каждом ряду 24 места. Сколько денег выручит кинотеатр за 3 сеанса, если цена билета m р. и на эти сеансы все билеты будут проданы?

Решение

3 * 16 * 24 * m

Задание 1065

Измерьте углы АОВ, ВОС, DMN, NME (рис. 201). Какие из этих углов равны?

Решение

∠AOB = ∠NME
∠BOC = ∠DMN

Задание 1066

Постройте угол АОВ в 140° и проведите луч ОМ так, чтобы он разделил угол АОВ на два угла, один из которых на 40° больше другого.

Решение

∠AOM − ∠MOB = 40°
∠AOM + ∠MOB = 140°
∠MOB = (140° − 40°) : 2 = 50°
∠AOM = 50°+ 40° = 90°

Задание 1067

Найдите объём прямоугольного параллелепипеда, если его длина 2,3 см, ширина 1,4 см, а высота 0,5 см.

Решение

V = a b c = 2,3 * 1,4 * 0,5 = 1,61 (см³) - объём прямоугольного параллелепипеда
Ответ: 1,61 см³.

Задание 1068

Длина прямоугольного параллелепипеда равна а см, ширина − на 2 см меньше длины, а высота равна 5 см. Составьте выражение для нахождения объёма этого параллелепипеда.

Решение

V = abc = a(a − 2) * 50 = 50a * (a − 2).

Задание 1069

Вычислите в арах площадь участка, изображённого на рисунке 202.

Решение

S = 44 * 18 + 56 * 18 = ( 44 + 56 ) * 18 = 1800 (м²) - площадь участка
1800 м² = 18 a
Ответ: 18 a.

Задание 1070

Начертите окружность и постройте два радиуса этой окружности так, чтобы угол между ними был равен 130°.

Решение

Задание 1071

Начертите отрезок МР, длина которого 4 см, и найдите две точки, удалённые от концов отрезка на 3 см.

Решение

Задание 1072

Расшифруйте надпись на крышке шкатулки, указывающую путь к тайнам математики:

Решение

Терпение и труд.

189-190 Задания для самопроверки

Страницы 189-190 Задания для самопроверки

№1

232 : 15 = 15 (ост.7)

№2

180° - развернутый угол
180 * 2/3 = 120° содержит угол

№3

1) 2 + 3 + 6 = 11 ( частей) - всего
2) 264 : 11 = 24 (г) - масса одной части коктейля
3) 24 * 3 = 72 (г) - сливок в коктейле
Ответ: 72 г сливок.

№4

0,0089
0,009
0,035
0,1

№5

а) 5 : х – 9 = 1
5 : х = 1 + 9
5 : х = 10
х = 10 * 5
х = 50

б) (х – 0,3) * 0,1 = 4,7
(х – 0,3) = 4,7 : 0,1
х – 0,3 = 47
х = 4,7 + 0,3
х = 5

в) 16х – 7х = 4,5
9х = 4,5
х = 4,5 : 9
х = 0,5

г) х + х – 1/2 = 1/2
2х – 1/2 = 1/2
2х = 1/2 + 1/2
2х = 1
х = 1 : 2 = 1/2

Ответ: В

№6

6,3 – 2,56 < 3,74

№7

Пусть х° угол ВОС,
тогда 4х° угол АОС.
Составим уравнение:
х + 4х = 115
5х = 115
х = 115 : 5
х = 23
Значи угол ВОС составляет 23° 
115 – 23 = 92° - угол АОС
Ответ: 92°.

№8

V = V1 + V2
V1 = 2 * 2 * 4 = 16
V2 = 1 * 2 * 2 = 4
V = 16 + 4 = 20

№9

1) 2 * 14,4 = 28,8 (км) - протяженность первого участка
2) 3 * 12,4 = 37,2 (км) - протяженность второго участка
3) 28,8 + 37,2 = 66 (км) - весь путь
4) 2 + 3 = 5 (ч) - время в пути
5) 66 : 5 = 13,2 (км/ч) - средняя скорость
Ответ: 13,2 км/ч.

№10

А {3, 6, 9, 12, 15, 18, 21, 24};
В {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24};
б) {6, 12, 13, 24}

 

                                     

Теперь, в конце учебного года, вам осталось пожелать лишь хороших каникул и до встречи в следующем учебном году.