В этих задачах используется свойство касательной и секущей к окружности. Касательная, это линия которая имеет лишь одну точку соприкосновения с окружностью, а секущая уже две. При этом у данных прямых есть одно из свойств, которое позволяет узнать номиналы расстояний если они измеряются от одной точки, вне тела окружности. Сейчас мы более подробно расскажем об этом, а также приведем возможные задачи из банка ФИПИ. 

Чтобы решить данную задачу, нужно вспомнить теорему о касательной и секущей. Звучит она следующим образом.

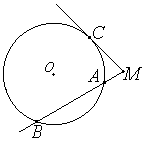
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC² = MA*MB.

Подставляем известные величины  и решаем. Таблица с корнями  двузначных чисел прилагается к бланку на экзамене.

Реальные задания по геометрии из банка ФИПИ

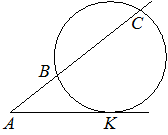
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=4, AC=64. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
AK²=4*64
AK²=256
AK=√256=16

Ответ: 16

A3FFD2

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
AK²=6*54
AK²=324
AK=√324=18

Ответ: 18

09F434

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=2, BC=6. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
АС=АВ+ВС=2+6=8
AK²=2*8
AK²=16
AK=√16=4

Ответ: 4

6F6C4D

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=2, BC=16. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
АС=АВ+ВС=2+16=18
AK²=2*18
AK²=36
AK=√36=6

Ответ: 6

C368B7

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=4, BC=12. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
АС=АВ+ВС=4+12=16
AK²=4*16
AK²=64
AK=√64=8

Ответ: 8

81DCF5

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=3, BC=24. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
АС=АВ+ВС=3+24=27
AK²=3*27
AK²=81
AK=√81=9

Ответ: 9

381796

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=5, BC=15. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
АС=АВ+ВС=5+15=20
AK²=5*20
AK²=100
AK=√100=10

Ответ: 10

20FD02

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=4, BC=32. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
АС=АВ+ВС=4+32=36
AK²=4*36
AK²=144
AK=√144=12

Ответ: 12

1A5A9C

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=7, BC=21. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
АС=АВ+ВС=7+21=28
AK²=7*28
AK²=196
AK=√196=14

Ответ: 14

F236D8

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=3, BC=72. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
АС=АВ+ВС=3+72=75
AK²=3*75
AK²=225
AK=√225=15

Ответ: 15

F9925F

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
АС=АВ+ВС=8+24=32
AK²=8*32
AK²=256
AK=√256=16

Ответ: 16

9069D8

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, BC=48. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
АС=АВ+ВС=6+48=54
AK²=6*54
AK²=324
AK=√324=18

Ответ: 18

5EA543

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=2, AC=8. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
AK²=2*8
AK²=16
AK=√16=4

Ответ: 4

D3E99D

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=3, AC=12. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
AK²=3*12
AK²=36
AK=√36=6

Ответ: 6

F93352

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=4, AC=16. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
AK²=4*16
AK²=64
AK=√64=8

Ответ: 8

D4A055

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=3, AC=27. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
AK²=3*27
AK²=81
AK=√81=9

Ответ: 9

F8417A

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=5, AC=20. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
AK²=5*20
AK²=100
AK=√100=10

Ответ: 10

E28079

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=24. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
AK²=6*24
AK²=144
AK=√144=12

Ответ: 12

C7F655

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=7, AC=28. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
AK²=7*28
AK²=196
AK=√196=14

Ответ: 14

E0E039

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=5, AC=45. Найдите AK.

Решение:

По теореме о касательной и секущей:
AK²=AB*AC
AK²=5*45
AK²=225
AK=√225=15

Ответ: 15

5D91D8