Задания про хорды окружности из открытого банка ФИПИ к ОГЭ по математике, которые могут вам попасться на реальном экзамене в этом году. Прежде о том, что такое хорда. Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы).
Реальные задания по геометрии из банка ФИПИ
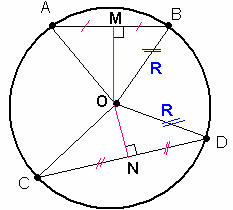
Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=10, а расстояния от центра окружности до хорд AB и CD равны соответственно 12 и 5.
Решение:
Проведем перпендикуляры к хордам. Тогда МВ = АВ/2 = 10/2 = 5.
А треугольник ∆ВМО = ∆OND так как тот и другой прямоугольный, и две стороны у них равные (OB=OD=R, MB=ON=5)
Отсюда следует, что катет треугольника ∆ВМО OM будет равен катету ∆OND ND то есть равен 12. А вся хорда CD в два раза больше.
CD=2-ND = 2*12=24
Ответ: 24
C96A5C
Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=12, а расстояния от центра окружности до хорд AB и CD равны соответственно 8 и 6.
Решение:
Проведем перпендикуляры к хордам. Тогда МВ = АВ/2 = 12/2 = 6.
А треугольник ∆ВМО = ∆OND так как тот и другой прямоугольный, и две стороны у них равные (OB=OD=R, MB=ON=6)
Отсюда следует, что катет треугольника ∆ВМО OM будет равен катету ∆OND ND то есть равен 8. А вся хорда CD в два раза больше.
CD=2-ND = 2*8=16
Ответ: 16
CFEE3D
Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=18, а расстояния от центра окружности до хорд AB и CD равны соответственно 12 и 9.
Решение:
Проведем перпендикуляры к хордам. Тогда МВ = АВ/2 = 18/2 = 9.
А треугольник ∆ВМО = ∆OND так как тот и другой прямоугольный, и две стороны у них равные (OB=OD=R, MB=ON=9)
Отсюда следует, что катет треугольника ∆ВМО OM будет равен катету ∆OND ND то есть равен 12. А вся хорда CD в два раза больше.
CD=2-ND = 2*12=24
Ответ: 24
CCD3C9
Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=16, а расстояния от центра окружности до хорд AB и CD равны соответственно 15 и 8.
Решение:
Проведем перпендикуляры к хордам. Тогда МВ = АВ/2 = 16/2 = 8.
А треугольник ∆ВМО = ∆OND так как тот и другой прямоугольный, и две стороны у них равные (OB=OD=R, MB=ON=8)
Отсюда следует, что катет треугольника ∆ВМО OM будет равен катету ∆OND ND то есть равен 15. А вся хорда CD в два раза больше.
CD=2-ND = 2*15=30
Ответ: 30
3F5FE3
Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=24, а расстояния от центра окружности до хорд AB и CD равны соответственно 16 и 12.
Решение:
Проведем перпендикуляры к хордам. Тогда МВ = АВ/2 = 24/2 = 12.
А треугольник ∆ВМО = ∆OND так как тот и другой прямоугольный, и две стороны у них равные (OB=OD=R, MB=ON=12)
Отсюда следует, что катет треугольника ∆ВМО OM будет равен катету ∆OND ND то есть равен 16. А вся хорда CD в два раза больше.
CD=2-ND = 2*16=32
Ответ: 32
141DCA
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=30, CD=40, а расстояние от центра окружности до хорды AB равно 20.
Решение:
Проведем перпендикуляры к хордам. Тогда МВ = АВ/2 = 30/2 = 15.
А треугольник ∆ВМО = ∆OND так как тот и другой прямоугольный, и две стороны, а именно гипотенузы, у них равные.
Отсюда делаем заключение, что МВ = ON = 15
Ответ: 15
DD14BB
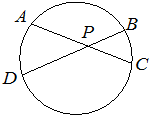
Хорды AC и BD окружности пересекаются в точке P, BP=15, CP=6, DP=10. Найдите AP.
Решение:
Отрезки хорд относительно точки пересечения Р и по свойству хорд: BP * DP = AP * PC, отсюда
АР = BP*DP
PC
AP = (15*10)/6=150/6=25
Ответ: 25
775913
Хорды AC и BD окружности пересекаются в точке P, BP=7, CP=14, DP=10. Найдите AP.
Решение:
Отрезки хорд относительно точки пересечения Р и по свойству хорд: BP * DP = AP * PC, отсюда
АР = BP*DP
PC
AP = (7*10)/14=70/14=5
Ответ: 5
987CB4
Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.
Решение:
Отрезки хорд относительно точки пересечения Р и по свойству хорд: BP * DP = AP * PC, отсюда
АР = BP*DP
PC
AP = (6*12)/8=72/8=9
Ответ: 9
C7865C
Хорды AC и BD окружности пересекаются в точке P, BP=4, CP=12, DP=21. Найдите AP.
Решение:
Отрезки хорд относительно точки пересечения Р и по свойству хорд: BP * DP = AP * PC, отсюда
АР = BP*DP
PC
AP = (4*21)/12=84/12=7
Ответ: 7
915B8A
Хорды AC и BD окружности пересекаются в точке P, BP=8, CP=24, DP=18. Найдите AP.
Решение:
Отрезки хорд относительно точки пересечения Р и по свойству хорд: BP * DP = AP * PC, отсюда
АР = BP*DP
PC
AP = (8*18)/24=144/24=6
Ответ: 6
A07BA0
Хорды AC и BD окружности пересекаются в точке P, BP=10, CP=8, DP=12. Найдите AP.
Решение:
Отрезки хорд относительно точки пересечения Р и по свойству хорд: BP * DP = AP * PC, отсюда
АР = BP*DP
PC
AP = (10*12)/8=120/8=15
Ответ: 15
6C233F
Хорды AC и BD окружности пересекаются в точке P, BP=12, CP=6, DP=13. Найдите AP.
Решение:
Отрезки хорд относительно точки пересечения Р и по свойству хорд: BP * DP = AP * PC, отсюда
АР = BP*DP
PC
AP = (12*13)/6=156/6=26
Ответ: 26
B0B284
Хорды AC и BD окружности пересекаются в точке P, BP=10, CP=14, DP=21. Найдите AP.
Решение:
Отрезки хорд относительно точки пересечения Р и по свойству хорд: BP * DP = AP * PC, отсюда
АР = BP*DP
PC
AP = (10*21)/14=210/14=15
Ответ: 15
56A3B8
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Решение:
Отрезки хорд относительно точки пересечения Р и по свойству хорд: BP * DP = AP * PC, отсюда
АР = BP*DP
PC
AP = (9*20)/15=180/15=12
Ответ: 12
4A7E13
Хорды AC и BD окружности пересекаются в точке P, BP=12, CP=15, DP=25. Найдите AP.
Решение:
Отрезки хорд относительно точки пересечения Р и по свойству хорд: BP * DP = AP * PC, отсюда
АР = BP*DP
PC
AP = (12*25)/15=300/15=20
Ответ: 20
97C312
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=14, CD=48, а расстояние от центра окружности до хорды AB равно 24.
Решение:
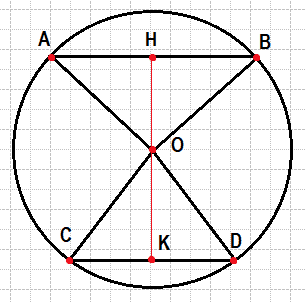
Проведём построения и введём обозначения, как показано на рисунке. Рассмотрим треугольники AOH и BOH, они прямоугольные, стороны AO и OB равны как радиусы окружностей, OH — общая, следовательно, треугольники AOH и HOB равны. Откуда
AH=BH=AB/2=14/2=7
Аналогично, равны треугольники COK и KOD, откуда СK=KD=CD/2=48/2=24. Рассмотрим треугольник BOH, найдём OB по теореме Пифагора:
$OB=\sqrt{HB^2+OH^2}\\OB=\sqrt{7^2+24^2}\\OB=\sqrt{49+576}\\OB=\sqrt{625}\\OB=25$
Рассмотрим треугольник OKD, он прямоугольный, из теоремы Пифагора найдём OK:
$OD^2=OK^2+KD^2\\OK^2=OD^2-KD^2\\OK=\sqrt{OD^2-KD^2}\\OK=\sqrt{25^2-24^2}\\OK=\sqrt{625-576}\\OK=7$
Таким образом, расстояние от центра окружности до хорды CD равно 7.
Ответ: 7.
0A27C6
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
Решение:
Проведём построения и введём обозначения, как показано на рисунке. Рассмотрим треугольники AOH и BOH, они прямоугольные, стороны AO и OB равны как радиусы окружностей, OH — общая, следовательно, треугольники AOH и HOB равны. Откуда
AH=BH=AB/2=14/2=7
Аналогично, равны треугольники COK и KOD, откуда СK=KD=CD/2=48/2=24. Рассмотрим треугольник BOH, найдём OB по теореме Пифагора:
$OB=\sqrt{HB^2+OH^2}\\OB=\sqrt{7^2+24^2}\\OB=\sqrt{49+576}\\OB=\sqrt{625}\\OB=25$
OB=OD=R. Рассмотрим треугольник OKD, он прямоугольный, из теоремы Пифагора найдём OK:
$OD^2=OK^2+KD^2\\OK^2=OD^2-KD^2\\OK=\sqrt{OD^2-KD^2}\\OK=\sqrt{25^2-24^2}\\OK=\sqrt{625-576}\\OK=7$
Таким образом, расстояние от центра окружности до хорды CD равно 7.
Ответ: 7.
DF648D
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=40, CD=42, а расстояние от центра окружности до хорды AB равно 21.
Решение:
Проведём построения и введём обозначения, как показано на рисунке. Рассмотрим треугольники AOH и BOH, они прямоугольные, стороны AO и OB равны как радиусы окружностей, OH — общая, следовательно, треугольники AOH и HOB равны. Откуда
AH=BH=AB/2=40/2=20
Аналогично, равны треугольники COK и KOD, откуда СK=KD=CD/2=42/2=21. Рассмотрим треугольник BOH, найдём OB по теореме Пифагора:
$OB=\sqrt{HB^2+OH^2}\\OB=\sqrt{20^2+21^2}\\OB=\sqrt{400+441}\\OB=\sqrt{841}\\OB=29$
OB=OD=R. Рассмотрим треугольник OKD, он прямоугольный, из теоремы Пифагора найдём OK:
$OD^2=OK^2+KD^2\\OK^2=OD^2-KD^2\\OK=\sqrt{OD^2-KD^2}\\OK=\sqrt{29^2-21^2}\\OK=\sqrt{841-441}\\OK=20$
Таким образом, расстояние от центра окружности до хорды CD равно 20.
Ответ: 20.
1B191C
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=36, CD=48, а расстояние от центра окружности до хорды AB равно 24.
Решение:
Проведём построения и введём обозначения, как показано на рисунке. Рассмотрим треугольники AOH и BOH, они прямоугольные, стороны AO и OB равны как радиусы окружностей, OH — общая, следовательно, треугольники AOH и HOB равны. Откуда
AH=BH=AB/2=36/2=18
Аналогично, равны треугольники COK и KOD, откуда СK=KD=CD/2=48/2=24. Рассмотрим треугольник BOH, найдём OB по теореме Пифагора:
$OB=\sqrt{HB^2+OH^2}\\OB=\sqrt{18^2+24^2}\\OB=\sqrt{324+576}\\OB=\sqrt{900}\\OB=30$
OB=OD=R. Рассмотрим треугольник OKD, он прямоугольный, из теоремы Пифагора найдём OK:
$OD^2=OK^2+KD^2\\OK^2=OD^2-KD^2\\OK=\sqrt{OD^2-KD^2}\\OK=\sqrt{30^2-24^2}\\OK=\sqrt{900-576}\\OK=18$
Таким образом, расстояние от центра окружности до хорды CD равно 18.
Ответ: 18.
83F622
