Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году. В задачах по биссектрисам углов A и B при боковой стороне AB трапеции ABCD пересекающихся в точке F необходимо найти сторону AB. 

Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2

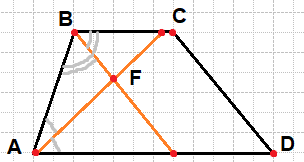
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=10.

Решение:

Введём обозначения, как показано на рисунке. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, следовательно:
2∠BAF + 2∠ABF=180° равносильно ∠BAF + ∠ABF=90º.
Рассмотрим треугольник ABF, сумма углов треугольника равна 180°, поэтому ∠AFB=180º-∠BAF-∠ABF=90 градусов, то есть треугольник ABF  — прямоугольный. Найдём AB по теореме Пифагора:
$AB^2=\sqrt{AF^2+BF^2}=\sqrt{24^2+10^2}=\sqrt{576+100}=\sqrt{676}=26$
Ответ: 26

6AD95A

Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=12, BF=5.

Решение:

Введём обозначения, как показано на рисунке. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, следовательно:
2∠BAF + 2∠ABF=180° равносильно ∠BAF + ∠ABF=90º.
Рассмотрим треугольник ABF, сумма углов треугольника равна 180°, поэтому ∠AFB=180º-∠BAF-∠ABF=90 градусов, то есть треугольник ABF  — прямоугольный. Найдём AB по теореме Пифагора:
$AB^2=\sqrt{AF^2+BF^2}=\sqrt{12^2+5^2}=\sqrt{144+25}=\sqrt{169}=13$
Ответ: 13

96E347

Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=12, BF=9.

Решение:

Введём обозначения, как показано на рисунке. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, следовательно:
2∠BAF + 2∠ABF=180° равносильно ∠BAF + ∠ABF=90º.
Рассмотрим треугольник ABF, сумма углов треугольника равна 180°, поэтому ∠AFB=180º-∠BAF-∠ABF=90 градусов, то есть треугольник ABF  — прямоугольный. Найдём AB по теореме Пифагора:
$AB^2=\sqrt{AF^2+BF^2}=\sqrt{12^2+9^2}=\sqrt{144+81}=\sqrt{225}=15$
Ответ: 13

9599CF

Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=15, BF=8.

Решение:

Введём обозначения, как показано на рисунке. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, следовательно:
2∠BAF + 2∠ABF=180° равносильно ∠BAF + ∠ABF=90º.
Рассмотрим треугольник ABF, сумма углов треугольника равна 180°, поэтому ∠AFB=180º-∠BAF-∠ABF=90 градусов, то есть треугольник ABF  — прямоугольный. Найдём AB по теореме Пифагора:
$AB^2=\sqrt{AF^2+BF^2}=\sqrt{15^2+8^2}=\sqrt{225+64}=\sqrt{289}=17$
Ответ: 17

4C7923

Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=16, BF=12.

Решение:

Введём обозначения, как показано на рисунке. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, следовательно:
2∠BAF + 2∠ABF=180° равносильно ∠BAF + ∠ABF=90º.
Рассмотрим треугольник ABF, сумма углов треугольника равна 180°, поэтому ∠AFB=180º-∠BAF-∠ABF=90 градусов, то есть треугольник ABF  — прямоугольный. Найдём AB по теореме Пифагора:
$AB^2=\sqrt{AF^2+BF^2}=\sqrt{16^2+12^2}=\sqrt{256+144}=\sqrt{400}=20$
Ответ: 20

92BF9C

Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=20, BF=15.

Решение:

Введём обозначения, как показано на рисунке. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, следовательно:
2∠BAF + 2∠ABF=180° равносильно ∠BAF + ∠ABF=90º.
Рассмотрим треугольник ABF, сумма углов треугольника равна 180°, поэтому ∠AFB=180º-∠BAF-∠ABF=90 градусов, то есть треугольник ABF  — прямоугольный. Найдём AB по теореме Пифагора:
$AB^2=\sqrt{AF^2+BF^2}=\sqrt{20^2+15^2}=\sqrt{400+225}=\sqrt{625}=25$
Ответ: 25

1EA262

Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=7.

Решение:

Введём обозначения, как показано на рисунке. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, следовательно:
2∠BAF + 2∠ABF=180° равносильно ∠BAF + ∠ABF=90º.
Рассмотрим треугольник ABF, сумма углов треугольника равна 180°, поэтому ∠AFB=180º-∠BAF-∠ABF=90 градусов, то есть треугольник ABF  — прямоугольный. Найдём AB по теореме Пифагора:
$AB^2=\sqrt{AF^2+BF^2}=\sqrt{24^2+7^2}=\sqrt{576+49}=\sqrt{625}=25$
Ответ: 25

AB214A

Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.

Решение:

Введём обозначения, как показано на рисунке. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, следовательно:
2∠BAF + 2∠ABF=180° равносильно ∠BAF + ∠ABF=90º.
Рассмотрим треугольник ABF, сумма углов треугольника равна 180°, поэтому ∠AFB=180º-∠BAF-∠ABF=90 градусов, то есть треугольник ABF  — прямоугольный. Найдём AB по теореме Пифагора:
$AB^2=\sqrt{AF^2+BF^2}=\sqrt{21^2+20^2}=\sqrt{441+400}=\sqrt{841}=21$
Ответ: 21

248EE7

Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=18.

Решение:

Введём обозначения, как показано на рисунке. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, следовательно:
2∠BAF + 2∠ABF=180° равносильно ∠BAF + ∠ABF=90º.
Рассмотрим треугольник ABF, сумма углов треугольника равна 180°, поэтому ∠AFB=180º-∠BAF-∠ABF=90 градусов, то есть треугольник ABF  — прямоугольный. Найдём AB по теореме Пифагора:
$AB^2=\sqrt{AF^2+BF^2}=\sqrt{24^2+18^2}=\sqrt{576+324}=\sqrt{900}=30$
Ответ: 30

DD7C92

Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=32, BF=24.

Решение:

Введём обозначения, как показано на рисунке. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, следовательно:
2∠BAF + 2∠ABF=180° равносильно ∠BAF + ∠ABF=90º.
Рассмотрим треугольник ABF, сумма углов треугольника равна 180°, поэтому ∠AFB=180º-∠BAF-∠ABF=90 градусов, то есть треугольник ABF  — прямоугольный. Найдём AB по теореме Пифагора:
$AB^2=\sqrt{AF^2+BF^2}=\sqrt{32^2+24^2}=\sqrt{1024+576}=\sqrt{1600}=40$
Ответ: 40

5A2C47