 Готовые домашние задания ко второй части учебника математики за четвёртый класс, авторы учебника Рудницкая В. Н., Кочурова Е. Э., Рыдзе О. А., седьмое издание. Программа Начальная школа 21 века.
Готовые домашние задания ко второй части учебника математики за четвёртый класс, авторы учебника Рудницкая В. Н., Кочурова Е. Э., Рыдзе О. А., седьмое издание. Программа Начальная школа 21 века.
Готовые домашние задания ко второй части учебника математики за четвёртый класс, авторы учебника Рудницкая В. Н., Кочурова Е. Э., Рыдзе О. А., седьмое издание. Программа Начальная школа 21 века.
Ответы ко 2 части учебника математики 4 класс, Рудницкая ("Начальная школа 21 века"):
Кликайте по вкладкам-страницам и смотрите ответы на задания.
Стр. 4
-
Ответы к странице 4 УЗНАЁМ НОВОЕ Умножение многозначного числа на двузначное число
1. Как выполнено умножение?
Для второго множителя перемножаем на число выше (первый множитель) вначале единицы. Вычисляем. Затем смещаем место записи результата на один разряд под вычисленным и умножаем на единицы десятков. Складываем суммы и получаем конечный результат.
2. Решите по одному примеру со своим соседом по парте, а затем проверьте работу друг друга.
162 · 58 851 · 16
162 · 58 = 9 396
*162
58
+1296
810
9396851 · 16 = 13 616
* 851
16
+5106
851
136163. Выполните умножение.
244 · 75 307 · 76 532 · 31
168 · 27 401 · 29 702 · 48
859 · 96 509 · 95 303 · 55*244
75
+1220
1708
18300*168
27
+1176
336
4536*859
96
+5154
7731
82464*307
76
+1842
2149
23332*401
29
+3609
802
11629*509
95
+2545
4581
48355*532
31
+532
1596
16492*702
48
+ 5616
2808
33696*303
55
+1515
1515
166654. Докажите, что равенство верно.
108 · 26 = 234 · 12
*108
26
+648
216
2808*234
12
+468
234
28082808 = 2808
Равенство верное.
5. Из листа стекла шириной 65 см и длиной 76 см нужно вырезать прямоугольный кусок размером 52 см на 37 см. Найдите площадь оставшейся части стекла.
1) 65 * 76 = 4990 (см²) – площадь листа стекла
2) 52 * 37 = 1924 (см²) – площадь вырезанного куска
3) 4990 – 1924 = 3016 (см²) – площадь оставшейся части стекла
Ответ: 3016 см². 5
-
Ответы к странице 5
6. Сравните записи. Какой способ записи умножения удобнее? Поясните свой ответ.
358 · 90 = ?358 · 90 = (358 · 9) · 10 = 3222 * 10 = 32220 удобнее, так как короче
7. Выполните умножение, используя удобный способ записи.
516 · 50 140 · 20 209 · 40
274 · 80 920 · 80 960 · 96
407 · 30 570 · 70 210 · 80516 · 50 = 25 800
*516
50
25800140 · 20 = 2 800
*140
20
2800209 · 40 = 8 360
* 209
40
8360274 · 80 = 21 920
*274
80
+21920920 · 80 = 73 600
*920
80
73600960 · 96 = 921 160
* 960
96
+576
864
92160407 · 30 = 12 210
*407
30
+12210570 · 70 = 39 900
*570
70
+39900210 · 80 = 16800
*210
80
+168008. Вычислите устно.
600 · 10 70 · 40 400 · 50
500 · 90 200 · 50 300 · 30600 · 10 = 6000
70 · 40 = 2 800
400 · 50 = 20 000
500 · 90 = 45 000
200 · 50 = 10 000
300 · 30 = 9 000
9. Выразите: в минутах: 12 ч, 150 ч, 400 ч; в секундах: 45 мин, 128 мин, 4 ч.
в минутах: 12 ч, 150 ч, 400 ч;
12 * 60 = 720 минут
150 * 60 = 9 000 минут
400 * 60 = 24 000 минут
в секундах: 45 мин, 128 мин, 4 ч.
45 * 60 = 2 700 сек
128 * 60 = 7680 сек
4 * 60 * 60 = 240 * 60 = 14 400 сек
6
-
Ответы к странице 6
10. Докажите, что равенство верно.
276 · 70 = 552 · 35
*276
70
19320*552
35
+2760
1656
1932019320 = 19320
Равенство верное.
11. Купили 15 столов и 20 табуреток. Цена стола 2 235 р., а цена табуретки в 5 раз меньше. Какова стоимость покупки? На сколько больше заплатили за столы, чем за табуретки?
1) 235 : 5 = 47 (руб.) – цена табуретки
2) 235 * 15 = 3525 (руб.) – стоят столы
3) 47 * 20 = (47 * 2) * 10 = 94 * 10 = 940 (руб.) – стоят табуретки
4) 3525 + 940 = 4465 (руб.) – стоимость покупки
5) 3525 – 940 = 2585 (руб.) – больше заплатили за столы, чем за табуретки
Ответ: 4465 руб., на 2585 руб. больше.12. Найдите значение выражения:
1) x · 38, если x = 96, 108, 517;x · 38, если
96 * 38 = 3648
* 96
38
+768
288
3648108 * 38 = 4104
*108
38
+864
324
4104517 * 38 = 19 646
*517
38
+4136
1551
196462) 156 · a – 42 · y, если a = 16, y = 53;
1 3 2
156 · 16 – 42 · 53 =10261)
*156
16
+936
156
24962)
*42
35
+210
126
14703)
-2496
1470
1026
3) 304 : x + 94 · y, если x = 38, y = 80.1 3 2
304 : 38 + 94 · 80 = 7 5281)
-304|38
304|8
02)
* 94
80
+75203)
7520 + 8 = 7528
13. Вычислите.
1 804 · 25 111 111 · 99
30 941 · 72 404 040 · 801 804 · 25 = 45 100
*1804
25
+ 9020
3608
45100111 111 · 99 = 10 999 989
* 111111
99
+ 999999
999999
1099998930 941 · 72 = 22 315 752
*30941
72
+ 61882
216587
22315752404 040 · 80 = 32 323 200
*404040
80
+32323200Проверьте результаты с помощью калькулятора.
14. Объясните, как выполнено умножение.
Для второго множителя перемножаем на число выше (первый множитель) вначале единицы. Вычисляем. Затем смещаем место записи результата на один разряд под вычисленным и умножаем на единицы десятков. Складываем суммы и получаем конечный результат.
7
-
Ответы к странице 7
15. Найдите значения выражений.
1 2 5 3 4
(107 + 96) · 43 + 480 : 12 · 54 = 10 8891) 107 + 96 = 203
2)
*203
43
+ 609
812
87293)
- 480|12
48 |40
0
4) 54 * 40 = 54 * 4 * 10 = 216 * 10 = 2160
5)
+8729
2160
108892 1 3 5 4
(890 – 36 · 4) · 37 – 106 · 8 = 26 7541) 36 * 4 = 30 * 4 + 6 * 4 = 120 + 24 = 144
2) 890 - 144 = 746
3)
*746
37
+5222
2238
276024) 106 * 8 = 100 * 8 + 6 * 8 = 800 + 48 = 848
5) 27602 - 848 = 26 754
-27602
848
26754
23 146 · 33 – 12 146 · 33 – 3 174 · 72 = (23146 - 12146) * 33 - 3174 * 72 = 11000 * 33 - 3174 * 72 = 363 000 - 3174 * 72 = 134 4721)
*3174
72
+6348
22218
2285282)
- 363000
228528
- 13447216. Бригада из 15 человек собрала 84 ящика винограда, по 14 кг в каждом. Сколько винограда собрали? Выразите результат в тоннах и килограммах. Какое данное в задаче лишнее?
14 * 84 = 1 176 (кг) – винограда собрали всего
1 176 кг = 1 т 176 кг
Ответ: 1 т 176 кг винограда.17. Улицу длиной 672 м и шириной 13 м покрыли асфальтом, расходуя на каждый квадратный метр 39 кг асфальта. Сколько асфальта потребовалось? Выразите результат в тоннах и килограммах.
1) 672 * 13 = 8 736 (м²) – площадь улицы
2) 8 736 * 39 = 340 704 (кг) = 340 т 704 кг – потребовалось асфальта
Ответ: 340 т 704 кг асфальта.18*. Восстановите записи.
*815
7
5705*348
13
+1044
348
45204
19. Два лыжника вышли из посёлка одновременно и пошли в противоположных направлениях. Один лыжник шёл со скоростью 200 м/мин, другой — со скоростью 167 м/мин. Какое расстояние будет между ними через 45 мин?
1) 200 + 167 = 367 (м/мин) – удаляются друг от друга
2) 367 * 45 = 16 515 (м) = 16 км 515 м – будет между ними через 45 мин.
Ответ: 16 км 515 м.20. Расстояние между городами 572 км. Из этих городов одновременно навстречу друг другу вышли два поезда. Через сколько часов поезда встретятся, если их скорости 65 км/ч и 78 км/ч?
1) 65 + 78 = 143 (км/ч) – скорость сближения поездов
2) 572 : 143 = 4 (ч.) – они встретятся
Ответ: через 4 часа. 8
-
Ответы к странице 8
21. В магазине было 430 пачек тетрадей, по 50 штук в каждой пачке. Сколько тетрадей осталось в магазине, если продали 7 494 штуки?
1) 430 * 50 = (43 * 5) * 10 * 10 = 215 * 100 = 21 500 (т.) – было всего
2) 21 500 – 7 494 = 14 006 (т.) – осталось в магазине
Ответ: 14 006 тетрадей осталось.22. Длина каждой стороны многоугольника 9 см. Периметр этого многоугольника равен 108 см. Как называется этот многоугольник?
108 : 9 = 12 (с.) – у многоугольника
Ответ: это двенадцатиугольник.23. Вычислите значения выражений.
1 3 2
512 · 7 + 488 · 7 = 70001)
*512
7
+35842)
*488
7
+34163)
+3584
3416
70001 3 2
800 · 4 – 450 · 4 = 14001) 800 * 4 = 3200
2) 450 * 4 = 1800
3) 3200 - 1800 = 1400
1 3 2
960 · 8 + 140 · 8 = 8 8001)
+960
8
76802)
*140
8
11203)
+ 7680
1120
88001 3 2
3 · 315 – 3 · 150 = 11451) 315 * 3 = 300 * 3 + 15 * 3 = 900 + 45 = 945
2) 3 * 150 = 300
3) 945 + 300 = 1245
24. Если неизвестное число увеличить на 248 и результат уменьшить на 362, то получится 567. Вычислите неизвестное число.
567 + 362 – 248 = 929 – 248 = 681
Ответ: 681.25. Если неизвестное число уменьшить в 7 раз, а затем результат увеличить в 9 раз, то получится 810. Какое это число?
810 : 9 * 7 = 90 * 7 = 630
Ответ: 630. 9
-
Ответы к странице 9
26. Андрей идёт на лыжах со скоростью 18 км/ч, а Борис — со скоростью 15 км/ч. Определите, сближаются лыжники или удаляются друг от друга и с какой скоростью, если они двигаются:
1) в противоположных направлениях от лыжной базы;
2) навстречу друг другу с двух лыжных баз;
3) от базы в одном направлении и Борис идёт за Андреем;
4) от базы в одном направлении и Андрей идёт за Борисом.Решение:
1) В противоположных направлениях от лыжной базы и Андрей идёт на лыжах со скоростью 18 км/час, а Борис-со скоростью 15 км/час:
Если они идут в разных направлениях, то они удаляются друг от друга со скоростью:
18 + 15 = 33 км/час;
2) Идут навстречу друг другу с двух лыжных баз, то они сближаются со скоростью:
18 + 15 = 33 км/час;
3) Вышли от базы в одном направлении и Борис идёт за Андреем:
Борис идет медленнее Андрея, поэтому догнать его не сможет, они удаляются друг от друга со скоростью:
18 - 15 = 3 км/час;
4) Вышли от базы в одном направлении и Андрей идёт за Борисом, они сближаются так как Андрей идет быстрее Бориса, скорость сближения:
18 - 15 = 3 км/час.
27. Выполните действия.
(362 + 458) · 7 = 820 * 7 = 800 * 7 + 20 * 7 = 5600 + 140 = 5740
(2 924 – 1 824) · 6 = 1100 * 6 = 6600
(2 864 + 936) · 5 = 3800 * 5 = 3000 * 5 + 800 * 5 = 15 000 + 4 000 = 19 000
(5 600 – 1 480) · 4 = 4120 * 4 = 4000 * 4 + 120 * 4 = 16 000 + 480 = 16 480
10
-
Ответы к странице 10
28. Купили 5 наволочек и столько же простыней. За наволочки заплатили на 925 р. меньше, чем за простыни. Какова цена наволочки, если цена простыни 285 р.?
1) 85 * 5 = 425 (р.) – заплатили за простыни
2) 425 – 200 = 225 (р.) – заплатили за наволочки
3) 225 : 5 = 45 (р.) – стоит наволочка
Ответ: 45 рублей.29. Фотоальбом в 5 раз дороже ручки и в 3 раза дешевле словаря. Цена ручки 24 р. Сколько рублей надо заплатить за покупку фотоальбома и словаря?
1) 24 * 5 = 120 (р.) – стоит фотоальбом
2) 120 : 3 = 40 (р.) – стоит словарь
3) 120 + 40 = 160 (р.) – заплатили за покупку фотоальбома и словаря
Ответ: 160 рублей.30*. По какому правилу записан ряд чисел? Назовите следующее число в ряду. 800, 1 600, 3 200, 6 400, … .
Каждый раз последующее число удваивается относительно предыдущего.
12800 следующее число
31*. Разговаривают племянник и дядя. — Дядя, сколько тебе лет? — Два раза по столько, сколько лет Оле. — А сколько лет Оле? — В три раза меньше, чем тёте Вале. — А сколько лет тёте Вале? — Тётя Валя на двадцать лет старше Алексея. — А сколько лет Алексею? — Алексей в пять раз старше Анечки. — А сколько лет Анечке? — Через год ей исполнится шесть лет. Сосчитайте, сколько лет дяде.
1) 6 – 1 = 5 (л.) – Анечке
2) 5 * 5 = 25 (л.) – Алексею
3) 25 + 20= 45 (л.) – тете Вале
4) 45 : 3 = 15 (л.) – Оле
5) 15 * 2 = 30 (л.) – дяде
Ответ: 30 лет. 11
-
Ответы к странице 11
32*. Конфеты трёх сортов расфасованы по полкилограмма. Купили по одной упаковке конфет этих сортов. Какова масса покупки? Сколько рублей стоит покупка, если конфеты каждого сорта продаются по цене 278 р. за килограмм?
Масса покупки – полтора килограмма
78 + 78 : 2 = 78 + 39 = 117 (р.) – стоит покупка
Ответ: 117 рублей.33. Не перемножая чисел 78 320 и 5, определите, сколькими нулями оканчивается запись числа, которое является произведением этих чисел.
Двумя нулями. Первый ноль сразу выносим из числа 78320, а второй ноль будет образован перемножением 2 * 5 = 10
Решите старинные задачи.
Задача 1. У крестьянина две лошади. Одну лошадь он купил 4 года назад, и ей тогда было 8 лет. Другую лошадь он купил 3 года назад, и ей тогда было 5 лет. На сколько лет одна лошадь моложе другой?1) 8 + 4 = 12 (л.) – первой лошади
2) 5 + 3 = 8 (л.) – второй лошади
3) 12 – 8 = 4 (г.) – одна лошадь моложе другой
Ответ: на 4 года.Задача 2. За перековку лошади кузнец берёт 80 копеек. За работу он кладёт 10 копеек с ноги. Во сколько кузнец оценивает новую подкову?
1) 10 * 2 = 20 (коп.) – кладет кузнец за работу
2) (80 – 20) : 2 = 60 : 2 = 30 (коп.) – стоит новая подкова
Ответ: 30 копеек. 12
-
Ответы к странице 12
34*. Изобразите такие фигуры в тетради, используя циркуль.
Срисовываем.
35*. Определите, деталь какой формы вырезали из доски.
Вырезали фигуру №3
13
-
Ответы к странице 13 УЗНАЁМ НОВОЕ Умножение многозначного числа на трёхзначное число
1. Расскажите, как выполнено умножение.
Для второго множителя перемножаем на число выше (первый множитель) вначале единицы. Вычисляем. Затем смещаем место записи результата на один разряд под вычисленным и умножаем на единицы десятков. Складываем суммы и получаем конечный результат.
2. Назовите числа, которые складывали при выполнении умножения.
972, 648, 324
3. Выполните умножение, делая записи столбиком.
115 · 163 1 294 · 216 64 · 952
236 · 374 2 139 · 151 650 · 125
563 · 113 6 431 · 333 160 · 270
264 · 856 9 075 · 152 900 · 420115 · 163 = 18 745
*115
163
+345
690
115
18745
1 294 · 216 = 279 504*1294
216
+7764
1294
2588
279504
64 · 952 = 60 928*64
952
+128
320
576
60928
236 · 374 = 88 264*236
374
+944
1652
708
88264
2 139 · 151 = 322 989*2139
151
+2139
10695
2139
322989
650 · 125 = 81 250*125
650
+625
650
81250
563 · 113 = 63 619* 563
113
+1689
563
563
63619
6 431 · 333 = 2 141 523* 6431
333
+19293
19293
19293
2141523160 · 270 = 43 200
*160
270
+112
32
43200
264 · 856 = 225 984*264
856
+1584
1320
2112
225984
9 075 · 152 = 1 379 400*9075
152
+18150
45375
9075
1379400
900 · 420 = 378 000*420
900
+3780004. Вычислите устно.
200 · 400 500 · 500 1 100 · 800
60 · 900 210 · 400 4 444 · 200200 · 400 = 2 * 4 * 10 000 = 8 * 10 000 = 80 000
500 · 500 = 5 * 5 * 10 000 = 250 000
1 100 · 800 = 11 * 8 * 10 000 = 880 000
60 · 900 = 6 * 9 * 1000 = 54 * 1000 = 54 000
210 · 400 = 21 * 4 * 1000 = 84 * 1000 = 84 000
4 444 · 200 = 4 444 * 2 * 100 = 8 888 * 100 = 888 800 14
-
Ответы к странице 14
5. Сравните записи. Какая из них удобнее? Ответ поясните.
Удобнее левая запись, так как на ней не учитываются ничего не значащие нули разряда десятков во втором множителе.
6. Выполните умножение.
207 · 503 107 · 208 10 920 · 203
609 · 305 409 · 907 3 570 · 602
708 · 504 308 · 803 21 250 · 307
909 · 808 706 · 706 12 609 · 800207 · 503 = 104121
*207
503
+621
1035
104121
107 · 208 = 22 256*107
208
+856
214
22256
10 920 · 203 = 2 216 760*10920
203
+3276
2184
2216760
609 · 305 = 185 745*609
305
+3045
1827
185745
409 · 907 = 370 963*409
907
+2863
3681
370963
3 570 · 602 = 2 149 140* 3570
602
+714
2142
2149140
708 · 504 = 356 832*708
504
+2832
3540
356832
308 · 803 = 247 324*308
803
+924
2464
247324
21 250 · 307 = 6 532 750* 21250
307
+14875
6375
6532750
909 · 808 = 733 664*908
808
+7264
7264
733664
706 · 706 = 498 436*706
706
+4236
4942
498436
12 609 · 800 = 10 087 200*12609
800
+100872007. Найдите значение выражения:
1) 506 · x + 207 · y, если x = 205, y = 70;
2) 1 290 + x · y, если x = 306, y = 405;
3) (217 + 583) · a, если a = 214, 387, 902;
4) (t + l) · 250, если t = 499, l = 201.Решение:
1) 506 · x + 207 · y, если x = 205, y = 70;
506 · 205 + 207 · 70 = 103 730 + 14 490 = 118 220
* 506
205
+2530
1012
103730*207
70
14490
2) 1 290 + x · y, если x = 306, y = 405;1 290 + 306 · 405 = 1290 + 123 930 = 125 220
* 306
405
+1530
1224
1239301290
+ 123930
125 2203) (217 + 583) · a, если a = 214, 387, 902;
(217 + 583) · 214 = 800 * 214 = 1 712
*214
800
1712(217 + 583) · 387 = 800 * 387 = 3 096
*387
800
3096(217 + 583) · 902 = 800 * 902 = 7 216
*902
800
7216
4) (t + l) · 250, если t = 499, l = 201.(499 + 201) · 250 = 700 * 250 = 175 000
*250
700
1750008. Найдите произведение чисел.
2 222 и 444 1 008 и 905
1 007 и 106 10 080 и 950Решение:
2 222 * 444 = 986 568
*2222
444
+8888
8888
8888
9865681 008 * 905 = 912 240
*1008
905
+5040
9072
9122401 007 * 106 = 106 742
*1007
106
+6042
1007
10674210 080 * 950 = 1 068
*10080
950
+5040
9072
1068
9. Найдите значения выражений.125 · 2 304 + 653 · 1 000 – 851 · 106
457 100 + 1 423 · (6 123 – 5 941) – 11 007
382 · 905 + 618 · 905 749 · 709 + 251 · 709
1 027 · 378 – 72 : 36 · 905 – 628 : 4
(650 · 15 + 350 · 15) · 0 + 800 : 32 – 25Решение:
1 4 2 5 3
125 · 2 304 + 653 · 1 000 – 851 · 106 = 941 0001) 125 * 2304 = 288 000
*2304
125
+11520
4608
2304
2880002) 653 * 1000 = 653 000
3) 851 * 106 = 90 206*851
106
+5106
851
902064) 288 000 + 653 000 = 941 000
5) 941 000 - 90 206 = 850 794
3 2 1 4
457 100 + 1 423 · (6 123 – 5 941) – 11 007 = 705 0791) 6 123 – 5 941 = 182
2) 1423 * 182 = 258 986*1423
182
+2846
11384
1423
2589863) 457100 + 258986 = 716086
+457100
258986
7160864) 716086 - 11 007 = 705 079
382 · 905 + 618 · 905 = (382 + 618) * 905 = 1000 * 905 = 905 000
749 · 709 + 251 · 709 = (749 + 251) * 709 = 1000 * 709 = 709 000
1 5 2 3 6 4
1 027 · 378 – 72 : 36 · 905 – 628 : 4 = 386 2391) 1 027 · 378 = 388 206
*1027
378
+8216
7189
3081
3882062) 72 : 36 = 2
3) 2 * 905 = 1810
4) 628 : 4 = 60 : 4 * 10 + 28 : 4 = 150 + 7 = 157
5) 388 206 - 1810 = 386 396
6) 386 396 - 157 = 386 239
1 3 2 4 6 5 7
(650 · 15 + 350 · 15) · 0 + 800 : 32 – 25 = 01)
2)
3)
4) по 4 действия не имеет смысла выполнять вычисления, так как скобки умножаются на 0, то есть будет 0
5) 800 : 32 = 25-800|32
64 |25
-160
160
06) 0 + 25 = 0
7) 25 - 25 = 0
15
-
Ответы к странице 15
10. Выполните умножение.
216 м · 320 м 18 дм · 200 см
420 км · 170 км 135 мм · 540 мм
51 см · 6 м 406 м · 307 м
65 мм · 84 см 9 км · 825 мРешение:
216 м · 320 м = 69120 м2
*216
320
+432
648
69120
18 дм · 200 см = 180 см * 200 см = 18 * 2 * 1000 = 36000 см2 = 3 м2 6000 см2
420 км · 170 км = 71 400 км2
*420
170
+ 294
42
71400
135 мм · 540 мм = 72900 мм2 = 729 см2
*135
540
+540
675
72900
51 см · 6 м = 51 см * 600 см = 51 * 6 * 100 = 30600 см2 = 30 м2 600 см2
406 м · 307 м = 124 642 м2
* 406
307
+ 2842
1218
124642
65 мм · 84 см = 65 мм * 840 мм = 54 600 мм2
*65
840
+260
520
54600
9 км · 825 м = 9000 * 825 = 7425 м2
*825
9000
7425000Карточка-помощница
46 см · 8 м
8 м = 800 см
46 см · 8 м = 36 800 см211. Ракета летела 102 с со скоростью 8 250 м/с. Какое расстояние пролетела ракета? Выразите результат в километрах и метрах.
8 250 * 102 = 841 500 м = 841 км 500 м – пролетела ракета
Ответ: 841 км 500 м.12. В магазине продали 124 фена по цене 865 р. Сколько денег выручил магазин за проданные фены? Не выполняя вычислений, определите по записи выполненного умножения:
1) cколько стоят 4 фена;
2) cколько стоят 20 фенов;
3) cколько стоят 100 фенов;
4) cколько стоят 124 фена.1) 865 * 124 = 107 260 (руб.) – выручил магазин
Ответ: 107 260 рублей.
1) 3 460 руб. стоят 4 фена
2) 17 300 руб. стоят 20 фенов
3) 86 500 руб. стоят 100 фенов
4) 107 260 руб. стоят 124 фена13. Тыквы растут на грядке, ширина которой 1 м 12 см, а длина в 3 раза больше ширины. Верно ли, что площадь грядки больше 3 м2 и меньше 4 м2?
1) 1 м 12 см = 112 см
2) 112 * 3 = 336 (см) – длина грядки
3) 112 * 336 = 37 632 (см²) – площадь грядки
Ответ: 37 632 см². 16
-
Ответы к странице 16
14. В магазин «Мебель» привезли a диванов по цене 9 375 р. и x столов по цене 5 400 р. На какую сумму привезли мебели в магазин? Составьте выражение и найдите его значение, если a = 105, x = 210.
Решение:
a * 9375 + x * 5400, если a = 105, x = 210, тогда
105 * 9375 + 210 * 5400 = 984 375 + 1 134 000 = 2 118 375
1)
*9375
105
+46875
9375
984375
2)
*210
5400
+84
105
1134000
3)
+1134000
984375
2118375
15. Чему равно произведение, если:1) один множитель равен 4 000, а другой 298;
2) каждый из двух множителей равен 125?
Решение:1)
4000 * 298 = 4 * 298 * 1000 = 1 192
* 298
4
1192
2)
125 * 125 = 15 625
*125
125
+625
250
125
15625
16*. При каком значении а произведение 196 · а равно а?
При а = 0
17. Сколькими нулями оканчивается произведение? Ответьте, не выполняя указанных вычислений.
1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 · 11 · 12 · 13 · 14 · 15 · 16 · 17 · 18 · 19 · 20четырьмя нулями
18. К какому пятизначному числу надо прибавить 1, чтобы получить шестизначное число? Из какого числа надо вычесть 3, чтобы получить 3 597? Какое число получится, если наибольшее четырёхзначное число умножить на наименьшее трёхзначное?Решение:
К какому пятизначному числу надо прибавить 1, чтобы получить шестизначное число? 99999
Из какого числа надо вычесть 3, чтобы получить 3 597? 3600
Какое число получится, если наибольшее четырёхзначное число умножить на наименьшее трёхзначное? 9999 * 100 = 999 900
19. Решите задачу устно. За 400 г творога заплатили 84 р. По какой цене продаётся творог?
Карточка-помощница
Сначала узнаём стоимость 100 г творога. Для этого надо…
Решение:
1) 84 : 4 = 21 (р.) стоит 100 г творога.
2) 21 * 10 = 210 (р.) стоит 1 кг творога.
Ответ: 210 рублей. 17
-
Ответы к странице 17
20*. Имеет ли задача решение? Сумма трёх чисел, следующих при счёте одно за другим, равна 40. Какие это числа?
Решение:
Эти числа, так как следуют одно за другим, должны быть максимально близки друг к другу.
То есть каждое из этих чисел должно равняться примерно 3 части от суммы.
В итоге получается, что из 40 мы можем взять 3 десятка, то есть 3 * 10 = 30 и у нас останется 10. 40 - 30 = 10.
И это число десять должно складываться из 3 значений по порядку. Но нет таких 3 целых чисел, из которых можно получить 10. Получается, что задача не имеет решения.21. На лучших пасеках Сибири с каждого улья получают 160 кг мёда высшего качества. Сколько мёда можно получить с двух сибирских пасек, если на одной пасеке 175 ульев, а на другой на 15 ульев больше?
1) 175 + 15 = 190 (ул.) – на второй пасеке
2) 160 * 175 + 160 * 190 = 160 * (175 + 190) = 160 * 365 = 58 400 (кг) – соберут с двух пасек
Ответ: 58 400 кг меда.22. Ширина прямоугольного участка земли 15 м 2 дм, а длина — 22 м 5 дм. Вычислите площадь участка и выразите её в квадратных метрах.
1) 15 м 2 дм = 152 дм
2) 22 м 5 дм = 225 дм
3) 152 * 225 = 34 200 (дм²) = 342 (м²) – площадь участка
Ответ: 342 м².23*. Восстановите записи.
*245
7
1715
* 348
63
+1044
2088
21924
*283
703
+849
1981
19894924. Докажите, выполнив вычисления, что значением выражения является число 1 945.
4 5 6 1 3 2
38 · 1 000 – 13 496 – (495 · 17 + 136 · 104) = 19451)
*495
17
+3465
495
8415
2)
*136
104
+544
136
14144
3)
+ 8415
14144
22559
4) 38 * 1000 = 38 000
5)
- 38000
13496
24504
6)
-24504
22559
1945
25. Выполните деление.
846 : 2 380 : 5 420 : 210
112 : 4 891 : 9 84 : 42
623 : 7 320 : 8 100 : 20Решение:
846 : 2 = 423 380 : 5 = 76 420 : 210 = 2
112 : 4 = 28 891 : 9 = 99 84 : 42 = 2
623 : 7 = 89 320 : 8 = 40 100 : 20 = 5 18
-
Ответы к странице 18
26*. Для борьбы с паводком на реке была построена плотина. На её стене через каждые 10 см нанесли отметки, которые показывают уровень воды в реке. Перед началом паводка вода находилась на отметке 2 м 20 см. Затем каждый час уровень воды повышался на 5 см. За какое время вода поднялась на 95 см? Сколько отметок выше 2 м 20 см за это время оказалось под водой?
Решение:
95 : 5 = 19 (ч) надо было, чтобы вода поднялась на 95 см.
В итоге под водой оказалось 18 отметок, с учетом, что 2 м 20 см было уже под водой и верхнюю отметку, тоже скрыло под водой.Решите старинную задачу. У хозяина смётано на лугу 2 стога сена. Из одного стога навили 30 возов, из другого — на 10 возов меньше. Всё сено перевезли на одной лошади, которая ходила за ним по 10 раз в день. За сколько дней перевезли всё сено?
1) 30 – 10 = 20 (в.) – навили из 2 стога
2) 30 + 20 = 50 (в.) – всего навили
3) 50 : 10 = 5 (дн.) – перевезли все сено
Ответ: за 5 дней.27. Назовите координаты центра окружности. Вне, внутри или на окружности лежит точка, которой соответствует пара чисел: (2, 2); (4, 4); (5, 4); (6, 6); (1, 4); (3, 5); (3, 4)?
Решение:
Центр (3, 4)
Точки вне: (2, 2); (6, 6)
Точки внутри: (4, 4); (3, 5); (3, 4)
Точки на окружности: (5, 4); (1, 4); 19
-
Ответы к странице 19
28. От двух станций одновременно в противоположных направлениях, удаляясь один от другого, отправились два поезда со скоростями 80 км/ч и 90 км/ч. Через 5 ч они были на расстоянии 970 км один от другого. Вычислите расстояние между станциями.
1) 5 * (80 + 90) = 5 * 170 = 850 (км) – удалились друг от друга поезда за 5 ч.
2) 970 – 850 = 120 (км) – расстояние между станциями
Ответ: 120 км.29. В океане плывут голубой кит массой 150 т и его детёныш, масса которого составляет две пятых массы кита. Какова масса обоих китов?
1) 160 : 5 * 2 = 60 (т) – масса детеныша кита
2) 150 + 60 = 210 (т) – масса обоих китов
Ответ: 210 т.30. В поваренной книге написано: «Для приготовления блинчиков взять три четверти килограмма муки...» Сколько граммов муки нужно взять?
1) 1 кг = 1 000 г
2) 1 000 : 4 : 3 = 250 * 3 = 750 (г) – муки нужно взять
Ответ: 750 г муки.31*. Масса ящика с вафлями 18 кг, 4 ящика с вафлями имеют такую же массу, как 6 ящиков с изюмом. Вычислите массу 15 ящиков с изюмом.
1) 18 * 4 = 72 (кг) – весят 4 ящика с вафлями
2) 72 : 6 = 12 (кг) – масса ящика с изюмом
3) 12 * 15 = 180 (кг) – масса 15 ящиков с изюмом
Ответ: 180 кг.32*. Машина сначала ехала 30 мин со скоростью 90 км/ч, а затем 1 ч 30 мин со скоростью 80 км/ч. Какое расстояние проехала машина?
1) 30 мин – это половина часа
2) 80 * 1 + 80 : 2 + 90 : 2 = 80 + 40 + 45 = 165 (км) – проехала машина
Ответ: 165 км.33. Турист прошёл 20 км, двигаясь со скоростью 5 км/ч. На остановки во время пути он затратил 45 мин. Сколько времени занял весь путь?
1) 20 : 5 = 4 (ч.) – шел турист
2) 4 ч + 45 мин = 4 ч 45 мин – занял весь путь
Ответ: 4 ч 45 мин. 20
-
Ответы к странице 20 УЗНАЁМ НОВОЕ
34. На каждые 50 км пути машина расходует 6 л бензина. Сколько бензина нужно для того, чтобы проехать 200 км?
200 : 50 * 6 = 4 * 6 = 24 (л) – бензина нужно
Ответ: 24 л бензина.35. Поезд прошёл без остановок 420 км со скоростью 70 км/ч, затем он сделал остановку на 14 мин, а остальные 300 км прошёл со скоростью 75 км/ч. Сколько времени было затрачено на весь путь?
1) 420 : 70 = 6 (ч) – он шел со скоростью 70 км/ч
2) 300 : 75 = 4 (ч) – он шел со скоростью 75 км/ч
3) 6 ч + 14 мин + 4 ч = 10 ч 14 мин – затратил на весь путь
Ответ: 10 ч 14 мин.36. Возьмите кубики и расположите их в один слой так, как показано на рисунках. Возьмите ещё кубики и сделайте из них второй слой. Сколько всего кубиков в каждой из получившихся фигур?
Решение:
1) 2 * 4 * 2 = 8 * 2 = 16 (куб.) в фигуре
2) 2 * 3 * 2 = 6 * 2 = 12 (куб.) в фигуре37. Сколько кубиков взяли, чтобы сложить такую фигуру?
3 * 3 * 2 = 9 * 2 = 18 (куб.) взяли.
Ответ: 18 кубиков.38. От станции до посёлка 210 км. Из посёлка на станцию выехала машина со скоростью 65 км/ч. На каком расстоянии от станции будет машина через 3 ч после выезда?
1) 65 * 3 = 195 (км) – проедет машина за 3 ч.
2) 210 –195 = 15 (км) – будет машина от станции
Ответ: 15 км. 21
-
Ответы к странице 21 УЗНАЁМ НОВОЕ Конус
1. Учительница завязала Пете глаза, дала в руки одну из фигур и попросила её охарактеризовать. Вот что сказал Петя: «В основании фигуры — круг. Боковая поверхность без рёбер. Есть вершина». Знаете ли вы, как называется эта фигура? Проверьте себя: найдите название данной фигуры среди слов: куб, пирамида, конус, шар.
КОНУС
2. Возьмите модель конуса и рассмотрите её. Какой фигурой является основание, вершина конуса?
Основание - круг. Вершина - точка.
22
-
Ответы к странице 22
3. Рассмотрите чертёж конуса. Назовите вершину и центр основания конуса. Основанием любого конуса является круг.
Изучаем чертеж.
4. Какие предметы или их части по форме похожи на боковую поверхность конуса?
Колпак, шляпа гриба, купол башни, нонла (вьетнамская шляпа)
23
-
Ответы к странице 23
5. Начертите круг радиусом 5 см. Отметьте его центр. Надрежьте круг по его радиусу до центра круга. Наложите края один на другой так, чтобы получилась фигура конической формы. Склейте края.
Выполняем задание по учебнику.
6. От рулона ткани продавец отрезал одну пятую часть, что составило 3 м. Сколько метров ткани было в рулоне первоначально?
3 * 5 = 15 (м) – ткани было в рулоне первоначально
Ответ: 15 м ткани.7. От деревни до города 32 км. Проехав четвёртую часть пути, велосипедист остановился отдохнуть. Сколько километров ему осталось проехать до города?
1) 32 : 4 = 8 (км) – проехал велосипедист
2) 32 – 8 = 24 (км) – осталось проехать
Ответ: 24 км.8. Выполните действия.
12 км – 7 км 60 м 126 км : 3
10 т 160 кг + 840 кг 304 м · 50
85 ц – 2 кг 17 р. 20 к. · 6
2 ч 30 мин – 45 мин 3 р. : 4Решение:
12 км – 7 км 60 м = 12000 м - 7060 м = 4 940 м = 4 км 940 м
10 т 160 кг + 840 кг = 10 160 кг + 840 кг = 11 000 кг = 11 т
85 ц – 2 кг = 8500 кг - 2 кг = 8498 кг = 84 ц 98 кг
2 ч 30 мин – 45 мин = 2 * 60 мин + 30 мин - 45 мин = 150 мин - 45 мин = 105 мин = 1 ч 45 мин
126 км : 3 = 42 км
304 м · 50 = 304 * 5 * 10 м = 15200 м = 15 км 200 м
17 р. 20 к. · 6 = 1720 к * 6 = 10 320 к = 103 р 20 к
3 р. : 4 = 300 к : 4 = 75 к 24
-
Ответы к странице 24
9. Как изменяется второй множитель в произведениях?
250 · 2 250 · 6
250 · 3 250 · 7
250 · 4 250 · 8
250 · 5 250 · 9
Вычислите значение первого выражения. Вычисляйте значение каждого следующего выражения, используя значение предыдущего выражения.Решение:
Второй множитель увеличивается каждый раз на 1, то есть значение произведения каждый от примера к примеру будет увеличиваться на значение первого множителя, то есть на 250.
250 · 2 = 500 250 · 6 = 1500
250 · 3 = 750 250 · 7 = 1750
250 · 4 = 1000 250 · 8 = 2000
250 · 5 = 1250 250 · 9 = 225010. Математический фокус. Запишите номер своего дома или квартиры и выполните следующие действия: умножьте это число на 2, затем прибавьте 3, полученное число умножьте на 50, к произведению прибавьте свой возраст и число 65, вычтите из результата 215. Проверьте себя: получится число, две последние цифры которого обозначают возраст, а оставшиеся — номер вашего дома или квартиры.
Пробуем посчитать!
11. Закончите предложения так, чтобы получились неверные высказывания.
Если сложить 25 и 35, то получится ... .
Частное чисел 24 и 8 равно ... .
Разность чисел 100 и 70 не равна ... .
Число 30 меньше числа 28 на ... .
Произведение чисел 400 и 5 не равно … .Решение:
25 + 35 = 60
24 : 8 = 3
100 - 70 = 30
30 - 28 = 2
400 * 5 = 2000 25
-
Ответы к странице 25 УЗНАЁМ НОВОЕ Задачи на движение в одном направлении
1. Из села в город выехали одновременно машина и автобус. Автобус двигался со скоростью 60 км/ч, а машина — со скоростью 85 км/ч. Ответьте на вопросы. Почему машина перегнала автобус? Увеличивается или уменьшается расстояние между ними каждый час? На сколько километров автобус отстал от машины за 1 ч? На сколько километров автобус отстанет от машины за 2 ч, если их скорости не изменятся? На каком расстоянии друг от друга будут машина и автобус через 4 ч после начала движения?
1) 85 – 60 = 25 (км) – за час автобус отстал от машины
2) 25 * 2 = 50 (км) – за 2 часа автобус отстанет от машины
3) 25 * 4 = 100 (км) – через 4 часа после начала движения автобус и машина будут на расстоянии 100 км друг от друга
Ответ: 100 км.2. Велосипедист и мотоциклист начали движение одновременно в одном направлении из одного пункта. Скорость велосипедиста 17 км/ч, скорость мотоциклиста в 5 раз больше. На сколько километров мотоциклист обгонит велосипедиста за 2 ч?
1) 17 * 5 = 85 (км/ч) – скорость мотоциклиста
2) 2 * (85 – 17) = 2 * 68 = 136 (км) – мотоциклист обгонит велосипедиста
Ответ: на 136 км. 26
-
Ответы к странице 26
3. Собака погналась за кошкой, которая находилась от неё на расстоянии 270 м. Кошка убегает от собаки со скоростью 320 м/мин, собака бежит со скоростью 350 м/мин. Ответьте на вопросы. Догонит ли собака кошку? Ответ поясните. На сколько метров уменьшается расстояние между собакой и кошкой каждую минуту? Через сколько минут собака может догнать кошку?
1) 350 – 320 = 30 (м) – сокращение расстояния между кошкой и собакой каждую минуту
2) 270 : 30 = 9 (мин.) – собака догонит кошку
Ответ: да, собака догонит кошку через 9 минут.4. От станции отошёл поезд со скоростью 70 км/ч. Через 2 ч в этом же направлении отошёл другой поезд со скоростью 90 км/ч. Какое расстояние будет между поездами через 3 ч после отправления второго поезда?
1) 70 * (2 + 3) = 70 * 5 = 350 (км) – пройдет 1 поезд
2) 90 * 3 = 270 (км) – пройдет 2 поезд
3) 350 – 270 = 80 (км) – будет между ними
Ответ: 80 км.5. Одна стрекоза летит со скоростью 12 м/с и догоняет другую, которая летит со скоростью 10 м/с. Вначале расстояние между ними было 6 м. Через сколько секунд первая стрекоза догонит вторую?
6 : (12 – 10) = 6 : 2 = 3 (с.) – первая стрекоза догонит вторую
Ответ: через 3 с.6. Собака стала догонять хозяина, когда расстояние между ними было 400 м. Собака бежала со скоростью 150 м/мин, а хозяин шёл со скоростью 70 м/мин. Через сколько минут собака догнала хозяина?
400 : (150 – 70) = 400 : 80 = 5 (мин.) – собака догнала хозяина
Ответ: 5 мин. 27
-
Ответы к странице 27
7. Коля шёл со скоростью 80 м/мин и уронил варежку. Таня, находясь от Коли на расстоянии 240 м, увидела, что он чтото уронил. Со скоростью 160 м/мин она добежала до варежки, подняла её и бросилась за Колей. Сколько времени Таня догоняла Колю?
240 : (160 – 80) = 240 : 80 = 3 (мин.) – Таня догоняла Колю
Ответ: 3 мин.8. Вычислите устно.
120 + 3 50 · 3 240 : 12
400 – 350 200 · 3 360 : 90
102 + 40 120 · 5 120 : 30
850 – 800 30 · 6 150 : 50
Решение:
120 + 3 = 123
400 – 350 = 50
102 + 40 = 142
850 – 800 = 50
50 · 3 = 150
200 · 3 = 600
120 · 5 = 600
30 · 6 = 180
240 : 12 = 20
360 : 90 = 4
120 : 30 = 4
150 : 50 = 39. Найдите значения выражений.
6 · 80 – 135 : 5 + 364 =
720 : 8 + 36 · 12 : 4 – 16 =
100 – 6 · (36 : 9) : 8 – 8 =
(235 – 135) · 23 – 644 : (98 : 7) =Решение:
6 · 80 – 135 : 5 + 364 = 480 - 27 + 364 = 453 + 364 = 817
720 : 8 + 36 · 12 : 4 – 16 = 90 + 108 - 16 = 198 - 16 = 182
*36
12
+72
36
432
100 – 6 · (36 : 9) : 8 – 8 = 100 - 6 * 4 : 8 - 8 = 100 - 3 - 8 = 89
(235 – 135) · 23 – 644 : (98 : 7) = 100 * 23 - 644 : 14 = 2300 - 46 = 2254-644|14
56 |46
- 84
84
010. Умножьте число 12 345 679 на каждое из чисел: 9, 18, 27, 36, 45, 54, 63, 72, 81. Проверьте себя: если вы правильно выполнили умножение, то должны получиться произведения, записанные одинаковыми цифрами: единицами, двойками, тройками, четвёрками, пятёрками, шестёрками, семёрками, восьмёрками и девятками.
Решение:
12345679*9=111111111
12345679*18=222222222
12345679*27=333333333
12345679*36=444444444
12345679*45=555555555
12345679*54=666666666
12345679*63=777777777
12345679*72=888888888
12345679*81=99999999911. Выполните умножение.
205 · 603 607 · 702 105 · 106
405 · 504 408 · 902 207 · 124
108 · 207 384 · 209 302 · 167
704 · 101 422 · 508 606 · 333Решение:
205 · 603 =123 615*205
603
+615
1230
123615405 · 504 = 204120
*405
504
+1620
2025
204120
108 · 207 = 22 356
*108
207
+756
216
22356
704 · 101 = 71 104
*704
101
+704
704
71104
607 · 702 = 426 114
* 607
702
+1214
4249
426114
408 · 902 = 368 016
*408
902
+816
3672
368016
384 · 209 = 80 256
*384
209
+3456
768
80256
422 · 508 = 214 376
* 422
508
+3376
2110
214376
105 · 106 = 11 130
*105
106
+630
105
11130
207 · 124 = 25 668
*124
207
+868
248
25668
302 · 167 = 50 434
*167
302
+334
501
50434
606 · 333 = 201 798
*333
606
+1998
1998
201798 28
-
Ответы к странице 28
12. Выполните деление с остатком.
46 : 8 78 : 19 361 : 9 425 : 21
60 : 9 124 : 5 276 : 8 836 : 17
85 : 4 56 : 13 418 : 7 526 : 15
Решение:
46 : 8 = 5 (остаток 6)
-46|8
40|5
6
78 : 19 = 4 (остаток 2)
-78|19
76|4
2
361 : 9 = 40 (остаток 1)
-361|9
36 |40
1
425 : 21 = 20 (остаток 5)
-425|21
42 |20
5
60 : 9 = 6 (остаток 6)-60|9
54|6
6
124 : 5 = 24 (остаток 4)-124|5
10 |24
- 24
20
4
276 : 8 = 34 (остаток 4)
-276|8
24 |34
-36
32
4
836 : 17 = 49 (остаток 1)
-836|17
68 |49
-156
153
3
85 : 4 = 21 (остаток 1)
-85|4
8 |21
-5
4
156 : 13 = (остаток 1)
-56|13
52|4
4
418 : 7 = 59 (остаток 5)
-418|7
35 |59
- 68
63
5
526 : 15 = 35 (остаток 1)
-526|15
45 |35
-76
75
113. Вычислите значения x в равенствах.
x + 257 = 1 280 9 701 + x = 10 070
x – 3 091 = 778 8 913 – x = 8 756
x · 8 = 96 625 : x = 25
x : 15 = 45 48 · x = 96
x · 250 = 750 1000 : x = 100Решение:
x + 257 = 1 280
х = 1280 - 257
х = 123
9 701 + x = 10 070
х = 1070 - 9701
х = 369
x – 3 091 = 778
х = 3 091 + 778
х = 3869
8 913 – x = 8 756
х = 8913 - 8756
х = 157
x · 8 = 96
х = 96 : 8
х = 12
625 : x = 25
х = 625 : 25
х = 25
x : 15 = 45
х = 45 * 15
х = 675
48 · x = 96
х = 96 : 48
х = 2
x · 250 = 750
х = 750 : 250
х = 3
1000 : x = 100
х = 1000 : 100
х = 1014. Подойдёт ли по размерам коробка для торта?
Да, подойдет! Все габариты коробки больше, чем габариты торта.
15. Прямоугольный брусок покрасили со всех сторон и разрезали на кубики. Сколько кубиков, у которых окрашены 2 грани, 3 грани?
3 грани у угловых кубиков, то есть у 8 штук. 2 грани у кубиков выходящих на ребро, то есть тоже у 8 штук.
16. Длина прямоугольной грядки 5 м, а ширина — 20 дм. Грядку удлинили на 1 м, оставив ту же ширину. Какой стала площадь грядки?
1) 20 дм = 2 м
2) 5 + 1 = 6 (м) – стала длина грядки
3) 6 * 2 = 12 (м²) – площадь грядки
Ответ: 12 м². 29
-
Ответы к странице 29
17. Вычислите площадь поля, размеры которого указаны на рисунке. Решите задачу двумя способами.
Решение:
1 способ
1) 430 * 560 = 240 800 (м2) - часть площади зеленой фигуры.
2) 850 - 560 = 290 (м) - разница между длиной сверху и снизу фигуры.
3) 290 * 180 = 52 200 (м2) - часть площади зеленой фигуры.
4) 240 800 + 52 200 = 293 000 (м2) - площадь фигуры.
Ответ: 293 000 м22 способ
1) 430 * 850 = 365 500 (м2) площадь фигуры без учета выреза.
2) 850 - 560 = 290 (м) - разница между длиной сверху и снизу фигуры.
3) 430 - 180 = 250 (м) - разница между шириной слева и справа.
4) 250 * 290 = 72 500 (м2) - площадь вырезанной фигуры.
5) 365 500 - 72 500 = 293 000 (м2) - площадь фигуры.
Ответ: 293 000 м2
18. От рулона ткани длиной 20 м отрезали полтора метра ткани. Сколько ткани осталось в рулоне? Выберите верный ответ. 19 м 60 см 18 м 50 см 20 м 21 м 50 смРешение:
2000 см - 150 см = 1850 см = 18 м 50 см
Правильный ответ 18 м 50 см.19. Верно ли утверждение? Поясните свой ответ на примерах.
1) Сумма двух любых двузначных чисел больше 20.
2) Не существует верных неравенств.
3) Любое трёхзначное число записывается тремя разными цифрами.
Решение:
1) Сумма двух любых двузначных чисел больше 20.
Нет не верно. Так как минимальное двузначное это 10. В итоге 10 + 10 = 20. При этом условии результат не больше 20.
2) Не существует верных неравенств.
Существуют. Скажем 3>2. Это неравенство и оно верное!
3) Любое трёхзначное число записывается тремя разными цифрами.
Нет, неверно. Скажем есть числа 300 или 333 и другие подобные.20*. За 20 мин поезд проходит 18 км. Чему равна скорость поезда?
1) 20 мин – это третья часть часа
2) 18 * 3 = 54 (км/ч) – скорость поезда
Ответ: 54 км/ч.21. Выполните действия.
18 ч 46 мин – 13 ч 29 мин = 18 ч - 13 ч + 46 мин - 29 мин = 5 ч + 17 мин = 5 ч 17 мин
8 ч 15 мин – 35 мин = 7 ч + 75 мин - 35 мин = 7 ч + 40 мин = 7 ч 40 мин
40 мин 35 с – 20 мин 48 с = 39 мин 95 c - 20 мин 48 с = 19 мин 47 с
14 ч 38 мин + 18 ч 46 мин = 14 ч + 18 ч + 38 мин + 46 мин = 32 ч + 24 мин + 1 ч = 33 ч 24 мин
1 ч – 29 мин = 31 мин
11 ч – 29 мин = 10 ч 31 мин 30
-
Ответы к странице 30 УЗНАЁМ НОВОЕ Истинные и ложные высказывания. Высказывания со словами «неверно, что»
В математике высказывания бывают истинными и ложными. Высказывание «185 больше 97» — истинное, а высказывание «47 минус 39 равно 18» — ложное.
1. Прочитайте высказывания. Какие из них истинные и какие ложные?
В июне 30 дней.
112 и 113 — двузначные числа.
47 – 39 = 8
324 < 305
185 > 97
Любой квадрат является прямоугольником.
Ответы:
В июне 30 дней. - истинное
112 и 113 — двузначные числа. - ложное
47 – 39 = 8 - истинное
324 < 305 - ложное
185 > 97 - истинное
Любой квадрат является прямоугольником. - ложное2. Прочитай те и выберите истинные высказывания.
В русском алфавите 33 буквы.
Длина измеряется только в метрах.
1 ч = 60 мин.
1 ч = 100 мин.
Буква М — гласная.
20 делится на 5 и на 4.
368 + 402 = 360 + 402.
Человек может идти со скоростью 60 км/ч.
Ответы:
В русском алфавите 33 буквы. - истинное
Длина измеряется только в метрах. - ложное
1 ч = 60 мин. - истинное
1 ч = 100 мин. - ложное
Буква М — гласная. - ложное
20 делится на 5 и на 4. - истинное
368 + 402 = 360 + 402. - ложное
Человек может идти со скоростью 60 км/ч. - ложное 31
-
Ответы к странице 31
3. Даны истинные высказывания. Орёл — птица. В неделе 7 дней. Февраль — зимний месяц. Слово «нос» — существительное. Каждое из этих высказываний замените другим высказыванием так, чтобы оно начиналось словами «неверно, что». Какое высказывание получилось — истинное или ложное?
Ответы:
Неверно, что орёл — птица.
Неверно, что в неделе 7 дней.
Неверно, что февраль — зимний месяц.
Неверно, что слово «нос» — существительное
Получились ложные высказывания.4. Даны ложные высказывания. В любом четырёхугольнике три вершины. Тонна — единица длины. Сумма 45 и 10 равна 54. Каждое из этих высказываний замените другим высказыванием так, чтобы оно начиналось словами «неверно, что». Какое высказывание получилось — истинное или ложное?
Неверно, что четырёхугольнике три вершины.
Неверно, что тонна — единица длины.
Неверно, что Сумма 45 и 10 равна 54.
Получились верные высказывания.5. Сравните два высказывания. Чем они отличаются?
1) Клён — лиственное дерево. Неверно, что клён — лиственное дерево.
2) В марте 30 дней. Неверно, что в марте 30 дней.
Ответы:
1)
Клён — лиственное дерево. истинное
Неверно, что клён — лиственное дерево. ложное
2)
В марте 30 дней. - ложное
Неверно, что в марте 30 дней. - истинное6. Выполните действия устно.
6 000 + 3 000 + 200 + 5 60 · 80
(14 350 – 350) : 100 2 360 – 300
18 000 + 5 000 + 300 750 + 20
60 · 3 + 120 960 : 320
Решение:
6 000 + 3 000 + 200 + 5 = 9 205
60 · 80 = 4 800
(14 350 – 350) : 100 = 14000 : 100 = 140
2 360 – 300 = 2 060
18 000 + 5 000 + 300 = 23 300
750 + 20 = 770
60 · 3 + 120 = 300
960 : 320 = 3 32
-
Ответы к странице 32
7. Выполните умножение.
1 250 · 35 405 · 270 20 007 · 14
810 · 630 108 · 502 40 400 · 301
Проверьте результаты умножения с помощью калькулятора.
Решение:
1 250 · 35 = 43 750
*1250
35
+625
375
43750
405 · 270 = 109 350
* 405
270
+2835
910
109350
20 007 · 14 = 280 098
*20007
14
+80028
20007
280098
810 · 630 = 510 300
*810
630
+ 243
486
510300
108 · 502 = 54 216
*108
502
+216
540
54216
40 400 · 301 = 12 160 400
* 40400
301
+404
1212
121604008. Из села в город выехал мотоциклист со скоростью 53 км/ч. В то же время из города в село навстречу ему выехал велосипедист со скоростью 18 км/ч. Какое расстояние будет между ними через 3 ч, если расстояние от города до села 220 км?
1) 53 * 3 = 159 (км) – проедет за 3 часа мотоциклист
2) 18 * 3 = 54 (км) – проедет за 3 часа велосипедист
3) 220 – (159 + 54) = 220 – 213 = 7 (км) – будет между ними
Ответ: 7 км.9. От пристани отплыл катер со скоростью 64 км/ч. Вслед за ним сразу отплыл теплоход со скоростью 26 км/ч. Через какое время между ними будет расстояние 76 км?
1) 64 – 26 = 38 (км/ч) – скорость удаления катера от теплохода
2) 76 : 38 = 2 (ч.) – между ними будет 76 км
Ответ: 76 км.10. Из города выехала грузовая машина со скоростью 60 км/ч. Одновременно с ней по тому же шоссе из города выехала легковая машина. Через 2 ч она обогнала грузовую на 40 км. С какой скоростью ехала легковая машина?
1) 60 * 2 = 120 (км) – проехала за 2 часа грузовая машина
2) 120 + 40 = 160 (км) – проехала за 2 часа легковая машина
3) 160 : 2 = 80 (км/ч) – скорость легковой машины
Ответ: 80 км/ч. 33
-
Ответы к странице 33
11. Прочитайте числовое выражение; выражение с буквой; числовое равенство; равенство с буквой.
x + 12 56 : a = 8 30 – 6 = 24 25 · 3
Решение:
x + 12 сумма икса и двенадцати
56 : a = 8 частное равно восьми при делимом пятьдесят шесть и делителе а
30 – 6 = 24 разность тридцати и шести равна двадцати четырем
25 · 3 произведение двадцати пяти и трех12. Лариса задумала число, разделила его на 5, к частному прибавила 80, сумму умножила на 6 и произведение разделила на 72. Получилось число 10. Какое число задумала Лариса?
((10 * 72) : 6 – 80) * 5 = (120 – 80) * 5 = 200 (ч.) – задумала Лариса
Ответ: число 200.13. Саша задумал число, прибавил к нему 60, сумму разделил на 15, частное умножил на 18 и произведение разделил на 90. Получилось число 2. Вычислите задуманное число.
2 * 90 : 18 * 15 – 60 = 10 * 15 – 60 = 150 – 60 = 90 – задуманное число
Ответ: 90.14. Как сосчитать, сколько кубиков потребовалось для каждой из фигур?
По факту каждая из фигур это объем, где единицей измерения является один кубик. То есть если узнать объем выраженный в кубиках, то это и будет сколько кубиков ушло на каждую фигуру. А мы знаем, что объем считается умножением всех сторон друг на друга. То есть получается:
4*3*5=60 (куб.) ушло на левую (зеленая) фигуру
3 * 3 * 3 = 27 (куб.) ушло на правую (синяя) фигуру 34
-
Ответы к странице 34
15. Чтобы связать один шарфик, нужно 75 г козьего пуха. Верно ли, что на 27 таких шарфиков использовали больше 2 кг пуха?
75 * 27 = 2 025 (г) – пуха потребуется на 27 шарфиков
2 025 г = 2 кг 25 г
Ответ: больше 2 кг пуха.16. Купили 200 г творога и заплатили за покупку 36 р. 80 к. Вычислите цену килограмма творога.
1) 200 г – это пятая часть килограмма
2) 36 р. 80 к. = 3680 к.
3) 3680 * 5 = 18 400 к = 184 (р.) – стоит кг кофе
Ответ: 184 р.17. Узнайте в магазине цены на следующие продукты: сливочное масло (за упаковку), зелёный горошек (за банку), хлеб (за батон), молоко (за пакет или бутылку), сахар (за пачку), конфеты (за коробку). Скопируйте таблицу и внесите в неё собранные данные. Затем рассчитайте стоимость двух разных наборов из этих продуктов.
Продукт Цена Набор 1 Набор 2 штук Стоимость штук Стоимость Сливочное масло 36 р. 2 72 р. 3 Зелёный горошек 3 2 Хлеб 2 2 Молоко 1 2 Сахар 4 5 Конфеты 2 1 Сумма: Сумма: Сумма: 35
-
Ответы к странице 35
18. Назовите координаты вершин ломаной АСВМK.
Решение:А (3,1);
С (5,3);
В (6,6);
М (10,10);
K (13,6);19. На рисунке изображена фотография в масштабе 1 : 10. Вычислите её действительные размеры.
Решение:
Надо умножить ее габариты на 10. 36
-
Ответы к странице 36 УЗНАЁМ НОВОЕ Составные высказывания
1. Прочитайте каждое высказывание и определите, истинно оно или ложно. 1. Ель — лиственное дерево. 2. Ель — хвойное дерево. Соединим эти два высказывания союзом или. Ель — лиственное дерево или ель — хвойное дерево. Это высказывание можно записать короче. Ель — лиственное или хвойное дерево. Истинное или ложное высказывание с союзом «или» получилось? Составное высказывание с союзом «или» истинно, если истинно хотя бы одно из двух составляющих его высказываний.
2. Определите, истинно или ложно составное высказывание с союзом «или», если:
1) первое высказывание истинно, а второе ложно;
2) первое высказывание ложно, а второе истинно;
3) оба высказывания истинные;
4) оба высказывания ложные.
Решение:
1) первое высказывание истинно, а второе ложно; истинное
2) первое высказывание ложно, а второе истинно; истинное
3) оба высказывания истинные; ложное
4) оба высказывания ложные. ложное 37
-
Ответы к странице 37
3. Прочитайте пары высказываний.
1) Буква Э — гласная. Буква Э — согласная. 2) Тринадцать больше тридцати. Тринадцать меньше тридцати. 3) В сутках 12 часов. В сутках 36 часов. 4) Число 6 делится на 2. Число 6 делится на 3. Истинно или ложно первое высказывание; второе высказывание? Соедините каждые два высказывания союзом «или». Какое высказывание получилось — истинное или ложное?Решение:
1) Буква Э — гласная. Буква Э — согласная. первое истинное, второе ложное
2) Тринадцать больше тридцати. Тринадцать меньше тридцати. первое ложное, второе истинное
3) В сутках 12 часов. В сутках 36 часов. первое ложное, второе ложное
4) Число 6 делится на 2. Число 6 делится на 3. первое истинное, второе истинноеСоединяем каждые два высказывания союзом «или»
1) Буква Э — гласная или Буква Э — согласная. истинное
2) Тринадцать больше тридцати или Тринадцать меньше тридцати. истинное
3) В сутках 12 часов или В сутках 36 часов. ложное
4) Число 6 делится на 2. Число 6 делится на 3. ложное
4. Из каких двух высказываний образовано каждое составное высказывание?
1) В одном часе 100 мин или 60 мин.
2) Март — первый месяц весны или лета.
3) Слоны обитают на Cеверном или на Южном полюсе.
4) Разность чисел 960 и 180 равна 780 или 880.
5) В одном метре 100 см или 10 дм.
6) Основанием пирамиды может быть квадрат или семиугольник. Истинно или ложно каждое из составных высказываний? Ответ поясните.
Решение:
1) В одном часе 100 мин. В одном часе 60 мин. первое ложное, второе истинное
2) Март — первый месяц весны. Март — первый месяц лета. первое истинное, второе ложное
3) Слоны обитают на Cеверном. Слоны обитают на Южном полюсе. первое ложное, второе ложное
4) Разность чисел 960 и 180 равна 780. Разность чисел 960 и 180 равна 880.
5) В одном метре 100 см. В одном метре 10 дм. первое истинное, второе истинное
6) Основанием пирамиды может быть квадрат. Основанием пирамиды может быть семиугольник. первое истинное, второе истинное5*. Приведите примеры истинных и ложных составных высказываний, образованных с помощью союза «или».
Истинные
Ель зеленая или оранжевая.
Береза лиственная или хвойноеЛожные
Ель желтая или оранжевая.
Береза вечнозеленое дерево или хвойное 38
-
Ответы к странице 38
6. Прочитайте каждое высказывание и определите, истинно оно или ложно.
1. Берёза — лиственное дерево.
2. Берёза — хвойное дерево.Соединим эти два высказывания союзом и. Берёза — лиственное и хвойное дерево. Истинное или ложное высказывание с союзом «и» получилось? Составное высказывание с союзом «и» истинно, если истинны оба составляющих его высказывания. В остальных случаях оно ложно.
Решение:
1. Берёза — лиственное дерево. истинное
2. Берёза — хвойное дерево. ложное
Берёза — лиственное и хвойное дерево. ложное7. Определите, истинно или ложно составное высказывание с союзом «и», если:
1) первое высказывание истинно, а второе ложно;
2) первое высказывание ложно, а второе истинно;
3) оба высказывания ложные;
4) оба высказывания истинные.Решение:
1) первое высказывание истинно, а второе ложно; ложное
2) первое высказывание ложно, а второе истинно; ложное
3) оба высказывания ложные; ложное
4) оба высказывания истинные. истинное8. Прочитайте пары высказываний.
1) Буква Ж — гласная. Буква Ж — согласная.
2) Килограмм — единица массы. Килограмм — единица длины.
3) В одном дециметре 100 см. В одном дециметре 10 мм.
4) Число 100 делится на 10. Число 100 делится на 5.
Истинно или ложно первое высказывание; второе высказывание? Соедините каждые два высказывания союзом «и». Какое высказывание получилось — истинное или ложное?
Решение:
1) Буква Ж — гласная. Буква Ж — согласная. первое ложное, второе истинное
2) Килограмм — единица массы. Килограмм — единица длины. первое истинное, второе ложное
3) В одном дециметре 100 см. В одном дециметре 10 мм. первое ложное, второе ложное
4) Число 100 делится на 10. Число 100 делится на 5. первое истинное, второе истинноеСоедините каждые два высказывания союзом «и».
1) Буква Ж — гласная и согласная. ложное
2) Килограмм — единица массы и единица длины. ложное
3) В одном дециметре 100 см. и 10 мм. ложное
4) Число 100 делится на 10 и на 5. истинное 39
-
Ответы к странице 39
9. Из каких двух высказываний образовано каждое составное высказывание?
1) Зайцы едят морковку и капусту.
2) Листья с деревьев опадают весной и осенью.
3) В четырёхугольнике ABCD 3 вершины и 3 стороны. Истинно или ложно каждое из составных высказываний? Ответ поясните.
Истинно или ложно каждое из составных высказываний? Ответ поясните.
Решение:
1) Зайцы едят морковку. Зайцы едят капусту. первое истина, второе истина
2) Листья с деревьев опадают весной. Листья с деревьев опадают осенью. первое ложное, второе истинное
3) В четырёхугольнике ABCD 3 вершины. В четырёхугольнике ABCD 3 стороны. первое ложное, второе ложное10*. Приведите примеры истинных и ложных составных высказываний, образованных с помощью союза «и».
Солнце светит и греет
Птица летает и поет.
Учеба трудна и полезна.11. Составное высказывание «Если А. С. Пушкин родился в 1799 году, то он родился в восемнадцатом веке» образовано из двух высказываний:
1. А. С. Пушкин родился в 1799 году.
2. Он родился в восемнадцатом веке. Первое высказывание истинно. Это можно установить, используя энциклопедию. Второе высказывание тоже истинно, так как в восемнадцатый век входят годы с 1701-го по 1800-й включительно. Составное высказывание «Если А. С. Пушкин родился в 1799 году, то он родился в восемнадцатом веке» истинно. 40
-
Ответы к странице 40
Истинно ли высказывание «Если А. С. Пушкин жил с 1799 по 1837 год, то он прожил 48 лет»?
12. Прочитайте два высказывания. Выясните, истинные они или ложные. Соедините эти два высказывания с помощью слов «если, то». Как вы думаете, истинное или ложное высказывание получилось?
1) Ворона — птица. Ворона летает.
2) Число 4 720 — четырёхзначное. После зачёркивания нуля в числе 4 720 получится двузначное число.Решение:
1) Ворона — птица. Ворона летает. первое истинное, второе истинное
2) Число 4 720 — четырёхзначное. После зачёркивания нуля в числе 4 720 получится двузначное число. первое истинное, второе ложноеСоедините эти два высказывания с помощью слов «если, то».
1) Если Ворона птица, летает. истинное
2) Если Число 4 720 четырёхзначное, то после зачёркивания нуля в числе 4 720 получится двузначное число. ложное13. Даны два высказывания:
1) Петя отвечал на уроке математики.
2) Он получил пятёрку. Известно, что первое высказывание истинное, а второе ложное. Истинно или ложно составное высказывание «Если Петя отвечал на уроке математики, то он получил пятёрку»? Составное высказывание, образованное с помощью слов «если, то», ложно, только если первое высказывание истинно, а второе ложно.Решение:
Если Петя отвечал на уроке математики, то он получил пятёрку. ложное14. Определите, истинны или ложны высказывания, из которых образовано составное высказывание. Истинно или ложно составное высказывание?
1) Если 18 делится на 2 и на 3, то оно делится на 5.
2) Если 6 · 5 = 30, то 30 : 5 = 6.
3) Если 12 – 5 = 7, то 7 > 12.
4) Если в четырёхугольнике ABCK все углы прямые, то четырёхугольник ABCK — прямоугольник.
Решение:
1) 18 делится на 2 и на 3. 18 делится 5. первое истинное, второе ложное
2) 6 · 5 = 30, 30 : 5 = 6. первое истинное, второе истинное
3) 12 – 5 = 7, 7 > 12. первое истинное, второе ложное
4) В четырёхугольнике ABCK все углы прямые. Четырёхугольник ABCK — прямоугольник. первое истинное, второе истинное (в учебнике имеется рисунок прямоугольника ABCK) 41
-
Ответы к странице 41
15. Используя рисунок, образуйте из данных высказываний составное высказывание с помощью слов «если, то» так, чтобы оно было ложным.
АВСМ — прямоугольник.
АВСМ — квадрат.Если АВСМ — прямоугольник, то АВСМ — квадрат.
16*. Приведите примеры истинных и ложных составных высказываний, образованных с помощью слов «если, то».
Истинные
Если у квадрата сторона 2 см, то площадь 4 см2
Если листья желтеют, то наступает осень.
Если не изучать материал, то его не будешь знать.
ЛожныхЕсли у квадрата сторона 2 см, то площадь 6 см2
Если листья желтеют, то наступает лето.
Если не изучать материал, то его будешь знать.17. Вычислите.
263 127 + 736 452 728 326 – 607 314
32 736 + 398 585 900 076 – 704 977
Решение:
263 127 + 736 452 = 999579
+263127
736452
999579
728 326 – 607 314 = 121 012
-728326
607314
121012
32 736 + 398 585 = 431321
+32736
398585
431321
900 076 – 704 977 = 195099
-900076
704977
195099 42
-
Ответы к странице 42
18. Найдите значения выражений.
(15 · (178 + 5) + 90) · 7 =
486 : 9 · (46 + 54) : 10 =
624 268 – 13 965 + 190 008 =
105 · (6 + 203) – 300 : 5 =
(6 275 – 1 829) · 0 + 3 500 =
0 : (17 068 + 91 374) + 10 000 =
Решение:
2 1 3 4
(15 · (178 + 5) + 90) · 7 = 19 845
1) 178 + 5 = 183
2) 15 * 183 = 2745
* 183
15
+915
183
2745
3) 2745 + 90 = 2835
4) 2835 * 7 = 19845
*2835
7
19845
2 3 1 4
486 : 9 · (46 + 54) : 10 = 560
1) 46 + 54 = 100
2) 486 : 9 = 56
- 486|9
45 |56
- 36
36
0
3) 56 * 100 = 5600
4) 5600 : 10 = 560
1 2
624 268 – 13 965 + 190 008 = 800 311
1) 624 268 – 13 965 = 610 303
-624268
13965
610303
2) 610303 + 190008 = 800311
+610303
190008
800311
2 1 4 3
105 · (6 + 203) – 300 : 5 = 21 886
1) 6 + 203 = 209
2) 105 * 209 = 21945
*105
209
+945
210
21945
3) 300 : 5 = 60
4) 21946 - 60 = 21886
(6 275 – 1 829) · 0 + 3 500 = 0 + 3500 = 3500
0 : (17 068 + 91 374) + 10 000 = 0 + 10 000 = 10 00019. Выполните вычисления и определите, какое из чисел 628, 100, 3 639, 5 300 является значением выражения:
1) 35 · 104 – (320 : 80 + 156) : 160;
2) 25 · (146 + 254) : 100.
Решение:
1) 35 · 104 – (320 : 80 + 156) : 160 = 35 · 104 – (4 + 156) : 160 = 35 · 104 – 1 = 3640 - 1 = 3639
2) 25 · (146 + 254) : 100 = 25 · (146 + 254) : 100 = 25 * 400 : 100 = 10 000 : 100 = 10020*. Сумма трёх чисел равна 30 217. Первое слагаемое — наименьшее пятизначное число, второе — наибольшее четырёхзначное число. Чему равно каждое из слагаемых суммы?
Решение:
10000 + 9999 + х = 30 217
х = 30217 - 19999
х = 10218
Ответ: 10 21821. Выполните умножение.
3 687 · 5 96 · 53 203 · 509
12 070 · 8 77 · 77 615 · 301
5 002 · 6 502 · 61 1 217 · 108
9 100 · 7 390 · 84 4 050 · 204
Проверьте результаты с помощью калькулятора.
Решение:
3 687 · 5 = 18 435
*3687
5
18435
96 · 53 = 5 088
*96
53
+288
480
5088
203 · 509 = 103 327
* 203
509
+ 1827
1015
103327
12 070 · 8 = 96 560
*12070
8
96560
77 · 77 = 5 929
*77
77
+539
539
5929615 · 301 = 185 115
*615
301
+ 615
1845
185115
5 002 · 6 = 30 012
*5002
6
+30012
502 · 61 = 30 622
* 502
61
+ 502
3012
306221 217 · 108 = 131 436
* 1217
108
+9736
1217
131436
9 100 · 7 = 63 700
*9100
7
63700
390 · 84 = 32 760
*390
84
+156
312
32760
4 050 · 204 = 826 200
*4050
204
+1620
810
82620022. Пешеход прошёл 16 км за 4 ч. На обратном пути он уменьшил скорость на 2 км/ч. Сколько времени потратил пешеход на обратный путь? Объясните, как составлено выражение для решения задачи: 16 : (16 : 4 – 2). Закончите решение задачи.
Решение:
16 : (16 : 4 – 2) - в скобках нашли скорость на обратном пути и поделили на расстояние 16 км. В итоге получили время на обратный путь.
16:(16:4-2)=16:2=8 (ч) - время на обратный путь
Ответ: 8 часов. 43
-
Ответы к странице 43
23. Из Москвы в дачный посёлок выехала грузовая машина со скоростью 43 км/ч. В то же время из этого посёлка в Москву выехала легковая машина со скоростью 56 км/ч. Расстояние по шоссе от Москвы до посёлка 198 км. Через сколько часов машины встретятся?
198 : (56 + 43) = 198 : 99 = 2 (ч.) – машины встретятся
Ответ: через 2 часа.24*. Из деревни в город на лошади выехал фермер. Расстояние до города 24 км. Лошадь двигалась со скоростью 8 км/ч. Собака, сопровождающая фермера, постоянно забегала вправо, влево от дороги, вперёд и возвращалась к лошади. Какое расстояние пробежала собака к моменту въезда фермера в город, если она всё время бежала со скоростью 12 км/ч?
1) 24 : 8 = 3 (ч.) – двигались лошадь и собака
2) 12 * 3 = 36 (км) – пробежала собака
Ответ: 36 км.25. Поезд отошёл от станции, прошёл 10 мин со скоростью 60 км/ч, а затем уменьшил скорость на 20 км/ч из-за ремонтных работ на путях. Поезд шёл с этой скоростью 15 мин до следующей станции. Каково расстояние между станциями? Объясните решение задачи.
1) 60 : 6 = 10 (км) - прошел поезд за 10 минут
2) 60 – 20 = 40 (км/ч) - скорость после ее уменьшения
3) 40 : 4 = 10 (км) - прошел поезд после снижения скорости
4) 10 + 10 = 20 (км) - от станции до станции.
Ответ: 20 км. 44
-
Ответы к странице 44
26. Из Москвы в Санкт-Петербург выехали одновременно две машины: одна со скоростью 90 км/ч, а другая со скоростью 78 км/ч. Какое расстояние будет между ними через полчаса; через час?
1) (90 – 78) : 2 = 12 : 2 = 6 (км) – будет между ними через полчаса
2) 90 – 78 = 12 (км) – будет между ними через час
Ответ: 12 км.27*. Для варки варенья из чёрной смородины на 2 кг ягод берут 3 кг сахара. Сколько килограммов ягод потребуется для варки варенья, если хозяйка возьмёт 12 кг сахара?
1) 12 : 3 = 4 (раза) по 2 кг ягод надо взять.
2) 4 * 2 = 8 (кг) ягод надо.
Ответ: 8 кг ягод.
28*. В двух амбарах было 3 090 кг зерна. Когда из первого амбара взяли 470 кг зерна, а из второго в 4 раза больше, то во втором амбаре зерна не осталось. Сколько зерна осталось в первом амбаре?1) 470 * 4 = 1 880 (кг) – взяли зерна из 2 амбара
2) 3 090 – 1 880 = 1 210 (кг) – зерна было в 1 амбаре
3) 1 210 + 470 = 1 680 (кг) – зерна осталось в 1 амбаре
Ответ: 1 680 кг.29. В 21 ч со станции отправился поезд со скоростью 72 км/ч. В 3 ч ночи он сделал остановку. Сколько километров прошёл поезд до этой остановки?
1) 24 – 21 + 3 = 6 (ч) – шел поезд до остановки
2) 72 * 6 = 432 (км) – прошел поезд до остановки
Ответ: 432 км.30. Какая часть каждой фигуры закрашена?
Слева - половина, по центру - 4/7, справа - 1/4.
31*. Начертите две окружности, радиусы которых 2 см и 3 см, так, чтобы расстояние между их центрами было равно: 1) 0 см; 2) 5 см; 3) 4 см; 4) 7 см.
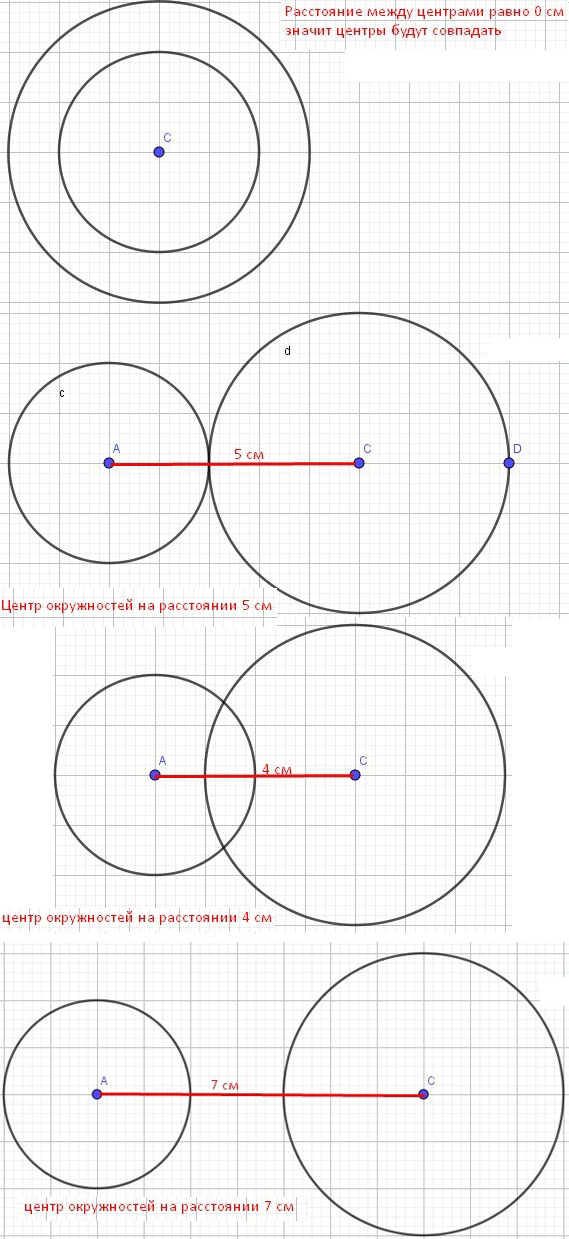
45
-
Ответы к странице 45
32*. Вычислите площадь прямоугольника. Начертите два других прямоугольника, каждый из которых имеет такую же площадь.
Решение:
Измеряем стороны - 3 и 6 см.
3 * 6 = 18 (см2) площадь прямоугольника.
Ответ: 18 см2Можно нарисовать два прямоугольника скажем с размерами:
2 и 9 см
4 и 4,5 см33. Перечертите квадрат на клетчатый лист бумаги. Вырежьте квадрат и разрежьте его на 5 частей так, как показано на рисунке. Закройте учебник. Перемешайте эти части, а затем снова сложите из них квадрат.
Перечерчиваем и складываем по памяти.
46
-
Ответы к странице 46 УЗНАЁМ НОВОЕ Задачи на перебор вариантов
1. Папа купил три книги. В каком порядке эти книги можно поставить на книжную полку? Чтобы перебрать все возможные варианты, то есть не пропустить ни одного и не назвать один и тот же вариант дважды, обычно придумывают определённый способ перебора. Рассмотрите таблицу и объясните, какой способ перебора всех вариантов расположения книг на полке предложен в этой таблице. А — книга Х. К. Андерсена Б — книга В. Бианки М — книга С. Михалкова
Вариант Левая Средняя Правая
книга книга книга
1 А Б М
2 А М Б
3 Б А М
4 Б М А
5 М А Б
6 М Б А 47
-
Ответы к странице 47
Прочитайте высказывания. Используя таблицу, определите, в каких случаях каждое высказывание истинное и в каких — ложное.
1) В середине стоит книга Х. К. Андерсена.
2) Книга В. Бианки стоит левее книги С. Михалкова.
3) Неверно, что справа стоит книга В. Бианки. В каких случаях книга С. Михалкова стоит слева, справа, в середине?Ответы:
1) В середине стоит книга Х. К. Андерсена.
Вариант Левая Средняя Правая
книга книга книга
1 А Б М ложное
2 А М Б ложное
3 Б А М истинное
4 Б М А ложное
5 М А Б истинное
6 М Б А ложное
2) Книга В. Бианки стоит левее книги С. Михалкова.
Вариант Левая Средняя Правая
книга книга книга
1 А Б М истинное
2 А М Б ложное
3 Б А М истинное
4 Б М А истинное
5 М А Б ложное
6 М Б А ложное3) Неверно, что справа стоит книга В. Бианки. В каких случаях книга С. Михалкова стоит слева, справа, в середине?
* - слева никогда, так как книга В. Бианки как раз и стоит слева, так как не справа!
Вариант Левая Средняя Правая
книга книга книга
1 А Б М истинное
2 А М Б ложное
3 Б А М истинное
4 Б М А истинное
5 М А Б ложное
6 М Б А ложное2. Имеются стакан, кружка и три напитка: простокваша, молоко и чай. Рассмотрите варианты наполнения разными напитками стакана и кружки. Попробуйте пояснить способ перебора вариантов.
П — простокваша
М — молоко
Ч — чай
Попробуйте составить и заполнить другую таблицу для решения этой же задачи. С — стакан К — кружка
Вариант Простокваша Молоко Чай
Решение:Вариант Простокваша Молоко Чай 1 С 2 С 3 С 4 К 5 К 6 К 48
-
Ответы к странице 48
Используя любую из этих таблиц, определите, в каких случаях истинно каждое высказывание.
1) В стакан налит чай.
2) В кружку налито не молоко.
3) В стакане чай или простокваша.
4) Молоко в кружке или в стакане.
5) Чай в стакане или в кружке.
6) Чай в кружке или в стакане.
7) Простокваша в кружке и в стакане.
8) Если в стакане чай, то в кружке молоко.Решение:
1) В стакан налит чай.Вариант Простокваша Молоко Чай 1 С 2 С 3 С истинное 4 К 5 К 6 К 2) В кружку налито не молоко.
Вариант Простокваша Молоко Чай 1 С 2 С 3 С 4 К истинное 5 К 6 К истинное 3) В стакане чай или простокваша.
Вариант Простокваша Молоко Чай 1 С истинное 2 С 3 С истинное 4 К 5 К 6 К 4) Молоко в кружке или в стакане.
Вариант Простокваша Молоко Чай 1 С 2 С истинное при выполнении второго условия 3 С 4 К 5 К истинное при выполнении второго условия 6 К 5) Чай в стакане или в кружке.
Вариант Простокваша Молоко Чай 1 С 2 С 3 С истинное 4 К 5 К 6 К истинное 6) Чай в кружке или в стакане.
Вариант Простокваша Молоко Чай 1 С 2 С 3 С истинное 4 К 5 К 6 К истинное 7) Простокваша в кружке и в стакане.
Вариант Простокваша Молоко Чай 1 С истинное 2 С 3 С 4 К истинное 5 К 6 К 8) Если в стакане чай, то в кружке молоко. * Высказывание ложное, так как нет зависимости чая от молока.
Вариант Простокваша Молоко Чай 1 С 2 С 3 С 4 К 5 К 6 К 3. Верно ли высказывание? Поясните свой ответ на примерах.
1) Среди трёхзначных чисел есть такие числа, которые делятся на 10.
2) Среди трёхзначных чисел нет наибольшего.
Решение:
1) Среди трёхзначных чисел есть такие числа, которые делятся на 10.
Да, верное. Скажем 100 или 110, 120, 220 и т.д.
2) Среди трёхзначных чисел нет наибольшего.
Неверное. Так как 999 самое большее трехзначное, все остальные меньше его.4*. Используя скобки, измените порядок действий так, чтобы выражение:
1) 630 + 270 : 90 : 2 имело значение 5;
2) 3 · 120 – 200 : 4 имело значение 210.
Решение:
(630+270):90:2=5
1) 630+270=900
2. 900:90=10
3. 10:2=53*(120-(200:4))=210
1. 200:4=50
2. 120-50=70
3. 70*3=2105. Произведение двух чисел равно 207. Чему будет равно новое произведение, если один из множителей увеличить в 3 раза, оставив другой без изменения? Как надо изменить один из множителей, чтобы произведение уменьшилось в 3 раза?
Ответ:
По если увеличить один из множителей в 3 раза, то результат увеличится тоже в 3 раза.
Чтобы уменьшить произведение в 3 раза, надо один из множителей уменьшить в 3 раза.6. От куска ткани отрезали два раза по 23 м, и в нём осталось 32 м. Сколько метров ткани было в куске?
2 * 23 + 32 = 46 + 32 = 78 (м) – ткани было в куске
Ответ: 78 м. 49
-
Ответы к странице 49
7. На рисунке дан график движения грибника. Пользуясь графиком, ответьте на вопросы. Что обозначают числа на каждой из осей? Сколько километров прошёл грибник: за первый час движения; через 2 ч после выхода из дома? За сколько часов грибник прошёл 10 км? Как время отдыха грибника обозначено на графике? Сколько времени он отдыхал? Вычислите, с какой скоростью шёл грибник до остановки на отдых и с какой скоростью он шёл после отдыха.
Ответы:
Что обозначают числа на каждой из осей?
По оси х время, по оси y путь.
Сколько километров прошёл грибник: за первый час движения; через 2 ч после выхода из дома?
Через час 4 км, через 2 - 8 км.
За сколько часов грибник прошёл 10 км?
за 5 часов
Как время отдыха грибника обозначено на графике?
Прямой параллельной оси х
Сколько времени он отдыхал?
2 часа
Вычислите, с какой скоростью шёл грибник до остановки на отдых и с какой скоростью он шёл после отдыха.
до остановки 4 км/ч, после 2 км/ч8. Длина участка 85 м, ширина 64 м. Дом, построенный на этом участке, занимает площадь 160 м2. Половина остальной площади занята садом. Какую площадь занимает сад?
1) 85 * 64 = 5 440 (м²) – площадь участка
2) (5 440 – 160) : 2 = 5 280 : 2 = 2640 (м²) – занимает сад
Ответ: 2640 м². 50
-
Ответы к странице 50
9. Прочитайте высказывания.
1) В слове «корова» шесть букв.
2) Март, апрель и май — весенние месяцы.
3) 1 — самое маленькое число.
4) А. С. Пушкин был врачом. Образуйте из каждого высказывания новое со словами «неверно, что». Какое получилось высказывание — истинное или ложное?
Ответы:
1) Неверно, что в слове «корова» шесть букв. ложное
2) Неверно, что март, апрель и май — весенние месяцы. ложное
3) Неверно, что 1 — самое маленькое число. Если брать только натуральные числа, то высказывание истинное
4) Неверно, что А. С. Пушкин был врачом истинное10. Истинно или ложно высказывание?
1) Неверно, что белые медведи живут на Юге.
2) Неверно, что любой прямоугольник является квадратом.
3) Неверно, что в неделе 7 дней.
Из каждого высказывания образуйте новое высказывание без слов «неверно, что». Определите, какое получилось высказывание — истинное или ложное.
Решение:
1) Неверно, что белые медведи живут на Юге. истинное
2) Неверно, что любой прямоугольник является квадратом. истинное
3) Неверно, что в неделе 7 дней. ложноеБелые медведи живут на Юге. ложное
Любой прямоугольник является квадратом. ложное
В неделе 7 дней. истинное11. Из данных высказываний образуйте составное высказывание с союзом «и». 1. Километр — единица массы. 2. Километр — единица длины. Какое получилось высказывание — истинное или ложное?
Решение:
1. Километр — единица массы и единица длины. ложное12. Истинно ли высказывание?
1) Если периметр квадрата на рисунке равен 12 см, то его площадь равна 6 см2.
2) Если площадь квадрата на рисунке равна 9 см2, то длина его стороны равна 3 см.Ответы:
1) Если периметр квадрата на рисунке равен 12 см, то его площадь равна 6 см2. ложное
2) Если площадь квадрата на рисунке равна 9 см2, то длина его стороны равна 3 см. истинное 51
-
Ответы к странице 51
13. Вырежьте такие треугольники и сложите из них один треугольник.
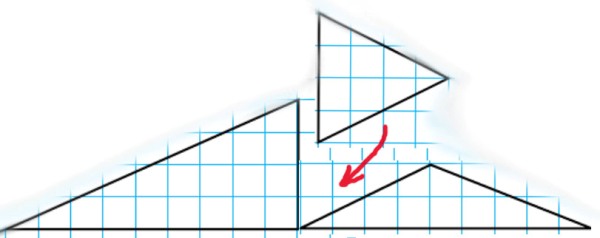
14. На какие три группы можно разделить данные фигуры?
1. Конусы и пирамиды.
2. Параллелограммы с прямыми углами.
3. Грани с прямоугольниками, но основания сложная фигура. 52
-
Ответы к странице 52
15. Длина взлётной полосы наиболее крупных аэродромов составляет 5 км, а ширина 360 м. Какова площадь такой взлётной полосы?
1) 5 км = 5 000 м
2) 5 000 * 360 = 2 100 000 (м²) – площадь взлетной полосы
Ответ: 2 100 000 м².16. Используя справочник или энциклопедию, найдите данные о площадях пяти самых крупных островов Европы (Великобритания, Ирландия, Новая Земля, Сицилия и Исландия). Найдите эти острова на карте. Назовите их в порядке увеличения площадей.
площадь Сицилии- 25 711 км²
площадь Ирландии- 70 273 км²
площадь о. Новая Земля - 83 000 км²
площадь Исландии - 103 125 км²
площадь Великобритании – 244 820 км ²17. Какую форму имеют сооружения, изображённые на фотоснимке?
Пирамиды
53
-
Ответы к странице 53 УЗНАЁМ НОВОЕ Деление суммы на число
1. В одной группе 30 туристов, а в другой — 60. Всех туристов рассадили поровну в 3 автобуса и повезли на экскурсию. Сколько туристов в каждом автобусе? Решая эту задачу, Волк и Заяц составили два разных выражения.
(30 + 60) : 3
30 : 3 + 60 : 3
Объясните, как рассуждал каждый из них. Вычислите значения выражений и сравните полученные результаты.Решение:
В первом случае нашли общее количество туристов, а затем поделив на 3 узнали сколько в каждом автобусе.
Во втором случае нашли третью часть от одной группы и третью часть от второй. Затем сложили эти третьи части и получили сколько было туристов в каждом автобусе.2. Сравните значения выражений.
(14 + 28) : 7 и 14 : 7 + 28 : 7
(40 + 16) : 8 и 40 : 8 + 16 : 8
(250 + 150) : 5 и 250 : 5 + 150 : 5
Сделайте вывод. Объясните, как можно разделить сумму двух чисел на какое-нибудь число, если каждое слагаемое делится на это число. Сравните свой ответ с текстом.
Решение:
(14 + 28) : 7 = 14 : 7 + 28 : 7 = 2 + 4 = 6
(40 + 16) : 8 = 40 : 8 + 16 : 8 = 5 + 2 = 7
(250 + 150) : 5 = 250 : 5 + 150 : 5 = 50 + 30 = 80Можно вычислить сумму и поделить на делитель, а можно каждое из слагаемых суммы поделить на делитель, а потом сложить полученные результаты.
Чтобы разделить сумму двух чисел на какое-нибудь число при условии, что каждое слагаемое делится на это число, можно разделить на это число каждое слагаемое и сложить полученные результаты.
54
-
Ответы к странице 54
Чтобы разделить сумму двух чисел на какое-нибудь число при условии, что каждое слагаемое делится на это число, можно разделить на это число каждое слагаемое и сложить полученные результаты.
3. Проверьте правило деления суммы на число.
(14 + 28) : 7
(320 + 160) : 8
Решение:
(14 + 28) : 7 = 42 : 7 = 6
14 : 7 + 28 : 7 = 2 + 4 = 6
(320 + 160) : 8 = 480 : 8 = 6
320 : 8 + 160 : 8 = 4 + 2 = 64. Запишите выражения, равные данным, используя правило деления суммы на число.
(16 + 24) : 8
(180 + 540) : 90
(49 + 14) : 7
(32 + 8) : 4КАРТОЧКА-ПОМОЩНИЦА
(12 + 18) : 2 = 12 : 2 + 18 : 2
Решение:
(16 + 24) : 8 = 16 : 8 + 24 : 8 = 2 + 3 = 5
(180 + 540) : 90 = 180 : 90 + 540 : 90 = 2 + 6 = 8
(49 + 14) : 7 = 49 : 7 + 14 : 7 = 7 + 2 = 9
(32 + 8) : 4 = 32 : 4 + 8 : 4 = 8 + 2 = 105. Используя правило деления суммы на число, найдите значения выражений.
(56 + 12) : 2 = 56 : 2 + 12 : 2 = 28 + 6 = 34
(360 + 80) : 40 = 360 : 40 + 80 : 40 = 9 + 2 = 11
(170 + 560) : 10 = 170 : 10 + 560 : 10 = 17 + 56 = 73
(120 + 300) : 60 = 120 : 60 + 300 : 60 = 2 + 5 = 7
(72 + 96) : 12 = 72 : 12 + 96 : 12 = 6 + 8 = 14
(280 + 280) : 70 = 280 : 70 + 280 : 70 = 4 + 4 = 8
(148 + 280) : 4 = 148 : 4 + 280 : 4 = 37 + 70 = 107
(150 + 450) : 50 = 150 : 50 + 450 : 50 = 3 + 9 = 116. Используя правило деления суммы на число, назовите сумму двух чисел и число, на которое её делят.
8 : 2 + 6 : 2
15 : 3 + 9 : 3
276 : 23 + 184 : 23
21 : 7 + 28 : 7
15 : 5 + 25 : 5
116 : 29 + 609 : 29Ответы:
8 : 2 + 6 : 2 сумма 8+6 = 14, число 2
15 : 3 + 9 : 3 сумма 15 +9 = 24, число 3
276 : 23 + 184 : 23 сумма 276 + 184 = 460, число 23
21 : 7 + 28 : 7 сумма 21 + 28 = 49, число 7
15 : 5 + 25 : 5 сумма 15 + 25 = 40, число 5
116 : 29 + 609 : 29 сумма 116 + 609 = 725, число 29 55
-
Ответы к странице 55
7. Приведите примеры, подтверждающие высказывание: «Если одно из двух слагаемых суммы делится на данное число, а другое не делится, то и сумма не разделится на это число».
Решение:
1 пример:
6 : 3 = 2
7 : 2 не делится
(6 + 7) = 13
13 не делится на 2
2 пример:
15:5=3
5 : 3 не делится
(15 + 5) = 20
20 : 3 не делится
8. Представьте делимое в виде суммы двух чисел так, чтобы каждое из них делилось на данное число. Вычислите значения выражений.
24 : 2 72 : 6 135 : 3 360 : 30
60 : 5 42 : 3 530 : 5 750 : 50
Решение:
24 : 2 = 10 : 2 + 14 : 2 = 5 + 7 = 12
72 : 6 = 60 : 6 + 12 : 6 = 10 + 2 = 12
135 : 3 = 90 : 3 + 45 : 3 = 30 + 15 = 45
360 : 30 = 300 : 30 + 60 : 30 = 10 + 2 = 12
60 : 5 = 50 : 5 + 10 : 5 = 10 + 2 = 12
42 : 3 = 30 : 3 + 12 : 3 = 10 + 4 = 14
530 : 5 = 500 : 5 + 30 : 5 = 100 + 6 = 106
750 : 50 = 500 : 50 + 250 : 50 = 10 + 5 = 159. При сборе винограда с одного ряда сняли 24 кг, а с другого — 48 кг. Весь виноград разложили в ящики по 8 кг. Сколько ящиков потребовалось?
(24 + 48) : 8 = 24 : 8 + 48 : 8 = 3 + 6 = 9 (ящ.) – потребовалось
Ответ: 9 ящиков.10. До обеда в саду собрали 444 кг груш, а после обеда — 348 кг. Собранные груши разложили в ящики по 12 кг. Сколько ящиков потребовалось?
(444 + 348) : 12 = 444 : 12 + 348 : 12 = 37 + 29 = 66 (ящ.) – потребовалось
Ответ: 66 ящиков.11. Приведите примеры:
1) истинного высказывания;
2) ложного высказывания;
3) предложения, которое не является высказыванием;
4) истинного высказывания со словами «неверно, что».
Ответы:
1) истинного высказывания; В году 12 месяцев.
2) ложного высказывания; В неделе 10 суток.
3) предложения, которое не является высказыванием; Вот это да!
4) истинного высказывания со словами «неверно, что». Неверно, что в неделе 10 суток12. Между какими двумя ближайшими числами (слева и справа) на числовом луче находится каждое из чисел: 565 999, 80 000, 7 509?
Решение:
565 998 565 999 566 000
79 999 80 000 80 001
7 508 7 509 7510 56
-
Ответы к странице 56
13. Вычислите значения выражений.
690 : 3 · 205 – 47 150 + 850 =
(238 145 – 237 776) : 41 + 327 : 3 · 7 =
10 000 – 120 · 80 + (900 – 750 : 25) · 7 =
Решение:
1 2 3 4
690 : 3 · 205 – 47 150 + 850 = 850
1) 690 : 3 = 230
2) 230 * 205 = 47 150
*205
230
+615
410
47150
3) 47150-47150 =04) 0 + 850 = 850
1 2 5 3 4
(238 145 – 237 776) : 41 + 327 : 3 · 7 = 763
1) 238 145 – 237 776 = 369
-238145
237776
3692) 369 : 41 = 9
3) 327 : 3 = 300 : 3 + 27 : 3 = 100 + 9 = 109
4) 109 * 7 = 763
5 3 6 2 1 4
10 000 – 120 · 80 + (900 – 750 : 25) · 7 = 6 490
1) 750 : 25 = 30
2) 900 - 30 = 870
3) 120 * 80 = 9600
4) 870 * 7 = 6090
5) 10 000 - 9600 = 400
6) 400 + 6090 = 649014. Сравните выражения в парах. Найдите значение первого выражения. Найдите значение второго выражения, используя значение первого.
25 · 4 и 25 000 · 4
13 · 5 и 130 000 · 5
Решение:
25 · 4 < 25 000 · 4
13 · 5 < 130 000 · 5
25 · 4 = 100
25 000 · 4 = 100 000
13 · 5 = 65
130 000 · 5 = 650 00015. Найдите значение второго выражения, используя значение первого.
2 · 360 = 720 (39 · 25) · 4 = 3 900
360 · 2 39 · (25 · 4)
Какие свойства умножения вы использовали?16. Выполните действия, применяя распределительное свойство умножения.
(90 + 30) · 4
(25 + 50) · 4
Решение:
(90 + 30) · 4 = 90 * 4 + 30 * 4 = 360 + 120 = 480
(25 + 50) · 4 = 25 * 4 + 50 * 4 = 100 + 200 = 30017. Сумму чисел 58 и 7 увеличьте в 11 раз. Разность чисел 87 и 23 уменьшите в 8 раз. Частное чисел 309 и 3 уменьшите на 33. Произведение чисел 124 и 70 увеличьте на 300.
Решение:
Сумму чисел 58 и 7 увеличьте в 11 раз (58 + 7) * 11 = 65 * 11 = 715
Разность чисел 87 и 23 уменьшите в 8 раз. (87 - 23) : 8 = 64 : 8 = 8
Частное чисел 309 и 3 уменьшите на 33. 309 : 3 - 33 103 - 33 = 70
Произведение чисел 124 и 70 увеличьте на 300. 124 * 70 + 300 = 8680 + 300 = 8980
18*. Велосипедист за 4 ч проехал 48 км. На обратном пути он увеличил скорость на 4 км/ч. Сколько времени потратил велосипедист на обратный путь? Как составлено выражение 48 : (48 : 4 + 4)? Закончите решение задачи.
1) 48 : 4 = 12 (км/ч) – скорость велосипедиста
2) 12 + 4 = 16 (км/ч) – скорость на обратном пути
3) 48 : 16 = 3 (ч) – затратил на обратный путь
Ответ: 3 часа. 57
-
Ответы к странице 57 УЗНАЁМ НОВОЕ Деление на 1 000, 10 000...
1. Как разделить число: на 10; на 100? Приведите примеры.
Ответ:
Деление на 10 или на 100 подразумевает уменьшение количества разрядов в числе на то количество, сколько нулей в делителе. Так скажем для 10 это на один разряд, для 100 два разряда.
Пример:
25 000 : 10 = 2 500
25 000 : 100 = 2502. Рассуждая так же, как при делении на 10 и на 100, попробуйте сформулировать правило деления на 1 000, 10 000 и 100 000. Найдите частное.
5 000 : 1 000 5 460 000 : 10 000
12 000 : 1 000 900 000 : 100 000
10 000 : 10 000 1 000 000 : 100 000
Решение:
5 000 : 1 000 = 5
5 460 000 : 10 000 = 5 460
12 000 : 1 000 = 12
900 000 : 100 000 = 9
10 000 : 10 000 = 1
1 000 000 : 100 000 = 103. Назовите тысячную долю каждого из чисел: 6 000, 13 000, 280 000, 700 000, 4 000 000.
Решение:
6 000 : 1000 = 6
13 000 : 1000 = 13
280 000 : 1000 = 28
700 000 : 1000 = 700
4 000 000 : 1000 = 4 0004. Как называется тысячная доля: килограмма; тонны; километра; метра?
Ответы:
тысячная доля:
килограмма - грамм
тонны - килограмм
километра - метр
метра - миллиметр5. Сколько граммов в 1 т? Какую часть тонны составляет 1 г? Тысячную долю грамма называют миллиграммом. Миллиграмм обозначают так: мг. В одном грамме 1 000 миллиграммов. 1 г = 1 000 мг В миллиграммах обычно выражают дозы лекарств. Например, масса аспирина в одной таблетке равна 20 мг.
Решение:
Сколько граммов в 1 т? 1 000 000 г
Какую часть тонны составляет 1 г? 1/1 000 000
6. Прочитайте записи: 5 мг, 10 мг, 25 мг, 200 мг, 685 г 120 мг, 1 кг 500 г 40 мг.
Ответ:
5 мг - пять миллиграмм,
10 мг - десять миллиграмм
25 мг - двадцать пять миллиграмм
200 мг - двести миллиграмм
685 г 120 мг - шестьсот восемьдесят пять грамм сто двадцать миллиграмм
1 кг 500 г 40 мг - один килограмм пятьсот грамм сорок миллиграмм 58
-
Ответы к странице 58
7. Во сколько раз: 1 мг меньше 1 г; 1 мг меньше 1 кг?
Ответы:
1 мг меньше 1 г в 1000 раз
1 мг меньше 1 кг в 1000 000 раз8. Рассмотрите набор гирь-разновесов. Найдите в нём гирьки массой 50 г, 20 г, 10 г, 5 г, 2 г, 1 г, 500 мг, 200 мг, 100 мг, 50 мг, 20 мг, 10 мг. Определите с помощью гирек и чашечных весов массу некоторых мелких предметов (конфеты, горошины, зёрнышка, ягоды рябины и других).
Самостоятельно используем имеющиеся гири и предметы.
9. Решите пары примеров и сравните результаты.
1) 800 : 400 2) 1 000 : 50 3) 240 : 80
8 : 4 100 : 5 24 : 8
Что вы заметили?
Ответ:
1) 800 : 400 = 2
8 : 4 = 2
2) 1 000 : 50 = 20
100 : 5 = 20
3) 240 : 80 = 3
24 : 8 = 310. Разделите 1 200 на 600. Какое число получилось? Разделите 1 200 на 100 и 600 на 100. Найдите частное полученных чисел. Какое число получилось? Сравните это число с частным чисел 1 200 и 600. Сделайте вывод. Сравните свой вывод с текстом учебника.
Решение:
1200 : 600 = 2
1200 : 100 = 12
600 : 100 = 6
Вывод:
Находя частное при делении без остатка, иногда удобно сначала разделить, если это возможно, делимое и делитель на одно и то же число, а затем найти частное полученных чисел. Результат не изменится. Пример. Разделим 600 на 120. Сразу видно, что 600 и 120 можно устно разделить на 60. Получим: 600 : 60 = 10, 120 : 60 = 2, Значит, 600 : 120 = 10 : 2 = 5.
59
-
Ответы к странице 59
Находя частное при делении без остатка, иногда удобно сначала разделить, если это возможно, делимое и делитель на одно и то же число, а затем найти частное полученных чисел. Результат не изменится. Пример. Разделим 600 на 120. Сразу видно, что 600 и 120 можно устно разделить на 60. Получим: 600 : 60 = 10, 120 : 60 = 2, Значит, 600 : 120 = 10 : 2 = 5.
11. На какое наибольшее число можно разделить делимое и делитель?
110 : 10 26 500 : 100
360 : 120 12 800 : 400
840 : 280 2 060 : 10
100 000 : 5 000 8 000 : 2 000
25 000 : 500 1 000 : 100Решение:
110 : 10 = 11 : 1 = 11 (на число 10).
360 : 120 = 3 : 1 = 3 (на число 120).
840 : 280 = 3 : 1 = 3 (на число 280).
100000 : 5000 = 2 : 1 = 2 (на число 5000).
25000 : 500 = 50 : 1 = 50 (на число 5000).
26500 : 100 = 265 : 1 = 265 (на число 100).
12800 : 400 = 32 : 1 = 32 (на число 400).
2060 : 10 = 206 : 1 = 206 (на число 10).
8000 : 2000 = 4 : 1 = 4 (на число 2000).
1000 : 100 = 10 : 1 = 10 (на число 100) .12. Разделите делимое и делитель на 5. Составьте и запишите равенства по образцу. 400 : 25 175 : 35 315 : 45 495 : 55
200 : 50 = 40 : 10
Решение:
400 : 25 = 80 : 5
175 : 35 = 35 : 7
315 : 45 = 63 : 15
495 : 55 = 99 : 1113. На складе было 25 000 кг капусты. Со склада часть капусты увезли на 7 машинах, погрузив на каждую 2 т. Сколько тонн капусты осталось?
1) 25 000 кг = 25 т
2) 25 – 2 * 7 = 25 – 14 = 11 (т) – капусты осталось
Ответ: 11 т.14. Может ли человек иметь: 1) массу 82 000 г ; 2) рост 1 920 мм? Ответ поясните.
Ответы:
1) массу 82 000 г , может так как это 82 кг
2) рост 1 920 мм, может, так как это 1 метр 92 см 60
-
Ответы к странице 60
15. Чему равно значение выражения 52 000 : a, если a = 10, 100, 1 000?
Решение:
52 000 : 10 = 5 200
52 000 : 100 = 520
52 000 : 1 000 = 5216. Чему равно частное? Как проверить результат с помощью умножения?
0 : 268 =
0 : 1 254 =
Решение
0 : 268 = 0
0 : 1 254 = 0
Проверить можно умножив на 0 и получив в результате делимое равное 0.17. Почему нельзя делить на 0? Поясните на примерах 12 : 0 и 0 : 0. Сравните свой ответ с текстом.
1) 12 : 0. Частное — это число, при умножении которого на 0 должно получиться 12. Такого числа нет.
2) 0 : 0. Частное — любое число. Какое бы число мы ни взяли, при умножении его на 0 получится 0.Делить на ноль нельзя, так как это ну существующее значение.
18. Оцените (верно, неверно) утверждение: «Частное нуля и любого числа равно 0». Как надо исправить его, чтобы оно стало верным? Дайте новую формулировку и сверьте её с данной в учебнике. Частное нуля и любого другого числа равно 0.
Ответы:
Частное нуля и любого числа равно 0. Это не верно!
Верное высказывание , - на ноль делить нельзя! 61
-
Ответы к странице 61
В математике это предложение записывают так. При любом значении а, кроме 0, верно равенство 0 : а = 0.
19. Истинно или ложно составное высказывание?
1) Если 15 + 5 = 20, то (15 + 5) · 2 = = 20 · 2.
2) Если длина стороны квадрата равна 2 см, то его периметр равен 6 см.
3) Значение выражения 250 – 50 · 4 равно числу 50 или числу 800.
4) Длина отрезка равна 3 см или 4 см.
Решение:
1) Если 15 + 5 = 20, то (15 + 5) · 2 = 20 · 2. истинное
2) Если длина стороны квадрата равна 2 см, то его периметр равен 6 см. ложное
3) Значение выражения 250 – 50 · 4 равно числу 50 или числу 800. истинное
4) Длина отрезка равна 3 см или 4 см. (смотрим рисунок и измеряем, у нас получилось 4 см, значит выражение истинное)
20. Составьте несколько задач, используя следующие данные, и решите их устно: из двух городов навстречу один другому вышли два поезда; расстояние между городами 1 200 км; первый поезд проходит это расстояние за 20 ч; второй поезд проходит расстояние между городами за 12 ч; скорость первого поезда 60 км/ч; скорость второго поезда 100 км/ч; скорость первого поезда на 40 км/ч меньше, чем скорость второго.
Задачи:
Из двух городов навстречу один другому вышли два поезда расстояние между городами 1 200 км первый поезд проходит это расстояние за 20 ч, а второй поезд проходит расстояние между городами за 12 ч. Через сколько часов поезда встретятся?
1) 1200 : 20 = 60 (км/ч) скорость первого поезда.
2) 1200 : 12 = 100 (км/ч) скорость второго поезда.
3) 100 + 60 = 160 (км/ч) скорость сближения.
4) 1200 : 160 = 7 остаток 5, то есть через 7 ч 30 минут встретятся поезда.
Ответ: 7 часов 30 минут
Из двух городов навстречу один другому вышли два поезда расстояние между городами 1 200 км скорость второго поезда 100 км/ч; скорость первого поезда на 40 км/ч меньше, чем скорость второго. Через сколько часов каждый из поездов пройдет весь путь?
1) 1200 : 100 = 12 (ч) надо первому поезду.
2) 100 - 40 = 60 (км/ч) скорость второго поезда.
3) 1200 : 60 = 20 (ч) надо второму поезду.
Ответ: 12 часов и 20 часов. 62
-
Ответы к странице 62
21. Выполните действия.
309 · 706 6 385 + 27 681
255 · 538 90 000 – 14 683
470 · 250 724 008 – 697 093
504 · 504 99 999 + 6 781
Проверьте результаты с помощью калькулятора.
Решение:
309 · 706 = 218 154* 309
706
+1854
2163
218154
255 · 538 = 137 190
*255
538
+2040
765
1275
137190
470 · 250 = 117 500
*470
250
+235
94
117500
504 · 504 = 254 016
* 504
504
+2016
2016
254016
6 385 + 27 681 = 34 066
+6385
27681
34066
90 000 – 14 683 = 75 317
-90000
14683
75317724 008 – 697 093 = 26 915
-724008
697093
26915
99 999 + 6 781 = 106 780
+99999
6781
10678022. Сколько времени показывают часы? Сколько минут прошло с того момента, когда часы показывали 1 ч? Сколько секунд прошло с того момента, когда часы показывали 1 ч 20 мин?
Ответы:
Сколько времени показывают часы? Часы показывают 4 часа 10 минут
Сколько минут прошло с того момента, когда часы показывали 1 ч? 3 часа 10 минут
Сколько секунд прошло с того момента, когда часы показывали 1 ч 20 мин? прошло 2 часа 50 минут23. Какие фигуры вы видите на рисунке? Скопируйте и заполните таблицу: отметьте знаком «+» изображённые на рисунке фигуры.
Номер рисунка Окружность Квадрат Треугольник Пятиугольник 1 + + + + 2 + + 3 + + + 4 + + 63
-
Ответы к странице 63
24. На диаграмме представлена информация о числе деревьев каждой из пяти пород, растущих в лесопарковой зоне города. Перенесите данные из диаграммы в таблицу. Каких деревьев больше: дубов или сосен; елей или рябин? Каких деревьев поровну? Каких меньше всего? На сколько берёз больше, чем елей; берёз больше, чем сосен? На сколько елей меньше, чем рябин? Сколько всего хвойных деревьев? Сколько всего лиственных деревьев?
Порода дерева Число деревьев Ель 100 Дуб 175 Сосна 75 Береза 250 Рябина 175 25. Верно ли равенство?
25 : 8 + 31 : 8 = 7
Решение:
Да, верно!
25 : 8 + 31 : 8 =(25 + 31) : 8 = 54 : 8 = 7 64
-
Ответы к странице 64 УЗНАЁМ НОВОЕ Карта
1. План города, области, государства, континента Земли называют картой. На карте имеется координатная сетка из параллелей и меридианов. Карта всегда одинаково ориентирована по отношению к сторонам света: сверху — север, снизу — юг, справа — восток, слева — запад. Рассмотрите карту. В каком масштабе выполнена эта карта? Что означает этот масштаб?
Масштаб 1 : 140 000 000
65
-
Ответы к странице 65
2. Запишите масштаб карты, если:
а) 1 см на карте соответствует 10 000 000 см на местности;
б) 1 см на карте соответствует 200 км на местности.
Ответы:
а) 1 см на карте соответствует 10 000 000 см на местности; 1 : 10 000 000
б) 1 см на карте соответствует 200 км на местности. 1 : 2003. Что означает масштаб карты: 1 : 6 000 000; 1 : 7 500 000; 1 : 300 000 000?
Ответы:
1 : 6 000 000 - 1 единица длины на карте соответствует 6 000 000 единицам длины на местности.
1 : 7 500 000 - 1 единица длины на карте соответствует 7 500 000 единицам длины на местности.
1 : 300 000 000 - 1 единица длины на карте соответствует 300 000 000 единицам длины на местности.4. Рассмотрите карту Подмосковья, выполненную в масштабе 1 : 1 000 000. Измерьте по карте и вычислите расстояние между городами:
а) Звенигород и Химки; б) Пушкино и Бронницы; в) Красногорск и Щёлково.Ответы:
Звенигород и Химки = 4 см 1:1 000 000 = 40 км
Пушкино и Бронницы = 7 см 1:1 000 000 = 70 км
Красногорск и Щёлково = 41 мм 1:1 000 000 = 41 км 66
-
Ответы к странице 66
5. Смешали по 1 кг конфет четырёх сортов по цене 175 р., 172 р., 180 р. и 185 р. за килограмм. Какова цена 1 кг полученного набора?
(175 + 172 + 180 + 185) : 4 = 712 : 4 = 178 (р.) – цена 1 кг набора
Ответ: 178 р.6. Цена 1 кг сыра — 600 р.; 5 кг сыра стоят столько же, сколько 10 кг творога. Какова цена 1 кг творога? Решите задачу двумя способами.
1) 600 * 5 : 10 = 3 000 : 10 = 300 (р.) – цена 1 кг чая
2) 600 : (10 : 5) = 600 : 2 = 300 (р.) – цена 1 кг чая
Ответ: 300 р.7. Стоимость девяти мотков пряжи на 450 р. больше, чем стоимость шести мотков этой пряжи. На костюм нужно 30 мотков пряжи. Сколько это будет стоить?
1) 450 : (9 – 6) = 450 : 3 = 150 (р.) – стоит 1 моток пряжи
2) 150 * 30 = 4 500 (р.) – будет стоить костюм
Ответ: 4 500 р.8. При сушке из 10 кг свежих яблок получается 1 кг 500 г сушёных. Сколько сушёных яблок получится из тонны свежих?
1) 1 т = 1 000 кг
2) 1 кг 500 г = 1 500 г
3) 1 000 : 10 = 100 (р.) – взяли больше свежих яблок
4) 1 500 * 100 = 150 000 (г) = 150 (кг) – получится сухих яблок
Ответ: 150 кг.9. Перелётные птицы за сутки преодолевают расстояние 200—300 км. Сколько километров пролетит стая птиц за 12 ч?
1) 24 : 12 = 2 (раза) - во столько 12 часов меньше суток
2) 200 : 2 = 100 (км) - пролетит стая птиц за 12 ч
3) 300 : 2 = 150 (км) - пролетит стая птиц за 12 ч
Ответ: 100-150 км.10. На две стройки отправили 8 одинаковых ящиков с гвоздями. Когда на обеих стройках израсходовали 60 кг гвоздей, то на одной стройке осталось 3 полных ящика, а на другой — 2. Сколько гвоздей было в каждом ящике?
1) 8 – (3 + 2) = 3 (ящ.) – гвоздей израсходовали
2) 60 : 3 = 20 (кг) – гвоздей в одном ящике
Ответ: 20 кг.11. Автомат заворачивает шоколадные конфеты в обёртки. Производительность автомата 45 конфет в минуту. Сколько конфет он завернёт за час? За какое время автомат завернёт 8 775 конфет
1) 45 * 60 = 270 (к.) – завернет за час
2) 8 775 : 45 = 195 (мин.) = 3 ч. 15 мин. – завернет 8 775 конфет
Ответ: за 3 ч. 15 мин. 67
-
Ответы к странице 67
12*. Современный спортивный лук для стрельбы имеет длину 1 580—1 770 мм, а стрела имеет длину 600—800 мм. Выразите длину лука в метрах и сантиметрах, а длину стрелы в сантиметрах.
1) 1 580 мм = 158 см = 1 м 58 см
2) 1 770 мм = 177 см = 1 м 77 см
3) 600 мм = 60 см
4) 800 мм = 80 см
Ответ: 1 м 58 см – 1 м 77 см; 60 – 80 см.13. Длина комнаты равна 4 м 20 см, а ширина — 3 м 50 см. В магазине продаются 4 ковра таких размеров. Выберите для этой комнаты ковёр наиболее подходящих размеров.
Размеры 1 2 3 4 Длина 5м 4м 4м 15см 4м 80см Ширина 3 м 2м 50 см 3 м 40 см 4м Ковер под номер 3 наиболее подходящий.
14*. Полкилограмма колбасы стоят 160 р. Какова стоимость 250 г, 750 г, 1 кг колбасы?
Полкилограмма – это 500 г
1) 160 : (500 : 250) = 160 : 2 = 80 (р.) – стоят 250 г колбасы
2) 80 * (750 : 250) = 80 * 3 = 240 (р.) – стоят 750 г колбасы
3) 160 * 2 = 320 (р.) – стоит 1 кг колбасы
Ответ: 320 р.15. От одной овцы тонкорунной породы настригают в год примерно 5 кг 200 г шерсти. Сколько шерсти можно получить при той же норме от отары овец, в которой 465 животных?
1) 5 кг 200 г = 5 200 г
2) 5 200 * 465 = 2 418 000 г = 2 148 кг = 2 т 318 кг – шерсти можно настричь
Ответ: 2 т 418 кг.16. Для изготовления канцелярской скрепки длиной 4 см 5 мм требуется кусок проволоки длиной 15 см. Сколько проволоки потребуется для изготовления 100 коробок таких скрепок, если в одну коробку кладут 75 штук?
15 * 75 * 100 = 112 500 мм = 11 250 см = 112 м 50 см – проволоки потребуется
Ответ: 112 м 50 см.17*. Вагончик подвесной канатной дороги проехал 1 км 200 м за 10 мин. Вычислите скорость движения вагончика в метрах в секунду.
1) 1 км 200 м = 1 200 м
2) 10 мин = 10 * 60 = 600 с
3) 1 200 : 600 = 2 (м/с) – скорость движения вагончика
Ответ: 2 м/с. 68
-
Ответы к странице 68 УЗНАЁМ НОВОЕ Цилиндр
1. Рассмотрите фигуры. Названия каких фигур вы уже знаете? Назовите эти фигуры. Знаете ли вы, как называется фигура под номером пять?
Найдите её название среди слов: конус, шар, цилиндр, куб. Запишите в тетради два раза слово «цилиндр» и запомните его написание.
Некоторые окружающие нас предметы по форме похожи на цилиндр: банки, вазы, детали машин, бидоны. В прошлом были в моде мужские шляпы, которые так и назывались — цилиндр. Цилиндр имеет два основания и боковую поверхность. Каждое из оснований представляет собой круг, а боковая поверхность — прямоугольник.
Ответы:
1 - куб, 2 - пирамида, 3 - шар, 4 - конус, 5 - цилиндр.
Фигура под номером 5 - цилиндр. 69
-
Ответы к странице 69
2. Какие предметы или их части имеют форму цилиндра?
бидон, банка от консервов, бревно, стакан, ведро
3. Возьмите модель цилиндра и рассмотрите её основания, боковую поверхность. Какую фигуру представляет каждое из двух оснований цилиндра и боковая поверхность?
Основания цилиндра это круги, а боковая поверхность это свернутый прямоугольник, по периметру основания - круг.
4. Возьмите стакан, в основании которого круг (см. задание 2), и налейте в него воду. Какую форму принимает вода в стакане?
вода принимает форму цилиндра
5. Перемножьте устно числа.
99 · 4 39 · 7 199 · 5
69 · 6 49 · 4 79 · 3Карточка-помощница
99 · 8 = (100 – 1) · 8 = 800 – 8 = 792
Решение:
99 · 4 = (100 – 1) * 4 = 400 - 4 = 396
39 · 7 = (40 - 1) * 7 = 280 - 7 = 273
199 · 5 = (200 - 1) * 5 = 1000 - 5 = 995
69 · 6 = (70 - 1) * 6 = 420 - 6 = 414
49 · 4 = (50 - 1) * 4 = 200 - 4 = 196
79 · 3 = (80 - 1) * 3 = 240 - 3 = 237 70
-
Ответы к странице 70
6. Решите задачу. Вариант 1 В бассейне длина дорожки равна 200 м. Пловец уже проплыл три четвёртых этой дорожки. Сколько метров ему осталось проплыть?
Вариант 2 Длина лыжной трассы 25 км. Лыжник прошёл четыре пятых пути. Сколько километров ему осталось пройти? Обменяйтесь тетрадями и проверьте работу друг друга.Вариант 1.
1) 200 : 4 * 3 = 50 * 3 = 150 (м) – проплыл пловец
2) 200 – 150 = 50 (м) – осталось проплыть
Ответ: 50 м.
Вариант 2.
1) 25 : 5 * 4 = 5 * 4 = 20 (км) – прошел лыжник
2) 25 – 20 = 5 (км) – осталось пройти
Ответ: 5 км.7. Вычислите значения выражений.
(260 : 40 + 540 : 40) · 6 + 184
750 : (50 · 3 – 25 · 3) · 30 + 70
Решение:
(260 : 40 + 540 : 40) · 6 + 184 = (260 + 540) : 40 * 6 + 184 = 800 : 40 * 6 + 184 = 20 * 6 + 184 = 120 + 184 = 304
750 : (50 · 3 – 25 · 3) · 30 + 70 = 750 :((50-25)*3) * 30 + 70 = 750 : 75 * 30 + 70 = 10 * 30 + 70 = 300 + 70 = 3708*. Из 30 учащихся отметку «5» за контрольную работу по математике получили 5 человек, отметок «4» было поставлено вдвое больше. Какая часть всех учащихся класса получила отличные и хорошие отметки?
Решение:
1) 5 * 2 = 10 (чел.) - получили 4.
2) 10 + 5 = 15 (чел.) получили 5 и 4.
3) 30 : 15 = 2 (раз) во столько меньше получили 4 и 5, чем было всего, то есть половина.
Ответ: половина учащихся получили 4 и 5.9.
1) На сколько 96 т больше 96 ц?
2) Какую часть часа составляют 6 мин, 10 мин, 15 мин, 20 мин, 30 мин?
3) Какую часть рубля составляют 1 к., 20 к., 50 к.?
4) Сколько копеек в 50 р., в 100 р.?
5) Сколько метров в 20 км, в 1 000 км?
6) Сколько центнеров в 40 т, в 100 т?
Решение:1 тонна - 1000 килограмм.
1 центнер - 100 килограмм.
1 час - 60 минут.
1 рубль - 100 копеек.
1 километр - 1000 метров.1)
96 тон - 96000 килограмм.
96 центнеров - 9600 килограмм.
96000-9600= 86400 килограмм, больше 96 тонн от 96 центнеров.
2)
60/6=10 десятую часть, от часа, составляют 6 минут.
60/10=6 шестую часть, от часа, занимает 10 минут.
60/15=4 четвертую часть, от часа, занимают 15 минут.
60/20=3 третью часть, от часа, занимают 20 минут.
60/30=2 вторую часть, от часа, занимают 30 минут.
3)
100/1=100 сотую часть, от рубля, занимает одна копейка.
100/20= 5 пятую часть, от рубля, занимает 20 копеек.
100/50= 2 вторую часть, от рубля, занимает 50 копеек.
4)
50*100=5000 копеек, в 50 рублях.
100*100=1000 копеек, в 100 рублях.
5)
20*1000==20000 метров, в 20 километрах.
1000*1000=1000000 метров, в 1000 километрах.
6)
40*10= 400 центнеров, в 40 тоннах.
100*10=1000 центнеров, в 100 тоннах. 71
-
Ответы к странице 71
10. Масса курантов, установленных на Спасской башне Московского Кремля, равна 25 000 000 г, диаметр каждого из четырёх циферблатов — 6 120 мм, длина часовой стрелки — 2 970 мм, а минутной — 3 280 мм. Выразите массу в тоннах, а длины — в метрах и сантиметрах.
Решение:
25 000 000 г = 25 т
6 120 мм = 6 м 12 см
2 970 мм = 2 м 97 см
3 280 мм = 3 м 28 см11. Найдите и объясните ошибки, которые допущены при умножении чисел.
*2360
9
21240*4108
150
+20540
4108
616200*607
208
+4856
1214
12625612. Какие высказывания ложные? Это не конус. Это не пирамида. Это пирамида. Это не прямоугольный параллелепипед.
Это не конус ложное, все остальные истинные.
72
-
Ответы к странице 72
13. Запишите в таблицу значения данных выражений, подставляя вместо буквы t числа: 10, 20, 30, 60, 150.
t 300 + t 300 - t 300 * t 300 : t 10 300 + 10 = 310 300 - 10 = 290 300 * 10 = 3 000 300 : 10 = 30 20 300 + 20 = 320 300 -20 = 280 300 * 20 = 6 000 300 : 20 = 15 30 300 + 30 = 330 300 - 30 = 270 300 * 30 = 9 000 300 : 30 = 10 60 300 + 60 = 360 300 - 60 = 240 300 * 60 = 18 000 300 : 60 = 5 150 300 + 150 = 450 300 - 150 = 150 300 * 150 = 45 000 300 : 150 = 2 14. Изобразите от руки кривые линии.
Копируем линии. Перерисовываем от руки.
15. Определите и назовите координаты центра окружности и точек А, С, М. В какой точке окружность касается оси Oх? Назовите координаты этой точки.
Ответы:
К (3, 2)
А (1, 2)
С (3, 4)
М (5, 2) 73
-
Ответы к странице 73 УЗНАЁМ НОВОЕ Деление на однозначное число
1. Вспомните и расскажите, как разделить 810 на 5. Объясните, как учащиеся выполнили деление.
-810|5
5 |162
- 31
30
10
10
0Работаем с каждым разрядом, начиная с большего и делим его на делимое. Как только у нас появляется возможность подобрать число, которое кратно делимому и можно вычесть из разряда, мы это делаем и работаем теперь с остатком по тому же принципу. Так в итоге разбираем все число.
74
-
Ответы к странице 74
2. Выполните деление.
62 785 : 5 52 278 : 3 6 083 : 4
236 270 : 5 638 145 : 9 22804 : 8
16 971 : 3 123 716 : 4 10 000 : 9
22 936 : 8 229 327 : 7 6 666 : 5
Проверьте результаты с помощью калькулятора.
Решение:
62 785 : 5 = 12 557
-62785|5
5 |12557
-12
10
-27
25
- 28
25
-35
35
0
52 278 : 3 = 17 426
-52278|3
3 |17426
- 22
21
-12
12
-7
6
-18
18
0
6 083 : 4 = 1520 (3 остаток)
-6083|4
4 |1520
-20
20
-8
8
3 остаток
236 270 : 5 = 47 254
-236270|5
20 |47254
-36
35
-12
10
-17
15
-20
20
0
638 145 : 9 = 7016
-638145|9
63 |70905
-81
81
-45
45
0
22804 : 8 = 2850 (4 остаток)
-22804|8
16 |2850
-68
64
-40
40
4 (остаток)
16 971 : 3 = 5 657
-16971|3
15 |5657
-19
18
-17
15
-21
21
0
123 716 : 4 = 30 929
-123716|4
12 |30929
-37
36
-11
8
-36
36
0
10 000 : 9 = 1 111 (1 остаток)
- 10000|9
-9 |1111
10
9
-10
9
-10
9
1 остаток
22 936 : 8 = 2867
-22936|8
16 |2867
-69
64
- 53
48
-56
56
0
229 327 : 7 = 32761
-229327|7
21 |32761
-19
14
-53
49
-42
42
-7
7
0
6 666 : 5 = 1333 (1 остаток)
-6666|5
5 |1333
-16
15
-16
15
- 16
15
1 остаток
3. Выполните действия. Проверьте умножение делением, а деление умножением.
3 687 · 8 12 345 · 7
529 671 : 3 92 808 : 4
Решение:
3 687 · 8 = 29 496
* 3687
8
29496Проверка:
-29496|8
24 |3687
-54
48
-69
64
- 56
56
0
12 345 · 7 = 86 415
*12345
7
86415
Проверка:-86415|7
7 |12345
-16
14
-24
21
-31
28
-35
35
0
529 671 : 3 = 176 577
-529671|3
3 |176557
- 22
21
-19
18
-16
15
-17
15
-21
21
0
Проверка:
*176557
3
529671
92 808 : 4 = 23 202
-92808|4
8 |23202
-12
12
-8
8
-8
8
0
Проверка:
*23202
4
928084. Вычислите значения выражений.
632 702 : 7 + 303 804 : 6 – 882 910 : 7 =
(240 328 : 8 + 654 084 + 20) : 7 =
(2 118 · 105 : 3 – 654 084 : 9) · 607 =
Решение:
1 4 2 5 3
632 702 : 7 + 303 804 : 6 – 882 910 : 7 = 14 890
1) 632 702 : 7 = 90 386
-632702|7
63 |90386
- 27
21
-60
56
-42
42
0
2) 303 804 : 6 = 50 634
3) 882 910 : 7 = 126 130
4) 90 386 + 50 634 = 141 020
5) 141 020 - 126 130 = 14 890
1 2 3 4
(240 328 : 8 + 654 084 + 20) : 7 = 97 735
1) 240 328 : 8 = 30 041
-240328|8
24 |30041
- 32
32
-8
8
0
2) 30 041 + 654 084 = 684 125
3) 684 125 + 20 = 684 145
4) 684 145 : 7 = 97 735
-684145|7
63 |97735
-54
49
-51
49
-24
21
- 35
35
0
1 2 4 3 5
(2 118 · 105 : 3 – 654 084 : 9) · 607 = 882 578
1) 2 118 · 105 = 222 390
2) 222 390 : 3 = 74 130
3) 654 084 : 9 = 72 676
4) 74130 - 72676 = 1 454
5) 1 454 * 607 = 882 5785. Каждое из данных равенств верно. Какими способами это можно доказать? Выполните вычисления.
29 764 : 5 = 5952 (ост. 4)
62 080 : 9 = 6897 (ост. 7)
Решение:5952 * 5 = 29 760
29760 + 4 = 29 764
6897 * 9 = 62 073
62073 + 7 = 62080
6. Проверьте, является ли число 3 значением буквы x в каждом равенстве.
712 020 : х = 237 340
12 228 : x = 3
Решение:712 020 : х = 237 340
712 020 : 3 = 237 040
237 040 = 237 040
да, является
12 228 : x = 3
12 228 : 3 = 4076
4076 не равно 3
нет, не является7. В хозяйстве 247 840 м2 посевной площади занято овощами, фруктовыми деревьями и зерновыми культурами. Пятая часть этой площади занята овощами, фруктовыми деревьями — площадь в 4 раза меньше, чем овощами. Остальная площадь занята зерновыми культурами. Какая площадь занята зерновыми культурами?
1) 247 840 : 5 = 49 568 (м²) – занято овощами
2) 49 568 : 4 = 12 392 (м²) – занято фруктовыми деревьями
3) 247 840 – (49 568 + 12 392) = 185 880 (м²) – занято зерновыми культурами
Ответ: 185 880 м². 75
-
Ответы к странице 75
8*. Площадь прямоугольника равна 2 133 м2, его ширина — 9 м. Найдите длину другого прямоугольника с такой же шириной, но площадью в 3 раза меньшей.
1) 2 133 : 3 = 711 (м²) – площадь другого прямоугольника
2) 711 : 9 = 79 (м) – длина другого прямоугольника
Ответ: 79 м.9. Цену на диван снижали два раза. Сначала на одну десятую часть за счёт экономии ткани, а затем ещё на четверть от новой цены за счёт замены дорогостоящей ткани более дешёвой. Какой стала новая цена на диван, если его первоначальная цена была 14 560 р.?
1) 4 560 : 10 = 456 (р.) – снизили в первый раз цену
2) 4 560 – 456 = 4 104 (р.) – стала цена после первого снижения
3) 4 104 : 4 = 1 026 (р.) – снизили цену во второй раз
4) 4 104 – 1026 = 3 078 (р.) – стала новая цена дивана
Ответ: 3 078 р.10. Чему равно частное? Сделайте вывод. Сделайте свой вывод: для всех ли чисел он верный? Сравните свой вывод с данным в учебнике. Если делитель равен 1, то частное равно делимому. В математике это предложение записывают так: при любом значении а верно равенство а : 1 = а.
Решение:
Если делитель 1, то частное всегда равно делимому. 76
-
Ответы к странице 76
11. Объясните, как получены цепочки верных равенств.
800 : 160 = 80 : 16 = 10 : 2
128 000 : 64 000 = 128 : 64 = 32 : 16 = 2 : 1
Решение:Сокращаем на число нолей в делимом и делителе. После проводим вычисление.
12. Верно ли высказывание: «Если сумма двух чисел делится на 2, то и каждое число делится на 2»? Поясните свой ответ на примерах.
Решение:
Нет не верное!
(1+1) : 2 = 2 : 2 = 1
1 :2 не делится без остатка.13. Верно ли высказывание: «Если каждое из двух чисел делится на 2, то и их сумма делится на 2»? Поясните свой ответ на примерах.
Решение:
Да, верное!
6 : 2 = 3
8 : 2 = 4
(6+8) : 2 = 14 : 2 = 714. Определите, какие из высказываний истинные и какие ложные.
1) Три не больше тридцати.
2) Неверно, что 42 : 7 = 8.
3) Неверно, что 9 · 4 = 36.
4) Если 0 разделить на 12, то получится 12.
Решение:
1) Три не больше тридцати. истинное
2) Неверно, что 42 : 7 = 8. истинное
3) Неверно, что 9 · 4 = 36. ложное
4) Если 0 разделить на 12, то получится 12. ложное15. В саду посадили 14 фруктовых деревьев: груши, сливы и яблони. Слив на 3 больше, чем груш, а яблонь меньше, чем груш. Сколько деревьев каждого вида посадили в саду? Решите задачу способом подбора. Сколько решений имеет задача?
Решение:
Рассуждаем. 14 - 3 = 11 (дер.) будет если слив и груш будет поровну. Если попытаться 11 поделить на 3, то ближайшее целое будет 9 с остатком 2. Так вот 9 делится на три вида деревьев, по 3 штуки на каждый вид. А остаток берем добавляем к грушам и сливам. То есть 3 + 1 = 4 дерева груши. Тогда 4 + 3 = 7 деревьев слив. 14 - 7 - 4 = 3 дерева яблони. Возможен еще один вариант, когда количество груш и слив будем увеличивать за счет яблок. Надо добавить по одному дереву, чтобы сохранилась зависимость с разностью в 3 штуки, то есть из яблони надо забрать число кратное 2. 3 - 2 = 1 яблоня. Тогда груш 4 + 1 = 5, а слив 7 + 1 = 8. Другие варианты не подходят, так как из яблонь больше не возьмешь "взаймы".
Вариант 1 - 4 дерева груши. 7 деревьев слив. 3 дерева яблони.
Вариант 2 - 5 груш, 8 слив, 1 яблоня.16. С помощью угольника и линейки начертите квадрат, длина стороны которого 4 см 8 мм, в масштабе 1 : 2; 2 : 1
Решение:
Чертим квадрат со стороной 2 см 4 мм и второй со стороной 8 см 16 мм. 77
-
Ответы к странице 77
17. Сравните:
1) четвёртую часть часа и 15 мин;
2) пятую часть минуты и 27 с;
3) восьмую часть килограмма и 250 г;
4) тысячную часть километра и 10 дм.
Решение:
1) четвёртую часть часа = 15 мин;
2) пятую часть минуты < 27 с;
3) восьмую часть килограмма < 250 г;
4) тысячную часть километра = 10 дм.18. На изготовление украшения ювелир израсходовал одну тысячную долю килограмма золота. Сколько золота нужно для изготовления пяти таких же украшений?
1) 1 кг = 1 000 г
2) 1 000 : 1 000 = 1 (г) – израсходовал на одну цепочку
3) 1 * 5 = 5 (г) – золота нужно для 5 цепочек
Ответ: 5 г.19*. Стиральный порошок продаётся в коробках по 650 г и 750 г. Мама хочет купить не более 2 кг порошка. Сколько и какие упаковки порошка она может купить?
Решение:
650 г
750 г
650 г + 650 г = 1300 г
650 г + 650 г + 650 г = 1950 г
650 г и 750 г = 1400 г
750 г + 750 г = 1500 г20. Выполните необходимые измерения и начертите такие прямоугольники, используя угольник и линейку.
Решение:
Измеряем стороны зеленого прямоугольника и желтого квадрата из учебного пособия и чертим точно с такими же размерами у себя в тетради.21. Во время уборки урожая собрали центнер картофеля. В большой мешок положили 46 кг, а остальной картофель разложили поровну в два мешка поменьше. Сколько килограммов картофеля положили в каждый из этих мешков?
1) 1 ц = 100 кг
2) 100 – 46 = 54 (кг) – положили в маленькие мешки
3) 54 : 2 = 27 (кг) – положили в каждый маленький мешок
Ответ: 27 кг. 78
-
Ответы к странице 78
22*. С какой скоростью шёл человек, если за 20 мин он прошёл 2 км?
1) 20 мин – это третья часть часа
2) 2 * 3 = 6 (км/ч) – скорость человека
Ответ: 6 км/ч.23. От двух станций, которые находятся на расстоянии 652 км, вышли одновременно навстречу друг другу два поезда и встретились через 4 ч. Скорость одного поезда 85 км/ч. С какой скоростью шёл другой поезд?
1) 85 * 4 = 340 (км) – прошел один поезд
2) 652 – 340 = 312 (км) – прошел другой поезд
3) 312 : 4 = 78 (км/ч) – скорость другого поезда
Ответ: 78 км/ч.24. Петя догоняет Серёжу, идущего со скоростью 100 м/мин. Сейчас расстояние между ними 300 м. Скорость Пети 160 м/мин. Через сколько минут Петя догонит Серёжу?
1) 160 – 100 = 60 (м/мин) – скорость сближения
2) 300 : 60 = 5 (мин.) – Петя догонит Сережу
Ответ: через 5 минут.25. На плодоовощной базе было 30 т свёклы. В овощные магазины свёклу развозили три грузовика. На первый погрузили 2 т 500 кг свёклы, на второй — 3 т, а на третий — 4 т 800 кг. Сколько свёклы осталось на базе?
1) 2 т 500 кг + 3 т + 4 т 800 кг = 9 т 1300 кг = 10 т 300 кг – увезли в магазины
2) 30 т – 10 т 300 кг = 19 т 700 кг – свеклы осталось на базе
Ответ: 19 т 700 кг.26. На изготовление 50 деталей мастер затрачивает 1 ч 40 мин, а его ученик работает в 2 раза медленнее. За сколько минут ученик делает одну деталь? Решите задачу двумя способами.
1 ч 40 мин = 100 мин
1 способ:
100 : 50 * 2 = 2 * 2 = 4 (мин) – ученик делает одну деталь
2 способ:
1) 1 ч 40 мин * 2 = 2 ч 80 мин = 3 ч 20 мин – потребуется ученику для изготовления 50 деталей
2) 3 ч 20 мин = 200 мин
3) 200 : 50 = 4 (мин) – ученик делает одну деталь
Ответ: 4 минуты.27*. Из аэропорта одновременно вылетели в противоположных направлениях два самолёта. Скорость одного самолёта 850 км/ч, а другого — 950 км/ч. Какое расстояние будет между ними через 30 мин после вылета?
1) 850 + 950 = 1 800 (км/ч) – скорость удаления самолетов
2) 30 мин – половина часа
3) 1 800 : 2 = 900 (км) – будет между ними
Ответ: 900 км. 79
-
Ответы к странице 79
28. Назовите координаты вершин четырёхугольника AВCM.
Решение:
A (1,4)
В (5,9)
C (9,6)
M (6,1)29. Какую форму имеют предметы или их части?
Решение:
Глобус - шар,
Термос - цилиндр,
Сачок - конус
Мяч - шар
Беседка (крыша) - пирамида
Аквариум - параллелограмм.30. Цена шубы была 30 000 р. Через некоторое время эту цену снизили на одну десятую часть. За сколько рублей можно теперь купить эту шубу?
1) 30 000 : 10 = 3 000 (р.) – снизили цену на шубу
2) 30 000 – 3 000 = 27 000 (р.) – можно купить шубу
Ответ: 27 000 р. 80
-
Ответы к странице 80 УЗНАЁМ НОВОЕ Деление на двузначное число
1. Как выполнил деление каждый учащийся?
Смотрим примеры в учебном пособии.
81
-
Ответы к странице 81
2. Выполните деление.
10 455 : 85 27 090 : 45 78 275 : 39
8 508 : 12 8 357 : 61 33 687 : 12
Решение:
10 455 : 85 = 123
-10455|85
85 |123
- 195
170
-255
255
0
27 090 : 45 = 602
-27090|45
270 |602
-90
90
0
78 275 : 39 = 2007 (2 остаток)
-78275|39
78 |2007
- 275
273
2
8 508 : 12 = 709
-8508|12
84 |709
-108
108
0
8 357 : 61 = 137
-8357|61
61 |137
- 225
183
-427
427
0
33 687 : 12 = 2807
-33687|12
24 |2807
- 96
96
-87
84
33. Выполните действия.
82 320 : 28 : 14 : 7 990 : 55 · 16 : 72 Проверьте результаты вычислений с помощью калькулятора.
Решение:
82 320 : 28 : 14 : 7 = 30
-82320|28
56 |2940
- 263
252
-112
112
0-2940|14
28 |210
-140
140
0
210 : 7 = 30
990 : 55 · 16 : 72 = 18
-990|55
55 |18
-440
440
04. Выполните деление.
268 800 : 84
121 000 : 11
196 196 : 14
144 144 : 12
Проверьте себя: найдите свои ответы среди чисел 3 200, 11 000, 14 014, 12 012.
Решение:
268 800 : 84 = 3200
-268800|84
252 |3200
-168
168
0
121 000 : 11 = 11 000
-121000|11
11 |11000
-11
11
0
196 196 : 14 = 14 014
-196196|14
14 |14014
-56
56
-19
14
-56
56
0
144 144 : 12 = 12 012
-144144|12
12 |12012
-24
24
-14
12
-24
24
05. Вычислите частное.
238 266 : 61 238 266 : 62 238 266 : 63 Проверьте себя: если сложить результаты деления, то получится число 11 531.
Решение:
238 266 : 61 = 3906
-238266|61
183 |3906
-552
549
-366
366
0
238 266 : 62 = 3843
-238266|62
186 |3843
-522
496
-266
248
- 186
186
0
238 266 : 63 = 3782
-238266|63
189 |3782
-492
441
-516
504
-126
126
03906 + 3843 + 3782 = 11531
6*. Площадь прямоугольника 4 225 дм2. Его ширина равна 6 м 5 дм. Найдите площадь другого прямоугольника, ширина которого составляет тринадцатую часть длины, а длина — пятую часть длины первого прямоугольника.
1) 6 м 5 дм = 65 дм
2) 4 225 : 65 = 65 (дм) – длина прямоугольника
3) 65 : 13 = 5 (дм) – ширина нового прямоугольника
4) 65 : 5 = 13 (дм) – длина нового прямоугольника
5) 5 * 13 = 65 (дм²) – площадь нового прямоугольника
Ответ: 65 дм².7. На одну машину погрузили 35 одинаковых ящиков с виноградом сорта «Изабелла», а на другую — 48 таких же ящиков с виноградом сорта «Мускат». Сколько имеется килограммов винограда каждого сорта, если всего на машины погрузили 1 т 162 кг винограда?
1) 1 т 162 кг = 1 162 кг
2) 1 162 : (35 + 48) = 1 162 : 83 = 14 (кг) – винограда в 1 ящике
3) 14 * 35 = 490 (кг) – винограда «Изабелла»
4) 14 * 48 = 672 (кг) – винограда «Мускат»
Ответ: 490 кг; 672 кг. 82
-
Ответы к странице 82
8. В 16 одинаковых мешках 768 кг моркови. Сколько килограммов моркови в 32 таких мешках? Решите задачу двумя способами.
1 способ.
768 : 16 * 32 = 48 * 32 = 1536 (кг) – моркови в 32 мешках
2 способ.
768 * (32 : 16) = 768 * 2 = 1536 (кг) – моркови в 32 мешках
Ответ: 1536 кг.9*. С первого поля собрали 56 мешков картофеля, а со второго — 84 таких же мешка. Со второго поля собрали на 1 т 400 кг картофеля больше, чем с первого. Сколько картофеля собрали с каждого поля?
1) 1 т 400 кг = 1 400 кг
2) 1 400 : (84 – 56) = 1 400 : 28 = 50 (кг) – картофеля в 1 мешке
3) 50 * 56 = 2800 (кг) = 2 т 800 кг – собрали с 1 поля
4) 50 * 84 = 4200 (кг) = 4 т 200 кг – собрали со 2 поля
Ответ: 2 т 800 кг; 4 т 200 кг.10. Вычислите значения выражений.
1 4 2 5 3 6
(4 826 : 38 + 62 · 11 – 2 398 : 22) : 35 = 20
1) 4 826 : 38 = 127
-4826|38
38 |127
-102
76
- 266
266
0
2) 62 * 11 = 682
3) 2 398 : 22 = 109
-2398|22
22 |109
-198
198
0
4) 127 + 682 = 809
5) 809 - 109 = 700
6) 700 : 35 = 20
3 1 4 2 5
(59 937 – 304 752 : 21 – 1 117 · 17) : 12 = 2203
1) 304 752 : 21 = 14 512
-304752|21
21 |14512
-94
84
-107
105
-25
21
-42
42
0
2) 1 117 · 17 = 18 989
*1117
17
+7819
1117
18989
3)
-59937
14512
45425
4)
-45425
18989
26436
5)
-26436|12
24 |2203
-24
24
-36
36
0
1 2 5 3 4
(25 287 + 48 589) : 92 – 92 · 10 : 2 = 343
1) 25 287 + 48 589 = 73 876
+25287
48589
73876
2) 73 876 : 92 = 803
-73876|92
736 |803
-276
276
0
3) 92 * 10 = 920
4) 920 : 2 = 460
5) 803 - 460 = 343
3 5 1 2 4
397 370 : 79 – (327 · 84 – 5 295) : 57 = 4 641
1) 327 * 84 = 27 468
*327
84
+1308
2616
27468
2) 27 468 - 5 295 = 22 173
- 27468
8295
22173
3) 397 370 : 79 = 5 030-397370|79
395 |5030
-237
237
04) 22 173 : 57 = 389
-22173|57
171 |389
-507
456
-513
513
0
5) 5 030 - 389 = 4 641
-5030
389
464111. Лыжник идёт по лыжне со скоростью 18 км/ч. Сколько метров в час проходит лыжник? Сколько метров в минуту проходит лыжник? Сколько метров в секунду проходит лыжник?
Решение:
1) 18 * 1000 = 18 000 (м) в час проходит лыжник.
2) 18 000 : 60 = 300 (м) в минуту проходит лыжник.
3) 300 : 60 = 5 (м) в секунду проходит лыжник.
Ответ: 18000 м в час, 300 м в минуту, 5 м в секунду проходит лыжник.12. Пешеход идёт со скоростью 6 км/ч. Выразите его скорость в метрах в минуту.
Решение:
6 * 1000 : 60 = 6000 : 60 = 100 (м/мин) скорость пешехода.
Ответ: 100 м/мин.13. Самолёт летит со скоростью 960 км/ч. Выразите его скорость в километрах в минуту.
Решение:
960 : 60 = 16 (км/мин) скорость самолета.
Ответ: 16 км/мин14. Автомобиль едет со скоростью 120 км/ч. Какова его скорость в метрах в минуту?
Решение:
120 * 1000 : 60 = 120 000 : 60 = 2 000 (м/мин) скорость автомобиля.
Ответ: 2000 м/мин15. По плану токарь должен изготовить 1 755 деталей за 27 дней. Ежедневно он изготавливал 68 деталей. Выполнял ли токарь дневную норму?
1 755 : 27 = 65 (д.) – дневная норма
65 < 68
Ответ: токарь выполнял дневную норму. 83
-
Ответы к странице 83
16. При делении одного числа на другое Ваня пропустил 0 в частном, и вместо числа 108 у него получилось число 18. Во сколько раз ответ Вани меньше правильного ответа?
108 : 18 = 6 (р.)
Ответ: в 6 раз.17. Автомобиль за 14 ч проехал 1 148 км. Сколько километров он проедет с той же скоростью за 19 ч?
1 148 : 14 * 19 = 82 * 19 = 1 558 (км) – проедет за 19 ч
Ответ: за 19 ч.18. Из двух городов навстречу друг другу выехали одновременно грузовая машина со скоростью 43 км/ч и легковая машина со скоростью 56 км/ч. Через сколько часов они встретятся, если расстояние между городами 693 км?
693 : (43 + 56) = 693 : 99 = 7 (ч.) – они встретятся
Ответ: через 7 часов.19. Вычислите устно.
56 + 7 12 + 9 93 : 3 120 : 6
28 + 9 36 + 5 124 : 4 810 : 9
45 + 8 72 + 6 88 : 4 155 : 5
Решение:
56 + 7 = 63
12 + 9 = 21
93 : 3 = 90 : 3 + 3 : 3 = 30 + 1 = 31
120 : 6 = 12 : 6 * 10 = 2 * 10 = 20
28 + 9 = 37
36 + 5 = 41
124 : 4 = 120 : 4 + 4 : 4 = 30 + 1 = 31
810 : 9 = 81 : 9 * 10 = 9 * 10 = 90
45 + 8 = 53
72 + 6 = 78
88 : 4 = 80 : 4 + 8 : 4 = 20 + 2 = 22
155 : 5 = 150 : 5 + 5 : 5 = 30 + 1 = 3120. Верно ли высказывание? Поясните свой ответ на примерах.
1) В любом многоугольнике вершин и сторон поровну.
2) Любая незамкнутая ломаная линия имеет столько же вершин, сколько звеньев.
3) Среди прямоугольников нет таких, у которых длина равна ширине.
4) Среди квадратов нет ни одного прямоугольника.
Решение:
1) В любом многоугольнике вершин и сторон поровну. истинное
2) Любая незамкнутая ломаная линия имеет столько же вершин, сколько звеньев. ложное
3) Среди прямоугольников нет таких, у которых длина равна ширине. ложное, если считать, что квадрат частный случай прямоугольника.
4) Среди квадратов нет ни одного прямоугольника. ложное, если считать, что квадрат частный случай прямоугольника. 84
-
Ответы к странице 84
21. Вычислите.
50 г 80 мг + 20 мг 3 кг 40 г + 960 г
1 г – 900 мг 200 мг · 4
2 кг 50 г : 5 1 г 8 мг : 2
Решение:
50 г 80 мг + 20 мг = 50 080 + 20 = 50 100 мг = 50 г 100 мг
3 кг 40 г + 960 г = 3 040 + 960 = 4 000 г = 4 кг
1 г – 900 мг = 1000 - 900 = 10 мг
200 мг · 4 = 800 мг
2 кг 50 г : 5 = 2 050 : 5 = 410 г
1 г 8 мг : 2 = 1008 : 2 = 504 мг22. Выполните деление.
10 170 : 5 242 432 : 8
406 630 : 7 960 038 : 2
480 270 : 6 6 013 200 : 3
1 010 097 : 9 89 991 : 9
Решение:
10 170 : 5 = 10 000 : 5 + 170 : 5 = 200 + 34 = 234
242 432 : 8 = 24 000 :8 + 2400 : 8 + 32 :8 = 3000 + 300 + 4 = 3304
406 630 : 7 = 58 090
-406630|7
35 |58090
-56
56
-63
63
0
960 038 : 2 = 900 000 : 2 + 6 000 : 2 + 38 :2 = 450 000 + 3000 + 19 = 453 019
480 270 : 6 = 480 000 : 6 + 240 : 6 + 30 : 6 = 80 000 + 40 + 5 = 80 045
6 013 200 : 3 = 6 000 000 : 3 + 12 000 : 3 + 1 200 : 3 = 2 000 000 + 4 000 + 400 = 2 004 400
1 010 097 : 9 = 112 233
- 1010097|9
9 |112233
-11
9
-20
18
-20
18
-29
27
-27
27
3
89 991 : 9 = 9 999-89991|9
81 |9999
-89
81
-89
81
- 89
81
-81
81
0
23. Найдите устно значения выражений.0 : 2 412 + 456 · 1 – 78 : 1 + 354 · 0 =
(678 – 125 · 5 + 781 · 0) · 1 =
1 000 – (456 · 104 + 8 907) · 0 =
0 : (4 567 – 4 399 + 56 · 42) =
Решение:
0 : 2 412 + 456 · 1 – 78 : 1 + 354 · 0 = 456 - 78 = 378
(678 – 125 · 5 + 781 · 0) · 1 = (678 - 600 + 0) * 1 = 78
1 000 – (456 · 104 + 8 907) · 0 = 1000 - 0 = 1000
0 : (4 567 – 4 399 + 56 · 42) = 024. Для приготовления оладий надо на 500 г муки взять 2 стакана молока, 2 яйца, полторы столовые ложки сахара, 3 столовые ложки сливочного масла, половину чайной ложки соли, 25 г дрожжей. Рассчитайте количество продуктов на 1 кг муки.
Решение:
1) 1000 : 500 = 2 (р.) больше надо продуктов на 1 кг, чем на 500 г.
2) 2 * 2 = 4 (ст.) молока.
3) 1,5 * 2 = 3 (л.) сахара.
4) 3 * 2 = 6 (л.) сливочного масла.
5) 0,5 *2 = 1 (ч. л.) соли.
6) 25 * 2 = 50 (г) дрожжей.
Ответ: на 1 кг муки надо, - 4 ст. молока, 3 ст. л. - сахара, 6 ст. л. сливочного масла, 1 ч. л. - соли, 50 г дрожжей.25. Для приготовления шашлыка на 500 г мяса нужно взять: 2 головки репчатого лука, 100 г зелёного лука, 200 г помидоров, половину лимона, одну столовую ложку уксуса и одну столовую ложку растительного масла. Рассчитайте количество продуктов на 2 кг мяса.
Решение:
1) 2000 : 500 = 4 (р.) больше надо продуктов на 2 кг, чем на пол килограмма.
2) 2 * 4 = 8 (г.) репчатого лука.
3) 100 * 4 = 400 (г.) укропа.
4) 200 * 4 = 800 (г.) помидор.
5) 0,5 * 4 = 2 лимона.
6) 1 * 4 = 4 (л.) столовая уксуса.
7) 1 * 4 = 4 (л.) столовая масла.
26*. Площадь прямоугольника 24 см2. В каком случае из этого прямоугольника можно вырезать квадрат, у которого длина стороны 4 см?Решение:
Одна из сторон должна быть минимум 4 см.
24 : 4 = 6 (см) должна быть вторая сторона прямоугольника.
В итоге получается, что можно вырезать квадрат в диапазоне, когда ширина изменяется от 4 см, до 6. Вторая сторона - длина будет как бы "отдавать" свой размер, также изменяясь, но в меньшую сторону от 6 см, до 4 см. Вот в процессе этих метаморфоз и можно вырезать квадрат со сторонами по 4 см. 85
-
Ответы к странице 85
27. Из двух городов одновременно навстречу друг другу выехали машина со скоростью 66 км/ч и велосипедист со скоростью 18 км/ч. Через 3 ч им осталось проехать до встречи 46 км. Вычислите расстояние между городами.
3 * (66 + 18) + 46 = 3 * 84 + 46 = 252 + 46 = 298 (км) – расстояние между городами
Ответ: 298 км.28. Какие числа можно записать вместо букв, чтобы неравенства были верными?
a < 5 х < 1 36 : с < 5
8 > m 12 + y < 16 8 · n < 40Решение: если это натуральные числа и 0, то
a < 5 a {1,2,3,4}
х < 1 x {0}
36 : с < 5 с {9, 12, 18, 36}
8 > m m {}
12 + y < 16 y {0, 1, 2, 3}
8 · n < 40 n {0, 1, 2, 3, 4}29. Из шалаша вышел охотник и направился в лес по тропинке со скоростью 96 м/мин. Через 30 мин он встретил друга, который возвращался к шалашу. Охотник попросил друга, когда тот дойдёт до шалаша, развести костёр. Через сколько минут после встречи друг охотника дойдёт до шалаша по той же дороге, если он идёт со скоростью 80 м/мин?
1) 96 * 30 = 2880 (м) – прошел охотник до встречи с другом
2) 2880 : 80 = 36 (мин) – друг охотника дойдет до шалаша
Ответ: через 36 минут.30. Пачка сливочного масла массой 250 г стоит 132 р. Сколько стоит 1 кг масла? Петя решил эту задачу так: умножил 132 на 4 и получил 528. Как рассуждал Петя?
Решение:
Петя решил, раз 250 г это 4 часть, так как 1000 : 250 = 4, то стоимость возрастет пропорционально массе, что верно. В итоге:
132 * 4 = 528 рублей.
Ответ: 528 рублей.31. Ртуть — единственный в природе металл, который в обычных условиях находится в жидком состоянии. Ртуть очень тяжёлая: 1 л ртути имеет массу, равную 13 кг 600 г. Какова масса 5 л ртути, 10 л ртути?
13 кг 600 г * 5 = 65 кг 3000 г = 68 (кг) – масса ртути в пятилитровом баллоне
Ответ: 68 кг. 86
-
Ответы к странице 86
32. Рассмотрите диаграмму. Назовите рост каждого из детей. Оля — 128 см Ответьте на вопросы. Кто из детей самый высокий? Кто по росту ниже Оли? Есть ли дети одинакового роста? Кто по росту выше Оли, но ниже Юры? На сколько сантиметров Ира ниже Зои? Кто из девочек выше всех других девочек? Верно ли, что из мальчиков самый высокий Яша? На сколько сантиметров Тая выше Иры?
Решение:
Оля - 128 см,
Юра - 140 см,
Зоя - 125 см,
Ира - 123 см,
Яша - 134 см,
Таня - 125 см
Кто из детей самый высокий? Юра
Кто по росту ниже Оли? Зоя, Ира, Таня
Есть ли дети одинакового роста? Да (Зоя, Таня)
Кто по росту выше Оли, но ниже Юры? Яша
На сколько сантиметров Ира ниже Зои? 125 - 123 = 2 см
Кто из девочек выше всех других девочек? Оля
Верно ли, что из мальчиков самый высокий Яша? Нет
На сколько сантиметров Таня выше Иры? 125 - 123 = 2 см33. Предложите способ устного вычисления суммы.
50 + 51 + 52 + 53 + 54 + 55 + 56 + 57 + 58 + 59 + 60
Решение:
Если складывать крайние значения, приближаясь к середине, то их сумма будет одинаковой. то есть 50 + 60 = 51 + 59 = 110. Таких значений 5. Значит 110 * 5 = 550 будет сумма выражения. 87
-
Ответы к странице 87
34. Начертите и вырежьте такие фигуры. Составьте из всех четырёх фигур прямоугольник.
Решение: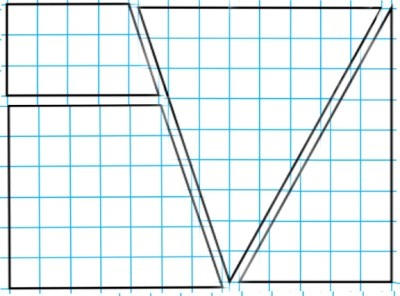
35. Цена телефона равна 8 500 р. На сколько дороже обойдётся покупателю приобретение этого телефона в рассрочку на 1 год, если нужно будет заплатить сразу десятую часть его цены и в течение следующих 11 месяцев выплачивать по 750 р. в месяц?
1) 8 500 : 10 = 850 (руб.) – десятая часть цены
2) 850 + 750 * 11 = 850 + 8 250 = 9 100 (руб.) – заплатит всего в рассрочку
3) 9 100 – 8 500 = 600 (руб.) – обойдется дороже
Ответ: на 600 рублей.36. Один из самых больших золотых самородков массой 36 200 г был добыт на Урале в 1842 году. Он хранится в Московском Кремле. Выразите массу этого самородка в килограммах и граммах.
Решение:
36 200 г = 36 кг 200 г 88
-
Ответы к странице 88 УЗНАЁМ НОВОЕ Деление на трёхзначное число
1. Как выполнено деление?
Решение:
Смотрим учебное пособие.2. Выполните деление.
23 166 : 429 20 412 : 378 64 983 : 684
20 319 : 521 19 536 : 444 36 346 : 153
69 471 : 837 19 869 : 537 957 330 : 209Решение:
23 166 : 429 = 54
-23166|429
2145 |54
-1716
1716
0
20 412 : 378 = 54
- 20412|378
1890 |54
-1512
1512
0
64 983 : 684 = 95 (остаток 3)
-64983|684
6156 |95
-3423
3420
3
20 319 : 521 = 39
- 20319|521
1563 |39
-4689
4689
0
19 536 : 444 = 44
-19536|444
1776 |44
-1776
1776
0
36 346 : 153 = 237 (85 остаток)
-36346|153
306 |237
-574
459
-1156
1071
85
69 471 : 837 = 83
-69471|837
6696 |83
-2511
2511
0
19 869 : 537 = 37
-19869|537
1611 |37
-3759
3759
0
957 330 : 209 = 4580 (110 остаток)
-957330|209
836 |4580
-1213
1045
-1683
1672
1103. Проверьте умножением, правильно ли выполнено деление.
162 409 : 403 = 403 27 336 : 402 = 608Решение:
162 409 : 403 = 403
-162409|403
1612 |403
-1240
1240
0
27 336 : 402 = 608
-27336|402
2412 |608
-3216
3216
0 89
-
Ответы к странице 89
4. Найдите значения выражений.
1) (1 494 + 1 854) : (1 104 – 1 077) · 378 =
2) 27 463 · 0 + 37 400 : 136 =
3) (76 114 : 19 – 3 928) · 751 + 60 521 =
4) 166 842 : 207 · 207 =
5) 203 · 604 – 140 904 : 456 + 0 : 33 987 =
6) (87 147 : 207 – 87 527 : 803) · 312 =
Решение:
1 3 2 4
(1 494 + 1 854) : (1 104 – 1 077) · 378 = 46872
1) 1 494 + 1 854 = 3 348
2) 1 104 – 1 077 = 27
3) 3 348 : 27 = 124
-3348|27
27 |124
-64
54
-108
108
0
4) 124 * 378 = 46 872
*124
378
+992
868
372
46872
1 3 2
27 463 · 0 + 37 400 : 136 = 275
1) 27 463 · 0 = 0
2) 37 400 : 136 = 275
-37400|136
272 |275
- 1020
952
-680
680
0
3)
1 2 3 4
(76 114 : 19 – 3 928) · 751 + 60 521 = 166 842
1) 76114 : 19 = 4006
-76114|19
76 |4006
-114
114
0
2) 4006 - 3928 = 78
3) 78 * 751 = 57 578
*751
78
+6008
5257
58578
4) 58578 + 60 521 = 119 099
+58578
60521
119099
166 842 : 207 · 207 = 166 842
1 4 2 5 3
203 · 604 – 140 904 : 456 + 0 : 33 987 = 122 303
1) 203 * 604 = 122 612
*203
604
+ 812
1218
122612
2) 140 904 : 456 = 309
-140904|456
1368 |309
-4104
4104
0
3) 0 : 33 987 = 0
4) 122 612 - 309 = 122 303
5) 122 303 + 0 = 122 303
1 3 2 4
(87 147 : 207 – 87 527 : 803) · 312 = 97 344
1) 87 147 : 207 = 421
-87147|207
828 |421
-434
414
- 207
207
0
2) 87 527 : 803 = 109
-87527|803
803 |109
-7227
7227
03) 421 - 109 = 312
4) 312 * 312 = 97 344
*312
312
+624
312
936
973445. Составьте выражение:
1) из суммы чисел 13 479 и 16 397, знака деления и разности 1 276 и 968;
2) из разности чисел 14 374 и 13 389, знака умножения и частного 9 300 и 372.
Найдите значения выражений.Решение:
1) из суммы чисел 13 479 и 16 397, знака деления и разности 1 276 и 968;
1 3 2
(13 479 + 16 397) : (1 276 - 968) = 97
1) 13 479 + 16 397 = 29876
2) 1 276 - 968 = 308
3) 29876 : 308 = 97
-29876|308
2772 |97
-2156
2156
0
2) из разности чисел 14 374 и 13 389, знака умножения и частного 9 300 и 372.
1 3 2
(14 374 - 13 389) * (9 300 : 372) = 24 625
1) 14 374 - 13 389 = 985
-14374
13389
985
2) 9300 : 372 = 25
-9300|372
744 |25
-1860
1860
0
3) 985 * 25 = 24 625
*985
25
+4925
1970
246256. Выполните деление.
230 202 : 378 84 854 : 406
32 922 : 279 460 756 : 508
2 231 100 : 670 4 087 140 : 102
631 350 : 305 529 156 : 503Решение:
230 202 : 378 = 609
-230202|378
2268 |609
-3402
3402
0
84 854 : 406 = 209
-84854|406
812 |209
-3654
3654
0
32 922 : 279 = 118
-32922|279
279 |118
-502
279
- 2232
2232
0
460 756 : 508 = 907
-460756|508
4572 |907
-3556
3556
0
2 231 100 : 670 = 3 330
-2231100|670
2010 |3330
-2211
2010
-2010
2010
0
4 087 140 : 102 = 40 070
-4087140|102
408 |40070
-714
714
0
631 350 : 305 = 2135
-631350|305
610 |2070
-2135
2135
0
529 156 : 503 = 1052
-529156|503
503 |1052
-2615
2515
-1006
1006
07. Найдите значение выражения 17 940 : y, если у = 115, 345, 690.
Решение:
17 940 : 115 = 156
-17940|115
115 |156
-644
575
-690
690
0
17 940 : 345 = 52
-17940|345
1725 |52
-690
690
0
17 940 : 690 = 52 : 2 = 26
последнее выражение было найдено из условия соотношения делителя и частного и на основании результата предыдущего примера - 690 : 345 = 2 и 52 : 2 = 26
8. Самолёт пролетел 1 900 км со скоростью 950 км/ч. Сколько часов самолёт был в пути?
1 900 : 950 = 2 (ч.) – самолет был в пути
Ответ: 2 часа.9. На овощной базе было а кг помидоров. На 7 машин погрузили по 160 кг помидоров и отвезли в магазины. Сколько килограммов помидоров осталось на базе? Составьте выражение для решения задачи и выполните вычисления, если а = 2 479.
1) а – 160 * 7 = а – 1 120
а = 2 479
2) 2 479 – 1 120 = 1 359 (кг) – помидоров осталось на базе
Ответ: 1 359 кг. 90
-
Ответы к странице 90
10. В пяти одинаковых кусках ткани было по 135 м ситца, а в девяти одинаковых кусках было по 25 м сатина. На сколько метров сатина меньше, чем ситца? Во сколько раз ситца больше, чем сатина?
1) 135 * 5 = 675 (м) – было ситца
2) 25 * 9 = 225 (м) – было сатина
3) 675 – 225 = 450 (м) – сатина меньше, чем ситца
4) 675 : 225 = 3 (р.) – ситца больше, чем сатина
Ответ: на 450 м меньше; в 3 раза больше.11. Самолёт пролетел 3 820 км со скоростью 955 км/ч, затем он уменьшил скорость до 950 км/ч и с этой скоростью пролетел ещё 1 900 км. Сколько времени затратил самолёт на весь рейс?
1) 3 820 : 995 = 4 (ч.) – летел до уменьшения скорости
2) 1 900 : 950 = 2 (ч.) – летел еще
3) 4 + 2 = 6 (ч.) – затратил самолет на весь рейс
Ответ: 6 часов.12. За сколько часов можно долететь от Москвы до Петропавловска-Камчатского на самолёте Ту-154, если скорость самолёта 850 км/ч? На карте, масштаб которой 1 : 40 000 000, расстояние между этими городами составляет 17 см.
1) 17 * 40 000 000 = 680 000 000 (см) = 6 800 (км) – расстояние между городами
2) 6 800 : 850 = 8 (ч.) – летит самолет
Ответ: 8 часов.13. Проверьте, верны ли равенства и неравенства.
706 + 43 = 749 270 · 2 : 10 > 54
769 – 45 = 724 880 : 44 · 10 > 100
45 + 432 = 477 488 – 135 < 353
Решение:
706 + 43 = 749, 749 = 749, верное
270 · 2 : 10> 54, 540 : 10 = 540, 540 > 54, верное
769 – 45 = 724, 724 = 724, верное
880 : 44 · 10> 100, 20 * 10 = 200, 200 > 100 верное
45 + 432 = 477, 477 = 477, верное
488 – 135< 353, 353 = 353, неверное14. Назовите результаты действий.
0 : 2 763 14 830 – 0
2 718 : 2 718 98 702 + 0
48 361 · 1 0 + 100 000
0 · 43 786 0 – (8 247 – 8 247)
4 888 – 800 6 735 + 5
2 900 + 100 90 470 – 300
Решение:
0 : 2 763 = 0
14 830 – 0 = 14 830
2 718 : 2 718 = 1
98 702 + 0 = 98 702
48 361 · 1 = 48 361
0 + 100 000 = 100 000
0 · 43 786 = 0
0 – (8 247 – 8 247) = 0
4 888 – 800 = 4088
6 735 + 5 = 6800
2 900 + 100 = 3000
90 470 – 300 = 90 170 91
-
Ответы к странице 91
15. Верно ли высказывание? Поясните свой ответ на примерах.
1) Среди ломаных есть замкнутые ломаные.
2) Нельзя начертить два пересекающихся луча.
3) Существуют треугольники с равными сторонами.
4) Существуют два числа, произведение которых равно 70.
Решение:
1) Среди ломаных есть замкнутые ломаные. истинное
2) Нельзя начертить два пересекающихся луча. ложное
3) Существуют треугольники с равными сторонами. истинное
4) Существуют два числа, произведение которых равно 70. истинное16*. В пакете 9 кг крупы. Как с помощью чашечных весов и гирь массой 50 г и 200 г развесить всю крупу в два пакета так, чтобы в одном было 2 кг, а в другом 7 кг, при условии, что можно сделать только три взвешивания?
В одной из египетских пирамид учёные обнаружили на каменной плите гробницы изображённое иероглифами число 2 520. Трудно точно сказать, за что выпала такая честь на долю этого числа. Может быть, за то, что оно без остатка делится на все числа от 1 до 10? Докажите, что это действительно так.
Решение:
Задание 1Разделить пополам эти 9 кг, т.е. уравновесить весы, на каждую чашу приходится 4500 гр крупы.(4500 гр. высыпаем в первый пакет)
1) 9000 : 2= 4 500 (г)
4500 гр крупы опять делим пополам на каждую чашу . Получается, что на каждую чашу положили по 2 кг 250 гр. (опять высыпаем в первый пакет ещё 2 250 гр. Там уже 6 кг 750гр)
2) 4500 : 2=2250 (г)
4) 4 500 +2 250 =6 750 (г)
От оставшихся 2 кг 250 грамм отсыпаем 250 гр. с помощью гирь. Получаем 2 кг во втором пакете. А эти 250 гр добавляем в первый пакет, получаем 7 кг
В итоге получили 2 кг. крупы, а вся остальная масса даст 7 кг.
Задание 2
В одной из египетских пирамид учёные обнаружили на каменной плите гробницы изображённое иероглифами число 2 520. Трудно точно сказать, за что выпала такая честь на долю этого числа. Может быть, за то, что оно без остатка делится на все числа от 1 до 10? Докажите, что это действительно такэто самое маленькое число, которое можно поделить без остатка на все целые числа до 10 включительно
1,2,3,4,5,6,7,8,9,10
действительно
2520:1 =2520
2520:2 =1260
2520:3 =840
2520:4 =630
2520:5 =504
2520:6 =420
2520:7 =360
2520:8 =315
2520:9 =280
2520:10=25217. По какому правилу записан ряд чисел: 15 300, 15 200, 15 100, ...? Назовите три следующих числа в этом ряду.
Решение:
15 300, 15 200, 15 100, 15 000, 14 900, 14 800 каждое последующее меньше предыдущего на 100. 92
-
Ответы к странице 92
18. Найдите значения выражений.
1 070 + 86 · 101 – 2 008 – 2 116 : 46 =
123 · 60 + 1 356 : 12 + 5 041 : 71 · 15 · 5 =
190 · 50 – 3 283 : 49 + 69 046 : 23 =
2 491 : 47 + 8 364 : 82 – 3 094 : 91 =
Решение:
3 1 4 5 2
1 070 + 86 · 101 – 2 008 – 2 116 : 46 = 7 702
1) 86 * 101 = 8 686
*86
101
+86
86
8686
2) 2 116 : 46 = 46
- 2116|46
184 |46
- 276
276
0
3) 1070 + 8686 = 9 756
4) 9756 - 2008 = 7 748
5) 7748 - 46 = 7 702
1 6 2 7 3 4 5
123 · 60 + 1 356 : 12 + 5 041 : 71 · 15 · 5 = 12 818
1)
*123
60
7380
2) 1356 : 12 = 113
-1356|12
12 |113
-15
12
-36
36
0
3)
-5041|71
497 |71
- 71
71
0
4) 71 * 15 = 1065
*71
15
+355
71
1065
5) 1065 * 5 = 5 325
6) 7 380 + 113 = 7 4937) 7 493 + 5 325 = 12 818
1 4 2 5 3
190 · 50 – 3 283 : 49 + 69 046 : 23 = 12 435
1) 190 · 50 = 9500
2) 3 283 : 49 = 67
-3283|49
294 |67
-343
343
0
3) 69 046 : 23 = 3002
-69046|23
69 |3002
-46
46
0
4) 9500 - 67 = 9 433
5) 9 433 + 3 002 = 12 435
1 4 2 5 3
2 491 : 47 + 8 364 : 82 – 3 094 : 91 = 121
1) 2 491 : 47 = 53
-2491|47
235 |53
-141
141
0
2) 8 364 : 82 = 102
-8364|82
82 |102
- 164
164
0
3) 3 094 : 91 = 34
-3094|91
273 |34
-364
364
0
4) 53 + 102 = 155
5) 155 - 34 = 12119. Выполните вычисления устно.
71 – 9
327 + 99
5 263 – 999
Карточка-помощница
36 – 9 = 36 – 10 + 1 = 26 + 1 = 27
Решение:
71 – 9 = 70 - 9 + 1 = 61 + 1 = 62
327 + 99 = 327 + 100 - 1 = 427 - 1 = 426
5 263 – 999 = 5 263 - 1000 + 1 = 4263 - 1 = 4262
20. Поиграйте в игру «Кто быстрее поднимется на гору».
1 631 – 331 2 463 – 163
1 000 – 2 1 000 – 7
2 461 + 9 3 896 + 4
115 + 103 245 + 130
Решение:
1 631 – 331 = 1962
1 000 – 2 = 998
2 461 + 9 = 2470
115 + 103 = 218
2 463 – 163 = 2300
1 000 – 7 = 993
3 896 + 4 = 3 900
245 + 130 = 37521*. Сколько путей ведут от озера к лесу, если идти по указанным тропинкам через деревню? Придумайте способы подсчёта возможных вариантов.
Решение:
Подсчитать варианты можно следующим образом. Скажем вначале брать количество вариантов до деревни, а потом к каждому из этих вариантов добавлять количество вариантов после деревни. В итоге все количество вариантов будет равно произведению до деревни и после нее.
1) 1 * 3 = 3 варианта
2) 2 * 3 = 6 вариантов
3) 3 * 2 = 6 вариантов
4) 3 * 3 = 9 вариантов 93
-
Ответы к странице 93
22*. В жёлтой, зелёной и красной коробках лежит по одному яблоку этих же цветов, но цвет яблока не совпадает с цветом коробки. Жёлтое яблоко лежит не в зелёной коробке. В какой коробке лежит каждое из яблок?
Решение:
1. Исходя из условий задачи, жёлтое яблоко лежит не в зелёной коробке и не в жёлтой. Значить оно лежит в красной коробке.
2. Зеленое яблоко, исходя из условий задачи, может лежать в красой или желтой коробке, но так как в красной коробке лежит жёлтое яблоко, то зеленое яблоко может лежать только в желтой коробке.
3. Так как в желтой коробке лежит зеленое яблоко, то красное яблоко может лежать только зеленой коробке.
Ответ: жёлтое яблоко лежит в красной коробке, зеленое яблоко лежит в желтой коробке, а красное яблоко лежит в зеленой коробке23*. Катя, Валя и Оля гуляют во дворе со своими собаками — таксой, пуделем и овчаркой. Собака Кати не такса. Собака Вали тоже не такса, но и не овчарка. Какой породы собака у каждой из девочек?
Решение:
Ответ:
У Кати- овчарка
У Вали - Пудель
У Оли - такса
У Вали не может быть такса и овчарка
Единственная оставшаяся пудель
Значит у Вали - пудель
У Кати не может быть такса значит либо пудель или овчарка, но как пудель у Вали значит у Кати овчарка.
У Оли такса потому что другие собаки заняты.24*. В стакан, в кружку и в чашку налиты разные напитки: кофе, молоко и сок. В стакане не кофе и не сок, в чашке не сок. Какой напиток в стакане, в кружке и в чашке?
Решение:
В стакане - МОЛОКО
В чашке - КОФЕ
В кружке - СОК25. Вспомните, как называются числа и результаты действий при сложении, вычитании, умножении и делении. Прочитайте равенства и скажите, как называется каждое из чисел.
25 + 64 = 89 96 – 15 = 81 70 · 2 = 140 630 : 70 = 9Решение:
25 + 64 = 89 сумма
96 – 15 = 81 разность
70 · 2 = 140 произведение
630 : 70 = 9 частное26. Как называются неизвестные числа в равенствах? Вычислите их устно.
_ + 120 = 200 92 + _ = 192
_ – 30 = 760 79 – _ = 6
_ · 6 = 480 150 · _ = 900
_ : 5 = 120 300 : _ = 50
Решение:
80 + 120 = 200 - 1 слагаемое
92 + 100 = 192 - 2 слагаемое
790 – 30 = 760 - уменьшаемое
79 – 73 = 6 - вычитаемое
80 · 6 = 480 - множитель
150 · 6 = 900 - множитель
700 : 5 = 120 - делимое
300 : 6 = 50 - делитель 94
-
Ответы к странице 94
27. Запишите предложение в виде равенства. Вычислите неизвестное число, обозначенное буквой.
1) Если к 86 прибавить b, то получится 109.
2) Если из 250 вычесть y, то получится 7.
3) Если x уменьшить на 9, то получится 999.
4) Еcли n разделить на 10, то получится 10.Решение:
1) Если к 86 прибавить b, то получится 109.
86 + b = 109
b = 109 - 86
b = 23
2) Если из 250 вычесть y, то получится 7.
250 - y = 7
y = 250 - 7
y = 243
3) Если x уменьшить на 9, то получится 999.
x - 9 = 999
x = 999 + 9
x = 1008
4) Еcли n разделить на 10, то получится 10.
n : 10 = 10
n = 10 * 10
n = 10028. Сумму чисел 4 000 и 1 000 уменьшите в 100 раз и результат увеличьте на 200. Сколько получилось?
Решение:
(4000 + 1000) : 100 + 200 = 5000 : 100 + 200 = 50 + 200 = 25029. Вычислите устно.
360 : 2 320 · 3 4 640 + 60
360 : 20 4 400 · 2 2 830 – 500
64 : 4 560 · 2 1 010 : 5
640 : 4 110 · 80 302 · 4Решение:
360 : 2 = 180
320 · 3 = 960
4 640 + 60 = 5000
360 : 20 = 18
4 400 · 2 = 8800
2 830 – 500 = 2330
64 : 4 = 16
560 · 2 = 1120
1 010 : 5 = 202
640 : 4 = 160
110 · 80 = 8800
302 · 4 = 120830. Автобус отошёл от автовокзала в 8 ч 48 мин и через 35 мин сделал остановку на 8 мин. В котором часу автобус отошёл от места остановки?
8 ч 48 мин + 35 мин + 8 мин = 9 ч 23 мин + 8 мин = 9 ч 31 мин
Ответ: 9 ч 31 мин.31*. Сначала поезд двигался со скоростью 80 м/мин. После разгона он увеличил скорость в 15 раз. Какую скорость набрал поезд в пути? Выразите её в километрах в час.
80 * 15 = 1 200 (м/мин) = 1200 * 60 : 1 000 = 72 000 : 1 000 = 72 (км/ч) – набрал поезд
Ответ: 72 км/ч.32*. Вагонетка грузовой подвесной дороги движется со скоростью 10 м/с. Протяжённость дороги 3 км. За какое время вагонетка проедет этот путь?
1) 3 км = 3 000 м
2) 3 000 : 10 = 300 (с) = 300 : 60 = 5 (мин) – проедет вагонетка
Ответ: за 5 минут.33*. Вчера облака двигались со скоростью 120 м/мин, а сегодня — 120 см/с. Когда облака двигались быстрее?
120 м/мин = 120 * 100 : 60 = 12 000 : 60 = 200 (см/с) – скорость первого облака
200 > 120
Ответ: первое облако быстрее. 95
-
Ответы к странице 95
34. В таблице указаны размеры спортивной формы и обуви игроков футбольной команды.
Фамилия Размер формы Размер обуви
Скворцов 46 42
Иванов 44 40
Цветков 48 39
Сорокин 44 39
Ершов 44 39
Степанов 48 41
Петров 46 40
Рыбкин 48 40
Белов 46 39
Смирнов 48 42
Крылов 46 40
Ответьте на вопросы. Сколько игроков в команде? Сколько игроков носит спортивную форму 44 размера; 46 размера; 48 размера? Кто из игроков носит обувь 40 размера; 39 размера? Есть ли футболисты, которые носят обувь 38 размера; 41 размера? У кого из игроков самый большой размер обуви? Какой размер формы и обуви у Цветкова, Смирнова, Ершова? Кто носит форму 48 размера и обувь 40 размера?
У кого размер формы 46, а обуви 42? У кого из игроков одинаковый размер обуви; одинаковый размер формы?
Решение:Сколько игроков в команде? - 11 игроков в команде
Сколько игроков носит спортивную форму 44 размера; 46 размера; 48 размера? - 3 игрока 44, 4 игрока 46, и 4 игрока 48 размера
Кто из игроков носит обувь 40 размера; 39 размера? - 40 размер носит Иванов, Петров, Рыбкин и Крылов, а 39 - Цветков, Сорокин, Ершов, Белов,
Есть ли футболисты, которые носят обувь 38 размера; 41 размера? - 38 размер не носит никто, а 41 носит Степанов
У кого из игроков самый большой размер обуви? - самый большой размер 42 у Скворцова и Смирнова
Какой размер формы и обуви у Цветкова, Смирнова, Ершова? - размер формы Цветкова 48 - обуви 39, Смирнов-48-42, Ершов 44-39,
Кто носит форму 48 размера и обувь 40 размера? - форму 48 размера носит Цветков, Степанов, Рыбкин, Смирнов, обувь 40 размера носит Иванов, Петров, Рыбкин, Крылов.
У кого размер формы 46, а обуви 42? - Скворцов
У кого из игроков одинаковый размер обуви; одинаковый размер формы? - одинаковый размер обуви 39 - Цветков, Сорокин, Ершов, Белов, 40 - Иванов, Петров, Рыбкин, Крылов, 42 - Скворцов, Смирнов; одинаковый размер формы 46 у Скворцов, Петров, Белов, Крылов, 44 - Иванов, Сорокин, Ершов, 48 - Цветков, Степанов, Рыбкин, Смирнов. 96
-
Ответы к странице 96
35. На какие две группы можно разделить данные фигуры?
Решение:
С основанием в виде круга и с основанием в виде многоугольника.36. По международным стандартам футбольное поле имеет форму прямоугольника длиной 100 – 110 м, а шириной 69 – 75 м. Вычислите площадь футбольного поля, указав её наибольшее и наименьшее значения.
1) 100 * 69 = 6 900 (м²) – наименьший размер поля
2) 110 * 75 = 8 250 (м²) – наибольший размер поля
Ответ: 6 900 м²; 8 250 м². 97
-
Ответы к странице 97 УЗНАЁМ НОВОЕ Деление отрезка на 2, 4, 8 равных частей с помощью циркуля и линейки
1. Трое учащихся получили задание разделить отрезок АВ пополам с помощью циркуля и линейки. Как выполнял задание каждый из учащихся? Кто выполнил задание правильно? Проверьте, используя циркуль. Объясните ошибки других учеников.
Решение:
Маша выполнила задачу правильно. Катя начертила слишком маленькие окружности, которые не пересекаются. Саша начертил окружности с разными диаметрами.2. Как с помощью циркуля и линейки разделить отрезок на две равные по длине части? Составьте план действий.
Решение:
1. Выберем раствор для радиуса окружности, чуть меньше длины отрезка, так чтобы он был гарантировано больше его половины.
2. Начертим две окружности, с центром в точках начала и конца отрезка.
3. Поставим точки пересечения окружностей.
4. Проведем отрезок по точкам пересечения окружностей.
5. Точка пересечения построенного отрезка и имеющегося и будет серединой имеющегося отрезка. 98
-
Ответы к странице 98
3. Постройте отрезок произвольной длины и разделите его пополам с помощью циркуля и линейки.
Решение:
Используем алгоритм:
1. Выберем раствор для радиуса окружности, чуть меньше длины отрезка, так чтобы он был гарантировано больше его половины.
2. Начертим две окружности, с центром в точках начала и конца отрезка.
3. Поставим точки пересечения окружностей.
4. Проведем отрезок по точкам пересечения окружностей.
5. Точка пересечения построенного отрезка и имеющегося и будет серединой имеющегося отрезка.4. Как с помощью циркуля и линейки разделить отрезок: 1) на 4 равные части; 2) на 8 равных частей?
Решение:
Делим отрезок пополам, потом еще пополам, это будет 4 часть.
Делим отрезок пополам, потом еще пополам, потом еще пополам, это будет 8 часть.5. Постройте в тетради такие треугольники. Разделите каждую из сторон треугольника пополам и отметьте точками середины сторон. Соедините отрезком каждую отмеченную точку с противолежащей вершиной треугольника. Что вы заметили? Проверьте замеченное свойство на любом другом треугольнике. Для этого начертите треугольник со сторонами любой длины и выполните аналогичные построения.
Решение:
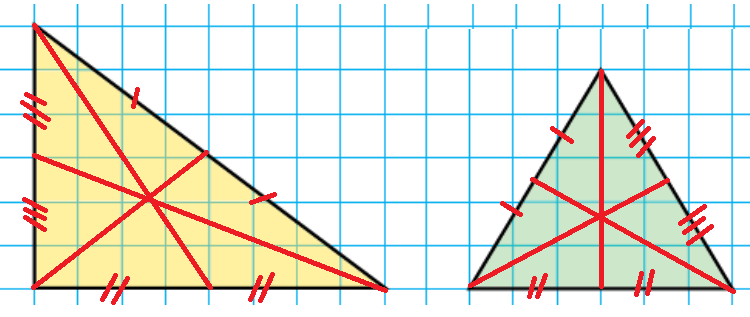
Заметили, что образуются биссектрисы. Все они пересекаются в одной точке, все они делят угол у вершины пополам.
6. Не выполняя указанных действий, прикиньте, больше или меньше числа 1 000 результаты действий.
2 475 – 876 903 · 20
603 + 495 4 270 : 70Решение:
2 475 – 876 больше
603 + 495 больше
903 · 20 больше
4 270 : 70 меньше 99
-
Ответы к странице 99
7. Во сколько раз 1 кг больше 100 г; 1 ц меньше 1 т; 1 ц больше 10 кг?
Решение:
1 кг больше 100 г; 1000 : 100 = 10 раз
1 ц меньше 1 т; 1000 : 100 = 10 раз
1 ц больше 10 кг 100 : 10 = 10 раз8. Какое свойство умножения выражает равенство? Сформулируйте каждое свойство.
1) 324 · 17 = 17 · 324
2) (12 · 8) · 30 = 12 · (8 · 30)
3) (165 + 38) · 70 = 165 · 70 + 38 · 70Решение:
1) 324 · 17 = 17 · 324 переместительное
2) (12 · 8) · 30 = 12 · (8 · 30) сочетательное
3) (165 + 38) · 70 = 165 · 70 + 38 · 70 распределительное9. Обувная фабрика за день выпустила 3 600 пар обуви. Детская обувь составила три четверти всей обуви, а остальная обувь — женская. Придумайте вопрос и решите задачу устно двумя способами.
Сколько пар женской обуви выпустила фабрика?
1) 3 600 : 4 * 3 = 900 * 3 = 2 700 (п.) – детская обувь
2) 3 600 – 2 700 = 900 (п.) – женская обувь
Ответ: 900 пар.10. За книгу заплатили 36 р. и ещё две трети её стоимости. Сколько рублей стоит книга?
1) 36 руб. составляет треть стоимости книги
2) 36 * 3 = 108 (руб.) – стоит книга
Ответ: 108 рублей.11. Ответьте на вопросы, используя данные таблицы. На сколько граммов литр нефти тяжелее литра керосина? Чему равна масса 2 л ртути? Что легче — 2 л бензина или 1 л ртути? Во сколько раз масса 80 л морской воды больше массы 1 л керосина?
Вещество Вместимость Масса
Бензин 1 л 690 г
Морская вода 1 л 1 кг 50 г
Нефть 1 л 840 г
Керосин 1 л 800 г
Ртуть 1 л 13 кг 600 гРешение:
На сколько граммов литр нефти тяжелее литра керосина? 840 - 800 = 40 граммов.
Чему равна масса 2 л ртути? 13 600 * 2 = 27 200 г или 27 кг 200 г
Что легче — 2 л бензина или 1 л ртути? 690 * 2 = 1380 г = 1 кг 380 г; 27 кг 200 г > 1 кг380 г 2 л бензина легче 1 л ртути
Во сколько раз масса 80 л морской воды больше массы 1 л керосина? 80 * 1050 = 84 000 г 84000 : 840 = 100 раз 100
-
Ответы к странице 100
12. Вычислите:
1) сумму чисел 3 407 и 19 007 856;
2) разность чисел 1 010 203 и 998 877;
3) произведение чисел 196 и 408;
4) частное чисел 123 140 и 524.
Решение:
1) сумму чисел 3 407 и 19 007 856;+19007856
3407
190112632) разность чисел 1 010 203 и 998 877;
-1010203
998877
113263) произведение чисел 196 и 408;
*196
408
+1568
784
799684) частное чисел 123 140 и 524.
-123140|524
1048 |235
-1834
1572
-2620
2620
013. Найдите значения выражений.
2 912 : 8 + 1 200 : 300 – 1 · 144 : 12 =
(51 855 + 9 857) : 532 : 58 : 2 · 10 000 =
102 867 – 867 · 90 + 57 000 : 380 =
(207 · 304 – 12 967 + 3 072 : 24) · 0 =
Решение:
1 5 2 6 3 4
2 912 : 8 + 1 200 : 300 – 1 · 144 : 12 = 356
1) 2 912 : 8 = 364
2) 1 200 : 300 = 4
3) 1 · 144 = 144
4) 144 : 12 = 12
5) 364 + 4 = 368
6) 368 - 12 = 356
1 2 3 4 5
(51 855 + 9 857) : 532 : 58 : 2 · 10 000 = 10 000
1) 51 855 + 9 857 = 61 712
2) 61 712 : 532 = 116
3) 116 : 58 = 2
4) 2 : 2 = 1
5) 1 * 10 000 = 10 000
3 1 4 2
102 867 – 867 · 90 + 57 000 : 380 = 24 987
1) 867 · 90 = 78 030
2) 57 000 : 380 = 150
3) 102 867 - 78 030 = 24 837
4) 24 837 + 150 = 24 987(207 · 304 – 12 967 + 3 072 : 24) · 0 = 0
14. Вычислите значение x.
605 : x = 121 x – 7 056 = 12 000
x · 75 = 900 30 010 – x = 89
Решение:
605 : x = 121
х = 605 : 121
х = 5
x – 7 056 = 12 000
х = 12 000 + 7 056
х = 19 056
x · 75 = 900
х = 900 : 75
х = 12
30 010 – x = 89
х = 30 010 - 89
х = 29 92115. Истинно или ложно высказывание?
1) Произведение чисел 30 и 8 больше 210.
2) Среди всех многоугольников треугольник имеет наименьшее число сторон.
3) Если 612 разделить на 3, то получится 34.
4) Если верно неравенство 24 > 10, то верно и неравенство 24 + 6 > 10 + 6.
5) Неверно, что частное чисел 300 и 5 равно 60.
6) Тысячная часть числа 2 500 000 равна 2 500.
Решение:
1) Произведение чисел 30 и 8 больше 210. 30 * 8 = 240 истинное
2) Среди всех многоугольников треугольник имеет наименьшее число сторон. истинное
3) Если 612 разделить на 3, то получится 34. 612 : 3 = 204 ложное
4) Если верно неравенство 24 > 10, то верно и неравенство 24 + 6 > 10 + 6. истинное
5) Неверно, что частное чисел 300 и 5 равно 60. ложное
6) Тысячная часть числа 2 500 000 равна 2 500. истинное16. Не выполняя умножения, прочитайте выражения в таком порядке, чтобы их значения увеличивались. Устно выполните вычисления.
1 100 · 4 8 · 1 100 6 · 1 100
1 100 · 9 10 · 1 100 2 · 1 100
Решение: порядок будет таким
2 · 1 100
1 100 · 4
6 · 1 100
8 · 1 100
1 100 · 9
10 · 1 100 101
-
Ответы к странице 101
17. Длина аллеи 540 м. От двух концов аллеи побежали одновременно навстречу друг другу Петя и его собака Пират. Через 2 мин Петя и Пират встретились. С какой скоростью бежал Петя, если скорость Пирата была 150 м/мин?
1) 150 * 2 = 300 (м) – пробежал Пират
2) 540 – 300 = 240 (м) – пробежал Петя
3) 240 : 2 = 120 (м/мин) – скорость Пети
Ответ: 120 м/мин.18. Каждое из чисел 8, 50, 32, 100 умножьте на 10 000. Назовите тысячную часть чисел: 1 000, 85 000, 124 000, 2 400 000. Разделите на миллион: 8 млн, 13 млн, 425 млн.
Решение:
Каждое из чисел 8, 50, 32, 100 умножьте на 10 000.
8*10 000 = 80 000
50 * 10 000 = 500 000
32 * 10 000 = 320 000
100 * 10 000 = 1 000 000
Назовите тысячную часть чисел: 1 000, 85 000, 124 000, 2 400 000.
1000 : 1000 = 1 одни
85 000 : 1000 = 85 восемьдесят пять
124 000 : 1000 = 124 сто двадцать четыре
2 400 000 : 1000 = 2 400 две тысячи четыреста
Разделите на миллион: 8 млн, 13 млн, 425 млн.
8 000 000 : 1 000 000 = 8
13 000 000 : 1 000 000 = 13
425 000 000 : 1 000 000 = 42519. Петя съел несколько порций мороженого и заболел. Врач выписал ему лекарство от кашля: в упаковке 20 таблеток, по 50 мг лекарства в каждой. Сколько граммов лекарства в упаковке?
50 * 20 = 1000 мг = 1 (г) - лекарства
Ответ: 1 г. 102
-
Ответы к странице 102
20. Дима, Коля и Таня по очереди помогают маме убирать квартиру. Рассмотрите таблицу и ответьте на вопросы. В какие дни дежурит каждый из детей? Кто убирает квартиру в среду, кто — во вторник? В какой день все дети отдыхают? В какие дни помогают маме мальчики? Составьте похожее расписание помощи маме по хозяйству.
Решение:Дима дежурит в пн и чт
Коля дежурит в вт и пт
Таня дежурит ср и сб
Кто убирает квартиру в среду, кто - во вторник?
в среду убирает Таня
во вторник убирает Коля
В какой день все дети отдыхают?
в воскресенье
В какие дни помогают маме мальчики?
в пн чт вт пт21. Прежде чем вычислять, прикиньте, сколько цифр будет в частном.
1 384 : 4 9 306 : 9
48 006 : 6 50 250 : 5Карточка-помощница
6'093 : 3 (4 цифры) 25'60 : 5 (3 цифры)
Решение:
1 384 : 4 = 346 (3 цифры)-1384|4
12 |346
-18
16
-24
24
0
9 306 : 9 = 1034
-9306|9
9 |1034
-30
27
-36
36
0
48 006 : 6 = 8 001
-48 006|6
48 |8001
-6
6
0
50 250 : 5 = 10 050
-50250|5
5 |10050
-250
250
022. Объясните ошибки в записях.
Решение:Слева направо.
1) 360 надо было сместить на один разряд вправо.
2) не пропущен разряд с 0, то есть не смещено влево число 5720
3) не произведено умножение по разрядам и не найдена сумма результатов.
4) не учтен 0 в результате, должно быть 9 193 000 103
-
Ответы к странице 103 УЗНАЁМ НОВОЕ
Нахождение неизвестного числа в равенствах вида x + 5 = 7, x · 5 = 15, x – 5 = 7, x : 5 = 15
1. Объясните, как можно вычислить неизвестное первое слагаемое.
Решение:Для того, чтобы вычислить неизвестное слагаемое, необходимо в одну сторону выражения перенести известные значения, а во вторую неизвестное.
2. Какое действие надо выполнить, чтобы найти неизвестное первое слагаемое в каждом из равенств?
a + 129 = 600 m + 1 534 = 2 000
y + 30 = 298 k + 910 = 1 300
Сформулируйте правило для нахождения неизвестного первого слагаемого. Сравните свой ответ с текстом. Чтобы найти неизвестное первое слагаемое, надо из суммы вычесть второе слагаемое.
Решение:
Чтобы найти неизвестное первое слагаемое, надо из суммы вычесть второе слагаемое.3. Пользуясь правилом, найдите неизвестное первое слагаемое.
x + 7 006 = 89 400 y + 12 345 = 31 006
Решение:
x + 7 006 = 89 400
х = 89 400 - 7 006
х = 82 394
y + 12 345 = 31 006
y = 31 006 - 12 345
y = 18 661 104
-
Ответы к странице 104
4. Запишите предложение в виде равенства. Найдите неизвестное число.
1) Если к неизвестному числу x прибавить 7 050, то получится 7 153.
2) Если неизвестное число a увеличить на 316, то получится 2 004.
Решение:
1) Если к неизвестному числу x прибавить 7 050, то получится 7 153.
х + 7 050 = 7 153
х = 7 153 - 7 050
х = 103
2) Если неизвестное число a увеличить на 316, то получится 2 004.
а + 316 = 2 004
а = 2 004 - 316
а = 1 6885. Дима задумал число, прибавил к нему 1 217 и получил 1 500. Какое число задумал Дима? План решения.
1) Обозначаю неизвестное число буквой x.
2) Составляю равенство по тексту задания.
3) Нахожу неизвестное число по правилу.Решение:
х + 1 217 = 1 500
х = 1 500 – 1 217
х = 283
Ответ: 283.
6. Катя задумала число, увеличила его на 75 и получила 1 500. Какое число задумала Катя?х + 75 = 1 500
х = 1 500 – 75
х = 1 425
Ответ: 1 425.7. В аквариуме было несколько рыбок. Когда в аквариум пустили ещё 8 рыбок, там стало 15 рыбок. Сколько рыбок было в аквариуме?
х – рыбок было в аквариуме
х + 8 = 15
х = 15 – 8
х = 7
Ответ: 7 рыбок.8. Объясните, как можно найти неизвестный первый множитель.
Решение:
х * 18 = 216
х = 216 : 18
х = 12
Для этого необходимо уменьшить результат произведения на соизмеримый показатель со вторым множителем в произведении. 105
-
Ответы к странице 105
9. Какое действие надо выполнить, чтобы найти неизвестный первый множитель в каждом из равенств?
a · 10 = 150 x · 45 = 90
y · 9 = 720 m · 102 = 306
Сформулируйте правило для нахождения неизвестного первого множителя. Сравните свой ответ с текстом. Чтобы найти неизвестный первый множитель, надо произведение разделить на второй множитель.Решение:
Чтобы найти неизвестный первый множитель, надо произведение разделить на второй множитель.
a · 10 = 150
а = 150 : 10
а = 15
x · 45 = 90
х = 90 : 45
х = 2
y · 9 = 720
у = 720 : 9
y = 80
m · 102 = 306
m = 306 : 102
m = 310. Используя правило, найдите неизвестный первый множитель.
x · 38 = 36 480 y · 4 = 8 060
Решение:
x · 38 = 36 480
х = 36 480 : 38
х = 960
y · 4 = 8 060
y = 8 060 : 4
y = 2 01511. Запишите предложение в виде равенства. Найдите неизвестное число.
1) Если неизвестное число t умножить на 107, то получится 22 042.
2) Если неизвестное число m увеличить в 50 раз, то получится 18 200.
Решение:
1) Если неизвестное число t умножить на 107, то получится 22 042.
t * 107 = 22 042
t = 22 042 : 107
t = 206
2) Если неизвестное число m увеличить в 50 раз, то получится 18 200.
m * 50 = 18 200
m = 18 200 : 50
m = 36412. Юра задумал число, умножил его на 365 и получил 44 530. Какое число задумал Юра?
х * 365 = 44 530
х = 44 530 : 365
х = 122
Ответ: 122.13. Коля задумал число, увеличил его в 25 раз и получил 625 000. Найдите задуманное число.
х * 25 = 625 000
х = 625 000 : 25
х = 25 000
Ответ: 25 000.14. Найдите устно неизвестное число.
x · 100 = 3 200 x · 5 = 300
a · 50 = 1 000 m · 80 = 800
Решение:
x · 100 = 3 200
x = 3 200 : 100
x = 32
x · 5 = 300
x = 300 : 5
x = 60
a · 50 = 1 000
a = 1 000 : 50
a = 20
m · 80 = 800
m = 800 : 80
m = 10 106
-
Ответы к странице 106
15. Объясните, как можно найти неизвестное уменьшаемое.
Решение:16. Какое действие надо выполнить, чтобы найти неизвестное уменьшаемое?
x – 450 = 999 y – 504 = 751
a – 1 234 = 2 800 c – 21 = 5 004
Сформулируйте правило для нахождения неизвестного уменьшаемого. Сравните свой ответ с текстом. Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Решение:
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
x – 450 = 999
x = 999 + 450
x = 1 449
y – 504 = 751
y = 751 + 504
y = 1255
a – 1 234 = 2 800
a = 2800 + 1234
a = 4034
c – 21 = 5 004
c = 5 004 + 21
c = 5 02517. Используя правило, найдите уменьшаемое.
а – 24 056 = 100 000
y – 339 = 18
m – 3 356 = 476
n – 12 758 = 6 907
Решение:
а – 24 056 = 100 000
a = 100 000 + 24 056
a = 124 056
y – 339 = 18
y = 18 + 339
y = 357
m – 3 356 = 476
m = 476 + 3 356
m = 3832
n – 12 758 = 6 907
n = 6 907 + 12 758
n = 19 66518. Запишите предложение в виде равенства. Найдите неизвестное число.
1) Если из неизвестного числа n вычесть 7 777, то получится 896.
2) Если неизвестное число y уменьшить на 509 871, то получится 18 059.
Решение:
1) Если из неизвестного числа n вычесть 7 777, то получится 896.
n - 7 777 = 896
n = 896 + 7 777
n = 8 673
2) Если неизвестное число y уменьшить на 509 871, то получится 18 059.
y - 509 871 = 18 059
y = 18 059 + 509 871
y = 527 930 107
-
Ответы к странице 107
19. Если задуманное число уменьшить на 5 627, то получится 12 996. Найдите задуманное число.
х – 5 627 = 12 996
х = 12 996 + 5 627
х = 18 623
Ответ: 18 623.20. В бочке была вода. Когда из неё взяли 75 л воды, там осталось 125 л воды. Сколько воды было в бочке?
х л – воды было в бочке
х – 75 = 125
х = 125 + 75
х = 200
Ответ: 200 л.21. Объясните, как можно найти неизвестное делимое.
x : 5 = 1 260
x = 1 260 · 5
Ответ: 6 300.22. Какое действие надо выполнить, чтобы найти неизвестное делимое?
m : 19 = 126 b : 36 = 72
a : 48 = 59 c : 180 = 360
Сформулируйте правило для нахождения неизвестного делимого. Сравните свой ответ с текстом. Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Решение:
m : 19 = 126
m = 126 * 19
m = 2394
b : 36 = 72
b = 72 * 36
b = 2 592
a : 48 = 59
a = 59 * 48
a = 2 832
c : 180 = 360
c = 360 * 180
c = 64 800
23. Запишите предложение в виде равенства. Найдите неизвестное число.
1) Если неизвестное число a разделить на 309, то получится 309.
2) Если неизвестное число t разделить на 104, то получится 52.
Решение:
1) Если неизвестное число a разделить на 309, то получится 309.
a : 309 = 309
a = 309 * 309
a = 95 481
2) Если неизвестное число t разделить на 104, то получится 52.
t : 104 = 52
t = 52 * 104
t = 5 408 108
-
Ответы к странице 108
24. Если неизвестное число разделить на 65, то получится 7 020. Какое это число?
х : 65 = 7 020
х = 7 020 * 65
х = 456 300
Ответ: 456 300.25. Если неизвестное число уменьшить в 4 500 раз, то получится 90. Найдите неизвестное число.
х : 4 500 = 90
х = 90 * 4 500
х = 405 000
Ответ: 405 000.26. Назовите результаты.
28 · 100 2 000 : 10
130 · 10 80 600 : 100
405 · 1 000 16 000 : 1 000
600 : 100 · 1 000 35 · 100 : 10
10 · 100 · 1 000 1 000 : 100 : 10
Решение:
28 · 100 = 2 800
2 000 : 10 = 200
130 · 10 = 1 300
80 600 : 100 = 806
405 · 1 000 = 405 000
16 000 : 1 000 = 16
600 : 100 · 1 000 = 6 000
35 · 100 : 10 = 35 000
10 · 100 · 1 000 = 1 000 000
1 000 : 100 : 10 = 127. Самолёт пролетел 3 800 км со скоростью 950 км/ч. Сколько часов самолёт был в пути?
3 800 : 950 = 4 (ч.) – самолет был в пути
Ответ: 4 часа.28. Один земельный участок имеет длину 32 м и ширину 20 м. Другой участок имеет ширину в 2 раза меньшую, чем длина первого участка, а длину в 3 раза большую, чем ширина первого участка. Какой из участков имеет большую площадь и на сколько?
1) 32 * 20 = 640 (м²) – площадь 1 участка
2) (32 : 2) * (20 * 3) = 16 * 60 = 960 (м²) – площадь 2 участка
3) 960 – 640 = 320 (м²) – больше площадь 2 участка
Ответ: на 320 м².29. Токарь изготавливал в каждый из восьми дней 23 детали и выполнил треть своего месячного задания. Сколько деталей он должен изготовить за месяц?
23 * 8 * 3 = 184 * 3 = 552 (д.) – должен изготовить за месяц
Ответ: 552 детали. 109
-
Ответы к странице 109
30. В речной порт доставили 18 234 кг зерна. Это зерно выгрузили за три дня, ежедневно выгружая одно и то же количество зерна. Половину зерна, выгруженного в третий день, отправили на мельницу. Сколько зерна отправили на мельницу?
1) 18 234 : 3 = 6 078 (кг) – зерна выгружали ежедневно
2) 6 078 : 2 = 3 026 (кг) – зерна отправили на мельницу
Ответ: 3 026 кг.31. Из двух городов навстречу друг другу идут два поезда: один со скоростью 55 км/ч, а другой со скоростью 65 км/ч. Какое расстояние будет между поездами за час до встречи?
1 * (55 + 65) = 1 * 120 = 120 (км) – будет между ними за час до встречи
Ответ: 120 км.32. Вычислите устно:
1) четверть числа: 80, 160, 164, 200;
2) пятую часть числа: 500, 150, 60, 25;
3) сотую часть числа: 300, 1 800, 66 000;
4) тысячную часть числа: 24 000, 240 000.
Решение:
1) четверть числа: 80, 160, 164, 200;
80 : 4 = 20
160 : 4 = 40
164 : 4 = 41
200 : 4 = 50
2) пятую часть числа: 500, 150, 60, 25;
500 : 5 = 100
150 : 5 = 30
60 : 5 = 12
25 : 5 = 5
3) сотую часть числа: 300, 1 800, 66 000;
300 : 100 = 3
1 800 : 100 = 18
66 000 : 100 = 660
4) тысячную часть числа: 24 000, 240 000.
24 000 : 1000 = 24
240 000 : 1000 = 24033. Составьте выражения и найдите их значения.
1) К 328 прибавить частное 414 и 46.
2) Из числа 901 вычесть произведение 16 и 15.
3) Из произведения 30 и 9 вычесть сумму 68 и 127.
4) Сумму 627 и 373 разделить на частное 250 и 50.
Решение:
1) К 328 прибавить частное 414 и 46.
328 + 414 :46 = 328 + 9 = 337
2) Из числа 901 вычесть произведение 16 и 15.
901 - 16 * 15 = 901 - 240 = 661
3) Из произведения 30 и 9 вычесть сумму 68 и 127.
30 * 9 - (68 + 127) = 270 - 195 = 75
4) Сумму 627 и 373 разделить на частное 250 и 50.
(627 + 373) : (250 : 50) = 1000 : 5 = 20034. Не выполняя вычислений, объясните, почему верно неравенство 2 568 – 395 > 2 568 – 593.
Решение:
Верное так как 395 < 593.35. Докажите, что при а, равном числу 315, верно равенство (3 685 + а) : 200 = 20.
Решение:
(3 685 + 315) : 200 = 4000 : 200 = 20
20 = 20. Верно! 110
-
Ответы к странице 110
36*. Выразите в квадратных сантиметрах.
7 дм2 2 м2 3 дм2
21 дм2 15 дм2 8 см2
6 м2 2 500 мм2
9 м2 80 000 мм2Решение:
7 дм2 = 700 см2
21 дм2 = 2100 см2
6 м2 = 60000 см2
9 м2 = 90000 см2
2 м2 3 дм2 = 20000 см2 + 300 см2 = 20 300 см2
15 дм2 8 см2 = 1500 см2 + 8 см2 = 1508 см2
2 500 мм2 = 25 см2
80 000 мм2 = 800 см2
37*. Выразите в квадратных дециметрах.
70 000 мм2 5 200 см2 60 м2
90 000 мм2 65 000 см2 13 м2Решение:
70 000 мм2 = 7дм2
90 000 мм2 = 9 дм2
5 200 см2 = 52 дм2
65 000 см2 = 650 дм2
60 м2 = 6000 дм2
13 м2 = 1300 дм238. Для каждого из чисел 597, 305, 489, 899, 112, 999 назовите ближайшее к нему число, состоящее только из сотен.
Решение:
597 ближайшее к нему число, состоящее только из сотен - 600
305 ближайшее к нему число, состоящее только из сотен - 300
489 ближайшее к нему число, состоящее только из сотен - 500
899 ближайшее к нему число, состоящее только из сотен - 900
112 ближайшее к нему число, состоящее только из сотен - 100
999 ближайшее к нему число, состоящее только из сотен - 100039. Вычислите площадь детали в квадратных сантиметрах.
20 * 36 – 8 * 12 = 720 – 96 = 624 (см²) – площадь детали
Ответ: 624 см². 111
-
Ответы к странице 111
40. На диаграмме представлены данные о долготе дня с 12 по 17 февраля в городе Москве. На сколько минут длиннее стал день 17 февраля по сравнению с каждым из дней: 15 февраля, 14 февраля, 12 февраля?
Решение:
1) по сравнению с 15 февраля: 9 ч 48 м -9 ч 43 м = 5 Ответ: на 5 минут
2) с 14 февраля: 9 ч 48 м - 9 ч 33 м = 15 мин Ответ: на 15 минут
3) с 12 февраля: 9 ч 48 мин - 9 ч 24 м = 24 мин Ответ: на 24 минуты 112
-
Ответы к странице 112
41. Прочитайте слова: ЗИМА, ВЕСНА, ЛЕТО, ОСЕНЬ. Какие из высказываний об этих словах истинны, а какие — ложны?
1) В словах ЗИМА и ЛЕТО по 4 буквы.
2) Нет слов, состоящих из 7 букв.
3) Нет слов с буквой В.
4) В некоторых словах есть буква С.
5) Каждое слово начинается с согласной буквы.
6) В слове ЗИМА первый звук мягкий.
7) Есть два слова с буквой Т.
8) В каждом из слов 4 или 5 букв.
9) В каждом из слов 5 или 6 букв.
10) Каждое слово обозначает время года.Решение:
1) В словах ЗИМА и ЛЕТО по 4 буквы. истинное
2) Нет слов, состоящих из 7 букв. истинное
3) Нет слов с буквой В. ложное
4) В некоторых словах есть буква С. истинное
5) Каждое слово начинается с согласной буквы. ложное
6) В слове ЗИМА первый звук мягкий. ложное
7) Есть два слова с буквой Т. ложное
8) В каждом из слов 4 или 5 букв. истинное
9) В каждом из слов 5 или 6 букв. ложное
10) Каждое слово обозначает время года. истинное42. Цена шарфика составляет сотую часть цены куртки. Куртка стоит 5 200 р. Какова цена шарфика? Какова стоимость куртки и шарфика?
1) 5 200 : 100 = 52 (р.) – стоит шарфик
2) 5 200 + 52 = 5 252 (р.) – стоит куртка с шарфиком
Ответ: 52 руб., 5 252 руб.43. Прежде чем выполнять деление, прикиньте, сколько цифр должно быть в частном.
690 : 46 90 000 : 45 5 260 : 1 052
3 040 : 76 203 700 : 97 11 082 : 3 694Карточка-помощница
24'84 : 12 (3 цифры)
Решение:
690 : 46 = 15 (2 цифры)
90 000 : 45 = 2 000 (3 цифры)
5 260 : 1 052 = 5 (1 цифра)
3 040 : 76 = 40 (2 цифры)
203 700 : 97 = 2 100 (4 цифры)
11 082 : 3 694 = 3 (1 цифра)44. Какие числа надо записать вместо букв, чтобы равенства были верными?
х · 8 = 944 1 020 – t = 874
y + 3 075 = 9 116 365 : s = 5
Решение:
х · 8 = 944
х = 944 : 8
х = 118
1 020 – t = 874
t = 1020 - 874
t = 146
y + 3 075 = 9
y = 9 + 3075
y = 3084
116 365 : s = 5
s = 116 365 : 5
s = 23 273 113
-
Ответы к странице 113 УЗНАЁМ НОВОЕ Угол и его обозначение
1. На рисунке изображены два угла. Сторонами угла являются два луча, исходящие из одной точки. Эту точку называют вершиной угла. Назовите вершину и стороны каждого угла. При записи обозначения угла слово «угол» заменяют знаком ∠. После этого знака пишут три заглавные буквы латинского алфавита, причём в середине всегда указывают букву, обозначающую вершину угла. Записи ∠AOB и ∠BOA — это разные обозначения одного и того же угла. Прочитайте и запишите обозначения другого угла.
Решение:
∠ KMC
∠ CMK2. Угол можно показать, вращая луч на плоскости — так, как стрелка часов вращается на циферблате. Приложите карандаш к одной из сторон угла (конец карандаша должен совпадать с вершиной угла, как на рисунке). Поворачивайте карандаш на плоскости до совмещения его с другой стороной угла.
Покажите вращением карандаша каждый из углов. 114
-
Ответы к странице 114
3. Запишите обозначение каждого угла двумя способами и прочитайте эти обозначения. Назовите стороны углов.
Решение:∠ АОВ ∠ BOA
∠ МКС ∠ CKM
∠ EDP ∠ PDE4*. Имеют ли общую вершину пары углов? Назовите эту вершину:
1) ∠АKО и ∠BKM;
2) ∠ABC и ∠DBC;
3) ∠ОАМ и ∠KВС;
4) ∠CDO и ∠ODC.Решение:
1) ∠АKО и ∠BKM; да, имеют
2) ∠ABC и ∠DBC; да, имеют
3) ∠ОАМ и ∠KВС; нет, не имеют
4) ∠CDO и ∠ODC. да, имеют 115
-
Ответы к странице 115
5*. Назовите общую сторону углов:
1) ∠KМВ и ∠KМО;
2) ∠ВАС и ∠МАС;
3) ∠АВС и ∠СВА.Решение:
1) ∠KМВ и ∠KМО; общая сторона KМ
2) ∠ВАС и ∠МАС; общая сторона АС
3) ∠АВС и ∠СВА. это один и тот же угол6. Используя кальку, вырежьте такие же углы, как на рисунке. Какой угол самый большой? Какой угол самый маленький? Выполните проверку способом наложения одного угла на другой. Для этого совместите вершины двух углов, сторону одного угла направьте вдоль стороны другого угла. Вторая сторона меньшего угла окажется между сторонами большего угла.
Решение:
Какой угол самый большой? оранжевый, самый правый
Какой угол самый маленький? желтый, самый левый7. Используя угольник, найдите среди углов на рисунке прямой угол. Какие из углов: больше прямого угла; меньше прямого угла?
Решение:
прямой ∠XOY или он же ∠YOX
меньше прямого ∠ABC или он же ∠CBA
больше прямого ∠ CDK или ∠KDC, ∠ AMB или ∠ BMA 116
-
Ответы к странице 116
8. Вычислите устно.
520 + 80 250 · 3 960 : 3
970 – 160 400 · 5 960 : 30
1 000 – 900 14 · 7 1 500 : 500
630 + 400 90 · 30 4 800 : 2
Решение:
520 + 80 = 600
250 · 3 = 750
960 : 3 = 32
970 – 160 = 810
400 · 5 = 2 000
960 : 30 = 32
1 000 – 900 = 100
14 · 7 = 98
1 500 : 500 = 3
630 + 400 = 1 030
90 · 30 = 2 700
4 800 : 2 = 2 4009. Найдите неизвестное число.
а – 986 = 3 974 m · 8 = 50 800
y + 1 138 = 4 000 a · 4 = 4 100
x – 2 765 = 7 081 x · 90 = 34 200
k + 40 521 = 50 521 y · 208 = 13 936
Решение:
а – 986 = 3 974
a = 3 974 + 986
a = 4 960
m · 8 = 50 800
m = 50 800 : 8
m = 6 350
y + 1 138 = 4 000
у = 4 000 - 1 138
у = 2 862
a · 4 = 4 100
а = 4 100 : 4
а = 1 025
x – 2 765 = 7 081
х = 7 081 + 2 765
х = 9 846
x · 90 = 34 200
х = 34 200 : 90
х = 380
k + 40 521 = 50 521
k = 50 521 - 40 521
k = 10 000
y · 208 = 13 936
y = 13 936 : 208
y = 6710. Найдите значения выражений.
9 480 : (300 – 285) · 1 000 – 109 · 197 =
85 625 : 25 – 1 104 : (73 992 – 804 · 92) =
(16 316 + 10 774) : 45 · 100 + 878 · 607 =
94 · 768 – (63 782 + 10 998 : 9) =
Решение:
2 1 3 5 4
9 480 : (300 – 285) · 1 000 – 109 · 197 = 610 527
1) 300 – 285 = 15
2) 9 480 : 15 = 632
-9480|15
90 |632
-48
45
-30
30
0
3) 632 * 1000 = 632 000
4) 109 * 197 = 21 473
*197
109
+1773
197
21473
5) 632 000 - 21 473 = 610 527
4 5 3 2 1
85 625 : 25 – 1 104 : (73 992 – 804 · 92) = 3 379
1) 804 * 92 = 73 968
2) 73 992 - 73 968 = 24
3) 1 104 : 24 = 46
-1104|24
96 |46
-144
144
0
4) 85 625 : 25 = 3 425
5) 3 425 - 46 = 3 379
1 2 3 5 4
(16 316 + 10 774) : 45 · 100 + 878 · 607 = 592 746
1) 16 316 + 10 774 = 26 910
2) 26 910 : 45 = 598
-26910|45
225 |598
-441
405
-360
360
0
3) 598 * 100 = 59 800
4) 878 * 607 = 532 946
5) 59 800 + 532 946 = 592 746
3 4 2 1
94 · 768 – (63 782 + 10 998 : 9) = 7 220
1) 10 998 : 9 = 1 222
-10998|9
9 |1222
-19
18
-19
18
-18
18
0
2) 63 752 + 1 222 = 64 972
3) 94 * 768 = 72 192
4) 72 192 - 64 972 = 7 22011. Из города в деревню через село турист на велосипеде ехал несколько часов со скоростью 18 км/ч. Сколько времени затратил турист на весь путь, если от города до села 30 км, а от села до деревни 60 км?
(30 + 60) : 18 = 90 : 18 = 5 (ч.) – затратил турист
Ответ: 5 часов. 117
-
Ответы к странице 117
12. Участок пути длиной 108 км автомобиль проехал со скоростью 54 км/ч. Следующий участок пути длиной 180 км он проехал со скоростью 60 км/ч. Сколько времени затратил автомобиль на весь путь?
108 : 54 + 180 : 60 = 2 + 3 = 5 (ч.) – затратил на весь путь
Ответ: 5 часов.13. Расстояние между двумя городами 345 км. В 11 ч утра из одного города выехала машина и прибыла в другой город в 17 ч того же дня. С какой скоростью ехала машина, если на остановки в пути шофёр затратил 1 ч?
1) 17 – 11 – 1 = 5 (ч.) – ехала машина
2) 345 : 5 = 69 (км/ч) – скорость машины
Ответ: 69 км/ч.14. Прямой участок шоссе длиной 600 м и шириной 13 м надо заасфальтировать. На каждые 100 м2 требуется 3 т 850 кг асфальта. Сколько потребуется асфальта, чтобы покрыть весь участок?
1) 600 * 13 = 7 800 (м²) – площадь участка шоссе
2) 3 т 850 кг = 3 850 кг
3) 7 800 : 100 * 3 850 = 78 * 3 850 = 300 300 кг = 300 т 300 кг – потребуется асфальта
Ответ: 300 т 300 кг.15. Используя рисунок, определите, истинно или ложно составное высказывание. 1) Если фигура ABCD — квадрат, то фигура ABCD — прямоугольник. 2) Если фигура MKOP — прямоугольник, то фигура MKOP — квадрат.
Решение:
1) Если фигура ABCD — квадрат, то фигура ABCD — прямоугольник. истинное
2) Если фигура MKOP — прямоугольник, то фигура MKOP — квадрат. ложное16. Расстояние на карте между двумя населёнными пунктами равно 3 см 2 мм. Масштаб карты 1 : 2 500 000. Какое расстояние между этими пунктами на местности? Выразите результат в километрах.
1) 3 см 2 мм = 32 мм
2) 32 * 2 500 000 = 80 000 000 мм = 80 (км) – расстояние на местности
Ответ: 80 км. 118
-
Ответы к странице 118
17. Из каких двух высказываний состоит составное высказывание? «Если в выражении 120 – 5 · (4 + 3) есть скобки, то действия выполняются слева направо по порядку». Истинно или ложно данное высказывание?
Решение:
Из каких двух высказываний состоит составное высказывание? из двух условий
«Если в выражении 120 – 5 · (4 + 3) есть скобки, то действия выполняются слева направо по порядку». Истинно или ложно данное высказывание? ложное18. Жук ползёт по кирпичу. Какое расстояние он преодолеет, если его путь показан красным цветом?
Решение:
10 + 25 + 5 = 40 см
19. Перед выполнением деления прикиньте, сколько цифр будет в частном.
43 680 : 840 1 241 240 : 124
509 040 : 126 67 488 : 888Карточка-помощница
720'00 : 360 (3 цифры)
Решение:
43 680 : 840 = 52 (2 цифры)
-4368|84
420 |52
-168
168
0
1 241 240 : 124 = 10 010-1241240|124
124 |10010
-124
124
0
509 040 : 126 = 10 010
-509040|126
504 |10010
-504
504
0
67 488 : 888 = 76
-67488|888
6216 |76
-5328
5328
020. Найдите и объясните ошибки в каждой из записей.
Решение:
Слева направо:
Левый пример: не учтен последний разряд. Ответ должен быть 670
По середине: не учтен разряд. Ответ должен быть 207
Справа: добавлен лишний разряд в ответе. Ответ должен быть 713 119
-
Ответы к странице 119 УЗНАЁМ НОВОЕ Виды углов
1. Найдите с помощью угольника прямой угол. Какой из остальных углов: меньше прямого угла; больше прямого угла? Угол, который меньше прямого, называют острым. Угол, который больше прямого, называют тупым.
Решение:
∠ под номером 2 прямой
∠ под номером 1 меньше прямого
∠ под номером 3 больше прямого2. Какие углы на рисунке: острые, прямые, тупые?
Решение:
∠ острые:
1, 4, 5∠ тупые:
2
∠ прямые:
3, 6 120
-
Ответы к странице 120
3. Начертите в тетради прямой угол, два острых угла и три тупых угла.
Решение:
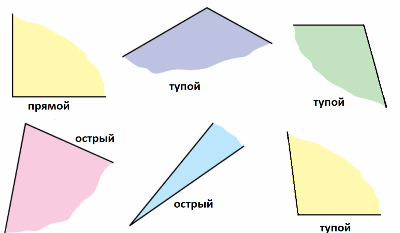
4. Найдите в многоугольниках прямые, острые, тупые углы.
Решение:
В многоугольнике OADC:∠ острые: ADC
∠ тупые: OAD OCD
∠ прямые: AOC
В многоугольнике KBM:
∠ острые: BMK BKM
∠ тупые: нет
∠ прямые: KBMВ многоугольнике EXPY:
∠ острые: EYP
∠ тупые: XEY
∠ прямые: EXP XPY5. Найдите неизвестное число.
x · 65 = 24 700 x : 17 = 17 340Решение:
x · 65 = 24 700
х = 24 700 : 65
х = 380
x : 17 = 17 340
х = 17 340 * 17
х = 294 7806. Выполните действия.
3 111 – 7 236 : 18 =
2 610 : 58 · 45 + 3 860 · 100 =
Решение:
2 1
3 111 – 7 236 : 18 = 2 709
1) 7 236 : 18 = 402
2) 3 111 - 402 = 2 7091 2 4 3
2 610 : 58 · 45 + 3 860 · 100 = 388 025
1) 2 610 : 58 = 45
-2610|58
232 |45
-290
290
0
2) 45 * 45 = 2 025
*45
45
+225
180
2025
3) 3 860 * 100 = 386 000
4) 2 025 + 386 000 = 388 0257. Для оклейки одной комнаты купили 7 рулонов обоев, а для оклейки второй — 12 таких же рулонов. Для второй комнаты купили на 50 м обоев больше, чем для первой. Сколько метров обоев пошло на каждую комнату?
1) 50 : (12 – 7) = 50 : 5 = 10 (м) – обоев в одном рулоне
2) 10 * 7 = 70 (м) – обоев пошло на 1 комнату
3) 10 * 12 = 120 (м) – обоев пошло на 2 комнату
Ответ: 70 м, 120 м.8. Может ли один человек быть старше другого в 600 раз? Проверьте свой ответ, используя данные: внуку 1 месяц, а дедушке 50 лет.
Решение:
1) 50 * 12 = 600 (мес.) дедушке.
2) 600 : 1 = 600 (р.) 1 месяц меньше 600.
Ответ: может. 121
-
Ответы к странице 121
9. Площадь прямоугольника равна 860 дм2, а его ширина 10 дм. Чему равен периметр прямоугольника?
1) 860 : 10 = 86 (дм) – длина прямоугольника
2) 2 * (10 + 86) = 2 * 96 = 192 (дм) – периметр прямоугольника
Ответ: 192 дм.10. Вычислите площадь квадрата, если длина его стороны равна: 12 см 5 мм; 1 дм 5 см 6 мм.
Решение:
12 см 5 мм = 125 мм
125 * 125 = 15 625 (мм2) площадь квадрата со стороной 125 мм
Ответ: 15 625 мм21 дм 5 см 6 мм = 156 мм
156 *156 = 24 336 (мм2) площадь квадрата со стороной 156 мм
Ответ: 24 336 мм211. Не выполняя вычислений, определите неизвестное число в каждом из равенств.
x – 125 = 625 – 125
x + 254 = 254 + 85Решение:
x – 125 = 625 – 125
х = 625
x + 254 = 254 + 85
х = 8512. Каждое из чисел 600, 8 000, 10 000: 1) увеличьте в 4 раза;2) уменьшите в 100 раз.
Решение:
1) увеличьте в 4 раза;
600 * 4 = 2400
8 000 * 4 = 32 000
10 000 * 4 = 40 000
2) уменьшите в 100 раз.
600 : 100 = 6
8 000 : 100 = 8
10 000 : 100 = 10013. Из города в противоположных направлениях выехали грузовик и мопед. Скорость грузовика 47 км/ч, а мопеда — 33 км/ч. Какое расстояние по шоссе будет между ними: через 1 ч; через 6 ч?
1) 1 * (47 + 33) = 1 * 80 = 80 (км) – будет между ними через 1 час
2) 6 * (47 + 33) = 6 * 80 = 480 (км) – будет между ними через 6 часов
Ответ: 80 км, 480 км.14. Из города в одном направлении выехали одновременно легковая машина и автобус. Скорость автобуса 65 км/ч, а машины — 75 км/ч. Какое расстояние по шоссе будет между ними: через 1 ч; через 6 ч?
1) 1 * (75 – 65) = 1 * 10 = 10 (км) – будет между ними через 1 час
2) 6 * (75 – 65) = 6 * 10 = 60 (км) – будет между ними через 6 часов
Ответ: 10 км, 60 км.15. На две стройки отправили 10 одинаковых ящиков с гвоздями. Когда на стройках использовали 60 кг гвоздей, на первой стройке осталось 5 полных ящиков, а на второй — 2 ящика. Сколько килограммов гвоздей в каждом ящике?
1) 10 – (5 + 2) = 10 – 7 = 3 (ящ.) – гвоздей потратили
2) 60 : 3 = 20 (кг) – гвоздей в каждом ящике
Ответ: 20 кг гвоздей. 122
-
Ответы к странице 122
16. Расстояние между двумя городами на плане равно 7 см. Масштаб плана 1 : 1 000 000. Каково расстояние между этими городами на местности?
7 * 1 000 000 = 7 000 000 см = 70 (км) – между городами на местности
Ответ: 70 км.17. Прямое шоссе длиной 12 км изображено на плане отрезком длиной 4 см. В каком масштабе выполнен план?
Решение:
12 км = 1 200 000 см1 200 000 : 4 = 300 000 (раз) разница между масштабами, то есть масштаб плана 1 : 300 000
18. От села до города 1 500 м. Каким будет это расстояние на плане, сделанном в масштабе 1 : 30 000?
1) 1 500 м = 150 000 см
2) 150 000 : 30 000 = 5 см
Ответ: 5 см.19. На рисунке дан график изменения температуры воздуха в разное время суток (с 8 ч до 17 ч). Сколько градусов показывал термометр в 9 ч утра; в полдень; в 15 ч? Когда температура была максимальной? В какой промежуток времени температура не изменялась?
Решение:
Сколько градусов показывал термометр в 9 ч утра; 10 °С
в полдень; в 15 ч? 15 °С
Когда температура была максимальной? в 14 часов
В какой промежуток времени температура не изменялась? с 15 до 16 часов 123
-
Ответы к странице 123
20. В таблице указаны сроки цветения цветковых растений средней полосы России. Ответьте на вопросы. У каких растений сроки цветения совпадают? Какие цветы цветут только один месяц? Какие цветы цветут в мае, какие — в июле и какие — в сентябре?
У какого цветка сроки цветения больше: лилии или настурции; настурции или хризантемы? Какие цветы отцветают последними? Какие цветы зацветают раньше всех? Какой цветок зацветает позже: гиацинт или крокус; нарцисс или незабудка? Сколько месяцев цветёт пион, ландыш, гвоздика, купальница? Назовите сроки цветения бархатцев, календулы, пиона.Решение:
Совпадают сроки цветения у крокуса и незабудки (апрель); гиацинта, крокуса, купальницы, ландыша, нарцисса, незабудки, тюльпана (май)... Один месяц цветут: гиацинт, ландыш, пион, тюльпан.
8 мае цветут: гиацинт, крокус, купальница, ландыш, нарцисс, незабудка, тюльпан, в июле...
Больше сроки цветения у лилии больше чем у настурции; у настурции больше чем у хризантемы. Последними цветут астры. Раньше всех зацветают крокусы и незабудки. Позже зацветает гиацинт чем крокус; нарцисс чем незабудка. Пион цветёт 1 месяц, ландыш 1 месяц, гвоздика 4 месяца, купальница 3 месяца.
Сроки цветения бархатцев: июль сентябрь; календулы: июль - сентябрь; пиона — июнь. 124
-
Ответы к странице 124
21. Расположите значения величин в порядке увеличения:
1) 2 км, 1 250 м, 999 м, 1 250 дм, 30 м 8 дм;
2) 16 кг, 5 300 г, 1 600 г, 280 г, 1 т, 6 ц.Решение:
1) 30 м 8 дм, 1 250 дм, 999 м, 1 250 м, 2 км,
2) 280 г, 1 600 г, 5 300 г, 16 кг, 6 ц, 1 т.22. Выразите время: в минутах: 28 800 с, 40 ч, 6 ч 12 мин; в сутках: 96 ч, 168 ч, 192 ч; в часах: 420 мин, 600 мин, 540 мин, 1 020 мин; в секундах: 9 мин 15 с, 2 ч 30 мин 15 с.
Решение:
в минутах: 28 800 с, 40 ч, 6 ч 12 мин;
28 800 с : 60 = 480 мин
40 ч * 60 = 2 400 мин
6 ч 12 мин = 6 * 40 мин + 12 мин = 240 + 18 = 256 мин
в сутках: 96 ч, 168 ч, 192 ч;
96 ч : 24 = 4 сут.
168 ч : 24 = 7 сут.
192 ч : 24 = 8 сут.
в часах: 420 мин, 600 мин, 540 мин, 1 020 мин;
420 мин : 60 = 7 ч.
600 мин : 60 = 10 ч.
540 мин : 60 = 9 ч.
1 020 мин : 60 = 17 ч
в секундах: 9 мин 15 с, 2 ч 30 мин 15 с.
9 мин 15 с = 9 * 60 с + 15 с = 540 с + 15 с = 555 сек.
2 ч 30 мин 15 с = 2 * 60 * 60 с + 30 * 60 с + 15 с = 7 200 с + 1 800 с + 15 с = 9 015 с23*. Скорость движения лодки в стоячей воде 3 752 м/ч. Скорость течения реки 1 976 м/ч. Найдите скорость движения лодки по течению реки и против течения.
Решение:
3 752 м/ч + 1 976 м/ч = 5 728 м/ч скорость по течению.
3 752 м/ч - 1 976 м/ч = 1 776 м/ч скорость против течения. 125
-
Ответы к странице 125 УЗНАЁМ НОВОЕ Нахождение неизвестного числа в равенствах вида 8 + x = 16, 8 · x = 16, 8 – x = 2, 8 : x = 2
1. Объясните, как можно вычислить неизвестное второе слагаемое.
Решение:
в одну сторону выражения перенести известные величины, в другую неизвестные, при переносе поменять знак на противоположный2. Какое действие надо выполнить, чтобы найти неизвестное второе слагаемое в каждом из равенств?
408 + a = 1 340 3 360 + x = 25 001
900 + y = 27 000 97 531 + n = 100 050
Сформулируйте правило для нахождения неизвестного второго слагаемого. Сравните свой ответ с текстом. Чтобы найти неизвестное второе слагаемое, надо из суммы вычесть первое слагаемое.Решение:
408 + a = 1 340
a = 1 340 - 408
a = 932
3 360 + x = 25 001
х = 25 001 - 3 360
х = 21 641
900 + y = 27 000
y = 27 000 - 900
y = 26 100
97 531 + n = 100 050
n = 100 050 - 97 531
n = 2 5193. Пользуясь правилом, найдите неизвестное второе слагаемое.
12 800 + m = 40 213 893 + k = 2 000Решение:
12 800 + m = 40
m = 12 800 - 40
m = 12 760
213 893 + k = 2 000
к = 213 893 - 2 000
к = 211 893 126
-
Ответы к странице 126
4. Запишите предложение в виде равенства. Найдите неизвестное число.
1) Если к числу 678 прибавить неизвестное число m, то получится 101 200.
2) Если к числу 5 080 прибавить неизвестное число t, то получится 6 117.Решение:
1) Если к числу 678 прибавить неизвестное число m, то получится 101 200.
678 + m = 101 200
m = 101 200 - 678
m = 100 522
2) Если к числу 5 080 прибавить неизвестное число t, то получится 6 117.
5 080 + t = 6 117
t = 6 117 - 5 080
t = 1 0375. Оля задумала число, прибавила его к числу 968 и получила 1 000. Какое число задумала Оля?
х + 968 = 1 000
х = 1 000 – 968
х = 32
Ответ: 32.6. На базе было 3 450 кг капусты. После того как на базу привезли ещё фургон капусты, там стало 8 700 кг капусты. Сколько капусты привезли на базу?
х кг капусты привезли на базу
3 450 + х = 8 700
х = 8 700 – 3 450
х = 5 250 (кг) – капусты привезли на базу
Ответ: 5 250 кг.7. Объясните, как можно вычислить неизвестный второй множитель.
Решение:
в одну сторону выражения перенести известные величины, в другую неизвестные, при переносе поменять знак на противоположный имеющемуся8. Какое действие надо выполнить, чтобы найти неизвестный второй множитель в каждом из равенств?
65 · a = 650 506 · b = 2 530
19 · x = 3 800 8 · m = 4 000
Сформулируйте правило для нахождения неизвестного второго множителя. Сравните свой ответ с текстом.Решение:
65 · a = 650
а = 650 : 65
а = 10
506 · b = 2 530
b = 2 530 : 506
b = 5
19 · x = 3 800
x = 3 800 : 19
х = 20
8 · m = 4 000
m = 4 000 : 8
m = 5 000 127
-
Ответы к странице 127
9. Запишите предложение в виде равенства. Найдите неизвестное число.
1) Если 28 умножить на неизвестное число a, то получится 103 432.
2) Если число 312 увеличить в n раз, то получится 4 992.Решение:
1) Если 28 умножить на неизвестное число a, то получится 103 432.
28 * a = 103 432
a = 103 432 : 28
а = 3 694
2) Если число 312 увеличить в n раз, то получится 4 992.
312 * n = 4 992
n = 4 992 : 312
n = 1610. Митя задумал число, умножил на него число 960 и получил 336 000. Какое число задумал Митя?
960 * х = 336 000
х = 336 000 : 960
х = 350
Ответ: 350.11. Объясните, как можно найти неизвестное вычитаемое.
Решение:
в одну сторону выражения перенести известные величины, в другую неизвестные, при переносе поменять знак на противоположный имеющемуся12. Какое действие надо выполнить, чтобы найти неизвестное вычитаемое в каждом из равенств?
250 – x = 36 500 – n = 144
1 900 – y = 855 4 014 – c = 382
Сформулируйте правило для нахождения неизвестного вычитаемого. Сравните свой ответ с текстом.
Решение:
250 – x = 36
x = 250 - 36
x = 214
500 – n = 144
n = 500 - 144
n = 356
1 900 – y = 855
y = 1 900 - 855
y = 1 045
4 014 – c = 382
c = 4 014 - 382
c = 3 632 128
-
Ответы к странице 128
13. Запишите предложение в виде равенства. Найдите неизвестное число.
1) Если из числа 10 120 вычесть a, то получится 983.
2) Если число 40 308 уменьшить на y, то получится 409.Решение:
1) Если из числа 10 120 вычесть a, то получится 983.
10 120 - а = 983
а = 10 120 - 983
а = 9 137
2) Если число 40 308 уменьшить на y, то получится 409.
40 308 - y = 409
y = 40 380 - 409
y = 39 97114. Если неизвестное число вычесть из 5 555, то получится 3 939. Чему равно неизвестное число?
5 555 – х = 3 939
х = 5 555 – 3 939
х = 1 616
Ответ: 1 616.15. У папы было 12 000 р. После покупки пылесоса у него осталось 8 440 р. Какова цена пылесоса?
х руб. – цена магнитофона
12 000 – х = 8 440
х = 12 000 – 8 440
х = 3 560
Ответ: 3 560 рублей.16. На мельнице было 15 450 кг пшеницы. После того как часть пшеницы смололи, осталось 8 600 кг пшеницы. Сколько пшеницы смололи?
х кг пшеницы смололи
15 450 – х = 8 600
х = 15 450 – 8 600
х = 6 850
Ответ: 6 850 кг.17. Объясните, как можно найти неизвестный делитель.
Решение: в одну сторону выражения перенести известные величины, в другую неизвестные, при переносе поменять знак на противоположный имеющемуся
129
-
Ответы к странице 129
18. Какое действие надо выполнить, чтобы найти неизвестный делитель в каждом из равенств?
126 : a = 42 2 700 : c = 900
625 : b = 5 5 400 : x = 54
Сформулируйте правило для нахождения неизвестного делителя. Сравните свой ответ с текстом. Чтобы найти неизвестный делитель, надо делимое разделить на частное.Решение:
126 : a = 42
a = 126 : 42
а = 3
2 700 : c = 900
с = 2 700 : 900
с = 3
625 : b = 5
b = 625 : 5
b = 125
5 400 : x = 54
x = 5 400 : 54
x = 10019. Запишите предложение в виде равенства. Найдите неизвестное число.
1) Если число 920 разделить на a, то получится 46.
2) Если число 2 100 уменьшить в b раз, то получится 35.Решение:
1) Если число 920 разделить на a, то получится 46.
920 : а = 46
а = 920 : 46
а = 20
2) Если число 2 100 уменьшить в b раз, то получится 35.
2100 : b = 35
b = 2100 : 35
b = 6020. На неизвестное число разделили число 14 168 и получили 92. Найдите неизвестное число.
х – неизвестное число
14 168 : х = 92
х = 14 168 : 92
х = 154
Ответ: 154.21. Выполните действия.
409 801 – 586 50 308 · 4 830 605 : 5
50 728 + 6 183 320 · 406 17 280 : 36
867 + 995 540 258 · 137 109 296 : 297Решение:
409 801 – 586
50 308 · 4
830 605 : 5
50 728 + 6
183 320 · 406
17 280 : 36
867 + 995
540 258 · 137
109 296 : 29722. Вычислите устно.
(100 – 1) · 8 99 · 7 101 · 7
(100 – 2) · 4 98 · 5 101 · 9
(100 – 1) · 6 99 · 9 1 001 · 4
(100 – 2) · 3 97 · 3 1 001 · 5Решение:
(100 – 1) · 8 = 100 * 8 - 1 * 8 = 800 - 8 = 792
(100 – 2) · 4 = 100 * 4 - 2 * 4 = 400 - 8 = 392
(100 – 1) · 6 = 100 * 6 - 1 * 6 = 600 - 6 = 594
(100 – 2) · 3 = 100 * 3 - 2 * 3 = 300 - 6 = 294
99 · 7 = (100 - 1) * 7 = 100 * 7 - 1 * 7 = 700 - 7 = 693
98 · 5 = (100 - 2) * 5 = 500 - 10 = 490
99 · 9 = (100 - 1) * 9 = 900 - 9 = 891
97 · 3 = (100 - 3) * 3 = 300 - 9 = 291
101 · 7 = (100 + 1) * 7 = 700 + 7 = 707
101 · 9 = (100 + 1) * 9 = 900 + 9 = 909
1 001 · 4 = (1000 + 1) * 4 = 4000 + 4 = 4004
1 001 · 5 = (1000 + 1) * 5 = 5000 + 5 = 5005 130
-
Ответы к странице 130
23. Найдите значения выражений.
64 · 35 + 106 · 402 – 128 : 64 =
(8 000 – 3 988) · 105 – 945 : 5 · 100 =
46 839 – (322 060 – 64 · 150) : 20 =
(753 · 486 – 82 · 105 – 37 048) : 100 =
(12 460 + 760 · 112) : 41 – 1 791 =
(34 · 28 – 952) · 161 829 + 5 463 · 60 =
Решение:
1 4 2 5 3
64 · 35 + 106 · 402 – 128 : 64 = 44 850
1) 64 * 35 = 2 240
2) 106 * 402 = 42 612
3) 128 : 64 = 2
4) 2 240 + 42 612 = 44 852
5) 44 852 - 2 = 44 850
1 2 5 3 4
(8 000 – 3 988) · 105 – 945 : 5 · 100 = 401 310
1) 8 000 - 3 998 = 4 002
2) 4 002 * 105 = 420 210
3) 945 : 5 = 189-945|5
5 |189
- 44
40
-45
45
0
4) 189 * 100 = 18 900
5) 420 210 - 18 900 = 401 310
4 2 1 3
46 839 – (322 060 – 64 · 150) : 20 = 31 216
1) 64 * 150 = 9600
2) 322 060 - 9 600 = 312 460
3) 312 460 : 20 = 15 623
-312460|20
20 |15623
-112
100
-124
120
-46
40
-60
60
0
4) 46 839 - 15 623 = 31 216
1 3 2 4 5
(753 · 486 – 82 · 105 – 37 048) : 100 = 3 203
1) 753 · 486 = 365 958
2) 82 · 105 = 8 610
3) 365 958 - 8 610 = 357 348
4) 357 348 - 37 048 = 320 300
5) 320 300 : 100 = 3 203
2 1 3 4
(12 460 + 760 · 112) : 41 – 1 791 = 589
1) 760 · 112 = 85 120
2) 12 460 + 85 120 = 97 580
3) 97 580 : 41 = 2380
-97580|41
82 |2380
-155
123
-328
328
0
4) 2380 - 1791 = 589
1 2 3 5 4
(34 · 28 – 952) · 161 829 + 5 463 · 60 = 327 780
1) 34 · 28 = 952
2) 952 - 952 = 0
3) 0 * 161 829 = 0
4) 5 463 · 60 = 327 780
5) 0 + 327 780 = 327 78024. Трое мастеров — Петров, Воробьёв и Зайцев — получили заказ на изготовление 324 матрёшек. Петров за день может сделать 18 матрёшек, Воробьёв — 20, а Зайцев — 16. За сколько дней мастера выполнят заказ, если возьмутся за работу одновременно?
324 : (18 + 20 + 16) = 324 : 54 = 6 (дн.) – выполняет заказ мастера
Ответ: за 6 дней.25. Два повара должны испечь 174 пирожка. За час работы один повар может испечь 30 пирожков, а другой — 28. За сколько часов, работая вместе, они испекут все пирожки?
174 6 (30 + 28) = 174 : 58 = 3 (ч.) – испекут все пирожки
Ответ: за 3 часа.26. Для варки варенья приготовили 45 кг ягод: крыжовник, малину и чёрную смородину. Крыжовника было 6 кг 500 г, а малины — втрое больше, чем крыжовника. Сколько чёрной смородины приготовили для варки варенья?
6 кг 500 г = 6 500 г
1) 6 500 * 3 = 19 500 (г) – приготовили малины
45 кг = 45 000 г
2) 45 000 – (6500 + 19500 ) = 19 000 (г) – приготовили чёрной смородины
19 000 г = 19 кг
Ответ: 19 кг.27. В двух резервуарах было 120 т нефти. Когда из одного резервуара взяли 35 т 600 кг нефти, а из другого — 46 т 400 кг нефти, в обоих резервуарах нефти осталось поровну. Сколько нефти было в каждом резервуаре первоначально?
1) 35 т 600 кг + 46 т 400 кг = 82 (кг) – всего взяли нефти
2) 120 – 82 = 38 (т) – нефти всего осталось
3) 38 : 2 = 19 (т) – нефти осталось в каждом резервуаре
4) 19 т + 35 т 600 кг = 54 т 600 кг – нефти было в 1 резервуаре
5) 19 т + 46 т 400 кг = 65 т 400 кг – нефти было во 2 резервуаре
Ответ: 54 т 600 кг, 65 т 400 кг. 131
-
Ответы к странице 131
28*. В 9 ч утра из города на шоссе выехала машина со скоростью 72 км/ч. Через полчаса вслед за ней выехал мотоциклист со скоростью 60 км/ч. На каком расстоянии вдоль шоссе они будут находиться друг от друга в 10 ч утра?
1) 72 * 1 = 72 (км) – проехала машина
2) 60 : 2 = 30 (км) – проехал мотоциклист
3) 72 – 30 = 42 (км) – будет между ними в 10 час
Ответ: 42 км.29. В упаковке 5 котлет, массой 120 г каждая. Какова масса четырёх таких упаковок котлет?
1) 120 * 5 * 4 = 600 * 4 = 2 400 г = 2 кг 400 г – масса четырех упаковок котлет
Ответ: 2 кг 400 г.30. Выполните действия.
20 ч 16 мин + 1 ч 44 мин =
10 ч 25 мин – 9 ч 35 мин =
17 ч 30 мин + 2 ч 40 мин =
4 мин 57 с + 12 мин 6 с =
16 ч 45 мин – 30 мин =
27 мин 36 с – 14 мин 42 с =
Решение:1 час = 60 минут
20 ч 16 мин + 1 ч 44 мин = (20 ч + 1 ч) + (16 мин. + 44 мин.) = 21 ч 60 мин. = 21 ч+1 ч = 22 ч
10 ч 25 мин - 9 ч 35 мин = 9 ч (60 мин. + 25 мин.) - 9 ч 35 мин. = 9 ч 85 мин. - 9 ч 35 мин. = (9 ч - 9 ч) + (85 мин. - 35 мин.) = 50 мин.
17 ч 30 мин + 2 ч 40 мин = (17 ч+ 2 ч) + (30 мин. + 40 мин.) = 19 ч 70 мин. = 19 ч (60 мин. + 10 мин.)=(19 ч +1 ч) + 10 мин. = 20 ч 10 мин.1 минута = 60 секунд
4 мин 57 с + 12 мин 6 с = (4 мин. + 12 мин.) + (57 с + 6 с) = 16 мин. 63 с = 16 мин. + (60 с+3 с) = (16 мин. + 1 мин.) + 3 с = 17 мин. 3 с
16 ч 45 мин - 30 мин = 16 ч + (45 мин. - 30 мин.) = 16 ч 15 мин.
27 мин 36 с - 14 мин 42 с = 26 мин. (60 с + 36 с) - 14 мин. 42 с = 26 мин. 96 с - 14 мин. 42 с = (26 мин. - 14 мин.) + (96 с - 42 с) = 12 мин. 54 с31. Выразите в километрах и метрах: 50 321 м, 8 111 м, 34 780 м, 800 000 м, 123 005 м.
Решение:
50321 м=50 км 321 м
8111 м=8 км 111 м
34780 м=34 км 780 м
800000 м=800 км
123005=123 км 5 м32. Выразите в метрах: 42 км 120 м, 49 км, 179 км 500 м, 86 км 35 м, 5 км 6 м.
Решение:
42 км 120 м =42
120 м 179 км
500 м = 179 500 м
86 км 35 м = 8635 м
49 км = 49 000 м
5 км 6 м = 5006 м33. Верно или неверно?
1) При делении числа на 7 в остатке может получиться число 9.
2) Частное 36 000 : 1 800 не изменится, если делимое и делитель разделить на 100.
3) Неверно, что произведение чисел 20 и 30 равно 600.
4) Сумма двух чисел может быть равной одному из слагаемых.Решение:
1) При делении числа на 7 в остатке может получиться число 9. ложное
2) Частное 36 000 : 1 800 не изменится, если делимое и делитель разделить на 100. истинное
3) Неверно, что произведение чисел 20 и 30 равно 600. ложное
4) Сумма двух чисел может быть равной одному из слагаемых. истинное 132
-
Ответы к странице 132
34. Назовите по два числа, которые при делении на 5 дают в остатке: 2, 3, 4.
Решение:
в остатке: 2,
12 и 102
3,
23 и 203
4
104 и 30435. Какие числа на числовом луче соответствуют отмеченным точкам?
Решение:
A 20 000
B 30 000
C 65 000
D 70 00036. На каком участке (А, Б, В, Г, Д, Е) числового луча находятся числа: 267 500, 102 800, 396 125, 184 000, 212 999?
Решение:
267 500 (участок Г)
102 800 (участок А)
396 125 (участок Е)
184 000 (участок Б)
212 999 (участок В)37*. Учительница показала ученикам модели трёх многогранников. Дима посмотрел на них сверху и вот что увидел. Какая из этих фигур является пирамидой; прямоугольным параллелепипедом? Какая из них может быть кубом? Почему?
Решение:
Какая из этих фигур является пирамидой; фигура 3
прямоугольным параллелепипедом? 1
Какая из них может быть кубом? Почему? 2 может быть, если у нее высота такая же как и сторона у сечения которое мы видим.38. Оля начертила квадрат. Зоя посмотрела на него и сказала, что это прямоугольник. Не ошиблась ли Зоя?
Решение:
Нет, не ошиблась, так как квадрат это прямоугольник в том числе. 133
-
Ответы к странице 133
39. Какие из высказываний об изображённом угле истинные?
1) ∠AOB не прямой.
2) ∠AOB не острый.
3) ∠AOB острый.
4) ∠AOB не тупой.
5) ∠AOB тупой.
6) ∠AOB острый или прямой.Решение:
1) ∠AOB не прямой. истинное
2) ∠AOB не острый. истинное
3) ∠AOB острый. ложное
4) ∠AOB не тупой. ложное
5) ∠AOB тупой. истинное
6) ∠AOB острый или прямой. ложное40. Определите, в каком из треугольников:
1) есть прямой угол;
2) есть тупой угол;
3) все углы острые;
4) есть не только острый угол, но и прямой;
5) нет прямого угла.Решение:
1) есть прямой угол; во 2
2) есть тупой угол; в 3
3) все углы острые; в 1
4) есть не только острый угол, но и прямой; во 2
5) нет прямого угла. 1 и 341. Измерьте и сравните длины сторон в каждом из треугольников. У какого из треугольников:
1) все стороны разной длины;
2) все стороны одной и той же длины;
3) только две стороны имеют одинаковую длину?Решение:
1) все стороны разной длины; у 1
2) все стороны одной и той же длины; у 3
3) только две стороны имеют одинаковую длину. у 2 134
-
Ответы к странице 134
42. Начертите три треугольника со сторонами разной длины так, чтобы в одном треугольнике был прямой угол, в другом — тупой угол, а в третьем — все углы были острыми.
Решение:
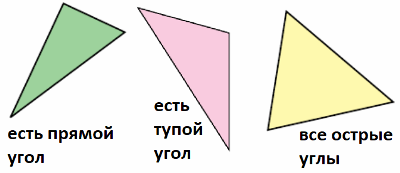
43. В конкурсе детской песни участвовали шестеро четвероклассников — Андреев, Серова, Павлов, Васильев, Белов и Галкина. На диаграмме показано, сколько баллов получил каждый из них. Кто из участников конкурса получил наибольшее число баллов и кто — наименьшее? Сколько баллов получила каждая из девочек? Сколько баллов получил Павлов? Кто получил больше баллов — Галкина или Васильев — и на сколько?
Решение:
сколько баллов получил каждый из них.
Галкина 4
Белов 3
Серова 6
Андреев 10
Павлов 8
Васильев 5
Кто из участников конкурса получил наибольшее число баллов и кто — наименьшее?
Наибольшее Андреев 10
Наименьшее Белов 3
Сколько баллов получила каждая из девочек?
Галкина 4
Серова 6
Сколько баллов получил Павлов?
Павлов 8
Кто получил больше баллов — Галкина или Васильев — и на сколько?
Васильев больше на 1 балл.44. Из данных чисел 0, 1, 2, 3, 4, 5, 6, 7, 8 укажите те, которые являются значениями x в неравенствах.
x < 3 x : 2 < 5
x > 4 3 · x > 10Решение:
x < 3 {0, 1, 2}
x > 4 {0, 1, 2, 3}
x : 2 < 5 {0, 1, 2, 3, 4, 5, 6, 7, 8}
3 · x > 10 {0, 1, 2, 3} 135
-
Ответы к странице 135 УЗНАЁМ НОВОЕ Виды треугольников
1. Определите вид углов в каждом треугольнике. Как вы думаете, почему красный треугольник называют остроугольным, синий — прямоугольным, а зелёный — тупоугольным? Треугольник, в котором все углы острые, называют остроугольным. Треугольник, в котором один из углов прямой, называют прямоугольным. Треугольник, в котором один из углов тупой, называют тупоугольным.
2. Определите вид каждого треугольника, используя угольник.
Решение:
розовый - тупоугольный
фиолетовый - прямоугольный
желтый - остроугольный 136
-
Ответы к странице 136
3. Измерьте длины сторон каждого треугольника. Есть ли в каждом из треугольников равные по длине стороны? Сколько их? Как вы думаете, почему красный треугольник называют разносторонним, синий — равнобедренным, а зелёный — равносторонним? Треугольник, в котором все стороны разной длины, называют разносторонним. Треугольник, в котором две стороны равны по длине, называют равнобедренным. Треугольник, в котором все стороны равны по длине, называют равносторонним.
Решение:
Есть ли в каждом из треугольников равные по длине стороны? Сколько их? в зеленом 3 стороны
Как вы думаете, почему красный треугольник называют разносторонним, синий — равнобедренным, а зелёный — равносторонним? Треугольник, в котором все стороны разной длины, называют разносторонним. Треугольник, в котором две стороны равны по длине, называют равнобедренным. Треугольник, в котором все стороны равны по длине, называют равносторонним.4. Можно ли равносторонний треугольник назвать равнобедренным? Можно ли равнобедренный треугольник назвать равносторонним? Поясните свои ответы.
Решение:
Можно ли равносторонний треугольник назвать равнобедренным? Да, можно, так как две стороны у него будут равны точно.
Можно ли равнобедренный треугольник назвать равносторонним? Нет, нельзя, так как третья сторона не равна двум другим.5. Верно ли высказывание? Поясните свой ответ на примерах.
1) Разносторонний треугольник не может быть прямоугольным.
2) Равнобедренный треугольник не может быть тупоугольным.
3) В треугольнике могут быть только два острых угла.Решение:
1) Разносторонний треугольник не может быть прямоугольным. ложное
2) Равнобедренный треугольник не может быть тупоугольным. ложное
3) В треугольнике могут быть только два острых угла. ложное, может быть три 137
-
Ответы к странице 137
6. Определите вид треугольника, измерив длины его сторон.
Решение:
желтый - равносторонний
фиолетовый - равнобедренный
зеленый - прямоугольный7. Периметр равнобедренного треугольника равен 25 см. Длина наибольшей из сторон равна 9 см. Найдите длины остальных сторон.
Решение:
1) 25 - 9 = 16 (см) длина двух оставшихся сторон, равных
2) 16 : 2 = 8 (см) длина любой из равных сторон.
Ответ: длины сторон 8, 8 и 9 см.8. Верно ли высказывание? Поясните свой ответ на примерах.
1) Среди прямоугольных треугольников есть равнобедренные.
2) Если треугольник тупоугольный, то он разносторонний.
3) Любой остроугольный треугольник является равносторонним.Решение:
1) Среди прямоугольных треугольников есть равнобедренные. истинное
2) Если треугольник тупоугольный, то он разносторонний. ложное
3) Любой остроугольный треугольник является равносторонним. ложное9. Периметр равностороннего треугольника равен 609 000 мм. Вычислите длину стороны треугольника в метрах.
609 000 м : 3 = 203 000 мм = 20 300 см = 203 (м) – длина стороны треугольника
Ответ: 203 м.10. Начертите в тетради прямоугольный равнобедренный треугольник. Длина каждой из равных сторон — 4 см 6 мм.
Решение:
Чертим по следующему алгоритму.
1) Проводим стороны 4 см 6 мм.
2) Отмеряем прямой угол и проводим вторую сторону 4 см 6 мм
3) Соединяем концы сторон между собой отрезком - основанием треугольника. 138
-
Ответы к странице 138
11. Мама купила 2 кг свёклы по цене 26 р. за килограмм и несколько бананов на 32 р. У неё осталось денег в 5 раз больше, чем она потратила. Сколько денег было у мамы?
1) 26 * 2 + 32 = 52 + 32 = 84 (р.) – потратила мама
2) 84 * 5 = 420 (р.) – осталось у мамы
3) 420 + 84 = 504 (р.) – было у мамы
Ответ: 504 рубля.12*. Человек идёт со скоростью 6 км/ч. Какое расстояние человек пройдёт: за 30 мин; за 20 мин; за 5 мин?
Решение:
1) 60 : 30 = 2 (раза) 30 минут меньше 1 часа
2) 6 : 2 = 3 (км) пройдет за пол часа.1) 60 : 20 = 3 (раза) 20 минут меньше 1 часа
2) 6 : 3 = 2 (км) пройдет за пол часа.1) 60 : 5 = 12 (раз) 5 минут меньше 1 часа
2) 6000 : 12 = 500 (м) пройдет за пол часа.13. Запишите выражение, состоящее:
1) из произведения 226 и 41, знака «плюс» и частного 3 120 и 390;
2) из произведения 27 и 307, знака «минус» и частного 4 685 и 937.Решение:
1) из произведения 226 и 41, знака «плюс» и частного 3 120 и 390;
226 * 41 + 3 120 : 390 = 9 266 + 8 = 9 274
2) из произведения 27 и 307, знака «минус» и частного 4 685 и 937.
27 * 307 - 4 685 : 937 = 8 289 - 5 = 8 28414*. Два поезда идут навстречу друг другу со скоростью 45 км/ч каждый. Длина каждого поезда 250 м. Сколько секунд пройдёт с момента встречи машинистов до момента встречи проводников, стоящих у последних дверей последних вагонов?
1) 45 км/ч = 45 * 1 000 м : 60 мин = 750 (м/мин) – скорости поездов
2) 750 * 2 : (250 * 2) = 1 500 : 500 = 3 (мин.) – пройдет
Ответ: 3 мин.. 139
-
Ответы к странице 139
15. В 12 ч дня из двух соседних сёл вышли два агронома и пошли навстречу друг другу по дороге длиной 6 км. Через 40 мин они встретились. Скорость движения одного агронома 80 м/мин. С какой скоростью шёл другой агроном?
1) 80 * 40 = 3 200 (м) – прошел первый агроном до встречи
2) 6 000 – 3 200 = 2 800 (м) – прошел до встречи другой агроном
3) 2 800 : 40 = 70 (м/мин) – скорость другого агронома
Ответ: 70 м/мин.16*. Охотник вышел из шалаша и пошёл к озеру. Полчаса он шёл со скоростью 5 км/ч. Пройденный путь составил треть расстояния от шалаша до озера. На каком расстоянии от шалаша находится озеро?
5 км/ч = 5000 м
1) 5 000 : 2 = 2 500 (м) – прошел охотник, это треть пути
2) 2 500 * 3 = 7 500 (м) – расстояние от шалаша до озера
7 500 м = 7 км 500 м
Ответ: 7 км 500 м.17. В несколько пятитонных и 8 трёхтонных грузовиков погрузили 54 000 кг арбузов. Сколько было пятитонных грузовиков?
1) 3 * 8 = 24 (т) – арбузов в трёхтонных грузовиках
54 000 кг = 54 т
2) 54 – 24 = 30 (т) – арбузов погрузили в пятитонные грузовики
3) 30 : 5 = 6 (г.) – пятитонных
Ответ: 6 пятитонных грузовиков.18. Для изготовления маленькой подушки нужно 800 г пуха. На большую подушку пуха нужно в 3 раза больше. Сколько пуха израсходуют для изготовления пяти больших подушек?
800 * 3 * 5 = 2 400 * 5 = 12 000 (г) – израсходуют на 5 больших подушек
12 000 г = 12 кг
Ответ: 12 кг пуха.19. Выполните действия.
639 · 185 302 · 408
4 308 + 28 765 148 431 – 139 648
45 494 : 43 35 042 : 7
9 408 : 98 25 578 : 63
1 008 · 206 67 266 : 222
Решение:639 · 185 = 118 215
*639
285
+3195
5112
1278
118215
302 · 408 = 123 216
*302
408
+2416
1208
123216
4 308 + 28 765 = 33 073
+4308
28765
33073
148 431 – 139 648 = 8 783
-148431
139648
8783
45 494 : 43 = 1058
-45494|43
43 |1058
-249
215
-344
344
0
35 042 : 7 = 5 006
-35042|7
35 |5006
-42
42
0
9 408 : 98 = 96
-9408|98
882 |96
-588
588
0
25 578 : 63 = 406
-25578|63
252 |406
-378
378
0
1 008 · 206 = 207 648
*206
1008
+1648
206
207648
67 266 : 222 = 303
-67266|222
666 |303
-666
666
0 140
-
Ответы к странице 140
20. Найдите значения выражений.
413 · 302 – 54 203 : 67 + 67 591 · 0 =
26 433 : 33 + 507 · 418 – 0 : 9 235 =
2 547 · 8 – 25 · 78 · 4 + 355 · 404 =
Решение:
1 4 2 5 3
413 · 302 – 54 203 : 67 + 67 591 · 0 = 123 917
1) 413 · 302 = 124 726
2) 54 203 : 67 = 809
-54203|67
536 |809
- 603
603
0
3) 67 591 · 0 = 0
4) 124 726 - 809 = 123 917
5) 123 917 + 0 = 123 917
1 4 2 5 3
26 433 : 33 + 507 · 418 – 0 : 9 235 = 212 727
1) 26 433 : 33 = 801
-26433|33
264 |801
-33
33
0
2) 507 * 418 = 211 926
3) 0 : 9 235 = 0
4) 801 + 211 926 = 212 727
5) 212 727 - 0 = 212 727
1 5 2 3 6 4
2 547 · 8 – 25 · 78 · 4 + 355 · 404 = 150 844
1) 2 547 · 8 = 20 376
2) 25 · 78 = 1950
*25
78
+200
175
1950
3) 1950 * 4 = 7800
4) 355 * 404 = 143 420
5) 20 376 - 7 800 = 7 424
6) 7 424 + 143 420 = 150 84421. Найдите неизвестное число.
4 350 – x = 2 874 180 · y = 9 000
a : 208 = 67 m + 3 008 = 14 873
Решение:
4 350 – x = 2 874
x = 4 350 - 2 874
х = 1 476
180 · y = 9 000
y = 9000 : 180
y = 50
a : 208 = 67
a = 67 * 208
a = 13 936
m + 3 008 = 14 873
m = 14 873 - 3 008
m = 11 86522. Вычислите периметр и площадь каждого из прямоугольников.
Решение:
ABCD размеры 4 * 6 см
Периметр: (4 + 6) * 2 = 10 * 2 = 20 (см)
Площадь: 4 * 6 = 24 (см2)
ADEM размеры 3 * 3
Периметр: 3 * 4 = 12 (см)
Площадь: 3 * 3 = 9 (см2)23. Какие из высказываний истинны?
1) Произведение чисел 700 и 200 равно 14 000.
2) 40 · 1 200 = 48 000.
3) Произведение 3 и 150 меньше произведения 30 и 15.
4) Число 200 делится без остатка не только на 4, но и на 40.
Решение:
1) Произведение чисел 700 и 200 равно 14 000. ложное
2) 40 · 1 200 = 48 000. истинное
3) Произведение 3 и 150 меньше произведения 30 и 15. ложное
4) Число 200 делится без остатка не только на 4, но и на 40. истинное24*. За 100 г орехов заплатили 24 р. Какова цена 1 кг орехов? Какова стоимость 400 г орехов?
Решение:
1) 1000 : 100 = 10 (раз) 100 г меньше 1000 г.
2) 24 * 10 = 240 (р.) стоит 1 кг орехов
3) 24 * 4 = 96 (р.) стоит 400 г орехов.
Ответ: 1 кг стоит 240 рублей. 96 рублей стоит 400 г. 141
-
Ответы к странице 141
25*. На 150 р. можно купить четверть килограмма кофе. Какова стоимость 100 г кофе?
1) 150 * 4 = 600 (руб.) – стоит 1 000 г кофе
2) 600 : (1 000 : 100) = 600 : 10 = 60 (р.) – стоимость 100 г кофе
Ответ: 60 рублей.26*. У Олега 2 500 р. Пятая часть этой суммы составляет десятую часть денег Андрея. Сколько денег у Андрея?
1) 2 500 : 5 = 500 (р.) – составляют десятую часть денег Андрея
2) 500 * 10 = 5 000 (р.) – у Андрея
Ответ: 5 000 рублей.27. Прочитайте определения понятий. Биссектриса — это луч, выходящий из вершины угла и делящий угол пополам. Гипотенуза — это сторона прямоугольного треугольника, лежащая против прямого угла. Выполните от руки рисунки, иллюстрирующие эти определения.
Решение:
Делаем рисунки.28. Используя рисунок, постройте треугольник.
Вариант 1 Вариант 2
В масштабе 1 : 2 В масштабе 2 : 1
Решение:При построении
В масштабе 1 : 2 уменьшаем значения сторон в два раза.
В масштабе 2 : 1 увеличиваем значения сторон в два раза.29. Выразите в указанных единицах:
16 000 мг в граммах; 4 380 мг в граммах и миллиграммах.Решение:
16 000 мг в граммах - 16 г;
4 380 мг в граммах и миллиграммах - 4 г 380 мг. 142
-
Ответы к странице 142 УЗНАЁМ НОВОЕ Точное и приближённое значения величины
1. Какое время показывают каждые часы? По каким часам наиболее точно можно определить время? По каким часам можно определить время с точностью: 1) до 5 минут; 2) до минуты; 3) до секунды?
Решение:
Какое время показывают каждые часы? первые 2 часа 20 минут, вторые 2 часа 21 минуту, третьи 2 часа 21 минуту 31 секунду
По каким часам наиболее точно можно определить время? по третьимПо каким часам можно определить время с точностью:
1) до 5 минут; первые часы
2) до минуты; вторые
3) до секунды? третьи2. С помощью каких весов можно точнее определить массу апельсина?
Решение:
с помощью электронных часов. 143
-
Ответы к странице 143
3. Длина отрезка AB равна 4 см 6 мм. Объясните, кто из учеников точнее указал длину отрезка AB. На сколько миллиметров ошибся каждый ученик?
Маша точнее. У нее погрешность 4 мм, а у Миши 6 мм.
4. Прочитайте записи. Какая запись выражает точное значение величины, а какая — приближённое? На сколько они отличаются друг от друга?
1) s = 16 км 200 м, s ≈ 16 км.
2) t = 3 мин 8 с, t ≈ 3 мин.
3) v = 27 км/ч, v ≈ 30 км/ч.Решение:
1)
s = 16 км 200 м, точное
s ≈ 16 км. приближенное
разница 16 200 - 16 000 = 200 м
2) t = 3 мин 8 с, точное
t ≈ 3 мин. приближенное
разница 3 мин 8 с - 3 мин = 8 с
3) v = 27 км/ч, точное
v ≈ 30 км/ч. приближенное
разница 30 - 27 = 3 км/ч 144
-
Ответы к странице 144
5. Масса тыквы на электронных весах равна 8 кг 657 г. Определите массу тыквы с помощью изображённых на рисунке чашечных весов. Запишите результат измерения. На сколько граммов отличаются эти результаты?
Решение:
На чашечных весах 8 кг 700 г.
8 700 - 8 657 = 43 (г) разница результатов.
Ответ: 43 грамма.6. Длина синего шнура равна 12 м 6 см, а жёлтого — 12 м 95 см. Укажите приближённое значение длины каждого шнура с точностью до метра.
Решение:
синий шнур 12 м 6 см, примерно 12 м
жёлтого 12 м 95 см, примерно 13 м7. Из листа фанеры можно вырезать 16 одинаковых квадратов. Сколько взять листов фанеры для того, чтобы вырезать 90 таких квадратов?
90 : 16 = 5 (ост. 10)
Ответ: 6 листов.8. Вычислите устно.
73 · 100 2 400 : 60
573 · 1 000 5 400 : 9
50 · 200 3 700 + 1 – 1 000
37 000 : 1 000 3 272 – 100 · 0
8 000 : 10 3 050 + 0 + 11Решение:
73 · 100 = 7 300
2 400 : 60 = 40
573 · 1 000 = 573 000
5 400 : 9 = 600
50 · 200 = 10 000
3 700 + 1 – 1 000 = 2 701
37 000 : 1 000 = 37
3 272 – 100 · 0 = 3 272
8 000 : 10 = 800
3 050 + 0 + 11 = 3 0619. На мельнице смололи 7 500 кг пшеницы. Из каждых 5 кг пшеницы получилось 4 кг муки. Сколько муки получилось из всей пшеницы?
7 500 : 5 * 4 = 2 500 * 4 = 10 000 (кг) – пшеницы получилось
10 000 кг = 10 т
Ответ: 10 т.10. Длина луга 150 м, ширина — 60 м. С каждых 100 м2 собрали 180 кг сена. Сколько сена собрали со всего луга?
1) 150 * 60 = 9 000 (м²) – площадь луга
2) 9 000 : 100 * 180 = 90 * 180 = 16 200 (кг) – сена собрали с луга
16 200 кг = 16 т 200 кг
Ответ: 16 т 200 кг. 145
-
Ответы к странице 145
11. Определите вид треугольников AXC, BXK, PXM: 1) по длинам сторон; 2) по видам углов. Проверьте, выполнив необходимые измерения, что прямая XY является осью симметрии каждого из указанных треугольников.
Решение:
AXC равнобедренный, тупоугольный
BXK, равнобедренный, остроугольный
PXM, равносторонний, остроугольный12. Прямоугольный участок земли имеет ширину 40 м и длину 50 м. Вычислите площадь и периметр участка. Начертите план этого участка, если 10 м соответствуют 1 см на плане.
Решение:
Чертим план 1 : 10 000, то есть 4 на 5 см. (8 на 10 клеток)
1) (4+5) * 2 = 9 * 2 = 18 (см) периметр
2) 4 * 5 = 20 (см2) площадь.
Ответ: 18 см периметр и 20 см2 площадь.13. Составьте три задачи, используя данные из таблицы.
Скорость Время Расстояние
70 км/ч 3 ч ? км
50 км/ч ? ч 350 км
? км/ч 2ч 1900 кмРешение:
1. Машина ехала со скоростью 70 км/ч 3 часа. Какое расстояние она проехала?
2. Автобус проехал 350 км со скорость 50 км/ч. Сколько по времени он ехал?
3. Самолет за 2 часа пролетел 1900 км. С какой скоростью он летел?14. Нужно выкроить одинаковые по размерам квадратные носовые платки у которых длина стороны 30 см. Ширина куска ткани такая, что на ней помещается 2 платка. Длина куска равна 1 м 20 см. Сколько платков получится?
1) 30 * 2 = 60 (см) – ширина куска ткани
1 м 20 см = 120 см
2) 120 : 30 = 4 (п.) – получится в длину
3) 4 * 2 = 8 (п.) – получится всего
Ответ: 8 платков. 146
-
Ответы к странице 146
Путешествие в прошлое
Рассказывают, что, когда будущему великому немецкому математику К. Ф. Гауссу исполнилось 9 лет, учитель предложил ему найти сумму всех чисел от 1 до 100. Гаусс быстро сообразил, каким простым способом можно выполнить это задание: надо складывать первое число с последним, второе с предпоследним и так далее. Сумма каждой такой пары чисел равна 101, и таких пар 50. Какое же число получил Гаусс?
101 * 50 = 5050
15*. Произведение двух чисел равно 705. Чему равно новое произведение, если один из множителей уменьшить в 5 раз, а другой оставить без изменения?
Решение:
705 : 5 = 141
Ответ: 14116*. Частное двух чисел равно 180. Чему равно новое частное, если делитель увеличить в 2 раза?
Решение:
180 * 2 = 360
Ответ: 360 147
-
Ответы к странице 147
17. Жильцы дома держат разных животных: черепах, кошек, хомяков, собак и попугаев. В каждой квартире живёт только одно из них. Рассмотрите диаграмму и ответьте на вопросы. Сколько в доме квартир, в которых живут попугаи, кошки, хомяки? Каких животных больше всего; меньше всего? Назовите животных в порядке увеличения их численности в доме. На сколько собак больше, чем кошек? На сколько попугаев меньше, чем кошек и собак? Во сколько раз черепах меньше, чем собак? Верно ли, что хомяков на 5 больше, чем черепах? Сколько всего животных живёт в доме?
Решение:
Сколько в доме квартир, в которых живут попугаи, кошки, хомяки?
30 + 35 + 25 = 90 (кв.)
Каких животных больше всего; меньше всего?
больше всего собак
меньше всего черепах
Назовите животных в порядке увеличения их численности в доме. На сколько собак больше, чем кошек?
черепахи, хомяки, попугаи, кошки, собаки
40 - 35 = 5 собак больше, чем кошек.
На сколько попугаев меньше, чем кошек и собак?
35 + 40 - 30 = 75 - 30 = 45 (поп.) меньше, чем кошек и собак.
Во сколько раз черепах меньше, чем собак?
40 : 20 = 2 (раза) черепах меньше, чем собак
Верно ли, что хомяков на 5 больше, чем черепах?
25 - 20 = 5 (хом.) на столько больше, чем черепах
5 = 5
Верно!
Сколько всего животных живёт в доме?
20 + 25 + 30 +35 + 40 = 150 животных18. Определите вид треугольника, если его периметр вычисляется так:
1) 15 · 2 + 24 = 54 (мм);
2) 25 · 3 = 75 (см).Решение:
1) 15 · 2 + 24 = 54 (мм); равнобедренный, стороны по 15 мм и основание 24 мм
2) 25 · 3 = 75 (см). равносторонний, все стороны 25 см 148
-
Ответы к странице 148
19. Запишите в тетради названия фигур.
Решение:
1 - конус,
2 - куб,
3 - цилиндр,
4 - пирамида20. Дима начертил треугольник и вычислил его периметр: 5 + 5 + 8 = 18 (см). Коля тоже начертил треугольник и вычислил его периметр: 7 · 3 = 21 (см). У кого из мальчиков равносторонний треугольник? Как называется другой треугольник?
Решение:
У Коли равносторонний, а у Димы равнобедренный.21. Определите вид каждого из углов (острый, прямой, тупой).
Решение:
1, 2, 4 - острый
3, 6 - прямой
5, 7 - тупой22. В ювелирном деле применяется единица массы, называемая каратом. Один карат равен 200 мг. В начале XVII века в Индии был найден всемирно известный алмаз «Орлов» массой 300 карат. Выразите его массу в граммах.
Решение:
200 * 300 = 60 000 мг = 60 г.
Ответ: 60 грамм. 149
-
Ответы к странице 149 УЗНАЁМ НОВОЕ Построение отрезка, равного данному
1. Не измеряя длину отрезка AB, нужно с помощью циркуля и линейки построить отрезок CK, равный отрезку AB. Как Миша решил эту задачу? Проверьте с помощью линейки, равен ли по длине отрезок CK отрезку AB. Расскажите, как построить с помощью циркуля и линейки отрезок, равный данному отрезку, не измеряя его длину.
Решение:
Миша измерил циркулем отрезок АВ, как говориться взял раствор. Провел луч и из нарисовал окружность, центр которой является начало луча, радиусом равным отрезку AB. Пересечение окружности и луча дало точку для отрезка на луче равному отрезку AB. 150
-
Ответы к странице 150
2. Не выполняя измерений, постройте в тетради отрезки, равные данным. Проверьте построение измерением.
Решение:
Чертим отрезки "на глаз". проверяем размеры.3. Найдите длину ломаной, выполняя только одно измерение.
Решение:
Строим луч и откладываем на нем отрезки равные отрезкам ломанной.4. Найдите периметр фигуры, выполняя только одно измерение.
Решение:
Задание выполняем аналогично заданию №3. Строим луч и откладываем на нем отрезки равные сторонам многоугольников. 151
-
Ответы к странице 151
5. Даша измерила длину рукава платья с точностью до сантиметра и получила 54 см. Точная длина рукава — 54 см 3 мм. На сколько приближённый результат, который получила Даша, отличается от точного значения длины рукава?
Решение:
54 см 3 мм - 54 см = 3 мм погрешность измерения.
Ответ: 3 мм6. Сделав покупки, Катя уже хотела уйти из магазина, но вспомнила, что забыла купить пирожки. Цена пирожка 15 р. Она взглянула на оставшиеся деньги и решила, что их достаточно для покупки 6 пирожков, но не хватает на 7 пирожков. Сколько денег могло остаться у Кати? Запишите ответ в виде: от … р. до … р.
Решение:
15 * 6 = 90 (руб.) точно должно быть
15 * 7 = 105 (руб.) нет, так как хватило бы на 7 пирожков.
Ответ: от 90 рублей, до 104 рублей было у Кати.7. Алёша проплыл 50 м по дорожке бассейна. Катя, глядя на циферблат часов с часовой и минутной стрелками, утверждает, что на всю дистанцию Алёша затратил 1 мин. Тренер, следивший за временем с секундомером, сообщил, что ошибка Кати составляет 20 с. За какое время в действительности Алёша мог проплыть дистанцию?
Решение:
60 - 20 = 40 (с) мог проплыть Алеша дистанцию 50 м.
60 + 20 = 80 (с) мог проплыть Алеша дистанцию 50 м.
Ответ: 40 или 80 секунд.8*. Корабль получил пробоину, и в трюм стала поступать вода. Каждые 7 мин в трюм поступает 5 т воды, а откачивают за это время 8 т 500 кг воды. Как изменяется масса воды в трюме — увеличивается или уменьшается и как быстро?
1) 8 т 500 кг – 5 т = 3 т 500 кг – уменьшается количество воды за 7 минут
2) 3 500 : 7 = 500 (кг) – в минуту уменьшается количество воды в трюме
Ответ: на 500 кг. 152
-
Ответы к странице 152
9. Масса Танечки составляет сотую часть тонны. Её брат Ванечка на одну тысячную тонны легче. Какова масса Ванечки?
1 т = 1 000 кг
1) 1 000 : 100 = 10 (кг) – масса Танечки
2) 1 000 : 1 000 = 1 (кг) – Ванечка легче Танечки
3) 10 – 1 = 9 (кг) – масса Ванечки
Ответ: 9 кг.10. Найдите значения выражений.
(484 260 – 1 020 · 34) : (133 350 : 105) =
22 680 : 54 : (12 873 – 112 · 114) =
3 640 : 28 · 2 + 8 · 2 010 =
(26 908 : 124 + 74 370 : 74) · 20 =
Решение:
2 1 4 3
(484 260 – 1 020 · 34) : (133 350 : 105) = 354
1) 1 020 · 34 = 34 680
* 1020
34
+408
306
34680
2) 484 260 - 34 680 = 449 580
3) 133350 : 105 = 1 270
-133350|105
105 |1270
-283
210
-735
735
0
4) 449 580 : 1 270 = 354
-449580|1270
3810 |354
-6858
6350
-5080
5080
0
3 4 2 1
22 680 : 54 : (12 873 – 112 · 114) = 4
1) 112 · 114 = 12 768
2) 12 873 - 12 768 = 105
3) 22 680 : 54 = 420
-22680|54
216 |420
-102
102
0
4) 420 : 105 = 4
1 2 4 3
3 640 : 28 · 2 + 8 · 2 010 = 16 340
1) 3 640 : 28 = 130
-3640|28
28 |130
-84
84
0
2) 130 * 2 = 260
3) 8 * 2 010 = 16 080
4) 260 + 16 080 = 16 340
1 3 2 4
(26 908 : 124 + 74 370 : 74) · 20 = 24 440
1) 26 908 : 124 = 217
-26908|124
248 |217
-210
124
-868
868
0
2) 74 370 : 74 = 1 005
-74370|74
74 |1005
-370
370
0
3) 217 + 1 005 = 1 222
4) 1 222 * 20 = 24 44011. Вычислите устно.
1) Частное чисел 8 000 и 20 уменьшите в 4 раза.
2) Разность чисел 9 500 и 2 500 разделите на 7.
3) Частное чисел 1 400 и 700 разделите на 2.
4) Сумму чисел 12 000 и 15 000 уменьшите в 1 000 раз.Решение:
1) Частное чисел 8 000 и 20 уменьшите в 4 раза.
(8 000 : 20) : 4 = 400 : 4 = 100
2) Разность чисел 9 500 и 2 500 разделите на 7.
(9500 - 2500) : 7 = 7000 : 7 = 1 000
3) Частное чисел 1 400 и 700 разделите на 2.
(1 400 : 700) : 2 = 2 : 2 = 1
4) Сумму чисел 12 000 и 15 000 уменьшите в 1 000 раз.
(12 000 + 15 000) : 1000 = 17 000 : 1 000 = 1712. Верно ли высказывание? Поясните свой ответ на примерах.
1) Среди равнобедренных треугольников есть равносторонние.
2) Существуют углы, которые больше прямого угла.
3) Из двух чисел одно всегда больше или меньше другого.
4) Не существует равнобедренных прямоугольных треугольников.Решение:
1) Среди равнобедренных треугольников есть равносторонние.
2) Существуют углы, которые больше прямого угла.
3) Из двух чисел одно всегда больше или меньше другого.
4) Не существует равнобедренных прямоугольных треугольников.13. Вычислите неизвестное число.
381 · x = 1 524 1 010 – y = 304
x : 88 = 102 629 + y = 1 258Решение:
381 · x = 1 524
x = 1 524 : 381
x = 4
1 010 – y = 304
y = 1 010 - 304
y = 706
x : 88 = 102
x = 102 * 88
x = 8 976
629 + y = 1 258
y = 1258 - 629
y = 629 153
-
Ответы к странице 153
14. Рассмотрите схему движения двух поездов, которые одновременно отправились из городов А и В и были в пути 6 часов. Составьте задачу и ответьте на вопросы. Как узнать:
1) на сколько километров за 6 ч удалится от пункта A поезд, который шёл со скоростью 50 км/ч;
2) на сколько километров за 6 ч удалится от пункта B поезд, который шёл со скоростью 60 км/ч;
3) какое расстояние будет между поездами через 6 ч после начала движения? Проверьте, правильно ли составлено выражение 50 · 6 + 60 · 6 + 175 для ответа на последний вопрос.
Решение:
Задача: Одновременно из двух городов А и В расположенных на расстоянии 175 км отправились два поезда в разные стороны, со скоростью 50 км/ч и 60 км/ч. Сколько км будет между ними через 6 часов.1) на сколько километров за 6 ч удалится от пункта A поезд, который шёл со скоростью 50 км/ч; 50 * 6 = 300 км
2) на сколько километров за 6 ч удалится от пункта B поезд, который шёл со скоростью 60 км/ч; 60 * 60 = 360 км
3) какое расстояние будет между поездами через 6 ч после начала движения? Проверьте, правильно ли составлено выражение 50 · 6 + 60 · 6 + 175 для ответа на последний вопрос.
Да, верно!
Прочитайте другой план решения задачи и, пользуясь этим планом, выполните вычисления.
1) На сколько километров удалятся поезда друг от друга за 1 ч?
2) На сколько километров удалятся поезда друг от друга за 6 ч?
3) Какое расстояние будет между поездами через 6 ч? Проверьте, правильно ли по этому плану составлено выражение (50 + 60) · 6 + 175.Решение:
1) На сколько километров удалятся поезда друг от друга за 1 ч? 50 + 60 = 110 км
2) На сколько километров удалятся поезда друг от друга за 6 ч? (50 +60) * 6 = 110 * 6 = 660 км
3) Какое расстояние будет между поездами через 6 ч? Проверьте, правильно ли по этому плану составлено выражение (50 + 60) · 6 + 175.
Да, верно! 154
-
Ответы к странице 154
15. Длина ленты 8 дм 6 см 3 мм. Саша измерил длину этой ленты с точностью до сантиметра, а Лена измерила длину этой же ленты с точностью до дециметра. У Саши получилось 8 дм 6 см, а у Лены — 9 дм. Кто из них точнее выполнил измерение? На сколько ошибся каждый?
Решение:
Саша выполнил измерения точнее. Саша ошибся на 3 мм, а Лена на 3 см 7 мм.16. От автовокзала в аэропорт отправился автобус со скоростью 64 км/ч. Через 30 мин до аэропорта ему осталось проехать 28 км. Сколько времени необходимо автобусу на обратный путь от аэропорта до автовокзала, если он уменьшит скорость на 4 км/ч?
30 мин – это половина часа
1) 64 : 2 = 32 (км) – проехал автобус за полчаса
2) 32 + 28 = 60 (км) – расстояние от аэропорта до автовокзала
3) 64 – 4 = 60 (км/ч) – скорость автобуса на обратном пути
4) 60 : 60 = 1 (ч) – потребуется автобусу на обратный путь
Ответ: 1 час.17. Мама подарила Маше копилку. В первый день Маша бросила туда 1 копейку. Каждый день она удваивала сумму денег в копилке. Сколько денег положила Маша в копилку на пятнадцатый день?
Решение:
Решение задачи:
1. Узнаем сколько денег положила Маша в копилку на пятнадцатый день.
1-й день - 1 копеек.
2-й день - 2 копеек.
3-й день - 4 копеек.
4-й день - 8 копеек.
5-й день - 16 копеек.
6-й день - 32 копейки.
7-й день - 64 копейки.
8-й день - 128 копеек.
9-й день - 256 копеек.
10-й день - 512 копеек.
11-й день - 1024 копейки.
12-й день - 2048 копеек.
13-й день - 4096 копеек.
14-й день - 8192 копейки
15-й день - 16384 копейки.
Ответ: Маша на пятнадцатый день положила в копилку сто шестьдесят три рубля и восемьдесят четыре копейки.18. Выполните действия.
(3 060 : 15 – 5) · (3 750 – 1 750 · 2) =
16 218 : 9 + 169 680 : 56 + 56 · (275 – 175) =
65 065 : 65 – 40 815 : (1 000 – 93) · 10 =
74 200 : (37 + 63) – 742 · 5 : 371 =Проверьте свои вычисления с помощью калькулятора.
Решение:
1 2 5 4 3
(3 060 : 15 – 5) · (3 750 – 1 750 · 2) = 49 750
1) 3 060 : 15 = 204
2) 204 - 5 = 199
3) 1750 * 2 = 3500
4) 3750 - 3500 = 250
5) 199 * 250 = 49 750
2 5 3 6 4 1
16 218 : 9 + 169 680 : 56 + 56 · (275 – 175) = 10 432
1) 275 - 175 = 100
2) 16 218 : 9 = 1 802
-16218|9
9 |1802
-72
72
-18
18
0
3) 169 680 : 56 = 3 030
-169680|56
168 |3030
-168
168
0
4) 56 * 100 = 5 600
5) 1 802 + 3 030 = 4 832
6) 4 832 + 5 600 = 10 432
1 5 3 2 4
65 065 : 65 – 40 815 : (1 000 – 93) · 10 = 551
1) 65 065 : 65 = 1 001
2) 1 000 – 93 = 907
3) 40 815 : 907 = 45
-40815|907
3628 |45
-4535
4535
0
4) 45 * 10 = 450
5) 1 001 - 450 = 551
2 1 5 3 4
74 200 : (37 + 63) – 742 · 5 : 371 = 732
1) 37 + 63 = 100
2) 74 200 : 100 = 742
3) 742 * 5 = 3710
4) 3710 : 371 = 10
5) 742 - 10 = 732
155
-
Ответы к странице 155
19*. Смешали 100 г цейлонского чая стоимостью 68 р. и 100 г индийского чая стоимостью 90 р. Какова стоимость 50 г смеси?
1) 28 + 30 = 58 (р.) – стоят 200 г смеси
58 р. = 5 800 коп.
2) 5 800 : 200 * 50 = 29 * 50 = 1450 (коп.) – стоят 50 г смеси
1450 коп. = 14 р. 50 коп.
Ответ: 14 р. 50 коп.20*. На столе стоят 6 стаканов, в которые налиты молоко и кефир, — по три стакана каждого напитка. Оля, Таня и Петя взяли по одному стакану. Составьте таблицу вариантов выбора напитков каждым из детей.
Решение:
Оля Таня Миша
Кефир Кефир Кефир
Кефир Кефир Молоко
Кефир Молоко Кефир
Кефир Молоко Молоко
Молоко Кефир Кефир
Молоко Молоко Кефир
Молоко Кефир Молоко
Молоко Молоко Молоко21*. Катер плывёт по течению реки со скоростью 24 км/ч. Скорость течения 2 км/ч. С какой скоростью катер будет плыть на обратном пути?
1) 24 – 2 = 22 (км/ч) – собственная скорость катера
2) 22 – 2 = 20 (км/ч) – скорость катера на обратном пути
Ответ: 20 км/ч.22. Постройте данный квадрат в масштабе 1 : 2.
Решение:
Квадрат со сторонами 9 клеток на 9 клеток. В масштабе 1 : 2 это будет 4,5 клетки на 4,5 клетки. Строим такой квадрат.23. Из одного города в другой одновременно по одной и той же дороге выехали машины «Волга» и «Газель». Через 4 ч «Газель» оказалась впереди «Волги» на 40 км. «Волга» ехала со скоростью 50 км/ч. С какой скоростью ехала «Газель»?
1) 40 : 4 = 10 (км/ч) – скорость «Газели» больше скорости «Волги»
2) 50 + 10 = 60 (км/ч) – скорость «Газели»
Ответ: 60 км/ч. 156
-
Ответы к странице 156
24*. На весы положили три одинаковые по массе дыни. Если одну из дынь снять и вместо неё положить арбуз, масса которого вдвое больше массы дыни, то весы покажут 16 кг. Какова масса одной дыни?
16 : 4 = 4 (кг) – масса одной дыни
Ответ: 4 кг.25. Петя прочитал в энциклопедии, что самое глубокое и большое озеро в мире Байкал достигает в длину 636 км, а в ширину 79 км. Найдя площадь озера умножением 636 на 79, он получил 50 244 км2. Петя удивился, что в энциклопедии указано другое число: 31 700 км2. В чём ошибка Пети?
Решение:
В том, что Петя посчитал озеро как правильную фигуру, - прямоугольник. На самом деле озеро имеет сложную форму с изогнутыми берегами, а это значит, что площадь считается тоже с учетом этих форм.6. Из 250 г мясного фарша выходит 4 одинаковые по массе котлеты. К обеду приготовили 12 котлет. Сколько фарша потребовалось? Решите задачу разными способами.
Решение:
способ 1
1) 12 : 4 = 3 (р.) больше надо фарша для 12 котлет, чем для 4
2) 250 * 3 = 750 (г) фарша надо.
Ответ: 750 г.
способ 2
1) 250 : 4 = 62,5 (г) фарша идет на одну котлету.
2) 62,5 * 12 = 750 (г) фарша надо.
Ответ: 750 г. 157
-
Ответы к странице 157
27. Велосипедист должен проехать 90 км. Он ехал 3 ч со скоростью р км/ч. Сколько километров ему осталось проехать? Составьте выражение и решите задачу, если p = 17 км/ч.
Решение:
90 - 3 * p
90 - 3 * 17 = 90 - 51 = 39 (км) осталось проехать.
Ответ: 39 км осталось проехать.28. Вычислите неизвестное число.
m : 8 = 134 924 c : 306 = 409
b : 29 = 1 060 k : 108 = 706Решение:
m : 8 = 134 924
m = 134 924 * 8
m = 1 079 392
c : 306 = 409
c = 409 * 306
c = 125 154
b : 29 = 1 060
b = 1 060 * 29
b = 30 740
k : 108 = 706
k = 706 * 108
k = 76 24829*. Выразите в метрах в минуту: 90 км/ч, 960 км/ч, 18 км/ч, 120 км/ч.
Решение:
90 км/ч = 90 * 1000 : 60 = 90 000 : 60 = 1 500 м/мин
960 км/ч = 960 * 1000 : 60 = 960 000 : 60 = 16 000 м/мин
18 км/ч = 18 * 1000 : 60 = 300 м/мин
120 км/ч = 120 * 1000 : 60 = 2 000 м/мин30. Вычислите неизвестное число.
x + 4 078 = 12 106
a – 9 999 = 101 010
c · 6 = 3 864
y : 9 = 81 810
91 356 + x = 100 000
60 015 – a = 4 326
15 · c = 153 075
10 800 : y = 40
Решение:
x + 4 078 = 12 106
x = 12 106 - 4 078
х = 8 028
a – 9 999 = 101 010
а = 101 010 + 9 999
а = 111 009
c · 6 = 3 864
с = 3 864 : 6
с = 644
y : 9 = 81 810
у = 81 810 * 9
у = 736 290
91 356 + x = 100 000
х = 100 000 - 91 356
х = 8 644
60 015 – a = 4 326
а = 60 015 - 4 326
а = 55 689
15 · c = 153 075
с = 153 075 : 15
с = 10 205
10 800 : y = 40
y = 10 800 : 40
y = 27031*. Килограмм абрикосов стоит 130 р. Какова стоимость 100 г, 500 г, 650 г абрикосов?
1 кг = 1 000 г
1) 130 : (1 000 : 100) = 130 : 10 = 13 (р.) – стоят 100 г абрикосов
2) 13 * (500 : 100) = 13 * 5 = 65 (р.) – стоят 500 г абрикосов
13 р. = 1 300 к.
3) 1 300 : 2 = 650 (к.) – стоят 50 г абрикосов
650 (к.) = 6 р. 50 к.
4) 650 г = 500 г + 100 г + 50 г
5) 65 р. + 13 р. + 6 р. 50 к. = 84 р. 50 к. – стоят 650 г абрикосов
Ответ: 13 р., 65 р., 84 р. 50 к.32. Расстояние от дома до школы, в которой учится Серёжа, равно 200 м. Изобразите это расстояние отрезком в масштабе 1 : 4 000.
Решение:
20 000 : 4 000 = 5 (см) длина отрезка.
Ответ: 5 см длина отрезка на плане.33. Для каждого из данных значений величины укажите его ближайшее приближённое значение.
8 кг 30 г ≈ кг 3 км 875 м ≈ км 9 ч 59 мин ≈ ч 16 м2 9 см2 ≈ м2
Решение:
8 кг 30 г ≈ 8 кг
3 км 875 м ≈ 4 км
9 ч 59 мин ≈ 10 ч
16 м2 9 см2 ≈ 16 м2


