Свойства изображения в плоском зеркале:
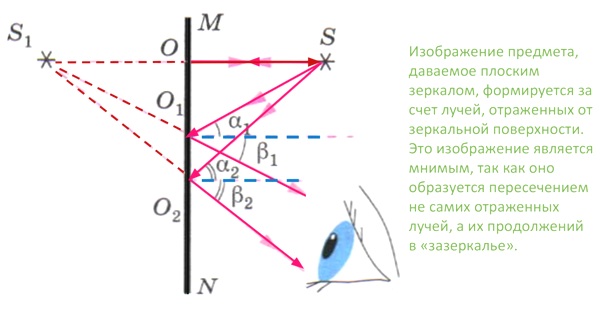
Изображение мнимое (лучи не сходятся за зеркалом, видны их продолжения).
Изображение симметрично объекту относительно плоскости зеркала.
Размер изображения равен размеру объекта.
Изображение прямое (не перевёрнутое).

Законы отражения:
Первый закон: Падающий луч, отражённый луч и нормаль к поверхности лежат в одной плоскости.
Второй закон: Угол падения равен углу отражения:

α=β

где α— угол между падающим лучом и нормалью, β — угол между отражённым лучом и нормалью.

Построение изображения:

Для точки: Проведите перпендикуляр от объекта к зеркалу и продлите его на такое же расстояние за зеркало.

Для протяжённого объекта (например, стрелки): Постройте изображение каждой точки и соедините их (рис. 1).

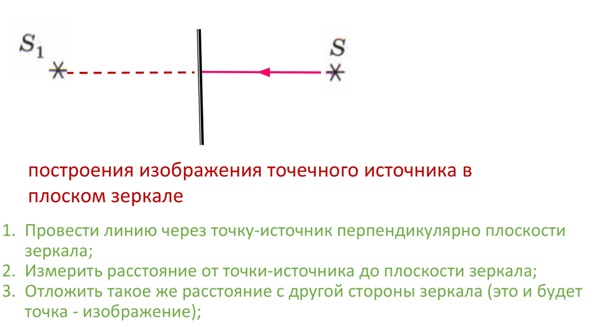
Рис. 1. Построение изображения объекта в плоском зеркале.

Формула расстояния:
Если объект находится на расстоянии d от зеркала, то изображение расположено на расстоянии d′=d за зеркалом:

d′=d

В системе отсчёта с положительным направлением в сторону зеркала: d′=−d (знак «минус» указывает на мнимое изображение).

Примеры задач:

Задача 1: Объект находится в 3 м от зеркала. На каком расстоянии от зеркала видно изображение?
Ответ: 3 м за зеркалом.

Задача 2: Какой минимальной высоты должно быть зеркало, чтобы человек ростом H увидел себя целиком?
Решение: Достаточно половины роста: h_зерк​=2H​.
Обоснование: Верхний край зеркала должен находиться на уровне между глазами и макушкой, нижний — между глазами и ступнями (рис. выше, где глаз под углом может смотреть условно в объем зеркала).

Особенности восприятия:

В зеркале происходит зеркальное отражение (лево и право меняются местами). Например, надпись «Привет» в зеркале будет выглядеть как «тевирП».

Вывод: Для решения задач ЕГЭ важно помнить симметрию, мнимость изображения, равенство углов падения и отражения, а также формулу расстояния d′=d. Тренируйтесь на задачах с построением лучей и расчётами!