Не буду вам рассказывать про всевозможные формулы, про то, как исключительно математическими средствами определят производную функцию, как из производной получить саму функцию… Такой нудной но весьма прагматичной информации вполне хватает на просторах интернета. Мне хотелось бы поговорить о применяемости этой самой производной, а ее смысле в нашей жизни, что собственно заодно кому-то «откроет глаза» что же все-таки такое производная и нафиг она собственно нужна!
Так вот если прям сразу и по теме, то если скорость чего-либо или кого-либо взять за условную функцию, то производная будет ускорением этого чего-то или кого-то. То есть производная отражает динамику изменения нашей функции. При этом динамика может быть как отрицательной, так и положительной и это естественно, ибо ничего в нашем мире нет постоянного.
Еще один пример можно привести и для финансовой системы, - где, скажем, функция это увеличение вклада на наших счетах при изменяющейся ставке от месяца к месяцу, когда банк ее меняет, а производная будет тем самым изменением, на которое меняется наш вклад за условные период времени относительно предыдущего значения. То есть опять же показатель изменения качества прибыли с наших средств в банке.

После подобных заявлений хотелось бы также немного охарактеризовать их визуально, ибо пословица о том, что лучше увидеть, чем быть наслышанным весьма актуальна и право зачастую оправдывает себя.

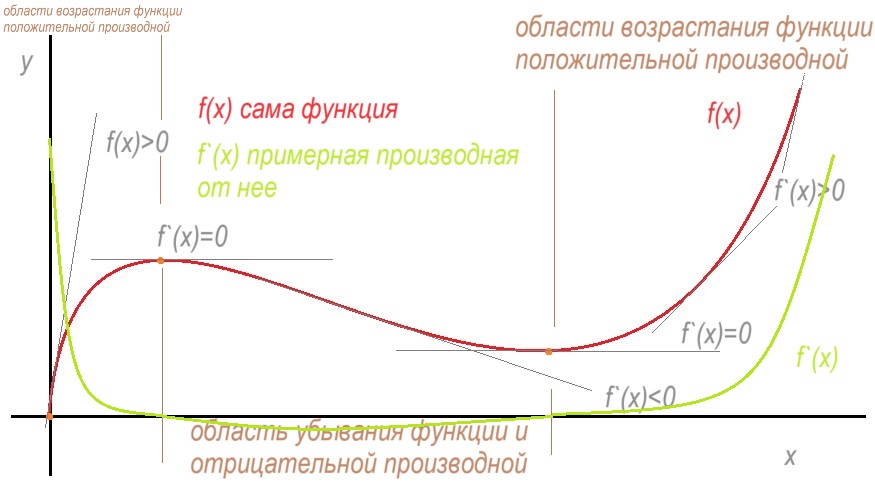
Итак смотрите, есть условная функция, не знаю какая у нее формула, так как начертил просто от руки, но она красная… У нее есть области: вначале роста, потом выход на точку максимума, такие точки называются вернее точками экстремума, так как максимум может быть условный, поскольку он не самый максимальный среди всех. Далее убывание и очередная точка экстремум в виде минимума, а дальше снова рост.
Так вот производная характеризуется серыми касательными к этой красной функции. И самое главное для производной не то насколько она высоко находится над осью x, сколько максимально большой угол между этой касательной и осью x, то есть стремление этой самой касательной вверх. Само собой, чем больше угол, тем более явное стремление, тем выше динамика, о которой я уже упоминал выше…
Что насчет функции производной, которая зеленая, то смотрите, вначале ее показатели были очень высокие так как касательные были как раз с большим углом относительно x, потом они начали снижаться, до тех пор, пока функция не пришла на экстремум максимума. И именно там произошел переломный момент для производной, она перестала расти, стала равна нулю в какой-то момент, так как касательная стала параллельна оси x, а далее угол стал уже условно отрицательным, так как касательная стала наклоняться в другую сторону. При этом и производная в таком случае считается отрицательной и тем более отрицательной, чем угол опять же будет более значимым. В итоге получаем отрицательные значения для функции производной (зеленой) в области, где наша исследуемая функция (красная) просто теряет динамику роста, то есть убывает.
Ну и опять же схожая ситуация, когда убывание функции (красной) заканчивается, то находится точка экстремума минимум, где производная функции (зеленая) равна нулю, а далее идет рост самой функции (красной), а вот производная выходит из отрицательных областей. (зеленая)

Какие выводы мы с вами сделаем?

Любое убывание функции автоматически выдает отрицательные значения для производной функции. Или наоборот, отрицательные значения производной говорят о том, что функция убывает.

Любое возрастание функции автоматически выдает положительные значения для производной функции. Или наоборот, положительные значения производной говорят о том, что функция растет.

Высокие показатели функции совсем не являются тождественными, что производная также имеет высокие значения. Ибо деньги без начисления процентов в банке, даже если их много, не прибывают, а динамика (прирост) и есть производная.

Пиковые значения функции, будь то минимум или максимум с дальнейшим изменением тенденции, то есть убывает, потом растет или растет, потом убывает, - меняют значения производной от минуса к плюсу или наоборот, так как в пиковых точках функции сама производная равна 0, а динамика нашего процесса меняется на противоположную.

Заключение

Все то, что я вам рассказал, имело своей целью не научить вас вычислять производную от функции или находить функцию от производной, а именно донести до вас понятия, какие алгоритмы и процессы затронуты в метафизических связях самой функции и её производной. Ведь нет никакого интереса ковыряться с бессмысленными вещами, а прагматичность наоборот наполняет нашу активность смыслом!