Как в свое время говорили, что кукуруза царица полей, так можно сказать и о математике, что математика, - это царица наук! Отчасти это утверждение справедливо, ведь даже в русском языке есть отдельная тема по числительным, которые надо писать логично, правильно, представляя прежде всего образ цифр...
 Ну мы не будем о практичности математики, ведь это на наш взгляд не требует какого-либо доказательства, мы поговорим о конкретном учебном издании, о задачнике. Задачник это книга с дополнительными упражнениями, задачами по предмету. Так вот в нашем случае это задачник с оранжевой обложкой, за 5 класс, автора Бунимович. И именно к нему мы и представим вам готовые ответы, как еще говорят школьники ГДЗ!  

 Сами ответы мы вам рекомендуем использовать как материал для сверки, когда вы все уже сделали сами.

ГДЗ ответы к задачнику по математике 5 класс Бунимович

Теперь выбираем нужную вам вкладку, которая соответствует номеру задачи, кликаем по ней и смотрим ответы.

  Как в свое время говорили, что кукуруза царица полей, так можно сказать и о математике, что математика, - это царица наук! Отчасти это утверждение справедливо, ведь даже в русском языке есть отдельная тема по числительным, которые надо писать логично, правильно, представляя прежде всего образ цифр...
 Ну мы не будем о практичности математики, ведь это на наш взгляд не требует какого-либо доказательства, мы поговорим о конкретном учебном издании, о задачнике. Задачник это книга с дополнительными упражнениями, задачами по предмету. Так вот в нашем случае это задачник с оранжевой обложкой, за 5 класс, автора Бунимович. И именно к нему мы и представим вам готовые ответы, как еще говорят школьники ГДЗ!  

 Сами ответы мы вам рекомендуем использовать как материал для сверки, когда вы все уже сделали сами.

ГДЗ ответы к задачнику по математике 5 класс Бунимович

Теперь выбираем нужную вам вкладку, которая соответствует номеру задачи, кликаем по ней и смотрим ответы.

 

Стр. 4

ГДЗ к части № 1. ЗАДАЧИ И УПРАЖНЕНИЯ

Натуральные числа

Ответы к теме Сравнение натуральных чисел

1. Сравните числа и запишите результат сравнения с помощью знака > или <:></:>

Решение

а) 564 < 654

б) 9561 < 9600

в) 11860 > 1869

г) 996 < 1096

д) 80990 > 8990

е) 36999 < 37000

ж) 1001001 > 1000101

з) 3000508 < 3001000

2. Сравните числа:
а) 1 млн и 10000000;
б) 1 млн 100 тыс. и 1010000;
в) 1 млрд и 1000000001;
г) 1 млрд 10 млн 100 тыс. и 1010110000.

Решение

а) 1 млн < 10000000

б) 1 млн 100 тыс. > 1010000

в) 1 млрд < 1000000001

г) 1 млрд 10 млн 100 тыс. < 1010110000

3. Расположите числа в порядке возрастания и запишите результат в виде двойного неравенства:
а) 699, 659 и 698;
б) 9019, 9190 и 9109;
в) 10010, 9999 и 10009.

Решение

а) 659 < 698 < 699

б) 9019 < 9109 < 9190

в) 9999 < 10009 < 10010

4. Сравните длины:
а) 975 см и 10 м;
б) 8929 м и 8 км;
в) 50 м и 4345 см;
г) 1000 мм и 10 см;
д) 3 м 4 дм и 35 дм;
е) 8 дм 6 см и 80 см.

Решение

а) 975 см < 10 м
975 см < (10 * 100) см
975 см < 1000 см

б) 8929 м > 8 км
8929 м > (8 * 1000) м
8929 м > 8000 м

в) 50 м > 4345 см
(50 * 100) см > 4345 см
5000 см > 4345 см

г) 1000 мм > 10 см
1000 мм > (10 * 10) мм
1000 мм > 100 мм

д) 3 м 4 дм < 35 дм
(3 * 10 + 4) дм < 35 дм
34 дм < 35 дм

е) 8 дм 6 см > 80 см
(8 * 10 + 6) см > 80 см
86 см > 80 см

5. Сравните массы:
а) 15 т и 15305 кг;
б) 495 кг и 5 ц;
в) 920 г и 1 кг;
г) 29000 кг и 30 т;
д) 1 кг 75 г и 1750 г;
е) 1700 г и 1 кг 700 г.

Решение

а) 15 т < 15305 кг
(15 * 1000) кг < 15305 кг
15000 кг < 15305 кг

б) 495 кг < 5 ц
495 кг < (5 * 100) кг
495 кг < 500 кг

в) 920 г < 1 кг
920 г < (1 * 1000) г
920 г < 1000 г

г) 29000 кг < 30 т
29000 кг < (30 * 1000) кг
29000 кг < 30000 кг

д) 1 кг 75 г < 1750 г
(1 * 1000 + 75) г < 1750 г
1075 г < 1750 г

е) 1700 г = 1 кг 700 г
1700 г = (1 * 1000 + 700) г
1700 г = 1700 г

6. Сравните промежутки времени:
а) 1 ч 3 мин и 63 мин;
б) 2 ч 15 мин и 215 мин;
в) 2 ч и 180 мин;
г) 300 мин и 5 ч;
д) 2 мин 15 с и 125 с;
е) 1 ч 30 мин 30 с и 90 мин 45 с.

Решение

а) 1 ч 3 мин = 63 мин
(1 * 60 + 3) мин = 63 мин
63 мин = 63 мин

б) 2 ч 15 мин < 215 мин
(2 * 60 + 15) мин < 215 мин
120 + 15 мин < 215 мин
135 мин < 215 мин

в) 2 ч < 180 мин
(2 * 60) мин < 180 мин
120 мин < 180 мин

г) 300 мин = 5 ч
300 мин = (5 * 60) мин
300 мин = 300 мин

д) 2 мин 15 с > 125 с
(2 * 60 + 15) с > 125 с
(120 + 15) с > 125 с
135 с > 125 с

е) 1 ч 30 мин 30 с < 90 мин 45 с
(60 + 30) мин + 30 с < 90 мин 45 с
90 мин + 30 с < 90 мин 45 с

7. Какие числа можно подставить вместо буквы x в данное неравенство, чтобы получилось верное числовое неравенство:
а) 45 < x < 52;
б) 991 < x < 1002?

Решение

а) 45 < x < 52
x = 46, 47, 48, 49, 50, 51.

б) 991 < x < 1002
x = 992, 993, 994, 995, 996, 997, 998, 999, 1000, 1001.

8. Даны числа 0, 12, 25, 28, 35, 36, 40. Какие из них можно подставить вместо буквы a в неравенство 30 < a + 5 < 45, чтобы получить верное числовое неравенство?
Назовите еще какое−нибудь число, при подстановке которого в данное неравенство получается верное числовое неравенство.

Решение

0 + 5 = 5;
12 + 5 = 17;
25 + 5 = 30;
28 + 5 = 33;
35 + 5 = 40;
36 + 5 = 41;
40 + 5 = 45.
30 < a + 5 < 45
a = 28, 35, 36.
Неравенство будет верно и при a = 29.

9. Перечислите все цифры, которые можно записать вместо звездочки, чтобы получившееся неравенство было верным:
а) 7*38 > 7238;
б) 96*4 > 9614;
в) 1596 > 159*;
г) 2438 < 2*38;
д) 478* > 4783;
е) 1686 < 1*86.

Решение

а) 7*38 > 7238;
7338 > 7238;
7438 > 7238;
7538 > 7238;
7638 > 7238;
7738 > 7238;
7838 > 7238;
7938 > 7238.
Ответ: 3, 4, 5, 6, 7, 8, 9.

б) 96*4 < 9614;
9604 < 9614.
Ответ: 0

в) 1596 > 159*;
1596 > 1590;
1596 > 1591;
1596 > 1592;
1596 > 1593;
1596 > 1594;
1596 > 1595.
Ответ: 0, 1, 2, 3, 4, 5.

г) 2438 < 2*38;
2438 < 2538;
2438 < 2638;
2438 < 2738;
2438 < 2838;
2438 < 2938.
Ответ: 5, 6, 7, 8, 9.

д) 478* > 4783;
4784 > 4783;
4785 > 4783;
4786 > 4783;
4787 > 4783;
4788 > 4783;
4789 > 4783.
Ответ: 4, 5, 6, 7, 8, 9.

е) 1686 < 1*86;
1686 < 1786;
1686 < 1886;
1686 < 1986.
Ответ: 7, 8, 9.

10. а) Расположите в порядке возрастания числа
32100, 32010, 32001, 3210, 2310, 3120.
б) Расположите в порядке убывания числа
37861, 820012, 23045, 23545, 82100, 37880.

Решение

а) 3120 < 3210 < 3310 < 32001 < 32010 < 32100

б) 820012 > 82100 > 37880 > 37861 > 23545 > 23045

5

11. Символом abc (с чертой наверху) обозначают трехзначное число, в котором a сотен, b десятков и c единиц. Расположите в порядке возрастания следующие числа:
____
abc0;
______
abc000;
___
abc;
_____
abc00.

Решение

___   ____     _____    ______
abc < abc0 < abc00 < abc000

12. Запишите:
а) наименьшее четное 10−значное число, в котором все цифры различны;
б) наибольшее нечетное 10−значное число, в котором все цифры различны.

Решение

а) 1023456798

б) 9876543201

13. Слова располагают в словарях в алфавитном порядке по следующему правилу:
если два слова начинаются с разных букв, то сначала пишут слово, первая буква которого идет в алфавите раньше;
если два слова начинаются с одной буквы, то сравнивают вторые буквы и сначала записывают то слово, в котором вторая буква идет в алфавите раньше;
если совпадают вторые буквы, то сравнивают третьи буквы и т.д.
1) Расположите в словарном порядке слова: отрезок, луч, колокол, ломаная, линия, квадрат, куб, прямая, конус.
2) Придумайте правило сравнения чисел с одинаковым количество цифр, похожее на правило расположения слов в словарях. Пользуясь этим правилом, расположите в порядке возрастания числа, каждое из которых содержит 8 цифр:
87650199;
90121911;
89999009;
89977747;
82946575;
90497816.
3) Можно ли упорядочить любые натуральные числа, поступая так же, как при расположении слов в словарях?

Решение

1) Квадрат, колокол, конус, куб, линия, ломаная, луч, отрезок, прямая.

2) Если 2 числа начинаются с разных цифр, то смотрим, какая цифра идет раньше. Если 2 числа начинаются с одной цифры, то сравнивают вторые цифры и сначала пишут число, у которого вторая цифра расположена на координатном луче раньше, если совпадают и вторые цифры, то сравнивают третьи и так далее. Это правило работает только в том случае, если количество цифр в числах одинаковое.
82946575 < 87650199 < 89977747 < 89999009 < 90121911 < 90497816

3) Нет, нельзя, так как натуральные числа могут содержать разное количество цифр.

ГДЗ к теме Округление натуральных чисел

14. Округлите числа:
а) 57, 93, 216, 381, 725, 1046, 2798, 23564 до десятков;
б) 538, 763, 2882, 3129, 1880, 3966, 107352 до сотен;
в) 6756000, 25397750, 1035127, 13500102 до миллионов.

Решение

а) 57 ≈ 60;
93 ≈ 90;
216 ≈ 220;
381 ≈ 380;
725 ≈ 730;
1046 ≈ 1050;
2798 ≈ 2800;
23564 ≈ 23560.

б) 538 ≈ 500;
763 ≈ 800;
2882 ≈ 2900;
3129 ≈ 3100;
1880 ≈ 1900;
3966 ≈ 4000;
107352 ≈ 107400.

в) 6756000 ≈ 7000000;
25397750 ≈ 25000000;
1035127 ≈ 1000000;
13500102 ≈ 14000000.

15. округлите каждое из чисел до старшего разряда:
а) 48, 71, 85, 725, 462, 851;
б) 8127, 6721, 2078, 25509, 19265.

Решение

а) 48 ≈ 50;
71 ≈ 70;
85 ≈ 90;
725 ≈ 700;
462 ≈ 500;
851 ≈ 900.

б) 8127 ≈ 8000;
6721 ≈ 7000;
2078 ≈ 2000;
25509 ≈ 30000;
19265 ≈ 20000.

16. округлите каждое из чисел до указанного разряда и запишите результат, используя сокращения (тыс., млн):
а) до тысяч: 8356, 74750, 204831, 38682, 10923, 75500;
б) до миллионов: 12031786, 8750627, 1931278, 12510000.
Образец.
Округлим до миллионов число 32741120: 32741120 ≈ 33000000 = 33 млн.

Решение

а) 8356 ≈ 8000 = 8 тыс.;
74750 ≈ 75000 = 75 тыс.;
204831 ≈ 205000 = 205 тыс.;
38682 ≈ 39000 = 39 тыс.;
10923 ≈ 11000 = 11 тыс.;
75500 ≈ 76000 = 76 тыс.

б) 12031786 ≈ 12000000 = 12 млн.;
8750627 ≈ 9000000 = 9 млн.;
1931278 ≈ 2000000 = 2 млн.;
12510000 ≈ 13000000 = 13 млн.

17. а) Масса груза 4790 кг. Сколько это примерно тонн?
б) Бегемот весит 4150 кг. Сколько это примерно тонн?
в) Масса пирога 960 г. Сколько это примерно килограммов?
г) Масса десятка пирожных 1056 г. Сколько это примерно килограммов?
Образец.
Сколько примерно тонн составляют 2640 кг? Так как 1 т = 1000 кг, то округлим 2640 до тысяч: 2640 кг ≈ 3000 кг = 3 т.

Решение

а) Так как 1 т = 1000 кг, то округлим 4790 до тысяч:
4790 кг ≈ 5000 кг = 5 т − масса груза.

б) Так как 1 т = 1000 кг, то округлим 4150 до тысяч:
4150 кг ≈ 4000 кг = 4 т − весит бегемот.

в) Так как 1 кг = 1000 г, то округлим 960 до тысяч:
960 г ≈ 1000 г = 1 кг − масса пирога.

г) Так как 1 кг = 1000 г, то округлим 1056 до тысяч:
1056 г ≈ 1000 г = 1 кг − масса десятка пирожных.

6

18. а) Расстояние от дома до реки 2750 м. Сколько это примерно километров?
б) Высота горы 3260 м. Сколько это примерно километров?
в) Длина доски 935 мм. Сколько это примерно сантиметров? А сколько примерно метров?
г) Длина провода 1246 мм. Сколько это примерно сантиметров? А сколько примерно метров?
Образец.
1) Сколько примерно километров составляют 6240 м?
6240 м ≈ 6000 м = 6 км.
2) Сколько примерно сантиметров составляют 524 мм?
524 мм ≈ 520 мм = 52 см.

Решение

а) 2750 м ≈ 3000 м = 3 км

б) 3260 м ≈ 3000 м = 3 км

в) 935 мм ≈ 940 мм = 94 см;
935 мм ≈ 1000 мм = 1 м.

г) 1246 мм ≈ 1250 мм = 125 см;
1246 мм ≈ 1000 мм = 1 м.

19. Выразите приближенно данное расстояние сначала в метрах, а потом в километрах:
а) 98466 см;
б) 186734 см;
в) 3665453 см.
Образец.
736512 см ≈ 736500 см = 7365 м ≈ 7000 м = 7 км.

Решение

а) 98466 см ≈ 98500 см = 985 м ≈ 1000 м = 1 км

б) 186734 см ≈ 186700 см = 1867 м ≈ 2000 м = 2 км

в) 3665453 см ≈ 3665500 см = 36655 м ≈ 37000 м = 37 км

20. Запишите ряд чисел, который получится, если последовательно округлять число 28741568 до десятков, сотен, тысяч и т.д., вплоть до старшего разряда.

Решение

28741568 ≈ 28741570 ≈ 28741600 ≈ 28742000 ≈ 28740000 ≈ 28700000 ≈ 29000000 ≈ 30000000

21. Найдите наименьшее число и наибольшее число, при округлении которого:
а) до десятков получится 640;
б) до сотен получится 7300;
в) до тысяч получится 3000;
г) до десятков тысяч получится 20000.

Решение

а) 635 − наименьшее;
644 − наибольшее.

б) 7250 − наименьшее;
7349 − наибольшее.

в) 2500 − наименьшее;
3499 − наибольшее.

г) 15000 − наименьшее;
24999 − наибольшее.

Самостоятельная работа № 1

Вариант 1

1. Расположите в порядке возрастания числа:
62890;
10000;
62900;
8985.

Решение

8985 > 10000 > 62890 > 62900

2. Сравните промежутки времени:
а) 600 с и 6 мин;
б) 5 ч 25 мин и 325 мин.

Решение

а) 600 с > 6 мин
600 с > (6 * 60) с
600 с > 360 с

б) 5 ч 25 мин = 325 мин
(5 * 60 + 25) мин = 325 мин
(300 + 25) мин = 325 мин
325 мин = 325 мин

3. Округлите до десятков, до сотен, до десятков тысяч число:
а) 7146358;
б) 531984.

Решение

а) 7146358 ≈ 7146360;
7146358 ≈ 7146400;
7146358 ≈ 7150000.

б) 531984 ≈ 531980;
531984 ≈ 532000;
531984 ≈ 530000.

Вариант 2

1. Расположите в порядке возрастания числа:
90000;
73550;
6400;
72880.

Решение

6400 < 72800 < 73550 < 90000

2. Сравните промежутки времени:
а) 3 мин и 180 с;
б) 450 мин и 6 ч 20 мин.

Решение

а) 3 мин = 180 с
(3 * 60) с = 180 с
180 с = 180 с

б) 450 мин > 6 ч 20 мин
450 мин > (6 * 60 + 20) мин
450 мин > (360 + 20) мин
450 мин > 380 мин

3. Округлите до десятков, до сотен, до десятков тысяч число:
а) 35185274;
б) 396507.

Решение

а) 35185274 ≈ 35185270;
35185274 ≈ 35185300;
35185274 ≈ 35190000.

б) 396507 ≈ 396510;
396507 ≈ 396500;
396507 ≈ 400000.

ГДЗ к теме Решение комбинаторных задач

22. Представьте число 10 в виде суммы двух слагаемых всеми возможными способами (суммы, отличающиеся только порядком слагаемых, считайте одинаковыми).

Решение

10 = 0 + 10;
10 = 1 + 9;
10 = 2 + 8;
10 = 3 + 7;
10 = 4 + 6;
10 = 5 + 5.

23. Представьте указанное число в виде произведения двух множителей всеми возможными способами (произведения, отличающиеся только порядком множителей, считайте одинаковыми):
а) 12;
б) 24;
в) 36;
г) 100.

Решение

а) 12 = 1 * 12;
12 = 2 * 6;
12 = 3 * 4.

б) 24 = 1 * 24;
24 = 2 * 12;
24 = 3 * 8;
24 = 4 * 6.

в) 36 = 1 * 36;
36 = 2 * 18;
36 = 3 * 12;
36 = 4 * 9;
36 = 6 * 6.

г) 100 = 1 * 100;
100 = 2 * 50;
100 = 4 * 25;
100 = 5 * 20;
100 = 10 * 10.

24. Код на замке чемодана состоит из четырех цифр. Его хозяин решил набрать четыре идущие подряд цифры, расположив их по порядку от меньшей к большей. Сколько существует вариантов такого кода?

Решение

0123;
1234;
2345;
3456;
4567;
5678;
6789.
Ответ: 7 вариантов.

7

25. Две волейбольные команды "Ласточка" и "Орленок" играют матч до трех побед. С каким счетом может закончиться их поединок, если в волейбол ничьих не бывает? Занесите все возможные исходы поединка в таблицу:

Решение

Ласточка Орленок
   3               0
   3               1
   3               2
   0               3
   1               3
   2               3

26. Сколько можно составить различных букетов из трех роз, если в продаже белые и красные роза?
Подсказка.
Чтобы было удобнее перебирать варианты, введите обозначения:
Б − белая роза,
К − красная роза.

Решение

1) ККК;
2) БББ;
3) ККБ;
4) ББК.
Ответ: 4 варианта.

27. Решите задачу, построив дерево возможных вариантов:
а) В школьной столовой на завтрак предлагают сок или компот, а также пирожки с мясом, яблоками или картошкой. Сколько вариантов завтрака из пирожка и напитка предлагают столовая?
б) Сколько трехзначных чисел можно составить из цифр 4,6 и 8 при условии, что цифра в записи числа не должна повторяться?
в) Сколько трехзначных чисел можно составить из двух цифр 1 и 9?

Решение

а) Пусть:
K − компот;
С − сок;
Пм − пирожки с мясом;
Пя − пирожки с яблоками;
Пк − пирожки с картошкой.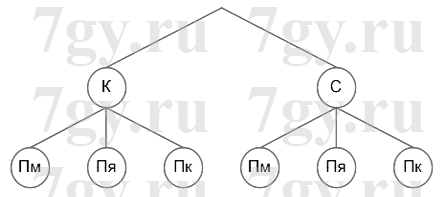

Ответ: 6 вариантов.

б)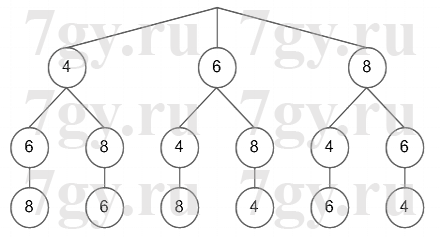 

Ответ: 6 чисел.

в)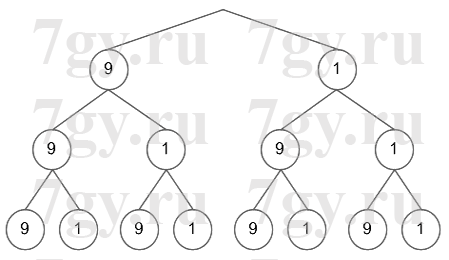

Ответ: 8 вариантов.

28. Сколько можно составить двузначных чисел:
а) если использовать только цифры 1, 4, 7;
б) если использовать только цифры 0, 4, 7;
в) если использовать только цифры 4, 7, 8, 9, причем не повторяя их в записи числа?
Указание.
Решите задачу двумя способами: с помощью построения дерева возможных вариантов и без использования дерева.

Решение

а) Способ 1.

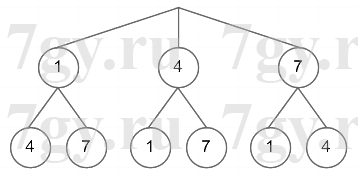
Способ 2.
14, 17, 47, 74, 71, 41.
Ответ: 6 чисел.

б) Способ 1.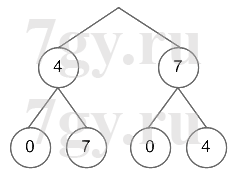

Способ 2.
40, 47, 74, 70.
Ответ: 4 числа.

в) Способ 1.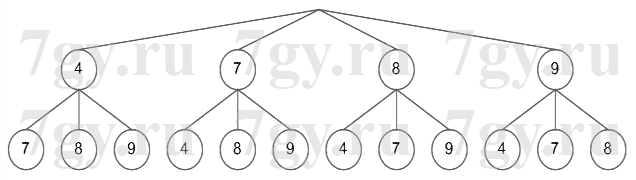

Способ 2.
47, 48, 49, 74, 78, 79, 84, 87, 89, 94, 97, 98.
Ответ: 12 чисел.

29. Сколько четных трехзначных чисел можно составить, используя только цифры 5 и 6?

Решение

556, 656, 666, 566.
Ответ: 4 числа.

30. Начертите горизонтальную прямую и отметьте на ней слева направо пять точек A, B, C, D и E. Сколько отрезков у вас получилось?

Решение

AB, AC, AD, AE, BC, BD, BE, CD, CE, DE.
Ответ: 10 отрезков.

31. Оля, Костя, Нина, Таня и Галя должны по очереди дежурить в классе, и им нужно составить расписание. Оля вызвалась дежурить первой, а Галя сказала, что будет дежурить последней. Сколько вариантов расписания при этих условиях они могут составить?

Решение

Пусть:
О − Оля;
К − Костя;
Н − Нина;
Т − Таня;
Г − Галя.
Тогда:
1) О, К, Н, Т, Г;
2) О, Н, Т, К, Г;
3) О, Т, К, Н, Г;
4) О, Т, Н, К, Г;
5) О, К, Н, Т, Г;
6) О, Н, К, Т, Г.
Ответ: 6 вариантов

32. Двенадцать ребят решили сыграть в футбол. Они разбились на две команды поровну и в каждой команде должны выбрать двух нападающих, трех защитников и вратаря. В одной из команд каждый из ребят хочет быть нападающим. Сколько вариантов выбора нападающих в этой команде?

Решение

Дадим номера от 1 до 6 членам команды, в которой каждый из ребят хочет быть нападающим, тогда возможны следующие варианты:
1,2; 1,3; 1,4; 1,5; 1,6;
2,3; 2,4; 2,5; 2,6;
3,4; 3,5; 3,6;
4,5; 4,6;
5,6.
Ответ: 15 вариантов.

33. Сколько четных чисел можно составить, если использовать только цифры 0, 1, 3, 5, причем каждую не более одного раза (т.е. один раз или ни разу)? Назовите самое большое из них.

Решение

5310;
5130;
3510;
1530;
1350;
510;
530;
350;
310;
150;
130;
50;
30;
10.
Самое большое число 5310.

8

Действия с натуральными числами
ГДЗ к теме Сложение и вычитание

34. Найдите сумму:
а) 4274 + 3226;
б) 9436 + 1468;
в) 3839 + 694;
г) 334 + 9679.

Решение

а) 4274 + 3226 = 7500

б) 9436 + 1468 = 10904

в) 3839 + 694 = 4533

г) 334 + 9679 = 10013

35. Найдите разность:
а) 3745 − 2743;
б) 4084 − 922;
в) 1648 − 678;
г) 5724 − 1656.

Решение

а) 3745 − 2743 = 1002

б) 4084 − 922 = 3162

в) 1648 − 678 = 970

г) 5724 − 1656 = 4068

36. Вычислите:
а) 1653 − 1345;
б) 9871 + 999;
в) 2823 + 269;
г) 2034 − 965.

Решение

а) 1653 − 1345 = 308

б) 9871 + 999 = 10870

в) 2823 + 269 = 3092

г) 2034 − 965 = 1069

37. Сложите числа:
а) 605 + 570 + 450 + 304 + 299;
б) 591 + 483 + 307 + 254 + 628.

Решение

а) 605 + 570 + 450 + 304 + 299 = 1175 + 450 + 304 + 299 = 1625 + 304 + 299 = 1929 + 299 = 2228

б) 591 + 483 + 307 + 254 + 628 = 1074 + 307 + 254 + 628 = 1381 + 254 + 628 = 1635 + 628 = 2263

38. Придумайте правило, по которому строится данная последовательность чисел, и восстановите три следующих и три предыдущих числа:
а) ...; 46; 55; 64; ...;
б) ...; 45; 40; 35; ... .

Решение

а) Закономерность: каждое последующее число на 9 больше предыдущего.
19; 28; 37; 46; 55; 64; 73; 82; 91.

б) Закономерность: каждое последующее число на 5 меньше предыдущего.
60; 55; 50; 45; 40; 35; 30; 25; 20.

39. Объясните, как найти неизвестное слагаемое. Найдите неизвестное слагаемое:
а) 648 + a = 1667;
б) x + 315 = 411;
в) 932 = a + 558.

Решение

Что найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

а) 648 + a = 1667
a = 1667 − 648
a = 1019

б) x + 315 = 411
a = 411 − 315
a = 96

в) 932 = a + 558
a = 932 − 558
a = 374

40. Объясните, как найти неизвестное уменьшаемое, вычитаемое. Найдите неизвестное уменьшаемое или вычитаемое:
а) 801 − a = 349;
б) x − 287 = 1006;
в) 460 − y = 287.
Решение правило
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.

Решение

а) 801 − a = 349
a = 801 − 349
a = 452

б) x − 287 = 1006
x = 1006 − 287
x = 719

в) 460 − y = 287
y = 460 − 287
y = 173

41. Найдите неизвестное число:
а) 348 + x = 816;
б) 327 − a = 125;
в) y − 107 = 904.

Решение

а) 348 + x = 816
x = 816 − 348
x = 468

б) 327 − a = 125
a = 327 − 125
a = 202

в) y − 107 = 904
y = 904 + 107
y = 1011

42. Используя округление, выполните прикидку результата, а затем выполните сложение:
а) 81 + 59;
б) 117 + 321;
в) 348 + 59;
г) 121 + 183.

Решение

а) 81 + 59 ≈ 80 + 60 = 140
81 + 59 = 140

б) 117 + 321 ≈ 120 + 320 = 440
117 + 321 = 438

в) 348 + 59 ≈ 350 + 60 = 410
348 + 59 = 407

г) 121 + 183 ≈ 120 + 180 = 300
121 + 183 = 304

43. Книгохранилище библиотеки занимает три комнаты. В одной комнате 8225 книг, в другой − 12918 книг, в третьей − 13673 книги. Сколько примерно тысяч книг находится в книгохранилище?
1) 10 тыс.;
2) 340 тыс.;
3) 33 тыс.;
4) 35 тыс.

Решение

8225 + 12918 + 13673 ≈ 8000 + 13000 + 14000 ≈ 21000 + 14000 = 35000 = 35 тыс.
Ответ: 4) 35 тыс.

44. Решите задачу, используя прикидку:
У покупателя имеется 1500 р. на покупку игрушек. Названия игрушек, продающихся в магазине, и их цены представлены в таблице:

Какие игрушки покупатель может купить, если они должны быть разными? Найдите несколько вариантов покупки.

Решение

Покупатель может купить:
1) машину, набор мебели для кукол;
2) куклу, настольную игру и набор мебели для кукол;
3) куклу, мяч, посуду для кухни и настольную игру;
4) набор мебели для кукол, посуду для кухни и настольную игру.

9

45. а) В начале пути спидометр автомобиля показывал 28639 км. Определите, каким будет показание спидометра через 834 км.
б) В начале пути спидометр автомобиля показывал 34863 км, а в конце − 35787 км. Какой путь проделал автомобиль?

Решение

а) 28639 + 834 = 29473 (км) − показание спидометра через 834 км.
Ответ: 29473 км

б) 35787 − 34863 = 924 (км) − путь, которой проделал автомобиль.
Ответ: 924 км

46. а) От Москвы до Новгорода по шоссе 520 км, а от Новгорода до Санкт−Петербурга на 310 км меньше. Сколько километров от Москвы до Санкт−Петербурга?
б) От Москвы до Ржева по железной дороге 220 км. В первый час поезд прошел 65 км, во второй − на 18 км больше. Сколько километров ему осталось пройти?

Решение

а) 1) 520 − 310 = 210 (км) − от Новгорода до Санкт−Петербурга;
2) 520 + 210 = 730 (км) − от Москвы до Санкт−Петербурга.
Ответ: 730 км

б) 1) 65 + 18 = 83 (км) − прошел поезд за второй час;
2) 65 + 83 = 148 (км) − прошел поезд за два часа;
3) 220 − 148 = 72 (км) − осталось пройти поезду.
Ответ: 72 км

47. Вычислите:
а) 22222 − 8888;
б) 59284 + 36917;
в) 44444 + 9999;
г) 20010 − 6517.

Решение

а) 22222 − 8888 = 13334

б) 59284 + 36917 = 96201

в) 44444 + 9999 = 54443

г) 20010 − 6517 = 13493

48. а) Составьте из чисел 999, 5555, 8008 всевозможные суммы и вычислите их.
б) Составьте из чисел 2357, 2802, 3100 всевозможные разности и вычислите их.

Решение

а) 999 + 5555 = 6554
999 + 8008 = 9007
5555 + 8008 = 13563
999 + 5555 + 8008 = 14562

б) 3100 − 2802 = 298
3100 − 2357 = 743
2802 − 2357 = 445

49. а) Запишите какие−нибудь два числа, сумма которых равна 200. Сколько таких пар чисел можно записать?
б) Запишите какие−нибудь два числа, разность которых равна 200. Сколько таких пар чисел можно записать?

Решение

а) 100 + 100 = 200;
110 + 90 = 200;
120 + 80 = 200.
Всего можно записать 100 таких пар.

б) 205 − 5 = 200;
210 − 10 = 200;
220 − 20 = 200.
Таких пар можно записать бесконечное множество.

50. Используя данное равенство, составьте еще два:
а) 945 + 848 = 1793;
б) 1325 − 516 = 809;
в) 1644 − 374 = 1270;
г) 761 + 1766 = 2527.
Образец.
Из равенства 2715 + 897 = 3612 следует, что 3612 − 897 = 2715, а также, что 3612 − 2715 = 897.

Решение

а) Из равенства 945 + 848 = 1793 следует, что 1793 − 945 = 848, а также, что 1793 − 848 = 945.

б) Из равенства 1325 − 516 = 809 следует, что 516 + 809 = 1325, а также, что 1325 − 809 = 516.

в) Из равенства 1644 − 374 = 1270 следует, что 1270 + 374 = 1644, а также, что 1644 − 1270 = 374.

г) Из равенства 761 + 1766 = 2527 следует, что 2527 − 1766 = 761, а также, что 2527 − 761 = 1766.

51. Найдите неизвестное число:
а) (x + 24) + 53 = 930;
б) (34 − x) + 23 = 27;
в) 35 + (x − 17) = 85;
г) 64 − (15 + x) = 28.

Решение

а) (x + 24) + 53 = 930
x + 24 = 930 − 53
x + 24 = 877
x = 877 − 24
x = 853

б) (34 − x) + 23 = 27
34 − x = 27 − 23
34 − x = 4
x = 34 − 4
x = 30

в) 35 + (x − 17) = 85
x − 17 = 85 − 35
x − 17 = 50
x = 50 + 17
x = 67

г) 64 − (15 + x) = 28
15 + x = 64 − 28
15 + x = 36
x = 36 − 15
x = 21

52. Определите, какое число задумано, если:
а) к задуманное числу прибавили 16, а затем еще 23 и получили 78;
б) к задуманному числу прибавили 120, затем вычли 75 и получили 80;
в) из задуманного числа вычли 16, затем прибавили 32 и получили 50;
г) из задуманного числа вычли 12, затем 23 и получили 49.

Решение

а) x + 16 + 23 = 78
x + 39 = 78
x = 78 − 39
x = 39
Ответ: задуманное число 39.

б) x + 120 − 75 = 80
x + 120 = 80 + 75
x + 120 = 155
x = 155 − 120
x = 35
Ответ: задуманное число 35.

в) x − 16 + 32 = 50
x = 50 + 16 − 32
x = 66 − 32
x = 34
Ответ: задуманное число 34.

г) x − 12 − 23 = 49
x = 49 + 12 + 23
x = 61 + 23
x = 84
Ответ: задуманное число 84.

53 (56 в новом задачнике, с.13). Пользуясь оценкой, сравните значение каждой суммы с данным числом:
а) 728 + 319 и 1000;
б) 587 + 892 и 1500;
в) 489 + 477 и 1000;
г) 923 + 619 и 1500.
Образец.
Сравните сумму 597 + 539 с числом 1200.
Решение:
597 + 539 < 600 + 600 = 1200, значит, 597 + 539 < 1200.

Решение

а) 728 + 319 < 700 + 300 = 1000, значит, 728 + 319 > 1000.

б) 587 + 892 < 600 + 900 = 1500, значит, 587 + 892 < 1500.

в) 489 + 477 < 500 + 500 = 1000, значит, 489 + 477 < 1000.

г) 923 + 619 > 900 + 600 = 1500, значит, 923 + 619 < 1500.

10

54 (57 в новом задачнике, с.13). Пользуясь оценкой, ответьте на вопрос задачи.
а) Хватит ли 150 р. на покупку гамбургера, плитки шоколада и бутылки фруктовой воды, если гамбургер стоит 69 р., плитка шоколада − 48 р. и бутылка фруктовой воды − 26 р.?
б) На диске записано четыре рассказа Г.К.Честертона. Хватит ли 2 ч, чтобы прослушать эти рассказы, если они звучат 33 мин, 42 мин, 36 мин и 43 мин?

Решение

а) 69 + 48 + 26 < 70 + 50 + 30 = 150, значит 69 + 48 + 26 < 150.
Ответ: 150 рублей хватит на покупку гамбургера, плитки шоколада и бутылки фруктовой воды.

б) 33 + 42 + 36 + 40 > 30 + 30 + 30 + 30 = 120, значит 33 мин + 42 мин + 36 мин + 40 мин > 2 ч
Ответ: 2 часов не хватит, чтобы послушать все рассказы.

55. а) В гараже транспортного предприятия 145 автобусов. Это на 30 больше, чем грузовых машин, а легковых машин на 12 меньше, чем грузовых. Сколько всего машин в гараже?
б) Фирма сшила для магазина блузки, платья и детские костюмы. На блузки пошло 115 м ткани. Это на 40 м больше, чем на платье, и на 120 м меньше, чем на детские костюмы. Сколько метров ткани израсходовано?

Решение

а) 1) 145 − 30 = 115 (машин) − было грузовых;
2) 115 − 12 = 103 (машины) − было легковых;
3) 145 + 115 + 103 = 363 (машины) − всего было в гараже.
Ответ: 363 машины.

б) 1) 115 − 40 = 75 (м) − пошло на платье;
2) 115 + 120 = 235 (м) − пошло на детские костюмы;
3) 115 + 75 + 235 = 190 + 235 = 425 (м) − всего израсходовано.
Ответ: 425 м.

56. Из Крюкова в Семеновское можно проехать на одном из двух автобусов: через Вороново или через Покровское. Определите, какой путь займет меньше времени, если известно, что из Крюкова в Вороново автобус идет 1 ч 50 мин, а из Воронова в Семеновское − 1 ч 15 мин; путь из Крюкова в Покровское занимает 35 мин, а из Покровского в Семеновское − 2 ч 35 мин. При этом в Воронове остановка длится 10 мин, а в Покровском − 18 мин.
Подсказка.
Сделайте схематический рисунок.

Решение

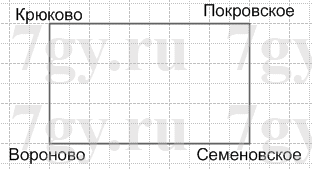
1) 1 ч 50 мин + 1 ч 15 мин + 10 мин = 2 ч 75 мин = 3 ч 15 мин − занимает путь Крюково − Вороново − Семеново;
2) 35 мин + 2 ч 35 мин + 18 мин = 2 ч 88 мин = 3 ч 28 мин − занимает путь Крюково − Покровское − Семеново;
3) 3 ч 15 мин < 3 ч 28 мин − значит, путь через Вороново займет меньше времени.
Ответ: путь через Вороново

57. а) В 5А и 5Б классах вместе 62 ученика, в 5Б и в 5В классах вместе 64 ученика. Сколько учеников в каждом из этих классов, если во всех трех вместе 93 ученика?
б) Гирлянда составлена из красных, синих, зеленых и желтых флажков. Красных, синих и зеленых флажков вместе 37 штук, синих, зеленых и желтых − 29 штук, красных, зеленых и желтых − 32 штуки. Всего в гирлянде 44 флажка. Сколько флажков каждого цвета в отдельности?

Решение

а) 1) 93 − 64 = 29 (учеников) − в 5А классе;
2) 62 − 29 = 33 (ученика) − в 5Б классе;
3) 64 − 33 = 31 (ученик) − в 5В классе.
Ответ: 29, 33 и 31 ученик.

б) 1) 44 − 37 = 7 (желтых) − флажков в гирлянде;
2) 44 − 29 = 15 (красных) − флажков в гирлянде;
3) 44 − 32 = 12 (синих) − флажков в гирлянде;
4) 44 − (7 + 15 + 12) = 44 − 34 = 10 (зеленых) − флажков в гирлянде.
Ответ: 7 желтых, 15 красных, 12 синих и 10 зеленых.

Самостоятельная работа № 2 (в новом задачнике на стр.13)

Вариант 1

1. 1) Выполните действие:
а) 463 + 23700;
б) 4516 − 428;
в) 20000 − 1750.

Решение

а) 463 + 23700 = 24163

б) 4516 − 428 = 4088

в) 20000 − 1750 = 18250

2. Найдите неизвестное число:
а) 135 + a = 210;
б) 400 − x = 325;
в) y − 230 = 600.

Решение

а) 135 + a = 210
a = 210 − 135
a = 75

б) 400 − x = 325
x = 400 − 325
x = 75

в) y − 230 = 600
y = 600 + 230
y = 830

3. Определите, какое расстояние короче и на сколько:
2 км 75 м или 2930 м.

Решение

1) 2 км 75 м = (2 * 1000 + 75) м = 2075 (м);
2) 2075 м < 2930 м;
3) 2930 − 2075 = 855 (м).
Ответ: на 855 м больше 2930 м, чем 2 км 75 м.

Вариант 2

1. Выполните действие:
а) 532 + 36800;
б) 6414 − 625;
в) 20000 − 1350.

Решение

а) 532 + 36800 = 37332

б) 6414 − 625 = 5789

в) 20000 − 1350 = 18650

2. Найдите неизвестное число:
а) a + 185 = 240;
б) x − 426 = 500;
в) 700 − y = 370.

Решение

а) a + 185 = 240
a = 240 − 185
a = 55

б) x − 426 = 500
x = 500 + 426
x = 926

в) 700 − y = 370
y = 700 − 370
y = 330

3. Определите, какое расстояние короче и на сколько:
3090 м или 3 км 450 м.

Решение

1) 3 км 450 м = (3 * 1000 + 450) м = 3450 (м);
2) 3090 < 3450;
3) 3450 − 3090 = 360 (м).
Ответ: на 360 м короче 3090 м, чем 3 км 450 м.

11

ГДЗ к теме Умножение и деление

58. Замените сложение умножением:
а) 35 + 35 + 35 + 35 + 35 + 35;
б) 120 + 120 + 120 + 120 + 120;
в) a + a + a + a;
г) x + x + x + x + x.

Решение

а) 35 + 35 + 35 + 35 + 35 + 35 = 35 * 6 = 210

б) 120 + 120 + 120 + 120 + 120 = 120 * 5 = 600

в) a + a + a + a = 4a

г) x + x + x + x + x = 5x

59. Выполните умножение:
а) 123 * 305;
б) 274 * 206;
в) 307 * 148;
г) 411 * 702.

Решение

а) 123 * 305 = 37515

б) 274 * 206 = 56444

в) 307 * 148 = 45436

г) 411 * 702 = 288522

60. Выполните умножение:
а) 39 * 3500;
б) 4800 * 27;
в) 15000 * 65;
г) 54 * 32000.

Решение

а) 39 * 3500 = 136500

б) 4800 * 27 = 129600

в) 15000 * 65 = 975000

г) 54 * 32000 = 1728000

Запись столбиком:

61. Выполните умножение:
а) 5040 * 160;
б) 3700 * 140;
в) 1200 * 7400;
г) 6080 * 2100.

Решение

а) 5040 * 160 = 806400

б) 3700 * 140 = 518000

в) 1200 * 7400 = 8880000

г) 6080 * 2100 = 12768000

Запись столбиком:

62. Используя данное равенство, найдите значения двух выражений:
а)
139 * 856 = 118984;
118984 : 856 = ;
118984 : 139 = .
б)
207 * 615 = 127305;
127305 : 207 = ;
127305 : 615 = .

Решение

а) 139 * 856 = 118984;
118984 : 856 = 139;
118984 : 139 = 856.

б) 207 * 615 = 127305;
127305 : 207 = 615;
127305 : 615 = 207.

63. Найдите частное:
а) 2816 : 11;
б) 7059 : 13;
в) 6168 : 12;
г) 7488 : 24.

Решение

а) 2816 : 11 = 256

б) 7059 : 13 = 543

в) 6168 : 12 = 514

г) 7488 : 24 = 312

Запись уголком:

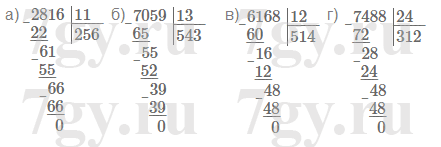
64. Найдите частное:
а) 20130 : 15;
б) 13512 : 24;
в) 72576 : 21;
г) 16692 : 52.

Решение

а) 20130 : 15 = 1342

б) 13512 : 24 = 563

в) 72576 : 21 = 3456

г) 16692 : 52 = 321

Запись уголком:

65. Найдите частное:
а) 5656 : 14;
б) 9933 : 11;
в) 7635 : 15;
г) 7700 : 25.

Решение

а) 5656 : 14 = 404

б) 9933 : 11 = 903

в) 7635 : 15 = 509

г) 7700 : 25 = 308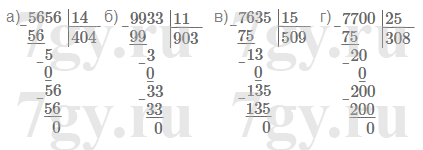

66. Найдите частное:
а) 39000 : 6;
б) 57600 : 9;
в) 53900 : 5;
г) 26000 : 4.

Решение

а) 39000 : 6 = 6500

б) 57600 : 9 = 6400

в) 53900 : 5 = 10780

г) 26000 : 4 = 6500

Запись уголком:

67. Найдите частное:
а) 89100 : 900;
б) 31250 : 250;
в) 10780 : 110;
г) 28600 : 440.

Решение

а) 89100 : 900 = 99

б) 31250 : 250 = 125

в) 10780 : 110 = 98

г) 28600 : 440 = 65

Запись уголком:

68. Вычислите:
а) 7351 * 26;
б) 6936 : 102;
в) 15655 : 31;
г) 402 * 1250.

Решение

а) 7351 * 26 = 191126

б) 6936 : 102 = 68

в) 15655 : 31 = 505

г) 402 * 1250 = 502500

Запись в тетради:

69. Запишите число, которое:
а) в 7 раз больше числа 209;
б) в 5 раз меньше числа 2045.

Решение

а) 209 * 7 = 1463
×209
      7
1463
Ответ: 1463

б) 2045 : 5 = 409
_2045 |5    
  20     |409
   _45
     45
       0
Ответ: 409.

70. Определите:
а) во сколько раз число 441559 больше числа 109;
б) во сколько раз число 306 меньше числа 674730.

Решение

71. Придумайте правило, по которому строится данная последовательность чисел, и найдите следующие три числа в этой последовательности:
а) 1; 4; 16; ...;
б) 729; 243; 81; ... .

Решение

а) Закономерность: каждое последующее число в 4 раза больше предыдущего.
1; 4; 16; 64; 256; 1024.

б) Закономерность: каждое последующее число в 3 раза меньше предыдущего.
729; 243; 81; 27; 9; 3.

72. Объясните, как найти неизвестный множитель. Найдите неизвестный множитель:
а) x * 81 = 891;
б) 18 * a = 270;
в) 2640 = b * 12;
г) 132 = 33 * y.

Решение

Чтобы найти неизвестный множитель, нужно произведение поделить на известный множитель.
а)
x * 81 = 891
x = 891 : 81
x = 11
_891 |81
  81   |11
  _81
    81
      0

б) 18 * a = 270
a = 270 : 18
a = 15
_270 |18
  18   |15
  _90
    90
     0

в) 2640 = b * 12
b = 2640 : 12
b = 220
_2640 |12  
  24     |220
  _24
    24
     0

г) 132 = 33 * y
y = 132 : 33
y = 4
_132 |33
  132 |4
     0

12

73. Объясните, как найти неизвестные делимое и делитель. Найдите неизвестное делимое или неизвестный делитель:
а) x : 17 = 21;
б) 168 : b = 6;
в) y : 8 = 24;
г) 525 : a = 15.

Решение

Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Чтобы найти неизвестный делитель, нужно делимое поделить на частное.

а) x : 17 = 21
x = 21 * 17
x = 357
×21
  17
147
21  
357

б) 168 : b = 6
b = 168 : 6
b = 28
_168 |6   
  12   |28
  _48
    48
     0

в) y : 8 = 24
y = 24 * 8
y = 192
×24
    8
192

г) 525 : a = 15
a = 525 : 15
a = 35
_525 |15
  45   |35
 _75
   75
     0

74. Найдите неизвестное число:
а) 8 * a = 416;
б) y : 18 = 50;
в) x * 9 = 531;
г) 6464 : b = 32.

Решение

а) 8 * a = 416
a = 416 : 8
a = 52
_416 |8   
  40   |52
 _16
   16
     0

б) y : 18 = 50
y = 50 * 18
y = 900
x50
18  
40
5    
900

в) x * 9 = 531
x = 531 : 9
x = 59
_531 |9  
  45   |59
  _81
    81
     0

г) 6464 : b = 32
b = 6464 : 32
b = 202
_6464 |32   
  64     |202
    _64
      64
       0

75. Для того, чтобы предвидеть, какой примерно результат должен получиться, часть используют прикидку с помощью округления. Выполните прикидку результата, затем вычислите произведение:
а) 41 * 98;
б) 19 * 52;
в) 399 * 49;
г) 296 * 21.
Образец.
112 * 46 ≈ 100 * 50 = 5000; выполнив умножение, получим 5152.

Решение

а) 41 * 98 ≈ 40 * 100 = 4000; выполнив умножение, получим 4606.
 × 47
    98
  376
423  
4606

б) 19 * 52 ≈ 20 * 50 = 1000; выполнив умножение, получим 988.
×19
  52
  38
95   
988

в) 399 * 49 ≈ 400 * 50 = 20000; выполнив умножение, получим 19551.
×  399
      49
  3591
1596  
19551

г) 296 * 21 ≈ 300 * 20 = 6000; выполнив умножение, получим 6216.
×296
    21
  296
592   
6216

76. Выполните прикидку суммы, затем вычислите ее точное значение:
а) 48 + 51 + 49 + 48 + 52 + 50;
б) 599 + 597 + 600 + 601 + 602.
Образец.
31 + 29 + 30 + 28 + 29 + 32 + 33 ≈ 30 * 7 = 210; вычислив сумму, получим 212.

Решение

а) 48 + 51 + 49 + 48 + 52 + 50 ≈ 50 * 6 = 300;
48 + 51 + 49 + 48 + 52 + 50 = 298.

б) 599 + 597 + 600 + 601 + 602 ≈ 600 * 5 = 3000;
599 + 597 + 600 + 601 + 602 = 2999.

77. Четыре ученика, отвечая у доски, получили следующие результаты:
1) 512 * 26 = 13312;
2) 34 * 317 = 10771;
3) 623 * 18 = 12214;
4) 405 * 25 = 10120.
Выясните, кто из них правильно выполнил умножение.
Подсказка. Сначала найдите неправильное решения по последней цифре результата; остальные равенства проверьте, выполнив умножение.

Решение

1) 2 * 6 = 12 − в первом результате последняя цифра верная;
2) 4 * 7 = 28 − во втором результате последняя цифра неверная;
3) 3 * 8 = 24 − в третьем результате последняя цифра верная;
4) 5 * 5 = 25 − в четвертом результате последняя цифра неверная;
5)
×  512
      26
  3072
1024  
13312
6)
×  623
      18
  4984
623    
11214
Ответ: первый ученик выполнил умножение правильно.

78. а) Сколько миллиметров в 52 см? в 23 дм? в 2 м 34 см?
б) Сколько сантиметров в 84 м? в 52 дм? в 2 м 34 см?
в) Сколько килограммов в 105 т? в 12 т 350 кг? в 4 ц 15 кг?
г) Сколько граммов в 26 кг? в 2 кг 250 г? в 3 ц 8 кг?

Решение

а) 52 см = (52 * 10) мм = 520 мм;
23 дм = (23 * 100) мм = 2300 мм;
2 м 34 см = (2 * 1000 + 34 * 10) мм = (2000 + 340) мм = 2340 мм.

б) 84 м = (84 * 100) см = 8400 см;
52 дм = (52 * 10) см = 520 см;
2 м 34 см = (2 * 100 + 34) см = 234 см.

в) 105 т = (105 * 1000) кг = 105000 кг;
12 т 350 кг = (12 * 1000 + 350) кг = 12350 кг;
4 ц 15 кг = (4 * 100 + 15) кг = 415 кг.

г) 26 кг = (26 * 1000) г = 26000 г;
2 кг 250 г = (2 * 1000 + 250) г = 2250 г;
3 ц 8 кг = (3 * 100000 + 8 * 1000) г = (300000 + 8000) г = 308000 г.

79. а) Сколько минут в 24 ч? в 48 ч? в 6 ч 15 мин?
б) Сколько секунд в 45 мин? в 6 ч? в 3 ч 10 мин?

Решение

а) 24 ч = (24 * 60) мин = 1440 мин;
48 ч = (48 * 60) мин = 2880 мин;
6 ч 15 мин = (6 * 60 + 15) мин = (360 + 15) мин = 375 мин.

б) 45 мин = (45 * 60) с = 2700 с;
6 ч = (6 * 60 * 60) с = (6 * 3600) с = 21600 с;
3 ч 10 мин = (3 * 60 * 60 + 10 * 60) с = (3 * 3600 + 600) с = (10800 + 600) с = 11400 с.

80. Определите, что больше и во сколько раз:
а) 10 км или 1000 м;
б) 5 кг или 500 г;
в) 30 ч или 300 мин;
г) 20 мин или 200 с.

Решение

а) 1) 10 км = (10 * 1000) м = 10000 м;
2) 10000 м > 1000 м;
3) 10000 : 1000 = 10.
Ответ: в 10 раз 10 км больше, чем 1000 м.

б) 1) 5 кг = (5 * 1000) г = 5000 г;
2) 5000 г > 500 г;
3) 5000 : 500 = 10.
Ответ: в 10 раз 5 кг больше, чем 500 г.

в) 1) 300 мин = (300 : 60) ч = 5 ч;
2) 30 ч > 5 ч;
3) 30 : 5 = 6.
Ответ: в 6 раз 30 ч больше, чем 300 мин.

г) 1) 20 мин = (20 * 60) с = 1200 с;
2) 1200 с > 200 с;
3) 1200 : 200 = 6.
Ответ: в 6 раз 20 мин больше, чем 200 с.

81. Замените сложение умножением:
а) $\underbrace{82 + 82 + ... + 82}_{10-раз}$;
б) $\underbrace{82 + 82 + ... + 82}_{100-раз}$;
в) $\underbrace{15 + 15 + ... + 15}_{n-раз}$;
г) $\underbrace{a + a + ... + a}_{n-раз}$.

Решение

а) $\underbrace{82 + 82 + ... + 82}_{10-раз} = 82 * 10 = 820$

б) $\underbrace{82 + 82 + ... + 82}_{100-раз} = 82 * 100 = 8200$

в) $\underbrace{15 + 15 + ... + 15}_{n-раз} = 15n$

г) $\underbrace{a + a + ... + a}_{n-раз} = an$

13

82. Замените сложением умножением и вычислите:
а) $\underbrace{10 + 10 + ... + 10}_{101-раз} + \underbrace{101 + 101 + ... + 101}_{10-раз}$;
б) $\underbrace{15 + 15 + ... + 15}_{200-раз} + \underbrace{100 + 100 + ... + 100}_{15-раз}$.
Образец.
$\underbrace{150 + 150 + ... + 150}_{20-раз} + \underbrace{20 + 20 + ... + 20}_{150-раз} = 150 * 20 + 20 * 150 = 150 * 20 * 2 = 6000$

Решение

а) $\underbrace{10 + 10 + ... + 10}_{101-раз} + \underbrace{101 + 101 + ... + 101}_{10-раз} = 10 * 101 + 101 * 10 = 101 * 10 * 2 = 1010 * 2 = 2020$

б) $\underbrace{15 + 15 + ... + 15}_{200-раз} + \underbrace{100 + 100 + ... + 100}_{15-раз} = 15 * 200 + 100 * 15 = 3000 + 1500 = 4500$

83. Выполните умножение:
а) 15683 * 82;
б) 160820 * 185;
в) 350 * 636 * 22;
г) 402 * 125 * 48.

Решение

а) 15683 * 82 = 1286006
x  15683
          82
    31366
125464  
1286006

б) 160820 * 185 = 29751700
x   160820
        185  
    80410
128656
16082       
29751700

в) 350 * 636 * 22 = 222600 * 22 = 4897200
  x 636
      350
  3180
1908    
222600

x 222600
       22   
   4452
4452      
4897200

г) 402 * 125 * 48 = 50250 * 48 = 2412000
x  125
    402
    250
500    
50250

x  50250
        48  
  40200
20100    
2412000

84. Пользуясь оценкой, сравните значение каждого произведения с данным числом:
а) 198 * 5 и 1000;
б) 253 * 4 и 1000;
в) 496 * 3 и 1500;
г) 253 * 6 и 1500.
Образец.
Сравните 284 * 4 и 1000.
Решение:
248 * 4 < 250 * 4 = 1000, значит, 248 * 4 < 1000.

Решение

а) 198 * 5 < 200 * 5 = 1000, значит, 198 * 5 < 1000.

б) 253 * 4 > 250 * 4 = 1000, значит, 253 * 4 > 1000.

в) 496 * 3 < 500 * 3 = 1500, значит, 496 * 3 < 1500.

г) 253 * 6 > 250 * 6 = 1500, значит, 253 * 6 > 1500.

!85. Найдите частное:
а) 833325 : 15;
б) 399996 : 18;
в) 271062 : 22;
г) 108025 : 25.

Решение

а) 833325 : 15 = 55555

б) 399996 : 18 = 22222

в) 271062 : 22 = 12321

г) 108025 : 25 = 4321

!86. Найдите частное:
а) 140126 : 14;
б) 320128 : 16;
в) 686868 : 34;
г) 421848 : 42.

Решение

а) 140126 : 14 = 10009

б) 320128 : 16 = 20008

в) 686868 : 34 = 20202

г) 421848 : 42 = 10044

!87. Выполните деление и результат проверьте умножением:
а) 727272 : 12;
б) 5012575 : 25;
в) 900900180 : 18;
г) 45030015 : 15.

Решение

а) 727272 : 12 = 60606
Проверка:
60606 * 12 = 727272

б) 5012575 : 25 = 200503
Проверка:
200503 * 25 = 5012575

в) 900900180 : 18 = 50050010
Проверка:
50050010 * 18 = 900900180

г) 45030015 : 15 = 3002001
Проверка:
3002001 * 15 = 45030015

88. Найдите три предыдущих и три следующих числа в последовательности чисел:
а) ...; 32; 64; 128; ...;
б) ...; 112; 224; 448; ... .

Решение

а) Закономерность: каждое последующее число в 2 раза больше предыдущего.
4; 8; 16; 32; 64; 128; 256; 512; 1024.

б) Закономерность: каждое последующее число в 2 раза больше предыдущего.
14; 28; 56; 112; 224; 448; 896; 1792; 3584.

89. а) Записали последовательность из четырех чисел, каждое из которых в 3 раза больше предыдущего. Последнее число равно 486. Найдите первое.
б) Записали последовательность из четырех чисел, каждое из которых в 6 раз меньше предыдущего. Последнее число равно 2. Найдите первое.

Решение

а) 1) 486 : 3 = 162 − третье число;
2) 162 : 3 = 54 − второе число;
3) 54 : 3 = 18 − первое число.
Ответ: 18

б) 1) 12 * 6 = 12 − третье число;
2) 12 * 6 = 72 − второе число;
3) 72 * 6 = 432 − первое число.
Ответ: 432

90. Используя данное равенство, составьте еще два равенства:
а) 28080 : 156 = 180;
б) 5780 : 17 = 340.

Решение

а) 28080 : 156 = 180
28080 : 180 = 156
180 * 156 = 28080

б) 5780 : 17 = 340
5780 : 340 = 17
340 * 17 = 5780

91. Найдите неизвестное число:
а) (x + 150) : 16 = 30;
б) 8 * (a − 35) = 208;
в) 180 : (x − 12) = 20;
г) (a + 43) * 9 = 747.

Решение

а) (x + 150) : 16 = 30
x + 150 = 30 * 16
x + 150 = 480
x = 480 − 150
x = 330

б) 8 * (a − 35) = 208
a − 35 = 208 : 8
a − 35 = 26
a = 26 + 35
a = 61

в) 180 : (x − 12) = 20
x − 12 = 180 : 20
x − 12 = 9
x = 9 + 12
x = 21

г) (a + 43) * 9 = 747
a + 43 = 747 : 9
a + 43 = 83
a = 83 − 43
a = 40

14

ГДЗ к теме Решение задач

92. Длину окружности можно приближенно найти, умножив ее радиус на 6. Решите задачу, используя этот факт.
а) Арена цирка имеет форму круга диаметром 13 м. Обезьянка пробежала круг по краю арены. Какое расстояние она пробежала?
б) Для скатерти мама выкроила из ткани круг радиусом 75 см. По краю скатерти он хочет пришить кружево. Какой длины кружево ей потребуется?

Решение

а) (13 * 6) : 2 = 78 : 2 = 39 (м) − пробежала обезьянка.
Ответ: 39 метров.

б) 75 * 6 = 450 (см) = 4 м 50 см − кружева потребуется.
Ответ: 4 м 50 см.

93. а) Танцевальная студия заказала 15 платьев для выступлений. Для отделки одного платья требуется 1 м 60 см кружева. Хватит ли 25 м кружева для их отделки?
б) Для первого класса нужно купить 24 учебника математики. Один учебник стоит 140 р. 50 к. Хватит ли 3300 р. для покупки учебников?

Решение

а) 1 м 60 см = 160 см
1) 15 * 160 = 2400 (см) = 24 (м) − кружева понадобится на 15 платьев;
2) 25 > 24, значит, кружева хватит.
Ответ: да, хватит.

б) 140 р. 50 к. = 14050 к.
1) 14050 * 24 = 337200 (к.) = 3372 (р.) − нужно для покупки 24 учебников;
2) 3372 > 3300 − значит, 3300 р. не хватит.
Ответ: нет, не хватит.

94. а) В книге 256 страниц. Андрей прочитал 192 страницы. Во сколько раз число прочитанных страниц больше, чем число непрочитанных?
б) Расстояние между городами равно 420 км. Автомобиль проехал 84 км и сделал остановку. Во сколько раз путь, который он проехал, меньше оставшегося пути?

Решение

а) 1) 256 − 192 = 64 (с.) − осталось прочитать;
2) 192 : 64 = в 3 (раза) − число прочитанных страниц больше, чем число непрочитанных.
Ответ: в 3 раза.

б) 1) 420 − 84 = 336 (км) − осталось проехать;
2) 336 : 84 = в 4 (раза) − путь, который проехал автомобиль, меньше оставшегося пути.
Ответ: в 4 раза.

95. а) В 8 больших коробках столько же карандашей, сколько в 12 маленьких. Сколько карандашей в одной маленькой коробке, если в одной большой коробке 18 карандашей?
б) Пластиковые папки для бумаги продают маленькими и большими упаковками. За 5 маленьких упаковок надо заплатить столько же, сколько за 3 большие. Сколько стоит одна большая упаковка, если цена маленькой 60 р.?

Решение

а) 1) 18 * 8 = 144 (к.) − всего в больших коробках;
2) 144 : 12 = 12 (к.) − в одной маленькой коробке.
Ответ: 12 карандашей.

б) 1) 5 * 60 = 300 (р.) − цена 5 маленьких упаковок;
2) 300 : 3 = 100 (р.) − цена одной большой упаковки.
Ответ: 100 рублей.

96. Заполните таблицу:...
Для каждого случая определите, о ком или о чем может идти речь в задаче.

Решение

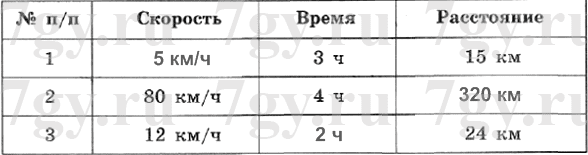
1) 15 : 3 = 5 (км/ч) − скорость туриста;
2) 80 * 4 = 320 (км) − проехал автомобиль;
3) 24 : 12 = 2 (ч) − ехал велосипедист.

97. а) Поезд проехал 400 км за 5 ч. Какое расстояние он проедет за 8 ч, если будет ехать с той же скоростью?
б) Велосипедист ехал 4 ч со скоростью 12 км/ч. За какое время он прошел бы это расстояние пешком, если бы шел со скоростью 6 км/ч?
в) Автобус проехал 120 км со скоростью 60 км/ч. С какой скоростью ему надо ехать, чтобы за это же время проехать 170 км?

Решение

а) 1) 400 : 5 = 80 (км/ч) − скорость поезда;
2) 80 * 8 = 640 (км) − проедет поезд за 8 часов.
Ответ: 640 км.

б) 1) 4 * 12 = 48 (км) − проехал велосипедист;
2) 48 : 6 = 8 (ч) − шел бы это расстояние велосипедист пешком.
Ответ: за 8 ч

в) 1) 120 : 60 = 2 (ч) − ехал автобус со скоростью 60 км/ч;
2) 170 : 2 = 85 (км/ч) − скорость, с которой надо ехать автобусу.
Ответ: 85 км/ч.

15

98. а) В России до 1924 г. использовались старинные русские меры длины: сажень, аршин, пядь, вершок. В 1 вершке примерно 4 см 5 мм, 1 пядь − это 4 вершка, 1 аршин − это 16 вершков, 1 сажень − это 3 аршина. Сколько примерно сантиметров в 1 пяди? в 1 аршине? в 1 сажени?
б) В США до сих пор вместо метрической системы единиц используются старинные меры. Длина измеряется в дюймах, футах, ярдах. В 1 дюйме примерно 2 см 5 мм, 1 фут − это 12 дюймов, 1 ярд − это 3 фута. Сколько примерно сантиметров в 1 футе? в 1 ярде?

Решение

а) 1) 4 см 5 мм * 4 = 45 мм * 4 = 180 мм = 18 (см) − в одной пяди;
2) 4 см 5 мм * 16 = 45 мм * 16 = 720 мм = 72 (см) − в одном аршине;
3) 72 * 3 = 216 (см) − в одной сажени.
Ответ: 18 см − в 1 пяди; 72 см − в 1 аршине; 216 см − в 1 одной сажени.

б) 1) 1 фут = 12 дюймов = 12 * 25 мм = 300 мм = 30 (см);
2) 1 ярд = 3 фута = 3 * 12 дюймов = 36 дюймов = 36 * 25 мм = 900 мм = 90 (см).
Ответ: 30 см − в 1 футе; 90 см − в 1 ярде.

99. а) Самую большую скорость в соревнованиях по бегу человек показывает на дистанциях 60 − 100 м. Лучшие бегуны среди людей пробегают 100 м примерно за 10 с. Выразите скорость, с которой они в это время бегут, в километрах в час.
б) Абсолютный чемпион в спринте среди современных млекопитающих − гепард. Известен случай, когда гепард преодолел расстояние около 600 м за 20 с. Какую скорость (в км/ч) развил в это время гепард?

Решение

а) 1 ч = 60 мин = 3600 с;
1 км = 1000 м.
100 м : 10 с = 10 м/с = (10 * 3600 : 1000) км/ч = 36000 : 1000 = 36 (км/ч) − скорость лучших бегунов.
Ответ: 36 км/ч.

б) 1 ч = 60 мин = 3600 с;
1 км = 1000 м.
1) 600 : 20 = 30 (м/с) − скорость гепарда;
2) 30 * 3600 : 1000 = 108000 : 1000 = 108 (км/ч) − скорость гепарда.
Ответ: 108 км/ч.

Самостоятельная работа № 3

Вариант 1

1. Найдите произведение:
а) 724 * 203;
б) 65 * 2800;
в) 4060 * 2100.

Решение

а) 724 * 203 = 146972
x    724
      203
    2172
1448       
146972

б) 65 * 2800 = 182000
х  65
    2800
  520
130      
182000

в) 4060 * 2100 = 8526000
х4060
    2100
  406
812        
8526000

2. Найдите частное:
а) 1404 : 13;
б) 56640 : 236.

Решение

а) 1404 : 13 = 108
_1404 |13   
  13     |108
 _104
   104
      0

б) 56640 : 236 = 240
_56640 |236
  472     |240
  _944
    944
        0

3. Определите, во сколько раз:
195 кг больше 600 г.

Решение

195 кг : 600 г = 195000 г : 600 г = 325
Ответ: в 325 раз 195 кг больше, чем 600 г.

_195000 |600
  1800     |325
 _1500
    1200
   _3000
     3000
           0

4. Найдите неизвестное число:
а) 7 * a = 378;
б) 160 : x = 32;
в) y : 23 = 46.

Решение

а) 7 * a = 378
a = 378 : 7
a = 54
_378 |7   
  35   |54
 _28
   28
     0

б) 160 : x = 32
x = 160 : 32
x = 5

в) y : 23 = 46
y = 46 * 23
y = 1058
×  46
    23
  138
  92    
1058

Вариант 2

1. Найдите произведение:
а) 583 * 302;
б) 34 * 7500;
в) 6040 * 1200.

Решение

а) 583 * 302 = 176066
  х  583
      302
    1166
1749    
176066

б) 34 * 7500 = 255000
х 34
   7500
  170
238      
255000

в) 6040 * 1200 = 7248000
х6040
    1200
1208
604        
7248000

2. Найдите частное:
а) 1498 : 14;
б) 51480 : 143.

Решение

а) 1498 : 14 = 107
_1498 |14   
  14     |107
  _98
    98
      0 

б) 51480 : 143 = 360
_51480 |143
  429     |360
  _858
    858
       0

3. Определите, во сколько раз:
800 г меньше 188 кг

Решение

188 кг : 800 г = 188000 г : 800 г = 235
Ответ: в 235 раз 800 г меньше, чем 188 кг
_188000 |800
  1600     |235
  _2800
    2400
   _4000
     4000
           0

4. Найдите неизвестное число:
а) a * 18 = 270;
б) x : 16 = 48;
в) 140 : y = 70.

Решение

а) a * 18 = 270
a = 270 : 18
a = 15
_270 |18
  18   |15
  _90
    90
      0

б) x : 16 = 48
x = 48 * 16
x = 768
×48
  16
288
48  
768

в) 140 : y = 70
y = 140 : 70
y = 2

ГДЗ к теме Порядок действий в вычислениях

100. Определите, правильно ли указан порядок действий. Если нет, то укажите правильный:
а) $24 \overset{3}{+} 15 \overset{2}{*} (40 \overset{1}{-} 31)$;
б) $12 \overset{1}{*} 40 \overset{2}{-} 128 \overset{3}{:} 8$;
в) $189 \overset{4}{-} 120 \overset{1}{:} 3 \overset{3}{-} 7 \overset{2}{*} 7$;
г) $16 \overset{3}{:} (112 \overset{2}{-} 27 \overset{1}{*} 4)$.

Решение

а) $24 \overset{3}{+} 15 \overset{2}{*} (40 \overset{1}{-} 31)$ − верно.

б) $12 \overset{1}{*} 40 \overset{2}{-} 128 \overset{3}{:} 8$ − неверно.
Правильный порядок:
$12 \overset{1}{*} 40 \overset{3}{-} 128 \overset{2}{:} 8$

в) $189 \overset{4}{-} 120 \overset{1}{:} 3 \overset{3}{-} 7 \overset{2}{*} 7$ − неверно.
Правильный порядок:
$189 \overset{3}{-} 120 \overset{1}{:} 3 \overset{4}{-} 7 \overset{2}{*} 7$

г) $16 \overset{3}{:} (112 \overset{2}{-} 27 \overset{1}{*} 4)$ − верно.

101. Найдите значения выражений и сравните их:
а) 5 * (8 + 14) и 5 * 8 + 14;
б) 5 * (6 + 4) * 25 и 5 * 6 + 4 * 25;
в) 12 + 60 : (6 : 2) и (12 + 60) : 6 : 2;
г) 5 * (20 − 6) + 40 и 5 * 20 − (6 + 40).

Решение

а) 5 * (8 + 14) = 5 * 22 = 110;
5 * 8 + 14 = 40 + 14 = 54;
110 > 54;
5 * (8 + 14) > 5 * 8 + 14.

б) 5 * (6 + 4) * 25 = 5 * 10 * 25 = 125 * 10 = 1250;
5 * 6 + 4 * 25 = 30 + 100 = 130;
1250 > 130;
5 * (6 + 4) * 25 > 5 * 6 + 4 * 25.

в) 12 + 60 : (6 : 2) = 12 + 60 : 3 = 12 + 20 = 32;
(12 + 60) : 6 : 2 = 72 : 6 : 2 = 12 : 2 = 6;
32 > 6;
12 + 60 : (6 : 2) > (12 + 60) : 6 : 2.

г) 5 * (20 − 6) + 40 = 5 * 14 + 40 = 70 + 40 = 110;
5 * 20 − (6 + 40) = 100 − 46 = 54;
110 > 54;
5 * (20 − 6) + 40 > 5 * 20 − (6 + 40).

16

102. Найдите значение выражения:
а) 3 * 408 − 384 : 6;
б) 224 : 4 + 5 * 201;
в) 672 : 28 * 45 − 898;
г) 1476 − 252 : 21 * 24.

Решение

103. Найдите значение выражения:
а) 11 * (1040 − 619) + 752;
б) 7200 − (298 + 142) * 15;
в) (980 − 879) * (436 − 379);
г) (201 − 4590 : 45) * 101.

Решение

!104. Найдите значение выражения:
а) 136 * (668 − 588) − 404 * 25;
б) 1540 : 11 + 1890 : 9 + 982;
в) 1953 + (17432 − 56 * 223) : 16;
г) 6010 − (130 * 52 − 68890 : 83).

Решение

а) $136 \overset{2}{*} (668 \overset{1}{-} 588) \overset{4}{-} 404 \overset{3}{*} 25 = 136 * 80 - 404 * 25 = 10880 - 10100 = 780$

б) $1540 \overset{1}{:} 11 \overset{3}{+} 1890 \overset{2}{:} 9 \overset{4}{+} 982 = 140 + 210 + 982 = 350 + 982 = 1332$

в) $1953 \overset{4}{+} (17432 \overset{2}{-} 56 \overset{1}{*} 223) \overset{3}{:} 16 = 1953 + (17432 - 12488) : 16 = 1953 + 4944 : 16 = 1953 + 309 = 2262$

г) $6010 \overset{4}{-} (130 \overset{1}{*} 52 \overset{3}{-} 68890 \overset{2}{:} 83) = 6010 - (6760 - 830) = 6010 - 5930 = 80$

105. Упростите выражение, убрав ненужные скобки, и найдите его значение:
а) (11 * 11) − (30 * 4);
б) (138 + (60 : 2)) − 150;
в) 50 − ((4 * 12) − 18);
г) 15 + (10 * (120 − 70)).
Образец.
20 * (15 − (12 : 3)) = 20 * (15 − 12 : 3) = 220.

Решение

а) (11 * 11) − (30 * 4) = 11 * 11 − 30 * 4 = 121 − 120 = 1

б) (138 + (60 : 2)) − 150 = 138 + 60 : 2 − 150 = 138 + 30 − 150 = 168 − 150 = 18

в) 50 − ((4 * 12) − 18) = 50 − (4 * 12 − 18) = 50 − (48 − 18) = 50 − 30 = 20

г) 15 + (10 * (120 − 70)) = 15 + 10 * (120 − 70) = 15 + 10 * 50 = 15 + 500 = 515

106. При нахождении значения одного из выражений допущена ошибка, она может быть обнаружена по последней цифре результата. Найдите это выражение.
1) 18 * 4 + 28 * 3 = 156;
2) 20 + 16 + 42 = 77;
3) 77 * 11 + 401 = 1248.

Решение

1) 18 * 4 + 28 * 3 = 156
8 * 4 = 32 − последняя цифра 2;
8 * 3 = 24 − последняя цифра 4;
2 + 4 = 6 − ответ правильный.

2) 20 + 16 + 42 = 77
0 + 6 + 2 = 8 − ответ неправильный.

3) 77 * 11 + 401 = 1248
7 * 1 = 7 − последняя цифра;
7 + 1 = 8 − ответ правильный.

!107. Запишите выражение и найдите его значение:
а) сумма частного чисел 108 и 3 и произведения чисел 25 и 12;
б) разность числа 670 и суммы чисел 195 и 76;
в) произведение суммы чисел 38 и 22 и разности чисел 132 и 52;
г) частное числа 680 и разности чисел 97 и 57.

Решение

а) $108 \overset{1}{:} 3 \overset{3}{+} 25 \overset{2}{*} 12 = 36 + 300 = 336$

б) $670 \overset{2}{-} (195 \overset{1}{+} 76) = 670 - 271 = 399$

в) $(38 \overset{1}{+} 22) \overset{3}{*} (132 \overset{2}{-} 52) = 60 * 80 = 4800$
1) 38 + 22 = 60
2) 132 − 52 = 80;
3) 60 * 80 = 4800.

г) $680 \overset{2}{:} (97 \overset{1}{-} 57) = 680 : 40 = 17$

108. Запишите разные выражения для вычисления длины ломаной (рис. 1).

Решение

а) 1) 5 + 5 + 10 + 10 + 15 + 15 + 20 + 20 + 25 = 125 (мм);
2) 2 * 5 + 10 * 2 + 15 * 2 + 20 * 2 + 25 = 10 + 20 + 30 + 40 + 25 = 125 (мм);
3) 2 * (5 + 10 + 15 + 20) + 25 = 2 * 50 + 25 = 125 (мм);
4) 5 * 25 = 125 (мм).

б) 1) 4 + 10 + 8 + 20 + 12 + 30 + 16 + 40 = 140 (мм);
2) 10 * 10 + 4 * 10 = 100 + 40 = 140 (мм).

109. Составьте выражение по условию задачи и решите ее.
а) Велосипедисты проехали в первый день 148 км, во второй − в 4 раза меньше, а в третий − на 90 км больше, чем во второй. Сколько километров проехали велосипедисты за 3 дня?
б) Турист во время путешествия отправился из одного города в другой. Сначала он 2 ч ехал на автобусе со скоростью 70 км/ч, потом 4 ч шел пешком со скоростью 4 км/ч, и после этого ему осталось пройти 12 км. Чему равно расстояние между городами?

Решение

а) 148 + 148 : 4 + (148 : 4 + 90) = 148 + 37 + (37 + 90) = 148 + 37 + 127 = 185 + 127 = 312 (км) − проехали велосипедисты за 3 дня.
Ответ: 312 км.

б) 2 * 70 + 4 * 4 + 12 = 140 + 16 + 12 = 156 + 12 = 168 (км) − расстояние между городами.
Ответ: 168 км.

17

110. Составьте выражение по условию задачи и решите ее.
а) Ирина и Наташа должны подписать 270 приглашений на школьный вечер. Ирина подписывает 40 приглашений в час, а Наташа − 50 приглашений. Они работают вместе. За какое время все приглашения будут подписаны?
б) Один автомат наполняет конфетами 70 коробок в час, а другой − 75 коробок. Их включают одновременно. За какое время будет заполнено конфетами 870 коробок?

Решение

а) 270 : (40 + 50) = 270 : 90 = 3 (ч) − будут подписывать приглашения Ирина и Наташа.
Ответ: за 3 часа.

б) 870 : (70 + 75) = 870 : 145 = 6 (ч) − будут заполняться конфетами 870 коробок.
Ответ: за 6 часов.

111. а) Толя вышел из школы и пошел на стадион со скоростью 90 м/мин. Через 10 мин ему осталось пройти 300 м. На каком расстоянии от школы находится стадион?
б) Николай вышел из дома в школу, расстояние до которой 1800 м. Через 12 мин ему осталось пройти 600 м. Определите скорость (в м/мин), с которой идет Николай.

Решение

а) 1) 90 * 10 = 900 (м) − прошел Толя за 10 мин;
2) 900 + 300 = 1200 (м) − расстояние между школой и стадионом.
Выражение:
90 * 10 + 300 = 900 + 300 = 1200 (м)
Ответ: 1200 м.

б) 1) 1800 − 600 = 1200 (м) − прошел Николай;
2) 1200 : 12 = 100 (м/мин) − скорость Николая.
Выражение:
(1800 − 600) : 12 = 1200 : 12 = 100 (м/мин)
Ответ: 100 м/мин.

112. а) Электричка идет из города Павловска со скоростью 55 км/ч. Пассажир сел в электричку на станции, находящейся в 27 км от Павловска. На каком расстоянии от города он будет через 2 ч?
б) Автомобиль выехал из одного города в другой и едет со скоростью 85 км/ч. Расстояние между городами 360 км. Сколько километров ему останется проехать после 3 ч пути?

Решение

а) 1) 55 * 2 = 110 (км) − проедет электричка за 2 часа;
2) 110 + 27 = 137 (км) − расстояние, на котором будет электричка от города через 2 часа.
Выражение:
55 * 2 + 27 = 110 + 27 = 137 (км)
Ответ: 137 км.

б) 1) 85 * 3 = 255 (км) − проедет автомобиль за 3 часа;
2) 360 − 255 = 105 (км) − останется проехать автомобилю после 3 часов пути.
Выражение:
360 − 85 * 3 = 360 − 255 = 105 (км)
Ответ: 105 км.

!113. Выполните действия:
а) 19857 − (29716 : 68 + 192 * 64);
б) 17775 + (601 * 508 − 11094 : 86);
в) (678 + 1125 : 75) * 64 − 32702;
г) 17814 + (2209 : 47 + 862) * 14.

Решение

а) $19857 \overset{4}{-} (29716 \overset{1}{:} 68 \overset{3}{+} 192 \overset{2}{*} 64) = 19857 - (437 + 12288) = 19857 - 12725 = 7132$

б) $17775 \overset{4}{+} (601 \overset{1}{*} 508 \overset{3}{-} 11094 \overset{2}{:} 86) = 17775 + (305308 - 129) = 17775 + 305179 = 322954$

в) $(678 \overset{2}{+} 1125 \overset{1}{:} 75) \overset{3}{*} 64 \overset{4}{-} 32702 = (678 + 15) * 64 - 32702 = 693 * 64 - 32702 = 44352 - 32702 = 11650$

г) $17814 \overset{4}{+} (2209 \overset{1}{:} 47 \overset{2}{+} 862) \overset{3}{*} 14 = 17814 + (47 + 862) * 14 = 17814 + 909 * 14 = 17814 + 12726 = 30540$

!114. Выполните действия:
а) 215 * (368 − 274) * (78 + 8664 : 76);
б) (8034 : 78 + 256) + 68 * (127 + 128);
в) 4080 − (352719 − 57837) : 98 + 307 * 107;
г) 988 + 1530 * (12 * 6 − 38) * 15.

Решение

а) $215 \overset{4}{*} (368 \overset{1}{-} 274) \overset{5}{*} (78 \overset{3}{+} 8664 \overset{2}{:} 76) = 215 * 94 * (78 + 114) = 20210 * 192 = 3880320$

б) $(8034 \overset{1}{:} 78 \overset{2}{+} 256) \overset{5}{+} 68 \overset{4}{*} (127 \overset{3}{+} 128) = (103 + 256) + 68 * 255 = 359 + 17340 = 17699$

в) $4080 \overset{4}{-} (352719 \overset{1}{-} 57837) \overset{2}{:} 98 \overset{5}{+} 307 \overset{3}{*} 107 = 4080 - 294882 : 98 + 307 * 107 = 4080 - 3009 + 32849 = 1071 + 32849 = 33920$

г) $988 \overset{5}{+} 1530 \overset{3}{*} (12 \overset{1}{*} 6 \overset{2}{-} 38) \overset{4}{*} 15 = 988 + 1530 * (72 - 38) * 15 = 988 + 1530 * 34 * 15 = 988 + 52020 * 15 = 988 + 780300 = 781288$

!115. Выполните действия:
а) (7470 : 18 − 319) + (103 * 20 − 24 * 45) : 28;
б) 21 * 55 + (107209 − 21696) − (78 + 8664 : 76);
в) (900 − 654 : 6) * 7 + 6 * (571 − 24 * 23);
г) (873 − 6036 : 12) * 12 − 2 * (48 * 7 + 344).

Решение

а) $(7470 \overset{1}{:} 18 \overset{2}{-} 319) \overset{7}{+} (103 \overset{3}{*} 20 \overset{5}{-} 24 \overset{4}{*} 45) \overset{6}{:} 28 = (415 - 319) + (2060 - 1080) : 28 = 96 + 980 : 28 = 96 + 35 = 131$

б) $21 \overset{4}{*} 55 \overset{5}{+} (107209 \overset{1}{-} 21696) \overset{6}{-} (78 \overset{3}{+} 8664 \overset{2}{:} 76) = 1155 + 85513 - (78 + 114) = 1155 + 85513 - 192 = 86668 - 192 = 86476$

в) $(900 \overset{2}{-} 654 \overset{1}{:} 6) \overset{5}{*} 7 \overset{7}{+} 6 \overset{6}{*} (571 \overset{4}{-} 24 \overset{3}{*} 23) = (900 - 109) * 7 + 6 * (571 - 552) = 791 * 7 + 6 * 19 = 5537 + 114 = 5651$

г) $(873 \overset{2}{-} 6036 \overset{1}{:} 12) \overset{5}{*} 12 \overset{7}{-} 2 \overset{6}{*} (48 \overset{3}{*} 7 \overset{4}{+} 344) = (873 - 503) * 12 - 2 * (336 + 344) = 370 * 12 - 2 * 680 = 4440 - 1360 = 3080$

116. а) Фирма за 30 дней должна была сшить 2400 пиджаков. На выполнение заказа были взяты дополнительные люди, поэтому в день шили на 20 пиджаков больше, чем планировали. На сколько дней раньше срока был выполнен этот заказ?
б) Семья Петровых часто ездит на автомобиле в гости к своим родственникам в соседний город, расстояние до которого 240 км. Обычно они тратят на дорогу 4 ч. На сколько меньше времени уходило бы у них на дорогу, если бы они ехали со скоростью, на 20 км/ч большей?

Решение

а) 1) 2400 : 30 = 80 (п.) − в день должна была шить фирма;
2) 80 + 20 = 100 (п.) − в день шила фирма;
3) 2400 : 100 = 24 (д.) − выполнялся заказ;
4) 30 − 24 = на 6 (д.) − раньше срока был выполнен заказ.
Ответ: на 6 дней.

б) 1) 240 : 4 = 60 (км/ч) − обычная скорость автомобиля;
2) 60 + 20 = 80 (км/ч) − увеличенная скорость автомобиля;
3) 240 : 80 = 3 (ч) − тратила бы семья Петровых на дорогу с увеличенной скоростью;
4) 4 − 3 = на 1 (ч) − меньше времени уходило бы на дорогу.
Ответ: на 1 час.

18

117. а) Электричка идет из города Солнечного в город Радужный, расстояние до которого 230 км, со скоростью 60 км/ч. Пассажир сел в электричку на станции, находящейся в 17 км от Солнечного. На каком расстоянии от города Радужного он будет через 3 ч?
б) Шоссе от Москвы до Санкт−Петербурга проходит через Тверь. Автобус выехал из Твери в сторону Санкт−Петербурга со скоростью 65 км/ч. На каком расстоянии от Санкт−Петербурга будет автобус через 5 ч, если расстояние от Москвы до Санкт−Петербурга равно 700 км, а до Твери − 170 км?

Решение

а) 1) 60 * 3 = 180 (км) − проедет электричка за 3 часа;
2) 180 + 17 = 197 (км) − от города Солнечного будет пассажир через 3 часа;
3) 230 − 197 = 33 (км) − расстояние, на котором будет пассажир от города Радужного через 3 часа.
Ответ: 33 км.

б) 1) 65 * 5 = 325 (км) − проедет автобус за 5 часов;
2) 700 − 170 = 530 (км) − расстояние от Твери до Санкт−Петербурга;
3) 530 − 325 = 205 (км) − расстояние, на котором будет автобус через 5 часов от Санкт−Петербурга.
Ответ: 205 км.

118. а) Два мастера работают на фабрике елочных украшений. Один из них расписывают 20 елочных шаров в час, а другой − 25. Успеют ли они выполнить заказ по раскрашиванию 1500 шаров, если первый будет работать 5 дней по 8 ч в день, а второй − 4 дня по 6 ч в день?
б) Два мастера работают на фабрике елочных украшений. Один из них работал 12 дней по 7 ч в день, другой − 10 дней по 8 ч, и вместе они расписали 2880 елочных шаров. Сколько шаров в час расписывал первый мастер, если второй расписывал по 15 шаров в час?

Решение

а) 1) 5 * 8 = 40 (ч) − будет работать первый мастер;
2) 20 * 40 = 800 (ш.) − сделает первый мастер за 5 дней;
3) 4 * 6 = 24 (ч) − будет работать второй мастер;
4) 25 * 24 = 600 (шариков) − сделает второй мастер за 4 дня;
5) 800 + 600 = 1400 (ш.) − сделают оба мастера;
6) 1400 < 1500 − значит, два мастера не успеют выполнить заказ.
Ответ: нет, не успеют.

б) 1) 12 * 7 = 84 (ч) − работал первый мастер;
2) 10 * 8 = 80 (ч) − работал второй мастер;
3) 15 * 80 = 1200 (ш.) − расписал второй мастер;
4) 2880 − 1200 = 1680 (ш.) − расписал первый мастер;
5) 1680 : 84 = 20 (ш.) − в час расписывал первый мастер.
Ответ: 20 шаров.

119. а) Пакет, в котором 4 яблока и 10 слив, весит 600 г, а пакет, в котором 2 яблока и 10 слив, весит 400 г. Сколько весит одно яблоко и сколько весит одна слива?
б) Известно, что 2 большие коробки яиц и 4 маленькие стоят на 52 р. меньше, чем 2 большие коробки и 6 маленьких. Сколько стоит одна большая коробка яиц и одна маленькая, если известно, что большая коробка на 8 р. дороже маленькой?

Решение

а) 1) 600 − 400 = 200 (г) − весят 2 яблока;
2) 200 : 2 = 100 (г) − весит 1 яблоко;
3) 400 − 200 = 200 (г) − весят 10 слив;
4) 200 : 10 = 20 (г) − весит 1 слива.
Ответ: 100 г весит яблоко; 20 г весит слива.

б) 1) 6 − 4 = 2 (маленькие коробки) − стоят 52 рубля;
2) 52 : 2 = 26 (р.) − стоит одна маленькая коробка;
3) 26 + 8 = 34 (р.) − стоит одна большая коробка.
Ответ: 26 р. и 34 р.

120. а) Компьютер и монитор вместе стоят 12000 р., монитор и принтер − 7000 р., а компьютер и принтер − 9400 р. Сколько стоят компьютер, принтер и монитор вместе?
б) Петя, Коля и Слава поочередно парами становились на весы. Петя и Коля вместе весят 55 кг, Коля и Слава вместе − 58 кг, а Петя и Слава − 59 кг. Сколько весит каждый мальчик?

Решение

а) 1) 12000 + 7000 + 9400 = 19000 + 9400 = 28400 (р.) − стоят два компьютера, два монитора и два принтера;
2) 28400 : 2 = 14200 (р.) − стоят компьютер, принтер и монитор вместе.
Ответ: 14200 рублей.

б) 1) 55 + 58 + 59 = 172 (кг) − удвоенный вес мальчиков;
2) 172 : 2 = 86 (кг) − весят мальчики вместе;
3) 86 − 55 = 31 (кг) − весит Слава;
4) 86 − 58 = 28 (кг) − весит Петя;
5) 86 − 59 = 27 (кг) − весит Коля.
Ответ: 31 кг − Слава; 28 кг − Петя; 27 кг − Коля.

Самостоятельная работа № 4

Вариант 1

1. Найдите значение выражения
15 * (300 − 252 : 14) : 9.

Решение

$15 \overset{3}{*} (300 \overset{2}{-} 252 \overset{1}{:} 14) \overset{4}{:} 9 = 15 * (300 - 18) : 9 = 15 * 282 : 9 = 4230 : 9 = 470$

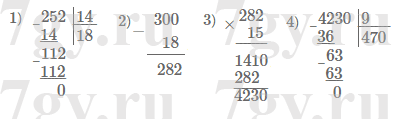
2. Запишите выражение и найдите его значение:
частное числа 855 и разности чисел 95 и 86.

Решение

855 : (95 − 86) = 855 : 9 = 95
1) 95 − 86 = 9;
2)
_855 |9  
  81   |95
 _45
   45
     0

3. Турист вышел из гостиницы и пошел к пристани со скоростью 60 м/мин. Через 15 мин ему осталось пройти 400 м. На каком расстоянии от пристани находится гостиница? Выразите расстояние в километрах и метрах.

Решение

1) 60 * 15 = 900 (м) − прошел турист за 15 минут;
2) 900 + 400 = 1300 (м) = 1 км 300 м − от пристани находится гостиница.
Выражение:
60 * 15 + 400 = 900 + 400 = 1300 (м)
Ответ: 1 км 300 м.

19

Вариант 2

1. Найдите значение выражения
6600 : (300 − 15 * 9) + 165.

Решение

$6600 \overset{3}{:} (300 \overset{2}{-} 15 \overset{1}{*} 9) \overset{4}{+} 165 = 6600 : (300 - 135) + 165 = 6600 : 165 + 165 = 40 + 165 = 205$

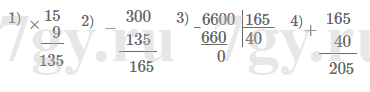
2. Запишите выражение и найдите его значение:
произведение суммы чисел 59 и 46 и меньшего из этих чисел.

Решение

(59 + 46) * 46 = 105 * 46 = 4830
1) +59
      46
    105
2) × 105
         46
       630
     420   
     4830

3. Студент вышел из института и пошел на стадион, расстояние до которого 1 км 300 м. Через 14 мин ему осталось пройти 250 м. Определите скорость (в м/мин), с которой шел студент.

Решение

1 км 300 м = 1300 м
1) 1300 − 250 = 1050 (м) − прошел студент за 14 минут;
2) 1050 : 14 = 75 (м/мин) − скорость студента.
Выражение:
(1300 − 250) : 14 = 1050 : 14 = 75 (м/мин)
Ответ: 75 м/мин.

ГДЗ к теме Степень числа

121. Запишите произведение в виде степени:
а) 5 * 5 * 5 * 5 * 5 * 5;
б) 10 * 10 * 10 * 10;
в) 2 * 2 * 2 * 2 * 2 * 2 * 2;
г) $\underbrace{3 * 3 * ... * 3}_{15-множ.}$;
д) $\underbrace{8 * 8 * ... * 8}_{100-множ.}$;
е) $\underbrace{10 * 10 * ... * 10}_{20-множ.}$.

Решение

а) $5 * 5 * 5 * 5 * 5 * 5 = 5^6$

б) $10 * 10 * 10 * 10 = 10^4$

в) $2 * 2 * 2 * 2 * 2 * 2 * 2 = 2^7$

г) $\underbrace{3 * 3 * ... * 3}_{15-множ.} = 3^{15}$

д) $\underbrace{8 * 8 * ... * 8}_{100-множ.} = 8^{100}$

е) $\underbrace{10 * 10 * ... * 10}_{20-множ.} = 10^{20}$

122. Какое из следующих выражений можно записать в виде степени $6^7$?
1) 6 + 6 + 6 + 6 + 6 + 6 + 6;
2) 7 * 7 * 7 * 7 * 7 * 7;
3) 6 * 6 * 6 * 6 * 6 * 6 * 6;
4) 6 * 7.

Решение

$6 * 6 * 6 * 6 * 6 * 6 * 6 = 6^7$

123. Запишите выражение и найдите его значение:
а) 2 в пятой степени;
б) 5 в четвертой степени;
в) 4 в квадрате;
г) 8 в кубе.

Решение

а) $2^5 = 2 * 2 * 2 * 2 * 2 = 4 * 4 * 2 = 16 * 2 = 32$

б) $5^4 = 5 * 5 * 5 * 5 = 25 * 25 = 625$

в) $4^2 = 4 * 4 = 16$

г) $8^3 = 8 * 8 * 8 = 64 * 8 = 512$

124. Запишите в виде произведения и вычислите:
а) $7^2$;
б) $6^3$;
в) $12^3$;
г) $11^3$.

Решение

а) $7^2 = 7 * 7 = 49$

б) $6^3 = 6 * 6 * 6 = 36 * 6 = 216$

в) $12^3 = 12 * 12 * 12 = 144 * 12 = 1728$

г) $11^3 = 11 * 11 * 11 = 121 * 11 = 1331$

125. Запишите в виде произведения и вычислите:
а) $90^2$;
б) $20^3$;
в) $120^2$;
г) $600^3$.

Решение

а) $90^2 = 90 * 90 = 8100$

б) $20^3 = 20 * 20 * 20 = 400 * 20 = 8000$

в) $120^2 = 120 * 120 = 14400$

г) $600^3 = 600 * 600 * 600 = 36000 * 600 = 21600000$

126. Сравните значения выражений:
а) $2^3$ и $3^2$;
б) $4^2$ и $2^4$;
в) $4^2$ и $3^3$;
г) $4^3$ и $5^3$.

Решение

а) $2^3 = 2 * 2 * 2 = 8$;
$3^2 = 3 * 3 = 9$;
8 < 9;
$2^3 < 3^2$.

б) $4^2 = 4 * 4 = 16$;
$2^4 = 2 * 2 * 2 * 2 = 4 * 4 = 16$;
16 = 16;
$4^2 = 2^4$.

в) $4^2 = 4 * 4 = 16$;
$3^3 = 3 * 3 * 3 = 9 * 3 = 27$;
16 < 27;
$4^2 < 3^3$.

г) $4^3 = 4 * 4 * 4 = 16 * 4 = 64$;
$5^3 = 5 * 5 * 5 = 25 * 5 = 125$;
64 < 125;
$4^3 < 5^3$.

127. Начертите в тетради таблицу и заполните ее:

Решение

20

128. Начертите в тетради таблицу и заполните ее:

Решение

$1^2 = 1 * 1 = 1$;
$1^3 = 1 * 1 * 1 = 1$.

$2^2 = 2 * 2 = 4$;
$2^3 = 2 * 2 * 2 = 8$.

$3^2 = 3 * 3 = 9$;
$3^3 = 3 * 3 * 3 = 27$.

$4^2 = 4 * 4 = 16$;
$4^3 = 4 * 4 * 4 = 16 * 4 = 64$.

$5^2 = 5 * 5 = 25$;
$5^3 = 5 * 5 * 5 = 25 * 5 = 125$.

$6^2 = 6 * 6 = 36$;
$6^3 = 6 * 6 * 6 = 36 * 6 = 216$.

$7^2 = 7 * 7 = 49$;
$7^3 = 7 * 7 * 7 = 49 * 7 = 343$.

$8^2 = 8 * 8 = 64$;
$8^3 = 8 * 8 * 8 = 64 * 8 = 512$.

$9^2 = 9 * 9 = 81$;
$9^3 = 9 * 9 * 9 = 81 * 9 = 729$.

$10^2 = 10 * 10 = 100$;
$10^3 = 10 * 10 * 10 = 1000$.

х         1 2 3   4    5    6     7     8     9     10
$х^2$ 1 4 9  16   25  36   49   64   81   100
$х^3$ 1 8 27 64 125 216 343 512 729 1000

129. а) Запишите в виде квадрата некоторого числа: 25; 144; 121; 225.
б) Запишите в виде куба некоторого числа: 1; 125; 512; 1000.

Решение

а) $25 = 5^2$;
$144 = 12^2$;
$121 = 11^2$;
$225 = 15^2$.

б) $1 = 1^3$;
$5 = 5^3$;
$512 = 8^3$;
$1000 = 10^3$.

130. Числовая последовательность состоит из пяти чисел и строится по такому правилу: первое число равно 10, а каждое следующее в 10 раз больше предыдущего. Запишите эту последовательность. Представьте ее члены:
а) в виде степеней числа 10;
б) в виде натуральных чисел.

Решение

а) $10; 10^2; 10^3; 10^4; 10^5$.

б) 10; 100; 1000; 10000; 10000.

131. Определите, по какому правилу составлена последовательность чисел, и запишите следующие три числа:
а) 1; 4; 9; 16; ...;
б) 1; 8; 27; ... .
Найдите сотое число в каждое последовательности.

Решение

а) Закономерность: записана последовательность квадратов натуральных чисел.
1; 4; 9; 16; 25; 36; 49.
$100^2 = 10000$ − сотое число.

б) Закономерность: записана последовательность кубов натуральных чисел.
1; 8; 27; 64, 125, 216.
$100^3 = 1000000$ − сотое число.

132. Представьте число в виде суммы разрядных слагаемых, используя степени числа 10:
а) 672;
б) 2534;
в) 1983;
г) 7045.

Решение

а) $672 = 6 * 100 + 7 * 10 + 2 = 6 * 10^2 + 7 * 10 + 2$

б) $2534 = 2 * 1000 + 5 * 100 + 3 * 10 + 4 = 2 * 10^3 + 5 * 10^2 + 3 * 10 + 4$

в) $1983 = 1 * 1000 + 9 * 100 + 8 * 10 + 3 = 1 * 10^3 + 9 * 10^2 + 8 * 10 + 3$

г) $7045 = 7 * 1000 + 0 * 10^2 + 4 * 10 + 5 = 7 * 10^3 + 4 * 10 + 5$

133. Запишите число, которое представлено в виде суммы разрядных слагаемых:
а) $5 * 10^2 + 4 * 10 + 8$;
б) $9 * 10^2 + 0 * 10 + 5$;
в) $2 * 10^3 + 8 * 10^2 + 7 * 10 + 3$;
г) $1 * 10^3 + 3 * 10^2 + 0 * 10 + 2$.

Решение

а) $5 * 10^2 + 4 * 10 + 8 = 548$

б) $9 * 10^2 + 0 * 10 + 5 = 905$

в) $2 * 10^3 + 8 * 10^2 + 7 * 10 + 3 = 2873$

г) $1 * 10^3 + 3 * 10^2 + 0 * 10 + 2 = 1302$

134. Найдите значение выражения:
а) $3 * 4^2$;
б) $6 * 2^4$;
в) $27 : 3^2$;
г) $250 : 5^3$.

Решение

а) $3 * 4^2 = 3 * 16 = 48$

б) $6 * 2^4 = 6 * 16 = 96$

в) $27 : 3^2 = 27 : 9 = 3$

г) $250 : 5^3 = 250 : 125 = 2$

135. Вычислите:
а) $79 + 11^3$;
б) $(113 - 108)^3$;
в) $3 * 15^2$;
г) $(3 * 6)^2$.

Решение

а) $79 + 11^3 = 79 + 121 * 11 = 79 + 1331 = 1410$

$\snippet{name: column_multiplication, x: 121, y: 11}$

б) $(113 - 108)^3 = 5^3 = 125$

в) $3 * 15^2 = 3 * 225 = 675$

г) $(3 * 6)^2 = 18^2 = 324$

136. Найдите значение выражения:
а) $100 - 12^2 : 3$;
б) $5 * 4^3 - 319$;
в) $25 * 11 - 16^2$;
г) $600 - 750 : 5^3$.

Решение

а) $100 - 12^2 : 3 = 100 - 144 : 3 = 100 - 48 = 52$

б) $5 * 4^3 - 319 = 5 * 64 - 319 = 320 - 319 = 1$

в) $25 * 11 - 16^2 = 275 - 256 = 19$

г) $600 - 750 : 5^3 = 600 - 750 : 125 = 600 - 6 = 594$

137. Найдите значение выражения:
а) $(76 - 66)^3 * 18$;
б) $(14 + 36) * 11^2$;
в) $(16 + 180 : 12)^2$;
г) $904 + (12 * 3)^2$.

Решение

а) $(76 - 66)^3 * 18 = 10^3 * 18 = 1000 * 18 = 18000$

б) $(14 + 36) * 11^2 = 50 * 121 = 6050$

в) $(16 + 180 : 12)^2 = (16 + 15)^2 = 31^2 = 961$

г) $904 + (12 * 3)^2 = 904 + 36^2 = 904 + 1296 = 2200$

138. Найдите значение выражения:
а) $1^2 + 2^2 + 3^2 + 4^2 + 5^2$;
б) $1^3 + 2^3 + 3^3 + 4^3 + 5^3$.

Решение

а) $1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 1 + 4 + 9 + 16 + 25 = 14 + 16 + 25 = 30 + 25 = 55$

б) $1^3 + 2^3 + 3^3 + 4^3 + 5^3 = 1 + 8 + 27 + 64 + 125 = 36 + 64 + 125 = 100 + 125 = 225$

139. Проверьте равенство:
а) $2^3 + 2^5 + 2^6 + 2^7 + 2^8 + 2^9 = 1000$;
б) $11^3 + 12^3 + 13^3 + 14^3 = 8000$.

Решение

а) $2^3 + 2^5 + 2^6 + 2^7 + 2^8 + 2^9 = 8 + 32 + 64 + 128 + 256 + 512 = 40 + 320 + 640 = 1000$
1000 = 1000 − равенство верно.

б) $11^3 + 12^3 + 13^3 + 14^3 = 121 * 11 + 144 * 12 + 169 * 13 + 196 * 14 = 1331 + 1728 + 2197 + 2744 = 3059 + 4941 = 8000$
8000 = 8000 − равенство верно.

140. Какой показатель степени надо вписать вместо звездочки, чтобы получилось верное равенство:
а) $8^* = 512$;
б) $2^* = 64$;
в) $3^* = 81$;
г) $7^* = 343$?

Решение

а) $8^3 = 8 * 8 * 8 = 64 * 8 = 512$

б) $2^6 = 2 * 2 * 2 * 2 * 2 * 2 = 8 * 8 = 64$

в) $3^4 = 81 = 3 * 3 * 3 * 3 = 9 * 9 = 81$

г) $7^3 = 7 * 7 * 7 = 49 * 7 = 343$

21

141. Выполните прикидку результата, округлив основание степени до старшего разряда:
а) $26^2$;
б) $18^2$;
в) $117^2$;
г) $485^2$.
Образец.
$59^2 ≈ 60^2 = 3600$

Решение

а) $26^2 ≈ 30^2 = 900$

б) $18^2 ≈ 20^2 = 400$

в) $117^2 ≈ 120^2 = 14400$

г) $485^2 ≈ 500^2 = 250000$

142. Используя прикидку, объясните, почему возведение в степень выполнено неверно:
а) $22^2 = 4084$;
б) $66^2 = 43056$;
в) $11^3 = 10331$;
г) $49^3 = 17649$.

Решение

а) $22^2 = 4084$
$22^2 ≈ 20^2 = 400$ − решение неверно.

б) $66^2 = 43056$
$66^2 ≈ 70^2 = 4900$ − решение неверно.

в) $11^3 = 10331$
$11^3 ≈ 10^3 = 1000$ − решение неверно.

г) $49^3 = 17649$
$49^3 ≈ 50^3 = 125000$ − решение неверно.

143. Определите, какой цифрой оканчиваются степени числа 6; степени числа 5. Пользуясь сделанным выводом, определите, какой цифрой оканчивается число $5^{10}; 35^7; 6^8; 236^5$.

Решение

$6^1 = 6$;
$6^2 = 36$;
$6^3 = 196$ − все степени числа 6 оканчиваются на 6, значит:
$6^8$ − оканчивается на 6;
$236^5$ − оканчивается на 6.

$5^1 = 5$;
$5^2 = 25$;
$5^3 = 125$ − все степени числа 5 оканчиваются на 5, значит:
$5^{10}$ − оканчивается на 5;
$35^7$ − оканчивается на 5.

144. 1) Определите, какой цифрой могут оканчиваться степени числа 2. Для этого выясните, какой цифрой оканчиваются значения степеней $2^1; 2^2; 2^3; 2^4; 2^5; 2^6$.
2) Подметьте закономерность в последовательности цифр в предыдущем задании и определите, какой цифрой оканчивается число $2^{10}; 2^{15}; 2^{17}$.

Решение

1) $2^1 = 2$;
$2^2 = 4$;
$2^3 = 8$;
$2^4 = 16$;
$2^5 = 32$;
$2^6 = 64$.
Степени числа 2 могут оканчиваться цифрами: 2, 4, 8, 6.

2) Закономерность: 2, 4, 8, 6, 2, 4, 8, 6, .... , то есть через каждые четыре цифры порядок повторяется.
Тогда:
$2^{10}$
10 : 4 = 2 (ост.2) − оканчивается на 4.
$2^{15}$
15 : 4 = 3 (ост.3) − оканчивается на 8.
$2^{17}$
17 : 4 = 4 (ост.1) − оканчивается на 2.

145. Определите, какой цифрой могут оканчиваться степени числа 4. Пользуясь подмеченной закономерностью, определите, какой цифрой оканчивается число $4^{9}; 4^{22}; 4^{101}; 4^{200}$.

Решение

$4^1 = 4$;
$4^2 = 16$;
$4^3 = 64$;
$4^4 = 256$.
Нечетная степень числа 4 оканчивается на 4, а четная степень на 6, тогда:
$4^{9}$ − оканчивается на 4;
$4^{22} - оканчивается на 6$;
$4^{101} - оканчивается на 4$;
$4^{200} - оканчивается на 6$.

Самостоятельная работа № 5

Вариант 1

1. Запишите выражение и найдите его значение:
а) три в четвертой степени;
б) восемь в квадрате.

Решение

а) $3^4 = 3 * 3 * 3 * 3 = 9 * 9 = 81$

б) $8^2 = 8 * 8 = 64$

2. Сравните значения выражений:
$5^3$ и $3^5$.

Решение

В учебнике опечатка, скорее всего пример должен выглядеть так:
$5^3 = 5 * 5 * 5 = 25 * 5 = 125$;
$3^5 = 3 * 3 * 3 * 3 * 3 = 9 * 9 * 3 = 81 * 3 = 243$;
125 < 243;
$5^3 < 3^5$.

3. Найдите значение выражения:
а) $16 + 4^2$;
б) $42 - 12^2 : 4$.

Решение

а) В учебнике опечатка, скорее всего пример должен выглядеть так:
$16 + 4^2 = 16 + 16 = 32$

б) В учебнике опечатка, скорее всего пример должен выглядеть так:
$42 - 12^2 : 4 = 42 - 144 : 4 = 42 - 36 = 6$

Вариант 2

1. Запишите выражение и найдите его значение:
а) два в пятой степени;
б) пять в кубе.

Решение

а) $2 * 5 = 2 * 2 * 2 * 2 * 2 = 4 * 4 * 2 = 16 * 2 = 32$

б) $5^3 = 5 * 5 * 5 = 25 * 5 = 125$

2. Сравните значения выражений:
$4^4$ и $8^2$

Решение

В учебнике опечатка, скорее всего пример должен выглядеть так:
$4^4 = 4 * 4 * 4 * 4$;
$8^2 = 8 * 8 = 4 * 2 * 4 * 2$;
4 * 4 * 4 * 4 > 4 * 2 * 4 * 2;
$4^4 > 8^2$.

3. Найдите значение выражения:
а) $33 - 3^3$;
б) $2 * 15^2 + 5$.

Решение

а) В учебнике опечатка, скорее всего пример должен выглядеть так:
$33 - 3^3 = 33 - 27 = 6$

б) В учебнике опечатка, скорее всего пример должен выглядеть так:
$2 * 15^2 + 5 = 2 * 225 + 5 = 450 + 5 = 455$

ГДЗ к теме Задачи на движение

146. Используя рисунок 2, вычислите для каждого случая скорость сближения или удаления.

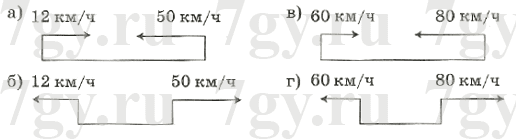
Решение

а) 12 + 50 = 62 (км/ч)
Ответ: 62 км/ч − скорость сближения.

б) 12 + 50 = 62 (км/ч)
Ответ: 62 км/ч − скорость удаления.

в) 60 + 80 = 140 (км/ч)
Ответ: 140 км/ч − скорость сближения.

г) 60 + 80 = 140 (км/ч)
Ответ: 140 км/ч − скорость удаления.

22

147. Со станции одновременно в противоположных направлениях отправились два поезда. Скорость одного из них 43 км/ч, другого − 56 км/ч. Какое расстояние будет между ними:
а) через 1 ч;
б) через 2 ч;
в) через 5 ч?
Для каждого случая запишите выражение.

Решение

а) (43 + 56) * 1 = 99 * 1 = 99 (км) − будет между поездами через 1 час.
Ответ: 99 км

б) (43 + 56) * 2 = 99 * 2 = 198 (км) − будет между поездами через 2 часа.
Ответ: 198 км

в) (43 + 56) * 5 = 99 * 5 = 495 (км) − будет между поездами через 5 часов.
Ответ: 495 км

148. От двух станций, расстояние между которыми 30 км, одновременно в противоположных направлениях, удаляясь друг от друга, отправляются два поезда. Один идет со скоростью 55 км/ч, другой − 70 км/ч. Какое расстояние будет между ними:
а) через 1 ч;
б) через 3 ч;
в) через 6 ч?

Решение

а) (55 + 70) * 1 + 30 = 125 * 1 + 30 = 125 + 30 = 155 (км) − будет между поездами через 1 ч.
Ответ: 155 км

б) (55 + 70) * 3 + 30 = 125 * 3 + 30 = 375 + 30 = 405 (км) − будет между поездами через 3 ч.
Ответ: 405 км

в) (55 + 70) * 6 + 30 = 125 * 6 + 30 = 750 + 30 = 780 (км) − будет между поездами через 6 ч.
Ответ: 780 км.

149. Из одного пункта в противоположных направлениях выезжают автобус и автомобиль. Скорость автобуса 45 км/ч, а автомобиля 55 км/ч. Через какое время расстояние между ними будет равно:
а) 200 км;
б) 300 км;
в) 400 км?

Решение

а) 200 : (45 + 55) = 200 : 100 = 2 (ч) − время, через которое между автобусом и автомобилем будет 200 км.
Ответ: через 2 часа.

б) 300 : (45 + 55) = 300 : 100 = 3 (ч) − время, через которое между автобусом и автомобилем будет 300 км.
Ответ: через 3 часа

в) 400 : (45 + 55) = 400 : 100 = 4 (ч) − время, через которое между автобусом и автомобилем будет 400 км.
Ответ: через 4 часа.

150. а) От железнодорожной станции до поселка 72 км. От станции и из поселка одновременно навстречу друг другу выехали два велосипедиста. Один из них едет со скоростью 13 км/ч, другой − 11 км/ч. Через сколько часов велосипедисты встретятся, если будут ехать без остановок?
б) Две моторные лодки одновременно отправляются навстречу друг другу от двух пристаней, расстояние между которыми 88 км. Одна из них движется со скоростью 24 км/ч, скорость другой на 4 км/ч меньше. Через сколько часов они встретятся?

Решение

а) 72 : (13 + 11) = 72 : 24 = 3 (ч) − время, через которое встретятся велосипедисты.
Ответ: через 3 часа.

б) 1) 24 − 4 = 20 (км/ч) − скорость второй лодки;
2) 88 : (24 + 20) = 88 : 44 = 2 (ч) − время, через которое встретятся лодки.
Ответ: через 2 часа.

151. а) Два автомобиля выехали одновременно навстречу друг другу и через 3 ч встретились. Один автомобиль ехал со скоростью 80 км/ч, другой − 90 км/ч. Какое расстояние было между ними в начале пути? Решите задачу двумя способами.
б) Два туриста вышли одновременно из двух пунктов и отправились по шоссе навстречу друг другу. Один шел пешком со скоростью 5 км/ч, другой ехал на велосипеде со скоростью на 10 км/ч большей. Какое расстояние было между ними в начале пути, если они встретились через 2 ч? Решите задачу двумя способами.

Решение

а) Способ 1.
1) 80 + 90 = 170 (км/ч) − скорость сближения автомобилей;
2) 170 * 3 = 510 (км) − расстояние между автомобилями в начале пути.
Ответ: 510 км.

Способ 2.
1) 80 * 3 = 240 (км) − проехал до встречи первый автомобиль;
2) 90 * 3 = 270 (км) − проехал до встречи второй автомобиль;
3) 240 + 270 = 510 (км) − расстояние между автомобилями в начале пути.
Ответ: 510 км.

б) Способ 1.
1) 5 + 10 = 15 (км/ч) − скорость велосипедиста;
2) 5 + 15 = 20 (км/ч) − скорость сближения;
3) 20 * 2 = 40 (км) − расстояние между туристами в начале пути.
Ответ: 40 км.

Способ 2.
1) 5 + 10 = 15 (км/ч) − скорость велосипедиста;
2) 5 * 2 = 10 (км) − прошел до встречи пешеход;
3) 15 * 2 = 30 (км) − прошел до встречи велосипедист.
4) 20 * 2 = 40 (км) − расстояние между туристами в начале пути.
Ответ: 40 км.

152. а) Из двух сел, расстояние между которыми 28 км, одновременно навстречу друг другу вышли два пешехода. Один шел со скоростью 4 км/ч, другой − со скоростью 5 км/ч. Какое расстояние будет между ними через 3 ч?
б) Два поезда движутся навстречу друг другу со скоростями 60 км/ч и 80 км/ч. На каком расстоянии друг от друга будут они за 1 ч до встречи? за 2 ч до встречи?

Решение

а) 1) 4 + 5 = 9 (км/ч) − скорость сближения пешеходов;
2) 9 * 3 = 27 (км) − пройдут пешеходы через 3 часа;
3) 28 − 27 = 1 (км) − будет между пешеходами через 3 часа.
Ответ: 1 км.

б) 1) 60 + 80 = 140 (км/ч) − скорость сближения;
2) 140 * 1 = 140 (км) − будет между поездами за 1 час до встречи;
3) 140 * 2 = 280 (км) − будет между поездами за 2 часа до встречи.
Ответ: 140 км; 280 км.

153. а) Расстояние между туристическими базами равно 36 км. Группы туристов преодолевают это расстояние на лыжах за 6 ч, а на скутерах в 2 раза быстрее. От этих баз одновременно навстречу друг другу отправляются две группы − одна на скутерах, другая на лыжах. Через какое время они встретятся?
б) Из двух городов навстречу друг другу вышли скорый и товарный поезда. Товарный поезд едет в 2 раза медленнее. Скорый поезд преодолевает расстояние между городами, равное 1080 км, за 9 ч. Через какое время поезда встретятся?

Решение

а) 1) 36 : 6 = 6 (км/ч) − скорость туристов на лыжах;
2) 6 * 2 = 12 (км/ч) − скорость туристов на скутерах;
3) 6 + 12 = 18 (км/ч) − скорость сближения групп;
4) 36 : 18 = 2 (ч) − время, через которое встретятся две группы.
Ответ: через 2 часа.

б) 1) 1080 : 9 = 120 (км/ч) − скорость скорого поезда;
2) 120 : 2 = 60 (км/ч) − скорость товарного поезда;
3) 120 + 60 = 180 (км/ч) − скорость сближения поездов;
4) 1080 : 180 = 6 (ч) − время, через которое поезда встретятся.
Ответ: через 6 часов.

23

154. От автобусной станции отошел автобус со скоростью 40 км/ч. Через час от этой же станции в противоположном направлении вышел другой автобус, скорость которого 60 км/ч.
1) Какое расстояние будет между автобусами через 3 ч после выхода первого автобуса?
2) Через какое время после второго автобуса расстояние между ними будет равно 140 км?
3) Через какое время после выхода первого автобуса расстояние между ними будет равно 240 км?

Решение

1. 1) 40 + 60 = 100 (км/ч) − скорость удаления автобусов;
    2) 40 * 1 = 40 (км) − будет между автобусами через 1 час после выезда первого;
    3) 3 − 1 = 2 (ч) − ехали автобусы одновременно;
    4) 100 * 2 = 200 (км) − проехали автобусы за 2−й и 3−й часы, после выезда первого;
    5) 200 + 40 = 240 (км) − будет между автобусами через 3 ч после выхода первого автобуса.
Ответ: 240 км

2. 1) 40 + 60 = 100 (км/ч) − скорость удаления автобусов;
    2) 40 * 1 = 40 (км) − будет между автобусами через 1 час после выезда первого;
    3) 140 − 40 = 100 (км) − нужно проехать автобусам вместе, чтобы расстояние между ними стало 140 км;
    4) 100 : 100 = 1 (ч) − после выезда второго автобуса расстояние между автобусами будет 140 км.
Ответ: через 1 час

3. 1) 40 + 60 = 100 (км/ч) − скорость удаления автобусов;
    2) 40 * 1 = 40 (км) − будет между автобусами через 1 час после выезда первого;
    3) 240 − 40 = 200 (км) − нужно проехать автобусам вместе, чтобы расстояние между ними стало 240 км;
    4) 200 : 100 = 2 (ч) − после выезда второго автобуса расстояние между автобусами будет 240 км;
    5) 1 + 2 = 3 (ч) − после выезда первого автобуса расстояние между автобусами будет 240 км.
Ответ: через 3 часа.

155. а) Расстояние между городами A и B равно 720 км. Из города A в город B вышел скорый поезд, который идет со скоростью 80 км/ч. Через 2 ч навстречу ему из города B в город A вышел пассажирский поезд со скоростью 60 км/ч. Через сколько часов после выхода пассажирского поезда эти поезда встретятся?
б) Андрей вышел из бассейна и направился к школе со скоростью 80 м/мин. Через 10 мин после выхода Андрея к бассейну из школы отправился Борис, скорость которого на 20 м/мин больше, чем скорость Андрея. Через сколько минут после своего выхода Андрей встретил Бориса, если расстояние между школой и бассейном равно 1 км 700 м?

Решение

а) 1) 80 * 2 = 160 (км) − прошел за скорый поезд до выхода пассажирского;
2) 720 − 160 = 560 (км) − было между поездами при выходе пассажирского поезда;
3) 80 + 60 = 140 (км/ч) − скорость сближения поездов;
4) 560 : 140 = 4 (ч) − время, через которое произойдет встреча, после выхода пассажирского поезда.
Ответ: через 4 часа.

б) 1 км 700 м = 1700 м
1) 80 * 10 = 800 (м) − прошел Андрей до выхода Бориса;
2) 1700 − 800 = 900 (м) − было между мальчиками на момент выхода Бориса;
3) 80 + 20 = 100 (м/мин) − скорость Бориса;
4) 100 + 80 = 180 (м/мин) − скорость сближения мальчиков;
5) 900 : 180 = 5 (мин) − время, через которое произошла встреча после выхода Бориса;
6) 10 + 5 = 15 (мин) − время, через которое произошла встреча после выхода Андрея.
Ответ: через 15 минут.

156. Из городов A и B одновременно навстречу друг другу вышли пассажирский поезд и поезд−экспресс. Через 2 ч они встретились, а еще через 3 ч пассажирский поезд прибыл в город B. Определите скорость экспресса, если пассажирский поезд шел со скоростью 60 км/ч.

Решение

1) 2 + 3 = 5 (ч) − ехал из одного города в другой пассажирский поезд;
2) 5 * 60 = 300 (км) − расстояние между городами;
3) 300 : 2 = 150 (км/ч) − скорость сближения поездов;
4) 150 − 60 = 90 (км/ч) − скорость поезда−экспресса.
Ответ: 90 км/ч.

157. Два туриста, один на мотоцикле, а другой на мопеде, двигаются по шоссе навстречу друг другу. Скорость мотоцикла 60 км/ч, и она в 2 раза больше скорости мопеда. В некоторый момент времени расстояние между ними равно 225 км. Через какое время оно окажется равным 45 км?

Решение

1) 60 : 2 = 30 (км/ч) − скорость мопеда;
2) 60 + 30 = 90 (км/ч) − скорость сближения туристов;

Случай 1. Туристы не доехали друг до друга 45 км.
3) 225 − 45 = 180 (км) − нужно проехать туристам;
4) 180 : 90 = 2 (ч) − время, через которое между туристами будет 45 км.

Случай 2. Туристы встретились и разъехались на 45 км.
5) 225 + 45 = 270 (км) − нужно проехать туристам;
6) 270 : 90 = 3 (ч) − время, через которое между туристами будет 45 км.
Ответ: через 2 ч; через 3 ч.

158. Два друга−охотника вышли из леса с двух сторон поля и оказались на расстоянии 450 м друг от друга. Один шел со скоростью 70 м/мин, а другой − со скоростью 80 м/мин. Собака одного из охотников побежала навстречу другому. Добежав до него, она вернулась к хозяину и, повернув, снова бросилась к его другу. Так она продолжала свой бег до встречи двух охотников. Определите:
а) сколько минут бегала собака между двумя охотниками;
б) какое расстояние она пробежала, если она бегала со скоростью 12 км/ч.

Решение

а) 1) 70 + 80 = 150 (м/мин) − скорость сближения охотников;
2) 450 : 150 = 3 (мин) − время, через которое охотники встретились, а значит это же время бегала собака.
Ответ: 3 минуты.

б) 1) 12 км/ч = 12 * 1000 : 60 = 12000 : 60 = 200 (м/мин) − скорость собаки;
2) 70 + 80 = 150 (м/мин) − скорость сближения охотников;
3) 450 : 150 = 3 (мин) − время, через которое охотники встретились, а значит это же время бегала собака;
4) 3 * 200 = 600 (м) − пробежала собака.
Ответ: 600 метров.

24

Самостоятельная работа № 6

Вариант 1

1. Из двух сел одновременно навстречу друг другу вышли два пешехода и встретились через 20 мин. Один шел со скоростью 80 м/мин, другой − со скоростью 60 м/мин. Какое расстояние было между ними в начале пути?

Решение

1) 60 + 80 = 140 (м/мин) − скорость сближения пешеходов;
2) 140 * 20 = 2800 (м) = 2 км 800 м − было между ними в начале пути.
Ответ: 2 км 800 м.

2. Два теплохода одновременно отправлятся от двух пристаней навстречу друг другу. Расстояние между пристанями 200 км. Скорость одного теплохода 24 км/ч, другого − 26 км/ч. Через сколько часов они встретятся?

Решение

1) 24 + 26 = 50 (км/ч) − скорость сближения теплоходов;
2) 200 : 50 = 4 (ч) − время, через которое теплоходы встретятся.
Ответ: через 4 часа.

Вариант 2

1. От двух станций одновременно навстречу друг другу отправляются два поезда. Скорость одного поезда 45 км/ч, другого − 60 км/ч. Поезда встретились через 3 ч. Найдите расстояние между станциями.

Решение

1) 45 + 60 = 105 (км/ч) − скорость сближения поездов;
2) 105 * 3 = 315 (км) − расстояние между станциями.
Ответ: 315 км.

2. Два пешехода вышли одновременно навстречу друг другу из двух сел, расстояние между которыми 6000 м. Один шел со скоростью 90 м/мин, другой − со скоростью 60 м/мин. Через сколько минут они встретятся?

Решение

1) 90 + 60 = 150 (м/мин) − скорость сближения пешеходов;
2) 6000 : 150 = 40 (мин) − время, через которое встретятся пешеходы.
Ответ: через 40 минут.

ГДЗ к теме Задачи на движение по реке

159. Скорость катера в стоячей воде равна 12 км/ч, скорость течения реки − 3 км/ч. Определите:
а) скорость катера по течению реки;
б) скорость катера против течения реки;
в) путь, которой пройдет катер по течению реки за 3 ч;
г) путь, который пройдет катер против течения реки за 3 ч.

Решение

а) 12 + 3 = 15 (км/ч) − скорость катера по течению реки.
Ответ: 15 км/ч.

б) 12 − 3 = 9 (км/ч) − скорость катера против течения реки.
Ответ: 9 км/ч.

в) (12 + 3) * 3 = 15 * 3 = 45 (км) − пройдет катер по течению реки за 3 ч.
Ответ: 45 км.

г) (12 − 3) * 3 = 9 * 3 = 27 (км) − пройдет катер против течения реки за 3 ч.
Ответ: 27 км.

160. Заполните таблицу:...

Решение

1 строка:
1) 12 + 4 = 16 (км/ч) − скорость по течению;
2) 12 − 4 = 8 (км/ч) − скорость против течения.
2 строка:
1) 28 − 25 = 3 (км/ч) − скорость течения;
2) 25 − 3 = 22 (км/ч) − скорость против течения.
3 строка:
1) 24 − 20 = 4 (км/ч) − скорость течения;
2) 24 + 4 = 28 (км/ч) − скорость по течению.
4 строка:
17 − 2 = 15 (км/ч) − собственная скорость;
15 − 2 = 13 (км/ч) − скорость против течения.
5 строка:
16 + 3 = 19 (км/ч) − собственная скорость;
19 + 3 = 22 (км/ч) − скорость по течению.
6 строка:
34 − 30 = 4 (км/ч) − скорость течения;
30 − 4 = 26 (км/ч) − скорость против течения.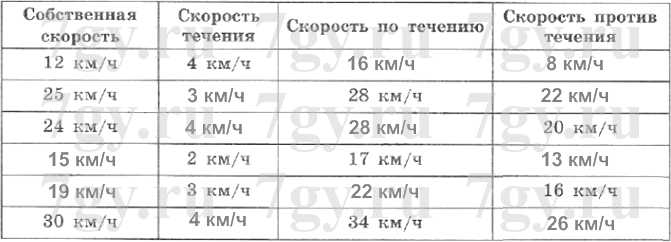

161. а) Собственная скорость катера − 13 км/ч, скорость течения реки равна 3 км/ч. Расстояние между двумя причалами 80 км. За какое время катер пройдет это расстояние, если будет плыть по течению реки? против течения реки?
б) В стоячей воде спортсмен плывет со скоростью 55 м/мин. За какое время он проплывет 280 м по реке, скорость течения которой 15 м/мин, если будет плыть по течению реки? против течения реки?

Решение

а) 1) 13 + 3 = 16 (км/ч) − скорость катера по течению реки;
2) 13 − 3 = 10 (км/ч) − скорость катера против течения реки;
3) 80 : 16 = 5 (ч) − будет плыть катер по течению реки;
4) 80 : 10 = 8 (ч) − будет плыть катер против течения реки.
Ответ: 5 ч; 8 ч.

б) 1) 55 + 15 = 70 (м/мин) − скорость спортсмена по течению реки;
2) 55 − 15 = 40 (м/мин) − скорость спортсмена против течения реки;
3) 280 : 70 = 4 (мин) − будет плыть спортсмен 280 метров по течению реки;
4) 280 : 40 = 7 (мин) − будет плыть спортсмен 280 метров против течения реки.
Ответ: 4 мин; 7 мин.

25

162. а) Катер прошел 72 км по течению реки и вернулся обратно. Какой путь занял у него больше времени и на сколько, если собственная скорость катера равна 21 км/ч, скорость течения реки − 3 км/ч?
б) Собственная скорость лодки 9 км/ч, скорость течения реки 3 км/ч. Сколько времени понадобится этой лодке, чтобы пройти 24 км по реке и вернуться обратно?

Решение

а) 1) 21 + 3 = 24 (км/ч) − скорость катера по течению;
2) 21 − 3 = 18 (км/ч) − скорость катера против течения;
3) 72 : 24 = 3 (ч) − плыл катер по течению;
4) 72 : 18 = 4 (ч) − плыл катер против течения;
5) 4 − 3 = на 1 (ч) − дольше плыл катер против течения, чем по течению.
Ответ: на 1 час дольше против течения.

б) 1) 9 + 3 = 12 (км/ч) − скорость лодки по течению;
2) 9 − 3 = 6 (км/ч) − скорость лодки против течения;
3) 24 : 12 = 2 (ч) − будет плыть лодка по течению;
4) 24 : 6 = 4 (ч) − будет плыть лодка против течения;
5) 2 + 4 = 6 (ч) − понадобится лодке, чтобы пройти 24 км по реке и вернуться обратно.
Ответ: 6 часов.

163. а) Лодка, имеющая собственную скорость 6 км/ч, шла 3 ч по течению реки и 5 ч против течения. Какое расстояние прошла лодка, если скорость течения реки равна 2 км/ч?
б) Пловец, скорость которого в стоячей воде равна 50 м/мин, плыл 12 мин против течения реки и 15 мин по течению. Какое расстояние проплыл пловец, если скорость течения реки 10 м/мин?

Решение

а) 1) 6 + 2 = 8 (км/ч) − скорость лодки по течению;
2) 6 − 2 = 4 (км/ч) − скорость лодки против течения;
3) 8 * 3 = 24 (км) − прошла лодка по течению;
4) 4 * 5 = 20 (км) − прошла лодка против течения;
5) 24 + 20 = 44 (км) − прошла лодка всего.
Ответ: 44 км.

б) 1) 50 + 10 = 60 (м/мин) − скорость пловца по течению;
2) 50 − 10 = 40 (м/мин) − скорость пловца против течения;
3) 60 * 15 = 900 (м) − проплыл пловец по течению;
4) 40 * 12 = 480 (м) − проплыл пловец против течения;
5) 900 + 480 = 1380 (м) = 1 км 380 м − проплыл пловец всего.
Ответ: 1 км 380 м.

164. а) Скорость лодки против течения реки 5 км/ч, собственная скорость лодки 7 км/ч. За какое время он пройдет 45 км по течению реки?
б) По течению реки теплоход "Ракета" идет со скоростью 24 км/ч, скорость течения реки 1 км/ч. Какое расстояние пройдет теплоход против течения реки за 4 ч?

Решение

а) 1) 7 − 5 = 2 (км/ч) − скорость течения реки;
2) 7 + 5 = 9 (км/ч) − скорость лодки по течению;
3) 45 : 9 = 5 (ч) − будет идти лодка 45 км по течению реки.
Ответ: 5 часов.

б) 1) 24 − 1 = 23 (км/ч) − собственная скорость теплохода;
2) 23 − 1 = 22 (км/ч) − скорость теплохода против течения;
3) 22 * 4 = 88 (км) − проедет теплоход по течению реки за 4 часа.
Ответ: 88 км.

165. а) Собственная скорость теплохода 25 км/ч. Расстояние между причалами 120 км. Если теплоход плывет вниз по реке, то это расстояние он проходит за 4 ч. Найдите скорость течения реки и время, за которое теплоход проходит это расстояние вверх по реке.
б) Рыболовы отправились на моторной лодке вверх по реке и отплыли от своего лагеря на расстояние, равное 3 км 600 м. Этот путь занял у них 24 мин. Сколько времени уйдет у них на обратный путь, если известно, что в стоячей воде лодка движется со скоростью 175 м/мин?

Решение

а) 1) 120 : 4 = 30 (км/ч) − скорость теплохода по течению;
2) 30 − 25 = 5 (км/ч) − скорость течения реки;
3) 25 − 5 = 20 (км/ч) − скорость теплохода против течения;
4) 120 : 20 = 6 (ч) − будет идти 120 км теплоход вверх по реке.
Ответ: 5 км/ч; 6 ч.

б) 3 км 600 м = 3600 м
1) 3600 : 24 = 150 (м/мин) − скорость лодки против течения;
2) 175 − 150 = 25 (м/мин) − скорость течения реки;
3) 175 + 25 = 200 (м/мин) − скорость лодки по течению;
4) 3600 : 200 = 18 (мин) − уйдет у рыболовов на обратный путь.
Ответ: 18 минут.

166. Скорость катера по течению реки 19 км/ч, а против течения 15 км/ч. Найдите:
а) скорость течения реки;
б) собственная скорость катера.

Решение

а) 1) 19 − 15 = 4 (км/ч) − удвоенная скорость течения реки;
2) 4 : 2 = 2 (км/ч) − скорость течения реки.
Ответ: 2 км/ч.

б) 1) 19 − 15 = 4 (км/ч) − удвоенная скорость течения реки;
2) 4 : 2 = 2 (км/ч) − скорость течения реки;
3) 19 − 2 = 17 (км/ч) − собственная скорость катера.
Ответ: 17 км/ч.

167. а) Скорость катера по течению реки 21 км/ч. Двигаясь против течения реки, этот катер преодолевает 60 км за 4 ч. Найдите скорость течения реки и собственную скорость катера.
б) Лодка проплывает по течению реки 24 км за 3 ч. Скорость ложки против течения реки 2 км/ч. Найдите скорость течения реки и собственную скорость лодки.

Решение

а) 1) 60 : 4 = 15 (км/ч) − скорость катера против течения реки;
2) (21 − 15) : 2 = 6 : 2 = 3 (км/ч) − скорость течения реки;
3) 15 + 3 = 18 (км/ч) − собственная скорость катера.
Ответ: 3 км/ч; 18 км/ч.

б) 1) 24 : 3 = 8 (км/ч) − скорость лодки по течению реки;
2) (8 − 2) : 2 = 6 : 2 = 3 (км/ч) − скорость течения реки;
3) 8 − 3 = 5 (км/ч) − собственная скорость лодки.
Ответ: 3 км/ч; 5 км/ч.

168. а) Теплоход за 2 ч проходит 56 км по течению реки, а против течения реки он проходит 66 км за 3 ч. Найдите скорость течения реки и собственную скорость теплохода.
б) Катер против течения реки проходит 126 км за 9 ч, а то же расстояние по течению реки за 7 ч. Найдите собственную скорость катера.

Решение

а) 1) 56 : 2 = 28 (км/ч) − скорость теплохода по течения;
2) 66 : 3 = 22 (км/ч) − скорость теплохода против течения;
3) (28 − 22) : 2 = 6 : 2 = 3 (км/ч) − скорость течения реки;
4) 28 − 3 = 25 (км/ч) − собственная скорость теплохода.
Ответ: 3 км/ч; 25 км/ч.

б) 1) 126 : 9 = 14 (км/ч) − скорость катера против течения;
2) 126 : 7 = 18 (км/ч) − скорость катера по течению;
3) (18 − 14) : 2 = 4 : 2 = 2 (км/ч) − скорость течения реки;
4) 18 − 2 = 16 (км/ч) − собственная скорость катера.
Ответ: 16 км/ч.

169. Расстояние между двумя пристанями равно 72 км. Катер проходит от одной пристани до другой по течению реки за 2 ч, а против течения за 3 ч. За сколько часов это расстояние проплывут плоты?
Указание.
Подумайте, как связаны между собой скорость, с которой плывут плоты, и скорость течения реки.

Решение

1) 72 : 2 = 36 (км/ч) − скорость катера по течению;
2) 72 : 3 = 24 (км/ч) − скорость катера против течения;
3) (36 − 24) : 2 = 12 : 2 = 6 (км/ч) − скорость течения реки;
4) 72 : 6 = 12 (ч) − расстояние между пристанями будут плыть плоты.
Ответ: 12 часов.

26

Использование свойств действий при вычислениях
ГДЗ к теме Преобразование выражений на основе свойств арифметических действий

170. Сгруппируйте слагаемые так, чтобы они дополняли друг друга до круглого числа, и вычислите сумму:
а) 17 + 6 + 5 + 24 + 3 + 25;
б) 12 + 13 + 7 + 8 + 5 + 35;
в) 16 + 15 + 15 + 14 + 17 + 13 + 10;
г) 11 + 16 + 18 + 14 + 19 + 12 + 40.
Образец.
7 + 6 + 5 + 4 + 3 + 5 + 9 = (7 + 3) + (6 + 4) + (5 + 5) + 9 = 10 + 10 + 10 + 9 = 39

Решение

а) 17 + 6 + 5 + 24 + 3 + 25 = (17 + 3) + (6 + 24) + (5 + 25) = 20 + 30 + 30 = 80

б) 12 + 13 + 7 + 8 + 5 + 35 = (12 + 8) + (13 + 7) + (5 + 35) = 20 + 20 + 40 = 80

в) 16 + 15 + 15 + 14 + 17 + 13 + 10 = (16 + 14) + (15 + 15) + 10 + (17 + 13) = 30 + 30 + 10 + 30 = 100

г) 11 + 16 + 18 + 14 + 19 + 12 + 40 = (11 + 19) + (16 + 14) + (18 + 12) + 40 = 30 + 30 + 30 + 40 = 130

171. Вычислите сумму, дополнив одно из слагаемых до круглого числа:
а) 96 + 47;
б) 57 + 198;
в) 75 + 98;
г) 296 + 25;
д) 88 + 95;
е) 397 + 44.
Образец.
199 + 63 = (199 + 1) + 62 = 200 + 62 = 262

Решение

а) 96 + 47 = (96 + 4) + (47 − 4) = 100 + 43 = 143

б) 57 + 198 = (57 − 2) + (198 + 2) = 55 + 200 = 255

в) 75 + 98 = (75 − 2) + (98 + 2) = 73 + 100 = 173

г) 296 + 25 = (296 + 4) + (25 − 4) = 300 + 21 = 321

д) 88 + 95 = (88 − 5) + (95 + 5) = 83 + 100 = 183

е) 397 + 44 = (397 + 3) + (44 − 3) = 400 + 41 = 441

172. Найдите удобный способ группировки множителей и вычислите произведение:
а) 5 * 5 * 8 * 8;
б) 12 * 4 * 5 * 5;
в) 11 * 4 * 25;
г) 18 * 2 * 50.
Образец.
6 * 6 * 5 * 5 = (6 * 5) * (6 * 5) = 30 * 30 = 900

Решение

а) 5 * 5 * 8 * 8 = (5 * 8) * (5 * 8) = 40 * 40 = 1600

б) 12 * 4 * 5 * 5 = (12 * 5) * (4 * 5) = 60 * 20 = 1200

в) 11 * 4 * 25 = 11 * (4 * 25) = 11 * 100 = 1100

г) 18 * 2 * 50 = 18 * (2 * 50) = 18 * 100 = 1800

173. Примените переместительное и сочетательное свойства умножения и вычислите произведение устно:
а) 2 * 11 * 5 * 9;
б) 7 * 2 * 3 * 5;
в) 25 * 17 * 4;
г) 3 * 4 * 23 * 25.

Решение

а) 2 * 11 * 5 * 9 = (2 * 5) * (11 * 9) = 10 * 99 = 990

б) 7 * 2 * 3 * 5 = (7 * 3) * (2 * 5) = 21 * 10 = 210

в) 25 * 17 * 4 = 17 * (25 * 4) = 17 * 100 = 1700

г) 3 * 4 * 23 * 25 = (3 * 23) * (4 * 25) = 69 * 100 = 6900

174. Преобразуйте произведение так, чтобы одним из множителей было круглое число, и выполните вычисления:
а) 15 * 4;
б) 35 * 12;
в) 44 * 25;
г) 75 * 16.
Образец.
16 * 15 = (8 * 2) * (3 * 5) = (8 * 3) * (2 * 5) = 240

Решение

а) 15 * 4 = (5 * 3) * (7 * 2) = (5 * 2) * (7 * 3) = 10 * 21 = 210

б) 35 * 12 = (5 * 7) * (6 * 2) = (5 * 2) * (7 * 6) = 10 * 42 = 420

в) 44 * 25 = (11 * 2 * 2) * (5 * 5) = 11 * (5 * 2) * (5 * 2) = 11 * 10 * 10 = 1100

г) 75 * 16 = (15 * 5) * (2 * 8) = (15 * 8) * (5 * 2) = 120 * 10 = 1200

175. Найдите разные способы вычисления данного произведения и запишите соответствующие цепочки равенств:
а) 36 * 25;
б) 32 * 125.

Решение

а) 1) 36 * 25 = 9 * 4 * 25 = 9 * 100 = 900;
2) 36 * 25 = 6 * 6 * 5 * 5 = 30 * 30 = 900.

б) 1) 32 * 125 = 5 * 25 * 4 * 8 = 40 * 100 = 4000;
2) 32 * 125 = 4 * 4 * 2 * 5 * 5 * 5 = 4 * 5 * 4 * 5 * 4 * 2 = 20 * 20 * 10 = 400 * 10 = 4000

176. Найдите значение выражения, применив распределительное свойство:
а) 14 * 4 + 16 * 4;
б) 18 * 3 + 12 * 3;
в) 13 * 7 + 7 * 17;
г) 68 * 18 − 68 * 8;
д) 74 * 16 − 74 * 15;
е) 33 * 52 − 31 * 52.

Решение

а) 14 * 4 + 16 * 4 = 4 * (14 + 16) = 4 * 30 = 120

б) 18 * 3 + 12 * 3 = 3 * (18 + 12) = 3 * 30 = 90

в) 13 * 7 + 7 * 17 = 7 * (13 + 17) = 7 * 30 = 210

г) 68 * 18 − 68 * 8 = 68 * (18 − 8) = 68 * 10 = 680

д) 74 * 16 − 74 * 15 = 74 * (16 − 15) = 74 * 1 = 74

е) 33 * 52 − 31 * 52 = 52 * (33 − 31) = 55 * 2 = 104

177. Вычислите, используя распределительное свойство:
а) $21^2 + 21 * 9$;
б) $37^2 + 37 * 63$;
в) $25^2 - 25 * 15$;
г) $45^2 - 45 * 35$.

Решение

а) $21^2 + 21 * 9 = 21 * (21 + 9) = 21 * 30 = 630$

б) $37^2 + 37 * 63 = 37 * (37 + 63) = 37 * 100 = 3700$

в) $25^2 - 25 * 15 = 25 * (25 - 15) = 25 * 10 = 250$

г) $45^2 - 45 * 35 = 45 * (45 - 35) = 45 * 10 = 450$

178. Вычислите произведение, воспользовавшись распределительным свойством:
а) 132 * 8;
б) 154 * 6;
в) 97 * 12;
г) 199 * 15.
Образец.
245 * 6 = (200 + 40 + 5) * 6 = 1200 + 240 + 30 = 1470;
98 * 14 = (100 − 2) * 14 = 1400 − 28 = 1372.

Решение

а) 132 * 8 = (100 + 30 + 2) * 8 = 800 + 240 + 16 = 1056

б) 154 * 6 = (100 + 50 + 4) * 6 = 600 + 300 + 24 = 924

в) 97 * 12 = (90 + 7) * 12 = 1080 + 84 = 1164

г) 199 * 15 = (100 + 90 + 9) * 15 = 1500 + 1350 + 135 = 2985

27

179. Найдите значение выражения, дважды воспользовавшись распределительным свойством:
а) 32 * 26 − 11 * 26;
б) 32 * 26 − 11 * 32;
в) 43 * 16 + 43 * 13;
г) 48 * 11 + 48 * 4.
Образец.
43 * 25 − 43 * 13 = 43 * (25 − 13) = 43 * 12 = 43 * (10 + 2) = 430 + 86 = 516

Решение

а) 32 * 26 − 11 * 26 = (32 − 11) * 26 = 21 * 26 = 26 * (20 + 1) = 520 + 26 = 546

б) 32 * 26 − 11 * 32 = 32 * (26 − 11) = 32 * 15 = 15 * (30 + 2) = 450 + 30 = 480

в) 43 * 16 + 43 * 13 = 43 * (16 + 13) = 43 * 29 = 43 * (30 − 1) = 1290 − 43 = 1247

г) 48 * 11 + 48 * 4 = 48 * (11 + 4) = 48 * 15 = 48 * (10 + 5) = 480 + 240 = 720

180. Найдите значение выражения:
а) 62 * 14 + 11 * 62 − 12 * 25;
б) 48 * 11 − 11 * 16 + 32 * 19;
в) 17 * 19 + 17 * 45 − 17 * 14;
г) 12 * 32 − 12 * 18 + 38 * 14.

Решение

а) 62 * 14 + 11 * 62 − 12 * 25 = 62 * (14 + 11) − 12 * 25 = 62 * 25 − 12 * 25 = 25 * (62 − 12) = 25 * 50 = 1250

б) 48 * 11 − 11 * 16 + 32 * 19 = 11 * (48 − 16) + 32 * 19 = 11 * 32 + 32 * 19 = 32 * (11 + 19) = 32 * 30 = 960

в) 17 * 19 + 17 * 45 − 17 * 14 = 17 * (19 + 45 − 14) = 17 * (19 + 31) = 17 * 50 = 850

г) 12 * 32 − 12 * 18 + 38 * 14 = 12 * (32 − 18) + 38 * 14 = 12 * 14 + 38 * 14 = 14 * (12 + 38) = 14 * 50 = 700

181. Разберите, как вычислена разность 46 * 75 − 70 * 45:
46 * 75 − 70 * 45 = (2 * 23) * (3 * 5 * 5) − (7 * 2 * 5) * (3 * 3 * 5) = 2 * 3 * 5 * 5 * (23 − 21) = 150 * 2 = 300
Вычислите, используя рассмотренный прием:
а) 14 * 55 + 38 * 35;
б) 34 * 35 − 14 * 75;
в) 75 * 26 + 30 * 35;
г) 75 * 38 − 50 * 33.

Решение

а) 14 * 55 + 38 * 35 = (2 * 7) * (5 * 11) + (2 * 19) * (5 * 7) = 2 * 5 * 7 * (11 + 19) = 2 * 5 * 7 * 30 = 70 * 30 = 2100

б) 34 * 35 − 14 * 75 = (2 * 17) * (5 * 7) − (2 * 7) * (5 * 15) = 2 * 7 * 5 * (17 − 15) = 2 * 7 * 5 * 2 = 20 * 7 = 140

в) 75 * 26 + 30 * 35 = (3 * 5 * 5) * (13 * 2) + (5 * 6) * (5 * 7) = 3 * 5 * 2 * (5 * 13 + 5 * 7) = 3 * 5 * 2 * 5 * (13 + 7) = 3 * 5 * 2 * 5 * 20 = 150 * 20 = 3000

г) 75 * 38 − 50 * 33 = (3 * 5 * 5) * (2 * 19) − (2 * 5 * 5) * (11 * 3) = 3 * 2 * 5 * 5 * (19 − 11) = 3 * 2 * 5 * 5 * 8 = 6 * 40 * 5 = 30 * 40 = 1200

182. Вычислите сумму, используя "прием Гаусса":
а) 1 + 2 + 3 + ... + 50;
б) 11 + 12 + 13 + ... + 60;
в) 1 + 3 + 5 + ... + 99;
г) 3 + 6 + 9 + ... + 90.

Решение

а) 1 + 2 + 3 + ... + 50 = (1 + 50) + (2 + 49) + ... + (25 + 26) = 25 * 51 = 1275

б) 11 + 12 + 13 + ... + 60 = (11 + 60) + (12 + 59) + ... + (35 + 36) = 71 * 25 = 1775

в) 1 + 3 + 5 + ... + 99 = (1 + 99) + (3 + 97) + ... + (49 + 51) = 100 * 25 = 2500

г) 3 + 6 + 9 + ... + 90 = (90 + 3) + (87 + 6) + ... (48 + 45) = 93 * 15 = 1395

183. Зная, что x + y = 10, найдите значение выражения:
а) x + 6 + y;
б) (x + 12) + (y + 8);
в) (y + x) * 4;
г) 5 * x + 5 * y.

Решение

а) x + 6 + y = (x + y) + 6 = 10 + 6 = 16

б) (x + 12) + (y + 8) = (x + y) + (12 + 8) = 10 + 20 = 30

в) (y + x) * 4 = 10 * 4 = 40

г) 5 * x + 5 * y = 5 * (x + y) = 5 * 10 = 50

184. Найдите сумму (a + b) + (b + c) + (c + a), если известно, что a + b + c = 8.

Решение

(a + b) + (b + c) + (c + a) = a + b + b + c + c + a = 2a + 2b + 2c = 2(a + b + c) = 2 * 8 = 16

185. а) Ученик задумал число, умножил его на 8, затем это же число умножил на 15 и результаты сложил. В сумме получилось 276. Какое число задумал ученик?
б) Ученик задумал число, умножил его на 16, затем это же число умножил на 9. Первое произведение оказалось на 42 больше второго. Какое число задумал ученик?

Решение

а) Пусть x − задуманное число, тогда:
x * 8 + x * 15 = 276
x * (8 + 15) = 276
x * 23 = 276
x = 276 : 23
x = 12
Ответ: 12 − задуманное число.

б) Пусть x − задуманное число, тогда:
x * 16 − x * 9 = 42
x * (16 − 9) = 42
x * 7 = 42
x = 42 : 7
x = 6
Ответ: 6 − задуманное число.

Самостоятельная работа № 7

Вариант 1

1. Преобразуйте выражение и вычислите его значение:
а) 86 + 37 + 14 + 23;
б) 4 * 6 * 12 * 25.

Решение

а) 86 + 37 + 14 + 23 = (86 + 14) + (37 + 23) = 100 + 60 = 160

б) 4 * 6 * 12 * 25 = (6 * 12) * (4 * 25) = 72 * 100 = 7200

2. Вычислите, используя распределительное свойство:
а) 16 * 91 − 16 * 71;
б) $35^2 + 35 * 65$.

Решение

а) 16 * 91 − 16 * 71 = 16 * (91 − 71) = 16 * 20 = 320

б) В учебнике опечатка, скорее всего пример выглядит так:
$35^2 + 35 * 65 = 35 * (35 + 65) = 35 * 100 = 3500$

Вариант 2

1. Преобразуйте выражение и вычислите его значение:
а) 58 + 79 + 12 + 21;
б) 20 * 17 * 5 * 3.

Решение

а) 58 + 79 + 12 + 21 = (58 + 12) + (79 + 21) = 70 + 100 = 170

б) 20 * 17 * 5 * 3 = (20 * 5) * (17 * 3) = 100 * 51 = 5100

2. Вычислите, используя распределительное свойство:
а) 34 * 7 + 16 * 7;
б) $742 - 74 * 64$.

Решение

а) 34 * 7 + 16 * 7 = 7 * (34 + 16) = 7 * 50 = 350

б) В учебнике опечатка, скорее всего пример выглядит так:
$74^2 - 74 * 64 = 74 * (74 - 64) = 74 * 10 = 740$

28

ГДЗ к теме Решение задач на части

186. Чтобы сварить варенье из вишни, на 2 части ягод берут 3 части сахара.
1) Сколько сахара следует взять, если приготовлено 2 кг 600 г ягод?
2) Сколько килограммов вишни надо взять, если имеется 4 кг 500 г сахара?

Решение

а) 2 кг 600 г = 2600 г
1) 2600 : 2 = 1300 (г) − составляет одна часть;
2) 1300 * 3 = 3900 (г) = 3 кг 900 г − сахара следует взять.
Ответ: 3 кг 900 г.

б) 4 кг 500 г = 4500 г
1) 4500 : 3 = 1500 (г) − составляет одна часть;
2) 1500 * 2 = 3000 (г) = 3 (кг) − вишни надо взять.
Ответ: 3 кг.

187. а) Мороженое содержит 5 частей воды, 2 части молочного жира и 3 части сахара. Сколько надо взять воды, молочного жира и сахара, чтобы приготовить 700 г мороженого?
б) Тесто для вареников содержит 16 частей творога, 3 части муки, 3 части сметаны и 3 части сахара. Найдите массу каждого продукта, необходимого для приготовления 1 кг теста.

Решение

а) 1) 5 + 2 + 3 = 10 (частей) − всего;
2) 700 : 10 = 70 (г) − составляет одна часть;
3) 5 * 70 = 350 (г) − воды надо взять;
4) 2 * 70 = 140 (г) − молочного жира надо взять;
5) 3 * 70 = 210 (г) − сахара надо взять.
Ответ: 350 г воды, 140 г молочного жира и 210 г сахара.

б) 1) 16 + 3 + 3 + 3 = 25 (частей) − всего;
2) 1000 : 25 = 40 (г) − составляет одну часть;
3) 16 * 40 = 640 (г) − творога необходимо;
4) 3 * 40 = 120 (г) − и муки, и сметаны, и сахара необходимо.
Ответ: 640 г творога; по 120 г сметаны, муки и сахара.

188. При помоле ржи на каждые 3 части муки приходится 1 часть отходов. Сколько смололи ржи, если муки получилось на 36 ц больше, чем отходов?

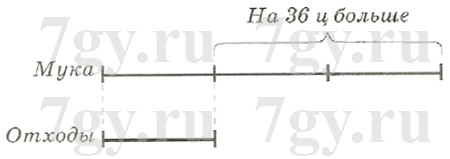
Подсказка.
Воспользуйтесь рисунком 3.

Решение

1) 3 − 1 = 2 (части) − муки получается больше, чем ржи;
2) 36 : 2 = 18 (ц) − составляет одна часть;
3) 18 * 1 = 18 (ц) − составляют отходы;
4) 18 * 3 = 54 (ц) − составляет мука;
5) 54 + 18 = 72 (ц) − смололи ржи.
Ответ: 72 центнера.

189. Для компота взяли 6 частей яблок, 5 частей груш и 3 части слив. Груш и слив вместе было 2 кг 400 г. Какова была общая масса всех фруктов?

Решение

2 кг 400 г = 2400 г
1) 5 + 3 = 8 (частей) − приходится на груши и сливы;
2) 2400 : 8 = 300 (г) − составляет одна часть;
3) 6 + 8 = 14 (частей) − всего;
4) 300 * 14 = 4200 (г) = 4 кг 200 г − общая масса фруктов.
Ответ: 4 кг 200 г.

190. а) В два пакета надо разложить 56 орехов так, чтобы в одном их было в 3 раза меньше, чем в другом. Сколько орехов надо положить в каждый пакет?
б) Для спортивного клуба купили 80 мячей − волейбольных и баскетбольных, причем волейбольных в 4 раза больше, чем баскетбольных. Сколько купили тех и других мячей в отдельности?

Решение

а) 1) 3 + 1 = 4 (части) − всего;
2) 56 : 4 = 14 (ор.) − составляет одна часть;
3) 14 * 1 = 14 (ор.) − в одном пакете;
4) 14 * 3 = 42 (ор.) − в другом пакете.
Ответ: 14 и 42 ореха.

б) 1) 4 + 1 = 5 (частей) − всего;
2) 80 : 5 = 16 (м.) − составляет одна часть;
3) 16 * 1 = 16 (м.) − баскетбольных купили;
4) 16 * 4 = 64 (м.) − волейбольных купили.
Ответ: 16 баскетбольных и 64 волейбольных мячей.

191. а) Ученик купил тетрадей в клетку в 3 раза больше, чем в линейку, причем тетрадей в клетку было на 18 больше, чем в линейку. Сколько всего тетрадей купил ученик?
б) В библиотеке на верхней полке стеллажа стояло на 12 учебников меньше, чем на нижней. Коля заметил, что на верхней полке в 4 раза меньше учебников, чем на нижней полке. Сколько учебников стояло на каждой полке?

Решение

а) 1) 3 − 1 = 2 (части) − тетрадей в клетку было больше, чем в линейку;
2) 18 : 2 = 9 (т.) − составляет одну часть;
3) 3 + 1 = 4 (части) − составляют все тетради;
4) 9 * 4 = 36 (т.) − всего купил ученик.
Ответ: 36 тетрадей

б) 1) 4 − 1 = 3 (части) − учебников на нижней полке больше, чем на верхней;
2) 12 : 3 = 4 (уч.) − составляет одна часть;
3) 4 * 1 = 4 (уч.) − стояло на верхней полке;
3) 4 * 4 = 16 (уч.) − стояло на нижней полке.
Ответ: 16 учебников на нижней полке и 4 учебника на верхней полке.

192. а) За 3 дня Оля прочитала 84 страницы, причем в первый день она прочитала в 3 раза больше, чем во второй, а в третий − 16 страниц. Сколько страниц прочитала Оля в первый день?
б) Кусок ткани длиной 76 м разрезали на 3 части. Первая из них имеет длину 25 м, а вторая в 2 раза короче третьей. Найдите длину третьей части.

Решение

а) 1) 84 − 16 = 68 (с.) − прочитала Оля за первые два дня;
2) 1 + 3 = 4 (части) − страниц приходится на первые 2 дня;
3) 68 : 4 = 17 (с.) − составляет 1 часть;
4) 3 * 17 = 51 (страницу) − прочитала Оля в первый день.
Ответ: 51 страницу.

б) 1) 76 − 25 = 51 (м) − длина второй и третьей части;
2) 1 + 2 = 3 (части) − приходится на вторую и третью части;
3) 51 : 3 = 17 (м) − составляет одна часть;
4) 17 * 2 = 34 (м) − длина третьей части.
Ответ: 34 метра.

29

193. а) В двух коробках 36 кусков мела. Когда из одной коробки израсходовали 12 кусков мела, то в ней стало в 3 раза меньше мела, чем в другой. Сколько кусков мела было в каждой коробке первоначально?
б) В двух банках 5 л молока. Когда в одну банку добавили 1 л, то в ней стало в 2 раза больше молока, чем в другой. Сколько литров молока было в каждой банке?

Решение

а) 1) 36 − 12 = 24 (к.) − осталось в двух коробках;
2) 3 + 1 = 4 (части) − составляют 24 куска;
3) 24 : 4 = 6 (к.) − составляет одна часть;
4) 6 * 3 = 18 (к.) − стало в первой коробке;
5) 6 * 1 = 6 (к.) − стало во второй коробке;
6) 6 + 12 = 18 (к.) − было во второй коробке изначально.
Ответ: в каждой коробке было по 18 кусков.

б) 1) 5 + 1 = 6 (л) − молока стало в двух банках;
2) 2 + 1 = 3 (части) − приходится на 6 литров;
3) 6 : 3 = 2 (л) − составляет одна часть;
4) 2 * 1 = 2 (л) − стало в первой банке;
5) 2 * 2 = 4 (л) − стало во второй банке;
6) 4 − 1 = 3 (л) − было во второй банке первоначально.
Ответ: 2 литра и 3 литра.

194. а) В трех больших пакетах и в четырех маленьких содержится 550 г карамели. Сколько граммов карамели в одном маленьком пакете и сколько в одном большом, если в маленький входит в 2 раза меньше карамели, чем в большой?
Подсказка.
Воспользуйтесь рисунком 4.

б) В шести маленьких и в двух больших коробках 40 карандашей. В одной маленькой коробке в 2 раз меньше карандашей, чем в большой. Сколько карандашей в маленькой коробке и сколько в большой?
Подсказка. Считайте, что карандаши в маленькой коробке составляют 1 часть.

Решение

а) 1) 4 + 3 * 2 = 4 + 6 = 10 (частей) − всего или 10 маленьких пакетов;
2) 550 : 10 = 55 (г) − карамели в маленьком пакете;
3) 55 * 2 = 110 (г) − карамели в большом пакете.
Ответ: 55 г и 110 г.

б) 1) 6 + 2 * 2 = 6 + 4 = 10 (частей) − всего или 10 маленьких коробок;
2) 40 : 10 = 4 (карандаша) − в маленькой коробке;
3) 4 * 2 = 8 (карандашей) − в большой коробке.
Ответ: 4 карандаша и 8 карандашей.

195. а) Мать в 2 раза старше дочери, а отец на 5 лет старше матери. Всем вместе 120 лет. Сколько лет отцу?
б) Митя в 5 раз моложе бабушки, а отец в 3 раза старше Мити. Всем вместе 108 лет. Сколько лет каждому из них?

Решение

а) 1) 120 − 5 = 115 (лет) − было бы им вместе, если бы отец и мать были ровесниками, тогда:
возраст дочери составляет 1 часть;
возраст матери составляет 2 части;
возраст отца составляет 2 части.
2) 1 + 2 + 2 = 5 (частей) − приходится на 115 лет;
3) 115 : 5 = 23 (года) − дочери;
4) 23 * 2 = 46 (лет) − матери;
5) 23 * 2 + 5 = 46 + 5 = 51 (год) − отцу.
Ответ: 23 года дочери, 46 лет матери, 51 год отцу.

б) 1) 1 + 3 + 5 = 9 (частей) − приходится на 108 лет;
2) 108 : 9 = 12 (лет) − Мите;
3) 12 * 3 = 36 (лет) − отцу;
4) 12 * 5 = 60 (лет) − бабушке.
Ответ: 12 лет Мите, 36 лет отцу, 60 лет бабушке.

Самостоятельная работа № 8

Вариант 1

1. Чтобы приготовить овощной салат, на 10 частей картофеля берут 3 части свеклы и 2 части моркови.
1) Сколько моркови надо взять, чтобы приготовить 1 кг 200 г салата?
2) Сколько картофеля надо взять, если для салата имеется 150 г свеклы?

Решение

1.   1 кг 200 г = 1200 г
    1) 10 + 3 + 2 = 15 (частей) − всего;
    2) 1200 : 15 = 80 (г) − составляет одну часть;
    3) 80 * 2 = 160 (г) − моркови надо взять.
Ответ: 160 г.

2. 1) 150 : 3 = 50 (г) − составляет одну часть;
    2) 50 * 10 = 500 (г) − картофеля надо взять.
Ответ: 500 г.

2. Кроссовки дороже футбольного мяча в 2 раза, а вместе они стоят 1650 р. Сколько стоит футбольный мяч?

Решение

1) 1 + 2 = 3 (части) − составляют 1650 р.;
2) 1650 : 3 = 550 (р.) − стоит футбольный мяч.
Ответ: 550 рублей.

Вариант 2

1. Чтобы приготовить фасолевый салат, на 7 частей фасоли берут 4 части курицы и 2 части сыра.
1) Сколько сыра надо взять, чтобы приготовить 650 г салата?
2) Сколько фасоли надо взять, если для салата имеется 360 г курицы?

Решение

1.  1) 7 + 4 + 2 = 13 (частей) − приходится на 650 г;
    2) 650 : 13 = 50 (г) − составляет одну часть;
    3) 2 * 50 = 100 (г) − сыра надо взять.
Ответ: 100 г.

2.  1) 360 : 4 = 90 (г) − составляет одна часть;
2) 90 * 7 = 630 (г) − фасоли надо взять.
Ответ: 630 г.

2. Альбом для рисования дороже карандаша в 10 раз, а вместе они стоят 275 р. Сколько стоит карандаш?

Решение

1) 1 + 10 = 11 (частей) − приходится на 275 р.;
2) 275 : 11 = 25 (р.) − стоит карандаш.
Ответ: 25 рублей.

30

ГДЗ к теме Решение задач на уравнивание

196. а) В соревнованиях приняли участие 117 спортсменов, причем юношей на 39 больше, чем девушек. Сколько юношей и сколько девушек участвовало в соревнованиях?
б) Журнал дороже газеты на 25 р., а вместе они стоят 43 р. Сколько стоят газета и журнал в отдельности?
в) Варежки дешевле шапки на 170 р., а вместе они стоят 340 р. Сколько стоят варежки и сколько стоит шапка?

Решение

а) 1) 117 − 39 = 78 (с.) − было бы, если бы юношей и девушек было одинаково;
2) 78 : 2 = 39 (девушек) − участвовало в соревнованиях;
3) 39 + 39 = 78 (юношей) − участвовало в соревнованиях.
Ответ: 78 юношей и 39 девушек.

б) 1) 43 − 25 = 18 (р.) − стоили бы журнал и газета, если бы стоили одинаково;
2) 18 : 2 = 9 (р.) − стоит газета;
3) 9 + 25 = 34 (р.) − стоит журнал.
Ответ: 9 р. стоит газета; 34 р. стоит журнал.

в) 1) 340 − 170 = 170 (р.) − стоили бы варежка и шапка, если бы стоили одинаково;
2) 170 : 2 = 85 (р.) − стоят варежки;
3) 85 + 170 = 255 (р.) − стоит шапка.
Ответ: 85 р. стоят варежки, 255 р. стоит шапка.

197. а) Сумма двух чисел 432, первое число больше второго на 18. Найдите эти числа.
б) Сумма двух чисел 537, первое число меньше второго на 131. Найдите эти числа.

Решение

а) 1) 432 − 18 = 414 − была бы сумма чисел, если бы числа были одинаковы;
2) 414 : 2 = 207 − меньшее слагаемое;
3) 207 + 18 = 225 − большее слагаемое.
Ответ: 207 и 225

б) 1) 537 − 131 = 406 − была бы сумма чисел, если бы числа были одинаковы;
2) 406 : 2 = 203 − меньшее слагаемое;
3) 203 + 131 = 334 − большее слагаемое.
Ответ: 203 и 334

198. а) Представьте число 175 в виде суммы двух слагаемых, одно из которых на единицу меньше другого.
б) Представьте число 193 в виде суммы двух слагаемых, одно из которых на единицу больше другого.

Решение

а) 1) 175 − 1 = 174 − уравняем числа по меньшему числу;
2) 174 : 2 = 87 − меньшее слагаемое;
3) 87 + 1 = 88 − большее слагаемое.
Ответ: 87 и 88.

б) 1) 193 − 1 = 192 − уравняем числа по меньшему числу;
2) 192 : 2 = 96 − меньшее слагаемое;
3) 96 + 1 = 97 − большее слагаемое.
Ответ: 96 и 97.

199. а) На двух полках стояло 12 книг. Когда с первой полки на вторую переставили 2 книги, то книг на полках стало поровну. Сколько книг первоначально стояло на каждой полке?
б) В двух рядах 30 спортсменов. Когда из первого ряда перешли во второй 3 спортсмена, то в каждом ряду оказалось одинаковое число спортсменов. Сколько спортсменов было в каждом ряду первоначально?
в) В двух коробках 48 карандашей. Когда из первой коробки переложили во вторую 8 карандашей, то карандашей в коробках стало поровну. Сколько карандашей было в каждой коробке первоначально?

Решение

а) 1) 12 : 2 = 6 (к.) − стало на каждой полке;
2) 6 + 2 = 8 (к.) − стояло на первой полке первоначально;
3) 6 − 2 = 4 (к.) − стояло на второй полке первоначально.
Ответ: 8 и 4 книги.

б) 1) 30 : 2 = 15 (с.) − стало в каждом ряду;
2) 15 + 3 = 18 (с.в) − было в первом ряду;
3) 15 − 3 = 12 (с.) − было во втором ряду.
Ответ: 18 и 12 спортсменов

в) 1) 48 : 2 = 24 (к.) − было в каждом коробке;
2) 24 + 8 = 32 (к.) − первоначально было в первой коробке;
3) 24 − 8 = 16 (к.) − первоначально было во второй коробке.
Ответ: 32 и 16 карандашей.

200. 1) Разберите, как решена следующая задача:
Мама купила сыну 12 карандашей по 5 р. и по 7 р. Всего за карандаши она заплатила 68 р. Сколько карандашей по 5 р. и сколько по 7 р. купила мама?
Решение.
Если бы мама купила все карандаши по 5 р., то она заплатила бы 5 * 12 = 60 (р.). Но она заплатила на 8 р. больше. Каждый более дорогой карандаш добавил в общую стоимость по 2 р.
Сколько было карандашей по 7 р.?
8 : 2 = 4
Сколько было карандашей по 5 р.?
12 − 4 = 8.
(Убедитесь в правильности ответа, подсчитав сумму стоимости карандашей.)
2) Решите самостоятельно аналогичную задачу:
Для новогодней елки купили 10 шаров по 25 р. и по 40 р. Все шары вместе стоили 340 р. Сколько купили тех и других шаров?

Решение

1.  7 * 4 + 5 * 8 = 28 + 40 = 68 (р.) − сумма стоимости карандашей.
Ответ: задача решена верно.

2. 1) 10 * 25 = 250 (р.) − стоили бы шары, если бы все они стоили 25 р.;
    2) 340 − 250 = 90 (р.) − добавочная стоимость шаров по 40 р.;
    3) 40 − 25 = 15 (р.) − добавил бы каждый шар по 40 р.;
    4) 90 : 15 = 6 (шаров) − по 40 р. купили;
    5) 10 − 6 = 4 (шара) − по 25 р. купили.
Проверка:
4 * 25 + 6 * 40 = 100 + 240 = 340 (р.) − сумма стоимости всех шаров.
Ответ: 6 шаров по 40 р. и 4 шара по 25 р.

31

201. Для детского сада купили 20 пирамид: больших − по 7 колец и маленьких − по 5 колец. У всех пирамид вместе 128 колец. Сколько купили больших пирамид?
Подсказка.
Уравняйте число колец, "сняв" с больших пирамид по 2 кольца. Сколько тогда всего будет колец?

Решение

1) 20 * 5 = 100 (к.) − было бы всего если бы все пирамиды были по 5 колец;
2) 128 − 100 = 28 (к.) − добавочных с пирамид по 7 колец;
3) 7 − 5 = 2 (к.) − добавила бы каждая 7−кольцовая пирамида;
4) 28 : 2 = 14 (п.) − было по 7 колец;
5) 20 − 14 = 6 (п.) − было по 5 колец.
Проверка:
14 * 7 + 6 * 5 = 98 + 30 = 128 (колец) − всего.
Ответ: 14 пирамид по 7 колец; 6 пирамид по 5 колец.

202. а) В заповеднике у носорогов и антилоп вместе 36 рогов. Сколько носорогов и сколько антилоп в заповеднике, если у них вместе 24 головы?
Подсказка.
Предположите, что у носорогов и антилоп по 1 рогу. Сколько в таком случае всего будет рогов?
б) В детском саду имеется 20 велосипедов − трехколесных и двух колесных. У всех велосипедов вместе 55 колес. Сколько тех и других велосипедов в детском саду?
Подсказка.
Предположите, что все велосипеды двухколесные. Сколько в таком случае всего будет колес?

Решение

а) 1) 24 * 1 = 24 (р.) − было бы всего, если бы у антилоп было бы тоже по 1 рогу;
2) 36 − 24 = 12 (р.) − добавляют рога антилоп;
3) 2 − 1 = 1 (р.) − добавляет каждая антилопа;
4) 12 * 1 = 12 (ж.) − антилоп было в заповеднике;
5) 24 − 12 = 12 (жю) − носорогов было в заповеднике.
Проверка:
12 * 1 + 12 * 2 = 12 + 24 = 36 (р.)
Ответ: 12 антилоп и 12 носорогов.

б) 1) 20 * 2 = 40 (к.) − было бы всего, если бы все велосипеды были бы двухколесные;
2) 55 − 40 = 15 (к.) − добавляют трехколесные велосипеды;
3) 3 − 2 = 1 (к.) − добавляет каждый трехколесный велосипед;
4) 15 * 1 = 15 (в.) − было трехколесных;
5) 20 − 15 = 5 (в.) − было двухколесных.
Проверка:
15 * 3 + 5 * 2 = 45 + 10 = 55 (к.)
Ответ: 15 трехколесных и 5 двухколесных велосипедов.

203. а) В классе учатся мальчики и девочки, всего 30 человек. Витя подсчитал, что если каждый мальчик принесет по 5 кг макулатуры, а каждая девочка − по 3 кг, то все учащиеся вместе соберут 122 кг макулатуры. Сколько в классе мальчиков?
б) На празднике 22 ученика, у каждого мальчика по 3 шара, у каждой девочки по 5 шаров. Всего надули 86 шаров. Кого на празднике больше − девочек или мальчиков и на сколько?

Решение

а) 1) 30 * 3 = 90 (кг) − макулатуры принесли бы всего, если бы каждый принес по 3 кг;
2) 122 − 90 = 32 (кг) − добавляют мальчики;
3) 5 − 3 = 2 (кг) − добавляет каждый мальчик;
4) 32 : 2 = 16 (мальчиков) − было в классе.
Ответ: 16 мальчиков.

б) 1) 22 * 3 = 66 (ш.) − надули бы всего, если бы у каждого было бы по 3 шара;
2) 86 − 66 = 20 (ш.в) − добавляют девочки;
3) 5 − 3 = 2 (ш.) − добавляет каждая девочка;
4) 20 : 2 = 10 (девочек) − было на празднике;
5) 22 − 10 = 12 (мальчиков) − было на празднике;
6) 12 − 10 = на 2 (мальчика) − было больше, чем девочек.
Ответ: на 2 мальчика было больше.

204. а) В двух бочках было 40 ведер воды. Когда из первой бочки перелили во вторую в 3 раза больше ведер, чем в ней уже было, воды в бочках стало поровну. Сколько ведер воды было в каждой бочке первоначально?
б) В двух корзинах 60 яблок. Когда из первой корзины переложили во вторую в 2 раза меньше яблок, чем там было, яблок в корзинах стало поровну. Сколько яблок было в каждой корзине?

Решение

а) 1) 40 : 2 = 20 (в.) − стало в каждой бочке;
2) 1 + 3 = 4 (части) − приходится на 20 ведер;
3) 20 : 4 = 5 (в.) − воды было во второй бочке;
4) 40 − 5 = 35 (в.) − воды было в первой бочке.
Ответ: 35 ведер и 5 ведер

б) 1) 60 : 2 = 30 (ябл.) − стало в каждой корзине;
2) 1 + 2 = 3 (части) − приходится на 30 яблок;
3) 30 : 3 = 10 (ябл.) − составляет одна часть;
4) 10 * 2 = 20 (ябл.) − было во второй корзине;
5) 60 − 20 = 40 (ябл.) − было в первой корзине.
Ответ: 40 яблок и 20 яблок.

Самостоятельная работа № 9

Вариант 1

1. В двух коробках 45 конфет, причем в первой на 11 конфет меньше, чем во второй. Сколько конфет в каждой коробке?

Решение

1) 45 − 11 = 34 (к.) − было бы всего, если бы конфет в коробках было бы поровну;
2) 34 : 2 = 17 (к.) − было в первой коробке;
3) 17 + 11 = 28 (к.) − было во второй коробке.
Ответ: 17 конфет и 28 конфет.

2. Арбуз тяжелее дыни на 700 г, а их общая масса 5 кг 500 г. Найдите массу арбуза.

Решение

5 кг 500 г = 5500 г
1) 5500 − 700 = 4800 (г) − весили бы арбуз и дыня, если бы их масса была одинакова;
2) 4800 : 2 = 2400 (г) = 2 кг 400 г − масса дыни;
3) 2400 + 700 = 3100 (г) = 3 кг 100 г − масса арбуза.
Ответ: 2 кг 400 г − масса дыни; 3 кг 100 г − масса арбуза.

Вариант 2

1. В двух ящиках 62 лимона, причем в первом на 12 лимонов больше, чем во втором. Сколько лимонов в каждом ящике?

Решение

1) 62 − 12 = 50 (л.) − было бы всего, если бы лимонов в ящиках было поровну;
2) 50 : 2 = 25 (л.) − было во втором ящике;
3) 25 + 12 = 37 (л.) − было в первом ящике.
Ответ: 37 лимонов и 25 лимонов

2. Кабачок легче тыквы на 1 кг 800 г, а их общая масса 3 кг. Найдите массу тыквы.

Решение

1 кг 800 г = 1800 г;
3 кг = 3000 г.
1) 3000 − 1800 = 1200 (г) − весили бы кабачок и тыква, если бы их масса была одинакова;
2) 1200 : 2 = 600 (г) − масса кабачка;
3) 1800 + 600 = 2400 (г) = 2 кг 400 г − масса тыквы.
Ответ: 600 г весит кабачок, 2 кг 400 г весит тыквы.

32

Делимость чисел
ГДЗ к теме Нахождение делителей и кратных

205. Среди чисел 1, 2, 3, 4, 5, 6, 7, 12, 30 найдите те, которые являются делителями числа:
а) 105;
б) 144;
в) 120;
г) 140.

Решение

а) 105 : 1, так как любое число делится на 1;
105 : 3, так как сумма цифр числа делится на 3;
105 : 5, так как число оканчивается на 5;
105 : 7, так как (10 − 5 * 2) − делится на 7.

б) 144 : 1, так как любое число делится на 1;
144 : 2, так как число четное;
144 : 3, так как сумма цифр числа делится на 3;
144 : 4, так как число составленное из двух последних чисел делится на 4;
144 : 6, так как число одновременно делится и на 2 и на 3;
144 : 12, так как число одновременно делится и на 3 и на 4.

в) 120 : 1, так как любое число делится на 1;
120 : 2, так как число четное;
120 : 3, так как сумма цифр числа делится на 3;
120 : 4, так как число составленное из двух последних чисел делится на 4;
120 : 5, так как число оканчивается на 0;
120 : 6, так как число одновременно делится и на 2 и на 3;
120 : 12, так как число одновременно делится и на 3 и на 4;
120 : 30, так как число заканчивается цифрой нуль и сумма цифр числа делится на 3.

г) 140 : 1, так как любое число делится на 1;
140 : 2, так как число четное;
140 : 4, так как число составленное из двух последних чисел делится на 4;
140 : 5, так как число оканчивается на 0;
140 : 7, так как (14 − 7 * 2) − делится на 7.

206. а) Число 252 представили в виде произведения: 252 = 12 * 21. О каких делителях числа 252 говорит равенство? Укажите еще два делителя этого числа.
б) Используя равенство 510 = 34 * 15, найдите четыре делителя числа 510.

Решение

а) 252 = 12 * 21
Делители числа 252: 12 и 21.
12 = 3 * 4 = 2 * 2 * 3 = 2 * 6;
21 = 3 * 7.
Значит, делителями числа 252 будут также числа 2, 3, 4, 6, 7.

б) 510 = 34 * 15
Делители числа 510: 34 и 15.
34 = 2 * 17;
15 = 3 * 5.
Значит, делителями числа 510 будут также числа; 2, 3, 5, 17.

207. Не выполняя арифметических действий, докажите, что:
а) произведение 12 * 63 делится на 42;
б) степень $12^3$ делится на 27;
в) произведение 75 * 14 делится на 50;
г) произведение $2 * 15^2$ делится на 50.
Образец.
Докажем, что произведение 12 * 30 делится на 8.
Решение.
Чтобы доказать это утверждение, выделим в произведении 12 * 30 множитель 8;
12 * 30 = (4 * 3) * (3 * 15) = 8 * (3 * 15).

Решение

а) 12 * 63 = (6 * 2) * (9 * 7) = (6 * 7) * (2 * 9) = 42 * (2 * 9)

б) $12^3 = 12 * 12 * 12 = 3 * 4 * 3 * 4 * 3 * 4 = (3 * 3 * 3) * (4 * 4 * 4) = 27 * (4 * 4 * 4)$

в) 75 * 14 = (25 * 3) * (14 * 2) = (25 * 2) * (14 * 3) = 50 * (14 * 3)

г) $2 * 15^2 = 2 * 15 * 15 = 2 * 5 * 3 * 5 * 3 = (2 * 5 * 5) * (3 * 3) = 50 * (3 * 3)$

208. Запишите по порядку, начиная с наименьшего, все делители числа:
а) 15;
б) 21;
в) 28;
г) 48;
д) 100.

Решение

а) делители числа 15: 1, 3, 5, 15.

б) делители числа 21: 1, 3, 7, 21.

в) делители числа 28: 2, 4, 7, 14, 28.

г) делители числа 48: 2, 4, 6, 8, 12, 24, 48.

д) делители числа 100: 2, 4, 5, 10, 20, 25, 50, 100.

209. Найдите наибольший общий делитель пары чисел:
а) 9 и 12;
б) 12 и 18;
в) 30 и 36;
г) 18 и 28.

Решение

а) НОД (9;12) = 3
Д(9) = {1; 3; 9};
Д(12) = {1; 3; 4; 6; 12}.

б) НОД (12;18) = 6
Д(12) = {1; 2; 3; 4; 6; 12};
Д(18) = {1; 2; 3; 6; 9; 18}.

в) НОД (30;36) = 6
Д(30) = {1; 2; 3; 5; 6; 10; 15; 30};
Д(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}.

г) НОД (18;28) = 2
Д(30) = {1; 2; 3; 6; 9; 18};
Д(36) = {1; 2; 4; 7; 14; 28}.

210. 1) Найдите наибольший общий делитель чисел:
а) 12 и 6;
б) 20 и 10;
в) 150 и 50;
г) 48 и 12.
2) Известно, что число a делится на число b. Чему равен НОД (a;b)?

Решение

1) а) НОД (12;6) = 6;
б) НОД (20;10) = 10;
в) НОД (150;50) = 50;
г) НОД (48;12) = 12.

2) НОД (a;b) = b.

211. 1) НОД (8;9) = 1. Убедитесь в этом, выписав все делители каждого из чисел 8 и 9.
2) Придумайте шесть пар чисел a и b, таких, что НОД (a;b) = 1.

Решение

1.  НОД (8;9) = 1
    Д(8) = {1; 2; 4; 8};
    Д(9) = {1; 3; 9}.

2. 1) НОД (9;10) = 1;
    2) НОД (10;11) = 1;
    3) НОД (11;17) = 1;
    4) НОД (9;23) = 1;
    5) НОД (7;22) = 1;
    6) НОД (20;31) = 1.

212. Запишите первые десять чисел, кратных числу:
а) 12;
б) 15;
в) 22;
г) 30.

Решение

а) 24, 36, 48, 60, 72, 84, 96, 108, 120, 132.

б) 30, 45, 60, 75, 90, 105, 120, 135, 150, 165.

в) 44, 66, 88, 110, 132, 154, 176, 198, 220, 242.

г) 60, 90, 120, 150, 180, 210, 240, 270, 300, 330.

213. Верно ли, что одно из двух чисел кратно другому:
а) 15 и 60;
б) 6 и 146;
в) 96 и 12;
г) 37 и 144?

Решение

а) 60 : 15 = 4 − верно

б) 146 : 6 = 24 (ост.2) − неверно
$\snippet{name: long_division, x: 146, y: 6}$

в) 96 : 12 = 8 − верно

г) 144 : 37 = 3 (ост.33) − неверно

214. Какие из чисел 24, 36, 48, 84, 96, 120 являются общими кратными чисел:
а) 6 и 8;
б) 12 и 8;
в) 3 и 4;
г) 8 и 3?

Решение

а) 24, 48, 96, 120.

б) 24, 48, 96, 120.

в) 24, 36, 48, 84, 96, 120.

г) 24, 48, 96, 120.

215. Найдите наименьшее общее кратное чисел:
а) 10 и 15;
б) 8 и 12;
в) 6 и 10;
г) 12 и 15.

Решение

а) 10: 10, 20, 30, 40, 50, ...;
15: 15, 30, 45, 60, ...;
НОК (10;15) = 30.

б) 8: 8, 16, 24, 32, ...;
12: 12, 24, 36, 48, ...;
НОК (8;12) = 24.

в) 6: 6, 12, 18, 24, 30, 36, ...;
10: 10, 20, 30, 40, 50, ...;
НОК (6;10) = 30.

г) 12: 12, 24, 36, 48, 60, 72, 84, ...;
15: 15, 30, 45, 60, 75, ...;
НОК (12,15) = 60.

216. 1) Найдите наименьшее общее кратное чисел:
а) 40 и 20;
б) 26 и 13;
в) 150 и 50;
г) 120 и 30.
2) Известно, что число a делится на число b. Чему равно НОК (a;b)?

Решение

1. а) 40: 40, 80, 120, 160, ...;
20: 20, 40, 80, 100, ...;
НОК (40;20) = 40.

б) 26: 26, 52, 78, ...;
13: 13, 26, 39, 52, ...;
НОК (26;13) = 26.

в) 150: 150; 300; 450; 600, ...;
50: 50, 100, 150, 200, ...;
НОК (150;50) = 150.

г) 120: 120, 240, 360, 480, ...;
30: 30, 60, 90, 120, 150, ... .
НОК (120;30) = 120.

2) НОК (a;b) = a.

33

217. Проверьте, что НОК (3;4) = 12. Придумайте еще пять пар чисел a и b, таких, что НОК (a;b) = a * b (т.е. наименьшее общее кратное этих чисел равно их произведению).

Решение

3: 3, 6, 9, 12, 15, ...;
4: 4, 8, 12, 16, ...;
НОК (3;4) = 12.
1) НОК (2;3) = 6;
2) НОК (4;5) = 20;
3) НОК (5;6) = 30;
4) НОК (6;7) = 42;
5) НОК (7;8) = 56.

218. Найдите общие делители и наибольший общий делитель чисел:
а) 84 и 56;
б) 225 и 180.

Решение

а) 84: 1, 2, 3, 6, 7, 12, 14, 28, 42, 84;
56: 1, 2, 4, 7, 8, 14, 16, 28, 56;
ОД: 1, 2, 4, 7, 14, 28;
НОД (84;56) = 28.

б) 225: 1, 3, 5, 9, 15, 25, 45, 75, 225;
180: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 30, 36, 45, 60, 90, 180;
ОД: 1, 3, 5, 9, 15, 45;
НОД (180;225) = 45.

219. Найдите несколько общих кратных и наименьшее общее кратное чисел:
а) 4, 6 и 12;
б) 3, 4 и 18;
в) 3, 6 и 9;
г) 10, 16 и 40;
д) 6, 9 и 10;
е) 12, 15 и 20.

Решение

а) ОК: 12, 24, 36, ...;
НОК (4;6;12) = 12.

б) ОК: 36, 72, 108, ...;
НОК (3;4;18) = 36.

в) ОК: 18, 36, 54, ...;
НОК (3;6;9) = 18.

г) ОК: 120, 240, 360, ...;
НОК (10;16;40) = 80.

д) ОК: 90, 180, 270, ...;
НОК (6;9;10) = 90.

е) ОК: 60, 120, 180, ...;
НОК (12;15;20) = 60.

220. Какая последняя цифра может быть у числа, кратного:
а) 10;
б) 15;
в) 11;
г) 16;
д) 13?

Решение

а) 0.

б) 0, 5.

в) 2, 4, 6, 8.

г) 0, 2, 4, 6, 8.

д) 2, 3, 6, 9.

221. Среди чисел 5, 10, 15, 20, 25, 40, 50, 75, 100 найдите все те, которые:
а) кратны 25;
б) не кратны 10;
в) делятся на 5 и на 4;
г) кратны 5 и не кратны 4;
д) являются делителем числа 500;
е) являются делителем числа 500 и не являются делителем числа 50.

Решение

а) 25, 50, 75, 100.

б) 5, 15, 25, 75.

в) 20, 40, 100.

г) 5, 15, 25, 50, 75.

д) 5, 10, 20, 25, 50, 100.

е) 20, 100.

ГДЗ к теме Простые и составные числа

222. Есть ли среди данных чисел простые? Выпишите их.
а) 1, 11, 21, 31, 41, 51, 61, 71, 81, 91;
б) 2, 12, 22, 32, 42, 52, 62, 72, 82, 92;
в) 3, 13, 23, 33, 43, 53, 63, 73, 83, 93;
г) 5, 15, 25, 35, 45, 55, 65, 75, 85, 95;
д) 7, 17, 27, 37, 47, 57, 67, 77, 87, 97;
е) 9, 19, 29, 39, 49, 59, 69, 79, 89, 99.

Решение

а) 11, 31, 41, 61, 71.

б) 2.

в) 3, 13, 23, 43, 53, 73, 83.

г) 5.

д) 7, 17, 37, 47, 67, 97.

е) 19, 29, 59, 79, 89.

223. Разложите на простые множители число:
а) 18;
б) 40;
в) 130;
г) 210.

Решение

а) $ \begin{array}{r|l} 18 & 2\\ 9 & 3\\ 3 & 3\\ 1 & \end{array} $
$18 = 2 * 3^2$

б) $ \begin{array}{r|l} 40 & 2\\ 20 & 2\\ 10 & 2\\ 5 & 5\\ 1 & \end{array} $
$40 = 2^3 * 5$

в) $ \begin{array}{r|l} 130 & 2\\ 65 & 5\\ 13 & 13\\ 1 & \end{array} $
$130 = 2 * 5 * 13$

г) $ \begin{array}{r|l} 210 & 2\\ 105 & 5\\ 21 & 7\\ 3 & 3\\ 1 & \end{array} $
$210 = 2 * 3 * 5 * 7$

224. Какое число разложено на простые множители:
а) $2 * 3^4 * 7$;
б) $2^3 * 3 * 5$;
в) $3^2 * 5 * 11^2$?

Решение

а) $2 * 3^4 * 7 = 2 * 81 * 7 = 81 * 14 = 1134$

б) $2^3 * 3 * 5 = 8 * 3 * 5 = 40 * 3 = 120$

в) $3^2 * 5 * 11^2 = 9 * 5 * 121 = 45 * 121 = 5445$

225. Пользуясь равенством 111 = 3 * 37, разложите на простые множители число:
а) 222;
б) 444;
в) 666;
г) 999.

Решение

а) 222 = 2 * 111 = 2 * 3 * 37

б) 444 = 4 * 111 = 2 * 2 * 3 * 37

в) 666 = 6 * 111 = 2 * 3 * 3 * 37

г) 999 = 9 * 111 = 3 * 3 * 3 * 37

226. Найдите несколько делителей числа, равного произведению:
а) $2 * 5 * 13$;
б) $2^2 * 3^2$;
в) $2 * 5^2 * 7$;
г) $2^2 * 3 * 5^2$.

Решение

а) $2 * 5 * 13 = 10 * 13 = 130$
некоторые из делителей:
2 * 5 = 10;
2 * 13 = 26;
5 * 13 = 65.

б) $2^2 * 3^2 = 4 * 9 = 36$
некоторые из делителей:
2 * 3 = 6;
3 * 3 = 9;
4 * 3 = 12;
2 * 3 * 3 = 18.

в) $2 * 5^2 * 7 = 2 * 25 * 7 = 50 * 7 = 350$
некоторые из делителей:
2 * 5 = 10;
2 * 7 = 14;
5 * 7 = 35;
2 * 5 * 7 = 70.

г) $2^2 * 3 * 5^2 = 4 * 3 * 25 = 3 * 100 = 300$
некоторые из делителей:
2 * 5 = 10;
2 * 2 * 5 = 20;
3 * 5 = 15;
3 * 5 * 5 = 75.

227. Найдите все делители числа a, если:
а) a = 2 * 3 * 5;
б) $a = 2 * 3^2$.

Решение

а) a = 2 * 3 * 5 = 6 * 5 = 30;
2 * 3 = 6;
2 * 5 = 10;
3 * 5 = 15.
Делители: 1, 2, 3, 5, 6, 10, 15, 30.

б) $a = 2 * 3^2 = 2 * 9 = 18$
2 * 3 = 6;
3 * 3 = 9.
Делители: 1, 2, 3, 6, 9, 18.

228. Представьте число 30 в виде суммы простых чисел всеми возможными способами. (Суммы, отличающиеся только порядком слагаемых, считайте одинаковыми.)

Решение

30 = 17 + 13;
30 = 11 + 19;
30 = 7 + 23;
30 = 1 + 29.

34

229. Представьте все четные числа от 12 до 20 в виде разности двух простых чисел.

Решение

12 = 23 − 11;
14 = 17 − 3;
16 = 29 − 13;
18 = 31 − 13;
18 = 29 − 11;
20 = 31 − 11;
20 = 23 − 3.

230. Может ли быть простым числом:
а) сумма двух простых чисел;
б) произведение двух простых чисел?

Решение

а) Сумма двух простых чисел может быть простым числом, например:
11 + 2 = 13.

б) Произведение двух простых чисел не может быть простым числом, так как у произведения будет минимум четыре делителя:
1;
перовое число;
второе число;
произведение этих чисел.

ГДЗ к теме Применение признаков делимости

231. На какие из чисел 2, 5, 10, 3, 9 делится данное число:
а) 135;
б) 504;
в) 708;
г) 4920?

Решение

а) 135 : 5, так как число оканчивается на 5;
135 : 3, так как сумма цифр числа делится на 3;
135 : 9, так как сумма цифр числа делится на 9.

б) 504 : 2, так как число четное;
504 : 3, так как сумма цифр числа делится на 3;
504 : 9, так как сумма цифр числа делится на 9.

в) 708 : 2, так как число четное;
708 : 3, так как сумма цифр числа делится на 3.

г) 4920 : 2, так как число четное;
4920 : 5, так как число оканчивается на 0;
4920 : 10, так как число оканчивается на 0.

232. Какие из чисел 188, 723, 918, 8025, 7776, 405, 835, 1236, 711 делятся:
а) на 3; на 3 и на 2; на 3 и на 5;
б) на 9; на 9 и на 2; на 9 и на 5?

Решение

а) Делятся на 3:
723, 918, 8025, 7776, 405, 1236, 711.
Делятся на 3 и на 2:
918, 7776, 1236.
Делятся на 3 и на 5:
8025, 405.

б) Делятся на 9:
918, 7776, 405, 711.
Делятся на 9 и на 2:
918, 7776.
Делятся на 9 и на 5:
405.

233. В четырехзначном числе 273* вместо последней цифры стоит звездочка. Какой может быть эта цифра, чтобы число делилось:
а) на 2;
б) на 5;
в) на 3;
г) на 9?

Решение

а) 2730 : 2;
2732 : 2;
2734 : 2;
2736 : 2;
2738 : 2.
Ответ: 0, 2, 4, 6, 8.

б) 2730 : 5;
2735 : 5.
Ответ: 0, 5.

в) 2730 : 3;
2733 : 3;
2736 : 3;
2739 : 3.
Ответ: 0, 3, 6, 9.

г) 2736 : 3.
Ответ: 6.

234. Запишите какое−нибудь четырехзначное число, которое делится на 9 и оканчивается цифрой:
0; 1; 2; 3; 4; 5; 6; 7; 8; 9.

Решение

3330;
3231;
3132;
3033;
3024;
3015;
3006;
2007;
1008;
9999.

235. Не выполняя действий, определите, делится ли на 5 значение выражения:
а) 470 + 755;
б) 215 + 113;
в) 330 − 28;
г) 935 − 85;
д) 445 * 710;
е) 416 * 300.

Решение

а) 470 + 755 − делится на 5, так как оба числа делятся на 5.

б) 215 + 113 − не делятся на 5, так как оба числа не делятся на 5.

в) 330 − 28 − не делятся на 5, так как оба числа не делятся на 5.

г) 935 − 85 − делится на 5, так как оба числа делятся на 5.

д) 445 * 710 − делится на 5, так как хотя бы один из множителей делится на 5.

е) 416 * 300 − делится на 5, так как хотя бы один из множителей делится на 5.

236. Докажите, что произведение:
а) 24 * 25 делится на 15;
б) 35 * 12 делится на 20;
в) 9 * 15 * 40 делится на 25;
г) 6 * 12 * 40 делится на 45.

Решение

а) 24 * 25 = 3 * 8 * 5 * 5 = (3 * 5) * (8 * 5) = 15 * (8 * 5)

б) 35 * 12 = 5 * 7 * 3 * 4 = (5 * 4) * (7 * 3) = 20 * (7 * 3)

в) 9 * 15 * 40 = 9 * 5 * 3 * 5 * 8 = (5 * 5) * (9 * 3 * 8) = 25 * (9 * 3 * 8)

г) 6 * 12 * 40 = 3 * 2 * 3 * 4 * 5 * 8 = (3 * 3 * 5) * (2 * 4 * 8) = 45 * (2 * 4 * 8)

237. Напишите наибольшее трехзначное число, которое делится:
а) на 2;
б) на 3;
в) на 2 и на 3;
г) на 15.

Решение

а) 998

б) 999

в) 996

г) 975

238. Припишите к числу 10 слева такую цифру, чтобы получившееся трехзначное число делилось на 15.

Решение

Чтобы число делилось на 15, надо чтобы число одновременно делилось и на 3 и на 5, тогда:
210 : 15;
510 : 15;
810 : 15.

239. К числу 10 надо приписать по одной цифре справа и слева так, чтобы полученное число делилось на 18. Сделайте это всеми возможными способами.
Подсказка.
Число должно делится на 2 и на 9. Сначала "обеспечивайте" делимость на 2, т.е. приписывайте справа цифры 0, 2 и т.д. Затем определяйте, какая цифра должна стоять слева.

Решение

Чтобы число делилось на 2, тогда оно должно быть четным, тогда число может быть:
*100;
*102;
*104;
*106;
*108.
Чтобы число делилось на 9, тогда сумма его цифр должно делиться на 9, тогда это число:
8100;
6102;
4104;
2106;
9108.

240. Верно ли утверждение: если число делится на 4 и на 6, то оно делится на 24?

Решение

6 * 4 = 24, значит утверждение верно.

241. Рассмотрите признак делимости на 4: число делится на 4 в том и только в том случае, если две его последние цифры образуют число, делящееся на 4. Определите, какие из чисел 164, 230, 1124, 2080, 3118 делятся на 4.

Решение

164 : 4, так как 64 : 4;
1124 : 4, так как 24 : 4;
2080 : 4, так как 80 : 4.

35

242. Рассмотрите признак делимости на 25: число делится на 25 в том и только в том случае, если оно оканчивается на 00, 25, 50 или 75. Определите, какие из чисел 6425, 3005, 12475, 8000, 7555 делятся на 25.

Решение

6425 : 25;
12475 : 25;
8000 : 25.

243. Запишите наименьшее 10−значное число, в котором:
а) все цифры различны и оно делится на 4;
б) все цифра различны и оно делится на 25.
Указание.
См. упр. 241 и 242.

Решение

а) 1023457896

б) 1023468975

244. Запишите наибольшее 10−значное число, в котором:
а) все цифры различны и оно делится на 4;
б) все цифра различны и оно делится на 25.
Указание.
См. упр. 241 и 242.

Решение

а) 9876543120

б) 9876432150

245. В записи числа 2438195760 использованы все 10 цифр, причем каждая по одному разу. Это число имеет много делителей. Докажите, что его делителем является любое из чисел от 1 до 18.

Решение

2438195760 : 1, так как любое число делится на 1;
2438195760 : 2, так как число четное;
2438195760 : 3, так как сумма цифр числа делится на 3 (2 + 4 + 3 + 8 + 1 + 9 + 5 + 7 + 6 + 0 = 45);
2438195760 : 4, так как число, составленное из двух последних цифр делится на 4;
2438195760 : 5, так как оканчивается на 0;
2438195760 : 6, так как число одновременно делится на 2 и на 3;
2438195760 : 7 = 348313680
2438195760 : 8, так как число одновременно делится на 2 и на 4;
2438195760 : 9, так как сумма цифр числа делится на 9 (2 + 4 + 3 + 8 + 1 + 9 + 5 + 7 + 6 + 0 = 45);
2438195760 : 10, так как оканчивается на 0;
2438195760 : 11, так как на 11 делятся те числа, у которых сумма цифр, стоящих на нечетных местах, либо равна сумме цифр, стоящих на четных местах, либо отличается от нее на число, делящееся на 11:
2 + 3 + 1 + 5 + 6 = 17;
4 + 8 + 9 + 7 + 0 = 28;
28 − 17 = 11.
2438195760 : 12, так как число одновременно делится на 3 и на 4;
2438195760 : 13 = 187553520
2438195760 : 14, так как число одновременно делится на 2 и на 7;
2438195760 : 15, так как число одновременно делится на 3 и на 5;
2438195760 : 16, так как число одновременно делится на 2 и на 8;
2438195760 : 17 = 143423280
2438195760 : 18, так как число одновременно делится на 2 и на 9.

246. Разберите признак делимости на 11:
чтобы узнать, делится ли число на 11, надо:
- сложить все цифры числа, стоящие на нечетных местах, начиная с разряда единиц (т.е. справа налево), и сделать то же самое для цифр, стоящих на четных местах;
- из большей полученной суммы вычесть меньшую и определить, делится ли разность на 11;
- если ответ "да", то и само число делится на 11; если "нет", то число на 11 не делится.
Используя признак делимости на 11, установите, делится ли число 4217532:
а) на 11;
б) на 33;
в) на 99.
Образец.
Определим, делится ли число 374715 на 11.
Решение:
5 + 7 + 7 = 19 и 1 + 4 + 3 = 8, 19 − 8 = 11;
11 делится на 11; следовательно, число 374715 делится на 11.

Решение

а) 4 + 1 + 5 + 2 = 12;
2 + 7 + 3 = 12;
12 − 12 = 0;
0 делится на 11; следовательно, число 4217532 делится на 11.

б) 4 + 2 + 1 + 7 + 5 + 3 + 2 = 24;
24 : 3, значит число 4217532 делится на 3 и одновременно на 11, а значит данное число делится на 33.

в) Число 4217532 делится на 3 и делится на 33, а значит оно делится и на 99, так как 3 * 33 = 99.

Самостоятельная работа № 10

Вариант 1

1. Найдите:
а) НОД (36;54);
б) НОК (9 и 12).

Решение

а) НОД (36;54) = 2 * 3 * 3 = 18;
36 = 4 * 9 = 2 * 2 * 3 * 3;
54 = 6 * 9 = 2 * 3 * 3 * 3.

б) НОК (9 и 12) = 3 * 3 * 2 * 2 = 36;
9 = 3 * 3;
12 = 3 * 2 * 2.

2. Разложите на простые множители число 210.

Решение

$ \begin{array}{r|l} 210 & 2\\ 105 & 5\\ 21 & 7\\ 3 & 3\\ 1 & \end{array} $
210 = 2 * 3 * 5 * 7

3. Какие из чисел 105, 108, 110, 115, 152, 160, 175, 190:
а) делятся на 2 и не делятся на 5;
б) делятся на 2 и на 5?

Решение

а) 108, 152.

б) 110, 160, 190.

Вариант 2

1. Найдите:
а) НОД (42;28);
б) НОК (10 и 8).

Решение

а) НОД (42;28) = 7 * 2 = 14;
42 = 7 * 2 * 3;
28 = 7 * 2 * 2.

б) НОК (10 и 8) = 5 * 2 * 2 * 2 = 40;
10 = 5 * 2;
8 = 2 * 2 * 2.

2. Разложите на простые множители число 150.

Решение

$ \begin{array}{r|l} 150 & 2\\ 75 & 5\\ 15 & 5\\ 3 & 3\\ 1 & \end{array} $
$150 = 2 * 3 * 5^2$

3. Какие из чисел 133, 141, 153, 264, 287, 495, 519:
а) делятся на 3 и не делятся на 9;
б) делятся на 3 и на 9?

Решение

а) 141, 264, 519.

б) 153, 495.

36

Дроби
ГДЗ к теме Доли

247. а) Как называют доли, получаемые при делении целого на 3, 5, 6, 8 равных частей?
б) На сколько равных частей разделили целое, если в результате получились четвертые доли? седьмые доли? десятые доли? двенадцатые доли?

Решение

а) третьи доли;
пятые доли;
шестые доли;
восьмые доли.

б) на четыре части;
не семь частей;
на десять частей;
на двенадцать частей.

248. Вставьте пропущенные слова:
а)
сантиметр − ... часть метра;
миллиметр − ... часть сантиметра;
метр − ... часть километра;
миллиметр − ... часть метра.
б)
грамм − ... часть килограмма;
килограмм − ... часть тонны;
килограмм − ... часть центнера;
центнер − ... часть тонны.

Решение

а) сантиметр − сотая часть метра;
миллиметр − десятая часть сантиметра;
метр − тысячная часть километра;
миллиметр − тысячная часть метра.

б) грамм − тысячная часть килограмма;
килограмм − тысячная часть тонны;
килограмм − сотая часть центнера;
центнер − десятая часть тонны.

249. 1) Сколько граммов содержится:
а) в половине килограмма;
б) в четверти килограмма?
2) Сколько минут содержится:
а) в половине часа;
б) в четверти часа?

Решение

1) 1 кг = 1000 г
а) 1000 : 2 = 500 (г) − содержится в половине килограмма;
б) 1000 : 4 = 250 (г) − содержится в четверти килограмма.

2) 1 ч = 60 мин
а) 60 : 2 = 30 (мин) − содержится в половине часа;
б) 60 : 4 = 15 (мин) − содержится в четверти часа.

250. Назовите время, которое показывают часы, используя слова "половина", "четверть" (рис.5).

Решение

1) четверть двенадцатого;
2) половина двенадцатого;
3) без четверти двенадцать.

251. У Андрея 90 марок, у Богдана на 30 меньше, а у Вадима третья часть числа всех марок Андрея и Богдана. Сколько марок у Вадима?

Решение

1) 90 − 30 = 60 (м.) − у Богдана;
2) 90 + 60 = 150 (м.к) − у Андрея и Богдана вместе;
3) 150 : 3 = 50 (м.) − было у Вадима.
Ответ: 50 марок

252. Туристы прошли 32 км, это составило четверть длины всего маршрута. Какова длина маршрута?

Решение

32 : 1 * 4 = 128 (км) − длина маршрута.
Ответ: 128 км.

253. Вставьте пропущенные слова:
а) 1 $см^2$ − это ... часть 1 $м^2$;
б) 1 $мм^2$ − это ... часть 1 $см^2$;
в) 1 $дм^2$ − это ... часть 1 $м^2$;
г) 1 $м^2$ − это ... часть 1 $км^2$.

Решение

а) 1 $см^2$ − это десятитысячная часть 1 $м^2$

б) 1 $мм^2$ − это сотая часть 1 $см^2$

в) 1 $дм^2$ − это сотая часть 1 $м^2$

г) 1 $м^2$ − это миллионная часть 1 $км^2$

254. а) В книге 78 страниц. В первый день Аня прочитала половину всей книги, а во второй день − треть числа оставшихся страниц. Сколько страниц ей осталось прочитать?
б) В книге 96 страниц. В первый день Аня прочитала треть книги, а за 2 первых дня − половину книгу. Сколько страниц прочитала Аня во второй день?

Решение

а) 1) 78 : 2 = 39 (с.) − прочитала Аня в первый день;
2) 39 : 3 = 13 (с.) − прочитала Аня во второй день;
3) 39 − 13 = 26 (с.) − осталось прочитать Ане.
Ответ: 26 страниц.

б) 1) 96 : 3 = 32 (с.) − прочитала Аня в первый день;
2) 96 : 2 = 48 (с.) − прочитала Аня за первые два дня;
3) 48 − 32 = 16 (с.) − прочитала Аня за второй день.
Ответ: 16 страниц.

255. а) Школьная футбольная команда за год сыграла 18 матчей в футбольных турнирах. Половину всех матчей она выиграла, шестую часть проиграла, остальные сыграла вничью. Сколько игр команда сыграла вничью?
б) Школьная футбольная команда, играя в течение года с командами других школ, половину всех матчей выиграла, 4 игры проиграла, что составило пятую часть всех сыгранных за год матчей, остальные сыграла вничью. Сколько игр команда сыграла вничью?

Решение

а) 1) 18 : 2 = 9 (и.) − команда выиграла;
2) 18 : 6 = 3 (и.) − команда проиграла;
3) 18 − (9 + 3) = 18 − 12 = 6 (и.) − команда сыграла вничью.
Ответ: 6 игр.

б) 1) 4 * 5 = 20 (и.) − команда сыграла за год;
2) 20 : 2 = 10 (и.) − команда выиграла;
3) 20 − (10 + 4) = 20 − 14 = 6 (и.) − команда сыграла вничью.
Ответ: 6 игр.

37

ГДЗ к теме Что такое дробь

256. Используя разные геометрические фигуры, изобразите дробь:
а) $\frac{1}{2}$;
б) $\frac{1}{3}$;
в) $\frac{1}{4}$;
г) $\frac{2}{3}$;
д) $\frac{3}{5}$;
е) $\frac{5}{6}$.

Решение

257. Запишите ответ в виде дроби:
а) Молоко разлили поровну в 6 стаканов. Какая часть молока поместилась в 1 стакан? в 3 стакана? в 5 стаканов?
б) Конфеты разложили поровну в 8 коробок. Какую часть конфет положили в 1 коробку? в 3 коробки? в 7 коробок?
в) Бассейн наполняется водой за 5 ч. Какая часть бассейна наполнится водой за 1 ч? за 2 ч? за 4 ч?
г) Комбайн убрал поле за 8 дней, выполняя за день один и тот же объем работы. Какая часть поля была убрана за 1 день? за 5 дней? за 7 дней?

Решение

а) 1) $1 : 6 = \frac{1}{6}$ (часть) − молока поместилась в 1 стакан;
2) $3 : 6 = \frac{3}{6}$ (часть) − молока поместилась в 3 стакана;
3) $5 : 6 = \frac{5}{6}$ (часть) − молока поместилась в 5 стаканов.
Ответ: $\frac{1}{6}, \frac{3}{6}, \frac{5}{6}.$

б) 1) $1 : 8 = \frac{1}{8}$ (часть) − конфет положили в 1 коробку;
2) $3 : 8 = \frac{3}{8}$ (часть) − конфет положили в 3 коробки;
3) $7 : 8 = \frac{7}{8}$ (часть) − конфет положили в 7 коробок.
Ответ: $\frac{1}{8}, \frac{3}{8}, \frac{7}{8}.$

в) 1) $1 : 5 = \frac{1}{5}$ (часть) − бассейна наполнится за 1 час;
2) $2 : 5 = \frac{2}{5}$ (часть) − бассейна наполнится за 2 часа;
3) $4 : 5 = \frac{4}{5}$ (часть) − бассейна наполнится за 4 часа.
Ответ: $\frac{1}{5}, \frac{2}{5}, \frac{4}{5}.$

г) 1) $1 : 8 = \frac{1}{8}$ (часть) − поля была убрана за 1 день;
2) $5 : 8 = \frac{5}{8}$ (часть) − поля была убрана за 5 дней;
3) $7 : 8 = \frac{7}{8}$ (часть) − поля была убрана за 7 дней.
Ответ: $\frac{1}{8}, \frac{5}{8}, \frac{7}{8}.$

258. а) На стол поставили 12 чашек: среди них 7 красных, остальные − синие. Какую часть всех чашек составляют красные чашки? синие чашки?
б) На соревнования по легкой атлетике поехала школьная команда из 15 человек, в которой 4 пятиклассника, остальные − шестиклассники. Какую часть всей команды составляют пятиклассники? шестиклассники?

Решение

а) 1) 12 − 7 = 5 (чашек) − синих на столе;
2) $7 : 12 = \frac{7}{12}$ (всех чашек) − составляют красные чашки;
3) $5 : 12 = \frac{5}{12}$ (всех чашек) − составляют синие чашки.
Ответ: $\frac{7}{12}; \frac{5}{12}$.

б) 1) 15 − 4 = 11 (шестиклассников) − было в команде;
2) $4 : 15 = \frac{4}{15}$ (команды) − составляли пятиклассники;
3) $11 : 15 = \frac{11}{15}$ (команды) − составляли шестиклассники.
Ответ: $\frac{4}{15}; \frac{11}{15}$.

259. а) В связке 11 воздушных шаров: 3 из них желтые, 4 − зеленые, остальные красные. Какую часть всех шаров составляют красные шары? желтые шары? зеленые шары?
б) В коробке 15 шариковых ручек: 7 из них синие, 5 − черные, остальные − зеленые. Какую часть всех ручек составляют синие и черные ручки вместе? синие и зеленые ручки вместе?

Решение

а) 1) 11 − (3 + 4) = 11 − 7 = 4 (шара) − было красных;
2) $4 : 11 = \frac{4}{11}$ (всех шаров) − составляют красные шары;
3) $3 : 11 = \frac{3}{11}$ (всех шаров) − составляют желтые шары;
4) $4 : 11 = \frac{4}{11}$ (всех шаров) − составляют зеленые шары.
Ответ: $\frac{4}{11}$ − красные; $\frac{3}{11}$ − составляют желтые; $\frac{4}{11}$ − составляют зеленые.

б) 1) 7 + 5 = 12 (ручек) − было синих и черных;
2) 15 − 12 = 3 (ручки) − было зеленых;
3) 7 + 3 = 10 (ручек) − было синих и зеленых;
4) $12 : 15 = \frac{12}{15}$ (всех ручек) − составляют синие и черные ручки вместе;
5) $10 : 15 = \frac{10}{15}$ (всех ручек) − составляют синие и зеленые ручки вместе.
Ответ: $\frac{12}{15}$ − синие и черные; $\frac{10}{15}$ − синие и зеленые.

260. Запишите:
а) три правильные и три неправильные дроби со знаменателем 6;
б) три правильные и три неправильные дроби с числителем 5.

Решение

а) Правильные:
$\frac{1}{6}, \frac{2}{6}, \frac{5}{6}$.
Неправильные:
$\frac{7}{6}, \frac{11}{6}, \frac{17}{6}$.

б) Правильные:
$\frac{5}{6}, \frac{5}{7}, \frac{5}{11}$.
Неправильные:
$\frac{5}{2}, \frac{5}{3}, \frac{5}{4}$.

261. В дробь $\frac{10}{b}$ вместо b подставляют числа 2, 13, 10, 7, 15, 4, 99, 9. При каких значениях b дробь является правильной? неправильной?

Решение

Дробь будет правильной при b > 10:
13, 15, 99.
Дробь будет неправильной при b ≤ 10:
2, 10, 7, 4, 9.

262. Сколько килограммов содержится в:
а) $\frac{1}{4}$ т;
б) $\frac{3}{4}$ т;
в) $\frac{3}{10}$ т;
г) $\frac{13}{10}$ т?

Решение

а) $\frac{1}{4} т = 1000 : 4 = 25$ (кг)

б) $\frac{3}{4} т = 1000 : 4 * 3 = 250 * 3 = 750$ (кг)

в) $\frac{3}{10} т = 1000 : 10 * 3 = 100 * 3 = 300$ (кг)

г) $\frac{13}{4} т = 1000 : 10 * 13 = 100 * 13 = 1300$ (кг)

38

263. Сколько сантиметров содержится в:
а) $\frac{1}{10}$ м, $\frac{7}{20}$ м, $\frac{17}{10}$ м, $\frac{7}{5}$ м;
б) $\frac{1}{10}$ дм, $\frac{4}{5}$ дм, $\frac{7}{2}$ дм, $\frac{6}{5}$ дм?

Решение

а) $\frac{1}{10} м = 100 : 10 = 10$ (см);
$\frac{7}{20} м = 7 * 100 : 20 = 700 : 20 = 35$ (см);
$\frac{17}{10} м = 17 * 100 : 10 = 1700 : 10 = 170$ (см);
$\frac{7}{5} м = 7 * 100 : 5 = 700 : 5 = 140$ (см).

б) $\frac{1}{10} дм = 1 * 10 : 10 = 10 : 10 = 1$ (см);
$\frac{4}{5} дм = 4 * 10 : 5 = 40 : 5 = 8$ (см);
$\frac{7}{2} дм = 7 * 10 : 2 = 70 : 2 = 35$ (см);
$\frac{6}{5} дм = 6 * 10 : 5 = 60 : 5 = 12$ (см).

264. а) Сколько минут содержится
в $\frac{1}{2}$ ч?
в $\frac{3}{4}$ ч?
в $\frac{6}{5}$ ч?
в $\frac{3}{2}$ ч?
б) Сколько секунд содержится
в $\frac{2}{3}$ мин?
в $\frac{1}{6}$ мин?
в $\frac{5}{2}$ мин?
в $\frac{11}{10}$ мин?

Решение

а) 1 ч = 60 мин
$\frac{1}{2} ч = 60 * 1 : 2 = 30$ (мин);
$\frac{3}{4} ч = 60 : 4 * 3 = 15 * 3 = 45$ (мин);
$\frac{6}{5} ч = 60 : 5 * 6 = 12 * 6 = 72$ (мин);
$\frac{3}{2} ч = 60 : 2 * 3 = 30 * 3 = 90$ (мин).

б) 1 мин = 60 с
$\frac{2}{3} мин = 60 : 3 * 2 = 20 * 2 = 40$ (с);
$\frac{1}{6} мин = 60 : 6 * 1 = 10 * 1 = 10$ (с);
$\frac{5}{2} мин = 60 : 2 * 5 = 30 * 5 = 150$ (с);
$\frac{11}{10} мин = 60 : 10 * 11 = 6 * 11 = 66$ (с).

265. а) Начертите координатную прямую, взяв единичный отрезок, равный 10 клеткам, и отметьте дроби:
$\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}, \frac{5}{5}, \frac{6}{5}, \frac{7}{5}, \frac{8}{5}$.
б) Начертите координатную прямую, взяв единичный отрезок, равный 12 клеткам, и отметьте дроби:
$\frac{1}{4}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{2}{2}, \frac{5}{4}, \frac{5}{3}$.

Решение

а)

$\frac{1}{5} = 10 : 5 * 1 = 2$ (клетки);
$\frac{2}{5} = 10 : 5 * 2 = 4$ (клетки);
$\frac{3}{5} = 10 : 5 * 3 = 2 * 6 = 12$ (клеток);
$\frac{4}{5} = 10 : 5 * 4 = 2 * 4 = 8$ (клеток);
$\frac{5}{5} = 10 : 5 * 5 = 2 * 5= 10$ (клеток);
$\frac{6}{5} = 10 : 5 * 6 = 2 * 6 = 12$ (клеток);
$\frac{7}{5} = 10 : 5 * 7 = 2 * 7 = 14$ (клеток);
$\frac{8}{5} = 10 : 5 * 8 = 2 * 8 = 16$ (клеток).

б)

$\frac{1}{4} = 12 : 4 * 1 = 3$ (клетки);
$\frac{1}{3} = 12 : 3 * 1 = 4$ (клетки);
$\frac{1}{2} = 12 : 2 * 1 = 6$ (клеток);
$\frac{2}{3} = 12 : 3 * 2 = 4 * 2 = 8$ (клеток);
$\frac{3}{4} = 12 : 4 * 3 = 3 * 3 = 9$ (клеток);
$\frac{2}{2} = 12 : 2 * 2 = 6 * 2 = 12$ (клеток);
$\frac{5}{4} = 12 : 4 * 5 = 3 * 5 = 15$ (клеток);
$\frac{5}{3} = 12 : 3 * 5 = 4 * 5 = 20$ (клеток).

266. а) Телепередача длится 90 мин, $\frac{2}{15}$ этого времени отводится на рекламу. Сколько минут отводится на рекламу?
б) Спектакль длится 3 ч, антракты составляют $\frac{3}{10}$ этого времени. Какова продолжительность антрактов?

Решение

а) 90 : 15 * 2 = 6 * 2 = 12 (мин) − отводится на рекламу.
Ответ: 12 минут.

б) 3 ч = 180 мин
180 : 10 * 3 = 18 * 3 = 54 (мин) − продолжительность антрактов.
Ответ: 54 минуты.

267. а) Для школьного праздника решили приготовить 24 подарка, а приготовили с запасом: $\frac{7}{6}$ этого количества. Сколько подарков приготовили для школьного праздника?
б) Таня распространили 30 объявлений, а ее брат − $\frac{8}{5}$ этого количества. Сколько объявлений распространил брат?

Решение

а) 24 : 6 * 7 = 4 * 7 = 28 (подарков) − приготовили для школьного праздника.
Ответ: 28 подарков.

б) 30 : 5 * 8 = 6 * 8 = 48 (объявлений) − распространил брат.
Ответ: 48 объявлений.

268. а) Будильник показывает 11 ч утра. Какая часть суток прошла? Какую часть суток составляет оставшееся до конца суток время?
б) В Машиной тетради 48 страниц. Из них 23 страницы заполнены, остальные − чистые. Какую часть всех страниц составляют заполненные страницы? Какую часть всех страниц составляют чистые страницы?

Решение

а) 1 сутки − 24 ч
1) 24 − 11 = 13 (ч) − оставшееся до конца суток время;
2) $\frac{11}{24}$ (суток) − прошла;
3) $\frac{13}{24}$ (суток) − оставшееся до конца суток время.
Ответ: $\frac{11}{24}$ суток; $\frac{13}{24}$ суток.

б) 1) 48 − 23 = 25 (страниц) − были чистыми;
2) $\frac{23}{48}$ (тетради) − составляют заполненные страницы;
3) $\frac{25}{48}$ (тетради) − составляют чистые страницы.
Ответ: $\frac{23}{48}$ тетради; $\frac{25}{48}$ тетради.

269. а) На книжной полке 35 книг, 27 из них − учебники, остальные − словари. Какую часть составляют словари?
б) В магазин привезли 200 лампочек, 7 из них оказались неисправными. Какую часть лампочек составляют исправные?

Решение

а) 1) 35 − 27 = 8 (словарей) − на книжной полке;
2) $\frac{8}{35}$ (книг) − составляют словари.
Ответ: $\frac{8}{35}$ книг.

б) 1) 200 − 7 = 193 (лампочек) − исправные;
2) $\frac{193}{200}$ (лампочек) − составляют исправные.
Ответ: $\frac{193}{200}$ лампочек.

39

270. Сколько квадратных сантиметров содержится в:
а) $\frac{3}{10} м^2$;
б) $\frac{50}{100} м^2$;
в) $\frac{2}{5} м^2$;
г) $\frac{3}{4} м^2$?

Решение

а) $\frac{3}{10} м^2 = 10000 : 10 * 3 = 1000 * 3 = 3000 (см^2)$

б) $\frac{50}{100} м^2 = 10000 : 100 * 50 = 100 * 50 = 5000 (см^2)$

в) $\frac{2}{5} м^2 = 10000 : 5 * 2 = 2000 * 2 = 4000 (см^2)$

г) $\frac{3}{4} м^2 = 10000 : 4 * 3 = 2500 * 3 = 7500 (см^2)$

271. а) Внутри прямоугольника со сторонами 2 см и 5 см закрасили прямоугольник со сторонами 1 см и 3 см (рис. 6,а). Какая часть пощади большого прямоугольника закрашена?
б) Внутри квадрата со стороной 10 см закрасили квадрат со стороной 7 см (рис. 6,б). Какая часть площади большого квадрата закрашена?

Решение

а) 1) 2 * 5 = 10 $(см^2)$ − площадь большого прямоугольника;
2) 1 * 3 = 3 $(см^2)$ − площадь закрашенной части;
3) $3 : 10 = \frac{3}{10}$ (большого прямоугольника) − закрашено.
Ответ: $\frac{3}{10}$ − большого прямоугольника

б) 1) 10 * 10 = 100 $(см^2)$ − площадь большого квадрата;
2) 7 * 7 = 49 $(см^2)$ − площадь закрашенного квадрата;
3) $49 : 100 = \frac{49}{100}$ − большого квадрата закрашено.
Ответ: $\frac{49}{100}$ − большого квадрата

272. В парке посадили 60 берез и рябин. Березы составили $\frac{7}{12}$ всех посаженных деревьев. Сколько посадили рябин?

Решение

1) 60 : 12 * 7 = 5 * 7 = 35 (д.) − берез посадили;
2) 60 − 35 = 25 (д.) − рябин посадили.
Ответ: 35 берез и 25 рябин.

273. Спортсмен за 10 с пробежал $\frac{2}{5}$ всей дистанции. За какое время он может пробежать всю дистанцию?

Решение

10 : 2 * 5 = 5 * 5 = 25 (с) − время, за которое спортсмен может пробежать всю дистанцию.
Ответ: за 25 секунд.

274. Автобус проехал четверть всего маршрута и сделал остановку. После остановки до конца маршрута он проехал 24 км. Какова длина маршрута?

Решение

1) 4 − 1 = 3 (четверти) − проехал автобус после остановки;
2) 24 : 3 = 8 (км) − четверть всего маршрута;
3) 8 * 4 = 32 (км) − длина всего маршрута.
Ответ: 32 км.

275. а) На столе лежало несколько книг. Когда взяли половину всех книг и еще одну книгу, то на столе осталось 4 книги. Сколько книг лежало на столе?
б) Петя отдал брату половину своих дисков и еще 3 диска. После этого у Пети осталось 8 дисков. Сколько дисков было у Пети первоначально?

Решение

а) 1) 4 + 1 = 5 (к.) − составляет половину книг;
2) 5 * 2 = 10 (к.) − лежало на столе.
Ответ: 10 книг.

б) 1) 8 + 3 = 11 (д.) − составляет половину;
2) 11 * 2 = 22 (д.) − было у Пети первоначально.
Ответ: 22 диска.

Самостоятельная работа № 11

Вариант 1

1. а) Начертите прямоугольник со сторонами 3 клетки и 5 клеток. Закрасьте:
$\frac{3}{5}$ прямоугольника.
б) Запишите, какая часть прямоугольника осталась незакрашенной.

Решение

а) 

б) $\frac{2}{5}$ (прямоугольника) − осталось незакрашенной.

2. Определите, сколько сантиметров содержится:
а) в $\frac{3}{10}$ м;
б) в $\frac{11}{25}$ м;
в) в $\frac{7}{5}$ м.

Решение

а) $\frac{3}{10} м = 100 : 10 * 3 = 10 * 3 = 30$ (см)

б) $\frac{11}{25} м = 100 : 25 * 11 = 4 * 11 = 44$ (см)

в) $\frac{7}{5} м = 100 : 5 * 7 = 20 * 7 = 140$ (см)

3. Начертите координатную прямую, взяв за единичный отрезок 12 клеток. Отметьте на координатной прямой дроби:
$\frac{1}{3}, \frac{5}{12}, \frac{5}{4}$.

Решение

$\frac{1}{3} = 12 : 3 * 1 = 4$ (клетки);
$\frac{5}{12} = 12 : 12 * 5 = 1 * 5 = 5$ (клеток);
$\frac{5}{4} = 12 : 4 * 5 = 3 * 5 = 15$ (клеток).

Вариант 2

1. а) Начертите прямоугольник со сторонами 3 клетки и 5 клеток. Закрасьте:
$\frac{2}{3}$ прямоугольника.
б) Запишите, какая часть прямоугольника осталась незакрашенной.

Решение

а) 

б) $\frac{1}{3}$ (прямоугольника) − осталось незакрашенной.

2. Определите, сколько сантиметров содержится:
а) в $\frac{7}{10}$ м;
б) в $\frac{3}{20}$ м;
в) в $\frac{5}{4}$ м.

Решение

а) $\frac{7}{10} м = 100 : 10 * 7 = 10 * 7 = 70$ (см)

б) $\frac{3}{20} м = 100 : 20 * 3 = 5 * 3 = 15$ (см)

в) $\frac{5}{4} м = 100 : 4 * 5 = 25 * 5 = 125$ (см)

3. Начертите координатную прямую, взяв за единичный отрезок 12 клеток. Отметьте на координатной прямой дроби:
$\frac{1}{2}, \frac{11}{12}, \frac{7}{6}$.

Решение

$\frac{1}{2} = 12 : 2 * 1 = 6$ (клеток);
$\frac{11}{12} = 12 : 12 * 11 = 1 * 11 = 11$ (клеток);
$\frac{7}{6} = 12 : 6 * 7 = 2 * 7 = 14$ (клеток).

40

ГДЗ к теме Приведение дробей к новому знаменателю

276. а) На какой множитель надо умножить число 4, чтобы в произведении получить число: 8; 24; 36; 52?
б) На какой множитель надо умножить число 6, чтобы в произведении получить число: 12; 18; 60; 72?

Решение

а) 8 : 2 = 4;
24 : 4 = 6;
36 : 4 = 9;
52 : 4 = 13.

б) 12 : 6 = 2;
18 : 6 = 3;
60 : 6 = 10;
72 : 6 = 12.

277. а) Приведите дробь $\frac{1}{4}$ к знаменателю 8; 12; 16; 20. Сколько восьмых, двенадцатых, шестнадцатых, двадцатых долей содержится в $\frac{1}{4}$?;
б) Приведите дробь $\frac{1}{5}$ к знаменателю 10; 15; 20; 100. Сколько десятых, пятнадцатых, двадцатых, сотых долей содержится в $\frac{1}{5}$?

Решение

а) $\frac{1}{4} = \frac{1 * 2}{4 * 2} = \frac{2}{8}$;
$\frac{1}{4} = \frac{1 * 3}{4 * 3} = \frac{3}{12}$;
$\frac{1}{4} = \frac{1 * 4}{4 * 4} = \frac{4}{16}$;
$\frac{1}{4} = \frac{1 * 5}{4 * 5} = \frac{5}{20}$.

б) $\frac{1}{5} = \frac{1 * 2}{5 * 2} = \frac{2}{10}$;
$\frac{1}{5} = \frac{1 * 3}{5 * 3} = \frac{3}{15}$;
$\frac{1}{5} = \frac{1 * 4}{5 * 4} = \frac{4}{20}$;
$\frac{1}{5} = \frac{1 * 20}{5 * 20} = \frac{20}{100}$.

278. Представьте дробь:
а) $\frac{1}{2}$ в виде дроби знаменателем 6; 18; 24; 30;
б) $\frac{5}{6}$ в виде дроби знаменателем 12; 24; 48; 120;
в) $\frac{2}{3}$ в виде дроби знаменателем 9; 21; 36; 150;
г) $\frac{4}{7}$ в виде дроби знаменателем 14; 28; 63; 140.

Решение

а) $\frac{1}{2} = \frac{1 * 3}{2 * 3} = \frac{3}{6}$;
$\frac{1}{2} = \frac{1 * 9}{2 * 9} = \frac{9}{18}$;
$\frac{1}{2} = \frac{1 * 12}{2 * 12} = \frac{12}{24}$;
$\frac{1}{2} = \frac{1 * 15}{2 * 15} = \frac{15}{30}$.

б) $\frac{5}{6} = \frac{5 * 2}{6 * 2} = \frac{10}{12}$;
$\frac{5}{6} = \frac{5 * 4}{6 * 4} = \frac{20}{24}$;
$\frac{5}{6} = \frac{5 * 8}{6 * 8} = \frac{40}{48}$;
$\frac{5}{6} = \frac{5 * 20}{6 * 20} = \frac{100}{120}$.

в) $\frac{2}{3} = \frac{2 * 3}{3 * 3} = \frac{6}{9}$;
$\frac{2}{3} = \frac{2 * 7}{3 * 7} = \frac{14}{21}$;
$\frac{2}{3} = \frac{2 * 12}{3 * 12} = \frac{24}{36}$;
$\frac{2}{3} = \frac{2 * 50}{3 * 50} = \frac{100}{150}$.

г) $\frac{4}{7} = \frac{4 * 2}{7 * 2} = \frac{8}{14}$;
$\frac{4}{7} = \frac{4 * 4}{7 * 4} = \frac{16}{28}$;
$\frac{4}{7} = \frac{4 * 9}{7 * 9} = \frac{36}{63}$;
$\frac{4}{7} = \frac{4 * 20}{7 * 20} = \frac{80}{140}$.

279. Приведите дроби:
а) $\frac{1}{4}, \frac{7}{6}, \frac{3}{8}, \frac{17}{12}$ к знаменателю 24;
б) $\frac{2}{3}, \frac{7}{5}, \frac{4}{9}, \frac{16}{15}$ к знаменателю 90;
в) $\frac{5}{12}, \frac{7}{9}, \frac{5}{6}, \frac{4}{4}$ к знаменателю 36;
г) $\frac{3}{5}, \frac{3}{4}, \frac{8}{25}, \frac{7}{50}$ к знаменателю 100.

Решение

а) $\frac{1}{4} = \frac{1 * 6}{4 * 6} = \frac{6}{24}$;
$\frac{7}{6} = \frac{7 * 4}{6 * 4} = \frac{28}{24}$;
$\frac{3}{8} = \frac{3 * 3}{8 * 3} = \frac{9}{24}$;
$\frac{17}{12} = \frac{17 * 2}{12 * 2} = \frac{34}{24}$.

б) $\frac{2}{3} = \frac{2 * 30}{3 * 30} = \frac{60}{90}$;
$\frac{7}{5} = \frac{7 * 18}{5 * 18} = \frac{126}{90}$;
$\frac{4}{9} = \frac{4 * 10}{9 * 10} = \frac{40}{90}$;
$\frac{16}{15} = \frac{16 * 6}{15 * 6} = \frac{96}{90}$.

в) $\frac{5}{12} = \frac{5 * 3}{12 * 3} = \frac{15}{36}$;
$\frac{7}{9} = \frac{7 * 4}{9 * 4} = \frac{28}{36}$;
$\frac{5}{6} = \frac{5 * 6}{6 * 6} = \frac{30}{36}$;
$\frac{4}{4} = \frac{4 * 9}{4 * 9} = \frac{36}{36}$.

г) $\frac{3}{5} = \frac{3 * 20}{5 * 20} = \frac{60}{100}$;
$\frac{3}{4} = \frac{3 * 25}{4 * 25} = \frac{75}{100}$;
$\frac{8}{25} = \frac{8 * 4}{25 * 4} = \frac{32}{100}$;
$\frac{7}{50} = \frac{7 * 2}{50 * 2} = \frac{14}{100}$.

280. Замените звездочку числом так, чтобы получилось верное равенство:
а) $\frac{4}{3} = \frac{*}{120}$;
б) $\frac{3}{4} = \frac{15}{*}$;
в) $\frac{5}{6} = \frac{*}{72}$;
г) $\frac{9}{7} = \frac{81}{*}$.

Решение

а) $\frac{4}{3} = \frac{*}{120}$
* = 120 : 3 * 4 = 40 * 4 = 160
$\frac{4}{3} = \frac{160}{120}$

б) $\frac{3}{4} = \frac{15}{*}$
* = 15 : 3 * 4 = 5 * 4 = 20
$\frac{3}{4} = \frac{15}{20}$

в) $\frac{5}{6} = \frac{*}{72}$
* = 72 : 6 * 5 = 12 * 5 = 60
$\frac{5}{6} = \frac{60}{72}$

г) $\frac{9}{7} = \frac{81}{*}$
* = 81 : 9 * 7 = 9 * 7 = 63
$\frac{9}{7} = \frac{81}{63}$

281. Запишите пять дробей, равных:
а) $\frac{5}{2}$;
б) $\frac{1}{12}$;
в) $\frac{3}{8}$;
г) $\frac{7}{10}$.

Решение

а) $\frac{5}{2} = \frac{10}{4} = \frac{20}{8} = \frac{40}{16} = \frac{80}{32} = \frac{160}{64}$

б) $\frac{1}{12} = \frac{2}{24} = \frac{4}{48} = \frac{8}{96} = \frac{16}{192} = \frac{32}{384}$

в) $\frac{3}{8} = \frac{6}{16} = \frac{12}{32} = \frac{24}{64} = \frac{48}{128} = \frac{96}{256}$

г) $\frac{7}{10} = \frac{14}{20} = \frac{28}{40} = \frac{56}{80} = \frac{108}{160} = \frac{216}{320}$

282. Можно ли представить в виде дроби со знаменателем 30 дробь:
$\frac{1}{2}; \frac{1}{3}; \frac{1}{4}; \frac{1}{5}; \frac{1}{9}; \frac{1}{10}; \frac{1}{100}; \frac{1}{300}?$
Если можно, то приведите дробь к указанному знаменателю.

Решение

$\frac{1}{2} = \frac{15}{30}$;
$\frac{1}{3} = \frac{10}{30}$;
$\frac{1}{4}$ − нельзя представить;
$\frac{1}{5} = \frac{6}{30}$;
$\frac{1}{9}$ − нельзя представить;
$\frac{1}{10} = \frac{3}{30}$;
$\frac{1}{100}$ − нельзя представить;
$\frac{1}{300}$ − нельзя представить.

41

ГДЗ к теме Сокращение дробей

283. Объясните, почему верно равенство:
а) $\frac{50}{60} = \frac{5}{6}$;
б) $\frac{40}{75} = \frac{8}{15}$;
в) $\frac{12}{48} = \frac{1}{4}$;
г) $\frac{16}{24} = \frac{2}{3}$.

Решение

а) $\frac{50}{60} = \frac{50 : 10}{60 : 10} = \frac{5}{6}$

б) $\frac{40}{75} = \frac{40 : 5}{75 : 5} = \frac{8}{15}$

в) $\frac{12}{48} = \frac{12 : 12}{48 : 12} = \frac{1}{4}$

г) $\frac{16}{24} = \frac{16 : 8}{24 : 8} = \frac{2}{3}$

284. Начертите координатную прямую с единичным отрезком, равным 10 клеткам, и отметьте на ней точки с координатами:
$\frac{1}{10}, \frac{2}{10}, \frac{5}{10}, \frac{7}{10}, \frac{9}{10}, \frac{12}{10}, \frac{15}{10}$.
Отметьте на этой координатной прямой точки с координатами:
$\frac{1}{2}, \frac{1}{5}, \frac{3}{2}, \frac{6}{5}$.

Решение

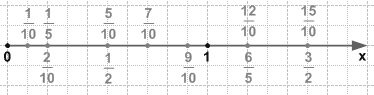
$\frac{1}{2} = \frac{5}{10}$;
$\frac{1}{5} = \frac{2}{10}$;
$\frac{3}{2} = \frac{15}{10}$;
$\frac{6}{5} = \frac{12}{10}$.

285. Сократите дробь:
а) $\frac{8}{12}, \frac{12}{16}, \frac{12}{18}, \frac{24}{40}, \frac{18}{27}, \frac{8}{36}$;
б) $\frac{20}{70}, \frac{30}{75}, \frac{15}{27}, \frac{26}{39}, \frac{15}{40}, \frac{22}{33}$.

Решение

а) $\frac{8}{12} = \frac{8 : 4}{12 : 4} = \frac{2}{3}$;
$\frac{12}{16} = \frac{12 : 4}{16 : 4} = \frac{3}{4}$;
$\frac{12}{18} = \frac{12 : 6}{18 : 6} = \frac{2}{3}$;
$\frac{24}{40} = \frac{24 : 8}{40 : 8} = \frac{3}{5}$;
$\frac{18}{27} = \frac{18 : 9}{27 : 9} = \frac{2}{3}$;
$\frac{8}{36} = \frac{8 : 4}{36 : 4} = \frac{2}{9}$.

б) $\frac{20}{70} = \frac{20 : 10}{70 : 10} = \frac{2}{7}$;
$\frac{30}{75} = \frac{30 : 15}{75 : 15} = \frac{2}{5}$;
$\frac{15}{27} = \frac{15 : 3}{27 : 3} = \frac{5}{9}$;
$\frac{26}{39} = \frac{26 : 13}{39 : 13} = \frac{2}{3}$;
$\frac{15}{40} = \frac{15 : 5}{40 : 5} = \frac{3}{8}$;
$\frac{22}{33} = \frac{22 : 11}{33 : 11} = \frac{2}{3}$.

286. Сократите дробь:
а) $\frac{3}{12}, \frac{5}{15}, \frac{4}{20}, \frac{5}{50}, \frac{9}{18}, \frac{10}{40}$;
б) $\frac{6}{12}, \frac{5}{25}, \frac{3}{18}, \frac{15}{60}, \frac{12}{48}, \frac{8}{24}$.

Решение

а) $\frac{3}{12} = \frac{3 : 3}{12 : 3} = \frac{1}{4}$;
$\frac{5}{15} = \frac{5 : 5}{15 : 5} = \frac{1}{3}$;
$\frac{4}{20} = \frac{4 : 4}{20 : 4} = \frac{1}{5}$;
$\frac{5}{50} = \frac{5 : 5}{50 : 5} = \frac{1}{10}$;
$\frac{9}{18} = \frac{9 : 9}{18 : 9} = \frac{1}{2}$;
$\frac{10}{40} = \frac{10 : 10}{40 : 10} = \frac{1}{4}$.

б) $\frac{6}{12} = \frac{6 : 6}{12 : 6} = \frac{1}{2}$;
$\frac{5}{25} = \frac{5 : 5}{25 : 5} = \frac{1}{5}$;
$\frac{3}{18} = \frac{3 : 3}{18 : 3} = \frac{1}{6}$;
$\frac{15}{60} = \frac{15 : 15}{60 : 15} = \frac{1}{4}$;
$\frac{12}{48} = \frac{12 : 12}{48 : 12} = \frac{1}{4}$;
$\frac{8}{24} = \frac{8 : 8}{24 : 8} = \frac{1}{3}$.

287. Сократите дробь:
а) $\frac{18}{20}, \frac{5}{30}, \frac{16}{12}, \frac{30}{20}, \frac{9}{12}, \frac{2}{8}$;
б) $\frac{65}{26}, \frac{17}{51}, \frac{12}{8}, \frac{24}{40}, \frac{15}{6}, \frac{10}{100}$.

Решение

а) $\frac{18}{20} = \frac{18 : 2}{20 : 2} = \frac{9}{10}$;
$\frac{5}{30} = \frac{5 : 5}{30 : 5} = \frac{1}{6}$;
$\frac{16}{12} = \frac{16 : 4}{12 : 4} = \frac{4}{3}$;
$\frac{30}{20} = \frac{30 : 10}{20 : 10} = \frac{3}{2}$;
$\frac{9}{12} = \frac{9 : 3}{12 : 3} = \frac{3}{4}$;
$\frac{2}{8} = \frac{2 : 2}{8 : 2} = \frac{1}{4}$.

б) $\frac{65}{26} = \frac{65 : 13}{26 : 13} = \frac{5}{2}$;
$\frac{17}{51} = \frac{17 : 17}{51 : 17} = \frac{1}{3}$;
$\frac{12}{8} = \frac{12 : 4}{8 : 4} = \frac{3}{2}$;
$\frac{24}{40} = \frac{24 : 8}{40 : 8} = \frac{3}{5}$;
$\frac{15}{6} = \frac{15 : 3}{6 : 3} = \frac{5}{2}$;
$\frac{10}{100} = \frac{10 : 10}{100 : 10} = \frac{1}{10}$.

288. Выпишите несократимые дроби:
$\frac{3}{5}, \frac{6}{8}, \frac{15}{25}, \frac{13}{14}, \frac{6}{7}, \frac{24}{35}, \frac{81}{90}, \frac{16}{48}.$

Решение

$\frac{3}{5}$ − несократимая дробь;
$\frac{6}{8} = \frac{3}{4}$;
$\frac{15}{25} = \frac{3}{5}$;
$\frac{13}{14}$ − несократимая дробь;
$\frac{6}{7}$ − несократимая дробь;
$\frac{24}{35}$ − несократимая дробь;
$\frac{81}{90} = \frac{9}{10}$;
$\frac{16}{48} = \frac{1}{3}$.
Ответ: $\frac{3}{5}, \frac{13}{14}, \frac{6}{7}, \frac{24}{35}.$

289. Запишите все правильные дроби со знаменателем 20. Сократите те из них, которые можно сократить.

Решение

$\frac{1}{20}$;
$\frac{2}{20} = \frac{1}{10}$;
$\frac{3}{20}$;
$\frac{4}{20} = \frac{1}{5}$;
$\frac{5}{20} = \frac{1}{4}$;
$\frac{6}{20} = \frac{3}{10}$;
$\frac{7}{20}$;
$\frac{8}{20} = \frac{2}{5}$;
$\frac{9}{20}$;
$\frac{10}{20} = \frac{1}{2}$;
$\frac{11}{20}$;
$\frac{12}{20} = \frac{3}{5}$;
$\frac{13}{20}$;
$\frac{14}{20} = \frac{7}{10}$;
$\frac{15}{20} = \frac{3}{4}$;
$\frac{16}{20} = \frac{4}{5}$;
$\frac{17}{20}$;
$\frac{18}{20} = \frac{9}{10}$;
$\frac{19}{20}$.

290. Выразите:
а) в метрах 20 см, 75 см, 45 см, 5 дм, 8 дм, 12 дм;
б) в километрах 200 м, 250 м, 350 м, 500 м;
в) в килограммах 120 г, 380 г, 750 г, 500 г.
Образец.
Выразим в метрах 30 см. Так как 1 см = $\frac{1}{100}$ м, то 30 см = $\frac{30}{100}$ м = $\frac{3}{10}$ м.

Решение

а) Выразим в метрах 20 см. Так как 1 см = $\frac{1}{100}$ м, то 20 см = $\frac{20}{100}$ м = $\frac{1}{5}$ м.
Выразим в метрах 75 см. Так как 1 см = $\frac{1}{100}$ м, то 75 см = $\frac{75}{100}$ м = $\frac{3}{4}$ м.
Выразим в метрах 45 см. Так как 1 см = $\frac{1}{100}$ м, то 45 см = $\frac{45}{100}$ м = $\frac{9}{20}$ м.
Выразим в метрах 5 дм. Так как 1 дм = $\frac{1}{10}$ м, то 5 дм = $\frac{5}{10}$ м = $\frac{1}{2}$ м.
Выразим в метрах 8 дм. Так как 1 дм = $\frac{1}{10}$ м, то 8 дм = $\frac{8}{10}$ м = $\frac{4}{5}$ м.
Выразим в метрах 12 дм. Так как 1 дм = $\frac{1}{10}$ м, то 12 дм = $\frac{12}{10}$ м = $\frac{6}{5}$ м.

б) Выразим в километрах 200 м. Так как 1 м = $\frac{1}{1000}$ км, то 200 м = $\frac{200}{1000}$ км = $\frac{1}{5}$ км.
Выразим в километрах 250 м. Так как 1 м = $\frac{1}{1000}$ км, то 250 м = $\frac{250}{1000}$ км = $\frac{1}{4}$ км.
Выразим в километрах 350 м. Так как 1 м = $\frac{1}{1000}$ км, то 350 м = $\frac{350}{1000}$ км = $\frac{7}{20}$ км.
Выразим в километрах 500 м. Так как 1 м = $\frac{1}{1000}$ км, то 500 м = $\frac{500}{1000}$ км = $\frac{1}{2}$ км.

в) Выразим в килограммах 120 г. Так как 1 г = $\frac{1}{1000}$ кг, то 120 г = $\frac{120}{1000}$ кг = $\frac{3}{25}$ кг.
Выразим в килограммах 380 г. Так как 1 г = $\frac{1}{1000}$ кг, то 380 г = $\frac{380}{1000}$ кг = $\frac{19}{50}$ кг.
Выразим в килограммах 750 г. Так как 1 г = $\frac{1}{1000}$ кг, то 750 г = $\frac{750}{1000}$ кг = $\frac{3}{4}$ кг.
Выразим в килограммах 500 г. Так как 1 г = $\frac{1}{1000}$ кг, то 500 г = $\frac{500}{1000}$ кг = $\frac{1}{2}$ кг.

291. Выразите:
а) в часах 30 мин, 25 мин, 12 мин, 40 мин;
б) в минутах 4 с, 10 с, 20 с, 40 с, 45 с.

Решение

а) Выразим в часах 30 мин. Так как 1 мин = $\frac{1}{60}$ ч, то 30 мин = $\frac{30}{60}$ ч = $\frac{1}{2}$ ч.
Выразим в часах 25 мин. Так как 1 мин = $\frac{1}{60}$ ч, то 25 мин = $\frac{25}{60}$ ч = $\frac{5}{12}$ ч.
Выразим в часах 12 мин. Так как 1 мин = $\frac{1}{60}$ ч, то 12 мин = $\frac{12}{60}$ ч = $\frac{1}{5}$ ч.
Выразим в часах 40 мин. Так как 1 мин = $\frac{1}{60}$ ч, то 40 мин = $\frac{40}{60}$ ч = $\frac{2}{3}$ ч.

б) Выразим в минутах 4 с. Так как 1 с = $\frac{1}{60}$ мин, то 4 с = $\frac{4}{60}$ мин = $\frac{1}{15}$ мин.
Выразим в минутах 10 с. Так как 1 с = $\frac{1}{60}$ мин, то 10 с = $\frac{10}{60}$ мин = $\frac{1}{6}$ мин.
Выразим в минутах 20 с. Так как 1 с = $\frac{1}{60}$ мин, то 20 с = $\frac{20}{60}$ мин = $\frac{1}{3}$ мин.
Выразим в минутах 40 с. Так как 1 с = $\frac{1}{60}$ мин, то 40 с = $\frac{40}{60}$ мин = $\frac{2}{3}$ мин.
Выразим в минутах 45 с. Так как 1 с = $\frac{1}{60}$ мин, то 45 с = $\frac{45}{60}$ мин = $\frac{3}{4}$ мин.

292. а) В школьном хоре 60 человек, 27 из них − мальчики. Какую часть числа всех участников хора составляют мальчики? Какую часть числа всех участников хора составляют девочки?
б) В коробке 12 красных, 28 синих и 18 зеленых карандашей. Какую часть всех карандашей составляют красные карандаши, какую − синие и какую − зеленые?

Решение

а) 1) 60 − 27 = 33 (девочки) − в хоре;
2) $\frac{27}{60} = \frac{9}{20}$ (хора) − составляют мальчики;
3) $\frac{33}{60} = \frac{11}{20}$ (хора) − составляют девочки.
Ответ: $\frac{9}{20}$ − мальчики; $\frac{11}{20}$ − девочки.

б) 1) 12 + 28 + 18 = 58 (к.) − всего;
2) $\frac{12}{58} = \frac{6}{29}$ (частей) − составляют красные карандаши;
3) $\frac{28}{58} = \frac{14}{29}$ (частей) − составляют синие карандаши;
4) $\frac{18}{58} = \frac{9}{29}$ (частей) − составляют зеленые карандаши.
Ответ: $\frac{6}{29}$ − красные; $\frac{14}{29}$ − синие; $\frac{9}{29}$ − зеленые.

42

293. а) Антон за выполнение некоторой работы должен был получить 2000 р. Какую часть всей работы выполнил Антон, если он получил 400 р.? 600 р.? 1500 р.?
б) Оля купила коробку корма для рыбок, которого хватает на 30 дней. Она расходует ежедневно одно и то же количество корма. Какую часть корма израсходует Оля за 5 дней? за 10 дней? за 24 дня?

Решение

а) 1) $\frac{400}{2000} = \frac{1}{5}$ (работы) − выполнил Антон, если он получил 400 р.;
2) $\frac{600}{2000} = \frac{3}{10}$ (работы) − выполнил Антон, если он получил 600 р.;
3) $\frac{1500}{2000} = \frac{3}{4}$ (работы) − выполнил Антон, если он получил 1500 р.
Ответ: $\frac{1}{5}; \frac{3}{10}; \frac{3}{4}.$

б) 1) $\frac{5}{30} = \frac{1}{6}$ (корма) − израсходует Оля за 5 дней;
2) $\frac{10}{30} = \frac{1}{3}$ (корма) − израсходует Оля за 10 дней;
3) $\frac{24}{30} = \frac{4}{5}$ (корма) − израсходует Оля за 24 дня.
Ответ: $\frac{1}{6}; \frac{1}{3}; \frac{4}{5}.$

294. Сократите дробь:
а) $\frac{32}{48}$;
б) $\frac{48}{120}$;
в) $\frac{60}{64}$;
г) $\frac{64}{112}$.

Решение

а) $\frac{32}{48} = \frac{32 : 16}{48 : 16} = \frac{2}{3}$

б) $\frac{48}{120} = \frac{48 : 24}{120 : 24} = \frac{2}{5}$

в) $\frac{60}{64} = \frac{60 : 4}{64 : 4} = \frac{15}{16}$

г) $\frac{64}{112} = \frac{64 : 16}{112 : 16} = \frac{4}{7}$

295. Сократите дробь:
а) $\frac{300}{560}$;
б) $\frac{165}{1320}$;
в) $\frac{168}{525}$;
г) $\frac{512}{1600}$.

Решение

а) $\frac{300}{560} = \frac{30}{56} = \frac{15}{28}$

б) $\frac{165}{1320} = \frac{33}{264} = \frac{1}{8}$

в) $\frac{168}{525} = \frac{56}{175} = \frac{8}{25}$

г) $\frac{512}{1600} = \frac{256}{800} = \frac{128}{400} = \frac{32}{100} = \frac{8}{25}$

296. а) Какую дробь сократили на 12, если в результате получили $\frac{3}{4}$? проверьте себя, выполнив сокращение.
б) Какую дробь сократили на 10, если в результате получили $\frac{7}{12}$?

Решение

а) $\frac{3}{4} = \frac{3 * 12}{4 * 12} = \frac{36}{48}$;
$\frac{36}{48} = \frac{36 : 12}{48 : 12} = \frac{3}{4}$.

б) $\frac{7}{12} = \frac{7 * 10}{12 * 10} = \frac{70}{120}$;
$\frac{70}{120} = \frac{70 : 10}{120 : 10} = \frac{7}{12}$.

297. Сократите дробь:
а) $\frac{8 * 3}{3 * 40}$;
б) $\frac{10 * 11 * 9}{12 * 10 * 11}$;
в) $\frac{6 * 12}{20 * 9}$;
г) $\frac{3 * 4 * 25}{24 * 15}$.

Решение

а) $\frac{8 * 3}{3 * 40} = \frac{8}{40} = \frac{1}{5}$

б) $\frac{10 * 11 * 9}{12 * 10 * 11} = \frac{9}{12} = \frac{3}{4}$

в) $\frac{6 * 12}{20 * 9} = \frac{2 * 3}{5 * 3} = \frac{2}{5}$

г) $\frac{3 * 4 * 25}{24 * 15} = \frac{3 * 5}{6 * 3} = \frac{5}{6}$

298. Сократите дробь:
а) $\frac{5^2}{5^3}$;
б) $\frac{3^3}{3^5}$;
в) $\frac{2 * 3^3}{2^2 * 3 * 5}$;
г) $\frac{2^3 * 5^2 * 7}{2^2 * 5^3}$.

Решение

а) $\frac{5^2}{5^3} = \frac{1}{5}$

б) $\frac{3^3}{3^5} = \frac{1}{3^2} = \frac{1}{9}$

в) $\frac{2 * 3^3}{2^2 * 3 * 5} = \frac{3^2}{2 * 5} = \frac{9}{10}$

г) $\frac{2^3 * 5^2 * 7}{2^2 * 5^3} = \frac{2 * 7}{5} = \frac{14}{5}$

299. а) На рисунке 7,а изображен план дачного участка. Какую часть площади участка занимает дом, цветник, сад, огород?
б) Квадрат, сторона которого равна 6 см, разбит на четыре прямоугольника (рис. 7,б). Какую часть площади квадрата составляет площадь каждого из этих прямоугольников?

Решение

а) 1) 30 * 40 = 1200 $(м^2)$ − общая площадь участка;
2) 10 * 10 = 100 $(м^2)$ − площадь дома;
3) $\frac{100}{1200} = \frac{1}{12}$ (участка) − занимает площадь дома;
4) 5 * (30 − 10) = 5 * 20 = 100 $(м^2)$ − площадь цветника;
5) $\frac{100}{1200} = \frac{1}{12}$ (участка) − занимает площадь цветника;
6) (40 − 15 − 5) * 30 = 20 * 30 = 600 $(м^2)$ − площадь сада с домом;
7) 600 − 100 = 500 $(м^2)$ − площадь сада;
8) $\frac{500}{1200} = \frac{5}{12}$ (участка) − занимает площадь сада;
9) 30 * (15 + 5) = 30 * 20 = 600 $(м^2)$ − площадь огорода вместе с цветником;
10) 600 − 100 = 500 $(м^2)$ − площадь огорода;
11) $\frac{500}{1200} = \frac{5}{12}$ (участка) − занимает площадь огорода.
Ответ:
$\frac{1}{12}$ − занимает площадь дома;
$\frac{1}{12}$ − занимает площадь цветника;
$\frac{5}{12}$ − занимает площадь сада;
$\frac{5}{12}$ − занимает площадь огорода.

б) 1) 6 * 6 = 36 $(см^2)$ − общая площадь квадрата;
2) 2 * 2 = 4 $(см^2)$ − площадь маленького квадрата;
3) $\frac{4}{36} = \frac{1}{9}$ (большого квадрата) − составляет площадь маленького квадрата;
4) (6 − 2) * (6 − 2) = 4 * 4 = 16 $(см^2)$ − площадь среднего квадрата;
5) $\frac{16}{36} = \frac{4}{9}$ (большого квадрата) − составляет площадь среднего квадрата;
6) (6 − 2) * 2 = 4 * 2 = 8 $(см^2)$ − площадь каждого из прямоугольников;
7) $\frac{8}{36} = \frac{2}{9}$ (большого квадрата) − составляет площадь каждого прямоугольника.
Ответ:
$\frac{1}{9}$ − составляет маленький квадрат;
$\frac{4}{9}$ − составляет средний квадрат;
$\frac{2}{9}$ − составляет каждый из прямоугольников.

43

Самостоятельная работа № 12

Вариант 1

1. Приведите дробь $\frac{3}{8}$ к знаменателю:
а) 32;
б) 40;
в) 72.

Решение

а) $\frac{3}{8} = \frac{3 * 4}{8 * 4} = \frac{12}{32}$

б) $\frac{3}{8} = \frac{3 * 5}{8 * 5} = \frac{15}{40}$

в) $\frac{3}{8} = \frac{3 * 9}{8 * 9} = \frac{27}{72}$

2. Определите, можно ли привести дробь к знаменателю 156, и если можно, сделайте это:
а) $\frac{6}{10}$;
б) $\frac{11}{26}$.

Решение

а) 156 : 10 = 15 (ост.6), значит дробь $\frac{6}{10}$ нельзя привести к знаменателю 156.

б) 156 : 26 = 6, значит:
$\frac{11}{26} = \frac{11 * 6}{26 * 6} = \frac{66}{156}$

3. Сократите дробь:
$\frac{6}{30}$;
$\frac{42}{48}$;
$\frac{16}{12}$.

Решение

$\frac{6}{30} = \frac{6 : 6}{30 : 6} = \frac{1}{5}$;
$\frac{42}{48} = \frac{42 : 6}{48 : 6} = \frac{7}{8}$;
$\frac{16}{12} = \frac{16 : 4}{12 : 4} = \frac{4}{3}$.

Вариант 2

1. Приведите дробь $\frac{3}{8}$ к знаменателю:
а) 24;
б) 48;
в) 64.

Решение

а) $\frac{3}{8} = \frac{3 * 3}{8 * 3} = \frac{9}{24}$

б) $\frac{3}{8} = \frac{3 * 6}{8 * 6} = \frac{18}{48}$

в) $\frac{3}{8} = \frac{3 * 8}{8 * 8} = \frac{24}{64}$

2. Определите, можно ли привести дробь к знаменателю 156, и если можно, сделайте это:
а) $\frac{7}{12}$;
б) $\frac{13}{20}$.

Решение

а) 156 : 12 = 13, значит:
$\frac{7}{12} = \frac{7 * 13}{12 * 13} = \frac{91}{156}$

б) 156 : 20 = 7 (ост.16), значит дробь $\frac{13}{20}$ нельзя привести к знаменателю 156.

3. Сократите дробь:
$\frac{6}{24}$;
$\frac{16}{40}$;
$\frac{20}{8}$.

Решение

$\frac{6}{24} = \frac{6 : 6}{24 : 6} = \frac{1}{4}$;
$\frac{16}{40} = \frac{16 : 8}{40 : 8} = \frac{2}{5}$;
$\frac{20}{8} = \frac{20 : 4}{8 : 4} = \frac{5}{2}$.

ГДЗ к теме Приведение дробей к общему знаменателю

300. Найдите несколько чисел, кратных двум данным числам. Укажите наименьшее общее кратное этих чисел:
а) 3 и 7;
б) 4 и 5;
в) 6 и 12;
г) 16 и 8;
д) 6 и 4;
е) 25 и 10.

Решение

а) 3: 3, 6, 9, 12, 15, 18, 21, ...;
7: 7, 14, 21, ... .
НОК(3;7) = 21

б) 4: 4, 8, 12, 16, 20, ...;
5: 5, 10, 15, 20, ... .
НОК(3;7) = 21

в) 6: 6, 12, 18, 24, ...;
12: 12, 24, ... .
НОК(6;12) = 24

г) 16: 16, 32, ...;
8: 8, 16, ... .
НОК(16;8) = 16

д) 6: 6, 12, ...;
4: 4, 8, 12, ... .
НОК(6;4) = 12

е) 25: 25, 50, ...;
10: 10, 20, 30, 40, 50, ... .
НОК(25;10) = 50

301. Найдите несколько общих знаменателей дробей, назовите их наименьший общий знаменатель:
а) $\frac{2}{3}$ и $\frac{1}{7}$;
б) $\frac{3}{5}$ и $\frac{5}{6}$;
в) $\frac{1}{6}$ и $\frac{1}{12}$;
г) $\frac{4}{3}$ и $\frac{10}{9}$;
д) $\frac{1}{6}$ и $\frac{5}{8}$;
е) $\frac{7}{10}$ и $\frac{4}{15}$.

Решение

а) $\frac{2}{3}$ и $\frac{1}{7}$
21, 42, 63, ... .
21 − наименьший общий знаменатель.

б) $\frac{3}{5}$ и $\frac{5}{6}$
30, 60, 90, ... .
30 − наименьший общий знаменатель.

в) $\frac{1}{6}$ и $\frac{1}{12}$
12, 24, 36, ... .
12 − наименьший общий знаменатель.

г) $\frac{4}{3}$ и $\frac{10}{9}$
9, 18, 27, ... .
9 − наименьший общий знаменатель.

д) $\frac{1}{6}$ и $\frac{5}{8}$
24, 48, 72, ... .
24 − наименьший общий знаменатель.

е) $\frac{7}{10}$ и $\frac{4}{15}$
30, 60, 90, ... .
30 − наименьший общий знаменатель.

302. Приведите к наименьшему общему знаменателю дроби:
а) $\frac{7}{9}$ и $\frac{4}{3}$;
б) $\frac{23}{100}$ и $\frac{8}{25}$;
в) $\frac{5}{16}$ и $\frac{5}{8}$;
г) $\frac{5}{6}$ и $\frac{2}{3}$;
д) $\frac{5}{2}$ и $\frac{19}{10}$;
е) $\frac{5}{18}$ и $\frac{5}{6}$.

Решение

а) $\frac{7}{9}$;
$\frac{4}{3} = \frac{12}{9}$.

б) $\frac{23}{100}$;
$\frac{8}{25} = \frac{32}{100}$.

в) $\frac{5}{16}$;
$\frac{5}{8} = \frac{10}{16}$.

г) $\frac{5}{6}$;
$\frac{2}{3} = \frac{4}{6}$.

д) $\frac{5}{2} = \frac{25}{10}$;
$\frac{19}{10}$.

е) $\frac{5}{18}$;
$\frac{5}{6} = \frac{15}{18}$.

303. Приведите к наименьшему общему знаменателю дроби:
а) $\frac{1}{2}$ и $\frac{3}{7}$;
б) $\frac{3}{5}$ и $\frac{2}{3}$;
в) $\frac{3}{2}$ и $\frac{7}{5}$;
г) $\frac{5}{4}$ и $\frac{4}{3}$;
д) $\frac{1}{3}$ и $\frac{9}{10}$;
е) $\frac{1}{6}$ и $\frac{1}{7}$.

Решение

а) $\frac{1}{2} = \frac{7}{14}$;
$\frac{3}{7} = \frac{6}{14}$.

б) $\frac{3}{5} = \frac{9}{15}$;
$\frac{2}{3} = \frac{10}{15}$.

в) $\frac{3}{2} = \frac{15}{10}$;
$\frac{7}{5} = \frac{14}{10}$.

г) $\frac{5}{4} = \frac{15}{12}$;
$\frac{4}{3} = \frac{16}{12}$.

д) $\frac{1}{3} = \frac{10}{30}$;
$\frac{9}{10} = \frac{27}{30}$.

е) $\frac{1}{6} = \frac{7}{42}$;
$\frac{1}{7} = \frac{6}{42}$.

304. Приведите к наименьшему общему знаменателю дроби:
а) $\frac{3}{4}$ и $\frac{7}{10}$;
б) $\frac{2}{15}$ и $\frac{1}{6}$;
в) $\frac{3}{8}$ и $\frac{5}{6}$;
г) $\frac{1}{6}$ и $\frac{1}{9}$;
д) $\frac{5}{12}$ и $\frac{3}{8}$;
е) $\frac{3}{25}$ и $\frac{1}{10}$.

Решение

а) $\frac{3}{4} = \frac{15}{20}$;
$\frac{7}{10} = \frac{14}{20}$.

б) $\frac{2}{15} = \frac{4}{30}$;
$\frac{1}{6} = \frac{5}{30}$.

в) $\frac{3}{8} = \frac{9}{24}$;
$\frac{5}{6} = \frac{20}{24}$.

г) $\frac{1}{6} = \frac{3}{18}$;
$\frac{1}{9} = \frac{2}{18}$.

д) $\frac{5}{12} = \frac{10}{24}$;
$\frac{3}{8} = \frac{9}{24}$.

е) $\frac{3}{25} = \frac{6}{50}$;
$\frac{1}{10} = \frac{5}{50}$.

44

305. Приведите к наименьшему общему знаменателю дроби:
а) $\frac{1}{2}, \frac{1}{3}, \frac{1}{4}$;
б) $\frac{1}{3}, \frac{1}{4}, \frac{1}{5}$;
в) $\frac{1}{2}, \frac{1}{4}, \frac{1}{16}$;
г) $\frac{1}{2}, \frac{1}{4}, \frac{1}{6}$;
д) $\frac{1}{15}, \frac{1}{10}, \frac{1}{5}$;
е) $\frac{1}{6}, \frac{1}{8}, \frac{1}{9}$.

Решение

а) $\frac{1}{2} = \frac{6}{12}$;
$\frac{1}{3} = \frac{4}{12}$;
$\frac{1}{4} = \frac{3}{12}$.

б) $\frac{1}{3} = \frac{20}{60}$;
$\frac{1}{4} = \frac{15}{60}$;
$\frac{1}{5} = \frac{12}{60}$.

в) $\frac{1}{2} = \frac{8}{16}$;
$\frac{1}{4} = \frac{4}{16}$;
$\frac{1}{16} = \frac{1}{16}$.

г) $\frac{1}{2} = \frac{6}{12}$;
$\frac{1}{4} = \frac{3}{12}$;
$\frac{1}{6} = \frac{2}{12}$.

д) $\frac{1}{15} = \frac{2}{30}$;
$\frac{1}{10} = \frac{3}{30}$;
$\frac{1}{5} = \frac{6}{30}$.

е) $\frac{1}{6} = \frac{12}{72}$;
$\frac{1}{8} = \frac{9}{72}$;
$\frac{1}{9} = \frac{8}{72}$.

306. Приведите к наименьшему общему знаменателю дроби:
а) $\frac{1}{12}, \frac{1}{18}, \frac{2}{3}, \frac{4}{15}$;
б) $\frac{5}{14}, \frac{3}{7}, \frac{8}{21}, \frac{1}{42}$.

Решение

а) $\frac{1}{12} = \frac{15}{180}$;
$\frac{1}{18} = \frac{10}{180}$;
$\frac{2}{3} = \frac{120}{180}$;
$\frac{4}{15} = \frac{48}{180}$.

б) $\frac{5}{14} = \frac{15}{42}$;
$\frac{3}{7} = \frac{18}{42}$;
$\frac{8}{21} = \frac{16}{42}$;
$\frac{1}{42}$.

307. Разберите, как выполнено приведение к наименьшему общему знаменателю дробей $\frac{5}{54}$ и $\frac{1}{45}$.
Общий знаменатель этих дробей должен делиться и на 54, и на 45. Так как 54 = 2 * 3 * 3 * 3 и 45 = 3 * 3 * 5, то общий знаменатель должен делиться на 2 один раз, 3 раза на 3 и на 5 один раз. Наименьшее число, удовлетворяющее этому условию, есть произведение 2 * 3 * 3 * 3 * 5 = 270. Дополнительный множитель для первой дроби равен 5, для второй − 2 * 3 = 6. Получаем
$\frac{5}{54} = \frac{5 * 5}{54 * 5} = \frac{25}{270}$,
$\frac{1}{45} = \frac{1 * 6}{45 * 6} = \frac{6}{270}$.
пользуясь разобранным приемом, приведите к наименьшему общему знаменателю дроби:
а) $\frac{13}{60}$ и $\frac{11}{24}$;
б) $\frac{8}{45}$ и $\frac{3}{40}$;
в) $\frac{4}{27}$ и $\frac{7}{24}$;
г) $\frac{5}{84}$ и $\frac{7}{36}$.

Решение

а) 60 = 6 * 10 = 3 * 2 * 2 * 5;
24 = 6 * 4 = 2 * 3 * 2 * 2.
Значит знаменатель должен делиться на 2 − три раза, на 3 − один раз и на 5.
2 * 2 * 2 * 3 * 5 = 24 * 5 = 120
Дополнительный множитель для первой дроби равен 2, для второй − 5. Получаем:
$\frac{13}{60} = \frac{13 * 2}{60 * 2} = \frac{26}{120}$;
$\frac{11}{24} = \frac{11 * 5}{24 * 5} = \frac{55}{120}$.

б) 45 = 5 * 9 = 5 * 3 * 3;
40 = 5 * 8 = 5 * 4 * 2 = 5 * 2 * 2 * 2.
Значит знаменатель должен делиться на 5 − один раз, на 2 − три раза и на 3 − два раза.
5 * 2 * 2 * 2 * 3 * 3 = 10 * 36 = 360
Дополнительный множитель для первой дроби равен 2 * 2 * 2 = 8, для второй − 3 * 3 = 9. Получаем:
$\frac{8}{45} = \frac{8 * 8}{45 * 8} = \frac{64}{360}$;
$\frac{3}{40} = \frac{3 * 9}{40 * 9} = \frac{27}{360}$.

в) 27 = 3 * 9 = 3 * 3 * 3;
24 = 3 * 8 = 3 * 2 * 4 = 3 * 2 * 2 * 2.
Значит знаменатель должен делиться на 3 − три раза, на 2 − три раза.
2 * 2 * 2 * 3 * 3 * 3 = 8 * 9 * 3 = 72 * 3 = 216
Дополнительный множитель для первой дроби равен 2 * 2 * 2 = 8, для второй − 3 * 3 = 9. Получаем:
$\frac{4}{27} = \frac{4 * 8}{27 * 8} = \frac{32}{216}$;
$\frac{7}{24} = \frac{7 * 9}{24 * 9} = \frac{63}{216}$.

г) 84 = 12 * 7 = 3 * 2 * 2 * 7;
36 = 2 * 2 * 3 * 3.
Значит знаменатель должен делиться на 3 − два раза, на 2 − два раза, на 7 − один раз.
2 * 2 * 3 * 3 * 7 = 4 * 9 * 7 = 28 * 9 = 252
Дополнительный множитель для первой дроби равен 3, для второй − 7. Получаем:
$\frac{5}{84} = \frac{5 * 3}{84 * 3} = \frac{15}{252}$;
$\frac{7}{36} = \frac{7 * 7}{36 * 7} = \frac{49}{252}$.

ГДЗ к теме Сравнение дробей

308. Начертите координатную прямую с единичным отрезком 12 клеток. С помощь координатной прямой покажите, что:
а) $\frac{5}{12} < \frac{11}{12}$;
б) $\frac{3}{4} > \frac{1}{4}$;
в) $\frac{2}{3} > \frac{7}{12}$;
г) $\frac{1}{6} < \frac{1}{4}$.

Решение

а) $\frac{5}{12} < \frac{11}{12}$


б) $\frac{3}{4} = \frac{9}{12}$;
$\frac{1}{4} = \frac{3}{12}$.
$\frac{3}{4} > \frac{1}{4}$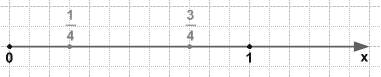


в) $\frac{2}{3} = \frac{8}{12}$.
$\frac{2}{3} > \frac{7}{12}$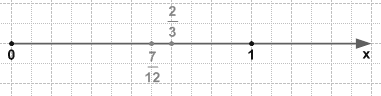


г) $\frac{1}{6} = \frac{2}{12}$;
$\frac{1}{4} = \frac{3}{12}$.
$\frac{1}{6} < \frac{1}{4}$

309. Сравните дроби и запишите ответ с помощью знака > или <:></:>

Решение

а) $\frac{6}{7} > \frac{3}{7}$

б) $\frac{11}{12} > \frac{7}{12}$

в) $\frac{4}{15} < \frac{7}{15}$

г) $\frac{7}{9} < \frac{17}{9}$

310. а) Расположите в порядке возрастания дроби $\frac{15}{17}, \frac{7}{17}, \frac{3}{17}, \frac{12}{17}, \frac{19}{17}$. Запишите какую−нибудь дробь, которая больше самой большой из этих дробей, и дробь, которая меньшая самой маленькой из них.
б) Расположите в порядке убывания дроби $\frac{3}{22}, \frac{17}{22}, \frac{25}{22}, \frac{7}{22}$. Запишите какую−нибудь дробь, которая больше самой большой из этих дробей, и дробь, которая меньшая самой маленькой из них.

Решение

а) $\frac{3}{17} < \frac{7}{17} < \frac{12}{17} < \frac{15}{17} < \frac{19}{17}$;
$\frac{25}{17}$ − больше самой большой из дробей;
$\frac{1}{17}$ − меньше самой маленькой из дробей.

б) $\frac{25}{22} > \frac{17}{22} > \frac{7}{22} > \frac{3}{22}$;
$\frac{27}{22}$ − больше самой большой из дробей;
$\frac{1}{22}$ − меньше самой маленькой из дробей.

45

311. а) Проехав $\frac{7}{10}$ всего пути, автобус сделал остановку. Какое расстояние меньше: то, которое автобус проехал, или то, которое ему осталось проехать?
б) От начала уроков прошло $\frac{2}{5}$ учебного времени. Что больше: время, которое уже прошло, или время, которое осталось?

Решение

а) 1) $1 - \frac{7}{10} = \frac{10}{10} - \frac{7}{10} = \frac{3}{10}$ (пути) − автобусу осталось проехать;
2) $\frac{3}{10} < \frac{7}{10}$.
Ответ: расстояние которое осталось проехать меньше расстояния которое автобус проехал.

б) 1) $1 - \frac{2}{5} = \frac{5}{5} - \frac{2}{5} = \frac{3}{5}$ (времени) − осталось;
2) $\frac{2}{5} < \frac{3}{5}$.
Ответ: оставшееся время больше, чем прошедшее.

312. Сравните дроби:
а) $\frac{3}{4}$ и $\frac{4}{5}$;
б) $\frac{2}{3}$ и $\frac{4}{7}$;
в) $\frac{4}{9}$ и $\frac{3}{7}$;
г) $\frac{7}{9}$ и $\frac{3}{5}$.

Решение

а) $\frac{3}{4} = \frac{15}{20}$;
$\frac{4}{5} = \frac{16}{20}$;
$\frac{15}{20} < \frac{16}{20}$;
$\frac{3}{4} < \frac{4}{5}$.

б) $\frac{2}{3} = \frac{14}{21}$;
$\frac{4}{7} = \frac{12}{21}$;
$\frac{14}{21} > \frac{12}{21}$;
$\frac{2}{3} > \frac{4}{7}$.

в) $\frac{4}{9} = \frac{28}{63}$;
$\frac{3}{7} = \frac{27}{63}$;
$\frac{28}{63} > \frac{27}{63}$;
$\frac{4}{9} > \frac{3}{7}$.

г) $\frac{7}{9} = \frac{35}{45}$;
$\frac{3}{5} = \frac{27}{45}$;
$\frac{35}{45} > \frac{27}{45}$;
$\frac{7}{9} > \frac{3}{5}$.

313. Сравните дроби:
а) $\frac{5}{6}$ и $\frac{7}{12}$;
б) $\frac{3}{8}$ и $\frac{17}{40}$;
в) $\frac{4}{9}$ и $\frac{1}{3}$;
г) $\frac{11}{20}$ и $\frac{3}{5}$.

Решение

а) $\frac{5}{6} = \frac{10}{12}$;
$\frac{10}{12} > \frac{7}{12}$;
$\frac{5}{6} > \frac{7}{12}$.

б) $\frac{3}{8} = \frac{15}{40}$;
$\frac{15}{40} < \frac{17}{40}$;
$\frac{3}{8} < \frac{17}{40}$.

в) $\frac{1}{3} = \frac{3}{9}$;
$\frac{4}{9} > \frac{3}{9}$;
$\frac{4}{9} = \frac{1}{3}$.

г) $\frac{3}{5} = \frac{12}{20}$;
$\frac{11}{20} < \frac{12}{20}$;
$\frac{11}{20} < \frac{3}{5}$.

314. Сравните дроби:
а) $\frac{7}{24}$ и $\frac{5}{16}$;
б) $\frac{5}{9}$ и $\frac{7}{12}$;
в) $\frac{11}{8}$ и $\frac{17}{12}$;
г) $\frac{27}{25}$ и $\frac{13}{10}$.

Решение

а) $\frac{7}{24} = \frac{14}{48}$;
$\frac{5}{16} = \frac{15}{48}$;
$\frac{14}{48} < \frac{15}{48}$;
$\frac{7}{24} < \frac{5}{16}$.

б) $\frac{5}{9} = \frac{20}{36}$;
$\frac{7}{12} = \frac{21}{36}$;
$\frac{20}{36} < \frac{21}{36}$;
$\frac{5}{9} < \frac{7}{12}$.

в) $\frac{11}{8} = \frac{33}{24}$;
$\frac{17}{12} = \frac{34}{24}$;
$\frac{33}{24} < \frac{34}{24}$;
$\frac{11}{8} < \frac{17}{12}$.

г) $\frac{27}{25} = \frac{54}{50}$;
$\frac{13}{10} = \frac{65}{50}$;
$\frac{54}{50} < \frac{65}{50}$;
$\frac{27}{25} < \frac{13}{10}$.

315. Не приводя дроби к общему знаменателю, определите, какая из них больше:
а) $\frac{1}{5}$ или $\frac{1}{4}$;
б) $\frac{1}{11}$ или $\frac{1}{14}$;
в) $\frac{3}{10}$ или $\frac{3}{7}$;
г) $\frac{7}{25}$ или $\frac{7}{26}$.

Решение

а) $\frac{1}{5} < \frac{1}{4}$

б) $\frac{1}{11} > \frac{1}{14}$

в) $\frac{3}{10} < \frac{3}{7}$

г) $\frac{7}{25} > \frac{7}{26}$

316. Определите, правильной или неправильной является каждая дробь, и сравните ее с 1:
$\frac{11}{15}, \frac{21}{20}, \frac{14}{9}, \frac{9}{14}, \frac{73}{110}, \frac{253}{250}.$

Решение

$\frac{11}{15} < 1$;
$\frac{21}{20} > 1$;
$\frac{14}{9} > 1$;
$\frac{9}{14} < 1$;
$\frac{73}{110} < 1$;
$\frac{253}{250} > 1$.

317. Сравните дроби:
а) $\frac{1}{3}$ и $\frac{3}{2}$;
б) $\frac{2}{7}$ и $\frac{4}{3}$;
в) $\frac{7}{5}$ и $\frac{8}{9}$;
г) $\frac{19}{20}$ и $\frac{20}{17}$.

Решение

а) $\frac{1}{3} < \frac{3}{2}$

б) $\frac{2}{7} < \frac{4}{3}$

в) $\frac{7}{5} > \frac{8}{9}$

г) $\frac{19}{20} < \frac{20}{17}$

318. Запишите дробь, равную $\frac{1}{2}$, меньшую $\frac{1}{2}$ и большую $\frac{1}{2}$, со знаменателем:
а) 10;
б) 24;
в) 30;
г) 8.

Решение

а) $\frac{1}{2} = \frac{5}{10}$;
$\frac{1}{2} > \frac{4}{10}$;
$\frac{1}{2} < \frac{6}{10}$.

б) $\frac{1}{2} = \frac{12}{24}$;
$\frac{1}{2} > \frac{5}{24}$;
$\frac{1}{2} < \frac{14}{24}$.

в) $\frac{1}{2} = \frac{15}{30}$;
$\frac{1}{2} > \frac{1}{30}$;
$\frac{1}{2} < \frac{29}{30}$.

г) $\frac{1}{2} = \frac{4}{8}$;
$\frac{1}{2} > \frac{3}{8}$;
$\frac{1}{2} < \frac{5}{8}$.

319. Отрезок между 0 и 1 на координатной прямой разделили точкой пополам. Определите, в какой половине единичного отрезка − в левой или правой − расположена точка, изображающая число:
а) $\frac{7}{8}$;
б) $\frac{3}{4}$;
в) $\frac{3}{10}$;
г) $\frac{5}{16}$.

Решение

а) $\frac{1}{2} = \frac{4}{8}$ − середина отрезка;
$\frac{4}{8} < \frac{7}{8}$.
Ответ: в правой.

б) $\frac{1}{2} = \frac{2}{4}$ − середина отрезка;
$\frac{2}{4} < \frac{3}{4}$.
Ответ: в правой.

в) $\frac{1}{2} = \frac{5}{10}$ − середина отрезка;
$\frac{5}{10} > \frac{3}{10}$.
Ответ: в левой

г) $\frac{1}{2} = \frac{8}{16}$ − середина отрезка;
$\frac{8}{16} > \frac{5}{16}$.
Ответ: в левой.

46

320. Меньше или больше половины литровой банки наполнится водой, если в нее налить:
а) $\frac{2}{5}$ л воды;
б) $\frac{75}{100}$ л воды?

Решение

а) 1) $\frac{1}{2} = \frac{5}{10}$ (банки) − составляет половину;
2) $\frac{2}{5} = \frac{4}{10}$ (банки) − наполнили;
3) $\frac{4}{10} < \frac{5}{10}$ − значит, меньше половины банки наполнится водой.
Ответ: меньше половины банки.

б) 1) $\frac{1}{2} = \frac{50}{100}$ (банки) − составляет половину;
2) $\frac{50}{100} < \frac{75}{100}$ − значит, больше половины банки наполнится водой.
Ответ: больше половины банки.

321. Расположите в порядке возрастания дроби:
а) $\frac{2}{7}, \frac{3}{5}, \frac{4}{9}$;
б) $\frac{2}{3}, \frac{3}{4}, \frac{7}{12}$;
в) $\frac{3}{4}, \frac{2}{5}, \frac{4}{7}$;
г) $\frac{7}{15}, \frac{7}{20}, \frac{9}{25}$.

Решение

а) $\frac{2}{7} = \frac{90}{315}$;
$\frac{3}{5} = \frac{189}{315}$;
$\frac{4}{9} = \frac{140}{315}$;
$\frac{90}{315} < \frac{140}{315} < \frac{189}{315}$;
$\frac{2}{7} < \frac{4}{9} < \frac{3}{5}$.

б) $\frac{2}{3} = \frac{8}{12}$;
$\frac{3}{4} = \frac{9}{12}$;
$\frac{7}{12}$;
$\frac{7}{12} < \frac{8}{12} < \frac{9}{12}$;
$\frac{7}{12} < \frac{2}{3} < \frac{3}{4}$.

в) $\frac{3}{4} = \frac{105}{140}$;
$\frac{2}{5} = \frac{56}{140}$;
$\frac{4}{7} = \frac{80}{140}$;
$\frac{56}{140} < \frac{80}{140} < \frac{105}{140}$;
$\frac{2}{5} < \frac{4}{7} < \frac{3}{4}$.

г) $\frac{7}{15} = \frac{140}{300}$;
$\frac{7}{20} = \frac{105}{300}$;
$\frac{9}{25} = \frac{108}{300}$;
$\frac{105}{300} < \frac{108}{300} < \frac{140}{300}$;
$\frac{7}{20} < \frac{9}{25} < \frac{7}{15}$.

322. Какая из дробей больше:
а) $\frac{1382}{1385}$ или $\frac{2445}{2298}$;
б) $\frac{999}{1000}$ или $\frac{2001}{2000}$?

Решение

а) $\frac{1382}{1385} < \frac{2445}{2298}$

б) $\frac{999}{1000} < \frac{2001}{2000}$

323. а) Два одинаковых ведра наполнили водой. Из одного вылили $\frac{1}{3}$ всей воды, а из другого − $\frac{1}{4}$. В каком ведре воды осталось больше?
б) Взяли три ленты одинаковой длины : белую, синюю и красную. От белой отрезали $\frac{1}{5}$ ее длины, от синей − $\frac{1}{7}$ ее длины, от красной − $\frac{1}{6}$ ее длины. Какая из лент стала короче других?

Решение

а) $\frac{1}{3} > \frac{1}{4}$ − значит из второго ведра воды вылили меньше, следовательно воды в нем осталось больше.
Ответ: во втором ведре

б) $\frac{1}{5} > \frac{1}{6} > \frac{1}{7}$ − значит от белой ленты отрезали больше, следовательно она стала короче других.
Ответ: белая лента

324. Какая из дробей $\frac{5}{8}, \frac{2}{5}, \frac{7}{6}, \frac{1}{4}$ самая маленькая? Какая самая большая? Расположите дроби в порядке возрастания.

Решение

$\frac{5}{8} = \frac{75}{120}$;
$\frac{2}{5} = \frac{48}{120}$;
$\frac{7}{6} = \frac{140}{120}$;
$\frac{1}{4} = \frac{30}{120}$;
$\frac{1}{4} < \frac{2}{5} < \frac{5}{8} < \frac{7}{6}$;
$\frac{1}{4}$ − самая маленькая дробь;
$\frac{7}{6}$ − самая большая дробь.

325. а) Запишите какое−нибудь число, которое больше $\frac{1}{4}$, но меньше $\frac{1}{3}$.
б) Запишите какие−нибудь три числа, которые больше $\frac{1}{2}$, но меньше $\frac{2}{3}$.

Решение

а) $\frac{1}{4} = \frac{6}{24}$;
$\frac{1}{3} = \frac{8}{24}$;
$\frac{6}{24} < \frac{7}{24} < \frac{8}{24}$;
$\frac{1}{4} < \frac{7}{24} < \frac{1}{3}$.

б) $\frac{1}{2} = \frac{12}{24}$;
$\frac{2}{3} = \frac{16}{24}$;
$\frac{12}{24} < \frac{13}{24} < \frac{14}{24} < \frac{15}{24} < \frac{16}{24}$;
$\frac{1}{2} < \frac{13}{24} < \frac{14}{24} < \frac{15}{24} < \frac{2}{3}$.

326. а) Запишите несколько чисел, которые меньше $\frac{1}{100}$. Сколько таких чисел можно найти?
б) Запишите несколько чисел, которые больше $\frac{99}{100}$. Сколько таких чисел можно найти?

Решение

а) $\frac{1}{100} > \frac{1}{1000} > \frac{1}{10000} > \frac{1}{100000}$
Чисел меньше $\frac{1}{100}$ можно найти бесконечное множество.

б) $\frac{99}{100} < \frac{109}{100} < \frac{209}{100} < \frac{990}{100}$
Чисел больше $\frac{99}{100}$ можно найти бесконечное множество.

327. а) Один автомобиль за 10 мин проехал 12 км, а другой за 8 мин − 10 км. Какой автомобиль ехал быстрее?
б) Баскетбольная команда школы №1 из 24 сыгранных игр выиграла 14, а баскетбольная команда школы №2 из 18 сыгранных игр выиграла 12. Какая команда играла лучше?

Решение

а) 1) $12 : 10 = \frac{12}{10}$ (км/ч) − скорость первого автомобиля;
2) $10 : 8 = \frac{10}{8}$ (км/ч) − скорость второго автомобиля;
3) $\frac{12}{10} = \frac{48}{40}$;
$\frac{10}{8} = \frac{50}{40}$;
$\frac{48}{40} < \frac{50}{40}$ − значит второй автомобиль ехал быстрее.
Ответ: второй автомобиль

б) 1) $14 : 24 = \frac{14}{24}$ (игр) − выиграла команда школы №1;
2) $12 : 18 = \frac{12}{18}$ (игр) − выиграла команда школы №2;
3) $\frac{14}{24} = \frac{7}{12}$;
$\frac{12}{18} = \frac{2}{3} = \frac{8}{12}$;
$\frac{7}{12} < \frac{8}{12}$ − значит команда школы №2 играла лучше.
Ответ: команда школы №2.

47

Самостоятельная работа № 13

Вариант 1

1. Приведите дроби к наименьшему общему знаменателю:
а) $\frac{1}{5}$ и $\frac{2}{7}$;
б) $\frac{5}{12}$ и $\frac{2}{3}$;
в) $\frac{1}{6}$ и $\frac{7}{15}$.

Решение

а) $\frac{1}{5} = \frac{7}{35}$;
$\frac{2}{7} = \frac{10}{35}$.

б) $\frac{5}{12}$;
$\frac{2}{3} = \frac{8}{12}$.

в) $\frac{1}{6} = \frac{5}{30}$;
$\frac{7}{15} = \frac{14}{30}$.

2. Сравните дроби:
а) $\frac{7}{15}$ и $\frac{11}{15}$;
б) $\frac{11}{16}$ и $\frac{5}{8}$.

Решение

а) $\frac{7}{15} < \frac{11}{15}$

б) $\frac{5}{8} = \frac{10}{16}$;
$\frac{11}{16} > \frac{10}{16}$;
$\frac{11}{16} > \frac{5}{8}$.

3. Сравните дроби, не приводя их к общему знаменателю:
а) $\frac{1}{20}$ и $\frac{1}{10}$;
б) $\frac{3}{7}$ и $\frac{3}{8}$;
в) $\frac{15}{17}$ и $\frac{17}{14}$.

Решение

а) $\frac{1}{20} < \frac{1}{10}$

б) $\frac{3}{7} > \frac{3}{8}$

в) $\frac{15}{17} < \frac{17}{14}$

4. Выпишите дроби больше $\frac{1}{2}$:
$\frac{1}{5}; \frac{4}{7}; \frac{4}{8}; \frac{7}{12}$.

Решение

$\frac{1}{2} = \frac{5}{10} = \frac{7}{14} = \frac{4}{8} = \frac{6}{12}$;
$\frac{1}{5} = \frac{2}{10} < \frac{5}{10}$;
$\frac{4}{7} = \frac{8}{14} > \frac{7}{14}$;
$\frac{4}{8} = \frac{1}{2}$;
$\frac{7}{12} > \frac{6}{12}$.
Ответ: $\frac{4}{7}, \frac{7}{12}$.

Вариант 2

1. Приведите дроби к наименьшему общему знаменателю:
а) $\frac{4}{9}$ и $\frac{1}{4}$;
б) $\frac{1}{6}$ и $\frac{5}{18}$;
в) $\frac{7}{20}$ и $\frac{3}{8}$.

Решение

а) $\frac{4}{9} = \frac{16}{36}$;
$\frac{1}{4} = \frac{9}{36}$.

б) $\frac{1}{6} = \frac{3}{18}$;
$\frac{5}{18}$.

в) $\frac{7}{20} = \frac{14}{40}$;
$\frac{3}{8} = \frac{15}{40}$.

2. Сравните дроби:
а) $\frac{9}{14}$ и $\frac{11}{14}$;
б) $\frac{4}{7}$ и $\frac{3}{5}$.

Решение

а) $\frac{9}{14} < \frac{11}{14}$

б) $\frac{4}{7} = \frac{20}{35}$;
$\frac{3}{5} = \frac{21}{35}$;
$\frac{20}{35} < \frac{21}{35}$;
$\frac{4}{7} < \frac{3}{5}$.

3. Сравните дроби, не приводя их к общему знаменателю:
а) $\frac{1}{5}$ и $\frac{1}{25}$;
б) $\frac{5}{11}$ и $\frac{5}{9}$;
в) $\frac{9}{7}$ и $\frac{7}{11}$.

Решение

а) $\frac{1}{5} > \frac{1}{25}$

б) $\frac{5}{11} < \frac{5}{9}$

в) $\frac{9}{7} > \frac{7}{11}$.

4. Выпишите дроби больше $\frac{1}{2}$:
$\frac{6}{11}; \frac{1}{9}; \frac{5}{8}; \frac{3}{6}$.

Решение

$\frac{1}{2} = \frac{11}{22} = \frac{9}{18} = \frac{4}{8} = \frac{3}{6}$;
$\frac{6}{11} = \frac{12}{22} > \frac{11}{22}$;
$\frac{1}{9} = \frac{2}{18} < \frac{9}{18}$;
$\frac{5}{8} > \frac{4}{8}$;
$\frac{3}{6} = \frac{1}{2}$.
Ответ: $\frac{6}{11}, \frac{5}{8}$.

---

Самостоятельная работа № 14

Вариант 1

1. Выполните деление:
а) 3 : 10;
б) 9 : 18;
в) 15 : 20;
г) 12 : 9.

Решение

а) $3 : 10 = \frac{3}{10}$

б) $9 : 18 = \frac{9}{18} = \frac{1}{2}$

в) $15 : 20 = \frac{15}{20} = \frac{3}{4}$

г) $12 : 9 = \frac{12}{9} = \frac{4}{3}$

2. Решите задачу:
Велосипедист проехал 5 км за 15 мин. Сколько километров в минуту проезжал велосипедист?

Решение

$5 : 15 = \frac{5}{15} = \frac{1}{3}$ (км/мин) − проезжал велосипедист.
Ответ: $\frac{1}{3}$ км/мин.

3. Представьте число 8 в виде дроби со знаменателем:
а) 1;
б) 5;
в) 9.

Решение

а) $8 = \frac{8}{1}$

б) $8 = \frac{40}{5}$

в) $8 = \frac{72}{9}$

4. Сравните частные:
а) 12 : 8 и 15 : 10;
б) 4 : 14 и 2 : 3.

Решение

а) $12 : 8 = \frac{12}{8} = \frac{3}{2}$;
$15 : 10 = \frac{15}{10} = \frac{3}{2}$;
$\frac{3}{2} = \frac{3}{2}$;
12 : 8 = 15 : 10.

б) $4 : 14 = \frac{4}{14} = \frac{12}{42}$;
$2 : 3 = \frac{2}{3} = \frac{28}{42}$;
$\frac{12}{42} < \frac{28}{42}$;
4 : 14 < 2 : 3.

Вариант 2

1. Выполните деление:
а) 1 : 5;
б) 8 : 24;
в) 15 : 21;
г) 9 : 6.

Решение

а) $1 : 5 = \frac{1}{5}$

б) $8 : 24 = \frac{8}{24} = \frac{1}{3}$

в) $15 : 21 = \frac{15}{21} = \frac{5}{7}$

г) $9 : 6 = \frac{9}{6} = \frac{3}{2}$

2. Решите задачу:
Спортсмен пробежал 4 км за 32 мин. Сколько километров в минуту он пробегал?

Решение

$4 : 32 = \frac{4}{32} = \frac{1}{8}$ (км/мин) − пробегал спортсмен.
Ответ: $\frac{1}{8}$ км/мин

3. Представьте число 8 в виде дроби со знаменателем:
а) 1;
б) 4;
в) 10.

Решение

а) $8 = \frac{8}{1}$

б) $8 = \frac{32}{4}$

в) $8 = \frac{80}{10}$

4. Сравните частные:
а) 3 : 4 и 10 : 16;
б) 10 : 8 и 25 : 20.

Решение

а) $3 : 4 = \frac{3}{4} = \frac{6}{8}$;
$10 : 16 = \frac{10}{16} = \frac{5}{8}$;
$\frac{6}{8} > \frac{5}{8}$;
3 : 4 > 10 : 16.

б) $10 : 8 = \frac{10}{8} = \frac{5}{4}$;
$25 : 20 = \frac{25}{20} = \frac{5}{4}$;
$\frac{5}{4} = \frac{5}{4}$;
10 : 8 = 25 : 20.

48

Действия с дробями
ГДЗ к теме Сложение и вычитание дробей

328. Сложите дроби и упростите результат:
а) $\frac{1}{8} + \frac{1}{8}$;
б) $\frac{4}{15} + \frac{1}{15}$;
в) $\frac{2}{9} + \frac{1}{9}$;
г) $\frac{4}{18} + \frac{5}{18}$;
д) $\frac{2}{21} + \frac{2}{21} + \frac{3}{21}$;
е) $\frac{2}{25} + \frac{4}{25} + \frac{4}{25}$.

Решение

а) $\frac{1}{8} + \frac{1}{8} = \frac{2}{8} = \frac{1}{4}$

б) $\frac{4}{15} + \frac{1}{15} = \frac{5}{15} = \frac{1}{3}$

в) $\frac{2}{9} + \frac{1}{9} = \frac{3}{9} = \frac{1}{9}$

г) $\frac{4}{18} + \frac{5}{18} = \frac{9}{18} = \frac{1}{2}$

д) $\frac{2}{21} + \frac{2}{21} + \frac{3}{21} = \frac{7}{21} = \frac{1}{3}$

е) $\frac{2}{25} + \frac{4}{25} + \frac{4}{25} = \frac{10}{25} = \frac{2}{5}$

329. Найдите разность:
а) $\frac{7}{15} - \frac{4}{15}$;
б) $\frac{15}{16} - \frac{7}{16}$;
в) $\frac{17}{21} - \frac{10}{21}$;
г) $\frac{42}{100} - \frac{17}{100}$.

Решение

а) $\frac{7}{15} - \frac{4}{15} = \frac{3}{15} = \frac{1}{5}$

б) $\frac{15}{16} - \frac{7}{16} = \frac{8}{16} = \frac{1}{2}$

в) $\frac{17}{21} - \frac{10}{21} = \frac{7}{21} = \frac{1}{3}$

г) $\frac{42}{100} - \frac{17}{100} = \frac{25}{100} = \frac{1}{4}$

330. Приведите дроби к общему знаменателю и выполните сложение:
а) $\frac{1}{2} + \frac{1}{8}$;
б) $\frac{2}{3} + \frac{4}{9}$;
в) $\frac{3}{4} + \frac{1}{12}$;
г) $\frac{2}{3} + \frac{1}{6}$.

Решение

а) $\frac{1}{2} + \frac{1}{8} = \frac{4}{8} + \frac{1}{8} = \frac{5}{8}$

б) $\frac{2}{3} + \frac{4}{9} = \frac{6}{9} + \frac{4}{9} = \frac{10}{9}$

в) $\frac{3}{4} + \frac{1}{12} = \frac{9}{12} + \frac{1}{12} = \frac{10}{12} = \frac{5}{6}$

г) $\frac{2}{3} + \frac{1}{6} = \frac{4}{6} + \frac{1}{6} = \frac{5}{6}$

331. Приведите дроби к общему знаменателю и выполните сложение:
а) $\frac{1}{3} + \frac{1}{4}$;
б) $\frac{2}{3} + \frac{1}{5}$;
в) $\frac{5}{7} + \frac{2}{3}$;
г) $\frac{1}{2} + \frac{1}{3}$.

Решение

а) $\frac{1}{3} + \frac{1}{4} = \frac{4}{12} + \frac{3}{12} = \frac{7}{12}$

б) $\frac{2}{3} + \frac{1}{5} = \frac{10}{15} + \frac{3}{15} = \frac{13}{15}$

в) $\frac{5}{7} + \frac{2}{3} = \frac{15}{21} + \frac{14}{21} = \frac{29}{21}$

г) $\frac{1}{2} + \frac{1}{3} = \frac{3}{6} + \frac{2}{6} = \frac{5}{6}$

332. Приведите дроби к общему знаменателю и выполните сложение:
а) $\frac{5}{6} + \frac{3}{8}$;
б) $\frac{9}{10} + \frac{3}{4}$;
в) $\frac{3}{10} + \frac{2}{15}$;
г) $\frac{2}{9} + \frac{1}{6}$.

Решение

а) $\frac{5}{6} + \frac{3}{8} = \frac{20}{24} + \frac{9}{24} = \frac{29}{24}$

б) $\frac{9}{10} + \frac{3}{4} = \frac{18}{20} + \frac{15}{20} = \frac{33}{20}$

в) $\frac{3}{10} + \frac{2}{15} = \frac{9}{30} + \frac{4}{30} = \frac{13}{30}$

г) $\frac{2}{9} + \frac{1}{6} = \frac{4}{18} + \frac{3}{18} = \frac{7}{18}$

333. Выполните вычитание и проверьте ответ сложением:
а) $\frac{5}{6} - \frac{2}{3}$;
б) $\frac{17}{18} - \frac{5}{6}$;
в) $\frac{5}{8} - \frac{5}{24}$;
г) $\frac{1}{2} - \frac{3}{10}$.

Решение

а) $\frac{5}{6} - \frac{2}{3} = \frac{5}{6} - \frac{4}{6} = \frac{1}{6}$
Проверка:
$\frac{1}{6} + \frac{2}{3} = \frac{1}{6} + \frac{4}{6} = \frac{5}{6}$

б) $\frac{17}{18} - \frac{5}{6} = \frac{17}{18} - \frac{15}{18} = \frac{2}{18} = \frac{1}{9}$
Проверка:
$\frac{1}{9} + \frac{5}{6} = \frac{2}{18} + \frac{15}{18} = \frac{17}{18}$

в) $\frac{5}{8} - \frac{5}{24} = \frac{15}{24} - \frac{5}{24} = \frac{10}{24} = \frac{5}{12}$
Проверка:
$\frac{5}{12} + \frac{5}{24} = \frac{10}{24} + \frac{5}{24} = \frac{15}{24} = \frac{5}{8}$

г) $\frac{1}{2} - \frac{3}{10} = \frac{5}{10} - \frac{3}{10} = \frac{2}{10} = \frac{1}{5}$
Проверка:
$\frac{1}{5} + \frac{3}{10} = \frac{2}{10} + \frac{3}{10} = \frac{5}{10} = \frac{1}{2}$

334. Вычислите разность:
а) $\frac{1}{4} - \frac{1}{5}$;
б) $\frac{7}{9} - \frac{1}{4}$;
в) $\frac{2}{3} - \frac{1}{7}$;
г) $\frac{2}{3} - \frac{2}{11}$.

Решение

а) $\frac{1}{4} - \frac{1}{5} = \frac{5}{20} - \frac{4}{20} = \frac{1}{20}$

б) $\frac{7}{9} - \frac{1}{4} = \frac{28}{36} - \frac{9}{36} = \frac{19}{36}$

в) $\frac{2}{3} - \frac{1}{7} = \frac{14}{21} - \frac{3}{21} = \frac{11}{21}$

г) $\frac{2}{3} - \frac{2}{11} = \frac{22}{33} = \frac{6}{33} = \frac{16}{33}$

335. Вычислите разность:
а) $\frac{5}{6} - \frac{1}{15}$;
б) $\frac{11}{12} - \frac{3}{8}$;
в) $\frac{5}{9} - \frac{1}{6}$;
г) $\frac{7}{6} - \frac{3}{10}$.

Решение

а) $\frac{5}{6} - \frac{1}{15} = \frac{25}{30} - \frac{2}{30} = \frac{23}{30}$

б) $\frac{11}{12} - \frac{3}{8} = \frac{22}{24} - \frac{9}{24} = \frac{13}{24}$

в) $\frac{5}{9} - \frac{1}{6} = \frac{10}{18} - \frac{3}{18} = \frac{7}{18}$

г) $\frac{7}{6} - \frac{3}{10} = \frac{35}{30} - \frac{9}{30} = \frac{26}{30} = \frac{13}{15}$

336. Найдите значение выражения:
а) $\frac{1}{3} + \frac{1}{6} + \frac{1}{18}$;
б) $\frac{1}{12} + \frac{1}{6} + \frac{3}{4}$;
в) $\frac{1}{20} + \frac{1}{4} + \frac{2}{5}$;
г) $\frac{1}{4} + \frac{2}{25} + \frac{3}{100}$.

Решение

а) $\frac{1}{3} + \frac{1}{6} + \frac{1}{18} = \frac{6}{18} + \frac{3}{18} + \frac{1}{18} = \frac{10}{18} = \frac{5}{9}$

б) $\frac{1}{12} + \frac{1}{6} + \frac{3}{4} = \frac{1}{12} + \frac{2}{12} + \frac{9}{12} = \frac{12}{12} = 1$

в) $\frac{1}{20} + \frac{1}{4} + \frac{2}{5} = \frac{1}{20} + \frac{5}{20} + \frac{8}{20} = \frac{14}{20} = \frac{7}{10}$

г) $\frac{1}{4} + \frac{2}{25} + \frac{3}{100} = \frac{25}{100} + \frac{8}{100} + \frac{3}{100} = \frac{36}{100} = \frac{9}{25}$

337. Найдите значение выражения:
а) $\frac{1}{2} + \frac{1}{3} + \frac{1}{5}$;
б) $\frac{1}{2} + \frac{1}{5} + \frac{3}{7}$;
в) $\frac{1}{2} + \frac{2}{3} + \frac{3}{5}$;
г) $\frac{2}{3} + \frac{1}{4} + \frac{1}{5}$.

Решение

а) $\frac{1}{2} + \frac{1}{3} + \frac{1}{5} = \frac{15}{30} + \frac{10}{30} + \frac{6}{30} = \frac{31}{30}$

б) $\frac{1}{2} + \frac{1}{5} + \frac{3}{7} = \frac{35}{70} + \frac{14}{70} + \frac{30}{70} = \frac{79}{70}$

в) $\frac{1}{2} + \frac{2}{3} + \frac{3}{5} = \frac{15}{30} + \frac{20}{30} + \frac{18}{30} = \frac{53}{30}$

г) $\frac{2}{3} + \frac{1}{4} + \frac{1}{5} = \frac{40}{60} + \frac{15}{60} + \frac{12}{60} = \frac{67}{60}$

49

338. Сравните с числом 1 сумму дробей:
а) $\frac{1}{4} + \frac{1}{4} + \frac{1}{4}$;
б) $\frac{5}{9} + \frac{5}{9}$;
в) $\frac{1}{5} + \frac{1}{5} + \frac{1}{5} + \frac{1}{5} + \frac{1}{5}$.

Решение

а) $\frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{3}{4} < 1$

б) $\frac{5}{9} + \frac{5}{9} = \frac{10}{9} > 1$

в) $\frac{1}{5} + \frac{1}{5} + \frac{1}{5} + \frac{1}{5} + \frac{1}{5} = \frac{5}{5} = 1$.

339. Представьте число 1 в виде суммы:
а) двух дробей со знаменателями, равными 7;
б) трех дробей со знаменателями, равными 10.

Решение

а) $\frac{3}{7} + \frac{4}{7} = \frac{7}{7} = 1$

б) $\frac{1}{10} + \frac{2}{10} + \frac{7}{10} = \frac{10}{10} = 1$

340. Найдите числа, которые должны быть записаны в пустых клетках таблицы:

Решение

1 таблица.
1) $\frac{1}{2} + \frac{2}{3} = \frac{3}{6} + \frac{4}{6} = \frac{7}{6}$;
2) $\frac{7}{8} - \frac{1}{2} = \frac{7}{8} - \frac{4}{8} = \frac{3}{8}$;
3) $\frac{1}{3} - \frac{1}{6} = \frac{2}{6} - \frac{1}{6} = \frac{1}{6}$.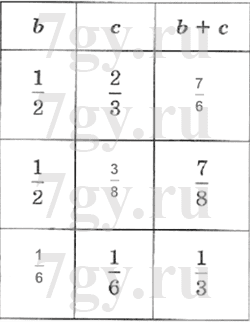


2 таблица.
1) $\frac{11}{14} - \frac{3}{7} = \frac{11}{14} - \frac{6}{14} = \frac{5}{14}$;
2) $\frac{2}{3} - \frac{4}{9} = \frac{6}{9} - \frac{4}{9} = \frac{2}{9}$;
3) $\frac{1}{2} + \frac{1}{5} = \frac{5}{10} + \frac{2}{10} = \frac{7}{10}$.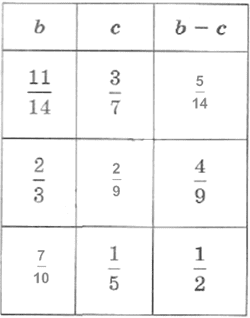

341. а) Оля прочитала $\frac{1}{4}$ всей книги. Какую часть книги ей осталось прочитать? Больше или меньше половины книги ей осталось прочитать?
б) До привала туристы прошли $\frac{1}{4}$ пути, после привала − еще $\frac{1}{2}$ всего пути. Какую часть пути они прошли? Какую часть им осталось пройти?

Решение

а) 1) $1 - \frac{1}{4} = \frac{4}{4} - \frac{1}{4} = \frac{3}{4}$ (книги) − осталось прочитать Оле;
2) $\frac{1}{2} = \frac{2}{4}$
$\frac{3}{4} > \frac{2}{4}$ − значит больше половины книги осталось прочитать Оле.
Ответ: $\frac{3}{4}$ книги; больше половины.

б) 1) $\frac{1}{4} + \frac{1}{2} = \frac{1}{4} + \frac{2}{4} = \frac{3}{4}$ (пути) − всего прошли туристы;
2) $1 - \frac{3}{4} = \frac{4}{4} - \frac{3}{4} = \frac{1}{4}$ (пути) − осталось пройти туристам.
Ответ: $\frac{3}{4}$ пути; $\frac{1}{4}$ пути.

342. Если открыть кран, то детский бассейн наполнится за 12 мин. Какая часть бассейна останется незаполненной, если открыть кран на 1 мин? на 2 мин?

Решение

1) $1 : 12 = \frac{1}{12}$ (бассейна) − заполняется за 1 минуту;
2) $\frac{1}{12} + \frac{1}{12} = \frac{2}{12} = \frac{1}{6}$ (бассейна) − заполнится за 2 минуты;
3) $1 - \frac{1}{12} = \frac{12}{12} - \frac{1}{12} = \frac{11}{12}$ (бассейна) − останутся незаполненными, если открыть кран на 1 мин;
4) $1 - \frac{1}{6} = \frac{6}{6} - \frac{1}{6} = \frac{5}{6}$ (бассейна) −останутся незаполненными, если открыть кран на 2 мин.
Ответ: $\frac{11}{12}$ бассейна; $\frac{5}{6}$ бассейна.

343. а) В одной коробке $\frac{1}{4}$ кг конфет, а в другой − на $\frac{1}{5}$ кг больше. Сколько конфет в двух коробках? Выразите ответ в граммах.
б) Туристы отправились на прогулку на лодке. До привала они плыли $\frac{3}{4}$ ч, обратный путь занял у них на $\frac{1}{3}$ ч больше. Сколько времени длилась прогулка, если привал занял $\frac{5}{6}$ ч? Ответ выразите в часах и минутах.

Решение

а) 1) $\frac{1}{4} + \frac{1}{5} = \frac{5}{20} + \frac{4}{20} = \frac{9}{20}$ (кг) − конфет в другой коробке;
2) $\frac{1}{4} + \frac{9}{20} = \frac{5}{20} + \frac{9}{20} = \frac{14}{20} = \frac{7}{10}$ (кг) − конфет в двух коробках;
3) 1000 : 10 * 7 = 100 * 7 = 700 (г) − конфет в двух коробках.
Ответ: 700 г.

б) 1) $\frac{3}{4} + \frac{1}{3} = \frac{9}{12} + \frac{4}{12} = \frac{13}{12}$ (ч) − занял путь обратно;
2) $\frac{3}{4} + \frac{13}{12} + \frac{5}{6} = \frac{9}{12} + \frac{13}{12} + \frac{10}{12} = \frac{32}{12} = \frac{8}{3}$ (ч) − длилась прогулка;
3) 60 : 3 * 8 = 20 * 8 = 160 (мин) = 2 ч 40 мин − длилась прогулка.
Ответ: 2 ч 40 мин.

50

344. Вычислите:
а) $\frac{11}{30} + \frac{7}{12}$;
б) $\frac{1}{27} + \frac{5}{18}$;
в) $\frac{5}{21} - \frac{5}{28}$;
г) $\frac{11}{18} - \frac{7}{12}$.

Решение

а) $\frac{11}{30} + \frac{7}{12} = \frac{22}{60} + \frac{35}{60} = \frac{57}{60} = \frac{19}{20}$

б) $\frac{1}{27} + \frac{5}{18} = \frac{2}{54} + \frac{15}{54} = \frac{17}{54}$

в) $\frac{5}{21} - \frac{5}{28} = \frac{20}{84} - \frac{15}{84} = \frac{5}{84}$

г) $\frac{11}{18} - \frac{7}{12} = \frac{22}{36} - \frac{21}{36} = \frac{1}{36}$

345. Вычислите:
а) $\frac{1}{8} - \frac{1}{10} + \frac{1}{4}$;
б) $\frac{3}{20} + \frac{1}{5} - \frac{1}{6}$;
в) $\frac{3}{4} - \frac{4}{25} - \frac{7}{20}$;
г) $\frac{3}{7} - \frac{1}{6} + \frac{5}{14}$.

Решение

а) $\frac{1}{8} - \frac{1}{10} + \frac{1}{4} = \frac{5}{40} - \frac{4}{40} + \frac{10}{40} = \frac{1}{40} + \frac{10}{40} = \frac{11}{40}$

б) $\frac{3}{20} + \frac{1}{5} - \frac{1}{6} = \frac{9}{60} + \frac{12}{60} - \frac{10}{60} = \frac{21}{60} - \frac{10}{60} = \frac{11}{60}$

в) $\frac{3}{4} - \frac{4}{25} - \frac{7}{20} = \frac{75}{100} - \frac{16}{100} - \frac{35}{100} = \frac{40}{100} - \frac{16}{100} = \frac{24}{40} = \frac{3}{5}$

г) $\frac{3}{7} - \frac{1}{6} + \frac{5}{14} = \frac{18}{42} - \frac{7}{42} + \frac{15}{42} + \frac{15}{42} = \frac{11}{42} + \frac{15}{42} = \frac{16}{42} = \frac{8}{21}$

346. Вычислите сумму, группируя дроби с одинаковыми знаменателями:
а) $\frac{3}{7} + \frac{4}{9} + \frac{4}{7} + \frac{5}{9}$;
б) $\frac{1}{11} + \frac{1}{5} + \frac{4}{11} + \frac{4}{5} + \frac{6}{11}$;
в) $\frac{1}{15} + \frac{4}{15} + \frac{1}{18} + \frac{5}{18} + \frac{2}{21} + \frac{5}{21} + \frac{1}{24} + \frac{7}{24}$;
г) $\frac{1}{8} + \frac{1}{12} + \frac{1}{16} + \frac{1}{20} + \frac{3}{8} + \frac{5}{12} + \frac{7}{16} + \frac{9}{20}$.

Решение

а) $\frac{3}{7} + \frac{4}{9} + \frac{4}{7} + \frac{5}{9} = (\frac{3}{7} + \frac{4}{7}) + (\frac{4}{9} + \frac{5}{9}) = \frac{7}{7} + \frac{9}{9} = 1 + 1 = 2$

б) $\frac{1}{11} + \frac{1}{5} + \frac{4}{11} + \frac{4}{5} + \frac{6}{11} = (\frac{1}{11} + \frac{4}{11} + \frac{6}{11}) + (\frac{1}{5} + \frac{4}{5}) = \frac{11}{11} + \frac{5}{5} = 1 + 1 = 2$

в) $\frac{1}{15} + \frac{4}{15} + \frac{1}{18} + \frac{5}{18} + \frac{2}{21} + \frac{5}{21} + \frac{1}{24} + \frac{7}{24} = $

$ = (\frac{1}{15} + \frac{4}{15}) + (\frac{1}{18} + \frac{5}{18}) + (\frac{2}{21} + \frac{5}{21}) + (\frac{1}{24} + \frac{7}{24}) = $
$ = \frac{5}{15} + \frac{6}{18} + \frac{7}{21} + \frac{8}{24} = \frac{1}{3} + \frac{1}{3} + \frac{1}{3} + \frac{1}{3} = \frac{4}{3}$

г) $\frac{1}{8} + \frac{1}{12} + \frac{1}{16} + \frac{1}{20} + \frac{3}{8} + \frac{5}{12} + \frac{7}{16} + \frac{9}{20} = $
$ = (\frac{1}{8} + \frac{3}{8}) + (\frac{1}{12} + \frac{5}{12}) + (\frac{1}{16} + \frac{7}{16}) + (\frac{1}{20} + \frac{9}{20}) = $
$ = \frac{4}{8} + \frac{6}{12} + \frac{8}{16} + \frac{10}{20} = \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = \frac{4}{2} = 2$

347. Представьте число 1 в виде суммы:
а) двух дробей со знаменателями, равными 3 и 6;
б) трех дробей со знаменателями, равными 2, 4 и 8.

Решение

а) $\frac{1}{3} + \frac{4}{6} = \frac{1}{3} + \frac{2}{3} = \frac{3}{3} = 1$

б) $\frac{1}{2} + \frac{2}{8} + \frac{1}{4} = \frac{2}{4} + \frac{1}{4} + \frac{1}{4} = \frac{4}{4} = 1$

348. Не выполняя вычислений, сравните значения выражений:
а) $\frac{1}{4} + \frac{1}{5} + \frac{1}{6}$ и $\frac{1}{5} + \frac{1}{6} + \frac{1}{7}$;
б) $\frac{1}{2} + \frac{1}{3} - \frac{1}{5}$ и $\frac{1}{2} + \frac{1}{3} - \frac{1}{4}$.

Решение

а) $\frac{1}{4} + \frac{1}{5} + \frac{1}{6} > \frac{1}{5} + \frac{1}{6} + \frac{1}{7}$

б) $\frac{1}{2} + \frac{1}{3} - \frac{1}{5} > \frac{1}{2} + \frac{1}{3} - \frac{1}{4}$

Самостоятельная работа № 15

Вариант 1

1. Вычислите:
а) $\frac{3}{5} + \frac{1}{4}$;
б) $\frac{8}{9} - \frac{1}{3}$;
в) $\frac{5}{8} + \frac{7}{10}$.

Решение

а) $\frac{3}{5} + \frac{1}{4} = \frac{12}{20} + \frac{5}{20} = \frac{17}{20}$

б) $\frac{8}{9} - \frac{1}{3} = \frac{8}{9} - \frac{3}{9} = \frac{5}{9}$

в) $\frac{5}{8} + \frac{7}{10} = \frac{25}{40} + \frac{28}{40} = \frac{53}{40}$

2. Найдите неизвестное число, обозначенное буквой:
а) $\frac{3}{7} + x = \frac{11}{15}$;
б) $x - \frac{1}{12} = \frac{7}{12}$.

Решение

а) $\frac{3}{7} + x = \frac{11}{15}$
$x = \frac{11}{15} - \frac{3}{7}$
$x = \frac{77}{105} - \frac{45}{105}$
$x = \frac{32}{105}$

б) $x - \frac{1}{12} = \frac{7}{12}$
$x = \frac{7}{12} + \frac{1}{12}$
$x = \frac{8}{12}$
$x = \frac{2}{3}$

3. Какое из чисел больше и на сколько:
$\frac{17}{24}$ или $\frac{5}{8}$?

Решение

$\frac{5}{8} = \frac{15}{24}$;
$\frac{17}{24} > \frac{15}{24}$;
$\frac{17}{24} - \frac{15}{24} = \frac{2}{24} = \frac{1}{12}$.
Ответ: $\frac{17}{24}$ на $\frac{1}{12}$ больше, чем $\frac{5}{8}$

Вариант 2

1. Вычислите:
а) $\frac{2}{5} + \frac{1}{2}$;
б) $\frac{5}{6} - \frac{2}{3}$;
в) $\frac{8}{15} + \frac{3}{10}$.

Решение

а) $\frac{2}{5} + \frac{1}{2} = \frac{4}{10} + \frac{5}{10} = \frac{9}{10}$

б) $\frac{5}{6} - \frac{2}{3} = \frac{5}{6} - \frac{4}{6} = \frac{1}{6}$

в) $\frac{8}{15} + \frac{3}{10} = \frac{16}{30} + \frac{9}{30} = \frac{25}{30} = \frac{5}{6}$

2. Найдите неизвестное число, обозначенное буквой:
а) $x + \frac{5}{8} = \frac{9}{8}$;
б) $x - \frac{2}{9} = \frac{5}{9}$.

Решение

а) $x + \frac{5}{8} = \frac{9}{8}$
$x = \frac{9}{8} - \frac{5}{8}$
$x = \frac{4}{8}$
$x = \frac{1}{2}$

б) $x - \frac{2}{9} = \frac{5}{9}$
$x = \frac{5}{9} + \frac{2}{9}$
$x = \frac{7}{9}$

3. Какое из чисел больше и на сколько:
$\frac{19}{36}$ или $\frac{7}{9}$?

Решение

$\frac{7}{9} = \frac{28}{36}$;
$\frac{19}{36} < \frac{28}{36}$;
$\frac{28}{36} - \frac{19}{36} = \frac{9}{36} = \frac{1}{4}$.
Ответ: число $\frac{7}{9}$ больше, чем $\frac{19}{36}$ на $\frac{1}{4}$

51

Самостоятельная работа № 16

Вариант 1

1. Выполнение задания по литературе заняло у Иры $\frac{3}{4}$ ч, а по биологии − на $\frac{1}{6}$ ч меньше.
а) Сколько времени ушло у Иры на оба задания?
б) Больше это или меньше 1 ч и на сколько?
в) Выразите полученную разницу в минутах.

Решение

1) $\frac{3}{4} - \frac{1}{6} = \frac{9}{12} - \frac{2}{12} = \frac{7}{12}$ (ч) − заняло выполнение задания по биологии;
2) $\frac{3}{4} + \frac{7}{12} = \frac{9}{12} + \frac{7}{12} = \frac{16}{12} = \frac{4}{3}$ (ч) − ушло у Иры на оба задания;
3) 60 : 3 * 4 = 20 * 4 = 80 (мин) = 1 ч 20 мин − ушло у Иры на оба задания;
4) $1 < \frac{4}{3}$
$\frac{4}{3} - \frac{3}{3} = \frac{1}{3}$ (ч) − больше, чем 1 ч заняло у Иры выполнение задания;
60 : 3 = на 20 (мин) − больше, чем 1 ч заняло у Иры выполнение задания.
Ответ:
а) 1 ч 20 мин;
б) больше на $\frac{1}{3}$ ч;
в) больше на 20 мин.

Вариант 2

1. Выполнение задания по географии заняло у Петра $\frac{7}{12}$ ч, а по истории − на $\frac{1}{10}$ ч меньше.
а) Сколько времени ушло у Петра на оба задания?
б) Больше это или меньше 1 ч и на сколько?
в) Выразите полученную разницу в минутах.

Решение

1) $\frac{7}{12} - \frac{1}{10} = \frac{35}{60} - \frac{6}{60} = \frac{29}{60}$ (ч) − заняло выполнение задания по географии;
2) $\frac{7}{12} + \frac{29}{60} = \frac{35}{60} + \frac{29}{60} = \frac{64}{60} = \frac{16}{15}$ (ч) − ушло у Петра на оба задания;
3) 60 : 15 * 16 = 4 * 16 = 64 (мин) = 1 ч 4 мин − ушло у Петра на оба задания;
3) $1 < \frac{16}{15}$
$\frac{16}{15} - 1 = \frac{16}{15} - \frac{15}{15} = \frac{1}{15}$ (ч) − больше, чем 1 ч ушло на оба задания;
4) 60 : 15 = на 4 (мин) − больше, чем 1 ч ушло на оба задания.
Ответ:
а) 1 ч 4 мин;
б) больше на $\frac{1}{15}$ ч;
в) больше на 4 мин.

ГДЗ к теме Смешанные дроби. Сложение смешанных дробей

349. Прочитайте смешанные дроби и покажите примерное положение каждой из них на координатной прямой:
а) $5\frac{1}{3}$ и $4\frac{1}{2}$;
б) $2\frac{3}{8}$ и $2\frac{5}{8}$;
в) $6\frac{1}{7}$ и $6\frac{1}{3}$;
г) $7\frac{2}{5}$ и $7\frac{3}{4}$.

Решение

а) $5\frac{1}{3}$ − пять целых одна третья;
$4\frac{1}{2}$ − четыре целых одна вторая.


б) $2\frac{3}{8}$ − две целых три восьмых;
$2\frac{5}{8}$ − две целых пять восьмых.


в) $6\frac{1}{7}$ − шесть целых одна седьмая;
$6\frac{1}{3}$ − шесть целых одна третья.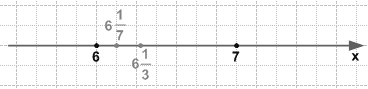


г) $7\frac{2}{5}$ − семь целых две пятых;
$7\frac{3}{4}$ − семь целых три четвертых.

350. Запишите неправильную дробь в виде смешанной дроби:
а) $\frac{5}{2}, \frac{17}{5}, \frac{20}{3}, \frac{51}{12}, \frac{111}{20}$;
б) $\frac{9}{4}, \frac{17}{3}, \frac{28}{5}, \frac{41}{10}, \frac{112}{25}$.

Решение

а) $\frac{5}{2} = 2\frac{1}{2}$;
$\frac{17}{5} = 3\frac{2}{5}$;
$\frac{20}{3} = 6\frac{2}{3}$;
$\frac{51}{12} = \frac{17}{4} = 4\frac{1}{4}$;
$\frac{111}{20} = 5\frac{11}{20}$.

б) $\frac{9}{4} = 2\frac{1}{4}$;
$\frac{17}{3} = 5\frac{2}{3}$;
$\frac{28}{5} = 5\frac{3}{5}$;
$\frac{41}{10} = 4\frac{1}{10}$;
$\frac{112}{25} = 4\frac{12}{25}$.

351. Запишите неправильную дробь в виде смешанной дроби:
а) $\frac{22}{10}, \frac{24}{9}, \frac{56}{16}, \frac{45}{18}, \frac{70}{6}$;
б) $\frac{24}{20}, \frac{33}{12}, \frac{55}{15}, \frac{56}{21}, \frac{63}{6}$.

Решение

а) $\frac{22}{10} = \frac{11}{5} = 2\frac{1}{5}$;
$\frac{24}{9} = \frac{8}{3} = 2\frac{2}{3}$;
$\frac{56}{16} = \frac{7}{2} = 3\frac{1}{2}$;
$\frac{45}{18} = \frac{5}{2} = 2\frac{1}{2}$;
$\frac{70}{6} = \frac{35}{3} = 11\frac{2}{3}$.

б) $\frac{24}{20} = \frac{6}{5} = 1\frac{1}{5}$;
$\frac{33}{12} = \frac{11}{4} = 2\frac{3}{4}$;
$\frac{55}{15} = \frac{11}{3} = 3\frac{2}{3}$;
$\frac{56}{21} = \frac{8}{3} = 2\frac{2}{3}$;
$\frac{63}{6} = \frac{21}{2} = 10\frac{1}{2}$.

352. Запишите смешанную дробь в виде неправильной дроби:
а) $3\frac{1}{3}, 2\frac{2}{5}, 7\frac{3}{4}, 4\frac{2}{9}, 1\frac{2}{17}$;
б) $4\frac{1}{2}, 1\frac{3}{11}, 2\frac{1}{6}, 3\frac{4}{9}, 5\frac{5}{14}$.

Решение

а) $3\frac{1}{3} = \frac{3 * 3 + 1}{3} = \frac{10}{3}$;
$2\frac{2}{5} = \frac{2 * 5 + 2}{5} = \frac{12}{5}$;
$7\frac{3}{4} = \frac{7 * 4 + 3}{4} = \frac{31}{4}$;
$4\frac{2}{9} = \frac{4 * 9 + 2}{9} = \frac{38}{9}$;
$1\frac{2}{17} = \frac{1 * 17 + 2}{17} = \frac{19}{17}$.

б) $4\frac{1}{2} = \frac{4 * 2 + 1}{2} = \frac{9}{2}$;
$1\frac{3}{11} = \frac{1 * 11 + 3}{11} = \frac{14}{11}$;
$2\frac{1}{6} = \frac{2 * 6 + 1}{6} = \frac{13}{6}$;
$3\frac{4}{9} = \frac{3 * 9 + 4}{9} = \frac{31}{9}$;
$5\frac{5}{14} = \frac{5 * 14 + 5}{14} = \frac{75}{14}$.

353. а) Ломаная состоит из трех равных звеньев (рис.8). Найдите длину каждого звена, если длина ломаной 10 см.
б) Периметр равнобедренного треугольника ABC равен 12 дм (рис.9). Длина основания AC равна 3 дм. Найдите длины сторон AB и BC.

Решение

а) $10 : 3 = \frac{10}{3} = 3\frac{1}{3}$ (см) − длина каждого звена.
Ответ: $3\frac{1}{3}$ см.

б) 1) 12 − 3 = 9 (дм) − сумма длин боковых сторон;
2) $9 : 2 = \frac{9}{2} = 4\frac{1}{2}$ (дм) − длина стороны AB и длина стороны BC.
Ответ: $AB = BC = 4\frac{1}{2}$ дм.

52

354. Сравните числа:
а) $\frac{10}{3}$ и $\frac{5}{2}$;
б) $\frac{15}{3}$ и $\frac{14}{4}$;
в) $\frac{100}{9}$ и 10;
г) 5 и $\frac{42}{10}$.
Образец.
Сравним $\frac{16}{3}$ и $\frac{22}{5}$. Выделим из каждой дроби целую часть:
$\frac{16}{3} = 5\frac{1}{3}$,
$\frac{22}{5} = 4\frac{2}{5}$.
Так как $5\frac{1}{3} > 4\frac{2}{5}$, то $\frac{16}{3} > \frac{22}{5}$.

Решение

а) Сравним $\frac{10}{3}$ и $\frac{5}{2}$. Выделим из каждой дроби целую часть:
$\frac{10}{3} = 3\frac{1}{3}$;
$\frac{5}{2} = 2\frac{1}{2}$.
Так как $3\frac{1}{3} > 2\frac{1}{2}$, то $\frac{10}{3} > \frac{5}{2}$.

б) Сравним $\frac{15}{3}$ и $\frac{14}{4}$. Выделим из каждой дроби целую часть:
$\frac{15}{3} = 5$;
$\frac{14}{4} = 3\frac{2}{4} = 3\frac{1}{2}$.
Так как $5 > 3\frac{1}{2}$, то $\frac{15}{3} > \frac{14}{4}$.

в) Сравним $\frac{100}{9}$ и 10. Выделим из дроби целую часть:
$\frac{100}{9} = 11\frac{1}{9}$.
Так как $11\frac{1}{9} > 10$, то $\frac{100}{9} > 10$.

г) Сравним 5 и $\frac{42}{10}$. Выделим из дроби целую часть:
$\frac{42}{10} = 4\frac{2}{10} = 4\frac{1}{5}$.
Так как $5 > 4\frac{1}{5}$, то $5 > \frac{42}{10}$.

355. Выразите в метрах:
а)
$5\frac{1}{10}$ км;
$3\frac{1}{5}$ км;
$7\frac{1}{2}$ км.
б)
$2\frac{7}{10}$ км;
$4\frac{3}{5}$ км;
$7\frac{3}{20}$ км.

Решение

а) $5\frac{1}{10}$ км = 5 * 1000 + 1000 : 10 = 5000 + 100 = 5100 м;
$3\frac{1}{5}$ км = 3 * 1000 + 1000 : 5 = 3000 + 200 = 3200 м;
$7\frac{1}{2}$ км = 7 * 1000 + 1000 : 2 = 7000 + 500 = 7500 м.

б) $2\frac{7}{10}$ км = 2 * 1000 + 1000 : 10 * 7 = 2000 + 100 * 7 = 2000 + 700 = 2700 м;
$4\frac{3}{5}$ км = 4 * 1000 + 1000 : 5 * 3 = 4000 + 200 * 3 = 4000 + 600 = 4600 м;
$7\frac{3}{20}$ км = 7 * 1000 + 1000 : 20 * 3 = 7000 + 50 * 3 = 7000 + 150 = 7150 м.

356. Выразите в килограммах:
а)
1 кг 300 г;
2 кг 400 г;
3 кг 750 г.
б)
5200 г;
2450 г;
1500 г.

Решение

а) 1 кг 300 г = $1\frac{300}{1000} = 1\frac{3}{10}$ кг;
2 кг 400 г = $2\frac{400}{1000} = 2\frac{4}{10} = 2\frac{2}{5}$ кг;
3 кг 750 г = $3\frac{750}{1000} = 3\frac{75}{100} = 3\frac{3}{4}$ кг.

б) 5200 г = $5\frac{200}{1000} = 5\frac{2}{10} = 5\frac{1}{5}$ кг;
2450 г = $2\frac{450}{1000} = 2\frac{45}{100} = 2\frac{9}{20}$ кг;
1500 г = $1\frac{500}{1000} = 1\frac{5}{10} = 1\frac{1}{2}$ кг.

357. Выразите в часах:
а)
1 ч 15 мин;
2 ч 12 мин;
3 ч 20 мин.
б)
80 мин;
150 мин;
105 мин.

Решение

а) 1 ч 15 мин = $1\frac{15}{60} = 1\frac{1}{4}$ ч;
2 ч 12 мин = $2\frac{12}{60} = 2\frac{1}{5}$ ч;
3 ч 20 мин = $3\frac{20}{60} = 3\frac{1}{3}$ ч.

б) 80 мин = 60 мин + 20 мин = $1\frac{20}{60} = 1\frac{1}{3}$ ч;
150 мин = 120 мин + 30 мин = $2\frac{30}{60} = 2\frac{1}{2}$ ч;
105 мин = 60 мин + 45 мин = $1\frac{45}{60} = 1\frac{3}{4}$ ч.

358. Выполните сложение и представьте результат в виде смешанной дроби:
а) $\frac{11}{14} + \frac{7}{14}$;
б) $\frac{5}{9} + \frac{2}{3}$;
в) $\frac{3}{5} + \frac{4}{7}$;
г) $\frac{14}{15} + \frac{1}{6}$.

Решение

а) $\frac{11}{14} + \frac{7}{14} = \frac{18}{14} = \frac{9}{7} = 1\frac{2}{7}$

б) $\frac{5}{9} + \frac{2}{3} = \frac{5}{9} + \frac{6}{9} = \frac{11}{9} = 1\frac{2}{9}$

в) $\frac{3}{5} + \frac{4}{7} = \frac{21}{35} + \frac{20}{35} = \frac{41}{35} = 1\frac{6}{35}$

г) $\frac{14}{15} + \frac{1}{6} = \frac{28}{30} + \frac{5}{30} = \frac{33}{30} = \frac{11}{10} = 1\frac{1}{10}$

359. Выполните сложение:
а) $3\frac{1}{2} + 1\frac{1}{4}$;
б) $2\frac{2}{3} + 7\frac{1}{6}$;
в) $\frac{5}{8} + 3\frac{5}{24}$;
г) $8\frac{1}{2} + \frac{1}{8}$.

Решение

а) $3\frac{1}{2} + 1\frac{1}{4} = (3 + 1) + (\frac{2}{4} + \frac{1}{4}) = 4 + \frac{3}{4} = 4\frac{3}{4}$

б) $2\frac{2}{3} + 7\frac{1}{6} = (2 + 7) + (\frac{4}{6} + \frac{1}{6}) = 9\frac{5}{6}$

в) $\frac{5}{8} + 3\frac{5}{24} = 3 + (\frac{15}{24} + \frac{5}{24}) = 3\frac{20}{24} = 3\frac{5}{6}$

г) $8\frac{1}{2} + \frac{1}{8} = 8 + (\frac{4}{8} + \frac{1}{8}) = 8\frac{5}{8}$

360. Выполните сложение:
а) $2\frac{1}{2} + 4\frac{5}{7}$;
б) $\frac{4}{5} + 6\frac{1}{6}$;
в) $3\frac{1}{2} + \frac{1}{3}$;
г) $1\frac{3}{10} + \frac{2}{3}$.

Решение

а) $2\frac{1}{2} + 4\frac{5}{7} = (2 + 4) + (\frac{7}{14} + \frac{10}{14}) = 6 + \frac{17}{14} = 6 + 1\frac{3}{14} = 7\frac{3}{14}$

б) $\frac{4}{5} + 6\frac{1}{6} = 6 + (\frac{24}{30} + \frac{5}{30}) = 6\frac{29}{30}$

в) $3\frac{1}{2} + \frac{1}{3} = 3 + (\frac{3}{6} + \frac{2}{6}) = 3\frac{5}{6}$

г) $1\frac{3}{10} + \frac{2}{3} = 1 + (\frac{9}{30} + \frac{20}{30}) = 1\frac{29}{30}$

361. Выполните сложение:
а) $\frac{1}{4} + 2\frac{5}{6}$;
б) $1\frac{3}{20} + \frac{7}{25}$;
в) $3\frac{2}{9} + 5\frac{1}{6}$;
г) $8\frac{5}{6} + 2\frac{3}{8}$.

Решение

а) $\frac{1}{4} + 2\frac{5}{6} = 2 + (\frac{3}{12} + \frac{10}{12}) = 2 + \frac{13}{12} = 2 + 1\frac{1}{12} = 3\frac{1}{12}$

б) $1\frac{3}{20} + \frac{7}{25} = 1 + (\frac{15}{100} + \frac{28}{100}) = 1\frac{43}{100}$

в) $3\frac{2}{9} + 5\frac{1}{6} = (3 + 5) + (\frac{4}{18} + \frac{3}{18}) = 8\frac{7}{18}$

г) $8\frac{5}{6} + 2\frac{3}{8} = (8 + 2) + (\frac{20}{24} + \frac{9}{24}) = 10 + \frac{29}{24} = 10 + 1\frac{5}{24} = 11\frac{5}{24}$

362. Масса котенка $\frac{3}{5}$ кг, а масса щенка $1\frac{3}{4}$ кг. Какими будут показания весов, если их поместить на весы вместе? Дайте ответ сначала в килограммах, а затем в килограммах и граммах.

Решение

1) $\frac{3}{5} + 1\frac{3}{4} = \frac{12}{20} + 1\frac{15}{20} = 1\frac{27}{20} = 2\frac{7}{20}$ (кг) − общая масса котенка и щенка;
2) $2\frac{7}{20}$ кг = 2 + 1000 : 20 * 7 = 2 + 350 = 2 кг 350 г − общая масса котенка и щенка.
Ответ: $2\frac{7}{20}$ кг или 2 кг 350 г

363. Вера и Коля вышли из своих домов, которые находятся на одной улице, и пошли навстречу друг другу. Вера прошла до встречи $1\frac{2}{5}$ км, а Коля − на $\frac{3}{10}$ км больше. Чему равно расстояние между домами Веры и Коли?

Решение

1) $1\frac{2}{5} + \frac{3}{10} = 1\frac{4}{10} + \frac{3}{10} = 1\frac{7}{10}$ (км) − прошел Коля;
2) $1\frac{7}{10} + 1\frac{2}{5} = 1\frac{7}{10} + 1\frac{4}{10} = 2\frac{11}{10} = 3\frac{1}{10}$ (км) − расстояние между домами Веры и Коли.
Ответ: $3\frac{1}{10}$ км

53

364. Турист ехал на автобусе $2\frac{1}{5}$ ч, потом на попутной машине $1\frac{3}{10}$ ч и еще шел пешком четверть часа. Сколько часов турист был в пути?

Решение

$2\frac{1}{5} + 1\frac{3}{10} + \frac{1}{4} = 2\frac{4}{20} + 1\frac{6}{20} + \frac{5}{20} = 3\frac{15}{20} = 3\frac{3}{4}$ (ч) − турист был в пути.
Ответ: $3\frac{3}{4}$ ч

365. а) Запишите последовательность из пяти чисел, в которой первое число равно 1, а каждое следующее − на $\frac{2}{3}$ больше предыдущего. Найдите сумму членов этой последовательности.
б) Первое число в последовательности равно $\frac{2}{3}$, а каждое следующее на $\frac{4}{5}$ больше предыдущего. Найдите шестое число в этой последовательности.

Решение

а) $1 + (1 + \frac{2}{3}) + (1 + \frac{2}{3} + \frac{2}{3}) + (1 + \frac{2}{3} + \frac{2}{3} + \frac{2}{3}) + (1 + \frac{2}{3} + \frac{2}{3} + \frac{2}{3} + \frac{2}{3}) = $
$ = 1 + 1\frac{2}{3} + 1\frac{4}{3} + 1\frac{6}{3} + 1\frac{8}{3} = 1 + 1\frac{2}{3} + 2\frac{1}{3} + 3 + 3\frac{2}{3} = $
$ = (1 + 1 + 2 + 3 + 3) + (\frac{2}{3} + \frac{1}{3} + \frac{2}{3}) = 10\frac{5}{3} = 11\frac{2}{3}$

б) $\frac{2}{3} + \frac{4}{5} + \frac{4}{5} + \frac{4}{5} + \frac{4}{5} + \frac{4}{5} = \frac{2}{3} + \frac{20}{3} = \frac{2}{3} + 4 = 4\frac{2}{3}$

366. а) Клумба имеет треугольную форму. Одна ее сторона равна $2\frac{2}{5}$ м, другая − $1\frac{7}{10}$ м, третья − 3 м. Хватит ли декоративной изгороди длиной 7 м для ограждения этой клумбы?
б) Косынка имеет форму равнобедренного треугольника. Каждая из двух равных сторон равна $\frac{4}{5}$ м, а большая сторона длиннее на $\frac{7}{20}$ м. Хватит ли трех метров тесьмы для окантовки этой косынки?

Решение

а) 1) $2\frac{2}{5} + 1\frac{7}{10} + 3 = 2\frac{4}{10} + 1\frac{7}{10} + 3 = 6\frac{11}{10} = 7\frac{1}{10}$ (м) − периметр клумбы;
2) $7\frac{1}{10} > 7$ − значит декоративной изгороди не хватит.
Ответ: нет, не хватит.

б) 1) $\frac{4}{5} + \frac{4}{5} + (\frac{4}{5} + \frac{7}{20}) = \frac{8}{5} + (\frac{16}{20} + \frac{7}{20}) = \frac{8}{5} + \frac{23}{20} = 1\frac{3}{5} + 1\frac{3}{20} = 1\frac{12}{20} + 1\frac{3}{20} = 2\frac{15}{20} = 2\frac{3}{4}$ (м) − периметр косынки;
2) $3 > 2\frac{3}{4}$ − значит трех метров тесьмы хватит.
Ответ: да, хватит.

Самостоятельная работа № 17

Вариант 1

1. Представьте неправильную дробь в виде смешанной дроби:
а) $\frac{5}{2}$;
б) $\frac{11}{10}$;
в) $\frac{40}{18}$.

Решение

а) $\frac{5}{2} = 2\frac{1}{2}$

б) $\frac{11}{10} = 1\frac{1}{10}$

в) $\frac{40}{18} = 2\frac{4}{18} = 2\frac{2}{9}$

2. Запишите смешанную дробь в виде неправильной дроби:
а) $1\frac{5}{6}$;
б) $2\frac{1}{8}$;
в) $3\frac{3}{4}$.

Решение

а) $1\frac{5}{6} = \frac{6 * 1 + 5}{6} = \frac{11}{6}$

б) $2\frac{1}{8} = \frac{2 * 8 + 1}{8} = \frac{17}{8}$

в) $3\frac{3}{4} = \frac{3 * 4 + 3}{4} = \frac{15}{4}$

3. Сравните:
$\frac{11}{3}$ и $\frac{17}{6}$;
$\frac{17}{8}$ и $\frac{9}{4}$.

Решение

$\frac{11}{3} = 3\frac{2}{3}$;
$\frac{17}{6} = 2\frac{5}{6}$;
$3\frac{2}{3} > 2\frac{5}{6}$;
$\frac{11}{3} > \frac{17}{6}$.

$\frac{17}{8} = 2\frac{1}{8}$;
$\frac{9}{4} = 2\frac{1}{4}$;
$2\frac{1}{8} < 2\frac{1}{4}$;
$\frac{17}{8} < \frac{9}{4}$.

Вариант 2

1. Представьте неправильную дробь в виде смешанной дроби:
а) $\frac{7}{2}$;
б) $\frac{9}{8}$;
в) $\frac{58}{16}$.

Решение

а) $\frac{7}{2} = 3\frac{1}{2}$

б) $\frac{9}{8} = 1\frac{1}{8}$

в) $\frac{58}{16} = \frac{29}{8} = 3\frac{5}{8}$

2. Запишите смешанную дробь в виде неправильной дроби:
а) $2\frac{3}{5}$;
б) $3\frac{1}{10}$;
в) $1\frac{2}{7}$.

Решение

а) $2\frac{3}{5} = \frac{2 * 5 + 3}{5} = \frac{13}{5}$

б) $3\frac{1}{10} = \frac{3 * 10 + 1}{10} = \frac{31}{10}$

в) $1\frac{2}{7} = \frac{1 * 7 + 2}{7} = \frac{9}{7}$

3. Сравните:
$\frac{12}{5}$ и $\frac{10}{3}$;
$\frac{13}{6}$ и $\frac{19}{9}$.

Решение

$\frac{12}{5} = 2\frac{2}{5}$;
$\frac{10}{3} = 3\frac{1}{3}$;
$2\frac{2}{5} < 3\frac{1}{3}$;
$\frac{12}{5} < \frac{10}{3}$.

$\frac{13}{6} = 2\frac{1}{6}$;
$\frac{19}{9} = 2\frac{1}{9}$;
$2\frac{1}{6} > 2\frac{1}{9}$;
$\frac{13}{6} > \frac{19}{9}$.

Самостоятельная работа № 18

Вариант 1

1. Выполните сложение и представьте результат в виде смешанной дроби:
а) $\frac{2}{7} + \frac{4}{5}$;
б) $\frac{5}{12} + \frac{3}{4}$.

Решение

а) $\frac{2}{7} + \frac{4}{5} = \frac{10}{35} + \frac{28}{35} = \frac{38}{35} = 1\frac{3}{35}$

б) $\frac{5}{12} + \frac{3}{4} = \frac{5}{12} + \frac{9}{12} = \frac{14}{12} = \frac{7}{6} = 1\frac{1}{6}$

2. Найдите сумму:
а) $3\frac{1}{8} + 1\frac{1}{4}$;
б) $4\frac{2}{3} + \frac{3}{8}$.

Решение

а) $3\frac{1}{8} + 1\frac{1}{4} = (3 + 1) + (\frac{1}{8} + \frac{2}{8}) = 4\frac{3}{8}$

б) $4\frac{2}{3} + \frac{3}{8} = 4 + (\frac{16}{24} + \frac{9}{24}) = 4 + \frac{25}{24} = 4 + 1\frac{1}{24} = 5\frac{1}{24}$

Вариант 2

1. Выполните сложение и представьте результат в виде смешанной дроби:
а) $\frac{2}{3} + \frac{7}{10}$;
б) $\frac{11}{18} + \frac{5}{6}$.

Решение

а) $\frac{2}{3} + \frac{7}{10} = \frac{20}{30} + \frac{21}{30} = \frac{41}{30} = 1\frac{11}{30}$

б) $\frac{11}{18} + \frac{5}{6} = \frac{11}{18} + \frac{15}{18} = \frac{26}{18} = \frac{13}{9} = 1\frac{4}{9}$

2. Найдите сумму:
а) $2\frac{1}{3} + 1\frac{4}{9}$;
б) $3\frac{3}{4} + \frac{4}{5}$.

Решение

а) $2\frac{1}{3} + 1\frac{4}{9} = (2 + 1) + (\frac{3}{9} + \frac{4}{9}) = 3\frac{7}{9}$

б) $3\frac{3}{4} + \frac{4}{5} = 3 + (\frac{15}{20} + \frac{16}{20}) = 3\frac{31}{20} = 4\frac{11}{20}$

54

Вычитание смешанных дробей

367. Вычислите разность:
а) 1−1/5;
б) 1−3/7;
в) 1−7/9;
г) 1−3/10.

Решение:

а) 1− 1/5 = 5/5 − 1/5 = 4/5;
б) 1 − 3/7 = 7/7 − 3/7 = 4/7;
в) 1 − 7/9 = 9/9 − 7/9 = 2/9;
г) 1 − 3/10 = 10/10 − 3/10 = 7/10.

368. Вычислите разность:

Решение:

а) $2-\frac12=1\frac22-\frac12=1\frac12$
б) $4-\frac45=3\frac55-\frac45=3\frac15$
в) $7-\frac47=6\frac77-\frac47=6\frac37$
г) $10-\frac9{11}=9\frac{11}{11}-\frac9{11}=9\frac2{11}$

369. Вычислите разность:

Решение:

а) $6-2\frac13=5\frac33-2\frac13=3\frac23$
б) $8-5\frac12=7\frac22-5\frac12=2\frac12$
в) $4-3\frac34=3\frac44-3\frac34=\frac14$
г) $5-2\frac38=4\frac88-2\frac38=2\frac58$

370. Найдите разность смешанных дробей:

Решение:

а) $3\frac34-1\frac14=2\frac24=2\frac12$
б) $1\frac56-1\frac16=\frac46=\frac23$
в) $4\frac59-3\frac29=1\frac39=1\frac13$
г) $5\frac{11}{12}-1\frac5{12}=4\frac6{12}=4\frac12$

371. Найдите разность смешанных дробей:

Решение:

а) $4\frac29-1\frac16=4\frac4{18}-1\frac3{18}=3\frac1{18}$
б) $7\frac38-7\frac14=7\frac38-7\frac28=\frac18$
в) $8\frac34-1\frac16=8\frac9{12}-1\frac2{12}=7\frac7{12}$
г) $7\frac49-4\frac13=7\frac49-4\frac39=3\frac19$

372. Выполните вычитание:

Решение:

а) $3\frac16-\frac56=2\frac76-\frac56=2\frac26=2\frac13$
б) $2\frac14-\frac34=1\frac54-\frac34=1\frac24=1\frac12$
в) $4\frac38-\frac58=3\frac{11}8-\frac58=3\frac68=3\frac34$
г) $5\frac5{12}-\frac{11}{12}=4\frac{17}{12}-\frac{11}{12}=4\frac6{12}=4\frac12$

373. Выполните вычитание:

Решение:

а) $3\frac17-1\frac57=2\frac87-1\frac57=1\frac37$
б) $4\frac13-3\frac23=3\frac43-3\frac23=\frac23$
в) $6\frac49-3\frac59=5\frac{13}9-3\frac59=2\frac89$
г) $7\frac15-3\frac35=6\frac65-3\frac35=3\frac35$

374. Найдем разность:

$4\frac49-\frac79=(4\frac49-1)+\frac29=3\frac49+\frac29=3\frac69=3\frac23$

Мы заменили вычитаемое числом 1 и, чтобы разность не изменилась, "вернули" 2/9. Воспользовавшись таким же приемом, выполните вычитание:

Решение:

а) $4\frac8{15}-\frac{14}{15}=(4\frac8{15}-1)+\frac1{15}=3\frac8{15}+\frac1{15}=3\frac9{15}=3\frac35$
б) $3\frac7{11}-\frac9{11}=(3\frac7{11}-1)+\frac2{11}=2\frac7{11}+\frac2{11}=2\frac9{11}$
в) $9\frac1{21}-5\frac{20}{21}=4\frac1{21}-\frac{20}{21}=(4\frac1{21}-1)+\frac1{21}=3\frac1{21}+\frac1{21}=3\frac2{21}$
г) $10\frac5{64}-3\frac{61}{64}=7\frac5{64}-\frac{61}{64}=(7\frac5{64}-1)+\frac3{64}=6\frac5{64}+\frac3{64}=6\frac8{64}=6\frac18$

375. Вычислите разность:

Решение:

а) $1\frac1{16}-\frac18=1\frac1{16}-\frac2{16}=(1\frac1{16}-1)+\frac{14}{16}=\frac1{16}+\frac{14}{16}=\frac{15}{16}$
б) $2\frac49-\frac23=2\frac49-\frac69=(2\frac49-1)+\frac39=1\frac49+\frac39=1\frac79$
в) $3\frac1{12}-2\frac34=3\frac1{12}-2\frac9{12}=1\frac1{12}-\frac9{12}=(1\frac1{12}-1)+\frac3{12}=\frac1{12}+\frac3{12}=\frac4{12}=\frac13$
г) $4\frac2{15}-1\frac23=4\frac2{15}-1\frac{10}{15}=3\frac2{15}-\frac{10}{15}=(3\frac2{15}-1)+\frac5{15}=2\frac2{15}+\frac5{15}=2\frac7{15}$

376. Вычислите разность:

Решение:

а) $2\frac16-\frac13=2\frac16-\frac26=(2\frac16-1)+\frac46=1\frac16+\frac46=1\frac56$
б) $3\frac15-1\frac14=2\frac4{20}-\frac5{20}=(2\frac4{20}-1)+\frac{15}{20}=1\frac4{20}+\frac{15}{20}=1\frac{19}{20}$
в) $4\frac23-\frac67=4\frac{14}{21}-\frac{18}{21}=(4\frac{14}{21}-1)+\frac3{21}=3\frac{14}{21}+\frac3{21}=3\frac{17}{21}$
г) $10\frac25-5\frac23=5\frac6{15}-\frac{10}{15}=(5\frac6{15}-1)+\frac5{15}=4\frac6{15}+\frac5{15}=4\frac{11}{15}$

377. Вычислите разность:

Решение:

а) $3\frac14-1\frac56=2\frac3{12}-\frac{10}{12}=(2\frac3{12}-1)+\frac2{12}=1\frac3{12}+\frac2{12}=1\frac5{12}$
б) $1\frac3{20}-\frac7{25}=1\frac{15}{100}-\frac{28}{100}=(1\frac{15}{100}-1)+\frac{72}{100}=\frac{15}{100}+\frac{72}{100}=\frac{87}{100}$
в) $4\frac16-3\frac38=1\frac4{24}-\frac9{24}=(1\frac4{24}-1)+\frac{15}{24}=\frac4{24}+\frac{15}{24}=\frac{19}{24}$
г) $10\frac3{10}-3\frac2{15}=7\frac9{30}-\frac4{30}=7\frac5{30}=7\frac16$

55

378. а) Собственная скорость теплохода равна 20_4/5 км/ч, а скорость течения реки − 1_1/2 км/ч. Найдите скорость теплохода по течению и против течения реки.
б) Скорость лодки по течению реки равна 15_1/2 км/ч, а скорость течения равна 2_3/5 км/ч. Найдите собственную скорость лодки и ее скорость против течения.
в) Скорость катера против течения реки равна 15_2/5 км/ч, а собственная скорость катера равна 19 км/ч. Найдите скорость течения реки и скорость катера по течению реки.

Решение:

а) 1) $20\frac45+1\frac12=20\frac8{10}+1\frac5{10}=21\frac{13}{10}=22\frac3{10}$ (км/ч) − скорость теплохода по течению;
     2) $20\frac45-1\frac12=20\frac8{10}-1\frac5{10}=19\frac3{10}$ (км/ч) − скорость теплохода против течения.
Ответ: $22\frac3{10}$ км/ч; $19\frac3{10}$ км/ч.

б) 1) $15\frac12-2\frac35=12\frac5{10}-\frac6{10}=(13\frac5{10}-1)+\frac4{10}=12\frac5{10}+\frac4{10}=12\frac9{10}$ (км/ч) − собственная скорость лодки;
    2) $12\frac9{10}-2\frac35=12\frac9{10}-2\frac6{10}=10\frac3{10}$ (км/ч) − скорость лодки против течения.
Ответ: $12\frac9{10}$ км/ч; $10\frac3{10}$ км/ч.

в) 1) $19-15\frac25=18\frac55-15\frac25=3\frac35$ (км/ч) − скорость течения;
    2) $19+3\frac35=22\frac35$ (км/ч) − скорость катера по течению.
Ответ: $3\frac35$ км/ч; $22\frac35$ км/ч.

379. Найдите значение выражения:

Решение:

а) $5\frac5{12}-2\frac59=3\frac{15}{36}-\frac{20}{36}=(3\frac{15}{36}-1)+\frac{16}{36}=2\frac{15}{36}+\frac{16}{36}=2\frac{31}{36}$
б) $8\frac14-7\frac5{18}=1\frac9{36}-\frac{10}{36}=(1\frac9{36}-1)+\frac{26}{36}=\frac9{36}+\frac{26}{36}=\frac{35}{36}$
в) $4\frac7{12}-1\frac58=3\frac{14}{24}-\frac{15}{24}=(3\frac{14}{24}-1)+\frac9{24}=2\frac{14}{24}+\frac9{24}=2\frac{23}{24}$
г) $3\frac7{18}-2\frac8{15}=1\frac{35}{90}-\frac{48}{90}=(1\frac{35}{90}-1)+\frac{42}{90}=\frac{35}{90}+\frac{42}{90}=\frac{77}{90}$

380. По какому правилу составлена последовательность чисел? Запишите три следующих числа этой последовательности, найдите сумму всех шести чисел:

а) $6,5\frac13,4\frac23,...$
б) $5\frac25,5,4\frac35,...$

Решение:

а) $6-5\frac13=5\frac33-5\frac13=\frac23$
$5\frac13-4\frac23=1\frac13-\frac23=(1\frac13-1)+\frac13=\frac13+\frac13=\frac23$
Закономерность: каждое последующее число на 2/3 меньше предыдущего.
$4\frac23-\frac23=4$
$4-\frac23=3\frac33-\frac23=3\frac13$
$3\frac13-\frac23=(3\frac13-1)+\frac13=2\frac13+\frac13=2\frac23$
$6,5\frac13,4\frac23,4,3\frac13,2\frac23$
$6+5\frac13+4\frac23+4+3\frac13+2\frac23=(6+4)+(5\frac13+4\frac23)+(3\frac13+2\frac23)=10+10+6=26$
Ответ: 26

б) $5\frac25-5=\frac25$
$5-4\frac35=4\frac55-4\frac35=\frac25$
Закономерность: каждое последующее число на 2/5 меньше предыдущего.
$4\frac35-\frac25=4\frac15$
$4\frac15-\frac25=(4\frac15-1)+\frac35=3\frac15+\frac35=3\frac45$
$3\frac45-\frac25=3\frac25$
$5\frac25,5,4\frac35,4\frac15,3\frac45,3\frac25$
$5\frac25+5+4\frac35+4\frac15+3\frac45+3\frac25=5+(5\frac25+4\frac35)+(4\frac15+3\frac45)+3\frac25=5+10+8+3\frac25=26\frac25$
Ответ: $26\frac25$.

381. а) Туристы шли по равнине 2_1/2 ч, а в гору на 1_1/3 ч меньше. Сколько времени занял этот путь? (Ответ выразите в часах и минутах.)
б) Туристы шли 2_1/4 ч в гору, а под гору на 3/5 ч меньше. По равнине они шли 11/20 ч. Сколько времени занял туристический маршрут?

Решение:

а) 1) $2\frac12-1\frac13=1\frac36-\frac26=1\frac16$ (ч) − туристы шли в гору;
    2) $2\frac12+1\frac16=2\frac36+1\frac16=3\frac46=3\frac23({\operatorname ч})=3\frac{40}{60}$ (ч) = 3 ч 40 мин − занял весь путь.
Ответ: 3 ч 40 мин.

б) 1) $2\frac14-\frac35=2\frac5{20}-\frac{12}{20}=(2\frac5{20}-1)+\frac8{20}=1\frac5{20}+\frac8{20}=1\frac{13}{20}$ (ч) − времени шли туристы под гору;
    2) $2\frac14+1\frac{13}{20}+\frac{11}{20}=2\frac5{20}+1\frac{13}{20}+\frac{11}{20}=3\frac{29}{20}=4\frac9{20}({\operatorname ч})=4\frac{27}{60}$ (ч) = 4 ч 27 мин − занял туристический маршрут.
Ответ: 4 ч 27 мин.

Самостоятельная работа № 19

Вариант 1

1. Найдите разность:

Решение:

а) $10-4\frac5{12}=9\frac{12}{12}-4\frac5{12}=5\frac7{12}$
б) $2\frac56-\frac13=2\frac56-\frac26=2\frac36=2\frac12$
в) $6\frac15-2=4\frac15$
г) $3\frac27-2\frac47=1\frac27-\frac47=(1\frac27-1)+\frac37=\frac27+\frac37=\frac57$

2. Вычислите:

Решение:

$3+\frac12-\frac45=3+\frac5{10}-\frac8{10}=3\frac5{10}-\frac8{10}=(3\frac5{10}-1)+\frac2{10}=2\frac5{10}+\frac2{10}=2\frac7{10}$

Вариант 2

1. Найдите разность:

Решение:

а) $10-6\frac38=9\frac88-6\frac38=3\frac58$
б) $3\frac79-\frac23=3\frac79-\frac69=3\frac19$
в) $5\frac14-3=2\frac14$
г) $3\frac25-1\frac45=2\frac25-\frac45=(2\frac25-1)+\frac15=1\frac25+\frac15=1\frac35$

2. Вычислите:

Решение:

$2+\frac13-\frac34=2\frac13-\frac34=2\frac4{12}-\frac9{12}=(2\frac4{12}-1)+\frac3{12}=1\frac4{12}+\frac3{12}=1\frac7{12}$

56

Умножение дробей

382. Выполните умножение:

Решение:

а) $\frac38\ast\frac12=\frac3{16}$
б) $\frac13\ast\frac25=\frac2{15}$
в) $\frac35\ast\frac17=\frac3{35}$
г) $\frac3{11}\ast\frac14=\frac3{44}$

383. Выполните умножение:

Решение:

а) $\frac56\ast\frac47=\frac53\ast\frac27=\frac{10}{21}$
б) $\frac37\ast\frac23=\frac17\ast\frac21=\frac27$
в) $\frac79\ast\frac35=\frac73\ast\frac15=\frac7{15}$
г) $\frac78\ast\frac{12}{17}=\frac72\ast\frac3{17}=\frac{21}{34}$

384. Вычислите степень:

Решение:

а) $(\frac17)^2=\frac17\ast\frac17=\frac1{49}$
б) $(\frac35)^2=\frac35\ast\frac35=\frac9{25}$
в) $(\frac1{10})^3=\frac1{10}\ast\frac1{10}\ast\frac1{10}=\frac1{1000}$
г) $(\frac25)^3=\frac25\ast\frac25\ast\frac25=\frac8{125}$
д) $(1\frac13)^2=(\frac43)^2=\frac43\ast\frac43=\frac{16}9=1\frac79$
е) $(1\frac12)^3=(\frac32)^3=\frac32\ast\frac32\ast\frac32=\frac{27}8=3\frac38$

385. Вычислите произведение:

Решение:

а) $\frac{44}{45}\ast\frac35\ast\frac{10}{11}=\frac4{15}\ast\frac11\ast\frac21=\frac8{15}$
б) $\frac{30}{77}\ast\frac{11}{18}\ast\frac3{25}=\frac17\ast\frac11\ast\frac15=\frac1{35}$
в) $\frac{20}{13}\ast\frac{39}{100}\ast\frac{10}{21}=\frac11\ast\frac11\ast\frac27=\frac27$

386. Выполните умножение:

Решение:

а) $\frac23\ast6=2\ast2=4$
б) $16\ast\frac18=2\ast1=2$
в) $30\ast\frac56=5\ast5=25$
г) $\frac35\ast15=3\ast3=9$
д) $\frac17\ast7=1\ast1=1$
е) $25\ast\frac15=5\ast1=5$

387. Выполните умножение:

Решение:

а) $3\frac15\ast3=\frac{16}5\ast3=\frac{48}5=9\frac35$
б) $5\ast2\frac17=5\ast\frac{15}7=\frac{75}7=10\frac57$
в) $3\frac13\ast6=\frac{10}3\ast6=10\ast2=20$
г) $8\ast1\frac14=8\ast\frac54=2\ast5=10$

388. Выполните умножение:

Решение:

а) $1\frac12\ast\frac29=\frac32\ast\frac29=\frac11\ast\frac13=\frac13$
б) $1\frac13\ast2\frac14=\frac43\ast\frac94=\frac11\ast\frac31=3$
в) $\frac78\ast5\frac13=\frac78\ast\frac{16}3=\frac71\ast\frac23=\frac{14}3=4\frac23$
г) $2\frac12\ast\frac35=\frac52\ast\frac35=\frac12\ast\frac31=\frac32=1\frac12$

389. При умножении смешанной дроби на натуральное число можно пользоваться распределительным свойством. Например:

$4\frac38\ast2=4\ast2+\frac38\ast2=8+\frac34=8\frac34$

Пользуясь этим приемом, найдите произведение:

Решение:

а) $3\frac58\ast2=3\ast2+\frac58\ast2=6+\frac54=6+1\frac14=7\frac14$
б) $15\frac78\ast4=15\ast4+\frac78\ast4=60+\frac72=60+3\frac12=63\frac12$
в) $10\frac23\ast9=10\ast9+\frac23\ast9=90+2\ast3=90+6=96$
г) $12\frac{11}{15}\ast5=12\ast5+\frac{11}{15}\ast5=60+\frac{11}3=60+3\frac23=63\frac23$
д) $11\frac35\ast10=11\ast10+\frac35\ast10=110+3\ast2=110+6=116$

390. Скорость велосипедиста 12 км/ч. Какое расстояние он проедет за 3 ч? за 3/4 ч? за 1_1/2 ч?

Решение:

1) 12 * 3 = 36 (км) − проедет велосипедист за 3 ч;
2) $12\ast\frac34=3\ast3=9$ (км) − проедет велосипедист за 3/4 ч;
3) 12\ast1\frac12=12\ast\frac32=6\ast3=18$$ (км) − проедет велосипедист за 1_1/2 ч.
Ответ: 36 км; 9 км; 18 км.

391. В одном часе 60 мин. Сколько минут составляет:
а) 1_1/3 ч;
б) 2_5/12 ч;
в) 3_3/4 ч;
г) 1_5/6 ч?

Решение:

а) $1\frac13\ast60=1\ast60+\frac13\ast60=60+20=80$ (мин) − составляет $1\frac13$ ч.
Ответ: 80 минут

б) $2\frac5{12}\ast60=2\ast60+\frac5{12}\ast60=120+5\ast5=120+25=145$ (мин) − составляет $2\frac5{12}$ ч.
Ответ: 145 минут

в) $3\frac34\ast60=3\ast60+\frac34\ast60=180+3\ast15=180+45=225$ (мин) − составляет $3\frac34$ ч.
Ответ: 225 минут

г) $1\frac56\ast60=1\ast60+\frac56\ast60=60+5\ast10=60+50=110$ (мин) − составляет $1\frac56$ ч.
Ответ: 110 мин

57

392. В одном километре 1000 м. Сколько метров содержится:
а) в 5_1/20 км;
б) в 3_7/10 км;
в) в 4_3/5 км;
г) в 1_3/4 км?

Решение:

а) $5\frac1{20}\ast1000=5\ast1000+\frac1{20}\ast1000=5000+50=5050$ (м) − содержится в $5\frac1{20}$ км.
Ответ: 5050 метров.

б) $3\frac7{10}\ast1000=3\ast1000+\frac7{10}\ast1000=3000+7\ast100=3000+700=3700$ (м) − содержится в $3\frac7{10}$ км.
Ответ: 3700 метров

в) $4\frac35\ast1000=4\ast1000+\frac35\ast1000=4000+3\ast200=4000+600=4600$ (м) − содержится в $4\frac35$ км.
Ответ: 4600 метров.

г) $1\frac34\ast1000=1\ast1000+\frac34\ast1000=1000+3\ast250=1000+750=1750$ (м) − содержится в $1\frac34$ км.
Ответ: 1750 метров.

393. а) Сколько часов длятся 5 уроков, если один урок длится 3/4 ч?
б) В сутках 24 ч. Поход продолжался 3_2/3 суток. Сколько это часов?

Решение:

а) $\frac34\ast5=\frac{15}4=3\frac34$ (ч) − длятся 5 уроков.
Ответ: $3\frac34$ ч.

б) $3\frac23\ast24=\frac{11}3\ast24=11\ast8=88$ (ч) − продолжался поход.
Ответ: 88 часов.

394. В сумку положили 1/2 кг сахара, а крупы − в полтора раза больше. Чему равна масса сахара и крупы вместе?

Решение:

1) $\frac12\ast1\frac12=\frac12\ast\frac32=\frac34$ (кг) − крупы положили в сумку;
2) $\frac12+\frac34=\frac24+\frac34=\frac54=1\frac14$ (кг) − масса сахара и крупы вместе.
Ответ: $1\frac14$ кг.

395. а) Спортивная площадка прямоугольной формы имеет размеры 10_1/2 м и 16 м. Чему равна площадь спортплощадки?
б) Чему равна площадь комнаты, размеры которой 5_1/2 м и 3_1/2 м?

Решение:

а) $16\ast10\frac12=16\ast10+16\ast\frac12=160+8=168({\operatorname м}^2)$ − площадь спортплощадки.
Ответ: 168 $м^2$.

б) $5\frac12\ast3\frac12=\frac{11}2\ast\frac72=\frac{77}4=19\frac14({\operatorname м}^2)$ − площадь комнаты.
Ответ: $19\frac14({\operatorname м}^2$.

396. В числовой последовательности первое число равно 2/3, а каждое следующее в полтора раза больше предыдущего. Запишите первые пять чисел этой последовательности. Найдите их сумму.

Решение:

$\frac23$ − первое число;
$1\frac12=\frac32$ − полтора.
$\frac23\ast\frac32=1$ − второе число;
$1\ast\frac32=\frac32=1\frac12$ − третье число;
$\frac32\ast\frac32=\frac94=2\frac14$ − четвертое число;
$\frac94\ast\frac32=\frac{27}8=3\frac38$ − пятое число;
$\frac23+1+1\frac12+2\frac14+3\frac38=\frac{16}{24}+1+1\frac{12}{24}+2\frac6{24}+3\frac9{24}=7\frac{43}{24}=8\frac{19}{24}$ − сумма пяти чисел.
Ответ: $8\frac{19}{24}$

397. Не выполняя вычислений, сравните значения выражений:

Решение:

а) $(\frac34)^2<1$
б) $1<(\frac87)^3$
в) $\frac37>(\frac37)^2$
г) $(\frac58)^3<(\frac58)^2$

398. Расположите в порядке возрастания:

Решение:

а) $(\frac12)^3<(\frac12)^2<\frac12$
б) $(\frac25)^3<(\frac25)^2<\frac25$
в) $\frac23<\frac32<(\frac32)^2$
г) $(\frac45)^2<\frac45<\frac54$

399. а) Веревку длиной 18 м надо разрезать на два куска так, чтобы один из них оказался в 3 раза больше другого. Сколько метров в каждом куске?
б) В двух ящиках 58 кг моркови, причем в одном из них моркови в 4 раза меньше, чем в другом. Сколько моркови в каждом ящике?

Решение:

а) Пусть меньший кусок составляет 1 часть, тогда:
1) 1 * 3 = 3 (части) − составляет второй кусок;
2) 1 + 3 = 4 (части) − всего;
3) $18:4=\frac{18}4=\frac92=4\frac12$ (м) − длина меньшего куска;
4) $4\frac12\ast3=4\ast3+\frac12\ast3=12\frac32=13\frac12$ (м) − длина большего куска.
Ответ: $4\frac12$ м, $13\frac12$ м.

б) Пусть морковь в одном ящике составляет 1 часть, тогда:
1) 1 * 4 = 4 (части) − составляет морковь в другом ящике;
2) 1 + 4 = 5 (частей) − всего;
3) $58:5=\frac{58}5=11\frac35$ (кг) − моркови в одном ящике;
4) $11\frac35\ast4=11\ast4+\frac35\ast4=44+\frac{12}5=44+2\frac25=46\frac25$ (кг) − моркови в другом ящике.
Ответ: $11\frac35$ кг, $46\frac25$ кг.

400. Больше или меньше 1 м² площадь:
а) квадрата со стороной 90 см;
б) квадрата со стороной 1_1/10 м;
в) прямоугольника со сторонами 1 м и 3/4 м;
г) прямоугольника со сторонами 2 м и 1/2 м?

Решение:

а) 1 м² = 10000 см²
1) 90 * 90 = 8100 см² − площадь квадрата;
2) 8100 < 10000 − площадь квадрата меньше 1 м².
Ответ: меньше.

б) 1) $1\frac1{10}\ast1\frac1{10}=\frac{11}{10}\ast\frac{11}{10}=\frac{121}{100}=1\frac{21}{100}({\operatorname м}^2)$ − площадь квадрата;
2) $1\frac{21}{100}>1$ − площадь квадрата больше 1 м².
Ответ: больше.

в) 1) $1\ast\frac34=\frac34({\operatorname м}^2)$ − площадь прямоугольника;
2) $\frac34<1$ − площадь прямоугольника меньше 1 м².
Ответ: меньше.

г) 1) $2\ast\frac12=1({\operatorname м}^2)$ − площадь прямоугольника;
2) 1 = 1 площадь прямоугольника равна 1 м².
Ответ: равна.

58

401. Имеются два листа фанеры, один имеет форму квадрата со стороной 1 м, другой − форму прямоугольника со сторонами 1_1/2 м и 3/4 м. Площадь какого листа больше?

Решение:

1) 1 * 1 = 1 (м^2) − площадь квадрата;
2) $1\frac12\ast\frac34=\frac32\ast\frac34=\frac98=1\frac18{\operatorname м}^2$ − площадь прямоугольника;
3) $1\frac18>1$ − площадь прямоугольного листа больше, чем площадь квадратного.
Ответ: площадь прямоугольного листа больше.

402. Пол комнаты прямоугольной формы покрасили краской 2 раза. В первый раз на каждый квадратный метр пошло 1/8 кг краски, а во второй − 3/40 кг. Сколько израсходовали краски, если длина пола 5 м, а ширина 4_1/2 м?

Решение:

1) $5\ast4\frac12=5\ast4+5\ast\frac12=20\frac52=22\frac12({\operatorname м}^2)$ − площадь пола;
2) $22\frac12\ast\frac18=\frac{45}2\ast\frac18=\frac{45}{16}=2\frac{13}{16}$ (кг) − краски израсходовали в первый раз;
3) $22\frac12\ast\frac3{40}=\frac{45}2\ast\frac3{40}=\frac92\ast\frac38=\frac{27}{16}=1\frac{11}{16}$ (кг) − краски израсходовали во второй раз;
4) $2\frac{13}{16}+1\frac{11}{16}=3\frac{24}{16}=3\frac32=4\frac12$ (кг) − краски израсходовали всего.
Ответ: $4\frac12$ кг.

403. Дно контейнера имеет форму прямоугольника, одна сторона которого равна 1_1/5 м, а другая на 1_-11/20 м длиннее. Найдите периметр дна контейнера и его площадь.

Решение:

1) $1\frac15+1\frac{11}{20}=1\frac4{20}+1\frac{11}{20}=2\frac{15}{20}=2\frac34$ (м) − длина другой стороны;
2) $(1\frac15+2\frac34)\ast2=(1\frac4{20}+2\frac{15}{20})\ast2=3\frac{19}{20}\ast2=3\ast2+\frac{19}{20}\ast2=6+\frac{19}{10}=6+1\frac9{10}=7\frac9{10}$ (м) − периметр дна контейнера;
3) $1\frac15\ast2\frac34=\frac65\ast\frac{11}4=\frac35\ast\frac{11}2=\frac{33}{10}=3\frac3{10}({\operatorname м}^2)$ − площадь дна контейнера.
Ответ: $7\frac9{10}$ м, $3\frac3{10}{\operatorname м}^2$.

404. Детская площадка имеет форму квадрата со стороной 6_3/4 м. Маша пробежала вокруг площадки 2 раза, вернувшись в исходную точку. Больше или меньше 50 м пробежала Маша?

Решение:

1) $6\frac34\ast4=6\ast4+\frac34\ast4=24+3=27$ (м) − периметр площадки;
2) 27 * 2 = 54 (м) − пробежала Маша;
3) 54 > 50 − больше 50 м пробежала Маша.
Ответ: больше 50 м.

405. Каждый рисунок (рис.10,а−б) задает некоторую задачу. Выясните, что известно, и найдите неизвестные величины.

Решение:

а)
1) $S=BC\ast CD=3\frac12\ast2\frac15=\frac72\ast\frac{11}5=\frac{77}{10}=7\frac7{10}({\operatorname м}^2)$ − площадь прямоугольника ABCD;
2) $P=(BC+CD)\ast2=(3\frac12+2\frac15)\ast2=(3\frac5{10}+2\frac2{10})\ast2=5\frac7{10}\ast2=5\ast2+\frac7{10}\ast2=10+\frac75=10+1\frac25=11\frac25$ (м) − периметр прямоугольника ABCD.
Ответ:
$S=7\frac7{10}{\operatorname м}^2$,
$P=11\frac25$

б)
1) $\frac P2=20:2=10$ (м) − полупериметр прямоугольника ABCD;
2) $AB=\frac P2-BC=10-6\frac12=9\frac22-6\frac12=3\frac12$ (м);
3) $S=AB\ast BC=3\frac12\ast6\frac12=\frac72\ast\frac{13}2=\frac{91}4=22\frac34({\operatorname м}^2)$ − площадь прямоугольника ABCD.
Ответ: $S=22\frac34{\operatorname м}^2$.

Самостоятельная работа № 20

Вариант 1

1. Найдите произведение:

Решение:

а) $\frac59\ast\frac3{20}=\frac13\ast\frac14=\frac1{12}$
б) $15\ast\frac{16}{25}=3\ast\frac{16}5=\frac{48}5=9\frac35$
в) $1\frac12\ast3=1\ast3+\frac12\ast3=3+\frac32=3+1\frac12=4\frac12$

2. Вычислите квадрат числа 3/5.

Решение:

$(\frac35)^2=\frac35\ast\frac35=\frac9{25}$

Вариант 2

1. Найдите произведение:

Решение:

а) $\frac7{12}\ast\frac8{21}=\frac13\ast\frac23=\frac29$
б) $18\ast\frac29=2\ast2=4$
в) $1\frac14\ast5=1\ast5+\frac14\ast5=5+\frac54=5+1\frac14=6\frac14$

2. Вычислите квадрат числа 5/6.

$(\frac56)^2=\frac56\ast\frac56=\frac{25}{36}$

59

Деление дробей

406. Запишите число, обратное данному:
а) 4/9;
б) 5/58;
в) 1/4;
г) 35;
д) 3_1/3;
е) 10_1/4.

Решение:

а) $\frac94=2\frac14$
б) $\frac{58}5=11\frac35$
в) $\frac41=4$
г) $\frac1{35}$
д) $3\frac13=\frac{10}3$
$\frac3{10}$
е) $10\frac14=\frac{41}4$
$\frac4{41}$

407. Выполните деление:

Решение:

а) $\frac23:\frac79=\frac23\ast\frac97=\frac21\ast\frac37=\frac67$
б) $\frac14:\frac16=\frac14\ast\frac61=\frac12\ast\frac31=\frac32=1\frac12$
в) $\frac49:\frac23=\frac49\ast\frac32=\frac23\ast\frac11=\frac23$
г) $\frac58:\frac12=\frac58\ast\frac21=\frac54\ast\frac11=1\frac14$

408. Выполните деление:

Решение:

а) $3:\frac35=3\ast\frac53=5$
б) $16:\frac23=16\ast\frac32=8\ast3=24$
в) $5:\frac14=5\ast4=20$
г) $1:\frac29=1\ast\frac92=4\frac12$

409. Выполните деление:

Решение:

а) $\frac37:21=\frac37\ast\frac1{21}=\frac17\ast\frac17=\frac1{49}$
б) $\frac59:45=\frac59\ast\frac1{45}=\frac19\ast\frac19=\frac1{81}$
в) $\frac{10}{21}:15=\frac{10}{21}\ast\frac1{15}=\frac2{21}\ast\frac13=\frac2{63}$
г) $\frac3{10}:30=\frac3{10}\ast\frac1{30}=\frac1{10}\ast\frac1{10}=\frac1{100}$

410. Выполните деление:

Решение:

а) $1\frac57:3\frac34=\frac{12}7:\frac{15}4=\frac{12}7\ast\frac4{15}=\frac47\ast\frac45=\frac{16}{35}$

б) $5\frac12:2\frac15=\frac{11}2:\frac{11}5=\frac{11}2\ast\frac5{11}=\frac12\ast\frac51=\frac52=2\frac12$

в) $4\frac12:3\frac34=\frac92:\frac{15}4=\frac92\ast\frac4{15}=\frac31\ast\frac25=\frac65=1\frac15$

г) $2\frac35:2\frac4{11}=\frac{13}5:\frac{26}{11}=\frac{13}5\ast\frac{11}{26}=\frac15\ast\frac{11}2=\frac{11}{10}=1\frac1{10}$

411. Заполните таблицу:

Решение:

а)
1) $bc=\frac38\ast\frac32=\frac9{16}$
2) $c=bc:b=\frac9{21}:\frac34=\frac37\ast\frac43=\frac17\ast\frac41=\frac47$
3) $b=bc:c=\frac{16}{21}:\frac23=\frac{16}{21}\ast\frac32=\frac87\ast\frac11=1\frac17$

б)
1) $b:c=\frac56:\frac49=\frac56\ast\frac94=\frac52\ast\frac34=\frac{15}8=1\frac78$
2) $c=b:(b:c)=\frac7{10}:\frac12=\frac7{10}\ast\frac21=\frac75\ast\frac11=1\frac25$
3) $b=(b:c)\ast c=\frac25\ast\frac54=\frac11\ast\frac12=\frac12$

412. а) Проволоку длиной 7_1/2 м разрезали на куски по 3/4 м. Сколько получилось кусков?
б) Расфасовали 54 кг винограда в упаковки по 1_1/2 кг в каждую. Сколько получилось таких упаковок?

Решение:

а) $7\frac12:\frac34=\frac{15}2\ast\frac43=5\ast2=10$ (к.) − получилось.
Ответ: 10 кусков.

б) $54:1\frac12=54:\frac32=54\ast\frac23=18\ast2=36$ (уп.) − получилось.
Ответ: 36 упаковок.

413. а) В чайнике 1_1/2 л воды. Один стакан вмещает 1/5 л воды. Сколько стаканов можно наполнить водой из чайника?
б) Для перевязки одной посылки требуется 2_1/2 м веревки. Сколько таких посылок можно перевязать, используя клубок, в котором 17 м веревки?

Решение:

а) $1\frac12:\frac15=\frac32\ast\frac51=\frac{15}2=7\frac12$ (ст.) − значит можно наполнить 7 стаканов.
Ответ: 7 стаканов.

б) $17:2\frac12=17:\frac52=17\ast\frac25=\frac{34}5=6\frac45$ (п.) − значит можно перевязать 6 посылок.
Ответ: 6 посылок.

60

414. а) Мама сварила 2 кг варенья и хочет разложить его в банки. У нее есть одинаковые банки, каждая из которых вмещает 3/5 кг варенья. Сколько таких банок ей потребуется?
б) В одну банку помещается 3/10 кг оливкового масла. Сколько понадобится банок, чтобы разлить 4 кг масла?

Решение:

а) $2:\frac35=2\ast\frac53=\frac{10}3=3\frac13$ (банки) − значит потребуется 4 банки, чтобы разложить все варенье.
Ответ: 4 банки.

б) $4:\frac3{10}=4\ast\frac{10}3=\frac{40}3=13\frac13$ (банок) − значит понадобится 14 банок, чтобы разлить 4 кг масла.
Ответ: 14 банок.

415. а) Скорость лодки 8_3/4 км/ч. За какое время она пройдет 7 км?
б) За 2/3 ч катер прошел 15_2/5 км. Найдите скорость катера.

Решение:

а) $7:8\frac34=7:\frac{35}4=7\ast\frac4{35}=\frac45({\operatorname ч})=\frac{48}{60}({\operatorname ч})$ = 48 (мин) − будет проходить лодка 7 км.
Ответ: 48 минут

б) $15\frac25:\frac23=\frac{77}5\ast\frac32=\frac{231}{10}=23\frac1{10}$ (км/ч) − скорость катера.
Ответ: $23\frac1{10}$ км/ч.

416. В числовой последовательности первое число равно 54, а каждое следующее в полтора раза меньше предыдущего. Запишите первые пять чисел этой последовательности. Найдите их сумму.

Решение:

54 − первое число;
$1\frac12=\frac32$ − полтора.
$54:\frac32=54\ast\frac23=18\ast2=36$ − второе число;
$36:\frac32=36\ast\frac23=12\ast2=24$ − третье число;
$24:\frac32=24\ast\frac23=8\ast2=16$ − четвертое число;
$16:\frac32=16\ast\frac23=\frac{32}3=10\frac23$ − пятое число;
$54+36+24+16+10\frac23=130+10\frac23=140\frac23$ − сумма.
Ответ: $140\frac23$.

417. а) За 1_1/5 ч поезд прошел 100 км. За какое время он проедет 180 км?
б) За 1_1/2 ч теплоход прошел 42 км. За какое время он пройдет 70 км?

Решение:

а)
1) $100:1\frac15=100:\frac65=100\ast\frac56=50\ast\frac53=\frac{250}3=83\frac13$ (км/ч) − скорость поезда;
2) $180:\frac{250}3=180\ast\frac3{250}=18\ast\frac3{25}=\frac{54}{25}=2\frac4{25}$ (ч) − проедет поезд 180 км.
Ответ: $2\frac4{25}$.

б)
1) $42:1\frac12=42:\frac32=42\ast\frac23=14\ast2=28$ (км/ч) − скорость теплохода;
2) $70:28=\frac{70}{28}=\frac52=2\frac12$ (ч) − пройдет теплоход 70 км.
Ответ: $2\frac12$.

418. а) На верхней книжной полке 27 книг. На средней полке книг в полтора раза меньше, чем на верхней, а на нижней в 2 раза больше, чем на средней. Сколько книг на трех книжных полках вместе?
б) В магазин для продажи поступили календари. Календарей с изображением цветов было 50 штук, с изображением моря − в 2_1/2 раза меньше, а с изображением натюрмортов − в полтора раза больше, чем с изображением моря. Сколько всего календарей поступило в продажу?

Решение:

а)
1) $27:1\frac12=27:\frac32=27\ast\frac23=9\ast2=18$ (к.) − на средней полке;
2) 18 * 2 = 36 (к.) − на нижней полке;
3) 27 + 18 + 36 = 45 + 36 = 81 (к.) − на трех книжных полках вместе.
Ответ: 81 книга.

б)
1) $50:2\frac12=50:\frac52=50\ast\frac25=10\ast2=20$ (к.) − было с изображением моря;
2) $20\ast1\frac12=20\ast\frac32=10\ast3=30$ (к.) − было с изображением натюрмортов;
3) 50 + 20 + 30 = 100 (к.) − всего поступило в продажу.
Ответ: 100 календарей.

419. а) Для наполнения 5 одинаковых сосудов требуется 3_3/4 мин. Сколько времени потребуется для наполнения 8 таких же сосудов?
б) Для изготовления 15 одинаковых коробок требуется 22_1/2 мин. Сколько времени потребуется для изготовления 8 таких же коробок?

Решение:

а)
1) $3\frac34:5=\frac{15}4\ast\frac15=\frac34$ (мин) − требуется для наполнения одного сосуда;
2) $\frac34\ast8=3\ast2=6$ (мин) − требуется для наполнения 8 сосудов.
Ответ: 6 минут.

б)
1) $22\frac12:15=\frac{45}2\ast\frac1{15}=\frac32=1\frac12$ (мин) − требуется дли изготовления одной коробки;
2) $\frac32\ast8=3\ast4=12$ (мин) − потребуется для изготовления 8 коробок.
Ответ: 12 минут.

420. На рисунке 11 изображен отрезок AB. Точка C делит отрезок AB, длина которого 10 дм на две части. Найдите длину каждой части, если длина одной из них на 2_1/2 дм больше другой.
А_____________С____________________________В

Решение:

1) $10-2\frac12=9\frac22-2\frac12=7\frac12$ (дм) − была бы длина отрезка AB, если бы AC было равно BC;
2) $7\frac12:2=\frac{15}2\ast\frac12=\frac{15}4=3\frac34$ (дм) − длина отрезка AC;
3) $3\frac34+2\frac12=3\frac34+2\frac24=5\frac54=6\frac14$ (дм) − длина отрезка CB.
Ответ: $3\frac34$, $6\frac14$.

61

Самостоятельная работа № 21

Вариант 1

1. Найдите частное:

Решение:

а) $\frac78:\frac7{36}=\frac78\ast\frac{36}7=\frac11\ast\frac41=4$
б) $20:\frac45=20\ast\frac54=5\ast5=25$
в) $\frac6{11}:9=\frac6{11}\ast\frac19=\frac2{11}\ast\frac13=\frac2{33}$

2. Вычислите:

Решение:

$\frac23\ast\frac16:\frac34=\frac23\ast\frac16\ast\frac43=\frac13\ast\frac13\ast\frac43=\frac4{27}$

3. Автомобиль проехал 50 км за 2/3 ч. С какой скоростью ехал автомобиль?

Решение:

$50:\frac23=50\ast\frac32=25\ast3=75$ (км/ч) − скорость автомобиля.
Ответ: 75 км/ч.

Вариант 2

1. Найдите частное:

Решение:

а) $\frac{16}{25}:\frac{12}{35}=\frac{16}{25}\ast\frac{35}{12}=\frac45\ast\frac73=\frac{28}{15}=1\frac{13}{15}$

б) $18:\frac35=18\ast\frac53=6\ast5=30$

в) $\frac47:12=\frac47\ast\frac1{12}=\frac17\ast\frac13=\frac1{21}$

2. Вычислите:

Решение:

$\frac25\ast\frac14:\frac3{10}=\frac25\ast\frac14\ast\frac{10}3=\frac11\ast\frac11\ast\frac13=\frac13$

3. Автобус проехал 30 км за 3/4 ч. С какой скоростью ехал автобус?

Решение:

$30:\frac34=30\ast\frac43=10\ast4=40$ (км/ч) − скорость автобуса.
Ответ: 40 км/ч.

Разные действия с дробями

421. Найдите значение выражения:

Решение:

а) $2\frac56-(1\frac59+\frac14)=2\frac{30}{36}-(1\frac{20}{36}+\frac9{36})=2\frac{30}{36}-1\frac{29}{36}=1\frac1{36}$

б) $\frac7{20}-(3\frac58-3\frac25)=\frac{14}{40}-(3\frac{25}{40}-3\frac{16}{40})=\frac{14}{40}-\frac9{40}=\frac5{40}=\frac18$

в) $\frac34-(\frac4{25}+\frac7{20})=\frac{75}{100}-(\frac{16}{100}+\frac{35}{100})=\frac{75}{100}-\frac{51}{100}=\frac{24}{100}=\frac6{25}$

422. Найдите значение выражения:

Решение:

а) $\frac12-\frac4{45}+\frac{13}{15}=\frac{45}{90}-\frac8{90}+\frac{78}{90}=\frac{37}{90}+\frac{78}{90}=\frac{115}{90}=\frac{23}{18}=1\frac5{18}$

б) $\frac{14}{15}+\frac{11}{12}-1\frac7{10}=\frac{56}{60}+\frac{55}{60}-1\frac{42}{60}=\frac{111}{60}-1\frac{42}{60}=1\frac{51}{60}-1\frac{42}{60}=\frac9{60}=\frac3{20}$

в) $3\frac7{20}-2\frac27+\frac3{28}=3\frac{49}{140}-2\frac{40}{140}+\frac{15}{140}=1\frac9{140}+\frac{15}{140}=1\frac{24}{140}=1\frac6{35}$

423. Найдите значение выражения:

Решение:

а) $\frac12-\frac4{45}+4=\frac{45}{90}-\frac8{90}+4=\frac{37}{90}+4=4\frac{37}{90}$

б) $5+\frac14-\frac56=5+\frac3{12}-\frac{10}{12}=5\frac3{12}-\frac{10}{12}=(5\frac3{12}-1)+\frac2{12}=4\frac3{12}+\frac2{12}=4\frac5{12}$

в) $3\frac59-2-\frac56=1\frac{10}{18}-\frac{15}{18}=(1\frac{10}{18}-1)+\frac3{18}=\frac{10}{18}+\frac3{18}=\frac{13}{18}$

424. Найдите значение выражения:

Решение:

а) $(\frac45-\frac{11}{15})\ast\frac5{11}=(\frac{12}{15}-\frac{11}{15})\ast\frac5{11}=\frac1{15}\ast\frac5{11}=\frac13\ast\frac1{11}=\frac1{33}$

б) $\frac7{88}\ast(\frac8{21}+\frac87)=\frac7{88}\ast(\frac8{21}+\frac{24}{21})=\frac7{88}\ast\frac{32}{21}=\frac1{11}\ast\frac43=\frac4{33}$

в) $(\frac14+\frac7{12})\ast\frac37=(\frac3{12}+\frac7{12})\ast\frac37=\frac{10}{12}\ast\frac37=\frac56\ast\frac37=\frac52\ast\frac17=\frac5{14}$

425. Найдите значение выражения:

Решение:

а) $1\frac1{45}:(\frac8{25}+\frac35)=\frac{46}{45}:(\frac8{25}+\frac{15}{25})=\frac{46}{45}:\frac{23}{25}=\frac{46}{45}\ast\frac{25}{23}=\frac29\ast\frac51=\frac{10}9=1\frac19$

б) $(1\frac12-\frac38):7=(1\frac48-\frac38):7=1\frac18\ast\frac17=\frac98\ast\frac17=\frac9{56}$

в) $(1\frac17+\frac5{14}):\frac5{28}=(1\frac2{14}+\frac5{14})\ast\frac{28}5=1\frac7{14}\ast\frac{28}5=\frac{21}{14}\ast\frac{28}5=\frac{21}1\ast\frac25=\frac{42}5=8\frac25$

426. Найдите значение выражения:

Решение:

а) $\frac14+\frac38\ast1\frac23=\frac14+\frac38\ast\frac53=\frac14+\frac18\ast\frac51=\frac28+\frac58=\frac78$

б) $1\frac16\ast\frac3{14}-\frac1{10}=\frac76\ast\frac3{14}-\frac1{10}=\frac12\ast\frac12-\frac1{10}=\frac14-\frac1{10}=\frac5{20}-\frac2{20}=\frac3{20}$

в) $\frac3{20}+\frac15:\frac16=\frac3{20}+\frac15\ast\frac61=\frac3{20}+\frac65=\frac3{20}+1\frac15=\frac3{20}+1\frac4{20}=1\frac7{20}$

427. Найдите значение выражения:

Решение:

а) $12-3\frac35:\frac{24}{25}=12-\frac{18}5\ast\frac{25}{24}=12-\frac31\ast\frac54=12-\frac{15}4=11\frac44-3\frac34=8\frac14$
б) $3\frac16\ast1\frac12-4=\frac{19}6\ast\frac32-4=\frac{19}2\ast\frac12-4=\frac{19}4-4=4\frac34-4=\frac34$
в) $5\frac23-3:1\frac45=5\frac23-3:\frac95=5\frac23-3\ast\frac59=5\frac23-1\ast\frac53=5\frac23-1\frac23=4$

428. Запишите числовое выражение и найдите его значение:
а) произведение суммы и разности дробей 1_1/2 и 3/4;
б) сумма произведения и частного дробей 1_1/2 и 3/4.

Решение:

а) $(1\frac12+\frac34)\ast(1\frac12-\frac34)=(1\frac24+\frac34)\ast(\frac32-\frac34)=1\frac54\ast(\frac64-\frac34)=\frac94\ast\frac34=\frac{27}{16}=1\frac{11}{16}$

б) $1\frac12\ast\frac34+1\frac12:\frac34=\frac32\ast\frac34+\frac32\ast\frac43=\frac98+\frac11\ast\frac21=1\frac18+2=3\frac18$

62

Для ответа на вопрос задачи составьте выражение и вычислите его значение (№429-431)

429. Длина ломаной равна 8 м (рис.12). Длина отрезка CD равна 2_1/5 м. Чему равна длина отрезка AB?

Решение:

$(8-2\frac15):2=(97\frac55-2\frac15):2=5\frac45:2=\frac{29}5\ast\frac12=\frac{29}{10}=2\frac9{10}$ (м) − длина отрезка AB.
Ответ: $2\frac9{10}$ м.

430. У Пети 6 красных палочек длиной 4_2/5 см и 10 синих длиной 5_1/2 см. Он сложил из них ломаную. Какова ее длина?

Решение:

$6\ast4\frac25+10\ast5\frac12=(6\ast4+6\ast\frac25)+10\ast\frac{11}2=(24+\frac{12}5)+5\ast11=(24+2\frac25)+55=26\frac25+55=81\frac25$(см) − длина ломаной.
Ответ: $81\frac25$ см.

431. В торговый зал магазин вынесли разложенные в пакеты конфеты. Всего было приготовлено 25 пакетов с ирисками по 3/10 кг в каждом и 20 пакетов с карамелью по 2/5 кг в каждом. На сколько масса карамели была больше, чем масса ирисок?

Решение:

$20\ast\frac25-25\ast\frac3{10}=4\ast2-5\ast\frac32=8-\frac{15}2=7\frac22-7\frac12=\frac12$ (кг) − масса карамели была больше, чем масса ирисок.
Ответ: на $\frac12$ кг.

432. Вычислите, используя распределительное свойство:

Решение:

а) $(\frac34+\frac38+\frac56)\ast24=\frac34\ast24+\frac38\ast24+\frac56\ast24=3\ast6+3\ast3+5\ast4=18+9+20=47$

б) $7\ast\frac23+7\ast\frac12+7\ast\frac56=7\ast(\frac23+\frac12+\frac56)=7\ast(\frac46+\frac36+\frac56)=7\ast\frac{12}6=7\ast2=14$

433. Найдите значение выражения:

Решение:

а) $(\frac56+\frac5{18})-(3\frac79-2\frac{13}{15})=(\frac{15}{18}+\frac5{18})-(3\frac{35}{45}-2\frac{39}{45})=\frac{20}{18}-(2\frac{80}{45}-2\frac{39}{45})=1\frac2{18}-\frac{41}{45}=1\frac19-\frac{41}{45}=1\frac5{45}-\frac{41}{45}=\frac{50}{45}-\frac{41}{45}=\frac9{45}=\frac15$

б) $(\frac{21}{22}-\frac5{11})+(\frac{22}{39}-\frac3{13})=(\frac{21}{22}-\frac{10}{22})+(\frac{22}{39}-\frac9{39})=\frac{11}{22}+\frac{13}{39}=\frac12+\frac13=\frac36+\frac26=\frac56$

434. Найдите значение выражения:

Решение:

а) $2\frac9{10}-(1\frac25+\frac3{10})+\frac7{20}=2\frac{18}{20}-(1\frac8{20}+\frac6{20})+\frac7{20}=2\frac{18}{20}-1\frac{14}{20}+\frac7{20}=1\frac4{20}+\frac7{20}=1\frac{11}{20}$
б) $4-(\frac{41}{84}-\frac5{21})+7\frac{11}{30}=4-(\frac{41}{84}-\frac{20}{84})+7\frac{11}{30}=4-\frac{21}{84}+7\frac{11}{30}=4-\frac3{12}+7\frac{11}{30}=11\frac{22}{60}-\frac{15}{60}=11\frac7{60}$

435. Найдите значение выражения:

Решение:

а) $(1-\frac14+\frac38):\frac34-\frac12=(\frac88-\frac28+\frac38)\ast\frac43-\frac12=\frac98\ast\frac43-\frac12=\frac32\ast\frac11-\frac12=\frac22=1$
б) $(1-\frac78+\frac7{10}):\frac38-\frac25=(\frac{40}{40}-\frac{35}{40}+\frac{28}{40})\ast\frac83-\frac25=\frac{33}{40}\ast\frac83-\frac25=\frac{11}5\ast\frac11-\frac25=2\frac15-\frac25=(2\frac15-1)+\frac35=1\frac15+\frac35=1\frac45$

436.

Решение:

а) $2\ast1\frac5{12}+4\ast1\frac18+1\frac19\ast1\frac14=2\ast\frac{17}{12}+4\ast\frac98+\frac{10}9\ast\frac54=\frac{17}6+\frac92+\frac59\ast\frac52=2\frac56+4\frac12+\frac{25}{18}=2\frac{15}{18}+4\frac9{18}+1\frac7{18}=7\frac{31}{18}=8\frac{13}{18}$

б) $70:(\frac58+\frac56)+(3\frac19-\frac13)=70:(\frac{15}{24}+\frac{20}{24})+(2\frac{10}9-\frac39)=70:\frac{35}{24}+2\frac79=70\ast\frac{24}{35}+2\frac79=2\ast24+2\frac79=48+2\frac79=50\frac79$

в) $(\frac16+\frac1{10}+\frac1{15}):(\frac35-\frac13-\frac14)=(\frac5{30}+\frac3{30}+\frac2{30}):(\frac{36}{60}-\frac{20}{60}-\frac{15}{60})=\frac{10}{30}:\frac1{60}=\frac13\ast\frac{60}1=20$

г) $(3-1\frac58)\ast(4-1\frac3{11}):(5-1\frac14)=(2\frac88-1\frac58)\ast(3\frac{11}{11}-1\frac3{11}):(4\frac44-1\frac14)=1\frac38\ast2\frac8{11}:3\frac34=\frac{11}8\ast\frac{30}{11}:\frac{15}4=\frac{11}8\ast\frac{30}{11}\ast\frac4{15}=\frac11\ast\frac11\ast\frac11=1$

63

Самостоятельная работа № 22

Вариант 1

1. Найдите значение выражения:

Решение:

$\frac98:(3\frac13-1\frac56)=\frac98:(3\frac26-1\frac56)=\frac98:(2\frac86-1\frac56)=\frac98:1\frac36=\frac98:1\frac12=\frac98:\frac32=\frac98\ast\frac23=\frac34\ast\frac11=\frac34$

2. Вычислите, используя распределительное свойство:

Решение:

$(\frac56+\frac7{16})\ast96=(\frac{40}{48}+\frac{21}{48})\ast96=\frac{61}{48}\ast96=61\ast2=122$

Вариант 2

1. Найдите значение выражения:

Решение:

$\frac54:(3\frac38-1\frac12)=\frac54:(2\frac{11}8-1\frac48)=\frac54:1\frac78=\frac54:\frac{15}8=\frac54\ast\frac8{15}=\frac11\ast\frac23=\frac23$

2. Вычислите, используя распределительное свойство:

Решение:

$(\frac5{15}+\frac1{12})\ast30=(\frac{20}{60}+\frac5{60})\ast30=\frac{25}{60}\ast30=\frac{25}2=12\frac12$

Задачи на нахождение части целого и целого по его части

437. а) От тесьмы, длина которой 10 м, отрезали 2/5 ее длины, чтобы завязать коробку с подарками. Сколько метров тесьмы отрезали? Сколько метров тесьмы осталось?
б) Автотуристы за 3 дня проехали 360 км. В первый день они проехали 2/5 , а во второй день − 3/ 8 всего пути. Сколько километров проехали автотуристы в каждый из дней? Сколько километров проехали автотуристы в третий день?

Решение:

а) 1) 10 ∗ 2/5 = 2 ∗ 2 = 4 (м) − тесьмы отрезали;
2) 10 − 4 = 6 (м) − тесьмы осталось.
Ответ: 4 м отрезали; 6 м осталось.

б) 1) 360 ∗ 2/5 = 72 ∗ 2 = 144 (км) − проехали автотуристы в первый день;
2) 360 ∗ 3/8 = 45 ∗ 3 = 135 (км) − проехали автотуристы во второй день;
3) 360 − (144 + 135) = 360 − 279 = 81 (км) − проехали автотуристы в третий день.
Ответ: 144 км, 135 км, 81 км.

438. а) В коробке 300 разноцветных шариков. Синие шарики составляют 4/15 всех шариков, красные − 3/20, желтые − 2/25. Сколько в коробке шариков каждого из этих цветов?
б) На странице 2000 букв, 1/20 всех букв составляет буква "а", 3/50 − буква "и", 3/100 − буква "м", 3/1000 − буква "ь". Сколько раз встречается на странице каждая из этих букв?

Решение:

1) 300 ∗ 4/15 = 20 ∗ 4 = 80 (ш.) − синих шариков в коробке;
2) 300 ∗ 3/20 = 15 ∗ 3 = 45 (ш.) − красных шариков в коробке;
3) 300 ∗ 2/25 = 12 ∗ 2 = 24 (ш.) − желтых шарика в коробке.
Ответ: 80 синих, 45 красных, 24 желтых шарика.

б) 1) 2000 ∗ 1/20 = 100 (букв "а");
2) 2000 ∗ 3/50 = 40 ∗
3 = 120 (букв "и");
3) 2000 ∗ 3/100 = 20 ∗ 3 = 60 (букв "м");
4) 2000 ∗ 3/1000 = 2 ∗ 3 = 6 (букв "ь").
Ответ: 100 − "а", 120 − "и", 60 − "м", 6 − "ь".

439. а) Таня выполняла домашнее задание 1_1/2 ч, причем 4/5 этого времени она потратила на решение задач. Сколько времени Таня решала задачи? Выразите ответ в часах, а затем в минутах.
б) Занятия в школе длятся 6_2/3 ч, причем 1/8 этого времени отводится на перемены. Сколько времени отводится на перемены? Выразите ответ в часах, а затем в минутах.

Решение:

а) $1\frac12\ast\frac45=\frac32\ast\frac45=\frac31\ast\frac25=\frac65=1\frac15({\operatorname ч})=\frac65({\operatorname ч})=\frac{72}{60}({\operatorname ч})=1\frac15(ч)=72$ (мин) − Таня решала задачи.
Ответ: $1\frac15ч=72$ или 72 минуты.

б) $6\frac23\ast\frac18=\frac{20}3\ast\frac18=\frac53\ast\frac12=\frac56({\operatorname ч})=\frac{50}{60}({\operatorname ч})=\frac56(ч)=50$ (мин) − отводится на перемены.
Ответ: $\frac56ч$ или 50 минут.

64

440. а) Какова сумма денег, если 48 р. составляют 3/4 этой суммы?
б) Определите длину отрезка, 3/5 которого составляют 45 см.
в) Дочери 14 лет. Ее возраст составляет 2/7 возраста матери. Сколько лет матери?

Решение:

а) $48:\frac34=48\ast\frac43=16\ast4=64$ (р.) − вся сумма денег.
Ответ: 64 рубля.
б) $45:\frac35=45\ast\frac53=15\ast5=75$ (см) − длина отрезка.
Ответ: 75 см.
в) $14:\frac27=14\ast\frac72=7\ast7=49$ (лет) − матери.
Ответ: 49 лет.

441. а) Прочитали 90 страниц. Это составило 3/5 всей книги. Сколько страниц осталось прочитать?
б) Ковер закрывает 3/4 площади пола комнаты. Площадь ковра 18 м². Чему равна площадь комнаты, не закрытая ковром?

Решение:

а)
1) $90:\frac35=90\ast\frac53=30\ast5=150$ (стр.) − в книге;
2) 150 − 90 = 60 (стр.) − осталось прочитать.
Ответ: 60 страниц.
б)
1) $18:\frac34=18\ast\frac43=6\ast4=24({\operatorname м}^2)$ − площадь комнаты;
2) 24 − 18 = 6 (м²) − площадь комнаты, не закрытая ковром.
Ответ: 6 м².

442. а) В первый день прочитали 3/4 книги, а во второй день − оставшиеся 35 страниц. Сколько всего страниц в книге?
б) В первый день Катя выучила 3/5 всех словарных слов, а во второй − 20 оставшихся слов. Сколько всего слов она выучила?

Решение:

а) Примем всю книгу за 1, тогда:
1) 1 − 3/4 = 1/4 (книги) − прочитали во второй день;
2) 35 : 1/4 = 35 ∗ 4 = 140 (страниц) − всего в книге.
Ответ: 140 страниц.

б) Примем все слова за 1, тогда:
1) 1 − 3/5 = 2/5 (слов) − выучила Катя во второй день;
2) 20 : 2/ 5 = 20 ∗ 5/2 = 10 ∗ 5 = 50 (слов) − всего выучила Катя.
Ответ: 50 слов.

443. В супермаркете "Прогресс" покупатель получает скидку в зависимости от стоимости покупки:
Стоим-ть
покупки в р.        Скидка
От 100 до 500     1/20 стоимости
От 500 до 1000   1/10 стоимости
Выше 1000 3/20 стоимости
Пользуясь данными таблицы, определите, сколько рублей покупатель заплатит за покупку, если ее стоимость составляет:
а) 340 р.;
б) 750 р.;
в) 2360 р.

Решение:

а) 1) 340 ∗ 1/20 = 17 (р.) − составит скидка;
2) 340 − 17 = 323 (р.) − покупатель заплатит за покупку.
Ответ: 323 рубля.

б) 1) 750 ∗ 1/10 = 75 (р.) − составит скидка;
2) 750 − 75 = 675 (р.) − покупатель заплатит за покупку.
Ответ: 675 рублей.

в) 1) 2360 ∗ 3/20 = 118 ∗ 3 = 354 (р.) − составит скидка;
2) 2360 − 354 = 2006 (р.) − покупатель заплатит за покупку.
Ответ: 2006 рублей.

444. а) Сыну 8 лет, его возраст составляет 2/9 возраста отца. Возраст отца составляет 3/5 возраста дедушки. Сколько лет дедушке?
б) Масса котенка 300 г, что составляет 2/5 массы щенка. А масса щенка составляет 3/20 массы взрослой собаки. Найдите массу взрослой собаки.

Решение:

а)
1) 8 : 2/9 = 8 ∗ 9/2 = 4 ∗ 9 = 36 (лет) − отцу;
2) 36 : 3/ 5 = 36 ∗ 5/3 = 12 ∗ 5 = 60 (лет) − дедушке.
Ответ: 60 лет.

б)
1) 300 : 2/5 = 300 ∗ 5/2 = 150 ∗ 5 = 750 (г) − масса щенка;
2) 750 : 3/20 = 750 ∗ 20/3 = 250 ∗ 20 = 5000 (г) = 5 (кг) − масса взрослой собаки.
Ответ: 5 кг.

445. а) На принтере сначала распечатали треть всей рукописи, потом еще 10 страниц. В результате распечатали половину всей рукописи. Сколько страниц в рукописи?
б) Покрасили четверть длины всего забора, а потом еще 8 м. В результате покрасили половину забора. Какова длина всего забора?

Решение:

а)
1) 1/2 − 1/3 = 3/6 − 2/6 = 1/6 (книги) − составляет 10 страниц;
2) 10 : 1/6 = 10 ∗ 6 = 60 (страниц) − в рукописи всего.
Ответ: 60 страниц.

б)
1) 1/2 − 1/4 = 2/4 − 1/4 = 1/4 (забора) − составляют 8 м;
2) 8 : 1/4 = 8 ∗ 4 = 32 (м) − длина забора.
Ответ: 32 метра.

65

446. а) В первый день прочитали 2/5, а во второй − 1/3 числа всех страниц книги. После этого осталось прочитать 80 страниц. Сколько всего страниц в книге?
б) Таня подсчитала, что 1/6 всего времени, которое потребовалось ей для выполнения домашних заданий, у нее ушло на математику, а 1/4 − на русский язык. Остальные уроки она сделала за 1 ч 10 мин. Сколько времени Таня выполняла домашние задания?

Решение:

а) Примем всю книгу за 1, тогда:
1) 1 − (2/5 + 1/3) = 1 − (6/15 + 5/15) = 1 − 11/15 = 4/15 (книги) − составляют 80 страниц;
2) 80 : 4/15 = 80 ∗ 15/4 = 20 ∗ 15 = 300 (стр.) − в книге всего.
Ответ: 300 страниц.

б)  Примем все время за 1, тогда:
1) 1 − (1/6 + 1/4) = 1 − (2/12 + 3/12) = 1 − 5/12 = 7/12 (времени) − составляют 1 ч 10 мин;
2) 1 ч 10 мин = 70 мин;
70 : 7/12 = 70 ∗ 12/7 = 10 ∗ 12 = 120 (мин) = 2 (ч) − Таня выполняла домашние задания.
Ответ: 2 ч.

447. а) Туристы прошли свой маршрут за 2 дня. В первый день они прошли до привала 7/20 маршрута и еще 15 км после привала, во второй день до привала − 2/5 маршрута и после привала 10 км. Чему равна длина маршрута?
б) Два пешехода вышли одновременно навстречу друг другу из пунктов A и B. При встрече оказалось, что один из них прошел 2/9 всего расстояния от A и B и еще 1_1/2 км, а другой прошел 1/3 всего расстояния от A до B и еще 2_1/2 км. Чему равно расстояние от пункта A до пункта B?

Решение:

а)
1) 7/20 + 2/5 = 7/20 + 8/20 = 15/20 = 3/4 (маршрута) − прошли туристы до привала за 2 дня;
2) 1 − 3/4 = 1/4 (маршрута) − прошли туристы после привала за 2 дня;
3) 15 + 10 = 25 (км) − прошли туристы после привала за 2 дня;
4) 25 : 1/4 = 25 ∗ 4 = 100 (км) − длина маршрута.
Ответ: 100 км.

б) Примем расстояние от пункта A до пункта B за 1, тогда:
1) 2/9 + 1/3 = 2/9 + 3/9 = 5/9 (расстояния) − прошли два пешехода;
2) $1\frac12+2\frac12=4$ (км) − прошли два пешехода;
3) 1 − 5/9 = 4/9 (расстояния) − составляет 4 км;
4) 4 : 4/9 = 4 ∗ 9/4 = 9 (км) − расстояние от пункта A до пункта B.
Ответ: 9 км.

Самостоятельная работа № 23

Вариант 1

1. Фильм из двух частей длится 120 мин. Длительность первой части составляет 3/5 общей длительности фильма. Сколько минут длится первая часть фильма и сколько вторая?

Решение:

1) 120 ∗ 3/5 = 24 ∗ 3 = 72 (мин) − длительность первой части фильма;
2) 120 − 72 = 48 (мин) − длительность второй части фильма.
Ответ: 72 мин и 48 мин.

2. Какова длина туристического маршрута, если 3/4 всего маршрута составляет 24 км?

Решение:

24 : 3/4 = 24 ∗ 4/3 = 8 ∗ 4 = 32 (км) − длина маршрута.
Ответ: 32 км.

Вариант 2

1. Комплект из плеера и диска стоит 980 р. Стоимость плеера составляет 5/7 стоимости всего комплекта. Сколько стоит плеер и сколько диск?

Решение:

1) 980 ∗ 5/7 = 140 ∗ 5 = 700 (р.) − стоит плеер;
2) 980 − 700 = 280 (р.) − стоит диск.
Ответ: 700 р. − плеер, 280 р. − диск.

2. Какова длина туристического маршрута, если 2/5 всего маршрута составляет 20 км?

Решение:

20 : 2/5 = 20 ∗ 5/2 = 10 ∗ 5 = 50 (км) − длина всего маршрута.
Ответ: 50 км.

66

Таблицы и диаграммы

Чтение и составление таблиц

448. В фирме работают три бригады по заготовке грибов. В таблице представлена информация о количестве грибов (в кг), сданных ими за 3 месяца.

1) Заполните пустые клетки таблицы.
2) используя таблицу, ответьте на вопросы:
а) Сколько килограммов грибов заготовила бригада №1 в июле?
б) Сколько всего килограммов грибов заготовила за 3 месяца бригада №2?
в) Сколько всего килограммов грибов заготовили за сентябрь три бригады?
3) Придумайте и задайте свои вопросы.

Решение:

1.
1) 48 + 34 + 59 = 82 + 59 = 141 (кг) − всего заготовила бригада №1;
2) 46 + 42 + 51 = 88 + 51 = 139 (кг) − всего заготовила бригада №2;
3) 60 + 53 + 49 = 113 + 49 = 162 (кг) − всего заготовила бригада №3;
4) 48 + 46 + 60 = 94 + 60 = 154 (кг) − грибов итого заготовлено в июле;
5) 34 + 42 + 53 = 76 + 53 = 129 (кг) − грибов итого заготовлено в августе;
6) 59 + 51 + 49 = 110 + 49 = 159 (кг) − грибов итого заготовлено в сентябре;
7) 141 + 139 + 162 = 280 + 162 = 442 (кг) − грибов всего заготовлено за 3 месяца.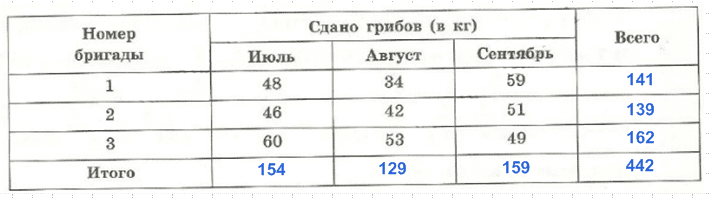


2.
а) 48 (кг) − заготовила бригада №1 в июле;
б) 139 (кг) − заготовила за 3 месяца бригада №2;
в) 159 (кг) − грибов заготовили за сентябрь три бригады.

3.
а) Сколько килограммов грибов заготовила бригада №2 в сентябре?
Ответ: 51 кг

б) Сколько всего килограммов грибов заготовила за 3 месяца бригада №1?
Ответ: 141 кг

в) Сколько всего килограммов грибов заготовили за август три бригады?
Ответ: 129 кг

449. В таблице представлены результаты пяти матчей по футболу трех команд, участвующих в чемпионате. Заполните столбцы:
В − выиграно матчей,
П − проиграно,
Н − сыграно вничью,
О − набрано очков.
За победу в матче команда получает 3 очка, за ничью − 1 очко, за проигрыш − 0 очков.

Ответьте на вопросы:
Сколько мячей забросила каждая команда в пяти матчах? Сколько мячей пропустила?

Решение:

1) 2 * 3 + 2 * 0 + 1 * 1 = 6 + 0 + 1 = 7 (очков) − набрала команда "Юпитер";
2) 1 * 3 + 2 * 0 + 2 * 1 = 3 + 0 + 2 = 5 (очков) − набрала команда "Сатурн";
3) 4 * 3 + 0 * 0 + 1 * 1 = 12 + 0 + 1 = 13 (очков) − набрала команда "Нептун".

4) 0 + 3 + 0 + 2 + 1 = 6 (мячей) − забила команда "Юпитер" в пяти матчах;
5) 1 + 0 + 1 + 2 + 1 = 5 (мячей) − забила команда "Сатурн" в пяти матчах;
6) 1 + 2 + 3 + 2 + 3 = 11 (мячей) − забила команда "Нептун" в пяти матчах;
7) 0 + 0 + 1 + 1 + 3 = 5 (мячей) − пропустила команда "Юпитер" в пяти матчах;
8) 2 + 3 + 1 + 2 + 0 = 8 (мячей) − пропустила команда "Сатурн" в пяти матчах;
9) 0 + 1 + 2 + 0 + 3 = 6 (мячей) − пропустила команда "Нептун" в пяти матчах.

450. Чтобы заказать в ателье новогодние костюмы, собраны данные о размере одежды членов драматического кружка: 42, 46, 40, 48, 40, 46, 46, 40, 46, 48, 44, 40, 42, 46, 46, 44, 46, 40, 48, 40, 48, 44, 46, 48, 46, 40, 40, 42.
Представьте эти данные в таблице.
Ответьте на вопросы:
а) Сколько человек занимается в кружке?
б) Какой размер одежды встречается чаще других?
в) Какой размер одежды встречается реже других?
г) Какого размера: 40 или 42 − надо заказать больше и на сколько?

Решение

Размер
одежды Количество
40           8
42           3
44           3
46           9
48           5
Всего: 28

а) 28 (человек) − занимается в кружке;
б) 48 (размер) − одежды встречается чаще всего;
в) 42 и 44 (размер) − одежды встречаются реже других;
г) 8 − 3 = на 5 (костюмов) − 40 размера нужно заработать больше, чем 42 размера.

67

451. Составьте таблицу и представьте в ней следующие данные о количестве учащихся в пятых классах трех школ города.
В школе №1 в 5А классе учатся 25 учащихся, в 5Б классе − 27, в 5В − 19;
в школе №2 в 5А классе учатся 18 учащихся, в 5Б классе − 21, в 5В − 23;
в школе №3 в 5А классе учатся 28 учащихся, в 5Б классе − 24, в 5В − 30.

Решение

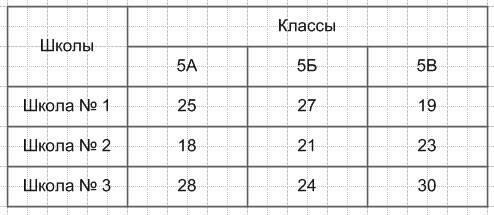
452. Сколько страниц в учебнике? Составьте таблицу и представьте в ней данные о количестве страниц в ваших учебниках для 5 класса.

Решение:

Учебники      Кол-во страниц
Математика        369
Русский язык       236
Английский язык 251
Литература          368
Биология              432

453. В каком году родились учащиеся вашего класса? Соберите эти данные и представьте их в таблице.

Решение:

Год рождения Кол-во учеников
2008                       4
2009                       25

Чтение и построение диаграмм

454. На диаграмме показана численность населения крупнейших стран мира (в млн человек, по данным на 2011 г.)

Используя диаграмму, ответьте на вопросы:
а) Какие страны входят в пятерку самых населенных стран мира?
б) Какая страна занимает по численности населения первое место в мире? Сколько человек в ней проживает?
в) На сколько человек население Китая больше населения Индии?
г) На каком месте по численности населения находится Россия? Сколько человек в ней проживает?
д) Верно ли, что в Пакистане и Нигерии вместе проживает примерно столько же человек, сколько в США?
е) Примерно во сколько раз численность России меньше, чем в США? Задайте свой вопрос.

Решение:

а) Китай, Индия, США, Индонезия, Бразилия.

б) Китай занимает первое место в мире по численности населения. В ней проживает 1338 млн человек.

в) 1138 млн − 1120 млн = 18 млн (человек) − население Китая больше населения Индии.
Ответ: на 18 млн человек

г) Россия занимает 9 место по численности населения в мире. В ней проживает 140 млн человек.

д) 149 млн + 174 млн = 323 млн (человек) − проживает в Пакистане и Нигерии вместе.
Ответ: верно, что в Пакистане и Нигерии вместе проживает примерно столько же человек, сколько в США

е) Примерно в 2 раза численность России меньше, чем в США.

Вопрос:
Какая страна замыкает десятку самых населенных стран мира. Сколько человек в ней проживает?
Ответ:
Япония замыкает десятку самых населенных стран мира. В ней проживает 127 млн человек.

455. В таблице указано количество отметок "2", "3", "4" и "5", полученные пятиклассниками за контрольную работу по математике.
Отметка 2 3 4 5
Число уч-ся 2 7 9 5
Используя эти данные, постройте столбчатую диаграмму. На горизонтальной оси укажите отметки. На вертикальной оси выберите удобную единицу измерения и отметьте число учащихся. Постройте соответствующие столбики.

Решение

68

456. Представьте на столбчатой диаграмме данные, полученные при выполнении задания:
а) № 452;
б) № 453.

Решение

а)

б) 

457. Постройте столбчатую диаграмму "Самые длинные реки России" по следующим данным:
Лена − 4400 км,
Обь − 3650 км,
Волга − 3531 км,
Енисей − 3487 км,
Амур − 2824 км,
Оленек − 2292 км,
Колыма − 2129 км.
Указание.
Пусть 1 см соответствует 1000 км.

Решение:

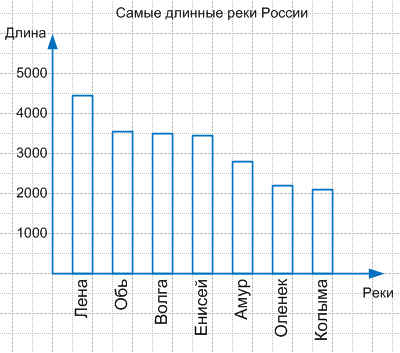
458. Постройте столбчатую диаграмму "Площадь оледенения в горах России" по следующим данным:
Большой Кавказ − 1424,
Алтай − 915,
горы Камчатки − 874,
Корякское нагорье − 260 (в км²).
Указание.
Пусть 1 клетка соответствует 250 км².

Решение

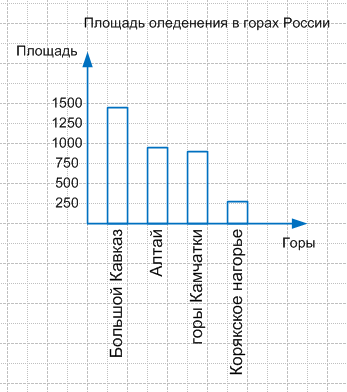
459. Постройте столбчатую диаграмму "Неблагоприятные погодные явления" по следующим данным:
ураганы, бури, смерчи − 66,
сильные дожди − 49,
сильные снегопады − 17,
сильные морозы − 10,
сильные метели − 9,
засухи − 7,
грозы, градобития − 3.

Решение

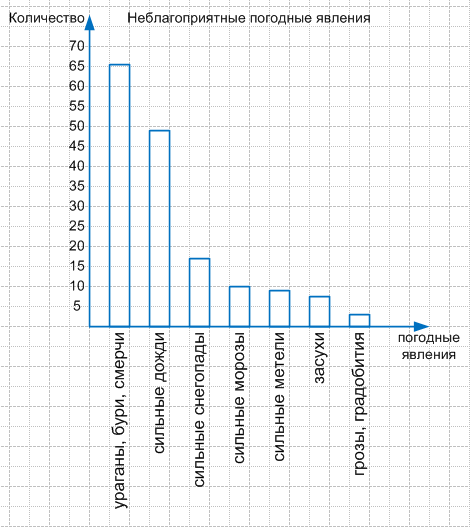
460. На диаграмме показана доля пород хвойных деревьев в лесах России.
Используя диаграмму, ответьте на вопросы:
а) Деревья каких пород преобладают в лесах нашей страны? Какую часть всех хвойных деревьев они составляют?
б) Каких деревьев больше: елей или сосен? Во сколько раз?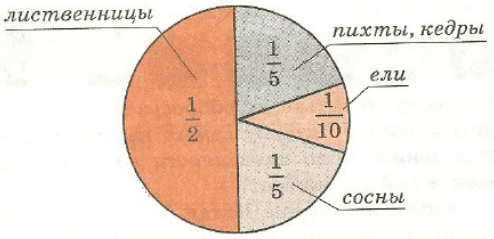

Решение

а) В лесах нашей страны преобладают лиственницы. Они составляют 1/2 часть всех деревьев.

б) 1/5 : 1/10 = 1/5 ∗ 10 = 2
Ответ: в 2 раза больше сосен, чем елей.

461. Иван провел среди одноклассников опрос на тему "Какое время года вы предпочитаете?". Им были получены следующие результаты:
лето − 8 человек,
зиму − 6 человек,
весну − 6 человек,
осень − 4 человека.
Ответьте на вопросы:
а) Сколько человек было опрошено?
б) Какая часть опрошенных предпочитает лето? зиму? весну? осень?
Представьте полученные результаты на круговой диаграмме.

Решение

а) 8 + 6 + 6 + 4 = 14 + 10 = 24 (человека) − было опрошено.
Ответ: 24 человека.

б) 
1) 8/24 = 1/3 (опрошенных) − предпочитает лето;
2) 6/24 = 1/4 (опрошенных) − предпочитает зиму;
3) 6/24 = 1/4 (опрошенных) − предпочитает весну;
4) 4/24 = 1/6 (опрошенных) − предпочитает осень.

Опрос общественного мнения

462. Проведите опрос "В какое время года отмечают день рождения ваши одноклассники?" и постройте по полученным данным столбчатую диаграмму.

Решение:

День рождения отмечают:
весной − 5 человек;
летом − 7 человек;
осенью − 9 человек;
зимой − 6 человек.

69

463. Проведите опрос на тему "Сколько братьев и сестер у учащихся вашего класса?". Составьте таблицу, указав в ней число учащихся, не имеющих братьев и сестер, имеющих одного брата или сестру, двух и т.д. Постройте по полученным данным столбчатую диаграмму.

Решение:

464. Проведите опрос среди одноклассников на тему "Какое время года вы предпочитаете?", заполните таблицу и постройте по полученным данным столбчатую диаграмму.

Решение:

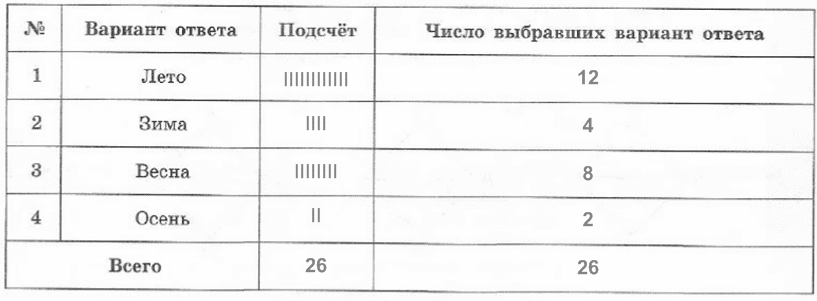
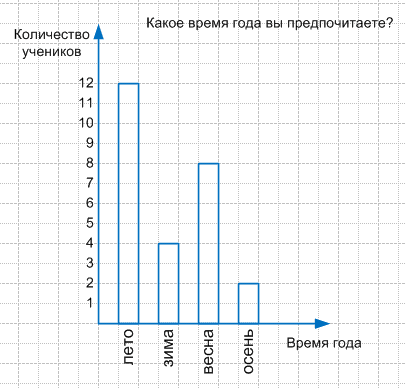
465. 1) Проведите опрос среди учащихся класса на тему "Кем бы вы хотели быть, когда вырастите?". Варианты ответа: юрист, экономист, программист, врач, бизнесмен, рабочий, инженер, военный, ученый, спортсмен, артист, музыкант, учитель, фермер. Постройте по полученным данным диаграмму.
2) Проведите опрос среди родителей вашего класса на тему "Кем бы вы хотели видеть вашего сына, дочь?". Постройте по полученным данным диаграмму.

Решение:

1) 

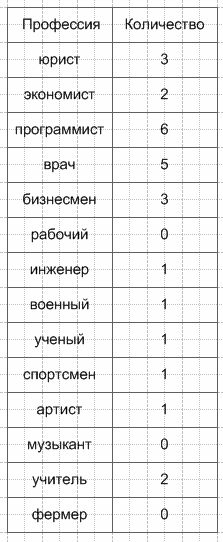
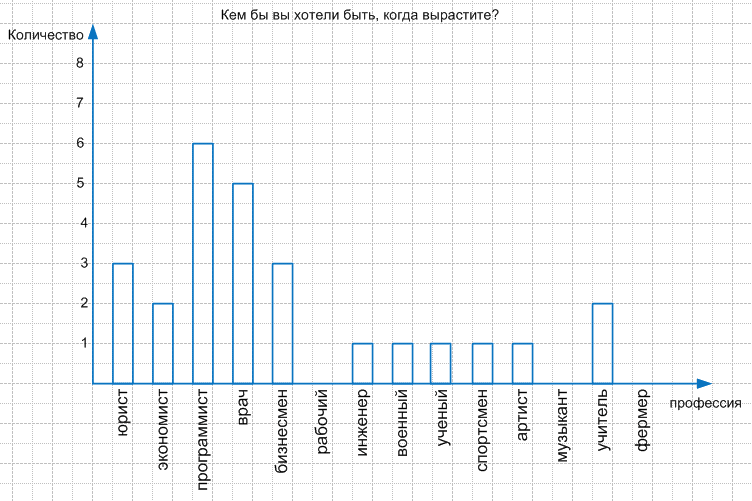
2) 

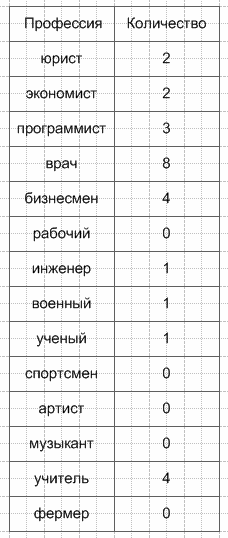
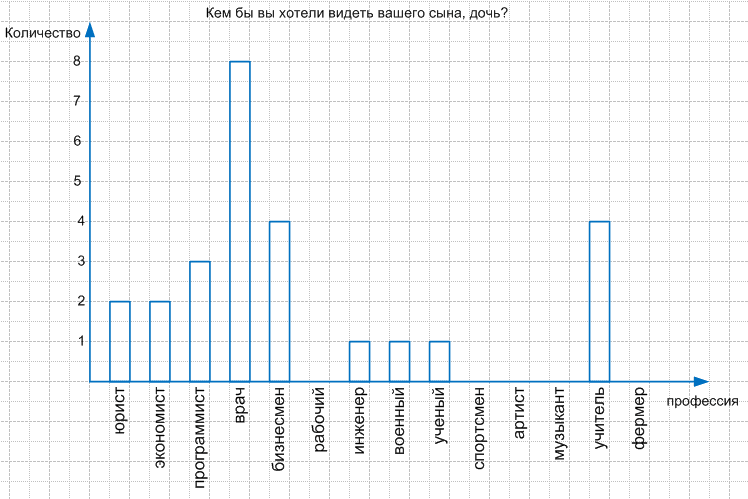
Самостоятельная работа № 24

Вариант 1

1. Используя таблицу, составленную по упражнению 451, определите, сколько пятиклассников в каждой из трех школ города. Постройте по этим данным столбчатую диаграмму.

Решение

1) 25 + 27 + 19 = 52 + 19 = 71 (пятиклассник) − в школе №1;
2) 18 + 21 + 23 = 39 + 23 = 62 (пятиклассника) − в школе №2;
3) 28 + 24 + 30 = 52 + 30 = 82 (пятиклассника) − в школе №3.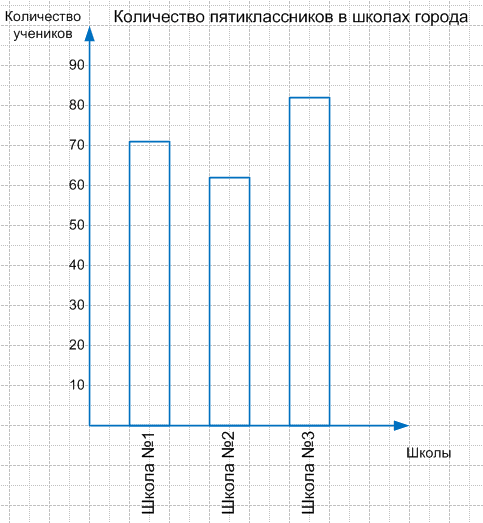

Вариант 2

1. Используя таблицу, составленную по упражнению 450, определите, сколько костюмов каждого размера требуется для кружка. Постройте по этим данным столбчатую диаграмму.

Решение:

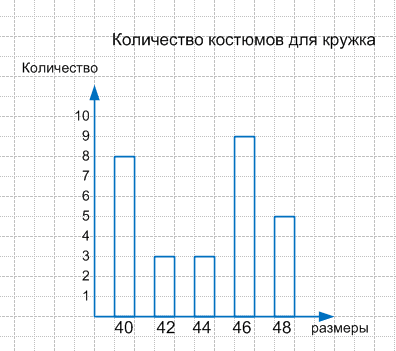
70

ЧАСТЬ 2. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ

Обводим линии

1. а) Вы начали движение из узла B (см.рис.1,а). Где вы закончите движение?
б) Удастся ли обвести одним росчерком линию, изображенную на рисунке 1,а, если начать движение из узла C? из узла D?

Решение:

а) Движение закончится в узле C.


б) Если начать движение из узла C, удастся обвести одним росчерком линию.

Если начать движение из узла D, не удастся обвести одним росчерком линию.

2. Назовите все узлы линии, изображенной на рисунке 2, начав с которых ее можно обвести одним росчерком, отметьте начало движения и покажите стрелками направление движения.

Решение:

Можно начать с узла B:


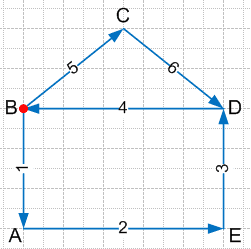
Можно начать с узла D: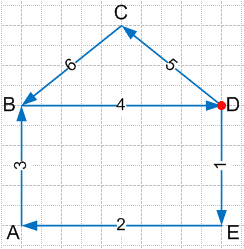

3. На рисунке 3 изображена линия, которую вы, наверное, умеете рисовать одним росчерком. Это звезда. Оказывается, хотя она и выглядит значительно более сложной, чем предыдущие линии, овести ее можно, причем начав с любого узла. Начертите звезду несколько раз, начиная движение из разных узлов.

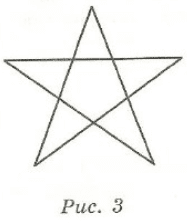
Решение:

Способ 1.


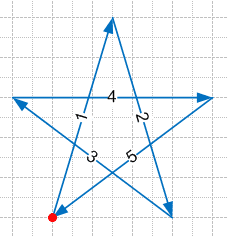
Способ 2.


Способ 3.


Способ 4.


Способ 5.

71

4. Линию, изображенную на рисунке 4, как и звезду, можно вычертить одним росчерком, начав движение из любого узла. Вычертите эту линию дважды: начав с узла, из которого выходят два отрезка, а затем с узла, из которого выходят четыре отрезка.
Начертите одним росчерком линию, изображенную на рисунке 5.

А теперь попробуйте обвести одним росчерком линию, изображенную на рисунке 6. Вам это сделать не удалось! Почему? Вы не смогли найти нужный узел? Нет! Дело в том, что это вообще невозможно. Проведем рассуждения, которые убедят нас в этом. Рассмотрим узел A. Начнем обводить линию с этого узла. Из него выходит три отрезка. Чтобы пройти по каждому из этих отрезков, мы должны выйти из узла A по одному из них, в процессе обводки обязательно вернуться в него по другому отрезку и тут же выйти по третьему. А так как выйти из него мы уже не сможем, то узел A в этом случае должен являться концом.
Итак, узел A должен быть или начальным, или конечным узлом вычерчивания. Но про три других узла нашей линии можно сказать то же самое. Однако как начальным узлом, так и конечным может быть только один из этих узлов. А значит, обвести эту линию одним росчерком невозможно.
Линию нельзя обвести одним росчерком, если она содержит более двух узлов, в которых сходится нечетное число отрезков.

Решение:

С узла, из которого выходят два отрезка:


С узла, из которого выходят четыре отрезка: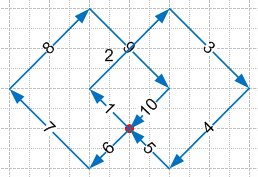

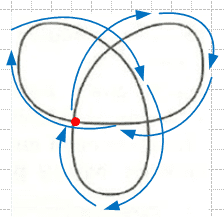
5. Какие линии, изображенные на рисунке 7, можно обвести одним росчерком, а какие нельзя?

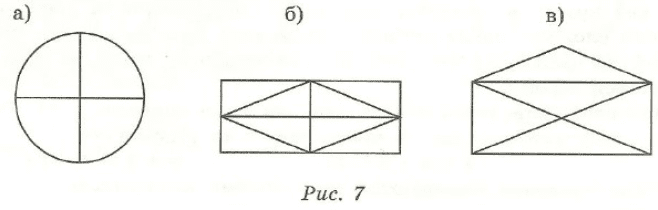
Решение:

а) Обвести одним росчерком невозможно, так как линия имеет более 2 узлов, в которых сходятся нечетное количество отрезков.
б) Обвести одним росчерком невозможно, так как линия имеет более 2 узлов, в которых сходятся нечетное количество отрезков.
в) Обвести одним росчерком возможно, так как линия имеет только 2 узла, в которых сходятся нечетное количество отрезков.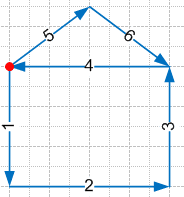

72

6. а) Можно ли согнуть каркас куба, изображенного на рисунке 8, из единого куска проволоки?
б) Можно ли сделать такой каркас из двух кусков проволоки, спаяв их в нескольких узлах?

Решение:

У куба 8 узлов в котором сходится нечетное количество отрезков. Поэтому даже разделив проволоку на два куска все равно в каком−то из кусков будет более двух таких узлов. Значит:
а) нельзя согнуть;
б) нельзя сделать.

7. Вспомните, как вы учились писать по прописям. Некоторые буквы вы писали, не отрывая ручки от бумаги, другие же нет.
а) Какие из букв, изображенных на рисунке 9, можно писать одним росчерком?
б) Придумайте свой способ написания букв Б, К, Ж, Ф, при котором их можно вычертить одним росчерком.

Решение:

а) Буквы А, В, Н, У можно написать одним росчерком.
б) Чтобы буквы Б, К, Ж, Ф можно было написать одним росчерком, то их можно написать такими:

73

Магические квадраты

1. Впишите в пустые клетки квадрата такие числа, чтобы квадрат стал магическим.
а)

2		6
	5	1
4

б)

18		14
	15
16

 

 Решение:

а) 

2		6
	5	1
4

4 + 5 + 6 = 15 − значит в каждой строке, столбце и диагонали сумма должна быть равна 15.
Тогда:
15 − (4 + 2) = 15 − 6 = 9 − число в первом столбце второй строке.
Получим:

2		6
9	5	1
4

15 − (2 + 6) = 15 − 8 = 7 − число во втором столбце первой строке.
Получим:

2	7	6
9	5	1
4

15 − (7 + 5) = 15 − 12 = 3 − число во втором столбце третьей строке.
Получим:

2	7	6
9	5	1
4	3

15 − (4 + 3) = 15 − 7 = 8 − число в третьем столбце третьей строке.
Ответ:

2	7	6
9	5	1
4	3	8

б) 

18		14
	15
16

16 + 15 + 14 = 45 − значит в каждой строке, столбце и диагонали сумма должна быть равна 45.
Тогда:
45 − (18 + 16) = 45 − 34 = 11 − число в первом столбце второй строке.
Получим:

18		14
11	15
16

45 − (18 + 14) = 45 − 32 = 13 − число во втором столбце первой строке.
Получим:

18	13	14
11	15
16

45 − (13 + 15) = 45 − 28 = 17 − число во втором столбце третьей строке.
Получим:

18	13	14
11	15
16	17

45 − (11 + 15) = 45 − 26 = 19 − число в третьем столбце во второй строке.
Получим:

18	13	14
11	15	19
16	17

45 − (16 + 17) = 45 − 33 = 12 − число в третьем столбце в третьей строке.
Ответ:

18	13	14
11	15	19
16	17	12

 

2. Восстановите магические квадраты.
а)

3		15	14
13	16
10	11
8		12	9

 
б)

		14	11
	15	8	10
16	2	9
13	12

 

Решение:

а) 

3		15	14
13	16
10	11
8		12	9

3 + 13 + 10 + 8 = 16 + 18 = 34 − сумма, которая должна быть в каждой строке, столбце и диагонали.
Тогда:
34 − (3 + 15 + 14) = 34 − 32 = 2 − число во втором столбце первой строке.
Получим:

3	2	15	14
13	16
10	11
8		12	9

34 − (8 + 12 + 9) = 34 − 29 = 5 − число во втором столбце третьей строке.
Получим:

3	2	15	14
13	16
10	11
8	5	12	9

34 − (8 + 11 + 14) = 34 − 33 = 1 − число в третьем столбце второй строке.
Получим:

3	2	15	14
13	16	1
10	11
8	5	12	9

34 − (15 + 1 + 12) = 34 − 28 = 6 − число в третьем столбце третьей строке.
Получим:

3	2	15	14
13	16	1
10	11	6
8	5	12	9

34 − (13 + 16 + 1) = 34 − 30 = 4 − число в четвертом столбце второй строке.
Получим:

3	2	15	14
13	16	1	4
10	11	6
8	5	12	9

34 − (10 + 11 + 6) = 34 − 27 = 7 − число в четвертом столбце третьей строке.
Ответ:

3	2	15	14
13	16	1	4
10	11	6	7
8	5	12	9

б) 

	14	11
	15	8	10
16	2	9
13	12

13 + 2 + 8 + 11 = 15 + 19 = 34 − сумма, которая должна быть в каждой строке, столбце и диагонали.
Тогда:
34 − (15 + 8 + 10) = 34 − 33 = 1 − число в первом столбце второй строке.
Получим:

		14	11
1	15	8	10
16	2	9
13	12

34 − (1 + 16 + 13) = 34 − 30 = 4 − число в первом столбце первой строке.
Получим:

4		14	11
1	15	8	10
16	2	9
13	12

34 − (4 + 14 + 11) = 34 − 29 = 5 − число во втором столбце первой строке.
Получим:

4	5	14	11
1	15	8	10
16	2	9
13	12

34 − (16 + 2 + 9) = 34 − 27 = 7 − число в четвертом столбце третьей строке.
Получим:

4	5	14	11
1	15	8	10
16	2	9	7
13	12

34 − (14 + 8 + 9) = 34 − 31 = 3 − число в третьем столбце четвертой строке.
Получим:

4	5	14	11
1	15	8	10
16	2	9	7
13	12	3

34 − (13 + 12 + 3) = 34 − 28 = 6 − число в четвертом столбце четвертой строке.
Ответ:

4	5	14	11
1	15	8	10
16	2	9	7
13	12	3	6

 

74

3. Убедитесь сами, что квадрат Дюрера является магическим, вычислив суммы по строкам, столбцам и диагоналям. Исследуйте другие свойства этого квадрата, посчитав сумму чисел центрального квадрата и каждого из угловых квадратов.

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

Как же составляют магические квадраты? Составим, например, магический квадрат из чисел от 1 до 9, как тот, что изображен на рисунке 2.

4	9	2
3	5	7
8	1	6

Рис.2

Для этого можно попробовать перебрать различные варианты расстановки чисел от 1 до 9 в клетках таблицы. Если повезет, вы получите магический квадрат. Однако при этом надо иметь в виду, что всего существует почти 400000 разных расстановок чисел в этом квадрате.
Гораздо интереснее составить такой магический квадрат с помощью рассуждений.
Сумма всех чисел от 1 до 9 равна 45. Всего в квадрате три строки. Значит, в каждой строке магического квадрата сумма чисел должна быть равна 45 : 3 = 15. Но тогда, чтобы квадрат был магическим, в каждом столбце и на каждой диагонали сумма чисел должна быть равна 15.
Выпишем все возможные представления числа 15 в виде суммы трех слагаемых от 1 до 9:
9 + 5 + 1
9 + 4 + 2
8 + 6 + 1
8 + 5 + 2
8 + 4 + 3
7 + 6 + 2
7 + 5 + 3
6 + 5 + 4
Заметим, что число, стоящее в центре таблицы, должно встречаться в выписанных суммах 4 раза (столбец, строка и две диагонали). Каждое число, стоящее в углу таблицы, должно встречаться в суммах 3 раза (строка, столбец, диагональ). А число, стоящее на одном из оставшихся четырех мест, должно встречаться в суммах только 2 раза (строка и столбец).
Поскольку в полученных суммах 4 раза встречается только число 5, оно и должно стоять в центре таблицы.
Трижды встречаются в суммах числа 2, 4, 6 и 8. Значит, они должны стоять в углах таблицы, причем так, чтобы 2 и 8 были на одной диагонали: 1, 3, 7 и 9. Их нужно поставить на свободные места, учитывая при этом, что сумма чисел в каждой строке должна быть равна 15.
Описанный способ дает несколько разных магических квадратов. Например, число 8 можно расположить в любом из четырех углов, что позволит получить разные по виду квадраты.

Решение:

Квадрат Дюрера

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

16 + 3 + 2 + 13 = 19 + 15 = 34 − сумма чисел первой строки;
5 + 10 + 11 + 8 = 15 + 19 = 34 − сумма чисел второй строки;
9 + 6 + 7 + 12 = 15 + 19 = 34 − сумма чисел третьей строки;
4 + 15 + 14 + 1 = 19 + 15 = 34 − сумма чисел четвертой строки;
16 + 5 + 9 + 4 = 21 + 13 = 34 − сумма чисел первого столбца;
3 + 10 + 6 + 15 = 13 + 21 = 34 − сумма чисел второго столбца;
2 + 11 + 7 + 14 = 13 + 21 = 34 − сумма чисел третьего столбца;
13 + 8 + 12 + 1 = 21 + 13 = 34 − сумма чисел четвертого столбца;
16 + 10 + 7 + 1 = 26 + 8 = 34 − сумма чисел первой диагонали;
4 + 6 + 11 + 13 = 10 + 24 = 34 − сумма чисел второй диагонали;
10 + 11 + 6 + 7 = 21 + 13 = 34 − сумма чисел центрального квадрата;
16 + 3 + 5 + 10 = 19 + 15 = 34 − сумма чисел верхнего левого квадрата;,
9 + 6 + 4 + 15 = 15 + 19 = 34 − сумма чисел нижнего левого квадрата;
2 + 13 + 11 + 8 = 15 + 19 = 34 − сумма чисел верхнего правого квадрата;
7 + 12 + 14 + 1 = 19 + 15 = 34 − сумма чисел нижнего правого квадрата.
Вывод: в квадрате Дюрера суммы чисел строк, столбцов, диагоналей, а также центрального квадрата и угловых квадратов равны.

4. Составьте сами все 8 различных магических квадратов из чисел от 1 до 9.

Решение:

1)

4	9	2
3	5	7
8	1	6

2)

2	7	6
9	5	1
4	3	8

3)

6	1	8
7	5	3
2	9	4

4)

8	3	4
1	5	9
6	7	2

5)

6	7	2
1	5	9
8	3	4

6)

2	9	4
7	5	3
6	1	8

7)

4	3	8
9	5	1
2	7	6

8)

8	1	6
3	5	7
4	9	2

 

5. Возьмите квадрат 4×4 и впишите в него числа от 1 до 16 по порядку. Теперь поменяйте местами числа, стоящие в противоположных углах квадрата. А затем поменяйте местами числа, стоящие в противоположных углах центрального квадрата. Если вы все сделали правильно, должен получиться магический квадрат. Проверьте.

Решение:

Впишем в квадрат числа от 1 до 16 по порядку:

1	2	3	4
5	6	7	8
9	10	11	12
13	14	15	16

Поменяем местами числа, стоящие в противоположных углах квадрата:

16	2	3	13
5	6	7	8
9	10	11	12
4	14	15	1

Поменяем местами числа, стоящие в противоположных углах центрального квадрата:

16	2	3	13
5	11	10	8
9	7	6	12
4	14	15	1

Проверим, получился ли магический квадрат:
16 + 2 + 3 + 13 = 18 + 16 = 34 − сумма чисел первой строки;
5 + 11 + 10 + 8 = 16 + 18 = 34 − сумма чисел второй строки;
9 + 7 + 6 + 12 = 16 + 18 = 34 − сумма чисел третьей строки;
4 + 14 + 15 + 1 = 18 + 16 = 34 − сумма чисел четвертой строки;
16 + 5 + 9 + 4 = 21 + 13 = 34 − сумма чисел первого столбца;
2 + 11 + 7 + 14 = 13 + 21 = 34 − сумма чисел второго столбца;
3 + 10 + 6 + 15 = 13 + 21 = 34 − сумма чисел третьего столбца;
13 + 8 + 12 + 1 = 21 + 13 = 34 − сумма чисел четвертого столбца;
16 + 11 + 6 + 1 = 27 + 7 = 34 − сумма чисел первой диагонали;
4 + 7 + 10 + 13 = 11 + 23 = 34 − сумма чисел второй диагонали;
11 + 10 + 7 + 6 = 21 + 13 = 34 − сумма чисел центрального квадрата;
16 + 2 + 5 + 11 = 18 + 16 = 34 − сумма чисел верхнего левого квадрата;
3 + 13 + 10 + 8 = 16 + 18 = 34 − сумма чисел верхнего правого квадрата;
9 + 7 + 4 + 14 = 16 + 18 = 34 − сумма чисел нижнего левого квадрата;
6 + 12 + 15 + 1 = 18 + 16 = 34 − сумма чисел нижнего правого квадрата.
Да, получился магический квадрат.

75

Последняя цифра

1. Найдите последнюю цифру суммы или произведения:
а) 151 + 152 + 153 + 154 + 155 + 156 + 157 + 158 + 159;
б) 151 * 152 * 153 * 154 * 155 * 156 * 157 * 158 * 159;
в) 11 + 12 + 13 + 14 + ... + 29;
г) 11 * 12 * 13 * ... * 29.

Решение:

а) 151 + 152 + 153 + 154 + 155 + 156 + 157 + 158 + 159
Сложим последние цифры каждого слагаемого:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 3 + 7 + 11 + 15 + 9 = 10 + 26 + 9 = 36 + 9 = 45 − значит последняя цифра суммы равна 5.
Ответ: 5

б) 151 * 152 * 153 * 154 * 155 * 156 * 157 * 158 * 159
Умножим последние цифры каждого множителя:
1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 = (2 * 5) * (1 * 3 * 4 * 6 * 7 * 8 * 9) = 10 * (1 * 3 * 4 * 6 * 7 * 8 * 9) − значит последняя цифра произведения равна 0, так как один из множителей равен 10.
Ответ: 0

в) 11 + 12 + 13 + 14 + ... + 29
Сложим последние цифры каждого слагаемого:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 2 * (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) = 2 * 45 = 90 − значит последняя цифра суммы равна 0.
Ответ: 0

г) 11 * 12 * 13 * ... * 29
Умножим последние цифры каждого множителя:
1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 0 * 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 = 0 − значит последняя цифра произведения равна 0.
Ответ: 0

2. Найдите последние цифры значений выражений:
а) 12 * 123 + 13 * 134 + 14 * 145 + 15 * 156 + 16 * 167 + 17 * 178;
б) 154 * 628 + 814 * 318 + 774 * 458 + 314 * 398 + 654 * 218.

Решение:

а) 12 * 123 + 13 * 134 + 14 * 145 + 15 * 156 + 16 * 167 + 17 * 178
Найдем последние цифры в каждом из произведений и получим:
6 + 2 + 0 + 0 + 2 + 6 = 16 − значит последняя цифра значения выражения равна 6.
Ответ: 6

б) 154 * 628 + 814 * 318 + 774 * 458 + 314 * 398 + 654 * 218
Найдем последние цифры в каждом из произведений и получим:
2 + 2 + 2 + 2 + 2 = 10 − значит последняя цифра значения выражения равна 0.
Ответ: 0

3. Найдите последние цифры значений выражений:
а) 12 * 123 − 13 * 134 + 14 * 1415 − 15 * 156 + 16 * 167;
б) 154 * 628 − 814 * 318 + 774 * 458 − 314 * 398 + 654 * 218.

Решение:

а) 12 * 123 − 13 * 134 + 14 * 1415 − 15 * 156 + 16 * 167
Найдем последние цифры в каждом из произведений и получим:
6 − 2 + 0 − 0 + 2 = 6 − значит последняя цифра значения выражения равна 6.
Ответ: 6

б) 154 * 628 − 814 * 318 + 774 * 458 − 314 * 398 + 654 * 218
Найдем последние цифры в каждом из произведений и получим:
2 − 2 + 2 − 2 + 2 = 2 − значит последняя цифра значения выражения равна 2.
Ответ: 2

4. Продолжите фразу:
а) Квадрат натурального числа может оканчиваться цифрами ...
б) Куб натурального числа может оканчиваться цифрами ...

Решение:

а) Так как последняя цифра натурального числа моежт быть от 0 до 9, то:
$0^2 = 0$
$1^2 = 1$
$2^2 = 4$
$3^2 = 9$
$4^2 = 16$
$5^2 = 25$
$6^2 = 36$
$7^2 = 49$
$8^2 = 64$
$9^2 = 81$
Значит:
Квадрат натурального числа может оканчиваться цифрами 0, 1, 4, 5, 6, 9.

б) Так как последняя цифра натурального числа моежт быть от 0 до 9, то:
$0^3 = 0$
$1^3 = 1$
$2^3 = 8$
$3^3 = 27$
$4^3 = 64$
$5^3 = 125$
$6^3 = 216$
$7^3 = 343$
$8^3 = 512$
$9^3 = 729$
Значит:
Куб натурального числа может оканчиваться цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

5. а) Среди чисел 18 * 96, 22 * 88, 51 * 97 одно является квадратом натурального числа. Какое?
б) Какое из чисел 76 * 19, 98 * 18, 85 * 20 не является квадратом натурального числа?

Решение:

а) Найдем последние цифры каждого произведения:
8 * 6 = 48 − значит последняя цифра произведния 18 * 96 равна 8;
2 * 8 = 16 − значит последняя цифра произведения 22 * 88 равна 6;
1 * 7 = 7 − значит последняя цифра произведения 51 * 97 равна 7.
Квадрат натурального числа может оканчиваться цифрами 0, 1, 4, 5, 6, 9, значит произведение чисел 22 * 88 является квадратом натурального числа.
Ответ: 22 * 88.

б) Найдем последние цифры каждого произведения:
6 * 9 = 54 − значит последняя цифра произведния 76 * 19 равна 4;
8 * 8 = 64 − значит последняя цифра произведния 98 * 18 равна 4;
5 * 0 = 0 − значит последняя цифра произведния 85 * 20 равна 0.
Квадрат натурального числа может оканчиваться цифрами 0, 1, 4, 5, 6, 9, однако он не может оканчиваться одним нулем, так как $10^2 = 100, 20^2 = 400$ и т.д. Поэтому произведение чисел 85 * 20 не является квадратом натурального числа.
Ответ: 85 * 20.

76

6. Замените многоточие любым числом так, чтобы получилось верное равенство (там, где это невозможно, объясните почему):
а) ...3 : ...8 = ...2;
б) ...4 : ...6 = ...4;
в) (...3 : ...9 : ...7) * ...4 : ...3 = ...6.

Решение:

а) ...3 : ...8 = ...2
Верное равенство получить невозможно, так как чтобы найти делимое, необходимо частное умножить на делитель. Так как 2 * 8 = 16, значит делитель должен оканчиваться на 6, а не на 3.

б) 224 : 16 = 14

в) (...3 : ...9 : ...7) * ...4 : ...3 = ...6
Верное равенство получить невозможно, так как:
1) Рассмотрим частное ...3 : ...9. При умножении последней цифры частного на последнюю цифру делителя должно получится произведение с последней цифрой 3, значит последняя цифра частного равна 7, так как 7 * 9 = 63.
2) Рассмотрим частное (...3 : ...9) : ...7. Мы выяснили, что последняя цифра частного (...3 : ...9) равна 7, значит последняя цифра частного (...3 : ...9) : ...7 равна 1.
3) Рассмотрим произведение (...3 : ...9 : ...7) * ...4. Мы выяснили, что последняя цифра частного (...3 : ...9) : ...7 равна 1, значит последняя цифра произведения (...3 : ...9 : ...7) * ...4 равна 4.
4) Рассмотрим частное (...3 : ...9 : ...7) * ...4 : ...3 = ...6. Мы выяснили, что последняя цифра произведения (...3 : ...9 : ...7) * ...4 равна 4. Но так как 6 * 3 = 18, то последняя цифра этого произведения должна быть равна 8. Поэтому верное равенство полчить невозможно.

7. Какой цифрой оканчивается:
а) сумма всех однозначных чисел;
б) сумма всех двузначных чисел;
в) сумма всех трехзначных чисел;
г) сумма всех стозначных чисел?

Решение:

а) 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 5 = 10 + 10 + 10 + 10 + 5 = 45 − значит сумма всех однозначных чисел оканчивается цифрой 5.
Ответ: 5

б) 10 + 11 + 12 + 13 ... + 97 + 98 + 99 = 10 + (11 + 99) + (12 + 98) + (13 + 97) + ... 55 = 10 + 110 + 110 + 110 + ... + 55 = ...5 − значит сумма всех двузначных чисел оканчивается цифрой 5.
Ответ: 5

в) 100 + 101 + 102 + 103 + ... + 997 + 998 + 999 = 100 + (101 + 999) + (102 + 998) + (103 + 997) + ... + 550 = 100 + 1100 + 1100 + 1100 + ... + 550 = ...0 − значит сумма всех трехзначных чисел оканчивается цифрой 0.
Ответ: 0

г) Первое стозначное число оканчивается нулем. Второе стозначное число оканчивается 1. Предпоследнее стозначное число оканчивается 9. Тогда сумма последних цифр стозначных чисел будет выглядеть следующим образом:
...0 + ...1 + ...2 + ...3 + ... + ...7 + ...8 + ...9 = ...0 + (...1 + ...9) + (...2 + ...8) + (...3 + ...7) + ... + ...0 = ...0 + ...0 + ...0 + ...0 + ... + ...0 = ...0 − значит сумма всех стозначных чисел оканчивается цифрой 0.
Ответ: 0

8. Какой цифрой оканчивается:
а) произведение всех однозначных чисел, не равных нулю;
б) произведение всех трехзначных чисел;
в) произведение всех стозначных чисел?

Решение:

а) 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 = (2 * 5) * (1 * 3 * 4 * 6 * 7 * 8 * 9) = 10 * (1 * 3 * 4 * 6 * 7 * 8 * 9) − значит произведение всех однозначных чисел, не равных нулю, оканчивается на 0, так как один из множителей оканчивается на 0.
Ответ: 0

б) 100 * 101 * 102 * 103 * ... * 997 * 998 * 999 − значит произведение всех трехзначных чисел, оканчивается на 0, так как один из множителей оканчивается на 0.
Ответ: 0

в) Первое стозначное число оканчивается на 0, значит и произведение всех стозначных чисел оканчивается на 0, так как один из множителей оканчивается на 0.
Ответ: 0

9. Найдите первую, не равную нулю цифру справа в произведении:
а) первых семи натуральных чисел;
б) первых десяти натуральных чисел;
в) первых шестнадцати натуральных чисел;
г) первых двадцати натуральных чисел.

Решение:

а) 1 * 2 * 3 * 4 * 5 * 6 * 7 = (2 * 5) * (3 * 4) * (6 * 7) = 10 * 12 * 42 = ...2 * ...2 * ...0 = ...40 − значит последняя цифра, не равная нулю справа в произведении первых семи натуральных чисел равна 4.
Ответ: 4

б) 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 = (3 * 4) * (6 * 7) * (8 * 9) * (2 * 5) * 10 = ...2 * ...2 * ...2 * ...0 * ...0 = ...800 − значит последняя цифра, не равная нулю справа в произведении первых десяти натуральных чисел равна 8
Ответ: 8

в) 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 * 11 * 12 * 13 * 14 * 15 * 16 = (2 * 5) * (4 * 15) * 10 * (3 * 6) * (7 * 8) * (9 * 11) * (12 * 13) * (14 * 16) = ...0 * ...0 * ...0 * ...8 * ...6 * ...9 * ...6 * ...4 = ...8 * ...4 * ...4 * ...000 = ...2 * ...4 * ...000 = ...8000 − значит 8 последняя цифра, не равная нулю справа в произведении первых шестнадцати натуральных чисел.
Ответ: 8

г) 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 * 11 * 12 * 13 * 14 * 15 * 16 * 17 * 18 * 19 * 20 = (2 * 5) * (4 * 15) * 10 * (3 * 6) * (7 * 8) * (9 * 11) * (12 * 13) * (14 * 16) * (17 * 18) * 19 * 2 * 10 = ...0 * ...0 * ...0 * ...8 * ...6 * ...9 * ...6 * ...4 * ...6 * ...9 = ...8 * ...4 * ...4 * ...9 * ...2 * ...0000 = ...2 * ...6 * ...2 * ...0000 = ...2 * ...2 * ...0000 = ...40000 − значит 4 последняя цифра, не равная нулю справа в произведении первых шестнадцати натуральных чисел.
Ответ: 4

10. Найдите последнюю цифру:
а) 1999 * 1999 * 1999 * 1999 * 1999 * 1999 * 1999;
б) $2009^5$;
в) $9999^{10}$.

Решение:

а)1999 * 1999 * 1999 * 1999 * 1999 * 1999 * 1999 = ...9 * ...9 * ...9 * ...9 * ...9 * ...9 * ...9 = ...1 * ...1 * ...1 * ...9 = ...9
Ответ: 9

б) $2009^5 = ...9 * ...9 * ...9 * ...9 * ...9 = ...1 * ...1 * ...9 = ...9$
Ответ: 9

в) $9999^{10} = ...9 * ...9 * ...9 * ...9 * ...9 * ...9 * ...9 * ...9 * ...9 * ...9 = ...1 * ...1 * ...1 * ...1 * ...1 * ...1 * ...1 * ...1 * ...1 * ...1 = ...1$
Ответ: 1

77

Фигурные числа

1. Изобразите в тетради первые восемь треугольных чисел, а затем выпишите числа в ряд одно за другим.
А можно ли продолжить выписывать треугольные числа, не обращаясь к рисунку? Сделать это совсем просто, если понять правило, по которому каждое следующее число получается из предыдущего. Посмотрите еще раз на рисунок: чтобы изобразить второе число, мы добавили к первому треугольнику 2 шара; чтобы изобразить третье число, мы добавили к предыдущему 3 шара; чтобы получить четвертое число, к предыдущему треугольнику добавили 4 шара и т.д. Понятно, что если мы хотим найти, например, девятое треугольное число, то надо к предыдущему, т.е. к в восьмому, треугольнику добавить 9 шаров.

Решение:

1, 3, 6, 10, 15, 21, 28, 36.

2. Пользуясь замеченной закономерностью, выпишите в ряд первые пятнадцать треугольных чисел.
а) Шары укладывают в равносторонние треугольники. В пятнадцатом треугольнике 120 шаров. Сколько шаров в шестнадцатом треугольнике? в четырнадцатом?
б) Заполните часть таблицы треугольных чисел.

​

Номер числа	17	18	19	20	21	22	23	24	25
Треугольное число				210

 

Решение:

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120.
а) 120 + 16 = 136 (шаров) − в шестнадцатом треугольнике.
     120 − 15 = 105 (шаров) − в четырнадцатом треугольнике.
б)

Номер числа	17	18	19	20	21	22	23	24	25
Треугольное число	153	171	190	210	231	253	276	300	325

 

78

3. а) Шары уложили в равносторонний треугольник, в котором 25 рядов. Сколько потребовалось шаров?
    б) Чему равно треугольное число с номером 35? с номером 50? с номером 1000?

Решение:

а) 1 + 2 + 3 + ... + 24 + 25 = ((25 + 1) * 25) : 2 = (26 * 25) : 2 = 650 : 2 = 325 (шаров) − потребовалось.
Ответ: 325 шаров

б) 1) 1 + 2 + 3 + ... + 34 + 35 = ((1 + 35) * 35) : 2 = (36 * 35) : 2 = 1260 : 2 = 630 − треугольное число с номером 35;
2) 1 + 2 + 3 + ... + 49 + 50 = ((1 + 50) * 50) : 2 = (51 * 50) : 2 = 2550 : 2 = 1275 − треугольное число с номером 50;
3) 1 + 2 + 3 + ... + 999 + 1000 = ((1 + 1000) * 1000) : 2 = (1001 * 1000) : 2 = 1001000 : 2 = 500500 − треугольное число с номером 1000.
Ответ: 35; 50; 1000.

4. Является ли треугольным число 64? число 91?

Решение:

Запишем ряд треугольных чисел:
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, ...
Значит:
число 64 − не является треугольным;
число 91 − является треугольным.

5. В каком порядке идут четные и нечетные числа в последовательности треугольных чисел? Четным или нечетным является число с номером 17, 18, 19, 20? Четным или нечетным является число с номером 60, 78, 35?

Решение:

Последовательность треугольных чисел начинается с двух нечетных чисел, затем идут два четных числа, затем два нечетных и так далее.
Получается, что через каждые четыре числа последовательность нечетных и четных чисел повторяется, поэтому, чтобы определить четным или нечетным является число его нужно поделить на 4. Если число делится с остатком 1 или 2, то оно нечетное. Если число делится с остатком 3, либо без остатка, то оно четное.
Тогда:
17 : 4 = 4 (ост.1) − число нечетное;
18 : 4 = 4 (ост.2) − число нечетное;
19 : 4 = 4 (ост.3) − число четное;
20 : 4 = 5 − число четное;
60 : 4 = 15 − число четное;
78 : 4 = 19 (ост.2) − число нечетное;
35 : 4 = 8 (ост.3) − число четное.

6. Представьте число 35 в виде суммы нескольких треугольных чисел. Сделайте рисунок.
■ Поговорим теперь о числах, называемых квадратными. На рисунке 2 изображены первые четыре квадратных числа 1: 1, 4, 9, 16. А как изобразить пятое квадратное число? Сделайте это.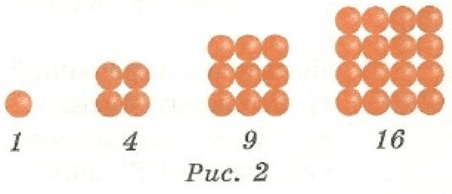

Решение:

1 + 3 + 6 + 10 + 15 = 35

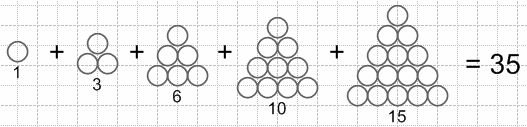
■ Чтобы изобразить пятое квадратное число нужно к четвертому квадратном числу прибавить одну строку и один столбец. В пятом квадратном числе должно быть 5 строк и 5 столбцов.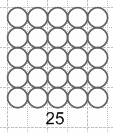

7. Запишите в тетради первые десять квадратных чисел.

Решение:

Номер числа	1	2	3	4	5	6	7	8	9	10
Квадратное число	1	4	9	16	25	36	49	64	81	100

 

8. Найдите двадцатое, двадцать пятое и сороковое квадратные числа.

Решение:

$20^2 = 400$ − двадцатое квадратное число;
$25^2 = 625$ − двадцать пятое квадратное число;
$40^2 = 1600$ − сороковое квадратное число.

9. Представьте число 30 в виде суммы нескольких квадратных чисел. Сделайте рисунок.
■ Великий древнегреческий ученый Диофант (III в. н.э.) нашел закономерность, связывающую треугольные числа с квадратными числами: если треугольное число умножить на 8 и к произведению прибавить 1, то получится квадратное число. Коротко это можно записать так:
треугольное число * 8 + 1 = квадратное число.
Проверьте эту закономерность для нескольких первых квадратных чисел. Вы видели, что треугольные числа получаются суммированием последовательных натуральных чисел. А квадратные числа получаются суммированием последовательных нечетных чисел. В самом деле,
1 + 3 = 4,
1 + 3 + 5 = 9,
1 + 3 + 5 + 7 = 16,
1 + 3 + 5 + 7 + 9 = 25 и т.д.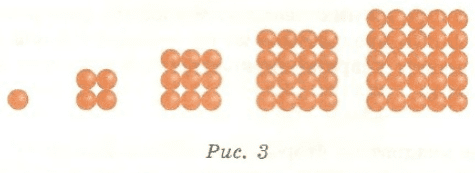

Решение:

1 + 4 + 9 + 16 = 30

■
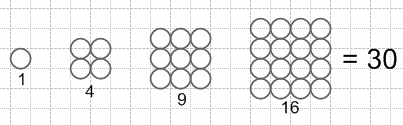
1 * 8 + 1 = 8 + 1 = 9
3 * 8 + 1 = 24 + 1 = 25
6 * 8 + 1 = 48 + 1 = 49
10 * 8 + 1 = 80 + 1 = 81

79

10. Представьте в виде суммы последовательных нечетных чисел квадратные числа 81, 100, 169.

Решение:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 11 + 13 + 15 + 17 = 81
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 11 + 13 + 15 + 17 + 19 = 100
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 = 169

Разрезаем квадрат

1. Начертите в тетради какой−нибудь квадрат и разрежьте его прямой на два одинаковых:
а) прямоугольника;
б) треугольника.
Проведите еще одну прямую так, чтобы разрезать квадрат на четыре одинаковые части.

Решение:

а)            б)

80

2. а) Найдите все возможные фигуры, которые можно составить из четырех одинаковых квадратов. Для этого начните с самого простого случая − "уложите" все четыре квадрата в один ряд, а затем рассмотрите другие варианты. Зарисуйте получившиеся фигуры. У вас должно получиться пять различных фигур.
б) Вырежьте по четыре экземпляра каждой фигуры (см.задание а) и попробуйте составить из них квадрат. Из каких фигур нельзя составить квадрат? Из каких фигур квадрат можно составить несколькими способами? Зарисуйте все варианты разрезания квадрата со стороной 4 клетки на четыре одинаковые части.

Решение:

а)

б) Квадрат можно составить из фигур:

Квадрат нельзя составить из фигуры:

Варианты разрезания квадрата:

3. Можно ли квадрат со стороной 5 клеток разрезать на две одинаковые части так, чтобы линия разреза проходила по сторонам клеток?

Решение:

5 * 5 = 25 клеток всего в квадрате со стороной 5 клеток.
25 − число нечетное, значит оно не делится без остатка на 2. Значит такой квадрат нельзя разрезать на две одинаковые части без разрезания хотя бы одной клетки пополам.
Ответ: нет, нельзя

4. Разрежьте квадрат (рис.2) на четыре одинаковые части, проводя линии разреза по сторонам клеток так, чтобы в каждой части было по одному крестику.

Решение:

а)             б)           в)

5. На какое наименьшее число квадратов вы можете разрезать квадрат со стороной 13 клеток, если разрезы следует проводить только по сторонам клеток? Наибольшее число, очевидно, равно 169 − числу отдельных клеток. Наименьшее число равно 11. Попробуйте найти это решение.

Решение:

81

Четно или нечетно

1. Четным или нечетным числом является сумма:
а) 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29;
б) 11 + 15 + 19 + 23 + 27 + 31 + 35;
в) 99 + 78 + 97 + 43 + 85 + 64 + 15 + 70?

Решение:

а) 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29
Сумма состоит из 10−и (четного количества) нечетных слагаемых, значит сумма является числом четным.
Ответ: четное.

б) 11 + 15 + 19 + 23 + 27 + 31 + 35
Сумма состоит из 7−и (нечетного количества) нечетных слагаемых, значит сумма является числом нечетным.
Ответ: нечетное.

в) 99 + 78 + 97 + 43 + 85 + 64 + 15 + 70 = (99 + 97 + 43 + 85 + 15) + (78 + 64 + 70)
99 + 97 + 43 + 85 + 15 − число нечетное, так как состоит из 5−и (нечетного количества) нечетных слагаемых;
78 + 64 + 70 − число четное, так как сумма четных слагаемых всегда число четное.
(99 + 97 + 43 + 85 + 15) + (78 + 64 + 70) − число нечетное, так как сумма нечетного и четного чисел, число нечетное.
Ответ: нечетное.

2. Четным или нечетным числом является сумма:
а) всех чисел от 1 до 100;
б) всех нечетных чисел от 1 до 90;
в) всех нечетных чисел от 1 до 49?

Решение:

а) 100 : 2 = 50 − нечетных чисел в ряде чисел от 1 до 100, значит сумма всех чисел от 1 до 100 является числом четным.

б) 90 : 2 = 45 − нечетных чисел в ряде чисел от 1 до 90, значит сумма всех чисел от 1 до 90 является числом нечетным.

в) 48 : 2 + 1 = 24 + 1 = 25 − нечетных чисел в ряде чисел от 1 до 49, значит сумма всех чисел от 1 до 49 является числом нечетным.

3. Четным или нечетным числом является произведение:
а) 11 * 13 * 15 * 17 * 19;
б) 11 * 12 * 13?

Решение:

а) 11 * 13 * 15 * 17 * 19 − число нечетное, так как произведение нечетных чисел число нечетное.

б) 11 * 12 * 13 = 11 * 2 * 6 * 13 = 2 * (11 * 6 * 13) − число четное, так как один из множитель равен 2.

82

4. Четным или нечетным будут сумма и произведение:
а) простых однозначных чисел;
б) двух последовательных натуральных чисел;
в) пяти последовательных нечетных чисел?

Решение:

а) Простые однозначные числа: 2, 3, 5, 7, тогда:
2 + 3 + 5 + 7 − число нечетное;
2 * 3 * 5 * 7 − число четное.

б) Так как два последовательных числа последовательны, значит одно числи четное, а второе нечетное. Поэтому:
сумма этих чисел − число нечетное;
произведение этих чисел − число четное.

в) Сумма пяти последовательных нечетных чисел будет числом нечетным, так как количество слагаемых нечетно.
Произведение пяти последовательных нечетных чисел будет числом нечетным, так как произведение нечетных чисел − число нечетное.

5. Что можно сказать о двух числах, если известно, что:
а) их сумма четна;
б) их произведение четно;
в) их сумма и произведение четны;
г) их сумма нечетна;
д) их произведение нечетно;
е) их сумма и произведение нечетны?

Решение:

а) Можно сказать, что это либо два четных, либо два нечетных числа.
б) Можно сказать, что из этих двух чисел как минимум одно число обязательно четное.
в) Можно сказать что это два четных числа.
г) Можно сказать, что одно число четное, а второе нечетное.
д) Можно сказать что это два нечетных числа.
е) Такое невозможно.

6. Сумма трех натуральных чисел − число четное. Четным или нечетным числом является их произведение? А что можно сказать о произведении трех чисел, если их сумма − число нечетное?

Решение:

Так как сумма трех натуральных чисел − число четное, значит сумма состоит из трех четных слагаемых, либо из одного четного и двух нечетных слагаемых.
Так как сумма трех натуральных чисел имеет как минимум одно четное слагаемое, значит произведение этих чисел − число четное.

Так как сумма трех натуральных чисел − число нечетное, значит сумма состоит из трех нечетных слагаемых, либо из двух четных и одного нечетного слагаемых.
Так как сумма трех натуральных чисел может иметь, а может не иметь четных слагаемых, значит произведение этих чисел может быть как четным, так и нечетным числом.

7. Какой знак ("+" или "−") стоит в выражении:
а) 87 − 86 + 85 − 84 + ... − 2 + 1 перед числом 35;
б) 68 − 66 + 64 − 62 + ... + 4 − 2 перед числом 38?

Решение:

а) 87 − 86 + 85 − 84 + ... − 2 + 1
В выражении перед четными числами стоит знак "−", а перед нечетными стоит знак "+" . Значит перед числом 35 стоит знак "+", так как это число нечетное.
Ответ: "+"

б) 68 − 66 + 64 − 62 + ... + 4 − 2
В выражении перед числами, кратными 4, стоит знак "+", а перед остальными знак "−". Значит перед число 38 стоит знак "−", так как это число не кратно 4.
Ответ: "−"

8. В последовательности натуральных чисел 1, 1, 2, 3, 5 ,8, 13, 21, ... каждое число, начиная с третьего, равно сумме двух предыдущих. Каких чисел больше среди первых 12 чисел этой последовательности − четных или нечетных? Четным или нечетным числом является число, стоящее в последовательности под номером:
а) 15;
б) 96;
в) 1000?

Решение:

В последовательности 1, 1, 2, 3, 5 ,8, 13, 21, ... каждое третье число четное, а остальные нечетные. То есть в каждой тройке чисел: 2 нечетных числа и одно четное. Значит среди первых 12 чисел больше нечетных чисел, чем четных. Так как четное число стоит под номером, кратным числу 3, то оно будет четным если порядковый номер числа будет делиться на 3 без остатка и нечетным, если на 3 без остатка оно делиться не будет.
Тогда:
а) 15 : 3 = 5 − значит число под номером 15 является четным;
б) 96 : 3 = 32 − значит число под номером 96 является четным;
в) 1000 : 3 = 333 (ост.1) − значит число под номером 100 является нечетным.
Ответ:
а) четное;
б) четное;
в) нечетное.

83

Построения на клетчатой бумаге

1. 1) Проведен отрезок AB и отмечена точка O (рис.4). Не пользуясь делениями линейки, постройте какой−нибудь отрезок, равный AB, один конец которого расположен в точке O, а другой − в узле сетки.
2) Найдите все такие отрезки.

Решение:

1) Отрезок AB является диагональю прямоугольника. Нарисуем его.
Нарисуем такой же прямоугольник так, чтобы точка O была одним из его углов, а противоположный угол находился в узле сетки.
Проведем диагональ из точки O в противоположный угол прямоугольника.


2) Найдем все такие отрезки поворачивая прямоугольник вокруг точки O.

2. Постройте отрезок AC так, чтобы угол BAC был прямым (см.рис.5).

Решение:

∠BAC = 90°

3. Отрезок AB (рис.6) − сторона квадрата. Постройте этот квадрат.

Решение:

4. Луч BC (рис.7) − сторона угла. Постройте угол ABC, равный 45°. (Указание. Сначала постройте квадрат со стороной BC.)

Решение:

5. Отрезок AB (рис.8) − боковая сторона равнобедренного треугольника. Перенесите рисунок в тетрадь и постройте какой−нибудь равнобедренный треугольник со стороной AB, вершины которого лежат в узлах квадратной сетки. Сколько таких треугольников можно построить?

Решение:

Можно построить четыре таких треугольника: ABC, ABD, ABE, ABF.

6. Постройте какие−нибудь точки C и O так, чтобы у четырехугольника ABCO были равны все четыре стороны (см.рис.8).

Решение:

7. Найдите середину отрезка AB (рис.9).

Решение:

Точка O − середина отрезка AB.

84

Находим НОД и НОК

1. Найдите наибольший общий делитель чисел: 875 и 1225; 60, 132 и 240.

Решение:

875 и 1225
$ \begin{array}{r|l} 875 & 5\\ 175 & 5\\ 35 & 5\\ 7 & 7\\ 1 & \end{array} $
875 = 5 * 5 * 5 * 7

$ \begin{array}{r|l} 1225 & 5\\ 245 & 5\\ 49 & 7\\ 7 & 7\\ 1 & \end{array} $
1225 = 5 * 5 * 7 * 7
НОД(875; 1225) = 5 * 5 * 7 = 25 * 7 = 175

60, 132 и 240
$ \begin{array}{r|l} 60 & 2\\ 30 & 2\\ 15 & 3\\ 5 & 5\\ 1 & \end{array} $
60 = 2 * 2 * 3 * 5

$ \begin{array}{r|l} 132 & 2\\ 66 & 2\\ 33 & 3\\ 11 & 11\\ 1 & \end{array} $
132 = 2 * 2 * 3 * 11

$ \begin{array}{r|l} 240 & 2\\ 120 & 2\\ 60 & 2\\ 30 & 2\\ 15 & 3\\ 5 & 5\\ 1 & \end{array} $
240 = 2 * 2 * 2 * 2 * 3 * 5
НОД(60; 132; 240) = 2 * 2 * 3 = 4 * 3 = 12

2. Найдите НОД (a;b) и НОК (a;b), если $a = 2^2 * 3^5 * 7, b = 2^3 * 3^3 * 7^2.$

Решение:

$a = 2^2 * 3^5 * 7$
$b = 2^3 * 3^3 * 7^2$
$НОД (a;b) = 2^2 * 3^3 * 7$
$НОК (a;b) = 2^3 * 3^5 * 7^2$

3. Найдите наименьшее общее кратное чисел:
а) 1764 и 1890;
б) 24, 75 и 80.

Решение:

а) 1764 и 1890
$ \begin{array}{r|l} 1764 & 2\\ 882 & 2\\ 441 & 3\\ 147 & 3\\ 49 & 7\\ 7 & 7\\ 1 & \end{array} $
$1764 = 2^2 * 3^2 * 7^2$

$ \begin{array}{r|l} 1890 & 2\\ 945 & 3\\ 315 & 3\\ 105 & 3\\ 35 & 5\\ 7 & 7\\ 1 & \end{array} $
$1890 = 2 * 3^3 * 5 * 7$
$НОК = 2^2 * 3^3 * 5 * 7^2 = 26460$

б) 24, 75 и 80.
$ \begin{array}{r|l} 24 & 2\\ 12 & 2\\ 6 & 2\\ 3 & 3\\ 1 & \end{array} $
$24 = 2^3 * 3$

$ \begin{array}{r|l} 75 & 3\\ 25 & 5\\ 5 & 5\\ 1 & \end{array} $
$75 = 3 * 5^2$

$ \begin{array}{r|l} 80 & 2\\ 40 & 2\\ 20 & 2\\ 10 & 2\\ 5 & 5\\ 1 & \end{array} $
$80 = 2^4 * 5$
$НОК = 2^4 * 3 * 5^2 = 1200$

4. Сравните дроби:
а) $\frac{23}{126}$ и $\frac{47}{330}$;
б) $\frac{59}{396}$ и $\frac{121}{840}$.

Решение:

а) $\frac{23}{126}$ и $\frac{47}{330}$
$ \begin{array}{r|l} 126 & 2\\ 63 & 3\\ 21 & 3\\ 7 & 7\\ 1 & \end{array} $
$126 = 2 * 3^2 * 7$

$ \begin{array}{r|l} 330 & 2\\ 165 & 3\\ 55 & 5\\ 11 & 11\\ 1 & \end{array} $
$330 = 2 * 3 * 5 * 11$
$НОК = 2 * 3^2 * 5 * 7 * 11 = 6930$
6930 : 126 = 55
$\frac{23}{126} = \frac{23 * 55}{126 * 55} = \frac{1265}{6930}$
6930 : 330 = 21
$\frac{47}{330} = \frac{47 * 21}{330 * 21} = \frac{987}{6930}$
$\frac{1265}{6930} > \frac{987}{6930}$, значит:
$\frac{23}{126} > \frac{47}{330}$

б) $\frac{59}{396}$ и $\frac{121}{840}$
$ \begin{array}{r|l} 396 & 2\\ 198 & 2\\ 99 & 3\\ 33 & 3\\ 11 & 11\\ 1 & \end{array} $
$396 = 2^2 * 3^2 * 11$

$ \begin{array}{r|l} 840 & 2\\ 420 & 2\\ 210 & 2\\ 105 & 3\\ 35 & 5\\ 7 & 7\\ 1 & \end{array} $
$840 = 2^3 * 3 * 5 * 7$
$НОК = 2^3 * 3^2 * 5 * 7 * 11 = 27720$
27720 : 396 = 70
$\frac{59}{396} = \frac{59 * 70}{396 * 70} = \frac{4130}{27720}$
27720 : 840 = 33
$\frac{121}{840} = \frac{121 * 33}{840 * 33} = \frac{3993}{27720}$
$\frac{4130}{27720} > \frac{3993}{27720}$, значит:
$\frac{59}{396} > \frac{121}{840}$

5. Найдите какое−нибудь число, расположенное между числами $\frac{41}{1680}$ и $\frac{19}{720}$.

Решение:

$\frac{41}{1680}$ и $\frac{19}{720}$
$ \begin{array}{r|l} 1680 & 2\\ 840 & 2\\ 420 & 2\\ 210 & 2\\ 105 & 3\\ 35 & 5\\ 7 & 7\\ 1 & \end{array} $
$1680 = 2^4 * 3 * 5 * 7$

$ \begin{array}{r|l} 720 & 2\\ 360 & 2\\ 180 & 2\\ 90 & 2\\ 45 & 3\\ 15 & 3\\ 5 & 5\\ 1 & \end{array} $
$720 = 2^4 * 3^2 * 5$
$НОК(720; 1680) = 2^4 * 3^2 * 5 * 7 = 5040$
5040 : 1680 = 3
$\frac{41}{1680} = \frac{41 * 3}{1680 * 3} = \frac{123}{5040}$
5040 : 720 = 7
$\frac{19}{720} = \frac{19 * 7}{720 * 7} = \frac{133}{5040}$
$\frac{123}{5040} < \frac{131}{5040} < \frac{133}{5040}$, значит:
$\frac{41}{1680} < \frac{131}{5040} < \frac{19}{720}$.

6. Числа a и b называют взаимно простыми, если НОД (a;b) = 1. Покажите, что числа 50 и 189 являются взаимно простыми. Найдите НОК (50;189). Чему равно НОК (a;b), если a и b − взаимно простые числа?

Решение:

$ \begin{array}{r|l} 50 & 2\\ 25 & 5\\ 5 & 5\\ 1 & \end{array} $
$50 = 2 * 5^2$

$ \begin{array}{r|l} 189 & 3\\ 63 & 3\\ 21 & 3\\ 7 & 7\\ 1 & \end{array} $
$189 = 3^3 * 7$
$НОК(50; 189) = 2 * 3^3 * 5^2 * 7 = 9450$
Наименьшим общим кратным взаимно простых чисел является произведение этих чисел.

85

Старинные задачи на дроби

1. Из папируса Ахмеса (Египет, ок.2000 лет до н.э.).
Приходит пастух с 70 быками. Его спрашивают:
−Сколько приводишь ты из своего многочисленного стада?
Пастух отвечает:
−Я привожу две трети от трети скота. Сочти, сколько быков в стаде.

Решение:

1) 70 : 2 * 3 = 35 * 3 = 105 (б.) − составляет треть скота;
2) 105 * 3 = 315 (б.) − всего в стаде.
Ответ: 315 быков.

2. В знаменитой книге "1001 ночь" мудрец задает юной деве следующую задачу: "Одна женщина отправилась в сад собирать яблоки. Чтобы выйти из сада, ей нужно было пройти через четыре двери, у каждой из которых стоял стражник. Стражнику у первых дверей женщина отдала половину сорванных ею яблок. Дойдя до второго стражника, женщина отдала половину сорванных ею яблок. Так же она поступила и с третьим стражником, а когда она поделилась яблоками со стражником у четвертых дверей, то у нее осталось лишь 10 яблок. Сколько яблок она собрала в саду?"

Решение:

1) 10 * 2 = 20 (ябл.) − оставалось у женщины после третьего стражника;
2) 20 * 2 = 40 (ябл.) − оставалось у женщины после второго стражника;
3) 40 * 2 = 80 (ябл.) − оставалось у женщины после первого стражника;
4) 80 * 2 = 160 (ябл.) − женщина собрала в саду.
Ответ: 160 яблок.

86

3. Из книги "Косс" Адама Ризе (XVIв.). Трое выиграли некоторую сумму денег. На долю первого пришлась $\frac{1}{4}$ этой суммы, на долю второго − $\frac{1}{7}$, а на долю третьего − 17 флоринов. Как велик весь выигрыш?

Решение:

Пусть вся сумма равна 1, тогда:
1) $1 - (\frac{1}{4} + \frac{1}{7}) = 1 - (\frac{7}{28} + \frac{4}{28}) = \frac{28}{28} - \frac{11}{28} = \frac{17}{28}$ (суммы) − составляют 17 флоринов;
2) $17 : \frac{17}{28} = 17 * \frac{28}{17} = 1 * \frac{28}{1} = 28$ (флоринов) − составляет весь выигрыш.
Ответ: 28 флоринов.

4. (Брахмагупта, Индия, около 600 г.) Слониха, слоненок и слон пришли к озеру, чтобы напиться воды. Слон может выпить озеро за 3 ч, слониха − за 5 ч, а слоненок − за 6 ч. За сколько времени они все вместе выпьют озеро?

Решение:

Все озеро равно 1, тогда:
1) $1 : 3 = \frac{1}{3}$ (оз.) − может выпить слон за 1 час;
2) $1 : 5 = \frac{1}{5}$ (оз.) − может выпить слониха за 1 час;
3) $1 : 6 = \frac{1}{6}$ (оз.) − может выпить слоненок за 1 час;
4) $\frac{1}{3} + \frac{1}{5} + \frac{1}{6} = \frac{10}{30} + \frac{6}{30} + \frac{5}{30} = \frac{21}{30} = \frac{7}{10}$ (оз.) − выпивают они втроем за 1 час;
5) $1 : \frac{7}{10} = 1 * \frac{10}{7} = 1\frac{3}{7}$ (ч) − время за которое они все вместе выпьют озеро.
Ответ: за $1\frac{3}{7}$ часа.

5. Из "Арифметики" Л.Ф.Магницкого (Россия, XVIII в.). Лошадь съедает воз сена за месяц, коза − за два месяца, овца − за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?

Решение:

Пусть весь воз сена равен 1, тогда:
1) 1 : 1 = 1 (воз) − сена съедает лошадь за 1 месяц;
2) $1 : 2 = \frac{1}{2}$ (воза) − сена съедает коза за 1 месяц;
3) $1 : 3 = \frac{1}{3}$ (воза) − сена съедает овца за 1 месяц;
4) $1 + \frac{1}{2} + \frac{1}{3} = 1 + \frac{3}{6} + \frac{2}{6} = 1\frac{5}{6}$ (воза) − сена съедают лошадь, коза и овца вместе за 1 месяц;
5) $1 : 1\frac{5}{6} = 1 : \frac{11}{6} = 1 * \frac{6}{11} = \frac{6}{11}$ (месяца) − потребуется лошади, козе и овце, чтобы вместе съесть стог сена.
Ответ: за $\frac{6}{11}$ месяца.

6. (Древняя Греция, Герон Александрийский, I в. н.э.) Бассейн может заполняться через четыре фонтана. Если открыть только первый фонтан, бассейн наполнится за день, только второй − за 2 дня, только третий − за 3 дня, только четвертый − за 4 дня. За какое время наполнится бассейн, если открыть все четыре фонтана?

Решение:

Пусть весь бассейн равен 1, тогда:
1) 1 : 1 = 1 (бассейн) − заполнит первый фонтан за день;
2) $1 : 2 = \frac{1}{2}$ (бассейна) − заполнит второй фонтан за день;
3) $1 : 3 = \frac{1}{3}$ (бассейна) − заполнит третий фонтан за день;
4) $1 : 4 = \frac{1}{4}$ (бассейна) − заполнит четвертый фонтан за день;
5) $1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} = 1 + \frac{6}{12} + \frac{4}{12} + \frac{3}{12} = 1 + \frac{13}{12} = 1 + 1\frac{1}{12} = 2\frac{1}{12}$ (бассейна) − наполнят все четыре фонтана за день;
6) $1 : 2\frac{1}{12} = 1 : \frac{25}{12} = 1 * \frac{12}{25} = \frac{12}{25}$ (дня) − потребуется четырем фонтанам, чтобы наполнить бассейн.
Ответ: за $\frac{12}{25}$ дня.

87

Модели многогранников

1. 1) На рисунке 1 показано, как можно сложить куб с длиной ребра 3 см из полоски бумаги шириной 3 см и длиной 21 см. Рассмотрите рисунок, вырежете полоску бумаги указанного размера и сложите из нее куб.
2) Сколько квадратов должна содержать полоска бумаги, окрашенная с одной стороны в красный цвет, чтобы сложить из нее куб с шестью красными гранями?

Решение:

1) Сложите куб по рисунку.
2) В задании 1 цветом было окрашено 7 квадратов, при этом две грани куба остались неокрашенными. Поэтому 9 квадратов должна содержать полоска бумаги, окрашенная с одной стороны в красный цвет, чтобы сложить из нее куб с шестью красными гранями.

2. Изготовьте модель треугольной пирамиды описанным выше способом.

Решение:

На рисунке 2,а изображена, как вы уже знаете развертка пирамиды. Но если из нее свернуть пирамиду, то некоторые ребра будут "открытыми". Чтобы избежать этого, нам потребуется вторая полоска (рис.2,б).
• Движением к себе слегка согните полоски по пунктирным линиям.
• Наложите одну полоску на другую так, чтобы у них совпало по одному треугольнику (рис.2,в).
• Согните нижнюю полоску в форме пирамиды.
• После этого верхний полоской оберните две рани получившейся пирамиды, а последний концевой треугольник заправьте в образовавшуюся щель.

3. 1) Возьмите три полоски бумаги разного цвета, одна из которых изображена на рисунке 3. Движением к себе слегка согните по внутренним линиям. Теперь попробуйте сплести из этих полосок куб.
2) Существует две возможности расположения граней одного цвета. В первом случае одинаково окрашенными оказываются противоположные грани куба, а во втором − соседние грани. Как на вашей модели расположились грани одного цвета? Сплетите еще одну модель с иным расположением граней.

Решение:

Сплетите модель куба и ответьте на вопрос. Плетем по принципу, как показано на рисунке 1.