Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году. В треугольнике ABC известны длины сторон, который вписан в окружность, надо найти значение от вершины до точки пересечения катета и прямой являющейся продолжением высоты к диаметру из другой вершины.

Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2

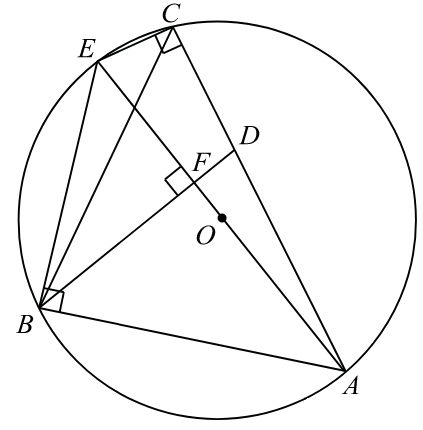
В треугольнике ABC известны длины сторон AB=84, AC=98, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

Решение:

Проведём построения, как показано на рисунке. Угол ABE  — вписанный и опирается на диаметр, значит, угол ABE  — прямой. Рассмотрим треугольники AEB и ABF, они прямоугольные, угол BAE  — общий, следовательно, эти треугольники подобны. Откуда:

$\frac{AE}{AB}=\frac{AB}{AF}\\AB^2=AE\ast AF$

Угол ECA  — вписанный и опирается на диаметр, следовательно, он прямой. Рассмотрим треугольники AEC и AFD, они прямоугольные, угол FAD  — общий, следовательно, эти треугольники подобны. Откуда

$\frac{AE}{AD}=\frac{AC}{AF}\\AD=AE\ast\frac{AF}{AC}$

Подставляя выше найденное равенство:

$AD=\frac{AB^2}{AC}=\frac{84^2}{98}=72$

CD=AC-AD=98-72=26

Ответ: 26

CBF1A6

В треугольнике ABC известны длины сторон AB=40, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

Решение:

Проведём построения, как показано на рисунке. Угол ABE  — вписанный и опирается на диаметр, значит, угол ABE  — прямой. Рассмотрим треугольники AEB и ABF, они прямоугольные, угол BAE  — общий, следовательно, эти треугольники подобны. Откуда:

$\frac{AE}{AB}=\frac{AB}{AF}\\AB^2=AE\ast AF$

Угол ECA  — вписанный и опирается на диаметр, следовательно, он прямой. Рассмотрим треугольники AEC и AFD, они прямоугольные, угол FAD  — общий, следовательно, эти треугольники подобны. Откуда

$\frac{AE}{AD}=\frac{AC}{AF}\\AD=AE\ast\frac{AF}{AC}$

Подставляя выше найденное равенство:

$AD=\frac{AB^2}{AC}=\frac{40^2}{64}=25$

CD=AC-AD=64-25=39

Ответ: 39

B844B3

В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

Решение:

Проведём построения, как показано на рисунке. Угол ABE  — вписанный и опирается на диаметр, значит, угол ABE  — прямой. Рассмотрим треугольники AEB и ABF, они прямоугольные, угол BAE  — общий, следовательно, эти треугольники подобны. Откуда:

$\frac{AE}{AB}=\frac{AB}{AF}\\AB^2=AE\ast AF$

Угол ECA  — вписанный и опирается на диаметр, следовательно, он прямой. Рассмотрим треугольники AEC и AFD, они прямоугольные, угол FAD  — общий, следовательно, эти треугольники подобны. Откуда

$\frac{AE}{AD}=\frac{AC}{AF}\\AD=AE\ast\frac{AF}{AC}$

Подставляя выше найденное равенство:

$AD=\frac{AB^2}{AC}=\frac{30^2}{100}=9$

CD=AC-AD=100-9=91

Ответ: 91

A5F365

В треугольнике ABC известны длины сторон AB=12, AC=72, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

Решение:

Проведём построения, как показано на рисунке. Угол ABE  — вписанный и опирается на диаметр, значит, угол ABE  — прямой. Рассмотрим треугольники AEB и ABF, они прямоугольные, угол BAE  — общий, следовательно, эти треугольники подобны. Откуда:

$\frac{AE}{AB}=\frac{AB}{AF}\\AB^2=AE\ast AF$

Угол ECA  — вписанный и опирается на диаметр, следовательно, он прямой. Рассмотрим треугольники AEC и AFD, они прямоугольные, угол FAD  — общий, следовательно, эти треугольники подобны. Откуда

$\frac{AE}{AD}=\frac{AC}{AF}\\AD=AE\ast\frac{AF}{AC}$

Подставляя выше найденное равенство:

$AD=\frac{AB^2}{AC}=\frac{12^2}{72}=2$

CD=AC-AD=72-2=70

Ответ: 70

108486

В треугольнике ABC известны длины сторон AB=36, AC=54, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

Решение:

Проведём построения, как показано на рисунке. Угол ABE  — вписанный и опирается на диаметр, значит, угол ABE  — прямой. Рассмотрим треугольники AEB и ABF, они прямоугольные, угол BAE  — общий, следовательно, эти треугольники подобны. Откуда:

$\frac{AE}{AB}=\frac{AB}{AF}\\AB^2=AE\ast AF$

Угол ECA  — вписанный и опирается на диаметр, следовательно, он прямой. Рассмотрим треугольники AEC и AFD, они прямоугольные, угол FAD  — общий, следовательно, эти треугольники подобны. Откуда

$\frac{AE}{AD}=\frac{AC}{AF}\\AD=AE\ast\frac{AF}{AC}$

Подставляя выше найденное равенство:

$AD=\frac{AB^2}{AC}=\frac{36^2}{54}=24$

CD=AC-AD=54-24=30

Ответ: 30

DC28AA

В треугольнике ABC известны длины сторон AB=28, AC=56, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

Решение:

Проведём построения, как показано на рисунке. Угол ABE  — вписанный и опирается на диаметр, значит, угол ABE  — прямой. Рассмотрим треугольники AEB и ABF, они прямоугольные, угол BAE  — общий, следовательно, эти треугольники подобны. Откуда:

$\frac{AE}{AB}=\frac{AB}{AF}\\AB^2=AE\ast AF$

Угол ECA  — вписанный и опирается на диаметр, следовательно, он прямой. Рассмотрим треугольники AEC и AFD, они прямоугольные, угол FAD  — общий, следовательно, эти треугольники подобны. Откуда

$\frac{AE}{AD}=\frac{AC}{AF}\\AD=AE\ast\frac{AF}{AC}$

Подставляя выше найденное равенство:

$AD=\frac{AB^2}{AC}=\frac{28^2}{56}=14$

CD=AC-AD=56-14=42

Ответ: 42

F69982

В треугольнике ABC известны длины сторон AB=60, AC=80, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

Решение:

Проведём построения, как показано на рисунке. Угол ABE  — вписанный и опирается на диаметр, значит, угол ABE  — прямой. Рассмотрим треугольники AEB и ABF, они прямоугольные, угол BAE  — общий, следовательно, эти треугольники подобны. Откуда:

$\frac{AE}{AB}=\frac{AB}{AF}\\AB^2=AE\ast AF$

Угол ECA  — вписанный и опирается на диаметр, следовательно, он прямой. Рассмотрим треугольники AEC и AFD, они прямоугольные, угол FAD  — общий, следовательно, эти треугольники подобны. Откуда

$\frac{AE}{AD}=\frac{AC}{AF}\\AD=AE\ast\frac{AF}{AC}$

Подставляя выше найденное равенство:

$AD=\frac{AB^2}{AC}=\frac{60^2}{80}=45$

CD=AC-AD=80-45=35

Ответ: 35

78449B

В треугольнике ABC известны длины сторон AB=15, AC=25, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

Решение:

Проведём построения, как показано на рисунке. Угол ABE  — вписанный и опирается на диаметр, значит, угол ABE  — прямой. Рассмотрим треугольники AEB и ABF, они прямоугольные, угол BAE  — общий, следовательно, эти треугольники подобны. Откуда:

$\frac{AE}{AB}=\frac{AB}{AF}\\AB^2=AE\ast AF$

Угол ECA  — вписанный и опирается на диаметр, следовательно, он прямой. Рассмотрим треугольники AEC и AFD, они прямоугольные, угол FAD  — общий, следовательно, эти треугольники подобны. Откуда

$\frac{AE}{AD}=\frac{AC}{AF}\\AD=AE\ast\frac{AF}{AC}$

Подставляя выше найденное равенство:

$AD=\frac{AB^2}{AC}=\frac{15^2}{25}=9$

CD=AC-AD=25-9=16

Ответ: 16

10B970

В треугольнике ABC известны длины сторон AB=14, AC=98, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

Решение:

Проведём построения, как показано на рисунке. Угол ABE  — вписанный и опирается на диаметр, значит, угол ABE  — прямой. Рассмотрим треугольники AEB и ABF, они прямоугольные, угол BAE  — общий, следовательно, эти треугольники подобны. Откуда:

$\frac{AE}{AB}=\frac{AB}{AF}\\AB^2=AE\ast AF$

Угол ECA  — вписанный и опирается на диаметр, следовательно, он прямой. Рассмотрим треугольники AEC и AFD, они прямоугольные, угол FAD  — общий, следовательно, эти треугольники подобны. Откуда

$\frac{AE}{AD}=\frac{AC}{AF}\\AD=AE\ast\frac{AF}{AC}$

Подставляя выше найденное равенство:

$AD=\frac{AB^2}{AC}=\frac{14^2}{98}=2$

CD=AC-AD=98-2=96

Ответ: 96

11E6E2

В треугольнике ABC известны длины сторон AB=18, AC=36, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

Решение:

Проведём построения, как показано на рисунке. Угол ABE  — вписанный и опирается на диаметр, значит, угол ABE  — прямой. Рассмотрим треугольники AEB и ABF, они прямоугольные, угол BAE  — общий, следовательно, эти треугольники подобны. Откуда:

$\frac{AE}{AB}=\frac{AB}{AF}\\AB^2=AE\ast AF$

Угол ECA  — вписанный и опирается на диаметр, следовательно, он прямой. Рассмотрим треугольники AEC и AFD, они прямоугольные, угол FAD  — общий, следовательно, эти треугольники подобны. Откуда

$\frac{AE}{AD}=\frac{AC}{AF}\\AD=AE\ast\frac{AF}{AC}$

Подставляя выше найденное равенство:

$AD=\frac{AB^2}{AC}=\frac{18^2}{36}=9$

CD=AC-AD=36-9=27

Ответ: 27

29FBB2