Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году.

Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2

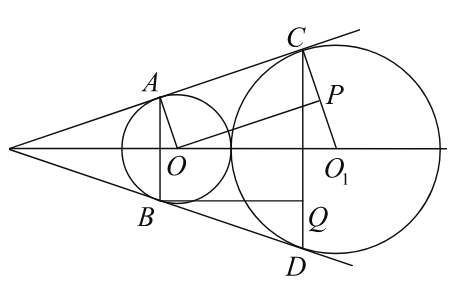
Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Решение:

Линия центров касающихся окружностей проходит через их точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов (100+25=125). Опустим перпендикуляр OP из центра меньшей окружности на радиус O₁C второй окружности. Тогда

O₁P = O₁C - PC = O₁С - OA = 100 - 25 = 75.

Из прямоугольного треугольника OPO₁ находим, что

$OP=\sqrt{OO_1^2-O_1P^2}=\sqrt{{(100+25)}^2-75^2}=\sqrt{15625-5625}=100$

Опустим перпендикуляр BQ из точки B на прямую CD. Прямоугольный треугольник BQD подобен прямоугольному треугольнику OPO1 по двум углам, поэтому:

BQ  =  OP
BD     OO₁

Следовательно,

$BQ=\frac{OP\ast BD}{OO1}=\frac{100\ast100}{125}=\frac{10000}{125}=80$

Ответ: 80

057560

Окружности радиусов 45 и 55 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Решение:

Линия центров касающихся окружностей проходит через их точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов (55+45=100). Опустим перпендикуляр OP из центра меньшей окружности на радиус O₁C второй окружности. Тогда

O₁P = O₁C - PC = O₁С - OA = 55 - 45 = 10.

Из прямоугольного треугольника OPO₁ находим, что

$OP=\sqrt{OO_1^2-O_1P^2}=\sqrt{{(45+55)}^2-10^2}=\sqrt{10000-100}=\sqrt{9900}$

Опустим перпендикуляр BQ из точки B на прямую CD. Прямоугольный треугольник BQD подобен прямоугольному треугольнику OPO1 по двум углам, поэтому:

BQ  =  OP
BD     OO₁

Следовательно,

$BQ=\frac{OP\ast BD}{OO_1}=\frac{\sqrt{9900}\ast\sqrt{9900}}{100}=\frac{9900}{100}=99$

Ответ: 99

6C7F1F

Окружности радиусов 42 и 84 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Решение:

Линия центров касающихся окружностей проходит через их точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов (42+84=126). Опустим перпендикуляр OP из центра меньшей окружности на радиус O₁C второй окружности. Тогда

O₁P = O₁C - PC = O₁С - OA = 84 - 42 = 42.

Из прямоугольного треугольника OPO₁ находим, что

$OP=\sqrt{OO_1^2-O_1P^2}=\sqrt{{(84+42)}^2-42^2}=\sqrt{15876-1764}=\sqrt{14112}$

Опустим перпендикуляр BQ из точки B на прямую CD. Прямоугольный треугольник BQD подобен прямоугольному треугольнику OPO1 по двум углам, поэтому:

BQ  =  OP
BD     OO₁

Следовательно,

$BQ=\frac{OP\ast BD}{OO_1}=\frac{\sqrt{14112}\ast\sqrt{14112}}{126}=\frac{15876}{126}=112$

Ответ: 112

897324

Окружности радиусов 4 и 60 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Решение:

Линия центров касающихся окружностей проходит через их точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов (60+4=64). Опустим перпендикуляр OP из центра меньшей окружности на радиус O₁C второй окружности. Тогда

O₁P = O₁C - PC = O₁С - OA = 60 - 4 = 56.

Из прямоугольного треугольника OPO₁ находим, что

$OP=\sqrt{OO_1^2-O_1P^2}=\sqrt{{(60+4)}^2-56^2}=\sqrt{4096-3136}=\sqrt{960}$

Опустим перпендикуляр BQ из точки B на прямую CD. Прямоугольный треугольник BQD подобен прямоугольному треугольнику OPO1 по двум углам, поэтому:

BQ  =  OP
BD     OO₁

Следовательно,

$BQ=\frac{OP\ast BD}{OO_1}=\frac{\sqrt{960}\ast\sqrt{960}}{64}=\frac{960}{64}=15$

Ответ: 15

CF289F

Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Решение:

Линия центров касающихся окружностей проходит через их точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов (45+90=135). Опустим перпендикуляр OP из центра меньшей окружности на радиус O₁C второй окружности. Тогда

O₁P = O₁C - PC = O₁С - OA = 90 - 44 = 45.

Из прямоугольного треугольника OPO₁ находим, что

$OP=\sqrt{OO_1^2-O_1P^2}=\sqrt{{(90+45)}^2-45^2}=\sqrt{18225-2025}=\sqrt{16200}$

Опустим перпендикуляр BQ из точки B на прямую CD. Прямоугольный треугольник BQD подобен прямоугольному треугольнику OPO1 по двум углам, поэтому:

BQ  =  OP
BD     OO₁

Следовательно,

$BQ=\frac{OP\ast BD}{OO_1}=\frac{\sqrt{16200}\ast\sqrt{16200}}{135}=\frac{16200}{135}=120$

Ответ: 120

BE20F1

Окружности радиусов 36 и 45 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Решение:

Линия центров касающихся окружностей проходит через их точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов (45+36=81). Опустим перпендикуляр OP из центра меньшей окружности на радиус O₁C второй окружности. Тогда

O₁P = O₁C - PC = O₁С - OA = 45 - 36 = 9.

Из прямоугольного треугольника OPO₁ находим, что

$OP=\sqrt{OO_1^2-O_1P^2}=\sqrt{{(36+45)}^2-9^2}=\sqrt{6561-81}=\sqrt{6480}$

Опустим перпендикуляр BQ из точки B на прямую CD. Прямоугольный треугольник BQD подобен прямоугольному треугольнику OPO1 по двум углам, поэтому:

BQ  =  OP
BD     OO₁

Следовательно,

$BQ=\frac{OP\ast BD}{OO_1}=\frac{\sqrt{6480}\ast\sqrt{6480}}{81}=\frac{6480}{81}=80$

Ответ: 80

288EAC

Окружности радиусов 33 и 99 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Решение:

Линия центров касающихся окружностей проходит через их точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов (33+99=132). Опустим перпендикуляр OP из центра меньшей окружности на радиус O₁C второй окружности. Тогда

O₁P = O₁C - PC = O₁С - OA = 99 - 33 = 66.

Из прямоугольного треугольника OPO₁ находим, что

$OP=\sqrt{OO_1^2-O_1P^2}=\sqrt{{(33+99)}^2-66^2}=\sqrt{17424-4356}=\sqrt{13068}$

Опустим перпендикуляр BQ из точки B на прямую CD. Прямоугольный треугольник BQD подобен прямоугольному треугольнику OPO1 по двум углам, поэтому:

BQ  =  OP
BD     OO₁

Следовательно,

$BQ=\frac{OP\ast BD}{OO_1}=\frac{\sqrt{13068}\ast\sqrt{13068}}{132}=\frac{13068}{132}=99$

Ответ: 99

FB531E

Окружности радиусов 12 и 20 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Решение:

Линия центров касающихся окружностей проходит через их точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов (12+20=32). Опустим перпендикуляр OP из центра меньшей окружности на радиус O₁C второй окружности. Тогда

O₁P = O₁C - PC = O₁С - OA = 20 - 12 = 8.

Из прямоугольного треугольника OPO₁ находим, что

$OP=\sqrt{OO_1^2-O_1P^2}=\sqrt{{(12+20)}^2-8^2}=\sqrt{1024-64}=\sqrt{960}$

Опустим перпендикуляр BQ из точки B на прямую CD. Прямоугольный треугольник BQD подобен прямоугольному треугольнику OPO1 по двум углам, поэтому:

BQ  =  OP
BD     OO₁

Следовательно,

$BQ=\frac{OP\ast BD}{OO_1}=\frac{\sqrt{960}\ast\sqrt{960}}{32}=\frac{960}{32}=30$

Ответ: 30

2FA692

Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Решение:

Линия центров касающихся окружностей проходит через их точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов (44+77=121). Опустим перпендикуляр OP из центра меньшей окружности на радиус O₁C второй окружности. Тогда

O₁P = O₁C - PC = O₁С - OA = 77 - 44 = 33.

Из прямоугольного треугольника OPO₁ находим, что

$OP=\sqrt{OO_1^2-O_1P^2}=\sqrt{{(77+44)}^2-33^2}=\sqrt{14641-1089}=\sqrt{13552}$

Опустим перпендикуляр BQ из точки B на прямую CD. Прямоугольный треугольник BQD подобен прямоугольному треугольнику OPO1 по двум углам, поэтому:

BQ  =  OP
BD     OO₁

Следовательно,

$BQ=\frac{OP\ast BD}{OO_1}=\frac{\sqrt{13552}\ast\sqrt{13552}}{121}=\frac{13552}{122}=112$

Ответ: 112

6F1598

Окружности радиусов 22 и 99 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Решение:

Линия центров касающихся окружностей проходит через их точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов (22+99=121). Опустим перпендикуляр OP из центра меньшей окружности на радиус O₁C второй окружности. Тогда

O₁P = O₁C - PC = O₁С - OA = 99 - 22 = 77.

Из прямоугольного треугольника OPO₁ находим, что

$OP=\sqrt{OO_1^2-O_1P^2}=\sqrt{{(22+99)}^2-77^2}=\sqrt{14641-5929}=\sqrt{8712}$

Опустим перпендикуляр BQ из точки B на прямую CD. Прямоугольный треугольник BQD подобен прямоугольному треугольнику OPO1 по двум углам, поэтому:

BQ  =  OP
BD     OO₁

Следовательно,

$BQ=\frac{OP\ast BD}{OO_1}=\frac{\sqrt{8712}\ast\sqrt{8712}}{121}=\frac{8712}{121}=72$

Ответ: 72

29F53E