В этой статье поговорим о довольно известной и между прочим актуальной на ОГЭ теме (9 класс), о касательной и секущей к окружности. Обратимся мы к этой теме с точки зрения дилетанта, то есть с условием, что мы как будто вовсе ничего не знаем об этом и вот сейчас перед нами стоит задача узнать что же такое это самая секущая, эта самая касательная и какие у них есть свойства, если провести эти два луча из одной из точек, где-то в пространстве. 
 Итак, как мы сказали начнем с определений и азов, а потом уже перейдем к практическим задачам, которые как раз и покажут нам примеры применения наших полученных знаний и актуализируют их для дальнейшего применения в возможных задачах по геометрии, будь то домашняя работа, ОГЭ или ЕГЭ. 

 и как мы и говорили начнем с определений, перейдем к свойствам, а потом переключимся на примеры.

Что такое касательная к окружности

 Даже из одного наименования уже можно догадаться, о чем идет речь, ведь часто общепринятое использование слова касательная, буквально совпадает с тем, с чем мы будем иметь дело.

Касательная к окружности это прямая, которая имеет одну общую точку соприкосновения с окружностью. 

Сами понимаете, что можно условно провести эту прямую с любой окружности, если можно так выразиться: слева, справа, сверху, снизу. При этом везде картина будет одна и та же, будет наша окружность и будет линия, чуть только коснувшаяся ее в одной точке. 

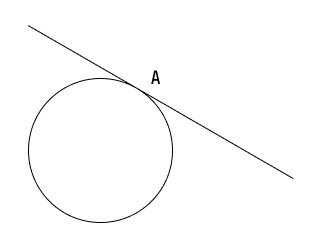
Собственно на рисунке все видно и как нам кажется весьма наглядно!

Что такое секущая к окружности

Теперь о секущей. Все прямые, которые проходят через тело круга и секут его, как раз и являются секущими. А если точнее...

Секущая к окружности, это прямая которая имеет две общие точки пересечения с окружностью. 

Сами понимаете, что часть прямой будет снаружи окружности, а часть внутри. Так вот часть внутри называют хордой окружности. Эта информация в дополнение к имеющемуся материалу. Визуально секущую на рисунке можно представить так.

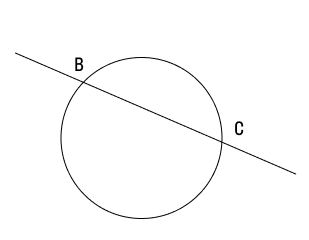
Тоже вполне понятно и логично. Теперь самое время перейти к свойствам касательной и секущей. 

Свойства касательной и секущей к окружности (соотношение)

Первое с чего хочется начать, так это с простого.

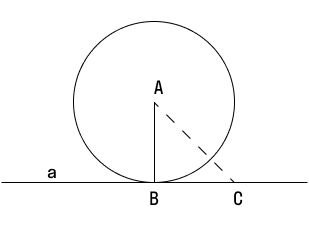
1 СВОЙСТВО. С леммы, что радиус проведенный к касательной является также перпендикуляром к этой касательной.

AB ⟂ а

Это доказательство взаимоисключающее, оно предполагает обратное, которое не подтверждается логическими заключениями. То есть: если мы предположим, что отрезок АВ являющийся радиусом не перпендикулярен, а есть условно истинный другой отрезок перпендикулярный к касательной, скажем АС, который показан утрировано неверно, то мы сможем сделать заключение о том, что отрезок АС будет иметь две разные точки пересечения с окружностью и прямой - касательной. И это как раз противоречит определению понятия касательной, так как именно одна единственная точка может быть общей у касательной и окружности. 

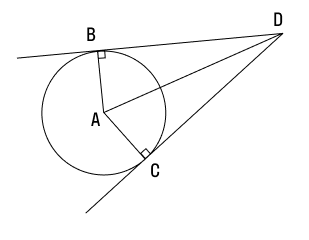
2 СВОЙСТВО. Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны

BD = DC

Еще одно свойство касается уже не только касательной, но и секущей.

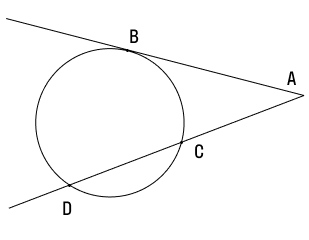
3 СВОЙСТВО. Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть

AB²=AD*CA

Это свойство часто вам будет пригождаться при решении задач.   И есть еще одно свойство

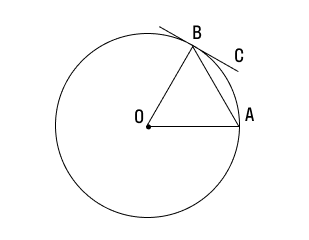
4 СВОЙСТВО. Угол между хордой и касательной, проходящей через конец хорды, равен половине градусной меры дуги, расположенной между концами хорды. 

∠ BOA = ∠ 2 CBA или ∠ 1/2 BOA = ∠ CBA

Это основные и собственно наиболее важные свойства касательной, секущей и хорды в окружности. Именно используя эти утверждения - свойства можно решить многие задачи, которые на первый взгляд будут казаться весьма сложными и неразрешимыми.