Продолжая наш экскурс в изучение свойств и особенностей различных геометрических фигур, мы подошли к фигуре - треугольник. Треугольник представляет собой одну из простейших геометрических фигур, у которой 3 стороны, три угла, все остальное иллюзорно. То есть углы могут быть самые различные, но при этом их сумма равна 180 градусам всегда. Длины сторон тоже могут быть самые разные.
 Нас же будет интересовать площадь треугольника, то есть формула по которой она высчитывается. Именно этой теме я бы и хотел посвятить эту статью. 

 Прежде, чем мы окунемся в процесс рассуждений как же нам быть с треугольником по поводу нахождения его площади, мне хотелось бы напомнить о том, как она вообще находится. Это важно, так как по факту уже является началом этих самых рассуждений в цепочки вычисления формулы площади треугольника.

 Итак, площадь это количество единиц ее измерения, будь то сантиметры, метры, километры, но ограниченной сторонами на поверхности. При этом простейший путь ее нахождения по формуле будет связан с путем перемножения двух перпендикулярных сторон, то есть когда стороны расположены под прямым углом друг к другу. То есть всегда просто найти площадь квадрата или прямоугольника, путем перемножения значений двух перпендикулярных сторон.

А вот с треугольниками возникает некоторая неувязочка, так как не всегда и не у всех сторон между сторонами треугольника прямой угол. Если он есть, то можно достроить треугольник до прямоугольника... Если его нет, то всегда можно разбить треугольники искусственно так, чтобы у нас был этот прямой угол, то есть получилось два прямоугольных треугольника. То есть мы должны работать с прямоугольными треугольниками. 

Что же, давайте посмотрим на картинку, так как визуально информация воспринимается порой куда лучше... На ней как раз видно, как получать прямоугольный треугольник, как достроить его до прямоугольника и как вычислить окончательную площадь.

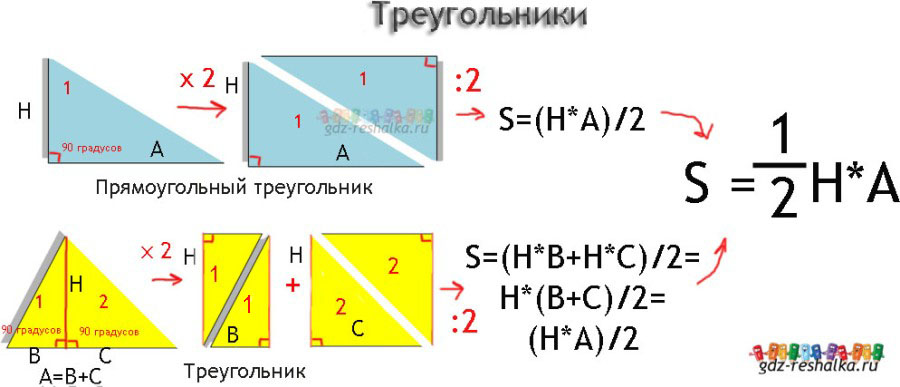
 Если вы уделили ей должное внимание и время, то дальнейшее пояснение по теме теряет смысл, но я все же поясню. Итак, смотрите, если имеется прямоугольный треугольник, то для нахождения площади искусственно берем два таких треугольника, получая прямоугольник. Потом, чтобы все же вернуться к значению площади одного треугольника, делим значение пополам.

С не прямоугольными треугольниками все тоже самое, разве что мы вначале искусственно получаем из любого непрямоугольного треугольника два прямоугольных, а сделать это можно всегда, а потом по тому же самому правилу как и с предыдущим примером находим площадь двух прямоугольников и корректируем делением на 2, чтобы вернуться к площади треугольника.

Собственно еще раз надо записать формулу нахождения площади треугольника.

S=H*A/2,
где H - высота проведенная из вершины перпендикулярно основанию. А - само основание, которое перпендикулярно высоте.

 На этом статью можно считать логически завершенной, а вы можете теперь не только рассчитывать площадь треугольника, но и осознавать, каким же путем вычисляется эта самая площадь, исходя из логических заключений.