 Вспоминаем, что по теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. А еще нужно вспомнить, что в равностороннем треугольнике биссектриса является медианой и высотой, то есть делит угол пополам, сторону пополам, к тому же вертикальна к этой стороне. Собственно, это вся теория, которую нужно знать для заданий, предложенных ФИПИ и изложенных ниже.
Вспоминаем, что по теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. А еще нужно вспомнить, что в равностороннем треугольнике биссектриса является медианой и высотой, то есть делит угол пополам, сторону пополам, к тому же вертикальна к этой стороне. Собственно, это вся теория, которую нужно знать для заданий, предложенных ФИПИ и изложенных ниже.
Реальные задания по геометрии из банка ФИПИ
Сначала задачи на чистую теорему Пифагора.
Катеты прямоугольного треугольника равны 20 и 21. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 202 + 212 = 400 + 441 = 841
гипотенуза = √841 = 29
Ответ: 29
9B2289
Катеты прямоугольного треугольника равны 10 и 24. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 102 + 242 = 100 + 576 = 676
гипотенуза = √676 = 26
Ответ: 26
36ECD2
Катеты прямоугольного треугольника равны 20 и 15. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 202 + 152 = 400 + 225 = 625
гипотенуза = √625 = 25
Ответ: 25
265E3E
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 122 + 162 = 144 + 256 = 400
гипотенуза = √400 = 20
Ответ: 20
D4ECD4
Катеты прямоугольного треугольника равны 7 и 24. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 72 + 242 = 49 + 576 = 625
гипотенуза = √625 = 25
Ответ: 25
7BF396
Катеты прямоугольного треугольника равны 18 и 24. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 182 + 242 = 324 + 576 = 900
гипотенуза = √900 = 30
Ответ: 30
A0EBE9
Катеты прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 82 + 152 = 64 + 225 = 289
гипотенуза = √289 = 17
Ответ: 17
760E4B
Катеты прямоугольного треугольника равны 9 и 12. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 92 + 122 = 81 + 144 = 225
гипотенуза = √225 = 15
Ответ: 15
0E7DA8
Катеты прямоугольного треугольника равны 12 и 5. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 122 + 52 = 144 + 25 = 169
гипотенуза = √169 = 13
Ответ: 13
7BFD23
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 302 + 402 = 900 + 1600 = 2500
гипотенуза = √2500 = 50
Ответ: 50
33759E
Катеты прямоугольного треугольника равны 60 и 80. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 602 + 802 = 3600 + 6400 = 10 000
гипотенуза = √10000 = 100
Ответ: 100
5256FC
Катеты прямоугольного треугольника равны 16 и 30. Найдите гипотенузу этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
гипотенуза2 = 162 + 302 = 256 + 900 = 1156
гипотенуза = √1156 = 34
Ответ: 34
1DFD1B
В прямоугольном треугольнике катет и гипотенуза равны 8 и 17 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 172 - 82 = √ 289 - 64 = √ 225 = 15
Ответ: 15
B1D433
В прямоугольном треугольнике катет и гипотенуза равны 16 и 20 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 202 - 162 = √ 400 - 256 = √ 144 = 12
Ответ: 12
6AB9FA
В прямоугольном треугольнике катет и гипотенуза равны 20 и 25 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 252 - 202 = √ 625 - 400 = √ 225 = 15
Ответ: 15
CC5DD4
В прямоугольном треугольнике катет и гипотенуза равны 12 и 20 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 202 - 122 = √ 400 - 144 = √ 256 = 16
Ответ: 16
38EF21
В прямоугольном треугольнике катет и гипотенуза равны 5 и 13 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 132 - 52 = √ 169 - 25 = √ 144 = 12
Ответ: 12
F35611
В прямоугольном треугольнике катет и гипотенуза равны 30 и 50 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 502 - 302 = √ 2500 - 900 = √ 1600 = 40
Ответ: 40
D544D6
В прямоугольном треугольнике катет и гипотенуза равны 40 и 50 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 502 - 402 = √ 2500 - 1600 = √ 900 = 30
Ответ: 30
BB7A45
В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 342 - 162 = √ 1156 - 256 = √ 900 = 30
Ответ: 30
328539
В прямоугольном треугольнике катет и гипотенуза равны 9 и 15 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 152 - 92 = √ 225 - 81 = √ 144 = 12
Ответ: 12
C3EEC0
В прямоугольном треугольнике катет и гипотенуза равны 9 и 41 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 412 - 92 = √ 1681 - 81 = √ 1600 = 40
Ответ: 40
26C62D
В прямоугольном треугольнике катет и гипотенуза равны 40 и 41 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 412 - 402 = √ 1681 - 1600 = √ 81 = 9
Ответ: 9
760845
В прямоугольном треугольнике катет и гипотенуза равны 7 и 25 соответственно. Найдите другой катет этого треугольника.

Решение:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит, катет будет равен корню квадратному из разности квадратов гипотенузы и катета.
√ 252 - 72 = √ 625 - 49 = √ 576 = 24
Ответ: 24
A74393
В следующих заданиях нужно увидеть, что образовался прямоугольный треугольник. Далее используем свойства биссектрисы/медианы и проводим вычисления по теореме Пифагора.
Сторона равностороннего треугольника равна 14√3. Найдите высоту этого треугольника.
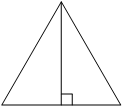
Решение:
Поскольку проведена высота, а высота перпендикулярна стороне, на которую проведена, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора. К тому же в равностороннем треугольнике высота является медианой, то есть делит сторону пополам. Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и высота - катетом.
с = 14√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 14√ 3 = 14 * 3/2 = 21
Ответ: 21
C404FC
Сторона равностороннего треугольника равна 16√3. Найдите медиану этого треугольника.
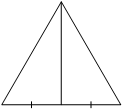
Решение:
Поскольку проведена медиана, а медиана в равностороннем треугольнике является высотой, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и медиана - катетом.
с = 16√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 16√ 3 = 16 * 3/2 = 24
Ответ: 24
A05CF1
Сторона равностороннего треугольника равна 12√3. Найдите биссектрису этого треугольника.
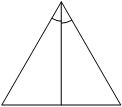
Решение:
Поскольку проведена биссектриса, а биссектриса в равностороннем треугольнике является высотой, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора. К тому же в равностороннем треугольнике биссектриса является медианой, то есть делит сторону пополам.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и биссектриса - катетом.
с = 12√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 12√ 3 = 12 * 3/2 = 18
Ответ: 18
ACC20D
Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.

Решение:
Поскольку проведена медиана, а медиана в равностороннем треугольнике является высотой, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и медиана - катетом.
с = 14√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 14√ 3 = 14 * 3/2 = 21
Ответ: 21
A911BB
Сторона равностороннего треугольника равна 16√3. Найдите биссектрису этого треугольника.

Решение:
Поскольку проведена биссектриса, а биссектриса в равностороннем треугольнике является высотой, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора. К тому же в равностороннем треугольнике биссектриса является медианой, то есть делит сторону пополам.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и биссектриса - катетом.
с = 16√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 16√ 3 = 16 * 3/2 = 24
Ответ: 24
A97C55
Сторона равностороннего треугольника равна 12√3. Найдите высоту этого треугольника.

Решение:
Поскольку проведена высота, а высота перпендикулярна стороне, на которую проведена, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора. К тому же в равностороннем треугольнике высота является медианой, то есть делит сторону пополам. Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и высота - катетом.
с = 12√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 12√ 3 = 12 * 3/2 = 18
Ответ: 18
D5802A
Сторона равностороннего треугольника равна 14√3. Найдите биссектрису этого треугольника.

Решение:
Поскольку проведена биссектриса, а биссектриса в равностороннем треугольнике является высотой, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора. К тому же в равностороннем треугольнике биссектриса является медианой, то есть делит сторону пополам.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и биссектриса - катетом.
с = 14√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 14√ 3 = 14 * 3/2 = 21
Ответ: 21
AF7118
Сторона равностороннего треугольника равна 16√3. Найдите высоту этого треугольника.

Решение:
Поскольку проведена высота, а высота перпендикулярна стороне, на которую проведена, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора. К тому же в равностороннем треугольнике высота является медианой, то есть делит сторону пополам. Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и высота - катетом.
с = 16√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 16√ 3 = 16 * 3/2 = 24
Ответ: 24
0F89BC
Сторона равностороннего треугольника равна 12√3. Найдите медиану этого треугольника.

Решение:
Поскольку проведена медиана, а медиана в равностороннем треугольнике является высотой, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и медиана - катетом.
с = 12√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 12√ 3 = 12 * 3/2 = 18
Ответ: 18
411EE5
Сторона равностороннего треугольника равна 10√3. Найдите медиану этого треугольника.

Решение:
Поскольку проведена медиана, а медиана в равностороннем треугольнике является высотой, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и медиана - катетом.
с = 10√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 10√ 3 = 10 * 3/2 = 15
Ответ: 15
02147B
Сторона равностороннего треугольника равна 10√3. Найдите высоту этого треугольника.

Решение:
Поскольку проведена высота, а высота перпендикулярна стороне, на которую проведена, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора. К тому же в равностороннем треугольнике высота является медианой, то есть делит сторону пополам. Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и высота - катетом.
с = 10√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 10√ 3 = 10 * 3/2 = 15
Ответ: 15
1A37BC
Сторона равностороннего треугольника равна 10√3. Найдите биссектрису этого треугольника.

Решение:
Поскольку проведена биссектриса, а биссектриса в равностороннем треугольнике является высотой, образовалось 2 прямоугольных треугольника. К любому из них можно применить теорему Пифагора. К тому же в равностороннем треугольнике биссектриса является медианой, то есть делит сторону пополам.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и биссектриса - катетом.
с = 10√ 3, b = с/2, а - ?
По теореме Пифагора а2 + b2 = с2
а2 = с2 - b2
$а^2=с^2-{(\frac с2)}^2=\frac{4с^2-с^2}4=\frac{3с^2}4=\frac34с^2$
$а=\sqrt{\frac34с^2}=\frac{\sqrt3}2c$
a = √3/2 * 10√ 3 = 10 * 3/2 = 15
Ответ: 15
BD0443
Высота равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике высота является медианой и биссектрисой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и высота - катетом.
а = 13√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 13√3 = 2 * 13 = 26
Ответ: 26
98F294
Медиана равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике медиана является высотой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и медиана - катетом.
а = 13√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 13√3 = 2 * 13 = 26
Ответ: 26
2B00D0
Биссектриса равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике биссектриса является медианой и высотой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и биссектриса - катетом.
а = 13√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 13√3 = 2 * 13 = 26
Ответ: 26
877976
Высота равностороннего треугольника равна 12√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике высота является медианой и биссектрисой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и высота - катетом.
а = 12√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 12√3 = 2 * 12 = 24
Ответ: 24
4E59F7
Медиана равностороннего треугольника равна 12√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике медиана является высотой и биссектрисой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и медиана - катетом.
а = 12√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 12√3 = 2 * 12 = 24
Ответ: 24
9F9A78
Биссектриса равностороннего треугольника равна 12√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике биссектриса является медианой и высотой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и биссектриса - катетом.
а = 12√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 12√3 = 2 * 12 = 24
Ответ: 24
52CB7E
Высота равностороннего треугольника равна 11√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике высота является медианой и биссектрисой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и высота - катетом.
а = 11√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 11√3 = 2 * 11 = 22
Ответ: 22
C200BE
Медиана равностороннего треугольника равна 11√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике медиана является высотой и биссектрисой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и медиана - катетом.
а = 11√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 11√3 = 2 * 11 = 22
Ответ: 22
EF0911
Биссектриса равностороннего треугольника равна 11√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике биссектриса является медианой и высотой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и биссектриса - катетом.
а = 11√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 11√3 = 2 * 11 = 22
Ответ: 22
79A610
Высота равностороннего треугольника равна 9√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике высота является медианой и биссектрисой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и высота - катетом.
а = 9√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 9√3 = 2 * 9 = 18
Ответ: 18
911A31
Медиана равностороннего треугольника равна 9√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике медиана является высотой и биссектрисой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и медиана - катетом.
а = 9√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 9√3 = 2 * 9 = 18
Ответ: 18
02E441
Биссектриса равностороннего треугольника равна 9√3. Найдите сторону этого треугольника.

Решение:
В равностороннем треугольнике биссектриса является медианой и высотой. Она делит этот треугольник на 2 прямоугольных треугольника.
Значит, сторона равностороннего треугольника будет гипотенузой прямоугольного треугольника, половинка стороны - катетом, и биссектриса - катетом.
а = 9√ 3, b = с/2, с - ?
По теореме Пифагора а2 + b2 = с2
$с^2=а^2+{(\frac с2)}^2$
$с^2-{(\frac с2)}^2=а^2$
$с^2-\frac{с^2}4=а^2$
$\frac{4с^2-с^2}4=а^2$
$\frac34с^2=а^2$
$с^2=\frac43а^2$
$с=\sqrt{\frac43а^2}$
$с=\frac2{\sqrt3}а$
c = 2/√3 * 9√3 = 2 * 9 = 18
Ответ: 18
D33BE4


