Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году. В этих задачах необходимо найти стороны треугольника в том случае, когда в треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину.
Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2
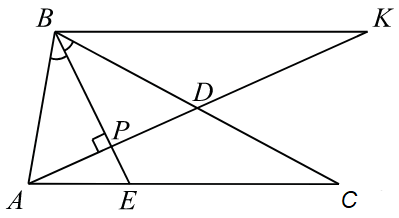
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 12. Найдите стороны треугольника ABC.
Решение:
Пусть P — точка пересечения отрезков BE и AD. Треугольник ABD — равнобедренный, так как его биссектриса BP является высотой. Поэтому AP = PD = 12/2=6
BC = 2BD = 2AB так как AD медиана.
По свойству биссектрисы треугольника.
$\frac{CE}{AE}=\frac{BC}{AB},\;так\;как\;BC\;больше\;AB\;в\;2\;раза,\;то\\\frac{CE}{AE}=2,\;\;а\;AC\;=\;3AE$
Проведём через вершину B прямую, параллельную AC. Пусть K — точка пересечения этой прямой с продолжением медианы AD. Тогда BK = AC = 3AE. Треугольники APE и KPB подобные (по 2 углам, вертикальные и накрест лежащие у параллельных прямых), а из этого следует, что:
$\frac{PE}{BP}=\frac{AE}{BK}=\frac13$
то есть BE можно поделить на 4 части, 3 из которых будут приходиться на BP, а одна на PE
PE = 12/4*1=3 и BP = 12/4*3=9
теперь зная BP и AP можем найти AB
$AB=\sqrt{BP^2\;+\;AP^2}=\sqrt{9^2+6^2}=\sqrt{81+36}=\sqrt{117}$ = 3√13
само собой BC из условия что оно в два раза больше BA будет BC=2√117=2*3√13=6√13
зная PE и AP можем найти AE
$AE=\sqrt{PE^2\;+\;AP^2}=\sqrt{3^2+6^2}=\sqrt{9+36}=\sqrt{45}$
тогда AC из условия что оно в 3 раза больше AE будет AE=3√45=3*3√5
Ответ: AB=3√13, BC=6√13, AE=9√5
89CAAE
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
Решение:
Пусть P — точка пересечения отрезков BE и AD. Треугольник ABD — равнобедренный, так как его биссектриса BP является высотой. Поэтому AP = PD = 44/2=22
BC = 2BD = 2AB так как AD медиана.
По свойству биссектрисы треугольника.
$\frac{CE}{AE}=\frac{BC}{AB},\;так\;как\;BC\;больше\;AB\;в\;2\;раза,\;то\\\frac{CE}{AE}=2,\;\;а\;AC\;=\;3AE$
Проведём через вершину B прямую, параллельную AC. Пусть K — точка пересечения этой прямой с продолжением медианы AD. Тогда BK = AC = 3AE. Треугольники APE и KPB подобные (по 2 углам, вертикальные и накрест лежащие у параллельных прямых), а из этого следует, что:
$\frac{PE}{BP}=\frac{AE}{BK}=\frac13$
то есть BE можно поделить на 4 части, 3 из которых будут приходиться на BP, а одна на PE
PE = 44/4*1=11 и BP = 44/4*3=33
теперь зная BP и AP можем найти AB
$AB=\sqrt{BP^2\;+\;AP^2}=\sqrt{33^2+22^2}=\sqrt{1089+484}=\sqrt{1573}$ = 11√13
само собой BC из условия что оно в два раза больше BA будет BC=22√13
зная PE и AP можем найти AE
$AE=\sqrt{PE^2\;+\;AP^2}=\sqrt{11^2+22^2}=\sqrt{121+484}=\sqrt{605}$
тогда AC из условия что оно в 3 раза больше AE будет AE=3√605
Ответ: AB=11√13, BC=22√13, AE=3√605
382962
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 16. Найдите стороны треугольника ABC.
Решение:
Пусть P — точка пересечения отрезков BE и AD. Треугольник ABD — равнобедренный, так как его биссектриса BP является высотой. Поэтому AP = PD = 16/2=8
BC = 2BD = 2AB так как AD медиана.
По свойству биссектрисы треугольника.
$\frac{CE}{AE}=\frac{BC}{AB},\;так\;как\;BC\;больше\;AB\;в\;2\;раза,\;то\\\frac{CE}{AE}=2,\;\;а\;AC\;=\;3AE$
Проведём через вершину B прямую, параллельную AC. Пусть K — точка пересечения этой прямой с продолжением медианы AD. Тогда BK = AC = 3AE. Треугольники APE и KPB подобные (по 2 углам, вертикальные и накрест лежащие у параллельных прямых), а из этого следует, что:
$\frac{PE}{BP}=\frac{AE}{BK}=\frac13$
то есть BE можно поделить на 4 части, 3 из которых будут приходиться на BP, а одна на PE
PE = 16/4*1=4 и BP = 16/4*3=12
теперь зная BP и AP можем найти AB
$AB=\sqrt{BP^2\;+\;AP^2}=\sqrt{12^2+8^2}=\sqrt{144+64}=\sqrt{208}$ =4√13
само собой BC из условия что оно в два раза больше BA будет BC=8√13
зная PE и AP можем найти AE
$AE=\sqrt{PE^2\;+\;AP^2}=\sqrt{4^2+8^2}=\sqrt{16+64}=\sqrt{80}$=4√5
тогда AC из условия что оно в 3 раза больше AE будет AE=12√5
Ответ: AB=4√13, BC=8√13, AE=12√5
C510C2
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 20. Найдите стороны треугольника ABC.
Решение:
Пусть P — точка пересечения отрезков BE и AD. Треугольник ABD — равнобедренный, так как его биссектриса BP является высотой. Поэтому AP = PD = 20/2=10
BC = 2BD = 2AB так как AD медиана.
По свойству биссектрисы треугольника.
$\frac{CE}{AE}=\frac{BC}{AB},\;так\;как\;BC\;больше\;AB\;в\;2\;раза,\;то\\\frac{CE}{AE}=2,\;\;а\;AC\;=\;3AE$
Проведём через вершину B прямую, параллельную AC. Пусть K — точка пересечения этой прямой с продолжением медианы AD. Тогда BK = AC = 3AE. Треугольники APE и KPB подобные (по 2 углам, вертикальные и накрест лежащие у параллельных прямых), а из этого следует, что:
$\frac{PE}{BP}=\frac{AE}{BK}=\frac13$
то есть BE можно поделить на 4 части, 3 из которых будут приходиться на BP, а одна на PE
PE = 20/4*1=5 и BP = 20/4*3=15
теперь зная BP и AP можем найти AB
$AB=\sqrt{BP^2\;+\;AP^2}=\sqrt{15^2+10^2}=\sqrt{225+100}=\sqrt{325}$ =5√13
само собой BC из условия что оно в два раза больше BA будет BC=10√13
зная PE и AP можем найти AE
$AE=\sqrt{PE^2\;+\;AP^2}=\sqrt{5^2+10^2}=\sqrt{25+100}=\sqrt{125}$=5√5
тогда AC из условия что оно в 3 раза больше AE будет AE=15√5
Ответ: AB=5√13, BC=10√13, AE=15√5
2FAD1C
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8. Найдите стороны треугольника ABC.
Решение:
Пусть P — точка пересечения отрезков BE и AD. Треугольник ABD — равнобедренный, так как его биссектриса BP является высотой. Поэтому AP = PD = 8/2=4
BC = 2BD = 2AB так как AD медиана.
По свойству биссектрисы треугольника.
$\frac{CE}{AE}=\frac{BC}{AB},\;так\;как\;BC\;больше\;AB\;в\;2\;раза,\;то\\\frac{CE}{AE}=2,\;\;а\;AC\;=\;3AE$
Проведём через вершину B прямую, параллельную AC. Пусть K — точка пересечения этой прямой с продолжением медианы AD. Тогда BK = AC = 3AE. Треугольники APE и KPB подобные (по 2 углам, вертикальные и накрест лежащие у параллельных прямых), а из этого следует, что:
$\frac{PE}{BP}=\frac{AE}{BK}=\frac13$
то есть BE можно поделить на 4 части, 3 из которых будут приходиться на BP, а одна на PE
PE = 8/4*1=2 и BP = 8/4*3=6
теперь зная BP и AP можем найти AB
$AB=\sqrt{BP^2\;+\;AP^2}=\sqrt{6^2+4^2}=\sqrt{36+16}=\sqrt{52}$ = 2√13
само собой BC из условия что оно в два раза больше BA будет 4√13
зная PE и AP можем найти AE
$AE=\sqrt{PE^2\;+\;AP^2}=\sqrt{2^2+4^2}=\sqrt{4+16}=\sqrt{20}$ = 2√5
тогда AC из условия что оно в 3 раза больше AE будет AE=6√5
Ответ: AB=2√13, BC=4√13, AE=6√5
951A66
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 24. Найдите стороны треугольника ABC.
Решение:
Пусть P — точка пересечения отрезков BE и AD. Треугольник ABD — равнобедренный, так как его биссектриса BP является высотой. Поэтому AP = PD = 24/2=12
BC = 2BD = 2AB так как AD медиана.
По свойству биссектрисы треугольника.
$\frac{CE}{AE}=\frac{BC}{AB},\;так\;как\;BC\;больше\;AB\;в\;2\;раза,\;то\\\frac{CE}{AE}=2,\;\;а\;AC\;=\;3AE$
Проведём через вершину B прямую, параллельную AC. Пусть K — точка пересечения этой прямой с продолжением медианы AD. Тогда BK = AC = 3AE. Треугольники APE и KPB подобные (по 2 углам, вертикальные и накрест лежащие у параллельных прямых), а из этого следует, что:
$\frac{PE}{BP}=\frac{AE}{BK}=\frac13$
то есть BE можно поделить на 4 части, 3 из которых будут приходиться на BP, а одна на PE
PE = 24/4*1=6 и BP = 24/4*3=18
теперь зная BP и AP можем найти AB
$AB=\sqrt{BP^2\;+\;AP^2}=\sqrt{18^2+12^2}=\sqrt{324+144}=\sqrt{468}$ =2√117
само собой BC из условия что оно в два раза больше BA будет BC=4√117
зная PE и AP можем найти AE
$AE=\sqrt{PE^2\;+\;AP^2}=\sqrt{6^2+12^2}=\sqrt{36+144}=\sqrt{180}$=2√45
тогда AC из условия что оно в 3 раза больше AE будет AE=6√45
Ответ: AB=2√117, BC=4√117, AE=6√45
29FC1C
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 28. Найдите стороны треугольника ABC.
Решение:
Пусть P — точка пересечения отрезков BE и AD. Треугольник ABD — равнобедренный, так как его биссектриса BP является высотой. Поэтому AP = PD = 28/2=14
BC = 2BD = 2AB так как AD медиана.
По свойству биссектрисы треугольника.
$\frac{CE}{AE}=\frac{BC}{AB},\;так\;как\;BC\;больше\;AB\;в\;2\;раза,\;то\\\frac{CE}{AE}=2,\;\;а\;AC\;=\;3AE$
Проведём через вершину B прямую, параллельную AC. Пусть K — точка пересечения этой прямой с продолжением медианы AD. Тогда BK = AC = 3AE. Треугольники APE и KPB подобные (по 2 углам, вертикальные и накрест лежащие у параллельных прямых), а из этого следует, что:
$\frac{PE}{BP}=\frac{AE}{BK}=\frac13$
то есть BE можно поделить на 4 части, 3 из которых будут приходиться на BP, а одна на PE
PE = 28/4*1=7 и BP = 28/4*3=21
теперь зная BP и AP можем найти AB
$AB=\sqrt{BP^2\;+\;AP^2}=\sqrt{21^2+14^2}=\sqrt{441+196}=\sqrt{637}$ =7√13
само собой BC из условия что оно в два раза больше BA будет BC=14√13
зная PE и AP можем найти AE
$AE=\sqrt{PE^2\;+\;AP^2}=\sqrt{7^2+14^2}=\sqrt{49+196}=\sqrt{245}$=7√5
тогда AC из условия что оно в 3 раза больше AE будет AE=21√5
Ответ: AB=7√13, BC=14√13, AE=21√5
C77754
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 32. Найдите стороны треугольника ABC.
Решение:
Пусть P — точка пересечения отрезков BE и AD. Треугольник ABD — равнобедренный, так как его биссектриса BP является высотой. Поэтому AP = PD = 32/2=16
BC = 2BD = 2AB так как AD медиана.
По свойству биссектрисы треугольника.
$\frac{CE}{AE}=\frac{BC}{AB},\;так\;как\;BC\;больше\;AB\;в\;2\;раза,\;то\\\frac{CE}{AE}=2,\;\;а\;AC\;=\;3AE$
Проведём через вершину B прямую, параллельную AC. Пусть K — точка пересечения этой прямой с продолжением медианы AD. Тогда BK = AC = 3AE. Треугольники APE и KPB подобные (по 2 углам, вертикальные и накрест лежащие у параллельных прямых), а из этого следует, что:
$\frac{PE}{BP}=\frac{AE}{BK}=\frac13$
то есть BE можно поделить на 4 части, 3 из которых будут приходиться на BP, а одна на PE
PE = 32/4*1=8 и BP = 32/4*3=24
теперь зная BP и AP можем найти AB
$AB=\sqrt{BP^2\;+\;AP^2}=\sqrt{24^2+16^2}=\sqrt{576+256}=\sqrt{832}$ =8√13
само собой BC из условия что оно в два раза больше BA будет BC=16√13
зная PE и AP можем найти AE
$AE=\sqrt{PE^2\;+\;AP^2}=\sqrt{8^2+16^2}=\sqrt{64+256}=\sqrt{320}$=8√5
тогда AC из условия что оно в 3 раза больше AE будет AE=24√5
Ответ: AB=8√13, BC=16√13, AE=24√5
9B997B
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 36. Найдите стороны треугольника ABC.
Решение:
Пусть P — точка пересечения отрезков BE и AD. Треугольник ABD — равнобедренный, так как его биссектриса BP является высотой. Поэтому AP = PD = 36/2=18
BC = 2BD = 2AB так как AD медиана.
По свойству биссектрисы треугольника.
$\frac{CE}{AE}=\frac{BC}{AB},\;так\;как\;BC\;больше\;AB\;в\;2\;раза,\;то\\\frac{CE}{AE}=2,\;\;а\;AC\;=\;3AE$
Проведём через вершину B прямую, параллельную AC. Пусть K — точка пересечения этой прямой с продолжением медианы AD. Тогда BK = AC = 3AE. Треугольники APE и KPB подобные (по 2 углам, вертикальные и накрест лежащие у параллельных прямых), а из этого следует, что:
$\frac{PE}{BP}=\frac{AE}{BK}=\frac13$
то есть BE можно поделить на 4 части, 3 из которых будут приходиться на BP, а одна на PE
PE = 36/4*1=9 и BP = 36/4*3=27
теперь зная BP и AP можем найти AB
$AB=\sqrt{BP^2\;+\;AP^2}=\sqrt{27^2+18^2}=\sqrt{729+324}=\sqrt{1053}$ =3√117
само собой BC из условия что оно в два раза больше BA будет BC=6√117
зная PE и AP можем найти AE
$AE=\sqrt{PE^2\;+\;AP^2}=\sqrt{9^2+18^2}=\sqrt{81+324}=\sqrt{405}$=3√45
тогда AC из условия что оно в 3 раза больше AE будет AE=9√45
Ответ: AB=3√117, BC=6√117, AE=9√45
25CB29
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 40. Найдите стороны треугольника ABC.
Решение:
Пусть P — точка пересечения отрезков BE и AD. Треугольник ABD — равнобедренный, так как его биссектриса BP является высотой. Поэтому AP = PD = 40/2=20
BC = 2BD = 2AB так как AD медиана.
По свойству биссектрисы треугольника.
$\frac{CE}{AE}=\frac{BC}{AB},\;так\;как\;BC\;больше\;AB\;в\;2\;раза,\;то\\\frac{CE}{AE}=2,\;\;а\;AC\;=\;3AE$
Проведём через вершину B прямую, параллельную AC. Пусть K — точка пересечения этой прямой с продолжением медианы AD. Тогда BK = AC = 3AE. Треугольники APE и KPB подобные (по 2 углам, вертикальные и накрест лежащие у параллельных прямых), а из этого следует, что:
$\frac{PE}{BP}=\frac{AE}{BK}=\frac13$
то есть BE можно поделить на 4 части, 3 из которых будут приходиться на BP, а одна на PE
PE = 40/4*1=10 и BP = 40/4*3=30
теперь зная BP и AP можем найти AB
$AB=\sqrt{BP^2\;+\;AP^2}=\sqrt{30^2+20^2}=\sqrt{900+400}=\sqrt{1300}$ =2√325
само собой BC из условия что оно в два раза больше BA будет BC=4√325
зная PE и AP можем найти AE
$AE=\sqrt{PE^2\;+\;AP^2}=\sqrt{10^2+20^2}=\sqrt{100+400}=\sqrt{500}$=2√125
тогда AC из условия что оно в 3 раза больше AE будет AE=6√125
Ответ: AB=2√325, BC=4√325, AE=6√125
994A4D
