Самая простая фигура, для которой можно найти площадь, это квадрат. Квадрат является частным случае параллелограмма. Кроме того, его собратьями будут такие фигуры как прямоугольник, ромб.
В общем, если в ним приглядеться, то родственная связь вполне прослеживается. Но об этом я еще расскажу, а сейчас мне хотелось бы сконцентрироваться о мысли, о чем будет рассказывать моя статья. Здесь все просто, практически я уже сказал о вводных. Ведь я собираюсь рассказать вам о том, как найти площадь прямоугольника, нет даже не так... Давайте более обобщенно, но при этом не сложнее задуманного! В статье я расскажу о том, как найти площадь четырехугольника.
Какие бывают четырехугольники или о частных случаях параллелограмма
Давайте еще раз о том, о чем я говорил, но в картинках. Ведь увидеть всегда лучше, чем прочитать.
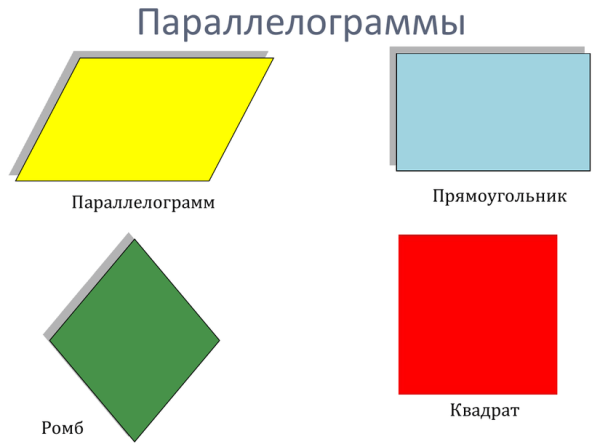
Здесь я думаю у вас не возникает вопросов и разногласий, по поводу того, что все фигуры четырехугольники и что все они родственные, назову их так. Теперь надо вспомнить как же находится площадь. Это весьма просто! Берем величины сторон в одном формате измерения, будь то см, мм, м, стулья в ряду и количество рядов, клетки в тетради вдоль и поперек, все что угодно, но в одном формате и для перпендикулярных направлений. Затем умножаем одну сторону на другую и получаем площадь нашу площадь.
Площадь прямоугольника или квадрата
То есть можно сразу сделать вывод, что вычислить скажем квадрат и прямоугольник очень просто, надо перемножить их стороны.
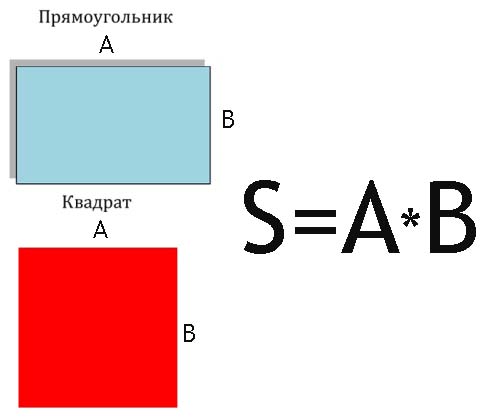
Что же, здесь все понятно. Это и так было просто.
А как же быть с четырехугольниками, где стороны расположены не под прямыми углами? Такие четырехугольники можно получить, если скажем по раме картине ударить в угол молотком. Тогда она все перекосится, при этом ее стороны напротив, так и останутся параллельными. Разве что изменят положение относительно ранее перпендикулярных рамок, поменяв прямой угол на острый или тупой. Однако как же теперь быть с нахождением площади, ведь стороны не перпендикулярны. Здесь надо включить свое воображение и разбить такие "перекошенные" фигуры на такие, чтобы из них можно было собрать прямоугольник с прямыми углами!
Поверьте мне, но сделать это всегда можно! В уме берем кусочек с одной стороны и переставляем на другую. Давайте опять обратимся к картинке, чтобы все было наглядно.
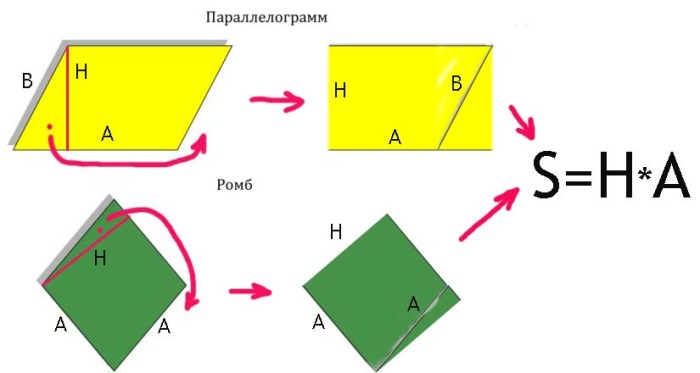
Смотрите, что для параллелограмма, что для ромба я без проблем сразу нашел вариант, как сделать из этих фигур четырехугольник с прямыми углами. При этом существует 4 способа как можно это сделать. Попробуйте найти каждый из них!
Ну а нам собственно и осталось посчитать площадь, так как теперь мы имеем дело с четырехугольником с прямыми углами. Вы помните, что находится площадь путем перемножения величины одной стороны, на другую, если стороны у нас перпендикулярны, а сейчас все именно так!
Единственное теперь нашей стороной стала не одна из сторон, а по факту высота H параллелограмма с той самой стороны, где мы взяли кусочек.
В итоге получили формулу пощади параллелограмма - S=H*A , где А одна из сторона, а H высота перпендикулярная данной стороне.
На этом тему нахождения площади четырехугольника можно считать закрытой. А если у вас остались какие-либо вопросы, то можете задать их в комментариях. Они не останутся без внимания.
