Одна из совершенных плоских фигур это круг. Ее совершенство выражается в какой-то законченности, простоте и прагматичности. В мире так много круглых предметов, которые между прочим были созданы исключительно природой, без участия человека. Скажем вы видели как падает капля любой жидкости на поверхность, пусть тот же дождь, когда он только начинается и мокрые капли хорошо видны!? Капли воды превращаются в круги, а их так много и они множатся до тех пор пока не покроют всю площадь вокруг нас... А да, кстати, о площади! Какая же интересно площадь у этих самых кругов? Как можно вычислить эту площадь, ведь она вроде как не очень просты по площади, там есть кривая, то есть этот самый контур, который является периметром круга.
Давайте-ка разберемся со всем этим по порядку.
Круг как геометрическая фигура и из чего она состоит
На самом деле, не смотря на то, что я так превозносил круг как совершенную фигуру, посчитать его площадь не так уж и просто. Ну это я к тому, что не так уж сразу и поймешь как это сделать. Мы привыкли считать площадь квадратами, прямоугольниками, в общем фигурами, у которых стороны перпендикулярны и параллельны.
А здесь смотрите что, круг весь закругляется со всех сторон. И как к нему подступиться даже и не знаешь. Круги и чертят обычно циркулем, ставят в одной точке иглу циркуля и вокруг этой точки с выбранным размером (называется раствором) чертят контур круга. Но кругом является все пространство в площади ограниченной от точки центра, до нашей получившейся линии.
Отсюда наверное уже можно и придумать какое-то определение для круга.
Круг - это множество точек расположенных в объеме от центра круга, до его периметра.
При этом точки конечно же не должны накладываться одна на другую и второе, нас в этом объеме интересует именно характеристика площади. Однако как мы уже заметили, сразу к этой площади так не подступиться, надо бы попробовать как-то разложить на более простые фигуры, что мы и постараемся сейчас сделать.
Раскладываем круг на более простые фигуры
На само деле, площадь круга можно разбить на площади треугольников. Можно представить всю площадь в виде прямоугольных или равнобедренных треугольников, это не принципиально. Единственное, здесь не будет учитываться разность основания треугольника, которая представлена прямой и дуга окружности круга. По факту эта погрешность растворяется в том случае, если брать треугольники с минимальным основанием, то есть брать как можно больше треугольников в площади круга.
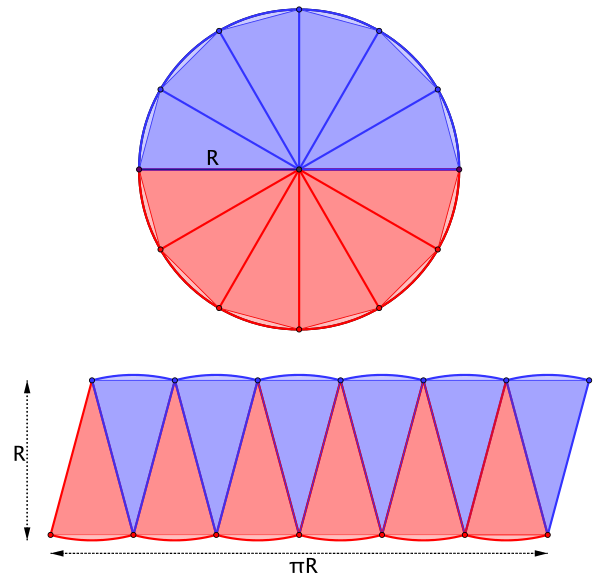
Чем больше треугольников возьмем, тем более точно будет рассчитана площадь. То есть смысл этого в том, чтобы сумма всех оснований треугольников была равна периметру круга! Тогда этот вопрос с погрешностью будет закрыт.
В этом случае остается воспользоваться простейшей формулой нахождения площади треугольника. Где в треугольнике R будет высотой, то есть R=H. Основание равно периметру круга, то есть π*R. Площадь же всех треугольников будет равна основание треугольника, умноженное на высоту и поделить все пополам. То есть (π*R*R)/2=π*R2.
Как найти площадь круга (формула)
Заметьте, по сути мы сами сейчас вывели формулу площади круга. Смотрите наши рассуждения выше.
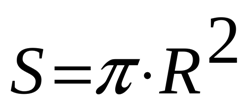
Поэтому, если вы все поняли, как и что, то нас наверное можно по интеллекту древнегреческого математика Пифагора! Что же, из этой формулы теперь можно выводить и другие, то есть скажем выражая не через радиус, а через диаметр окружности. Это уже не принципиально!
Онлайн калькулятор нахождения площади круга
