 В этой статье речь пойдет о ГДЗ по математике первой части учебника автора Петерсона. Сразу же скажем, что всего частей 3, и сразу же повторимся, здесь только первая!
В этой статье речь пойдет о ГДЗ по математике первой части учебника автора Петерсона. Сразу же скажем, что всего частей 3, и сразу же повторимся, здесь только первая!
Что же, как нам кажется это самая продуктивная, то есть самая сложная и само собой самая полезная программа по математике для начальных классов. Именно в учебных пособиях Петерсона можно найти наиболее сложные и интересные и заковыристые задания! Она охватывает максимально объемный курс для начальных классов, то есть все что должны изучать школьники в этом возрасте и даже чуть больше. Все это нам кажется весьма полезным и перспективным, так как конечно же сказывается на развитии и знании наших учеников! Что же, перестаем хвалить саму программу и переходим уже к ответам!
Сами ответы в этой статье приведены все также, как и в других наших статьях. Весь учебник разбит на страницы, в соответствии с его реальными страницами, вот и все!
Вторая часть учебника СМОТРЕТЬ
Ответы к домашним заданиям для учебника по математике за 3 класс автора Петерсон, 1 часть
3
-
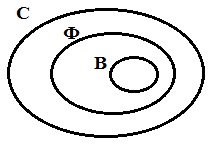
Урок 1 Множество и его элементы, страница 3
1 Придумай названия для предметов и животных, собранных вместе:Коллекция марок, Коробка карандашей, Стая гусей,
Набор посуды, Букет цветов, Стадо коров.Множество
Когда какие-нибудь объекты собирают вместе, в математике для их названия используют общее слово – множество. Сказать «стадо чашек» нельзя, а множество чашек – можно. Можно сказать: множество коров, множество птиц, множество цветов, множество марок, множество учеников и т. д.
а) Как может называться множество овец? отара
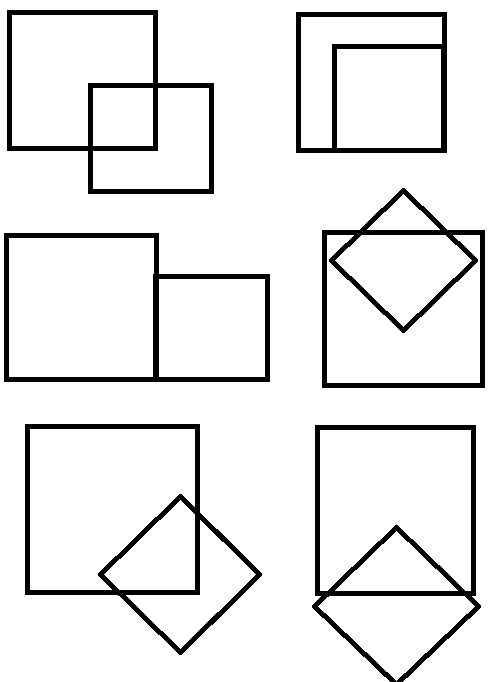
б) Как может называться множество лошадей? табун
в) Как может называться множество пчёл, летящих вместе? рой
г) Как может называться множество футболистов, собравшихся вместе для игры? командаКакие ещё командные игры ты знаешь? волейбол, баскетбол, хоккей
д) Как может называться множество кораблей, плывущих вместе? эскадраЭлементы множества
Предметы или живые существа, входящие в множество, называют элементами этого множества. Например, берёза – элемент множества деревьев, ласточка – элемент множества птиц. В то же время лист берёзы не является элементом множества деревьев, а хвост ласточки не является элементом множества птиц.
4
-
Урок 1, страница 4
Множество и его элементы3. Опиши множества, который можно назвать: хор, оркестр, бригада, класс, коллекция, библиотека.
хор - множество певцов поющих одну песню, оркестр - музыканты играющие оду мелодию, класс - ученики изучающие одну учебную программу с одним классным руководителем, библиотека - книги собранные в одном месте.
4 Назови двух учеников твоего класса. Элементами какого множества они являются? Принадлежат ли этому множеству портфели учеников?Скажем Витя и Таня. Они являются элементами множества класс, при этом портфели не относятся к этому множеству.
5 Перечисли членов твоей семьи. Принадлежишь ли ты этому множеству? А твой друг?Я принадлежу к множеству моей семьи (мама, папа, я), а друг нет, так как у него есть своя семья.
6. На рисунке изображены портреты семьи Ивановых. Перечисли элементы этого множества.
Множество: Петя, Ирина Семеновна, Сергей Васильевич, Иван Сергеевич, Елена Александровна, Анна
Из каких элементов состоит множество детей этой семьи, множество взрослых этой семьи?
Дети: Анна, Петя
Взрослые: Ирина Семеновна, Сергей Васильевич, Иван Сергеевич, Елена АлександровнаКак будут звать Петю, когда он вырастет? Петр Сергеевич
Как будут звать Аню? Анна Сергеевна
Чьим отцом является Сергей Васильевич? Ивана Сергеевича
Чьей бабушкой является Ирина Семёновна? Пети и Ани
7 С каких деревьев взяты эти листья? Клен, дуб, липа
Назови ещё три элемента множества видов деревьев. Рябина, сосна, тополь
Всегда ли на деревьях есть листья? Нет, не всегда.
У всех ли деревьев есть листья? Нет, не на всех.
8 По какому признаку подобраны слова: роза, фиалка, гвоздика, василёк, тюльпан? Это множество цветов.
Назови ещё 2 элемента множества цветов. ромашка, гладиолус
Принадлежат ли ему сосна, баран, ромашка, шипы от розы? Нет.
Какие цветы растут на клумбах? Городские
Какие растут в поле? Полевые
Какие растут на лугу? Луговые
9 На рисунке изображены некоторые элементы множества плодов. На зови их. яблоко, груша, виноград, вишня, сливаВ каких из этих плодов одно семечко или одна косточка, а в каких – много семян или косточек?
Одна: вишня, слива.
Много: виноград, груша, яблокоВсе ли плоды растут на деревьях?
Нет, не все.
Какие ещё элементы множества плодов ты знаешь?
Банан, персик, помидор, огурец, тыква, арбуз, дыня
5
-
Урок 1, страница 5
10.а) Ласточка пролетает в час 70 км, а стриж – в 2 раза больше. Сколько километров в час пролетает стриж?
70*2=140 (км) пролетает за час стриж.
Ответ: 140 км.б) Сосна живёт примерно 600 лет. Это на 250 лет больше, чем живёт ель. Сколько лет живёт ель?
600-250=350 (л.) живет ель.
Ответ: 350 лет.в) Для нормальной жизни рыбок скалярий им требуется по 3 л воды на каждую. Сколько рыбок могут нормально жить в аквариуме, вмещающем 24 л воды?
24:3=8 (р.) могут нормально жить в аквариуме.
Ответ: 8 рыбок.
г) Масса пингвина папы 42 кг, пингвина мамы – 32 кг, а их детёныша – 8 кг. Чему равна масса этой пингвиньей семьи? На сколько папа тяжелее, чем мама с детёнышем вместе?1) 42+32+8=82 (кг) масса семьи пингвинов.
2) 32+8=40 (кг) весит мама пингвин с детенышем.
3) 42-40=2 (кг) папа тяжелее, чем мама с детенышем.
Ответ: масса семьи пингвинов 82 кг, папа тяжелее мамы и детеныша на 2 кг.Придумай и реши свою задачу о жизни растений и животных.
Каждый год семья кроликов из 4 штук увеличивалась в 2 раза. Сколько кроликов станет на 3 год?
1) 4*2=8 (кр.) стало во 2 год.
2) 8*2=16 (кр.) стало на 3 год.
Ответ: 16 кроликов.
11. Сравни выражения. Что в них интересного? Найди устно их значения. Какое выражение следующее?
32 + 8 = 40 32 + 18 = 50 32 + 28 = 60 32 + 38 = 70 32 + 48 = 80Каждое последующее выражение больше предыдущего на 1 десяток.
32 + 58 = 90 - следующее выражение.
12. Пират нашёл клад из 900 монет. Чтобы побыстрее его унести, он положил 186 монет в шапку, 215 — в правый карман, 74 — в левый карман, 125 — в правую ладонь, а 68 — в левую. Сколько монет он не смог унести?
1) 186+215+74+125+68=668 (м.) унес пират.
2) 900-668=232 (м.) не смог унести пират
Ответ: 232 монеты.13 Реши уравнения:
х + 215 = 612
х = 612 - 215
х = 397500 – х = 346
х = 500-346
х = 154х – 485 = 197
х = 485 + 197
х = 68214 Составь программу действий и вычисли:
1 2 5 3 4
а) 21 : 3 · 6 – (18 + 14) : 8 = 381) 21 : 3 = 7
2) 7 * 6 = 42
3) 18 + 14= 32
4) 32 : 8 = 4
5) 42 - 4 = 382 1 6 3 4 5
б) 63 : (3 · 3) + (8 · 7 – 2) : 6 = 161) 3 * 3 = 9
2) 63 : 9 = 7
3) 8 * 7 = 56
4) 56 - 2 = 54
5) 54 : 6 = 9
6) 7 + 9 = 16
15 Задача-шутка
Два мальчика, Дима и Миша, отправились в булочную. По дороге они нашли 20 рублей. Сколько бы денег нашёл один Дима, если бы отправился в булочную?20 рублей
16 Сколько двузначных чисел содержат в своей записи хотя бы одну цифру 7?70, 71, 72, 73, 74, 75, 76, 77, 78, 79 - 10 чисел
17, 27, 37, 47, 57, 67, 87, 97 - 8 чисел
Итого: 10+8 = 18 двузначных чисел содержит цифру 7 6
-
Урок 2, страница 6
Способы задания множествНайди общее свойство всех предметов, изображённых на рисунке:
а) вещи созданные людьми
б) красные вещи
в) инструменты
г) одежда
а) Назови 5 элементов множества ягод.Смородина, клубника, малина, вишня
б) Назови 3 элемента множества грибов.Подберезовик, Опенок, Белый гриб
Какие съедобные грибы ты знаешь?
Подберезовик, опенок, белый гриб, масленок, лисичка
Какие грибы несъедобные?
Бледная поганка, мухомор
в) Назови 2 элемента множества книг."Снежная королева", "Буратино"
Есть ли у тебя любимые книги?
Да, есть. "Чук и Гек"
г) Назови 4 элемента множества растений.Василек, Ромашка, Лопух, Крапива
Объясни, почему надо беречь растения.
Растения являются средой обитания для насекомых и микроорганизмов. Они вырабатывают кислород и ими питаются домашние животные. Без растений мы бы не смогли прожить, поэтому их надо беречь!
д) Задай какое-нибудь множество с помощью свойства. Назови один предмет, который принадлежит этому множеству, и один предмет, который ему не принадлежит.Скажем съедобное. Один из элементов этого множества - это сыр, а не принадлежит этому множеству шапка.
3. Что сдавала в багаж дама из стихотворения С. Я. Маршака? Назови все элементы этого множества. Принадлежит ли ему стол?Диван, Чемодан, Саквояж, Картину, Корзину, Картонку И маленькую собачонку. Стол не принадлежит этому множеству.
Что общего между чемоданом и диваном? А между корзиной и собачонкой? Почему они собраны вместе?
Все это багаж!
4. Перечисли множество предметов, которые лежат у тебя в портфеле.Тетрадь, учебник, пенал, ручка, карандаш, ластик.
Принадлежат ли ему арбуз, самолёт, ручка?арбуз - нет, самолет - нет, ручка - да.
7
-
Урок 2, страница 7
Способы задания множеств
5. Всегда ли все согласны, что суп вкусный? Какая пословица об этом говорит?
Речь без пословицы, что суп без соли.
Из хорошего мяса — хороший суп.Почему нельзя точно назвать элементы множества вкусных супов?
Потому что супы все сделаны из разных ингредиентов, которые порой не сочетаются.
Обозначь множество буквой и задай общим свойством его элементов по образцу. Задай множество перечислением:
6.а) Перечисли множество летних месяцев.
б) Перечисли множество вторых классов в твоей школе.
в) Придумай множество, в котором легко перечислить элементы.7. Обозначь множество буквой и задай общим свойством его элементов по образцу.
а) А{0; 1; 2; 3; 4; 5; 6; 7; 8; 9};
б) Б{0; 2; 4; 6; 8};
в) В{а; я; у; ю; э; е; о; ё; ы; и}.
8. Задай множество перечислением:а) А – множество букв в слове «лиса»; А{л; и; с; а};
б) В – множество однозначных чисел, меньших 5; В{0;1;2;3;4}
в) С – множество двузначных чисел, кратных 10; С{10; 20; 30; 40; 50; 60; 70; 80; 90}
г) D – множество трёхзначных чисел, больших 603, но меньших 608 D{604;605;606;607} 8
-
Страница 8
Способы задания множества
9. Вычисли устно. Какие правила действий с числами ты вспоминаешь?
6 + 9 =15 20 + 8 = 28 17 + 8 = 25 39 + 57 = 96
9 + 6 = 15 8 + 20 = 28 8 + 17 = 25 57 + 39 = 96
15 – 6 = 9 28 – 20 = 8 25 – 17 = 8 96 – 39 = 57
15 – 9 = 6 28 – 8 = 20 25 – 8 = 17 96 – 57 = 39
10. В первый день Ира прочитала 21 страницу, во второй – в 2 раза больше, чем в первый, а в третий на 15 страниц меньше, чем во второй день. Сколько страниц прочитала Ира за все три дня?1) 21 * 2 = 42 (стр.) Ира прочитала во второй день.
2) 42 - 15 = 27 (стр.) Ира прочитала в 3 день.
3) 21 + 27 + 42 = 90 (стр.) Ира прочитала за 3 дня.
Ответ: 90 страниц.
11. Измерь своими шагами ширину класса. Как изменится результат измерения, если шаг увеличить, уменьшить?Если шаг уменьшить, то количество шагов увеличиться, если увеличить, то уменьшится.
Зачем нужны общие для всех единицы длины?
Чтобы у всех был одинаковый стандарт измерения длин.
Какие единицы длины ты знаешь?
мм, см, м, км
12. Вырази в сантиметрах и вычисли:
а) 3 м 7 дм 6 см + 4 м 3 дм 8 см = 376 + 438 = 814 см
б) 1 м 6 дм 9 см + 47 дм 2 см = 169 + 472 = 641 см
в) 9 м 72 см – 5 дм 9 см = 972 - 59 = 913 см
г) 7 м 4 см – 32 дм 6 см = 704 - 326 = 378 см
13. Периметр треугольника равен 7 дм 8 см. Длина первой стороны равна 2 дм 1 см, длина второй стороны – 3 дм 4 см. Найди длину третьей стороны этого треугольника.7 дм 8 см = 78 см
2 дм 1 см = 21 см
3 дм 4 см = 34 см1) 21 + 34 = 55 (см) длина 1 и 2 стороны треугольника.
2) 78 - 55 = 23 (см) длина 3 стороны треугольника.
Ответ: 23 см.14. Найди пропущенные цифры и сделай проверку
+82
15
97 Проверка 97 - 15 = 82+12
30
42 Проверка 42 - 12 = 30+ 38
60
98 Проверка 98 - 60 = 38+56
14
70 Проверка 70 - 14 = 56+40
25
65 Проверка 65 - 25 = 4015. Выполни действия. Положи на точки прозрачную плёнку и соедини последовательно ответы примеров. Что получилось
1) 20* 9 = 180
2) 34 * 5 = 170
3) 360 : 4 = 90
4) 480 : 60 = 8
5) 52 : 4 = 13
6) 86 : 43 = 2Смотри рисунок.
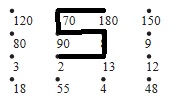
16. Составь множество трёхзначных чисел, которые можно записать с помощью цифр 3 и 6 (цифры в записи числа могут повторяться).
333, 336, 363, 366, 633, 636, 663, 666
* Задания учебника с пропусками выполняются в тетради
9
-
Страница 9
Способы задания множеств Равные множества. Пустое множество
Урок 3
1.а) Сравни элементы множеств в первом и во втором рядах.
Есть ли в первом ряду элемент, которого нет во втором ряду? Нет, нету.
Есть ли во втором ряду элемент, которого нет в первом ряду?
Нет, нету.б) Сравни множества в первом и во втором рядах. В каком ряду есть лишни элемент?
Во втором есть лишни "элемент" мышка.
Равные множества (смотрит текст - определение в учебнике)Два множества равны, если они состоят из одних и тех же
элементов. Если множества А и В равны, то пишут А = В, а если
они не равны, то пишут А не равно В.
Пример:
Пусть А = {малина; земляника; смородина},
В = {земляника; малина; смородина},
С = {смородина; малина; вишня},
D = {малина; земляника; смородина; крыжовник}.
А = В (в них одни и те же элементы, но стоят в разном порядке);
А не равно С (в А есть земляника, а в С её нет);
А не равно D (в D есть крыжовник, а в А его нет).2.
D = {а; квадрат; 5}. Верно ли, что D = { квадрат ;5; а }?
Да, верно!
Сколько имеется различных способов записи множества D с помощью фигурных скобок?
6 способа записи {а; квадрат; 5}, {а; 5; квадрат}, { квадрат; 5; а }, { квадрат; а; 5 } { 5; квадрат; а; } { 5; а; квадрат; }
3.
А = {0; 1; 2}. Какие из множеств В = {2; 0; 1}, C = {1; 0}, D = {3; 2; 1; 0} равны множеству А, а какие ему не равны? Сделай записи.А = B, А не равно С, А не равно D,
10
-
Страница 10
4. Верны ли записи? Обоснуй свой ответ.
а) Да, в этом случае множества равны, так как количество элементов и они сами одинаковы.
б) Нет не равны. Так как количество элементов различно.
в) Множества равны. Количество элементов и они сами одинаковы.
5. Запиши множества всеми возможными способами.а) Смотри рисунок -
б) {а, б, в}{а, в, б}{б, а, в}{б, в, а}{в, а, б}{в, б, а}
6. Сколько элементов содержит:
а) множество дней недели;
7 элементов
б) множество букв русского алфавита;
33 элемента
в) множество хвостов у кошки Мурки;
1 элемент
г) множество носов у Пети;
1 элемент
д) множество коров, пасущихся на Луне?
0 элементов7.
а) Растут ли около вашей школы тропические пальмы? Каким является множество пальм, растущих около вашей школы?
Пустое множество
б) Каким является множество шестиногих лошадей? Пустое множество.Двухлетних детей в вашем классе? Пустое.
Крокодилов в Москве-реке? Пустое множество.
в) Назови свой пример описания пустого множества.
Множество двоечников в нашем классе.8. Найди правильное обозначение пустого множества: 2 вариант, - то есть круг без скобок, перечеркнутый снизу слева вверх вправо.
9. Как найти площадь прямоугольника? Как найти его неизвестную сторону? Найди х по рисункам:
1 слева
16:8=2 см
Ответ: х = 2 см2 слева
6*3=18 см2
Ответ: х = 18 см23 слева
20 : 4=5 (см)
Ответ: х = 5 см10.
а) Длина прямоугольника равна 6 см, а ширина – 2 см. Построй этот прямоугольник, найди его периметр и площадь.
Строим прямоугольник со сторонами 6 и 2 см.
1) (6+2)*2= 8 * 2 = 16 (см) периметр прямоугольника.
2) 6 * 2 = 12 (см2) площадь прямоугольника.
Ответ: 16 см периметр и 12 см2 площадь прямоугольника.
б) Площадь прямоугольного участка земли равна 600 м2, а ширина – 20 м. Найди длину этого прямоугольника.600:20=30 (м) длина прямоугольника.
Ответ: 30 метров. 11
-
Страница 11
Построй графическую модель и реши уравнения с комментированием:
х • 8 = 72
х = 72 : 8
х = 928 : х = 4
х = 28 : 4
х = 7х : 7 = 5
х = 7 * 5
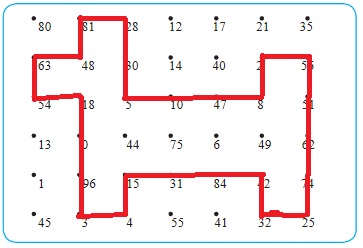
х = 3512. Положи на точки прозрачную плёнку и соедини последовательно ответы примеров. Отгадай, кто это.
1) 7 * 9 = 63
2) 8 * 6 = 48
3) 9 * 9 = 81
4) 7 * 4 = 28
5) 30 : 6 = 5
6) 40 :5 = 8
7) 14 :7 = 2
8) 7 * 8 = 56
9) 5 * 5 = 25
10) 4 * 8 = 32
11) 6 * 7 = 42
12) 3 * 5 = 15
13) 2 * 6 : 3 = 4
14) 6 * 4 : 8 = 3
15) 27 : 3 * 2 = 18
16) 36 : 4 * 6 = 54
17) 3 * 7 * 3 = 63Смотри рисунок.
13. Составь выражение и найди его значение, если a = 12, b = 3, c = 2: «Володя высадил на первой грядке a кустов клубники, на второй грядке – на b кустов больше, чем на первой, а на третьей – на c кустов меньше, чем на первой грядке. Сколько всего кустов клубники посадил Володя?»
Составляем выражение: а + (а + в) + (а - с) =
12 + (12 +3) + (12 - 2 ) = 12 + 15 + 10 = 37 (к.) клубники посадил Володя.
Ответ: 37 кустов.14. Справа нарисована фигура, составленная из клеточек. Что нельзя вырезать из этой фигуры?
Нельзя вырезать фигуру Е.
12
-
Страница 12
Урок 4 Решение задач
1.
а) Запиши множество А гласных и множество В согласных букв в слове «малина».А {А, И, А}
B {М, Л, Н}
б) Задай каждое из указанных множеств общим свойством:
С = {12; 21; 30},
D = {51; 52; 53; 54; 55; 56; 57; 58; 59; 60}.2. Выполни действия и объясни приёмы вычислений:
37 * 2 = 74 58 : 2 = 29 36 : 12 = 3 62 • 40 = 2480 180 : 9 = 20
5 * 18 = 90 72 : 4 = 18 60 : 15 = 4 200 * 3 = 600 630 : 70 = 93.
а) Во сколько раз 56 больше, чем 8?56 : 8 = 7 раз
Во сколько раз 8 меньше, чем 56?
56 : 8 = 7 раз
б) На сколько 56 больше, чем 8?
56 - 8 = 48
На сколько 8 меньше, чем 56?
56 - 8 = 48
4. На садовом участке огород занимает 84 м2. Площадь цветника на 36 м2 меньше площади огорода. Площадь фруктового сада в 5 раз больше площади цветника. Чему равна площадь фруктового сада?
1) 84 - 36 = 48 (м2) площадь цветника.
2) 48 * 5 = 240 (м2) площадь фруктового сада.
Ответ: 240 м2 площадь фруктового сада.5. Сравни числа
7<104 345>294 156>154
215>98 728<730 972>9276. Составь программу действий и вычисли. Проверь результаты с помощью калькулятора.
2 1 3
а) 526 - (401 - 294) + 381 = 526 - 207 + 381 = 7001 3 2 4
б) (694 + 76) - (253 + 472) + 146 = 770 - 725 + 146 = 45 + 146 = 1917. Найди пропущенные цифры. Сделай проверку, используя связь между сложением и вычитанием
+297
305
602-817
463
354+256
248
504-407
381
26
8. Вычисли устно:
7 + 8 =15 16 + 4 = 20 9 + 15 = 24 27 + 43 = 60 36 + 17 = 53
12 – 5 = 7 30 – 9 = 21 42 – 8 = 34 50 – 32 = 18 85 – 39 = 46 13
-
Страница 13
Решение задач Урок 4
9. Объясни по рисункам смысл равенств. Что ты замечаешь? Как можно использовать эти равенства для проверки правильности вычислений?
В варианте "а" равенства представляют собой сумму, а в случае "б", это произведение.
Первые два примера в каждом случае указывают на возможность перестановки элементов (переместительное свойство)
Вторые два примера в случае можно отнести к примерам для проверки.10. Выполни вычитание 731 – 296 и проверь выполненное действие тремя разными способами.
731 – 296 = 435
Проверка:
731 – 435 = 296
435 + 296 = 731
296 + 435 = 73111. Реши уравнения с комментированием:
х * 20 = 160
х = 160 : 20
х = 8х : 7 = 42
х = 42 * 7
х = 29492 : х = 46
х = 92 : 46
х = 2
12. БЛИЦтурнир*
а) Масса арбуза а кг, а масса тыквы на 2 кг меньше. Какова общая масса арбуза и тыквы?а + (а-2)
б) Шапка стоит b р., а пальто – в 9 раз дороже. Сколько стоят пальто и шапка вместе?b + b*9
в) В ведро входит с л воды, а в кастрюлю – в 7 раз меньше. На сколько объём этого ведра больше объёма этой кастрюли?c - c:7
г) В куске было d м ткани. Из этой ткани сшили 8 одинаковых платьев, расходуя на каждое платье по n м. Сколько метров осталось в куске?d - 8 * n
13 Периметр квадрата равен 36 м. Чему равна его площадь?
1) 36 : 4 = 9 (м) длина стороны квадрата.
2) 9 * 9 = 81 (м2) площадь квадрата.
Ответ: 81 м2 площадь квадрата.
14 Запиши множество чётных трёхзначных чисел, сумма цифр которых равна 3.{102, 120, 210, 300}
15. Из 18 спичек составлены 6 одинаковых квадратов. Убери 2 спички так, чтобы осталось:
а) 4 таких же квадрата;
б) 5 таких же квадратов.
Попробуй найти разные решения.Смотри рисунок.
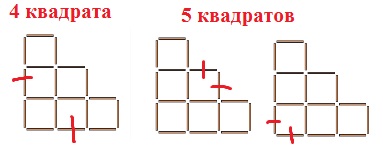
14
-
Страница 14
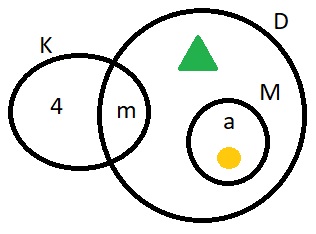
1. Назови каждый элемент множества В = {2; m; зеленый квадрат }.
Элементы: 2, m, зеленый квадрат.
Принадлежит ли этому множеству число 2, буква а?Число 2 принадлежит множеству.
Буква а не принадлежит множеству.2. На рисунке изображена диаграмма множества А. Какие элементы принадлежат множеству А, а какие ему не принадлежат? Сделай записи, используя знаки
Смотри рисунок.

3. Нарисуй диаграмму множества С и отметь на ней элементы
Смотри рисунок.
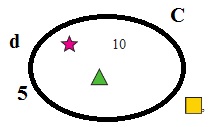
4. Имеется множество. Используя знаки, составь и прочитай верные записи: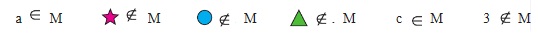
15
-
Страница 15
Диаграмма Эйлера–Венна. Знаки и Урок 5
5. D – множество двузначных чисел.
а) Принадлежат ли множеству числа 26, 307, 8, 940, 15, 60? Отметь их на диаграмме множества .
Сделай записи, используя знаки.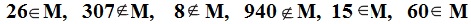
б) Сколько элементов содержит множество?3 элемента
в) Укажи самое маленькое и самое большое число, принадлежащее множеству.Самое маленькое - 15;
Самое большое - 60.
6. Запиши множество трёхзначных чисел, у которых все три цифры одинаковые. Сколько существует таких чисел?К {111, 222, 333, 444, 555, 666, 777, 888, 999}
9 чисел.
7. Найди общее свойство элементов множества А и общее свойство элементов множества В.Сколько девочек принадлежит А, но не принадлежит B?
4 девочки
Сколько девочек принадлежит В, но не принадлежит А?
3 девочки
Сколько общих элементов у множеств А В?
1 девочка
8. Объясни по чертежу, как выполнено деление с остатком. Назови делимое, делитель, частное и остаток.Делимое 35, делитель 8, остаток 3
Запиши равенства в тетради.
35 = 8 * 4 + 3
35 : 8 = 4 (ост. 3)9. Выполни деление с остатком, используя:
а) числовой луч;
б) алгоритм
Какой способ ты считаешь наиболее удобным? Более удобным считаю алгоритм.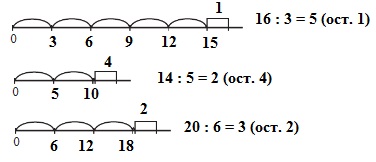
10. Выполни деление с остатком.19 : 3 = 6 (ост. 3)
21 : 8 = 2 (ост. 5)
34 : 7 = 4 (ост. 6)
75 : 9 = 8 (ост. 3)
56 : 6 = 9 (ост. 2) 16
-
Страница 16
Урок 5 Диаграмма Эйлера–Венна. Знаки
11. Бабушка Гамми приготовила 45 л яблочного сока и 85 л вишнёвого. Из них на завтрак медведи израсходовали 18 л, а на обед – в 2 раза больше, чем на завтрак. Сколько сока у медведей ещё осталось?1) 45 + 85 = 130 (л.) сока приготовила бабушка Гамми.
2) 18 * 3 = 54 (л.) сока израсходовали медведи на завтрак и обед.
3) 130 - 54 = 76 (л.) сока осталось у медведей.
Ответ: 76 литров сока.
12. Вычисли устно и объясни приёмы вычислений:5 • 100 = 500 800 : 10 = 80 200 • 3 = 600 560 : 7 = 80 270 : 90 = 3
10 • 70 = 700 400 : 100 = 4 40 • 18 = 720 400 : 5 = 80 320 : 160 = 2
13. Найди значения выражений:2 3 7 4 1 8 5 6
а) 360 : 6 • 5 – 450 : (25 • 2) – 70 • 6 : 3 = 1521) 25 * 2 = 50
2) 360 : 6 = 60
3) 60 * 5 = 300
4) 450 : 50 = 9
5) 70 * 6 = 420
6) 420 : 3 = 140
7) 300 - 9 = 292
8) 292 - 140 = 1524 1 7 5 6 8 3 2
б) 4 • (30 • 8) – 9 • 8 : 12 – (100 – 8 • 8) = 9181) 30 * 8 = 240
2) 8 * 8 = 64
3) 100 - 64 = 36
4) 4 * 240 = 960
5) 9 * 8 = 72
6) 72 : 12 = 6
7) 960 - 6 = 954
8) 954 - 36 = 918
14. БЛИЦтурнир
а) У Вадима а открыток. Их в 2 раза меньше, чем у Алёши. Сколько открыток у Алёши?а*2
б) У Лены b марок. Их на с марок меньше, чем у её сестры. Сколько марок у них вместе?
b + (b + c)
в) Артём нашёл n ягод земляники. Из них сестре он подарил k ягод, а бабушке – в 3 раза больше. Сколько ягод у него осталось?n - k - k * 3
г) Из x белых и у красных гвоздик сделали букеты по 5 гвоздик в каждом. Сколько получилось букетов?
(x + y) : 5
15. Определи, какие знаки действий можно вставить вместо звёздочек. Есть ли другие решения?
31 * 1 = 31 25 + 0 = 25 0 * 26 = 0
1 * 58 = 58 0 + 49 = 49 74 * 0 = 0Других вариантов нет.
16. Три купца хотят поделить между собой 21 бочонок кваса, из которых 7 полных, 7 наполовину полных и 7 пустых. Как им это сделать, не переливая квас, чтобы у каждого оказалось одинаковое количество кваса и бочонков (вместимость всех бочонков одинаковая)?
По логике задача решается так:
Если нам в конечном счете надо получить равное количество бочонков, при равном количестве кваса, то исходя из того, что пустые бочонки не влияют на объем кваса их сразу отбросим. Будем использовать их в конце для правильного создания количества бочонков кваса.
В итоге имеем 7 полных и 7 полупустых на 3 купцов. Этот объем кваса надо разделить на 3.
7 * 1 + 7 * 0,5 = 10. 5 объемов бочек всего
10.5 : 3 = 3.5 объема бочки кваса должен получить каждый купец.Начинаем раздавать бочки:
Из 7 полных у каждого получится 7 : 3 = 2 бочки (остаток 1), то есть у двух купцов по 1 * 2 = 2 объема , у третьего 1 * 3 = 3 объема бочки.
Начинаем делить бочки с половиной кваса. У того у кого уже есть 3 объема, надо дать одну полупустую бочку и все, у него будет полный объем кваса рассчитанный ранее, то есть 3,5. Остальное разделить между 2 купцами
Получится в итоге так:
У одного купца 3 полных бочки и 1 полупустая, то есть 4 бочки
У двух купцов 2 полных бочки и 3 полупустых, то есть по 5 бочек.Теперь у нас остались пустые бочки, которые мы оставляли напоследок ими уравновешиваем количество бочек. У того у кого 4 бочки даем 3 бочки, а двум другим по 2 бочки.
В итоге получаем:
У одного купца 3 полных бочки, 1 полупустая и 3 пустых.
У двух купцов 2 полных бочки, 3 полупустых и 2 пустых.
У каждого получилось 3,5 объема бочки кваса и всего 7 бочек.Если логика вам не подходит, то просто пытаемся решить задачу методом подбора!!!
17
-
Страница 17
Решение задач Урок 6
1. Определи, по какому признаку составлено множество:
а) А = {0; 2; 4; 6; 8}; четные цифры до 10
б) В = {1; 3; 5; 7; 9}; нечетные цифры до 10
в) С = {март; апрель; май}; весенние месяцы
г) D = {Атос; Портос; Арамис}; мушкетеры
д) Е = {Ш; П; А; Г}; использовано слово ШПАГ
е) К = {+; –; · ; : }; арифметические операции
ж) L = {30; 31; 32; 33; 34; 35; 36; 37; 38; 39}; числа с 30 до 39
з) М = {Москва}. столица России2. А – множество двузначных чисел, сумма цифр которых равна 5. Принадлежат ли этому множеству числа 5, 14, 25, 32, 50? Сделай записи, используя знаки
5 ∈A, 14∈А, 25∈ А, 32 ∈ А, 50 ∈А
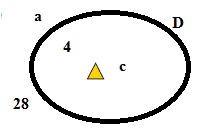
3. Прочитай записи. Построй диаграмму множества D и отметь на ней элементы. Смотри рисунок.
4. Фермер купил 64 саженца фруктовых деревьев. Из них 40 саженцев – для сада, а остальные – для трёх земельных участков поровну. Сколько фруктовых деревьев посадили на каждом из этих участков
1) 64 - 40 = 24 (саж.) были куплены для 3 участков.
2) 24 : 3 = 8 (саж.) были посажены на каждый из 3 участков.
Ответ: 3 саженца.5. Выполни деление с остатком и сделай проверку:
39 : 5 = 7 (ост. 4)
Проверка: 5 * 7 + 4 = 3548 : 7 = 6 (ост. 6)
Проверка: 7 * 6 + 6 = 4825 : 2 = 12 (ост. 1)
Проверка: 12 * 2 + 1 = 2563 : 4 = 15 (ост. 3)
Проверка: 4 * 15 + 3 = 63
92 : 7 = 13 (ост. 1)
Проверка: 7 * 13 + 1 = 926.
а) Пользуясь числовым лучом, составь множество двузначных чисел, кратных 11.
Пусть это будет множество А, тогда
А {11, 22, 33, 44, 55, 66, 77, 88, 99}
б) Выполни деление с остатком:
25 : 11 = 2 (ост. 3)
39 : 11 = 3 (ост. 6)
54 : 11 = 4 (ост. 10)
75 : 11 = 6 (ост. 9)
90 : 11 = 8 (ост. 2)
в) Выучи двузначные числа, кратные 11. Проверь себя, работая в паре. Самостоятельно.
18
-
Страница 18
7. В каждой из двух групп чисел найди «лишнее» число. Смотрите рисунок.

8. Составь выражения. Найди их значения при данных значениях а и b. Что ты замечаешь?
а) Мама купила к празднику а конфет. Из них b конфет она положила в вазу, а остальные раздала поровну двум детям. Сколько конфет досталось каждому из них? (а = 30, b = 24)(30 - 24) : 2 = 6 : 2 = 3 (конф.) досталось каждому.
Ответ: 3 конфеты.б) В мешке было а кг крупы. Из них израсходовали b кг, а остальную крупу рассыпали поровну в 2 пакета. Сколько килограммов крупы в каждом из этих пакетов? (а = 42, b = 36)
(42 - 36) : 2 = 6 : 3 (кг) в каждом пакете.
Ответ: 3 кг.в) Во 2 классе а человек. Из них b человек заболели, а остальные разделились поровну на две команды для игры в КВН. Сколько человек в каждой команде?
(а = 28, b = 4)(28 - 4) : 2 = 24 : 2 = 12 (чел.) в каждой команде.
Ответ: 12 человек.Все выражения составлены по одной схеме.
9. Составь задачу, которая решается так: (а – b) : 2 Подбери для а и b подходящие значения и найди ответ.
У Вити и Кати было 100 рублей, 20 рублей они потратили на газировку, а остальные деньги поделили между собой. Сколько досталось каждому?
(100 - 20) : 2 = 80 : 2 = 40 (руб.) досталось каждому.
Ответ: 40 рублей.10. Вспомни правила действий с 0 и 1. Допиши равенства в тетради:
а + 0 = а
а • 0 = 0
а : 1 = а
а – 0 = а
0 : а = 0
а : а = 1
а – а = 0
а • 1 = а
а : 0 - делить на 0 нельзя!11. Составь программу действий и вычисли:
3 4 7 1 2 5 8 6
а) 5 • 0 : 25 + (72 : 1 – 0) : 9 + 6 : 6 = 91) 72 : 1 = 72
2) 72 - 0 = 72
3) 5 * 0 = 0
4) 0 : 25 = 0
5) 72 : 9 = 8
6) 6 : 6 = 1
7) 0 + 8 = 8
8) 8 + 1 = 94 1 7 2 3 5 8 6
б) 24 : (3 • 8) – (7 • 0 + 1) • 1 + 8 : 1 = 81) 3 * 8 = 24
2) 7 * 0 = 0
3) 0 + 1 = 1
4) 24 : 24 = 1
5) 1 * 1 = 1
6) 8 : 1 = 8
7) 1 - 1 = 0
8) 0 + 8 = 812. Рассмотри уравнения. Какие из них имеют решения, а какие – нет?
Сколько решений? Назови их.
х + 0 = 8, х = 8 одно решение!
х – х = 5, не имеет решения, так как не логично
х • 0 = 7, не имеет решения, так как не логично
0 : х = 0, не имеет решения, так как подходит любое число 19
-
Страница 19
13. Назови фигуры на рисунке. Запиши с помощью фигурных скобок:
1) множество А фигур, расположенных внутри замкнутой линии:А = а, b, f, e
2) множество В фигур, расположенных снаружи замкнутой линии:
В = d, с
Что общего у всех этих фигур?
Они объемные
14. Запиши множества С и D с помощью фигурных скобок. Найди общее свойство элементов каждого из этих множеств.
C {c, e, a, b, d, f}
D {a, b}Какое из множеств С и D является частью другого? D является частью С.
Принадлежат ли элементы множества С множеству D? Да, но только часть.
А наоборот? Да, все элементы D принадлежат C.15. Найди общее свойство фигур множества А, множества В, общей части (пересечения) множеств А и В
По размеру большие, по форме квадраты.
Сделай записи в тетради, используя знаки и :
а ∈ А c ∈ A f ∈ А k ∈ A
а ∈ В c ∈ B f ∈ В k ∈ B16. В одной вазе лежат апельсин, мандарин и банан, в другой – яблоко и груша, а в третьей – персик и слива. Найди все способы, которыми можно взять два фрукта – по одному из разных ваз. Сколько всего различных способов?
1. апельсин-яблоко-персик
2. апельсин-яблоко-слива
3. апельсин-груша-персик
4. апельсин-груша-слива
5. мандарин-яблоко-персик
6. мандарин-яблоко-слива
7. мандарин-груша-персик
8. мандарин-груша-слива
9. банан-яблоко-персик
10. банан-яблоко-слива
11. банан-груша-персик
12. банан-груша-слива
Всего 12 способов 20
-
Страница 20
1. Пусть А – множество зайцев, В – множество животных. На диаграмме изображены некоторые элементы этих множеств.
Каждый ли заяц является животным?
Да, каждый!
Всякое ли животное является зайцем?
Нет, не всякое!
Какое из этих множеств является частью другого?
Зайцы являются множеством животных.
2. Задай свойством множества, изображённые на рисунках. Какое из них является подмножеством другого? Сделай записи.a) C ∈ M
б) B ∈ D
в) K ∈ P
г) F ∈ EКак расположены относительно друг друга диаграммы множества и подмножества?
Подмножества всегда внутри множества.
21
-
Страница 21
3. Определи по диаграмме, какое из множеств является подмножеством другого:
a) M ∈ P
б) A ∈ C, B ∈ C, B ∈ A
в) F ∈ K, F ∈ E, E ∈ K
г) S ∈ D, T ∈ D, S ∈ T4. Определи, какое из указанных двух множеств является подмножеством другого. Сделай записи и нарисуй диаграммы Эйлера–Венна.
а) В – множество учеников некоторой школы, С – множество отличников этой школы.
б) D – множество девочек некоторого класса, Е – множество всех учеников этого класса.
в) К – множество рыб, О – множество окуней.
г) N – множество натуральных чисел, М – множество чётных чисел.
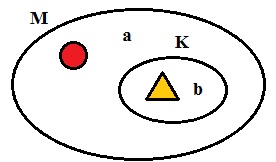
5. М = {a; b; треугольник желтый; красный круг; +} и К = {b; треугольник желтый}. Нарисуй диаграмму Эйлера–Венна множеств М и К и отметь на ней элементы этих множеств. Какое из них является подмножеством другого? Запиши с помощью знака и прочитай разными способами.
6. Придумай примеры множества и его подмножества. Нарисуй диаграмму Эйлера–Венна
7. Квадрат разбит на части. Назови каждый элемент множества получившихся геометрических фигур.
В множество квадрата входит два прямоугольника, треугольник, пятиугольник, четырехугольник.
8. Построй прямоугольник со сторонами 3 см и 7 см. Построй квадрат с тем же периметром. Сравни их по площади.
1) (3 + 7) * 2=10 * 2=20 (см) - периметр прямоугольника.
2) 20 : 4=5 (см) - должна быть сторона квадрата, чтобы получился периметр 20 см.
3) 5 * 5 = 25 (см2) - площадь квадрата.
4) 3 * 7 = 21 (см2) - площадь прямоугольника.25 см2 > 21 см2
Ответ: площадь квадрата больше, чем площадь прямоугольника.
22
-
Страница 22
9. Составь задачу по картинке и реши её:
Витя купил 5 яблок и 2 груши, заплатив за покупку 108 рублей. Маша купила 2 яблока и 2 груши, заплатив 72 рубля. Сколько стоит 1 яблоко и 1 груша?
На сколько рублей груша дороже яблока? Во сколько раз яблоко дешевле груши?
Решение:
1) 108-72=36 (р.) стоит 3 яблока.
2) 36 : 3 = 12 (р.) стоит 1 яблоко.
3) 12 * 2 = 24 (р.) стоит 2 яблока.
4) 72 - 24 = 48 (р.) стоит 2 груши.
5) 48 : 2 = 24 (р.) стоит 1 груша.
6) 24 - 12 = 12 (р.) груша дороже яблока.
7) 24 : 12 = 2 (р.) груша дороже яблока.Ответ: груша стоит 24 рубля, яблоко 12 рублей, при этом груша дороже на 12 рублей и в 2 раза.
10. Составь выражение и найди его значение:
а) На одной улице 18 одноэтажных домов и 3 двухэтажных. Во сколько раз одноэтажных домов на этой улице больше, чем двухэтажных?
18 :3 = 6 (р.) больше одноэтажных домов, чем двухэтажных.
Ответ: в 6 раз.б) В одном доме 10 квартир. Это в 5 раз меньше, чем в другом. Сколько квартир в этих двух домах?
10 : 5 + 10 = 12 (кв.) в двух домах.
Ответ: 12 квартир.в) На каждом этаже 7 этажного дома по 6 квартир, а на каждом этаже 9 этажного дома по 4 квартиры. В каком из этих домов больше квартир и на сколько?
7 * 6 - 9 * 6 = 42 - 36 = 6 (кв.) больше в 7 этажном доме.
Ответ: на 6 квартир больше в 7 этажном доме, чем в 9 этажном.г) В первом доме 56 квартир, а во втором – в 7 раз меньше. На сколько квартир в первом доме больше, чем во втором?
56 - 56 : 7 = 56 - 8 = 48 (кв.) на столько больше в первом доме.
Ответ: на 48 квартир больше в первом доме11.
а) 91 : 7 = 13
б) 80 : 5 = 16
в) 64 : 4 = 18
г) 78 : 3 = 26
д) (39 + 29) : 4 = 17
е) (60 – 5) : 5 = 11
ж) 63 : (3 • 7) = 63 : 21 = 3
з) 240 : (80 : 2) = 240 : 40 = 8
и) 19 + 17 • 3 – 46 = 19 + 51 - 46 = 24
к) 54 – 26 + 38 • 3 = 54 - 26 + 114 = 142
л) 48 : 2 + 60 : 2 = 24 + 30 = 54
м) (19 · 5 – 5) : 30 = (95 - 5) :30 = 90 : 30 = 312. Найди значения х и составь таблицу в тетради. Расположи ответы в порядке убывания и расшифруй слово. Что это?
a 4 8 10 15 25 37 x 79 119 139 74 174 294 САТУРН
23
-
Страница 23
1.
а) Прочитай задачу, назови её условие и вопрос:
«Три одинаковых яблока стоят 42 рубля. Сколько рублей стоят 5 таких яблок?»Условие: три одинаковых яблока стоят 42 рубля. Вопрос: сколько рублей стоят 5 таких яблок?
Реши задачу, используя схему и таблицу:
1) 42 : 3 = 14 (р.) стоит 1 яблоко.
2) 14 * 5 = 70 (р.) стоит 5 яблок.
Ответ: 70 рублей.б) Почему задачи такого типа называют задачами «на приведение к единице»? Как их удобнее решать – с помощью схемы или таблицы?
Называют так потому, что итоговое значение находится через значение приведенное в одной единице исчисления чего-либо.
2.
а) В 7 одинаковых ящиках 56 кг винограда. Сколько килограммов винограда в 10 таких ящиках?
1) 56 : 7 = 8 (кг) в 1 ящике.
2) 8 * 10 = 80 (кг) в 10 ящиках.
Ответ: 80 кг.б) Составь задачу по выражению и реши её: (16 : 8) • 6.
В ящике 16 кг апельсин расфасованных в 8 пакетов. Сколько кг апельсин в 6 таких пакетах?
(16 : 8) • 6 = 2 * 6 = 12 (кг) апельсин в 6 пакетах.
Ответ: 12 кг.3.
а) Из 36 метров ткани можно сшить 9 одинаковых костюмов. Сколько метров этой ткани потребуется на 15 таких костюмов?1) 36 : 9 = 4 (м) ткани надо на 1 костюм.
2) 4 * 15 = 60 (м) ткани надо на 15 костюмов.
Ответ: 60 метров.б) За 7 билетов в театр заплатили 2100 р. Сколько денег надо заплатить за 12 таких билетов, если цена билетов одинаковая?
1) 2100 :7 = 300 (р.) стоит 1 билет.
2) 300 *12 = 3600 (р.) надо заплатить за 12 билетов.
Ответ: 3600 рублей.4.
а) В трёх одинаковых банках 15 л мёда. Сколько литров в бочонке, вмещающем 12 таких банок?1) 15 : 3 = 5 (л) в одной банке.
2) 5 * 12 = 60 (л) меда в 12 банках.
Ответ: 60 литров меда.б) Для строительства двух одинаковых домов требуется 120 м3 леса. Сколько кубических метров леса потребуется для строительства 6 таких домов?
1) 120 :2 = 60 (м3) требуется леса для 1 дома.
2) 60 * 6 = 360 (м3) потребуется для 6 домов.
Ответ: 360 м3 леса.5.
Реши уравнения с комментированием:3 • х = 57
х = 57 : 3
х = 19х : 68 = 4
х = 68 * 4
х = 272540 : х = 90
х = 540 : 90
х = 66.
Назови какое-нибудь подмножество:
а) множества учеников школы; девочки
б) множества птиц; воробьи
в) множества легковых автомобилей; Жигули
г) множества натуральных чисел. от 1 до 10. 24
-
Страница 24
Урок 8
Задачи на приведение к единице
7. На диаграмме отмечены все элементы множеств А, В и С.
а) Запиши эти множества с помощью фигурных скобок.А = {д;е}
B = {м;к;д;е}
C = {а;р;м}б) Найди подмножества. Сделай записи, вставляя знаки ⊂ или ⊄:
А ⊂ В С ⊄ В А ⊄ СЗнак ∈ ставится между элементом и множеством, а знак ⊂ ставится между двумя множествами.
Например, к ∈ В, А ⊂ В.8. Пусть А = {?; ☆ ; а; b}, B = {а; b}. Найди и прочитай верные записи:
А ⊂ B - не верно
А ⊄ B - верно
А ∉ B - не верно
B ⊂ B - верно
B ⊄ B - не верно, так как множество принадлежит само себе
B ∉ B - не верно, так как знак применяется для элементов, а не для множеств.
☆ ∈ A - верно
☆ ∉ B - верно, не принадлежит этому множеству
☆ ⊂ A - неверно, так как тут элемент и множество, а значит знак должен быть другим.9. Вычисли и расположи ответы в порядке возрастания. Кто это?
40 : 4 = 10
10 - 7 = 3
3 * 9 = 27П
18 : 3 =6
6 + 9 =15
15 • 5 = 75Д
500 : 5 =100
100 – 64 = 36
36 • 2 = 72Р
5 • 80 = 400
400 – 120 = 280
280 : 40 = 7Е
140 – 60 = 80
80 : 40 = 2
2 + 68 = 70А
68 : 17 = 4
4 • 8 = 32
32 – 32 = 0Г
ГЕПАРД
10.
а) Пользуясь числовым лучом, составь множество двузначных чисел, кратных 12.
А = {12;24;36;48;60;72;84;96}
б) Выполни деление с остатком:
37 : 12 = 3 (ост. 1)
50 : 12 = 4 (ост. 2)
68 : 12 = 5 (ост. 8)
75 : 12 = 6 (ост. 3)
99 : 12 = 8 (ост. 3)
в) Выучи двузначные числа, кратные 12. Проверь себя, работая в паре.
11. Составь выражение и найди его значение, если m = 15, k = 20:
«В магазин привезли m двухколёсных и k трёхколёсных велосипедов. Сколько всего колёс у всех этих велосипедов?»15 * 2 + 20 * 3 = 30 + 60 = 90 (кол.) у всех велосипедов.
Ответ: 90 колес. 25
-
Страница 25
Урок 8
Задачи на приведение к единице
12. Сравни выражения*:
х – 315 > х – 415
m • 3 > m : 3
a • 8 + a • 6 < 15 • a
у + 205 < 502 + у
с : 38 > с : 46
b • 24 – b • 10 > b • 7
48 – t < 200 – t
512 : d > 312 : d
6 • c + 3 • c = c • 913. Определи для каждого случая, какая фигура является пересечением двух треугольников.
а) треугольник
в) линия
д) четырехугольник
б) шестиугольник
г) точка
е) пятиугольник
14. Выполни действия. Расположи ответы примеров в порядке убывания и расшифруй слово. Что оно означает?
Л 387 + 512 + 78 = 948
У 46 + 58 + 724 = 828
О 61 + 445 + 189 = 695
Т 35 + 619 + 55 = 709
Н 248 + 23 + 302 + 95 = 573
П 8 + 88 + 888 = 984ПЛУТОН
15. Для запуска 4-местного и 8-местного космических кораблей в отряд космонавтов набрали группу из 52 человек. К полёту на 4-местном корабле готовятся 3 команды. Сколько команд готовятся для полёта на 8-местном корабле?
на 4-местном на 8-местном
|___________|_____________________________|Решение:
1) 4 * 3 = 12 (ч.) готовят для полета на 4 местных кораблях.
2) 52 - 12 =40 (ч.) готовят для полета на 8 местных кораблях.
3) 40 :8 = 5 (ком.) готовят на 8 местные корабли.
Ответ: 5 команд.16. В первом аквариуме на 16 рыбок больше, чем во втором. Сколько рыбок надо переселить из первого аквариума во второй, чтобы рыбок в них стало поровну?
Решение:
Получается, что у нас разница в 16 рыбок, которых и предстоит разделить поровну. 16:2 = 8 рыбок надо пересадить, а 8 оставить.
26
-
Страница 26
Урок 9
Решение задач
1. Реши задачи двумя способами:
а) Антон прошёл 240 м за 4 минуты. Сколько метров он пройдёт за 8 минут, если будет идти с той же скоростью?
1 способ
1) 240 : 4 = 60 (м) Антон проходит за минуту.
2) 60 * 8 - 480 (м) пройдет за 8 минут.
Ответ: 480 метров.2 способ
1) 8:4=2 (р.) на столько он будет дольше идти по времени 8 минут, относительно 4 минут.
2) 240 * 2 = 480 (м) пройдет за 8 минут.
Ответ: 480 метров.б) Рабочий сделал за 2 часа 18 одинаковых деталей. Сколько деталей, работая так же, он изготовит за 8 часов?
1 способ
1) 18 : 2 = 9 (д.) рабочий делает за час.
2) 9 * 8 = 72 (д.) сделает за 8 часов.
Ответ: 72 детали.2 способ
1) 8 : 2 = 4 (р.) во столько 8 часов больше 2 часов.
2) 18 * 4 = 72 (д.) сделает за 8 часов.
Ответ: 72 детали.2. Составь программу действий и вычисли:
3 1 4 8 5 6 9 7 2
а) 3 • (9 : 9) • 10 – 0 : 5 • 18 – 6 • (4 : 1) = 61) 9 : 9 = 1
2) 4 : 1 = 4
3) 3 * 1 = 3
4) 3 * 10 = 30
5) 0 : 5 = 0
6) 0 * 18 = 0
7) 6 * 4 = 24
8) 30 - 0 = 30
9) 30 - 24 = 61 2 5 8 6 3 9 7 4
б) (7 • 9 – 0) : 21 + 6 • (0 : 8) – 45 : (15 • 1) = 01) 7 * 9 = 63
2) 63 - 0 = 63
3) 0 : 8 = 0
4) 15 * 1 = 15
5) 63 : 21 = 3
6) 6 * 0 = 0
7) 45 : 15 = 3
8) 3 + 0 = 3
9) 3 - 3 = 03. Пользуясь диаграммой Эйлера–Венна, запиши множества А и В с помощью фигурных скобок. Заполни пропуски, используя знаки ∈, ∉, ⊂, ⊄ :
А ⊄ В m ∈ A
В ⊂ А m ∈ В
2 ∈ А 9 ∉ А
2 ∉ В 9 ∉ В4.
С – множество всех спортсменов,
Ф – множество футболистов,
В – множество вратарей футбольных команд.Нарисуй на одном рисунке диаграммы множеств С, Ф и В. Найди подмножества и сделай записи с помощью знака ⊂.
В ⊂ Ф Ф ⊂ С
5.
а) Определи по диаграмме Эйлера–Венна элементы множеств М и К.
0, 1, 2, 3, 4, 6, 8
Какие элементы принадлежат обоим множествам одновременно?
2, 4
Где расположены эти элементы?
В области этих двух множеств, то есть на площади их пересечения.
б) Пользуясь диаграммой, найди пропущенные знаки ∈ и ∉ . Сделай записи. Что ты замечаешь?
1 ∈ М 4 ∈ М 8 ∉ М 15 ∉ М
1 ∉ К 4 ∈ К 8 ∈ К 15 ∉ К 27
-
Страница 27
Урок 9
Решение задач
6. Вычисли устно:
700 – 160 : 2 = 700 - 320 = 380
(525 – 525) • (396 + 489) = 0 * (396 + 489) = 0
584 + 0 : 216 = 584 + 0 = 584
(800 – 200 + 40) : (201 – 200) = 640 : 1 = 6407. Составь выражения. Найди их значения при данных значениях букв:
а) В трёх одинаковых коробках n кг изюма. Сколько изюма в 8 таких коробках? (n = 12)
12 : 3 * 8 = 4 * 8 = 32 (кг) изюма в 8 коробках.
Ответ: 32 килограмма изюма в 8 коробках.б) Для изготовления а одинаковых компьютеров требуется 30 кг металла. Сколько металла пойдёт на изготовление b таких компьютеров? (а = 10, b = 7)
30 : 10 * 7 = 3 * 7 = 21 (кг) металла пойдёт на изготовление b таких компьютеров.
Ответ: 21 килограмм металла.8. Сарай имеет форму прямоугольного параллелепипеда. Длина сарая равна 10 м, ширина – 4 м, а высота – 3 м. Найди объём этого сарая и площадь его стен.
1) 10 * 4 * 3 = 40 * 3 = 120 (м3) объем сарая.
2) (10 * 4 + 10 * 3 + 4 * 3) * 2 = (40 + 30 + 12) * 2 = 154 (м2) площадь стен сарая.
Ответ: 120 м3 объем и 154 м2 площадь стен сарая.9. Реши уравнения с комментированием и сделай проверку:
х – 38 = 712
х = 712 + 38
х = 750Проверка: 750 - 3 8 = 712
524 – х = 198
х = 524 - 198
х = 326Проверка: 326 + 198 = 524
х + 275 = 900
х = 900 - 275
х = 625Проверка: 625 + 275 = 900
10. Вычисли. Расположи ответы в порядке убывания, и ты узнаешь имя созвездия в Северном полушарии.
40 : 5 * 3 : 6 + 46 = 50
(72 : 8 + 11) : 5 * 9 = 36
(28 : 7 * 8 + 8) : 10 = 4
(63 : 9 + 23) : 6 * 7 = 35
36 : 4 * 5 + 15 - 13 = 47
(42 : 6 + 17) : 3 * 20 = 160ДРАКОН
11. Подбери вместо звёздочек цифры так, чтобы равенство было верно:
* + * = **
Сколько решений имеет эта задача?1 + 9 = 10
2 + 8 = 10
3 + 7 = 10
4 + 6 = 10
5 + 5 = 10
5 + 6 = 11
5 + 7 = 12
5 + 8 = 13
5 + 9 = 14
6 + 6 = 12
6 + 7 = 13
6 + 8 = 14
6 + 9 = 15
7 + 4 = 11
7 + 5 = 12
7 + 6 = 13
7 + 7 = 14
7 + 8 = 15
7 + 9 = 16
8 + 3 = 11
8 + 4 = 12
8 + 5 = 13
8 + 6 = 14
8 + 7 = 15
8 + 8 = 16
8 + 9 = 17
9 + 2 = 11
9 + 3 = 12
9 + 4 = 13
9 + 5 = 14
9 + 6 = 15
9 + 7 = 16
9 + 8 = 17
9 + 9 = 1834 решения, при условии, что используются числа лишь один раз, без их перестановки, то есть 2 + 8 заменят в том числе и 8 + 2.
28
-
Страница 28
Урок 10
Пересечение множеств. Знак ∩
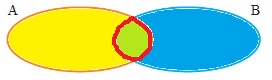
1. Построй в тетради, как показано на рисунке, диаграммы множеств А и В. Раскрась жёлтым цветом область А, а синим – область В.
Какую часть этих областей пришлось закрасить дважды? Обведи её границу красным цветом. Это – пересечение, или общая часть, двух областей.
2. К – множество детей на дне рождения у Коли, а Т – множество детей на дне рождения у Тани. Из каких элементов они состоят?
K = {Шура; Надя; Петя} T = {Петя; Маша; Лена}
Найди пересечение множеств K и Т.
К ∩ Т = Петя
Как можно найти пересечение множеств К и Т, не рисуя диаграммы? Сделай вывод.
Общий элемент встречающийся в одном и другом множестве будет результатом пересечения этих множеств.
3.
А – множество учеников, изучающих английский язык.
F – множество учеников, изучающих французский язык.
Что представляет собой множество А ∩ F?А ∩ F = Ø при условии что каждый из учеников изучает лишь только один иностранный язык.
29
-
Страница 29
Урок 10
Пересечение множеств. Знак ∩
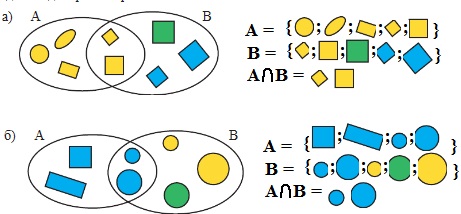
4. Найди общее свойство элементов каждого из множеств А, В, А ∩ В. Где на диаграмме расположены их элементы?
5. Назови элементы множеств М и К. Найди их пересечение М ∩ К. Построй диаграмму этих множеств и отметь их элементы. Обведи на диаграмме множество М ∩ К.
а)
М = {а; б; ?; ☆ }
К = {?; а; в}
М ∩ К = ?; аб)
М = {15; 25; 30; 40}
К = {23; 24; 25}
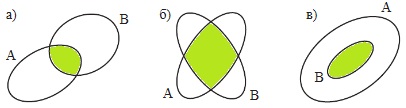
М ∩ К = 256. Нарисуй в тетради диаграмму множеств А и В. Закрась на ней множество А ∩ В.
7. Докажи, что множества А и В на рисунке не имеют общих элементов. Объясни смысл равенства: А ∩ В = ∅
У них нет общих элементов!
Такие множества называются непересекающимися. Приведи свои примеры непересекающихся множеств.
Ученики разных школ, скажем 11 и 25 не образуют общие элементы множеств этих школ!
8. Начерти два треугольника так, чтобы их пересечением были:
а) шестиугольник;
б) пятиугольник;
в) четырёхугольник;
г) треугольник;
д) отрезок;
е) точка;
ж) пустое множество.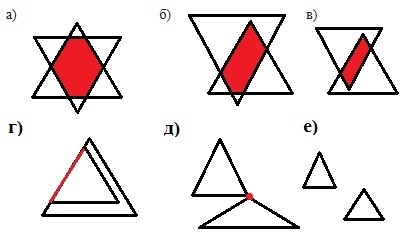
9. Улитка проползла утром 3 см 6 мм, днём – 1 дм 4 мм, а вечером – на 4 см меньше, чем утром и днём вместе. Какое расстояние проползла улитка за всё это время?
I II III
|____|________|_______|Решение:
1) 36 + 14 = 50 (мм) улитка проползла утром и днем.
2) 50 - 40 = 10 (мм) улитка проползла вечером.
3) 50 + 10 = 60 (мм) всего проползла улитка.
Ответ: 60 мм 30
-
Страница 30
Урок 10
10. Подбери корни уравнений:
а) 15 • а = 15 : а
a = 1б) x • 10 = x : 10
x = 1в) y + y = y • y
y = 0г) b + b + b = b • b
b = 111. БЛИЦтурнир
а) Оля испекла а пирожков, а её сестра – b пирожков. Эти пирожки они разложили поровну на 3 тарелки. Сколько пирожков в каждой тарелке?
(a+b) : 3
б) В 7 одинаковых банках d литров сока. Сколько сока в 20 таких банках?
d : 7 * 20
в) С первой грядки собрали с огурцов, а со второй – на b огурцов меньше. Во сколько раз больше огурцов собрано с первой грядки, чем со второй?
с : (с - b)
г) В коробке было n конфет. Четверо ребят взяли по а конфет. Сколько конфет осталось в коробке?
n - 4*a
д) В вазе лежало с яблок, а груш – в 3 раза больше, чем яблок. Сколько всего яблок и груш лежало в вазе?
c + c * 3
12. Найди значения выражений:
а) 76 • 5 = 380
б) 8 • 49 = 392
в) 130 • 6 = 780
г) 3 • 290 = 870
д) 48 : 3 = 16
е) 52 : 4 = 13
ж) 950 : 5 = 190
з) 660 : 6 = 100
и) 80 : 16 = 5
к) 57 : 19 = 3
л) 780 : 13 = 60
м) 560 : 140 = 4
н) 75 : 25 + 3 • 17 = 3 + 51 = 54
о) 200 – 80 : 5 = 200 - 16 = 184
п) (160 – 70) : 18 = 90 : 18 = 5
р) (29 + 25) : (72 : 8) = 54 : 9 = 613. Через три с половиной часа наступит полдень. А сейчас который час?
Сейчас 8 : 30
14. От Бабы Яги до Кощея ведут 3 дороги, а от Кощея до Кикиморы – 4 дороги. Сколькими способами можно дойти от Бабы Яги до Кикиморы по этим дорогам?
3 + 4 = 7 способами.
Ответ: 7 способов. 31
-
Страница 31
Урок 11
Свойства пересечения множеств
1.
а) Назови записанные свойства сложения и умножения. В чём их смысл?
а + b = b + a
а • b = b • a
(а + b) + c = a + (b + c)
(а • b) • c = a • (b • c)В том, что при выполнении вычислений этих выражений не важен порядок действий и возможно использовать перестановки.
б) Обладают ли этими свойствами вычитание и деление? Обоснуй свой ответ.
Нет, не обладает. Для этого лучше всего привести пример.
9 : 3 ≠ 3 : 9
9 - 3 ≠ 3 - 9
2. А = {1; 2; 3; 4}, В = {3; 4; 5}. Запиши с помощью фигурных скобок множества А ∩ В и В ∩ А. Покажи их на диаграмме Эйлера–Венна. Что ты замечаешь?
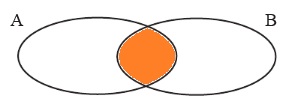
А ∩ В = {3; 4} B ∩ A = {3; 4}
Сделай вывод.
Пересечение элементов двух множеств одно и тоже, не важно берем ли мы пересечение первого множества во втором или второго в первом.
3. Нарисуй диаграмму множеств А, В и С. Закрась на ней сначала А ∩ В, потом С, а затем обведи их пересечение (А ∩ В) ∩ C. Аналогично построй диаграмму множества А ∩ (В ∩ C).
(А ∩ В) ∩ C =
А ∩ (В ∩ C) =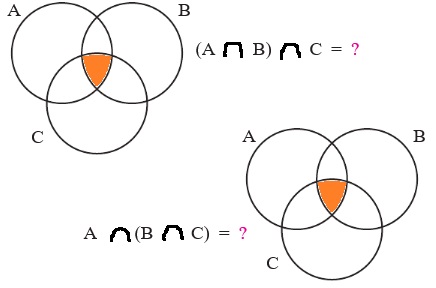
Сравни полученные множества. Что ты замечаешь? Сделай вывод
Свойства пересечения множеств
Пересечение множеств обладает переместительным и сочетательным свойствами.
Переместительное свойство: А ∩ В = В ∩ А
Сочетательное свойство: (А ∩ В) ∩ C = А ∩ (В ∩ C)Значит, результат пересечения множеств не зависит от порядка множеств и от порядка действий.
4. Допиши в тетради равенства, выражающие свойства пересечения множеств. Назови эти свойства и объясни их смысл.
М ∩ К = К ∩ М (М ∩ К) ∩ Т = Т ∩ (М ∩ К)
32
-
Страница 32
Урок 11
Свойства пересечения множеств
5. В – множество машин марки «Волга», С – множество синих машин, М – множество машин у жителей Москвы. Что представляют собой множества:
а) М ∩ В; (машины "Волга" в Москве)
б) В ∩ С; (синие машины "Волга" )
в) М ∩ С; (синие машины в Москве)
г) (М ∩ В) ∩ С? (синие машины "Волга" в Москве)
6. Выполни действия наиболее удобным способом. Какие свойства чисел при этом используются?
а)
(298 + 386) + 102 = 400 + 386 = 786489 + (256 + 11) = 500 + 256 = 756
258 + 475 + 42 + 125 = 300 + 600 = 900
б)
19 • 2 • 5 = 190 * 10 = 190
8 • 2 • 25 = 8 * 100 = 800
14 • 45 = 2 * 7 * 45 = 7 * 90 = 6307. Найди значения х и составь таблицу в тетради. Расположи ответы в порядке убывания и расшифруй слово. Кто это?
B Е О У К И Д Т С
а 1 2 3 4 5 6 7 8 9 х 160 320 480 640 800 354 434 286 594 КУСОДИЕВ *
* - Русский советский художник. Академик живописи ИАХ. Член Ассоциации художников революционной России. Портретист, театральный художник, декоратор. (Родился: 7 марта 1878 г., Астрахань, Российская империя)
8. Составь выражения. Найди их значения при данных значениях букв:
а) В студии рисования с девочек, а мальчиков – в 3 раза меньше. На сколько девочек в этой студии больше, чем мальчиков? (с = 15, 21, 27)
при с = 15, 15 : 3 = 5 раз
при с = 21, 21 : 3 = 7 раз
при с = 27, 27 : 3 = 9 разб) В 4 одинаковых банках m литров сока. Сколько литров сока в 9 таких банках? (m = 8, 12, 20)
при m = 8, 8 : 4 * 9 = 18 литров
при m = 12, 12 : 4 * 9 = 27 литров
при m = 20, 20 : 4 * 9 = 45 литров9. В начале лета рост щенка Тимошки был равен 2 дм 7 см. В июне Тимошка вырос на 6 см, в июле – на 2 см меньше, чем в июне. На сколько сантиметров вырос Тимошка в августе, если в конце лета его рост составил 4 дм?
4 дм – 2 дм 7 см
июнь июль август
|_____|__|________|Решение:
1) 27 + 6 = 33 (см) рост Тимошки в июне.
2) 6 - 2 = 4 (см) вырос в июле.
3) 33 + 4 = 37 (см) рост Тимошки в июле.
4) 40 - 37 = 3 (см) Тимошка вырос в августе.
Ответ: 3 см.10. Общий вес Миши, Саши и Тани равен 54 кг. Миша весит столько же, сколько Саша и Таня вместе. Сколько весит Миша?
Решение: Так как Миша весит столько же как и Саша и Таня, то можно считать, что общий вес это два веса Миши.
54 : 2 = 27 (кг) весит Миша
Ответ: 27 кг. 33
-
Страница 33
Урок 12
Решение задач
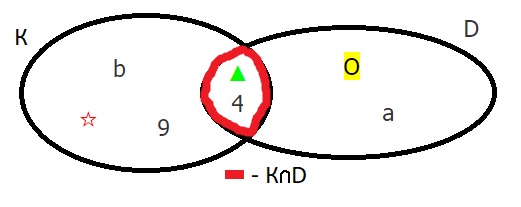
1. Известно, что К = {▲; b; 4; ☆ ; 9}, D = {а; ▲ ; 4; О }. Найди их пересечение К ∩ D. Построй диаграмму множеств К и D и отметь их элементы. Обведи множество К ∩ D.
К ∩ D = {▲ ; 4;}
2. Составь выражения. Найди их значения при данных значениях букв:
а) В четырёх одинаковых подъездах дома n квартир. Сколько квартир в 6 таких же подъездах этого дома? (n = 64)
64 : 4 * 6 = 18 * 6 = 108 (кв.) в 6 подъездах.
Ответ: 108 квартир.б) На k одинаковых этажах дома 56 окон. Сколько окон на r таких же этажах этого дома? (k = 7, r = 12)
56 : 7 * 12 = 8 * 12 = 96 (ок.) на 12 этажах
Ответ: 96 окон.3. Вычисли удобным способом:
а) 427 + (84 + 173) = 600 + 84 = 684
в) 2 • 16 • 5 • 6 = 10 * 16 * 6 = 10 * 96 = 960
б) 35 + 541 + 19 + 165 = 200 + 560 = 760
г) 25 • 2 • 18 = 50 * 18 = 50 * 10 * 8 = 9004. БЛИЦтурнир
а) На первой ёлке с игрушек, а на второй – на 15 игрушек меньше. Во сколько раз больше игрушек на первой ёлке, чем на второй?
с : (с - 15)
б) В первом доме d жильцов, а во втором – в 4 раза больше. На сколько меньше жильцов в первом доме, чем во втором?
d * 4 - d
в) Мама заготовила на зиму а двухлитровых и b трёхлитровых банок варенья. Сколько всего литров варенья заготовила мама?
a * 2 + b * 3
5. Найди значения выражений. Проверь результаты по действиям с помощью калькулятора.
а) 29 • 2 + 26 = 58 + 26 = 84
б) 37 + 42 • 4 = 37 + 168 = 205
в) 72 : 3 – 17 = 24 - 17 = 7
г) 63 + 100 : 4 = 63 + 25 = 88
д) 540 : 9 + 280 : (14 • 5) = 60 + 280 : 70 = 60 + 4 = 64
е) 300 : (5 • 60) • (78 : 13) = 300 : 300 * 6 = 1 * 6 = 66. Составь уравнение, реши его и сделай проверку:
а) Из какого числа надо вычесть 394, чтобы получить 286?
х - 394 = 286
х = 286 + 394
х = 680б) На сколько надо уменьшить число 604, чтобы получить 178?
604 - х = 178
х = 604 - 178
х = 426в) Какое число надо увеличить на 573, чтобы получить 850?
х + 573 = 850
х = 850 - 573
х = 2777. Найди значения выражений:
2 1 6 7 3 5 4
а) (13 + 8 • 4) : 5 – (27 : 3 – 0 • 6) = 01) 8 * 4 = 32
2) 32 + 13 = 45
3) 27 : 3 = 9
4) 0 * 6 = 0
5) 9 - 0 = 9
6) 45 : 5 = 9
7) 9 - 9 = 04 1 7 5 3 2 8 6
б) 40 : (24 : 6) + 7 • (12 – 2 • 2) – 5 • 5 = 411) 24 : 6 = 4
2) 2 * 2 = 4
3) 12 - 4 = 8
4) 40 : 4 = 10
5) 7 * 8 = 56
6) 5 * 5 = 25
7) 10 + 56 = 66
8) 66 - 25 = 41 34
-
Страница 34
Урок 12
Решение задач
8. Рассмотри рисунок. Сравни по площади фигуры А и В, В и С, А и С.
1) Верно ли, что на рисунке все фигуры равны между собой? Нет. А - 11 клеток, B и D - 9 клеток, С - 10 клеток.
2) Верно ли, некоторые фигуры равны между собой? Да, B и D.
3) Имеются ли фигуры, площадь которых равна 11 клеточкам? Да, фигура А.
4) Верно ли, что площадь каждой фигуры больше 10 клеточек? Нет, так как B и D по 9 клеток.Обоснуй свой ответ.
9.
а) Пользуясь числовым лучом, составь множество двузначных чисел, кратных 13.Скажем это будет множество А, тогда А = {13, 26, 39, 52, 65, 78, 91}
б) Выполни деление с остатком:
28 : 13 = 2 (ост. 2)
40 : 13 = 3 (ост. 1)
56 : 13 = 4 (ост. 4)
72 : 13 = 5 (ост. 7)
94 : 13 = 7 (ост. 3)в) Выучи двузначные числа, кратные 13. Проверь себя, работая в паре. Самостоятельно
10. Практическая работа
Вырежи из плотной бумаги два квадрата: один со стороной 3 см, а другой – со стороной 2 см. Начерти различные случаи пересечения квадратов, обводя модели карандашом.
Примеры:
11. Как расположить 4 элемента на диаграммах множеств А и В, чтобы в каждом из них было соответственно:
а) 2 и 4 элемента;
б) по 3 элемента;
в) 4 и 3 элемента;
г) 0 и 4 элемента;
д) по 4 элемента;
е) по 2 элемента?
Смотрим рисунок.
12. Послезавтра будет четверг. Позавчера у Тани был день рождения. Какой это был день недели?
Сегодня вторник, а день рождения был в воскресенье.
35
-
Страница 35
Урок 13
Обратные задачи на приведение к единице
1. Реши задачи, составляя выражения. Сравни их. Что ты замечаешь?
В трёх одинаковых наборах 36 пуговиц. Сколько пуговиц в 5 таких наборах?
3 наб. — 36 п.
5 наб. — ? п.
1 наб. — ? п.1) 36 : 3 = 12 (п.) в одном наборе.
2) 12 * 5 = 60 (п.) в 5 наборах.
Ответ: 60 пуговиц.В трёх одинаковых наборах 36 пуговиц. Во скольких таких наборах 60 пуговиц?
3 наб. — 36 п.
? наб. — 60 п.
1 наб. — ? п1) 36 : 3 = 12 (п.) в одном наборе.
2) 60 : 12 = 5 (н.) в 60 пуговицах.
Ответ: 5 наборов.Почему такие задачи называют взаимно обратными?
Так как находим величины зависящие друг от друга, но все же разные.
Чем отличаются их краткие записи и решения?
Различными единицами измерения и неизвестными
2.
а) Реши задачу, используя схему и таблицу. Какой способ удобнее? «На 2 м2 земли посадили 16 кустов клубники. На какой площади, высаживая клубнику так же, можно разместить 80 кустов?»
2 м2 — 16 к.
? м2 — 80 к.
1 м2 — ? к.1) 16 : 2 = 8 (к.) можно посадить на 1м2
2) 80 : 8 = 10 (м2) надо для 80 кустов.
Ответ: 10 м2б) Составь и реши обратную задачу.
«На 2 м2 земли посадили 16 кустов клубники. Сколько кустов можно посадить на 10 м2?»
2 м2 — 16 к.
? м2 — 10 м2.
1 м2 — ? к.1) 16 : 2 = 8 (к.) можно посадить на 1м2
2) 8 * 10 = 80 (к.) можно посадить на 10 м2
Ответ: 80 кустов.3. Составь и реши задачи на приведение к единице по выражениям: (15 : 5) • 9 и 27 : (15 : 5). Что ты замечаешь?
(15 : 5) • 9 = 3 * 9 = 27
27 : (15 : 5) = 27 : 3 = 9
Эти выражения подобраны по принципу обратных задач.
4.
а) За 5 одинаковых конвертов заплатили 45 р. Сколько таких конвертов можно купить на 72 р.?
1) 45 : 5 = 9 (р.) стоит 1 конверт.
2) 72 : 9 = 8 (кон.) можно купить за 72 рубля.
Ответ: 8 конвертов.б) Из 27 м ткани сшили 9 одинаковых платьев. Сколько таких платьев можно сшить из 60 м этой ткани?
1) 27 : 9 = 3 (м) идет на 1 платье.
2) 60 : 3 = 20 (пл.) можно сшить из 60 м ткани.
Ответ: 20 платьев.5. Построй два отрезка так, чтобы их пересечением были:
а) отрезок;
б) точка;
в) пустое множество.
6. Пусть М = {а; о }, К = {m; 4}, D = {а; m; о ; ▲ }.
а) Являются ли множества М и К подмножествами D?
Сделай записи, используя знаки ⊂ и ⊄ .
М ⊂ D
К ⊄ Dб) Нарисуй диаграмму Эйлера–Венна множеств М, К и D. Отметь на ней элементы этих множеств.
36
-
Страница 36
Урок 13
Обратные задачи на приведение к единице
7. Реши уравнения с комментированием и сделай проверку:
14 • х = 840
х= 840 : 14
х = 60х : 70 = 13
х = 70 * 13
х = 910960 : х = 160
х = 960 : 160
х = 68. Реши примеры. Расшифруй и отгадай загадку:
Х32 + 51 = 83
О82 – 40 = 42
Р47 + 33 = 80
Д90 – 46 = 44
Ы25 + 36 = 61
Н52 – 18 = 34
Я35 : 7 • 9 = 45
Б54 : 6 • 2 = 18
Е48 : 6 • 5 = 40
Г56 : 8 • 9 = 63
Ю64 : 8 • 9 = 72
С30 : 6 • 5 = 25
У(6 + 3) • 9 = 81
Ь6 + 3 • 9 = 33
Т10 • 3 – 2 = 28
П180 : 90 = 2
А45 : 15 = 3
Л70 : 14 = 5
В64 : 16 = 4
Ё78 : 6 = 13
К51 : 3 = 17
Ж38 : 2 = 19
И84 : 7 = 12
М48 : 3 = 16
Ц92 : 4 = 23ОН ПАДАЕТ С ГРОХОТОМ СЛОВНО СКАЛА СВЕРКАЯ НА СОЛНЦЕ КАК ГЛЫБА СТЕКЛА ПРОХОДЯТ ВЕКА ПРОБЕГАЮТ ГОДА И ВСЕ ЖЕ ЕМУ НЕ УПАСТЬ НИКОГДА
ОТВЕТ: ВОДОПАД
9. Задача-шутка
Два отца и два сына делили 3 апельсина. Возможен ли случай, когда каждому достанется по одному апельсину?
Да, возможно! Если это дедушка, папа и внук!
37
-
Страница 37
Урок 14
Объединение множеств. Знак ∪
1. Построй в тетради диаграмму множеств А и В. Раскрась область А жёлтым цветом, а область В – синим. Обведи красным карандашом всю закрашенную область. Это – объединение множеств А и В.
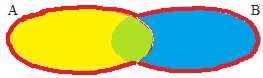
2. В классе проводился шахматно-шашечный турнир. А – множество победителей шахматного турнира, а В – шашечного турнира. Назови элементы множеств А и В.
Множество A = {Петя, Миша, Коля};
Множество B = {Коля, Саша, Дима}.Чему равно их объединение?
Их объединения это победители шашечного и шахматного турнира. Все победители турниров: Петя, Миша, Коля, Саша и Дима.
А вот если б надо было найти пересечение множеств, то это был бы один элемент: Коля победитель всех турниров.
Как можно найти объединение множеств А и В, не рисуя диаграммы? Сделай вывод.
Сложить все элементы множеств.
3. А – множество людей, умеющих плавать, В – множество людей, умеющих играть на скрипке. Что представляют собой множества А ∪ В и А ∩ В?
А ∪ В = умеющих плавать или играть на скрипке.
А ∩ В = умеющих плавать и играющих при этом на скрипке.
38
-
Страница 38
Урок 14
Объединение множеств. Знак ∪
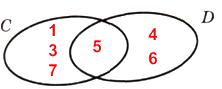
4. Известно, что С = {1; 3; 5; 7}, D = {4; 5; 6}. Найди их объединение С ∪ D. Построй диаграмму множеств С и D и отметь их элементы. Обведи на диаграмме множество С ∪ D.
С ∪ D = {1; 3; 4; 5; 6; 7}
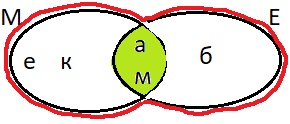
5. Известно, что М = {а; е; м; к}, E = {а; б; м}. Найди их пересечение М ∩ E и объединение М ∪ E. Нарисуй диаграмму множеств М и E и отметь их элементы. Закрась множество М ∩ E и обведи М ∪ E.
М ∩ E = {а; е; м; к; б; м}.
М ∪ E = {а; м}
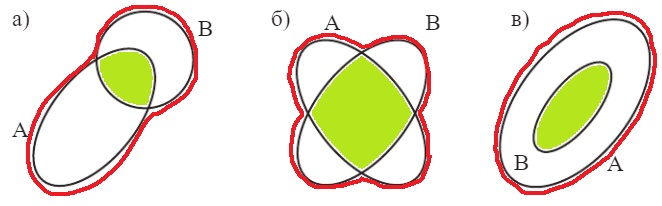
6. Нарисуй в тетради диаграмму множеств А и В. Закрась на ней множество А ∩ В и обведи А ∪ В.
7. Реши задачи, составляя выражения:
а) С трёх одинаковых овец состригли 18 кг шерсти. Сколько таких овец надо постричь, чтобы получить 72 кг шерсти?
72 : (18 : 3) = 12 (ов.) надо подстричь, чтобы получить 72 кг шерсти.
Ответ: 12 овец.б) С трёх одинаковых овец состригли 18 кг шерсти. Сколько килограммов шерсти можно состричь с 12 таких овец?
18:3*12=72 (кг) шерсти будет с 12 овец.
Ответ: 72 кг шерстиСравни задачи. Чем они похожи и чем различаются? Как называют такие задачи?
Эти задачи являются обратными. Они схожи номинальными значениями параметров, но различаются постановкой задачи и тем что мы ищем.
8. Составь и реши взаимно обратные задачи по выражениям: (28 : 4) • 8 и 56 : (28 : 4).
28 бутылок стояли в 4 ящиках. Сколько бутылок будет в 8 ящиках?
(28 : 4) • 8 = 56 (бут.) будет в 8 ящиках.
Ответ: 56 бутылок.28 бутылок стояли в 4 ящиках. Сколько ящиков надо для 56 бутылок?
56 : (28 : 4) = 8 (ящ.) надо для 56 бутылок.
Ответ: 8 ящиков.9.
а) Реши задачу, составляя выражение: «Велосипедист проехал за 2 часа 30 км. За сколько часов, двигаясь так же, он преодолеет 90 км?»
90 : (30 : 2) = 90 : 15 = 6 (ч.) надо велосипедисту, чтобы проехать 90 км.
Ответ: 6 часов.б) Составь обратную задачу, которая решается так: (30 : 2) • 15. (* - здесь у авторов скорее всего ошибка, вместо 15 должно быть 6)
Велосипедист проехал за 2 часа 30 км. Сколько километров велосипедист проедет за 15 часов? (* - за 6 часов)
10. Составь выражения. Найди их значения при данных значениях букв:
а) В зоопарке пони съедает в неделю с кг травы. На сколько дней для пони хватит запаса травы в d кг (расход травы в день одинаковый)? (с = 98, d = 420)
Решение:
d : (c : 7) = 420 : (98 : 7) = 420 : 14 = 30 (дн.) на столько хватит пони 420 кг травы.
Ответ: на 30 дней.б) В n одинаковых бочек вошло 96 кг огурцов. Сколько таких бочек потребуется для засолки а кг огурцов? (n = 3, а = 320)
а: (96 : n) = 320 : (96 : 3) = 320 : 32 = 10 (б.) потребуется для для 320 кг огурцов.
Ответ: 10 бочек. 39
-
Страница 39
Урок 14
11. Вычисли. Объясни для каждого столбика приёмы вычислений:
48 • 5 = 240 40*5+8*5=200 + 40 = 240
92 : 4 = 23 80 : 4 + 12 : 4 = 20 + 3 = 23
56 : 14 = 4 40 : 10 + 16 : 4 = 10 + 4= 14
30 • 9 = 270 3*9*10=27*10=270
850 : 5 = 150 500:5 + 350:5 = 100+70 =170
3 • 74 = 222 3*70 + 3 * 4 = 210 + 12 = 222
84 : 7 = 12 70 : 7 + 14 : 7 = 10 + 2 = 12
98 : 49 = 2 80 : 40 = 2 и 18 : 9 = 2
8 • 120 = 960 8 *100 + 8 * 20 = 800 + 160 = 960
720 : 60 = 12 600 : 60 + 120 : 60 = 10 + 2 = 1212.
а) Пользуясь числовым лучом, составь множество двузначных чисел, кратных 14.
14, 28, 42, 56, 70, 84, 98
б) Выполни деление с остатком:
45 : 14 = 2 (ост. 3)
60 : 14 = 4 (ост. 4)
78 : 14 = 5 (ост. 8)
86 : 14 = 6 (ост. 2)в) Выучи двузначные числа, кратные 14. Проверь себя, работая в паре.
13. Составь программу действий и вычисли:
1 4 6 2 5 3
а) (714 – 649) • 7 – (95 : 19) • (68 : 2) = 2851) 714 - 649 = 65
2) 95 : 19 = 5
3) 68 : 2 = 34
4) 65 * 7 = 455
5) 5 * 34 = 170
6) 455 - 170 = 2854 1 7 3 2 5 6
б) 6 • (532 – 478) + (300 – 38 • 7) : 17 • 100 = 5241) 532 - 478 = 54
2) 38 * 7 = 266
3) 300 - 266 = 34
4) 6 * 54 = 324
5) 34 : 17 = 2
6) 2 * 100 = 200
7) 324 + 200 = 52414.
а) Множество М содержит 5 элементов, множество К – 4 элемента, а их пересечение М ∩ К – 2 элемента. Сколько элементов содержит объединение М ∪ К этих множеств?
5 + 4 - 2 = 7 (эл.)
Объединение М ∪ К содержит 7 элементов.
б) Множества А и В содержат соответственно а и b элементов, а их пересечение А ∩ В – с элементов. Сколько элементов содержит объединение А ∪ В этих множеств?
объединение А ∪ В содержит а + b - с
15. В классе английский язык изучают 25 детей, а немецкий – 27 детей. Из них 18 детей изучают одновременно английский и немецкий языки. Сколько всего детей в классе изучают эти иностранные языки? Сколько детей изучают только один из этих языков?
1) 25+27-18 = 52 - 18 = 34 (уч.) изучают языки.
2) 34 - 18 = 16 (уч.) изучают лишь 1 язык.
Ответ: 34 ученика изучают языки, и 16 учеников изучает лишь 1 иностранный язык.16. Сколько элементов содержит множество букв в высказывании: «Учить – ум точить»? Запиши это множество с помощью фигурных скобок.
Пусть это будет множество А, тогда а = {У,ч,и,т,ь,у,м,т,о,ч,и,т,ь}. Получается множество из 13 элементов. (если брать только буквы)
40
-
Страница 40
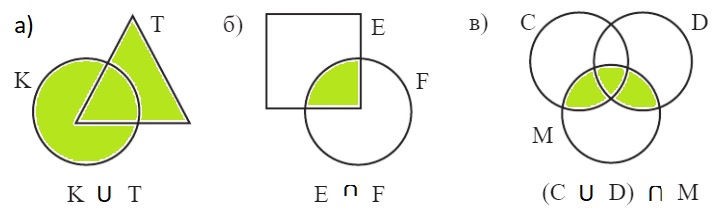
Урок 15 Решение задач
1. Нарисуй диаграмму в тетради и раскрась указанное множество:
K ∪ T E ∩ F (C ∪ D) ∩ M
2. А = {3; 6; 9; 12}, В = {2; 4; 6}.
Запиши с помощью фигурных скобок пересечение и объединение множеств А и В. Построй диаграмму этих множеств и отметь на ней их элементы.
А ∪ В = {2; 3; 4; 6; 9; 12}
А ∩ В = {6}
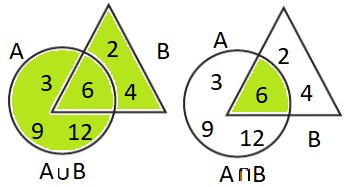
* - дополнительно цветом выделены результаты.
3. Реши задачи, составляя выражения. Сравни их. Что ты замечаешь? Как называют такие задачи?
а) В 4 одинаковых ящика разложили 20 кг вишни. Сколько вишни уместится в 15 таких ящиках?20 : 4 * 15 = 5 * 15 = 75 (кг) вишни поместится в 15 таких ящиках.
Ответ: 75 кг вишни.б) В 4 одинаковых ящика разложили 20 кг вишни. Сколько таких ящиков потребуется для того, чтобы разложить 75 кг вишни?
75 : (20 : 4) = 75 : 5 = 15 (ящ.) потребуется для 75 кг вишни.
Ответ: 15 ящиков.Это взаимно обратные задачи.
4. Составь и реши взаимно обратные задачи по выражениям: (56 : 4) • 5 и 70 : (56 : 4)
В 4 одинаковых коробках 56 пачек масла. Сколько пачек масла в 5 таких коробках?
(56 : 4) • 5 = 14 * 5 = 70 (пач.) в 5 коробках.
Ответ: 70 пачек.В 4 одинаковых коробках 56 пачек масла. Сколько надо коробок для 70 пачек масла?
70 : (56 : 4) = 70 : 14 = 5 (кор.) надо для 70 пачек масла.
Ответ: 5 коробок.5. БЛИЦтурнир
а) Трём кроликам на месяц требуется а кг корма. Сколько килограммов корма потребуется на месяц 8 таким кроликам?
a : 3 * 8
б) Лошадь съедает за неделю b кг овса. За сколько дней при таком же расходе она съест с кг овса?
c : (b : 7)
в) Поезд за 3 часа проехал d км. Сколько километров он проедет за 10 часов, двигаясь с той же скоростью?
d : 3 * 10
г) На двух одинаковых автобусах можно перевезти k пассажиров. Сколько таких автобусов требуется, чтобы перевезти m пассажиров?
m : (k : 2)
6. Найди значения выражений. Объясни для каждого столбика приёмы вычислений:
86 • 3 = 80 * 3 + 6 * 3 = 240 + 18 = 258
96 : 6 = 60 : 6 + 36 : 6 = 10 + 6 = 16
7 • 40 = 7 * 4 * 10 = 28 * 10 = 280
720 : 90 = 72 : 9 = 8
76 : 19 = 4
9 • 57 = 9 * 50 + 9 * 7 = 450 + 63 = 513
75 : 5 = 50 : 5 + 25 : 5 = 10 + 5 = 15
80 • 8 = 8 * 8 * 10 = 64 * 10 = 640
300 : 5 = 30 : 5 * 10 = 6 * 10 = 60
112 : 28 = 4 41
-
Страница 41
Урок 15 Решение задач
7. Выполни действия и узнай, какая это звезда:
(30 + 20) * 2 : 20 + 19 = 24
((60 + 30) : 3 + 15) : 9 = 5
(100 - 90) * 8 : 20 + 17 = 21
(((80 - 50) : 15) + 19) * 3 = 63
((50 - 6) : 11 + 16) : 10 = 2
((40 - 36) * 12) : 8 * 11 = 6663 2 66 21 63 5 24 А Л Ь Т А И Р 8. Первая сторона треугольника равна 60 см, вторая – в 3 раза меньше первой. Третья сторона на 27 см меньше суммы первой и второй сторон вместе. Чему равен периметр треугольника?
1) 60 : 3 = 20 (см) - длина второй стороны
2) 60 + 20 = 80 (см) - сумма длин первой и второй сторон
3) 80 - 27 = 53 (см) - длина третьей стороны
4) 80 + 53 = 133 (см) - периметр треугольника
Ответ: 133 см.9. Сравни:
4 м 3 дм > 5 дм 8 см
8 дм 73 мм > 15 см 6 мм
3 м 6 дм 4 см > 27 дм 9 см
1 м > 984 мм10. А = {а; ☆; 9}, В = {9; а; ▲ ; ☆ ; с}.
а) Назови элементы множеств А и В. Построй их диаграмму. Какое из множеств А и В является подмножеством другого?
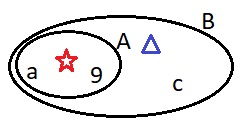
Сделай записи, вставляя знаки ∈, ∉, ⊂ или ⊄.
9 ∈ А ▲ ∉ А ? ∉ А А ⊂ В
9 ∈ В ▲ ∈ В ? ∉ В В ⊄ Аб) Найди объединение и пересечение множеств А и В. Что ты замечаешь? Сделай вывод:
Если А ⊂ В, то А ∪ В = В = {9; а; ▲; ☆ ; с}, А ∩ В = А = {а; ☆; 9}
42
-
Страница 42
Урок 16 Умножение чисел в столбик: 24 • 8
1. Вычисли. Какие способы сложения и вычитания трёхзначных чисел ты знаешь? Чем удобна запись в столбик?
378 + 127 = 300 + 100 + 78 + 27 = 400 + 105 = 505
513 – 69 = 400 + 113 - 69 = 400 + 44 = 444
Можно раскладывать на разряды и производить вычисления с ними. Запись в столбик хороша тем, что разряды находятся друг напротив друга, что удобно!
2. Как умножить сумму на число? Пользуясь рисунком, допиши равенство:
(а + b) • с = a * c + b * c
3. В рамке записано умножение чисел 24 • 8 в столбик. Объясни с помощью рисунка, как получена эта запись:
Вначале разложили множитель на десятки и единицы, потом умножили на второй множитель каждое из чисел и результаты сложили.
24 * 8 = 20 * 8 + 4 * 8 = 192
4. Выполни в тетради умножение в столбик:
*56
7
+42
35
392*95
4
+20
36
380*79
4
+36
28
316*68
9
+72
54
612*32
5
+10
15
1605. Вычисли, используя запись в столбик:
98 • 5
*98
5
+40
45
49027 • 7
*27
7
+49
14
18986 • 8
*86
8
+48
64
68856 • 6
*56
6
+36
30
33674 • 4
*74
4
+16
28
2966. Запиши с помощью фигурных скобок:
а) множество двузначных чисел, меньших 14;
Скажем это множество А, тогда А = {12; 10}
б) множество трёхзначных чисел, больших 998;
Скажем это множество А, тогда А = {999}
в) множество трёхзначных чисел, составленных из цифр 5, 8, 1 (цифры в записи числа не повторяются).
Скажем это множество А, тогда А = {158; 185; 518; 581; 815; 851}
7. С = {b; ★ ; о ; m}, D = { ★; m; ▲ }.
а) Построй диаграмму множеств С и D и отметь на ней их элементы. Найди множества С ∩ D и С ∪ D.
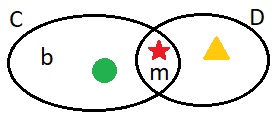
С ∩ D = {★; m;}
С ∪ D = {b; ★ ; о ; m; ▲}
б) Обведи на диаграмме красным карандашом множество С ∩ D и раскрась жёлтым цветом С ∪ D

43
-
Страница 43
Урок 16 Умножение чисел в столбик: 24 • 8
8. Как увеличить число на 3 единицы (прибавить 3), в 10 раз (умножить на 10)? Как уменьшить число на 5 единиц (вычесть 5), в 2 раза (разделить на 2)? Составь и заполни таблицу в тетради:
а 14 28 40 52 66 98 а + 3 17 31 43 55 69 101 а • 10 140 280 400 520 660 980 а – 5 9 23 35 48 61 93 а : 2 7 14 20 26 33 49 9. В трёх автобусах едут 99 человек. В первом автобусе едут 42 человека. Это на 6 человек больше, чем во втором автобусе. Во сколько раз в третьем автобусе меньше людей, чем в первом?
1) 42 - 6 = 36 (чел.) во втором автобусе.
2) 99 - 42 - 36 = 21 (чел.) в третьем автобусе.
3) 42 : 21 = 2 (р.) в первом больше человек, чем в третьем.
Ответ: в 2 раза.10. Составь программу действий и вычисли:
1 5 2 6 3 7 4
а) 1 : 1 – 0 • 0 + 1 • 0 – 1 • 1 = 1 - 0 + 1 - 1 = 12 5 3 1 6 4
б) 325 : 325 – 0 : (764 + 136) + 1 • 999 = 1 - 0 + 999 = 100011. БЛИЦтурнир
а) Сергей нашёл а грибов, а Вадим – в 4 раза больше. На сколько грибов меньше нашёл Сергей, чем Вадим?
а * 4 - а
б) На первой полке b книг, а на второй – на 8 книг меньше. Во сколько раз на первой полке книг больше, чем на второй?
b :(b - 8)
в) Турист прошёл в первый день n км, во второй день – в 2 раза меньше, а в третий – на 5 км больше, чем в первый день. Сколько километров прошёл турист за эти 3 дня?
n + n : 2 + (n + 5)
12. Реши уравнения с комментированием и сделай проверку:
х • 60 = 480
х = 480 : 60
х = 8
Проверка: 5* 60 = 480540 : х = 9
х = 540 : 9
х = 60
Проверка: 60 * 9 = 540х : 7 = 80
х = 7 * 80
х = 560
Проверка: 560 : 7 = 8013. В мешке лежат яблоки 3 сортов. Какое минимальное число яблок надо взять из мешка не глядя, чтобы:
а) среди них было не менее 2 яблок одного сорта;
минимум 2 яблока.
б) среди них было хотя бы 5 яблок одного сорта.
минимум 5 яблок
14. Объясни, как это может быть: 2 матери, 3 дочки, 2 сестры, а всего – 4 женщины?
Бабушка, мама и две дочери мамы.
44
-
Страница 44
Урок 17 Свойства объединения множеств
1. Сравни равенства в каждом столбце, каждой строке. Что в них общего? Какие свойства они выражают?
а + b = b + a
a • b = b • a
A ∩ B = B ∩ A
(а + b) + c = a + (b + c)
(a • b) • c = a • (b • c)
(A ∩ B) ∩ C = A ∩ (B ∩ C)Все ли операции над числами обладают этими свойствами?
2. А = {к; м; п}, В = {а; м; к; р}. Запиши с помощью фигурных скобок множества А ∪ В и В ∪ А. Покажи их на диаграмме Эйлера–Венна. Что ты замечаешь?
А ∪ В = {к; м; п; а; р}
В ∪ А = {к; м}
Сделай вывод.
При объединении множеств в результате фигурируют все элементы этих множеств, а при пересечении лишь общие элементы, встречающиеся в одном и другом множестве.
3. Нарисуй диаграмму множеств А, В и С. Раскрась на ней сначала множество А ∪ В, потом множество С, а затем обведи их объединение (А ∪ В) ∪ C. Аналогично построй диаграмму множества А ∪ (В ∪ C).
(А ∪ В) ∪ C =
А ∪ (В ∪ C) =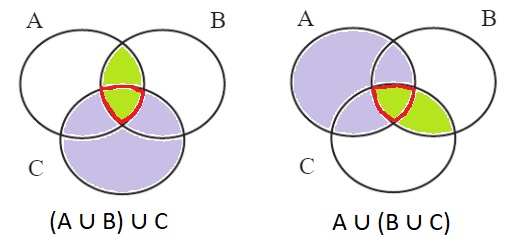
Сравни полученные множества. Что ты замечаешь? Сделай вывод.
Свойства объединения множеств
Объединение множеств обладает переместительным и сочетательным свойствами.
Переместительное свойство: А ∪ В = В ∪ А
Сочетательное свойство: (А ∪ В) ∪ C = А ∪ (В ∪ C)
Значит, результат объединения множеств не зависит от порядка множеств и от порядка действий.4. Допиши в тетради равенства, выражающие свойства объединения множеств. Назови эти свойства и объясни их смысл.
М ∪ К =K ∪ M
(М ∪ К) ∪ Т = М ∪ (К ∪ Т)
45
-
Страница 45
Урок 17 Свойства объединения множеств
5. С помощью знаков ∩ и ∪ запиши, какие множества закрашены.
слева - А ∩ В, по центру - D ∪ E, справа - (К ∩ M) ∪ N
6.
а) Пусть А – множество машин, В – множество легковых машин, С – множество машин красного цвета, D – множество гаражей. Найди на диаграмме, где какое множество расположено. Что означает раскрашенное множество?
Раскрашенное множество обозначает легковые красные машины.
б) Пусть А – множество цветов, В – множество роз, С – множество жёлтых цветов, D – множество деревьев. Нарисуй диаграмму множеств А, В, С и D. Раскрась на ней множество жёлтых роз.

* - диаграмма аналогична предыдущему варианту.
7. Выполни действия наиболее удобным способом. Какие свойства чисел при этом используются?
а)
(373 + 56) + 127 = 500 + 56 = 556
602 + (98 + 245) = 700 + 245 = 94584 + 71 + 429 + 16 = 100 + 500 = 600
б)
2 • 39 • 2 • 5 • 5 = 39 * 100 = 3900
25 • 7 • 4 = 7 * 100 = 700
16 • 35 = 560
8.
а) В 4 одинаковых коробках 24 карандаша. Сколько карандашей в 9 таких коробках?24 : 4 * 9 = 6 * 9 = 54 (кар.) в 9 коробках.
Ответ: 54 карандашаб) На 5 одинаковых костюмов пошло 35 м ткани. Сколько таких костюмов можно сшить из 56 м этой ткани?
56 : (35 : 5) = 56 : 7 = 8 (кост.) можно сшить из 56 м ткани.
Ответ: из 56 м можно сшить 8 костюмов.
в) Около дома растёт 8 тополей, а лип – в 2 раза меньше. Сколько лип и тополей растёт около дома?8 : 2 + 8 = 12 (дер.) растет возле дома.
Ответ: 12 лип и тополейг) Саша купил 4 пирожка по 16 р. и 2 буханки хлеба по 18 р. Сколько денег заплатил он за всю покупку?
4 * 16 + 2 * 18 = 64 + 36 = 100 (р.) заплатил за покупку.
Ответ: 100 рублей.9. В равенствах вместо некоторых цифр стоят звёздочки. Объясни, почему эти равенства не верны.
* + 2 * = * при прибавлении к двухзначному не может получится однозначное
* + * = 6 * - при сложении двух однозначных числе не может получиться двухзначное с 6 десятками
* 5 + * 7 = * 8 при сложении чисел у которых в единицах 5 и 7 не может получиться число с разрядом единиц 8
* * 5 + * 7 = * 2 при сложении трехзначного и двухзначного не получится двухзначное
3 * * – * * = * * при вычитании из трехзначного с 3 сотнями и двухзначного не получится двухзначное
* * 9 – * 4 = * * 3 при вычитании из числа с разрядом единиц 9 числа с разрядом единиц 4 не получится 3 46
-
Страница 46
Урок 17 Свойства объединения множеств
10.
а) Пользуясь числовым лучом, составь множество двузначных чисел, кратных 15.
15, 30, 45, 60, 75, 90
б) Выполни деление с остатком:
34 : 15 = 2 (ост. 4)
47 : 15 = 3 (ост. 2)
76 : 15 = 5 (ост. 1)
98 : 15 = 6 (ост. 8)
в) Выучи двузначные числа, кратные 15. Проверь себя, работая в паре.
Самостоятельно.
11. Найди значения выражений:
1 3 2 4 6 5 7
а) (80 : 4 – 60 : 30) • 5 + 96 : 3 – 117 = 51) 80 : 4 = 20
2) 60 : 30 = 2
3) 20 - 2 = 18
4) 18 * 5 = 90
5) 96 : 3 = 32
6) 90 + 32 = 122
7) 122 - 117 = 54 7 5 1 3 2 8 6
б) 56 : 4 + 2 • (120 : 6 – 80 : 20) + 17 • 8 = 1821) 120 : 6 = 20
2) 80 : 20 = 4
3) 20 - 4 = 16
4) 56 : 4 = 14
5) 2 * 16 = 32
6) 17 * 8 = 136
7) 14 + 32 = 46
8) 46 + 136 = 18212. Составь верное высказывание: «В квадрате Е закрашена ровно треть клеточек».
13. Построй прямоугольник, ширина которого равна 3 клеточкам, а длина – 4 клеточкам. Закрась на нём ровно:
а) половину клеточек
б) треть клеточек
в) четверть клеточек
г) шестую часть клеточек
14. Какие фигуры надо поставить вместо вопросительных знаков?
47
-
Страница 47
Урок 18 Разбиение множества на части
1. Сосчитай число элементов в множестве А и его подмножествах. Что ты замечаешь? Сделай вывод.
Количества элементов множества, равно количеству всех элементов подмножеств.
2. Разбей множества А и В на части: съедобные и несъедобные предметы. Сколько предметов в каждой части, во всём множестве? Что ты замечаешь?
А (съедобные) = {белый гриб; лисички} А (несъедобные) = {бабочка; стрекоза; мухомор}
B (съедобные)= {груша; яблоко; помидор; огурец} B (несъедобные)= {бабочка; стрекоза}В каждом множестве по 6 элементов, при этом множества A и B имеют общее пересечение. Общее количество элементов любого из множеств равно количеству элементов подмножеств.
Можно ли разбить множество А на части: несъедобные предметы и грибы?
Нельзя, так как часть грибов несъедобная, а также останутся и другие неиспользованные элементы.
Можно ли разбить множество В на части: овощи и фрукты? Почему?
Нельзя, так как останутся и другие неиспользованные элементы.
Разбиение множества на части по свойству (классификация)
Множество разбито на части, если каждый его элемент попадает ровно в одну часть. Разбиение множества на части по некоторому свойству является своеобразным «наведением порядка» в множестве. Это разбиение называют также классификацией. Свойство, по которому множество разбито на части, называют основанием классификации.
1) Все элементы множества A распределены в группы по цвету.
2) Каждый элемент множества А попал только в одну такую группу.
Пример. Классификация элементов множества A по цвету. Основанием классификации в данном случае является цвет 48
-
Страница 48
Урок 18 Разбиение множества на части
3. В каких множествах «наведён порядок»? Докажи. Как об этом можно сказать иначе?
Если исходить из правил классификации, то порядок наведен в множествах А и X. Так как:
1) Все элементы множества распределены в группы.
2) Каждый элемент множества попал только в одну такую группу.4. Разбей на части множество чисел А = {5, 50, 84, 104, 435, 507, 930}. Найди несколько решений. Для каждого решения укажи основание классификации, полученные группы и их название.
Образец:
Основание классификации: делится на 2
I группа: {50, 84, 104, 930} – чётные числа
II группа: {5, 435, 507} – нечётные числа5. Назови элементы множества фигур на рисунке. Нарисуй его в тетради и разбей на части по форме. Составь 4 равенства.
I группа: {▲;▲;▲} – маленькие треугольники
II группа: {?} – маленькие квадраты
III группа: {▲} – большие треугольники
IV группа: {?} – большие квадратыНа какие ещё части можно разбить множество этих фигур?
Можно разбить по цветам.
6. Множества A, B, С и D содержат соответственно a, b, с и d элементов. Найди пропущенные буквы:
a + b + с = d
d – c – b = а
d – a = b + с
d – a – b = c
a + c = d – b
c + b = d – a
b = d – a – c
d – c = a + b 49
-
Страница 49
Урок 18 Разбиение множества на части
7. Собралось 6 охотников и 9 рыбаков, а всего 10 человек. Как это может быть?
9 рыбаков, 6 охотников из 10 человек, значит 5 человек и охотники и рыбаки.
8.
а) Охотник убегает от медведя после осечки ружья. За 5 секунд он пробежал 30 м. Сейчас он находится на расстоянии 360 м от домика лесника. Сколько времени нужно охотнику, чтобы добежать до лесника, если скорость его не изменится?
1) 30 : 5 = 6 (м/с) скорость охотника.
2) 360 : 6 = 60 (с) надо охотнику.
Ответ: 60 секунд.б) Павлину в зоопарке за неделю добавляют в корм 350 г пшеницы. Сколько пшеницы при том же расходе в день съедает павлин в зоопарке за месяц (30 дней)?
1) 350 : 7 = 50 (г) пшеницы павлину добавляют в день.
2) 50 * 30 = 1500 (г) пшеницы съедает павлин за 30 дней.
Ответ: 1500 г или 1,5 кг.9. Вычисли. Объясни для каждого столбика приёмы вычислений:
39 • 8 = 30 * 8 + 9 * 8 = 240 + 72 = 31217 • 50 = 50 * 10 + 7 * 50 = 850
540 : 3 = 300 : 3 + 240 : 3 = 100 + 80 = 180
700 : 35 = 70 : 35 * 10 = 2 *10 = 20
56 : 9 = 6 (ост. 2)
5 • 76 = 5 * 70 + 5 * 6 = 350 + 30 = 380
280 • 2 = 28 *2 * 10 = 56 * 10 = 560
860 : 2 = 86 : 2 * 10 = 43 * 10 = 430
600 : 120 = 5
38 : 15 = 2 (ост. 8)
10. Выполни умножение, используя запись в столбик:
72 • 9
*72
9
+18
63
6486 • 85
*85
6
+30
48
51094 • 6
*94
6
+24
36
384268 • 3
*268
3
804124 • 7
*124
7
86811. Реши уравнения с комментированием и сделай проверку:
х + 93 = 517
х = 517 - 93
х = 424
Проверка: 424 + 93 = 517204 – х = 156
х = 204 - 156
х = 48
Проверка: 204 – 48 = 156х – 429 = 361
х = 429 + 361
х = 790
Проверка: 790 - 429 = 36112. A – множество детских игрушек, B – множество кукол, C – множество пирамидок, D – множество игрушек в магазине «Малыш». Построй диаграмму множеств A, B, C и D. Раскрась множество кукол в магазине «Малыш».
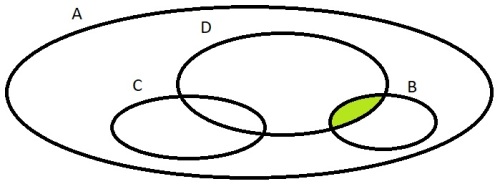
13. Ученики 3 класса ездили на экскурсии в Суздаль и Владимир. В Суздале побывали 12 учеников, а во Владимире – 18 учеников, причём в обоих городах побывали четверо ребят. Сколько учеников приняли участие в этих двух экскурсиях? Что ещё можно спросить?
1) 12 +18 = 30 (поездок) было сделано
2) 30 - 4 = 26 (уч.) приняли участие.
Ответ: 26 учеников.14. Вычисли, используя запись в столбик. Узнай, как прочитать эти числа:
а) 12 345 + 98 765
+ 12 345
98 765
111110в) 101 010 – 20 202
- 101010
20202
80808б) 77 777 + 7777
+77777
7777
855554г) 100 000 – 99 999
-100000
99999
1 50
-
Страница 50
Урок 19 Решение задач
1. А = {карандаш, ручка, чашка, мел, блюдце}. Разбей множество А на части по назначению.
I группа: {карандаш, ручка, мел} – школьные принадлежности
II группа: {чашка, блюдце} – посуда2. Множество В = {5, 6, 23, 42, 50, 51, 60} разбито на части. Укажи основание классификации.
а) {5, 6} и {23, 42, 50, 51, 60} - однозначные и двухзначные числа
б) {5, 23, 50} и {6, 42, 51, 60} - сумма разрядов чисел равна 5 и 6
в) {50, 60} и {5, 6, 23, 42, 51} - числа с круглыми десятками и с единицами в разряде
г) {6, 42, 50, 60} и {5, 23, 51} - четные и нечетные3. Выполни умножение в столбик:
42 • 7
*42
7
29494 • 5
*94
5
47073 • 6
*73
6
43889 • 4
*89
4
3564. Составь выражения и найди их значения:
а) В 4 ящиках 64 кг яблок. Сколько килограммов яблок в 7 таких ящиках?
64 : 4 * 7 = 18 * 7 = 126 (кг) яблок в 7 ящиках.
Ответ: 126 кг яблок.б) Кадушка вмещает 72 л воды, а бочка – 160 л. Кадушку наполняют 9 вёдер воды. Сколько таких вёдер нужно, чтобы наполнить бочку?
160 : (72 : 9) = 20 (вед.) надо для того, чтобы наполнить бочку.
Ответ: 20 ведер.5. Объясни, что означают записанные свойства. Какое свойство пропущено? Запиши его в тетради.
Сложение Умножение Переместительное свойство а + b = b + а а • b = b • a Сочетательное свойство (а + b) + c = a + (b + c) (а * b) * c = a * (b * c) 6.
а) Проанализируй равенства и объясни способ умножения круглых чисел:
8 • 60 = 8 • (6 • 10) = (8 • 6) • 10 = 48 • 10 = 480
20 • 30 = (2 • 10) • (3 • 10) = (2 • 3) • (10 • 10) = 6 • 100 = 600Если есть число с нулем на конце, то его можно не учитывать в расчетах, а держать в голове. После расчетов добавить столько нулей, сколько убрали перед началом расчетов.
Пользуясь этим способом, объясни, почему умножение круглых чисел в столбик записывают так:
х 310 х26
3 20
930 520Потому что ноль можно не учитывать при вычислении, но не забывать про него в результате. Он добавляет один порядок к результату, то есть увеличивает его в 10 раз.
б) Запиши в тетради примеры в столбик и вычисли:
28 • 30*28
30
840490 • 2
*490
2
98036 • 20
*36
20
720160 • 6
*160
6
96025 • 40
*25
40
1000 51
-
Страница 51
Урок 19 Решение задач
7. Андрей поймал 20 раков, Вася – в 2 раза меньше Андрея, Юля – на 12 раков меньше, чем Андрей и Вася вместе, а Даша поймала на 4 рака больше Васи. Сколько всего раков поймали ребята? Кто поймал больше раков – мальчики или девочки, и на сколько?
1) 20 : 2 = 10 (р.) поймал Вася.
2) 20 +10 = 30 (р.) поймал Андрей и Вася, то есть мальчики.
3) 30 - 12 = 18 (р.) поймала Юля.
4) 10 + 4 = 14 (р.) поймала Даша.
5) 20 + 10 + 18 + 14 = 62 (р.) поймали ребята.
6) 14 + 18 = 32 (р.) поймала Даша и Юля, то есть девочки.
7) 32 - 30 = 2 (р.) больше поймали девочки, чем мальчики.Ответ: 62 рака поймали ребята, при этом девочки поймали больше раков, чем мальчики на 2 рака.
8. Составь программу действий и вычисли:
4 1 5 9 2 3 6 10 7 8
а) 48 : (36 : 6) : 1 + (0 • 4 + 3) • 9 – 0 : 12 • 3 = 35
1) 36/6=6
2) 48/6=8
3) 8/1=8
4) 0*4=0
5) 3*9=27
6) 0/12=0
7) 0*3=0
8) 8+27=35
9) 0+3=3
10) 35-0=355 1 3 2 10 6 4 7 11 8 9
б) 16 : (72 : 8 + 7 • 1) – 0 : (8 • 8) : 1 + 56 : 56 • 4 = 51) 72:8=9
2) 7*1=7
3) 9+7=16
4) 16:16=1
5) 8*8=64
6) 0:64=0
7) 0:1=0
8) 56:56=1
9) 1*4=4
10) 1-0=1
11) 1+4=59. А = {4, 8, 12, 16, 20}, В = {8, 16, 24}. Найди пересечение и объединение множеств А и В. Построй диаграмму этих множеств и отметь на ней их элементы.
10. Объясни решение примеров, записанных в столбик. Используя полученные результаты, устно найди ответы остальных примеров.
+318
485
803319 + 485 = 803
318 + 484 = 803
319 + 484 = 803328 + 485 = 813
803 – 485 = 318
903 – 585 = 318-952
587
365953 – 587 = 366
952 – 588 = 364
953 – 588 = 365
852 – 587 = 265
952 – 687 = 165
365 + 587 = 65211. В множестве А два элемента, в множестве В три элемента. При каком условии множество А В будет содержать 2 + 3 = 5 элементов?
При объединении множеств A и B. А ∪ В
12. Как расположить 5 элементов на диаграммах множеств А и В, чтобы в каждом из множеств было соответственно:
а) 2 и 4 элемента;
б) по 4 элемента;
в) 4 и 5 элементов;
г) по 5 элементов;
д) 3 и 2 элемента;
е) по 3 элемента?
52 - 64
-
Страница 52 - 64
Урок 20 - 21 Как люди научились считать
Нет заданий.
65
-
Страница 65
Урок 22 Нумерация многозначных чисел
1.
а) Для чего служат натуральные числа? Назови первые 5 чисел натурального ряда. Чем интересно число 999? Назови подряд следующие 5 чисел.
Натуральные числа служат для осуществления расчетов с реальными значениями.
1, 2, 3, 4, 5
999 это самое большое трехзначное число
1000, 1001, 1002, 1003, 1004
б) Попробуй прочитать число: 456980. Как читают многозначные числа?
Четыреста пятьдесят шесть тысяч девятьсот восемьдесят.
Для чтения натуральных чисел их разбивают, начиная справа, на группы по 3 цифры в каждой. Эти группы называют классами. Первые четыре класса в записи натуральных чисел – единицы, тысячи, миллионы и миллиарды, а так же разрядные единицы этих классов.
66
-
Страница 66
Урок 22 Нумерация многозначных чисел
2. Прочитай числа, записанные в таблице. Что обозначает цифра 8 в их записи?
* - в скобках будет указано то, что определяет цифра 8 в числе
805 Восемьсот пять (сотни)
980 девятьсот восемьдесят (десятки)
8 319 Восемь тысяч триста девятнадцать (тысячи)
50 000 Пятьдесят тысяч
86 705 Восемьдесят шесть тысяч семьсот пять (десятки тысяч)
500 000 Пятьсот тысяч
813 673 Восемьсот тринадцать тысяч шестьсот семьдесят три (сотни тысяч)
9 721 210 Девять миллионов семьсот двадцать одна тысяча двести десять
и так далее...3.Прочитай числа. Сколько в них классов, разрядов? Найди число, в разряде десятков тысяч которого стоит цифра 5.
а) 3512, 6032, 8907, 6200, 5555, 8812;
б) 12 063, 106 727, 30 009, 485 226;
в) 7 396 824, 429 157 340, 25 571 630 748.по аналогии с предыдущим заданием
67
-
Страница 67
Урок 22 Нумерация многозначных чисел
4. Сосчитай:
а) от 7398 до 7405
б) от 15 002 до 14 996
в) от 200 004 до 199 998
г) от 3 516 997 до 3 517 0035. Придумай задачу, которая решается так:
20 + 20 : 4 - В 4 одинаковых ящиках 20 коробок. Сколько коробок будет в 5 таких ящиках?
(n : 2) • 9 - В ящике n пачек масла, при этом они разложены в 2 коробки поровну. Сколько пачек масла в 9 таких коробках?
35 : (а : 6) - В ящике а пачек масла упакованных в коробки по 6 штук. Сколько таких коробок можно упаковать, если есть 35 пачек масла?
6. БЛИЦтурнир
а) За 4 одинаковых батона заплатили а р. Сколько денег надо заплатить за 6 таких батонов?
(a : 4) * 6
б) За 4 одинаковых батона заплатили а р. Сколько таких батонов можно купить на с р.?
c : (а * 4)
в) У Маши было b р. Она купила 5 кексов по d р. Сколько денег у неё осталось?
b - 5 * d
г) Игорь купил 2 мороженых по х р. и 3 пирожных по у р. Сколько денег он заплатил за покупку?
x * 2 + y * 3
д) У Пети было а р. Мама дала ему ещё b р. Во сколько раз больше у него стало денег, чем было?
(a + b) : а
7. Ручка стоит 27 р., она в 3 раза дороже карандаша. Тетрадь на 7 р. дешевле ручки. Сможет ли Оля купить ручку, карандаш и тетрадь, если у неё есть 60 р.?
1) 27 : 3 = 9 (р.) стоит карандаш
2) 27 - 7 = 20 (р.) стоит тетрадь.
3) 27 + 20 + 9 = 56 (р.) надо на ручку, карандаш и тетрадь60>56
Ответ: да сможет.
8. Выполни умножение в столбик и прочитай полученные числа:
а)
32 • 7
*32
7
224Двести двадцать четыре
51 • 9
* 51
9
459Четыреста пятьдесят девять
б) 78 • 6
*78
6
468Четыреста шестьдесят восемь
94 • 5
*94
5
470Четыреста семьдесят
в) 8300 • 4
*8300
4
25200Двадцать пять тысяч двести
27 • 800
* 27
8000
216000Двести шестнадцать тысяч
г) 68 000 • 9
*68000
9
612000Шестьсот двенадцать тысяч
75 • 2000
*75
2000
150000Сто пятьдесят тысяч
9. Найди пропущенные цифры. Проверь с помощью калькулятора.
а)
+495
354
849б)
- 542
163
379в)
-820
457
363г)
-742
285
45710. Продолжи ряд на 4 числа, сохраняя закономерность:
1) 0, 25, 50, 75, 100, 125, 150, 175
2) 10, 9, 11, 8, 12, 7, 13, 6, 14, 5
11.
АВ = 3 см 8 мм,
ВС = 2 см 5 мм,
СD = 3 см.
Начерти отрезки АВ, ВС и СD, если они:
а) лежат на одной прямой;
б) образуют ломаную линию.
12. Сколько месяцев в году имеют в названии ровно 6 букв?
январь - 6 букв
апрель - 6 букв
август - 6 букв
ноябрь - 6 букв4 месяца!
68
-
Страница 68
Урок 23 Сравнение натуральных чисел
1. Сравни числа. Какие правила сравнения чисел ты знаешь?
78 < 203
160 > 9
804 > 812
В первую очередь обращаем внимание на самые значимые разряды и сравниваем по ним, если они равны, то переходим к менее значимым и т.д.
2. Прочитай числа. Сколько в них классов, разрядов?
579 318 Пятьсот семьдесят девять тысяч триста восемнадцать - 6 разрядов, 2 класса
3 642 003 Три миллиона шестьсот сорок две тысячи три - 7 разрядов, 3 класса
18 060 785 Восемнадцать миллионов шестьдесят тысяч семьсот восемьдесят пять - 8 разрядов, 3 класса
760 300 014 Семьсот шестьдесят миллионов триста тысяч четырнадцать - 9 разрядов, 3 класса
6 581 007 500 Шесть миллиардов пятьсот восемьдесят один миллион семь тысяч пятьсот - 10 разрядов, 4 класса
27 990 320 407 Двадцать семь миллиардов девятьсот девяносто миллионов триста двадцать тысяч четыреста семь - 11 разрядов, 4 класса
620 007 000 083 Шестьсот двадцать миллиардов семь миллионов восемьдесят три - 12 разрядов, 4 классаВ каких разрядах отсутствуют разрядные единицы?
6 581 007 500
Как ты думаешь, какое из чисел таблицы самое маленькое, а какое – самое большое?
Самое большое
620 007 000 083
Самое маленькое
579 318
3. Прочитай числа, назови предыдущее и последующее число. Попробуй найти среди этих чисел самое большое и самое маленькое.
50 090 Пятьдесят тысяч девяносто. Предыдущее - 50 089 Пятьдесят тысяч восемьдесят девять. Последующее - 50 091 Пятьдесят тысяч девяносто один.
50 009 Пятьдесят тысяч девять (самое маленькое). Предыдущее 50 008 - Пятьдесят тысяч восемь. Последующее - 50 010 Пятьдесят тысяч десять
90 500 Девяносто тысяч пятьсот (самое большое). Предыдущее 90 499 - Девяносто тысяч четыреста девяносто девять. Последующее 90 501 - Девяносто тысяч пятьсот один
59 000 Пятьдесят девять тысяч. Предыдущее - 58 999 Пятьдесят восемь тысяч девятьсот девяносто девять. Последующее - 59 001 Пятьдесят девять тысяч один.
Как можно сравнить многозначные числа?
Правила сравнения натуральных чисел
Правило 1. Если количество цифр разное, то больше число, у которого цифр больше, и наоборот.
Правило 2. Если количество цифр одинаковое, то больше число, у которого больше первая несовпавшая цифра слева, и наоборот.4. Сравни числа:
789 < 1002 815 104 > 815 036
5806 > 5680 750 023 > 99 998
3914 < 3921 37 948 609 > 37 948 096
26 450 > 26 409 444 444 444 > 2 222 222 222 69
-
Страница 69
Урок 23 Сравнение натуральных чисел
5. Вычисли устно:
а) 50 + 40
: 30
• 50
– 100
50
б) 30 + 70
: 10
• 15
– 150
0в) (100 - 70)
• 3
– 18
: 36
2
г) 67 – 23
: 11
• 25
– 19
816. Чем похожи и чем различаются выражения:
(30 – d) : 3 и 30 – d : 3?
Эти значения имеют одинаковые числа и операции, но разные по порядку выполнения вычисления.
Прочитай эти выражения и найди их значения при d = 0, 6, 18, 30. Что ты замечаешь?
При 0
(30 – 0) : 3 = 10
30 – 0 : 3 = 30При 6
(30 – 6) : 3 = 8
30 – 6 : 3 = 28При 18
(30 – 18) : 3 = 4
30 – 18 : 3 = 24При 30
(30 – 30) : 3 = 0
30 – 30 : 3 = 20Разряд единиц в получившихся результатах один и тот же.
7. БЛИЦтурнир
а) В 5 одинаковых банках а л сока. Сколько литров сока в 12 таких банках?
(а : 5) * 12
б) В 5 одинаковых банках a л сока. Сколько потребуется таких банок, чтобы разлить в них 12 литров сока?
12 : (а : 5)
в) В первом мешке с кг крупы, а во втором – в 3 раза больше. На сколько килограммов крупы меньше в первом мешке, чем во втором?
с * 3 - с
г) В магазин привезли m кг картошки по 20 кг в мешке и n кг моркови по 30 кг в мешке. Сколько мешков картошки и моркови привезли в магазин?
m : 20 + n : 30
8.
а) Составь в тетради таблицу, заполняя пропуски:
V X L C D M CCIX LXXII MDLX 5 10 50 100 500 1000 209 72 1560 б) Запиши арабскими цифрами числа: СССLХII, MDCCXLIV.
362, 1744
в) Запиши римскими цифрами числа: 25, 96, 140, 2001.
XXV, XCVI, СXL, MMI
9. Через четыре с половиной часа наступит полночь. А сейчас который час?
Восьмой
10. Сегодня 10 декабря, среда. Какой день будет послезавтра? Как назывался позапрошлый месяц?
Послезавтра 12 - пятница. Позапрошлый месяц - октябрь.
70
-
Страница 70
Урок 24 Решение задач
1. Прочитай число: 572 031 006 800.
Пятьсот семьдесят два миллиарда тридцать один миллион шесть тысяч восемьсот
Сколько классов в его записи? Назови их.
4 класса: единицы, тысячи, миллионы, миллиарды
Сколько разрядов?
12 разрядов
Назови разряды, в которых стоят цифры: 3, 6, 2, 8.
3 - десятки миллионов;
6 - тысячи;
2 - миллиарды;
8 - сотни.2. Разбей на классы и прочитай числа:
а)
7 961, Семь тысяч девятьсот шестьдесят один (2 класса единицы и тысячи)
8 520, Восемь тысяч пятьсот двадцать (2 класса единицы и тысячи)
93 067, Девяносто три тысячи шестьдесят семь (2 класса единицы и тысячи)
200 721, Двести тысяч семьсот двадцать один (2 класса единицы и тысячи)
8 629 356; Восемь миллионов шестьсот двадцать девять тысяч триста пятьдесят шесть (3 класса единицы, тысячи и миллионы)б)
324 508 764, Триста двадцать четыре тысячи пятьсот восемь тысяч семьсот шестьдесят четыре (3 класса единицы, тысячи и миллионы)
94 351 084 922, Девяносто четыре миллиарда триста пятьдесят один миллион восемьдесят четыре тысячи девятьсот двадцать два (4 класса единицы, тысячи, миллионы и миллиарды)
775 613 204 380. Семьсот семьдесят пять миллиардов шестьсот тринадцать миллионов двести четыре тысячи триста восемьдесят (4 класса единицы, тысячи, миллионы и миллиарды)3. Запиши число:
а) 2 млн 48 тыс. 5 ед. Подчеркни класс тысяч. 2 048 005
б) 36 млн 7 тыс. 94 ед. Подчеркни разряд единиц миллионов. 36 007 094
в) 5 млрд 19 млн 208 ед. Подчеркни класс миллиардов. 5 019 000 218
г) 912 млрд 6 млн 45 тыс. Подчеркни разряд десятков тысяч. 912 006 045 0004. Сравни числа:
598 < 2103 8 888 888 > 11 111 111
704 000 > 700 600 345 000 690 > 345 002 0005.
а) Какое число следует за числом:
99, - 100
899, - 900
999, - 1000
4367, - 4368
7599, - 7600
20 300, 20 301
38 126, - 38 127
52 999, - 53 000
999 999? - 1 000 000б) Какое число предшествует числу:
40, - 39
650, - 649
1000, - 999
8324, - 8323
9680, - 9679
14 399, - 14 398
26 700, - 26 699
80 000, - 79 999
10 000 000? - 9 999 999в) Назови «соседей» числа:
5349, - 5348 и 5350
60 237, - 60236 и 60238
589 600. - 589 599 и 589 6016. Периметр четырёхугольника равен 3 м. Первая его сторона равна 72 см, вторая – на 16 см больше первой, а третья – в 2 раза меньше второй. Найди четвёртую сторону этого четырёхугольника.
Р = 3 м = 300 см
1) 72 + 16 = 88 (см) длина второй стороны.
2) 88 : 2 = 44 (см) длина третьей стороны.
3) 72 + 88 + 44 = 204 (см) длина трех сторон.
4) 300 - 204 = 96 (см) длина четвертой стороны
Ответ: 96 см.7. Все ли выражения сравнили верно? Если есть ошибки, исправь их в тетради.
а • 8 + а • 3 > а • 10 52 – c > 25 – c (было неверно) 720 : k > 702 : k
b • 5 – b = 4 • b (было неверно) d – 48 > d – 402 m : 111 < m : 99 (было неверно) 71
-
Страница 71
Урок 24 Решение задач
8. Вычисли. Объясни для каждого столбика приёмы вычислений:
а)
56 : 7 = 8
54 : 9 = 6
45 : 5 = 9табличные значения
б)
68 : 2 = 60 : 2 + 8 : 2 = 30 + 4 = 34
42 : 3 = 30 : 3 + 12 : 3 = 10 + 4 = 14
96 : 4 = 80 : 4 + 16 : 4 = 20 + 4 = 24разбили делимое на удобные для нас числа и поделили их на делимое, результаты сложили
в)
84 : 12 = 7
91 : 13 = 7
77 : 11 = 7подбором
г)
35 : 8 = 32 : 8 + 3 = 4 (ост. 3)
29 : 6 = 24 : 6 + 5 = 4 (ост. 5)
17 : 4 = 16 : 4 + 1 = 4 (ост. 1)деление с остатком
д)
72 : 17 = 4 (ост. 4 )
80 : 15 = 4 (ост. 10)
57 : 18 = 3 (ост. 3)деление с остатком
9.
а) Пользуясь числовым лучом, составь множество двузначных чисел, кратных 16.
16, 32, 48, 64, 80, 96
б) Выполни деление с остатком:
37 : 16 = 2 (ост. 5)
49 : 16 = 3 (ост. 1)
68 : 16 = 4 (ост. 4)
82 : 16 = 5 (ост. 2)
в) Выучи двузначные числа, кратные 16. Проверь себя, работая в паре.
Самостоятельно
10. Вычисли. Расшифруй названия птиц. Найди о них информацию в энциклопедии или Интернете.
Р 72 – 37 = 35
Ф 49 : 7 • 8 = 56
С 7 • 9 – 8 • 4 = 63 - 32 = 31
И 500 – 475 = 25
А 6 • 8 : 4 = 12
Т 54 : 6 + 9 • 8 = 9 + 72 = 81
Л 18 • 4 + 0 = 72
Д 64 : 8 • 12 = 96
Е 35 • 2 – 38 : 2 = 51
Я 25 • 5 – 0 = 125
О 96 : 24 • 20 = 80
Ж 94 : 2 + 70 : 14 = 5296 125 81 51 72
ДЯТЕЛ
31 81 35 25 52
СТРИЖ
96 35 80 56 12
ДРОФА
11. А – множество натуральных чисел, меньших 9, но больших или равных 5. Запиши множество А с помощью фигурных скобок.
А = {5, 6, 7, 8}
12. На какие части можно разбить множество всех слов русского языка?
Все слова русского языка можно разбить на части но следующим свойствам:
1) по одинаковой первой или второй или последней и т.д. букве;
2) по частям речи;
3) по одинаковому количеству слогов;
4) по одинаковому числу букв;
5) по одинаковому количеству гласных/согласных.Можно ли его разбить на части: «существительные» и «слова, которые начинаются с буквы М»? Почему?
Нельзя разбить все слова русского языка на части: «существительные» и «слова, начинающиеся с буквы «м», так как многие имена существительные начинаются с этой буквы, эти множества будут пересекаться между собой, поэтому групп не получится.
72
-
Страница 72
Урок 25 Сумма разрядных слагаемых
1. Запиши числа:
а) девять тысяч триста пять; 9 305
б) девять тысяч тридцать пять; 9 035
в) девять тысяч триста пятьдесят; 9 350
г) восемьдесят тысяч пятнадцать; 80 015
д) девятьсот две тысячи восемь; 902 008
е) шесть миллионов двадцать четыре тысячи восемьсот девять; 6 024 809
ж) триста пять миллионов пятьсот шестьдесят тысяч восемьсот; 305 560 800
з) двенадцать миллиардов четыреста двадцать миллионов триста сорок семь тысяч сто семьдесят пять. 12 420 347 1752.
а) Прочитай числа.
43 сорок три
430 четыреста тридцать
403 четыреста три43 000 сорок три тысячи
40 300 сорок тысяч триста
40 030 сорок тысяч тридцать400 030 четыреста тысяч тридцать
40 003 000 сорок миллионов три тысячи
400 300 000 четыреста миллионов триста тысячСколько единиц в разряде десятков у чисел первого столбика?
7
Сколько в каждом всего десятков?
в первом столбике в числах 7 десятков
во втором 3 десятка
в третьем 3 десятковб) Сколько единиц в разряде сотен тысяч у чисел третьего столбика?
7
Сколько в каждом всего сотен тысяч?
для первого столбика 0
для второго столбика 0
для третьего столбика 7 сотен тысяч во всех числахв) Запиши числа второй строки в виде суммы разрядных слагаемых. Сделай вывод.
400 + 30 40 000 + 300 40 000 000 + 3 000
73
-
Страница 73
Урок 25 Сумма разрядных слагаемых
3. Сосчитай сумму. В каких разрядах отсутствуют единицы?
а) 8000 + 400 + 30 + 5 = 8435
в этой сумме в каждом разряде есть единицы
30 000 + 6000 + 80 + 1 = 36 081
отсутствуют в разряде сотен
б) 900 000 + 70 000 + 500 = 970 500
отсутствуют в разряде единиц, десятков, тысяч
4 000 000 + 9000 + 80 = 4 009 080
отсутствуют в разряде единиц, сотен, десятков тысяч и сотен тысяч.
4. Запиши числа в виде суммы разрядных слагаемых:
42 075 = 40 000 + 2 000 + 70 + 5
200 097 = 200 000 + 90 + 7
384 794 = 300 000 + 80 000 + 4 000 +700 + 90 + 4
7 056 448 = 7 000 000 + 50 000 + 6 000 + 400 + 40 + 8
5. БЛИЦтурнир
а) На одном сеансе в кинотеатре побывали а человек, а на другом – на 70 человек меньше. Сколько всего человек побывали на обоих сеансах?
а + (а - 70)
б) В первом пансионате отдыхает b человек, а во втором – в 3 раза больше. На сколько меньше отдыхающих в первом пансионате, чем во втором?
b * 3 - b
в) В автобусе ехало n человек. На остановке вышли c человек, а вошли d человек. Сколько человек стало в автобусе?
n - c + d
г) Выставку детских рисунков за 3 дня посетили а человек. В первый день её посетили b человек, а во второй день – в 2 раза больше. Сколь ко человек посетили выставку в третий день?
a - b + (b * 2)
д) В пяти одинаковых автобусах можно разместить х человек. Сколько человек можно разместить в восьми таких автобусах?
x : 5 * 8
6. Как найти целое? Как найти часть? Составь все возможные равенства из чисел: 251, 319, 570.
251 = 200 + 50 + 1, 251 = 250 + 1, 251 = 200 + 51
319 = 300 +10 + 9, 319 = 310 + 9, 319 = 300 + 19
570 = 500 +707. Реши уравнения с комментированием и сделай проверку:
х – 374 = 546
х = 546 + 374
х = 920687 + х = 814
х = 814 - 687
х = 127432 – х = 396
х = 432 - 396
х = 368. Составь программу действий и вычисли:
1 3 7 4 5 8 6 2
а) (17 + 43) : 2 – 9 • 8 : 4 + 70 : (7 + 7) = 171) 17 + 43=60
2) 7 + 7=14
3) 60 : 2 = 30
4) 9 * 8 = 72
5) 72 : 4 = 18
6) 70 : 14 = 5
7) 30 - 18 = 12
8) 12 + 5 = 173 4 7 5 1 8 2 6
б) 96 : 2 : 12 + 15 • (78 : 13) – (33 + 54) : 3 = 651) 78 : 13 = 6
2) 33 + 54 = 87
3) 96 : 2 = 48
4) 48 : 12 = 4
5) 15 × 6 = 90
6) 87 : 3 = 29
7) 4 + 90 = 94
8) 94 - 29 = 659. Найди значения выражений (20 + х) : 2 и 20 + х : 2, если х = 8, 12, 26, 42. Что ты замечаешь? Как это можно объяснить?
При 8
(20 + 8) : 2 = 14
20 + 8 : 2 = 24При 12
(20 + 12) : 2 = 16
20 + 12 : 2 = 26При 26
(20 + 26) : 2 = 23
20 + 26 : 2 = 33При 42
(20 + 42) : 2 = 31
20 + 42 : 2 = 4110. Составь множество цифр, входящих в запись числа:
* - представим, что для каждого случая у нас это будет множество A, тогда.
а) 135 906 247;
А = {0;1;2;3;4;5;6;7;9}
б) 3 333 333 333;
А = {3}
в) 20 260 600 000.
А = {0;2;6}
74
-
Страница 74
Урок 26 Сложение и вычитание многозначных чисел
1.
а) Прочитай числа. Сколько единиц у этих чисел в разряде сотен миллионов? Сколько всего в них сотен миллионов?
млрд млн тыс. ед.
2 348 697 864 Два миллиарда триста сорок восемь миллионов шестьсот девяносто семь тысяч восемьсот шестьдесят четыре (единиц в разряде сотен миллионов: 3 всего сотен миллионов:23)
383 635 999 875 Триста восемьдесят три миллиарда шестьсот тридцать пять миллионов девятьсот девяносто девять тысяч восемьсот семьдесят пять (единиц в разряде сотен миллионов: 6 всего сотен миллионов:3836)
906 503 409 707 Девятьсот шесть миллиардов пятьсот три миллиона четыреста девять тысяч семьсот семь (единиц в разряде сотен миллионов: 5 всего сотен миллионов:9065)
73 420 360 000 Семьдесят три миллиарда четыреста двадцать миллионов триста шестьдесят тысяч (единиц в разряде сотен миллионов: 4 всего сотен миллионов:734)млрд млн тыс. ед.
86 710 000 800 Восемьдесят шесть миллиардов семьсот десять миллионов тысяч восемьсот (единиц в разряде сотен миллионов: 7 всего сотен миллионов:867)
7 200 075 000 Семь миллиардов двести миллионов семьдесят пять тысяч (единиц в разряде сотен миллионов: 2 всего сотен миллионов:72)
63 057 000 005 Шестьдесят три миллиарда пятьдесят семь миллионов пять (единиц в разряде сотен миллионов: 0 всего сотен миллионов:630)
1 070 000 000 Один миллиард семьдесят миллионов (единиц в разряде сотен миллионов: 0 всего сотен миллионов:10)б) Найди число, в разряде десятков тысяч которого стоит цифра 7. Запиши его в виде суммы разрядных слагаемых.
7 200 075 000
7 000 000 000 + 200 000 000 + 75 000 = 7 200 075 000
2. Найди разряды, в которых отсутствуют единицы. Запиши цифрами числа:
а) 24 тыс. 715 ед. 24 715
б) 4 тыс. 5 ед. 4 005 (отсутствуют единицы: в десятках и сотнях)
в) 812 тыс. 34 ед. 812 034 (отсутствуют единицы в десятках)
г) 2 млн 3 тыс. 18 ед. 2 003 018 (отсутствуют единицы: в сотнях, в десятках тысяч, сотнях тысяч)
д) 17 млн 623 ед. 17 000 623 (отсутствуют единицы в единицах тысяч, в десятках тысяч, в сотнях тысяч)
е) 9 млн 4 тыс. 7 ед. 9 004 007 (отсутствуют единицы: в десятках, в сотнях, в десятках тысяч, в сотнях тысяч)3. Сравни числа:
7422 < 7428
6315 < 6351
3090 > 3009
24 106 > 14 278
55 505 > 55 055
369 999 < 400 0004. Что ты уже умеешь делать с многозначными числами? Чему надо научиться? Попробуй сложить и вычесть два многозначных числа по своему выбору. Сделай вывод.
+3 568 123
1 254 256
4 822 379 75
-
Страница 75
Урок 26 Сложение и вычитание многозначных чисел
5. Найди значения выражений:
а) 5214 + 4723
+5214
4723
9937б) 26 348 + 91 570
+26348
91570
117918в) 8359 – 6042
-8359
6042
2317г) 357 906 – 74 014
-357906
74014
283882д) 1378 + 9615
+1378
9615
10993е) 42 630 – 1806
-42630
1806
408246. Выполни действия. Проверь результаты с помощью калькулятора.
а) 235 287 + 8609
+235287
8609
243896б) 638 095 – 52 008
-638095
52008
586087в) 56 084 + 174 269
+56084
174269
2303537. Заяц (0), Ёж (▲) и Медведь (?) решали примеры. Проверь, верны ли их решения. Если есть ошибки, исправь их в тетради.
Все решили неправильно. Правильное решение такое:
-700012
52918
6470948. Реши уравнения с комментированием:
х : 25 = 80
х = 80 * 25
х = 2000960 : х = 4
х = 960 : 4
х = 24035 • х = 700
х = 700 : 35
х = 209. БЛИЦтурнир
а) Банан стоит а р., а ананас на b р. дороже. Во сколько раз банан дешевле ананаса?
(a + b) : a
б) На с р. можно купить 5 кг яблок. Сколько рублей надо заплатить за 8 кг таких же яблок?
c : 5 * 8
в) На с р. можно купить 5 кг яблок. Сколько килограммов таких яблок можно купить на d рублей?
d : (c : 5)
г) Стол стоит х р., а стул — у р. Сколько стоят 2 таких стола и 8 стульев?
2 * х + 8 * y
д) Карандаш стоит а р. Сколько надо заплатить за 2 коробки таких карандашей, если в одной из них m штук, а в другой — n штук карандашей?
a * m + a * n
е) Оля истратила b р., а осталось у неё в 2 раза больше, чем она истратила. Сколько было денег у Оли вначале?
b + b * 2 или 3b
10. Какие трёхзначные числа можно составить из цифр 0, 3, 5, если цифры в записи числа:
а) не повторяются;
305
350
503
530
4 числаб) могут повторяться?
300
303
305
330
333
335
350
353
355
500
503
505
530
533
535
550
553
555
18 чиселСколько таких чисел?
76
-
Страница 76
Урок 27 Решение задач
1. Разбей числа на классы и прочитай их:
а) 5075; 5 075 Пять тысяч семьдесят пять
б) 20068; 20 068 Двадцать тысяч шестьдесят восемь
в) 418093; 418 093 Четыреста восемнадцать тысяч девяносто три
г) 540780; 540 078 Пятьсот сорок тысяч семьсот восемьдесят
д) 8012505; 8 012 505 Восемь миллионов двенадцать тысяч пятьсот пять
е) 36015724; 36 015 724 Тридцать шесть миллионов пятнадцать тысяч семьсот двадцать четыре
ж) 29300006; 29 300 006 Двадцать девять миллионов триста тысяч шесть
з) 756818042; 756 818 042 Семьсот пятьдесят шесть миллионов восемьсот восемнадцать тысяч сорок два
и) 9560002729. 9 560 002 729 Девять миллиардов пятьсот шестьдесят миллионов две тысячи семьсот двадцать девять2. Дополни предложения так, чтобы получились верные высказывания:
а) В числе 82 500 816 содержится всего 825 сотен тысяч, а в разряде сотен тысяч стоит цифра 5
б) За числом 6 049 999 следует число 6 050 000
в) Перед числом 5 704 000 000 идёт число 5 703 999 999
г) Самое маленькое семизначное число 1 000 000
д) Самое большое шестизначное число 999 9993. Вычисли. Проверь результаты с помощью калькулятора.
а) 2 956 307 + 18 769+2956307
18769
2975076б) 4 600 805 – 576 095
-4600805
576095
4024710в) 85 297 + 3 644 905
+ 85297
3644905
3730202г) 10 000 000 – 93 918
-10000000
93918
99060824. Запиши числа в виде суммы разрядных слагаемых:
а) 7302 = 7000+300+2
б) 90 548 = 90 000 + 500 + 40 + 8
в) 300 090 = 300 000 + 90
г) 7 000 050 004 = 7 000 000 000 + 50 000 + 45. Реши задачи, составляя выражения. Сравни их. Что ты замечаешь? Как называют такие задачи?
а) Из 24 м ткани сшили 8 одинаковых скатертей. Сколько ткани потребуется для пошива 15 таких скатертей?
24 : 8 * 15 = 3 * 15 = 45 (м) надо на 15 скатертей.
Ответ: 45 метров.б) Из 24 м ткани сшили 8 одинаковых скатертей. Сколько таких скатертей можно сшить из 45 м ткани?
45 : 24 : 8 = 45 : 3 = 15 (ск.) можно сшить.
Ответ: 15 скатертей.Такие задачи называются обратные.
6. Придумай задачи по выражениям:
а) (60 : 6) • 4;
В 6 коробках было 60 конфет. Сколько конфет в 4 таких коробках?
(60 : 6) • 4 = 10 * 4 = 40 (кон.) в 4 коробках.
Ответ: 40 конфетб) 72 : (48 : 6).
В 6 коробках было 48 конфет. Сколько коробок можно заполнить 72 конфетами?
72 : (48 : 6) = 72 : 8 = 9 (кор.) можно заполнить.
Ответ: 9 коробок.7. Запиши примеры в столбик и вычисли:
а) 39 • 8
*39
8
312
б) 7 • 58*58
7
406в) 420 • 6
*420
6
2520г) 83 • 900
* 83
900
747008.
а) Пользуясь числовым лучом, составь множество двузначных чисел, кратных 17.17, 34, 51, 68, 85
б) Выполни деление с остатком:
38 : 17 = 2 (ост. 4)
56 : 17 = 3 (ост. 5)
70 : 17 = 4 (ост. 3)
91 : 17 = 5 (ост. 6)в) Выучи двузначные числа, кратные 17. Проверь себя, работая в паре.
Самостоятельно.
77
-
Страница 77
Урок 27 Решение задач
9. Cравни, не вычисляя. Обоснуй свой ответ.
264 • 98 > 95 • 264 так как 98 больше 95
7 • (39 + 2) = 7 • 2 + 7 • 39 раскрыли скобки
(7 • 15) • 4 = 7 • (4 • 15) изменен порядок действий
(9 + 14) • 8 > 8 • 9 + 12 • 8 так как 14 больше 12
10. Вычисли. Наложи прозрачную плёнку и соедини ответы по порядку. Что получилось?
1. (71 – 19) : 13 = 4 6. 42 • 2 – 25 • 3 = 9 11. (58 + 26) : 14 = 6
2. (19 + 9) • 3 = 84 7. 15 • 5 + 50 : 2 = 100 12. 24 : 6 + 36 = 40
3. 100 – 16 : 4 = 96 8. (75 – 74) • 5 • 9 = 45 13. 91 : 13 • 8 : 14 = 4
4. (44 + 33) : 7 = 11 9. 6 • (72 – 32) : 8 = 30 14. 80 : 16 • 9 : 15 = 3
5. (36 + 48) : 12 = 7 10. 32 + 48 : 8 • 3 = 50 15. 72 : 12 • 9 : 27 = 2
11. Используя связь между числами первой строки, найди неизвестное число во второй строке:
а)
18 60 42
26 45 19* - крайние цифры в сумме дают среднее
б)
35 38 73
17 48 65* - первые две слева дают правое число
в)
12 48 4
23 115 5* - произведение крайних дает среднее
12. Составь множество двузначных чисел, в записи которых используются лишь цифры 2, 5 и 8. Найди пересечение этого множества с множеством чётных чисел.
Числа:
А = {22, 25, 28, 52, 55, 58, 82, 85, 88}
Четные:
B = {22; 28; 52; 58; 82; 88}
Пересечение:
A U В = B = {22; 28; 52; 58; 82; 88}
78
-
Страница 78
Урок 28 Преобразование единиц счёта
1. Прочитай числа. Сколько единиц у каждого из них в разряде десятков тысяч? Сколько всего десятков тысяч?
млрд млн тыс. ед.
6 009 916 480 Шесть миллиардов девять миллионов девятьсот шестнадцать тысяч четыреста восемьдесят (единиц в разряде десятков тысяч: 1 всего десятков тысяч: 600 991)
32 730 000 020 Тридцать два миллиарда семьсот тридцать миллионов двадцать (единиц в разряде десятков тысяч: 0 всего десятков тысяч: 3 273 000)млрд млн тыс. ед.
93 001 082 564 Девяносто три миллиарда один миллион восемьдесят две тысячи пятьсот шестьдесят четыре (единиц в разряде десятков тысяч: 8 всего десятков тысяч: 9 300 108)
800 026 740 005 Восемьсот миллиардов двадцать шесть миллионов семьсот сорок тысяч пять (единиц в разряде десятков тысяч: 4 всего десятков тысяч: 800 021 674)2. Запиши и прочитай числа:
а) 7 тыс. 38 ед. 7 038 Семь тысяч тридцать восемь
б) 406 тыс. 2 ед. 406 002 Четыреста шесть тысяч два
в) 2 млн 405 тыс. 9 ед. Два миллиона четыреста пять тысяч девять
г) 53 млрд 8 млн 16 ед. Пятьдесят три миллиарда восемь миллионов шестнадцать.3. Модели каких чисел изображены? Вырази эти числа в сотнях и единицах, десятках и единицах.
а)
248
(в сотнях и единицах: 2 сотни + 48 ед., десятках и единицах: 24 дес. + 8 ед.)
б)
306
(в сотнях и единицах: 3 сот. + 6 ед. десятках и единицах: 30 дес. + 6 ед.)
в)
580
(в сотнях и единицах: 5 сот + 80 ед., десятках и единицах: 58 дес. + 0 ед.)
4. Сколько сотен и единиц в числе 36 007?
360 сотен и 7 единиц
Сделай вывод: как выразить любое натуральное число в заданных единицах счёта?
Алгоритм записи числа в заданных единицах счёта
Подчеркнуть указанные разряды.
Провести справа от них черту
Прочитать / записать ответ (нули перед числом не пишут)5. Вырази числа в указанных единицах счёта:
а) 5070 в тысячах и десятках; 50 сотен 7 дес.
б) 24 803 в тысячах и единицах; 24 тыс. 803 ед.
в) 6 319 000 в миллионах и тысячах; 6 млн. 319 тысяч
г) 31 584 702 в миллионах, тысячах и единицах; 31 млн. 584 тыс. 702 ед.
д) 49 305 064 в сотнях тысяч, сотнях и единицах; 493 сот. тыс. 50 сот. 64 ед.
е) 58 120 900 в миллионах, тысячах и десятках. 58 млн. 120 тыс. 90 дес.
79
-
Страница 79
Урок 28 Преобразование единиц счёта
6. Вырази числа в тысячах и единицах, а длины – в километрах и метрах. Что ты замечаешь?
а) 6328 = 6 тыс. 328 ед.
6328 м = 6 км 328 м
б) 25 043 = 25 тыс. 43 ед.
25 043 м = 25 км 43 м
в) 88 808 = 88 тыс. 808 ед.
88 808 м = 88 км 808 м
г) 975 004 = 975 тыс. 4 ед.
975 004 м = 975 км 4 м
7. Запиши цифрами числа, а длины вырази в метрах. Сравни примеры каждого столбика. Что ты замечаешь?
а) 4 тыс. 17 ед. = 4 017
4 км 17 м = 4017 м
б) 37 тыс. 258 ед. = 37 258
37 км 258 м = 37 258 м
в) 752 тыс. 9 ед. = 752 009
752 км 9 м = 752 009 м
г) 94 тыс. = 94 000
94 км = 94 000 м
8. Выполни действия. Проверь результаты с помощью калькулятора.
а) 9072 + 389
+9072
389
9461б) 578 254 – 129 496
-578254
129496
448758в) 38 829 + 64 217
+38829
64217
103046г) 167 104 – 3970
-167104
3970
163134д) 372 005 – 86 918
-372005
86918
285087е) 93 948 + 159 307
+93948
159307
2532559. Запиши и прочитай наибольшее семизначное число и наименьшее десятизначное число. Какие числа им предшествуют? Какие числа за ними следуют?
9 999 999 Девять миллионов девятьсот девяносто девять тысяч девятьсот девяносто девять (предшествует 9 999 998, последующее 10 000 000)
1 000 000 Один миллион (предшествует 999 999, последующее 1 000 001)
10.
а) Стороны прямоугольного участка земли равны 90 м и 15 м. Найди площадь этого участка.
90 *15 = 1350 (м2) площадь участка.
Ответ: 1350 м2
б) Площадь прямоугольника 70 дм2, а его ширина – 5 дм. На сколько дециметров длина прямоугольника больше его ширины?
1) 70 : 5 = 14 (дм) длина прямоугольника.
2) 14 - 5 = 9 (дм) на столько длина больше ширины.
Ответ: на 9 дм.11. Реши уравнения с комментированием, сделай проверку:
26 • х = 52
х = 52 : 26
х = 278 : х = 3
х = 78 : 3
х = 26х • 17 = 51
х = 51 : 17
х = 3х : 240 = 4
х = 240 * 4
х = 96012. Определи, какие точки принадлежат прямой l, а какие ей не принадлежат. Сделай записи, используя знаки ∈ и ∉.
l ∈ А, М
l ∉ С, B, D, K
13. А – множество городов России, В – множество городов Европы. Что представляет собой множество А ∩ В? Назови несколько элементов этого множества.
Москва, Брянск, Курск, Тверь
14. Найди множество трёхзначных чисел, в записи которых используются только цифры 1 и 3 (вместе или по отдельности). Чему равна разность наибольшего и наименьшего из этих чисел?
А {111; 113; 131, 133, 311, 313, 331, 333}
разность наибольшего и наименьшего из этих чисел: 333 - 111 = 222
80
-
Страница 80
Урок 29 Решение задач
1. Запиши цифрами числа:
а) 2 тыс. 82 ед. 2 082
б) 48 тыс. 5 ед. 48 005
в) 574 тыс. 574000
г) 97 млн 97 000 000
д) 3 млн 56 ед. 3 000 056
е) 7 млрд 45 тыс. 8 ед. 7 000 045 0082. Прочитай числа и определи, сколько единиц каждого разряда в них содержится:
а) 5378; Пять тысяч триста семьдесят восемь (единиц в тысячах: 5 в сотнях: 3 в десятках: 7 в единицах: 8)
б) 32 609; Тридцать две тысячи шестьсот девять (единиц в десятках тысячах: 3 в тысячах: 2 в сотнях: 6 в десятках: 0 в единицах: 9)
в) 940 615. Девятьсот сорок тысяч шестьсот пятнадцать (единиц в сотнях тысячах: 9 в десятках тысяч: 4 в тысячах: 0 в сотнях: 6 в десятках: 1 в единицах: 5)Для каждого из этих чисел определи, сколько всего в нём единиц, десятков, сотен, тысяч, десятков тысяч.
3. Вырази число 2 003 916 в указанных единицах счёта:
а) в миллионах, тысячах и единицах;
2 млн 3 тыс. 916
б) в десятках тысяч, сотнях и единицах.
200 дес. тыс. 39 сот. 16 ед.
4. Объясни решение примеров. Как выполнить вычитание многозначных чисел, когда в разрядах уменьшаемого не хватает единиц?
Когда не хватает единиц в разряде, то "занимаем" единицы из более высокого разряда, при этом учитывая это при дальнейшем вычислении и получении результата.
5. Найди значения выражений. Проверь с помощью калькулятора.
а) 4000 – 257
-4000
257
3743б) 50 000 – 12 400
-50000
12400
37600в) 710 096 + 99 939
-710096
99939
610157г) 302 034 – 5626
-302034
5626
296408д) 26 105 002 – 297 307
-26105002
297307
25807695е) 8297 + 1 994 758
+ 8297
1994758
20030556. Реши уравнения. Сделай проверку с помощью калькулятора.
х – 3066 = 72 527
х = 72527 + 3066
х = 7559315 470 – х = 8315
х = 15470+8315
х = 23785х + 824 = 2000
х = 2000 - 824
х = 11767. В первых трёх классах Таня записала в свой словарь 1274 английских слова. Из них 82 слова она записала в первом классе, а во втором классе – в 4 раза больше слов, чем в первом. Сколько слов записала Таня в свой словарь в третьем классе?
1) 82 * 4 = 328 (сл.) записала во втором классе.
2) 328 + 82 = 410 (сл.) записала в 1 и во 2 классе.
3) 1274 - 410 = 864 (сл.) записала в 3 классе.
Ответ: 864 слова.8. Сравни числа:
32 624 > 9316
777 < 7000
5812 < 6812
3324 > 3243
86 000 > 85 099
932 758 = 932 785 81
-
Страница 81
Урок 29 Решение задач
9. Викторина «В мире птиц»
1) Вычисли. Расшифруй название птицы-строителя, которая вьёт гнёзда, похожие на чулки.
K - 50
А - 20
И - 40
Т - 0
Ч - 58ТКАЧИК
2) Пользуясь алгоритмом, найди значения х. Расшифруй название птицы, которая вообще не вьёт гнёзда, а выкапывает норки в земле.
а 1 2 5 9 11 12 14 х 75 175 475 875 85 95 115 К И Д Р О М З 115 175 95 85 875 85 475 85 75 З И М О Р О Д О К 10. Выполни деление с остатком и сделай проверку:
а) 59 : 7 = 8 (ост. 3)
б) 25 : 8 = 3 (ост. 1)
в) 47 : 5 = 9 (ост. 2)
г) 64 : 3 = 21 (ост. 1)
д) 55 : 17 = 3 (ост. 4)
11. Сравни выражения. Что в них общего? Выполни умножение в столбик:
390 • 80
*390
80
3120052 • 60
* 52
60
3120780 • 50
*780
50
390004300 • 7
*4300
7
30100Общее в низ то, что ноли при вычислении не учитываем, но не забываем про них в результате.
12. Старинные задачи-шутки
а) Шла баба в Москву и повстречала 3 мужиков. Каждый из них нёс по мешку, в каждом мешке по коту. Сколько всего существ направлялось в Москву?Если мужики шли тоже в Москву, то 3 кота, 3 мужика и баба. Итого 7 существ, но это с учетом, что больше никто в Москву не шел.
б) Длина бревна 5 аршин. В одну минуту от этого бревна отпиливают по одному аршину. Через сколько минут будет распилено всё бревно?
Через 4 минуты, так как последний рез сразу разделит бревно на две равные части по аршину.
82
-
Страница 82
Урок 30 Свойства действий с многозначными числами
1. (Устно.) Вычисли удобным способом:
23 + 24 + 25 + 26 + 27 = (23 + 27) + 25 + (24+26) = 125
(36 + 25) + 75 + (64 + 100) = (64 + 36) + (25 + 75) + 100 = 300
Какие свойства сложения помогли упростить вычисления? Можно ли распространить их на многозначные числа? Почему?
Перестановка слагаемых. Да, можно применить и к многозначным числам. Для многозначных чисел сохраняются все изученные ранее свойства и правила действий с числами (правила порядка действий, свойства арифметических действий и т. д.).
2. (Устно.) Вычисли удобным способом. Обоснуй свой ответ.
а) 71 300 + 2996 + 4 + 700 = 72 000 + 3 000 = 75 000
б) 9998 + 405 + 2 + 95 + 2500 = 10 000 + 500 = 10 500
в) (18 607 + 458) – 17 607 = 1000 + 458 = 1458
г) 32 584 – (32 564 + 19) = 20 - 19 = 13. Вычисли. Проверь результаты с помощью калькулятора.
а) 55 796 208 + 603 917+55796208
603917
56400125б) 41 002 600 – 25 624
-41002600
25624
409769764. При каких значениях букв верны равенства:
а + 16 504 = 16 504, при а = 0
34 290 + b = 34 290, при b = 0
7 009 072 – с = 0, при с = 7 009 072
Назови свойства сложения и вычитания с нулём.
При прибавлении или вычитании нуля результат равен тому значению к которому прибавляли или из которого вычитали ноль.
5. Составь выражение и найди его значение:
а) Из числа 67 546 вычесть сумму чисел 5624 и 14 976.
67546 - (5624 + 14976) = 46 946
б) Разность чисел 80 000 и 46 980 увеличить на 7589.
(80 000 - 46 980) + 7589 = 40 609
6. Составь программу действий. Что ты замечаешь?
3 1 4 6 5 2
1) a : (b – c) • d + k • (m : n)3 6 4 2 1 5
2) а : b – с • (d + k • m) : n3 2 1 6 4 5
3) а : (b – с • d) + k • m : n1 2 4 6 5 3
4) (а : b – с) • d + k • (m : n)Не смотря на то, что в выражениях одни и те же символы и одинаковое количество действий, результаты вычислений будут разные (если все значение элементов, конечно, не равны 0)
7. Составь программу действий и вычисли:
2 1 3
а) 100 000 – (5020 + 72 396) – 2973 = 25 557
1) 5020 + 72 396 = 77416
2) 100 000 - 77 416 = 22584
3) 22584 - 2973 = 25 5571 3 2
б) (206 400 – 40 287) – (50 266 + 103 924) = 11 923
1) 206 400 – 40 287 = 166 113
2) 50 266 + 103 924 = 154 190
3) 166 113 - 154 190 = 11 9238. В трёх школах учится 3600 человек. В первой школе учится 1265 человек, а во второй школе – на 348 человек больше, чем в первой. Сколько учеников в третьей школе? На сколько учеников в третьей школе меньше, чем в первой?
1) 1265 + 348 = 1613 (ч.) учится во второй школе.
2) 3600 - 1613 = 1987 (ч.) учится в третьей школе.
Ответ: 1987 человек. 83
-
Страница 83
Урок 30 Свойства действий с многозначными числами
9.
а) Пользуясь числовым лучом, составь множество двузначных чисел, кратных 18.
18, 36, 54, 72, 90
б) Выполни деление с остатком:
39 : 18 = 2 (ост. 3)
55 : 18 = 3 (ост. 1)
62 : 18 = 3 (ост. 8)
76 : 18 = 4 (ост. 4)в) Выучи двузначные числа, кратные 18. Проверь себя, работая в паре.
Самостоятельно
10. Вычисли. Расшифруй и отгадай загадку:
Т 38 : 2 = 19
У 75 : 3 = 25
Б 68 : 4 = 17
К 96 : 6 = 16
И 60 : 5 = 12
П 36 : 18 = 2
Ш 99 : 9 = 11В 34 • 2 = 68
Е 24 • 3 = 72
Д 19 • 4 = 76
Ё 18 • 5 = 90
Р 12 • 7 = 84
С 28 • 2 = 56
Ъ 9 + 9 = 18З (96 – 26) : 14 = 5
О (63 – 35) : 7 = 4
Г 25 • 1 + 25 : 25 = 26
А 36 : 1 – 24 • 0 = 36
Л 80 : 2 + 80 : 40 = 42
Ы 72 – 48 : 6 · 3 = 48
Н 4 • (23 – 8) : 10 = 6СИДИТ ДЕД ВО СТО ШУБ ОТДЕТ КТО ЕГО РАЗДЕВАЕТ ТОТ СЛЕЗЫ ПРОЛЕВАЕТ
84
-
Страница 84
Урок 30 Свойства действий с многозначными числами
11. Сравни выражения:
а – 25 > а – 205
42 + b > b + 24
306 – с = 360 – с
270 : d > 27 : d
81 • х < х • 83 – х
у : 52 < у : 212.
а) Длина прямоугольника 17 дм, а ширина на 8 дм меньше длины. Найди площадь и периметр этого прямоугольника.
1) 17 - 8 = 9 (дм) ширина прямоугольника.
2) 17 * 9 = 153 (см2) площадь прямоугольника.
3) (17 +9) * 2 = 52 (см) периметр прямоугольника.
Ответ: 52 см периметр и 153 см2 площадь.б) Площадь прямоугольника равна 290 см2, а его длина – 29 см. Чему равен периметр этого прямоугольника?
1) 290 : 29 = 10 (см) ширина прямоугольника.
2) (29 +10) * 2 = 78 (см) периметр прямоугольника.
Ответ: 78 см.в) Найди площадь квадрата, периметр которого равен 36 м.
1) 36 : 4 = 9 (см) сторона квадрата.
2) 9*9 = 81 (см) периметр квадрата.
Ответ: 81 см.13. Конверт стоит 5 рублей, а марка – m рублей, где m > 5.
1) Верно ли, что конверт дороже марки на m – 5 рублей?
Да.
2) Верно ли, что 4 конверта и 6 марок стоят m · 6 + 20 рублей?
Да.
3) Могут ли 3 конверта и 2 марки стоить 38 рублей?
Да.
14. К – множество кругов, С – множество фигур синего цвета. Что представляет собой пересечение этих множеств С ∩ К?
синие круги
15. По диаграмме Эйлера–Венна определи, какие знаки пропущены: ∈ , ∉ , ⊂ или ⊄ . Сделай записи в тетради.
2 ∈ A
2 ∉ B
2 ∈ D
2 ∉ E
B ⊂ A
C ⊂ A
D ⊄ C
E ⊄ A16. Старинные задачи
а) Летела стая гусей: один гусь впереди, а два позади; один позади и два впереди; один между двумя и три в ряд. Сколько было гусей?
3 + 3 + 3 + 3 = 12 гусей
б) Коля и его сестра Шура хвалились своими успехами в арифметике. Отец сказал: «Хвалиться может каждый. А вот попробуйте решить мои задачи». И дал детям по записке.
Коля прочитал: «Если к моим деньгам прибавить их половину, то получится 81 рубль. Сколько у меня денег?». А Шура прочитала: «Если мама положит в кошелёк ещё треть денег, находящихся в нём, то в кошельке станет 68 рублей. Сколько денег в кошельке?». Но ни Коля, ни Шура задачи решить не смогли. Не поможешь ли ты в их затруднительном положении?Для Коли:
81 : 3 * 2 = 54 (р.) у папы.
Ответ: 54 рубля.Для Шуры:
68 : 2 * 3 = 102 (р.) в кошельке.
Ответ: 102 рубля. 85
-
Страница 85
Урок 31 Решение задач
1. Запиши цифрами числа:
а) 28 тыс. 12 ед. 28 012
б) 15 млн 2 тыс. 320 ед. 15 002 320
в) 58 млн 6 тыс. 58 006 000
2.
а) Вырази число 17 000 в десятках; 1 700 дес.
в сотнях; 170 сот.
в тысячах. 17 тыс.
б) Вырази число 5 320 000 в десятках; 532 000 дес.
в тысячах; 5 320 тыс.
в десятках тысяч. 532 дес. тыс
3. (Устно.) Найди значения выражений:
639 999 + 1 = 640 000 87 905 – 300 = 87 605 53 997 + 840 + 3 + 160 = 54 000 + 1000 = 55 000
3 200 000 – 1 = 3 199 000 218 520 + 40 000 = 258 520 9 000 000 + 70 000 + 400 + 10 = 9 070 400
4. Вычисли суммы. Проверь результаты с помощью калькулятора.
а) 325 + 7260 + 68 =
в) 6084 + 25 615 + 82 + 705 = 7 653
б) 9593 + 724 + 32 807 = 43 124
г) 80 088 + 232 + 7509 + 67 = 95 896
5. Составь программу действий и вычисли:
2 1
а) 6058 + (73 942 – 35 092) =1) 73 942 – 35 092 = 38 850
2) 6058 + 38 850 = 44 9082 1 3
б) 802 620 – (20 000 – 4634) + 64 589 =1) 20 000 – 4634 = 15 366
2) 802 620 – 15 366 = 787 254
3) 787 254 + 64 589 = 851 8436. По железной дороге от Бреста до Москвы 1099 км, от Москвы до Екатеринбурга – 1667 км, от Екатеринбурга до Новосибирска – 1524 км, а от Новосибирска до Иркутска – 1851 км. Чему равно расстояние от Бреста до Иркутска по этой железной дороге?
1) 1099 + 1667 + 1524 +1851 = 6 141 (км) от Бреста до Иркутска.
Ответ: 6 141 км.7. Реши уравнения с комментированием и сделай проверку:
х : 72 = 10
х = 72 * 10
х = 720600 : х = 100
х = 600 : 100
х = 6х • 10 = 350
х = 350 : 10
х = 35540 : х = 54
х = 540 : 54
х = 108. Длина прямоугольника равна 12 см, а ширина – в 2 раза меньше длины. Найди площадь квадрата с тем же периметром, что и у данного прямоугольника.
1) 12 : 2 = 6 (см) ширина прямоугольника.
2) (12 + 6) *2 = 36 (см) периметр прямоугольника.
3) 36 : 4 = 9 (см) должна быть сторона квадрата.
4) 9 * 9 = 81 (см2) должна быть площадь квадрата.
Ответ: 81 см29. Нарисуй прямую АВ и отметь на ней точку С. Сколько образовалось лучей? Назови их.
Два луча. СВ и СА.

86
-
Страница 86
Урок 31 Решение задач
10. Что общего в выражениях:
1 группа
а • 15 + а
7 • а + 8 • а
2 группа
5 • (3 • b)
На какие группы их можно разбить?
В одной группе есть операция сложения, во второй только умножение.
11. БЛИЦтурнир
а) С одной грядки собрали а кабачков, а с другой – b кабачков. Их разложили в корзины по 10 кабачков в каждую. Сколько корзин потребовалось?
(а + b) : 10
б) Папа привёз для сада саженцы яблонь. После того как посадили 2 ряда по n яблонь в каждом, осталось ещё m саженцев. Сколько саженцев яблонь привёз папа?
2 * n + m
12. Выполни действия. Что общего в примерах каждого столбика?
6 • 8 = 48
7 • 5 = 3554 : 9 = 6
42 : 7 = 824 • 3 = 72
5 • 18 = 9058 : 2 = 29
87 : 3 = 2996 : 16 = 6
96 : 12 = 837 : 4 = 9 (ост. 1)
73 : 8 = 9 (ост. 1)13. Вычисли. Расшифруй названия птиц. Найди о них информацию в энциклопедии или Интернете.
К 80 : 5 + 28 = 44
А 4 • 16 – 38 = 26
Н 68 : (13 – 9) = 17
Б (49 + 29) : 6 = 13
М 18 + 32 : 2 = 34
Е (18 + 32) : 2 = 25
Ч 100 – 18 • 3 = 46
Т (100 – 18) • 3 = 246
Г 91 : 13 • 10 = 70
О 8 • (72 : 24) = 24
Л 60 : 3 – 75 : 5 = 5
Ы 42 : 3 + 27 · 3 = 95ЧЕГЛОК * ЧОМГА ** БАКЛАН***
* - Чегло́к — небольшая хищная птица из семейства соколиных, обитающая на обширной территории Евразии и в Северной Африке. Предпочитает светлые леса в сочетании с открытыми ландшафтами. На большей части ареала перелётная птица, зимует в Африке и тропической Азии. Питается насекомыми и мелкими птицами, которых ловит на лету. Достаточно распространённый вид.
** - Больша́я пога́нка, или чо́мга — вид водных птиц из семейства поганковых. Размером чомга немного меньше утки. Это птица с тонкой шеей и удлинённым прямым клювом. Спина буровато-рыжая, живот, шея и голова белые. В весеннем оперении на голове у чомги вырастают два тёмных пучка перьев, похожих на «ушки», и рыжий «воротничок» вокруг шеи.
*** - Бакла́ны — род морских птиц семейства баклановых. Широко распространены по всему миру с большим биологическим разнообразием в тропическом и умеренном климате. Обитают на морских побережьях континентов и островов, а также по берегам рек, озёр, на заболоченных территориях.
14. Задача-шутка
Продолжи ряд на 2 буквы, сохраняя закономерность: О, Д, Т, Ч, П, …
Последовательность букв О–Д–Т–Ч–П на первый взгляд кажется загадочной, однако разгадать ее все же можно. Это первые буквы названий чисел, которые образуют натуральный ряд: один–два–три–четыре–пять и т. д. Естественно, что продолжением показанного ряда будут буквы Ш–С–В (шесть–семь–восемь).
87
-
Страница 87
Урок 32 Решение задач
1. Запиши цифрами числа:
а) 367 тыс. 4 ед. 367 004
б) 214 млн 56 ед. 214 056
в) 4 млрд 85 млн 4 085 000 0002. Запиши числа в виде суммы разрядных слагаемых:
а) 7802 7000 + 800 + 2
б) 470 502 400 000 + 70 000 + 500 + 2
в) 1 006 090 1 000 000 + 6 000 + 903. Найди сумму:
а) 5000 + 200 + 40 + 1 = 5214
б) 8000 + 600 + 5 = 8605
в) 20 000 + 4000 + 600 + 30 + 4 = 24 634
г) 900 000 + 3000 + 200 + 70 = 903 270
д) 4 000 000 + 50 000 + 80 + 6 = 4 050 086
е) 10 000 000 + 600 000 + 400 + 5 = 10 600 4054. Сравни:
8549 < 31 047
4 * * * * > 1 * * * *
22 222 < 55 555
* * 9 < * * * 8
60 384 016 > 60 184 029
6 * * * > 2 * * * *5. Выполни действия. Проверь результаты с помощью калькулятора.
а) 20 000 – 2075 = 17 925
б) 906 020 – 99 804 = 806 216
в) 2 940 759 + 83 246 = 3 024 005
г) 5 200 740 – 260 938 = 4 939 8026. Ширина прямоугольника 9 дм, а длина – на 2 дм больше. Найди площадь квадрата с тем же периметром, что и у данного прямоугольника.
1) 9 + 2 = 11 (дм) длина прямоугольника.
2) (9 + 11) * 2 = 40 (дм) периметр прямоугольника.
3) 40 : 4 = 10 (дм) сторона квадрата.
4) 10 * 10 = 100 (дм) площадь квадрата, с тем же периметром, что у прямоугольника.
Ответ: 100 дм.7. Реши уравнения с комментированием и сделай проверку:
520 : х = 40
х = 520 : 40
х = 13
Проверка: 520 : 13 = 40х • 38 = 760
х = 760 : 38
х = 20
Проверка: 38 * 20 = 760х : 23 = 400
х = 400 * 23
х = 9200
Проверка: 9200 : 23 = 4008. Выполни деление с остатком и сделай проверку:
а) 15 : 9 = 1 (ост. 6)
б) 32 : 6 = 5 (ост. 2)
в) 57 : 4 = 4 (ост. 1)
г) 73 : 14 = 5 (ост. 3)9. БЛИЦтурнир
а) Дети собрали 4 банки малины по d кг в каждой банке. На варенье израсходовали с кг. Сколько килограммов малины ещё осталось?
d * 4 - c
б) Мама купила а яблок. Из них b яблок были ещё зелёные, и она их отложила. Остальные яблоки она разделила поровну между четырьмя детьми. Сколько яблок досталось каждому ребёнку?
(a - b) : 4
88
-
Страница 88
Урок 32 Решение задач
10. Запиши множества с помощью фигурных скобок или знака ∅:
а) А – множество летних месяцев года; А{июнь; июль; август}
б) В – множество пальцев одной руки; В{мизинец, безымянный, средний, указательный, большой}
в) D – множество крылатых зайцев; D{пустое множество}
г) F – множество делителей числа 12; F{1; 2; 3; 4; 6; 12}
д) Е – множество двузначных чисел, кратных 15; Е{30, 45, 60, 75, 90}
е) С – множество букв в слове «математика». С{м;а;т;е;и;к}11. Составь программу действий и вычисли:
1 3 2 4 6 5
а) (80 : 4 – 60 : 30) • 5 + 96 : 3 = 57
1) 80 : 4 = 20
2) 60 : 30 = 2
3) 20 - 2 = 18
4) 18 * 5 = 90
5) 96 : 3 =32
6) 90 - 32 = 574 6 5 1 3 2
б) 56 : 4 + 2 • (120 : 6 – 80 : 20) = 48
1) 120 : 6 = 20
2) 80 : 20 = 4
3) 20 - 4 = 16
4) 56 : 4 = 14
5) 2 * 16 = 32
6) 14 + 32 = 4812. Найди на рисунке все пары пересекающихся прямых. Имеются ли на этом рисунке параллельные прямые, перпендикулярные прямые?
Пары пересекающихся:
а и с; a и d; b и с; b и d; с и d
Пара перпендикулярных прямых:
а и с; b и с;
Пары параллельных:
а и b
13. Известно, что 25 • 12 = 300. Используя данное равенство, найди значения выражений:
300 : 25 = 12
25 • 13 = 325
25 • 11 = 275
12 • 24 = 288
300 : 12 = 25
13 • 25 = 325
11 • 25 = 275
24 • 12 = 28814. Где надо поставить скобки, чтобы равенства стали верными?
а) 90 : 2 • (5 – 5) = 0
в) 80 : (8 + 12) • 4 = 16
б) (60 : 5 – 2) • 7 = 70
г) 40 : (2 • 4 + 2) • 5 = 20
15. Старинная задача
Один господин встретил знакомую семью, состоящую из деда, отца и сына, и спросил, сколько им лет. «Нам всем вместе 100 лет», – ответил за всех дед. Тогда господин спросил отца: «Скажите же, сколько вам лет?» – «Мне вместе с сыном 45 лет, – ответил отец, – а сын на 25 лет моложе меня». Так любопытному господину и не пришлось узнать, сколько лет каждому из них. Не сообразишь ли ты?
Всем троим 100 лет, отцу с сыном - 45 на двоих, значит, деду:
100 - 45 = 55 (лет).Сын на 25 лет моложе отца, тогда сыну:
(45 - 25): 2 = 10 (лет).Отцу: 10 + 25 = 35 (лет).
Ответ: Деду - 55 лет, отцу - 35, а сыну - 10. 89
-
Страница 89
Урок 33 Умножение на 10, 100, 1000...
1.
а) Прочитай равенства разными способами и объясни их смысл:
а • b = b • a
(а • b) • c = a • (b • c)При перемене последовательности операции в случае с операциями умножения и сложения, результат не меняется!
б) Вспомни правило умножения на 10 и на 100. Вычисли:
5 • 10 = 50
5 • 100 = 500Установи с помощью свойств умножения, сохранится ли это правило при умножении на 1000, 10 000 и т. д. Сделай вывод.
Умножение числа на 10, 100, 1000...
При умножении числа на 10, 100, 1000 и т. д. можно приписать к этому числу справа соответственно 1 нуль, 2 нуля, 3 нуля и т. д.2. Вычисли устно:
36 • 10 = 360
100 • 4 = 400
70 • 10 = 700
29 • 100 = 2900
10 • 300 = 3000
56 • 100 = 5600
8 • 1000 = 8000
10 000 • 3 = 30 000
90 • 100 = 9000
1000 • 64 = 64 0003. Вычисли произведения и прочитай полученные числа:
а) 172 • 100 = 17 200 семнадцать тысяч двести
б) 3500 • 10 = 35 000 тридцать пять тысяч
в) 1000 • 460 = 460 000 четыреста шестьдесят тысяч
г) 58 • 1000 = 58 000 пятьдесят восемь тысяч
д) 840 • 1000 = 840 000 восемьсот сорок тысяч
е) 2700 • 1000 = 2 700 000 два миллиона семьсот тысяч
ж) 10 • 50 000 = 500 000 пятьсот тысяч
з) 40 200 • 10 000 = 402 000 000 четыреста два миллиона4. Найди значения выражений:
а) 95 • 100 = 9 500
б) 10 • 400 = 4 000
в) 100 • 320 = 32 000
г) 245 • 1000 = 245 000
д) 74 • 10 000 = 740 000
е) 1800 • 1000 = 1 800 000
ж) 1000 • 6000 = 6 000 000
з) 20 500 • 100 = 2 050 0005.
а) Запиши подряд пять раз цифру 7. Прочитай получившееся число.
77 777 семьдесят семь тысяч семьсот семьдесят семь
б) Запиши подряд три раза число 80. Какое число получилось?
808 080 восемьсот восемь тысяч восемьдесят
в) Какое число получится, если записать число 287 четыре раза подряд?
287 287 287 287 двести восемьдесят семь миллиардов двести восемьдесят семь миллионов двести восемьдесят семь тысяч двести восемьдесят семь
6. Вырази каждое число в десятках тысяч, сотнях и единицах:
а) 96 394
9 дес. тыс. 63 сот 94 ед.б) 508 062
50 дес. тыс. 80 сот. 62 ед.в) 7 040 850
704 дес. тыс. 8 сот. 50 ед. 90
-
Страница 90
Урок 33 Умножение на 10, 100, 1000...
7. Реши первый пример каждого столбика письменно, а остальные – устно:
870 305 + 62 915 = 933 220 607 435 – 5236 = 602 199
875 306 + 62 915 = 938 221 607 436 – 5236 = 602 200
875 305 + 62 914 = 938 219 607 435 – 5237 = 602 198
875 306 + 62 914 = 938 220 607 436 – 5237 = 602 1998. Составь программу действий и вычисли:
1 3 2
а) (12 384 – 7205) – (526 + 2079) = 2 574
1) 12 384 – 7205 = 5 179
2) 526 + 2079 = 2 605
3) 5 179 - 2 605 = 2 5742 1 3
б) 10 612 – (40 570 – 35 596) + 19 412 = 25 050
1) 40 570 – 35 596 = 4 974
2) 10 612 - 4 974 = 5 638
3) 5 638 + 19 412 = 25 0509.
а) Расстояние от дома до школы 920 м, а от дома до стадиона – 1400 м. На сколько метров расстояние от дома до школы меньше, чем расстояние от дома до стадиона?
1400 - 920 = 480 (м) на столько расстояние от дома до школы меньше, чем расстояние от дома до стадиона.
Ответ: 480 мб) В трёх посёлках 18 200 жителей. В первом посёлке живёт 4570 человек, а во втором – на 1635 человек больше, чем в первом. Сколько человек живёт в третьем посёлке?
1) 4 570 + 1 635 = 6205 (ж.) живет во втором поселке.
2) 6 205 + 4 570 = 10 775 (ж.) живет в первом и втором поселке.
3) 18 200 - 10 775 = 7 425 (ж.) живет в третьем поселке.
Ответ: 7 425 жителей.10. Найди значения х. Расположи их в порядке убывания – и ты узнаешь название одной из самых красивых птиц наших лесов.
а 100 200 300 400 500
х Г Л Е О ЩЩЕГОЛ
11. Запиши примеры в столбик и вычисли:
а) 75 • 8
*75
8
600б) 9 • 36
*36
9
324
в) 42 • 50
*42
50
2100г) 30 • 84
*84
30
252012. Старинная задача
Торговка, сидя на рынке, соображала: «Если бы к моим яблокам прибавить половину их да ещё десяток, то у меня была бы целая сотня!» Сколько яблок у неё было?
Решить эту задачу нам удалось, начав с её конца. От 100 мы отняли 10 яблок. Осталось 90 яблок, а это значит, что в это количество входят 3 части (2 части и ещё 1 часть, которую торговка хочет прибавить). 90 делим на 3 части, узнаём 1 треть = 30 яблокам. Значит, у торговки на рынке было 30*2=60 яблок.
Решение
100-10=90 — яблок без последнего десятка
мои яблоки плюс половину их
мои яблоки — это две половины и плюс еще одна, всего три половины
Значит половина яблок это 90/3=30
А было 2 половины, т.е. 60 яблок
Классически уравнением: было яблок х, половина х/2
всего
х+х/2+10=100
3/2х=90
х=90:3*2
х=60
ответ 60 яблок 91
-
Страница 91
Урок 34 Умножение круглых чисел
1. а) Допиши в тетради равенства, выражающие свойства умножения. Назови эти свойства и объясни их смысл.
а • b = … (а • b) • c = …
б) Объясни, как выполнено умножение круглых чисел: 6000 • 300 = (6 • 1000) • (3 • 100) = (6 • 3) • (1000 • 100) = = 18 • 100 000 = 1 800 000 Как это можно сделать быстрее? Сделай вывод.
Умножение круглых чисел
Круглые числа можно умножить, не глядя на нули, а затем приписать справа столько нулей, сколько в обоих множителях вместе.2. Найди значения произведений:
а) 30 • 50 = 1 500
в) 8 • 300 = 2 400
д) 800 • 8 = 6 400
ж) 60 • 400 = 24 000
б) 70 • 90 = 6 300
г) 600 • 5 = 3 000
е) 3 • 7000 = 21 000
з) 200 • 900 = 180 000
3. Выполни действия:
а) 90 • 400 = 36 000
б) 7 • 8000 = 56 000
в) 3000 • 20 = 60 000
г) 600 • 900 = 540 000
д) 160 • 500 = 80 000
е) 2000 • 350 = 700 000
ж) 80 000 • 40 = 3 200 000
з) 15 • 600 000 = 9 000 0004. Объясни, как выполнено умножение круглых чисел в столбик:
Выполни умножение в столбик:
а) 940 • 400
*940
400
376000б) 7600 • 70
*7600
70
532000в) 470 • 5000
*470
5000
2350000г) 38 000 • 800
*38000
800
304000005. Составь и реши 3 собственных примера на умножение круглых чисел.
25 * 10 000 = 250 000
2000 * 5 = 10 000
100 * 5000 = 500 0006. Запиши и прочти:
а) наименьшее трёхзначное число; 100
б) наибольшее четырёхзначное число; 9 999
в) наименьшее пятизначное число; 10 000
г) наибольшее шестизначное число. 999 999Какие числа им предшествуют? Какие числа за ними следуют?
92
-
Страница 92
Урок 34 Умножение круглых чисел
7. Выполни действия:
а) 21 000 – 15 849 = 5 151
б) 86 010 – 4356 = 81 654
в) 873 284 + 36 970 = 910 254
г) 615 972 – 244 018 = 371 954
д) 52 : 4 = 13
е) 520 : 4 = 130
ж) 520 : 40 = 13
з) 52 : 13 = 4
и) 50 : 6 = 8 (ост. 2)
к) 34 : 8 = 4 (ост. 2)
л) 59 : 7 = 8 (ост. 3)
м) 31 : 9 = 3 (ост. 4)8. БЛИЦтурнир
а) Турист прошёл за 3 дня а км, причём в первый день он прошёл b км, а во второй день – с км. Сколько километров прошёл турист в третий день?
а - (b + c)
б) Лена нашла m грибов, а Коля – n грибов. Из них k грибов оказались несъедобными. Сколько съедобных грибов нашли Лена и Коля?
(m + n) - k
в) В автобусе ехали d пассажиров. На остановке х пассажиров вышли, а у пассажиров вошли. Сколько пассажиров стало в автобусе?
d - x + a
9. Найди значения выражений. Проверь с помощью калькулятора.
а) 14 006 – (20 300 – 8012) = 14006 - 12 288 = 1 718
б) 259 600 – (967 + 53 878) – 14 695 = 259 600 - 54 845 = 204 755
10. Реши уравнения с комментированием и сделай проверку:
х : 40 = 600
х = 600 : 40
х = 15720 000 : х = 900
х = 720 000 : 900
х = 800х • 100 = 3 500 000
х = 3 500 000 : 100
х = 350 00011. Задачи-шутки
а) Сколько концов у 4 палок, у 5 палок, у 5 с половиной палок?у 4 - 8 концов, у 5 и 5 с половиной - 10 концов.
б) Раздели на бумаге число двенадцать на две равные части так, чтобы одна из частей была семь.
∨II = VII - семь римская
∧II = ∧IIв) Как разделить 188 на две равные части, чтобы в каждой из них получилось 100?
I00 = 100
I00 = 100Надо провести черту по центру числа, как бы перечеркнув его, тогда верхняя часть будет похоже на число 100 и нижняя на 100.
12. Нарисуй в тетради диаграмму множеств А, В и С. Раскрась на ней множество:
а) А ∩ В
б) В ∩ С
в) А ∩ С
г) А ∩ В ∩ С
д) А ∪ В
е) В ∪ С
ж) А ∪ С
з) А ∪ В ∪ С
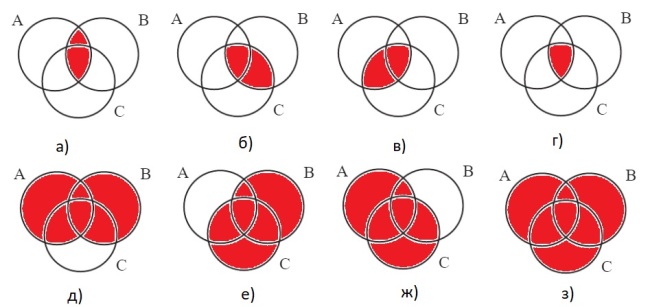
93
-
Страница 93
Урок 35 Решение задач
1. Вычисли:
а) 90 • 100 = 9000
б) 1000 • 28 = 28 000
в) 40 • 10 000 = 400 000
г) 7000 • 1000 = 7 000 000
д) 300 • 20 = 6 000
е) 5000 • 6 = 30 000
ж) 80 • 4000 = 320 000
з) 200 • 90 000 = 18 000 000
2. Запиши примеры в столбик и вычисли:
а) 24 • 500
*24
5000
120000б) 750 • 70
*750
70
52500в) 4900 • 9
*4900
9
44100г) 8300 • 6000
*8300
6000
498000003. Автомобилист проехал от Москвы до Самары 1138 км, а от Самары до Томска – 2894 км. Чему равно расстояние от Москвы до Томска через Самару? На сколько километров расстояние от Москвы до Самары меньше, чем расстояние от Самары до Томска?
1) 1138 + 2894 = 4 032 (км) от Москвы до Томска
2) 2894 - 1138 = 1756 (км) на столько больше расстояние от Томска до Самары, чем от Самары до Москвы.
Ответ: 4032 км от Москвы до Томска и 1756 км на столько больше расстояние от Томска до Самары, чем от Самары до Москвы.4. Назови число:
а) следующее за числом 19 999 - 20 000
в) на 1 большее числа 349 999 350 000
б) предшествующее числу 1200 - 1199
г) на 1 меньшее числа 25 000 - 24 999
5. Сравни числа:
276 < 726
9345 < 9348
5002 < 5010
2406 < 24 000
38 000 < 37 000 000
60 606 > 9999
52 407 < 52 470
278 652 > 256 8726. БЛИЦтурнир
а) В банку входит k литров воды, а в ведро – в 4 раза больше. Сколько литров воды входит в ведро?
k * 4
б) Мама купила себе на платье b м ткани, а на платье дочке – в 3 раза меньше. На сколько метров мамин отрез ткани длиннее, чем у дочки?
b - b : 3
в) Блузка стоит d р., а свитер на 240 р. дороже. Во сколько раз блузка дешевле, чем свитер?
(d + 240) : d
7. Продолжи ряд на 3 числа, сохраняя закономерность:
а) 8712, 8708, 8704 … 8700, 8696, 8692
в) 55, 5555, 555 555 … 55 555 555, 5 555 555 555, 555 555 555 555
б) 9106, 9083, 9060 … 9037, 9014, 8991
г) 89, 7890, 678 900 … 56 789 000, 4 567 890 000, 345 678 900 000
94
-
Страница 94
Урок 35 Решение задач
8. Выполни действия:
а) 2349 + 34 758 = 37 107
б) 40 210 – 5643 = 34 567
в) 800 500 – 64 916 = 735 584
г) 3 219 686 + 1 780 314 = 5 000 000
д) 324 • 100 = 32 400
и) 2600 : 100 = 26
е) 1000 • 85 = 85 000
ж) 970 • 10 000 = 9 700 000
з) 100 • 530 000 = 53 000 000
и) 2600 : 100 = 26
к) 38 000 : 10 = 3 800
л) 450 000 : 10 = 45 000
м) 500 000 : 100 = 5 000
9.
а) Площадь прямоугольника равна 140 см2, а его длина – 20 см. Чему равен периметр этого прямоугольника?
1) 140 : 20 = 7 (см) ширина прямоугольника.
2) (20 + 7) * 2 = 54 (см) периметр прямоугольника.
Ответ: 54 см.б) Измерь в метрах длину и ширину классной комнаты. Найди площадь её пола, потолка и общую площадь стен.
Самостоятельно.
10.
а) Пользуясь числовым лучом, составь множество двузначных чисел, кратных 19.
19, 38, 57, 76, 90
б) Выполни деление с остатком:
25 : 19 = 1 (ост. 6)
40 : 19 = 2 (ост. 2)
54 : 19 = 2 (ост. 16)
77 : 19 = 3 (ост. 18)
91 : 19 = 5 (ост. 1)
в) Выучи двузначные числа, кратные 19. Проверь себя, работая в паре.
Самостоятельно
11. Игра «Математические горки» Сосчитай суммы. Какая из этих сумм больше?
1
21
321
4321
54321
654321
7654321
87654321
987654321
1083676269
9
89
789
6789
56789
456789
3456789
23456789
123456789
150891621
1083676269 > 150891621Ответ: сумма в левой горке больше.
12. Расположи 2 элемента в множествах А, В и С так, чтобы каждое из них содержало соответственно:
а) по 2 элемента;
б) 2, 2 и 1 элемент;
в) 2, 1 и 1 элемент;
г) 2, 1 и 0 элементов;
д) 2, 2 и 0 элементов;
е) по 1 элементу.
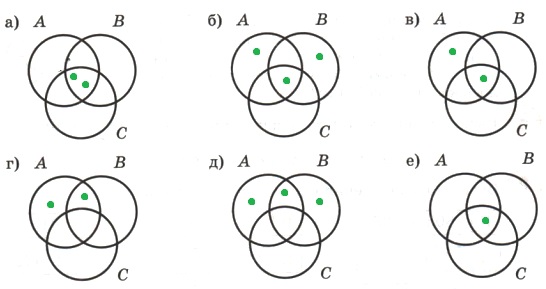
95
-
Страница 95
Урок 36 Деление на 10, 100, 1000...
1. Найди неизвестную операцию. Какие операции называют взаимно обратными?
4 + 5 = 9 и 9 - 5 = 4
6 * 2 = 12 и 12 : 2 = 6
2.
а) Вспомни правило деления на 10 и на 100.
Вычисли:
360 : 10 = 36
800 : 100 = 8
б) Используя схемы, выполни деление на 1000, на 10 000:
28 000 : 1000 = 28
600 000 : 10 000 = 60
Что ты замечаешь? Сделай вывод.
Деление числа на 10, 100, 1000... При делении числа на 10, 100, 1000 и т. д. можно отбросить справа соответственно 1 нуль, 2 нуля, 3 нуля и т. д.
3. Выполни действия:
а)
5600 : 10 = 560
8400 : 100 = 84
42 000 : 1000 = 42б)
60 000 : 10 = 6000
75 000 : 100 = 750
290 000 : 1000 = 290в)
170 000 : 1000 = 17 000
9 800 000 : 10 000 = 980
3 250 000 : 100 = 32 5004. Вычисли. Составь и реши следующий пример:
а)
250 : 10 = 25
3000 : 100 = 30
35000 : 1000 = 35
400000 : 10000 = 40
4500000 : 100000 = 45б)
550 : 10 = 55
4400 : 100 = 44
33000 : 1000 = 33
220000 : 10000 = 22
1100000 : 100000 = 115. Найди значения выражений. Что ты замечаешь?
9 • 90 = 810
800 • 8 = 6400
70 • 700 = 49 000
6 • 60 000 = 360 000
Какой пример может быть следующим? Обоснуй свой ответ.50 * 50000 = 2500 000 Каждый раз количество нулей прибавлялось и понижалось число в первом разряде.
96
-
Страница 96
Урок 36 Деление на 10, 100, 1000...
6. Запиши примеры в столбик и вычисли:
а) 92 • 50
*92
50
4600б) 6900 • 8
*6900
8
55200в) 6300 • 40
*6300
40
252000г) 54 000 • 700
*54000
700
37 800 0007. Костя дома делал уроки 135 минут. Из них 25 минут он вспоминал, что задали, и 36 минут мечтал о мороженом. Затем он искал ручку половину того времени, что мечтал, а остальное время делал задания. Сколько времени ушло у Кости на выполнение заданий?
1) 25 + 36 = 61 (мин.) ушла на вспоминания и мечты.
2) 36 : 2 = 18 (мин.) искал ручку.
3) 135 - (61 + 18) = 56 (мин.) делал задания.
Ответ: 56 минут.8. Реши уравнения и сделай проверку:
х : 700 = 8000
х = 700 * 8000
х = 5 600 000630 : х = 9
х = 630 : 9
х = 70х • 60 = 480
х = 480 : 60
х = 89. Реши задачи. Что в них общего и чем они различаются? Придумай свои задачи на разные виды деления.
а) В классе 28 человек. Они разбились на 4 равные группы. Сколько человек в каждой группе?28 : 4 = 7 (чел.) в группе
Ответ: 7 человек.б) В классе 28 человек. Они разбились на группы по 4 человека в каждой. Сколько получилось групп?
28 : 4 = 7 (гр.) получилось
Ответ: 7 групп.10. На диаграмме отмечены элементы множеств А и В. Запиши с помощью фигурных скобок, из каких элементов состоят множества А, В, А ∩ В, А ∪ В
11. Найди значения выражений:
а) 80 590 – 4825 = 75 765
б) 925 070 + (30 602 – 7384) = 925 070 + 23 218 = 948 288
12. Начерти два луча, пересечением которых являются:
а) точка;
б) отрезок;
в) луч;
г) пустое множество.
13. Чайнворд
1. Многоугольник.
2. Группа цифр в записи числа.
3. Наименьшее трёхзначное число.
4. Геометрическая фигура.
5. Прямоугольник с равными сторонами.
6. Наименьшее четырёхзначное число.
7. Старая русская мера длины.
8. Знак, показывающий отсутствие единиц какого-либо разряда.Ответы:
Чайнворд - разновидность кроссворда, в котором последняя буква слова является первой буквой следующего слова. В данном случае речь идет о чайнворде математическом - все вопросы так или иначе относятся к разделам математики.
1. прямоугольник
2. класс
3. сто
4. остроугольник - фигура у которой все углы острые
5. квадрат
6. тысяча
7. аршин
8. ноль 97
-
Страница 97
Урок 37 Деление круглых чисел
1. Закончи решение примеров и сравни их:
а) 36 : 4 = 9
360 : 40 = 36 д. : 4 д. = 9
3600 : 400 = 36 с. : 4 с. = 9
36 000 : 4000 = 36 т. : 4 т. = 9б) 54 : 9 = 6
540 : 9 = 54 д. : 9 = 6
5400 : 9 = 54 с. : 9 = 6
54 000 : 9 = 54 т. : 9 = 6Сделай вывод.
Деление круглых чисел
Правило 1
При делении круглых чисел (без остатка) можно отбросить в делимом и делителе поровну нулей.
Правило 2
При делении круглых чисел (без остатка) можно отбросить в делимом нули справа, а потом приписать их к частному.2. Выбери правило и сосчитай. Сделай записи по образцу.
Образец: 42 000 : 700 = 420 : 7 = 60
а)
240 : 60 = 4
360 : 90 = 4
5600 : 700 = 8
28 000 : 4000 = 7б)
4500 : 5 = 900
6300 : 70 = 90
72 000 : 80 = 900
180 000 : 2000 = 90в)
3000 : 500 = 6
1400 : 20 = 70
27 000 : 3000 = 9
480 000 : 600 = 8003. Выполни деление и обоснуй свой ответ:
а) 3500 : 70 = 50
в) 500 : 50 = 10
д) 560 000 : 80 = 7 000
ж) 10 000 : 5000 = 2
б) 6400 : 800 = 8
г) 54 000 : 60 = 9 000
е) 490 000 : 700 = 700
з) 20 000 : 400 = 50
4. Реши уравнения с комментированием и сделай проверку:
х : 80 = 800
х = 800 * 80
х = 64 000
Проверка 64 000 : 80 = 8002500 : х = 500
х = 2500 : 500
х = 5
Проверка: 5 * 500 = 2500х • 40 = 1600
х = 1600 : 40
х = 40
Проверка 40 * 40 = 16005. Найди значение выражения а + b, если:
а) а = 347, b = 6893
347 +6893 = 7 240б) а = 5750, b = 29 362
5750 +29362 = 35112 98
-
Страница 98
Урок 37 Деление круглых чисел
6. Найди значение выражения а – b, если:
а) а = 4210, b = 677
4210 - 677 = 3 533б) а = 18 532, b = 7608
18 532 - 7608 = 10 9247. Чему равен периметр треугольника со сторонами а см, b см и с см? Найди ответ при а = 456, b = 718, с = 932.
456 + 718 + 932 = 2106 (см) - периметр треугольника.
Ответ: 2106 см8. Первая сторона треугольника равна 20 м, вторая – в 4 раза больше первой, а третья – на 12 м меньше второй. Чему равен периметр этого треугольника?
1) 20 * 4 = 80 (м) вторая сторона треугольника.
2) 80 - 12 = 68 (м) третья сторона.
3) 20 + 80 + 68 = 168 (м) периметр треугольника.
Ответ: 168 метров.9. Найди периметр и площадь закрашенной фигуры. Сравни их с периметром и площадью прямоугольника ABCD.
10. Выполни действия:
а)
250 • 1000 = 250 000
78 000 : 100 = 780б)
130 • 700 = 91 000
40 000 • 15 = 600 000в)
17 : 15 = 1 (ост. 2)
59 : 14 = 4 (ост. 3)г)
9507 – 819 = 8 688
5648 + 4352 = 10 00011. Объясни, почему каждое выражение может быть лишним:
а • 2 + 95 44 : 4 + 4 58 + 6 31 – 7 • 3
а*2+95 -может быть лишним, так как один из множителей в данном выражении является неизвестным, в других выражениях все члены - числовые значения;
44:4+4 - может быть лишним, так как только в этом выражении используется действие - деление, или может быть лишним, так как все цифры в этом выражении одинаковые;
31-7*3 - может быть лишним, так как одно из действий в данном выражении - вычитание, в остальных - это сложение;
56+8 - может быть лишним, так как здесь всего одно арифметическое действие, в остальных их два.12. А = {▲; 2; 3; ? }, В = {n; 3; ? }. Построй диаграмму Эйлера–Венна множеств А и В, отметь на ней их элементы. Найди множества А ∩ В и А ∪ В. Закрась на диаграмме А ∩ В и обведи А ∪ В.
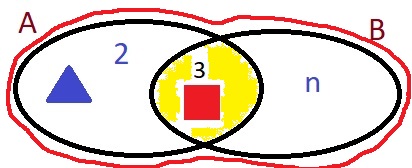
А ∩ В {3; ? }
А ∪ В {▲; 2; 3; ? ; n}
13. Выполни действия. Проверь результаты с помощью калькулятора.
а) 600 038 – 218 053 = 381 985
б) (641 265 + 8735) – 28 472 = 621 528
14. Возраст старика Хоттабыча записывается числом с разными цифрами. Известно, что:
а) если первую и последнюю цифру зачеркнуть, то получится наименьшее из двузначных чисел, сумма цифр которых равна 13;
б) первая цифра больше последней в 4 раза. Сколько лет Хоттабычу?Ответ: Из условия "если первую и последнюю цифры зачеркнуть, то получится двузначное число, которое при сумме цифр равной 13, является наибольшим" следует, что это число 94. А из условия "первая цифра больше последней в 4 раза" можно получить всего два варианта: 4 и 1, 8 и 2. Учитывая, что все цифры в искомом числе должны быть разными, подходит только второй вариант. Т. е. ответ 8942.
99
-
Страница 99
Урок 38 Решение задач
1. Запиши число 18 млрд 72 млн 2 тыс. 418 ед. Какая цифра стоит в разряде единиц миллионов этого числа? Сколько в нём всего миллионов?
2. Вычисли:
а) 9000 : 1000
б) 75 300 000 : 100
в) 27 000 : 90
д) 3 200 000 : 800
г) 490 000 : 7000
е) 600 000 : 15003. Найди периметр и площадь закрашенной фигуры:
4. Составь программу действий и вычисли:
2 6 3 4 7 5 1
а) 64 : 4 + 3 • 9 • 7 – 91 : (28 : 4) = 1921) 28:4=7
2) 64:4=16
3) 3*9=27
4) 27*7=189
5) 91:7=13
6) 16+189=205
7) 205-13=1921 3 2 4 7 5 6
б) (69 • 2 – 6 • 8) : 5 + 170 • 3 : 10 = 691) 69*2=138
2) 6*8=48
3)138-48=90
4) 90:5=18
5) 170*3=510
6) 510:10=51
7) 18+51=695. Реши уравнения с комментированием и сделай проверку:
х – 9382 = 719
х = 9382 + 719
х = 10 101
Проверка: 10 101 - 9382 = 719300 000 – х = 47 475
х = 300 000 - 47 475
х = 252 525
Проверка: 299 953 + 47 475 = 252 525х + 116 084 = 208 003
х = 208 003 - 116 084
х = 91 9196. Прочитай выражения разными способами и вычисли. Что ты замечаешь?
а)
73 – 13 • 5 = 8
(73 – 13) • 5 = 300б)
80 : 16 + 4 = 9
80 : (16 + 4) = 4в)
15 • 4 – 3 • 2 = 54
15 • (4 – 3) • 2 = 307. БЛИЦтурнир
а) В одной банке 3 л сока. Сколько сока в k таких банках?
3 * к
б) b литров молока разлили в 2-литровые банки. Сколько таких банок потребовалось?
b : 2
в) с кг картошки разложили поровну в 4 мешка. Сколько килограммов картошки в каждом мешке?
с : 4
г) После того как израсходовали d кг муки, осталось муки в 5 раз больше, чем израсходовали. Сколько муки было вначале?
d + d * 5
д) х кг печенья разложили в коробки по 6 кг, а у кг – в коробки по 8 кг. Сколько всего коробок с печеньем получилось?
х : 6 + у : 8
100
-
Страница 100
Урок 38 Решение задач
8. Выполни действия:
а)
10 000 • 390 = 3 900 000
8 020 000 : 1000 = 8 020б)
2600 • 300 = 780 000
72 000 : 80 = 900в)
96 : 19 = 5 (ост. 6)
60 : 16 = 3 (ост. 12)г)
28 075 + 6493 = 34 568
60 000 – 4945 = 55 0559. Пусть А – множество учащихся школы, В – множество учеников 3 «А» класса этой школы, С – множество мальчиков 3 «А» класса этой школы, D – множество отличников в этой школе.
Какие из множеств являются подмножествами множества А, множества В? Нарисуй диаграмму Эйлера–Венна множеств А, B, C и D.
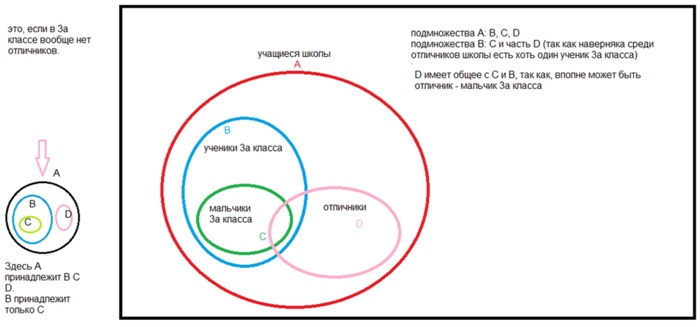
10. Построй в тетради фигуру, равную данной. Чему равна её площадь в квадратных сантиметрах? В клеточках?
Можно построить прямоугольник 3 на 4 см, при этом площадь в см3 будет равна 3 * 4 = 12, а в клетка 12 * 4 = 48 клеток.
11. Четыре подруги пришли на каток, каждая со своим братом. Они разбились на пары и начали кататься. Оказалось, что в каждой паре «кавалер» выше «дамы» и никто не катается со своей сестрой. Самый высокий из компании – Юра Воробьёв, следующий по росту – Андрей Егоров, потом Люся Егорова, Серёжа Петров, Оля Петрова, Дима Крымов, Инна Крымова и Аня Воробьёва. Кто с кем катался?
Подсказка
С кем катается Люся Егорова — самая высокая среди девочек?Решение
Самая высокая из девочек — Люся Егорова, и по условию она катается с мальчиком, который выше её. Таких мальчиков двое, но один из них её брат. Значит, Люся Егорова катается с Юрой Воробьёвым. Рассуждая аналогично, устанавливаем, что Оля Петрова катается с Андреем Егоровым, Инна Крымова — с Серёжей Петровым, а Аня Воробьёва — с Димой Крымовым.Ответ
Люся Егорова и Юра Воробьёв, Оля Петрова и Андрей Егоров, Инна Крымова и Серёжа Петров, Аня Воробьёва и Дима Крымов.12. Какую фигуру надо поставить вместо знака вопроса?
101
-
Страница 101
Урок 39 Единицы длины
1. Используя таблицу, ответь на вопросы:
а) Сколько в 1 километре метров, дециметров, сантиметров, миллиметров?
1 км = 1000 м; 1 км = 10 000 дм; 1 км = 100 000 см; 1 км = 1 000 000 мм
б) Сколько в 1 метре дециметров, сантиметров, миллиметров?
1 м = 100 см; 1 м = 1000 мм;
в) Сколько в 1 дециметре сантиметров, миллиметров?
1 дм = 10 см; 1 дм = 100 мм.
г) Сколько в 1 сантиметре миллиметров?
1 см = 10 мм
Какое действие надо выполнить при переходе от больших мерок к меньшим?
умножение
А при обратном движении?
деление
При переходе к меньшим меркам выполняется умножение, а при переходе к большим меркам – деление.
2. Вырази в сантиметрах:
а) 5 дм 3 см = 53 см
в) 6 м 8 дм 7 см = 687 см
д) 4 м 5 см = 405 см
ж) 8 км = 800 000 см
б) 7 м = 700 см
г) 9 м 12 см = 912 см
е) 2 м 6 дм = 260 см
з) 16 000 мм = 1 600 см3. Вырази в миллиметрах:
а) 3 см 9 мм = 39 мм
в) 2 дм 5 см 7 мм = 257 мм
д) 5 м 82 см = 5082 мм
ж) 2 км = 2 000 000 мм
б) 8 дм 3 мм = 803 мм
г) 1 дм 8 см = 180 мм
е) 4 м 2 дм 7 мм = 4 207 мм
з) 64 см = 640 мм4. Вырази в метрах:
а) 4 км 700 м = 4700 м
в) 12 км 50 м = 12 050 м
д) 280 дм = 28 м
б) 6 км 18 м = 6018 м
г) 1 км 4 м = 1004 м
е) 35 000 см = 350 м5. Сравни:
3 м 7 см > 6 дм 8 см
9 км 300 м > 9030 м
5 дм 30 мм = 53 см
7 м 86 см > 78 дм 5 см 102
-
Страница 102
Урок 39 Единицы длины
6. Выполни действия:
а) 5 м 94 см + 6 дм 8 см = 594 + 68 = 662 см
в) 9 м 6 дм 5 см – 5 м 8 см = 965 - 508 = 457 см
б) 7 м 2 дм – 42 дм 3 см = 720 - 423 = 297 см
г) 34 дм – 2 м 37 см = 340 - 237 = 1037.
а) Из 24 мотков шерсти связали 3 одинаковые кофты. Сколько мотков шерсти потребуется, чтобы связать 8 таких кофт?24 : 3 * 8 = 64 (м.) надо для 8 кофт.
Ответ: 64 мотка.б) Из 14 м ткани сшили 7 одинаковых юбок. Сколько таких юбок можно сшить из 30 м ткани?
30 : (14 : 7) = 30 : 2 = 15 (юб.) можно сшить из 30 м.
Ответ: 15 юбок.8. Составь выражения и найди их значения:
а) Уменьшаемое 208 400, вычитаемое выражено разностью чисел 18 000 и 9762.
208 400 - (18 000 - 9762) = 208 400 - 8232 = 200 162
б) Из разности чисел 720 048 и 97 256 вычесть сумму чисел 36 809 и 250 249.
(720 048 - 97 256) - (36 809 + 250 249) = 622 792 - 287 058 = 335 734
в) К сумме чисел 777 777 и 66 666 прибавить разность чисел 111 111 и 99 999.
(777 777 + 66 666) + (111 111 - 99 999) = 844 443 + 11 112 = 855 555
9. БЛИЦтурнир
а) Петя прошёл полем а км, а лесом — в 2 раза меньше. Сколько всего километров прошёл Петя полем и лесом?
а + а : 2
б) Аня шла в школу b мин, а возвращалась домой с мин. На сколько меньше времени она затратила на дорогу в школу, чем на дорогу домой?
c - b
в) Первая перемена длится n мин, вторая – на 5 мин дольше первой. А третья перемена в 2 раза короче первой. Сколько времени длятся все эти три перемены вместе?
n + (n + 5) + (n : 2)
г) Учительница принесла в класс х тетрадей. Из них у тетрадей она отложила, а остальные раздала поровну 20 ученикам. Сколько тетрадей получил каждый ученик?
(х - у) : 20
д) В буфет привезли а кг конфет. В течение 3 дней расходовали по b кг конфет в день. Сколько килограммов конфет ещё осталось?
а - 3 * b
10. Реши уравнения с комментированием и сделай проверку:
х + 518 = 9004
х = 9004 - 518
х = 8 486
Проверка: 8486 + 518 = 9004х – 768 = 32
х = 768 + 32
х = 800
Проверка 800 - 768 = 3257 100 – х = 236
х = 57100 - 236
х = 56864
Проверка 57100-56864 = 236 103
-
Страница 103
Урок 39 Единицы длины
11. На зиму Медвежонок заготовил три бочонка мёда. В первом бочонке было 72 кг, во втором бочонке – в 3 раза меньше, чем в первом, а в третьем – на 68 кг больше, чем во втором. Сколько килограммов мёда заготовил Медвежонок на зиму?
1) 72 : 3 = 24 (кг) меда во втором бочонке.
2) 24 + 68 = 92 (кг) меда в третьем бочонке.
3) 72 + 24 + 92 = 188 (кг) заготовил всего меда.
Ответ: 188 кг меда.12.
а) Составь выражение, значение которого равно 150.(45 * 2) + 60 = 150
б) Составь произведение суммы и разности, значение которого равно 24.
(4 + 2) * (12 - 8) = 6 * 4 = 24
13. Вычисли. Наложи прозрачную плёнку и соедини ответы по порядку. Что получилось?
1. 45 800 : 100 • 10 = 4 580
2. 1000 · 24 : 100 = 240
3. 600 · 10 : 1000 = 6
4. 3600 : 10 · 100 = 36 000
5. 52 · 1000 : 100 = 520
6. 90 · 40 = 360
7. 5 · 80 = 400
8 600 · 8 = 4800
9. 9 · 700 = 6300
10. 60 · 50 = 3000
11. 810 : 90 = 9
12. 2800 : 700 = 4
13. 3500 : 50 = 70
14. 1800 : 900 = 2
15. 420 : 70 = 6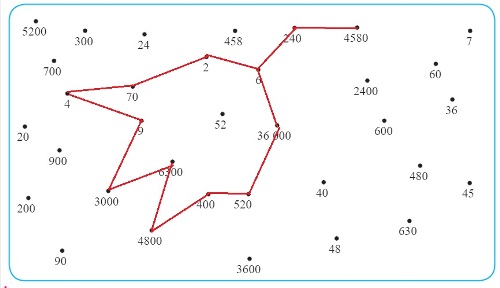
14. Запиши множество всех четырёхзначных чисел, у которых:
а) все цифры одинаковые;
A{1111; 2222; 3333; 4444; 5555; 6666; 7777; 8888; 9999}
б) сумма цифр равна 3.
A{1110; 1101; 1011; 1200; 1020; 1002; 2100; 2010; 2001; 3000}
104
-
Страница 104
Урок 40 Решение задач
1. Определи по схеме, сколько миллиметров в 1 дециметре?
1 дм = 100 мм
Сколько дециметров в 1 километре?
1 км = 10 000 дм
Что означают стрелки? Как преобразовать единицы длины?
стрелки обозначают переход от одной величины к другой
2. Вырази в указанных единицах измерения. Что ты замечаешь?
а) 205 = 20 д. 5 ед.
205 см = 20 дм 5 см
205 мм = 20 см 5 мм
б) 8020 = 8 тыс. 20 ед.
8020 м = 8 км 20 м
8020 мм = 8 м 20 мм3. Вырази:
а) в сантиметрах:
40 мм = 4 см;
3 дм 6 см = 36 см;
58 м = 580 см;
2 м 3 см = 203 см;
б) в миллиметрах:7 см = 70 мм;
1 см 5 мм = 15 мм;
4 дм = 400 мм;
6 дм 2 мм = 602 мм;в) метрах:
3 км = 3000 м;
5 км 14 м = 5014 м;
82 км 5 м = 82 005 м;
9000 см = 9 м.4. Выполни действия:
а) 4 дм 2 см + 9 см 6 мм
б) 3 м – 2 дм 5 см
в) 1 км 3 м – 89 м
г) 5 дм 9 см 3 мм + 47 мм
д) 7 м 2 дм 5 см + 24 м 72 см
е) 6 км – 4 км 32 м
ж) 90 м 2 см – 6 м 4 дм 2 см
з) 2 дм 98 мм + 4 м 2 мм5. Прочитай выражения разными способами:
а + 3 · b и (а + 3) · b
Найди их значения, если а = 5, b = 10. Что ты замечаешь?
5 + 3 · 10 = 35
(5 + 3) · 10 = 806. БЛИЦтурнир
а) У Гриши было d моделей машин, а моделей самолётов – на 8 меньше. Во сколько раз меньше моделей самолётов, чем машин, было у Гриши?
d : (d : 8)
б) В 3 одинаковых коробках b конфет. Сколько конфет в 7 таких коробках?
b : 3 * 7
в) В 4 одинаковых банках k литров варенья. Сколько банок нужно, чтобы разлить в них m литров варенья?
Ь : (к : 4)
105
-
Страница 105
Урок 40 Решение задач
7.
а) Отметь три точки А, В и С. Начерти треугольник АВС. Измерь его стороны и найди периметр.
Чертим треугольник, измеряем стороны и считаем его периметр.
б) Выполни то же задание для четырёхугольника DЕFK.
По аналогии с предыдущим заданием.
8. Известно, что АВ = 3 см 6 мм, ВС = 5 см 4 мм. Начерти отрезки АВ и ВС так, чтобы:
1) В ∈ АС
2) В ∉ АС
В каждом из этих случаев сравни длину отрезка АС с суммой длин отрезков АВ и ВС. Что ты замечаешь? Как можно объяснить полученный результат?
В первом случае, когда В ∈ АС, точка B является точкой на стыке отрезков. Во втором, Тока В лежит вне отрезка AC, то есть отрезки наложены один на другой.
9. Выполни действия:
а) 396 579 + 83 624 = 480 203
б) 530 217 – 482 635 = 47 582
в) 2 039 455 + 82 167 + 714 305 = 2 835 927
г) 7 004 210 – 34 514
д) 7800 • 7 = 54 600
е) 820 • 800 = 656 000
ж) 90 • 6800 = 612 000
з) 95 000 • 300 = 28 500 000
и) 3000 : 6 = 500
к) 2500 : 50 = 50
л) 200 000 : 4000 = 50
м) 35 000 : 700 = 5010. Прочитай задачи. Можно ли их решить? Почему?
а) Андрей купил 4 конфеты. Сколько денег он заплатил? Добавляем, что конфеты были по 5 рублей.
4 * 5 = 20 (р.) стоили 4 конфеты.
Ответ: 20 рублей.б) Сколько платьев можно сшить из 60 м ткани? Добавляем, если на каждое идет по 5 метров.
60 : 5 = 12 (п.) можно сшить.
Ответ: 12 платьев.в) Игорю – 8 лет, а Денису – 10 лет. На сколько сантиметров Денис выше Игоря? Добавляем, что Денис 123 см, а Игорь 115 см.
123 - 115 = 8 (см) Денис выше Игоря.
Ответ: на 8 см.Определи, каких данных недостает. Придумай для них значения и реши эти задачи.
11. Составь программу действий и вычисли:
5 6 9 1 7 10 8 2 4 3
а) 9 • 4 : 6 + (18 + 22) : 8 – 48 : (3 • 8 – 2 • 9) = 31) 18+22=40
2) 3*8=24
3) 2*9=18
4) 24-18= 6
5) 9*4=36
6) 36:6=6
7) 40:8=5
8) 48:6=8
9) 6+5=11
10) 11-8=35 2 1 9 3 6 4 10 7 8
б) 5 • (30 – 7 • 3) – (50 – 18) : (28 : 7) + 81 : 9 • 7 = 4231) 7·3=21
2) 30-21=9
3) 50-18=32
4) 28:7=4
5) 5·9=45
6) 45·32=1 440
7) 1 440:4=360
8) 81:9=9
9) 9·7=63
10) 360+63=42312. Какую фигуру надо поставить вместо знака вопроса?
106
-
Страница 106
Урок 41 Единицы массы
1. Чему равна масса арбуза?
2 + 1 + 5 = 7 кг
Чему равна масса одного яблока (все яблоки имеют одинаковую массу)?
1000 : 5 = 200 гр
Какие более мелкие, чем килограмм, единицы массы ты знаешь?
грамм, миллиграмм
Какие более крупные единицы?
центнеры, тонны
Единицы массы
Для измерения массы предметов, кроме килограмма, используют более мелкую единицу – грамм, а также более крупные единицы – центнер и тонна.
2. Определи, чему равна масса винограда и масса дыни:
2 + 1 = 3 (кг) масса винограда.
5000 + 500 +100 - 1000 = 4600 (г) масса дыни. или 4 кг 600 г.
3. Вырази в килограммах:
а) 6000 г = 6 кг
б) 28 000 г = 28 кг
в) 3 ц = 300 кг
г) 5 ц = 500 кг
д) 4 т = 4000 кг
е) 9 т = 9000 кг
ж) 4 ц 32 кг = 432 кг
з) 18 ц 7 кг = 1807 кг
и) 5 т 2 ц 8 кг = 5208 кг
к) 6 т 15 кг = 6015 кг4. Вырази в граммах:
а) 4 кг = 4000 г
б) 127 кг = 127 000 г
в) 5 кг 200 г = 5200 г
г) 5 кг 20 г = 5020 г
д) 5 кг 2 г = 5002 г 107
-
Страница 107
Урок 41 Единицы массы
5. Вырази в килограммах и граммах:
а) 9675 г = 9 кг 675 г
б) 14 300 г = 14 кг 300 г
в) 7004 г = 7 кг 4 г
г) 5628 г = 5 кг 628 г6. Вырази в центнерах:
а) 800 кг = 8 ц
б) 9000 кг = 90 ц
в) 36 т = 360 ц
г) 8 т 3 ц = 83 ц7. Вырази в тоннах:
а) 30 ц = 3 т
б) 50 000 кг =50 т
в) 400 ц = 40 т
г) 2 000 000 г = 2 т8.
а) Самое крупное животное на Земле – голубой кит. Его масса 120 т. Во сколько раз кит тяжелее слона, масса которого 5 т?
120 : 5 = 24 (р. ) кит тяжелее слона.
Ответ: в 24 раза.б) В одном куске колбасы 1 кг 300 г, а в другом – на 400 г меньше. Сколько колбасы в обоих кусках вместе?
1) 1300 - 400 = 900 (г) во втором куске колбасы.
2) 1300 + 900 = 2300 (г) масса колбасы в обоих кусках.
Ответ: 2300 г9. Вычисли устно. Что ты замечаешь? Где нарушена закономерность?
9 • 8 = 72
72 : 9 = 8
72 : 8 = 9
16 • 3 = 48
48 : 16 = 3
48 : 3 = 16
5 • 19 = 95
95 : 5 = 19
95 : 19 = 5
6 • 90 = 540 - здесь нарушена закономерность
5400 : 6 = 900 - здесь нарушена закономерность
5400 : 90 = 60 - здесь нарушена закономерность
70 • 40 = 2 800
2800 : 40 = 70
2800 : 70 = 4010. Реши примеры. Расположи ответы примеров в порядке возрастания. Расшифруй название животного и узнай о нём информацию.
Р 420 : 6 = 70
И 160 : 2 = 80
П 350 : 7 = 50
Г 40 • 5 = 200
К 9 • 600 = 5400
О 80 • 60 = 4800
С 280 : 7 = 40
Б 800 : 2 = 400
Н 300 : 3 = 100СПРИНГБОК
* - Спри́нгбок, или антило́па-прыгу́н (лат. Antidorcas marsupialis) — африканская антилопа из подсемейства настоящих антилоп (Antilopinae).
11. Реши уравнения с комментированием и сделай проверку:
х – 5916 = 18 124
x = 18124 + 5916
x = 24 04070 815 – х = 2129
х = 70815 + 2129
х = 72944х + 79 105 = 403 560
х= 403560-79105
х= 32445512. Какую фигуру надо поставить вместо знака вопроса?
108
-
Страница 108
Урок 42 Решение задач
1. Запиши число 3 млрд 754 млн 28 ед.
3 754 000 028
Какая цифра стоит в разряде сотен миллионов этого числа?
7
Сколько в нём всего сотен миллионов?
37
2.
а) Вырази число 9274 в десятках и единицах; 927 дес. 4 ед.
сотнях и единицах; 92 сот. 74 ед.
тысячах и единицах. 9 тыс. 274 ед.б) Вырази 9274 мм в сантиметрах и миллиметрах; 928 см 4 мм
дециметрах и миллиметрах; 92 дм 74 мм
метрах и миллиметрах. 9 м 274 ммв) Вырази 9274 кг в центнерах и килограммах; 92 ц 74 кг
тоннах и килограммах. 9 т 274 кгЧто ты замечаешь?
Величины отличаются друг от друга порядком в цифровом значении.
3. Определи по схеме, в каких единицах можно выразить килограмм, центнер, тонну?
4. Вырази в указанных единицах измерения:
а) 30 005 г = 30 кг 5 г
в) 5 ц 4 кг = 504 кг
д) 9 т 28 кг = 9028 кг
б) 12 кг 9 г = 12009 г
г) 70 000 кг = 70 т
е) 4 т 6 ц = 4600кг5. Выполни действия:
а) 4 ц 7 кг + 2 т 98 кг = 407 + 2098 = 2505
б) 5 т – 9 ц 44 кг = 5000 - 944 = 4056
в) 7 кг 64 г – 5 кг 8 г = 7064 - 5008 = 2056
г) 1 т 2 ц – 9 ц 64 кг = 1200 - 964 = 2366. Сравни:
3 кг > 999 г
7 т > 8 ц 256 кг
15 кг 900 г < 16 кг 400 г
14 ц 6 кг < 5 т 2 кг7. БЛИЦтурнир
а) В 5 наборах цветной бумаги всего k листов. Сколько листов бумаги в 7 таких наборах?
k : 5 * 7
б) Из b астр сделали 4 одинаковых букета. Сколько таких букетов можно сделать из d астр?
d : (b : 4)
в) В первый день около школы посадили n лип, а во второй – в 3 раза меньше. На сколько лип больше посадили в первый день, чем во второй?
n - n : 3
г) В корзинке a грибов, из них с белых. Во сколько раз белых грибов в этой корзинке меньше, чем остальных?
(а - с) : с
109
-
Страница 109
Урок 42 Решение задач
8.
а) На одной чашке весов лежит кусок сыра в 700 г, а на другой – гиря в 1 кг. Какие гири можно положить на первую чашку, чтобы весы были в равновесии?
Гири массой в 300 грамм. Скажем 100 и 200 грамм или три по 100 грамм.
б) На одной чашке весов лежит арбуз массой 4 кг 800 г, а на другой – дыня массой 5 кг. Какими гирями можно их уравновесить?
Гири массой в 200 грамм. Скажем 100 и 100 грамм.
в) У продавца есть одна гиря в 100 г и две гири по 200 г. Какую ещё гирю ему нужно взять, чтобы получился килограмм?
Надо взять 500 грамм.
9.
а) Петя купил 1 кг 700 г винограда, а Вася – на 500 г больше. Сколько винограда купили они вместе?
1) 1700 + 500 = 2200 (г) купил винограда Вася.
2) 1700 + 2200 = 3900 (г) купили винограда вместе Петя и Вася.
Ответ 3900 грамм.б) В двух мешках 78 кг 400 г муки. В первом мешке 35 кг 600 г муки. На сколько второй мешок тяжелее первого?
1) 78400 - 35600 = 42800 (г) весит второй мешок.
2) 42800 - 35600 = 7200 (г) на столько тяжелее один мешок другого.
Ответ: 7200 г10. Реши уравнения с комментированием:
х • 70 = 4900
х = 4900 : 70
х = 70х : 80 = 700
х = 80 * 700
х = 56 00064 000 : х = 40
х = 64 000 : 40
х = 160011. Выполни действия:
а) 380 658 + 9542 = 390 200
б) 1 800 340 – 685 539 = 1 114 801
в) 56 387 014 – 4 914 658 = 51 472 356
г) 5600 • 4 = 22400
д) 9700 • 30 = 291 000
е) 90 • 800 = 72 000
ж) 28 : 8 = 3 (ост. 4)
з) 83 : 9 = 9 (ост. 2)
и) 75 : 7 = 10 (ост. 5)
к) 6300 : 700 = 9
л) 40 000 : 80 = 500
м) 840 000 : 210 = 400012. В классе 25 учеников уже прочитали повесть о Малыше и Карлсоне, а 23 ученика – повесть о Винни-Пухе. Причём 18 человек прочитали обе эти повести. Сколько всего учеников в классе, если каждый ученик прочитал хотя бы одну из этих книг?
1) 25-18=7 (уч.) прочитали только одну книгу про Малыша и Карлсона.
2) 23-18=5 (уч.) прочитали только книгу про Винни-пуха.
3) 18+7+5=30 (уч.) всего в классе
Ответ: 30 учеников.13. Подбери, если возможно, значения х, при которых верны равенства:
х • х – 25 = 0
х • х + 1 = 0
(х – х) • 4 = 0Всегда ли есть решение? Существует ли несколько решений?
Для х • х – 25 = 0
х*х-25=0
х*х=25
х=5Для х • х + 1 = 0
х*х+1=0
х*х=-1 х-подобрать невозможно, т.к. число в квадрате не может иметь отрицательный результатДля (х – х) • 4 = 0
(х-х)*4=0
х-х=0:4
х-х=0х=любому числу
110
-
Страница 110
Урок 43 Решение задач
1. Прочитай число: 45 630 817 294. Назови цифру в разряде сотен миллионов этого числа. Сколько в нём всего сотен миллионов?
Сорок пять миллиардов шестьсот тридцать миллионов восемьсот семнадцать тысяч двести девяносто четыре
в разряде сотен миллионов этого числа - 6
всего сотен миллионов - 45 632. Запиши цифрами число: 5 млрд 36 тыс. 800 ед. Подчеркни цифру в разряде десятков тысяч. Сколько в нём всего десятков тысяч?
5 000 036 800
Всего десятков тысяч - 500 003
3. Выполни действия:
а) 1000 • 240 = 240 000
в) 180 • 300 = 54 000
д) 78 000 : 100 = 780
ж) 20 000 : 4000 = 5
б) 90 • 600 = 54 000
г) 40 • 5000 = 200 000
е) 6300 : 90 = 70
з) 320 000 : 160 = 2 0004. Вырази в указанных единицах измерения:
а)
8400 дм = 840 м
5 дм 3 мм = 503 мм
10 м 8 см = 1080 см
9 км 36 м = 9036 мб)
7000 г = 7 кг
3 т 9 кг = 3009 кг
15 000 кг = 15 т
8302 кг = 8 т 3 ц 2 кг5. БЛИЦтурнир
а) Аня вышила а красных крестиков, а зелёных – в 4 раза больше. На сколько меньше красных крестиков, чем зелёных, вышила Аня?
а * 4 - а
б) Длина прямоугольника b см, а ширина – на 24 см меньше. Во сколько раз длина прямоугольника больше его ширины?
b : (b - 24)
в) 4 одинаковых стула стоят m р. Сколько рублей надо заплатить за 6 таких стульев?
m : 4 * 6
г) На пошив 3 одинаковых платьев пошло d м ткани. Сколько таких платьев можно сшить из 72 м этой ткани?
72 : (d : 3)
6. Найди значения выражений. Проверь с помощью калькулятора.
а) 2 047 639 – 459 086 = 1 588 553
б) 305 286 – 72 058 = 233 228
в) (2316 + 8739) – (10 210 – 6862) = 11055 - 3348 = 7 707
г) 400 000 – (216 319 + 98 757) + 16 086 = 400 000 - 315076 + 16086 = 101 010
7. Выполни действия:
а) 8 дм 3 см 5 мм – 2 дм 6 мм = 835 - 206 = 629
б) 14 км 98 м + 902 м = 14098 + 902 = 15000
в) 4 кг 283 г – 2 кг 605 г = 4283 - 2605 = 1678
г) 5 т – 6 ц 38 кг = 5000 - 638 = 43628. Имеются стандартные гири массой меньше 1 кг. Каким наименьшим возможным числом таких гирь можно взвесить предметы массой:
Надо начать с того, какие гири являются стандартными: 1 г, 2 г, 25 г, 50г, 100 г, 200г, 300 г, 500 г, - какие еще бывают стандартные гири?
а) 26 г = 25 + 1
б) 94 г =
в) 125 г = 100 +25
г) 347 г =
д) 600 г = 100 + 500
е) 870 г =
ж) 950 г = 500 + 300 + 100 +50 111
-
Страница 111
Урок 43 Решение задач
9. Масса пустой миски равна 420 г. Найди по рисункам массу яблок и массу арбуза:
4100 - 420 = 3680 (г) масса яблок
3300 - 420 = 2880 (г) масса арбуза
10. Реши уравнения с комментированием и сделай проверку:
х • 50 = 350
х = 350 : 50
х = 7
Проверка: 7 * 50 = 350х : 600 = 80
х = 80 * 600
х = 48 000
Проверка: 48 000 : 80 = 60096 000 : х = 600
х = 96 000 : 600
х = 160
Проверка: 160 * 600 = 96 00011. Найди объём фигур на рисунке, если объём каждого кубика равен 1 см3 (кубическому сантиметру).
Слева верхняя 1 * 2 * 3 = 6 см3
Слева нижняя 2 * 2 * 3 = 12 см3
Посредине 2 * 3 * 5 = 30 см3
Справа 2 * 3 * 4 = 24 см312. На лесной опушке собрались а зайчиков и b белочек, а остальных зверей – в 3 раза меньше, чем зайчиков и белочек вместе. Сколько всего зверей было на опушке? Составь выражение и найди его значение при а = 17 и b = 19.
(17 + 19) + (17 + 19) : 3 = 36 + 12 = 48 (зв.) всего.
Ответ: 48 зверей.13. А = {4, ★, а, 5}, В = {b, 4, ★ }. Запиши с помощью фигурных скобок пересечение и объединение множеств А и В. Построй диаграмму Эйлера–Венна этих множеств. Раскрась на ней множество А ∩ В и обведи А ∪ В.
А ∩ В = {4, ★}
А ∪ В = {4, ★, а, 5; b}
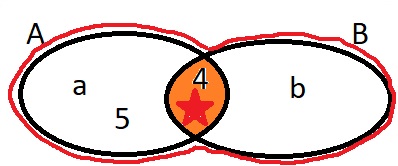
14. Задача-шутка
Бримазище нашёл 96 шклидулок, а бримазёнок – на 64 шклидулки меньше. Сколько шклидулок нашли они вместе? Во сколько раз больше шклидулок нашёл бримазище, чем бримазёнок?Решение
Бримазёнок нашел 96-64=32 шклидулки
32+96=128 шклидулок нашли вместе
96 :3 2=3 раза больше.Ответ: 128 шклидулок нашли вместе и в 3 раза больше нашёл Бримазище, чем Бримазёнок
15. От домика Кенги к домику Винни-Пуха ведут 4 тропинки, а от домика Винни-Пуха к домику Пятачка – 5 тропинок. Сколькими способами можно пройти от Кенги к Пятачку, зайдя по дороге к Винни-Пуху? Реши задачу с помощью «дерева возможностей».
3*2=6 способов дойти
AA1
BA1
CA1
AB1
BB1
CB1На этом первая часть заканчивается! Ураа!


