![]()
 Плеяда наших учебников с ответами пополнилась еще одним решебником с ГДЗ ответами онлайн. Сама по себе математика предмет нужный, полезный, прагматичный и применяемый во всех областях нашей жизни. По крайнем мере математика за 6 класс уж точно является предметом практичным. Ведь здесь самый простые и насущные арифметические операции и теоремы находящие отклики в нашей повседневности.
Плеяда наших учебников с ответами пополнилась еще одним решебником с ГДЗ ответами онлайн. Сама по себе математика предмет нужный, полезный, прагматичный и применяемый во всех областях нашей жизни. По крайнем мере математика за 6 класс уж точно является предметом практичным. Ведь здесь самый простые и насущные арифметические операции и теоремы находящие отклики в нашей повседневности.
Ну что же, раз так, то самое время перейти уже к конкретно нашей теме, которая будет о учебнике Математики за 6 шестой класс, авторы учебника Никольский, Потапов, Решетников.
Темы учебника это изучение дробей, сначала обыкновенные, потом десятичные, решение задач с формулой пути, решение уравнений с одним неизвестным. Азы геометрии, с вычислением площадей, но об этом мало...
Выбирайте нужную страницу ГДЗ на вкладках, чтобы посмотреть ответы на нужные задания.
ГДЗ - ответы по математике 6 класс к учебнику Никольского:
Кликаем и смотрим
Страница 6
-
Отношения, пропорции, проценты
Отношения чисел и величинОтветы к стр. 6
1. Что называют:
а) отношением числа α к числу b; б) членами отношения?
Приведите примеры.а) отношением числа α к числу b называют частное двух не равных нулю чисел, например 8/51 является отношением числа 8 к числу 51, 8/9 : 4/7 является отношением числа 8/9 к числу 4/7;
б) в отношении чисел α и b членами отношения называют числа α и b, например 8/51 является отношением числа 8 к числу 51 — числа 8 и 51 являются членами отношения, 8/9 : 4/7 является отношением числа 8/9 к числу 4/7 — 8/9 и 4/7 являются членами отношения. 7
-
Ответы к стр. 7
2. Чем является отношение величин:
а) одного наименования; б) разных наименований?
Приведите примеры.а) отношение величин одного наименования (длин, скоростей, стоимостей, выраженных одинаковыми единицами измерения) есть число, например 800 см : 4 м = 8 м : 4 м = 2 — отношение длины (800 см) к длине (4 м) есть число 2;
б) отношение величин разных наименований (пути и времени, массы тела и его объёма) есть новая величина, например: 20 км : 2 ч = 10 км/ч — отношение расстояния (20 км) ко времени (2 ч) есть новая величина скорость (10 км/ч).
3. Используя слово отношение прочитайте запись:
а) 7 : 2; б) 3/5; в) 1 : 5; г) 1/6.а) отношение числа семь к числу два;
б) отношение числа три к числу пять;
в) отношение числа один к числу пять;
г) отношение числа один к числу шесть.
4. Запишите отношение, назовите его члены:
а) 7 к 3; б) 5 к 9; в) 12 к 4; г) 10 к 1000.а) 7/3, члены отношения 7 и 3;
б) 5/9, члены отношения 5 и 9;
в) 12/4, члены отношения 12 и 4;
г) 10/1000, члены отношения 10 и 1000.
5. Найдите отношение:
а) 3 к 1/2; б) 5 к 10/13; в) 7/8 к 21/32; г) 12/17 к 48/51.a) 3 : 1/2 = 3/1 : 1/2 = 3/1 • 2/1 = 3•2/1•1 = 6/1 = 6;
б) 5 : 10/13 = 5/1 : 10/13 = 5/1 • 13/10 = 5•13/1•10 = 1•13/1•2 = 13/2;
в) 7/8 : 21/32 = 7/8 • 32/21 = 7•32/8•21 = 1•4/1•3 = 4/3;
г) 12/17 : 48/51 = 12/17 • 51/48 = 12•51/17•48 = 1•3/1•4 = 3/4.
6. Прочитайте отношение, назовите его члены, упростите отношение с помощью свойства отношения:
а) 40 : 50 = 4 : 5; б) 99 : 18; в) 450 : 250; г) 720 : 81.
В чём заключается свойство отношения?40 : 50 — это отношение сорока к пятидесяти, члены отношения 40 и 50.
Свойство отношения — отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю: 40 : 50 = (40 : 10) : (50 : 10) = 4 : 5.б) 99 : 18 — это отношение девяноста девяти к восемнадцати, члены отношения 99 и 18, (99 : 9) : (18 : 9) = 11 : 2;
в) 450 : 250 — это отношение четырёхсот пятидесяти к двумстам пятидесяти, члены отношения 450 и 250, (450 : 50) : (250 : 50) = 9 : 5;
г) 720 : 81 — это отношение семьсот двадцати к восьмидесяти одному, члены отношения 720 и 81 = (720 : 9) : (81 : 9) = 80 : 9.
7. Запишите отношение в виде дроби (там, где можно, упростите отношение):
а) 3 : 5; б) 49 : 28; в) 35 : 700; г) 5 : 7; д) 520 : 460; е) 27 : 81.а) 3 : 5 = 3/5;
б) 49 : 28 = 49/28 = 7•7/4•7 = 7/4;
в) 35 : 700 = 35/700 = 1•35/20•35 = 1/20;
г) 5 : 7 = 5/7;
д) 520 : 460 = 520/460 = 26•20/23•20 = 26/23;
е) 27 : 81 = 27/81 = 1•27/3•27 = 1/3.
8. Можно ли выразить натуральным числом отношение:
а) 40 : 20; б) 30 : 60; в) 1000 : 100;
г) 600 : 30; д) 20 : 40; е) 100 : 1000.а) 40 : 20 = (40 : 10) : (20 : 10) = 4 : 2 = 2 — можно;
б) 30 : 60 = (30 : 30) : (60 : 30) = 1 : 2 = 1/2 — нельзя;
в) 1000 : 100 = (1000 : 100) : (100 : 100) = 10 : 1 = 10 — можно;
г) 600 : 30 = (600 : 10) : (30 : 10) = 60 : 3 = 20 — можно;
д) 20 : 40 = (20 : 20) : (40 : 20) = 1 : 2 = 1/2 — нельзя;
е) 100 : 1000 = (100 : 100) : ( 1000 : 100) = 1 : 10 = 1/10 — нельзя.
9. Замените отношение дробных чисел равным ему отношением натуральных чисел по образцу:
а) 1/2 : 1/3. I способ. 1/2 : 1/3 = 1/2 • 3/1 = 1•3/2•1 = 3/2.
II способ. Умножим каждый член отношения на 6:
1/2 : 1/3 = 6/2 : 6/3 = 3 : 2.
б) 1/4 : 1/5; в) 3/7 : 4/5; г) 2/5 : 3/7; д) 12/17 : 1 1/2; е) 1 1/2 : 3/8; ж) 2 1/2 : 1 2/3.б) 1/4 : 1/5. I способ. 1/4 : 1/5 = 1/4 • 5/1 = 5/4.
II способ. Умножим каждый член отношения на 20:
1/4 : 1/5 = 20/4 : 20/5 = 5 : 4.в) 3/7 : 4/5. I способ. 3/7 : 4/5 = 3/7 • 5/4 = 3•5/7•4 = 15/28.
II способ. Умножим каждый член отношения на 35:
3/7 : 4/5 = 105/7 : 140/5 = 15 : 28.г) 2/5 : 3/7. I способ. 2/5 : 3/7 = 2/5 • 7/3 = 2•7/5•3 = 14/15.
II способ. Умножим каждый член отношения на 35:
2/5 : 3/7 = 70/5 : 105/7 = 14 : 15.д) 12/17 : 1 1/2. I способ. 12/17 : 1 1/2 = 12/17 : 3/2 = 12/17 • 2/3 = 12•2/17•3 = 24/51 = 8•3/17•3 = 8/17.
II способ. Умножим каждый член отношения на 34:
12/17 : 1 1/2 = 12/17 : 3/2 = 204/17 : 102/2 = 24 : 51 = (24 : 3) : (51 : 3) = 8 : 17.е) 1 1/2 : 3/8. I способ. 1 1/2 : 3/8 = 3/2 : 3/8 = 3/2 • 8/3 = 3•8/2•3 = 24/6 = 4/1 = 4.
II способ. Умножим каждый член отношения на 8:
1 1/2 : 3/8 = 3/2 : 3/8 = 24/2 : 24/8 = 12 : 3 = 4 : 1 = 4.ж) 2 1/2 : 1 2/3. I способ. 2 1/2 : 1 2/3 = 5/2 : 5/3 = 5/2 • 3/5 = 5•3/2•5 = 15/10 = 3•5/2•5 = 3/2.
II способ. Умножим каждый член отношения на 6:
2 1/2 : 1 2/3 = 5/2 : 5/3 = 30/2 : 30/3 = 15 : 10 = (15 : 5) : (10 : 5) = 3 : 2.10. Упростите отношение величин (10-11):
а) 35м/28м; б) 45кг/36кг; в) 420км/720км; г) 450т/540т; д) 320ч/48ч; е) 480мин/840мин.а) 35м/28м = 5•7м/4•7м = 5/4;
б) 45кг/36кг = 5•9кг/4•9кг = 5/4;
в) 420км/720км = 7•60км/12•60км = 7/12;
г) 450т/540т = 5•90т/6•90т = 5/6;
д) 320ч/48ч = 20•16ч/3•16ч = 20/3;
е) 480мин/840мин = 4•120мин/7•120мин = 4/7.
11. а) 12м/15дм; б) 18кг/540г; в) 490см/35дм;
г) 450кг/2т; д) 3500см3/21дм3; е) 9900дм3/18м3.а) 12м/15дм = 120дм/15дм = 8•15дм/15дм = 8;
б) 18кг/540г = 18000г/540г = 100•180г/3•180г = 100/3;
в) 490см/35дм = 490см/350см = 7•70см/5•70см = 7/5;
г) 450кг/2т = 450кг/2000кг = 9•50кг/40•50кг = 9/40;
д) 3500см3/21дм3 = 3500см3/21000см3 = 1•3500см3/6•3500см3 = 1/6;
е) 9900дм3/18м3 = 9900дм3/18000дм3 = 11•900дм3/20•900дм3 = 11/20.
8
-
Ответы к стр. 8
12. Упростите отношение величин по образцу:
а) 350км/5ч = 350/5 км/ч = 70 км/ч;
б) 720км/8ч; в) 360м/3мин; г) 420кг/4м3;
д) 2250кг/3м3; е) 720м/20с; ж) 450г/5см3.б) 720км/8ч = 720/8 км/ч = 90 км/ч;
в) 360м/3мин = 360/3 м/мин = 120 м/мин;
г) 420кг/4м3 = 420/4 кг/м3 = 105 кг/м3;
д) 2250кг/3м3 = 2250/3 кг/м3 = 750 кг/м3;
е) 720м/20с = 720/20 м/с = 36 м/с;
ж) 450г/5см3 = 450/5 г/см3 = 90 г/см3.
13. Найдите пройденный путь s, если известны скорость ν и время равномерного движения t:
а) ν = 2 м/с, t = 3 с; б) ν = 2 м/с, t = 1/20 мин.а) s = ν • t = 2 м/с • 3 c = (2 • 3) м•с/с = 6 м
Ответ: 6 м.б) s = ν • t = 2 м/с • 1/20 мин = 2 м/с • 60/20 с = 2 м/с • 3 c = (2 • 3) м•с/с = 6 м
Ответ: 6 м.14. Найдите скорость равномерного движения ν, если известны пройденный путь s и время движения t:
а) s = 6 м, t = 3 с; б) s = 6 м, t = 1/20 ч.а) ν = s : t = (6 : 3) м/c = 2 м/с
Ответ: 2 м/с.б) ν = s : t = 6 м : 1/20 ч = 6 м : 60/20 мин = (6 : 3) м/мин = 2 м/мин
Ответ: 2 м/мин.15. Скорость пешехода 5 1/5 км/ч. Найдите путь пройденный пешеходом за:
а) 2 ч; б) 1 1/2 ч; в) 45 мин; г) 125 мин.а) 5 1/5 км/ч • 2 ч = 26/5 км/ч • 2 ч = 26•2/5 км•ч/ч = 52/5 км = 10 2/5 км
Ответ: 10 2/5 км.б) 5 1/5 км/ч • 1 1/2 ч = 26/5 км/ч • 3/2 ч = 26•3/5•2 км•ч/ч = 78/10 км = 39•2/5•2 км = 39/5 км = 7 4/5 км
Ответ: 7 4/5 км.в) 5 1/5 км/ч • 45 мин = 26/5 км/ч • 45/60 ч = 26/5 км/ч • 3•15/4•15 ч = 26/5 км/ч • 3/4 ч = 26•3/5•4 км•ч/ч = 78/20 км = 39•2/10•2 км = 39/10 км = 3 9/10 км
Ответ: 3 9/10 км.г) 5 1/5 км/ч • 125 мин = 26/5 км/ч • 125/60 ч = 26/5 км/ч • 25•5/12•5 ч = 26/5 км/ч • 25/12 ч = 26•25/5•12 км•ч/ч = 650/60 км = 65•10/6•10 км = 65/6 км = 10 5/6 км
Ответ: 10 5/6 км.16. Расстояние в 1 1/2 км пешеход прошел за 20 мин. Найдите скорость пешехода. Ответ запишите в следующих единицах:
а) км/ч; б) км/мин; в) м/ч; г) м/мин; д) м/с.а)1 1/2 км : 20 мин = 3/2 км : 20/60 ч = 3/2 км : 20/3•20 ч = 3/2 км : 1/3 ч = 3/2 км • 3/1 ч = 3•3/2•1 км/ч = 9/2 км/ч = 4 1/2 км/ч
Ответ: 4 1/2 км/ч.б) 1 1/2 км : 20 мин = 3/2 км • 1/20 мин = 3•1/2•20 км/мин = 3/40 км/мин
Ответ: 3/40 км/мин.в) 1 1/2 км : 20 мин = 3/2 км : 20/60 ч = 3•1000/2 м • 60/20 ч = 1500 • 3 м/ч = 4500 м/ч
Ответ: 4500 м/ч.г) 1 1/2 км : 20 мин = 3•1000/2 м : 20 мин = 1500 м : 20 мин = 75 м/мин
Ответ: 75 м/мин.д) 1 1/2 км : 20 мин = 3•1000/2 м : (20 • 60) с = 1500 м : 1200 с = 15•100/12•100 м/с = 15/12 м/с = 5•3/4•3 м/с = 5/4 м/с = 1 1/4 м/с
Ответ: 1 1/4 м/с.17. Скорость легковой автомашины 72 км/ч. Какой путь она проедет за:
а) 2/3 ч; б) 45 мин; в) 50 мин; г) 165 мин.а) 72 км/ч • 2/3 ч = 72•2/3 км•ч/ч = 144/3 км = 48 км
Ответ: 48 км.б) 72 км/ч • 45 мин = 72 км/ч • 45/60 ч = 72 км/ч • 3/4 ч = 72•3/4 км•ч/ч = 216/4 км = 54 км
Ответ: 54 км.в) 72 км/ч • 50 мин = 72 км/ч • 50/60 ч = 72 км/ч • 5/6 ч = 72•5/6 км•ч/ч = 360/6 км = 60 км
Ответ: 60 км.г) 72 км/ч • 165 мин = 72 км/ч • 165/60 ч = 72 км/ч • 11/4 ч = 72•11/4 км•ч/ч = 792/4 км = 198 км
Ответ: 198 км.18. Скорость легковой машины 1200 м/мин. За сколько часов машина проедет:
а) 144 км; б) 36 км; в) 8 км; г) 54 км.1200 м/мин = 1200•60/1000 км/ч = 72 км/ч
а) 144 км : 72 км/ч = 144/72 км•ч/км = 2 ч
Ответ: 2 ч.б) 36 км : 72 км/ч = 36/72 км•ч/км = 36/2•36 ч = 1/2 ч
Ответ: 1/2 ч.в) 8 км : 72 км/ч = 8/72 км•ч/км = 8/9•8 ч = 1/9 ч
Ответ: 1/9 ч.г) 54 км : 72 км/ч = 54/72 км•ч/км = 18•3/18•4 ч = 3/4 ч
Ответ: 3/4 ч.19. Найдите скорость автомашины, если 80 км она проезжает:
а) за 1 ч; б) за 4/5 ч; в) за 4/3 ч; г) за 8/7 ч;
д) за 50 мин; е) за 65 мин; ж) за 90 мин; з) за 100 мин.а) 80 км : 1 ч = 80 км/ч
Ответ: 80 км/ч.б) 80 км : 4/5 ч = 80 км • 5/4 ч = 80•5/4 км/ч = 400/4 км/ч = 100 км/ч
Ответ: 100 км/ч.в) 80 км : 4/3 ч = 80 км • 3/4 ч = 80•3/4 км/ч = 240/4 км/ч = 60 км/ч
Ответ: 60 км/ч.г) 80 км : 8/7 ч = 80 км • 7/8 ч = 80•7/8 км/ч = 560/8 км/ч = 70 км/ч
Ответ: 70 км/ч.д) 80 км : 50 мин = 80 км : 50/60 ч = 80 км : 5/6 ч = 80 км • 6/5 ч = 80•6/5 км/ч = 480/5 км/ч = 96 км/ч
Ответ: 96 км/ч.е) 80 км : 65 мин = 80 км : 65/60 ч = 80 км : 13/12 ч = 80 км • 12/13 ч = 80•12/13 км/ч = 960/13 км/ч = 73 11/13 км/ч
Ответ: 73 11/13 км/ч.ж) 80 км : 90 мин = 80 км : 90/60 ч = 80 км : 3/2 ч = 80 км • 2/3 ч = 80•2/3 км/ч = 160/3 км/ч = 53 1/3 км/ч
Ответ: 53 1/3 км/ч.з) 80 км : 100 мин = 80 км : 100/60 ч = 80 км : 5/3 ч = 80 км • 3/5 ч = 80•3/5 км/ч = 240/5 км/ч = 48 км/ч
Ответ: 48 км/ч.20. Два конькобежца одновременно стартовали на дистанцию 10 000 м по замкнутой дорожке, длина которой равна 400 м. Скорость первого конькобежца 20 км/ч, а скорость второго 21 км/ч. Обгонит ли второй конькобежец первого на круг до конца дистанции? А на два круга?
1) 10 000 : 400 = 25 (кругов) — надо пробежать каждому конькобежцу
2) 400 м : 20 км/ч = 400 м : 20 000 м/ч = 400/20000 ч = 1/50 ч — потратит I конькобежец на один круг
3) 400 м : 21 км/ч = 400 м : 21 000 м/ч = 400/21000 ч = 2/105 ч — потратит II конькобежец на один круг
4) 1/50 — 2/105 = 21-20/1050 = 1/1050 (ч) — разница по времени между конькобежцами за один круг
5) 1/1050 • 25 = 25/1050 = 1/42 (ч) — разница по времени между конькобежцами за 25 кругов
6) 1/42 : 1/50 = 1/42 • 50/1 = 42/50 = 1 21/84 = 1 4/21 (круга) — на столько обгонит II конькобежец
Ответ: II конькобежец обгонит I конькобежца на 1 4/21 круга, то есть на 1 круг обгонит, а на 2 круга — нет. 10
-
Отношения, пропорции, проценты
МасштабОтветы к стр. 10
21. Что показывает численный масштаб:
а) 1 : 100; б) 1 : 1000; в) 1 : 20 000.а) расстояние на карте в 100 раз меньше расстояния на местности;
б) расстояние на карте в 1000 раз меньше расстояния на местности;
в) расстояние на карте в 20 000 раз меньше расстояния на местности.22. Определите численный масштаб, если известно, что 1 см на плане (географической карте) изображает отрезок длиной:
а) 10 см; б) 50 см; в) 6 дм; г) 10 м;
д) 100 м; е) 1 км; ж) 6 км; з) 10 км.а) 1 : 10;
б) 1 : 50;
в) 1 : 60, так как 6 дм = 60 см;
г) 1 : 1000, так как 10 м = 1000 см;
д) 1 : 10 000, так как 100 м = 10 000 см;
е) 1 : 100 000, так как 1 км = 100 000 см;
ж) 1 : 600 000, так как 6 км = 600 000 см;
з) 1 : 1 000 000, так как 10 км = 1 000 000 см.23. Расстояние между двумя городами равно 200 км. Определите расстояние между изображениями этих городов на карте, если численный масштаб карты равен:
а) 1 : 1 000 000; б) 1 : 200 000; в) 1/5000000.а) 200 км = 20 000 000 см
1 : 1 000 000 = 1/1000000
20 000 000 см • 1/1000000 = 20000000/1000000 см = 20 см
Ответ: 20 см.б) 200 км = 20 000 000 см
1 : 200 000 = 1/200000
20 000 000 см • 1/200000 = 20000000/200000 см = 100 см
Ответ: 100 см.в) 200 км = 20 000 000 см
20000000 см • 1/5000000 = 20000000/5000000 см = 4 см
Ответ: 4 см.24. Масштаб карты равен 1/50000. Определите расстояние на местности, если на карте оно равно:
а) 1 см; б) 5 см; в) 22 см; г) 37 мм; д) 1 1/5 дм; е) 146 мм.а) 1 см : 1/50000 = 1 см • 50000/1 = 50 000 см = 500 м
Ответ: 500 м.б) 5 см : 1/50000 = 5 см • 50000/1 = 250 000 см = 2500 м = 2 км 500 м
Ответ: 2 км 500 м.в) 22 см : 1/50000 = 22 см • 50000/1 = 1 100 000 см = 11 000 м = 11 км
Ответ: 11 км.г) 37 мм = 37/10 см
37/10 см : 1/50000 = 37/10 см • 50000/1 = 37•50000/10 см = 37 см•5000/1 = 185 000 см = 1850 м = 1 км 850 м
Ответ: 1 км 850 м.д) 1 1/5 дм = 6/5 дм = 6/5 • 10 см = 6•10/5 см = 60/5 см = 12 см
12 см : 1/50000 = 12 см • 50000/1 = 600 000 см = 6000 м = 6 км
Ответ: 6 км.е) 146 мм = 146/10 см = 73/5 см
73/5 см : 1/50000 = 73/5 см • 50000/1 = 73•50000/5 см = 73 см•10000/1 = 730 000 см = 7300 м = 7 км 300 м
Ответ: 7 км 300 м.25. План комнаты имеет вид прямоугольника со сторонами 40 мм и 31 мм. Определите длину и ширину комнаты, если численный масштаб плана равен 1 : 200.
1 : 200 = 1/200
Длина α = 40 мм : 1/200 = 40 мм • 200/1 = 8000 мм = 800 см = 8 м
Ширина b = 31 мм : 1/200 = 31 мм • 200/1 = 6200 мм = 620 см = 6 м 20 см
Ответ: длина α = 8 м, ширина b = 6 м 20 см.26. Огород имеет вид прямоугольника, длина которого 340 м, а ширина 220 м. Какие размеры будет иметь изображение этого огорода на плане, выполненном в масштабе 1 : 500?
1 : 500 = 1/500
Длина α = 340 м • 1/500 = 340/500 м = 34/50 м = 17/25 м = 1700/25 см = 68 см
Ширина b = 220 м • 1/500 = 220/500 м = 22/50 м = 11/25 м = 1100/25 см = 44 см
Ответ: длина изображение на плане α = 68 см, ширина изображения на плане b = 44 см.27. Прямоугольник со сторонами 12 см и 6 см изображает на плане поле, занятое под овёс. Определите масштаб плана, если бóльшая сторона поля имеет длину 360 м. Определите меньшую сторону поля.
Масштаб М = 12 см : 360 м = 12 см : 36 000 см = 12/36000 = 1/3000 = 1 : 3000
Ширина b = 6 см : 1/3000 = 6 см • 3000/1 = 18 000 см = 180 м
Ответ: масштаб 1 : 3000, ширина поля b = 180 м.28. Используя план местности (рис. 2) определите:
а) расстояние от А до B;
б) расстояние от А и от B до моста через реку;
в) расстояние от B до смешанного леса.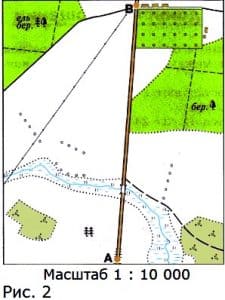
а) 1 : 10 000 = 1/10000
расстояние на плане от А до B примерно 70 мм = 7 см
расстояние на местности от А до B: s = 7 см : 1/10000 = 7 см • 10000/1 = 70 000 см = 700 м.
Ответ: от А до В 700 м.б) 1 : 10000 = 1/10000
расстояние на плане от А до моста через реку примерно 20 мм = 2 см
расстояние на плане от В до моста через реку примерно 50 мм = 5 см
расстояние на местности от А до моста через реку: s = 2 см : 1/10000 = 2 см • 10000/1 = 20 000 см = 200 м
расстояние на местности от В до моста через реку: s = 5 см : 1/10000 = 5 см • 10000/1 = 50 000 см = 500 м.
Ответ: от А до моста 200 м, от В до моста 500 м.в) 1 : 10000 = 1/10000
расстояние на плане от B до смешанного леса примерно 15 мм = 15/10 см = 3/2 см
расстояние на местности от B до смешанного леса: s = 3/2 : 1/10000 = 3/2 • 10000/1 = 30000/2 = 15 000 см = 150 м.
Ответ: от В до смешанного леса 150 м. 11
-
Ответы к стр. 11
29. За сколько часов туристы преодолеют расстояние от A до B (рис.3), если будут двигаться со скоростью:
а) 5 км/ч; б) 4 км/ч.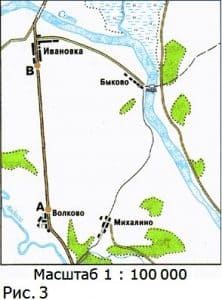
а) 1 : 100 000 = 1/100000
расстояние на плане от А до B примерно 40 мм = 4 см
расстояние на местности от А до B: s = 4 см : 1/100000 = 4 см • 100000/1 = 400 000 см = 4000 м = 4 км
t = s : ν = 4 км : 5 км/ч = 4/5 ч
Ответ: за 4/5 ч.б) 1 : 100 000 = 1/100000
расстояние на плане от А до B примерно 40 мм = 4 см
расстояние на местности от А до B: s = 4 см : 1/100000 = 4 см • 100000/1 = 400 000 см = 4000 м = 4 км
t = s : ν = 4 км : 4 км/ч = 1 ч
Ответ: за 1 ч.30. Начертите план класса в масштабе 1 : 100.
длина класса α = 11 м = 1100 см
ширина класса b = 7 м = 700 см
1 : 100 = 1/100
длина класса на плане: 1100 см • 1/100 = 1100/100 см = 11 см
ширина класса на плане: 700 см • 1/100 = 700/100 см = 7 см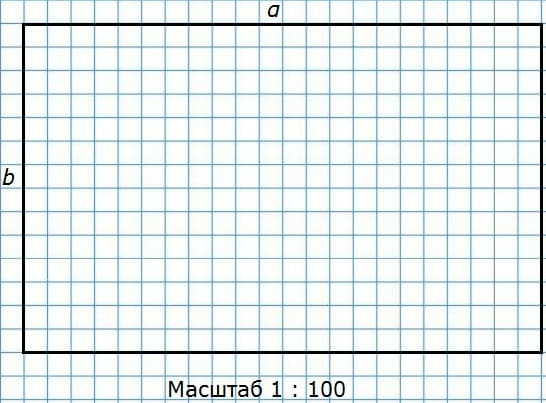
31. а) начертите план своей комнаты в масштабе 1 : 50;
б) начертите план школьного здания в масштабе 1 : 250.а) длина комнаты α = 4 м 50 см = 450 см
ширина комнаты b = 2 м 80 см = 280 см
1 : 50 = 1/50
длина комнаты на плане: 450 см • 1/50 = 450/50 см = 9 см
ширина комнаты на плане: 280 см • 1/50 = 280/50 см = 5 30/50 см = 5 3/5 см
б) 1 : 250 = 1/250
школьное здание состоит из четырёх блоков, два из которых соединены переходом:
— первый блок:
длина α1 = 18 м = 1800 см
ширина b1 = 15 м = 1500 см
длина на плане: 1800 см • 1/250 = 1800/250 см = 7 50/250 см = 7 1/5 см
ширина на плане: 1500 см • 1/250 = 1500/250 см = 6 см
— второй блок:
длина α2 = 21 м = 2100 см
ширина b2 = 17 м = 1700 см
длина на плане: 2100 см • 1/250 = 2100/250 см = 8 100/250 см = 8 2/5 см
ширина на плане: 1700 см • 1/250 = 1700/250 см = 6 200/250 см = 6 4/5 см
— третий блок:
длина α3 = 19 м = 1900 см
ширина b3 = 15 м = 1500 см
длина на плане: 1900 см • 1/250 = 1900/250 см = 7 150/250 см = 7 3/5 см
ширина на плане: 1500 см • 1/250 = 1500/250 см = 6 см
— четвёртый блок:
длина α4 = 23 м = 2300 см
ширина b4 = 17 м = 1700 см
длина на плане: 2300 см • 1/250 = 2300/250 см = 9 50/250 см = 9 1/5 см
ширина на плане: 1700 см • 1/250 = 1700/250 см = 6 200/250 см = 6 4/5 см
— переход между вторым и четвёртым блоками:
длина αп = 10 м = 1000 см
ширина bп = 7 м = 700 см
длина на плане: 1000 см • 1/250 = 1000/250 см = 4 см
ширина на плане: 700 см • 1/250 = 700/250 см = 2 200/250 см = 6 4/5 см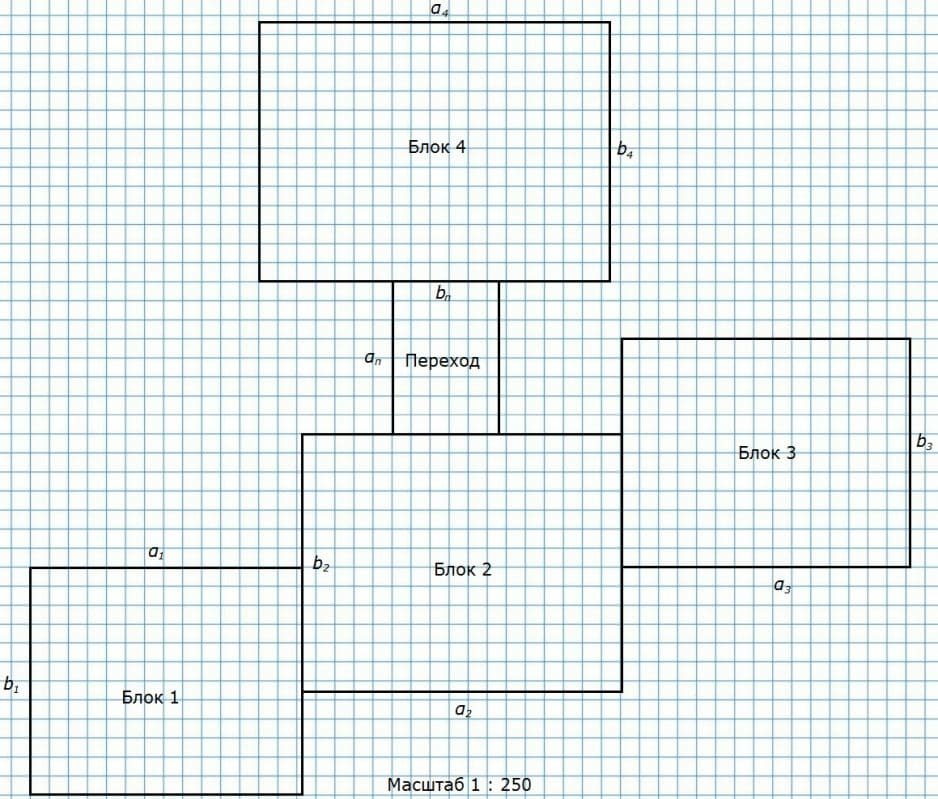
32. Можно ли начертить план здания (прямоугольной формы в основании) длиной 50 м и шириной 20 м на странице тетради, если использовать масштаб 1 : 50? Какой масштаб следует использовать, чтобы план поместился на странице тетради?
длина страницы тетради = 20 см
ширина страницы тетради = 16 см
длина здания α = 50 м = 5000 см
ширина здания b = 20 м = 2000 см
1 : 50 = 1/50
длина здания на плане: 5000 см • 1/50 = 5000/50 см = 100 см
ширина здания на плане: 2000 см • 1/50 = 2000/50 см = 40 см
Так как длина и ширина здания на плане больше длины и ширины страницы тетради, то начертить план здания нельзя.
Обозначим масштаб через х и найдём масштаб на плане для длины и ширины здания на тетрадной станице:
— для длины здания на плане: 5000 см • х = 20 см, х = 20/5000 = 1/250 = 1 : 250
— для ширины здания на плане: 2000 см • х = 16 см, х = 16/2000 = 1/125 = 1 : 125
Из двух получившихся масштабов выбираем наименьший, то есть 1 : 250. Тогда длина здания на плане будет 20 см, а ширина здания на плане будет 2000 см • 1/250 = 2000/250 см = 8 см.33. На рисунке 4 изображен комар в масштабе 4 : 1. Определите истинную длину крыла комара.
4 : 1 = 4/1
длина крыла комара на рисунке α = 14 мм = 14/10 см
истинная длина крыла комара: 14/10 см : 4/1 = 14/10 см • 1/4 = 14/40 см = 7/20 см
Ответ: длина крыла комара 7/20 см.34. Определите увеличен или уменьшен предмет, если он изображён в масштабе:
а) 1 : 100; б) 10 : 1;
в) 1 : 20; г) 4 : 1.а) уменьшен в 100 раз;
б) увеличен в 10 раз;
в) уменьшен в 20 раз;
г) увеличен в 4 раза.Придумываем задачу
35. На материале других школьных предметов придумайте две задачи с использованием масштаба и решите их.
а) Какое расстояние необходимо пройти туристам до привала, если расстояние до него на карте 20 см, а масштаб карты 1 : 100 000.
1 : 100 000 = 1/100000
20 см : 1/100000 = 20 см • 100000/1 = 2 000 000 см = 20 000 м = 20 км
Ответ: до привала 20 км.б) На чертеже прямоугольной детали длина её изображения 20 см, а ширина — 10 см. Определите истинные размеры детали, если масштаб чертежа 1 : 5.
1 : 5 = 1/5
истинная длина детали: 20 см : 1/5 = 20 см • 5/1 = 100 см = 1 м
истинная ширина детали: 10 см : 1/5 = 10 см • 5/1 = 50 см
Ответ: длина детали 1 м, ширина — 50 см. 13
-
Отношения, пропорции, проценты
Деление числа в данном отношенииОтветы к стр. 13
36. Разделите 900 р. в отношении: а) 5 : 4; б) 2 : 3.
а) 900•5/5+4 = 900•5/9 = 100 • 5 = 500 (р.)
900•4/5+4 = 900•4/9 = 100 • 4 = 400 (р.)
Ответ: 500 р. и 400 р.б) 900•2/2+3 = 900•2/5 = 180 • 2 = 360 (р.)
900•3/2+3 = 900•3/5 = 180 • 3 = 540 (р.)
Ответ: 360 р. и 540 р.37. Разделите число:
а) 12 в отношении 1 : 3; б) 15 в отношении 2 : 3;
в) 48 в отношении 1/3 и 1/5; г) 100 в отношении 1/2 и 1/3.а) 12•1/1+3 = 12•1/4 = 3 • 1 = 3
12•3/1+3 = 12•3/4 = 3 • 3 = 9
Ответ: 3 и 9.б) 15•2/2+3 = 15•2/5 = 3 • 2 = 6
15•3/2+3 = 15•3/5 = 3 • 3 = 9
Ответ: 6 и 9.в) 48 : (1/3 + 1/5) • 1/3 = 48 : 8/15 • 1/3 = 48 • 15/8 • 1/3 = 48•15•1/8•3 = 6•5•1/1•1 = 30
48 : (1/3 + 1/5) • 1/5 = 48 : 8/15 • 1/5 = 48 • 15/8 • 1/5 = 48•15•1/8•5 = 6•3•1/1•1 = 18
Ответ: 30 и 18.г) 100 : (1/2 + 1/3) • 1/2 = 100 : 5/6 • 1/2 = 100 • 6/5 • 1/2 = 100•6•1/5•2 = 20•3•1/1•1 = 60
100 : (1/2 + 1/3) • 1/3 = 100 : 5/6 • 1/3 = 100 • 6/5 • 1/3 = 100•6•1/5•3 = 20•2•1/1•1 = 40
Ответ: 60 и 40.8. Объясните, как разделить число 24 в отношении 1 : 2 : 3.
Отношение 1 : 2 : 3 означает, что первое число состоит из одной части, второе — из двух частей, а третье — из трёх одинаковых частей. Для того чтобы разделить число 24 в отношении 1 : 2 : 3 необходимо воспользоваться формулой: с/α+b+d • α, с/α+b+d • b и с/α+b+d • d, где с – данное число, α, b и d — значения отношений.
24•1/1+2+3 = 24•1/6 = 4 • 1 = 424•2/1+2+3 = 24•2/6 = 4 • 2 = 8
24•3/1+2+3 = 24•3/6 = 4 • 3 = 12
Ответ: 4, 8 и 12.39. Первая машинистка печатает 10 страниц в час, вторая — 8 страниц в час. Как разделить между ними рукопись в 90 страниц, чтобы они закончили работу одновременно?
1) 90•10/10+8 = 90•10/18 = 5 • 10 = 50 (стр.) – первой машинистке
2) 90•8/10+8 = 90•8/18 = 5 • 8 = 40 (стр.) – второй машинистке
Ответ: первой машинистке необходимо дать 50 страниц, а второй — 40 страниц.40. Чтобы приготовить стекло берут 10 частей поташу, 31 часть песку и 2 части мелу. Сколько нужно этих материалов на 86 пудов стекла?
1) 86•10/10+31+2 = 86•10/43 = 2 • 10 = 20 (пудов) — поташ
2) 86•31/10+31+2 = 86•31/43 = 2 • 31 = 62 (пуда) — песок
3) 86•2/10+31+2 = 86•2/43 = 2 • 2 =4 (пуда) — мел
Ответ: поташ 20 пудов, песок 62 пуда, мел 4 пуда. 14
-
Ответы к стр. 14
41. Скорость велосипедиста в 5 раз больше скорости пешехода. Однажды они отправились одновременно навстречу друг другу из пунктов, расстояние между которыми 30 км. Какой путь проедет велосипедист до встречи с пешеходом?
30•5/5+1 = 30•5/6 = 5 • 5 = 25 (км) — проедет велосипедист
Ответ: 25 км проедет велосипедист.42. Мотоциклист может проехать расстояние между пунктами за 2 ч, а велосипедист — за 6 ч. Однажды они одновременно отправились навстречу друг другу из этих пунктов. Сколько километров проехал каждый до встречи, если расстояние между пунктами 60 км? Решите задачу двумя способами.
I способ
1) 2 : 6 = 1 : 3 — отношение скорости мотоциклиста к скорости велосипедиста
2) 1 + 3 = 4 (части) — на столько нужно разделить расстояние
3) 60 : 4 = 15 (км) — приходится на одну часть
4) 15 • 1 = 15 (км) — проедет до встречи велосипедист
5) 15 • 3 = 45 (км) — проедет до встречи мотоциклистII способ
1) 2 : 6 = 1 : 3 — отношение скорости мотоциклиста к скорости велосипедиста
2) 60•1/3+1 = 60•1/4 = 15 • 1 = 15 (км) — проедет велосипедист3) 60•3/3+1 = 60•3/4 = 15 • 3 = 45 (км) — проедет мотоциклист
Ответ: мотоциклист проедет 45 км, а велосипедист — 15 км.
43. Над выполнением задания 3 дня работала первая бригада из 5 плотников и 4 дня вторая бригада из 6 плотников. За работу заплатили 39 000 р. Какую сумму получит первая бригада, если все плотники работали с одинаковой производительностью?
1) 5 • 3 = 15 (чел./дней) — производительность I бригады
2) 6 • 4 = 24 (чел./дней) — производительность II бригады
3) 39000•15/15+24 = 39000•15/39 = 1000 • 15 = 15 000 (р.) — получит I бригада
Ответ: первая бригада получит 15 000 р.44. Из «Арифметики» А. П. Киселёва. а) Разделить 84 на три части пропорционально числам 7, 5 и 2.
б) Разделить 125 на такие части, чтобы первая относилась ко второй, как 2 : 3, вторая к третьей, как 3 : 5, а третья к четвертой, как 5 : 6.
в) Разделить 125 на такие части, чтобы первая относилась ко второй, как 2 : 3, вторая к третьей, как 4 : 5, а третья к четвертой, как 6 : 11.
г) Три купца составили товарищество для ведения некоторого торгового дела. Первый купец внёс для этой цели 15 000 р., второй — 10 000 р., третий — 12 500 р. По окончании торгового дела они получили общей прибыли 7500 руб. Спрашивается, сколько из этой прибыли придётся получить каждому купцу.
д) На железной дороге работало 3 артели; в первой было 27 рабочих, во второй — 32, в третьей — 15; первая работала 20 дней, вторая — 18, третья — 16; все три артели получили за работу 4068 руб. Сколько придется получить каждой артели?а) 1) 84•7/7+5+2 = 84•7/14 = 42
2) 84•5/7+5+2 = 84•5/14 = 30
3) 84•2/7+5+2 = 84•2/14 = 12
Ответ: 42, 30 и 12.б) Необходимо сравнить отношения частей.
I часть : II часть = 2 : 3
II часть : III часть = 3 : 5
III часть : IV часть = 5 : 6
или I часть : II часть : III часть : IV часть = (2 : 3) : (3 : 5) : (5 : 6).
Поскольку в равенстве (3 : 5) : (5 : 6) подчёркнутые цифры равны, то можно записать отношение частей в виде 3 : 5 : 6. Далее сравним (2 : 3) и (3 : 5 : 6) — подчёркнутые цифры равны, записываем отношение частей в виде: 2 : 3 : 5 : 6.
Тогда:
1) 125•2/2+3+5+6 = 125•2/16 = 125/8 = 15 5/82) 125•3/2+3+5+6 = 125•3/16 = 375/16 = 23 7/16
3) 125•5/2+3+5+6 = 125•5/16 = 625/16 = 39 1/16
4) 125•6/2+3+5+6 = 125•6/16 = 125•3/8 = 375/8 = 46 7/8
Ответ: 15 5/8, 23 7/16, 39 1/16 и 46 7/8.в) Необходимо сравнить отношения частей.
I часть : II часть = 2 : 3
II часть : III часть = 4 : 5
III часть : IV часть = 6 : 11
или I часть : II часть : III часть : IV часть = (2 : 3) : (4 : 5) : (6 : 11).
Поскольку в равенстве (4 : 5) : (6 : 11) подчёркнутые цифры не равны, то нужно найти их наименьшее общее кратное. НОК 5 и 6 будет 30, следовательно, (4 : 5) нужно умножить на 6, а (6 : 11) нужно умножить на 5. Получим: (24 : 30) : (30 : 55) — подчёркнутые цифры равны, тогда можно записать отношение частей в виде 24 : 30 : 55. Далее, сравним (2 : 3) и (24 : 30 : 55). Подчёркнутые цифры не равны — нужно найти их НОК. НОК 3 и 24 будет 24, следовательно, (2 : 3) нужно умножить на 8, а (24 : 30 : 55) нужно умножить на 1. Получим (16 : 24) : (24 : 30 : 55) — подчёркнутые цифры равны, тогда можно записать отношение частей в виде: 16 : 24 : 30 : 55.
Тогда:
1) 125•16/16+24+30+55 = 125•16/125 = 162) 125•24/16+24+30+55 = 125•24/125 = 24
3) 125•30/16+24+30+55 = 125•30/125 = 30
4) 125•55/16+24+30+55 = 125•55/125 = 55
Ответ: 16, 24, 30 и 55.г) Запишем внесённые купцами деньги в виде отношения: 15 000 : 10 000 : 12 500 = 150 : 100 : 125 = 6 : 4 : 5. Тогда:
1) 7500•6/6+4+5 = 7500•6/15 = 500 • 6 = 3000 (р.) — получит I купец
2) 7500•4/6+4+5 = 7500•4/15 = 500 • 4 = 2000 (р.) — получит II купец
3) 7500•5/6+4+5 = 7500•5/15 = 500 • 5 = 2500 (р.) — получит III купец
Ответ: 3000 р., 2000 р. и 2500 р.д) 1) 27 • 20 = 540 (чел./дней) — производительность I артели
2) 32 • 18 = 576 (чел./дней) — производительность II артели
3) 15 • 16 = 240 (чел./дней) — производительность III артели4) 4068•540/540+576+240 = 4068•540/1356 = 3 • 540 = 1620 (р.) — получит I артель
5) 4068•576/540+576+240 = 4068•576/1356 = 3 • 576 = 1728 (р.) — получит II артель
6) 4068•240/540+576+240 = 4068•240/1356 = 3 • 240 = 720 (р.) — получит III артель
Ответ: 1620 р., 1728 р. и 720 р. 16
-
Отношения, пропорции, проценты
ПропорцииОтветы к стр. 16
45. Что называют пропорцией? Приведите пример, назовите крайние и средние члены пропорции. Сформулируйте основное свойство пропорции.
Пропорцией называется равенство двух отношений, например 200/50 = 32/8 — 200 и 8 крайние члены, а 50 и 32 средние члены пропорции. Основное свойство пропорции — произведение крайних членов пропорции равно произведению её средних членов: 200 • 8 = 50 • 32.
46. Запишите в виде пропорции:
а) 2 относится к 3, как 10 относится к 15;
б) 1/3 относится к 6, как 1 относится к 18;
в) 3 во столько же раз больше 2, во сколько раз 6 больше 4;
г) 7 больше 3 1/2 во столько же раз, во сколько раз 9 больше 9/2.а) 2/3 = 10/15;
б) 1/3 : 6 = 1 : 18;
в) 3/2 = 6/4;
г) 7 : 3 1/2 = 9 : 9/2.
47. Можно ли составить пропорцию из отношений:
а) 6 : 3 и 24 : 12; б) 1 : 5 и 17 : 85;
в) 2 : 5 и 10 : 24; г) 20 : 8 и 35 : 14.а) 6 : 3 = 2, 24 : 12 = 2, 2 = 2 — следовательно, пропорцию составить можно;
б) 1 : 5 = 1/5, 17 : 85 = 17/85 = 1/5, 1/5 = 1/5 — следовательно, пропорцию составить можно;
в) 2 : 5 = 2/5, 10 : 24 = 10/24 = 5/12, 2/5 ≠ 5/12 — следовательно, пропорцию составить нельзя;
г) 20 : 8 = 20/8 = 5/2, 35 : 14 = 35/14 = 5/2, 5/2 = 5/2 — следовательно, пропорцию составить можно.48. Верно ли равенство (48-50):
а) 3/4 = 15/20; б) 7 : 5 = 77/55; в) 12/18 = 14 : 21?а) 3/4 = 15/20, 3 • 20 = 4 • 15, 60 = 60 – следовательно, равенство верно;
б) 7 : 5 = 77/55, 7 : 5 = 77 : 55, 7 • 55 = 5 • 77, 385 = 385 – следовательно, равенство верно;
в) 12/18 = 14 : 21, 12 : 18 = 14 : 21, 12 • 21 = 18 • 14, 252 = 252 – следовательно, равенство верно.49. а) 2/3 : 4/5 = 10 : 12; б) 3/7 : 4/9 = 27 : 28;
в) 4/11 : 5/6 = 48 : 110; г) 1/2 : 2/3 = 4 : 3?а) 2/3 : 4/5 = 10 : 12, 2/3 • 12 = 4/5 • 10, 8 = 8 — равенство верно;
б) 3/7 : 4/9 = 27 : 28, 3/7 • 28 = 4/9 • 27, 3•28/7 = 27•4/9, 3 • 4 = 3 • 4, 12 = 12 — равенство верно;
в) 4/11 : 5/6 = 48 : 110, 4/11 • 110 = 5/6 • 48, 4•110/11 = 5•48/6, 4 • 10 = 5 • 8, 40 = 40 — равенство верно;
г) 1/2 : 2/3 = 4 : 3, 1/2 • 3 = 2/3 • 4, 3/2 ≠ 8/3 — равенство неверно.
50. а) 1/7 : 3/4 = 1/14 : 3/8; б) 2/3 : 4/5 = 1/3 : 2/5;
в) 1 1/2 : 5 = 3 : 10; г) 1 4/5 : 2 = 10 : 9?а) 1/7 : 3/4 = 1/14 : 3/8, 1/7 • 3/8 = 3/4 • 1/14, 3/56 = 3/56 — равенство верно;
б) 2/3 : 4/5 = 1/3 : 2/5, 2/3 • 2/5 = 4/5 • 1/3, 4/15 = 4/15 — равенство верно;
в) 1 1/2 : 5 = 3 : 10, 3/2 • 10 = 5 • 3, 30/2 = 15, 15 = 15 — равенство верно;
г) 1 4/5 : 2 = 10 : 9, 9/5 • 9 = 2 • 10, 81/5 ≠ 20 — равенство неверно.
17
-
Ответы к стр. 17
51. Замените пропорцией равенство:
а) 12 • 2 = 6 • 4; б) 15 • 6 = 9 • 10;
в) 42 • 4 = 84 • 2; г) 24 • 10 = 2 • 120.а) 12 • 2 = 6 • 4 → 12 : 6 = 4 : 2;
б) 15 • 6 = 9 • 10 → 15 : 9 = 10 : 6;
в) 42 • 4 = 84 • 2 → 42 : 84 = 2 : 4;
г) 24 • 10 = 2 • 120 → 24 : 2 = 120 : 10.52. Из данной пропорции получите новую, поменяв местами крайние члены (средние члены):
а) 25/13 = 50/26; б) 28 : 25 = 84 : 75.а) меняем крайние члены: 26/13 = 50/25,
меняем средние члены: 25/50 = 13/26;б) меняем крайние члены: 75 : 25 = 84 : 28;
меняем средние члены: 28 : 84 = 25 : 75.53. Решите пропорцию (53-58):
а) х/2 = 3/7; б) х/3 = 2/5; в) х/12 = 7/10; г) х/16 = 9/32.а) х/2 = 3/7
х • 7 = 2 • 3
7х = 6
х = 6/7
Ответ: 6/7.б) х/3 = 2/5
х • 5 = 2 • 3
5х = 6
х = 6/5 = 1 1/5
Ответ: 1 1/5.в) х/12 = 7/10
х • 10 = 12 • 7
10х = 84
х = 84/10 = 42/5 = 8 2/5
Ответ: 8 2/5.г) х/16 = 9/32
х • 32 = 16 • 9
32х = 144
х = 144/32 = 9/2 = 4 1/2
Ответ: 4 1/2.54. а) 7/8 = х/6; б) 13/15 = х/10; в) 12/21 = х/14; г) 48/51 = х/34.
а) 7/8 = х/6
7 • 6 = 8 • x
8х = 42
х = 42/8 = 21/4 = 5 1/4
Ответ: 5 1/4.б) 13/15 = х/10
13 • 10 = 15 • x
15х = 130
х = 130/15 = 26/3 = 8 2/3
Ответ: 8 2/3.в) 12/21 = х/14
12 • 14 = 21 • x
21х = 168
х = 168/21 = 24/3 = 8
Ответ: 8.г) 48/51 = х/34
48 • 34 = 51 • x
51х = 1632
х = 1632/51 = 32
Ответ: 32.55. а) 15/х = 5/8; б) 24/х = 8/7; в) 12/х = 4/5; г) 25/х = 5/7.
а) 15/х = 5/8
15 • 8 = x • 5
5x = 120
х = 120/5 = 24
Ответ: 24.б) 24/х = 8/7
24 • 7 = x • 8
8x = 168
х = 168/8 = 21
Ответ: 21.в) 12/х = 4/5
12 • 5 = x • 4
4x = 60
х = 60/4 = 15
Ответ: 15.г) 25/х = 5/7
25 • 7 = x • 5
5x = 175
х = 175/5 = 35
Ответ: 35.56. а) 3/5 = 7/х; б) 8/7 = 15/х; в) 7/1 = 12/х; г) 8/1 = 3/х.
а) 3/5 = 7/х,
3 • х = 5 • 7
3х = 35
х = 35/3 = 11 2/3
Ответ: 11 2/3.б) 8/7 = 15/х
8 • х = 7 • 15
8х = 105
х = 105/8 = 13 1/8
Ответ: 13 1/8.в) 7/1 = 12/х
7 • х = 1 • 12
7х = 12
х = 12/7 = 1 5/7
Ответ: 1 5/7.г) 8/1 = 3/х
8 • х = 1 • 3
8х = 3
х = 3/8
Ответ: 3/8.57. а) х : 1/2 = 3 : 5; б) х : 2/3 = 3 : 4;
в) х : 5 = 7 : 1/2; г) х : 6 = 1/3 : 8.а) х : 1/2 = 3 : 5
х • 5 = 1/2 • 3
5х = 3/2
х = 3/2 : 5 = 3/2 • 1/5 = 3/10
Ответ: 3/10.б) х : 2/3 = 3 : 4
х • 4 = 2/3 • 3
4х = 6/3 = 2
х = 2 : 4 = 2/4 = 1/2
Ответ: 1/2.в) х : 5 = 7 : 1/2
х • 1/2 = 5 • 7
1/2 х = 35
х = 35 : 1/2 = 35 • 2 = 70
Ответ: 70.г) х : 6 = 1/3 : 8
х • 8 = 6 • 1/3
8х = 6/3 = 2
х = 2 : 8 = 2/8 = 1/4
Ответ: 1/4.58. а) 14 : 15 = 3 : х; б) 12 : 29 = 1/58 : х;
в) 12 : 25 = 7/15 : х; г) 144 : 125 = 1 1/2 : х.а) 14 : 15 = 3 : х
14 • х = 15 • 3
14х = 45
х = 45/14 = 3 3/14
Ответ: 3 3/14.б) 12 : 29 = 1/58 : х
12 • х = 29 • 1/58
12х = 29/58 = 1/2
х = 1/2 : 12 = 1/2 • 1/12 = 1/24
Ответ: 1/24.в) 12 : 25 = 7/15 : х
12 • х = 25 • 7/15
12х = 175/15 = 35/3
х = 35/3 : 12 = 35/3 • 1/12 = 35/36
Ответ: 35/36.г) 144 : 125 = 1 1/2 : х
144 • х = 125 • 3/2
144х = 375/2
х = 375/2 : 144 = 375/2 • 1/144 = 375/288 = 125/96 = 1 29/96
Ответ: 1 29/96.Доказываем
59. Докажите, что если α/b = c/d, то:
а) d/b = c/α; б) d/c = b/α; в) α+c/b+d = c/d; г) α/b = α+c/b+d.а) α/b = c/d — по основному свойству пропорции αd = bc, разделим обе части выражения на αb:
αd/αb = bc/αb
d/b = c/αб) α/b = c/d — по основному свойству пропорции αd = bc, разделим обе части выражения на αc:
αd/αc = bc/αc
d/c = b/αв) α/b = c/d — по основному свойству пропорции αd = bc, прибавим к обеим частям выражения cd:
αd + cd = bc + cd
d(α + c) = c(b + d) и по основному свойству пропорции получим:
α+c/b+d = c/dг) α/b = c/d — по основному свойству пропорции αd = bc, прибавим к обеим частям выражения αb:
αd + αb = bc + αb
α(d + b) = b(c + α) и по основному свойству пропорции получим:
α/b = α+c/b+d60. Решите пропорцию (60-61):
а) 2x/3 = 4/9; б) 3x/5 = 9/10; в) 8/15 = 6х/9; г) 12/13 = 18х/39.а) 2x/3 = 4/9
2x • 9 = 3 • 4
18х = 12
х = 12/18 = 2/3
Ответ: 2/3.б) 3x/5 = 9/10
3x • 10 = 5 • 9
30х = 45
х = 45/30 = 3/2 = 1 1/2
Ответ: 1 1/2.в) 8/15 = 6х/9
8 • 9 = 15 • 6х
90х = 72
х = 72/90 = 8/10 = 4/5
Ответ: 4/5г) 12/13 = 18х/39
12 • 39 = 13 • 18х
234х = 468
х = 468 : 234
х = 2
Ответ: 2.61. а) 1/5 = 2 : 3х; б) 2/7 = 3/4х; в) 21/25 = 49/50х; г) 16/19 = 32 : 38х.
а) 1/5 = 2 : 3х
1 • 3х = 5 • 2
3х = 10
х = 10/3 = 3 1/3
Ответ: 3 1/3.б) 2/7 = 3/4х
2 • 4х = 7 • 3
8х = 21
х = 21/8 = 2 5/8
Ответ: 2 5/8.в) 21/25 = 49/50х
21 • 50х = 25 • 49
1050х = 1225
х = 1225/1050 = 49/42 = 1 7/42 = 1 1/6
Ответ: 1 1/6.г) 16/19 = 32 : 38х
16 • 38х = 19 • 32
608х = 608
х = 608 : 608
х = 1
Ответ: 1. 20
-
Отношения, пропорции, проценты
Прямая и обратная пропорциональностьОтветы к стр. 20
62. Какие величины называют:
а) прямо пропорциональными;
б) обратно пропорциональными?
Приведите примеры.а) Две величины называют прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз. Например, один карандаш стоит 5 рублей, два карандаша стоят 10 рублей и так далее.
б) Две величины называют обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз. Например, машина проехала путь со скоростью 50 км/ч за 2 часа, а мотоцикл тот же путь проехал со скоростью 25 км/ч за 4 часа — время движения обратно пропорционально скорости движения на одном и том же участке пути: с увеличением скорости время уменьшается.
63. За несколько одинаковых карандашей заплатили 8 р. Сколько нужно заплатить за такие же карандаши, если их:
а) в 2 раза больше;
б) в 2 раза меньше?а) Стоимость карандашей прямо пропорциональна их количеству, поэтому за них заплатили в 2 раза больше: 8 р. • 2 = 16 р.
б) Стоимость карандашей прямо пропорциональна их количеству, поэтому за них заплатили в 2 раза меньше: 8 р. : 2 = 4 р.
64. За несколько одинаковых карандашей заплатили 8 р. Сколько нужно заплатить за такое же количество карандашей, каждый из которых:
а) в 2 раза дороже; б) в 2 раза дешевле?а) Стоимость карандашей при их постоянном количестве прямо пропорциональна их цене, поэтому заплатят в 2 раза больше: 8 р. • 2 = 16 р.
б) Стоимость карандашей при их постоянном количестве прямо пропорциональна их цене, поэтому заплатят в 2 раза меньше: 8 р. : 2 = 4 р.
65. На имеющиеся деньги можно купить 30 карандашей.
а) Сколько тетрадей можно купить на те же деньги, если тетрадь дешевле карандаша в 2 раза?
б) Сколько ручек можно купить на те же деньги, если ручка дороже карандаша в 10 раз?а) Стоимость обратно пропорциональна количеству, поэтому при уменьшении стоимости в 2 раза, количество возрастёт в 2 раза: 30 • 2 = 60 тетрадей.
б) Количество обратно пропорционально стоимости, поэтому при увеличении стоимости в 10 раз, количество уменьшится в 10 раз: 30 : 10 = 3 ручки.
66. Велосипедист за несколько часов проехал 36 км.
а) Сколько километров пройдёт за то же время пешеход, скорость которого в 3 раза меньше скорости велосипедиста?
б) Сколько километров проедет за то же время мотоциклист, скорость которого в 5 раз больше скорости велосипедиста?а) Скорость прямо пропорциональна расстоянию, поэтому при уменьшении скорости в 3 раза расстояние также уменьшится в 3 раза: 36 км : 3 = 12 км — пройдёт пешеход.
б) Скорость прямо пропорциональна расстоянию, поэтому при увеличении скорости в 5 раз расстояние также увеличится в 5 раз: 36 км • 5 = 210 км — проедет мотоциклист.
67. Расстояние от села до города велосипедист проехал за 3 ч.
а) За сколько часов это расстояние пройдёт пешеход, скорость которого в 3 раза меньше скорости велосипедиста?
б) За сколько часов это расстояние проедет мотоциклист, скорость которого в 5 раз больше скорости велосипедиста?а) Скорость обратно пропорциональна времени, поэтому при уменьшении скорости в 3 раза, время в пути увеличится в 3 раза: 3 ч • 3 = 9 часов — потребуется пешеходу.
б) Скорость обратно пропорциональна времени, поэтому при увеличении скорости в 5 раз, время в пути уменьшится в 5 раз: 3 ч : 5 = 3/5 часа — потребуется мотоциклисту.
68. Какова зависимость между:
а) ценой карандаша и стоимостью нескольких таких карандашей при постоянном их количестве;
б) количеством карандашей одного сорта и их стоимостью при постоянной их цене;
в) количеством карандашей и их ценой при постоянной стоимости покупки?а) прямо пропорциональная — чем больше цена карандаша, тем больше общая стоимость карандашей при их постоянном количестве;
б) прямо пропорциональная — чем больше количество карандашей, тем больше их стоимость;
в) обратно пропорциональная — чем больше карандашей, тем меньше стоит один карандаш при постоянной стоимости покупки.
69. Какова зависимость между:
а) скоростью и расстоянием при постоянном времени движения;
б) временем и расстоянием при постоянной скорости движения;
в) временем и скоростью при постоянном пути?а) прямо пропорциональная — чем больше скорость, тем больше пройденное расстояние при постоянном времени движения;
б) прямо пропорциональная — чем больше затрачено времени, тем больше пройденное расстояние при постоянной скорости движения;
в) обратно пропорциональная — чем больше затрачено времени на путь, тем меньше скорость движения при постоянном пути.
21
-
Ответы к стр. 21
70. Какова зависимость между:
а) количеством одинаковых тракторов и площадью, которую они вспашут за один день;
б) числом дней работы трактора и площадью, которую он вспашет;
в) количеством одинаковых тракторов и числом дней, за которые они вспашут поле?а) прямо пропорциональная — чем больше количество тракторов, тем большую площадь они вспашут;
б) прямо пропорциональная — чем больше дней трактор будет пахать, тем большую площадь он вспашет;
в) обратно пропорциональная — чем больше будет количество тракторов, тем меньшее количество дней уйдёт у них на вспашку.
71. а) Покупают одинаковые тетради. Какова зависимость между количеством тетрадей и стоимостью всей покупки?
б) Некто хочет проехать расстояние между двумя городами с постоянной скоростью. Какова зависимость между скоростью и временем движения?а) прямо пропорциональная — чем больше количество одинаковых тетрадей, тем больше стоимость всей покупки;
б) обратно пропорциональная — чем больше скорость, тем меньше времени уйдёт на поездку.
72. За 6 ч поезд прошел 480 км. Сколько километров поезд прошел за первые 2 часа, двигаясь с постоянной скоростью?
↑ 6 ч — 480 км ↑
↑ 2 ч — х км ↑
Время движения поезда прямо пропорционально пройденному расстоянию, тогда:
6/2 = 480/х
х = 2•480/6 = 2 • 80 = 160 (км)
Ответ: 160 км прошел поезд за первые два часа.73. Для варки варенья из вишни на 6 кг ягод берут 4 кг сахарного песку.
Сколько килограммов сахарного песку надо взять на 12 кг ягод?↓ 6 кг ягод — 4 кг сахара ↓
↓ 12 кг ягод — х кг сахара ↓
Масса ягод прямо пропорциональна массе сахарного песка, тогда:
6/12 = 4/х
х = 12•4/6 = 2 • 4 = 8 (кг)
Ответ: 8 кг сахарного песка нужно взять.74. Для варки варенья из вишни на 6 кг ягод берут 4 кг сахарного песка. Сколько килограммов ягод надо взять на 12 кг сахарного песка?
↑ 6 кг ягод — 4 кг сахара ↑
↑ х кг ягод — 12 кг сахара ↑
Масса сахарного песка прямо пропорциональна массе ягод, тогда:
6/х = 4/12
х = 6•12/4 = 6 • 3 = 18 (кг)
Ответ: 18 кг ягод нужно взять.75. а) В 100 г раствора содержится 4 г соли. Сколько соли содержится в 300 г этого раствора
б) В 4000 г раствора содержится 80 г соли. Сколько соли содержится в 200 г этого раствора?а)↓ 100 г раствора — 4 г соли ↓
↓ 300 г раствора — х г соли ↓
Масса раствора прямо пропорциональна массе соли, тогда:
100/300 = 4/х
х = 300•4/100 = 3 • 4 = 12 (г)
Ответ: 12 г соли содержится.б)↑ 4000 г раствора — 80 г соли ↑
↑ 200 г раствора — х г соли ↑
Масса раствора прямо пропорциональна массе соли, тогда:
4000/200 = 80/х
х = 200•80/4000 = 80 : 20 = 4 (г)
Ответ: 4 г соли содержится.76. Расстояние между двумя городами первый поезд прошёл со скоростью 80 км/ч за 3 ч. За сколько часов второй поезд пройдёт то же расстояние со скоростью 60 км/ч?
↑ 80 км/ч — 3 ч ↓
↑ 60 км/ ч — х ч ↓
Скорость движения поезда обратно пропорциональна времени в пути, тогда:
80/60 = х/3
х = 3•80/60 = 80 : 20 = 4 (ч)
Ответ: 4 часа потребуется второму поезду.77. Пять маляров могли бы покрасить забор за 8 дней. За сколько дней тот же забор покрасят:
а) 10 маляров; б) 1 маляр.а)↓ 5 маляров — 8 дней ↑
↓ 10 маляров — х дней ↑
Количество маляров обратно пропорционально количеству дней, тогда:
10/5 = 8/х
х = 5•8/10 = 40 : 10 = 4 (дня)
Ответ: 4 дня потребуется 10 малярам.б)↑ 5 маляров — 8 дней ↓
↑ 1 маляров — х дней ↓
Количество маляров обратно пропорционально количеству дней, тогда:
5/1 = х/8
х = 5•8/1 = 40 (дней)
Ответ: 40 дней потребуется одному маляру.78. 8 м сукна стоят столько же, сколько стоят 63 м ситца. Сколько метров ситца можно купить вместо 14 м сукна?
↓ 8 м сукна — 63 м ситца ↓
↓ 14 м сукна — х м ситца ↓
Количество сукна прямо пропорционально количеству ситца, тогда:
8/14 = 63/х
х = 14•63/8 = 882/8 = 441/4 = 110 1/4 м
Ответ: 110 1/4 м ситца можно купить.79. В жаркий день 6 косцов выпили бочонок кваса за 8 ч. Нужно узнать, сколько косцов за 3 ч выпьют такой же бочонок кваса.
↓ 6 косцов — 8 часов ↑
↓ х косцов — 3 часа ↑
Количество косцов обратно пропорционально времени распития кваса, тогда:
х/6 = 8/3
х = 6•8/3 = 2 • 8 = 16 (косцов)
Ответ: 16 косцов выпьют квас за 3 часа.80. Из «Арифметики» А. П. Киселёва. 8 аршин сукна стоят 30 р. Сколько стоят 15 аршин этого сукна?
↓ 8 аршин сукна — 30 р. ↓
↓ 15 аршин сукна — х р. ↓
Количество сукна прямо пропорционально его стоимости, тогда:
8/15 = 30/х
х = 15•30/8 = 450/8 = 225/4 = 56 1/4 (р.)
1/4 р. = 1/4 • 100 коп. = 100/4 коп. = 25 коп.
Ответ: 56 1/4 р. или 56 р. 25 коп. стоят 15 аршин сукна.81. Со скоростью 80 км/ч товарный поезд прошел 720 км. Какое расстояние пройдет за то же время пассажирский поезд, скорость которого 60 км/ч?
↑ 80 км/ч — 720 км ↑
↑ 60 км/ч — х км ↑
Скорость поезда прямо пропорциональна пройденному расстоянию, тогда:
80/60 = 720/х
х = 720•60/80 = 9 • 60 = 540 (км)
Ответ: 540 км пройдет пассажирский поезд. 22
-
Ответы к стр. 22
82. а) Грузовик со скоростью 60 км/ч проехал расстояние между городами за 8 ч. За сколько часов то же расстояние проедет легковой автомобиль со скоростью 80 км/ч?
б) Бригада из 4 человек может выполнить задание за 10 дней. За сколько дней выполнит такое же задание другая бригада из 5 человек, если все 9 человек работают одинаково хорошо?а) ↓ 60 км/ч — 8 ч ↑
↓ 80 км/ч — х ч ↑
Скорость движения обратно пропорциональна времени в пути, тогда:
80/60 = 8/х
х = 60•8/80 = 60 : 10 = 6 (ч)
Ответ: 6 ч потребуется легковому автомобилю на преодоление пути.б) ↓ 4 человека — 10 дней ↑
↓ 5 человек — х дней ↑
Количество человек обратно пропорционально количеству рабочих дней, тогда:
5/4 = 10/х
х = 4•10/5 = 4 • 2 = 8 (дней)
Ответ: 8 дней потребуется бригаде из 5 человек.83. Один килограмм металлолома заменяет 2 1/2 кг богатой железом руды. Сколько руды заменяют 4 т металлолома?
4 т = 4000 кг
↓ 1 кг металлолома — 2 1/2 кг руды ↓
↓ 4 т металлолома — х кг руды ↓
Масса металлолома прямо пропорционально массе руды, тогда:
1/4000 = 2 1/2 : х
х = (4000 • 2 1/2) : 1 = 4000 • 5/2 = 4000•5/2 = 2000 • 5 = 10000 (кг) = 10 (т )
Ответ: 10 т руды.84. а) Автомобилист заметил, что со скоростью 60 км/ч он проехал мост через реку за 40 с. На обратном пути он проехал этот же мост за 30 с. Определите скорость автомобиля на обратном пути.
б) Автомобилист заметил, что со скоростью 60 км/ч он проехал тоннель за 1 мин. За сколько минут он проехал бы этот тоннель со скоростью 50 км/ч?а) ↓60 км/ч — 40 с ↑
↓ х км/ч — 30 с ↑
Скорость движения обратно пропорциональна времени в пути, тогда:
х/60 = 40/30
х = 60•40/30 = 2 • 40 = 80 (км/ч)
Ответ: 80 км/ч скорость на обратном пути.б) ↑ 60 км/ч — 1 мин ↓
↑ 50 км/ч — х мин ↓
Скорость движения обратно пропорциональна времени в пути, тогда:
60/50 = х/1
х = 60•1/50 = 6/5 = 1 1/5 (мин.)
1/5 мин = 1/5 • 60 с = 60/5 с = 12 с
Ответ: 1 1/5 мин или 1 мин 12 с.85. Две шестеренки сцеплены зубьями. Первая, имеющая 60 зубьев, за минуту делает 50 оборотов. Сколько оборотов за минуту делает вторая, имеющая 40 зубьев?
↑ 60 зубьев — 50 оборотов ↓
↑ 40 зубьев — х оборотов ↓
Количество зубьев обратно пропорционально количеству оборотов, тогда:
60/40 = х/50
х = 60•50/40 = 3•50/2 = 3•25/1 = 75 (оборотов)
Ответ: 75 оборотов.86. За одно и то же время токарь делает 6 деталей, а его ученик — 4 детали.
а) Сколько деталей сделает ученик токаря за то же время, за которое токарь сделает 27 деталей?
б) Сколько времени потратит ученик токаря на задание, которое токарь выполняет за 1 ч?а) ↓ 6 деталей токарь — 4 детали ученик ↓
↓ 27 деталей токарь — х деталей ученик ↓
Количество деталей токаря прямо пропорционально количеству деталей ученика, тогда:
6/27 = 4/х
х = 27•4/6 = 9•4/2 = 9•2/1 = 18 (деталей)
Ответ: 18 деталей сделает ученик.б) Если исходить из условия, что за 1 час токарь делает 6 деталей (хотя нигде в условии этого не сказано), то:
↑ 6 деталей — 1 ч токарь ↓
↑ 4 деталей — х ч ученик ↓
Количество деталей изготовляемых учеником за одно время с токарем обратно пропорционально времени выполнения учеником задания токаря, тогда:
6/4 = x/1
x = 6•1/4 = 3/2 = 1 1/2 ч
1/2 ч = 1/2 • 60 мин = 60/2 мин = 30 мин
Более правильно сравнить работу токаря и ученика за одинаковое время: 6 деталей : 4 детали = 6/4 = 3/2 раза — медленнее работает ученик, чем токарь. Следовательно, ученик на выполнение задания потратит в 3/2 раза больше времени, чем токарь: 1 ч • 3/2 = 3/2 ч = 1 1/2 ч = 1 ч 30 мин.
Ответ: 1 1/2 ч или 1 ч 30 мин потратит ученик на то же самое задание, которое токарь делает за 1 час.87. За одно и то же время пешеход прошел 6 км, а велосипедист проехал 18 км.
а) Сколько километров проехал велосипедист за то же время, за которое пешеход прошел 10 км?
б) Сколько времени потратил велосипедист на тот путь, который пешеход прошел за 2 ч?а) ↓ 6 км пешеход — 18 км велосипедист ↓
↓ 10 км пешеход — x км велосипедист ↓
Расстояние, пройденное пешеходом, прямо пропорционально расстоянию, преодоленному велосипедистом, тогда:
6/10 = 18/x
x = 10•18/6 = 10 • 3 = 30 (км)
Ответ: 30 км проедет велосипедист.б) Если исходить из условия, что за 2 часа пешеход прошёл 6 км (хотя нигде в условии этого не сказано), то:
↑ 6 км пешеход — 2 ч пешеход ↓
↑ 18 км велосипедист — x ч велосипедист ↓
Расстояние обратно пропорционально времени в пути, тогда:
6/18 = x/2
x = 6•2/18 = 12/18 = 2/3 (ч)
2/3 ч = 2/3 • 60 мин = 2•60/3 мин = 2 • 20 мин = 40 мин
Более правильно сравнить расстояние, которое преодолевают пешеход и велосипедист за одинаковое время: 18 км : 6 км = 18/6 = 3 раза — медленнее передвигается пешеход, чем велосипедист. Следовательно, велосипедист на путь, пройденный пешеходом, потратит в 3 раза меньше времени, чем пешеход: 2 ч : 3 = 2/3 ч = 40 мин.
Ответ: 2/3 ч или 40 мин потратит велосипедист.88. Некоторую работу 6 человек сделают за 18 дней. За сколько дней сделают ту же работу 9 человек, работающих так же успешно, как и первые?
↓ 6 человек — 18 дней ↑
↓ 9 человек — х дней ↑
Количество человек обратно пропорционально количеству рабочих дней, тогда:
6/9 = х/18
х = 6•18/9 = 6 • 2 = 12 (дней)
Ответ: 9 человек выполнят работу за 12 дней.89. а) Шесть маляров выполняют работу за 5 дней. Сколько еще маляров надо пригласить, чтобы все вместе они выполнили то же задание за 3 дня?
б) Двое рабочих могли выполнить задание за 10 дней. Сколько еще рабочих надо пригласить, чтобы все вместе они выполнили то же задание за 4 дня?а) ↓ 6 маляров — 5 дней ↑
↓ х маляров — 3 дня ↑
Количество маляров обратно пропорционально количеству рабочих дней, тогда:
1) 6/х = 3/5
х = 6•5/3 = 2 • 5 = 10 (маляров) — выполнят работу за 10 дней
2) 10 — 6 = 4 (маляра)
Ответ: необходимо пригласить 4 маляра.б) ↓ 2 рабочих — 10 дней ↑
↓ х рабочих — 4 дня ↑
Количество рабочих обратно пропорционально количеству рабочих дней, тогда:
1) 2/х = 4/10
х = 2•10/4 = 10/2 = 5 (рабочих) — выполнят работу за 4 дня
2) 5 — 2 = 3 (рабочих)
Ответ: необходимо пригласить 3 рабочих. 23
-
Ответы к стр. 23
90. Из «Арифметики» Л. Ф. Магницкого. Некий господин позвал плотника и велел двор построить. Дал ему двадцать человек работников и спросил, в сколько дней построят они его двор. Плотник ответил: в тридцать дней. А господину надобно в 5 дней построить, и ради того спросил он плотника: сколько человек тебе надо иметь, дабы с ними ты построил двор в 5 дней; и плотник, недоумевая, спрашивает тебя, арифметик: сколько человек ему надо иметь, чтобы построить тот двор в 5 дней?
↓ 20 работников — 30 дней ↑
↓ х работников — 5 дней ↑
Количество работников обратно пропорционально количеству рабочих дней, тогда:
20/х = 5/30
х = 20•30/5 = 4 • 30 = 120 (работников)
Ответ: 120 работников потребуется для постройки двора за 5 дней.91. Из «Сборника задач и упражнений по арифметике» С. А. Пономарёва и Н. И. Сырнева. а) Скорость парохода относится к скорости течения как 36 : 5. Пароход двигался по течению 5 ч 10 мин. Сколько времени потребуется ему чтобы вернуться обратно?
б) Катер проходит определенное расстояние в стоячей воде за 12 ч. То же расстояние он может пройти по течению за 10 ч. Против течения катер идёт со скоростью 24 км/ч. Определите скорость катера по течению.а) 5 ч 10 мин = 310 мин
36 + 5 = 41 часть — составляет скорость по течению
36 — 5 = 31 часть — составляет скорость против течения
↓ 310 мин — 41 часть ↑
↓ х мин — 31 часть ↑
Время в пути обратно пропорционально скорости парохода, тогда:
310/х = 31/41
х = 310•41/31 = 10 • 41 = 410 (мин)
410 мин = 410/60 ч = 6 50/60 ч = 6 5/6 ч = 6 часов 50 минут
Ответ: 6 часов 50 минут потребуется пароходу на путь обратно.б) 12 : 10 — отношение скорости катера по течению к скорости катера в стоячей воде
12 — 10 = 2 части — составляет скорость течения
10 — 2 = 8 частей — составляет скорость катера против течения
↓ 24 км/ч — 8 частей ↓
↓ х км/ч — 12 частей ↓
Скорость катера против течения прямо пропорциональна скорости катера по течению, тогда:
24/х = 8/12
х = 24•12/8 = 3 • 12 = 36 (км/ч)
Ответ: скорость катера по течению 36 км/ч.Ищем информацию
92. Найдите в учебнике, справочной литературе или Интернете, как решали задачи напрямую и обратную пропорциональности во времена Л. Ф. Магницкого и в средневековой Европе. Придумайте задачу на прямую или обратную пропорциональность и решите её старинным способом.
Во времена Леонтия Магницкого задачи на прямую и обратную пропорциональность решали методом тройного правила. Это правило называли строкой потому, что для простоты вычислений данные записывались в строку. Правильность такого решения целиком зависела от правильности записи данных задачи: порядок записи для задач на прямую и обратную пропорциональности отличался.
Тройное правило: перемножить второе и третье число и произведение разделить на первое.
Тройное правило применяли при решении задач в средние века.Прямая пропорциональность. Мотоциклист проехал 100 км за 2 ч. Какой путь он проедет за 5 часов?
Запись в строку: 2 – 100 – 5.
Вычисление: 100 • 5 : 2 = 500 : 2 = 250 (км)
Ответ: за 5 часов мотоциклист проедет 250 км.Обратная пропорциональность. Мотоциклист проехал путь со скоростью 40 км/ч за 3 ч. За какое время он проедет этот же путь со скоростью 60 км/ч?
Запись в строку: 60 – 3 – 40.
Вычисление: 3 • 40 : 60 = 120 : 60 = 2 (ч)
Ответ: со скоростью 60 км/ч мотоциклист проедет путь за 2 часа. 25
-
Отношения, пропорции, проценты
Понятие о процентеОтветы к стр. 25
93. Что называют процентом?
Сотую часть числа (величины) называют процентом этого числа (величины).
94. Как найти несколько процентов числа?
Чтобы найти p процентов от числа (величины) А, надо найти р/100 от А, то есть вычислить р/100 • А.
26
-
Ответы к стр. 26
95. Запишите проценты в виде дроби:
1 %, 5 %, 70 %, 100 %, 120 %, 150 %, 200 %, 1020 %.1 % = 1 : 100 = 1 • 1/100 = 1/100;
5 % = 5 : 100 = 5 • 1/100 = 5/100 = 1/20;
70 % = 70 : 100 = 70 • 1/100 = 70/100 = 7/10;
100 % = 100 : 100 = 100 • 1/100 = 100/100 = 1;
120 % = 120 : 100 = 120 • 1/100 = 120/100 = 6/5 = 1 1/5;
150 % = 150 : 100 = 150 • 1/100 = 150/100 = 3/2 = 1 1/2;
200 % = 200 : 100 = 200 • 1/100 = 200/100 = 2;
1020 % = 1020 : 100 = 1020 • 1/100 = 1020/100 = 102/10 = 10 1/5.
96. Прочитайте предложение, запишите число процентов в виде дроби, прочитайте полученное предложение:
а) Число 25 составляет 25 % от 100;
6) Число 20 составляет 50 % от 40;
в) Число 500 увеличили на 10 % и получили 550.а) Число двадцать пять составляет двадцать пять процентов от ста.
25 % = 25 • 1/100 = 25/100 = 1/4
Число 25 составляет 1/4 от 100 ⇔ Число двадцать пять составляет одну четвёртую от ста.б) Число двадцать составляет пятьдесят процентов от сорока.
50 % = 50 • 1/100 = 50/100 = 1/2
Число 20 составляет 1/2 от 40 ⇔ Число двадцать составляет одну вторую от сорока.в) Число пятьсот увеличили на десять процентов и получили пятьсот пятьдесят.
10 % = 10 • 1/100 = 10/100 = 1/10
Число 500 увеличили на 1/10 и получили 550 ⇔ Число пятьсот увеличили на одну десятую и получили пятьсот пятьдесят.97. Запишите дроби в виде процентов:
а) 1/100, 3/100, 5/100, 10/100, 1/10, 1/20; б) 1/50, 1/5, 1/2, 1/4, 2, 1 15/100.а) 1/100 • 100 = 100/100 = 1 %,
3/100 • 100 = 300/100 = 3 %,
5/100 • 100 = 500/100 = 5 %,
10/100 • 100 = 1000/100 = 10 %,
1/10 • 100 = 100/10 = 10 %,
1/20 • 100 = 100/20 = 5 %;
б) 1/50 • 100 = 100/50 = 2 %,
1/5 • 100 = 100/5 = 20 %,
1/2 • 100 = 100/2 = 50 %,
1/4 • 100 = 100/4 = 25 %,
2 • 100 = 200 %;
1 15/100 • 100 = 115/100 • 100 = 115 %.
98. В начале XX века в России из каждых 100 человек, занятых в хозяйстве, 9 человек работали в промышленности, 75 работали в сельском хозяйстве, 9 человек работали в торговле. Выразите в процентах долю работников, занятых в промышленности, сельском хозяйстве и в торговле, от общего числа занятых в хозяйстве.
9/100 — доля работающих в промышленности,
9/100 • 100 % = 9 % работали в промышленности;75/100 — доля работающих в сельском хозяйстве,
75/100 • 100 % = 75 % работали в сельском хозяйстве;9/100 — доля работающих в торговле,
9/100 • 100 % = 9 % работали в торговле.Ответ: 9 % работали в промышленности, 75 % работали в сельском хозяйстве, 9 % работали в торговле.
99. Найдите 1 % от:
а) 1 метра; б) 1 центнера; в) 1 килограмма.а) 1 м = 100 см,
100 см • 1/100 = 100/100 см = 1 см;б) 1 ц = 100 кг,
100 кг • 1/100 = 100/100 кг = 1 кг;в) 1 кг = 1000 г,
1000 г • 1/100 = 1000/100 г = 10 г.100. Найдите 5 %, 17 %, 23 % от:
а) 1 метра;
б) 1 центнера;
в) 1 килограмма.а) 1 метр = 100 см,
100 см • 5/100 = 500/100 см = 5 см,100 см • 17/100 = 1700/100 см = 17 см.
100 см • 23/100 = 2300/100 см = 23 см;
б) 1 центнер = 100 кг,
100 кг • 5/100 = 500/100 кг = 5 кг,100 кг • 17/100 = 1700/100 кг = 17 кг,
100 кг • 23/100 = 2300/100 кг = 23 кг;
в) 1 кг = 1000 г,
1000 г • 5/100 = 5000/100 кг = 50 г,1000 г • 17/100 = 17000/100 кг = 170 г,
1000 г • 23/100 = 23000/100 кг = 230 г.
101. Найдите:
а) 1 % от 100; б) 1 % от 300; в) 5 % от 40;
г) 7 % от 200; д) 20 % от 15; е) 25 % от 48;
ж) 100 % от 49; з) 120 % от 250; и) 200 % от 300.а) 1/100 • 100 = 100/100 = 1;
б) 1/100 • 300 = 300/100 = 3;
в) 5/100 • 40 = 200/100 = 2;
г) 7/100 • 200 = 1400/100 = 14;
д) 20/100 • 15 = 300/100 = 3;
е) 25/100 • 48 = 1200/100 = 12;
ж) 100/100 • 49 = 4900/100 = 49;
з) 120/100 • 250 = 30000/100 = 300;
и) 200/100 • 300 = 60000/100 = 600.
102. Служащий вложил 500 р. в акции своего предприятия и получил 20% дохода. Сколько рублей дохода он получил?
20/100 • 500 = 10000/100 = 100 (р.)
Ответ: 100 рублей дохода получил служащий.103. Какую часть числа составляют его:
а) 1 %; б) 5 %; в) 10 %; г) 20 %;
д) 25 %; е) 50 %; ж) 75 %; з) 100 %?а) 1 % = 1 • 1/100 = 1/100 — числа составляет 1 %;
б) 5 % = 5 • 1/100 = 5/100 = 1/20 — числа составляет 5 %;
в) 10 % = 10 • 1/100 = 10/100 = 1/10 — числа составляет 10 %;
г) 20 % = 20 • 1/100 = 20/100 = 1/5 — числа составляет 20 %;
д) 25 % = 25 • 1/100 = 25/100 = 1/4 — числа составляет 25 %;
е) 50 % = 50 • 1/100 = 50/100 = 1/2 — числа составляет 50 %;
ж) 75 % = 75 • 1/100 = 75/100 = 3/4 — числа составляет 75 %;
з) 100 % = 100 • 1/100 = 100/100 = 1 числа составляет 100 %.
104. Вычислите:
а) 50 % от 400; б) 10 % от 20; в) 25 % от 16; г) 75 % от 8.а) 50 % • 1/100 • 400 = 50•400/100 = 50 • 4 = 200;
б) 10% • 1/100 • 20 = 10•20/100 = 20/10 = 2;
в) 25% • 1/100 • 16 = 25•16/100 = 16/4 = 4;
г) 75% • 1/100 • 8 = 75•8/100 = 3•8/4 = 3 • 2 = 6.
105. Из сахарной свёклы получают сахар, масса которого составляет 18 % массы свеклы. Сколько сахара получится при переработке:
а) 40 т свёклы; б) 30 т свёклы; в) 500 т свёклы.а) 18 • 1/100 • 40 = 18•40/100 = 18•2/5 = 36/5 = 7 1/5 (т)
1/5 т = 1/5 • 1000 кг = 1000/5 кг = 200 кг
Ответ: 7 1/5 т или 7 т 200 кг сахара.б) 18 • 1/100 • 30 = 18•30/100 = 18•3/10 = 54/10 = 27/5 = 5 2/5 (т)
2/5 т = 2/5 • 1000 кг = 2000/5 кг = 400 кг
Ответ: 5 2/5 т или 5 т 400 кг сахара.в) 18 • 1/100 • 500 = 18•500/100 = 18 • 5 = 90 (т)
Ответ: 90 т сахара.106. Магнитный железняк содержит 70% чистого железа. Сколько тонн железа в 13 т железняка?
70 • 1/100 • 13 = 70•13/100 = 7•13/10 = 91/10 = 9 1/10 (т)
Ответ: 9 1/10 т железняка.107. Сплав содержит 62% олова и 38% свинца. Сколько граммов олова и сколько свинца в 400 г сплава?
1) 62 • 1/100 • 400 = 62•400/100 = 62 • 4 = 248 (г) — олова в 400 г сплава
2) 38 • 1/100 • 400 = 38•400/100 = 38 • 4 = 152 (г) — свинца в 400 г сплава
Ответ: 248 г олова и 152 г свинца в 400 г сплава. 27
-
Ответы к стр. 27
108. Папа потратил 2000 р. на подарки маме и нам — детям. На подарок маме он потратил 40 % этой суммы, мне и моей сестре по 30 %. Все ли деньги потратил папа? Нет ли в задаче лишних данных?
40 % + 30 % + 30 % = 100 % — всех денег потратил папа, а так как все его деньги составляют 100 %, значит он потратил все деньги
Ответ: папа потратил все деньги, 2000 р. — лишнее данное.109. а) 25% учащихся класса соревновались в прыжках в высоту, еще 75% — в прыжках в длину. Все ли учащиеся класса участвовали в соревнованиях?
б) Туристы проехали 80% намеченного маршрута на поезде и 15% — на автобусе. Весь ли маршрут они проехали?
в) Маша потратила 70% имевшихся у неё денег на книги и 30% на тетради. Все ли деньги потратила Маша.а) 25 % + 75 % = 100 % учащихся участвовали в соревнованиях, а так как все учащиеся класса составляют 100 %, значит все учащиеся класса участвовали в соревнованиях
Ответ: все учащиеся класса участвовали в соревнованиях.б) 1) 80 % + 15 % = 95 % — маршрута проехали туристы
2) 100 % — 95 % = 5 % — маршрута туристы не проехали
Ответ: туристы проехали не весь маршрут.в) 70 % + 30 % = 100 % — денег потратила Маша, а так как все её деньги составляют 100 %, значит она потратила все деньги
Ответ: Маша потратила все деньги.110. Учительница сказала: «С контрольной работой справились 100% учащихся нашего класса». Как это понимать?
Все учащиеся класса составляют 100 %, а так как 100 % учащихся справились с контрольной работой, значит все учащиеся класса справились с контрольной работой.
Ответ: все учащиеся класса справились с контрольной работой.111. а) Потратили 80 % суммы. Сколько процентов этой суммы осталось?
б) Мужчины составляют 75 % всех работников завода. Сколько процентов составляют женщины?
в) Девочки составляют 40 % класса. Сколько процентов класса составляют мальчики?а) вся сумма составляет 100 %
100 % — 80 % = 20 %
Ответ: 20 % суммы осталось.б) все работники завода составляют 100%
100 % — 75 % = 25 %
Ответ: 25 % женщин работает на заводе.в) все дети класса составляют 100%
100 % — 40 % = 60 %
Ответ: 60 % мальчиков учится в классе.112. а) Найдите 15 % числа 36.
б) Найдите число, 15 % которого равны 36.а) 15 • 1/100 • 36 = 15•36/100 = 3•36/20 = 3•9/5 = 27/5 = 5 2/5.
б) 36/15 • 100 = 3600/15 = 240.
113. Найдите число:
а) 1 % которого равен 3; б) 10 % которого равны 40;
в) 15 % которого равны 30; г) 50 % которого равны 250.а) 3/1 • 100 = 300;
б) 40/10 • 100 = 4 • 100 = 400;
в) 30/15 • 100 = 2 • 100 = 200;
г) 250/50 • 100 = 5 • 100 = 500.
114. Запишите дробь в виде процентов:
а) 4/5; б) 5/4; в) 3/4; г) 13/25; д) 17/20; е) 4/3.а) 4/5 = 4/5 • 100 = 400/5 = 80 %;
б) 5/4 = 5/4 • 100 = 500/4 = 125 %;
в) 3/4 = 3/4 • 100 = 300/4 = 75 %;
г) 13/25 = 13/25 • 100 = 13•100/25 = 13 • 4 = 52 %;
д) 17/20 = 17/20 • 100 =17•100/20 = 17 • 5 = 85 %;
е) 4/3 = 4/3 • 100 = 400/3 = 133 1/3 %.
28
-
Ответы к стр. 28
115. а) В магазин привезли партию лампочек. Среди них оказалось 16 разбитых лампочек, что составило 2 % от общего числа. Сколько лампочек привезли в магазин?
б) Посадили семена гороха, 270 из них взошли. Это составило 90 % от всех посаженных семян. Сколько семян посадили?а) 16/2 • 100 = 8 • 100 = 800 (лампочек)
Ответ: 800 лампочек привезли в магазин.б) 270/90 • 100 = 3 • 100 = 300 (семян)
Ответ: 300 семян гороха всего посадили.116. Из 16 кг свежих груш получили 4 кг сушёных. Какую часть от массы свежих груш составляет масса сушённых? Выразите эту часть в процентах. Сколько процентов массы теряется при сушке?
1) 4 кг : 16 кг = 1/4 — составляет масса сушенных груш от массы свежих
2) 1/4 • 100 = 100/4 = 25 % — составляет масса сушенных груш от массы свежих
3) 100 % — масса свежих груш, 25 % — масса груш после сушки
100 % — 25 % = 75 % — массы груш теряется при сушке
Ответ: 1/4 или 25 % составляет масса сушенных груш от массы свежих, 75 % массы груш теряется при сушке.117. Сколько процентов числа 50 составляет число 40? Сколько процентов числа 40 составляет число 50?
40/50 • 100 = 4•100/5 = 4 • 20 = 80%.
50/40 • 100 = 5•100/4 = 5 • 25 = 125%.
118. а) Посадили 50 семян, 47 из них взошли. Определите процент всхожести семян.
б) В школе 400 учащихся, 12 из них учатся на «5». Сколько процентов учащихся школы учится на «5»?а) 47/50 • 100 = 47•100/50 = 47 • 2 = 94 (%)
Ответ: всхожесть семян 94 %.б) 12/400 • 100 = 12•100/400 = 12/4 = 3 (%)
Ответ: 3 % учащихся учатся на «5».119. Маша прочитала 120 страниц, и ей ещё осталось прочитать 130 страниц книги.
а) Сколько процентов всех страниц она прочитала?
б) Сколько процентов всех страниц ей осталось прочитать?120 + 130 = 250 — всего страниц в книге
а) 120/250 • 100 = 120•100/250 = 12 • 4 = 48 (%) — книги прочитано
б) 130/250 • 100 = 130•100/250 = 13 • 4 = 52 (%) — книги не прочитано
Ответ: прочитано 48% всех страниц, осталось прочитать 52% всех страниц.120. В июле было 12 солнечных и 18 пасмурных дней. Сколько процентов составили:
а) солнечные дни;
б) пасмурные дни.12 + 18 = 30 — всего дней в июле
а) 12/30 • 100 = 12•100/30 = 120/3 = 40 (%) — солнечных дней
б) 18/30 • 100 = 18•100/30 = 180/3 = 60 (%) — пасмурных дней
Ответ: 40% солнечных дней, 60% пасмурных дней.121. В одном килограмме сыра содержится 200 г белка. Сколько процентов белка содержится в сыре?
1 кг = 1000 г
200/1000 • 100 = 200•100/1000 = 200/10 = 20 (%)
Ответ: 20% белка содержится в сыре. 29
-
Отношения, пропорции, проценты
Задачи на процентыОтветы к стр. 29
122. а) В магазин привезли 2500 кг лука. Продали 30% всего лука. Сколько килограммов лука осталось продать?
б) В школе 400 учащихся, 52 % этого числа составляют девочки. Сколько мальчиков в школе?а) 30 % = 30/100
2500 • 30/100 = 2500•30/100 = 25 • 30 = 750 (кг) – лука продано
2500 − 750 = 1750 (кг) — лука осталось продатьили
100 – 30 = 70 (%) – лука осталось продать
2500 • 70/100 = 2500•70/100 = 25 • 70 = 1750 (кг) – лука осталось продатьили
100 – 30 = 70 (%) – лука осталось продать
↓ 2500 кг – 100 % ↓
↓ х кг – 70 % ↓
2500/х = 100/70
х = 2500•70/100 = 25 • 70 = 1750 (кг) – лука осталось продать
Ответ: 1750 кг лука осталось продать.б) 52 % = 52/100
400 • 52/100 = 400•52/100 = 4 • 52 = 208 (уч.) – девочки
400 − 208 = 192 (уч.) — мальчикиили
100 – 52 = 48 (%) – мальчики
400 • 48/100 = 400•48/100 = 4 • 48 = 192 (уч.) – мальчикиили
100 – 52 = 48 (%) – мальчики
↓ 400 уч. – 100 % ↓
↓ х уч. – 48 % ↓
400/х = 100/48
х = 400•48/100 = 4 • 48 = 192 (уч.) – мальчики
Ответ: 192 мальчика в школе.123. Масса сушёных груш составляет 20 % массы свежих. Сколько килограммов сушёных груш получится из 100 кг; 350 кг; 25 кг свежих? Сколько процентов массы свежих груш теряется при сушке?
100 кг • 20 % = 100 • 20/100 = 20 (кг)
350 кг • 20 % = 350 • 20/100 = 350/5 = 70 (кг)
25 кг • 20 % = 25 • 20/100 = 20/4 = 5 (кг)
100 % — 20 % = 80 % — массы груш теряется при сушке
Ответ: получится 20 кг; 70 кг; 5 кг сушёных груш, 80 % массы теряется при сушке. 30
-
Ответы к стр. 30
124. Виноград при сушке теряет 70 % своей массы. Сколько изюма (сушёного винограда) получится из 100 кг; 250 кг; 80 кг свежего винограда?
100 % — 70 % = 30 % — составляет масса изюма от свежего винограда
100 кг • 30% = 100 • 30/100 = 30 (кг) — изюма
250 кг • 30% = 250 • 30/100 = 25 • 3 = 75 (кг) — изюма
80 кг • 30% = 80 • 30/100 = 8 • 3 = 24 (кг) — изюма
Ответ: получится 30 кг; 75 кг; 24 кг изюма.125. Припой содержит 40 % олова, 2% сурьмы, остальную часть составляет свинец. Сколько граммов олова, свинца и сурьмы в 300 г припоя?
1) 100 % — (40 % + 2 %) = 58 % — свинца содержится в припое
2) 300 г • 40 % = 300 • 40/100 = 3 • 40 = 120 (г) — олова содержится в припое
3) 300 г • 2 % = 300 • 2/100 = 3 • 2 = 6 (г) — сурьмы содержится в припое
4) 300 г • 58 % = 300 • 58/100 = 3 • 58 = 174 (г) — свинца содержится в припое
Ответ: 120 г олова, 6 г сурьмы и 174 г свинца в 300 г припоя.126. Токарь до обеденного перерыва обточил 24 детали, что составляет 60 % сменной нормы. Сколько деталей должен обточить токарь за смену?
↑ 24 детали — 60 % ↑
↑ х деталей — 100 % ↑
24/х = 60/100
х = 24•100/60 = 4 • 10 = 40 (деталей)
Ответ: 40 деталей должен обточить токарь за смену.127. а) Туристы прошли 75% маршрута, и им осталось пройти ещё 5 км. Какова длина всего маршрута?
б) Туристы прошли 5% маршрута, и им осталось пройти ещё 19 км. Какова длина всего маршрута?а) 100 % — 75 % = 25 % — маршрута осталось пройти
↓ 5 км — 25 % ↓
↓ х км — 100 % ↓
5/х = 25/100
х = 5•100/25 = 5 • 4 = 20 (км)
Ответ: длина всего маршрута 20 км.б) 100 % — 5 % = 95 % — маршрута осталось пройти
↓ 19 км — 95 % ↓
↓ х км — 100 % ↓
19/х = 95/100
х = 19•100/95 = 19•20/19 = 20 (км)
Ответ: длина всего маршрута 20 км.128. Что больше:
а) 30 % от 40 или 40 % от 30; б) 80 % от 60 или 60 % от 70?а) 40 • 30 % = 40 • 30/100 = 40•30/100 = 4 • 3 = 12,
30 • 40 % = 30 • 40/100 = 30•40/100 = 3 • 4 = 12,
12 = 12, следовательно, 30 % от 40 = 40 % от 30;б) 60 • 80 % = 60 • 80/100 = 60•80/100 = 6 • 8 = 48,
70 • 60 % = 70 • 60/100 = 70•60/100 = 7 • 6 = 42,
48 > 42, следовательно, 80 % от 60 > 60 % от 70.129. Определите без вычислений, что больше:
а) 12 % от 34 или 13 % от 34; б) 12 % от 49 или 12 % от 50.а) 12 % от 34 < 13 % от 34, так как 12 % < 13 %;
б) 12 % от 49 < 12 % от 50, так как 49 < 50.130. Товар стоил 500 р. Его цена повысилась на 20 %. На сколько рублей повысилась цена?
500 • 20 % = 500 • 20/100 = 500•20/100 = 5 • 20 = 100 (р.)
Ответ: на 100 рублей повысилась цена.131. У Алёши 80 марок, у Бори на 20% больше, чем у Алёши. У Вовы на 25% меньше, чем у Алёши. Сколько марок у Бори и Вовы в отдельности?
1) 80 • 20 % = 80 • 20/100 = 8 • 2 = 16 (марок) — составляют 20 % от марок Алёши
2) 80 + 16 = 96 (марок) — у Бори
3) 80 • 25 % = 80 • 25/100 = 80/4 = 20 (марок) — составляют 25 % от марок Алёши
4) 80 — 20 = 60 (марок) — у Вовы
Ответ: 96 марок у Бори, 60 марок у Вовы.132. Увеличьте число:
а) 60 на 10 %; б) 80 на 25 %;
в) 40 на 50 %; г) 425 на 4%.а) 60 + 60 • 10 % = 60 + 60 • 10/100 = 60 + 6 = 66;
б) 80 + 80 • 25 % = 80 + 80 • 25/100 = 80 + 80/4 = 80 + 20 = 100;
в) 40 + 40 • 50 % = 40 + 40 • 50/100 = 40 + 40/2 = 40 + 20 = 60;
г) 425 + 425 • 4 % = 425 + 425 • 4/100 = 425 + 425/25 = 425 + 17 =442.133. Уменьшите число:
а) 60 на 10 %; 6) 80 на 25 %; в) 90 на 50 %; г) 125 на 20 %.а) 60 — 60 • 10 % = 60 — 60 • 10/100 = 60 — 6 = 54;
б) 80 — 80 • 25 % = 80 — 80 • 25/100 = 80 — 80/4 = 80 — 20 = 60;
в) 90 — 90 • 50 % = 90 — 90 • 50/100 = 90 — 90/2 = 90 — 45 = 45;
г) 125 — 125 • 20 % = 125 — 125 • 20/100 = 125 — 125/5 = 125 — 25 = 100.134. а) Увеличьте число 80 на 20 %; 30 %; 65 %; 80 %.
б) Уменьшите число 60 на 15 %; 20 %; 25 %; 75 %.а) 80 + 80 • 20 % = 80 + 80 • 20/100 = 80 + 8 • 2 = 80 + 16 = 96;
80 + 80 • 30 % = 80 + 80 • 30/100 = 80 + 8 • 3 = 80 + 24 = 104;
80 + 80 • 65 % = 80 + 80 • 65/100 = 80 + 8•13/2 = 80 + 4 • 13 = 80 + 52 = 132;
80 + 80 • 80 % = 80 + 80 • 80/100 = 80 + 8 • 8 = 80 + 64 = 144.б) 60 — 60 • 15 % = 60 — 60 • 15/100 = 60 — 60•3/20 = 60 — 3 • 3 = 60 — 9 = 51;
60 — 60 • 20 % = 60 — 60 • 20/100 = 60 — 6 • 2 = 60 — 12 = 48;
60 — 60 • 25 % = 60 — 60 • 25/100 = 60 — 60/4 = 60 — 15 = 45;
60 — 60 • 75% = 60 — 60 • 75/100 = 60 — 60•3/4 = 60 — 15 • 3 = 60 — 45 = 15.135. Мясо при варке теряет 40 % своей массы
а) Сколько варёного мяса получится из 6 кг свежего?
б) Сколько свежего мяса нужно взять, чтобы получить 6 кг варёного?а) 100 % — 40 % = 60 % — массы мяса останется после варки
↑ 6 кг — 100 % ↑
↑ х кг — 60 % ↑
6/х = 100/60
х = 6•60/100 = 36/10 = 18/5 = 3 3/5 (кг)
Ответ: 3 3/5 кг мяса останется после варки.б) 100 % — 40 % = 60 % — массы мяса останется после варки
↓ 6 кг — 60 % ↓
↓ х кг — 100 % ↓
6/х = 60/100
х = 6•100/60 = 1 • 10 = 10 (кг)
Ответ: 10 кг свежего мяса нужно взять.Придумываем задачу
136. Найдите в справочной литературе, школьных учебниках по другим предметам, периодической печати или Интернете примеры применения процентов. Составьте задачу на проценты и решите её.
Примеры применения процентов:
— самая длинная кость в скелете человека – бедренная: ее длина составляет обычно 27 % от роста человека;
— общая мышечная масса мужчины составляет около 40 % от веса тела, а женщины — около 30 %;
— медузы на 98-99 % состоят из воды, хотя они не растворяются в море и их можно взять в руки;
— страна с самым большим количеством озёр — Канада: 60 % всех озёр мира находятся на её территории и занимают 9 % канадских земель;
— самая засушливая страна — Ливия: 99 % её территории составляют пустыни;
— в Сибири растёт примерно 25 % мировых лесов.Примеры задач:
Самая длинная кость в скелете человека — бедренная: ее длина составляет обычно 27 % от роста человека. Вычислите длину бедренной кости человека, рост которого составляет 170 см.
170 • 27/100 = 17•27/10 = 459/10 = 45 9/10 (см)
Ответ: 45 9/10 см длина бедренной кости.Общая мышечная масса мужчины составляет около 40 % от веса тела. Какова мышечная масса мужчины весом 85 кг?
85 • 40/100 = 85•4/10 = 340/10 = 34 (кг)
Ответ: мышечная масса 34 кг. 32
-
Отношения, пропорции, проценты
Круговые диаграммыОтветы к стр. 32
137. Сколько градусов содержит развёрнутый угол? Сколько градусов содержит полный угол?
Развёрнутый угол — 180°, полный угол — 360°.
138. Используя круговую диаграмму (рис. 9) скажите, сколько в доме однокомнатных квартир; двухкомнатных; трёхкомнатных.
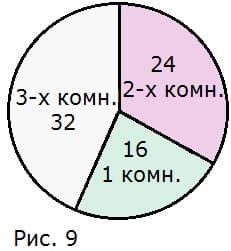
Ответ:
16 однокомнатных квартир; 24 двухкомнатных квартир; 32 трёхкомнатных квартир.
139. На круговой диаграмме (рис. 10) показан процентный состав населения города N. Сколько мужчин, женщин и детей живёт в городе N, если всего в нем 48 тыс. жителей?
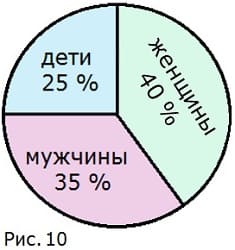
48 000 • 35/100 = 48000•35/100 = 480 • 35 = 16 800 (чел.) — мужчин
48 000 • 40/100 = 48000•40/100 = 480 • 40 = 19 200 (чел.) — женщин
48 000 • 25/100 = 48000•25/100 = 480 • 25 = 12 000 (чел.) — детей
Ответ: 16 800 мужчин, 19 200 женщин, 12 000 детей.140. На круговой диаграмме (рис. 11) показано содержание металлов в сплаве. Сколько граммов олова, свинца и других металлов содержится в 200 г такого сплава?
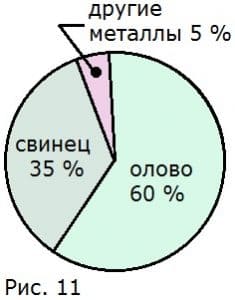
1) 200 • 60/100 = 2 • 60 = 120 (г) — олова содержится в сплаве
2) 200 • 35/100 = 2 • 35 = 70 (г) свинца содержится в сплаве
3) 200 • 5/100 = 2 • 5 = 10 (г) — других металлов содержится в сплаве
Ответ: 120 г олова, 70 г свинца, 10 г других металлов.141. Постройте круговую диаграмму, отражающую результаты выполнения контрольной работы по русскому языку в 7 классе: «5» получили 3 человека, «4» − 12 человек, «3» − 15 человек («2» и «1» нет).
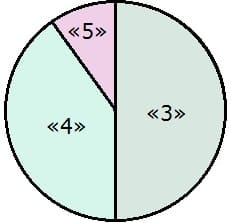
360° — все ученики в классе
1) 3 + 12 + 15 = 30 (чел.) — всего учатся в классе
2) 360° : 30 = 12° — соответствует 1 ученику на диаграмме
3) 12° • 3 = 36° — соответствует ученикам, получившим «5»
4) 12° • 12 = 144° — соответствует ученикам, получившим «4»
5) 12° • 15 = 180° — соответствует ученикам получившим «3»
Ответ: 36° — «5», 144° — «4», 180° — «3».142. Постройте круговую диаграмму «Мой режим дня».
Мой режим дня:
Подъем и сбор в школу — 7.00-7.30
Дорога в школу — 7.30-8.00
Занятия в школе — 8.00-14.30
Дорога из школы — 14.30-15.00
Обед — 15.00-15.30
Отдых, прогулка, посещение секций 15.30-17.30
Ужин 17.30-18.00
Приготовление домашних заданий 18.00-21.30
Приготовление ко сну 21.30-22.00
Сон 22.00-7.00Всего в сутках 24 часа, из них 9 часов уходят на сон и не учитываются в расчёте, то есть в распорядке дня учитываются 24 – 9 = 15 часов. Эти 15 часов соответствуют 360° на диаграмме.
360° : 15 = 24° — соответствует 1 час на диаграмме
Подъем и сбор в школу, дорога в школу, дорога из школы, обед, ужин, приготовление ко сну занимают 30 минут или 1/2 часа: 24 • 1/2 = 24/2 = 12° — соответствует на диаграмме.
Занятия в школе занимают 6 часов 30 минут или 6 1/2 часа: 24 • 6 1/2 = 24•13/2 = 156° – соответствует на диаграмме.
Отдых, прогулка, посещение секций занимают 2 часа: 24 • 2 = 48° – соответствует на диаграмме.
Приготовление домашних заданий занимает 3 часа 30 минут или 3 1/2 часа: 24 • 3 1/2 = 24•7/2 = 84° — соответствует на диаграмме.
Придумываем задачу
143. Используя данные из других школьных предметов, периодической печати или Интернета, придумайте задачу на составление круговой диаграммы.
На склад привезли 5 т цемента, 15 т песка, 3 т кирпичей, 13 т извести, 4 т шифера. Постройте круговую диаграмму, отражающую состав привезённых материалов.
1) 5 + 15 + 3 + 13 + 4 = 40 (т) — всего материалов привезли на склад
2) 360° : 40 = 9° — соответствует 1 т материала на диаграмме
3) 9° • 5 = 45° — соответствует массе цемента на диаграмме
4) 9° • 15 = 135° — соответствует массе песка на диаграмме
5) 9° • 3 = 27° — соответствует массе кирпичей на диаграмме
6) 9° • 13 = 117° — соответствует массе извести на диаграмме
7) 9° • 4 = 36° — соответствует массе шифера на диаграмме 34
-
Отношения, пропорции, проценты
Задачи на перебор всех возможных вариантовОтветы к стр. 34
144. Запишите все двузначные числа, в записи которых используются цифры:
а) 1, 3, 9 без повторения; б) 1, 3, 9 с повторением;
в) 2, 4, 6 без повторения; г) 2, 4, 6 с повторением.а) На первое место можно поставить любую из трёх цифр, на второе место можно поставить только одну из двух оставшихся цифр, то есть имеется 3 • 2 = 6 возможных вариантов записи двузначного числа: 13, 19, 31, 39, 91, 93;
б) На первое место можно поставить любую из трёх цифр, на второе место можно поставить также одну из трёх цифр, то есть имеется 3 • 3 = 9 возможных вариантов записи двузначного числа: 11, 13, 19, 31, 33, 39, 91, 93, 99;
в) На первое место можно поставить любую из трёх цифр, на второе место можно поставить только одну из двух оставшихся цифр, то есть имеется 3 • 2 = 6 возможных вариантов записи двузначного числа: 24, 26, 42, 46, 62, 64;
г) На первое место можно поставить любую из трёх цифр, на второе место можно поставить также одну из трёх цифр, то есть имеется 3 • 3 = 9 возможных вариантов записи двузначного числа: 22, 24, 26, 42, 44, 46, 62, 64, 66.145. Запишите все двузначные числа, в записи которых используются цифры 0, 1, 5: а) без повторения; б) с повторением.
а) На первое место можно поставить любую из трёх цифр, кроме нуля (то есть любую из двух цифр), на второе место можно поставить только одну из двух оставшихся цифр, то есть имеется 2 • 2 = 4 возможных вариантов записи двузначного числа: 10, 15, 50, 51;
б) На первое место можно поставить любую из трёх цифр, кроме нуля (то есть любую из двух цифр), на второе место можно поставить также одну из трёх цифр, то есть имеется 2 • 3 = 6 возможных вариантов записи двузначного числа: 10, 11, 15, 50, 51, 55.
146. Сколько двузначных чисел можно записать цифрами 9, 8, 7: а) с повторением цифр; б) без повторения цифр?
а) На первое место можно поставить любую из трёх цифр, на второе место можно поставить также одну из трёх цифр, то есть имеется 3 • 3 = 9 возможных вариантов записи двузначного числа: 77, 78, 79, 87, 88, 89, 97, 98, 99.
б) На первое место можно поставить любую из трёх цифр, на второе место можно поставить только одну из двух оставшихся цифр, то есть имеется 3 • 2 = 6 возможных вариантов записи двузначного числа: 78, 79, 87, 89, 97, 98.
147. Сколько двузначных чисел можно записать цифрами 0, 2, 4, 6: а) с повторением цифр; б) без повторения цифр?
а) На первое место можно поставить любую из четырёх цифр, кроме нуля (то есть любую из трёх цифр), на второе место можно поставить также одну из четырёх цифр, то есть имеется 3 • 4 = 12 возможных вариантов записи двузначного числа: 20, 22, 24, 26, 40, 42, 44, 46, 60, 62, 64, 66;
б) На первое место можно поставить любую из четырёх цифр, кроме нуля (то есть любую из трёх цифр), на второе место можно поставить только одну из трёх оставшихся цифр, то есть имеется 3 • 3 = 9 возможных вариантов записи двузначного числа: 20, 24, 26, 40, 42, 46, 60, 62, 64.
148. Четыре подружки купили 4 билета в кино. Сколькими различными способами они могут занять свои места в зрительном зале?
Первая девочка может сесть на одно из четырёх мест, вторая девочка может выбрать себе одно из трёх оставшихся мест, третья девочка может выбрать себе одно из двух оставшихся мест, четвертая девочка может выбрать себе одно оставшееся место, то есть 4 • 3 • 2 • 1 = 24 способа занять места.
149. Сколько двузначных; трёхзначных; четырёхзначных чисел можно составить, используя цифры 1, 2, 3, 4, 5 без повторения?
На первое место можно поставить любую из пяти цифр, на второе место можно поставить только одну из четырёх оставшихся цифр, то есть имеется 5 • 4 = 20 возможных вариантов записи двузначного числа.
На первое место можно поставить любую из пяти цифр, на второе место можно поставить только одну из четырёх оставшихся цифр, на третье место можно поставить только одну из трёх оставшихся цифр, то есть имеется 5 • 4 • 3 = 60 возможных вариантов записи трёхзначного числа.
На первое место можно поставить любую из пяти цифр, на второе место можно поставить только одну из четырёх оставшихся цифр, на третье место можно поставить только одну из трёх оставшихся цифр, на четвёртое место можно поставить только одну из двух оставшихся цифр, то есть имеется 5 • 4 • 3 • 2 = 120 возможных вариантов записи четырёхзначного числа.
150. Сколько двузначных; трёхзначных; четырёхзначных чисел можно составить, используя цифры 1, 2, 3, 4, 5 с повторением?
На первое место можно поставить любую из пяти цифр, на второе место можно поставить также любую из пяти цифр, то есть имеется 5 • 5 = 25 возможных вариантов записи двузначного числа.
На первое место можно поставить любую из пяти цифр, на второе и третье место можно поставить также любую из пяти цифр, то есть имеется 5 • 5 • 5 = 125 возможных вариантов записи трёхзначного числа.
На первое место можно поставить любую из пяти цифр, на второе, третье и четвёртое место можно поставить также любую из пяти цифр, то есть имеется 5 • 5 • 5 • 5 = 625 возможных вариантов записи четырёхзначного числа.
151. а) Все четырёхзначные числа, записанные цифрами 1, 2, 3, 4 без повторения, занумеровали в порядке возрастания чисел. Какой номер имеет число 4312?
б) Все пятизначные числа, записанные цифрами 1, 2, 3, 4, 5 без повторения, занумеровали в порядке возрастания чисел. Какой номер имеет число 54 312?
в) Все пятизначные числа, записанные цифрами 1, 2, 3, 4, 5 без повторения, выписывают в порядке возрастания. Сколько чисел в этом списке? Каким по счету в этом списке будет число 54 231?а) На первое место можно поставить любую из четырёх цифр, на второе место можно поставить только одну из трёх оставшихся цифр, на третье место можно поставить только одну из двух оставшихся цифр, на четвёртое место можно поставить только одну последнюю оставшеюся цифру, то есть имеется 4 • 3 • 2 • 1 = 24 возможных вариантов записи четырёхзначного числа. Число 4321 является наибольшим, а значит имеет 24 порядковый номер. Число 4312 идёт перед ним, следовательно, оно имеет 23 порядковый номер.
б) На первое место можно поставить любую из пяти цифр, на второе место можно поставить только одну из четырёх оставшихся цифр, на третье место можно поставить только одну из трёх оставшихся цифр, на четвёртое место можно поставить только одну из двух оставшихся цифр, на пятое место можно поставить только одну последнюю оставшеюся цифру, то есть имеется 5 • 4 • 3 • 2 • 1 = 120 возможных вариантов записи пятизначного числа. Число 54 321 является наибольшим, а значит имеет 120 порядковый номер. Число 54 312 идёт перед ним, следовательно, оно имеет 119 порядковый номер.
в) На первое место можно поставить любую из пяти цифр, на второе место можно поставить только одну из четырёх оставшихся цифр, на третье место можно поставить только одну из трёх оставшихся цифр, на четвёртое место можно поставить только одну из двух оставшихся цифр, на пятое место можно поставить только одну последнюю оставшеюся цифру, то есть имеется 5 • 4 • 3 • 2 • 1 = 120 возможных вариантов записи пятизначного числа. Число 54 321 является наибольшим, а значит имеет 120 порядковый номер. Число 54 312 идёт перед ним, следовательно, оно имеет 119 порядковый номер. А затем идёт число 54 231 под 118 порядковым номером.
35
-
Ответы к стр. 35
152. У круглого стола поставили четыре стула. Сколькими способами можно рассадить на эти стулья:
а) четырёх детей; б) трёх детей; в) двух детей?а) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, четвёртый ребёнок может сесть только на один оставшийся стул , то есть имеется 4 • 3 • 2 • 1 = 24 возможных способа рассадить четырёх детей на стулья.
б) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, третий ребёнок может сесть на любой из двух оставшихся стульев, один стул остаётся свободным, то есть имеется 4 • 3 • 2 = 24 возможных способа рассадить трёх детей на стулья.
в) Первый ребёнок может сесть на любой из четырёх стульев, второй ребёнок может сесть на любой из трёх оставшихся стульев, два стула остаются свободными, то есть имеется 4 • 3 = 12 возможных способа рассадить двух детей на стулья.
153. Мальчика и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?
Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, а с другой стороны — находиться пустой стул.
Мальчик может сесть на любой из четырёх стульев, первая девочка может сесть на любой из двух оставшихся стульев рядом с мальчиком (но только не напротив него), вторая девочка может сесть на оставшийся стул рядом с мальчиком (но только не напротив него), то есть имеется 4 • 2 • 1 = 8 возможных способов рассадить детей.154. Двух мальчиков и двух девочек надо рассадить за круглым столом с четырьмя стульями так, чтобы девочки не оказались рядом. Сколькими способами это можно сделать?
Чтобы девочки не оказались рядом, между ними, с одной стороны должен сидеть мальчик, и с другой стороны тоже сидеть мальчик.
Первая девочка может сесть на любой из четырёх стульев, первый мальчик может сесть на любой из двух оставшихся стульев рядом с девочкой (но только не напротив неё), вторая девочка может сесть на стул рядом с мальчиком и напротив первой девочки, второй мальчик может сесть на оставшийся стул, то есть имеется 4 • 2 • 1 • 1 = 8 возможных способов рассадить детей.155. Бросили два игральных кубика. На первом выпало 3 очка, на втором — 6 очков. (рис. 14). Сколькими разными способами может выпасть сумма в 9 очков? Сколькими различными способами могут выпасть очки на этих кубиках?
Сумму 9 можно получить: 3 + 6 и 4 + 5. На первом кубике может выпасть любое из четырёх чисел (3, 4, 5 или 6), на втором кубике может выпасть только одно число, дополняющее число, выпавшее на первом кубике до суммы, равной 9 (3 + 6, 6 + 3, 4 + 5, 5 + 4), то есть имеется 4 • 1 = 4 возможных способа получить сумму в 9 очков.
На первом кубике может выпасть любое из шести чисел, на втором кубике может также выпасть любое из шести чисел, то есть имеется 6 • 6 = 36 возможных способов.
156. а) На окружности отметили 6 точек (рис. 15). Сколько получится отрезков, если соединить каждую точку с каждой?
б) Встретились шесть друзей (рис. 16), каждый пожал руку каждому. Сколько было рукопожатий?
а) Из точки А выходит 5 отрезков. Из точки В выходит тоже 5 отрезков, но отрезок ВА — это тот же отрезок АВ. Если продолжить построение отрезков, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 отрезков.
б) Алёша пожал руку Фёдору, Егору, Диме, Саше и Вове — всего 5 рукопожатий. Фёдор пожал руку Алёше, Егору, Диме, Саше и Вове — всего тоже 5 рукопожатий. Но рукопожатие Алёша-Фёдор и Фёдор-Алёша — это одно рукопожатие. Если продолжить рассматривать рукопожатия, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (6 • 5) : 2 = 15 рукопожатий.
157. Восемь друзей решили провести турнир по шашкам так, чтобы каждый сыграл с каждым одну партию. Сколько партий будет сыграно?
Всего 8 друзей, значит, каждый сыграет одну партию с каждым из семи оставшихся друзей. Но, например, если Витя сыграет с Лёшей и Лёша сыграет с Витей — это одна и та же партия. Если продолжить рассматривать количество сыгранных партий, то можно убедиться, что половина из них будет повторяться, следовательно, всего получится (8 • 7) : 2 = 28 партий.
36
-
Ответы к стр. 36
Исследуем
158. Несколько приятелей при встрече обменялись рукопожатиями. Только Вася Угрюмов был не в духе и пожал руку не всем своим приятелям. Всего было 13 рукопожатий. Скольким приятелям Вася пожал руку?
Подсчитаем, сколько рукопожатий могли сделать приятели без Васи Угрюмова:
— предположим, было 3 приятеля: 3 • 2 : 2 = 3 рукопожатия,
— предположим, было 4 приятеля: 4 • 3 : 2 = 6 рукопожатий,
— предположим, было 5 приятелей: 5 • 4 : 2 = 10 рукопожатий,
— предположим, было 6 приятелей: 6 • 5 : 2 = 15 рукопожатий — такого быть не может, поскольку по условию рукопожатий было 13.
Если приятелей без Васи было 5, то они сделали 10 рукопожатий. С Васей они сделали 13 рукопожатий (а должны бы были сделать 15 рукопожатий), следовательно, Вася сделал 13 — 10 = 3 рукопожатия, то есть не пожал руку 15 — 13 = 2 приятелям. А всего было 5 + 1 = 6 приятелей.159. Несколько приятелей при встрече обменялись рукопожатиями. Только Петя Веселов был так рад встрече, что дважды пожал руку некоторым из приятелей (но не всем). Всего было b рукопожатий. Скольким приятелям Петя пожал руку дважды?
Решите задачу, если:
а) b = 17; б) b = 18; в) b = 19.а) Подсчитаем, сколько рукопожатий могли сделать все приятели:
— предположим, было 3 приятеля: 3 • 2 : 2 = 3 рукопожатия,
— предположим, было 4 приятеля: 4 • 3 : 2 = 6 рукопожатий,
— предположим, было 5 приятелей: 5 • 4 : 2 = 10 рукопожатий,
— предположим, было 6 приятелей: 6 • 5 : 2 = 15 рукопожатий,
— предположим, было 7 приятелей: 7 • 6 : 2 = 21 рукопожатие — такого быть не может, поскольку по условию рукопожатий было 17.
Если приятелей было 6, то они сделали 15 рукопожатий. Но по условию рукопожатий было 17, следовательно, Вася сделал 17 — 15 = 2 рукопожатия дважды, то есть пожал руку двум приятелям дважды. А всего было 6 приятелей.б) Подсчитаем, сколько рукопожатий могли сделать все приятели:
— предположим, было 3 приятеля: 3 • 2 : 2 = 3 рукопожатия,
— предположим, было 4 приятеля: 4 • 3 : 2 = 6 рукопожатий,
— предположим, было 5 приятелей: 5 • 4 : 2 = 10 рукопожатий,
— предположим, было 6 приятелей: 6 • 5 : 2 = 15 рукопожатий,
— предположим, было 7 приятелей: 7 • 6 : 2 = 21 рукопожатие — такого быть не может, поскольку по условию рукопожатий было 18.
Если приятелей было 6, то они сделали 15 рукопожатий. Но по условию рукопожатий было 18, следовательно, Вася сделал 18 — 15 = 3 рукопожатия дважды, то есть пожал руку трём приятелям дважды. А всего было 6 приятелей.в) Подсчитаем, сколько рукопожатий могли сделать все приятели:
— предположим, было 3 приятеля: 3 • 2 : 2 = 3 рукопожатия,
— предположим, было 4 приятеля: 4 • 3 : 2 = 6 рукопожатий,
— предположим, было 5 приятелей: 5 • 4 : 2 = 10 рукопожатий,
— предположим, было 6 приятелей: 6 • 5 : 2 = 15 рукопожатий,
— предположим, было 7 приятелей: 7 • 6 : 2 = 21 рукопожатие — такого быть не может, поскольку по условию рукопожатий было 19.
Если приятелей было 6, то они сделали 15 рукопожатий. Но по условию рукопожатий было 19, следовательно, Вася сделал 19 — 15 = 4 рукопожатия дважды, то есть пожал руку четырём приятелям дважды. А всего было 6 приятелей.160. Постройте многоугольник, имеющий n сторон, если:
а) n = 4; б) n = 5; в) n = 6; г) n = 7; д) n = 8.
В каждом случае проведите все диагонали многоугольника. Объясните, почему число d всех диагоналей вычисляется по формуле d = n(n−3)/2.
Многоугольник, имеющий n сторон, имеет также n вершин. Из одной вершины можно провести (n — 1) отрезков к другим вершинам. Поскольку два из этих отрезков будут сторонами многоугольника, соединяющими две соседние вершины, и не могут считаться диагоналями, то всего диагоналей будет n • (n — 1 — 2) = n(n — 3). Каждая диагональ соединяет две вершины, поэтому среди диагоналей есть попарно совпадающие (см. задание 156,а на стр. 35), следовательно, полученное количество диагоналей нужно разделить на 2: n(n — 3)/2.
а) d = 4(4-3)/2 = 4/2 = 2;
б) d = 5(5-3)/2 = 10/2 = 5;
в) d = 6(6-3)/2 = 18/2 = 9;
г) d = 7(7-3)/2 = 28/2 = 14;
д) d = 8(8-3)/2 = 40/2 = 20.161. Ученица нарисовала многоугольник и провела 20 диагоналей. Ей осталось провести меньше половины всех диагоналей этого многоугольника. Сколько диагоналей ей осталось провести?
Количество диагоналей многоугольника находится по формуле: d = n(n — 3)/2. По условию задачи количество диагоналей в многоугольнике больше 20 и не может быть больше 39, так как 20 + 19 = 39.
Допустим что в многоугольнике 8 сторон, тогда количество диагоналей в нем равно: d = 8(8 — 3)/2 = 40/2 = 20 — не подходит, так как количество диагоналей должно быть больше 20.
Допустим что в многоугольнике 9 сторон, тогда количество диагоналей в нем равно: d = 9(9 — 3)/2 = 54/2 = 27 — подходит условию задачи. 27 — 20 = 7 диагоналей осталось провести.
Допустим что в многоугольнике 10 сторон, тогда количество диагоналей в нем равно: d = 10(10 — 3)/2 = 70/2 = 35 — подходит условию задачи. 35 — 20 = 15 диагоналей осталось провести.
Допустим что в многоугольнике 11 сторон, тогда количество диагоналей в нем равно: d = 11(11 — 3)/2 = 88/2 = 44 — не подходит, так как 44 > 39.
Ответ: ученице осталось провести 15 диагоналей, если она нарисовала многоугольник с 10 сторонами, и 7 диагоналей, если она нарисовала многоугольник с 9 сторонами.
39
-
Отношения, пропорции, проценты
Вероятность событияОтветы к стр. 39
162. Бросают игральный кубик. Подсчитайте вероятность события:
а) А: «выпадет 5 очков»;
б) B: «выпадает четное число очков»;
в) С: «выпадает нечетное число очков»;
г) D: «выпадает число очков, кратное 3».Вероятностью события А называют отношение количества случаев, благоприятствующих событию А, к числу всех равновозможных случаев, один из которых обязательно произойдет.
а) Всего на кубике 6 граней, то есть число всех равновозможных случаев равно 6. 5 очков находится только на одной грани, то есть количество случаев, благоприятствующих событию, равно 1. Тогда вероятность события А (выпадение 5 очков) равна 1/6.
б) Всего на кубике 6 граней, то есть число всех равновозможных случаев равно 6. На трёх гранях расположены чётные очки: 2, 4, 6, поэтому количество случаев, благоприятствующих событию, равно 3. Тогда вероятность события В (выпадение чётного числа очков) равна 3/6 = 1/2.
в) Всего на кубике 6 граней, то есть число всех равновозможных случаев равно 6. На трёх гранях расположены нечётные очки: 1, 3, 5, поэтому количество случаев, благоприятствующих событию, равно 3. Тогда вероятность события С (выпадение нечётного числа очков) равна 3/6 = 1/2.
г) Всего на кубике 6 граней, то есть число всех равновозможных случаев равно 6. На двух гранях расположены очки кратные трём: 3, 6, поэтому количество случаев, благоприятствующих событию, равно 2. Тогда вероятность события D (выпадение числа очков, кратного 3), равна 2/6 = 1/3.
163. Задачи Даламбера. а) Монета бросается два раза. Какова вероятность того, что хотя бы один раз выпадет герб?
б) Монета бросается три раза. Какова вероятность того, что герб выпадет по крайней мере один раз?а) В результате двух последовательных подбрасываний монеты возможно 4 исхода:
1) герб, герб;
2) герб, цифра;
3) цифра, герб;
4) цифра, цифра.
Из них в трёх случаях (1, 2 и 3) выпадает герб. Следовательно, вероятность выпадения герба равна 3/4.б) В результате трёх последовательных подбрасываний монеты возможно 8 исходов:
1) герб, герб, герб;
2) герб, герб, цифра;
3) герб, цифра, герб;
4) герб, цифра, цифра;
5) цифра, герб, герб;
6) цифра, герб, цифра;
7) цифра, цифра, герб;
8) цифра, цифра, цифра.
Из них в семи случаях (1, 2, 3, 4, 5, 6, 7) выпадает герб. Следовательно, вероятность выпадения герба равна 7/8.164. Из ящика, где находятся 2 чёрных и 5 белых шаров, вынут наугад один шар. Какова вероятность того, что вынут:
а) чёрный шар; б) белый шар.Число всех равновозможных случаев равно 7, так как в ящике всего 7 шаров.
а) Количество случаев, благоприятствующих выпадению чёрного шара равно 2, так как в ящике 2 чёрных шара. Вероятность выпадения чёрного шара равна 2/7.
б) Количество случаев, благоприятствующих выпадению белого шара равно 5, так как в ящике 5 белых шаров. Вероятность выпадения белого шара равна 5/7.
165. Подбросьте монету 50 раз. Сколько раз выпал орёл?
Вероятность выпадения орла 1/2, то есть он должен выпасть 25 раз.
166. На двух карточках написали буквы А и Д, положили карточки на стол буквами вниз в произвольном порядке (рис. 19, а). Какова вероятность того, что после переворачивания карточек получится слово «ДА» (рис. 19, б)?
Так как карточки могут сформировать либо слово «АД», либо слово «ДА», то число всех равновозможных случаев, одно из которых обязательно произойдёт при переворачивании карточек равно 2.
Количество случаев, благоприятствующих формированию слова «ДА» равно 1, тогда вероятность формирования слова «ДА» равна 1/2.167. На трёх карточках написали буквы Е, Н, Т, положили карточки на стол буквами вниз в произвольном порядке. Какова вероятность того, что после переворачивания карточек получится слово «НЕТ».
При переворачивании первой карточки на ней может оказаться одна из трёх букв. На второй карточке может оказаться одна из двух оставшихся букв, а на третьей — последняя оставшаяся буква. Тогда общее количество полученных сочетаний букв будет 3 • 2 • 1 = 6 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при переворачивании карточек, равно 6.
Количество случаев, благоприятствующих формированию слова «НЕТ» равно 1, тогда вероятность формирования слова «НЕТ» равна 1/6.168. На четырёх карточках написали буквы К, О, Л, Я, положили карточки на стол буквами вниз в произвольном порядке. Какова вероятность того, что после переворачивания карточек получится имя КОЛЯ?
При переворачивании первой карточки на ней может оказаться одна из четырёх букв. На второй карточке может оказаться одна из трёх оставшихся букв, на третьей — одна из двух оставшихся букв и на четвёртой — последняя оставшаяся буква. Тогда общее количество полученных сочетаний букв будет 4 • 3 • 2 • 1 = 24 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при переворачивании карточек, равно 24.
Количество случаев, благоприятствующих формированию слова «КОЛЯ» равно 1, тогда вероятность формирования слова «КОЛЯ» равна 1/24.169. На четырёх карточках написали буквы А, С, А, Ш, положили карточки на стол буквами вниз в произвольном порядке. Какова вероятность того, что после переворачивания карточек получится имя САША?
При переворачивании первой карточки на ней может оказаться одна из четырёх букв. На второй карточке может оказаться одна из трёх оставшихся букв, на третьей — одна из двух оставшихся букв и на четвёртой — последняя оставшаяся буква. Тогда общее количество полученных сочетаний букв будет 4 • 3 • 2 • 1 = 24 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при переворачивании карточек, равно 24.
Количество случаев, благоприятствующих формированию слова «САША» равно 2, так как буква «А» встречается 2 раза. Тогда вероятность формирования слова «САША» равна 2/24 = 1/12170. Синоптики обещают на следующей неделе 2 солнечных дня и 5 пасмурных. Какое событие более вероятно: «воскресенье − солнечный день» или «воскресенье − пасмурный день»?
Число всех равновозможных случаев, одно из которых обязательно произойдет на неделе равно 2 + 5 = 7 дней.
Количество случаев, благоприятствующих условию «воскресенье — солнечный день» равно 2, так как солнечный день может быть 2 раза в неделю. Количество случаев, благоприятствующих условию «воскресенье — пасмурный день» равно 5, так как пасмурный день может быть 5 раз в неделю.
Вероятность события «воскресенье — солнечный день» = 2/7.
Вероятность события «воскресенье — пасмурный день» = 5/7.
5/7 > 2/7, следовательно, выше вероятность события «воскресенье — пасмурный день».171. Из 28 костей домино выбирают наугад одну кость (на рисунке 20 изображена кость с суммой очков 11). Какова вероятность выбрать кость с суммой очков:
а) 0; б) 2; в) 6; г) 10.
Число всех равновозможных случаев, одно из которых обязательно произойдет при выборе кости домино равно 28, так как всего костей домино 28.
а) Количество случаев, благоприятствующих выбору кости с 0 очков равна 1, так как только 1 кость имеет такое количество очков, поэтому вероятность равна 1/28.
б) Количество случаев, благоприятствующих выбору кости с 2 очками равна 2, так как 2 кости имеют такое количество очков: 0 + 2 и 1 + 1, поэтому вероятность равна 2/28 = 1/14.
в) Количество случаев, благоприятствующих выбору кости с 6 очками равна 4, так как 4 кости имеют такое количество очков: 0 + 6, 1 + 5, 2 + 4, 3 + 3, поэтому вероятность равна 4/28 = 1/7.
г) Количество случаев, благоприятствующих выбору кости с 10 очками равна 2, так как 2 кости имеют такое количество очков: 4 + 6, 5 + 5, поэтому вероятность равна 2/28 = 1/14.
40
-
Ответы к стр. 40
172. Бросают игральный кубик. Какова вероятность того, что выпадет число очков:
а) делящееся и на 2, и на 3;
б) делящееся на 2 и не делящееся на 3;
в) делящееся на 3 и не делящееся на 2;
г) не делящееся ни на 2, ни на 3;
д) делящееся или на 2, или на 3?
У к а з а н и е. Решите задачу, используя рисунок 21.
На рисунке в первом круге числа 2, 4 и 6 делятся на 2. Во втором круге числа 6 и 3 делятся на 3. Число 6 в пересечении кругов делится и на 2, и на 3. Числа 2 и 4 в первом круге делятся только на 2. Числа 1 и 5 за кругом не делятся ни на 2, ни на 3.
Число всех равновозможных случаев, одно из которых обязательно произойдет при бросании кубика равно 6, так на кубике 6 граней.
а) Количество случаев, благоприятствующих выпадению числа делящегося и на 2 и на 3 равно 1, так как такое число только одно — 6. Вероятность события равна 1/6.
б) Количество случаев, благоприятствующих выпадению числа, делящегося на 2 и не делящегося на 3 равно 2, так как таких чисел два: 2 и 4. Вероятность события равна 2/6 = 1/3.
в) Количество случаев, благоприятствующих выпадению числа, делящегося на 3 и не делящееся на 2 равно 1, так как такое число только одно — 3. Вероятность события равна 1/6.
г) Количество случаев, благоприятствующих выпадению числа, не делящееся ни на 2, ни на 3 равно 2, так как таких чисел два: 1 и 5. Вероятность события равна 2/6 = 1/3.
д) Количество случаев, благоприятствующих выпадению числа, делящегося или на 2, или на 3 равно 4, так как таких чисел четыре: 2, 3, 4 и 6. Вероятность события равна 4/6 = 2/3.
173. Бросают два игральных кубика. Какова вероятность события:
а) A: «сумма очков равна 2»;
б) B: «сумма очков равна 10»;
в) C: «сумма очков равна 12»;
г) D: «сумма очков равна 13»;
д) E: «сумма очков равна 1»;
е) F: «сумма очков равна одному из натуральных чисел 2, 3, …, 11, 12»?Число всех равновозможных случаев, одно из которых обязательно произойдет при бросании кубика равно 6, так как на кубике 6 граней. Так как кубика два, то число всех равновозможных случаев, одно из которых обязательно произойдет, будет 6 • 6 = 36.
а) Чтобы сумма очков была 2, может быть 1 вариант: 1 + 1. Тогда вероятность события равна 1/36.
б) Чтобы сумма очков была 10, могут быть 3 варианта: 4 + 6, 5 + 5 и 6 + 4. Тогда вероятность события равна 3/36 = 1/12.
в) Чтобы сумма очков была 12, может быть 1 вариант: 6 + 6. Тогда вероятность события равна 1/36.
г) Максимальная сумма очков на двух кубиках равна 12, поэтому сумма 13 очков получиться не может, следовательно, количество случаев, благоприятствующих выпадению суммы в 13 очков, равно 0. Тогда вероятность события равна 0/36 = 0.
д) Минимальная сумма очков на двух кубиках равна 2, поэтому сумма 1 очко получится не может, следовательно, количество случаев, благоприятствующих выпадению суммы в 1 очко, равно 0. Тогда вероятность события равна 0/36 = 0.
е) При сложении чисел на двух гранях кубика всегда получится сумма очков, равная одному из натуральных чисел 2, 3, …, 11, 12, поэтому количество случаев, благоприятствующих выпадению данной суммы равно 36. Тогда вероятность события равна 36/36 = 1.
174. В первом ряду микроавтобуса имеется только 3 места. На них собираются сесть двое мужчин и одна женщина. Какова вероятность того, что мужчины окажутся рядом?
Число всех равновозможных случаев, одно из которых обязательно произойдет при рассадке пассажиров равно 3: мужчина-мужчина-женщина, мужчина-женщина-мужчина, женщина-мужчина-мужчина. Так как для того, чтобы мужчины оказались рядом, женщина обязательно должна сидеть на крайнем сидении, то количество благоприятствующих для этого случаев равно 2. Тогда вероятность того, что мужчины окажутся рядом равна 2/3.
175. Бросают две монеты. Если выпадут два орла, то выиграл 1-й, если выпадут орёл и решка, то выиграл 2-й. Справедлива ли эта игра?
В результате подбрасывания двух монет возможно 4 исхода:
1) орёл, орёл;
2) орёл, решка;
3) решка, орёл;
4) решка, решка.
Из них в одном случае (1) выпадает два орла. Следовательно, вероятность события равна 1/4.
В двух случаях (2 и 3) выпадает орёл и решка. Следовательно, вероятность события равна 2/4.
1/4 < 2/4, то есть игра не справедлива (больше шансов выиграть у второго игрока).176. Бросают два игральных кубика. Если сумма очков 11 − выиграл 1-й, если сумм очков 12 − выиграл 2-й. Справедлива ли эта игра?
Число всех равновозможных случаев, одно из которых обязательно произойдет при бросании кубика равно 6, так как на кубике 6 граней. Так как кубика два, то число всех равновозможных случаев, одно из которых обязательно произойдет, будет 6 • 6 = 36.
Чтобы сумма очков была 11, могут быть 2 варианта: 5 + 6 и 6 + 5. Тогда вероятность события равна 2/36.
Чтобы сумма очков была 12, может быть 1 вариант: 6 + 6. Тогда вероятность события равна 1/36.
2/36 > 1/36, то есть игра не справедлива (больше шансов выиграть у первого игрока).
Придумываем задачу
177. Придумайте справедливую и несправедливую игру:
а) с двумя игральными кубиками; б) с двумя монетами.а) Справедливая. Бросают два игральных кубика. Если сумма очков 2 − выиграл 1-й, если сумм очков 12 − выиграл 2-й.
Число всех равновозможных случаев, одно из которых обязательно произойдет при бросании кубика равно 6, так как на кубике 6 граней. Так как кубика два, то число всех равновозможных случаев, одно из которых обязательно произойдет, будет 6 • 6 = 36.
Чтобы сумма очков была 2, может быть 1 вариант: 1 + 1. Тогда вероятность события равна 1/36.
Чтобы сумма очков была 12, может быть 1 вариант: 6 + 6. Тогда вероятность события равна 1/36.
1/36 = 1/36, то есть игра справедлива.
а) Несправедливая. Бросают два игральных кубика. Если сумма очков 10 − выиграл 1-й, если сумм очков 12 − выиграл 2-й.
Число всех равновозможных случаев, одно из которых обязательно произойдет при бросании кубика равно 6, так как на кубике 6 граней. Так как кубика два, то число всех равновозможных случаев, одно из которых обязательно произойдет, будет 6 • 6 = 36.
Чтобы сумма очков была 10, могут быть 3 варианта: 4 + 6, 5 + 5 и 6 + 4. Тогда вероятность события равна 3/36.
Чтобы сумма очков была 12, может быть 1 вариант: 6 + 6. Тогда вероятность события равна 1/36.
3/36 > 1/36, то есть игра не справедлива (больше шансов выиграть у первого игрока).
б) Справедливая. Бросают две монеты. Если выпадут два орла, то выиграл 1-й, если выпадут две решки, то выиграл 2-й.
В результате подбрасывания двух монет возможно 4 исхода:
1) орёл, орёл;
2) орёл, решка;
3) решка, орёл;
4) решка, решка.
Из них в одном случае (1) выпадает два орла. Следовательно, вероятность события равна 1/4.
В одном случае (4) выпадает две решки. Следовательно, вероятность события равна 1/4.
1/4 = 1/4, то есть игра справедлива.б) Несправедливая. Бросают две монеты. Если выпадут два орла, то выиграл 1-й, если выпадет хотя бы одна решка, то выиграл 2-й.
В результате подбрасывания двух монет возможно 4 исхода:
1) орёл, орёл;
2) орёл, решка;
3) решка, орёл;
4) решка, решка.
Из них в одном случае (1) выпадает два орла. Следовательно, вероятность события равна 1/4.
В трёх случаях (2, 3 и 4) выпадает хотя бы одна решка. Следовательно, вероятность события равна 3/4.
1/4 < 3/4, то есть игра не справедлива (больше шансов выиграть у второго игрока).178. Витя задумал число, записанное цифрами 1, 2, 3, 4, 5 без повторения. Коля пытается это число угадать. Какова вероятность того что Коля угадает число с первого раза, если это число:
а) двузначное; б) трёхзначное; в) четырёхзначное?а) На первом месте числа может оказаться одна из пяти цифр. На втором месте может оказаться одна из четырёх оставшихся цифр. Тогда общее количество полученных сочетаний цифр будет 5 • 4 = 20 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 20, так как 20 двузначных чисел можно составить из цифр 1, 2, 3, 4, 5 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Коля должен с первого раза. Тогда вероятность того, что Коля угадает двузначное число с первого раза равна 1/20.б) На первом месте числа может оказаться одна из пяти цифр. На втором месте может оказаться одна из четырёх оставшихся цифр, а на третьем — одна из трёх оставшихся. Тогда общее количество полученных сочетаний цифр будет 5 • 4 • 3 = 60 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 60, так как 60 трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Коля должен с первого раза. Тогда вероятность того, что Коля угадает трёхзначное число с первого раза равна 1/60.в) На первом месте числа может оказаться одна из пяти цифр. На втором месте может оказаться одна из четырёх оставшихся цифр. На третьем месте может оказаться одна из трёх оставшихся цифр, а на четвёртом — одна из двух оставшихся. Тогда общее количество полученных сочетаний цифр будет 5 • 4 • 3 • 2 = 120 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 120, так как 120 четырёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Коля должен с первого раза. Тогда вероятность того, что Коля угадает четырёхзначное число с первого раза равна 1/120.179. Коля задумал число, записанное цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9 без повторения. Витя пытается это число угадать. Какова вероятность того, что Витя угадает число с первого раза, если это число:
а) двузначное; б) трёхзначное; в) четырёхзначное?а) На первом месте числа может оказаться одна из девяти цифр. На втором месте может оказаться одна из восьми оставшихся цифр. Тогда общее количество полученных сочетаний цифр будет 9 • 8 = 72 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 72, так как 72 двузначных числа можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Витя должен с первого раза. Тогда вероятность того, что Витя угадает двузначное число с первого раза равна 1/72.б) На первом месте числа может оказаться одна из девяти цифр. На втором месте может оказаться одна из восьми оставшихся цифр, а на третьем — одна из семи оставшихся. Тогда общее количество полученных сочетаний цифр будет 9 • 8 • 7 = 504 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 504, так как 504 трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Витя должен с первого раза. Тогда вероятность того, что Витя угадает трёхзначное число с первого раза равна 1/504.в) На первом месте числа может оказаться одна из девяти цифр. На втором месте может оказаться одна из восьми оставшихся цифр. На третьем месте может оказаться одна из семи оставшихся цифр, а на четвёртом — одна из шести оставшихся. Тогда общее количество полученных сочетаний цифр будет 9 • 8 • 7 • 6 = 3024 способов. То есть и число всех равновозможных случаев, одно из которых обязательно произойдет при составлении числа равно 3024, так как 3024 четырёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 без повторения.
Количество случаев, благоприятствующих условию равно 1, так угадать число Витя должен с первого раза. Тогда вероятность того, что Витя угадает четырёхзначное число с первого раза равна 1/3024. 42
-
Отношения, пропорции, проценты
Занимательные задачиОтветы к стр. 42
180. Пруд зарастает лилиями — за неделю площадь, занятая лилиями, удваивается. За сколько недель пруд покрылся лилиями наполовину, если полностью лилиями он покрылся за 8 недель?
Так как площадь, занятая лилиями, каждую неделю удваивается, то наполовину пруд был покрыт лилиями неделю назад, то есть 8 — 1 = 7 недель.
Ответ: за 7 недель.181. Некоторый вид бактерий размножается со скоростью 1 деление в минуту (каждую минуту бактерия раздваивается). Если посадить 1 бактерию в пустой сосуд, то он наполнится за 1 ч. За какое время наполнится сосуд, если в него сначала посадить две бактерии?
Одна бактерия делится на две за 1 минуту. И через 1 минуту в сосуде будет две бактерии. Таким образом для того, чтобы рассчитать, за сколько минут заполнится сосуд, если в него положить сразу две бактерии, необходимо:
1 ч — 1 мин. = 60 мин. — 1 мин. = 59 мин.
Ответ: за 59 минут.182. 3 курицы за 3 дня снесли 3 яйца. Сколько яиц снесут 12 куриц за 12 дней?
1) 3 (яйца) : 3 (курицы) = 1 (яйцо) — сносит одна курица за 3 дня
2) 12 (дней) : 3 (дня) = 4 (яйца) — снесет курица за 12 дней
3) 4 (яйца) • 12 (куриц) = 48 (яиц) — снесут 12 куриц за 12 дней
Ответ: 48 яиц.183. 100 синиц за 100 дней съедает 100 кг зерна. Сколько килограммов зерна съедят 10 синиц за 10 дней?
1) 100 (кг) : 100 (синиц) = 1 (кг) — зерна съедает 1 синица за 100 дней
2) 1 кг : 10 = 1/10 (кг) — съедает 1 синица за 10 дней
3) 1/10 (кг) • 10 (синиц) = 1 (кг) — съедает 10 синиц за 10 дней
Ответ: 1 кг.184. 3 маляра за 5 дней могут покрасить 60 окон. Сколько окон покрасят 5 маляров за 4 дня?
1) 60 (окон) : 3 (маляра) = 20 (окон) — покрасит 1 маляр за 5 дней
2) 20 (окон) : 5 (дней) = 4 (окна) — покрасит 1 маляр за 1 день
3) 4 (окна) • 4 (дня) = 16 (окон) — покрасит 1 маляр за 4 дня
4) 16 (окон) • 5 (маляров) = 80 (окон) — покрасит 5 маляров за 4 дня
Ответ: 80 окон. 43
-
Ответы к стр. 43
185. 2 землекопа за 2 ч выкопают 2 м канавы. Сколько землекопов за 5 ч выкопают 5 м канавы?
1) 2 (м) : 2 (ч) = 1 (м) — выкопают 2 землекопа за 1 час
2) 1 (м) : 2 (землекопа) = 1/2 (м) — выкопает 1 землекоп за 1 час
3) 1/2 (м) • 5 (ч) = 2 1/2 (м) — выкопает 1 землекоп за 5 часов
4) 5 (м) : 2 1/2 (м) = 5 : 5/2 = 5 • 2/5 = 10/5 = 2 (землекопа) — выкопаю 5 метров канавы за 5 часов
Ответ: 2 землекопа.186. Из «Всеобщей арифметики» И. Ньютона. Если писец может за 8 дней написать 15 листов, сколько понадобится писцов, чтобы написать 405 листов за 9 дней?
1) 15 (листов) : 8 (дней) = 15/8 (листов) — напишет 1 писец за 1 день
2) 15/8 (листов) • 9 (дней) = 135/8 (листов) — напишет 1 писец за 9 дней
3) 405 (листов) : 135/8 (листов) = 405 • 8/135 = 3 • 8 = 24 (писца) — напишут 405 листов за 9 дней
Ответ: 24 писца.187. Переписчик в течение 4 дней может переписать 40 листов, работая по 9 ч в день. Во сколько дней он перепишет 60 листов, работая по 12 ч в день?
1) 40 (листов) : 4 (дня) = 10 (листов) — переписчик перепишет за один 9-ти часовой рабочий день
2) 10 (листов) : 9 (часов) = 10/9 (листов) — перепишет переписчик за 1 час
3) 10/9 (листов) • 12 (часов) = 40/3 (листов) — перепишет переписчик за 12-и часовой рабочий день
4) 60 (листов) : 40/3 (листов) = 60 • 3/40 = 9/2 = 4 1/2 (дня) — 12-и часовых рабочих дня потребуется переписчику чтобы переписать 60 листов
Ответ: 4 1/2 дня.188. У хозяйки спросили: «Хорошо ли несутся ваши куры?» − «Считайте сами, − был ответ, − полторы курицы за полтора дня несут полтора яйца, а всего у меня 12 кур». Сколько яиц несут куры в день?
Полтора — это 1 1/2
1) 1 1/2 (яйца) : 1 1/2 (курицы) = 1 (яйцо) — сносит 1 курица за полтора дня
2) 1 яйцо : 1 1/2 дня = 1 : 3/2 = 1 • 2/3 = 2/3 (яйца) — сносит 1 курица за 1 день
3) 2/3 (яйца) • 12 (куриц) = 2 • 4 = 8 (яиц) — снесут 12 куриц за 1 день
Ответ: 8 яиц.189. Зарплата в 100 условных единиц, повысилась на 10 %, потом еще на 10 %. На сколько процентов повысилась зарплата за 2 раза?
10 % — это 1/10 числа
1) 100 + 100 • 1/10 = 100 + 100/10 = 100 + 10 = 110 (условных единиц) — составила заработная плата после первого повышения
2) 110 + 110 • 1/10 = 110 + 110/10 = 110 + 11 = 121 (условных единиц) — составила заработная плата после второго повышения
3) 121/100 • 100 % — 100 % = 121 % — 100 % = 21 % — повысилась заработная плата после двух повышений
Ответ: на 21 %.190. Цена товара в 100 условных единиц, понизилась на 10 %, потом еще на 10 %. На сколько процентов понизилась цена товара за 2 раза?
10 % − это 1/10 числа
1) 100 — 100 • 1/10 = 100 — 100/10 = 100 — 10 = 90 (условных единиц) — составила цена после первого понижения
2) 90 — 90 • 1/10 = 90 — 90/10 = 90 — 9 = 81 (условных единиц) — составила цена после второго понижения
3) 100 % — 81/100 • 100 % = 100 % — 81 % = 19 % — понизилась цена после двух понижений
Ответ: на 19 %.191. Цена товара в 100 условных единиц сначала понизилась на 10 %, потом повысилась на 10 %. На сколько процентов понизилась или повысилась цена товара за 2 раза?
10 % — это 1/10 числа
1) 100 — 100 • 1/10 = 100 — 100/10 = 100 — 10 = 90 (условных единиц) — составила цена после понижения
2) 90 + 90 • 1/10 = 90 + 90/10 = 90 + 9 = 99 (условных единиц) — составила цена после повышения
3) 100 % — 99/100 • 100 % = 100 % — 99 % = 1 % — понизилась цена после двух изменений
Ответ: на 1 % понизилась.192. Цена товара в 100 условных единиц сначала повысилась на 10 %, потом понизилась на 10 %. На сколько процентов понизилась или повысилась цена товара за 2 раза?
10 % − это 1/10 числа
1) 100 + 100 • 1/10 = 100 + 100/10 = 100 + 10 = 110 (условных единиц) — составила цена после повышения
2) 110 — 110 • 1/10 = 110 — 110/10 = 110 — 11 = 99 (условных единиц) — составила цена после понижения
3) 100 % — 99/100 • 100 % = 100 % — 99 % = 1 % — понизилась цена после двух изменений
Ответ: на 1 % понизилась.193. Известно, что площади равных фигур равны и площадь фигуры равна сумме площадей составляющих её частей. Вычислите площадь (рис. 22): а) прямоугольника ABCD; б) треугольника ABC; в) треугольника ADC.
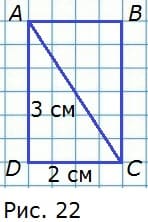
Площадь прямоугольника равна произведению его сторон: SABCD = 2 см • 3 см = 6 см2.
Площадь прямоугольника ABCD = площадь треугольника ABC + площадь треугольника ADC. Треугольники ABC и ADC равны.
6 см2 : 2 = 3 см2 — площадь треугольника ABC;
6 см2 : 2 = 3 см2 — площадь треугольника ADC.194. Вычислите площадь многоугольника (длины сторон в сантиметрах указаны на рисунке 23).
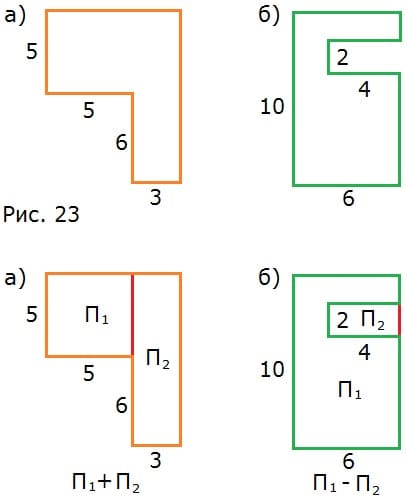
а) 5 • 5 + (6 + 5) • 3 = 25 + 33 = 58 (см2);
б) 10 • 6 — 2 • 4 = 60 — 8 = 52 (см2). 44
-
Ответы к стр. 44
Исследуем
195. Две фигуры называют равновеликими если их площади равны.
а) Постройте прямоугольник со сторонами 6 см и 4 см. Постройте два прямоугольника, равновеликие с построенным.
б) Какие стороны может иметь прямоугольник, равновеликий квадрату со стороной 8 см?
в) Какой наибольший периметр имеет прямоугольник, равновеликий квадрату со стороной 10 см?
Стороны прямоугольника выражаются натуральными числами.а) 6 см • 4 см = 24 см2 — площадь прямоугольника
Стороны равновеликого ему прямоугольника могут иметь стороны:
24 см2 = 2 см и 12 см;
24 см2 = 3 см и 8 см.
б) Стороны квадрата равны, тогда: 8 см • 8 см = 64 см2 — площадь квадрата со стороной 8 см.
Стороны равновеликого ему прямоугольника могут иметь стороны:
64 см2 = 1 см и 64 см;
64 см2 = 2 см и 32 см;
64 см2 = 16 см и 4 см.в) Стороны квадрата равны, тогда: 10 см • 10 см = 100 см2 — площадь квадрата со стороной 10 см.
Стороны равновеликого ему прямоугольника могут иметь стороны:
100 см2 = 1 см и 100 см;
100 см2 = 2 см и 50 см;
100 см2 = 4 см и 25 см.
Периметр прямоугольника равен сумме длин всех его сторон, тогда:
2 • (1 см + 100 см) = 202 см;
2 • (2 см + 50 см) = 104 см;
2 • (4 см + 25 см) = 58 см.
Периметр прямоугольника со сторонами 1 см и 100 см наибольший.Доказываем
196. Две равные фигуры наложили друг на друга (рис. 24). Докажите, что площади закрашенных фигур равны.
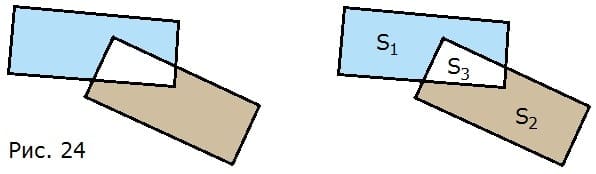
Обозначим площадь голубой части как S1, площадь серой части как S2, площадь белой части как S3, тогда:
— площадь первого прямоугольника равна S1 + S3;
— площадь второго прямоугольника равна S2 + S3.
Так как по условию задачи прямоугольники равны, то:
S1 + S3 = S2 + S3
S1 = S2 + S3 — S3
S1 = S2 — то есть площади закрашенных фигур равны.197. Вычислите площадь треугольника (рис. 25).
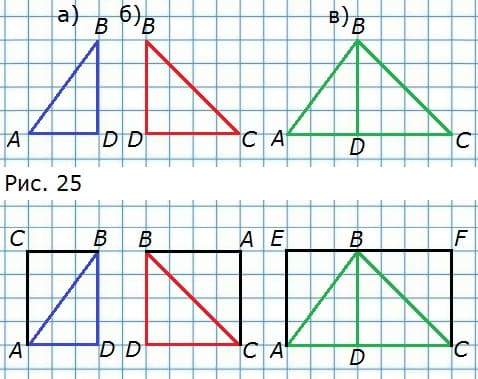
а) AD = 15 мм, DB = 20 мм.
Достраиваем треугольник ABD до прямоугольника ACBD.
Площадь прямоугольника равна: SACBD = AD • DB = 15 мм • 20 мм = 300 мм2.
Прямоугольник состоит из двух равных треугольников, тогда площадь треугольника ABD равна: 300 мм2 : 2 = 150 мм2.б) DC = 20 мм, DB = 20 мм.
Достраиваем треугольник DBC до прямоугольника DBAC. Так как DC = DB, то получился квадрат со стороной 20 мм.
Площадь квадрата равна: SDBAC = DC • DB = 20 мм • 20 мм = 400 мм2.
Квадрат состоит из двух равных треугольников, тогда площадь треугольника BDC равна: 400 мм2 : 2 = 200 мм2.в) AD = 15 мм, DB = 20 мм.
Достраиваем треугольник ABD до прямоугольника AEBD.
Площадь прямоугольника равна: SAEBD = AD • DB = 15 мм • 20 мм = 300 мм2.
Прямоугольник состоит из двух равных треугольников, тогда площадь треугольника ABD равна: 300 мм2 : 2 = 150 мм2.
DC = 20 мм, DB = 20 мм.
Достраиваем треугольник DBC до прямоугольника DBFC. Так как DC = DB, то получился квадрат со стороной 20 мм.
Площадь квадрата равна: SDBFC = DC • DB = 20 мм • 20 мм = 400 мм2.
Квадрат состоит из двух равных треугольников, тогда площадь треугольника BDC равна: 400 мм2 : 2 = 200 мм2.
Площадь фигуры равна сумме площадей составляющих её частей, следовательно, площадь треугольника ABC = площадь треугольника ABD + площадь треугольника BDC = 150 мм2 + 200 мм2 = 350 мм2.198. На рисунке 26 изображен параллелограмм (четырёхугольник, противоположные стороны которого попарно параллельны). Вычислите его площадь, если AD = 3 см, BK = 2 см.
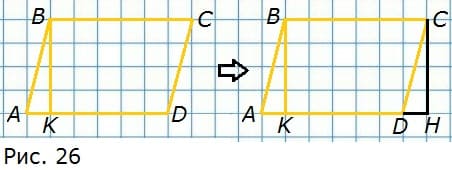
Из точки C проведём отрезок CH параллельный и равный отрезку BK. Треугольники ABK и CDH равны, тогда прямоугольники ABCD и BCHK равновеликие, то есть их площади равны.
AD = BC = 3 см, BK = CH = 2 см.
Площадь BCHK = BC • CH = 3 см • 2 см = 6 см2.
Площадь ABCD = площадь BCHK = 6 см2.199. На рисунке 27 изображена трапеция (четырёхугольник, две стороны которого параллельны, а две другие — не параллельны). Вычислите её площадь, если AD = 5 см, BC = 2 см, BK = 2 см.
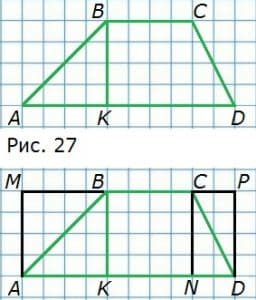
Достроим трапецию до прямоугольника AMPD.
BK = PD = 2 см.
Площадь прямоугольника AMPD = AD • PD = 5 см • 2 см = 10 см2.
Площадь прямоугольника BCNK = BC • BK = 2 см • 2 см = 4 см2.
Сумма площадей прямоугольников AMBK и CPDN равна разности площадей прямоугольников AMPD и BCNK = 10 см2 — 4 см2 = 6 см2.
Сумма площадей треугольников ABK и CDN = Сумма площадей прямоугольников AMBK и CPDN : 2 = 6 см2 : 2 = 3 см2.
Площадь трапеции ABCD = Площадь прямоугольника BCNK + сумма площадей треугольников ABK и CDN = 4 см2 + 3 см2 = 7 см2. 46
-
Целые числа
Отрицательные целые числаОтветы к стр. 46
200. Можно ли проиллюстрировать на ряде неотрицательных чисел вычитание: а) 7 — 4; б) 7 — 7; в) 7 — 8?
Если уменьшаемое больше или равно вычитаемому, то проиллюстрировать вычитание на ряде неотрицательных чисел можно. Если уменьшаемое меньше вычитаемого, то проиллюстрировать нельзя.
а) …, 2, 3, 4, 5, 6, 7, 8, …
↑ -4 |
7 > 4 — проиллюстрировать на ряде можно;
б) 0, 1, 2, 3, 4, 5, 6, 7, 8, …
↑ -7 |
7 = 7 — проиллюстрировать на ряде можно;в) 7 < 8 — проиллюстрировать на ряде нельзя.
201. Как получить ряд целых чисел?
Чтобы получить ряд целых чисел необходимо к ряду натуральных (целых положительных) чисел добавить целые отрицательные числа и число нуль.
47
-
Ответы к стр. 47
202. Как называют числа, расположенные в ряду целых чисел:
а) справа от нуля; б) слева от нуля.а) числа расположенные в ряду целых чисел справа от нуля называют натуральными или целыми положительными;
б) числа расположенные в ряду целых чисел слева от нуля называют целыми отрицательными.
203. Является ли число 0: а) положительным; б) отрицательным.
а) нет;
б) нет.204. Прочитайте числа +2, -3, 0, +7, -9.
а) Какие из этих чисел расположены в ряду целых чисел справа от нуля; слева от нуля?
б) Какие из этих чисел являются положительными; отрицательными.Плюс два, минус три, нуль, плюс семь, минус девять.
а) Числа расположенные в ряду целых чисел справа от нуля называют натуральными или целыми положительными. Числа расположенные в ряду целых чисел слева от нуля называют целыми отрицательными.
Справа от нуля расположены числа: +2; +7
Слева от нуля расположены числа: -3; -9.б) положительные: +2, +7;
отрицательные: -3, -9.205. Прочитайте записи и объясните их смысл:
Москва -2°, Калуга -8°, Тверь +3°.Москва минус два градуса, Калуга минус восемь градусов, Тверь плюс три градуса.
В Москве 2 градуса мороза, в Калуге 8 градусов мороза, в Твери 3 градуса тепла.206. Используя знаки «+» и «-», запишите:
а) 3° тепла; б) 4° тепла; в) 6° тепла;
г) 2° мороза; д) 5° ниже нуля; е) 1° холода.На уличном термометре числа выше нуля читаются как градусы тепла (перед ними ставится знак «+»), а числа ниже нуля — как градусы мороза (перед ними ставится знак «-»).
а) +3°; б) +4°; в) +6°;
г) −2°; д) −5°; е) −1°.207. Приведите пример:
а) конечного множества чисел;
б) бесконечного множества чисел.а) числа от 0 до 100 или от −100 до 100 или от -100 до 0;
б) числа от 100 и больше или положительные или отрицательные. 48
-
Ответы к стр. 48
208. Какие числа называют противоположными? Приведите примеры противоположных чисел.
Числа, которые отличаются только знаком, называют противоположными. Например, -10 и +10 или +1000 и -1000.
209. Какое число противоположно числу 0?
Число 0 противоположно самому себе: 0 = -0 = +0.
210. Что получится если перед целым числом поставить:
а) знак «+»; б) знак «-»?а) положительное число;
б) отрицательное число.211. Что называют модулем:
а) положительного целого числа;
б) отрицательного целого числа;
в) числа нуль?Модулем положительного числа называют само это число: |+3| = +3.
Модулем отрицательного числа называют противоположное ему (положительное) число: |-3| = +3.
Модулем число 0 является число 0: |0| = 0.212. Какие числа имеют одинаковый модуль? Приведите примеры.
Противоположные числа имеют одинаковый модуль: |-3| = |+3| = +3.
213. Для какого числа модуль — противоположное ему число?
Модулем отрицательного числа называют противоположное ему (положительное) число: |-3| = +3.
49
-
Ответы к стр. 49
214. Запись -(-2) читают так: «число, противоположное минус двум» или «минус минус 2». Прочитайте запись числа и упростите её по образцу:
а) +(+2) = +2; б) -(-2) = +2;
в) +(-2); г) +(-3); д) -(+3); е) -(-3); ж) -(+8); з) -(-10).в) число, соответствующее числу минус два или плюс минус два, +(-2) = -2;
г) число, соответствующее числу минус три или плюс минус три, +(-3) = -3;
д) число, противоположное плюс трём или минус плюс три, -(+3) = -3;
е) число, противоположное минус трём или минус минус три, -(-3) = +3;
ж) число, противоположное плюс восьми или минус плюс восемь, -(+8) = -8;
з) число, противоположное минус десяти или минус минус десять, -(-10) = +10.215. Какие числа получатся, если перед числами -1, 3, 0, -6, 7 поставить: а) знак «+»; б) знак «-»?
а) +(-1) = -1;
+3 = 3;
+0 = 0;
+(-6) = -6;
+7 = 7.б) -(-1) = 1;
-3 = -3;
-0 = 0;
-(-6) = 6;
-7 = -7.216. Какие из чисел -5, 6, 8, -10, 0, +4, -0 являются:
а) положительными; б) отрицательными?а) 6, 8, 4;
б) -5, -10.217. Заполните пропуски, прочитайте полученную запись:
а) |+1| = …; б) |-6| = …; в) |0| = …;
г) |-3| = …; д) |+7| = …; е) |-8| = ….а) |+1| = 1 — модулем числа плюс один является число один;
б) |-6| = 6 — модулем числа минус шесть является число шесть;
в) |0| = 0 — модулем числа нуль является число нуль;
г) |-3| = 3 — модулем числа минус три является число три;
д) |+7| = 7 — модулем числа плюс семь является число семь;
е) |-8| = 8 — модулем числа минус восемь является число восемь.218. Найдите модули чисел: +2, -2, +5, -5, +8, -10, +100, +0, -3.
|+2| = 2;
|-2| = 2;
|+5| = 5;
|-5| = 5;
|+8| = 8;
|-10| = 10;
|+100| = 100;
|+0| = 0;
|-3| = 3.219. Укажите два различных числа, модули которых равны.
7 и -7, так как противоположные числа имеют одинаковый модуль: |7| = 7 и |-7| = 7.
220. Для каждого из чисел 2, 5, -3, 10, -17 укажите другое число, имеющее тот же модуль.
-2, так как |2| = 2 и |-2| = 2,
-5, так как |5| = 5 и |-5| = 5,
3, так как |-3| = 3 и |3| = 3,
-10, так как |10| = 10 и |-10| = 10,
17, так как |-17| = 17 и |17| = 17.221. Назовите два противоположных числа, имеющих модуль:
а) 2; б) 7; в) 9; г) 8.а) -2 и 2, так как |-2| = 2 и |2| = 2;
б) -7 и 7, так как |-7| = 7 и |7| = 7;
в) -9 и 9, та как |-9| = 9 и |9| = 9;
г) -8 и 8, так как |-8| = 8 и |8| = 8.222. Выполните действия (222-224).
а) |+6| + |+7|; б) |-9| + |-8|;
в) |-6| + |+7|; г) |+8| + |+9|.а) |+6| + |+7| = 6 + 7 = 13;
б) |-9| + |-8| = 9 + 8 = 17;
в) |-6| + |+7| = 6 + 7 = 13;
г) |+8| + |+9| = 8 + 9 = 17.223. Выполните действия (222-224).
а) |-9| — |-6|; б) |-5| — |+3|;
в) |-20| — |-6|; г) |-17| — |-8|.а) |-9| — |-6| = 9 — 6 = 3;
б) |-5| — |+3| = 5 — 3 = 2;
в) |-20| — |-6| = 20 — 6 = 14;
г) |-17| — |-8| = 17 — 8 = 9.224. Выполните действия (222-224).
а) |-7| + |+5| + |+8| + |-10|;
б) |+12| + |-2| — |+10| + |-9|;
в) |+18| + |-2| — |-5| — |-15|;
г) |-10| + |-2| — |-8| + |-5|.а) |-7| + |+5| + |+8| + |-10| = 7 + 5 + 8 + 10 = 30;
б) |+12| + |-2| — |+10| + |-9| = 12 + 2 — 10 + 9 = 13;
в) |+18| + |-2| — |-5| — |-15| = 18 + 2 — 5 — 15 = 0;
г) |-10| + |-2| — |-8| + |-5| = 10 + 2 — 8 + 5 = 9.225. Назовите число модуль которого равен:
а) +5; б) +8; в) +1; г) 0.
Сколько таких чисел можно назвать?Можно назвать два числа, кроме г).
а) -5 и 5, так как |-5| = +5 и |5| = +5;
б) -8 и 8, так как |-8| = +8 и |8| = +8;
в) -1 и 1, так как |-1| = +1 и |1| = +1;
г) 0, так как |0| = 0.226. Если целое число обозначено буквой α, то противоположное ему число обозначают —α. Заполните таблицу.
α 5 -3 2 -6 7 8 -9 —α -5 3 -2 6 -7 -8 9 50
-
Ответы к стр. 50
227. Всегда ли модуль числа равен самому числу, т. е. |α| = α? Для каких чисел это равенство верно?
Модулем положительного числа называют само это число, а модулем числа 0 является число 0, поэтому равенство верно только для положительных чисел и для нуля.
228. Всегда ли модуль числа равен противоположному числу, т. е. |α| = —α? Для каких чисел это верно?
Модулем отрицательного числа называют противоположное ему (положительное) число, а модулем числа 0 является число 0, поэтому равенство верно только для отрицательных чисел и для нуля.
229. Для какого числа выполняются оба условия: |α| = α и |α| = —α?
Модулем числа 0 является число 0, поэтому оба условия верны только для нуля.
230. Верно ли, что |-α| = |α|?
Модули противоположных чисел равны, следовательно равенство верно.
231. Маша по ошибке считает, что (-α) — это запись отрицательного числа. Назовите такое число a, чтобы число (-α) было:
а) положительным; б) отрицательным; в) нулём.Если перед целым числом поставить знак «-», то получится число ему противоположное.
а) Пусть α = -5, тогда —α будет числом ему противоположным и равным 5, т. е. положительным.
б) Пусть α = 5, тогда —α будет числом ему противоположным и равным -5, т. е. отрицательным.
в) Пусть α = 0, а так как число 0 является противоположным самому себе, то и —α будет равно 0. 51
-
Ответы к стр. 51
232. Сравните натуральные числа
а) 425 и 452; б) 999 и 1000; в) 579 и 957;
г) 12 456 и 12 459; д) 1300 и 1297; е) 13 547 и 1354.а) 425 < 452 (425 меньше 452);
б) 999 < 1000 (999 меньше 1000);
в) 579 < 957 (579 меньше 957);
г) 12 456 < 12 459 (12 456 меньше 12 459);
д) 1300 > 1297 (1300 больше 1297);
е) 13 547 > 1354 (13 547 больше 1354).233. Как сравнивают целые числа?
Из двух целых чисел больше то, которое в ряду целых чисел стоит правее.
234. Какие числа: а) больше нуля; б) меньше нуля.
а) положительные числа больше 0;
б) отрицательные числа меньше 0.235. Какое число больше: положительное или отрицательное?
Положительное.
236. Сформулируйте правило сравнения:
а) целого числа с нулём;
б) положительного числа с отрицательным;
в) отрицательного числа с отрицательным.а) любое положительное число больше нуля, а любое отрицательное число меньше нуля;
б) любое положительное число больше отрицательного;
в) из двух отрицательных чисел больше то, у которого модуль меньше.237. Существует ли:
а) наибольшее натуральное число;
б) наименьшее натуральное число;
в) наибольшее отрицательное целое число;
г) наименьшее отрицательное целое число;
д) наибольшее целое число;
е) наименьшее целое число.а) натуральных чисел бесконечно много, поэтому наибольшего целого числа не существует;
б) из двух натуральных (положительных) чисел больше то, которое в ряду натуральных чисел стоит правее, поэтому наименьшим будет самое ближнее к 0 число, то есть 1;
в) из двух отрицательных чисел больше то, у которого модуль меньше, то есть, наибольшим отрицательным числом будет -1;
г) отрицательных чисел бесконечно много, поэтому наименьшего отрицательного числа не существует;
д) целых чисел бесконечно много, поэтому наибольшего целого числа не существует;
е) целых чисел бесконечно много, поэтому наименьшего целого числа не существует.238. Сравните числа (238-240):
а) 5 и 0; б) -5 и 0; в) 7 и 0;
г) -7 и 0; д) 8 и -7; е) -3 и 100.а) 5 > 0; б) -5 < 0; в) 7 > 0;
г) -7 < 0; д) 8 > -7; е) -3 < 100.239. Сравните числа (238-240):
а) -9 и -6; б) -3 и -20; в) -7 и -15;
г) -25 и -1; д) -20 и 0; е) 0 и -40;
ж) -8 и 13; з) 128 и -300; и) -5 и -6.а) -9 < -6; б) -3 > -20; в) -7 > -15;
г) -25 < -1; д) -20 < 0; е) 0 > -40;
ж) -8 < 13; з) 128 > -300; и) -5 > -6.240. Сравните числа (238-240):
а) 728 и 800; б) -296 и 1; в) -999 и 2;
г) 0 и -500; д) 725 и 0; е) -600 и -5;
ж) -856 и -100; з) -51 и -510; и) 326 и 32.а) 728 < 800; б) -296 < 1; в) -999 < 2;
г) 0 > -500; д) 725 > 0; е) -600 < -5;
ж) -856 < -100; з) -51 > -510; и) 326 > 32.241. Запишите числа в порядке возрастания:
а) 400, -400, 0, 236, -528; б) 752, 0, -35, -257, 432.а) -528, -400, 0, 236, 400;
б) -257, -35, 0, 432, 752.242. Запишите числа в порядке убывания:
а) -250, 367, 0, -8, 12, -400;
б) -790, 790, 0, -9, -12, 425.а) 367, 12, 0, -8, -250, -400;
б) 790, 425, 0, -9, -12, -790.243. Найдите разность:
а) |+5| — |-5|; б) |-5| — |+5|;
в) |+3| — |-3|; г) |-3| — |+3|.а) |+5| — |-5| = 5 — 5 = 0;
б) |-5| — |+5| = 5 — 5 = 0;
в) |+3| — |-3| = 3 — 3 = 0;
г) |-3| — |+3| = 3 — 3 = 0.244. Верно ли утверждение: если α > b, то |α| > |b|?
Так как из двух отрицательных чисел больше то, у которого модуль меньше, то утверждение будет неверным для отрицательных α и b.
245. Верно ли утверждение: если α > b, то |α| < |b|?
Так как модулем положительного числа называют само это число и из двух положительных чисел больше то, которое в ряду целых чисел стоит правее, то утверждение будет неверным для положительных α и b.
246. Может ли быть так, чтобы α ≠ b, но |α| = |b|? Приведите примеры. Как называют такие числа α и b?
Так как одинаковый модуль имеют противоположные числа, то равенство верно для противоположных чисел.
Например:
-10 ≠ 10, но |-10| = 10 и |10| = 10, следовательно, |-10| = |10|;
-23 ≠ 23, но |-23| = 23 и |23| = 32, следовательно, |-23| = |23|;
-570 ≠ 570, но |-570| = 570 и |570| = 570, следовательно, |-570| = |570|. 52
-
Ответы к стр. 52
247. Объясните с помощью ряда неотрицательных чисел, почему если для целых чисел α, b и с верны неравенства α > b и b > c, то верно неравенство α > c.
Из двух положительных чисел больше то, которое в ряду целых чисел стоит правее. Поэтому если α > b, то α в ряду целых чисел стоит правее b. Если b > c, то b стоит правее c. Таки образом ряд целых чисел примет следующий вид : …, c, b, α, ….
Так как α стоит правее c, следовательно, α > c. 54
-
Ответы к стр. 54
248. С помощью ряда целых чисел определите сумму:
а) (+3) + (+2); б) (+3) + (-2); в) (-3) + (+2); г) (-3) + (-2).а) …, 2, 3, 4, 5, 6, …
| +2 ↑
или (+3) + (+2) = 3 + 2 = 5б) …, 0, 1, 2, 3, 4, …
↑ -2 |
или (+3) + (-2) = 3 — 2 = 1в) …, -4, -3, -2, -1, 0, …
| +2 ↑
или (-3) + (+2) = -3 + 2 = -1г) …, -6, -5, -4, -3, -2, …
↑ -2 |
или (-3) + (-2) = -(3 + 2) = -5249. Как сложить два числа:
а) с одинаковыми знаками; б) с разными знаками?а) чтобы сложить два числа одинаковых знаков, надо сложить их модули и поставить перед суммой знак слагаемых;
б) чтобы сложить два числа разных знаков и с разными модулями, надо из большего модуля вычесть меньший и перед разностью поставить знак слагаемого с большим модулем.250. Чему равна сумма противоположных чисел?
Сумма противоположных чисел равна 0.
251. Чему равна сумма целого числа и нуля?
Сумма целого числа и нуля равна самому целому числу.
252. Используя правило сложения, вычислите:
а) +7 + (+9) = + (7 + 9) = …; б) -4 + (-6) = -(6 + 4) = …;
в) -5 + (-6); г) -5 + (-9); д) -6 + (-1); е) -1 + (-6).а) +7 + (+9) = +(7 + 9) = +16;
б) -4 + (-6) = -(6 + 4) = -10;
в) -5 + (-6) = -(5 + 6) = -11;
г) -5 + (-9) = -(5 + 9) = -14;
д) -6 + (-1) = -(6 + 1) = -7;
е) -1 + (-6) = -(1 + 6) = -7.253. Вычислите (253-254):
а) -1 + (-2); б) -2 + (-1); в) -2 + (-4);
г) -5 + (-1); д) -3 + (-8); е) -4 + (-11).а) -1 + (-2) = -(1 + 2) = -3;
б) -2 + (-1) = -(2 + 1) = -3;
в) -2 + (-4) = -(2 + 4) = -6;
г) -5 + (-1) = -(5 + 1) = -6;
д) -3 + (-8) = -(3 + 8) = -11;
е) -4 + (-11) = -(4 + 11) = -15.254. Вычислите (253-254):
а) -9 + (-2); б) -7 + (-3); в) -13 + (-8);
г) +12 + (+23); д) -25 + (-7); е) +18 + (+42).а) -9 + (-2) = -(9 + 2) = -11;
б) -7 + (-3) = -(7 + 3) = -10;
в) -13 + (-8) = -(13 + 8) = -21;
г) +12 + (+23) = +(12 + 23) = +35;
д) -25 + (-7) = -(25 + 7) = -32;
е) +18 + (+42) = +(18 + 42) = +60.255. Используя правила сложения, вычислите:
а) +7 + (-6) = +(7 — 6) = +1, так как |7| > |-6|;
б) -18 + (+12) = -(18 — 12) = -6, так как |-18| > |12|;
в) -8 + (+9); г) +8 + (-9); д) +12 + (-15);
е) -13 + (+18); ж) -2 + (+18); з) +25 + (-32).в) -8 + (+9) = +(9 — 8) = +1, так как |9| > |-8|;
г) +8 + (-9) = -(9 — 8) = -1, так как |-9| > |8|;
д) +12 + (-15) = -(15 — 12) = -3, так как |-15| > |12|;
е) -13 + (+18) = +(18 — 13) = +5, так как |18| > |-13|;
ж) -2 + (+18) = +(18 — 2) = +16, так как |18| > |-2|;
з) +25 + (-32) = -(32 — 25) = -7, так как |-32| > |25|.256. Найдите сумму:
а) -1 + (+2); б) +5 + (-2); в) -4 + (+1);
г) -8 + (+2); д) +7 + (-9); е) -10 + (+4).а) -1 + (+2) = +(2 — 1) = +1, так как |2| > |-1|;
б) +5 + (-2) = +(5 — 2) = +3, так как |5| > |-2|;
в) -4 + (+1) = -(4 — 1) = -3, так как |-4| > |1|;
г) -8 + (+2) = -(8 — 2) = -6, так как |-8| > |2|;
д) +7 + (-9) = -(9 — 7) = -2, так как |-9| > |7|;
е) -10 + (+4) = -(10 — 4) = -6, так как |-10| > |4|. 55
-
Ответы к стр. 55
Замечание. Для упрощения записи суммы у положительных слагаемых обычно опускают знак «+» и скобки. Например, вместо +3 + (+8) пишут 3 + 8, т. е.
+3 + (+8) = 3 + 8.
Аналогично — 5 + (+9) = -5 + 9.257. Упростите запись суммы:
а) -5 + (+7) = -5 + 7; б) -8 + (+9); в) -9 + (+7);
г) +3 + (+7); д) +8 + (-13); е) +9 + (-17).а) -5 + (+7) = -5 + 7;
б) -8 + (+9) = -8 + 9;
в) -9 + (+7) = -9 + 7;
г) +3 + (+7) = 3 + 7;
д) +8 + (-13) = 8 — 13;
е) +9 + (-17) = 9 — 17.258. Назовите знак каждого слагаемого:
а) -5 + 8; б) 5 + 7; в) -13 +(-9); г) -91 + 26; д) -95 + (-13).а) -5 + 8, «минус» 5, «плюс» 8;
б) 5 + 7, «плюс» 5, «плюс» 7;
в) -13 +(-9), «минус» 13, «минус» 9;
г) -91 + 26, «минус» 91, «плюс» 26;
д) -95 + (-13), «минус» 95, «минус» 13.Вычислите по образцу (259-263):
-755 + (-983) = -(755 + 983) = -1738 | +755
| 983
| 1783259. а) -102 + (-98); б) -33 + (-167); в) -128 + (-12);
г) 688 + 957; д) -172 + (-118); е) 694 + 738.а) -102 + (-98) = -(102 + 98) = -200
+102
98
200б) -33 + (-167) = -(33 + 167) = -200
+ 33
167
200в) -128 + (-12) = -(128 + 12) = -140
+128
12
140г) 688 + 957 = 1645
+ 688
957
1645д) -172 + (-118) = -(172 + 118) = -290
+172
118
290е) 694 + 738 = 1432
+ 694
738
1432260. а) -354 + (-293); б) -293 + (-354); в) 784 + 951;
г) -728 + (-256); д) 487 + 954; е) (-259) + (-728).а) -354 + (-293) = -(354 + 293) = -647
+354
293
647б) -293 + (-354) = -(293 + 354) = -647
+293
354
647в) 784 + 951 = 1735
+784
951
1735г) -728 + (-256) = -(728 + 256) = -984
+728
256
984д) 487 + 954 = 1441
+ 487
954
1441е) (-259) + (-728) = -(259 + 728) = -987
+259
728
987261. а) -7825 + (-3517); б) 7903 + 484; в) -35 + (-8094)
а) -7825 + (-3517) = -(7825 + 3517) = -11342
+ 7825
3517
11342б) 7903 + 484 = 8387
+7903
484
8387в) -35 + (-8094) = -(35 + 8094) = 8129
+ 35
8094
8129262. а) 359 + (-483); б) -703 + 117; в) -14 + 864;
г) 151 + (-87); д) 17 + (-256); е) 476 + (-253).а) 359 + (-483) = -(483 — 359) = -124
—483
359
124б) -703 + 117 = -(703 — 117) = -586
—703
117
586в) -14 + 864 = +(864 — 14) = 850
—864
14
850г) 151 + (-87) = +(151 — 87) = 64
—151
87
64д) 17 + (-256) = -(256 — 17) = 239
—256
17
239е) 476 + (-253) = +(476 — 253) = 223
—476
253
223263. а) -170 + (-250); б) -350 + 480; в) 7805 + (-454);
г) 1306 + (-2514); д) -8576 + (-1720); е) -6060 + 3903.а) -170 + (-250) = -(170 + 250) = -420
+170
250
420б) -350 + 480 = +(480 — 350) = 130
—480
350
130в) 7805 + (-454) = 7805 — 454 = 7351
—7805
454
7351г) 1306 + (-2514) = -(2514 — 1306) = -1208
—2514
1306
1208д) -8576 + (-1720) = -(8576 + 1720) = -10296
+ 8576
1720
10296е) -6060 + 3903 = -(6060 — 3903) = -2157
—6060
3903
2157264. Вычислите по образцу:
а) -5 + (-3) + 2 = -(5 + 3) + 2 = -8 + 2 = -6;
б) 3 + (-7) + (-8) + 6 = -4 + (-8) + 6 = -12 + 6 = -6;
в) -8 + 3 + (-1); г) -7 + (-2) + (-10);
д) 8 + (-9) + (-7); е) -3 + (-4) + (-5) + (-6);
ж) -4 + 8 +(-9) + 3; з) 8 + (-10) + (-12) + 3.в) -8 + 3 + (-1) = -(8 + 1) + 3 = -9 + 3 = -6;
г) -7 + (-2) + (-10) = -(9) + (-10) = -19;
д) 8 + (-9) + (-7) = -(9 + 7) + 8 = -16 + 8 = -8;
е) -3 + (-4) + (-5) + (-6) = -7 + (-5) + (-6) = -12 + (-6) = -18;
ж) -4 + 8 +(-9) + 3 = -(4 + 9) + (8 + 3) = -13 + 11 = -2;
з) 8 + (-10) + (-12) + 3 = (8 + 3) — (10 + 12) = 11 − 22 = -11. 56
-
Ответы к стр. 56
265. Запишите для целых чисел α и b переместительный закон сложения, сформулируйте его.
α + b = b + α
Сумма двух целых чисел не зависит от порядка слагаемых.266. Запишите для целых чисел α, b и c сочетательный закон сложения, сформулируйте его.
(α + b) + c = α + (b + с)
Чтобы к сумме двух целых чисел прибавить третье целое число, можно к первому числу прибавить сумму второго и третьего — результат будет тот же. 57
-
Ответы к стр. 57
267. Вычислите, применяя законы сложения:
а) 5 + 798 + 35; б) (723 + 59) + 17;
в) 357 + 48 + 13; г) 488 + (596 + 12).а) 5 + 798 + 35 = (5 + 35) + 798 = 40 + 798 = 838;
б) (723 + 59) + 17 = (723 + 17) + 59 = 740 + 59 = 799;
в) 357 + 48 + 13 = (357 + 13) + 48 = 370 + 48 = 418;
г) 488 + (596 + 12) = (488 + 12) + 596 = 500 + 596 = 1096.
268. Выполните сложение и сравните результаты:
а) -5 + (-9) и -9 + (-5); б) 48 + (-36) и -36 + (48);
в) -25 + (16) и 16 + (-25); г) -8 + (18 + (-7)) и (-8 + 18) + (-7);
д) 13 + (-6 + (-7)) и (13 + (-6)) + (-7).а) -5 + (-9) = -(5 + 9) = -14,
-9 + (-5) = -(9 + 5) = -14,
-14 = -14;б) 48 + (-36)= 48 — 36 = 12,
-36 + (48) = -36 + 48 = 12,
12 = 12;в) -25 + (16) = -(25 — 16) = -9,
16 + (-25) = -(25 — 16) = -9,
9 = 9;г) -8 + (18 + (-7)) = -8 + (18 — 7) = -8 + 11 = 3,
(-8 + 18) + (-7) = (18 — 8) — 7 = 10 — 7 = 3,
3 = 3;д) 13 + (-6 + (-7)) = 13 — (6 + 7) = 13 — 13 = 0,
(13 + (-6)) + (-7) = (13 — 6) — 7 = 7 — 7 = 0,
0 = 0.269. Примените переместительный закон сложения:
а) -45 + (-10) = -10 + (-45)
б) 8 + (-35); в) -13 + 49; г) -17 + (-23).б) 8 + (-35) = -35 + 8;
в) -13 + 49 = 49 + (-13);
г) -17 + (-23) = -23 + (-17).270. Примените сочетательный закон сложения:
а) 42 + (-3 + 7) = (42 + (-3)) + 7;
б) 56 + (-16 + 7); в) (-52 + 17) + (-9); г) -13 + (-8 + 25).б) 56 + (-16 + 7) = (56 + (- 16)) + 7;
в) (-52 + 17) + (-9) = -52 + (17 + (-9));
г) -13 + (-8 + 25) = (-13 + (-8)) + 25.271. Заполните пропуски:
а) 3 + 5 + (-8) = 3 + (-8) + …;
б) 6 + … + (-1) = (-1) + (6 + (-2));
в) -1 + … + 3 = (3 + (-7)) + …;
г) -4 + … + (-7) = 2 + (… +(-4)).а) 3 + 5 + (-8) = 3 + (-8) + 5;
б) 6 + (-2) + (-1) = (-1) + (6 + (-2));
в) -1 + (-7) + 3 = (3 + (-7)) + (-1);
г) -4 + 2 + (-7) = 2 + (-7 + (-4)).272. Вычислите применяя законы сложения:
а) 49 + ((-49) + 22); б) -12 + (12 + (-29));
в) (47 + (-58)) + (-47); г) (124 + 59) + (-24);
д) -56 + 17 + (-27); е) 49 + (-72) + 62;
ж) 36 + (-51) + 14; з) -48 + (-19) + 28.а) 49 + ((-49) + 22) = (49 + (-49)) + 22 = 0 + 22 = 22;
б) -12 + (12 + (-29)) = ((-12) + 12) + (-29) = 0 + (-29) = -29;
в) (47 + (-58)) + (-47) = (47 + (-47)) + (-58) = 0 + (-58) = -58;
г) (124 + 59) + (-24) = (124 + (-24)) + 59 = 100 + 59 = 159;
д) -56 + 17 + (-27) = -56 + ((-27) + 17) = -56 + (-10) = -66;
е) 49 + (-72) + 62 = 49 + ((-72) + 62) = 49 + (-10) = 39;
ж) 36 + (-51) + 14 = (36 + 14) + (-51) = 50 + (-51) = -1;
з) -48 + (-19) + 28 = ((-48) + 28) + (-19) = -20 + (-19) = -39.
273. Вычислите по образцу:
а) -1 + 2 + (-3) + 5 = (2 + 5) + ((-1) + (-3)) = 7 + (-4) = …;
б) -2 + (-4) + 2 + 5 + (-3) + 1 + (-3);
в) 20 + (-8) + 2 + 5 + (-10) + (-1) + (-3);
г) -4 + (-1) + 3 + (-2) + (-3) + 9;
д) -17 + 17 + (-8) + 6 + (-2) + 8;
е) 4 + (-6) + (-1) + (-4) + 6 + (-3) + 1.а) -1 + 2 + (-3) + 5 = (2 + 5) + ((-1) + (-3)) = 7 + (-4) = 3;
б) -2 + (-4) + 2 + 5 + (-3) + 1 + (-3) = (2 + 5 + 1) + ((-2) + (-4) + (-3) + (-3)) = 8 + (-12) = -4;
в) 20 + (-8) + 2 + 5 + (-10) + (-1) + (-3) = (20 + 2 + 5) + ((-8) + (-10) + (-1) + (-3)) = 27 + (-22) = 5;
г) -4 + (-1) + 3 + (-2) + (-3) + 9 = (3 + 9) + ((-4) + (-1) + (-2) + (-3)) = 12 + (-10) = 2;
д) -17 + 17 + (-8) + 6 + (-2) + 8 = (17 + 6 + 8) + ((-17) + (-8) + (-2)) = 31 + (-27) = 4;
е) 4 + (-6) + (-1) + (-4) + 6 + (-3) + 1 = (4 + 6 + 1) + ((-6) + (-1) + (-4) + (-3)) = 11 + (-14) = -3.
274. Вычислите, применяя законы сложения (274-275):
а) (-1) + (-2) + (-3) + (-4) + 4 + 3 + 2 + 1;
б) (-7) + (-5) + (-3) + (-1) + 1 + 3 + 5 + 7;
в) (-10) + (-9) + (-8) + (-7) + … + 7 + 8 + 9 + 10;
г) (-100) + (-99) + (-98) + … + 98 + 99 + 100.а) (-1) + (-2) + (-3) + (-4) + 4 + 3 + 2 + 1 = ((-1) + 1) + ((-2) + 2) + ((-3) + 3) + ((-4) + 4) = 0 + 0 + 0 + 0 = 0;
б) (-7) + (-5) + (-3) + (-1) + 1 + 3 + 5 + 7 = ((-7) + 7) + ((-5) + 5) + ((-3) + 3) + ((-1) + 1) = 0 + 0 + 0 + 0 = 0;
в) (-10) + (-9) + (-8) + (-7) + … + 7 + 8 + 9 + 10 = ((-10) + 10) + ((-9) + 9) + ((-8) + 8) + ((-7) + 7) + … + ((-1) + 1) = 0 + 0 + 0 + 0 + … + 0 = 0;
г) (-100) + (-99) + (-98) + … + 98 + 99 + 100 = ((-100) + 100) + ((-99) + 99) + ((-98) + 98)+ … + ((-1) + 1) = 0 + 0 + 0 + … + 0 = 0.
58
-
Ответы к стр. 58
275. Вычислите, применяя законы сложения (274-275):
а) 1 + (-2) + 3 + (-4) + … + 9 + (-10);
б) 1 + (-2) + 3 + (-4) + … + 99 + (-100);
в) (-1) + 2 + (-3) + 4 + … + (-9) + 10;
г) (-1) + 2 + (-3) + 4 + … + (-99) + 100.а) Всего 10 чисел, разобьём их по парам: 1 + (-2), 3 + (-4) и так далее – всего 5 пар (10 : 2 = 5). Тогда:
1 + (-2) + 3 + (-4) + … + 9 + (-10) = (1 + (-2)) + (3 + (-4)) + … + (9 + (-10)) = -1 + (-1) + … + (-1) = -5, так как получится 5 пар со значением -1;б) Всего 100 чисел, разобьём их по парам: 1 + (-2), 3 + (-4) и так далее – всего 50 пар (100 : 2 = 50). Тогда:
1 + (-2) + 3 + (-4) + … + 99 + (-100) = (1 + (-2)) + (3 + (-4)) + … + (99 + (-100)) = -1 + (-1) + … + (-1) = -50, так как получится 50 пар со значением -1;в) Всего 10 чисел, разобьём их по парам: -1 + 2, -3 + 4 и так далее – всего 5 пар (10 : 2 = 5). Тогда:
(-1) + 2 + (-3) + 4 + … + (-9) + 10 = ((-1) + 2) + ((-3) + 4) + … + ((-9) + 10) = 1 + 1 + … + 1 = 5, так как получится 5 пар со значением 1;г) Всего 100 чисел, разобьём их по парам: -1 + 2, -3 + 4 и так далее – всего 50 пар (100 : 2 = 50). Тогда:
(-1) + 2 + (-3) + 4 + … + (-99) + 100 = ((-1) + 2) + ((-3) + 4) + … + ((-99) + 100) = 1 + 1 + … + 1 = 50, так как получится 50 пар со значением 1.276. Даны числа: 9, -11, 10. Убедитесь, что сумма любых двух соседних чисел отрицательна, а сумма всех трёх чисел положительна. Напишите в строчку три числа так, чтобы сумма двух соседних чисел была положительна, а сумма трёх числа была отрицательна.
Соседние числа в ряду 9 и -11, -11 и 10.
9 + (-11) = -(11 — 9) = -2 — сумма двух соседних чисел отрицательна
-11 + 10 = -(11 — 10) = -1 — сумма двух соседних чисел отрицательна
9 + (-11) + 10 = 19 — 11 = 8 — сумма всех трёх чисел положительнаВозьмем ряд чисел -9, 11, -10, тогда:
-9 + 11 = 11 — 9 = 2 — сумма двух соседних чисел положительна
11 + (-10) = 11 — 10 = 1 — сумма двух соседних чисел положительна
-9 + 11 + (-10) = 11 + (-9 + (-10)) = 11 + (-19) = -8 — сумма всех трёх чисел отрицательна.277. Убедитесь, что для чисел 5, -4, -2, 5, -4, -2, 5 сумма любых трёх соседних чисел отрицательна, а сумма всех чисел положительна. Напишите в строчку семь чисел так, чтобы сумма любых трех соседних чисел была положительна, а сумма всех чисел отрицательна.
Соседние три числа в ряду: 5, -4, -2; -4, -2, 5; -2, 5, -4; 5, -4, -2; -4, -2, 5.
5 + ((-4) + (-2)) = 5 + (-6) = -1;
-4, -2, 5 = ((-4) + (-2)) + 5 = -6 + 5 = -1;
-2, 5, -4 = ((-2) + (-4)) + 5 = -6 + 5 = -1;
5, -4, -2 = 5 + ((-4) + (-2)) = 5 + (-6) = -1;
((-4) + (-2)) + 5 = -6 + 5 = -1;
Получается, что сумма любых трёх соседних чисел отрицательна. Набор любых трёх соседних чисел содержит одинаковые числа 5, -4 и -2 в разном порядке.
5 + (-4) + (-2) + 5 + (-4) + (-2) + 5 = (5 + 5 + 5) + ((-4) + (-2) + (-4) + (-2)) = 15 + (-12) = 3 — сумма всех чисел положительна.Возьмем ряд чисел -5, 4, 2, -5, 4, 2, -5.
Соседние три числа в ряду: -5, 4, 2; 4, 2, -5; 2, -5, 4; -5, 4, 2; 4, 2, -5.
-5 + (4 + 2) = -5 + 6 = 1;
(4 + 2) + (-5) = 6 + (-5) = 1;
2 + (-5) + 4 = -5 + (2 + 4) = -5 + 6 = 1;
-5 + (4 + 2) = -5 + 6 = 1;
(4 + 2) + (-5) = 6 + (-5) = 1;
Получается, что сумма любых трёх соседних чисел положительна. Набор любых трёх соседних чисел содержит одинаковые числа -5, 4 и 2 в разном порядке.
-5 + 4 + 2 + (-5) + 4 + 2 + (-5) = ((-5) + (-5) + (-5)) + (3 + 2 + 4 + 2) = -15 + 12 = -3 — сумма всех чисел отрицательна.278. Запишите и вычислите:
а) сумму чисел 17 и -23;
б) сумму чисел -20 и 4;
в) сумму числа, противоположного -13, и числа -225;
г) сумму числа -26 и числа, противоположного -12.а) 17 + (-23) = -6;
б) -20 + 4 = -16;
в) противоположным числу -13 является число 13, тогда: 13 + (-225) = -212;
г) противоположным числу -12 является число 12, тогда: -26 + 12 = -14.279. К числу α прибавьте число, противоположное b:
а) α = 12, b = -7; б) α = 13, b = 16; в) α = 15, b = 7;
г) α = 24, b = 13; д) α = -14, b = 7; е) α = -29, b = 40;
ж) α = -24, b = -13; з) α = -16; b= -18.а) противоположным числу -7 является число 7, тогда: 12 + 7 = 19;
б) противоположным числу 16 является число -16, тогда: 13 + (-16) = -3;
в) противоположным числу 7 является число -7, тогда: 15 + (-7) = 8;
г) противоположным числу 13 является число -13, тогда: 24 + (-13) = 11;
д) противоположным числу 7 является число -7, тогда: -14 + (-7) = -(14 + 7) = -21;
е) противоположным числу 40 является число -40, тогда: -29 + (-40) = -(29 + 40) = -69;
ж) противоположным числу -13 является число 13, тогда: -24 + 13 = -11;
з) противоположным числу -18 является число 18, тогда: -16 + 18 = 2.
280. Перепишите, заменив х числом так, чтобы получилось верное равенство:
а) (-6) + (-7) = х; б) -8 + х = -10; в) -8 + х = -3;
г) -8 + х = 0; д) -8 + х = -8; е) х + 5 = 10;
ж) х + 5 = 0; з) х + 5 = -3; и) х + 5 = -8.а) х = -13, (-6) + (-7) = -13;
б) х = -2, -8 + (-2) = -10;
в) х = 5, -8 + 5 = -3;
г) х = 8, -8 + 8 = 0;
д) х = 0, -8 + 0 = -8;
е) х = 5, 5 + 5 = 10;
ж) х = -5, -5 + 5 = 0;
з) х = -8, -8 + 5 = -3;
и) х = -13, -13 + 5 = -8. 59
-
Ответы к стр. 59
281. Что называют разностью чисел α и b?
Разность α — b есть сумма числа α и числа, противоположного числу b.
282. Какой сумме равна разность α — b?
α — b = α + (-b)
283. Применяя, определение разности, проверьте, верно ли равенство:
а) +28 — (+9) = 14; б) +7 — (+12) = -5;
в) -2 — (-3) = 1; г) -12 — (+1) = -11.а) +28 — (+9) = 28 + (-9) = 28 — 9 = 19, 19 ≠ 14 — равенство неверно;
б) +7 — (+12) = 7 + (-12) = -(12 — 7) = -5, -5 = -5 — равенство верно;
в) -2 — (-3) = -2 + 3 = 3 — 2 = 1, 1 = 1 — равенство верно;
г) -12 — (+1) = -12 + (-1) = -(12 + 1) = -13, -13 ≠ -11, равенство неверно.
284. Назовите уменьшаемое, вычитаемое и число, противоположное вычитаемому:
а) +45 — (+63); б) +27 — (-52); в) -4 — (+19);
г) -41 — (+95); д) -59 — (-11); е) +32 — (-16).а) +45 — уменьшаемое, +63 — вычитаемое, -63 — число противоположное вычитаемому;
б) +27 — уменьшаемое, -52 — вычитаемое, +52 — число противоположное вычитаемому;
в) -4 — уменьшаемое, +19 — вычитаемое, -19 — число противоположное вычитаемому;
г) -41 — уменьшаемое, +95 — вычитаемое, -95 — число противоположное вычитаемому;
д) -59 — уменьшаемое, -11 — вычитаемое, +11 — число противоположное вычитаемому;
е) +32 — уменьшаемое, -16 — вычитаемое, +16 — число противоположное вычитаемому.
285. Замените разность чисел суммой уменьшаемого и числа, противоположному вычитаемому:
а) +25 — (-6) = +25 + (+6); б) (-9) — (+45) = (-9) + (-45);
в) +47 — (+58); г) (-36) — (+12);
д) +13 — (-27); е) (-45) — (-59).в) +47 — (+58) = +47 + (-58);
г) (-36) — (+12) = (-36) + (-12);
д) +13 — (-27) = +13 + 27;
е) (-45) — (-59) = (-45) + 59. 60
-
Ответы к стр. 60
Замечание. Для упрощения записи разности у положительных уменьшаемого и вычитаемого опускают скобки и знак «+».
Например, +9 — (+3) = 9 — 3; -9 — (+3) = -9 — 3; +9 — (-3) = 9 — (-3).286. Замените разность суммой:
а) -5 — (+2) = -5 + (-2); б) 12 — (-7) = 12 + 7;
в) -6 — (-3); г) 9 — (+13); д) 17 — (+24);
е) -13 — (-19); ж) 13 — (-27); з) -15 — (+10).в) -6 — (-3) = -6 + 3;
г) 9 — (+13) = 9 + (-13);
д) 17 — (+24) = 17 + (-24);
е) -13 — (-19) = -13 + 19;
ж) 13 — (-27) = 13 + 27;
з) -15 — (+10) = -15 + (-10).287. Вычислите по образцу (287-288):
а) 9 — 10 = 9 + (-10) = -(10 — 9) = -1;
б) 6 — 8; в) 4 — 10; г) 5 — 20; д) 6 — 11;
е) 8 — 13; ж) 8 — 24; з) 24 — 48; и) 35 — 47;
к) 64 — 71; л) 91 — 119; м) 62 — 89; н) 67 — 105.б) 6 — 8 = 6 + (-8) = -(8 — 6) = -2;
в) 4 — 10 = 4 + (-10) = -(10 — 4) = -6;
г) 5 — 20 = 5 + (-20) = -(20 — 5) = -15;
д) 6 — 11 = 6 + (-11) = -(11 — 6) = -5;
е) 8 — 13 = 8 + (-13) = -(13 — 8) = -5;
ж) 8 — 24 = 8 + (-24) = -(24 — 8) = -16;
з) 24 — 48 = 24 + (-48) = -(48 — 24) = -24;
и) 35 — 47 = 35 + (-47) = -(47 — 35) = -12;
к) 64 — 71 = 64 + (-71) = -(71 — 64) = -7;
л) 91 — 119 = 91 + (-119) = -(119 — 91) = -28;
м) 62 — 89 = 62 + (-89) = -(89 — 62) = -27;
н) 67 — 105 = 67 + (-105) = -(105 — 67) = -38.288. Вычислите по образцу (287-288):
а) -3 — 7 = -3 + (-7) = -(3 + 7) = -10;
б) -4 — 8; в) -5 — 2; г) -8 — 14; д) -10 — 10;
е) -20 — 60; ж) -11 — 23; з) -28 — 17; и) -5 — 91;
к) -92 — 18; л) -240 — 14; м) -50 — 105; н) -200 — 400.б) -4 — 8 = -4 + (-8) = -(4 + 8) = -12;
в) -5 — 2 = -5 + -2) = -(5 + 2) = -7;
г) -8 — 14 = -8 + (-14) = -(8 + 14) = -22;
д) -10 — 10 = -10 + (-10) = -(10 + 10) = -20;
е) -20 — 60 = -20 + (-60) = -(20 + 60) = -80;
ж) -11 — 23 = -11 + (-23) = -(11 + 23) = -34;
з) -28 — 17 = -28 + (-17) = -(28 + 17) = -45;
и) -5 — 91 = -5 + (-91) = -(5 + 91) = -96;
к) -92 — 18 = -92 + (-18) = -(92 + 18) = -110;
л) -240 — 14 = -240 + (-14) = -(240 + 14) = -254;
м) -50 — 105 = -50 + (-105) = -(50 + 105) = -155;
н) -200 — 400 = -200 + (-400) = -(200 + 400) = -600.289. Вычислите:
а) -5 — 2; б) -1 — 3; в) -15 — 12; г) -6 — 14; д) -100 — 200.а) -5 — 2 = -5 + (-2) = -(5 + 2) = -7;
б) -1 — 3 = -1 + (-3) = -(1 + 3) = -4;
в) -15 — 12 = -15 + (-12) = -(15 + 12) = -27;
г) -6 — 14 = -6 + (-14) = -(6 + 14) = -20;
д) -100 — 200 = -100 + (-200) = -(100 + 200) = -300.290. Вычислите по образцу (290-291):
а) -1 — (-4) = -1 + 4 = 3;
б) -2 — (-2); в) -3 — (-4); г) -5 — (-2); д) -8 — (-6); е) 9 — (-5).б) -2 — (-2) = -2 + 2 = 0;
в) -3 — (-4) = -3 + 4 = 1;
г) -5 — (-2) = -5 + 2 = -3;
д) -8 — (-6) = -8 + 6 = -2;
е) 9 — (-5) = 9 + 5 = 14.291. Вычислите по образцу (290-291):
а) -794 — (-581) = -794 + 581 = -(794 — 581) = -213;| — 794
| 581
| 213
б) -824 — (-642); в) -498 — (-402); г) -864 — (-164);
д) -1240 — (-200); е) -1000 — (-2500); ж) 80 — (-1800).б) -824 — (-642) = -824 + 642 = -(824 — 642) = -182
— 824
642
182в) -498 — (-402) = -498 + 402 = -(498 — 402) = -96
— 498
402
96г) -864 — (-164) = -864 + 164 = -(864 — 164) = -700
— 864
164
700д) -1240 — (-200) = -1240 + 200 = -(1240 — 200) = -1040
— 1240
200
1040е) -1000 — (-2500) = -1000 + 2500 = 2500 — 1000 = 1500
— 2500
1000
1500ж) 80 — (-1800) = 80 + 1800 = 1880
+1800
80
1880292. Запишите сумму чисел без скобок по образцу:
а) (-25) + (-42) = -25 — 42;
б) (-45) + (-12); в) 17 + (-3); г) (-28) + (-49); д) 13 + (-45).а) (-25) + (-42) = -25 — 42;
б) (-45) + (-12) = -45 — 12;
в) 17 + (-3) = 17 — 3;
г) (-28) + (-49) = -28 — 49;
д) 13 + (-45) = 13 — 45.293. Вычислите сумму чисел:
а) 49 + (-23); б) 56 + (-63); в) (-15) + (-40); г) (-66) + (-28).а) 49 + (-23) = 49 — 23 = 26;
б) 56 + (-63) = 56 — 63 = -(63 — 56) = -7;
в) (-15) + (-40) = -15 + (-40) = -(15 + 40) = -55;
г) (-66) + (-28) = -66 + (-28) = -(66 + 28) = -94.294. Вычислите:
а) (-5 + 8) + 9; б) (14 — 18) — 7; в) 96 — (-72 + 13);
г) -75 — (-75 + 8); д) 79 + (48 — 79); е) 14 — (15 — 94).а) (-5 + 8) + 9 = -5 + 8 + 9 = (8 + 9) — 5 = 17 — 5 = 12;
б) (14 — 18) — 7 = 14 — 18 — 7 = (-18 — 7) + 14 = -(18 + 7) + 14 = -25 + 14 = -(25 — 14) = -11;
в) 96 — (-72 + 13) = 96 + 72 — 13 = (96 — 13) + 72 = 83 + 72 = 155;
г) -75 — (-75 + 8) = — 75 + 75 — 8 = (-75 + 75) — 8 = 0 — 8 = -8;
д) 79 + (48 — 79) = 79 + 48 — 79 = (79 — 79) + 48 = 0 + 48 = 48;
е) 14 — (15 — 94)= 14 — 15 + 94 = 94 + (14 — 15) = 94 — (15 — 14) = 94 — 1 = 93.
61
-
Ответы к стр. 61
295. Если α и b — натуральные числа, то верно ли, что их сумма и разность также являются натуральными числами?
Сумма натуральных чисел α и b всегда является натуральным (положительным) числом.
Разность натуральных чисел α и b не всегда является натуральным (положительным) числом, так как если b > α, то b — α = отрицательное число.296. Если α и b — целые числа, то верно ли, что их сумма и разность также являются целыми числами?
Сумма и разность двух целых чисел всегда будет равна целому числу.
297. Вычислите наиболее простым способом (297-298):
а) -1 — 2 — 3 — 4 — 5 — 6 + 5 + 4 + 3 + 2 + 1;
б) -8 — 7 — 5 — 3 — 1 + 0 + 1 + 3 + 5 + 7 + 8 + 9.а) -1 — 2 — 3 — 4 — 5 — 6 + 5 + 4 + 3 + 2 + 1 = (-1 + 1) + (-2 + 2) + (-3 + 3) + (-4 + 4) + (-5 + 5) — 6 = 0 + 0 + 0 + 0 + 0 — 6 = -6;
б) -8 — 7 — 5 — 3 — 1 + 0 + 1 + 3 + 5 + 7 + 8 + 9 = (-8 + 8) + (-7 + 7) + (-5 + 5) + (-3 + 3) + (-1 + 1) + 0 + 9 = 0 + 0 + 0 + 0 + 0 + 0 + 9 = 9.
298. Вычислите наиболее простым способом (297-298):
а) -9 — 8 — 7 — … — 1 + 0 + 1 + … + 7 + 8 + 9 + 10;
б) -101 — 100 — 99 — 98 — … + 98 + 99 + 100;
в) 1 — 2 + 3 — 4 + … + 9 — 10 + 11;
г) 1 — 2 + 3 — 4 + … + 99 — 100.а) Сложим сначала попарно все противоположные числа, затем оставшиеся 0 и 10:
-9 — 8 — 7 — … — 1 + 0 + 1 + … + 7 + 8 + 9 + 10 = (-9 + 9) + (-8 + 8) + (-7 + 7) + (-6 + 6) + (-5 + 5) + (-4 + 4) + (-3 + 3) + (-2 + 2) + (-1 + 1) + (0 + 10) = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 10 = 10 ;б) Сложим сначала попарно все противоположные числа, затем оставшиеся 0 и -101:
-101 — 100 — 99 — 98 − … + 98 + 99 + 100 = (-100 + 100) + (-99 + 99) + … + (-1 + 1) + (-101 + 0) = 0 + … + 0 + (-101) = -101;в) Сложим сначала попарно все соседние числа начиная с 1 (всего 5 пар) и прибавим к ним оставшееся без пары 11:
1 — 2 + 3 — 4 + … + 9 — 10 + 11 = (1 — 2) + (3 — 4) + … + (9 — 10) + 11 = (-1) + (-1) + … (-1) + 11 = -(1 + 1 + 1 + 1 + 1) + 11 = -5 + 11 = 11 — 5 = 6, так как получится 5 пар со значением -1;г) Всего 100 чисел, разобьём их по парам: 1 + (-2), 3 + (-4) и так далее – всего 50 пар (100 : 2 = 50). Тогда:
1 — 2 + 3 — 4 + … + 99 — 100 = (1 — 2) + (3 — 4) + … + (9 — 10) = (-1) + (-1) + … + (-1) = -50, так как получится 50 пар со значением -1.299. Для какого числа х верно равенство (299-300)?
а) x + 13 = 7, |
x = 7 — 13, | 7 — 13 = -(13 — 7) = -6
x = -6; |
б) х + 8 = -7; в) -7 + х = 9; г) х — (-8) = 13; д) -15 — х = 7.б) x + 8 = -7,
x = -7 — 8, | -7 — 8 = -(7 + 8) = -(15) = -15
x = -15;в) -7 + x = 9,
x = 9 — (-7), | 9 — (-7) = 9 + 7 = 16
x = 16;г) x — (-8) = 13,
x = 13 + (-8), | 13 + (-8) = 13 — 8 = 5
х = 5;д) -15 — x = 7,
x = -15 — 7, | -15 — 7 = -(15+7) = -22
x = -22.300. Для какого числа х верно равенство (299-300)?
а) -498 — x = -175, | —498
x = -498 — (-175), | 175
х = -498 + 175, | 323
x = -323;
б) 79 + x = -356; в) x — 57 = -493;
г) 167 — x = 39; д) -542 + x = 542.б) 79 + x = -356,
x = -356 — 79,
x = -435;
+356
79
435в) x — 57 = -493,
x = -493 + 57,
x = -436;
— 493
57
436г) 167 — x = 39,
x = 167 — 39,
x = 128;
— 167
39
128д) -542 + x = 542,
x = 542 + 542,
x = 1084.
+ 542
542
1084301. Найдите сумму нескольких одинаковых слагаемых:
а) (-5) + (-5) + … + (-5); б) (-7) + (-7) + … + (-7);
⌊ ⌋ ⌊ ⌋
6 8
в) (-10) + (-10) + … + (-10); г) (-6) + (-6) + … + (-6);
⌊ ⌋ ⌊ ⌋
9 11а) -(5 + 5 + 5 + 5 + 5 + 5) = -(30) = -30;
б) -(7 + 7 + 7 + 7 + 7 + 7 + 7 + 7) = -(56) = -56;
в) -(10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10) = -(90) = -90;
г) -(6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6) = -(66) = -66.
63
-
Произведение целых чисел
Ответы к стр. 63
302. а) Что называют произведением двух целых не равных нулю чисел?
б) Чему равно произведение любого целого числа и нуля?
в) Что называют степенью числа α с натуральным показателем n?а) Произведением двух целых не равных нулю чисел называют произведение их модулей, взятое со знаком «+», если эти числа одинаковых знаков, и со знаком «-», если они разных знаков.
б) Произведение любого целого числа и нуля равно нулю.
в) Степенью числа α с натуральным показателем n называют произведение n множителей, каждый из которых равен α.
303. Справедливы ли переместительный и сочетательный законы умножения для целых чисел? Сформулируйте их.
Справедливы.
Переместительный закон: от перемены мест множителей произведение не меняется.
Сочетательный закон: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.304. Что получится, если число умножить на (-1)?
При умножении любого числа на (-1) меняется только знак этого числа, то есть получается противоположное ему число.
305. Вычислите столбиком:
а) 123 • 9; б) 357 • 8; в) 256 • 32;
г) 457 • 48; д) 521 • 32; е) 439 • 528.а) × 123
9
1107;б) × 357
8
2856;в) × 256
32
+ 512
768
8192;г) × 457
48
+ 3656
1828
21936;д) × 521
32
+ 1042
1563
16672;е) × 439
528
3512
+ 878
2195
231792.306. Вычислите, применяя законы умножения:
а) 24 • 2 • 5; б) 47 • 4 • 25; в) 53 • 8 • 125;
г) 2 • 37 • 5; д) 25 • 57 • 4; е) 8 • 39 • 125.а) 24 • 2 • 5 = 24 • (2 • 5) = 24 • 10 = 240;
б) 47 • 4 • 25 = 47 • (4 • 25) = 47 • 100 = 4700;
в) 53 • 8 • 125 = 53 • (8 • 125) = 53 • 1000 = 53 000;
г) 2 • 37 • 5 = (2 • 5) • 37 = 10 • 37 = 370;
д) 25 • 57 • 4 = (25 • 4) • 57 = 100 • 57 = 5700;
е) 8 • 39 • 125 = 39 • (8 • 125) = 39 • 1000 = 39 000.307. Вычислите: а) 122; б) 93; в) 44; г) 25.
а) 122 = 12 • 12 = 144;
б) 93 = 9 • 9 • 9 = 729;
в) 44 = 4 • 4 • 4 • 4 = 256;
г) 25 = 2 • 2 • 2 • 2 • 2 = 32.308. Определите знак произведения. Выполните умножение:
а) (-2) • (+3); б) (+8) • (-3); в) (+6) • (-5);
г) (-7) • (+4); д) (-2) • (-1); е) (-8) • (-8);
ж) (-7) • (-9); з) (+9) • (+8); и) (+10) • (+77).а) (-2) • (+3) = -6;
б) (+8) • (-3) = -24;
в) (+6) • (-5) = -30;
г) (-7) • (+4) = -28;
д) (-2) • (-1) = 2;
е) (-8) • (-8) = 64;
ж) (-7) • (-9) = 63;
з) (+9) • (+8) = 72;
и) (+10) • (+77) = 770.309. Выполните умножение:
а) 0 • (-5); б) (+3) • 0; в) (-6) • 0;
г) (+49) • 0; д) 0 • (-54); е) 0 • (+48).а) 0 • (-5) = 0;
б) (+3) • 0 = 0;
в) (-6) • 0 = 0;
г) (+49) • 0 = 0;
д) 0 • (-54) = 0;
е) 0 • (+48) = 0.310. Выполните умножение по образцу:
(-56) ∗ (-13) = +(56 ∗ 13) = … |×56
| 13
| …
а) (+45) • (-13); б) (+230) • (-48); в) (-505) • (-8);
г) (-358) • (-5); д) (-24) • (-35); е) (-125) • (-160);
ж) (-405) • (+28); з) (-72) • (+101); и) (+15) • (+16).а) (+45) • (-13) = -(45 • 13) = -585;
× 45
13
+135
45
585б) (+230) • (-48) = -(230 • 48) = -11 040;
× 230
48
+1840
920
11040в) (-505) • (-8) = +(505 • 8) = 4040;
×505
8
4040г) (-358) • (-5) = +(358 • 5) = 1790;
×358
5
1790д) (-24) • (-35) = +(24 • 35) = 840;
× 24
35
+120
72
840е) (-125) • (-160) = +(125 • 160) = 20 000;
× 125
160
0
+ 750
125
20000ж) (-405) • (+28) = -(405 • 28) = -11 340;
× 405
28
+ 3240
810
11340з) (-72) • (+101) = -(72 • 101) = -7272;
× 72
101
72
+ 0
72
7272и) (+15) • (+16) = +(15 • 16) = 240.
× 15
16
+ 90
15
240Замечание. Для упрощения записи у положительных множителей знак «+» и скобки можно опускать, но этот знак надо учитывать, определяя знак произведения.
Например, (-3) • (+17) = (-3) • 17 = -51, (+2) • (-48) = 2 • (-48) = -96.311. Упростите запись произведения в предыдущем задании.
а) (+45) • (-13) = 45 • (-13);
б) (+230) • (-48) = 230 • (-48);
в) (-505) • (-8) = +(505 • 8) = 505 • 8;
г) (-358) • (-5) = +(358 • 5) = 358 • 5;
д) (-24) • (-35) = +(24 • 35) = 24 • 35;
е) (-125) • (-160) = +(125 • 160) = 125 • 160;
ж) (-405) • (+28) = (-405) • 28;
з) (-72) • (+101) = (-72) • 101;
и) (+15) • (+16) = 15 • 16.312. Определите знак произведения:
а) (-1) • (-1); б) (-1) • (-1) • (-1); в) (-1) • (-1) • (-1) • (-1);
г) (-1) • (-1) • (-1) • (-1) • (-1) • (-1) • (-1).а) (-1) • (-1) = 1;
б) (-1) • (-1) • (-1) = ((-1) • (-1)) • (-1) = 1 • (-1) = -1;
в) (-1) • (-1) • (-1) • (-1) = ((-1) • (-1)) • ((-1) • (-1)) = 1 • 1 = 1;
г) (-1) • (-1) • (-1) • (-1) • (-1) • (-1) • (-1) = ((-1) • (-1)) • ((-1) • (-1)) • ((-1) • (-1)) • (-1) = 1 • 1 • 1 • (-1) = -1. 64
-
Ответы к стр. 64
313. Определите знак произведения и вычислите это произведение:
а) (-3) • (-2) • (-1) • 4; б) (-2) • 3 • (-4) • (-6).а) (-3) • (-2) • (-1) • 4 = -(3 • 2 • 1 • 4) = -24;
б) (-2) • 3 • (-4) • (-6) = -(2 • 3 • 4 • 6) = -144.314. Сколько отрицательных множителей может содержать произведение, чтобы оно было:
а) положительным; б) отрицательным?а) 2 или 4 или 6 и так далее — чётное количество;
б) 1 или 3 или 5 и так далее — нечётное количество.315. Используя законы умножения, вычислите по образцу:
(-16) • (-7) • (-25) = -(16 • 25 • 7) = -(4 • 4 • 25 • 7) = -(100 • 4 • 7) = -(100 • 28) = -2800;
а) 2 • (-3) • (-10); б) (-4) • 17 • 25; в) 8 • (-25) • (-3);
г) (-6) • (-5) • (-7); д) 8 • (-17) • 125; е) (-3) • 16 • (-125).а) 2 • (-3) • (-10) = +(2 • 3 • 10) = +(6 • 10) = 60;
б) (-4) • 17 • 25 = -(4 • 17 • 25) = -(100 • 17) = -1700;
в) 8 • (-25) • (-3) = +(8 • 25 • 3) = +(4 • 2 • 25 • 3) = +(100 • 6) = 600;
г) (-6) • (-5) • (-7) = -(6 • 5 • 7) = -(3 • 2 • 5 • 7) = -(21 • 10) = -210;
д) 8 • (-17) • 125 = -(8 • 17 • 125) = -(1000 • 17) = -17 000;
е) (-3) • 16 • (-125) = +(3 • 16 • 125) = +(3 • 2 • 8 • 125) = +(6 • 1000) = 6000.316. Если α и b — целые числа, то верно ли, что:
а) если α > 0 и b > 0, то α • b > 0;
б) если α < 0 и b < 0, то α • b < 0;
в) если α • b > 0, то α > 0 и b > 0;
г) если α • b < 0, то α > 0 и b < 0.а) если α > 0 и b > 0, то α • b > 0 — верно, так как α и b имеют одинаковые знаки, а значит знак произведения будет «+»;
б) если α < 0 и b < 0, то α • b < 0 — неверно, так как α и b имеют одинаковые знаки, а значит знак произведения будет «+»;
в) если α • b > 0, то α > 0 и b > 0 — верно, так как α и b имеют одинаковые знаки, а значит знак произведения будет «+»;
г) если α • b < 0, то α > 0 и b < 0 — верно, так как α и b имеют разные знаки, а значит знак произведения будет «-».317. Произведение трёх чисел положительно. Можно ли утверждать, что все три числа положительные? Приведите примеры.
Утверждать нельзя, так как произведение трёх чисел будет положительным и тогда, когда оно будет содержать один положительный множитель и два отрицательных: -8 • (-10) • 5 = +(8 • 10) • 5 = 80 • 5 = 400.
318. Произведение двух чисел равно нулю. Докажите, что среди этих чисел есть хотя бы один нуль.
По условию задачи α • b = 0. Допустим, что b ≠ 0 или α ≠ 0, тогда α = 0 : b = 0 или b = 0 : α = 0 – то есть хотя бы один из множителей равен нулю.
319. Вычислите:
а) (-1)2; б) (-1)3; в) (-1)4; г) (-1)5;
д) (-3)2; е) (-2)2; ж) (-4)2; з) (-5)2;
и) (-2)3; к) (-3)3; л) (-4)3; м) (-5)3.а) (-1)2 = (-1) • (-1) = 1;
б) (-1)3 = (-1) • (-1) • (-1) = -1;
в) (-1)4 = (-1) • (-1) • (-1) • (-1) = 1;
г) (-1)5 = (-1) • (-1) • (-1) • (-1) • (-1) = -1;
д) (-3)2 = (-3) • (-3) = 9;
е) (-2)2 = (-2) • (-2) = 4;
ж) (-4)2 = (-4) • (-4) = 16;
з) (-5)2 = (-5) • (-5) = 25;
и) (-2)3 = (-2) • (-2) • (-2) = -8;
к) (-3)3 = (-3) • (-3) • (-3) = -27;
л) (-4)3 = (-4) • (-4) • (-4) = -64;
м) (-5)3 = (-5) • (-5) • (-5) = -125.320. Определите знак степени:
а) (-1)2; б) (-1)5; в) (-1)6; г) (-1)11;
д) (-1)8; е) (-1)9; ж) (-1)10; з) (-24)5;
и) (-33)50; к) (-103)46; л) (-12)100; м) (-41)33.Если произведение содержит чётное количество отрицательных множителей, то знак произведения будет «+», если же количество отрицательных множителей нечётное, то знак произведения будет «-». Таким образом, получается: если степень числа n — чётное, то знак степени будет «+», а если степень числа n — не чётное, то знак степени будет «-».
а) +; б) -; в) +; г) -; д) +; е) -; ж) +; з) -; и) +; к) +; л) +; м) -.321. Вычислите:
а) (-1)11 — (-1)11; б) (-2)5 — (-3)3;
в) (-1)4 — (-1)2 — (-1)2; г) (-1)2 + (-1)3 + (-1)4.а) (-1)11 — (-1)11 = (-1) — (-1) = (-1) + 1 = 0;
б) (-2)5 — (-3)3 = (-32) — (-27) = (-32) + 27 = -(32 — 27) = -5;
в) (-1)4 — (-1)2 — (-1)2 = 1 — 1 — 1 = -1;
г) (-1)2 + (-1)3 + (-1)4 = 1 — 1 + 1 = 1.322. Убедитесь, что верно равенство: 72 — 4 • (-3) = 72 + (-4) • (-3).
72 — 4 • (-3) = 72 + (-4) • (-3),
72 — (-12) = 72 + 12,
72 + 12 = 84,
84 = 84 — равенство верно.323. Вычислите:
а) 48 — 12 • (-5); б) 69 — (-12) • (-5); в) 129 — 15 • 9;
г) 456 — 45 • (-6); д) 158 — 45 • 7; е) 258 — 13 • (-7).а) 48 — 12 • (-5) = 48 — (-60) = 48 + 60 = 108;
б) 69 — (-12) • (-5) = 69 — 60 = 9;
в) 129 — 15 • 9 = 129 — 135 = -(135 — 129) = -6;
г) 456 — 45 • (-6) = 456 — (-270) = 456 + 270 = 726;
д) 158 — 45 • 7 = 158 — 315 = -(315 — 158) = -157;
е) 258 — 13 • (-7) = 258 — (-91) = 258 + 91 = 349.324. Какое число больше:
а) 3 • 3 • 3 или (-3) • (-3) • (-3);
б) -5 • 5 или (-5) • (-5);
в) (-7) • (-7) или 7 • (-7);
г) -2 • 2 • 2 • 2 или (-2) • (-2) • (-2) • (-2)?а) 3 • 3 • 3 = 27,
(-3) • (-3) • (-3) = -27,
27 > -27, следовательно, 3 • 3 • 3 > (-3) • (-3) • (-3);б) -5 • 5 = -25,
(-5) • (-5) = 25,
-25 < 25, следовательно, -5 • 5 < (-5) • (-5);в) (-7) • (-7) = 49,
7 • (-7) = -49,
49 > -49, следовательно, (-7) • (-7) > 7 • (-7);г) -2 • 2 • 2 • 2 = -16,
(-2) • (-2) • (-2) • (-2) = 16,
-16 < 16, следовательно, -2 • 2 • 2 • 2 < (-2) • (-2) • (-2) • (-2). 65
-
Ответы к стр. 65
325. Запишите выражение разными способами по образцу:
а) (-8)3 = (-8) • (-8) • (-8) = -(8 • 8 • 8) = -(83) = -83;
б) -63; в) (-5)4; г) -54; д) -72; е) (-18)2.б) -63 = (-6) • (-6) • (-6) = -(6 • 6 • 6) = -(63) = (-6)3;
в) (-5)4 = (-5) • (-5) • (-5) • (-5) = +(5 • 5 • 5 • 5) = 54;
г) -54 = -(5 • 5 • 5 • 5) = -(54);
д) -72 = -(7 • 7) = -(72);
е) (-18)2 = (-18) • (-18) = +(18 • 18) = 182.326. Какое число больше:
а) -22 или (-2)2; б) -32 или -23;
в) (-3)2 или (-2)3; г) (-4)3 или -34.а) -22 = -(2 • 2) = -4,
(-2)2 = (-2) • (-2) = 4,
-4 < 4, следовательно, -22 < (-2)2;б) -32 = -(3 • 3) = -9,
-23 = -(2 • 2 • 2) = -8,
-9 < -8, следовательно, -32 < -23;в) (-3)2 = (-3) • (-3) = 9,
(-2)3 = (-2) • (-2) • (-2) = -8,
9 > -8, следовательно, (-3)2 > (-2)3;г) (-4)3 = (-4) • (-4) • (-4) = -64,
-34 = -(3 • 3 • 3 • 3) = -81,
-64 > -81, следовательно, (-4)3 > -34.327. Запишите:
а) квадрат числа -2; б) произведение -4 и 7;
в) сумму чисел -7 и 7; г) куб числа -10;
д) четвертую степень -5; е) разность чисел -4 и -12.а) (-2)2;
б) -4 • 7;
в) -7 + 7;
г) (-10)3;
д) (-5)4;
е) -4 — (-12).328. Вычислите, предварительно указав порядок действий:
а) 3 • (-2)2; б) -4 • (-3)3; в) -(-3)4;
г) -(-2)3; д) -(-5)2; е) -4 • (-3)2.2 1
а) 3 • (-2)2 = 3 • 4 = 12;
2 1
б) -4 • (-3)3 = -4 • (-27) = 108;
2 1
в) -(-3)4 = -(+81) = -81;
2 1
г) -(-2)3 = -(-8) = 8;
2 1
д) -(-5)2 = -(+25) = -25;
2 1
е) -4 • (-3)2 = -4 • 9 = -36.329. Найдите число одинаковых слагаемых:
а) (-2) + (-2) + … + (-2) = -12; б) (-8) + (-8) + … + (-8) = -80;
в) (-4) + (-4) + … + (-4) = -20; г) (-3) + (-3) + … + (-3) = -39.а) |-12| : |-2| = 12 : 2 = 6 – шесть одинаковых слагаемых;
б) |-80| : |-8| = 80 : 8 = 10 – десять одинаковых слагаемых;
в) |-20| : |-4| = 20 : 4 = 5 – пять одинаковых слагаемых;
г) |-39| : |-3| = 39 : 3 = 13 – тринадцать одинаковых слагаемых.330. Какие одинаковые слагаемые сложили:
а) … + … + … + … + … = -25;
б) … + … + … + … = -40;
в) … + … + … + … + … + … = -36?а) -25 : 5 = -5;
б) -40 : 4 = -10;
в) -36 : 6 = -6. 66
-
Ответы к стр. 66
331. Чему равно частное от деления отличных от нуля целого числа α на целое число b, если |α| делится нацело на |b|?
Частное чисел α и b равно частному их модулей, взятому со знаком «+», если эти числа одинаковых знаков, и со знаком «-», если они разных знаков.
332. Чему равно частное от деления нуля на любое целое, не равное нулю число?
Частное от деления нуля на любое целое, не равное нулю число α равно 0.
333. Можно ли делить на нуль?
На 0 делить нельзя.
334. Выполните действия:
а) 234 : 6; б) 744 : 8; в) 1794 : 23;
г) 2997 : 37; д) 9268 : 331; е) 21 333 : 547.а) —234|6
18 |39
—54
54
0б) —744|8
72 |93
—24
24
0в) —1794|23
161 |78
—184
184
0г) —2997|37
296 |8
—37
37
0д) —9268|331
662 |28
—2648
2648
0е) —21333|547
1641 |39
—4923
4923
0335. Вычислите:
а) 576 • 23 — 766 • 35; б) 849 • 18 — 783 • 28;
в) 136 • 13 — (8416 + 1234); г) 4736 : 4 − 1245 • 5.а) 576 • 23 — 766 • 35 = 13 248 — 26 810 = -(26 810 — 13 248) = -13 562;
× 576 × 766
23 35
+1728 + 3830
1152 2298
13248 26810б) 849 • 18 — 783 • 28 = 15 282 — 21 924 = -(21 924 — 15 282) = -6642;
× 849 × 783
18 28
+ 6792 + 6264
849 1566
15282 21924в) 136 • 13 — (8416 + 1234) = 1768 — 9650 = -(9650 — 1768) = -7882;
×136 +8416
13 1234
+ 408 9650
136
1768г) 4736 : 4 — 1245 • 5 = 1184 — 6225 = -(6225 — 1184) = -5041.
—4736|4 ×1245
4 |1184 5
—7 6225
4
—33
32
—16
16
0336. Определите знак числа x:
а) x • (-8) = 400; б) (-10) • x = -420;
в) x • 15 = -60; г) 12 • x = 144.а) x • (-8) = 400, x = 400 : (-8), следовательно, x будет иметь знак «-»;
б) (-10) • x = -420, x = (-420) : (-10), следовательно, x будет иметь знак «+»;
в) x • 15 = -60, x = (-60) : 15, следовательно, x будет иметь знак «-»;
г) 12 • x = 144, x = 144 : 12, следовательно, x будет иметь знак «+».337. Определите знак частного:
а) 400 : (-8); б) (-420) : (-10);
в) (-60) : 15; г) 144 : 12.а) -; б) +; в) -; г) +.
338. Выполните деление (338-339):
а) (+60) : (-10) = -(60 : 10) = -6;
б) (-20) : 5; в) (-50) : 10; г) (-80) : (-20);
д) (-100) : (-25); е) 30 : (-15); ж) 64 : (-8).б) (-20) : 5 = -(20 : 5) = -4;
в) (-50) : 10 = -(50 : 10) = -5;
г) (-80) : (-20) = +(80 : 20) = 4;
д) (-100) : (-25) = +(100 : 25) = 4;
е) 30 : (-15) = -(30 : 15) = -2;
ж) 64 : (-8) = -(64 : 8) = -8.339. Выполните деление (338-339):
а) 200 : (-40); б) (-500) : 100; в) 720 : (-90);
г) (-810) : (-9); д) (-560) : (-70); е) (-480) : 60.а) 200 : (-40) = -(200 : 40) = -5;
б) (-500) : 100 = -(500 : 100) = -5;
в) 720 : (-90) = -(720 : 90) = -8;
г) (-810) : (-9) = +(810 : 9) = 90;
д) (-560) : (-70) = +(560 : 70) = 8;
е) (-480) : 60 = -(200 : 40) = -8. 67
-
Ответы к стр. 67
340. Выполните деление по образцу:
7227 : (-9) = -(7227 : 9) = — … | 7227|9
| | …
а) (-711) : 9; б) 1332 : (-3); в) (-2316) : (-12);
г) (-1302) : 42; д) (-2205) : (-7); е) 3208 : (-8).а) (-711) : 9 = -(711 : 9) = -79;
—711|9
63 |79
—81
81
0б) 1332 : (-3) = -(1332 : 3) = -444;
—1332|3
12 |444
—13
12
—12
12
0в) (-2316) : (-12) = +(2316 : 12) = 193;
—2316|12
12 |193
—111
108
—36
36
0г) (-1302) : 42 = -(1302 : 42) = -31;
—1302|42
126 |31
—42
42
0д) (-2205) : (-7) = +(2205 : 7) = 315;
—2205|7
21 |315
—10
7
—35
35
0е) 3208 : (-8) = -(3208 : 8) = -401.
—3208|8
32 |401
—8
8
0341. Найдите число х, для которого верно равенство:
а) х • (-12) = 36; б) (-13) • х = -143; в) х • (-15) = 465;
г) 14 • х = -294; д) х : 8 = 7; е) х : 6 = -42;
ж) х : (-7) = -9; з) х : (-11) = -352; и) 48 : х = 6;
к) 56 : х = -8; л) (-64) : х = 8; м) (-68) : х = -4.а) х • (-12) = 36,
х = 36 : (-12),
х = -3;б) (-13) • х = -143,
х = (-143) : (-13),
х = 11;в) х • (-15) = 465,
х = 465 : (-15),
х = -31;г) 14 • х = -294,
х = (-294) : 14,
х = -21;д) х : 8 = 7,
х = 7 • 8,
х = 56;е) х : 6 = -42,
х = (-42) • 6,
х = -252;ж) х : (-7) = -9
х = (-9) • (-7)
х = 63;з) х : (-11) = -352
х = (-352) • (-11)
х = 3872;и) 48 : х = 6
х = 48 : 6
х = 8;к) 56 : х = -8
х = 56 : (-8)
х = -7;л) (-64) : х = 8
х = (-64) : 8
х = -8;м) (-68) : х = -4
х = (-68) : (-4)
х = 17.342. Выполните действия по образцу:
а) 13 • 15 — 28 • 25 = -505;
1) ×13 2) ×28 3) 195 — 700 = -505 | -700
15 25 | 195
+ 65 +140 | 505
13 56
195 700
б) 679 • 13 — 846 • 15; в) 849 • 18 — 684 : 19;
г) 4074 : 42 — 12 • 59; д) 3612 : 12 — 8445 : 15.б) 679 • 13 — 846 • 15 = 8827 — 12 690 = -3863;
1) ×679 2)×846
13 15
+2037 +4230
679 846
8827 126903) 8827 — 12 690 = -3863
—12690
8827
3963в) 849 • 18 — 684 : 19 = 15 282 — 36 = 15 246;
1)×849 2) —684|19
18 57 |36
+ 6792 —114
849 114
15282 03) 15 282 — 36 = 15 246
—15282
36
15246г) 4074 : 42 — 12 • 59 = 97 — 708 = -611;
1) —4074|42 2) ×12
378 |97 59
—294 +108
294 60
0 7083) 97 — 708 = -611
—708
97
611д) 3612 : 12 — 8445 : 15 = 301 — 563 = -262.
1) —3612|12 2) —8445|15
36 |301 75 |563
0 —94
—12 90
12 —45
0 45
0
3) 301 — 563 = -262
—563
301
262343. Вычислите:
а) 43 212 : 78 — 407 • 720 + 350 • 509;
б) 164 • 756 + 148 916 — 564 • 702 + 48 762 : 86;
в) (24 968 + 11 648) : (768 — 1564);
г) 37 115 : 65 — 72 675 : 85.а) 43 212 : 78 — 407 • 720 + 350 • 509 = 554 — 293 040 + 178 150 = -114 336;
1) —43212|78 2) ×407
390 |554 720
—421 + 814
390 2849
—312 293040
312
03)×509 4) —293040 5) —292486
350 554 178150
+ 2545 292486 114336
1527
178150б) 164 • 756 + 148 916 — 564 • 702 + 48 762 : 86 = 123 984 + 148 916 — 395 928 + 567 = -122 461;
1) ×164 2)×564
756 702
984 1128
+ 820 + 0
1148 3948
123984 3959283) —48762|86 4) +123984
430 |567 148916
—576 272900
516
—602
602
05) —395928 6) —123098
272900 567
123028 122461в) (24 968 + 11 648) : (768 — 1564) = 36 616 : (-796) = -46;
1) +24968 2) —1564
11648 768
36616 7963) —36616|796
3184 |46
—4776
4776
0г) 37 115 : 65 — 72 675 : 85 = 571 — 855 = -284.
1) —37115|65 2) —72675|85
325 |571 680 |855
—461 —467
455 425
—65 —425
65 425
0 03) —855
571
284 68
-
Ответы к стр. 68
344. Запишите произведение в виде суммы (разности):
а) 5 • (38 + 17) = 5 • 38 + 5• 17;
б) 17 • (31 + 16); в) (28 + 37) • 56; г) (72 + 98) • 12;
д) (49 — 17) • 12; е) 8 • (57 — 38); ж) 17 • (28 + 31).б) 17 • (31 + 16) = 17 • 31 + 17 • 16;
в) (28 + 37) • 56 = 28 • 56 + 37 • 56;
г) (72 + 98) • 12 = 72 • 12 + 98 • 12;
д) (49 — 17) • 12 = 49 • 12 — 17 • 12;
е) 8 • (57 — 38) = 8 • 57 — 8 • 38;
ж) 17 • (28 + 31) = 17 • 28 + 17 • 31.345. Вынесите общий множитель за скобки:
а) 15 • 12 + 15 • 49 = 15 • (12 + 49);
б) 57 • 39 + 57 • 64; в) 39 • 12 + 28 • 12; г) 73 • 57 + 79 • 57;
д) 13 • 95 — 13 • 41; е) 27 • 48 — 19 • 48; ж) 54 • 88 — 54 • 87.б) 57 • 39 + 57 • 64 = 57 • (38 + 64);
в) 39 • 12 + 28 • 12 = 12 • (39 + 28);
г) 73 • 57 + 79 • 57 = 57 • (73 + 79);
д) 13 • 95 — 13 • 41 = 13 • (95 — 41);
е) 27 • 48 — 19 • 48 = 48 • (27 — 19);
ж) 54 • 88 — 54 • 87 = 54 • (88 — 87).346. Вычислите удобным способом:
а) 350 • 46 + 250 • 46; б) 728 • 49 — 528 • 49;
в) 52 • 100 — 52 • 99; г) 99 • 48 + 1 • 48;
д) 4300 — 43 • 99; е) 999 • 156 + 156;
ж) 128 • 32 + 872 • 32 — 1000 • 31; з) 999 • 999 — 999 • 989 — 9990;
и) 728 • 359 — 628 • 359 + 641 • 1000.а) 350 • 46 + 250 • 46 = 46 • (350 + 250) = 46 • 600 = 27 600;
б) 728 • 49 — 528 • 49 = 49 • (728 — 528) = 49 • 200 = 9800;
в) 52 • 100 — 52 • 99 = 52 • (100 — 99) = 52 • 1 = 52;
г) 99 • 48 + 1 • 48 = (99 + 1) • 48 = 100 • 48 = 4800;
д) 4300 — 43 • 99 = 43 • 100 — 43 • 99 = 43 • (100 — 99) = 43 • 1 = 43;
е) 999 • 156 + 156 = 999 • 156 + 1 • 156 = (999 + 1) • 156 = 1000 • 156 = 156 000;
ж) 128 • 32 + 872 • 32 — 1000 • 31 = (128 + 872) • 32 — 1000 • 31 = 1000 • 32 — 1000 • 31 = 1000 • (32 — 31) = 1000 • 1 = 1000;
з) 999 • 999 — 999 • 989 — 9990 = 999 • 999 — 999 • 989 — 999 • 10 = 999 • (999 — 989 — 10) = 999 • 0 = 0;
и) 728 • 359 — 628 • 359 + 641 • 1000 = (728 — 628) • 359 + 641 • 1000 = 100 • 359 + 641 • 10 • 100 = 100 • (359 + 6410) = 100 • 6769 = 676 900.
347. Запишите распределительный закон для целых чисел α, b, c, сформулируйте его.
(α + b) • c = α • c + b • c
Чтобы целое число c умножить на сумму целых чисел α и b, можно число c умножить вначале на число α, за тем число c умножить на число b и полученные результаты сложить.348. Как называют переход от суммы α • c + b • c к произведению (α + b) • c?
Вынесение общего множителя за скобки.
349. Проверьте выполнение распределительного закона для чисел α, b, c:
а) α = -5, b = 3, c = -10; б) α = -5, b = -3, c = 6.(α + b) • c = α • c + b • c
а) (-5 + 3) • (-10) = (-5) • (-10) + 3 • (-10),
(-2) • (-10) = 50 + (-30),
20 = 20 — распределительный закон выполнен;б) (-5 + (-3)) • 6 = (-5) • 6 + (-3) • 6,
(-8) • 6 = (-30) + (-18)
-48 = -48 — распределительный закон выполнен. 69
-
Ответы к стр. 69
350. Запишите произведение в виде суммы по образцу:
а) (-5) • (-12 + 16) = (-5) • (-12) + (-5) • 16;
б) 6 • (8 + (-17)); в) (-7) • ((-15) + (-12);
г) 16 • (8 — 17); д) (-17) • (-15 — 12);
е) (25 + 16) • (-9); ж) (45 — 17) • (-11);
з) (-15 — 42) • 13; и) (-28 — 37) • (-3).б) 6 • (8 + (-17)) = 6 • 8 + 6 • (-17);
в) (-7) • ((-15) + (-12) = (-7) • (-15) + (-7) • (-12);
г) 16 • (8 — 17) = 16 • 8 + 16 • (-17);
д) (-17) • (-15 — 12) = (-17) • (-15) + (-17) • (-12);
е) (25 + 16) • (-9) = 25 • (-9) + 16 • (-9);
ж) (45 — 17) • (-11) = 45 • (-11) + (-17) • (-11);
з) (-15 — 42) • 13 = (-15) • 13 + (-42) • 13;
и) (-28 — 37) • (-3) = (-28) • (-3) + (-37) • (-3).351. Верно ли применен распределительный закон:
а) (-2) • (5 + 7) = -10 — 14; б) (-7 + 5 — 8) • (-2) = 14 — 10 + 16;
в) (7 — 8) • (-3) = -21 — 24; г) 6 • ((-4) + (-12)) = -24 — 72?а) (-2) • (5 + 7) = -10 — 14,
(-2) • 5 + (-2) • 7 = -10 — 14,
-10 + (-14) = -10 — 14,
-10 — 14 = -10 — 14 — распределительный закон применен верно;б) (-7 + 5 — 8) • (-2) = 14 — 10 + 16,
(-7) • (-2) + 5 • (-2) + (-8) • (-2) = 14 — 10 + 16,
14 + (-10) + 16 = 14 — 10 + 16,
14 — 10 + 16 = 14 — 10 + 16 — распределительный закон применен верно;в) (7 — 8) • (-3) = -21 – 24,
7 • (-3) + (-8) • (-3) = -21 — 24,
-21 + 24 ≠ -21 — 24 — распределительный закон применен неверно;г) 6 • ((-4) + (-12)) = -24 — 72,
6 • (-4) + 6 • (-12) = -24 — 72,
-24 + (-72) = -24 — 72,
-24 — 72 = -24 — 72 — распределительный закон применен верно.352. Вместо знака [] поставьте знак «+» или «-» так, чтобы равенство было верным:
а) 3 • (2 — 7) = []3 • 2 [] 3 • 7; б) (-5) • (-6 — 7) = []5 • 6 [] 5 • 7;
в) (-2) • (6 + 9) = []2 • 6 [] 2 • 9; г) (-2) • (6 — 9) = []2 • 6 [] 2 • 9.а) 3 • (2 — 7) = 3 • 2 + 3 • (-7) = +3 • 2 — 3 • 7;
б) (-5) • (-6 — 7) = (-5) • (-6) + (-5) • (-7) = +5 • 6 + 5 • 7;
в) (-2) • (6 + 9) = (-2) • 6 + (-2) • 9 = —2 • 6 — 2 • 9;
г) (-2) • (6 — 9) = (-2) • 6 + (-2) • (-9) = —2 • 6 + 2 • 9.353. Упростите числовое выражение (353-355):
а) (-8) • (-7 + 5) — 5 • (-8); б) 3 • (-98 + 2) + 3 • 98;
в) (-8) • (-47 + 125) — 47 • 8; г) (-25) • (45 — 100) + 25 • 45;
д) 83 • (-98 — 1) + 98 • 83; е) (-15) • (-7 + 15) — 7 • 15.а) (-8) • (-7 + 5) — 5 • (-8) = -8 • (-7 + 5 — 5) = -8 • (-7) = 56;
б) 3 • (-98 + 2) + 3 • 98 = 3 • (-98 + 2 + 98) = 3 • 2 = 6;
в) (-8) • (-47 + 125) — 47 • 8 = -8 • (-47 + 125 + 47) = -8 • 125 = -1000;
г) (-25) • (45 — 100) + 25 • 45 = -25 • (45 — 100 — 45) = -25 • (-100) = 2500;
д) 83 • (-98 — 1) + 98 • 83 = 83 • (-98 — 1 + 98) = 83 • (-1) = -83;
е) (-15) • (-7 + 15) — 7 • 15 = -15 • (-7 + 15 + 7) = -15 • 15 = -225.
354. Упростите числовое выражение (353-355):
а) (12 — 27) • (-1); б) (-1) • (35 — 88);
в) (-1) • (56 — 74); г) (-1) • (-28 — 112).а) (12 — 27) • (-1) = 12 • (-1) + (-27) • (-1) = -12 + 27 = 15;
б) (-1) • (35 — 88) = (-1) • 35 + (-1) • (-88) = -35 + 88 = 53;
в) (-1) • (56 — 74) = (-1) • 56 + (-1) • (-74) = -56 + 74 = 18;
г) (-1) • (-28 — 112) = (-1) • (-28) + (-1) • (-112) = 28 + 112 = 140.355. Упростите числовое выражение (353-355):
а) 4 • (-25 + 76 + 24); б) (25 — 62 — 38) • (-4);
в) (7 — 125 + 13) • (-8); г) 8 • (-8 + 100 — 22 + 25).а) 4 • (-25 + 76 + 24) = 4 • (-25 + 100) = 4 • (-25) + 4 • 100 = -100 + 400 = 300;
б) (25 — 62 — 38) • (-4) = (25 — 100) • (-4) = 25 • (-4) + (-100) • (-4) = -100 + 400 = 300;
в) (7 — 125 + 13) • (-8) = (-125 + 20) • (-8) = (-125) • (-8) + 20 • (-8) = 1000 — 160 = 840;
г) 8 • (-8 + 100 — 22 + 25) = 8 • (-30 + 125) = 8 • (-30) + 8 • 125 = -240 + 1000 = 760.
356. Вынесите общий множитель за скобки по образцу:
а) 45 • 13 — 45 • 81 = 45 • (13 — 81);
б) 49 • 57 — 49 • 570; в) 58 • 64 — 99 • 64;
г) (-53) • 48 — (-53) • 59; д) (-45) • 12 + 95 • (-45);
е) -53 • 48 — 57 • 48; ж) -45 • 13 — 45 • 27.б) 49 • 57 — 49 • 570 = 49 • (57 — 570);
в) 58 • 64 — 99 • 64 = 64 • (58 — 99);
г) (-53) • 48 — (-53) • 59 = -53 • (48 — 59);
д) (-45) • 12 + 95 • (-45) = -45 • (12 + 95);
е) -53 • 48 — 57 • 48 = 48 • (-53 — 57);
ж) -45 • 13 — 45 • 27 = -45 • (13 + 27).357. Вынесите общий множитель за скобки со знаком «+»:
а) 4 • 52 — 4 • (-95) = 4 • (52 — (-95)) = 4 • (52 + 95);
б) -16 • 17 — 16 • 18; в) 49 • 19 — 19 • 91; г) -88 • 35 — 77 • 35;
д) 73 • 37 — 73 • 73; е) -57 • 33 + 48 • 33; ж) 99 • 98 + 99 • 100.б) -16 • 17 — 16 • 18 = 16 • (-17 — 18);
в) 49 • 19 — 19 • 91 = 19 • (49 — 91);
г) -88 • 35 — 77 • 35 = 35 • (-88 — 77);
д) 73 • 37 — 73 • 73 = 73 • (37 — 73);
е) -57 • 33 + 48 • 33 = 33 • (-57 + 48);
ж) 99 • 98 + 99 • 100 = 99 • (98 + 100).358. Вынесите общий множитель за скобки со знаком «-»:
а) 4 • 52 — 4 • (-95) = (-4) • (-52 — 95);
б) -16 • 17 — 16 • 18; в) 49 • 19 — 19 • 91; г) -88 • 35 — 77 • 35;
д) 73 • 37 — 73 • 73; е) -57 • 33 + 48 • 33; ж) 99 • 98 + 99 • 100.б) -16 • 17 — 16 • 18 = (-16) • (17 + 18);
в) 49 • 19 — 19 • 91 = (-19) • (-49 + 91);
г) -88 • 35 — 77 • 35 = (-35) • (88 + 77);
д) 73 • 37 — 73 • 73 = (-73) • (-37 + 73);
е) -57 • 33 + 48 • 33 = (-33) • (57 — 48);
ж) 99 • 98 + 99 • 100 = (-99) • (-98 — 100). 70
-
Ответы к стр. 70
359. Вычислите:
а) 59 • 64 + 59 • 36; б) 72 • 128 — 72 • 228;
в) 63 • 356 — 556 • 63; г) -99 • 12 — 99 • 88;
д) -67 • 85 — 67 • 115; е) 41 • 91 — 91 • 51.а) 59 • 64 + 59 • 36 = 59 • (64 + 36) = 59 • 100 = 5900;
б) 72 • 128 — 72 • 228 = 72 • (128 — 228) = 72 • (-100) = -7200;
в) 63 • 356 — 556 • 63 = 63 • (356 — 556) = 63 • (-200) = -12 600;
г) -99 • 12 — 99 • 88 = -99 • (12 + 88) = -99 • 100 = -9900;
д) -67 • 85 — 67 • 115 = -67 • (85 + 115) = -67 • 200 = -13 400;
е) 41 • 91 — 91 • 51 = 91 • (41 — 51) = 91 • (-10) = -910.360. Докажите, что:
а) 43 • 15 — 55 • 15 + 34 • 15 делится на 22;
б) 12 • 17 — 16 • 17 + 13 • 17 делится на 9;
в) 99 • 51 — 99 • 91 + 69 • 99 делится на 29;
г) 63 • 23 — 32 • 63 + 22 • 63 делится на 13.Если хотя бы один из множителей произведения делится на некоторое число без остатка, то и само произведение делится на это число без остатка.
а) 43 • 15 — 55 • 15 + 34 • 15 = 15 • (43 — 55 + 34) = 15 • 22, 22 делится на 22 без остатка;б) 12 • 17 — 16 • 17 + 13 • 17 = 17 • (12 — 16 + 13) = 17 • 9, 9 делится на 9 без остатка;
в) 99 • 51 — 99 • 91 + 69 • 99 = 99 • (51 — 91 + 69) = 99 • 29, 29 делится на 29 без остатка;
г) 63 • 23 — 32 • 63 + 22 • 63 = 63 • (23 — 32 + 22) = 63 • 13, 13 делится на 13 без остатка.
361. Вычислите:
а) 42 • 53 — 32 • 53 — 42 • 63 + 32 • 63;
б) 79 • 45 + 79 • 55 — 89 • 45 — 89 • 55;
в) 88 • 75 — 12 • 45 + 12 • 75 — 88 • 45;
г) 392 • 23 — 492 • 23 + 392 • 77 — 492 • 77.а) 42 • 53 — 32 • 53 — 42 • 63 + 32 • 63 = 53 • (42 — 32) — 63 • (42 — 32) = (42 — 32) • (53 — 63) = 10 • (-10) = -100;
б) 79 • 45 + 79 • 55 — 89 • 45 — 89 • 55 = 79 • (45 + 55) — 89 • (45 + 55) = (45 + 55) • (79 — 89) = 100 • (-10) = -1000;
в) 88 • 75 — 12 • 45 + 12 • 75 — 88 • 45 = 88 • 75 + 12 • 75 — 12 • 45 — 88 • 45 = 75 • (88 + 12) — 45 • (12 + 88) = (88 + 12) • (75 — 45) = 100 • 30 = 3000;
г) 392 • 23 — 492 • 23 + 392 • 77 — 492 • 77 = 392 • 23 + 392 • 77 — 492 • 23 — 492 • 77 = 392 • (23 + 77) — 492 • (23 + 77) = (23 + 77) • (392 — 492) = 100 • (-100) = -10 000.
71
-
Ответы к стр. 71
362. Сформулируйте правило раскрытия скобок, перед которыми стоит знак: а) «+»; б) «-».
а) если сумма заключена в скобки, перед которыми стоит знак «+», то при раскрытии скобок знаки слагаемых оставляют без изменения;
б) если сумма заключена в скобки, перед которыми стоит знак «-», то при раскрытии скобок знаки слагаемых меняют на противоположные.
363. По какому правилу заключают в скобки сумму, если перед скобками ставят знак : а) «+»; б) «-»?
а) если сумма заключается в скобки, перед которыми стоит знак «+», то знаки слагаемых, заключаемых в скобки, оставляют без изменения;
б) если сумма заключается в скобки, перед которыми стоит знак «-», то знаки слагаемых, заключаемых в скобки, меняют на противоположные.
364. Раскройте скобки, объясняя свои действия (364-366):
а) +(5 + 7); б) +(3 — 8 + 7);
в) +(-3 + 8 + 7); г) +(-10 — 12 + 1).Если сумма заключена в скобки, перед которыми стоит знак «+», то при раскрытии скобок знаки слагаемых оставляют без изменения.
а) +(5 + 7) = 5 + 7;
б) +(3 -8 + 7) = 3 — 8 + 7;
в) +(-3 + 8 + 7) = -3 + 8 + 7;
г) +(-10 — 12 + 1) = -10 — 12 + 1.365. Раскройте скобки, объясняя свои действия (364-366):
а) -(5 + 7); б) -(3 — 8 + 7);
в) -(-3 + 8 + 7); г) -(-10 — 12 + 1).Если сумма заключена в скобки, перед которыми стоит знак «-», то при раскрытии скобок знаки слагаемых меняют на противоположные.
а) -(5 + 7) = -5 — 7;
б) -(3 — 8 + 7) = -3 + 8 — 7;
в) -(-3 + 8 + 7) = 3 — 8 — 7;
г) -(-10 — 12 + 1) = 10 + 12 — 1.366. Раскройте скобки, объясняя свои действия (364-366):
а) +(α — b — c); б) -(α — b — c);
в) +(-α + b + c); г) -(-α + b + c),
где α, b, и с − целые числа.а) Если сумма заключена в скобки, перед которыми стоит знак «+», то при раскрытии скобок знаки слагаемых оставляют без изменения: +(a — b — c) = a — b — c;
б) Если сумма заключена в скобки, перед которыми стоит знак «-», то при раскрытии скобок знаки слагаемых меняют на противоположные: -(a — b — c) = -a + b + c;
в) Если сумма заключена в скобки, перед которыми стоит знак «+», то при раскрытии скобок знаки слагаемых оставляют без изменения: +(-a + b + c) = -a + b + c;
г) Если сумма заключена в скобки, перед которыми стоит знак «-», то при раскрытии скобок знаки слагаемых меняют на противоположные: -(-a + b + c) = a — b — c.
72
-
Ответы к стр. 72
367. Раскройте скобки (367-370):
а) +(56 + 42); б) +(7 • 8 + 42); в) +(63 + 42);
г) +(63 + 6 • 7); д) +(61 — 98); е) +(-88 + 99).а) +(56 + 42) = 56 + 42;
б) +(7 • 8 + 42) = 7 • 8 + 42;
в) +(63 + 42) = 63 + 42;
г) +(63 + 6 • 7) = 63 + 6 • 7;
д) +(61 — 98) = 61 — 98;
е) +(-88 + 99) = -88 + 99.368. Раскройте скобки (367-370):
а) -(41 + 19); б) -(44 + 57); в) -(45 — 35);
г) -(45 — 7 • 5); д) -(45 — 53); е) -(9 • 5 — 53).а) -(41 + 19) = -41 — 19;
б) -(44 + 57) = -44 — 57;
в) -(45 — 35) = -45 + 35;
г) -(45 — 7 • 5) = -45 + 7 • 5;
д) -(45 — 53) = -45 + 53;
е) -(9 • 5 — 53) = -9 • 5 + 53.369. Раскройте скобки (367-370):
а) +(48 — 93) — 8; б) -(96 — 35) — 6;
в) -(7 • 8 — 20) + 7 • 8; г) +(99 — 5 + 8) — 17.а) +(48 — 93) — 8 = 48 — 93 — 8;
б) -(96 — 35) — 6 = -96 + 35 — 6;
в) -(7 • 8 — 20) + 7 • 8 = -7 • 8 + 20 + 7 • 8;
г) +(99 — 5 + 8) — 17 = 99 — 5 + 8 — 17.370. Раскройте скобки (367-370):
а) -(2 • 5 + 48) + 23; б) -(32 — 74) — 74;
в) +(-120 — 9 • 9) — 81; г) +(120 — 92) + 81.а) -(2 • 5 + 48) + 23 = -2 • 5 — 48 + 23;
б) -(32 — 74) — 74 = -32 + 74 — 74;
в) +(-120 — 9 • 9) — 81 = -120 — 9 • 9 — 81;
г) +(120 — 92) + 81 = 120 — 92 + 81.371. Раскройте скобки и вычислите сумму:
а) -(-72 + 39) + 39 = 72 — 39 + 39 = 72;
б) +(398 — 700) + 700; в) -(754 — 1200) — 1200;
г) +(-32 — 491) + 32; д) -(-129 + 59) — 129.б) +(398 — 700) + 700 = 398 — 700 + 700 = 398;
в) -(754 — 1200) — 1200 = -754 + 1200 — 1200 = -754;
г) +(-32 — 491) + 32 = -32 — 491 + 32 = -491;
д) -(-129 + 59) — 129 = 129 — 59 — 129 = -59.Замечание. Знак «+» перед скобками часто не пишут, но учитывают его при раскрытии скобок.
372. Вычислите (372-373):
а) (456 — 75) — 25; б) -(728 — 49) + 51;
в) (-238 + 742) — 42; г) -(-356 + 145) — 56.а) (456 — 75) — 25 = 456 — 75 — 25 = 456 — (75 + 25) = 456 — 100 = 356;
б) -(728 — 49) + 51 = -728 + 49 + 51 = -728 + (49 + 51) = -728 + 100 = -628;
в) (-238 + 742) — 42 = -238 + 742 — 42 = -238 + (742 — 42) = -238 + 700 = 462;
г) -(-356 + 145) — 56 = 356 — 145 — 56 = (356 — 56) — 145 = 300 — 145 = 155.373. Вычислите (372-373):
а) (7 • 95 — 900) — 7 • 95; б) -(795 — 9 • 99) — 99 • 9;
в) (-48 + 101 — 29) — 101 + 29; г) -(-79 — 39 + 81) + 81 — 39.а) (7 • 95 — 900) — 7 • 95 = 7 • 95 — 900 — 7 • 95 = -900;
б) -(795 — 9 • 99) — 99 • 9 = -795 + 9 • 99 — 99 • 9 = -795;
в) (-48 + 101 — 29) — 101 + 29 = -48 + 101 — 29 — 101 + 29 = -48;
г) -(-79 — 39 + 81) + 81 — 39 = 79 + 39 — 81 + 81 — 39 = 79.374. Перепишите, заполняя пропуски:
а) 45 — 36 = +(45 — 36);
б) 45 — 36 = -(…); в) -79 + 11 = +(…);
г) -79 + 11 = -(…); д) 38 + 59 = +(…);
е) -17 — 81 = -(…); ж) 39 — 70 = +(…).б) 45 — 36 = -(-45 + 36);
в) -79 + 11 = +(-79 + 11);
г) -79 + 11 = -(79 — 11);
д) 38 + 59 = +(38 + 59);
е) -17 — 81 = -(17 + 81);
ж) 39 — 70 = +(39 — 70).375. Заключите первые два слагаемых в скобки, перед скобками поставьте знак «+»:
а) 79 — 48 + 15 — 8; б) -56 + 38 — 12 + 100;
в) 43 + 59 — 35 — 11; г) -43 — 59 + 35 + 11;
д) 42 — 79 + 13 — 1; е) -57 + 48 — 17 + 23.а) 79 — 48 + 15 — 8 = +(79 — 48) + 15 — 8;
б) -56 + 38 — 12 + 100 = +(-56 + 38) — 12 + 100;
в) 43 + 59 — 35 — 11 = +(43 + 59) — 35 — 11;
г) -43 — 59 + 35 + 11 = +(-43 — 59) + 35 + 11;
д) 42 — 79 + 13 — 1 = +(42 — 79) + 13 — 1;
е) -57 + 48 — 17 + 23 = +(-57 + 48) — 17 + 23.376. Заключите первые два слагаемых в скобки, перед скобками поставьте знак «-»:
а) 79 — 48 + 15 — 8; б) -56 + 38 — 12 + 100;
в) 43 + 59 — 35 — 11; г) -43 — 59 + 35 + 11;
д) 42 — 79 + 13 — 1; е) -57 + 48 — 17 + 23.а) 79 — 48 + 15 — 8 = -(-79 + 48) + 15 — 8;
б) -56 + 38 — 12 + 100 = -(56 — 38) — 12 + 100;
в) 43 + 59 — 35 — 11 = -(-43 — 59) — 35 — 11;
г) -43 — 59 + 35 + 11 = -(43 + 59) + 35 + 11;
д) 42 — 79 + 13 — 1 = -(-42 + 79) + 13 — 1;
е) -57 + 48 — 17 + 23 = -(57 — 48) — 17 + 23. 73
-
Ответы к стр. 73
377. По каким правилам раскрывают скобки в суммах?
В суммах, в которых стоящие перед скобками знаки «+» или «-» обозначают действия сложения или вычитания применимы правила раскрытия скобок:
α + (b — c) = α + b — c,
α — (b — c) = α — b + c.378. Какие правила и законы применяют для вычисления суммы нескольких слагаемых?
Для вычисления суммы нескольких слагаемых применяют правила раскрытия скобок и заключения в скобки, законы сложения.
379. Раскройте скобки:
а) 49 — (38 — 5); б) -32 + (78 — 9);
в) 72 + (-32 + 9); г) -63 — (-63 + 1);
д) (79 — 39) — (79 — 48); е) (37 — 49) — (87 — 59);
ж) -(45 — 64) + (38 — 24); з) -(-35 + 2) + (-35 — 8).а) 49 — (38 — 5) = 49 — 38 + 5;
б) -32 + (78 — 9) = -32 + 78 — 9;
в) 72 + (-32 + 9) = 72 — 32 + 9;
г) -63 — (-63 + 1) = -63 + 63 — 1;
д) (79 — 39) — (79 — 48) = 79 — 39 — 79 + 48;
е) (37 — 49) — (87 — 59) = 37 — 49 — 87 + 59;
ж) -(45 — 64) + (38 — 24) = -45 + 64 + 38 — 24;
з) -(-35 + 2) + (-35 — 8) = 35 — 2 — 35 — 8.380. Раскройте скобки и вычислите:
а) 108 — (108 — 5); б) -49 — (-49 + 2);
в) -56 + (-98 + 56); г) 100 — (-5 + 100);
д) (79 — 81) — (39 — 81); е) (-78 + 23) + (27 + 78);
ж) (-39 + 15) — (5 — 39); з) (105 — 48) — (62 + 105).а) 108 — (108 — 5) = 108 — 108 + 5 = 5;
б) -49 — (-49 + 2) = -49 + 49 — 2 = -2;
в) -56 + (-98 + 56) = -56 — 98 + 56 = -98;
г) 100 — (-5 + 100) = 100 + 5 — 100 = 5;
д) (79 — 81) — (39 — 81) = 79 — 81 — 39 + 81 = 40;
е) (-78 + 23) + (27 + 78) = -78 + 23 + 27 + 78 = 50;
ж) (-39 + 15) — (5 — 39) = -39 + 15 — 5 + 39 = 10;
з) (105 — 48) — (62 + 105) = 105 — 48 — 62 — 105 = -110. 74
-
Ответы к стр. 74
381. Вычислите, раскрывая скобки только в тех случаях, когда это облегчает вычисления:
а) 79 — (63 + 7); б) 43 + (23 + 77); в) 79 — (79 — 7);
г) 43 + (77 — 43); д) 102 — (56 + 44); е) 102 — (102 — 5);
ж) 93 — (68 + 93); з) -72 — (99 + 1); и) 48 — (11 + 19);
к) 48 — (18 + 19); л) -56 + (96 + 9); м) 59 + (96 + 4);
н) 52 — (32 — 41); о) 73 — (68 — 8); п) -25 — (-45 + 19).а) 79 — (63 + 7) = 79 — 70 = 9;
б) 43 + (23 + 77) = 43 + 100 = 143;
в) 79 — (79 — 7) = 79 — 79 + 7 = 7;
г) 43 + (77 — 43) = 43 + 77 — 43 = 77;
д) 102 — (56 + 44) = 102 — 100 = 2;
е) 102 — (102 — 5) = 102 — 102 + 5 = 5;
ж) 93 — (68 + 93) = 93 — 68 — 93 = -68;
з) -72 — (99 + 1) = -72 — 100 = -172;
и) 48 — (11 + 19) = 48 — 30 = 18;
к) 48 — (18 + 19) = 48 — 18 — 19 = 30 — 19 = 11;
л) -56 + (96 + 9) = -56 + 96 + 9 = 40 + 9 = 49;
м) 59 + (96 + 4) = 59 + 100 = 159;
н) 52 — (32 — 41) = 52 — 32 + 41 = 20 + 41 = 61;
о) 73 — (68 — 8) = 73 — 60 = 13;
п) -25 — (-45 + 19) = -25 + 45 — 19 = 20 — 19 = 1.382. Заключите два последних слагаемых в скобки двумя способами (со знаком «+» и со знаком «-» перед скобками):
а) 37 + 12 + 13; б) 45 — 2 — 12; в) 5 — 28 + 22; г) 76 + 38 — 52.а) 37 + 12 + 13 = 37 + (12 + 13) = 37 — (-12 — 13);
б) 45 — 2 — 12 = 45 + (-2 — 12) = 45 — (2 + 12);
в) 5 — 28 + 22 = 5 + (-28 + 22) = 5 — (28 — 22);
г) 76 + 38 — 52 = 76 + (38 — 52) = 76 — (-38 + 52).383. Вычислите двумя способами (применяя и не применяя правила раскрытия скобок или заключения в скобки):
а) 48 — 19 — 1; б) 93 — 7 — 13; в) 48 — (28 — 43); г) 88 — (18 — 30).а) 48 — 19 — 1 = 29 — 1 = 28,
48 — 19 — 1 = 48 — (19 + 1) = 48 — 20 = 28;б) 93 — 7 — 13 = 86 — 13 = 73,
93 — 7 — 13 = (93 — 13) — 7 = 80 — 7 = 73;в) 48 — (28 — 43) = 48 — (-15) = 48 + 15 = 63,
48 — (28 — 43) = 48 — 28 + 43 = 20 + 43 = 63;г) 88 — (18 — 30) = 88 — (-12) = 88 + 12 = 100,
88 — (18 — 30) = 88 — 18 + 30 = 70 + 30 = 100.384. Вычислите, выбирая удобный способ:
а) 84 — (44 + 28); б) 94 — (44 + 26); в) 826 — (231 + 269);
г) 728 — (328 — 179); д) 83 — 23 — 29; е) 83 — 21 — 29;
ж) 236 — 136 — 92; з) 236 — 108 — 92.а) 84 — (44 + 28) = 84 — 44 — 28 = 40 — 28 = 12;
б) 94 — (44 + 26) = 94 — 70 = 24;
в) 826 — (231 + 269) = 826 — 500 = 326;
г) 728 — (328 — 179) = 728 — 328 + 179 = 400 + 179 = 579;
д) 83 — 23 — 29 = 60 — 29 = 31;
е) 83 — 21 — 29 = 83 — (21 + 29) = 83 — 50 = 33;
ж) 236 — 136 — 92 = 100 — 92 = 8;
з) 236 — 108 — 92 = 236 — (108 + 92) = 236 — 200 = 36.385. Вычислите :
а) -(98 + 49) — (102 — 49); б) (123 — 254) — (23 — 354);
в) (149 + 237) — (137 + 49); г) -(95 + 105) — (398 — 98);
д) (49 + 35) — (49 — 35); е) (48 + 15) — (48 — 15);
ж) (76 + 28) — (76 — 28); з) (72 + 29) — (72 — 29).а) -(98 + 49) — (102 — 49) = -98 — 49 — 102 + 49 = (-49 + 49) — (102 + 98) = 0 — 200 = -200;
б) (123 — 254) — (23 — 354) = 123 — 254 — 23 + 354 = (123 — 23) — (254 — 354) = 100 — (-100) = 100 + 100 = 200;
в) (149 + 237) — (137 + 49) = 149 + 237 — 137 — 49 = (149 — 49) + (237 — 137) = 100 + 100 = 200;
г) -(95 + 105) — (398 — 98) = -200 — 300 = -500;
д) (49 + 35) — (49 — 35) = 49 + 35 — 49 + 35 = (49 — 49) + (35 + 35) = 0 + 70 = 70;
е) (48 + 15) — (48 — 15) = 48 + 15 — 48 + 15 = (48 — 48) + (15 + 15) = 0 + 30 = 30;
ж) (76 + 28) — (76 — 28) = 76 + 28 — 76 + 28 = (76 — 76) + (28 + 28) = 0 + 56 = 56;
з) (72 + 29) — (72 — 29) = 72 + 29 — 72 + 29 = (72 — 72) + (29 + 29) = 0 + 58 = 58. 75
-
Ответы к стр. 75
386. Что называют:
а) координатной осью;
б) положительной координатной полуосью;
в) отрицательной координатной полуосью?а) прямую, на которой заданы начало отсчёта, направление отсчёта и единичный отрезок, называют координатной осью;
б) луч, идущий вправо от нуля на координатной оси называют положительной координатной полуосью;
в) луч, идущий влево от нуля на координатной оси называют положительной координатной полуосью.
387. Как называют точку, изображающую число нуль?
Точку, изображающую число нуль, называют начальной точкой или началом отсчёта.
388. Как найти расстояние между точками m и n координатной оси (m > n)?
Расстояние находится по формуле m — n (из координаты точки, расположенной правее, вычитают координату точки, расположенной левее на координатной оси).
389. Какие точки находятся на одинаковом расстоянии от точки нуль, но на разных полуосях?
Точки, координаты которых являются противоположными числами.
76
-
Ответы к стр. 76
390. Дана координатная ось (рис. 32), некоторые её точки обозначены буквами A, B, C, D, E. Укажите координаты этих точек.

А(4), В(-3), С(-5), D(6), Е(1).
391. Вычислите длину отрезка (рис. 32):
а) OA; б) OB; в) OC; г) OD; д) AC;
е) AE; ж) OE; з) CB; и) DA; к) BE.а) OA = 4 — 0 = 4;
б) OB = 0 — (-3) = 0 + 3 = 3;
в) OC = 0 — (-5) = 0 + 5 = 5;
г) OD = 6 — 0 = 6;
д) AC = 4 — (-5) = 4 + 5 = 9;
е) AE = 4 — 1 = 3;
ж) OE = 1 — 0 = 1;
з) CB = -3 — (-5) = -3 + 5 = 2;
и) DA = 6 — 4 = 2;
к) BE = 1 — (-3) = 1 + 3 = 4.392. Изобразите координатную ось (единичный отрезок 1 см). Отметьте на ней точки A(-5), B(7); C(4); D(-4). Вычислите длину отрезка:
а) OA; б) OB; в) BC; г) BD; д) AD.
Результаты проверьте с помощью линейки.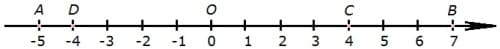
а) OA = 0 — (-5) = 5 см;
б) OB = 7 — 0 = 7 см;
в) BC = 7 — 4 = 3см;
г) BD = 7 — (-4) = 7 + 4 = 11 см;
д) AD = -4 — (-5) = -4 + 5 = 1 см.393. Изобразите координатную ось (единичный отрезок 1 клетка тетради). Отметьте на ней точки O(0), A(5), B(-8), C(9), D(-2). Вычислите длину отрезка:
а) OA; б) OB; в) AB; г) AC; д) DC.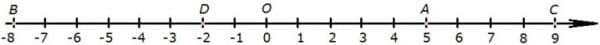
а) OA = 5 — 0 = 5 клеток;
б) OB = 0 — (-8) = 0 + 8 = 8 клеток;
в) AB = 5 — (-8) = 5 + 8 = 13 клеток;
г) AC = 9 — 5 = 4 клетки;
д) DC = 9 — (-2) = 9 + 2 = 11 клеток.394. Определите расстояние между точками m и n координатной оси, если:
а) m = 7, n = -3; б) m = 3, n = -7;
в) m = -8, n = 0; г) m = -8, n = 8.а) 7 — (-3) = 7 + 3 = 10;
б) 3 — (-7) = 3 + 7 = 10;
в) 0 — (-8) = 0 + 8 = 8;
г) 8 — (-8) = 8 + 8 = 16.395. На координатной оси отмечены точки 0 и 3. С помощью циркуля покажите на оси точки -3, 6, -6, 9, -9.

80
-
Дополнения к главе 2
Ответы к стр. 80
396. Какая точка координатной оси симметрична относительно начала координат точке:
а) 5;
б) −7;
в) 0?Две точки удаленные на одинаковое расстояние от начала координат являются симметричными.
Две точки, координаты которых противоположные числа, находятся на одинаковом расстоянии от начала координат, но на разных полуосях.
а) точке с координатой 5 симметрична относительно начала координат точка −5;
б) точке с координатой −7 симметрична относительно начала координат точка 7;
в) Точка 0 симметрична сама себе.
Ответ:
а) −5;
б) 7;
в) 0.397. Объясните, какие две точки называют симметричными относительно точки O.
Ответ: Точки A и B называются симметричными относительно точки O, если эти точки A, B и O лежат на одной прямой и точка O является серединой отрезка AB.
398. По рисунку 50 определите, какая точка симметрична относительно точки О точке:
а) А;
б) В;
в) С;
г) D;
д) M;
е) N;
ж) О.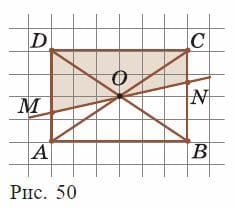
Точки А и В называются симметричными относительно точки О, если эти точки А, В и О лежат на одной прямой и точка О является серединой отрезка АВ.
а) точке А относительно точки О симметрична точка С;
б) точке B относительно точки О симметрична точка D;
в) точке C относительно точки О симметрична точка A;
г) точке D относительно точки О симметрична точка B;
д) точке M относительно точки О симметрична точка N;
е) точке N относительно точки О симметрична точка M;
ж) Точка О симметрична сама себе.
Ответ:
а) С;
б) D;
в) A;
г) B;
д) N;
е) M;
ж) О.399. ПО рисунку 50 определить, какой отрезок симметричен относительно точки O отрезку:
а) AB;
б) AD;
в) BC;
г) AO;
д) BO;
е) OC;
ж) BD;
з) MN.
а) точкам A и B относительно точки O симметричны точки C и D, следовательно, отрезку AB относительно точки O симметричен отрезок CD;
б) точкам A и D относительно точки O симметричны точки C и B, следовательно, отрезку AD относительно точки O симметричен отрезок CB;
в) точкам B и C относительно точки O симметричны точки D и A, следовательно, отрезку BC относительно точки O симметричен отрезок DA;
г) точкам A и O относительно точки O симметричны точки C и O, следовательно, отрезку AO относительно точки O симметричен отрезок CO;
д) точкам B и O относительно точки O симметричны точки D и O, следовательно, отрезку BO относительно точки O симметричен отрезок DO;
е) точкам O и C относительно точки O симметричны точки O и A, следовательно, отрезку OC относительно точки O симметричен отрезок OA;
ж) точкам B и D относительно точки O симметричны точки D и B, следовательно, отрезку BD относительно точки O симметричен отрезок DB;
з) точкам M и N относительно точки O симметричны точки N и M, следовательно, отрезку MN относительно точки O симметричен отрезок NM.
Ответ:
а) CD;
б) CB;
в) DA;
г) CO;
д) DO;
е) OA;
ж) DB;
з) NM. 81
-
Ответы к стр. 81
400. По рисунку 50 определите, какой фигуре симметричен относительно точки O:
а) треугольник BCO;
б) треугольник ADC;
в) треугольник CNO;
г) прямоугольник ABCD;
д) четырёхугольник DCNM.
Две фигуры называются симметричными если каждой точке одной фигуры соответствует симметричная точка другой фигуры.
а) точкам B, C, O относительно точки O симметричны точки D, A, O, следовательно, треугольник BCO относительно точки O симметричен треугольнику DAO;
б) точкам A, D, C относительно точки O симметричны точки C, B, A, следовательно, треугольник ADC относительно точки O симметричен треугольнику CBA;
в) точкам C, N, O относительно точки O симметричны точки A, M, O, следовательно, треугольник CNO относительно точки O симметричен треугольнику AMO;
г) точкам A, B, C, D относительно точки O симметричны точки C, D, A, B, следовательно, прямоугольник ABCD относительно точки O симметричен прямоугольнику CDAB;
д) точкам D, C, N, M относительно точки O симметричны точки B, A, M, N, следовательно, четырёхугольник DCNM относительно точки O симметричен четырехугольнику BAMN.
Ответ:
а) треугольнику DAO;
б) треугольнику CBA;
в) треугольнику AMO;
г) прямоугольнику CDAB;
д) четырехугольнику BAMN.401. На клетчатой бумаге изображен прямоугольник 3 * 4 (рис.51). Найдите пять способов разрезания прямоугольника на две равные части так, чтобы линия разреза шла по линиям клетчатой бумаги.
Ответ:
402. На клетчатой бумаге изобразите прямоугольник 3 * 5, из которого удалён центральный квадрат (рис.52). Найдите пять способов разрезания оставшейся фигуры на две равные части так, чтобы линия разреза шла по линиям клетчатой бумаги.
Ответ:

403. На клетчатой бумаге изображен квадрат 6 * 6. Найдите шесть способов разрезания квадрата на две равные части так, чтобы линия разреза шла по линиям клетчатой бумаги.
Ответ:
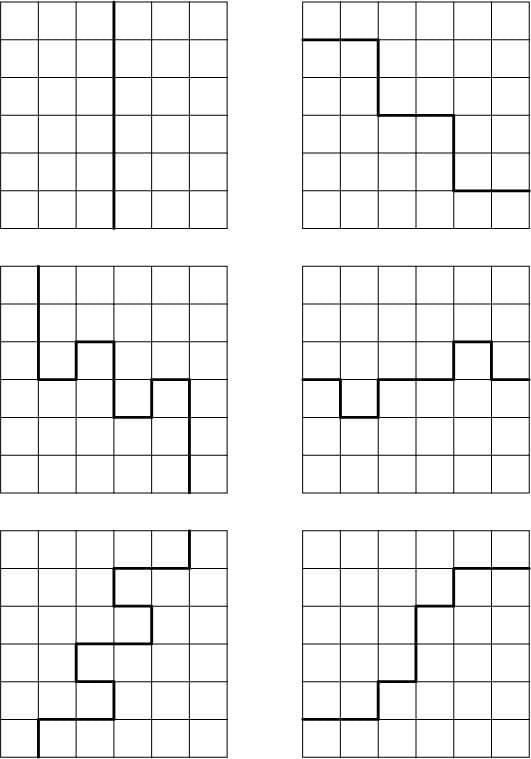
404. Можно ли квадрат 5 * 5, изображенный на клетчатой бумаге, разрезать на две равные части так, чтобы линия разреза шла по линиям клетчатой бумаги?
Площадь квадрата 5 * 5 = 25 клеток. Если квадрат разделить пополам, то в каждой половине будет
25 : 2 = 12 1 2, то есть какую−то клетку придется делить не по линии клетчатой бумаги.
Ответ: нет, нельзя.Доказываем
405. Докажите, что любая прямая, проходящая через центр симметрии прямоугольника, делит его на две равные части.
Возьмем прямоугольник ABCD и проведем через его центр симметрии прямую. Раз прямая проведена через центр симметрии то получается, что точка A симметрична точке B относительно точки M, а точка D симметрична точке C относительно точки N, следовательно:
AM = MB;
DN = NC.
Таким образом если прямоугольник AMND развернуть на 180 градусов относительно отрезка MN, то прямоугольник AMND совместится с прямоугольником MBCN и отсюда следует что прямоугольник AMND = прямоугольнику MBCN.406. Докажите, что любая прямая, проходящая через центр симметрии фигуры, делит её на две равные части.
Точки A и B называются симметричными относительно точки O, если эти точки A, B и O лежат на одной прямой и точка O является серединой отрезка AB. Таким образом, если через центр симметрии фигуры провести прямую, то между симметричными точками и центром симметрии можно построить два равных отрезка. Например: AO = OB. Такие же равные отрезки можно построить, используя все множество симметричных точек из которых состоит фигура. Следовательно, если одну половину фигуры развернуть на 180 градусов относительно прямой, проходящей через центр симметрии, то первая половина совместится со второй половиной фигуры, а это значит что две половины равны.
407. Постройте окружность с центром O. Отметьте на ней точку M. Постройте точку N, симметричную точке M относительно точки O. Верно ли, что окружность симметрична относительно своего центра?
Да, верно. Окружность симметрична относительно своего центра, так как MO = ON. Такие же равные отрезки можно построить, используя все множество симметричных точек из которых состоит окружность и если одну половину окружности развернуть на 180 градусов относительно прямой, проходящей через центр симметрии, то первая половина совместится со второй половиной окружности, а это значит что две половины равны.
408. Постройте круг с центром O. Отметьте внутри круга точку M. Постройте точку N, симметричную точку M относительно точки O. Верно ли, что круг симметричен относительно своего центра?
Да, верно. Окружность симметрична относительно своего центра, так как MO = ON. Такие же равные отрезки можно построить, используя все множество симметричных точек из которых состоит окружность и если одну половину окружности развернуть на 180 градусов относительно прямой, проходящей через центр симметрии, то первая половина совместится со второй половиной окружности, а это значит что две половины равны.
82
-
Ответы к стр. 82
409. Дан отрезок AB и точка O вне этого отрезка. Постройте отрезок A B 1, так чтобы точки A и A 1, B и B 1 были симметричны относительно точки O. Соедините точки A и B 1, A 1 и B. Укажите все пары отрезков, симметричных друг другу относительно точки O. Какие из построенных отрезков симметричны сами себе относительно точки O?
Пары отрезков симметричные друг другу относительно точки O:
AB иA 1 B 1 ;
A B 1 и A 1 B ;
AO и A 1 O ;
BO и B 1 O .
Отрезки симметричные сами себе относительно точки O:
A A 1 ;
B 1 B .410. Дан треугольник ABC. Постройте треугольник, симметричный треугольнику ABC относительно точки A.
411. Постройте треугольник, симметричный треугольнику ABC относительно точки O, лежащей на стороне AB.
Ответ:
412. Из прямоугольника вырезали квадрат (рис.53). Постройте прямую, которая делит площадь закрашенной фигуры пополам.
Прямая которая проходит через центр симметрии фигуры делит ее пополам. И в прямоугольнике и в квадрате центром симметрии является точка пересечения диагоналей, следовательно, прямая MN, проведенная через точки пересечения диагоналей, делит обе фигуры пополам.
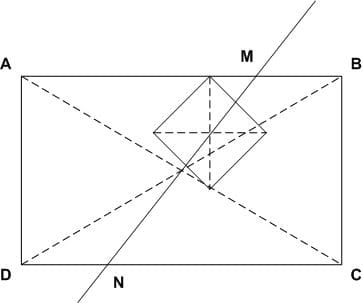
413. Вороне как−то Бог послал кусочек сыра... Предположим, что, в отличие от героини известной басни, наша Ворона захотела разделить сыр поровну с Лисицей. Как она должна разрезать по прямой кусок сыра, если этот кусок имеет форму прямоугольника с круглой дыркой (рис.54)? (Толщина куска сыра во всех местах одна и та же).
Прямая которая проходит через центр симметрии фигуры делит ее пополам. Центром симметрии прямоугольника является точка пересечения его диагоналей. Центром пересечения круга является точка пересечения его диаметров. Таким образом, чтобы разделить сыр пополам необходимо провести диагональ, одновременно проходящую и через центр симметрии прямоугольника и через центр симметрии круга
Ответ:
83
-
Ответы к стр. 83
414. Запишите в строчку 5 таких чисел, чтобы сумма любых двух соседних чисел была положительна, а сумма всех чисел была отрицательна.
−9, 10, −4, 5, −3
−9 + 10 = 1 сумма положительная,
10 + (−4) = 10 − 4 = 6 сумма положительная,
−4 + 5 = 1 сумма положительная,
5 + (−3) = 5 − 3 = 2 сумма положительная,
−9 + 10 + (−4) + 5 + (−3) = (10 + 5) + (−9 − 4 − 3) = 15 + (−16) = −1 сумма отрицательная.
Ответ: −9, 10, −4, 5, −3415. Можно ли записать в строчку 6 таких чисел, чтобы сумма любых двух соседних чисел была положительна, а сумма всех чисел была отрицательна?
Такие числа записать нельзя. Если сумма двух соседних чисел положительна, то взяв эти числа попарно и найдя сумму этих пар, получим, что сумма всех шести чисел тоже положительна.
Ответ: нет, записать такие числа нельзя.416. Можно ли записать в строчку 7 таких чисел, чтобы сумма любых двух соседних чисел была положительна, а сумма всех чисел была отрицательна?
−9, 10, −9, 10, −9, 10, −9
−9 + 10 = 1 сумма положительная,
10 − 9 = 1 сумма положительная,
−9 + 10 = 1 сумма положительная,
10 − 9 = 1 сумма положительная,
−9 + 10 = 1 сумма положительная,
10 − 9 = 1 сумма положительная,
−9 + 10 + (−9) + 10 + (−9) + 10 + (−9) = (10 + 10 + 10) + (−9 − 9 − 9 − 9) = 30 + (−36) = −6 сумма отрицательная.
Ответ: −9, 10, −9, 10, −9, 10, −9. 84
-
Ответы к стр. 84
417. Можно ли записать в строчку 9 таких чисел, чтобы сумма любых трех соседних чисел была положительна, а сумма всех чисел была отрицательна?
Такие числа записать нельзя, так как можно разбить эти числа на три последовательные тройки. По условию сумма этих троек положительная, поэтом если сложить значения этих трёх сумм мы также получим положительную сумму всех 9 чисел.
Ответ: такие числа записать нельзя.418. Можно ли расставить в клетках таблицы, состоящей из трёх строк и четырёх столбцов, целые числа так, чтобы сумма чисел:
а) в каждой строке была равна −20, а в каждом столбце −15;
б) в каждой строке была равна −20, а в каждом столбце −16;
в) в каждой строке была положительной, а в каждом столбце − отрицательной?Выполнить условие задачи можно лишь только в том случае, если сумма чисел во всех строках таблица равна сумме чисел во всех столбцах таблицы.
а) −20 * 3 = −60 сумма чисел во всех строках таблицы,
−15 * 4 = −60 сумма чисел во всех столбцах таблицы,
−60 = −60, расставить числа можно.
б) −20 * 3 = −60 сумма чисел во всех строках таблицы,
−16 * 4 = −64 сумма чисел во всех столбцах таблицы,
− 60 ≠ − 64, расставить числа нельзя.
в) расставить числа нельзя, так как сумма во всех строках таблицы будет положительной, а сумма во всех столбцах таблицы будет отрицательной, а положительное число не может быть равным отрицательному числу.
Ответ:
а) можно;
б) нельзя;
в) нельзя.419. В строчку записаны несколько чисел так, чтобы сумма любых трёх соседних чисел положительна. Можно ли утверждать, что сумма всех чисел положительна, если чисел:
а) 18;
б) 19;
в) 20?Для того чтобы найти верный ответ необходимо разбить числа на последовательные тройки чисел. Сумма каждой тройки по условию положительная, следовательно, тот ряд чисел, который делится на последовательные тройки без остатка, записать по условию задачи можно. Тот же ряд чисел, который не делится на последовательные тройки без остатка, записать нельзя, так как оставшиеся числа могут быть отрицательными и по модулю могут быть больше результата сложения сумм последовательных троек чисел. Поэтому:
а) 18 : 3 = 6 троек чисел, по условию сумма каждой тройки положительная, поэтому и сумма результатов сложения всех 6 троек также положительна.
б) записать нельзя, так как 19 : 3 = 6 последовательных троек и еще 1 число. Это последнее число может быть отрицательным и по модулю быть больше чем сумма результатов сложения всех 6−и троек, поэтому сумма всех 19 чисел может быть отрицательной.
Например: −8, −8, 17, −8, −8, 17, −8, −8, 17, −8, −8, 17, −8, −8, 17, −8, −8, 17, −8
Каждая последовательная тройка имеет вид: −8, −8, 17, ее сумма равна:
−8 + (−8) + 17 = −16 + 17 = 1
сумма результатов сложения всех 6 троек равна:
1 * 6 = 6
Последнее 19−ое число −8 и |−8|>|6|, следовательно, сумма всех 19 чисел отрицательна.
в) нельзя, так как сумма последние 2 числа могут быть отрицательными и их сумма по модулю может быть больше чем сумма результатов сложения всех 6−и троек, следовательно, сумма всех 20 чисел будет отрицательной.
Например: −8, −8, 17, −8, −8, 17, −8, −8, 17, −8, −8, 17, −8, −8, 17, −8, −8, 17, −8, −8
Каждая последовательная тройка имеет вид: −8, −8, 17, ее сумма равна:
−8 + (−8) + 17 = −16 + 17 = 1
сумма результатов сложения всех 6 троек равна:
1 * 6 = 6
Сумма последних двух чисел равна:
−8 + (−8) = −16, |−16|>|6|, следовательно, сумма всех 20 чисел отрицательна.
Ответ:
а) можно;
б) нельзя;
в) нельзя.420. В непрозрачном мешке лежат 10 белых и 5 черных шаров. Какое наименьшее число шаров нужно вынуть из мешка не глядя, чтобы среди них было 2 шара:
а) белых;
б) черных;
в) разных цветов;
г) одного цвета?а) первые 5 вынутых шаров могут быть черными, а значит в мешке останутся только белые шары. Поэтому за два последующих вынимания мы выполним условие задачи, следовательно:
5 + 2 = 7 шаров нужно вынуть, чтобы можно было утверждать что среди них обязательно есть 2 белых шара;
б) первые 10 вынутых шаров могут быть белыми, а значит в мешке останутся только черные шары. Поэтому за два последующих вынимания мы выполним условие задачи, следовательно:
10 + 2 = 12 шаров нужно вынуть, чтобы можно было утверждать что среди них обязательно есть 2 белых шара;
в) первые 10 вынутых шаров могут быть белыми, а значит в мешке останутся только черные шары. Поэтому за следующее вынимание мы выполним условие задачи, следовательно:
10 + 1 = 11 шаров нужно вынуть, чтобы можно было утверждать что среди них обязательно есть 2 разноцветных шара;
д) первые 2 вынутых шара могут быть разноцветными, поэтому за следующее вынимание мы выполним условие задачи, следовательно:
2 + 1 = 3 шара нужно вынуть, чтобы можно было утверждать что среди них обязательно есть 2 шара одинакового цвета.
Ответ:
а) 7 шаров;
б) 12 шаров;
в) 11 шаров;
г) 3 шара.421. В непрозрачном мешке лежат 679 белых и 679 чёрных шаров. Какое наименьшее число шаров нужно вынуть из мешка не глядя, чтобы среди них было 2 шара:
а) белых;
б) чёрных;
в) разных цветов;
г) одного цвета?а) первые 679 вынутых шаров могут быть черными, а значит в мешке останутся только белые шары. Поэтому за два последующих вынимания мы выполним условие задачи, следовательно:
679 + 2 = 681 шар нужно вынуть, чтобы можно было утверждать что среди них обязательно есть 2 белых шара;
б) первые 679 вынутых шаров могут быть белыми, а значит в мешке останутся только черные шары. Поэтому за два последующих вынимания мы выполним условие задачи, следовательно:
679 + 2 = 681 шар нужно вынуть, чтобы можно было утверждать что среди них обязательно есть 2 белых шара;
в) первые 679 вынутых шаров могут быть одноцветными, а значит в мешке останутся только шары другого цвета. Поэтому за следующее вынимание мы выполним условие задачи, следовательно:
679 + 1 = 680 шаров нужно вынуть, чтобы можно было утверждать что среди них обязательно есть 2 разноцветных шара;
д) первые 2 вынутых шара могут быть разноцветными, поэтому за следующее вынимание мы выполним условие задачи, следовательно:
2 + 1 = 3 шара нужно вынуть, чтобы можно было утверждать что среди них обязательно есть 2 шара одинакового цвета.
Ответ:
а) 681 шар;
б) 681 шар;
в) 680 шаров;
г) 3 шара.422. Имеется 3 комнаты с разными замками и 3 ключа от этих комнат. Какое наименьшее число проб нужно сделать, чтобы определить, какой ключ от какой комнаты?
Если первые два ключа не подошли к первой комнате, то и без пробы можно определить что третий ключ подходит к первой комнате, поэтому наименьшее количество проб которое нужно сделать для того чтобы определить ключ для первой комнаты равно 2.
Для первой комнаты ключ уже определен и его мы не используем. Остается два ключа и если первый из этих ключей не подойдет ко второй комнате, то и без пробы можно сказать что второй из оставшихся ключей подходит ко второй комнате, поэтому наименьшее количество проб которое нужно сделать для того чтобы определить ключ для второй комнаты равно 1.
Для первых двух комнат ключи уже определены, поэтому и без проб ясно, что последний оставшийся ключ подходит для третей комнаты, поэтому наименьшее количество проб которое нужно сделать для того чтобы определить ключ для третей комнаты равно 0.
Наименьшее количество проб которое нужно сделать для того чтобы определить ключ для каждой из трёх комнат равно: 2 + 1 + 0 = 3 пробы.
Ответ: 3 пробы.423. Вася возвел натуральное число в квадрат и получил число, оканчивающееся цифрой 2. Не ошибся ли Вася?
Если натуральное число оканчивается на 0, то последняя цифра в квадрате это числа равна 0, так как 02 = 0;
если натуральное число оканчивается на 1, то последняя цифра в квадрате это числа равна 1, так как 12 = 1;
если натуральное число оканчивается на 2, то последняя цифра в квадрате это числа равна 4, так как 22 = 4;
если натуральное число оканчивается на 3, то последняя цифра в квадрате это числа равна 9, так как 32 = 9;
если натуральное число оканчивается на 4, то последняя цифра в квадрате это числа равна 6, так как 42 = 16;
если натуральное число оканчивается на 5, то последняя цифра в квадрате это числа равна 5, так как 52 = 25;
если натуральное число оканчивается на 6, то последняя цифра в квадрате это числа равна 6, так как 62 = 36;
если натуральное число оканчивается на 7, то последняя цифра в квадрате это числа равна 9, так как 72 = 49;
если натуральное число оканчивается на 8, то последняя цифра в квадрате это числа равна 4, так как 82 = 64;
если натуральное число оканчивается на 9, то последняя цифра в квадрате это числа равна 1, так как 92 = 81.
Таким образом квадраты натуральных чисел могут оканчиваться только на цифры: 0, 1, 4, 5, 6, 9, так как среди этих цифр нет цифры 2, то Вася ошибся.
Ответ: Вася ошибся.424. Ведущий телевизионной игры спросил игрока:
− Верите ли Вы, что я не курю уже 20 дней?
− Верю, − ответил игрок.
− А вот и неверно, я не курю уже 24 дня!
Правильно ли ведущий оценил ответ игрока?Если ведущий не курит 24 дня, то он не курит и меньшее число дней, например 17 или 16, следовательно, ведущий неверно оценил ответ игрока, так как 20 дней меньше 24 дней.
Ответ: неверно.425. Встретились три подруги − Белова, Краснова и Чернова. На одной из них было чёрное платье, на другой − красное, на третьей белое. Девочка в белом платье говорит Черновой: "Нам надо меняться платьями, а то цвет наших платьев не соответствует фамилиям". Кто в каком платье был?
Чернова была в красном платье, так как в чёрном она не могла быть, потому что чёрный цвет соответствует её фамилии, а в белом платье она не могла быть, так как по условию задачи к ней обращается девочка в белом платье.
Белова была в чёрном платье, так как в белом она не могла быть, потому что белый цвет соответствует её фамилии, а в красном платье была Чернова.
Краснова была в белом платье, так как в красном она не могла быть, потому что красный цвет соответствует её фамилии, а в черном платье была Белова.
Ответ: Чернова была в красном платье, Белова в чёрном, а Красонова в белом. 85
-
Ответы к стр. 85
426. Коля, Боря, Вова и Юра заняли первые четыре места в соревновании. На вопрос, какие места они заняли, трое из них ответили:
1) Коля ни первое, ни четвертое;
2) Боря второе;
3) Вова не был последним.
Какое место занял каждый мальчик?Боря занял 2 место по условию задачи;
Коля занял 3 место, так как второе занял Боря, а Коля сказал что его место было ни первым, ни последним;
Вова занял 1 место, так он сказал что его место было не последним, а 2 и 3 места заняли Боря и Коля.
Юра занял оставшиеся 4 место.
Ответ: Вова − 1 место; Боря − 2 место; Коля − 3 место; Юра − 4 место.427. Имеется три мешка с монетами. В двух из них настоящие монеты, массой 10 г каждая, а в одном фальшивые монеты, массой 9 г каждая. Есть весы, показывающие общую массу положенных на них монет. Как с помощью одного взвешивания определить, в каком мешке фальшивые монеты, если из мешков можно брать любое число монет?
Нужно взять 1 монету из первого мешка и 2 монеты из второго мешка, если при взвешивании вес монет будет равен:
30 г (10 + 2 * 10), то фальшивые монеты в третьем мешке;
29 г (9 + 2 * 10), то фальшивые монеты в первом мешке;
28 г (10 + 2 * 9), то фальшивые монеты во втором мешке.428. Имеется:
а) четыре мешка с монетами;
б) пять мешков с монетами;
в) десять мешков с монетами.
Во всех мешках, кроме одного, настоящие монеты, массой 10 г каждая, а в одном фальшивые монеты, массой 9 г каждая. Есть весы, показывающие общую массу положенных на них монет. Как с помощью одного взвешивания определить, в каком мешке фальшивые монеты, если из мешков можно брать любое число монет?а) Возьмем из первого мешка 1 монету, из второго мешка 2 монеты, из третьего мешка 3 монеты. Если при взвешивании вес монет будет равен:
60г = 10г + 2 * 10г + 3 * 10г, то фальшивые монеты в четвертом мешке;
59г = 9г + 2 * 10г + 3 * 10г, то фальшивые монеты в первом мешке;
58г = 10г + 2 * 9г + 3 * 10г, то фальшивые монеты во втором мешке;
57г = 10г + 2 * 10г + 3 * 9г, то фальшивые монеты в третьем мешке;б) Возьмем из первого мешка 1 монету, из второго мешка 2 монеты, из третьего мешка 3 монеты, из 4 мешка 4 монеты. В каком мешке будут находиться фальшивые монеты, если вес 10 взятых монет составит:
100г = 10г + 2 * 10г + 3 * 10г + 4 * 10г, то фальшивые монеты в пятом мешке;
99г = 9г + 2 * 10г + 3 * 10г + 4 * 10г, то фальшивые монеты в первом мешке;
98г = 10г + 2 * 9г + 3 * 10г + 4 * 10г, то фальшивые монеты во втором мешке;
97г = 10г + 2 * 10г + 3 * 9г + 4 * 10г, то фальшивые монеты в третьем мешке;
96г = 10г + 2 * 10г + 3 * 10г + 4 * 9г, то фальшивые монеты в четвертом мешке.в) Возьмем из первого мешка 1 монету, из второго мешка 2 монеты, из третьего мешка 3 монеты, из 4 мешка 4 монеты, ..., из 9 мешка 9 монет. В каком мешке будут находиться фальшивые монеты, если вес взятых монет составит:
450г = 10г + 2 * 10г + 3 * 10г + 4 * 10г + 5 * 10г + 6 * 10г + 7 * 10г + 8 * 10г + 9 * 10г, то фальшивые монеты будут в десятом мешке;
449г = 9г + 2 * 10г + 3 * 10г + 4 * 10г + 5 * 10г + 6 * 10г + 7 * 10г + 8 * 10г + 9 * 10г, то фальшивые монеты будут в первом мешке;
448г = 10г + 2 * 9г + 3 * 10г + 4 * 10г + 5 * 10г + 6 * 10г + 7 * 10г + 8 * 10г + 9 * 10г, то фальшивые монеты будут во втором мешке.
И аналогично, если вес составит:
447г, то фальшивые монеты будут в третьем мешке;
446г, то фальшивые монеты будут в четвертом мешке;
445г, то фальшивые монеты будут в пятом мешке;
444г, то фальшивые монеты будут в шестом мешке;
443г, то фальшивые монеты будут в седьмом мешке;
442г, то фальшивые монеты будут в восьмом мешке;
441г, то фальшивые монеты будут в девятом мешке.429. В коробке лежат три пилотки − одна синяя и две красные. Учитель вызывает к доске двух учеников, которые становятся лицом к классу и закрывают глаза. Учитель надевает каждому из них на голову пилотку, а оставшиеся прячет в коробку. Ученики открывают глаза, и каждый видит пилотку своего товарища, но не видит своей. Может ли кто−нибудь из них определить цвет своей пилотки? Рассмотрите два случая:
а) надеты одна синяя и одна красная пилотка;
б) надеты две красные пилотки.а) если ученик видит на голове своего товарища синюю пилотку, то значит у него своя пилотка обязательно красная, так как синих больше не осталось;
б) если ученик видит на голове своего товарища красную пилотку, то значит у него своя пилотка либо красная, либо синяя, поэтому определить цвет своей пилотки в этом случае нельзя.
Ответ:
а) может определить;
б) не может определить.430. В коробке лежат пять пилоток − две синие и три красные. Учитель вызывает к доске трёх учеников, которые становятся лицом к классу и закрывают глаза. Учитель надевает каждому из них на голову пилотку, а оставшиеся прячет в коробку. Ученики открывают глаза, и каждый видит пилотку своего товарища, но не видит своей. Может ли кто−нибудь из них определить цвет своей пилотки? Какие случаи следует рассмотреть?
1 случай: ученик видит что на двух его товарищах одеты две синие пилотки, следовательно, на своей голове у него красная пилотка, так как синих больше не осталось;
2 случай: ученик видит что на двух его товарищах одеты две красные пилотки, следовательно, определить цвет своей пилотки он не может, так как остались две синие и одна красная пилотка;
3 случай: ученик видит что на двух его товарищах одеты одна красная и одна синяя пилотка, следовательно, определить цвет своей пилотки он не может, так как остались две красные и одна синяя пилотка.
Ответ: цвет своей пилотки ученик может определить только в том случае, когда на головах своих товарищей он видит две синие пилотки.431. Приехав в город, Ходжа Насреддин постучал в ворота первого дома и попросил хозяина пустить его переночевать. Денег у Насреддина не было, но была золотая цепочка из семи звеньев. Хозяин согласился приютить путника на семь дней с такими условиями:
1) за один день Насреддин платит одним звеном цепочки;
2) расплачиваться он должен ежедневно;
3) хозяин соглашался принять не более одного распиленного звена.(имеется ввиду, что в процессе оплаты у хозяина на руках не может одновременно находится два и более отдельных одинарных звена цепочки).
Смог ли Ходжа Насреддин расплатиться с хозяином?Насреддин распилил звено на три части: с одним звеном; с двумя звеном; с четырьмя.
1 день − Насреддин расплатился цепочкой из одного звена;
2 день − Насреддин расплатился цепочкой двух звеньев и получил на сдачу цепочку из одного звена;
3 день − Насреддин расплатился цепочкой из одного звена;
4 день − Насреддин расплатился цепочкой из четырёх звеньев и получил на сдачу цепочку из одного звена и цепочку из двух звеньев;
5 день − Насреддин расплатился цепочкой из одного звена;
6 день − Насреддин расплатился цепочкой из двух звеньев и получил на сдачу цепочку из одного звена;
7 день − Насреддин расплатился цепочкой из одного звена.
Ответ: да, смог. 86
-
Ответы к стр. 86
432. В одной коробке лежат два белых шара, в другой − два черных, в третьих − один белый и один чёрный. На каждой коробке имеется табличка, но она неправильно указывает содержимое коробки (рис. 55). Из какой коробки не глядя надо вынуть шар, чтобы можно было определить содержимое каждой коробки?
1 случай: из коробки "БЧ" достали белый шар, тогда:
− в коробке "БЧ" и второй шар будет белым, так как если он будет чёрным, то содержимое коробки "БЧ" будет соответствовать названию коробки, что неприемлемо по условию задачи;
− в коробке "ЧЧ" будет 1 белый шар, а второй чёрный, так как мы определили, что два белых шара лежат в коробке "БЧ", а два черных шара не могут находиться в коробке "ЧЧ", так как тогда содержимое коробки будет соответствовать её названию.
− в коробке "ББ" будут находиться два чёрных шара, так в коробке "БЧ" находятся два белых шара, а в коробке "ЧЧ" находятся один белый и один черный шар.
2 случай: из коробки "БЧ" достали черный шар, тогда:
− в коробке "БЧ" и второй шар будет черным, так как если он будет белым, то содержимое коробки "БЧ" будет соответствовать названию коробки, что неприемлемо по условию задачи;
− в коробке "ББ" будет 1 белый шар, а второй чёрный, так как мы определили, что два черных шара лежат в коробке "БЧ", а два белых шара не могут находиться в коробке "ББ", так как тогда содержимое коробки будет соответствовать её названию.
− в коробке "ЧЧ" будут находиться два белых шара, так в коробке "БЧ" находятся два черных шара, а в коробке "ББ" находятся один белый и один черный шар.
Ответ: из коробки "БЧ".433. Три друга Коля, Олег и Петя играли во дворе, и один из них случайно разбил мячом оконное стекло. Коля сказал: "Это не я разбил стекло", Олег сказал: "Это Петя разбил стекло". Позднее выяснилось, что одно из этих утверждений верное, а другое нет. Кто из мальчиков разбил стекло?
Допустим что утверждение Олега верно, а Коли неверно, тогда по словам Олега получается что стекло разбил Петя, а по утверждению Коли, что он сам это сделал. Получается что по словам двух мальчиков стекло разбил не один человек, что по условию задачи неверно.
Допустим что утверждение Олега неверно, а Коли верно, тогда по словам Олега получается что стекло разбил либо Коля, либо Олег, а по утверждению Коли либо Петя, либо Олег. Ни Коля, ни Петя не могли разбить стекло, так в этих случаях утверждения Коли и Олега будут расходиться, следовательно, стекло разбил Олег.
Ответ: Олег.434.Задачи С.А. Рачинского.
а) В будущем (1892) году думаю провести в Петербурге столько минут, сколько часов проведу в деревне. Сколько времени я проведу в Петербурге? (Время на переезды не учитываются);
б) У меня пять детей. Дал я им пряников поровну. Трое из них съели по 5 пряников, и тогда у всех троих осталось столько пряников, сколько у двух остальных. Сколько всех пряников роздано?
в) От Москвы до Тамбова 450 верст. Выехали одновременно навстречу друг другу из Москвы почтовый, а из Тамбова товарный поезд. Второй мог бы пройти весь путь за 18 ч, а первый вдвое быстрее. Через сколько часов они встретятся?
г) Дочь ткёт по 3 аршина в день, 4 дня она ткала одна, но затем стала ткать и мать, которая ткёт по 5 аршинов в день. Когда их тканья стало поровну они прекратили работу. Сколько соткали они вдвоем?а) 1892 год високосный, так как 1892 делится на 4 без остатка.
В високосном году 366 суток, 366 * 24 = 8784 часа, 8784 * 60 = 527040 минут.
Пусть время проведенное в Петербурге будет равно x минут, тогда время проведенное в деревне будет равно 60 * x минут, следовательно:
60 * x + x = 527040
x * (60 + 1) = 527040
x * 61 = 527040
x = 527040 : 61
x = 8640 минут проведет в Петербурге.
8640 : 60 = 144 часа проведет в Петербурге.
144 : 24 = 6 дней проведет в Петербурге.
Ответ: 6 дней.
б) Пусть изначально каждому ребенку раздали по x пряников, тогда изначально у детей было
x + x + x + x + x пряников.
Трое из детей съело по 5 пряников, тогда всего они съели 5 * 3 = 15 пряников и у них осталось x + x + x − 15 пряников, равное количеству пряников оставшихся у двух оставшихся детей, то есть:
x + x + x − 15 = x + x
x + x + x − x − x = 15
(x − x) + (x − x) + x = 15
x = 15 пряников изначально раздали каждому ребенку.
x * 5 = 15 * 5 = 75 пряников всего было роздано.
Ответ: 75 пряников.в) Дано:
s = 450 вёрст
t2 = 18 часов
Найти:
t3 - ?
Решение:
v2 = s : t2 = 450 : 18 = 25 вёрст в час скорость второго поезда.
v1 = v2 * 2 = 25 * 2 = 50 вёрст в час скорость первого поезда.
v3 = v1 + v2 = 25 + 50 = 75 вёрст в час скорость сближения поездов.
t3 = s : v3 = 450 : 75 = 6 часов, время через которое поезда встретятся.
Ответ: 6 часов.
г) 4 * 3 = 12 аршин соткала дочь, пока работала,
5 − 3 = на 2 аршина в день мать ткет ткани больше матери,
12 : 2 = 6 дней потребуется матери чтобы догнать дочь,
6 * 5 = 30 аршин ткани соткала мать за время своей работы,
4 + 6 = 10 дней всего проработала дочь,
10 * 3 = 30 аршин ткани соткала дочь за время своей работы,
30 + 30 = 60 аршин ткани соткали мать и дочь за время своей работы.
Ответ: 60 аршин. 89
-
Рациональные числа
Отрицательные дробиОтветы к стр. 89
435. Запишите три отрицательные дроби.
— 4/6, — 3/2, — 5/5.
436. Какие числа называют противоположными? Приведите примеры.
Числа, отличающиеся только знаком, называют противоположными: — 4/6 и 4/6, — 3/2, и 3/2, — 5/5 и 5/5.
437. Какое число противоположно:
а) числу нуль;
б) положительному числу;
в) отрицательному числу?а) нуль противоположен сам себе;
б) положительному числу противоположно отрицательное число;
в) отрицательному числу противоположно положительное число.438. Что называют модулем:
а) положительной дроби; б) отрицательной дроби; в) нуля?а) саму эту дробь;
б) противоположную ей (положительную) дробь;
в) число нуль.439. Какие из дробей являются положительными, какие отрицательными: 1/6, — 1/3, 0/4, — 2/7, 3/1, — 0/2?
Отрицательные дроби: — 1/3, — 2/7, — 0/2.
Положительные дроби: 1/6, 0/4, 3/1.440. Назовите дроби, противоположные дробям: 1/2, 2/9, — 1/3, — 3/7, -4/11.
дробь — 1/2 противоположна дроби 1/2;
дробь — 2/9 противоположна дроби 2/9;
дробь 1/3 противоположна дроби — 1/3;
дробь 3/7 противоположна дроби — 3/7;
дробь 4/11 противоположна дроби -4/11.441. Какое число противоположно самому себе?
Число нуль противоположно само себе.
Упростите запись по образцу (442-443):
442. а) |8| = 8; б) |-7| = 7; в) |1/9| = 1/9; г) |-2/3| = 2/3;
д) |2|; е) |-3|; ж) |0|; з) |1/4|;и) |- 1/5|; к) |2/7|.д) |2| = 2;
е) |-3| = 3;
ж) |0| = 0;
з) |1/4| = 1/4;
и) |- 1/5| = 1/5;
к) |2/7| = 2/7.443. а) |-1/4|;б) |-2/9|;в) |-1/8|;г) |-8/15|;
д) |- 3/8|;е) |- 8/9|;ж) — |- 1/2|;з) — |- 1/5|.а) |-1/4| = 1/4;
б) |-2/9| = 2/9;
в) |-1/8| = 1/8;
г) |-8/15| = 8/15;
д) |- 3/8| = 3/8;
е) |- 8/9| = 8/9;
ж) — |- 1/2| = — 1/2;
з) — |- 1/5| = — 1/5.444. Сравните:
а) |2/3| и |- 2/3|; б) |-5| и |- 1/2|; в) |- 1/5| и |1/4|.а) |2/3| = 2/3, |- 2/3| = 2/3,
2/3 = 2/3, следовательно, |2/3| = |- 2/3|;б) |-5| = 5, |- 1/2| = 1/2,
5 > 1/2, следовательно, |-5| > |- 1/2|;в) |- 1/5| = 1/5, |1/4| = 1/4,
1/5 < 1/4, следовательно, |- 1/5| < |1/4|.445. Запишите дробь так, чтобы знак «-» стоял в числителе по образцу:
а) — 3/4 = -3/4; б) — 5/7; в) — 7/3; г) — 4/9; д) — 1/9; е) — 13/12.б) — 5/7 = -5/7;
в) — 7/3 = -7/3;
г) — 4/9 = -4/9;
д) — 1/9 = -1/9;
е) — 13/12 = -13/12.446. Запишите дробь так, чтобы знак «-» стоял в знаменателе по образцу:
а) — 3/4 = 3/-4; б) — 6/5; в) — 7/8; г) — 8/9; д) — 17/18; е) — 18/17.б) — 6/5 = 6/-5;
в) — 7/8 = 7/-8;
г) — 8/9 = 8/-9;
д) — 17/18 = 17/-18;
е) — 18/17 = 18/-17. 90
-
Ответы к стр. 90
447. Запишите дроби -2/7, -6/11, -2/13, 5/-7, 4/-9, 12/-7 так, чтобы знак «-» стоял перед чертой дроби.
-2/7 = — 2/7;
-6/11 = — 6/11;
-2/13 = — 2/13;
5/-7 = — 5/7;
4/-9 = — 4/9;
12/-7 = — 12/7.448. Равны ли дроби:
а) — 2/3 и -2/3; б) -5/8 и — 5/8; в) 4/9 и -4/9; г) — 5/7 и 5/7?а) — 2/3 = -2/3 – равны;
б) -5/8 = — 5/8 – равны;
в) 4/9 > -4/9 – не равны;
г) — 5/7 < 5/7 – не равны.449. Найдите модуль числа:
а) — 1/2; б) -2/3; в) 3/4; г) 5/-9; д) 0; е) — 5/4.а) |- 1/2| = 1/2;
б) |-2/3| = 2/3;
в) |3/4| = 3/4;
г) |5/-9| = 5/9;
д) |0| = 0;
е) |- 5/4| = 5/4.450. Вычислите:
а) |- 1/2| + |1/2|; б) |2/3| + |- 1/3|; в) |- 13/23| — |13/23|;
г) |-32/3| — |-22/3|; д) |-31/3| • |-22/5|; е) |23/5| : |-51/5|.а) |- 1/2| + |1/2| = 1/2 + 1/2 = 1+1/2 = 2/2 = 1;
б) |2/3| + |- 1/3| = 2/3 + 1/3 = 2+1/3 = 3/3 = 1;
в) |- 13/23| — |13/23| = 13/23 — 13/23 = 0;
г) |-32/3| — |-22/3| = 32/3 — 22/3 = (3 — 2) + (2/3 — 2/3) = 1;
д) |-31/3| • |-22/5| = 31/3 • 22/5 = 10/3 • 12/5 = 10•12/3•5 = 2•4/1•1 = 8;
е) |23/5| : |-51/5| = 23/5 : 51/5 = 13/5 : 26/5 = 13/5 • 5/26 = 13•5/5•26 = 1•1/1•2 = 1/2.
92
-
Рациональные числа
Рациональные числаОтветы к стр. 92
451. Какое число называют рациональным? Назовите несколько рациональных чисел.
Число, которое можно записать в виде p/q, где p и q — целые числа и q не равно нулю, называют рациональным числом или дробью: 1/3, 3/-8, -2/-1.
452. Является ли натуральное число рациональным?
Является — любое натуральное число α можно представить в виде α/1.
453. Является ли целое число рациональным?
Является — любое целое число α можно представить в виде α/1.
454. Является ли положительная дробь рациональным числом?
Является, как и отрицательная дробь.
455. Сформулируйте основное свойство дроби. Приведите пример использования основного свойства дроби для приведения дроби к новому знаменателю.
Если числитель и знаменатель дроби умножить на одно и тоже целое, не равное нулю число, то получится равная ей дробь: p/q = p•n/q•n. Например: 1/3 = 1•4/3•4 = 4/12.
456. В каком случае дробь можно сократить? На основании какого свойства сокращают дроби? Приведите примеры.
Если числитель и знаменатель дроби имеют общий множитель n — целое, не равное нулю, число, то дробь можно сократить на n. Дробь сокращают на основании основного свойства дроби.
8/10 = 4•2/5•2 = 4/5457. В каком случае дробь положительна? отрицательна? Приведите примеры.
Дробь p/q отрицательна, если числа p и q разных знаков.
Дробь p/q положительна, если числа p и q одного знака.
-1/3, 1/-4 − отрицательные дроби.
-2/-3, 10/11 − положительные дроби.458. Любую ли дробь можно привести к положительному знаменателю?
Пользуясь основным свойством дроби, можно любую дробь привести к положительному знаменателю.
459. Сократите дроби 8/20, 35/36, 42/48, 764/828, 792/891.
8/20 = 2•4/5•4 = 2/5;
35/36 — дробь сократить нельзя;
42/48 = 7•6/8•6 = 7/8;
764/828 = 191•4/207•4 = 191/207;
792/891 = 8•99/9•99 = 8/9.
93
-
Ответы к стр. 93
460. Приведите дроби к знаменателю 48: 1/2, 2/3, 3/4, 5/6, 7/8, 11/12, 15/16.
1/2 = 1•24/2•24 = 24/48;
2/3 = 2•16/3•16 = 32/48;
3/4 = 3•12/4•12 = 36/48;
5/6 = 5•8/6•8 = 40/48;
7/8 = 7•6/8•6 = 42/48;
11/12 = 11•4/12•4 = 44/48;
15/16 = 15•3/16•3 = 45/48.
461. Приведите дробь к положительному знаменателю:
а) 1/-2; б) 1/-3; в) -2/-3; г) -2/-5; д) 7/-4; е) 12/-7.а) 1/-2 = 1•(-1)/-2•(-1) = -1/2;
б) 1/-3 = 1•(-1)/-3•(-1) = -1/3;
в) -2/-3 = -2•(-1)/-3•(-1) = 2/3;
г) -2/-5 = -2•(-1)/-5•(-1) = 2/5;
д) 7/-4 = 7•(-1)/-4•(-1) = -7/4;
е) 12/-7 = 12•(-1)/-7•(-1) = -12/7.
462. Приведите дроби -1/2 и — 1/4 к знаменателю: а) 8; б) 28; в) 36.
а) -1/2 = -1•4/2•4 = -4/8,
— 1/4 = — 1•2/4•2 = — 2/8;б) -1/2 = -1•14/2•14 = -14/28,
— 1/4 = — 1•7/4•7 = — 7/28;в) -1/2 = -1•18/2•18 = -18/36,
— 1/4 = — 1•9/4•9 = — 9/36.463. Приведите к знаменателю 60 дробь:
а) — 1/2; б) — 2/3; в) -4/5; г) -11/12; д) 13/-15; е) 19/-20.а) — 1/2 = — 1•30/2•30 = — 30/60;
б) — 2/3 = — 2•20/3•20 = — 40/60;
в) -4/5 = -4•12/5•12 = -48/60;
г) -11/12 = -11•5/12•5 = -55/60;
д) 13/-15 = 13•4/-15•4 = 52/-60;
е) 19/-20 = 19•3/-20•3 = 57/-60.
464. Упростите запись рационального числа:
а) -1/-2; б) -3/-4; в) -49/56; г) 72/-67;
д) — 81/-72; е) — 96/-143; ж) — -15/42; з) -55/-75;
и) — -125/625; к) 100/-8; л) 32/-512; м) -32/-128.а) -1/-2 = -1•(-1)/-2•(-1) = 1/2;
б) -3/-4 = -3•(-1)/-4•(-1) = 3/4;
в) -49/56 = -7•7/8•7 = -7/8 = — 7/8;
г) 72/-67 = — 72/67;
д) — 81/-72 = -9•9/-8•9 = —9•(-1)/-8•(-1) = 9/8;
е) — 96/-143 = -96•(-1)/-143•(-1) = 96/143;
ж) — -15/42 = -5•3/-14•3 = -5•(-1)/-14•(-1) = 5/14;
з) -55/-75 = -11•5/-15•5 = -11•(-1)/-15•(-1) = 11/15;
и) — -125/625 = -1•125/-5•125 = -1•(-1)/-5•(-1) = 1/5;
к) 100/-8 = 25•4/-2•4 = 25/-2 = — 25/2;
л) 32/-512 = 1•32/-16•32 = 1/-16 = — 1/16;
м) -32/-128 = -1•32/-4•32 = -1•(-1)/-4•(-1) = 1/4.
465. Сократите дробь, запишите результат в виде дроби с положительным знаменателем:
а) -8/-12; б) -35/21; в) 36/-45; г) 45/-63;
д) — 35/77; е) -96/-128; ж) -124/-196; з) 252/-444.а) -8/-12 = -2•4/-3•4 = -2•(-1)/-3•(-1) = 2/3;
б) -35/21 = -5•7/3•7 = -5/3;
в) 36/-45 = 4•9/-5•9 = 4•(-1)/-5•(-1) = -4/5;
г) 45/-63 = 5•9/-7•9 = 5•(-1)/-7•(-1) = -5/7;
д) — 35/77 = -5•7/11•7 = -5/11;
е) -96/-128 = -3•32/-4•32 = -3•(-1)/-4•(-1) = 3/4;
ж) -124/-196 = -31•4/-49•4 = -31•(-1)/-49•(-1) = 31/49;
з) 252/-444 = 21•12/-37•12 = 21•(-1)/-37•(-1) = -21/37.
466. Найдите число x, для которого верно равенство:
а) -1/3 = x/3; б) -4/5 = x/20; в) — 2/3 = x/9;
г) — 5/6 = x/30; д) — 4/5 = -20/x; е) — x/3 = -12/18.а) -1/3 = x/3,
-1 = x,
x = -1;б) -4/5 = x/20,
-4•4/5•4 = x/20,
-16/20 = x/20,
-16 = x,
x = -16;в) — 2/3 = x/9,
-2•3/3•3 = x/9,
-6/9 = x/9,
-6 = x,
x = -6;г) — 5/6 = x/30,
-5•5/6•5 = x/30,
-25/30 = x/30,
-25 = x,
x = -25;д) — 4/5 = -20/x,
-4•5/5•5 = -20/x,
-20/25 = -20/x,
25 = x,
x = 25;е) — x/3 = -12/18,
x/-3 = -2•6/3•6,
x/-3 = -2•(-1)/3•(-1),
x/-3 = 2/-3,
x = 2.Упростите запись (467-468):
467. а) — -5/7; б) — 4/-3; в) — -3/7; г) — 9/-10.
а) — -5/7 = -5/-7 = -5•(-1)/-7•(-1) = 5/7;
б) — 4/-3 = -4/-3 = -4•(-1)/-3•(-1) = 4/3;
в) — -3/7 = -3/-7 = -3•(-1)/-7•(-1) = 3/7;
г) — 9/-10 = -9/-10 = -9•(-1)/-10•(-1) = 9/10.
468. а) — (-7/9) = — -7/9 = -(-7)/9 = 7/9;
б) — (- 4/9); в) — (- -1/3); г) — (- 2/-13); д) — (- -1/-2).б) — (- 4/9) = — -4/9 = -(-4)/9 = 4/9;
в) — (- -1/3) = — -(-1)/3 = — 1/3;
г) — (- 2/-13) = — 2/-(-13) = — 2/13;
д) -(- -1/-2) = — -(-1)/-2 = — 1/-2 = 1/-(-2) = 1/2.
94
-
Ответы к стр. 94
469. Равны ли рациональные числа:
а) 1/4 и -8/-32; б) -75/100 и 3/-4; в) 24/-40 и -27/45; г) -77/-88 и 63/72.а) -8/-32 = -1•8/-4•8 = -1•(-1)/-4•(-1) = 1/4, а так как 1/4 = 1/4, то 1/4 = -8/-32;
б) -75/100 = -3•25/4•25 = — 3/4 = 3/-4, а так как 3/-4 = 3/-4, то -75/100 = 3/-4;
в) 24/-40 = 3•8/-5•8 = 3/-5 = — 3/5, -27/45 = -3•9/5•9 = -3/5 = — 3/5, а так как — 3/5 = — 3/5, то 24/-40 = -27/45;
г) -77/-88 = -7•11/-8•11 = -7•(-1)/-8•(-1) = 7/8, 63/72 = 7•9/8•9 = 7/8, а так как 7/8 = 7/8, то -77/-88 = 63/72.
470. Запишите в виде целого числа дробь:
а) 2/1; б) -13/1; в) 0/2; г) -14/7; д) -32/-4; е) 44/-11.а) 2/1 = 2;
б) -13/1 = — 13/1 = -13;
в) 0/2 = 0;
г) -14/7 = — 14/7 = -2;
д) -32/-4 = -32•(-1)/-4•(-1) = 32/4 = 8;
е) 44/-11 = — 44/11 = -4.
471. Даны рациональные числа: -17/9; 37/-48; -15/-5; 0/-7; -17/-1; 16/-8; — -46/-23; -20/-30.
Выпишите числа, являющееся: а) натуральными; б) целыми.а) натуральные числа:
-15/-5 = -15•(-1)/-5•(-1) = 15/5 = 3;
-17/-1 = -17•(-1)/-1•(-1) = 17;б) целые числа:
-15/-5 = -15•(-1)/-5•(-1) = 15/5 = 3;
0/-7 = 0;
-17/-1 = -17•(-1)/-1•(-1) = 17;
— -46/-23 = -(-46)/-23 = 46/-23 = — 46/23 = -2;
16/-8 = — 16/8 = -2.472. Найдите равные среди рациональных чисел:
— 3/9; -5/-10; 4/-8; -25/50; 0/100; 17/34; 0/-72; 100/-300.— 3/9 = 100/-300, так как — 3/9 = — 1•3/3•3 = — 1/3, 100/-300 = — 100/300 = — 1•100/3•100 = — 1/3, а — 1/3 = — 1/3;
-5/-10 = 17/34, так как -5/-10 = -1•5/-2•5 = -1•(-1)/-2•(-1) = 1/2, 17/34 = 1•17/2•17 = 1/2, а 1/2 = 1/2;
4/-8 = -25/50, так как 4/-8 = 1•4/-2•4 = 1/-2 = — 1/2, -25/50 = -1•25/2•25 = -1/2 = — 1/2, — 1/2 = — 1/2;
0/100 = 0/-72, так как 0/100 = 0, 0/-72 = 0, а 0 = 0.
473. Запишите три дроби с положительным знаменателем, равные числу: а) 5; б) -2; в) -28; г) 0.
а) 5 = 15/3 = 25/5 = 60/12;
б) -2 = -12/6 = -20/10 = -42/21;
в) -28 = -84/3 = -140/5 = -224/8;
г) 0 = 0/1 = 0/10 = 0/32.
474. Является ли дробь положительной, отрицательной:
а) 3/5; б) -5/9; в) 4/-3; г) 0/-1; д) -6/-8; е) — -1/3; ж) — 7/9; з) -9/17.а) 3/5 − положительная дробь;
б) -5/9 = — 5/9 − отрицательная дробь;
в) 4/-3 = — 4/3 − отрицательная дробь;
г) 0/-1 = 0 − не является положительной или отрицательной дробью;
д) -6/-8 = -6•(-1)/-8•(-1) = 6/8 − положительная дробь;
е) — -1/3 = -(-1)/3 = 1/3 − положительная дробь;
ж) — 7/9 − отрицательная дробь;
з) -9/17 = — 9/17 − отрицательная дробь.
475. Назовите и запишите дробь, противоположную дроби:
а) — 1/5; б) -1/3; в) 4/7; г) — 5/6; д) — 7/8; е) -1/-3.а) отрицательной дроби — 1/5 противоположны положительные дроби 1/5, -1/-5;
б) отрицательной дроби -1/3 противоположны положительные дроби 1/3, -1/-3;
в) положительной дроби 4/7 противоположны отрицательные дроби -4/7, 4/-7, — 4/7;
г) отрицательной дроби — 5/6 противоположны положительные дроби 5/6, -5/-6;
д) отрицательной дроби — 7/8 противоположны положительные дроби 7/8, -7/-8;
е) положительной дроби -1/-3 противоположны отрицательные дроби -1/3, 1/-3, — 1/3.476. Одинаковые или разные знаки имеют числа m и n (mn ≠ 0), если верно равенство: а) |m/n| = m/n; б) |m/n| = − m/n.
а) |m/n| > 0, поэтому для того, чтобы равенство было верным, дробь m/n должна быть положительной и, следовательно, числа m и n должны иметь одинаковые знаки;
б) |m/n| > 0, поэтому для того, чтобы равенство было верным, дробь m/n должна быть отрицательной и, следовательно, числа m и n должны иметь разные знаки, так как если m/n < 0, то — m/n > 0.
95
-
Рациональные числа
Сравнение рациональных чиселОтветы к стр. 95
477. Как сравнивают две дроби:
а) с общим положительным знаменателем;
б) с разными знаменателями?а) Из двух дробей с общим положительным знаменателем больше та, у которой числитель больше.
б) Чтобы сравнить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сравнить полученные дроби.
478. Сформулируйте правило сравнения: положительной дроби с нулём; отрицательной дроби с нулём; положительной дроби с отрицательной.
Любая положительная дробь больше нуля; любая отрицательная дробь меньше нуля; любая положительная дробь больше отрицательной.
Сравните числа (479-484):
479. а) 15 и -45; б) 79 и 0;
в) -81 и 0; г) 48 и -1000;
д) -999 и -1; е) 46 и -46.а) 15 > -45;
б) 79 > 0;
в) -81 < 0;
г) 48 > -1000;
д) -999 < -1;
е) 46 > -46.480. а) 3/7 и 4/7; б) 49/50 и 4/5; в) 11/20 и 17/30.
а) 3/7 < 4/7;
б) 49/50 > 4/5, так как 4/5 = 4•10/5•10 = 40/50;
в) 11/20 < 17/30, так как 11/20 = 11•3/20•3 = 33/60, 17/30 = 17•2/30•2 = 34/60.
96
-
Ответы к стр. 96
Сравните числа (479-484):
481. а) 37/452 и 207/388; б) 456/729 и 895/891; в) 999/1000 и 1000/1001.
а) Чтобы сравнить две положительные дроби между собой, можно сравнить каждую из них с дробью 1/2. Для того чтобы сравнить любую положительную дробь с дробью 1/2, нужно умножить числитель этой дроби на 2. Если получившееся число больше числа в знаменателе дроби, значит дробь больше 1/2, если же получившееся число меньше числа в знаменателе, то значит дробь меньше 1/2.
37/452 • 2 = 74/452, 74 < 452 — то есть, эта дробь меньше 1/2,207/388 • 2 = 414/388, 414 > 388 — то есть, эта дробь больше 1/2,
следовательно, 37/452 < 207/388;
б) Чтобы сравнить две положительные дроби между собой, можно сравнить каждую из них с 1. Если числитель дроби больше знаменателя, то эта дробь больше 1. Если числитель дроби меньше знаменателя, то эта дробь меньше 1.
456 < 729, значит 456/729 < 1,895 > 891, значит 895/891 > 1,
следовательно, 456/729 < 895/891;
в) 999/1000 = 999•1001/1000•1001 = 999999/1001000,
1000/1001 = 1000•1000/1001•1000 = 1000000/1001000,
999999/1001000 < 1000000/1001000,
следовательно, 999/1000 < 1000/1001.
482. а) 6/7 и 8/7; б) 1 и 7/8; в) 1 и 9/8; г) 1/2 и 1/3.
а) из двух дробей с общим положительным знаменателем больше та, у которой числитель больше: 6/7 < 8/7;
б) дробь, у которой числитель меньше знаменателя, называется правильной, а любая правильная дробь меньше 1: 1 > 7/8;
в) дробь, у которой числитель больше знаменателя, называется неправильной, а любая неправильная дробь больше 1: 1 < 9/8;
г) из двух дробей с одинаковыми числителями больше та, знаменатель которой меньше: 1/2 > 1/3.
483. а) -1 и -2; б) -12 и -7; в) — 1/2 и 0; г) 0 и -3/4.
Из двух отрицательных чисел больше то, у которого модуль меньше.
а) -1 > -2;
б) -12 < -7;Любое отрицательное число меньше нуля.
в) — 1/2 < 0;
г) -3/4 = — 3/4, 0 > — 3/4, следовательно, 0 > -3/4.484. а) — 1/2 и 1/2; б) — 4/5 и — 3/5; в) — 1/7 и -3/7; г) -3/8 и 5/-8.
Из двух дробей с общим положительным знаменателем больше та, у которой числитель больше.
а) — 1/2 = -1/2, -1 < 1, то есть, -1/2 < 1/2, тогда — 1/2 < 1/2;б) — 4/5 = -4/5, — 3/5 = -3/5, -4 < -3, то есть -4/5 < -3/5, тогда — 4/5 < — 3/5;
в) — 1/7 = -1/7, -1 > -3, то есть -1/7 > -3/7, тогда — 1/7 > -3/7;
г) 5/-8 = — 5/8 = -5/8, -3 > -5, то есть -3/8 > -5/8, тогда -3/8 > 5/-8.
485. Запишите в порядке возрастания числа:
— 1/8, — 5/8, — 6/8, — 2/8, — 9/8, — 1, — 3/8, — 4/8.Из двух дробей с общим положительным знаменателем больше та, у которой числитель больше.
— 1 = — 8/8= -8/8, тогда:— 9/8, — 1, — 6/8, — 5/8, — 4/8, — 3/8, — 2/8, — 1/8.
486. Запишите в порядке убывания числа: — 7/4, — 1/4, — 15/4, — 3/4, — 2.
Из двух дробей с общим положительным знаменателем больше та, у которой числитель больше.
— 2 = — 8/4 = -8/4, тогда:— 1/4, — 3/4, — 7/4, — 2, — 15/4.
487. Найдите дробь которая больше одной из данных дробей, но меньше другой:
а) — 1/5 и — 4/5; б) — 9/10 и — 3/10; в) -12/13 и 4/-13;
г) -8/11 и — 5/11; д) — 1/8 и — 7/8; е) — 3/7 и — 5/7.а) — 1/5 > — 3/5 > — 4/5;
б) — 9/10 < — 4/10 < — 3/10;
в) -12/13 < — 7/13 < 4/-13;
г) -8/11 < — 6/11 < — 5/11;
д) — 1/8 > — 4/8 > — 7/8;
е) — 3/7 > — 4/7 > — 5/7.
488. Сравните числа:
а) — 1/2 и — 1/3; б) — 1/5 и — 1/2; в) — 1/6 и — 4/11;
г) — 1/2 и — 3/4; д) — 3/5 и — 7/10; е) — 5/9 и — 2/3;
ж) — 11/24 и — 1/2; з) — 5/28 и — 1/7; и) — 25/32 и — 5/8;
к) — 9/10 и — 14/15; л) — 1/4 и — 7/8; м) — 13/24 и — 17/36.а) — 1/2 < — 1/3, так как — 1/2 = -3/6, — 1/3 = -2/6, а -3/6 < -2/6;
б) — 1/5 > — 1/2, так как — 1/5 = -2/10, — 1/2 = -5/10, а -2/10 > -5/10;
в) — 1/6 > — 4/11, так как — 1/6 = -11/66, — 4/11 = -24/66, а -11/66 > -24/66;
г) — 1/2 > — 3/4, так как — 1/2 = -2/4, — 3/4 = -3/4, а -2/4 > -3/4;
д) — 3/5 > — 7/10, так как — 3/5 = -6/10, — 7/10 = -7/10, а -6/10 < -7/10;
е) — 5/9 > — 2/3, так как — 5/9 = -5/9, — 2/3 = -6/9, а -5/9 > -6/9;
ж) — 11/24 > — 1/2, так как — 11/24 = -11/24, — 1/2 = -12/24, а -11/24 > -12/24;
з) — 5/28 < — 1/7, так как — 5/28 = -5/28, — 1/7 = -4/28, а -5/28 < -4/28;
и) — 25/32 < — 5/8, так как — 25/32 = -25/32, — 5/8 = -20/32, а -25/32 < -20/32;
к) — 9/10 > — 14/15, так как — 9/10 = -27/30, — 14/15 = -28/30, а -27/30 > -28/30;
л) — 1/4 > — 7/8, так как — 1/4 = -2/8, — 7/8 = -7/8, а -2/8 > -7/8;
м) — 13/24 < — 17/36, так как — 13/24 = -39/72, — 17/36 = -36/72, а -39/72 < -36/72.
489. Запишите дроби — 1/2, — 2/3, — 3/4 в порядке возрастания.
— 1/2 = — 1•6/2•6 = — 6/12,
— 2/3 = — 2•4/3•4 = — 8/12,
— 3/4 = — 3•3/4•3 = — 9/12,
в порядке возрастания: — 3/4, — 2/3, — 1/2.490. Запишите дроби — 1/2, — 5/6, — 1/3 в порядке убывания.
— 1/2 = — 1•3/2•3 = — 3/6,
— 1/3 = — 1•2/3•2 = — 2/6,
в порядке убывания: — 1/3, — 1/2, — 5/6.491. Верно ли, что если — 4/7 > — 2/3 и — 2/3 > — 4/5, то — 4/7 > — 4/5?
— 4/7 > — 2/3, так как — 4/7 = — 60/105, — 2/3 = — 70/105, а — 60/105 > — 70/105,
— 2/3 > — 4/5, так как — 2/3 = — 70/105, — 4/5 = — 84/105, а — 70/105 > — 84/105,
— 4/7 > — 4/5, так как — 60/105 > — 84/105 — следовательно, утверждение верно.
97
-
Ответы к стр. 97
492. Существуют ли дроби p/q, для которых верно неравенство — 2/5 < p/q < — 1/5? Если существуют, то найдите три такие дроби.
— 2/5 = — 2•4/5•4 = — 8/20,
— 1/5 = — 1•4/5•4 = — 4/20, тогда:
— 8/20 < — 7/20 < — 4/20,
— 8/20 < — 6/20 < — 4/20,
— 8/20 < — 5/20 < — 4/20,
493. Можно ли назвать 10 дробей, бóльших одной из данных дробей, но меньше другой:
а) — 39/40 и — 1/40; б) — 3/4 и — 1/4?
Можно ли назвать 100, 1000, 10 000 таких дробей?а) условие — 39/40 < p/q < — 1/40 выполняется для любой отрицательной дроби со знаменателем 40 и числителем, модуль которого меньше 39 и больше 1: — 38/40, — 37/40, — 36/40, — 35/40, — 34/40, — 33/40, — 32/40, — 31/40, — 30/40, — 29/40;
б) — 3/4 = — 30/40, — 1/4 = — 10/40, таким образом условие — 3/4 < p/q < — 1/4 выполняется для любой отрицательной дроби со знаменателем 40 и числителем, модуль которой меньше 30 и больше 10: — 29/40, — 28/40, — 27/40, — 26/40, — 25/40, — 24/40, — 23/40, — 22/40, — 21/40, — 20/40.
Также можно назвать и 100, и 1000, и 10 000 дробей. Для это нужно привести дроби к бóльшему знаменателю.494. Найдите дробь, которая больше одной из данных дробей, но меньше другой:
а) — 1/5 и — 1/3; б) — 5/6 и — 2/3; в) — 3/8 и — 3/4;
г) — 3/20 и — 7/30; д) — 3/7 и — 2/9; е) — 10/11 и — 19/20.а) — 1/5 = — 3/15, — 1/3 = — 5/15, тогда:
— 3/15 > — 4/15 > — 5/15, значит — 1/5 > — 4/15 > — 1/3;б) — 5/6 = — 10/12, — 2/3 = — 8/12, тогда:
— 10/12 < — 9/12 < — 8/12, значит — 5/6 < — 9/12 < — 2/3;в) — 3/4 = — 6/8, тогда:
— 3/8 > — 5/8 > — 6/8, значит — 3/8 > — 5/8 > — 3/4;г) — 3/20 = — 9/60, — 7/30 = — 14/60, тогда:
— 9/60 > — 11/60 > — 12/60, значит — 3/20 > — 11/60 > — 7/30;д) — 3/7 = — 27/63, — 2/9 = — 14/63, тогда:
— 27/63 < — 18/63 < — 14/63, значит — 3/7 < — 18/63 < — 2/9;е) — 10/11 = — 200/220, — 19/20 = — 209/220, тогда:
— 200/220 > — 203/220 > — 209/220, значит — 10/11 > — 203/220 > — 19/20.495. Сравните числа:
а) — 1/2 и -1; б) — 8/8 и -1; в) — 9/8 и -1; г) — 498/497 и — 1.а) — 1/2 > -1, так как -1 = — 2/2, а — 1/2 > — 2/2;
б) — 8/8 = -1, так как -1 = — 8/8, а — 8/8 = — 8/8;
в) — 9/8 < -1, так как -1 = — 8/8, а — 9/8 < — 8/8;
г) — 498/497 < -1, так как -1 = — 497/497, а — 498/497 < — 497/497.
496. Как можно сравнить дроби, не приводя их к общему положительному знаменателю, если числители этих дробей одинаковые положительные целые числа?
Из двух дробей с положительными знаменателями и положительными одинаковыми числителями будет больше та, у которой меньше знаменатель.
99
-
Рациональные числа
Сложение и вычитание дробейОтветы к стр. 99
497. Сформулируйте правила сложения и вычитания дробей с общим положительным знаменателем.
Сумма двух дробей с общим положительным знаменателем есть дробь с тем же знаменателем и числителем равным сумме числителей: p/q + r/q = p+r/q.
Разность двух дробей с общим положительным знаменателем есть дробь с тем же знаменателем и числителем, равным разности числителей уменьшаемого и вычитаемого: p/q — r/q = p—r/q.
498. Чему равна сумма противоположных дробей?
Сумма противоположных дробей равна нулю.
499. Как вычислить сумму или разность дробей с разными знаменателями?
Чтобы вычислить сумму или разность дробей с разными знаменателями, нужно привести эти дроби к общему положительному знаменателю и выполнить вычисления по правилу сложения и вычитания дробей с общим положительным знаменателем.
Выполните действия (500-501):
500. а) 8/9 + 5/9; б) 17/25 — 8/25; в) 31/32 + 63/64; г) 23/68 — 5/17; д) 50/49 + 15/56.
а) 8/9 + 5/9 = 8+5/9 = 13/9;
б) 17/25 — 8/25 = 17-8/25 = 9/25;
в) 31/32 + 63/64 = 62/64 + 63/64 = 62+63/64 = 125/64;
г) 23/68 — 5/17 = 23/68 — 20/68 = 23-20/68 = 3/68;
д) 50/49 + 15/56 = 400/392 + 105/392 = 400+105/392 = 505/392.
501. а) (-56) + 17; б) 42 + (-29); в) (-39) + (-57);
г) (-48) + 81; д) 37 + (-82); е) (-68) + (-51).а) (-56) + 17 = -56 + 17 = -39;
б) 42 + (-29) = 42 — 29 = 13;
в) (-39) + (-57) = -39 — 57 = -96;
г) (-48) + 81 = -48 + 81 = 33;
д) 37 + (-82) = 37 — 82 = -45;
е) (-68) + (-51) = -68 — 51 = -119.502. По каким формулам можно складывать и вычитать дроби?
Дроби любого знака p/q и r/s можно складывать и вычитать по формулам:
p/q + r/s = p•s+q•r/q•sp/q — r/s = p•s—q•r/q•s
Вычислите (503-514):
503. а) -1/2 + -1/2; б) -1/3 + -1/3; в) -2/3 + -1/3; г) -2/7 + -5/7; д) -7/12 + -1/12.
а) -1/2 + -1/2 = -1+(-1)/2 = -1-1/2 = -2/2 = -1;
б) -1/3 + -1/3 = -1+(-1)/3 = -1-1/3 = -2/3 = — 2/3;
в) -2/3 + -1/3 = -2+(-1)/3 = -2-1/3 = -3/3 = -1;
г) -2/7 + -5/7 = -2+(-5)/7 = -2-5/7 = -7/7 = -1;
д) -7/12 + -1/12 = -7+(-1)/12 = -7-1/12 = -8/12 = — 2/3.
100
-
Ответы к стр. 100
Вычислите (503-514):
504. а) -1/3 + 2/3; б) — 1/4 + 3/4; в) 1/5 + -3/5;
г) 3/7 + -4/7; д) 8/13 + -12/13; е) 19/25 + -24/25.а) -1/3 + 2/3 = -1+2/3 = 1/3;
б) — 1/4 + 3/4 = -1+3/4 = 2/4 = 1/2;
в) 1/5 + -3/5 = 1-3/5 = -2/5 = — 2/5;
г) 3/7 + -4/7 = 3-4/7 = -1/7 = — 1/7;
д) 8/13 + -12/13 = 8-12/13 = -4/13 = — 4/13;
е) 19/25 + -24/25 = 19-24/25 = -5/25 = — 1/5.
505. а) 1/2 + -1/2; б) -5/6 + 5/6; в) -2/3 + 2/3.
а) 1/2 + -1/2 = 1-1/2 = 0/2 = 0;
б) -5/6 + 5/6 = -5+5/6 = 0/6 =0;
в) -2/3 + 2/3 = -2+2/3 = 0/3 = 0.
506. а) 1/3 — 2/3; б) 1/4 — 3/4; в) 2/7 — 5/7;
г) 7/12 — 11/12; д) -8/11 — 3/11; е) — 5/17 — 10/17.а) 1/3 — 2/3 = 1-2/3= -1/3 = — 1/3;
б) 1/4 — 3/4 = 1-3/4 = -2/4 = — 1/2;
в) 2/7 — 5/7 = 2-5/7 = -3/7 = — 3/7;
г) 7/12 — 11/12 = 7-11/12 = -4/12 = — 1/3;
д) -8/11 — 3/11 = -8-3/11 = -11/11 = -1;
е) — 5/17 — 10/17 = -5-10/17 = -15/17 = — 15/17.
507. а) -2/7 — -5/7; б) -4/9 — -8/9; в)- 1/10 — -7/10;
г) — 12/19 — 7/19; д) -4/5 — -3/5; е) — 1/24 — 11/24.а) -2/7 — -5/7 = -2-(-5)/7 = -2+5/7 = 3/7;
б) -4/9 — -8/9 = -4-(-8)/9 = -4+8/9 = 4/9;
в) — 1/10 — -7/10 = -1-(-7)/10 = -1+7/10 = 6/10 = 3/5;
г) — 12/19 — 7/19 = -12-7/19 = -19/19 = -1;
д) -4/5 — -3/5 = -4-(-3)/5 = -4+3/5 = -1/5 = — 1/5;
е) — 1/24 — 11/24 = -1-11/24 = -12/24 = — 1/2.
508. а) -1/2 + -1/4; б) -1/3 + 1/6; в) — 1/2 + 1/6; г) 1/8 + -1/4; д) 3/10 + -7/100.
а) -1/2 + -1/4 = -2/4 + -1/4 = -2-1/4 = -3/4 = — 3/4;
б) -1/3 + 1/6 = -2/6 + 1/6 = -2+1/6 = -1/6 = — 1/6;
в) — 1/2 + 1/6 = -3/6 + 1/6 = -3+1/6 = -2/6 = — 1/3;
г) 1/8 + -1/4 = 1/8 + -2/8 = 1-2/8 = -1/8 = — 1/8;
д) 3/10 + -7/100 = 30/100 + -7/100 = 30-7/100 = 23/100.
509. а) — 3/5 — 9/10; б) — 15/24 — 3/8; в) -2/3 — 5/6;
г) — 7/6 — 5/24; д) 2/5 — 13/50; е) — 50/160 — 9/16.а) — 3/5 — 9/10 = -6/10 — 9/10 = -6-9/10 = -15/10 = — 3/2 = -1 1/2;
б) — 15/24 — 3/8 = -15/24 — 9/24 = -15-9/24 = -24/24 = -1;
в) -2/3 — 5/6 = -4/6 — 5/6 = -4-5/6 = -9/6 = — 3/2 = -1 1/2;
г) — 7/6 — 5/24 = -28/24 — 5/24 = -28-5/24 = -33/24 = — 11/8 = -1 3/8;
д) 2/5 — 13/50 = 20/50 — 13/50 = 20-13/50 = 7/50;
е) — 50/160 — 9/16 = -5/16 — 9/16 = -5-9/16 = -14/16 = — 7/8.
510. а) — 1/6 + 1/9; б) 3/10 — 2/15; в) — 2/10 — 6/15;
г) 3/8 — 2/9; д) — 5/12 + 4/15; е) 2/16 — -3/39.а) — 1/6 + 1/9 = -3/18 + 2/18 = -3+2/18 = -1/18 = — 1/18;
б) 3/10 — 2/15 = 9/30 — 4/30 = 9-4/30 = 5/30 = 1/6;
в) — 2/10 — 6/15 = -6/30 — 12/30 = -6-12/30 = -18/30 = — 3/5;
г) 3/8 — 2/9 = 27/72 — 16/72 = 27-16/72 = 11/72;
д) — 5/12 + 4/15 = -25/60 + 16/60 = -25+16/60 = -9/60 = — 3/20;
е) 2/16 — -3/39 = 78/624 — -48/624 = 78-(-48)/624 = 78+48/624 = 126/624 = 21/104.
511. а) 5/8 + (- 9/8); б) — 3/13 + (- 8/13); в) — 2/5 + 4/5;
г) 3/8 + (- 3/4); д) — 7/15 + (- 2/3); е) — 7/8 — 15/16;
ж) 1/3 + (- 1/2); з) — 1/4 + 1/3; и) — 2/21 + 3/14.а) 5/8 + (- 9/8) = 5/8 — 9/8 = 5-9/8 = -4/8 = — 1/2;
б) — 3/13 + (- 8/13) = -3/13 — 8/13 = -3-8/13 = -11/13 = — 11/13;
в) — 2/5 + 4/5 = -2/5 + 4/5 = -2+4/5 = 2/5;
г) 3/8 + (- 3/4) = 3/8 — 3/4 = 3/8 — 6/8 = 3-6/8 = -3/8 = — 3/8;
д) — 7/15 + (- 2/3) = -7/15 — 2/3 = -7/15 — 10/15 = -7-10/15 = -17/15 = -1 2/15;
е) — 7/8 — 15/16 = -14/16 — 15/16 = -14-15/16 = -29/16 = -1 13/16;
ж) 1/3 + (- 1/2) = 1/3 — 1/2 = 2/6 — 3/2 = 2-3/6 = -1/6 = — 1/6;
з) — 1/4 + 1/3 = -3/12 + 4/12 = -3+4/12 = 1/12;
и) — 2/21 + 3/14 = -4/42 + 9/42 = -4+9/42 = 5/42.
512. а) — 9/180 — 7/120; б) — 4/210 + 5/140; в) -7/480 + 8/180.
а) — 9/180 — 7/120 = -18/360 — 21/360 = -18-21/360 = -39/360 = — 13/120;
б) — 4/210 + 5/140 = -8/420 + 15/420 = -8+15/420 = 7/420 = 1/60;
в) -7/480 + 8/180 = -21/1440 + 64/1440 = -21+64/1440 = 43/1440.
513. а) — 7/15 + 2/15 — 1/5; б) — 1/6 — 5/12 — 7/24; в) — 3/13 — 5/13 + 3/26;
г) 9/28 — 4/7 — 1/4; д) 10/27 — 5/18 + 8/9; е) 2/5 + 1/6 + 1/15.а) — 7/15 + 2/15 — 1/5 = -7/15 + 2/15 — 3/15 = -7+2-3/15 = -8/15 = — 8/15;
б) — 1/6 — 5/12 — 7/24 = -4/24 — 10/24 — 7/24 = -4-10-7/24 = -21/24 = — 7/8;
в) — 3/13 — 5/13 + 3/26 = -6/26 — 10/26 + 3/26 = -6-10+3/26 = -13/26 = — 1/2;
г) 9/28 — 4/7 — 1/4 = 9/28 — 16/28 — 7/28 = 9-16-7/28 = -14/28 = — 1/2;
д) 10/27 — 5/18 + 8/9 = 20/54 — 15/54 + 48/54 = 20-15+48/54 = 53/54;
е) 2/5 + 1/6 + 1/15 = 12/30 + 5/30 + 2/30 = 12+5+2/30 = 19/30.
101
-
Ответы к стр. 101
Вычислите (503-514):
514. а) — 1/5 + 3/10 — 7/20; б) — 3/20 — 7/30 + 2/40; в) 11/60 — 23/30 — 17/20.
а) — 1/5 + 3/10 — 7/20 = -4/20 + 6/20 — 7/20 = -4+6-7/20 = -5/20 = — 1/4;
б) — 3/20 — 7/30 + 2/40 = -9/60 — 14/60 + 3/60 = -9-14+3/60 = -20/60 = — 1/3;
в) 11/60 — 23/30 — 17/20 = 11/60 — 46/60 — 51/60 = 11-46-51/60 = -86/60 = -43/30 = -1 13/30.
515. Найдите число х, для которого верно равенство:
а) х + 1/8 = — 5/8; б) 1/7 + х = — 3/7; в) х — 1/4 = — 1/2;
г) х — 1/6 = 1/3; д) 2/3 — х = — 1/7; е) 1/6 — х = — 4/9.а) х + 1/8 = — 5/8,
х = — 5/8 — 1/8,
х = -5-1/8,
х = -6/8,
х = — 3/4;б) 1/7 + х = — 3/7,
х = — 3/7 — 1/7,
х = -3-1/7,
х = -4/7,
х = — 4/7;в) х — 1/4 = — 1/2,
х = — 1/2 + 1/4,
х = — 2/4 + 1/4,
х = -2+1/4,
х = -1/4,
х = — 1/4;г) х — 1/6 = 1/3,
х = 1/3 + 1/6,
х = 2/6 + 1/6,
х = 2+1/6,
х = 3/6,
х = 1/2;д) 2/3 — х = — 1/7,
х = 1/7 + 2/3,
х = 3/21 + 14/21,
х = 3+14/21,
х = 17/21;е) 1/6 — х = — 4/9,
х = 4/9 + 1/6,
х = 8/18 + 3/18,
х = 8+3/18,
х = 11/18.516. Найдите число, которое:
а) на 1/2 больше числа — 1/2; б) на 1/4 меньше числа 1/6.а) Обозначим неизвестное число как х, тогда, если из х вычесть 1/2, то получится — 1/2:
х — 1/2 = — 1/2,
х = -1/2 + 1/2,
х= -1+1/2,
х = 0/2,
х = 0;б) Обозначим неизвестное число как х, тогда, если к х прибавить 1/4, то получится 1/6:
х + 1/4 = 1/6,
х = 1/6 — 1/4,
х = 2/12 — 3/12,
х = 2-3/12,
х = — 1/12.517. Запишите разность дробей в виде равной ей суммы дробей:
а) 1/3 — 4/3; б) — 1/5 — 1/5; в) -4/7 — -8/7.а) 1/3 — 4/3 = 1/3 + (- 4/3);
б) — 1/5 — 1/5 = — 1/5 + (- 1/5);
в) -4/7 — -8/7 = -4/7 + (- -8/7) = -4/7 + 8/7.
518. Вычислите, предварительно заменив разность дробей равной ей суммой:
а) 1/2 — (- 1/3); б) 4/9 — (- 7/9); в) — 9/16 — (- 3/8);
г) — 1/2 — (- 3/8); д) — 9/10 — (- 15/16); е) 25/26 — (- 11/13).а) 1/2 — (- 1/3) = 1/2 + 1/3 = 3/6 + 2/6 = 3+2/6 = 5/6;
б) 4/9 — (- 7/9) = 4/9 + 7/9 = 4+7/9 = 11/9 = 1 2/9;
в) — 9/16 — (- 3/8) = — 9/16 + 3/8 = — 9/16 + 6/16 = -9+6/16 = — 3/16;
г) — 1/2 — (- 3/8) = — 1/2 + 3/8 = — 4/8 + 3/8 = -4+3/8 = — 1/8;
д) — 9/10 — (- 15/16) = — 9/10 + 15/16 = — 72/80 + 75/80 = -72+75/80 = 3/80;
е) 25/26 — (- 11/13) = 25/26 + 11/13 = 25/26 + 22/26 = 47/26 = 1 21/26.
103
-
Рациональные числа
Умножение и деление дробейОтветы к стр. 103
519. По каким правилам умножают и делят дроби любого знака?
Дроби любого знака умножают и делят по тем же правилам, что и положительные дроби:
p/q • r/s = p•r/q•s,p/q : r/s = p•s/q•r, где r ≠ 0.
520. Как умножить дробь на целое число?
Чтобы дробь умножить на целое число, можно её числитель умножить на это число, а знаменатель оставить прежним.
521. Как разделить дробь на целое число, не равное нулю?
Чтобы разделить дробь на целое число, не равное нулю, можно знаменатель дроби умножить на это число, а числитель оставить прежним.
522. Какие числа называют взаимно обратными?
Числа, произведение которых равно 1: p/q и q/p.
104
-
Ответы к стр. 104
Выполните действие (523-525):
523. а) 75 • (-64); б) (-57) • (-129); в) (-144) • 55;
г) 912 : (-48); д) (-1596) : 57; е) (-2701) : (-37).а) 75 • (-64) = -4800;
×75
64
+ 300
450
4800б) (-57) • (-129) = 7353;
×129
57
+ 903
645
7353в) (-144) • 55 = -7920;
×144
55
+ 720
720
7920г) 912 : (-48) = -19;
—912|48
48 |19
—432
432
0д) (-1596) : 57 = -28;
—1596|57
114 |28
—456
456
0
е) (-2701) : (-37) = 73.—2701|37
259 |73
—111
111
0524. а) 161 784 : (-321); б) -2 164 320 : 432;
в) -4 101 630 : (-507); г) -1 936 980 : (-918).а) 161 784 : (-321) = -504;
—161784|321
1605 |504
—1284
1284
0б) -2 164 320 : 432 = -5010;
—2164320|432
2160 |5010
—432
432
0в) -4 101 630 : (-507) = 8090;
—4101630|507
4056 |8090
—4563
4563
0г) -1 936 980 : (-918) = 2110.
—1936980|918
1836 |2110
—1009
918
—918
918
0525. а) 34/35 : 51/55; б) 37/38 • 57/148; в) 54/125 • 35;
г) 115/116 : 62; д) 351/625 • 250/182; е) 99 : 143/120.а) 34/35 : 51/55 = 34/35 • 55/51 = 2•11/7•3 = 22/21 = 1 1/21;
б) 37/38 • 57/148 = 1•3/2•4 = 3/8;
в) 54/125 • 35 = 54/125 • 35/1 = 54•7/25•1 = 378/25 = 15 3/25;
г) 115/116 : 62 = 115/116 • 1/62 = 115•1/116•62 = 115/7192;
д) 351/625 • 250/182 = 27•1/5•7 = 27/35;
е) 99 : 143/120 = 99/1 • 120/143 = 9•120/1•13 = 1080/13 = 83 1/13.
Сократите дробь (526-528):
526. а) 36•(-112)/126•(-63); б) 184•(-49)/84•(-69); в) (-315)•57/114•(-108);
г) (-105)•84/196•125; д) (-111)•(-9)/78•74; е) (-888)•55/77•999.а) 36•(-112)/126•(-63) = 4•56/63•7 = 4•8/63•1 = 32/63;
б) 184•(-49)/84•(-69) = 8•7/12•3 = 2•7/3•3 = 14/9;
в) (-315)•57/114•(-108) = 35•1/2•12 = 35/24;
г) (-105)•84/196•125 = — 21•3/7•25 = — 3•3/1•25 = — 9/25;
д) (-111)•(-9)/78•74 = 3•3/26•2 = 9/52;
е) (-888)•55/77•999 = — 8•5/7•9 = — 40/63.
527. а) (-1)•3/6•(-4); б) (-3)•4/6•(-5); в) (-4)•10/(-30)•14;
г) (-8)•18/(-28)•6; д) (-12)•(-5)/(-21)•10; е) (-75)•(-24)/(-32)•(-100).а) (-1)•3/6•(-4) = 1•1/2•4 = 1/8;
б) (-3)•4/6•(-5) = 1•4/2•5 = 1•2/1•5 = 2/5;
в) (-4)•10/(-30)•14 = 2•1/3•7 = 2/21;
г) (-8)•18/(-28)•6 = 2•3/7•1 = 6/7;
д) (-12)•(-5)/(-21)•10 = — 4•1/7•2 = — 2•1/7•1 = — 2/7;
е) (-75)•(-24)/(-32)•(-100) = 3•3/4•4 = 9/16.
528. а) -3•8•(-6)/18•(-4); б) -7•16/-14•(-2)•(-10); в) -2•(-3)•(-6)/-3•(-8)•(-10);
г) -96•(-125)/-75•(-128); д) 56•(-77)/-121•(-49); е) -128•(-92)/-256•(-48).а) -3•8•(-6)/18•(-4) = — 3•8/3•4 = — 8/4 = -2;
б) -7•16/-14•(-2)•(-10) = 1•16/2•2•10 = 8/2•10 = 4/10 = 2/5;
в) -2•(-3)•(-6)/-3•(-8)•(-10) = 1•1•6/1•4•10 = 3/2•10 = 3/20;
г) -96•(-125)/-75•(-128) = 3•5/3•4 = 1•5/1•4 = 5/4;
д) 56•(-77)/-121•(-49) = — 8•7/11•7 = — 8•1/11•1 = — 8/11;
е) -128•(-92)/-256•(-48) = 1•23/2•12 = 23/24.
529. Вычислите произведение по образцу:
(- 1/2) • 2/3 = -1/2 • 2/3 = -1•2/2•3 = -1/3 = — 1/3;
а) -3/7 • 5/9; б) -3/8 • -4/5; в) -9/10 • -1/-2;
г) -7/2 • 4/-35; д) -5/6 • 3/10; е) -7/32 • 4/-21;
ж) — 2/5 • (- 75/2); з) 4/3 • (- 9/16); и) — 18/5 • (- 4/81).а) -3/7 • 5/9 = -3•5/7•9 = -1•5/7•3 = -5/21 = — 5/21;
б) -3/8 • -4/5 = -3•(-4)/8•5 = -3•(-1)/2•5 = 3/10;
в) -9/10 • -1/-2 = -9•(-1)/10•(-2) = 9/-20 = — 9/20;
г) -7/2 • 4/-35 = -7•4/2•(-35) = -1•2/1•(-5) = 2/5;
д) -5/6 • 3/10 = -5•3/6•10 = -1•1/2•2= -1/4 = — 1/4;
е) -7/32 • 4/-21 = -7•4/32•(-21) = -1•1/8•(-3) = -1/-24 = 1/24;
ж) — 2/5 • (- 75/2) = -2/5 • -75/2 = -2•(-75)/5•2 = -1•(-15)/1•1 = 15/1 = 15;
з) 4/3 • (- 9/16) = 4/3 • -9/16 = 4•(-9)/3•16 = 1•(-3)/1•4 = -3/4 = — 3/4;
и) — 18/5 • (- 4/81) = -18/5 • -4/81 = -18•(-4)/5•81 = -2•(-4)/5•9 = 8/45.
Вычислите (530-531):
530. а) — 1/2 • 2/5; б) 3/4 • (- 2/9); в) — 4/5 • (- 10/3);
г) — 1/7 • (- 3/4); д) 2/5 • (- 3/4); е) — 3/8 • 4/5.а) — 1/2 • 2/5 = -1/2 • 2/5 = -1•2/2•5 = -1•1/1•5 = -1/5 = — 1/5;
б) 3/4 • (- 2/9) = 3/4 • -2/9 = 3•(-2)/4•9 = 1•(-1)/2•3 = -1/6 = — 1/6;
в) — 4/5 • (- 10/3) = -4/5 • -10/3 = -4•(-10)/5•3 = -4•(-2)/1•3 = 8/3 = 2 2/3;
г) — 1/7 • (- 3/4) = -1/7 • -3/4 = -1•(-3)/7•4 = 3/28;
д) 2/5 • (- 3/4) = 2/5 • -3/4 = 2•(-3)/5•4 = 1•(-3)/5•2 = -3/10 = — 3/10;
е) — 3/8 • 4/5 = -3/8 • 4/5 = -3•4/8•5 = -3•1/2•5 = -3/10 = — 3/10.
105
-
Ответы к стр. 105
Вычислите (530-531):
531. а) — 1/3 • 2; б) 7 • (- 1/2); в) -4 • (- 1/6);
г) 3/4 • (-8); д) 25/28 • (- 14); е) — 12 • (- 13/24).а) — 1/3 • 2 = — 1•2/3 = — 2/3;
б) 7 • (- 1/2) = — 7•1/2 = — 7/2 = -3 1/2;
в) -4 • (- 1/6) = — -4•(-1)/6 = 4/6 = 2/3;
г) 3/4 • (-8) = 3•(-8)/4 = 3•(-2)/1 = -6/1 = -6;
д) 25/28 • (-14) = 25•(-14)/28 = 25•(-1)/2 = -25/2 = -12 1/2;
е) -12 • (- 13/24) = -12•(-13)/24 = 1•13/2 = 6 1/2.
532. Запишите частное в виде дроби с положительным знаменателем, сократите полученную дробь:
а) -2 : 6; б) -5 : 15; в) -10 : (-20); г) -4 : (-16).а) -2 : 6 = -2/6 = -1•2/6 = -1•1/3 = -1/3;
б) -5 : 15 = -5/15 = -1•5/15 = -1•1/3 = -1/3;
в) -10 : (-20) = -10/-20 = -1•10/-1•20 = 10/20 = 1/2;
г) -4 : (-16) = -4/-16 = -1•4/-1•16 = 4/16 = 1/4.
533. Являются ли взаимно обратными числа:
а) -1/2 и — 4/2; б) 2/-3 и 3/2; в) — 1/4 и -4;
г) — 5/6 и 6/-5; д) -2 и -1/2; е) -1 и 1.а) -1/2 = — 1/2, — 4/2 = — 2/1, а — 1/2 и — 2/1 — взаимно обратные числа, следовательно, -1/2 и — 4/2 — взаимно обратные числа;
б) 2/-3 = — 2/3, а — 2/3 и 3/2 — не взаимно обратные числа, следовательно, 2/-3 и 3/2 — не взаимно обратные числа;
в) -4 = — 4/1, а — 1/4 и — 4/1 — взаимно обратные числа, следовательно, — 1/4 и -4 — взаимно обратные числа;
г) 6/-5 = — 6/5, а — 5/6 и — 6/5 — взаимно обратные числа, следовательно, — 5/6 и 6/-5 — взаимно обратные числа;
д) -2 = — 2/1, -1/2 = — 1/2, а — 2/1 и — 1/2 — взаимно обратные числа, следовательно, -2 и -1/2 — взаимно обратные числа;
е) взаимно обратные числа не могут быть разных знаков, следовательно, -1 и 1 — не взаимно обратные числа.
534. Назовите делимое и делитель, найдите дробь, обратную делителю, замените деление умножением на дробь, обратную делителю:
а) 3/5 : 2/3; б) — 4/5 : 3/8; в) -4 : -2/3; г) — 3/7 : (-9).а) 3/5 — делимое, 2/3 — делитель, 3/2 — дробь, обратная делителю,
3/5 : 2/3 = 3/5 • 3/2;б) — 4/5 — делимое, 3/8 — делитель, 8/3 — дробь, обратная делителю,
— 4/5 : 3/8 = — 4/5 • 8/3;в) -4 — делимое, -2/3 — делитель, 3/-2 — дробь, обратная делителю,
-4 : -2/3 = -4 • 3/-2;г) — 3/7 — делимое, -9 — делитель, — 1/9 — дробь, обратная делителю,
— 3/7 : (-9) = — 3/7 • (- 1/9).Вычислите (535-540):
535. а) -3/5 : 5/-9; б) 16/-25 : 8/-15; в) 9/-10 : 1/2; г) 2/3 : 6/-7.
а) -3/5 : 5/-9 = -3/5 • -9/5 = -3•(-9)/5•5 = 27/25 = 1 2/25;
б) 16/-25 : 8/-15 = 16/-25 • -15/8 = -1•16•15/-1•25•8 = 2•3/5•1 = 6/5 = 1 1/5;
в) 9/-10 : 1/2 = 9/-10 • 2/1 = 9•2/-10•1 = — 9•1/5 = — 9/5 = -1 4/5;
г) 2/3 : 6/-7 = 2/3 • -7/6 = 2•(-7)/3•6 = 1•(-7)/3•3 = — 7/9.
536. а) — 3/7 : 5/6; б) 16/-25 : (- 8/15); в) — 9/20 : (- 18/25);
г) 28/63 : (- 9/7); д) — 15/16 : (- 10/24); е) — 15/17 : 25/34.а) — 3/7 : 5/6 = — 3/7 • 6/5 = — 3•6/7•5 = — 18/35;
б) 16/-25 : (- 8/15) = 16/-25 • (- 15/8) = 16•15/25•8 = 2•3/5•1 = 6/5 = 1 1/5;
в) — 9/20 : (- 18/25) = — 9/20 • (- 25/18) = 9•25/20•18 = 1•5/4•2 = 5/8;
г) 28/63 : (- 9/7) = 28/63 • (- 7/9) = — 28•7/63•9 = — 28•1/9•9 = — 28/81;
д) — 15/16 : (- 10/24) = — 15/16 • (- 24/10) = 15•24/16•10 = 3•3/2•2 = 9/4 = 2 1/4;
е) — 15/17 : 25/34 = — 15/17 • 34/25 = — 15•34/17•25 = — 3•2/1•5 = — 6/5 = -1 1/5.
537. а) 32/75 : (- 48/25); б) — 38/75 : (- 19/100); в) — 32/77 : (- 64/55);
г) — 125/196 : 50/52; д) 228/245 : (- 57/125); е) — 132/1000 : (- 143/1000).а) 32/75 : (- 48/25) = 32/75 • (- 25/48) = — 32•25/75•48 = — 4•1/3•6 = — 2•1/3•3 = — 2/9;
б) — 38/75 : (- 19/100) = — 38/75 • (- 100/19) = 38•100/75•19 = 2•4/3•1 = 8/3 = 2 2/3;
в) — 32/77 : (- 64/55) = — 32/77 • (- 55/64) = 32•55/77•64 = 1•5/7•2 = 5/14;
г) — 125/196 : 50/52 = — 125/196 • 52/50 = — 125•52/196•50 = — 5•13/49•2 = — 65/98;
д) 228/245 : (- 57/125) = 228/245 • (- 125/57) = — 228•125/245•57 = — 4•25/49•1 = — 100/49 = -2 2/49;
е) — 132/1000 : (- 143/1000) = — 132/1000 • (- 1000/143) = 132•1000/1000•143 = 12•1/1•13 = 12/13.
538. а) — 1/2 : 2; б) — 1/3 : 2; в) — 2/5 : (-3); г) 3/7 : (-9);
д) -4 : 1/2; е) (-3) : (- 1/2); ж) 5 : (- 3/10); з) -8 : 4/5.а) — 1/2 : 2 = — 1/2 • 1/2 = — 1•1/2•2 = — 1/4;
б) — 1/3 : 2 = — 1/3 • 1/2 = — 1•1/3•2 = — 1/6;
в) — 2/5 : (-3) = — 2/5 • (- 1/3) = 2•1/5•3 = 2/15;
г) 3/7 : (-9) = 3/7 • (- 1/9) = — 3•1/7•9 = — 1•1/7•3 = — 1/21;
д) — 4 : 1/2 = -4 • 2/1 = -4 • 2 = -8;
е) (-3) : (- 1/2) = -3 • (- 2/1) = -3 • (-2) = 6;
ж) 5 : (- 3/10) = 5 • (- 10/3) = — 5•10/3 = — 50/3 = -16 2/3;
з) -8 : 4/5 = -8 • 5/4 = — 8•5/4 = — 2•5/1 = -10.
539. а) 48 : (- 1/2); б) -55 : (- 2/5); в) -72 : 36/37;
г) (- 16/35) : 64; д) — 12/13 : 24; е) 15/32 : (-20).а) 48 : (- 1/2) = 48 • (- 2/1) = 48 • (-2) = -96;
б) -55 : (- 2/5) = -55 • (- 5/2) = 55•5/2 = 275/2 = 137 1/2;
в) -72 : 36/37 = -72 • 37/36 = — 72•37/36 = — 2•37/1 = -74;
г) (- 16/35) : 64 = — 16/35 • 1/64 = — 16•1/35•64 = — 1•1/35•4 = — 1/140;
д) — 12/13 : 24 = — 12/13 • 1/24 = — 12•1/13•24 = — 1•1/13•2 = — 1/26;
е) 15/32 : (-20) = 15/32 • (- 1/20) = — 15•1/32•20 = — 3•1/32•4 = — 3/128.
106
-
Ответы к стр. 106
Вычислите (535-540):
540. а) — 3/5 • (- 2/5); б) 2/3 • (- 5/7); в) — 3/7 : (- 4/5); г) 3/5 : (- 2/3);
д) — 15/16 • (- 48/25); е) — 5/3 : 25/27; ж) — 3/4 • (- 4/5); з) — 2/3 : (- 4/5).а) — 3/5 • (- 2/5) = 3•2/5•5 = 6/25;
б) 2/3 • (- 5/7) = — 2•5/3•7 = — 10/21;
в) — 3/7 : (- 4/5) = — 3/7 • (- 5/4) = 3•5/7•4 = 15/28;
г) 3/5 : (- 2/3) = 3/5 • (- 3/2) = — 3•3/5•2 = — 9/10;
д) — 15/16 • (- 48/25) = 15•48/16•25 = 3•3/1•5 = 9/5 = 1 4/5;
е) — 5/3 : 25/27 = — 5/3 • 27/25 = — 5•27/3•25 = — 1•9/1•5 = — 9/5 = -1 4/5;
ж) — 3/4 • (- 4/5) = 3•4/4•5 = 3•1/1•5 = 3/5;
з) — 2/3 : (- 4/5) = — 2/3 • (- 5/4) = 2•5/3•4 = 1•5/3•2 = 5/6.
541. Найдите число х, для которого верно равенство:
а) х • 3/5 = — 4/15; б) — 2/3 • х = 4/7; в) х : 1/2 = — 1/4; г) 2/7 : х = — 22/21.а) х = — 4/15 : 3/5 = — 4/15 • 5/3 = — 4•5/15•3 = — 4•1/3•3 = — 4/9;
б) х = 4/7 : (- 2/3) = 4/7 • (- 3/2) = — 4•3/7•2 = — 2•3/7•1 = — 6/7;
в) х = — 1/4 • 1/2 = — 1•1/4•2 = — 1/8;
г) х = 2/7 : (- 22/21) = 2/7 • (- 21/22) = — 2•21/7•22 = — 1•3/1•11 = — 3/11.
542. Вычислите:
а) (-2/3)3; б) (3/-4)2; в) (1/-10)3; г) (-5/6)2; д) (- 6/7)2;
е) (- 3/4)3; ж) (- 3/10)4; з) (- 1/2)5; и) (- 1/3)3.а) (-2/3)3 = -2•(-2)•(-2)/3•3•3 = — 8/27;
б) (3/-4)2 = 3•3/-4•(-4) = 9/16;
в) (1/-10)3 = 1•1•1/-10•(-10)•(-10) = — 1/1000;
г) (-5/6)2 = -5•(-5)/6•6 = 25/36;
д) (- 6/7)2 = 6•6/7•7 = 36/49;
е) (- 3/4)3 = — 3•3•3/4•4•4 = — 27/64;
ж) (- 3/10)4 = 3•3•3•3/10•10•10•10 = 81/10000;
з) (- 1/2)5 = — 1•1•1•1•1/2•2•2•2•2 = — 1/32;
и) (- 1/3)3 = — 1•1•1/3•3•3 = — 1/27.
543. Положительным или отрицательным числом является степень отрицательной дроби:
а) с чётным показателем; б) с нечётным показателем?а) положительным;
б) отрицательным.Определите порядок действий, вычислите (544-546):
544. а) (- 1/2)2 — 1/2; б) 1/3 — (- 1/3)2; в) (- 1/3)3 — 1/9; г) 1/2 — (- 1/2)3.
а) (- 1/2)2 — 1/2 = — 1/4;
1) (- 1/2)2 = (-1/2)2 = -1•(-1)/2•2 = 1/4,
2) 1/4 — 1/2 = 1/4 — 2/4 = 1-2/4 = -1/4 = — 1/4,
б) 1/3 — (- 1/3)2 = 2/9;
1) (- 1/3)2 = (-1/3)2 = -1•(-1)/3•3 = 1/9,
2) 1/3 — 1/9 = 3/9 — 1/9 = 3-1/9 = 2/9,
в) (- 1/3)3 — 1/9 = — 4/27;
1) (- 1/3)3 = (-1/3)3 = -1•(-1)•(-1)/3•3•3 = -1/27,
2) -1/27 — 1/9 = -1/27 — 3/27 = -1-3/27 = -4/27 = — 4/27,
г) 1/2 — (- 1/2)3 = 5/8.
1) (- 1/2)3 = (-1/2)3 = -1•(-1)•(-1)/2•2•2 = -1/8,
2) 1/2 — -1/8 = 4/8 — -1/8 = 4-(-1)/8 = 5/8.
545. а) 1/2 • (- 2/3) + (- 1/2)2; б) — 3/4 • 12/7 — (- 1/7)2;
в) — 1/3 • 6/5 — 5/6 • 3/25; г) 3/10 • (- 5/6) + 2/3 • (- 3/8).а) 1/2 • (- 2/3) + (- 1/2)2 = — 1/12;
1) (- 1/2)2 = (-1/2)2 = -1•(-1)/2•2 = 1/4,
2) 1/2 • (- 2/3) = — 1•2/2•3 = — 1•1/1•3 = — 1/3,
3) — 1/3 + 1/4 = -4/12 + 3/12 = -4+3/12 = -1/12 = — 1/12,
б) — 3/4 • 12/7 — (- 1/7)2 = — 1 15/49;
1) (- 1/7)2 = (-1/7)2 = -1•(-1)/7•7 = 1/49,
2) — 3/4 • 12/7 = — 3•12/4•7 = — 3•3/1•7 = — 9/7,
3) — 9/7 — 1/49 = -63/49 — 1/49 = -63-1/49 = -64/49 = — 1 15/49,
в) — 1/3 • 6/5 — 5/6 • 3/25 = — 1/2;
1) — 1/3 • 6/5 = — 1•6/3•5 = — 1•2/1•5 = — 2/5,
2) 5/6 • 3/25 = 5•3/6•25 = 1•1/2•5 = 1/10,
3) — 2/5 — 1/10 = — 4/10 — 1/10 = -4-1/10 = -5/10 = — 1/2,
г) 3/10 • (- 5/6) + 2/3 • (- 3/8) = — 1/2.
1) 3/10 • (- 5/6) = — 3•5/10•6 = — 1•1/2•2 = — 1/4,
2) 2/3 • (- 3/8) = — 2•3/3•8 = — 1•1/1•4 = — 1/4,
3) — 1/4 + (- 1/4) = —1/4 + —1/4 = -1+(-1)/4 = -2/4 = — 1/2.
546. а) — 5/9 • (- 18/25) — 14/27 • (- 18/35); б) — 27/20 • (- 5/9) — 5/24 • (- 22/5);
в) 21/20 • (- 8/21) + 7/72 • (- 36/5); г) — 36/60 • (- 5/18) — (- 21/56) • (- 1/3).а) — 5/9 • (- 18/25) — 14/27 • (- 18/35) = 2/3;
1) — 5/9 • (- 18/25) = 5•18/9•25 = 1•2/1•5 = 2/5,
2) 14/27 • (- 18/35) = — 14•18/27•35 = — 2•2/3•5 = — 4/15,
3) 2/5 — (- 4/15) = 6/15 + 4/15 = 6+4/15 = 10/15 = 2/3,
б) — 27/20 • (- 5/9) — 5/24 • (- 22/5) = 1 2/3;
1) — 27/20 • (- 5/9) = 27•5/20•9 = 3•1/4•1 = 3/4,
2) 5/24 • (- 22/5) = — 5•22/24•5 = — 1•11/12•1 = — 11/12,
3) 3/4 — (- 11/12) = 9/12 + 11/12 = 9+11/12 = 20/12 = 5/3 = 1 2/3,
в) 21/20 • (- 8/21) + 7/72 • (- 36/5) = — 1 1/10;
1) 21/20 • (- 8/21) = — 21•8/20•21 = — 1•2/5•1 = — 2/5,
2) 7/72 • (- 36/5) = — 7•36/72•5 = — 7•1/2•5 = — 7/10,
3) — 2/5 + (- 7/10) = -4/10 + -7/10 = -4+(-7)/10 = -11/10 = — 1 1/10,
г) — 36/60 • (- 5/18) — (- 21/56) • (- 1/3) = 1/24.
1) — 36/60 • (- 5/18) = 36•5/60•18 = 2•1/12•1 = 2/12 = 1/6,
2) (- 21/56) • (- 1/3) = 21•1/56•3 = 7•1/56•1 = 1•1/8•1 = 1/8,
3) 1/6 — 1/8 = 4/24 — 3/24 = 4-3/24 = 1/24.
107
-
Рациональные числа
Законы сложения и умноженияОтветы к стр. 107
547. Для рациональных чисел α, b, и c запишите и сформулируйте:
а) переместительный закон сложения;
б) сочетательный закон сложения;
в) переместительный закон умножения;
г) сочетательный закон умножения;
д) распределительный закон.а) от перестановки слагаемых сумма не меняется: α + b = b + α;
б) для того, чтобы к сумме двух чисел α и b прибавить третье число с, можно к числу α прибавить сумму чисел b и c: (α + b) + c = α + (b + с);
в) от перестановки множителей произведение не меняется: α • b = b • α;
г) для того чтобы произведение двух чисел α и b умножить на число c, можно число α умножить на произведение чисел b и c: (α • b) • c = α • (b • c);
д) для того чтобы сумму двух чисел α и b умножить на третье число с можно каждое из слагаемых α и b умножить на число с и полученные результаты сложить: (α + b) • c = α • c + b • с.
Вычислите, применяя законы сложения и умножения (548-550):
548. а) 80 • 359 • (-125); б) 457 + 985 — 57;
в) 45 • (-39) + 55 • (-39); г) 76 • 45 — 26 • 45;
д) 157 • (-13) — 17 • (-13); е) (-124) • 35 + 24 • 35.а) 80 • 359 • (-125) = 359 • (80 • (-125)) = 359 • (-10 000) = -3 590 000;
б) 457 + 985 — 57 = (457 — 57) + 985 = 400 + 985 = 1385;
в) 45 • (-39) + 55 • (-39) = -39 • (45 + 55) = -39 • 100 = -3900;
г) 76 • 45 — 26 • 45 = 45 • (76 — 26) = 45 • 50 = 2250;
д) 157 • (-13) — 17 • (-13) = -13 • (157 − 17) = -13 • 140 = -1820;
е) (-124) • 35 + 24 • 35 = 35 • (-124 + 24) = 35 • (-100) = -3500.549. а) 4/15 + 5/36 + 11/15 + 31/36; б) 7/25 + 32/33 — 7/25;
в) 39/40 • 124/125 : 124/125; г) 4/35 • 17/18 + 17/18 • 31/35;
д) 45/46 • 49/51 — 45/46 • 3/51; е) 72/73 • 34/65 + 72/73 • 39/65.а) 4/15 + 5/36 + 11/15 + 31/36 = (4/15 + 11/15) + (5/36 + 31/36) = 15/15 + 36/36 = 1 + 1 = 2;
б) 7/25 + 32/33 — 7/25 = (7/25 — 7/25) + 32/33 = 0 + 32/33 = 32/33;
в) 39/40 • 124/125 : 124/125 = 39/40 • 124/125 • 125/124 = 39/40 • (124/125 • 125/124) = 39/40 • 1 = 39/40;
г) 4/35 • 17/18 + 17/18 • 31/35 = 17/18 • (4/35 + 31/35) = 17/18 • 35/35 = 17/18 • 1 = 17/18;
д) 45/46 • 49/51 — 45/46 • 3/51 = 45/46 • (49/51 — 3/51) = 45/46 • 46/51 = 45•46/46•51 = 15•1/1•17 = 15/17;
е) 72/73 • 34/65 + 72/73 • 39/65 = 72/73 • (34/65 + 39/65) = 72/73 • 73/65 = 72•73/73•65 = 72•1/1•65 = 72/65 = 1 7/65.
108
-
Рациональные числа
Законы сложения и умноженияОтветы к стр. 108
Вычислите, применяя законы сложения и умножения (548-550):
550. а) 23•35+38•35/17•61+18•61; б) 49•99+28•99/12•154+21•154;
в) 75•27+75•37/37•48-12•48; г) 679•846+679•54/679•846-679•46.а) 23•35+38•35/17•61+18•61 = 35•(23+38)/61•(17+18) = 35•61/61•35 = 1•1/1•1 = 1;
б) 49•99+28•99/12•154+21•154 = 99•(49+28)/154•(12+21) = 99•77/154•33 = 3•1/2•1 = 3/2 = 1 1/2;
в) 75•27+75•37/37•48-12•48 = 75•(27+37)/48•(37-12) = 75•64/48•25 = 3•8/6•1 = 24/6 = 4;
г) 679•846+679•54/679•846-679•46 = 679•(846+54)/679•(846-46) = 679•900/679•800 = 1•9/1•8 = 9/8 = 1 1/8.
Вычислите (551-555):
551. а) — 7/25 — 11/25 — 2/25; б) — 1/72 — 7/72 — 18/72;
в) — 19/55 — 18/55 + 4/55; г) 25/64 — 17/64 — 15/64.а) — 7/25 — 11/25 — 2/25 = -7-11-2/25 = -20/25 = — 4/5;
б) — 1/72 — 7/72 — 18/72 = -1-7-18/72 = -26/72 = — 13/36;
в) — 19/55 — 18/55 + 4/55 = -19-18+4/55 = -33/55 = — 3/5;
г) 25/64 — 17/64 — 15/64 = 25-17-15/64 = -7/64 = — 7/64.
552. а) — 1/5 + 6/25 — 8/25; б) — 1/7 + 2/21 — 3/7;
в) — 8/49 — 5/7 — 9/49; г) 7/10 — 4/15 — 11/30.а) — 1/5 + 6/25 — 8/25 = — 5/25 + 6/25 — 8/25 = -5+6-8/25 = -7/25 = — 7/25;
б) — 1/7 + 2/21 — 3/7 = — 3/21 + 2/21 — 9/21 = -3+2-9/21 = -10/21 = — 10/21;
в) — 8/49 — 5/7 — 9/49 = — 8/49 — 35/49 — 9/49 = -8-35-9/49 = -52/49 = -1 3/49;
г) 7/10 — 4/15 — 11/30 = 21/30 — 8/30 — 11/30 = 21-8-11/30 = 2/30 = 1/15.
553. а) — 33/80 + (3/16 — 39/80); б) 2/45 + (- 3/45 + 7/9); в) 7/15 — (4/15 — 1/5);
г) — 5/16 — (1/16 — 7/8); д) — 1/27 + (7/9 — 2/3); е) (- 2/15 — 4/5) + 3/10;
ж) (- 2/15 + 4/5) — 3/10; з) -(5/8 — 5/12) + 1/24.а) — 33/80 + (3/16 — 39/80) = — 33/80 + 15/80 — 39/80 = -33+15-39/80 = — 57/80;
б) 2/45 + (- 3/45 + 7/9) = 2/45 — 3/45 + 35/45 = 2-3+35/45 = 34/45;
в) 7/15 — (4/15 — 1/5) = 7/15 — 4/15 + 3/15 = 7-4+3/15 = 6/15 = 2/5;
г) — 5/16 — (1/16 — 7/8) = — 5/16 — 1/16 + 14/16 = -5-1+14/16 = 8/16 = 1/2;
д) — 1/27 + (7/9 — 2/3) = — 1/27 + 21/27 — 18/27 = -1+21-18/27 = 2/27;
е) (- 2/15 — 4/5) + 3/10 = — 4/30 — 24/30 + 9/30 = -4-24+9/30 = — 19/30;
ж) (- 2/15 + 4/5) — 3/10 = — 4/30 + 24/30 — 9/30 = -4+24-9/30 = 11/30;
з) -(5/8 — 5/12) + 1/24 = — 15/24 + 10/24 + 1/24 = -15+10+1/24 = — 4/24 = — 1/6.
554. а) 3/8 — 2/7 + 5/8 — 5/7; б) 11/14 — 7/10 — 21/100 — 13/14;
в) — 12/19 — 15/26 + 3/19 + 9/19; г) 2/7 — 5/9 — 4/9 — 4/7.а) 3/8 — 2/7 + 5/8 — 5/7 = (3/8 + 5/8) — (2/7 + 5/7) = 8/8 — 7/7 = 1 — 1 = 0;
б) 11/14 — 7/10 — 21/100 — 13/14 = (11/14 — 13/14) — (7/10 + 21/100) = — 2/14 — (70/100 + 21/100) = — 1/7 — 91/100 = —100-637/700 = — 737/700 = -1 37/700;
в) — 12/19 — 15/26 + 3/19 + 9/19 = (- 12/19 + 3/19 + 9/19) — 15/26 = 0 — 15/26 = — 15/26;
г) 2/7 — 5/9 — 4/9 — 4/7 = (2/7 — 4/7) — (5/9 + 4/9) = — 2/7 — 9/9 = — 2/7 — 1 = — 1 2/7.
555. а) 2 • (1/4 — 1/2); б) (1/9 — 1/3) • (-3); в) 1/2 • (2/3 — 2/5); г) — 1/3 • (3/4 — 3/5).
а) 2 • (1/4 — 1/2) = 2 • (1/4 — 2/4) = 2 • (- 1/4) = — 2/4 = — 1/2;
б) (1/9 — 1/3) • (-3) = (1/9 — 3/9) • (-3) = — 2/9 • (-3) = 6/9 = 2/3;
в) 1/2 • (2/3 — 2/5) = 1/2 • (10/15 — 6/15) = 1/2 • 4/15 = 1•4/2•15 = 1•2/1•15 = 2/15;
г) — 1/3 • (3/4 — 3/5) = — 1/3 • (15/20 — 12/20) = — 1/3 • 3/20 = — 1•3/3•20 = — 1•1/1•20 = — 1/20.
556. Определите знак произведения:
а) (-1) • (- 2/3) • (- 7/13); б) (- 1/3) • 1/2 • (-1) • (-7/-9);
в) (- -8/9) • (- 5/-9) • (- 1/5); г) (- -1/-5) • (- 1/4) • 1/5 • (-8/7).а) (-1) • (- 2/3) • (- 7/13) = — 1•2•7/3•13 — нечётное число знаков «-» в выражении;
б) (- 1/3) • 1/2 • (-1) • (-7/-9) = 1•1•1•7/3•2•9 — чётное число знаков «-» в выражении;
в) (- -8/9) • (- 5/-9) • (- 1/5) = — 8•5•1/9•9•5 — нечётное число знаков «-» в выражении;
г) (- -1/-5) • (- 1/4) • 1/5 • (-8/7) = — 1•1•1•8/5•4•5•7 — нечётное число знаков «-» в выражении.
557. Вычислите:
а) (- 2/3) • (- 1/2) • 3/4; б) (- 4/5) • (- 3/4) • (- 1/2).а) (- 2/3) • (- 1/2) • 3/4 = 2•1•3/3•2•4 = 1•1•1/1•1•4 = 1/4;
б) (- 4/5) • (- 3/4) • (- 1/2) = — 4•3•1/5•4•2 = — 1•3•1/5•1•2 = — 3/10.
558. Сколько отрицательных множителей может содержать произведение, чтобы оно было: а) положительным; б) отрицательным?
а) чётное количество отрицательных множителей;
б) нечётное количество отрицательных множителей. 109
-
Ответы к стр. 109
559. а) Произведение пяти множителей — положительное число. Можно ли утверждать, что все множители — положительные числа?
б) Произведение четырёх множителей — положительное число. Можно ли утверждать, что все множители — положительные числа?а) Произведение положительных чисел есть число положительное, но кроме пяти положительных множителей есть следующие варианты для получения в произведении положительного числа: два множителя — отрицательные числа, три множителя — положительные числа; четыре множителя — отрицательные числа, один множитель — положительное число.
б) Произведение положительных чисел есть число положительное, но кроме четырёх положительных множителей есть следующие варианты для получения в произведении положительного числа: два множителя — отрицательные числа, два множителя — положительные числа; четыре множителя — отрицательные числа.Доказываем
560. Сформулируйте и докажите свойства деления рациональных чисел, которые выражаются следующими равенствами:
а) α : b = (α • n) : (b • n); б) α : b = (α : n) : (b : n);
в) (α + b) : n = α : n + b : n, где b ≠ 0 и n ≠ 0.а) если делимое и делитель умножить на одно и то же число, то частное не изменится: α : b = (α • n) : (b • n) = α•n/b•n = α•1/b•1 = α/b = α : b;
б) если делимое и делитель разделить на одно и то же число, то частное не изменится: α : b = (α : n) : (b : n) = α/n : b/n = α/n • n/b = α•n/n•b = α•1/1•b = α/b = α : b;
в) для того, чтобы сумму разделить на какое-либо число, можно каждое слагаемое разделить на это число и полученные результаты сложить: (α + b) : n = α : n + b : n = α/n + b/n = α+b/n = (α + b) : n.
Вычислите (561-563):
561. а) — 3/4 : 5/6 + 15/16 • 2/5 — 1 : 1/9; б) 2 : (- 3/5) + 3/5 : 2 — 3/2 : 6 + 6 : 3/2;
в) 11/4 : (2/5 — 3/2) + (3/4 + 5/6) : (- 25/8); г) (2/15 + 19/12) • 30/103 — (1 : 9/4) • (- 9/16).а) — 3/4 : 5/6 + 15/16 • 2/5 — 1 : 1/9 = — 3/4 • 6/5 + 15•2/16•5 — 1 • 9/1 = — 3•6/4•5 + 3•1/8•1 — 9 = — 3•3/2•5 + 3/8 — 9 = — 9/10 + 3/8 — 9 = — 36/40 + 15/40 — 9 = — 21/40 — 9 = -9 21/40;
б) 2 : (- 3/5) + 3/5 : 2 — 3/2 : 6 + 6 : 3/2 = 2 • (- 5/3) + 3/5 • 1/2 — 3/2 • 1/6 + 6 • 2/3 = — 10/3 + 3/10 — 3/12 + 12/3 = — 200/60 + 18/60 — 15/60 + 4 = — 197/60 + 4 = -3 17/60 + 4 = 43/60;
в) 11/4 : (2/5 — 3/2) + (3/4 + 5/6) : (- 25/8) = 11/4 : (4/10 — 15/10) + (9/12 + 10/12) • (- 8/25) = 11/4 : (- 11/10) + 19/12 • (- 8/25) = 11/4 • (- 10/11) — 19•8/12•25 = — 11•10/4•11 — 19•2/3•25 = — 1•5/2•1 — 38/75 = — 375/150 — 76/150 = — 451/150 = -3 1/150;
г) (2/15 + 19/12) • 30/103 — (1 : 9/4) • (- 9/16) = (8/60 + 95/60) • 30/103 — (1 • 4/9) • (- 9/16) = 103/60 • 30/103 — 4/9 • (- 9/16) = 103•30/60•103 + 4•9/9•16 = 1•1/2•1 + 1•1/1•4 = 1/2 + 1/4 = 2/4 + 1/4 = 3/4.
562. а) 8/9 • 7/24 — 8/9 • 5/24; б) 3/25 • (- 5/49) + 22/25 • (- 5/49).
а) 8/9 • 7/24 — 8/9 • 5/24 = 8/9 • (7/24 — 5/24) = 8/9 • 2/24 = 8/9 • 1/12 = 2•1/9•3 = 2/27;
б) 3/25 • (- 5/49) + 22/25 • (- 5/49) = — 5/49 • (3/25 + 22/25) = — 5/49 • 25/25 = — 5/49.
563. а) — 1/2 • (- 2/3) • (- 3/4) • (- 4/5); б) — 10/11 • (- 11/12) • (- 12/13) • (- 13/14) • (- 14/15).
а) — 1/2 • (- 2/3) • (- 3/4) • (- 4/5) = 1•2•3•4/2•3•4•5 = 1/5;
б) — 10/11 • (- 11/12) • (- 12/13) • (- 13/14) • (- 14/15) = — 10•11•12•13•14/11•12•13•14•15 = — 10/15 = — 2/3.
110
-
Рациональные числа
Смешанные дроби произвольного знакаОтветы к стр. 110
564. Представьте отрицательную неправильную дробь в виде отрицательной смешанной дроби:
а) — 4/3; б) — 13/5; в) — 41/15; г) — 45/16.а) — 4/3 = -1 1/3;
б) — 13/5 = -2 3/5;
в) — 41/15 = -2 11/15;
г) — 45/16 = -2 13/16.
565. Запишите частное в виде обыкновенной или смешанной дроби:
а) -17 : (-18); б) 13 : (-25); в) -19 : (-5); г) 29 : (-15).а) -17 : (-18) = 17/18;
б) 13 : (-25) = — 13/25;
в) -19 : (-5) = 19/5 = 3 4/5;
г) 29 : (-15) = — 29/15 = -1 14/15.
566. Сравните числа:
а) — 1/2 и -1 1/2; б) — 3/2 и -1 1/4;
в) -1 1/5 и -1 1/6; г) — 12/11 и -1 1/13.а) — 1/2 > -1 1/2, так как — 1 1/2 = — 3/2, а — 1/2 > — 3/2;
б) — 3/2 < -1 1/4, так как — 3/2 = — 6/4, -1 1/4 = — 5/4, а — 6/4 < — 5/4;
в) -1 1/5 < -1 1/6, так как -1 1/5 = — 6/5 = — 36/30, -1 1/6 = — 7/6 = — 35/30, а — 36/30 < — 35/30;
г) — 12/11 < -1 1/13, так как — 12/11 = — 156/143, -1 1/13 = — 14/13 = — 154/143, а — 156/143 < — 154/143.
111
-
Рациональные числа
Смешанные дроби произвольного знакаОтветы к стр. 111
Вычислите (567-571):
567. а) -3 2/5 + (-1 1/5); б) -7 1/3 + (-1 2/3); в) -12 5/7 + (-4 4/7);
г) -3 8/19 + (-1 11/19); д) -4 2/3 + (-1 1/3); е) (-8 2/3) + (-9 2/3).а) -3 2/5 + (-1 1/5) = -(3 2/5 + 1 1/5) = -(4 + 3/5) = -4 3/5;
б) -7 1/3 + (-1 2/3) = -(7 1/3 + 1 2/3) = -(8 + 3/3) = -(8 + 1) = -9;
в) -12 5/7 + (-4 4/7) = -(12 5/7 + 4 4/7) = -(16 + 9/7) = -(16 + 1 2/7) = -17 2/7;
г) -3 8/19 + (-1 11/19) = -(3 8/19 + 1 11/19) = -(4 + 19/19) = -(4 + 1) = -5;
д) -4 2/3 + (-1 1/3) = -(4 2/3 + 1 1/3) = -(5 + 3/3) = -(5 + 1) = -6;
е) (-8 2/3) + (-9 2/3) = -(8 2/3 + 9 2/3) = -(17 + 4/3) = -(17 + 1 1/3) = — 18 1/3.
568. а) 18 5/9 + (-22 2/9); б) 25 3/4 + (-51 1/4); в) -6 2/9 + 1 2/3;
г) 7 1/12 + (-8 3/4); д) 18 5/6 + (-7 1/2); е) 2 1/5 + (- 4/15).а) 18 5/9 + (-22 2/9) = 18 5/9 — 22 2/9 = -(22 2/9 — 18 5/9) = -(4 2/9 — 5/9) = -(3 + 11/9 — 5/9) = -(3 + 6/9) = -3 2/3;
б) 25 3/4 + (-51 1/4) = 25 3/4 — 51 1/4 = -(51 1/4 — 25 3/4) = -(26 1/4 — 3/4) = -(25 + 5/4 — 3/4) = -(25 + 2/4) = -25 1/2;
в) -6 2/9 + 1 2/3 = -(6 2/9 — 1 2/3) = -(6 2/9 — 1 2/3) = -(5 2/9 — 2/3) = -(4 + 11/9 — 6/9) = -(4 + 5/9) = — 4 5/9;
г) 7 1/12 + (-8 3/4) = 7 1/12 — 8 3/4 = -(8 3/4 — 7 1/12) = -(1 3/4 — 1/12) = -(1 + 9/12 — 1/12) = — (1 + 8/12) = -1 2/3;
д) 18 5/6 + (-7 1/2) = 18 5/6 — 7 1/2 = 11 5/6 — 1/2 = 11 + 5/6 — 3/6 = 11 + 2/6 = 11 1/3;
е) 2 1/5 + (- 4/15) = 2 1/5 — 4/15 = 1 + 6/5 — 4/15 = 1 + 18/15 — 4/15 = 1 + 14/15 = 1 14/15.
569. а) -3 — 2 1/5; б) -8 + 2/13; в) -7 1/3 — 4; г) 4/17 — 15.
а) -3 — 2 1/5 = -(3 + 2 1/5) = -5 1/5;
б) -8 + 2/13 = -(8 — 2/13) = -(7 + 13/13 — 2/13) = -(7 + 11/13) = -7 11/13;
в) -7 1/3 — 4 = -(7 1/3 + 4) = -11 1/3;
г) 4/17 — 15 = -(15 — 4/17) = -(14 + 17/17 — 4/17) = -(14 + 13/17) = -14 13/17.
570. а) 1 1/3 — 3 2/3; б) 7 2/5 — (-1 1/5); в) -6 3/7 + 1 2/7;
г) 7 2/9 — 9 8/9; д) 4 1/2 — 8 1/3; е) 6 9/10 — 12 1/100;
ж) -4 2/5 — 1 1/2; з) -5 1/3 — 8 2/9; и) -2 1/5 — 14 1/10.а) 1 1/3 — 3 2/3 = -(3 2/3 — 1 1/3) = -(2 2/3 — 1/3) = -2 1/3;
б) 7 2/5 — (-1 1/5) = 7 2/5 + 1 1/5 = 8 + 3/5 = 8 3/5;
в) -6 3/7 + 1 2/7 = -(6 3/7 — 1 2/7) = -(5 3/7 — 2/7) = -(5 + 3/7 — 2/7) = -(5 + 1/7) = -5 1/7;
г) 7 2/9 — 9 8/9 = -(9 8/9 — 7 2/9) = -(2 8/9 — 2/9) = -(2 + 8/9 — 2/9) = -(2 + 6/9) = -2 2/3;
д) 4 1/2 — 8 1/3 = -(8 1/3 — 4 1/2) = -(4 1/3 — 1/2) = -(3 + 4/3 — 1/2) = -(3 + 8/6 — 3/6) = -(3 + 5/6) = -3 5/6;
е) 6 9/10 — 12 1/100 = -(12 1/100 — 6 9/10) = -(6 1/100 — 9/10) = -(5 + 101/100 — 90/100) = -(5 + 11/100) = -5 11/100;
ж) -4 2/5 — 1 1/2 = -(4 2/5 + 1 1/2) = -(5 + 2/5 + 1/2) = -(5 + 4/10 + 5/10) = -(5 + 9/10) = -5 9/10;
з) -5 1/3 — 8 2/9 = -(5 1/3 + 8 2/9) = -(13 + 1/3 + 2/9) = -(13 + 3/9 + 2/9) = -(13 + 5/9) = -13 5/9;
и) -2 1/5 — 14 1/10 = -(2 1/5 + 14 1/10) = -(16 + 1/5 + 1/10) = -(16 + 2/10 + 1/10) = -(16 + 3/10) = -16 3/10.
571. а) 1/2 — 1/3 + 1/7 — 2 1/3; б) 7/9 — 2/3 — 3 1/6 — 1.
а) 1/2 — 1/3 + 1/7 — 2 1/3 = 1/2 + 1/7 — 1/3 — 2 1/3 = (7/14 + 2/14) — (1/3 + 7/3) = 9/14 — 8/3 = -(8/3 — 9/14) = -(112/42 — 27/42) = — 85/42 = -2 1/42;
б) 7/9 — 2/3 — 3 1/6 — 1 = (7/9 — 2/3) — (3 1/6 + 1) = (7/9 — 6/9) — (19/6 + 6/6) = 1/9 — 25/6 = -(25/6 — 1/9) = -(75/18 — 2/18) = — 73/18 = -4 1/18.
572. Вычислите по образцу:
а) -4 1/2 + 5 3/7 + 4/7 = -4 1/2 + (5 3/7 + 4/7) = -4 1/2 + 6 = 6 — 4 1/2 = 1 1/2;
б) -1 1/3 + 8 1/2 + 1/3; в) 3 2/5 — 7 1/2 + 2 3/5;
г) -5/9 + 2 1/3 + 1 2/3; д) 7/15 — 2 — 1/5.б) -1 1/3 + 8 1/2 + 1/3 = (-1 1/3 + 1/3) + 8 1/2 = -1 + 8 1/2 = 8 1/2 — 1 = 7 1/2;
в) 3 2/5 — 7 1/2 + 2 3/5 = (3 2/5 + 2 3/5) — 7 1/2 = 6 — 7 1/2 = -(7 1/2 — 6) = -1 1/2;
г) -5/9 + 2 1/3 + 1 2/3 = — 5/9 + (2 1/3 + 1 2/3) = — 5/9 + 4 = 4 — 5/9 = 3 4/9;
д) 7/15 — 2 — 1/5 = (7/15 — 1/5) — 2 = (7/15 — 3/15) — 2 = 4/15 — 2 = -(2 — 4/15) = -1 11/15.
573. Упростите выражение, раскрывая скобки по образцу:
а) 7 1/2 + (3 2/3 — 2 1/2) = 7 1/2 + 3 2/3 — 2 1/2 = 5 + 3 2/3 = 8 2/3;
б) 8 3/5 — (7 1/3 — 11 2/5) = 8 3/5 — 7 1/3 + 11 2/5 = 20 — 7 1/3 = 12 2/3;
в) 5/12 + (1 1/2 — 5/12); г) 2 — (2/5 — 7 1/2);
д) 4 2/7 — (7 1/2 + 4 2/7); е) 9 7/9 — (2 1/2 — 2/9).в) 5/12 + (1 1/2 — 5/12) = 5/12 + 1 1/2 — 5/12 = 0 + 1 1/2 = 1 1/2;
г) 2 — (2/5 — 7 1/2) = 2 — 2/5 + 7 1/2 = 9 1/2 — 2/5 = 9 5/10 — 4/10 = 9 1/10;
д) 4 2/7 — (7 1/2 + 4 2/7) = 4 2/7 — 7 1/2 — 4 2/7 = 0 — 7 1/2 = -7 1/2;
е) 9 7/9 — (2 1/2 — 2/9) = 9 7/9 — 2 1/2 + 2/9 = 10 — 2 1/2 = 7 1/2.
112
-
Ответы к стр. 112
Вычислите (574-577)
574. Вычислите
а) $2\frac12\ast\frac2{-75}=-\frac52\ast\frac2{75}=-\frac{1\ast1}{1\ast15}=-\frac1{15}$
б) $1\frac13\ast\frac{-9}{16}=-\frac43\ast\frac9{16}=-\frac{1\ast3}{1\ast4}=-\frac34$
в) $3\frac13\ast\frac{-7}{-100}=\frac{10}3\ast\frac7{100}=\frac{1\ast7}{3\ast10}=\frac7{30}$
г) $\frac{-5}9\ast4\frac12=-\frac59\ast\frac92=-\frac{5\ast1}{1\ast2}=-\frac52=-2\frac12$
д) $-\frac35\ast1\frac14=-\frac35\ast\frac54=-\frac{3\ast1}{1\ast4}=-\frac34$
е) $3\frac14\ast(-\frac{24}{39})=-\frac{13}4\ast\frac{24}{39}=-\frac{1\ast6}{1\ast3}=-\frac63=-2$
ж) $-\frac34\ast2\frac15=-\frac34\ast\frac{11}5=-\frac{3\ast11}{4\ast5}=-\frac{33}{20}=-1\frac{13}{20}$
з) $2\frac17\ast(-\frac{14}{15})=-\frac{15}7\ast\frac{14}{15}=-\frac{1\ast2}{1\ast1}=-2$
и) $3\frac17\ast(-\frac5{11})=-\frac{22}7\ast\frac5{11}=-\frac{2\ast5}{7\ast1}=-\frac{10}7=-1\frac17$575. Вычислите
а) $-\frac13\ast(-1)=\frac13$
б) $-1\ast\frac35=-\frac35$
в) $-1\ast(-1\frac12)=1\frac12$
г) $-3\frac15\ast(-1)=3\frac15$
д) $-2\ast\frac34=-\frac{2\ast3}4=-\frac64=-\frac32=-1\frac12$
е) $-1\frac12\ast(-4)=\frac{3\ast4}2=\frac{3\ast2}1=6$
ж) $-5\ast\frac{-3}{10}=\frac{5\ast3}{10}=\frac{1\ast3}2=\frac32=1\frac12$
з) $-9\ast(-1\frac16)=-9\ast(-\frac76)=\frac{9\ast7}6=\frac{3\ast7}2=\frac{21}2=10\frac12$
576. Вычислите
а) $(-1\frac13)\ast\frac9{10}=(-\frac43)\ast\frac9{10}=-\frac{4\ast9}{3\ast10}=-\frac{2\ast3}{1\ast5}=-\frac{2\ast3}{1\ast5}=-\frac65=-1\frac15$
б) $(-\frac27)\ast3\frac12=(-\frac27)\ast\frac72=-\frac{7\ast2}{7\ast2}=-\frac{1\ast1}{1\ast1}=-1$
в) $(-5\frac12)\ast(-\frac{32}{33})=(-\frac{11}2)\ast(-\frac{32}{33})=\frac{11\ast32}{2\ast33}=\frac{1\ast16}{1\ast3}=\frac{16}3=5\frac13$
г) $4\frac16\ast(-\frac{24}{25})=\frac{25}6\ast(-\frac{24}{25})=-\frac{25\ast24}{6\ast25}=-\frac{24}6=-4$
577. Вычислите
а) $(-5)\ast\frac23=-\frac{5\ast2}3=-\frac{10}3=-3\frac13$
б) $7\ast(-1\frac12)=7\ast(-\frac32)=-\frac{7\ast3}2=-\frac{21}2=-10\frac12$
в) $(-3)\ast(-1\frac14)=(-3)\ast(-\frac54)=\frac{3\ast5}4=\frac{15}4=3\frac34$
г) $(-2\frac34)\ast(-1\frac17)=(-\frac{11}4)\ast(-\frac87)=\frac{11\ast8}{4\ast7}=\frac{11\ast8}{4\ast7}=\frac{22}7=3\frac17$
д) $(-1\frac13)\ast2\frac25=-\frac43\ast\frac{12}5=-\frac{4\ast12}{3\ast5}=-\frac{16}5=-3\frac15$
е) $4\frac12\ast(-5\frac13)=\frac92\ast-\frac{16}3=-\frac{9\ast16}{2\ast3}=-3\ast8=-24$
578. Вычислите, предварительно указав порядок действий:
а) 1) $-1\frac13\ast\frac12=-\frac43\ast\frac12=-\frac{4\ast1}{3\ast2}=-\frac46=-\frac23;$
2) $(-\frac25)\ast2\frac12=(-\frac25)\ast\frac52=-\frac{2\ast5}{5\ast2}=-1;$
3) $-1\ast-\frac23=\frac23.$б) 1) $5\frac13\ast(-\frac34)=\frac{16}3\ast(-\frac34)=-\frac{16\ast3}{3\ast4}=-4;$
2) $(-\frac27)\ast(-4)=\frac{2\ast4}7=\frac87;$
3) $\frac87\ast\frac79=\frac89.$в) 1) $\frac92\ast(-1\frac15)=\frac92\ast(-\frac65)=-\frac{9\ast6}{2\ast5}=-\frac{27}5;$
2) $\frac29\ast(-\frac{27}5)=-\frac{2\ast27}{9\ast5}=-\frac{2\ast27}{9\ast5}=-\frac{2\ast3}{1\ast5}=-\frac65;$
3) $-\frac65\ast(-2)=\frac{6\ast2}5=\frac{12}5=2\frac25.$г) 1) $3\frac13\ast2\frac14=\frac{10}3\ast\frac94=\frac{10\ast9}{3\ast4}=\frac{5\ast3}{1\ast2}=\frac{15}2;$
2) $(-\frac12)\ast\frac45=-\frac{1\ast4}{2\ast5}=-\frac25;$
3) $\frac{15}2\ast(-\frac25)=-3.$579. Вычислите
а) $2\frac13\ast(-\frac79)\ast\frac97=2\frac13\ast(-1)=-2\frac13;$
б) $(-\frac89)\ast2\frac4{17}\ast(-\frac98)=1\ast2\frac4{17}=2\frac4{17};$
в) $2\frac14\ast(-\frac23)\ast(-1\frac12)=2\frac14\ast(-\frac23)\ast(-\frac32)=2\frac14\ast1=2\frac14;$
г) $(-\frac45)\ast(2\frac12\ast(-1\frac13))=(-\frac45)\ast(\frac52\ast(-\frac43))=(-\frac45)\ast(-\frac{5\ast4}{2\ast3})=(-\frac45)\ast(-\frac{10}3)=\frac83=2\frac23;$
д) $5\frac79\ast(-\frac89)\ast(-2\frac14)=\frac{52}9\ast(-\frac89)\ast(-\frac94)=\frac{52}9\ast\frac{8\ast9}{9\ast4}=\frac{52}9\ast2=\frac{52\ast2}9=\frac{104}9=11\frac59;$
е) $4\frac15\ast(3\frac12\ast(-\frac57))=\frac{21}5\ast(\frac72\ast(-\frac57))=\frac{21}5\ast(-\frac52)=-\frac{21}2=-10\frac12.$
580. Докажите, что:
а) ( − 1/7 ) ∗ 8/9 ∗ 1 3/4 > 2/− 3 ∗ 2 1/4 ∗ 1/6 ;
б) ( 7/12 − 7/18 ) ∗ ( − 6/7 ) < ( − 25/36 ) : 5/− 12 ∗ − 1/11.а) $(-\frac17)\ast\frac89\ast1\frac34=(-\frac12)\ast\frac89\ast\frac74=-\frac{1\ast8\ast7}{7\ast9\ast4}=-\frac{1\ast2\ast1}{1\ast9\ast1}=-\frac29=-\frac8{36}$
$\frac2{-3}\ast2\frac14\ast\frac16=\frac2{-3}\ast\frac94\ast\frac16=-\frac{2\ast9\ast1}{3\ast4\ast6}=-\frac{1\ast1\ast1}{1\ast4\ast1}=-\frac14=-\frac9{36}$
$-\frac8{36}>-\frac9{36};$б) $(\frac7{12}-\frac7{18})\ast(-\frac67)=\frac{21-14}{36}\ast(-\frac67)=\frac7{36}\ast(-\frac67)=-\frac16=-\frac{33}{198}$
$(-\frac{25}{36}):\frac5{-12}\ast\frac{-1}{11}=(-\frac{25}{36})\ast\frac{-12}5\ast\frac{-1}{11}=-\frac{25\ast12\ast1}{36\ast5\ast11}=-\frac{5\ast1\ast1}{3\ast1\ast11}=-\frac5{33}=-\frac{30}{198}$
$-\frac{33}{198}<-\frac{30}{198}$ 113
-
Ответы к стр. 113
581. Не проводя вычислений, сравните результат с нулём, а затем вычислите:
а) 5 1/2 ∗ ( − 1/4 ) ;
б) − 3/7 ∗ 2 1/3 ;
в) ( − 7/9 ) ∗ − 8/5 ;
г) − 8 /− 9 ∗ − 3 /− 7 ∗ − 7 /− 8 ;
д) ( − 1/2 ) : ( − 7 ) : ( − 3 ) ;
е) ( − 4/5 ) 2 .а) 5 1/2 ∗ ( − 1/4 ) < 0 ;
5 1/2 ∗ ( − 1/4 ) = 11/2 ∗ ( − 1/4 ) = − 11 ∗ 1/2 ∗ 4 = − 11/8 = − 1 3/8 ;
б) − 3/7 ∗ 2 1/3 < 0 ;
− 3/7 ∗ 2 1/3 = − 3/7 ∗ 7/3 = − 1 ;
в) ( − 7/9 ) ∗ − 8/5 > 0 ;
( − 7/9 ) ∗ − 8/5 = 7 ∗ 8/9 ∗ 5 = 56/45 = 1 11/45 ;
г) − 8/− 9 ∗ − 3/− 7 ∗ − 7/− 8 > 0 ;
− 8/− 9 ∗ − 3/− 7 ∗ − 7/− 8 = 8 ∗ 3 ∗ 7/9 ∗ 7 ∗ 8 = 3/9 = 1/3 ;
д) ( − 1/2 ) : ( − 7 ) : ( − 3 ) < 0 ;
( − 1/2 ) : ( − 7 ) : ( − 3 ) = ( − 1/2 ) ∗ ( − 1/7 ) : ( − 1/3 ) = − 1 ∗ 1 ∗ 1/2 ∗ 7 ∗ 3 = − 1/42 ;
е) ( − 4/5 ) 2 > 0 ;
( − 4/5 ) 2 = ( − 4/5 ) ∗ ( − 4/5 ) = 16/25 .582. Определите без вычислений, значение какого выражения больше:
а) 4 1/2 ∗ ( − 7/5 ) ∗ ( − 3/19 ) или 5 7/9 : ( − 4/17 ) : 8/13 ;
б) ( − 1/2 ) ∗ ( − 1/3 ) ∗ ( − 1/4 ) или ( − 1/4 ) : ( − 1/2 ) : 1/3 ;
в) ( − 1 1/3 ) ∗ ( − 2 2/7 ) ∗ ( − 3 3/5 ) или ( − 1/2 ) ∗ ( − 1/10 ) ∗ ( − 1/100 )а) 4 1/2 ∗ ( − 7/5 ) ∗ ( − 3/19 ) > 5 7/9 : ( − 4/17 ) : 8/13, так как значение первого выражения положительное (содержит четное количество отрицательных множителей), а значение второго выражения отрицательное (содержит нечетное количество отрицательных множителей)
б) ( − 1/2 ) ∗ ( − 1/3 ) ∗ ( − 1/4 ) < ( − 1/4 ) : ( − 1/2 ) : 1/3, так как значение первого выражения отрицательное (содержит нечетное количество отрицательных множителей), а значение второго выражения положительное (содержит четное количество отрицательных множителей)
в) ( − 1 1/3 ) ∗ ( − 2 2/7 ) ∗ ( − 3 3/5 ) < ( − 1/2 ) ∗ ( − 1/10 ) ∗ ( − 1/100 ), так как первое выражение содержит целые части, а значит модуль результата первого произведения будет больше модуля результата второго произведения, а так как результаты обоих произведений будут отрицательными, то результат второго выражения будет больше результата второго выражения.583. Вычислитель степень, предварительно указав основание и показатель степени:
а) ( − 1/2 ) 2 ;
б) ( − 1/2 ) 3 ;
в) ( − 1/3 ) 2 ;
г) ( − 1/3 ) 3 .а) − 1/2 − основание степени, 2 − показатель степени,
( − 1/2 ) 2 = ( − 1/2 ) ∗ ( − 1/2 ) = 1/4 ;
б) − 1/2 − основание степени, 3 − показатель степени,
( − 1/2 ) 3 = ( − 1/2 ) ∗ ( − 1/2 ) ∗ ( − 1/2 ) = − 1/8 ;
в) − 1/3 − основание степени, 2 − показатель степени,
( − 1/3 ) 2 = ( − 1/3 ) ∗ ( − 1/3 ) = 1/9 ;
г) − 1/3 − основание степени, 3 − показатель степени,
( − 1/3 ) 3 = ( − 1/3 ) ∗ ( − 1/3 ) ∗ ( − 1/3 ) = − 1/27 .584. Сравните с нулём, затем вычислите:
а) ( − 3/4 ) 3;
б) ( − 1/2 ) 5;
в) ( − 2/3 ) 4;
г) ( − 4/5 ) 3.а) ( − 3/4 ) 3 < 0 , ( − 3/4 ) 3 = ( − 3/4 ) ∗ ( − 3/4 ) ∗ ( − 3/4 ) = − 3 ∗ 3 ∗ 3/4 ∗ 4 ∗ 4 = − 27/64
Ответ: ( − 3/4 ) 3 < 0 , − 27/64
б) ( − 1/2 ) 5 < 0 , ( − 1/2 ) 5 = ( − 9 1/2 ) ∗ ( − 1/2 ) ∗ ( − 1/2 ) ∗ ( − 1/2 ) ∗ ( − 1/2 ) = − 1 ∗ 1 ∗ 1 ∗ 1 ∗ 1/2 ∗ 2 ∗ 2 ∗ 2 ∗ 2 = − 1/32
Ответ: ( − 1/2 ) 5 < 0 , − 1/32
в) ( − 2/3 ) 4 > 0 , ( − 2/3 ) 4 = ( − 2/3 ) ∗ ( − 2/3 ) ∗ ( − 2/3 ) ∗ ( − 2/3 ) = 2 ∗ 2 ∗ 2 ∗ 2/3 ∗ 3 ∗ 3 ∗ 3 = 16/81
Ответ: ( − 2/3 ) 4 > 0 , 16/81
г) ( − 4/5 ) 3 < 0 , ( − 4/5 ) 3 = ( − 4/5 ) ∗ ( − 4/5 ) ∗ ( − 4/5 ) = − 4 ∗ 4 ∗ 4/5 ∗ 5 ∗ 5 = − 64/125585. Вычислите:
а) 3 2/3 : − 11/12;
б) 8/15 : 16 − 25;
в) − 7/9 : 2 1/3;
г) − 9/− 16 : 1 13/32;
д) − 1 1/3 : 2/3;
е) 7/8 : ( − 1 5/8 );
ж) − 4/5 : ( − 1 1/5 );
з) − 4/3 : ( − 1 5/6 );
и) 4 : ( − 1 1/3 );
к) ( − 2 2/5 ) : 10;
л) − 6 : 3 3/5;
м) − 2 5/7 : ( − 38 ).a) 3 2/3 : − 11/12 = 11/3 ∗ − 12/11 = − 12/3 = − 4
Ответ: −4
б) 8/15 : 16 − 25 = 8/15 ∗ − 25/16 = − 1 ∗ 5/3 ∗ 2 = − 5/6
Ответ: − 5/6
в) − 7/9 : 2 1/3 = − 7/9 : 7/3 = − 7/9 ∗ 3/7 = − 3/9 = − 1/3
Ответ: − 1/3
г) − 9 − 16 : 1 13/32 = 9/16 : 45/32 = 9/16 ∗ 32/45 = 1 ∗ 2/1 ∗ 5 = 2/5
Ответ: 2/5
д) − 1 1/3 : 2/3 = − 4/3 ∗ 3/2 = − 4/2 = − 2
Ответ: −2
е) 7/8 : ( − 1 5/8 ) = 7/8 : − 13/8 = 7/8 ∗ − 8 13 = − 7/13
Ответ: − 7 13
ж) − 4/5 : ( − 1 1/5 ) = − 4/5 : − 6/5 = − 4/5 ∗ − 5/6 = 4/6 = 2/3
Ответ: 2/3
з) − 4/3 : ( − 1 5/6 ) = − 4/3 : − 11/6 = − 4/3 ∗ − 6/11 = 4 ∗ 2/1 ∗ 11 = 8/11
Ответ: 8/11
и) 4 : ( − 1 1/3 ) = 4 : − 4/3 = 4 ∗ − 3/4 = − 1 ∗ 3/1 ∗ 1 = − 3
Ответ: −3
к) ( − 2 2/5 ) : 10 = − 12/5 ∗ 1/10 = − 6 ∗ 1/5 ∗ 5 = − 6/25
Ответ: − 6/25
л) − 6 : 3 3/5 = − 6 : 18/5 = − 6 ∗ 5/18 = − 1 ∗ 5/1 ∗ 3 = − 5/3 = − 1 2/3
Ответ: − 1 2/3
м) − 2/5/7 : ( − 38 ) = − 19/7 ∗ − 1/38 = 1 ∗ 1/7 ∗ 2 = 1/14
Ответ: 1/14586. Вычислите:
а) 1 1/2 : ( − 1 1/6 ) ;
б) − 2 1/3 : ( − 1/5/6 ) ;
в) − 1 1/3 : 2/7/8 ;
г) − 2 1/8 : ( − 3 1/16 ) ;
д) 1 13/15 : ( − 1 2/5 ) ;
е) ( − 2 2/21 ) : ( − 1 4/7 ) .а) 1 1/2 : ( − 1 1/6 ) = 3/2 : ( − 7/6 ) = 3/2 ∗ ( − 6/7 ) = − 3 ∗ 6/2 ∗ 7 = − 3 ∗ 3/1 ∗ 7 = − 9/7 = − 1 2/7 ;
б) − 2 1/3 : ( − 1 5/6 ) = − 7/3 : ( − 11/6 ) = − 7/3 ∗ ( − 6/11 ) = 7 ∗ 6/3 ∗ 11 = 7 ∗ 2/1 ∗ 11 = 14/11 = 1 3/11 ;
в) − 1 1/3 : 2 7/8 = − 4/3 : 23/8 = − 4/3 ∗ 8/23 = − 4 ∗ 8/3 ∗ 23 = − 32/69 ;
г) − 2 1/8 : ( − 3 1/16 ) = − 17/8 : ( − 49/16 ) = − 17/8 * ( − 16/49 ) = 17 ∗ 16/8 ∗ 49 = 17 ∗ 2 / 1 ∗ 49 = 34/49 ;
д) 1 13/15 : ( − 1 2/5 ) = 28 15 : ( − 7/5 ) = 28/15 ∗ ( − 5/7 ) = − 28 ∗ 5/15 ∗ 7 = − 4 ∗ 1/3 ∗ 1 = − 4/3 = − 1 1/3 ;
е) ( − 2 2/21 ) : ( − 1 4/7 ) = ( − 44/21 ) : ( − 11/7 ) = ( − 44/21 ) ∗ ( − 7/11 ) = 44 ∗ 7/21 ∗ 11 = 4 ∗ 1/3 ∗ 1 = 4/3 = 1 1/3 114
-
Ответы к стр. 114
587. Вычислите:
а) 7 2/9 ∗ 8 2/3 − 7 2/9 ∗ 6 2/3 = 7 2/9 ∗ ( 8 2/3 − 6 2/3 ) = 65/9 ∗ 2 = 130/9 = 14 4/9 ;
б) 12 35/44 ∗ 4 1/10 − 8 35/44 ∗ 4 1/10 = 4 1/10 ∗ ( 12 35/44 − 8 35/44 ) = 41/10 ∗ 4 = 41 ∗ 2/5 = 82/5 = 16/2/5 ;
в) 7 1/3 ∗ 2 1/5 + 7 1/3 ∗ 1 4/5 = 7 1/3 ∗ ( 2 1/5 + 1 4/5 ) = 22/3 ∗ 4 = 88/3 = 29 1/3 ;
г) ( − 3 1/9 ) ∗ 7 4/7 + ( − 3 1/9 ) ∗ ( − 2 3/7 ) = ( − 3 1/9 ) ∗ ( 7 4/7 + ( − 2 3/7 ) ) = ( − 28/9 ) ∗ 5 1/7 = ( − 28/9 ) ∗ 36/7 = − 28 ∗ 36/9 ∗ 7 = − 4 ∗ 4/1 ∗ 1 = − 16 ;
д) 2 6/7 ∗ 4 2/5 − 2 6/7 ∗ 4 = 2 6/7 ∗ ( 4 2/5 − 4 ) = 20/7 ∗ 2/5 = 20 ∗ 2/7 ∗ 5 = 4 ∗ 2/7 ∗ 1 = 8/7 = 1 1/7 ;
е) ( − 2 3/7 ) ∗ ( − 5 ) + 2 3/7 ∗ ( − 2 2/3 ) = 2 3/7 ∗ ( 5 − 2 2/3 ) = 17/7 ∗ 2 1/3 = 17/7 ∗ 7/3 = 17/3 = 5 2/3 .588. Вычислите:
а) 7 1/2 ∗ ( − 1/5 ) + ( − 1 2/3 ) ∗ ( − 9/10 ) − 17 29/30 = 15/2 ∗ ( − 1/5 ) + ( − 5/3 ) ∗ ( − 9/10 ) − 17 29/30 = − 3/2 + 3/2 − 17 29/30 = 0 − 17 29/30 = − 17 29/30 ;
б) ( − 2 13/25 ) : ( − 2 7/10 ) − 17 25/47 : ( − 17 25/47 ) − 4 3/5 = ( − 63/25 ) : ( − 27/10 ) + 1 − 4 3/5 = ( − 63/25 ) ∗ ( − 10/27 ) − 3 3/5 = 63 ∗ 10/25 ∗ 27 − 3 3/5 = 7 ∗ 2/5 ∗ 3 − 3 3/5 = 14/15 − 3 3/5 = 14/15 − 18/5 = 14 − 54/15 = − 40/15 = − 8/3 = − 2 2/3 . 117
-
Ответы к стр. 117
589. Где на координатной оси расположены точки, изображающие:
а) положительные дроби;
б) отрицательные дроби.Ответ:
а) точки, изображающие положительные дроби, расположены на положительной полуоси.
б) точки, изображающие отрицательные дроби, расположены на отрицательной полуоси.590. Если а и b − рациональные числа и а < b, то:
а) как расположены на координатной оси точки а и b координатной оси;
б) как найти расстояние между точками а и b координатной оси;
в) как найти координату середины отрезка между точками а и b координатной оси?Ответ:
а) точка b расположена правее точки а;
б) b − a;
в) a + b/2.591. Что называют средним арифметическим нескольких чисел? Приведите пример.
Ответ:
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Например:
(5 + 6 + 10 + 11) : 4 = 8.592. Изобразите на координатной оси с единичным отрезком 8 см точки:
0 , 1/8 , 2/8 , 3/8 , 4/8 , 5/8 , 6/8 , 7/8 , 8/8 , 9/8 , 10/8 , 11/8 , 12/8 .
593. Изобразите на координатной оси точки:
0 , 1/6 , 2/6 , 3/6 , 4/6 , 5/6 , 6/6 , 7/6 , 8/6 , 9/6 , 10/6 , 11/6 , 12/6 .
Какой единичный отрезок удобно взять?
594. Выберите удобный единичный отрезок и отметьте на координатной оси точки:
а) 0 , 1 , 2 , 3 , 1/2 , 1 1/2 ;
б) 0 , 1/4 , 1/2 , 3/4 , 2 , 2 1/4 , 2 1/2 , 2 3/4 .
595. Изобразите на координатной оси точки
A ( 1/2 ), B ( 2 ), С ( 2 3/4 ) .
Найдите длины отрезков AB, BC, AC.
А В = В − А = 2 − 1/2 = 1 1/2 ;
В С = С − В = 2 3/4 − 2 = 3/4 ;
А С = С − А = 2 3/4 − 1/2 = 2 3/4 − 2/4 = 2 1/4 .596. Изобразите на координатной оси с единичным отрезком 4см точки:
а) 0 , 1/2 , 1/4 , 2/4 , 3/4 , 4/4 , 1 1/4 , 1/8 , 5/8 ;
б) − 1 , − 1/2 , − 2/2 , − 1/4 , − 2/4 , − 3/4 , − 5/4 .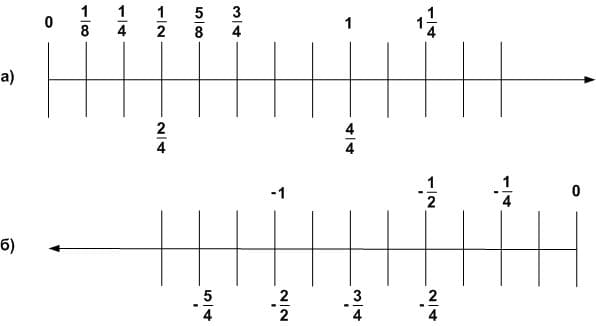
597. Выберите удобный единичный отрезок и изобразите на координатной оси точки:
а) − 1 1/2 , − 2 1/2 , − 3 1/2 , − 4 1/2 ;
б) − 1/3 , − 2/3 , − 1 1/3 , − 1 2/3 , − 2 1/3 , − 2 2/3 .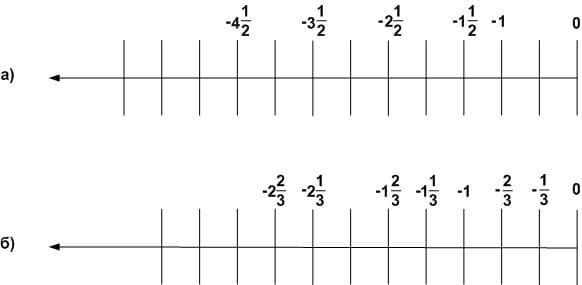
598. На координатной оси отметьте точку:
а) А ( − 2 1/4 ) ;
б) B ( − 1 1/5 ) ;
в) C ( − 3 1/2 ) ;
г) D ( − 4 1/2 ) .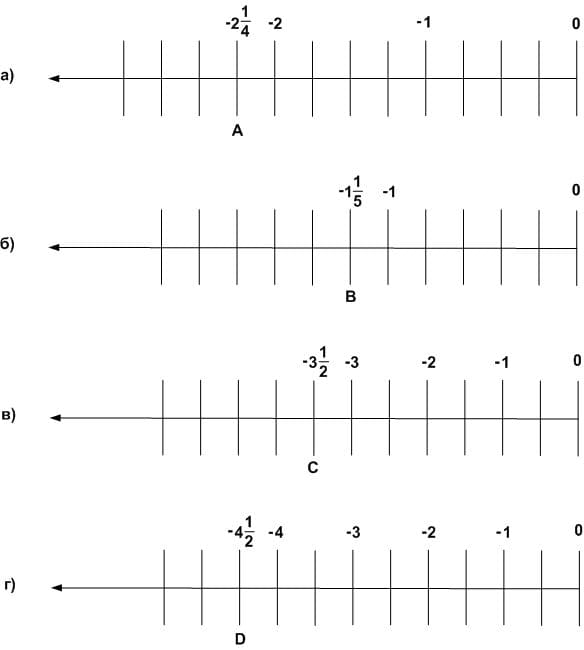
118
-
Ответы к стр. 118
599. Найдите координату середины отрезка, соединяющего точки:
а) 1/2 и 1/3;
б) 3/5 и 4/7;
в) 2 1/4 и 5/8;
г) 3 1/2 и 3 1/4.а) ( 1/2 + 1/3 ) : 2 = 3 + 2/6 : 2 = 5/6 ∗ 1/2 = 5/12
Ответ: 5/12
б) ( 3/5 + 4 7 ) : 2 = 21 + 20/35 : 2 = 41/35 ∗ 1/2 = 41/70
Ответ: 41/70
в) ( 2 1/4 + 5/8 ) : 2 = ( 9/4 + 5/8 ) : 2 = 18 + 5/8 : 2 = 23/8 ∗ 1/2 = 23/16 = 1 7/16
Ответ: 1 7/16
г) ( 3 1/2 + 3 1/4 ) : 2 = ( 7/2 + 13/4 ) : 2 = 14 + 13/4 : 2 = 27/4 ∗ 1 2 = 27/8 = 3 3/8
Ответ: 3 3/8600. Даны точки A(2) и B ( 2 1 2 ) . Найдите координату точки C − середины отрезка AB, координату точки D − середины отрезка CB, координату точки E − середины отрезка CD. Изобразите эти точки на координатной оси.
C = A + B/2 = ( 2 + 2 1/2 ) : 2 = 4 1/2 : 2 = 9/2 ∗ 1/2 = 9/4 = 2 1/4 ;
D = C + B/2 = ( 2 1/4 + 2 1/2 ) : 2 = ( 2 1/4 + 2 2/4 ) : 2 = 4 3/4 : 2 = 19/4 ∗ 1/2 = 19/8 = 2 3/8 ;
E = C + D/2 = ( 2 1/4 + 2 3/8 ) : 2 = ( 2 2/8 + 2 3/8 ) : 2 = 4 5/8 : 2 = 37/8 ∗ 1/2 = 37/16 = 2 5/16 .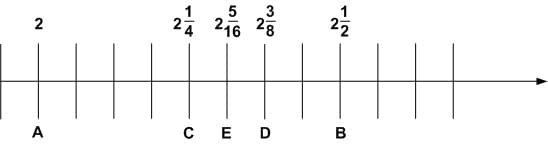
C ( 2 1/4 ) , D ( 2 3/8 ) , E ( 2 5/16 ).601. Найдите координату точки B по координатам точки А и точки С − середины отрезка AB, если:
а) A ( 2 ) , С ( 5 ) ;
б) A ( 1/2 ) , С ( 3 ) ;
в) A ( 1/4 ) , С ( 2/3 ) .А + В/2 = С,
B = С ∗ 2 − А, тогда:
а) B = 5 ∗ 2 − 2 = 8 ;
б) B = 3 ∗ 2 − 1/2 = 5 1/2 ;
в) B = 2/3 ∗ 2 − 1/4 = 4/3 − 1/4 = 16 − 3/12 = 13/12 = 1 1/12 .
Ответ:
а) B ( 8 ) ;
б) B ( 5 1/2 ) ;
в) B ( 1 1/12 ) .602. Найдите координаты точек, делящих отрезок AB на три равные части, если:
а) A ( 5 ) , B ( 9 1/2 );
б) A ( 1/3 ) , B ( 2/9 );
в) A ( 1/2 ) , B ( 3 1/6 ).а) ( 9 1/2 − 5 ) = 4 1/2 − длина отрезка АВ,
4 1/2 : 3 = 9/2 ∗ 1/3 = 3/2 = 1 1/2 − длина одной из трёх равных частей отрезка АВ.
5 + 1 1/2 = 6 1/2 − координата первой точки, делящей отрезок АВ на три равные части,
6 1/2 + 1 1/2 = 8 − координата второй точки, делящей отрезок АВ на три равные части.
Ответ: ( 6 1/2 ) и ( 8 )
б) 1/3 − 2/9 = 3/9 − 2/9 = 1/9 − длина отрезка АВ,
1/9 : 3 = 1/9 ∗ 1/3 = 1/27 − длина одной из трёх равных частей отрезка АВ.
2/9 + 1/27 = 6/27 + 1/27 = 7/27 − координата первой точки, делящей отрезок АВ на три равные части,
7/27 + 1/27 = 8/27 − координата второй точки, делящей отрезок АВ на три равные части.
Ответ: ( 7/27 ) и ( 8/27 )
в) 3 1/6 − 1/2 = 3 1/6 − 3/6 = 2 7/6 − 3/6 = 2 4/6 = 2 2/3 − длина отрезка АВ,
2 2/3 : 3 = 8/3 ∗ 1/3 = 8/9 − длина одной из трёх равных частей отрезка АВ.
1/2 + 8/9 = 9/18 + 16/18 = 25/18 = 1 7/18 − координата первой точки, делящей отрезок АВ на три равные части,
1 7/18 + 8/9 = 1 7/18 + 16/18 = 1 23/18 = 2 5/18 − координата второй точки, делящей отрезок АВ на три равные части.
Ответ: ( 1 7/18 ) и ( 2 5/18 )603. Определите расстояние между точками:
а) A ( − 3 1/2 ) и B ( 2 ) ;
б) A ( − 4 ) и B ( − 2 1/2 ) ;
в) A ( − 3 1/4 ) и B ( − 4 1/8 ) ;
г) A ( − 4 7/8 ) и B ( − 6 1/2 ) .а) 2 − ( − 3 1/2 ) = 2 + 3 1/2 = 5 1/2 ;
б) − 2 1/2 − ( − 4 ) = − 2 1/2 + 4 = 1 1/2 ;
в) − 3 1/4 − ( − 4 1/8 ) = − 3 1/4 + 4 1/8 = − 3 2/8 + 4 1/8 = 1 1/8 − 2/8 = 9/8 − 2/8 = 7/8 ;
г) − 4 7/8 − ( − 6 1/2 ) = − 4 7/8 + 6 1/2 = 2 1/2 − 7/8 = 2 4/8 − 7/8 = 1 12/8 − 7/8 = 1 5/8 .
Ответ:
а) 5 1/2 ;
б) 1 1/2 ;
в) 7/8 ;
г) 1 5/8 .604. Найдите среднее арифметическое чисел:
а) 4 и 6 ;
б) 1/2 и 3 ;
в) 1/2 и 1 1/8 ;
г) 2 1/4 и 2/3 .а) ( 4 + 6 ) : 2 = 10 : 2 = 5 ;
б) ( 1/2 + 3 ) : 2 = 3 1/2 : 2 = 7/2 ∗ 1/2 = 7/4 = 1 3/4 ;
в) ( 1/2 + 1 1/8 ) : 2 = ( 1/2 + 9/8 ) : 2 = 4 + 9/8 : 2 = 13/8 ∗ 1/2 = 13/16 ;
г) ( 2 1/4 + 2/3 ) : 2 = ( 9/4 + 2/3 ) : 2 = 27 + 8/12 ∗ 1/2 = 35/12 ∗ 1/2 = 35/24 = 1 11/24 .
Ответ:
а) 5 ;
б) 1 3/4 ;
в) 13/16 ;
г) 1 11/24 .605. Найдите среднее арифметическое чисел:
а) 1/3 и − 1/5 ;
б) 1/4 и − 3/5 ;
в) − 16 и − 8 ;
г) − 16 и 8.а) ( 1/3 + ( − 1/5 ) ) : 2 = 5 − 3/15 : 2 = 2/15 ∗ 1/2 = 1/15 ;
б) ( 1/4 + ( − 3/5 ) ) : 2 = 5 − 12/20 : 2 = − 7/20 ∗ 1/2 = − 7/40 ;
в) ( − 16 + ( − 8 ) ) : 2 = − 24 : 2 = − 12 ;
г) ( − 16 + 8 ) : 2 = − 8 : 2 = − 4.
Ответ:
а) 1/15 ;
б) − 7/40 ;
в) − 12 ;
г) − 4.606. Найдите среднее арифметическое чисел:
а) 1, 3, 4;
б) −5, 8, 13;
в) 10, 12, 14, 16;
г) −19, −9, 1, 11;
д) −2, 0, 2, 5, 10;
е) −2, −1, 0, 1, 2.а) ( 1 + 3 + 4 ) : 3 = 8 : 3 = 8/3 = 2 2/3 ;
б) ( − 5 + 8 + 13 ) : 3 = 16 : 3 = 16/3 = 5 1/3 ;
в) ( 10 + 12 + 14 + 16 ) : 4 = 52 : 4 = 13 ;
г) ( − 19 − 9 + 1 + 11 ) : 4 = − 16 : 4 = − 4 ;
д) ( − 2 + 0 + 2 + 5 + 10 ) : 5 = 15 : 5 = 3 ;
е) ( − 2 − 1 + 0 + 1 + 2 ) : 5 = 0 : 5 = 0.607. Определите координату середины отрезка AB, если:
а) A ( − 4 ) , B ( − 1 ) ;
б) A ( − 8 ) , B ( 3 ) ;
в) A ( − 7/10 ), B ( − 1/10 ) ;
г) A ( − 1/3 ), B ( 1/6 ) .а) ( − 4 + ( − 1 ) ) : 2 = − 5 : 2 = − 5/2 = − 2 1/2 ;
б) ( − 8 + 3 ) : 2 = − 5 : 2 = − 5/2 = − 2 1/2 ;
в) ( ( − 7/10 ) + ( − 1/10 ) ) : 2 = − 8/10 ∗ 1/2 = − 4/10 = − 2/5 ;
г) ( ( − 1/3 ) + ( 1/6 ) ) : 2 = − 2 + 1/6 ∗ 1/2 = − 1/6 ∗ 1/2 = − 1/12 .
Ответ:
а) − 2 1/2 ;
б) − 2 1/2 ;
в) − 2/5 ;
г) − 1/12 .608. Точка C − середина отрезка AB. Определите координату точки B, если:
а) A ( − 2 ) , C ( 1 ) ;
б) A ( − 5 ) , C ( − 1 ) ;
в) A ( − 3/10 ) , C ( 9/10 ) ;
г) A ( 0 ) , C ( 12/13 ) .A + B/2 = C,
B = C ∗ 2 − A, тогда:
а) B = 1 ∗ 2 − ( − 2 ) = 1 ∗ 2 + 2 = 4 ;
б) B = − 1 ∗ 2 − ( − 5 ) = − 1 ∗ 2 + 5 = 3 ;
в) B = 9/10 ∗ 2 − ( − 3/10 ) = 9/10 ∗ 2 + 3/10 = 18/10 + 3/10 = 21/10 = 2 1/10 ;
г) B = 12/13 ∗ 2 − 0 = 24/13 ∗ 2 = 1 11/13 ;
Ответ:
а) B ( 4 ) ;
б) B ( 3 ) ;
в) B ( 2 1/10 ) ;
г) B ( 1 1/13 ) . 119
-
Ответы к стр. 119
609. На координатном луче отмечены числа. С помощью циркуля отметьте на координатном луче число:
а) a + 2 (рис.61,а);
б) a + 4 (рис.61,б).
Ответ:
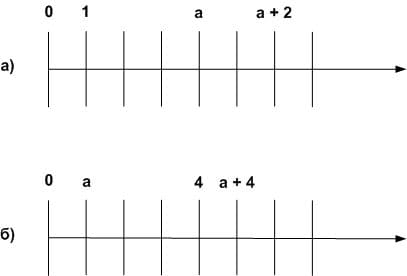
610. Для чисел a и b выполняется равенство 5 − a = b. С помощью циркуля отметьте на координатном луче число a + b (рис.62).

5 − a = b, следовательно, a + b = 5.
Ответ: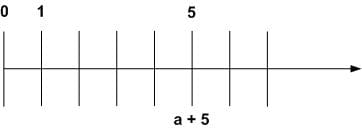
611. Для чисел a и b выполняется равенство a − 3 = b. С помощью циркуля отметьте на координатном луче число а (рис.63).

a − 3 = b, следовательно, a = b + 3.
Ответ: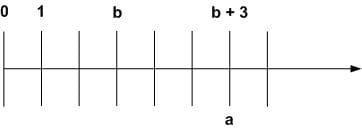
612. На координатной оси отмечены точки с координатами: 0, 1, b (рис.64). С помощью циркуля постройте точки с координатами:
−1, −b, b + 1, b − 1, 1 − b, −b − 1.
Ответ:

613. На координатной оси точки с координатами: 0, a, b.
С помощью циркуля постройте точки с координатами: −a, −b, a + b, a − b, b − a, −a − b (рис.65).
Ответ:

614. На рисунке 66 указаны координаты точек A и B. Найдите координату точки C.
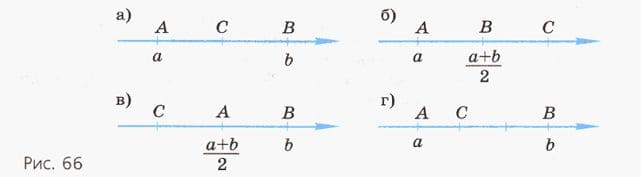
а) C − середина отрезка AB, поэтому C ( a + b/2 ) ;
б) Точка B середина отрезка AC, то есть координата точки B равна среднему арифметическому координат точек A и C, тогда:
а + C/2 = а + b/2
а + C = а + b
C ( а + b − а )
C ( b ) ;
в) Точка A середина отрезка CB, то есть координата точки A равна среднему арифметическому координат точек C и B, тогда:
C + b/2 = а + b/2
C + b = а + b
C ( b + а − b )
C ( а )
г) b − a длина отрезка AB,
b − a/3 длина отрезка AC,
C ( а + b − a/3 = 3 а + b − a/3 = 2 а + b/3 )
Ответ:
а) C ( a + b/2 ) ;
б) C ( b ) ;
в) C ( а ) ;
г) C ( 2 а + b/3 ) . 120
-
Ответы к стр. 120
615. Определите координаты точек, делящих отрезок AB на четыре равные части, если:
а) А ( 2 2/8 ) , B ( 4 ) ;
б) А ( − 5/7 ) , B ( 1/7 ) .
а) 4 − 2 2/8 = 3 8/8 − 2 2/8 = 1 6/8 = 1 3/4 − длина отрезка АВ,
1 3/4 : 4 = 7/4 ∗ 1/4 = 7/16 − длина одной из четырёх равных частей отрезка АВ.
2 2/8 + 7/16 = 2 4/16 + 7/16 = 2 11/16 − координата первой точки, делящей отрезок АВ на четыре равные части,
2 11/16 + 7/16 = 2 18/16 = 3 2/16 = 3 1/8 − координата второй точки, делящей отрезок АВ на четыре равные части.
3 2/16 + 7/16 = 3 9/16 − координата третьей точки, делящей отрезок АВ на четыре равные части.
Ответ: 2 11/16 , 3 1/8 , 3 9/16.
б) 1/7 − ( − 5/7 ) = 1/7 + 5/7 = 6/7 − длина отрезка АВ,
6/7 : 4 = 6/7 ∗ 1/4 = 6/28 = 3/14 − длина одной из четырёх равных частей отрезка АВ.
− 5/7 + 3/14 = − 10/14 + 3/14 = − 7/14 = − 1/2 − координата первой точки, делящей отрезок АВ на четыре равные части,
− 7/14 + 3/14 = − 4/14 = − 2/7 − координата второй точки, делящей отрезок АВ на четыре равные части.
− 4/14 + 3/14 = − 1/14 − координата третьей точки, делящей отрезок АВ на четыре равные части.
Ответ: − 1/2 , − 2/7 , − 1/14.616. а) Среднее арифметическое чисел 4 1/3 и a равно 2 1/2. Найдите число а.
б) Среднее арифметическое чисел a и − 1/3 равно 5/6. Найдите число а.
а) ( 4 1/3 + а ) : 2 = 2 1/2
( 4 1/3 + а ) = 5/2 ∗ 2
а = 5 − 4 1/3
а = 2/3
б) ( а + ( − 1/3 ) ) : 2 = 5/6
( а − 1/3 ) = 5/6 ∗ 2
а = 5/3 + 1/3
а = 6/3
а = 2.
Ответ:
а) 2/3 ;
б) 2.617. Отрезок, соединяющий точки 0 и 1 на координатной оси, разделили пополам − получили два отрезка. Правый отрезок разделили пополам − получили еще два отрезка. Правый из них разделили пополам и т.д. Запишите координаты пяти первых полученных таким образом точек. Определите без вычислений координаты следующих пяти точек.
0 + 1/2 = 1/2 координата первой получившейся точки,
1/2 + 1/2 = 3/2 ∗ 1/2 = 3/4 координата второй получившейся точки,
3/4 + 1/2 = 7/4 ∗ 1/2 = 7/8 координата третьей получившейся точки,
7/8 + 1/2 = 15/8 ∗ 1/2 = 15/16 координата четвертой получившейся точки,
15/16 + 1/2 = 31/16 ∗ 1/2 = 31/32 координата пятой получившейся точки.
Для того, чтобы рассчитать координаты каждой последующей точки, необходимо знаменатель координаты предыдущей точки умножить на 2, и получившийся результат записать в знаменатель координаты искомой точки. Затем из знаменателя координаты искомой точки вычесть 1 и записать результат в числитель координаты искомой точки. То есть координата шестой точки будет равна:
32 ∗ 2 − 1/32 ∗ 2 = 63/64, тогда:
координата 7 точки 127/128 ;
координата 8 точки 255/256 ;
координата 9 точки 511/512 ;
координата 10 точки 1023/1024 .
Ответ: 1/2 , 3/4 , 7/8 , 15/16 , 31/32 , 63/64 , 127/128 , 255/256 , 511/512 , 1023/1024 . 122
-
Рациональные числа
УравненияОтветы к стр. 122
618. Является ли число 2 корнем уравнения:
а) x — 2 = 0; б) x + 4 = 0; в) 2x = 4;
г) 3x — 4 = x; д) x + 3 = 2x + 1; е) 3x + 4 = 6x — 2?Подставим в уравнение вместо х число 2.
а) 2 — 2 = 0,
0 = 0 — является;б) 2 + 4 = 0,
6 ≠ 0 — не является;в) 2 • 2 = 4,
4 = 4 — является;г) 3 • 2 — 4 = 2,
2 = 2 — является;д) 2 + 3 = 2 • 2 + 1,
5 = 5 — является;е) 3 • 2 + 4 = 6 • 2 — 2,
10 = 10 — является.Решите уравнение (619-629):
619. а) х — 2 = 0; б) х + 4 = 0; в) 100 + х = 0; г) х — 5 = 6;
д) х + 2 = 5; е) х — 11 = -7; ж) 12 + х = 17; з) х + 7 = 7.а) х — 2 = 0,
х = 0 + 2,
х = 2;б) х + 4 = 0,
х = 0 — 4,
х = -4;в) 100 + х = 0,
х = 0 — 100,
х = -100;г) х — 5 = 6,
х = 6 + 5,
х = 11;д) х + 2 = 5,
х = 5 — 2,
х = 3;е) х — 11 = -7,
х = -7 + 11,
х = 4;ж) 12 + х = 17,
х = 17 — 12,
х = 5;з) х + 7 = 7,
х = 7 — 7,
х = 0.620. а) 5 + x = 3; б) -7 + x = -2; в) x + 3 = -6;
г) 12 + x = -8; д) x + 18 = 18; е) -13 + x = -5;
ж) x — 1/5 = 2; з) x — 2 = 1/2; и) x — 4 = 1 1/3.а) 5 + x = 3,
x = 3 — 5,
x = -2;б) -7 + x = -2,
x = -2 + 7,
x = 5;в) x + 3 = -6,
x = -6 — 3,
x = -9;г) 12 + x = -8,
x = -8 — 12,
x = -20;д) x + 18 = 18,
x = 18 — 18,
x = 0;е) -13 + x = -5,
x = -5 + 13,
x = 8;ж) x — 1/5 = 2,
x = 2 + 1/5,
x = 2 1/5;з) x — 2 = 1/2,
x = 1/2 + 2,
x = 2 1/2;и) x — 4 = 1 1/3,
x = 1 1/3 + 4,
x = 5 1/3.621. а) x — 1/2 = 1/2; б) x — 1/3 = 1/4; в) x — 1/18 = 1/12;
г) x — 1 = — 1/3; д) 1/7 + x = 11; е) 1 1/5 + x = 1;
ж) x — 6 1/3 = -3 2/3; з) 7/9 + x = 2 1/2; и) x — 2 1/2 = -1 3/5.а) x — 1/2 = 1/2,
x = 1/2 + 1/2,
x = 2/2,
х = 1;б) x — 1/3 = 1/4,
x = 1/4 + 1/3,
x = 3+4/12,
х = 7/12;в) x — 1/18 = 1/12,
x = 1/12 + 1/18,
x = 3+2/36,
х = 5/36;г) x — 1 = — 1/3,
x = — 1/3 + 1,
x = 2/3;д) 1/7 + x = 11,
x = 11 — 1/7,
x = 10 6/7;е) 1 1/5 + x = 1,
x = 1 — 1 1/5,
x = — 1/5;ж) x — 6 1/3 = -3 2/3,
x = -3 2/3 + 6 1/3,
x = 2 2/3;з) 7/9 + x = 2 1/2,
x = 2 1/2 — 7/9,
x = 2 9/18 — 14/18,
х = 1 27/18 — 14/18,
х = 1 13/18;и) x — 2 1/2 = -1 3/5,
x = -1 3/5 + 2 1/2,
x = -1 6/10 + 2 5/10,
х = 1 15/10 — 1 6/10,
х = 9/10.622. а) 2x = 4; б) 6x = 24; в) 7x = -14;
г) -5x = 100; д) -2x = -8; е) 12x = -36.а) 2x = 4,
x = 4 : 2,
х = 2;б) 6x = 24,
x = 24 : 6,
х = 4;в) 7x = -14,
x = -14 : 7,
х = -2;г) -5x = 100,
x = -100 : 5,
х = -20;д) -2x = -8,
x = -8 : (-2),
х = 4;е) 12x = -36,
x = -36 : 12,
х = -3.623. а) 3x = 2; б) 6x = -7; в) -2x = -13; г) 2x = 0;
д) -5x = 0; е) —x = 2; ж) —x = 0; з) —x = -5.а) 3x = 2,
x = 2/3;б) 6x = -7,
x = — 7/6,
х = -1 1/6;в) -2x = -13,
x = -13/-2,
х = 6 1/2;г) 2x = 0,
x = 0 : 2,
х = 0;д) -5x = 0,
x = 0 : (-5),
х = 0;е) —x = 2,
x = 2 : (-1),
х = -2;ж) —x = 0,
x = 0 : (-1),
х = 0;з) —x = -5,
x = -5 : (-1),
х = 5.624. а) 2x = 1/2; б) 3x = — 1/4; в) -2x = 1/4;
г) 1/2 x = 3; д) 3/4 x = 1; е) — 1/3 x = -3;
ж) — 2/7 x = 0; з) -4x = 8/25; и) 2x = 1 1/3.а) 2x = 1/2,
x = 1/2 : 2,
х = 1/2 • 1/2,
х = 1/4;б) 3x = — 1/4,
x = — 1/4 : 3,
х = — 1/4 • 1/3,
х = — 1/12;в) -2x = 1/4,
x = 1/4 : (-2),
х = 1/4 • (- 1/2),
х = — 1/8;г) 1/2 x = 3,
x = 3 : 12,
х = 3 • 2,
х = 6;д) 3/4 x = 1,
x = 1 : 3/4,
х = 1 • 4/3,
х = 4/3,
х = 1 1/3;е) — 1/3 x = -3,
x = -3 : (- 1/3),
х = -3 • (- 3/1),
х = 9/1,
х = 9;ж) — 2/7 x = 0,
x = 0 : (- 2/7),
х = 0;з) -4x = 8/25,
x = 8/25 : (-4),
х = 8/25 • (- 1/4),
х = — 2•1/25•1,
х = — 2/25;и) 2x = 1 1/3,
x = 1 1/3 : 2,
х = 4/3 • 1/2,
х = 2•1/3•1,
х = 2/3.625. а) 2x — 6 = 0; б) 12 + 3x = 0; в) —x + 7 = 0; г) 15 — 3x = 0;
д) 3x + 1 = 7; е) 5 — 2x = 1; ж) 5x — 2 = 1; з) -5x — 2 = -12.а) 2x — 6 = 0,
2x = 0 + 6,
х = 6 : 2,
х = 3;б) 12 + 3x = 0,
3x = 0 — 12,
х = -12 : 3,
х = -4;в) —x + 7 = 0,
—x = 0 — 7,
х = -7 : (-1),
х = 7;г) 15 — 3x = 0,
-3x = 0 — 15,
х = -15 : (- 3),
х = 5;д) 3x + 1 = 7,
3x = 7 — 1,
х = 6 : 3,
х = 2;е) 5 — 2x = 1,
-2x = 1 — 5,
-2х = -4,
x = -4 : (-2),
х = 2;ж) 5x — 2 = 1,
5x = 1 + 2,
x = 3/5;з) -5x — 2 = -12,
-5x = -12 + 2,
х = -10 : (-5),
х = 2.626. а) 3x + 2x = 10; б) 5x + x = 6; в) 4x + 2x — 7 = 5;
г) 7x + x + 3 = 19; д) 5 = 4x — 3x; е) 8 = 3x — x;
ж) 3x — 1 = 2x; з) 3x — 6 = x.а) 3x + 2x = 10,
(3 + 2)х = 10,
5x = 10,
x = 10 : 5,
х = 2;б) 5x + x = 6,
(5 + 1)х = 6,
6x = 6,
x = 6 : 6,
х = 1;в) 4x + 2x — 7 = 5,
(4 + 2)х = 5 + 7,
6x = 12,
x = 12 : 6,
х = 2;г) 7x + x + 3 = 19,
(7 + 1)х = 19 — 3,
8x = 16,
x = 16 : 8,
х = 2;д) 5 = 4x — 3x,
5 = (4 — 3)х,
x = 5;е) 8 = 3x — x,
8 = (3 — 1)х,
8 = 2x,
x = 8 : 2,
х = 4;ж) 3x — 1 = 2x,
3x — 2x = 1,
(3 — 2)х = 1,
x = 1;з) 3x — 6 = x,
3x — x = 6,
(3 — 1)х = 6,
2x = 6,
x = 6 : 2,
х = 3.627. а) x + 3 = 3x — 7; б) 3 — x = 1 + x; в) 7x + 2 = 3x — 10;
г) 5x — 8 = 3x — 8; д) 1/2 x — 3 = 2 — 1/3 x; е) 5x — 2 1/4 = 1/2 x;
ж) 2/5 x — 1 = 3/4 x — 6; з) 2x — 3/5 = 3/4 x — 1/2.а) x + 3 = 3x — 7,
3 + 7 = 3x — x,
10 = (3 — 1)х,
10 = 2х,
х = 10 : 2,
х = 5;б) 3 — x = 1 + x,
3 — 1 = x + x,
2 = (1 + 1)х,
2 = 2х,
х = 2 : 2,
х = 1;в) 7x + 2 = 3x — 10,
7x — 3x = -10 — 2,
(7 — 3)х = -12,
4x = -12,
x = -12 : 4,
x = -3;г) 5x — 8 = 3x — 8,
5x — 3x = -8 + 8,
(5 — 3)х = 0,
2х = 0,
х = 0 : 2,
х = 0;д) 1/2 x — 3 = 2 — 1/3 x,
1/2 x + 1/3 x = 2 + 3,
3/6 x + 2/6 x = 5,
5/6 x = 5,
x = 5 : 5/6,
х = 5 • 6/5,
х = 6;е) 5x — 2 1/4 = 1/2 x,
5x — 1/2 x = 2 1/4,
(5 — 1/2)х = 2 1/4,
4 1/2 x = 2 1/4,
x = 2 1/4 : 4 1/2,
х = 9/4 • 2/9,
х = 1/2;ж) 2/5 x — 1 = 3/4 x — 6,
2/5 x — 3/4 x = -6 + 1,
(8/20 — 15/20)х = -5,
— 7/20 х = -5,
х = -5 : (- 7/20),
х = -5 • (- 20/7),
х = 100/7,
х = 14 2/7;з) 2x — 3/5 = 3/4 x — 1/2,
2x — 3/4 x = — 1/2 + 3/5,
(2 — 3/4)x = — 5/10 + 6/10,
1 1/4 x = 1/10,
х = 1/10 : 5/4,
х = 1/10 • 4/5,
х = 1•2/5•5,
х = 2/25.628. а) 2(x — 5) = 9; б) 12 + 3(x — 1) = 0; в) -(x + 8) = 3;
г) 1 — 5(2 — 3x) = 6; д) 7 — 3(x + 1) = 6; е) 5 — 2(3 — x) = 11;
ж) 2x — (7 + x) = 2; з) -3 — 3(3 — 2x) = 1.а) 2(x — 5) = 9,
2x — 10 = 9,
2x = 9 + 10,
x = 19/2,
х = 9 1/2;б) 12 + 3(x — 1) = 0,
12 + 3x — 3 = 0,
3x = 0 — 12 + 3,
x = -9 : 3,
х = -3;в) -(x + 8) = 3,
—x — 8 = 3,
—x = 3 + 8,
x = 11 : (-1),
х = -11;г) 1 — 5(2 — 3x) = 6,
1 — 10 + 15x = 6,
15x = 6 — 1 + 10,
x = 15 : 15,
х = 1;д) 7 — 3(x + 1) = 6,
7 — 3x — 3 = 6,
-3x = 6 — 7 + 3,
x = 2 : (-3),
х = — 2/3;е) 5 — 2(3 — x) = 11,
5 — 6 + 2x = 11,
2x = 11 — 5 + 6,
x = 12 : 2,
х = 6;ж) 2x — (7 + x) = 2,
2x — 7 — x = 2,
(2 — 1)x = 2 + 7,
х = 9;з) -3 — 3(3 — 2x) = 1,
-3 — 9 + 6x = 1,
6x = 1 + 3 + 9,
x = 13/6,
х = 2 1/6. 123
-
Ответы к стр. 123
Решите уравнение (619-629):
629. а) 3(x + 2) — x = 10; б) 8 = 3(x — 4) — x;
в) 4x + 3(x — 7) = 5; г) 3(x — 1) + x = 2x;
д) 5 — x = 4(x — 3); е) 5(x + 4) + x = 6;
ж) 7 — (2x + 3) = 9; з) 3(x — 7) — 6x = —x;
и) 1/2(x — 4) + 3x = 5; к) 2(x + 3/5) — x = 3 1/5;
л) 5x — (1/2 x + 9) = 18; м) -2(1/3 x + 7) = -21.а) 3(x + 2) — x = 10,
3x + 6 — x = 10,
(3 — 1)x = 10 — 6,
2x = 4,
x = 4 : 2,
х = 2;б) 8 = 3(x — 4) — x,
8 = 3x — 12 — x,
8 + 12 = (3 — 1)х,
20 = 2х,
x = 20 : 2,
х = 10;в) 4x + 3(x — 7) = 5,
4x + 3x — 21 = 5,
(4 + 3)x = 5 + 21,
7x = 26,
x = 26/7,
х = 3 5/7;г) 3(x — 1) + x = 2x,
3x — 3 + x = 2x,
3x + x — 2x = 3,
(3 + 1 — 2)x = 3
2x = 3,
x = 3/2,
х = 1 1/2;д) 5 — x = 4(x — 3),
5 — x = 4x — 12,
5 + 12 = x + 4x,
17 = (1 + 4)х,
17 = 5x,
х = 17/5,
x = 3 2/5;е) 5(x + 4) + x = 6,
5x + 20 + x = 6,
5x + x = 6 — 20,
(5 + 1)x = -14,
6x = -14,
x = -14/6,
х = -2 1/3;ж) 7 — (2x + 3) = 9,
7 — 2x — 3 = 9,
-2x = 9 — 7 + 3,
-2x = 5,
x = 5/-2,
х = -2 1/2;з) 3(x — 7) — 6x = —x,
3x — 21 — 6x = —x,
3x — 6x + x = 21,
-2x = 21,
x = 21/-2,
х = -10 1/2;и) 1/2(x — 4) + 3x = 5,
1/2 x — 2 + 3x = 5,
1/2 x + 3x = 5 + 2,
3 1/2 x = 7,
x = 7 : 3 1/2,
х = 7 • 2/7,
х = 2;к) 2(x + 3/5) — x = 3 1/5,
2x + 6/5 — x = 3 1/5,
2x — x = 2 6/5 — 6/5,
(2 — 1)х = 2,
х = 2;л) 5x — (1/2 x + 9) = 18,
5x — 1/2 x — 9 = 18,
5x — 1/2 x = 18 + 9,
(5 — 1/2)х = 27,
4 1/2 x = 27,
x = 27 : 4 1/2,
х = 27 • 2/9,
х = 6;м) -2(1/3 x + 7) = -21,
— 2/3 x — 14 = -21,
— 2/3 x = -21 + 14,
— 2/3 x = -7,
x = -7 : (- 2/3),
х = -7 • (- 3/2),
х = 21/2,
х = 10 1/2. 124
-
Рациональные числа
Решение задач с помощью уравненийОтветы к стр. 124
Обозначьте одну из величин через х и выразите через х ответ на вопрос задачи (630-633):
630. а) Когда Маша прочитала несколько страниц книги, то ей осталось прочитать на 40 страниц больше, чем она уже прочитала. Сколько страниц в книге?
б) Когда было пройдено несколько километров, то осталось пройти на 10 км меньше, чем уже пройдено. Определите всё расстояние.
в) В многоэтажном доме двухкомнатных квартир в 3 раза больше, чем однокомнатных. Сколько всего в этом доме двухкомнатных и однокомнатных квартир?
г) В некотором поселке имеются только одноэтажные и двухэтажные дома, причем двухэтажных домов в 10 раз меньше, чем одноэтажных. Сколько всего домов в этом поселке?а) Пусть х — страниц книги Маша прочитала, тогда х + 40 — страниц осталось прочитать:
х + (х + 40) = 2х + 40 — всего страниц в книге.
Ответ: 2х + 40 — всего страниц в книге.б) Пусть х — пройдено километров, тогда х — 10 — километров осталось пройти:
х + (х — 10) = 2х — 10 км — всё расстояние.
Ответ: 2х — 10 км — общее расстояние.в) Пусть х — количество однокомнатных квартир, тогда 3х — количество двухкомнатных квартир:
3х + х = 4х — всего квартир в доме.
Ответ: 4х — всего квартир в доме.г) Пусть х — двухэтажных домов, тогда 10х — количество одноэтажных домов:
10х + х = 11х — всего домов в поселке.
Ответ: 11х — всего домов в поселке.631. В вазе лежало 15 яблок. Даша угостила трёх подруг, дав всем яблок поровну. Сколько яблок осталось в вазе?
Пусть x — количество яблок, которое дали одной из подруг, тогда 3x — количество яблок, которое Даша раздала трём подругам:
15 — 3x — количество яблок, которое осталось в вазе.
Ответ: 15 — 3x — количество яблок, которое осталось в вазе. 125
-
Ответы к стр. 125
Обозначьте одну из величин через х и выразите через х ответ на вопрос задачи (630-633):
632. а) Папа в 3 раза старше сына. На сколько лет сын моложе папы?
б) Дочь в 4 раза младше мамы. На сколько лет мама старше своей дочери?
в) Папа на 28 лет старше сына. Во сколько раз он старше сына?
г) Мама на 24 года старше дочери. Во сколько раз она старше дочери?а) Пусть х — лет сыну, тогда 3х — возраст папы:
3х — х = 2х — на 2х лет сын моложе папы.
Ответ: на 2х лет.б) Пусть х — лет дочери, тогда 4х — возраст мамы:
4х — х = 3х — на 3х лет мама старше дочери.
Ответ: на 3х лет.в) Пусть х — лет сыну, тогда х + 28 — возраст папы:
х+28/х = х/х + 28/х = 1 + 28/х — в 1 + 28/х лет папа старше сына.
Ответ: в 1 + 28/х лет.г) Пусть х — лет дочери, тогда х + 24 — возраст мамы:
х+24/х = х/х + 24/х = 1 + 24/х — в 1 + 24/х лет мама старше дочери.
Ответ: в 1 + 24/х лет.633. а) Ученик задумал число, увеличил его в 3 раза и уменьшил результат на 5. Какое число он получил?
б) Ученик задумал число, уменьшил его на 3 и увеличил результат в 5 раз. Какое число он получил?а) Пусть х — задуманное число, тогда:
х • 3 — 5 = 3х — 5 — полученное число.
Ответ: 3х — 5.б) Пусть х — задуманное число, тогда:
(х — 3) • 5 = 5х — 15 — полученное число.
Ответ: 5х — 15.634. Обозначьте неизвестное число буквой и составьте уравнение по условию задачи:
а) Задумали число, прибавили к нему 8 и получили 33.
б) Задумали число, умножили его на 4 и получили 52.
в) Задумали число, умножили его на 7, к произведению прибавили 12 и получили 26.
г) Задумали число, вычли из него 4, умножили разность на 5 и получили 35.а) Пусть х — задуманное число, тогда уравнение:
x + 8 = 33;б) Пусть х — задуманное число, тогда уравнение:
4x = 52;в) Пусть х — задуманное число, тогда уравнение:
7x + 12 = 26;г) Пусть х — задуманное число, тогда уравнение:
(x — 4) • 5 = 35.635. Одно число на 6 больше другого, а их сумма равна 18. Составьте уравнение по условию задачи, обозначив буквой:
а) меньшее число; б) большее число.а) Пусть х — меньшее число, тогда х + 6 — большее число, а уравнение:
х + (х + 6) = 18;б) Пусть х — большее число, тогда х — 6 — меньшее число, а уравнение:
х + (х — 6) = 18.636. Одно число на 4 меньше другого, а их сумма равна 22. Составьте уравнение по условию задачи, обозначив буквой:
а) меньшее число; б) большее число.а) Пусть х — меньшее число, тогда х + 4 — большее число, а уравнение:
х + (х + 4) = 22;б) Пусть х — большее число, тогда х — 4 — меньшее число, а уравнение:
х + (х — 4) = 22.Составьте уравнение по условию задачи, обозначив буквой неизвестное число, и решите его (637-652):
637. а) Одно число в 5 раз больше другого, а их сумма равна 42.
б) Одно число в 3 раза меньше другого, а их сумма равна 28.
в) Одно число в 4 раза больше другого, а их разность равна 39.
г) Одно число в 7 раз меньше другого, а их разность равна 54.а) Пусть х — меньшее число, тогда 5х — большее число, а уравнение:
x + 5x = 42,
6x = 42,
x = 42 : 6,
х = 7;б) Пусть х — меньшее число, тогда 3х — большее число, а уравнение:
x + 3x = 28,
4x = 28,
x = 28 : 4,
х = 7;в) Пусть х — меньшее число, тогда 4х — большее число, а уравнение:
4x — x = 39,
3x = 39,
x = 39 : 3,
х = 13;г) Пусть х — меньшее число, тогда 7х — большее число, а уравнение:
7x — x = 54,
6x = 54,
x = 54 : 6,
х = 9.638. а) Брат нашёл в 3 раза больше белых грибов, чем сестра. Всего они нашли 24 белых гриба. Сколько белых грибов нашёл брат и сколько сестра?
б) На двух полках 63 книги, причём на одной в 2 раза меньше книг, чем на другой. Сколько книг на каждой полке?а) Пусть х — грибов нашла сестра, тогда 3x — грибов нашёл брат, а уравнение:
3x + x = 24,
4x = 24,
x = 24 : 4,
х = 6 — грибов собрала сестра
3 • 6 = 18 — грибов собрал брат
Ответ: 6 грибов собрала сестра, 18 грибов собрал брат.б) Пусть х — книг на одной полке, тогда 2x — книг на другой полке, а уравнение:
2x + x = 63,
3x = 63,
x = 63 : 3,
х = 21 — книга находится на одной полке
21 • 2 = 42 — книги находится на второй полке
Ответ: 21 книга находится на одной полке и 42 книги находится на другой полке. 126
-
Ответы к стр. 126
Составьте уравнение по условию задачи, обозначив буквой неизвестное число, и решите его (637-652):
639. а) В книжке 60 страниц. Прочитали в 2 раза больше страниц, чем осталось прочитать. Сколько страниц осталось прочитать?
б) На автомобильной стоянке стоит 72 автомобиля, причём легковых автомобилей в 7 раз больше, чем грузовых. Сколько грузовых автомобилей на автостоянке?а) Пусть х — страниц осталось прочитать, тогда 2х — число прочитанных страниц, а уравнение:
2х + х = 60,
3х = 60,
х = 60 : 3,
х = 20 — страниц осталось прочитать
Ответ: 20 страниц осталось прочитать.б) Пусть х — число грузовых машин, тогда 7х — число легковых машин, а уравнение:
7х + х = 72,
8х = 72,
х = 72 : 8,
х = 9 — грузовых машин на стоянке
Ответ: 9 грузовых машин.640. а) У хозяйки было 20 кур и цыплят. Кур был в 4 раза меньше, чем цыплят. Сколько цыплят было у хозяйки?
б) У хозяйки было 16 уток и утят. Уток было в 3 раза меньше, чем утят. Сколько утят было у хозяйки?а) Пусть x — количество кур, тогда 4x — количество цыплят, а уравнение:
4x + x = 20,
5x = 20,
х = 20 : 5,
х = 4 — курицы было у хозяйки
4 • 4 = 16 — цыплят было у хозяйки
Ответ: 16 цыплят.б) Пусть x — количество уток, тогда 3x — количество утят, а уравнение:
3x + x = 16,
4x = 16,
x = 16 : 4,
х = 4 — утки было у хозяйки
3 • 4 = 12 — утят было у хозяйки
Ответ: 12 утят.641. а) Кусок полотна в 124 м надо разрезать на две части так, чтобы длина одной части была на 12 м больше, чем другой. По скольку метров полотна будет в каждой части?
б) Кусок лески длиной 16 м надо разрезать на две части так, чтобы длина одной части была на 1 м больше, чем другой. По скольку метров лески будет в каждой части?а) Пусть х — метров длина одной части, тогда х + 12 — метров длина второй части, а уравнение:
х + (х + 12) = 124,
х + х + 12 = 124,
2х = 124 — 12,
2х = 112,
х = 112 : 2,
х = 56 — метров длина одной части
56 + 12 = 68 — метров длина второй части
Ответ: 56 метров и 68 метров.б) Пусть х — метров длина одной части, тогда х + 1 — метров длина второй части, а уравнение:
х + (х + 1) = 16,
х + х + 1 = 16,
2х = 16 — 1,
2х = 15,
х = 15/2,
х = 7 1/2 — метров длина одной части
7 1/2 + 1 = 8 1/2 — метров длина второй части
Ответ: 7 1/2 метров и 8 1/2 метров.642. а) В школу привезли 690 столов и стульев. Стульев было на 230 больше, чем столов. Сколько столов и стульев в отдельности привезли в школу?
б) В соревнованиях по лыжам участвовали 53 человека. Девочек было на 17 меньше, чем мальчиков. Сколько мальчиков и девочек в отдельности участвовало в соревнованиях?а) Пусть х — количество столов, тогда х + 230 — количество стульев, а уравнение:
х + (х + 230) = 690,
х + х + 230 = 690,
2х = 690 — 230,
х = 460 : 2,
х = 230 — столов привезли
230 + 230 = 460 — стульев привезли
Ответ: 230 столов и 460 стульев.б) Пусть х — было девочек, тогда х + 17 — было мальчиков, а уравнение:
х + (х + 17) = 53,
х + х + 17 = 53,
2х = 53 — 17,
х = 36 : 2,
х = 18 — девочек было на соревнованиях
18 + 17 = 35 — мальчиков было на соревнованиях
Ответ: 18 девочек и 35 мальчиков.643. Двое должны поделить между собой 15 р. так, чтобы одному досталось на 4 р. больше, чем другому. Сколько достанется каждому?
Пусть х — рублей досталось одному, тогда х + 4 рублей досталось другому, а уравнение:
х + (х + 4) = 15,
х + х + 4 = 15,
2х = 15 — 4,
х = 11/2,
х = 5 1/2 — рублей или 5 рублей 50 копеек досталось одному
5 1/2 + 4 = 9 1/2 — рублей или 9 рублей 50 копеек досталось другому
Ответ: 5 рублей 50 копеек и 9 рублей 50 копеек.644. а) За конфеты заплатили в 3 раза больше, или на 6 р. больше, чем за печенье. Сколько заплатили за печенье?
б) За тетради заплатили в 4 раза больше, или на 7 р. 20 к. больше, чем за линейки. Сколько заплатили за линейки?а) Пусть x — рублей заплатили за печенье, тогда 3x или x + 6 — рублей заплатили за конфеты, а уравнение:
3х = х + 6,
3х — х = 6,
2х = 6,
х = 6 : 2,
х = 3 — рубля заплатили за печенье
Ответ: 3 рубля.б) Пусть x — рублей заплатили за линейки, тогда 4x или x + 7 р. 20 к. — заплатили за тетради (7р. 20 коп. = 7 20/100 р. = 7 1/5 р.), а уравнение:
4х = х + 7 1/5,
4х — х = 7 1/5,
3х = 7 1/5,
х = 7 1/5 : 3,
х = 36/5 • 1/3,
х = 12•1/5•1,
х = 12/5,
х = 2 2/5 — рубля или 2 рубля 40 копеек заплатили за линейки (2 2/5 р. = 2 р. 40/100 к. = 2 р. 40 к.).
Ответ: 2 рубля 40 копеек заплатили за линейки.645. а) Папа в 8 раз старше дочери, а дочь на 28 лет младше папы. Сколько лет папе?
б) Мама в 6 раз старше сына, а сын на 25 лет младше мамы. Сколько лет маме?а) Пусть х — возраст дочери, тогда 8х или х + 28 лет — возраст папы, а уравнение:
8х = х + 28,
8х — х = 28,
7х = 28,
х = 28 : 7,
х = 4 — года дочери
8 • 4 = 32 года папе
Ответ: 32 года папе.б) Пусть х — возраст сына, тогда 6х или х + 25 — возраст мамы, а уравнение:
6х = х + 25,
6х — х = 25,
5х = 25,
х = 25 : 5
х = 5 — лет сыну
6 • 5 = 30 — лет маме
Ответ: маме 30 лет.646. На солнышке грелись несколько кошек. У них вместе лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?
Пусть х — количество кошек, у каждой кошки по 4 лапы и по 2 уха, тогда 4х — количество лап, 2х — количество ушей, а уравнение:
4х — 2х = 10,
2х = 10,
х = 10 : 2,
х = 5 — кошек
О т в е т 5 кошек.647. Десяти собакам и кошкам скормили 56 галет. Каждой собаке досталось 6 галет, а каждой кошке — 5 галет. Сколько было собак и сколько кошек?
Пусть х — количество кошек, тогда 10 — x — количество собак и 5x галет скормили кошкам, а 6(10 — x) галет скормили собакам.
5x + 6(10 — x) = 56,
5x + 60 — 6x = 56,
—x = 56 — 60,
x = -4 : (-1),
х = 4 — кошки
10 — 4 = 6 — собак
Ответ: 4 кошки и 6 собак. 127
-
Ответы к стр. 127
Составьте уравнение по условию задачи, обозначив буквой неизвестное число, и решите его (637-652):
648. В хозяйстве имеются куры и овцы. Сколько тех и других, если известно, что у них всех вместе:
а) 19 голов и 46 ног; б) 30 голов и 74 ноги?а) У куриц и овец по одной голове, значит, всего животных было 19.
Пусть х — количество куриц, тогда 19 — х — количество овец, 2х — количество ног у куриц, 4(19 — х) — количество ног у овец, а уравнение:
2х + 4(19 — х) = 46,
2х + 76 — 4х = 46,
-2х = 46 — 76,
х = -30 : (-2),
х = 15 — куриц
19 — 15 = 4 — овцы
Ответ: 15 куриц и 4 овцы.б) У куриц и овец по одной голове, значит всего животных было 30.
Пусть х — количество куриц, тогда 30 — х — количество овец, 2х — количество ног у куриц, 4(30 — х) — количество ног у овец, а уравнение:
2х + 4(30 — х) = 74,
2х + 120 — 4х = 74,
-2х = 74 — 120,
х = -46 : (-2),
х = 23 — курицы
30 — 23 = 7 — овец
Ответ: 23 курицы и 7 овец.649. У пятнадцати треугольников и четырёхугольников 53 угла. Сколько треугольников и четырёхугольников в отдельности?
Пусть х — количество четырёхугольников, тогда 15 — х — количество треугольников, 4х — было всего углов у всех четырёхугольников, 3(15 — х) — было всего углов у всех треугольников, а уравнение:
4х + 3(15 — х) = 53,
4х + 45 — 3х = 53,
х = 53 – 45,
х = 8 — четырёхугольников
15 — 8 = 7 — треугольниковили
Пусть х — количество треугольников, тогда 15 — х — количество четырёхугольников, 3х — было всего углов у всех треугольников, 4(15 — х) — было всего углов у всех четырёхугольников, а уравнение:
3х + 4(15 — х) = 53,
3х + 60 — 4х = 53,
—х = 53 — 60,
х = -7 : (-1),
х = 7 — треугольников
15 — 7 = 8 — четырёхугольниковОтвет: 8 четырёхугольников и 7 треугольников.
650. а) Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было монет по 2 р.?
б) Если разменять 27 рублей на гривенники и двугривенные1 так, чтобы всех монет было 170, то сколько будет гривенников и сколько двугривенных?
1Гривенник и двугривенный — старинные названия монет в 10 и 20 копеек.а) Пусть х — количество 2-x рублевых монет, тогда 19 — x — количество 5-и рублевых монет, 2x — общая сумма 2-x рублевых монет, 5(19 — x) — общая сумма 5-и рублевых монет, а уравнение:
2x + 5(19 — x) = 74,
2x + 95 — 5x = 74,
-3x = 74 — 95,
x = -21 : (-3),
х = 7 — 2-x рублевых монет
Ответ: 7 2-x рублевых монет было.б) Пусть х — количество гривенников, тогда 170 — x — количество двугривенных, 10x — общая сумма гривенников (один гривенник равен 10 копейкам), 20(170 — x) — общая сумма двугривенных (один двугривенный равен 20 копейкам), а уравнение (27 рублей = 2700 копеек):
10x + 20(170 — x) = 2700,
10x + 3400 — 20x = 2700,
-10x = 2700 — 3400,
x = -700 : (-10),
х = 70 — гривенников
170 — 70 = 100 — двугривенных
Ответ: 70 гривенников и 100 двугривенных.651. Из «Арифметики» Л. Ф .Магницкого. Спросил некто учителя:
— Сколько имеешь учеников у себя в учении, ибо хочу отдать тебе в учение своего сына?
Учитель же отвечал ему:
— Если придёт ко мне ещё столько, сколько имею, да ещё половина и ещё четверть и ещё твой сын, то будет у меня 100 учеников.
Сколько учеников было у учителя?Пусть х — было учеников у учителя, тогда х — пришло столько же, 1/2 х — пришла половина, 1/4 х — пришла четверть, 1 человек — пришёл сын, а уравнение:
x + x + 1/2 x + 1/4 x + 1 = 100,
4/4 x + 4/4 х + 2/4 x + 1/4 x = 100 — 1,
11/4 x = 99,
x = 99 : 11/4,
х = 99 • 4/11,
х = 36 — учеников было у учителя
Ответ: 36 учеников.652. (Греция.)
Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?
— Вот сколько, — ответил философ, — половина изучает математику, четверть музыку, седьмая часть пребывает в молчании и, кроме того, есть ещё три женщины.Пусть х — всего учеников, тогда 1/2 x — изучает математику, 1/4 x — изучает музыку, 1/7 x — пребывает в молчании, 3 человека — количество женщин, а уравнение:
1/2 x + 1/4 x + 1/7 x + 3 = x,
14/28 x + 7/28 x + 4/28 x — 28/28 x = -3,
— 3/28 x = -3,
х = -3 : (- 3/28),
х = -3 • (- 28/3),
х = 28 — учеников занимается у Пифагора
Ответ: 28 учеников. 128
-
Рациональные числа
Буквенные выраженияОтветы к стр. 128
653. Замените число 5 буквой α в числовом выражении:
а) 7 • 5 — 1; б) 2 • 5 — 5 : 3.
Запишите полученное буквенное выражение.а) 7 • α — 1 или 7α -1;
б) 2 • α — α : 3 или 2α — α : 3.654. Приведите примеры буквенных выражений.
3α + 8, 5α, 6 : α — 2, α + b.
655. Подставьте вместо буквы α в буквенное выражение α + 3 число:
а) 5; б) 3; в) 1; г) 0; д) -1; е) -3.а) 5 + 3;
б) 3 + 3;
в) 1 + 3;
г) 0 + 3;
д) -1 + 3;
е) -3 + 3.656. Найдите значение буквенного выражения 7 + х при х, равном:
а) 0; б) 3 ;в) -1; г) -4; д) -7; е) -10.а) 7 + 0 = 7;
б) 7 + 3 = 10;
в) 7 + (-1) = 7 — 1 = 6;
г) 7 + (-4) = 7 — 4 = 3;
д) 7 + (-7) = 7 — 7 = 0;
е) 7 + (-10) = 7 — 10 = -3.657. Выражение α + 2 — это сумма α и 2, выражение 3 — x — это разность 3 и x. Прочитайте буквенные выражения:
а) 5 + α; б) 7 — α; в) 4 — x; г) α +12;
д) 2α; е) 7b; ж) -3α; з) α + (-3).а) 5 + α — это сумма 5 и α;
б) 7 — α — это разность 7 и α;
в) 4 — x — это разность 4 и x;
г) α + 12 — это сумма α и 12;
д) 2α — это произведение 2 и α;
е) 7b — это произведение 7 и b;
ж) -3α — это произведение -3 и α;
з) α + (-3) — это сумма α и -3.658. Вычислите значение буквенного выражения по образцу:
а) 10 — 4х при х = -5.
Решение. При х = -5 10 — 4х = 10 — 4 • (-5) = 10 + 20 = 30.
б) 2х + 1 при х = 5; в) 6 + 8х при х = -1;
г) 5 — 4α при α = 2; д) 3 — 7b при b = -2.б) при х = 5 2х + 1 = 2 • 5 + 1 = 10 + 1 = 11;
в) при х = -1 6 + 8х = 6 + 8 • (-1) = 6 + (-8) = -2;
г) при α = 2 5 — 4α = 5 — 4 • 2 = 5 — 8 = -3;
д) при b = -2 3 — 7b = 3 — 7 • (-2) = 3 + 14 = 17. 129
-
Ответы к стр. 129
Найдите значение буквенного выражения (659-660):
659. а) α + b при α = 1, b = 3; б) α — b при α = -2, b = 4;
в) 2х — y при х = 5, y = 6; г) 3х — 2y при х = -1, y = -4.а) при α = 1, b = 3 α + b = 1 + 3 = 4;
б) при α = -2, b = 4 α — b = -2 — 4 = -6;
в) при х = 5, y = 6 2х — y = 2 • 5 — 6 = 4;
г) при х = -1, y = -4 3х — 2y = 3 • (-1) — 2 • (-4) = -3 + 8 = 5.660. а) αb при α = 3/4, b = 1 3/5; б) 2(α + b) при α = 3/10, b = 1 1/2;
в) αbс при α = 1/3, b = 1 1/2, c = 2.а) при α = 3/4, b = 1 3/5 αb = 3/4 • 1 3/5 = 3/4 • 8/5 = 3•2/1•5 = 6/5 = 1 1/5;
б) при α = 3/10, b = 1 1/2 2(α + b) = 2 • (3/10 + 1 1/2) = 2 • (3/10 + 15/10) = 2 • 18/10 = 2•9/5 = 18/5 = 3 3/5;
в) при α = 1/3, b = 1 1/2, c = 2 αbс = 1/3 • 1 1/2 • 2 = 1/3 • 3/2 • 2 = 1•3•2/3•2 = 1.
Найдите значение каждого буквенного выражения при указанных значениях х (661-662):
661.
х 1 3 0 -1 -5 1/3 х — 1 0 2 -1 -2 -6 — 2/3 2х + 1 3 7 1 -1 -9 1 2/3 3 — 3х 0 -6 3 6 18 2 1 + 1/2 х 1 1/2 2 1/2 1 1/2 -1 1/2 1 1/6 662.
х 1 2 5 0 -2 -4 2х 2 4 10 0 -4 -8 х2 1 4 25 0 4 16 663. Стороны прямоугольника α и b. Запишите формулу периметра прямоугольника. Вычислите периметр при:
а) α = 2 см, b = 3 см; б) α = 7 см, b = 9 см;
в) α = 1 1/5 см, b = 3 4/5 см; г) α = 2 1/2 см, b = 3 1/4 см.Периметр прямоугольника равен: 2(α + b).
а) Р = 2 • (2 + 3) = 2 • 5 = 10 см;
б) Р = 2 • (7 + 9) = 2 • 16 = 32 см;
в) Р = 2 • (1 1/5 + 3 4/5) = 2 • (6/5 + 19/5) = 2 • 5 = 10 см;
г) Р = 2 • (2 1/2 + 3 1/4) = 2 • (5/2 + 13/4) = 2 • (10/4 + 13/4) = 2 • 23/4 = 23/2 = 11 1/2 см.664. Стороны прямоугольника α и b. Запишите формулу площади прямоугольника. Вычислите площадь при:
а) α = 2 см, b = 7 см; б) α = 4 см, b = 5 см;
в) α = 3 1/2 см, b = 2 2/5 см; г) α = 3 1/5 см, b = 1 1/4 см.Площадь прямоугольника равна: α • b.
а) S = 2 • 7 = 14 см2;
б) S = 4 • 5 = 20 см2;
в) S = 3 1/2 • 2 2/5 = 7/2 • 12/5 = 7•6/1•5 = 42/5 = 8 2/5 см2;
г) S = 3 1/5 • 1 1/4 = 16/5 • 5/4 = 4•1/1•1 = 4 см2.665. Сторона квадрата α. Запишите формулы периметра и площади квадрата. Вычислите периметр и площадь квадрата при:
а) α = 3 см; б) α = 8 см; в) α = 10 см;
г) α = 1/2 дм; д) α = 3 1/2 см; е) α = 2 3/4 см.Периметр квадрата равен: 4α, площадь квадрата равна: α2.
а) P = 4 • 3 = 12 см, S = 32 = 3 • 3 = 9 см2;
б) P = 4 • 8 = 32 см, S = 82 = 8 • 8 = 64 см2;
в) P = 4 • 10 = 40 см, S = 102 = 10 • 10 = 100 см2;
г) P = 4 • 1/2 = 4/2 = 2 дм, S = (1/2)2 = 1/2 • 1/2 = 1/4 дм2;
д) P = 4 • 3 1/2 = 4 • 7/2 = 2•7/1 = 14 см, S = (3 1/2)2 = 7/2 • 7/2 = 49/4 = 12 1/4 см2;
е) P = 4 • 2 3/4 = 4 • 11/4 = 11 см, S = (2 3/4)2 = 11/4 • 11/4 = 121/16 = 7 9/16 см2. 130
-
Рациональные числа
Буквенные выраженияОтветы к стр. 130
666. Длина, ширина и высота прямоугольного параллелепипеда α, b, c. Запишите формулу объёма прямоугольного параллелепипеда. Вычислите объём при:
а) α = 2 см, b = 3 см, с = 5 см; б) α = 2/5 см, b = 4 см, с = 5 см.Объём прямоугольного параллелепипеда равен: α • b • c.
а) V = 2 • 3 • 5 = 30 см3;
б) V = 2/5 • 4 • 5 = 2•4•5/5 = 8 см3.667. Ребро куба α. Запишите формулу объёма куба. Вычислите объём при:
а) α = 4 см; б) α = 5 см; в) α = 10 см.Объём куба равен: α3.
а) V = 43 = 4 • 4 • 4 = 64 см3;
б) V = 53 = 5 • 5 • 5 = 125 см3;
в) V = 103 = 10 • 10 • 10 = 1000 см3.668. Составьте буквенное выражение для вычисления площади S фигуры (рис. 67).
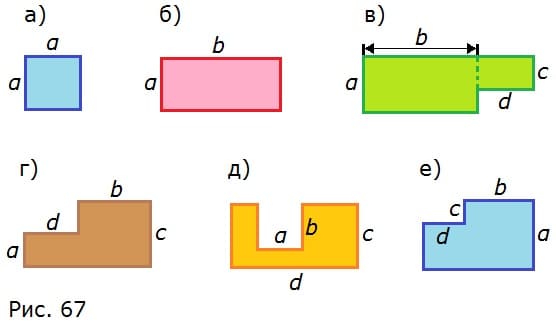
а) α2;
б) α • b;
в) α • b + d • c;
г) α • d + b • c;
д) с • d — α • b;
е) α • b + d • (α — c) = αb + αd — cd = α • (b + d) — сd.Решите задачу, составляя числовое выражение (669 — 671):
669. а) Купили 7 тетрадей по 50 к. и 2 ручки по 3 р. Сколько заплатили за покупку?
б) Купили 4 линейки по 40 к. и 3 угольника по 80 к. Сколько сдачи получили с 5 р.?а) 50 к. = 50/100 рубля, тогда:
7 • 50/100 + 2 • 3 = 350/100 + 6 = 3 50/100 + 6 = 9 50/100 — рубля или 9 рублей 50 копеек
Ответ: 9 рублей 50 копеек.б) 40 к. = 40/100 рубля, 80 к. = 80/100 рубля, тогда:
5 — (4 • 40/100 + 3 • 80/100) = 5 — (160/100 + 240/100) = 5 — 400/100 = 5 — 4 = 1 — рубль сдачи получили
Ответ: 1 рубль.670. а) Турист ехал 2 ч на поезде со скоростью 60 км/ч и шёл пешком 3 ч со скоростью 5 км/ч. Какое расстояние преодолел турист за 5 ч?
б) Длина маршрута 400 км. Турист ехал 4 ч поездом со скоростью 65 км/ч и 2 ч автобусом со скоростью 60 км/ч. За сколько часов он пройдет остаток пути пешком, если будет идти со скоростью 5 км/ч?а) 2 • 60 + 3 • 5 = 120 + 15 = 135 км.
Ответ: 135 км.б) 4 • 65 + 2 • 60 — путь на поезде и автобусе
400 — (4 • 65 + 2 • 60) — путь, который нужно пройти пешком
(400 — (4 • 65 + 2 • 60)) : 5 = (400 — (260 + 120)) : 5 = (400 — 380) : 5 = 20 : 5 = 4 — часа потребуется туристу, чтобы пройти остаток пути
Ответ: 4 часа. 131
-
Ответы к стр. 131
Решите задачу, составляя числовое выражение (669 — 671):
671. а) В бригаде 8 маляров, каждый за 2 ч может покрасить одно окно. За сколько часов бригада покрасит 24 окна?
б) Бригаде из 8 маляров нужно покрасить 40 окон. Каждый маляр за 2 ч может покрасить одно окно. Сколько окон останется покрасить через 8 ч работы бригады?а) 8 — количество окон, которое может покрасить бригада за 2 часа
8 : 2 – количество окон, которое может покрасить бригада за 1 час
24 : (8 : 2) = 24 : 4 = 6 — часов потребуется бригаде на покраску 24 окон
Ответ: 6 часов.б) 8 — количество окон, которое может покрасить бригада за 2 часа
8 : 2 — количество окон, которое может покрасить бригада за 1 час
8 : 2 • 8 − количество окон которое, покрасит бригада за 8 часов
40 — (8 : 2 • 8 ) = 40 — 32 = 8 — окон останется покрасить бригаде через 8 часов работы
Ответ: 8 окон.Решите задачу, составив буквенное выражение (672 — 673):
672. а) Книга стоит x р. Сколько стоят 8 таких книг?
б) Купили 10 тетрадей по x р. и 3 ручки по 3 р. Сколько заплатили за покупку?
в) Купили x линеек по 40 к. и 4 тетради по 50 к. Сколько сдачи получили с 5 р.?а) 8x — рублей стоит 8 книг;
б) 10x + 3 • 3 = 10x + 9 — рублей заплатили за покупку;
в) 5 — (40/100 x + 4 • 50/100) = 5 — (40/100 x + 200/100) = 5 — 2 — 40/100 x = 3 — 40/100 x = 3 — 2/5 x — рублей получится сдачи.673. а) Турист ехал x ч на поезде со скоростью 50 км/ч и шёл пешком 2 ч со скоростью 4 км/ч. Какое расстояние преодолел турист за всё время?
б) Длина маршрута 400 км. Турист ехал 4 ч поездом со скоростью x км/ч и 3 ч автобусом со скоростью 70 км/ч. За сколько часов он пройдёт остаток пути пешком, если будет идти со скоростью 4 км/ч?а) 50x + 2 • 4 = 50x + 8 — км преодолел турист за все время движения
Ответ: 50x + 8 км.б) (400 — (4x + 3 • 70)) : 4 = (400 — 4x — 210) : 4 = (190 — 4x) : 4 = 190/4 — x = 47 1/2 — x — часа потребуется туристу на преодоление остатка пути
Ответ: 47 1/2 — x часа.674. Через одну трубу можно наполнить бассейн за а мин, а через другую — за b мин. Через сколько минут наполнится бассейн, если открыть обе трубы? Составьте буквенное выражение для получения ответа, найдите его значение при:
а) α = 30, b = 20; б) α = 70, b = 30; в) α = 60, b = 90.1-я труба заполняет бассейн за α минут или 1/α бассейна за 1 минуту.
2-я труба заполняет бассейн за b минут или 1/b бассейна за 1 минуту.
Обе трубы одновременно заполняют бассейн за 1 минуту на 1/α + 1/b = b+α/αb, а весь бассейн за 1 : b+α/αb = 1 • αb/α+b = αb/α+b минут.
а) 30•20/30+20 = 600/50 = 12 минут;
б) 70•30/70+30 = 2100/100 = 21 минута;
в) 60•90/60+90 = 5400/150 = 36 минут.Составив буквенное выражение, решите задачи (675 — 676):
675. Сестра нашла x грибов, а брат в 2 раза больше. Сколько грибов нашёл брат? Сколько грибов они нашли вместе?
2x — грибов нашел брат
х + 2x = 3x — грибов нашли они вместе
Ответ: 2x и 3x.676. а) На решение примеров Вася затратил x мин, а на решение задачи на 10 мин больше. Сколько минут Вася затратил на всё задание?
б) В классе x девочек, а мальчиков на 4 меньше, чем девочек. Сколько всего учащихся в классе?а) x + x + 10 = 2x + 10 — минут затратил Вася на всё задание
Ответ: 2x + 10 минут.б) x + x — 4 = 2x — 4 — всего учащихся в классе
Ответ: 2x — 4 учащихся.Доказываем
677. Докажите, что если из суммы двух чисел вычесть их разность, то получится удвоенное меньшее число, т.е. для любых чисел α и b (α > b) верно равенство (α + b) — (α — b) = 2b.
(α + b) — (α — b) = α + b — α + b = 2b
678. Докажите, что для любых чисел α и b (α > b) верно равенство:
(α + b) + (α — b) = 2α.
Сформулируйте доказанное свойство суммы и разности двух числе в виде правила.Если к сумме двух чисел прибавить их разность, то получится удвоенное большее число:
(α + b) + (α — b) = α + b + α — b = 2α 132
-
Ответы к стр. 132
Доказываем
679. В старину для решения задач пользовались такими правилами: чтобы по сумме и разности двух чисел найти большее число, надо к полусумме двух чисел прибавить их полуразность; чтобы найти меньшее число, надо из полусуммы двух чисел вычесть их полуразность. Докажите равенства:
а) α+b/2 + α—b/2 = α; б) α+b/2 — α—b/2 = b.а) α+b/2 + α—b/2 = α+b+α—b/2 = 2α/2 = α;
б) α+b/2 — α—b/2 = α+b—α+b/2 = 2b/2 = b.680. а) Сумма двух чисел равна 37, а разность 13. Найдите эти числа.
б) Сумма двух чисел равна 48, а разность 12. Найдите эти числа.а) (α + b) — (α — b) = 2b, (α + b) + (α — b) = 2α, α + b = 37, α — b = 13, тогда:
37 — 13 = 2b, 37 + 13 = 2α,
24 = 2b, 50 = 2α,
b = 12 α = 25
Ответ: 12 и 25.б) (α + b) — (α — b) = 2b, (α + b) + (α — b) = 2α, α + b = 48, α — b = 12, тогда:
48 — 12 = 2b, 48 + 12 = 2α,
36 = 2b, 60 = 2α,
b = 18 α = 30
Ответ: 18 и 30.681. Найдите числа, сумма и разность которых равны соответственно:
а) 49 и 17; б) 72 и 48; в) 57 и 39; г) 38 и 2.а) (α + b) — (α — b) = 2b, (α + b) + (α — b) = 2α, α + b = 49, α — b = 17, тогда:
49 — 17 = 2b, 49 + 17 = 2α,
32 = 2b, 66 = 2α,
b = 16 α = 33
Ответ: 16 и 33.б) (α + b) — (α — b) = 2b, (α + b) + (α — b) = 2α, α + b = 72, α — b = 48, тогда:
72 — 48 = 2b, 72 + 48 = 2α,
24 = 2b, 120 = 2α,
b = 12 α = 60
Ответ: 12 и 60.в) (α + b) — (α — b) = 2b, (α + b) + (α — b) = 2α, α + b = 57, α — b = 39, тогда:
57 — 39 = 2b, 57 + 39 = 2α,
18 = 2b, 96 = 2α,
b = 9 α = 48
Ответ: 9 и 48.г) (α + b) — (α — b) = 2b, (α + b) + (α — b) = 2α, α + b = 38, α — b = 2, тогда:
38 — 2 = 2b, 38 + 2 = 2α,
36 = 2b, 40 = 2α,
b = 18 α = 20
Ответ: 18 и 20.682. а) Сумма двух чисел равна 304, одно из них больше другого на 50. Найдите эти числа.
б) Сумма двух чисел 760. Одно меньше другого на 98. Найдите эти числа.а) (α + b) — (α — b) = 2b, (α + b) + (α — b) = 2α, α + b = 304, α — b = 50, тогда:
304 — 50 = 2b, 304 + 50 = 2α,
254 = 2b, 354 = 2α,
b = 127 α = 177
Ответ: 127 и 177.б) (α + b) — (α — b) = 2b, (α + b) + (α — b) = 2α, α + b = 760, α — b = 98, тогда:
760 — 98 = 2b, 760 + 98 = 2α,
662 = 2b, 858 = 2α,
b = 331 α = 429
Ответ: 331 и 429.683. Если собственную скорости лодки обозначить x км/ч, а скорость течения y км/ч, то что можно найти, вычислив x + y; x — y?
x + y — это скорость лодки, плывущей по течению;
x — y — это скорость лодки, плывущей против течения.684. Если скорость лодки по течению x км/ч, а скорость течения y км/ч, то что такое x — y; x — 2y?
x — y — это скорость лодки, плывущей в стоячей воде;
x — 2y — это скорость лодки, плывущей против течения.685. Если скорость лодки против течения x км/ч, а скорость течения у км/ч, то что такое x + y; x + 2y?
x + y — это скорость лодки, плывущей в стоячей воде;
x + 2y — это скорость лодки, плывущей по течению. 136
-
Фигуры на плоскости, симметричные относительно прямой
Ответы к стр. 136
686. Какие две фигуры называют симметричными относительно прямой а?
Две фигуры называют симметричными относительно прямой а, плоскость рисунка перегнуть относительно прямой а, разделяющую эти фигуры на рисунке друг от друга, и эти фигуры совместятся.
687. По рисунку 79 определите, какая точка симметрична относительно прямой а точке:
а) A;
б) B;
в) C;
г) D;
д) M.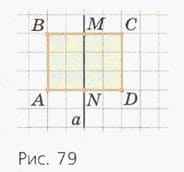
Ответ:
а) D;
б) C;
в) B;
г) A;
д) M.688. По рисунку 79 определите, какой отрезок симметричен относительно прямой а отрезку:
а) AB;
б) BM;
в) BC;
г) CD;
д) AN;
е) ND;
ж) AD.
Ответ:
а) DC;
б) CM;
в) CB;
г) BA;
д) DN;
е) NA;
ж) DA.689. Какой фигуре симметричен относительно прямой а (рис. 79) прямоугольник:
а) ABMN;
б) MCDN;
в) ABCD.
Ответ:
а) DCMN;
б) MBAN;
в) DCBA.690. Какую фигуру называют симметричной относительно прямой а?
Ответ: Фигуру называют симметричной относительно прямой а, если плоскость фигуры перегнуть относительно прямой а, делящую эту фигуры пополам, и эта плоскость половины фигуры совместится с плоскостью второй половины фигуры.
691. Постройте на клетчатой бумаге прямоугольник 4 * 6 и все его оси симметрии. Сколько осей симметрии имеет прямоугольник?
Ответ: 2 оси симметрии.
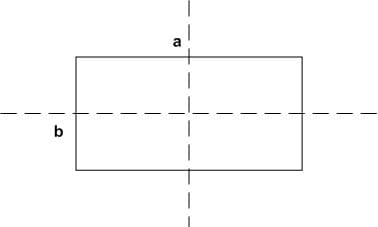
692. Постройте на клетчатой бумаге квадрат 6 * 6 и все его оси симметрии. Сколько осей симметрии имеет квадрат?
Ответ: 4 оси симметрии.
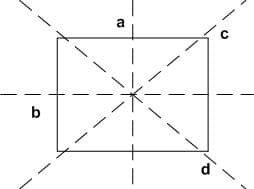
693. Постройте окружность с центром О и три её оси симметрии. Сколько осей симметрии имеет окружность?
Ответ: Любая прямая, проходящая через центр окружности будет являться её осью симметрии. Окружность будет иметь бесконечное количество осей симметрии.
694. Перерисуйте в тетрадь те буквы алфавита, у которых есть оси симметрии. Для каждой из них укажите число осей симметрии.
Ответ:
695. Нарисуйте в тетради фигуру, имеющую:
а) одну ось симметрии;
б) две оси симметрии.Ответ:
696. Перегните лист бумаги пополам, вырежьте ножницами какую−нибудь фигуру, имеющую ось симметрии.
Ответ:
697. Перегните лист бумаги как показано на рисунке 80. Из полученного треугольника вырежьте выделенные цветом части. Сколько осей симметрии имеет полученная "снежинка"?
Ответ: 4 оси симметрии.
137
-
Ответы к странице 137
698. Вырежьте из бумаги "снежинку", имеющую восемь осей симметрии.
Ответ:
699. Дан отрезок AB и прямая b, не пересекающая этот отрезок. Постройте отрезок MN, симметричный отрезку AB относительно прямой b.
Ответ:
700. Дана прямая b и отрезок AB, пересекающий эту прямую. Постройте отрезок MN, симметричный отрезку AB относительно прямой b. Где лежит точка пересечения отрезков AB и MN? Как это объяснить?
Ответ:
Отрезок AB симметричен MN, значит для точки пересечения отрезка AB и прямой b должна быть симметричная точка на отрезке MN, а так как две точки называются симметричными относительно точки O, если эти точки лежат на одной прямой и точка O является серединой отрезка которые эти точки образует, то точка пересечения отрезков AB и MN лежит на прямой b в месте пересечения отрезков AB и MN.
701. Дан треугольник АВС и прямая b, не пересекающая стороны этого треугольника. Постройте треугольник, симметричный треугольнику АВС относительно прямой b.
Ответ:
702. Дан треугольник АВС и прямая b, пересекающая стороны этого треугольника. Постройте треугольник, симметричный треугольнику АВС относительно прямой b.
Ответ:
703. Дана прямая b и окружность, пересекающая эту прямую. Постройте окружность, симметричную данной окружности относительно прямой b.
Ответ:
704. На плане (рис.81) показана железная дорога и два города A и B. Укажите место на железной дороге, где надо построить станцию C, чтобы суммарная длина дороги от A до C и от C до B была наименьшей.
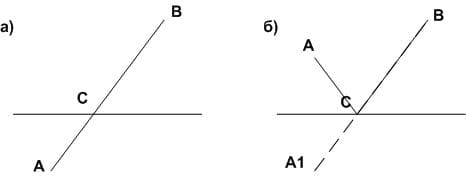
а) Кратчайшее расстояние это прямая, поэтому суммарная длина дороги от A до C и от C до B будет наименьшей, если точка C будет находиться на пересечении отрезка между городами A и B и железной дороги.
б) Для того, чтобы суммарная длина дороги от A до C и от C до B была наименьшей, необходимо построить точку A1, симметричную точке A, относительно железной дороги и поставить точку C в месте пересечения железной дороги и отрезка A1B.705. В жаркий день медвежонок направился из своего дома (А) в гости к ослику (В), но сначала решил подойти к реке попить воды. Укажите кратчайший путь от А до В с заходом к реке (рис.82).
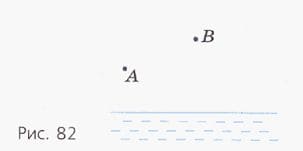
Ответ: Для того, чтобы путь от А до В был кратчайшим, необходимо построить точку А1, симметричную точке А, относительно реки и поставить точку в месте пересечения реки и отрезка А1В.
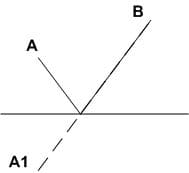
706. Другой раз медвежонок направился из дома (A) в гости к ослику (B), но сначала решил подойти к реке попить воды, а потом поесть малины. Укажите кратчайший путь от A до B с заходом к реке и к кустам малины (рис.83)
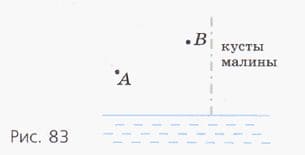
Ответ: Для того, чтобы путь от A до B был кратчайшим, необходимо:
1. Построить точку A1, симметричную точке A, относительно реки;
2. Построить точку B1, симметричную точке B, относительно кустам малины;
3. Провести отрезок A1B1
4. В местах пересечения отрезком A1B1 поставить соответственно точки C и D
5. Соединить точки ACBD, который и будет кратчайшим маршрутом медвежонка.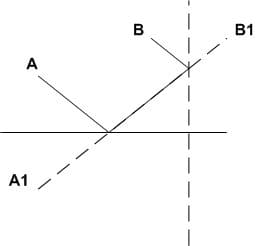
138
-
Ответы к странице 138
707. а) Рыба весит 5 кг и еще полрыбы. Сколько весит рыба?
б) Книга стоит 30 р. и еще полкниги. Сколько стоит книга?а) Пусть x − вес рыбы, тогда из условия получим:
5 + 1/2 x = x
1/2 x − x = − 5
1/2 x = 5
x = 5 : 1/2 = 5 ∗ 2 = 10.
Ответ: 10 кг.
б) Пусть книга стоит x, тогда по условию получим:
30 + 1/2 x = x
1/2 x − x = − 30
1/2 x = 30
x = 30 : 1/ 2 = 30 ∗ 2 = 60
Ответ: 60 рублей.708. Один автолюбитель рассказывал: "Я отправился путешествовать на "Москвиче", имея одно запасное колесо.
а) Время от времени я заменял колёса, и оказалось, что первое колесо проехало 1000 км, второе − 900 км, третье − 800 км, четвертое − 700 км и пятое − 600 км". Сколько километров проехал автомобиль?
б) Может ли автомобилист так менять колёса, чтобы первое колесо проехало 1400 км, второе − 1200 км, третье − 1000 км, четвертое − 800 км и пятое − 600 км?а) Раз одно из колёс проехало 1000 км, то значит и машина как минимум проехала 1000 км.
Максимальное расстояние которое машина могла проехать равно:
(1000 + 900 + 800 +700 + 600) : 4 = 4000 : 4 = 1000 км.
Максимальное и минимальное расстояние пройденное машиной совпадают, следовательно, машина проехала 1000 км.
Ответ: 1000 км.б) Раз одно из колёс проехало 1000 км, то значит и машина как минимум проехала 1400 км.
Максимальное расстояние которое машина могла проехать равно:
(1400 + 1200 + 1000 + 800 + 600) : 4 = 5000 : 4 = 1250 км.
Максимальное расстояние меньше минимального, а значит машина не может проехать расстояние с заданными условиями.
Ответ: не может. 139
-
Ответы к странице 139
709. Среди математиков каждый седьмой − философ, а среди философов каждый девятый − математик. Кого больше: философов или математиков?
Пусть:
a − люди, которые знают только математику,
b − люди, которые знают только философию,
c − люди, которые знают и математику и философию.
Тогда всего:
a + c − математиков,
b + c − философов,
c=1/7 ( a + c ) − философов среди математиков,
c= 1/9 ( b + c ) − математиков среди философов.
1/7 ( a + с ) = 1/9 ( b + c )
( a + c ) = 1/9 ( b + c ) : 1/7
( a + c ) = 1/9 ( b + c ) ∗ 1/7
( a + c ) = 7/9 ( b + c )
Сравним математиков (a + c) и философов (b + c):
( a + c ) − ( b + c ) = 7/9 ( b + c ) − ( b + c ) = ( 7/9 − 1 ) ∗ ( b + c ) = − 2/9 ( b + c ) < 0, то есть философов больше, так как вычитая из количества математиков количество философов получилось большее число.
Ответ: больше философов.710. Восемь подружек решили обменяться фотографиями так, чтобы у каждой из них оказались фотографии остальных подруг. Сколько фотографий для этого потребуется?
Чтобы раздать каждой подруге по фотографии, каждой девочке необходимо принести 7 фотографий. Всего подружек 8, поэтому:
8 * 7 = 56 фотографий потребуется.
Ответ: 56 фотографий потребуется.711. В нашем классе каждая девочка дружит ровно с тремя мальчиками, а каждый мальчик дружит ровно с двумя девочками. Сколько учащихся в нашем классе, если мальчиков на 5 больше, чем девочек?
Пусть девочек х, тогда:
мальчиков х + 5,
дружеских пар девочек 3х,
дружеских пар мальчиков 2(х + 5)
3х = 2(х + 5)
3х = 2х + 10
х = 10 девочек в классе,
10 + 5 = 15 мальчиков в классе,
10 + 15 = 25 детей всего в классе.
Ответ: 25 детей.712. В первенстве по футболу принимают участие 8 команд. Каждая команда играет с каждой по одному разу. За выигрыш команда получает 2 очка, за ничью − 1 очко, за проигрыш − 0 очков. Какая наибольшая и какая наименьшая разница очков может быть между первым и последним местом, если известно, что первое место заняла одна команда и последнее место заняла одна команда?
Каждая команда в течении первенства сыграет по 7 матчей.
Максимальное количество очков, которое может набрать команда победитель равно:
7 * 2 = 14 очков.
Минимальное количество очков, которое может набрать команда, занявшая последнее место равно:
7 * 0 = 0 очков.
14 − 0 = 14 очков наибольшая разница, которая может разделить команду, занявшую первое место и команду, занявшую последнее место.
Найдем минимальную разницу, которая может разделить команду, занявшую первое место и команду, занявшую последнее место.
Разница не может быть равна 0 и 1, так как тогда нарушится условие задачи, что только одна команда заняла первое место, и одна команда заняла последнее место. Проверим, может ли разница составить 2 очка.
Для того, чтобы разница составила 2 очка, необходимо, чтобы остальные 6 команд, кроме победителя и команды, занявшей последнее место, набрали одинаковое количество очков, а значит сыграли все свои матчи в ничью.
Раз 6 команд сыграли все свои игры в ничью, то у команды победителя будет 6 ничьих и у команды, занявшей последнее место, будет так же 6 ничьих. Всего в первенстве каждая команда сыграет по 7 матчей, значит в матче между командой − победителем и командой, занявшей последнее место выиграл команда победитель. Турнирная таблица тогда примет следующий вид:
1 место: 1 победа 6 ничьих 0 поражений = 1 * 2 + 6 * 1 + 0 = 2 + 6 = 8 очков.
2 − 7 место: 0 побед 7 ничьих 0 поражений = 0 + 7 * 1 + 0 = 7 очков.
8 место: 0 побед 6 ничьих 1 поражение = 0 + 6 * 1 + 0 = 6 очков.
8 − 6 = 2 очка минимальная разница, которая может разделить команду, занявшую первое место и команду, занявшую последнее место.
Ответ:
Максимальная разница = 14 очков;
Минимальная разница = 2 очка.713. Большая коробка конфет в 2 раза дороже маленькой. Хотят купить 3 большие коробки и 2 маленькие, но если купить 2 большие коробки и 3 маленькие, то покупка будет дешевле на 15 р. Сколько стоит каждая коробка?
Пусть маленькая коробка стоит х рублей, тогда:
2х рублей стоит большая коробка,
3 * 2х + 2х = 2 * 2х + 3х + 15
6х + 2х − 4х − 3х = 15
х = 15 рублей стоит маленькая коробка,
2 * 15 = 30 рублей стоит большая коробка.
Ответ:
маленькая коробка стоит 15 рублей;
большая коробка стоит 30 рублей.714. Один экскаватор может вырыть траншею за 30 ч, другой − за 20 ч. Первый проработал 9 ч, потом второй закончил работу. За сколько часов была выполнена работа?
Первый экскаватор за 1 час выкапывает
1/30 траншеи.
1/30 ∗ 9 = 9/30 = 3/10 траншеи выкопал первый экскаватор за 9 часов.
1 − 3/10 = 7/10 траншеи осталось выкопать второму экскаватору.
Второй экскаватор за 1 час выкапывает 1 20 траншеи.
7/10 : 1/20 = 7/10 ∗ 1/20 = 7 ∗ 2 = 14 ч потребуется 2 экскаватору чтобы выполнить свою часть работы.
9 + 14 = 23 часа ушло на работу двух экскаваторов.
Ответ: 23 часа.715. (Индия, XIв.)
Есть кадамба цветок,
На один лепесток
Пчелок пятая часть опустилась,
Рядом тут же росла
Вся в цвету симегенда,
И на ней третья часть поместилась.
Разность их ты найди,
Ее трижды сложи
И тех пчел на Кутай посади.
Лишь одна не нашла себе места нигде.
Всё летала то взад, то вперед и везде
Ароматом цветов наслаждалась.
Назови теперь мне,
Подсчитавши в уме,
Сколько пчелок всего здесь собралось.Пусть всего было x пчел, тогда:
1/5 x пчел опустилось на кадамбы цветок,
1/3 x пчел опустилось на симегенду,
3 ( 1/3 x − 1/5 x ) пчел село на Кутай,
1 пчела не нашла себе место.
1/5 x + 1/3 x + 3 ( 1/3 x − 1/5 x ) + 1 = x
1/5 x + 1/3 x + x − 3/5 x − x = − 1
3/15 x + 5/15 x + x − 9/15 x − x = − 1
− 1/15 x = − 1
x = − 1 : − 1/15
x = 15 пчел было всего.
Ответ: 15 пчел. 140
-
Ответы к странице 140
716. (Армения, VII в.) Один купец прошел через три города, и взыскали с него в первом городе пошлины половину и треть имущества, во втором городе половину и треть (с того, что осталось) и в третьем городе снова взыскали половину и треть (с того, что у него было), и когда он прибыл домой, у него осталось 11 дахеканов (денежных единиц). Итак, узнай, сколько всего дахеканов было в начале у купца.
Пусть всего было x дахеканов, тогда:
1/2 x + 1/3 x взыскали в первом городе,
x − ( 1/2 x + 1/3 x ) = x − 3+2/6 x = x − 5/6 x = 1/6 x осталось дахеканов после первого города;
1/6 x ∗ 1/2 + 1/6 x ∗ 1/3 = 1/6 x ( 1/2 + 1/3 ) = 1/6 x ∗ 5/6 = 5/36 x взыскали во втором городе;
1/6 x − 5/36 x = 6 − 5/36 x = 1/36 x дахеканов осталось после посещения второго города;
1/36 x ∗ 1/2 + 1/36 x ∗ 1/3 = 1/36 x ( 1/2 + 1/3 ) = 1/36 x ∗ 5/6 = 5/216 x взыскали в третьем городе;
1/36 x − 5/216 x = 6 − 5/216 x = 1/216 x дахеканов осталось после посещения третьего города.
1/216 x = 11
x = 11 : 1/216 = 11 ∗ 216 = 2376 дахеканов было изначально.
Ответ: 2376 дахеканов.717. Из Акимского папируса (VIв.) Некто взял из сокровищницы 1/13. Другой взял 1/17 из того, что осталось, оставил же в сокровищнице 150. Мы хотим узнать, сколько было в сокровищнице первоначально.
Пусть изначально в сокровищнице было x, тогда:
Первый взял (1/13 x) и в сокровищнице осталось x − 1/13 x = 12/13 x.
Второй взял 1/17 ∗ 12/13 x = 12/221 x и в сокровищнице осталось:
12/13 x − 12/221 x = 204 − 12/221 x = 192/221 x.
192/221 x = 150
x = 150 : 192/221 = 150 ∗ 221/192 = 25 ∗ 221/32 = 5525/32 = 172 21/32 изначально было в сокровищнице.
Ответ: 172 21/32.718. Из "Арифметики" Л.Ф.Магницкого. Некто пришёл в ряд, купил игрушек для малых ребят: за первую игрушку заплатил 1/5 часть всех своих денег, за другую 3/7 остатка от первой покупки, за треть игрушку заплатил 3/5 остатка от второй покупки, а по приезду в дом нашел остальных в кошельке денег 1 р. 92 к. Спрашивается, сколько в кошельке денег было и сколько за которую игрушку денег заплачено.
Пусть всего денег было x, тогда за первую игрушку заплатили 1/5 x,
x − 1/5 x = 4/5 x всех денег осталось в кошельке после первой покупки;
3/7 ∗ 4/5 x = 12/35 x заплатили за вторую игрушку,
4/5 x − 12/35 x = 28 − 12/35 x = 16/35 x всех денег осталось в кошельке после второй покупки;
3/5 ∗ 16/35 x = 48/175 x заплатили за третью игрушку,
16/35 x − 48/175 x = 80 − 48/175 x = 32/175 x всех денег осталось в кошельке после третьей покупки;
1 р. 92 к. = 1 92/100 рубля.
32/175 x = 1 92/100
x = 192/100 : 32/175 = 192/100 ∗ 175/32 = 6/4 ∗ 7/1 = 3 ∗ 7/2 = 21/2 = 1050/100 = 10 50/100 = 10 рублей 50 копеек было, тогда:
10 50/100 ∗ 1/5 = 1050/100 ∗ 1/5 = 210/100 = 2 10/100 = 2 рубля 10 копеек заплатили за первую игрушку;
10 50/100 ∗ 12/35 = 1050/100 ∗ 12/35 = 30 ∗ 12/100 = 360/100 = 3 60/100 = 3 рубля 60 копеек заплатили за вторую игрушку;
10 50/100 ∗ 48/175 = 1050/100 ∗ 48/175 = 6 ∗ 48/100 = 288/100 = 2 88/100 = 2 рубля 88 копеек заплатили за третью игрушку.
Ответ:
Всего было: 10 рублей 50 копеек;
за первую игрушку заплатили 2 рубля 10 копеек;
за вторую игрушку заплатили 3 рубля 60 копеек;
за третью игрушку заплатили 2 рубля 88 копеек.719. Для перевозки 25 зеркал нанят извозчик с условием заплатить ему по 1 р. 50 к. за доставку каждого зеркала в целости и вычесть с него по 5 р. за каждое разбитое им зеркало. На дороге извозчик действительно разбил несколько зеркал и за перевозку получил только 18 р. Сколько зеркал он доставил в целости?
Пусть разбили x зеркал, тогда:
25 − x − доставлено целых зеркал;
1 р. 50 к. = 1 50/100 = 1 1/2 рубля.
3/2 ∗ ( 25 − x ) − 5 x = 18
75/2 − 3/2 x − 5 x = 18
− 3/2 x − 5 x = 18 − 37 1/2
− 5 3/2 x = − 19 1/2
x = − 19 1/2 : − 5 3/2
x = 39/2 : 13/2
x = 39/2 ∗ 2/13 = 3 зеркала разбили.
25 − 3 = 22 зеркала доставили целыми.
Ответ: 22 зеркала.720. Первый мастер шьёт шубу за 5 дней, а второй за 3 дня. Как распределить между ними заказ на пошив 9 шуб, чтобы каждый сшил целое число шуб и заказ был выполнен в кратчайший срок?
Найдите x в уравнении x : 1/5 = ( 9 − x ) : 1/3 и укажите, сколько шуб должен сшить 1 мастер, чтобы закончить свою работу одновременно со вторым мастером:
x = 3 3/8+
x = 3 5/8
x = 3 7/8
x = 3 1/8
1. Раскройте скобки;
2. Перенесите слагаемые с x в левую часть уравнения, а слагаемые без x в правую часть уравнения (при переносе не забываем менять знак).
3. Выполните вычисления.1/5 шубы за 1 день шьёт первый мастер;
1/3 шубы за 1 день шьёт второй мастер;
Пусть первый сошьет x шуб, тогда:
9 − x шуб сошьет второй.
Кратчайший срок исполнения заказа будет в том случае, если оба мастера закончат работу одновременно, тогда:
x : 1/5 = ( 9 − x ) : 1/3
x ∗ 5/1 = ( 9 − x ) ∗ 3/1
5 x = 27 − 3 x
5 x + 3 x = 27
8 x = 27
x = 27/8 = 3 3/8 шубы необходимо дать первому мастеру и 3 5/8 шубы второму мастеру, чтобы они закончили свою работу одновременно и работа была закончена в кратчайший срок. По условию задачи количество шуб должно быть целым, тогда первому мастеру даём ближайшее целое число к 3 3/8, а это 3. Тогда второму мастеру достанется 9 − 3 = 6 шуб.
3 : 1/5 = 3 ∗ 5 = 15 дней первый мастер будет шить 3 шубы;
мастеру достанется 9 − 3 = 6 шуб.
6 : 1/3 = 6 ∗ 3 = 18 дней второй мастер будет шить 6 шуб.
Так как мастера работают одновременно, то срок выполнения заказа составит 18 дней.
Ответ:
Первому мастеру 3 шубы;
Второму мастеру 6 шуб;
Заказ будет выполнен за 18 дней.721. Три пирата Джон, Джек и Билл откопали кувшин с золотыми. Джон хотел взять себе треть всех золотых и половину остатка дать Джеку. Джек хотел взять себе половину всех золотых и треть остатка дать Джону. На каком варианте дележа они остановились, Билл не помнит, но он точно знает, что ему досталось 50 золотых. Сколько золотых было в кувшине?
Пусть всего монет в кувшине было x, тогда:
1 вариант:
1/3 x монет взял себе Джон,
x − 1/3 x = 2 3 x монет осталось в кувшине, после того как Джон взял свою долю;
2/3 x : 2 = 2/3 x ∗ 1/2 = 1/3 x − монет досталось Джеку;
x − 1/3 x − 1/3 x = 50
1/3 x = 50
x = 50 : 1/3 = 50 ∗ 3 = 150 монет было в кувшине.2 вариант:
1/2 x монет взял себе Джек,
x − 1/2 x = 1 2 x монет осталось в кувшине, после того как Джек взял свою долю;
1/2 x : 3 = 1/2 x ∗ 1/3 = 1/6 x − монет досталось Джону;
x − 1/2 x − 1/6 x = 50
x − 3/6 x − 1/6 x = 50
x − 4/6 x = 50
x − 2/3 x = 50
1/3 x = 50
x = 50 : 1/3 = 50 ∗ 3 = 150 монет было в кувшине.
Ответ: в обоих случаях в кувшине было 150 монет. 141
-
Ответы к странице 141
722. Имея полный бак топлива, рыбак может проплыть на моторной лодке 20 км против течения или 30 км по течению реки. На какое наибольшее расстояние он может отплыть по реке при условии, что топлива должно хватить и на обратный путь? Движение с выключенным мотором не рассматривается.
1/20 бака тратится на 1 км пути против течения;
1/30 бака тратится на 1 км пути по течению;
Путь в одну сторону равен пути в другую сторону, поэтому пусть этот отрезок реки будет равен x км, тогда:
1/20 x + 1/30 x = 1
5/60 x = 1
x = 1 : 5/60 = 1 ∗ 60/5 = 1 ∗ 12 = 12 к м − наибольшее расстояние на которое может отплыть рыбак.
Ответ: 12 км.723. Остап купил 4 новых колеса для своего автомобиля. Он знает, что передние колеса, автомобиля изнашиваются через 12 тыс.км пробега, а задние − через 8 тыс. км пробега. Какой наибольший путь может проехать автомобиль, если Остап догадается вовремя поменять задние колеса с передними?
Пусть ресурс колеса равен 1, тогда:
переднее колесо изнашивается на1/12 за каждую тысячу километров;
заднее колесо изнашивается на 1 8 за каждую тысячу километров.
Пусть проехали x километров до смены шин и y километров после смены шин, тогда:
x + у − общий путь пройденный автомобилем;
1 − 1/12 x − остаток ресурса передних колес после смены;
1 − 1/8 x − остаток ресурса задних колес после смены;
1 − 1/12 x − 1/8 y − остаток ресурса передних колес после всего пройденного расстояния;
1 − 1/8 x − 1/12 y − остаток ресурса задних колес после всего пройденного расстояния.
Машина проедет максимально расстояние, если колеса износятся полностью, то есть:
1 − 1/12 x − 1/8 y = 0
1/12 x + 1/8 y = 1
2 x + 3 y/24 x = 1
2 x + 3 y = 24
и 1 − 1/8 x − 1/12 y = 0
1/8 x + 1/12 y = 1
3 x + 2 y 24 x = 1
3 x + 2 y = 24
2 x + 3 y + 3 x + 2 y = 24 + 24
5 x + 5 y = 48
5 ( x + y ) = 48
x + y = 48/5 = 9 3/5 = 9 600/1000 тыс.км = 9600 км.
Ответ: 9600 км. 144
-
Десятичные дроби
Понятие положительной десятичной дробиОтветы к стр. 144
724. Запишите и обыкновенные и смешанные дроби в виде десятичных и прочитайте полученные записи:
а) 3 1/10, 2 9/10, 15 4/10, 3/10, 5/10, 11/10, 27/10;
б) 5 12/100, 7 20/100, 6 91/100, 13/100, 85/100, 7/100, 111/100;
в) 5 135/1000, 17 399/1000, 8 999/1000, 777/1000, 123/1000, 87/1000, 2011/1000;
г) 4 8899/10000, 1 5678/10000, 1234/10000, 6969/10000, 98/10000, 2012/10000.а) 3 1/10 = 3,1 — три целых одна десятая,
2 9/10 = 2,9 — две целых девять десятых,
15 4/10 = 15,4 — пятнадцать целых четыре десятых,
3/10 = 0,3 — нуль целых три десятых,
5/10 = 0,5 — нуль целых пять десятых,
11/10 = 1,1 — одна целая одна десятая,
27/10 = 2,7 — две целых семь десятых;б) 5 12/100 = 5,12 — пять целых двенадцать сотых,
7 20/100 = 7,2 — семь целых две десятых,
6 91/100 = 6,91 — шесть целых девяносто одна сотая,
13/100 = 0,13 — нуль целых тринадцать сотых,
85/100 = 0,85 — нуль целых восемьдесят пять сотых,
7/100 = 0,07 — нуль целых семь сотых,
111/100 = 1,11 — одна целая одиннадцать сотых;в) 5 135/1000 = 5,135 — пять целых сто тридцать пять тысячных,
17 399/1000 = 17,399 — семнадцать целых триста девяносто девять тысячных,
8 999/1000 = 8,999 — восемь целых девятьсот девяносто девять тысячных,
777/1000 = 0,777 – нуль целых семьсот семьдесят семь тысячных,
123/1000 = 0,123 – нуль целых сто двадцать три тысячных,
87/1000 = 0,087 – нуль целых восемьдесят семь тысячных,
2011/1000 = 2,011 – две целых одиннадцать тысячных;г) 4 8899/10000 = 4,8899 – четыре целых восемь тысяч восемьсот девяносто девять десятитысячных,
1 5678/10000 = 1,5678 – одна целая пять тысяч шестьсот семьдесят восемь десятитысячных,
1234/10000 = 0,1234 – нуль целых одна тысяча двести тридцать четыре десятитысячных,
6969/10000 = 0,6969 – нуль целых шесть тысяч девятьсот шестьдесят девять десятитысячных,
98/10000 = 0,0098 – нуль целых девяносто восемь десятитысячных,
2012/10000 = 0,2012 – нуль целых две тысячи двенадцать десятитысячных.725. Прочитайте дроби, запишите их в виде обыкновенных или смешанных дробей:
а) 3,2; 7,3; 3,5; 0,1; 0,9;
б) 7,12; 9,23; 10,34; 0,45; 0,56;
в) 12,333; 16,596; 0,887; 0,379; 0,111;
г) 2,1111; 5,1995; 4,1996; 0,1997; 0,1998.а) 3,2 (три целых две десятых) = 3 2/10;
7,3 (семь целых три десятых) = 7 3/10;
3,5 (три целых пять десятых) = 3 5/10;
0,1 (нуль целых одна десятая) = 1/10;
0,9 (нуль целых девять десятых) = 9/10;б) 7,12 (семь целых двенадцать сотых) = 7 12/100;
9,23 (девять целых двадцать три сотых) = 9 23/100;
10,34 (десять целых тридцать четыре сотых) = 10 34/100;
0,45 (нуль целых сорок пять сотых) = 45/100;
0,56 (нуль целых пятьдесят шесть сотых) = 56/100;в) 12,333 (двенадцать целых триста тридцать три тысячных) = 12 333/1000;
16,596 (шестнадцать целых пятьсот девяносто шесть тысячных) = 16 596/1000;
0,887 (нуль целых восемьсот восемьдесят семь тысячных) = 887/1000;
0,379 (нуль целых триста семьдесят девять тысячных) = 379/1000;
0,111 (нуль целых сто одиннадцать тысячных) = 111/1000;г) 2,1111 (две целых одна тысяча сто одиннадцать десятитысячных) = 2 1111/10000;
5,1995 (пять целых одна тысяча девятьсот девяносто пять десятитысячных) = 5 1995/10000;
4,1996 (четыре целых одна тысяча девятьсот девяносто шесть десятитысячных) = 4 1996/10000;
0,1997 (нуль целых одна тысяча девятьсот девяносто семь десятитысячных) = 1997/10000;
0,1998 (нуль целых одна тысяча девятьсот девяносто восемь десятитысячных) = 1998/10000.726. Запишите обыкновенные и смешанные дроби в виде десятичных и прочитайте полученные записи:
а) 4 1/100; 215 3/100; 9/100; 2/100; 11/100; 21 17/100;
б) 3 1/1000; 7 12/1000; 8/1000; 81/1000; 32 7/1000; 113/1000;
в) 6 5/10000; 2 13/10000; 356/10000; 679/10000; 2011/10000; 15 17/10000;
г) 7 7/100000; 100 46/100000; 627/100000; 1111/100000; 98 2012/100000.а) 4 1/100 = 4,01 – четыре целых одна сотая;
215 3/100 = 215,03 – двести пятнадцать целых три сотых;
9/100 = 0,09 – нуль целых девять сотых;
2/100 = 0,02 – нуль целых две сотых;
11/100 = 0,11 – нуль целых одиннадцать сотых;
21 17/100 = 21,17 – двадцать одна целая семнадцать сотых;б) 3 1/1000 = 3,001 – три целых одна тысячная;
7 12/1000 = 7,012 – семь целых двенадцать тысячных;
8/1000 = 0,008 – нуль целых восемь тысячных;
81/1000 = 0,081 – нуль целых восемьдесят одна тысячная;
32 7/1000 = 32,007 – тридцать две целых семь тысячных;
113/1000 = 0,113 – нуль целых сто тринадцать тысячных;в) 6 5/10000 = 6,0005 – шесть целых пять десятитысячных;
2 13/10000 = 2,0013 – две целых тринадцать десятитысячных;
356/10000 = 0,0356 – нуль целых триста пятьдесят шесть десятитысячных;
679/10000 = 0,0679 – нуль целых шестьсот семьдесят девять десятитысячных;
2011/10000 = 0,2011 – нуль целых две тысячи одиннадцать десятитысячных;
15 17/10000 = 15,0017 – пятнадцать целых семнадцать десятитысячных;г) 7 7/100000 = 7,00007 – семь целых семь стотысячных;
100 46/100000 = 100,00046 – сто целых сорок шесть стотысячных;
627/100000 = 0,00627 – нуль целых шестьсот двадцать семь стотысячных;
1111/100000 = 0,01111 – нуль целых одна тысяча сто одиннадцать стотысячных;
98 2012/100000 = 98,02012 – девяносто восемь целых две тысячи двенадцать стотысячных.727. Запишите в виде неправильной дроби:
а) 12,3; б) 1,23; в) 10,123; г) 987,6; д) 98,76;
е) 9,876; ж) 2,2222; з) 22,222; и) 222,22.а) 12,3 = 123/10;
б) 1,23 = 123/100;
в) 10,123 = 10123/1000;
г) 987,6 = 9876/10;
д) 98,76 = 9876/100;
е) 9,876 = 9876/1000;
ж) 2,2222 = 22222/10000;
з) 22,222 = 22222/1000;
и) 222,22 = 22222/100.728. Прочитайте дроби:
а) 5,05; 7,01; 12,07; 0,01; 0,09;
б) 19,004; 6,016; 8,008; 0,001; 0,022;
в) 13,0007; 2,0089; 16,0999; 0,0001; 0,0022;
г) 31,00009; 7,00099; 0,00001; 0,00666.а) 5,05 — пять целых пять сотых;
7,01 — семь целых одна сотая;
12,07 — двенадцать целых семь сотых;
0,01 — нуль целых одна сотая;
0,09 — нуль целых девять сотых;б) 19,004 — девятнадцать целых четыре тысячных;
6,016 — шесть целых шестнадцать тысячных;
8,008 — восемь целых восемь тысячных;
0,001 — нуль целых одна тысячная;
0,022 — нуль целых двадцать две тысячных;в) 13,0007 — тринадцать целых семь десятитысячных;
2,0089 — две целых восемьдесят девять десятитысячных;
16,0999 — шестнадцать целых девятьсот девяносто девять десятитысячных;
0,0001 — нуль целых одна десятитысячная;
0,0022 — нуль целых двадцать две десятитысячных;г) 31,00009 — тридцать одна целая девять стотысячных;
7,00099 — семь целых девяносто девять стотысячных;
0,00001 — нуль целых одна стотысячная;
0,00666 — нуль целых шестьсот шестьдесят шесть стотысячных. 145
-
Десятичные дроби
Понятие положительной десятичной дробиОтветы к стр. 145
729. Почитайте дроби, назовите их целые части, назовите цифры разрядов десятых, сотых и т. д.
а) 16,789; 0,1234; 100,56789; б) 0,023; 7,00526; 0,00017.а) 16,789 — шестнадцать целых семьсот восемьдесят девять тысячных, целая часть – шестнадцать, разряд десятых – семь, разряд сотых – восемь, разряд тысячных – девять;
0,1234 — нуль целых одна тысяча двести тридцать четыре десятитысячных, целая часть – нуль, разряд десятых – один, разряд сотых – два, разряд тысячных – три, разряд десятитысячных – четыре;
100,56789 — сто целых пятьдесят шесть тысяч семьсот восемьдесят девять стотысячных, целая часть – сто, разряд десятых – пять, разряд сотых – шесть, разряд тысячных – семь, разряд десятитысячных – восемь, разряд стотысячных — девять;
б) 0,023 — нуль целых двадцать три тысячных, целая часть – нуль, разряд десятых – нуль, разряд сотых – два, разряд тысячных – три;
7,00526 — семь целых пятьсот двадцать шесть стотысячных, целая часть – семь, разряд десятых – нуль, разряд сотых – нуль, разряд тысячных – пять, разряд десятитысячных – два, разряд стотысячных — шесть;
0,00017 — нуль целых семнадцать стотысячных, целая часть – нуль, разряд десятых – нуль, разряд сотых – нуль, разряд тысячных – нуль, разряд десятитысячных – один, разряд стотысячных – семь.
730. Запишите в виде десятичной дроби по образцу:
а) 18/30 = 3•6/3•10 = 6/10 = 0,6; б) 27/90, 24/120, 24/40, 48/60;
в) 15/500, 160/400, 36/900, 140/700; г) 11/11000, 81/3000, 144/40000, 8888/400000.б) 27/90 = 9•3/9•10 = 3/10 = 0,3,
24/120 = 12•2/12•10 = 2/10 = 0,2,
24/40 = 4•6/4•10 = 6/10 = 0,6,
48/60 = 6•8/6•10 = 8/10 = 0,8;в) 15/500 = 5•3/5•100 = 3/100 = 0,03,
160/400 = 40•4/40•10 = 4/10 = 0,4,
36/900 = 9•4/9•100 = 4/100 = 0,04,
140/700 = 70•2/70•10 = 2/10 = 0,2;г) 11/11000 = 11•1/11•1000 = 1/1000 = 0,001,
81/3000 = 3•27/3•1000 = 27/1000 = 0,027,
144/40000 = 4•36/4•10000 = 36/10000 = 0,0036,
8888/400000 = 4•2222/4•100000 = 2222/100000 = 0,02222.731. Запишите в виде десятичной дроби по образцу:
а) 1/4 = 1•25/4•25 = 25/100 = 0,25; б) 1/2, 1/5, 2/5, 3/5, 4/5;
в) 3/4, 1/25, 3/25, 24/25, 7/25; г) 1/20, 1/50, 21/50, 3/40, 9/200;
д) 16/10, 324/100, 99/10, 1234/1000; е) 168/40, 328/80, 9999/900, 1648/160;
ж) 3/2, 6/5, 17/4, 39/25; з) 13/20, 14/20, 14/700, 35/500, 36/500.б) 1/2 = 1•5/2•5 = 5/10 = 0,5,
1/5 = 1•2/5•2 = 2/10 = 0,2,
2/5 = 2•2/5•2 = 4/10 = 0,4,
3/5 = 3•2/5•2 = 6/10 = 0,6,
4/5 = 4•2/5•2 = 8/10 = 0,8;в) 3/4 = 3•25/4•25 = 75/100 = 0,75,
1/25 = 1•4/25•4 = 4/100 = 0,04,
3/25 = 3•4/25•4 = 12/100 = 0,12,
24/25 = 24•4/25•4 = 96/100 = 0,96,
7/25 = 7•4/25•4 = 28/100 = 0,28;г) 1/20 = 1•5/20•5 = 5/100 = 0,05,
1/50 = 1•2/50•2 = 2/100 = 0,02,
21/50 = 21•2/50•2 = 42/100 = 0,42,
3/40 = 3•25/40•25 = 75/1000 = 0,075,
9/200 = 9•5/200•5 = 45/1000 = 0,045;д) 16/10 = 1 6/10 = 1,6,
324/100 = 3 24/100 = 3,24,
99/10 = 9 9/10 = 9,9,
1234/1000 = 1 234/1000 = 1,234;е) 168/40 = 4 8/40 = 4 4•2/4•10 = 4 2/10 = 4,2,
328/80 = 4 8/80 = 4 8•1/8•10 = 4 1/10 = 4,1,
9999/900 = 11 99/900 = 11 9•11/9•100 = 11 11/100 = 11,11,
1648/160 = 10 48/160 = 10 16•3/16•10 = 10 3/10 = 10,3;ж) 3/2 = 1 1/2 = 1 1•5/2•5 = 1 5/10 = 1,5,
6/5 = 1 1/5 = 1 1•2/5•2 = 1 2/10 = 1,2,
17/4 = 4 1/4 = 4 1•25/4•25 = 4 25/100 = 4,25,
39/25 = 1 14/25 = 1 14•4/25•4 = 1 56/100 = 1,56;з) 13/20 = 13•5/20•5 = 65/100 = 0,65,
14/20 = 14•5/20•5 = 70/100 = 0,7,
14/700 = 7•2/7•100 = 2/100 = 0,02,
35/500 = 5•7/5•100 = 7/100 = 0,07,
36/500 = 36•2/500•2 = 72/1000 = 0,072.732. Выразите в метрах и дециметрах по образцу:
а) 3,2 м = 3 м 2 дм; б) 4,9 м; в) 6,1 м.б) 4,9 м = 4 м 9 дм;
в) 6,1 м = 6 м 1 дм.733. Выразите в метрах и сантиметрах:
а) 3,12 м; б) 8,54 м; в) 6,02 м; г) 6,2 м.а) 3,12 м = 3 м 12 см;
б) 8,54 м = 8 м 54 см;
в) 6,02 м = 6 м 2 см;
г) 6,2 м = 6 м 20 см.734. Выразите в рублях и копейках по образцу:
а) 3,45 р. = 3 р. 45 к.; б) 3,56 р.; в) 5,6 р.;
г) 6,05 р.; д) 6,1 р.; е) 0,25 р.б) 3,56 р. = 3 р. 56 к.;
в) 5,6 р. = 5 р. 60 к.;
г) 6,05 р. = 6 р. 5 к.;
д) 6,1 р. = 6 р. 10 к.;
е) 0,25 р. = 25 к.735. Выразите в килограммах и граммах:
а) 8,537 кг; б) 8,037 кг; в) 8,007 кг; г) 8,530 кг; д) 8,500 кг.а) 8,537 кг = 8 кг 537 г;
б) 8,037 кг = 8 кг 37 г;
в) 8,007 кг = 8 кг 7 г;
г) 8,530 кг = 8 кг 530 г;
д) 8,500 кг = 8 кг 500 г.736. Выразите в тоннах и килограммах:
а) 0,435 т; б) 4,350 т, в) 5,024 т; г) 6,030 т; д) 7,008 т.а) 0,435 т = 435 кг;
б) 4,350 т = 4 т 350 кг;
в) 5,024 т = 5 т 24 кг;
г) 6,030 т = 6 т 30 кг;
д) 7,008 т = 7 т 8 кг.737. Запишите величину, используя десятичные дроби, по образцу:
а) 23 см 2 мм = 23 2/10 см = 23,2 см;
б) 5 м 6 дм; в) 7 м 54 см; г) 8 м 4 см;
д) 11 ц 52 кг; е) 11 ц 50 кг; ж) 11 ц 5 кг;
з) 5 р. 48 к.; и) 5 р. 50 к.; к) 3 р. 5 к.б) 5 м 6 дм = 5 6/10 м = 5,6 м;
в) 7 м 54 см = 7 54/100 м = 7,54 м;
г) 8 м 4 см = 8 4/100 м = 8,04 м;
д) 11 ц 52 кг = 11 52/100 ц = 11,52 ц;
е) 11 ц 50 кг = 11 50/100 ц = 11,5 ц;
ж) 11 ц 5 кг = 11 5/100 ц = 11,05 ц;
з) 5 р. 48 к. = 5 48/100 р = 5,48 р.;
и) 5 р. 50 к. = 5 50/100 р = 5,5 р.;
к) 3 р. 5 к = 3 5/100 р = 3,05 р. 146
-
Ответы к стр. 146
738. Выполните действия:
а) 8,23 м + 3,56 м; б) 7,39 р. − 6,27 р.;
в) 0,3 дм • 0,2 дм; г) 1,3 м • 0,02 м;
д) 4,62 км : 2 с; е) 12 км : 5 ч.а) 8,23 м + 3,56 м = 8 23/100 м + 3 56/100 м = 11 79/100 м = 11,79 м;
б) 7,39 р. − 6,27 р. = 7 39/100 р. – 6 27/100 р. = 1 12/100 р. = 1,12 р.;
в) 0,3 дм • 0,2 дм = 3/10 дм • 2/10 дм = 6/100 дм2 = 0,06 дм2;
г) 1,3 м • 0,02 м = 130/100 м • 2/100 м = 260/10000 = 0,026 м2;
д) 4,62 км : 2 с = 462/100 км : 2 с = 462/100 км • 1/2 с = 462/200 км/с = 231/100 км/с = 2,31 км/с;
е) 12 км : 5 ч = 12 км • 1/5 ч = 12/5 км/ч = 24/10 км/ч = 2,4 км/ч.
147
-
Десятичные дроби
Сравнение положительных десятичных дробейОтветы к стр. 147
739. Что получится, если у десятичной дроби в дробной части приписать справа нули? Приведите примеры.
Если у десятичной дроби в дробной части приписать справа нули, тот получится дробь, равная данной:
0,81 = 0,810 = 0,8100 = 0,81000.740. Что получится, если у десятичной дроби в дробной части отбросить справа нули? Приведите примеры.
Если у десятичной дроби в дробной части отбросить справа нули, тот получится дробь, равная данной:
0,81000 = 0,8100 = 0,810 = 0,81.741. Какая из двух положительных десятичных дробей больше? Приведите примеры.
Из двух десятичных положительных дробей больше та, у которой целая часть больше; при равенстве целых частей больше та дробь, у которой цифра разряда десятых больше; при равенстве целых частей и цифр разряда десятых больше та дробь, у которых цифра разряда сотых больше, и т. д.:
8,1 > 7,1; 8,23 > 8,22.742. Уравняйте число цифр после запятой у дробей:
а) 1,2 и 3,51; б) 0,23 и 0,123; в) 0,6 и 3,02;
г) 7,125 и 0,48007; д) 6,23 и 7,5; е) 8,2001 и 9,00007.а) 1,20 и 3,51;
б) 0,230 и 0,123;
в) 0,60 и 3,02;
г) 7,12500 и 0,48007;
д) 6,23 и 7,50;
е) 8,20010 и 9,00007.743. Сколько десятых, сотых, тысячных содержит дробь:
а) 1,235; б) 1,27; в) 3,51; г) 0,5?а) две десятых, три сотых, пять тысячных;
б) две десятых, семь сотых, нуль тысячных;
в) пять десятых, одна сотая, нуль тысячных;
г) пять десятых, нуль сотых, нуль тысячных.744. Какая из дробей больше:
а) 6,35 или 5,19; б) 7,48 или 7,51;
в) 2,52 или 2,53; г) 17,49 или 17,5?а) 6,35 > 5,19, так как целая часть первой дроби (шесть) больше целой части второй дроби (пять);
б) 7,48 < 7,51, так как целые части дробей равны, а цифра разряда десятков первой дроби (четыре) меньше цифры разряда десятков второй дроби (пять);
в) 2,52 < 2,53, так как целые части и цифра разряда десятков дробей равны, а цифра разряда сотен первой дроби (два) меньше цифры разряда сотен второй дроби (три);
г) 17,49 < 17,5, так как целые части дробей равны, а цифра разряда десятков первой дроби (четыре) меньше цифры разряда десятков второй дроби (пять).
745. Используя знаки = и ≠, сравните дроби:
а) 7,5 и 7,50; б) 8,5 и 9,1; в) 0,48 и 0,4;
г) 0,25 и 0,2500; д) 7,48 и 7,481; е) 3,1 и 2,99.а) 7,5 = 7,50;
б) 8,5 ≠ 9,1;
в) 0,48 ≠ 0,4;
г) 0,25 = 0,2500;
д) 7,48 ≠ 7,481;
е) 3,1 ≠ 2,991.Используя знаки > и <, сравните дроби (746-748):
746. а) 3,59 и 7,1; б) 6,28 и 6,9; в) 0,4 и 0,51;
г) 72,7 и 7,27; д) 4,1234 и 4,1231; е) 12,39 и 1,2399.а) 3,59 < 7,1;
б) 6,28 < 6,9;
в) 0,4 < 0,51;
г) 72,7 > 7,27;
д) 4,1234 > 4,1231;
е) 12,39 > 1,2399.747. а) 2,078 и 2,780; б) 3,205 и 3,025; в) 7,250 и 7,205;
г) 4,290 и 4,295; д) 12,4 и 12,41; е) 15,129 и 15,1.а) 2,078 < 2,780;
б) 3,205 > 3,025;
в) 7,250 > 7,205
г) 4,290 < 4,295;
д) 12,4 < 12,41;
е) 15,129 > 15,1.748. а) 6,92 и 6,9; б) 1,2 и 1,19; в) 72,3 и 7,239; г) 0,48 и 0,471.
а) 6,92 > 6,9;
б) 1,2 > 1,19;
в) 72,3 > 7,239;
г) 0,48 > 0,471.Укажите число, большее одного из данных чисел, но меньшее другого (749-751):
749. а) 4000 и 5000; б) 4200 и 4300;
в) 4250 и 4260; г) 4290 и 4300.а) 4000 < 4350 < 5000;
б) 4200 < 4250 < 4300;
в) 4250 < 4256 < 4260;
г) 4290 < 4294 < 4300.750. а) 0,600 и 0,700; б) 0,650 и 0,660;
в) 0,650 и 0,655; г) 0,655 и 0,660.а) 0,600 < 0,655 < 0,700;
б) 0,650 < 0,656 < 0,660;
в) 0,650 < 0,653 < 0,655;
г) 0,655 < 0,656 < 0,660.751. а) 0,6 и 0,7; б) 0,48 и 0,49;
в) 0,65 и 0,66; г) 0,325 и 0,326.а) 0,6 < 0,66 < 0,7;
б) 0,48 < 0,484 < 0,49;
в) 0,65 < 0,655 < 0,66;
г) 0,325 < 0,3257 < 0,326. 148
-
Ответы к стр. 148
752. Расположите дроби в порядке возрастания:
а) 0,8; 1,17; 0,789; 1,7; б) 3,5; 0,35; 3,35; 0,335.а) 0,789; 0,8; 1,17; 1,7;
б) 0,335; 0,35; 3,35; 3,5.753. Расположите дроби в порядке убывания:
а) 7,4; 6,98; 7,199; 6,899; б) 0,449; 0,49; 0,5; 0,499.а) 7,4; 7,199; 6,98; 6,899;
б) 0,5; 0,499; 0,49; 0,449.754. Изобразите на координатной прямой числа:
а) 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1,0;
б) 0,2; 0,4; 0,6; 0,8; 1,0; 1,2; 1,4; 1,6; 1,8; 2,0.
755. В каком порядке (слева направо) на координатной прямой расположены точки:
а) А(1,2), В(0,2), C(1,13); б) М(7,48), N(4,78), К(7,8)?а) В(0,2), C(1,13), А(1,2);
б) N(4,78), М(7,48), К(7,8).756. Запишите величины с помощью десятичных дробей и сравните их:
а) 7 кг 485 г и 6 кг 90 г; б) 5 м 48 см и 5 м 40 см;
в) 7 км 740 м и 7 км 74 м; г) 8 т 5 кг и 8 т 500 кг.а) 7 кг 485 г = 7,485 кг, 6 кг 90 г = 6,9 кг,
7,485 кг > 6,9 кг;б) 5 м 48 см = 5,48 м, 5 м 40 см = 5,4 м,
5,48 м > 5,4 м;в) 7 км 740 м = 7,74 км, 7 км 74 м = 7,074 км,
7,74 км > 7,074 км;г) 8 т 5 кг = 8,005 т, 8 т 500 кг = 8,5 т,
8,005 т < 8,5 т.757. Запишите в метрах и сантиметрах:
а) 6,79 м; 12,48 м; 16,06 м; б) 19,01 м; 7,40 м; 7,4 м; 8,1 м.а) 6,79 м = 6 м 79 см;
12,48 м = 12 м 48 см;
16,06 м = 16 м 6 см;б) 19,01 м = 19 м 1 см;
7,40 м = 7 м 40 см;
7,4 м = 7 м 40 см;
8,1 м = 8 м 10 см.758. Запишите в тоннах и килограммах:
а) 3,569 т; 6,760 т; 6,070 т; б) 6,007 т; 4,480 т; 4,48 т; 9,4 т.а) 3,569 т = 3 т 569 кг;
6,760 т = 6 т 760 кг;
6,070 т = 6 т 70 кг;б) 6,007 т = 6 т 7 кг;
4,480 т = 4 т 480 кг;
4,48 т = 4 т 480 кг;
9,4 т = 9 т 400 кг. 149
-
Десятичные дроби
Сложение и вычитание положительных десятичных дробейОтветы к стр. 149
Вычислите (759-761):
759. а) 1,5 + 2,3; б) 3,7 + 1,4; в) 12,3 + 1,23;
г) 7,84 + 8,9; д) 125,34 + 12,534; е) 7,53 + 8,624.а) +1,5
2,3
3,81
б) +3,7
1,4
5,1в) +12,30
1,23
13,531
г) + 7,84
8,90
16,74д) +125,340
12,534
137,8741
е) + 7,530
8,624
16,154760. а) 6,48 − 2,35; б) 7,26 − 3,19; в) 2,528 − 1,9;
г) 7,2 − 3,148; д) 6,98 − 3,99; е) 7,25 − 3,261.а) −6,48
2,35
4,13•
б) −7,26
3,19
4,07•
в) −2,528
1,900
0,628•
г) −7,200
3,148
4,052• •
д) −6,98
3,99
2,99• • •
е) −7,250
3,261
3,989761. а) 38 + 0,56; б) 7,39 + 11; в) 0,736 + 25;
г) 8,248 − 6; д) 7,2 − 1,899; е) 5 − 3,78.а) +38,00
0,56
38,56б) + 7,39
11,00
18,39в) + 0,736
25,000
25,736г) −8,248
6,000
2,248д) −7,200
1,899
5,301е) −5,00
3,78
1,22 150
-
Ответы к стр. 150
Вычислите, применяя законы сложения и правила раскрытия скобок (762-763):
762. а) 7,48 + 3,19 + 1,12 + 6,81; б) 6,2 + 7,49 + 1,8 + 1,29;
в) 16,28 + 5,395 − 1,18 − 4,305; г) 7,358 + 8,24 − 6,458 − 2,84.а) 7,48 + 3,19 + 1,12 + 6,81 = (7,48 + 1,12) + (3,19 + 6,81) = 8,6 + 10 = 18,6;
+7,48 + 3,16 + 8,6
1,12 6,81 10,00
8,60 10,00 18,60б) 6,2 + 7,49 + 1,8 + 1,29 = (6,2 + 1,8) + (7,49 + 1,29) = 8 + 8,78 = 16,78;
+6,2 +7,49 + 8,00
1,8 1,29 8,78
8,0 8,78 16,78в) 16,28 + 5,395 − 1,18 − 4,305 = (16,28 − 1,18) + (5,395 — 4,305) = 15,1 + 1,09 = 16,19;
−16,28 −5,395 +15,10
1,18 4,305 1,09
15,10 1,090 16,19г) 7,358 + 8,24 − 6,458 − 2,84 = (7,358 − 6,458) + (8,24 − 2,84) = 0,9 + 5,4 = 6,3.
−7,358 −8,24 +0,90
6,458 2,84 5,40
0,900 5,40 6,30763. а) 5,236 + (4,664 − 2,6); б) 4,756 − (2,395 − 1,244).
а) 5,236 + (4,664 − 2,6) = (5,236 + 4,664) − 2,6 = 9,9 − 2,6 = 7,3.
+5,236 −9,9
4,664 2,6
9,900 7,3б) 4,756 − (2,395 − 1,244) = (4,756 + 1,244) − 2,395 = 6 — 2,395 = 3,605.
+4,756 −6,000
1,244 2,395
6,000 3,605764. Заменив десятичную дробь обыкновенной, вычислите:
а) 2,5 + 3 1/2; б) 7 3/4 − 2,25; в) 0,2 • 3;
г) 4,8 : 4; д) 6 : 0,6; е) 12 : 0,3.а) 2,5 + 3 1/2 = 2 5/10 + 3 1/2 = 2 1/2 + 3 1/2 = 6;
б) 7 3/4 − 2,25 = 7 75/100 – 2 25/100 = 5 50/100 = 5 1/2;
в) 0,2 • 3 = 2/10 • 3 = 6/10 = 3/5;
г) 4,8 : 4 = 48/10 • 1/4 = 12/10 = 1 2/10 = 1 1/5;
д) 6 : 0,6 = 6 : 6/10 = 6 • 10/6 = 10.
е) 12 : 0,3 = 12 : 3/10 = 12 • 10/3 = 40.765. Заменив обыкновенную дробь десятичной, вычислите:
а) 1/10 + 2,5; б) 7 3/100 − 2,15; в) 4,12 – 1 1/5;
г) 9,1 + 3 1/2; д) 17,3 – 9 1/4; е) 6,09 + 2 1/25.а) 1/10 + 2,5 = 0,1 + 2,5 = 2,6;
б) 7 3/100 − 2,15 = 7,03 − 2,15 = 4,88;
в) 4,12 – 1 1/5 = 4,12 – 1 2/10 = 4,12 − 1,2 = 2,92;
г) 9,1 + 3 1/2 = 9,1 + 3 5/10 = 9,1 + 3,5 = 12,6;
д) 17,3 – 9 1/4 = 17,3 – 9 25/100 = 17,3 − 9,25 = 8,05;
е) 6,09 + 2 1/25 = 6,09 + 2 4/100 = 6,09 + 2,04 = 8,13.766. Вычислите периметр прямоугольника, если:
а) его ширина равна 2,3 см, а длина на 1,9 см больше;
б) его ширина равна 2,48 дм, а длина на 1,6 дм больше;
в) его длина равна 12,1 см, а ширина на 4,8 см меньше;
г) его длина равна 18 дм, а ширина на 4,7 дм меньше.а) 1) 2,3 + 1,9 = 4,2 (см) – длина
2) 2,3 + 2,3 + 4,2 + 4,2 = 13 (см) — периметр
Ответ: периметр 13 см.б) 1) 2,48 + 1,6 = 4,08 (дм) – длина
2) 2,48 + 2,48 + 4,08 + 4,08 = 13,12 (дм) — периметр
Ответ: периметр 13,12 дм.в) 1) 12,1 – 4,8 = 7,3 (см) – ширина
2) 12,1 + 12,1 + 7,3 + 7,3 = 38,8 (см) — периметр
Ответ: периметр 38,8 см.г) 1) 18 – 4,7 = 13,3 (дм) – ширина
2) 18 + 18 + 13,3 + 13,3 = 62,6 (дм) — периметр
Ответ: периметр 62,6 дм.767. Вычислите по образцу:
а) 1,2 дм + 1,2 см = 1,2 дм + 0,12 дм = 1,32 дм;
б) 16 см + 4,35 дм; в) 7,35 м + 4,9 дм; г) 2 * 4,8 дм;
д) 4,8 дм : 2; е) 12,3 дм − 42 см; ж) 34 дм − 34 см.б) 16 см + 4,35 дм = 1,6 дм + 4,35 дм = 5,95 дм;
в) 7,35 м + 4,9 дм = 73,5 дм + 4,9 дм = 78,4 дм;
г) 2 • 4,8 дм = 2 • 48 см = 96 см = 9,6 дм;
д) 4,8 дм : 2 = 48 см : 2 = 24 см = 2,4 дм;
е) 12,3 дм − 42 см = 12,3 дм − 4,2 дм = 8,1 дм;
ж) 34 дм − 34 см = 34 дм − 3,4 дм = 30,6 дм.768. Вычислите периметр треугольника, имеющего стороны:
а) 490 мм, 48 см, 4,7 дм; б) 23 мм, 3,4 см, 0,48 дм;
в) 3,5 см, 0,38 дм, 0,041 м; г) 0,125 м, 1,З дм, 14,5 см.а) 490 мм + 48 см + 4,7 дм = 49 см + 48 см + 47 см = 144 (см) — периметр
Ответ: периметр 144 см.б) 23 мм + 3,4 см + 0,48 дм = 2,3 см + 3,4 см + 4,8 см = 10,5 (см) — периметр
Ответ: периметр 10,5 см.в) 3,5 см + 0,38 дм + 0,041 м = 3,5 см + 3,8 см + 4,1 см = 11,4 (см) — периметр
Ответ: периметр 11,4 см.г) 0,125 м + 1,3 дм + 14,5 см = 12,5 см + 13 см + 14,5 см = 40 (см) — периметр
Ответ: периметр 40 см.769. В квартире две комнаты. Одна комната имеет площадь 16,3 м2, а другая на 1,9 м2 меньше. Какова площадь двух комнат?
1) 16,3 – 1,9 = 14,4 (м2) — площадь второй комнаты
2) 16,3 + 14,4 = 30,7 (м2) − площадь двух комнат
Ответ: площадь комнат 30,7 м2.770. В квартире три комнаты общей площадью 44,8 м2. Одна комната имеет площадь 11,3 м2, другая на 3,5 м2 больше. Найдите площадь третьей комнаты.
1) 11,3 + 3,5 = 14,8 (м2) – площадь второй комнаты
2) 11,3 + 14,8 = 26,1 (м2) – площадь первой и второй комнат
3) 44,8 – 26,1 = 18,7 (м2) − площадь третьей комнаты
Ответ: 18,7 м2.771. Щенок весит 2,5 кг, а котёнок на 2,1 кг меньше. Сколько весят котёнок и щенок вместе?
1) 2,5 – 2,1 = 0,4 (кг) – весит котёнок
2) 2,5 + 0,4 = 2,9 (кг) − весят котёнок и щенок вместе
Ответ: 2,9 кг.772. Турист проехал на автобусе 48,4 км − это на 25,8 км больше, чем он прошёл пешком. Какое расстояние турист преодолел на автобусе и пешком?
1) 48,4 – 25,8 = 22,6 (км) – прошёл пешком
2) 48,4 + 22,6 = 71 (км) — преодолел турист на автобусе и пешком
Ответ: 71 км.773. Боря собрал 12,6 кг яблок − это на 2,8 кг больше, чем собрал Алёша, и на 1,4 кг меньше, чем собрал Серёжа. Сколько килограммов яблок собрали мальчики вместе?
1) 12,6 – 2,8 = 9,8 (кг) – яблок собрал Алёша
2) 12,6 + 1,4 = 14 (кг) – яблок собрал Серёжа
3) 12,6 + 9,8 + 14 = 36,4 (кг) – яблок собрали мальчики вместе
Ответ: 36,4 кг яблок. 151
-
Ответы к стр. 151
774. В кассе была некоторая сумма денег. Поступило в кассу 480,5 р., а выдано из кассы 538,1 р. После чего в кассе осталось 1230,8 р. Сколько денег было в кассе первоначально?
х р. – было в кассе денег сначала, х + 480,5 р. – стало после поступления, х + 480,5 – 538,1 р. – стало после выдачи, что равно 1230,8 р. Тогда:
х + 480,5 − 538,1 = 1230,8;
х = 1230,8 − 480,5 + 538,1;
х = 750,3 + 538,1;
х = 1288,4 — рубля было в кассе
Ответ: 1288,4 рубля.775. Скорость течения реки 4,2 км/ч, а собственная скорость лодки 7,5 км/ч. Определите скорость лодки по течению и против течения.
4,2 + 7,5 = 11,7 (км/ч) − скорость лодки по течению
7,5 − 4,2 = 3,3 (км/ч) − скорость лодки против течения
Ответ: 11,7 км/ч − скорость лодки по течению, 3,3 км/ч − скорость лодки против течения.776. Скорость катера по течению 22,5 км/ч, а против течения 18,5 км/ч. Какова собственная скорость катера?
Разность скорости по течению и скорости против течения есть удвоенная скорость течения: Vпо т. – Vпр. т. = 2Vт., тогда:
2Vт. = 22,5 – 18,5;
2Vт. = 4;
Vт. = 4 : 2;
Vт. = 2 (км/ч) – скорость течения
22,5 – 2 = 20,5 (км/ч) – собственная скорость катераили
х км/ч – скорость катера, а y км/ч – скорость течения, тогда x + y − скорость катера по течению, х − y − скорость катера против течения:
х + y + х − y = 22,5 + 18,5;
2х = 41;
х = 41 : 2;
х = 20,5 (км/ч) — собственная скорость катера
Ответ: 20,5 км/ч. 152
-
Десятичные дроби
Перенос запятой в положительной десятичной дробиОтветы к стр. 152
777. В какую сторону и на сколько цифр надо перенести запятую, чтобы увеличить десятичную дробь:
а) в 10 раз; б) в 100 раз; в) в 1000 раз;
г) в 10 000 раз; д) в 100 000 раз; е) в 1 000 000 раз.а) вправо на 1 цифру;
б) вправо на 2 цифры;
в) вправо на 3 цифры;
г) вправо на 4 цифры;
д) вправо на 5 цифр;
е) вправо на 6 цифр.778. В какую сторону и на сколько цифр надо перенести запятую, чтобы уменьшить десятичную дробь:
а) в 10 раз; б) в 100 раз; в) в 1000 раз;
г) в 10 000 раз; д) в 100 000 раз; е) в 1 000 000 раз.а) влево на 1 цифру;
б) влево на 2 цифры;
в) влево на 3 цифры;
г) влево на 4 цифры;
д) влево на 5 цифр;
е) влево на 6 цифр.779. Как изменится дробь, если в её десятичной записи запятую перенести на 3 цифры вправо? на 3 цифры влево?
Увеличится в 1000 раз; уменьшится в 1000 раз.
780. Как изменится дробь, если:
а) запятую в её десятичной записи перенести сначала на 2 цифры вправо, а затем на 3 цифры влево;
б) запятую в её десятичной записи перенести сначала на 3 цифры влево, а затем на 2 цифры вправо?а) 2 вправо − 3 влево = 1 влево — значит, уменьшится в 10 раз;
б) 3 влево − 2 вправо = 1 влево — значит, уменьшится в 10 раз.781. Как изменится положение запятой в записи десятичной дроби, если эту дробь:
а) сначала увеличить в 10 раз, потом ещё в 100 раз;
б) сначала увеличить в 10 раз, потом уменьшить в 100 раз;
в) сначала уменьшить в 10 раз, потом ещё в 100 раз;
г) сначала уменьшить в 10 раз, а потом увеличить в 100 раз?а) увеличить в 10 раз − вправо на 1, потом еще в 100 раз − вправо на 2, тогда 1 вправо + 2 вправо = 3 вправо – переместится на 3 вправо;
б) увеличить в 10 раз − вправо на 1, потом уменьшить в 100 раз − влево на 2, 1 вправо – 2 влево = 1 влево – переместится на 1 влево;
в) уменьшить в 10 раз − влево на 1, потом ещё в 100 раз − влево на 2, 1 влево + 2 влево = 3 влево – переместится на 3 влево;
г) уменьшить в 10 раз − влево на 1, а потом увеличить в 100 раз − вправо на 2, 1 влево – 2 вправо = 1 вправо – переместится на 1 вправо.
782. Какое число больше и во сколько раз;
а) 32,549 или 325,49; б) 2,7543 или 2754,3;
в) 47,58 или 4,758; г) 123,45 или 1,2345?а) 325,49 больше 32,549 в 10 раз;
б) 2754,3 больше 2,7543 в 1000 раз;
в) 47,58 больше 4,758 в 10 раз;
г) 123,45 больше 1,2345 в 100 раз.783. Какое число меньше и во сколько раз:
а) 0,4853 или 4853; б) 0,296 или 0,00296;
в) 480 или 0,48; г) 200 или 0,02?а) 0,4853 меньше 4853 в 10 000 раз;
б) 0,00296 меньше 0,296 в 100 раз;
в) 0,48 меньше 480 в 1000 раз;
г) 0,02 меньше 200 в 10 000 раз.784. Увеличьте следующие дроби в 10, 100, 1000 раз:
а) 7,3459; б) 8,279; в) 9,13; г) 7,2.а) 73,459, 734,59, 7345,9;
б) 82,79, 827,9, 8279;
в) 91,3, 913, 9130;
г) 72, 720, 7200.785. Выразите в сантиметрах по образцу:
а) 4,25 дм = 42,5 см; б) 4,2 мм = 0,42 см;
в) 5,21 дм; г) 3,2 дм; д) 13,2 мм; е) 2,1 мм.в) 5,21 дм = 52,1 см;
г) 3,2 дм = 32 см;
д) 13,2 мм = 1,32 см;
е) 2,1 мм = 0,21 см. 153
-
Ответы к стр. 153
786. Выразите в дециметрах:
а) 4,84 м; б) 3,5 м;
в) 396,7 см; г) 2,5 см;
д) 13 мм; е) 25,4 мм.а) 4,84 м = 48,4 дм;
б) 3,5 м = 35 дм;
в) 396,7 см = 39,67 дм;
г) 2,5 см = 0,25 дм;
д) 13 мм = 0,13 дм;
е) 25,4 мм = 0,254 дм.787. Выразите в метрах:
а) 20 см; б) 34,1 см;
в) 15,6 дм; г) 3,4 дм;
д) 0,5265 км; е) 1,4356 км.а) 20 см = 0,2 м;
б) 34,1 см = 0,341 м;
в) 15,6 дм = 1,56 м;
г) 3,4 дм = 0,34 м;
д) 0,5265 км = 526,5 м;
е) 1,4356 км = 1435,6 м.788. Выразите в килограммах:
а) 1,246 ц; б) 12,46 ц; в) 124,6 ц; г) 15 ц;
д) 1,5245 т; е) 15,245 т; ж) 152,45 т; з) 0,0485 т;
и) 7548 г; к) 238 г; л) 45 г; м) 5 г.а) 1,246 ц = 124,6 кг;
б) 12,46 ц = 1246 кг;
в) 124,6 ц = 12 460 кг;
г) 15 ц = 1500 кг;
д) 1,5245 т = 1524,5 кг;
е) 15,245 т = 15 245 кг;
ж) 152,45 т = 152 450 кг;
з) 0,0485 т = 48,5 кг;
и) 7548 г = 7,548 кг;
к) 238 г = 0,238 кг;
л) 45 г = 0,045 кг;
м) 5 г = 0,005 кг.789. Выразите в квадратных километрах (км2):
а) 1245 га; б) 125 га; в) 1256 га; г) 145 га.а) 1245 га = 12,45 км2;
б) 125 га = 1,25 км2;
в) 1256 га = 12,56 км2;
г) 145 га = 1,45 км2.790. Выразите в квадратных сантиметрах (см2):
а) 3,548 дм2; б) 3,9 дм2; в) 635 мм2; г) 23 мм2.а) 3,548 дм2 = 354,8 см2.
б) 3,9 дм2 = 390 см2.
в) 635 мм2 = 6,35 см2.
г) 23 мм2 = 0,23 см2.791. Выразите в кубических метрах (м3):
а) 4754 дм3; б) 723 дм3; в) 35 дм3; г) 7 дм3.а) 4754 дм3 = 4,754 м3;
б) 723 дм3 = 0,723 м3;
в) 35 дм3 = 0,035 м3;
г) 7 дм3 = 0,007 м3.792. Выразите в кубических миллиметрах (мм3):
а) 0,3574 см3; б) 2,3915 см3; в) 7,29 см3; г) 4,325 см3.а) 0,3574 см3 = 357,4 мм3;
б) 2,3915 см3 = 2391,5 мм3;
в) 7,29 см3 = 7290 мм3;
г) 4,325 см3 = 4325 мм3. 154
-
Десятичные дроби
Умножение положительных десятичных дробейОтветы к стр. 154
793. Сформулируйте правило умножения двух десятичных дробей.
Чтобы перемножить две десятичные дроби, достаточно перемножить их как натуральные числа, не обращая внимания на запятые, а в полученном произведении отделить запятой справа столько цифр, сколько их было после запятых в обоих множителях вместе.
Вычислите произведение (794-799):
794. а) 0,02 • 10; б) 3,2 • 100; в) 0,3 • 1000;
г) 2,39 • 1000; д) 0,041 • 100; е) 0,0005 • 1000.а) 0,02 • 10 = 0,2;
б) 3,2 • 100 = 320;
в) 0,3 • 1000 = 300;
г) 2,39 • 1000 = 2390;
д) 0,041 • 100 = 4,1;
е) 0,0005 • 1000 = 0,5.795. а) 2,4 • 2; б) 3,1 • 3; в) 0,5 • 2;
г) 2,5 • 4; д) 1,25 • 8; е) 0,072 • 2;
ж) 5,2 • 0,4; з) 7,1 • 0,9; и) 0,08 • 0,13.а) ×2,4
2
4,8б) ×3,1
3
9,3в) ×0,5
2
1,0г) × 2,5
4
10,0д) × 1,25
8
10,00е) ×0,072
2
0,144ж) × 5,2
0,4
2,08з) × 7,1
0,9
6,39и) × 0,13
0,08
0,0104796. а) 6,5 • 0,004; б) 0,09 • 0,18; в) 7,6 • 0,005;
г) 0,048 • 0,09; д) 0,7 • 0,0085; е) 0,009 • 0,78;
ж) 80,8 • 0,7; з) 0,09 • 5,007; и) 0,6 • 3,054.а) × 6,5
0,004
0,026б) × 0,18
0,09
0,0162в) × 7,6
0,005
0,038г) × 0,048
0,09
0,00432д) ×0,0085
0,7
0,00595е) × 0,78
0,009
0,00702ж) ×80,8
0,7
56,56з) ×5,007
0,09
0,45063и) ×3,054
0,6
1,8324797. а) 3,59 • 0,1; б) 2,3 • 0,1; в) 0,0235 • 0,1;
г) 63,2 • 0,01; д) 3,5 • 0,01; е) 2,32 • 0,01;
ж) 723,1 • 0,001; з) 79,4 • 0,001; и) 3,8 • 0,001.а) 3,59 • 0,1 = 0,359;
б) 2,3 • 0,1 = 0,23;
в) 0,0235 • 0,1 = 0,00235;
г) 63,2 • 0,01 = 0,632;
д) 3,5 • 0,01 = 0,035;
е) 2,32 • 0,01 = 0,0232;
ж) 723,1 • 0,001 = 0,7231;
з) 79,4 • 0,001 = 0,0794;
и) 3,8 • 0,001 = 0,0038.798. а) 4,381 • 0,2; б) 7,713 • 0,8; в) 0,07 • 620,4;
г) 0,2569 • 0,6; д) 0,3 • 2,451; е) 67,19 • 0,05;
ж) 42,25 • 0,4; з) 362,5 • 0,8; и) 512,5 • 0,08.а) ×4,381
0,2
0,8762б) ×7,713
0,8
6,1704в) ×620,4
0,07
43,428г) ×0,2569
0,6
0,15414д) ×2,451
0,3
0,7353е) ×67,19
0,05
3,3595ж) ×42,25
0,4
16,9з) ×362,5
0,8
290,00и) ×512,5
0,08
41,000 155
-
Ответы к стр. 155
Вычислите произведение (794-799):
799. а) 2,3 • 1,1; б) 4,3 • 1,2; в) 0,22 • 3,3;
г) 53 • 0,31; д) 0,68 • 61; е) 0,72 • 0,015;
ж) 4,355 • 2,2; з) 3,2 • 0,25; и) 0,084 • 0,55.а) ×2,3
1,1
+ 23
23
2,53б) ×4,3
1,2
+ 86
43
5,16в) ×0,22
3,3
+ 66
66
0,726г) × 53
0,31
+ 53
159
16,43д) ×0,68
61
+ 68
408
41,48е) × 0,72
0,015
+360
72
0,01080ж) ×4,355
2,2
+ 8710
8710
9,5810з) × 3,2
0,25
+160
64
0,800и) ×0,084
0,55
+ 420
420
0,04620800. Вычислите, применяя законы умножения:
а) 0,25 • 0,3 • 4; б) 0,2 • 0,13 • 50; в) 0,8 • 0,11 • 1,25;
г) 0,125 • 3 • 0,8; д) 0,5 • 7,3 • 2,2; е) 0,25 • 1,7 • 1,6.а) 0,25 • 0,3 • 4 = (0,25 • 4) • 0,3 = 1 • 0,3 = 0,3;
×0,25
4
1,00б) 0,2 • 0,13 • 50 = (0,2 • 50) • 0,13 = 10 • 0,13 = 1,3;
×0,2
50
10,0в) 0,8 • 0,11 • 1,25 = (0,8 • 1,25) • 0,11 = 1 • 0,11 = 0,11;
×1,25
0,8
1,000г) 0,125 • 3 • 0,8 = (0,125 • 0,8) • 3 = 0,1 • 3 = 0,3;
×0,125
0,8
0,1000д) 0,5 • 7,3 • 2,2 = (0,5 • 2,2) • 7,3 = 1,1 • 7,3 = 8,03;
×2,2 ×7,3
0,5 1,1
1,10+ 73
73
8,03е) 0,25 • 1,7 • 1,6 = (0,25 • 1,6) • 1,7 = 0,4 • 1,7 = 0,68.
×0,25 ×1,7
1,6 0,4
+150 0,68
25
0,400Вычислите (801-805):
801. а) 2,4 • 4,8 + 2,6 • 4,8; б) 30,5 • 20,3 − 30,5 • 0,3;
в) 5,1 • 1,8 − 1,8; г) 4,9 • 6,2 + 6,2.а) 2,4 • 4,8 + 2,6 • 4,8 = 4,8 • (2,4 + 2,6) = 4,8 • 5 = 24;
+2,4 ×4,8
2,6 5
5,024,0б) 30,5 • 20,3 − 30,5 • 0,3 = 30,5 • (20,3 − 0,3) = 30,5 • 20 = 610;
—20,3 ×30,5
0,3 20
20,0 610,0в) 5,1 • 1,8 − 1,8 = 1,8 • (5,1 − 1) = 1,8 • 4,1 = 7,38;
—5,1 ×1,8
1 4,1
4,1 + 18
72
7,38г) 4,9 • 6,2 + 6,2 = 6,2 • (4,9 + 1) = 6,2 • 5,9 = 36,58.
+4,9 ×6,2
1 5,9
5,9 +558
310
36,58802. а) 0,1 • 0,1; б) 0,2 • 0,2 • 0,2; в) 0,3 • 0,3 • 0,3 • 0,3;
г) 0,05 • 0,05; д) 0,6 • 0,6 • 0,6; е) 0,08 • 0,08;
ж) (0,5 + 0,2)2; з) (0,7 + 0,3)3; и) (0,9 − 0,4)3;
к) 0,8 + 1,12; л) 1,22 − 1,2; м) 1,52 − 0,25.При возведении в степень десятичной дроби количество цифр после запятой в ответе будет равно произведению количества цифр после запятой в исходной дроби и степени, в которую мы возводим эту дробь. То есть достаточно возвести в степень число, записанное без запятой, а потом отсчитать справа необходимое количество цифр (добавляя при необходимости нули) и поставить запятую.
а) 0,1 • 0,1 = 0,12 = 0,01;
1 • 1 = 1 → 0,01
количество цифр после запятой в дроби 0,1 = 1, степень, в которую возводится дробь 0,1 = 2, тогда 1 • 2 = 2 – после запятой две цифры, последняя из которых 1б) 0,2 • 0,2 • 0,2 = 0,23 = 0,008;
2 • 2 • 2 = 8 → 0,008
количество цифр после запятой в дроби 0,2 = 1, степень, в которую возводится дробь 0,2 = 3, тогда 1 • 3 = 3 – после запятой три цифры, последняя из которых 8в) 0,3 • 0,3 • 0,3 • 0,3 = 0,34 = 0,0081;
3 • 3 • 3 • 3 = 84 → 0,0081
количество цифр после запятой в дроби 0,3 = 1, степень, в которую возводится дробь 0,3 = 4, тогда 1 • 4 = 4 – после запятой четыре цифры, последние из которых 81г) 0,05 • 0,05 = 0,052 = 0,0025;
5 • 5 = 25 → 0,0025
количество цифр после запятой в дроби 0,05 = 2, степень, в которую возводится дробь 0,05 = 2, тогда 2 • 2 = 4 – после запятой четыре цифры, последние из которых 25д) 0,6 • 0,6 • 0,6 = 0,63 = 0,216;
6 • 6 • 6 = 0,216
количество цифр после запятой в дроби 0,6 = 1, степень, в которую возводится дробь 0,6 = 3, тогда 1 • 3 = 3 – после запятой три цифры, последние из которых 216е) 0,08 • 0,08 = 0,082 = 0,0064;
8 • 8 = 64 → 0,0064;
количество цифр после запятой в дроби 0,08 = 2, степень, в которую возводится дробь 0,08 = 2, тогда 2 • 2 = 4 – после запятой четыре цифры, последние из которых 64ж) (0,5 + 0,2)2 = 0,72 = 0,49;
7 • 7 = 49 → 0,49
количество цифр после запятой в дроби 0,7 = 1, степень, в которую возводится дробь 0,7 = 2, тогда 1 • 2 = 2 – после запятой две цифры, последние из которых 49з) (0,7 + 0,3)3 = 13 = 1 • 1 • 1 = 1;
и) (0,9 − 0,4)3 = 0,53 = 0,125;
5 • 5 • 5 = 125 → 0,125
количество цифр после запятой в дроби 0,5 = 1, степень, в которую возводится дробь 0,5 = 3, тогда 1 • 3 = 3 – после запятой три цифры, последние из которых 125к) 0,8 + 1,12 = 0,8 + 1,1 • 1,1 = 0,8 + 1,21 = 2,01;
×1,1 +1,21
1,1 0,8
+ 11 2,01
11
1,21л) 1,22 − 1,2 = 1,2 • 1,2 −1,2 = 1,44 − 1,2 = 0,24
×1,2 —1,44
1,2 1,2
+ 24 0,24
12
1,44м) 1,52 − 0,25 = (1,5 • 1,5) − 0,25 = 2,25 − 0,25 = 2.
×1,5 —2,25
1,5 0,25
+ 75 2,00
15
2,25803. а) 9,51 • 18; б) 66,3 • 26; в) 8,47 • 0,64;
г) 7,3 • 5,42; д) 0,85 • 2,06; е) 8,07 • 0,016.а) ×9,51
18
+ 7608
951
171,18б) ×66,3
26
+ 3978
1326
1723,8в) ×8,47
0,64
+ 3388
5082
5,4208г) ×5,42
7,3
+ 1626
3794
39,566д) ×2,06
0,85
+ 1030
1648
1,7510е) × 8,07
0,016
+ 4842
807
0,12912804. а) 3,32 • 0,101; б) 3,02 • 6,48; в) 3,21 • 0,562;
г) 95,5 • 3,17; д) 0,861 • 0,242; е) 0,999 • 0,732.а) × 3,32
0,101
+ 332
332
0,33532б) ×6,48
3,02
+ 1296
1944
19,5696в) × 3,21
0,562
642
+ 1926
1605
1,80402г) ×95,5
3,17
6685
+ 955
2865
302,735д) ×0,861
0,242
1722
+ 3444
1722
0,208362е) ×0,999
0,732
1998
+ 2997
6993
0,731268805. а) 7,668 • 24 − 9,68; б) 35,22 + 45,83 • 2,6;
в) 5,306 • 42 + 5,36 • 82; г) 1,654 • 3,4 + 6,4 • 9,5;
д) 2,4 • 98 + 4,8; е) 35,4 • 1,99 + 35,4;
ж) 3,2 • 103 − 9,6; з) 1,22 • 97 + 3,66.а) 7,668 • 24 − 9,68 = 184,032 − 9,68 = 174,352;
×7,668 —184,032
24 9,68
+ 30672 174,352
15336
184,032б) 35,22 + 45,83 • 2,6 = 35,22 + 119,158 = 154,378.
×45,83 +119,158
2,6 35,22
+ 27498 154,378
9166
119,158в) 5,306 • 42 + 5,36 • 82 = 222,852 + 439,52 = 662,372;
×5,306 ×5,36
42 82
+ 10612 + 1072
21224 4288
222,852 439,52+222,852
439,52
662,372г) 1,654 • 3,4 + 6,4 • 9,5 = 5,6236 + 60,8 = 66,4236;
×1,654 ×6,4
3,4 9,5
+ 6616 + 320
4962 576
5,6236 60,80+60,8
5,6236
66,4236д) 2,4 • 98 + 4,8 = 2,4 • 98 + 2 • 2,4 = 2,4 • (98 + 2) = 2,4 • 100 = 240;
е) 35,4 • 1,99 + 35,4 = 35,4 • (1,99 + 1) = 35,4 • 2,99 = 105,846;
×35,4
2,99
3186
+3186
708
105,846ж) 3,2 • 103 − 9,6 = 3,2 • 103 – 3 • 3,2 = 3,2 • (103 − 3) = 3,2 • 100 = 320;
з) 1,22 • 97 + 3,66 = 1,22 • 97 + 3 • 1,22 = 1,22 • (97 + 3) = 1,22 • 100 = 122.
806. Известно, что 8 • 125 = 1000. Вычислите:
а) 8 • 12,5; б) 0,08 • 125; в) 0,8 • 12,5;
г) 8 • 0,125; д) 0,8 • 1,25; е) 0,08 • 12,5.а) 8 • 12,5 = 100;
б) 0,08 • 125 = 10;
в) 0,8 • 12,5 = 10;
г) 8 • 0,125 = 1;
д) 0,8 • 1,25 = 1;
е) 0,08 • 12,5 = 1.807. Пешеход идёт со скоростью 4,4 км/ч. Какой путь он пройдет за:
а) 2 ч; б) 0,5 ч; в) 1,5 ч?а) V = 4,4 км/ч;
t = 2 ч;
S − ?Решение:
S = V • t
4,4 • 2 = 8,8 (км)
×4,4
2
8,8
Ответ: 8,8 км.б) V = 4,4 км/ч;
t = 0,5 ч;
S − ?Решение:
S = V • t
4,4 • 0,5 = 2,2 (км)
×4,4
0,5
2,20
Ответ: 2,2 км.в) V = 4,4 км/ч;
t = 1,5 ч;
S − ?Решение:
S = V • t
4,4 • 1,5 = 6,6 (км)
×4,4
1,5
+220
44
6,60
Ответ: 6,6 км.808. Собственная скорость моторной лодки 12,6 км/ч, а скорость течения реки 1,8 км/ч. Какой путь пройдёт лодка по течению и против течения за:
а) 3 ч; б) 2,5 ч; в) 0,5 ч?а) Vлодки = 12,6 км/ч;
Vтечения = 1,8 км/ч;
t = 3 ч;
Sпо течению − ?
Sпротив течения − ?Решение:
Sпо течению = (Vлодки + Vтечения) • t
(12,6 + 1,8) • 3 = 43,2 (км)
+12,6 ×14,4
1,8 3
14,4 43,2Sпротив течения = (Vлодки — Vтечения) • t
(12,6 − 1,8) • 3 = 32,4 (км)
—12,6 ×10,8
1,8 3
10,8 32,4
Ответ: Sпо течению = 43,2 км, Sпротив течения = 32,4 км.
б) Vлодки = 12,6 км/ч;
Vтечения = 1,8 км/ч;
t = 2,5 ч;
Sпо течению − ?
Sпротив течения − ?Решение:
Sпо течению = (Vлодки + Vтечения ) • t
(12,6 + 1,8) • 2,5 = 36 (км)
+12,6 ×14,4
1,8 2,5
14,4 + 720
288
36,00Sпротив течения = (Vлодки — Vтечения) • t
(12,6 − 1,8) • 2,5 = 27 (км)
—12,6 ×10,8
1,8 2,5
10,8 + 540
216
27,00
Ответ: Sпо течению = 36 км, Sпротив течения = 27 км.
в) Vлодки = 12,6 км/ч;
Vтечения = 1,8 км/ч;
t = 0,5 ч;
Sпо течению − ?
Sпротив течения − ?Решение:
Sпо течению = (Vлодки + Vтечения) • t
(12,6 + 1,8) • 0,5 = 7,2 (км)
+12,6 ×14,4
1,8 0,5
14,4 7,20Sпротив течения = (Vлодки — Vтечения) • t
(12,6 − 1,8) • 0,5 = 5,4 (км)
—12,6 ×10,8
1,8 0,5
10,8 5,40
Ответ: Sпо течению = 7,2 км, Sпротив течения = 5,4 км. 156
-
Десятичные дроби
Умножение положительных десятичных дробейОтветы к стр. 156
809. Вычислите площадь прямоугольника со сторонами α и b:
а) α = 3,6 см; b = 4 см; б) α = 5 дм; b = 3,13 дм;
в) α = 3,12 дм; b = 3,5 дм; г) α = 6,25 м; b = 1,6 м.а) α = 3,6 см;
b = 4 см;
S — ?
Решение:
S = α • b
3,6 • 4 = 14,4 (см2)
×3,6
4
14,4
Ответ: S = 14,4 см2.б) α = 5 дм;
b = 3,13 дм;
S — ?
Решение:
S = α • b
5 • 3,13 = 15,65 (дм2)
×3,13
5
15,65
Ответ: S = 15,65 дм2.в) α = 3,12 дм;
b = 3,5 дм;
S — ?
Решение:
S = α • b
3,12 • 3,5 = 10,92 (дм2)
×3,12
3,5
+1560
936
10,920
Ответ: S = 10,92 дм2.г) α = 6,25 м;
b = 1,6 м;
S — ?
Решение:
S = α • b
6,25 • 1,6 = 10 (м2)
×6,25
1,6
+3750
625
10,000
Ответ: S = 10 м2.810. Вычислите объём прямоугольного параллелепипеда, длина, ширина, высота которого α, b, c:
а) α = 4,5 см; b = 2,3 см; c = 10 см;
б) α = 3,2 дм; b = 1,5 дм; c = 2,5 дм;
в) α = 12 см; b = 2,5 дм; c = 10 см.а) α = 4,5 см;
b = 2,3 см;
c = 10 см;
V — ?
Решение:
V = α • b • c
4,5 • 2,3 • 10 = 10,35 • 10 = 103,5 (см3)
×4,5
2,3
+135
90
10,35
Ответ: V = 103,5 см3.б) α = 3,2 дм;
b = 1,5 дм;
c = 2,5 дм;
V — ?
Решение:
V = α • b • c
3,2 • 1,5 • 2,5 = 1,5 • 8 = 12 (дм3)
×3,2 ×1,5
2,5 8
+160 12,064
8,00
Ответ: V = 12 дм3.в) α = 12 см;
b = 2,5 дм;
c = 10 см;
V — ?
Решение:
V = α • b • c
2,5 дм = 25 см
12 • 25 • 10 = 300 • 10 = 3000 (см3)
×25
12
+50
25
300
Ответ: V = 3000 см3.811. Масса 1 м3 воздуха 1,29 кг. Определите массу воздуха в вашем классе.
α = 22 м;
b = 10 м;
c = 3,5 м;
mвоздуха — ?
Решение:
1) V = α • b • c
22 • 10 • 3,5 = 77 • 10 = 770 (м3) — объём класса
×3,5
22
+ 70
70
77,02) 770 • 1,29 = 993,3 (кг)
×1,29
770
+903
903
993,30
Ответ: mвоздуха = 993,3 кг.812. Масса 1 см3 алюминия 2,7 г, масса 1 см3 свинца 11,3 г. Какой кубик тяжелее − алюминиевый с ребром 3 см или свинцовый с ребром 2 см?
V = α3
1) 33 = 3 • 3 • 3 = 27 (см3) − объём алюминиевого кубика
2) 23 = 2 • 2 • 2 = 8 (см3) − объём свинцового кубика
3) 27 • 2,7 = 72,9 (г) − масса алюминиевого кубика
×27
2,7
+189
54
72,94) 8 • 11,3 = 90,4 (г) − масса свинцового кубика
×11,3
8
90,490,4 г > 72,9 г – свинцовый кубик тяжелее
Ответ: свинцовый кубик тяжелее алюминиевого.813. Использование 1 т макулатуры позволяет получить 0,7 т бумаги и заменить при этом 4,4 м3 древесины. Сколько бумаги можно получить из 7,5 т макулатуры? Сколько при этом экономится древесины?
1) 7,5 • 0,7 = 5,25 (т) — бумаги получится из 7,5 т макулатуры
×7,5
0,7
5,252) 4,4 • 7,5 = 33 (м3) — древесины экономится
×7,5
4,4
+ 300
300
33,00
Ответ: 5,25 т бумаги получится, 33 м3 древесины экономится. 158
-
Десятичные дроби
Деление положительных десятичных дробейОтветы к стр. 158
814. Выразите частное в виде обыкновенной дроби:
а) 3 : 0,7; б) 3,5 : 1,2; в) 1,25 : 1,4.а) 3 : 0,7 = 3 : 7/10 = 3•10/7 = 30/7;
б) 3,5 : 1,2 = 35/10 : 12/10 = 35•10/10•12 = 35/12;
в) 1,25 : 1,4 = 125/100 : 14/10 = 125•10/100•14 = 125/140 = 25/28.
815. По какому правилу делят десятичную дробь на натуральное число?
Деление десятичной дроби на натуральное число выполняется также, как деление натуральных чисел, но после окончания деления целой части десятичной дроби надо в частном поставить запятую.
816. По какому правилу делят десятичные дроби?
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и делителе перенести запятую на столько цифр вправо, сколько их после запятой в делителе, и затем выполнить деление на натуральное число.
817. Всегда ли при делении десятичных дробей частное можно записать в виде десятичной дроби? Приведите примеры.
Обыкновенную дробь, знаменатель которой нельзя привести к числу, являющемуся степенью числа 10, нельзя представить в виде десятичной дроби. Следовательно, не всегда, при делении десятичных дробей, частное можно записать в виде десятичной дроби: 0,5 : 0,3 = 5/10 : 3/10 = 50/30 = 5/3 – число в знаменателе 30 можно привести к 10 путём деления на 3, но число в числителе 50 не делится на 3, а число в знаменателе 3 нельзя привести к числу, являющемуся степенью числа 10.
Вычислите (818-821):
818. а) 12,5 : 10; б) 72,6 : 100; в) 173,56 : 100;
г) 0,3 : 100; д) 0,73 : 1000; е) 1,664 : 10 000.а) 12,5 : 10 = 1,25;
б) 72,6 : 100 = 0,726;
в) 173,56 : 100 = 1,7356;
г) 0,3 : 100 = 0,003;
д) 0,73 : 1000 = 0,00073;
е) 1,664 : 10 000 = 0,0001664.819. а) 783 : 10; б) 988 : 100; в) 54 000 : 10 000;
г) 7800 : 1000; д) 3 : 1000; е) 5 : 100 000.а) 783 : 10 = 78,3;
б) 988 : 100 = 9,88;
в) 54 000 : 10 000 = 5,4;
г) 7800 : 1000 = 7,8;
д) 3 : 1000 = 0,003;
е) 5 : 100 000 = 0,00005. 159
-
Ответы к стр. 159
Вычислите (818-821):
820. а) 3,6 : 3; б) 75,5 : 5; в) 1,24 : 4;
г) 2,53 : 11; д) 7,81 : 11; е) 13,2 : 24.а) —3,6 |3
3 |1,2
—6
6
0б) —75,5|5
5 |15,1
—25
25
—5
5
0в) —1,24 |4
12 |0,31
—4
4
0г) —2,53 |11
22 |0,23
—33
33
0д) —7,81 |11
77 |0,71
—11
11
0е) —13,2 |24
120 |0,55
—120
120
0821. а) 0,48 : 8; б) 0,84 : 21; в) 0,001 : 5;
г) 0,002 : 4; д) 0,125 : 25; е) 0,0625 : 25.а) —0,48 |8
0 |0,06
—4
0
—48
48
0б) —0,84 |21
0 |0,04
—8
0
—84
84
0в) —0,0010 |5
0 |0,0002
—0
0
—0
0
—1
0
—10
10
0г) —0,0020 |4
0 |0,0005
—0
0
—0
0
—2
0
—20
20
0д) —0,125 |25
0 |0,005
—1
0
—12
0
—125
125
0е) —0,0625 |25
0 |0,0025
—0
0
—6
0
—62
50
—125
125
0822. Выполните деление и проверьте полученный результат:
а) 3,1 : 0,1; б) 7,21 : 0,01; в) 6,3571 : 0,01;
г) 4,729 : 0,001; д) 4,29 : 0,1; е) 7,1 : 0,001.а) 3,1 : 0,1 = 31 : 1 = 31
проверка: 31 • 0,1 = 3,1;б) 7,21 : 0,01 = 721 : 1 = 721
проверка: 721 • 0,01 = 7,21;в) 6,3571 : 0,01 = 635,71 : 1 = 635,71
проверка: 635,71 • 0,01 = 6,3571;г) 4,729 : 0,001 = 4729 : 1 = 4729
проверка: 4729 • 0,001 = 4,729;д) 4,29 : 0,1 = 42,9 : 1 = 42,9
проверка: 42,9 • 0,1 = 4,29;е) 7,1 : 0,001 = 7100 : 1 = 7100
проверка: 7100 • 0,001 = 7,1.Вычислите (823-824):
823. а) 6 : 0,1; б) 7 : 0,001; в) 8 : 0,001;
г) 35 : 0,1; д) 49 : 0,01; е) 56 : 0,001.а) 6 : 0,1 = 60 : 1 = 60;
б) 7 : 0,001 = 7000 : 1 = 7000;
в) 8 : 0,001 = 8000 : 1 = 8000;
г) 35 : 0,1 = 350 : 1 = 350;
д) 49 : 0,01 = 4900 : 1 = 4900;
е) 56 : 0,001 = 56 000 : 1 = 56 000.824. а) 1 : 0,2; б) 1 : 0,25; в) 1 : 0,125; г) 1 : 0,4; д) 1 : 0,5.
а) 1 : 0,2 = 10 : 2 = 5;
б) 1 : 0,25 = 100 : 25 = 4;
в) 1 : 0,125 = 1000 : 125 = 8;
г) 1 : 0,4 = 1 : 4/10 = 1 • 10/4 = 250/100 = 2,5;
д) 1 : 0,5 = 10 : 5 = 2.825. Как изменится частное, если:
а) делимое увеличить в 5 раз;
б) делитель увеличить в 3 раза;
в) делимое и делитель увеличить в одинаковое число раз?а) увеличится в 5 раз;
б) уменьшится в 3 раза;
в) останется неизменным.Вычислите (826-827):
826. а) 48 : 4,8; б) 536 : 5,36; в) 921 : 92,1;
г) 39 : 0,39; д) 4 : 0,4; е) 999 : 99,9.а) 48 : 4,8 = 480 : 48 = 10;
б) 536 : 5,36 = 53 600 : 536 = 100;
в) 921 : 92,1 = 9210 : 921 = 10;
г) 39 : 0,39 = 3900 : 39 = 100
д) 4 : 0,4 = 40 : 4 = 10;
е) 999 : 99,9 = 9990 : 999 = 10.827. а) 53,6 : 5,36; б) 5,36 : 0,01; в) 72,34 : 7,234;
г) 7,234 : 0,01; д) 372,9 : 3,729; е) 3,729 : 0,1.а) 53,6 : 5,36 = 5360 : 536 = 10;
б) 5,36 : 0,01 = 536 : 1 = 536;
в) 72,34 : 7,234 = 72 340 : 7234 = 10;
г) 7,234 : 0,01 = 723,4 : 1 = 723,4;
д) 372,9 : 3,729 = 372 900 : 3729 = 100;
е) 3,729 : 0,1 = 37,29 : 1 = 37,29.Выполните деление, проверьте результат (828-829):
828. а) 4 : 0,5; б) 3 : 0,2; в) 2 : 0,02;
г) 14 : 0,07; д) 12 : 0,004; е) 10 : 0,005.а) 4 : 0,5 = 40 : 5 = 8
проверка: 8 • 0,5 = 4;б) 3 : 0,2 = 30 : 2 = 15
проверка: 15 • 0,2 = 3;в) 2 : 0,02 = 200 : 2 = 100
проверка: 100 • 0,02 = 2г) 14 : 0,07 = 1400 : 7 = 200
проверка: 200 • 0,07 = 14;д) 12 : 0,004 = 12 000 : 4 = 3000
проверка: 3000 • 0,004 = 12;е) 10 : 0,005 = 10 000 : 5 = 2000
проверка: 2000 • 0,005 = 10.829. а) 7,6 : 0,2; б) 6,3 : 0,3; в) 0,64 : 3,2;
г) 0,49 : 0,7; д) 0,01 : 0,05; е) 0,004 : 0,8.а) 7,6 : 0,2 = 76 : 2 = 38
проверка: 38 • 0,2 = 7,6;б) 6,3 : 0,3 = 63 : 3 = 21
проверка: 21 • 0,3 = 6,3;в) 0,64 : 3,2 = 6,4 : 32 = 0,2
проверка: 0,2 • 3,2 = 0,64г) 0,49 : 0,7 = 4,9 : 7 = 0,7
проверка: 0,7 • 0,7 = 0,49;д) 0,01 : 0,05 = 1 : 5 = 0,2
проверка: 0,2 • 0,05 = 0,01;е) 0,004 : 0,8 = 0,04 : 8 = 0,005
проверка: 0,005 • 0,8 = 0,004.Вычислите (830-833):
830. а) 0,21 : 0,84; б) 0,19 : 0,095; в) 3,76 : 0,4;
г) 7,05 : 1,5; д) 3,5 : 0,4; е) 25,9 : 3,7.а) —21 |84
0 |0,25
—210
168
—420
420
0б) —190 |95
190 |2
0в) —37,6 |4
36 |9,4
—16
16
0г) —70,5 |15
60 |4,7
—105
105
0д) —35 |4
32 |8,75
—30
28
—20
20
0е) —259 |37
259 |7
0831. а) 1,75 : 1,4; б) 18,4 : 7,36; в) 16,92 : 4,23;
г) 86,1 : 2,46; д) 21,875 : 3,125; е) 183,96 : 5,256.а) —17,5 |14
14 |1,25
—35
28
—70
70
0б) —1840 |736
1472 |2,5
—3680
3680
0в) —1692 |423
1692 |4
0г) —8610 |246
738 |35
—1230
1230
0д) —21875 |3125
21875 |7
0е) —183960 |5256
15768 |35
—26280
26280
0832. а) 0,25 : 4 + 15,3 : 5 + 12,4 : 8 + 0,15 : 3;
б) 96,7 : 10 + 0,045 : 5 + 140,4 : 12 + 1,53 : 15.а) 0,25 : 4 + 15,3 : 5 + 12,4 : 8 + 0,15 : 3 = 4,7225;
—0,25 |4
0 |0,0625
—2
0
—25
24
—10
8
—20
20
0—15,3 |5
15 |3,06
—3
0
—30
30
0—12,4 |8
8 |1,55
—44
40
—40
40
0—0,15 |3
0 |0,05
—1
0
—15
15
00,0625
+3,06
1,55
0,05
4,7225б) 96,7 : 10 + 0,045 : 5 + 140,4 : 12 + 1,53 : 15 = 21,481.
96,7 : 10 = 9,67—0,045 |5
0 |0,009
—0
0
—4
0
—45
45
0—140,4 |12
12 |11,7
—20
20
—84
84
0—1,53 |15
0 |0,102
—15
15
—3
0
—30
30
09,67
+ 0,009
11,7
0,102
21,481833. а) 4,912 : 16 + (18,305 : 7 + 0,0368 : 4);
б) 72,492 : 12 + 78,156 : 36 − 120,03 : 15;
в) 1,35 : 2,7 + 6,02 − 5,9 + 0,4 : 2,5 • (4,2 − 0,075);
г) 4,3 − 3,5 + 1,44 : 3,6 + 3,6 : 1,44 • (0,1 − 0,02).а) 4,912 : 16 + (18,305 : 7 + 0,0368 : 4) = 2,9312;
—18,305 |7
14 |2,615
—43
42
—10
7
—35
35
0—0,0368 |4
0 |0,0092
—0
0
—3
0
—36
36
—8
8
0+2,615
0,0092
2,6242—4,912 |16
0 |0,307
—49
48
—11
0
—112
112
0+0,307
2,6242
2,9312б) 72,492 : 12 + 78,156 : 36 − 120,03 : 15 = 0,21;
—72,492 |12
72 |6,041
—4
0
—49
48
—12
12
0—78,156 |36
72 |2,171
—61
36
—255
252
—36
36
0—120,03 |15
120 |8,002
—0
0
—3
0
—30
30
0+6,041
2,171
8,212—8,212
8,002
0,21в) 1,35 : 2,7 + 6,02 − 5,9 + 0,4 : 2,5 • (4,2 − 0,075) = 1,28;
—4,2
0,075
4,125—13,5 |27
0 |0,5
—135
135
0—4 |25
0 |0,16
—40
25
—150
150
0×4,125
0,16
+24750
4125
0,66000+0,5
6,02
6,52—6,52
5,9
0,62+0,62
0,66
1,28г) 4,3 − 3,5 + 1,44 : 3,6 + 3,6 : 1,44 • (0,1 − 0,02) = 1,4.
—0,1
0,02
0,08—14,4 |36
0 |0,4
—144
144
0—360 |144
288 |2,5
—720
720
0× 2,5
0,08
0,200—4,3
3,5
0,8+0,8
0,4
1,2+1,2
0,2
1,4834. Сколько сотых содержится в числе:
а) 3/4; б) 2/5; в) 1/2; г) 7/20; д) 3/25.а) 3/4 = 75/100 = 0,75 − 75 сотых;
б) 2/5 = 40/100 = 0,40 − 40 сотых;
в) 1/2 = 50/100 = 0,50 − 50 сотых;
г) 7/20 = 35/100 = 0,35 − 35 сотых;
д) 3/25 = 12/100 = 0,12 − 12 сотых.
160
-
Ответы к стр. 160
835. Не выполняя вычислений, сравните:
а) 19,95 • 199,6 и 1,995 • 1996; б) 19,96 • 1,997 и 199,6 • 19,97;
в) 199,7 • 199,8 и 1,997 • 1,998; г) 1,998 • 199,9 и 1,998 • 1999.Из двух чисел, состоящих из одинаковых цифр и расположенных в одинаковом порядке, большим будет то число, количество знаков после запятой у которого меньше.
а) в произведении чисел 19,95 • 199,6 будет 3 знака после запятой, в произведении чисел 1,995 • 1996 будет 3 знака после запятой, следовательно, 19,95 • 199,6 = 1,995 • 1996;
б) в произведении чисел 19,96 • 1,997 будет 5 знаков после запятой, в произведении чисел 199,6 • 19,97 будет 3 знака после запятой, следовательно, 19,96 • 1,997 < 199,6 • 19,97;
в) в произведении чисел 199,7 • 199,8 будет 2 знака после запятой, в произведении чисел 1,997 • 1,998 будет 6 знаков после запятой, следовательно, 199,7 • 199,8 > 1,997 • 1,998;
г) в произведении чисел 1,998 • 199,9 будет 4 знака после запятой, в произведении чисел 1,998 • 1999 будет 3 знака после запятой, следовательно, 1,998 • 199,9 < 1,998 • 1999.
Придумываем задачу
836. Не выполняя вычислений, объясните, почему верно равенство 35,48 • 2,937 = 0,3548 • 293,7. Придумайте несколько аналогичных верных равенств.
Два числа, состоящие из одинаковых цифр расположенных в одинаковом порядке, будут равны, если количество знаков после запятой у них будет равно.
В произведение чисел 35,48 • 2,937 будет 5 знаков после запятой, в произведении чисел 0,3548 • 293,7 будет 5 знаков после запятой, следовательно, 35,48 • 2,937 = 0,3548 • 293,7.
Верные равенства:
2,359 • 896,7 и 23,59 • 89,67;
56,89 • 2,987 и 5,689 • 29,87.837. Не выполняя вычислений, объясните, почему верно неравенство: 2,318 • 12,547 > 23,17 • 1,2547. Придумайте несколько аналогичных верных неравенств.
В произведении чисел 2,318 • 12,547 будет 5 знаков после запятой, в произведении чисел 23,17 • 1,2547 также будет иметь 5 знаков после запятой, следовательно, сравнивать произведение данных пар чисел можно не обращая внимания на запятые. Сравним первые и вторые множители попарно : 2318 > 2317, 12547 = 12547, значит, 2318 • 12547 > 2317 • 12547.
Верные неравенства:
5,687 • 13,58 > 56,87 • 1,357;
68,95 • 234,5 < 689,5 • 24,45.838. Вычислите:
а) 12,3•3,21/1,23•32,1; б) 0,123•321/1,23•3,21;
в) 12,3•3,21/1,23•3,21; г) 0,123•0,321/1,23•3,21.а) в произведение чисел 12,3 • 3,21 будет 3 знака после запятой, в произведении чисел 1,23 • 32,1 будет 3 знака после запятой, следовательно, 12,3 • 3,21 = 1,23 • 32,1 и 12,3•3,21/1,23•32,1 = 1/1 = 1;
б) в произведении чисел 0,123 • 321 будет 3 знака после запятой, в произведении чисел 1,23 • 3,21 будет 4 знака после запятой, следовательно, числитель в 10 раз больше знаменателя и 0,123•321/1,23•3,21 = 10/1 = 10;
в) в произведении чисел 12,3 • 3,21 будет 3 знака после запятой, в произведении чисел 1,23 • 3,21 будет 4 знака после запятой, следовательно, числитель в 10 раз больше знаменателя и 12,3•3,21/1,23•3,21 = 10/1 = 10;
г) в произведении чисел 0,123 • 0,321 будет 6 знаков после запятой, в произведении чисел 1,23 • 3,21 будет 4 знака после запятой, следовательно, числитель в 100 раз меньше знаменателя и 0,123•0,321/1,23•3,21 = 1/100 = 0,01.
839. На прямолинейном участке железнодорожного пути уложены рельсы длиной 12,5 м. Сколько рельсов уложено на 1 км пути?
1 км = 1000 м
1000 : 12,5 = 80 (рельс) – уложено в один ряд
—10000 |125
1000 |80
0
Рельсы укладываются в два ряда параллельно, значит, их уложено в 2 раза больше:
80 • 2 = 160 (рельс) — уложено всего
Ответ: 160 рельс уложено на 1 км пути.840. Слон тяжелее бегемота на 0,7 т, а их общая масса 8,3 т. Какова масса каждого животного?
Пусть х т — масса слона, тогда x − 0,7 т − масса бегемота, а х + (х – 0,7) т – их общая масса, которая по условию задачи равна 8,3 т.
x + (x − 0,7) = 8,3
2x − 0,7 = 8,3
2x = 8,3 + 0,7
2x = 9
x = 9 : 2
х = 4,5 т — масса слона
4,5 − 0,7 = 3,8 (т) — масса бегемота
Ответ: масса слона 4,5 т, масса бегемота – 3,8 т.841. Вычислите скорость движения пешехода, который:
а) за 2,4 ч прошёл 10,8 км; б) за 1,8 ч прошёл 9,9 км.а) Дано:
S = 10,8 км
t = 2,4 ч
Найти:
Ʋ − ?
Решение:
Ʋ = S : t
10,8 : 2,4 = 4,5 (км/ч)
—108 |24
96 |4,5
—120
120
0
Ответ: скорость пешехода 4,5 км/ч.б) Дано:
S = 9,9 км
t = 1,8 ч
Найти:
Ʋ − ?
Решение:
Ʋ = S : t
9,9 : 1,8 = 5,5 (км/ч)
—99 |18
90 |5,5
—90
90
0
Ответ: скорость пешехода 5,5 км/ч.842. На производство 1 т бумаги расходуется 250 т воды. Это в 12,5 раза больше, чем расходуется на производство 1 т стали, и в 6 раз меньше, чем на производство 1 т аммиака. Сколько тонн воды расходуется на производство 1 т стали? 1 т аммиака?
1) 250 : 12,5 = 20 (т) — воды расходуется на производство 1 т стали
—2500 |125
250 |20
0
2) 250 • 6 = 1500 (т) — воды расходуется на производство 1 т аммиака
Ответ: 20 т воды расходуется на производство 1 т стали, 1500 т воды расходуется на производство 1 т аммиака.843. Площадь первой комнаты на 5,2 м2 больше площади второй комнаты, а сумма их площадей 34,8 м2. Определите площадь каждой комнаты.
Пусть х м2 — площадь второй комнаты, тогда x + 5,2 м2 − площадь первой комнаты, а х + (х + 5,2) м2 – их общая площадь, которая по условию задачи равна 34,8 м2.
Составим уравнение:
x + (x + 5,2) = 34,8
2x + 5,2 = 34,8
2x = 34,8 − 5,2
2x = 29,6
x = 29,6 : 2
х = 14,8 м2 — площадь второй комнаты
14,8 + 5,2 = 20 (м2) — площадь первой комнаты
Ответ: 14,8 м2 площадь второй комнаты, 20 м2 — площадь первой комнаты.844. Расстояние между пунктами 14,4 км. Пешеход прошел в 2 раза больше, чем ему осталось пройти. Сколько километров прошел пешеход?
Пусть х км — осталось пройти пешеходу, тогда 2x км – уже прошёл пешеход, а всего надо пройти х + 2х км, что по условию задачи равно 14,4 км.
Составим уравнение:
x + 2x = 14,4
3x = 14,4
x = 14,4 : 3
х = 4,8 км — осталось пройти пешеходу
2 • 4,8 = 9,6 (км) – прошёл пешеход
Ответ: пешеход прошёл 9,6 км.845. На 66,5 р. купили 4 пачки печенья и 3 коробки конфет. Каждая коробка конфет стоила в 5 раз дороже пачки печенья. Сколько стоила коробка конфет?
Пусть х р. стоила пачка печенья, тогда 5x р. — стоила коробка конфет, всего купили печенья на 4х р. и конфет на 3 • 5х = 15х р., а общая стоимость покупки 4х + 15х, что по условию задачи равно 66,5 р.
Составим уравнение:
4x + 15x = 66,5
19x = 66,5
x = 66,5 : 19
х = 3,5 р. — стоила пачка печенья
3,5 • 5 = 17,5 (р.) — стоила коробка конфет
Ответ: 17,5 р. 161
-
Ответы к стр. 161
846. Из "Сборника задач и упражнений по арифметике" С.А.Пономарева и Н.И.Сырнева (Задача−шутка). Крестьянин поехал на луга за сеном и взял с собой трёх сыновей: 15 лет, 12 лет и 10 лет. Обратный путь в 13,5 км мальчики по очереди ехали на возу, причем расстояние распределили обратно пропорционально возрасту. Сколько километров проехал каждый из них на возу.
Пусть x км проехал средний сын, тогда:
12/15 x − проехал старший сын;
12/10 x − проехал младший сын.
12/15 x + x + 12/10 x = 13,5
24/30 x + x + 36/30 x = 13,5
60/30 x + x = 13,5
2 x + x = 13,5
3 x = 13,5
x = 13,5 : 3
х = 4,5 км проехал средний сын.
12/15 ∗ 4,5 = 12/15 ∗ 45/10 = 12 ∗ 3/1 ∗ 10 = 36/10 = 3,6 км проехал старший сын.
12/10 ∗ 4,5 = 12/10 ∗ 45/10 = 540/100 = 54/10 = 5,4 км проехал младший сын.
Ответ:
4,5 км проехал средний сын;
3,6 км проехал старший сын;
5,4 км проехал младший сын.847. Придумайте и решите 6 разных задач на движение по реке, в условиях которых были бы использованы десятичные дроби.
Задача 1.Скорость лодки в стоячей воде 10 км/ч, укажите за какое время лодка проплывет 10,5 км?
Дано:
U = 10 км/ч
S = 10,5 км
Найти:
t − ?
Решение:
t = S : U = 10,5 : 10 = 1,05 часа потребуется лодке, чтобы проплыть 10,5 км.
Ответ: 1,05 часа.
Задача 2. Скорость течения реки 5 км/ч, скорость лодки в стоячей воде 10 км/ч, укажите за какое время лодка проплывет 10,5 км по течению?
Дано:
U лодки = 10 км/ч
U течения = 5 км/ч
S = 10,5 км
Найти:
t − ?
Решение:
t = S : (U лодки + U течения) = 10,5 : (10 + 5) = 10,5 : 15 = 0,7 часа потребуется лодке, чтобы проплыть 10,5 км по течению.
Ответ: 0,7 часа.
Задача 3. Скорость течения реки 5 км/ч, скорость лодки в стоячей воде 10 км/ч, укажите за какое время лодка проплывет 10,5 км против течения?
Дано:
U лодки = 10 км/ч
U течения = 5 км/ч
S = 10,5 км
Найти:
t − ?
Решение:
t = S : (U лодки − U течения) = 10,5 : (10 − 5) = 10,5 : 5 = 2,1 часа потребуется лодке, чтобы проплыть 10,5 км против течения.
Ответ: 2,1 часа.
Задача 4. Скорость течения реки 5 км/ч, скорость лодки в стоячей воде 10 км/ч, укажите за какое время лодка проплывет 10,5 км по течению и вернется обратно?
Дано:
U лодки = 10 км/ч
U течения = 5 км/ч
S = 10,5 км
Найти:
t − ?
Решение:
t = S : (U лодки − U течения) + S : (U лодки − U течения) = 10,5 : (10 + 5) + 10,5 : (10 − 5)= 10,5 : 15 + 10,5 : 5 = 1,05 + 2,1 = 3,15 часа потребуется лодке, чтобы проплыть 10,5 км по течению и вернуться обратно.
Ответ: 3,15 часа.
Задача 5. Скорость течения реки 5 км/ч, скорость лодки в стоячей воде 10 км/ч, укажите за какое время лодка проплывет 10,5 км по течению и вернется обратно, при чём при движении по течению лодка сплавлялась с выключенным мотором?
Дано:
U лодки = 10 км/ч
U течения = 5 км/ч
S = 10,5 км
Найти:
t − ?
Решение:
t = S : U течения + S : (U лодки − U течения) = 10,5 : 5 + 10,5 : (10 − 5)= 2,1 + 2,1 = 4,2 часа потребуется лодке, чтобы проплыть 10,5 км по течению и вернуться обратно, при чём при движении по течению лодка будет сплавляться с выключенным мотором.
Ответ: 4,2 часа.
Задача 6. Скорость течения реки 5 км/ч, скорость лодки в стоячей воде 10 км/ч, укажите во сколько раз меньше затратит лодка на преодоление пути по течению, чем против течения?
Дано:
U лодки = 10 км/ч
U течения = 5 км/ч
S = 10,5 км
Найти:
t против течения : t по течению − ?
Решение:
t = S : (U лодки + U течения) = 10,5 : (10 + 5) = 10,5 : 15 = 0,7 часа потребуется лодке, чтобы проплыть 10,5 км по течению.
t = S : (U лодки − U течения) = 10,5 : (10 − 5) = 10,5 : 5 = 2,1 часа потребуется лодке, чтобы проплыть 10,5 км против течения.
t против течения : t по течению = 2,1 : 1,05 = в 2 раза меньше затратит лодка на преодоление пути по течению, чем против течения.
Ответ: в 2 раза.848. Вычислите:
а) 13,7 ∗ 2,2 − 5,9 ∗ 2,2 + 7,82 ;
б) 2,62 ∗ 13,58 + 3,8 ∗ 13,58 + 6,422 .а) 13,7 ∗ 2,2 − 5,9 ∗ 2,2 + 7,82 = 30,14 − 12,98 + 60,84 = 17,16 + 60,84 = 78
Ответ: 78
б) 2,62 ∗ 13,58 + 3,8 ∗ 13,58 + 6,422 = 13,58 ∗ ( 2,62 + 3,8 ) + 6,422 = 13,58 ∗ 6,42 + 6,422 = 6,42 ∗ ( 13,58 + 6,42 ) = 6,42 ∗ 20 = 128,4
Ответ: 128,4849. Вычислите:
а) 1,476 + 2,08 ∗ 4,05/49,938 : 24,36 − 0,25 ;
б) 4,58 + 6,275 : 1,25/49,533 : 16,5 − 2,522 .
а) $\frac{1,476+2,08\ast4,05}{49,938:24,36-0,25}=\frac{1,476+8,424}{2,05-0,25}=\frac{9,9}{1,8}=5,5;$
б) $\frac{4,58+6,275:1,25}{49,533:16,5-2,522}=\frac{4,58+5,02}{3,002-2,522}=\frac{9,6}{0,48}=20.$850. Вычислите:
а) 1/2 + 0,5 ;
б) 1/4 + 0,3 ;
в) 2/5 − 0,4 ;
г) 3/4 − 0,25 ;
д) 7/25 + 0,13 ;
е) 6/25 − 0,02.а) 1/2 + 0,5 = 0,5 + 0,5 = 1.
б) 1/4 + 0,3 = 0,25 + 0,3 = 0,55.
в) 2/5 − 0,4 = 0,4 − 0,4 = 0.
г) 3/4 − 0,25 = 0,75 − 0,25 = 0,5.
д) 7/25 + 0,13 = 0,28 + 0,13 = 0,41.
е) 6/25 − 0,02 = 0,24 − 0,02 = 0,22.851. Вычислите:
а) 1 1/2 − 3 1/4 ∗ 0,2 ;
б) 1 1/5 : 1,6 − 4/5 ∗ 0,125 ;
в) 4 1/2 ∗ 0,4 : 0,15 ∗ 1 2/3 ;
г) 3 1/3 ∗ 0,3 + 19 : 0,5 ∗ 1/4 .а) 1 1/2 − 3 1/4 ∗ 0,2 = 1,5 − 3,25 ∗ 0,2 = 1,5 − 0,65 = 0,85
б) 1 1/5 : 1,6 − 4/5 ∗ 0,125 = 1,2 : 1,6 − 0,8 ∗ 0,125 = 0,75 − 0,1 = 0,65
в) $4\frac12\ast0,4:0,15\ast1\frac23=\frac92\ast\frac4{10}:\frac{15}{100}\ast\frac53=\frac{9\ast4\ast5}{2\ast10\ast3}\ast\frac{100}{15}=2\ast10=20$
г) $3\frac13\ast0,3+19:0,5\ast\frac14=\frac{10}3\ast\frac3{10}+19:\frac5{10}\ast\frac14=1+19\ast\frac{10}5\ast\frac14=1+19\ast\frac12=1+9,5=10,5$852. Вычислите:
а) ( 1 3/8 + 1 3/4 − 0,411 ) : 0,59 ;
б) ( 6 7/15 − 1,4 ) : ( 2 4/5 + 1,2 ) ;
в) 12,8 ∗ 1 4 : ( 3/4 − 0,125 ) ;
г) 1 17/18 ∗ ( 3 1/4 − 2,95 ) : 3,5.а) ( 1 3/8 + 1 3/4 − 0,411 ) : 0,59 = ( 1,375 + 1,75 − 0,411 ) : 0,59 = ( 3,125 − 0,411 ) : 0,59 = 2,714 : 0,59 = 4,6
б) $(6\frac7{15}-1,4):(2\frac45+1,2)=(\frac{97}{15}-\frac{14}{10}):(\frac{14}5+\frac{12}{10})=\frac{194-42}{30}:\frac{28+12}{10}=\frac{152}{30}\ast\frac{10}{40}=\frac{38}{30}=\frac{19}{15}=1\frac4{15}$
в) 12,8 ∗ 1/4 : ( 3/4 − 0,125 ) = 12,8 ∗ 0,25 : ( 0,75 − 0,125 ) = 3,2 : 0,625 = 5,12
г) $1\frac{17}{18}\ast(3\frac14-2,95):3,5=\frac{35}{18}\ast(\frac{13}4-\frac{295}{100}):\frac{35}{10}=\frac{35}{18}\ast\frac{325-295}{100}\ast\frac{10}{35}=\frac{35}{18}\ast\frac{30}{100}\ast\frac{10}{35}=\frac{3\ast1}{18\ast1}=\frac16$853. Решите уравнение:
а) x − 3 1/2 = 6,1 ;
б) 2,5 x + 6,3 = 7 1/3 ;
в) 2 2/3 x − 5,1 = 3,7 ;
г) 1,5 x + 2 1/3 = 2,5.а) x − 3 1/2 = 6,1
x − 3,5 = 6,1
x = 6,1 + 3,5 = 9,6
Ответ: 9,6.
б) 2,5 x + 6,3 = 7 1/3
25/10 x + 63/10 = 22/3
25/10 x = 22/3 − 63/10
x = 31/30 : 25/10
х = 31/30 ∗ 10/25
х = 31/75
Ответ: 31/75
в) 2 2/3 x − 5,1 = 3,7
8/3 x − 51/10 = 37/10
8/3 x = 37/10 + 51/10
8/3 x = 88/10 : 8/3
х = 88/10 ∗ 3/8
х = 33/10 = 3 3/10
Ответ: 3 3/10
г) 1,5 x + 2 1/3 = 2,5
15/10 x + 7/3 = 25/10
15/10 x = 25/10 − 7/3
x = 75 − 70/30 : 15/10 = 5/30 ∗ 10/15 = 1/9
Ответ: 1/9854. Решите пропорцию:
а) x/4,9 = 1,5/2,1 ;
б) 1,8/x = 0,36/3,2 ;
в) 2,7/25 = x/1,25 ;
г) x : 4,2 = 3/2 : 6,3 ;
д) x : 3,8 = 4/5 : 1,9 ;
е) 2,5 : x = 3 1/3 : 1,2 ;
ж) 2 1/3 : x = 3,5 : 1,5 ;
з) 2 x : 3,5 = 8 : 7 ;
и) 1,2 x : 8 = 0,36 : 5.а) x/4,9 = 1,5/2,1
x = 4,9 ∗ 1,5/2,1 = 3,5
Ответ: 3,5.
б) 1,8/x = 0,36/3,2
x = 1,8 ∗ 3,2/0,36
х = 16
Ответ: 16.
в) 2,7/25 = x/1,25
x = 2,7 ∗ 1,25/25
х = 0,135
Ответ: 0,135.
г) x : 4,2 = 3/2 : 6,3
x = 4,2 ∗ 1,5/6,3
х = 1
Ответ: 1.
д) x : 3,8 = 4/5 : 1,9
x = 3,8 ∗ 0,8/1,9
х = 1,6
Ответ: 1,6.
е) 2,5 : x = 3 1/3 : 1,2
x = 25/10 ∗ 12/10 : 10/3
х = 25/10 ∗ 12/10 ∗ 3/10
х = 25 ∗ 12 ∗ 3/10 ∗ 10 ∗ 10
х = 900/1000 = 9/10 = 0,9
Ответ: 0,9.
ж) 2 1/3 : x = 3,5 : 1,5
x = 7/3 ∗ 15/10 : 35/10
х = 7/3 ∗ 15/10 ∗ 10/35
х = 1 ∗ 3 ∗ 1/3 ∗ 1 ∗ 1 = 1
Ответ: 1.
з) 2 x : 3,5 = 8 : 7
2 x = 3,5 ∗ 8 7
x = 4 : 2 = 2
Ответ: 2.
и) 1,2 x : 8 = 0,36 : 5
1,2 x = 8 ∗ 0,36 5
x = 0,576 : 1,2 = 0,48
Ответ: 0,48. 162
-
Десятичные дроби и проценты
Ответы к стр. 162
855. Найдите 27% числа:
а) 200;
б) 290;
в) 45;
г) 38.а) 200 * 27% = 200 * 0,27 = 54
Ответ: 54
б) 290 * 27% = 290 * 0,27 = 78,3
Ответ: 78,3
в) 45 * 27% = 45 * 0,27 = 12,15
Ответ: 12,15
г) 38 * 27% = 38 * 0,27 = 10,26
Ответ: 10,26856. Найдите число, 27% которого равны:
а) 540;
б) 300;
в) 243;
г) 2727.а) 540 : 27% = 540 : 0,27 = 2000
Ответ: 2000
б) 300 : 27
Ответ: 1111 1/9
в) 243 : 27% = 243 : 0,27 = 900
Ответ: 900
г) 2727 : 27% = 2727 : 0,27 = 10100
Ответ: 10100857. Сколько процентов числа 350 составляет число:
а) 35;
б) 385;
в) 315;
г) 679.а) 35/350 ∗ 100
Ответ: 10%.
б) 385/350 ∗ 100
Ответ: 110%.
в) 315/350 ∗ 100
Ответ: 90%.
г) 679/350 ∗ 100
Ответ: 194%. 163
-
Ответы к стр. 163
858. Масса сушёных яблок составляет 25% массы свежих. Сколько сушёных яблок получили из 200 кг; 360 кг; 4,5 т свежих? Сколько процентов массы свежих яблок теряется при сушке?
200 * 25% = 200 * 0,25 = 50 кг сушеных яблок;
360 * 25% = 360 * 0,25 = 90 кг сушеных яблок;
4,5 * 25% = 4,5 * 0,25 = 1,125 т сушеных яблок;
100% − 25% = 75% массы свежих яблок теряется при сушке.
Ответ:
50 кг сушеных яблок;
90 кг сушеных яблок;
1,125 т сушеных яблок;
75% массы свежих яблок теряется при сушке.859. Виноград при сушке теряет 65% своей массе. Сколько изюма (сушеного винограда) получится из 400 кг; 350 кг; 1,8 т свежего винограда?
Масса свежего винограда составляет 100%, а масса потерь при сушке составляет 65%, тогда:
100% − 65% = 35% составляет масса изюма в массе винограда.
400 * 35% = 400 * 0,35 = 140 кг изюма получится из 400 кг винограда;
350 * 35% = 350 * 0,35 = 122,5 кг изюма получится из 350 кг винограда;
1,8 * 35% = 1,8 * 0,35 = 0,63 т изюма получится из 1,8 т винограда.
Ответ:
140 кг изюма получится из 400 кг винограда;
122,5 кг изюма получится из 350 кг винограда;
0,63 т изюма получится из 1,8 т винограда.860. Трава при сушке теряет 85% своей массы.
а) Сколько сена получится из 600 кг; 1500 кг; 11,8 т свежей травы?
б) Сколько травы надо накосить, чтобы насушить 1500 кг; 3300 кг; 3,6 т сена?а) Масса свежей травы составляет 100%, а масса потерь сушке составляет 85%, тогда:
100% − 85% = 15% составляет масса сена в массе свежей травы.
600 * 15% = 600 * 0,15 = 90 кг сена получится из 600 кг травы;
1500 * 15% = 1500 * 0,15 = 225 кг сена получится из 1500 кг травы;
11,8 * 15% = 11,8 * 0,15 = 1,77 т сена получится из 11,8 т травы.
Ответ:
90 кг сена получится из 600 кг травы;
225 кг сена получится из 1500 кг травы;
1,77 т сена получится из 11,8 т травы.
б) Масса свежей травы составляет 100%, а масса потерь сушке составляет 85%, тогда:
100% − 85% = 15% составляет масса сена в массе свежей травы.
1500 : 0,15 = 10000 кг = 10 т травы надо накосить, чтобы насушить 1500 кг сена;
3300 : 0,15 = 22000 кг = 22 т травы надо накосить, чтобы насушить 3300 кг сена;
3,6 : 0,15 = 24 т травы надо накосить, чтобы насушить 3,6 т сена.
Ответ:
10 т травы надо накосить, чтобы насушить 1500 кг сена;
22 т травы надо накосить, чтобы насушить 3300 кг сена;
24 т травы надо накосить, чтобы насушить 3,6 т сена.861. Что больше:
а) 45% от 72 или 72% от 45;
б) 38% от 80 или 60% от 45.а) 72 * 45% = 72 * 0,45 = 32,4;
45 * 72% = 45 * 0,72 = 32,4;
32,4 = 32,4, следовательно, 45% от 72 = 72% от 45.
Ответ: 45% от 72 = 72% от 45.
б) 80 * 38% = 80 * 0,38 = 30,4;
45 * 60% = 45 * 0,6 = 27;
30,4 > 27, следовательно, 38% от 80 > 60% от 45.
Ответ: 38% от 80 > 60% от 45.862. Товар стоил 150 р. Его цена повысилась на 12%. Сколько теперь стоит этот товар?
150 * 12% = 150 * 0,12 = на 18 р. повысилась цена товара.
150 + 18 = 168 р. стоит теперь товар.
Ответ: 168 р.863. Увеличьте число:
а) 80 на 20%;
б) 480 на 25%;
в) 50 на 10%;
г) 25 на 100%.а) 80 * 20% = 80 * 0,2 = 16
80 + 16 = 96
Ответ: 96
б) 480 * 25% = 480 * 0,25 = 120
480 + 120 = 600
Ответ: 600
в) 50 * 10% = 50 * 0,1 = 5
50 + 5 = 55
Ответ: 55
г) 25 * 100% = 25 * 1 = 25
25 + 25 = 50
Ответ: 50864. Уменьшите число:
а) 60 на 10%;
б) 500 на 28%;
в) 90 на 50%;
г) 125 на 40%.а) 60 * 10% = 60 * 0,1 = 6
60 − 6 = 54
Ответ: 54
б) 500 * 28% = 500 * 0,28 = 140
500 − 140 = 360
Ответ: 360
в) 90 * 50% = 90 * 0,5 = 45
90 − 45 = 45
Ответ: 45
г) 125 * 40% = 125 * 0,4 = 50
125 − 50 = 75
Ответ: 75865. Можно ли цену товара:
а) увеличить на 101%;
б) уменьшить на 101%?а) Пусть цена товара равна x, тогда:
1,01x − размер изменения цены товара;
x + 1,01x = x(1 + 1,01) = 2,01x новая цена товара, следовательно, на 101% центу товара можно повысить.
Ответ: можно.
б) Пусть цена товара равна x, тогда:
1,01x − размер изменения цены товара;
x − 1,01x = x(1 − 1,01) = −0,01x не может быть новой ценой товара, так как значение цены отрицательное.
Ответ: нельзя. 165
-
Сложные задачи на проценты
Ответы к стр. 165
866. Число 200 увеличили на 20%, полученный результат уменьшили на 20%. Получится ли в результате число 200? Какое число получится?
200 + 200 * 20% = 200 + 200 * 0,2 = 200 + 40 = 240 после увеличения,
240 − 240 * 20% = 240 − 240 * 0,2 = 240 − 48 = 192 результат двух изменений.
Ответ: 192.867. а) Число а увеличили на 20%, полученное число увеличили еще на 20%. Во сколько раз увеличилось число а? На сколько процентов увеличилось число а за два раза?
б) Цену товара уменьшили на 10%, полученную цену уменьшили еще на 10%. На сколько процентов уменьшили цену товара за два раза?а) (a + 0,2a) + (a + 0,2a) * 0,2 = 1,2a * (1 + 0,2) = 1,2a * 1,2 = 1,44a число после двух изменений.
1,44a : a = в 1,44 раза увеличилось число a;
(1,44a : a * 100) − 100 = на 44 % увеличилось число a.
Ответ:
в 1,44 раза увеличилось число a;
на 44 % увеличилось число a.
б) Пусть цена товара равна x, тогда:
x − 0,1x − 0,1 * (x − 0,1x) = 0,9x − 0,1 * 0,9x = 0,9x − 0,09x = 0,81x составила цена товара после двух изменений.
100 − 0,81x/x ∗ 100 = на 19% уменьшилась цена товара после двух изменений.
Ответ: на 19% уменьшилась цена товара. 166
-
Ответы к стр. 166
868. а) Число a больше числа b в 1,25 раза; в 1,32 раза; в 1,5 раза.
На сколько процентов число а больше числа b?
б) Число a больше числа b на 25%; на 48%; на 60%. Во сколько раз число а больше числа b?а) Число a = 1,25b, тогда:
1,25 b/b ∗ 100 − 100 = на 25% число a больше числа b.
Число a = 1,32b, тогда:
1,32 b/b ∗ 100 − 100 = на 32% число a больше числа b.
Число a = 1,5b, тогда:
1,5 b/b ∗ 100 − 100 = на 50% число a больше числа b.
Ответ: на 25%; на 32%; на 50%.
б) Число a = b + 0,25b = 1,25b, тогда:
1,25 b/b = в 1,25 раза число a больше числа b;
Число a = b + 0,48b = 1,48b, тогда:
1,48 b/b = в 1,48 раза число a больше числа b;
Число a = b + 0,6b = 1,6b, тогда:
1,6 b/b = в 1,6 раза число a больше числа b.
Ответ: в 1,25 раза; в 1,48 раз; в 1,6 раз.869. а) Некоторую сумму положили в банк под 20% годовых. Во сколько раз увеличится вложенная сумма за 5 лет, если начисляют простые проценты?
б) Некоторую сумму положили в банк под 20% годовых. Во сколько раз увеличится вложенная сумма за 4 года, если начисляют сложные проценты?а) Пусть сумма вклада равна a, тогда:
S = a ∗ ( 1 + n ∗ p/100 ) = a ∗ ( 1 + 5 ∗ 20/100 ) = a ∗ ( 1 + 1 ) = 2 a составила сумма вклада за 5 лет.
2 а а = в 2 раза увеличилась сумма вклада в банке за 5 лет.
Ответ: в 2 раза.
б) Пусть сумма вклада равна a, тогда:
S = a ∗ ( 1 + p/100 ) n = a ∗ ( 1 + 20/100 ) 4 = a ∗ ( 1,2 ) 4 = 2,0736 a составила сумма вклада за 4 года.
2,0736 a/a = в 2,0736 раза увеличилась сумма вклада в банке за 4 года.
Ответ: в 2,0736 раза.870. Сбербанк России с 1 октября 1993 года начислял доход из расчёта: 150% за хранение денег в банке в течение года; 65% за хранение денег в банке в течение 6 месяцев; 30% за хранение денег в банке в течение 3 месяцев. Каким образом при этих условиях можно было получить наибольший доход на сумму 100 000 р. в течение года? Каков этот наибольший доход?
Рассмотрим вариант начисления простых процентов:
S = a ∗ ( 1 + n ∗ p/100 )
Вклад на 1 год: = 100000 ∗ ( 1 + 1 ∗ 150/100 ) = 100000 ∗ 2,5 = 250000 рублей составит сумма вклада через год.
250000 − 100000 = 150000 р. составит сумма дохода.
Вклад на 6 месяцев: = 100000 ∗ ( 1 + 2 ∗ 65/100 ) = 100000 ∗ 2,3 = 230000 рублей составит сумма вклада через год.
230000 − 100000 = 130000 р. составит сумма дохода.
Вклад на 3 месяца: = 100000 ∗ ( 1 + 4 ∗ 30/100 ) = 100000 ∗ 2,2 = 220000 рублей составит сумма вклада через год.
220000 − 100000 = 120000 р. составит сумма дохода.
При начислении простых процентов наибольшего дохода можно будет достигнуть положив вклад сразу на год.
Рассмотрим вариант начисления сложных процентов:
S = a ∗ ( 1 + p 100 ) n
Вклад на 1 год: = 100000 ∗ ( 1 + 150/100 ) 1 = 100000 ∗ 2,5 = 250000 рублей составит сумма вклада через год.
250000 − 100000 = 150000 р. составит сумма дохода.
Вклад на 6 месяцев: = 100000 ∗ ( 1 + 65/100 ) 2 = 100000 ∗ 2,7225 = 272250 рублей составит сумма вклада через год.
272250 − 100000 = 172250 р. составит сумма дохода.
Вклад на 3 месяца: = 100000 ∗ ( 1 + 30/100 ) 4 = 100000 ∗ 2,8561 = 285610 рублей составит сумма вклада через год.
285610 − 100000 = 185610 р. составит сумма дохода.
Ответ: максимальный доход в течение года будет достигнут в случае вклада на 3 месяца под начисление сложных процентов.871. Компания X выплачивает доход по своим акциям ежегодно из расчета 40% годовых. Компания Y выплачивает доход по акциям 1 раз в полгода из того же расчета. В акции какой компании выгоднее вложить деньги на 1 год?
Пусть вклад равен а, тогда через год размер вклада в компании X составит
S = a ∗ ( 1 + n ∗ p/100 ) = a ∗ ( 1 + 1 ∗ 40/100 ) = 1,4 a,
1,4a − a = 0,4a составит размер выплаты за год;
в компании Y размер вклада через полгода составит S = a ∗ ( 1 + n ∗ p/100 ) = a ∗ ( 1 + 0,5 ∗ 40/100 ) = 1,2 a,
1,2 − a = 0,2a составит размер выплаты за полгода,
0,2a * 2 = 0,4a составит размер выплаты за год.
Ответ: годовой размер выплаты в обеих компаниях будет одинаковым, а значит в акции какой компании вкладывать деньги разницы нет.872. Обломов похудел на 25%, потом прибавил в весе на 20%, похудел на 10%, потом прибавил в весе на 20%. Прибавил Обломов в весе или похудел?
Пусть Обломов весил x, тогда:
x * (1 − 0,25) * (1 + 0,2) * (1 − 0,1) * (1 + 0,2) = x * 0,75 * 1,2 * 0,9 * 1,2 = 0,972x
x > 0,972, а значит Обломов похудел.
Ответ: Обломов похудел.873. Служащая фирмы сказала: "Производство продукции нашей фирмы увеличится на 200%, или в 2 раза". Исправьте её ошибку, если верно условие:
а) на 200%;
б) в 2 раза.а) Пусть объём производства продукции был равен x, тогда:
x + 2x = 3x объём производства продукции после его увеличения на 200%.
3x : x = в 3 раза вырос объём производства продукции, а не в 2 раза.
Ответ: объём производства продукции вырос в 3 раза, а не в 2 раза.
б) Пусть объём производства продукции был равен x, тогда:
x * 2 = 2x объём производства продукции после его увеличения в 2 раза.
(2x : x − 1) * 100 = на 100% вырос объём производства продукции, а не на 200%.
Ответ: объём производства продукции вырос на 100%, а не на 200%.874. Две противоположные стороны прямоугольника увеличили на 10%. На сколько процентов увеличилась его площадь? Зависит ли результат от того, какую пару сторон увеличили на 10%?
Пусть стороны прямоугольника a и b, тогда площадь прямоугольника равна:
S = a * b = ab
Пусть a увеличили на 10%:
a + 0,1a = 1,1a
S = 1,1a * b = 1,1ab
( 1,1 a b/a b − 1 ) ∗ 100 = на 10% увеличилась площадь.
Пусть b увеличили на 10%:
b + 0,1b = 1,1b
S = a * 1,1b = 1,1ab
( 1,1 a b/a b − 1 ) ∗ 100 = на 10% увеличилась площадь.
Ответ: площадь увеличилась на 10%. Результат не зависит от выбора пары сторон.875. а) Все стороны прямоугольника увеличили на 10%. На сколько процентов увеличилась его площадь?
б) Две противоположные стороны прямоугольника увеличили на 20%, две другие − уменьшили на 20%. Как изменилась площадь прямоугольника?а) Пусть стороны прямоугольника a и b, тогда площадь прямоугольника равна:
S = a * b = ab
Пусть каждую сторону увеличили на 10%, тогда:
a + 0,1a = 1,1a
b + 0,1b = 1,1b
S = 1,1a * 1,1b = 1,21ab
( 1,21 a b/a b − 1 ) ∗ 100 = на 21% увеличилась площадь.
Ответ: на 21% увеличилась площадь.
б) Пусть стороны прямоугольника a и b, тогда площадь прямоугольника равна:
S = a * b = ab
Пусть ширину a увеличили на 20%:
a + 0,2a = 1,2a
а длину уменьшили на 20%:
b − 0,2b = 0,8b
S = 1,2a * 0,8b = 0,96ab
( 1 − 0,96 a b/a b ) ∗ 100 = на 4% уменьшилась площадь.
Ответ: на 4% уменьшилась площадь.876. Две противоположные стороны прямоугольника увеличили на 20%, две другие − уменьшили на 10%. На сколько процентов увеличилась площадь прямоугольника?
Пример
Размер увеличения равен произведению исходного размера на процент изменения размера.Пусть стороны прямоугольника a и b, тогда площадь прямоугольника равна:
S = a * b = ab
Пусть ширину a увеличили на 20%:
a + 0,2a = 1,2a
а длину уменьшили на 10%:
b − 0,1b = 0,9b
S = 1,2a * 0,9b = 1,08ab
( 0,96 a b/a b − 1 ) ∗ 100 = на 8% увеличилась площадь.
Ответ: на 8% увеличилась площадь.877. Длину прямоугольника уменьшили на 20%. На сколько процентов надо увеличить ширину прямоугольника, чтобы его площадь не изменилась?
Пусть стороны прямоугольника а (ширина) и b (длина), тогда площадь прямоугольника равна:
S = a * b = ab
Пусть b уменьшили на 20%:
b − 0,2b = 0,8b
На сколько процентов изменилась а неизвестно, но известно, что площадь прямоугольника после изменений размеров его сторон осталась неизменной, тогда:
a * b = xa * 0,8b
$x=\frac{a\ast b}{0,8b}:a=\frac{a\ast b}{0,8b\ast a}=\frac1{0,8}=1,25$
( 1,25 a/a − 1 ) ∗ 100 = на 25% необходимо увеличить ширину прямоугольника, чтобы площадь осталась неизменной.
Ответ: необходимо увеличить ширину на 25%. 167
-
Ответы к стр. 167
878. В драмкружке число мальчиков составляет 80% от числа девочек. Сколько процентов составляет число девочек от числа мальчиков в этом кружке?
Пусть девочек было x, тогда:
0,8x − было мальчиков,
x/0,8 x ∗ 100 = 1,25 ∗ 100 = 125 составляют девочки от числа мальчиков.
Ответ: 125% составляют девочки от числа мальчиков.879. Имеется 600 г раствора, содержащего 15% соли. Сколько воды требуется добавить в раствор, чтобы он стал содержать 10% соли?
Содержание соли обратно пропорционально количеству раствора, то есть чем больше раствора, тем меньше в нем содержание соли, поэтому:
↑600 г раствора − 15% соли ↓
↑x г раствора − 10% соли ↓
600/x = 10/15
x = 600 ∗ 15/10
х = 900
в 900 г раствора будет содержаться 10% соли.
900 − 600 = 300 г раствора необходимо добавить.
Ответ: 300 г.880. Сколько граммов воды нужно добавить к 120 г раствора, в котором содержится 30% сахара, чтобы получить раствор, содержащий 20% сахара?
Содержание сахара обратно пропорционально количеству раствора, то есть чем больше раствора, тем меньше в нем содержание сахара, поэтому:
↑120 г раствора − 30% соли ↓
↑x г раствора − 20% соли ↓
120/x = 20/30
x = 120 ∗ 30/20
х = 180
в 180 г раствора будет содержаться 20% сахара.
180 − 120 = 60 г раствора необходимо добавить.
Ответ: 60 г.881. Кусок сплава массой 700 г, содержащий 80% олова, сплавили с куском олова весом 300 г. Определите процентное содержание олова в полученном сплаве.
700 * 80% = 700 * 0,8 = 560 г олова содержится в куске сплава массой 700 г,
700 + 300 = 1000 г стал весить кусок сплава после добавления 300 г олова,
560 + 300 = 860 г олова содержится в куске сплава после сплавки,
860 : 1000 * 100% = 86% олова содержится в куске сплава после сплавки.
Ответ: 86%.882. Имеется 500 г раствора, содержащего 40% кислоты. Сколько воды требуется добавить в раствор, чтобы он стал содержать 25% кислоты?
Содержание кислоты обратно пропорционально количеству раствора, то есть чем больше раствора, тем меньше в нем содержание кислоты, поэтому:
↑500 г раствора − 40% кислоты ↓
↑x г раствора − 25% кислоты ↓
500/x = 25/40
x = 500 ∗ 40/25
х = 800
в 800 г раствора будет содержаться 25% кислоты.
800 − 500 = 300 г раствора необходимо добавить.
Ответ: 300 г.883. В первый день рабочий перевыполнил дневное задание на 2%, во второй день он перевыполнил дневное задание на 4%. На сколько процентов рабочий перевыполнил задание двух дней?
Пусть норма в день равна х, тогда:
x + x * 2% = x * (1 + 0,02) = 1,02x выполнил рабочий в первый день,
x + x * 4% = x * (1 + 0,04) = 1,04x выполнил рабочий во второй день,
1,02x + 1,04x = 2,06x выполнил рабочий за 2 дня,
2x − норма рабочего за два дня,
( 2,06 x/2 x − 1 ) ∗ 100 = 3%
на 3% рабочий перевыполнил норму двух дней.
Ответ: на 3%.884. В спортивной секции девочки составляют 60% числа мальчиков. Сколько процентов всех участников секции составляют девочки?
Пусть в секции х мальчиков, тогда:
0,6x − девочки;
x + 0,6x = 1,6x − всего детей в секции;
0,6 x/1,6 x ∗ 100 составляют девочки от общего числа детей в секции.
Ответ: 37,5%. 168
-
Десятичные дроби произвольного знака
Ответы к стр. 168
885. Вычислите:
а) 2,1 + (−3,5);
б) (−4,9) + (−1,3);
в) 4,8 − 9,9;
г) 6,2 − (−1,7);
д) −7,9 − (−1,8);
е) −1,2 − 3,5.a) 2,1 + (−3,5) = −(3,5 − 2,1) = −1,4.
Ответ: −1,4.
б) (−4,9) + (−1,3) = −(4,9 + 1,3) = −6,2.
Ответ: −6,2.
в) 4,8 − 9,9 = −(9,9 − 4,8) = −5,1.
Ответ: −5,1.
г) 6,2 − (−1,7) = 6,2 + 1,7 = 7,9.
Ответ: 7,9.
д) −7,9 − (−1,8) = −7,9 + 1,8 = −(7,9 − 1,8) = −6,1.
Ответ: −6,1.
е) −1,2 − 3,5 = −1,2 + (−3,5) = −(1,2 + 3,5) = −4,7.
Ответ: −4,7.886. Вычислите:
а) 1,56 + (−8,28);
б) −7,53 − 6,48;
в) −13,75 − 5;
г) 12,51 − 17,23;
д) 12,285 − 13,999;
е) 13,4 − 17,48.а) 1,56 + (−8,28) = −(8,28 − 1,56) = −6,72
Ответ: 6,72
б) −7,53 − 6,48 = −7,53 + (−6,48) = −(7,53 + 6,48) = −14,01
Ответ: −14,01
в) −13,75 − 5 = −13,75 + (−5) = −(13,75 + 5) = −18,75
Ответ: −18,75
г) 12,51 − 17,23 = 12,51 + (−17,23) = −(17,23 − 12,51) = −4,72
Ответ: −4,72
д) 12,285 − 13,999 = 12,285 + (−13,999) = −1,714
Ответ: −1,714
е) 13,4 − 17,48 = 13,4 + (−17,48) = −4,08
Ответ: −4,08887. Вычислите:
а) (−1,2) * 5;
б) (−4,9) : 7;
в) (−6,4) : (−0,8);
г) 72 : (0,6);
д) (−4,8) : 0,16;
е) (−1,28) : (−6,4).а) (−1,2) * 5 = −(1,2 * 5) = −6
Ответ: −6
б) (−4,9) : 7 = −(4,9 : 7) = −0,7
Ответ: −0,7
в) (−6,4) : (−0,8) = 6,4 : 0,8 = 0,8
Ответ: 0,8
г) 72 : (−0,6) = −(72 : 0,6) = −120
Ответ: −120
д) (−4,8) : 0,16 = −(4,8 : 0,16) = −30
Ответ: −30
е) (−1,28) : (−6,4) = 1,28 : 6,4 = 0,2
Ответ: 0,2888. Вычислите:
а) 4,16 − 5,1 * 3,2;
б) 7,39 − 1,21 : 1,1;
в) (−44,44) : 11 + 1,1;
г) (−6,25) : 2,5 + 2,5;
д) 0,48 : 1,6 − 4,8;
е) 12,5 * (−4) : (−2).а) 4,16 − 5,1 * 3,2 = 4,16 − 16,32 = −12,16
Ответ: −12,16
б) 7,39 − 1,21 : 1,1 = 7,39 − 1,1 = 6,29
Ответ: 6,29.
в) (−44,44) : 11 + 1,1 = −4,04 + 1,1 = −2,94
Ответ: −2,94
г) (−6,25) : 2,5 + 2,5 = −2,5 + 2,5 = 0
Ответ: 0
д) 0,48 : 1,6 − 4,8 = 0,3 − 4,8 = −4,5
Ответ: −4,5.
е) 12,5 * (−4) : (−2) = −50 : (−2) = 25
Ответ: 25.889. Вычислите:
а) 44 : (−2,5) − 6 * (4,3 * 0,8 − 3,7);
б) (−11,2 : (−2,8) − 3,6 + 2,4) : (−0,4);
в) −3,6 * (−0,5) − (−3,2 + 0,8) * 1,05.а) 44 : (−2,5) − 6 * (4,3 * 0,8 − 3,7) = −17,6 − 6 * (3,44 − 3,7) = −17,6 − 6 * (−0,26) = −17,6 + 1,56 = −16,04
Ответ: −16,04
б) (−11,2 : (−2,8) − 3,6 + 2,4) : (−0,4) = (4 − 3,6 + 2,4) : (−0,4) = (0,4 + 2,4) : (−0,4) = 2,8 : (−0,4) = −7
Ответ: −7
в) −3,6 * (−0,5) − (−3,2 + 0,8) * 1,05 = −3,6 * (−0,5) + 2,4 * 1,05 = 1,8 + 2,52 = 4,32.
Ответ: 4,32.890. Вычислите:
а) (4,28 + 3,6 * (−0,85)) : (−0,4);
б) 7,68 − 6,4 : (−1,2 − 0,4);
в) (4,7 + 2,3) * (−3,5) − 8,7 + 0,3;
г) 5,41 − 8,1 : (3,6 − 6,3).а) (4,28 + 3,6 * (−0,85)) : (−0,4) = (4,28 + (−3,06)) : (−0,4) = 1,22 : (−0,4) = −3,05
Ответ: −3,05
б) 7,68 − 6,4 : (−1,2 − 0,4) = 7,68 − 6,4 : (−1,6) = 7,68 + 4 = 11,68
Ответ: 11,68.
в) (4,7 + 2,3) * (−3,5) − 8,7 + 0,3 = 7 * (−3,5) − 8,7 + 0,3 = −24,5 − 8,7 + 0,3 = −33,2 + 0,3 = −32,9
Ответ: −32,9
г) 5,41 − 8,1 : (3,6 − 6,3) = 5,41 − 8,1 : (−2,7) = 5,41 + 3 = 8,41.
Ответ: 8,41.891. Вычислите:
а) (0,05 − 2,2 + 0,53) : 1,8 + 0,4;
б) 0,2 * (0,4 − 1,08 + 0,15) + 0,2;
в) (0,4 * 0,01 − 0,01) : 0,25 − 0,231;
г) −0,8 + 4,2 * (0,002 : 0,04 − 4,1).а) (0,05 − 2,2 + 0,53) : 1,8 + 0,4 = (−2,15 + 0,53) : 1,8 + 0,4 = −1,62 : 1,8 + 0,4 = −0,9 + 0,4 = −0,5
Ответ: −0,5.
б) 0,2 * (0,4 − 1,08 + 0,15) + 0,2 = 0,2 * (−0,68 + 0,15) + 0,2 = 0,2 * (−0,53) + 0,2 = −0,106 + 0,2 = 0,094
Ответ: 0,094
в) (0,4 * 0,01 − 0,01) : 0,25 − 0,231 = (0,004 − 0,01) : 0,25 − 0,231 = −0,006 : 0,25 − 0,231 = −0,024 − 0,231 = −0,255
Ответ: −0,255
г) −0,8 + 4,2 * (0,002 : 0,04 − 4,1) = −0,8 + 4,2 * (0,05 − 4,1) = −0,8 + 4,2 * (−4,05) = −0,8 − 17,01 = −17,81.
Ответ: −17,81892. Решите уравнение:
а) 0,4x = 3;
б) 2x = 1,8;
в) 0,3x = −2,7;
г) 1,5x = −10,5;
д) −0,002x = 25;
е) −1,4x = 2,842.а) 0,4x = 3
x = 3 : 0,4
х = 7,5
Ответ: 7,5
б) 2x = 1,8
x = 1,8 : 2
х = 0,9
Ответ: 0,9
в) 0,3x = −2,7
x = −2,7 : 0,3
х = −9
Ответ: −9
г) 1,5x = −10,5
x = −10,5 : 1,5
х = −7
Ответ: −7
д) −0,002x = 25
x = 25 : (−0,002)
х = −12500
Ответ: −12500
е) −1,4x = 2,842
x = 2,842 : (−1,4)
х = −2,03
Ответ: −2,03893. Вычислите:
а) (−654,84 : 32,1 − 35,568 : (−3,42)) : 2,5;
б) (−3,17 − 25,9632 : 4,32) : (−74,358 : 24,3);
в) (2763,36 : (−30,4) − 70,7) : (714,07 : 7,07).а) (−654,84 : 32,1 − 35,568 : (−3,42)) : 2,5 = (−20,4 − 35,568 : (−3,42)) : 2,5 = (−20,4 + 10,4) : 2,5 = −10 : 2,5 = −4
б) (−3,17 − 25,9632 : 4,32) : (−74,358 : 24,3) = (−3,17 − 6,01) : (−3,06) = (−9,18) : (−3,06) = 3
в) (2763,36 : (−30,4) − 70,7) : (714,07 : 7,07) = (−90,9 − 70,7) : 101 = −161,6 : 101 = −1,6894. Вычислите:
а) ( 2,75 : 3 2/3 − 2 1/3 : 1,75 ) ∗ 3 2/21 ;
б) ( 3,24 : 9 7 − 3 1/5 : 1 1/3 ) : ( − 0,9 ) ;
в) ( − 4,5 ) ∗ 5 1/3 + ( − 5,5 ) ∗ 5 1/3 ;
г) 3 1/7 ∗ 7,425 + ( − 6,425 ) ∗ 3 1/7 .а) $(2,75:3\frac23-2\frac13:1,75)\ast3\frac2{21}=(\frac{275}{100}:\frac{11}3-\frac73:\frac{175}{100})\ast\frac{65}{21}=(\frac{11}4\ast\frac3{11}-\frac73\ast\frac47)\ast\frac{65}{21}=(\frac34-\frac43)\ast\frac{65}{21}=\frac{9-16}{12}\ast\frac{65}{21}=-\frac{7\ast65}{12\ast21}=-\frac{65}{36}=-1\frac{29}{36}$
б) $(3,24:\frac97-3\frac15:1\frac13):(-0,9)=(\frac{324}{100}:\frac97-\frac{16}5:\frac43):(-\frac9{10})=(\frac{81}{25}\ast\frac79-\frac{16}5\ast\frac34)\ast(-\frac{10}9)=(\frac{63}{25}-\frac{12}5)\ast(-\frac{10}9)=\frac{63-60}{25}\ast(-\frac{10}9)=\frac3{25}\ast(-\frac{10}9)=-\frac2{15}$
в) $(-4,5)\ast5\frac13+(-5,5)\ast5\frac13=\frac{16}3\ast(-4,5-5,5)=\frac{16}3\ast(-10)=-\frac{160}3=-53\frac13$
г) $3\frac17\ast7,425+(-6,425)\ast3\frac17=3\frac17\ast(7,425-6,425)=3\frac17\ast1=3\frac17$ 169
-
Ответы к стр. 169
895. Вычислите:
а) $\frac{-0,125\ast5}{(1\frac{28}{63}-\frac{17}{21})\ast7\frac78}$ ;
б) $\frac{(\frac{21}{40}-\frac{19}{24})\ast0,7+0,04}{0,675\ast3,4-2,02}$ ;
в) $\frac{(13,25-2\frac5{27}-10\frac56)\ast230,04+46,75}{(1\frac37+3\frac13):(12\frac13-14\frac27)}$ .а) $\frac{-0,125\ast5}{(1\frac{28}{63}-\frac{17}{21})\ast7\frac78}=\frac{-0,625}{(\frac{91}{63}-\frac{51}{63})\ast\frac{63}8}=\frac{-0,625}{\frac{40}{63}\ast\frac{63}8}=\frac{-0,625}5=-0,125$
б) $\frac{(\frac{21}{40}-\frac{19}{24})\ast0,7+0,04}{0,675\ast3,4-2,02}=\frac{\frac{63-95}{120}\ast\frac7{10}+0,04}{0,675\ast3,4-2,02}=\frac{\frac{-14}{75}+\frac4{100}}{2,295-2,02}=\frac{\frac{-56+12}{300}}{0,275}=\frac{\frac{-44}{300}}{\frac{275}{1000}}=-\frac{44}{300}\ast\frac{1000}{275}=-\frac{44}3\ast\frac{10}{275}=-\frac{44}3\ast\frac2{55}=-\frac{88}{165}=-\frac8{15}$
в) $\frac{(13,25-2\frac5{27}-10\frac56)\ast230,04+46,75}{(1\frac37+3\frac13):(12\frac13-14\frac27)}=\frac{(\frac{1325}{100}-\frac{59}{27}-\frac{65}6)\ast230,04+46,75}{(\frac{10}7+\frac{10}3):(\frac{37}3-\frac{100}7)}=\frac{\frac{35775-5900-29250}{2700}\ast230,04+46,75}{\frac{30+70}{21}:\frac{259-300}{21}}=\frac{\frac{625}{2700}\ast\frac{23004}{100}+\frac{4675}{100}}{\frac{100}{21}\ast\frac{-21}{41}}=\frac{\frac{213}4+\frac{4675}{100}}{\frac{-100}{41}}=\frac{\frac{5325+4675}{100}}{\frac{-100}{41}}=100\ast\frac{-41}{100}=-41$ 170
-
Приближение десятичных дробей
Ответы к стр. 170
896. Что показывает знак "
≈"? Как читают запись а ≈ а 1 ?
Ответ:
≈ − знак приближенного равенства;
а ≈ а 1 − число а приближенно равно числу а 1 или а 1 есть приближение числа а.897. Назовите приближение числа 0,2638:
а) с недостатком с точностью до одной десятой;
б) с избытком с точностью до одной сотой;
в) с округлением с точностью до одной тысячной.а) Ответ: 0,2
б) Ответ: 0,27
в) Ответ: 0,264898. Какие цифры называют значащими в записи числа в виде десятичной дроби?
Ответ: значащей цифрой десятичной дроби называют её первую (слева направо) отличную от нуля цифру, а также все следующие за ней цифры.
171
-
Ответы к стр. 171
899. Что значит округлить число с точностью до второй значащей цифры?
Ответ: это значит округлить его до того разряда, где находится вторая значащая цифра, заменив следующие цифры нулями.
900. Найдите приближение числа а с недостатком с точностью до единицы третьего разряда после запятой:
а) а = 0,3456;
б) а = 0,76543;
в) а = 0,02325;
г) а = −0,34354.а) Ответ: 0,345
б) Ответ: 0,765
в) Ответ: 0,023
г) Ответ: −0,343901. Найдите приближение числа а с избытком с точностью до единицы второго разряда после запятой:
а) а = 1,2345;
б) а = 3,56789;
в) а = 2,577;
г) а = 2,555.а) Ответ: 1,24
б) Ответ: 3,57
в) Ответ: 2,58
г) Ответ: 2,56902. Округлите число а с точностью до 0,01:
а) а = 1,24851;
б) а = 1,24158;
в) а = −7,02303;
г) а = 0,12528.а) Ответ: 1,25
б) Ответ: 1,24
в) Ответ: −7,02
г) Ответ: −0,13903. Округлите число а с точностью до 0,001:
а) а = 8,91011...;
б) а = −8,91011...;
в) а = 0,2626;
г) а = 0,6265.а) Ответ: 8,91
б) Ответ: −8,91
в) Ответ: 0,263
г) Ответ: 0,627904. Подчеркните значащие цифры числа:
а) 3,52;
б) 0,352;
в) 0,03520;
г) 7,405;
д) 4,203;
е) 0,005;
ж) 0,0420;
з) 7,0003;
и) 10,0050;
к) 6,700;
л) 0,00067;
м) 0,0100.а) 3,52;
б) 0,352;
в) 0,03520;
г) 7,405;
д) 4,203;
е) 0,005;
ж) 0,0420;
з) 7,0003;
и) 10,0050;
к) 6,700;
л) 0,00067;
м) 0,0100.905. Округлите число 1995,1996:
а) до десятых;
б) до сотых;
в) до тысячных;
г) до единиц;
д) до десятков;
е) до сотен.а) 1995,1996 ≈ 1995,2
Ответ: 1995,2
б) 1995,1996 ≈ 1995,2
Ответ: 1995,2
в) 1995,1996 ≈ 1995,2
Ответ: 1995,2
г) 1995,1996 ≈ 1995
Ответ: 1995
д) 1995,1996 ≈ 2000
Ответ: 2000
е) 1995,1996 ≈ 2000
Ответ: 2000906. Округлите число 1039,9301 до семи; шести; пяти; четырёх; трёх значащих цифр.
Ответ:
до семи значащих цифр 1039,93;
до шести значащих цифр 1039,93;
до пяти значащих цифр 1039,9;
до четырёх значащих цифр 1040;
до трёх значащих цифр 1040. 173
-
Приближение суммы, разности, произведения и частного двух чисел
Ответы к стр. 173
907. Сформулируйте правило приближенного сложения двух чисел, заданных десятичными дробями и округленных с точностью до одной тысячной.
Ответ: Чтобы вычислить приближенную сумму двух чисел, заданных десятичными дробями и округленных с точностью до одной тысячной, надо округлить эти числа с одинаковой точностью до одной тысячной, затем сложить полученные приближения.
908. Сформулируйте правило приближенного вычитания двух чисел, заданных десятичными дробями и округленных с точностью до одной десятой.
Ответ: Чтобы вычислить приближенную разность двух чисел, заданных десятичными дробями и округленных с точностью до одной десятой, надо округлить эти числа с одинаковой точностью до одной десятой, затем вычесть полученные приближения.
909. Сформулируйте правило приближенного умножения чисел, заданных десятичными дробями и округленных с точностью до третьей значащей цифры.
Ответ: Чтобы вычислить приближённо произведение двух чисел, заданных десятичными дробями и округленных с точностью до третьей значащей цифры, надо округлить эти числа до третьей значащей цифры, перемножить полученные приближения и результат округлить до третьей значащей цифры.
910. Сформулируйте правило приближенного деления чисел, заданных десятичными дробями и округленных с точностью до четвертой значащей цифры.
Ответ: Чтобы вычислить приближённо частное двух чисел, заданных десятичными дробями и округленных с точностью до четвертой значащей цифры, надо округлить эти числа до четвертой значащей цифры, разделить полученные приближения и результат округлить до четвертой значащей цифры.
911. Округлите числа а и b с точностью до 0,1 и вычислите приближенно их сумму а + b и разность а − b:
а) а = 3,26, b = 0,11;
б) а = −1,256, b = 2,555;
в) а = 0,010010, b = 0,2;
г) а = 2,7235, b = −3,42426;
д) а = −7,17, b = −0,33;
е) а = −6,373, b = −8,765.а) 3,26 ≈ 3,3
0,11 ≈ 0,1
3,3 + 0,1 = 3,4
3,3 − 0,1 = 3,2
Ответ: 3,4; 3,2.
б) − 1,256 ≈ − 1,3
2,555 ≈ 2,6
−1,3 + 2,6 = 1,3
−1,3 − 2,6 = −3,9
Ответ: 1,3; −3,9.
в) 0,010010 ≈ 0
0,2 ≈ 0,2
0 + 0,2 = 0,2
0 − 0,2 = −0,2
Ответ: 0,2; −0,2.
г) 2,7235 ≈ 2,7
− 3,42426 ≈ − 3,4
2,7 − 3,4 = −0,7
2,7 + 3,4 = 6,1
Ответ: −0,7; 6,1.
д) − 7,17 ≈ − 7,2
− 0,33 ≈ − 0,3
−7,2 − 0,3= −7,5
−7,2 + 0,3 = −6,9
Ответ: −7,5; −6,9.
е) − 6,373 ≈ − 6,4
− 8,765 ≈ − 8,8
−6,4 − 8,8 = −15,2
−6,4 + 8,8 = 2,4
Ответ: −15,2; 2,4.912. Округлите числа а и b с точностью до 0,01 и вычислите приближенно их сумму а + b и разность а − b:
а) а = 1,4545, b = −1,203;
б) а = 2,1264, b = −3,1145;
в) а = −5,777, b = 2,536;
г) а = 0,5642, b = −3,573;
д) а = −12,454, b = 10,111;
е) а = −9,5273, b = −11,1928.а) 1,4545 ≈ 1,45
− 1,203 ≈ − 1,2
1,45 − 1,2 = 0,25
1,45 + 1,2 = 2,65
Ответ: 0,25; 2,65.
б) 2,1264 ≈ 2,13
− 3,1145 ≈ − 3,11
2,13 − 3,11 = −0,98
2,13 + 3,11 = 5,24
Ответ: −0,98; 5,24.
в) − 5,777 ≈ − 5,78
2,536 ≈ 2,54
−5,78 + 2,54 = −3,24
−5,78 − 2,54 = −8,32
Ответ: −3,24; −8,32.
г) 0,5642 ≈ 0,56
− 3,573 ≈ − 3,57
0,56 − 3,57 = −3,01
0,56 + 3,57 = 4,13
Ответ: −3,01; 4,13.
д) − 12,454 ≈ − 12,45
10,111 ≈ 10,11
−12,45 + 10,11 = −2,34
−12,45 − 10,11 = −22,56
Ответ: −2,34; −22,56.
е) − 9,5273 ≈ − 9,53
− 11,1928 ≈ − 11,19
−9,53 − 11,19 = −20,72
−9,53 + 11,19 = 1,66
Ответ: −20,72; 1,66.913. Округлив числа а и b с точностью до третьей значащей цифры, вычислите приближенно их произведение а * b и частное а : b:
а) а = −2,435, b = 1,923;
б) а = 2,1458, b = 0,78788;
в) а = −2,131, b = −0,009293;
г) а = 0,03531, b = 357,693.а) − 2,435 ≈ − 2,44
1,923 ≈ 1,92
− 2,44 ∗ 1,92 ≈ − 4,68
− 2,44 : 1,92 ≈ − 1,27
Ответ: −4,68; −1,27.
б) 2,1456 ≈ 2,15
0,78788 ≈ 0,788
2,15 ∗ 0,788 ≈ 1,69
2,15 : 0,788 ≈ 2,73
Ответ: 1,69; 2,73.
в) − 2,131 ≈ − 2,13
− 0,009293 ≈ − 0,00929
− 2,13 ∗ − 0,00929 ≈ 0,0198
− 2,13 : − 0,00929 ≈ 229
Ответ: 0,0198; 229.
г) 0,03531 ≈ 0,0353
357,693 ≈ 358
0,0353 ∗ 358 ≈ 12,6
0,0353 : 358 ≈ 0,0000986
Ответ: 12,6; 0,0000986.914. Округлив числа а и b с точностью до второй значащей цифры, вычислите приближенно их произведение а * b и частное а : b:
а) а = 0,253, b = 0,75;
б) а = 3,5781, b = −0,00494;
в) а = −0,045, b = −0,593;
г) а = 382,231, b = 0,002434.а) 0,253 ≈ 0,25
0,75 ≈ 0,75
0,25 ∗ 0,75 ≈ 0,19
0,25 : 0,75 ≈ 0,33
Ответ: 0,19; 0,33.
б) 3,5781 ≈ 3,6
− 0,00494 ≈ − 0,0049
3,6 ∗ − 0,0049 ≈ − 0,018
3,6 : − 0,0049 ≈ 730
Ответ: −0,018; 730.
в) − 0,045 ≈ − 0,045
− 0,593 ≈ 0,59
− 0,045 ∗ − 0,59 ≈ 0,027
− 0,045 : − 0,59 ≈ 0,076
Ответ: 0,027; 0,076.
г) 382,231 ≈ 380
0,002434 ≈ 0,0024
− 0,045 ∗ − 0,59 ≈ 0,91
− 0,045 : − 0,59 ≈ 160000
Ответ: 0,91; 160000. 177
-
Вычисления с помощью калькулятора
Ответы к стр. 177
915. Вычислите с помощью калькулятора:
а) 3,56 + 7,031;
б) 4,27 − 2,999;
в) 3,25 * 4,8;
г) 8,8 : 0,55.а) 3,56 + 7,031 = 10,591
Ответ: 10,591
б) 4,27 − 2,999 = 1,271
Ответ: 1,271
в) 3,25 * 4,8 = 15,6
Ответ: 15,6
г) 8,8 : 0,55 = 16
Ответ: 16916. Вычислите с помощью калькулятора:
а) 6,325 + 1,5031;
б) 7,1 − 6,3456;
в) 6,25 * 1,92;
г) 14,4 : 0,048.а) 6,325 + 1,5031 = 7,8281
Ответ: 7,8281
б) 7,1 − 6,3456 = 0,7544
Ответ: 0,7544
в) 6,25 * 1,92 = 12
Ответ: 12
г) 14,4 : 0,048 = 300
Ответ: 300917. Вычислите с помощью калькулятора:
а) 4,295 + 7,35;
б) 7,2391 − 3,957;
в) 9,58 * 0,45;
г) 7,896 : 0,48.а) 4,295 + 7,35 = 11,645
Ответ: 11,645
б) 7,2391 − 3,957 = 3,2821
Ответ: 3,2821
в) 9,58 * 0,45 = 4,311
Ответ: 4,311
г) 7,896 : 0,48 = 16,45
Ответ: 16,45918. Вычислите с помощью калькулятора:
а) 5,728 * 4,25 − 20,134;
б) 87,162 : 4,38 + 13,78;
в) 6,236 * 12,5 : 0,625;
г) 0,729 : 0,027 * 3,126;
д) 14,9445 : 4,05 − 5,69;
е) 0,016 * 0,3125 − 0,05.а) 5,728 * 4,25 − 20,134 = 24,344 − 20,134 = 4,21
Ответ: 4,21
б) 87,162 : 4,38 + 13,78 = 19,9 + 13,78 = 33,68
Ответ: 33,68
в) 6,236 * 12,5 : 0,625 = 77,95 : 0,625 = 124,72
Ответ: 124,72
г) 0,729 : 0,027 * 3,126 = 27 * 3,126 = 84,402
Ответ: 84,402
д) 14,9445 : 4,05 − 5,69 = 3,69 − 5,69 = −2
Ответ: −2
е) 0,016 * 0,3125 − 0,05 = 0,005 − 0,05 = −0,045
Ответ: −0,045919. С помощью калькулятора найдите приближения обыкновенных дробей с недостатком по образцу:
а) 6/9 ≈ 0,6666666;
б) 7/9;
в) 8/9;
г) 1/9;
д) 13/99;
е) 25/99;
ж) 79/99;
з) 5/99.б) 7/9 ≈ 0,7777777
Ответ: 0,7777777
в) 8/9 ≈ 0,8888888
Ответ: 0,8888888
г) 1/9 ≈ 0,1111111
Ответ: 0,1111111
д) 13/99 ≈ 0,1313131
Ответ: 0,1313131
е) 25/99 ≈ 0,2525252
Ответ: 0,2525252
ж) 79/99 ≈ 0,7979797
Ответ: 0,7979797
з) 5/99 ≈ 0,050505
Ответ: 0,050505920. Вычислите с помощью калькулятора:
а) 1 : 9 * 9;
б) 4 : 7 * 7.
Точный или приближенный результат получился? Каков точный ответ?а) 0,999999999 при расчете с помощью калькулятора ответ получился приближенный, так как 1/9 ∗ 9 = 1 − точный ответ.
Ответ:
0,999999999 − приближенный ответ;
1 − точный ответ.
б) 3,999999997 при расчете с помощью калькулятора ответ получился приближенный, так как 4/7 ∗ 7 = 4 − точный ответ.
Ответ:
3,999999997 − приближенный ответ;
4 − точный ответ.921. Вычислите с помощью калькулятора:
а) 891 : 297;
б) 297 : 891;
в) 999,9999 * 9;
г) 7777,7777 : 1,4.а) 891 : 297 = 3
Ответ: 3
б) 297 : 891 ≈ 0,333333333
Ответ: ≈ 0,333333333
в) 999,9999 * 9 = 8999,9991
Ответ: 8999,9991
г) 7777,7777 : 1,4 = 5555,5555
Ответ: 5555,5555 179
-
Процентные расчеты с помощью калькулятора
Ответы к стр. 179
922. а) Найдите 36% числа 500.
б) В школе 540 учащихся. Мальчики составляют 55% числа всех учащихся. Сколько в школе мальчиков?а) 500 * 36% = 500 * 0,36 = 180
Ответ: 180.
б) 540 * 54% = 540 * 0,54 = 297 мальчиков учится в школе.
Ответ: 297 мальчиков.923. Товар стоил 45 р. На сколько рублей повысится цена товара, если её повышение составит:
а) 10%;
б) 12%;
в) 20%;
г) 25%.а) 45 * 10% = 45 * 0,1 = на 4,5 р повысится цена товара.
Ответ: на 4,5 р.
б) 45 * 12% = 45 * 0,12 = на 5,4 р повысится цена товара.
Ответ: на 5,4 р.
в) 45 * 20% = 45 * 0,2 = на 9 р повысится цена товара.
Ответ: на 9 р.
г) 45 * 25% = 45 * 0,25 = на 11,25 р повысится цена товара.
Ответ: на 11,25 р.924. Магазин повышает цены на некоторые товары на 15%. Перечертите таблицу в тетрадь и заполните её, определив, на сколько рублей повысилась цена каждого товара и какой она стала.
1 случай:
200 * 15% = 200 * 0,15 = 30 р. размер повышения цены товара,
200 + 30 = 230 р. новая цена товара;
2 случай:
150 * 15% = 150 * 0,15 = 22,5 р. размер повышения цены товара,
150 + 22,5 = 172,5 р. новая цена товара;
3 случай:
420 * 15% = 420 * 0,15 = 63 р. размер повышения цены товара,
420 + 63 = 483 р. новая цена товара.
Ответ:
Цена товара На сколько Новая цена
до повыш, р. повыс. цена, р. товара, р.
200 30 230
150 22,5 172,5
420 63 483925. Банк по срочным вкладам начисляет ежемесячный доход в размере 3% от суммы вклада. Определите величину вклада через месяц.
Задание рисунок 11 случай:
700 + 700 * 3% = 700 * (1 + 0,03) = 700 * 1,03 = 721 р. составил размер вклада через месяц.
2 случай:
950 + 950 * 3% = 950 * (1 + 0,03) = 950 * 1,03 = 978,5 р. составил размер вклада через месяц.
3 случай:
320 + 320 * 3% = 320 * (1 + 0,03) = 320 * 1,03 = 329,6 р. составил размер вклада через месяц.
Ответ:
Величина вклада Величина вклада
в начале мес., р. через месяц, р.
700 721
950 978,5
320 329,6926. Найдите число, 18% которого равны 720.
720 : 18% = 720 : 0,18 = 4000
Ответ: 4000927. Из посаженных семян подсолнечника взошло 176 семян, что составило 88% от числа посаженных. Сколько семян подсолнечника было посажено?
176 : 88% = 176 : 0,88 = 200 семян подсолнечника было посажено.
Ответ: 200 семян подсолнечника было посажено.928. На предновогодней распродаже магазин снизил цены на все товары на 12%. Определите, какой стала цена каждого товара.
1 случай: 40 − 40 * 12% = 40 * (1 − 0,12) = 40 * 0,88 = 35,2 р. стала составлять цена товара после её понижения на 12%.
2 случай: 300 − 300 * 12% = 300 * (1 − 0,12) = 300 * 0,88 = 264 р. стала составлять цена товара после её понижения на 12%.
3 случай: 120 − 120 * 12% = 120 * (1 − 0,12) = 120 * 0,88 = 120 р. стала составлять цена товара после её понижения на 12%.
Ответ:
Цена товара Новая цена
до понижения, р. товара, р.
40 35,2
300 264
120 105,6 180
-
Ответы к стр. 180
929. Банк по срочным вкладам начисляет ежемесячный доход в размере 5% от суммы вклада, имевшейся в начале месяца. В начале месяца на счёт положили 500 р. Определите величину вклада через:
а) 1 месяц;
б) 2 месяца;
в) 3 месяца,
если доход начисляется по формуле сложных процентов.а) S = a ∗ ( 1 + p/100 ) n = 500 ∗ ( 1 + 5/100 ) 1 = 500 ∗ 1,05 = 525р. составит сумма вклада через месяц.
Ответ: 525 р.
б) S = a ∗ ( 1 + p/100 ) n = 500 ∗ ( 1 + 5/100 ) 2 = 500 ∗ 1,1025 = 551,25р. составит сумма вклада через 2 месяца.
Ответ: 551,25 р.
в) S = a ∗ ( 1 + p/100 ) n = 500 ∗ ( 1 + 5/100 ) 3 = 500 ∗ 1,157625 = 578,8125р. составит сумма вклада через 3 месяца.
Ответ: 578,8125 р.930. Сколько процентов составляет число 80 от:
а) 100;
б) 320;
в) 240;
г) 60.а) 80/100 ∗ 100
Ответ: 80%.
б) 80/320 ∗ 100
Ответ: 25%.
в) 80/240 ∗ 100
Ответ: 33 1/3 %.
г) 80/60 ∗ 100
Ответ: 133 1/3 %.931. Из 120 посаженных семян подсолнечника взошло 102. Сколько процентов семян подсолнечника взошло?
102/120 ∗ 100 семян подсолнечника взошло.
Ответ: 85%.932. В автоинспекции города N подсчитали, что число легковых автомобилей в городе увеличивалось в последние года на 15% ежегодно. Во сколько раз увеличится число легковых автомобилей за 5 лет, если эта тенденция сохранится?
1,15 5 ≈ 2,011357 ≈примерно в 2 раза увеличится число легковых автомобилей за 5 лет.
Ответ: примерно в 2 раза.933. Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10% за каждый месяц. На сколько процентов выросли цены за 3 месяца?
В месяц цены на продукты растут в 1,1 раз, тогда:
1,1 3 = в 1,331 раза выросли цены на продукты за 3 месяца,
1,331 * 100% = 133,1% стали составлять цены на продукты через 3 месяца от начальной цены,
133,1% − 100% = на 33,1% выросли цены на продукты за 3 месяца.
Ответ: на 33,1%.934. Деньги, вложенные в акции известной фирмы, приносят ежегодно 20% дохода. Через сколько лет вложенная сумма удвоится, если доход начисляется по формуле сложных процентов?
Пусть начальный вклад был x, тогда по формуле сложных процентов:
x ∗ ( 1,2 ) n = 2 x
( 1,2 ) n = 2
Представим, что вклад удвоится за 2 года, тогда:
( 1,2 ) 2 = 1,44 ≠ 2;
за три года ( 1,2 ) 3 = 1,728 ≠ 2;
за четыре года ( 1,2 ) 4 = 2,0736 ≈ 2.
Ответ: вклад удвоится за 4 года. 183
-
Фигуры в пространстве, симметричные относительно плоскости
Ответы к стр. 183
935. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины равны:
а) 3 см, 4 см, 5 см;
б) 3 см, 4 см, 4 см;
в) 4 см, 4 см, 4 см.
Сколько плоскостей симметрии у этого прямоугольного параллелепипеда?а) Ответ: 3 плоскости.
б) Ответ: 5 плоскостей.
в) Ответ: 9 плоскостей.
936. Сколько плоскостей симметрии у цилиндра, конуса, шара?
Ответ: у всех фигур бесконечное количество осей симметрии.
937. На клетчатой бумаге несложно нарисовать кубики. На рисунке 95 изображены две фигуры, которые можно из трёх равных кубиков при условии, что каждый из них должен иметь хотя бы одну общую грань с остальными кубиками. Назовем их трикубиками. Убедитесь, что имеется только две фигуры трикубиков. Сколько плоскостей симметрии у каждой из них?
Ответ: 1 фигура имеет 5 плоскостей симметрии, 2 фигура имеет 2 плоскости симметрии.
938. Нарисуйте все фигуры тетракубиков, полученные из четырёх кубиков по тому же правилу, что и для трикубиков. Убедитесь, что существует только восемь фигур тетракубиков. Сколько плоскостей симметрии имеет каждая из них?

939. Имеются ли плоскости симметрии у правильной пирамиды (если да, то сколько?), если она:
а) треугольная (рис.96);
б) шестиугольная (рис.97)?
а) Ответ: 3 плоскости симметрии.
б) Ответ: 3 плоскости симметрии.
940. Петя получил записки с непонятными словами (рис.98 и 99). Он догадался, как прочитать их с помощью зеркала. Придумайте слова, которые можно зашифровать тем же способом и прочитать с помощью зеркала.

Ответ:
Зашифрованные слова, которые можно прочитать с помощью зеркала, если они будут записаны по горизонтали: НОС, ФОН, СОН, КОН;
Зашифрованные слова, которые можно прочитать с помощью зеркала, если они будут записаны по вертикали: ТОН, ШАХ, ТОПОТ, ФОН, ТОМ. 185
-
Занимательные задачи
Ответы к стр. 185
941. Арбуз весил 20 кг, в нём содержалось 99% воды. Через несколько дней он немного усох и содержание воды уменьшилось до 98%. Сколько теперь весит арбуз?
100% − 99% = 1% процентное содержание "сухого" вещества в арбузе.
20 * 1% = 20 * 0,01 = 0,2 кг масса "сухого" вещества в арбузе.
100% − 98% = 2% процентное содержание "сухого" вещества в арбузе, после его усыхания.
Вес "сухого" вещества равен 0,2 кг, что составляет 2% от нового веса арбуза, поэтому необходимо найти число, 2% которого равны 0,2.
0,2 : 2% = 0,2 : 0,02 = 10 кг вес арбуза после усыхания.
Ответ: 10 кг.942. Некий леспромхоз решил вырубить сосновый лес, но экологи запротестовали. Тогда директор леспромхоза всех успокоил, сказав: "В нашем лесу 99% сосны. После рубки сосна будет составлять 98% всех деревьев". Какую часть леса может вырубить леспромхоз?
Пусть всего деревьев было х, тогда:
х * 99% = 0,99х − было сосен и 0,01х − остальных деревьев.
Пусть вырубили y сосен, тогда:
х − y − осталось всего деревьев в лесу,
100% − 98% = 2% − процентное содержание остальных деревьев в лесу после рубки сосен,
(х − y) * 2% = 0,02(х − y)
0,02(х − y) = 0,01х
0,02х − 0,02y = 0,01х
0,02х − 0,01х = 0,02y
0,01х = 0,02y
х/y = 1/2 = 0,5, то есть отношение вырубленных сосен к начальному числу всех деревьев равно 0,5, а это значит, что вырубили половину леса.
Ответ: вырубили половину леса. 186
-
Ответы к стр. 186
943. На коробке с вермишелью написано: "Масса нетто 500 г при влажности 13%" Какова масса вермишели, если она хранится при влажности 25%?
100% − 13% = 87% процентное содержание "сухого" продукта,
500 * 87% = 500 * 0,87 = 435 г масса "сухого" продукта,
100% − 25% = 75% процентное содержание "сухого" продукта при влажности 25%,
Вес "сухого" вещества равен 435 г, что составляет 75% от новой массы вермишели, поэтому необходимо найти число, 75% которого равны 435:
435 : 75% = 435 : 0,75 = 580 г масса вермишели при влажности 25%.
Ответ: 580 г.944. Для получения томат−пасты протертую массу томатов выпаривают в специальных машинах. Сколько тонн томат−пасты, содержащей 30% воды, получится из 28 т протертой массы томатов, содержащей 95% воды?
100% − 95% = 5% − "сухого" вещества содержится в томат−пасте, содержащей 95% воды,
28 * 5% = 28 * 0,05 = 1,4 т "сухого" вещества содержится в 28 т протертой массы томатов, содержащей 95% воды.
100% − 30% = 70% − "сухого" вещества содержится в томат−пасте, содержащей 30% воды,
Вес "сухого" вещества равен 1,4 т, что составляет 70% от массы томат−пасты, содержащей 30% воды, поэтому необходимо найти число, 70% которого равны 1,4:
1,4 : 70% = 1,4 * 0,7 = 2 т томат−пасты, содержащей 30% воды, получится из 28 т протертой массы томатов, содержащей 95% воды.
Ответ: 2 т.945. Производительность труда повысили на 25%. На сколько процентов уменьшится время выполнения задания?
N ∗ t0 = A, где N − производительность, t − время, А − совершенная работа.
N * 25% = 1,25N
1,25 N ∗ t1 = A
1,25 N ∗ t1 = N ∗ t0
t1/t0 = 1/1,25 = 0,8
(1 − 0,8) * 100% = на 20% уменьшилось время выполнения задания.
Ответ: на 20% уменьшилось.946. Папа и сын плывут на лодке против течения. В какой−то момент сын уронил за борт папину шляпу. Только через 25 мин папа заметил пропажу, быстро развернул лодку, и они поплыли вниз по течению с той же собственной скоростью. Через сколько минут они догонят шляпу?
Пусть скорость лодки равна х, а скорость течения y, тогда:
х + y − скорость лодки по течению,
х − y − скорость лодки против течения,
(х − y) * 25 − проплыла лодка после потери шляпы,
25y − проплыла шляпа по течению, до момента обнаружения пропажи
(х + y) − y = х − скорость с которой лодка догоняет шляпу.
$t=\frac{({\operatorname х}-y)\ast25+25y}{\operatorname х}=\frac{25{\operatorname х}-25y+25y}{\operatorname х}=\frac{25{\operatorname х}}{\operatorname х}=25$ минут потребуется лодке чтобы догнать шляпу.947. Папа купил себе дипломат с двумя кодовыми замками. На каждом из этих замков устанавливают код − набор из трёх цифр от 0 до 9 (рис.100). Дипломат закрывают и на его наружной панели устанавливают произвольные наборы цифр. Каждый замок откроется лишь тогда, когда будет правильно набран его код.
а) Саша установил новый код на каждый замок, но забыл сообщить об этом папе и ушел в школу. Сколько времени может занять открывание замков у папы в худшем случае, если он будет последовательно проверить коды для каждого замка и на проверку каждого кода будет тратить 1 с?
б) Какова вероятность открыть с первой попытки один кодовый замок? оба замка?
в) Саша установил новый код на каждый замок и через некоторое время забыл, в каком порядке цифры 1,2 и 3 образуют эти два кода. Сколько кодов в худшем случае придётся проверить Саше, чтобы открыть оба замка?
г) Саша установил два новых кода на замках дипломата и чрез некоторое время забыл их. Он помнит, что в каждый код входят цифры 1, 2 и какая−то третья цифра (не 1 и не 2). Сколько кодов в худшем случае придётся проверить Саше, чтобы открыть один замок? оба замка?
123 987а) 10 * 10 * 10 = 1000 равновозможных случаев, одно из которых обязательно произойдет при правильном подборе цифр на одном замке.
1000 * 1 = 1000 секунд может потребоваться, чтобы открыть один замок,
1000 * 2 = 2000 секунд может потребоваться, чтобы открыть оба замка.
Ответ: 2000 секунд.
б) 10 * 10 * 10 = 1000 числу всех равновозможных случаев, одно из которых обязательно произойдет при правильном подборе цифр.
1/1000 − вероятность подбора правильного набора цифр в одном замке, а следовательно и вероятность открытия первого замка с одной попытки.
1/1000 ∗ 1/1000 = 1/1000000 − вероятность открытия обоих замков с одной попытки.
Ответ:
1/1000 − вероятность открытия первого замка с одной попытки.
1/1 000 000 − вероятность открытия обоих замков с одной попытки.
в) Ответ:
Код состоит из цифр 1,2,3, при чем цифры не повторяются, тогда:
для 1−ого диска мы можем выбрать цифру 3 способами;
для 2−ого диска мы можем выбрать цифру 2 способами;
для 3−ого диска мы можем выбрать цифру 1 способом.
3 * 2 * 1 = 6 способами, в худшем случае, можно подобрать код на одном замке,
6 * 2 = 12 способами, в худшем случае, можно подобрать код на обоих замках.
Ответ: 12 кодов.
г) Код состоит из цифр 1,2, и третьей цифры, при чем цифры не повторяются, тогда:
для 1−ого диска мы можем выбрать цифру 3 способами;
для 2−ого диска мы можем выбрать цифру 2 способами;
для 3−ого диска мы можем выбрать цифру 1 способом.
3 * 2 * 1 = 6 способами можно установить цифры для одного замка.
В каждом из способов два диска уже заняты цифрами 1 и 2, и только для третьего диска может быть выбрано 8 вариантов цифр, поэтому каждый из 6 способов может иметь 8 вариантов цифр.
6 * 8 = 48 кодов будет необходимо подобрать в худшем случае, чтобы открыть один замок.
48 * 2 = 96 кодов будет необходимо подобрать в худшем случае, чтобы открыть оба замка.
Ответ:
48 кодов будет необходимо подобрать в худшем случае, чтобы открыть один замок.
96 кодов будет необходимо подобрать в худшем случае, чтобы открыть оба замка. 187
-
Ответы к стр. 187
948. В школе 20 классов. В ближайшем к школе доме живут 23 ученика этой школы. Можно ли утверждать, что среди них обязательно найдутся хотя бы два одноклассника?
Для того, чтобы среди детей не было одноклассников, необходимо чтобы в каждом из классов было не больше одного ученика живущего в этом доме, тогда:
20 классов * 1 ученик = 20 − это максимальное количество детей, которое может жить в одном доме, чтобы среди них не было одноклассников.
Так как 23 > 20, то можно утверждать, что среди детей живущих в доме, обязательно есть одноклассники.
Ответ: Да, можно.949. В школе учится 370 человек. Докажите, что среди всех учащихся найдутся хотя бы два ученика, празднующие свой день рождения в один и тот же день.
Количество дней в високосном году равно 366.
370 > 366, следовательно, в школе обязательно найдутся ученики, празднующие свой день рождения в один и тот же день.950. Коля подсчитал, что на завтрак, обед и ужин он съел 10 конфет. Докажите, что хотя бы один раз он съел не меньше четырёх конфет.
Предположим, что Коля съедал в каждый прием пищи равное и целое количество конфет, тогда:
10 : 3 = 3 1/3 ≈ 3 конфеты съедал бы Коля за один прием пищи.
3 * 3 = 9 конфет съедал бы Коля в день в этом случае, следовательно, для того чтобы съесть 10 конфет в день Коле обязательно бы пришлось съесть в один прием пищи хотя бы 4 конфеты.951. В классе 37 человек. Докажите, что из них найдутся хотя бы 4 человека, родившиеся в один месяц.
Предположим, что в каждом месяце родилось одинаковое количество человек, тогда:
37 : 12 = 3 1/12 ≈ 3 именинника было бы в каждом месяце.
3 * 12 = 36 учеников в классе было бы в этом случае, следовательно, для того чтобы бы в классе было 37 учеников, необходимо чтобы в каком то месяце было 4 именинника.952. В коллекции имеется 25 монет по 1, 2, 3 и 5 копеек. Есть ли среди них 7 монет одинакового достоинства?
Предположим, что в коллекции находится равное количество монет разного достоинства, тогда:
25 : 4 = 6 1/4 ≈ 6 монет каждого из номиналов содержалось бы в коллекции.
6 * 4 = 24 монеты всего было бы в этом случае в коллекции, следовательно, для того чтобы бы в коллекции было 25 монет, необходимо чтобы количество монет какого−то из номиналов было бы больше 6.953. Учительница объявила результаты диктанта. Больше всех ошибок было у Пети − 13. Докажите, что среди 28 учащихся, допустивших ошибки, найдутся 3 человека с одинаковым числом ошибок.
Предположим, что в классе одинаковое количество учеников совершили по 1 ошибке, по 2 ошибке, ... по 13 ошибок, тогда:
28 : 13 = 2 2/13 ≈ 2 ученика совершили бы одинаковое количество ошибок.
2 * 13 = 26 детей было бы тогда в классе, что неверно. Следовательно, в классе обязательно найдутся 3 человека, совершивших одинаковое количество ошибок.954. За 3 года Вася стал старше на 25%. Сколько теперь Васе лет?
Пусть Васе было x, тогда:
1,25x − лет сейчас Васе,
1,25x : x = в 1,25 лет Вася стал старше за 3 года,
x + 3/x = 1,25
x + 3 = 1,25x
1,25x − x = 3
0,25x = 3
x = 3 : 0,25
х = 12 лет было Васе.
12 + 3 = 15 лет Васе сейчас.
Ответ: 15 лет.955. а) Сейчас Ваня на 20% старше, чем 2 года назад. Сколько теперь Ване лет?
б) Два года назад Маша была на 20% моложе, чем сейчас. Сколько лет Маше сейчас?а) Пусть Ване было x, тогда:
1,2x − лет сейчас Ване,
1,2x : x = в 1,2 раза стал старше Ваня за 2 года,
x + 2/x = 1,2
x + 2 = 1,2x
1,2x − x = 2
0,2x = 2
x = 2 : 0,2 = 10 лет было Ване.
10 + 2 = 12 лет Ване сейчас.
Ответ: 12 лет.
б) Пусть Маше сейчас x лет, тогда:
x * (1 − 0,2) = 0,8x лет было Маше 2 года назад.
0,8x + 2 = x
x − 0,8x = 2
0,2x = 2
x = 2 : 0,2 = 10 лет Маше сейчас.
Ответ: 10 лет. 189
-
Ответы к странице 189
956. Конечную десятичную дробь записали в виде обыкновенной несократимой дроби. Может ли знаменатель этой дроби иметь простые делители отличные от 2 и 5?
Если конечную десятичную дробь записать в виде обыкновенной несократимой дроби p/q, то ее знаменатель q не имеет других простых делителей, кроме 2 и 5.
Ответ: не может. 190
-
Обыкновенные и десятичные дроби
Разложение положительной обыкновенной дроби в конечную десятичную дробь
Ответы к странице 190
957. Какие делители должен иметь знаменатель обыкновенной несократимой дроби, чтобы она разлагалась в конечную десятичную дробь? Приведите примеры.
Если знаменатель q несократимой дроби p/q не имеет других простых делителей, кроме 2 и 5, то эта дробь разлагается в конечную десятичную.
$\frac12=\frac{1\ast5}{2\ast5}=\frac5{10}=0,5$
$\frac15=\frac{1\ast2}{5\ast2}=\frac2{10}=0,2$
$\frac18=\frac1{2\ast2\ast2}=\frac{1\ast5\ast5\ast5}{2\ast2\ast2\ast5\ast5\ast5}=\frac{125}{1000}=0,125$
$\frac1{16}=\frac1{2\ast2\ast2\ast2}=\frac{1\ast5\ast5\ast5\ast5}{2\ast2\ast2\ast2\ast5\ast5\ast5\ast5}=\frac{625}{10000}=0,0625$958. Какими способами можно разложить обыкновенную дробь в десятичную? Приведите примеры.
1 способ: Для того, чтобы разложить обыкновенную дробь в десятичную можно и числитель и знаменатель дроби умножить на соответствующую степень числа 2 или числа 5, для того чтобы знаменатель приведенной дроби стал равным степени числа 10, а затем представить эту дробь в виде десятичной:
$\frac12=\frac{1\ast5}{2\ast5}=\frac5{10}=0,5$
$\frac15=\frac{1\ast2}{5\ast2}=\frac2{10}=0,2$
2 способ: Для того, чтобы разложить обыкновенную дробь в десятичную можно числитель дроби поделить на ее знаменатель уголком:
1 |2
-10 |0.5
0
1 |5
-10 |0.2
0959. Какие простые множители содержит знаменатель дроби:
а) 1/64;
б) 1/48;
в) 1/56;
г) 1/24;
д) 1/128;
е) 1/78;
ж) 1/256;
з) 1/625;
и) 1/10;
к) 1/100;
л) 1/1000;
м) 1/10000.а) 64 = 26
Ответ: 2
б) 48 = 24 ∗ 3
Ответ: 2 и 3.
в) 56 = 23 ∗ 7
Ответ: 2 и 7.
г) 24 = 23 ∗ 3
Ответ: 2 и 3.
д) 128 = 27
Ответ: 2
е) 78 = 2 ∗ 3 ∗ 13
Ответ: 2, 3, 13
ж) 256 = 28
Ответ: 2
з) 625 = 54
Ответ: 5
и) 10 = 2 ∗ 5
Ответ: 2 и 5
к) 100 = 22 ∗ 52
Ответ: 2 и 5
л) 1000 = 23 ∗ 53
Ответ: 2 и 5
м) 1000 = 24 ∗ 54
Ответ: 2 и 5960. Сократите дробь:
а) 24/60;
б) 15/20;
в) 65/100;
г) 94/100;
д) 21/30;
е) 16/400;
ж) 8/100;
з) 8/1000.а) 24/60 = 4/10 = 2/5
Ответ: 2/5
б) 15/20 = 3/4
Ответ: 3/4
в) 65/100 = 13/20
Ответ: 13/20
г) 94/100 = 47/50
Ответ: 47/50
д) 21/30 = 7/10
Ответ: 7/10
е) 16/400 = 4/100 = 1/25
Ответ: 1/25
ж) 8/100 = 2/25
Ответ: 2/25
з) 8/1000 = 1/125
Ответ: 1/125961. Запишите в виде обыкновенной несократимой дроби:
а) 0,4;
б) 0,12;
в) 0,125;
г) 1,2;
д) 0,45;
е) 0,04;
ж) 1,008;
з) 0,0018.а) 0,4 = 4/10 = 2/5
Ответ: 2/5
б) 0,12 = 12/100 = 3/25
Ответ: 3/25
в) 0,125 = 125/1000 = 1/8
Ответ: 1/8
г) 1,2 = 12/10 = 6/5
Ответ: 6/5
д) 0,45 = 45/100 = 9/20
Ответ: 9/20
е) 0,04 = 4/100 = 1/25
Ответ: 1/25
ж) 1,008 = 1008/1000 = 126/125
Ответ: 126/125
з) 0,0018 = 18/10000 = 9/5000
Ответ: 9/5000962. Приведите дробь к знаменателю 10, или 100, или 1000:
а) 1/2;
б) 1/4;
в) 3/5;
г) 1/25;
д) 11/20;
е) 9/8;
ж) 3/8;
з) 7/40.а) 1/2 = 5/10
1/2 = 50/100
1/2 = 500/1000
б) 1/4 = 25/100
1/4 = 250/1000
в) 3/5 = 6/10
3/5 = 60/100
3/5 = 600/1000
г) 1/25 = 4/100
1/25 = 40/1000
д) 11/20 = 55/100
11/20 = 550/1000
е) 9/8 = 1125/1000
ж) 3/8 = 375/1000
з) 7/40 = 175/1000963. Разложите двумя способами в десятичную дробь:
а) 1/4;
б) 4/5;
в) 24/15;
г) 15/24.а) 1/4 = 25/100 = 0,25
1 : 4 = 0,25
Ответ: 0,25
б) 4/5 = 8/10 = 0,8
4 : 5 = 0,8
Ответ: 0,8
в) 24/15 = 8/5 = 16/10 = 1,6
24 : 15 = 1,6
Ответ: 1,6
г) 15/24 = 5/8 = 625/1000 = 0,625
15 : 24 = 0,625
Ответ: 0,625964. Разложите обыкновенную дробь в десятичную делением числителя на знаменатель уголком:
а) 7/5;
б) 3/16;
в) 48/15;
г) 3/2000;
д) 17/40;
е) 28/140;
ж) 3/12;
з) 7/56.а)
7 |5 -5 |1.4 20 -20 0
Ответ: 1,4
б)3 |16 -16 |0.1875 140 -128 120 -112 80 -80 0
Ответ: 0,1875
в)48 |15 -45 |3.2 30 -30 0
Ответ: 3,2
г)3 |2000 -2000 |0.0015 10000 -10000 0
Ответ: 0,0015
д)17 |40 -160 |0.425 100 -80 200 -200 0
Ответ: 0,425
е)28 |140 -280 |0.2 0
Ответ: 0,2
ж)3 |12 -24 |0.25 60 -60 0
Ответ: 0,25
з)7 |56 -56 |0.125 140 -112 280 -280 0
Ответ: 0,125965. Разложите обыкновенную дробь в десятичную делением числителя на знаменатель уголком:
а) 6/24;
б) 7/4;
в) 3/2;
г) 9/5;
д) 3/25;
е) 12/75;
ж) 17/200;
з) 123/20.а)
6 |24 -48 |0.25 120 -120 0
Ответ: 0,25
б)7 |4 -4 |1.75 30 -28 20 -20 0
Ответ: 1,75
в)3 |2 -2 |1.5 10 -10 0
Ответ: 1,5
г)9 |5 -5 |1.8 40 -40 0
Ответ: 1,8
д)3 |25 -25 |0.12 50 -50 0
Ответ: 0,12
е)12 |75 -75 |0.16 450 -450 0
Ответ: 0,16
ж)17 |200 -1600 |0.085 1000 -1000 0
Ответ: 0,085
з)123 |20 -120 |6.15 30 -20 100 -100 0
Ответ: 6,15 191
-
Ответы к странице 191
966. Разложите обыкновенную дробь в десятичную делением числителя на знаменатель уголком:
а) 783/40;
б) 324/25;
в) 625/125;
г) 860/400;
д) 33/60;
е) 1024/256;
ж) 804/400;
з) 624/120.а)
783 |40 -40 |19.575 383 -360 230 -200 300 -280 200 -200 0
Ответ: 19,575
б)324 |25 -25 |12.96 74 -50 240 -225 150 -150 0
Ответ: 12,96
в)625 |125 -625 |5 0
Ответ: 5
г)860 |400 -800 |2.15 600 -400 2000 -2000 0
Ответ: 2,15
д)33 |60 -300 |0.55 300 -300 0
Ответ: 0,55
е)1024 |256 -1024 |4 0
Ответ: 4
ж)804 |400 -800 |2.01 400 -400 0
Ответ: 2,01
з)624 |120 -600 |5.2 240 -240 0
Ответ: 5,2967. Можно ли разложить данную обыкновенную дробь в конечную десятичную дробь (ответ обосновать):
а) 1/7;
б) 6/48;
в) 7/352;
г) 12/56;
д) 120/38;
е) 12/96;
ж) 21/75;
з) 7/300.а) 1/7 = 1/1 ∗ 7; нельзя, так как знаменатель имеет простой делитель равный 7, отличный от 2 и 5.
Ответ: нельзя.
б) 6/48 = 1/8 = 1/23; можно, так как знаменатель имеет простой делитель равный 2.
Ответ: можно.
в) 7/352 = 7/11 ∗ 25; нельзя, так как знаменатель имеет простой делитель равный 11, отличный от 2 и 5.
Ответ: нельзя.
г) 12/56 = 12/7 ∗ 23; нельзя, так как знаменатель имеет простой делитель равный 7, отличный от 2 и 5.
Ответ: нельзя.
д) 120/38 = 120/19 ∗ 2; нельзя, так как знаменатель имеет простой делитель равный 19, отличный от 2 и 5.
Ответ: нельзя.
е) 12/96 = 1/8 = 1/23; можно, так как знаменатель имеет простой делитель равный 2.
Ответ: можно.
ж) 21/75 = 7/25 = 7/52; можно, так как знаменатель имеет простой делитель равный 5.
Ответ: можно.
з) 7/300 = 7/3 ∗ 22 ∗ 52; нельзя, так как знаменатель имеет простой делитель равный 3, отличный от 2 и 5.
Ответ: нельзя. 193
-
Бесконечные периодические десятичные дроби
Ответы к странице 193
968. В каком случае несократимая обыкновенная дробь не разлагается в конечную десятичную дробь?
Ответ: Если знаменатель q несократимой дроби p/q имеет простой делитель, кроме 2 и 5, то эта дробь не разлагается в конечную десятичную.
969. Каким способом любую обыкновенную дробь можно разложить в десятичную?
Ответ: Любую обыкновенную дробь можно разложить в десятичную, если числитель дроби поделить на ее знаменатель уголком.
970. Какие десятичные дроби можно получить при делении уголком числителя обыкновенной дроби на её знаменатель?
Ответ: При делении уголком числителя обыкновенной дроби на её знаменатель можно получить либо конченые десятичные дроби, либо бесконечные периодические дроби.
971. Как узнать, в какую десятичную дробь разлагается обыкновенная дробь − в конечную или в бесконечную? Приведите примеры.
Если знаменатель q несократимой дроби p/q не имеет других простых делителей, кроме 2 и 5, то эта дробь разлагается в конечную десятичную дробь.
1/20 = 1/5 ∗ 22 = 0,05
1/40 = 1/5 ∗ 23 = 0,025
Если знаменатель q несократимой дроби p q имеет другие простые делители, кроме 2 и 5, то эта дробь разлагается в бесконечную периодическую десятичную дробь.
1/15 = 1/3 ∗ 5 = 0,0 ( 6 )
1/30 = 1/3 ∗ 5 ∗ 2 = 0,0 ( 3 ) 194
-
Ответы к странице 194
972. Как можно записать конечную десятичную дробь или натуральное число в виде бесконечной периодической десятичной дроби? Приведите примеры.
Приписывая к целому числу (после запятой) или к конечной десятичной дроби бесконечно много нулей, мы превращаем ее в равную ей бесконечную периодическую десятичную дробь с периодом 0.
0,15 = 0,150000... = 0,15(0)
15 = 15,00000... = 15(0)973. Запишите число в виде периодической дроби, назовите ее период:
а) 1/3;
б) 2/9;
в) 12/5;
г) 12;
д) 24/30;
е) 36/48;
ж) 4/7;
з) 45/63;
и) 1/6;
к) 2/6;
л) 3/6;
м) 4/6;
н) 20/41;
о) 15/37;
п) 5/21.а) 1/3 = 0,( 3 ); период 3.
Ответ: 0,(3); период 3.
б) 2/9 = 0,( 2 ); период 2.
Ответ: 0,(2); период 2.
в) 12/5 = 2,4 ( 0 ); период 0.
Ответ: 2,4(0); период 0.
г) 12 = 12,(0); период 0.
Ответ: 12,(0); период 0.
д) 24/30 = 0,8 ( 0 ); период 0.
Ответ: 0,8(0); период 0.
е) 36/48 = 0,75 ( 0 ); период 0.
Ответ: 0,75(0); период 0.
ж) 4/7 = 0,( 571428 ); период 571428.
Ответ: 0,(571428); период 571428.
з) 45/63 = 0,( 714285 ); период 714285.
Ответ: 0,(714285); период 714285.
и) 1/6 = 0,1 ( 6 ); период 6.
Ответ: 0,1(6); период 6.
к) 2/6 = 0,( 3 ); период 3.
Ответ: 0,(3); период 3.
л) 3/6 = 0,5 ( 0 ); период 0.
Ответ: 0,5(0); период 0.
м) 4/6 = 0,6 ( 0 ); период 0.
Ответ: 0,6(0); период 0.
н) 20/41 = 0,( 48780 ); период 48780.
Ответ: 0,(48780); период 48780.
о) 15/37 = 0,( 405 ); период 405.
Ответ: 0,(405); период 405.
п) 5/21 = 0,( 238095 ); период 238095.
Ответ: 0,(238095); период 238095.974. Разложите обыкновенную дробь в периодическую делением числителя на знаменатель уголком:
а) 1/9;
б) 2/9;
в) 3/9;
г) 4/9.
а) Ответ: 0,(1)
б) Ответ: 0,(2)
в) Ответ: 0,(3)
г) Ответ: 0,(4)975. Разложите обыкновенную дробь в периодическую:
а) 5/9;
б) 6/9;
в) 7/9;
г) 8/9.
а) Ответ: 0,(5)
б) Ответ: 0,(6)
в) Ответ: 0,(7)
г) Ответ: 0,(8)976. Разложите обыкновенную дробь в десятичную и назовите её период:
а) 12/99;
б) 23/99;
в) 34/99;
г) 45/99.
а) Ответ: 0,(12); период 12.
б) Ответ: 0,(23); период 23.
в) Ответ: 0,(34); период 34.
д) Ответ: 0,(45); период 45.977. Разложите обыкновенную дробь в периодическую:
а) 56/99;
б) 67/99;
в) 78/99;
г) 89/99.
а) Ответ: 0,(56); период 56.
б) Ответ: 0,(67); период 67.
в) Ответ: 0,(78); период 78.
г) Ответ: 0,(89); период 89.978. Используя предыдущие задания, запишите периодическую дробь в виде обыкновенной:
а) 0,(1);
б) 0,(3);
в) 0,(5);
г) 0,(7);
д) 0,(25);
е) 0,(37);
ж) 0,(10);
з) 0,(05).а) 0,( 1 ) = 1/9
Ответ: 1/9
б) 0,( 3 ) = 3/9
Ответ: 3/9
в) 0,( 5 ) = 5/9
Ответ: 5/9
г) 0,( 7 ) = 7/9
Ответ: 7/9
д) 0,( 25 ) = 25/99
Ответ: 25/99
е) 0,( 37 ) = 37/99
Ответ: 37/99
ж) 0,( 10 ) = 10/99
Ответ: 10/99
з) 0,( 5 ) = 5/99
Ответ: 5/99979. а) Запишите три любые обыкновенные дроби со знаменателем 999 в виде периодических десятичных дробей.
б) Запишите три любые периодические дроби с периодом, состоящим из трёх цифр, в виде обыкновенных дробей.а) 458/999 = 0,( 458 )
45/9999 = 0,( 0045 )
5/9999 = 0,( 0005 )
б) 0,( 123 ) = 123/999
0,( 003 ) = 3/999
0,( 0003 ) = 3/9999 198
-
Периодичность десятичного разложения обыкновенной дроби
Ответы к странице 198
980. Какие остатки могут получиться при делении натуральных чисел на:
а) 2;
б) 3;
в) 4;
г) 5;
д) 9;
е) 11?а) Ответ: 0; 1.
б) Ответ: 0; 1; 2.
в) Ответ: 0; 1; 2; 3.
г) Ответ: 0; 1; 2; 3; 4.
д) Ответ: 0; 1; 2; 3; 4; 5; 6; 7; 8.
е) Ответ: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10.981. Докажите, что при делении натурального числа p на натуральное число q (q > 1) получается бесконечная периодическая десятичная дробь с периодом, состоящим не более чем из (q − 1) цифры.
Возникающий при делении остаток может быть любым натуральным числом, но это число будет обязательно меньше делителя, то есть возникающий остаток при делении числа p на число q будет находиться в диапазоне от 0 до числа равного q − 1.
Возникновение при делении уголком остатка добавляет нам дополнительный знак после запятой в частном. В случае выпадения остатка одинакового предыдущим период десятичной дроби зациклится, следовательно, при делении натурального числа p на натуральное число q (q > 1) получается бесконечная периодическая десятичная дробь с периодом, состоящим не более чем из (q − 1) цифры.982. а) Сколько цифр может быть в периоде десятичного разложения обыкновенной несократимой дроби со знаменателем 7?
б) В каком случае разложение обыкновенной дроби в десятичную является: конечным; бесконечным?
в) Почему десятичное разложение дроби 3 7 периодическое?а) При делении натурального числа p на натуральное число q (q > 1) получается бесконечная периодическая десятичная дробь с периодом, состоящим не более чем из (q − 1) цифры.
7 − 1 = не более 6 цифр может быть в периоде десятичного разложения обыкновенной несократимой дроби со знаменателем 7.
Ответ: не более 6.
б) Ответ:
Если знаменатель q несократимой дроби p/q не имеет других простых делителей, кроме 2 и 5, то эта дробь разлагается в конечную десятичную дробь.
Если знаменатель q несократимой дроби p/q имеет другие простые делители, кроме 2 и 5, то эта дробь разлагается в бесконечную периодическую десятичную дробь.
в) 3/7 = 3/7 ∗ 1 = 0,( 428571 ), так как знаменатель дроби 3/7 имеет отличные от 2 и 5 простые делители, разложение дроби 3/7 является бесконечным периодическим.983. Разложите обыкновенную дробь в десятичную делением числителя на знаменатель уголком:
а) 1/11;
б) 2/11;
в) 1/12;
г) 5/12;
д) 1/7;
е) 5/7;
ж) 2/7;
з) 1/33.
а) Ответ: 0,(09)
б) Ответ: 0,(18)
в) Ответ: 0,08(3)
г) Ответ: 0,41(6)
д) Ответ: 0,(142857)
е) Ответ: 0,(714285)
ж) Ответ: 0,(285714)
з) Ответ: 0,(03)984. Запишите периодическую дробь в виде обыкновенной дроби:
а) 1,(8);
б) 0,(3);
в) 0,(7);
г) 3,(5);
д) 0,1(2);
е) 1,12(3);
ж) 7,5,(4);
з) 0,(35);
и) 0,(59);
к) 0,(12);
л) 1,0(12);
м) 8,7(21).а) x = 1,(8)
100x = 188,(8)
10x = 18,(8)
90x = 188,(8) − 18,(8)
x = 170/90 = 17/9 = 1 8/9
Ответ: 1 8/9
б) x = 0,(3)
100x = 33,(3)
10x = 3,(3)
90x = 33,(3) − 3,(3)
x = 30/90 = 3/9 = 1/3
Ответ: 1/3
в) x = 0,(7)
100x = 77,(7)
10x = 7,(7)
90x = 77,(7) − 7,(7)
x = 70/90 = 7/9
Ответ: 7/9
г) x = 3,(5)
100x = 355,(5)
10x = 35,(5)
90x = 355,(5) − 35,(5)
x = 320/90 = 32/9 = 3 5/9
Ответ: 3 5/9
д) x = 0,1(2)
100x = 12,(2)
10x = 1,(2)
90x = 12,(2) − 1,(2)
x = 11/90
Ответ: 11/90
е) x = 1,12(3)
1000x = 1123,(3)
100x = 112,(3)
900x = 1123,(3) − 112,(3)
x = 1011/900 = 337/300 = 1 37/300
Ответ: 1 37/300
ж) x = 7,5(4)
100x = 754,(4)
10x = 75,(4)
90x = 679
x = 679/90 = 7 49/90
Ответ: 7 49/90
з) x = 0,(35)
100x = 35,(35)
99x = 35,(35) − 0,(35)
x = 35/99
Ответ: 35/99
и) x = 0,(59)
100x = 59,(59)
99x = 59,(59) − 0,(59)
x = 59/99
Ответ: 59/99
к) x = 0,(12)
100x = 12,(12)
99x = 12,(12) − 0,(12)
x = 12/99 = 4/33
Ответ: 4/33
л) x = 1,0(12)
100000x = 101212,(12)
1000x = 1012,(12)
99000x = 101212,(12) − 1012,(12)
x = 100200/99000 = 1002/990 = 334/330 = 167/165 = 1 2/165
Ответ: 1 2/165
м) x = 8,7(21)
1000x = 8721,(21)
10x = 87,(21)
990x = 8721,(21) − 87,(21)
x = 8634/990 = 2878/330 = 1439/165 = 8 119/165
Ответ: 8 119/165985. Покажите, что периодическая дробь с периодом 9 равна конечной десятичной дроби:
а) 0,3(9) = 0,4;
б) 1,2(9) = 1,3.а) x = 0,3(9)
100x = 39,(9)
10x = 3,(9)
90x = 39,(9) − 3,(9)
x = 36/90 = 4/10 = 0,4
Ответ: 0,3(9) = 0,4
б) x = 1,2(9)
100x = 129,(9)
10x = 12,(9)
90x = 129,(9) − 12,(9)
x = 117/90 = 13/10 = 1,3
Ответ: 1,2(9) = 1,3 199
-
Непериодические бесконечные десятичные дроби
Ответы к странице 199
986. Какое число называют:
а) рациональным;
б) иррациональным;
в) действительным?а) Число, которое можно записать в виде p/q, где p и q − целые числа и q не равно нулю, называют рациональным числом или дробью.
1/2;
12 = 12/1;
12,( 9 ) = 13 = 13/1.
б) Число, которое можно записать в виде бесконечной непериодической бесконечной десятичной дроби, называют иррациональным числом.
1,0100100010000...;
1,0200200020000....
в) Рациональные и иррациональные числа называют действительными числами, поэтому все ответы верны.987. Любое ли, иррациональное число является действительным?
Ответ: любое.
988. Придумайте какие−нибудь пять бесконечных непериодических дробей (иррациональных чисел).
Ответ:
0,2121121112...
0,3383833383...
5,7574737271...
8,6656665666...
4,4144144414...989. Существует ли рациональное число, равное бесконечной непериодической дроби?
Ответ: нет, так как любое действительное число представляется в виде бесконечной десятичной дроби. Если число рациональное, то дробь периодическая, если число иррациональное, то дробь непериодическая.
990. Каким числом (рациональным или иррациональным) является число:
а) 0,275;
б) 0,(2);
в) 1,32323232...;
г) 1,15(45);
д) 3,10110111011110...;
е) 0,12345678...?а) Ответ: 0,275 − рациональное число.
б) Ответ: 0,(2) − рациональное число.
в) Ответ: 1,32323232... − рациональное число.
г) Ответ: 1,15(45) − рациональное число.
д) Ответ: 3,10110111011110... − иррациональное число.
е) Ответ: 0,12345678... − иррациональное число.991. Запишите четыре числа:
а) натуральных;
б) положительных;
в) отрицательных;
г) целых;
д) рациональных;
е) иррациональных;
ж) чётных;
з) нечётных;
и) простых;
к) составных;
л) кратных 3;
м) кратных 2 и 5.а) Ответ: 1; 3; 5; 7.
б) Ответ: 1; 5;1/2; 0,1.
в) Ответ: −7; −1,(2); −0,010010001...; −1,5.
г) Ответ: 1; 3; 5; −7.
д) Ответ:1/2; 0,1; −1,5; −1,(2).
е) Ответ: 0,2121121112...; 0,3383833383...; 5,7574737271...; −0,010010001....
ж) Ответ: 2; 4; 6; −8.
з) Ответ: 1; 3; 5; −7.
и) Ответ: 2; 3; 5; 7.
к) Ответ: 4; 8; 9; 12.
л) Ответ: 99; 303; 6; 27.
м) Ответ: 20; 50; 10; 120. 200
-
Ответы к странице 200
992. Запишите два числа:
а) рациональных и отрицательных;
б) целых и кратных 5;
в) целых и положительных;
г) простых и больших 30;
д) нечетных и кратных 7;
е) составных и чётных.а) Ответ: −1; −1,(2).
б) Ответ: 10; −5.
в) Ответ: 10; 18.
г) Ответ: 31; 67.
д) Ответ: 21; 63.
е) Ответ: 66; 24. 202
-
Действительные числа
Ответы к странице 202
993. Что называют целой частью положительной бесконечной десятичной дроби?
Ответ: Число до запятой у положительной бесконечной десятичной дроби называют целой частью этой дроби.
994. Назовите цифры пятого, шестого, седьмого разрядов после запятой у дроби:
а) 13,(27);
б) 17,12345678...;
в) 0,000(12).а) Ответ: 2; 7; 2.
б) Ответ: 5; 6; 7.
в) Ответ: 2; 1; 2.995. Какие числа называют противоположными? Приведите примеры.
Ответ: Числа, отличающиеся только знаком, называют противоположными, например:
1 и −1
1,0(5) и −1,0(5)996. Как обозначают число, противоположное числу a?
Число противоположное числу а равно −a.
Ответ: −a.997. Если число обозначено через −a, значит ли это, что оно отрицательное? Приведите примеры.
Нет, не обязательно.
Допустим a = 2, тогда −а = −2 − отрицательное число;
допустим a = −2, тогда −а = −(−2) = 2 − положительное число.
Ответ: Нет, не обязательно.998. Что называют модулем (абсолютной величиной) действительного числа? Приведите примеры.
Модуль действительно числа a обозначают |a| и определяют:
|a| = a, если a положительное.
|a| = 0, если a = 0.
|a| = −a, если а отрицательное.
|1,(3)| = 1,(3)
|−1,(3)| = −(−1,(3)) = 1,(3)
|0| = 0999. Как сравнить два действительных числа? Приведите примеры.
Из двух положительных действительных чисел больше то, чей модуль больше.
1,5 < 1,(5)
Любое положительное действительное число больше 0.
0 < 1,(5)
Любое отрицательное действительное число меньше 0.
−1,5 < 0
Из двух отрицательных действительных чисел больше то, у которого модуль меньше.
−1,5 > −1,(5)
Любое положительное действительное число больше отрицательного.
1,5(5) > −1,(5)1000. Если |a| < |b|, то всегда ли верно неравенство a < b?
Ответ:
Неравенство: если |a| < |b|, то a < b, может быть верно в следующих случаях:
a − отрицательное число, а b − положительное число;
a равно 0, а b − положительное число;
a и b положительные числа.1001. Пусть |a| = |b|, в каких случаях a = b и в каких a = −b?
Ответ:
Равенство a = b, при |a| = |b| может быть верно в следующих случаях:
a и b положительные числа;
a и b отрицательные числа;
a и b равны нулю.
Равенство a = −b, при |a| = |b| может быть верно в следующих случаях:
a − положительное число, а b − отрицательное число;
a − отрицательное число, а b − положительное число;
a и b равны нулю.1002. Поясните, как надо понимать записи:
а) a ≤ b;
б) a < b < c;
в) a ≤ b < c;
г) a ≤ b ≤ c.а) Ответ: b больше или равно a.
б) Ответ: b больше a и меньше с.
в) Ответ: b больше или равно a и меньше c.
г) Ответ: b больше или равно a и меньше или равно c. 203
-
Ответы к странице 203
1003. Для каких чисел верно равенство:
а) |a| = a;
б) |a| = −a.а) Ответ:
Равенство |a| = a верно для:a ≥ 0
для a = 0
б) Ответ:
Равенство |a| = −a верно для:a ≤ 0
для a = 01004. Найдите модуль (абсолютную величину) числа:
а) −2,(3);
б) −0,5777;
в) −12,0(12);
г) 3,0(13).а) |−2,(3)| = 2,(3)
Ответ: 2,(3)
б) |−0,5777| = 0,5777
Ответ: 0,5777
в) |−12,0(12)| = 12,0(12)
Ответ: 12,0(12)
г) |3,0(13)| = 3,0(13)
Ответ: 3,0(13)1005. Найдите число, противоположное числу:
а) 2,5(3);
б) −1,(72);
в) 3,1(12);
г) 3,0(13).а) Ответ: −2,5(3).
б) Ответ: −1,(72).
в) Ответ: −3,1(12).
г) Ответ: −3,0(13).1006. Сравните числа:
а) 3,5 и 3,(5);
б) −2,14 и −2,1(4);
в) −3,(2) и 4,11;
г) −5,(43) и −5,(4).а) Из двух положительных действительных чисел больше то, чей модуль больше.
|3,5| = 3,5
|3,(5)| = 3,(5), следовательно, 3,5 < 3,(5).
Ответ: 3,5 < 3,(5).
б) Из двух отрицательных действительных чисел больше то, у которого модуль меньше.
|−2,14| = 2,14
|−2,1(4)| = 2,1(4), следовательно, −2,14 > −2,1(4).
Ответ: −2,14 > −2,1(4).
в) Любое положительное действительное число больше отрицательного, следовательно, −3,(2) < 4,11.
Ответ: −3,(2) < 4,11.
г) Из двух отрицательных действительных чисел больше то, у которого модуль меньше.
|−5,(43)| = 5,(43)
|−5,(4)| = 5,(4), следовательно, −5,(43) > −5,(4).
Ответ: −5,(43) > −5,(4).1007. Округлите числа а и b с точностью до 0,1 и вычислите приближенно разность а − b, если:
а) а = 12,32, b = 0,1;
б) а = 0,(2), b = −2,323;
в) а = 4,2, b = 1,(1);
г) а = 45,6(12), b = 10,(2).а) 12,3 ≈ 12,2
0,1 ≈ 0,1
12,3 − 0,1 = 12,2
Ответ: 12,2.
б) 0,( 2 ) ≈ 0,2
− 2,323 ≈ − 2,3
0,2 − (−2,3) = 0,2 + 2,3 = 2,5
Ответ: 2,5
в) 4,2 ≈ 4,2
1,( 1 ) ≈ 1,1
4,2 − 1,1 = 3,1
Ответ: 3,1
г) 45,6 ( 12 ) ≈ 45,6
10,( 2 ) ≈ 10,2
45,6 − 10,2 = 35,4
Ответ: 35,41008. Найдите приближенную сумму чисел, беря слагаемые с точностью до 0,01:
а) 3,5 + 3,(5);
б) 1,359 + 3,2(6);
в) 12,351 + 0,(3);
г) 7,(41) + 5,(36).а) 3,5 ≈ 3,5
3,( 5 ) ≈ 3,56
3,5 + 3,56 = 7,06
Ответ: 7,06
б) 1,359 ≈ 1,36
3,2 ( 6 ) ≈ 3,27
1,36 + 3,27 = 4,63
Ответ: 4,63
в) 12,351 ≈ 12,35
0,( 3 ) ≈ 0,33
12,35 + 0,33 = 12,68
Ответ: 12,68
г) 7,( 41 ) ≈ 7,41
5,( 36 ) ≈ 5,36
7,41 + 5,36 = 12,77
Ответ: 12,771009. Найдите приближенно разность чисел, беря уменьшаемое и вычитаемое с точностью до 0,001:
а) 11,(4) − 7,3;
б) 12,(15) − 3,7236;
в) 7,(93) − 2,(39);
г) 3,3297 − 6,(8).а) 11,( 4 ) ≈ 11,444
7,3 ≈ 7,3
11,444 − 7,3 = 4,144
Ответ: 4,144
б) 12,( 15 ) ≈ 12,152
3,7236 ≈ 3,724
12,152 − 3,724 = 8,428
Ответ: 8,428
в) 7,( 93 ) ≈ 7,939
2,( 39 ) ≈ 2,394
7,939 − 2,394 = 5,545
Ответ: 5,545
г) 3,3297 ≈ 3,33
6,( 8 ) ≈ 6,889
3,33 − 6,889 = −3,559
Ответ: −3,5591010. Найдите приближенно произведение чисел, беря множители с точностью до второй значащей цифры:
а) 1,3 * 12,(1);
б) 0,56 * 0,(3);
в) 9,(1) * 6,(2);
г) 12,(45) * 1,(1).а) 1,3 ≈ 1,3
12,( 1 ) ≈ 12
1,3 ∗ 12 ≈ 16
Ответ: 16.
б) 0,56 ≈ 0,56
0,( 3 ) ≈ 0,33
0,56 ∗ 0,33 ≈ 0,18
Ответ: 0,18
в) 9,( 1 ) ≈ 9,1
6,( 2 ) ≈ 6,2
9,1 ∗ 6,2 ≈ 56
Ответ: 56
г) 12,( 45 ) ≈ 12
1,( 1 ) ≈ 1,1
12 ∗ 1,1 ≈ 13
Ответ: 131011. Найдите приближенно частное чисел, беря делимое и делитель с точностью до третьей значащей цифры:
а) 3,2 : 0,(2);
б) 0,(5) : 2;
в) 3,(82) : 2,(3);
г) 35,0(8) : 4,(02).а) 3,2 ≈ 3,2
0,( 2 ) ≈ 0,222
3,2 : 0,( 2 ) ≈ 14,4
Ответ: 14,4
б) 0,( 5 ) ≈ 0,556
2 ≈ 2
0,556 : 2 ≈ 0,278
Ответ: 0,278
в) 3,( 82 ) ≈ 3,83
2,( 3 ) ≈ 2,33
3,83 : 2,33 ≈ 1,64
Ответ: 1,64
г) 35,0 ( 8 ) ≈ 35,1
4,( 02 ) ≈ 4,02
35,1 : 4,02 ≈ 8,73
Ответ: 8,731012. а) Что получится, если к числу прибавить 0?
б) Чему равна сумма противоположных чисел?
в) Можно ли разность a − b записать в виде суммы?
г) Что получится, если число умножить на 1?
д) Что получится, если число умножить на 0?а) a + 0 = a
Ответ: само число.
б) a + (−a) = a − a = 0
Ответ: 0
в) a − b = a + (−b)
Ответ: можно.
г) a * 1 = a
Ответ: само число.
д) a * 0 = 0
Ответ: 01013. Докажите, пользуясь свойствами действительных чисел, что:
а) если a < b и c − отрицательное число, то a * c > b * c
б) если 0 < a < b, то a 2 < b 2;
в) если a < b < 0, то a 2 > b 2.а) a − b < 0, так как a < b
(a − b) * c > 0, так как a − b < 0 и c < 0
(a − b) * c > 0
В соответствии с распределительным законом умножения:
a * c − b * c > 0
Переносим −b * c в правую часть неравенства и получаем:
a * c > b * c
б) Если обе части неравенства умножить на одно и тоже положительное число, то знак неравенства не поменяется, тогда:
a 2 < a * b
a * b < b 2
a 2< ab <b 2
a 2<b 2
в) Если обе части неравенства умножить на одно и тоже отрицательное число, то знак неравенства меняется на противоположный, тогда:
a 2 > a * b
a * b > b 2
a 2> ab <b 2
a 2>b 2 204
-
Ответы к странице 204
1014. Какими свойствами арифметических действий воспользовались при вычислениях:
а) 125 * 7 * 8 * 3 = 125 * 8 * 7 * 3 = 1000 * 21 = 21000;
б) 4 2 3 ∗ 7 1 3 + 2 2 3 ∗ 4 2 3 = 4 2 3 ∗ ( 7 1 3 + 2 2 3 ) = 4 2 3 ∗ 10 = 14 ∗ 10 3 = 46 2 3;
в) 4 2 5 ∗ 7 13 19 ∗ 5 22 = 22 5 ∗ 5 22 ∗ 7 13 19 = 7 13 19?а) Ответ: сочетательный и переместительный законы ab = ba и (ab)c = ab(c)
б) Ответ: распределительный закон ab + ac = a(b + c)
в) Ответ: сочетательный и переместительный законы ab = ba и (ab)c = ab(c)1015. Известно, что если a < b, то a + c < b + c для любого действительного числа c. Проиллюстрируйте это свойство действительных чисел на примере, взяв a = −4,7, b = −5,25, с = −2,3.
a > b, так как −4,7 > −5,24,
a + c = −(4,7 + 2,3) = −7,
b + c = −(5,25 + 2,3) = −7,55,
a + c > b + c, так как −7 > −7,55.1016. Найдите два числа x, удовлетворяющие условию:
а) |x − 5,3| = 1;
б) |x − 5,3| < 1;
в) |x − 5,3| > 1;
Сколько таких чисел можно найти в каждом случае?а) |x − 5,3| = 1, равносильно
x1 − 5,3 = 1 или x 2 − 5,3 = − 1, тогда:
x1 − 5,3 = 1
x1 = 1 + 5,3 = 6,3
x2 − 5,3 = − 1
x2 = − 1 + 5,3 = 4,3
Ответ: Для условия |x − 5,3| = 1 верны только два значения х: 6,3 и 4,3.
б)
|x − 5,3| < 1, равносильно x − 5,3 < 1 или x − 5,3 > −1, тогда:
x − 5,3 < 1
x < 1 + 5,3
x < 6,3
x − 5,3 > −1
x > −1 + 5,3
x > 4,3
Ответ: Бесконечное количество чисел, удовлетворяющих условию 4,3 > x < 6,3.
в) |x − 5,3| > 1, равносильно x − 5,3 > 1 или x − 5,3 < −1, тогда:
x − 5,3 > 1
x > 1 + 5,3
x > 6,3
x − 5,3 < −1
x < −1 + 5,3
x < 4,3
Ответ: Бесконечное количество чисел, удовлетворяющих условию x > 6,3 или x < 4,3.1017. Вычислите (1017−1020):
а) 68 * 48 + 68 * 52;
б) 59 * 37 + 59 * 63;
в) 87 * 29 + 87 * 71;
г) 17 * 73 − 63 * 17;
д) 382 * 400 − 500 * 382;
е) 756 * 350 + 756 * 650.а) 68 * 48 + 68 * 52 = 68 * (48 + 52) = 68 * 100 = 6800
б) 59 * 37 + 59 * 63 = 59 * (37 + 63) = 59 * 100 = 5900
в) 87 * 29 + 87 * 71 = 87 * (29 + 71) = 87 * 100 = 8700
г) 17 * 73 − 63 * 17 = 17 * (73 − 63) = 17 * 10 = 170
д) 382 * 400 − 500 * 382 = 382 * (400 − 500) = 382 * −100 = −38200
е) 756 * 350 + 756 * 650 = 756 * (350 + 650) = 756 * 1000 = 7560001018. Вычислите (1017−1020):
а) 32 * 18 : 9;
б) 748 * 12 : 6;
в) 126 * 96 : 32;
г) 172 * 128 : 64.а) 32 * 18 : 9 = 32 * (18 : 9) = 32 * 2 = 64
б) 748 * 12 : 6 = 748 * (12 : 6) = 748 * 2 = 1496
в) 126 * 96 : 32 = 126 * (96 : 32) = 126 * 3 = 378
г) 172 * 128 : 64 = 172 * (128 : 64) = 172 * 2 = 3441019. Вычислите (1017−1020):
а) 25 * 7 * 8;
б) 13 * 12 * 25;
в) 2 1/2 ∗ 3 1/3;
г) 1/7 ∗ 8 1/6 ∗ 6;
д) 78 : 3 ∗ ( 1/8 − 2 1/8 );
е) ( 75 − 100/1 2 ) ∗ 0,04.а) 28 * 7 * 8 = (25 * 8) * 7 = 200 * 7 = 1400
б) 13 * 12 * 25 = 13 * (12 * 25) = 13 * 300 = 3900
в) 5/2 ∗ 10/3 = 5 ∗ 5/3 = 25/3 = 8 1/3
г) 1/7 ∗ 8 1/6 ∗ 6 = 1/7 ∗ ( 6 ∗ 49/6 ) = 1/7 ∗ 49 = 7
д) 78 : 3 ∗ ( 1/8 − 2 1/8 ) = 26 ∗ ( − 2 ) = − 52
е) ( 75 − 100 1/2 ) ∗ 0,04 = − 25 1/2 ∗ 4/100 = − 51/2 ∗ 4/100 = − 51 ∗ 2/100 = − 102/100 = − 1 1/501020. Вычислите (1017−1020):
а) 12,5(67) − 12,5(67);
б) 6,7(89) * 0;
в) 4,51(2) : 1;
г) 0 : 0,0(654).а) 12,5(67) − 12,5(67) = 0
б) 6,7(89) * 0 = 0
в) 4,51(2) : 1 = 4,51(2)
г) 0 : 0,0(654) = 0 207
-
Длина отрезка
Ответы к странице 207
1021. На рисунке 108 изображены отрезки BC, AD, KP. Определите на глаз длину каждого отрезка в сантиметрах. Проверьте свой глазомер с помощью линейки.
Ответ:
BC = 5 см
AD = 3,5 см
KP = 5 см1022. Постройте в тетради три произвольных отрезка и выполните предыдущее задание.
Строим любые отрезки по линейке и пишем их длину.
1023. Постройте в тетради отрезки длиной 3,5 см, 5 см и 6,5 см. Разделите на глаз каждый отрезок на 3 равные части. Проверьте свой глазомер с помощью линейки.
3,5 : 3 = 1,1(6) см длина третьей части 1 отрезка;
5 : 3 = 1,(6) см длина третьей части 2 отрезка;
6,5 : 3 = 2,1(6) длина третьей части 3 отрезка.1024. Постройте отрезок длиной 8,5 см. Разделите на глаз этот отрезок:
на 5 равных частей;
на 6 равных частей.8,5 : 5 = 1,7 см длина пятой части отрезка;
8,5 : 6 = 1,41(6) см длина шестой части отрезка.1025. На рисунке 109 изображены отрезки AB и CD. Приняв за единицу измерения отрезок CD, измерьте на глаз отрезок AB с точностью до 1 с недостатком. Проверьте свой глазомер с помощью циркуля.
Ответ: AB
≈ 5 длин отрезка CD.
1026. Длина отрезка AB выражена числом 5,375. Запишите приближённую длину отрезка AB с точностью до 1; до 0,1; до 0,01 с недостатком.
Ответ: 5; 5,3; 5,37.
1027. Длина отрезка AB равна:
а) 3 1/8;
б) 2 5/16;
в) 3 61/99;
г) 4 14/27.
Выразите длину отрезка десятичной дробью с точностью до 1; до 0,1; до 0,01 с недостатком.а) 3 1/8 = 3 125/1000 = 3,125 ≈ 3
3 1/8 = 3 125/1000 = 3,1 ≈ 3
3 1/8 = 3 125/1000 = 3,12 ≈ 3
Ответ: 3; 3,1; 3,12.
б) 2 5/16 = 2 3125/10000 = 2,3125 ≈ 2
2 5/16 = 2 3125/10000 = 2,3125 ≈ 2,3
2 5/16 = 2 3125/10000 = 2,3125 ≈ 2,31
Ответ: 2; 2,3; 2,31.
в) 3 61/99 = 3,( 61 ) ≈ 3
3 61/99 = 3,( 61 ) ≈ 3,6
3 61/99 = 3,( 61 ) ≈ 3,61
Ответ: 3; 3,6; 3,61.
г) 4 14/27 = 4,( 518 ) ≈ 4
4 14/27 = 4,( 518 ) ≈ 4,5
4 14/27 = 4,( 518 ) ≈ 4,51
Ответ: 4; 4,5; 4,51.1028. Выразите длину отрезка AB десятичной дробью с точностью до 0,1; 0,01; 0,001; 0,0001 с недостатком, если AB = 3 19 99:
3 19/99 = 3,( 19 ) ≈ 3,1
3 19/99 = 3,( 19 ) ≈ 3,19
3 19/99 = 3,( 19 ) ≈ 3,191
3 19/99 = 3,( 19 ) ≈ 3,1919
Ответ: 3,1; 3,19; 3,191; 3,1919. 209
-
Длина окружности. Площадь круга
Ответы к странице 209
1029. а) Чему равно отношение длины окружности к длине её диаметра?
б) Чему равно отношение длины окружности к длине её радиуса?а) Ответ:
π ≈ 3,14
б) r − радиус, d − диаметр, с − длина окружности.
r = d/2, тогда:
c/2 r = π
c/r = 2 π
Ответ: 2π.1030. Напишите формулу для вычисления:
а) длины окружности;
б) площади круга.а) Ответ: C = 2πR
б) Ответ: S = π R 21031. Вычислите длину окружности радиуса:
а) З см;
б) 0,06 м;
в) 0,4 дм.а) C = 2πR = 2π * 3 = 6π = 6 * 3,14 = 18,84 см
Ответ: 18,84 см
б) C = 2πR = 2π * 0,06 = 0,12π = 0,12 * 3,14 = 0,3768 м = 37,68 см
Ответ: 37,68 см
в) C = 2πR = 2π * 0,4 = 0,8π = 0,8 * 3,14 = 2,512 дм
Ответ: 2,512 дм.1032. Вычислите площадь круга радиуса:
а) З см;
б) 4,6 дм;
в) 0,2 м.а) S = π R 2 = π ∗ 3 2 = 9 π = 9 ∗ 3,14 = 28,26 см2
Ответ: 28,26 см2
б) S = π R 2 = π ∗ 4,6 2 = 21,16 π = 21,16 ∗ 3,14 = 66,4424 дм2
Ответ: 66,4424 дм2
в) S = π R 2 = π ∗ 0,2 2 = 0,04 π = 0,04 ∗ 3,14 = 0,1256 м2
Ответ: 0,1256 м21033. Как изменится длина окружности, если её радиус:
а) увеличить в 3 раза;
б) уменьшить в 2 раза?а) C = 2πR − длина окружности с радиусом R,
R * 3 = 3R − радиус окружности при увеличении его в 3 раза,
C = 2π3R = 6πR длина окружности с радиусом 3R,
6 π R/2 π R = 3 − кратность увеличения длины окружности при увеличении её радиуса в 3 раза.
Ответ: увеличится в 3 раза.
б) C = 2πR − длина окружности c радиусом R,
C : 2 = 1/2 R − радиус окружности при уменьшении его b 2 раза,
C = 2 π 1/2 R = πR длина окружности с радиусом 1 2 R,
π R/2 π R = 1/2 − кратность увеличения длины окружности при уменьшении её радиуса в 2 раза.
Ответ: уменьшится в 2 раза.1034. Как изменится радиус окружности, если её длину:
а) увеличить в 5 раз;
б) уменьшить в 7 раз?а) С = 2πR − длина окружности с радиусом R,
R = С/2 π при длине окружности С,
С * 5 = 5С − длина окружности, после ее увеличения в 5 раз,
R = 5 С/2 π при длине окружности 5С
5 С/2 π : С/2 π = 5 С/2 π ∗ 2 π/С = 5 − кратность увеличения радиуса окружности при увеличении её длины в 5 раз.
Ответ: увеличится в 5 раз.
б) С = 2πR − длина окружности с радиусом R,
R = С/2 π при длине окружности С,
С : 7 = 1/7 C − длина окружности, после ее уменьшения в 7 раз,
R = С/14 π при длине окружности 1/7 C,
С/14 π : С/2 π = С/14 π ∗ 2 π/С = 1/7 − кратность увеличения радиуса окружности при уменьшении её длины в 7 раз.
Ответ: уменьшится в 7 раз.1035. Как изменится длина окружности, если её радиус:
а) увеличить на 3 см;
б) уменьшить на 3 см?а) С = 2πR − длина окружности с радиусом R,
R + 3 = радиус окружности при увеличении его на 3 см,
С = 2π(R + 3) = длина окружности с радиусом R + 3,
2π(R + 3) − 2πR = 2πR + 6π − 2πR = 6π = 6 * 3,14 = на 18,84 см увеличится длина окружности если ее радиус увеличить на 3 см.
Ответ: увеличится на 18,84 см.
б) С = 2πR − длина окружности с радиусом R,
R − 3 = радиус окружности при уменьшении его на 3 см,
С = 2π(R − 3) = длина окружности с радиусом R − 3,
2π(R − 3) − 2πR = 2πR − 6π − 2πR = −6π = −6 * 3,14 = −18,84 см, на 18,84 уменьшится длина окружности если ее радиус уменьшить на 3 см.
Ответ: уменьшилась на 18,84 см.1036. Как изменится радиус окружности, если её длину:
а) увеличить на 6,28 см;
б) уменьшить на 9,42 дм?а) С = 2πR − длина окружности с радиусом R,
R = С/2 π при длине окружности С,
C + 6,28 − длина окружности, после ее увеличения на 6,28 см,
R = C + 6,28/2 π при длине окружности C + 6,28
C + 6,28/2 π − С/2 π = C + 6,28 − С/2 π = 3,14/π = на 1 см увеличится радиус окружности при увеличении ее длины на 6,28 см.
Ответ: увеличится на 1 см.
б) С = 2πR − длина окружности с радиусом R,
R = С/2 π при длине окружности С,
C − 9,42 − длина окружности, после ее уменьшения на 9,42 дм,
R = C − 9,42/2 π при длине окружности C − 9,42
C − 9,42/2 π − С/2 π = C − 9,42 − С/2 π = − 4,71/π = − 1,5 на 1,5 дм уменьшится радиус окружности при уменьшении ее длины на 9,42 дм.
Ответ: уменьшится на 9,42 дм.1037. Как изменится площадь круга, если его радиус:
а) увеличить в 3 раза;
б) уменьшить в 2 раза?а) S = π R2 − площадь окружности с радиусом R,
R * 3 = 3R − радиус окружности при увеличении его в 3 раза,
S = π ( 3 R2 ) = π 9 R 2 площадь окружности с радиусом 3R,
π 9 R2/π R2 = 9 − кратность увеличения площади окружности при увеличении её радиуса в 3 раза.
Ответ: увеличится в 9 раз.
б) S = π R2 − площадь окружности с радиусом R,
R : 2 = 1/2 R − радиус окружности при уменьшении его в 2 раза,
S = π R2 /4 площадь окружности с радиусом 1 2 R,
π R2 /4 : π R2 = π R2 /4 ∗ 1/π R2 = 1/4 − кратность увеличения площади окружности при уменьшении её радиуса в 2 раза, то есть площадь окружности уменьшится в 4 раза.
Ответ: уменьшится в 4 раза.1038. Сравните длины красной и синей линий, являющихся половинами окружностей (рис. 111).
а) Пусть длина AM = x, тогда:
MB = 3x, AB = 4x;
R = d : 2, тогда:
R полуокружности AM = x/2;
R полуокружности MB = 3 x/2;
R полуокружности AB = 4 x/2 = 2 x;
Длина полуокружности = 2πR : 2 = πR, тогда:
длина полуокружности AM = π x/2;
длина полуокружности MB = 3 π x/2;
длина полуокружности AB = 2πх;
Длина красной линии = длина полуокружности AM + длина полуокружности MB = π x/2 + 3 π x/2 = 4 π x/2 = 2 π x
Длина синей линии = длина полуокружности AB = 2πx, следовательно, длины красной и синей линий равны.
Ответ: длины линий равны.
б) Пусть длина AM = x, тогда:
MB = x, AB = 2x;
R = d : 2, тогда:
R полуокружности AM = x/2;
R полуокружности MB = x/2;
R полуокружности AB = х;
Длина полуокружности = 2πR : 2 = πR, тогда:
длина полуокружности AM = π x/2;
длина полуокружности MB = π x/2;
длина полуокружности AB = πх;
Длина красной линии = длина полуокружности AM + длина полуокружности MB = π x/2 + π x/2 = π x
Длина синей линии = длина полуокружности AB = πx, следовательно, длины красной и синей линий равны.
Ответ: длины линий равны.1039. Докажите, что ответ в предыдущей задаче не зависит от положения точки M на отрезке AB.
AB = AM + MB
R полуокружности AM = A M/2;
R полуокружности MB = M B/2;
Длина полуокружности AM = π ∗ A M/2;
Длина полуокружности MB = π ∗ M B/2;
Длина красной линии = ${\operatorname\pi}\ast\frac{AM}2+{\operatorname\pi}\ast\frac{MB}2={\operatorname\pi}\ast(\frac{AM}2+\frac{MB}2)=\frac12{\operatorname\pi}(AM+MB)=\frac12{\operatorname\pi}(AB)$, при перемещении точки M длина отрезка AB, а следовательно и длина красной линии не изменится, поэтому длина синей линии будет равна длине красной линии, независимо от положения точки M.1040. Вычислите площадь закрашенной фигуры (рис. 112). Сторона квадрата равна 4 см, дуги − четвёртые части окружности радиуса 4 см.
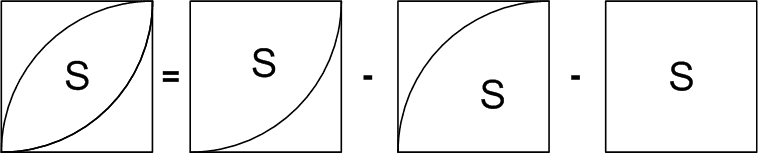
S квадрата = а2 = 42 = 16 см2
S четвертой части окружности равна = $\frac{{\operatorname\pi}R^2}4=\frac{{\operatorname\pi}4^2}4=\frac{16{\operatorname\pi}}4=4{\operatorname\pi}$
S закрашенной фигуры равна = 4π + 4π − 16 = 8π − 16 = 8 * 3,14 − 16 = 25,12 − 16 = 9,12 см2
Ответ: 9,12 см2 210
-
Ответы к странице 210
1041. На сторонах квадрата как на диаметрах построили полуокружности внутри квадрата. Вычислите площадь закрашенной фигуры (рис. 113). Сторона квадрата равна 4 см.

S квадрата = а2 = 42 = 16 см2
S полуокружности равна = $\frac{{\operatorname\pi}R^2}2=\frac{{\operatorname\pi}2^2}2=\frac{4{\operatorname\pi}}2=2{\operatorname\pi}$
S закрашенной фигуры равна = 2π * 4 − 16 = 8π − 16 = 8 * 3,14 − 16 = 25,12 − 16 = 9,12 см2
Ответ: 9,12 см21042. На сторонах квадрата как на диаметрах построили полукруги вне квадрата. Получили первую фигуру (рис. 114, а). Потом каждую сторону такого же квадрата разделили на 2 равные части и на каждой из них как на диаметрах построили полукруги вне квадрата. Получили вторую фигуру (рис. 114,б). Потом каждую сторону такого же квадрата разделили на 3 равные части и т. д. Вычислите периметр и площадь каждой из первых четырёх фигур, если сторона квадрата равна 12 см.
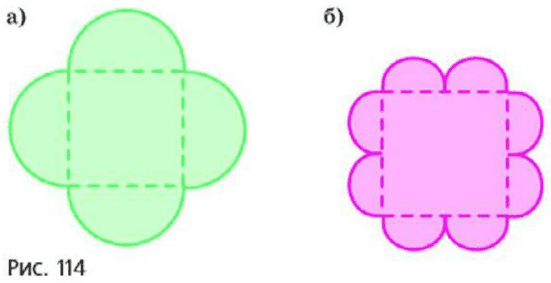

Ответ:
P1 = P2 = P3 = P4 = 24 π;
S1 = 144 + 72 π
S2 = 144 + 36 π
S3 = 144 + 24 π
S4 = 144 + 18 π1043. Земной шар стянули обручем по экватору. Затем увеличили обруч на 1 м. Пролезет ли кошка в образовавшийся зазор?
С = 2πR − длина окружности (обруча) с радиусом R,
R = С/2 π при длине окружности (обруча) С,
C + 1 − длина окружности (обруча), после ее увеличения на 1 м,
R = C + 1/2 π при длине окружности C + 1
$\frac{C+1}{2{\operatorname\pi}}-\frac{\operatorname С}{2{\operatorname\pi}}=\frac{C+1-{\operatorname С}}{2{\operatorname\pi}}=\frac1{2{\operatorname\pi}}=\frac1{2\ast3,14}=\frac1{6,28}=1:6,28\approx0,159{\operatorname м}=15,9{\operatorname с}{\operatorname м}$ зазор, образовавшийся между исходным и увеличенным обручем.
Ответ: кошка в зазор размером 15,9 см должна пролезть. 212
-
Координатная ось
Ответы к странице 212
1044. Что называют координатной осью?
Ответ: прямую на которой заданы начало отсчёта, направление отсчёта и единичный отрезок, называют координатной осью.
1045. Что называют координатой точки на координатной оси?
Ответ: Число, показывающее положение точки на координатной оси, называют координатой этой точки.
1046. Какие точки координатной оси называют:
а) рациональными;
б) иррациональными?а) Ответ: точки координатной оси называют рациональными, если они имеют рациональные координаты.
б) Ответ: точки координатной оси называют иррациональными, если они имеют иррациональные координаты.1047. Как надо понимать утверждение: множество всех точек координатной оси находится во взаимно однозначном соответствии со множеством всех действительных чисел?
Ответ:
1. Каждой точки оси соответствует действительное число − координата этой точки.
2. Две различные точки A и B оси x имеют разные координаты x1 и x2.
3. Каждое действительное число есть координата некоторой точки оси x.1048. Расположите координатную ось сначала горизонтально, потом вертикально. Отметьте на ней числа:
а) 2; 3; 4; 5;
б) −1; −2; −3; −4.а) Ответ:
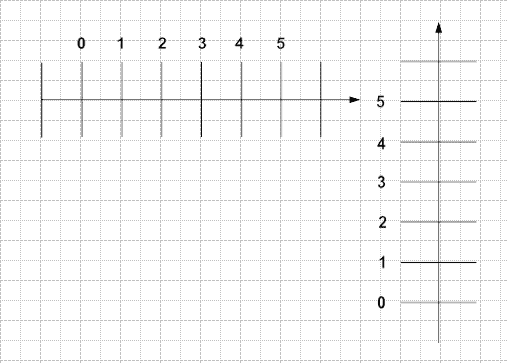
б) Ответ: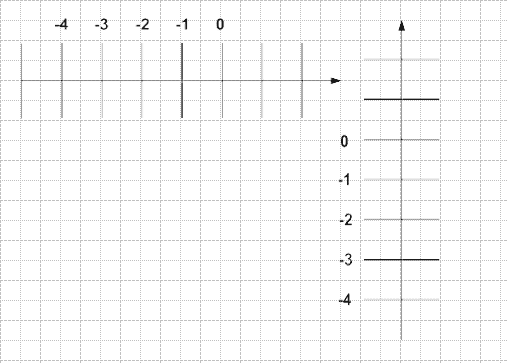
1049. Отметьте на координатной оси точки:
а) 0; 1; −1; 2; −2; 3; −3; 4; −4;
б) 0; 1; −2; 3; −4; 5; −6; 7; −8.а) Ответ:
б) Ответ:
1050. Начертите в тетради координатную ось с единичным отрезком 1 см (2 клетки). Укажите на этой оси числа:
а) 1/2 ; 2/2 ; 3/2 ; 4/2 ; 5/2 ; 6/2 ; 7/2;
б) − 1/2 ; − 2/2 ; − 3/2 ; − 4/2 ; − 5/2 ; − 6/2 ; − 7/2.а) Ответ:
б) Ответ:
1051. Начертите в тетради координатную ось с единичным отрезком 5 см. Укажите на оси числа:
а) 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9;
б) −0,1; −0,2; −0,3; −0,4; −0,5; −0,6; −0,7; −0,8; −0,9.а) Ответ:
б) Ответ:
1052. Начертите координатную ось и укажите на ней следующие числа, выбрав удобный для работы единичный отрезок и положение начальной точки координатной оси:
а) 1/4 ; − 1/4 ; 1/2 ; − 1/2 ; 3/4 ; 4/4 ; 5/4 ; 6/4 ; 7/4 ; − 3/4;
б) 1/5 ; − 1/5 ; 2/5 ; − 2/5 ; 3/5 ; − 3/5 ; − 4/5 ; − 1 ; − 1 1/5 ; 1 2/5;
в) − 1/3 ; 1/3 ; 2/3 ; 4/3 ; 5/3 ; 2 ; 7/3 ; 8/3 ; 3 ; 10/3 ; 11/3 ; 4;
г) 0,5; −0,5; −1; 1,5; −1,5; −2; −2,5; −3; −3,5.а) Ответ:
б) Ответ:
в) Ответ:
г) Ответ: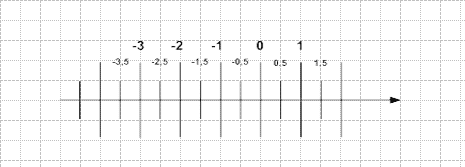
213
-
Ответы к странице 213
1053. Укажите на координатной оси точки:
а) 10; 11; 12; 13;
б) −25; −24; −23; −22;
в) 100; 101; 102; 103;
г) −257; −256; −255; −254;
д) 60; 70; 80; 90; 100;
е) −30; −20; −10; 0; 10.Между линиями делайте любое одинаковое количество клеточек (например, 1 или 2)
а) Ответ: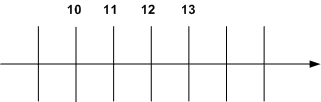
б) Ответ: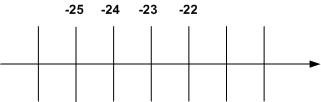
в) Ответ: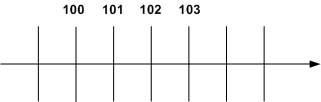
г) Ответ:
д) Ответ:
е) Ответ:
1054. Укажите на координатной оси точки:
а) 2; 2,1; 2,2; 2,3; 2,4;
б) −3,2; −3,1; −3; −2,9; −2,8;
в) 0,01; 0,02; 0,03;
г) −0,04; −0,05; −0,06;
д) 4,053; 4,054; 4,055;
е) −10,01; −10,02; −10,03.Между линиями делайте любое одинаковое количество клеточек (например, 1 или 2)
а) Ответ:
б) Ответ: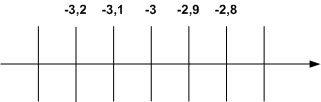
в) Ответ: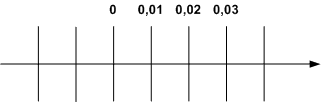
г) Ответ: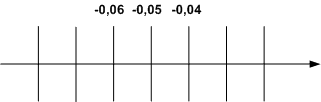
д) Ответ: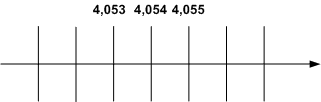
е) Ответ: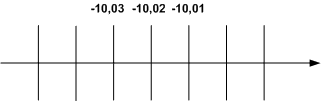
1055. Покажите на оси х числа, которые:
а) больше 3;
б) меньше −2;
в) больше 1,5;
г) меньше 7,2;
д) больше 4;
е) меньше −3;
ж) больше −1, но меньше 0;
з) больше −2, но меньше 5;
и) больше 0, но меньше 2;
к) больше −3, но меньше 3.а) Ответ:
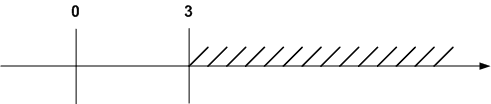
б) Ответ: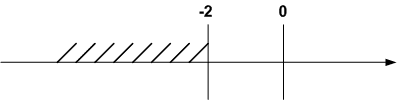
в) Ответ: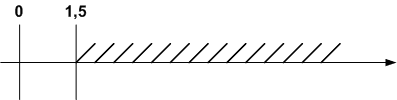
г) Ответ: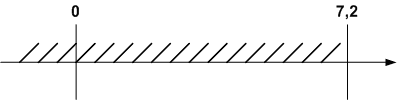
д) Ответ: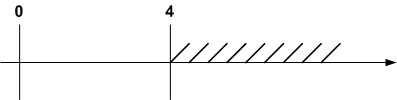
е) Ответ: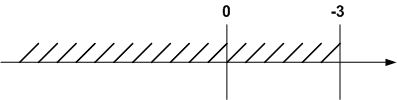
ж) Ответ: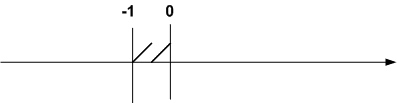
з) Ответ: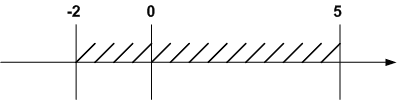
и) Ответ: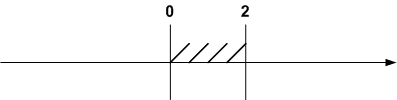
к) Ответ: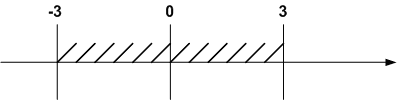
216
-
Обыкновенные и десятичные дроби
Декартова система координат на плоскостиОтветы к стр. 216
1056. На рисунке 121 изображены точки A (2;3), B (0;4), C(3;0), D (−4;−2). Назовите абсциссу и ординату каждой точки. Запишите координаты точек M, N, K, L. В каких координатных углах расположены точки A, D, L, K?
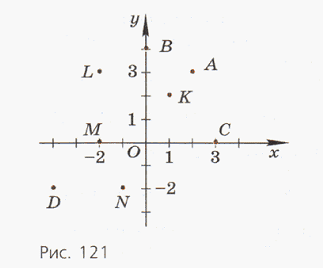
Ответ:
Абсциссы: A: 2; B: 0; C: 3; D: −4.
Ординаты: A: 3; B: 4; C: 0; D: −2.
M(−2; 0); N (−1; −2); K(1; 2); L(−2; 3).
В I координатном углу расположены точки A и K;
во II координатном углу расположена точка L;
в III координатном углу расположена точка D.1057. а) Где находятся точки, абсциссы которых равны нулю?
б) Где находятся точки, ординаты которых равны нулю?а) Ответ: на оси ординат.
б) Ответ: на оси абсцисс.1058. Каким свойством обладают координаты точек I, II, III, IV четвертей?
Ответ:
I четверть: x > 0; y > 0;
II четверть: x < 0; y > 0;
III четверть: x < 0; y < 0;
IV четверть: x > 0; y < 0.1059. В каких координатных углах находятся точки, абсциссы которых положительны?
Ответ: точки, абсциссы которых положительны будут находиться в I и IV четвертях.
1060. В каких координатных углах находятся точки, ординаты которых положительны?
Ответ: точки, ординаты которых положительны будут находиться в I и II четвертях.
1061. Как надо понимать утверждение: между точками координатной плоскости и упорядоченными парами чисел имеет место взаимно однозначное соответствие?
Ответ:
1. каждой точке плоскости поставлена в соответствие упорядоченная пара чисел (координаты точек)
2. разным точкам плоскости поставлены в соответствие разные упорядоченная пара чисел соответствует некоторой одной точке плоскости
3. каждая упорядоченная пара чисел соответствует некоторой одной точке плоскости.1062. Определите координаты точек, изображённых на рисунке 122.
Ответ:
А (3; 0);
B (−3; 0);
C (−1; 2);
D (0; −3);
E (2; −1);
F (1; 3);
H (−3; 2);
K (3; −2);
M (0; 1);
N (−3; 4).1063. Постройте систему координат и отметьте точки:
A (4; 3);
B (2; 4);
C (−5; 2);
D (4; −3);
E (−5; −1);
M (1; 3);
N (3; 0);
K (0; 4).Ответ:
1064. Постройте систему координат и отметьте точки:
A (5; 1);
B (−4; 2);
S (−3; −2);
Q (1; −4);
C (−5; −4);
D (4; −2);
Z (−3; 0);
P (0; 4).
217
-
Ответы к стр. 217
1065. Назовите абсциссы и ординаты точек, постройте точки в системе координат:
а) A (−3; 4), B (4; −2), C (−2; −4), D (5; 2);
б) E (0; 4), F (0; −4), M (3; 0), N (−3; 0).
а)
абсцисса ордината A −3 4 B 4 −2 C −2 −4 D 5 2 б)
абсцисса ордината E 0 4 F 0 −4 M 3 0 N −3 0 1066. Постройте в системе координат точки (2; 1), (2; 5), (6; 5), (5; 4), (6; 3), (2; 3). Соедините отрезками первую точку со второй, вторую с третьей и т. д. Какая фигура получилась?
Ответ: флаг.
1067. Постройте по данным точкам в системе координат фигуры, соединяя точки, как в предыдущем задании:
а) (0; 4), (−2;−2), (3; 2), (−3; 2), (2; −2), (0; 4);
б) (2; 3), (−2; 3), (−2; 5), (3; 5), (5; 3), (2; 3), (2; −5), (0; − 5), (0; 3);
в) (0; −4), (0; 0), (3; 3), (6; 0), (6; − 4), (0; −4), (6; 0), (0; 0), (6; −4).
Ответ: звезда, молоток, конверт.
1068. Постройте фигуру животного по точкам: (4; −3), (2; −3), (2; −2), (4; −2), (4; −1), (3; 1), (2; 1), (1; 2), (0; 0), (−3; 2), (−4; 5), (0; 8), (2; 7), (6; 7), (8; 8), (10; 6), (10; 2), (7; 0), (6; 2), (6; −2), (5; −3), (4; −3), (4; −5), (3; −9), (0; −8), (1; −5), (1; −4), (0; −4), (0; −9), (−3; −9), (−3; −3), (−7; −3), (−7; −7), (−8; −7), (−8; −8), (−11; −8), (−10; −4), (−11; −1), (−14; −3), (−12; −1), (−11; 2), (−8; 4), (−4; 5).
Постройте отдельно две точки: (2; 4), (6; 4) − это глаза животного.
Ответ: слон.
1069. Постройте отрезки AB и CD, если A (−3; 4), B (2; −1), C (−2; 0), D (4; 3). Найдите координаты точки пересечения отрезков AB и CD.
Ответ: отрезки AB и CD пересекаются в точке Е (0; 1).
1070. Постройте прямые AB и CD, если A (−1; 1), B (1; 2), C (−3; 0), D (2; 1). Найдите координаты точки пересечения прямых AB и CD.
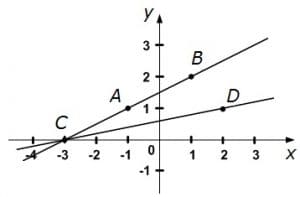
Ответ: прямые AB и CD пересекаются в точке С (−3; 0).
Придумываем задачу
1071. Придумайте задачу на построение фигур по точкам, заданным своими координатами.
Постройте по данным точкам в системе координат фигуру, соединяя точки последовательно: (0; 0), (1; 2), (2; 0), (4; 2), (2; -3), (-2; -3), (-4; 2), (-2; 0), (-1; 2), (0; 0).
Ответ: корона.
220
-
Обыкновенные и десятичные дроби
Столбчатые диаграммы и графикиОтветы к стр. 220
1072. Пользуясь столбчатой диаграммой (рис. 129), определите, сколько мальчиков и сколько девочек в 6 «А» и в 6 «Б» классах; сколько мальчиков в двух этих классах; сколько девочек в двух этих классах; сколько всего учащихся в двух классах.
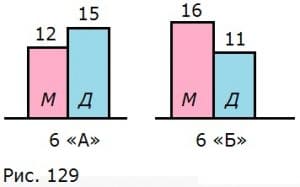
В 6 «А» 12 мальчиков и 15 девочек, в 6 «Б» 16 мальчиков и 11 девочек;
12 + 16 = 28 — мальчиков в двух классах;
15 + 11 = 26 — девочек в двух классах;
28 + 26 = 54 — учащихся в двух классах.1073. В таблице приведены результаты выполнения контрольной работы по математике. Постройте столбчатую диаграмму, отражающую эти результаты.
Оценка «5» «4» «3» «2» Число учащихся 4 10 12 2 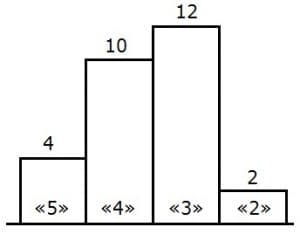
1074. На рисунке 130 показан график изменения температуры Т (в градусах по Цельсию) воды в чайнике. Какой была температура воды через 3 мин, 5 мин, 7 мин после включения? В какой момент чайник выключили? Сколько минут он кипел?
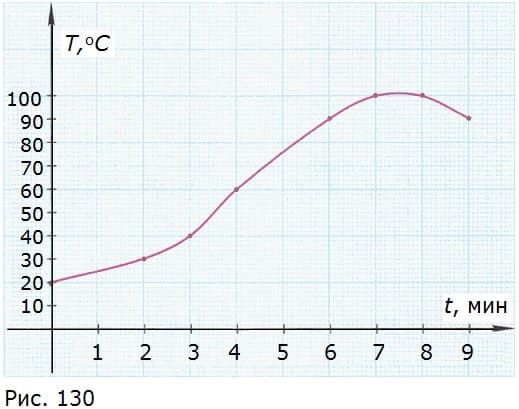
40°С − температура воды в чайнике через 3 минуты;
75°С − температура воды в чайнике через 5 минут;
100°С − температура воды в чайнике через 7 минут.
Через 8 минут выключили чайник, так температура в этот момент времени начала опускаться.
Вода закипела через 7 минут, так как вода закипает при 100°С. Вода перестала кипеть через 8 минут, так как после 8-ой минуты температура опустилась ниже 100°С. 8 − 7 = 1 минуту кипел чайник. 221
-
Обыкновенные и десятичные дроби
Столбчатые диаграммы и графикиОтветы к стр. 221
1075. В 6 ч утра из посёлка на озеро, находящееся в 5 км от посёлка, отправились рыбачить отец и сын. Туда они пошли пешком, а обратно ехали на попутной машине. На рисунке 131 изображён график их движения. Определите с помощью графика:
а) В какое время рыболовы пришли к озеру?
б) Что они делали с 7 ч до 8 ч 45 мин?
в) Сколько времени занял у них обратный путь?
г) С какой скоростью они шли пешком?
д) С какой скоростью ехала машина?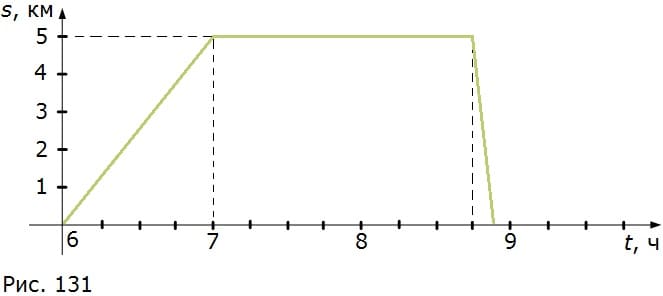
а) Рыболовы пришли к озеру в 7 часов, так как в это время они прошли расстояние в 5 км.
б) С 7 ч до 8 ч 45 мин расстояние между рыболовами и поселком не изменялось, следовательно, они ловили рыбу на озере.
в) В 8 ч 45 минут рыболовы отправились домой (расстояние до поселка на графике в этот момент времени начало изменяться), а в 8 ч 52,5 минуты (единичный отрезок на графике равен 1 ч : 4 = 60 мин : 4 = 15 мин) рыболовы добрались до дома (расстояние до поселка на графике в этот момент времени стало равно нулю): 8 ч 52,5 мин − 8 ч 45 мин = 7,5 минут занял путь домой.
г) Рыболовы вышли из посёлка в 6 часов, а пришли к озеру в 7 часов, тогда 7 ч – 6 ч = 1 ч — занял путь до озера. До озера 5 км, тогда 5 км : 1 ч = 5 км/ч — составила скорость движения пешком.
д) Рыболовы добирались от озера до дома на попутной машине 7,5 минут или 7,5 : 60 = 0,125 ч и преодолели 5 км, поэтому 5 км : 0,125 ч = 40 км/ч − скорость движения машины.
222
-
Ответы к стр. 222
1076. На рисунке 132 приведён график изменения температуры воздуха в течение суток. Измерения проводились через 2 ч.
а) Какая температура была в 4 ч, 8 ч, 12 ч, 21 ч, 23 ч?
б) В какие часы температура была выше 0 °С?
в) В какие часы температура была ниже 0 °С?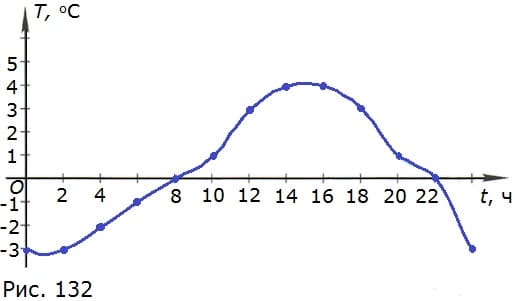
а) в 4 часа: −2 °С, в 8 часов: 0 °С, в 12 часов: +3 °С, в 21 час: +0,5 °С, в 23 часа: −2 °С;
б) с 8 ч до 22 ч;
в) с 0 ч до 8 ч и с 22 ч до 24 ч.1077. По данным, приведённым в таблице, постройте график изменения температуры воздуха: Т − температура воздуха в градусах по Цельсию, t − время в часах. Сколько часов температура была выше 0 °С? ниже 0 °С?
t,ч 8 9 10 11 12 13 14 15 16 17 18 19 21 21 Т,°С -6 -5 -4 -2 0 1 2 5 4 3 1 0 -2 -4 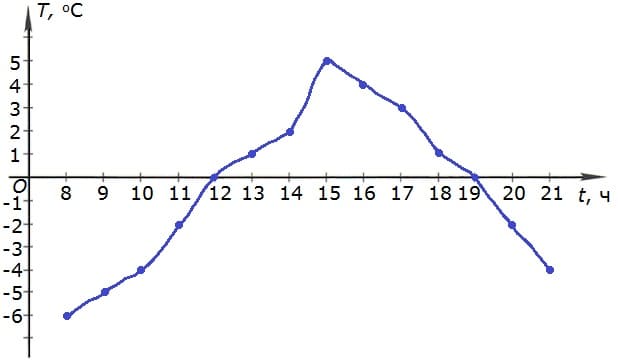
С 12 ч до 19 ч температура воздуха была выше 0°С, то есть в течение 19 ч — 12 ч = 7 ч.
С 8 ч до 12 ч и с 19 ч до 21 ч температура воздуха была ниже 0°С, то есть в течение (12 ч — 8 ч) + (21 ч — 19 ч) = 6 ч.1078. На рисунке 133 показан график движения двух пешеходов, вышедших из пунктов A и B навстречу друг другу.
а) Через сколько часов после выхода первого пешехода из пункта A второй пешеход вышел из пункта B?
б) Через сколько часов после выхода первого пешехода из пункта A они встретились?
в) С какой скоростью шёл первый пешеход?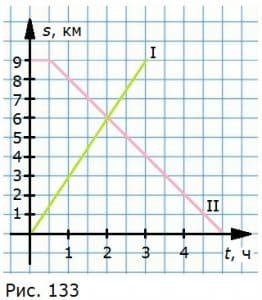
а) Примем, что первый пешеход вышел в 0 ч, так как расстояние, пройденное им, с этого момента стало изменяться. Тогда второй пешеход вышел в 0,5 ч, так как расстояние, пройденное им, с этого момента стало изменяться. Значит, 0,5 ч – 0 ч = 0,5 ч — разница во времени между выходом первого и второго пешеходов.
б) Точка пересечения графиков, то есть точка встречи двух пешеходов, имеет координаты s(6) и t(2). Поскольку принято, что первый пешеход вышел в 0 ч, то и время до точки встречи составляет: 2 ч – 0 ч = 2 ч (для второго пешехода 2 ч – 0,5 ч = 1,5 ч).
в) Всего первый пешеход прошел 9 км, что заняло у него 3 ч, тогда 9 км : 3 ч = 3 км/ч — скорость движения первого пешехода.
225
-
Обыкновенные и десятичные дроби
Задачи на составление и разрезание фигурОтветы к стр. 225
1079. У шахматной доски отрезали две противоположные угловые клетки (рис. 143). Можно ли эту доску разрезать на фигуры домино, покрывающие две клетки доски?
Видимо на рисунке в учебнике ошибка — обрезанные клетки не могут быть жёлтого цвета, они коричневые.
После обрезания доски на ней осталось 32 жёлтых и 30 коричневых клеток. Фигуры домино будут состоять из двух цветов: одной клетки коричневого цвета и одной клетки жёлтого цвета, так как на доске соседние клетки имеют разные цвета. Тогда каждая фигура домино будет убавлять от доски одинаковое количество коричневых и жёлтых клеток, а поскольку коричневых клеток на 2 меньше, чем жёлтых и соседние клетки не могут быть одинакового цвета, разрезать доску на фигуры домино невозможно.
1080. Прямоугольник 2 × 4 состоит из 8 квадратов. Разрежьте прямоугольник на две равные части так, чтобы линия разреза шла по сторонам квадратов. Найдите три способа разрезания.
1081. Квадрат 4 × 4 состоит из 16 квадратов. Разрежьте его на: а) две; б) четыре равные части так, чтобы линия разреза шла по сторонам квадратов. Сколько способов разрезания вы найдёте?
1082. Прямоугольник 4 × 6 состоит из 24 квадратов. Разрежьте его на шесть равных частей так, чтобы линия разреза шла по сторонам квадратов.
1083. Разрежьте фигуру, состоящую из квадратов (рис. 144), на три равные части так, чтобы линия разреза шла по сторонам квадратов.
1084. Разрежьте фигуру, состоящую из квадратов (рис. 145), на четыре равные части так, чтобы линия разреза шла по сторонам квадратов.
1085. Разрежьте фигуру, состоящую из квадратов (рис. 146), на четыре равные части так, чтобы линия разреза шла по сторонам квадратов.
226
-
Ответы к стр. 226
1086. Из трёх различных фигур пентамино составьте прямоугольник 3 × 5. Сколько различных решений имеет задача?
Существует только 12 разных фигур пентамино, а задача имеет 7 различных решений.
1087. Из фигур тримино, домино и одного квадрата (рис. 147) сложите квадрат 3 × 3. Сколькими способами это можно сделать?
Задача имеет 5 различных решений.
1088. Из фигур тетрамино, тримино и домино (рис. 148) составьте прямоугольник 4 × 7. Найдите 10 различных решений.
1089. Разрежьте фигуру, изображённую на рисунке 149, на восемь равных частей так, чтобы линия разреза шла по сторонам квадратов.
228
-
Обыкновенные и десятичные дроби
Занимательные задачиОтветы к стр. 228
1090. Купили конфеты и печенье. 1 кг конфет дороже 1 кг печенья на 50%, но их купили на 50% меньше, чем печенья. За что заплатили больше?
Пусть купили x кг печенья по y р. за 1 кг − всего на xy р. Тогда конфет купили 0,5x кг по 1,5y р. за 1 кг − всего на 0,5x • 1,5y = 0,75xy р. Так как xy > 0,75xy, то за печенье заплатили больше, чем за конфеты.
Ответ: за печенье заплатили больше, чем за конфеты.1091. Мама не доверяет банкам и хранит сбережения дома. Крупная премия пролежала дома с зимы до лета. За это время цены в магазине выросли на 25%. На сколько процентов уменьшилась покупательная способность отложенных денег?
Пусть на α р. зимой можно было купить одну единицу товара. Летом этот товар уже стоил α + 0,25α = 1,25α, т. е. летом на те же α р. можно купить α : 1,25α = 0,8 единицы того же товара. Это на 1 − 0,8 = 0,2 единицы товара, или на 20 %, меньше, чем зимой.
Ответ: покупательная способность отложенных денег уменьшилась на 20 %.1092. Некто купил зимой акции АО NNN по 60 р. за акцию. К лету стоимость акций поднялась на 20 р. за акцию, а цены на товары за то же время увеличились на 20 %. На сколько процентов увеличилась покупательная способность денег, вложенных в акции?
Пусть купили n акций, тогда α = n • 60 = 60n — сумма вложенных в акции денег.
60 + 20 = 80 р. стала стоить 1 акция к лету, тогда 80n — стало вложенных денег, то есть сумма вложенных средств возросла в 80n/60n = 4/3 раза.
Пусть изначальная стоимость цены товара равна α р. (сумма вложенных в акции денег).
α + 0,2α = 1,2α — стала стоить единица товара к лету, то есть стоимость товара возросла в 1,2α/α=1,2 раза.
4/3 : 1,2 = 4/3 : 6/5 = 4/3 • 5/6 = 10/9 − кратность увеличения покупательной способности денег (10/9 единиц товара теперь можно купить).
10/9 • 100 % = 111 1/9 % — составила покупательная способность денег летом от их исходной способности.
111 1/9 – 100 = 11 1/9 % − увеличение покупательной способности денег.
Ответ: на 11 1/9 %.1093. Мальчики составляют 45 % всех учащихся школы. Известно, что 30 % всех мальчиков и 40 % всех девочек учатся без троек. Сколько процентов всех учащихся школы учатся без троек?
Пусть х — всего учеников, тогда 0,45x – мальчиков и 0,55x – девочек.
0,3 • 0,45x = 0,135x — мальчиков учится без троек,
0,4 • 0,55x = 0,22x — девочек учится без троек,
0,135x + 0,22x = 0,355x — учеников учится без троек, где 0,355 – доля от всех учеников или 0,355 • 100 % = 35,5 % учеников учится без троек.
Ответ: 35,5 % учащихся учится без троек.1094. Рядовой Сидоров почистил бак картошки за 4 ч, и у него 20 % всей картошки ушло в очистки. За сколько часов он начистит такой же (по массе) бак картошки?
Пусть x − масса нечищеной картошки, а 100 % − 20 % = 80 % — чищеной картошки остается, тогда 80% • x = 0,8x — масса чищеной картошки в баке.
x/0,8x = 1,25 – во столько раз больше нужно почистить Сидорову картошки, чтобы получить x чищеной картошки (и во столько же раз по времени).
4 • 1,25 = 5 (ч) — потребуется Сидорову для того, чтобы получить x (бак) чищеной картошки.
Ответ: за 5 ч.1095. Когда подвели итоги голосования по половине всех бюллетеней, то оказалось, что объединение «Ананас» получило 10% голосов избирателей. Подсчитайте, какое наибольшее и какое наименьшее число процентов голосов избирателей может набрать объединение «Ананас» на выборах после подсчёта всех бюллетеней.
Пусть x — всего бюллетеней, а y − голоса за объединение «Ананас». Тогда после подсчёта половины бюллетеней:
y = 50 % • x • 10 % = 0,5x • 0,1 = 0,05x или 5 % — голосов набрало объединение «Ананас» после подсчёта половины бюллетеней.
Если во второй половине бюллетеней за объединение «Ананас» не будет ни одного голоса, то останется 5% голосов из первой половины бюллетеней.
Если после подсчета второй половины бюллетеней все голоса будут отданы за объединение «Ананас», то оно получит:
0,5x + 0,05x = 0,55x • 100 % = 55 % голосов.
Ответ: минимум 5 %, максимум 55 %. 229
-
Ответы к стр. 229
1096. Дан отрезок AB. Провели две пересекающиеся окружности одинакового радиуса с центрами в точках A и B. Точки пересечения окружностей обозначили буквами M и N. Докажите, что точки A и B симметричны относительно прямой MN.
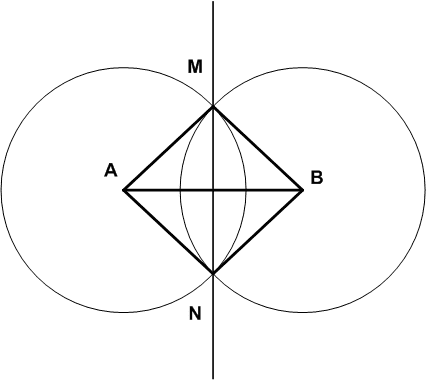
Если треугольники △AMN и △BMN будут симметричны относительно прямой MN, то и точки A и B будут симметричны относительно прямой MN.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
AM = MB, AN = NB так как они являются радиусами своих окружностей. По условию задачи радиусы двух окружностей равны.
MN − сторона треугольников, следовательно, треугольники △AMN и △BMN равны, а так как они имеют одно основание, при перегибании плоскости рисунка относительно прямой MN указанные треугольники наложатся друг на друга. Следовательно, △AMN и △BMN симметричны относительно прямой MN, а значит и точки A и B будут симметричны относительно прямой MN.1097. Серединным перпендикуляром к отрезку называют прямую, перпендикулярную отрезку и делящую его пополам. Докажите, что любая точка серединного перпендикуляра к отрезку одинаково удалена от концов этого отрезка.
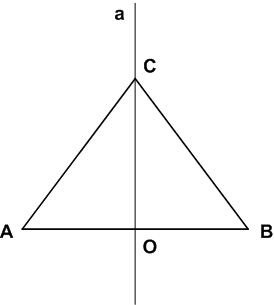
Возьмем на прямой а (средний перпендикуляр) произвольную точку C и соединим AC и AB. Точка пересечения прямой а и отрезка AB − точка O.
Докажем что △AOC = △BOC:
1. AO = OB, так как точка O является серединой отрезка AB, так как прямая а является серединным перпендикуляром;
2. ∠AOC равен ∠COB, так прямая а перпендикулярна отрезку AB.
3. CO − общая сторона треугольников △AOC и △BOC.
△AOC = △BOC, так как две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника.
Раз △AOC = △BOC, то значит и AC = BC, а так как точка C взята произвольно, то любая точка на прямой а будет равноудалена от A и B.1098. Задача Леонардо да Винчи. Докажите, что если две равные окружности пересекаются друг с другом, то любая точка прямой, проходящей через точки пересечения окружностей, одинаково удалена от того и другого центра.
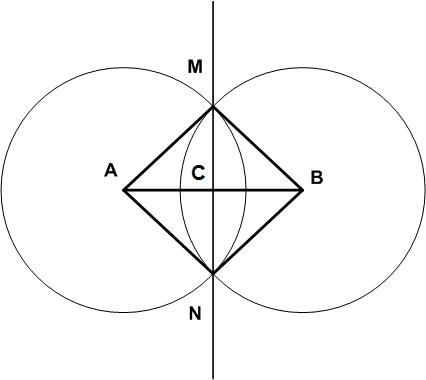
Необходимо доказать, что прямая, проходящей через точки пересечения окружностей, является серединным перпендикуляром к отрезку, соединяющего центры двух окружностей.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
AM = MB, AN = NB так как они являются радиусами своих окружностей. По условию задачи радиусы двух окружностей равны.
MN − сторона треугольников, следовательно, треугольники △AMN и △BMN равны.
Докажем, что △MAC = △MBC:
1. ∠AMC = ∠CMB, так как △AMN и △BMN равны;
2. MC − общая сторона
3. AM = MB, так как △AMN и △BMN равны.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны, следовательно, △MAC = △MBC.
∠MCB = ∠MCA, так как △MAC = △MBC.
∠ACB = 180°, ∠MCB = ∠MCA = 180° : 2 = 90°, следовательно, прямая MN перпендикулярна отрезку AB и AC = CB, так как △MAC = △MBC, а значит прямая MN является серединным перпендикуляром к отрезку AB.
Любая точка серединного перпендикуляра к отрезку, соединяющего центры двух окружностей, будет равно удалена от центров данных окружностей.1099. Даны точки A и B. Постройте ось симметрии точек A и B.

Если треугольники △AMN и △BMN будут симметричны относительно прямой MN, то и точки A и B будут симметричны относительно прямой MN.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
AM = MB, AN = NB так как они являются радиусами своих окружностей. По условию задачи радиусы двух окружностей равны.
MN − сторона треугольников, следовательно, треугольники △AMN и △BMN равны, а так как они имеют одно основание, при перегибании плоскости рисунка относительно прямой MN указанные треугольники наложатся друг на друга. Следовательно, △AMN и △BMN симметричны относительно прямой MN, а значит и точки A и B будут симметричны относительно прямой MN, а значит прямая MN будет осью симметрии для точек A и B.1100. Разделите отрезок пополам циркулем и линейкой.
Докажите, что любая точка серединного перпендикуляра к отрезку одинаково удалена от концов этого отрезка.
1. Постройте отрезок;
2. С помощью циркуля постройте две равных окружности, центрами которых будут являться концы отрезка, с радиусом больше, чем половина длины отрезка.
3. Проведите прямую через точки пересечения двух окружностей, точка пересечения данной прямой с отрезком и будет серединой отрезка.Ответ:
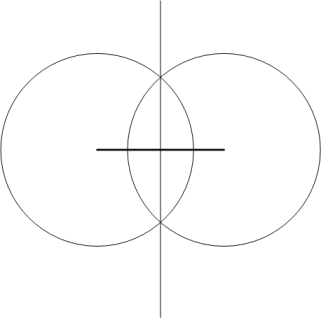
1101. Велосипедист проехал путь от A до B и обратно с некоторой постоянной скоростью. Пешеход прошёл путь от A до B со скоростью, в 2 раза меньшей скорости велосипедиста, но зато возвращался на автобусе со скоростью, в 4 раза большей скорости велосипедиста. Сколько времени затратил каждый из них на путь туда и обратно, если один был в пути на 0,5 ч дольше другого?
Пусть скорость пешехода V, тогда:
скорость велосипедиста 2V;
скорость автобуса 8V.
Пусть S расстояние от A до B, тогда:
S/2 V ∗ 2 = S/V − времени затратил велосипедист на дорогу туда и обратно;
S/V + S/8 V = 8 S + S/8 V = 9 S/8 V = 9/8 * S/V − времени затратил пешеход на дорогу туда и обратно;
9/8 * S/V > S/V, следовательно, пешеход потратил больше времени на 0,5 ч, чем велосипедист.
9/8 * S/V − S/V = 0,5
S/V ( 9/8 − 1 ) = 1/2
1/8 * S/V = 1/2
S/V = 1/2 : 1/8 = 1/2 ∗ 8/1 = 4 часа затратил на путь туда и обратно велосипедист.
4 + 0,5 = 4,5 ч затратил на путь туда и обратно пешеход.
Ответ:
4 часа затратил на путь туда и обратно велосипедист;
4,5 ч затратил на путь туда и обратно пешеход.1102. Задача аль−Каши. Плата работнику за 30 дней 10 динаров и платье. Он работал 3 дня и заработал платье. Сколько динаров стоит платье?
Пусть платье стоит x динаров, тогда:
10 + x/30 плата работнику за 1 день;
3 ∗ 10 + x/30 = x
10 + x/10 = x
10 + x = 10 x
9 x = 10
x = 10/9 = 1 1/9 динара стоит платье.
Ответ: 1 1/9 динара стоит платье.1103. Из книги «Косс» К. Рудольфа (XVI в.). Некто согласился работать с условием получить в конце года одежду и 10 флоринов. Но по истечении 7 месяцев прекратил работу и при расчёте получил одежду и 2 флорина. Во сколько ценилась одежда?
Пусть одежда стоит x флоринов, тогда:
x + 10 − заработок рабочего за 12 месяцев;
x + 10/12 − заработок рабочего за 1 месяц;
7 ∗ x + 10/12 = x + 2
7 ( x + 10 ) = 12 ( x + 2 )
7 x + 70 = 12 x + 24
5 x = 46
x = 46/5 = 9 1/5 − флорина ценилась одежда.
Ответ: 9 1/5 флорина.1104. Из «Арифметики» Л. Ф. Магницкого. Некий человек нанял работника на год, обещал ему дать 12 р. и кафтан. Но тот, отработав 7 месяцев, захотел уйти и просил достойной платы с кафтаном. Хозяин дал ему по достоинству расчёт 5 р. и кафтан. Спрашивается, а какой цены тот кафтан был.
Пусть кафтан стоил x р., тогда:
12 + x− заработок работника за 12 месяцев;
x + 12/12 − заработок работника за 1 месяц;
7 ∗ x + 12/12 = x + 5
7 ( x + 12 ) = 12 ( x + 5 )
7 x + 84 = 12 x + 60
5 x = 24
x = 24/5 = 4 4/5 = 4 80/100 = 4 р. 80 коп. стоил кафтан.
Ответ: 4 р. 80 коп. стоил кафтан.1105. Несколько работников получило 120 р. Если б их было четырьмя меньше, то каждый из них получил бы втрое больше. Сколько было работников?
Пример
Укажите правильно составленное уравнение по условию задачи:
120/x − 4 = 3 ∗ 120/x +
120/x + 4 = 120/x
120/x = 3 ∗ 120/x
120/x − 4 = 120/x
Заработок каждого работника, после того как их стало меньше возрос в 3 раза.
Решение:
Пусть было x работников, тогда:
120 x р. получал каждый работник,
120/x − 4 = 3 ∗ 120/x
1/x − 4 = 3/x
x = 3 ( x − 4 )
x = 3 x − 12
2 x = 12
x = 6 работников было.
Ответ: 6 работников. 230
-
Ответы к стр. 230
1106. Принёс крестьянин на рынок продавать яйца. Подходит к нему торговец и спрашивает: «Сколько стоит десяток яиц?» Крестьянин ответил замысловато: «Двадцать пять яиц без полушки стоят пять полушек без пяти яиц». Сосчитайте, по какой цене продавал крестьянин десяток яиц. (1 полушка =1/2 деньги; 1 деньга = 1/2 копейки)
Пусть одно яйцо стоит x, тогда:
25x − 1 = 5 − 5x
30x = 6
x = 6/30 = 1/5 полушки стоит 1 яйцо;
10 x = 10 ∗ 1/5 = 2 полушки стоит десяток яиц.
1 полушка = 1/2 деньги; 1 деньга = 1/2 копейки, значит:
1/2 ∗ 1/2 = 1/4 копейки составляла полушка, тогда:
2 ∗ 1/4 = 1/2 копейки стоил десяток яиц.
Ответ: десяток яиц стоит 2 полушки или 1/2 копейки.1107. Двадцать пять яиц с полуденьгой стоят столько, сколько 3 деньги без 5 яиц. Сколько яиц приходится на 1 деньгу?
Пусть яйцо стоит x денег, тогда:
25x − стоит 25 яиц;
5x − стоит 5 яиц;
25 x + 1/2 = 3 − 5 x
30 x = 2 1/2
x = 2 1/2 : 30 = 5/2 ∗ 1/30 = 1/12 деньги стоит 1 яйцо;
1 : 1/12 = 1 ∗ 12/1 = 12 яиц приходится на 1 деньгу.
Ответ: 12 яиц.1108. Один араб перед смертью завещал трём своим сыновьям 17 верблюдов, с тем чтобы старший получил половину, средний − треть, младший − девятую часть всех верблюдов. После смерти отца сыновья никак не могли разделить верблюдов по завещанию, и они позвали главу племени. Этот глава приехал на собственном верблюде и, узнав, в чём дело, предложил присоединить к их верблюдам своего и поделить их по завещанию. Братья обрадовались предложению главы племени. Но каково же было их удивление, когда оказалось, что, выполнив в точности завещание отца, они получили на самом деле не 18, а 17 верблюдов, вследствие чего им пришлось вернуть главе племени его верблюда. Почему так получилось?
Изначально сыновья не могли поделить верблюдов, потому что число 17 является простым и не делится без остатка ни на 2, ни на 3, ни на 9.
После того как верблюдов стало 18, то:
18 ∗ 1/2 = 9 верблюдов получил старший сын;
18 ∗ 1/3 = 6 верблюдов получил средний сын;
18 ∗ 1/9 = 2 верблюда получил младший сын.
9 + 6 + 2 = 17 верблюдов досталось братьям.1109. Шли три путника с грузом.
− Если бы кто−нибудь сейчас продал нам мула, я бы отдал за него половину его стоимости, − сказал первый путник.
− А я бы добавил треть его стоимости, − сказал второй.
− И я добавил бы четверть, − произнёс третий.
Вдруг перед ними появился погонщик мулов, который согласился продать мула за 13 монет. Так как 13 не делится ни на 2, ни на 3, ни на 4, то путники долго спорили, кто сколько монет должен дать. Тогда погонщик сказал:
− Я согласен, чтобы каждый из вас дал мне соответственно половину, треть и четверть не от 13, а от 12 монет. Каждый из путников понял, что даст меньше, чем обещал, и поэтому все они согласились на такое распределение платы за мула. Сколько монет получил погонщик?12 ∗ 1/2 = 6 монет отдал первый путник;
12 ∗ 1/3 = 4 монеты отдал второй путник;
12 ∗ 1/4 = 3 монеты отдал третий путник.
6 + 4 + 3 = 13 монет получил погонщик.
Ответ: 13 монет. 231
-
Задания для повторения
Ответы к стр. 231
1110. Найдите значение числового выражения:
а) 14957 − (2586 + 4298);
б) 598 * 99 : 299;
в) 758 * 809 − 180492 : 356;
г) 682 − 480 : (123 + 37).а) 14957 − (2586 + 4298) = 14957 − 6884 = 8073
б) 598 * 99 : 299 = (598 : 299) * 99 = 2 * 99 = 198
в) 758 * 809 − 180492 : 356 = 613222 − 507 = 612715
г) 682 − 480 : (123 + 37) = 682 − 480 : 160 = 682 − 3 = 6791111. Найдите значение числового выражения:
а) 795 * 848 : 848;
б) 456 * 759 : 759;
в) 6111 : 679 * 679;
г) 6768 : 846 * 846.а) 795 * 848 : 848 = 795 * (848 : 848) = 795 * 1 = 795
б) 456 * 759 : 759 = 456 * (759 : 759) = 456 * 1 = 456
в) 6111 : 679 * 679 = 6111
г) 6768 : 846 * 846 = 67681112. Найдите значение числового выражения:
а) 48 − 48 : (17 − 9) + 40;
б) 54 − (48 − 39) * 5 − 5;
в) 67 − (62 − 38) : 6 − 4;
г) 48 : (31 − 19) : 2 + 2.а) 48 − 48 : (17 − 9) + 40 = 48 − 48 : 8 + 40 = 48 − 6 + 40 = 42 + 40 = 82
б) 54 − (48 − 39) * 5 − 5 = 54 − 9 * 5 − 5 = 54 − 45 − 5 = 9 − 5 = 4
в) 67 − (62 − 38) : 6 − 4 = 67 − 24 : 6 − 4 = 67 − 4 − 4 = 63 − 4 = 59
г) 48 : (31 − 19) : 2 + 2 = 48 : 12 : 2 + 2 = 4 : 2 + 2 = 2 + 2 = 41113. Найдите значение числового выражения:
а) (7529 + 4356) + (644 + 1901);
б) 753 + (2747 + 3998) + 1002;
в) (8935 + 6639) + (7361 + 125);
г) 4957 + (8243 + 495) + 7205.а) (7529 + 4356) + (644 + 1901) = (7529 + 1901) + (644 + 4356) = 9430 + 5000 = 14430
б) 753 + (2747 + 3998) + 1002 = (753 + 2747) + (3998 + 1002) = 3500 + 5000 = 8500
в) (8935 + 6639) + (7361 + 125) = (7361 + 6639) + (8935 + 125) = 14000 + 9060 = 23060
г) 4957 + (8243 + 495) + 7205 = (4957 + 8243) + (495 + 7205) = 13200 + 7700 = 209001114. Найдите значение числового выражения:
а) 468 − 396 : (42 − 42 : 7) + 8;
б) 324 − 297 : (36 − 36 : 4) + 5;
в) 4221 − 294 : (98 : 14 − 5);
г) 5864 − 79 : (72 : 9 − 7) + 1001.а) 468 − 396 : (42 − 42 : 7) + 8 = 468 − 396 : 36 + 8 = 468 − 11 + 8 = 457 + 8 = 465
б) 324 − 297 : (36 − 36 : 4) + 5 = 324 − 297 : 27 + 5 = 324 − 11 + 5 = 313 + 5 = 318
в) 4221 − 294 : (98 : 14 − 5) = 4221 − 294 : 2 = 4221 − 147 = 4074
г) 5864 − 79 : (72 : 9 − 7) + 1001 = 5864 − 79 : 1 + 1001 = 5785 + 1001 = 67861115. Найдите значение числового выражения:
а) (756 − 242 + 326 * 9) * 0;
б) 14304 : 596 * (777 : 7 − 888 : 8).а) (756 − 242 + 326 * 9) * 0 = 0
б) 14304 : 596 * (777 : 7 − 888 : 8) = 14304 : 596 * (111 − 111) = 14304 : 596 * 0 = 01116. Найдите значение числового выражения:
а) 248 : 2 − 124 + 963 : 3 − 321 + 4;
б) 808 : 8 − 909 : 9 + 424 : 2 − 636 : 3 + 5.а) 248 : 2 − 124 + 963 : 3 − 321 + 4 = 124 − 124 + 321 − 321 + 4 = 0 + 0 + 4 = 4
б) 808 : 8 − 909 : 9 + 424 : 2 − 636 : 3 + 5 = 101 − 101 + 212 − 212 + 5 = 0 + 0 + 5 = 51117. Вычислите, применяя законы арифметических действий:
а) 239 * 324 − 156 * 315 + 156 * 315;
б) 31905 : 45 + 571 * 33 − 33 * 571;
в) 22796 : 41 + 505 * 707 − 22796 : 41;
г) 896 * 127 + 9702 : 77 − 127 * 896.а) 239 * 324 − 156 * 315 + 156 * 315 = 239 * 324 − 156 * (315 − 315) = 239 * 324 − 0 = 77436
б) 31905 : 45 + 571 * 33 − 33 * 571 = 31905 : 45 + 571 * (33 − 33) = 31905 : 45 = 709
в) 22796 : 41 + 505 * 707 − 22796 : 41 = 505 * 707 + (22796 : 41 − 22796 : 41) = 357035 + 0 = 357035
г) 896 * 127 + 9702 : 77 − 127 * 896 = 9702 : 77 + (896 * 127 − 127 * 896) = 9702 : 77 + 0 = 1261118. Вычислите, применяя законы арифметических действий:
а) 35 + 33 + 31 + 29 + 27 + 25;
б) 36 * 35 − 35 * 34 + 34 * 33 − 33 * 32 + 32 * 31 − 31 * 30 + 30 * 29 − 29 * 28 + 28 * 27 − 27 * 26 + 26 * 25 − 25 * 24.а) 35 + 33 + 31 + 29 + 27 + 25 = (35 + 25) + (31 + 29) + (33 + 27) = 60 + 60 + 60 = 180
б) 36 * 35 − 35 * 34 + 34 * 33 − 33 * 32 + 32 * 31 − 31 * 30 + 30 * 29 − 29 * 28 + 28 * 27 − 27 * 26 + 26 * 25 − 25 * 24 = 35 * (36 − 34) + 33 * (34 − 32) + 31 * (32 − 30) + 29 * (30 − 28) + 27 * (28 − 26) + 25 * (26 − 24) = 2 * (35 + 33 + 31 + 29 + 27 + 25) = 2 * 180 = 3601119. а) Вычислите:
7 * 11;
24 * 101;
378 * 1001;
7 * 22 − 2 * 77;
24 * 1313 − 13 * 2424.
б) Докажите, не выполняя всех вычислений, что:
275 * 346346 − 346 * 275275 = 0;
1996 * 19971997 − 1997 * 19961996 = 0.а) 7 * 11 = 77;
24 * 101 = 2424;
378 * 1001 = 378378;
7 * 22 − 2 * 77 = 154 − 154 = 0;
24 * 1313 − 13 * 2424 = 0.
Ответ: 77; 2424; 378378; 0; 0.
б) 275 * 346346 − 346 * 275275 = 275 * (346346 − 346 * 1001) = 275 * 0 = 0;
1996 * 19971997 − 1997 * 19961996 = 1996 * (19971997 − 1997 * 10001) = 1996 * 0 = 0.1120. Проверьте справедливость равенств:
10 2 + 11 2 + 12 2 = 13 2 + 14 2; 3 3 + 4 3 + 5 3 = 6 3.
Используя данные равенства, вычислите:
а) ( 10 2 + 11 2 + 12 2 + 13 2 + 14 2 ) : 365;
б) ( З 3 + 4 3 + 5 3 + 6 3 ) : 54.а) 10 2 + 11 2 + 12 2 = 13 2 + 14 2
100 + 121 + 144 = 169 + 196
365 = 365
( 13 2 + 14 2 + 13 2 + 14 2 ) : ( 13 2 + 14 2 ) = 2 ∗ ( 13 2 + 14 2 ) : ( 13 2 + 14 2 ) = 2
Ответ: 2
б) 3 3 + 4 3 + 5 3 = 27 + 64 + 125 = 216
6 3 = 216
216 = 216
( З 3 + 4 3 + 5 3 + 6 3 ) : 54 = ( 6 3 + 6 3 ) : 54 = 2 ∗ 6 3 : 54 = 2 ∗ 216 : 54 = 432 : 54 = 8
Ответ: 81121. Проверьте справедливость равенств:
1 3 + 6 3 + 8 3 = 9 3;
11 3 + 12 3 + 13 3 + 14 3 = 20 3;
108 2 + 109 2 + 110 2 = 133 2 + 134 2;
Используя данные равенства, вычислите:
а) ( 1 3 + 6 3 + 8 3 + 9 3 ) : 27;
б) ( 11 3 + 12 3 + 13 3 + 14 3 + 20 3 ) : 1000;
в) ( 108 2 + 109 2 + 110 2 − 133 2 − 134 2 ) : 365.а) 1 3 = 1
6 3 = 216
8 3 = 512
1 3 + 6 3 + 8 3 = 1 + 216 + 512 = 729
9 3 = 729
729 = 729
( 1 3 + 6 3 + 8 3 + 9 3 ) : 27 = ( 9 3 + 9 3 ) : 27 = 2 ∗ 9 3 : 27 = 2 ∗ 729 : 27 = 54
Ответ: 54
б) 11 3 = 1331
12 3 = 1728
13 3 = 2197
14 3 = 2744
11 3 + 12 3 + 13 3 + 14 3 = 1331 + 1728 + 2197 + 2744 = 8000
20 3 = 8000
8000 = 8000
( 11 3 + 12 3 + 13 3 + 14 3 + 20 3 ) : 1000 = ( 20 3 + 20 3 ) : 1000 = 2 ∗ 8000 : 1000 = 16
Ответ: 16
в) 108 2 = 11664
109 2 = 11881
110 2 = 12100
108 2 + 109 2 + 110 2 = 11664 + 11881 + 12100 = 35645
133 2 = 17689
134 2 = 17956
133 2 + 134 2 = 17689 + 17956 = 35645
( 108 2 + 109 2 + 110 2 − 133 2 − 134 2 ) : 365 = ( 133 2 + 134 2 − 133 2 − 134 2 ) : 365 = 0 : 365 = 0
Ответ: 0 232
-
Ответы к стр. 232
1122. Найдите значение числового выражения:
а) −640 : (−80) − 560 : 7 + 490 : 7;
б) −540 : 9 + (−450) : 5 + 160;
в) 720 : (−36) − 840 : (−42) − 753;
г) −860 : 20 − 625 : 25 + 75.а) −640 : (−80) − 560 : 7 + 490 : 7 = 8 − 80 + 70 = −2
б) −540 : 9 + (−450) : 5 + 160 = −60 − 90 + 160 = 10
в) 720 : (−36) − 840 : (−42) − 753 = −20 + 20 − 753 = −753
г) −860 : 20 − 625 : 25 + 75 = −43 − 25 + 75 = −68 + 75 = 71123. Найдите значение числового выражения:
а) 222 : (−3996 : 54) + 333;
б) 256 * (37 * (−9) + 33) : (−1200);
в)−2376 : (−625 : 25 + 49);
г) 5100 : (−2279 : 53 + 26) * (−17).а) 222 : (−3996 : 54) + 333 = 222 : (−74) + 333 = −3 + 333 = 330
б) 256 * (37 * (−9) + 33) : (−1200) = 256 * (−333 + 33) : (1200) = 256 * (−300) : (1200) = −76800 : (−1200) = 64
в) −2376 : (−625 : 25 + 49) = −2376 : (−25 + 49) = −2376 : 24 = −99
г) 5100 : (−2279 : 53 + 26) * (−17) = 5100 : (−43 + 26) * (−17) = 5100 : (−17) * (−17) = 51001124. Найдите значение числового выражения:
а) 49 * 68 + 51 * 68 + 49 * 12 + 51 * 12;
б) 87 * 52 − 17 * 52 + 87 * 38 − 17 * 38;
в) 77 * 99 + 23 * 99 − 77 * 29 − 23 * 29;
г) 108 * 86 − 86 * 18 − 108 * 56 + 18 * 56;
д) 428 * 356 + 72 * 356 + 144 * 428 + 72 * 144.а) 49 * 68 + 51 * 68 + 49 * 12 + 51 * 12 = 49 * (68 + 12) + 51 * (68 + 12) = 70 * (49 + 51) = 70 * 100 = 7000
б) 87 * 52 − 17 * 52 + 87 * 38 − 17 * 38 = 52 * (87 − 17) + 38 * (87 − 17) = 70 * (52 + 38) = 70 * 90 = 6300
в) 77 * 99 + 23 * 99 − 77 * 29 − 23 * 29 = 99 * (77 + 23) − 29 * (77 + 23) = 100 * (99 − 29) = 100 * 70 = 7000
г) 108 * 86 − 86 * 18 − 108 * 56 + 18 * 56 = 108 * (86 − 56) − 18 * (86 − 56) = 30 * (108 − 18) = 30 * 90 = 2700
д) 428 * 356 + 72 * 356 + 144 * 428 + 72 * 144 = 356 * (428 + 72) + 144 * (428 + 72) = 500 * (356 + 144) = 500 + 500 = 2500001125. Два ученика по очереди пишут цифры десятизначного числа.
а) Может ли второй ученик добиться того, чтобы это число делилось на 3, если первый старается ему помешать?
б) Может ли первый ученик добиться того, чтобы это число делилось на 9, если второй старается ему помешать?а) Число делится на 3, если сумма всех цифр числа делится на 3.
Так как последнюю цифру десятизначного числа будет ставить второй ученик, то он сможет поставить такую цифру, чтобы сумма всех цифр десятизначного числа делилась на 3.
Ответ: сможет.
б) Число делится на 9, если сумма всех цифр числа делится на 9.
Так как последнюю цифру десятизначного числа будет ставить второй ученик, то он сможет поставить такую цифру, чтобы сумма всех цифр десятизначного числа не делилась на 9.
Ответ: не сможет.1126. Делится ли число 12345678910111213...979899 на 3? на 9?
Число делится на 3, если сумма всех цифр числа делится на 3;
Число делится на 9, если сумма всех цифр числа делится на 9.
1 + 2 + 3 + 4 + ... + 97 + 98 + 99 = (1 + 99) + (2 + 98) + (3 + 97) + (4 + 96) + ... + (48 + 52) + (49 + 51) + 50 = 100 * 50 + 50 = 5050
5 + 0 + 5 + 0 = 10 не делится ни на 3, ни на 9.
Ответ: не делится ни на 3, ни на 9.1127. Докажите, что если в трёхзначном числе средняя цифра равна сумме крайних, то число кратно 11.
Пусть наше число abc, и b = a + c.
х ас
11
ас
ас
а(а+с)с
=b
где а+с <10
Так как b = a + c, то ac * 11 = a(a + c) = abc, следовательно, abc будет делиться на 11.1128. Разность двух нечётных чисел равна 8. Докажите, что эти числа взаимно простые.
Предположим, что эти числа не взаимно простые, т.е. их можно представить в виде a * c и b * c, где с − общий простой делитель, не равный 1. Очевидно, что этот делитель также нечетный, поскольку среди делителей нечетных чисел не может быть четных простых делителей. Числа a и b − также нечетные. Получаем:
ac − bc = 8; или (a − b)c = 8;
Разность двух нечетных чисел есть четное число, то есть (a − b) − четное число, а с − нечетное число, таким образом получается, что равенство (a − b)c = 8 будет верно только в том случае, если число 8 можно представить в виде произведения четного (a − b) и нечетного (с) чисел, но это невозможно, кроме случая с = 1. Значит, рассматриваемые числа могут быть только взаимно простыми.1129. Чтобы узнать, является ли число 2503 простым, его стали последовательно делить на простые числа: 2, 3, 5, 7, 11, 13 На каком простом числе можно прекратить испытание?
Проверяя делится ли число 2503 на какое − то другое число кроме самого себя и единицы мы производим следующее вычисление:
2503/а = с, где а − это простые числа 2, 3, 5, 7 и так далее, и проверяем получится ли при делении число с целым. Число а можно будет не подбирать если оно станет больше числа с.
472 = 2209, а 532 = 2809, следовательно, 47 − это последнее простое число, при котором а < c.
Ответ: на числе 47 можно прекратить испытание.1130. Из утверждений «A делится на 2», «А делится на 4», «A делится на 8», «A делится на 16» три верных, а одно неверное. Какое? Объясните ваш ответ.
4 = 2 * 2
8 = 2 * 2 * 2 = 2 * 4
16 = 2 * 2 * 2 * 2 = 8 * 2 = 4 * 4
Допустим, что утверждение «A делится на 16» верное, тогда число A будет обязательно делится и на 2 и на 4 и на 8, и значит 4 утверждения будут верными, что не соответствует условию задачи.
Ответ: «А делится на 16» − неверное.1131. Сколько чисел от 1 до 100 не делится ни на 2, ни на 3?
Для того, чтобы найти ответ на поставленный вопрос необходимо из 100 убрать:
1. Все четные числа, так как они делятся на 2;
2. Нечетные числа, которые делятся на 3;
3. Единицу.
Все четные числа делятся на 2, поэтому:
100 − 50 = 50 нечетных чисел осталось.
В диапазоне чисел от 1 до 100 каждое третье нечетное число будет делиться на 3, поэтому:
50 : 3 = 16,(6) = 16 целых нечетных чисел которые делятся на 3.
100 − 50 − 16 − 1 = 33 числа содержится в диапазоне чисел от 0 до 100, которые не делятся ни на 2, ни на 3.
Ответ: 33 числа.1132. Сравните дроби 12 13 и 16 17, не приводя их к общему знаменателю.
1 − 12/13 = 1/13 не хватает до единицы дроби 12/13;
1 − 16/17 = 1/17 не хватает до единицы дроби 16/17;
Из двух положительных обыкновенных дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше, поэтому:
1/13 > 1/17, следовательно:
12/13 < 16/17, так как дроби 12/13 до единицы не хватает больше, чем дроби 16/17.
Ответ: 12/13 < 16/171133. Сравните дроби:
а) 2323/6464 и 23/64;
б) 71/98 и 7171/9898.а) 2323/6464 = 23/64, так как 2323/6464 = 23 ∗ 101/64 ∗ 101
Ответ: 2323/6464 = 23/64
б) 71/98 = 7171/9898, так как 7171/9898 = 71 ∗ 101/98 ∗ 101
Ответ: 71/98 = 7171/98981134. Найдите значение числового выражения:
а) 11/15 ∗ ( 4 1/2 − 3 2/5 : 17/20 ) + 1 11/20;
б) 5 4/7 : 1 5/21 − ( 5 2/15 ∗ 3/22 + 1 14/15 );
в) 7 2/3 + 4 1/6 ∗ ( 6 2/7 − 3 5/7 );
г) 4 2/7 : 1 5/21 + ( 4 3/13 ∗ 14/15 − 3 1/3 ).а) $\frac{11}{15}\ast(4\frac12-3\frac25:\frac{17}{20})+1\frac{11}{20}=\frac{11}{15}\ast(\frac92-\frac{17}5\ast\frac{20}{17})+\frac{31}{20}=\frac{11}{15}\ast(\frac92-4)+\frac{31}{20}=\frac{11}{15}\ast\frac12+\frac{31}{20}=\frac{11}{30}+\frac{31}{20}=\frac{22+93}{60}=\frac{115}{60}=\frac{23}{12}=1\frac{11}{12}$
б) $5\frac47:1\frac5{21}-(5\frac2{15}\ast\frac3{22}+1\frac{14}{15})=\frac{39}7:\frac{26}{21}-(\frac{77}{15}\ast\frac3{22}+\frac{29}{15})=\frac{39}7\ast\frac{21}{26}-(\frac7{10}+\frac{29}{15})=\frac92-\frac{21+58}{30}=\frac{135-79}{30}=\frac{56}{30}=\frac{28}{15}=1\frac{13}{15}$
в) $7\frac23+4\frac16\ast(6\frac27-3\frac57)=\frac{23}3+\frac{25}6\ast(\frac{44}7-\frac{26}7)=\frac{23}3+\frac{25}6\ast\frac{18}7=\frac{23}3+\frac{25}6\ast\frac{18}7=\frac{23}3+\frac{75}7=\frac{161+225}{21}=\frac{386}{21}=18\frac{18}{21}$
г) $4\frac27:1\frac5{21}+(4\frac3{13}\ast\frac{14}{15}-3\frac13)=\frac{30}7:\frac{26}{21}+(\frac{55}{13}\ast\frac{14}{15}-\frac{10}3)=\frac{30}7\ast\frac{21}{26}+(\frac{154}{39}-\frac{10}3)=\frac{45}{13}+\frac{154-130}{39}=\frac{135+24}{39}=\frac{159}{39}=\frac{53}{13}=4\frac1{13}$ 233
-
Ответы к стр. 233
1135. Найдите значение числового выражения:
а) 3 3/7 ∗ 3 1/2 : ( 1 1/11 − 27/55 );
б) ( 2 1/2 : 10 + 10 : 2 1/2 − 2 1/6 ) ∗ 36/125;
в) 3 1/8 : ( ( 4 5/12 − 3 13/24 ) ∗ 4/7 + ( 3 1/18 − 2 7/12 ) ∗ 1 10/17 ).а) $3\frac37\ast3\frac12:(1\frac1{11}-\frac{27}{55})=\frac{24}7\ast\frac72:(\frac{12}{11}-\frac{27}{55})=12:\frac{60-27}{55}=12\ast\frac{55}{33}=12\ast\frac53=20$
б) $(2\frac12:10+10:2\frac12-2\frac16)\ast\frac{36}{125}=(\frac52\ast\frac1{10}+10\ast\frac25-\frac{13}6)\ast\frac{36}{125}=(\frac14+4-\frac{13}6)\ast\frac{36}{125}=(\frac{17}4-\frac{13}6)\ast\frac{36}{125}=\frac{51-26}{12}\ast\frac{36}{125}=\frac{25}{12}\ast\frac{36}{125}=\frac35$
в) $3\frac18:((4\frac5{12}-3\frac{13}{24})\ast\frac47+(3\frac1{18}-2\frac7{12})\ast1\frac{10}{17})=\frac{25}8:((\frac{53}{12}-\frac{85}{24})\ast\frac47+(\frac{55}{18}-\frac{31}{12})\ast\frac{27}{17})=\frac{25}8:(\frac{106-85}{24}\ast\frac47+\frac{110-93}{36}\ast\frac{27}{17})=\frac{25}8:(\frac12+\frac34)=\frac{25}8:\frac{2+3}4=\frac{25}8\ast\frac45=\frac52=2\frac12$1136. Найдите значение числового выражения:
а) ( 7/8 + 1/6 + 23/24 ) ∗ 177 : 118;
б) 129 ∗ ( 7/9 + 5/6 + 7/18 + 5 ) : 86;
в) ( 1/2 + 1/3 + 1/6 + 3 ) ∗ 119 : 68;
г) 3456 : ( 2/3 + 4/5 + 8/15 + 7 ) : 16.а) $(\frac78+\frac16+\frac{23}{24})\ast177:118=\frac{21+4+23}{24}\ast\frac{177}{118}=2\ast\frac{177}{118}=3$
б) $129\ast(\frac79+\frac56+\frac7{18}+5):86=129\ast(\frac{14+15+7}{18}+5):86=129\ast7:86=\frac{903}{86}=10\frac{43}{86}=10\frac12$
в) $(\frac12+\frac13+\frac16+3)\ast119:68=(\frac{3+2+1}6+3)\ast119:68=4\ast\frac{119}{68}=\frac{119}{17}=7$
г) $3456:(\frac23+\frac45+\frac8{15}+7):16=3456:(\frac{10+12+8}{15}+7):16=3456:9:16=384:16=24$1137. Найдите значение числового выражения:
а) ( 1/2 + 11/12 + 3/4 + 5/6 ) ∗ ( − 5 ) + ( − 756 ) : ( − 36 );
б) ( 19/20 + 1/2 + 3/4 + 4/5 ) ∗ ( − 123 ) − ( − 5029 ) : 76.а) $(\frac12+\frac{11}{12}+\frac34+\frac56)\ast(-5)+(-756):(-36)=\frac{6+11+9+10}{12}\ast(-5)+21=-15+21=6$
б) $(\frac{19}{20}+\frac12+\frac34+\frac45)\ast(-123)-(-5029):76=\frac{19+10+15+16}{20}\ast(-123)-(-67)=3\ast(-123)+67=-369+67=-302$1138. Найдите значение числового выражения:
а) 256 : 48 − 156 : 36;
б) 399 : 49 + 664 : 56;
в) 816 : 88 − 819 : 99;
г) 460 : 52 + 123 : 39;
д) 48 : 7 − 45 : 14/45 : 7 − 48 : 14;
е) 56 : 13 + 100 : 26/100 : 13 + 56 : 26.а) $256:48-156:36=\frac{256}{48}-\frac{156}{36}=\frac{32}6-\frac{26}6=\frac{32-26}6=\frac66=1$
б) $399:49+664:56=\frac{399}{49}+\frac{664}{56}=\frac{57}7+\frac{83}7=\frac{57+83}7=\frac{140}7=20$
в) $816:88-819:99=\frac{816}{88}-\frac{819}{99}=\frac{102}{11}-\frac{91}{11}=\frac{102-91}{11}=\frac{11}{11}=1$
г) $460:52+123:39=\frac{460}{52}+\frac{123}{39}=\frac{115}{13}+\frac{41}{13}=\frac{115+41}{13}=\frac{156}{13}=12$
д) $\frac{48:7-45:14}{45:7-48:14}=(\frac{48}7-\frac{45}{14}):(\frac{45}7-\frac{48}{14})=\frac{96-45}{14}:\frac{90-48}{14}=\frac{51}{14}\ast\frac{14}{42}=\frac{51}{42}=\frac{17}{14}=1\frac3{14}$
е) $\frac{56:13+100:26}{100:13+56:26}=(\frac{56}{13}+\frac{100}{26}):(\frac{100}{13}+\frac{56}{26})=\frac{112+100}{26}:\frac{200+56}{26}=\frac{212}{26}\ast\frac{26}{256}=\frac{212}{256}=\frac{53}{64}$1139. Найдите значение числового выражения:
$\frac{3\frac23+1\frac47}{3\frac23-1\frac47}:\frac{13\frac13-3\frac1{13}}{13\frac13+3\frac1{13}}:\frac{5\frac12+1\frac38}{5\frac12-1\frac38}$Для удобства разобьем вычисление выражения на составные части, а именно найдем сначала значение каждого члена частного в отдельности:
1. $\frac{3\frac23+1\frac47}{3\frac23-1\frac47}=\frac{3\frac{14}{21}+1\frac{12}{21}}{3\frac{14}{21}-1\frac{12}{21}}=\frac{5\frac5{21}}{2\frac2{21}}=\frac{110}{21}\ast\frac{21}{44}=\frac{110}{44}=\frac52$
2. $\frac{13\frac13-3\frac1{13}}{13\frac13+3\frac1{13}}=\frac{13\frac{13}{39}-3\frac3{39}}{13\frac{13}{39}+3\frac3{39}}=\frac{10\frac{10}{39}}{16\frac{16}{39}}=\frac{400}{39}\ast\frac{39}{640}=\frac{400}{640}=\frac58$
3. $\frac{5\frac12+1\frac38}{5\frac12-1\frac38}=\frac{5\frac48+1\frac38}{5\frac48-1\frac38}=\frac{6\frac78}{4\frac18}=\frac{55}8\ast\frac8{33}=\frac{55}{33}=\frac53$
$\frac52:\frac58:\frac53=\frac52\ast\frac85\ast\frac35=\frac{12}5=2\frac25$
Ответ: 2 2/51140. Найдите значение числового выражения:
а) $\frac{3\frac34:1\frac12+1\frac12:3\frac34\ast2\frac12}{2:3\frac15+3\frac14:13:\frac23}$;
б) $\frac{15:\frac5{18}:3\frac38\ast(\frac1{16}+\frac{11}{36}+\frac5{48}+\frac5{18})}{(11\frac5{11}-8\frac{21}{22}):1\frac23}$.а) $\frac{3\frac34:1\frac12+1\frac12:3\frac34\ast2\frac12}{2:3\frac15+3\frac14:13:\frac23}=\frac{\frac{15}4:\frac32+\frac32:\frac{15}4\ast\frac52}{2:\frac{16}5+\frac{13}4:13:\frac23}=\frac{\frac{15}4\ast\frac23+\frac32\ast\frac4{15}\ast\frac52}{2\ast\frac5{16}+\frac{13}4\ast\frac1{13}\ast\frac32}=\frac{\frac52+1}{\frac58+\frac38}=\frac{\frac72}1=3\frac12$
б) $\frac{15:\frac5{18}:3\frac38\ast(\frac1{16}+\frac{11}{36}+\frac5{48}+\frac5{18})}{(11\frac5{11}-8\frac{21}{22}):1\frac23}=\frac{15\ast\frac{18}5\ast\frac8{27}\ast(\frac3{48}+\frac{11}{36}+\frac5{48}+\frac{10}{36})}{(11\frac{10}{22}-8\frac{21}{22})\ast\frac35}=\frac{15\ast\frac{18}5\ast\frac8{27}\ast(\frac16+\frac7{12})}{2\frac{11}{22}\ast\frac35}=\frac{15\ast\frac{18}5\ast\frac8{27}\ast\frac{2+7}{12}}{\frac52\ast\frac35}=\frac{15\ast\frac{18}5\ast\frac8{27}\ast\frac34}{\frac32}=\frac{12}{\frac32}=12\ast\frac23=8$1141. Найдите значение числового выражения:
а) $\frac{20:2\frac2{15}+25\frac57:2\frac2{35}}{20\frac79:4\frac25-\frac59}$;
б) $\frac{6\frac34:9+24:\frac67-\frac19:\frac4{21}}{53\frac23-22\frac{14}{15}:2\frac23}$.а) $\frac{20:2\frac2{15}+25\frac57:2\frac2{35}}{20\frac79:4\frac25-\frac59}=\frac{20:\frac{32}{15}+\frac{180}7:\frac{72}{35}}{\frac{187}9:\frac{22}5-\frac59}=\frac{20\ast\frac{15}{32}+\frac{180}7\ast\frac{35}{72}}{\frac{187}9\ast\frac5{22}-\frac59}=\frac{\frac{75}8+\frac{100}8}{\frac{85}{18}-\frac59}=\frac{\frac{175}8}{\frac{85-10}{18}}=\frac{175}8:\frac{75}{18}=\frac{175}8\ast\frac{18}{75}=\frac{21}4=5\frac14$
б) $\frac{6\frac34:9+24:\frac67-\frac19:\frac4{21}}{53\frac23-22\frac{14}{15}:2\frac23}=\frac{\frac{27}4\ast\frac19+24\ast\frac76-\frac19\ast\frac{21}4}{53\frac{10}{15}-\frac{344}{15}\ast\frac38}=\frac{\frac34+28-\frac7{12}}{53\frac{10}{15}-\frac{129}{15}}=\frac{28\frac16}{53\frac{10}{15}-8\frac9{15}}=\frac{\frac{169}6}{45\frac1{15}}=\frac{169}6\ast\frac{15}{676}=\frac{1\ast5}{2\ast4}=\frac58$1142. Сократите дробь:
а) 36 ∗ 25/50 ∗ 24;
б) 38 ∗ 17/34 ∗ 21;
в) 64 ∗ 48/56 ∗ 72;
г) 38 ∗ 45/60 ∗ 95;
д) 25 − 12/12 ∗ 13;
е) 26 + 13/13 ∗ 26;
ж) 7 + 28/7 ∗ 28;
з) 45 + 5/5 ∗ 45.а) $\frac{36\ast25}{50\ast24}=\frac{\overset3{\cancel{(36)}}\ast\overset1{\cancel{(25)}}}{\underset2{\cancel{50}}\ast\underset2{\cancel{24}}}=\frac34$
б) $\frac{38\ast17}{34\ast21}=\frac{\overset{19}{\cancel{(38)}}\ast\overset1{\cancel{(17)}}}{\underset1{\cancel{34}}\ast21}=\frac{19}{21}$
в) $\frac{64\ast48}{56\ast72}=\frac{\overset8{\cancel{(64)}}\ast\overset2{\cancel{(48)}}}{\underset7{\cancel{56}}\ast\underset3{\cancel{72}}}=\frac{16}{21}$
г) $\frac{38\ast45}{60\ast95}=\frac{\overset2{\cancel{(38)}}\ast\overset3{\cancel{(45)}}}{\underset4{\cancel{60}}\ast\underset5{\cancel{19}}}=\frac{\overset3{\cancel{(6)}}}{\underset{10}{\cancel{20}}}=\frac3{10}$
д) $\frac{25-12}{12\ast13}=\frac{\overset1{\cancel{(13)}}}{12\ast\underset1{\cancel{13}}}=\frac1{12}$
е) $\frac{26+13}{13\ast26}=\frac{\overset3{\cancel{(39)}}}{\underset1{\cancel{13}}\ast26}=\frac3{26}$
ж) $\frac{7+28}{7\ast28}=\frac{\overset5{\cancel{(35)}}}{\underset1{\cancel7}\ast28}=\frac5{28}$
з) $\frac{45+5}{5\ast45}=\frac{\overset2{\cancel{(50)}}}{\underset1{\cancel5}\ast\underset9{\cancel{45}}}=\frac29$1143. Сократите дробь:
а) ( 17 − 12 ) ∗ 8/15 ∗ 16;
б) ( 25 − 9 ) ∗ 25/75 ∗ ( 38 − 22 );
в) ( 41 − 5 ) ∗ 19/( 23 − 4 ) ∗ 36;
г) 17 ∗ 8 − 12 ∗ 8/80;
д) 25 ∗ 25 − 9 ∗ 25/3 ∗ 50;
е) 16 ∗ 23 + 9 ∗ 23/17 ∗ 25 + 6 ∗ 25.а) $\frac{(17-12)\ast8}{15\ast16}=\frac{\overset1{\cancel{(5)}}\ast\overset1{\cancel{(8)}}}{\underset3{\cancel{15}}\ast\underset2{\cancel{16}}}=\frac{1\ast1}{3\ast2}=\frac16$
б) $\frac{(25-9)\ast25}{75\ast(38-22)}=\frac{\overset1{\cancel{(16)}}\ast\overset1{\cancel{(25)}}}{\underset3{\cancel{75}}\ast\underset1{\cancel{16}}}=\frac13$
в) $\frac{(41-5)\ast19}{(23-4)\ast36}=\frac{\overset1{\cancel{(36)}}\ast\overset1{\cancel{(19)}}}{\underset1{\cancel{19}}\ast\underset1{\cancel{36}}}=1$
г) $\frac{17\ast8-12\ast8}{80}=\frac{8\ast(17-12)}{80}=\frac{\overset1{\cancel{(8)}}\ast\overset1{\cancel{(8)}}}{\underset2{\cancel{80}}}=\frac12$
д) $\frac{25\ast25-9\ast25}{3\ast50}=\frac{25\ast(25-9)}{3\ast50}=\frac{\overset1{\cancel{(25)}}\ast\overset8{\cancel{(16)}}}{3\ast\underset1{\cancel{50}}}=\frac83=2\frac23$
е) $\frac{16\ast23+9\ast23}{17\ast25+6\ast25}=\frac{23\ast(16+9)}{25\ast(17+6)}=\frac{\overset1{\cancel{(23)}}\ast\overset1{\cancel{(25)}}}{\underset1{\cancel{25}}\ast\underset1{\cancel{23}}}=1$ 234
-
Ответы к стр. 234
1144. Вычислите:
а) 45 ∗ 56 + 45 ∗ 14/70 ∗ 72;
б) 38 ∗ 53 − 38 ∗ 25/19 ∗ 42;
в) 395 ∗ 43 + 5 ∗ 43/695 ∗ 86 + 86 ∗ 105;
г) 359 ∗ 23 − 59 ∗ 23/758 ∗ 69 − 158 ∗ 69.а) $\frac{45\ast56+45\ast14}{70\ast72}=\frac{45\ast(56+14)}{70\ast72}=\frac{\overset5{\cancel{(45)}}\ast\overset1{\cancel{(70)}}}{\underset1{\cancel{70}}\ast\underset8{\cancel{72}}}=\frac58$
б) $\frac{38\ast53-38\ast25}{19\ast42}=\frac{38\ast(53-25)}{19\ast42}=\frac{\overset2{\cancel{(38)}}\ast\overset2{\cancel{(28)}}}{\underset1{\cancel{19}}\ast\underset3{\cancel{42}}}=\frac43=1\frac13$
в) $\frac{395\ast43+5\ast43}{695\ast86+86\ast105}=\frac{43\ast(395+5)}{86\ast(695+105)}=\frac{\overset1{\cancel{(43)}}\ast\overset1{\cancel{(400)}}}{\underset2{\cancel{86}}\ast\underset2{\cancel{800}}}=\frac14$
г) $\frac{359\ast23-59\ast23}{758\ast69-158\ast69}=\frac{23\ast(359-59)}{69\ast(758-158)}=\frac{\overset1{\cancel{(23)}}\ast\overset1{\cancel{(300)}}}{\underset3{\cancel{69}}\ast\underset2{\cancel{600}}}=\frac16$1145. Вычислите по образцу:

б) 954 * 35 : 742 * 9;
в) 5292 : 63 : 28 * 999;
г) 4189 : 71 * 26 : 118;
д) 1125 * 808 : 375 * 33 : 1111.б) $954\ast35:742\ast9=\frac{954\ast35\ast9}{742}=\frac{954\ast5\ast9}{106}=9\ast5\ast9=405$
в) $5292:63:28\ast999=\frac{5292\ast999}{63\ast28}=\frac{84\ast999}{1\ast28}=3\ast999=2997$
г) $4189:71\ast26:118=\frac{4189\ast26}{71\ast118}=\frac{1\ast26}{1\ast2}=13$
д) $1125\ast808:375\ast33:1111=\frac{1125\ast808\ast33}{375\ast1111}=\frac{3\ast8\ast3}{1\ast1}=72$1146. Проверьте равенство:
а) $\frac1{3+\frac12}=\frac27$;
б) $\frac1{2+\frac1{3+\frac14}}=\frac{13}{30}$.а) $\frac1{3+\frac12}=\frac1{3\frac12}=\frac1{\frac72}=\frac27$.
б) $\frac1{2+\frac1{3+\frac14}}=\frac1{2+\frac1{3\frac14}}=\frac1{2+\frac1{\frac{13}4}}=\frac1{2+\frac4{13}}=\frac1{\frac{30}{13}}=\frac{13}{30}$.1147. Вычислите:
а) $\frac1{1+\frac1{2+\frac13}}$;
б) $\frac1{2+\frac1{2+\frac12}}$;
в) $\frac1{3+\frac1{3+\frac13}}$.а) $\frac1{1+\frac1{2+\frac13}}=\frac1{2+\frac1{3\frac14}}=\frac1{1+\frac1{\frac73}}=\frac1{1+\frac37}=\frac1{\frac{10}7}=\frac7{10}$
б) $\frac1{2+\frac1{2+\frac12}}=\frac1{2+\frac1{2\frac12}}=\frac1{2+\frac1{\frac52}}=\frac1{2+\frac25}=\frac1{\frac{12}5}=\frac5{12}$
в) $\frac1{3+\frac1{3+\frac13}}=\frac1{3+\frac1{3\frac13}}=\frac1{3+\frac1{\frac{10}3}}=\frac1{3+\frac3{10}}=\frac1{\frac{33}{10}}=\frac{10}{33}$1148. а) Найдите натуральные числа x, y, z, для которых верно равенство:
$\frac1{x+\frac1{y+\frac1z}}=\frac7{30}$
б) Найдите целые числа x, y, z, для которых верно то же равенство.а) $\frac1{x+\frac1{y+\frac1z}}=\frac1{x+\frac1{\frac{zy+1}z}}=\frac1{x+\frac z{zy+1}}=\frac{xyz+x+x}{zy+1}=\frac{zy+1}{xyz+x+x}=\frac7{30}$
Пусть z = 2; y = 3, тогда:
6x + x + 2 = 30
7x = 30 − 2
7x = 28
x = 28 : 7 = 4
Пусть z = 3; y = 2, тогда:
6x + x + 3 = 30
7x = 30 − 3
7x = 27
x = 27/7 − не натуральное число.
Пусть z = 1; y = 6, тогда:
6x + x + 1 = 30
7x = 30 − 1
7x = 29
x = 29/7 − не натуральное число.
Пусть z = 6; y = 1, тогда:
6x + x + 6 = 30
7x = 30 − 6
7x = 24
x = 24/7 − не натуральное число.
Получается, что только при z = 2; y = 3; x = 4 равенство будет верным.
Ответ:
x = 4;
y = 3;
z = 2.
б) Пример
$\frac1{x+\frac1{y+\frac1z}}=\frac1{x+\frac1{\frac{zy+1}z}}=\frac1{x+\frac z{zy+1}}=\frac{xyz+x+x}{zy+1}=\frac{zy+1}{xyz+x+x}=\frac7{30}$
Решение:
$\frac1{x+\frac1{y+\frac1z}}=\frac1{x+\frac1{\frac{zy+1}z}}=\frac1{x+\frac z{zy+1}}=\frac{xyz+x+x}{zy+1}=\frac{zy+1}{xyz+x+x}=\frac7{30}$
Пусть z = 2; y = 3, тогда:
6x + x + 2 = 30
7x = 30 − 2
7x = 28
x = 28 : 7 = 4
Пусть z = 3; y = 2, тогда:
6x + x + 3 = 30
7x = 30 − 3
7x = 27
x = 27/7 − не целое число.
Пусть z = 1; y = 6, тогда:
6x + x + 1 = 30
7x = 30 − 1
7x = 29
x = 29/7 − не целое число.
Пусть z = 6; y = 1, тогда:
6x + x + 6 = 30
7x = 30 − 6
7x = 24
x = 24/7 − не целое число.
Пусть z = −1; y = −6, тогда:
6x + x − 1 = 30
7x = 30 + 1
7x = 31
x = 31/7 − не целое число.
Пусть z = −6; y = −1, тогда:
6x + x − 6 = 30
7x = 30 + 6
7x = 36
x = 36/7 − не целое число.
Пусть z = −2; y = −3, тогда:
6x + x − 2 = 30
7x = 30 + 2
7x = 32
x = 32/7 − не целое число.
Пусть z = −3; y = −2, тогда:
6x + x − 3 = 30
7x = 30 + 3
7x = 33
x = 33/7 − не целое число.
Получается, что только при z = 2; y = 3; x = 4 равенство будет верным.
Ответ:
x = 4;
y = 3;
z = 2.1149. Вычислите:
а) 4,35 * 3,08 − 16,119 : 4,05 + 0,95 * 40;
б) (454,5 : 5 − 0,3636 : 0,09) : 4,343.а) 4,35 * 3,08 − 16,119 : 4,05 + 0,95 * 40 = 13,398 − 3,98 + 38 = 47,418
б) (454,5 : 5 − 0,3636 : 0,09) : 4,343 = (90,9 − 4,04) : 4,343 = 20. 235
-
Ответы к стр. 235
1150. Вычислите наиболее простым способом:
а) 5759 + 43,25 + 6,75;
б) 42,3 + 7,29 + 57,7 + 0,51;
в) 3,17 * 125 * 8;
г) 1,25 * 13 * 4 * 8 * 2,5;а) 5759 + 43,25 + 6,75 = 5759 + (43,25 + 6,75) = 5759 + 50 = 5809
б) 42,3 + 7,29 + 57,7 + 0,51 = (42,3 + 57,7) + (7,29 + 0,51) = 100 + 7,8 = 107,8
в) 3,17 * 125 * 8 = 3,17 * (125 * 8) = 3,17 * 1000 = 3170
г) 1,25 * 13 * 4 * 8 * 2,5 = (1,25 * 8) * 13 * (4 * 2,5) = 10 * 13 * 10 = 13001151. Вычислите наиболее простым способом :
а) 2 7/9 ∗ 2/3 ∗ 1 1/2;
б) 2/5 ∗ ( 2 1/2 ∗ 5,4 );
в) 765 * 59 + 235 * 59;
г) ( 3 1/3 − 1 1/4 ) ∗ 12;
д) 4 1/2 ∗ 7 2/3 + 4 1/2 ∗ 2 1/3;
е) 42 * 43,8 − 42 * 3,8.а) 2 7/9 ∗ 2/3 ∗ 1 1/2 = 2 7/9 ∗ ( 2/3 ∗ 3/2 ) = 2 7/9 ∗ 1 = 2 7/9
б) 2/5 ∗ ( 2 1/2 ∗ 5,4 ) = ( 2/5 ∗ 5/2 ) ∗ 5,4 = 1 ∗ 5,4 = 5,4
в) 765 * 59 + 235 * 59 = 59 * (765 + 235) = 59 * 1000 = 59000
г) ( 3 1/3 − 1 1/4 ) ∗ 12 = 10/3 ∗ 12 − 5/4 ∗ 12 = 40 − 15 = 25
д) 4 1/2 ∗ 7 2/3 + 4 1/2 ∗ 2 1/3 = 9/2 ∗ ( 7 2/3 + 2 1/3 ) = 9/2 ∗ 10 = 45
е) 42 * 43,8 − 42 * 3,8 = 42 * (43,8 − 3,8) = 42 * 40 = 16801152. Вычислите наиболее простым способом:
а) 4,8 ∗ 2,12 ∗ 0,25
10,6 ∗ 0,96 ∗ 2,5;
б) 3,2 ∗ 0,72 ∗ 5,05
3,6 ∗ 6,4 ∗ 4,04;
в) 6,25 ∗ 0,49 ∗ 0,88
7,7 ∗ 3,5 ∗ 0,125;
г) 18,18 ∗ 6,8 ∗ 4,3
0,86 ∗ 0,34 ∗ 9,09.а) $\frac{4,8\ast2,12\ast0,25}{10,6\ast0,96\ast25}=\frac{\overset1{\cancel{480}}\ast\overset1{\cancel{212}}\ast\overset1{\cancel{25}}}{\underset1{\cancel{1060}}\ast\underset1{\cancel{96}}\ast\underset{10}{\cancel{250}}}=\frac1{10}=0,1$
б) $\frac{3,2\ast0,72\ast5,05}{3,6\ast6,4\ast4,04}=\frac{\overset1{\cancel{320}}\ast\overset1{\cancel{72}}\ast\overset1{\cancel{505}}}{\underset1{\cancel{360}}\ast\underset2{\cancel{640}}\ast\underset4{\cancel{404}}}=\frac18=0,125$
в) $\frac{6,25\ast0,49\ast0,88}{7,7\ast3,5\ast0,125}=\frac{\overset1{\cancel{6250}}\ast\overset1{\cancel{490}}\ast\overset1{\cancel8}}{\underset1{\cancel{7700}}\ast\underset{10}{\cancel{3500}}\ast\underset1{\cancel{125}}}=\frac8{10}=0,8$
г) $\frac{18,18\ast6,8\ast4,3}{0,86\ast0,34\ast9,09}=\frac{\overset1{\cancel{1818}}\ast\overset{20}{\cancel{680}}\ast\overset{10}{\cancel{430}}}{\underset1{\cancel{86}}\ast\underset1{\cancel{34}}\ast\underset1{\cancel{909}}}=200$1153. Вычислите:
а) (−24,3) : (4,5 − 4,5 * (−0,8)) : 0,5;
б) 12,5 * (−3,6 + 3,6 * (−1,5)) * (−0,8).а) (−24,3) : (4,5 − 4,5 * (−0,8)) : 0,5 = (−24,3) : (4,5 + 3,6) : 0,5 = (−24,3) : 8,1 : 0,5 = (−3) : 0,5 = −6
б) 12,5 * (−3,6 + 3,6 * (−1,5)) * (−0,8) = 12,5 * (−3,6 − 5,4) * (−0,8) = 12,5 * (−9) * (−0,8) = −112,5 * (−0,8) = 901154. Вычислите наиболее простым способом:
а) 751 − 387 − 551 + 387 − 600;
б) (4,7 − 4,9) + (4,9 − 5,1) − (−5,1 − 5,3).а) 751 − 387 − 551 + 387 − 600 = (751 − 551) + (387 − 387) − 600 = 200 − 600 = −400
б) (4,7 − 4,9) + (4,9 − 5,1) − (−5,1 − 5,3) = 4,7 − 4,9 + 4,9 − 5,1 + 5,1 + 5,3 = (4,7 + 5,3) + (−4,9 + 4,9) + (−5,1 + 5,1) = 10 + 0 + 0 = 101155. Вычислите наиболее простым способом:
а) 4,6 * 7,3 + 5,4 * 8,5 + 4,6 * 8,5 + 5,4 * 7,3;
б) 9,8 * 17,42 + 9,8 * 5,58 − 1,8 * 17,42 − 1,8 * 5,58;
в) 15,37 * 7,88 − 9,37 * 7,88 + 15,37 * 2,12 − 9,37 * 2,12;
г) 4,54 * 77,7 − 4,54 * 7,7 + 7,46 * 77,7 − 7,46 * 7,7;
д) 75,9 * 42,3 − 65,9 * 42,3 + 628 * 1,77 − 528 * 1,77.а) 4,6 * 7,3 + 5,4 * 8,5 + 4,6 * 8,5 + 5,4 * 7,3 = 7,3 * (4,6 + 5,4) + 8,5 * (5,4 + 4,6) = 7,3 * 10 + 8,5 * 10 = 10 * (7,3 + 8,5) = 10 * 15,8 = 158
б) 9,8 * 17,42 + 9,8 * 5,58 − 1,8 * 17,42 − 1,8 * 5,58 = 9,8 * (17,42 + 5,58) − 1,8 * (17,42 + 5,58) = 9,8 * 23 − 1,8 * 23 = 23 * (9,8 − 1,8) = 23 * 8 = 184
в) 15,37 * 7,88 − 9,37 * 7,88 + 15,37 * 2,12 − 9,37 * 2,12 = 7,88 * (15,37 − 9,37) + 2,12 * (15,37 − 9,37) = 7,88 * 6 + 2,12 * 6 = 6 * (7,88 + 2,12) = 6 * 10 = 60
г) 4,54 * 77,7 − 4,54 * 7,7 + 7,46 * 77,7 − 7,46 * 7,7 = 4,54 * (77,7 − 7,7) + 7,46 * (77,7 − 7,7) = 4,54 * 70 + 7,46 * 70 = 70 * (4,54 + 7,46) = 70 * 12 = 840
д) 75,9 * 42,3 − 65,9 * 42,3 + 628 * 1,77 − 528 * 1,77 = 42,3 * (75,9 − 65,9) + 1,77 * (628 − 528) = 42,3 * 10 + 1,77 * 100 = 423 + 177 = 6001156. Вычислите:
а) 1/4 + 2,7;
б) 4,1 ∗ 2/5;
в) 2,9 − 1 3/4;
г) 4,5 : 2 1/2;
д) 3 2/3 − 0,25;
е) 2 1/7 ∗ 0,7;
ж) 1/2 : 0,3;
з) 2 1/2 : 4,5.а) $\frac14+2,7=\frac14+2\frac7{10}=\frac5{20}+2\frac{14}{20}=2\frac{19}{20}$
б) $4,1\ast\frac25=4\frac1{10}\ast\frac25=\frac{41}{10}\ast\frac25=\frac{41}{25}=1\frac{16}{25}$
в) $2,9-1\frac34=2\frac9{10}-1\frac34=2\frac{18}{20}-1\frac{15}{20}=1\frac3{20}$
г) $4,5:2\frac12=4\frac5{10}:\frac52=\frac{45}{10}\ast\frac25=\frac95=1\frac45$
д) $3\frac23-0,25=3\frac23-\frac14=3\frac8{12}-\frac3{12}=3\frac5{12}$
е) $2\frac17\ast0,7=\frac{15}7\ast\frac7{10}=\frac32=1\frac12$
ж) $\frac12:0,3=\frac12:\frac3{10}=\frac12\ast\frac{10}3=\frac53=1\frac23$
з) $2\frac12:4,5=\frac52:4\frac12=\frac52\ast\frac29=\frac59$1157. Вычислите:
а) ( 1,545 : 1,5 − 1 ) ∗ 2 2/3 + 0,5 ∗ 4/15;
б) ( 2,678 : 1,3 − 2 ) ∗ 3 1/3 + 0,3 ∗ 7/15.а) $(1,545:1,5-1)\ast2\frac23+0,5\ast\frac4{15}=(1,03-1)\ast\frac83+\frac12\ast\frac4{15}=\frac3{100}\ast\frac83+\frac2{15}=\frac2{25}+\frac2{15}=\frac{6+10}{75}=\frac{16}{75}$
б) $(2,678:1,3-2)\ast3\frac13+0,3\ast\frac7{15}=(2,06-2)\ast\frac{10}3+\frac3{10}\ast\frac7{15}=\frac3{50}\ast\frac{10}3+\frac7{50}=\frac{10}{50}+\frac7{50}=\frac{17}{50}$1158. Вычислите:
а) 2/7 : 8 + 5 : 0,7 − 3/4 : 21;
б) 3 : 4 1/5 + 5,4 : 7,2 − 2/7 : 0,8;
в) 4,5 ∗ 2/3 − 1 5/7 : 1,2 + 3 1/5 ∗ 3 1/8;
г) 6,25 : 5/3 − 2,5 : 1,5 + 7 1/2 − 8 1/3.а) $\frac27:8+5:0,7-\frac34:21=\frac27\ast\frac18+\frac{50}7-\frac1{28}=\frac1{28}+\frac{50}7-\frac1{28}=7\frac17$
б) $3:4\frac15+5,4:7,2-\frac27:0,8=3\ast\frac5{21}+0,75-\frac27\ast\frac54=\frac57+\frac34-\frac5{14}=\frac{20+21-10}{28}=\frac{31}{28}=1\frac3{28}$
в) $4,5\ast\frac23-1\frac57:1,2+3\frac15\ast3\frac18=\frac92\ast\frac23-\frac{12}7\ast\frac56+\frac{16}5\ast\frac{25}8=3-\frac{10}7+10=11\frac47$
г) $6,25:\frac53-2,5:1,5+7\frac12-8\frac13=\frac{25}4\ast\frac35-\frac52\ast\frac23+7\frac12-8\frac13=\frac{15}4-\frac53+7\frac12-8\frac13=\frac{45}{12}-\frac{20}{12}+7\frac6{12}-8\frac4{12}=\frac{25}{12}-\frac{10}{12}=\frac{15}{12}=\frac54=1\frac14$1159. Вычислите:
а) ( 8 1/4 − 3,51 ) : 2,37
1/5 ∗ 3,17 − 2,205 : 3 1/2;
б) ( 3 1/3 − 2,5 ) ∗ 6,6
15,717 : 3,1 − 1/7 ∗ 0,49.а) $\frac{(8\frac14-3,51):2,37}{\frac15\ast3,17-2,205:3\frac12}=\frac{(8,25-3,51):2,37}{0,2\ast3,17-2,205:3,5}=\frac{4,74:2,37}{0,634-0,63}=\frac2{0,004}=500$
б) $\frac{(3\frac13-2,5)\ast6,6}{15,717:3,1-\frac17\ast0,49}=\frac{(3\frac13-2\frac12)\ast\frac{66}{10}}{5,07-\frac17\ast\frac{49}{100}}=\frac{\frac56\ast\frac{66}{10}}{5,07-0,07}=\frac{\frac{11}2}5=\frac{11}2\ast\frac15=\frac{11}{10}=1\frac1{10}=1,1$ 236
-
Ответы к стр. 236
1160. Вычислите:
а) 3 3/4 : 0,03 − 4,52 ∗ 8 1/2;
б) 3 3/8 − ( 7 1/2 − 4,25 ) : 9/20;
в) 3 2/5 : 5,1 − 4 2/3 : 6,3;
г) − 3 3/5 : 2,7 + 2,7 : 3 3/5.а) $3\frac34:0,03-4,52\ast8\frac12=3,75:0,03-4,52\ast8,5=125-38,42=86,58$
б) $3\frac38-(7\frac12-4,25):\frac9{20}=3\frac38-(7\frac12-4\frac14)\ast\frac{20}9=3\frac38-(7\frac24-4\frac14)\ast\frac{20}9=3\frac38-3\frac14\ast\frac{20}9=3\frac38-\frac{13}4\ast\frac{20}9=3\frac38-\frac{65}9=3\frac{27}{72}-7\frac{16}{72}=-3\frac{61}{72}$
в) $3\frac25:5,1-4\frac23:6,3=3\frac25:5\frac1{10}-4\frac23:6\frac3{10}=\frac{17}5\ast\frac{10}{51}-\frac{14}3\ast\frac{10}{63}=\frac23-\frac{20}{27}=\frac{18}{27}-\frac{20}{27}=-\frac2{27}$
г) $-3\frac35:2,7+2,7:3\frac35=-3\frac35:2\frac7{10}+2\frac7{10}:3\frac35=-\frac{18}5\ast\frac{10}{27}+\frac{27}{10}\ast\frac5{18}=-\frac43+\frac34=-\frac{16}{12}+\frac9{12}=-\frac7{12}$1161. Вычислите наиболее простым способом:
а) 4,526 + 12 1/5 − ( 4 2/3 ∗ 1,8 + 4,526 );
б) 3 1/3 : 2,4 + 9,888 − ( 1/18 + 7,888 );
в) 4,51 ∗ 3 1/2 − 7 2/3 − ( − 5,49 ∗ 3 1/2 + 10 1/3 );
г) 4,573 + 2 2/7 ∗ 3 1/8 − ( 2,073 − 1 5/7 ∗ 3 1/8 ).а) $4,526+12\frac15-(4\frac23\ast1,8+4,526)=4,526+\frac{61}5-\frac{14}3\ast\frac95-4,526=\frac{61}5-\frac{14}3\ast\frac95=\frac{61}5-\frac{42}5=\frac{19}5=3\frac45$
б) $3\frac13:2,4+9,888-(\frac1{18}+7,888)=\frac{10}3:\frac{12}5+9,888-\frac1{18}-7,888=\frac{10}3\ast\frac5{12}+2-\frac1{18}=\frac{25}{18}-\frac1{18}+2=\frac43+2=1\frac13+2=3\frac13$
в) $4,51\ast3\frac12-7\frac23-(-5,49\ast3\frac12+10\frac13)=4,51\ast\frac72-7\frac23+5,49\ast\frac72-10\frac13=\frac72\ast(4,51+5,49)-7\frac23-10\frac13=\frac72\ast10-18=35-18=17$
г) $4,573+2\frac27\ast3\frac18-(2,073-1\frac57\ast3\frac18)=4,573+\frac{16}7\ast\frac{25}8-2,073+\frac{12}7\ast\frac{25}8=\frac{25}8\ast(\frac{16}7+\frac{12}7)+4,573-2,073=\frac{25}8\ast4+2,5=\frac{25}2+2,5=12,5+2,5=15$1162. Вычислите:
а) ( 15 : 3,75 + 10,5 : 1,5 ∗ 3/14 ) : ( 1 33/52 − 1 1/4 );
б) ( 10 : 2,5 + 7,5 : 10 ) ∗ ( 3/40 + 7/12 − 157/360 ).а) $(15:3,75+10,5:1,5\ast\frac3{14}):(1\frac{33}{52}-1\frac14)=(15\ast\frac{100}{375}+\frac{105}{10}\ast\frac{10}{15}\ast\frac3{14}):(1\frac{33}{52}-1\frac{13}{52})=(4+7\ast\frac3{14}):\frac5{13}=(4+\frac32):\frac5{13}=\frac{11}2\ast\frac{13}5=\frac{143}{10}=14,3$
б) $(10:2,5+7,5:10)\ast(\frac3{40}+\frac7{12}-\frac{157}{360})=(4+0,75)\ast\frac{27+210-157}{360}=4\frac34\ast\frac29=\frac{19}4\ast\frac29=\frac{19}{18}=1\frac1{18}$1163. Решите пропорцию:
а) x : 7 = 5 : 8;
б) x : 3 = 4 : 5;
в) 2 : x = 3 : 4;
г) 1 : x = 7 : 8.а) x : 7 = 5 : 8
8x = 7 * 5
x = 35/8 = 4 3/8
Ответ: 4 3/8
б) x : 3 = 4 : 5
5x = 3 * 4
x = 12/5 = 2 2/5
Ответ: 2 2/5
в) 2 : x = 3 : 4
3x = 2 * 4
x = 8/3 = 2 2/3
Ответ: 2 2/3
г) 1 : x = 7 : 8
7x = 1 * 8
x = 8/7 = 1 1/7
Ответ: 1 1/71164. Решите пропорцию:
а) x/9 = 5/7;
б) 5/x = 0,2 / 3;
в) 6x / 5 = 18/7;
г) 7,5 : (2x) = 3 : 0,8;
д) x − 3/5 = 4/7;
е) x+1 / 3 = x−1 / 2.а) x/9 = 5/7
7x = 9 * 5
x = 45/7 = 6 3/7
Ответ: 6 3/7
б) 5/x = 0,2/3
0,2x = 5 * 3
x = 15/0,2 = 75
Ответ: 75
в) $\frac{6x}5=\frac{18}7$
42x = 5 * 18
x = 90/42 = 15/7 = 2 1/7
Ответ: 2 1/7
г) 7,5 : (2x) = 3 : 0,8
6x = 7,5 * 0,8
x = 6/6 = 1
Ответ: 1
д) $\frac{x-3}5=\frac47$
7(x − 3) = 5 * 4
7x − 21 = 20
7x = 20 + 21
7x = 41
x = 41/7 = 5 6/7
Ответ: 5 6/7
е) $\frac{x+1}3=\frac{x-1}2$
2(x + 1) = 3(x − 1)
2x + 2 = 3x − 3
2x − 3x = −3 − 2
−x = −5
x = −5/−1 = 5
Ответ: 51165. Упростите выражение:
а) 4x − 5 + 1,5 + 2;
б) 8x − (3x + 5) + (2x − 9);
в) 5(x − 0,4) − 7(2x + 1,5);
г) 2,3x − (2,3x + 0,5) − 0,2(5x − 3).а) 4x − 5 + 1,5 + 2 = 4x − 1,5
б) 8x − (3x + 5) + (2x − 9) = 8x − 3x − 5 + 2x − 9 = 7x − 14
в) 5(x − 0,4) − 7(2x + 1,5) = 5x − 2 − 14x − 10,5 = −9x − 12,5
г) 2,3x − (2,3x + 0,5) − 0,2(5x − 3) = 2,3x − 2,3x − 0,5 − x + 0,6 = −x + 0,11166. Упростите выражение:
а) 3(x − 8) + 2(x + 3) + 24;
б) 3,2(2x + 1) + 1,6(4x + 2) + 1,7;
в) 2(x − 1) − 3(x − 2) + x;
г) 7,5(x − 4) − 2,5(3x − 12) + 5.а) 3(x − 8) + 2(x + 3) + 24 = 3x − 24 + 2x + 6 + 24 = 5x + 6
б) 3,2(2x + 1) + 1,6(4x + 2) + 1,7 = 6,4x + 3,2 + 6,4x + 3,2 + 1,7 = 12,8x + 8,1
в) 2(x − 1) − 3(x − 2) + x = 2x − 2 − 3x + 6 + x = 4
г) 7,5(x − 4) − 2,5(3x − 12) + 5 = 7,5x − 30 − 7,5x + 30 + 5 = 51167. Упростите выражение:
а) 2,4 x + 1 5/7 − 2 2/3 x − 5;
б) 7,1x + (3,5 − x) − (5,9x − 1);
в) − 3 x − 2 ( x − 9 ) + 3 ( 2 x + 2/3 ).а) $2,4x+1\frac57-2\frac23x-5=2\frac25x+1\frac57-2\frac23x-5=\frac{6-10}{15}x-3\frac27=-\frac4{15}x-3\frac27$
б) 7,1x + (3,5 − x) − (5,9x − 1) = 7,1x + 3,5 − x − 5,9x + 1 = 0,2x + 4,5
в) $-3x-2(x-9)+3(2x+\frac23)=-3x-2x+18+6x+2=x+20$1168. Упростите выражение:
а) 3(x − 5) + 5(x + 1) + 10;
б) 1,2(2x − 1) + 3,5(x − 2) + 10,2;
в) 5(x − 1) − 2(x + 3) − 3x;
г) 2,5(x − 0,2) − 5(2x − 0,4) + 0,5x.а) 3(x − 5) + 5(x + 1) + 10 = 3x − 15 + 5x + 5 + 10 = 8x
б) 1,2(2x − 1) + 3,5(x − 2) + 10,2 = 2,4x − 1,2 + 3,5x − 7 + 10,2 = 5,9x − 8,2 + 10,2 = 5,9x + 2
в) 5(x − 1) − 2(x + 3) − 3x = 5x − 5 − 2x − 6 − 3x = −11
г) 2,5(x − 0,2) − 5(2x − 0,4) + 0,5x = 2,5x − 0,5 − 10x + 2 + 0,5x = −7x + 1,5 237
-
Ответы к стр. 237
1169. Найдите значение выражения:
а) 5x − 39 при x = 10; 0; 3;
б) −3,5x + 6 при x = 2; −3; 0,4;
в) x − 1/3 при x = 5 ; 2 1/2 ; − 0,5;
г) 1/2 − 2/3 x при x = 0,5 ; − 6 ; 4.а) 5x − 39 = 5 * 10 − 39 = 50 − 39 = 11;
5x − 39 = 5 * 0 − 39 = 0 − 39 = −39;
5x − 39 = 5 * 3 − 39 = 15 − 39 = −24.
Ответ: 11; −39; −24.
б) б) −3,5x + 6 = −3,5 * 2 + 6 = −7 + 6 = −1;
−3,5x + 6 = −3,5 * −3 + 6 = 10,5 + 6 = 16,5;
−3,5x + 6 = −3,5 * 0,4 + 6 = −1,4 + 6 = 4,6.
Ответ: −1; 16,5; 4,6.
в) x − 1/3 = 5 − 1/3 = 4 2/3
x − 1/3 = 2 1/2 − 1/3 = 2 3/6 − 2/6 = 2 1/6;
x − 1/3 = − 0,5 − 1/3 = − 1/2 − 1/3 = − 3/6 − 2/6 = − 5/6.
Ответ: 4 2/3 ; 2 1/6 ; − 5/6.
г) $\frac12-\frac23x=\frac12-\frac23\ast0,5=\frac12-\frac23\ast\frac12=\frac12-\frac13=\frac36-\frac26=\frac16$;
$\frac12-\frac23x=\frac12-\frac23\ast(-6)=\frac12+4=4\frac12$;
$\frac12-\frac23x=\frac12-\frac23\ast4=\frac12-\frac83=\frac36-\frac{16}6=-\frac{13}6=-2\frac16$.
Ответ: 1/6 ; 4 1/2 ; − 2 1/6.1170. Найдите значение выражения:
а) 25x − 50 + 44x − 88 при x = 2;
б) 13x + 39 + 21x + 63 при x = −3;
в) 128 − 4x + 356 − 8x при x = 7;
г) 121 − 11x + 456 − 10x при x = 11.а) 25x − 50 + 44x − 88 = 69x − 138 = 69 * 2 − 138 = 138 − 138 = 0
Ответ: 0
б) 13x + 39 + 21x + 63 = 34x + 102 = 34 * (−3) + 102 = −102 + 102 = 0
Ответ: 0
в) 28 − 4x + 356 − 8x = 484 − 12x = 484 − 12 * 7 = 484 − 84 = 400
Ответ: 400
г) 121 − 11x + 456 − 10x = 577 − 21x = 577 − 21 * 11 = 577 − 231 = 346
Ответ: 3461171. Найдите значение выражения:
а) 4,2x − 84 + 2,3x − 46 + x при x = 20;
б) 2,1x + 6,3 − 2,4x − 6,2 − 5 при x = −3;
в) 3,2(x − 3,2) + 5,5(x − 2,2) при x = 3,2;
г) 6,3(x + 2,4) − 9,1(x + 1,4) при x = −1,4.а) 4,2x − 84 + 2,3x − 46 + x = 7,5x − 130 = 7,5 * 20 − 130 = 150 − 130 = 20
Ответ: 20
б) 2,1x + 6,3 − 2,4x − 6,2 − 5 = −0,3x − 4,9 = −0,3 * (−3) − 4,9 = 0,9 − 4,9 = −4
Ответ: −4
в) 3,2(x − 3,2) + 5,5(x − 2,2) = 3,2(3,2 − 3,2) + 5,5(3,2 − 2,2) = 3,2 * 0 + 5,5 * 1 = 5,5
Ответ: 5,5
г) 6,3(x + 2,4) − 9,1(x + 1,4) = 6,3(−1,4 + 2,4) − 9,1(−1,4 + 1,4) = 6,3 * 1 − 9,1 * 0 = 6,3
Ответ: 6,31172. Решите уравнение:
а) 4 1/2 x = 9,9;
б) 5,5x = −66;
в) − 3,6 x = 14 2/5;
г) −2,2x = −4,84.а) $4\frac12x=9,9$
$x=9\frac9{10}:4\frac12=\frac{99}{10}\ast\frac29=\frac{11}5=2\frac15$
Ответ: 11/5
б) 5,5x = −66
x = −66 : 5,5 = −12
Ответ: −12
в) − 3,6 x = 14 2/5
x = 14 2/5 : ( − 3 3/5 ) = 72/5 ∗ ( − 5/18 ) = 4
Ответ: −4
г) −2,2x = −4,84
x = −4,84 : (−2,2) = 2,2
Ответ: 2,21173. Решите уравнение:
а) 3x = 5;
б) 0,7x = −2;
в) −2,1x = 3,6;
г) 6x − 7 = 0,2;
д) 0,6x + 0,5 = 3;
е) −5x + 1,2 = −5,1.а) 3x = 5
x = 5/3 = 1 2/3
Ответ: 1 2/3
б) 0,7x = −2
x = − 2 : 0,7 = − 2 : 7 10 = − 2 ∗ 10/7 = − 20/7 = − 2 6/7
Ответ: − 2 6/7
в) −2,1x = 3,6
$x=-\frac{3,6}{2,1}=-\frac{36}{21}=-\frac{12}7=-1\frac57$
Ответ: − 1 5/7
г) 6x − 7 = 0,2
6x = 0,2 + 7 = 7,2
x = 7,2 : 6 = 1,2
Ответ: 1,2
д) 0,6x + 0,5 = 3
0,6x = 3 − 0,5 = 2,5
$x=\frac{2,5}{0,6}=\frac{25}6=4\frac16$
Ответ: 4 1/6
е) −5x + 1,2 = −5,1
−5x = −5,1 − 1,2 = −6,3
$x=\frac{-6,3}{-5}=\frac{63}{50}=1\frac{13}{50}$
Ответ: 1 13/501174. Решите уравнение:
а) 5x − 9 = 2,3x + 1;
б) 7,3 x − 1/3 = − 1,2 x + 3;
в) 6(x − 3) + 2(x + 2) = 1;
г) 5(x − 1) − 4(x − 2) = 10;
д) 3(x − 9) + 5(x − 4) = 1;
е) 7(x − 9) − (3x + 1) = 9.а) 5x − 9 = 2,3x + 1 = 5x − 2,3x = 1 + 9
2,7x = 10
x = 10 2,7 = 100/27 = 3 19/27
Ответ: 3 19/27
б) 7,3 x − 1/3 = − 1,2 x + 3
7,3 x + 1,2 x = 3 + 1/3
8,5 x = 3 1/3
x = 3 1/3 : 8 1/2 = 10/3 : 17/2 = 10/3 ∗ 2/17 = 20/51
Ответ: 20/51
в) 6(x − 3) + 2(x + 2) = 1
6x − 18 + 2x + 4 = 1
6x + 2x = 1 + 18 − 4
8x = 15
x = 15/8 = 1 7/8
Ответ: 1 7/8
г) 5(x − 1) − 4(x − 2) = 10
5x − 5 − 4x + 8 = 10
5x − 4x = 10 + 5 − 8
x = 7
Ответ: 7
д) 3(x − 9) + 5(x − 4) = 1
3x − 27 + 5x − 20 = 1
3x + 5x = 1 + 27 + 20
8x = 48
x = 48 : 8 = 6
Ответ: 6
е) 7(x − 9) − (3x + 1) = 9
7x − 63 − 3x − 1 = 9
7x − 3x = 9 + 63 + 1
4x = 73
x = 73/4 = 18 1/4
Ответ: 18 1/41175. Решите уравнение:
а) 4,5(x − 1) − 2,3(x + 2) = 2,1x;
б) 2/3 ( x − 5 ) + 1 1/3 ( x + 1 ) = 9;
в) x + 1/2 x + 1/3 x = 33;
г) x + x + 1/2 x + 1/4 x + 1 = 100.а) 4,5(x − 1) − 2,3(x + 2) = 2,1x
4,5x − 4,5 − 2,3x − 4,6 = 2,1x
4,5x − 2,3x − 2,1x = 4,5 + 4,6
0,1x = 9,1
x = 9,1 : 0,1 = 91
Ответ: 91
б) $\frac23(x-5)+1\frac13(x+1)=9$
$\frac23x-\frac{10}3+1\frac13x+1\frac13=9$
$\frac23x+1\frac13x=9+\frac{10}3-1\frac13$
$2x=9+3\frac13-1\frac13=9+2=11$
$x=\frac{11}2=5\frac12$
Ответ: 5 1/2
в) $x+\frac12x+\frac13x=33$
$x+\frac36x+\frac26x=33$
$1\frac56x=33$
$x=33:\frac{11}6=33\ast\frac6{11}=18$
Ответ: 18
г) $x+x+\frac12x+\frac14x+1=100$
$2x+\frac24x+\frac14x=100-1$
$2\frac34x=99$
$x=99:\frac{11}4=99\ast\frac4{11}=36$
Ответ: 361176. Решите уравнение:
а) 2(2x − 1) − 3(x − 2) = 6 + 4(3 − 2x);
б) 2(x + 2) − 3(x − 2) = 5 − 4(3x − 1).а) 2(2x − 1) − 3(x − 2) = 6 + 4(3 − 2x)
4x − 2 − 3x + 6 = 6 + 12 − 8x
4x − 3x + 8x = 6 + 12 + 2 − 6
9x = 14
x = 14/9 = 1 5/9
Ответ: 1 5/9
б) 2(x + 2) − 3(x − 2) = 5 − 4(3x − 1)
2x + 4 − 3x + 6 = 5 − 12x + 4
2x + 12x − 3x = 5 + 4 − 4 − 6
11x = −1
x = − 1/11
Ответ: − 1/111177. Бак вмещает 1000 л воды. Каждый день расходуют 600 л, а ночью доливают половину того количества, что находилось в баке утром. Хватит ли воды в баке на четверг, если утром в понедельник бак был полон?
Понедельник: 1000 − 600 + 1000 : 2 = 400 + 500 = 900 л
Вторник: 900 − 600 + 900 : 2= 300 + 450 = 750 л
Среда: 750 − 600 + 750 : 2 = 150 + 375 = 525 л
Четверг: 525 − 600 = −75 л
Ответ: не хватит.1178. В булочную привезли 654 кг чёрного и белого хлеба. После того как продали 215 кг чёрного и 287 кг белого хлеба, того и другого сорта осталось поровну. Сколько чёрного и белого хлеба в отдельности привезли в булочную?
Пусть привезли x кг белого хлеба, тогда:
654 − x кг привезли черного хлеба,
654 − x − 215 кг − осталось черного хлеба,
x − 287 кг − осталось белого хлеба,
654 − x − 215 = x − 287
−2x = −287 − 654 + 215
−2x = −726
x = −726 : (−2) = 363 кг привезли белого хлеба.
654 − 363 = 291 кг привезли черного хлеба.
Ответ: 363 кг белого и 291 кг черного. 238
-
Ответы к стр. 238
1179. В двух магазинах было 452 холодильника. После того как оба магазина продали холодильников поровну, в одном осталось 72, а в другом − 84 холодильника. Сколько холодильников было в каждом магазине первоначально?
Пусть в первом магазине было x холодильников, тогда:
452 − x холодильников было во втором магазине,
x − 72 холодильников продали в первом магазине,
452 − x − 84 холодильников продали во втором магазине,
x − 72 = 452 − x − 84
x + x = 452 − 84 + 72
2x = 440
x = 440 : 2 = 220 холодильников изначально было в первом магазине,
452 − 220 = 232 холодильника было во втором магазине.
Ответ:
в первом магазине было 220 холодильников;
во втором магазине было 232 холодильника.1180. Первый цех железобетонных изделий расходует в день 25 т цемента. Сколько цемента расходует в день второй цех завода, если привезённых 870 т цемента хватит на 15 дней их совместной работы?
Пусть второй цех расходует x т цемента в день, тогда:
25 + x цемента т в день расходуют оба цеха,
(25 + x) * 15 = 870
375 + 15x = 870
15x = 870 − 375
15x = 495
x = 495 : 15 = 33 т цемента в день расходует второй цех завода.
Ответ: 33 т1181. Завод по плану должен изготовить 7920 приборов за 24 дня. За сколько дней завод выполнит это задание, если будет изготавливать в день на 30 приборов больше, чем намечено по плану?
7920 : 24 = 330 приборов изготавливает по плану завод в день,
330 + 30 = 360 приборов будет изготавливать завод в день,
7920 : 360 = 22 дня будет выполнять план завод, при увеличении планового задания на 30 приборов.
Ответ: 22 дня.1182. Токарь должен за 6 ч обточить 96 деталей. Применяя усовершенствованный резец, он может обтачивать в час на 8 деталей больше. Сколько времени сэкономит токарь на обточке 96 деталей, применяя усовершенствованный резец?
96 : 6 = 16 деталей в час обтачивает токарь, используя старый резец;
16 + 8 = 24 детали в час сможет обтачивать токарь используя усовершенствованный резец;
96 : 24 = 4 часа потребуется токарю на обточку 96 деталей пи использовании усовершенствованного резца.
6 − 4 = 2 ч сэкономит токарь.
Ответ: 2 ч1183. Нужно проверить 360 тетрадей диктанта. Первый учитель может проверить за 15 ч, второй − за 10 ч, третий − за 6 ч. За сколько времени проверят они тетради втроём?
360 : 15 = 24 тетради в час проверяет первый учитель;
360 : 10 = 36 тетрадей в час проверяет второй учитель;
360 : 6 = 60 тетрадей в час проверяет третий учитель;
24 + 36 + 60 = 120 тетрадей в час проверяют три учителя;
360 : 120 = 3 часа потребуется трём учителям на проверку 360 тетрадей.
Ответ: 3 часа.1184. A, B и C сыграли три партии, причём проигравший обязан был удваивать суммы, принадлежащие остальным в начале партии. Проиграли последовательно A, B и C, и в результате у всех троих оказалось по 48 р. Сколько денег было у каждого из них вначале?
Рассмотрим ситуацию с конца:
После 3−ей партии:
А = 48 р.;
В = 48 р.;
C = 48 р.
После 2−ой партии:
А = 48 : 2 = 24 р.;
В = 48 : 2 = 24 р.;
C = 48 + 24 + 24 = 96 р.
После 1−ой партии:
А = 24 : 2 = 12 р.;
В = 24 + 12 + 48 = 84 р.;
C = 96 : 2 = 48 р.
На начало игры:
А = 12 + 42 + 24 = 78 р.;
В = 84 : 2 = 42 р.;
C = 48 : 2 = 24 р.
Ответ:
А = 78 р.;
В = 42 р.;
C = 24 р.1185. A, B, C и D сыграли четыре партии, причём проигравший обязан был удваивать суммы, принадлежащие остальным в начале партии. Проиграли последовательно A, B, C и D, и в результате у всех четверых оказалось по 48 р. Сколько денег было у каждого из них вначале?
Рассмотрим ситуацию с конца:
Конец игры:
A = 48 р.;
B = 48 р.;
C = 48 р.;
D = 48 р.
Начало 4 партии:
A = 48 : 2 = 24 р.;
B = 48 : 2 = 24 р.;
C = 48 : 2 = 24 р.;
D = 48 + 24 + 24 + 24 = 120 р.
Начало 3 партии:
A = 24 : 2 = 12 р.;
B = 24 : 2 = 12 р.;
C = 24 + 12 + 12 + 60 = 108 р.;
D = 120 : 2 = 60 р.
Начало 2 партии:
A = 12 : 2 = 6 р.;
B = 12 + 6 + 54 + 30 = 102 р.;
C = 108 : 2 = 54 р.;
D = 60 : 2 = 30 р.
Начало игры:
A = 6 + 51 + 27 + 15 = 99 р.;
B = 102 : 2 = 51 р.;
C = 54 : 2 = 27 р.;
D = 30 : 2 = 15 р.
Ответ:
A = 99 р.;
B = 51 р.;
C = 27 р.;
D = 15 р.1186. а) У крестьянина было несколько поросят и несколько ягнят. Три поросёнка и два ягнёнка весят 23 кг, а два поросёнка и три ягнёнка весят 22 кг. Сколько весят один поросёнок и один ягнёнок в отдельности?
б) В трёх маленьких и четырёх больших коробках 150 цветных карандашей, а в четырёх маленьких и трёх больших коробках 144 цветных карандаша. Сколько цветных карандашей в большой коробке?а) Пусть поросенок весит x, ягненок y, тогда:
3x + 2y = 23
2x + 3y = 22
3x + 2y + 2x + 3y = 23 + 22
5x + 5y = 45
5(x + y) = 45
x + y = 45 : 5 = 9
x = 9 − y
3(9 − y) + 2y = 23
27 − y + 2y = 23
−y = 23 − 27
y = 4 кг весит ягненок,
x = 9 − 4 = 5 кг весит поросенок.
Ответ:
4 кг весит ягненок,
5 кг весит поросенок.
б) Пусть в маленькой коробке x карандашей, а в большой y карандашей y, тогда:
3x + 4y = 150
4x + 3y = 144
3x + 4y + 4x + 3y = 150 + 144
7x + 7y = 294
7(x + y) = 294
x + y = 294 : 7 = 42
x = 42 − y
3(42 − y) + 4y = 150
126 − 3y + 4y = 150
y = 150 − 126 = 24 карандаша в большой коробке.
Ответ: 24 карандаша.1187. а) Скорость течения реки 2 км/ч. На сколько километров в час скорость лодки по течению реки больше скорости против течения? Зависит ли ответ от собственной скорости лодки?
б) Скорость лодки по течению реки больше скорости лодки против течения на 6 км/ч. Какова скорость течения?а) Пусть собственная скорость лодки x км/ч, тогда:
x + 2 км/ч − скорость лодки по течению;
x − 2 км/ч − скорость лодки против течения.
x + 2 − (x − 2) = x + 2 − x + 2 = на 4 км/ч скорость лодки по течению больше скорости лодки против течения. Ответ не зависит от собственной скорости лодки.
Ответ: На 4 км/ч скорость лодки по течению больше скорости лодки против течения. Ответ не зависит от собственной скорости лодки.
б) Пусть собственная скорость лодки x км/ч, скорость течения реки y км/ч, тогда:
x + y − скорость лодки по течению;
x − y − скорость лодки против течения.
(x + y) − (x − y) = 6
x + y − x + y = 6
2y = 6
y = 6 : 2 = 3 км/ч скорость течения.
Ответ: 3 км/ч 239
-
Ответы к стр. 239
1188. Расстояние, равное 3,6 км, проплыли по течению за 30 мин, а против течения за 40 мин. Определите скорость течения реки. За сколько часов это же расстояние проплывут плоты?
30 : 60 = 1/2 часа;
40 : 60 = 2/3 часа.
3,6 : 1/2 = 36/10 ∗ 2 = 72/10 = 7,2 км/ч скорость по течению.
3,6 : 2 3 = 36/10 ∗ 3/2 = 54/10 = 5,4 км/ч скорость против течения.
(7,2 − 5,4) : 2 = 1,8 : 2 = 0,9 км/ч скорость течения.
3,6 : 0,9 = 4 ч потребуется плотам на преодоление расстояния.
Ответ:
0,9 км/ч скорость течения;
4 ч потребуется плотам на преодоление расстояния.1189. Пассажир метро, стоящий на ступеньке эскалатора, поднимается вверх за З мин. За сколько минут поднимется пассажир, если будет идти вверх со скоростью 25 м/мин и длина эскалатора 150 м?
150 : 3 = 50 м/мин скорость эскалатора.
50 + 25 = 75 м/мин скорость пассажира идущего по эскалатору.
150 : 75 = 2 мин потребуется пассажиру на подъём.
Ответ: 2 мин.1190. Стоя неподвижно на ступени эскалатора метро, человек поднимается вверх за 1 мин. Тот же человек, взбегая по ступеням неподвижного эскалатора, поднимается вверх за 40 с. За какое время тот же человек взбежит вверх по движущемуся эскалатору?
1 мин = 60 секунд.
Пусть длина эскалатора равна 1 единице, тогда:
1/60 ед./с. − скорость эскалатора;
1/40 ед./с. − скорость человека;
1/60 + 1/40 = 5/120 = 1/24 ед./с. − скорость бегущего по эскалатору человека.
1 : 1/24 = 1 ∗ 24 = 24 сек. потребуется человеку чтобы взбежать по эскалатору.
Ответ: 24 секунды.1191. Дачник пришёл от своей дачи на станцию как раз к отходу электрички. Если бы он на каждый километр тратил на 3 мин меньше, то пришёл бы на 12 мин раньше. Далеко ли от станции живёт дачник?
Пусть S км расстояние от дачи до станции, а t время прохождения этого расстояния, тогда:
t/S время за которое проходит дачник 1 км пути.
( t/S − 3 ) ∗ S = t − 12
t − 3S = t − 12
−3S = −12 + t − t
3S = 12
S = 12 : 3 = 4 км расстояние от дачи до станции.
Ответ: 4 км.1192. а) Колонна автобусов с детьми длиной 1 км двигалась по шоссе со скоростью 50 км/ч. Автоинспектору, машина которого замыкала колонну, понадобилось подъехать к головному автобусу. Сколько минут уйдёт у инспектора на путь туда и обратно, если он будет ехать со скоростью 70 км/ч?
б) Колонна солдат длиной 250 м движется со скоростью 4,5 км/ч. Из конца колонны в её начало отправляется сержант со скоростью 5,5 км/ч, затем с той же скоростью он возвращается в конец колонны. Сколько минут затратит сержант на путь туда и обратно?а) 70 − 50 = 20 км/ч относительная скорость машины автоинспектора к головному автобусу,
1/20 ч потребуется машине автоинспектора, чтобы подъехать к головному автобусу.
70 + 50 = 120 км/ч относительная скорость машины автоинспектора к концу колонны,
1/120 ч потребуется машине автоинспектора, чтобы вернуться в конец колонны.
1/20 + 1/120 = 7/120 = 3,5/60 ч или 3,5 минуты потребуется автоинспектору, что преодолеть путь туда и обратно.
б) 250 м = 250/1000 = 1/4 км
5,5 − 4,5 = 1 км/ч относительная скорость сержанта к началу колонны,
1/4 : 1 = 1/4 ч потребуется сержанту на путь к началу колонны.
5,5 + 4,5 = 10 км/ч относительная скорость машины сержанта к концу колонны,
1/4 : 10 = 1/4 ∗ 1/10 = 1/40 ч потребуется сержанту на путь к концу колонны.
1/4 + 1/40 = (10 + 1) :40 = 11/40 ч или 11/40 ∗ 60 = 11 ∗ 3 : 2 = 33/2 = 16,5 минут потребуется сержанту на путь туда и обратно.
Ответ: 16,5 мин.1193. а) Два поезда вышли одновременно навстречу друг другу с двух станций, удалённых друг от друга на 520 км. Через какое время расстояние между поездами будет равно 65 км, если их скорости 60 км/ч и 70 км/ч?
б) Два поезда, расстояние между которыми 685 км, вышли одновременно навстречу друг другу. Через какое время расстояние между поездами будет равно 95 км, если их скорости 55 км/ч и 45 км/ч?а)
Дано:
S = 520 км
S1 = 65 к м
U1 = 60 к м / ч
U2 = 70 к м / ч
Найти:
t
Решение:
S − S1 = 520 − 65 = 455 км суммарно необходимо проехать двум поездам до того момента как расстояние между ними составит 65 км.
U1 + U2 = 60 + 70 = 130 км/ч суммарная скорость двух поездов.
t = 455 : 130 = 3,5 ч будут ехать поезда, до того момента как расстояние между ними составит 65 км.
Ответ: 3,5 ч.
б) Дано:
S = 685 км
S1 = 95 к м
U1 = 55 к м / ч
U2 = 45 к м / ч
Найти:
t
Решение:
S − S1 = 685 − 95 = 590 км суммарно необходимо проехать двум поездам до того момента как расстояние между ними составит 95 км.
U1 + U2 = 55 + 45 = 100 км/ч суммарная скорость двух поездов.
t = 590 : 100 = 5,9 ч будут ехать поезда, до того момента как расстояние между ними составит 95 км.
Ответ: 5,9 ч.1194. После четырёх стирок от куска мыла осталась только третья часть. На сколько стирок хватит оставшейся части?
1 − 1/2 = 2/3 мыла было израсходовано за 4 стирки
2/3 : 4 = 2/3 ∗ 1/4 = 1/6 часть мыла расходуется на 1 стирку.
1/3 : 1/6 = 1/3 ∗ 6 = 2, на 2 стирки хватит оставшейся части.
Ответ: на 2 стирки.1195. Двум ученикам поручено подклеить в библиотеке несколько книг. Когда они закончили работу, то первый сказал, что подклеил 3/5 всех книг, а второй сказал, что подклеил 2/3 всех книг. Их товарищ заметил, что ребята ошиблись в расчётах. Как он догадался?
Все количество книг которое было поручено подклеить двум ученикам равно 1.
3/5 + 2/3 = 9 + 10/15 = 19/15 = 1 4/15
1 4/15 ≠ 1, следовательно, ребята ошиблись в расчетах. 240
-
Ответы к стр. 240
1196. В классе каждый ученик выполнил нормативы по бегу или по метанию мяча. Половина класса сдала норматив по бегу, 2/3 класса − по метанию мяча. Какая часть класса выполнила нормативы и по бегу, и по метанию мяча?
$(\frac12+\frac23)-1=\frac{3+4}6-1=\frac16$ класса выполнила норматив и по бегу и по метанию мяча.
Ответ: 1/61197. Часть студентов института изучает английский язык, часть − французский. Какая часть студентов изучает оба языка, если 3/4 всех студентов изучает английский и 1/3 французский?
$(\frac34+\frac13)-1=\frac{9+4}{12}-1=\frac{13}{12}-1=\frac1{12}$
Ответ: 1/121198. Масса наибольшего количества соли, которое растворяется в воде, составляет 9/25 массы воды. Сколько килограммов соли растворится в 5/6 ведра воды, если ведро вмещает 12 кг воды?
12 ∗ 5/6 = 2 ∗ 5 = 10 кг масса воды в ведре.
9/25 ∗ 10 = 18/5 = 3 3/5 кг может растворится в 5/6 ведра воды.
Ответ: 3 3/5 кг.1199. Из «Арифметики» Л. Н. Толстого. Муж и жена брали деньги из одного сундука, и ничего не осталось. Муж взял 7/10 всех денег, а жена 690 р. Сколько было всех денег?
1 − 7/10 = 3/10 всех денег взяла жена.
Пусть денег было x р., тогда:
3/10 x = 690
x = 690 : 3/10 = 690 ∗ 10/3 = 2300 р. было в сундуке.
Ответ: 2300 р.1200. Купивши комод за 36 р., я потом вынужден был продать его за 7/12 цены. Сколько рублей я потерял при этой продаже?
36 ∗ 7/12 = 3 ∗ 7 = 21 р. составила цена продажи.
36 − 21 = 15 р. было потеряно при продаже.
Ответ: 15 рублей.1201. Мастер сплавил 3 куска серебра в 1/4 фунта, в 1/6 фунта и в 1/8 фунта, сделал из него ложки и продал их. Сколько получил он денег, если фунт серебра ценил в 24 р. да за работу взял 8 р.?
$\frac14+\frac16+\frac18=\frac{6+4+3}{24}=\frac{13}{24}$ фунта суммарная масса сплавленного серебра.
24 ∗ 13/24 = 13 р. стоимость серебра.
13 + 8 = 21 р. получил мастер за ложки.
Ответ: 21 р.1202. Из первого крана за 2,5 мин наливается столько воды, сколько из второго за 3 мин. За сколько минут можно наполнить бак объёмом 66 л через эти два крана, если через второй кран в минуту наливается 15 л воды?
15 * 3 = 45 л наливается в бак из второго крана за 3 минуты;
45 : 2,5 = 18 л/мин − скорость потока воды из первого крана;
18 + 15 = 33 л/мин − суммарная скорость потока воды из обоих кранов;
66 : 33 = 2 мин будет заполняться бак.
Ответ: 2 мин.1203. Одна бригада за день выполняет 1/6 задания, другая 1/12 задания. За сколько дней при совместной работе бригады выполнят это задание?
$\frac16+\frac1{12}=\frac{2+1}{12}=\frac3{12}=\frac14$ задания выполняют за 1 день обе бригады.
Все задание равно 1, тогда:
1 : 1/4 = 1 ∗ 4 = 4 дня потребуется бригадам на выполнение задания.
Ответ: 4 дня.1204. Через одну трубу за минуту 1/50 наполняется бассейна, через другую 1/75 бассейна. За сколько минут бассейн наполнится через обе трубы?
$\frac1{50}+\frac1{75}=\frac{3+2}{150}=\frac5{150}=\frac1{30}$ бассейна заполняется за 1 минуту через обе трубы.
Весь объем бассейна равен 1, тогда:
1 : 1/30 = 1 ∗ 30 = 30 минут потребуется на заполнение бассейна через обе трубы.
Ответ: 30 минут. 241
-
Ответы к стр. 241
1205. а) Заготовленного корма хватило бы корове на 60 дней или овцам на 90 дней. Рассчитайте, на сколько дней хватит заготовленного корма и корове, и овцам вместе.
б) Крестьянин подсчитал, что заготовленного сена хватит для коровы на 80 дней или для овец на 120 дней. Рассчитайте, на сколько дней хватит заготовленного сена и корове, и овцам вместе.а) Весь корм = 1, тогда:
1/60 часть корма съедают коровы за 1 день;
1/90 часть корма съедают овцы за 1 день;
$\frac1{60}+\frac1{90}=\frac{3+2}{180}=\frac5{180}=\frac1{36}$ часть корма съедают коровы и овцы вместе.
1 : 1/36 = 1 ∗ 36 = 36 дней запас корма для коров и овец.
Ответ: на 36 дней.
б) Всё сено = 1, тогда:
1/80 часть сена съедают коровы за 1 день;
1/120 часть сена съедают овцы за 1 день;
$\frac1{80}+\frac1{120}=\frac{3+2}{240}=\frac5{240}=\frac1{48}$ часть сена съедают коровы и овцы вместе.
1 : 1/48 = 1 ∗ 48 = 48 дней запас сена для коров и овец.
Ответ: на 48 дней.1206. Из села в город вышел пешеход. Одновременно с ним из города в село выехал велосипедист. Пешеход пришёл в город через 6 ч, а велосипедист приехал в село через 3 ч. Через сколько часов после начала движения они встретились?
Пусть расстояние между городом и селом равно S, тогда:
S/6 − скорость пешехода;
S/3 − скорость велосипедиста;
$\frac S6+\frac S3=\frac{S+2S}6=\frac{3S}6=\frac S2$ скорость сближения пешехода и велосипедиста.
S : S/2 = S ∗ 2/S = 2 ч пройдет до встречи пешехода и велосипедиста.
Ответ: 2 ч.1207. Из пункта A в пункт B отправили плот вниз по реке. Одновременно с ним из пункта B в пункт A вышел катер, который прибыл в пункт A через 5 ч. Через сколько часов катер встретил плот, если плот прибыл в пункт B через 20 ч после начала движения?
Пусть расстояние между пунктами A и B равно S, тогда:
S/5 − скорость катера;
S/20 − скорость плота;
$\frac S5+\frac S{20}=\frac{4S+S}{20}=\frac S4$ скорость сближения катера и плота.
S : S/4 = S ∗ 4/S = 4 ч пройдет до встречи катера и плота.
Ответ: 4 ч.1208. Опытный токарь выполнит задание за 1 ч 20 мин, а его ученик − за 4 ч. За сколько минут они выполнят задание при совместной работе?
1 ч 20 мин = 80 мин; 4 ч = 240 мин;
Все задание равно 1, тогда:
1/80 − скорость работы токаря;
1/240 − скорость работы ученика;
$\frac1{80}+\frac1{240}=\frac{3+1}{240}=\frac1{60}$
1 : 1/60 = 60 минут потребуется токарю и ученику на выполнение задания.
Ответ: 60 мин.1209. Первый турист может пройти расстояние между городами за 4 ч, а второй − за 6 ч. Как−то раз они вышли одновременно из этих городов навстречу друг другу. Хватит ли им 2,5 ч на движение до встречи?
Пусть расстояние между городами равно S, тогда:
S/4 скорость первого туриста;
S/6 скорость второго туриста;
$\frac S4+\frac S6=\frac{3S+2S}{12}=\frac{5S}{12}$ скорость сближения туристов;
$S:\frac{5S}{12}=S\ast\frac{12}{5S}=\frac{12}5=\frac{24}{10}=2,4$ ч. пройдет до встречи двух туристов.
2,4 < 2,5, следовательно, 2,5 часа хватит на движение до встречи.
Ответ: хватит.1210. Первая бригада может выполнить задание за 5 недель, а вторая − за 3 недели. Хватит ли им двух недель на выполнение задания при совместной работе?
Все задание равно 1, тогда:
1/5 − скорость работы токаря;
1/3 − скорость работы ученика;
$\frac15+\frac13=\frac{3+5}{15}=\frac8{15}$
1 : 8/15 = 1 ∗ 15/8 = 1 7/8 недель потребуется обеим бригадам на выполнение задания.
1 7/8 < 2, следовательно, двух недель на выполнение задания обеими бригадами хватит.
Ответ: хватит.1211. Задача Я. И. Перельмана. Переписка доклада поручена двум машинисткам. Более опытная из них могла бы выполнить всю работу в 2 ч, менее опытная − в 3 ч. Во сколько времени перепишут они доклад, если разделят между собой работу так, чтобы выполнить её в кратчайший срок?
Весь доклад равен 1, тогда:
1/2 скорость работы более опытной машинистки;
1/3 скорость работы менее опытной машинистки;
$\frac12+\frac13=\frac{3+2}6=\frac56$ совместная скорость работы обеих машинисток;
$1:\frac56=1\ast\frac65=1\frac15=1\frac2{10}=1,2$ ч потребуется двум машинисткам на совместное выполнение задания.
Ответ: 1,2 ч.1212. Имеющихся денег хватит на школьные завтраки на 24 учебных дня или на обеды на 12 дней. На сколько дней хватит этих денег, если завтракать и обедать в школе?
Пусть денег было x, тогда:
x/24 стоит завтрак;
x/12 стоит обед.
$\frac x{24}+\frac x{12}=\frac{x+2x}{24}=\frac{3x}{24}=\frac x8$ общая стоимость обеда и завтрака.
$x:\frac x8=x\ast\frac8x$ = на 8 дней хватит денег если обедать и завтракать в школе.
Ответ: 8 дней.1213. Мама с дочкой потратили на уборку квартиры 30 мин. Одна мама убрала бы квартиру за 50 мин. За сколько минут убрала бы квартиру дочь?
Вся уборка квартиры равна 1, тогда:
1/30 − совместная скорость уборки;
1/50 − скорость уборки мамы;
$\frac1{30}-\frac1{50}=\frac{5-3}{150}=\frac2{150}=\frac1{75}$ − скорость уборки дочери.
1 : 1/75 = 75 минут потребуется дочери на уборку квартиры.
Ответ: 75 минут.1214. (Греция.) Бассейн наполняется четырьмя трубами, из которых первая может наполнить бассейн за 1 день, вторая − за 1 день, третья − за 3, четвёртая − за 4. За какое время наполнится бассейн через четыре трубы?
Весь объём бассейна равен 1, тогда:
1/1 − скорость потока из 1 трубы;
1/1 − скорость потока из 2 трубы;
1/3 − скорость потока из 3 трубы;
1/4 − скорость потока из 4 трубы;
$\frac11+\frac11+\frac13+\frac14=\frac{12+12+4+3}{12}=\frac{31}{12}$ − суммарная скорость потока из 4 труб.
1 : 31/12 = 1 * 12/31 = 12/31 дня потребуется на заполнения бассейна четырьмя трубами.
Ответ: 12/31 242
-
Ответы к стр. 242
1215. Две машины выехали одновременно навстречу друг другу из городов A и B и встретились через 3 ч. Ещё через 2 ч легковая машина прибыла в город B. За сколько часов грузовая машина доехала от города B до города A?
Пусть расстояние между городами равно S, тогда:
S/3 − скорость сближения автомобилей;
3 + 2 = 5 часов потребовалось на преодоления расстояния легковой машине;
S/5 − скорость легковой автомобиля;
$\frac S3-\frac S5=\frac{5S-3S}{15}=\frac{2S}{15}$ − скорость грузового автомобиля;
$S:\frac{2S}{15}=S\ast\frac{15}{2S}=\frac{15}2=7\frac12=7,5$ часа потребуется грузовому автомобилю на преодоление расстояния.
Ответ: 7,5 часа.1216. В хозяйстве под картофель занята площадь в 3 раза большая, чем под капусту. Под капусту занято на 36 га меньше, чем под картофель. Какая площадь занята под картофель?
Пусть под капусту занято x га, тогда:
3x га занято под картофель и x + 36 га занято под картофель.
3x = x + 36
2x = 36
x = 36 : 2 = 18 га занято под капусту;
18 + 36 = 54 га занято под картофель.
Ответ: 54 га.1217. Первая глава книги содержит в 3 раза меньше страниц, чем две другие, вместе взятые. Три главы вместе содержат 276 страниц. Сколько страниц в первой главе?
Пусть в первой главе x страниц, тогда:
3x страниц содержат две другие главы;
x + 3x = 276
4x = 276
x = 276 : 4 = 69 страниц в первой главе.
Ответ: 69 страниц.1218. Мост длиной 324 м имеет четыре пролёта, из которых два в 2 раза короче двух других, имеющих одинаковую длину. Определите длины пролётов моста.
Пусть длина двух коротких пролетов x м, тогда:
2x м длина двух длинных пролетов.
x + 2x = 324
3x = 324
x = 108 м длина двух коротких пролетов,
108 : 2 = 54 м длина каждого из коротких пролетов,
54 * 2 = 108 м длина каждого из длинных пролетов.
Ответ: 54 м и 108 м.1219. Кенгуру прыгает в длину на расстояние, в 4 раза большее, или на 9 м большее, чем в высоту. На какое расстояние кенгуру прыгает в длину?
Пусть в высоту кенгуру прыгает на x м, тогда:
на 4x м и x + 9 м прыгает кенгуру в длину.
4x = x + 9
3x = 9
x = 9 : 3 = 3 м высота прыжка кенгуру,
4 * 3 = 12 м длина прыжка кенгуру.
Ответ: 12 м.1220. Слон в 5 раз тяжелее белого медведя. Белый медведь на 3,6 т легче слона. Сколько весит каждое животное?
Пусть медведь весит x т, тогда:
5x т или x + 3,6 т весит слон.
5x = x + 3,6
4x = 3,6
x = 3,6 : 4 = 0,9 т весит медведь,
5 * 0,9 = 4,5 т весит слон.
Ответ:
0,9 т весит медведь,
4,5 т весит слон.1221. Для участия в эстафете ребята разделились на две команды. Чтобы участников эстафеты в командах стало поровну, учитель перевёл 3 человека из одной команды в другую. На сколько человек первоначально в одной команде было больше, чем в другой?
Пример
Укажите правильно составленное уравнение по условию задачи:
x − 3 = y + 3
x + 3 = y − 3
x + 3 = y + 3
x − 3 = y − 3
После того, как 3 человека перевили из одной команды в другую, количество человек в командах сравнялось.Решение:
Пусть в одной команде было x человек, а в другой y, тогда:
x − 3 человек осталось в одной команде после того, как из нее забрали 3 человека.
y + 3 человека стало в другой команде после того, как в нее добавили 3 человека.
Так как количество человек в командах стало поровну, то:
x − 3 = y + 3
x − y = 3 + 3 = 6 человек разница между командами, которая была изначально.
Ответ: 6 человек.1222. У Саши и Вити вместе 160 марок. После того как Саша дал Вите 15 марок, а Витя дал Саше 19 марок, число марок у мальчиков стало одинаковым. Сколько марок было у каждого мальчика первоначально?
Пусть у Саши было x марок, тогда:
160 − x марок было у Вити;
x − 15 + 19 = x + 4 марки стало у Саши;
160 − x + 15 − 19 = 156 − x марок стало у Вити;
x + 4 = 156 − x
x + x = 156 − 4
2x = 152
x = 152 : 2 = 76 марок было у Саши первоначально,
160 − 76 = 84 марки было у Вити.
Ответ:
76 марок было у Саши,
84 марки было у Вити.1223. В двух мешках 250 телефонных жетонов. Если из одного мешка переложить в другой 25 жетонов, то количества жетонов в мешках сравняются. Сколько жетонов в каждом мешке?
Пусть в первом мешке x жетонов, тогда:
250 − x жетонов во втором мешке.
x − 25 жетонов осталось в первом мешке,
250 − x + 25 = 275 − x жетонов стало во втором мешке, тогда:
x − 25 = 275 − x
x + x = 275 + 25
2x = 300
x = 300 : 2 = 150 жетонов было в первом мешке,
250 − 150 = 100 жетонов было во втором мешке.
Ответ: 150 и 100 жетонов.1224. а) Сумма числителя и знаменателя дроби равна 32, числитель на 2 меньше знаменателя. Найдите эту дробь.
б) Числитель на 8 больше знаменателя, сумма числителя и знаменателя равна 34. Найдите эту дробь.а) Пусть искомая дробь равна a/b, тогда:
a + b = 32
a + 2 = b
a + a + 2 = 32
2a = 32 − 2
2a = 30
a = 30 : 2 = 15
b = 15 + 2 = 17, следовательно, искомая дробь равна 15/17
Ответ: 15/17.
б) Пусть искомая дробь равна a/b, тогда:
a + b = 34
a − 8 = b
a + a − 8 = 34
2a = 34 + 8
2a = 42
a = 42 : 2 = 21
b = 21 − 8 = 13, следовательно, искомая дробь равна 21/13
Ответ: 21/13.1225. Между городами A и B расстояние 331 км. На пути из A в B есть город C, расстояние от которого до города A на 17 км больше, чем до города B. Найдите расстояние от A до C и от B до C.
Пусть расстояние между городами A и C равно S, тогда:
331 − S км или S − 17 − расстояние от C до B, следовательно:
331 − S = S − 17
−2S = −17 − 331
2S = 348
S = 348 : 2 = 174 км расстояние от A до C,
174 − 17 = 157 км расстояние от C до B.
Ответ:
174 км расстояние от A до C,
157 км расстояние от C до B. 243
-
Ответы к стр. 243
1226. а) Книга в переплёте стоит 5 р. Книга на 4 р. дороже переплёта. Сколько стоит переплёт? б) Бутылка масла стоит 10 р. Масло на 9 р. дороже бутылки. Сколько стоит масло?
а) Пусть переплет стоит x, тогда:
x + 4 р. стоит книга;
x + x + 4 = 5
2x = 5 − 4
2x = 1
x = 1 : 2 = 0,5 р. или 50 копеек стоит переплет.
Ответ: 50 копеек.
б) Пусть масло стоит x, тогда:
x − 9 р. стоит бутылка;
x + x − 9 = 10
2x = 10 + 9
2x = 19
x = 19 : 2 = 9,5 р. или 9 рублей 50 копеек стоит масло.
Ответ: 9 р. 50 копеек.1227. Три доярки обслуживают на ферме 125 коров. Сколько доярок потребуется для обслуживания 625 коров при той же норме?
125 : 3 = 125/3 коров обслуживает одна доярка,
625 : 125/3 = 625 ∗ 3/125 = 5 ∗ 3 = 15 доярок понадобится для обслуживания 625 коров.
Ответ: 15 доярок.1228. С конвейера автозавода каждые полторы минуты сходит один автомобиль. Сколько автомобилей выпускает завод за 1 ч?
1/1,5 = 10/15 = 2/3 части автомобиля выпускается в минуту.
1 ч = 60 мин, тогда:
60 ∗ 2/3 = 20 ∗ 2 = 40 автомобилей сходит с конвейера за час.
Ответ: 40 автомобилей.1229. На некотором участке заменили старые рельсы длиной 8 м новыми рельсами длиной 12 м.
а) Сколько потребуется новых рельсов, если сняли 240 старых рельсов?
б) Сколько сняли старых рельсов, если установили 240 новых рельсов?а) 240 * 8 = 1920 м общая длина старых рельс;
1920 : 12 = 160 новых рельс потребуется.
Ответ: 160 рельс.
б) 240 * 12 = 2880 м общая длина новых рельс;
2880 : 8 = 360 старых рельс сняли.
Ответ: 360 рельс.1230. Колесо, окружность которого 1,5 м, сделало на некотором расстоянии 96 оборотов. Сколько оборотов на том же расстоянии сделает колесо, окружность которого 2,4 м?
1,5 * 96 = 144 м проехало колесо окружностью 1,5 м;
144 : 2,4 = 60 оборотов сделает колесо, окружность которого 2,4 м.
Ответ: 60 оборотов.1231. Для 16 голов скота на 36 дней требуется 1,92 т сухой подстилки. Сколько сухой подстилки требуется для 20 голов скота на 40 дней?
1,92 : 16 = 0,12 т сухой подстилки требуется на 1 голову на 36 дней;
0,12 : 36 = 0,12/36 = 12/3600 = 1/300 т сухой подстилки требуется на 1 голову в день.
1/300 ∗ 20 = 2/30 = 1/15 т сухой подстилки требуется на 20 голов в день;
1/15 ∗ 40 = 8/3 = 2 2/3 т сухой подстилки требуется на 20 голов на 40 дней.
Ответ: 2 2/3 т1232. Из A в B вышел пешеход со скоростью 4,8 км/ч. Одновременно с ним из B в A выехал велосипедист со скоростью 10 км/ч, который доехал до A, повернул назад и поехал с той же скоростью. Догонит ли велосипедист пешехода до его прихода в B?
Пусть расстояние от A до B равно S, тогда:
$\frac S{4,8}=\frac{10S}{48}=\frac5{24}S$ ч потребуется пешеходу чтобы пройти расстояние от A до B.
$\frac S{10}\ast2=\frac15S$ ч потребуется велосипедисту, чтобы доехать от B до A и вернуться обратно.
$\frac5{24}S=\frac{25}{120}$, а $\frac15S=\frac{24}{120}S$, тогда:
25/120 > 24/120, следовательно, пешеход затратил на дорогу времени больше, чем велосипедист, а это значит что велосипедист догонит пешехода.
Ответ: догонит.1233. а) За 1 ч бригада маляров покрасила половину стены дома. Оставшуюся часть стены покрасил один человек за 4 ч. Сколько маляров в бригаде?
б) Бригада за полдня выполнила 3/4 задания. Оставшуюся часть задания выполнил один человек за полдня. Сколько человек в бригаде?
в) Бригада плотников выполнила 3/5 задания за полдня. Оставшуюся часть задания выполнил один плотник за день. Сколько плотников в бригаде?
г) Задача Л. Н. Толстого. Косцы должны выкосить два луга. Начав с утра косить большой луг, они после полудня разделились: одна половина осталась на первом луге и к вечеру его докосила, а другая − перешла косить на второй луг, площадью вдвое меньше первого. Сколько было косцов, если известно, что в течение следующего дня оставшуюся часть работы выполнил один косец?а) Вся стена равна 1, тогда:
1/2 − половина стены,
1 − 1/2 = 1/2 стены осталось покрасить,
1/2 : 4 = 1/2 ∗ 1/4 = 1/8 стены красит 1 маляр за 1 час.
1/2 : 1/8 = 1/2 ∗ 8 = 4 маляра было в бригаде.
Ответ: 4 маляра.
б) Все задание равно 1, тогда:
1 − 3/4 = 1/4 задания доделывал 1 человек полдня, то есть 1 4 это скорость выполнения задания 1 человеком за полдня,
3/4 : 1/4 = 3/4 ∗ 4 = 3 человека было в бригаде.
Ответ: 4 человека.
в) Все задание равно 1, тогда:
1 − 3/5 = 2/5 задания доделывал 1 человек 1 день,
2/5 : 2 = 2/5 ∗ 1/ 2 = 2/10 = 1/5 задания выполняет 1 человек за полдня.
3/5 : 1/5 = 3/5 ∗ 5 = 3 человека было в бригаде.
Ответ: 3 человека.
г) Пусть:
косцов было x;
скорость одного косца v скашиваемой площади в день, тогда:
xv − площадь скашиваемого участка всеми косцами в день.
$\frac{xv}2$ − площадь скашиваемого участка всеми косцами за полдня.
$\frac{xv}2+\frac12\ast\frac{xv}2=\frac{xv}2+\frac{xv}4=\frac{2xv+1xv}4=\frac{3xv}4$ − площадь большого луга;
$\frac12\ast\frac{xv}2+v=\frac{xv}4+v=\frac{xv+4v}4$ − площадь маленького луга.
Так как, по условию задачи площадь большого луга в 2 раза больше первого, то:
$\frac{3xv}4:\frac{xv+4v}4=2$
$\frac{3xv}4\ast\frac4{xv+4v}=2$
$\frac{3xv}{xv+4v}=2$
3xv = 2(xv + 4v)
3xv = 2xv + 8v
3xv − 2xv = 8v
xv = 8v
x = 8v : v = 8 косцов было.
Ответ: 8 косцов. 244
-
Ответы к стр. 244
1234. 10 ветряных мельниц смололи 200 четвертей ржи в 12 дней, работая в день по 14 ч. По сколько часов в день должны работать 8 таких же мельниц, чтобы в 21 день смолоть 300 четвертей ржи?
12 * 14 = 168 часов работали мельницы за 12 дней.
200 : 10 = 20 четвертей ржи смолола 1 мельница за 168 ч.
20 : 168 = 20/168 = 5/42 четверти в час производительность одной мельницы.
8 ∗ 5/42 = 20/21 четверти производительность 8 мельниц в час.
Пусть мельницы будут работать по x часов, тогда:
20/21 x − четверти производительность 8 мельниц в день.
20/21 x ∗ 21 = 300
20x = 300
x = 300 : 2 = 15 часов в день должны работать 8 мельниц, чтобы перемолоть 300 четвертей ржи.
Ответ: 15 часов.1235. а) Картофель содержит 20% крахмала. Сколько картофеля надо взять для получения 200 кг крахмала?
б) При помоле ржи получается 75% муки. Сколько ржи надо взять, чтобы получить 200 кг муки?
в) При помоле пшеницы получается 80% муки. Сколько пшеницы надо взять, чтобы получить 200 кг муки?
г) Получаемый при сушке винограда изюм составляет 32 % от массы винограда. Из скольких килограммов винограда получится 4 кг изюма?а) 20% = 0,2
200 : 0,2 = 1000 кг картофеля надо взять для получения 200 кг крахмала.
Ответ: 1000 кг.
б) 75% = 0,75
200 : 0,75 = 200 : 75/100 = 200 ∗ 100/75 = 800/3 = 266 2/3 кг ржи надо взять, чтобы получить 200 кг муки.
Ответ: 266 2/3 кг.
в) 80% = 0,8
200 : 0,8 = 250 кг пшеницы надо взять, чтобы получить 200 кг муки.
Ответ: 250 кг.
г) 32% = 0,32
4 : 0,32 = 12,5 кг винограда надо взять, чтобы получить 24 кг изюма.
Ответ: 12,5 кг.1236. а) Найдите число, 20 % которого составляют 50 % от 200.
б) Найдите число, 10% которого составляют 60% от 300.а) 200 * 50% = 200 * 0,5 = 100
100 : 0,2 = 500
Ответ: 500
б) 300 * 60% = 300 * 0,6 = 180
180 : 0,1 = 1800
Ответ: 18001237. В 800 г воды растворили 20 г соли. Какова концентрация раствора в процентах?
800 + 20 = 820 г масса раствора
20/820 ∗ 100% концентрация соли в процентах.
Ответ: 2 18/41%1238. а) Рубашка стоила 150 р. После снижения цены она стоит 120 р. На сколько процентов снижена цена рубашки?
б) Товар стоил 690 р. После снижения цены он стоит 621 р. На сколько процентов снижена цена товара?а) 150 − 120 = 30 р. снижение цены рубашки.
30/150 ∗ 100 снижение цены рубашки.
Ответ: на 20%
б) 690 − 621 = 69 р. снижение цены товара.
69/690 ∗ 100 снижение цены товара.
Ответ: на 10%1239. Агроном подсчитал, что имеющиеся в хозяйстве удобрения составляют 80% того, что потребуется в текущем году. На сколько процентов надо увеличить имеющийся запас удобрений, чтобы полностью обеспечить потребности хозяйства?
Пусть необходимо х удобрений, тогда:
0,8х удобрений имеется,
$\frac{\operatorname х}{0,8{\operatorname х}}\ast100=\frac{10}8\ast100$ на 125% надо увеличить имеющийся запас удобрений, чтобы полностью обеспечить потребности хозяйства.
Ответ: на 125%1240. Два мальчика собрали 420 марок, и у одного из них оказалось на 10% больше марок, чем у другого. Сколько марок было у другого?
Пусть у мальчика с меньшим количеством марок было x марок, тогда:
420 − x марок было у другого мальчика,
(420 − x) − x = 0,1x
420 − x − x = 0,1x
−x − x − 0,1x = −420
−2,1x = −420
x = −420 : (−2,1) = 200 марок было у мальчика с меньшим количеством марок.
420 − 200 = 220 марок было у другого мальчика.
Ответ: 200 и 220.1241. На заводе 35 % всех работающих − женщины, а остальные − мужчины, которых на 504 человека больше, чем женщин. Сколько всего рабочих на заводе?
100% − 35% = 65% мужчин.
Пусть всего x рабочих, тогда:
0,35x − женщины;
0,65x − мужчины.
0,65x − 0,35x = 504
0,3x = 504
x = 504 : 0,3 = 1680 человек работаю на заводе.
Ответ: 1680 человек.1242. а) Разность чисел равна 20. Одно из них больше другого на 40%. Найдите меньшее число.
б) Разность чисел равна 20. Одно из них меньше другого на 40%. Найдите меньшее число.а) Пусть искомые числа а и b, где a > b, тогда:
a − b = 20;
a больше b на 40% поэтому:
a = b + 0,4b = 1,4b.
1,4b − b = 20
0,4b = 20
b = 20 : 0,4 = 50
Ответ: 50
б) Пусть искомые числа а и b, где a > b, тогда:
a − b = 20;
b меньше a на 40% поэтому:
b = a − 0,4a = 0,6a.
a − 0,6a = 20
0,4a = 20
a = 20 : 0,4 = 50
50 − b = 20
b = 50 − 20 = 30
Ответ: 301243. В коллекции имеется 12 жуков и пауков. У всех вместе у них 80 ног. Сколько в коллекции жуков и сколько пауков? (У жука 6 ног, у паука 8.)
Пусть жуков x, тогда:
12 − x пауков.
6x − ног у всех жуков;
(12 − x) * 8 = 96 − 8x − ног у всех пауков.
6x + 96 − 8x = 80
−2x = 80 − 96
2x = 16
x = 8 жуков.
12 − 8 = 4 паука.
Ответ: 8 жуков и 4 паука. 245
-
Ответы к стр. 245
1244. Задача Д. Пойи. Торговец продаёт орехи двух сортов: одни по 90 центов, другие по 60 центов за килограмм. Он хочет получить 50 кг смеси по 72 цента за килограмм. Сколько для этого потребуется орехов каждого сорта?
Пусть в смеси x кг по 90 центов за кг, тогда:
50 − x кг орехов по 60 центов за кг.
90x − стоимость орехов первого типа;
(50 − x) * 60 = 3000 − 60x − стоимость орехов второго типа.
50 * 72 = 3600 стоимость смеси.
90x + 3000 − 60x = 3600
90x − 60x = 3600 − 3000
30x = 600
x = 600 : 30 = 20 кг орехов по 90 центов за кг будет в смеси.
50 − 20 = 30 кг орехов по 60 центов за кг будет в смеси.
Ответ: 20 кг орехов по 90 центов за кг и 30 кг орехов по 60 центов за кг будет в смеси.1245. Пешеход прошёл расстояние между сёлами со скоростью 4 км/ч. Если бы он проходил в час на 1 км больше, то ему потребовалось бы на тот же путь на 1 ч меньше. Сколько времени шёл пешеход и какой путь он прошёл?
Пусть расстояние равно S, тогда:
S/4 ч время за которое пешеход прошел расстояние со скоростью 4 км/ч,
4 + 1 = 5 км/ч − новая скорость пешехода.
S/5 ч время за которое пешеход прошел расстояние со скоростью 5 км/ч.
S/4 − S/5 = 1
$\frac{5S-4S}{20}=1$
S/20 = 1
S = 1 * 20 = 20 км расстояние между селами.
20 : 4 = 5 ч шел пешеход со скоростью 4 км/ч,
20 : 5 = 4 ч шел пешеход со скоростью 5 км/ч.
Ответ:
расстояние 20 км;
5 ч шел пешеход со скоростью 4 км/ч,
4 ч шел пешеход со скоростью 5 км/ч.1246. Поезд прошёл расстояние между двумя городами со скоростью 80 км/ч. Если бы его скорость была на 20 км/ч меньше, то ему потребовалось бы на эту поездку на 1 ч больше. Найдите расстояние между двумя городами.
Пусть расстояние равно S, тогда:
S/80 ч время за которое поезд проехал расстояние со скоростью 80 км/ч,
80 − 20 = 60 км/ч − новая скорость поезда.
S/60 ч время за которое поезд проехал расстояние со скоростью 60 км/ч.
S/60 − S/80 = 1
$\frac{4S-3S}{240}=1$
S/240 = 1
S = 1 * 240 = 240 км расстояние между городами.
Ответ: 240 км1247. Тракторист может вспахать поле за 5 дней. Увеличив выработку на 2,5 га в день, он выполнил работу за 4 дня. Какова площадь поля?
Пусть площадь поля x га, тогда:
x/5 га производительность тракториста в день при работе 5 дней,
x/4 га производительность тракториста в день при работе 4 дня.
x/4 − x/5 = 2,5
$\frac{5x-4x}{20}=2,5$
x/20 = 2,5
x = 2,5 * 20 = 50 га.
Ответ: 50 га1248. Чтобы выполнить задание к сроку, цех должен был в день изготавливать по 30 приборов. Повысив производительность труда, рабочие цеха стали изготавливать в день по 34 прибора и выполнили задание на 2 дня раньше срока. Сколько приборов нужно было изготовить по плану и за сколько дней?
Пусть задание надо было выполнить за x дней, тогда:
x − 2 дней работал цех при производительности 34 прибора в день.
30x приборов всего изготовил цех при производительности 30 приборов в день.
34(x − 2) = 34x − 68 приборов всего изготовил цех при производительности 34 прибора в день.
Так как и при первой и при второй производительности цех изготовил одинаковое количество приборов, то:
30x = 34x − 68
30x − 34x = −68
−4x = −68
x = −68 : (−4) = 17 дней работал цех при производительности 30 приборов в день.
17 * 30 = 510 приборов необходимо было изготовить по плану
Ответ: за 17 дней цех должен изготовить 510 приборов.1249. Завод получил заказ на изготовление некоторого числа машин к определённому сроку. Если завод будет выпускать ежедневно по 250 машин, то к сроку будет изготовлено на 1000 машин меньше, чем заказано. Если же завод будет выпускать ежедневно по 320 машин, то к сроку будет изготовлено на 400 машин больше, чем заказано. Сколько машин надо изготавливать в день, чтобы выполнить заказ в срок?
Пусть заказано x машин, тогда:
x − 1000 машин будет изготовлено при производительности 250 машин в день,
x + 400 машин будет изготовлено при производительности 320 машин в день.
$\frac{x-1000}{250}$ количество дней работы завода при производительности 250 машин в день,
$\frac{x+400}{320}$ количество дней работы завод при производительности 320 машин в день.
Так как срок заказа был неизменным, то:
$\frac{x-1000}{250}=\frac{x+400}{320}$
320x − 320000 = 250x + 100000
320x − 250x = 100000 + 320000
70x = 420000
x = 420000 : 70 = 6000 машин было заказано.
Пусть необходимо изготавливать y машин в день, тогда:
6000/y количество дней работы завода при правильной производительности.
Так как срок заказа был неизменным, то:
$\frac{6000}y=\frac{6000-1000}{250}$
$\frac{6000}y=\frac{5000}{250}$
6000 * 250 = 5000y
$y=\frac{6000\ast250}{5000}=6\ast50=300$ машин в день необходимо изготавливать.
Ответ: 300 машин в день.1250. Если раздать учащимся по 1 тетради, останется 36 тетрадей, а если раздать по 3 тетради, не хватит 12. Сколько тетрадей и сколько учащихся?
Пусть всего x учащихся, тогда:
x * 1 + 36 − общее количество тетрадей,
x * 3 + 12 − общее количество тетрадей, следовательно:
x + 36 = 3x − 12
x − 3x = −12 − 36
−2x = −48
x = −48 : (−2) = 24 учащимся раздавали тетради.
24 + 36 = 60 тетрадей было.
Ответ: 24 учащихся и 60 тетрадей.1251. Ученики собираются выписать газету. Если они соберут с каждого по 15 к., то им не хватит 2 р., а если каждый внесёт по 25 к., то получится лишних 2 р. Сколько было учеников? Сколько стоит подписка на газету?
2 р. = 200 коп.
Пусть всего x учеников, тогда:
x * 15 + 200 − необходимое количество денег на подписку газеты,
x * 25 − 200 − необходимое количество денег на подписку газеты, следовательно:
15x + 200 = 25x − 200
15x − 25x = −200 − 200
−10x = −400
x = −400 : (−10) = 40 учеников было.
40 * 15 + 200 = 600 + 200 = 800 коп. = 8 р. стоит подписка на газету.
Ответ: 40 учеников и 8 рублей.1252. (Китай, 1в.) Сообща покупают вещь. Если каждый человек внесёт по 8 (денежных единиц), то избыток равен 3. Если каждый человек внесёт по 7, то недостаток равен 4. Спрашивается количество людей и стоимость вещи.
Пусть всего x человек, тогда:
x * 8 − 3 − цена вещи,
x * 7 + 4 − цена вещи, следовательно:
8x − 3 = 7x + 4
8x − 7x = 4 + 3
x = 7 человек было.
8 * 7 − 3 = 56 − 3 = 53 денежные единицы цена вещи.
Ответ: было 7 человек, 53 денежные единицы цена вещи. 246
-
Ответы к стр. 246
1253. (Китай, II в.) Сообща покупают курицу. Если каждый человек внесёт по 9 (денежных единиц), то останется 11, если же каждый внесёт по 6, то не хватит 16. Найти число людей и стоимость курицы.
Пусть всего x человек, тогда:
x * 9 − 11 − цена курицы,
x * 6 + 16 − цена курицы, следовательно:
9x − 11 = 6x + 16
9x − 6x = 16 + 11
3x = 27
x = 27 : 3 = 9 человек было.
9 * 9 − 11 = 81 − 11 = 70 денежных единиц цена курицы.
Ответ: было 9 человек, 70 денежных единиц цена курицы.1254. Задача Я. И. Перельмана. Двое очистили 400 штук картофеля; один очищал 3 штуки в минуту, другой − 2. Второй работал на 25 мин больше, чем первый. Сколько времени работал каждый?
Пусть первый работал x мин., тогда:
x + 25 мин. работал второй
3x − количество картофеля, почищенного первым человеком,
2(x + 25) = 2x + 50 − количество картофеля, почищенного вторым человеком.
3x + 2x + 50 = 400
5x = 400 − 50
x = 350 : 5 = 70 мин. работал первый человек.
70 + 25 = 95 мин. работал второй человек.
Ответ: первый − 70 мин., второй − 95 мин.1255. Слон может бежать со скоростью, на 25 км/ч большей, чем медведь. Скорость медведя составляет 2/7 скорости слона. С какой скоростью может бежать каждое животное?
Пусть скорость слона x км/ч, тогда:
x − 25 или 2/7 x км/ч составляет скорость медведя.
x − 25 = 2/7 x
x − 2/7 x = 25
5/7 x = 25
x = 25 : 5/7 = 25 ∗ 7/5 = 5 ∗ 7 = 35 км/ч скорость слона.
35 − 25 = 10 км/ч скорость медведя.
Ответ:
35 км/ч − скорость слона;
10 км/ч − скорость медведя.1256. Первая бригада может выполнить задание за 56 ч, а вторая − за 112 ч. Мастер рассчитал, что работу можно организовать так, что сначала над выполнением задания будет работать первая бригада несколько дней (по 8 ч), а затем − вторая. При этом задание будет выполнено за 8 дней. Сколько дней должна работать каждая бригада?
56 : 8 = 7 дней потребуется первой бригаде на выполнение задания.
112 : 8 = 14 дней потребуется второй бригаде на выполнение задания.
Пусть все задание равно 1, тогда:
1/7 − производительность первой бригады в день;
1/14 − производительность второй бригады в день.
Пусть первая бригада будет работать x дней, тогда:
8 − x дней будет работать вторая бригада.
x/7 часть задания которую выполнит первая бригада,
1/14 ( 8 − x ) = 8/14 − x/14 = 4/7 − x/14 часть задания которую выполнит вторая бригада.
Так как в сумме обе бригады выполнят все задание, то:
x/7 + 4/7 − x/14 = 1
$\frac{2x}{14}-\frac x{14}=1-\frac47$
x/14 = 3/7
x = 3/7 ∗ 14 = 6 дней будет работать первая бригада.
8 − 6 = 2 дня будет работать вторая бригада.
Ответ:
6 дней будет работать первая бригада;
2 дня будет работать вторая бригада.1257. На пришкольном участке один класс откопал 7/20 всех деревьев, другой 3/5 остатка, а третий остальные 52 дерева. Сколько деревьев на пришкольном участке?
Пусть всего было x деревьев, тогда:
7/20 x деревьев откопал первый класс.
$\frac35(x-\frac7{20}x)=\frac35\ast\frac{13}{20}x=\frac{39}{100}x$ деревьев откопал второй класс.
$\frac7{20}x+\frac{39}{100}x+52=x$
$\frac7{20}x+\frac{39}{100}x-x=-52$
$\frac{35}{100}x+\frac{39}{100}x-x=-52$
$\frac{74}{100}x-x=-52$
$-\frac{26}{100}x=-52$
$x=-52:-\frac{26}{100}=52\ast\frac{100}{26}=2\ast100=200$ деревьев было.
Ответ: 2001258. Рабочий израсходовал 2/35 зарплаты на уплату за квартиру, 5/22 оставшихся денег на покупку вещей. После этого у него осталось на 320 р. больше, чем он израсходовал. Какова зарплата рабочего?
Пусть зарплата x р., тогда:
2/35 x р. рабочий заплатил за квартиру,
x − 2/35 x = 33/35 x р. денег осталось.
33/35 x ∗ 5/22 = 3/14 x р. рабочий потратил на покупку вещей.
$\frac2{35}x+\frac3{14}x=\frac{4+15}{70}x=\frac{19}{70}x$ р. израсходовал рабочий.
19/70 x + 320 р. у рабочего осталось.
19/70 x + 19/70 x + 320 = x
19/35 x − x = − 320
− 16/35 x = − 320
x = − 320 : ( − 16/35 ) = 320 ∗ 35/16 = 20 ∗ 35 = 700 р . зарплата рабочего.
Ответ: 700 р.1259. В два магазина завезли яблок поровну. В первом магазине продали треть всех яблок и ещё 30 кг, во втором магазине продали четверть всех яблок и ещё 40 кг. После чего оказалось, что яблок в магазинах продали поровну. Сколько яблок завезли в каждый магазин первоначально?
Пусть в каждый магазин завезли по x кг яблок, тогда:
1/3 x + 30 кг яблок продали в первом магазине;
1/4 x + 40 кг яблок продали во втором магазине.
Так как яблок в обоих магазинах продали поровну, то:
1/3 x + 30 = 1/4 x + 40
1/3 x + 1/4 x = 40 − 30
$\frac{4-3}{12}x=10$
1/12 x = 10
x = 10 : 1/12 = 10 ∗ 12 = 120 кг яблок было изначально в каждом магазине.
Ответ: 120 яблок.1260. В нашем классе мальчиков и девочек поровну. На школьный вечер пришли половина всех мальчиков и ещё 3 мальчика, треть всех девочек и ещё 6 девочек. Оказалось, что на школьный вечер пришло мальчиков и девочек поровну. Сколько всего учащихся в нашем классе?
Так как количество мальчиков и девочек равно, то пусть количество мальчиков равно x и количество девочек равно x, тогда:
1/2 x + 3 мальчика пришло на вечер;
1/3 x + 6 девочек пришло на вечер.
Так как на школьный вечер мальчиков и девочек пришло поровну, то:
1/2 x + 3 = 1/3 x + 6
1/2 x − 1/3 x = 6 − 3
1/6 x = 3
x = 3 : 1/6 = 3 ∗ 6 = 18 мальчиков и 18 девочек учится в классе.
18 + 18 = 36 учеников в классе.
Ответ: 36 учеников.1261. На вопрос: «Который час?» − был дан ответ: «2/5 прошедших часов от полуночи до сего времени равны 2 3 часов, оставшихся до полудня». Спрашивается, сколько сейчас времени.
Пусть от полуночи прошло x часов, тогда:
12 − x часов осталось до полудня.
2/5 x,
2/3 ( 12 − x ) = 2/3 ∗ 12 − 2/3x = 8 − 2/3 x.
2/5 x = 8 − 2/3 x
2/5 x + 2/3 x = 8
6 + 10/15 x = 8
16/15 x = 8
x = 8 : 16/15 = 8 ∗ 15/16 = 15/2 = 7 1/2 = 7,5ч или 7 часов 30 минут утра.
Ответ: 7 ч 30 минут утра. 247
-
Ответы к стр. 247
1262. Верёвку длиной 28 м надо разрезать на 3 части так, чтобы вторая часть была в 3,5 раза, а третья − в 2,5 раза больше первой. Найдите длину каждой части.
Пусть длина первой части веревки равна x м, тогда:
3,5x м длина второй части веревки;
2,5x м длина третей части веревки.
x + 3,5x + 2,5x = 28
7x = 28
x = 28 : 7 = 4 м длина первой части веревки,
3,5 * 4 = 14 м длина второй части веревки,
2,5 * 4 = 10 м длина третьей части веревки.
Ответ:
4 м длина первой части веревки,
14 м длина второй части веревки,
10 м длина третьей части веревки.1263. Один человек спросил своего приятеля:
− Сколько лет твоему сыну?
− Если к возрасту моего сына прибавить столько же да ещё половину, то будет 10 лет. Сколько же лет сыну?Пусть сыну x лет, тогда:
1/2 x половина лет сына.
x + x + 1/2 x = 10
5/2 x = 10
x = 10 : 5/2 = 10 ∗ 2/5 = 4 года сыну.
Ответ: 4 года.1264. Одного человека спросили: «Сколько Вам лет?» На что он ответил: «Когда я проживу ещё половину, да треть, да четверть моих теперешних лет, тогда мне будет 100 лет». Сколько лет этому человеку?
Пусть человеку x лет, тогда:
1/2 x половина лет человека;
1/3 x треть лет человека;
1/4 x четверть лет человека;
x + 1/2 x + 1/3 x + 1/4 x = 100
12 + 6 + 4 + 3/12 x = 100
25/12 x = 100
x = 100 : 25/12 = 100 ∗ 12/25 = 4 ∗ 12 = 48 лет человеку.
Ответ: 48 лет.1265. Летит стая гусей и навстречу ей один гусь.
− Здравствуйте, сто гусей! − сказал гусь.
− Нас не сто, − ответил вожак стаи.− Вот если бы нас было столько, ещё столько, да полстолько, да четверть столько, да ещё ты, гусь, с нами − вот тогда бы нас было сто гусей. Сколько гусей было в стае?Пусть в стае было x гусей, тогда:
1/2 x половина гусей;
1/4 x четверть гусей;
x + x + 1/2 x + 1/4 x + 1 = 100
$\frac{4+4+2+1}4x=100-1$
11/4 x = 99
x = 99 : 11/4 = 99 ∗ 4/11 = 9 ∗ 4 = 36 гусей было в стае.
Ответ: 36 гусей.1266. У мальчика в коллекции было 210 российских марок и 65 иностранных. Когда ему подарили ещё 25 марок, то российских марок стало в 3 раза больше, чем иностранных. Сколько российских марок подарили мальчику?
Пусть подарили x российских марок, тогда:
25 − x подарили иностранных марок.
210 + x стало российских марок,
65 + 25 − x = 90 − x стало иностранных марок,
$\frac{210+x}{90-x}=3$
210 + x = 3 ( 90 − x )
210 + x = 270 − 3 x
x + 3 x = 270 − 210
4 x = 60
x = 60 : 4 = 15 российских марок подарили.
Ответ: 15 российских марок.1267. Отцу 32 года, сыну 8 лет. Через сколько лет отец будет:
а) в 3 раза старше сына;
б) в 5 раз старше сына?а) Пусть отец станет старше сына в 3 раза через x лет, тогда:
32 + x лет будет отцу;
8 + x лет будет сыну;
$\frac{32+x}{8+x}=3$
32 + x = 3(8 + x)
32 + x = 24 + 3x
x − 3x = 24 − 32
−2x = −8
x = −8 : (−2) = 4, то есть через 4 года отец будет в три раза старше сына.
Ответ: через 4 года.
б) Пусть отец станет старше сына в 5 раз через x лет, тогда:
32 + x лет будет отцу;
8 + x лет будет сыну;
$\frac{32+x}{8+x}=5$
32 + x = 5(8 + x)
32 + x = 40 + 5x
x − 5x = 40 − 32
−4x = 8
x = 8 : (−4) = −2, следовательно, то есть отец был старше сына в 5 раз 2 года назад.
Ответ: отец был старше сына в 5 раз 2 года назад.1268. Брату 12 лет, он в 3 раза старше своей сестры. Через сколько лет он будет в 2 раза старше своей сестры?
12 : 3 = 4 года сестре;
Пусть брат станет старше сестры в 2 раза через x лет, тогда:
12 + x лет будет брату;
4 + x лет будет сестре;
$\frac{12+x}{4+x}=2$
12 + x = 2(4 + x)
12 + x = 8 + 2x
x − 2x = 8 − 12
−x = −4
x = 4, то есть через 4 года брат будет в два раза старше сестры.
Ответ: через 4 года.1269. а) Сейчас мама в 8 раз старше своей дочери, а через 4 года она будет старше дочери в 4 раза. Сколько лет дочери сейчас?
б) Брат в 3 раза старше сестры, а через 5 лет он будет в 2 раза старше сестры. Сколько сейчас лет брату и сколько лет сестре?а) Пусть дочери x лет, тогда:
8x лет маме,
8x + 4 лет будет маме через 4 года,
x + 4 лет будет дочери через 4 года,
$\frac{8x+4}{x+4}=4$
8x + 4 = 4(x + 4)
8x + 4 = 4x + 16
8x − 4x = 16 − 4
4x = 12
x = 12 : 4 = 3 года дочери.
Ответ: 3 года дочери.
б) Пусть сестре x лет, тогда:
3x лет брату,
3x + 5 лет будет брату через 5 лет,
x + 5 лет будет сестре через 5 лет,
$\frac{3x+5}{x+5}=2$
3x + 5 = 2(x + 5)
3x + 5 = 2x + 10
3x − 2x = 10 − 5
x = 5 лет сейчас сестре,
5 * 3 = 15 лет сейчас брату.
Ответ:
5 лет сейчас сестре,
15 лет сейчас брату.1270. Отец старше сына на 24 года. Сейчас он старше сына в 3 раза. Через сколько лет отец будет:
а) в 2 раза старше сына;
б) в 5 раз старше сына?а) Пусть сыну x лет, тогда:
x + 24 или 3x лет сейчас отцу,
x + 24 = 3x
x − 3x = −24
−2x = −24
x = −24 : (−2) = 12 лет сейчас сыну,
12 + 24 = 36 лет сейчас отцу.
Пусть через y лет отец станет старше сына в 2 раза, тогда:
12 + y лет будет сыну;
36 + y лет будет отцу.
$\frac{36+y}{12+y}=2$
36 + y = 2(12 + y)
36 + y = 24 + 2y
y − 2y = 24 − 36
−y = −12
y = 12, то есть через 12 лет отец станет старше сына в 2 раза.
Ответ: через 12 лет.
б) Пусть сыну x лет, тогда:
x + 24 или 3x лет сейчас отцу,
x + 24 = 3x
x − 3x = −24
−2x = −24
x = −24 : (−2) = 12 лет сейчас сыну,
12 + 24 = 36 лет сейчас отцу.
Пусть через y лет отец станет старше сына в 5 раз, тогда:
12 + y лет будет сыну;
36 + y лет будет отцу.
$\frac{36+y}{12+y}=5$
36 + y = 5(12 + y)
36 + y = 60 + 5y
y − 5y = 60 − 36
−4y = 24
y = 24 : (−4) = −6, то есть 6 лет назад отец был старше сына в 5 раз.
Ответ: 6 лет назад отец был старше сына в 5 раз1271. В двух бидонах 70 л молока. После того как из каждого бидона продали по 20 л молока, в одном осталось в 2 раза больше молока, чем в другом. Сколько молока было в каждом бидоне первоначально?
Пусть в первом бидоне было x л молока, тогда:
70 − x л было во втором бидоне.
x − 20 л осталось в первом бидоне после продажи,
70 − x − 20 = 50 − x л осталось во втором бидоне после продажи.
Допустим, что в первом бидоне было больше молока, чем во втором, тогда:
$\frac{x-20}{50-x}=2$
x − 20 = 2(50 − x)
x − 20 = 100 − 2x
x + 2x = 100 + 20
3x = 120
x = 120 : 3 = 40 л было в первом бидоне,
70 − 40 = 30 л было во втором бидоне.
Допустим, что во втором бидоне было больше молока, чем в первом, тогда:
$\frac{50-x}{x-20}=2$
50 − x = 2(x − 20)
50 − x = 2x − 40
−x − 2x = −40 − 50
−3x = −90
x = −90 : (−3) = 30 л было в первом бидоне,
70 − 30 = 40 л было во втором бидоне.
Ответ: 30 л и 40 л1272. Двое ели сливы. Один сказал другому: «Дай мне свои две сливы, тогда у нас слив будет поровну», на что другой ответил: «Нет, лучше ты дай мне свои две сливы − тогда у меня будет в два раза больше, чем у тебя». Сколько слив у каждого?
Пусть у первого было x слив, а у второго y слив, тогда:
x + 2 слив стало у первого, когда второй отдал ему 2 сливы,
y − 2 слив стало у второго, когда он отдал первому две сливы.
Так как, слив стало поровну, то:
x + 2 = y − 2
x = y − 2 − 2 = y − 4
x − 2 слив стало у первого, когда он отдал второму 2 сливы,
y + 2 слив стало у второго, когда первый отдал ему 2 сливы.
Так как у второго слив стало в 2 раза больше, то:
$\frac{y+2}{x-2}=2$
y + 2 = 2(x − 2)
y + 2 = 2x − 4
y − 2x = −4 − 2
y − 2(y − 4) = −6
y − 2y + 8 = −6
−y = −6 − 8
y = 14 слив было у второго,
14 − 4 = 10 слив было у первого.
Ответ: 10 слив у первого и 14 слив у второго. 248
-
Ответы к стр. 248
1273. Задача Бхаскары. Некто сказал другу: «Дай мне 100 рупий, и я буду вдвое богаче тебя». Друг ответил: «Дай ты мне только 10, и я стану в 6 раз богаче тебя». Сколько было у каждого?
Пусть у первого было x рупий, а у второго y рупий, тогда:
x + 100 рупий стало у первого после того, как второй отдал ему 100 рупий;
y − 100 рупий стало у второго после того, как он отдал первому 100 рупий.
Так как у первого стало в два раза больше рупий, чем у второго, то:
$\frac{x+100}{y-100}=2$
x + 100 = 2(y − 100)
x + 100 = 2y − 200
−2y = −200 − x − 100
2y = 200 + x + 100
y = 150 + x 2
x − 10 рупий стало у первого после того, как он отдал второму 10 рупий;
y + 10 рупий стало у второго после того, как первый отдал ему 10 рупий.
Так как, у второго стало в 6 раз больше рупий, то:
$\frac{y+10}{x-10}=6$
$\frac{150+\frac x2+10}{x-10}=6$
150 + x 2 + 10 = 6 ( x − 10 )
160 + x 2 = 6 x − 60
x/2 − 6 x = − 60 − 160
− 5 x/2 = − 220
11/2 x = 220
x = 220 : 11/2 = 220 ∗ 2/11 = 20 ∗ 2 = 40 рупий изначально было у первого;
150 + 40 : 2 = 150 + 20 = 170 рупий изначально было у второго.
Ответ: 40 и 170 рупий.1274. (Греция.) Ослица и мул шли вместе, нагруженные мешками равного веса. Ослица жаловалась на тяжесть ноши. «Чего ты жалуешься, − сказал мул, − если ты мне дашь один твой мешок, моя ноша станет вдвое больше твоей, а если я дам тебе один мешок, наши грузы только сравняются». Сколько мешков было у каждого?
Пусть у ослицы было x мешков, а у мула y мешков, тогда:
x − 1 мешков стало у ослицы после того, как она отдала ему мулу 1 мешок;
y + 1 мешков стало у мула после того, как ослица отдала ему 1 мешок.
Так как, у мула стало в 2 раза больше мешков, чем у ослицы, то:
$\frac{y+1}{x-1}=2$
y + 1 = 2(x − 1)
y + 1 = 2x − 2
y = 2x − 2 − 1
y = 2x − 3
x + 1 мешков стало у ослицы после того, как мул отдал ей 1 мешок;
y − 1 мешков стало у мула после того, как он отдал ослице 1 мешок.
Так как, количество мешков сравнялось, то:
$\frac{y-1}{x+1}=1$
$\frac{2x-3-1}{x+1}=1$
2x − 3 − 1 = x + 1
2x − x = 1 + 3 + 1
x = 5 мешков изначально было у ослицы,
2 * 5 − 3 = 10 − 3 = 7 мешков изначально было у мула.
Ответ: 5 мешков было у ослицы и 7 мешков было у мула.1275. Задача Л. Эйлера. Мул и осёл несли груз весом в несколько сотен каких−то единиц. Осёл, жалуясь на свою судьбу, сказал мулу: «Мне нужно только сто единиц твоей ноши, чтобы моя стала вдвое тяжелее твоей». На это мул ему ответил: «Да, это так, но если бы ты мне отдал сто единиц из твоей ноши, то я был бы нагружен втрое больше тебя». Какого веса была ноша осла и ноша мула?
Пусть осёл нёс x ед. ноши, а мул y ед. ноши, тогда:
x + 100 ед. ноши стало у осла после того, как мул отдал ему 100 ед. ноши;
y − 100 ед. ноши стало у мула после того, как он отдал ослу 100 ед. ноши.
Так как, у осла ноша стала в 2 раза тяжелее, чем у мула, то:
$\frac{x+100}{y-100}=2$
x + 100 = 2(y − 100)
x + 100 = 2y − 200
x = 2y − 300
x − 100 ед. ноши стало у осла после того, как он отдал мулу 100 ед. ноши;
y + 100 ед. ноши стало у мула после того, как осёл отдал ему 100 ед. ноши.
Так как, ноша мула стала в 3 раза тяжелее, чем ноша осла, то:
$\frac{x+100}{y-100}=3$
y + 100 = 3(x − 100)
y + 100 = 3(x − 100)
y + 100 = 3x − 300
y + 100 = 3(2y − 300) − 300
y + 100 = 6y − 900 − 300
y − 6y = −900 − 300 − 100
−5y = −1300
y = −1300 : (−5) = 260 ед. ноши было у мула.
2 * 260 − 300 = 220 ед. ноши было у осла.
Ответ: 260 ед. ноши было у мула и 220 ед. ноши было у осла.1276. Мне теперь вдвое больше лет, чем было тогда, когда мой брат был в моём возрасте. Когда мне будет столько лет, сколько теперь брату, то нам вместе будет 98 лет. Сколько лет каждому?
Пусть одному брату x лет, а второму брату y лет, тогда:
y − x разнице в возрасте.
x − (y − x) лет было первому брату, когда второй брат был в его возрасте.
Так как сейчас первому брату в два раза больше лет, чем было когда второй брат был в его нынешнем возрасте, то:
$\frac x{x-(y-x)}=2$
x = 2(x − (y − x))
x = 2(x − y + x)
x = 2x − 2y + 2x
2y = 2x + 2x − x
2y = 3x
y = 3/2 x
x + (y − x) лет будет первому брату, как сейчас второму брату.
x + (y − x) + (y − x) лет будет второму брату, когда первому брату столько же лет сколько сейчас второму брату.
Так как в это время им будет вместе 98 лет, то:
x + (y − x) + x + (y − x) + (y − x) = 98
x + y − x + x + y − x + y − x = 98
3y − x = 98
3 ∗ 3/2 x − x = 98
9/2 x − x = 98
7/2 x = 98
x = 98 : 7/2 = 98 ∗ 2/7 = 14 ∗ 2 = 28 лет сейчас первому брату,
3/2 ∗ 28 = 3 ∗ 14 = 42 года сейчас второму брату.
Ответ: 28 лет первому брату и 42 года второму брату.1277. Кузнечик прыгает по прямой большими прыжками по 12 см и малыми прыжками по 7 см. Сможет ли кузнечик из одной точки прямой попасть в другую, если расстояние между ними 3 см?
2 * 12 − 3 * 7 = 24 − 21 = 3 см
Ответ: сможет если он прыгнет на три больших прыжка в перед и на 3 малых прыжка назад.1278. Кузнечик прыгает по плоскости в любом направлении прыжками по 12 см. Сможет ли кузнечик из одной точки плоскости попасть в другую, если расстояние между ними 10 см?
Сможет, если будет двигаться по данной схеме:
1279. Разрежьте прямоугольник по прямой линии на две части так, чтобы из них можно было сложить треугольник. Найдите два различных решения задачи.
1280. а) Тротуар шириной 3 м и длиной 60 м выстилают бетонными плитами, каждая из которых имеет форму квадрата со стороной 50 см. Сколько потребуется плит?
б) Пол в ванной комнате выстилают керамическими плитками, каждая из которых имеет форму квадрата со стороной 12 см. Сколько нужно купить упаковок плиток по 48 плиток в каждой, если размеры пола ванной комнаты 1 м 80 см и 1 м 50 см? Учтите, что в ванной комнате мастера делают бортик высотой в полплитки и умеют резать керамические плитки на части.а) 50 см = 0,5 м
3 : 0,5 = 6 плиток надо уложить в ширину
60 : 0,5 = 120 плиток надо уложить в длину
6 * 120 = 720 плиток надо уложить всего.
Ответ: 720 плиток.
б) 1 м 80 см = 180 см
1 м 50 см = 150 см
180 : 12 = 15 плиток надо уложить в длину
150 : 12 = 12,5 плитки надо уложить в ширину
15 * 12,5 = 187,5 плитки всего нужно уложить на пол.
2 * 180 + 2 * 150 = 360 + 300 = 660 см периметр ванной комнаты.
660 : 12 : 2 = 27,5 плиток понадобится на бортики.
187,5 + 27,5 = 215 плиток понадобится всего.
215 : 48 = 4 23/48 упаковок плиток понадобится, а так упаковки продаются целыми, то понадобится 5 упаковок.
Ответ: 5 упаковок. 249
-
Ответы к стр. 249
1281. а) Коробка имеет форму прямоугольного параллелепипеда. Её длина равна 28 см, ширина составляет 0,5 длины, а высота составляет 1/7 ширины. Найдите объём коробки.
б) Длина строительного кирпича 25 см, ширина составляет 0,48 длины, а высота составляет 0,26 длины. Выразите объём кирпича в кубических дециметрах.а) 28 * 0,5 = 14 см ширина коробки
14 ∗ 1/7 = 2 см высота коробки
28 ∗ 14 ∗ 2 = 784 см3 объём коробки
Ответ: 784 см3
б) 25 * 0,48 = 12 см ширина кирпича
25 * 0,26 = 6,5 см высота кирпича
25 ∗ 12 ∗ 6,5 = 1950 см3
1950 : 1000 = 1,95 дм3
Ответ: 1,95 дм31282. В килограммовой пачке сахара содержится 180 кусков сахара. Какова масса каждого куска?
1 кг = 1000 г
1000 : 180 = 1000/180 = 50/9 = 5 5/9 г вес одного куска.
Ответ: 5 5/9 г1283. Выразите объём пачки сахара, размеры которой 5,5 см, 11,5 см и 17,5 см, в кубических дециметрах. Ответ округлите до сотых.
5,5 ∗ 11,5 ∗ 17,5 = 1106,875 см3
1106,875 : 1000 см3 = 1,106875 ≈ 1,11 дм3
Ответ: 1,11 дм3.1284. а) Можно ли написать 45 различных двузначных чисел так, чтобы среди них не было двух чисел, дающих в сумме 100?
б) Можно ли написать 55 различных двузначных чисел так, чтобы среди них не было двух чисел, дающих в сумме 100?а) Для того чтобы сумма двух любых двузначных чисел была не равна 100, необходимо чтобы это были числа меньше 50 или больше 50
Возьмем такие двузначные числа, сумма любых двух чисел из которых будет меньше 100 − это числа от 10 до 50.
50 − 10 + 1 = 41 двузначное число, сумма любых двух из которых будет меньше 100.
Возьмем такие двузначные числа, сумма любых двух чисел из которых будет больше 100 − это числа от 50 до 99.
99 − 50 + 1 = 50 двузначных чисел, сумма любых двух из которых будет больше 100.
Таким образом, чтобы выполнить условие задачи необходимо взять числа от 50 до 99.
Ответ: можно, если взять числа из диапазона от 50 до 99.
б) Каждое двузначное число из диапазона от 10 до 49 имеет такое число из диапазона 51 − 90 сумма с которым будет равна 100.
Числа 50, а также от 91 до 99 не имеют такой пары − всего 10 таких чисел,
49 − 10 + 1 = 40 чисел в диапазоне от 10 до 49
90 − 51 + 1 = 40 чисел в диапазоне от 51 до 90
Получается, что можно взять только 40 + 10 = 50 чисел, сумма двух любых из которых не будет равна 100.
Ответ: нельзя.1285. а) В коробке лежат 5 красных и 5 зелёных карандашей. Какое наименьшее число карандашей нужно взять из коробки не глядя, чтобы среди них оказалось 2 карандаша одного цвета? 2 карандаша разных цветов?
б) В коробке лежат 5 красных, 5 зелёных и 5 синих карандашей. Какое наименьшее число карандашей нужно взять из коробки не глядя, чтобы среди них оказалось 2 карандаша одного цвета? 2 карандаша разных цветов?а) При наихудшей ситуации первые 2 взятых карандаша будут разных цветов, а значит что любой следующий взятый карандаш будет одного цвета с одним из двух карандашей взятых ранее. Следовательно, нужно взять минимум 2 + 1 = 3 карандаша.
При наихудшей ситуации первые 5 взятых карандашей будут одного цвета, а значит в коробке останутся карандаши только второго цвета. Следовательно, нужно взять минимум 5 + 1 = 6 карандашей.
Ответ: 3 карандаша; 6 карандашей.
б) При наихудшей ситуации первые 3 взятых карандаша будут разных цветов, а значит что любой следующий взятый карандаш будет одного цвета с одним из трех карандашей взятых ранее. Следовательно, нужно взять минимум 3 + 1 = 4 карандаша.
При наихудшей ситуации первые 5 взятых карандашей будут одного цвета, а значит в коробке останутся карандаши только других цветов. Следовательно, нужно взять минимум 5 + 1 = 6 карандашей.
Ответ: 4 карандаша; 6 карандашей.1286. Студент за 5 лет учёбы сдал 31 экзамен. В каждом следующем году он сдавал больше экзаменов, чем в предыдущем. На пятом курсе экзаменов было втрое больше, чем на первом. Сколько экзаменов было на четвёртом курсе?
Пусть на первом курсе студент сдал x экзаменов, тогда:
3x экзаменов сдал студент на пятом курсе;
Найдем максимальное количество экзаменов, которое мог сдать студент на первом курсе, тогда количество экзаменов:
на 1 курсе x;
на 2 курсе x + 1;
на 3 курсе x + 2;
на 4 курсе x + 3;
на 5 курсе 3x.
x + x + 1 + x + 2 + x + 3 + 3x = 31
7x = 31 − 6
7x = 25
x = 25/7 = 3 4/7 максимальное количество экзаменов, которое мог сдать студент на первом курсе, так как количество экзаменов обязательно целое число, то максимум 3 экзамена.
Найдем минимальное количество экзаменов, которое мог сдать студент на первом курсе, тогда количество экзаменов:
на 1 курсе x;
на 2 курсе 3x − 3;
на 3 курсе 3x − 2;
на 4 курсе 3x − 1;
на 5 курсе 3x.
x + 3x − 3 + 3x − 2 + 3x − 1 + 3x = 31
13x = 31 + 3 + 2 + 1
13x = 37
x = 37/13 = 2 11/13 минимальное количество экзаменов, которое мог сдать студент на первом курсе, так как количество экзаменов обязательно целое число, то минимум 3 экзамена.
3 * 3 = 9 экзаменов сдавал студент на 5 курсе.
31 − (3 + 9) = 31 − 12 = 19 экзаменов всего сдал студент на 2, 3 и 4 курсе.
Пусть на 4 курсе он сдал 7 экзаменов, тогда на 19 − 7 = 12 экзаменов он сдал на 2 и 3 курсе.
12 нельзя разложить на два разных слагаемых, чтобы они были меньше 7(количество предполагаемых экзаменов на 4 курсе) и больше 3(количество экзаменов на 1 курсе), следовательно, 7 экзаменов для 4 курса не подходит.
Пусть на 4 курсе он сдал 8 экзаменов, тогда на 19 − 8 = 11 экзаменов он сдал на 2 и 3 курсе.
11 = 5 + 6, следовательно, на 2 курсе студент сдал 5 экзаменов, а на 3 курсе 6 экзаменов.
Ответ: 8 экзаменов.1287. Предание повествует, что царь Гиерон поручил мастеру изготовить корону и приказал выдать ему необходимое количество золота и серебра. Когда корона была доставлена, взвешивание показало, что она весит столько же, сколько весили золото и серебро. Однако правителю донесли, что мастер утаил часть золота, заменив его серебром. Гиерон призвал Архимеда и предложил ему определить, сколько золота и серебра заключает изготовленная корона. Архимед решил задачу, исходя из того, что чистое золото при взвешивании в воде теряет двадцатую долю своего веса, а серебро − десятую долю. Определите, сколько золота утаил мастер, если ему выдали 8 кг золота и 2 кг серебра, а корона весила в воде 9 1/4кг.
Пусть мастер утаил х кг золота, тогда он заменил его на х серебра, тогда:
8 − х кг золота использовал мастер при изготовлении короны;
2 + х кг серебра использовал мастер при изготовлении короны.
1 − 1/20 = 19/20 своего веса весит в воде золото;
1 − 1/10 = 9/10 своего веса весит в воде серебро.
$\frac{19}{20}(8-{\operatorname х})=\frac{38}5-\frac{19}{20}{\operatorname х}$ вес золота в воде;
$\frac9{10}(2+{\operatorname х})=\frac95+\frac9{10}{\operatorname х}$ вес серебра в воде, тогда:
$\frac{38}5-\frac{19}{20}{\operatorname х}+\frac95+\frac9{10}{\operatorname х}=9\frac14$
$-\frac{19}{20}{\operatorname х}+\frac9{10}{\operatorname х}=9\frac14-\frac{38}5-\frac95$
$-\frac{19}{20}{\operatorname х}+\frac{18}{20}{\operatorname х}=9\frac14-9\frac25$
$-\frac1{20}{\operatorname х}=9\frac5{20}-9\frac8{20}$
$-\frac1{20}{\operatorname х}=-\frac3{20}$
${\operatorname х}=-\frac3{20}:(-\frac1{20})=-\frac3{20}\ast(-20)=3$ кг золота утаил мастер.
Ответ: 3 кг.


