
Один из популярных, востребованных и нужных школьных предметов математика. Математика, которая нужна нам каждый день, каждый час, практически в каждом жизненном случае. Это и вычисления и логика и алгоритмы...Именно о математике, о учебнике авторов А.Г. Мерзляк, В.Б. Полонский, М.С Якир за 6 класс, речь и пойдет в нашей статье.
Надо заметить, что под такой вод зеленой обложкой, есть издания рабочей тетради, это 1 и 2 часть и издание учебника, который идет на весь год. (В нашем случае ГДЗ - ответы на весь год) Рабочие тетради тоже есть на нашем сайте, вам лишь надо выбрать раздел "Математика 6 класс". Но в данном случае речь все же об учебнике.
Итак, учебник в первую очередь начинается с повторений, ведь за лето многие детки теряют навыки и их надо просто-напросто восстановить хотя бы до майских. Далее начинаются новые темы.
Но самое главное, что мы вам предложим в этом учебнике, так это еще и ответы к нему. Из-за чего собственно все и затевалось.
ГДЗ ответы для учебника по математике 6 класс Мерзляк
Для того чтобы посмотреть нужные вам задания, вам всего лишь надо выбрать нужную вкладку.
Страница 6
-
Ответы к странице 6
Задание № 1. Верно ли утверждение:
1) число 6 является делителем числа 24; верно
2) число 6 кратно числу 24; неверно
3) число 5 является делителем числа 51; неверно
4) число 9 является делителем числа 99; верно
5) число 18 кратно числу 3; верно
6) число 28 кратно числу 8. неверноЗадание № 2. Какие из чисел 2, 3, 4, 6, 8, 9, 10, 12, 15, 16, 18, 30 являются:
1) делителями 24;
2) кратными 6;
3) делителями 20 и 24;
4) делителями 24 и кратными 4?Ответ 7 гуру
1) 2, 3, 4, 6, 8, 12.
2) 6, 12, 18, 30.
3) 2, 4.
4) 4, 8, 12.Задание № 3. Чему равняется:
1) наибольший делитель числа 19735;
2) наименьший делитель числа 19735;
3) наименьшее кратное числа 19735?Ответ
1) 19735
2) 1
3) 19735Задание № 4. Запишите все делители числа:
1) 18;
2) 8;
3) 13;
4) 56.Ответ
1) 18, 9, 6, 3, 2, 1.
2) 1, 2, 4, 8.
3) 13, 1.
4) 56, 28, 14, 8, 7, 4, 2, 1.Задание № 5. Запишите все делители числа:
1) 30;
2) 12;
3) 23;
4) 72.Ответ
1) 30, 15, 10, 6, 5, 3, 2, 1.
2) 12, 6, 4, 3, 2, 1.
3) 23, 1.
4) 72, 36, 24, 18, 12, 9, 8, 6, 4, 3, 2, 1.Задание № 6. Запишите пять чисел, кратных числу:
1) 7;
2) 30;
3) 100;
4) 34.Ответ
1) 7, 14, 21, 28, 35.
2) 30, 60, 90, 120, 150.
3) 100, 200, 300, 500, 1000.
4) 34, 68, 102, 136, 170.Задание № 7. Запишите четыре числа, кратных числу:
1) 16;
2) 12;
3) 150;
4) 47.Ответ
1) 16, 32, 48, 64.
2) 12, 24, 36, 48.
3) 150, 300, 450, 600.
4) 47, 94, 141, 188.Задание № 8. Из чисел 28, 36, 48, 64, 92, 100, 108, 110 выпишите те, которые:
1) кратны 4;
2) не кратны 6.Решение
1) 28, 36, 48, 64, 92, 100, 108.
2) 28, 64, 92, 100, 110.Задание № 9. Запишите все числа, являющиеся делителями каждого из чисел:
1) 15 и 20;
2) 7 и 21;
3) 24 и 36;
4) 20 и 21.Ответ
1) 5, 1.
2) 7, 1.
3) 1, 2, 3, 4, 6, 12.
4) 1Задание № 10. Запишите все числа, являющиеся делителями каждого из чисел:
1) 12 и 18;
2) 60 и 90;
3) 22 и 35;
4) 9 и 27.Ответ
1) 2, 3, 6.
2) 1, 2, 3, 6, 10, 15, 30.
3) 1.
4) 1, 3, 9.Задание № 11. Запишите какое−либо число, кратное каждому из чисел:
1) 3 и 4;
2) 6 и 12;
3) 4 и 6.Ответ
1) 12
2) 72
3) 24Задание № 12. Запишите какое−либо число, кратное каждому из чисел:
1) 5 и 9;
2) 8 и 32;
3) 8 и 12.Ответ
1) 45
2) 32
3) 96Задание № 13. Запишите все двузначные числа, кратные 19;
1) все двузначные числа, кратные 19;
2) все трёхзначные числа, кратные 105.Ответ
1) 19, 38, 57, 76, 95.
2) 105, 210, 315, 420, 525, 630, 735, 840, 942.Задание № 14. Запишите все двузначные числа, кратные 23.
Ответ
23, 46, 69, 92.
Задание № 15. Запишите все значения x, кратные числу 4, при которых верно неравенство 18 < x < 36.
Ответ
20, 24, 28, 32.
Задание № 16. Запишите все значения x, кратные числу 6, при которых верно неравенство 25 < x < 60.
Ответ
30, 36, 42, 48, 54.
Задание № 17. Запишите все значения x, являющиеся делителями числа 80, при которых верно неравенство 7 < x < 40.
Ответ
8, 10, 16, 20.
7
-
Страница 7
Задание № 18. Запишите все значения x, являющиеся делителями числа 98, при которых верно неравенство 14 < x < 50.
Ответ
49
Задание № 19. Найдите число, кратное числам 9 и 11, которое больше 100. Сколько существует таких чисел?
Ответ
Таких чисел бесконечное множество.
Задание № 20. Найдите число, кратное числам 9 и 12, которое меньше 100. Сколько существует таких чисел?
Ответ 7 гуру
Всего два числа: 36, 72.
Задание № 21. Верно ли утверждение:
1) если число a кратно 6, то оно кратно 3;
1) если число a кратно 3, то оно кратно 6;
1) если число a кратно 3 и 4, то оно кратно 12;
1) если число a кратно 4 и 6, то оно кратно 24;
Ответ проиллюстрируйте примерами.Решение
1) верно
12 : 6 = 2; 12 : 3 = 4.
2) неверно
9 кратно 3, но не кратно 6.
3) верно
24 : 3 = 8; 24 : 4 = 6; 24 : 12 = 2.
4) верно
48 : 4 = 12; 48 : 6 = 8; 48 : 24 = 2.Задание № 22. Известно, что сумма натуральных чисел a и b делится нацело на 5.
Верно ли, что:
1) каждое из чисел a и b делится нацело на 5;
2) одно из чисел делится нацело на 5, а другое − нет?
Ответ проиллюстрируйте примерами.Решение
1) неверно
18 + 2 = 20 сумма натуральных чисел a и b делится нацело на 5, каждое из чисел a и b не делится нацело на 5
2) неверно
18 + 2 = 20 сумма натуральных чисел a и b делится нацело на 5, ни одно из чисел a и b не делится нацело на 5Задание № 23. Известно, что каждое из чисел a и b не делится нацело на 3.
Верно ли, что их сумма также не делится нацело на 3?Решение
Неверно
При a = 2 и b = 4 их сумма делится нацело на 3. (2 + 4) : 3 = 2Задание № 24. Найдите три натуральных числа, для которых кратным будет число:
1) 65;
2) 121.
Укажите все варианты выбора таких трех чисел.Ответ
1) 1, 5, 65.
2) 1, 11, 121.Задание № 25. При делении числа a на 7 получили остаток 4. Какому условию должно удовлетворять число b, чтобы сумма a + b была кратна 7?
Ответ
Наименьшее число b = 3, каждое следующее на 7 больше.
Задание № 26. При делении числа a на 9 получили остаток 5. Какому условию должно удовлетворять число b, чтобы сумма a − b была кратна 9?
Ответ
Наименьшее число b = 5, каждое следующее на 9 больше.
Задание № 27. При каких натуральных значениях n значение выражения 15n кратно числу:
1) 3;
2) 5;
3) 10;
4) 11?Ответ
1) 1, 2, 3, 4, 5, ...
2) 1, 2, 3, 4, 5, ...
3) 2, 4, 6, 8, 10, 12, ...
4) 11, 22, 33, 44, 55, ...Задание № 28. При каких натуральных значениях n значение выражения:
1) 3n + 2 кратно числу 2;
2) 4n + 3 кратно числу 3?Ответ
1) 2, 4, 6, 8, 10, ...
2) 3, 6, 9, 12, 15, ...Задание № 29. Докажите, что:
1) двузначное число, записанное двумя одинаковыми цифрами, кратно 11;
2) трёхзначное число, записанное тремя одинаковыми цифрами, кратно 37.Решение
1) Такое число можно представить в виде произведения 11 и какого−либо числа меньшего 10, значит оно кратно 11.
2) 111 кратно 37, так как 37 * 3 = 111. Это значит, что любое трехзначное число, записанное тремя одинаковыми цифрами, будет кратно 37, так как это число можно представить в виде произведения 111 и какого−либо числа меньшего 10.Задание № 30. К однозначному числу дописали одну цифру, в результате чего оно увеличилось в 41 раз. Какую цифру и к какому числу дописали?
Ответ
К числу 1 дописали цифру 4, получилось 41.
Задание № 31. В двузначном числе зачеркнули одну цифру, в результате чего оно уменьшилось в 17 раз. Какую цифру и в каком числе зачеркнули?
Ответ
В числе 17 зачеркнули цифру 7.
8
-
Страница 8
Задание № 32. Первая на Руси школа, как написано в "Повести временных лет", была открыта в Киеве в 988 году при князе Владимире Святославовиче. В 1701 г. указом императора Петра I была создана первая в России государственная светская школа − Школа математических и навигацких наук, или, как чаще ее называли, Навигацкая школа. Первоначально школу возглавил боярин Федор Головин, а затем − выдающийся русский математик−педагог Леонтий Филиппович Магницкий (1669 − 1739), проработавший в школе 38 лет − со дня ее открытия в 1701 г. до последних дней своей жизни. Перу Л.Ф.Магницкого принадлежал первый изданный в России в 1703 г. учебник по математике, на долгие годы ставший основным учебником российских школ. В навигацкой школе обучали чтению, письму арифметике, геометрии, тригонометрии, черчению, географии, астрономии, навигации и другим предметам. Через сколько лет после открытия первой на Руси школы была открыта Навигацкая школа? На сколько лет Ваша школа "младше" Навигацкой школы?
Решение
1701 − 988 = 723 года, то есть через 723 года после открытия первой на Руси школы была открыта Навигацкая школа.
2017 − 1701 = на 316 лет наша школа "младше" Навигацкой школы.Задание № 33. Упростите выражение:
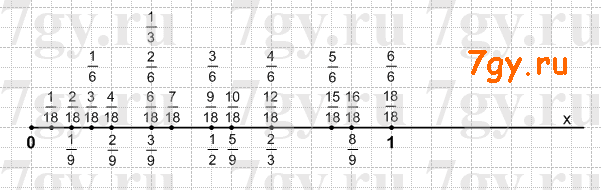
1) 0,2a * 50b, если a = 4, b = 3,6;
2) 0,4x * 25y, если x = 2,4, b = 3.Решение
1) 0,2a * 50b = 10 ab
Если a = 4; b = 3,6, то 10 * 3,6 * 4 = 36 * 4 = 144
2) 0,4x * 25y = 10 * y
Если х = 2,4, y = 3, 10 * 3 * 2,4 = 30 * 2,4 = 72Задание № 34. Решите уравнение:
1) 2,48х + 3,52х = 1,26;
2) 4,63х + 3,37х = 1,92;Решение уравнения
1) 2,48х + 3,52х = 1,26
6х = 1,26
х = 1,26 : 6 = 0,21
2) 4,63х + 3,37х = 1,92
8х = 1,92
х = 1,92 : 8 = 0,24Задача№ 35. В столовую завезли 146 кг овощей: 6 ящиков помидоров и 8 ящиков огурцов. Найдите, сколько килограммов огурцов было в каждом ящике, если помидоров в каждом ящике было 7,8 кг, а массы огурцов во всех ящиках одинаковы.
Решение задачи
7,8 * 6 = 46,8 (кг) - общая масса помидоров.
146 − 46,8 = 99,2 (кг) - огурцов в 8 ящиков.
99,2 : 8 = 12,4 (кг) - огурцов в каждом ящике.
Ответ: 12,4 кг.Задание № 36. Запишите в виде суммы разрядных слагаемых число:
1) 278;
2) 5093.Решение
1) 278 = 200 + 70 + 8
2) 5093 = 5000 + 90 + 3Задание № 37. Выполните деление с остатком:
1) 429 : 2;
2) 5001 : 2;
3) 768 : 10;
4) 9123 : 10;
5) 134 : 5;
6) 2867 : 5.Решение

9
-
Страница 9
Задание № 38. Выразите делимое через неполное частное, делитель и остаток в виде равенства a = bq + r, где a − делимое, b − делитель, q − неполное частное, r − остаток:
1) 83 : 7;
2) 171 : 17.Решение
1) 83 : 7 = 11 * 7 + 6
2) 171 : 17 = 10 * 17 + 1Задача от мудрой совы
Задача № 39. Сложите из шести спичек четыре равносторонних треугольника со стороной, равной длине одной спички.
Решение
Выкладываем на столе треугольник из 3-х спичек. Затем в каждый угол ставим по спичке и наклоняем их другим концом друг на друга. Получится треугольная пирамида. Её стороны - 4 треугольника.

11
-
Страница 11
Задание № 40. Заполните таблицу (поставьте знак "+" в случае утвердительно ответа или знак "−" в ином случае).

Задание № 41. Из чисел 34, 467, 435, 860, 648, 5465, 8216, 2405, 1020, 246370 выпишите те, которые делятся нацело:
1) на 2;
2) на 5;
3) на 10.Решение
1) 34, 860, 648, 8216, 1020, 246370.
2) 435, 860, 5465, 2405, 1020, 246370.
3) 860, 1020, 246370.Задание № 42. Какие из чисел 68, 395, 760, 943, 1270, 2625, 9042, 7121, 1734:
1) не делится нацело на 2;
2) кратны 10;
3) делятся нацело на 5, но не делятся нацело на 10?Решение
1) 395, 943, 2625, 7121.
2) 760, 1270.
3) 395, 2625.Задание № 43. Верно ли утверждение:
1) сумма двух четных чисел является четным числом;
2) сумма двух нечетных чисел, является нечетным числом;
3) сумма четного и нечетного чисел является нечетным числом;
4) если сумма двух чисел является четным числом, то и слагаемые − четные числа;
5) произведение двух четных является четным числом;
6) произведение двух нечетных чисел является нечетным числом;
7) произведение четного и нечетного чисел является нечетным числом?Решение
1) верно
2) неверно
3) верно
4) неверно
5) верно
6) верно
7) неверно 12
-
Страница 12
Задание № 44
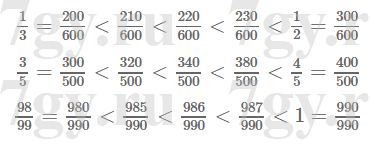
Запишите все нечетные значения x, при которых верно неравенство:
1) 273 < x < 290;
2) 2725 < x < 2737.Ответ 7 гуру
1) х = {275, 277, 279, 281, 283, 285, 287, 289}
2) х = {2727, 2729, 2731, 2733, 2735}Задание № 45
Запишите все четные значения x, при которых верно неравенство:
1) 134 < x < 160;
2) 489 < x < 502.Ответ
1) х = {136, 138, 140, 142, 144, 146, 148, 150, 152, 154, 156, 158}
2) х = {490, 492, 494, 496, 498, 500}Задание № 46
Найдите все четные значения x, кратные числу 5, при которых верно неравенство:
1) 38 < x < 75;
2) 3720 < x < 3754.Ответ
1) х = {40, 45, 50, 55, 60, 65, 70}
2) х = {3725, 3730, 3735, 3740, 3745, 3750}Задание № 47
Найдите все четные значения x, кратные числу 10, при которых верно неравенство:
1) 279 < x < 320;
2) 1465 < x < 1510.Ответ
1) х = {280, 290, 300, 310}
2) х = {1470, 1480, 1490, 1500}Задание № 48
Запишите все четырехзначные числа, кратные числу 5, для записи которых используют цифру 0, 3, 5, 7 (цифры не могут повторятся).
Ответ
3075, 3705, 3750, 3570, 3570, 7530, 7350, 7035, 7305, 5730, 5370.
Задание № 49
Найдите все цифры, которые можно дописать справа к числу 793, чтобы получить число, кратное:
1) 2;
2) 5;
3) 10.Ответ
1) 0, 2, 4, 6, 8.
2) 0, 5.
3) 0Задание № 50
Запишите наибольшее:
1) четырехзначное число, кратное 2;
2) пятизначное число, кратное 5;
3) шестизначное число, кратное 10.
Цифры в записи числа не могут повторяться.Ответ
1) 9876
2) 9875
3) 987650Задание № 51
1) Запишите шесть первых натуральных чисел, кратных 100. Обратите внимание на две последние цифры этих чисел. Сформулируйте признак делимости на 100.
2) Запишите восемь первых натуральных чисел, кратных 25. Обратите внимание на две последние цифры этих чисел. Сформулируйте признак делимости на 25.Решение
1) 100, 200, 300, 400, 500, 600.
Число делится на 100 без остатка в том случае, если оканчивается на 00.
2) 25, 50, 75, 100, 125, 150, 175, 200
Если число, составленное из двух последних цифр числа, делится на 25, то и число делится на 25.Задание № 52
Найдите наибольшее двузначное число x, при котором значение выражения х − 32 делится нацело на 5.
Решение
х = 97;
97 − 32 = 65 : 5 = 13Задание № 53
Найдите наименьшее трехзначное число y, при котором значение выражения 327 + y является числом, кратным 10.
Решение
y = 103;
(103 + 327) : 10 = 430 : 10 = 43Задание № 54
Может ли число, в записи которого все цифры равны 1, делиться нацело на число, в записи которого все цифры равны 2?
Ответ
Нет, не может.
Задание № 55
Может ли число, в записи которого все цифры равны 2, делиться нацело на число, в записи которого все цифры равны:
1) 1;
2) 5?Ответы
1) да, может
2) нетЗадание № 56
1) Сумма двух натуральных чисел является нечетным числом. Четным или нечетным числом будет их произведение?
2) Сумма двух натуральных чисел является четным числом. Обязательно ли их произведение будет четным числом.Ответы
1) Произведение будет четным.
2) Нет, не обязательно. 13
-
Страница 13
Задание № 57. Четной ил нечетной будет сумма натуральных слагаемых, если:
1) четыре слагаемых четные, а остальные − нечетные;
2) четыре слагаемых нечетные, а остальные четные?Ответ 7 гуру
1) Нечетная сумма
2) Четная суммаЗадание № 58. Сумма девяти натуральных слагаемых равна 1000. Можно ли утверждать, что их произведение − четное число? Ответ объясните.
Решение
Нельзя. В сумме количество нечетных слагаемых − число четное.
Произведение четного числа нечетных слагаемых − число нечетное.Задание № 59. Можно ли разложить 50 яблок на пять кучек, в каждой из которых нечетное количество яблок?
Решение
Нельзя, так как сумма которая складывается из 5 кучек нечетного количества яблок − число нечетное.
Задание № 60. Существует ли прямоугольник, длины сторон которого выражены натуральными числами в сантиметрах, причем одна из них на 1 см длиннее другой, и площадь которого равна 12345 см2
Ответ
Не существует, так как площадь прямоугольника равна произведению длины на ширину, а произведение четного и нечетного числа − число четное.
Задание № 61. Известно, что n − натуральное число. Является ли четным числом значение выражение:
1) 2n;
2) 2n + 1;
3) n(n + 1);
4) (2n − 1)(2n + 3);
5) (2n + 5)(4n − 2)(2n + 7)?Ответ
1) четное
2) нечетное
3) четное
4) нечетное
5) четноеЗадание № 62. В школе работают два ночных охранника − Иван Иванович и Петр Петрович. Они дежурят по очереди с вечера до утра следующего дня. Иван Иванович заступил на дежурство 1 сентября, а Петр Петрович − 2 сентября. Кто из них заступит на дежурство 18 сентября? 29 сентября? 1 октября? 30 октября? 31 октября? По каким числам − четный или нечетным − будет дежурить Иван Иванович в ноября? Кто из них будет дежурить в ночь на Новый год?
Решение
Иван Иванович дежурит в сентябре по нечетным числам, а Петр Петрович по четным;
Иван Иванович дежурит в октябре по нечетным числам, а Петр Петрович по четным;
Иван Иванович дежурит в ноябре по четным числам, а Петр Петрович по нечетным, так как в октябре 31 день и при переходе на ноябрь график четности−нечетности сменится;
Иван Иванович дежурит в декабре по четным числам, а Петр Петрович по нечетным, следовательно будут дежурить:
18 сентября − Петр Петрович;
29 сентября − Иван Иванович;
1 октября − Иван Иванович;
30 октября − Петр Петрович;
31 октября − Иван Иванович;
31 декабря − Петр Петрович.Задание № 63. Верно ли, что из любых трех натуральных чисел два таких, сумма которых делится нацело на 2?
Ответ
Верно.
Задание № 64. Сколькими нулями оканчивается запись числа, которое равно произведению:
1) 1 * 2 * 3 * ... * 15 * 16;
2) 1 * 2 * 3 * ... * 25 * 26?Ответ
1) Тремя нулями
2) Пятью нулямиЗадание № 65. Сумма двух натуральных чисел равно 700. Первое из них оканчивается цифрой 7. Если ее зачеркнуть, то получим второе число. Найдите эти числа.
Решение
Пусть первое число **7, которое можно представить в виде 100x + 10y + 7, то второе число будет 10х + y, тогда:
100x + 10y + 7 + 10x + y = 700
Так как у числа 700 последняя цифра 0, y = 10 − 7 = 3, тогда:
100x + 30 + 7 + 10x + 3 = 700
110x + 40 = 700
110х = 700 − 40 = 660
х = 660 : 110 = 6, тогда:
первое число: 600 + 30 + 7 = 637;
второе число: 60 + 3 = 63.Задание № 66. Сколько существует двузначных чисел, для записи которых использованы:
1) четные цифры;
2) нечетные цифры?Ответ
1) 20
2) 25Задание № 67. Можно ли в выражении 1 + 2 + 3 + ... + 8 + 9 заменить некоторые знаки "+" на знаки "−" так, чтобы значение полученного числового выражения было равным 18?
Решение
Нельзя, так в данном выражении нечетное количество нечетных слагаемых, а число 18 четное.
Задание № 68. Докажите, что:
1) 14168 кратно 28;
2) 1878 не кратно 24;
3) 73 является делителем 14892;
4) 56 не является делителем 5172.Решение

14
-
Страница 14
Задание № 69. По состоянию на 2008 год в России было 57 естественнонаучных и научно−технических музеев. Сколько всего музеев каждого из этих видов, если научно−технических музеев в 2 раза меньше, чем естественнонаучных?
Решение
Пусть научно−технических музеев х, тогда естественнонаучных 2х всего музеев всего музеев 57.
х + 2х = 57
3х = 57
х = 19 научно−технических музеев;
2х = 19 * 2 = 38 естественнонаучных музеев.Задание № 70. По состоянию на 2008 год в России был 141 государственный природный заповедник и национальный парк. Сколько в России природных заповедников и сколько национальных парков, если заповедников на 61 больше, чем парков?
Решение
Пусть всего парков было х, тогда заповедников х + 61.
Составим уравнение:
х + (х + 61) = 141
2х = 141 − 61
х = 80 : 2 = 40 парков.
х + 61 = 40 + 61 = 101 заповедников.Задание № 71. Выполните действия:
1) (69 * 0,63 − 10,098 : 5,4 − 20,54) : 0,324;
2) 0,98 * 3,8 − 0,132 : 5,5 − 2,45.Ответ
(69 * 0,63 − 10,098 : 5,4 − 20,54) : 0,324 = (43,47 − 1,87 − 20,54) : 0,324 = 21,06 : 0,324 = 65
0,98 * 3,8 − 0,132 : 5,5 − 2,45 = 3,724 − 0,024 − 2,45 = 3,7 − 2,45 = 1,25
Записываем решение по действиям:
Задача от мудрой совы
Задание № 72. В клетках таблицы размером 3 Х 3 стоят нули. Разрешается выбрать любой квадрат размером 2 Х 2 клетки и увеличить числа во всех его клетках на единицу. Можно ли после нескольких таких операций получить таблицу, изображенную на рисунке 1?
4 6 5
7 18 9
6 10 7Решение
В центре таблицы число 18, значит было произведено 18 операций.
Тогда сумма чисел по углам должна быть равна 18, а она равна 4 + 5 + 6 + 7 = 22.
Значит получить таблицу, изображенную на рисунке 1, нельзя. 15
-
Страница 15
Задание № 73. Заполните таблицу (поставьте знак "+" в случае утвердительного ответа или знак "−" в ином случае).

Задание № 74. Заполните таблицу (поставьте знак "+" в случае утвердительного ответа или знак "−" в ином случае).

16
-
Страница 16
Задание № 75
Из чисел 8937, 6565, 37828, 44292, 9462, 58395, 23646 выпишите те, которые делятся нацело:
1) на 3;
2) на 9;
3) на 3 и на 2.Ответ от 7 гуру
1) 8937, 6565, 44292, 9462, 58395, 23646.
2) 8937
3) 44292, 9467, 23646.Задание № 76
Из чисел 7826, 1215, 4075, 2880, 3921, 9319, 6072, 8142 выпишите те, которые делятся нацело:
1) на 3;
2) на 9;
3) на 9 и на 5.Ответ
1) 1215, 2880, 3921, 6072, 8142.
2) 1215, 2880.
3) 1215, 2880.Задание № 77
Найдите все значения y, кратные:
1) числу 3, при которых верно неравенство 143 < y < 162;
2) числу 9, при которых верно неравенство 92 < y < 128.Ответ
1) 144, 147, 150, 153, 156, 159.
2) 99, 108, 117, 126.Задание № 78
Найдите все значения m, кратные:
1) числу 3, при которых верно неравенство 324 < m < 345;
2) числу 9, при которых верно неравенство 423 < m < 480.Ответ
1) 327, 330, 333, 336, 339, 342.
2) 432, 441, 450, 459, 468, 477.Задание № 79
Вместо звездочки поставьте такую цифру, чтобы получилось число, кратное 3 (рассмотрите все возможные случаи):
1) 5484;
2) 36393;
3) 79*8.Ответ
1) 54840; 54843; 54846; 54849.
2) 306393; 336393; 366393; 396393.
3) 7908; 7938; 7968; 7998.Задание № 80
Вместо звездочки поставьте такую цифру, чтобы получилось число, кратное 9 (рассмотрите все возможные случаи):
1) 628*1;
2) 57*582;
3) 7*51.Ответ
1) 62811
2) 570582; 579582.
3) 7551Задание № 81
Запишите:
1) Наименьшее число, для записи которого используется только цифра 2 и которое делится нацело на 3;
2) наименьшее трехзначное число, которое делится нацело на 9.Ответ
1) 222
2) 108Задание № 82
Какую цифру можно поставить вместо звездочки в записи 627*, чтобы полученное число делилось нацело на 3, и на 5?
Ответ
0
Задание № 83
Какую цифру можно поставить вместо звездочки в записи 2185*, чтобы полученное число делилось нацело на 3, но не делилось нацело на 2?
Ответ
5
Задание № 84
Какую цифру можно поставить вместо звездочки в записи 347*, чтобы полученное число делилось нацело и на 2, и на 3?
Ответ
4
Задание № 85
Запишите наименьшее:
1) четырехзначное число, кратное 3;
2) пятизначное число, кратное 9;
3) шестизначное число, кратное 3 и 2;
4) четырехзначное число, кратное 5 и 9.
Цифры в записи числа не могут повторяться.Ответ
1) 1023
2) 10249
3) 102354
4) 10395Задание № 86
Запишите наибольшее четырехзначное число, которое делится нацело:
1) на 2 и на 3;
2) на 3 и на 5;
3) на 3 и на 10;
4) на 2 и на 9.Ответ
1) 9996
2) 9990
3) 9990
4) 9990Задание № 87
Какое наименьшее число надо прибавить к данному, чтобы получить число, кратное 9:
1) 1275;
2) 333;
3) 25718;
4) 987652;
5) 1020300;
6) 19191919191?Ответ
1) 3
2) 9
3) 4
4) 8
5) 8
6) 3 17
-
Страница 17
Задание № 88. Запишите, используя по одному разу каждый из цифр 0, 1, 4, 7, наибольшее и наименьшее четырехзначные числа, кратные 15.
Ответ от 7 гуру
7410, 1470.
Задание № 89. К числу 15 допишите слева и справа по одной цифре так, чтобы получившееся число было кратно 15. Сколько решений имеет задача?
Решение
Шесть решений: 1155, 4155, 7155, 3150, 9150, 6150.
Задание № 90. К числу 34 припишите слева и справа по одной цифре так, чтобы получившееся число было кратно 45. Сколько решений имеет задача?
Решение
Два решения: 2340; 6345.
Задание № 91. Вместо звездочек поставьте такие цифры, чтобы четырехзначное число 74 делилось нацело на 18. Найдите все решения.
Ответ
7740, 5742, 3744, 1746.
Задание № 92. Вместо звездочек поставьте такие цифры, чтобы четырехзначное число 34 делилось нацело на 9. Найдите все решения.
Ответ
3042, 3249, 3240, 3348, 3843, 3942, 3447, 3744, 3546, 3645.
Задание № 93. Галина Васильевна купила три пакета кефира, пачку масла за 45 р., несколько буханок хлеба по 24 р., шесть коробок спичек. Может ли вся покупка стоить 260 р.?
Решение
Стоимость хлеба и спичек четные числа. Если прибавить стоимость масла будет нечетное число. Чтобы получить четную общую стоимость покупки 260 р., стоимость кефира должна быть нечетным числом.
Ответ: Возможно, если стоимость кефира будет нечетным числом.Задание № 94. Сначала вычислили сумму цифр числа, равного произведению 1 * 2 * 3 * ... * 999 * 1000. Потом вычислили сумму цифр полученного числа. Так поступали до тех пор, пока не получили однозначное число. Что это за число?
Решение
Это число 9, так как произведение будет кратно 9, как и любое следующее число.
Задание № 95. Рома и Дима записывают девятнадцатизначное число, используя только цифры 1, 2 и 4. Первую цифру пишет Рома, вторую − Дима, третью − снова Рома и так далее по очереди. Рома хочет получить в результате число, кратное 3. Может и Дима помешать ему это сделать?
Решение
Да, может, так как числа 1, 2, 4 − не кратны трем. Поэтому Дима может сделать сумму не кратной трем.
Задание № 96. Как изменится − увеличится или уменьшится − и на сколько девятизначное число, последняя цифра которого 0, а предпоследняя − 5, если эти две цифры поменять местами?
Решение
Число уменьшится на 45
Задание № 97. Река Иртыш на 598 км длиннее реки Оби. Найдите длину каждой их этих рек, если их общая длина равна 7898 км.
Решение
Пусть длина реки Обь х км, тогда длина Иртыша х + 598 км.
Составим уравнение:
х + х + 598 = 7898
2х = 7898 − 598
х = 7300 : 2 = 3650 км длина Оби;
х + 598 = 3650 + 598 = 4248 км длина Иртыша.Задание № 98. По маршруту Орел − Тула − Москва выехал автомобиль. Какое расстояние между Орлом и Тулой, если оно на 5 км больше расстояния между Тулой и Москвой, а длина всего маршрута составляет 345 км?
Решение
Пусть между Тулой и Москвой х км, тогда между Орлом и Тулой х + 5 км.
Составим уравнение:
х + (х + 5) = 345
2х + 5 = 345
2х = 345 − 5
х = 340 : 2 = 170 км расстояние между Тулой и Москвой.
х + 5 = 170 + 5 = 175 км между Орлом и Тулой.Задание № 99. Вычислите:
1) 6,29 : 0,85 + (53 − 48,184) : 5,6;
2) 5,33 : 0,65 − (1,9218 − 0,8118) : 3.Ответ
6,29 : 0,85 + (53 − 48,184) : 5,6 = 7,4 + 4,816 : 5,6 = 7,4 + 0,86 = 8,26
5,33 : 0,65 − (1,9218 − 0,8118) : 3 = 8,2 − 1,11 : 3 = 8,2 − 0,37 = 7,83
Пишем решение по действиям: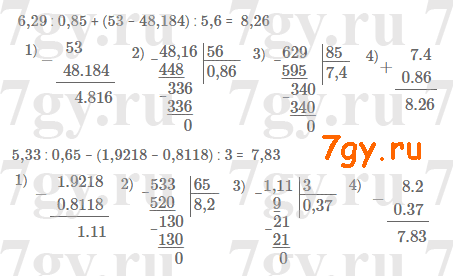
18
-
Страница 18
Задание № 100. Упростите выражение, заменив произведение одинаковых множителей степенью:
1) 7 * 7 * 7 * 7 * 7; 2) 10 * 10 * 10; 3) a * a * a * a; 4) x * x * x * x * x * x.Решение
7 * 7 * 7 * 7 * 7 = 75
10 * 10 * 10 = 103
a * a * a * a = a4
x * x * x * x * x * x = x6Задание № 101. Найдите значение выражения: 1) 25 ; 2) 72 ; 3) 0,62 ; 4) 0,53 ; 5) 1,54 ; 6) 1,23 ; 7) 06 ; 8) 112 .
Решение
25 = 2 * 2 * 2 * 2 * 2 = 32
72 = 7 * 7 = 49
0,62 = 0,6 * 0,6 = 0,36
0,53 = 0,5 * 0,5 * 0,5 = 0,125
1,54 = 1,5 * 1,5 * 1,5 * 1,5 = 5,0625
1,23 = 1,2 * 1,2 * 1,2 = 1,728
06 = 0
112 = 1Задание № 102. Запишите число 64 в виде степени с основанием:
1) 8;
2) 4;
3) 2.Решение
1) 64 = 82
64 = 43
64 = 26Задача от мудрой совы
Задание № 103. В чемпионате страны по футболу принимают участие 16 команд, каждая из которых имеет свой стадион. Все команды должны сыграть между собой, причем в каждом туре проводится 8 игр. Можно ли ставить расписание туров так, чтобы каждая команда по очереди играла на своем стадионе и на стадионе соперника?
Решение
Нет, нельзя.
Если попытаться составить календарь в соответствии с требованиями задачи, то в первом туре первая восьмерка играет дома, вторая восьмерка - на выезде, во втором туре та же первая восьмерка играет на выезде, вторая восьмерка - дома. Если будет продолжаться так дальше, то команды из первой восьмерки и команды из второй восьмерки между собой никогда не сыграют. Поэтому таким способом составить расписание туров невозможно. 23
-
Страница 23
Задание № 104
Среди чисел 1, 3, 6, 7, 12, 13, 21, 23, 24, 28, 29, 33, 45, 47 укажите:
1) простые;
2) составные.Ответ 7 гуру
1) 3, 7, 13, 23, 29, 47 - простые
2) 6, 12, 21, 24, 28, 45, 46, 33- составныеЗадание № 105
Запишите все делители числа, подчеркните те из них, которые являются простыми числами:
1) 21; 2) 30; 3) 48; 4) 54.Ответ
1) Д(21) = {1 , 3 , 7 , 21}
2) Д(30) = {1 , 2 , 3 , 5 , 6 , 10 , 15 , 30}
3) Д(48) = {1 , 2 , 3 , 6 , 4 , 8 , 12 , 24 , 48}
4) Д(54) = {1 , 2 , 3 , 6 , 9 , 18 , 27 , 54}Задание № 106
Разложите на простые множители число:
1) 12;
2) 42;
3) 216;
4) 450;
5) 920;
6) 2280;
7) 10850.Решение

Задание № 107
Разложите на простые множители число:
1) 27;
2) 56;
3) 625;
4) 820;
5) 2772;
6) 702;
7) 1224.Решение

Задание № 108
Запишите:
1) все простые числа, которые больше 10 и меньше 25;
2) все составные числа, которые больше 35 и меньше 49.Ответ
1) 10 < x < 25 , х - простое
х = {11, 13, 17, 19, 23}
2) 35 < а < 49 , а - составное
а = {36, 38, 39, 40, 42, 44, 45, 46, 48}Задание № 109
Запишите:
1) все простые числа, которые больше 22 и меньше 38;
2) все составные числа, которые больше 60 и меньше 78.Ответ
1) 22 < x < 38 , х - простое
х = {23, 29, 31, 37}
2) 60 < а < 78 , а - составное
а = {62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77}Задание № 110
Простым или составным числом является произведение:
1) 13 * 1;
2) 14 * 1;
3) 4 * 7;
4) 11 * 13;
5) 43 * 1;
6) 1 * 1.Ответ
1) простым
2) составным
3) составным
4) составным
5) простым
6) простымЗадание № 111
Запишите все делители числа, равного произведению:
1) 2 * 2 * 5;
2) 3 * 5 * 7.Ответ
1) 2 * 2 * 5 = 20
Д(20) = {1, 2, 4, 5, 10, 20}
2) 3 * 5 * 7 = 105
Д(105) = {1, 3, 5, 7, 15, 21, 35, 105}Задание № 112
Запишите все делители числа, равного произведению:
1) 2 * 5 * 13;
2) 3 * 3 * 3* 7.Решение
1) 2 * 5 * 13 = 130
Д(130) = {1, 2, 5, 10, 13, 26, 65, 130}
2) 3 * 3 * 3* 7 = 189
Д(189) = {1, 3, 9, 21, 27, 63, 189}Задание № 113
Чему равно частное от деления числа a на число b, если:
1) a = 2 * 2 * 2 * 3 * 3 * 7, b = 2 * 2 * 3 * 7;
2) a = 3 * 5 * 5 * 13 * 17 * 19, b = 3 * 13 * 19.Решение
1) a : b = (2 * 2 * 2 * 3 * 3 * 7) : (2 * 2 * 3 * 7) = (2 * 3) : 1 = 6
2) a : b = (3 * 5 * 5 * 13 * 17 * 19) : (3 * 13 * 19) = (5 * 5 * 17) : 1 = 425Задание № 114
Чему равно частное от деления числа a на число b, если:
1) a = 2 * 3 * 5 * 5 * 7 * 11 * 13, b = 2 * 5 * 13;
2) a = 2 * 2 * 3 * 5 * 23 * 37, b = 2 * 3 * 37.Решение
1) a : b = (2 * 3 * 5 * 5 * 7 * 11 * 13) : (2 * 5 * 13) = (3 * 5 * 7 * 11) : 1 = 1155
2) a : b = (2 * 2 * 3 * 5 * 23 * 37) : (2 * 3 * 37) = (2 * 5 * 23) : 1 = 230Задание № 115
Запишите все двузначные числа, в разложении которых на простые множители один из множителей равен:
1) 7;
2) 17;
3) 23.Решение
1) 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98.
2) 34, 51, 68, 85.
3) 46, 69, 92.Задание № 116
Запишите все двузначные числа, разложение которых на простые множители состоит:
1) из двух одинаковых множителей;
2) из трех одинаковых множителей.Ответ
1) 25, 49.
2) 27Задание № 117
Сколько существует чисел, которые можно разложить на два двузначных простых множителя, один из которых на 2 больше другого?
Воспользуйтесь таблицей простых чисел.Решение
Шесть простых чисел:
143 = 11 * 13;
323 = 17 * 19;
899 = 29 * 31;
1763 = 41 * 43;
3599 = 59 * 61;
5183 = 71 * 73.Задание № 118
Найдите все числа, которые можно разложить на два двузначных простых множителя, разность которых равна 4. Воспользуйтесь таблицей простых чисел.
Решение
Шесть чисел:
13 * 17 = 221;
19 * 23 = 437;
37 * 41 = 1517;
43 * 47 = 2021;
67 * 71 = 4757;
79 * 83 = 6557.Задание № 119
Задумали простое число. Известно, что следующее за ним натуральное число тоже простое. Какое число задумали?
Ответ
Число 2
24
-
Страница 24
Задание № 120. Может ли сумма двух простых чисел быть простым числом? В случае утвердительного ответа приведите пример.
Ответ 7 гуру
Да: 2 + 3 = 5
Задание № 121. Может ли быть простым числом:
1) произведение двух различных чисел;
2) значение площади квадрата, длина стороны которого выражается натуральным числом?
Ответ обоснуйте.Ответ
1) Да: 1 * 17 = 17 − все числа простые
2) Нет, так как значение площади равно длине стороны возведенной в квадрат, следовательно делителей у числа будет больше двух.Задание № 122. Может ли сумма двух составных чисел быть простым числом? В случае утвердительного ответа приведите примеры.
Ответ
Да:
8 + 9 = 17;
15 + 8 = 23.Задание № 123. Существует ли прямоугольник, длины сторон которого выражаются натуральными числами, а периметр − простым числом (длины сторон и периметр прямоугольника выражены в одних и тех же единицах измерения)? Ответ обоснуйте.
Ответ
Такого прямоугольника не существует. Периметр прямоугольника всегда четное число, так как периметр равен сумме длин всех четырех сторон.
Задание № 124. Может ли произведение ста различных простых чисел делиться нацело:
1) на 3;
2) на 9?Ответ
1) Да, если хотя бы 1 множитель равен 3.
2) Нет, так как 9 = 3 * 3, то есть в произведении должно быть два одинаковых числа 3.Задание № 125. Существуют ли три последовательных натуральных числа:
1) каждое из которых является простым;
2) ни одно из которых не является составным?
Ответ обоснуйте.Ответ
1) Нет, не существует. Одно число будет четным, а оно не является простым.
2) Да, например: 1, 2, 3.Задание № 126. При каком натуральном значении n простым числом значение выражения:
1) 2n;
2) n2;
3) n(n + 1)?Ответ
1) n = 1
2) нет такого числа
3) n = 1Задание № 127. Натурально число a,. которое больше 1 и меньше 100, не делится нацело ни на одно из чисел 2, 3, 5 и 7. Верно ли, что число a − простое?
Ответ обоснуйте.Ответ
Да, так как оно нечетное и не делится на 4, 6, 8, 9, то есть не делится на числа первой десятки. А так как оно меньше 100, то оно может быть представлено только в виде 1 * a, а значит число a − простое.
Задание № 128. Простое число, большее 1000, поделили на 6. Чему может быть равным остаток?
Ответ
Остаток может быть равен 1 или 5.
Задание № 129. Найдите все пары простых чисел, разность которых равна 17.
Ответ
Одна пара: 2 и 19.
Задание № 130. Квадрат со стороной 1,6 см и прямоугольник, ширина которого 0,8 см, имеют равные площади. Найдите длину прямоугольника.
Решение
1,6 * 1,6 = 2,56 см2 − площадь квадрата;
2,56 : 0,8 = 3,2 см2 − длина прямоугольника.Задание № 131. Решите уравнение:
1) 4x + 5x + 4,7 = 16,4;
2) 0,7x − 0,4x + 46 = 211;
3) (35,8 − x) : 2,1 = 1,3;
4) 0,9(283 − x) = 17,01.Решение
1) 4x + 5x + 4,7 = 16,4
9х = 16,4 − 4,7 = 11,7
х = 11,7 : 9 = 1,3
2) 0,7х − 0,4х + 46 = 211
0,3х = 211 − 46
0,3х = 165
х = 165 : 0,3 = 550
3) (35,8 − х) : 2,1 = 1,3
35,8 − х = 1,3 * 2,1
35,8 − х = 2,73
х = 35,8 − 2,73
х = 33,07
4) 0,9(283 − х) = 17,01
283 − х = 17,01 : 0,9
х = 283 − 17,01 : 0,9
х = 283 − 18,9
х = 264,1Задание № 132. Запишите пять чисел, кратных:
1) числу 8;
2) числу 18;
3) числу n.Решение
1) 8, 80, 88, 800, 8000.
2) 18, 36, 54, 180, 360.
3) 2n, 5n, 7n, 8n, 9n.Задание № 133. При делении нацело числа a на 15 получили число, кратное 6. Делится ли нацело число a на 10? Ответ обоснуйте.
Ответ
Да, так как 15 = 3 * 5; 6 = 2 * 3; a = 5 * 2 = 10.
Задание № 134. При делении нацело числа a на 6 получили число, кратное 12. Делится ли нацело число a на 9? Ответ обоснуйте.
Ответ
Да, так как 6 = 2 * 3; 12 = 3 * 4; a = 3 * 3 = 9.
25
-
Страница 25
Задание № 135. Найдите значение степени: 1) 34 ; 2) 62 ; 3) 53 ; 4) 27 ; 5) 73 ; 6) 112 .
Решение
34 = 81
62 = 36
53 = 75
27 = 128
73 = 343
112 = 121Задание № 136. Из чисел 348, 975, 1026, 2531, 12120, 43674, 58121 выпишите те, которые делятся нацело:
1) на 2;
2) на 3;
3) на 5.Решение
1) 348, 1026, 12120, 43674.
2) 348, 975, 1026, 12120, 43674.
3) 975, 12120.Задача от мудрой совы
Задание № 137. Шахматный конь начинает свой маршрут в левом нижнем углу доски, а заканчивает в правом верхнем углу. Может ли конь при этом побывать на всех полях доски по одному разу?
Решение
Нет, не может.
За каждый ход конь меняет цвет клетки. Для прохождения необходимо 63 хода (всего на шахматной доске 64 клетки, на одной из них конь уже стоит), то есть нечетное число ходов. А это значит, что последняя клетка не будет того же цвета, что и начальная, а по условию задачи последняя клетка того же цвета, что и начальная. 30
-
Страница 30
Задание № 138
Найдите наибольший общий делитель чисел:
1) 12 и 18;
2) 24 и 30;
3) 6 и 36;
4) 48 и 64;
5) 35 и 18;
6) 14, 21 и 28.Решение

Задание № 139
Найдите наибольший общий делитель чисел:
1) 16 и 24;
2) 15 и 60;
3) 10 и 15;
4) 45 и 56;
5) 21 и 49;
6) 12, 18 и 24.Решение

Задание № 140
Найдите наибольший общий делитель чисел a и b:
1) a = 2 * 2 * 3 * 5 * 7 * 19 и b = 2 * 3 * 3 * 7 * 11 * 13;
2) a = 23 * 32 * 73 * 112 * 19 и b = 22 * 35 * 112 * 193.Решение
1) НОД(a;b) = 2 * 3 * 7 = 42
2) НОД(a;b) = 22 * 32 * 112 * 19 = 82764Задание № 141
Найдите наибольший общий делитель чисел:
1) 72 и 120;
2) 792 и 1188;
3) 924 и 396;
4) 116 и 111.Решение

Задание № 142
Найдите наибольший общий делитель чисел:
1) 42 и 105;
2) 588 и 252;
3) 680 и 612.Решение

Задание № 143
Среди данных пар чисел выберите пары взаимно простых чисел:
1) 14 и 21;
2) 54 и 65;
3) 42 и 55;
4) 14 и 70;
5) 28 и 39;
6) 63 и 42.Решение

Задание № 144
Составьте все пары взаимно простых чисел 12, 14, 33, 25.
Решение
Взаимно простые числа:
12 и 25;
33 и 25;
14 и 25;
14 и 33.
12 | 2
6 | 2
3 | 3
1
14 | 2
7 | 7
1
33 | 3
11 | 11
1
25 | 5
5 | 5
1Задание № 145
Составьте все пары взаимно простых чисел 15, 16, 21, 77.
Решение
Взаимно простые числа:
16 и 21;
15 и 16;
15 и 77;
16 и 77.
15 | 3
5 | 5
1
16 | 2
8 | 2
4 | 2
2 | 2
1
21 | 3
7 | 7
1
77 | 7
11 | 11
1Задание № 146
Запишите все правильные дроби со знаменателем 15, у которых числитель и знаменатель − взаимно простые числа.
Решение
1 2 4 7 8 11 13 14
15 15 15 15 15 15 15 15Задание № 147
Запишите все неправильные дроби с числителем 16, у которых числитель и знаменатель − взаимно простые числа.
Решение
16 16 16 16 16 16 16 16
1 3 5 7 9 11 13 15Задание № 148
Докажите, что:
1) числа 364 и 495 − взаимно простые;
2) числа 380 и 399 не являются взаимно простыми.Решение
1) НОД(364;495) = 1 взаимно простые.
364 | 2
182 | 2
91 | 7
13 | 13
1
495 | 3
165 | 3
55 | 5
11 | 11
1
НОД(380;399) = 19 числа не взаимно простые.
380 | 2
190 | 2
95 | 5
19 | 19
1
399 | 3
133 | 7
19 | 19
1Задание № 149
Докажите, что:
1) числа 945 и 572 − взаимно простые;
2) числа 1095 и 738 не являются взаимно простыми.Решение
1) НОД(945;572) = 1 взаимно простые.
945 | 3
315 | 3
105 | 3
35 | 5
7 | 7
1
572 | 2
286 | 2
143 | 13
11 | 11
1
НОД(1095;738) = 3 числа не взаимно простые.
1095 | 3
365 | 5
73 | 73
1
738 | 2
369 | 3
123 | 3
41 | 41
1Задание № 150
Используя цифры 2, 3, 4, запишите все возможные двузначные числа (цифры в каждом двузначном числе должны быть различными). Из полученных чисел выпишите пары взаимно простых чисел.
Решение
43; 42; 24; 23; 32; 34.
Взаимно простые:
23 и 24;
24 и 43;
23 и 32;
32 и 43;
23 и 34;
34 и 43;
23 и 42;
42 и 43;
23 и 43. 31
-
Страница 31
Задание № 151. Напишите три пары составных чисел такие, что в парах числа являются взаимно простыми.
Решение
8 и 15; 9 и 40; 15 и 44.
Задача № 152. Между учениками 6 класса поделили поровну 155 тетрадей и 62 ручки. Сколько в этом классе учеников?
Решение задачи
НОД(155;62) = 31 (уч.)
155 | 5
31 | 31
1
62 | 2
31 | 31
1
Ответ: 31 ученик в классе.Задача № 153. На автомобили погрузили 96 контейнеров с картофелем и 64 контейнера с капустой. Сколько всего автомобилей, если известно, что их не меньше 20 и на всех автомобилях было одинаковое количество контейнеров с картофелем и одинаковое количество контейнеров с капустой?
Решение задачи
НОД(96;64) = 25 = 32 (ав.)
96 | 2
48 | 2
24 | 2
12 | 2
6 | 2
3 | 3
1
64 | 2
32 | 2
16 | 2
8 | 2
4 | 2
2 | 2
1
Ответ: 32 автомобиля.Задача № 154. Между школьными библиотеками 92 толковых и 138 орфографических словарей русского языка. Сколько было школ, если известно, что их не менее 25 и все школы получили одинаковые комплекты, состоящие из словарей двух видов?
Решение задачи
НОД(92;138) = 2 * 23 = 46 (ш.)
92 | 2
46 | 2
23 | 23
1
138 | 2
69 | 3
23 | 23
1
Ответ: 46 школ.Задача № 155. Для новогодних подарков приобрели 96 шоколадок, 72 апельсина и 84 банана. Какое наибольшее количество одинаковых подарков можно из них составить, если необходимо использовать все продукты? Сколько в отдельности шоколадок, апельсинов и бананов будет в каждом подарке?
Решение задачи
НОД(96;7;84) = 22*3 = 12 подарков будет всего.
В каждом подарке:
96 : 12 = 8 шоколадок,
72 : 12 = 6 апельсинов,
84 : 12 = 7 бананов.
92 | 2
48 | 2
24 | 2
6 | 2
3 | 3
1
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1
84 | 2
42 | 2
21 | 3
7 | 7
1Задание № 156. Из 156 желтых, 234 белых и 390 красных роз составляли букеты. Какое наибольшее количество одинаковых букетов можно составить, если необходимо использовать все цветы?
Решение
НОД(156;234;390) = 2 * 3 * 13 = 78 букетов
156| 2
78 | 2
39 | 3
13 | 13
1
234 | 2
117 | 3
39 | 3
13 | 13
1
390 | 2
195 | 3
65 | 5
13 | 13
1Задание № 157. Используя цифры 2, 5 и 9 (цифры не могут повторяться), запишите трехзначное число, которое:
1) кратно 2;
2) кратно 5.
Можно ли с помощью этих цифр записать число, кратное 3?Решение
1) 952
Сумма цифр не делится на 9, следовательно и число не делится на 9.
2) 925
Сумма цифр не делится на 9, следовательно и число не делится на 9.Задание № 158. Какую цифру можно поставить вместо звездочки в записи 1*8, чтобы полученное число делилось нацело на 18?
Решение
Цифру 0. 108 : 18 = 6
Задание № 159. Запишите число 19 в виде суммы трех простых чисел.
Решение
19 = 3 + 5 + 11
Задание № 160. Если к некоторому двузначному числу справа дописать нуль, то данное число увеличится на 432. Найдите это число.
Решение
Число 48.
480 − 48 = 432Задание № 161. Найдите числа, которых недостает в цепочке вычислений:
Решение
1) 0,05; 2,24; 0,04.
2) 1,5; 0,4; 0,05.Задача от мудрой совы
Задача № 162. Барон Мюнхгаузен рассказывал, что он разрезал арбуз на четыре части, а после того, как его съели, осталось пять корок. Может ли такое быть, если корки не ломать?
Решение
Да, можно. Нужно сначала в центре арбуза насквозь вырезать цилиндр, который будет иметь 2 корки снизу и сверху.
Оставшийся арбуз разрезается на ровные 3 части, каждая из которых будет иметь по одной корке.
Таким образом получится 4 части и 5 корок. 34
-
Страница 34
Задание № 163. Найдите наименьшее общее кратное чисел:
1) 8 и 12;
2) 12 и 16;
3) 6 и 12;
4) 10 и 21;
5) 24 и 36;
6) 6,8 и 12.Решение

Задание № 164. Найдите наименьшее общее кратное чисел:
1) 6 и 10;
2) 9 и 12;
3) 14 и 28;
4) 8 и 9;
5) 32 и 48;
6) 8,9 и 15.Решение

Задание № 165. Найдите наибольший общий делитель и наименьшее общее кратное чисел a и b:
1) a = 23 * 3 * 5 и b = 2 * 32 * 5 ;
2) a = 24 * 3 * 11 и b = 22 * 33 * 13 .Решение
1) НОД (a;b) = 2 * 3 * 5 = 30
НОК (a;b) = 23 * 32 * 5 = 360
2) НОД (a;b) = 22 * 3 = 12
НОК (a;b) = 24 * 33 * 11 * 13 = 61776Задание № 166. Найдите наибольший общий делитель и наименьшее общее кратное чисел a и b:
1) a = 3 * 52 и b = 3 * 5 * 7 ;
2) a = 23 * 32 * 54 и b = 22 * 33 * 52 .Решение
1) НОД(a;b) = 3 * 5 = 15
НОК ( a ; b ) = 3 * 52 * 7 = 525
2) НОД ( a ; b ) = 22 * 32 * 52 = 900
НОК ( a ; b ) = 23 * 33 * 54 = 135000Задание № 167. Найдите наименьшее общее кратное чисел:
1) 56 и 70;
2) 78 и 792;
3) 320 и 720;
4) 252 и 840.Решение

Задание № 168. Найдите наименьшее общее кратное чисел:
1) 42 и 63;
2) 120 и 324;
3) 675 и 945;
4) 924 и 396.Решение

35
-
Страница 35
Задание № 169. Найдите наименьшее общее кратное знаменателей дробей: 1) 11/12 и 4/15 ; 2) 97/100 и 1/125 .
Решение

Задание № 170. Найдите наименьшее общее кратное знаменателей дробей:
1) 8/9 и 7/6;
2) 11/20 и 24/25.Решение

Задание № 171. Найдите наименьшее общее кратное:
1) первых пяти натуральных чисел;
2) первых пяти нечетных чисел;
3) первых пяти простых чисел.Решение
1) НОК ( 1 ; 2 ; 3 ; 4 ; 5 ) = 22 * 3 * 5 = 60
2) НОК ( 1 ; 3 ; 5 ; 7 ; 9 ) = 32 * 5 * 7 = 315
3) НОК ( 2 ; 3 ; 5 ; 7 ; 11 ) = 11 * 7 * 5 * 3 * 2 = 2310Задание № 172. Найдите наименьшее общее кратное:
1) первых пяти чётных чисел;
2) первых четырех составных чисел.Решение
1) НОК ( 2 ; 4 ; 6 ; 8 ; 10 ) = 5 * 3 * 23 = 120
2) НОК ( 4 ; 6 ; 8 ; 9 ) = 23 * 32 = 72Задача № 173. Длина шага Чебурашки равна 15 см, а крокодила Гены − 50 см. Какое из них наименьшее одинаковое расстояние должен пройти каждый из них, чтобы они сделали по целому числу шагов?
Решение задачи
НОК(15;50) = 2 * 3 * 25 = 150 см
15 | 3
5 | 5
1
50 | 2
25 | 5
5 | 5
1
Ответ: 150 см.Задача № 174. С одного места в одном направлении по велотреку одновременно стартовали два велосипедиста. Один из них делает круг за 1 мин, а другой − за 45 с. Через какое наименьшее количество минут после начала движения они вновь окажутся в месте старта? Сколько кругов по велотреку при этом сделает каждый из них?
Решение задачи
60 | 2
30 | 2
15 | 3
5 | 5
1
45 | 3
15 | 3
5 | 5
1
НОК(15;50) = 22 * 32 * 5 = 180 с = 3 (мин.)
180 : 60 = 3 (к.) сделает первый велосипедист;
180 : 45 = 4 (к.) сделает второй велосипедист.
Ответ: 3 круга, 4 круга.Задача № 175. Дима и Петя отправились в поход из одного пункта в одном направлении.Петя делал остановку для отдыха через каждые 2400 м, а Дима − через каждые 2800 м. На каком наименьшим расстоянии от пункта отправления места их остановок совпадут?
Решение задачи
НОК(2400;2800)=25 * 3 * 52 * 7 = 16800 (м)
2400 | 2
1200 | 2
600 | 2
300 | 2
150 | 2
75 | 3
25 | 5
5 | 5
1
2800 | 2
1400 | 2
700 | 2
350 | 2
175 | 5
35 | 5
7 | 7
1
Ответ: 16800 м.Задание № 176. В ящике лежит меньше 80 мандаринов. Известно, что их можно делить поровну между двумя, тремя или пятью детьми, но нельзя разделить поровну между четырьмя детьми. Сколько мандаринов лежит в ящике?
Решение
НОК (2;3;5) = 2 * 3 * 5 = 30 (м.) - лежит в ящике.
Ответ: 30 мандаринов.Задача № 177. Саша ходит в бассейн один раз в три дня, Коля − раз в четыре дня, Петя − раз в пять дней. Мальчики встретились в бассейне во вторник. Через сколько дней и в какой день недели они встретятся в следующий раз?
Решение задачи
НОК (3;4;5) = 3 * 4 * 5 = 60 (д.) пройдет до встречи.
60 : 7 = 56 и 4 в остатке. Получается что:
56 день будет понедельник;
57 день − вторник;
58 день − среда;
59 день − четверг;
60 день − пятница, то есть мальчики встретятся через 60 дней в пятницу.
Ответ: через 60 дней, в пятницу.Задача № 178. Готовя подарки к Новому году, члены родительского комитета 6 класса увидели, что имеющиеся конфеты можно разложить поровну по 15 штук или по 20 штук в один подарок. Сколько было конфет, если известно, что их было больше 600 и меньше 700?.
Решение
НОК (15;20) = 22 * 3 * 5 = 60 (к.) минимальное число в подарке
Наибольшее число меньше 700 и больше 600 делящееся нацело на 60 будет 660, таким образом было 660 конфет в 660 : 60 = 11 подарках.
15 | 3
5 | 5
1
20 | 2
10 | 2
5 | 5
1
Ответ: 660 конфет. 36
-
Страница 36
Задание № 179. Если к данному числу прибавить 2, то полученное число будет кратно 5. Чему равен остаток от деления данного числа на 5?
Ответ 7 гуру
5 − 2 = 3 − остаток от деления данного числа на 5.
Задача № 180. Белый аист пролетел 48 км со скоростью 40 км/ч. Сколько взмахов крыльями сделал при этом аист, если каждую секунду он делает два взмаха?
Решение задачи
48 : 40 = 1,2 часа * 3600 = 4320 (с.) летел аист
4320 * 2 = 8640 (вз.) крыльями сделал при этом аист.
Ответ: 4320 секунд, 8640 взмахов.Задача № 181. В коробке лежит 14 шаров, из которых 5 − синего цвета. Какую часть всех шаров составляют синие?
Ответ
5
14 всех шаров составляют синие.Задача № 182. В коробке лежит 14 шаров, из которых 3/7 составляют шары красного цвета. Сколько красных шаров в коробке?
Решение задачи
14 * 3 = 6 (ш.) - красных в коробке.
7
Ответ: 6 шаров.Задача № 183. В коробке лежат шары, 6 из которых белого цвета. Сколько всего шаров в коробке, если белые составляют 3/7 всех шаров?
Решение
6 : 3/7 = 6 * 7/3 = 2 * 7 = 14 (ш.) всего в коробке.
Ответ: 14 шаров.Задание № 184. Укажите, какие из дробей 12/17,12/7, 5/13,374/10,53/8,53/54,72/71:
1) правильные;
2) неправильные.
Неправильные дроби преобразуйте в смешанные числа.Решение
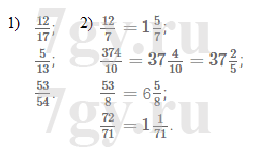
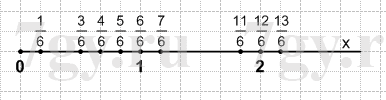
Задание № 185. Начертите координатный луч, взяв за единичный отрезок, длина которого в раз больше стороны клетки тетради. Отметьте на луче точки, соответствующие числам: 1/6;3/6;4/6;5/6;6/6;7/6;11/6;12/6;13/6.
Задача от мудрой совы
Задание № 186. На чудо дереве садовник вырастил 85 бананов и 70 апельсинов. Каждый день он срывает два плода, и сразу на дереве вырастает один новый. Если садовник срывает два одинаковых фрукта, то вырастает апельсин, а если два разных − то банан. Каким окажется последний фрукт на этом дереве?
Решение задачи
Останется банан, так как количество бананов всегда будет нечетно.
42
-
Страница 42
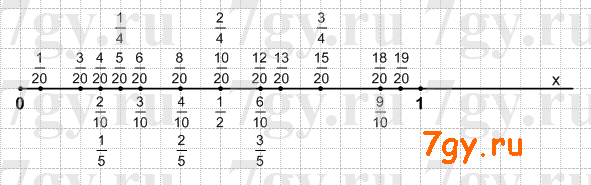
Задание № 187. Начертите координатный луч, взяв за единичный отрезок, длина которого в 20 раз больше стороны клетки тетради. Отметьте на луче точки, соответствующие числам...
Задание № 188. Начертите координатный луч, взяв за единичный отрезок, длина которого в 18 раз больше стороны клетки тетради. Отметьте на луче точки, соответствующие числам...
Задание № 189. Умножьте на 4 числитель и знаменатель каждой из дробей:
1/2, 1/3, 5/6, 4/7, 10/19.Решение

Задание № 190. Разделите на 3 числитель и знаменатель каждой из дробей:
3/9, 12/33, 30/45, 15/36, 99/240.Решение

43
-
Страница 43
Задание № 191. Укажите пропущенное значение числителя или знаменателя, при котором данная запись будет верной...
Решение
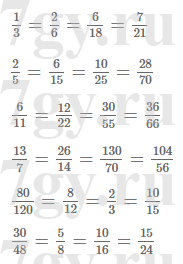
Задание № 192. Объясните, почему верно равенство:
1) 1/6=7/42;
2) 100/240=5/12;
3) 3/4=33/44;
4) 6/54=1/9.Решение
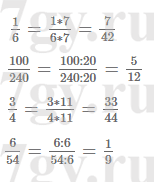
Задание № 193. Запишите три дроби равные:
1) 1/7;
2) 2/5;
3) 7/11;
4) 3/12.Решение
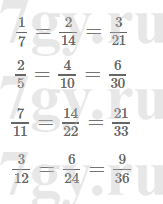
Задание № 194. Какие из данных равенств неверны:
1) 3/8=9/24;
2) 4/5=16/25;
3) 72/90=8/9;
4) 42/49=6/7.Решение

Задание № 195. Каждую из данных дробей замените равной ей дробью, знаменатель которой равен 42:
1) 1/6;
2) 3/7;
3) 5/14;
4) 2/3;
5) 16/21;
6) 1/2.Решение
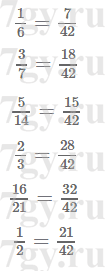
Задание № 196. Каждую из данных дробей замените равной ей дробью, знаменатель которой равен 72:
1) 2/3;
2) 5/4;
3) 1/6;
4) 8/9;
5) 17/36;
6) 11/8.Решение
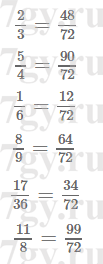
Задание № 197. Запишите:
1) число 3 в виде дроби, знаменатель которой равен 6;
2) число 13 в виде дроби, знаменатель которой равен 5;
3) число 1 в виде дроби, знаменатель которой равен 29.Решение
3 = 18
6
13 = 65
5
1 = 29
29Задание № 198. Запишите:
1) число 5 в виде дроби, знаменатель которой равен 8;
2) число 10 в виде дроби, знаменатель которой равен 14;
3) число 16 в виде дроби, знаменатель которой равен 16.Решение
40 = 5
8
140 = 10
14
256 = 16
16Задание № 199. Пользуясь основным свойством дроби, найдите значение a, при котором верно равенство:
1) a/6=9/54;
2) 7/a=49/28;
3) 27/45=3/a;
4) a/32=5/8.Решение
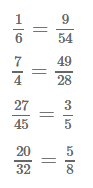
Задание № 200. Пользуясь основным свойством дроби, найдите значение a, при котором верно равенство:
1) a/5=6/15;
2) 1/12=4/a;
3) 56/70=8/a;
4) a/60=6/5.Решение
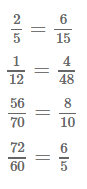
1) а = 2
2) а = 48
3) а = 10
4) а = 72 44
-
Страница 44
Задание № 201. Решите уравнение.
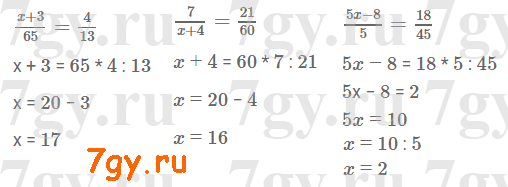
Задание № 202. Решите уравнение.
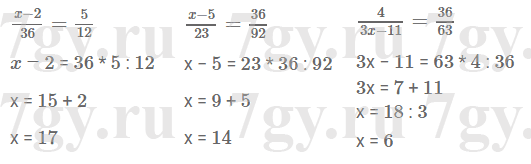
Задача № 203. Леденец стоит 16 р. У Димы есть 20 монет по 10 р. Какое наибольшее количество леденцов может купить Дима, чтобы продавцу не нужно было давать ему сдачу?
Решение задачи
20 * 10 = 200 (р.) - всего у Димы;
Для того, чтобы продавцу не надо было сдавать сдачу, сумма, которую отдаст Дима за леденцы, должна нацело делится на 10. Наибольшая такая сумма равна 160 рублей.
160 : 16 = 10 (л.) - может купить Дима, чтобы продавцу не нужно было давать ему сдачу.
Ответ: 10 леденцов.Задание № 204. Число делится нацело на 2, на 5 и на 9. Каким числам кратно это число?
Решение
НОК (2;5;9) = 90
90 кратно 18, 10, 45.Задача № 205. В среднем сердце человека делает 75 ударов в минуту. Сколько ударов делает сердце в течение суток? Сколько литров крови оно перекачивает за 1 мин, если сердце перекачивает за сутки 8640 л крови?
Решение задачи
75 * 60 мин * 24 ч = 108000 (уд.) - делает сердце в стуки.
8640 : 24 : 60 = 6 (л.) крови перекачивает сердце за 1 минуту.
Ответ: 108000 ударов, 6 литров крови.Задание № 206. Начертите острый угол ABC. Проведите луч BD так, чтобы угол ABD был прямым, а угол CBD:
1) тупым;
2) острым.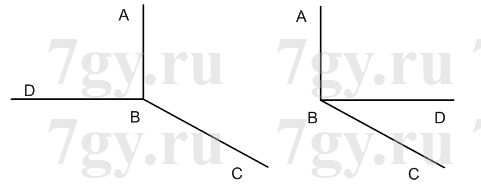
Задача № 207. От пристани отправился теплоход со скоростью 18 км/ч. Через 3 ч после этого от пристани в том же направлении отправился второй теплоход, который догнал первый через 9 ч после своего выхода. Найдите скорость второго теплохода.
Решение задачи
18 * 3 = 54 (км) - проплыл первый теплоход за 3 часа.
54 : 9 + 18 = 24 (км/ч) - скорость второго теплохода.
Ответ: 24 км/ч.Задача № 208. Из одного города в другой со скоростью 60 км/ч выехал автомобиль. Через 3 ч из другого города навстречу ему выехал второй автомобиль. Они встретились через 7 ч после начала движения первого автомобиля. Найдите скорость второго автомобиля, если расстояние между городами равно 700 км.
Решение задачи
60 * 3 = 180 (км) − проехал 1 автомобиль до начала движения второго.
700 − 180 = 520 (км) - прошли оба автомобиля с момента выезда второго.
520 : (7 − 4) = 520 : 4 = 130 (км/ч) - скорость сближения автомобилей.
130 − 60 = 70 (км/ч) - скорость второго автомобиля.
Ответ: 70 км/ч.Задача от мудрой совы
Задание № 209. На поле размером 10 Х 10 клеток для игры в "Морской бой" поставили корабль в прямоугольник размером 1 Х 3 клетки. Можно ли, сделав 33 выстрела, наверняка в него попасть?
Решение
Можно, так как всего клеток 10 * 10 = 100, то делая каждый выстрел через 2 клетки за 33 выстрела можно покрыть 33 * 3 = 99 клеток, что значит наверняка попасть в корабль.
46
-
Страница 46
Задание № 210. Сократите дробь.
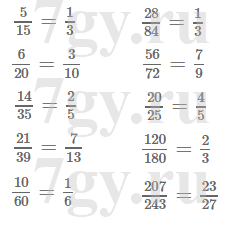
Задание № 211. Сократите дробь.
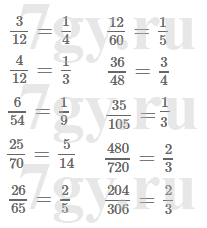
Задание № 212. Какие из дробей 11/12; 7/42; 9/111; 5/42; 12/68; 13/36 несократимы?
Ответ 7 гуру
11/2 и 5/42 − несократимы, так как не имеют общего делителя.
47
-
Страница 47
Задание № 213. Какие из дробей 15/25;24/99;28/45;26/51;16/42;22/69 несократимы?
Ответ 7 гуру
28/45, 26/51 и 22/69 − несократимы, так как не имеют общего делителя.
Задание № 214. Запишите десятичную дробь в виде обыкновенной дроби и результат, если возможно, сократите:
1) 0,4;
2) 0,5;
3) 0,12;
4) 0,84;
5) 0,16;
6) 0,59;
7) 0,128;
8) 0,96;
9) 0,2348;
10) 0,975.Решение
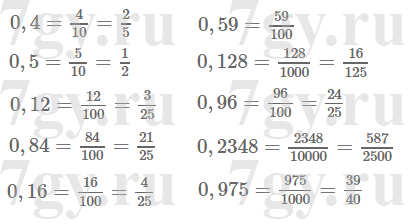
Задание № 215. Найдите среде данных дробей равные между собой.
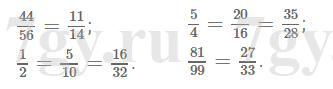
Задание № 216. Найдите среде данных дробей
24/27, 1/10, 6/60, 8/9, 40/45 равные между собой и запишите соответствующие равенства.Решение
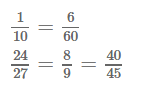
Задание № 217. Какую часть часа составляют:
1) 4 мин;
2) 10 мин;
3) 36 мин;
4) 54 мин;
5) 72 мин?Решение

Задание № 218. Какую часть суток составляют:
1) 3 ч;
2) 8 ч;
3) 12 ч;
4) 16 ч;
5) 21 ч?Решение
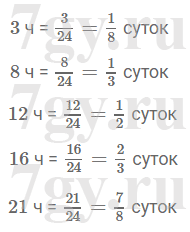
Задание № 219. Какую часть развернутого угла составляет угол, градусная мера которого равна:
1) 4°;
2) 12°;
3) 27°;
4) 126°;
5) 153°.Решение
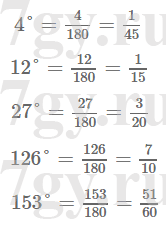
Задание № 220. Какую часть прямого угла составляет угол, градусная мера которого равна:
1) 2°;
2) 15°;
3) 36°;
4) 75°;
5) 54°.Решение
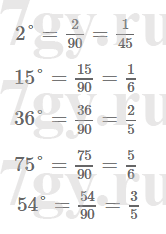
Задание № 221. Выполните действия и сократите результат.
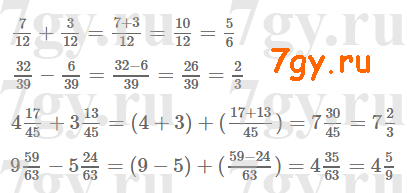
Задание № 222. Выполните действия и сократите результат.
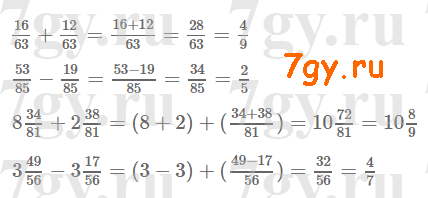
Задание № 223. Запишите все правильные и несократимые дроби со знаменателем 18.
Решение
1/18; 5/18; 7/18; 11/18; 13/18; 17/18.
Задание № 224. Запишите все неправильные и несократимые дроби с числителем 20.
Решение
20/1; 20/3; 20/7; 20/9; 20/11; 20/13; 20/17; 20/19.
Задание № 225. Сократите.

48
-
Страница 48
Задание № 226. Сократите.
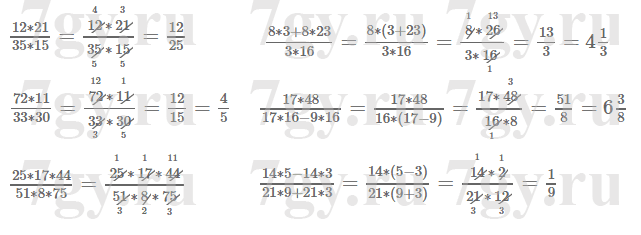
Задание № 227. Сократите (буквами обозначены натуральные числа).
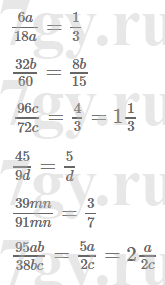
Задание № 228. Дробь x/6 сократили на 2 и получили дробь 2/y. Найдите значения x и y.
Решение
x : 2 = 2
x = 2 * 2 = 4;
6 : 2 = y
y = 3.Задание № 229. После сокращения дроби 21/a на 3 получили дробь b/4. Найдите значения a и b.
Решение
21 : 3 = b
b = 7;
a : 3 = 4
a = 3 * 4 = 12.Задание № 230. Запишите, используя каждую цифру от 0 до 9 только один раз:
1) наименьшее число, кратное 2;
2) наибольшее число, кратное 18.Ответ 7 гуру
1) 4
2) 9876543210Задание № 231. К какому числу надо прибавить 5,7, чтобы произведение полученной суммы и числа 3,6 было равно 120,6?
Решение
Пусть неизвестное число равно x, тогда:
(x + 5,7) * 3,6 = 120,6
x + 5,7 = 120,6 : 3,6
x + 5,7 = 33,5
х = 33,5 − 5,7
х = 27,8Задание № 232. Из какого числа надо вычесть 3,8, чтобы произведение полученной разности и числа 5,5 было равно 34,1?
Решение
Пусть неизвестное число равно x, тогда:
(x − 3,8) * 5,5 = 34,1
x − 3,8 = 34,1 : 5,5
x − 3,8 = 6,2
x = 6,2 + 3,8
x = 10Задание № 233. Расположите в порядке возрастания дроби: 9/19;1/19;16/19;5/19;14/19;10/19.
Решение
1 5 9 10 14 16
19 19 19 19 19 19Задание № 234. Сравните:
1) 10/21 и 8/21;
2) 8/19 и 8/9;
3) 4/7 и 1;
4) 7/4 и 1;
5) 1 и 11/15;
6) 11/15 и 15/11;
7) 2 и 5/3;
8) 2 и 7/3.Ответ
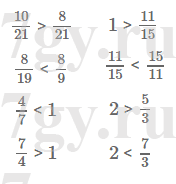
49
-
Страница 49
Задача от мудрой совы
Задача № 235. Из старинной книги выпала часть страниц, идущих подряд. Первая выпавшая страница имеет номер 251, а номер последней записан теми же цифрами в другом порядке. Какой номер последней выпавшей страницы?
Ответ к задаче
Существует два решения:
1) страница № 512;
2) страница № 521.
Поскольку первая выпавшая из книги страница - это уже 251, то следующие выпавшие не могут начинаться ни на 1**, ни на 21*, а значит, это будет 5**. Подставляем оставшиеся цифры, получаем 512 и 521. 51
-
Страница 51
Задание № 236. Приведите дроби:
1) 1/2;3/4;4/5;9/10 к знаменателю 20;
2) 3/4;1/6;7/18;8/9 к знаменателю 36;
3) 1/2;2/4;3/8;5/32 к знаменателю 64;
4) 1/5;1/4;7/25;63/50 к знаменателю 100.Решение
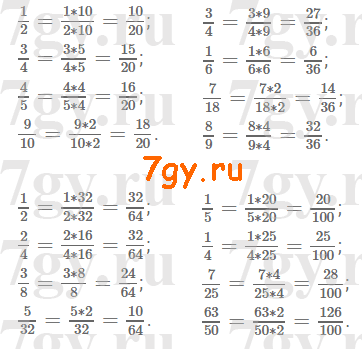
Задание № 237. Приведите дробь:
1) 7/9 к знаменателю 27;
2) 3/5 к знаменателю 40;
3) 4/13 к знаменателю 78;
4) 12/17 к знаменателю 102;
5) 4/23 к знаменателю 69;
6) 5/24 к знаменателю 144.Решение
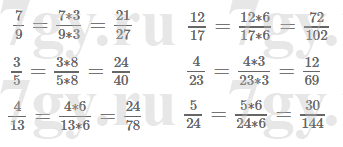
52
-
Страница 52
Задание № 238. Среди дробей 5/6;5/8;3/10;7/16;9/24;11/18;8/28;10/12;10/3;5/4;13/36;1/14
найдите те, которые можно привести к знаменателю 48. Найденные дроби приведите к указанному знаменателю.Решение
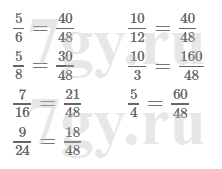
Задание № 239. Приведите к наименьшему общему знаменателю дроби:
1) 1/4 и 1/6;
2) 4/9 и 7/12;
3) 5/6 и 7/18;
4) 3/8 и 4/15;
5) 2/15 и 11/12;
6) 1/12 и 1/18;
7) 1/24 и 1/18;
8) 3/10,3/8 и 3/4.Решение
3/12 и 2/12
16/36 и 21/36
15/18 и 7/18
45/120 и 32/120
8/60 и 55/60
3/36 и 2/36
3/72 и 4/72
12/40,15/40 и 30/40.Задание № 240. Приведите к наименьшему общему знаменателю дроби:
1) 3/8 и 5/12;
2) 2/15 и 3/10;
3) 10/17 и 13/34;
4) 4/13 и 3/4;
5) 9/14 и 2/21;
6) 1/20 и 1/30;
7) 1/9,1/4 и 1/6;
8) 3/28,9/14 и 7/8.Решение
9/24 и 10/24
4/30 и 9/30
20/34 и 13/34
16/52 и 39/52
27/42 и 4/42
3/60 и 2/60
4/36, 9/36 и 6/36
6/56, 36/56 и 49/56Задание № 241. Сравните дроби:
1) 5/7 и 7/9;
2) 11/20 и 17/30;
3) 2/9 и 1/6;
4) 5/6 и 3/4;
5) 8/38 и 4/19;
6) 7/9 и 8/11;
7) 8/25 и 7/20;
8) 5/12 и 4/9.Решение
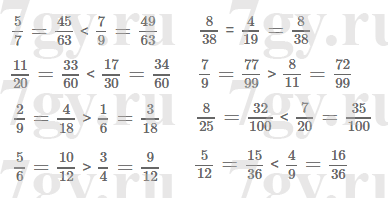
Задание № 242. Сравните дроби:
1) 5/6 и 7/11;
2) 7/13 и 7/16;
3) 3/8 и 1/6;
4) 5/8 и 7/10;
5) 3/7 и 9/21;
6) 3/5 и 5/8;
7) 7/12 и 11/18;
8) 10/21 и 9/14.Решение
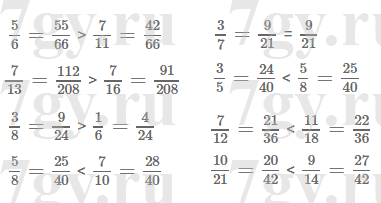
Задание № 243. Укажите какую−либо дробь, которая меньше 1/2 и знаменатель которой равен:
1) 6;
2) 10;
3) 22.Ответ
1) 2/6
2) 4/10
3) 7/22Задание № 244. Укажите какую−либо дробь, которая больше 1/6 и знаменатель которой равен:
1) 12;
2) 30;
3) 66.Ответ
1) 11/12
2) 25/30
3) 40/66Задание № 245. Расположите в порядке возрастания числа:
1) 7/12,3/8,1/4,5/6;
2) 3/4,8/15,5/12,9/20.Ответ
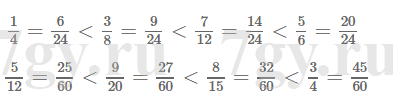
53
-
Страница 53
Задание № 246. Расположите в порядке убывания числа:
1) 4/9,1/4,7/12,13/18;
2) 28/45,5/9,7/10,13/18,8/15.Ответ 7 гуру
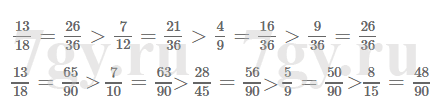
Задача № 247. Лакомка съедает 7 пирожных за 12 мин, а Сладкоежка − 13 пирожных за 20 мин. У кого аппетит лучше − у Лакомки или у Сладкоежки?
Решение

Задача № 248. Головку сыра массой 9 кг разделили на 16 равных кусков, а головку массой 13 кг − на 20 равных кусков. Кусок какой головки сыра, первой или второй, вы посоветуете съесть мышонку Джерри, который очень его любит?
Решение

Задание № 249. Расстояние между двумя городами легковой автомобиль преодолевает за 4 ч, а грузовой − за 7 ч. Какой автомобиль проедет большее расстояние: легковой за 3 ч или грузовой за 5 ч?
Решение

Задание № 250. Теплоход проходит расстояние между двумя пристанями за 9 ч, а катер − за 6 ч. Сравните расстояния: пройденное теплоходом за 7 ч и пройденное катером за 5 ч.
Решение

Задание № 251. Какие из дробей 3/7,11/28,1/2,13/42,23/70 больше дроби 5/14?
Решение

Задание № 252. Какие из дробей 43/112,9/28,3/14,3/8,1/4 меньше дроби 19/56?
Решение

Задание № 253. Найдите все натуральные значения x, при которых верно неравенство:
1) 8/19<x/19<1;
2) 1/3<x/18<5/6.Ответ
1) 9; 10; 11; 12; 13; 14; 15; 16; 17; 18.
2) 7; 8; 9; 10; 11; 12; 13; 14.Задание № 254. Найдите все натуральные значения x, при которых верно неравенство:
1) 12/23<x/23<1;
2) 4/9<x/36<11/12.Ответ
1) 13; 14; 15; 16; 17; 18; 19; 20; 21; 22.
2) 17; 18; 19; 20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 30; 31; 32.Задание № 255. Какие из дробей 1/2,3/8,5/6,9/16,7/24,11/24 можно поставить вместо x, чтобы было верно неравенство 11/48<x<2948/?
Ответ

Задание № 256. Какие из дробей 3/7,6/7,9/14,5/8,15/28,11/14 можно поставить вместо x, чтобы было верно неравенство 19/56<x<37/56?
Решение

Задание № 257. Найдите все дроби со знаменателем 48, которые больше 1/4, но меньше 1/3.
Решение

Задание № 258. Укажите два числа, каждое из которых:
1) больше 1/5, но меньше 1/4;
2) больше 1/7, но меньше 1/6;
3) больше 1/10, но меньше 1/9;
4) больше 3/7, но меньше 5/7.Решение

54
-
Страница 54
Задание № 259. Укажите три числа, каждое из которых:
1) больше 1/3, но меньше 1/2;
2) больше 3/5, но меньше 4/5;
3) больше 98/99, но меньше 1.Решение
Задание № 260. Сравните дроби
171/181 и 171171/181181.Решение
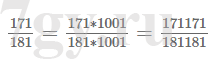
Задание № 261.Найдите все натуральные значения x, при которых верно неравенство:
1) x/17<8/51;
2) x/65<1/13;
3) x/5<3/15;
4) 1/16<x/8.Решение

Задание № 262. Дробь сначала сократили на 2, затем на 3, потом на 7. На какое число можно было сократить эту дробь сразу.
Ответ
Дробь можно было сразу сократить на 42 = 2 * 3 * 7
Задание № 263. Запишите все правильные дроби со знаменателем 12. Сократите те из них, которые не являются несократимыми.
Решение
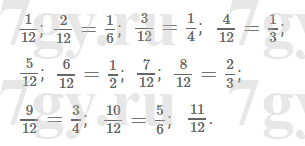
Задание № 264. Сумма двух чисел равна 374. Последней цифрой одного из этих чисел является нуль. Если его отбросить, то получим второе число. Найдите эти числа.
Решение
Пусть искомые числа будут x и y, тогда по условию получаем следующее уравнение:
x + y = 374, при этом x = 10y, тогда
10y + y = 374
11y = 374
y = 374 : 11 = 34
x = 10y = 10 * 34 = 340Задание № 265. Вычислите...
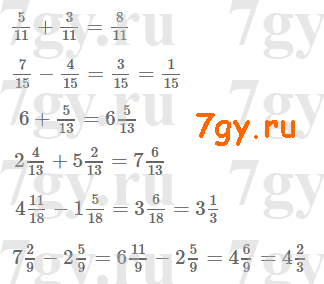
Задание № 266. Решите уравнение...
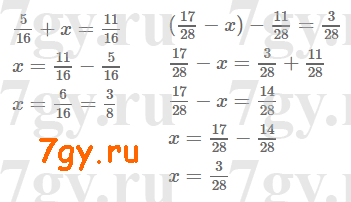
Задача от мудрой совы
Задание № 267. Из чашки с молоком одну ложку молока переливают в чашку с кофе и тщательно размешивают. После этого одну ложку смеси переливают в чашку с молоком. Чего теперь больше: кофе в чашке с молоком или молока в чашке с кофе?
Решение
Молока в чашке с кофе больше, чем кофе в чашке с молоком. Так как в чашку с кофе налили ложку только молока, а в чашку с молоком налили ложку смеси (кофе + молоко).
57
-
Страница 57
Задание № 268. Вычислите:
1) 3/7+4/9;
2) 8/9−7/8;
3) 13/15−2/3;
4) 20/21+3/7;
5) 17/18−11/12;
6) 7/16+1/6;
7) 2/9+5/6;
8) 10/21+9/14;9) 7/9−4/15;
10) 9/14−3/7+15/28;
11) 1/6+1/4−1/8;
12) 13/18−29/45+8/15.Ответы 7 гуру

Задание № 269. Вычислите:
1) 1/4+3/5;
2) 9/11−2/5;
3) 13/16−9/32;
4) 3/28+5/14;
5) 14/15−7/10;
6) 3/8+1/6;
7) 9/25−7/20;
8) 37/42−17/24;
9) 11/24−3/16;
10) 9/16+7/24−3/8;
11) 1/3−1/6+1/4;
12) 2/5+4/15−5/9.Решение
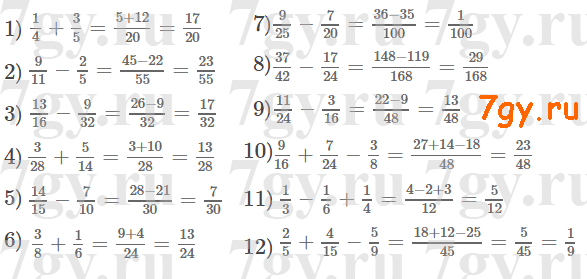
Задание № 270. Найдите значение выражения, предварительно сократив дроби:
1) 25/80+45/60;
2) 20/45+26/54;
3) 36/300+12/40−350/1000;
4) 14/24−39/90+15/100;
5) 42/120+20/32−28/160;
6) 45/72−33/144−20/64.Решение
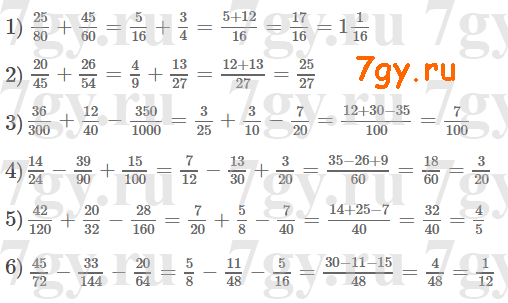
Задача № 271. В одной банке было 3/10 л сметаны, а в другой − 4/15 л. В какой банке было больше сметаны и на сколько литров?
Решение задачи

Ответ: в первой на 1/30 л больше.Задача № 272. Окунев поймал рыбу длиной 8/25 м, а Щукин − длиной 13/40м. Кто из них поймал рыбу длиннее и на сколько метров?
Решение от 7 гуру

Ответ: Щукин поймал рыбу длиннее на 1/200 метра.Задача № 273. Золушка 11/20 ч убирала комнаты, что на 2/15 ч больше времени, которое она затратила на мытье посуды. Сколько времени заняли у Золушки уборка и мытье посуды?
Решение задачи

Ответ: 58 минут. 58
-
Страница 58
Задача № 274. На завтрак Винни−Пух съел 2/9 горшочка меда, что на 2/15 горшочка меньше, чем он съел на обед. Какую часть горшочка меда Винни−Пух съел на завтрак и на обед?
Решение задачи

Ответ: 16, 26.
45 45Задание № 275. Найдите сумму:
1) 4 5/9 + 7 1/6;
2) 6 11/12 + 8 13/18;
3) 2 3/16 +1 7/24 + 3 1/12.Решение
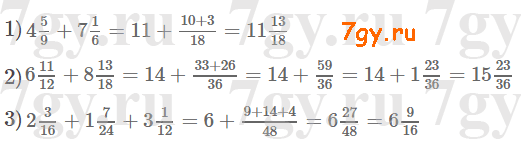
Задание № 276. Найдите сумму:
1) 5 7/8 + 6 3/10;
2) 6 3/8 + 2 5/9;
3) 1 8/21 + 4 3/14 + 2 2/7.Решение
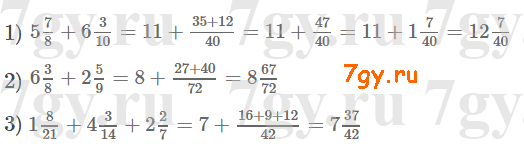
Задание № 277. Вычислите значение выражения:
1) 8 9/14 − 3 3/7;
2) 7 5/12 − 3 7/24;
3) 12 11/12 − 5 13/18.Решение от 7gy.ru
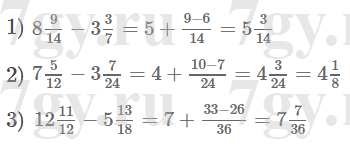
Задание № 278. Вычислите:
1) 1 − 17/29;
2) 4 − 7/19;
3) 13 − 7 3/16;
4) 15 − 12 16/17.Решение

Задание № 279. Вычислите:
1) 1 − 13/55;
2) 6 − 9/20;
3) 10 − 5 12/35;
4) 8 − 4 5/22.Решение
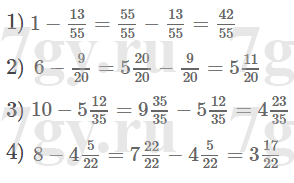
Задание № 280. Выполните вычитание:
1) 3 1/12 − 1/6;
2) 8 7/30 − 2 9/20;
3) 7 10/51 − 4 21/34;
4) 5 1/4 − 1 3/8.Решение
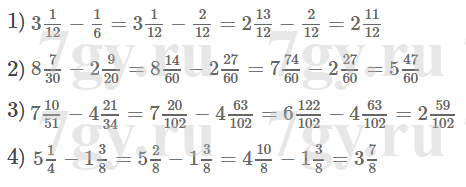
Задание № 281. Выполните вычитание:
1) 4 3/16 − 5/8;
2) 6 4/9 − 3 6/7;
3) 10 11/24 − 8 19/36;
4) 9 1/6 − 5 3/4.Решение
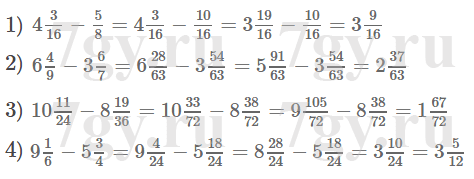
Задание № 282. Решите уравнение:
1) x + 7 4/15 = 9 7/10;
2) 8 9/14 − x = 4 3/7;
3) x − 3 8/9 = 5 1/12.Решение от 7 гуру
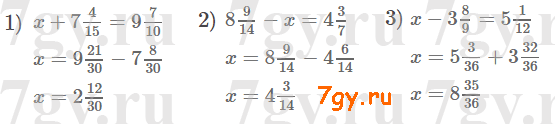
Задание № 283. Решите уравнение:
1) 6 3/11 + x = 10 6/7;
2) 9 5/36 − x = 2 4/9;
3) x − 5 17/60 = 7 9/20.Решение
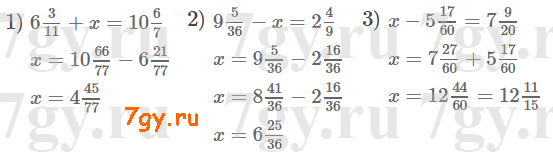
Задание № 284. Преобразуйте десятичные дроби в обыкновенные и вычислите:
1) 0,8 − 5/7;
2) 0,36 + 8/15;
3) 7 7/8 − 3,18;
4) 4,75 − 2 3/16.Решение
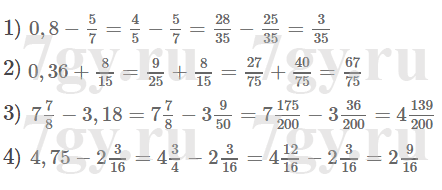
Задание № 285. Преобразуйте десятичные дроби в обыкновенные и вычислите:
1) 0,5 + 1/3;
2) 2/3 − 0,25;
3) 0,125 + 5/12;
4) 3,25 − 2 9/14.Решение
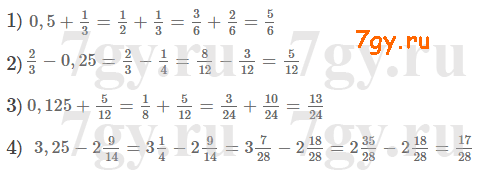
59
-
Страница 59
Задача № 286. Собственная скорость теплохода составляет 20 2/7 км/ч, а скорость течения реки − 2 11/14 км/ч. Найдите скорость теплохода по течению реки и его скорость против течения.
Решение задачи

Задача № 287. Скорость катера по течению составляет 27 1/3 км/ч, а скорость течения − 1 4/9 км/ч. Найдите собственную скорость катера и скорость катера против течения реки.
Решение задачи

Задание № 288. Расшифруйте фамилию выдающегося русского математика, жившего на рубеже XIX и XX вв., академика Петербургской Академии наук, вице−президента Академии наук СССР, основателя школы математической физики, чьё имя носит Математический институт Российской академии наук в Москве. Номер примера соответствует месту, на котором стоит буква в слове.
1) 2/9 + 5/6;
2) 1 − 5/17;
3) 6 − 1 4/9;
4) 2 1/3 − 1 1/2;
5) 1 1/7 + 2 3/28;
6) 5 1/6 − 4 1/4;
7) 1/4+1/12+2/3.Решение от 7 гуру
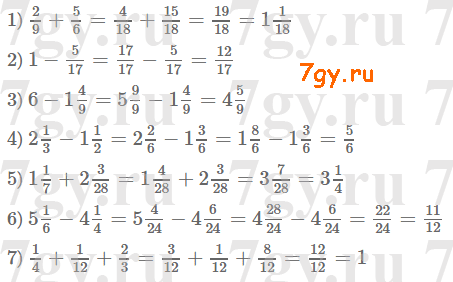
Фамилия математика: СТЕКЛОВ.Задание № 289. Вычислите значение выражения наиболее удобным способом:
1) 3/7 + 14/19 + 4/7 + 5/19;
2) 7/16 + 11/42 + 9/16 + 17/42;
3) 5/18 + 4/81 + 7/18 + 5/81;
4) 9/40 + 13/50+ 12/50 + 11/40;
5) 3 5/11 + 1 3/16 + 2 5/16 + 4 6/11;
6) 1 17/24 + 3 1/36 + 5 4/24 + 2 8/36.Решение
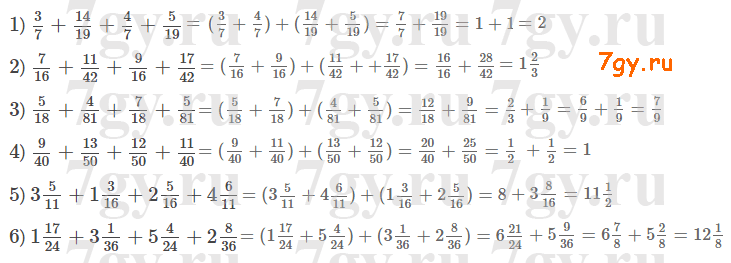
Задание № 290. Решите уравнение:
1) (x + 5/12) − 9/20 = 11/15;
2) (x − 11/30) − 16/45 = 2/9;
3) (x − 7/15) + 5/8 = 17/24;
4) 4/5 − (x+ 1/60)= 2/3;
5) 4 3/4 − (x − 2 5/8) = 3 5/6;
6) 9 9/28 − (4 5/21 − x) = 6 2/7.Решение

60
-
Страница 60
Задание № 291. Решите уравнение:
1) (x + 4/21) − 4/15 = 16/35;
2) (x − 8/19) − 4/57 = 2/3;
3) (x − 8/9) + 3/8 = 19/36;
4) 3 1/6 − (x + 1 1/12) = 1/4;
5) 6 5/27 − (x − 1 2/9) = 3 20/81;
6) 3 5/36 − (1 4/9 − x) = 1 17/18.Решение уравнений

Задание № 292. Выполните действия:
1) 7 7/9 − 4 1/12 + 2 3/4;
2) 17 2/3 − 6 1/36 + 4 3/8;
3) 10 9/16 − (3 11/12 + 4 4/9);
4) (20 − 7 23/36) − (14 4/27 − 6 1/18).Ответ
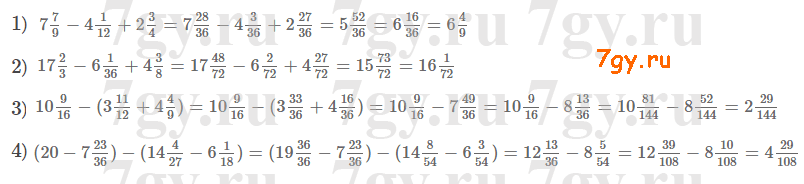
Задание № 293. Выполните действия:
1) 5 5/9 + 3 1/6 − 6 4/27;
2) 1 5/7 + 3 11/14 − 2 1/4;
3) 12 13/48 − (9 17/32 − 4 5/24);
4) (18 − 10 18/35) − (3 9/28 + 2 3/20).Ответы от 7 гуру
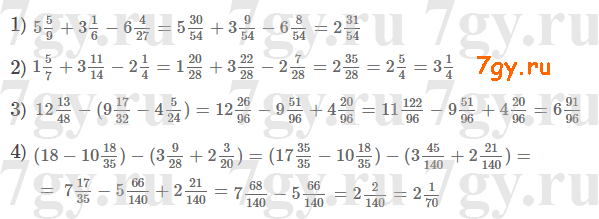
Задача № 294. В трех ящиках было 36 9/16 кг апельсинов. В первом и втором ящиках было 28 7/8 кг апельсинов, а в первом и третьем − 24 3/4 кг. Сколько килограммов апельсинов было в каждом ящике?
Решение задачи
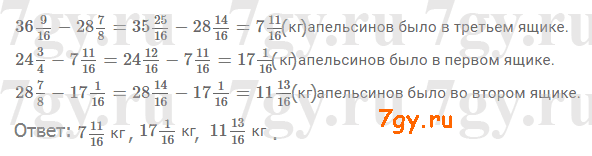
Задача № 295. На компьютере обработали три задачи в течении 30 мин. На первую и вторую задачи было затрачено 24 14/15 мин, а на вторую и третью − 18 19/45 мин. Сколько минут было затрачено на обработку каждой задачи?
Решение задачи

Задача № 296. Для приготовления 6 1/2 кг крема кулинар взял 3 8/15 кг молока, 7/12 кг какао и сахар. Сколько килограммов сахара взял кулинар для приготовления крема?
Решение задачи

Задача № 297. Для приготовления 12 кг мороженого взяли 7 4/15 кг воды, 2 11/20 кг молочного жира, 1 23/30 кг сахара и фруктовой сироп. Сколько килограммов сиропа взяли для изготовления мороженого?
Решение

61
-
Страница 61
Задача № 298. Длина одной из сторон треугольника равна 12 3/8 см, что на 4 5/24 см больше длины второй стороны и на 3 2/3 см меньше длины третьей. Вычислите периметр треугольника.
Решение задачи

Задача № 299. Периметр треугольника равен 42 см, а длина одной из сторон − 10 7/15 см, что на 2 5/6 см меньше длины второй. Найдите длину третьей стороны треугольника.
Решение от 7 гуру
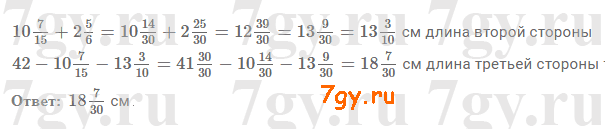
Задача № 300. Филипок потратил 1/2 своих денег на приобретение книги "Занимательная математика", 1/4 − на книгу "Занимательная физика", 1/12 − на карандаши, а оставшиеся деньги − на конфеты. Какую часть своих денег Филипок потратил на конфеты?
Решение задачи

Задача № 301. Золотов, Серебров, Платинов и Бриллиантов нашли клад. Золотову досталась 1/6 клада, Сереброву − 2/9, Платинову − 5/18, а остальное − Бриллиантову. Какую часть клада получил Бриллиантов?
Решение

Задача № 302. Ивасик−Телесик может вспахать поле за 6 ч, а Катигорошек − за 4 ч. Какую часть поля они вспашут, работая вместе, за 1ч? За 2 ч?
Решение задачи

Задача № 303. Первый маляр может покрасить забор за 15 ч, второй − за 12 ч, а третий − за 10 ч. Какую часть забора они покрасят вместе за 1 ч? За 2 ч? За 4 ч?
Решение

Задание№ 304. 1) Миша может съесть арбуз за 12 мин, а Коля − за 16 мин. Какая часть арбуза останется через 1 мин, если мальчики одновременно начнут есть его вместе?
2) Бассейн можно наполнить водой за 6 ч через одну трубу и слить воду за 10 ч через другую. Бассейн был пуст, когда Иван Забывайкин открыл краны одновременно на двух трубах. Какая часть бассейна останется незаполненной водой через 1 ч после того, как открыли краны?Решение задач

Задача № 305. Петр Ленивцев может покрасить стену за 24 ч, а Иван Трудолюб − за 8 ч. Какая часть стены останется неокрашенной после 1 ч совместной работы Ленивцева и Трудолюба?
Решение задачи
Вся стена равна 1, тогда:
1/24 стены покрасит Петр Ленивцев за 1 ч;
1/8 стены покрасит Иван Трудолюб за 1 ч;
1−1/24−1/8=24/24−1/24−3/24=20/24=5/6 (стены) останется неокрашенной после 1 ч совместной работы Ленивцева и Трудолюба.
Ответ: 5/6 стены.Задача № 306. Елена и Мария могут вместе набрать на компьютере текст рукописи за 6 ч. Какую часть рукописи наберет Елена за 1 ч, если Мария может набрать текст всей рукописи за 9 ч?
Решение задачи
Вся рукопись равна 1, тогда:
1/6 рукописи наберут Елена и Мария за 1 ч;
1/9 рукописи наберет Мария за 1 ч;
1/6−1/9=3/18−2/18=1/18 часть рукописи наберет Елена за 1 ч.
Ответ: 1/18 часть рукописи.Задача № 307. Через две трубы бассейн можно наполнить водой за 3 ч. Какую часть бассейна можно наполнить за 1 ч через одну из этих труб, если через другую трубу его можно наполнить за 5 ч?
Решение задачи
Весь бассейн равен 1, тогда:
1/3 часть бассейна можно наполнить через две трубы за 1 ч;
1/5 часть бассейна можно наполнить через одну трубу за 1 ч;
1/3−1/5=5/15−3/15=2/15 части бассейна можно наполнить за 1 ч через вторую трубу.
Ответ: 2/15 части бассейна. 62
-
Страница 62
Задание № 308. Увеличится или уменьшится сумма и на сколько, если:
1) одно из слагаемых увеличить на 2 3/8, а другое уменьшить на 1 11/12;
2) одно из слагаемых увеличить на 4 6/11, а другое уменьшить на 5 5/22.Ответ 7 гуру
Задание № 309. Увеличится или уменьшится разность и на сколько, если:
1) уменьшаемое увеличить на 14 7/83;
2) вычитаемое увеличить на 4 13/57;
3) уменьшаемое увеличить на 4/21, а вычитаемое − на 9/14;
4) уменьшаемое уменьшить на 1 1/6, а вычитаемое увеличить на 2/3?Ответ
Задание № 310. Увеличится или уменьшится разность и на сколько, если:
1) уменьшаемое уменьшить на 6 19/91;
2) вычитаемое уменьшить на 5 1/58;
3) уменьшаемое уменьшить на 14/45, а вычитаемое − на 3/10;
4) уменьшаемое увеличить на 7 3/28, а вычитаемое уменьшить на 8 5/8?Ответы
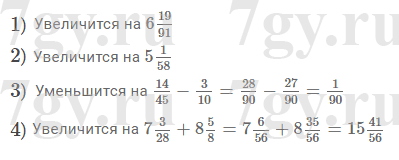
Задание № 311. Найдите значение выражения, выбирая удобный порядок вычислений:
1) (9 3/7 + 2 9/16) − 5 3/7;
2) (4 5/8 + 1 6/11) − 6/11;
3) 10 5/14 − (3 5/14 + 2 9/34);
4) 7 1/7 − (2 6/13 + 3 1/7).Решение
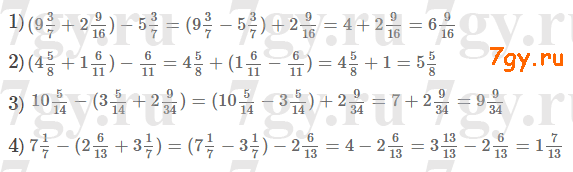
Задание № 312. Найдите значение выражения, выбирая удобный порядок вычислений:
1) (12 19/24 + 5 19/28) − 3 19/24;
2) 6 4/9 − (1 7/24 + 4 4/9).Решение
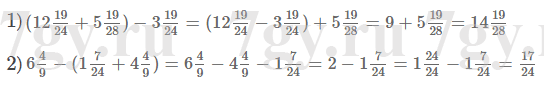
Задание № 313. Сравните дроби, не приводя их к общему знаменателю:
1) 61/62 и 62/63;
2) 1003/1007 и 103/107.Ответ
1) Можно сравнить части, которые не хватает до целого - 1/62 > 1/63. В первой дроби не хватает до целого больше, значит она меньше.
61/62 < 62/63
2) До целого не хватает: 4/1007 < 4/107, следовательно
1003/1007 > 103/107Задание № 314. Упростите выражение (буквами обозначены натуральные числа):
1) 3a/8b−a/5b;
2) 4m/9n+5m/12n;
3) 7x/6y−4x/15y.Решение
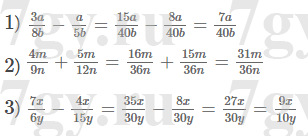
Задание № 315. Упростите выражение (буквами обозначены натуральные числа):
1) 3/a+9/2a;
2) 11c/14d+c/21d;
3) 17p/18q−11p/12q.Решение
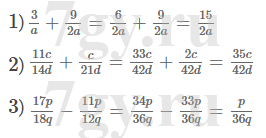
63
-
Страница 63
Задание № 316. Какое натуральное число является корнем уравнения:
1) a + 1/a = 7 1/7;
2) b − 1/b= 14 14/15?Ответ от 7 гуру
1) a = 7
2) b = 15Задание № 317. При каких наименьших натуральных значениях a и b верно равенство:
1) 1/2 * 3 = a/2 − b/3;
2) 4/3 * 5 = a/3 − b/5?Ответ
1) a = b = 1 или a = 3, b = 4.
2) a = b = 2 или a = 5, b = 7.Задание № 318. Увеличится или уменьшится значение дроби и на сколько, если ее числитель увеличить на знаменатель?
Ответ
Увеличится на 1.
Задание № 319. Вычислите значение выражения:
1/2*3 + 1/3*4 + 1/4*5 +...+ 1/19*20.Ответ
Задание № 320. Вычислите значение выражения:
2/3*5 + 2/5*7 +... + 2/29*31.Ответ
Задание № 321. Докажите, что
1/10 + 1/11 + 1/12 +...+ 1/18 > 1/2.Решение
Задание № 322. Докажите, что
1/31 + 1/32 + 1/33+...+ 1/39 + 1/40 > 1/4.Решение
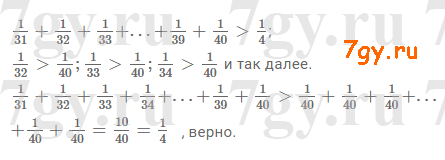
Задание № 323. Укажите пять чисел, каждое из которых имеет только три разных делителя. Можно ли утверждать, что таких чисел бесконечно много?
Решение
4 делится на 1, 2, 4.
25 делится на 1, 5, 25.
77 делится на 1, 7, 77.
9 делится на 1, 3, 9.
49 делится на 1, 7, 49.
Можно утверждать, что таких чисел бесконечно много.Задание № 324. Не выполняя вычислений, определите, простым или составным числом является значение выражения
11+222+333.Решение
11 − число нечетное;
222 − число четное;
333 − число нечетное, следовательно значение выражения
11+222+333 число четное, а значит составное.Задача № 325. За 55 мин бревно распилили на равные части длиной 30 см. Какой длины было бревно, если каждое распиливание длилось 1 мин?
Решение
Сделали 5 распилов, значит получили 6 частей.
6 * 30 = 180 см длина бревна.
Ответ: 180 см.Задача № 326. Расстояние между двумя пристанями по реке равно 36,6 км. От пристани, расположенной выше по течению, отплыл плот. Через 0,8 ч после начала движения плота навстречу ему от другой пристани отправился катер, собственная скорость которого равна 25 км/ч. Через сколько часов после начала движения плота они встретятся, если скорость течения реки составляет 2 км/ч?
Решение задачи
По условию задачи составим выражение:
36,6 − 0,8 * 2 = 36,6 − 1,6 = 35 (км) - оставшийся путь.
Найдем, какое время движутся вместе плот и катер:
$35:25=\frac{35}{25}=1\frac25$ (ч.)
Ответ: $1\frac25$ часа.Задание № 327. Какую часть площади прямоугольника ABCD составляет площадь закрашенного прямоугольника (рис. 6)?
Решение
11 * 8 = 88 клеток площадь прямоугольника ABCD;
5 * 3 = 15 клеток площадь закрашенной части;
15/ 88 площади прямоугольника ABCD составляет площадь закрашенного прямоугольника. 64
-
Страница 64
Задание № 328. Найдите произведение дробей 3/5 и 3/4, предварительно преобразовав их в десятичные. Результат запишите в виде обыкновенной дроби.
Решение от 7 гуру
3 = 6 = 0,6
5 10
3 = 75 = 0,75
4 100
0,6 * 0,75 = 0,45 = 45 = 9
100 20Задание № 329. Упростите выражение:
1) 12 * 3a;
2) 0,6a * 7b;
3) 0,8m * 0,5n * 4p.Решение
1) 2 * 3a = 6a
2) 0,6a * 7b = 4,2ab
3) 0,8m * 0,5n * 4p = 1,6mnpЗадание № 330. Раскройте скобки:
1) 2(x + 7);
2) 7(5 − a);
3) (c − 0,4) * 1,2.Ответ
1) 2(x + 7) = 2x + 14
2) 7(5 − a) = 35 − 7a
3) (c − 0,4) * 1,2 = 1,2с − 0,48Задание № 331. Упростите выражение:
1) 1,6b − 0,5b;
2) 3x + 17x − 5x;
3) 5,6a + 0,4a − 2.Ответ
1) 1,6b − 0,5b = 1,1b
2) 3x + 17x − 5x = 15x
3) 5,6a + 0,4a − 2 = 6a − 2Задача от мудрой совы
Задание № 332. Сережа и Саша играют в такую игру: они по очереди берут камешки из кучки, в которой лежит 100 камешков. За один ход каждому разрешается взять или 1 камешек, или 3. Кто из них возьмет последний камешек, если игру начинает Сережа?
Решение задачи
После хода у Сережи всегда будет получаться нечетное число камешков, следовательно 100−й камень возьмет Саша.
67
-
Страница 67
Ответы к параграфу 11. Умножение дробей
Задание 333. Выполните умножение:
1) 2/13 ∗ 5;
2) 4/17 ∗ 3;
3) 8/9 ∗ 2;
4) 4/49 ∗ 7;
5) 7 ∗ 3/40;
6) 6 ∗ 15/18;
7) 7/12 ∗ 24;
8) 45 ∗ 8/15.Решение 7 гуру
1) $\frac2{13}\ast5=\frac2{13}\ast\frac51=\frac{10}{13}$
2) $\frac4{17}\ast3=\frac4{17}\ast\frac31=\frac{12}{17}$
3) $\frac89\ast2=\frac89\ast\frac21=\frac{16}9=1\frac79$
4) $\frac4{49}\ast7=\frac4{49}\ast\frac71=\frac47$
5) $7\ast\frac3{40}=\frac71\ast\frac3{40}=\frac{21}{40}$
6) $6\ast\frac{15}{18}=\frac61\ast\frac{15}{18}=\frac{15}3=5$
7) $\frac7{12}\ast24=\frac7{12}\ast\frac{24}1=7\ast2=14$
8) $45\ast\frac8{15}=\frac{45}1\ast\frac8{15}=3\ast8=24$Задание 334. Выполните умножение:
1) 9/35 ∗ 8;
2) 7/24 ∗ 16;
3) 42 ∗ 4/7;
4) 6/19 ∗ 57.Решение
1) $\frac9{35}\ast8=\frac{72}{35}=2\frac2{35}$
2) $\frac7{24}\ast16=\frac73\ast2=\frac{14}3=4\frac23$
3) $42\ast\frac47=6\ast4=24$
4) $\frac6{19}\ast57=6\ast3=18$Задание 335. Найдите произведение:
1) 2/7 ∗ 3/5;
2) 3/4 ∗ 5/6;
3) 4/7 ∗ 7/9;
4) 15/16 ∗ 48/55;
5) 22/25 ∗ 10/77;
6) 13/24 ∗ 16/39;
7) 6/35 ∗ 14/15;
8) 36/85 ∗ 34/39.Решение
1) $\frac27\ast\frac35=\frac6{35}$
2) $\frac34\ast\frac56=\frac{15}{24}$
3) $\frac47\ast\frac79=\frac41\ast\frac19=\frac49$
4) $\frac{15}{16}\ast\frac{48}{55}=\frac31\ast\frac3{11}=\frac9{11}$
5) $\frac{22}{25}\ast\frac{10}{77}=\frac25\ast\frac27=\frac4{35}$
6) $\frac{13}{24}\ast\frac{16}{39}=\frac13\ast\frac23=\frac29$
7) $\frac6{35}\ast\frac{14}{15}=\frac25\ast\frac25=\frac4{25}$
8) $\frac{36}{85}\ast\frac{34}{39}=\frac{12}5\ast\frac2{13}=\frac{24}{65}$Задание 336. Найдите произведение:
1) 6/11 ∗ 4/7;
2) 7/20 ∗ 10/21;
3) 8/9 ∗ 27/32;
4) 23/28 ∗ 49/46;
5) 34/86 ∗ 43/51;
6) 7/18 ∗ 90/77;
7) 63/64 ∗ 48/91;
8) 19/100 ∗ 5/38.Решение
1) $\frac6{11}\ast\frac47=\frac{24}{77}$
2) $\frac7{20}\ast\frac{10}{21}=\frac12\ast\frac13=\frac16$
3) $\frac89\ast\frac{27}{32}=\frac11\ast\frac34=\frac34$
4) $\frac{23}{28}\ast\frac{49}{46}=\frac14\ast\frac72=\frac78$
5) $\frac{34}{86}\ast\frac{43}{51}=\frac22\ast\frac13=\frac13$
6) $\frac7{18}\ast\frac{90}{77}=\frac11\ast\frac5{11}=\frac5{11}$
7) $\frac{63}{64}\ast\frac{48}{91}=\frac94\ast\frac3{13}=\frac{27}{52}$
8) $\frac{19}{100}\ast\frac5{38}=\frac1{20}\ast\frac12=\frac1{40}$Задание 337. Выполните умножение:
Решение
1) $9\frac37\ast\frac5{22}=\frac{66}7\ast\frac5{22}=\frac37\ast\frac51=\frac37\ast\frac51=\frac{15}7=2\frac17$
2) $6\frac38\ast\frac{16}{17}=\frac{51}8\ast\frac{16}{17}=\frac31\ast\frac21=6$
3) $2\frac13\ast1\frac15=\frac73\ast\frac65=\frac71\ast\frac25=\frac{14}5=2\frac45$
4) $19\frac12\ast1\frac59=\frac{39}2\ast\frac{14}9=\frac{13}1\ast\frac73=\frac{91}3=30\frac13$
5) $2\frac14\ast2\frac2{27}=\frac94\ast\frac{56}{27}=\frac11\ast\frac{14}3=4\frac23$
6) $2\frac8{11}\ast5\frac2{15}=\frac{30}{11}\ast\frac{77}{15}=\frac21\ast\frac71=14$
7) $\frac79\ast1\frac1{14}\ast5\frac25=\frac79\ast\frac{15}{14}\ast\frac{27}5=\frac11\ast\frac32\ast\frac31=\frac92=4\frac12$
8) $2\frac23\ast1\frac1{24}\ast5\frac25=\frac83\ast\frac{25}{24}\ast\frac{27}5=\frac11\ast\frac51\ast\frac31=15$ 68
-
Страница 68
Задание 338. Выполните умножение:
1) 9 3/5 ∗ 10/21;
2) 3 11/12 ∗ 9/94;
3) 1 5/7 ∗ 6 1/8;
4) 3 5/9 ∗ 5 1/4;
5) 1 13/15 ∗ 5/8 ∗ 2 2/7;
6) 2 1/4 ∗ 16/27 ∗ 4 1/3.Решение
1) $9\frac35\ast\frac{10}{21}=\frac{48}5\ast\frac{10}{21}=\frac{16}1\ast\frac27=\frac{32}7=4\frac47$
2) $3\frac{11}{12}\ast\frac9{94}=\frac{47}{12}\ast\frac9{94}=\frac14\ast\frac32=\frac38$
3) $1\frac57\ast6\frac18=\frac{12}7\ast\frac{49}8=\frac31\ast\frac72=\frac{21}2=10\frac12$
4) $3\frac59\ast5\frac14=\frac{32}9\ast\frac{21}4=\frac83\ast\frac71=\frac{56}3=18\frac23$
5) $1\frac{13}{15}\ast\frac58\ast2\frac27=\frac{28}{15}\ast\frac58\ast\frac{16}7=\frac43\ast\frac11\ast\frac21=\frac83=2\frac23$
6) $2\frac14\ast\frac{16}{27}\ast4\frac13=\frac94\ast\frac{16}{27}\ast\frac{13}3=\frac11\ast\frac43\ast\frac{13}3=\frac{52}9=5\frac79$Задание 339. Найдите произведение:
1) 0,4 ∗ 5/9;
2) 8/27 ∗ 0 , 75;
3) 1,5 ∗ 1/6;
4) 2 1/7 ∗ 2,8.Решение
1) $0,4\ast\frac59=\frac25\ast\frac59=\frac21\ast\frac19=\frac29$
2) $\frac8{27}\ast0,75=\frac8{27}\ast\frac34=\frac29\ast\frac11=\frac29$
3) $1,5\ast\frac16=\frac32\ast\frac16=\frac12\ast\frac12=\frac14$
4) $2\frac17\ast2,8=\frac{15}7\ast\frac{14}5=\frac31\ast\frac21=6$Задание 340. Найдите произведение:
1) 0,8 ∗ 7/12;
2) 1 2/3 ∗ 0,6;
3) 1,25 ∗ 32/45;
4) 4,5 ∗ 3 1/3.Решение
1) $0,8\ast\frac7{12}=\frac45\ast\frac7{12}=\frac15\ast\frac73=\frac7{15}$
2) $1\frac23\ast0,6=\frac53\ast\frac35=1$
3) $1,25\ast\frac{32}{45}=\frac54\ast\frac{32}{45}=\frac11\ast\frac89=\frac89$
4) $4,5\ast3\frac13=\frac92\ast\frac{10}3=\frac31\ast\frac51=15$Задание 341. Найдите значение выражения:
Решение
1) $(\frac{11}{18}-\frac49)\ast\frac3{16}=(\frac{11}{18}-\frac8{18})\ast\frac3{16}=\frac3{18}\ast\frac3{16}=\frac12\ast\frac1{16}=\frac1{32}$
2) $\frac{11}{18}-\frac49\ast\frac3{16}=\frac{11}{18}-\frac13\ast\frac14=\frac{11}{18}-\frac1{12}=\frac{22}{36}-\frac3{36}=\frac{19}{36}$
3) $1\frac35\ast(\frac34+1\frac38)=\frac85\ast(\frac68+1\frac38)=\frac85\ast\frac{17}8=\frac{17}5=3\frac25$
4) $1\frac35\ast\frac34+1\frac38=\frac85\ast\frac34+1\frac38=\frac25\ast\frac31+1\frac38=1\frac15+1\frac38=1\frac8{40}+1\frac{15}{40}=2\frac{23}{40}$
5) $13\frac45-3\frac15\ast3\frac34=13\frac45-\frac{16}5\ast\frac{15}4=13\frac45-\frac41\ast\frac31=13\frac45-12=1\frac45$
6) $1\frac3{25}\ast2\frac17-2\frac19\ast\frac{27}{190}=\frac{28}{25}\ast\frac{15}7-\frac{19}9\ast\frac{27}{190}=\frac45\ast\frac31-\frac11\ast\frac3{10}=2\frac25-\frac3{10}=2\frac4{10}-\frac3{10}=2\frac1{10}$
7) $4\frac7{12}\ast1\frac3{11}+1\frac1{15}\ast\frac{45}{64}=\frac{55}{12}\ast\frac{14}{11}+\frac{16}{15}\ast\frac{45}{64}=\frac56\ast\frac71+\frac13\ast\frac54=\frac{35}6+\frac5{12}=\frac{70}{12}+\frac5{12}=\frac{75}{12}=6\frac3{12}=6\frac14$
8) $(8-2\frac17\ast3\frac19)\ast\frac{27}{44}=(8-\frac{15}7\ast\frac{28}9)\ast\frac{27}{44}=(8-\frac51\ast\frac43)\ast\frac{27}{44}=(8-\frac{20}3)\ast\frac{27}{44}=(7\frac33-6\frac23)\ast\frac{27}{44}=\frac43\ast\frac{27}{44}=\frac11\ast\frac9{11}=\frac9{11}$
9) $(\frac45+\frac47)\ast(7\frac{11}{12}-5\frac79)=(\frac{28}{35}+\frac{20}{35})\ast(7\frac{33}{36}-5\frac{28}{36})=\frac{48}{35}\ast2\frac5{36}=\frac{48}{35}\ast\frac{77}{36}=\frac45\ast\frac{11}3=\frac{44}{15}=2\frac{14}{15}$
10) $\frac45+\frac47\ast(7\frac{11}{12}-5\frac79)=\frac45+\frac47\ast(7\frac{33}{36}-5\frac{28}{36})=\frac45+\frac47\ast\frac{77}{36}=\frac45+\frac11\ast\frac{11}9=\frac{36}{45}+\frac{55}{45}=\frac{91}{45}=2\frac1{45}$Задание 342. Найдите значение выражения:
Решение
1) $15\frac49-4\frac49\ast3\frac38=15\frac49-\frac{40}9\ast\frac{27}8=15\frac49-\frac51\ast\frac31=15\frac49-15=\frac49$
2) $\frac{81}{88}\ast(6-1\frac{13}{15}\ast1\frac{19}{21})=\frac{81}{88}\ast(6-\frac{28}{15}\ast\frac{40}{21})=\frac{81}{88}\ast(6-1\frac{13}{15}\ast1\frac{19}{21})=\frac{81}{88}\ast(6-\frac43\ast\frac83)=\frac{81}{88}\ast(5\frac99-3\frac59)=\frac{81}{88}\ast\frac{22}9=\frac94\ast\frac11=2\frac14$
3) $(5\frac1{16}-1\frac18)\ast(\frac56+\frac3{14})=(4\frac{17}{16}-1\frac2{16})\ast(\frac{35}{42}+\frac9{42})=3\frac{15}{16}\ast\frac{44}{42}=\frac{63}{16}\ast\frac{22}{21}=\frac38\ast\frac{11}1=\frac{33}8=4\frac18$
4) $5\frac1{16}-1\frac18\ast(\frac56+\frac3{14})=5\frac1{16}-\frac98\ast(\frac{35}{42}+\frac9{42})=5\frac1{16}-\frac98\ast\frac{22}{21}=5\frac1{16}-\frac34\ast\frac{11}7=5\frac1{16}-\frac{33}{28}=5\frac1{16}-1\frac5{28}=4\frac1{16}-\frac5{28}=4\frac7{112}-\frac{20}{112}=3\frac{119}{112}-\frac{20}{112}=3\frac{99}{112}$Задание 343. Какой путь пройдет поезд за 5/6 ч, если его скорость составляет 66 км/ч?
Решение
$66\ast\frac56=11\ast5=55$ (км)
Ответ: 55 км пройдет поезд.Задание 344. Какое расстояние проедет автомобиль со скоростью 72 км/ч за 2 1/4 ч?
Решение
$72\ast2\frac14=72\ast\frac94=18\ast9=162$ (км)
Ответ: 162 км проедет автомобиль.Задание 345. Сколько стоят 3 3/5 кг бананов, если цена 1 кг бананов составляет 27 1/2 р.?
Решение
$3\frac35\ast27\frac12=\frac{18}5\ast\frac{55}2=\frac91\ast\frac{11}1=99$ (р.)
Ответ: 99 рублей стоят $3\frac35$ кг банановЗадание 346. Сколько стоят 6 1/4 кг конфет, если 1 кг конфет стоит 70 2/5 р.?
Решение
$6\frac14\ast70\frac25=\frac{25}4\ast\frac{352}5=\frac51\ast\frac{88}1=440$ (р.)
Ответ: 440 рублей стоят $6\frac14$ кг конфет.Задание 347. Выполните умножение:
Решение
1) $\frac{11}{15}\ast\frac{21}{22}\ast\frac9{28}\ast\frac89=\frac15\ast\frac11\ast\frac11\ast\frac11=\frac15$
2) $2\frac12\ast3\frac13\ast4\frac15\ast\frac8{35}=\frac52\ast\frac{10}3\ast\frac{21}5\ast\frac8{35}=\frac11\ast\frac11\ast\frac11\ast\frac81=8$
3) $\frac38\ast1\frac57\ast\frac49\ast2\frac13=\frac38\ast\frac{12}7\ast\frac49\ast\frac73=\frac11\ast\frac11\ast\frac23\ast\frac11=\frac23$
4) $1\frac45\ast1\frac23\ast2\frac17\ast4\frac23=\frac95\ast\frac53\ast\frac{15}7\ast\frac{14}3=\frac31\ast\frac11\ast\frac51\ast\frac21=30$ 69
-
Страница 69
Задание 348. Выполните умножение:
Решение
1) $\frac5{16}\ast\frac45\ast\frac9{25}\ast\frac59=\frac14\ast\frac11\ast\frac15\ast\frac11=\frac1{20}$
2) $\frac{19}{25}\ast\frac{40}{57}\ast\frac5{36}\ast\frac9{16}=\frac11\ast\frac11\ast\frac1{12}\ast\frac12=\frac1{24}$
3) $2\frac23\ast\frac15\ast\frac34\ast10=\frac83\ast\frac15\ast\frac34\ast10=\frac21\ast\frac11\ast\frac11\ast2=4$
4) $18\frac13\ast1\frac2{11}\ast1\frac45\ast15=\frac{55}3\ast\frac{13}{11}\ast\frac95\ast15=\frac11\ast\frac{13}1\ast\frac31\ast15=585$Задание 349. Найдите значение степени:
Решение 7 гуру
1) $(\frac12)^4=\frac12\ast\frac12\ast\frac12\ast\frac12=\frac1{16}$
2) $(\frac25)^3=\frac25\ast\frac25\ast\frac25=\frac8{125}$
3) $(1\frac13)^4=\frac43\ast\frac43\ast\frac43\ast\frac43=\frac{256}{27}=9\frac{13}{27}$
4) $(2\frac23)^2=\frac83\ast\frac83=\frac{64}9=7\frac19$Задание 350. Найдите значение степени:
1) $(\frac13)^5$;
2) $(\frac37)^3$;
3) $(1\frac25)^2$;
4) $(3\frac14)^2$.Решение
1) $(\frac13)^5=\frac13\ast\frac13\ast\frac13\ast\frac13\ast\frac13=\frac1{243}$
2) $(\frac37)^3=\frac37\ast\frac37\ast\frac37=\frac{27}{343}$
3) $(1\frac25)^2=\frac75\ast\frac75=\frac{49}{25}=1\frac{24}{25}$
4) $(3\frac14)^2=\frac{13}4\ast\frac{13}4=\frac{169}{16}=10\frac9{16}$Задание 351. Найдите значение выражения:
Решение
1) $5\frac34\ast8-2\frac13\ast1\frac3{14}-1\frac{37}{48}\ast2\frac2{15}=\frac{23}4\ast8-\frac73\ast\frac{17}{14}-\frac{85}{48}\ast\frac{32}{15}=\frac{23}1\ast2-\frac13\ast\frac{17}2-\frac{17}3\ast\frac23=46-\frac{17}6-\frac{34}9=46-2\frac56-3\frac79=44\frac{36}{18}-2\frac{15}{18}-3\frac{14}{18}=39\frac7{18}$
2) $1\frac3{22}\ast2\frac{14}{15}-(1\frac58+2\frac18\ast\frac{11}{17})\ast\frac37=\frac{25}{22}\ast\frac{44}{15}-(1\frac58+\frac{17}8\ast\frac{11}{17})\ast\frac37=\frac51\ast\frac23-(1\frac58+\frac{11}8)\ast\frac37=\frac{10}3-(1\frac58+1\frac38)\ast\frac37=3\frac13-3\ast\frac37=3\frac13-\frac97=3\frac13-1\frac27=3\frac7{21}-1\frac6{21}=2\frac1{21}$
3) $6\frac25\ast1\frac9{16}-(2\frac14)^2=\frac{32}5\ast\frac{25}{16}-(\frac94\ast\frac94)=\frac21\ast\frac51-\frac{81}{16}=10-5\frac1{16}=4\frac{15}{16}$
4) $(2\frac7{10}-1\frac8{15})^2\ast\frac9{14}=(2\frac{21}{30}-1\frac{16}{30})^2\ast\frac9{14}=(1\frac16)^2\ast\frac9{14}=(\frac76\ast\frac76)\ast\frac9{14}=\frac{49}{36}\ast\frac9{14}=\frac74\ast\frac12=\frac78$Задание 352. Найдите значение выражения:
Решение
1) $4\frac23\ast6-1\frac{23}{42}\ast3\frac1{13}+2\frac18\ast1\frac{29}{51}=\frac{14}3\ast6-\frac{65}{42}\ast\frac{40}{13}+\frac{17}8\ast\frac{80}{51}=28-\frac5{21}\ast\frac{20}1+\frac11\ast\frac{10}3=28-4\frac{16}{21}+3\frac13=27\frac{21}{21}-4\frac{16}{21}+3\frac7{21}=26\frac47$
2) $(5\frac3{10}-3\frac45\ast\frac{13}{38})\ast\frac5{84}+2\frac1{12}\ast\frac4{15}=(5\frac3{10}-\frac{19}5\ast\frac{13}{38})\ast\frac5{84}+\frac{25}{12}\ast\frac4{15}=(5\frac3{10}-\frac15\ast\frac{13}2)\ast\frac5{84}+\frac53\ast\frac13=(5\frac3{10}-1\frac3{10})\ast\frac5{84}+\frac59=4\ast\frac5{84}+\frac59=\frac5{21}+\frac59=\frac{15}{63}+\frac{35}{63}=\frac{50}{63}$
3) $(3\frac13)^2-2\frac{13}{16}\ast2\frac25=\frac{10}3\ast\frac{10}3-\frac{45}{16}\ast\frac{12}5=\frac{100}9-\frac94\ast\frac31=11\frac19-\frac{27}4=11\frac4{36}-6\frac{27}{36}=10\frac{40}{36}-6\frac{27}{36}=4\frac{13}{36}$
4) $(\frac5{12}+\frac{13}{20})^2\ast1\frac{13}{32}=(\frac{25}{60}+\frac{39}{60})^2\ast\frac{45}{32}=\frac{16}{15}\ast\frac{16}{15}\ast\frac{45}{32}=\frac15\ast\frac81\ast\frac11=\frac85=1\frac35$Задание 353. Найдите значение выражения, используя распределительное свойство умножения:
Решение
1) $15\ast(1+\frac13-\frac15)=15\ast1+15\ast\frac13-15\ast\frac15=15+5-3=17$
2) $48\ast(\frac{19}{24}-\frac7{12}+\frac38)=48\ast\frac{19}{24}-48\ast\frac7{12}+48\ast\frac38=2\ast19-4\ast7+6\ast3=38-28+18=28$
3) $\frac79\ast(\frac67-\frac9{14})=\frac79\ast\frac67-\frac79\ast\frac9{14}=\frac13\ast\frac21-\frac11\ast\frac12=\frac23-\frac12=\frac46-\frac36=\frac16$
4) $(\frac{15}{16}-\frac5{12}+2\frac12)\ast\frac45=\frac{15}{16}\ast\frac45-\frac5{12}\ast\frac45+\frac52\ast\frac45=\frac34\ast\frac11-\frac13\ast\frac11+\frac11\ast\frac21=\frac34-\frac13+2=\frac9{12}-\frac4{12}+2=2\frac5{12}$Задание 354. Найдите значение выражения, используя распределительное свойство умножения:
Решение
1) $18\ast(\frac13-\frac19)=18\ast\frac13-18\ast\frac19=6-2=4$
2) $(2-\frac34-\frac45)\ast20=2\ast20-\frac34\ast20-\frac45\ast20=40-15-16=9$
3) $(1-\frac13-\frac16-\frac19)\ast18=1\ast18-\frac13\ast18-\frac16\ast18-\frac19\ast18=18-6-3-2=7$
4) $(\frac56+\frac59)\ast\frac{18}{25}=\frac56\ast\frac{18}{25}+\frac59\ast\frac{18}{25}=\frac11\ast\frac35+\frac11\ast\frac25=\frac35+\frac25=1$Задание 355. Вычислите значение выражения наиболее удобным способом:
Решение
1) $3\frac5{14}\ast\frac79-2\frac3{14}\ast\frac79=(3\frac5{14}-2\frac3{14})\ast\frac79=1\frac17\ast\frac79=\frac87\ast\frac79=\frac89$
2) $7\frac15\ast2\frac18+7\frac15\ast1\frac58=\frac{36}5\ast(2\frac18+1\frac58)=\frac{36}5\ast3\frac34=\frac{36}5\ast\frac{15}4=\frac91\ast\frac31=27$
3) $\frac34\ast1\frac35+1\frac35\ast1\frac38-1\frac12\ast1\frac35=\frac85\ast(\frac68+1\frac38-1\frac48)=\frac85\ast\frac58=1$
4) $3\frac9{14}\ast0,3-0,3\ast1\frac{10}{21}+0,3\ast1\frac16=\frac3{10}\ast(3\frac{27}{42}-1\frac{20}{42}+1\frac7{42})=\frac3{10}\ast3\frac13=\frac3{10}\ast\frac{10}3=1$ 70
-
Страница 70
Задание 356. Вычислите значение выражения наиболее удобным способом:
Решение
1) $4\frac49\ast\frac58+\frac58\ast3\frac59=\frac58\ast(4\frac49+3\frac59)=\frac58\ast8=5$
2) $3\frac78\ast\frac45-1\frac58\ast\frac45=(3\frac78-1\frac58)\ast\frac45=2\frac14\ast\frac45=\frac94\ast\frac45=\frac95=1\frac45$
3) $2\frac{11}{15}\ast1\frac1{19}-1\frac1{19}\ast\frac3{10}-1\frac16\ast1\frac1{19}=(2\frac{11}{15}-\frac3{10}-1\frac16)\ast\frac{20}{19}=(2\frac{22}{30}-\frac9{30}-1\frac5{30})\ast\frac{20}{19}=\frac{19}{15}\ast\frac{20}{19}=\frac1{15}\ast\frac{20}1=\frac43=1\frac13$
4) $4\frac79\ast1\frac{13}{14}-3\frac7{12}\ast1\frac{13}{14}+1\frac{13}{14}\ast1\frac{13}{18}=(4\frac{28}{36}-3\frac{21}{36}+1\frac{26}{36})\ast1\frac{13}{14}=2\frac{11}{12}\ast1\frac{13}{14}=\frac{35}{12}\ast\frac{27}{14}=\frac54\ast\frac92=\frac{45}8=5\frac58$Задание 357. Упростите выражение:
Решение
1) $\frac7{27}m\ast\frac9{28}n=\frac13m\ast\frac14n=\frac1{12}mn$
2) $5\frac35k\ast1\frac4{21}p=\frac{28}5k\ast\frac{25}{21}p=\frac41k\ast\frac53p=\frac{20}3kp=6\frac23kp$
3) $20x\ast\frac{11}{35}y=4x\ast\frac{11}7y=\frac{44}7xy=6\frac27xy$
4) $3\frac4{15}x\ast1\frac{17}{28}y\ast\frac47z=\frac11x\ast\frac31y\ast\frac11z=3xyz$Задание 358. Упростите выражение:
Решение
1) $\frac58a\ast\frac4{15}b=\frac12a\ast\frac13b=\frac16ab$
2) $6\frac34x\ast1\frac{11}{45}y=\frac{27}4x\ast\frac{56}{45}y=\frac31x\ast\frac{14}5y=\frac{42}5xy=8\frac25xy$
3) $\frac{13}{24}d\ast32c=\frac{13}3d\ast4c=\frac{52}3dc=17\frac13dc$
4) $18\frac13a\ast1\frac2{11}b\ast\frac9{13}c=\frac{55}3a\ast\frac{13}{11}b\ast\frac9{13}c=\frac51a\ast\frac11b\ast\frac31c=15abc$Задание 359. Упростите выражение:
Решение
1) $\frac23a+\frac58a+\frac16a=\frac{16}{24}a+\frac{15}{24}a+\frac4{24}a=\frac{35}{24}a=1\frac{11}{24}a$
2) $\frac45b-\frac23b+\frac4{15}b=\frac{12}{15}b-\frac{10}{15}b+\frac4{15}b=\frac6{15}b=\frac25b$
3) $\frac25x+\frac47x-\frac5{14}x=\frac{28}{70}x+\frac{40}{70}x-\frac{25}{70}x=\frac{43}{70}x$
4) $\frac7{12}y-\frac3{16}y+\frac5{24}y=\frac{28}{48}y-\frac9{48}y+\frac{10}{48}y=\frac{29}{48}y$
5) $\frac57m+\frac34m-\frac58m=\frac{40}{56}m+\frac{42}{56}m-\frac{35}{56}m=\frac{47}{56}m$
6) $\frac{11}{15}c-\frac5{18}c-0,4{\operatorname с}=\frac{66}{90}c-\frac{25}{90}c-\frac{36}{90}c=\frac5{90}c=\frac1{18}c$Задание 360. Упростите выражение и найдите его значение:
Решение
1) $\frac38x+\frac49x-\frac5{12}x=\frac{27}{72}x+\frac{32}{72}x-\frac{30}{72}x=\frac{29}{72}x=\frac{29}{72}\ast3\frac3{29}=\frac{29}{72}\ast\frac{90}{29}=\frac14\ast\frac51=\frac54=1\frac14$
2) $\frac9{10}{\operatorname с}-\frac2{15}{\operatorname с}-\frac35{\operatorname с}=\frac{27}{30}{\operatorname с}-\frac4{30}{\operatorname с}-\frac{18}{30}{\operatorname с}=\frac5{30}{\operatorname с}=\frac16{\operatorname с}=\frac16\ast2,4=\frac16\ast\frac{24}{10}=\frac11\ast\frac4{10}=\frac25$
3) $3\frac35y-2\frac13y-\frac1{15}y=3\frac9{15}y-2\frac5{15}y-\frac1{15}y=1\frac15y=\frac65\ast10=6\ast2=12$Задание 361. Упростите выражение и найдите его значение:
Решение
1) $\frac12a+\frac13a-\frac14a=\frac6{12}a+\frac4{12}a-\frac3{12}a=\frac7{12}a=\frac7{12}\ast1\frac57=\frac7{12}\ast\frac7{12}=1$
2) $\frac47b+\frac5{21}b-\frac23b=\frac{12}{21}b+\frac5{21}b-\frac{14}{21}b=\frac3{21}b=\frac17b=\frac17\ast2\frac13=\frac17\ast\frac73=\frac13$
3) $1\frac5{12}m+2\frac7{18}m-1\frac29m=1\frac{15}{36}m+2\frac{14}{36}m-1\frac8{36}m=2\frac7{12}m=\frac{31}{12}\ast1\frac{17}{31}=\frac{31}{12}\ast\frac{48}{31}=\frac11\ast\frac41=4$Задание 362. Докажите, что значение выражения не зависит от значения переменной:
Решение
1) $0,5x+1,4-\frac7{18}x-\frac19x=(\frac12x-\frac7{18}x-\frac19x)+1,4=(\frac9{18}x-\frac7{18}x-\frac2{18}x)+1,4=0+1,4=1,4$
2) $0,5x+\frac17x+7,4-\frac9{14}x=(\frac12x+\frac17x-\frac9{14}x)+7,4=(\frac7{14}x+\frac2{14}x-\frac9{14}x)+7,4=0+7,4=7,4$
3) $1\frac{17}{18}a+1-1,5a-\frac49a=(1\frac{17}{18}a-1,5a-\frac49a)+1=(1\frac{17}{18}a-1\frac12a-\frac49a)+1=(1\frac{17}{18}a-1\frac9{18}a-\frac8{18}a)+1=0+1=1$
4) $2,4+1,25b+\frac56b-2\frac1{12}b=2,4+(1\frac14b+\frac56b-2\frac1{12}b)=2,4+(1\frac3{12}b+\frac{10}{12}b-2\frac1{12}b)=2,4+0=2,4$ 71
-
Страница 71
Задание 363. Раскройте скобки:
Решение
1) $6\ast(\frac23a+\frac5{12}b)=6\ast\frac23a+6\ast\frac5{12}b=4a+\frac52b=4a+2\frac12b$
2) $\frac13\ast(\frac9{11}m-\frac67n)=\frac13\ast\frac9{11}m-\frac13\ast\frac67n=\frac3{11}m-\frac27n$
3) $12\ast(\frac34x+\frac{13}{18}y-\frac1{24}z)=12\ast\frac34x+12\ast\frac{13}{18}y-12\ast\frac1{24}z=9x+\frac{26}3y-\frac12z=9x+8\frac23y-\frac12z$
4) $1\frac17\ast(7p+\frac{21}{24}q-1\frac34)=\frac87\ast7p+\frac87\ast\frac{21}{24}q-\frac87\ast\frac74=8p+q-2$Задание 364. Раскройте скобки:
Решение
1) $14\ast(\frac12m+\frac37n)=14\ast\frac12m+14\ast\frac37n=7m+6n$
2) $\frac16\ast(\frac{12}{17}b-\frac{18}{23}c)=\frac16\ast\frac{12}{17}b-\frac16\ast\frac{18}{23}c=\frac2{17}b-\frac3{23}c$
3) $8\ast(\frac14p-\frac5{24}q+\frac7{12}t)=8\ast\frac14p-8\ast\frac5{24}q+8\ast\frac7{12}t=2p-\frac53q+\frac{14}3t=2p-1\frac23q+4\frac23t$
4) $1\frac34\ast(4a+\frac{16}{21}b-2\frac23)=\frac74\ast4a+\frac74\ast\frac{16}{21}b-\frac74\ast\frac83=7a+\frac43b-\frac{14}3=7a+1\frac13b-4\frac23$Задание 365. Длина прямоугольного параллелепипеда равна 8 1/3 см, что на 5/6 см больше его ширины и в 3 3/5 раза меньше его высоты. Вычислите объем прямоугольного параллелепипеда.
Решение 7 гуру
1) $8\frac13-\frac56=7\frac86-\frac56=7\frac36=7\frac12$ (см) - ширина параллелепипеда;
2) $8\frac13\ast3\frac35=\frac{25}3\ast\frac{18}5=5\ast6=30$ (см) - высота параллелепипеда;
3) $8\frac13\ast7\frac12\ast30=\frac{25}3\ast\frac{15}2\ast30=\frac{25}1\ast\frac51\ast15=25\ast5\ast15=1875$ ($см^3$)
Ответ: 1875 $см^3$ объем прямоугольного параллелепипеда.Задание 366.Одна из сторон прямоугольника равна 3 1/5 м, а соседняя − в 1 1/4 раза больше. Вычислите площадь прямоугольника.
Решение задачи
1) $3\frac15\ast1\frac14=\frac{16}5\ast\frac54=4$ (м) - длина соседней стороны прямоугольника;
2) $3\frac15\ast4=\frac{16}5\ast4=\frac{64}5=12\frac45$ ($м^2$) - площадь прямоугольника.
Ответ: $12\frac45м^2$.Задание 367. Турист шел пешком 5 1/3 ч со скоростью 4 1/8 км/ч и ехал на велосипеде 1 7/15 ч со скоростью 12 1/2 км/ч. Какое расстояние больше: то, которое турист преодолел пешком, или то, которое он проехал на велосипеде, и на сколько километров?
Решение задачи
1) $5\frac13\ast4\frac18=\frac{16}3\ast\frac{33}8=2\ast11=22$ (км) - турист шел пешком;
2) $1\frac7{15}\ast12\frac12=\frac{22}{15}\ast\frac{25}2=\frac{11}3\ast\frac51=\frac{55}3=\frac{55}3=18\frac13$ (км) - турист ехал на велосипеде
3) $22-18\frac13=21\frac33-18\frac13=3\frac23$ (км) - на столько больше турист преодолел пешком, чем проехал на велосипеде.
Ответ: на $3\frac23$ км.Задание 368. Мальвина купила 4 3/5 кг апельсинов по цене 7 1/2 сольдо за килограмм и 5 1/4 кг яблок по цене 3 1/5 сольдо. За какие фрукты − апельсины или яблоки − Мальвина заплатила больше и на сколько сольдо?
Решение задачи
1) $4\frac35\ast7\frac12=\frac{23}5\ast\frac{15}2=\frac{23}1\ast\frac32=\frac{69}2=34\frac12$ (сольдо) - заплатила Мальвина за апельсины;
2) $5\frac14\ast3\frac15=\frac{21}4\ast\frac{16}5=\frac{21}1\ast\frac45=\frac{84}5=16\frac45$ (сольдо) - заплатила Мальвина за яблоки;
3) $34\frac12-16\frac45=33\frac{15}{10}-16\frac85=17\frac7{10}$ (сольдо) - на столько Мальвина заплатила больше за апельсины, чем за яблоки.
Ответ: на $17\frac7{10}$ сольдо.Задание 369. Велосипедист Андрей ехал со скоростью 8 3/4 км/ч, а велосипедист Богдан − со скоростью в 1 1/7 раза больше. Каким было расстояние между велосипедистами сначала, если Богдан догнал Андрея через 3 4/5 ч после того, как они одновременно начали двигаться?
Решение задачи
1) $8\frac34\ast1\frac17=\frac{35}4\ast\frac87=5\ast2=10$ (км/ч) - скорость Богдана.
2) $10-8\frac34=1\frac14$ (км/ч) - скорость с которой Богдан догонял Андрея;
3) $3\frac45\ast1\frac14=\frac{19}5\ast\frac54=\frac{19}4=4\frac34$ (км) - было расстояние между велосипедистами сначала.
Ответ: $4\frac34$ км.Задание 370. Из двух городов одновременно навстречу друг другу отправились велосипедист и мотоциклист. Велосипедист ехал со скоростью 10 4/5 км/ч, а мотоциклист − со скоростью в 5 5/12 раза большей. Найдите расстояние между городами, если велосипедист и мотоциклист встретились через 3 1/3 ч после начала движения.
Решение задачи
1) $10\frac45\ast5\frac5{12}=\frac{54}5\ast\frac{65}{12}=\frac91\ast\frac{13}2=\frac{117}2=58\frac12$ (км/ч) - скорость мотоциклиста;
2) $10\frac45+58\frac12=10\frac8{10}+58\frac5{10}=69\frac3{10}$ (км/ч) - скорость сближения;
3) $3\frac13\ast69\frac3{10}=\frac{10}3\ast\frac{693}{10}=231$ (км) - расстояние между городами.
Ответ: 231 км. 72
-
Страница 72
Задание 371. Лодка плыла 3/5 ч против течения реки и 1 1/2 ч по течению. Какой путь преодолела лодка за все время движения, если собственная скорость лодки равна 18 км/ч, а скорость течения − 1 1/3 км/ч?
Решение
1) $18-1\frac13=16\frac23$ (км/ч) - скорость лодки против течения;
2) $18+1\frac13=19\frac13$ (км/ч) - скорость лодки по течению;
3) $\frac35\ast16\frac23=\frac35\ast\frac{50}3=10$ (км) - плыла лодка против течения;
4) $1\frac12\ast19\frac13=\frac32\ast\frac{58}3=29$ (км) - плыла лодка по течению;
5) 10 + 29 = 39 (км) - преодолела лодка за все время движения.
Ответ: 39 км.Задание 372. Теплоход шел 3 ч против течения и 1 3/5 ч по течению реки. На сколько километров меньше прошел теплоход по течению, чем против течения, если скорость течения составляет 2 1/4 км/ч, а собственная скорость теплохода − 22 1/3 км/ч?
Решение
1) $22\frac13-2\frac14=22\frac4{12}-2\frac3{12}=20\frac1{12}$ (км/ч) - скорость теплохода против течения;
2) $22\frac13+2\frac14=22\frac4{12}+2\frac3{12}=24\frac7{12}$ (км/ч) - скорость теплохода по течению;
3) $3\ast20\frac1{12}=3\ast\frac{241}{12}=60\frac14$ (км) - шел теплоход против течения;
4) $1\frac35\ast24\frac7{12}=\frac85\ast\frac{295}{12}=\frac21\ast\frac{59}3=\frac{118}3=39\frac13$ (км) - шел теплоход по течению;
5) $60\frac14-39\frac13=59\frac{15}{12}-39\frac4{12}=20\frac{11}{12}$ (км) - на столько меньше прошел теплоход по течению, чем против течения.
Ответ: на $20\frac{11}{12}$ км.Задание 373. Одна швея может выполнить заказ за 4 ч, а другая − за 6 ч. Какую часть заказа они выполнят за 3/4 ч, работая вместе? Хватит ли им 3 ч, чтобы, работая вместе, выполнить заказ?
Решение
Весь заказ равен единице, тогда 1/4 часть заказа выполнит первая швея за 1 час;
1/6 часть заказа выполнит вторая швея за 1 час.
1) $\frac14+\frac16=\frac3{12}+\frac2{12}=\frac5{12}$ заказа выполнят обе швеи за 1 ч;
2) $\frac34\ast\frac5{12}=\frac14\ast\frac54=\frac5{16}$ заказа выполнят обе швеи за 3/4ч;
3) $3\ast\frac5{12}=\frac54=1\frac14$ заказа выполнят обе швеи за 3 часа, следовательно им хватит 3 часов на выполнение заказа.
Ответ: 3 ч хватит.Задание 374. Один рабочий может выполнить производственное задание за 5 ч, а другой − за 15 ч. Какую часть задания они выполнят, если будут работать вместе 1 1/4 ч? Успеют ли они, работая вместе, выполнить задание за 3 ч?
Решение
Пусть все задание равно единице, тогда 1/5 часть задания может выполнить первый рабочий за 1 ч;
1/15 часть задания может выполнить второй рабочий за 1 ч.
1) $\frac15+\frac1{15}=\frac3{15}+\frac1{15}=\frac4{15}$ часть задания могут выполнить оба рабочих за 1 ч;
2) $\frac4{15}\ast1\frac14=\frac4{15}\ast\frac54=\frac13$ часть задания выполнят оба рабочих за $1\frac14$ ч;
3) $\frac4{15}\ast3=\frac{12}{15}$ задания выполнят рабочие за 3 ч, это меньше 1, следовательно они не успеют выполнить задание.
Ответ: не успеют.Задание 375. Выполните умножение:
Решение
1) $\frac{2x}9\ast\frac3{4y}=\frac x3\ast\frac1{2y}=\frac x{6y}$
2) $\frac{7ab}8\ast\frac{6c}{35a}=\frac b4\ast\frac{3c}5=\frac{3bc}{20}$
3) $\frac{5m}{4n}\ast\frac{4m}{5n}=\frac mn\ast\frac mn=\frac{m^2}{n^2}$
4) $\frac{18xy}{13z}\ast\frac{26z}{27x}=\frac{2y}1\ast\frac23=\frac{4y}3=1\frac13y$Задание 376. Не выполняя умножения сравните:
Решение
1) $200\ast\frac6{13}$ < 200
2) $\frac78\ast\frac34=\frac74\ast\frac38$
3) $\frac{13}{20}>\frac{13}{20}\ast\frac78$Задание 377. Не выполняя умножения сравните:
Решение
1) 1000 > $1000\ast\frac23$
2) $\frac{19}6\ast\frac55=\frac{19}6$
3) $\frac7{12}<\frac7{12}\ast\frac98$Задание 378. Игорь переложил из одного ящика в другой 2 1/3 кг яблок, после чего в каждом ящике стало по 20 кг. Сколько килограммов яблок было в каждом ящике первоначально?
Решение
1) $20-2\frac13=17\frac23$ (кг) - яблок, первоначально было в одном ящике;
2) $20+2\frac13=22\frac13$ (кг) - яблок, первоначально было во втором ящике.
Ответ: $17\frac23$ кг, $22\frac13$ кг.Задание 379. Запишите все правильные дроби с числителем 3, которые больше 3/7.
Решение
$\frac36;\frac35;\frac34$.
Задание 380. Фермер решил посадить кусты смородины. Он мог посадить их или в четыре ряда, или в шесть. Сколько кустов смородины он решил посадить, если известно, что их было больше 85, но меньше 100?
Решение
По условию задачи число кустов должно быть кратно и 4 и 6. Это число 96. Следовательно 96 кустов смородины решил посадить фермер.
73
-
Страница 73
Задание 381. С одного аэродрома в одном направлении с интервалом 0,4 ч вылетели два самолета. Первый самолет летел со скоростью 640 км/ч, а второй − 720 км/ч. Через сколько часов после своего вылета второй самолет будет впереди первого на расстоянии 24 км?
Решение задачи
1) 0,4 * 640 = 256 (км) пролетел первый самолет до вылета первого;
2) 256 + 24 = 280 (км) необходимо сократить второму самолету, чтобы быть на 24 км впереди первого;
3) 720 − 640 = 80 (км/ч) скорость приближения второго самолета к первому;
4) $280:80=\frac{28}8=\frac72=3\frac12$ ч потребуется пролететь второму самолету, чтобы быть на 24 км впереди первого.
Ответ: $3\frac12$ ч.Задание 382. Сколько равносторонних треугольников изображено на рисунке 9?
Ответ
13 равносторонних треугольников.
Задание 383. Сравните:
1) 14/3 и 4;
2) 12/5 и 3;
3) 6 и 35/6.Решение от 7 гуру
1) $\frac{14}3=4\frac23$ > 4
2) $\frac{12}5=2\frac25$ < 3
3) 6 > $\frac{35}6=5\frac56$Задание 384. Сократите дробь:
1) 124/279;
2) 324/378;
3) 888/999;
4) 1111/111111;
5) 2323/3434;
6) 121212/191919.Решение
1) $\frac{124}{279}=\frac49$
2) $\frac{324}{378}=\frac{162}{189}=\frac67$
3) $\frac{888}{889}=\frac{888}{999}=\frac89$
4) $\frac{1111}{111111}=\frac{101}{10101}$
5) $\frac{2323}{3434}=\frac{23}{34}$
6) $\frac{121212}{191919}=\frac{12}{19}$Задание 385. Запишите в виде десятичной дроби:
1) 7%;
2) 26%;
3) 60%;
4) 180%.Решение
1) 7% = 0,07
2) 26% = 0,26
3) 60% = 0,6
4) 180% = 1,8Задание 386. Запишите в виде обыкновенной дроби:
1) 6%;
2) 36%;
3) 80%;
4) 140%.Решение
1) 6% = $\frac6{100}=\frac3{50}$
2) 36% = $\frac{36}{100}=\frac9{25}$
3) 80% = $\frac{80}{100}=\frac45$
4) 140% = $\frac{140}{100}=\frac75=1\frac25$Задание 387. Запишите в процентах:
1) 0,12;
2) 0,05;
3) 0,5;
4) 0,324;
5) 0,467;
6) 4;
7) 1,12;
8) 1 1/25.Решение
1) 0,12 = 12%
2) 0,05 = 5%
3) 0,5 = 50%
4) 0,324 = 32,4%
5) 0,467 = 46,7%
6) 4 = 400%
7) 1,12 = 112%
8) $1\frac1{25}=1,04=104$%Задание 388. Задача от мудрой совы. На доске написаны три двузначных числа. Первая слева цифра одного из них − 5, второго − 6, а третьего − 7. Учитель попросил троих учащихся сложить любые два из этих чисел. Первый учащийся получил в сумме число 147, второй и третий − разные трехзначные числа, первые слева две цифры которых 1 и 2. Какие числа написаны на доске?
Решение задачи
У первого ученика могут быть числа 59, 69 и 79. Складываем их попарно: 59 + 69 ≠ 147. Остается 6* + 7* = 147, то есть 69 + 78 = 147 или 68 + 79 = 147.
Второй ученик складывал 5* + 69, третий 5* + 78, то есть подбором получаем число 51. 75
-
Страница 75
Задание 389. Найдите:
1) 3/5 от числа 60;
2) 0,16 от числа 20;
3) 5/6 от числа 3/20;
4) 24/65 от числа 39/40;
5) 3/7 от числа 5 3/5;
6) 3/8 от числа 2 2/3.Решение
1) $\frac35\ast60=3\ast12=36$
2) 0,16 * 20 = 3,2
3) $\frac56\ast\frac3{20}=\frac12\ast\frac14=\frac18$
4) $\frac{24}{65}\ast\frac{39}{40}=\frac35\ast\frac35=\frac9{25}$
5) $\frac37\ast5\frac35=\frac37\ast\frac{28}5=\frac31\ast\frac45=\frac{12}5=2\frac25$
6) $\frac38\ast2\frac23=\frac38\ast\frac83=1$Задание 390. Найдите:
1) 14% от числа 60;
2) 40% от числа 32;
3) 8% от числа 3/16;
4) 180% от числа 3 1/3.Решение
1) 0,14 * 60 = 8,4
2) 0,4 * 32 = 12,8
3) $0,08\ast\frac3{16}=\frac2{25}\ast\frac3{16}=\frac1{25}\ast\frac38=\frac3{200}$
4) $1,8\ast3\frac13=\frac95\ast\frac{10}3=\frac31\ast\frac21=6$Задание 391. Сколько градусов содержит угол, который составляет:
1) 2/15 прямого угла;
2) 13/20 развернутого угла.Решение
1) $\frac2{15}\ast90°=2\ast6=12°$
2) $\frac{13}{20}\ast180°=13\ast9=117°$Задание 392. Сколько градусов содержит угол, который составляет:
1) 23/18 прямого угла;
2) 11/12 развернутого угла.Решение
1) $\frac{23}{18}\ast90°=23\ast5=115°$
2) $\frac{11}{12}\ast180°=11\ast15=165°$Задание 393. Миша собрал 260 грибов, из них 5/13 составляли белые. Сколько белых грибов собрал Миша?
Решение задачи
$260\ast\frac5{13}=20\ast5=100$ (г.) - белых собрал Миша.
Ответ: 100 белых грибов.Задание 394. Оля испекла 45 пирожков, из них 4/9 составляли пирожки с вишнями. Сколько пирожков с вишнями испекла Оля?
Решение задачи
$45\ast\frac49=5\ast4=20$ (п.) - с вишнями испекла Оля.
Ответ: 20 пирожков с вишнями.Задание 395. Магазин продал 480 кг огурцов и помидоров, причем масса огурцов составляла 85% массы этих овощей. Сколько килограммов огурцов продали?
Решение задачи
480 * 85% = 480 * 0,85 = 408 (кг) - огурцов продали.
Ответ: 408 кг огурцов. 76
-
Страница 76
Задание 396. Отряд из 120 человек отправился в поход на лодках. В каждую лодку село 12,5% отряда. Сколько человек было в каждой лодке? На скольких лодках отряд отправился в поход?
Решение
1) 120 * 12,5% = 120 * 0,125 = 15 (ч.) - было в каждой лодке.
2) 120 : 15 = 8 (л.) - отправилось в поход.
Ответ: на 8 лодках.Задание 397. Агрофирма владеет 140 га земли, 16% которой занимает яблоневый сад. Найдите площадь сада.
Решение задачи
140 * 16% = 140 * 0,16 = 22,4 (га) - занимает яблоневый сад.
Ответ: 2,4 га.Задание 398. Медь составляет 4/7 массы сплава. Сколько килограммов меди содержится в 280 кг такого сплава?
Решение задачи
$280\ast\frac47=40\ast40=160$ (кг) - меди содержится в сплаве.
Ответ: 160 кг.Задание 399. Соль составляет 5/9 массы раствора. Сколько килограммов соли содержится в 18 кг такого раствора?
Решение задачи
$18\ast\frac59=2\ast5=10$ (кг) - соли содержится в растворе.
Ответ: 10 кг.Задание 400
Продали m порций мороженого, 5/8 которых составляло эскимо. Составьте выражение для нахождения количества порций эскимо и вычислите его значение при m = 120.
Решение задачи и образец правильной записи
$\frac58$ от m порций
$\frac58\ast m=\frac58m$ (порций) - количество порций эскимо
Если m = 120, то $\frac58\ast120=\frac58\ast\frac{120}1=\frac{5\ast\cancel{120}^{15}}{{\cancel8}_1}=75$
Ответ: $\frac58m$, 75 порций.Задание 401. В саду растет a кустов роз. 3/14 которых составляют розовые. Составьте выражение для нахождения количества кустов розовых роз и вычислите его значение при a = 210.
Решение
$\frac3{14}a=\frac3{14}\ast210=3\ast15=45$ (к.) - розовых роз растет в саду.
Ответ: 45 кустов.Задание 402. В дом отдыха привезли 1440 кг апельсинов и мандаринов. Апельсины составляли 7/12 массы привезенных фруктов. Сколько килограммов мандаринов привезли в дом отдыха?
Решение
1) $1440\ast\frac7{12}=120\ast7=840$ (кг) - апельсинов привезли в дом отдыха.
2) 1440 − 840 = 600 (кг) - мандаринов привезли в дом отдыха.
Ответ: 840 кг.Задание 403. Построили 192 коттеджа, из них 7/16 − двухэтажные, а остальные − трехэтажные. Сколько построили трехэтажных коттеджей?
Решение
1) $192\ast\frac7{16}=12\ast7=84$ (к.) - двухэтажных;
2) 192 − 84 = 108 (к.) - трехэтажных.
Ответ: 108 коттеджей.Задание 404
На сколько 3,5% от числа 32 больше, чем 2/9 от числа 0,45?
Решение задачи и образец правильной записи
1) 3,5% от 32
3,5 = 0,035
0,035 * 32 = 1,12
х0,035
32
0070
0105
01,120 = 1,12
2) $\frac29$ от 0,45
$\frac29$ * 0,45 = $\frac29\ast\frac{\cancel{45}^9}{{\cancel{100}}_{20}}=\frac{\cancel2^1}{{\cancel9}_1}\ast\frac{\cancel9^1}{{\cancel{20}}_{10}}=\frac1{10}=0,1$
3) 1,12 - 0,1 = 1,02 - на столько 3,5% от 32 больше, чем 2/9 от 0,45
Ответ: на 1,02.Задание 405. На сколько 8/27 от числа 5,4 больше, чем 4 2/3% от числа 6/7?
Решение
$\frac8{27}\ast5,4-4\frac23\ast\frac1{100}\ast\frac67=\frac8{27}\ast\frac{27}5-\frac{14}3\ast\frac1{100}\ast\frac67=\frac81\ast\frac15-\frac11\ast\frac1{25}\ast\frac11=\frac85-\frac1{25}=\frac{40}{25}-\frac1{25}=\frac{39}{25}=1\frac{14}{25}$
Ответ: на $1\frac{14}{25}$ больше.Задание 406. Учебники составляют 1/3 всех книг школьной библиотеки, а учебники по математике − 6/25 всех учебников. Какую часть всех книг, имеющихся в библиотеке, составляют учебники по математике?
Решение задачи от 7 гуру
$\frac6{25}\ast\frac13=\frac2{25}\ast\frac11=\frac2{25}$ (к.)
Ответ: $\frac2{25}$ всех книг, имеющихся в библиотеке, составляют учебники по математике.Задание 407. Каштаны составляют 5/18 всех деревьев, растущих в парке, а дубы − 9/10 количества каштанов. Какую часть всех деревьев в парке составляют дубы?
Решение
$\frac9{10}\ast\frac5{18}=\frac12\ast\frac12=\frac14$
Ответ: $\frac14$ часть всех деревьев в парке составляют дубы. 77
-
Страница 77
Задание 408. Трое рабочих изготовили 216 деталей. Первый рабочий изготовил 7/18 этих деталей, а второй − 13/36. Сколько деталей изготовил третий рабочий?
Решение задачи
1) $216\ast\frac7{18}=12\ast7=84$ (д.) - изготовил первый рабочий;
2) $216\ast\frac{13}{36}=6\ast13=78$ (д.) - изготовил второй рабочий;
3) 216 − 84 − 78 = 54 (д.) - изготовил третий рабочий.
Ответ: 54 детали.Задание 409. Барон Мюнхгаузен рассказывал, что, посланный с важным донесением из Москвы в Париж, он проскакал на коне 2460 км за четыре дня. В первый день он преодолел 3/20 расстояния, во второй − 4/15, в третий − 7/30. Сколько километров проскакал барон Мюнхгаузен в четвертый день?
Решение задачи
1) $2460\ast\frac3{20}=123\ast3=369$ (км) - проскакал Мюнхгаузен в первый день;
2) $2460\ast\frac4{15}=164\ast4=656$ (км) - проскакал Мюнхгаузен во второй день;
3) $2460\ast\frac7{30}=82\ast7=574$ (км) - проскакал Мюнхгаузен в третий день;
4) 2460 − 369 − 656 − 574 = 861 (км) - проскакал Мюнхгаузен в четвертый день.
Ответ: 861 км.Задание 410
Железный Дровосек нарубил $9\frac38{\operatorname м}^3$ дров. В первый день он нарубил 2/5 всего объема дров, а во второй − 4/9 остатка. Сколько кубометров дров нарубил Железный Дровосек во второй день?
Решение задачи и образец правильной записи
1) $\frac25$ от $9\frac38$ м3
$9\frac38\ast\frac25=\frac{75}8\ast\frac25=\frac{\cancel{75}^{15}\ast\cancel2^1}{{\cancel8}_4\ast{\cancel5}_1}=\frac{15}4=3\frac34$ $(м^3)$ - объем дров, нарубленных в I день;
2) $9\frac{{}^{1)}3}8-3\frac{{}^{2)}3}4=8\frac{11}8-3\frac68=5\frac58$ $(м^3)$ - остаток дров после первого дня;
3) $\frac49$ от $5\frac58$ м3
$5\frac58\ast\frac49=\frac{45}8\ast\frac49=\frac{\cancel{45}^5\ast\cancel4^1}{{\cancel8}_2\ast{\cancel9}_1}=\frac52=2\frac12$ $(м^3)$ - объем дров, нарубленных во II день.
Ответ: $2\frac12 м^3$.Задание 411. За три недели продали 324 коробки конфет. За первую неделю продали 5/18 этого количества, за вторую − 15/26 остатка. Сколько коробок конфет продали за третью неделю?
Решение задачи
1) $324\ast\frac5{18}=18\ast5=90$ (кор.) - конфет продали за первую неделю;
2) 324 − 90 = 234 (кор.) - осталось после первой недели;
3) $234\ast\frac{15}{26}=9\ast15=135$ (кор.) - продали во вторую неделю;
4) 324 − 90 − 135 = 99 (кор.) - продали за третью неделю.
Ответ: 99 коробок.Задание 412. Том Сойер покрасил забор прямоугольной формы, длина которого равна 9 1/3 фута (1 фут = 30,48 см), а высота составляет 5/14 длины. Сколько фунтов краски израсходовал Том, если на 1 квадратный фут пошло 4 1/2 фунта (1 фунт ≈ 454 г) краски?
Решение задачи
1) $9\frac13\ast\frac5{14}=\frac{28}3\ast\frac5{14}=\frac23\ast\frac51=\frac{10}3=3\frac13$ (футов) - высота забора;
2) $9\frac13\ast3\frac13=\frac{28}3\ast\frac{10}3=\frac{280}9=31\frac19$ (кв. футов) - площадь забора;
3) $31\frac19\ast4\frac12=\frac{280}9\ast\frac92=140$ (фунтов) - краски израсходовал Том.
Ответ: 140 фунтов краски.Задание 413. Для банка заказали новый сейф, имеющий форму прямоугольного параллелепипеда. Длина сейфа равна 3 м, ширина составляет 13/50 длины, а высота − 15/26 ширины. Сколько слитков золота, имеющих форму куба с ребром 6 см, можно положить в этот сейф?
Решение задачи от 7 гуру
1) $3\ast\frac{13}{50}=\frac{39}{50}=\frac{78}{100}$ (м) = 78 см - ширина сейфа;
2) $\frac{39}{50}\ast\frac{15}{26}=\frac3{10}\ast\frac32=\frac9{20}=\frac{45}{100}$ (м) = 45 см - высота сейфа;
3) 300 : 6 = 50 (сл.) - поместится в длину;
4) 78 : 6 = 13 (ряд.) - в ширину;
5) $45:6=\frac{45}6=\frac{15}2=7\frac12$ (слоев) - можно уложить только 7 слоев;
6) 50 * 13 * 7 = 4550 (сл.) можно положить в сейф.
Ответ: 4550 слитков.Задание 414. Банк "Ломаный грош" получил в июне 200 сольдо прибыли, в июле − 0,65 прибыли июня, в августе − 16/13 прибыли июля. Сколько сольдо составляла прибыль банка за три летних месяца?
Решение задачи
1) 200 * 0,65 = 130 (сольдо) - прибыль в июле;
2) $130\ast\frac{16}{13}=10\ast16=160$ (сольдо) - прибыль в августе;
3) 200 + 130 + 160 = 490 (сольдо) - прибыль банка за три летних месяца.
Ответ: 490 сольдо.Задание 415. Акционерное общество "Поле чудес" имело в декабре 1200 сольдо убытков, в январе − 135% от убытков декабря, в феврале − 25/18 убытков января. Сколько сольдо составили убытки АО "Поле чудес" за три зимних месяца?
Решение задачи
1) 1200 * 135% = 1200 * 1,35 = 1620 (сольдо) - в январе;
2) $1620\ast\frac{25}{18}=90\ast25=2250$ (сольдо) - в декабре;
3) 1200 + 1620 + 2250 = 5070 (сольдо) - составили убытки АО "Поле чудес" за три зимних месяца.
Ответ: 5070 сольдо.Задание 416. В столовую привезли 405 кг овощей: капусту, морковь и картофель. Морковь составляла 32% массы капусты, картофель − 138% массы капусты. Сколько килограммов капусты привезли в столовую?
Решение
Пусть капусты привезли x кг.
x + 0,32x + 1,3x = 405
2,7x = 405
x = 405 : 2,7
х = 150
Ответ: 150 кг капусты привезли в столовую. 78
-
Страница 78
Задание 417. Федоров, Иванов и Петров выиграли вместе в лотерею 1800 р. Выигрыш Иванова составил 64% выигрыша Федорова, а выигрыш Петрова − 76% выигрыша Федорова. Сколько рублей составлял выигрыш каждого из них?
Решение задачи
Путь Федоров выиграл x р, тогда:
x + 0,64x + 0,76x = 1800
2,4x = 1800
x = 1800 : 2,4
x = 750 (р.) - выиграл Федоров.
750 * 64% = 750 * 0,64 = 480 (р.) - выиграл Иванов;
750 * 76% = 750 * 0,76 = 570 (р.) - выиграл Петров.
Ответ: 750 рублей, 480 рублей и 570 рублей.Задание 418. С поля площадью 14 2/7 га собрали урожай сахарной свеклы по 280 ц с каждого гектара. На сахарный завод отвезли 9/16 урожая. Сколько центнеров сахара произвел завод из этой свеклы, если выход сахара составляет 1/6 массы переработанной свеклы?
Решение задачи
1) $14\frac27\ast280=\frac{100}7\ast280=100\ast40=4000$ (ц) - собрали всего.
2) $4000\ast\frac9{16}=250\ast9=2250$ (ц) - отвезли на завод;
3) $2250\ast\frac16=375$ (ц) - сахара произвел завод из привезенной свеклы.
Ответ: 375 ц сахара.Задание 419. С поля площадью 11 1/4 га собрали урожай семян подсолнечника по 21 1/3 ц с каждого гектара. На масло переработали 33/40 собранной массы семян. Сколько центнеров масла получили, если его выход составляет 1/3 массы переработанных семян?
Решение задачи от 7 гуру
1) $11\frac14\ast21\frac13=\frac{45}4\ast\frac{64}3=\frac{15}1\ast\frac{16}1=240$ (ц) - семян всего собрали;
2) $240\ast\frac{33}{40}=6\ast33=198$ (ц) - переработали на масло;
3) $198\ast\frac13=66$ (ц) - масла получили.
Ответ: 66 центнеров масла.Задание 420. Казак Данила сварил кулеш. Сам съел 1/4 казана, казаку Чубу дал 1/3 остатка, казаку Белоусу − 1/2 нового остатка, а казаку Ворону − остальное. После обеда казаки никак не могли выяснить, кому из них досталось больше кулеша. Помогите им разобраться.
Решение задачи
Пусть весь кулеш равен 1, тогда:
1) $1-\frac14=\frac34$ (кулеша) - осталось после того, как Данила съел свою долю;
2) $\frac34\ast\frac13=\frac14$ (кулеша) - досталось Чубу;
3) $\frac34-\frac14=\frac24=\frac12$ (кулеша) - осталось после того, как Чуб съел свою долю;
4) $\frac12\ast\frac12=\frac14$ (кулеша) - досталась Белоусу;
5) $\frac12-\frac14=\frac24-\frac14=\frac14$ (кулеша) - досталась Ворону.
Ответ: всем казакам кулеша досталось поровну.Задание 421. Числа a и b не равны 0. Какое из них больше, если:
1) 3/4 числа a равны 2/3 числа b;
2) 2/5 числа a равны 5/7 числа b.Решение
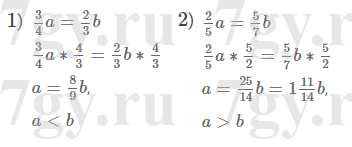
Задание 422. От шнура длиной 10 м отрезали 1/5 его длины, затем − 1/25 начальной длины, а потом − 1/19 того, что осталось. Сколько метров шнура осталось после этих трех операций?
Решение задачи
1) $10\ast\frac15=2$ (м) - отрезали вначале.
2) $10\ast\frac1{25}=\frac25$ (м) - отрезали во второй раз;
3) $10-2-\frac25=7\frac35$ (м) - осталось после двух обрезов;
4) $7\frac35\ast\frac1{19}=\frac{38}5\ast\frac1{19}=\frac25\ast\frac11=\frac25$ (м) - отрезали в третий раз.
5) $10-(2+\frac25+\frac25)=10-2\frac45=7\frac15$ (м) - шнура осталось после трех операций.
Ответ: $7\frac15$ м.Задание 423. Докажите, что a% от числа b равны b% от числа a.
Решение
$\frac a{100}\ast b=\frac b{100}\ast a$
a * b = b * a, верно.Задание 424. Известно, что 1/2 одного числа равна 1/3 другого. Какое из этих чисел больше (данные числа отличны от 0)?
Решение
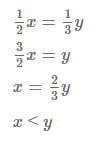
Задание 425. Контрольную работу по математике писали менее 50 шестиклассников. Оценку "5" получили 1/7 учащихся, писавших работу, оценку "4" − 1/3 учащихся, оценку "3" − 1/2 учащихся. Остальные, к сожалению, получили оценку "2". Сколько учащихся получили оценку "2"?
Решение задачи
Пусть количество писавших работу учеников равно 1, тогда:
1) $1-(\frac6{42}+\frac{14}{42}+\frac{21}{42})=1-\frac{41}{42}=\frac1{42}$
Ответ: всего писало работу 42 ученика, один из которых получил оценку "2". 79
-
Страница 79
Задание 426. Вода при замораживании увеличивает свой объем на 1/11. На какую часть уменьшится объем льда при превращении его в воду?
Решение задачи
Пусть первоначальный объем воды равен 1, тогда:
1) $1+\frac1{11}=1\frac1{11}$ объем замороженной воды;
2) $\frac1{11}:1\frac1{11}=\frac1{11}\ast\frac{11}{12}=\frac1{12}$ часть занимает объем льда от объема замороженной воды.
Ответ: на 1/12 уменьшится объем льда при превращении его в воду.Задание 427. На футбольный матч "Зенит" − ЦСКА из Москвы приехали 13 автобусов с болельщиками. На стадионе их разделили на две равные группы. Сколько болельщиков приехало, если 11/17 всех московских болельщиков не превышает 300, а в каждом автобусе ехало одинаковое количество пассажиров?
Решение задачи от 7 гуру
Если 11/17 всех московских болельщиков не превышает 300, то всё количество болельщиков не превышает $\frac{300\;\ast\;17}{11}=463\frac4{11}$,
значит болельщиков было не больше чем 463.
Кроме этого, количество болельщиков кратно числам 2 (их можно разделить на 2 группы), 13 (по числу автобусов) и 17 (число частей в целом), а значит и числу 2 * 13 * 17 = 442.
Ответ: 442 болельщика.Задание 428. В саду растут груши и яблони всего 100 деревьев. Сколько яблонь растет в саду, если 20% их количества равно 60% количества груш?
Решение задачи
Пусть яблонь было x, тогда груш 100 − x.
Составим уравнение:
0,2x = 0,6(100 − x)
0,2x = 60 − 0,6x
0,8x = 60
x = 60 : 0,8
х = 75
Ответ: 75 яблонь растет в саду.Задание 429. Количество отсутствующих в классе учащихся составляло 1/6 количества присутствующих. После того, как один ученик вышел из класса, количество отсутствующих составило 1/5 количества присутствующих. Сколько всего учащихся в классе?
Решение 7 гуру
Сначала количество отсутствующих составляло 1/7 часть класса. Когда один ученик вышел, количество отсутствующих стало составлять 1/6 часть класса. Тогда 1 ученик составляет
$\frac16-\frac17=\frac7{42}-\frac6{42}=\;\frac1{42}$ часть класса,
а значит в классе 42 ученика.
Ответ: 42 ученика.Задание 430. Сравните:
Решение
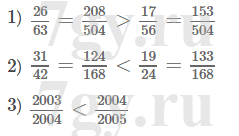
Задание 431. Найдите значение выражения:
$4\frac49\ast1\frac1{32}\ast1\frac15-(2\frac{11}{14}-2\frac2{35})\ast4\frac23$Решение
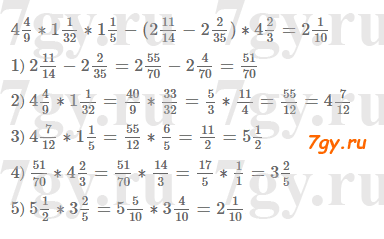
Задание 432. Что больше и на сколько: разность чисел 1 1/9 и 3/8 или их произведение?
Решение
$1\frac19-\frac38=\frac{80}{72}-\frac{27}{72}=\frac{53}{72}$
$1\frac19\ast\frac38=\frac{10}9\ast\frac38=\frac53\ast\frac14=\frac5{12}=\frac{30}{72}$
$\frac{53}{72}-\frac{30}{72}=\frac{23}{72}$
Ответ: на $\frac{23}{72}$ разность больше произведения.Задание 433. Задача от мудрой совы. Черепаха ползет по плоскости с постоянной скоростью, изменяя направление движения на 90° через каждые 15 мин. Докажите, что вернуться в точку "старта" она сможет только через целое количество часов после начала движения.
Решение
Чтобы вернуться в точку старта, черепахе придется повернуть на 360°.
360° : 90° = 4 раза ей надо повернуть.
15 * 4 = 60 минут = 1 ч потребуется черепахе для того, чтобы сделать 4 поворота. 81
-
Страница 81
Ответы к параграфу 13. Взаимно обратные числа
Задание 434. Являются ли взаимно обратными числа:
Решение

Задание 435. Укажите число, обратное числу:
1) 3/5;
2) 12;
3) 3 2/9;
4) 0,16;
5) 1/17;
6) 2,3.Решение
1) 5/3
2) 1/12
3) 9/29
4) $\frac{100}{16}=\frac{25}4=6\frac14$
5) 17
6) 10/23Задание 436.Укажите число, обратное числу:
1) 7/11;
2) 6;
3) 2 2/5;
4) 0,23;
5) 1/9;
6) 3,6.Решение
82-83
-
Страница 82-83
Задание 437. Вычислите наиболее удобным способом:
Решение
1) $\frac{12}{19}\ast(1\frac7{12}\ast4\frac{13}{21})=(\frac{12}{19}\ast\frac{19}{12})\ast4\frac{13}{21}=1\ast4\frac{13}{21}=4\frac{13}{21}$
2) $(3\frac27\ast25,8)\ast\frac7{23}=(\frac{23}7\ast\frac7{23})\ast25,8=1\ast25,8=25,8$Задание 438. Вычислите наиболее удобным способом:
Решение
1) $(6\frac8{11}\ast\frac45)\ast1\frac14=6\frac8{11}\ast(\frac45\ast\frac54)=6\frac8{11}\ast1=6\frac8{11}$
2) $2\frac56\ast(17,8\ast\frac6{17})=(\frac{17}6\ast\frac6{17})\ast17,8=1\ast17,8=17,8$Задание 439. Найдите число, обратное:
1) сумме чисел 7/18 и 7/12;
2) сумме чисел 2 13/14 и 1 20/21;
3) разности чисел 13/60 и 7/40;
4) произведению чисел 22/35 и 11/44.Решение
1) $\frac7{18}+\frac7{12}=\frac{14}{36}+\frac{21}{36}=\frac{35}{36}$, обратное число $\frac{36}{35}=1\frac1{35}$
2) $2\frac{13}{14}+1\frac{20}{21}=2\frac{39}{42}+1\frac{40}{42}=3\frac{79}{42}=\frac{205}{42}$, обратное число $\frac{42}{205}$
3) $\frac{13}{60}-\frac7{40}=\frac{26}{120}-\frac{21}{120}=\frac5{120}=\frac1{24}$, обратное число 24
4) $\frac{22}{35}\ast\frac{11}{44}=\frac1{35}\ast\frac{11}2=\frac{11}{70}$, обратное число $\frac{70}{11}=6\frac4{11}$Задание 440. Найдите число, обратное:
1) разности чисел 8 3/4 и 7 5/6;
2) произведению чисел 1 1/15 и 5/16.Решение
1) $8\frac34-7\frac56=8\frac{18}{24}-7\frac{20}{24}=7\frac{42}{24}-7\frac{20}{24}=\frac{22}{24}=\frac{11}{12}$, обратное число $\frac{12}{11}=1\frac1{11}$
2) $1\frac1{15}\ast\frac5{16}=\frac{16}{15}\ast\frac5{16}=\frac13$, обратное число 3Задание 441. 1) Первое число составляет 1/2 второго. Во сколько раз второе число больше первого?
2) Первое число составляет 3/2 второго. Какую часть первого числа составляет второе?Решение
Поскольку целое - это единица, ответом будет обратное число.
1) в 2 раза.
2) 2/3 части.Задание 442. Найдите среди чисел $1,4;1\frac25;\frac{28}{20};1,04;1\frac6{15};\frac75;\frac{35}{30};1\frac27$ равные.
Решение
$1,4=1\frac4{10}=1\frac25=\frac75=\frac{28}{20}=\frac{21}{15}=1\frac6{15}$, значит
$1,4=1\frac25=\frac75=\frac{28}{20}=1\frac6{15}$Задание 443. Расстояние между городами A и B равно 63 км. Из города A в город B выехал велосипедист со скоростью 12 км/ч. Через 3 ч после отъезда велосипедиста из города A в город B выехал мотоциклист, который догнал велосипедиста на расстоянии 42 км от города A. На каком расстоянии от города B будет велосипедист, когда туда приедет мотоциклист?
Решение
1) 3 * 12 = 36 (км) - успел проехать велосипедист до момента выезда мотоциклиста;
2) 42 − 36 = 6 (км) - успел проехать велосипедист пока его не догнал мотоциклист;
3) 42 : 6 = 7 (раз) - скорость мотоциклиста больше скорости велосипедиста;
4) 12 * 7 = 84 (км/ч) - скорость мотоциклиста;
5) 63 − 42 = 21 (км) - остается проехать мотоциклисту до города B после встречи с велосипедистом;
6) $21:84=\frac{21}{84}=\frac14$ (ч) - потребуется мотоциклисту чтобы проехать оставшиеся 21 км.
7) $12\ast\frac14=3$ (км) - успеет проехать велосипедист после встречи, до того момента как мотоциклист приедет в город B;
8) 63 − (42 + 3) = 18 (км) - не доедет велосипедист до города B, когда туда приедет мотоциклист.
Ответ: на расстоянии 18 км.Второй вариант решения:
1) 63 - 42 = 21 (км) - оставшееся расстояние до города В после встречи
2) 12 * 3 = 36 (км) - проехал велосипедист за 3 часа
3) 42 - 36 = 6 (км) - проехал велосипедист до встречи с мотоциклистом
4) 6 : 12 = 0.5 (ч) - время движения велосипедиста до того как его догнали
5) 42 : 0.5 = 84 (км\ч) - скорость мотоциклиста
6) 21 : 84 = 0.25 (ч) время пути мот до в
7) 0.25 * 12 = 3 (км) - проедет велосипедист
8) 21 - 3 = 18 (км) - останется велосепедисту, когда мотоциклист приедет в город В
Ответ: на расстоянии 18 км.Задание 444. Решите уравнение:
Решение
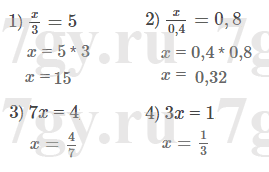
Задание 445. Вася и Саша играют в такую игру: они по очереди (Вася первым) ломают шоколадку, имеющую 6 X 8 квадратных долек. За один ход разрешается сделать прямолинейный разлом любого куска вдоль углубления между дольками шоколадки. Проигрывает тот, кто в очередной раз не сможет этого сделать. Кто из них выиграет?
Решение
8 * 6 = 48 долек всего, и для того чтобы разломать шоколадку полностью потребуется 47 разломов.
Так как число разломов нечетное, то выиграет (последним отломит дольку) тот, кто начнет первым, значит выиграет Вася. 85
-
Страница 85
Ответы к параграфу 14. Деление дробей
Задание 446. Выполните деление:
Решение
1) $\frac37:\frac56=\frac37\ast\frac65=\frac{18}{35}$
2) $\frac3{14}:\frac2{21}=\frac3{14}\ast\frac{21}2=\frac32\ast\frac32=\frac94=2\frac14$
3) $\frac7{16}:\frac{42}{43}=\frac7{16}\ast\frac{43}{42}=\frac1{16}\ast\frac{43}6=\frac{43}{96}$
4) $\frac34:\frac{21}{40}=\frac34\ast\frac{40}{21}=\frac11\ast\frac{10}7=1\frac37$
5) $\frac9{25}:\frac{27}{50}=\frac9{25}\ast\frac{50}{27}=\frac11\ast\frac23=\frac23$
6) $\frac{45}{56}:\frac{63}{64}=\frac{45}{56}\ast\frac{64}{63}=\frac57\ast\frac87=\frac{40}{49}$
7) $\frac23:\frac16=\frac23\ast\frac61=2\ast2=4$
8) $\frac{65}{98}:\frac{26}{49}=\frac{65}{98}\ast\frac{49}{26}=\frac{65}2\ast\frac1{26}=\frac{65}{52}=1\frac{13}{52}$Задание 447. Выполните деление:
Решение
1) $\frac{11}{15}:\frac38=\frac{11}{15}\ast\frac83=\frac{88}{45}=1\frac{43}{45}$
2) $\frac6{35}:\frac{18}{25}=\frac6{35}\ast\frac{25}{18}=\frac17\ast\frac53=\frac5{21}$
3) $\frac{12}{55}:\frac{48}{77}=\frac{12}{55}\ast\frac{77}{48}=\frac15\ast\frac74=\frac7{20}$
4) $\frac{21}{40}:\frac34=\frac{21}{40}\ast\frac43=\frac7{10}\ast\frac11=\frac7{10}$
5) $\frac{27}{50}:\frac9{25}=\frac{27}{50}\ast\frac{25}9=\frac32\ast\frac11=1\frac12$
6) $\frac{63}{64}:\frac{45}{56}=\frac{63}{64}\ast\frac{56}{45}=\frac78\ast\frac75=\frac{49}{40}=1\frac9{40}$
7) $\frac58:\frac5{32}=\frac58\ast\frac{32}5=\frac11\ast\frac41=4$
8) $\frac{14}{55}:\frac15=\frac{14}{55}\ast\frac51=\frac{14}{11}\ast\frac11=1\frac3{11}$Задание 448. Найдите частное:
Решение от 7 гуру
1) $10:\frac56=10\ast\frac65=2\ast6=12$
2) $12:\frac{15}{16}=12\ast\frac{16}{15}=4\ast\frac{16}5=\frac{64}5=12\frac45$
3) $\frac34:2=\frac34\ast\frac12=\frac38$
4) $\frac{10}{11}:10=\frac{10}{11}\ast\frac1{10}=\frac1{11}$
5) $1:\frac78=1\ast\frac87=1\frac17$
6) $7\frac35:\frac{19}{25}=\frac{38}5\ast\frac{25}{19}=\frac21\ast\frac51=10$
7) $1\frac78:2\frac{11}{32}=\frac{15}8\ast\frac{32}{75}=\frac11\ast\frac45=\frac45$
8) $5\frac13:1\frac59=\frac{16}3\ast\frac9{14}=\frac81\ast\frac37=\frac{24}7=3\frac37$Задание 449. Найдите частное:
Решение
1) $6:\frac79=6\ast\frac97=\frac{54}7=7\frac57$
2) $16:\frac4{11}=16\ast\frac{11}4=4\ast11=44$
3) $13:\frac{26}{29}=13\ast\frac{29}{26}=\frac{29}2=14\frac12$
4) $\frac79:5=\frac79\ast\frac15=\frac7{45}$
5) $\frac9{16}:6=\frac9{16}\ast\frac16=\frac3{16}\ast\frac12=\frac3{32}$
6) $1\frac59:1\frac8{27}=\frac{14}9\ast\frac{27}{35}=\frac21\ast\frac35=\frac65=1\frac15$
7) $2\frac{10}{13}:3\frac3{26}=\frac{36}{13}\ast\frac{26}{81}=\frac41\ast\frac29=\frac89$
8) $2\frac47:1\frac1{35}=\frac{18}7\ast\frac{35}{36}=\frac11\ast\frac52=2\frac12$ 86
-
Страница 86
Задание 450
Найдите значение выражения:
Решение
1) $3\frac34:\frac38:1\frac37=\frac{15}4\ast\frac83\ast\frac7{10}=\frac11\ast\frac11\ast\frac71=7$
2) $3\frac34:(\frac38:1\frac37)=\frac{15}4:(\frac38\ast\frac7{10})=\frac{15}4:\frac{21}{80}=\frac{15}4\ast\frac{80}{21}=\frac51\ast\frac{20}7=\frac{100}7=14\frac27$
3) $1\frac79\ast\frac{15}{32}:1\frac{19}{36}=\frac{16}9\ast\frac{15}{32}\ast\frac{36}{55}=\frac11\ast\frac11\ast\frac6{11}=\frac6{11}$
4) $1\frac79\ast(\frac{15}{32}:1\frac{19}{36})=\frac{16}9\ast(\frac{15}{32}\ast\frac{36}{55})=\frac{16}9\ast(\frac38\ast\frac9{11})=\frac{16}9\ast\frac{27}{88}=\frac21\ast\frac3{11}=\frac6{11}$
5) $3\frac47:1\frac17\ast\frac23=\frac{25}7\ast\frac78\ast\frac23=\frac{25}1\ast\frac14\ast\frac13=\frac{25}{12}=2\frac1{12}$
6) $3\frac47:(1\frac17\ast\frac23)=\frac{25}7:(\frac87\ast\frac23)=\frac{25}7:\frac{16}{21}=\frac{25}7\ast\frac{21}{16}=\frac{25}1\ast\frac3{16}=\frac{75}{16}=4\frac{11}{16}$
7) $(\frac5{12}+\frac18):\frac38=(\frac{10}{24}+\frac3{24}):\frac38=\frac{13}{24}\ast\frac83=\frac{13}3\ast\frac13=\frac{13}9=1\frac49$
8) $\frac5{12}+\frac18:\frac38=\frac5{12}+\frac18\ast\frac83=\frac5{12}+\frac13=\frac5{12}+\frac4{12}=\frac9{12}=\frac34$
9) $2\frac67:(\frac56-\frac9{14})=2\frac67:(\frac{35}{42}-\frac{27}{42})=2\frac67:\frac4{21}=\frac{20}7\ast\frac{21}4=\frac51\ast\frac31=15$
10) $2\frac67:\frac56-\frac9{14}=\frac{20}7\ast\frac65-\frac9{14}=\frac47\ast\frac61-\frac9{14}=\frac{48}{14}-\frac9{14}=\frac{39}{14}=2\frac{11}{14}$
11) $2\frac14:1\frac4{11}-\frac38:\frac78=\frac94\ast\frac{11}{15}-\frac38\ast\frac87=\frac34\ast\frac{11}5-\frac31\ast\frac17=\frac{33}{20}-\frac37=\frac{231}{140}-\frac{60}{140}=\frac{171}{140}=1\frac{31}{140}$
12) $(3\frac16-5\frac16:4\frac2{15})\ast\frac3{92}=(3\frac16-\frac{31}6\ast\frac{15}{62})\ast\frac3{92}=(3\frac16-\frac12\ast\frac52)\ast\frac3{92}=(3\frac16-\frac54)\ast\frac3{92}=(2\frac{28}{24}-1\frac6{24})\ast\frac3{92}=1\frac{22}{24}\ast\frac3{92}=\frac{23}{12}\ast\frac3{92}=\frac14\ast\frac14=\frac1{16}$Задание 451
Найдите значение выражения:
Решение
1) $12:3\frac38-1\frac14:\frac{15}{32}=12\ast\frac8{27}-\frac54\ast\frac{32}{15}=4\ast\frac89-\frac11\ast\frac83=\frac{32}9-\frac{24}9=\frac89$
2) $1\frac{31}{35}:(2-\frac89:1\frac{19}{45})=\frac{66}{35}:(2-\frac89\ast\frac{45}{64})=\frac{66}{35}:(2-\frac11\ast\frac58)=\frac{66}{35}:(2-\frac58)=\frac{66}{35}:1\frac38=\frac{66}{35}\ast\frac8{11}=\frac6{35}\ast\frac81=\frac{48}{35}=1\frac{13}{35}$
3) $(1\frac1{35}:\frac45-1\frac8{35})\ast3\frac13=(\frac{36}{35}\ast\frac54-1\frac8{35})\ast\frac{10}3=(\frac97\ast\frac11-1\frac8{35})\ast\frac{10}3=(1\frac{10}{35}-1\frac8{35})\ast\frac{10}3=\frac2{35}\ast\frac{10}3=\frac27\ast\frac23=\frac4{21}$
4) $(7-1\frac59:\frac7{24}):\frac{20}{27}=(7-\frac{14}9\ast\frac{24}7)\ast\frac{27}{20}=(7-\frac23\ast\frac81)\ast\frac{27}{20}=(7-5\frac13)\ast\frac{27}{20}=\frac53\ast\frac{27}{20}=\frac11\ast\frac94=2\frac14$Задание 452
Решите уравнение:
Решение

Задание 453
Решите уравнение:
Решение
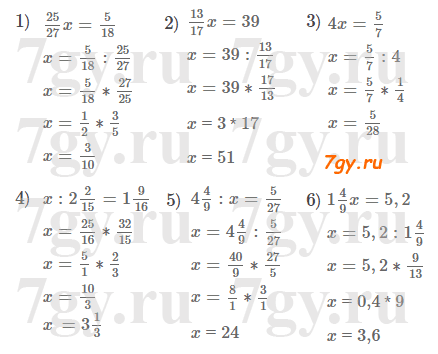
Задание 454
Найдите скорость поезда, если за 8/15 ч он проехал 34 2/3 км.
Решение
$34\frac23:\frac8{15}=\frac{104}3\ast\frac{15}8=\frac{13}1\ast\frac51=65$ (км/ч) - скорость поезда.
Ответ: 65 км/ч.Задание 455
За какое время автобус проедет 63 км, если его скорость составляет 50 2/5 км/ч?
Решение
$63:50\frac25=63\ast\frac5{252}=1\ast\frac54=1\frac14$ (ч) - потребуется автобусу, чтобы проехать 63 км.
Ответ: за $1\frac14$ ч.Задание 456
Сколько стоит 1 кг конфет, если за 2 1/5 кг заплатили 220р.?
Решение
$220:2\frac15=220\ast\frac5{11}=100$ (р.) стоит 1 кг конфет.
Ответ: 100 рублей.Задание 457
Какова масса 1 $дм^3$ сплава, если масса $5\frac13 дм^3$ этого сплава равна $3\frac59$ кг?
Решение
$3\frac59:5\frac13=\frac{32}9\ast\frac3{16}=\frac23\ast\frac11=\frac23$ (кг) - масса сплава.
Ответ: $\frac23$ кг.Задание 458
В двух цистернах 120 т нефти. Сколько тонн нефти в каждой цистерне, если в одной из них в 1 2/9 раза больше нефти, чем в другой?
Решение
Пусть в одной цистерне х тонн, тогда во второй $1\frac29{\operatorname х}$
Составим уравнение:
$1\frac29{\operatorname х}+x=120$
$2\frac29{\operatorname х}=120$
$x=120:2\frac29$
$x=120\ast\frac9{20}$
x = 6 ∗ 9
х = 54 (т) нефти в первой цистерне.
120 − 54 = 66 (т) нефти во второй цистерне.
Ответ: 54 т и 66 т. 87
-
Страница 87
Задание № 459
В двух контейнерах 90 кг яблок. Сколько килограммов яблок в каждом контейнере, если в одном из них в 2 1/3 раза меньше, чем в другом?
Решение
Пусть в одном контейнере x кг яблок, тогда в другом $2\frac13x$ кг яблок.
Составим уравнение:
$x+2\frac13x=90$
$\frac{10}3x=90$
$x=90:\frac{10}3$
$x=90\ast\frac3{10}$
x = 9 * 3
х = 27 (кг) яблок в одном контейнере;
90 − 27 = 53 (кг) яблок в другом контейнере.
Ответ: 27 кг и 53 кг.Задание № 460
Найдите среднее арифметическое чисел:
1) 5/6 и 7/20
2) 1 3/7 и 2 5/21;
3) 2 3/5, 3 3/10 и 2 1/2;
4) 7 5/24, 6 7/24 и 8 1/6.Решение
1) $(\frac56+\frac7{20}):2=(\frac{50}{60}+\frac{21}{60}):2=\frac{71}{60}\ast\frac12=\frac{71}{120}$
2) $(1\frac37+2\frac5{21}):2=(1\frac37+2\frac5{21}):2=(1\frac9{21}+2\frac5{21})\ast\frac12=3\frac23\ast\frac12=\frac{11}3\ast\frac12=\frac{11}6=1\frac56$
3) $(2\frac35+3\frac3{10}+2\frac12):3=(2\frac6{10}+3\frac3{10}+2\frac5{10}):3=8\frac25:3=\frac{42}5\ast\frac13=\frac{14}5=2\frac45$
4) $(7\frac5{24}+6\frac7{24}+8\frac16):3=(7\frac5{24}+6\frac7{24}+8\frac4{24}):3=21\frac23\ast\frac13=\frac{65}3\ast\frac13=\frac{65}9=7\frac29$461. Найдите значение выражения:
1) $(2\frac{13}{48}+2\frac5{12}):3\frac34-9\frac34:12=4\frac{33}{48}\ast\frac4{15}-\frac{39}4\ast\frac1{12}=4\frac{11}{16}\ast\frac45-\frac34\ast\frac14=\frac{75}{16}\ast\frac4{15}-\frac34\ast\frac14=\frac54\ast\frac11-\frac34\ast\frac14=\frac54-\frac3{16}=\frac{20}{16}-\frac3{16}=\frac{17}{16}=1\frac1{16}$
2) $(8:2\frac{10}{19}-1\frac{13}{15}\ast1\frac6{49}):(3\frac1{12}-1\frac{25}{36})=(8\ast\frac{19}{48}-\frac{28}{15}\ast\frac{55}{49}):(2\frac{39}{36}-1\frac{25}{36})=(1\ast\frac{19}6-\frac43\ast\frac{11}7):1\frac{14}{36}=(\frac{19}6-\frac{44}{21}):1\frac7{18}=(\frac{133}{42}-\frac{88}{42}):\frac{18}{25}=\frac{45}{42}\ast\frac{18}{25}=\frac97\ast\frac35=\frac{27}{35}$Задание № 462
Найдите значение выражения:
1) $(2\frac59-1\frac{20}{21}):1\frac8{49}+1\frac89:6=(1\frac{98}{63}-1\frac{60}{63}):\frac{57}{49}+\frac{17}9\ast\frac16=(1\frac{98}{63}-1\frac{60}{63}):\frac{57}{49}+\frac{17}9\ast\frac16=\frac{38}{63}\ast\frac{49}{57}+\frac{17}{54}=\frac29\ast\frac73+\frac{17}{54}=\frac{14}{27}+\frac{17}{54}=\frac{28}{54}+\frac{17}{54}=\frac{45}{54}=\frac56$
2) $(1\frac{17}{18}\ast1\frac{13}{14}-2\frac58:1\frac{19}{20}):(2\frac{25}{78}-1\frac1{26})=(\frac{35}{18}\ast\frac{27}{14}-\frac{21}8:\frac{39}{20}):(2\frac{25}{78}-1\frac3{78})=(\frac52\ast\frac32-\frac{21}8\ast\frac{20}{39}):1\frac{11}{39}=(\frac{15}4-\frac72\ast\frac5{13}):\frac{50}{39}=(\frac{15}4-\frac{35}{26})\ast\frac{39}{50}=(\frac{195}{52}-\frac{70}{52})\ast\frac{39}{50}=\frac{125}{52}\ast\frac{39}{50}=\frac5{52}\ast\frac{39}2=\frac{195}{104}=1\frac{91}{104}=1\frac78$Задание № 463
Решите уравнение:
1) $5\frac{11}{14}x-\frac8{15}=\frac5{21}$
2) $7\frac3{10}+\frac{25}{28}x=8\frac{13}{35}$
3) $3\frac13-1\frac1{20}x=1\frac{14}{15}$
4) $\frac38x+\frac7{12}x-\frac56x=\frac9{32}$
5) $2\frac13:x-1\frac16=1\frac59$
6) $2\frac13:(x+1\frac16)=1\frac59$
7) $27:(31\frac37-2\frac{11}{14}x)=1\frac18$
8) $48:(3\frac45x-25)=1\frac12$Решение

Задание № 464 с ответами
Решите уравнение:

Задание № 465
Автомобиль едет со скоростью 80 км/ч. Сколько километров он проезжает за 1 мин? Выразите скорость автомобиля в метрах в минуту.
Решение
1) $80:60=\frac{80}{60}=\frac86=\frac43=1\frac13$ (км/мин)
2) $1\frac13\ast1000=\frac{4000}3=1333\frac13$ (м/мин)
Ответ: $1\frac13 км/мин, 1333\frac13 м/мин$.Задание № 466
Пешеход двигался со скоростью 5 км/ч. Выразите его скорость в метрах в минуту и в метрах в секунду.
Решение
5 км = 5000 м, тогда:
5000 м : 60 мин = $\frac{5000}{60}=83\frac13$ м/мин.
$\frac{5000}{60\ast60}=\frac{5000}{3600}=\frac{50}{36}=\frac{25}{18}=1\frac7{18}$ (м/с)
Ответ: $83\frac13$ м/мин, $1\frac7{18}$ м/с. 88
-
Страница 88
Задание № 467
Из села до места рыбалки Иван Петрович проплыл на плоту 10 4/5 км, а возвращался на лодке, которая двигалась со скоростью 4 1/20 км/ч, потратив на обратный путь на 1 5/6 ч меньше. Найдите скорость течения реки.
Решение
1) $10\frac45:4\frac1{20}=\frac{54}5\ast\frac{20}{81}=\frac21\ast\frac43=\frac83=2\frac23$ (ч) Иван Петрович возвращался на лодке.
2) $2\frac23+1\frac56=2\frac46+1\frac56=3\frac96=4\frac12$ (ч) Иван Петрович плыл на плоту.
3) $10\frac45:4\frac12=\frac{54}5:\frac92=\frac{54}5\ast\frac29=\frac65\ast\frac21=\frac{12}5=2\frac25$ (км/ч) скорость плота, а значит и скорость течения реки.
Ответ: $2\frac25$ км/ч.Задание № 468
Теплоход проходит 40 1/2 км по течению реки за 1 1/2 ч. На сколько больше времени уйдет на обратный путь, если скорость течения равна 3 3/8 км/ч?
Решение
1) $40\frac12:1\frac12=\frac{81}2:\frac32=\frac{81}2\ast\frac23=\frac{27}1\ast\frac11=27$ (км/ч) - скорость теплохода по течению реки;
2) $27-3\frac38=23\frac58$ (км/ч) - собственная скорость теплохода;
3) $23\frac58-3\frac38=20\frac14$ (км/ч) - скорость теплохода против течения реки;
4) $40\frac12:20\frac14=\frac{81}2:\frac{81}4=\frac{81}2\ast\frac4{81}=2$ (ч) - потребуется теплоходу на обратный путь;
5) $2-1\frac12=\frac12$ (ч) - или на 30 минут на обратный путь уйдет времени больше.
Ответ: на 30 минут больше.Задание № 469
Длина трамвайного маршрута 15 3/4 км. На маршруте есть 12 остановок, на каждой из которых трамвай стоит 1 1/6 мин. За какое время трамвай преодолеет весь маршрут, если его скорость равна 13 1/8 км/ч?
Решение
1) $15\frac34:13\frac18=\frac{63}4:\frac{105}8=\frac{63}4\ast\frac8{105}=\frac31\ast\frac25=\frac65=1\frac15$ (ч)
2) $\frac65=\frac65\ast60=6\ast12=72$ (мин.)
3) $1\frac16\ast12=\frac76\ast12=7\ast2=14$ (мин.) затратит трамвай на остановки.
4) 72 + 14 = 86 (мин) или 1 ч 26 минут потребуется трамваю на преодоление всего маршрута с остановками.
Ответ: за 1 ч 26 минут.Задание № 470
Длина маршрута, который автобус проезжает за 7/10 ч равна 20 1/4 км. Автобус движется по маршруту со скоростью 45 км/ч и делает 10 остановок. Сколько времени длится каждая остановка автобуса, если на каждой остановке он стоит одинаковое время?
Решение
1) $20\frac14:45=\frac{81}4\ast\frac1{45}=\frac94\ast\frac15=\frac9{20}$ (ч)
2) $\frac9{20}\ast60=9\ast3=27$ (мин.) требуется автобусу на преодоление маршрута без остановок.
3) $\frac7{10}\ast60=7\ast6=42$ (мин.) требуется автобусу на преодоление маршрута с остановками.
4) 42 − 27 = 15 (мин.) затрачивает автобус на остановки.
5) $15:10=\frac{15}{10}=1\frac12$ (мин.) или 1 минуту 30 секунд длится каждая остановка автобуса.
Ответ: 1 минуту 30 секунд.Задание № 471
Необходимо расфасовать 32 1/2 кг сахара в пакеты по 3/4 кг в каждом. Сколько получится полных пакетов?
Решение
$32\frac12:\frac34=\frac{65}2\ast\frac43=\frac{65}1\ast\frac23=\frac{130}3=43\frac13$
Ответ: получим 43 полных пакета.Задание № 472
Для перевязывания одной пачки книг требуется 1 1/3 м веревки. На сколько таких пачек хватит 18 м веревки?
Решение
$18:1\frac13=18\ast\frac34=9\ast\frac32=\frac{27}2=13\frac12$
Ответ: 13 полных пачек.Задание № 473
Какое наименьшее количество банок емкостью 0,3 л необходимо взять, чтобы разлить в них 5 л варенья?
Решение
$5:0,3=5:\frac3{10}=5\ast\frac{10}3=\frac{50}3=16\frac23$
Ответ: потребуется 17 банок.Задание № 474
Какое наименьшее количество бидонов емкостью 6 2/3 л необходимо взять, чтобы разлить в них 70 л молока?
Решение
$70:6\frac23=70\ast\frac3{20}=\frac{21}2=10\frac12$
Ответ: потребуется 11 бидонов.Задание № 475
Мастер Иван Иванович может отремонтировать кабинет математики за 24 ч, а мастер Петр Петрович − за 48 ч. За сколько часов, работая вместе, они отремонтируют этот кабинет?
Решение
Пусть полный ремонт кабинета равен 1, тогда
1/24 кабинета отремонтирует Петр Петрович за 1 ч;
1/48 кабинета отремонтирует Иван Иванович за 1 ч;
$\frac1{24}+\frac1{48}=\frac2{48}+\frac1{48}=\frac3{48}=\frac1{16}$ (часть) кабинета отремонтируют обра работника за 1 ч;
$1:\frac1{16}=1\ast16=16$ (часов) потребуется на ремонт кабинета.
Ответ: за 16 часов.Задание № 476
Кот Том съедает жареную Индейку за 20 мин, а мышонок Джерри − за 30 мин. За сколько минут Том и Джерри съедят индейку вместе?
Решение
Пусть вся индейка равна 1, тогда
1/20 индейки съест Том за 1 минуту;
1/30 индейки съест Джерри за 1 минуту;
$1:(\frac1{20}+\frac1{30})=1:(\frac3{60}+\frac2{60})=1:\frac1{12}=1\ast12=12$ (мин.) потребуется Тому и Джерри чтобы съесть индейку.
Ответ: за 12 мин.Задание № 477
Первый рабочий может выполнить задание за 30 ч, а второй для этого необходимо в 1 1/2 раза больше времени, чем первому. За сколько часов они выполнят это задание, работая вместе? Какую часть задания при этом выполнит каждый из них?
Решение
$30\ast1\frac12=30\ast\frac32=15\ast3=45$ часов потребуется второму рабочему на выполнение задание.
Все задание равно 1, тогда:
1/30 задания выполнит первый рабочий за 1 ч;
1/45 задания выполнит второй рабочий за 1 ч;
$1:(\frac1{30}+\frac1{45})=1:(\frac3{90}+\frac2{90})=1:\frac1{18}=1\ast18=18$ (ч) потребуется обоим рабочим на выполнение задания.
$\frac{18}{30}=\frac35$ (часть) задания выполнит первый рабочий
$\frac{18}{45}=\frac25$ (часть) задания выполнит второй рабочий.
Ответ: за 18 часов, $\frac35 и \frac25$ часть задания. 89
-
Страница 89
Задание № 478
Первый тракторист может вспахать поле за 12 дней, второму на это требуется в 1 1/5 раза меньше времени, чем первому, а третьему − в 1 1/2 раза больше, чем второму. За сколько дней они вместе могут вспахать поле? Какую часть поля при этом вспашет каждый из них?
Решение
$12:1\frac15=12\ast\frac56=2\ast5=10$ (д.) потребуется второму трактористу на вспашку поля;
$10\ast1\frac12=10\ast\frac32=5\ast3=15$ (д.) потребуется третьему трактористу на вспашку поля;
1/12 поля вспашет первый тракторист за 1 день;
1/10 поля вспашет второй тракторист за 1 день;
1/15 поля вспашет третий тракторист за 1 день.
$1:(\frac1{12}+\frac1{10}+\frac1{15})=1:(\frac5{60}+\frac6{60}+\frac4{60})=1:\frac14=1\ast4=4$ (дня) потребуется трем трактористам чтобы вспахать поле
$\frac4{12}=\frac13$ часть поля вспашет первый тракторист;
$\frac4{10}=\frac25$ часть поля вспашет второй тракторист;
$\frac4{15}$ части поля вспашет третий тракторист;
Ответ: $\frac13, \frac25 и \frac4{15}$ части поля.Задание № 479
Через первую трубу бассейн можно наполнить водой за 10 ч. Наполнение бассейна через вторую трубу потребует в 1 1/4 раза меньше времени. За какое время наполнится бассейн, если открыть одновременно обе трубы? Какую часть бассейна наполнит при этом каждая труба?
Решение
$10:1\frac14=10\ast\frac45=2\ast4=8$ часов потребуется, чтобы заполнить бассейн через вторую трубу, тогда:
1/10 бассейна наполнится через первую трубу за 1 ч;
1/8 бассейна наполнится через вторую трубу за 1 ч.
$1:(\frac1{10}+\frac18)=1:(\frac4{40}+\frac5{40})=1:\frac9{40}=1\ast\frac{40}9=4\frac49$ часа потребуется на заполнение бассейна двумя трубами
$4\frac49:10=\frac{40}9\ast\frac1{10}=\frac49$ часть бассейна наполнит первая труба;
$4\frac49:8=\frac{40}9\ast\frac18=\frac59$ часть бассейна наполнит вторая труба.
Ответ: за $4\frac49$ часа, $\frac49 и \frac59$ части бассейна.Задание № 480
Двое рабочих работая вместе, могут выполнить некоторую работу за 6 ч. Один из них, работая самостоятельно, может выполнить эту работу за 15 ч. За сколько часов ее может выполнить самостоятельно другой рабочий?
Решение
1) $\frac6{15}=\frac25$ (часть) работы выполнит первый рабочий.
2) $1-\frac25=\frac35$ (часть) работы выполнит второй рабочий.
3) $\frac35:6=\frac35\ast\frac16=\frac15\ast\frac12=\frac1{10}$ (часть) работы выполнит второй рабочий за 1 час.
4) $1:\frac1{10}=1\ast10=10$ (ч) потребуется на выполнение работы второму рабочему.
Ответ: за 10 часов.Задание № 481
Пассажирский поезд проходит расстояние между двумя городами за 36 ч. Если одновременно из этих городов выйдут навстречу друг другу пассажирский и товарный поезда, то они встретятся через 20 ч после начала движения. За какое время товарный поезд может преодолеть расстояние между городами?
Решение
1) $\frac{20}{36}=\frac59$ (части) пути проедет до встречи пассажирский поезд;
2) $1-\frac59=\frac49$ (части) пути проедет до встречи товарный поезд;
3) $20:\frac49=20\ast\frac94=5\ast9=45$ (ч) потребуется товарному поезду на преодоление расстояния между городами.
Ответ: за 45 часов.Задание № 482
Через первую трубу бассейн можно наполнить водой за 3 ч, а через вторую − за 6 ч. Сначала 2 ч была открыта первая труба, затем ее закрыли и открыли вторую трубу. За сколько часов был наполнен бассейн?
Решение
2/3 бассейна наполнит первая труба, следовательно:
1) $1-\frac23=\frac13$ (части) бассейна наполнит вторая труба.
2) $6\ast\frac13=2$ (ч) будет наполнять свою часть бассейна вторая труба, тогда:
3) 2 + 2 = 4 (ч) потребуется на полное заполнение бассейна.
Ответ: 4 часа.Задание № 483
Первая бригада может выполнить заказ за 9 дней, а вторая − за 12 дней. Сначала три дня работала первая бригада, а затем ее заменила вторая. За сколько дней был выполнен заказ?
Решение
1) $\frac39=\frac13$ заказа выполнила первая бригада
2) $1-\frac13=\frac23$ заказа выполнила вторая бригада.
3) $12\ast\frac23=4\ast2=8$ (д.) потребуется второй бригаде на выполнение своей части заказа.
4) 3 + 8 = 11 (д.) потребуется на выполнение всего заказа.
Ответ: за 11 дней.Задание № 484
Выполните деление (буквами обозначены натуральные числа):
1) $\frac{2a}{21}:\frac{4b}{49}=\frac{2a}{21}\ast\frac{49}{4b}=\frac a3\ast\frac7{2b}=\frac{7a}{6b}=1\frac a{6b}$
2) $\frac{11m}{9n}:\frac{22n}{27m}=\frac{11m}{9n}\ast\frac{27m}{22n}=\frac mn\ast\frac{3m}{2n}=\frac{3m^2}{2n^2}=1\frac{m^2}{2n^2}$
3) $\frac{36ab}{17c}:\frac{21b}{34c}=\frac{36ab}{17c}\ast\frac{34c}{21b}=\frac{12a}1\ast\frac27=\frac{24a}7=3\frac{3a}7$
4) $\frac{51x}{32y}:\frac{17x}{16y}=\frac{51x}{32y}\ast\frac{16y}{17x}=\frac32\ast\frac11=1\frac12$Задание № 485
Найдите наименьшее натуральное число, при делении которого на 4/5 и на 6/7 в результате получим натуральные числа.
Решение
Число должно нацело делится на 4 и на 6, тогда:
НОК(4;6) = 12Задание № 486
Который сейчас час, если до конца суток осталось 4/5 того времени, что уже прошло от начала суток?
Решение
Пусть прошло x ч, тогда $\frac45x$ осталось.

Задание № 487
Найдите наименьшее натуральное число, при делении которого на 6/11, на 8/17 и на 12/19 в результате получим натуральные числа.
Решение
Число должно нацело делится на 6, на 8 и на 12, тогда:
НОК(6;8;12) = 24 90
-
Страница 90
Задание № 488 с ответами
Найдите значение выражения:
1) $1-\frac2{3+\frac12}=1-\frac2{3\frac12}=1-2:3\frac12=1-2\ast\frac27=1-\frac47=\frac37$
2) $\frac{8-\frac1{\frac12-\frac13}}{8+\frac1{\frac12-\frac13}}=\frac{8-\frac1{\frac16}}{8+\frac1{\frac56}}=\frac{8-6}{8+\frac56}=\frac2{9\frac15}=2:\frac{47}5=2\ast\frac5{47}=\frac{10}{47}$
3) $\frac1{1+\frac1{1+\frac1{1+\frac12}}}=\frac1{1+\frac1{1+\frac1{\frac32}}}=\frac1{1+\frac1{\frac53}}=\frac1{1+\frac35}=\frac1{1\frac35}=\frac1{\frac85}=\frac58$Задание можно оформлять двумя способами. Ориентируйтесь на требования вашего учителя. Примеры оформления третьего примера из задания №488:


Задание № 489 с ответами
Вычислите:
1) $2+\frac1{1+\frac2{1+\frac13}}=2+\frac1{1+\frac2{\frac43}}=2+\frac1{1+\frac32}=2+\frac1{\frac52}=2\frac25$
2) $\frac{2-\frac{\frac12-\frac14}2}{2+\frac{\frac12-\frac14}2}=\frac{2-\frac{\frac14}2}{2+\frac{\frac14}2}=\frac{2-\frac18}{2+\frac18}=\frac{15}{17}$
3) $\frac1{2-\frac1{2-\frac1{2-\frac13}}}=\frac1{2-\frac1{2-\frac1{\frac53}}}=\frac1{2-\frac1{2-\frac35}}=\frac1{2-\frac1{\frac75}}=\frac1{2-\frac57}=\frac1{\frac97}=\frac79$Задание № 490
Увеличится или уменьшится значение дроби и во сколько раз, если к ее знаменателю прибавить число равное этому знаменателю?
Решение
Пусть дробь $\frac{\operatorname х}y$, после увеличения знаменателя дробь примет вид $\frac{\operatorname х}{y+y}=\frac{\operatorname х}{2y}$, тогда:
$\frac{\operatorname х}y:\frac{\operatorname х}{2y}=\frac{\operatorname х}y\ast\frac{2y}{\operatorname х}=2$ , то есть дробь уменьшится в 2 раза.
Ответ: уменьшится в 2 раза.Задание № 491
Лодка проплывает некоторое расстояние по озеру за 6 ч, а по течению реки то же расстояние − за 5 ч. За сколько часов такое же расстояние проплывет плот по реке?
Решение
Все расстояние равно 1, тогда:
1/6 скорость лодки по озеру;
1/5 скорость лодки по течению реки;
1) $\frac15-\frac16=\frac6{30}-\frac5{30}=\frac1{30}$ скорость течения реки.
2) $1:\frac1{30}=1\ast30=30$ (ч) потребуется плоту, чтобы проплыть такое же расстояние по реке.
Ответ: за 30 ч.Задание № 492
Некоторое расстояние по течению реки катер проходит за 3 ч, а плот − за 15 ч. За сколько часов катер проходит такое же расстояние против течения реки?
Решение
Все расстояние равно 1, тогда:
1/3 скорость катера по течению;
1/15 скорость плота;
1) $\frac13-\frac1{15}=\frac5{15}-\frac1{15}=\frac4{15}$ скорость катера.
2) $\frac4{15}-\frac1{15}=\frac3{15}=\frac15$ скорость катера против течения.
3) $1:\frac15=1\ast5=5$ (ч) потребуется катеру, чтобы проплыть такое же расстояние против течения реки.
Ответ: за 5 часов.Задание № 493
Теплоход проходит некоторое расстояние по течению реки за 2 ч, а против течения − за 3 ч. За сколько часов это же расстояние проплывет плот?
Решение
Все расстояние равно 1, тогда:
1/2 скорость теплохода по течению;
1/3 скорость теплохода против течения;
1) $\frac12-\frac13=\frac36-\frac26=\frac16$ удвоенная скорость течения реки.
2) $\frac16:2=\frac16\ast\frac12=\frac1{12}$ скорость течения реки, а значит и скорость плота.
3) $1:\frac1{12}=1\ast12=12$ (ч) потребуется плоту на прохождение того же расстояния, что и теплоход.
Ответ: за 12 часов.Задание № 494
В первый день туристы прошли 5/12 намеченного пути, во второй − 30% пути, а в третий − остальной путь. Какую часть пути прошли туристы за третий день?
Решение
Все расстояние равно 1, тогда:
30 % = 3/10 пути прошли туристы во второй день;
$1-(\frac5{12}+\frac3{10})=1-(\frac{25}{60}+\frac{18}{60})=1-\frac{43}{60}=\frac{17}{60}$ пути прошли туристы в третий день.
Ответ: $\frac{17}{60}$ части пути.Задание № 495
Угол ABC − прямой, луч BM проведен так, что ∠MBC = 120°, луч BK − биссектриса угла ABC. Вычислите градусную меру угла MBK. Сколько решений имеет задача?
Решение
Задача имеет два решения:
1)
∠CBK = 90° : 2 = 45°
∠MBK = ∠MBC + ∠CBK = 120° + 45° = 165°
2)
∠CBK = 90° : 2 = 45°
∠MBK = ∠MBC − ∠CBK = 120° − 45° = 75°Задание № 496
Задача от мудрой совы. В один ряд расположены 1000 фишек. Любые две фишки, расположенные через одну, разрешается поменять местами. Можно ли переставить фишки в обратном порядке?
Решение
Нет, нельзя. По условию, местами можем поменять или только четные, или только нечетные фишки. Последняя фишка: 1000 − четная, первая: 1 − нечетная, поэтому они не могут поменяться местами.
92
-
Страница 92
Ответы к параграфу 15. Нахождение числа по заданному значению его дроби
Задание № 497
Найдите число, если:
1) 1/3;
2) 1/4;
3) 0,4;
4) 4/9;
5) 12/13;
6) 24/25 его равняется 48.Решение
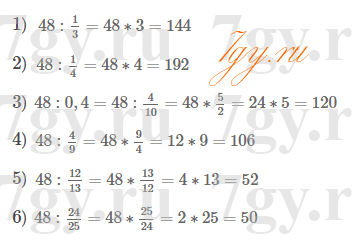
Задание № 498
Найдите число, если:
1) 1/2;
2) 0,2;
3) 2/3;
4) 7/8;
5) 8/11;
6) 14/13 его равняется 56.Решение
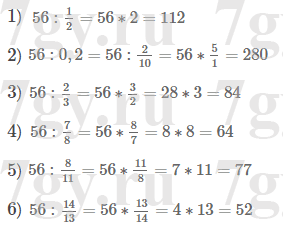
Задание № 499
Найдите число:
1) 3/4 которого равны 12;
2) 6/13 которого равны 24;
3) 7/9 которого равны 63;
4) 0,9 которого равны 81;
5) 9/7 которого равны 7 1/14;
6) 5/7 которого равны 5/7.Решение
Задание № 500
Найдите число:
1) 8/15 которого равны 40;
2) 5/27 которого равны 4 4/9;
3) 15/8 которого равны 120;
4) 3/5 которого равны 9/10.Решение
Задание № 501
Найдите число, если:
1) 24% этого числа равны 48;
2) 75% этого числа равны 1/4;
3) 3 1/3% этого числа равны 5;
4) 108% этого числа равны 86,4.Решение
1) 48 : 24% = 48 : 0,24 = 200
2) $\frac14:75\%=\frac14:\frac{75}{100}=\frac14:\frac43=\frac13$
3) $5:3\frac13\%=5:(\frac{10}3\ast\frac1{100})=5:\frac1{30}=5\ast330=150$
4) 86,4 : 108% = 86,4 : 1,08 = 80Задание № 502
Найдите число, если:
1) 13% этого числа равны 52;
2) 80% этого числа равны 3/5.Решение
1) 52 : 13% = 52 : 0,13 = 400
2) $\frac35:80$%=$\frac35:\frac8{10}=\frac35\ast\frac{10}8=\frac68=\frac34$ 93
-
Страница 93
Задание № 503
В зрительном зале Пермского театре оперы и балета 972 места, что составляет 81/148 количества мест для зрителей в Большом зале Новосибирского театра оперы и балет. Сколько мест для зрителей в Большом зале Новосибирского театра оперы и балета?
Решение
$972:\frac{81}{148}=972\ast\frac{148}{81}=12\ast148=1776$ (мест) для зрителей в Большом зале Новосибирского театра оперы и балета.
Ответ: 1776 мест.Задание № 504
Миша прочитал 144 страницы, что составило 3/5 количества страниц в книге. Сколько страниц в книге.
Решение
$144:\frac35=144\ast\frac53=48\ast5=240$ (стр.)
Ответ: 240 страниц в книге.Задание № 505
Команда шестиклассников выиграла соревнования о футболу. Ее лучший бомбардир забил 16 голов, что составляло 4/15 всех голов, забитых этой командой. Сколько всего голов забила команда шестиклассников?
Решение
$16:\frac4{15}=16\ast\frac{15}4=4\ast15=60$ (г.)
Ответ: 60 голов забила команда шестиклассников.Задание № 506
Чему равно расстояние между двумя городами, если 36 км составляет 15% этого расстояния?
Решение
36 : 15 % = $36:\frac{15}{100}=36\ast\frac{100}{15}=12\ast\frac{20}1=240$ (км)
Ответ: расстояние между двумя городами 240 км.Задание № 507
На приобретение книг для школьной библиотеки выделили определенную сумму денег, 8% которой потратили на приобретение словарей. Какую сумму выделили на приобретение книг, если на словари потратили 1200 р.?
Решение
1200 : 8 % $=1200:\frac8{100}=600\ast\frac{25}1=15000$ (р.)
Ответ: 15000 рублей выделили на приобретение книг.Задание № 508
На завтрак Винни−Пух съел 6/17 бочонка меда, а на обед − остальные 22 кг. Сколько килограммов меда было в бочонке?
Решение
1) $22-\frac6{17}=\frac{11}{17}$ бочонка меда Винни−Пух съел на обед.
2) $22:\frac{11}{17}=22\ast\frac{17}{11}=2\ast17=34$ (кг) меда было в бочонке.
Ответ: 34 кг меда было в бочонке.Задание № 509
В магазин привезли груши. В первый день продали 13/21 всех груш, а во второй − остальные 128 кг. Сколько килограммов груш продали за два дня?
Решение
1) $1-\frac{13}{21}=\frac8{21}$ часть груш продали во второй день;
2) $128:\frac8{21}=128\ast\frac{21}8=16\ast21=336$ (кг) груш продали за два дня.
Ответ: 336 кг груш продали за два дня.Задание № 510
1) Одно из двух слагаемых равно 320, что составляет 40/51 их суммы. Найдите второе слагаемое.
2) Найдите разность двух чисел, если вычитаемое равно 49, что составляет 7/12 уменьшаемого.Решение
1) $320:\frac{40}{51}=320\ast\frac{51}{40}=8\ast51=408$ - сумма двух слагаемых.
480 − 320 = 160 - второе слагаемое.
2) $49:\frac7{12}=49\ast\frac{12}7=7\ast12=84$ − уменьшаемое;
84 − 49 = 35 − разность. 94
-
Страница 94
Задание № 511
1) Одно из двух слагаемых равно 42, что составляет 6/23 второго слагаемого. Найдите их сумму.
2) Найдите разность двух чисел, если уменьшаемое равно 90 и составляет 9/5 вычитаемого.Решение
1) $42:\frac6{23}=42\ast\frac{23}6=7\ast23=161$ − второе слагаемое;
42 + 161 = 203 − сумма
2) $90:\frac95=90\ast\frac59=10\ast5=50$ − уменьшаемое;
90 − 50 = 40 − разностьЗадание № 512
В школьном хоре поют 24 девочки, что составляет 3/4 количества мальчиков, поющих в хоре. Сколько всего детей в этом хоре?
Решение
1) $24:\frac34=24\ast\frac43=8\ast4=32$ (д.) мальчики в хоре;
2) 32 + 24 = 56 (д.) всего в хоре.
Ответ: 56 детей.Задание № 513
Одна из сторон прямоугольника равна 2 5/8 дм, что составляет 7/6 длины соседней стороны. Найдите периметр и площадь прямоугольника.
Решение
1) $2\frac58:\frac76=\frac{21}8\ast\frac67=\frac34\ast\frac31=\frac94=2\frac14$ (см) длина второй стороны.
2) $(2\frac58+2\frac14)\ast2=(2\frac58+2\frac28)\ast2=4\frac78\ast2=\frac{39}8\ast2=\frac{39}4=9\frac34$ (см) периметр прямоугольника.
3) $2\frac58\ast2\frac14=\frac{21}8\ast\frac94=\frac{189}{32}=5\frac{29}{32} (см^2)$ площадь прямоугольника.
Ответ: $9\frac34 см и 5\frac{29}{32} см^2$.Задание № 514
Длина прямоугольного параллелепипеда равна 45 см, ширина составляет 4/9 длины и 12/7 высоты. Вычислите объем прямоугольного параллелепипеда.
Решение
1) $45\ast\frac49=5\ast4=20$ (см) ширина прямоугольного параллелепипеда.
2) $20:\frac{12}7=20\ast\frac7{12}=5\ast\frac73=\frac{35}3=11\frac23$ (см) высота прямоугольного параллелепипеда.
3) $45\ast20\ast11\frac23=45\ast20\ast\frac{35}3=15\ast20\ast35=1050\;({\operatorname с}{\operatorname м}^3)$ объем прямоугольного параллелепипеда.
Ответ: 1050 $см^3$.Задание № 515
Периметр треугольника равен 56 см. Длина одной из его сторон составляет 5/14 периметра и 15/8 длины другой стороны. Найдите стороны треугольника.
Решение
1) $56\ast\frac5{14}=4\ast5=20$ (см) длина первой стороны треугольника;
2) $20:\frac{15}8=20\ast\frac8{15}=4\ast\frac83=\frac{32}3=10\frac23$ (см) длина второй стороны треугольника;
3) $56-20-10\frac23=26-\frac23=25\frac13$ (см) длина третьей стороны треугольника.Задание № 516
Периметр прямоугольника равен 15 1/3 см, что составляет 23/6 длины прямоугольника. Найдите ширину прямоугольника.
Решение
1) $15\frac13:\frac{23}6=\frac{46}3:\frac{23}6=\frac{46}3\ast\frac6{23}=\frac21\ast\frac21=4$ (см) - длина прямоугольника;
2) $15\frac13:2-4=\frac{46}3\ast\frac12-4=\frac{23}3-4=7\frac23-4=3\frac23$ (см) - ширина прямоугольника.
Ответ: $3\frac23$ см.Задание № 517
Ученики 6 класса посадили возле школы деревья. Фруктовые деревья составляют 11/15 посаженных деревьев. Вишни составляют 4/11 фруктовых деревьев. Сколько всего деревьев посадили шестиклассники, если вишен посадили 12?
Решение
1) $12:\frac4{11}=12\ast\frac{11}4=3\ast11=33$ (д.) фруктовых;
2) $33:\frac{11}{15}=33\ast\frac{15}{11}=3\ast15=45$ (д.) посадили всего.
Ответ: 45 деревьев.Задание № 518
На птицеферме разводят кур, уток и индеек. Утки составляют 0,42 всех птиц, а индейки − 9/28 уток. Сколько всего птиц на ферме, если индеек − 54?
Решение
1) $54:\frac9{28}=54\ast\frac{28}9=6\ast28=168$ (птиц) уток было на птицеферме;
2) $168:0,42=168:\frac{21}{50}=168\ast\frac{50}{21}=8\ast50=400$ (птиц) всего на ферме.
Ответ: 400 птиц.Задание № 519
В детский санаторий привезли апельсины, мандарины и яблоки. Апельсины составляют 7/18 массы всех фруктов, мандарины − 5/12, а яблоки − остальные 28 кг. Сколько килограммов фруктов привезли в санаторий?
Решение
Все фрукты равно 1, тогда:
1) $1-\frac7{18}-\frac5{12}=\frac{36}{36}-\frac{14}{36}-\frac{25}{36}=\frac7{36}$ всех фруктов составляют яблоки.
2) $28:\frac7{36}=28\ast\frac{36}7=4\ast36=144$ (кг) фруктов привезли всего в санаторий.
Ответ: 144$ кг.Задание № 520
Известно, что 7/20 армии царя Гороха составляли стрелецкие полки, 13/30 армии − драгунские полки, а остальные 26 полков − казацкие. Сколько полков было в армии царя Гороха?
Решение
Вся армия равна 1, тогда:
1) $1-\frac7{20}-\frac{13}{30}=\frac{60}{60}-\frac{21}{60}-\frac{26}{60}=\frac{13}{60}$ армии составляли казацкие полки.
2) $26:\frac{13}{60}=26\ast\frac{60}{13}=2\ast60=120$ (полков) всего было в армии царя Гороха.
Ответ: 120 полков.Задание № 521
Петр, Федор и Иван собирали яблоки. Иван собрал 23% яблок, Петр − 39%, а Федор − остальные 190 кг. Сколько килограммов яблок они собрали вместе?
Решение
1) 100% − 23% − 39% = 38% яблок собрал Федор.
2) 190 : 38% = 190 : $\frac{38}{100}=190\ast\frac{50}{19}=10\ast50$ = 500 (кг) яблок собрали.
Ответ: 500 кг яблок. 95
-
Страница 95
Задание № 522
Сколько килограммов овощей привезли в магазин, если огурцы составляют 27% массы овощей, картофель − 42%, остальные 496 кг − капуста?
Решение
1) 100% − 27% − 42% = 31% капусты привезли в магазин.
2) 496 : 31 % = $496 : \frac{31}{100}=496\ast\frac{100}{31}=16\ast100=1600$ (кг)
Ответ: 1600 кг овощей привезли в магазин.Задание № 523
Готовясь к олимпиаде по математике, Максим в субботу и воскресенье решал задачи. В субботу он решил 7/18 всех задач, а в воскресенье − 2/9 всех задач и остальные 14 задач. Сколько всего задач решил Максим за два дня?
Решение
1) $1-\frac7{18}-\frac29=\frac{18}{18}-\frac7{18}-\frac4{18}=\frac7{18}$ составляют оставшиеся 14 задач.
2) $14:\frac7{18}=14\ast\frac{18}7=2\ast18=36$ (задач) решил Максим за два дня.
Ответ: 36 задач.Задание № 524
Готовясь к олимпиаде по английскому языку, Галина занималась переводом текста. За один день она перевела 5/12 всех страниц и еще 10 страниц, после чего ей осталось перевести 3/8 страниц текста. Сколько всего страниц составляет текст?
Решение
1) $1-\frac5{12}-\frac38=\frac{24}{24}-\frac{10}{24}-\frac9{24}=\frac5{24}$ составляют оставшиеся 10 страниц.
2) $10:\frac5{24}=10\ast\frac{24}5=2\ast24=48$ (стр.) составляет текст.
Ответ: 48 страниц.Задание № 525
Рассказывают, что на вопрос, сколько учеников в его школе, великий древнегреческий ученый Пифагор ответил: "Половина изучает математику, четверть − музыку, седьмая часть проводит время в молчаливых размышлениях, кроме того, есть еще три женщины". Сколько учеников было в школе Пифагора?
Решение
1) $1-\frac12-\frac14-\frac17=\frac{28}{28}-\frac{14}{28}-\frac7{28}-\frac4{28}=\frac3{28}$ составляют женщины.
2) $3:\frac3{28}=3\ast\frac{28}3=28$ (уч.) было в школе Пифагора.
Ответ: 28 учеников.Задание № 526
Найдите число, 10/13 которого равны 11/14 от числа 280.
Решение
1) $280\ast\frac{11}{14}=20\ast11=220$
2) $220:\frac{10}{13}=220\ast\frac{13}{10}=22\ast13=286$
Ответ: 286 − искомое число.Задание № 527
Найдите 7/24 числа, 3/8 которого составляют 36.
Решение
1) $36:\frac38=36\ast\frac83=12\ast8=96$
2) $96\ast\frac7{24}=4\ast7=28$
Ответ: 28 − искомое число. 96
-
Страница 96
Задание № 528
Буратино потратил 13/28 своих денег на покупку учебников, а на покупку конфет − 11/18 оставшихся денег. После этого у него осталось 35 сольдо. Сколько сольдо было у Буратино сначала?
Решение
1) $35:(1-\frac{11}{18})=35:\frac7{18}=35\ast\frac{18}7=5\ast18=90$ (с.) оставалось у Буратино после покупки конфет.
2) $90:(1-\frac{13}{28})=90:\frac{15}{28}=90\ast\frac{28}{15}=6\ast28=168$ (с.) было у Буратино сначала.
Ответ: 168 сольдо.Задание № 529
Три мышонка нашли головку сыра. Один мышонок съел 7/12 головки, второй − 7/15 остатка, а третий − остальные 1 2/3 кг сыра. Какова была масса головки сыра?
Решение
1) $1\frac23:(1-\frac7{15})=\frac53\ast\frac{15}{18}=\frac{25}8=3\frac18$ (кг) оставалось сыра после того, как свою часть съел первый мышонок.
2) $3\frac18:(1-\frac7{12})=\frac{25}8\ast\frac{12}5=\frac{15}2=7\frac12$ (кг) была масса головки сыра.
Ответ: $7\frac12$ кг.Задание № 530
В первый день в магазине продали 5/9 завезенной ткани, во второй − 35% остатка, а в третий − остальные 52 м. Сколько метров ткани завезли в магазин?
Решение
1) 52 : (100% − 35%) = 52 : 65% = $52:\frac{65}{100}=52:\frac{13}{20}=52\ast\frac{20}{13}=4\ast20=80$ (м) ткани оставалось после первого дня продажи;
2) $80:\frac59=80\ast\frac95=16\ast9=144$ (м) ткани завезли.
Ответ: 144 м.Задание № 531
За первый месяц отремонтировали 55% дороги, за второй − 3/8 остатка, а за третий − остальные 45 км. Сколько километров дороги отремонтировали за три месяца?
Решение
1) $45:(1-\frac38)=45:\frac58=45\ast\frac85=9\ast8=72$ (км) оставалось отремонтировать после первого месяца работы;
2) 72 : (100% − 55%) = $72:\frac{45}{100}=72\ast\frac{20}9=8\ast20=160$ (км) дороги отремонтировали за три месяца.
Ответ: 160 километров.Задание № 532
Альпинисты в первый день преодолели 1/3 высоты горы, во второй − 1/3 оставшейся высоты, в третий − снова 1/3 оставшейся высоты, а в четвертый − преодолели остальные 800 м и достигли вершины. Найдите высоту этой горы.
Решение
1) $800:(1-\frac13)=800:\frac23=800\ast\frac32=400\ast3=1200$ м оставалось преодолеть после двух дней восхождения;
2) $1200:(1-\frac13)=1200:\frac23=1200\ast\frac32=600\ast3=1800$ м оставалось преодолеть после первого дня восхождения;
3) $1800:(1-\frac13)=1800:\frac23=1800\ast\frac32=900\ast3=2700$ м высота этой горы.
Ответ: 2700 м.Задание № 533
Найдите значение выражения:
1) $\frac59+\frac49\ast3\frac16\ast(\frac4{19}+1\frac5{38}-\frac{75}{76})=\frac59+\frac49\ast\frac{19}6\ast(\frac{16}{76}+\frac{86}{76}-\frac{75}{76})=\frac59+\frac49\ast\frac{19}6\ast\frac{27}{76}=\frac59+\frac11\ast\frac12\ast\frac11=\frac59+\frac12=\frac{10}{18}+\frac9{18}=\frac{19}{18}=1\frac1{18}$
2) $(1\frac5{54}-\frac{11}{36})\ast3\frac35\ast2\frac27-1\frac27\ast1\frac59=(\frac{118}{108}-\frac{33}{108})\ast\frac{18}5\ast\frac{16}7-\frac97\ast\frac{14}9=\frac{85}{108}\ast\frac{18}5\ast\frac{16}7-\frac11\ast\frac21=\frac{17}3\ast\frac11\ast\frac87-2=\frac{136}{21}-2=6\frac{10}{21}-2=4\frac{10}{21}$Задание № 534
Решите уравнение:
1) 2/3 x = 1;
2) 5x = 1/6;
3) 4x = 1/4;
4) 7x = 20.Решение
Задание № 535
Найдите координату точки A (рис.11).

Решение
а) $A(\frac16)$
б) $A(\frac78)$
в) $A(\frac{11}{12})$ 97
-
Страница 97
Задание № 536
Вместо звездочек поставьте такие цифры, чтобы трехзначное число 8 делилось нацло на 9. Найдите все возможные решения.
Решение
180; 189; 981; 288; 882; 387; 783; 486; 684; 585.
Задание № 537
Из чисел 20, 45, 50, 64, 505 выберите те, разложение которых на простые множители содержит только числа 2 и 5.
Решение
20; 50; 125; 64.
Задание № 538
Можно ли несократимую дробь со знаменателем 3 привести к дроби со знаменателем 10? 100? 1000? Ответ обоснуйте.
Решение
Нет. Числа: 10; 100; 1000 не являются кратными числу 3.
Задание № 539
Задача от мудрой совы. После того как кусок мыла, имеющего форму прямоугольного параллелепипеда, использовали для стирки семь раз, его длина, ширина и высота уменьшились вдвое. На сколько стирок хватит оставшегося куска мыла?
Решение задачи
Наглядно кусок мыла можно представить так:

Если каждую сторону поделить пополам и убрать лишние кубики (их 7), останется 1 из 8. Если 7 кубиков хватило на 7 стирок, то 1-го кубика хватит на 1 стирку.
1) 2 * 2 * 2 = в 8 раз после семи стирок уменьшился объем мыла, следовательно осталось 1/8 объема мыла.
2) $1-\frac18=\frac78$ объема мыла истратили за семь стирок.
3) $\frac78:7=\frac78\ast\frac17=\frac18$ объема мыла тратится за одну стирку, следовательно остатка мыла хватит на одну стирку.
Ответ: на 1 стирку. 99
-
Страница 99
Ответы к параграфу 16. Преобразование обыкновенной дроби в десятичную
Задание № 540
Какие из данных обыкновенных дробей можно преобразовать в десятичные:
1) 4/5;
2) 2/3;
3) 7/8;
4) 13/400;
5) 9/125;
6) 18/150.Решение

Задание № 541
Какие из данных обыкновенных дробей можно преобразовать в десятичные:
1) 11/16;
2) 17/200;
3) 5/12;
4) 14/625;
5) 23/600;
6) 84/140.Решение
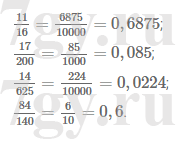
Задание № 542
Преобразуйте в десятичную дробь:
1) 13/20;
2) 3/25;
3) 9/40;
4) 7/16;
5) 97/80;
6) 42/15.Решение
1) $\frac{13}{20}=\frac{13\ast5}{20\ast5}=\frac{65}{100}=0,65$
2) $\frac3{25}=\frac{3\ast4}{25\ast4}=\frac{12}{100}=0,12$
3) $\frac9{40}=\frac{9\ast25}{40\ast25}=\frac{225}{1000}=0,225$
4) $\frac7{16}=\frac{7\ast625}{16\ast625}=\frac{4375}{10000}=0,4375$
5) $\frac{97}{80}=\frac{97\ast125}{80\ast125}=\frac{12125}{10000}=1,2125$
6) $\frac{42}{15}=\frac{14}5=\frac{28}{10}=2,8$Задание № 543
Преобразуйте в десятичную дробь:
1) 3/8;
2) 32/125;
3) 159/200;
4) 1/25;
5) 53/50;
6) 56/175.Решение
1) $\frac38=\frac{3\ast125}{8\ast125}=\frac{375}{1000}=0,375$
2) $\frac{32}{125}=\frac{32\ast8}{125\ast8}=\frac{256}{1000}=0,256$
3) $\frac{159}{200}=\frac{159\ast5}{200\ast5}=\frac{795}{1000}=0,795$
4) $\frac1{25}=\frac{1\ast4}{25\ast4}=\frac4{100}=0,04$
5) $\frac{53}{50}=\frac{53\ast2}{50\ast2}=\frac{106}{100}=1,06$
6) $\frac{56}{175}=\frac8{25}=\frac{32}{100}=0,32$Задание № 544
Преобразуйте обыкновенные дроби в десятичные и вычислите :
1) 0,29 + 6/25;
2) 4 5/8 − 3,94;
3) 8,22 − 4 7/50;
4) 15,63 + 1 9/16.Решение
1) $0,29+\frac6{25}=0,29+\frac{24}{100}=0,29+0,24=0,53$
2) $4\frac58-3,94=4\frac{625}{1000}-3,94=4,625-3,94=0,685$
3) $8,22-4\frac7{50}=8,22-4\frac{14}{100}=8,22-4,14=4,08$
4) $15,63+1\frac9{16}=15,63+1\frac{5625}{10000}=15,63+1,5625=17,7925$ 100
-
Страница 100
Задание № 545
Преобразуйте обыкновенные дроби в десятичные и вычислите :
1) 6/25 − 0,238;
2) 237/250 + 0,052;
3) 0,35 + 1 7/8;
4) 9 329/500 − 8,658.Решение
1) $\frac6{25}-0,238=\frac{24}{100}-0,238=0,24-0,238=0,002$
2) $\frac{237}{250}+0,052=\frac{948}{1000}+0,052=0,948+0,052=1$
3) $0,35+1\frac78=0,35+1\frac{875}{1000}=0,35+1,875=2,225$
4) $9\frac{329}{500}-8,658=9\frac{658}{1000}-8,658=9,658-8,658=1$Задание № 546
Найдите значение выражения:
$(0,5:1,25+1,4\ast\frac7{11}-\frac3{11})\ast4\frac18$Решение
$(0,5:1,25+1,4\ast\frac7{11}-\frac3{11})\ast4\frac18=(\frac12:1\frac14+\frac75\ast\frac7{11}-\frac3{11})\ast\frac{33}8=(\frac12\ast\frac45+\frac{49}{55}-\frac{15}{55})\ast\frac{33}8=(\frac{22}{55}+\frac{34}{55})\ast\frac{33}8=\frac{56}{55}\ast\frac{33}8=\frac75\ast\frac31=\frac{21}5=4\frac15$
Задание № 547
Одна сторона треугольника равна 32 см, вторая составляет 45% первой, а третья − 11/16 первой. Вычислите периметр треугольника.
Решение
1) 32 * 45% = $32\ast\frac{45}{100}=32\ast\frac9{20}=8\ast\frac95=\frac{72}5=\frac{144}{10}=14,4$ (см) длина второй стороны;
2) $32\ast\frac{11}{16}=2\ast11=22$ (см) длина третьей стороны;
3) 32 + 14,4 + 22 = 68,4 см периметр треугольника.
Ответ: 68,4 см.Задание № 548
Сравните:
1) 6,4 и 6,42;
2) 0,4 и 0,08;
3) 0,075 и 0,1.Решение
1) 6,4 < 6,42
2) 0,4 > 0,08
3) 0,075 < 0,1Задание № 549
Задача от мудрой совы. Каждая грань куба окрашена в белый или в черный цвет. Докажите, что найдется две грани с общим ребром, окрашенные в один цвет.
Решение
В каждой вершине куба сходятся 3 грани. Грани окрашены в 2 цвета: черный и белый. Следовательно, в каждой из вершин сойдутся цвета:
либо черный, белый, черный;
либо белый, черный, белый.
Грани, сходящиеся в вершине, имеют общие ребра. Следовательно, обязательно найдутся две грани с общим ребром, окрашенные в один цвет. 102
-
Страница 102
Ответы к параграфу 17. Бесконечные периодические десятичные дроби
Задание № 550
Прочитайте периодическую дробь и назовите ее период:
1) 0,(5);
2) 2,4(3);
3) 0,0(2);
4) 0,(32);
5) 1,(976);
6) 9,0(45);
7) 0,444...;
8) 3,424242...;
9) 0,567567...;
10) 0,137474...;
11) 4,101010...;
12) 2,1231212....Решение
1) 0 целых 5 в периоде, период 5.
2) 2 целых 4 десятых и 3 в периоде, период 3.
3) 0 целых 2 сотых в периоде, период 2.
4) 0 целых 32 в периоде, период 32.
5) 1 целая 976 в периоде, период 976.
6) 9 целых 0 десятых 45 в периоде, период 45.
7) 0 целых 4 в периоде, период 4.
8) 3 целых 42 в периоде, период 42.
9) 0 целых 567 в периоде, период 567.
10) 0 целых 13 сотых и 74 в периоде, период 74.
11) 4 целых 10 в периоде, период 10.
12) 2 целых 123 тысячных и 12 в периоде, период 12.Задание № 551
Запишите в виде бесконечной периодической десятичной дроби частное:
1) 1 : 9;
2) 4 : 11;
3) 47 : 12;
4) 12,4 : 27.Решение
1) $1:9=\frac19=0,(1)$
2) $4:11=\frac4{11}=0,(36)$
3) $47:12=\frac{47}{12}=3,91(6)$
4) $12,4:27=\frac{124}{270}=0,4(592)$Задание № 552
Запишите в виде бесконечной периодической десятичной дроби частное:
1) 5 : 6;
2) 19 : 11;
3) 86 : 15;
4) 6,32 : 18.Решение
1) $5:6=\frac56=0,8(3)$
2) $19:11=\frac{19}{11}=1,(72)$
3) $86:15=\frac{86}{15}=5,7(3)$
4) $6,32:18=\frac{632}{1800}=0,35(1)$Задание № 553
Преобразуйте обыкновенную дробь в бесконечную периодическую десятичную дробь и укажите ее период:
1) 7/9;
2) 11/30;
3) 13/18;
4) 31/33;
5) 49/54.Решение
1) $\frac79=0,(7)$
2) $\frac{11}{30}=0,3(6)$
3) $\frac{13}{18}=0,7(2)$
4) $\frac{31}{33}=0,(93)$
5) $\frac{49}{54}=0,9(074)$Задание № 554
Преобразуйте обыкновенную дробь в бесконечную периодическую десятичную дробь и укажите ее период:
1) 5/12;
2) 11/15;
3) 9/11;
4) 19/36;
5) 39/44.Решение
1) $\frac5{12}=0,41(6)$
2) $\frac{11}{15}=0,7(3)$
3) $\frac9{11}=0,(81)$
4) $\frac{19}{36}=0,52(7)$
5) $\frac{39}{44}=0,88(63)$ 103
-
Страница 103
Задание № 555
Сравните дроби, записав предварительно обыкновенные дроби в виде десятичной дроби или бесконечной периодической десятичной дроби:
1) 1/6 и 0,2;
2) 4/7 и 5/8;
3) 22/7 и 3,14;
4) 5/13 и 387/1000.Решение
1) $\frac16=0,1(6)<0,2$
2) $\frac47=0,(571428)<\frac58=0,625$
3) $\frac{22}7=3,(142857)>3,14$
4) $\frac5{13}=0,(384615)<\frac{387}{1000}=0,387$Задание № 556
Сравните дроби, записав предварительно обыкновенные дроби в виде десятичной дроби или бесконечной периодической десятичной дроби:
1) 3/11 и 0,269;
2) 7/9 и 77/100;
3) 11/12 и 19/20;
4) 47/15 и 119/36.Решение
1) $\frac3{11}=0,(27)>0,269$
2) $\frac79=0,(7)>\frac{77}{100}$
3) $\frac{11}{12}=0,91(6)<\frac{19}{20}=0,95$
4) $\frac{47}{15}=3,1(3)<\frac{119}{36}=3,30(5)$Задание № 557
Найдите значение выражения:
1) $\frac5{16}:1,25\ast0,36:1\frac45=\frac5{16}:\frac54\ast\frac9{25}:\frac95=\frac5{16}\ast\frac45\ast\frac9{25}\ast\frac59=\frac14\ast\frac11\ast\frac15\ast\frac11=\frac1{20}$
2) $\frac78:(0,75\ast\frac{14}{15}:1,2)=\frac78:(\frac34\ast\frac{14}{15}:\frac65)=\frac78:(\frac12\ast\frac75\ast\frac56)=\frac78:(\frac12\ast\frac71\ast\frac16)=\frac78:\frac7{12}=\frac78\ast\frac{12}7=\frac12\ast\frac31=\frac32=1\frac12$Задание № 558
Из двух городов расстояние между которыми 108 км, одновременно навстречу друг другу выехали царь Салтан и царевич Гвидон. Карета царя Салтана двигалась со скоростью 10 км/ч, что составляло 5/7 скорости, с которой на коне ехал царевич Гвидон. Через сколько часов после выезда они встретятся?
Решение
1) $10:\frac57=10\ast\frac75=2\ast7=14$ км/ч скорость кареты;
2) 14 + 10 = 24 км/ч скорость приближения;
3) $108:24=\frac{108}{24}=\frac92=4\frac12$ (ч) или 4,5 часа - через столько часов карета царя Салтана встретится с царевичем Гвидоном.
Ответ: через 4,5 часа.Задание № 559
Округлите дроби:
1) 9,486; 12,78; 0,5498; 10,333; 1,89 до десятых;
2) 3,405; 4,326; 82,2048; 0,2349; 0,999 до сотых;
3) 0,6372; 2,2981; 6,55555; 4,6767 до тысячных.Решение
1)
9,486 ≈ 9,5;
12,78 ≈ 12,8;
0,5498 ≈ 0,5;
10,333 ≈ 10,3;
1,89 ≈ 1,9.
2)
3,405 ≈ 3,41;
4,326 ≈ 4,33;
82,2048 ≈ 82,20;
0,2349 ≈ 0,23;
0,999 ≈ 1,00.
3)
0,6372 ≈ 0,637;
2,2981 ≈ 2,298;
6,55555 ≈ 6,556;
4,6767 ≈ 4,677.Задание № 560
Задача от мудрой совы. На доске написаны числа 1, 0, 1, 0, 0, 1, 0, 0. Разрешается к любым двум записанным числам прибавить одно и то же натуральное число. Можно ли, выполнив такую операции. несколько раз, достичь того, чтобы все записанные числа оказались равными?
Решение
Нет. Сумма всех чисел, написанных на доске, не четна. При прибавлении того же числа она будет оставаться нечетной. Чтобы все числа стали равны, сумма должна быть четной.
105
-
Страница 105
Ответы к параграфу 18. Десятичное приближение обыкновенной дроби
Задание № 561
Найдите десятичное приближение:
1) 1/16;
2) 6/17;
3) 9/40;
4) 2 1/3;
5) 5 4/11;
6) 1 17/200.Решение
1) $\frac1{16}=0,0625\approx0,06$
2) $\frac6{17}=0,35291...\approx0,35$
3) $\frac9{40}=0,225\approx0,23$
4) $2\frac13=2,333...\approx2,33$
5) $5\frac4{11}=5,3636...\approx5,36$
6) $1\frac{17}{200}=1,085\approx1,08$Задание № 562
Найдите десятичное приближение:
1) 12/23;
2) 6/43;
3) 8/9;
4) 5 5/16;
5) 1 2/7;
6) 3 1/625.Решение
1) $\frac{12}{23}=0,52173\approx0,522$
2) $\frac6{43}=0,13953...\approx1,140$
3) $\frac89=0,8888...\approx0,889$
4) $5\frac5{16}=5,3125\approx5,313$
5) $1\frac27=1,28571...\approx1,286$
6) $3\frac1{625}=3,0016\approx3,002$Задание № 563
Найдите десятичное приближение частного до указанного разряда:
1) 36,8 : 7 − до десятых;
2) 24,16 : 11 − до десятых;
3) 29 : 6 − до сотых;
4) 5 : 13 − до сотых;
5) 2 : 3 − до тысячных;
6) 26,7 : 14 − до сотых;
7) 52 : 15 − до тысячных;
8) 10 : 17 − до десятитысячных.Решение
1) 36,8 : 7 = 5,257... ≈ 5,3
2) 24,16 : 11 = 2,19(63) ≈ 2,2
3) 29 : 6 = 4,8(3) ≈ 4,83
4) 5 : 13 = 0,3846... ≈ 0,38
5) 2 : 3 = 0,(6) ≈ 0,667;
6) 26,7 : 14 = 1,90(714285) ≈ 1,91
7) 52 : 15 = 3,4(6) ≈ 3,467
8) 10 : 17 = 0,(5882352941176470) ≈ 0,5882Задание № 564
Найдите десятичное приближение частного до указанного разряда:
1) 43,3 : 9 − до десятых;
2) 78,32 : 18 − до десятых;
3) 38 : 11 − до сотых;
4) 10 : 18 − до сотых;
5) 5 : 9 − до тысячных;
6) 64,45 : 19 − до сотых;
7) 90 : 22 − до тысячных;
8) 65 : 23 − до десятитысячных.Решение
1) 43,3 : 9 = 4,8(1) ≈ 4,8
2) 78,32 : 18 = 4,35(1) ≈ 4,4
3) 38 : 11 = 3,(45) ≈ 3,45
4) 10 : 18 = 0,(5) ≈ 0,56
5) 5 : 9 = 0,(5) ≈ 0,556
6) 64,45 : 19 = 3,392105... ≈ 3,39
7) 90 : 22 = 4,(09) ≈ 4,091
8) 65 : 23 = 2,(826086956) ≈ 2,8261Задание № 565
В 7 пакетов развесили поровну 16 кг сахара. Сколько килограммов сахара в каждом пакете? Ответ запишите в виде десятичного приближения до сотых.
Решение
16 : 7 = 2,(285714) ≈ 2,29 кг сахара в каждом пакете.
Ответ: приблизительно 2,29 кг.Задание № 566
Среднее расстояние от Солнца до ближайшей к нему планеты Меркурий составляет 57,9 млн. км, а до самой отдаленной планеты Нептун − 4504,4 млн. км. Во сколько раз меркурий расположен ближе к Солнцу, чем Нептун? Ответ запишите в виде десятичного приближения до единиц.
Решение
4504,4 : 57,9 = 77,796... ≈ 78, то есть в 78 раз меркурий расположен ближе к Солнцу, чем Нептун.
Задание № 567
В 9 банок поровну налили 25 кг меда. Сколько килограммов меда налили в каждую банку? Ответ запишите в виде десятичного приближения до десятых.
Решение
25 : 9 = 2,(7) ≈ 2,8 кг меда налили в каждую банку.
Ответ: приблизительно 2,8 кг.Задание № 568
Найдите десятичное приближение до сотых корня уравнения:
1) 9x = 5;
2) 8 : x = 125;
3) 3x = 4;
4) 2/7 x = 1 1/6.Решение
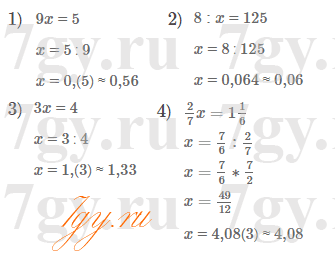
Задание № 569
Найдите десятичное приближение до сотых корня уравнения:
1) 12x = 7;
2) 5 : x = 8;
3) 7x = 16;
4) 3/8 x = 1 9/16.Решение

106
-
Страница 106
Задание № 570 с ответами
Преобразуйте обыкновенные дроби в десятичные, округлите их до сотых и выполните вычисления:
1) $\frac37+0,69\approx0,43+0,69=1,12$
2) $4\frac79-3\frac5{12}+4,96\operatorname{=≈}4,78-3,42+4,96=6,32$Задание № 571 с ответами
Преобразуйте обыкновенные дроби в десятичные, округлите их до сотых и выполните вычисления:
1) $\frac6{13}-0,28\approx0,46-0,28=0,18$
2) $12\frac{10}{19}-4,54-5\frac16\approx12,53-4,54-5,17=2,82$Задание № 572
Увеличится или уменьшится дробь и во сколько раз, если ее числитель увеличить в 4 раза, а знаменатель уменьшить в 3 раза?
Решение
Пусть изначальная дробь равна 1/1, тогда:
$\frac11\ast\frac41:\frac13=1\ast4\ast3=12$
Ответ: дробь увеличится в 12 раз.Задание № 573 с решением
Найдите значение выражения:
$(3,6-1\frac23):(4\frac1{15}-2\frac79)\ast2,6=(3\frac35-1\frac23):(3\frac{16}{15}-2\frac79)\ast2\frac35=(2\frac{24}{15}-1\frac{10}{15}):(3\frac{48}{45}-2\frac{35}{45})\ast2\frac35=1\frac{14}{15}:1\frac{13}{45}\ast2\frac35=\frac{29}{15}\ast\frac{45}{58}\ast\frac{13}5=\frac11\ast\frac32\ast\frac{13}5=\frac{39}{10}=3,9$
Задание № 574
Увеличится или уменьшится частное и во сколько раз, если:
1) делимое увеличить в 4 раза;
2) делитель уменьшить в 3 раза;
3) делимое увеличить в 6 раз, а делитель − в 2 раза?
4) делимое уменьшить в 10 раз, а делитель увеличить в 5 раз?Решение
1) увеличится в 4 раза
2) увеличится в 3 раза
3) увеличится в 3 раза
4) уменьшится в 10 * 5 = 50 разЗадание № 575
Задача от мудрой совы. Из натурального числа, которое не больше 100, вычли сумму его цифр. Из полученного числа снова вычли сумму его цифр, и так делали насколько раз. После 11 таких вычитаний впервые получили 0. Найдите исходное число.
Решение
Число 99.
99 − 18 = 81;
81 − 9 = 72;
72 − 9 = 63;
63 − 9 = 54;
54 − 9 = 45;
45 − 9 = 36;
36 − 9 = 27;
27 − 9 = 18;
18 − 9 = 9;
9 − 9 = 0. 114
-
Страница 114
Глава 3. Отношения и пропорции
Ответы к параграфу 19. ОтношенияЗадание № 576
Запишите с помощью знака деления ":" отношение чисел:
1) 7 и 3;
2) 4 и 28;
3) 2,1 и 3,4;
4) 2 1/3 и 7 3/5.Решение
1) 7 : 3
2) 4 : 28
3) 2,1 : 3,4
4) $2\frac13:7\frac35$Задание № 577
Запишите с помощью черты дроби отношение чисел:
1) 13 и 50;
2) 5 и 2;
3) 8 и 4,6;
4) 7/9 и 2/3.Решение
1) $\frac{13}{50}$
2) $\frac52$
3) $\frac8{4,6}=\frac{80}{46}=\frac{40}{23}$
4) $\frac79:\frac23=\frac79\ast\frac32=\frac73\ast\frac12=\frac76$Задание № 578
Найдите отношение:
1) 1,8 : 5,4;
2) 2,4 : 0,08;
3) 3,5 : 49;
4) 9,6 : 0,16;
5) 3 дм : 5 см;
6) 8 м : 1 км;
7) 12 м : 1,8 км;
8) 24 кг : 480 г;
9) 360 г : 5,4 кг;
10) 14,4 дм : 160 см;
11) 1 ч : 24 мин;
12) $78 см^2 : 2,6 дм^2$.Решение

Задание № 579
Найдите отношение:
1) 45 к 5;
2) 4 к 24;
3) 2 1/7 к 1 11/14;
4) 4,8 к 0,12;
5) 1,8 м к 30 см;
6) 1 кг к 125 г.Решение
1) 45 : 5 = 9
2) $4:24=\frac4{24}=\frac16$
3) $2\frac17:1\frac{11}{14}=\frac{15}7:\frac{25}{14}=\frac{15}7\ast\frac{14}{25}=\frac31\ast\frac25=\frac65=1\frac15$
4) $4,8:0,12=\frac{480}{12}=40$
5) $1,8{\operatorname м}:30{\operatorname с}{\operatorname м}=\frac{180}{30}=6$
6) $1{\operatorname к}{\operatorname г}:125{\operatorname г}=\frac{1000}{125}=8$Задание № 580
В спортивных соревнованиях участвовали 72 школьника, среди которых было 18 девочек. Во сколько раз всех участников соревнований было больше, чем девочек? Какую часть всех участников составляли девочки?
Решение
1) 72 : 18 = 4, то есть в 4 раза всех участников соревнований было больше, чем девочек;
2) $18:72=\frac{18}{72}=\frac14$ часть всех участников составляли девочки.
Ответ: $\frac14$ часть.Задание № 581
В сплаве, масса которого равна 250 кг, содержится 20 кг меди. Во сколько раз масса сплава больше, чем масса меди, содержащейся в нем? Какую часть сплава составляет медь?
Решение
1) $250:20=\frac{25}2=12\frac12$ (раз) - в 12,5 раза масса сплава больше, чем масса меди;
2) $20:250=\frac{20}{250}=\frac2{25}$ (части) сплава составляет медь.
Ответ: $\frac2{25}$ составляет медь.Задание № 582
Равны ли отношения:
1) 16 : 4 и 0,8 : 0,2;
2) 34/85 и 27/45;
3) 0,3 : 0,06 и 1 1/7 : 4/21;
4) 4,2/0,7 и 9/1,5.Решение

Задание № 583
Во сколько раз расстояние на карте меньше расстояния на местности, если масштаб карты 1 : 200000?
Решение
Расстояние на карте меньше расстояния на местности в 200000 раз.
Задание № 584
Во сколько раз расстояние на местности больше расстояния на карте, если масштаб карты 1 : 40000?
Решение
Расстояние на местности больше расстояния на карте в 40000 раз.
Задание № 585
Расстояние между городами Париж и Тулуза на карте, масштаб которой 1 : 9000000, равно 6,7 см. Вычислите расстояние между этими городами на местности.
Решение
6,7 * 9000000 = 60300000 см = 603000 м = 603 км расстояние между этими городами на местности.
Задание № 586
Расстояние между городами Яблоневое и Грушевое равно 240 км. Каким будет расстояние между этими городами на карте с масштабом 1 : 600000?
Решение
240 : 600000 = 0,0004 км = 0,4 м = 40 см расстояние между этими городами на карте.
115
-
Страница 115
Задание № 587
Расстояние между городами Зеленогорский и Синеозерный равно 320 км. Каким будет расстояние между этими городами на карте с масштабом 1 : 4000000?
Решение
320 : 4000000 = 0,00008 км = 0,08 м = 8 см расстояние между этими городами на карте.
Задание № 588
Замените данное отношение отношением натуральных чисел:
1) 1 : 3/8;
2) 5/12 : 17/18;
3) 3/4 : 5/18;
4) 1 2/3 : 11/3.Решение
1) $1:\frac38=1\ast\frac83=\frac83$
2) $\frac5{12}:\frac{17}{18}=\frac5{12}\ast\frac{18}{17}=\frac52\ast\frac3{17}=\frac{15}{34}$
3) $\frac34:\frac5{18}=\frac34\ast\frac{18}5=\frac32\ast\frac95=\frac{27}{10}$
4) $1\frac23:1\frac13=\frac53:\frac43=\frac53\ast\frac34=\frac54$Задание № 589
Замените отношение дробных чисел отношением натуральных чисел:
1) 4/9 : 11/9;
2) 0,8 : 0,03;
3) 2 5/8 : 3 1/6;
4) 3 1/2 : 3,6.Решение
1) $\frac49:\frac{11}9=\frac49\ast\frac9{11}=\frac4{11}$
2) $0,8:0,03=\frac{80}3$
3) $2\frac58:3\frac16=\frac{21}8:\frac{19}6=\frac{21}8\ast\frac6{19}=\frac{21}4\ast\frac3{19}=\frac{63}{76}$
4) $3\frac12:3,6=\frac72:\frac{18}5=\frac72\ast\frac5{18}=\frac{35}{36}$Задание № 590
Увеличится или уменьшится отношение и во сколько раз, если:
1) предыдущий член увеличить в 4 раза;
2) последующий член увеличить в 2,4 раза;
3) предыдущий и последующий члены увеличить в 10 раз;
4) последующий член увеличить в 7 раз, а предыдущий уменьшить в 3 раза;
5) предыдущий член уменьшить в 9 раз, а последующий − в 4,5 раза?Решение
1) увеличится в 4 раза
2) уменьшится в 2,4 раза
3) не изменится
4) уменьшится в 7 * 3 = 21 раз
5) уменьшится в 2 разаЗадание № 591
Увеличится или уменьшится отношение и во сколько раз, если:
1) предыдущий член уменьшить в 5 раз;
2) последующий член уменьшить в 6 раз;
3) предыдущий член увеличить в 9 раз, а последующий уменьшить в 2 раза;
4) последующий и предыдущий члены увеличить соответственно в 4 и 12 раз?Решение
1) уменьшится в 5 раз
2) увеличится в 6 раз
3) увеличится в 9 * 2 = 18 раз
4) увеличится в 12 : 3 = 4 разаЗадание № 592
Расстояние между двумя городами на местности равно 435 км, а на карте − 14,5 см. Найдите масштаб карты.
Решение
435 км = 435000000 мм;
14,5 см = 145 мм.
$\frac{145}{435000000}=\frac1{3000000}$ масштаб карты.Задание № 593
Расстояние между двумя городами на местности равно 120 км, а на карте − 7,5 см. Найдите масштаб карты.
Решение
120 км = 120000000 мм;
7,5 см = 75 мм.
$\frac{75}{120000000}=\frac1{1600000}$ − масштаб карты.Задание № 594
Размеры участка прямоугольной формы составляют 48 м и 30 м. Начертите в тетради план этого участка в масштабе 1 : 600.
Решение
48 м = 4800 см;
$\frac{4800}{600}=8$ (см) длина участка на плане.
30 м = 3000 см;
$\frac{3000}{600}=5$ (см) ширина участка на плане.
Задание № 595
На плане, масштаб которого равен 1 : 15000, длина прямоугольного участка равна 12 см, а ширина − 8 см. Сколько тонн семян пшеницы надо, чтобы засеять этот участок, если на 1 га земли высевают 0,24 т семян?
Решение
1) 12 * 15000 = 180000 (см) - длина участка на местности;
180000 см = 1800 м
2) 8 * 15000 = 120000 (см) - ширина участка на местности;
120000 см = 1200 м
3) 1800 * 1200 = 2160000 ($м^2$) - площадь участка на местности;
2160000 $м^2$ = 216 га
4) 216 * 0,24 = 51,84 (т) - семян пшеницы надо, чтобы засеять этот участок.
Ответ: 51,84 тонны семян.Задание № 596
Расстояние между селениями Приречное и Приозерное на местности составляет 288 км, а на карте − 9,6 см. Какое расстояние между селениями Кленовое и Калиновое на этой же карте, если расстояние на местности между ними равно 324 км?
Решение
288 км = 288000000 мм;
9,6 см = 96 мм.
$\frac{96}{288000000}=\frac1{3000000}$ масштаб карты.
324 км = 32400000 см.
$\frac{32400000}{3000000}=\frac{324}{30}=\frac{108}{10}=10,8$ см расстояние между селениями Кленовое и Калиновое на этой карте.
Ответ: 10,8 см. 116
-
Страница 116
Задание № 597
Расстояние между селами Рябиновка и Ольшанка на местности равно 98 км, а на карте − 4,9 см. Расстояние между селами Крапивня и Камышовое на этой же карте равно 7,6 см. Какое расстояние между селами Крапивня и Камышовое на местности?
Решение
98 км = 98000000 мм;
4,9 см = 49 мм.
$\frac{49}{98000000}=\frac1{2000000}$ - масштаб карты;
7,6 * 2000000 = 15200000 (см) - расстояние между селами Крапивня и Камышовое на местности.
15200000 см = 152 км
Ответ: 152 км.Задание № 598
Число 414 кратно числу 18. Найдите:
1) три числа, следующих за 414 и кратных 18;
2) два числа, предыдущих 414 и кратных 18.Решение
1)
414 + 18 = 432;
432 + 18 = 450;
450 + 18 = 468.
2)
414 − 18 = 396;
396 − 18 = 378.Задание № 599
Петя и Дима, работая вместе, могут прополоть огород за 2,4 ч. Петя может сделать это самостоятельно за 4 ч. Сколько времени требуется Диме, чтобы самостоятельно прополоть огород?
Решение
1) $2,4:4=\frac{12}5:4=\frac{12}5\ast\frac14=\frac35$ огорода прополол Петя за 2,4 часа;
2) $1-\frac35=\frac25$ огорода прополол Дима за 2,4 ч;
3) $2,4:\frac25=\frac{12}5:\frac25=\frac{12}5\ast\frac52=\frac61\ast\frac11=6$ (ч) потребуется Диме, чтобы самостоятельно прополоть огород.
Ответ: 6 часов.Задание № 600 с ответами
Найдите значение выражения:
$(2,04:\frac1{25}-36,1:\frac{19}{20})\ast\frac5{13}-0,6:0,9=(\frac{51}{25}:\frac1{25}-\frac{361}{10}:\frac{19}{20})\ast\frac5{13}-\frac35:\frac9{10}=(\frac{51}{25}\ast\frac{25}1-\frac{361}{10}\ast\frac{20}{19})\ast\frac5{13}-\frac35\ast\frac{10}9=(\frac{51}1\ast\frac11-\frac{19}1\ast\frac21)\ast\frac5{13}-\frac11\ast\frac23=(51-38)\ast\frac5{13}-\frac23=13\ast\frac5{13}-\frac23=5-\frac23=4\frac13$
Задание № 601
Витя купил тетрадь объемом 96 листов и пронумеровал все страницы по порядку от 1 до 192. Вася вырвал из этой тетради 5 листов и сложил все 70 чисел, которые на них были написаны. Могла ли полученная сумма быть равной 3500?
Решение
Не может, так как сумма номеров страниц на одном листе будет нечетной (четное + нечетное = нечетное). Количество листов тоже нечетно. В итоге получается начетное число, а число 3500 − четное.
119
-
Страница 119
Ответы к параграфу 20. Пропорции
Задание № 602
Прочитайте пропорцию, назовите ее крайние и средние члены:
1) 5 : 3 = 20 : 12;
2) 13 : 4 = 39 : 12;
3) 18/63 = 16/56;
4) 16/12 = 68/51;
5) x : 9 = 2 : 23;
6) 8/y = 64/15.Решение
1) Отношение 5 к 3 равно отношению 20 к 12;
Крайние члены пропорции: 5 и 12;
Средние члены пропорции: 3 и 20.
2) Отношение 13 к 4 равно отношению 39 к 12;
Крайние члены пропорции: 13 и 12;
Средние члены пропорции: 4 и 39.
3) Отношение 18 к 63 равно отношению 16 к 56;
Крайние члены пропорции: 18 и 56;
Средние члены пропорции: 63 и 16.
4) Отношение 16 к 12 равно отношению 68 к 51;
Крайние члены пропорции: 16 и 51;
Средние члены пропорции: 12 и 68.
5) Отношение x к 9 равно отношению 2 к 23;
Крайние члены пропорции: x и 23;
Средние члены пропорции: 9 и 2.
6) Отношение 8 к y равно отношению 64 к 15;
Крайние члены пропорции: 8 и 15;
Средние члены пропорции: y и 64.Задание № 603
Запишите в виде пропорции утверждение:
1) 2 относится к 7, как 6 относится к 21;
2) отношение 7,2 к 0,8 равно отношению 0,09 к 0,01;
3) 2/3 относится к 1 1/9, как 4/21 относится к 20/63.Решение
1) 2 : 7 = 6 : 21
2) 7,2 : 0,8 = 0,09 : 0,01
3) $\frac23:1\frac19=\frac4{21}:\frac{20}{63}$Задание № 604
Вычислив данные отношения, установите, можно ли из них составить пропорцию:
1) 2,8 : 0,7 и 152 : 38;
2) 6/11 : 3/22 и 12/17 : 5/34.
В случае утвердительного ответа запишите эту пропорцию.Решение
1) 2,8 : 0,7 = 4;
152 : 38 = 4;
4 = 4, следовательно пропорцию:
2,8 : 0,7 = 152 : 38 составить можно.
2) $\frac6{11}:\frac3{22}=\frac6{11}\ast\frac{22}3=\frac21\ast\frac21=4$
$\frac{12}{17}:\frac5{34}=\frac{12}{17}\ast\frac{34}5=\frac{12}1\ast\frac25=\frac{24}5=4\frac45$
$4\neq4\frac45$
пропорцию составить нельзя.Задание № 605
Вычислив данные отношения, установите, можно ли из них составить пропорцию:
1) 15 : 1,8 и 15/16 : 3/20;
2) 5 1/4 : 3 1/16 и 1 11/19 : 35/38.
В случае утвердительного ответа запишите эту пропорцию.Решение

120
-
Страница 120
Задание № 606
Не вычисляя данные отношения, установите, можно ли из них составить пропорцию:
1) 1,6 : 3,6 и 0,5 : 1,125;
2) 2 7/16 : 5/13 и 1 41/50 : 24/65.Решение
1) нельзя
2) нельзяЗадание № 607
Не вычисляя данные отношения, установите, можно ли из них составить пропорцию:
1) 3,8 : 2,7 и 5,7 : 4,6;
2) 3 : 1 7/8 и 2/3 : 5/12.Решение
1) Нельзя
2) Можно: $3:1\frac78=\frac23:\frac5{12}$Задание № 608
Решите уравнение:
1) 6 : x = 36 : 30;
2) 12 : 7 = 3 : x;
3) 4,9 : 0,35 = x : 35;
4) x/21 = 9/14;
5) x/16 =3/8;
6) 108/90 = 42/b.Решение

Задание № 609
Найдите неизвестный член пропорции:
1) x : 5 = 21 : 15;
2) 12/x = 8/18;
3) 4,5 : 0,6 = x : 2,4;
4) 3,4/5,1 =1,4/x.Решение
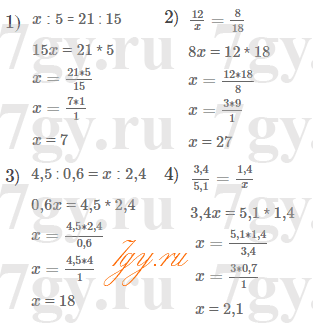
Задание № 610
Решите с помощью пропорции задачу:
1) Для изготовления 8 одинаковых приборов необходимо 18 кг металла. Сколько таких приборов можно изготовить из 27 кг металла?
2) За 5 ч турист прошел 24 км. Какое расстояние он пройдет за 8 ч с той же скоростью?
3) Из 140 кг свежих вишен получают 21 кг сушеных. Сколько килограммов сушеных вишен получится из 160 кг свежих? Сколько килограммов свежих вишен необходимо взять, чтобы получить 31,5 кг сушеных?
4) Объем бруска, изготовленного из древесины вишни, равен 800 см3, а его масса − 528 г. Какова масса бруска, изготовленного из этого же материала, если его объем равен 1500 см3?
5) Из 45 т железной руды выплавляют 25 т железа. Сколько требуется тонн руды, чтобы выплавить 10 т железа?
6) Площадь поля 480 га. Пшеницей засеяли 24% площади поля. Сколько гектаров земли засеяли пшеницей?
7) За первый час автомобиль проехал 70 км, что составило 14% всего пути. Сколько километров составляет весь путь?
8) Сплав содержит 12% цинка. Сколько килограммов цинка содержится в 80 кг сплава?Решение
1) Пусть из 27 кг металла возможно изготовить x приборов.
К-во приборов Масса металла
↓ 8 18 кг ↓
х 27 кг
$\frac8x=\frac{18}{27}$
18x = 8 * 27
$x=\frac{8\ast27}{18}$
$x=\frac{4\ast3}1$
x = 12
Значит, 12 приборов можно изготовить из 27 кг металла
Ответ: 12 приборов.
2) Пусть x км пройдет турист за 8 ч.
Время Путь
↓ 5 ч 24 км ↓
8 ч х км
$\frac58=\frac{24}x$
5x = 8 * 24
$x=\frac{8\ast24}5$
$x=\frac{192}5$
$x=38\frac25=38,4$
Значит, 38,4 км пройдет турист за 8 ч с той же скоростью
Ответ: 38,4 км.
3) Пусть из 160 кг свежих вишен возможно получить x кг сухих вишен.
Масса свеж. Масса сух
↓ 140 кг 21 кг ↓
160 кг х кг
$\frac{21}x=\frac{140}{160}$
140x = 160 * 21
$x=\frac{160\ast21}{140}$
$x=\frac{8\ast3}1$
x = 24
Значит, 24 кг сушеных вишен получится из 160 кг свежих
Пусть из x кг свежих вишен необходимо взять, чтобы получить 31,5 кг сухих вишен.
$\frac{21}{31,5}=\frac{140}x$
21x = 31,5 * 140
$x=\frac{31,5\ast140}{21}$
$x=\frac{1,5\ast140}1$
x = 210
Значит, 210 кг свежих вишен необходимо взять, чтобы получить 31,5 кг сухих вишен
Ответ: 24 кг; 210 кг.
4) Пусть x г масса бруска, если его объем равен 1500 см3.
$\frac{800}{1500}=\frac{528}x$
800x = 1500 * 528
$x=\frac{1500\ast528}{800}$
$x=\frac{15\ast66}1$
x = 990
Значит, 990 г масса бруска, если его объем равен 1500 см3.
Ответ: 990 г .
5) Пусть x т руды требуется, чтобы выплавить 10 т железа.
$\frac{45}x=\frac{25}{10}$
25x = 45 * 10
$x=\frac{45\ast10}{25}$
$x=\frac{9\ast2}1$
x = 18
Значит, 18 т руды требуется, чтобы выплавить 10 т железа.
Ответ: 18 т руды.
6) Пусть x га земли засеяли пшеницей.
$\frac{480}x=\frac{100}{24}$
100x = 480 * 24
$x=\frac{480\ast24}{100}$
$x=\frac{96\ast6}5$
$x=\frac{576}5=115\frac15=115,2$
Значит, 115,2 га земли засеяли пшеницей.
Ответ: 115,2 га земли.
7) Пусть x км составляет весь путь.
$\frac{70}x=\frac{14}{100}$
14x = 70 * 100
$x=\frac{70\ast100}{14}$
$x=\frac{5\ast100}1$
x = 500
Значит, 500 км составляет весь путь.
Ответ: 500 км.
8) Пусть x кг цинка содержится в 80 кг сплава.
$\frac{80}x=\frac{100}{12}$
100x = 80 * 12
$x=\frac{80\ast12}{100}$
$x=\frac{4\ast12}5$
$x=\frac{48}5=\frac{96}{10}=9,6$
Значит, 9,6 кг цинка содержится в 80 кг сплава
Ответ: 9,6 кг цинка.Задание № 611
Решите с помощью пропорции задачу.
1) На пошив 14 одинаковых костюмов израсходовали 49 м ткани. Сколько таких костюмов можно сшить из 84 м ткани?
2) За 7 ч в бассейн налилось 224 л воды. За какое время в него нальется 288 л воды?
3) Из 150 кг картофеля получают 27 кг крахмала. Сколько килограммов крахмала получат из 420 кг картофеля? Сколько килограммов картофеля необходимо, чтобы получить 30,6 кг крахмала?
4) В саду растет 320 деревьев, из которых 40% составляют яблони. Сколько яблонь растет в саду?
5) Масса соли составляет 24% массы раствора. Сколько килограммов раствора необходимо взять, чтобы он содержал 96 кг соли?Решение
1) Пусть x костюмов можно сшить из 84 м ткани.
$\frac{14}x=\frac{49}{84}$
4x = 14 * 84
$x=\frac{14\ast84}{49}$
$x=\frac{2\ast12}1$
x = 24
Значит, 24 костюма можно сшить из 84 м ткани.
Ответ: 24 костюма.
2) Пусть за x часов в бассейн нальется 288 л воды.
$\frac7x=\frac{224}{288}$
224x = 7 * 288
$x=\frac{7\ast288}{224}$
$x=\frac{1\ast72}8$
x = 9
Значит, 9 часов в бассейн будет наливаться 288 л воды.
Ответ: 9 часов.
3) Пусть x кг крахмала получат из 420 кг картофеля.
$\frac{27}x=\frac{150}{420}$
150x = 27 * 420
$x=\frac{27\ast420}{150}$
$x=\frac{27\ast14}5$
$x=\frac{378}5$
$x=\frac{756}{10}=75,6$
Значит, 75,6 кг крахмала получат из 420 кг картофеля.
Ответ: 75,6 кг крахмала.Пусть x кг картофеля необходимо, чтобы получить 30,6 кг крахмала.
$\frac{27}{30,6}=\frac{150}x$
27x = 30,6 * 150
$x=\frac{30,6\ast150}{27}$
$x=\frac{3,4\ast50}1$
x = 170
Значит, 170 кг картофеля необходимо, чтобы получить 30,6 кг крахмала.
Ответ: 170 кг картофеля.
4) Пусть x яблонь растет в саду.
К-во деревьев Проценты
320 д 100 %
х д 40 %
$\frac{320}x=\frac{100}{40}$
100x = 320 * 40
$x=\frac{320\ast40}{100}$
$x=\frac{32\ast4}1$
x = 128
Значит, 128 яблонь растет в саду
Ответ: 128 яблонь.
5) Пусть x килограммов раствора необходимо взять, чтобы он содержал 96 кг соли.
$\frac{100}{24}=\frac x{96}$
24x = 100 * 96
$x=\frac{100\ast96}{24}$
$x=\frac{100\ast4}1$
x = 400
Значит, 400 килограммов раствора необходимо взять, чтобы он содержал 96 кг соли.
Ответ: 400 кг. 121
-
Страница 121
Задание № 612
1) Расстояние между двумя городами на карте равно 17 см. Каково расстояние между этими городами на местности, если масштаб карты − 1 : 300000?
2) Расстояние между двумя поселками на местности равно 245 км, а на карте − 3,5 см. Найдите масштаб карты.Решение
1) Пусть 17 см на карте равны x см на местности.
На местн. На карте
↓300000 см 1 см ↓
х см 17 см
$\frac{300000}x=\frac1{17}$
x = 300000 * 17
x = 5100000
Значит, 5100000 см - расстояние между городами на местности.
5100000 см = 51 км
Ответ: 51 км.
2) 245 км = 24500000 см.
Пусть 1 см на карте равен x см на местности.
На карте На местн.
↑ 35 см 24500000 см ↑
1 см х см
$\frac{3,5}1=\frac{24500000}x$
3,5x = 24500000 * 1
$x=\frac{24500000}{3,5}$
$x=\frac{245000000}{35}$
x = 7000000
Значит, 7000000 см на местности равен 1 см на карте, следовательно масштаб карты равен 1 : 7000000.
Ответ: 1 : 7000000.Задание № 613
1) Расстояние между двумя городами на местности равно 240 км. Какое расстояние между ними на карте, масштаб которой 1 : 6000000?
2) Расстояние между городами A и B на местности равно 315 км, а на карте − 4,2 см. Какое расстояние между городами C и D на этой карте, если расстояние на местности между ними составляет 135 км?Решение
1) 240 км = 24000000 см.
Пусть x см на карте равно 24000000 см на местности.
$\frac x{24000000}=\frac1{6000000}$
6000000x = 24000000 * 1
$x=\frac{24000000}{6000000}$
$x=\frac{24}6$
x = 4 (см)
Значит, расстояние между двумя городами на карте 4 см.
Ответ: 4 см.
2) 315 км = 31500000 см.
Пусть x см на местности равно 1 см на карте.
$\frac{4,2}{31500000}=\frac1x$
4,2x = 31500000 * 1
$x=\frac{315000000}{42}$
x = 7500000
Значит, 7500000 см на местности равно 1 см на карте, то есть масштаб карты равен 1 : 7500000.
135 км = 13500000 см.
Пусть x см на карте будет 13500000 см на местности.
$\frac x{13500000}=\frac1{7500000}$
7500000x = 13500000 * 1
$x=\frac{13500000}{7500000}$
$x=\frac95$
$x=1\frac45=1,8$
Значит, расстояние между городами C и D на карте 1,8 см.
Ответ: 1,8 см.Задание № 614
Используя данные числа, составьте пропорцию:
1) 12; 7; 42; 2;
2) 0,2; 1,6; 0,72; 0,09.Решение
1) $\frac{42}7=\frac{12}2$
2) $\frac{0,2}{1,6}=\frac{0,09}{0,72}$Задание № 615
Составьте все возможные пропорции, которые следуют из равенства 4 * 9 = 18 * 2.
Решение

Задание № 616
Используя пропорцию 2 : 14 = 5 : 35, запишите еще три пропорции.
Решение
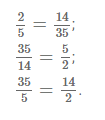
Задание № 617
Найдите отношение a к b, если:
1) b/a=3/7;
2) 16/b=9/a.Решение
1) $\frac ab=\frac73=2\frac13$
2) $\frac ab=\frac9{16}$Задание № 618
Найдите отношение a к b, если:
1) a/39=b/8;
2) 7/a=6/b.Решение
1) $\frac ab=\frac{39}8=4\frac78$
2) $\frac ab=\frac76=1\frac16$Задание № 619
Решите уравнение:
1) $\frac34:x=1\frac15:1\frac13$
2) $\frac2{x-0,4}=\frac1{0,4}$
3) $\frac{2x-1}3=\frac12$
4) $\frac34=\frac{x-1}{3,2}$
5) $2,5x:14=\frac17:30$
6) $36:35=\frac15x:\frac1{12}$Решение
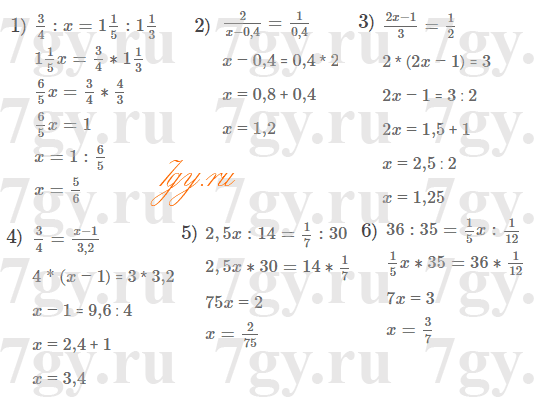
Задание № 620 с ответами
Решите уравнение:
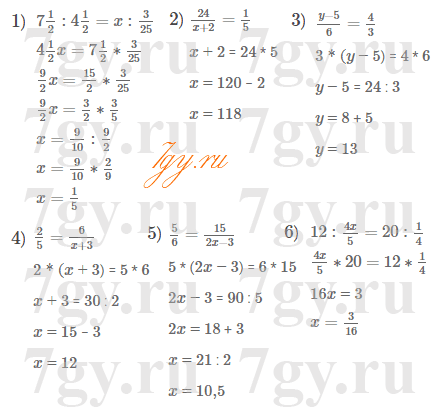
122
-
Страница 122
Задание № 621
Чтобы сварить четыре порции манной каши, нужно 220 г манной крупы, 960 г молока и 50 г сахара. Сколько необходимо взять продуктов каждого вида, чтобы сварить 18 порций каши?
Решение
18 : 4 = 4,5, то есть количество продуктов для 18 порций каши необходимо увеличить в 4,5 раза, тогда для приготовления 18 порций каши потребуется:
220 * 4,5 = 990 (г) манной крупы;
960 * 4,5 = 4320 (г) молока;
4320 г = 4 кг 320 г
50 * 4,5 = 225 (г) сахара.
Ответ: 990 г манной крупы; 4 кг 320 г молока; 225 г сахара.Задание № 622
Чтобы получить 120 кг мельхиора, необходимо сплавить 18 кг никеля, 24 кг цинка, а остальное − медь. Сколько килограммов каждого металла необходимо взять, чтобы получить 164 кг мельхиора?
Решение
$164:120=\frac{164}{120}=\frac{41}{30}$ то есть в 41/30 раза необходимо увеличить количество каждого металла, чтобы получить 164 кг мельхиора.
Таким образом потребуется:
$18\ast\frac{41}{30}=6\ast\frac{41}{10}=\frac{246}{10}=24,6$ (кг) никеля;
$24\ast\frac{41}{30}=8\ast\frac{41}{10}=\frac{328}{10}=32,8$ (кг) цинка;
164 − 24,6 − 32,8 = 106,6 кг меди.
Ответ: 24,6 кг никеля; 32,8 кг цинка; 106,6 кг меди.Задание № 623
Нарушится ли пропорция, если:
1) оба члена одного из отношений умножить на 8;
2) оба члена одного отношения разделить на 2, а оба члена другого отношения умножить на 5;
3) оба средних члена разделить на 3,6?Решение
1) нет
2) нет
3) даЗадание № 624
Нарушится ли пропорция, если:
1) оба члена одного из отношений разделить на 4;
2) оба крайних члена умножить на 10;
3) один из крайних членов и один из средних членов умножить на 6?Решение
1) нет
2) да
3) нетЗадание № 625
Докажите, что если a/b=c/d, то:
1) $\frac{a-b}b=\frac{c-d}d$
2) $\frac a{a+b}=\frac c{c+d}$Решение
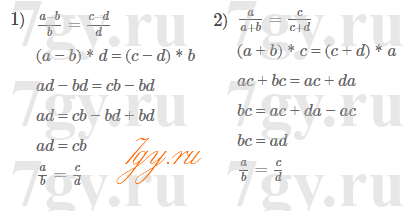
Задание № 626
Девять кокосов стоят столько дублонов, сколько кокосов можно купить за 1 дублон. Сколько стоят 15 кокосов?
Решение
9 кокосов стоят 1 дублон;
15 кокосов стоят x дублонов, тогда:
$\frac9{15}=\frac1x$
9x = 15
$x=\frac{15}9$
$x=\frac53=1\frac23$ (д.)
Ответ: $1\frac23$ дублонов стоят 15 кокосов.Задание № 627
Во сколько раз число:
1) 1/6;
2) 3/5;
3) 0,6 меньше обратного ему числа?Решение
1) В $6:\frac16=6\ast6=36$ (раз)
2) В $\frac53:\frac35=\frac53\ast\frac53=\frac{25}9=2\frac79$ (раза)
3) В $\frac{10}6:\frac6{10}=\frac53\ast\frac53=\frac{25}9=2\frac79$ (раза)Задание № 628
Из сел Заречное и Заозерное одновременно навстречу друг другу вышли два мальчика и встретились через 10 мин после начала движения. Затем мальчики продолжили движение в тех де направлениях, и один из них пришел в Заозерное через 8 мин после встречи. Через сколько минут после своего выхода из Заозерного второй мальчик придет в Заречное?
Решение
$10:8=\frac{10}8=\frac54$ , то есть в 5/4 раза скорость мальчика из Заозерного больше, чем скорость мальчика из Заречного;
$18\ast\frac54=9\ast\frac52=\frac{45}2=22,5$ , то есть через 22,5 минуты после своего выхода из Заозерного второй мальчик придет в Заречное.
Ответ: через 22,5 минуты.Задание № 629 с ответами
Найдите значение выражения:
1) $(3\frac13+2,5)\ast(4,6-2\frac13)=(3\frac13+2\frac12)\ast(4\frac35-2\frac13)=(3\frac26+2\frac36)\ast(4\frac9{15}-2\frac5{15})=5\frac56\ast2\frac4{15}=\frac{35}6\ast\frac{34}{15}=\frac73\ast\frac{17}3=\frac{119}9=13\frac29$
2) $(4,5\ast1\frac23-6,75)\ast(1\frac13)^3=(\frac92\ast\frac53-6\frac34)\ast(\frac43\ast\frac43\ast\frac43)=(7\frac12-6\frac34)\ast\frac{64}{27}=(6\frac64-6\frac34)\ast\frac{64}{27}=\frac34\ast\frac{64}{27}=\frac11\ast\frac{16}9=1\frac79$Задание № 630
В саду растет 56 деревьев, из них 14 деревьев составляют яблони. Какую часть деревьев сада составляют яблони?
Решение
$\frac{14}{56}=\frac14$ (часть)
Ответ: $\frac14$ часть деревьев сада составляют яблони. 123
-
Страница 123
Задание № 631
В саду растет 56 деревьев, из них 14 деревьев составляют яблони, а остальные деревья − груши. Какую часть от количества груш составляет количество яблонь?
Решение
56 − 14 = 42 груш растет в саду;
$\frac{14}{42}=\frac13$ (часть)
Ответ: $\frac13$ часть от количества груш составляет количество яблонь.Задание № 632
Задача от мудрой совы. На столе лежат четыре черные палочки разной длины, причем сумма их длин равна 40 см, и пять белых палочек, сумма длин которых также равна 40 см. Можно ли разрезать те и другие палочки так, чтобы потом расположить их парами, в каждой из которых длины палочек будут одинаковыми, а цвета разными?
Решение
Да, можно.
Сначала смотрим, есть ли среди палочек одинаковые по длине, но разного цвета. Если да, откладываем их в пару. Теперь выбираем самую короткую палочку одного цвета и обрезаем до нужной длины короткую палочку другого цвета. Откладываем их в пару. Продолжаем действовать таким же образом до последней пары палочек. 125
-
Страница 125
Задание № 633
Сколько процентов числа составляет его:
1) половина;
2) четверть;
3) десятая часть;
4) пятая часть?Решение
1) 1/2 * 100 = 50 (%)
2) 1/4 * 100 = 25 (%)
3) 1/10 * 100 = 10 (%)
4) 1/5 * 100 = 20 (%)Задание № 634
Сколько процентов составляет:
1) число 4 от числа 8;
2) число 2 от числа 10;
3) число 12 от числа 48;
4) число 45 от числа 300;
5) число 64 от числа 400;
6) число 138 от числа 120.Решение
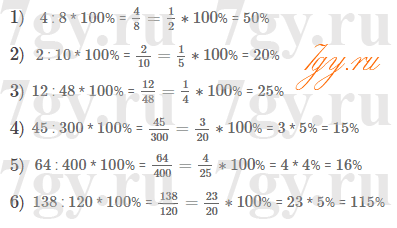
Задание № 635
Сколько процентов число 40 составляет от числа:
1) 100;
2) 80;
3) 160;
4) 10?Решение
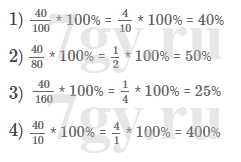
Задание № 636
1) Вика прочитала 169 страниц книги, в которой 260 страниц. Сколько процентов страниц книги прочитала Вика?
2) У Маши было 340 р. За 238 р. она купила подарок маме. Какой процент денег истратила Маша на подарок?
3) Найдите процент содержания олова в руде, если 80 т этой руды содержит 6,4 т олова?
4) За каникулы Витя планировал решить 60 задач по математике, а решил 102 задачи. На сколько процентов Витя выполнил "план по решению задач"?
5) Определите процент содержания сахара в растворе, если 250 г раствора содержит 115 г сахара.Решение

Задание № 637
1)Из 36 учеников 6 класса девять учащихся получили за контрольную работу по математике оценку "5". Сколько процентов учащихся получили оценку "5"?
2) Найдите процент содержания соли в растворе, если 400 г раствора содержат 34 г соли?
3) Посеяли 240 семян, из которых взошло 228. Найдите процент всхожести семян.Решение

126
-
Страница 126
Задание № 638
На сколько процентов изменилось значение величины, если она изменилась:
1) от 3 кг до 6 кг;
2) от 2 м до 3 м;
3) от 40 к. до 70 к.;
4) от 80 м до 72 м;
5) от 100 р. до 115 р.;
6) от 60 мин до 42 мин?Решение
1) 6 − 3 = 3 величина изменения значения;
3/3 * 100 = 100 (%)
2) 3 − 2 = 1 величина изменения значения;
1/2 * 100 = 50 (%)
3) 70 − 40 = 30 величина изменения значения;
30/40 * 100 = 75 (%)
4) 80 − 72 = 8 величина изменения значения;
8/80 * 100 = 10 (%)
5) 115 − 100 = 15 величина изменения значения;
15/100 * 100 = 15 (%)
6) 60 − 42 = 18 величина изменения значения;
18/60 * 100 = 30 (%)Задание № 639
1) Цена товара повысилась со 140 р. до 175 р. На сколько процентов повысилась цена товара?
2) Цена товара снизилась со 175 р. до 140 р. На сколько процентов снизилась цена товара?Решение
1) 175 − 140 = 35 рублей величина повышения цены товара;
35/140 * 100 = 1/4 * 100 = 25 (%), то есть на 25% повысилась цена товара.
2) 175 − 140 = 35 рублей величина снижения цены товара;
35/175 * 100 = 1/5 * 100 = 20 (%), то есть на 20% понизилась цена товара.Решение через пропорции
1)
140 р. - 100 %
175 р. - х %
140/175 = 100/х
140х = 100 * 175
х = 17500/140
х = 125
125 - 100 = 25 (%)
Ответ: на 25% повысилась цена товара.
2)
175 р. - 100 %
140 р. - х %
175/140 = 100/х
175х = 100 * 140
х = 14000/175
х = 80
100 - 80 = 20 (%)
Ответ: на 20% понизилась цена товара.Задание № 640
Известно, что 380 кг руды первого вида содержит 68,4 кг железа, а 420 кг руды второго вида − 96,6 кг железа. В какой руде, первого или второго вида, выше процентное содержание железа?
Решение
68,4/380 * 100 = 684/38 = 18 (%) - содержание железа в руде первого вида;
96,6/420 * 100 = 966/42 = 23 (%) - содержание железа в руде второго вида;
23 − 18 = 5 (%) - на столько содержание железа в руде второго вида больше содержания железа в руде первого вида.
Ответ: на 5% содержание железа в руде второго вида больше.Задание № 641
Известно, что 280 г первого раствора содержит 98 г соли, а 220 г второго раствора − 88 г соли. В каком растворе, первом или втором, выше процентное содержание соли?
Решение
98/280 * 100 = 7/20 * 100 = 7 * 5 = 35 (%) - содержание соли в первом растворе;
88/220 * 100 = 2/5 * 100 = 2 * 20 = 40 (%) - содержание соли во втором растворе;
40 − 35 = 5 (%) - содержание соли в первом растворе больше содержания соли во втором растворе.
Ответ: на 5 %.Задание № 642
По данным на первое полугодие 2009 г., общая численность населения Российской Федерации составляла 141,91 млн. человек, из них 103,71 млн − жители городов. Сколько процентов всего населения России составляет городское население? Ответ округлите до десятых.
Решение
103,71/141,91 * 100 = 10371/14191 * 100 ≈ 73,1 (%) населения России составляет городское население.
Ответ: 73,1%.Задание № 643
Костюм стоил 1800 р. Сначала его цену повысили на 20%, а потом новую цену снизили на 10%. Какой стала цена костюма после этих изменений? На сколько процентов изменилась начальная цена костюма?
Решение
1800 р. - 100 %
х р. - 20 %
1800/х = 100/20
100х = 1800 * 20
х = 360
1800 + 360 = 2160 (р.) - цена после повышения на 20 %
2160 р. - 100 %
х р. - 10 %
2160/х = 100/10
100х = 2160 *10
х = 216
2160 - 216 = 1944 (р.) - стал стоить костюм после понижения цены
1944 − 1800 = 144 (р.) - величина изменения начальной цены костюма;
144/1800 * 100 = 12/150 * 100 = 2/25 * 100 = 8 (%),
Ответ: на 8 % изменилась начальная цена костюма.Задание № 644
Шкаф стоил 4800 р. Сначала его цену снизили на 10%, а потом новую цену повысили на 25%. Какой стала цена шкафа после этих изменений? На сколько процентов изменилась начальная цена шкафа?
4800 р. - 100 %
х р. - 10 %
4800/х = 100/10
100х = 4800 * 10
х = 480
4800 − 480 = 4320 (р.) - стал стоить шкаф после понижения цены;
4320 р . - 100 %
х р. - 25 %
4320/х = 100/25
100 х = 4320 * 25
х = 1080
4320 + 1080 = 5400 (р.) - стал стоить шкаф после повышения цены;
5400 − 4800 = 600 рублей величина изменения начальной цены шкафа;
600/4800 * 100 = 1/8 * 100 = 12,5 (%)
Ответ: на 12,5 % изменилась начальная цена шкафа.Задача из старого учебника:
Шкаф стоил 2400 р. Сначала его цену снизили на 10%, а потом новую цену повысили на 25%. Какой стала цена шкафа после этих изменений? На сколько процентов изменилась начальная цена шкафа?
Решение
2400 р. - 100 %
х р. - 10 %
2400/х = 100/10
100х = 2400 * 10
х = 240
2400 − 240 = 2160 (р.) - стал стоить шкаф после понижения цены;
2160 р . - 100 %
х р. - 25 %
2160/х = 100/25
100 х = 2160 * 25
х = 540
2160 + 540 = 2700 (р.) - стал стоить шкаф после повышения цены;
2700 − 2400 = 300 рублей величина изменения начальной цены шкафа;
300/2400 * 100 = 1/8 * 100 = 12,5 (%)
Ответ: на 12,5 % изменилась начальная цена шкафа.Задание № 645
С 1995 по 2008 г. количество профессиональных театров в России возросло на 116, и в 2008 г. их было 586. На сколько процентов увеличилось количество профессиональных театров за указанный период? Ответ округлите до десятых.
Решение
586 − 116 = 470 (т.) - было в 1995 году;
116/470 * 100 ≈ 24,7 (%)
Ответ: на 24,7% возросло количество театров.Задание № 646
К сплаву массой 600 г, содержавшему 20% меди, добавили 40 г меди. Каким стало процентное содержание меди в новом сплаве?
Решение
600 г - 100 %
х г - 20 %
600/х = 100/20
100х = 600 * 20
х = 120
Значит, 120 г меди изначально содержалось в сплаве
120 + 40 = 160 (г) - меди стало содержаться в сплаве после добавления
600 + 40 = 640 (г) - масса сплава после добавления меди
160/640 * 100 = 1/4 * 100 = 25 (%) меди содержится в новом сплаве.
Ответ: 25% меди.Задание № 647
Было 300 г 6%−го раствора соли. Через некоторое время 60 г воды испарилось. Каким стало процентное содержание соли в растворе?
Решение
300 г - 100 %
х г - 6 %
300/х = 100/6
100х = 300 * 6
х = 18
Значит, 18 г соли было в растворе изначально.
300 − 60 = 240 (г) - раствора осталось после испарения;
18/240 * 100 = 3/40 * 100 = 30/4 = 7,5 (%) - содержание соли в новом растворе
Ответ: 7,5%.Задание № 648
К 620 г 40%−го раствора соли долили 180 г воды. Найдите процентное содержание соли в новом растворе.
Решение
620 г - 100 %
х г - 40 %
620/х = 100/40
100х = 620 * 40
х = 248
Значит, 248 г соли было в растворе изначально.
620 + 180 = 800 (г) - масса раствора после добавления воды;
248/800 * 100 = 31/100 * 100 = 31 (%)
Ответ: содержание соли в новом растворе 31%. 127
-
Страница 127
Задание № 649
Количество кленов составляет 40% от количества дубов, растущих в парке. Сколько процентов составляет количество дубов от количества кленов?
Решение
Пусть количество дубов в парке x, тогда количество кленов 0,4x, тогда:
$\frac x{0,4x}\ast100\%=\frac{10x}{4x}\ast100\%=10\ast25\%=250\%$
Ответ: 250 % составляет количество дубов от количества кленов.Задание № 650
На сколько процентов увеличится число при увеличении его в 2,4 раза?
Решение
Пусть начальное число равно x, тогда число после увеличения 2,4x;
2,4x − x = 1,4x величина увеличения значения числа;
$\frac{1,4x}x$ * 100% = 1,4 * 100% = 140%
Ответ: на 140% увеличится число при увеличении его в 2,4 раза.Задание № 651
На сколько процентов уменьшится число при уменьшении его в 2,5 раза?
Решение
Пусть число после уменьшения равно x, тогда тогда начальное число равно 2,5x;
2,5x − x = 1,5x величина уменьшения значения числа;
$\frac{1,5x}{2,5x}$ * 100% = 1,5 * 40% = 60%
Ответ: на 60% уменьшится число при уменьшении его в 2,5 раза.Задание № 652
Мальчик купил две книги. Одна была на 50% дороже другой. На сколько процентов вторая книга дешевле первой?
Решение
Пусть дешевая книга стоила x, тогда вторая x + 0,5x = 1,5x;
$\frac x{1,5x}\ast100\%=\frac{1000x}{15x}\%=\frac{200x}{3x}\%=66\frac23\%$
Ответ: на $66\frac23$ % одна книга дешевле второй.Задание № 653
Число x составляет 1% от числа y. Как надо изменить число y, чтобы число составило от него 2%?
Решение
Пусть y после изменения равно Y, тогда:
$\frac12=\frac yY$
Y = 2y, следовательно:
$\frac{2y}y=2$
Ответ: в 2 раза необходимо увеличить число y, чтобы x составило от него 2%.Задание № 654
К числам 100 и 1000 дописали справа цифру 1. Какое из чисел увеличилось на большее количество процентов?
Решение
К числу 100 дописали справа цифру 1, получилось число 1001, тогда:
1001/100 * 100% = 1001% увеличения числа 100;
к числу 1000 дописали справа цифру 1, получилось число 10001, тогда:
10001/1000 * 100% = 1000,1% увеличения числа 100, следовательно первое число увеличилось на большее количество процентов.Задание № 655
К некоторому числу прибавили 10% этого числа, а затем вычли 10% суммы и получили 990. Найдите это число.
Решение
Пусть искомое число будет x, тогда:
после увеличения это число стало: x + 0,1x = 1,1x;
после вычитания данное число стало: 1,1x − 0,1 * 1,1x = 1,1x * (1 − 0,1) = 1,1x * 0,9 = 0,99x.
Составим уравнение:
0,99x = 990
x = 990 : 0,99
$x=990\ast\frac{100}{99}$
x = 1000 − искомое число.
Ответ: 1000.Задание № 656
Найдите числа, которых недостает в цепочке вычислений:

Решение
$\frac38;1\frac15;9\frac16;9\frac18$
Задание № 657
Из городов Солнечный и Счастливый одновременно навстречу друг другу отправились пешеход и велосипедист, которые встретились через 2 ч после начала движения. Через 4 ч после встречи пешеход прибыл в город Счастливый. Сколько времени затратил велосипедист на путь из Счастливого в Солнечный?
Решение
2 + 4 = 6 (ч) шел пешеход всего;
$\frac26=\frac13$ (пути) прошел пешеход до встречи с велосипедистом;
$1-\frac13=\frac23$ (пути) проехал велосипедист до встречи с пешеходом потратив на это 2 ч.
$2:\frac23=2\ast\frac32=3$ (ч) затратил велосипедист на путь из Счастливого в Солнечный.
Ответ: 3 часа.Задание № 658
Сторона первого квадрата равна 3 см, а второго − 6 см. Во сколько раз:
1) сторона второго квадрата больше стороны первого;
2) периметр второго квадрата больше периметра первого;
3) площадь второго квадрата больше площади первого?Решение
1) В 6 : 3 = 2 (раза) сторона второго квадрата больше стороны первого.
2) 3 ∗ 4 = 12 (см) - периметр первого квадрата
6 ∗ 4 = 24 (см) - периметр второго квадрата
$\frac{P_2}{P_1}=\frac{24}{12}=2$ (раза)
Ответ: в 2 раза периметр второго квадрата больше периметра первого.
3) 3 ∗ 3 = 9 (см2) - площадь первого квадрата
6 ∗ 6 = 36 (см2) - площадь второго квадрата
$\frac{S_2}{S_1}=\frac{36}9=4$
Ответ: в 4 раза площадь второго квадрата больше площади первого.Задание № 659
Вычислите значение y по формуле y = 0,2x, если:
1) x = 5;
2) x = 1,2.
Найдите, используя данную формулу, значение x, если y = 4.Решение
1) При x = 5:
y = 0,2x = 0,2 * 5 = 1.
2) При x = 1,2:
y = 0,2x = 0,2 * 1,2 = 0,24.
При y = 4:
y = 0,2x
4 = 0,2x
x = 4 : 0,2
x = 20 128
-
Страница 128
Задание № 660
Из пункта А в 6 часов утра вышел турист. Вечером он дошел до пункта B и, переночевав, снова в 6 ч утра отправился в пункт А. Докажите, что на маршруте есть такой пункт С, в котором турист оказался в одно и то же время как в первый, так и во второй день (скорость туриста на маршруте могла меняться).
Решение
Поскольку скорость туриста могла меняться, такой пункт С существует.
Турист вышел в 6 утра из пункта А и из пункта B, значит, он затратил одинаковое время до пункта C, хотя расстояния AB и AC разные. 134
-
Страница 134
Ответы к параграфу 22. Прямая и обратная пропорциональная зависимость
Задание № 661
За некоторое время поезд прошел 320 км. Какое расстояние пройдет поезд за то же время, если его скорость:
1) увеличить в 3 раза;
2) уменьшить в 4 раза.Решение
1) 320 * 3 = 960 (км) пройдет поезд при увеличении скорости в 3 раза.
2) 320 : 4 = 80 (км) пройдет поезд при уменьшении скорости в 4 раза.Задание № 662
Площадь прямоугольника равна 60 см2. Какой станет его площадь, если ширина останется без изменений, а длину:
1) увеличить в 5 раз;
2) уменьшить в 12 раз?Решение
1) 60 * 5 = 300 (см2) станет площадь прямоугольника после увеличения его длины в 5 раз.
2) 60 : 12 = 5 (см2) станет площадь прямоугольника после уменьшения его длины в 12 раз.Задание № 663
За несколько метров ткани заплатили 540 р. Сколько надо было бы заплатить за такую ткань, если бы ее купили:
1) в 6 раз меньше;
2) в 2 раза больше?Решение
1) 540 : 6 = 90 (р.) надо было бы заплатить за такую ткань, если бы ее купили в 6 раз меньше.
2) 540 * 2 = 1080 (р.) надо было бы заплатить за такую ткань, если бы ее купили в 2 раза больше.Задание № 664
Двое рабочих изготовили за некоторое время 24 детали.
1) Скольким рабочим необходимо работать, чтобы за то же время изготовить 48 деталей; 120 деталей?
2) Сколько деталей изготовят эти двое рабочих за время в 3 раза большее? в 4 раза меньшее?
Дайте ответы на поставленные вопросы, считая, что производительность труда всех рабочих одинакова.Решение
1) Пусть x рабочих изготовили 48 деталей.
↓ 2 р. - 24 д. ↓
х р. - 48 д.
$\frac2x=\frac{24}{48}$
24x = 48 * 2
x = 96 : 24
x = 4 рабочим необходимо работать, чтобы за то же время изготовить 48 деталей.
Пусть x рабочих изготовили 120 деталей.
↓ 2 р. - 24 д. ↓
х р. - 120 д.
$\frac2x=\frac{24}{120}$
24x = 120 * 2
x = 240 : 24
x = 10
Значит, 10 рабочим необходимо работать, чтобы за то же время изготовить 120 деталей.
Ответ: 10 рабочим.
2) 24 * 3 = 72 детали изготовят эти двое рабочих за время в 3 раза большее;
24 : 4 = 6 деталей изготовят эти двое рабочих за время в 4 раза меньшее.Задание № 665
В таблице приведены соответствующие значения величин x и y. Установите, являются ли эти величины прямо пропорциональными.
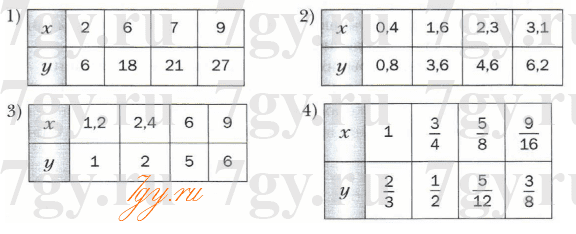
Решение
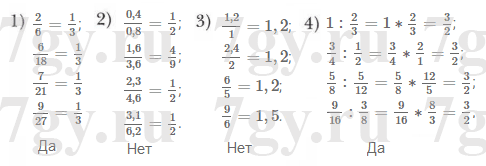
135
-
Страница 135
Задание № 666
Автомобиль проезжает некоторое расстояние за 10 ч. За какое время он проедет это же расстояние если его скорость:
1) увеличится в 2 раза;
2) уменьшится в 1,2 раза?Решение
1) 10 : 2 = 5 (ч)
2) 10 * 1,2 = 12 (ч)
Ответ: за 5 ч, за 12 ч.Задание № 667
Длина прямоугольника равна 30 см. Какой станет длина, если при неизменной площади ширину прямоугольника:
1) увеличить в 1,5 раза;
2) уменьшить в 3,2 раза?Решение
1) 30 : 1,5 = 20 см
2) 30 * 3,2 = 96 смЗадание № 668
Заполните таблицу, если величина y прямо пропорциональна величине x.
Решение
9,6 : 3,2 = 3, то есть 3x = y, тогда:
0,3 * 3 = 0,9;
8 * 3 = 24;
2,7 : 3 = 0,9;
42 : 3 = 14.
Задание № 669
Заполните таблицу, если величина y прямо пропорциональна величине x.
Решение
4 : 1,6 = 2,5, то есть x = 2,5y, тогда:
15 : 2,5 = 6;
8 * 2,5 = 20;
20 * 2,5 = 50;
1,2 : 2,5 = 0,48.
Задание № 670
За m кг конфет заплатили p р. Пользуясь таблицей, определите цену 1 кг конфет. Заполните таблицу:
Задайте формулой зависимость p от m.Решение
225 : 3 = 75 рублей стоит 1 кг конфет или p = 75m, тогда:
8 * 75 = 600 руб.;
300 : 75 = 4 кг.;
1,2 * 75 = 90 руб.;
60 : 75 = 0,8 кг.
136
-
Страница 136
Задание № 671
Поезд движется со скоростью 60 км/ч. Заполните таблицу, в первой строке которой указано время движения t, а во второй − пройденный путь s.
Задайте формулой зависимость s от t.Решение
S = Vt = 60t, тогда:
60 * 2 = 120 км;
0,5 * 60 = 30 км;
90 : 60 = 1,5 ч;
3,2 * 60 = 192 км;
240 : 60 = 4 ч;
156 : 60 = 2,6 ч.
Задание № 672
Пешеход прошел 24 км. Заполните таблицу, в первой строке которой указана скорость пешехода, а во второй − время движения.
Задайте формулой зависимость t от v.Решение

Задание № 673
Объем прямоугольного параллелепипеда равен 48 см2. Заполните таблицу, в первой строке которой указана площадь его основания, а во второй − высота.
Задайте формулой зависимость h от S.Решение
h = 48/S, тогда:
48 : 16 = 3 (см)
48 : 8 = 6 (см2)
48 : 9,6 = 5 (см)
48 : 240 = 0,2 (см)
48 : 4,8 = 10 (см2)
Задание № 674
Бригада из 15 рабочих может отремонтировать школу за 46 дней. Сколько требуется рабочих, чтобы отремонтировать эту школу за 30 дней, если производительность труда всех рабочих одинакова?
Решение
Пусть x рабочих отремонтирует школу за 30 дней.
↓ 15 р. - 46 д. ↑
х р. - 30 д.
$\frac{15}x=\frac{30}{46}$
30x = 15 * 46
$x=\frac{15\ast46}{30}$
$x=\frac{1\ast46}2$
x = 23
Значит, 23 рабочих могут отремонтировать эту школу за 30 дней.
Ответ: 23 рабочих.Задание № 675
Геракл заготовил для 240 коней царя Авгия кормов на 19 дней. На сколько дней хватит этих кормов, если коней у царя Авгия станет 304, а все кони потребляют одинаковое количество корма?
Решение
Пусть на х дней хватит кормов для 304 коней
↓ 240 к. - 19 д. ↑
304 к. - х д.
$\frac{240}{304}=\frac x{19}$
304x = 240 * 19
$x=\frac{240\ast19}{304}$
x = 15
Значит, на 15 дней хватит этих кормов 304 коням.
Ответ: на 15 дней.Задание № 676
Найдите число:
1) половина которого равна 1/6;
2) треть которого равна 1/2;
3) 2/3 которого равны 2/3;
4) 1/4 которого равна 1/8.Решение
1) $2\ast\frac16=\frac26=\frac13$
2) $3\ast\frac12=\frac32=1\frac12$
3) $\frac32\ast\frac23=1$
4) $4\ast\frac18=\frac48=\frac12$ 137
-
Страница 137
Задание № 677
Масса Земли составляет 182% массы Меркурия, а масса Сатурна − 9401% массы Земли. Сколько процентов массы Меркурия составляет масса Сатурна?
Решение
Пусть масса Меркурия равна x, тогда:
масса Земли = 1,82x;
масса Сатурна = 94,01 * 1,82x = 171,0982x, следовательно:
$\frac{171,0982x}x$ * 100% = 17109,82% массы Меркурия составляет масса Сатурна.
Ответ: 17109,82%.Задание № 678
Есть четыре цветка: роза, гвоздика, гладиолус и тюльпан. Сколько есть способов составить букет из трех цветков?
Решение
Есть два варианта составления букета:
1 вариант:
Если цветы в букете должны находится в том же порядке как и в условии задачи, тогда при каждом составлении букета из цветов, мы будем убирать поочередно один из предложенных цветов, следовательно есть 4 способа составить букет из трех цветков.
2 вариант:
Если нет разности в каком порядке цветы будут в букете, тогда:
первый цветок в букет можно выбрать из 4 цветков;
второй цветок из оставшихся трёх;
третий цветок из оставшихся двух, тогда:
4 * 3 * 2 = 24
Ответ: существует 24 способа составить букет из трех цветков.Задание № 679
Задача от мудрой совы. Андрей задумал натуральное число и умножил его на 19. Сережа зачеркнул последнюю цифру числа, полученного Андреем, и в результате получил 32. Какое число задумал Андрей?
Решение
После того, как Сережа зачеркнул последнюю цифру произведения число стало двузначным, значит произведение 19 на какое то число имело вид 32*, то есть было трехзначным.
Только при умножении 19 на 17 результат произведения будет начинаться на 32, следовательно искомое число 17. 19 * 17 = 323. 138
-
Страница 138
Ответы к параграфу 23. Деление числа в данном отношении
Задание № 680
Разделите:
1) число 138 в отношении 18 : 5;
2) число 70 в отношении 3 : 6 : 8 : 11.Решение
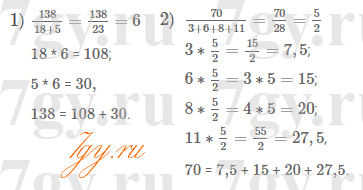
Задание № 681
Разделите:
1) число 72 в отношении 7 : 11;
2) число 92 в отношении 2 : 3 : 5.Решение
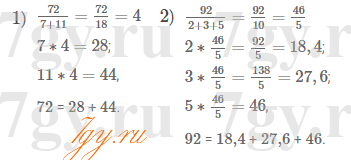
Задание № 682
Для изготовления сока берут 12 частей ягод и 17 частей воды (все части имеют одинаковую массу). Сколько килограммов ягод необходимо взять, чтобы получить 232 кг сока?
Решение
12 + 17 = 29 (ч.)
$\frac{232}{29}=8$ (кг) весит 1 часть, тогда:
12 * 8 = 96 (кг) ягод
Ответ: 96 кг ягод необходимо взять.Задание № 683
Для царя Гороха изготовили новую корону из сплава, состоящего из 7 частей золота и 5 частей платины (все части имеют одинаковую массу). Сколько граммов каждого металла взяли, если масса короны равна 2 кг 460 г?
Решение
2 кг 460 г = 2460 г.
7 + 5 = 12 (ч.)
$\frac{2460}{12}=205$ г весит 1 часть короны, тогда:
7 * 205 = 1435 г = 1 кг 435 г золота взяли;
5 * 205 = 1025 г = 1 кг 25 г платины взяли. 139
-
Страница 139
Задание № 684
Периметр треугольника равен 48 см, а его стороны относятся как 7 : 9 : 8. Найдите стороны треугольника.
Решение
7+9+8 = 24 (ч.)
$\frac{48}{24} * 7 = 14$ (см) - длина первой стороны треугольника;
$\frac{48}{24} * 9 = 18$ (см) - длина второй стороны треугольника;
$\frac{48}{24} * 8 = 16$ (см) - длина третьей стороны треугольника.
Ответ: 14 см, 18 см, 16 см.Задание № 685
Стороны треугольника относятся как 5 : 7 : 11, а сумма наибольшей и наименьшей сторон равна 80 см. Вычислите периметр треугольника.
Решение
$\frac{80}{5+11}=\frac{80}{16}=5$ (см) длина одной части периметра, тогда:
5 * (5 + 7 + 11) = 5 * 23 = 115 (см) периметр треугольника.
Ответ: 115 см.Задание № 686
Начертите развернутый угол ABC и проведите луч BD так, чтобы градусные меры углов ABD и CBD относились как 5 : 13.
Решение
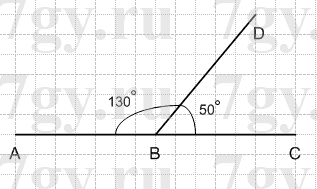
$\frac{180}{5+13}=\frac{180}{18}=10$° одна часть развернутого угла ABC;
∠ABD = 5 * 10° = 50°;
∠CBD = 13 * 10° = 130°.Задание № 687
Начертите угол MKE, градусная мера которого равна 130°. Между сторонами этого угла проведите луч KO так, чтобы градусные меры углов MKO и EKO относились как 19 : 7.
Решение
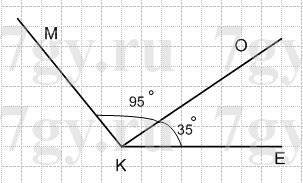
$\frac{130}{19+7}=\frac{120}{26}=5$° одна часть угла MKE;
∠MKO = 19 * 5° = 95°;
∠EKO = 7 * 5° = 35°.Задание № 688
Найдите такие значения x и y, чтобы числа x, y и 24 были соответственно пропорциональны числам:
1) 3, 5 и 6;
2) 1/8,1/36 и 1/9.Решение
1) $\frac{24}6=4$, следовательно:
x = 3 * 4 = 12;
y = 5 * 4 = 20.
2) $24:\frac19=24\ast9=216$
$x=\frac18\ast216=27$
$y=\frac1{36}\ast216=6$Задание № 689
Найдите такие значения a и b, чтобы числа a, 10 и b были соответственно пропорциональны числам 2, 1/6 и 3/4.
Решение
$10:\frac16=10\ast6=60$
a = 2 * 60 = 120;
$b=\frac34\ast60=3\ast15=45$Задание № 690
Трое штукатуров работали с одинаковой производительностью труда и получили за выполненную работу 8000 р. Сколько рублей получил каждый штукатур, если первый из них работал 16 ч, второй − 24 ч, а третий − 40 ч?
Решение
$\frac{8000}{16+24+40}=\frac{8000}{80}=100$ (р.) стоимость одного часа работы, тогда:
16 * 100 = 1600 (р.) получил первый штукатур;
24 * 100 = 2400 (р.) получил второй штукатур;
40 * 100 = 4000 (р.) получил третий штукатур.Задание № 691
Для трех ферм заготовили 540 т сена. Сколько тонн сена требуется доставить на каждую ферму, если на первой ферме 28 коров, на второй − 42 коровы, а на третьей − 65 коров (количество сена для каждой коровы требуется одинаковое)?
Решение
$\frac{540}{28+42+65}=\frac{540}{135}=4$ (т) сена необходимо на одну корову, тогда:
28 * 4 = 112 (т) сена требуется доставить на первую ферму;
42 * 4 = 168 (т) сена требуется доставить на вторую ферму;
65 * 4 = 260 (т) сена требуется доставить на третью ферму.Задание № 692
Представьте число 219 в виде суммы трех слагаемых x, y и z так, чтобы x : y = 4 : 9, а y : z = 15 : 2 2/3
Решение

Задание № 693
Сумма четырех чисел равна 386. Найдите эти числа, если первое относится ко второму как 2 : 5, второе к третьему − как 3 : 4, а третье к четвертому − как 6 : 7.
Решение
Пусть:
первое число равно a;
второе число равно b;
третье число равно c;
четвертое число равно d, тогда: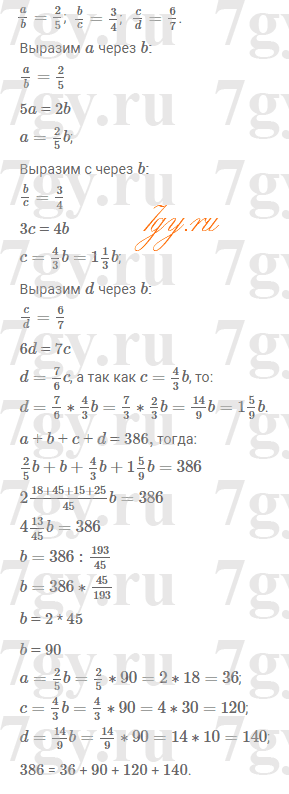
Задание № 694
Одна бригада отремонтировала 20 км дороги, а другая − 14 км. На сколько процентов длины дороги вторая бригада отремонтировала меньше, чем первая?
Решение

Ответ: на $17\frac{11}{17}$% дороги меньше отремонтировала 2 бригада.Задание № 695 с ответом
Найдите значение выражения:
$(1\frac1{12}+1\frac14)\ast1\frac{19}{56}+2\frac58\ast1\frac37\ast1\frac19=(\frac{13}{12}+\frac54)\ast\frac{75}{56}+\frac{21}8\ast\frac{10}7\ast\frac{10}9=(\frac{13}{12}+\frac{15}{12})\ast\frac{75}{56}+\frac12\ast\frac51\ast\frac53=\frac73\ast\frac{75}{56}+4\frac16=\frac11\ast\frac{25}8+4\frac16=3\frac18+4\frac16=3\frac3{24}+4\frac4{24}=7\frac7{24}$
140
-
Страница 140
Задание № 696
Начертите прямую и отметьте на ней произвольную точку O. Найдите на прямой все точки, удаленные от точки O на 3 см.
Решение

AO = OB = 3 смЗадание № 697
Отметьте на плоскости произвольную точку O. Отметьте четыре точки, удаленные от точки O на 2 см. Сколько еще можно отметить таких точек?
Решение
Таких точек можно отметить бесконечное множество.Задание № 698
На доске написано число 23. Каждую минуту число стирают и записывают на этом месте новое число, равное произведению цифр старого числа, увеличенного на 12. Какое число будет написано на доске через час?
Решение
Вычислим несколько первых чисел:
1−я минута: 2 * 3 + 12 = 18;
2−я минута: 1 * 8 + 12 = 20;
3−я минута: 2 * 0 + 12 = 12;
4−я минута: 1 * 2 + 12 = 14;
5−я минута: 1 * 4 + 12 = 16;
1 * 6 + 12 = 18, то есть получается, что через каждые 5 минут цикл цифр начинает повторяться.
60 : 5 = 12 ровных циклов пройдет через час, а на доске будет написано число 16. 144
-
Страница 144
Ответы к параграфу 24. Окружность и круг
Задание 699
Укажите радиус, хорду и диаметр окружности с центром B, изображенной на рисунке 33. Сколько радиусов и сколько хорд изображено на этом рисунке?
Решение
Три радиуса: AB; BK; BM;
Две хорды: MP; MK;
Диаметр: MP.Задание 700
Какие из точек, обозначенных на рисунке 34:
1) лежат на окружности;
2) принадлежит кругу;
3) не лежат на окружности;
4) не принадлежит кругу?
Решение
1) D; M; C.
2) D; M; C; B; K; O; F.
3) P; E; A; B; K; O; F.
4) P; E; A.Задание 701
Найдите диаметр окружности, радиус которой равен:
1) 14 см;
2) 4 см 5 мм;
3) 3,6 дм.Решение
1) 14 см * 2 = 28 см
2) 4 см 5 мм = 45 мм
45 * 2 = 90 мм = 9 см
3) 3,6 дм * 2 = 7,2 дмЗадание 702
Найдите диаметр окружности, радиус которой равен:
1) 8 см;
2) 5 см;
3) 9,2 дм.Решение
1) 8 см * 2 = 16 см
2) 5 см * 2 = 10 см
3) 9,2 дм * 2 = 18,4 дмЗадание 703
Начертите окружность радиуса 2 см 5 мм с центром M. Вычислите диаметр этой окружности.
Решение
d = 2r = 2,5 см * 2 = 5 см.Задание 704
Начертите окружность радиуса 3 см 2 мм с центром K. Вычислите диаметр этой окружности.
Решение
d = 2r = 3,2 см * 2 = 6,4 см. = 6 см 4 ммЗадание 705
Отметьте две произвольные точки A и B, измерьте расстояние между ними. Постройте окружность с центром A, проходящую через точку B, и окружность с центром B, проходящую через точку A. Чему равен радиус каждой из построенных окружностей? Отметьте точки пересечения окружностей. Каково расстояние от этих точек до центров окружностей?
Решение
AB = AC = AD = CB = DB = 3 смЗадание 706
Начертите отрезок AB, длина которого равна 5 см. Постройте окружность радиуса 3 см с центром A и окружность радиуса 4 см с центром B. Сколько существует точек пересечения окружностей? Чему равно расстояние от каждой из этих точек до точки A? До точки B?
Решение
Две точки пересечения C и D.
AC = AD = 3 см;
BC = BD = 4 см. 145
-
Страница 145
Задание 707
Начертите произвольный отрезок AB. Постройте окружность так, чтобы этот отрезок был ее диаметром.
Решение
AB = 5 см.Задание 708
Найдите периметр четырехугольника O1AO2B (рис.35), если радиусы окружностей равны 5 см и 3 см.
Решение
O1A=O1B=5см;
O2A=O2B=3см;
PO1AO2B=2∗(5+3)=2∗8=16 см.Задание 709
Начертите три окружности, имеющие общий центр, радиусы которых соответственно равны 2 см, 3 см и 4 см.
Решение
Задание 710
Начертите окружность, диаметр которой равен 7 см. Отметьте на окружности точку A. Найдите на окружности точки, удаленные от точки A на 4 см.
Решение
Бесконечное множество точек, удаленных от точки A на 4 см, будет лежать на окружности с центром в точке A.Задание 711
Начертите окружность и отметьте на ней три точки A, B и C. Сколько дуг при этом образовалось?
Решение
Три дуги: AB; BC; AC.Задание 712
Начертите окружность с центром O, радиус которой равен 3 см. Проведите луч с началом в точке O и отметьте на нем точку A, удаленную от точки O на 5 см. Проведите окружность с центром в точке A, радиус которой:
1) 2 см;
2) 2 см 5 мм;
3) 1 см 5 мм.
Сколько общих точек имеют окружности в каждом из этих случаев?Решение
1)
Одна общая точка.
2)
Две общих точки.
3)
Нет общих точки.Задание 713
Начертите окружность и треугольник так, чтобы стороны треугольника были хордами окружности.
Решение
Задание 714
Начертите окружность, проведите ее диаметр AB, отметьте на окружность точки C и D. Соедините точки C и D c концами диаметра AB и найдите градусные меры углов ACB и ADB.
Решение
∠ACB = 90°;
∠ADB = 90°.Задание 715
Радиус окружности с центром A равен 9 см, а радиус окружности с центром B − 2 см. Найдите расстояние между центрами этих окружностей (рис.36).
Решение
а) AB = 9 + 2 = 11 см
б) AB = 9 − 2 = 7 см 146
-
Страница 146
Задание 716
На рисунке 37 OC = 6 см, BD = 2,5 см. Найдите длину отрезка OK.
Решение
OB = OC − BD = 6 − 2,5 = 3,5 см;
OK = OB − BD = 3,5 − 2,5 = 1 см.Задание 717
Начертите произвольный треугольник. Проведите три окружности так, чтобы стороны треугольника были их диаметрами.
Решение
Задание 718
Начертите квадрат со стороной 3 см. Проведите четыре окружности так, чтобы стороны квадрата были их диаметрами.
Решение
Задание 719
1) Начертите отрезок AB, длина которого равна 3 см. Найдите точку, удаленную от каждого из концов отрезка AB на 2 см. Сколько существует таких точек?
2) Начертите отрезок CD, длина которого равна 3 см 5 мм. Найдите точку, удаленную от точки C на 2 см 5 мм, а от точки D - на 3 см.
Сколько существует таких точек?Решение
1)
Две точки: C и D;
AC = CB = BD = AD = 2 см.
2)
Две точки: A и B;
AD = DB = 3 см;
AС = СB = 2 см 5 мм.Задание 720
С помощью циркуля и линейки постройте треугольник со сторонами:
1) 3 см, 3 см и 4 см;
2) 3 см; 4 см и 5 см.Решение
1) 1 действие: строим отрезок AB = 4 см;
2 действие: строим две окружности, радиус которых равен 3 см, с центрами в точках A и B.
3 действие: точку С ставим в одной любой точке пересечения окружностей;
4 действие: проводим отрезки AC = BC = 3 см.
2) 1 действие: строим отрезок AB = 3 см;
2 действие: строим окружность, с радиусом равным 4 см, с центром в точке A;
3 действие: строим окружность, с радиусом равным 5 см, с центром в точке B;
4 действие: точку С ставим в одной любой точке пересечения окружностей;
5 действие: проводим отрезки AC = 4 см и BC = 5 см.
Задание 721
С помощью циркуля и линейки постройте треугольник со сторонами:
1) 5 см, 6 см и 4 см;
2) 2 см; 2 см и 2 см.Решение
1) 1 действие: строим отрезок AB = 6 см;
2 действие: строим окружность, с радиусом равным 5 см, с центром в точке A;
3 действие: строим окружность, с радиусом равным 4 см, с центром в точке B;
4 действие: точку С ставим в одной любой точке пересечения окружностей;
5 действие: проводим отрезки AC = 5 см и BC = 4 см.
2) 1 действие: строим отрезок AB = 2 см;
2 действие: строим две окружности, радиус которых равен 2 см, с центрами в точках A и B.
3 действие: точку С ставим в одной любой точке пересечения окружностей;
4 действие: проводим отрезки AC = BC = 2 см.
Задание 722
Установите, можно ли построить треугольник со сторонами:
1) 2 см, 6 см и 7 см;
2) 2 см, 6 см и 8 см;
3) 2 см, 6 см и 9 см.Решение
1) Для того, чтобы построить треугольник, каждая сторона треугольника должна быть меньше суммы двух других сторон.
2 < 6 + 7;
6 < 2 + 7;
7 < 2 + 6, следовательно треугольник с данными сторонами построить можно.
2) Для того, чтобы построить треугольник, каждая сторона треугольника должна быть меньше суммы двух других сторон.
2 < 6 + 8;
6 < 2 + 8;
8 = 2 + 6, следовательно треугольник с данными сторонами построить нельзя.
3) Для того, чтобы построить треугольник, каждая сторона треугольника должна быть меньше суммы двух других сторон.
2 < 6 + 9;
6 < 2 + 9;
9 > 2 + 6, следовательно треугольник с данными сторонами построить нельзя.Задание 723
В круге с центром O отметили точку M. Как разрезать этот круг:
1) на три части;
2) на две части − так, чтобы из них можно было составить новый круг, в котором отмеченная точка M была бы его центром?Решение
1) 1 действие:
Необходимо вырезать два круга с центром в точках O и M, причем радиус вырезаемых кругов должен быть меньше радиуса исходного круга более, чем в три раза.
2 действие:
Вырезанные круги необходимо поменять местами.
2) 1 действие:
Необходимо построить круг с центром в точке M и радиусом равным радиусу исходного круга с центром в точке O.
2 действие:
Разрезать круг с центром в точке O по дуге, образованной кругом с центром в точке O.
3 действие:
Отрезанные части приложить друг к другу с обратной стороны.Задание 724
На торте кондитер расположил семь кремовых розочек (рис.38). Как тремя прямолинейными разрезами разделить торт на семь порций, на каждой из которых была бы одна розочка?
Решение
Задание 725
Вычислите:
1) $7^2=7\ast7=49$
2) $0,4^2=0,4\ast0,4=0,16$
3) $1,2^2=1,2\ast1,2=1,44$
4) $(\frac13)^2=\frac13\ast\frac13=\frac19$
5) $(2\frac29)^2=\frac{20}9\ast\frac{20}9=\frac{400}{81}=4\frac{76}{81}$ 147
-
Страница 147
Задание 726
В первый день продали 500 кг яблок, а во второй − 420 кг. На сколько процентов меньше продали яблок во второй день, чем в первый?
Решение
$\frac{420}{500}$ * 100% = $\frac{420}{5}$ = 84% составляют продажи во второй день от продаж в первый день.
100% − 84% = 16%, то есть на 16% меньше продали яблок во второй день, чем в первый.Задание 727
Вычислите:
$(6,8-5\frac59):(2\frac{13}{30}-2\frac1{12})\ast3,6=(6\frac45-5\frac59):(2\frac{26}{60}-2\frac5{60})\ast\frac{18}5=(6\frac{36}{45}-5\frac{25}{45}):\frac7{20}\ast\frac{18}5=\frac{56}{45}:\frac7{20}\ast\frac{18}5=\frac{56}{45}\ast\frac{20}7\ast\frac{18}5=\frac85\ast\frac41\ast\frac21=\frac{64}5=12\frac45$
Задание 728
У командира в подчинении находятся трое солдат. Сколько существует способов расставить их на три поста?
Решение
Первого солдата можно поставить на любой из 3 постов (3 способа),
Второго солдата можно поставить на любой из 2 оставшихся постов (2 способа),
Третьего солдата можно поставить на один оставшийся свободным пост (1 способ), тогда:
3 * 2 * 1 = 6, то есть существует 6 способов чтобы расставить трех солдат на три поста.Задание 729
Диагональ AC квадрата ABCD увеличили в 3 раза и построили квадрат AMKN (рис. 39). Во сколько раз периметр квадрата AMKN больше периметра квадрата ABCD?
Решение
Пусть сторона квадрата ABCD = x, тогда сторона квадрата AMKN = 3x, тогда:
PABCD=4x;
PAMKN=4∗3x=12x;
$\frac{P_{AMKN}}{P_{ABCD}}=\frac{12x}{4x}=3$, то есть в 3 раза периметр квадрата AMKN больше периметра квадрата ABCD.Задание 730
Дети собирали в лесу грибы. Выйдя из леса, они построились парами − мальчик с девочкой, причем у мальчика грибов или вдвое больше, или вдвое меньше, чем у девочки. Возможно ли, что все дети вместе собрали 500 грибов?
Решение
Допусти у мальчика x грибов, тогда у девочки 2x грибов, а у них вместе:
x + 2x = 500
3х = 500
x=500/3, а так как 500 не делится нацело на 3, значит невозможно чтобы вместе дети набрали 500 грибов. 150
-
Страница 150
Ответы к параграфу 25. Длина окружности. Площадь круга
Задание 731
Вычислите длину окружности, диаметр которой равен:
1) 3,2 см;
2) 4,5 см.Решение
1) l = 2πr = πd = 3,14 * 3,2 = 10,048 см
2) l = 2πr = πd = 3,14 * 4,5 = 13,13 смЗадание 732
Вычислите длину окружности, радиус которой равен:
1) 6 см;
2) 1,8 м.Решение
1) l = 2πr = 2 * 3,14 * 6 = 37,68 см
2) l = 2πr = 2 * 3,14 * 1,8 = 11,304 мЗадание 733
Вычислите площадь круга, радиус которого равен:
1) 8 см;
2) 14 дм.Решение
1) $S={\operatorname\pi}r^2=3,14\ast8^2=3,14\ast64=200,96{\operatorname с}{\operatorname м}^2$
2) $S={\operatorname\pi}r^2=3,14\ast14^2=3,14\ast196=615,44{\operatorname д}{\operatorname м}^2$Задание 734
Вычислите площадь круга, диаметр которого равен:
1) 18 см;
2) 3,6 м.Решение
1) $r=\frac d2=\frac{18}2=9$ см, тогда:
$S={\operatorname\pi}r^2=3,14\ast9^2=3,14\ast81=254,34{\operatorname с}{\operatorname м}^2$.
2) $r=\frac d2=\frac{3,6}2=1,8$ м, тогда:
$S={\operatorname\pi}r^2=3,14\ast1,8^2=3,14\ast3,24=10,1736{\operatorname м}^2$Задание 735
Вычислите радиус окружности, длина которой равна:
1) 18,84 см;
2) 47,1 дм.Решение
1) l = 2πr
$r=\frac l{2{\operatorname\pi}}=\frac{18,84}{2\ast3,14}=\frac{18,84}{6,28}=3$ см
2) l = 2πr
$r=\frac l{2{\operatorname\pi}}=\frac{47,1}{2\ast3,14}=\frac{47,1}{6,28}=7,5$Задание 736
Найдите радиус круга, площадь которого равна 314 $см^2$.
Решение
$S={\operatorname\pi}r^2$
$r^2=\frac S{\operatorname\pi}=\frac{314}{3,14}=100$
r = 10 смЗадание 737
Проехав 400 м, колесо сделало 150 оборотов. Найдите радиус колеса в сантиметрах. Ответ округлите до единиц.
Решение
$\frac{400}{150}=\frac83=2\frac23$ м длина окружности колеса;
l = 2πr
$r=\frac l{2{\operatorname\pi}}=\frac83:6,28=\frac83:\frac{157}{25}=\frac83\ast\frac{25}{157}=\frac{200}{471}$ ≈ 0,4246 м ≈ 42,46 см ≈ 42 см радиус колесаЗадание 738
Длина окружности равна 100,48 см. Найдите площадь круга, ограниченного этой окружностью.
Решение
l = 2πr
$r=\frac l{2{\operatorname\pi}}=\frac{100,48}{6,28}=16$ (см)
$S=\operatorname\pi r^2=3,14\ast16^2=803,84(см^2)$ площадь круга.Задание 739
Выполните необходимые измерения и вычислите площадь закрашенного кольца (рис. 42).
Решение
r1=0,5см;
r2=1,5см;
$S=S_2-S_1=\operatorname\pi r_2^2-\operatorname\pi r_1^2=\operatorname\pi\ast(r_2^2-r_1^2)=3,14\ast(1,5^2-0,5^2)=3,14\ast(2,25-0,25)=3,14\ast2=6,28(см^2)$ - площадь закрашенного кольца.Задание 740
1) Радиус первой окружности равен 6 см, а радиус второй − 2 см. Во сколько раз длина первой окружности больше длины второй?
2) Радиус первой окружности в 4 раз больше радиуса второй. Во сколько раз длина первой окружности больше длины второй?Решение
1) l1=2π6;
l2=2π2;
Длина первой окружности больше длины второй в
$\frac{l_1}{l_2}=\frac{2{\operatorname\pi}6}{2{\operatorname\pi}2}=\frac62=3$ раза.
2) Пусть радиус меньшей окружности равен r, тогда большой 4r
l1=2πr;
l2=2π4r=8πr;
Длина большой окружности больше длины маленькой в
$\frac{l_2}{l_1}=\frac{8{\operatorname\pi}r}{2{\operatorname\pi}r}=\frac82=4$ раза.Задание 741
Диаметр обода зеркала оптического телескопа (рефлектора), расположенного в поселке Научный (Крым), равен 2,6 м. Диаметр обода зеркала самого большого оптического телескопа в России, находящегося в горах Западного Кавказа (Архыз), равен 6 м. Найдите отношение длин ободов зеркал этих телескопов.
Решение
l = 2πr = πd, тогда:
lкрым=2,6π;
lархыз=6π.
$\frac{l_{\operatorname а\operatorname р\operatorname х\operatorname ы\operatorname з}}{l_{\operatorname к\operatorname р\operatorname ы\operatorname м}}=\frac6{2,6}=\frac{60}{26}=\frac{30}{13}=2\frac4{13}$ отношение длин ободов зеркал этих телескопов.Задание 742
Радиус окружности увеличили на 1 см. На сколько увеличилась при этом длина окружности?
Решение
l = 2πr, после увеличения l = 2π(r + 1) = 2πr + 2π, тогда:
(2πr + 2π) − 2πr = 2πr + 2π − 2πr = 2π, то есть длина окружности увеличилась на 2π.Задание 743
Как изменится радиус окружности, если длину увеличить на 9,42 см?
Решение
l = 2πr, тогда
$r=\frac l{2{\operatorname\pi}}$.
После увеличения
$r=\frac{l+9,42}{2{\operatorname\pi}}$, следовательно радиус увеличится на:
$\frac{l+9,42}{2{\operatorname\pi}}-\frac l{2{\operatorname\pi}}=\frac{l+9,42-l}{2{\operatorname\pi}}=\frac{9,42}{2\ast3,14}=\frac32=1,5$ (см)Задание 744
Найдите длину дуги, составляющей 0,6 окружности, радиус которой равен 3,5 см.
Решение
l = 2πr = 2 * 3,14 * 3,5 = 21,98 см длина окружности, тогда:
0,6l = 0,6 * 21,98 = 13,188 см длина дуги.Задание 745
Найдите длину дуги, составляющей 5/12 окружности, радиус которой равен 36 дм.
Решение
l = 2πr = 2 * 3,14 * 36 = 226,08 дм длина окружности, тогда:
$\frac5{12}l=\frac5{12}\ast226,08=5\ast18,84=94,2$ (дм) длина дуги. 151
-
Страница 151
Задание 746
Вычислите длину красной линии, изображенной на рисунке 43.
Решение
а) Найдем длину окружности с диаметром 6 см:
l = 2πr = πd = 3,14 * 6 = 18,84 см, тогда длина красной линии равна:
9 * 2 + 18,84 = 18 + 18,84 = 36,84 см.
б) Найдем длину окружности с диаметром 8 см:
l = 2πr = πd = 3,14 * 8 = 25,12 см.
Так на рисунке 3 полуокружности с диаметром 8 см, то суммарная длина данных полуокружностей равна:
25,12 : 2 * 3 = 37,68 см.
Найдем длину окружности с диаметром 4 см:
l = 2πr = πd = 3,14 * 4 = 12,56 см, тогда длина красной линии равна:
37,68 + 12,56 = 50,24 см.Задание 747
Найдите площадь круга, если 2/3 длины окружности этого круга равны 24,8 см (число π округлите до десятых).
Решение
π ≈ 3,1 по условию нужно округлить до десятых.
$l=24,8:\frac23=24,8\ast\frac32=12,4\ast3=37,2$ см длина окружности;
$r=\frac l{2{\operatorname\pi}}=\frac{37,2}{2\ast3,1}=\frac{12}{2\ast1}=6$ см радиус окружности.
$S=\operatorname\pi r^2=3,1\ast6^2=3,1\ast36=111,6(см^2)$Задание 748
На сколько квадратных сантиметров площадь квадрата больше площади круга (рис.44), если сторона квадрата равна 8 см?

Решение
$S_{\operatorname к\operatorname в\operatorname а\operatorname д\operatorname р\operatorname а\operatorname т\operatorname а}=a^2=8^2=8\ast8=64(см^2)$
$r_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}=8:2=4$ (см)
$S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}=\operatorname\pi r^2=3,14\ast4^2=3,14\ast16=50,24(см^2)$
$S_{\operatorname к\operatorname в\operatorname а\operatorname д\operatorname р\operatorname а\operatorname т\operatorname а}-S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}=64-50,24=13,76(см^2)$
Ответ: на 13,76 $см^2$ площадь квадрата больше площади круга.Задание 749
Начертите прямоугольник со сторонами 3 см и 4 см. Проведите диагонали прямоугольника. Приняв точку пересечения диагоналей за центр окружности, а половину диагонали − за радиус, проведите эту окружность. Измерьте линейкой диаметр полученной окружности (в сантиметрах, с точностью до единиц). На сколько квадратных сантиметров площадь круга, ограниченного этой окружностью, больше площади прямоугольника?
Решение

Задание 750
Вычислите площадь закрашенной фигуры, изображенной на рисунке 45.
Решение

152
-
Страница 152
Задание 751
Вычислите площадь закрашенной фигуры (рис. 46), если длина стороны клетки равна 1 см.
Решение
а) $S_{квадрата}=a^2=8^2=8\ast8=64(см^2)$
$S_{круга}={\operatorname\pi}r^2=3,14\ast1^2=3,14(см^2)$
На рисунке 4 одинаковых круга, поэтому их суммарная площадь:
$S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}\ast4=3,14\ast4=12,56{\operatorname с}{\operatorname м}^2$
$S_{\operatorname ф\operatorname и\operatorname г\operatorname у\operatorname р\operatorname ы}=S_{\operatorname к\operatorname в\operatorname а\operatorname д\operatorname р\operatorname а\operatorname т\operatorname а}-4\ast S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}=64-12,56=51,44{\operatorname с}{\operatorname м}^2$
б)$S_{\operatorname к\operatorname в\operatorname а\operatorname д\operatorname р\operatorname а\operatorname т\operatorname а}=a^2=1^2=1{\operatorname с}{\operatorname м}^2$
Треугольник на фигуре можно разделить пополам и сложить из этих половинок квадрат со стороной 1 см;
Прямоугольник состоит из 2 квадратов со стороной 1 см;
$S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}={\operatorname\pi}r^2=3,14\ast3^2=3,14\ast9=28,26{\operatorname с}{\operatorname м}^2$
$S_{\operatorname ф\operatorname и\operatorname г\operatorname у\operatorname р\operatorname ы}=S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}-5\ast S_{\operatorname к\operatorname в\operatorname а\operatorname д\operatorname р\operatorname а\operatorname т\operatorname а}=28,26-5=23,26{\operatorname с}{\operatorname м}^2$Задание 752
Пицца, диаметр которой равен 30 см, стоит столько же, сколько две пиццы диаметром 20 см. В каком случае Дима съест больше пиццы: если купит одну большую или две маленькие, если все пиццы имеют одинаковую толщину?
Решение
r1 = 30 : 2 = 15 (см) диаметр большой пиццы;
r2 = 20 : 2 = 10 (см) диаметр маленькой пиццы;
$S_1={\operatorname\pi}r_1^2=3,14\ast15^2=3,14\ast225=706,5{\operatorname с}{\operatorname м}^2$ − площадь большой пиццы;
$S_2={\operatorname\pi}r_2^2=3,14\ast10^2=3,14\ast100=314{\operatorname с}{\operatorname м}^2$ − площадь маленькой пиццы, следовательно: 314 * 2 = 628 $см^2$ − суммарная площадь двух маленьких пицц.
706,5 − 628 = 78,5 ($см^2$)
Ответ: Дима съест на 78,5 $см^2$ больше, если купит одну большую пиццу.Задание 753
Диаметр колеса автомобиля равен 65 см. Автомобиль движется с такой скоростью, что колеса делают шесть оборотов в секунду. Найдите скорость автомобиля в километрах в час. Ответ округлите до десятых.
Решение
l = 2πr = πd = 3,14 * 65 = 204,1 см длина окружности колеса;
204,1 * 6 = 1224,6 см/сек скорость автомобиля в сантиметрах в секунду.
1 ч = 60 мин * 60 с = 3600 секунд;
1 км = 1000 м * 100 см = 100000 см, тогда:
$\frac{1224,6\ast3600}{100000}$ = 44,0856 ≈ 44,1 км/ч.Задание 754
Диаметр колеса вагона равен 78 см. За 2,5 мин колесо делает 1000 оборотов. Найдите скорость поезда метро в километрах в час. Ответ округлите до десятых.
Решение
l = 2πr = πd = 3,14 * 78 = 244,92 см длина окружности колеса;
244,92 * 1000 : 2,5 = 97968 см/мин скорость поезда метро в сантиметрах в минуту.
1 ч = 60 мин;
1 км = 1000 м * 100 см = 100000 см, тогда:
$\frac{97968\ast60}{100000}$ = 58,7808 ≈ 58,8 км/ч.Задание 755
Найдите длину дуги, которую описывает часовая стрелка длиной 6 см за 1 ч.
Решение
r = длина часовой стрелки = 6 см;
l = 2πr = 2 * 3,14 * 6 = 37,68 см длина окружности циферблата;
На циферблате 12 дуг по 1 часу, тогда:
37,68 : 12 = 3,14 см длина дуги, которую описывает часовая стрелка длиной 6 см за 1 ч.Задание 756
Найдите длину дуги, которую описывает минутная стрелка длиной 24 см за 40 мин.
Решение
r = длина часовой стрелки = 24 см;
l = 2πr = 2 * 3,14 * 24 = 150,72 (см) - длина окружности циферблата;
На циферблате 60 дуг по 1 минуте, тогда:
$\frac{40}{60}=\frac23$ - часть циферблата занимает искомая дуга, следовательно:
$150,72\ast\frac23=50,24\ast2=100,48$ (см) - длина дуги, которую описывает минутная стрелка длиной 24 см за 40 мин.Задание 757
Вычислите площадь закрашенной фигуры, изображенной на рисунке 47.
Решение
Найдем площадь не закрашенного участка отмеченного цифрой 1. Данная площадь равна площадь квадрата со стороной 5 см вычесть 1/4 площади окружности со радиусом 5 см, тогда:
$S_1=S_{\operatorname к\operatorname в\operatorname а\operatorname д\operatorname р\operatorname а\operatorname т\operatorname а}-\frac14S_{\operatorname о\operatorname к\operatorname р\operatorname у\operatorname ж\operatorname н\operatorname о\operatorname с\operatorname т\operatorname и}=5^2-\frac14\ast3,14\ast5^2=25-\frac{78,5}4=25-19,625=5,375$
Так как, таких не закрашенных участков 8, то 8 * 5,375 = 43 $см^2$ - площадь не закрашенной области на рисунке 47.
Площадь закрашенной фигуры = площадь квадрата со стороной 10 см − площадь не закрашенной области = $10^2-43=100-43=57(см^2)$Задание 758
Все вершины квадрата (рис. 48), диагональ которого равна 6 см, лежат на окружности. Вычислите площадь квадрата, не измеряя его стороны. На сколько площадь квадрата меньше площади круга, ограниченного данной окружностью?
Решение
Диагональ = диаметр окружности, тогда:
r = 6 : 2 = 3 см;
$S_{круга}=\operatorname\pi r^2=3,14\ast3^2=3,14\ast9=28,26(см^2)$;
Квадрат состоит из двух треугольников, площадь каждого из которого равна
$\frac12ah$, где a − основание треугольника, а h − высота треугольника, тогда:
$S_{треугольника}=\frac12\ast6\ast3=3\ast3=9(см^2)$;
$S_{квадрата}=9\ast2=18(см^2)$;
$S_{круга}-S_{квадрата}=28,26-18=10,26(см^2)$
Ответ: на 10,26 $см^2$ площадь квадрата меньше площади круга, ограниченного данной окружностью. 153
-
Страница 153
Задание 759
Докажите, что сумма длин красных дуг равна сумме длин зеленых дуг (рис.49).
Решение
И красные и зеленые дуги являются полуокружностями длина которой равна πr, тогда:
сумма длин красных дуг равна
πr1+πr2+πr3=π(r1+r2+r3);
сумма длин зеленых дуг равна
πr4+πr5+πr6+πr7=π(r4+r5+r6+r7), а так как: r1 + r2 + r3 = r4 + r5 + r6 + r7, следовательно сумма длин красных дуг равна сумме длин зеленых дуг.Задание 760
Задача Гиппократа. (Гиппократ Хиосский − древнегреческий геометр (V в. до н.э.).) Докажите, что сумма площадей закрашенных фигур ("луночек") равна площади прямоугольника (рис.50).
Решение
Найдем площадь не закрашенных участков, которая равна разнице площади окружности с диаметром 5 см и площади прямоугольника:
r=d:2=5:2=2,5;
$S_{\operatorname н\operatorname е\operatorname з\operatorname а\operatorname к\operatorname р.}={\operatorname\pi}r^2-ab=3,14\ast2,5^2-3\ast4=3,14\ast6,25-12=19,625-12=7,625{\operatorname с}{\operatorname м}^2$
Площадь "луночек" = сумма площадей двух полуокружностей с диаметром 3 см и двух полуокружностей с диаметром 4 см − площадь не закрашенных участков, тогда:
$2\ast\frac12{\operatorname\pi}2^2+2\ast\frac12{\operatorname\pi}1,5^2-7,625=3,14\ast(4\ast2,25)-7,625=3,14\ast6,25-7,625=19,625-7,625=12{\operatorname с}{\operatorname м}^2$,
значит сумма площадей закрашенных фигур ("луночек") равна площади прямоугольника.Задание 761
Два квадрата со стороной 1 см имеют общий центр (центр квадрата − точка пересечения его диагоналей)(рис.51). Докажите, что площадь их общей части больше π/4.
Решение
В общую часть квадратов можно вписать круг.
$r=d:2=\frac12$
$S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}={\operatorname\pi}r^2={\operatorname\pi}\ast\frac12^2=\frac{\operatorname\pi}4$, а так как площадь круга меньше общей части квадратов, то общая часть квадратов больше π/4.Задание 762
На рисунке 52 проиллюстрирован старинный способ вычисления площади круга. Объясните, почему произведение rl приближенно равно площади круга.
Решение
$S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}={\operatorname\pi}r^2$;
l = 2πr, а так как на прямоугольнике синие сектора перевернуты, в отличии их расположения на круге, то l на прямоугольнике равна $\frac{2{\operatorname\pi}r}2={\operatorname\pi}r$, тогда:
${\operatorname\pi}r\ast r={\operatorname\pi}r^2=S_{\operatorname к\operatorname р\operatorname у\operatorname г\operatorname а}$ 154
-
Страница 154
Задание 763
Масса сплава меди и серебра равна 7,2 кг. Масса серебра составляет 80% массы меди. Сколько килограммов меди в сплаве?
Решение
Пусть масса меди равна x, тогда масса серебра равна 0,8x.
Составим уравнение:
x + 0,8x = 7,2
1,8x = 7,2
x = 7,2 : 1,8
x = 4 кг составляет масса меди в сплаве.Задание 764
Решите уравнение:
1) $\frac13x+\frac15x+\frac16x=\frac{21}{40}$
2) $\frac14x+\frac16x+\frac18x=\frac{39}{56}$Решение
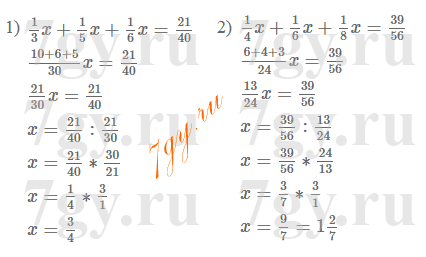
Задание 765
Цена товара дважды повышалась и каждый раз на 50%. Какой стала цена товара, если сначала она составляла 160 р.?
Решение
160 + 160 * 50% = 160 * (1 + 0,5) = 160 * 1,5 = 240 рублей стала цена товара после первого повышения;
240 + 240 * 50% = 240 * (1 + 0,5) = 240 * 1,5 = 360 рублей стала цена товара после второго повышения.Задание 766
В каждую клетку таблицы размером 3 X 3 клетки записывают некоторое число. Таблицу, в которой все записанные числа различны, а суммы чисел во всех строках, столбцах и по диагоналям одинаковые, называют магическим квадратом. Например, таблица изображенная на рисунке 53, является магическим квадратом. Существует ли магический квадрат, заполненный числами, обратными натуральным?
Решение
Да, для этого нужно каждое число из магического квадрата разделить на произведение 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9.
158
-
Страница 158
Ответы к параграфу 26. Цилиндр, конус, шар
Задание 767
Приведите примеры предметов, имеющих форму:
1) цилиндра;
2) конуса;
3) шара.Решение
1) Бочка, кружка, труба.
2) Колпак, морковь, стаканчик мороженого, пожарное ведро.
3) Яблоко, мяч, мыльный пузырь.Задание 768
На рисунке 65 изображен цилиндр. Укажите:
1) образующую цилиндра;
2) радиус нижнего основания цилиндра;
3) радиус верхнего основания цилиндра.
Решение
1) AB − образующая цилиндра
2) OA − радиус нижнего основания цилиндра
3) O1B − радиус верхнего основания цилиндраЗадание 769
Радиус основания цилиндра равен 6 см, а его образующая − 8 см. Найдите площадь боковой поверхности цилиндра.
Решение
Sб = 2πrl = 2π∗6∗8 = 96π $см^2$ ≈ 301,44 $см^2$
Задание 770
Найдите площадь боковой поверхности цилиндра, развертка которого изображена на рисунке 66 (длины отрезков даны в сантиметрах).
Решение
Sб = 2πrl = 2π∗5∗7 = 70π $см^2$ ≈ 219,8 $см^2$
Задание 771
На рисунке 67 изображен конус. Укажите:
1) вершину конуса;
2) центр его основания;
3) образующую конуса;
4) радиус основания конуса;
5) высоту конуса.
Решение
1) M − вершина конуса
2) O − центр основания конуса
3) MK − образующая конуса
4) OK − радиус основания конуса
5) OM − высота конусаЗадание 772
Радиус шара равен 6 см. Вычислите площадь сечения шара плоскостью, проходящей через центр шара.
Решение
Sсечения = πr2 = π∗62 = 36π $см^2$ ≈ 113,04 $см^2$
Задание 773
Длина окружности, ограничивающей сечение шара плоскостью, проходящей через его центр, равна 12,56 см. Чему равен радиус шара?
Решение
l = 2πr, тогда:
$r=\frac l{2{\operatorname\pi}}=\frac{12,56}{6,28}=2$ см радиус шара.Задание 774
Какие наименьшие размеры, выраженные целым числом сантиметров, должен иметь прямоугольный лист бумаги, чтобы им можно было обклеить боковую поверхность цилиндра с радиусом основания 5 см и высотой, равной диаметру основания?
Решение
r = 5 см, тогда:
l = 2r = 2 * 5 = 10 см;
Sб = 2πrl = 2π∗5∗10 = 100π $см^2$ ≈ 314 $см^2$;
314 : 10 = 31,4 см, а это значит, что прямоугольный лист бумаги должен иметь размеры 10 см на 32 см. 159
-
Страница 159
Задание 775
Диаметр отверстия трубы равен 40 см, а толщина ее стенок − 2 см. Хватит ли 2,5 кг краски, чтобы покрасить снаружи 10 м этой трубы, если на 1 $м^2$ ее поверхности расходуется 200 г краски?
Решение
Наружный диаметр трубы равен сумме диаметра отверстия трубы и толщине двух ее стенок, тогда:
d = 40 + 2 * 2 = 44 см;
r = 44 : 2 = 22 см = 0,22;
Sб = 2πrl = 2π∗0,22∗10 = 3,14∗440 = 13,816 $м^2$ площадь, которую необходимо покрасить;
200 г = 0,2 кг;
13,816 * 0,2 ≈ 2,76 кг краски необходимо, чтобы покрасить 10 м трубы;
2,5 кг < 2,76 кг, следовательно краски не хватит.Задание 776
Прямоугольник, площадь которого равна 40 $см^2$, вращают вокруг одной из его сторон. Вычислите площадь боковой поверхности образовавшегося цилиндра.
Решение
Sпрямоугольника=ab, а так как прямоугольник вращают вокруг одной из его сторон то
Sпрямоугольника=rl, а
Sб=2πrl, следовательно при любых размерах сторон прямоугольника площадь боковой поверхности образовавшегося цилиндра будет одним и тем же.
Пусть прямоугольник имеет стороны 4 см и 10 см, тогда:
Sб = 2πrl = 2π∗4∗10 = 3,14∗80 = 251,2 $см^2$ площадь боковой поверхности образовавшегося цилиндра.Задание 777
Хватит ли купленной ковровой дорожки для трех коридоров длиной 22,6 м, 24,7 м и 12,8 м, если купили 2 куска дорожки по 15,8 м и 2 куска по 14,6 м?
Решение
22,6 + 24,7 + 12,8 = 60,1 м суммарная длина коридоров;
2 * 15,7 + 2 * 14,6 = 2 * (15,7 + 14,6) = 2 * 30,4 = 60,8 м суммарная длина дорожки;
60,8 м > 60,1 м, значит дорожки хватит на все три коридора.Задание 778
Оля живет в двенадцатиэтажном доме в квартире № 189. В каком подъезде и на каком этаже живет Оля, если в ее доме на каждом этаже находится по четыре квартиры?
Решение
12 * 4 = 48 квартир в одном подъезде;
$\frac{189}{48}=3\frac{45}{48}$, следовательно Оля живет в 4 подъезде;
$\frac{45}{48}=11\frac3{48}$, следовательно Оля живет на 12 этаже.Задание 779
Известно, что a и b − различные простые числа. Запишите все делители числа m, если:
1) m = ab;
2) m = $a^2b$;
3) m = $a^2b^2$.Решение
1) 1; a; b; m.
2) $1;a;b;a^2;ab;m.$
3) $1;a;b;a^2;b^2;ab;a^2b;ab^2;m.$.Задание 780
В середине XVI в. в Москве проживало 100000 жителей и она была самым многолюдным городом Московского государства. После столицы по числу жителей выделялись города Великий Новгород и Псков. Количество жителей Пскова составляло 20% от количества жителей Москвы и 80% от количества жителей Великого Новгорода. Сколько людей проживало в середине XVI в. в Великом Новгороде?
Решение
100000 * 20% = 100000 * 0,2 = 20000 жителей было в Пскове;
20000 : 80% = 20000 : 0,8 = 25000 жителей было в Великом Новгороде.Задание 781
Пусть столбик, высота которого равна стороне клетки тетради, соответствует 1 году жизни человека. Нарисуй столбик, высота которого соответствует твоему возрасту.
Решение
Нарисуй столбик высотой столько клеток, сколько тебе полных лет.
Задание 782
Изобразите круг, разделите его двумя диаметрами на четыре равных сектора. Сколько процентов площади круга составляет площадь одного сектора?
Решение
Весь круг 100%, тогда:
100% : 4 = 25% площади круга составляет площадь одного сектора.Задание 783
Используя только цифры 1, 2, 3, 4, записали два неравных четырехзначных числа, у каждого из которых все цифры различны. Может ли одно из этих чисел делиться нацело на другое?
Решение
Нет, не может. Если бы это было возможно, то в частном могло получиться либо 2, либо 3. Но при умножении чисел 2 или 3 на цифры, данные в задаче, мы получим цифры, которые не даны, например 6, 8 или 9.
162
-
Страница 162
Ответы к параграфу 27. Диаграммы
Задание 784
На диаграмме (см.рис.71) показано количество спутников у планет Солнечной системы. Пользуясь диаграммой, установите:
1) у каких планет наибольшее количество спутников;
2) есть ли планеты, не имеющие спутников;
3) есть ли планеты с одинаковым количеством спутников;
4) во сколько раз у Юпитера больше спутников, чем у Нептуна;
5) на сколько у Земли меньше спутников, чем у Урана.
Решение
1) У Урана и Сатурна по 18 спутников.
2) Венера и Меркурий не имеют спутников.
3) У Урана и Сатурна по 18 спутников, а у Венеры и Меркурия по 0 спутников.
4) 16 : 8 = 2, то есть у Юпитера больше спутников, чем у Нептуна в 2 раза.
5) 18 : 1 = 18, то есть у Земли меньше спутников, чем у Урана в 18 раз.Задание 785
На диаграмме (рис. 72) приведена выборочная информация о природно−заповедном фонде России. Пользуясь диаграммой, установите:
1) сколько в России биосферных заповедников; зоологических парков;
2) на сколько больше природных заказников федерального значения, чем памятников природы федерального значения;
3) во сколько раз природных заповедников больше, чем национальных природных парков.
Решение
1) 39 биосферных заповедников;
33 зоологических парка.
2) 69 − 39 = 30, то есть на 30 природных заказников федерального значения больше, чем памятников природы федерального значения.
3) $\frac{69}{40}=1\frac{29}{40}$,
Ответ: природных заповедников больше, чем национальных природных парков в $1\frac{29}{40}$ раз.Задание 786
Пользуясь диаграммой, на которой приведена информация о площади наибольших водохранилищ России (рис. 73), установите:
1) у какого из данных водохранилищ самая большая площадь;
2) у какого из данных водохранилищ наименьшая площадь.
3) площадь какого водохранилища, Рыбинского или Волгоградского, больше.
Решение
1) У Кубышевского водохранилища самая большая площадь.
2) У Саяно−Шушенского водохранилища самая маленькая площадь.
3) Площадь Рыбинского водохранилища больше. 164
-
Страница 164
Задание 787
Пользуясь диаграммой, на которой изображено процентное содержание соли в воде некоторых морей (рис. 74), установите:
1) в каком из данных морей самая соленая вода;
2) в каком из данных морей наименее соленая вода;
3) в каком из морей, Средиземном или Красном, вода солонее.
Решение
1) В Мертвом море самая соленая вода.
2) В Черном море наименее соленая вода.
3) В Красном море вода солонее, чем в Средиземном. 165
-
Страница 165
Задание 788
На рисунке 75 приведена диаграмма количества пользователей Интернета в мире в процентах по отношению к общему количеству населения с 1995 по 2010 г. В течении какого года произошел наименьший прирост количества пользователей? Наибольший прирост?
Решение
Прирост населения по годам:
1995: 0,4%;
1996: 0,9 − 0,4 = 0,5%;
1997: 1,7 − 0,9 = 0,8%;
1998: 3,6 − 1,7 = 1,9%;
1999: 4,1 − 3,6 = 0,5%;
2000: 7,4 − 4,1 = 3,3%;
2001: 8,6 − 7,4 = 1,2%;
2002: 9,4 − 8,6 = 0,8%;
2003: 11,1 − 9,4 = 1,7%;
2004: 12,7 − 11,1 = 1,6%;
2005: 15,7 − 12,7 = 3%;
2006: 16,7 − 15,7 = 1%;
2007: 20 − 16,7 = 3,3%;
2008: 21,9 − 20 = 1,9%;
2009: 26,6 − 21,9 = 4,7%;
2010: 28,7 − 26,6 = 2,1%, следовательно:
наименьший прирост населения в 1995 году = 0,4%;
наибольший прирост населения в 2009 году = 4,7%.Задание 789
На круговой диаграмме (рис. 76) приведены результаты выборов мэра Солнечного города (в процентах). Пользуясь диаграммой, установите:
1) сколько процентов избирателей участвовало в голосовании;
2) на сколько процентов больше избирателей проголосовало за Знайку, чем за Незнайку;
3) сколько процентов избирателей проголосовало против Незнайки.
Решение
1) 100% − 7% = 93% процентов избирателей участвовало в голосовании.
2) 85% − 5% = 80%, то есть на 80% больше избирателей проголосовало за Знайку, чем за Незнайку.
3) 85% + 3% = 88% избирателей проголосовало против Незнайки.Задание 790
На круговой диаграмме (рис. 77) приведено распределение использования учеником 6 класса Петром Ивановым свободного от учебы времени. Установите:
1) сколько процентов свободного времени Петр проводит на свежем воздухе;
2) сколько процентов свободного времени он проводит с пользой для здоровья;
3) во сколько раз больше времени он тратит на просмотр телевизионных программ и игру на компьютере, чем на помощь родителям.
Посоветовали бы вы Петру что−то изменить в распределении свободного времени?Решение
1) 100% − 24% − 15% − 35% − 20% − 2% = 4% свободного времени Петр проводит на свежем воздухе.
2) Польза здоровью приносит пребывание на свежем воздухе и занятия спортом, а значит:
15% + 4% = 19%
3) $\frac{24+35}2=\frac{59}2=29,5$, то есть в 29,5 раз Петр больше времени он тратит на просмотр телевизионных программ и игру на компьютере, чем на помощь родителям. 166
-
Страница 166
Задание 791
На диаграмме, изображенной на рисунке 78, представлено распределение учеников по секциям спортивной школы.
1) Сколько процентов учеников спортивной школы составляют баскетболисты?
2) Сколько легкоатлетов в этой школе, если общее количество учащихся составляет 300 человек?
Решение
1) 100% − 65% − 5% − 15% = 15% учеников спортивной школы составляют баскетболисты.
2) 300 * 65% = 300 * 0,65 = 195 легкоатлетов в школе.Задание 792
Учащиеся 6 классов посещают разные спортивные секции. Используя диаграмму (рис. 79), установите:
1) какую секцию посещает больше всего шестиклассников;
2) какие секции посещает одинаковое количество шестиклассников;
3) какую часть количества футболистов составляет количество легкоатлетов;
4) сколько процентов количество гандболистов составляет от количества баскетболистов.Решение
1) футбольную секцию посещает больше всего шестиклассников
2) баскетбольную и волейбольную
3) $\frac{45}{75}=\frac35$ количества футболистов составляет количество легкоатлетов
4) $\frac{23}{30}=\frac{23}{30}$ * 100% = 0,51% 167
-
Страница 167
Задание 793
Пользуясь таблицей средних годовых температур воздуха в отдельных городах России, постройте соответствующую столбчатую диаграмму.
Решение
Задание 794
Пользуясь таблицей развития метрополитена в Санкт−Петербурге, постройте соответствующую столбчатую диаграмму.
Решение
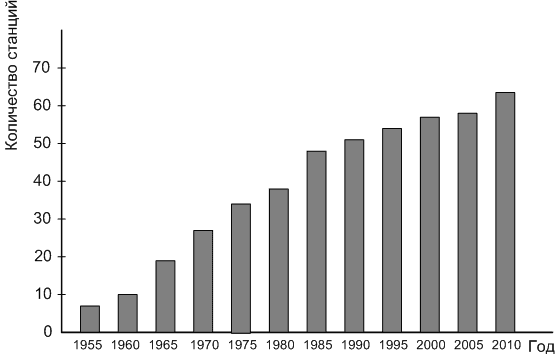
Задание 795
В таблице приведены высочайшие вершины некоторых горных систем Европы. Округлите высоту каждой вершины до сотен метров. Для изображения высоты 100 м возьмите отрезок, длина которого равна 1 мм, и постройте столбчатую диаграмму высот приведенных вершин горных систем.
Решение
168
-
Страница 168
Задание 796
С помощью таблицы, отражающей увеличение количества пользователей Интернета в мире, постройте соответствующую столбчатую диаграмму, округлив предварительно количество пользователей до десятков миллионов и взяв для изображения 10 млн человек отрезок длиной 1 мм.
Решение
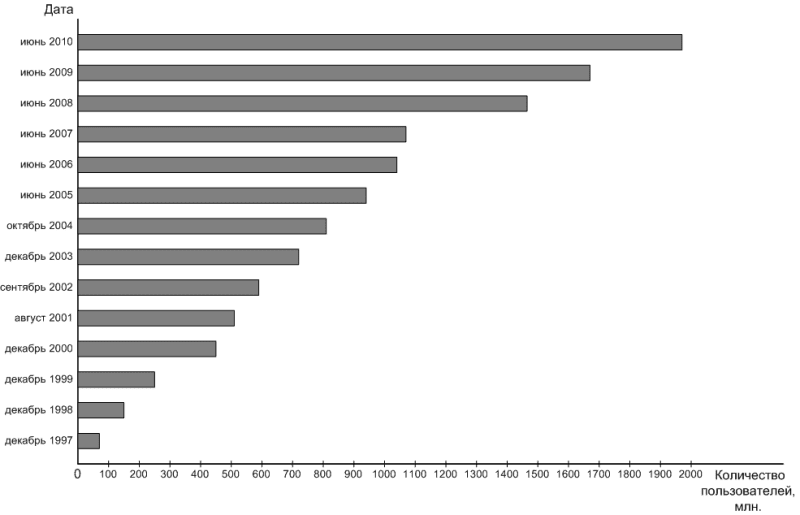
169
-
Страница 169
Задание 797
В таблице приведена распространенность некоторых химических элементов в земной коре.
Постройте столбчатую диаграмму распространенности приведенных элементов, взяв для изображения 0,1% отрезок, длина которого равна 1 мм.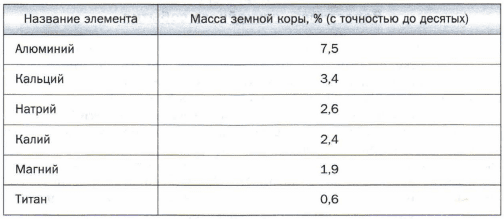
Решение
Задание 798
Максимальная масса белого медведя 800 кг, что составляет 2/15 максимальной массы индийского слона или 640% максимальной массы льва. Найдите максимальную массу:
1) индийского слона;
2) льва.Решение
1) $800:\frac2{15}=800\ast\frac{15}2=400\ast15=6000$ кг = 6 т масса индийского слона.
2) 800 : 640% = 800 : 6,4 = 125 кг масса льва.Задание 799
В Московском государственном университете имени М.В.Ломоносова учится около 40000 студентов. Количество студентов Кембриджского университета (Великобритания) составляет 30% количества студентов Московского университета или 3/7 количества студентов Гёттингенского университета (Германия). Сколько студентов учится в Гёттингенском университете?
Решение40000 * 30% = 40000 * 0,3 = 12000 студентов учится в Кембридже;
$12000:\frac37=12000\ast\frac73=4000\ast7=28000$ студентов учится в Гёттингенском университете.Задание 800
Используя цифры 4, 5, 6, записали два разных трехзначных числа. Может ли произведение этих чисел быть равным числу, записанному с помощью только цифр 0, 2, 3, 5, 6, 8? (В записи чисел цифры не повторяются.)
Решение
Нет, так как в произведении 465 * 546 = 253890 есть цифра 9, а в данных цифрах такой цифры нет.
Задание 801
В США дату обычно записывают так: месяц, число и год. Например, дату рождения A.C. Пушкина американец записал бы так: 5.26.1799. В Европе же сначала записывают число, потом месяц и год. Сколько в году дней, дату которых нельзя прочитать однозначно, не зная каким способом она записана?
Решение
Если число меньше или равно 12, то такую дату невозможно прочитать однозначно, так как будет непонятно месяц это или день.
В месяце таких дней 12, а в году 12 * 12 = 144 дня.
Ответ: 144 дня. 173
-
Страница 173
Ответы к параграфу 28. Случайные события. Вероятность случайного события
Задание 802
Приведите примеры экспериментов, результатами которых являются случайные события.
Решение
Подбрасывание монеты, выигрыш в лотерею, бросание игрального кубика.
Задание 803
Приведите примеры экспериментов, результатами которых являются события, по вашему мнению:
1) маловероятные;
2) очень вероятные.Решение
1) выигрыш в лотерею
2) выпадение любой цифры кроме 6, при вытаскивании из полного мешочка бочонка лото.Задание 804
Приведите примеры экспериментов, результатами которых являются:
1) достоверные события;
2) невозможные события.Решение
1) при подбрасывании монеты выпадет либо орел, либо решка.
2) при бросании игрального кубика выпадет цифра 7.Задание 805
Какие из следующих событий являются достоверными, а какие невозможными:
1) из корзины, в которой лежат только яблоки, достали персик;
2) в выбранном наугад слове русского языка обнаружили три подряд идущие буквы "и";
3) складывая два последовательных натуральных числа, получили нечетное число;
4) заглянув в календарь, обнаружили, что в следующем году ваш день рождения выпадет на среду?Решение
1) невозможное
2) невозможное
3) достоверное
4) достоверноеЗадание 806
Все ли равновероятные события имеют вероятность, равную 1/2?
РешениеЕсли этих событий два, то да (например подбрасывание монеты).
Если этих событий больше двух, то нет (например бросание игрального кубика).Задание 807
Приведите примеры экспериментов, результатами которых являются равновероятные события.
Решение
Подбрасывание монеты; бросание игрального кубика.
Задание 808
Приведите примеры экспериментов, результатами которых не являются равновероятные события.
Решение
Осень на дереве осталось 2 красных и 3 желтых листка, падение листка определенного цвета не является равновероятным событием.
В мешке 5 белых и 2 черных шарика, выпадение шарика определенного цвета не будет являтся равновероятным событием.Задание 809
Какова вероятность того, что при бросании игрального кубика выпадет количество очков, равное:
1) двум;
2) пять;
3) нечетному числу;
4) числу, которое кратно 6.Решение
1) благоприятных исходов 1 (цифра 2);
равновозможных исходов 6 (любая из шести цифр);
вероятность 1/6.
Ответ: 1/6.
2) благоприятных исходов 1 (цифра 5);
равновозможных исходов 6 (любая из шести цифр);
вероятность 1/6.
Ответ: 1/6.
3) благоприятных исходов 3 (цифры 2; 4; 6);
равновозможных исходов 6 (любая из шести цифр);
вероятность 3/6=1/2.
Ответ: 1/2.
4) благоприятных исходов 1 (цифра 6);
равновозможных исходов 6 (любая из шести цифр);
вероятность 1/6.
Ответ: 1/6.Задание 810
Какова вероятность того, что при бросании игрального кубика выпадет:
1) четное число;
2) число, которое не делится нацело на 4;
3) число, которое не делится нацело на 3;
4) число, кратное 7.Решение
1) благоприятных исходов 3 (цифры 2; 4; 6);
равновозможных исходов 6 (любая из шести цифр);
вероятность 3/6=1/2.
Ответ: 1/2.
2) благоприятных исходов 5 (цифры 1; 2; 3; 5; 6);
равновозможных исходов 6 (любая из шести цифр);
вероятность 5/6.
Ответ: 5/2.
3) благоприятных исходов 4 (цифры 1; 2; 4; 5);
равновозможных исходов 6 (любая из шести цифр);
вероятность 4/6=2/3.
Ответ: 2/3.
4) благоприятных исходов 0;
равновозможных исходов 6 (любая из шести цифр);
вероятность 0/6=0.
Ответ: 0.Задание 811
Чтобы сдать экзамен по математике, нужно выучить 30 билетов. Ученик выучил 25 билетов. Какова вероятность того, что он вытянет билет, ответ на который знает?
Решение
благоприятных исходов 25;
равновозможных исходов 30;
вероятность 25/30=5/6.
Ответ: 5/6. 174
-
Страница 174
Задание 812
Чтобы сдать экзамен по истории, нужно выучить 25 билетов. Ученик не выучил только один билет. Какова вероятность того, что он вытянет именно этот билет?
Решение
благоприятных исходов 1;
равновозможных исходов 25;
вероятность 1/25.
Ответ: 1/25.Задание 813
В классе учатся 12 девочек и 17 мальчиков. Один учащийся этого класса опоздал в школу. Какова вероятность того, что это:
1) был мальчик;
2) была девочка?Решение
1) 12 + 17 = 29 детей учатся в классе;
благоприятных исходов 17;
равновозможных исходов 29;
вероятность 17/29.
Ответ: 17/29.
2) 12 + 17 = 29 детей учатся в классе;
благоприятных исходов 12;
равновозможных исходов 29;
вероятность 12/29.
Ответ: 12/29.Задание 814
В лотерее 20 выигрышных билетов и 480 билетов без выигрыша. Какова вероятность выиграть в эту лотерею, если купить один билет.
Решение
20 + 480 = 500 билетов всего в розыгрыше;
благоприятных исходов 20;
равновозможных исходов 500;
вероятность 20/500=1/25.
Ответ: 1/25.Задание 815
Три грани кубика покрасили в красный цвет, а остальные три − в синий. Какова вероятность того, что при бросании кубика выпадет красная грань?
Решение
6 граней всего у кубика;
благоприятных исходов 3;
равновозможных исходов 6;
вероятность 3/6=1/2.
Ответ: 1/2.Задание 816
Две грани кубика покрасили в черный цвет, а остальные − в белый. Какова вероятность того, что при бросании кубика выпадет:
1) черная грань;
2) белая грань?Решение
1) 6 граней всего у кубика;
благоприятных исходов 2;
равновозможных исходов 6;
вероятность 2/6=1/3.
Ответ: 1/3.
2) 6 − 2 = 4 грани покрасили в белый цвет;
благоприятных исходов 4;
равновозможных исходов 6;
вероятность 4/6=2/3.
Ответ: 2/3.Задание 817
Из коробки шахмат случайно выпала одна фигура. Какова вероятность того, что эта фигура:
1) белый король;
2) черный ферзь;
3) король;
4) черная ладья;
5) конь;
6) белая пешка;
7) пешка;
8) белая фигура;
9) не пешка;
10) не король;
11) не белый ферзь;
12) не пешка и не король;
13) не слон и не ферзь;
14) не конь, не король и не ладья?Решение
1) Всего 32 шахматные фигуры, из них 1 белый король, тогда:
благоприятных исходов 1;
равновозможных исходов 32;
вероятность 1/32.
Ответ: 1/32.
2) Всего 32 шахматные фигуры, из них 1 черный ферзь, тогда:
благоприятных исходов 1;
равновозможных исходов 32;
вероятность 1/32.
Ответ: 1/32.
3) Всего 32 шахматные фигуры, из них 2 короля, тогда:
благоприятных исходов 2;
равновозможных исходов 32;
вероятность 2/32=1/16.
Ответ: 1/16.
4) Всего 32 шахматные фигуры, из них 2 черных ладьи, тогда:
благоприятных исходов 2;
равновозможных исходов 32;
вероятность 2/32=1/16.
Ответ: 1/16.
5) Всего 32 шахматные фигуры, из них 4 коня, тогда:
благоприятных исходов 4;
равновозможных исходов 32;
вероятность 4/32=1/8.
Ответ: 1/8.
6) Всего 32 шахматные фигуры, из них 8 белых пешек, тогда:
благоприятных исходов 8;
равновозможных исходов 32;
вероятность 8/32=1/4.
Ответ: 1/4.
7) Всего 32 шахматные фигуры, из них 16 пешек, тогда:
благоприятных исходов 16;
равновозможных исходов 32;
вероятность 16/32=1/2.
Ответ: 1/2.
8) Всего 32 шахматные фигуры, из них 16 белых фигур, тогда:
благоприятных исходов 16;
равновозможных исходов 32;
вероятность 16/32=1/2.
Ответ: 1/2.
9) Всего 32 шахматные фигуры, из них 16 пешек, тогда:
32 − 16 = 16 фигур не пешки;
благоприятных исходов 16;
равновозможных исходов 32;
вероятность 16/32=1/2.
Ответ: 1/2.
10) Всего 32 шахматные фигуры, из них 2 короля, тогда:
32 − 2 = 30 фигур не короли;
благоприятных исходов 30;
равновозможных исходов 32;
вероятность 30/32=15/16.
Ответ: 15/16.
11) Всего 32 шахматные фигуры, из них 1 белый ферзь, тогда:
32 − 1 = 31 фигура не белый ферзь;
благоприятных исходов 31;
равновозможных исходов 32;
вероятность 31/32.
Ответ: 31/32.
12) Всего 32 шахматные фигуры, из них 16 пешек и 2 короля, тогда:
32 − (16 + 2) = 32 − 18 = 14 фигур не пешка и не король;
благоприятных исходов 14;
равновозможных исходов 32;
вероятность 14/32=7/16.
Ответ: 7/16.
13) Всего 32 шахматные фигуры, из них 4 слона и 2 ферзя, тогда:
32 − (4 + 2) = 32 − 6 = 26 фигур не слон и ферзь;
благоприятных исходов 26;
равновозможных исходов 32;
вероятность 26/32=13/16.
Ответ: 13/16.
14) Всего 32 шахматные фигуры, из них 4 коня, 2 короля и 4 ладьи, тогда:
32 − (4 + 2 + 4) = 32 − 10 = 22 фигуры не конь, не король и не ладья;
благоприятных исходов 22;
равновозможных исходов 32;
вероятность 22/32=11/16.
Ответ: 11/16.Задание 818
В коробке было 19 карточек, пронумерованных числами от 1 до 19. Из коробки наугад взяли одну карточку. Какова вероятность того, что на ней написано число:
1) 12;
2) 21;
3) четное;
4) нечетное;
5) кратное 3;
6) кратное 7;
7) простое;
8) двузначное;
9) в записи которого есть цифра 9;
10) в записи которого есть цифра 1;
11) в записи которого отсутствует цифра 5;
12) сумма цифр которого делится нацело на 5;
13) при делении которого на 7 остаток равен 5;
14) в записи которого отсутствует цифра 1?Решение
1) Цифра 12 написана только на одной карточке, тогда:
благоприятных исходов 1;
равновозможных исходов 19;
вероятность 1/19.
Ответ: 1/19.
2) Цифры 21 нет ни на одной карточке, тогда:
благоприятных исходов 0;
равновозможных исходов 19;
вероятность 0/19=0.
Ответ: 0.
3) Карточек с четными цифрами 9 (2; 4; 6; 8; 10; 12; 14; 16; 18), тогда:
благоприятных исходов 9;
равновозможных исходов 19;
вероятность 9/19.
Ответ: 9/19.
4) Карточек с четными цифрами 10 (1; 3; 5; 7; 9; 11; 13; 15; 17; 19), тогда:
благоприятных исходов 10;
равновозможных исходов 19;
вероятность 10/19.
Ответ: 10/19.
5) Карточек с цифрой кратной трем 6 (3; 6; 9; 12; 15; 18), тогда:
благоприятных исходов 6;
равновозможных исходов 19;
вероятность 6/19.
Ответ: 6/19.
6) Карточек с цифрой кратной семи 2 (7; 14), тогда:
благоприятных исходов 2;
равновозможных исходов 19;
вероятность 2/19.
Ответ: 2/19.
7) Карточек с простыми цифрами 8 (2; 3; 5; 7; 11; 13; 17; 19), тогда:
благоприятных исходов 8;
равновозможных исходов 19;
вероятность 8/19.
Ответ: 8/19.
8) Карточек с двузначными цифрами 10 (10; 11; 12; 13; 14; 15; 16; 17; 18; 19), тогда:
благоприятных исходов 10;
равновозможных исходов 19;
вероятность 10/19.
Ответ: 10/19.
9) Карточек с числом в записи которого есть цифра девять 2 (9; 19), тогда:
благоприятных исходов 2;
равновозможных исходов 19;
вероятность 2/19.
Ответ: 2/19.
10) Карточек с числом в записи которого есть цифра один 11 (1; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19), тогда:
благоприятных исходов 11;
равновозможных исходов 19;
вероятность 11/19.
Ответ: 11/19.
11) Карточек с числом в записи которого присутствует цифра пять 2 (5; 15), поэтому 19 − 2 = 17 карточек с числом в записи которого отсутствует цифра пять, тогда:
благоприятных исходов 17;
равновозможных исходов 19;
вероятность 17/19.
Ответ: 17/19.
12) Карточек с числом сумма цифр которого делится нацело на пять 3 (5; 14; 19), тогда:
благоприятных исходов 3;
равновозможных исходов 19;
вероятность 3/19.
Ответ: 3/19.
13) Карточек с числом при делении которого на 7 остаток равен пяти 2 (12; 19), тогда:
благоприятных исходов 2;
равновозможных исходов 19;
вероятность 2/19.
Ответ: 2/19.
14) Карточек с числом в записи которого отсутствует цифра один 8 (2; 3; 4; 5; 6; 7; 8; 9), тогда:
благоприятных исходов 8;
равновозможных исходов 19;
вероятность 8/19.
Ответ: 8/19.Задание 819
Какова вероятность того, что на открытой наугад странице перекидного календаря (каждому дню года отводится отдельная страница) следующего года будет записано:
1) 7 число;
2) 31 число;
3) 29 число.Решение
1) В году 365 дней, в високосном 366 дней.
В месяц одно число 12, тогда:
1 * 12 = 12 чисел двенадцать в году;
благоприятных исходов 12;
равновозможных исходов:
в не високосном году 365;
в високосном году 366;
вероятность:
в не високосном году 12/365;
в високосном 12/366.
Ответ: 12/365 или 12/366.
2) В году 365 дней, в високосном 366 дней.
В году 7 месяцев с числом 31 (январь, март, май, июль, август, октябрь, декабрь) тогда:
1 * 12 = 12 чисел двенадцать в году;
благоприятных исходов 7;
равновозможных исходов:
в не високосном году 365;
в високосном году 366;
вероятность:
в не високосном году 7/365;
в високосном 7/366.
Ответ: 7/365 или 7/366.
3) В году 365 дней, в високосном 366 дней.
В месяц одно число 29, кроме февраля для не високосного года, тогда:
в не високосном году 1 * 11 = 11 чисел 29 в году;
в високосном году 1 * 12 = 12 чисел 29 в году;
благоприятных исходов:
в не високосном году 11;
в високосном году 12;
равновозможных исходов:
в не високосном году 365;
в високосном году 366;
вероятность:
в не високосном году 11/365;
в високосном 12/366=2/61.
Ответ: 11/365 или 2/61. 175
-
Страница 175
Задание 820
В коробке лежат пять красных и три желтых шара. Какова вероятность того, что выбранный наугад шар окажется:
1) желтым;
2) красным;
3) синим?Решение
1) 5 + 3 = 8 шаров всего в коробке, из них 3 желтых, тогда:
благоприятных исходов 3;
равновозможных исходов 8;
вероятность 3/8.
Ответ: 3/8.
2) 5 + 3 = 8 шаров всего в коробке, из них 5 красных, тогда:
благоприятных исходов 5;
равновозможных исходов 8;
вероятность 5/8.
Ответ: 5/8.
3) 5 + 3 = 8 шаров всего в коробке, из них 0 синих, тогда:
благоприятных исходов 0;
равновозможных исходов 8;
вероятность 0/8=0.
Ответ: 0.Задание 821
В ящике было 45 шаров, из которых 17 − белых. Потеряли два не белых шара. Какова вероятность того, что взятый наугад один шар будет белым?
Решение
45 − 2 = 43 шара всего осталось, из них 17 белых, тогда:
благоприятных исходов 17;
равновозможных исходов 43;
вероятность 17/43.
Ответ: 17/43.Задание 822
Карточки с номерами 1, 2, 3 положили в ряд. Какова вероятность того, что карточки с нечетными номерами окажутся рядом?
Решение
На первое место в ряду можно положить любую из трех карточек, на второе место любую из оставшихся двух, а на третье одну оставшуюся карточку, следовательно:
3 * 2 * 1 = 6 вариантов раскладок карточек существует.
Возможны 4 варианта того, что карточки с нечетными номерами окажутся рядом:
132; 312; 213; 231, тогда:
благоприятных исходов 4;
равновозможных исходов 6;
вероятность 4/6=2/3.
Ответ: 2/3.Задание 823
В коробке лежат два синих шара и несколько красных. Сколько красных шаров в коробке, если вероятность того, что выбранный наугад шар:
1) окажется синим, равна 2/5;
2) окажется красным, равна 4/5.Решение
1) $2:\frac25=2\ast\frac52=5$ шаров всего в коробке;
5 − 2 = 3 красных шара.
Ответ: 3 шара.
2) $1-\frac45=\frac15$ вероятность того, что шар окажется синим, тогда:
$2:\frac15=2\ast\frac51=10$ шаров всего в коробке;
10 − 2 = 8 красных шаров.
Ответ: 8 шаров.Задание 824
Грани кубика окрашены в два цвета − синий и желтый (каждая грань в один цвет). Вероятность того, что при бросании кубика выпадет синяя грань, равна 2/3. Сколько синих и сколько желтых граней у кубика?
Решение
Всего у кубика 6 граней, тогда:
$6\ast\frac23=2\ast2=4$ синих граней у кубика;
6 − 4 = 2 желтых грани у кубика.
Ответ: 4 синих; 2 желтых.Задание 825
В коробке лежат три зеленых и шесть синих шаров. Какое наименьшее количество шаров нужно вынуть наугад, чтобы вероятность того, что среди вынутых шаров хотя бы один окажется зеленого цвета, была равной 1?
Решение
Допустим, что первые 6 вынутых шаров оказались синими, тогда с вероятностью равной 1 можно утверждать, что следующий шар будет зеленого цвета. Следовательно нужно вынуть 7 шаров.
Ответ: 7 шаров.Задание 826
Один тракторист может вспахать поле за 18 ч, а другой − за 12 ч. Какую часть поля они вспашут вместе, если первый будет работать 5 ч, а второй − 7 ч?
Решение
Пусть все поле равно единице, тогда:1/18 поля вспашет первый тракторист за 1 час;
$5\ast\frac1{18}=\frac5{18}$ поля вспашет первый тракторист за 5 часов;
1/12 поля вспашет второй тракторист за 1 час;
$7\ast\frac1{12}=\frac7{12}$ поля вспашет второй тракторист за 7 часов;
$\frac5{18}+\frac7{12}=\frac{10+21}{36}=\frac{31}{36}$ поля вспашут трактористы вместе, если первый будет работать 5 ч, а второй − 7 ч.
Ответ: 31/36 поля.Задание 827
Цену товара сначала увеличили на 50%, а потом уменьшили на 50%. Какой стала цена товара, если сначала она составляла 2000 р.?
Решение
2000 + 2000 * 0,5 = 2000 + 1000 = 3000 рублей стал стоить товар после повышения цены;
3000 − 3000 * 0,5 = 3000 − 1500 = 1500 рублей стал стоить товар после понижения цены.
Ответ: 1500 р. стал стоить товар.Задание 828
Заполните цепочку вычислений:

Решение
$2\frac13:5\frac56=\frac73:\frac{35}6=\frac73\ast\frac6{35}=\frac11\ast\frac25=\frac25$
$\frac25\ast15=2\ast3=6$
$6-2\frac{13}{17}=5\frac{17}{17}-2\frac{13}{17}=3\frac4{17}$
$3\frac4{17}\ast1\frac6{11}=\frac{55}{17}\ast\frac{17}{11}=\frac51\ast\frac11=5$
Ответ: $\frac25$ → 6 → $3\frac4{17}$ → 5Задание 829
Футбольный мяч плотно обтянут сеткой. Из каждого узла сетки выходит три веревки. Может ли в этой сетке быть 999 узлов?
Решение
Так как сетка, обтягивающая футбольный мяч имеет замыкается в форму мяча, и при этом из каждого узла выходит по три веревки, также можно и сказать, что в каждый узел приходит по три веревки. То есть для того, чтобы сетка была замкнутой для каждого узла должен быть парный узел, то есть количество узлов обязательно будет четным. Получается 999 узлов быть не может.
Ответ: не может. 180
-
Страница 180
Глава 4. Рациональные числа и действия над ними.
Ответы к параграфу 29. Положительные и отрицательные числа.Задание 830
Какие из чисел
3;−6;−2 1/3;4,7;9/16;0;−5,2;−9 3/7;10,14;5/8:
1) являются положительными;
2) являются отрицательными;
3) не являются ни положительными, ни отрицательными?Решение
1) положительные:
3; 4, 7; 9/16; 10,14; 5/8.
2) отрицательные:
−6; −2 1/3; −5,2; −9 3/7.
3) не положительно и не отрицательное: 0.Задание 831
Запишите с помощью знаков "+" и "−" информацию Гидрометцентра:
1) 18° тепла;
2) 7° мороза;
3) 12° ниже нуля;
4) 16° выше нуля.Решение
1) +18°
2) −7°
3) −12°
4) +16°Задание 832
С помощью положительных и отрицательных чисел запишите высоты и глубины, приведенные в таблице:

Решение
Говерла (Карпаты) +2061;
Желоб Пуэрто−Рико (Атлантический океан) −8742;
Канченджанга (Гималаи) +8585 м;
Эльбрус (Кавказ) +5642 м;
Зондский желоб (Индийский океан);
Гренландское море −5527 м.Задание 833
Запишите шесть отрицательных дробей со знаменателем 5.
Решение
$-\frac15;-\frac25;-\frac35;-\frac45;-\frac65;-\frac75$
Задание 834
Запишите четыре отрицательные десятичные дроби с одной цифрой после запятой.
Решение
−0,2; −1,5; −100,1; −121,8.
Задание 835
Запишите показания термометров, изображенных на рисунке 82.
Решение
а) +6°
б) −4°Задание 836
Какую температуру будет показывать термометр, изображенный на рисунке 82, а, если:
1) его столбик опустится на 8 делений;
2) его столбик поднимется на 4 деления;
3) температура повысится на 5°C;
4) температура понизится на 6°C;
5) температура понизится на 10°C?
Решение
1) 6°C − 8°C = −2°C
2) 6°C + 4°C = +10°C
3) 6°C + 5°C = +11°C
4) 6°C − 6°C = 0°C
5) 6°C − 10°C = −4°CЗадание 837
Какую температуру будет показывать термометр, изображенный на рисунке 82, б, если:
1) его столбик поднимется на 2 деления;
2) его столбик опустится на 3 деления;
3) температура повысится на 6°C;
4) температура понизится на 5°C?
Решение
1) −4°C + 2°C = −2°C
2) −4°C − 3°C = −7°C
3) −4°C + 6°C = +2°C
4) −4°C − 5°C = −9°C 181
-
Страница 181
Задание 838
В 10 ч термометр показывал температуру −2°C. За два часа температура воздуха изменилась на 5°C. Какой стала температура воздуха?
Решение
1 вариант:
температура повысилась на 5°C, тогда:
−2°C + 5°C = +3°C стала температура воздуха.
2 вариант:
температура понизилась на 5°C, тогда:
−2°C − 5°C = −7°C стала температура воздуха.
Ответ: +3°C или −7°CЗадание 839
В 20 ч термометр показывал температуру −3°C. Через три часа температура воздуха изменилась на 4°C. Какой стала температура воздуха?
Решение
1 вариант:
температура повысилась на 4°C, тогда:
−3°C + 4°C = +1°C стала температура воздуха.
2 вариант:
температура понизилась на 4°C, тогда:
−3°C − 4°C = −7°C стала температура воздуха.
Ответ: +1°C или −7°CЗадание 840
В парке растет 150 кленов, дубов больше на 2/15 количества кленов, березы составляют 23/34 количества дубов, а липы − 20/87 общего количества кленов дубов и берез. Сколько всего указанных деревьев растет в парке?
Решение
1) $150+150\ast\frac2{15}=150+10\ast2=150+20=170$ (шт.) - дубов растет в парке;
2) $\frac{23}{34}\ast170=23\ast5=115$ (шт.) - берез растет в парке;
3) $\frac{20}{87}\ast(150+170+115)=\frac{20}{87}\ast435=20\ast5=100$ (шт.) - лип растет в парке.
4) 150 + 170 + 115 + 100 = 535 (дер.) - растет в парке.
Ответ: 535 деревьев.Задание 841
Найдите значение выражения:
$(1,02:\frac1{50}-7,26:\frac{11}{70}):3\frac15+0,4:0,36=2\frac{11}{18}$
1) $1,02:\frac1{50}=\frac{102}{100}:\frac1{50}=\frac{51}{50}\ast\frac{50}1=51$
2) $7,26:\frac{11}{70}=\frac{726}{100}:\frac{11}{70}=\frac{363}{50}\ast\frac{70}{11}=\frac{33}5\ast\frac71=\frac{231}5=46\frac15$
3) $51-46\frac15=50\frac55-46\frac15=4\frac45$
4) $4\frac45:3\frac15=\frac{24}5:\frac{16}5=\frac{24}5\ast\frac5{16}=\frac31\ast\frac12=\frac32=1\frac12$
5) $0,4:0,36=\frac4{10}:\frac{36}{100}=\frac25\ast\frac{25}9=\frac21\ast\frac59=\frac{10}9=1\frac19$
6) $1\frac12+1\frac19=2\frac{9+2}{18}=2\frac{11}{18}$Задание 842
Каковы координаты точек A, B, C, D, E на рисунке 83?
Решение
$A(2);B(3);C(\frac15);D(1\frac25);E(3\frac45)$
Задание 843
Начертите координатный луч, единичный отрезок которого равен 3 см. Отметьте на нем точки $A(1);B(2);C(\frac16);D(1\frac56);E(2\frac13);F(1,5)$
Решение
Задание 844
Начертите горизонтальную прямую, отметьте на ней точку O и точки M, N, K, P, которые расположены так:
1) точка M на 4 клетки правее точки O;
2) точка N на 3 клетки левее точки O;
3) точка K на 7 клеток левее точки O;
4) точка P на 5 клеток правее точки O.Решение

182
-
Страница 182
Задание 845
Задача от мудрой совы
Двое мальчиков находились в лодке у берега реки. К ним обратилась группа туристов с просьбой помочь переправиться на противоположный берег. В лодке помещаются или два мальчика, или один турист. Смогут ли мальчики помочь туристам?
Решение
Действие 1:
Оба мальчика переплывают на другой берег;
Действие 2:
Один мальчик возвращается обратно;
Действие 3:
Один турист переплывает на другой берег;
Действие 4:
Второй мальчик возвращает лодку на первый берег;
Действие 5:
Снова оба мальчика переплывают на другой берег.
Таким образом можно повторить этот цикл бесконечно и перевезти любое количество туристов.
Ответ: Мальчики смогут помочь туристам. 183-184
-
Страница 183-184
Ответы к параграфу 30. Координатная прямая
Задание 846
Запишите координаты точек A, B, C, D, E, F, M, K, изображенных на рисунке 86.
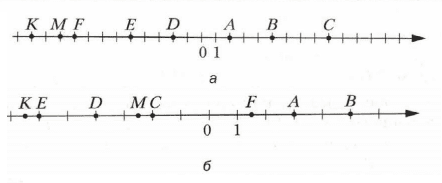
Решение
a) A(2); B(4); C(8); D(−2); E(−5); F(−9); M(−10); K(13).
б) A(3); B(5); C(−2); D(−4); E(−6); F(1,5); M(−2,5); K(−6,5).Задание 847
Запишите координаты точек A, B, C, D, E, F, M, K, изображенных на рисунке 87.
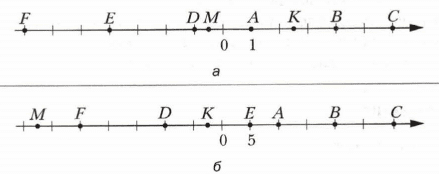
Решение
a) A(1);B(4);C(6);D(−1);E(−4);F(−7);M(−1/2);K(2,5).
б) A(10); B(20); C(30); D(−10); E(5); F(−25); M(−32,5); K(−2,5).Задание 848
Начертите координатную прямую и отметьте на ней числа: 0; 1; 4; −3; 6; −2; −5; 2,5; −4,5.
Решение

Задание 849
Начертите координатную прямую и отметьте на ней числа: 0; 1; −2; 7; 5; −4; −2,5; −5,5; −6.
Решение

Задание 850
Начертите координатную прямую, взяв за единичный такой отрезок, длина которого в 6 раз больше стороны клетки тетради. Отметьте точки $A(1),B(-1),C(-0,5),D(\frac23),E(-1\frac16),F(2\frac13),M(-1\frac23),P(-2\frac16),R(-\frac13)$
Решение

Задание 851
Начертите координатную прямую, взяв за единичный такой отрезок, длина которого в 4 раза больше стороны клетки тетради. Отметьте точки $A(2),B(\frac12),C(1\frac14),D(-2),E(-\frac14),F(-1,75),Q(-2\frac18),S(0,25),T(-1,5),N(1,25)$
Решение
Задание 852
Длина единичного отрезка координатной прямой равна 1 см. Чему равно расстояние между точками:
1) A(2) и B(6);
2) С(−3) и D(−1);
3) M(−4) и N(2)?Решение
1) 6 − 2 = 4 см
2) −1 − (−3) = −1 + 3 = 2 см
3) 2 − (−4) = 2 + 4 = 6 см 185
-
Страница 185
Задание 853
Длина единичного отрезка координатной прямой равна 5 мм. Чему равно расстояние между точками:
1) C(−5) и O(0);
2) A(−10) и B(−3);
3) D(−2) и E(2)?Решение
1) (2 − (−3)) * 5 = (2 + 3) * 5 = 5 * 5 = 25 мм
2) (−3 − (−10)) * 5 = (−3 + 10) * 5 = 7 * 5 = 35 мм
3) (2 − (−2)) * 5 = (2 + 2) * 5 = 4 * 5 = 20 ммЗадание 854
Начертите координатную прямую и отметьте на ней точки A(−1) и B(5). Найдите на прямую точку, которая является серединой отрезка AB, и определите ее координату.
Решение
Ответ: С(2).Задание 855
Начертите координатную прямую и отметьте на ней точки M(−6) и C(−2). Найдите на прямую точку N такую, что точка C − середина отрезка MN, и определите координату точки N.
Решение

Ответ: N(2).Задание 856
Начертите координатную точку прямую и отметьте на ней точки K(−1) и F(5). Найдите на прямой точку E такую, что точка K − середина отрезка EF, и определите координату точки E.
Решение

Ответ: E(−7).Задание 857
Начертите координатную прямую, отметьте на ней точку B(−4). Отметьте на этой прямой точку, удаленную от точки B:
1) в положительной направлении на 8 единиц;
2) в отрицательном направлении на 3 единицы.Решение
1)

Ответ: С(4)
2)
Ответ: K(−7)Задание 858
Начертите координатную прямую, отметьте на ней точку K(2). Отметьте на этой прямой точку, удаленную от точки K:
1) в отрицательном направлении на 2 единицы;
2) в положительном направлении на 4 единицы.Решение
1)
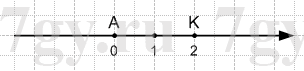
Ответ: A(0)
2)
Ответ: B(6)Задание 859
Запишите какие−нибудь три числа, лежащие на координатной прямой:
1) левее числа 2;
2) правее числа 3,6;
3) левее числа −100;
4) правее числа −25.Решение
1) −1; −5; −6.
2) 4; 5,2; 8.
3) −200; −250; −1000.
4) −20; −15; 15.Задание 860
Запишите какие−нибудь четыре числа, лежащие на координатной прямой между числами −1 и 0.
Решение
−0,7; −0,5; −0,3; −0,1.
Задание 861
Запишите какие−нибудь два числа, лежащие на координатной прямой:
1) левее числа −240;
2) правее числа −0,5;
3) между числами −9 и −8;
4) между числами −0,1 и 0,1.Решение
1) −243; −247.
2) 0; 2.
3) −8,6; −8,5.
4) 0; 0,06.Задание 862
Запишите числа, удаленные на 7 единиц от числа:
1) 80;
2) 4;
3) 0;
4) −3;
5) −12;
6) −7.Решение
1) 80 + 7 = 87;
80 − 7 = 73.
Ответ: 87; 73.
2) 4 + 7 = 11;
4 − 7 = −3.
Ответ: 11; −3.
3) 0 + 7 = 7;
0 − 7 = −7.
Ответ: 7; −7.
4) −3 + 7 = 4;
−3 − 7 = −10.
Ответ: 4; −10.
5) −12 + 7 = −5;
−12 − 7 = −19.
Ответ: −5; −19.
6) −7 + 7 = 0;
−7 − 7 = −14.
Ответ: 0; −14.Задание 863
На координатной прямой отметили числа −8 и 12 (рис.88). Какая из точек A, B, C или D является началом отсчета?
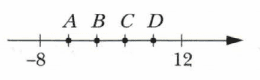
Решение
(12 − (−8)) : 5 = (12 + 8) : 5 = 4 − единичный отрезок;
−8 + 4 * 2 = −8 + 8 = 0
Ответ: B(0).Задание 864
Найдите координату точки C (рис.89).

Решение
5 − 3 = 2 − единичный отрезок;
3 − 5 * 2 = 3 − 10 = −7.
Ответ: С(−7). 186
-
Страница 186
Задание 865
На координатной прямой отметили точки A(2) и B(8). Какую координату должна иметь точка M, чтобы отрезок BM был в 2 раза длиннее отрезка AM? Сколько решений имеет задача?
Решение
1)

2)
Ответ: M(20) или M(4).Задание 866
Начертите две окружности, радиусы которых равны 2 см, так, чтобы они:
1) имели две общие точки;
2) имели одну общую точку;
3) не имели общих точек.Решение
1)
2)
3)
Задание 867
Из некоторого числа вычли 5/17 этого числа и получили 480. Найдите это число.
Решение
Пусть x − искомое число, тогда:
$x-\frac5{17}x=480$
$\frac{12}{17}x=480$
$x=480:\frac{12}{17}$
$x=480\ast\frac{17}{12}$
x = 40 * 17
x = 680 − искомое число.
Ответ: 680.Задание 868
Все учащиеся 6 класса занимаются или в секции тенниса, или в секции плавания. Некоторые из них занимаются и теннисом, и плаванием: 1/6 теннисистов занимаются плаванием, а 1/5 пловцов − теннисом. Кого в классе больше − теннисистов или пловцов?
Решение
Пусть x − теннисистов и y − пловцов в классе, тогда:
$\frac16x$ теннисистов занимаются плаванием;
$\frac15y$ пловцов занимаются теннисом;
$\frac16x=\frac15y$
$\frac x6=\frac y5$
5x = 6y
$\frac xy=\frac65>1$, следовательно теннисистов в классе больше.
Ответ: теннисистов в классе больше.Задание 869
Число 50 увеличили на 500%. Во сколько раз полученное число больше 50?
Решение
50 + 50 * 500% = 50 + 50 * 5 = 50 + 250 = 300 − число после увеличения;
300 : 50 = 6, то есть в 6 раз полученное число больше 50.
Ответ: в 6 раз.Задание 870
На столе стоят семь стаканов − все вверх дном. За один ход разрешается перевернуть любые четыре стакана. Можно ли за несколько ходов добиться того, чтобы все стаканы стояли правильно?
Решение
Так как стаканов нечетное количество, то для того, чтобы все стаканы стояли правильно, их нужно перевернуть нечетное количество раз. По условию задачи, за один раз можно перевернуть четное число стаканов − 4. Следовательно, таким образом нельзя перевернуть все стаканы.
Ответ: перевернуть стаканы по условию задачи нельзя. 188
-
Страница 188
Ответы к параграфу 31. Целые числа. Рациональные числа
Задание 871
Назовите число, противоположное числу:
1) 6;
2) −7;
3) 0,9;
4) 0;
5) 7,2;
6) −23;
7) −13,4.Решение
1) −6
2) 7
3) 0,9
4) 0
5) 7,2
6) 23
7) 13,4Задание 872
Заполните таблицу:

189
-
Страница 189
Задание 873
Являются ли противоположными числа:
1) 0,6 и −3/5;
2) 2,5 и 5/2;
3) −1,25 и 5/4;
4) −1,5 и −2/3?Решение
1) 0,6=6/10=3/5, следовательно 0,6 и −3/5 противоположные числа.
2) нет, так как оба числа положительные.
3) −1,25=−125/100=−5/4, следовательно −1,25 и 5/4 противоположные числа.
4) нет, так как оба числа отрицательные.Задание 874
Верно ли утверждение:
1) 4/15 − положительное число;
2) 4/15 − рациональное число;
3) −4 − отрицательное число;
4) −4 − натурально число;
5) −4 − целое число;
6) −4 − рациональное число;
7) 0 − натуральное число;
8) 0 − целое число;
9) 0 − рациональное число;
10) 0 − положительное число.Решение
1) верно
2) верно
3) не верно
4) не верно
5) верно
6) верно
7) не верно
8) верно
9) верно
10) не верноЗадание 875
Выберите из чисел 5;−7;0;1/2;−3,7;8,6;−125;324;15 3/7;−27 11/19;−2;35;13,65;−79;976.
1) натуральные;
2) целые;
3) положительные;
4) неположительные;
5) целые отрицательные;
6) дробные неотрицательные.Решение
1) 5; 324; 35; 976.
2) 5; −7; 0; −125; 324; −2;35; −79; 976.
3) 5; 1/2; 8, 6; 324; 15 3/7; 35; 13, 65; 976.
4) −7; 0; −3,7; −125; −27 11/19; −2; −79.
5) −7; −125; −2; −79.
6) 1/2; 8, 6; 15 3/7; 13,65.Задание 876
Найдите значение p, если:
1) −p = 8;
2) −p = −18;
3) −p = −0,1;
4) −p = 0.Решение
1) −p = 8
p = −8
2) −p = −18
p = 18
3) −p = −0,1
p = 0,1
4) −p = 0
p = 0Задание 877
Найдите значение −x, если:
1) x = 7,9;
2) x = −0,15;
3) x = −10;
4) x = 49.Решение
1) x = 7,9
−x = −7,9
2) x = −0,15
−x = 0,15
3) x = −10
−x = 10
4) x = 49
−x = −49Задание 878
Решите уравнение:
1) −y = 11;
2) −y = −31;
3) −y = 0;
4) −y=−(−1/3).Решение
1) −y = 11
y = −11
2) −y = −31
y = 31
3) −y = 0
y = 0
4) $-y=-(-\frac13)$
$y=-\frac13$Задание 879
Заполните таблицу:

Задание 880
Запишите все целые положительные числа, меньше 5 3/4 и числа, противоположные им. Отметьте все эти числа на координатной прямой.
Решение

Ответ: −5; −4; −3; −2; −1; 0; 1; 2; 3; 4; 5.Задание 881
Запишите шесть целых чисел, которые не являются натуральными.
Решение
−1; −3; −5; −8; −10; −15.
Задание 882
Какие целые числа расположены на координатной прямой между числами:
1) 4 и 9;
2) −4 и 2;
3) −8,2 и 0;
4) −3 и 3;
5) −1,9 и 2,1;
6) −8/9 и 8/9?Решение
1) 5; 6; 7; 8.
2) −3; −2; −1; 0; 1.
3) −8; −7; −6; −5; −4; −3; −2; −1.
4) −2; −1; 0; 1; 2.
5) −1; 0; 1; 2.
6) 0. 190
-
Страница 190
Задание 883
Сколько целых чисел расположено на координатной прямой между числами:
1) −22 и 43;
2) −54 и 16?Решение
1)
Между -22 и 0 находится 21 число, между 43 и 0 находится 42 числа, да еще посчитаем 0, потому что этот тоже целое число.
21 + 42 + 1 = 64
2) 53 + 15 + 1 = 69Задание 884
Положительным или отрицательным является число a, если число −a является:
1) положительным;
2) отрицательным;
3) нулем?Решение
1) отрицательным
2) положительным
3) нулемЗадание 885
Может ли число a быть равным числу −a?
Решение
Да, если это число 0.
Задание 886
Какое из чисел a или −a расположено справа от нуля на координатной прямой?
Решение
1 вариант:
Если a положительное число, то число a расположено справа от нуля на координатной прямой.
2 вариант:
Если a отрицательное число, то число −a расположено справа от нуля на координатной прямой.Задание 887
Укажите какие−нибудь три значения a, для которых между числами −a и a на координатной прямой лежит только целое число.
Решение
0,2; 0,6; 0,9.
Задание 888
Существует ли такое значение a, при котором между числами −a и a на координатной прямой лежит тысяча целых чисел?
Решение
Нет, так как 1000 четное число, а между противоположными числами лежит нечетное количество целых чисел, так как есть число нуль.
Задание 889
Отец и сын могут вместе покрасить забор за 6 ч. За сколько часов отец может сам покрасить забор, если сыну для этого надо 24 ч?
Решение
Пусть весь забор равен единице, тогда: 1/6 забора могут вместе покрасить отец и сын за 1 час; 1/24 забора может покрасить сын за 1 час;
$\frac16-\frac1{24}=\frac{4-1}{24}=\frac3{24}=\frac18$ забора может покрасить отец за 1 час;
$1:\frac18=1\ast\frac81=8$ часов потребуется отцу, чтобы покрасить весь забор в одиночку.
Ответ: 8 часов.Задание 890
На базе хранились 1 т апельсинов и мандаринов. Апельсины составляли 99% массы этих фруктов. Сколько килограммов апельсинов вывезли с базы, если их осталось 98% от остатка фруктов?
Решение
1 т = 1000 кг.
1000 кг - 100 %
х кг - 99 %
1000/х = 100/99
100х = 1000*99
х = 990
Значит, 990 кг апельсинов хранилось на базе.
1000 - 990 = 10 (кг) - мандаринов хранилось на базе
100 - 98 = 2 (%) - мандаринов стало, когда вывезли часть апельсинов
Пусть x кг апельсинов осталось на базе.
х кг - 98 %
10 кг - 2 %
х/10 = 98/2
2х = 98 * 10
x = 490
Значит, 490 кг осталось на базе.
990 - 490 = 500 (кг) - апельсинов вывезли с базы
Ответ: 500 кг.Задание 891
Найдите значение выражения:
1) $\frac{5\frac17\ast\frac35:3\frac35}{12\frac14:1\frac34}=\frac{\frac{36}7\ast\frac35\ast\frac5{18}}{\frac{49}4\ast\frac47}=\frac{\frac27\ast\frac31\ast\frac11}{\frac71\ast\frac11}=\frac{\frac67}7=\frac67\ast\frac17=\frac6{49}$
2) $\frac{2\frac27\ast2,4\ast1\frac59\ast1\frac9{16}}{3\frac13\ast1,125\ast1\frac57\ast1\frac79}=\frac{\frac{16}7\ast\frac{12}5\ast\frac{14}9\ast\frac{25}{16}}{\frac{10}3\ast\frac98\ast\frac{12}7\ast\frac{16}9}=\frac{\frac11\ast\frac41\ast\frac23\ast\frac51}{\frac51\ast\frac11\ast\frac17\ast\frac{16}1}=\frac{40}3:\frac{80}7=\frac{40}3\ast\frac7{80}=\frac13\ast\frac72=\frac76=1\frac16$Задание 892
Отметили три точки, не лежащие на одной прямой. Сколько существует ломаных с вершинами в этих точках?
Решение
Ответ: 3 ломаных.
Задание 893
Для заболевшего Димы врач оставил шесть внешне одинаковых таблеток − по две каждого из трех видов лекарств. Диме нужно принять три таблетки утром (по одной каждого вида) и три вечером. Однако Дима перепутал все таблетки. Сможет ли он выполнить назначение врача?
Решение
6 таблеток выписал врач всего.
3 + 3 = 6 таблеток выпьет Дима, значит он выполнит предписание врача, так как выпьет все таблетки.
Ответ: да, сможет. 194-195
-
Страница 194-195
Ответы к параграфу 32. Модуль числа
Задание 894
Найдите модуль каждого из чисел:
2;−3;4,3;12,6;−17;−17 1/7;−36;0;5 11/16;−129. Запишите соответствующие равенства.Решение
|2| = 2;
|−3| = 3;
|4,3| = 4,3;
|12,6| = 12,6;
|−17| = 17;
$\vert-17\frac17\vert=17\frac17$;
|−36| = 36;
|0| = 0;
$\vert5\frac{11}{16}\vert=5\frac{11}{16}$;
|−129| = 129.Задание 895
Найдите значение выражения:
1) |5,1|+|−9,9|;
2) |−7/9|−|−4/15|;
3) |−9,6|:|32|;
4) |8/9|∗|−27/32|.Решение
1) |5,1|+|−9,9|=5,1+9,9=15
2) $\vert-\frac79\vert-\vert-\frac4{15}\vert=\frac79-\frac4{15}=\frac{35}{45}-\frac{12}{45}=\frac{23}{45}$
3) |−9,6|:|32|=9,6:32=0,3
4) $\vert\frac89\vert\ast\vert-\frac{27}{32}\vert=\frac89\ast\frac{27}{32}=\frac11\ast\frac34=\frac34$Задание 896
Найдите значение выражения:
1) |−3,5|−|2,6|;
2) |20/21|+|−5/7|;
3) |−2,1|∗|−3,7|;
4) |−1/16|:|−1 1/4|.Решение
1) |−3,5|−|2,6|=3,5−2,6=0,9
2) $\vert\frac{20}{21}\vert+\vert-\frac57\vert=\frac{20}{21}+\frac57=\frac{20+15}{21}=\frac{35}{21}=\frac53=1\frac23$
3) |−2,1|∗|−3,7|=2,1∗3,7=7,77
4) $\vert-\frac1{16}\vert:\vert-1\frac14\vert=\frac1{16}:\frac54=\frac1{16}\ast\frac45=\frac14\ast\frac15=\frac1{20}$Задание 897
Вычислите значение выражения |a| : |b|, если:
1) a=−5 1/3,b=1 5/9;
2) a = 1,38, b = −0,4.Решение
1) $\vert-5\frac13\vert:\vert1\frac59\vert=\frac{16}3:\frac{14}9=\frac{16}3\ast\frac9{14}=\frac81\ast\frac37=\frac{24}7=3\frac37$
2) |1,38| : |−0,4| = 1,38 : 0,4 = 3,45Задание 898
Вычислите значение выражения |a| − |b|, если:
1) a = −0,14, b = 0,1;
2) a = −2 11/12, b= −1 17/18.Решение
1) |−0,14| − |0,1| = 0,14 − 0,1 = 0,04
2) $\vert-2\frac{11}{12}\vert-\vert-1\frac{17}{18}\vert=2\frac{11}{12}-1\frac{17}{18}=2\frac{33}{36}-1\frac{34}{36}=1\frac{69}{36}-1\frac{34}{36}=\frac{35}{36}$Задание 899
Укажите положительное число, модуль которого равен:
1) 14;
2) 4,6.Решение
1) |14| = 14
Ответ: 14
2) |4,6| = 4,6
Ответ: 4,6Задание 900
Укажите отрицательное число, модуль которого равен:
1) 16;
2) 0,8.Решение
1) |−16| = 16
Ответ: −16
2) |−0,8| = 0,8
Ответ: −0,8Задание 901
Решите уравнение:
1) |x| = 12;
2) |x| = −8;
3) |x| = 0;
4) |−x| = 2,4.Решение
1) |x| = 12
x1=12
x2=−12
2) |x| = −8
нет решения, так как модуль числа не может быть отрицательным.
3) |x| = 0
x = 0
4) |−x| = 2,4
x1=2,4
x2=−2,4Задание 902
Отметьте на координатной прямой числа, модуль которых равен:
1) 5;
2) 7;
3) 2,5;
4) 0;
5) 3,5;
6) 4.Решение
1) |5| = 5;
|−5| = 5.
2) |7| = 7;
|−7| = 7.
3) |2,5| = 2,5;
|−2,5| = 2,5.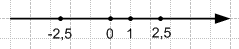
4) |0| = 0.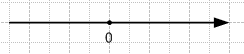
5) |3,5| = 3,5;
|−3,5| = 3,5.
6) |4| = 4;
|−4| = 4.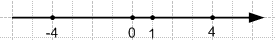
Задание 903
Решите уравнение:
1) |x| = 3,7;
2) |x| = −7,4;
3) |x| = 0,1.Решение
1) |x| = 3,7
x1=3,7
x2=−3,7
2) |x| = −7,4
нет решения, так как модуль числа не может быть отрицательным.
3) |x| = 0,1
x1=0,1
x2=−0,1Задание 904
Расположите числа −2,2; 8,6; 0,9; −6,8; −17,6; 0; 15 в порядке убывания их модулей.
Решение
|−17,6| = 17,6;
|15| = 15;
|8,6| = 8,6;
|−6,8| = 6,8;
|−2,2| = 2,2;
|0,9| = 0,9;
|0| = 0.
Ответ: −17,6; 15; 8,6; −6,8; −2,2; 0,9; 0.Задание 905
Расположите числа −9,4; 3; 4,7; −2,8; 0,4; −10,5 в порядке возрастания их модулей.
Решение
|0,4| = 0,4;
|−2,8| = 2,8;
|3| = 3;
|4,7| = 4,7;
|−9,4| = 9,4;
|−10,5 = 10,5.
Ответ: 0,4; −2,8; 3; 4,7; −9,4; −10,5.Задание 906
Запишите все целые числа, модули которых меньше 3,6.
Решение
|−3| = 3 < 3,6;
|−2| = 2 < 3,6;
|−1| = 1 < 3,6;
|0| = 0 < 3,6;
|1| = 1 < 3,6;
|2| = 2 < 3,6;
|3| = 3 < 3,6.
Ответ: −3; −2; −1; 0; 1; 2; 3.Задание 907
Запишите три положительных и три отрицательных числа, модули которых больше 9,2.
Решение
|10| = 10 > 9,2;
|11| = 11 > 9,2;
|15| = 15 > 9,2;
|−10| = 10 > 9,2;
|−11| = 11 > 9,2;
|−15| = 15 > 9,2.
Ответ: 10; 11; 15; −10; −11; −15.Задание 908
Отметьте на координатной прямой целые значения x, при которых верно неравенство:
1) |x| < 4;
2) 1,2 < |x| < 5.Решение
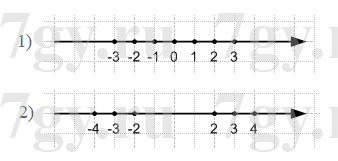
Задание 909
Отметьте на координатной прямой целые значения x, при которых верно неравенство:
1) |x| < 6,1;
2) 3,4 < |x| < 5,2.Решение
Задание 910
Для какого числа одновременно выполняются равенства |a| = a и |a| = −a?
Решение
Для a = 0.
Задание 911
Существует ли такое число a, что:
1) |a| = −|a|;
2) |−a| = −|a|?Решение
1) a = 0
2) a = 0 196
-
Страница 196
Задание 912
Верно ли утверждение:
1) если a = b, то |a| = |b|;
2) если |a| = |b|, то a = b;
3) если a = −b, то |a| = |b|;
4) если a = b, то |a| = b;
5) если |a| = |b|, то a = b или a = −b;
6) если a − целое число, то |a| − натуральное число?Решение
1) верно
2) неверно
3) верно
4) неверно
5) верно
6) неверноЗадание 913
За 1 ч напечатали 5/8 рукописи. За сколько часов напечатают всю рукопись?
Решение
$1:\frac58=1\ast\frac85=1\frac35$ ч потребуется, чтобы напечатать всю рукопись.
Ответ: $1\frac35$ ч.Задание 914
Найдите расстояние между двумя городами, если 4/9 этого расстояния на 20 км меньше всего расстояния.
Решение
Пусть x км расстояние между двумя городами, тогда:
$x-\frac49x=20$
$\frac59x=20$
$x=20:\frac59$
$x=20\ast\frac95$
x = 4 * 9
x = 36 км расстояние между двумя городами.
Ответ: 36 км.Задание 915
Вычислите значение выражения:
$0,9\ast(1\frac59-\frac49:(\frac58+\frac38:3))=\frac9{10}\ast(1\frac59-\frac49:(\frac58+\frac38\ast\frac13))=\frac9{10}\ast(1\frac59-\frac49:(\frac58+\frac18))=\frac9{10}\ast(1\frac59-\frac49:\frac34)=\frac9{10}\ast(1\frac59-\frac49\ast\frac43)=\frac9{10}\ast(1\frac59-\frac{16}{27})=\frac9{10}\ast(\frac{42}{27}-\frac{16}{27})=\frac9{10}\ast\frac{26}{27}=\frac15\ast\frac{13}3=\frac{13}{15}$
Задание 916
Сравните числа:
1) 6/7 и 17/21;
2) 7/12 и 11/15;
3) 5/9 и 4/7;
4) 3,4 и 3,38;
5) 0,02 и 0,019;
6) 0,001 и 0.Решение
1) $\frac67=\frac{18}{21}>\frac{17}{21}$
2) $\frac7{12}=\frac{35}{60}<\frac{11}{15}=\frac{44}{60}$
3) $\frac59=\frac{35}{63}<\frac47=\frac{36}{63}$
4) 3,4 > 3,38
5) 0,02 > 0,019
6) 0,001 > 0Задание 917
Расположите в порядке возрастания числа 5 5/8;5 3/5;5,7;4 1/2;6,1;4 9/16.
Решение
$5\frac58=5\frac{25}{40}$
$5\frac35=5\frac{24}{40}$
$5,7=5\frac7{10}=5\frac{28}{40}$
$4\frac12=4\frac8{16}$
Ответ: $4\frac12<4\frac9{16}<5\frac35<5\frac58<5,7<6,1$.Задание 918
В некотором весеннем месяце понедельников больше, чем вторников, а воскресений больше, чем суббот. Какой день недели был 7−го числа этого месяца? Какой это месяц?
Решение
В месяце 4 недели, а в неделе 7 дней, тогда:
7 * 4 = 28 дней.
Так как понедельников и воскресений больше, то:
28 + 1 + 1 = 30 дней в месяце, следовательно это апрель, так как в марте и мае по 31 день.
Ответ: апрель. 198
-
Страница 198
Ответы к параграфу 33. Сравнение чисел
Задание 919
Сравните числа:
1) 135 и −136;
2) −74 и 0;
3) −3,4 и −3,8;
4) −0,2 и −0,2001;
5) −7/13 и −7/16.Решение
1) 135 > −136
2) −74 < 0
3) −3,4 > −3,8
4) −0,2 > −0,2001
5) $-\frac7{13}<-\frac7{16}$Задание 920
Сравните числа:
1) −58 и 43;
2) 0 и −35;
3) −92 и −89;
4) −1,1 и −1,099;
5) −5/7 и −9/14.Решение
1) −58 < 43
2) 0 > −35
3) −92 < −89
4) −1,1 < −1,099
5) $-\frac57=-\frac{10}{14}<-\frac9{14}$Задание 921
Расположите в порядке убывания числа −10,9; 7; −4,8; 0; −4,9; 8,9; 9,5.
Решение
Ответ: 9,5 > 8,9 > 7 > 0 > −4,8 > −4,9 > −10,9.
Задание 922
Расположите в порядке возрастания числа −6; 5,3; 0,5; −5,9; 0; −11; 4,5.
Решение
Ответ: −11 > −6 > −5,9 > 0 > 0,5 > 4,5 > 5,3.
Задание 923
Расположите в таблице указанные вещества в порядке возрастания температуры их кипения.
Ответ

199
-
Страница 199
Задание 924
Запишите в виде неравенства утверждение:
1) 9 − положительное число;
2) −20 − отрицательное число;
3) −6 − неположительное число;
4) m − отрицательное число;
5) n − неотрицательное число;
6) c − положительное число.Решение
1) 9 > 0
2) −20 < 0
3) −6 ⩽ 0
4) m < 0
5) n ⩾ 0
6) c > 0Задание 925
Найдите все целые значения x, при которых верно неравенство:
1) −5,3 ⩽ x ⩽ 2,5;
2) −3,6 < x < 4,9;
3) −43 < x ⩽ −38;
4) −274,6 < x < −270,8.Решение
1) −5; −4; −3; −2; −1; 0; 1; 2.
2) −3; −2; −1; 0; 1; 2; 3; 4.
3) −42; −41; −40; −39; −38.
4) −274; −273; −272; −271.Задание 926
Найдите все целые значения x, при которых верно неравенство:
1) −5,6 ⩽ x ⩽ 2;
2) −0,61 ⩽ x < 4;
3) |x| ⩽ 0.Решение
1) −5; −4; −3; −2; −1; 0; 1; 2.
2) 0; 1; 2; 3.
3) 0.Задание 927
Найдите наименьшее целое число, при котором верно неравенство:
1) −9 < x < 3;
2) x ⩾ −10;
3) x ⩾ −2,6.Решение
1) −8
2) −10
3) −2Задание 928
Найдите наибольшее целое число, при котором верно неравенство:
1) −5 < x ⩽ 5,6;
2) x < −13;
3) x ⩽ −64,3.Решение
1) 5
2) −14
3) −65Задание 929
Между какими соседними числами лежит на координатной прямой число:
1) 5 9/17;
2) −8,4;
3) 0,45;
4) −0,17?Решение
1) $5<5\frac9{17}<6$
2) −9 < −8,4 < −8
3) 0 < 0,45 < 1
4) −1 < −0,17 < 0Задание 930
Напишите три последовательных целых числа, меньшее из которых равно:
1) 3;
2) −4;
3) −2.Решение
1) 3; 4; 5.
2) −4; −3; −2.
3) −2; −1; 0.Задание 931
Напишите четыре последовательных целых числа, большее из которых равно:
1) −8;
2) 0;
3) 3.Решение
1) −8; −9; −10; −11.
2) 0; −1; −2; −3.
3) 3; 2; 1; 0.Задание 932
Может ли число быть меньше 5, а его модуль − больше 5?
Решение
Может, например число −7 < 5, а |−7| > 5.
Задание 933
Какую цифру можно поставить вместо звездочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи):
1) −5,03 < −5,1;
2) −0,972 < −0,9872;
3) −9,36 > −9,332;
4) −2,09 < −27,1?Решение
1) −5,03 < −5,01
Ответ: 0.
2) −0,9972 < −0,9872
Ответ: 9.
3) −9,306 > −9,332;
−9,316 > −9,332;
−9,326 > −9,332.
Ответ: 0; 1; 2.
4) −28,09 < −27,1;
−29,09 < −27,1.
Ответ: 8; 9.Задание 934
Какую цифру можно поставить вместо звездочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
1) −6,46 > −6,415;
2) −32,1 < −32,17?Решение
1) −6,406 > −6,415
Ответ: 0
2) −32,18 < −32,17;
−32,19 < −32,17.
Ответ: 8; 9.Задание 935
На координатной прямой отметили числа a, b, m и n (рис.96). Сравните:
1) b и n;
2) m и a;
3) 0 и n;
4) a и 0;
5) m и n;
6) b и a;
7) −b и 0;
8) 0 > −a;
9) −a и m;
10) −b и n.
Решение
1) b > n
2) m > a
3) 0 < n
4) a < 0
5) m < n
6) b < a
7) −b < 0
8) 0 < −a
9) −a > m
10) −b < n 200
-
Страница 200
Задание 936
На каком из рисунков 97 (a − d) изображены числа a и b такие, что:
1) число a − отрицательное, число b − положительное;
2) числа a и b − положительные, |a| > |b|;
3) числа a и b − отрицательные, |a| < |b|?
Решение
1) а
2) д
3) бЗадание 937
Верно ли утверждение:
1) если a > 3, то a − положительное число;
2) если b < 1, то b − отрицательное число;
3) если c > −1, то c − положительное число;
4) если d < −2, то d − отрицательное число?Решение
1) верно
2) неверно
3) неверно
4) верноЗадание 938
Найдите все целые значения x, при которых верны одновременно оба двойных неравенства:
1) −7 < x < 3 и −5 ⩽ x ⩽ 9;
2) −3,8 ⩽ x ⩽ 4 и −2,6 < x < 6,3.Решение
1) −5; −4; −3; −2; −1; 0; 1; 2.
2) −2; −1; 0; 1; 2; 3; 4.Задание 939
Сравните числа −a и b, если:
1) числа a и b − положительные;
2) числа a и b − отрицательные.Решение
1) −a < b
2) −a > bЗадание 940
В записи чисел стерли несколько цифр и вместо них оставили звездочки. Сравните эти числа:
1) −4,2** и −4,6;
2) −0,628 и −0,627;
3) 0 и −,*.Решение
1) −4,2** > −4,6**
2) −0,628 < −0,627**
3) 0 > −,*Задание 941
В записи чисел стерли несколько цифр и вместо них оставили звездочки. Сравните эти числа:
1) −98* и −1;
2) −,* и −,;
3) −98,** и −4,*.Решение
1) −98* > −1***
2) −,** > −,
3) −98,** < −4,*Задание 942
Найдите два числа, каждое из которых:
1) больше 4/11, но меньше 5/11;
2) больше −5/11, но меньше −4/11.Решение

Задание 943
Верно ли утверждение:
1) если |a| > |b|, то a > b;
2) если |a| > b, то a > b;
3) если |a| < |b|, то a < b;
4) если a < b, то |a| < b?Решение
1) неверно
2) неверно
3) неверно
4) неверноЗадание 944
Сравните:
1) a и −a;
2) |a| и a;
3) |a| и −a.Решение
1) при a ⩾ 0:
a ⩾ −a;
при a < 0:
a < −a.
2) |a| ⩾ a
3) |a| ⩾ −a 201
-
Страница 201
Задание 945
С помощью записи [a] обозначают наибольшее целое число, которое не больше a. Например [3,2] = 3. Найдите:
1) [0,3];
2) [4];
3) [−3,2];
4) [−0,2].Решение
1) [0,3] = 0
2) [4] = 4
3) [−3,2] = −4
4) [−0,2] = −1Задание 946
Используя сторону равностороннего треугольника как диаметр, построили полуокружность (рис. 98). Чему равна длина красной линии, если сторона треугольника равна 6 см?
Решение
Диаметр полуокружности = 6 см, так как равен стороне треугольника;
6 : 2 = 3 см радиус полуокружности;
C = 2πr − длина окружности, тогда:
$C=\frac{2{\operatorname\pi}r}2={\operatorname\pi}r=3,14\ast3=9,42$ см длина полуокружности;
6 + 6 = 9,42 = 21,42 см длина красной линии.
Ответ: 21,42 см.Задание 947
Средний рост десяти баскетболистов равен 200 см, а средний рост шести из них составляет 190 см. Чему равен средний рост остальных четырех баскетболистов?
Решение
200 * 10 = 2000 см суммарный рост десяти баскетболистов;
190 * 6 = 1140 см суммарный рост шести баскетболистов;
2000 − 1140 = 860 см суммарный рост четырех баскетболистов;
860 : 4 = 215 см средний рост четырех баскетболистов.
Ответ: 215 см.Задание 948
Найдите значение выражения:
$2\frac14-1\frac14\ast(\frac27+3\frac17\ast\frac13):0,7$Решение
$2\frac14-1\frac14\ast(\frac27+3\frac17\ast\frac13):0,7=\frac56$
1) $3\frac17\ast\frac13=\frac{22}7\ast\frac13=\frac{22}{21}$
2) $\frac27+\frac{22}{21}=\frac{6+22}{21}=\frac{28}{21}=\frac43$
3) $1\frac14\ast\frac43=\frac54\ast\frac43=\frac51\ast\frac13=\frac53=1\frac23$
4) $2\frac14-1\frac23=2\frac3{12}-1\frac8{12}=1\frac{15}{12}-1\frac8{12}=\frac7{12}$
5) $\frac7{12}:0,7=\frac7{12}:\frac7{10}=\frac7{12}\ast\frac{10}7=\frac16\ast\frac51=\frac56$Задание 949
Какое число должно быть записано на координатной прямой в том месте, куда указывает стрелка (рис. 99)?

Решение
а) 34 + 8 = 42
Ответ: 42
б) 120 − 34 = 86
Ответ: 86Задание 950
Какое число должно быть записано на координатной прямой в том месте, откуда указывает стрелка (рис. 100)?

Решение
а) 41 − 6 = 35
Ответ: 35
б) 96 + 18 = 114
Ответ: 114 202
-
Страница 202
Задание 951
У нескольких бревен длиной 4 м и 5 м общая длина 45 м. Какое наибольшее количество распилов необходимо сделать, чтобы распилить все бревна на чурбаки длиной 1 м? (Каждым распилом разрезают только одно бревно.)
Решение
Наибольшее количество распилов нужно будет сделать, если бревен разной длины будет равное количества, то есть 5 бревен по 4 м и 5 бревен по 5 м.
Для того, чтобы распилить четырехметровое бревно на чурбаки длиной 1 м нужно сделать 3 распила, а пятиметровое нужно сделать 4 распила, тогда:
3 * 5 + 4 * 5 = 15 + 20 = 35 распилов всего необходимо сделать.
Ответ: 35 распилов. 205
-
Страница 205
Ответы к параграфу 34. Сложение рациональных чисел
Задание 952
Заполните таблицу:
Решение
−5 + (−3) = −(5 + 3) = −8;
−8 + (−9) = −(8 + 9) = −17;
−0,5 + (−0,7) = −(0,5 + 0,7) = −1,2;
12 + (−8) = 12 − 8 = 4;
−12 + 8 = −(12 − 8) = −4;
5 + (−3) = 5 − 3 = 2;
−8 + 9 = 9 − 8 = 1;
−0,5 + 0,3 = −(0,5 − 0,3) = −0,2;
−12 + 12 = 12 − 12 = 0;
0 + (−5) = −(5 − 0) = −5.
Задание 953
Утром температура воздуха была −4°C. Вечером:
1) потеплело на 3°C;
2) похолодало на 3°C;
3) потеплело на 4°C;
4) потеплело на 6°C.
Запишите в каждом случае вечернюю температуру в виде суммы и вычислите ее.Решение
1) −4 + 3 = −(4 − 3) = −1°C
Ответ: −1°C
2) −4 − 3 = −(4 + 3) = −7°C
Ответ: −7°C
3) −4 + 4 = −(4 − 4) = 0°C
Ответ: 0°C
4) −4 + 6 = 6 − 4 = 2°C
Ответ: 2°CЗадание 954
Выполните сложение:
1) −9 + 6;
2) 4 + (−1);
3) −6 + 20;
4) 20 + (−40);
5) −2,3 + 1,4;
6) 1,6 + (−4,1);
7) −0,8 + 1;
8) −1,8 + 1,8.Решение
1) −9 + 6 = −(9 − 6) = −3
2) 4 + (−1) = 4 − 1 = 3
3) −6 + 20 = 20 − 6 = 14
4) 20 + (−40) = −(40 − 20) = −20
5) −2,3 + 1,4 = −(2,3 − 1,4) = −0,9
6) 1,6 + (−4,1) = −(4,1 − 1,6) = −2,5
7) −0,8 + 1 = 1 − 0,8 = 0,2
8) −1,8 + 1,8 = 1,8 − 1,8 = 0Задание 955
Выполните сложение:
1) −7 + 12;
2) 13 + (−18);
3) −19 + 15;
4) 40 + (−20);
5) −1,7 + 3;
6) 2,8 + (−5,5);
7) 5 + (−6,9);
8) 2,7 + (−2,7).Решение
1) −7 + 12 = 12 − 7 = 5
2) 13 + (−18) = −(18 − 13) = −5
3) −19 + 15 = −(19 − 15) = −4
4) 40 + (−20) = 40 − 20 = 20
5) −1,7 + 3 = 3 − 1,7 = 1,3
6) 2,8 + (−5,5) = −(5,5 − 2,8) = −2,7
7) 5 + (−6,9) = −(6,9 − 5) = −1,9
8) 2,7 + (−2,7) = 2,7 − 2,7 = 0 206
-
Страница 206
Задание 956
Найдите сумму:
1) −6 + (−5);
2) −0,7 + (−2,8);
3) −0,82 + (−0,18);
4) −5/7+(−9/14);
5) −1/4+(−1/6);
6) −3/8+0.Решение
1) −6 + (−5) = −(6 + 5) = −11
2) −0,7 + (−2,8) = −(0,7 + 2,8) = −3,5
3) −0,82 + (−0,18) = −(0,82 + 0,18) = −1
4) $-\frac57+(-\frac9{14})=-(\frac57+\frac9{14})=-(\frac{10}{14}+\frac9{14})=-\frac{19}{14}=-1\frac5{14}$
5) $-\frac14+(-\frac16)=-(\frac14+\frac16)=-(\frac3{12}+\frac2{12})=-\frac5{12}$
6) $-\frac38+0=-\frac38$Задание 957
Найдите сумму:
1) −9 + (−13);
2) −3,6 + (−1,5);
3) −5/16+(−7/16);
4) −3/7+(−4/9).Решение
1) −9 + (−13) = −(9 + 13) = −22
2) −3,6 + (−1,5) = −(3,6 + 1,5) = −5,1
3) $-\frac5{16}+(-\frac7{16})=-(\frac5{16}+\frac7{16})=-\frac{12}{16}=-\frac34$
4) $-\frac37+(-\frac49)=-(\frac37+\frac49)=-(\frac{27}{63}+\frac{28}{63})=-\frac{55}{63}$Задание 958
Вычислите значение выражения:
1) $\frac2{15}+(-\frac3{10})=\frac4{30}+(-\frac9{30})=-(\frac9{30}-\frac4{30})=-\frac5{30}=-\frac16$
2) $-\frac23+\frac{13}{15}=-\frac{10}{15}+\frac{13}{15}=\frac{13}{15}-\frac{10}{15}=\frac3{15}=\frac15$
3) $\frac{13}{16}+(-\frac9{32})=\frac{26}{32}+(-\frac9{32})=\frac{26}{32}-\frac9{32}=\frac{17}{32}$
4) $-4\frac59+(-7\frac16)=-4\frac{10}{18}+(-7\frac3{18})=-(4\frac{10}{18}+7\frac3{18})=-11\frac{13}{18}$
5) $-5\frac78+(-6\frac3{10})=-5\frac{35}{40}+(-6\frac{12}{40})=-(5\frac{35}{40}+6\frac{12}{40})=-11\frac{47}{40}=-12\frac7{40}$
6) $-5\frac{13}{18}+12\frac{11}{12}=12\frac{33}{36}-5\frac{26}{36}=7\frac7{36}$
7) $-13+7\frac3{16}=-(12\frac{16}{16}-7\frac3{16})=-5\frac{13}{16}$
8) $-2\frac38+(-1\frac59)=-(2\frac{27}{72}+1\frac{40}{72})=-3\frac{67}{72}$
9) $-8+4\frac5{22}=-(7\frac{22}{22}-4\frac5{22})=-3\frac{17}{22}$
10) $-2\frac9{20}+5\frac7{30}=5\frac{14}{60}-2\frac{27}{60}=4\frac{74}{60}-2\frac{27}{60}=2\frac{47}{60}$
11) $-5\frac14+1\frac38=-(5\frac28-1\frac38)=-(4\frac{10}8-1\frac38)=-3\frac78$
12) $4\frac37+(-8\frac9{14})=-(8\frac9{14}-4\frac6{14})=-4\frac3{14}$Задание 959
Вычислите значение выражения:
1) $-\frac14+\frac35=-\frac5{20}+\frac{12}{20}=\frac7{20}$
2) $\frac9{11}+(-\frac25)=\frac{45}{55}+(-\frac{22}{55})=\frac{23}{55}$
3) $-\frac{20}{21}+\frac37=-\frac{20}{21}+\frac9{21}=-(\frac{20}{21}-\frac9{21})=-\frac{11}{21}$
4) $-8\frac9{14}+3\frac37=-8\frac9{14}+3\frac6{14}=-(8\frac9{14}-3\frac6{14})=-5\frac3{14}$
5) $7\frac5{12}+(-3\frac7{24})=7\frac{10}{24}-3\frac7{24}=4\frac3{24}=4\frac18$
6) $-6\frac{11}{12}+(-8\frac{13}{18})=-(6\frac{33}{36}+8\frac{26}{36})=-14\frac{59}{36}=-15\frac{23}{36}$
7) $-5\frac{12}{35}+10=9\frac{35}{35}-5\frac{12}{35}=4\frac{23}{35}$
8) $-11\frac79+8\frac2{15}=-(11\frac{35}{45}-8\frac6{45})=-3\frac{29}{45}$
9) $-3\frac1{12}+\frac16=-(3\frac1{12}-\frac2{12})=-(2\frac{13}{12}-\frac2{12})=-2\frac{11}{12}$
10) $3\frac67+(-6\frac49)=-(6\frac{28}{63}-3\frac{54}{63})=-(5\frac{91}{63}-3\frac{54}{63})=-2\frac{37}{63}$
11) $9\frac16+(-5\frac34)=9\frac2{12}-5\frac9{12}=8\frac{14}{12}-5\frac9{12}=3\frac5{12}$
12) $-3\frac89+(-2\frac1{12})=-(3\frac{32}{36}+2\frac3{36})=-5\frac{35}{36}$Задание 960
Самая низкая температура, полученная в лабораторных условиях, равна −273,14°C, что на 4,21°C ниже температуры кипения гелия. Чему равна температура кипения гелия?
Решение
−273,14 + 4,21 = −(273,14 − 4,21) = −268,93°C температура кипения гелия.
Ответ: −268,93°CЗадание 961
Представьте в виде сумм двух равных слагаемых число:
1) −12;
2) 7;
3) −9.Решение
1) −12 = −6 + (−6)
2) 7 = 3,5 + 3,5
3) −9 = −4,5 + (−4,5)Задание 962
Составьте числовое выражение и вычислите его значение:
1) к сумме чисел 7 и −20 прибавить число 18;
2) к числу 7,9 прибавить сумму чисел 2,1 и −10;
3) к сумме чисел 3 11/16 и −2 5/16 прибавить сумму чисел 4 17/36 и −1 11/36.Решение
1) (7 + (−20)) + 18 = −13 + 18 = 5
2) 7,9 + (2,1 + (−10)) = 7,9 + (−7,9) = 0
3) $(3\frac{11}{16}+(-2\frac5{16}))+(4\frac{17}{36}+(-1\frac{11}{36}))=1\frac6{16}+3\frac6{36}=1\frac38+3\frac2{12}=1\frac9{24}+3\frac4{24}=4\frac{13}{24}$ 207
-
Страница 207
Задание 963
Составьте числовое выражение и вычислите его значение:
1) к сумме чисел −6 и −19 прибавить число 15;
2) к числу −3,6 прибавить сумму чисел −7,2 и 4,5;
3) к сумме чисел −1,4 и −1,8 прибавить сумму чисел −5,2 и 8,1.Решение
1) (−6 + (−19)) + 15 = −25 + 15 = −10
2) −3,6 + (−7,2 + 4,5) = −3,6 + (−2,7) = −6,3
3) (−1,4 + (−1,8)) + (−5,2 + 8,1) = −3,2 + 2,9 = −0,3Задание 964
В кассе было 5000 р. В течении дня кассир несколько раз выдавал и принимал деньги, делая записи: −120 р., −300 р., 460 р., 530 р., −1270 р., −650 р. Сколько рублей осталось в кассе в конце дня?
Решение
5000 − 120 − 300 + 460 + 530 − 1270 − 650 = 3650 рублей осталось в кассе в конце дня.
Ответ: 3650 рублей.Задание 965
Водолаз достиг отметки −34 м. Выполняя работу он изменял глубину погружения на 6 м, 12 м, −17 м, −3 м, 20 м, −5 м. На какой глубине оказался водолаз после окончания работы?
Решение
−34 + 6 + 12 − 17 − 3 + 20 − 5 = −21 м − глубина на которой оказался водолаз после окончания работы.
Ответ: −21 м.Задание 966
При a = −6,3, b = 2,7 найдите значение выражения:
1) a + b;
2) |a| + b;
3) a + |b|;
4) |a + b|;
5) |a| + |b|.Решение
1) a + b = −6,3 + 2,7 = −3,6
2) |a| + b = |−6,3| + 2,7 = 6,3 + 2,7 = 9
3) a + |b| = −6,3 + |2,7| = −6,3 + 2,7 = −3,6
4) |a + b| = |−6,3 + 2,7| = |−3,6| = 3,6
5) |a| + |b| = |−6,3| + |2,7| = 6,3 + 2,7 = 9Задание 967
Найдите значение выражения |x + y| + x, если:
1) x = 2,8, y = −3,9;
2) x = −4,5, y = 7,2;
3) x = −2,3, y = −6,2;
4) x = −1 4/15,y = 2 7/18.Решение
1) |x + y| + x = |2,8 + (−3,9)| + 2,8 = |−1,1| + 2,8 = 1,1 + 2,8 = 3,9
2) |x + y| + x = |−4,5 + 7,2| + (−4,5) = |2,7| + (−4,5) = 2,7 + (−4,5) = −1,8
3) |x + y| + x = |−2,3 + (−6,2)| + (−2,3) = |−8,5| + (−2,3) = 8,5 − 2,3 = 6,2
4) $\vert x+y\vert+x=\vert-1\frac4{15}+2\frac7{18}\vert+(-1\frac4{15})=\vert-1\frac{24}{90}+2\frac{35}{90}\vert+(-1\frac{24}{90})=\vert1\frac{11}{90}\vert+(-1\frac{24}{90})=1\frac{11}{90}+(-1\frac{24}{90})=-\frac{13}{90}$Задание 968
Найдите значение выражений |a| + |b| и |a + b|, если:
1) a = −3, b = −7;
2) a = −4, b = 10;
3) a = 7,2, b = 2,8.
Какими должны быть числа a и b, чтобы выполнялось равенство |a + b| = |a| + |b|?Решение
1) |a| + |b| = |−3| + |−7| = 3 + 7 = 10;
|a + b| = |−3 + (−7)| = |−10| = 10.
2) |a| + |b| = |−4| + |10| = 4 + 10 = 14;
|a + b| = |−4 + 10| = |6| = 6.
3) |a| + |b| = |7,2| + |2,8| = 7,2 + 2,8 = 10;
|a + b| = |7,2 + 2,8| = |10| = 10.
Для того, чтобы выполнялось равенство |a + b| = |a| + |b|, числа a и b должны быть либо оба положительными, либо оба отрицательными.Задание 969
Может ли сумма двух чисел быть меньше каждого из слагаемых? В случае утвердительного ответа приведите пример. Какими числами должны быть в этом случае слагаемые? Какими числами должны быть слагаемые, чтобы их сумма была больше каждого из них?
Решение
Сумма двух чисел может быть меньше каждого из слагаемых, если оба слагаемых отрицательные числа, например:
−5 + (−2) = −7, где −7 < −5 и −7 < −2.
Сумма двух чисел может быть больше каждого из слагаемых, если оба слагаемых положительные числа, например:
5 + 2 = 7, где 7 > 5 и 7 > 2.Задание 970
При каких значениях x верно неравенство:
1) |x| > x;
2) |x| < x?Решение
1) неравенство |x| > x верно при x < 0
2) неравенство |x| < x не будет верно ни при каких xЗадание 971
По одной дороге в одном направлении ехали Емеля на печи и Иван Царевич на Сером Волке. В 10 ч 50 мин расстояние между ними было 51 км. Скорость печи, двигавшейся впереди, равна 12 км/ч, что составляет 18/35 скорости, с которой бежал Волк. В котором часу Иван Царевич догонит Емелю?
Решение
1) $12:\frac{18}{35}=12\ast\frac{35}{18}=2\ast\frac{35}3=\frac{70}3=23\frac13$ (км/ч) - скорость Волка;
2) $23\frac13-12=11\frac13$ (км/ч) - скорость сближения Волка и печи;
3) $51:11\frac13=51:\frac{34}3=51\ast\frac3{34}=3\ast\frac32=\frac92=4,5$ = 4 ч 30 мин - потребуется Иван Царевичу, чтобы догнать Емелю;
10 ч 50 мин + 4 ч 30 мин = 14 ч 80 мин = 15 ч 20 мин время в которое Иван Царевич догонит Емелю.
Ответ: в 15 ч 20 мин.Задание 972
Дима съел треть конфет, которые были в коробке, и еще четыре конфеты. После этого в коробке осталось 12 конфет. Сколько конфет было в коробке сначала?
Решение
Пусть x конфет было в коробке сначала, тогда:
$$ конфет съел Дима.
Так как в коробке осталось 12 конфет, то:
$x-(\frac13x+4)=12$
$x-\frac13x-4=12$
$\frac23x=12+4$
$x=16:\frac23$
$x=16\ast\frac32$
x = 8 * 3
x = 24 конфеты было в коробке сначала.
Ответ: 24 конфеты.Задание 973
В записи числа 3728954106 зачеркните три цифры так, чтобы оставшиеся цифры в том же порядке составили наименьшее из возможных чисел.
Решение
$\cancel3\cancel728\cancel954106$, тогда наименьшее число равно 2854106.
Ответ: 2854106. 208
-
Страница 208
Задание 974
Выполните сложение, выбирая удобный порядок вычислений:
1) (1,65 + 0,158) + 2,35;
2) 4,12 + 6,24 + 3,76 + 5,88.Решение
1) (1,65 + 0,158) + 2,35 = (1,65 + 2,35) + 0,158 = 4 + 0,158 = 4,158
2) 4,12 + 6,24 + 3,76 + 5,88 = (4,12 + 5,88) + (6,24 + 3,76) = 10 + 10 = 20Задание 975
Каждый участник шахматного турнира, играя белыми фигурами, выиграл столько партий, сколько все остальные вместе, играя черными. Докажите, что все участники одержали одинаковое количество побед.
Решение
Пусть каждый участник турнира сыграл n партий белыми фигурами, тогда по условию задачи, каждый участник турнира выиграл белыми n/2 партий и проиграл белыми n/2 партий. Так как количество побед и поражений у каждого участника одинаковое, следовательно все участники одержали одинаковое количество побед.
209
-
Страница 209
Ответы к параграфу 35. Свойства сложения рациональных чисел
Задание 976
Вычислите, используя свойства сложения:
1) (−5 + 19) + (−19);
2) (−16 + (−17)) + 17;
3) −0,4 + 0,8 + 0,4;
4) (−2/7+1)+(−5/7);
5) 4/15+(−8/25)+(−4/15);
6) 9 + (−12) + (−9) + 20.Решение
1) (−5 + 19) + (−19) = −5 + (19 − 19) = −5 + 0 = −5
2) (−16 + (−17)) + 17 = −16 + (17 − 17) = −16 + 0 = −16
3) −0,4 + 0,8 + 0,4 = (0,4 − 0,4) + 0,8 = 0 + 0,8 = 0,8
4) $(-\frac27+1)+(-\frac57)=(-\frac27+(-\frac57))+1=-\frac77+1=-1+1=0$
5) $\frac4{15}+(-\frac8{25})+(-\frac4{15})=(\frac4{15}-\frac4{15})+(-\frac8{25})=0+(-\frac8{25})=-\frac8{25}$
6) 9 + (−12) + (−9) + 20 = (9 − 9) + (20 − 12) = 0 + 8 = 8Задание 977
Выполните сложение, выбирая удобный порядок вычислений:
1) 7,29 + (−5,126) + (−6,29) + 5,126;
2) 24,35 + (−72,61) + 42,61 + (−13,35).Решение
1) 7,29 + (−5,126) + (−6,29) + 5,126 = (7,29 − 6,29) + (5,126 − 5,126) = 1 + 0 = 1
2) 24,35 + (−72,61) + 42,61 + (−13,35) = (24,35 − 13,35) + (−72,61 + 42,61) = 11 + (−30) = −19Задание 978
Выполните сложение, выбирая удобный порядок вычислений:
1) −6,38 + (−1,73) + 5,38 + 1,73;
2) −3,72 + 9,84 + 1,72 + (−20,84).Решение
1) −6,38 + (−1,73) + 5,38 + 1,73 = (−6,38 + 5,38) + (1,73 − 1,73) = −1 + 0 = −1
2) −3,72 + 9,84 + 1,72 + (−20,84) = (−3,72 + 1,72) + (−20,84 + 9,84) = −2 + (−11) = −13Задание 979
Найдите значение выражения:
1) −78 + 36 + 19 + (−22) + (−25);
2) 0,74 + (−9,39) + 3,26 + (−10,61) + 5,25;
3) 7/16+(−11/42)+(−9/16)+17/42;
4) −9/40+13/50+(−23/50)+19/40;
5) −3 31/36+(−1 17/24)+5 4/36+(−2 4/24).Решение
1) −78 + 36 + 19 + (−22) + (−25) = (−78 + (−22)) + (36 + 19 − 25) = −100 + 30 = −70
2) 0,74 + (−9,39) + 3,26 + (−10,61) + 5,25 = (−10,61 + (−9,39)) + (0,74 + 3,26) + 5,25 = −20 + 4 + 5,25 = −20 + 9,25 = −10,75
3) $\frac7{16}+(-\frac{11}{42})+(-\frac9{16})+\frac{17}{42}=(\frac7{16}+(-\frac9{16}))+(\frac{17}{42}-\frac{11}{42})=-\frac2{16}+\frac6{42}=-\frac18+\frac17=-\frac7{56}+\frac8{56}=\frac1{56}$
4) $-\frac9{40}+\frac{13}{50}+(-\frac{23}{50})+\frac{19}{40}=(\frac{19}{40}-\frac9{40})+(-\frac{23}{50}+\frac{13}{50})=\frac{10}{40}+(-\frac{10}{50})=\frac14+(-\frac15)=\frac5{20}+(-\frac4{20})=\frac1{20}$
5) $-3\frac{31}{36}+(-1\frac{17}{24})+5\frac4{36}+(-2\frac4{24})=(-3\frac{31}{36}+4\frac{40}{36})+(-1\frac{17}{24}+(-2\frac4{24}))=1\frac9{36}+(-3\frac{21}{24})=1\frac14+(-3\frac78)=1\frac28+(-3\frac78)=-2\frac58$ 210
-
Страница 210
Задание 980
Найдите значение выражения:
1) 43 + (−60) + 12 + 39 + (−21);
2) −1,23 + 2,14 + 7,38 + (−5,77) + 1,62;
3) −3/7+14/19+(−4/7)+3 5/19;
4) −5/18+(−4/81)+7/18+13/81;
5) −3 5/11+1 3/8+2 5/16+(−4 6/11).Решение
1) 43 + (−60) + 12 + 39 + (−21) = (43 + 12 + 39) + (−60 + (−21)) = 94 + (−81) = 13
2) −1,23 + 2,14 + 7,38 + (−5,77) + 1,62 = (7,38 + 1,62) + (−5,77 + (−1,23)) + 2,14 = 9 + 2,14 + (−7) = 11,14 − 7 = 4,14
3) $-\frac37+\frac{14}{19}+(-\frac47)+3\frac5{19}=(-\frac37+(-\frac47))+(\frac{14}{19}+3\frac5{19})=-\frac77+3\frac{19}{19}=-1+4=3$
4) $-\frac5{18}+(-\frac4{81})+\frac7{18}+\frac{13}{81}=(-\frac5{18}+\frac7{18})+(-\frac4{81}+\frac{13}{81})=\frac2{18}+\frac9{81}=\frac19+\frac19=\frac29$
5) $-3\frac5{11}+1\frac38+2\frac5{16}+(-4\frac6{11})=(-3\frac5{11}+(-4\frac6{11}))+(1\frac38+2\frac5{16})=-7\frac{11}{11}+(1\frac6{16}+2\frac5{16})=-8+3\frac{11}{16}=-7\frac{16}{16}+3\frac{11}{16}=-4\frac5{16}$Задание 981
Упростите выражение и найдите его значение:
1) 7,44 + a + (−3,5) + (−5,44) + (−12,5) + b, если a = 9,6; b = −5,7;
2) −5 9/35 + p + 4 11/28 + 6 2/35 + (−5 18/28) + k, если p = −2 19/30, k = 9.Решение
1) 7,44 + a + (−3,5) + (−5,44) + (−12,5) + b = (7,44 + (−5,44)) + (−3,5 + (−12,5)) + a + b = 2 + (−16) + a + b = −14 + a + b
При a = 9,6; b = −5,7
−14 + a + b = −14 + 9,6 + (−5,7) = 4,4 + (−5,7) = −10,1
2) $-5\frac9{35}+p+4\frac{11}{28}+6\frac2{35}+(-5\frac{18}{28})+k=(-5\frac9{35}+5\frac{37}{35})+(4\frac{11}{28}+(-5\frac{18}{28}))+p+k=\frac{28}{35}+(-1\frac7{28})+p+k=\frac45+(-1\frac14)+p+k=\frac{16}{20}+(-1\frac5{20})+p+k=\frac{16}{20}+(-\frac{25}{20})+p+k=-\frac9{20}+p+k$
При p = $-2\frac{19}{30}$, k = 9
$-\frac9{20}+(-2\frac{19}{30})+9=-\frac{27}{60}+(-2\frac{38}{60})+9=-2\frac{65}{60}+9=-3\frac5{60}+9=-3\frac1{12}+9=5\frac{11}{12}$Задание 982
Упростите выражение и найдите его значение:
1) −2,8 + x + 5,36 + (−7,2) + y + (−7,36), если x = −13, y = 54;
2) m + (−2 4/9) + 8 13/24 + n + (−3 2/9) + (−4 5/24), если m = −3 5/6,n = −2 11/12.Решение
1) −2,8 + x + 5,36 + (−7,2) + y + (−7,36) = (−2,8 + (−7,2)) + (5,36 + (−7,36)) + x + y = −10 + (−2) + x + y = −12 + x + y
При x = −13, y = 54
−12 + (−13) + 54 = −25 + 54 = 29
2) $m+(-2\frac49)+8\frac{13}{24}+n+(-3\frac29)+(-4\frac5{24})=(-2\frac49+(-3\frac29))+(8\frac{13}{24}+(-4\frac5{24}))+m+n=-5\frac69+4\frac8{24}+m+n=-5\frac23+4\frac13+m+n=-1\frac13+(-3\frac56)+(-2\frac{11}{12})=-1\frac4{12}+(-3\frac{10}{12})+(-2\frac{11}{12})=-6\frac{25}{12}=-8\frac1{12}$Задание 983
В течении шести дней уровень воды в водохранилище изменялся соответственно на: −3,2 дм; 1,6 дм; 4,3 дм; −2,2 дм; −1,9 дм и −0,8 дм. На сколько дециметров изменился уровень воды за шесть дней?
Решение
−3,2 + 1,6 + 4,3 − 2,2 − 1,9 − 0,8 = 5,9 − 8,1 = −2,2 дм, значит уровень воды понизился на 2,2 дм.
Ответ: на 2,2 дм понизился уровень воды.Задание 984
Найдите сумму всех целых чисел:
1) расположенных на координатной прямой между числами −8 и 11;
2) удовлетворяющих неравенству −9,8 < x < 6.Решение
1) −7 + (−6) + (−5) + (−4) + (−3) + (−2) + (−1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (−7 + 7) + (−6 + 6) + (−5 + 5) + (−4 + 4) + (−3 + 3) + (−2 + 2) + (−1 + 1) + 0 + 8 + 9 + 10 = 27
2) −9 + (−8) + (−7) + (−6) + (−5) + (−4) + (−3) + (−2) + (−1) + 0 + 1 + 2 + 3 + 4 + 5 = −9 + (−8) + (−7) + (−6) + (−5 + 5) + (−4 + 4) + (−3 + 3) + (−2 + 2) + (−1 + 1) + 0 = −30Задание 985
Запишите наибольшее и наименьшее отрицательные целые числа, в записи которых использованы две цифры.
Решение
−10 наибольшее число;
−99 наименьшее число.Задание 986
Найдите сумму двух чисел, одно из которых обратно числу 3, а второе − противоположно числу 3.
Решение
1/3 обратно числу 3;
−3 противоположно числу 3, тогда:
$\frac13+(-3)=-2\frac23$Задание 987
Положительным или отрицательным является число a, если:
1) −2 + a > −2;
2) −2 + a < −2;
3) −2 + (−a) > −2?Решение
1) −2 + a > −2
a > −2 + 2
a > 0
Ответ: положительным.
2) −2 + a < −2
a < −2 + 2
a < 0
Ответ: отрицательным.
3) −2 + (−a) > −2
−a > −2 + 2
−a > 0
a < 0
Ответ: отрицательным.Задание 988
Найдите периметр четырехугольника, если его стороны пропорциональны числам 3, 4, 5 и 8, а наибольшая сторона на 10,5 см больше наименьшей.
Решение
Пусть k − коэффициент пропорциональности, тогда:
8k − 3k = 10,5
5k = 10,5
k = 10,5 : 5
k = 2,1, следовательно теперь можно найти длины сторон:
3k = 3 * 2,1 = 6,3 см длина первой стороны;
4k = 4 * 2,1 = 8,4 см длина второй стороны;
5k = 5 * 2,1 = 10,5 см длина третьей стороны;
8k = 8 * 2,1 = 16,8 см длина четвертой стороны.
P = 6,3 + 8,4 + 10,5 + 16,8 = 42 см периметр четырехугольника.
Ответ: 42 см.Задание 989
Сергей Иванович положил в банк 4000 р. под 5% годовых. Какая сумма будет у него на счете через:
1) 1 год;
2) 2 года;
3) 3 года?Решение
1) 4000 + 4000 * 5% = 4000 + 4000 * 0,05 = 4000 * 1,05 = 4200 рублей будет на счете у Сергей Ивановича через 1 год.
2) 4200 * 1,05 = 4410 рублей будет на счете у Сергей Ивановича через 2 года.
3) 4410 * 1,05 = 4630 рублей будет на счете у Сергей Ивановича через 3 года.
Ответ: 4200 р.; 4410 р.; 4630 р.Задание 990
Флаги некоторых стран состоят из трех горизонтальных полос разного цвета. Сколько разных флагов с белой, синей и красной полосами можно составить?
Решение
Флаги будут отличаться порядком следования полос, тогда:
первый цвет можно выбрать один из трех, то есть тремя вариантами;
второй цвет можно выбрать один из оставшихся двух цветов, то есть двумя вариантами;
третий цвет можно выбрать одним вариантом, так неиспользованным остался только один цвет.
3 * 2 * 1 = 6 комбинаций флагов можно составить из трех разных цветов.
Ответ: 6 разных флагов. 211
-
Страница 211
Задание 991
Используя действие сложения, проверьте, верно ли выполнено вычитание:
1) 13,62 − 4,12 = 9,5;
2) 11/24−3/8=1/12.Решение
1) 9,5 + 4,12 = 13,62
Ответ: верно
2) $\frac1{12}+\frac38=\frac2{24}+\frac9{24}=\frac{11}{24}$
Ответ: верноЗадание 992
У электромонтера есть два куска провода, общая длина которых 25 м. От них он планирует отрезать необходимые для работы куски в 1 м, 2 м, 3 м, 6 м, 12 м. Сможет ли электромонтер отрезать необходимые для работы куски провода?
Решение
Так как 25 : 2 = 12,5 м, следовательно один из кусков провода будет обязательно больше 12 метров, а значит 12 м отрезать можно.
25 − 12 = 13 м длина оставшихся двух кусков.
13 : 2 = 6,5 м, следовательно один из кусков провода будет обязательно больше 6 м, а значит можно отрезать 6 метров.
13 − 6 = 7 м длина оставшихся двух кусков.
7 : 2 = 3,5 м, следовательно один из кусков провода будет обязательно больше 3 м, а значит можно отрезать 3 метра.
7 − 3 = 4 м длина оставшихся двух кусков.
4 : 2 = 2 м, следовательно один из кусков провода будет обязательно равен или больше 2 м, а значит можно отрезать 2 метра.
4 − 2 = 2 м длина оставшихся двух кусков.
2 : 1 = 1 м, следовательно один из кусков провода будет обязательно равен или больше 1 м, а значит можно отрезать 1 метр.
Ответ: может. 212-213
-
Страница 212-213
Ответы к параграфу 36. Вычитание рациональных чисел
Задание 993
Выполните вычитание:
1) 10 − 16;
2) 5 − 12;
3) −5 − 3;
4) −6 − 8;
5) 9 − (−2);
6) 4 − (−10);
7) −3 − (−8);
8) −11 − (−6);
9) 12,3 − (−6,8);
10) 2,4 − 5,6;
11) 0 − 13,4;
12) −1,4 − 1,2;
13) −10,2 − (−4,9);
14) 0 − (−99,4);
15) −8 − (−8).Решение
1) 10 − 16 = −6
2) 5 − 12 = −7
3) −5 − 3 = −8
4) −6 − 8 = −14
5) 9 − (−2) = 9 + 2 = 11
6) 4 − (−10) = 4 + 10 = 14
7) −3 − (−8) = −3 + 8 = 5
8) −11 − (−6) = −11 + 6 = −5
9) 12,3 − (−6,8) = 12,3 + 6,8 = 19,1
10) 2,4 − 5,6 = −3,2
11) 0 − 13,4 = −13,4
12) −1,4 − 1,2 = −2,6
13) −10,2 − (−4,9) = −10,2 + 4,9 = −5,3
14) 0 − (−99,4) = 0 + 99,4 = 99,4
15) −8 − (−8) = −8 + 8 = 0Задание 994
Выполните вычитание:
1) 3,5 − (−9,7);
2) 1,9 − 3,2;
3) 0 − 7,25;
4) −5,3 − 3,7;
5) −2,8 − (−5,2);
6) 0 − (−0,08).Решение
1) 3,5 − (−9,7) = 3,5 + 9,7 = 13,2
2) 1,9 − 3,2 = −1,3
3) 0 − 7,25 = −7,25
4) −5,3 − 3,7 = −9
5) − 2,8 − (−5,2) = − 2,8 + 5,2 = 2,4
6) 0 − (−0,08) = 0 + 0,08 = 0,08Задание 995
Выполните вычитание:
1) $\frac59-(-\frac16)=\frac59+\frac16=\frac{10}{18}+\frac3{18}=\frac{13}{18}$
2) $\frac3{16}-\frac{11}{24}=\frac9{48}-\frac{22}{48}=-\frac{13}{48}$
3) $-\frac79-\frac2{15}=-\frac{35}{45}-\frac6{45}=-\frac{41}{45}$
4) $-\frac{14}{25}-(-\frac7{10})=-\frac{14}{25}+\frac7{10}=-\frac{28}{50}+\frac{35}{50}=\frac7{50}$
5) $2\frac37-(-1\frac25)=2\frac37+1\frac25=2\frac{15}{35}+1\frac{14}{35}=3\frac{29}{35}$
6) $5\frac{12}{35}-10=5\frac{12}{35}-9\frac{35}{35}=-4\frac{23}{35}$
7) $2\frac9{20}-4\frac{17}{30}=2\frac{27}{60}-4\frac{34}{60}=-2\frac7{60}$
8) $-3\frac89-4\frac1{12}=-3\frac{32}{36}-4\frac3{36}=-7\frac{35}{36}$
9) $-4\frac3{16}-(-5\frac58)=-4\frac3{16}+5\frac58=-4\frac3{16}+5\frac{10}{16}=1\frac7{16}$Задание 996
Выполните вычитание:
1) $\frac78-(-\frac3{10})=\frac78+\frac3{10}=\frac{35}{40}+\frac{12}{40}=\frac{47}{40}=1\frac7{40}$
2) $\frac{11}{12}-\frac{17}{18}=\frac{33}{36}-\frac{34}{36}=-\frac1{36}$
3) $-\frac37-\frac9{14}=-\frac6{14}-\frac9{14}=-\frac{15}{14}=-1\frac1{14}$
4) $-\frac59-(-\frac34)=-\frac59+\frac34=-\frac{20}{36}+\frac{27}{36}=\frac7{36}$
5) $3\frac{11}{12}-(-4\frac49)=3\frac{11}{12}+4\frac49=3\frac{33}{36}+4\frac{16}{36}=7\frac{49}{36}=8\frac{13}{36}$
6) $4\frac5{17}-6=4\frac5{17}-5\frac{17}{17}=1\frac{12}{17}$
7) $1\frac38-3\frac14=1\frac38-3\frac28=1\frac38-2\frac{10}8=-1\frac78$
8) $-2\frac{14}{15}-1\frac{19}{45}=-2\frac{42}{45}-1\frac{19}{45}=-3\frac{61}{45}=-4\frac{16}{45}$
9) $-3\frac16-(-1\frac14)=-3\frac16+1\frac14=-3\frac2{12}+1\frac3{12}=-2\frac{14}{12}+1\frac3{12}=-1\frac{11}{12}$Задание 997
Решите уравнение:
1) x + 7 = 4;
2) 20 − x = 35;
3) x + 2,6 = −1,7;
4) −4,5 − x = 9;
5) x − 0,9 = −1,4;
6) 7 − x = −5;
7) −20 − x = −13;
8) −0,76 − x = −0,83.Решение
1) x + 7 = 4
x = 4 − 7
x = −3
2) 20 − x = 35
x = 20 − 35
x = −15
3) x + 2,6 = −1,7
x = −1,7 − 2,6
x = −4,3
4) −4,5 − x = 9
x = −4,5 − 9
x = −13,5
5) x − 0,9 = −1,4
x = −1,4 + 0,9
x = −0,5
6) 7 − x = −5
x = 7 + 5
x = 12
7) −20 − x = −13
x = −20 + 13
x = −7
8) −0,76 − x = −0,83
x = −0,76 + 0,83
x = 0,07Задание 998
Решите уравнение:
1) x + 19 = 10;
2) 12,4 − x = 16;
3) x + 3,4 = −5,8;
4) −1,2 − x = 0,6;
5) x − 3,8 = −1,9;
6) 11 − x = −14.Решение
1) x + 19 = 10
x = 10 − 19
x = −9
2) 12,4 − x = 16
x = 12,4 − 16
x = −3,6
3) x + 3,4 = −5,8
x = −5,8 − 3,4
x = −9,2
4) −1,2 − x = 0,6
x = −1,2 − 0,6
x= −1,8
5) x − 3,8 = −1,9
x = −1,9 + 3,8
x = 1,9
6) 11 − x = −14
x = 11 + 14
x = 25Задание 999
Мертвое море расположено на высоте −425 м относительно уровня Мирового океана. Каспийское море, которое является самым большим в мире озером, находится на высоте −28 м относительно уровня Мирового океана. На сколько метров уровень воды в Каспийском море выше ровня воды в Мертвом море?
Решение
−28 − (−425) = −28 + 425 = 397 м разница уровня воды в Каспийском и Мертвом морях.
Ответ: выше на 397 м.Задание 1000
Абсолютный максимум температуры воздуха 45,4°C в России был зафиксирован 12 июля 2010 г. на метеостанции Утта (Калмыкия). Абсолютный минимум температуры −69,8°C был зафиксирован на протяжении трех дней 5−7 февраля 1892 г. в Верхоянске (Якутия). Найдите разность абсолютных максимума и минимума температур.
Решение
45,4 − (−69,8) = 45,4 + 69,8 = 115,2°C разность абсолютных максимума и минимума температур.
Ответ: 115,2°C.Задание 1001
Самая низкая температура воздуха, зафиксированная в пустыне Сахара, равна −5°C, а самая высокая −55,4°C. Определите максимальный перепад температур воздуха в Сахаре.
Решение
55,4 − (−5) = 55,4 + 5 = 60,4°C максимальный перепад температур воздуха в Сахаре.
Ответ: 60,4°C. 214
-
Страница 214
Задание 1002
Ртуть плавится при температуре −38,9°C, а медь − при температуре 1083,4°C. На сколько градусов температура плавления меди выше температуры плавления ртути?
Решение
1083,4 − (−38,9) = 1083,4 + 38,9 = 1122,3°C разница температур плавления меди и ртути.
Ответ: 1122,3°C.Задание 1003
Самая низкая зафиксированная на поверхности Земли температура была равной −89,2°C, что на 70,8°C выше самой низкой температуры, измеренной на поверхности Луны. Чему равна самая низкая температура, зафиксированная на Луне?
Решение−89,2 − 70,80 = −160°C самая низкая температура, зафиксированная на Луне.
Ответ: −160°C.Задание 1004
Найдите значение выражения:
1) −27 + 13 − 34 + 21;
2) 1,7 − 3,4 − 2,5 + 4,1;
3) −0,65 − (−0,44) + (−1,23) + 8,1;
4) 3 1/6+(−2 4/9)−(−1 2/3);
5) 4 5/9+(−5 7/12)−(−2 1/6)−1 1/3+3 3/4+(−13/18).Решение
1) −27 + 13 − 34 + 21 = (−27 − 34) + (13 + 21) = −61 + 34 = −27
2) 1,7 − 3,4 − 2,5 + 4,1 = (−3,4 − 2,5) + (1,7 + 4,1) = −5,9 + 5,8 = −0,1
3) −0,65 − (−0,44) + (−1,23) + 8,1 = −0,65 + 0,44 − 1,23 + 8,1 = (−0,65 − 1,23) + (0,44 + 8,1) = −1,88 + 8,54 = 6,66
4) $3\frac16+(-2\frac49)-(-1\frac23)=3\frac16-2\frac49+1\frac23=(3\frac3{18}+1\frac{12}{18})-2\frac8{18}=4\frac{15}{18}-2\frac8{18}=2\frac7{18}$
5) $4\frac59+(-5\frac7{12})-(-2\frac16)-1\frac13+3\frac34+(-\frac{13}{18})=4\frac59-5\frac7{12}+2\frac16-1\frac13+3\frac34-\frac{13}{18}=(4-5+2-1+3)+(\frac{20}{36}-\frac{21}{36}+\frac6{36}-\frac{12}{36}+\frac{27}{36}-\frac{26}{36})=3+(-\frac6{36})=3-\frac16=2\frac56$Задание 1005
Найдите значение выражения:
1) 16 − 29 + 14 − 48;
2) −3,2 − 7,8 − 5,4 + 4,6;
3) −4,28 − 1,53 − (−7,85) + (−9,06);
4) −5 3/8+4 5/6−(−2 1/4);
5) −3 3/5+(−2 1/3)+4 8/15−1 5/6−(−6 7/10)+1/2.Решение
1) 16 − 29 + 14 − 48 = (−29 − 48) + (16 + 14) = −77 + 30 = −47
2) −3,2 − 7,8 − 5,4 + 4,6 = −16,4 + 4,6 = −11,8
3) −4,28 − 1,53 − (−7,85) + (−9,06) = −4,28 − 1,53 + 7,85 − 9,06 = −14,87 + 7,85 = −7,02
4) $-5\frac38+4\frac56-(-2\frac14)=-5\frac9{24}+4\frac{20}{24}+2\frac6{24}=-5\frac9{24}+6\frac{26}{24}=1\frac{17}{24}$
5) $-3\frac35+(-2\frac13)+4\frac8{15}-1\frac56-(-6\frac7{10})+\frac12=-3\frac35-2\frac13+4\frac8{15}-1\frac56+6\frac7{10}+\frac12=(-3-2+4-1+6)+(\frac{-18-10+16-25+21+15}{30})=4-\frac1{30}=3\frac{29}{30}$Задание 1006
Найдите значение выражения −a + b + c − d, если:
1) a = −4, b = 12, c = −6, d = 8;
2) a = 1,5, b = −3,2, с = −1,8, d = −2,4;
3) a=3 1/3,b=2 1/2,c=−1 5/6,d=5;
4) a=−2 1/7,b=−1 3/14,c=3 19/28,d=1 3/4.Решение
1) −a + b + c − d = −(−4) + 12 + (−6) − 8 = 4 + 12 − 6 − 8 = 16 − 14 = 2
2) −a + b + c − d = −1,5 + (−3,2) + (−1,8) − (−2,4) = −1,5 − 3,2 − 1,8 + 2,4 = −6,5 + 2,4 = −4,1
3) $-a+b+c-d=-3\frac13+2\frac12+(-1\frac56)-5=-3\frac13+2\frac12-1\frac56-5=-3\frac26+2\frac36-1\frac56-5=-2\frac46-5=-2\frac23-5=-7\frac23$
4) $-a+b+c-d=-(-2\frac17)+(-1\frac3{14})+3\frac{19}{28}-1\frac34=2\frac4{28}-1\frac6{28}+3\frac{19}{28}-1\frac{21}{28}=3-\frac4{28}=3-\frac17=2\frac67$Задание 1007
Составьте числовое выражение и вычислите его значение:
1) из числа 3,6 вычесть сумму чисел −12,6 и 5,3;
2) к разности чисел −2,4 и −3,8 прибавить сумму чисел 5,6 и −10.Решение
1) 3,6 − (−12,6 + 5,3) = 3,6 − (−7,3) = 3,6 + 7,3 = 10,9
2) (−2,4 − (−3,8)) + (5,6 + (−10)) = (−2,4 + 3,8) + (5,6 − 10) = 1,4 + (−4,4) = 1,4 − 4,4 = −3Задание 1008
Составьте числовое выражение и вычислите его значение:
1) к числу −1,4 прибавить разность чисел 2,5 и 4,1;
2) из суммы чисел −8,2 и 14 вычесть разность чисел 0,7 и −5,4.Решение
1) −1,4 + (2,5 − 4,1) = −1,4 + (−1,6) = −3
2) (−8,2 + 14) − (0,7 − (−5,4)) = 5,8 − (0,7 + 5,4) = 5,8 − 6,1 = −0,3Задание 1009
Найдите координату точки на координатной прямой, удаленной:
1) от точки A(4,6) на 10 единиц;
2) от точки B(−1 1/3) на 2 1/6 единицы;
3) от точки C(−3 2/7) на 3 2/7 единицы.Решение
1) 4,6 + 10 = 14,6;
4,6 − 10 = −5,4.
Ответ: 14,6 или −5,4.
2) $-1\frac13+2\frac16=-1\frac26+2\frac16=\frac56$
$-1\frac13-2\frac16=-1\frac26-2\frac16=-3\frac36=-3\frac12$
Ответ: 5/6 или $-3\frac12$.
3) $-3\frac27+3\frac27=0$
$-3\frac27-3\frac27=-6\frac47$
Ответ: 0 или $-6\frac47$. 215
-
Страница 215
Задание 1010
Упростите выражение:
1) −16 + a + 33 + b − a;
2) 7,2 − m − n − 8,9 − 1,1 + m;
3) −x+y−3/14+2/7−5/6+x;
4) p−k+3/8−9/16+7/32−p+k.Решение
1) −16 + a + 33 + b − a = (−16 + 33) + (a − a) + b = 17 + b
2) 7,2 − m − n − 8,9 − 1,1 + m = (7,2 − 8,9 − 1,1) + (m − m) − n = −2,8 − n
3) $-x+y-\frac3{14}+\frac27-\frac56+x=(-\frac9{42}+\frac{12}{42}-\frac{35}{42})+(x-x)+y=-\frac{32}{42}+y=-\frac{16}{21}+y$
4) $p-k+\frac38-\frac9{16}+\frac7{32}-p+k=(\frac{12}{32}-\frac{18}{32}+\frac7{32})+(p-p)+(k-k)=\frac1{32}$Задание 1011
Решите уравнение:
1) |x| + 2,8 = 5;
2) |x| − 3,1 = 4,4;
3) |x| − 0,4 = −0,29;
4) |x| − 6 = −9;
5) 15 − |x| = −2;
6) |x + 2,5| = 1.Решение
1) |x| + 2,8 = 5
|x| = 5 − 2,8
|x| = 2,2
x1=2,2;
x2=−2,2.
2) |x| − 3,1 = 4,4
|x| = 4,4 + 3,1
|x| = 7,5
x1=7,5;
x2=−7,5.
3) |x| − 0,4 = −0,29
|x| = −0,29 + 0,4
|x| = 0,11
x1=0,11;
x2=−0,11.
4) |x| − 6 = −9
|x| = −9 + 6
|x| = −3, нет решения, так как модуль числа не может быть числом отрицательным.
5) 15 − |x| = −2
|x| = 15 + 2
|x| = 17
x1=17;
x2=−17.
6) |x + 2,5| = 1
x + 2,5 = 1
x = 1 − 2,5
x1=−1,5;
|x + 2,5| = −1
x + 2,5 = −1
x = −1 − 2,5
x2=−3,5.Задание 1012
Решите уравнение:
1) |x| + 3 = 8;
2) |x| − 1,3 = 1,2;
3) |x| − 0,8 = −0,1;
4) |x| + 2,1 = 1;
5) 13 − |x| = 6;
6) |x + 2,1| = 3.Решение
1) |x| + 3 = 8
|x| = 8 − 3
|x| = 5
x1 = 5;
x2 = − 5.
2) |x| − 1,3 = 1,2
|x| = 1,2 + 1,3
|x| = 2,5
x1 = 2 , 5;
x2 = − 2 , 5.
3) |x| − 0,8 = −0,1
|x| = −0,1 + 0,8
|x| = 0,7
x1 = 0 , 7;
x2 = − 0 , 7.
4) |x| + 2,1 = 1
|x| = 1 − 2,1
|x| = −1,1, нет решения, так как модуль числа не может быть числом отрицательным.
5) 13 − |x| = 6
|x| = 13 − 6
|x| = 7
x1 = 7;
x2 = − 7.
6) |x + 2,1| = 3
x + 2,1 = 3
x = 3 − 2,1
x1 = 0, 9
x + 2,1 = −3
x = −3 − 2,1
x2 = − 5 , 1.Задание 1013
Не выполняя вычислений сравните:
1) сумму чисел −9,34 и −12,78 и их разность;
2) разность чисел 48 и 73 и сумму чисел −46 и 59;
3) разность чисел −16,5 и −2,37 и разность чисел −4,3 и −8,1.Решение
1) −9,34 + (−12,78) < −9,34 − (−12,78), так как разность данных чисел число положительное, а сумма число отрицательное.
2) 48 − 73 < −46 + 59, так как сумма число положительное, а разность число отрицательное.
3) −16,5 − (−2,37) < −4,3 − (−8,1), так как разность первых двух чисел число отрицательное, а разность вторых двух чисел число положительное.Задание 1014
Не выполняя вычислений сравните:
1) сумму чисел 81,9 и −74,6 и сумму чисел 80,4 и −83,5;
2) разность чисел 52 и 74 и сумму чисел −102 и 102;
3) разность чисел −96,3 и −96,3 и сумму чисел 0,872 и −0,872.Решение
1) 81,9 + (−74,6) > 80,4 + (−83,5), так как сумма первых двух чисел число положительное, а сумма вторых двух чисел число отрицательное.
2) 52 − 74 < −102 + 102, так как разность первых двух чисел число отрицательное, а сумма вторых двух чисел равна нулю.
3) −96,3 − (−96,3) = 0,872 + (0,872), так как и сумма и разность равны 0.Задание 1015
Решите уравнение:
1) ||x| − 8| = 2;
2) ||x| + 2| = 7.Решение
1) ||x| − 8| = 2
|x| − 8 = 2
|x| = 2 + 8
|x| = 10
x 1 = 10;
x 2 = − 10;
|x| − 8 = −2
|x| = −2 + 8
|x| = 6
x 3 = 6;
x 4 = − 6.
2) ||x| + 2| = 7
|x| + 2 = 7
|x| = 7 − 2
|x| = 5
x 1 = 5;
x 2 = − 5;
|x| + 2 = −7
|x| = −7 − 2
|x| = −9, нет корней, так как модуль числа не может быть отрицательным.Задание 1016
Можно ли указать наибольшее и наименьшее значения выражения:
1) |x| − 8,5;
2) −5,2 − |x|?
В случае утвердительного ответа укажите это значение и значение x, при котором выражение его принимает.Решение
1) Выражение |x| − 8,5 принимает наименьшее значение −8,5 при x = 0;
Наибольшее значение указать невозможно.
2) Выражение −5,2 − |x| принимает наибольшее значение −5,2 при x = 0;
Наименьшее значение указать невозможно.Задание 1017
Можно ли указать наибольшее и наименьшее значения выражения:
1) |x| + 3,9;
2) 7,6 − |x|?
В случае утвердительного ответа укажите это значение и значение x, при котором выражение его принимает.Решение
1) Выражение |x| + 3,9 принимает наименьшее значение 3,9 при x = 0;
Наибольшее значение указать невозможно.
2) Выражение 7,6 − |x| принимает наибольшее значение 7,6 при x = 0;
Наименьшее значение указать невозможно.Задание 1018
Первое число составляет 80% второго. Сколько процентов первого числа составляет второе число?
Решение
Пусть x первое число, тогда:
0,8x второе число.
$\frac x{0,8x}=\frac1{0,8}=\frac{10}8=\frac54=1,25=125$ % первого числа составляет второе число.
Ответ: 125%. 216
-
Страница 216
Задание 1019
В тире Вася сделал 48 выстрелов, из которых шесть не попали в цель. Найдите процент попаданий в цель.
Решение
48 − 6 = 42 выстрела не попали в цель;
$\frac{42}{48}$ * 100% = $\frac78$ * 100% = 87,5% попаданий в цель.
Ответ: 87,5%.Задание 1020
У Миши было 36 кроликов разной масти: белые, серые и бурые. Бурые составляли 1/3 всех кроликов, серых было 8. Какова вероятность того, что наугад выбранный кролик будет белым?
Решение
1) $36\ast\frac13=12$ (к.) - бурых
2) 36 − (12 + 8) = 36 − 20 = 16 (к.) - белых
3) $\frac{16}{36}=\frac49$
Ответ: $\frac49$.Задание 1021
Дмитрий Григорьевич взял с собой в командировку три рубашки, одну пару туфель, одни брюки, один обычный галстук и один галстук−бабочку. Дмитрий Григорьевич всегда носит туфли, брюки, рубашку и галстук. Сколько разных комплектов одежды он может составить?
Решение
Рубашку можно выбрать одну из трех, то есть 3 способами;
Туфли можно выбрать одним способом;
Брюки можно выбрать одним способом;
Галстук можно выбрать один из двух, то есть 2 способами.
3 * 1 * 1 * 2 = 6 разных комплектов одежды может составить Дмитрий Григорьевич.
Ответ: 6 комплектов.Задание 1022
Запишите в виде произведения сумму:
1) 1/2+1/2+1/2+1/2+1/2+1/2+1/2;
2) 2,3 + 2,3 + 2,3 + 2,3.Решение
1) $\frac12+\frac12+\frac12+\frac12+\frac12+\frac12+\frac12=7\ast\frac12$
2) 2,3 + 2,3 + 2,3 + 2,3 * 4 * 2,3Задание 1023
Докажите, что в любой компании из шести человек найдется трое попарно знакомых или трое попарно незнакомых.
Решение
Раз это компания, то минимум 2 человека знакомы и каждый из них знаком хотя бы еще с одним из людей этой компании. Значит, если первый знаком со вторым, а второй с третьим, то и первый и третий знакомы со вторым.
Аналогично, если первый не знаком со вторым, а второй с третьим, то это три пары незнакомых людей. 219
-
Страница 219
Ответы к параграфу 34. Умножение рациональных чисел
Задание 1024
Выполните умножение:
1) −12 * 5 = −60
2) −0,4 * 1,5 = −0,6
3) 3,4 * (−1,8) = −6,12
4) $-\frac34\ast(-\frac56)=-\frac14\ast(-\frac52)=\frac58$
5) $-\frac{15}{16}\ast(-\frac{48}{55})=-\frac31\ast(-\frac3{11})=\frac9{11}$
6) $-\frac{13}{24}\ast\frac{16}{39}=-\frac13\ast\frac23=-\frac29$
7) $\frac6{35}\ast(-\frac{14}{15})=\frac25\ast(-\frac25)=-\frac4{25}$
8) $-\frac7{12}\ast24=-\frac71\ast2=-14$
9) $45\ast(-\frac8{15})=3\ast(-\frac81)=-24$
10) $\frac{16}{17}\ast(-6\frac38)=\frac{16}{17}\ast(-\frac{51}8)=\frac21\ast(-\frac31)=-6$
11) $-3\frac59\ast(-5\frac14)=-\frac{32}9\ast-\frac{21}4=-\frac83\ast-\frac71=\frac{56}3=18\frac23$
12) $-1\frac57\ast6\frac18=-\frac{12}7\ast\frac{49}8=-\frac31\ast\frac72=-\frac{21}2=-10\frac12$Задание 1025
Выполните умножение:
1) 16 * (−3) = −48
2) −8 * (−7) = 56
3) −2,3 * (−1,4) = 3,22
4) $\frac67\ast(-\frac47)=-\frac{24}{49}$
5) $-\frac47\ast\frac79=-\frac41\ast\frac19=-\frac49$
6) $-6\ast(-\frac5{24})=-1\ast(-\frac54)=\frac54=1\frac14$
7) $-\frac6{19}\ast(-57)=-\frac61\ast(-3)=18$
8) $-9\frac35\ast(-\frac{10}{21})=-\frac{48}5\ast(-\frac{10}{21})=-\frac{16}1\ast(-\frac27)=\frac{32}7=4\frac47$Задание 1026
Найдите значение степени:
1) $(-2)^5=-32$
2) $(-0,6)^2=0,36$
3) $(-1\frac15)^3=(-\frac65)^3=-\frac{216}{125}=-1\frac{91}{125}$
4) $(-1\frac12)^2=(-\frac32)^2=\frac94=2\frac14$
5) $(-1)^{10}=1$
6) $(-1)^{23}=-1$Задание 1027
Найдите значение степени:
1) $(-7)^2=49$
2) $(-7)^3=-343$
3) $(-\frac12)^4=\frac1{16}$
4) $(-\frac13)^5=-\frac1{243}$Задание 1028
Выполните действия:
1) −3,2 * 0,4 + 2,6 * (−0,5) = −1,28 + (−1,3) = −2,58
2) 5,2 * (−0,8) − (−1,5) * (−3,4) = −4,16 − 5,1 = −9,26
3) (7,6 − 20) * (−3,14 + 5,24) = −12,4 * 2,1 = −26,04
4) $(-1\frac3{25})\ast2\frac17+(-2\frac19)\ast(-\frac{27}{190})=(-\frac{28}{25})\ast\frac{15}7+(-\frac{19}9)\ast(-\frac{27}{190})=(-\frac45)\ast\frac31+(-\frac11)\ast(-\frac3{10})=-\frac{12}5+\frac3{10}=-\frac{24}{10}+\frac3{10}=-\frac{21}{10}=-2,1$
5) $(8+2\frac17\ast(-3\frac19))\ast(-\frac{27}{44})=(8+\frac{15}7\ast(-\frac{28}9))\ast(-\frac{27}{44})=(8+\frac51\ast(-\frac43))\ast(-\frac{27}{44})=(8-\frac{20}3)\ast(-\frac{27}{44})=(8-6\frac23)\ast(-\frac{27}{44})=1\frac13\ast(-\frac{27}{44})=\frac43\ast(-\frac{27}{44})=\frac11\ast(-\frac9{11})=-\frac9{11}$
6) $(-5\frac1{16}+1\frac18)\ast(-\frac56-\frac3{14})=(-5\frac1{16}+1\frac2{16})\ast(-\frac{35}{42}-\frac9{42})=-3\frac{15}{16}\ast-\frac{44}{42}=-\frac{63}{16}\ast-\frac{22}{21}=-\frac38\ast-\frac{11}1=\frac{33}8=4\frac18$ 220
-
Страница 220
Задание 1029
Выполните действия:
1) $−2,7 * (−1,2) + 3,5 * (−2,8) = 3,24 − 9,8 = −6,56$
2) $−7,4 * 0,6 − 3,8 * (−2,3) = −4,44 + 8,74 = 4,3$
3) $(−9,3 − 1,7) * (2,6 + (−5,9)) = −11 * 3,3 = −36,3$
4) $4\frac7{12}\ast(-1\frac3{11})-(-1\frac1{15})\ast(-\frac{45}{64})=\frac{55}{12}\ast(-\frac{14}{11})-(-\frac{16}{15})\ast(-\frac{45}{64})=\frac56\ast(-\frac71)-(-\frac11)\ast(-\frac34)=-\frac{35}6-\frac34=-5\frac56-\frac34=-5\frac{10}{12}-\frac9{12}=-5\frac{19}{12}=-6\frac7{12}$
5) $-\frac{81}{88}\ast(-6+(-1\frac{13}{15})\ast(-1\frac{19}{21}))=-\frac{81}{88}\ast(-6+(-\frac{28}{15})\ast(-\frac{40}{21}))=-\frac{81}{88}\ast(-6+(-\frac43)\ast(-\frac83))=-\frac{81}{88}\ast(-6+\frac{32}9)=-\frac{81}{88}\ast(-6+3\frac59)=-\frac{81}{88}\ast-2\frac49=-\frac{81}{88}\ast-\frac{22}9=-\frac94\ast-\frac11=\frac94=2\frac14$
6) $(-\frac45-\frac47)\ast(5\frac79-7\frac{11}{12})=(-\frac{28}{35}-\frac{20}{35})\ast(5\frac{28}{36}-7\frac{33}{36})=-\frac{48}{35}\ast-2\frac5{36}=-\frac{48}{35}\ast-\frac{77}{36}=-\frac45\ast-\frac{11}3=\frac{44}{15}=2\frac{14}{15}$Задание 1030
Не выполняя вычислений, сравните:
1) $(-7,2)^2>0$
2) $0>(-5,3)^3$
3) $(-10)^7<(-0,1)^4$
4) $-5^9=(-5)^9$
5) $(-8)^{12}>-8^{12}$
6) $0,3^{13}>(-216)^5$Задание 1031
Не выполняя вычислений, сравните значения выражений:
1) −2,4 * (−3,6) * 7,8 и 9,6 * (−4,1) * 1,8;
2) 5 1/3∗(−7 14/19)∗(−6 1/7)∗4 11/12 и 9 1/8∗(−3/14)∗0∗(−1 1/9);
3) −7,13 * (−2) * (−14) * (−19) * 17 и −13 * (−21) * (−2136);
4) 139 * (−216) * 0 * 518 и 135 * 418 * (−5132).Решение
1) −2,4 * (−3,6) * 7,8 > 9,6 * (−4,1) * 1,8
2) $5\frac13\ast(-7\frac{14}{19})\ast(-6\frac17)\ast4\frac{11}{12}>9\frac18\ast(-\frac3{14})\ast0\ast(-1\frac19)$
3) −7,13 * (−2) * (−14) * (−19) * 17 > −13 * (−21) * (−2136)
4) 139 * (−216) * 0 * 518 > 135 * 418 * (−5132)Задание 1032
Выполните действия:
1) $(-5\frac34)\ast8+(-2\frac13)\ast(-1\frac3{14})-1\frac{37}{48}\ast(-2\frac2{15})=(-\frac{23}4)\ast8+(-\frac73)\ast(-\frac{17}{14})-\frac{85}{48}\ast(-\frac{32}{15})=(-\frac{23}1)\ast2+(-\frac13)\ast(-\frac{17}2)-\frac{17}3\ast(-\frac23)=-\frac{46}1+\frac{17}6+\frac{34}9=-46+2\frac56+3\frac79=-45\frac{18}{18}+2\frac{15}{18}+3\frac{14}{18}=-45\frac{18}{18}+6\frac{11}{18}=-39\frac7{18}$
2) $(6,75+(-4,5)\ast1\frac23)\ast(-1\frac13)^3=(6\frac34+(-\frac92)\ast\frac53)\ast(-\frac43)^3=(6\frac34+(-\frac32)\ast\frac51)\ast(-\frac{64}{27})=(6\frac34+(-\frac{15}2))\ast(-\frac{64}{27})=(6\frac34+(-7\frac12))\ast(-\frac{64}{27})=(6\frac34+(-6\frac64))\ast(-\frac{64}{27})=-\frac34\ast(-\frac{64}{27})=\frac{16}9=1\frac79$Задание 1033
Выполните действия:
1) $(-2\frac18)\ast(-1\frac{29}{51})+(-1\frac{23}{42})\ast3\frac1{13}-(-4\frac23)\ast6=(-\frac{17}8)\ast(-\frac{80}{51})+(-\frac{65}{42})\ast\frac{40}{13}-(-\frac{14}3)\ast6=(-\frac11)\ast(-\frac{10}3)+(-\frac5{21})\ast\frac{20}1-(-\frac{14}1)\ast2=3\frac13+(-4\frac{16}{21})-(-28)=3\frac7{21}+(-4\frac{16}{21})+28=-1\frac9{21}+28=-1\frac9{21}+27\frac{21}{21}=26\frac{12}{21}=26\frac47$
2) $(-\frac{11}{18}+(-2\frac29)\ast(-0,2))^3\ast(-1,2)=(-\frac{11}{18}+(-\frac{20}9)\ast(-\frac15))^3\ast(-\frac65)=(-\frac{11}{18}+\frac49\ast(-\frac11))^3\ast(-\frac65)=(-\frac{11}{18}+\frac8{18})^3\ast(-\frac65)=(-\frac16)^3\ast(-\frac65)=-\frac1{216}\ast(-\frac65)=-\frac1{36}\ast(-\frac15)=\frac1{180}$Задание 1034
Составьте числовое выражение и найдите его значение:
1) разность куба числа −5 и квадрата числа −8;
2) разность квадратов чисел −1 1/3 и 5/6;
3) разность произведений чисел −1,2 и −0,4 и чисел 1,6 и 0,6;
4) произведение суммы чисел 2,8 и −3,4 и суммы чисел −1,6 и 4,2.Решение
1) $(-5)^3-(-8)^2=-125-64=-189$
2) $(-1\frac13)^2-(\frac56)^2=(-\frac43)^2-(\frac56)^2=\frac{16}9-\frac{25}{36}=\frac{64}{36}-\frac{25}{36}=\frac{39}{36}=\frac{13}{12}=1\frac1{12}$
3) −1,2 * (−0,4) − 1,6 * 0,6 = 0,48 − 0,96 = −0,48
4) (2,8 + (−3,4)) * (−1,6 + 4,2) = −0,6 * 2,6 = −1,56Задание 1035
Составьте числовое выражение и найдите его значение:
1) куб разности чисел 7 и 10;
2) произведение суммы чисел 6 и −10 и их разности;
3) сумма произведений чисел −8/9 и −27/32 и чисел 23/28 и −49/46;
4) произведение разности чисел 4,5 и 6 и разности чисел 1,8 и −3,4.Решение
1) $(7-10)^3=(-3)^3=-27$
2) (6 + (−10)) * (6 − (−10)) = (6 − 10) * (6 + 10) = −4 * 16 = −64
3) $(-\frac89\ast(-\frac{27}{32}))+(\frac{23}{28}\ast(-\frac{49}{46}))=(-\frac11\ast(-\frac34))+(\frac14\ast(-\frac72))=\frac34+(-\frac78)=\frac68+(-\frac78)=-\frac18$
4) (4,5 − 6) * (1,8 − (−3,4)) = −1,5 * (1,8 + 3,4) = −1,5 * 5,2 = −7,8 221
-
Страница 221
Задание 1036
Найдите значение выражения:
1) $18x^2$, если x = − 1/9;
2) $(24x)^3$, если x = − 1/6;
3) $(x + y)^4$, если x = −0,9, y = 0,8;
4) 4x − 3y, если x = − 2 1/4 , y = − 7 1/3.Решение
1) $18x^2=18\ast(-\frac19)^2=18\ast\frac1{81}=2\ast\frac19=\frac29$
2) $(24x)^3=(24\ast(-\frac16))^3=(-4)^3=-64$
3) $(x+y)^4=(-0,9+0,8)^4=(-0,1)^4=0,0001$
4) $4x-3y=4\ast(-2\frac14)-3\ast(-7\frac13)=4\ast(-\frac94)-3\ast(-\frac{22}3)=1\ast(-\frac91)-1\ast(-\frac{22}1)=-9-(-22)=-9+22=13$Задание 1037
Найдите значение выражения:
1) $23−с^4$, если c = −3;
2) $x^2−x^3$, если x = −0,2;
3) (0,8a + 0,3b)(0,6b − 1,2a), если a = 2 1/12,b = −1 1/9.Решение
1) $23-{\operatorname с}^4=23-(-3)^4=23-81=-58$
2) $x^2-x^3=(-0,2)^2-(-0,2)^3=0,04-(-0,008)=0,04+0,008=0,048$
3) $(0,8a+0,3b)(0,6b-1,2a)=(0,8\ast2\frac1{12}+0,3\ast(-1\frac19))\ast(0,6\ast(-1\frac19)-1,2\ast2\frac1{12})=(\frac45\ast\frac{25}{12}+\frac3{10}\ast(-\frac{10}9))\ast(\frac35\ast(-\frac{10}9)-\frac65\ast\frac{25}{12})=(\frac11\ast\frac53+\frac11\ast(-\frac13))\ast(\frac11\ast(-\frac23)-\frac11\ast\frac52)=(\frac53-\frac13)\ast(-\frac23-\frac52)=\frac43\ast(-\frac46-\frac{15}6)=\frac43\ast(-\frac{19}6)=\frac23\ast(-\frac{19}3)=-\frac{38}9=-4\frac29$Задание 1038
Решите уравнение:
1) 3x = 0;
2) −6,8(x − 4) = 0;
3) (x + 7,2)(x − 8,1) = 0;
4) −5|x| = 0.Решение
1) 3x = 0
x = 0 : 3
x = 0
2) −6,8(x − 4) = 0
x − 4 = 0
x = 4
3) (x + 7,2)(x − 8,1) = 0
x + 7,2 = 0
x1=−7,2;
x − 8,1 = 0
x2=8,1.
4) −5|x| = 0
|x| = 0
x = 0Задание 1039
Решите уравнение:
1) −5 12/x=0;
2) 5,4(x + 6,3) = 0;
3) (x−3)(x+4)=0;
4) 23,5|x|=0.Решение
1) $-\frac5{12}x=0$
$x=0:(-\frac5{12})$
x = 0
2) 5,4(x + 6,3) = 0
x + 6,3 = 0
x = −6,3
3) (x − 3)(x + 4) = 0
x − 3 = 0
x1=3;
x + 4 = 0
x2=−4.
4) 23,5|x| = 0
|x| = 0
x = 0Задание 1040
Найдите все натуральные значения x, при которых верно неравенство:
1) −6x > −36;
2) −7x ⩾ −70;
3) −5x ⩾ −18;
4) −0,8x > −6,4.Решение
1) −6x > −36
x < −36 : (−6)
x < 6
Ответ: 5; 4; 3; 2; 1.
2) −7x ⩾ −70
x ⩽ −70 : (−7)
x ⩽ 10
Ответ: 10; 9; 8; 7; 6; 5; 4; 3; 2; 1.
3) −5x ⩾ −18
x ⩽ −18 : (−5)
x ⩽ 3,6
Ответ: 3; 2; 1.
4) −0,8x > −6,4
x < −6,4 : (−0,8)
x < 8
Ответ: 7; 6; 5; 4; 3; 2; 1.Задание 1041
Найдите все целые отрицательные значения x, при которых верно неравенство:
1) −5x < 20;
2) −9x ⩽ 45;
3) −4x ⩽ 35;
4) −0,3x < 1,2.Решение
1) −5x < 20
x > 20 : (−5)
x > −4
Ответ: −3; −2; −1.
2) −9x ⩽ 45
x ⩾ 45 : (−9)
x ⩾ −5
Ответ: −5; −4; −3; −2; −1.
3) −4x ⩽ 35
x ⩾ 35 : (−4)
x ⩾ −8,75
Ответ: −8; −7; −6; −5; −4; −3; −2; −1.
4) −0,3x < 1,2
x > 1,2 : −0,3
x > −4
Ответ: −3; −2; −1.Задание 1042
Какое из выражений $−x^2$,$(−x)^2$,$x^3$ при любых значениях x принимает такие значения:
1) положительные;
2) отрицательные;
3) неотрицательные;
4) неположительные?Решение
1) нет таких
2) нет таких
3) $(−x)^2$
4) $−x^2$Задание 1043
Положительным или отрицательным является значение выражения:
1) ab − 9c, если a, b и c − отрицательные числа;
2) 10p − mn, если m, n и p − отрицательные числа?Решение
1) ab − 9c = ab + (−9c), тогда:
ab − положительное, так как это произведение двух отрицательных чисел,
−9 − положительное, так как это произведение двух отрицательных чисел, следовательно
значение выражения ab − 9c положительное.
Ответ: положительные.
2) 10p − mn = 10p + (−mn), тогда:
10p − отрицательное, так как это произведение положительного и отрицательного числа;
−mn − отрицательное, так как это произведение положительного и отрицательного числа, следовательно значение выражения 10p − mn отрицательное.
Ответ: отрицательное.Задание 1044
Решите уравнение:
1) x(x + 9,4)(x − 6,5) = 0;
2) (x − 21)(x + 12,4) = 0.Решение
1) x(x + 9,4)(x − 6,5) = 0
x 1 = 0;
x + 9,4 = 0
x 2 = − 9 , 4;
x − 6,5 = 0
x 3 = 6 , 5.
2) (x − 21)(x + 12,4) = 0
x − 21 = 0
x 1 = 21;
x + 12,4 = 0
x 2 = − 12 , 4.Задание 1045
Решите уравнение:
1) (x + 1,2)(x + 5)(x − 10) = 0;
2) (x + 1)(x − 2) = 0.Решение
1) (x + 1,2)(x + 5)(x − 10) = 0
x + 1,2 = 0
x 1 = − 1 , 2;
x + 5 = 0
x 2 = − 5;
x − 10 = 0
x 3 = 10.
2) (x + 1)(x − 2) = 0
x + 1 = 0
x 1 = − 1;
x − 2 = 0
x 2 = 2.Задание 1046
Найдите наименьшее значение выражения:
1) $x^2−8$;
2) $7+x^2$.
При каком значении x выражение принимает наименьшее значение?Решение
1) При x = 0:
$x^2-8=0-8=-8$ − наименьшее значение.
2) При x = 0:
$7+x^2=7+0=7$ − наименьшее значение.Задание 1047
Найдите наибольшее значение выражения:
1) $4−x^2$;
2) $−x^2+10$.
При каком значении x выражение принимает наибольшее значение?Решение
1) При x = 0:
4 − $x^2$ = 4 − 0 = 4 − наибольшее значение.
2) При x = 0:
−$x^2$ + 10 = 0 + 10 = 10 − наибольшее значение. 222
-
Страница 222
Задание 1048
Во сколько раз:
1) 1/48 положительного числа меньше, чем 1/6 этого числа;
2) 5/6 положительного числа больше, чем 60% этого числа?Решение

Задание 1049
Галина и Ольга могут вместе налепить пельмени за 1 2/3 ч. На сколько часов больше нужно для этого Галине, чем Ольге, если Галина может налепить это количество пельменей за 3 3/4 ч?
Решение
Пусть все пельмени равны единице, тогда:
$1:1\frac23=1:\frac53=\frac35$ всех пельменей в час могут налепить вместе Галина и Ольга;
$1:3\frac34=1:\frac{15}4=\frac4{15}$ всех пельменей в час может налепить Галина;
$\frac35-\frac4{15}=\frac9{15}-\frac4{15}=\frac5{15}=\frac13$ всех пельменей в час может налепить Ольга;
$1:\frac13=3$ часа нужно Ольге, чтобы налепить все пельмени;
$3\frac34-3=\frac34$, то есть на 3/4 часа Галине нужно больше времени, чем Ольге, чтобы налепить все пельмени.
Ответ: на 3/4 часа.Задание 1050
За время, нужное Пончику, чтобы съесть шесть пирожков, Карлсон съедает 60 ватрушек. Винни−Пух съедает полгоршочка меда за время, нужное Карлсону, чтобы съесть 20 ватрушек. Сколько пирожков съест Пончик за время, необходимое Винни−Пуху, чтобы съесть горшочек меда?
Решение
20 * 2 = 40 ватрушек съест Карлсон за то время пока Винни−Пух съест горшочек меда;
$\frac{40}{60}=\frac23$ ватрушек съест Карлсон за то время пока Винни−Пух съест горшочек меда;
$6\ast\frac23=2\ast\frac21=4$ пирожка съест Пончик за время, необходимое Винни−Пуху, чтобы съесть горшочек меда.
Ответ: 4 пирожка.Задание 1051
За время, нужное бабушке, чтобы связать шесть носков. Ира успевает связать 2/3 носка. Сколько носков успеет связать бабушка за время, необходимое Ире, чтобы связать один носок?
Решение
$6:\frac23=6\ast\frac32=3\ast3=9$, то есть в девять раз бабушка вяжет быстрее Иры;
1 * 9 = 9 носков успеет связать бабушка за время, необходимое Ире, чтобы связать один носок.
Ответ: 9 носков.Задание 1052
Вычислите удобным способом:
1) 0,2 * 16,7 * 5;
2) 0,25 * 42,6 * 4.Решение
1) 0,2 * 16,7 * 5 = (0,2 * 5) * 16,7 = 1 * 16,7 = 16,7
2) 0,25 * 42,6 * 4 = (0,25 * 4) * 42,6 = 1 * 42,6 = 42,6Задание 1053
Упростите выражение:
1) 0,6a * 0,2b;
2) 4/5 m ∗ 5/16 n.Решение
1) 0,6a * 0,2b = 0,12ab
2) $\frac45m\ast\frac5{16}n=\frac11m\ast\frac14n=\frac14mn$Задание 1054
В Российской футбольной премьер−лиге принимает участие 16 команд. Докажите, что в любой момент чемпионата есть две команды, сыгравшие одинаковое количество матчей. (Команды, не сыгравшие ни одного матча, считают сыгравшими одинаковое количество матчей.)
Решение
Предположим, что это неверно и все команды сыграли разное число матчей. Т.к. команд 16, то больше 15 матчей команда сыграть не могла, получается, что количество сыгранных матчей у каждой из команд это число от 0 до 15. Но тогда получается, что команда, сыгравшая 15 матчей, сыграла с каждой из команд, а команда с 0 матчей не сыграла не разу, что невозможно. Следовательно в любой момент чемпионата есть две команды, сыгравшие одинаковое количество матчей.
225-226
-
Страница 225-226
Ответы к параграфу 38. Переместительное и сочетательное свойства умножения рациональных чисел. Коэффициент
Задание 1055
Выполните умножение:
1) $-\frac19\ast(-\frac17)\ast\frac15\ast(-\frac13)\ast3\ast(-5)\ast7\ast9=(-\frac19\ast9)\ast(-\frac17\ast7)\ast(\frac15\ast(-5))\ast(-\frac13\ast3)=-1\ast(-1)\ast(-1)\ast(-1)=1$
2) $8\ast(-6)\ast4\ast(-10)\ast\frac14\ast(-\frac13)\ast(-\frac15)\ast(-\frac12)=8\ast(4\ast\frac14)\ast(-6\ast(-\frac13)\ast(-\frac12))\ast(10\ast(-\frac15))=8\ast1\ast(-1)\ast-2=16$
3) 0,2 * (−0,25) * (−0,5) * 5 * (−4) * (−2) = (0,2 * 5) * (−0,25 * (−4)) * (−0,5 * (−2)) = 1 * 1 * 1 = 1Задание 1056
Назовите коэффициент выражения:
1) 6a;
2) −7,2b;
3) −xy;
4) 1,8mn;
5) 3/5 abc;
6) −2 1/3 p;
7) xyz;
8) 4 4/11 mk.Решение
1) 6
2) −7,2
3) −1
4) 1,8
5) 3
5
6) $-2\frac13$
7) 1
8) $4\frac4{11}$Задание 1057
Упростите выражение и укажите его коэффициент:
1) 4a * (−1,2);
2) −0,2b * (−0,14);
3) −6a * 8b;
4) −3,2p * (−0,5k);
5) −3/28 x ∗ 7/18 ∗ (−y);
6) 1 1/7 k ∗ 1 3/4 p ∗ (−1/2 m).Решение
1) 4a * (−1,2) = −4,8a
коэффициент −4,8
2) −0,2b * (−0,14) = 0,028b
коэффициент 0,028
3) −6a * 8b = −48ab
коэффициент −48
4) −3,2p * (−0,5k) = 1,6pk
коэффициент 1,6
5) $-\frac3{28}x\ast\frac7{18}\ast(-y)=-\frac14x\ast\frac16\ast(-y)=\frac1{24}xy$
коэффициент 1/24
6) $1\frac17k\ast1\frac34p\ast(-\frac12m)=\frac87k\ast\frac74p\ast(-\frac12m)=\frac11k\ast\frac11p\ast(-\frac11m)=kpm$
коэффициент 1Задание 1058
Упростите выражение и укажите его коэффициент:
1) −3m * (−2,1);
2) 3,6 * (−5x);
3) 10m * (−1,7) * n;
4) −7a * 3b * (−6c);
5) 16x ∗ (−8/15 b) ∗ 45/64 k;
6) −0,2t * (−5a) * (−b).Решение
1) −3m * (−2,1) = 6,3m
коэффициент 6,3
2) 3,6 * (−5x) = −18x
коэффициент −18
3) 10m * (−1,7) * n = −17mn
коэффициент −17
4) −7a * 3b * (−6c) = 126abc
коэффициент 126
5) $16x\ast(-\frac8{15}b)\ast\frac{45}{64}k=x\ast(-\frac21b)\ast\frac31k=-6xbk$
коэффициент −6
6) −0,2t * (−5a) * (−b) = −abt
коэффициент −1Задание 1059
Вычислите наиболее удобным способом:
1) −4 * 23 * (−0,5) = (−4 * (−0,5)) * 23 = 2 * 23 = 46
2) −0,4 * (−250) * 5 * (−0,2) = (−0,4 * (−250)) * (5 * (−0,2)) = 100 * (−1) = −100
3) $\frac7{13}\ast(-6,5)\ast0,4\ast(-1\frac67)=(\frac7{13}\ast(-\frac{13}7))\ast(-6,5\ast0,4)=-1\ast-2,6=2,6$
4) $\frac6{23}\ast(-2\frac13)\ast(-69)\ast\frac37=(\frac6{23}\ast(-69))\ast(-\frac73\ast\frac37)=(\frac61\ast(-3))\ast(-\frac11\ast\frac11)=18$
5) $-0,7\ast2,5\ast1\frac37\ast(-4)=(-\frac7{10}\ast\frac{10}7)\ast(2,5\ast(-4))=(-\frac11\ast\frac11)\ast(-10)=10$
6) $-\frac5{18}\ast(-\frac4{13})\ast\frac9{25}\ast(-26)=(-\frac5{18}\ast\frac9{25})\ast(-\frac4{13}\ast(-26))=(-\frac12\ast\frac15)\ast(-\frac41\ast(-2))=-\frac1{10}\ast8=-0,8$Задание 1060
Вычислите наиболее удобным способом:
1) −1,25 * (−3,47) * (−8);
2) −0,001 * (−54,8) * 50 * (−2);
3) 9/16∗11/35∗(−32)∗(−70);
4) 4,8∗(−2 1/6)∗(−5/24)∗(−6/13).Решение
1) −1,25 * (−3,47) * (−8) = (−1,25 * (−8)) * (−3,47) = 10 * (−3,47) = −34,7
2) −0,001 * (−54,8) * 50 * (−2) = (−0,001 * (50 * (−2)) * (−54,8) = (−0,001 * (−100)) * (−54,8) = 1 * (−54,8) = −54,8
3) $\frac9{16}\ast\frac{11}{35}\ast(-32)\ast(-70)=(\frac9{16}\ast(-32))\ast(\frac{11}{35}\ast(-70))=(\frac91\ast(-2))\ast(\frac{11}1\ast(-2))=-18\ast-22=396$
4) $4,8\ast(-2\frac16)\ast(-\frac5{24})\ast(-\frac6{13})=(4,8\ast(-\frac5{24}))\ast(-2\frac16\ast(-\frac6{13}))=(\frac{24}5\ast(-\frac5{24}))\ast(-\frac{13}6\ast(-\frac6{13}))=-1\ast1=-1$Задание 1061
Чему равно произведение всех целых чисел, которые больше −20 и меньше 20?
Решение
Произведение равно 0, так как среди множителей есть число 0.
Задание 1062
Положительным, отрицательным или нулем является произведение пяти чисел, если:
1) два числа положительные, а остальные − отрицательные;
2) два числа отрицательные, а остальные − положительные;
3) четыре числа отрицательные;
4) два числа отрицательные, два числа − положительные, а одно − нуль?Решение
1) отрицательным, так как количество отрицательных множителей нечетное.
2) положительным, так как количество отрицательных множителей четное.
3) положительным, так как количество отрицательных множителей четное.
4) нулем, так как среди множителей есть нуль.Задание 1063
Упростите выражение и найдите его значение:
1) −8/15 a ∗ 3 3/4 b, если a=−1/3,b=1/6;
2) −7/20 x ∗ (−1 1/14) ∗ y ∗ (−2 2/3 z), если x=−3 3/7,y=14,z=−5/16.Решение
1) $-\frac8{15}a\ast3\frac34b=-\frac8{15}a\ast\frac{15}4b=-\frac21a\ast\frac11b=-2ab=-2\ast(-\frac13)\ast\frac16=-1\ast(-\frac13)\ast\frac13=\frac19$
2) $-\frac7{20}x\ast(-1\frac1{14})\ast y\ast(-2\frac23z)=-\frac7{20}x\ast(-\frac{15}{14})\ast y\ast(-\frac83z)=-\frac11x\ast(-\frac11)\ast y\ast(-\frac11z)=-xyz=-(-3\frac37\ast14\ast-\frac5{16})=-(-\frac{24}7\ast14\ast-\frac5{16})=-(-\frac31\ast1\ast-\frac51)=-15$ 227
-
Страница 227
Задание 1064
Упростите выражение и найдите его значение:
1)200m * (−0,4n), если m = −0,25, n = 0,2;
2) −1/3 m ∗ (−3/4 n) ∗ 20p, если m=−3/20,p=4/9,n=−30.Решение
1) 200m * (−0,4n) = −80mn = −80 * (−0,25) * 0,2 = 20 * 0,2 = 4
2) $-\frac13m\ast(-\frac34n)\ast20p=-\frac11m\ast(-\frac11n)\ast5p=5mnp=5\ast(-\frac3{20})\ast(-30)\ast\frac49=5\ast(-\frac11)\ast(-1)\ast\frac21=10$Задание 1065
Сумма двадцати чисел, каждое из которых равно 1 или −1, равно 0. Найдите произведение этих двадцати чисел.
Решение
Произведение двадцати чисел, каждое из которых равно 1 или −1 состоит из десяти множителей 1 и десяти множителей −1, а так как количество отрицательных множителей четное, то произведение будет положительным и равно 1.
Ответ: 1.Задание 1066
Верно ли утверждение:
1) если a > 0 и b > 0, то ab > 0;
2) если a < 0 и b < 0, то ab < 0;
3) если ab > 0, a > 0 и b > 0;
4) если ab < 0, a > 0 и b < 0?Решение
1) верно
2) не верно
3) не обязательно, может быть a < 0 и b < 0
4) не обязательно, может быть a < 0 и b > 0Задание 1067
На сколько произведение чисел −4,2 и −3,5 больше:
1) большего из них;
2) их суммы?Решение
1) (−4,2 * (−3,5)) − (−3,5) = 14,7 + 3,5 = 18,2
2) (−4,2 * (−3,5)) − (−4,2 + (−3,5)) = 14,7 − (−7,7) = 14,7 + 7,7 = 22,4Задание 1068
На сколько произведение чисел −1,6 и 2,5 меньше:
1) меньшего из них;
2) их суммы?Решение
1) −1,6 − (−1,6 * 2,5) = −1,6 + 4 = 2,4
2) (−1,6 + 2,5) − (−1,6 * 2,5) = 0,9 + 4 = 4,9Задание 1069
Представьте в виде суммы двух дробей с числителем 1 дробь:
1) 5/6;
2) 7/12;
3) 9/20;
4) 4/9;
5) 1/2.Решение
1) $\frac56=\frac36+\frac26=\frac12+\frac13$
2) $\frac7{12}=\frac4{12}+\frac3{12}=\frac13+\frac14$
3) $\frac9{20}=\frac4{20}+\frac5{20}=\frac15+\frac14$
4) $\frac49=\frac19+\frac39=\frac19+\frac13$
5) $\frac12=\frac24=\frac14+\frac14$Задание 1070
За месяц завод изготовил продукции на 644 тыс.р., что на 15% больше, чем было запланировано. На какую сумму планировали изготовить продукции на заводе?
Решение
Пусть на x тыс.руб. было запланировано выпустить продукции, тогда:
x + 0,15x = 644
1,15x = 644
x = 644 : 1,15
x = 560 тыс.руб. запланированная стоимость продукции.
Ответ: 560 тыс.руб.Задание 1071
Вычислите значение выражения наиболее удобным способом:
1) 3,18 * 7,8 + 3,18 * 2,2;
2) 2 7/15 ∗ 4/9 + 2 7/15 ∗ 5/9.Решение
1) 3,18 * 7,8 + 3,18 * 2,2 = 3,18 * (7,8 + 2,2) = 3,18 * 10 = 31,8
2) $2\frac7{15}\ast\frac49+2\frac7{15}\ast\frac59=2\frac7{15}\ast(\frac49+\frac59)=2\frac7{15}\ast1=2\frac7{15}$Задание 1072
Раскройте скобки:
1) 8(a + 4);
2) 3(b + 4);
3) 0,4(x − 5).Решение
1) 8(a + 4) = 8a + 32
2) 3(b + 4) = 3b + 12
3) 0,4(x − 5) = 0,4x − 2Задание 1073
Упростите выражение:
1) 5m + 7m;
2) 6n + 3n + n;
3) 9y − 3y − y.Решение
1) 5m + 7m = 12m
2) 6n + 3n + n= 10n
3) 9y − 3y − y = 5yЗадание 1074
Четыре мальчика соревновались в нескольких (более одного) видах спорта. В каждом из видов спорта за одно и то же место начислялось одинаковое количество баллов (выраженных натуральным числом), причем каждое из мест (1−е, 2−е, 3−е, 4−е) мог занять только один из участников. В конце этих соревнований выяснилось, что мальчики получили 16, 14, 13 и 12 баллов соответственно. Выясните, в скольких видах спорта они соревновались.
Решение
16 + 14 + 13 + 12 = 55 баллов всего получили мальчики.
55 = 5 * 11, следовательно мальчики набрали или 5 баллов в 11 видах спорта (что невозможно) или 11 баллов в 5 видах спорта.
Ответ: 5 видов спорта. 230
-
Страница 230
Ответы к параграфу 39. Распределительное свойство умножения
Задание 1075
Верно ли применено распределительное свойство умножения:
1) −3(4 + 8) = −12 − 24;
2) (−5 − 6) * 7 = −35 − 42;
3) (m − n) * (−2) = −2m − 2n;
4) −5(p − k + 9) = 5p + 5k − 45;
5) −(0,2 + c) = −0,2 + c;
6) −(−a − b) = a − b?
В случае отрицательного ответа укажите, в чем состоит ошибка.Решение
1) верно
2) верно
3) неверно, (m − n) * (−2) = −2m + 2n.
4) неверно, −5(p − k + 9) = −5p + 5k − 45.
5) неверно, −(0,2 + c) = −0,2 − c.
6) неверно, −(−a − b) = a + b.Задание 1076
Раскройте скобки:
1) 2(a + 3b − 7c);
2) 0,4(1,3x − 0,5y − 1,3);
3) (a − 4d + 3p) * (−0,8);
4) −0,4a(−4b + 3p − 1,1c);
5) −m(−k + 29n − 38,9);
6) (0,1 + 0,3x − 2y) * (−10a).Решение
1) 2(a + 3b − 7c) = 2a + 6b − 14c
2) 0,4(1,3x − 0,5y − 1,3) = 0,52x − 0,2y − 0,52
3) (a − 4d + 3p) * (−0,8) = −0,8a + 3,2d − 2,4p
4) −0,4a(−4b + 3p − 1,1c) = 1,6ab − 1,2ap + 0,44ac
5) −m(−k + 29n − 38,9) = mk − 29mn + 38,9m
6) (0,1 + 0,3x − 2y) * (−10a) = −a − 3ax + 20xyЗадание 1077
Раскройте скобки:
1) −3(4 + 5m − 6n);
2) −0,2(−14t + z − 25y);
3) (−3,1x + 7,8y − 9,6) * 0,1;
4) (0,7x − 0,6y + 0,5z) * (−1,5p).Решение
1) −3(4 + 5m − 6n) = −12 − 15m + 18n
2) −0,2(−14t + z − 25y) = 2,8t − 0,2z + 5y
3) (−3,1x + 7,8y − 9,6) * 0,1 = −0,31x + 0,78y − 0,96
4) (0,7x − 0,6y + 0,5z) * (−1,5p) = −1,5xp + 0,9py − 0,75pzЗадание 1078
Раскройте скобки и найдите значение выражения:
1) 12,14 − (3,5 + 6,14);
2) 2,67 − (8,04 − 7,33);
3) 4,3 + (9,2 − 4,3 + 3,8);
4) (3,98 − 7,36) − (5,98 − 10,36).Решение
1) 12,14 − (3,5 + 6,14) = 12,14 − 3,5 − 6,14 = (12,14 − 6,14) − 3,5 = 6 − 3,5 = 2,5
2) 2,67 − (8,04 − 7,33) = 2,67 − 8,04 + 7,33 = (2,67 + 7,33) − 8,04 = 10 − 8,04 = 1,96
3) 4,3 + (9,2 − 4,3 + 3,8) = 4,3 + 9,2 − 4,3 + 3,8 = (4,3 − 4,3) + (9,2 + 3,8) = 13
4) (3,98 − 7,36) − (5,98 − 10,36) = 3,98 − 7,36 − 5,98 + 10,36 = (10,36 − 7,36) + (3,98 − 5,98) = 3 + (−2) = 1Задание 1079
Раскройте скобки и найдите значение выражения:
1) 9,38 − (−10 + 5,38);
2) −8,76 − (−3,25 − 10,76);
3) −6,19 + (−1,5 + 5,19);
4) −(−21,4 + 12,7) + (−20,4 + 12,7).Решение
1) 9,38 − (−10 + 5,38) = 9,38 + 10 − 5,38 = (9,38 − 5,38) + 10 = 4 + 10 = 14
2) −8,76 − (−3,25 − 10,76) = −8,76 + 3,25 + 10,76 = (10,76 − 8,76) + 3,25 = 2 + 3,25 = 5,25
3) −6,19 + (−1,5 + 5,19) = −6,19 − 1,5 + 5,19 = (−6,19 + 5,19) − 1,5 = −1 − 1,5 = −2,5
4) −(−21,4 + 12,7) + (−20,4 + 12,7) = 21,4 − 12,7 − 20,4 + 12,7 = (21,4 − 20,4) + (−12,7 + 12,7) = 1Задание 1080
Раскройте скобки и упростите выражение:
1) m − (n + m);
2) x + (−x + y);
3) (x + 3,2) − (x + 6,4);
4) −(m − 4,7 + n) − (10,3 − m).Решение
1) m − (n + m) = m − n − m = (m − m) − n = −n
2) x + (−x + y) = x − x + y = (x − x) + y = y
3) (x + 3,2) − (x + 6,4) = x + 3,2 − x − 6,4 = (x − x) + (3,2 − 6,4) = −3,2
4) −(m − 4,7 + n) − (10,3 − m) = −m + 4,7 − n − 10,3 + m = (−m + m) + (4,7 − 10,3) − n = −5,6 − nЗадание 1081
Раскройте скобки и упростите выражение:
1) −(a − b) − b;
2) −c + (c − d);
3) −(2,7 − a) + (−a + 1,8);
4) −(−6,2 + a + b) − (a − b + 10,9).Решение
1) −(a − b) − b = −a + b − b = −a + (b − b) = −a
2) −c + (c − d) = −c + c − d = (c − c) − d = −d
3) −(2,7 − a) + (−a + 1,8) = −2,7 + a − a + 1,8 = (a − a) + (−2,7 + 1,8) = −0,9
4) −(−6,2 + a + b) − (a − b + 10,9) = 6,2 − a − b − a + b − 10,9 = (−a − a) + (b − b) + (6,2 − 10,9) = −2a − 4,7Задание 1082
Запишите сумму двух выражений и упростите ее:
1) −8 − a и a + 23;
2) 1,3 + m и −4 − m;
3) p − m + k и −p + m + k;
4) 3,7 − 2,6 + 4,2 и −12,5 + 2,6 − 4,2.Решение
1) (−8 − a) + (a + 23) = −8 − a + a + 23 = (a − a) + (23 − 8) = 15
2) (1,3 + m) + (−4 − m) = 1,3 + m − 4 − m = (m − m) + (1,3 − 4) = −2,7
3) (p − m + k) + (−p + m + k) = p − m + k − p + m + k = (p − p) + (m m) + (k + k) = 2k
4) (3,7 − 2,6 + 4,2) + (−12,5 + 2,6 − 4,2) = 3,7 − 2,6 + 4,2 − 12,5 + 2,6 − 4,2 = (4,2 − 4,2) + (2,6 − 2,6) + (−12,5 + 3,7) = −8,8Задание 1083
Запишите разность двух выражений и упростите ее:
1) −8,4 + a и a + 14,9;
2) 42 − b и −b + 36,4;
3) m − n и −n + m − p;
4) −2,2 + 4,9 − c и 4,9 − c − 1,3.Решение
1) (−8,4 + a) − (a + 14,9) = −8,4 + a − a − 14,9 = (a − a) + (−8,4 − 14,9) = −23,3
2) (42 − b) − (−b + 36,4) = 42 − b + b − 36,4 = (b − b) + (42 − 36,4) = 5,6
3) (m − n) − (−n + m − p) = m − n + n − m + p = (m − m) + (n − n) + p = p
4) (−2,2 + 4,9 − c) − (4,9 − c − 1,3) = −2,2 + 4,9 − c − 4,9 + c + 1,3 = (c − c) + (4,9 − 4,9) + (−2,2 + 1,3) = −0,9 231
-
Страница 231
Задание 1084
Приведите подобные слагаемые:
1) 7x − 18x + 25x − 6x;
2) −0,3b − 1,4b + 3,1b + 0,7b;
3) 11a − 16b − 18a + 9b;
4) −0,8k + 0,9p − 1,7k + 0,5k + 1,4p.Решение
1) 7x − 18x + 25x − 6x = 8x
2) −0,3b − 1,4b + 3,1b + 0,7b = 2,1b
3) 11a − 16b − 18a + 9b = (11a − 18a) + (−16b + 9b) = −7a − 7b
4) −0,8k + 0,9p − 1,7k + 0,5k + 1,4p = (−0,8k − 1,7k + 0,5k) + (0,9p + 1,4p) = −2k + 2,3pЗадание 1085
Приведите подобные слагаемые:
1) −4a + 12a + 13a − 27a;
2) 4,2x − 4,8x − 6,3x − 2,4x;
3) −17x + 19y − 15y + 13x;
4) 0,9n − 0,8m − 0,7m + 3,5n − 1,9n.Решение
1) −4a + 12a + 13a − 27a = −6a
2) 4,2x − 4,8x − 6,3x − 2,4x = −9,3x
3) −17x + 19y − 15y + 13x = (−17x + 13x) + (19y − 15y) = −4x + 4y
4) 0,9n − 0,8m − 0,7m + 3,5n − 1,9n = (0,9n + 3,5n − 1,9n) + (−0,8m − 0,7m) = 2,5n − 1,5mЗадание 1086
Раскройте скобки и приведите подобные слагаемые:
1) 3(5a + 4) − 11a;
2) −0,2(4b − 7) + 1,4b;
3) 3a(7 − b) − 7(b − 3a);
4) −4(2k − 9) − 3(6k + 1);
5) (3x − 11) * 0,2 − 5(0,4 − 0,3x);
6) 1/6(18m−24n)−(5m+2n);
7) −3,5(3a − 2b) + 2(1,3a − b);
8) −(8a − 13) + 3(4 − 3a).Решение
1) 3(5a + 4) − 11a = 15a + 12 − 11a = 4a + 12
2) −0,2(4b − 7) + 1,4b = −0,8b + 1,4 + 1,4b = 0,6b + 1,4
3) 3a(7 − b) − 7(b − 3a) = 21a − 3ab − 7b + 21a = 42a − 3ab − 7b
4) −4(2k − 9) − 3(6k + 1) = −8k + 36 − 18k − 3 = −26k + 33
5) (3x − 11) * 0,2 − 5(0,4 − 0,3x) = 0,6x − 2,2 − 2 + 1,5x = 2,1x − 4,2
6) $\frac16(18m-24n)-(5m+2n)=3m-4n-5m-2n=-2m-6n$
7) −3,5(3a − 2b) + 2(1,3a − b) = −10,5a + 7b + 2,6a − 2b = −7,9a + 5b
8) −(8a − 13) + 3(4 − 3a) = −8a + 13 + 12 − 9a = −17a + 25Задание 1087
Раскройте скобки и приведите подобные слагаемые:
1) −4x − 8(9 − 2x);
2) 1/3(12−2,1y)+0,3y;
3) 6(3x − 2) + 4(5x − 1);
4) −7(3 − 4c) + 14(0,5 + 2c);
5) 3(2,1x − y) − 2,8(2x − 3y);
6) 0,4(8t + 7) − 1,6(2t − 3).Решение
1) −4x − 8(9 − 2x) = −4x − 72 + 16x = 12x − 72
2) $\frac13(12-2,1y)+0,3y=4-0,7y+0,3y=4-0,4y$
3) 6(3x − 2) + 4(5x − 1) = 18x − 12 + 20x − 4 = 38x − 16
4) −7(3 − 4c) + 14(0,5 + 2c) = −21 + 28c + 7 + 28c = 56c − 14
5) 3(2,1x − y) − 2,8(2x − 3y) = 6,1x − 3y − 5,6x + 8,4y = 0,7x + 5,4y
6) 0,4(8t + 7) − 1,6(2t − 3) = 3,2t + 2,8 − 3,2t + 4,8 = 7,6Задание 1088
Вынесите за скобки общий множитель:
1) 5a + 5b;
2) ax − bx;
3) −6a + 6b − 6;
4) 12a − 6b + 18c;
5) 0,3ab + 1,3ac − a;
6) 9m − 6n + 12k − 15.Решение
1) 5a + 5b = 5(a + b)
2) ax − bx = x(a − b)
3) −6a + 6b − 6 = −6(a − b + 1)
4) 12a − 6b + 18c = 6(2a − b + 3c)
5) 0,3ab + 1,3ac − a = a(0,3b + 1,3c − 1)
6) 9m − 6n + 12k − 15 = 3(3m − 2n + 4k − 5)Задание 1089
Вынесите за скобки общий множитель:
1) 3c − 3d;
2) mx − my;
3) 7a − 7b − 7c;
4) −12x − 8y + 20.Решение
1) 3c − 3d = 3(c − d)
2) mx − my = m(x − y)
3) 7a − 7b − 7c = 7(a − b − c)
4) −12x − 8y + 20 = −4(3x + 2y − 5)Задание 1090
Запишите выражение, значение которого противоположно значению данного выражения при любом значении a:
1) a − 8;
2) a + 8;
3) −a + 8;
4) −a − 8.Решение
1) −(a − 8) = 8 − a
2) −(a + 8) = −a − 8
3) −(−a + 8) = a − 8
4) −(−a − 8) = a + 8Задание 1091
Раскройте скобки:
1) $-12(\frac56a-\frac14b+\frac7{24}c-\frac1{12})=-10a+3b-\frac72c+1=-10a+3b-3\frac12c+1$
2) $(16a+8b-\frac59c-\frac49d)\ast(-\frac9{32}n)=-\frac92an-\frac94bn+\frac5{32}cn+\frac18dn=-4\frac12an-2\frac14bn+\frac5{32}cn+\frac18dn$
3) $-\frac4{15}bc(-45a-30d+3\frac34m-\frac38)=-\frac4{15}bc(-45a-30d+\frac{15}4m-\frac38)=12abc+8bcd-bcm+\frac1{10}bc$
4) (−3,6ab + 20a − b − 100) * (−5xy) = 18abxy − 100axy + 5bxy + 500xyЗадание 1092
Раскройте скобки:
1) $\frac37b(-14t-\frac79y+2\frac13c)=\frac37b(-14t-\frac79y+\frac73c)=-6bt-\frac13by+bc$
2) $-1,2xy(5m-6c+\frac16t-\frac56)=-6mxy+7,2cxy-0,2txy+xy$
3) $0,3mn(1,5-6bc+7b-10c)=0,45mn-1,8mnbc+2,1bmn-3cmn$ 232
-
Страница 232
Задание 1093
Вычислите наиболее удобным способом:
1) $6,72\ast(-2\frac13)+3,72\ast2\frac13=-2\frac13\ast(6,72-3,72)=-\frac73\ast3=-7$
2) $-7,2\ast2\frac2{15}-7,2\ast3\frac7{15}-7,2\ast(-4\frac4{15})=-7,2\ast(2\frac2{15}+3\frac7{15}-4\frac4{15})=-7,2\ast1\frac13=-\frac{36}5\ast\frac43=-\frac{12}5\ast\frac41=-\frac{48}5=-9,6$
3) $-3\frac9{14}\ast0,3-0,3\ast(-1\frac{10}{21})+0,3\ast1\frac16=0,3\ast(-3\frac9{14}+1\frac{10}{21}+1\frac16)=0,3\ast(-3\frac{27}{42}+1\frac{20}{42}+1\frac7{42})=0,3\ast(-1)=-0,3$Задание 1094
Вычислите наиболее удобным способом:
1) $-32,3\ast7\frac{10}{13}+2\frac3{13}\ast(-32,3)=-32,3\ast(7\frac{10}{13}+2\frac3{13})=-32,3\ast10=-323$
2) $1,6\ast(-5,3)-2,4\ast(-5,3)-4\frac45\ast5,3=-5,3\ast(1,6-2,4+4,8)=-5,3\ast4=-21,2$
3) $-5,6\ast4\frac23+6\frac{47}{48}\ast5,6+2\frac5{16}\ast(-5,6)=-5,6\ast(4\frac23-6\frac{47}{48}+2\frac5{16})=-5,6\ast(4\frac{32}{48}-6\frac{47}{48}+2\frac{15}{48})=-5,6\ast0=0$Задание 1095
Приведите подобные слагаемые:
1) $-\frac16x+\frac14y+\frac19x-\frac12y=(-\frac16x+\frac19x)+(\frac14y-\frac12y)=(-\frac3{18}x+\frac2{18}x)+(\frac14y-\frac24y)=-\frac1{18}x-\frac14y$
2) $\frac37a-\frac2{15}b-\frac5{14}a+\frac7{30}b=(\frac37a-\frac5{14}a)+(-\frac2{15}b+\frac7{30}b)=(\frac6{14}a-\frac5{14}a)+(-\frac4{30}b+\frac7{30}b)=\frac1{14}a+\frac3{30}b=\frac1{14}a+\frac1{10}b$
3) $-\frac{15}{16}m+\frac7{12}n+\frac5{12}m-\frac38p-\frac58n-\frac14p=(-\frac{15}{16}m+\frac5{12}m)+(\frac7{12}n-\frac58n)+(-\frac38p-\frac14p)=(-\frac{45}{48}m+\frac{20}{48}m)+(\frac{14}{24}n-\frac{15}{24}n)+(-\frac38p-\frac28p)=-\frac{25}{48}m-\frac1{24}n-\frac58p$
4) $\frac7{18}b-\frac{13}{28}c-\frac5{14}c-\frac{23}{36}b+\frac47c+\frac49b=(\frac7{18}b-\frac{23}{36}b+\frac49b)+(-\frac{13}{28}c-\frac5{14}c+\frac47c)=(\frac{14}{36}b-\frac{23}{36}b+\frac{16}{36}b)+(-\frac{13}{28}c-\frac{10}{28}c+\frac{16}{28}c)=\frac7{36}b-\frac7{28}c=\frac7{36}b-\frac14c$Задание 1096
Упросите выражение и найдите его значение:
1) 0,8y + 0,5y − 0,9y − 0,7y, если y = −1,8;
2) 20a − 15b − 10a + 6b, если a = −0,3, b = 0,7;
3) a * (−2,4) + 3,2a − (−4,8), если a = −0,2;
4) 6,2 * b − b * (−7,3) − (−4,5) * (−b), если b = −1,4.Решение
1) 0,8y + 0,5y − 0,9y − 0,7y = −0,3y = −0,3 * (−1,8) = 0,54
2) 20a − 15b − 10a + 6b = (20a − 10a) + (−15b + 6b) = 10a − 9b = 10 * (−0,3) − 9 * 0,7 = −3 − 6,3 = −9,3
3) a * (−2,4) + 3,2a − (−4,8) = (−2,4a + 3,2a) + 4,8 = 0,8a + 4,8 = 0,8 * (−0,2) + 4,8 = −0,16 + 4,8 = 4,64
4) 6,2 * b − b * (−7,3) − (−4,5) * (−b) = 6,2b + 7,3b − 4,5b = 9b = 9 * (−1,4) = −12,6Задание 1097
Упростите выражение и найдите его значение:
1) −0,6x − 1,2x + 3,2x − 5,6x, если x = 3,5;
2) −2,7x + 3,6y + 4,5x − 5,8y, если
x=−1 1/9,y=−4/11.Решение
1) −0,6x − 1,2x + 3,2x − 5,6x = −4,2x = −4,2 * 3,5 = −14,7
2) $-2,7x+3,6y+4,5x-5,8y=1,8x-2,2y=1,8\ast(-1\frac19)-2,2\ast(-\frac4{11})=\frac95\ast(-\frac{10}9)-\frac{11}5\ast(-\frac4{11})=\frac11\ast(-\frac21)-\frac15\ast(-\frac41)=-2+\frac45=-1\frac15$Задание 1098
Раскройте скобки и приведите подобные слагаемые:
1) $\frac23(-\frac38x+6)-\frac37(28-\frac7{12}x)=-\frac28x+4-12+\frac3{12}x=(-\frac14x+\frac14x)+(4-12)=-8$
2) $-\frac29(2,7x-1\frac12y)-1\frac16(2,4x-1\frac57y)=-\frac29(2,7x-\frac32y)-\frac76(2,4x-\frac{12}7y)=-0,6x+\frac13y-2,8x+2y=2\frac13y-3,4x$Задание 1099
Найдите значение выражения:
1) −6(2a − 7) + 4(5a − 6) при a = −2,5;
2) −1,1(2m − 4) − (2 − 3m) − 0,4(1 − m) при m = − 4;
3) 1 1/9(3y−9)−8 1/3(y−6) при y = 3,6.Решение
1) −6(2a − 7) + 4(5a − 6) = −12a + 42 + 20a − 24 = 8a + 18 = 8 * (−2,5) + 18 = −20 + 18 = −2
2) −1,1(2m − 4) − (2 − 3m) − 0,4(1 − m) = −2,2m + 4,4 − 2 + 3m − 0,4 + 0,4m = 1,2m + 2 = 1,2 * (−4) + 2 = −4,8 + 2 = −2,8
3) $1\frac19(3y-9)-8\frac13(y-6)=\frac{10}9(3y-9)-\frac{25}3(y-6)=\frac{10}3y-10-\frac{25}3y+50=40-\frac{15}3y=40-5y=40-5\ast3,6=40-18=22$Задание 1100
Найдите значение выражения:
1) 7(3 − 4b) − 5(3b + 4) при b = −0,2;
2) −2(3,1x − 1) + 3(1,2x + 1) − 8(0,3x + 3) при x = 0,8;
3) −2 4/13(13−p)+1 1/13(26−p) при p=3 1/4.Решение
1) 7(3 − 4b) − 5(3b + 4) = 21 − 28b − 15b − 20 = −43b + 1 = −43 * (−0,2) + 1 = 8,6 + 1 = 9,6
2) −2(3,1x − 1) + 3(1,2x + 1) − 8(0,3x + 3) = −6,2x + 2 + 3,6x + 3 − 2,4x − 24 = −5x − 19 = −5 * 0,8 − 19 = −4 − 19 = −23
3) $-2\frac4{13}(13-p)+1\frac1{13}(26-p)=-\frac{30}{13}(13-p)+\frac{14}{13}(26-p)=-30+\frac{30}{13}p+28-\frac{14}{13}p=\frac{16}{13}p-2=\frac{16}{13}\ast\frac{13}4-2=4-2=2$ 233
-
Страница 233
Задание 1101
Вынесите за скобки общий множитель:
1) 6ax − 12a + 9ay;
2) 7ab + 14ac − 28a;
3) −8mn − 6mk − 10m;
4) 8abc − 24abd − 6ab.Решение
1) 6ax − 12a + 9ay = 3a(2x − 4 + 3y)
2) 7ab + 14ac − 28a = 7a(b + 2c − 4)
3) −8mn − 6mk − 10m = −2m(4n + 3k + 5)
4) 8abc − 24abd − 6ab = 2ab(4c − 12d − 3)Задание 1102
Вынесите за скобки общий множитель:
1) −1,2pc − 0,2mc + c;
2) −35ac − 15bc + 20abc;
3) −6ax − 30ay − 42az;
4) 9mnp + 45mnk − 27mn.Решение
1) −1,2pc − 0,2mc + c = −c(1,2p + 0,2m − 1)
2) −35ac − 15bc + 20abc = −5c(7a + 3b − 4ab)
3) −6ax − 30ay − 42az = −6a(x + 5y + 7z)
4) 9mnp + 45mnk − 27mn = 9mn(p + 5k − 3)Задание 1103
Докажите, что значение выражения не зависит от значения переменной:
1) 4(a − 3) − 3(6 − a) + (20 − 7a);
2) (3m − 7) * 0,6 − 0,8(4m − 5) − (−1,7 − 1,4m).Решение
1) 4(a − 3) − 3(6 − a) + (20 − 7a) = 4a − 12 − 18 + 3a + 20 − 7a = (4a + 3a − 7a) + (−12 − 18 + 20) = 0 − 10 = −10
2) (3m − 7) * 0,6 − 0,8(4m − 5) − (−1,7 − 1,4m) = 1,8m − 4,2 − 3,2m + 4 + 1,7 + 1,4m = (1,8m + 1,4m − 3,2m) + (−4,2 + 4 + 1,7) = 0 + 1,5 = 1,5Задание 1104
Докажите, что при любом значении переменной:
1) выражение 3(5,1k − 2,5) − 0,9(17k + 5) принимает отрицательное значение;
2) выражение −0,2(36x + 15) + 0,6(12x + 7) принимает положительное значение.Решение
1) 3(5,1k − 2,5) − 0,9(17k + 5) = 15,3k − 7,5 − 15,3k − 4,5 = (15,3k − 15,3k) + (−7,5 − 4,5) = 0 − 12 = −12 < 0
2) −0,2(36x + 15) + 0,6(12x + 7) = −7,2x − 3 + 7,2x + 4,2 = (7,2x − 7,2x) + (4,2 − 3) = 0 + 1,2 = 1,2Задание 1105
Докажите, что при любом натуральном значении n значение выражения:
1) 5(4n − 4,2) − 7(2n − 3) кратно 6;
2) 9(3n − 8) + 2(36 − 11n) кратно 5.Решение
1) 5(4n − 4,2) − 7(2n − 3) = 20n − 21 − 14n + 21 = (20n − 14n) + (21 − 21) = 6n, так как один из множителей равен 6, то следовательно значение выражения кратно 6.
2) 9(3n − 8) + 2(36 − 11n) = 27n − 72 + 72 − 22n = (27n − 22n) + (72 − 72) = 5n, так как один из множителей равен 5, то следовательно значение выражения кратно 5.Задание 1106
Найдите значение выражения:
1) −4(n − k), если k − n = −7;
2) 4m − (m + 3n), если m − n = −0,8;
3) −3a − (8b − 15a), если 3a − 2b = −0,25;
4) 6(2x − 3y) − 2(x + y), если 2y − x = −17,8;
5) 7a(3b+4c)−3a(b+1/3c), если a=−3 1/3,3c+2b=−1,6.Решение
1) −4(n − k) = −4n + 4k = 4(k − n) = 4 * (−7) = −28
2) 4m − (m + 3n) = 4m − m − 3n = 3m − 3n = 3(m − n) = 3 * (−0,8) = −2,4
3) −3a − (8b − 15a) = −3a − 8b + 15a = 12a − 8b = 4(3a − 2b) = 4 * (−0,25) = −1
4) 6(2x − 3y) − 2(x + y) = 12x − 18y − 2x − 2y = 10x − 20y = −10(2y − x) = −10 * (−17,8) = −178
5) $7a(3b+4c)-3a(b+\frac13c)=21ab+28ac-3ab-ac=18ab+27ac=9a(3c+2b)=9\ast(-3\frac13)\ast(-1,6)=9\ast(-\frac{10}3)\ast(-1,6)=-30\ast(-1,6)=48$Задание 1107
Чем равно значение выражения:
1) 5a − (3a − 10b), если a + 5b = 1,7;
2) −0,9x − (0,6x + 0,5y), если 3x + y = −0,2;
3) 2m(n − 4p) + 5mp, если m = 4, 3p − 2n = −0,4?Решение
1) 5a − (3a − 10b) = 5a − 3a + 10b = 2a + 10b = 2(a + 5b) = 2 * 1,7 = 3,4
2) −0,9x − (0,6x + 0,5y) = −0,9x − 0,6x − 0,5y = −1,5x − 0,5y = −0,5(3x + y) = −0,5 * (−0,2) = 0,1
3) 2m(n − 4p) + 5mp = 2mn − 8mp + 5mp = 2mn − 3mp = −m(3p − 2n) = −4 * (−0,4) = 1,6Задание 1108
Запишите выражение без знака модуля:
1) |π − 3,14|;
2) |3 − π|;
3) |3,142 − π|;
4) |π − 3,15|.Решение
1) |π − 3,14| = π − 3,14
2) |3 − π| = 3 − π
3) |3,142 − π| = 3,142 − π
4) |π − 3,15| = π − 3,15Задание 1109
Знак какого арифметического действия надо поставить вместо звездочки, чтобы получилось верное равенство:
1) 6/7∗1 1/6=1;
2) 2/9∗5/9=2/5;
3) 3∗2 2/11=9/11;
4) 1,2∗5/6=1.Решение
1) $\frac67⋅1\frac16=\frac67⋅\frac76=1$
2) $\frac29:\frac59=\frac29⋅\frac95=\frac25$
3) $3-2\frac2{11}=2\frac{11}{11}-2\frac2{11}=\frac9{11}$
4) $1,2⋅\frac56=\frac65⋅\frac56=1$ 234
-
Страница 234
Задание 1110
Представьте в виде разности двух дробей с числителем 1 дробь:
1) 1/12;
2) 2/63;
3) 1/4;
4) 3/28;
5) 1/24.Решение
1) $\frac1{12}=\frac4{12}-\frac3{12}=\frac13-\frac14$
2) $\frac2{63}=\frac9{63}-\frac7{63}=\frac17-\frac19$
3) $\frac14=\frac24-\frac14=\frac12-\frac14$
4) $\frac3{28}=\frac7{28}-\frac4{28}=\frac14-\frac17$
5) $\frac1{24}=\frac4{24}-\frac3{24}=\frac16-\frac18$Задание 1111
До снижения цен стул стоил 1600 р. Какой стала цена стула после двух последовательных снижений, первое из которых было на 5%, а второе − на 10%?
Решение
1600 − 1600 * 0,05 = 1600 * (1 − 0,05) = 1600 * 0,95 = 1520 р. стал стоить стул после первого снижения;
1520 − 1520 * 0,1 = 1520 * (1 − 0,1) = 1520 * 0,9 = 1369 р. стал стоить стул после двух последовательных снижений.
Ответ: 1369 р.Задание 1112
По одной дороге в противоположных направлениях двигаются всадник со скоростью 14 км/ч и пешеход со скоростью 4 км/ч. Каким будет расстояние между ними через 15 мин, если сейчас между ними 3 км? Сколько решений имеет задача?
Решение
15 мин = $\frac{15}{60}=\frac14$ ч.
1 вариант: всадник и пешеход двигаются друг от друга.
$14\ast\frac14=\frac72=3,5$ км проедет всадник за 15 минут;
$4\ast\frac14=1$ км пройдет пешеход за 15 минут;
3,5 + 1 = 4,5 км совместно преодолеют всадник и пешеход.
Так как изначально между всадником и пешеходом было 3 км, то:
4,5 + 3 = 7,5 км будет между всадником и пешеходом через 15 минут.
2 вариант: всадник и пешеход двигаются друг к другу.
$14\ast\frac14=\frac72=3,5$ км проедет всадник за 15 минут;
$4\ast\frac14=1$ км пройдет пешеход за 15 минут;
3,5 + 1 = 4,5 км совместно преодолеют всадник и пешеход.
Так как изначально между всадником и пешеходом было 3 км, то:
4,5 − 3 = 1,5 км будет между всадником и пешеходом через 15 минут.
Ответ: 7,5 км или 1,5 км.Задание 1113
Используя действие умножения, проверьте, верно ли выполнено деление:
1) 0,12 : 0,3 = 0,4;
2) 1 1/3:1 7/9=3/4.Решение
1) 0,4 * 0,3 = 0,12
Ответ: верно.
2) $\frac34\ast1\frac79=\frac34\ast\frac{16}9=\frac11\ast\frac43=1\frac13$
Ответ: верно.Задание 1114
В вершинах куба записаны восемь различных чисел. Докажите, что хотя бы одно из них меньше среднего арифметического трех соседних чисел (соседними называют числа, записанные на концах одного ребра).
Решение
Пусть x − наименьшее число в одной из вершин, тогда:
x + a, x + b, x + c − соседние числа, где a, b, c − некоторые числа.
$\frac{x+a+x+b+x+c}3=\frac{3x+a+b+c}3=\frac{3x}3+\frac{a+b+c}3=(x+\frac{a+b+c}3)>x$ что и требовалось доказать. 236
-
Страница 236
Ответы к параграфу 40. Деление рациональных чисел
Задание 1115
Заполните таблицу:
Решение
12 : (−3) = −4;
−12 : 3 = −4;
−12 : (−3) = 4;
25 : (−5) = −5;
−40 : (−8) = 5;
−9 : (−9) = 1;
−8 : 8 = −1;
0 : (−6) = 0.
Задание 1116
Выполните деление:
1) 24 : (−8) = −3
2) −72 : (−6) = 12
3) −11,34 : (−42) = 5,67
4) 17 : (−5) = −3,4
5) −2 : 8 = −0,25
6) −1 : 25 = −0,04
7) −0,72 : (−0,8) = 0,9
8) $-\frac6{35}:\frac{18}{25}=-\frac6{35}\ast\frac{25}{18}=-\frac17\ast\frac53=-\frac5{21}$
9) $22:(-\frac{11}{17})=22\ast(-\frac{17}{11})=2\ast(-\frac{17}1)=-34$
10) $-\frac{14}{15}:21=-\frac{14}{15}\ast\frac1{21}=-\frac2{15}\ast\frac13=-\frac2{45}$
11) $\frac{19}{25}:(-7\frac35)=\frac{19}{25}:(-\frac{38}5)=\frac{19}{25}\ast(-\frac5{38})=\frac15\ast(-\frac12)=-\frac1{10}$
12) $-1\frac59:2\frac{13}{18}=-\frac{14}9:\frac{49}{18}=-\frac{14}9\ast\frac{18}{49}=-\frac21\ast\frac27=-\frac47$Задание 1117
Выполните деление:
1) −36 : 9 = −4
2) −45 : (−5) = 9
3) −78,2 : (−34) = 2,3
4) −13 : 2 = −6,5
6) −21 : (−14) = 1,5
6) 6 : (−12) = −0,5
7) −8,4 : 0,07 = −120
8) $\frac3{14}:(-\frac2{21})=\frac3{14}\ast(-\frac{21}2)=\frac32\ast(-\frac32)=-\frac94=-2\frac14$
9) $-12:(-\frac67)=-12\ast(-\frac76)=-2\ast(-\frac71)=14$
10) $-\frac34:(-5)=-\frac34\ast(-\frac15)=\frac3{20}$
11) $-1\frac8{27}:(-1\frac59)=-\frac{35}{27}:(-\frac{14}9)=-\frac{35}{27}\ast(-\frac9{14})=-\frac53\ast(-\frac12)=\frac56$
12) $-3\frac3{26}:(-2\frac{10}{13})=-\frac{81}{26}:(-\frac{36}{13})=-\frac{81}{26}\ast(-\frac{13}{36})=-\frac92\ast(-\frac14)=\frac98=1\frac18$Задание 1118
Решите уравнение:
1) 9x = −54;
2) 1,2x = −6;
3) 13x = −6;
4) −21x = 48;
5) 2 1/7x=−1 11/14;
6) −3,78 : x = −0,6;
7) x:(−1 3/13)=−0,26;
8) 18 : (−x) = 0,6.Решение
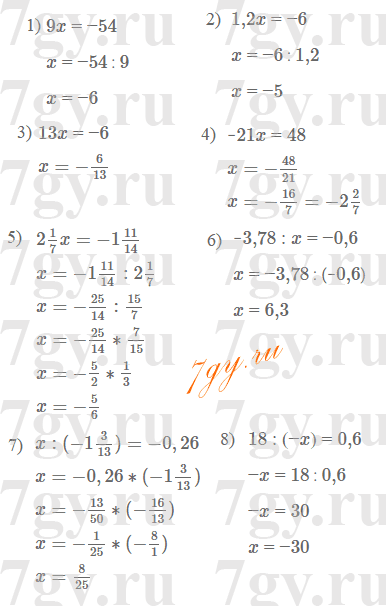
Задание 1119
Решите уравнение:
1) −5x = 30;
2) −0,8x = −5,6;
3) −7x = 4;
4) −6x = −8;
5) 2/3 x=−3/8;
6) 40,5 : x = −9;
7) −32/63:x=8/21;
8) x:2/7=−1,4.Решение
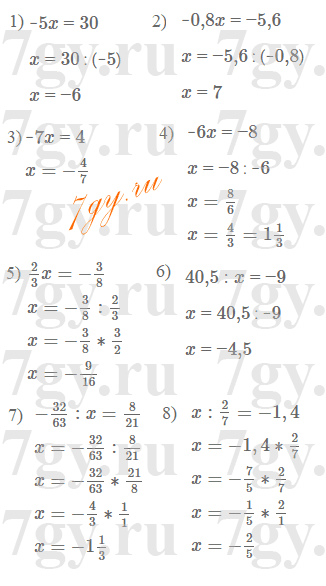
237
-
Страница 237
Задание 1120
Какие из дробей
−a/b,−a/−b,a/−b,a/b,−a/b равны?Решение
$-\frac ab=\frac a{-b}=\frac{-a}b$
$\frac{-a}{-b}=\frac ab$Задание 1121
Выполните действия:
1) 3,2 : (−8) + (−4,8) : (−6);
2) 2,1 * (−4) − 7,8 : (−6);
3) 14,4 : (−0,18) − 8,5 : (6,3 − 8).Решение
1) 3,2 : (−8) + (−4,8) : (−6) = −0,4 + 0,8 = 0,4
2) 2,1 * (−4) − 7,8 : (−6) = −8,4 + 1,3 = −7,1
3) 14,4 : (−0,18) − 8,5 : (6,3 − 8) = −80 − 8,5 : (−1,7) = −80 + 5 = −75Задание 1122
Выполните действия:
1) −5,4 : 0,6 + 9,6 : (−0,8);
2) −3,5 * 6 − 0,8 : (−0,16);
3) −21,6 : (−0,12) + 9,6 : (8,9 − 11,3).Решение
1) −5,4 : 0,6 + 9,6 : (−0,8) = −9 − 12 = −21
2) −3,5 * 6 − 0,8 : (−0,16) = −21 + 5 = −16
3) −21,6 : (−0,12) + 9,6 : (8,9 − 11,3) = 180 + 9,6 : (−2,4) = 180 − 4 = 176Задание 1123
Найдите значение выражения:
1) $(-\frac4{15}+\frac59):(-\frac{26}{45})=(-\frac{12}{45}+\frac{25}{45})\ast(-\frac{45}{26})=\frac{13}{45}\ast(-\frac{45}{26})=\frac11\ast(-\frac12)=-\frac12$
2) $-12:(-2\frac1{13})+1\frac14:(-\frac{15}{46})=-12:(-\frac{27}{13})+\frac54:(-\frac{15}{46})=-12\ast(-\frac{13}{27})+\frac54\ast(-\frac{46}{15})=-4\ast(-\frac{13}9)+\frac12\ast(-\frac{23}3)=\frac{52}9-\frac{23}6=\frac{104}{18}-\frac{69}{18}=\frac{35}{18}=1\frac{17}{18}$
3) $(-3\frac3{10}-1\frac8{15}):(-1\frac2{27})=(-3\frac9{30}-1\frac{16}{30}):(-\frac{29}{27})=-4\frac56\ast(-\frac{27}{29})=-\frac{29}6\ast(-\frac{27}{29})=-\frac12\ast(-\frac91)=\frac92=4\frac12$
4) $(\frac9{20}-\frac78):(-\frac7{45}-\frac29)=(\frac{18}{40}-\frac{35}{40}):(-\frac7{45}-\frac{10}{45})=-\frac{17}{40}:(-\frac{17}{45})=-\frac{17}{40}\ast(-\frac{45}{17})=-\frac18\ast(-\frac91)=\frac98=1\frac18$Задание 1124
Вычислите:
1) $(-\frac3{14}-\frac8{21}):\frac{20}{21}=(-\frac9{42}-\frac{16}{42}):\frac{20}{21}=-\frac{25}{42}\ast\frac{21}{20}=-\frac52\ast\frac14=-\frac58$
2) $\frac38:(-\frac58)-(-2\frac14):(-1\frac4{11})=\frac38:(-\frac58)-(-\frac94):(-\frac{15}{11})=\frac38\ast(-\frac85)-(-\frac94)\ast(-\frac{11}{15})=\frac31\ast(-\frac15)-(-\frac34)\ast(-\frac{11}5)=-\frac35-\frac{33}{20}=-\frac{12}{20}-\frac{33}{20}=-\frac{45}{20}=-\frac94=-2\frac14$
3) $(-4\frac1{12}+3\frac9{10}):3\frac3{10}=(-3\frac{65}{60}+3\frac{54}{60}):\frac{33}{10}=-\frac{11}{60}\ast\frac{10}{33}=-\frac16\ast\frac13=-\frac1{18}$
4) $(\frac{11}{14}-\frac56):(\frac{11}{14}-\frac34)=(\frac{33}{42}-\frac{35}{42}):(\frac{22}{28}-\frac{21}{28})=-\frac2{42}:\frac1{28}=-\frac1{21}\ast\frac{28}1=-\frac13\ast\frac41=-\frac43=-1\frac13$Задание 1125
Решите уравнение:
1) |x| : (−1,2) = −4;
2) −0,72 : |x| = −0,9.Решение
1) |x| : (−1,2) = −4
|x| = −4 * (−1,2)
|x| = 4,8
x 1 = 4 , 8;
x 2 = − 4 , 8.
2) −0,72 : |x| = −0,9
|x| = −0,72 : (−0,9)
|x| = 0,8
x 1 = 0 , 8;
x 2 = − 0 , 8.Задание 1126
Решите уравнение:
1) −3y − 9y + 5y = 2,1;
2) −2,4m + 3,8m + 1,2m = −0,052;
3) −3/7 a + 5/6 a − 8/21 a = −1/49;
4) −8 7/16 c + 10 19/24 c − 3 3/8 c = −3 1/16;
5) 2,3x − (−7,2) * x + x * (−1,5) = −2,4;
6) 3,4y + y * (−8,1) − (−2,2) * y = −10.Решение
1) −3y − 9y + 5y = 2,1
−7y = 2,1
y = 2,1 : (−7)
y = −0,3
2) −2,4m + 3,8m + 1,2m = −0,052
2,6m = −0,052
m = −0,052 : 2,6
m = −0,02
3) $-\frac37a+\frac56a-\frac8{21}a=-\frac1{49}$
$-\frac{18}{42}a+\frac{35}{42}a-\frac{16}{42}a=-\frac1{49}$
$\frac1{42}a=-\frac1{49}$
$a=-\frac1{49}:\frac1{42}$
$a=-\frac1{49}\ast\frac{42}1$
$a=-\frac17\ast\frac61$
$a=-\frac67$
4) $-8\frac7{16}c+10\frac{19}{24}c-3\frac38c=-3\frac1{16}$
$-8\frac{21}{48}c+10\frac{38}{48}c-3\frac{18}{48}c=-\frac{49}{16}$
$-1\frac1{48}c=-\frac{49}{16}$
$-1\frac1{48}c=-\frac{49}{16}:(-\frac{49}{48})$
$c=-\frac{49}{16}\ast(-\frac{48}{49})$
$c=-\frac11\ast(-\frac31)$
с = 3
5) 2,3x − (−7,2) * x + x * (−1,5) = −2,4
2,3x + 7,2x − 1,5x = −2,4
8x = −2,4
x = −2,4 : 8
x = −0,3
6) 3,4y + y * (−8,1) − (−2,2) * y = −10
3,4y − 8,1y + 2,2y = −10
−2,5y = −10
y = −10 : −2,5
y = 4Задание 1127
Решите уравнение:
1) −7x + 4x − 8x = −9,9;
2) 0,6y − 1,9y − 0,5y = 0,54;
3) 1/8x−2/3 x + 1/2 x = −5/18;
4) −9 5/6 b + 2 3/4 b + 1 5/12 b = 1 7/27.Решение
1) −7x + 4x − 8x = −9,9
−11x = −9,9
x = −9,9 : (−11)
x = 0,9
2) 0,6y − 1,9y − 0,5y = 0,54
−1,8y = 0,54
y = 0,54 : (−1,8)
y = −0,3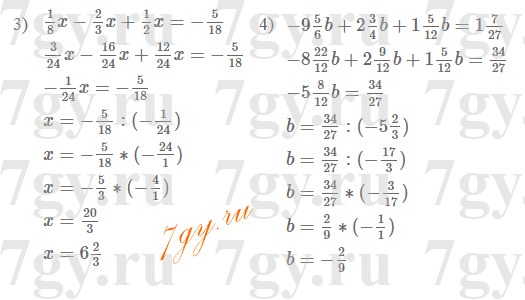
238
-
Страница 238
Задание 1128
Выполните действия:
1) −84 : 2,1 − 4,64 : (−5,8) − 6 : 24 + 1,4 : (−0,28);
2) (−32,64 : 0,8 + 4,324 : (−0,46)) * 1,5 + 28,16.Решение
1) −84 : 2,1 − 4,64 : (−5,8) − 6 : 24 + 1,4 : (−0,28) = −40 + 0,8 − 0,25 − 5 = −44,45
2) (−32,64 : 0,8 + 4,324 : (−0,46)) * 1,5 + 28,16 = (−40,8 − 9,4) * 1,5 + 28,16 = −50,2 * 1,5 + 28,16 = −75,3 + 28,16 = −47,14Задание 1129
Вычислите:
1) 2,46 : (−4,1) − 15 : 0,25 − 40 : (−25) + (−14,4) : (−0,32);
2) (−12,16 : (−0,4) + 4,62 : (−0,3)) * (−2,4) − 93,7.Решение
1) 2,46 : (−4,1) − 15 : 0,25 − 40 : (−25) + (−14,4) : (−0,32) = −0,6 − 60 + 1,6 + 45 = −14
2) (−12,16 : (−0,4) + 4,62 : (−0,3)) * (−2,4) − 93,7 = (30,4 − 15,4) * (−2,4) − 93,7 = 15 * (−2,4) − 93,7 = −36 − 93,7 = −129,7Задание 1130
Найдите значение выражения:
1) $(2\frac{13}{48}-(-2\frac5{12})):(-3\frac34)+9\frac34:(-13)=(2\frac{13}{48}+2\frac{20}{48}):(-\frac{15}4)+\frac{39}4:(-13)=4\frac{11}{16}\ast(-\frac4{15})+\frac{39}4\ast(-\frac1{13})=\frac{75}{16}\ast(-\frac4{15})+\frac{39}4\ast(-\frac1{13})=\frac54\ast(-\frac11)+\frac34\ast(-\frac11)=-\frac54-\frac34=-\frac84=-2$
2) $(1\frac23-3,6):(-2\frac79+4\frac1{15})\ast(-2,6)=(1\frac23-3\frac35):(-2\frac79+4\frac1{15})\ast(-2,6)=(1\frac{10}{15}-2\frac{24}{15}):(-2\frac{35}{45}+3\frac{48}{45})\ast(-2,6)=-1\frac{14}{15}:1\frac{13}{45}:(-2,6)=-\frac{29}{15}:\frac{58}{45}\ast(-\frac{13}5)=-\frac{29}{15}\ast\frac{45}{58}\ast(-\frac{13}5)=-\frac11\ast\frac32\ast(-\frac{13}5)=\frac{39}{10}=3,9$Задание 1131
Выполните действия:
1) $(-2\frac59+1\frac{20}{21}):1\frac8{49}-1\frac79:(-6)=(-1\frac{98}{63}+1\frac{60}{63}):\frac{57}{49}-\frac{16}9:(-6)=-\frac{38}{63}\ast\frac{49}{57}-\frac{16}9\ast(-\frac16)=-\frac29\ast\frac73-\frac89\ast(-\frac13)=-\frac{14}{27}+\frac8{27}=-\frac6{27}=-\frac29$
2) $(5\frac59-6,8):(2\frac{13}{30}-2\frac1{12})\ast3,6=(5\frac59-6\frac45):(2\frac{26}{60}-2\frac5{60})\ast\frac{18}5=(5\frac{25}{45}-6\frac{36}{45}):\frac{21}{60}\ast\frac{18}5=-1\frac{11}{45}:\frac7{20}\ast\frac{18}5=-\frac{56}{45}\ast\frac{20}7\ast\frac{18}5=-\frac85\ast\frac41\ast\frac21=-\frac{64}5=-12\frac45$Задание 1132
При каких значениях a и b верно равенство:
1) a : b = 1;
2) a : b = −1;
3) a : b = 0?Решение
1) a : b = 1
a = 1 * b
a = b
Ответ: при a = b
2) a : b = −1
a = −1 * b
a = −b
Ответ: при a = −b
3) a : b = 0
a = 0 * b
a = 0;
b ≠ a : 0
b ≠ 0.
Ответ: при a = 0 и b ≠ 0.Задание 1133
Вместо звездочек поставьте такие цифры (вместо одной звездочки − одну цифру), чтобы:
1) число 4 делилось нацело на 3, и на 10;
2) число 124 делилось нацело на 9 и на 5;
3) число 67* делилось нацело на 2 и на 3.
Найдите все возможные решения.Решение
1) Целое число делится нацело на 10, если оно оканчивается цифрой 0, тогда:
число 4 примет вид *40.
Целое число делится нацело на 3, если сумма его цифр нацело делится на 3, тогда:
6 = 2 + 4 + 0;
9 = 5 + 4 + 0;
12 = 8 + 4 + 0.
Ответ: 240; 540; 840.
2) Целое число делится нацело на 5, если оно оканчивается цифрой 0 или 5, тогда:
число 124 примет вид 1240 или 1245.
Целое число делится нацело на 9, если сумма его цифр нацело делится на 9, тогда:
9 = 1 + 2 + 2 + 4 + 0;
18 = 1 + 2 + 6 + 4 + 5.
Ответ: 12240; 12645.
3) Целое число делится нацело на 2, если оно четное, тогда:
число 67* может принять следующие виды:
670;
672;
674;
676;
678.
Целое число делится нацело на 3, если сумма его цифр нацело делится на 3, тогда:
15 = 6 + 7 + 2;
21 = 6 + 7 + 8.
Ответ: 672; 678.Задание 1134
Мухтар начал догонять преступника, когда тот был на расстоянии 1,2 км от него, и поймал его через 3 мин. С какой скоростью бежал пес, если злоумышленник пытался убежать со скоростью 0,2 км/мин?
Решение
0,2 * 3 = 0,6 км пробежал за 3 минуты злоумышленник;
1,2 + 0,6 = 1,8 км пробежал Мухтар до злоумышленника;
1,8 : 3 = 0,6 км/мин скорость Мухтара.
Ответ: 0,6 км/мин.Задание 1135
В шкафу висели рубашки, из которых 1/3 были белого цвета, а 5 рубашек − черного. Сколько всего рубашек было в шкафу, если 50% из них было ни белыми, ни черными?
Решение
Пусть x рубашек было всего, тогда:
0,5x рубашек, было белого и черного цветов;
$\frac13x$ рубашек белого цвета;
$\frac12x-\frac13x=\frac36x-\frac26x=\frac16x$ рубашек черного цвета.
Так как черных рубашек было 5, то:
$\frac16x=5$
$x=5:\frac16$
$x=5\ast\frac61$
x = 30 рубашек было всего.
Ответ: 30 рубашек.Задание 1136
Коля выбрал в библиотеке три книги. Однако домой он может взять только две из них. Сколько вариантов выбора двух книг есть у Коли?
Решение
3 варианта:
1−ю и 2−ю;
1−ю и 3−ю;
2−ю и 3−ю.
Ответ: 3 варианта.Задание 1137
Масса арбуза на 1 кг 200 г больше 60% его массы. Какова масса арбуза?
Решение
Пусть x кг масса арбуза, тогда:
0,6x кг 60% массы арбуза.
1 кг 200 г = 1200 г.
Так как масса арбуза на 1 кг 200 г больше 60% его массы, то:
x − 0,6x = 1200
0,4x = 1200
x = 1200 : 0,4
x = 3000 г = 3 кг масса арбуза.
Ответ: 3 кг.Задание 1138
В семье Петровых девять детей и двое родителей. Средний возраст всех детей составляет 6 лет, а средний возраст всех членов семьи − 12 лет. Каков средний возраст родителей?
Решение
9 * 6 = 54 года суммарный возраст детей;
9 + 2 = 11 членов семьи;
11 * 12 = 132 года суммарный возраст всех членов семьи;
132 − 54 = 78 суммарный возраст родителей;
78 : 2 = 39 лет средний возраст родителей.
Ответ: 39 лет. 239
-
Страница 239
Задание 1139
Является ли корнем уравнения 4(x + 6) = x + 9 число:
1) −3;
2) 0;
3) 2;
4) −5?Решение
1) 4(−3 + 6) = −3 + 9
4 * 3 = 6
12 ≠ 6, следовательно x = −3 не является корнем уравнения.
Ответ: нет.
2) 4(0 + 6) = 0 + 9
4 * 6 = 9
12 ≠ 9, следовательно x = 0 не является корнем уравнения.
Ответ: нет.
3) 4(2 + 6) = 2 + 9
4 * 8 = 11
32 ≠ 11, следовательно x = 2 не является корнем уравнения.
Ответ: нет.
4) 4(−5 + 6) = −5 + 9
4 * 1 = 4
4 = 4, следовательно x = −5 является корнем уравнения.
Ответ: да.Задание 1140
Является ли корнем уравнения $x^2$ = 2x + 3 число:
1) 3;
2) −2;
3) −1;
4) 4?Решение
1) $3^2$ = 2 ∗ 3 + 3
9 = 6 + 3
9 = 9, следовательно x = 3 является корнем уравнения.
Ответ: да.
2) $(−2)^2$ = 2 ∗ (−2) + 3
4 = −4 + 3
4 ≠ −1, следовательно x = −2 не является корнем уравнения.
Ответ: нет.
3) $(−1)^2$ = 2 ∗ (−1) + 3
1 = −2 + 3
1 = 1, следовательно x = −1 является корнем уравнения.
Ответ: да.
4) $4^2$ = 2 ∗ 4 + 3
16 = 8 + 3
16 ≠ 11, следовательно x = 4 не является корнем уравнения.
Ответ: нет.Задание 1141
Какие из приведенных уравнений имеют бесконечно много корней, а какие − не имеют корней:
1) 2x − 1 = 3;
2) 3x + 2 = 2;
3) x + 2 = x + 2;
4) 2x + 2 = 2(x + 1);
5) x + 2 = 3 + x;
6) 0 * x = 3?Решение
1) 2x − 1 = 3
2x = 3 + 1
x = 4 : 2
x = 2, один корень.
2) 3x + 2 = 2
3x = 2 − 2
3x = 0
x = 0, один корень.
3) x + 2 = x + 2
x − x = 2 − 2
0 = 0, бесконечно много корней.
4) 2x + 2 = 2(x + 1)
2x + 2 = 2x + 2
2x − 2x = 2 − 2
0 = 0, бесконечно много корней.
5) x + 2 = 3 + x
x − x = 3 − 2
0 ≠ 1, не имеет корней.
6) 0 * x = 3
0 ≠ 3, не имеет корней.Задание 1142
В стране Севентаун семь городов, каждый из которых соединен дорогами более чем с двумя городами. Докажите, что из любого города можно доехать до любого другого (возможно, проезжая через другие города).
Решение
Возьмем два города не соединенных между собой. Каждый из них соединен как минимум с тремя городам, тогда получается две отдельные друг от друга ветки по 4 города, то есть 4 + 4 = 8 городов, то невозможно по условию задачи. Значит хотя бы один город из этих двух веток является общим, а значит из любого города можно доехать до любого другого (возможно, проезжая через другие города).
241
-
Страница 241
Ответы к параграфу 41. Решение уравнений
Задание 1143
Решите уравнение:
1) 7x = −30 + 2x;
2) 16 − 18x = −25x − 12;
3) −17x + 20 = 7x − 28;
4) 20 − 2x = 27 + x;
5) 0,2x + 4,3 = 0,4x − 6,5;
6) 0,6x + 100 = 0,9x + 1;
7) −9/14 x + 18 = −2/3 x + 17;
8) −8/15 x − 11 = 4/9 x + 11.Решение
1) 7x = −30 + 2x
7x − 2x = −30
5x = −30
x = −30 : 5
x = −6
2) 16 − 18x = −25x − 12
−18x + 25x = −12 − 16
7x = −28
x = −28 : 7
x = −4
3) −17x + 20 = 7x − 28
−17x − 7x = −28 − 20
−24x = −48
x = −48 : (−24)
x = 2
4) 20 − 2x = 27 + x
−2x − x = 27 − 20
−3x = 7
$x=-\frac73=-2\frac13$
5) 0,2x + 4,3 = 0,4x − 6,5
0,2x − 0,4x = −6,5 − 4,3
−0,2x = −10,8
x = −10,8 : (−0,2)
x = 54
6) 0,6x + 100 = 0,9x + 1
0,6x − 0,9x = 1 − 100
−0,3x = −99
x = −99 : (−0,3)
x = 330
Задание 1144
Чему равен корень уравнения:
1) 3x = 28 − x;
2) 5x + 12 = 8x + 30;
3) 33 + 8x = −5x + 72;
4) 6x − 19 = −x − 10;
5) 0,7 − 0,2x = 0,3x − 1,8;
6) 0,1x + 9 = 0,2x − 4?Решение
1) 3x = 28 − x
3x + x = 28
4x = 28
x = 28 : 4
x = 7
2) 5x + 12 = 8x + 30
5x − 8x = 30 − 12
−3x = 18
x = 18 : (−3)
x = −6
3) 33 + 8x = −5x + 72
8x + 5x = 72 − 33
13x = 39
x = 39 : 13
x = 3
4) 6x − 19 = −x − 10
6x + x = −10 + 19
7x = 9
$x=\frac97=1\frac27$
5) 0,7 − 0,2x = 0,3x − 1,8
−0,2x − 0,3x = −1,8 − 0,7
−0,5x = −2,5
x = −2,5 : (−0,5)
x = 5
6) 0,1x + 9 = 0,2x − 4
0,1x − 0,2x = −4 − 9
−0,1x = −13
x = −13 : (−0,1)
x = 130Задание 1145
Решите уравнение:
1) −6(x + 2) = 4x − 17;
2) (18x − 19) − (4 − 7x) = −73;
3) 10x + 3(7 − 2x) = 13 + 2x;
4) −3(4 − 5y) + 2(3 − 6y) = −3,9.Решение
1) −6(x + 2) = 4x − 17
−6x − 12 = 4x − 17
−6x − 4x = −17 + 12
−10x = −5
x = −5 : (−10)
x = 0,5
2) (18x − 19) − (4 − 7x) = −73
18x − 19 − 4 + 7x = −73
18x + 7x = −73 + 19 + 4
25x = −50
x = −50 : 25
x = −2
3) 10x + 3(7 − 2x) = 13 + 2x
10x + 21 − 6x = 13 + 2x
10x − 6x − 2x = 13 − 21
2x = −8
x = −8 : 2
x = −4
4) −3(4 − 5y) + 2(3 − 6y) = −3,9
−12 + 15y + 6 − 12y = −3,9
3y = −3,9 + 12 − 6
3y = 2,1
y = 2,1 : 3
y = 0,7Задание 1146
Найдите корень уравнения:
1) 9(x − 1) = x + 15;
2) (11x + 14) − (5x − 8) = 25;
3) 12 − 4(x − 3) = 39 − 9x;
4) 2(3x + 5) − 3(4x − 1) = 11,8.Решение
1) 9(x − 1) = x + 15
9x − 9 = x + 15
9x − x = 15 + 9
8x = 24
x = 24 : 8
x = 3
2) (11x + 14) − (5x − 8) = 25
11x + 14 − 5x + 8 = 25
11x − 5x = 25 − 14 − 8
6x = 3
x = 3 : 6
x = 0,5
3) 12 − 4(x − 3) = 39 − 9x
12 − 4x + 12 = 39 − 9x
−4x + 9x = 39 − 12 − 12
5x = 15
x = 15 : 5
x = 3
4) 2(3x + 5) − 3(4x − 1) = 11,8
6x + 10 − 12x + 3 = 11,8
−6x = 11,8 − 10 − 3
−6x = −1,2
x = −1,2 : (−6)
x = 0,2Задание 1147
Решите уравнение:
1) 0,8(4x + 5) = −3,2;
2) −2,4(7 − 9y) = −48.Решение
1) 0,8(4x + 5) = −3,2
3,2x + 4 = −3,2
3,2x = −3,2 − 4
3,2x = −7,2
x = −7,2 : 3,2
x = -72 : 32
х = -2,25
2) −2,4(7 − 9y) = −48
−16,8 + 21,6y = −48
21,6y = −48 + 16,8
21,6y = −31,2
y = −31,2 : 21,6
y = −312 : 216
$y=-\frac{13}9$
$y=-1\frac49$ 242
-
Страница 242
Задание 1148
Решите уравнение:
1) −7(2 − 3x) = 56;
2) (5 + 7a) * 15 = −30.Решение
1) −7(2 − 3x) = 56
−14 + 21x = 56
21x = 56 + 14
21x = 70
$x=\frac{70}{21}$
$x=\frac{10}3=3\frac13$
2) (5 + 7a) * 15 = −30
75 + 105a = −30
105a = −30 − 75
105a = −105
a = −105 : 105
a = −1Задание 1149
Найдите корень уравнения:
1) 0,3m + 2(0,2m − 0,3) = 0,8 − 0,7(m − 2);
2) 0,6 − (1,3x + 1) = 2,8x − 13,52;
3) 1/8(8/9 y + 8)− 1/5(5/6 y + 1 2/3) = 2.Решение
1) 0,3m + 2(0,2m − 0,3) = 0,8 − 0,7(m − 2)
0,3m + 0,4m − 0,6 = 0,8 − 0,7m + 1,4
0,3m + 0,4m + 0,7m = 0,8 + 1,4 + 0,6
1,4m = 2,8
m = 2,8 : 1,4
m = 2
2) 0,6 − (1,3x + 1) = 2,8x − 13,52
0,6 − 1,3x − 1 = 2,8x − 13,52
−1,3x − 2,8x = −13,52 − 0,6 + 1
−4,1x = −13,12
x = −13,12 : (−4,1)
x = 3,2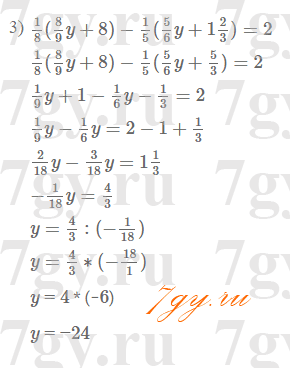
Задание 1150
Решите уравнение:
1) 0,4(x − 3) − 1,6 = 5(0,1x − 0,5);
2) 1,5(2x − 5) + 2x = 5(0,5x − 1,5) − 10;
3) 2/3(1 1/2 x + 3/5) − 4/5(5/12 x − 1/2) = 1 3/5.Решение
1) 0,4(x − 3) − 1,6 = 5(0,1x − 0,5)
0,4x − 1,2 − 1,6 = 0,5x − 2,5
0,4x − 0,5x = −2,5 + 1,2 + 1,6
−0,1x = 0,3
x = 0,3 : (−0,1)
x = −3
2) 1,5(2x − 5) + 2x = 5(0,5x − 1,5) − 10
3x − 7,5 + 2x = 2,5x − 7,5 − 10
3x + 2x − 2,5x = −7,5 − 10 + 7,5
2,5x = −10
x = −10 : 2,5
x = −4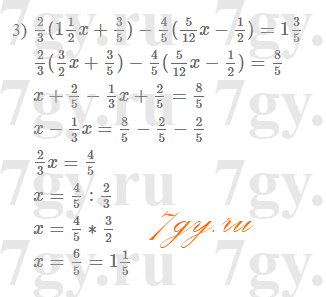
Задание 1151
Чему равен корень уравнения:
1) −9(6x + 1) = −45(2x + 2,6);
2) 0,6(2x + 1) = −1,8(3x − 4)?Решение
1) −9(6x + 1) = −45(2x + 2,6)
−54x − 9 = −90x − 117
−54x + 90x = −117 + 9
36x = −108
x = −108 : 36
x = −3
2) 0,6(2x + 1) = −1,8(3x − 4)
1,2x + 0,6 = −5,4x + 7,2
1,2x + 5,4x = 7,2 − 0,6
6,6x = 6,6
x = 6,6 : 6,6
x = 1Задание 1152
Решите уравнение:
1) −1,4(x − 6) = 7(4x + 1,2);
2) 2,6(0,4x − 1,4) = −3,9(1,2x − 0,9)?Решение
1) −1,4(x − 6) = 7(4x + 1,2)
−1,4x + 8,4 = 28x + 8,4
−1,4x − 28x = 8,4 − 8,4
−29,4x = 0
x = 0
2) 2,6(0,4x − 1,4) = −3,9(1,2x − 0,9)
1,04x − 3,64 = −4,68x + 3,51
1,04x + 4,68x = 3,51 + 3,64
5,72x = 7,15
x = 7,15 : 5,72
x = 1,25Задание 1153
Решите уравнение:
1) $\frac{x+0,4}8=\frac{0,7-x}3$
2) $\frac56=\frac{5x+6}{2x+3,2}$Решение
1) $\frac{x+0,4}8=\frac{0,7-x}3$
3(x + 0,4) = 8(0,7 − x)
3x + 1,2 = 5,6 − 8x
3x + 8x = 5,6 − 1,2
11x = 4,4
x = 4,4 : 11
x = 0,4
2) $\frac56=\frac{5x+6}{2x+3,2}$
5(2x + 3,2) = 6(5x + 6)
10x + 16 = 30x + 36
10x − 30x = 36 − 16
−20x = 20
x = 20 : (−20)
x = −1Задание 1154
Найдите чему равен корень уравнения:
1) $\frac{x-8}{x+2}=\frac73$;
2) $\frac4{x-1,2}=\frac{15}{x-10}$.Решение
1) $\frac{x-8}{x+2}=\frac73$
3(x − 8) = 7(x + 2)
3x − 24 = 7x + 14
3x − 7x = 14 + 24
−4x = 38
$x=-\frac{38}4$
$x=-\frac{19}2=-9\frac12$
2) $\frac4{x-1,2}=\frac{15}{x-10}$
4(x − 10) = 15(x − 1,2)
4x − 40 = 15x − 18
4x − 15x = −18 + 40
−11x = 22
x = 22 : (−11)
x = −2Задание 1155
Решите уравнение:
1) $\frac x{12}-\frac x8=\frac76$
2) $\frac{13x}{21}+\frac{9x}{14}=-1$
3) $-\frac{3x}{10}-\frac7{15}=\frac x6$Решение

Задание 1156
Найдите корень уравнения:
1) $\frac x3+\frac x{12}=\frac{15}4$
2) $\frac{7x}9-\frac{3x}4=\frac5{12}$
3) $1-\frac{8x}{15}=\frac{4x}9$Решение
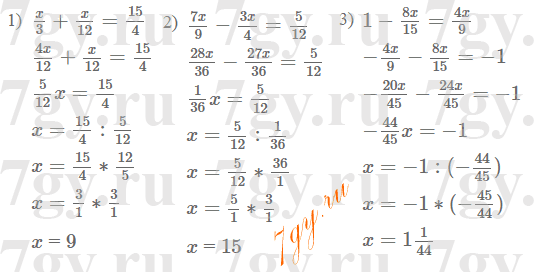
Задание 1157
При каком значении переменной:
1) значение выражения 5x − 0,4(7x − 9) равно 2,94;
2) выражения 0,4(6 − 4y) и 0,5(7 − 3y) − 1,9 принимают равные значения;
3) значение выражения −3(2,1x − 4) − 1,6 на 2,6 больше значения выражения 1,2(0,5 − 5x);
4) значение выражения a + 8 в 7 раз меньше значения выражения 90 − 3a?Решение
1) 5x − 0,4(7x − 9) = 2,94
5x − 2,8x + 3,6 = 2,94
2,2x = 2,94 − 3,6
2,2x = −0,66
x = −0,66 : 2,2
x = −0,3
2) 0,4(6 − 4y) = 0,5(7 − 3y) − 1,9
2,4 − 1,6y = 3,5 − 1,5y − 1,9
−1,6y + 1,5y = 3,5 − 1,9 − 2,4
−0,1y = 3,5 − 4,3
−0,1y = −0,8
y = −0,8 : (−0,1)
y = 8
3) −3(2,1x − 4) − 1,6 − 1,2(0,5 − 5x) = 2,6
−6,3x + 12 − 1,6 − 0,6 + 6x = 2,6
−6,3x + 6x = 2,6 − 12 + 1,6 + 0,6
−0,3x = −7,2
x = −7,2 : (−0,3)
x = 24
4) 7(a + 8) = 90 − 3a
7a + 56 = 90 − 3a
7a + 3a = 90 − 56
10a = 34
a = 34 : 10
a = 3,4Задание 1158
При каком значении переменной:
1) значение выражения 2,5x + 3(0,5x − 1,8) равно −3,8:
2) выражения 7 − 2x и 9x − 8(x + 1) принимают равные значения;
3) значение выражения 3(m + 1,4) − 6,4 на 0,7 меньше значения выражения 8m − 15(m − 1,1);
4) значение выражения 5n − 1 в 6 раз больше значения выражения 2n − 13?Решение
1) 2,5x + 3(0,5x − 1,8) = −3,8
2,5x + 1,5x − 5,4 = −3,8
2,5x + 1,5x = −3,8 + 5,4
4x = 1,6
x = 1,6 : 4
x = 0,4
2) 7 − 2x = 9x − 8(x + 1)
7 − 2x = 9x − 8x − 8
−2x − 9x + 8x = −8 − 7
−3x = −15
x = −15 : (−3)
x = 5
3) 8m − 15(m − 1,1) − (3(m + 1,4) − 6,4) = 0,7
8m − 15m + 16,5 − 3m − 4,2 + 6,4 = 0,7
8m − 15m − 3m = 0,7 − 16,5 + 4,2 − 6,4
−10m = −18
m = −18 : (−10)
m = 1,8
4) 6(2n − 13) = 5n − 1
12n − 78 = 5n − 1
12n − 5n = 78 − 1
7n = 77
n = 77 : 7
n = 11 243
-
Страница 243
Задание 1159
При каком значении a уравнение:
1) 5ax = 14 − x имеет корень, равный числу 4;
2) (2a + 1)x = −6a + 2x − 13 имеет корень, равный числу −1?Решение
1) 5a * 4 = 14 − 4
20a = 10
a = 10 : 20
a = 0,5
2) (2a + 1) * (−1) = −6a + 2 * (−1) − 13
−2a − 1 = −6a − 2 − 13
−2a + 6a = −2 − 13 + 1
4a = −14
a = −14 : 4
a = −3,5Задание 1160
При каком значении a уравнение:
1) 4ax = 84 имеет корень, равный числу −3;
2) (a − 7)x = 6 + 5a имеет корень, равный числу 1?Решение
1) 4a * (−3) = 84
−12a = 84
a = 84 : (−12)
a = −7
2) (a − 7) * 1 = 6 + 5a
a − 7 = 6 + 5a
a − 5a = 6 + 7
−4a = 13
$a=-\frac{13}4=-3\frac14$Задание 1161
Решите уравнение:
1) 3(6x − 1) = 2(9x + 1) − 10;
2) 1,4(2 − 5x) = 15 − (7x + 12,2).Решение
1) 3(6x − 1) = 2(9x + 1) − 10
18x − 3 = 18x + 2 − 10
18x − 18x = 3 + 2 − 10
0 ≠ −5, уравнение не имеет корней.
2) 1,4(2 − 5x) = 15 − (7x + 12,2)
2,8 − 7x = 15 − 7x − 12,2
7x − 7x = 15 − 12,2 − 2,8
0 = 0, уравнение имеет бесконечно много корней.Задание 1162
Решите уравнение:
1) 20 − 4x = 8(3x + 2,5) − 28x;
2) 4x + 9 = 5(2x − 7) − 6x.Решение
1) 20 − 4x = 8(3x + 2,5) − 28x
20 − 4x = 24x + 20 − 28x
−4x − 24x + 28x = 20 − 20
0 = 0, уравнение имеет бесконечно много корней.
2) 4x + 9 = 5(2x − 7) − 6x
4x + 9 = 10x − 35 − 6x
4x − 10x + 6x = −35 − 9
0 ≠ −44, уравнение имеет бесконечно много корней.Задание 1163
При каких значениях a уравнение не имеет корней:
1) ax = 1;
2) (a − 2)x = 3?Решение
1) 0 * x = 1
0 ≠ 1, то есть при а = 0 уравнение не имеет корней.
2) (a − 2)x = 3
a − 2 = 0
a = 2, то есть при а = 2 уравнение не имеет корней.Задание 1164
Найдите все целые значения a, при которых корень уравнения является целым числом:
1) ax = −14;
2) (a − 2)x = 12.Решение
1) ax = −14
$x=-\frac{14}a$, следовательно корень уравнения будет целым числом при a = 1; −1; 2; −2; 7; −7; 14; −14.
2) (a − 2)x = 12
$x=-\frac{12}{a-2}$, следовательно корень уравнения будет целым числом при a = 0; 1; 3; 4; 5; 8; 14; −1; −2; −4; −10.Задание 1165
Найдите все целые значения m, при которых корень уравнения является натуральным числом:
1) mx = 20;
2) (m + 3)x = −18.Решение
1) mx = 20
$x=\frac{20}m$, следовательно корень уравнения будет натуральным числом при m = 1; 3; 4; 5; 10; 20.
2) (m + 3)x = −18.
$x=-\frac{18}{m+3}$, следовательно корень уравнения будет натуральным числом при m = −21; −12; −9; −6; −5; −4.Задание 1166
Сколько процентов число 4 составляет от обратного ему числа?
Решение
1/4 обратное число числу 4, тогда:
$(4:\frac14)\ast100$ % = 4 * 4 * 100% = 1600%
Ответ: 1600%.Задание 1167
Сколько процентов число 5, составляет от числа, являющегося его квадратом?
Решение
$5^2$ = 25, тогда:
5 : 25 * 100% = 0,2 * 100% = 20%
Ответ: 20%.Задание 1168
Некоторое число сначала увеличили на 10%, а потом уменьшили результат на 10%. Установите, полученное число больше или меньше исходного и на сколько процентов.
Решение
Пусть x − первоначальное число, тогда:
x + 0,1x = 1,1x − число после увеличения;
1,1x − 0,1 * (1,1x) = 1,1x − 0,11x = 0,99x число после уменьшения.
(x − 0,99x) = 0,01x, следовательно полученное число меньше исходного на 1%.
Ответ: меньше на 1%.Задание 1169
На столе стояла коробка с конфетами. Женя взял половину конфет, а Катя − треть остальных, после чего в коробке осталось 6 конфет. Сколько конфет было в коробке сначала?
Решение
Пусть x конфет было всего, тогда:
$x-\frac12x=\frac12x$ конфет осталось после Жени;
$\frac12x\ast\frac13x=\frac16x$ конфет взяла Катя.
Так как в коробке осталось 6 конфет, то:
$x-\frac12x-\frac16x=6$
$\frac66x-\frac36x-\frac16x=6$
$\frac26x=6$
$\frac13x=6$
$x=6:\frac13$
$x=6\ast\frac31$
x = 18 конфет было в коробке сначала.
Ответ: 18 конфет.Задание 1170
Из шести девочек и троих мальчиков надо выбрать одного ученика для дежурства в школьной столовой. Какова вероятность того, что дежурным будет мальчик?
Решение
6 + 3 = 9 (уч.) - всего;
$\frac39=\frac13$ - вероятность того, что дежурным будет мальчик.
Ответ: 1/3.Задание 1171
Двузначное число, первая цифра которого 5, разделили на однозначное и получили в остатке 8. Найдите делимое и делитель.
Решение
Так как остаток 8, то однозначное число (делитель) будет больше остатка, значит 9.
Число кратное 9, первая цифра которого 5 равно 54, следовательно делимое будет равно 54 − 1 = 53.
Ответ: 53 − делимое, 9 − делитель. 244
-
Страница 244
Задание 1172
Задача от мудрой совы
В шахматной доске размером 8 × 8 клеток вырезали крайнюю левую верхнюю и крайнюю правую нижнюю клетки. Можно ли оставшуюся часть доски замостить косточками домино, покрывая одной косточкой ровно две клетки доски?
Решение
Вырезанные клетки белого цвета, значит на доске осталось 32 черных и 30 белых клеток.
Косточка домино покрывает обязательно 1 черную и 1 белую клетку одновременно, следовательно невозможно замостить косточками домино, покрывая одной косточкой ровно две клетки доски.
Ответ: нельзя. 245
-
Страница 245
Ответы к параграфу 42. Решение задач с помощью уравнений
Задание 1173
Лиса Алиса и кот Базилио наловили 215 окуньков, причем Алиса поймала в 4 раза больше, чем Базилио. Сколько окуньков поймал каждый из них?
Решение
Пусть x окуньков поймал Базилио, тогда:
4x окуньков поймала Алиса.
Так как всего они поймали 215 окуньков, то:
4x + x = 215
5x = 215
x = 215 : 5
x = 43 окунька поймал Базилио;
4x = 4 * 43 = 172 окунька поймала Алиса.
Ответ: 43 и 172 окунька.Задание 1174
Буратино заплатил за дневник и учебник "Арифметика" 96 сольдо, причем дневник стоил в 5 раз меньше, чем учебник. Сколько сольдо заплатил Буратино за дневник и сколько за учебник?
Решение
Пусть x сольдо заплатил Буратино за дневник, тогда:
5x сольдо заплатил Буратино за учебник.
Так как всего Буратино заплатил 96 сольдо, то:
5x + x = 96
6x = 96
x = 96 : 6
x = 16 сольдо заплатил Буратино за дневник;
5x = 5 * 16 = 80 сольдо заплатил Буратино за учебник.
Ответ: 16 и 80 сольдо. 246
-
Страница 246
Задание 1175
Масса выращенной моркови в 3 раза меньше, чем масса выращенной капусты. Сколько килограммов капусты вырастили, если известно, что ее было на 42 кг больше, чем моркови?
Решение
Пусть x кг вырастили моркови, тогда 3x кг вырастили капусты, а капусты вырастили на 42 кг больше.
Составим уравнение:
3x − x = 42;
2x = 42;
x = 42 : 2;
x = 21.
Значит, 21 кг вырастили моркови;
3 * 21 = 63 (кг) - вырастили капусты.
Ответ: 21 кг и 63 кг.Задание 1176
Заготовили липовый и гречишный мед, причем липового меда было в 9 раз больше, чем гречишного. Сколько всего килограммов меда заготовили, если гречишного заготовили на 56 кг меньше, чем липового?
Решение
Пусть x кг заготовили гречишного меда, тогда 9x кг заготовили липового меда, а гречишного мёда заготовили на 56 кг меньше.
Составим уравнение:
9x − x = 56;
8x = 56;
x = 56 : 8;
x = 7.
Значит, 7 кг гречишного мёда заготовили;
9x = 9 * 7 = 63 (кг) - липового мёда.
63 + 7 = 70 (кг) - меда всего заготовили.
Ответ: 70 кг мёда.Задание 1177
За первое полугодие Кирилл и Вася получили вместе 43 оценки "5" по математике, причем Кирилл получил на девять таких оценок больше, чем Вася. Сколько оценок "5" получил каждый мальчик?
Решение
Пусть x оценок "5" получил Вася, тогда (x + 9) оценок "5" получил Кирилл, а всего мальчики получили 43 оценки.
Составим уравнение:
x + x + 9 = 43;
2x = 43 − 9;
x = 34 : 2;
x = 17.
Значит, 17 оценок "5" получил Вася;
x + 9 = 17 + 9 = 26 оценок "5" получил Кирилл.
Ответ: 17 и 26 оценок.Задание 1178
Галя и Маша собрали 24,6 кг клубники, причем Галя собрала на 4,8 кг меньше, чем Маша. Сколько килограммов клубники собрала каждая девочка?
Решение
Пусть x кг клубники собрала Галя, тогда (x + 4,8) кг клубники собрала Маша, а всего девочки собрали 24,6 кг клубники.
Составим уравнение:
x + x + 4,8 = 24,6;
2x = 24,6 − 4,8;
2x = 19,8;
x = 19,8 : 2;
x = 9,9.
Значит, 9,9 кг клубники собрала Галя;
x + 4,8 = 9,9 + 4,8 = 14,7 (кг) - клубники собрала Маша.
Ответ: 9,9 и 14,7 кг.Задание 1179
Периметр прямоугольника равен 12,8 см, а одна из его сторон на 2,4 см меньше другой. Найдите площадь прямоугольника.
Решение
Пусть x см одна сторона, тогда (x + 2,4) см вторая сторона, а периметр прямоугольника равен 12,8 см.
Составим уравнение:
2(x + x + 2,4) = 12,8;
2(2x + 2,4) = 12,8;
4x + 4,8 = 12,8;
4x = 12,8 − 4,8;
x = 8 : 4;
x = 2.
Значит, 2 см одна сторона;
x + 2,4 = 2 + 2,4 = 4,4 (см) - вторая сторона.
S = 4,4 * 2 = 8,8 ($см^2$) - площадь прямоугольника.
Ответ: 8,8 $см^2$.Задание 1180
Одна из сторон прямоугольника в 15 раз больше другой, а его периметр равен 19,2. Найдите площадь прямоугольника.
Решение
Пусть x см одна сторона, тогда 15x см вторая сторона, а периметр прямоугольника равен 19,2 см.
Составим уравнение:
2(x + 15x) = 19,2;
2 * 16x = 19,2;
32x = 19,2;
x = 19,2 : 32;
x = 0,6.
Значит, 0,6 см одна сторона;
15x = 15 * 0,6 = 9 (см) - вторая сторона.
S = 9 * 0,6 = 5,4 ($см^2$) - площадь прямоугольника.
Ответ: 5,4 $см^2$.Задание 1181
На изготовление мечей для Ильи Муромца, Алеши Поповича и Добрыни Никитича пошло 250 пудов железа. Меч Ильи Муромца в 2 раза тяжелее меча Алеши Поповича, а меч Добрыни Никитича − на 14 пудов тяжелее меча Алеши Поповича. Сколько пудов железа пошло на меч Ильи Муромца?
Решение
Пусть x пудов весит меч Алеши Поповича, тогда 2x пудов весит меч Ильи Муромца, (x + 14) пудов весит меч Добрыни Никитича, а на изготовление мечей пошло 250 пудов железа.
Составим уравнение:
x + 2x + x + 14 = 250
4x = 250 − 14;
x = 236 : 4;
x = 59.
Значит, 59 пудов весит меч Алеши Поповича;
2x = 2 * 59 = 118 (п.) - железа пошло на меч Ильи Муромца.
Ответ: 118 пудов.Задание 1182
Суммарная масса фрекен Бок, Карлсона и Малыша равна 174 кг. Масса Малыша в 4 раза меньше массы фрекен Бок и на 30 кг меньше массы Карлсона. Найдите массу каждого из них.
Решение
Пусть x кг масса Малыша, тогда (4x) кг масса фрекен Бок, (x + 30) кг масса Карлсона, а суммарная масса равна 174 кг
Составим уравнение:
x + 4x + x + 30 = 174;
6x = 174 − 30;
x = 144 : 6;
x = 24.
Значит, 24 кг масса Малыша;
4x = 4 * 24 = 96 (кг) - масса фрекен Бок;
x + 30 = 24 + 30 = 54 (кг) - масса Карлсона.
Ответ: 24 кг, 96 кг, 54 кг.Задание 1183
Периметр треугольника равен 166 см. Одна из его сторон в 5 раз больше второй, которая на 68 см меньше третьей. Вычислите длины сторон треугольника.
Решение
Пусть x см вторая сторона, тогда 5x см первая сторона, (x + 68) см третья сторона, апериметр треугольника равен 166 см.
Составим уравнение:
x + 5x + x + 68 = 166;
7x = 166 − 68;
x = 98 : 7;
x = 14.
Значит, 14 см вторая сторона;
5x = 5 * 14 = 70 (см) - первая сторона;
x + 68 = 14 + 68 = 82 (см) - третья сторона.
Ответ: 70 см, 14 см, 82 см.Задание 1184
Одна сторона треугольника в 7 раз меньше второй и на 66 см меньше третьей. Найдите стороны треугольника, если его периметр равен 174 см.
Решение
Пусть x см первая сторона, тогда (7x) см вторая сторона, (x + 66) см третья сторона, а периметр треугольника равен 174 см.
Составим уравнение:
x + 7x + x + 66 = 174;
9x = 174 − 66;
x = 108 : 9;
x = 12.
Значит, 12 см - первая сторона;
7x = 7 * 12 = 84 (см) - вторая сторона;
x + 66 = 12 + 66 = 78 (см) - третья сторона.
Ответ: 12 см, 84 см, 78 см.Задание 1185
Килограмм апельсинов дороже килограмма яблок на 16 р. За 5 кг апельсинов заплатили столько, сколько за 9 кг яблок. Сколько стоит 1 кг апельсинов? 1 кг яблок?
Решение
Пусть x рублей стоит килограмм яблок, тогда (x + 16) рублей стоит килограмм апельсинов, 9x рублей заплатили за 9 кг яблок, (5(x + 16)) рублей заплатили за 5 кг апельсинов, а за 5 кг апельсинов заплатили столько, сколько за 9 кг яблок.
Составим уравнение:
5(x + 16) = 9x;
5x + 80 = 9x;
5x − 9x = −80;
−4x = −80;
x = −80 : (−4);
x = 20.
Значит, 20 рублей стоит килограмм яблок;
x + 16 = 20 + 16 = 36 (р.) - стоит килограмм апельсинов.
Ответ: 20 р., 36 р.Задание 1186
За 6 кг мармелада заплатили столько, сколько за 4,8 кг шоколадных конфет. Какова цена каждого вида сладостей, если 1 кг мармелада дешевле 1 кг шоколадных конфет на 20 р.?
Решение
Пусть x р. стоит 1 кг мармелада, тогда (x + 20) р. стоит 1 кг конфет, 6x р. стоит 6 кг мармелада, (4,8(x + 20)) р. стоит 4,8 кг конфет, а за 6 кг мармелада заплатили столько, сколько за 4,8 кг шоколадных конфет.
Составим уравнение:
6x = 4,8(x + 20);
6x = 4,8x + 96;
6x − 4,8x = 96;
1,2x = 96 : 1,2;
x = 80.
Значит, 80 рублей стоит 1 кг мармелада;
x + 20 = 80 + 20 = 100 (р.) - стоит 1 кг конфет.
Ответ: 80 р.; 100 р.Задание 1187
Машина бабушка засолила 122 кг капусты в 7 больших и 4 маленьких кадках. Сколько килограммов капусты входило в каждую кадку, если в большой кадке было на 8 кг капусты больше, чем в маленькой?
Решение
Пусть x кг капусты было в маленькой кадке, тогда (x + 8) кг капусты было в большой кадке, 4x кг капусты было в 4 маленьких кадках, (7(x + 8)) кг капусты было в 7 больших кадках, а всего бабушка засолила 122 кг.
Составим уравнение:
4x + 7(x + 8) = 122;
4x + 7x + 56 = 122;
11x = 122 − 56;
x = 66 : 11;
x = 6.
Значит, 6 кг капусты было в маленькой кадке;
x + 8 = 6 + 8 = 14 (кг) - капусты было в большой кадке.
Ответ: 6 кг; 14 кг. 247
-
Страница 247
Задание 1188
Фермер продал 8 кг свинины и 15 кг говядины за 7650 р. Сколько стоил 1 кг свинины и сколько 1 кг говядины, если свинина дешевле говядины на 50 р. за килограмм?
Решение
Пусть x р. стоил 1 кг свинины, тогда:
x + 50 р. стоил 1 кг говядины;
8x р. стоило 8 кг свинины;
15(x + 50) р. стоило 15 кг говядины.
Так как все мясо было продано за 7650 р., то:
8x + 15(x + 50) = 7650
8x + 15x + 750 = 7650
23x = 7650 − 750
x = 6900 : 23
x = 300 р. стоил 1 кг свинины;
x + 50 = 300 + 50 = 350 р. стоил 1 кг говядины.
Ответ: 300 р.; 350 р.Задание 1189
Пешеход преодолел расстояние между двумя поселками за 7 ч, а всадник − за 3 ч. Найдите скорости пешехода и всадника, если скорость пешехода на 5,6 км/ч меньше скорости всадника.
Решение
Пусть x км/ч скорость пешехода, тогда:
x + 5,6 км/ч скорость всадника.
7x км расстояние которое прошел пешеход;
3(x + 5,6) км расстояние которое проехал всадник.
Так как всадник и пешеход преодолели равное расстояние, то:
7x = 3(x + 5,6)
7x = 3x + 16,8
7x − 3x = 16,8
4x = 16,8
x = 16,8 : 4
x = 4,2 км/ч скорость пешехода;
x + 5,6 = 4,2 + 5,6 = 9,8 км/ч скорость всадника.
Ответ: 4,2 км/ч; 9,8 км/ч.Задание 1190
Для перевозки школьников в спортивный лагерь надо заказать 12 микроавтобусов или 5 больших автобусов. Сколько школьников нужно перевезти, если в большом автобусе на 35 мест больше, чем в микроавтобусе (в автобусах не должно быть свободных мест).
Решение
Пусть x мест в микроавтобусе, тогда:
x + 35 мест в большом автобусе;
12x школьников можно разместить в микроавтобусах;
5(x + 35) школьников можно разместить в больших автобусах.
Так как и в микроавтобусах и в больших автобусах можно разместить одинаковое количество школьников, то:
12x = 5(x + 35)
12x = 5x + 175
12x − 5x = 175
7x = 175
x = 175 : 7
x = 25 мест в микроавтобусе;
12x = 12 * 25 = 300 школьников нужно перевезти.
Ответ: 300 школьников.Задание 1191
Гриша и Федя собирали грибы. Гриша собрал в 5 раз больше грибов, чем Федя. В лесу они встретили Машу и Наташу. Гриша подарил Маше 19 грибов, а Наташа подарила Феде 29 грибов. После этого грибов у мальчиков стало поровну. Сколько грибов нашел каждый мальчик?
Решение
Пусть x грибов собрал Федя, тогда:
5x грибов собрал Гриша;
5x − 19 грибов осталось у Гриши;
x + 29 грибов стало у Феди.
Так как у мальчиков стало одинаковое количество грибов, то:
5x − 19 = x + 29
5x − x = 29 + 19
4x = 48
x = 48 : 4
x = 12 грибов собрал Федя;
5x = 5 * 12 = 60 грибов собрал Гриша.
Ответ: 12 и 60 грибов.Задание 1192
Белочки Рыженькая и Желтенькая собирали орехи, причем Рыженькая собрала в 8 раз меньше орехов, чем Желтенькая. Тогда Желтенькая отдала Рыженькой 42 своих ореха, после чего орехов у белочек стало поровну. Сколько орехов собрала каждая белочка?
Решение
Пусть x орехов собрала Рыженькая, тогда:
8x орехов собрала Желтенькая;
x + 42 орехов стало у Рыженькой;
8x − 42 орехов стало у Желтенькой.
Так как орехов у белочек стало поровну, то:
x + 42 = 8x − 42
x − 8x = −42 − 42
−7x = −84
x = −84 : (−7)
x = 12 орехов собрала Рыженькая;
8x = 8 * 12 = 96 орехов собрала Желтенькая.
Ответ: 12 и 96 орехов.Задание 1193
За три дня яхта капитана Врунгеля преодолела 222 км, причем за второй день она преодолела 7/8 расстояния, пройденного за первый день, а за третий − 90% того, что прошла за первый. Сколько километров проходила яхта каждый день?
Решение
Пусть x км прошла яхта в первый день, тогда:
$\frac78x$ км прошла яхта во второй день;
0,9x км прошла яхта в третий день.
Так как всего яхта прошла 222 км, то:
$x+\frac78x+0,9x=222$
$x+\frac78x+\frac9{10}x=222$
$\frac{40}{40}x+\frac{35}{40}x+\frac{36}{40}x=222$
$\frac{111}{40}x=222$
$x=222:\frac{111}{40}$
$x=222\ast\frac{40}{111}$
x = 2 * 40
x = 80 км прошла яхта в первый день;
$\frac78x=\frac78\ast80=7\ast10=70$ км прошла яхта во второй день;
0,9x = 0,9 * 80 = 72 км прошла яхта в третий день.
Ответ: 80 км; 70 км; 72 км.Задание 1194
Четверо рабочих изготовили 152 детали. Второй рабочий изготовил 5/6 количества деталей, изготовленных первым, третий − 90% того, что изготовил второй, а четвертый − на 8 деталей меньше, чем третий. Сколько деталей изготовил каждый рабочий?
Решение
Пусть x деталей изготовил первый рабочий, тогда:
$\frac56x$ деталей изготовил второй рабочий;
$0,9\ast\frac56x=\frac9{10}\ast\frac56x=\frac32\ast\frac12x=\frac34x$ деталей изготовил третий рабочий;
$\frac34x-8$ деталей изготовил четвертый рабочий.
Так как всего было изготовлено 152 детали, то:
$x+\frac56x+\frac34x+\frac34x-8=152$
$\frac{12}{12}x+\frac{10}{12}x+\frac9{12}x+\frac9{12}x=152+8$
$\frac{40}{12}x=160$
$x=160:\frac{40}{12}$
$x=160\ast\frac{12}{40}$
x = 4 * 12 = 48 деталей изготовил первый рабочий;
$\frac56x=\frac56\ast48=5\ast8=40$ деталей изготовил второй рабочий;
$\frac34x=\frac34\ast48=3\ast12=36$ деталей изготовил третий рабочий рабочий;
36 − 8 = 28 детали изготовил четвертый рабочий.
Ответ: 48, 40, 36 и 28 деталей.Задание 1195
Аладдин купил сливочное мороженое по 12 драхм за порцию и шоколадное − по 18 драхм. Сколько порций каждого вида мороженого приобрел Аладдин, если всего он купил 24 порции, заплатив за всю покупку 372 драхмы?
Решение
Пусть x порций было сливочного мороженого, тогда:
24 − x порций было шоколадного мороженого;
12x драхм было заплачено за сливочное мороженое;
18(24 − x) драхм заплачено за шоколадное мороженое.
Так как всего заплатили 372 драхмы, то:
12x + 18(24 − x) = 372
12x + 432 − 18x = 372
12x − 18x = 372 − 432
−6x = −60
x = −60 : (−6)
x = 10 порций было сливочного мороженого;
24 − x = 24 − 10 = 14 порций было шоколадного мороженого.
Ответ: 10 и 14 порций.Задание 1196
Карлсон купил 16 пирожных по 10 и по 16 крон, заплатив всего 202 кроны. Сколько пирожных каждого вида купил Карлсон?
Решение
Пусть x пирожных по 10 крон купил Карлсон, тогда:
16 − x пирожных по 16 крон купил Карлсон;
10x крон заплатил Карлсон за пирожные по 10 крон;
16(16 − x) крон заплатил Карлсон за пирожные по 16 крон.
Так как всего было заплачено 202 кроны, то:
10x + 16(16 − x) = 202
10x + 256 − 16x = 202
−6x = 202 − 256
x = −54 : (−6)
x = 9 пирожных по 10 крон купил Карлсон;
16 − x = 16 − 9 = 7 пирожных по 16 крон купил Карлсон.
Ответ: 9 и 7 пирожных.Задание 1197
Двум школам выделили на ремонт одинаковую сумму. Когда купили строительные материалы для первой школы стоимостью 200000 р., а для второй − стоимостью 120000 р., то в распоряжении второй школы осталось денег в 9 раз больше, чем в распоряжении первой. Сколько рублей было выделено каждой школе на ремонт?
Решение
Пусть х рублей выделили каждой школе, тогда:
x − 200000 р. осталось у первой школы;
x − 120000 р. осталось у второй школы.
Так как, в распоряжении второй школы осталось денег в 9 раз больше, чем в распоряжении первой, то:
9(x − 200000) = x − 120000
9x − 1800000 = x − 120000
9x − x = −120000 + 1800000
8x = 1680000
x = 1680000 : 8
x = 210000 рублей было выделено каждой школе на ремонт.
Ответ: 210000 рублей. 248
-
Страница 248
Задание 1198
В две бочки для полива огорода налили одинаковое количество воды. Когда из первой бочки использовали 47 л воды, а из второй − 23 л, то в первой осталось в 3 раза меньше воды, чем во второй. Сколько литров воды было в каждой бочке вначале?
Решение
Пусть x литров воды налили в каждую бочку, тогда:
x − 47 л воды осталось в первой бочке;
x − 23 л воды осталось во второй бочке.
Так как, в первой бочке осталось в 3 раза меньше воды, чем во второй, то:
3(x − 47) = x − 23
3x − 141 = x − 23
3x − x = 141 − 23
2x = 118
x = 118 : 2
x = 59 литров воды налили в каждую бочку.
Ответ: 59 литров.Задание 1199
У Андрея было в 5 раз больше денег, чем у Лены. Когда Андрей купил книгу за 240 р., а Лена − куклу за 80 р., то у Лены осталось на 320 р. меньше, чем у Андрея. Сколько денег было у каждого из них вначале?
Решение
Пусть x р. было у Лены, тогда:
5x р. было у Андрея;
x − 80 р. осталось у Лены;
5x − 240 р. осталось у Андрея.
Так как, у Лены осталось на 320 р. меньше, чем у Андрея, то:
5x − 240 − (x − 80) = 320
5x − 240 − x + 80 = 320
5x − x = 320 + 240 − 80
4x = 480
x = 480 : 4
x = 120 р. было у Лены;
5x = 5 * 120 = 600 р. было у Андрея.
Ответ: 120 р. и 600 р.Задание 1200
В одной кадке было в 4 раза больше меда, чем в другой. Когда из первой кадки взяли 210 кг меда, а из второй − 10 кг, то во второй осталось на 20 кг больше, чем в первой. Сколько килограммов меда было в каждой кадке вначале?
Решение
Пусть x кг меда было во второй кадке, тогда:
4x кг меда было в первой кадке;
4x − 210 кг меда осталось в первой кадке;
x − 10 кг меда осталось во второй кадке.
4x − 210 кг меда осталось в первой кадке.
Так как, во второй кадке осталось на 20 кг больше, чем в первой, то:
x − 10 − (4x − 210) = 20
x − 10 − 4x + 210 = 20
x − 4x = 20 + 10 − 210
−3x = −180
x = −180 : (−3)
x = 60 кг меда было во второй кадке;
4x = 4 * 60 = 240 кг меда было в первой кадке.
Ответ: 240 кг и 60 кг.Задание 1201
Из одного города выехал автомобиль со скоростью 65 км/ч, а через 2 ч после этого из другого навстречу ему выехал второй автомобиль со скоростью 75 км/ч. Найдите время, которое потратил на дорогу каждый автомобиль до момента встречи, если расстояние между городами равно 690 км.
Решение
Пусть x часов ехал до встречи второй автомобиль, тогда:
x + 2 часов ехал до встречи первый автомобиль;
65(x + 2) км проехал до встречи первый автомобиль;
75x км проехал до встречи второй автомобиль.
Так как, суммарное расстояние, которое проехали до встречи автомобили, равно расстоянию между городами, то:
65(x + 2) + 75x = 690
65x + 130 + 75x = 690
140x = 690 − 130
140x = 560
x = 560 : 140
x = 4 часа ехал до встречи второй автомобиль;
x + 2 = 4 + 2 = 6 часов ехал до встречи первый автомобиль.
Ответ: 6 ч и 4 ч.Задание 1202
Из села в направлении города выехал мотоциклист со скоростью 80 км/ч. Через 1,5 ч из города в село выехал велосипедист со скоростью 16 км/ч. Сколько часов ехал до встречи каждый из них, если расстояние между городом и селом равно 216 км?
Решение
Пусть x часов ехал до встречи велосипедист, тогда:
x + 1,5 часов ехал до встречи мотоциклист;
80(x + 1,5) км проехал до встречи мотоциклист;
16x км проехал до встречи велосипедист.
Так как, суммарное расстояние, которое проехали до встречи мотоциклист и велосипедист, равно расстоянию между городом и селом, то:
80(x + 1,5) + 16x = 216
80x + 120 + 16x = 216
96x = 216 − 120
96x = 96
x = 96 : 96
x = 1 час ехал до встречи велосипедист;
x + 1,5 = 2,5 часа ехал до встречи мотоциклист.
Ответ: 1 ч и 2,5 ч.Задание 1203
В одном баке было 140 л воды, а в другом − 108 л. В баках одновременно открыли краны. Из первого бака ежеминутно вытекает 5 л воды, а из второго − 6 л. Через сколько минут во втором баке останется в 2,5 раза меньше воды, чем в первом?
Решение
Пусть x минут пройдет, до того момента когда во втором баке останется в 2,5 раза меньше воды, чем в первом, тогда:
5x л воды выльется из первого бака;
6x л воды выльется из второго бака;
140 − 5x л воды останется в первом баке;
108 − 6x л воды останется во втором баке.
Так как, во втором баке останется в 2,5 раза меньше воды, чем в первом, то:
2,5(108 − 6x) = 140 − 5x
270 − 15x = 140 − 5x
−15x + 5x = 140 − 270
−10x = −130
x = −130 : (−10)
x = 13 минут пройдет, до того момента когда во втором баке останется в 2,5 раза меньше воды, чем в первом.
Ответ: 13 минут.Задание 1204
Виталику нужно решить 95 задач, а Мише − 60. Виталик ежедневно решает 7 задач, а Миша − 6. Через сколько дней у Виталика останется вдвое больше нерешенных задач, чем у Миши, если они начали решать задачи в один и тот же день?
Решение
Пусть x дней пройдет до момента, когда у Виталика останется вдвое больше нерешенных задач, чем у Миши, тогда:
7x задач решит Виталик;
6x задач решит Миша;
95 − 7x задач останется решить Виталику;
60 − 6x задач останется решить Мише.
Так как у Виталика останется вдвое больше нерешенных задач, чем у Миши, то:
2(60 − 6x) = 95 − 7x
120 − 12x = 95 − 7x
−12x + 7x = 95 − 120
−5x = −25
x = −25 : (−5)
x = 5 дней пройдет до момента, когда у Виталика останется вдвое больше нерешенных задач, чем у Миши.
Ответ: 5 дней.Задание 1205
Лодка плыла 1,4 ч по течению реки и 1,7 ч против течения. Путь, который проплыла лодка по течению, оказался на 2,2 км меньше пути, который она проплыла против течения. Найдите скорость течения реки, если скорость лодки в стоячей воде равна 28 км/ч.
Решение
Пусть x км/ч скорость течения, тогда:
28 + x км/ч скорость лодки по течению;
28 − x км/ч скорость лодки против течения;
1,4(28 + x) км проплыла лодка по течению;
1,7(28 − x) км проплыла лодка против течения.
Так как, путь, который проплыла лодка по течению, оказался на 2,2 км меньше пути, который она проплыла против течения, то:
1,7(28 − x) − 1,4(28 + x) = 2,2
47,6 − 1,7x − 39,2 − 1,4x = 2,2
−1,7x − 1,4x = 2,2 − 47,6 + 39,2
−3,1x = −6,2
x = −6,2 : (−3,1)
x = 2 км/ч скорость течения реки.
Ответ: 2 км/ч.Задание 1206
Туристы на байдарке плыли 2,4 ч по течению реки и 1,8 ч против течения. Путь, который байдарка проплыла по течению, был на 14,1 км больше, чем путь, пройденный против течения. Найдите скорость байдарки в стоячей воде, если скорость течения равна 2,5 км/ч.
Решение
Пусть x км/ч скорость байдарки в стоячей воде, тогда:
x + 2,5 км/ч скорость байдарки по течению;
x − 2,5 км/ч скорость байдарки против течения;
2,4(x + 2,5) км проплыли туристы по течению;
1,8(x − 2,5) км проплыли туристы против течения.
Так как, путь, который байдарка проплыла по течению, был на 14,1 км больше, чем путь, пройденный против течения, то:
2,4(x + 2,5) − 1,8(x − 2,5) = 14,1
2,4x + 6 − 1,8x + 4,5 = 14,1
0,6x = 14,1 − 6 − 4,5
x = 3,6 : 0,6
x = 6 км/ч скорость байдарки в стоячей воде.
Ответ: 6 км/ч.Задание 1207
Готовясь к экзамену, ученик планировал ежедневно решать 12 задач. Однако он решал ежедневно на 4 задачи больше, и уже за три дня до экзамена ему осталось решить 8 задач. Сколько дней ученик планировал готовиться к экзамену?
Решение
Пусть x дней ученик планировал готовиться к экзамену, тогда:
12x задач должен решить ученик всего;
12 + 4 = 16 задач в день решал ученик;
x − 3 дней решал задачи ученик;
16(x − 3) задач решил ученик.
Так как, за три дня до экзамена ему осталось решить 8 задач, то:
12x − 16(x − 3) = 8
12x − 16x + 48 = 8
−4x = 8 − 48
−4x = −40
x = −40 : −4
x = 10 дней ученик планировал готовиться к экзамену.
Ответ: 10 дней. 249-250
-
Страница 249-250
Задание 1208
Мастер планировал ежедневно изготавливать по 24 детали, чтобы выполнить заказ вовремя. Но поскольку он изготавливал ежедневно на 15 деталей больше, то уже за шесть дней до окончания срока работы он изготовил 21 деталь сверх заказа. Сколько дней мастер должен был работать над заказом?
Решение
Пусть x дней мастер должен был работать над заказом, тогда:
24x деталей всего должен изготовить мастер;
24 + 15 = 39 деталей в день изготавливал мастер;
x − 6 дней работал мастер;
39(x − 6) деталей изготовил мастер.
Так как мастер изготовил на 21 деталь больше, чем было заказано, то:
39(x − 6) − 24x = 21
39x − 234 − 24x = 21
39x − 24x = 21 + 234
15x = 255
x = 255 : 15
x = 17 дней мастер должен был работать над заказом.
Ответ: 17 дней.Задание 1209
В первой цистерне было 900 л воды, а во второй − 700 л. Когда из второй цистерны взяли воды вдвое больше, чем из первой, то в первой осталось воды в 3 раза больше, чем во второй. Сколько литров воды взяли из каждой цистерны?
Решение
Пусть x литров воды взяли из первой цистерны, тогда:
2x литров воды взяли из второй цистерны;
900 − x литров воды осталось в первой цистерне;
700 − 2x литров воды осталось во второй цистерне.
Так как, в первой цистерне осталось воды в 3 раза больше, чем во второй, то:
3(700 − 2x) = 900 − x
2100 − 6x = 900 − x
−6x + x = 900 − 2100
−5x = −1200
x = −1200 : (−5)
x = 240 литров воды взяли из первой цистерны;
2x = 2 * 240 = 480 литров воды взяли из второй цистерны.
Ответ: 240 и 480 литров.Задание 1210
В первой упаковке было 60 кг конфет, а во второй − 100 кг. Когда из второй упаковки продали в 4 раза больше конфет, чем из первой, то в первой осталось в 2 раза больше конфет, чем во второй. Сколько килограммов конфет продали из каждой упаковки?
Решение
Пусть x кг конфет продали из первой упаковки, тогда:
4x кг конфет продали из второй упаковки;
60 − x кг конфет осталось в первой упаковке;
100 − 4x кг конфет осталось во второй упаковке.
Так как, в первой упаковке осталось в 2 раза больше конфет, чем во второй, то:
2(100 − 4x) = 60 − x
200 − 8x = 60 − x
−8x + x = 60 − 200
−7x = −140
x = −140 : (−7)
x = 20 кг конфет продали из первой упаковки;
4x = 4 * 20 = 80 кг конфет продали из второй упаковки.
Ответ: 20 кг и 80 кг.Задание 1211
Каждую минуту в первую бочку из крана наливалось 3 л воды, а во вторую из другого крана − 2 л. В 12 ч в первой бочке было 21 л воды, а во второй − 54 л. Определите, в котором часу в первой бочке было в 4 раза меньше литров воды, чем во второй.
Решение
Пусть x минут наливалась вода, тогда:
3x литров воды налилось в первую бочку;
2x литров воды налилось во вторую бочку;
21 − 3x литров воды было в первой бочке x минут назад;
54 − 2x литров воды было во второй бочке x минут назад.
Так как, в первой бочке было в 4 раза меньше литров воды, чем во второй, то:
4(21 − 3x) = 54 − 2x
84 − 12x = 54 − 2x
−12x + 2x = 54 − 84
−10x = −30
x = −30 : (−10)
x = 3 минуты назад или в 11 ч 57 минут в первой бочке было в 4 раза меньше литров воды, чем во второй.
Ответ: в 11 ч 57 минут.Задание 1212
В магазине продается три вида чашек и два вида блюдец. Сколькими способами можно купить чашку с блюдцем?
Решение
Чашку можно выбрать одну из трех, то есть 3 способами;
Блюдце можно выбрать одно из двух, то есть 2 способами, тогда:
3 * 2 = 6 способами можно купить чашку с блюдцем.
Ответ: 6 способов.Задание 1213
В школе 6 классов. В 6 "Б" классе учащихся на одного больше, чем в 6"А", в 6"В" − на одного больше, чем в 6 "Б", и так далее. Укажите, каким из следующих чисел обязательно будет общее количество шестиклассников:
1) простым числом;
2) четным числом;
3) нечетным числом.Решение
Пусть x учеников в 6"А" классе, тогда:
x + 1 учеников в 6"Б" классе;
x + 2 учеников в 6"В" классе;
x + 3 учеников в 6"Г" классе;
x + 4 учеников в 6"Д" классе;
x + 5 учеников в 6"Е" классе, тогда всего учеников в этих классах:
x + x + 1 + x + 2 + x + 3 + x + 4 + x + 5 = 6x + 15.
6x − четное число, так как при произведение четного числа и натурального числа число четное, тогда:
6x + 15 всегда нечетное число, так как сумма четного и нечетного чисел число нечетное.
Ответ: нечетным числом.Задание 1214
В записи двузначного числа зачеркнули одну цифру, и оно уменьшилось в 31 раз. Какую цифру и в каком числе зачеркнули?
Решение
1 * 31 = 31
2 * 31 = 62
3 * 31 = 93
Ответ:
в числе 31 зачеркнули цифру 3;
в числе 62 зачеркнули цифру 6;
в числе 93 зачеркнули цифру 9.Задание 1215
Найдите значение выражения:
1) $(-2,04:\frac1{25}-3,61:(-\frac{19}{40})):(-2\frac45)+0,6:(-0,9)=(-\frac{51}{25}:\frac1{25}-\frac{361}{100}:(-\frac{19}{40})):(-\frac{14}5)+\frac35:(-\frac9{10})=(-\frac{51}{25}\ast\frac{25}1-\frac{361}{100}\ast(-\frac{40}{19}))\ast(-\frac5{14})+\frac35\ast(-\frac{10}9)=(-\frac{51}1\ast\frac11-\frac{19}5\ast(-\frac21))\ast(-\frac5{14})+\frac11\ast(-\frac23)=(-51+7\frac35)\ast(-\frac5{14})-\frac23=-43\frac25\ast(-\frac5{14})-\frac23=-\frac{217}5\ast(-\frac5{14})-\frac23=-\frac{31}1\ast(-\frac12)-\frac23=15\frac12-\frac23=15\frac36-\frac46=14\frac56$
2) $(7,7:(-\frac{11}{40})-3,8:(-\frac1{20}))\ast(-\frac5{16})-0,4:(-0,36)=(\frac{77}{10}:(-\frac{11}{40})-\frac{19}5:(-\frac1{20}))\ast(-\frac5{16})-\frac25:(-\frac9{25})=(\frac{77}{10}\ast(-\frac{40}{11})-\frac{19}5\ast(-\frac{20}1))\ast(-\frac5{16})-\frac25\ast(-\frac{25}9)=(\frac71\ast(-\frac41)-\frac{19}1\ast(-\frac41))\ast(-\frac5{16})-\frac21\ast(-\frac59)=(-28+76)\ast(-\frac5{16})+\frac{10}9=48\ast(-\frac5{16})+1\frac19=3\ast(-\frac51)+1\frac19=-15+1\frac19=-13\frac89$Задание 1216
В записи числа 689123401 зачеркните три цифры так, чтобы оставшиеся цифры в том же порядке составили наибольшее из возможных чисел.
Решение
$689\cancel12\cancel34\cancel01$
Ответ: 689541.Задание 1217
Из вершины B развернутого угла ABC провели луч BK так, что ∠ABK = 108°. Луч BD − биссектриса угла CBK. Вычислите градусную меру угла DBK.
Решение
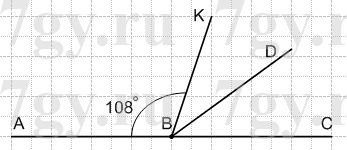
Так угол ABC развернутый, следовательно он равен 180°, тогда:
∠CBK = ∠ABC − ∠ABK = 180° − 108° = 72°
Так как, луч BD − биссектриса угла CBK, то:
∠DBK = ∠CBK : 2 = 72° : 2 = 36°
Ответ: ∠DBK = 36°Задание 1218
Существует ли 1005 натуральных чисел (не обязательно разных), сумма которых равна их произведению?
Решение
Сумма: 2 + 1005 + (1 + 1 + ... + 1) = 1007 + 1003 = 2010
Произведение: 2 * 1005 * (1 * 1 * ... * 1) = 2010
Ответ: да, существует. 253
-
Страница 253
Ответы к параграфу 43. Перпендикулярные прямые
Задание 1219
На рисунке 118 изображен квадрат MNKP. Запишите все пары перпендикулярных прямых.
Решение
MN⊥NK; NK⊥KP; KP⊥PM; PM⊥MN; NP⊥MK.
Задание 1220
Найдите на рисунке 119 пары перпендикулярных прямых и запишите их.
Решение
AC⊥KE; FT⊥MD.
Задание 1221
Перерисуйте в тетрадь рисунок 120. Проведите через точку M прямую, перпендикулярную прямой a.
Решение
Задание 1222
Проведите прямую d и отметьте точку M, ей не принадлежащую. Проведите через точку M прямую, перпендикулярную прямой d.
Решение
254
-
Страница 254
Задание 1223
Проведите прямую c и отметьте точку K, принадлежащую ей. Проведите через точку K прямую, перпендикулярную прямой c.
Решение
Задание 1224
Начертите прямоугольник ABCD, соедините точки A и C. Проведите через точку B прямую, перпендикулярную прямой AC.
Решение
Задание 1225
Начертите треугольник:
1) остроугольный;
2) тупоугольный;
3) прямоугольный.
Проведите через каждую вершину треугольника прямую, перпендикулярную противоположной стороне.Решение
1)
2)
3)
Задание 1226
Начертите угол ABK, градусная мера которого равна:
1) 73°;
2) 146°.
Отметьте на луче BK точку C и проведите через нее прямые, перпендикулярные прямым AB и BK.Решение
1)
2)
Задание 1227
Перерисуйте в тетрадь рисунок 121. Проведите через точку O прямые, перпендикулярные прямым AB, CD и EF.
Решение
Задание 1228
Начертите остроугольный треугольник и отметьте внутри него точку. Проведите через эту точку прямые, перпендикулярные сторонам треугольника.
Решение
Задание 1229
Начертите четырехугольник ABCD, в котором:
1) AB⊥AD;
2) AB⊥AD, AB⊥BC;
3) AB⊥AD, BC⊥CD.Решение
1)
2)
3)
Задание 1230
С помощью угольника определите, какие из прямых, изображенных на рисунке 122, перпендикулярны.
Решение
a⊥m; b⊥r; c⊥s; d⊥p.
Задание 1231
Начертите два перпендикулярных отрезка так, чтобы они:
1) пересекались;
2) не имели общих точек;
3) имели общий конец.Решение
1)
2)
3)
Задание 1232
Начертите два перпендикулярных луча так, чтобы они:
1) пересекались;
2) не имели общих точек.Решение
1)
2)
Задание 1233
На рисунке 123 AB⊥CD, ∠MOC + ∠BOK = 130°, COK = 42°. Найдите:
1) ∠MOK;
2) ∠MOD.
Решение
1) Так как, AB⊥CD, то ∠COB = 90°, тогда:
∠KOB = ∠COB − ∠COK = 90° − 42° = 48°.
∠MOC + ∠BOK = 130°, тогда:
∠MOC = 130° − ∠BOK = 130° − 42° = 82°.
∠MOK = ∠MOC + ∠COK = 82° + 42° = 124°.
Ответ: ∠MOK = 124°
2) Так как, AB⊥CD, то ∠COB = 90°; ∠AOC = 90°, тогда:
∠AOB = ∠COB + ∠AOC = 90° + 90° = 180°;
∠AOM = ∠AOB − (∠MOC + ∠BOK) − ∠COK = 180° − 130° − 42° = 8°.
Так как, AB⊥CD, то ∠AOD = 90°, тогда:
∠MOD = ∠AOD + ∠AOM = 90° + 8°= 98°.
Ответ: ∠MOD = 98° 255
-
Страница 255
Задание 1234
На рисунке 124 AС⊥DK, OB⊥BF, ∠DBO = 54°. Вычислите градусную меру угла ABF.
Решение
∠DBK развернутый и равен 180°.
Так как, OB⊥BF, то ∠OBF = 90°, тогда:
∠KBF = ∠DBK − ∠DBO − ∠OBF = 180° − 54° − 90° = 36°.
Так как, AС⊥DK, то ∠ABK = 90°, тогда:
∠ABF = ∠ABK + ∠KBF = 90° + 36° = 126°
Ответ: ∠ABF = 126°Задание 1235
Как построить перпендикулярные прямые, пользуясь шаблоном угла, который равен:
1) 15°;
2) 18°?Решение
1) 90 : 15 = 6, следовательно необходимо шаблоном угла 15° отложить 6 последовательных углов.
2) 90 : 18 = 5, следовательно необходимо шаблоном угла 18° отложить 5 последовательных углов.Задание 1236
Пользуясь угольником и шаблоном угла 17°, постройте угол, градусная мера которого:
1) 5°;
2) 12°?Решение
1)
90° − 17° * 5 = 90° − 85° = 5°
2)
17° * 6 − 90° = 102° − 90° = 12°Задание 1237
Пользуясь угольником и шаблоном угла 20°, постройте угол, градусная мера которого 10°.
Решение
90° − 20° * 4 = 90° − 80° = 10°Задание 1238
Сумма цифр двузначного числа равна 8, количество десятков в 3 раза меньше количества единиц. Найдите это число.
Решение
Пусть x количество десятков, тогда:
3x количество единиц.
Так как, сумма цифр двузначного числа равна 8, то:
3x + x = 8
4x = 8
x = 8 : 4
x = 2 количество десятков;
3x = 3 * 2 = 6 количество единиц, следовательно искомое число 26.
Ответ: 26.Задание 1239
Из семи учащихся четверо хорошо поют, двое выразительно читают стихи, а один красиво танцует. Сколькими способами из этих учащихся можно организовать концертную бригаду, состоящую из певца, чтеца и танцора?
Решение
В концертную бригаду можно выбрать:
одного из четырех певцов (4 способа);
одного из двух чтецов (2 способа);
одного танцора (1 способ), тогда:
4 * 2 * 1 = 8 способами можно организовать концертную бригаду.
Ответ: 8 способов.Задание 1240
Заполните пропуски в цепочке вычислений при:
1) x = 1 1/8;
2) x = 1 1/4.
Решение
1) $x\ast\frac2{15}=1\frac18\ast\frac2{15}=\frac98\ast\frac2{15}=\frac34\ast\frac15=\frac3{20}$
$\frac3{20}-\frac18=\frac6{40}-\frac5{40}=\frac1{40}$
$\frac1{40}<\frac1{30}$
$\frac1{40}:\frac78=\frac1{40}\ast\frac87=\frac15\ast\frac17=\frac1{35}$
$\frac1{35}-\frac27=\frac1{35}-\frac{10}{35}=-\frac9{35}$
2) $x\ast\frac2{15}=1\frac14\ast\frac2{15}=\frac54\ast\frac2{15}=\frac12\ast\frac13=\frac16$
$\frac16-\frac18=\frac4{24}-\frac3{24}=\frac1{24}$
$\frac1{24}>\frac1{30}$
$\frac1{24}:\frac7{12}=\frac1{24}\ast\frac{12}7=\frac12\ast\frac17=\frac1{14}$
$\frac1{14}-\frac37=\frac1{14}-\frac6{14}=-\frac5{14}$
Задание 1241
Сегодня Василию Ивановичу исполнилось 80 лет, а его детям − 34, 36 и 40. Сколько лет прошло с того времени, когда возраст отца был в 2 раза больше суммы возрастов его детей?
Решение
Пусть x лет прошло, тогда:
80 − x лет было Василию Ивановичу;
34 − x лет было первому ребенку;
36 − x лет было второму ребенку;
40 − x лет было третьему ребенку.
Так как, возраст отца был в 2 раза больше суммы возрастов его детей, то:
2(34 − x + 36 − x + 40 − x) = 80 − x
2(−3x + 110) = 80 − x
−6x + 220 = 80 − x
−6x + x = 80 − 220
−5x = −140
x = −140 : (−5)
x = 28 лет прошло.
Ответ: 28 лет.Задание 1242
Верно ли, что |a| + a = 2a при любом значении a?
Решение
Неверно, так как при отрицательном значении a равенство не будет верным, например a = −5, тогда:
|−5| + (−5) = 2 * (−5)
5 − 5 = −10
0 ≠ −10Задание 1243
На шахматную доску пролили краску. Может ли количество залитых клеток быть на 17 меньше количества клеток, оставшихся чистыми?
Решение
Пусть x клеток залили, тогда:
64 − x клеток остались чистыми.
Представим, что количество залитых клеток на 17 меньше чистых, тогда:
(64 − x) − x = 17
64 − x − x = 17
−2x = 17 − 64
x = −47 : (−2)
x = 23,5 клеток залили, что невозможно, так как количество клеток должно быть натуральным числом, следовательно залитых клеток не может быть на 17 меньше количества клеток, оставшихся чистыми.
Ответ: не может. 259
-
Страница 259
Ответы к параграфу 44. Осевая и центральная симметрия
Задание 1244
Прямая l проходит через середину отрезка AB. Обязательно ли точки A и B симметричны относительно прямой l?
Решение
Точки A и B будут симметричны относительно прямой l, только в том случае прямая l, проходящая через середину отрезка AB, будет перпендикулярна отрезку AB.
Ответ: не обязательно.Задание 1245
Используя линейку и угольник, определите, симметричны ли относительно прямой l (рис. 142) точки:
1) A и B;
2) M и K;
3) E и F;
4) C и D.
Решение
1) нет
2) нет
3) нет
4) нет 260
-
Страница 260
Задание 1246
Начертите прямую m и отметьте точки P и S по разные стороны от нее. Постройте точки, симметричные точкам P и S относительно прямой m.
Решение
Задание 1247
Перерисуйте рисунок 143 в тетрадь и постройте отрезки, симметричные отрезкам AB и CD относительно прямой a.
Решение
Задание 1248
Перерисуйте рисунок 144 в тетрадь и постройте отрезок, симметричный отрезку AB относительно прямой m.
Решение
Задание 1249
Симметричны ли изображенные на рисунке 145 фигуры относительно прямой l?
Решение
а) да
б) нет
в) нет
г) даЗадание 1250
На рисунке 146 отмечены точки A, B, C, D, E, F. С помощью линейки определите, симметричны ли точки:
1) A и E относительно точки C;
2) B и D относительно точки C;
3) C и F относительно точки E;
4) A и F относительно точки E.
Решение
1) да
2) нет
3) да
4) нет 261
-
Страница 261
Задание 1251
Перерисуйте рисунок 147 в тетрадь и постройте точку, симметричную точке:
1) A относительно точки B;
2) K относительно точки B;
3) B относительно точки K;
4) M относительно точки B;
5) M относительно точки K;
6) A относительно точки K.
Решение
1)
2)
3)
4)
5)
6)
Задание 1252
Начертите координатную прямую и отметьте на ней точки M (4) и K(−3). Постройте точки, симметричные точкам M и K относительно начала отсчета. Определите координаты полученных точек.
Решение

Ответ: M1(−4); K1(3).Задание 1253
Начертите координатную прямую и отметьте на ней точки A(5), B(1) и C(−2). Постройте точку, симметричную точке:
1) A относительно точки B;
2) C относительно точки B;
3) B относительно точки C;
4) B относительно точки A.
Определите координаты полученных точек.Решение
1)

Ответ: A1(−3).
2)
Ответ: C1(4).
3)
Ответ: B1(−5).
4)
Ответ: B1(9).Задание 1254
Какие из отмеченных точек окружности (рис.148) образуют пары точек, симметричных относительно ее центра O?
Решение
точка B симметрична точке E относительно O;
точка A симметрична точке D относительно O. 262
-
Страница 262
Задание 1255
Постройте точки, симметричные точкам M, N, K, P окружности (рис.149) относительно ее центра O.
Решение
Задание 1256
Начертите отрезок BD и отметьте точку A вне этого отрезка. Постройте отрезок, симметричный отрезку BD относительно точки A. Сравните полученный отрезок и отрезок BD.
Решение
Задание 1257
Перерисуйте рисунок 150 в тетрадь и постройте треугольник, симметричный треугольнику ABC относительно прямой l.
Решение
Задание 1258
Перерисуйте рисунок 151 в тетрадь и постройте треугольник, симметричный треугольнику ABC относительно прямой l.
Решение
Задание 1259
Сколько осей симметрии имеет фигура, изображенная на рисунке 152?
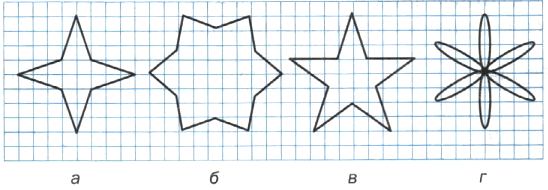
Решение
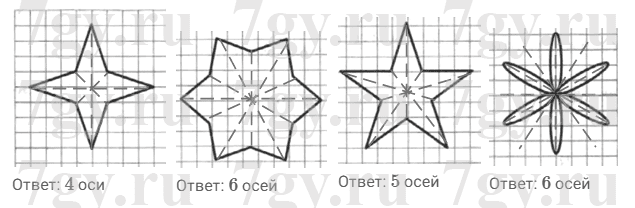
Задание 1260
Какие печатные буквы русского алфавита имеют:
1) вертикальную ось симметрии;
2) горизонтальную ось симметрии;
3) вертикальную и горизонтальную ось симметрии?Решение
1)

Только вертикальная ось симметрии:
2)
Только горизонтальная ось симметрии:
3)
И вертикальная, и горизонтальная ось симметрии:Задание 1261
Перерисуйте в тетрадь фигуру, изображенную на рисунке 153. Проведите все оси симметрии данной фигуры.
Решение
263
-
Страница 263
Задание 1262
Перерисуйте в тетрадь фигуру, изображенную на рисунке 154. Проведите все оси симметрии данной фигуры.
Решение
Задание 1263
На рисунке 155 изображены сторона AB и ось симметрии l треугольника ABC. Перерисуйте рисунок в тетрадь и постройте треугольник ABC. Определите вид треугольника ABC.
Решение
Так как AB симметрична BC, то AB = BC, следовательно ΔABC равнобедренный.
Все углы треугольника меньше 90°, следовательно ΔABC остроугольный.
Ответ: ΔABC равнобедренный, остроугольный.Задание 1264
На рисунке 156 изображены сторона AB и ось симметрии l четырехугольника ABCD. Перерисуйте рисунок в тетрадь и постройте четырехугольник ABCD.
Решение
Задание 1265
На рисунке 157 изображены стороны AB и BC и ось симметрии l шестиугольника ABCDEF. Перерисуйте рисунок в тетрадь и постройте шестиугольник ABCDEF.
Решение
Задание 1266
Перерисуйте рисунок 158 в тетрадь и постройте фигуру, симметричную треугольнику ABC относительно точки O.
Решение
264
-
Страница 264
Задание 1267
Перерисуйте рисунок 159 в тетрадь и постройте фигуру, симметричную треугольнику ABC:
1) относительно точки O;
2) относительно точки D.
Решение
Задание 1268
Начертите треугольник ABC. Постройте фигуру, симметричную этому треугольнику относительно точки C.
Решение
Задание 1269
Начертите квадрат ABCD. Постройте фигуру, симметричную этому квадрату относительно точки С.
Решение
Задание 1270
На рисунке 160 изображены сторона AB и центр симметрии O четырехугольника ABCD. Перерисуйте рисунок в тетрадь и постройте четырехугольник ABCD.
Решение
Задание 1271
На рисунке 161 изображены стороны AB и BC и центр симметрии O шестиугольника ABCDEF. Перерисуйте рисунок в тетрадь и постройте шестиугольник ABCDEF.
Решение
Задание 1272
Есть две одинаковые полоски в клетку (рис. 162). Два мальчика играют в такую игру: за один ход можно зачеркнуть любое количество клеток, но в одной полоске. Проигрывает тот, кому уже нечего зачеркнуть. Кто из двух игроков может обеспечить себе выигрыш и как это сделать?
Решение
Если второй будет закрашивать те же самые клетки, что и первый, но только в другой полоске, то второй будет последним кто зачеркнет клетки, а следовательно он обеспечит себе выигрыш.
Ответ: второй.Задание 1273
Два мальчика по очереди кладут одинаковые монетки на круглый стол так, чтобы они не накладывались друг на друга. Проигрывает тот, кто не может сделать ход. Кто из двух игроков может обеспечить себе выигрыш и как это сделать?
Решение
Выиграет первый, если положит первым ходом монету в центр стола. После хода второго игрока первый должен класть свою монету симметрично монете положенной вторым относительно центра. Таким образом, пока возможен ход второго игрока у первого всегда будет возможность положить монету, следовательно первый и победит.
Ответ: победит первый игрок.Задание 1274
В 1792 г. ученые Парижской академии наук измерили длину земного меридиана, проходящего через Париж. Одна десятимиллионная доля четверти Парижского меридиана составляла 1 м. Найдите длину земного меридиана, проходящего через Париж.
Решение
Пусть x м длина земного меридиана, проходящего через Париж, тогда:
$\frac14x$ четверть Парижского меридиана;
$\frac1{10000000}\ast\frac14x=\frac1{40000000}x$ одна десятимиллионная доля четверти Парижского меридиана.
Так как, одна десятимиллионная доля четверти Парижского меридиана составляла 1 м, то:
$\frac1{40000000}x=1$
$x=1:\frac1{40000000}$
$x=1\ast\frac{40000000}1$
x = 40000000 м = 40000 км длина земного меридиана, проходящего через Париж.
Ответ: 40000 км. 265
-
Страница 265
Задание 1275
Укажите трехзначное число:
1) первая цифра которого 6 и которое делится нацело на 5 и на 9, но не делится нацело на 2;
2) первая цифра которого 5 и которое делится нацело на 2, на 5 и на 9.Решение
1) Так как первая цифра числа равна 6, то число имеет вид 6*.
Так как число делится нацело на 5, то последняя цифра числа равна либо 0, либо 5. Но так как, оно не делится нацело на 2, то последняя цифра не может быть нулем, а значит она равна 5, и число имеет вид 65.
Так как число делится нацело на 9, то сумма цифр числа должна делится на 9, тогда:
6 + * + 5 = 9 * 2
* = 18 − 6 − 5
* = 7
Ответ: число 675.
2) Так как первая цифра числа равна 5, то число имеет вид 5*.
Так как число делится нацело на 5, то последняя цифра числа равна либо 0, либо 5. Но так как, оно делится нацело на 2, то последняя цифра не может быть 5, а значит она равна 0, и число имеет вид 50.
Так как число делится нацело на 9, то сумма цифр числа должна делится на 9, тогда:
5 + * + 0 = 9
* = 9 − 5 − 0
* = 4
Ответ: число 540.Задание 1276
Найдите значение выражения:
1) $(6\frac7{12}-3\frac{17}{36})\ast2,5-4\frac13:0,65=(6\frac{21}{36}-3\frac{17}{36})\ast\frac52-\frac{13}3:\frac{13}{20}=3\frac19\ast\frac52-\frac{13}3\ast\frac{20}{13}=\frac{28}9\ast\frac52-\frac{13}3\ast\frac{20}{13}=\frac{14}9\ast\frac51-\frac13\ast\frac{20}1=\frac{70}9-\frac{20}3=\frac{70}9-\frac{60}9=\frac{10}9=1\frac19$
2) $3\frac34\ast1\frac15+(2,55+2,7):(0,1-\frac1{80})=\frac{15}4\ast\frac65+5,25:(\frac1{10}-\frac1{80})=\frac32\ast\frac31+\frac{21}4:(\frac8{80}-\frac1{80})=\frac92+\frac{21}4:\frac7{80}=4\frac12+\frac{21}4\ast\frac{80}7=4\frac12+\frac31\ast\frac{20}1=4\frac12+60=64\frac12$Задание 1277
Перерисуйте в тетрадь рисунок 163. Через каждую из точек A и B проведите прямую, перпендикулярную прямой a.
Решение
Задание 1278
Перерисуйте в тетрадь рисунок 164. Через точку M проведите прямую b, перпендикулярную прямой a, и прямую c, перпендикулярную прямой b.

Решение
Задание 1279
На прямой отметили несколько точек. Затем между каждыми двумя соседними точками поставили еще по точке, и так поступили несколько раз. Докажите, что после каждой такой операции общее количество точек на прямой будет нечетным.
Решение
Так как каждый раз будет проставляться на одну точку меньше, чем было изначально, то количество, точек проставляемое в каждом отдельном представлении будет меняться с четного количества на нечетный, то есть:
допустим первый раз поставили четное количество точек, тогда:
четное количество − изначально;
нечетное количество − 1 проставление;
четное количество − 2 проставление;
нечетное количество − 3 проставление и т.д.
Так как после каждого проставления четное количество точек будет складываться с нечетным количеством, то сумма всех точек всегда будет нечетной.
Аналогичный расчет будет и в том случае, если первый раз проставили нечетное количество точек. 268
-
Страница 268
Ответ к параграфу 45. Параллельные прямые
Задание 1280
Перерисуйте в тетрадь рисунок 173. Проведите через каждую из точек A и B прямую, параллельную прямой m.
Решение
Задание 1281
Определите на глаз, а потом проверьте с помощью угольника и линейки, какие из прямых, изображенных на рисунке 174, параллельны.
Решение
а) a||c
б) a||c; b||d.Задание 1282
Перерисуйте в тетрадь рисунок 175. Проведите через точку O прямые, параллельные прямым k и p.
Решение
Задание 1283
Начертите угол MKE, градусная мера которого равна:
1) 58°;
2) 116°;
3) 90°.
Отметьте между сторонами угла точку P и проведите через эту точку прямые, параллельные сторонам угла.Решение
269
-
Страница 269
Задание 1284
Начертите треугольник и проведите через каждую его вершину прямую, параллельную противоположной стороне.
Решение
Задание 1285
Перерисуйте в тетрадь рисунок 176. Проведите прямые BC, CE, AD, DF, BE и AF. Определите, какие из этих прямых параллельны.
Решение
Ответ: AF||BE; BD||CE; BC||AD.Задание 1286
Начертите четырехугольник, у которого:
1) две стороны параллельны, а две другие − не параллельны;
2) противоположные стороны параллельны.Решение
Задание 1287
Начертите:
1) пятиугольник, две стороны которого параллельны;
2) шестиугольник, у которого каждая сторона параллельна какой−либо другой стороне.Решение
Задание 1288
Начертите шестиугольник, две стороны которого лежат на одной прямой, а каждая из четырех остальных сторон параллельна какой−либо другой стороне.
Решение
Задание 1289
Сколько точек пересечения могут иметь три прямые на плоскости?
Изобразите все случаи.Решение
Три прямые на плоскости могут иметь следующее количество точек пересечения на плоскости:

0 точек
1 точку
2 точки
3 точкиЗадание 1290
Составили одинаковые большие и одинаковые маленькие букеты роз. В двух маленьких и пяти больших букетах было 55 роз, а в шести маленьких и пяти больших − 75 роз. Сколько роз было в каждом букете?
Решение
Пусть x роз было в маленьком букете, y роз было в большом букете, тогда:
2x + 5y = 55 количество роз в первой комбинации;
6x + 5y = 75 количество роз во второй комбинации.
(6x + 5y) − (2x + 5y) = 75 − 55
6x + 5y − 2x − 5y = 20
6x − 2x = 20
4x = 20, то есть 20 роз содержится в 4 маленьких букетах;
x = 20 : 4
x = 5 роз содержится в каждом маленьком букете.
2x + 5y = 55
2 * 5 + 5y = 55
10 + 5y = 55
5y = 55 − 10
y = 45 : 5
y = 9 роз было в каждом большом букете.
Ответ: 5 роз в маленьком букете, 9 роз в большом букете. 270
-
Страница 270
Задание 1291
При обработки детали ее масса уменьшилась с 240 кг до 204 кг. На сколько процентов уменьшилась масса детали?
Решение
$\frac{204}{240}$ ∗ 100 = 17 ∗ 5 = 85 % составляет 204 кг от 240 кг.
100% − 85% = 15%, значит на 15% уменьшилась масса детали.
Ответ: на 15%.Задание 1292
Влажность травы составляет 80%, а сена − 20%. Сколько килограммов сена получат из 4 т травы?
Решение
$\frac{20}{80}$ ∗ 100 % = $\frac14$ ∗ 100 % = 25% составляет влажность сена от влажности травы, тогда:
4 * 25% = 4 * 0,25 = 1 т сена получится из 4 тонн травы.
Ответ: 1 т сена.Задание 1293
Найдите значение выражения:
$(8,25\ast\frac{10}{11}-10)\ast(11\frac23:2\frac29-6,15)+12,7:(-2\frac12)=(\frac{33}4\ast\frac{10}{11}-10)\ast(\frac{35}3:\frac{20}9-6,15)+\frac{127}{10}:(-\frac52)=(\frac{33}4\ast\frac{10}{11}-10)\ast(\frac{35}3\ast\frac9{20}-6,15)+\frac{127}{10}\ast(-\frac25)=(\frac32\ast\frac51-10)\ast(\frac71\ast\frac34-6,15)+\frac{127}5\ast(-\frac15)=(\frac{15}2-10)\ast(\frac{21}4-6,15)-\frac{127}{25}=(7,5-10)\ast(5,25-6,15)-5,08=-2,5\ast(-0,9)-5,08=2,25-5,08=-2,83$
Задание 1294
Отметьте на координатной прямой точку A(−3). Найдите на этой прямой точки, удаленные от точки A на пять единичных отрезков, и укажите их координаты.
Решение

−3 + 5 = 2, значит координата первой точки B(2);
−3 − 5 = −8, значит координата второй точки C(−8).Задание 1295
Все жители города A всегда говорят правду, а все жители города B всегда лгут. Известно, что жители города A бывают в городе B и наоборот. Путешественник попал в один из этих городов, но не знает, в какой. Какой один вопрос он должен задать первому встречному, чтобы выяснить, в каком городе он находится?
Решение
Можно задать следующие вопросы:
1. Вы бывали в городе B?
2. Вы бывали в городе A?
3. Вы проживаете в городе A или в городе B?
Ответ "нет" будет обозначать, что путешественник попал в город B, и наоборот. 274
-
Страница 274
Ответы к параграфу 46. Координатная плоскость
Задание 1296
Найдите координаты точек A, B, C, D, E, F, K, M, N, изображенных на рисунке 186.
Решение
Ответ: A(3;2); B(−1;4); C(−6;2); D(−5;−2); E(2;−2); F(0;3); K(4;0); M(−2;−4); N(5;4).
Задание 1297
Найдите координаты точек A, B, C, D, E, F, K, M, N, изображенных на рисунке 187.
Решение
Ответ: A(2;2); B(5;1); C(0;−5); D(2;−3); E(−1;−1); F(−5;0); K(−4;3); M(−3;2); N(−4;−3).
Задание 1298
На координатной плоскости отметьте точки: A(2;3),B(4;−5),C(−3;7),D(−2;2),F(−4;−2),K(2;−2),M(0;2),N(−3;0),P(1;6).
Решение
275
-
Страница 275
Задание 1299
На координатной плоскости отметьте точки: A(5;1),B(2;−1),C(−7;−1),D(−5;3),E(1;0),F(0;−4),S(−1;−3),T(−6;2),Q(3;2).
Решение
Задание 1300
Постройте отрезки AB и CD и найдите координаты точки пересечения этих отрезков, если A(−1;−3),B(3;1),C(0;4),D(3;−2).
Решение
Ответ: E(2;0)Задание 1301
Постройте отрезки AB и CD и найдите координаты точки пересечения этих отрезков, если A(−5;−2),B(1;4),C(−3;2),D(2;−3).
Решение
Ответ: E(−2;1)Задание 1302
Начертите на координатной плоскости треугольник EFK, если E(3;−2), F(−3;1), K(1;5). Найдите координаты точек пересечения стороны EF с осью x и стороны FK с осью y.
Решение
Ответ: A(−1;0); B(0;4).Задание 1303
Начертите на координатной плоскости четырехугольник PQRS, если P(−4;2), Q(−2;4), R(4;1),
S(−2;−2). Найдите координаты точек пересечения стороны QR с осью y и стороны PS с осью x.Решение
Ответ: A(0;3); B(−3;0).Задание 1304
Найдите координаты точки B, симметричной точке A(−1;−4) относительно:
1) оси абсцисс;
2) начала координат.Решение
1)
Ответ: B (−1;4)
2)
Ответ: B (1;4)Задание 1305
Найдите координаты точки M, симметричной точке N(−5;2) относительно:
1) оси ординат;
2) начала координат.Решение
1)
Ответ: M(5;2)
2)
Ответ: M(5;−2)Задание 1306
Отметьте на координатной плоскости точки M(4;3), K(−2;5), E(0;−3), F(−4;−2). Постройте точки, симметричные данным относительно:
1) начала координат;
2) оси ординат;
3) оси абсцисс.
Определите координаты полученных точек.Решение
1)
Ответ: M1 (− 4; − 3) ; K1 (2; − 5); E1 (0; 3); F1 (4 ; 2).
2)
Ответ: M1 (− 4; 3) ; K1 (2; 5); E1 (0; − 3); F1 (4; − 2).
3)
Ответ: M1 (4; − 3) ; K1 (− 2; − 5); E1 (0; 3); F1 (− 4; 2).Задание 1307
Отметьте на координатной плоскости точки Q(−3;0), S(1;−4). Постройте точки, симметричные данным относительно:
1) начала координат;
2) оси ординат;
3) оси абсцисс.
Определите координаты полученных точек.Решение
1)
Ответ: Q1(3;0); S1(−1;4).
2)
Ответ: Q1(3;0); S1(−1;−4).
3)
Ответ: Q1(−3;0); S1(1;4).Задание 1308
Даны координаты вершин прямоугольника ABCD: A(−3;−1), B(−3;3) и D(5;−1).
1) Начертите этот прямоугольник.
2) Найдите координаты вершины С.
3) Найдите координаты точки пересечения диагоналей прямоугольника.
4) Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.Решение
1)
2)
Ответ: С(5;3).
3)
Ответ: E(1;1).
4) AB = CD = 4 см;
BС = AD = 8 см, тогда:
S = 4 * 8 = 32 $см^2$ − площадь прямоугольника;
P = 2 * (8 + 4) = 2 * 12 = 24 см − периметр прямоугольника.Задание 1309
На координатной плоскости проведена линия (рис.188).
1) Найдите ординату точки, принадлежащей этой линии, абсцисса которой равна: 2; −3; −1.
2) Найдите абсциссу точки, принадлежащей этой линии, ордината которой равна: 3; 0; −2.
Решение
1)
Ответ: (2;4); (−3;−1); (−1;0).
2)
Ответ: (1;3); (−1;0); (−4;−2). 276
-
Страница 276
Задание 1310
На координатной плоскости проведена окружность (рис.189).
1) Найдите ординату точки, принадлежащей этой линии, абсцисса которой равна: 5; −4.
2) Найдите абсциссу точки, принадлежащей этой линии, ордината которой равна: −5; 3; 0.
Решение
1)
Ответ: (5;0); (−4;3) и (−4;−3).
2)
Ответ: (0;−5); (4;3) и (−4;3); (5;0) и (−5;0).Задание 1311
На координатной плоскости проведена линия (рис.190).
1) Найдите ординату точки, принадлежащей этой линии, абсцисса которой равна: −2; 3; 2.
2) Найдите абсциссу точки, принадлежащей этой линии, ордината которой равна: −4; −3; 0.
Решение
1)
Ответ: (−2;0); (3;5); (2;0).
2)
Ответ: (0;−4); (1;−3) и (−1;−3); (2;0) и (−2;0).Задание 1312
Постройте окружность с центром в точке M(3;2), проходящую через точку K(2;−1). Какие из точек принадлежат окружности: A(2;5), B(0;3), C(1;−1), D(3;−2), E(4;−1), F(5;0)?
Решение
Ответ: окружности принадлежат точки A, B, K, E, F.Задание 1313
Постройте окружность с центром в точке A(−4;0), проходящую через начало координат. Скольким единичным отрезкам равен радиус этой окружности? Укажите координаты каких−нибудь двух точек, одна из которых принадлежит кругу, ограниченному этой окружностью, а вторая находится вне его.
Решение
Ответ:
радиус окружности равен 4 единичным отрезкам;
точка M(−6;2) принадлежит окружности;
точка E(−2;5) не принадлежит окружности.Задание 1314
Отметьте на координатной плоскости точки M(2;1), A(1;−2) и B(−2;1). Проведите прямую AB. Через точку M проведите прямую, параллельную AB, и прямую, перпендикулярную AB.
Решение
Задание 1315
Отметьте на координатной плоскости точки A(−7;2) и B(−3;−4). Пользуясь линейкой и угольником, проведите ось симметрии этих точек.
Решение
Задание 1316
Отметьте на координатной плоскости точки C(3;−3) и D(−1;6). Пользуясь линейкой и угольником, проведите ось симметрии этих точек.
Решение
Задание 1317
Постройте на координатной плоскости треугольник MKP, если M(1;3), K(3;4), P(2;1). Постройте треугольник, симметричный данному относительно:
1) оси y;
2) оси x;
3) начала координат.
Определите координаты вершин полученного треугольника.Решение
1)
Ответ: M1 (− 1; 3) , K1 (− 3; 4) , P1 (− 2; 1)
2)
Ответ: M1 (1; − 3) , K1 (3; − 4) , P1 (2; − 1)
3)
Ответ: M1 (− 1; − 3) , K1 (− 3; − 4) , P1 (− 2; − 1) 277
-
Страница 277
Задание 1318
Начертите на координатной плоскости треугольник ABC, если A(−3;2), B(−1;4), C(2;3). Постройте треугольник, симметричный данному относительно:
1) начала координат;
2) точки P(2;2).
Найдите координаты вершин полученного треугольника.Решение
1)
Ответ: A 1 ( 3 ; − 2 ) , B 1 ( 1 ; − 4 ) , C 1 ( − 2 ; − 3 )
2)
Ответ: A 1 ( 7 ; 2 ) , B 1 ( 5 ; 0 ) , C 1 ( 2 ; 1 )Задание 1319
В какой четверти лежит точка A(x;y), если:
1) x > 0, y > 0;
2) x > 0, y < 0;
3) x < 0, y < 0;
4) x < 0, y > 0?Решение
1) в I четверти
2) в IV четверти
3) в III четверти
4) вo II четвертиЗадание 1320
Выше или ниже оси x расположена точка B(x;y), если:
1) y > 0, x − произвольное число;
2) y < 0, x − произвольное число?Решение
1) выше оси x
2) ниже оси xЗадание 1321
Справа или слева от оси y расположена точка C(x;y), если:
1) x < 0, y − произвольное число;
2) x > 0, y − произвольное число?Решение
1) слева оси y
2) справа оси yЗадание 1322
Из точек A(2;4), B(1;−10), C(0;−20), D(−4;−50), E(47;0), F(0;7), Q(−1;−1), S(−9;7), P(−6;0) выберите точки, лежащие:
1) выше оси х;
2) левее оси y;
3) на оси x;
4) на оси y.Решение
1) выше оси х лежат точки: A(2;4), F(0;7), S(−9;7), так как у этих точек y > 0.
2) левее оси y лежат точки: D(−4;−50), Q(−1;−1), S(−9;7), P(−6;0), так как у этих точек x < 0.
3) на оси x лежат точки: E(47;0), P(−6;0), так как у этих точек y = 0.
4) на оси y лежат точки: C(0;−20), F(0;7), так как у этих точек x = 0.Задание 1323
Начертите на координатной плоскости ломаную, последовательными вершинами которой являются точки с координатами: (8;0), (6;2), (0;6), (1;4), (−1;4), (−3;3), (−6;0), (−8;0), (−6;−1), (−6;−2,5), (−5;−1), (−1;−1), (0;1), (3;0), (2;−1), (5;−1), (6;−2), (7;−2), (9;−3), (8;−1). Отметьте точку (7;−1).
Решение
Задание 1324
Начертите на координатной плоскости две замкнутые ломаные, последовательными вершинами которых являются точки с координатами: (−5;3), (−2;1), (1;2), (2;3), (6;4), (−2;6) и (−3;3), (−3;4), (−2;5), (−2;3), четыре отрезка с концами в точках (−6;7) и (−2;6), (2;7) и (−2;6), (5;3) и (7;5), (5;5) и (7;3).
Решение
Задание 1325
Изобразите на координатной плоскости все точки (x;y) такие, что:
1) x = −3, y − произвольное число;
2) y = −5, x − произвольное число.Решение
1)
2)
Задание 1326
Изобразите на координатной плоскости все точки (x;y) такие, что:
1) x = 4, y − произвольное число;
2) y = 2, x − произвольное число.Решение
1)
2)
Задание 1327
Изобразите на координатной плоскости все точки, у которых:
1) абсцисса и ордината равны;
2) абсцисса и ордината − противоположные числа.Решение
1)
2)
Задание 1328
Изобразите на координатной плоскости все точки (x;y) такие, что:
1) y = 0, x < 3;
2) −4 < y < 4, x ⩾ 0;
3) |x| ⩽ 1, y ⩾ 1;
4) |x| > 2, y < −2.Решение
1)
2)
3)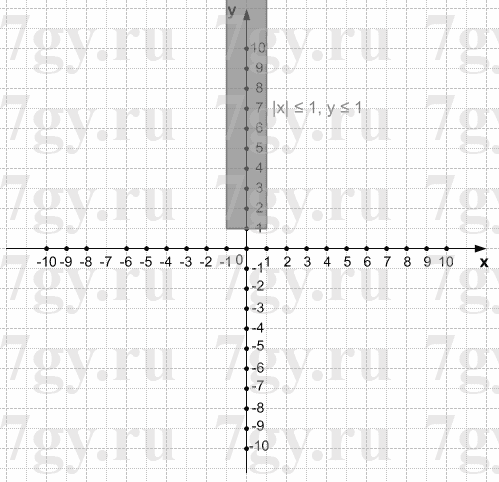
4)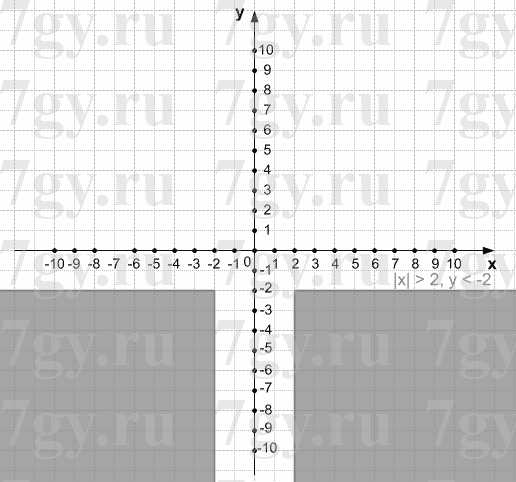
Задание 1329
Изобразите на координатной плоскости все точки (x;y) такие, что:
1) x = 0, y ⩾ −3;
2) −2 ⩽ x ⩽ 3, y − произвольное число;
3) |y| ⩽ 2, x − произвольное число;
4) |x| ⩽ 3, |y| ⩽ 1.Решение
1)
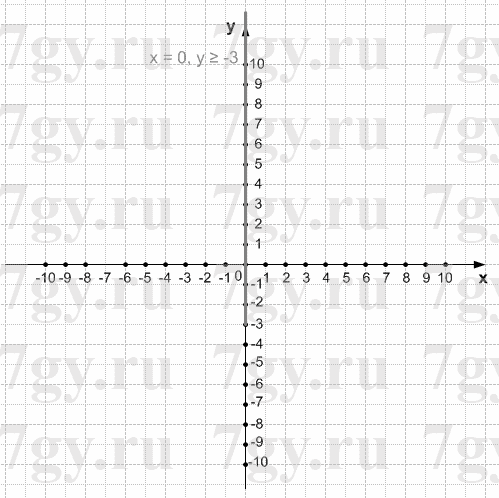
2)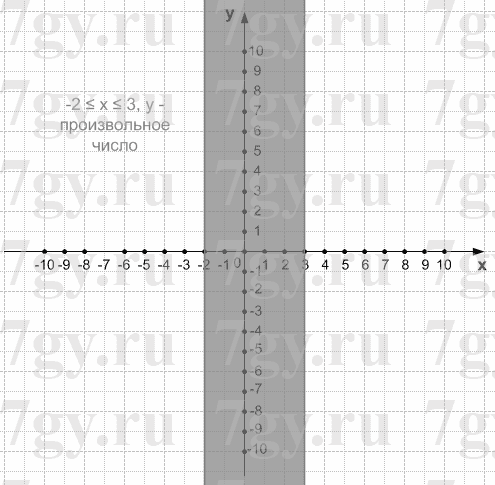
3)
4)
278
-
Страница 278
Задание 1330
Перерисуйте в тетрадь рисунок 191, проведите через каждую из точек B и M прямую, перпендикулярную прямой AD, а через точку K − прямую перпендикулярную прямой CD.
Решение
Задание 1331
В понедельник лакомка Наташа купила 12 конфет и с большим удовольствием съела их. В четверг она выиграла в лотерею деньги, сумма которых превышала потраченную ею в понедельник в 1 1/3 раза. Решив купить на эти деньги опять конфет. Наташа узнала, что цена конфет увеличилась в 1 3/5 раза. Сколько конфет сможет купить Наташа?
Решение
Пусть x р., стоила 1 конфета, тогда:
12x р. потратила Наташа в понедельник;
$1\frac13\ast12x=\frac43\ast12x=4\ast4x=16x$ рублей выиграла Наташа в лотерею;
$1\frac35x$ р. стала стоить 1 конфета после повышения.
$16x:1\frac35x=16x\ast\frac5{8x}=2\ast\frac51=10$ конфет сможет купить Наташа.
Ответ: 10 конфет.Задание 1332
Свежие яблоки содержат 75% воды, а сушеные − 12%. Сколько килограммов сушеных яблок получится из 264 кг свежих?
Решение
$\frac{75}{12}=\frac{25}4=6\frac14=6,25$, то есть в 6,25 раза свежие яблоки содержат больше воды, чем сушеные.
264 : 6,25 = 42,24 кг сушеных яблок получится из 264 кг свежих.
Ответ: 42,24 кг.Задание 1333
Белочка решила проверить свой запас орехов. Когда она считала их десятками, то не хватило двух орехов до целого числа десятков, а когда начала считать дюжинами, то осталось восемь орехов. Сколько орехов было у белочки, если известно, что их больше 300, но меньше 350?
Решение
По условию количество орехов больше 300, но меньше 350, следовательно количество орехов число трехзначное.
Так как не хватило 2 орехов, до целого числа десятков, то 10 − 2 = 8 − последняя цифра в количестве орехов, следовательно нам могут подойти числа: 308; 318; 328; 338; 348.
Из этих чисел только 308 делится на 12 с остатком 8, 308 : 12 = 12 * 25 + 8, следовательно 308 орехов было у белочки.
Ответ: 308 орехов.Задание 1334
В одной кучке лежит 171 камешек, а в другой − 172 камешка. Игроку за один ход разрешается взять любое количество камешков, но только из одной кучки. Проиграет тот, кому будет нечего брать. Кто из двух игроков выиграет при правильной стратегии − тот, кто начинает, или второй игрок?
Решение
Выиграет второй, если будет брать такое же количество камушек из той же кучки, что и первый. Если в какой то кучке останется 1 камушек, то второму нужно взять из другой кучки все камушки кроме одного. Тогда останется в каждой кучке по одному камушку, и после того как первый из одной кучки камешек заберет, то у второго станется последний ход. Если же в одной кучке первый возьмет последний камушек, то второму нужно забрать все камушки во второй кучке.
282-283
-
Страница 282-283
Ответы к параграфу 47. Графики
Задание 1335
На рисунке 198 изображен график изменения температуры воздуха на протяжении суток.
Пользуясь этим графиком, установите:
1) какой была температура воздуха в 4 ч; в 6 ч; в 10 ч; в 18 ч; в 22 ч;
2) в котором часу температура воздуха была 5°C; −2°C;
3) в котором часу температура воздуха была нулевой;
4) какой была самая низкая температура и в каком часу;
5) какой была самая высокая температура и в каком часу;
6) на протяжении каких промежутков времени температура воздуха была ниже 0°C; выше 0°C;
7) на протяжении каких промежутков времени температура воздуха повышалась; понижалась.
Решение
1) −4°C; −5°C; −2°C; 5°C; 0°C.
2) 5°C было в 13 ч и в 18 ч;
−2°C было в 3 ч, в 10 ч и в 23 ч.
3) 0°C было в 2 ч, в 11 ч и в 22 ч.
4) самая низкая температура −5°C была в 6 часов.
5) самая высокая температура 7°C была в 16 часов.
6) с 2 ч до 11 ч и с 22 ч до 24 ч температура воздуха была ниже 0°C;
с 0 ч до 2 ч и с 11 ч до 22 ч температура воздуха была выше 0°C.
7) с 6 ч до 16 ч температура воздуха повышалась;
с 0 ч до 6 ч и с 16 ч до 24 ч температура воздуха понижалась.Задание 1336
На рисунке 199 изображен график изменения температуры воздуха на протяжении суток.
Пользуясь графиком, установите:
1) какой была температура воздуха в 2 ч; в 8 ч; в 12 ч; в 16 ч; в 22 ч;
2) в котором часу температура воздуха была −3°C; −6°C; 0°C;
3) какой была самая низкая температура и в каком часу;
4) какой была самая высокая температура и в каком часу;
5) на протяжении каких промежутков времени температура воздуха была ниже 0°C; выше 0°C;
6) на протяжении каких промежутков времени температура воздуха повышалась; понижалась.
Решение
1) −5°C; −6°C; −4°C; 0°C; −1°C.
2) −3°C было в 14 ч;
−6°C было в 2 ч 30 мин, в 8 ч;
0°C было в 16 ч, в 21 ч.
3) самая низкая температура −10°C была в 6 часов.
4) самая высокая температура 4°C была в 19 часов.
5) с 0 ч до 16 ч и с 21 ч до 24 ч температура воздуха была ниже 0°C;
с 16 ч до 21 ч температура воздуха была выше 0°C.
6) с 6 ч до 21 ч температура воздуха повышалась;
с 0 ч до 6 ч и с 21 ч до 24 ч температура воздуха понижалась. 284
-
Страница 284
Задание 1337
На рисунке 200 изображен график изменения температуры раствора во время химического опыта.
Установите:
1) какой была начальная температура раствора;
2) какой была температура раствора через 30 минут после начала опыта; через полтора часа;
3) какой была самая высокая температура раствора и через сколько минут после начала опыта;
4) через сколько минут после начала опыта температура раствора была 35°C.
Решение
1) 10°C была начальная температура раствора
2) 30°C была температура раствора через 30 минут после начала опыта;
15°C была температура раствора через полтора часа после начала опыта.
3) 45°C была самая высокая температура раствора и через 60 минут после начала опыта
4) через 40 и через 70 минут после начала опыта температура раствора была 35°C 285
-
Страница 285
Задание 1338
Мотоциклист выехал из дома и через некоторое время вернулся назад. В дороге он 2 раза останавливался для отдыха. На рисунке 201 изображен график изменения расстояния от дома в зависимости от времени (график движения мотоциклиста).
1) Какое расстояние проехал мотоциклист за первый час движения?
2) На каком расстоянии от дома мотоциклист остановился для первого отдыха? Для второго отдыха?
3) Сколько длился первый отдых? Второй отдых?
4) На каком расстоянии от дома был мотоциклист через 5 ч после начала движения?
5) С какой скоростью двигался мотоциклист последние полчаса?
Решение
1) 60 км проехал мотоциклист за первый час движения.
2) на расстоянии 120 км от дома мотоциклист остановился для первого отдыха;
на расстоянии 75 км от дома мотоциклист остановился для второго отдыха.
3) 3 ч − 2 ч = 1 ч длился первый отдых;
4,5 ч − 4 ч = 0,5 ч = 30 мин длился второй отдых.
4) На расстоянии 60 км от дома был мотоциклист через 5 ч после начала движения.
5) $45{\operatorname к}{\operatorname м}:\frac12{\operatorname ч}=45{\operatorname к}{\operatorname м}\ast\frac21{\operatorname ч}=90$ км/ч скорость мотоциклиста в последние полчаса.Задание 1339
На рисунке 202 изображен график движения туриста.
1) На каком расстоянии от дома был турист через 10 ч после начала движения?
2) Сколько времени он затратил на остановку?
3) Через сколько часов после выхода турист был на расстоянии 8 км от дома?
4) С какой скоростью шел турист до остановки?
5) С какой скоростью шел турист последние два часа?
Решение
1) На расстоянии 10 км от дома был турист через 10 ч после начала движения
2) 7 ч − 4 ч = 3 ч затратил турист на остановку
3) Через 2 ч и через 11 часов после выхода турист был на расстоянии 8 км от дома
4) 16 км : 4 ч = 4 км/ч скорость туриста до остановки
5) 6 км : 2 ч = 3 км/ч скорость туриста последние два часа 286
-
Страница 286
Задание 1340
В таблице приведены данные измерения температуры воздуха на протяжении суток через каждый час. Используя эти данные, постройте график изменения температуры.
Пользуясь графиком, найдите, на протяжении какого времени температура повышалась и на протяжении какого времени понижалась.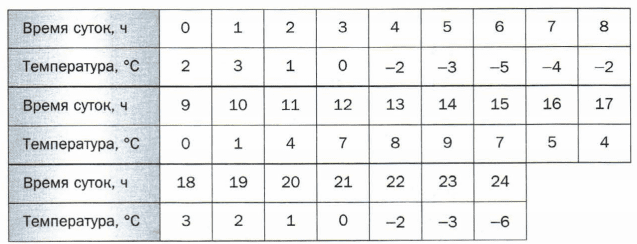
Решение
Температура повышалась с 0 до 1 ч и с 6 до 14 ч;
Температура понижалась с 1 до 6 ч и с 14 до 24 ч.Задание 1341
Велосипедист выехал из дома на прогулку. Сначала он ехал 2 ч со скоростью 12 км/ч, а потом отдохнул час и вернулся домой со скоростью 8 км/ч. Постройте график движения велосипедиста.
Решение
2 * 12 = 24 км проехал велосипедист за 2 ч;
24 : 8 = 3 ч возвращался домой велосипедист.Задание 1342
Постройте график зависимости переменной y от переменной x, которая задается формулой y = −2x.
Решение
х 1 2
у -2 -4
287
-
Страница 287
Задание 1343
У почтальона Печкина есть три разные конверта и четыре разные почтовые марки. Сколько у него вариантов выбора конверта с маркой?
Решение
Конверт можно выбрать один из трех (3 способа);
Марку можно выбрать одну из четырех (4 способа), тогда:
3 * 14 = 12 вариантов выбора конверта с маркой.
Ответ: 12 вариантов.Задание 1344
Вася прочитал 24% страниц книги, а потом еще 7/15 страниц книги. После этого ему осталось прочитать 44 страницы. Сколько страниц в книге?
Решение
Пусть x страниц в книге, тогда:
0,24x страниц прочитал Вася сначала;
$\frac7{15}x$ страниц прочитал Вася потом.
Так как, ему осталось прочитать 44 страницы, то:
$x-0,24x-\frac7{15}x=44$
$x-\frac6{25}x-\frac7{15}x=44$
$\frac{75}{75}x-\frac{18}{75}x-\frac{35}{75}x=44$
$\frac{22}{75}x=44$
$x=44:\frac{22}{75}$
$x=44\ast\frac{75}{22}$
$x=2\ast\frac{75}1$
x = 150 страниц в книге.
Ответ: 150 страниц.Задание 1345
Найдите значение выражения:
1) a : b − ab, если a = −0,5, b = $\frac23$;
2) $\frac{b+c}{b-c}$, если $b=\frac27,{\operatorname с}=-\frac49$;
3) $\frac{x^2+y^2}{x-y}$, если x = −0,3, y = −0,4.Решение
1) $a:b-ab=-0,5:\frac23-(-0,5\ast\frac23)=-\frac12\ast\frac32-(-\frac12\ast\frac23)=-\frac34-(-\frac11\ast\frac13)=-\frac34+\frac13=-\frac9{12}+\frac4{12}=-\frac5{12}$
2) $\frac{b+c}{b-c}=\frac{\frac27-\frac49}{\frac27+\frac49}=\frac{\frac{18}{63}-\frac{28}{63}}{\frac{18}{63}+\frac{28}{63}}=\frac{-\frac{10}{63}}{\frac{46}{63}}=-\frac{10}{63}\ast\frac{63}{46}=-\frac51\ast\frac1{23}=-\frac5{23}$
3) $\frac{x^2+y^2}{x-y}=\frac{(-0,3)^2+(-0,4)^2}{-0,3-(-0,4)}=\frac{0,09+0,16}{-0,3+0,4}=\frac{0,25}{0,1}=2,5$Задание 1346
В каждую клетку квадрата размером 6 × 6 клеток вписали одно из чисел −1, 0, 1. Могут ли суммы чисел, записанных в каждой строке, в каждом столбце и по двум большим диагоналям, быть разными?
Решение
2 диагонали + 6 строк + 6 столбцов = 14 вариантов расположения чисел длиной 6 клеток.
Вариантов сумм 6 чисел (где числа могут быть только −1, 0, 1) 13 от −6 до 6, следовательно суммы чисел, записанных в каждой строке, в каждом столбце и по двум большим диагоналям, быть разными не могут, хотя бы в двух вариантах суммы будут одинаковы.


