 Одно из видов заданий из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, которые могут вам попасться на реальном экзамене в этом году.
Одно из видов заданий из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, которые могут вам попасться на реальном экзамене в этом году.
Задания по геометрии из банка ФИПИ
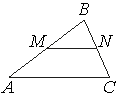
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
Решение:
Треугольники ABC и MBN подобны по двум углам: ∠B — общий, ∠BMN = ∠BAC — соответственные при секущей AB, MN и AC параллельны.
Из подобия треугольников следует:
BM = MN
AB AC , поэтому
BM = MN/AC * AB = 8/18 * 9 = 4, тогда
AM = AB − BM = 9 − 4 = 5
Ответ: 5
D60018

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
Решение:
Треугольники ABC и MBN подобны по двум углам: ∠B — общий, ∠BMN = ∠BAC — соответственные при секущей AB, MN и AC параллельны.
Из подобия треугольников следует:
BM = MN
AB AC , поэтому
BM = MN/AC * AB = 14/21 * 24 = 16, тогда
AM = AB − BM = 24 - 16 = 8
Ответ: 8
096C5B

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=24, MN=18. Найдите AM.
Решение:
Треугольники ABC и MBN подобны по двум углам: ∠B — общий, ∠BMN = ∠BAC — соответственные при секущей AB, MN и AC параллельны.
Из подобия треугольников следует:
BM = MN
AB AC , поэтому
BM = MN/AC * AB = 18/24 * 28 = 21, тогда
AM = AB − BM = 28 - 21 = 7
Ответ: 7
D3DF8C

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=33, AC=27, MN=18. Найдите AM.
Решение:
Треугольники ABC и MBN подобны по двум углам: ∠B — общий, ∠BMN = ∠BAC — соответственные при секущей AB, MN и AC параллельны.
Из подобия треугольников следует:
BM = MN
AB AC , поэтому
BM = MN/AC * AB = 18/27 * 33 = 22, тогда
AM = AB − BM = 33 - 22 = 11
Ответ: 11
E30A8E

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=25, AC=30, MN=12. Найдите AM.
Решение:
Треугольники ABC и MBN подобны по двум углам: ∠B — общий, ∠BMN = ∠BAC — соответственные при секущей AB, MN и AC параллельны.
Из подобия треугольников следует:
BM = MN
AB AC , поэтому
BM = MN/AC * AB = 12/30 * 25 = 10, тогда
AM = AB − BM = 25 - 10 = 15
Ответ: 15
1E6C42

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=16, MN=12. Найдите AM.
Решение:
Треугольники ABC и MBN подобны по двум углам: ∠B — общий, ∠BMN = ∠BAC — соответственные при секущей AB, MN и AC параллельны.
Из подобия треугольников следует:
BM = MN
AB AC , поэтому
BM = MN/AC * AB = 12/16 * 28 = 21, тогда
AM = AB − BM = 28 - 21 = 7
Ответ: 7
8CB097

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=40, AC=36, MN=27. Найдите AM.
Решение:
Треугольники ABC и MBN подобны по двум углам: ∠B — общий, ∠BMN = ∠BAC — соответственные при секущей AB, MN и AC параллельны.
Из подобия треугольников следует:
BM = MN
AB AC , поэтому
BM = MN/AC * AB = 27/36 * 40 = 30, тогда
AM = AB − BM = 40 - 30 = 10
Ответ: 10
5B7B2B

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=54, AC=48, MN=40. Найдите AM.
Решение:
Треугольники ABC и MBN подобны по двум углам: ∠B — общий, ∠BMN = ∠BAC — соответственные при секущей AB, MN и AC параллельны.
Из подобия треугольников следует:
BM = MN
AB AC , поэтому
BM = MN/AC * AB = 40/48 * 54 = 45, тогда
AM = AB − BM = 54 - 45 = 9
Ответ: 9
562FD1

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44, MN=24. Найдите AM.
Решение:
Треугольники ABC и MBN подобны по двум углам: ∠B — общий, ∠BMN = ∠BAC — соответственные при секущей AB, MN и AC параллельны.
Из подобия треугольников следует:
BM = MN
AB AC , поэтому
BM = MN/AC * AB = 24/44 * 66 = 36, тогда
AM = AB − BM =66 - 36 = 30
Ответ: 30
91469C

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=76, AC=38, MN=28. Найдите AM.
Решение:
Треугольники ABC и MBN подобны по двум углам: ∠B — общий, ∠BMN = ∠BAC — соответственные при секущей AB, MN и AC параллельны.
Из подобия треугольников следует:
BM = MN
AB AC , поэтому
BM = MN/AC * AB = 28/38 * 76 = 56, тогда
AM = AB − BM = 76 - 56 = 20
Ответ: 20
6CEB39


