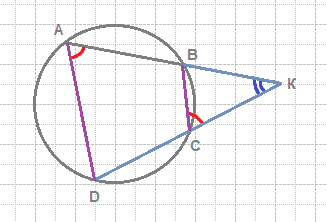
Один из видов заданий из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, которые могут вам попасться на реальном экзамене в этом году.

Вспоминаем, что описанная окружность — окружность, проходящая через все четыре вершины четырехугольника. Описанная окружность единственна. Можно описать окружность около: 1) любого прямоугольника (частный случай квадрат) 2) любой равнобедренной трапеции 3) любого четырехугольника, у которого сумма противоположных углов равна 180°. (См. рисунок: ∠A+∠C=∠B+∠D=180°)

Вспоминаем первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Реальные задания по геометрии из банка ФИПИ

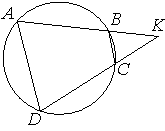
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.

Решение:

По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности).
Т.е. ∠BAD+∠BCD=180°
∠BCD=180°-∠BAD
∠KCB является смежным углу BCD, следовательно:
∠KCB+∠BCD=180°
Подставляем значение угла BCD:
∠KCB+(180°-∠BAD)=180°
∠KCB+180°-∠BAD=180°
∠KCB+180°-180°=∠BAD
∠KCB=∠BAD
Т.е. эти углы равны.

Рассмотрим треугольники AKD и BKC.
∠BKC - общий.
∠KCB=∠BAD (это мы определили ранее)
Следовательно, данные треугольники подобны (по первому признаку подобия).

Тогда:
BK = BC
DK    AD

AD = DK*BC
            BK

AD = 12*6
            8
AD = 9

Ответ: 9

048C03

Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=7, DK=14, BC=10. Найдите AD.

Решение:

По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности).
Т.е. ∠BAD+∠BCD=180°
∠BCD=180°-∠BAD
∠KCB является смежным углу BCD, следовательно:
∠KCB+∠BCD=180°
Подставляем значение угла BCD:
∠KCB+(180°-∠BAD)=180°
∠KCB+180°-∠BAD=180°
∠KCB+180°-180°=∠BAD
∠KCB=∠BAD
Т.е. эти углы равны.

Рассмотрим треугольники AKD и BKC.
∠BKC - общий.
∠KCB=∠BAD, это мы определили ранее.
Следовательно, данные треугольники подобны (по первому признаку подобия).

Тогда:
BK = BC
DK    AD

AD = DK*BC
            BK

AD = 14*10
             7

AD = 20

Ответ: 20

320015

Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=18, DK=9, BC=16. Найдите AD.

Решение:

По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности).
Т.е. ∠ABC+∠ADC=180°
∠ADC=180°-∠ABC
∠KDA является смежным углу ADC, следовательно:
∠KDA+∠ADC=180°
Подставляем значение угла ADC:
∠KDA+(180°-∠ABC)=180°
∠KDA+180°-∠ABC=180°
∠KDA+180°-180°=∠ABC
∠KDA=∠ABC
Т.е. эти углы равны.

Рассмотрим треугольники AKD и BKC.
∠BKC - общий.
∠KDA=∠ABC (это мы определили ранее).
Следовательно, данные треугольники подобны (по первому признаку подобия).

Тогда:

BK = BC
DK    AD

AD = DK*BC
            BK

AD = 9*16
           18

AD = 8

Ответ: 8

797303

Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=6, DK=10, BC=12. Найдите AD.

Решение:

По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности).
Т.е. ∠BAD+∠BCD=180°
∠BCD=180°-∠BAD
∠KCB является смежным углу BCD, следовательно:
∠KCB+∠BCD=180°
Подставляем значение угла BCD:
∠KCB+(180°-∠BAD)=180°
∠KCB+180°-∠BAD=180°
∠KCB+180°-180°=∠BAD
∠KCB=∠BAD
Т.е. эти углы равны.

Рассмотрим треугольники AKD и BKC.
∠BKC - общий.
∠KCB=∠BAD, это мы определили ранее.
Следовательно, данные треугольники подобны (по первому признаку подобия).

Тогда:
BK = BC
DK    AD

AD = DK*BC
            BK

AD = 10*12
             6

AD = 20

Ответ: 20

1D1BB8

Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=4, DK=12, BC=21. Найдите AD.

Решение:

По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности).
Т.е. ∠BAD+∠BCD=180°
∠BCD=180°-∠BAD
∠KCB является смежным углу BCD, следовательно:
∠KCB+∠BCD=180°
Подставляем значение угла BCD:
∠KCB+(180°-∠BAD)=180°
∠KCB+180°-∠BAD=180°
∠KCB+180°-180°=∠BAD
∠KCB=∠BAD
Т.е. эти углы равны.

Рассмотрим треугольники AKD и BKC.
∠BKC - общий.
∠KCB=∠BAD, это мы определили ранее.
Следовательно, данные треугольники подобны (по первому признаку подобия).

Тогда:
BK = BC
DK    AD

AD = DK*BC
            BK

AD = 12*21
             4

AD = 63

Ответ: 63

E373CB

Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.

Решение:

...
Ответ: ...

6DE641

Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=10, DK=6, BC=15. Найдите AD.

Решение:

По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности).
Т.е. ∠ABC+∠ADC=180°
∠ADC=180°-∠ABC
∠KDA является смежным углу ADC, следовательно:
∠KDA+∠ADC=180°
Подставляем значение угла ADC:
∠KDA+(180°-∠ABC)=180°
∠KDA+180°-∠ABC=180°
∠KDA+180°-180°=∠ABC
∠KDA=∠ABC
Т.е. эти углы равны.

Рассмотрим треугольники AKD и BKC.
∠BKC - общий.
∠KDA=∠ABC (это мы определили ранее).
Следовательно, данные треугольники подобны (по первому признаку подобия).

Тогда:

BK = BC
DK    AD

AD = DK*BC
            BK

AD = 6*15
           10

AD = 9

Ответ: 9

8AEF27

Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=14, DK=10, BC=21. Найдите AD.

Решение:

По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности).
Т.е. ∠ABC+∠ADC=180°
∠ADC=180°-∠ABC
∠KDA является смежным углу ADC, следовательно:
∠KDA+∠ADC=180°
Подставляем значение угла ADC:
∠KDA+(180°-∠ABC)=180°
∠KDA+180°-∠ABC=180°
∠KDA+180°-180°=∠ABC
∠KDA=∠ABC
Т.е. эти углы равны.

Рассмотрим треугольники AKD и BKC.
∠BKC - общий.
∠KDA=∠ABC (это мы определили ранее).
Следовательно, данные треугольники подобны (по первому признаку подобия).

Тогда:

BK = BC
DK    AD

AD = DK*BC
            BK

AD = 10*21
           14

AD = 15

Ответ: 15

55615A

Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.

Решение:

По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности).
Т.е. ∠ABC+∠ADC=180°
∠ADC=180°-∠ABC
∠KDA является смежным углу ADC, следовательно:
∠KDA+∠ADC=180°
Подставляем значение угла ADC:
∠KDA+(180°-∠ABC)=180°
∠KDA+180°-∠ABC=180°
∠KDA+180°-180°=∠ABC
∠KDA=∠ABC
Т.е. эти углы равны.

Рассмотрим треугольники AKD и BKC.
∠BKC - общий.
∠KDA=∠ABC (это мы определили ранее).
Следовательно, данные треугольники подобны (по первому признаку подобия).

Тогда:

BK = BC
DK    AD

AD = DK*BC
            BK

AD = 15*12
           20

AD = 9

Ответ: 9

E538A8

Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=12, DK=16, BC=24. Найдите AD.

Решение:

По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по свойству описанной окружности).
Т.е. ∠BAD+∠BCD=180°
∠BCD=180°-∠BAD
∠KCB является смежным углу BCD, следовательно:
∠KCB+∠BCD=180°
Подставляем значение угла BCD:
∠KCB+(180°-∠BAD)=180°
∠KCB+180°-∠BAD=180°
∠KCB+180°-180°=∠BAD
∠KCB=∠BAD
Т.е. эти углы равны.

Рассмотрим треугольники AKD и BKC.
∠BKC - общий.
∠KCB=∠BAD, это мы определили ранее.
Следовательно, данные треугольники подобны (по первому признаку подобия).

Тогда:
BK = BC
DK    AD

AD = DK*BC
            BK

AD = 16*24
             12

AD = 32

Ответ: 32

77C1B1