Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году.
Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году.
Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2
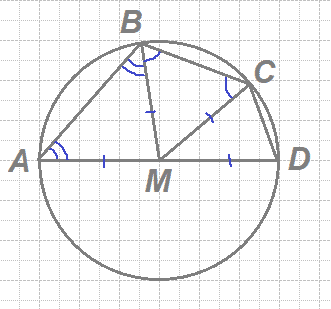
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=10, а углы B и C четырёхугольника равны соответственно 112° и 113°.
Решение:
1 способ
Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность. Четырёхугольник вписан в окружность, следовательно, суммы противоположных углов равны 180°:
∠BAD + ∠BCD =180°
∠BAD = 180° - ∠BCD
∠BAD = 180° - 113° = 67°
Отрезки AM,BM и CM равны как радиусы окружности, поэтому треугольники ABM и BMC — равнобедренные, откуда
∠BAD = ∠ABM = 67° и
∠ВCМ = ∠MBC = ∠ABC - ∠ABM = 112° - 67° = 45°
Рассмотрим треугольник BMC. Сумма углов в треугольнике равна 180°, откуда
∠BMC = 180° - ∠MBC - ∠ BCM = 180° - 45° - 45° = 90°
По теореме синусов найдём сторону BM из треугольника BMC:
BC/sinBMC =BM/sinBCM
BM = ВС * sinBCM/sinBMC
sin45° = √2/2
sin90° = 1
BM = 10 * √2/2
BM = 5√2
Сторона AD — диаметр описанной окружности, поэтому
AD = 2BM = 2 * 5√2 = 10√2
Ответ: 10√2
2 способ
Точка М равноудалена от вершин. Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность.
AD - диаметр.
дуга АС = 2 ∠В = 2 ∙ 112° = 224°
дуга ВD = 2 ∠С = 2 ∙ 113° = 226°
Cумма всех дуг окружности 360°
ВС + АС + BD – 180° = 360°
BC + 224° + 226° - 180° = 360°
BC + 270° = 360°
BC = 90°
∠BMC опирается на дугу ВС,
∠BMC = ВС = 90°
∆BMC прямоугольный равнобедренный треугольник, ВС = 10
По теореме Пифагора
а2 + а2 = 102
2а2 = 102
а = 5√2
АЕ = 2а = 2 ∙ 5√2 = 10√2
Ответ: 10√2
1B79A1
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=12, а углы B и C четырёхугольника равны соответственно 115° и 95°.
Решение:
Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность. Четырёхугольник вписан в окружность, следовательно, суммы противоположных углов равны 180°:
∠BAD + ∠BCD =180°
∠BAD = 180° - ∠BCD
∠BAD = 180° - 95° = 85°
Отрезки AM,BM и CM равны как радиусы окружности, поэтому треугольники ABM и BMC — равнобедренные, откуда
∠BAD = ∠ABM = 85° и
∠ВCМ = ∠MBC = ∠ABC - ∠ABM = 115° - 85° = 30°
Рассмотрим треугольник BMC. Сумма углов в треугольнике равна 180°, откуда
∠BMC = 180° - ∠MBC - ∠ BCM = 180° - 30° - 30° = 120°
По теореме синусов найдём сторону BM из треугольника BMC:
BC/sinBMC =BM/sinBCM
BM = ВС * sinBCM/sinBMC
$BM=\frac{12\ast\sin30^\circ}{\sin120^\circ}=\frac{12\ast{\displaystyle\frac12}}{\displaystyle\frac{\sqrt3}2}=4\sqrt3$
Сторона AD — диаметр описанной окружности, поэтому
AD = 2BM = 2 * 4√3 = 8√3
Ответ: 8√3
2 способ
Точка М равноудалена от вершин. Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность.
AD - диаметр.
дуга АС = 2 ∠В = 2 ∙ 115° = 230°
дуга ВЕ = 2 ∠С = 2 ∙ 95° = 190°
Сумма всех дуг окружности 360°
ВС + АС + BE – 180° = 360°
BC + 230° + 190° - 180° = 360°
BC + 240° = 360°
BC = 120°
∠BMC опирается на дугу ВС, ∠BMC = ВС = 120°
∆BMC равнобедренный треугольник, ВС = 12, ∠BMC = 120°
по т. косинусов
BC2 = a2 + a2 – 2 ∙ a ∙ a ∙ cos 120°
BC2 = a2 + a2 – 2 ∙ a ∙ a ∙ ( – 1/2)
BC2 = a2 + a2 + a2
BC2 = 3a2
a2 = BC2/3
a2 = 122/3
a2 = 144/3
а2 = 48
а = 4√3
АЕ = 2а = 2 ∙ 4√3 = 8√3
Ответ: 8√3
BD1CD0
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=9, а углы B и C четырёхугольника равны соответственно 116° и 94°.
Решение:
Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность. Четырёхугольник вписан в окружность, следовательно, суммы противоположных углов равны 180°:
∠BAD + ∠BCD =180°
∠BAD = 180° - ∠BCD
∠BAD = 180° - 94° = 86°
Отрезки AM,BM и CM равны как радиусы окружности, поэтому треугольники ABM и BMC — равнобедренные, откуда
∠BAD = ∠ABM = 86° и
∠ВCМ = ∠MBC = ∠ABC - ∠ABM = 116° - 86° = 30°
Рассмотрим треугольник BMC. Сумма углов в треугольнике равна 180°, откуда
∠BMC = 180° - ∠MBC - ∠ BCM = 180° - 30° - 30° = 120°
По теореме синусов найдём сторону BM из треугольника BMC:
BC/sinBMC =BM/sinBCM
BM = ВС * sinBCM/sinBMC
$BM=\frac{9\ast{\displaystyle\frac12}}{\displaystyle\frac{\sqrt3}2}=9\ast\frac{\sqrt3}3=3\sqrt3$
Сторона AD — диаметр описанной окружности, поэтому
AD = 2BM = 2 * 3√3 = 6√3
Ответ: 6√3
C0E083
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=19, а углы B и C четырёхугольника равны соответственно 95° и 115°.
Решение:
Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность. Четырёхугольник вписан в окружность, следовательно, суммы противоположных углов равны 180°:
∠BAD + ∠BCD =180°
∠BAD = 180° - ∠BCD
∠BAD = 180° - 115° = 65°
Отрезки AM,BM и CM равны как радиусы окружности, поэтому треугольники ABM и BMC — равнобедренные, откуда
∠BAD = ∠ABM = 65° и
∠ВCМ = ∠MBC = ∠ABC - ∠ABM = 95° - 65° = 30°
Рассмотрим треугольник BMC. Сумма углов в треугольнике равна 180°, откуда
∠BMC = 180° - ∠MBC - ∠ BCM = 180° - 30° - 30° = 120°
По теореме синусов найдём сторону BM из треугольника BMC:
BC/sinBMC =BM/sinBCM
BM = ВС * sinBCM/sinBMC
$BM=\frac{19\ast{\displaystyle\frac12}}{\displaystyle\frac{\sqrt3}2}=19\ast\frac{\sqrt3}3$
Сторона AD — диаметр описанной окружности, поэтому
AD = 2BM = 2 * 19√3/3 = 38√3/3
Ответ: 38√3/3
0F4C38
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 129° и 96°.
Решение:
Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность. Четырёхугольник вписан в окружность, следовательно, суммы противоположных углов равны 180°:
∠BAD + ∠BCD =180°
∠BAD = 180° - ∠BCD
∠BAD = 180° - 96° = 84°
Отрезки AM,BM и CM равны как радиусы окружности, поэтому треугольники ABM и BMC — равнобедренные, откуда
∠BAD = ∠ABM = 84° и
∠ВCМ = ∠MBC = ∠ABC - ∠ABM = 129° - 84° = 45°
Рассмотрим треугольник BMC. Сумма углов в треугольнике равна 180°, откуда
∠BMC = 180° - ∠MBC - ∠ BCM = 180° - 45° - 45° = 90°
По теореме синусов найдём сторону BM из треугольника BMC:
BC/sinBMC =BM/sinBCM
BM = ВС * sinBCM/sinBMC
BM = 8 * √2/2
BM = 4√2
Сторона AD — диаметр описанной окружности, поэтому
AD = 2BM = 2 * 4√2 = 8√2
Ответ: 8√2
3D4F8C
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=11, а углы B и C четырёхугольника равны соответственно 126° и 99°.
Решение:
Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность. Четырёхугольник вписан в окружность, следовательно, суммы противоположных углов равны 180°:
∠BAD + ∠BCD =180°
∠BAD = 180° - ∠BCD
∠BAD = 180° - 99° = 81°
Отрезки AM,BM и CM равны как радиусы окружности, поэтому треугольники ABM и BMC — равнобедренные, откуда
∠BAD = ∠ABM = 81° и
∠ВCМ = ∠MBC = ∠ABC - ∠ABM = 126° - 81° = 45°
Рассмотрим треугольник BMC. Сумма углов в треугольнике равна 180°, откуда
∠BMC = 180° - ∠MBC - ∠ BCM = 180° - 45° - 45° = 90°
По теореме синусов найдём сторону BM из треугольника BMC:
BC/sinBMC =BM/sinBCM
BM = ВС * sinBCM/sinBMC
BM = 11 * √2/2
BM = 11√2/2
Сторона AD — диаметр описанной окружности, поэтому
AD = 2BM = 2 * 11√2/2 = 11√2
Ответ: 11√2
3272C4
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=6, а углы B и C четырёхугольника равны соответственно 124° и 116°.
Решение:
Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность. Четырёхугольник вписан в окружность, следовательно, суммы противоположных углов равны 180°:
∠BAD + ∠BCD =180°
∠BAD = 180° - ∠BCD
∠BAD = 180° - 116° = 64°
Отрезки AM,BM и CM равны как радиусы окружности, поэтому треугольники ABM и BMC — равнобедренные, откуда
∠BAD = ∠ABM = 64° и
∠ВCМ = ∠MBC = ∠ABC - ∠ABM = 124° - 64° = 60°
Рассмотрим треугольник BMC. Сумма углов в треугольнике равна 180°, откуда
∠BMC = 180° - ∠MBC - ∠ BCM = 180° - 60° - 60° = 60°
По теореме синусов найдём сторону BM из треугольника BMC:
BC/sinBMC =BM/sinBCM
BM = ВС * sinBCM/sinBMC
BM = ВС = 6
Сторона AD — диаметр описанной окружности, поэтому
AD = 2BM = 2 * 6 = 12
Ответ: 12
66B052
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=14, а углы B и C четырёхугольника равны соответственно 110° и 100°.
Решение:
Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность. Четырёхугольник вписан в окружность, следовательно, суммы противоположных углов равны 180°:
∠BAD + ∠BCD =180°
∠BAD = 180° - ∠BCD
∠BAD = 180° - 100° = 80°
Отрезки AM,BM и CM равны как радиусы окружности, поэтому треугольники ABM и BMC — равнобедренные, откуда
∠BAD = ∠ABM = 80° и
∠ВCМ = ∠MBC = ∠ABC - ∠ABM = 110° - 80° = 30°
Рассмотрим треугольник BMC. Сумма углов в треугольнике равна 180°, откуда
∠BMC = 180° - ∠MBC - ∠ BCM = 180° - 30° - 30° = 120°
По теореме синусов найдём сторону BM из треугольника BMC:
BC/sinBMC =BM/sinBCM
BM = ВС * sinBCM/sinBMC
BM = 14 * √3/3
BM = 14√3/3
Сторона AD — диаметр описанной окружности, поэтому
AD = 2BM = 2 * 14√3/3 = 28√3/3
Ответ: 28√3/3
048981
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=3, а углы B и C четырёхугольника равны соответственно 94° и 131°.
Решение:
Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность. Четырёхугольник вписан в окружность, следовательно, суммы противоположных углов равны 180°:
∠BAD + ∠BCD =180°
∠BAD = 180° - ∠BCD
∠BAD = 180° - 131° = 49°
Отрезки AM,BM и CM равны как радиусы окружности, поэтому треугольники ABM и BMC — равнобедренные, откуда
∠BAD = ∠ABM = 49° и
∠ВCМ = ∠MBC = ∠ABC - ∠ABM = 94° - 49° = 45°
Рассмотрим треугольник BMC. Сумма углов в треугольнике равна 180°, откуда
∠BMC = 180° - ∠MBC - ∠ BCM = 180° - 45° - 45° = 90°
По теореме синусов найдём сторону BM из треугольника BMC:
BC/sinBMC =BM/sinBCM
BM = ВС * sinBCM/sinBMC
BM = 3 * √2/2
BM = 3√2/2
Сторона AD — диаметр описанной окружности, поэтому
AD = 2BM = 2 * 3√2/2 = 3√2
Ответ: 3√2
C2FA52
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=18, а углы B и C четырёхугольника равны соответственно 132° и 93°.
Решение:
Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность. Четырёхугольник вписан в окружность, следовательно, суммы противоположных углов равны 180°:
∠BAD + ∠BCD =180°
∠BAD = 180° - ∠BCD
∠BAD = 180° - 93° = 87°
Отрезки AM,BM и CM равны как радиусы окружности, поэтому треугольники ABM и BMC — равнобедренные, откуда
∠BAD = ∠ABM = 87° и
∠ВCМ = ∠MBC = ∠ABC - ∠ABM = 132° - 87° = 45°
Рассмотрим треугольник BMC. Сумма углов в треугольнике равна 180°, откуда
∠BMC = 180° - ∠MBC - ∠ BCM = 180° - 45° - 45° = 90°
По теореме синусов найдём сторону BM из треугольника BMC:
BC/sinBMC =BM/sinBCM
BM = ВС * sinBCM/sinBMC
sin45° = √2/2
sin90° = 1
BM = 18 * √2/2
BM = 9√2
Сторона AD — диаметр описанной окружности, поэтому
AD = 2BM = 2 * 9√2 = 18√2
Ответ: 18√2
94CC89