Следующие задачи на эту тему предлагает открытый банк заданий ФИПИ к ОГЭ по математике (раздел геометрия). Любое из них может вам попасться на ОГЭ в этом году.

Задания по геометрии из банка ФИПИ 

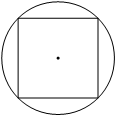
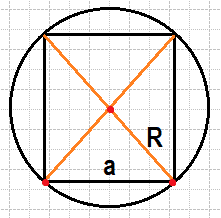
Сторона квадрата равна 4√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести диагонали в квадрате, который вписан в окружность, то радиус окружности будет равен половине диагонали квадрата. Отсюда по теореме Пифагора можно выразить неизвестный нам радиус, который является катетом для равнобедренного треугольника с гипотенузой - стороной квадрата. И так как гипотенуза нам известна, то можно выразить будет этот самый радиус R.

Получаем:
a²=R²+R²
a²=2R²
R=a/√2

Теперь подставляя в полученное равенство известную нам сторону квадрата находим радиус окружности.

R=a/√2=4√2/√2=4

Ответ: 4

1F54D7

Сторона квадрата равна 8√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести диагонали в квадрате, который вписан в окружность, то радиус окружности будет равен половине диагонали квадрата. Отсюда по теореме Пифагора можно выразить неизвестный нам радиус, который является катетом для равнобедренного треугольника с гипотенузой - стороной квадрата. И так как гипотенуза нам известна, то можно выразить будет этот самый радиус R.

Получаем:
a²=R²+R²
a²=2R²
R=a/√2

Теперь подставляя в полученное равенство известную нам сторону квадрата находим радиус окружности.

R=a/√2=8√2/√2=8

Ответ: 8

994045

Сторона квадрата равна 12√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести диагонали в квадрате, который вписан в окружность, то радиус окружности будет равен половине диагонали квадрата. Отсюда по теореме Пифагора можно выразить неизвестный нам радиус, который является катетом для равнобедренного треугольника с гипотенузой - стороной квадрата. И так как гипотенуза нам известна, то можно выразить будет этот самый радиус R.

Получаем:
a²=R²+R²
a²=2R²
R=a/√2

Теперь подставляя в полученное равенство известную нам сторону квадрата находим радиус окружности.

R=a/√2=12√2/√2=12

Ответ: 12

BD4933

Сторона квадрата равна 14√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести диагонали в квадрате, который вписан в окружность, то радиус окружности будет равен половине диагонали квадрата. Отсюда по теореме Пифагора можно выразить неизвестный нам радиус, который является катетом для равнобедренного треугольника с гипотенузой - стороной квадрата. И так как гипотенуза нам известна, то можно выразить будет этот самый радиус R.

Получаем:
a²=R²+R²
a²=2R²
R=a/√2

Теперь подставляя в полученное равенство известную нам сторону квадрата находим радиус окружности.

R=a/√2=14√2/√2=14

Ответ: 14

093734

Сторона квадрата равна 24√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести диагонали в квадрате, который вписан в окружность, то радиус окружности будет равен половине диагонали квадрата. Отсюда по теореме Пифагора можно выразить неизвестный нам радиус, который является катетом для равнобедренного треугольника с гипотенузой - стороной квадрата. И так как гипотенуза нам известна, то можно выразить будет этот самый радиус R.

Получаем:
a²=R²+R²
a²=2R²
R=a/√2

Теперь подставляя в полученное равенство известную нам сторону квадрата находим радиус окружности.

R=a/√2=24√2/√2=24

Ответ: 24

01D606

Сторона квадрата равна 32√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести диагонали в квадрате, который вписан в окружность, то радиус окружности будет равен половине диагонали квадрата. Отсюда по теореме Пифагора можно выразить неизвестный нам радиус, который является катетом для равнобедренного треугольника с гипотенузой - стороной квадрата. И так как гипотенуза нам известна, то можно выразить будет этот самый радиус R.

Получаем:
a²=R²+R²
a²=2R²
R=a/√2

Теперь подставляя в полученное равенство известную нам сторону квадрата находим радиус окружности.

R=a/√2=32√2/√2=32

Ответ: 32

E27C4D

Сторона квадрата равна 16√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести диагонали в квадрате, который вписан в окружность, то радиус окружности будет равен половине диагонали квадрата. Отсюда по теореме Пифагора можно выразить неизвестный нам радиус, который является катетом для равнобедренного треугольника с гипотенузой - стороной квадрата. И так как гипотенуза нам известна, то можно выразить будет этот самый радиус R.

Получаем:
a²=R²+R²
a²=2R²
R=a/√2

Теперь подставляя в полученное равенство известную нам сторону квадрата находим радиус окружности.

R=a/√2=32√2/√2=32

Ответ: 32

ED6F3D

Сторона квадрата равна 18√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести диагонали в квадрате, который вписан в окружность, то радиус окружности будет равен половине диагонали квадрата. Отсюда по теореме Пифагора можно выразить неизвестный нам радиус, который является катетом для равнобедренного треугольника с гипотенузой - стороной квадрата. И так как гипотенуза нам известна, то можно выразить будет этот самый радиус R.

Получаем:
a²=R²+R²
a²=2R²
R=a/√2

Теперь подставляя в полученное равенство известную нам сторону квадрата находим радиус окружности.

R=a/√2=18√2/√2=18

Ответ: 18

7134CE

Сторона квадрата равна 38√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести диагонали в квадрате, который вписан в окружность, то радиус окружности будет равен половине диагонали квадрата. Отсюда по теореме Пифагора можно выразить неизвестный нам радиус, который является катетом для равнобедренного треугольника с гипотенузой - стороной квадрата. И так как гипотенуза нам известна, то можно выразить будет этот самый радиус R.

Получаем:
a²=R²+R²
a²=2R²
R=a/√2

Теперь подставляя в полученное равенство известную нам сторону квадрата находим радиус окружности.

R=a/√2=38√2/√2=38

Ответ: 38

211998

Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести диагонали в квадрате, который вписан в окружность, то радиус окружности будет равен половине диагонали квадрата. Отсюда по теореме Пифагора можно выразить неизвестный нам радиус, который является катетом для равнобедренного треугольника с гипотенузой - стороной квадрата. И так как гипотенуза нам известна, то можно выразить будет этот самый радиус R.

Получаем:
a²=R²+R²
a²=2R²
R=a/√2

Теперь подставляя в полученное равенство известную нам сторону квадрата находим радиус окружности.

R=a/√2=40√2/√2=40

Ответ: 40

BA3134

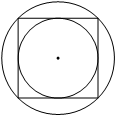
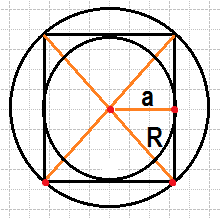
Радиус вписанной в квадрат окружности равен 2√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности, которая нам известна. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\R^2=2a^2$
R=a*√2

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

R=2√2*√2=2*2=4

Ответ: 4

B706F4

Радиус вписанной в квадрат окружности равен 4√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности, которая нам известна. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\R^2=2a^2$
R=a*√2

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

R=4√2*√2=4*2=8

Ответ: 8

CA3CE5

Радиус вписанной в квадрат окружности равен 6√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности, которая нам известна. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\R^2=2a^2$
R=a*√2

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

R=6√2*√2=6*2=12

Ответ: 12

829B45

Радиус вписанной в квадрат окружности равен 7√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности, которая нам известна. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\R^2=2a^2$
R=a*√2

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

R=7√2*√2=7*2=14

Ответ: 14

A74857

Радиус вписанной в квадрат окружности равен 22√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности, которая нам известна. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\R^2=2a^2$
R=a*√2

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

R=22√2*√2=22*2=44

Ответ: 44

1BEBBB

Радиус вписанной в квадрат окружности равен 26√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности, которая нам известна. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\R^2=2a^2$
R=a*√2

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

R=26√2*√2=26*2=52

Ответ: 52

E141CB

Радиус вписанной в квадрат окружности равен 10√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности, которая нам известна. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\R^2=2a^2$
R=a*√2

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

R=10√2*√2=10*2=20

Ответ: 20

9E173B

Радиус вписанной в квадрат окружности равен 16√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности, которая нам известна. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\R^2=2a^2$
R=a*√2

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

R=16√2*√2=16*2=32

Ответ: 32

C41908

Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности, которая нам известна. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\R^2=2a^2$
R=a*√2

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

R=24√2*√2=24*2=48

Ответ: 48

394240

Радиус вписанной в квадрат окружности равен 20√2. Найдите радиус окружности, описанной около этого квадрата.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности, которая нам известна. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\R^2=2a^2$
R=a*√2

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

R=20√2*√2=20*2=40

Ответ: 40

DDDB5C 

Радиус окружности, описанной около квадрата, равен 4√2. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности, который нам известен R. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности a, которую надо найти. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\2a^2=R^2\\a^2=\frac{R^2}2\\a=\frac R{\sqrt2}$

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

a=R/√2=4√2/√2=4

Ответ: 4

2FD244

Радиус окружности, описанной около квадрата, равен 6√2. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности, который нам известен R. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности a, которую надо найти. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\2a^2=R^2\\a^2=\frac{R^2}2\\a=\frac R{\sqrt2}$

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

a=R/√2=6√2/√2=6

Ответ: 6

46A3A9

Радиус окружности, описанной около квадрата, равен 14√2. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности, который нам известен R. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности a, которую надо найти. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\2a^2=R^2\\a^2=\frac{R^2}2\\a=\frac R{\sqrt2}$

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

a=R/√2=14√2/√2=14

Ответ: 14

DC3FCE

Радиус окружности, описанной около квадрата, равен 24√2. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности, который нам известен R. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности a, которую надо найти. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\2a^2=R^2\\a^2=\frac{R^2}2\\a=\frac R{\sqrt2}$

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

a=R/√2=24√2/√2=24

Ответ: 24

68C561

Радиус окружности, описанной около квадрата, равен 28√2. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности, который нам известен R. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности a, которую надо найти. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\2a^2=R^2\\a^2=\frac{R^2}2\\a=\frac R{\sqrt2}$

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

a=R/√2=28√2/√2=28

Ответ: 28

9631AF

Радиус окружности, описанной около квадрата, равен 44√2. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности, который нам известен R. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности a, которую надо найти. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\2a^2=R^2\\a^2=\frac{R^2}2\\a=\frac R{\sqrt2}$

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

a=R/√2=44√2/√2=44

Ответ: 44

64D33D

Радиус окружности, описанной около квадрата, равен 56√2. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности, который нам известен R. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности a, которую надо найти. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\2a^2=R^2\\a^2=\frac{R^2}2\\a=\frac R{\sqrt2}$

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

a=R/√2=56√2/√2=56

Ответ: 56

86368B

Радиус окружности, описанной около квадрата, равен 64√2. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности, который нам известен R. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности a, которую надо найти. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\2a^2=R^2\\a^2=\frac{R^2}2\\a=\frac R{\sqrt2}$

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

a=R/√2=64√2/√2=64

Ответ: 64

180516

Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности, который нам известен R. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности a, которую надо найти. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\2a^2=R^2\\a^2=\frac{R^2}2\\a=\frac R{\sqrt2}$

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

a=R/√2=38√2/√2=38

Ответ: 38

48A336

Радиус окружности, описанной около квадрата, равен 42√2. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

Если провести в квадрате диагонали, от точки пересечения этих диагоналей до вершин квадрата получится радиус описанной окружности, который нам известен R. А если провести из точки пересечения диагоналей высоту к одному из 4 получившихся равнобедренных прямоугольных треугольников, то получим радиус вписанной окружности a, которую надо найти. Теперь руководствуясь этими выводами можно вывести соотношение радиусов вписанной и описанной окружности используя теорему Пифагора.

Получаем:
$R^2=a^2+a^2\\2a^2=R^2\\a^2=\frac{R^2}2\\a=\frac R{\sqrt2}$

Теперь подставляя в полученное равенство известную нам величину (радиус вписанной окружности), мы получаем радиус описанной окружности.

a=R/√2=42√2/√2=42

Ответ: 42

C0FB9A 

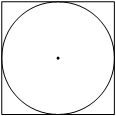
Сторона квадрата равна 6. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

 Если провести две средние линии для квадрата, когда та и другая будут пересекать середины перпендикулярных сторон квадрата, то каждая из таких линий будет являться диаметром вписанной окружности, а 4 получившихся квадрата будут со сторонами равными радиусу вписанной окружности. При этом все 4 квадрата будут одинаковые, а сторона каждого маленького квадрата будет равна половине стороны квадрата в котором они находятся. Получается нам надо разделить сторону большого квадрата пополам и мы узнаем радиус вписанной в этот квадрат окружности.

6:2=3

Ответ: 3

E5A7D3

Сторона квадрата равна 16. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

 Если провести две средние линии для квадрата, когда та и другая будут пересекать середины перпендикулярных сторон квадрата, то каждая из таких линий будет являться диаметром вписанной окружности, а 4 получившихся квадрата будут со сторонами равными радиусу вписанной окружности. При этом все 4 квадрата будут одинаковые, а сторона каждого маленького квадрата будет равна половине стороны квадрата в котором они находятся. Получается нам надо разделить сторону большого квадрата пополам и мы узнаем радиус вписанной в этот квадрат окружности.

16:2=8

Ответ: 8

D82EE3

Сторона квадрата равна 26. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

 Если провести две средние линии для квадрата, когда та и другая будут пересекать середины перпендикулярных сторон квадрата, то каждая из таких линий будет являться диаметром вписанной окружности, а 4 получившихся квадрата будут со сторонами равными радиусу вписанной окружности. При этом все 4 квадрата будут одинаковые, а сторона каждого маленького квадрата будет равна половине стороны квадрата в котором они находятся. Получается нам надо разделить сторону большого квадрата пополам и мы узнаем радиус вписанной в этот квадрат окружности.

26:2=13

Ответ: 13

D1ADF4

Сторона квадрата равна 34. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

 Если провести две средние линии для квадрата, когда та и другая будут пересекать середины перпендикулярных сторон квадрата, то каждая из таких линий будет являться диаметром вписанной окружности, а 4 получившихся квадрата будут со сторонами равными радиусу вписанной окружности. При этом все 4 квадрата будут одинаковые, а сторона каждого маленького квадрата будет равна половине стороны квадрата в котором они находятся. Получается нам надо разделить сторону большого квадрата пополам и мы узнаем радиус вписанной в этот квадрат окружности.

34:2=17

Ответ: 17

9FA314

Сторона квадрата равна 46. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

 Если провести две средние линии для квадрата, когда та и другая будут пересекать середины перпендикулярных сторон квадрата, то каждая из таких линий будет являться диаметром вписанной окружности, а 4 получившихся квадрата будут со сторонами равными радиусу вписанной окружности. При этом все 4 квадрата будут одинаковые, а сторона каждого маленького квадрата будет равна половине стороны квадрата в котором они находятся. Получается нам надо разделить сторону большого квадрата пополам и мы узнаем радиус вписанной в этот квадрат окружности.

46:2=23

Ответ: 23

D8BC0B

Сторона квадрата равна 48. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

 Если провести две средние линии для квадрата, когда та и другая будут пересекать середины перпендикулярных сторон квадрата, то каждая из таких линий будет являться диаметром вписанной окружности, а 4 получившихся квадрата будут со сторонами равными радиусу вписанной окружности. При этом все 4 квадрата будут одинаковые, а сторона каждого маленького квадрата будет равна половине стороны квадрата в котором они находятся. Получается нам надо разделить сторону большого квадрата пополам и мы узнаем радиус вписанной в этот квадрат окружности.

48:2=24

Ответ: 24

8C437E

Сторона квадрата равна 22. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

 Если провести две средние линии для квадрата, когда та и другая будут пересекать середины перпендикулярных сторон квадрата, то каждая из таких линий будет являться диаметром вписанной окружности, а 4 получившихся квадрата будут со сторонами равными радиусу вписанной окружности. При этом все 4 квадрата будут одинаковые, а сторона каждого маленького квадрата будет равна половине стороны квадрата в котором они находятся. Получается нам надо разделить сторону большого квадрата пополам и мы узнаем радиус вписанной в этот квадрат окружности.

22:2=11

Ответ: 11

078FAF

Сторона квадрата равна 24. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

 Если провести две средние линии для квадрата, когда та и другая будут пересекать середины перпендикулярных сторон квадрата, то каждая из таких линий будет являться диаметром вписанной окружности, а 4 получившихся квадрата будут со сторонами равными радиусу вписанной окружности. При этом все 4 квадрата будут одинаковые, а сторона каждого маленького квадрата будет равна половине стороны квадрата в котором они находятся. Получается нам надо разделить сторону большого квадрата пополам и мы узнаем радиус вписанной в этот квадрат окружности.

24:2=12

Ответ: 12

565F9D

Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

 Если провести две средние линии для квадрата, когда та и другая будут пересекать середины перпендикулярных сторон квадрата, то каждая из таких линий будет являться диаметром вписанной окружности, а 4 получившихся квадрата будут со сторонами равными радиусу вписанной окружности. При этом все 4 квадрата будут одинаковые, а сторона каждого маленького квадрата будет равна половине стороны квадрата в котором они находятся. Получается нам надо разделить сторону большого квадрата пополам и мы узнаем радиус вписанной в этот квадрат окружности.

56:2=28

Ответ: 28

FF0C20

Сторона квадрата равна 62. Найдите радиус окружности, вписанной в этот квадрат.

Решение:

Если провести две средние линии для квадрата, когда та и другая будут пересекать середины перпендикулярных сторон квадрата, то каждая из таких линий будет являться диаметром вписанной окружности, а 4 получившихся квадрата будут со сторонами равными радиусу вписанной окружности. При этом все 4 квадрата будут одинаковые, а сторона каждого маленького квадрата будет равна половине стороны квадрата в котором они находятся. Получается нам надо разделить сторону большого квадрата пополам и мы узнаем радиус вписанной в этот квадрат окружности.

62:2=31

Ответ: 31

A9C7B1

 

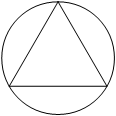
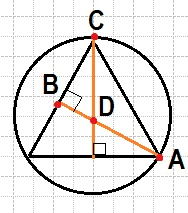
Сторона равностороннего треугольника равна 2√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Достраиваем в нашем равностороннем треугольнике две высоты, которые также являются и биссектрисами. В итоге каждый угол из которого выходит высота делится пополам и для равностороннего треугольника становится равен 60º/2=30º
При этом высота перпендикулярна к основанию и мы получаем прямоугольный треугольник. А в прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы. То есть BC=AC/2.
Но также при пересечении высот мы получаем и еще один меньший прямоугольный треугольник BCD, где также есть угол в 30 градусов. И опять же делаем заключение, что CD=2*BD, а CD является радиусом описанной окружности. Теперь выражаем радиус через сторону используя теорему Пифагора.

$R^2=\left(\frac{AC}2\right)^2+\left(\frac R2\right)^2\\R^2-\left(\frac R2\right)^2=\left(\frac{AC}2\right)^2\\\frac{4R^2}4-\frac R4^2=\frac{AC^2}4\\\frac{3R^2}4=\frac{AC^2}4\\3R^2=AC^2\\R^2=\frac{AC^2}3\\R=\frac{AC}{\sqrt3}\\\\\\$

Подставляем значение и вычисляем.

R = 2√3/√3=2
Ответ: 2 

 

44F7E4

Сторона равностороннего треугольника равна 4√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Достраиваем в нашем равностороннем треугольнике две высоты, которые также являются и биссектрисами. В итоге каждый угол из которого выходит высота делится пополам и для равностороннего треугольника становится равен 60º/2=30º
При этом высота перпендикулярна к основанию и мы получаем прямоугольный треугольник. А в прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы. То есть BC=AC/2.
Но также при пересечении высот мы получаем и еще один меньший прямоугольный треугольник BCD, где также есть угол в 30 градусов. И опять же делаем заключение, что CD=2*BD, а CD является радиусом описанной окружности. Теперь выражаем радиус через сторону используя теорему Пифагора.

$R^2=\left(\frac{AC}2\right)^2+\left(\frac R2\right)^2\\R^2-\left(\frac R2\right)^2=\left(\frac{AC}2\right)^2\\\frac{4R^2}4-\frac R4^2=\frac{AC^2}4\\\frac{3R^2}4=\frac{AC^2}4\\3R^2=AC^2\\R^2=\frac{AC^2}3\\R=\frac{AC}{\sqrt3}\\\\\\$

Подставляем значение и вычисляем.

R = 4√3/√3=4
Ответ: 4 

2B335C

Сторона равностороннего треугольника равна 6√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Достраиваем в нашем равностороннем треугольнике две высоты, которые также являются и биссектрисами. В итоге каждый угол из которого выходит высота делится пополам и для равностороннего треугольника становится равен 60º/2=30º
При этом высота перпендикулярна к основанию и мы получаем прямоугольный треугольник. А в прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы. То есть BC=AC/2.
Но также при пересечении высот мы получаем и еще один меньший прямоугольный треугольник BCD, где также есть угол в 30 градусов. И опять же делаем заключение, что CD=2*BD, а CD является радиусом описанной окружности. Теперь выражаем радиус через сторону используя теорему Пифагора.

$R^2=\left(\frac{AC}2\right)^2+\left(\frac R2\right)^2\\R^2-\left(\frac R2\right)^2=\left(\frac{AC}2\right)^2\\\frac{4R^2}4-\frac R4^2=\frac{AC^2}4\\\frac{3R^2}4=\frac{AC^2}4\\3R^2=AC^2\\R^2=\frac{AC^2}3\\R=\frac{AC}{\sqrt3}\\\\\\$

Подставляем значение и вычисляем.

R = 6√3/√3=6
Ответ: 6 

D1DC53

Сторона равностороннего треугольника равна 8√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Достраиваем в нашем равностороннем треугольнике две высоты, которые также являются и биссектрисами. В итоге каждый угол из которого выходит высота делится пополам и для равностороннего треугольника становится равен 60º/2=30º
При этом высота перпендикулярна к основанию и мы получаем прямоугольный треугольник. А в прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы. То есть BC=AC/2.
Но также при пересечении высот мы получаем и еще один меньший прямоугольный треугольник BCD, где также есть угол в 30 градусов. И опять же делаем заключение, что CD=2*BD, а CD является радиусом описанной окружности. Теперь выражаем радиус через сторону используя теорему Пифагора.

$R^2=\left(\frac{AC}2\right)^2+\left(\frac R2\right)^2\\R^2-\left(\frac R2\right)^2=\left(\frac{AC}2\right)^2\\\frac{4R^2}4-\frac R4^2=\frac{AC^2}4\\\frac{3R^2}4=\frac{AC^2}4\\3R^2=AC^2\\R^2=\frac{AC^2}3\\R=\frac{AC}{\sqrt3}\\\\\\$

Подставляем значение и вычисляем.

R = 8√3/√3=8
Ответ: 8 

B0A54A

Сторона равностороннего треугольника равна 10√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Достраиваем в нашем равностороннем треугольнике две высоты, которые также являются и биссектрисами. В итоге каждый угол из которого выходит высота делится пополам и для равностороннего треугольника становится равен 60º/2=30º
При этом высота перпендикулярна к основанию и мы получаем прямоугольный треугольник. А в прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы. То есть BC=AC/2.
Но также при пересечении высот мы получаем и еще один меньший прямоугольный треугольник BCD, где также есть угол в 30 градусов. И опять же делаем заключение, что CD=2*BD, а CD является радиусом описанной окружности. Теперь выражаем радиус через сторону используя теорему Пифагора.

$R^2=\left(\frac{AC}2\right)^2+\left(\frac R2\right)^2\\R^2-\left(\frac R2\right)^2=\left(\frac{AC}2\right)^2\\\frac{4R^2}4-\frac R4^2=\frac{AC^2}4\\\frac{3R^2}4=\frac{AC^2}4\\3R^2=AC^2\\R^2=\frac{AC^2}3\\R=\frac{AC}{\sqrt3}\\\\\\$

Подставляем значение и вычисляем.

R = 10√3/√3=10
Ответ: 10 

1962E6

Сторона равностороннего треугольника равна 12√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Достраиваем в нашем равностороннем треугольнике две высоты, которые также являются и биссектрисами. В итоге каждый угол из которого выходит высота делится пополам и для равностороннего треугольника становится равен 60º/2=30º
При этом высота перпендикулярна к основанию и мы получаем прямоугольный треугольник. А в прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы. То есть BC=AC/2.
Но также при пересечении высот мы получаем и еще один меньший прямоугольный треугольник BCD, где также есть угол в 30 градусов. И опять же делаем заключение, что CD=2*BD, а CD является радиусом описанной окружности. Теперь выражаем радиус через сторону используя теорему Пифагора.

$R^2=\left(\frac{AC}2\right)^2+\left(\frac R2\right)^2\\R^2-\left(\frac R2\right)^2=\left(\frac{AC}2\right)^2\\\frac{4R^2}4-\frac R4^2=\frac{AC^2}4\\\frac{3R^2}4=\frac{AC^2}4\\3R^2=AC^2\\R^2=\frac{AC^2}3\\R=\frac{AC}{\sqrt3}\\\\\\$

Подставляем значение и вычисляем.

R = 12√3/√3=12
Ответ: 12 

7435CB

Сторона равностороннего треугольника равна 14√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Достраиваем в нашем равностороннем треугольнике две высоты, которые также являются и биссектрисами. В итоге каждый угол из которого выходит высота делится пополам и для равностороннего треугольника становится равен 60º/2=30º
При этом высота перпендикулярна к основанию и мы получаем прямоугольный треугольник. А в прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы. То есть BC=AC/2.
Но также при пересечении высот мы получаем и еще один меньший прямоугольный треугольник BCD, где также есть угол в 30 градусов. И опять же делаем заключение, что CD=2*BD, а CD является радиусом описанной окружности. Теперь выражаем радиус через сторону используя теорему Пифагора.

$R^2=\left(\frac{AC}2\right)^2+\left(\frac R2\right)^2\\R^2-\left(\frac R2\right)^2=\left(\frac{AC}2\right)^2\\\frac{4R^2}4-\frac R4^2=\frac{AC^2}4\\\frac{3R^2}4=\frac{AC^2}4\\3R^2=AC^2\\R^2=\frac{AC^2}3\\R=\frac{AC}{\sqrt3}\\\\\\$

Подставляем значение и вычисляем.

R = 14√3/√3=14
Ответ: 14 

4F371C

Сторона равностороннего треугольника равна 16√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Достраиваем в нашем равностороннем треугольнике две высоты, которые также являются и биссектрисами. В итоге каждый угол из которого выходит высота делится пополам и для равностороннего треугольника становится равен 60º/2=30º
При этом высота перпендикулярна к основанию и мы получаем прямоугольный треугольник. А в прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы. То есть BC=AC/2.
Но также при пересечении высот мы получаем и еще один меньший прямоугольный треугольник BCD, где также есть угол в 30 градусов. И опять же делаем заключение, что CD=2*BD, а CD является радиусом описанной окружности. Теперь выражаем радиус через сторону используя теорему Пифагора.

$R^2=\left(\frac{AC}2\right)^2+\left(\frac R2\right)^2\\R^2-\left(\frac R2\right)^2=\left(\frac{AC}2\right)^2\\\frac{4R^2}4-\frac R4^2=\frac{AC^2}4\\\frac{3R^2}4=\frac{AC^2}4\\3R^2=AC^2\\R^2=\frac{AC^2}3\\R=\frac{AC}{\sqrt3}\\\\\\$

Подставляем значение и вычисляем.

R = 16√3/√3=16
Ответ: 16 

D20CD3

Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Достраиваем в нашем равностороннем треугольнике две высоты, которые также являются и биссектрисами. В итоге каждый угол из которого выходит высота делится пополам и для равностороннего треугольника становится равен 60º/2=30º
При этом высота перпендикулярна к основанию и мы получаем прямоугольный треугольник. А в прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы. То есть BC=AC/2.
Но также при пересечении высот мы получаем и еще один меньший прямоугольный треугольник BCD, где также есть угол в 30 градусов. И опять же делаем заключение, что CD=2*BD, а CD является радиусом описанной окружности. Теперь выражаем радиус через сторону используя теорему Пифагора.

$R^2=\left(\frac{AC}2\right)^2+\left(\frac R2\right)^2\\R^2-\left(\frac R2\right)^2=\left(\frac{AC}2\right)^2\\\frac{4R^2}4-\frac R4^2=\frac{AC^2}4\\\frac{3R^2}4=\frac{AC^2}4\\3R^2=AC^2\\R^2=\frac{AC^2}3\\R=\frac{AC}{\sqrt3}\\\\\\$

Подставляем значение и вычисляем.

R = 18√3/√3=18
Ответ: 18 

C3CA4A

Сторона равностороннего треугольника равна 20√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Достраиваем в нашем равностороннем треугольнике две высоты, которые также являются и биссектрисами. В итоге каждый угол из которого выходит высота делится пополам и для равностороннего треугольника становится равен 60º/2=30º
При этом высота перпендикулярна к основанию и мы получаем прямоугольный треугольник. А в прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы. То есть BC=AC/2.
Но также при пересечении высот мы получаем и еще один меньший прямоугольный треугольник BCD, где также есть угол в 30 градусов. И опять же делаем заключение, что CD=2*BD, а CD является радиусом описанной окружности. Теперь выражаем радиус через сторону используя теорему Пифагора.

$R^2=\left(\frac{AC}2\right)^2+\left(\frac R2\right)^2\\R^2-\left(\frac R2\right)^2=\left(\frac{AC}2\right)^2\\\frac{4R^2}4-\frac R4^2=\frac{AC^2}4\\\frac{3R^2}4=\frac{AC^2}4\\3R^2=AC^2\\R^2=\frac{AC^2}3\\R=\frac{AC}{\sqrt3}\\\\\\$

Подставляем значение и вычисляем.

R = 20√3/√3=20
Ответ: 20

CC527C

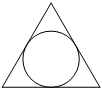
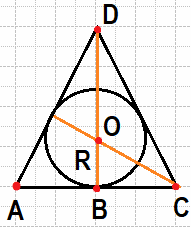
Сторона равностороннего треугольника равна 2√3. Найдите радиус окружности, вписанной в этот треугольник.

Решение:

Проведем две высоты. При этом точка пересечения высот O является центром окружностей, из свойств равностороннего треугольника. Также высота будет являться биссектрисой, а значит угол BCO в прямоугольном треугольнике равен 30º Мы знаем, что катет в прямоугольном треугольнике против угла в 30 градусов равен половине гипотенузы OC = 2R. Теперь используя теорему Пифагора для прямоугольного треугольника выразим R, через сторону AC. Получаем.

$\left(\frac{AC}2\right)^2+R^2\;=\left(2R\right)^2\\\left(\frac{AC}2\right)^2=4R^2-R^2\\\left(\frac{AC}2\right)^2=3R^2\\R^2=\frac{AC}4^2\ast\frac13\\R=\frac{AC}{2\sqrt3}\\\\\\$

Подставляем в формулу значение и считаем.

R=AC/2√3=2√3/2√3=1

Ответ: 1

6B6C6E

Сторона равностороннего треугольника равна 4√3. Найдите радиус окружности, вписанной в этот треугольник.

Решение:

Проведем две высоты. При этом точка пересечения высот O является центром окружностей, из свойств равностороннего треугольника. Также высота будет являться биссектрисой, а значит угол BCO в прямоугольном треугольнике равен 30º Мы знаем, что катет в прямоугольном треугольнике против угла в 30 градусов равен половине гипотенузы OC = 2R. Теперь используя теорему Пифагора для прямоугольного треугольника выразим R, через сторону AC. Получаем.

$\left(\frac{AC}2\right)^2+R^2\;=\left(2R\right)^2\\\left(\frac{AC}2\right)^2=4R^2-R^2\\\left(\frac{AC}2\right)^2=3R^2\\R^2=\frac{AC}4^2\ast\frac13\\R=\frac{AC}{2\sqrt3}\\\\\\$

Подставляем в формулу значение и считаем.

R=AC/2√3=4√3/2√3=2

Ответ: 2

F83E67

Сторона равностороннего треугольника равна 6√3. Найдите радиус окружности, вписанной в этот треугольник.

Решение:

Проведем две высоты. При этом точка пересечения высот O является центром окружностей, из свойств равностороннего треугольника. Также высота будет являться биссектрисой, а значит угол BCO в прямоугольном треугольнике равен 30º Мы знаем, что катет в прямоугольном треугольнике против угла в 30 градусов равен половине гипотенузы OC = 2R. Теперь используя теорему Пифагора для прямоугольного треугольника выразим R, через сторону AC. Получаем.

$\left(\frac{AC}2\right)^2+R^2\;=\left(2R\right)^2\\\left(\frac{AC}2\right)^2=4R^2-R^2\\\left(\frac{AC}2\right)^2=3R^2\\R^2=\frac{AC}4^2\ast\frac13\\R=\frac{AC}{2\sqrt3}\\\\\\$

Подставляем в формулу значение и считаем.

R=AC/2√3=6√3/2√3=3

Ответ: 3

7BA393

Сторона равностороннего треугольника равна 8√3. Найдите радиус окружности, вписанной в этот треугольник.

Решение:

Проведем две высоты. При этом точка пересечения высот O является центром окружностей, из свойств равностороннего треугольника. Также высота будет являться биссектрисой, а значит угол BCO в прямоугольном треугольнике равен 30º Мы знаем, что катет в прямоугольном треугольнике против угла в 30 градусов равен половине гипотенузы OC = 2R. Теперь используя теорему Пифагора для прямоугольного треугольника выразим R, через сторону AC. Получаем.

$\left(\frac{AC}2\right)^2+R^2\;=\left(2R\right)^2\\\left(\frac{AC}2\right)^2=4R^2-R^2\\\left(\frac{AC}2\right)^2=3R^2\\R^2=\frac{AC}4^2\ast\frac13\\R=\frac{AC}{2\sqrt3}\\\\\\$

Подставляем в формулу значение и считаем.

R=AC/2√3=8√3/2√3=4

Ответ: 4

68AB10

Сторона равностороннего треугольника равна 10√3. Найдите радиус окружности, вписанной в этот треугольник.

Решение:

Проведем две высоты. При этом точка пересечения высот O является центром окружностей, из свойств равностороннего треугольника. Также высота будет являться биссектрисой, а значит угол BCO в прямоугольном треугольнике равен 30º Мы знаем, что катет в прямоугольном треугольнике против угла в 30 градусов равен половине гипотенузы OC = 2R. Теперь используя теорему Пифагора для прямоугольного треугольника выразим R, через сторону AC. Получаем.

$\left(\frac{AC}2\right)^2+R^2\;=\left(2R\right)^2\\\left(\frac{AC}2\right)^2=4R^2-R^2\\\left(\frac{AC}2\right)^2=3R^2\\R^2=\frac{AC}4^2\ast\frac13\\R=\frac{AC}{2\sqrt3}\\\\\\$

Подставляем в формулу значение и считаем.

R=AC/2√3=10√3/2√3=5

Ответ: 5

911082

Сторона равностороннего треугольника равна 12√3. Найдите радиус окружности, вписанной в этот треугольник.

Решение:

Проведем две высоты. При этом точка пересечения высот O является центром окружностей, из свойств равностороннего треугольника. Также высота будет являться биссектрисой, а значит угол BCO в прямоугольном треугольнике равен 30º Мы знаем, что катет в прямоугольном треугольнике против угла в 30 градусов равен половине гипотенузы OC = 2R. Теперь используя теорему Пифагора для прямоугольного треугольника выразим R, через сторону AC. Получаем.

$\left(\frac{AC}2\right)^2+R^2\;=\left(2R\right)^2\\\left(\frac{AC}2\right)^2=4R^2-R^2\\\left(\frac{AC}2\right)^2=3R^2\\R^2=\frac{AC}4^2\ast\frac13\\R=\frac{AC}{2\sqrt3}\\\\\\$

Подставляем в формулу значение и считаем.

R=AC/2√3=12√3/2√3=6

Ответ: 6

F90F80

Сторона равностороннего треугольника равна 14√3. Найдите радиус окружности, вписанной в этот треугольник.

Решение:

Проведем две высоты. При этом точка пересечения высот O является центром окружностей, из свойств равностороннего треугольника. Также высота будет являться биссектрисой, а значит угол BCO в прямоугольном треугольнике равен 30º Мы знаем, что катет в прямоугольном треугольнике против угла в 30 градусов равен половине гипотенузы OC = 2R. Теперь используя теорему Пифагора для прямоугольного треугольника выразим R, через сторону AC. Получаем.

$\left(\frac{AC}2\right)^2+R^2\;=\left(2R\right)^2\\\left(\frac{AC}2\right)^2=4R^2-R^2\\\left(\frac{AC}2\right)^2=3R^2\\R^2=\frac{AC}4^2\ast\frac13\\R=\frac{AC}{2\sqrt3}\\\\\\$

Подставляем в формулу значение и считаем.

R=AC/2√3=14√3/2√3=7

Ответ: 7

5F2721

Сторона равностороннего треугольника равна 16√3. Найдите радиус окружности, вписанной в этот треугольник.

Решение:

Проведем две высоты. При этом точка пересечения высот O является центром окружностей, из свойств равностороннего треугольника. Также высота будет являться биссектрисой, а значит угол BCO в прямоугольном треугольнике равен 30º Мы знаем, что катет в прямоугольном треугольнике против угла в 30 градусов равен половине гипотенузы OC = 2R. Теперь используя теорему Пифагора для прямоугольного треугольника выразим R, через сторону AC. Получаем.

$\left(\frac{AC}2\right)^2+R^2\;=\left(2R\right)^2\\\left(\frac{AC}2\right)^2=4R^2-R^2\\\left(\frac{AC}2\right)^2=3R^2\\R^2=\frac{AC}4^2\ast\frac13\\R=\frac{AC}{2\sqrt3}\\\\\\$

Подставляем в формулу значение и считаем.

R=AC/2√3=16√3/2√3=8

Ответ: 8

54EED4

Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, вписанной в этот треугольник.

Решение:

Проведем две высоты. При этом точка пересечения высот O является центром окружностей, из свойств равностороннего треугольника. Также высота будет являться биссектрисой, а значит угол BCO в прямоугольном треугольнике равен 30º Мы знаем, что катет в прямоугольном треугольнике против угла в 30 градусов равен половине гипотенузы OC = 2R. Теперь используя теорему Пифагора для прямоугольного треугольника выразим R, через сторону AC. Получаем.

$\left(\frac{AC}2\right)^2+R^2\;=\left(2R\right)^2\\\left(\frac{AC}2\right)^2=4R^2-R^2\\\left(\frac{AC}2\right)^2=3R^2\\R^2=\frac{AC}4^2\ast\frac13\\R=\frac{AC}{2\sqrt3}\\\\\\$

Подставляем в формулу значение и считаем.

R=AC/2√3=18√3/2√3=9

Ответ: 9

B04F9A

Сторона равностороннего треугольника равна 20√3. Найдите радиус окружности, вписанной в этот треугольник.

Решение:

Проведем две высоты. При этом точка пересечения высот O является центром окружностей, из свойств равностороннего треугольника. Также высота будет являться биссектрисой, а значит угол BCO в прямоугольном треугольнике равен 30º Мы знаем, что катет в прямоугольном треугольнике против угла в 30 градусов равен половине гипотенузы OC = 2R. Теперь используя теорему Пифагора для прямоугольного треугольника выразим R, через сторону AC. Получаем.

$\left(\frac{AC}2\right)^2+R^2\;=\left(2R\right)^2\\\left(\frac{AC}2\right)^2=4R^2-R^2\\\left(\frac{AC}2\right)^2=3R^2\\R^2=\frac{AC}4^2\ast\frac13\\R=\frac{AC}{2\sqrt3}\\\\\\$

Подставляем в формулу значение и считаем.

R=AC/2√3=20√3/2√3=10

Ответ: 10

256E4F 

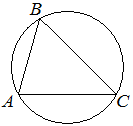
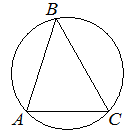
В треугольнике ABC угол C равен 45°, AB=6√2. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}\\\\\\$
Подставляем в формулу значение:

R=AB/2sin∠C=

= 6√2 *2___
  2*√2   =6

Ответ: 6

78B615

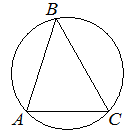
В треугольнике ABC угол C равен 60°, AB=12√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}\\\\\\$
Подставляем в формулу значение:

R=AB/2sin∠C=

= 12√3 *2
      2√3       = 12

Ответ: 12

541118

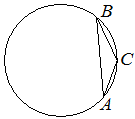
В треугольнике ABC угол C равен 135°, AB=14√2. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}\\\\\\$
Подставляем в формулу значение:

R=AB/2sin∠C=

= 14√2 *2
      2√2       = 14

Ответ: 14

6C9EF4

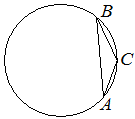
В треугольнике ABC угол C равен 30°, AB=16. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}\\\\\\$
Подставляем в формулу значение:

R=AB/2sin∠C=

= 16 *2
      2*1       = 16

Ответ: 16

DAE6A6

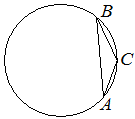
В треугольнике ABC угол C равен 150°, AB=26. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}\\\\\\$
Подставляем в формулу значение:

R=AB/2sin∠C=

= 26 *1
      2*1       = 26

Ответ: 14

6C273B

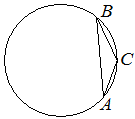
В треугольнике ABC угол C равен 120°, AB=18√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}\\\\\\$
Подставляем в формулу значение:

R=AB/2sin∠C=

= 18√3 *2
      2√3       = 18

Ответ: 18

F216F4

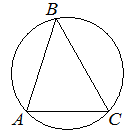
В треугольнике ABC угол C равен 45°, AB=8√2. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}\\\\\\$
Подставляем в формулу значение:

R=AB/2sin∠C=

= 8√2 *2
      2√2       = 8

Ответ: 8

16B266

В треугольнике ABC угол C равен 60°, AB=10√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}\\\\\\$
Подставляем в формулу значение:

R=AB/2sin∠C=

= 10√3 *2
      2√3       = 10

Ответ: 10

1D31C1

В треугольнике ABC угол C равен 150°, AB=4. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}\\\\\\$
Подставляем в формулу значение:

R=AB/2sin∠C=

= 4 *2
    2*1       = 4

Ответ: 4

69CD50

В треугольнике ABC угол C равен 120°, AB=22√3. Найдите радиус окружности, описанной около этого треугольника.

Решение:

Обобщенная теорема синусов гласит, стороны треугольника пропорциональны синусам противолежащих углов. При этом для треугольника АВС с радиусом описанного круга R верно соотношение:
$\frac{AB}{\sin\angle C}=2R\\R=\frac{AB}{2\sin\angle C}\\\\\\$
Подставляем в формулу значение:

R=AB/2sin∠C=

= 22√3 *2
      2√3       = 22

Ответ: 22

D93BBC

В треугольнике ABC известно, что AC=8, BC=15, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:

Найдем радиус описанной около этого треугольника окружности. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.

AB = √(AC² + BC²) = √(8² + 15²) = √(64 + 225) = √289 = 17

Найдем радиус.

R = 1/2 * AB = 1/2 * 17 = 17/2 = 8.5

Ответ: R = 8.5.

246FA5

В треугольнике ABC известно, что AC=12, BC=5, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:

Найдем радиус описанной около этого треугольника окружности. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.

AB = √(AC² + BC²) = √(5² + 12²) = √(25 + 144) = √169 = 13

Найдем радиус.

R = 1/2 * AB = 1/2 * 13 = 13/2 = 6.5

Ответ: R = 6.5

B1C05F

В треугольнике ABC известно, что AC=20, BC=21, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:

Найдем радиус описанной около этого треугольника окружности. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.

AB = √(AC² + BC²) = √(20² + 21²) = √(400 + 441) = √841 = 29

Найдем радиус.

R = 1/2 * AB = 1/2 * 29 = 29/2 = 14.5

Ответ: 14.5

1A1A54

В треугольнике ABC известно, что AC=10, BC=24, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:

Найдем радиус описанной около этого треугольника окружности. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.

AB = √(AC² + BC²) = √(10² + 24²) = √(100 + 576) = √676 = 26

Найдем радиус.

R = 1/2 * AB = 1/2 * 26 = 26/2 = 13

Ответ: 13

6A4430

В треугольнике ABC известно, что AC=40, BC=30, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:

Найдем радиус описанной около этого треугольника окружности. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.

AB = √(AC² + BC²) = √(20² + 21²) = √(400 + 441) = √841 = 29

Найдем радиус.

R = 1/2 * AB = 1/2 * 29 = 29/2 = 14.5

Ответ: 14.5

341F31

В треугольнике ABC известно, что AC=7, BC=24, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:

Найдем радиус описанной около этого треугольника окружности. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.

AB = √(AC² + BC²) = √(7² + 24²) = √(49 + 576) = √625 = 25

Найдем радиус.

R = 1/2 * AB = 1/2 * 25 = 25/2 = 12.5

Ответ: 12.5

B59D28

В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:

Найдем радиус описанной около этого треугольника окружности. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.

AB = √(AC² + BC²) = √(6² + 8²) = √(36 + 64) = √100 = 10

Найдем радиус.

R = 1/2 * AB = 1/2 * 10 = 10/2 = 5

Ответ: 5

446ABB

В треугольнике ABC известно, что AC=30, BC=16, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:

Найдем радиус описанной около этого треугольника окружности. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.

AB = √(AC² + BC²) = √(16² + 30²) = √(256 + 900) = √1156 = 34

Найдем радиус.

R = 1/2 * AB = 1/2 * 34 = 34/2 = 17

Ответ: 17

4FB9C5

В треугольнике ABC известно, что AC=16, BC=12, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:

Найдем радиус описанной около этого треугольника окружности. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.

AB = √(AC² + BC²) = √(12² + 16²) = √(144 + 256) = √400 = 20

Найдем радиус.

R = 1/2 * AB = 1/2 * 20 = 20/2 = 10

Ответ: 10

CA080B

В треугольнике ABC известно, что AC=40, BC=9, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.

Решение:

Найдем радиус описанной около этого треугольника окружности. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. А значит найдем гипотенузу АВ треугольника АВС по теореме Пифагора и разделим ее пополам.

AB = √(AC² + BC²) = √(9² + 40²) = √(81 + 1600) = √1681 = 41

Найдем радиус.

R = 1/2 * AB = 1/2 * 41 = 41/2 = 20.5

Ответ: 20.5

3C935

Задания с развернутым ответом

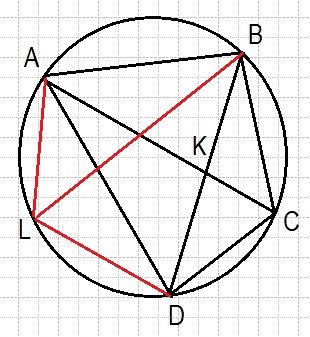
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Решение:

Проведём через точку D прямую, параллельную диагонали AC. Дуги AL и CD равны, следовательно, равны и стягивающие их хорды: AL = CD = 16.
Вертикальные углы AKB и CKD равны. Углы CKD и LDK равны как накрест лежащие: ∠CKD =∠LDK = 60º.
Четырёхугольник ABDL вписан в окружность, сумма его противолежащих углов равна 180°: ∠LAB = 180º -∠LDK = 180º-60º = 120º. Рассмотрим треугольник ABL. По теореме косинусов
$BL=\sqrt{AL^2+AB^2-2AL\cos120}\;=\sqrt{256+625-2\ast16\ast25\cos120}\;=\sqrt{1281}$

Далее по теореме синусов найдем радиус, выразив его через сторону и синус угла напротив нее

$R=\frac{BL}{2\sin\angle BAL}=$√1281/2sin∠BAL=

= √1281 *2
     2 * √3   = √427

Ответ: √427

2BB17F

Четырёхугольник ABCD со сторонами AB=5 и CD=17 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Решение:

Проведём через точку D прямую, параллельную диагонали AC. Дуги AL и CD равны, следовательно, равны и стягивающие их хорды: AL = CD = 17.
Вертикальные углы AKB и CKD равны. Углы CKD и LDK равны как накрест лежащие: ∠CKD =∠LDK = 60º.
Четырёхугольник ABDL вписан в окружность, сумма его противолежащих углов равна 180°: ∠LAB = 180º -∠LDK = 180º-60º = 120º. Рассмотрим треугольник ABL. По теореме косинусов
$BL=\sqrt{AL^2+AB^2-2AL\cos120}\;=\sqrt{25+289-2\ast5\ast17\cos120}\;=\sqrt{399}$

Далее по теореме синусов найдем радиус, выразив его через сторону и синус угла напротив нее

$R=\frac{BL}{2\sin\angle BAL}=$√399/2sin∠LAB=

= √399 *2
     2 * √3   = √133

Ответ: √133

602BF1

Четырёхугольник ABCD со сторонами AB=39 и CD=12 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Решение:

Проведём через точку D прямую, параллельную диагонали AC. Дуги AL и CD равны, следовательно, равны и стягивающие их хорды: AL = CD = 12.
Вертикальные углы AKB и CKD равны. Углы CKD и LDK равны как накрест лежащие: ∠CKD =∠LDK = 60º.
Четырёхугольник ABDL вписан в окружность, сумма его противолежащих углов равна 180°: ∠LAB = 180º -∠LDK = 180º-60º = 120º. Рассмотрим треугольник ABL. По теореме косинусов
$BL=\sqrt{AL^2+AB^2-2AL\cos120}\;=\sqrt{144+1521-2\ast39\ast12\cos120}\;=\sqrt{2133}$

Далее по теореме синусов найдем радиус, выразив его через сторону и синус угла напротив нее

$R=\frac{BL}{2\sin\angle BAL}=$√2133/2sin∠LAB=

= √2133 *2
     2 * √3   = √711

Ответ: √711

AE3879

Четырёхугольник ABCD со сторонами AB=43 и CD=4 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Решение:

Проведём через точку D прямую, параллельную диагонали AC. Дуги AL и CD равны, следовательно, равны и стягивающие их хорды: AL = CD = 4.
Вертикальные углы AKB и CKD равны. Углы CKD и LDK равны как накрест лежащие: ∠CKD =∠LDK = 60º.
Четырёхугольник ABDL вписан в окружность, сумма его противолежащих углов равна 180°: ∠LAB = 180º -∠LDK = 180º-60º = 120º. Рассмотрим треугольник ABL. По теореме косинусов
$BL=\sqrt{AL^2+AB^2-2AL\cos120}\;=\sqrt{16+1849-2\ast43\ast4\cos120}\;=\sqrt{2037}$

Далее по теореме синусов найдем радиус, выразив его через сторону и синус угла напротив нее

$R=\frac{BL}{2\sin\angle BAL}=$√2037/2sin∠LAB=

= √2037 *2
     2 * √3   = √679

Ответ: √679

3ECA01

Четырёхугольник ABCD со сторонами AB=34 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Решение:

Проведём через точку D прямую, параллельную диагонали AC. Дуги AL и CD равны, следовательно, равны и стягивающие их хорды: AL = CD = 22.
Вертикальные углы AKB и CKD равны. Углы CKD и LDK равны как накрест лежащие: ∠CKD =∠LDK = 60º.
Четырёхугольник ABDL вписан в окружность, сумма его противолежащих углов равна 180°: ∠LAB = 180º -∠LDK = 180º-60º = 120º. Рассмотрим треугольник ABL. По теореме косинусов
$BL=\sqrt{AL^2+AB^2-2AL\cos120}\;=\sqrt{1156+484-2\ast34\ast22\cos120}\;=\sqrt{2388}$

Далее по теореме синусов найдем радиус, выразив его через сторону и синус угла напротив нее

$R=\frac{BL}{2\sin\angle BAL}=$√2388/2sin∠LAB=

= √2388 *2
     2 * √3   = √796

Ответ: √796

97889E

Четырёхугольник ABCD со сторонами AB=11 и CD=41 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Решение:

Проведём через точку D прямую, параллельную диагонали AC. Дуги AL и CD равны, следовательно, равны и стягивающие их хорды: AL = CD = 41.
Вертикальные углы AKB и CKD равны. Углы CKD и LDK равны как накрест лежащие: ∠CKD =∠LDK = 60º.
Четырёхугольник ABDL вписан в окружность, сумма его противолежащих углов равна 180°: ∠LAB = 180º -∠LDK = 180º-60º = 120º. Рассмотрим треугольник ABL. По теореме косинусов
$BL=\sqrt{AL^2+AB^2-2AL\cos120}\;=\sqrt{121+1681-2\ast11\ast41\cos120}\;=\sqrt{2253}$

Далее по теореме синусов найдем радиус, выразив его через сторону и синус угла напротив нее

$R=\frac{BL}{2\sin\angle BAL}=$√2388/2sin∠LAB=

= √2253 *2
     2 * √3   = √751

Ответ: √751

30181B

Четырёхугольник ABCD со сторонами AB=44 и CD=8 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Решение:

Проведём через точку D прямую, параллельную диагонали AC. Дуги AL и CD равны, следовательно, равны и стягивающие их хорды: AL = CD = 8.
Вертикальные углы AKB и CKD равны. Углы CKD и LDK равны как накрест лежащие: ∠CKD =∠LDK = 60º.
Четырёхугольник ABDL вписан в окружность, сумма его противолежащих углов равна 180°: ∠LAB = 180º -∠LDK = 180º-60º = 120º. Рассмотрим треугольник ABL. По теореме косинусов
$BL=\sqrt{AL^2+AB^2-2AL\cos120}\;=\sqrt{64+1936-2\ast8\ast44\cos120}\;=\sqrt{2352}$

Далее по теореме синусов найдем радиус, выразив его через сторону и синус угла напротив нее

$R=\frac{BL}{2\sin\angle BAL}=$√2352/2sin∠LAB=

= √2352 *2
     2 * √3   = √784

Ответ: √784

F10ABA

Четырёхугольник ABCD со сторонами AB=12 и CD=30 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Решение:

Проведём через точку D прямую, параллельную диагонали AC. Дуги AL и CD равны, следовательно, равны и стягивающие их хорды: AL = CD = 30.
Вертикальные углы AKB и CKD равны. Углы CKD и LDK равны как накрест лежащие: ∠CKD =∠LDK = 60º.
Четырёхугольник ABDL вписан в окружность, сумма его противолежащих углов равна 180°: ∠LAB = 180º -∠LDK = 180º-60º = 120º. Рассмотрим треугольник ABL. По теореме косинусов
$BL=\sqrt{AL^2+AB^2-2AL\cos120}\;=\sqrt{144+900-2\ast12\ast30\cos120}\;=\sqrt{1404}$

Далее по теореме синусов найдем радиус, выразив его через сторону и синус угла напротив нее

$R=\frac{BL}{2\sin\angle BAL}=$√1404/2sin∠LAB=

= √1404 *2
     2 * √3   = √468

Ответ: √468

8FDA75

Четырёхугольник ABCD со сторонами AB=39 и CD=6 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Решение:

Проведём через точку D прямую, параллельную диагонали AC. Дуги AL и CD равны, следовательно, равны и стягивающие их хорды: AL = CD = 6.
Вертикальные углы AKB и CKD равны. Углы CKD и LDK равны как накрест лежащие: ∠CKD =∠LDK = 60º.
Четырёхугольник ABDL вписан в окружность, сумма его противолежащих углов равна 180°: ∠LAB = 180º -∠LDK = 180º-60º = 120º. Рассмотрим треугольник ABL. По теореме косинусов
$BL=\sqrt{AL^2+AB^2-2AL\cos120}\;=\sqrt{36+1521-2\ast6\ast39\cos120}\;=\sqrt{1791}$

Далее по теореме синусов найдем радиус, выразив его через сторону и синус угла напротив нее

$R=\frac{BL}{2\sin\angle BAL}=$√1791/2sin∠LAB=

= √1791 *2
     2 * √3   = √597

Ответ: √597

3F455F

Четырёхугольник ABCD со сторонами AB=40 и CD=10 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Решение:

Проведём через точку D прямую, параллельную диагонали AC. Дуги AL и CD равны, следовательно, равны и стягивающие их хорды: AL = CD = 10.
Вертикальные углы AKB и CKD равны. Углы CKD и LDK равны как накрест лежащие: ∠CKD =∠LDK = 60º.
Четырёхугольник ABDL вписан в окружность, сумма его противолежащих углов равна 180°: ∠LAB = 180º -∠LDK = 180º-60º = 120º. Рассмотрим треугольник ABL. По теореме косинусов
$BL=\sqrt{AL^2+AB^2-2AL\cos120}\;=\sqrt{100+1600-2\ast10\ast40\cos120}\;=\sqrt{2100}$

Далее по теореме синусов найдем радиус, выразив его через сторону и синус угла напротив нее

$R=\frac{BL}{2\sin\angle BAL}=$√1791/2sin∠LAB=

= √2100 *2
     2 * √3   = √700

Ответ: √700

A172F9

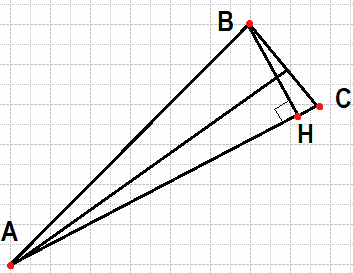
В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.

Решение:

Обозначим BH высоту, проведённую из вершины  B. Биссектриса, проведённая из угла A, делит высоту в отношении, равному отношению сторон треугольника AB и AH. Значит, 

cos∠BAC = AB = 3   
                 AH    5

Так как треугольник прямоугольный, то соотношение третей стороны можно вычислить по теореме Пифагора

х=√(5²-3²)=√(25-9)=√16=4 тогда исходя из того, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе получаем:

sin∠BAC = 4
                5

Теперь зная отношение сторон выраженную в синусе и принимая во внимание известную сторону применим обобщенную теорему синусов из которой:

2R=   BC__       R =    8*5 =  40  =   5
      2sin∠BAC              2*4      8

Ответ: 5

84B967

В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 5:4, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=18.

Решение:

Обозначим BH высоту, проведённую из вершины  B. Биссектриса, проведённая из угла A, делит высоту в отношении, равному отношению сторон треугольника AB и AH. Значит, 

cos∠BAC = AB = 4   
                 AH    5

Так как треугольник прямоугольный, то соотношение третей стороны можно вычислить по теореме Пифагора

х=√(5²-4²)=√(25-16)=√9=3 тогда исходя из того, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе получаем:

sin∠BAC = 3
                5

Теперь зная отношение сторон выраженную в синусе и принимая во внимание известную сторону применим обобщенную теорему синусов из которой:

2R=   BC__       R =     18*5 =  90  =   15
      2sin∠BAC                2*3        6

Ответ: 15

BC032E

В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.

Решение:

Обозначим BH высоту, проведённую из вершины  B. Биссектриса, проведённая из угла A, делит высоту в отношении, равному отношению сторон треугольника AB и AH. Значит, 

cos∠BAC = AB = 3   
                 AH    5

Так как треугольник прямоугольный, то соотношение третей стороны можно вычислить по теореме Пифагора

х=√(5²-3²)=√(25-9)=√16=4 тогда исходя из того, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе получаем:

sin∠BAC = 4
                5

Теперь зная отношение сторон выраженную в синусе и принимая во внимание известную сторону применим обобщенную теорему синусов из которой:

2R=   BC__      R =      16*5 =  80  =   10
      2sin∠BAC               2*4        8

Ответ: 10

E55CD0

В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 41:40, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=18.

Решение:

Обозначим BH высоту, проведённую из вершины  B. Биссектриса, проведённая из угла A, делит высоту в отношении, равному отношению сторон треугольника AB и AH. Значит, 

cos∠BAC = AB = 40   
                 AH    41

Так как треугольник прямоугольный, то соотношение третей стороны можно вычислить по теореме Пифагора

х=√(41²-40²)=√(1681-1600)=√81=9 тогда исходя из того, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе получаем:

sin∠BAC = 9
                41

Теперь зная отношение сторон выраженную в синусе и принимая во внимание известную сторону применим обобщенную теорему синусов из которой:

2R=   BC__       R =     18*41 =  738  =   41
      2sin∠BAC               2*9         18

Ответ: 41

C4C611

В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.

Решение:

Обозначим BH высоту, проведённую из вершины  B. Биссектриса, проведённая из угла A, делит высоту в отношении, равному отношению сторон треугольника AB и AH. Значит, 

cos∠BAC = AB = 15   
                 AH    17

Так как треугольник прямоугольный, то соотношение третей стороны можно вычислить по теореме Пифагора

х=√(17²-15²)=√(289-225)=√64=8 тогда исходя из того, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе получаем:

sin∠BAC =  8
                17

Теперь зная отношение сторон выраженную в синусе и принимая во внимание известную сторону применим обобщенную теорему синусов из которой:

2R=   BC__      R =      16*17 =  272  =   17
      2sin∠BAC               2*8        16

Ответ: 17

C18F47

В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 5:4, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=12.

Решение:

Обозначим BH высоту, проведённую из вершины  B. Биссектриса, проведённая из угла A, делит высоту в отношении, равному отношению сторон треугольника AB и AH. Значит, 

cos∠BAC = AB = 4   
                 AH    5

Так как треугольник прямоугольный, то соотношение третей стороны можно вычислить по теореме Пифагора

х=√(5²-4²)=√(25-16)=√9=3 тогда исходя из того, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе получаем:

sin∠BAC = 3
                5

Теперь зная отношение сторон выраженную в синусе и принимая во внимание известную сторону применим обобщенную теорему синусов из которой:

2R=   BC__       R =    12*5 =  60  =   10
      2sin∠BAC              2*3      6

Ответ: 10

022418

В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 5:4, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=6.

Решение:

Обозначим BH высоту, проведённую из вершины  B. Биссектриса, проведённая из угла A, делит высоту в отношении, равному отношению сторон треугольника AB и AH. Значит, 

cos∠BAC = AB = 4   
                 AH    5

Так как треугольник прямоугольный, то соотношение третей стороны можно вычислить по теореме Пифагора

х=√(5²-4²)=√(25-16)=√9=3 тогда исходя из того, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе получаем:

sin∠BAC = 3
                5

Теперь зная отношение сторон выраженную в синусе и принимая во внимание известную сторону применим обобщенную теорему синусов из которой:

2R=   BC__       R =    6*5 =  30  =   5
      2sin∠BAC              2*3      6

Ответ: 5

03EA6C

В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 13:12, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=20.

Решение:

Обозначим BH высоту, проведённую из вершины  B. Биссектриса, проведённая из угла A, делит высоту в отношении, равному отношению сторон треугольника AB и AH. Значит, 

cos∠BAC = AB = 12   
                 AH    13

Так как треугольник прямоугольный, то соотношение третей стороны можно вычислить по теореме Пифагора

х=√(13²-12²)=√(169-144)=√25=5 тогда исходя из того, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе получаем:

sin∠BAC =  5
                13

Теперь зная отношение сторон выраженную в синусе и принимая во внимание известную сторону применим обобщенную теорему синусов из которой:

2R=   BC__       R =    20*13 =  260  =   26
      2sin∠BAC              2*5         10

Ответ: 26

7D21C3

В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 25:24, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=14.

Решение:

Обозначим BH высоту, проведённую из вершины  B. Биссектриса, проведённая из угла A, делит высоту в отношении, равному отношению сторон треугольника AB и AH. Значит, 

cos∠BAC = AB = 24   
                 AH    25

Так как треугольник прямоугольный, то соотношение третей стороны можно вычислить по теореме Пифагора

х=√(25²-24²)=√(625-576)=√49=7 тогда исходя из того, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе получаем:

sin∠BAC =  7
                25

Теперь зная отношение сторон выраженную в синусе и принимая во внимание известную сторону применим обобщенную теорему синусов из которой:

2R=   BC__       R =    14*25 =  25
      2sin∠BAC               2*7      

Ответ: 25

CCDD0E

В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 13:12, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=10.

Решение:

Обозначим BH высоту, проведённую из вершины  B. Биссектриса, проведённая из угла A, делит высоту в отношении, равному отношению сторон треугольника AB и AH. Значит, 

cos∠BAC = AB = 12   
                 AH    13

Так как треугольник прямоугольный, то соотношение третей стороны можно вычислить по теореме Пифагора

х=√(13²-12²)=√(169-144)=√25=5 тогда исходя из того, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе получаем:

sin∠BAC = 5
                13

Теперь зная отношение сторон выраженную в синусе и принимая во внимание известную сторону применим обобщенную теорему синусов из которой:

2R=   BC__       R =    10*13 =  130  =  13
      2sin∠BAC              2*5         10

Ответ: 13

42942C

В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.

Решение:

Продолжим стороны AB и CD до их пересечения в точке E. Угол AEC равен 90°, поскольку сумма углов EAD и EDA равна 90°. Рассмотрим треугольники AED и BEC, они прямоугольные, углы ECB и EDA равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны, откуда 

$\frac{AE}{BE}=\;\frac{AB+BE}{BE}=\;\frac{AD}{BC}$

отсюда выразим BE

$\frac{AB+BE}{BE}=\;\frac{AD}{BC}\\BC(AB+BE)\;=AD\ast BE\\BC\ast AB+BC\ast BE\;=AD\ast BE\\AD\ast BE-BC\ast BE\;=BC\ast AB\\BE\;(AD-BC)\;=BC\ast AB\\BE\;=\;\frac{BC\ast AB}{AD-BC}$

Подставляем значение находим BE

BE=(BC*AB)/(AD-BC) = (21*20)/(49-21)=420/28=15

Пусть окружность касается прямой CD в точке F, причём точка F может лежать или на стороне CD или на её продолжении. Отрезок OF перпендикулярен прямой CD, как радиус проведённый в точку касания, OA,OB и OF  — радиусы.
Треугольник AOB  — равнобедренный, OH  — высота, следовательно, OH является медианой и биссектрисой. Четырехугольник OHEF  — прямоугольник, потому что все его углы прямые. Откуда:

R=OF=HE=HB+BE=AB/2+BE=10+15=25

Ответ: 25

3FA333

В трапеции ABCD основания AD и BC равны соответственно 18 и 6, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=10.

Решение:

Продолжим стороны AB и CD до их пересечения в точке E. Угол AEC равен 90°, поскольку сумма углов EAD и EDA равна 90°. Рассмотрим треугольники AED и BEC, они прямоугольные, углы ECB и EDA равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны, откуда 

$\frac{AE}{BE}=\;\frac{AB+BE}{BE}=\;\frac{AD}{BC}$

отсюда выразим BE

$\frac{AB+BE}{BE}=\;\frac{AD}{BC}\\BC(AB+BE)\;=AD\ast BE\\BC\ast AB+BC\ast BE\;=AD\ast BE\\AD\ast BE-BC\ast BE\;=BC\ast AB\\BE\;(AD-BC)\;=BC\ast AB\\BE\;=\;\frac{BC\ast AB}{AD-BC}$

Подставляем значение находим BE

BE=(BC*AB)/(AD-BC) = (6*10)/(18-6)=60/12=5

Пусть окружность касается прямой CD в точке F, причём точка F может лежать или на стороне CD или на её продолжении. Отрезок OF перпендикулярен прямой CD, как радиус проведённый в точку касания, OA,OB и OF  — радиусы.
Треугольник AOB  — равнобедренный, OH  — высота, следовательно, OH является медианой и биссектрисой. Четырехугольник OHEF  — прямоугольник, потому что все его углы прямые. Откуда:

R=OF=HE=HB+BE=AB/2+BE=5+5=10

Ответ: 10

4D1DBB

В трапеции ABCD основания AD и BC равны соответственно 33 и 11, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.

Решение:

Продолжим стороны AB и CD до их пересечения в точке E. Угол AEC равен 90°, поскольку сумма углов EAD и EDA равна 90°. Рассмотрим треугольники AED и BEC, они прямоугольные, углы ECB и EDA равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны, откуда 

$\frac{AE}{BE}=\;\frac{AB+BE}{BE}=\;\frac{AD}{BC}$

отсюда выразим BE

$\frac{AB+BE}{BE}=\;\frac{AD}{BC}\\BC(AB+BE)\;=AD\ast BE\\BC\ast AB+BC\ast BE\;=AD\ast BE\\AD\ast BE-BC\ast BE\;=BC\ast AB\\BE\;(AD-BC)\;=BC\ast AB\\BE\;=\;\frac{BC\ast AB}{AD-BC}$

Подставляем значение находим BE

BE=(BC*AB)/(AD-BC) = (11*20)/(33-11)=220/22=10

Пусть окружность касается прямой CD в точке F, причём точка F может лежать или на стороне CD или на её продолжении. Отрезок OF перпендикулярен прямой CD, как радиус проведённый в точку касания, OA,OB и OF  — радиусы.
Треугольник AOB  — равнобедренный, OH  — высота, следовательно, OH является медианой и биссектрисой. Четырехугольник OHEF  — прямоугольник, потому что все его углы прямые. Откуда:

R=OF=HE=HB+BE=AB/2+BE=10+10=20

Ответ: 20

1C7299

В трапеции ABCD основания AD и BC равны соответственно 32 и 24, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=7.

Решение:

Продолжим стороны AB и CD до их пересечения в точке E. Угол AEC равен 90°, поскольку сумма углов EAD и EDA равна 90°. Рассмотрим треугольники AED и BEC, они прямоугольные, углы ECB и EDA равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны, откуда 

$\frac{AE}{BE}=\;\frac{AB+BE}{BE}=\;\frac{AD}{BC}$

отсюда выразим BE

$\frac{AB+BE}{BE}=\;\frac{AD}{BC}\\BC(AB+BE)\;=AD\ast BE\\BC\ast AB+BC\ast BE\;=AD\ast BE\\AD\ast BE-BC\ast BE\;=BC\ast AB\\BE\;(AD-BC)\;=BC\ast AB\\BE\;=\;\frac{BC\ast AB}{AD-BC}$

Подставляем значение находим BE

BE=(BC*AB)/(AD-BC) = (24*7)/(32-24)=168/8=21

Пусть окружность касается прямой CD в точке F, причём точка F может лежать или на стороне CD или на её продолжении. Отрезок OF перпендикулярен прямой CD, как радиус проведённый в точку касания, OA,OB и OF  — радиусы.
Треугольник AOB  — равнобедренный, OH  — высота, следовательно, OH является медианой и биссектрисой. Четырехугольник OHEF  — прямоугольник, потому что все его углы прямые. Откуда:

R=OF=HE=HB+BE=AB/2+BE=3.5+21=24.5

Ответ: 24.5

EE7854

В трапеции ABCD основания AD и BC равны соответственно 34 и 14, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=12.

Решение:

Продолжим стороны AB и CD до их пересечения в точке E. Угол AEC равен 90°, поскольку сумма углов EAD и EDA равна 90°. Рассмотрим треугольники AED и BEC, они прямоугольные, углы ECB и EDA равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны, откуда 

$\frac{AE}{BE}=\;\frac{AB+BE}{BE}=\;\frac{AD}{BC}$

отсюда выразим BE

$\frac{AB+BE}{BE}=\;\frac{AD}{BC}\\BC(AB+BE)\;=AD\ast BE\\BC\ast AB+BC\ast BE\;=AD\ast BE\\AD\ast BE-BC\ast BE\;=BC\ast AB\\BE\;(AD-BC)\;=BC\ast AB\\BE\;=\;\frac{BC\ast AB}{AD-BC}$

Подставляем значение находим BE

BE=(BC*AB)/(AD-BC) = (14*12)/(34-14)=168/20=8.4

Пусть окружность касается прямой CD в точке F, причём точка F может лежать или на стороне CD или на её продолжении. Отрезок OF перпендикулярен прямой CD, как радиус проведённый в точку касания, OA,OB и OF  — радиусы.
Треугольник AOB  — равнобедренный, OH  — высота, следовательно, OH является медианой и биссектрисой. Четырехугольник OHEF  — прямоугольник, потому что все его углы прямые. Откуда:

R=OF=HE=HB+BE=AB/2+BE=6+8.4=14.4

Ответ: 14.4

A24A8E

В трапеции ABCD основания AD и BC равны соответственно 48 и 24, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=13.

Решение:

Продолжим стороны AB и CD до их пересечения в точке E. Угол AEC равен 90°, поскольку сумма углов EAD и EDA равна 90°. Рассмотрим треугольники AED и BEC, они прямоугольные, углы ECB и EDA равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны, откуда 

$\frac{AE}{BE}=\;\frac{AB+BE}{BE}=\;\frac{AD}{BC}$

отсюда выразим BE

$\frac{AB+BE}{BE}=\;\frac{AD}{BC}\\BC(AB+BE)\;=AD\ast BE\\BC\ast AB+BC\ast BE\;=AD\ast BE\\AD\ast BE-BC\ast BE\;=BC\ast AB\\BE\;(AD-BC)\;=BC\ast AB\\BE\;=\;\frac{BC\ast AB}{AD-BC}$

Подставляем значение находим BE

BE=(BC*AB)/(AD-BC) = (24*13)/(48-24)=312/24=13

Пусть окружность касается прямой CD в точке F, причём точка F может лежать или на стороне CD или на её продолжении. Отрезок OF перпендикулярен прямой CD, как радиус проведённый в точку касания, OA,OB и OF  — радиусы.
Треугольник AOB  — равнобедренный, OH  — высота, следовательно, OH является медианой и биссектрисой. Четырехугольник OHEF  — прямоугольник, потому что все его углы прямые. Откуда:

R=OF=HE=HB+BE=AB/2+BE=6.5+13=19.5

Ответ: 19.5

E4D760

В трапеции ABCD основания AD и BC равны соответственно 36 и 12, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=13.

Решение:

Продолжим стороны AB и CD до их пересечения в точке E. Угол AEC равен 90°, поскольку сумма углов EAD и EDA равна 90°. Рассмотрим треугольники AED и BEC, они прямоугольные, углы ECB и EDA равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны, откуда 

$\frac{AE}{BE}=\;\frac{AB+BE}{BE}=\;\frac{AD}{BC}$

отсюда выразим BE

$\frac{AB+BE}{BE}=\;\frac{AD}{BC}\\BC(AB+BE)\;=AD\ast BE\\BC\ast AB+BC\ast BE\;=AD\ast BE\\AD\ast BE-BC\ast BE\;=BC\ast AB\\BE\;(AD-BC)\;=BC\ast AB\\BE\;=\;\frac{BC\ast AB}{AD-BC}$

Подставляем значение находим BE

BE=(BC*AB)/(AD-BC) = (13*12)/(36-12)=156/24=6.5

Пусть окружность касается прямой CD в точке F, причём точка F может лежать или на стороне CD или на её продолжении. Отрезок OF перпендикулярен прямой CD, как радиус проведённый в точку касания, OA,OB и OF  — радиусы.
Треугольник AOB  — равнобедренный, OH  — высота, следовательно, OH является медианой и биссектрисой. Четырехугольник OHEF  — прямоугольник, потому что все его углы прямые. Откуда:

R=OF=HE=HB+BE=AB/2+BE=6.5+6.5=13

Ответ: 13

7D84CB

В трапеции ABCD основания AD и BC равны соответственно 32 и 4, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=14.

Решение:

Продолжим стороны AB и CD до их пересечения в точке E. Угол AEC равен 90°, поскольку сумма углов EAD и EDA равна 90°. Рассмотрим треугольники AED и BEC, они прямоугольные, углы ECB и EDA равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны, откуда 

$\frac{AE}{BE}=\;\frac{AB+BE}{BE}=\;\frac{AD}{BC}$

отсюда выразим BE

$\frac{AB+BE}{BE}=\;\frac{AD}{BC}\\BC(AB+BE)\;=AD\ast BE\\BC\ast AB+BC\ast BE\;=AD\ast BE\\AD\ast BE-BC\ast BE\;=BC\ast AB\\BE\;(AD-BC)\;=BC\ast AB\\BE\;=\;\frac{BC\ast AB}{AD-BC}$

Подставляем значение находим BE

BE=(BC*AB)/(AD-BC) = (4*14)/(32-4)=56/28=2

Пусть окружность касается прямой CD в точке F, причём точка F может лежать или на стороне CD или на её продолжении. Отрезок OF перпендикулярен прямой CD, как радиус проведённый в точку касания, OA,OB и OF  — радиусы.
Треугольник AOB  — равнобедренный, OH  — высота, следовательно, OH является медианой и биссектрисой. Четырехугольник OHEF  — прямоугольник, потому что все его углы прямые. Откуда:

R=OF=HE=HB+BE=AB/2+BE=7+2=9

Ответ: 9

8C4A28

В трапеции ABCD основания AD и BC равны соответственно 34 и 2, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=24.

Решение:

Продолжим стороны AB и CD до их пересечения в точке E. Угол AEC равен 90°, поскольку сумма углов EAD и EDA равна 90°. Рассмотрим треугольники AED и BEC, они прямоугольные, углы ECB и EDA равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны, откуда 

$\frac{AE}{BE}=\;\frac{AB+BE}{BE}=\;\frac{AD}{BC}$

отсюда выразим BE

$\frac{AB+BE}{BE}=\;\frac{AD}{BC}\\BC(AB+BE)\;=AD\ast BE\\BC\ast AB+BC\ast BE\;=AD\ast BE\\AD\ast BE-BC\ast BE\;=BC\ast AB\\BE\;(AD-BC)\;=BC\ast AB\\BE\;=\;\frac{BC\ast AB}{AD-BC}$

Подставляем значение находим BE

BE=(BC*AB)/(AD-BC) = (2*24)/(34-2)=48/32=1.5

Пусть окружность касается прямой CD в точке F, причём точка F может лежать или на стороне CD или на её продолжении. Отрезок OF перпендикулярен прямой CD, как радиус проведённый в точку касания, OA,OB и OF  — радиусы.
Треугольник AOB  — равнобедренный, OH  — высота, следовательно, OH является медианой и биссектрисой. Четырехугольник OHEF  — прямоугольник, потому что все его углы прямые. Откуда:

R=OF=HE=HB+BE=AB/2+BE=12+1.5=13.5

Ответ: 13.5

1C2090

В трапеции ABCD основания AD и BC равны соответственно 28 и 4, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=15.

Решение:

Продолжим стороны AB и CD до их пересечения в точке E. Угол AEC равен 90°, поскольку сумма углов EAD и EDA равна 90°. Рассмотрим треугольники AED и BEC, они прямоугольные, углы ECB и EDA равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны, откуда 

$\frac{AE}{BE}=\;\frac{AB+BE}{BE}=\;\frac{AD}{BC}$

отсюда выразим BE

$\frac{AB+BE}{BE}=\;\frac{AD}{BC}\\BC(AB+BE)\;=AD\ast BE\\BC\ast AB+BC\ast BE\;=AD\ast BE\\AD\ast BE-BC\ast BE\;=BC\ast AB\\BE\;(AD-BC)\;=BC\ast AB\\BE\;=\;\frac{BC\ast AB}{AD-BC}$

Подставляем значение находим BE

BE=(BC*AB)/(AD-BC) = (4*15)/(28-4)=60/24=2.5

Пусть окружность касается прямой CD в точке F, причём точка F может лежать или на стороне CD или на её продолжении. Отрезок OF перпендикулярен прямой CD, как радиус проведённый в точку касания, OA,OB и OF  — радиусы.
Треугольник AOB  — равнобедренный, OH  — высота, следовательно, OH является медианой и биссектрисой. Четырехугольник OHEF  — прямоугольник, потому что все его углы прямые. Откуда:

R=OF=HE=HB+BE=AB/2+BE=7.5+2.5=10

Ответ: 10

6EF2E3