Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году. В прямоугольном треугольнике проведена вершина из прямого угла, необходимо найти одну из сторон.
Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году. В прямоугольном треугольнике проведена вершина из прямого угла, необходимо найти одну из сторон.
Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2
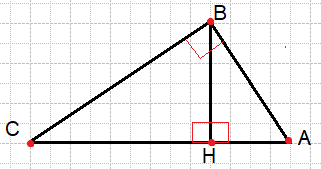
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.
Решение:
По факту нам известны значение от точки А до H и значение гипотенузы, надо найти один из катетов. Если провести высоту из прямого угла, то получим два прямоугольных треугольника. Причем эти два треугольника будут подобны, между собой и будут подобны исходному исходя из свойств высоты проведенной из прямого угла.
(Доказательство простое ∠ABH = 90º - ∠BAH и ∠BCA (BCH) = 90º - ∠BAH, получается ∠ABH = ∠BCH, о есть в треугольника два угла равные, а значит они подобные)
Исходя из подобия треугольников, можно утверждать, что соответствующий катет в каждом из треугольников к гипотенузе будет относится в той же пропорции. Делаем вывод, принимая х за значение коэффициента, что маленький катет BH в большем треугольнике CBH будет на х больше, чем опять же маленький катет HA в треугольнике HBA.
И также верно утверждение, что большой катет в маленьком треугольнике меньше на тот же коэффициент x к большому катету в большом треугольнике.
При этом мы знаем, что малый катет в маленьком треугольнике равен 6, а большой катет в большом треугольнике равен 24-6=18
Тогда можем составить равенство соотношений, которое выражает, что маленький известный нам катет настолько меньше маленького катета в большом треугольнике, насколько известный нам большой катет в большом треугольнике больше большого катета в малом. Получается так.
6*х=18/х
х =√3 (наш коэффициент отношений треугольников) Теперь находим AB, беря известное нам значение малого катета и зная, что второй катет являющийся малым катетом большого треугольника больше на этот самый вычисленный коэффициент
$BA^2=AH^2+BH^2\\BA\;=\sqrt{6^2+{(6\ast\sqrt3)}^2}\\BA\;=\sqrt{36+36\ast3}\\BA\;=\;\sqrt{144}\;=12$
Ответ: 12
9CB749
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=7, AC=28.
Решение:
По факту нам известны значение от точки А до H и значение гипотенузы, надо найти один из катетов. Если провести высоту из прямого угла, то получим два прямоугольных треугольника. Причем эти два треугольника будут подобны, между собой и будут подобны исходному исходя из свойств высоты проведенной из прямого угла.
(Доказательство простое ∠ABH = 90º - ∠BAH и ∠BCA (BCH) = 90º - ∠BAH, получается ∠ABH = ∠BCH, о есть в треугольника два угла равные, а значит они подобные)
Исходя из подобия треугольников, можно утверждать, что соответствующий катет в каждом из треугольников к гипотенузе будет относится в той же пропорции. Делаем вывод, принимая х за значение коэффициента, что маленький катет BH в большем треугольнике CBH будет на х больше, чем опять же маленький катет HA в треугольнике HBA.
И также верно утверждение, что большой катет в маленьком треугольнике меньше на тот же коэффициент x к большому катету в большом треугольнике.
При этом мы знаем, что малый катет в маленьком треугольнике равен 7, а большой катет в большом треугольнике равен 28-7=21
Тогда можем составить равенство соотношений, которое выражает, что маленький известный нам катет настолько меньше маленького катета в большом треугольнике, насколько известный нам большой катет в большом треугольнике больше большого катета в малом. Получается так.
7*х=21/х
х =√3 (наш коэффициент отношений треугольников) Теперь находим AB, беря известное нам значение малого катета и зная, что второй катет являющийся малым катетом большого треугольника больше на этот самый вычисленный коэффициент
$BA^2=AH^2+BH^2\\BA\;=\sqrt{7^2+{(7\ast\sqrt3)}^2}\\BA\;=\sqrt{49+49\ast3}\\BA\;=\;\sqrt{196}\;=14$
Ответ: 14
6380F3
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=8, AC=32.
Решение:
По факту нам известны значение от точки А до H и значение гипотенузы, надо найти один из катетов. Если провести высоту из прямого угла, то получим два прямоугольных треугольника. Причем эти два треугольника будут подобны, между собой и будут подобны исходному исходя из свойств высоты проведенной из прямого угла.
(Доказательство простое ∠ABH = 90º - ∠BAH и ∠BCA (BCH) = 90º - ∠BAH, получается ∠ABH = ∠BCH, о есть в треугольника два угла равные, а значит они подобные)
Исходя из подобия треугольников, можно утверждать, что соответствующий катет в каждом из треугольников к гипотенузе будет относится в той же пропорции. Делаем вывод, принимая х за значение коэффициента, что маленький катет BH в большем треугольнике CBH будет на х больше, чем опять же маленький катет HA в треугольнике HBA.
И также верно утверждение, что большой катет в маленьком треугольнике меньше на тот же коэффициент x к большому катету в большом треугольнике.
При этом мы знаем, что малый катет в маленьком треугольнике равен 8, а большой катет в большом треугольнике равен 32-8=24
Тогда можем составить равенство соотношений, которое выражает, что маленький известный нам катет настолько меньше маленького катета в большом треугольнике, насколько известный нам большой катет в большом треугольнике больше большого катета в малом. Получается так.
8*х=24/х
х =√3 (наш коэффициент отношений треугольников) Теперь находим AB, беря известное нам значение малого катета и зная, что второй катет являющийся малым катетом большого треугольника больше на этот самый вычисленный коэффициент
$BA^2=AH^2+BH^2\\BA\;=\sqrt{8^2+{(8\ast\sqrt3)}^2}\\BA\;=\sqrt{64+64\ast3}\\BA\;=\;\sqrt{256}\;=16$
Ответ: 16
E45C8A
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=45.
Решение:
По факту нам известны значение от точки А до H и значение гипотенузы, надо найти один из катетов. Если провести высоту из прямого угла, то получим два прямоугольных треугольника. Причем эти два треугольника будут подобны, между собой и будут подобны исходному исходя из свойств высоты проведенной из прямого угла.
(Доказательство простое ∠ABH = 90º - ∠BAH и ∠BCA (BCH) = 90º - ∠BAH, получается ∠ABH = ∠BCH, о есть в треугольника два угла равные, а значит они подобные)
Исходя из подобия треугольников, можно утверждать, что соответствующий катет в каждом из треугольников к гипотенузе будет относится в той же пропорции. Делаем вывод, принимая х за значение коэффициента, что маленький катет BH в большем треугольнике CBH будет на х больше, чем опять же маленький катет HA в треугольнике HBA.
И также верно утверждение, что большой катет в маленьком треугольнике меньше на тот же коэффициент x к большому катету в большом треугольнике.
При этом мы знаем, что малый катет в маленьком треугольнике равен 5, а большой катет в большом треугольнике равен 45-5=40
Тогда можем составить равенство соотношений, которое выражает, что маленький известный нам катет настолько меньше маленького катета в большом треугольнике, насколько известный нам большой катет в большом треугольнике больше большого катета в малом. Получается так.
5*х=40/х
х =√8 (наш коэффициент отношений треугольников) Теперь находим AB, беря известное нам значение малого катета и зная, что второй катет являющийся малым катетом большого треугольника больше на этот самый вычисленный коэффициент
$BA^2=AH^2+BH^2\\BA\;=\sqrt{5^2+{(5\ast\sqrt8)}^2}\\BA\;=\sqrt{25+25\ast8}\\BA\;=\;\sqrt{225}\;=15$
Ответ: 15
D35E73
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=10, AC=40.
Решение:
По факту нам известны значение от точки А до H и значение гипотенузы, надо найти один из катетов. Если провести высоту из прямого угла, то получим два прямоугольных треугольника. Причем эти два треугольника будут подобны, между собой и будут подобны исходному исходя из свойств высоты проведенной из прямого угла.
(Доказательство простое ∠ABH = 90º - ∠BAH и ∠BCA (BCH) = 90º - ∠BAH, получается ∠ABH = ∠BCH, о есть в треугольника два угла равные, а значит они подобные)
Исходя из подобия треугольников, можно утверждать, что соответствующий катет в каждом из треугольников к гипотенузе будет относится в той же пропорции. Делаем вывод, принимая х за значение коэффициента, что маленький катет BH в большем треугольнике CBH будет на х больше, чем опять же маленький катет HA в треугольнике HBA.
И также верно утверждение, что большой катет в маленьком треугольнике меньше на тот же коэффициент x к большому катету в большом треугольнике.
При этом мы знаем, что малый катет в маленьком треугольнике равен 10, а большой катет в большом треугольнике равен 40-10=30
Тогда можем составить равенство соотношений, которое выражает, что маленький известный нам катет настолько меньше маленького катета в большом треугольнике, насколько известный нам большой катет в большом треугольнике больше большого катета в малом. Получается так.
10*х=30/х
х =√3 (наш коэффициент отношений треугольников) Теперь находим AB, беря известное нам значение малого катета и зная, что второй катет являющийся малым катетом большого треугольника больше на этот самый вычисленный коэффициент
$BA^2=AH^2+BH^2\\BA\;=\sqrt{10^2+{(10\ast\sqrt3)}^2}\\BA\;=\sqrt{10+100\ast3}\\BA\;=\;\sqrt{400}\;=20$
Ответ: 20
53FFC0
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=9, AC=36.
Решение:
По факту нам известны значение от точки А до H и значение гипотенузы, надо найти один из катетов. Если провести высоту из прямого угла, то получим два прямоугольных треугольника. Причем эти два треугольника будут подобны, между собой и будут подобны исходному исходя из свойств высоты проведенной из прямого угла.
(Доказательство простое ∠ABH = 90º - ∠BAH и ∠BCA (BCH) = 90º - ∠BAH, получается ∠ABH = ∠BCH, о есть в треугольника два угла равные, а значит они подобные)
Исходя из подобия треугольников, можно утверждать, что соответствующий катет в каждом из треугольников к гипотенузе будет относится в той же пропорции. Делаем вывод, принимая х за значение коэффициента, что маленький катет BH в большем треугольнике CBH будет на х больше, чем опять же маленький катет HA в треугольнике HBA.
И также верно утверждение, что большой катет в маленьком треугольнике меньше на тот же коэффициент x к большому катету в большом треугольнике.
При этом мы знаем, что малый катет в маленьком треугольнике равен 9, а большой катет в большом треугольнике равен 36-9=27
Тогда можем составить равенство соотношений, которое выражает, что маленький известный нам катет настолько меньше маленького катета в большом треугольнике, насколько известный нам большой катет в большом треугольнике больше большого катета в малом. Получается так.
9*х=27/х
х =√3 (наш коэффициент отношений треугольников) Теперь находим AB, беря известное нам значение малого катета и зная, что второй катет являющийся малым катетом большого треугольника больше на этот самый вычисленный коэффициент
$BA^2=AH^2+BH^2\\BA\;=\sqrt{9^2+{(9\ast\sqrt3)}^2}\\BA\;=\sqrt{81+81\ast3}\\BA\;=\;\sqrt{324}\;=18$
Ответ: 20
273438
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=20.
Решение:
По факту нам известны значение от точки А до H и значение гипотенузы, надо найти один из катетов. Если провести высоту из прямого угла, то получим два прямоугольных треугольника. Причем эти два треугольника будут подобны, между собой и будут подобны исходному исходя из свойств высоты проведенной из прямого угла.
(Доказательство простое ∠ABH = 90º - ∠BAH и ∠BCA (BCH) = 90º - ∠BAH, получается ∠ABH = ∠BCH, о есть в треугольника два угла равные, а значит они подобные)
Исходя из подобия треугольников, можно утверждать, что соответствующий катет в каждом из треугольников к гипотенузе будет относится в той же пропорции. Делаем вывод, принимая х за значение коэффициента, что маленький катет BH в большем треугольнике CBH будет на х больше, чем опять же маленький катет HA в треугольнике HBA.
И также верно утверждение, что большой катет в маленьком треугольнике меньше на тот же коэффициент x к большому катету в большом треугольнике.
При этом мы знаем, что малый катет в маленьком треугольнике равен 5, а большой катет в большом треугольнике равен 20-5=15
Тогда можем составить равенство соотношений, которое выражает, что маленький известный нам катет настолько меньше маленького катета в большом треугольнике, насколько известный нам большой катет в большом треугольнике больше большого катета в малом. Получается так.
5*х=15/х
х =√3 (наш коэффициент отношений треугольников) Теперь находим AB, беря известное нам значение малого катета и зная, что второй катет являющийся малым катетом большого треугольника больше на этот самый вычисленный коэффициент
$BA^2=AH^2+BH^2\\BA\;=\sqrt{5^2+{(5\ast\sqrt3)}^2}\\BA\;=\sqrt{25+25\ast3}\\BA\;=\;\sqrt{100}\;=10$
Ответ: 20
E6B259
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=3, AC=27.
Решение:
По факту нам известны значение от точки А до H и значение гипотенузы, надо найти один из катетов. Если провести высоту из прямого угла, то получим два прямоугольных треугольника. Причем эти два треугольника будут подобны, между собой и будут подобны исходному исходя из свойств высоты проведенной из прямого угла.
(Доказательство простое ∠ABH = 90º - ∠BAH и ∠BCA (BCH) = 90º - ∠BAH, получается ∠ABH = ∠BCH, о есть в треугольника два угла равные, а значит они подобные)
Исходя из подобия треугольников, можно утверждать, что соответствующий катет в каждом из треугольников к гипотенузе будет относится в той же пропорции. Делаем вывод, принимая х за значение коэффициента, что маленький катет BH в большем треугольнике CBH будет на х больше, чем опять же маленький катет HA в треугольнике HBA.
И также верно утверждение, что большой катет в маленьком треугольнике меньше на тот же коэффициент x к большому катету в большом треугольнике.
При этом мы знаем, что малый катет в маленьком треугольнике равен 3, а большой катет в большом треугольнике равен 27-3=24
Тогда можем составить равенство соотношений, которое выражает, что маленький известный нам катет настолько меньше маленького катета в большом треугольнике, насколько известный нам большой катет в большом треугольнике больше большого катета в малом. Получается так.
3*х=24/х
х =√8 (наш коэффициент отношений треугольников) Теперь находим AB, беря известное нам значение малого катета и зная, что второй катет являющийся малым катетом большого треугольника больше на этот самый вычисленный коэффициент
$BA^2=AH^2+BH^2\\BA\;=\sqrt{3^2+{(3\ast\sqrt8)}^2}\\BA\;=\sqrt{9+9\ast8}\\BA\;=\;\sqrt{81}\;=9$
Ответ: 9
F50997
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=4, AC=16.
Решение:
По факту нам известны значение от точки А до H и значение гипотенузы, надо найти один из катетов. Если провести высоту из прямого угла, то получим два прямоугольных треугольника. Причем эти два треугольника будут подобны, между собой и будут подобны исходному исходя из свойств высоты проведенной из прямого угла.
(Доказательство простое ∠ABH = 90º - ∠BAH и ∠BCA (BCH) = 90º - ∠BAH, получается ∠ABH = ∠BCH, о есть в треугольника два угла равные, а значит они подобные)
Исходя из подобия треугольников, можно утверждать, что соответствующий катет в каждом из треугольников к гипотенузе будет относится в той же пропорции. Делаем вывод, принимая х за значение коэффициента, что маленький катет BH в большем треугольнике CBH будет на х больше, чем опять же маленький катет HA в треугольнике HBA.
И также верно утверждение, что большой катет в маленьком треугольнике меньше на тот же коэффициент x к большому катету в большом треугольнике.
При этом мы знаем, что малый катет в маленьком треугольнике равен 4, а большой катет в большом треугольнике равен 16-4=12
Тогда можем составить равенство соотношений, которое выражает, что маленький известный нам катет настолько меньше маленького катета в большом треугольнике, насколько известный нам большой катет в большом треугольнике больше большого катета в малом. Получается так.
4*х=12/х
х =√3 (наш коэффициент отношений треугольников) Теперь находим AB, беря известное нам значение малого катета и зная, что второй катет являющийся малым катетом большого треугольника больше на этот самый вычисленный коэффициент
$BA^2=AH^2+BH^2\\BA\;=\sqrt{4^2+{(4\ast\sqrt3)}^2}\\BA\;=\sqrt{16+16\ast3}\\BA\;=\;\sqrt{64}\;=8$
Ответ: 8
C3F608
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=3, AC=12.
Решение:
По факту нам известны значение от точки А до H и значение гипотенузы, надо найти один из катетов. Если провести высоту из прямого угла, то получим два прямоугольных треугольника. Причем эти два треугольника будут подобны, между собой и будут подобны исходному исходя из свойств высоты проведенной из прямого угла.
(Доказательство простое ∠ABH = 90º - ∠BAH и ∠BCA (BCH) = 90º - ∠BAH, получается ∠ABH = ∠BCH, о есть в треугольника два угла равные, а значит они подобные)
Исходя из подобия треугольников, можно утверждать, что соответствующий катет в каждом из треугольников к гипотенузе будет относится в той же пропорции. Делаем вывод, принимая х за значение коэффициента, что маленький катет BH в большем треугольнике CBH будет на х больше, чем опять же маленький катет HA в треугольнике HBA.
И также верно утверждение, что большой катет в маленьком треугольнике меньше на тот же коэффициент x к большому катету в большом треугольнике.
При этом мы знаем, что малый катет в маленьком треугольнике равен 3, а большой катет в большом треугольнике равен 12-3=9
Тогда можем составить равенство соотношений, которое выражает, что маленький известный нам катет настолько меньше маленького катета в большом треугольнике, насколько известный нам большой катет в большом треугольнике больше большого катета в малом. Получается так.
3*х=9/х
х =√3 (наш коэффициент отношений треугольников) Теперь находим AB, беря известное нам значение малого катета и зная, что второй катет являющийся малым катетом большого треугольника больше на этот самый вычисленный коэффициент
$BA^2=AH^2+BH^2\\BA\;=\sqrt{3^2+{(3\ast\sqrt3)}^2}\\BA\;=\sqrt{9+9\ast3}\\BA\;=\;\sqrt{36}\;=6$
Ответ: 6
2038C3