Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году. В статье приведены задачи типа, - пряма параллельная одному из оснований пересекает боковые стороны, найти номинал отрезка образованного между этими сторонами.
Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2
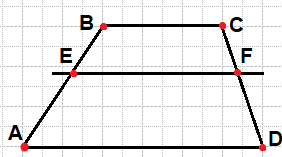
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Решение:
Мы знаем, что средняя линия трапеции равна среднему значению оснований, и расположена посредине боковых сторон. Это позволяет нам сделать вывод, что смещение относительно центра прямо пропорционально изменению размера. Так если мы за всю высоту возьмем 7 частей, которые учитываются в пропорции 4:3, то условно средняя линия будет смещена в сторону какого-либо значения, насколько отличается от среднего значения принятых нами частей. А у нас получается, что из 7 частей, среднее это 7/2=3,5 части, то есть на 0,5 части у нас смещение относительно оснований. Но так как наша целая часть это 1/7, то пол части будет 1/7*1/2=1/14 именно на столько надо прибавить (из-за того что смещена вниз) значение к средней линии, чтобы получить значение EF, тогда
EF= (BC+AD)/2+(AD-BC)1/14=56/2+28*1/14=28+2=30
...заметьте, что поправку делаем для разности между номиналами оснований AD-BC, ведь именно в этом диапазоне изменяется наша условно средняя линия на высчитанный показатель частей (от меньшего размера меньшего основания, до большего размера большего расстояния)Ответ: 30
55CB45
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
Решение:
Мы знаем, что средняя линия трапеции равна среднему значению оснований, и расположена посредине боковых сторон. Это позволяет нам сделать вывод, что смещение относительно центра прямо пропорционально изменению размера. Так если мы за всю высоту возьмем 5 частей, которые учитываются в пропорции 3:2, то условно средняя линия будет смещена в сторону какого-либо значения, насколько отличается от среднего значения принятых нами частей. А у нас получается, что из 5 частей, среднее это 5/2=2,5 части, то есть на 0,5 части у нас смещение относительно оснований. Но так как наша целая часть это 1/5, то пол части будет 1/5*1/2=1/10 именно на столько надо прибавить (из-за того что смещена вниз) значение к средней линии, чтобы получить значение EF, тогда
EF= (BC+AD)/2+(AD-BC)1/10=40/2+10*1/10=20+1=21
...заметьте, что поправку делаем для разности между номиналами оснований AD-BC, ведь именно в этом диапазоне изменяется наша условно средняя линия на высчитанный показатель частей (от меньшего размера меньшего основания, до большего размера большего расстояния)
Ответ: 21
DCE2BA
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=44, BC=24, CF:DF=3:1.
Решение:
Мы знаем, что средняя линия трапеции равна среднему значению оснований, и расположена посредине боковых сторон. Это позволяет нам сделать вывод, что смещение относительно центра прямо пропорционально изменению размера. Так если мы за всю высоту возьмем 4 части, которые учитываются в пропорции 3:1, то условно средняя линия будет смещена в сторону какого-либо значения, насколько отличается от среднего значения принятых нами частей. А у нас получается, что из 4 частей, среднее это 4/2=2 части, то есть на 1 часть у нас смещение относительно оснований. Но так как наша целая часть это 1/4, то пол часть и будет 1/4, именно на столько надо прибавить (из-за того что смещена вниз) значение к средней линии, чтобы получить значение EF, тогда
EF= (BC+AD)/2+(AD-BC)1/10=68/2+20*1/4=34+5=39
...заметьте, что поправку делаем для разности между номиналами оснований AD-BC, ведь именно в этом диапазоне изменяется наша условно средняя линия на высчитанный показатель частей (от меньшего размера меньшего основания, до большего размера большего расстояния)Ответ: 39
89A535
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=33, BC=18, CF:DF=2:1.
Решение:
Мы знаем, что средняя линия трапеции равна среднему значению оснований, и расположена посредине боковых сторон. Это позволяет нам сделать вывод, что смещение относительно центра прямо пропорционально изменению размера. Так если мы за всю высоту возьмем 3 части, которые учитываются в пропорции 2:1, то условно средняя линия будет смещена в сторону какого-либо значения, насколько отличается от среднего значения принятых нами частей. А у нас получается, что из 3 частей, среднее это 3/2=1,5 части, то есть на 0,5 части у нас смещение относительно оснований. Но так как наша целая часть это 1/3, то пол части будет 1/3*1/2=1/6 именно на столько надо прибавить (из-за того что смещена вниз) значение к средней линии, чтобы получить значение EF, тогда
EF= (BC+AD)/2+(AD-BC)1/10=51/2+15*1/6=25,5+2,5=28
...заметьте, что поправку делаем для разности между номиналами оснований AD-BC, ведь именно в этом диапазоне изменяется наша условно средняя линия на высчитанный показатель частей (от меньшего размера меньшего основания, до большего размера большего расстояния)
Ответ: 28
5D0CC5
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=45, BC=20, CF:DF=4:1.
Решение:
Мы знаем, что средняя линия трапеции равна среднему значению оснований, и расположена посредине боковых сторон. Это позволяет нам сделать вывод, что смещение относительно центра прямо пропорционально изменению размера. Так если мы за всю высоту возьмем 5 частей, которые учитываются в пропорции 4:1, то условно средняя линия будет смещена в сторону какого-либо значения, насколько отличается от среднего значения принятых нами частей. А у нас получается, что из 5 частей, среднее это 5/2=2,5 части, то есть на 1,5 части у нас смещение относительно оснований. Но так как наша целая часть это 1/5, то полторы части будет 1/5*1 1/2=1/5*3/2=3/10 именно настолько надо прибавить (из-за того что смещена вниз) значение к средней линии, чтобы получить значение EF, тогда
EF= (BC+AD)/2+(AD-BC)1/10=65/2+25*3/10=32,5+7,5=40
...заметьте, что поправку делаем для разности между номиналами оснований AD-BC, ведь именно в этом диапазоне изменяется наша условно средняя линия на высчитанный показатель частей (от меньшего размера меньшего основания, до большего размера большего расстояния)
Ответ: 40
D90C6D
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=36, BC=18, CF:DF=7:2.
Решение:
Мы знаем, что средняя линия трапеции равна среднему значению оснований, и расположена посредине боковых сторон. Это позволяет нам сделать вывод, что смещение относительно центра прямо пропорционально изменению размера. Так если мы за всю высоту возьмем 9 частей, которые учитываются в пропорции 7:2, то условно средняя линия будет смещена в сторону какого-либо значения, насколько отличается от среднего значения принятых нами частей. А у нас получается, что из 9 частей, среднее это 9/2=4,5 части, то есть на 2,5 части у нас смещение относительно оснований. Но так как наша целая часть это 1/9, то 2,5 части будет 1/9*2 1/2=1/9*5/2=5/18 именно на столько надо прибавить (из-за того что смещена вниз) значение к средней линии, чтобы получить значение EF, тогда
EF= (BC+AD)/2+(AD-BC)1/10=54/2+18*5/18=27+5=32
...заметьте, что поправку делаем для разности между номиналами оснований AD-BC, ведь именно в этом диапазоне изменяется наша условно средняя линия на высчитанный показатель частей (от меньшего размера меньшего основания, до большего размера большего расстояния)
Ответ: 32
B53A99
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=35, BC=21, CF:DF=5:2.
Решение:
Мы знаем, что средняя линия трапеции равна среднему значению оснований, и расположена посредине боковых сторон. Это позволяет нам сделать вывод, что смещение относительно центра прямо пропорционально изменению размера. Так если мы за всю высоту возьмем 7 частей, которые учитываются в пропорции 5:2, то условно средняя линия будет смещена в сторону какого-либо значения, насколько отличается от среднего значения принятых нами частей. А у нас получается, что из 7 частей, среднее это 7/2=3,5 части, то есть на 1,5 части у нас смещение относительно оснований. Но так как наша целая часть это 1/7, то 1,5 части будет 1/7*1 1/2=1/7*3/2=3/14 именно на столько надо прибавить (из-за того что смещена вниз) значение к средней линии, чтобы получить значение EF, тогда
EF= (BC+AD)/2+(AD-BC)1/10=56/2+14*3/14=28+3=31
...заметьте, что поправку делаем для разности между номиналами оснований AD-BC, ведь именно в этом диапазоне изменяется наша условно средняя линия на высчитанный показатель частей (от меньшего размера меньшего основания, до большего размера большего расстояния)
Ответ: 31
C2A1CF
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=48, BC=16, CF:DF=5:3.
Решение:
Мы знаем, что средняя линия трапеции равна среднему значению оснований, и расположена посредине боковых сторон. Это позволяет нам сделать вывод, что смещение относительно центра прямо пропорционально изменению размера. Так если мы за всю высоту возьмем 8 частей, которые учитываются в пропорции 5:3, то условно средняя линия будет смещена в сторону какого-либо значения, насколько отличается от среднего значения принятых нами частей. А у нас получается, что из 8 частей, среднее это 8/2=4 части, то есть на 1 части у нас смещение относительно оснований. Но так как наша целая часть это 1/8, именно настолько надо прибавить (из-за того что смещена вниз) значение к средней линии, чтобы получить значение EF, тогда
EF= (BC+AD)/2+(AD-BC)1/10=64/2+32*1/8=32+4=36
...заметьте, что поправку делаем для разности между номиналами оснований AD-BC, ведь именно в этом диапазоне изменяется наша условно средняя линия на высчитанный показатель частей (от меньшего размера меньшего основания, до большего размера большего расстояния)
Ответ: 36
3D72D5
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=45, BC=27, CF:DF=5:4.
Решение:
Мы знаем, что средняя линия трапеции равна среднему значению оснований, и расположена посредине боковых сторон. Это позволяет нам сделать вывод, что смещение относительно центра прямо пропорционально изменению размера. Так если мы за всю высоту возьмем 9 частей, которые учитываются в пропорции 5:4, то условно средняя линия будет смещена в сторону какого-либо значения, насколько отличается от среднего значения принятых нами частей. А у нас получается, что из 9 частей, среднее это 9/2=4,5 части, то есть на 0.5 части у нас смещение относительно оснований. Но так как наша целая часть это 1/9,а пол части 1/9*1/2=1/18 именно настолько надо прибавить (из-за того что смещена вниз) значение к средней линии, чтобы получить значение EF, тогда
EF= (BC+AD)/2+(AD-BC)1/10=72/2+18*1/18=36+1=37
...заметьте, что поправку делаем для разности между номиналами оснований AD-BC, ведь именно в этом диапазоне изменяется наша условно средняя линия на высчитанный показатель частей (от меньшего размера меньшего основания, до большего размера большего расстояния)
Ответ: 37
292E1E
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=50, BC=30, CF:DF=7:3.
Решение:
Мы знаем, что средняя линия трапеции равна среднему значению оснований, и расположена посредине боковых сторон. Это позволяет нам сделать вывод, что смещение относительно центра прямо пропорционально изменению размера. Так если мы за всю высоту возьмем 10 частей, которые учитываются в пропорции 7:3, то условно средняя линия будет смещена в сторону какого-либо значения, насколько отличается от среднего значения принятых нами частей. А у нас получается, что из 10 частей, среднее это 10/2=5 части, то есть на 2 части у нас смещение относительно оснований. Но так как наша целая часть это 1/10,а 2 части 2/10 именно настолько надо прибавить (из-за того что смещена вниз) значение к средней линии, чтобы получить значение EF, тогда
EF= (BC+AD)/2+(AD-BC)1/10=80/2+20*2/10=40+4=44
...заметьте, что поправку делаем для разности между номиналами оснований AD-BC, ведь именно в этом диапазоне изменяется наша условно средняя линия на высчитанный показатель частей (от меньшего размера меньшего основания, до большего размера большего расстояния)
Ответ: 44
60A16B
