Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году. Решаем в статье задачи о трапеции, где известно одно основание и два угла, а надо найти боковую сторону.

Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2

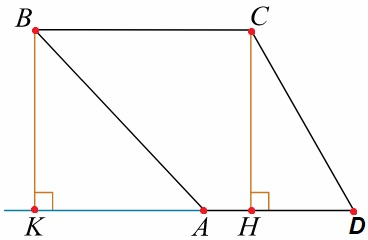
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.

Решение:

Проведем две высоты из точек BC, при этом получив треугольник CHD, который получился равнобедренный, так как у него есть прямой угол, а угол HCD=135-90=45° , значит и CDH = 45°, а если углы у основания равны, то стороны тоже, CH = HD.
Значит можно найти значение катета, а в итоге и высоты.

$36^2=CH^2+CH^2\\1296\;=\;2CH^2\\CH^2=\frac{1296}2\\CH\;=\;\sqrt{648}$

Рассмотрим теперь треугольник BKA, в нем угол KBA  = 90-60=30º

А в прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Значит зная значение высоты, то есть катета BK, все остальные стороны можно выразить через гипотенузу, так как у них есть зависимость и соответственно найти ее по теореме Пифагора.

$BA^2=\left(\frac12BA\right)^2+\sqrt{648}^2\\BA^2=\frac14BA^2+648\\\frac34BA^2=\;648\\BA^2=\frac{648\ast4}3\\BA=\sqrt{864}$

Ответ: √864

683F49

Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=24.

Решение:

Проведем две высоты из точек BC, при этом получив треугольник CHD, который получился равнобедренный, так как у него есть прямой угол, а угол HCD=135-90=45° , значит и CDH = 45°, а если углы у основания равны, то стороны тоже, CH = HD.
Значит можно найти значение катета, а в итоге и высоты.

$24^2=CH^2+CH^2\\576\;=\;2CH^2\\CH^2=\frac{576}2\\CH\;=\;\sqrt{288}$

Рассмотрим теперь треугольник BKA, в нем угол KBA  = 90-60=30º

А в прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Значит зная значение высоты, то есть катета BK, все остальные стороны можно выразить через гипотенузу, так как у них есть зависимость и соответственно найти ее по теореме Пифагора.

$BA^2=\left(\frac12BA\right)^2+\sqrt{288}^2\\BA^2=\frac14BA^2+288\\\frac34BA^2=288\\BA^2=\frac{288\ast4}3\\BA=\sqrt{384}$

Ответ: √384

F3229F

Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 135°, а CD=29.

Решение:

Проведем две высоты из точек BC, при этом получив треугольник CHD, который получился равнобедренный, так как у него есть прямой угол, а угол HCD=135-90=45° , значит и CDH = 45°, а если углы у основания равны, то стороны тоже, CH = HD.
Значит можно найти значение катета, а в итоге и высоты.

$29^2=CH^2+CH^2\\841\;=\;2CH^2\\CH^2=\frac{841}2\\CH\;=\;\sqrt{420.5}$

Рассмотрим теперь треугольник BKA, в нем угол KBA  = 90-30=60º, а значит KAB = 30º

А в прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Значит 

$BA=2\sqrt{420.5}$


Ответ: $BA=2\sqrt{420.5}$

099B90

Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 135°, а CD=17.

Решение:

Проведем две высоты из точек BC, при этом получив треугольник CHD, который получился равнобедренный, так как у него есть прямой угол, а угол HCD=135-90=45° , значит и CDH = 45°, а если углы у основания равны, то стороны тоже, CH = HD.
Значит можно найти значение катета, а в итоге и высоты.

$17^2=CH^2+CH^2\\289\;=\;2CH^2\\CH^2=\frac{289}2\\CH\;=\;\sqrt{144.5}$

Рассмотрим теперь треугольник BKA, в нем угол KBA  = 90-30=60º, а значит KAB = 30º

А в прямоугольном треугольнике против угла в 30 градусов лежит катет равный половине гипотенузы. Значит 

$BA=2\sqrt{144.5}$


Ответ: $BA=2\sqrt{144.5}$

382F20

Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.

Решение:

Проведем две высоты из точек BC, при этом получив треугольник CHD, который получился равнобедренный, так как у него есть прямой угол, а угол HCD=150-90=60° , значит и CDH = 30°, тогда СH=33/2

Рассмотрим теперь треугольник BKA, в нем угол KBA = 90-60=30º, а значит КА = 1/2 BA

По теореме Пифагора

$BA^2=\left(\frac12BA\right)^2+\left(\frac{33}2\right)^2\\BA^2=\frac14BA^2+\frac{1089}4\\\frac34BA^2=\frac{1089}4\\BA^2=\frac{1089}3\\BA=\sqrt{363}$


Ответ: √363

CC279D

Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.

Решение:

Проведем две высоты из точек BC, при этом получив треугольник CHD, который получился равнобедренный, так как у него есть прямой угол, а угол HCD=150-90=60° , значит и CDH = 30°, тогда СH=32/2=16

Рассмотрим теперь треугольник BKA, он равнобедренный, так как углы у гипотенузы по 45 градусов.

По теореме Пифагора

$BA^2=16^2+16^2\\BA^2=256+256\\BA=\sqrt{512}\\$

Ответ: √512

1C1CFA