Задание 14 ОГЭ по математике: арифметическая прогрессия

: Категория: ОГЭ по математике

Задание 14 ОГЭ по математике - найти логику и алгоритм вычисления числовой последовательности, как ее еще называют прогрессии. Задания приведенные здесь являются реальными и вполне могут попасться вам на экзамене, так как они из банка заданий ФИПИ. А значит стоит обратить внимание и даже решить их, дабы быть уверенным в том, что если они попадутся вам, то вы сможете решить их.
Арифметическая прогрессия – это последовательность чисел, каждый следующий член которой можно найти, прибавив к предыдущему одно и то же число d, при этом d называется разностью арифметической прогрессии. Оно может быть отрицательным, тогда прогрессия будет считаться убывающей.

Теперь немного об этих прогрессиях, а далее сами задания. Арифметическая прогрессия, это такая конструкция: «каждый следующий НА одно и то же число больше/меньше предыдущего». Или что-то подобное с предлогом НА.

На бланках ОГЭ будут формулы, которые можно и нужно использовать в решении таких задач: формула n-го члена арифметической прогрессии и формула суммы первых n членов арифметической прогрессии; формула суммы первых n членов геометрической прогрессии.

Формула n-го члена арифметической прогрессии (a_n ) первый член которой равен a₁и разность равна d.
a_n =a₁ + d(n-1)

Формула суммы первых n членов арифметической прогрессии:
$S_n=\frac{a_1+a_n}2n$

Формула n-го члена геометрической прогрессии (b_n ) первый член которой равен b₁и знаменатель равен q.
b_n=b_1*q^n-1

Формула суммы первых n членов геометрической прогрессии:
$S_n=\frac{(q_n-1)b_1}{q-1}$

a₁, a₂, ... a_n - члены прогрессии.

10 типов заданий: амфитеатр с известной разницей рядов; с неизвестной разницей рядов; распад изотопа - 2 типа; биологический эксперимент; змейка на клетчатой бумаге; кафе с квадратными столиками; опыт с охлаждением вещества; скачущий мячик; камень бросают в ущелье.

110 заданий.

Задания на числовую последовательность из ОГЭ по математике

Микроорганизмы в чашке Петри

В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 13 мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 90 минут после начала эксперимента. Ответ дайте в миллиграммах.

Решение:

b_n=b_1*q^n-1
b₄=13*3³=351 мг

Ответ: 351

Другой вариант решения.

Через 30 минут масса колонии станет 13*3=39,
через 60 минут — 39*3=117 ,
через 90 минут масса станет 117*3 = 351 мг.
Ответ: 351

A3E245

В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 18 мг. За каждые 20 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 60 минут после начала эксперимента. Ответ дайте в миллиграммах.

Решение:

b_n=b_1*q^n-1
b₄=18*3³=486 мг

Ответ: 486

8EC646

В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 10 мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 150 минут после начала эксперимента. Ответ дайте в миллиграммах.

Решение:

b_n=b_1*q^n-1
b₆=10*3⁵=2430 мг

Ответ: 2430

F2E006

В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 3 мг. За каждые 20 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 80 минут после начала эксперимента. Ответ дайте в миллиграммах.

Решение:

b_n=b_1*q^n-1
b₅=3*3⁴=243 мг

Ответ: 243

1AB01B

В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 8 мг. За каждые 20 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 80 минут после начала эксперимента. Ответ дайте в миллиграммах.

Решение:

b_n=b_1*q^n-1
b₅=8*3⁴=648 мг

Ответ: 648

53BBD2

В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 17 мг. За каждые 20 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 60 минут после начала эксперимента. Ответ дайте в миллиграммах.

Решение:

b_n=b_1*q^n-1
b₄=17*3³=459 мг

Ответ: 459

81F6DE

В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 14 мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 90 минут после начала эксперимента. Ответ дайте в миллиграммах.

Решение:

b_n=b_1*q^n-1
b₄=14*3³=378 мг

Ответ: 378

EEB25C

В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 4 мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 120 минут после начала эксперимента. Ответ дайте в миллиграммах.

Решение:

b_n=b_1*q^n-1
b₅=4*3⁴=324 мг

Ответ: 324

1A17AF

В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 16 мг. За каждые 20 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 60 минут после начала эксперимента. Ответ дайте в миллиграммах.

Решение:

b_n=b_1*q^n-1
b₄=16*3³=1296 мг

Ответ: 1296

85A862

В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 5 мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 120 минут после начала эксперимента. Ответ дайте в миллиграммах.

Решение:

b_n=b_1*q^n-1
b₅=5*3⁴=405 мг

Ответ: 405

8D0831

Попрыгунчики-мячики

У Ксюши есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 480 см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше 10 см?

Решение:

1й отскок - 480 см
2й отскок - 480/2
3й отскок - 240/2
4й отскок - 120/2
5й отскок - 60/2
6й отскок - 30/2
7й отскок - 15/2 < 10

Ответ: 7

B3AB64

У Лены есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 320 см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше 7 см?

Решение:

1й отскок - 320 см
2й отскок - 320/2
3й отскок - 160/2
4й отскок - 80/2
5й отскок - 40/2
6й отскок - 20/2
7й отскок - 10/2 < 7

Ответ: 7

54B8DF

У Алины есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 360 см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше 25 см?

Решение:

1й отскок - 360 см
2й отскок - 360/2
3й отскок - 180/2
4й отскок - 90/2
5й отскок - 45/2 <25

Ответ: 5

C4D018

У Светы есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 560 см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше 20 см?

Решение:

1й отскок - 560 см
2й отскок - 560/2
3й отскок - 280/2
4й отскок - 140/2
5й отскок - 70/2
6й отскок - 35/2 <20

Ответ: 6

C7F273

У Кати есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 400 см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше 20 см?

Решение:

1й отскок - 400 см
2й отскок - 400/2=200
3й отскок - 200/2=100
4й отскок - 100/2=50
5й отскок - 50/2=25
6й отскок - 25/2 <20

Ответ: 6

6FB00A

У Яны есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 240 см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше 5 см?

Решение:

1й отскок - 240 см
2й отскок - 240/2
3й отскок - 120/2
4й отскок - 60/2
5й отскок - 30/2
6й отскок - 15/2
7й отскок - 7,5/2 < 5

Ответ: 7

8EFD83

У Тани есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 360 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 15 см?

Решение:

Изменение высоты отскока мячика представляет собой геометрическую прогрессию с первым членом b₁=360 см и знаменателем q=1/3. По формуле n-ого члена bn=b₁*q^n-1 найдем, после какого по счету отскока высота, на которую подлетит мячик, станет меньше 15 см.

b_n < 15 ⇔ b₁q^n-1 < 15 ⇔ 360 * (¹/₃)^n-1 < 15 ⇔ (¹/₃)^n-1< ¹/₂₄

Следовательно, n=4 — минимальное целое значение, которое удовлетворяет неравенство, или счет отскока, после которого высота, на которую подлетит мячик, станет меньше 15 см.

Ответ: 4

Решение на пальцах.

С каждым отскоком высота мяча снижается. Здесь прошу обратить ваше внимание, что после первого отскока высота мяча 360 см. Получим:
после первого отскока - 360
после второго 360 : 3 = 120
после третьего 120 : 3 = 40
после четвертого40 : 3 = 13 < 15

Ответ: 4

4C0E02

У Юли есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 450 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 20 см?

Решение:

С каждым отскоком высота мяча снижается. Здесь прошу обратить ваше внимание, что после первого отскока высота мяча 450 см. Получим:
после первого отскока - 450
после второго 450 : 3 = 150
после третьего 150 : 3 = 50
после четвертого 50 : 3 = 16,(6) < 20

Ответ: 4

Решение через геометрическую прогрессию описано в задаче про Таню.

5F5DDD

У Ани есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 630 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 25 см?

Решение:

С каждым отскоком высота мяча снижается. Здесь прошу обратить ваше внимание, что после первого отскока высота мяча 630 см. Получим:
после первого отскока - 630
после второго 630 : 3 = 210
после третьего 210 : 3 = 70
после четвертого 70 : 3 = 23,(3) < 25

Ответ: 4

Решение через геометрическую прогрессию описано в задаче про Таню.

308876

У Кати есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 540 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 10 см?

Решение:

С каждым отскоком высота мяча снижается. Здесь прошу обратить ваше внимание, что после первого отскока высота мяча 540 см. Получим:
после первого отскока - 540
после второго 540 : 3 = 180
после третьего 180 : 3 = 60
после четвертого 60 : 3 = 20
после пятого 20 : 3 = 6,(6) < 10

Ответ: 5

Решение через геометрическую прогрессию описано в задаче про Таню.

F62180

Змейка

На клетчатой бумаге с размером клетки 1×1 нарисована «змейка», представляющая из себя ломаную, состоящую из чётного числа звеньев, идущих по линиям сетки. На рисунке изображён случай, когда последнее звено имеет длину 10. Найдите длину ломаной, построенной аналогичным образом, последнее звено которой имеет длину 120.

Решение:

Длина змейки, изображенной на рисунке, составляет 10 + 10 + 9 + 9 + 8 + ... + 3 + 2 + 2 + 1 + 1 и представляет арифметическую прогрессию, члены которой учтены два раза, первый член a₁=10, а разность d=1.

Найдем сумму арифметической прогрессии для змейки, последнее звено которой 120

$S_n=\frac{a_1+a_n}2n=\frac{120+1}2\ast120=121\ast60=7260$

Каждый член прогрессии должен быть учтен дважды, следовательно, длина змейки S=2S_n=14520.

Ответ: 14520

Лайфхак:

умножаем длину последнего звена на число на 1 больше этой длины.
В нашей задаче это 120 * 121 = 14520

Ответ: 14520

0BECFF

Решение:

Длина змейки, изображенной на рисунке, составляет 1 + 1 + 2 + 2 + 3 + ... + 9 + 9 + 10 + 10 и представляет арифметическую прогрессию, члены которой учтены 2 раза.

Формула суммы арифметической прогрессии:

$S_n=\frac{a_1+a_n}2n$

Первый член a₁=1 (начало змейки), разность d=1, n_{последнего члена}=10, a_n=10 (видим, что нумерация звеньев совпадает с длиной).

С учетом того, что в змейке члены прогрессии нужно учесть 2 раза, длина ломаной будет соответствовать 2S_n:

2S_n=(a₁+a_n)*n

Поскольку a₁=1; a_n=длине последнего звена;n=длине последнего звена,
получается, что умножаем длину последнего звена на число на 1 больше этой длины.

Найдем сумму арифметической прогрессии для змейки, последнее звено которой 190

2S_n=(a₁+1)*n=191*190=36290

Ответ: 36290

Лайфхак:

умножаем длину последнего звена на число на 1 больше этой длины.
В нашей задаче это 190 * 191 = 36290

Ответ: 36290

6A7CF2

Решение:

Длина змейки, изображенной на рисунке, составляет 1 + 1 + 2 + 2 + 3 + ... + 9 + 9 + 10 + 10 и представляет арифметическую прогрессию, члены которой учтены 2 раза.

Формула суммы арифметической прогрессии:

$S_n=\frac{a_1+a_n}2n$

Первый член a₁=1 (начало змейки), разность d=1, n_{последнего члена}=10, a_n=10 (видим, что нумерация звеньев совпадает с длиной).

С учетом того, что в змейке члены прогрессии нужно учесть 2 раза, длина ломаной будет соответствовать 2S_n:

2S_n=(a₁+a_n)*n

Поскольку a₁=1; a_n=длине последнего звена;n=длине последнего звена,
получается, что умножаем длину последнего звена на число на 1 больше этой длины.

Найдем сумму арифметической прогрессии для змейки, последнее звено которой 160

2S_n=(a₁+1)*n=161*160=25760

Ответ: 25760

Лайфхак:

умножаем длину последнего звена на число на 1 больше этой длины.
В нашей задаче это 160 * 161 = 25760

Ответ: 25760

212309

Решение:

Длина змейки, изображенной на рисунке, составляет 1 + 1 + 2 + 2 + 3 + ... + 9 + 9 + 10 + 10 и представляет арифметическую прогрессию, члены которой учтены 2 раза.

Формула суммы арифметической прогрессии:

$S_n=\frac{a_1+a_n}2n$

Первый член a₁=1 (начало змейки), разность d=1, n_{последнего члена}=10, a_n=10 (видим, что нумерация звеньев совпадает с длиной).

С учетом того, что в змейке члены прогрессии нужно учесть 2 раза, длина ломаной будет соответствовать 2S_n:

2S_n=(a₁+a_n)*n

Поскольку a₁=1; a_n=длине последнего звена;n=длине последнего звена,
получается, что умножаем длину последнего звена на число на 1 больше этой длины.

Найдем сумму арифметической прогрессии для змейки, последнее звено которой 100

2S_n=(a₁+1)*n=101*100=10100

Ответ: 10100

Лайфхак:

умножаем длину последнего звена на число на 1 больше этой длины.
В нашей задаче это 100 * 101 = 10100

Ответ: 10100

90FA7D

Решение:

Длина змейки, изображенной на рисунке, составляет 1 + 1 + 2 + 2 + 3 + ... + 9 + 9 + 10 + 10 и представляет арифметическую прогрессию, члены которой учтены 2 раза.

Формула суммы арифметической прогрессии:

$S_n=\frac{a_1+a_n}2n$

Первый член a₁=1 (начало змейки), разность d=1, n_{последнего члена}=10, a_n=10 (видим, что нумерация звеньев совпадает с длиной).

С учетом того, что в змейке члены прогрессии нужно учесть 2 раза, длина ломаной будет соответствовать 2S_n:

2S_n=(a₁+a_n)*n

Поскольку a₁=1; a_n=длине последнего звена;n=длине последнего звена,
получается, что умножаем длину последнего звена на число на 1 больше этой длины.

Найдем сумму арифметической прогрессии для змейки, последнее звено которой 170

2S_n=(a₁+1)*n=171*170=29070

Ответ: 29070

Лайфхак:

умножаем длину последнего звена на число на 1 больше этой длины.
В нашей задаче это 170 * 171 = 29070

Ответ: 29070

0FB2CE

Решение:

Длина змейки, изображенной на рисунке, составляет 1 + 1 + 2 + 2 + 3 + ... + 9 + 9 + 10 + 10 и представляет арифметическую прогрессию, члены которой учтены 2 раза.

Формула суммы арифметической прогрессии:

$S_n=\frac{a_1+a_n}2n$

Первый член a₁=1 (начало змейки), разность d=1, n_{последнего члена}=10, a_n=10 (видим, что нумерация звеньев совпадает с длиной).

С учетом того, что в змейке члены прогрессии нужно учесть 2 раза, длина ломаной будет соответствовать 2S_n:

2S_n=(a₁+a_n)*n

Поскольку a₁=1; a_n=длине последнего звена;n=длине последнего звена,
получается, что умножаем длину последнего звена на число на 1 больше этой длины.

Найдем сумму арифметической прогрессии для змейки, последнее звено которой 130

2S_n=(a₁+1)*n=131*130=17030

Ответ: 17030

Лайфхак:

умножаем длину последнего звена на число на 1 больше этой длины.
В нашей задаче это 130 * 131 = 17030

Ответ: 17030

D88BCE

Решение:

Длина змейки, изображенной на рисунке, составляет 1 + 1 + 2 + 2 + 3 + ... + 9 + 9 + 10 + 10 и представляет арифметическую прогрессию, члены которой учтены 2 раза.

Формула суммы арифметической прогрессии:

$S_n=\frac{a_1+a_n}2n$

Первый член a₁=1 (начало змейки), разность d=1, n_{последнего члена}=10, a_n=10 (видим, что нумерация звеньев совпадает с длиной).

С учетом того, что в змейке члены прогрессии нужно учесть 2 раза, длина ломаной будет соответствовать 2S_n:

2S_n=(a₁+a_n)*n

Поскольку a₁=1; a_n=длине последнего звена;n=длине последнего звена,
получается, что умножаем длину последнего звена на число на 1 больше этой длины.

Найдем сумму арифметической прогрессии для змейки, последнее звено которой 150

2S_n=(a₁+1)*n=151*150=22650

Ответ: 22650

Лайфхак:

умножаем длину последнего звена на число на 1 больше этой длины.
В нашей задаче это 150 * 151 = 22650

Ответ: 22650

97C3C9

Решение:

Длина змейки, изображенной на рисунке, составляет 1 + 1 + 2 + 2 + 3 + ... + 9 + 9 + 10 + 10 и представляет арифметическую прогрессию, члены которой учтены 2 раза.

Формула суммы арифметической прогрессии:

$S_n=\frac{a_1+a_n}2n$

Первый член a₁=1 (начало змейки), разность d=1, n_{последнего члена}=10, a_n=10 (видим, что нумерация звеньев совпадает с длиной).

С учетом того, что в змейке члены прогрессии нужно учесть 2 раза, длина ломаной будет соответствовать 2S_n:

2S_n=(a₁+a_n)*n

Поскольку a₁=1; a_n=длине последнего звена;n=длине последнего звена,
получается, что умножаем длину последнего звена на число на 1 больше этой длины.

Найдем сумму арифметической прогрессии для змейки, последнее звено которой 180

2S_n=(a₁+1)*n=181*180=32580

Ответ: 32580

Лайфхак:

умножаем длину последнего звена на число на 1 больше этой длины.
В нашей задаче это 180 * 181 = 32580

Ответ: 32580

D467E3

Решение:

Длина змейки, изображенной на рисунке, составляет 1 + 1 + 2 + 2 + 3 + ... + 9 + 9 + 10 + 10 и представляет арифметическую прогрессию, члены которой учтены 2 раза.

Формула суммы арифметической прогрессии:

$S_n=\frac{a_1+a_n}2n$

Первый член a₁=1 (начало змейки), разность d=1, n_{последнего члена}=10, a_n=10 (видим, что нумерация звеньев совпадает с длиной).

С учетом того, что в змейке члены прогрессии нужно учесть 2 раза, длина ломаной будет соответствовать 2S_n:

2S_n=(a₁+a_n)*n

Поскольку a₁=1; a_n=длине последнего звена;n=длине последнего звена,
получается, что умножаем длину последнего звена на число на 1 больше этой длины.

Найдем сумму арифметической прогрессии для змейки, последнее звено которой 140

2S_n=(a₁+1)*n=141*140=19740

Ответ: 19740

Лайфхак:

умножаем длину последнего звена на число на 1 больше этой длины.
В нашей задаче это 140 * 141 = 19740

Ответ: 19740

C8FD64

Решение:

Длина змейки, изображенной на рисунке, составляет 1 + 1 + 2 + 2 + 3 + ... + 9 + 9 + 10 + 10 и представляет арифметическую прогрессию, члены которой учтены 2 раза.

Формула суммы арифметической прогрессии:

$S_n=\frac{a_1+a_n}2n$

Первый член a₁=1 (начало змейки), разность d=1, n_{последнего члена}=10, a_n=10 (видим, что нумерация звеньев совпадает с длиной).

С учетом того, что в змейке члены прогрессии нужно учесть 2 раза, длина ломаной будет соответствовать 2S_n:

2S_n=(a₁+a_n)*n

Поскольку a₁=1; a_n=длине последнего звена;n=длине последнего звена,
получается, что умножаем длину последнего звена на число на 1 больше этой длины.

Найдем сумму арифметической прогрессии для змейки, последнее звено которой 110

2S_n=(a₁+1)*n=111*110=12210

Ответ: 12210

Лайфхак:

умножаем длину последнего звена на число на 1 больше этой длины.
В нашей задаче это 110 * 111 = 12210

Ответ: 12210

64C23B

Столики в кафе

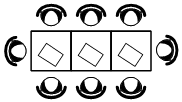
В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 16 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.
По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 16 член прогрессии:
a₁₆= 4 + 2 * (16 - 1) = 34.

Ответ: 34

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (16 - 2) * 2 = 6 + 28 = 34 человека.

Ответ: 34

5A3DF7

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 21 квадратный столик вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 21 член прогрессии:
a₂₁= 4 + 2 * (21 - 1) = 44.

Ответ: 44

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (21 - 2) * 2 = 6 + 38 = 44 человека.

Ответ: 44

D0F50E

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 19 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 19 член прогрессии:
a₁₉= 4 + 2 * (19 - 1) = 40.

Ответ: 40

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (19 - 2) * 2 = 40 человек.

Ответ: 40

17ABB5

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 20 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 20 член прогрессии:
a₂₀= 4 + 2 * (20 - 1) = 42.

Ответ: 42

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (20 - 2) * 2 = 42 человека.

Ответ: 42

97D5B4

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 18 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 18 член прогрессии:
a₁₈= 4 + 2 * (18 - 1) = 38.

Ответ: 38

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (18 - 2) * 2 = 38 человека.

Ответ: 38

A21B12

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 15 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 15 член прогрессии:
a₁₅= 4 + 2 * (15 - 1) = 32.

Ответ: 32

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (15 - 2) * 2 = 32 человека.

Ответ: 32

B26F2E

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 23 квадратных столика вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 23 член прогрессии:
a₂₃= 4 + 2 * (23 - 1) = 48.

Ответ: 48

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (23 - 2) * 2 = 48 человека.

Ответ: 48

27A42B

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 24 квадратных столика вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 24 член прогрессии:
a₂₄= 4 + 2 * (24 - 1) = 50.

Ответ: 50

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (24 - 2) * 2 = 50 человек.

Ответ: 50

922753

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 17 квадратных столиков вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 17 член прогрессии:
a₁₇= 4 + 2 * (17 - 1) = 36.

Ответ: 36

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (17 - 2) * 2 = 36 человек.

Ответ: 36

DF0BE2

В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 22 квадратных столика вдоль одной линии?

Решение:

Постепенное соединение столиков представляет собой арифметическую прогрессию с первым членом
a₁=4, a₂=6 и a₃=8, разность d=2.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 22 член прогрессии:
a₂₂= 4 + 2 * (22 - 1) = 46.

Ответ: 46

Задачу можно решить иначе.

Если сдвинуть столики вдоль одной линии, то за каждый столик, стоящий на конце линии (таких столиков всего два), смогут сесть по три человека, а за каждый из остальных столиков — по два человека. Следовательно, всего за столики смогут сесть
2 * 3 + (22 - 2) * 2 = 46 человек.

Ответ: 46

A907EE

Камень в ущелье

Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 9 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд?

Решение:

Растущая скорость камня представляет собой арифметическую прогрессию с первым членом a₁=9 м и разностью d=10 м.
a_n=a₁ + d(n-1)
a₅=9 + 10(5-1)=49

Найдем сумму этой прогрессии:

$S_n=\frac{a_1+a_n}2n$
$S_5=\frac{9+49}25=29\ast5=145$ м.

Ответ: 145.

1D0F07

Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 8 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые шесть секунд?

Решение:

1я секунда - 8 м
2 - 18
3 - 28
4 - 38
5 - 48
6 - 58
8 + 18 + 28 + 38 + 48 + 58 = 198 м

Ответ: 198

Решение по формулам.
Растущая скорость камня представляет собой арифметическую прогрессию с первым членом a₁=8 м и разностью d=10 м.

a_n =a₁ + d(n-1)
a₄ =8 + 10(6-1)=58 м пролетит камень за шестую секунду
$S_n=\frac{a_1+a_n}2n$
S_n=(8+58)6=198
2
Ответ: 198

1354B0

Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 15 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые четыре секунды?

Решение:

1я секунда - 15 м
2 - 25
3 - 35
4 - 45
15 + 25 + 35 + 45 = 120 м

Ответ: 120

Решение по формулам.

a_n =a₁ + d(n-1)
a₄ =15 + 10(4-1)=45 м пролетит камень за четвертую секунду
$S_n=\frac{a_1+a_n}2n$
S_n=(15+45)4=120
2
Ответ: 120

D16820

Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 7 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые шесть секунд?

Решение:

1я секунда - 7 м
2 - 17
3 - 27
4 - 37
5 - 47
6 - 57
7 + 17 + 27 + 37 + 47 + 57 = 192 м

Ответ: 120

Решение по формулам.

a_n =a₁ + d(n-1)
a₄ =7 + 10(6-1)=57 м пролетит камень за шестую секунду
$S_n=\frac{a_1+a_n}2n$
S_n=(7+57)6=192
2
Ответ: 192

731CD5

Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 11 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд?

Решение:

1я секунда - 11 м
2 - 21
3 - 31
4 - 41
5 - 51
11 + 21 +31 + 41 + 51 = 155 м

Ответ: 155

Решение по формулам.

a_n =a₁ + d(n-1)
a₄ =11 + 10*(5-1)=51 м пролетит камень за пятую секунду
$S_n=\frac{a_1+a_n}2n$
S_n=(11+51)5=155
2
Ответ: 155

C5D9D6

Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 14 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые четыре секунды?

Решение:

1я секунда - 14 м
2 - 24
3 - 34
4 - 44
14 + 24 +34 + 44 = 116 м

Ответ: 116

Решение по формулам.

a_n =a₁ + d(n-1)
a₄ =14 + 10*(4-1)=44 м пролетит камень за четвертую секунду
$S_n=\frac{a_1+a_n}2n$
S_n=(14+44)4=116
2
Ответ: 116

73505C

Решение:

1я секунда - 11 м
2 - 21
3 - 31
4 - 41
11 + 21 +31 + 41 = 104 м

Ответ: 104

Решение по формулам.

a_n =a₁ + d(n-1)
a₄ =11 + 10*(4-1)=41 м пролетит камень за четвертую секунду
$S_n=\frac{a_1+a_n}2n$
S_n=(11+41)4=104
2
Ответ: 104

422F95

Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 13 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд?

Решение:

1я секунда - 13 м
2 - 23
3 - 33
4 - 43
5 - 53
13 + 23 +33 + 43 + 53 = 165 м

Ответ: 165

Решение по формулам.

a_n =a₁ + d(n-1)
a₄ =13 + 10*(5-1)=53 м пролетит камень за пятую секунду
$S_n=\frac{a_1+a_n}2n$
S_n=(13+53)5=165
2
Ответ: 165

0C1662

Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 12 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые четыре секунды?

Решение:

1я секунда - 12 м
2 - 22
3 - 32
4 - 42
12 + 22 +32 + 42 = 108 м

Ответ: 108

Решение по формулам.

a_n =a₁ + d(n-1)
a₄ =12 + 10*(4-1)=42 м пролетит камень за четвертую секунду
$S_n=\frac{a_1+a_n}2n$
S_n=(12+42)4=108
2
Ответ: 108

26AA35

Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 6 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд?

Решение:

1я секунда - 6 м
2 - 16
3 - 26
4 - 36
5 - 46
6 + 16 +26 + 36 + 46 = 130 м

Ответ: 130

Решение по формулам.

a_n =a₁ + d(n-1)
a₄ =6 + 10*(5-1)=46 м пролетит камень за пятую секунду
$S_n=\frac{a_1+a_n}2n$
S_n=(6+46)5=130
2
Ответ: 130

A6EE88

Охлаждаем вещество

При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 6° C. Найдите температуру вещества (в градусах Цельсия) через 4 минуты после начала проведения опыта, если его начальная температура составляла − 7° C .

Решение:

Заметим, что значения температуры вещества представляют собой арифметическую прогрессию с разностью −6. При этом температура вещества в начальный момент времени будет первым членом прогрессии, температура вещества через одну минуту — вторым членом, а температура вещества через 4 минуты — пятым членом прогрессии, следовательно, она может быть найдена по формуле

a_n=a₁ + d (n - 1)
a₅=a₁ + d (5 - 1) = -7 + (-6) * 4= -31.

Ответ: -31

Другой вариант решения.

Через минуту температура вещества станет - 7 - 6 = -12 , через две минуты — - 7 - 12 =-19 , ..., через 4 минуты температура вещества станет - 7 - 24 = -31 ^оC.

Ответ: -31

AC63F5

При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 9° C. Найдите температуру вещества (в градусах Цельсия) через 4 минуты после начала проведения опыта, если его начальная температура составляла − 5° C .

Решение:

a_n =a₁ + d(n-1), a₁ - начальная температура, d - разность, n - количество контрольных точек, включая первую, когда только начали охлаждать.
a₅ =-5 + (-9)(5-1)=-31
Ответ:-31

5F9E7C

При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 5° C. Найдите температуру вещества (в градусах Цельсия) через 9 минут после начала проведения опыта, если его начальная температура составляла − 8° C .

Решение:

a_n =a₁ + d(n-1), a₁ - начальная температура, d - разность, n - количество контрольных точек, включая первую, когда только начали охлаждать.
a10 =-8 + (-5)(10-1)=-53
Ответ:-53

219613

При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 8° C. Найдите температуру вещества (в градусах Цельсия) через 6 минут после начала проведения опыта, если его начальная температура составляла − 6° C .

Решение:

a_n =a₁ + d(n-1), a₁ - начальная температура, d - разность, n - количество контрольных точек, включая первую, когда только начали охлаждать.
a₇ =-6 + (-8)(7-1)=-62
Ответ:-62

58DB2C

При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 5° C. Найдите температуру вещества (в градусах Цельсия) через 7 минут после начала проведения опыта, если его начальная температура составляла − 9° C .

Решение:

a_n =a₁ + d(n-1), a₁ - начальная температура, d - разность, n - количество контрольных точек, включая первую, когда только начали охлаждать.
a₈ =-9 + (-5)(8-1)=-44
Ответ:-44

912224

При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 9° C. Найдите температуру вещества (в градусах Цельсия) через 6 минут после начала проведения опыта, если его начальная температура составляла − 6° C .

Решение:

a_n =a₁ + d(n-1), a₁ - начальная температура, d - разность, n - количество контрольных точек, включая первую, когда только начали охлаждать.
a₇ =-6 + (-9)(7-1)=-60
Ответ:-60

02ABD8

При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 7 ° C. Найдите температуру вещества (в градусах Цельсия) через 5 минут после начала проведения опыта, если его начальная температура составляла − 7 ° C .

Решение:

a_n =a₁ + d(n-1), a₁ - начальная температура, d - разность, n - количество контрольных точек, включая первую, когда только начали охлаждать.
a₆ =-7 + (-7)(6-1)=-42
Ответ:-42

BF8E53

При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 8° C. Найдите температуру вещества (в градусах Цельсия) через 7 минут после начала проведения опыта, если его начальная температура составляла − 6° C .

Решение:

a_n =a₁ + d(n-1), a₁ - начальная температура, d - разность, n - количество контрольных точек, включая первую, когда только начали охлаждать.
a₈ =-6 + (-8)(8-1)=-62
Ответ:-62

4093C4

При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 6° C. Найдите температуру вещества (в градусах Цельсия) через 7 минут после начала проведения опыта, если его начальная температура составляла − 9° C .

Решение:

a_n =a₁ + d(n-1), a₁ - начальная температура, d - разность, n - количество контрольных точек, включая первую, когда только начали охлаждать.
a₈ =-9 + (-6)(8-1)=-51
Ответ:-51

0BBBCB

При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 7° C. Найдите температуру вещества (в градусах Цельсия) через 6 минут после начала проведения опыта, если его начальная температура составляла − 8° C .

Решение:

a_n =a₁ + d(n-1), a₁ - начальная температура, d - разность, n - количество контрольных точек, включая первую, когда только начали охлаждать.
a₇ =-8 + (-7)(7-1)=-50
Ответ:-50

D1616D

Ряды в амфитеатре

В амфитеатре 10 рядов. В первом ряду 25 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько мест в восьмом ряду амфитеатра?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=25 и разностью d=3. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a₈, имеем:
a₈=a₁+d(8-1)=25+3*7=46

Ответ: 46

Другой вариант решения.

Такую задачу можно решить и на пальцах, не зная формулы (на ОГЭ ведь нужен только ответ).
1 ряд - 25, 2 - 28, 3 - 31, 4 - 34, 5 - 37, 6 - 40, 7 - 43, 8 - 46.

Ответ: 46

1F7343

В амфитеатре 14 рядов. В первом ряду 20 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=20 и разностью d=3. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a₁₀, имеем:
a₁₀=a₁+d(10-1)=20+3*9=47
Ответ: 47

5F1149

В амфитеатре 11 рядов. В первом ряду 16 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение:

a₁=16, d=3
a_n =a₁ + d(n-1)
a₁₁=16 + 3(11-1)=46
$S_n=\frac{a_1+a_n}2n$
$S_{11}=\frac{16+46}2\ast11=31\ast11=341$

Ответ: 341

Решение на пальцах
1 ряд - 16, 2 - 19, 3 - 22, 4 - 25, 5 - 28, 6 - 31, 7 - 34, 8 - 37, 9 - 40, 10 - 43, 11 - 46.

(19+31) + (22+28) + (46+34) + (37+43) + 40 + 25 + 16 = 341

Ответ: 341

656145

В амфитеатре 11 рядов. В первом ряду 17 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение:

a₁=17, d=3
a_n =a₁ + d(n-1)
a₁₁=17 + 3(11-1)=47
$S_n=\frac{a_1+a_n}2n$
$S_{11}=\frac{17+47}2\ast11=31\ast11=352$

Ответ: 352

28DDF4

В амфитеатре 12 рядов. В первом ряду 21 место, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в одиннадцатом ряду амфитеатра?

Решение:

a₁=21, d=2
a_n =a₁ + d(n-1)
a₁₁=21 + 2(11-1)=41

Ответ: 41

6EAFF6

В амфитеатре 16 рядов. В первом ряду 19 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в тринадцатом ряду амфитеатра?

Решение:

19 + 2*(13-1)=43

Ответ: 43

DDFA05

В амфитеатре 14 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду 27 мест, а в восьмом ряду 36 мест. Сколько мест в последнем ряду амфитеатра?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с пятым членом a₅=27 и восьмым a₈=36,
a_n =a₁ + d(n-1) ⇒ разность равна $d=\frac{a_n-a_1}{n-1}$
можно заменить a₁ на a₅, но тогда и единицу в знаменателе не забываем заменить на 5.
$d=\frac{a_8-a_5}{8-5}=\frac{36-27}3=3$

a_n =a₁ + d(n-1) ⇒ a₁ = a_n - d(n-1)
a₁ = a₅ - d (n - 1) = 27 - 3 * 4 = 15.

По формуле n-го члена a_n= a₁ + d * (n - 1) найдем 14-й член прогрессии:

a₁₄= 15 + 3 * (14 - 1) = 54.

Ответ: 54

A55400

В амфитеатре 10 рядов. В первом ряду 19 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение:

a₁=19, d=3
a_n =a₁ + d(n-1)
a₁₀=19 + 3(10-1)=46
$S_n=\frac{a_1+a_n}2n$
$S_{10}=\frac{19+46}2\ast10=325$

Ответ: 325

682F09

В амфитеатре 16 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В четвёртом ряду 23 места, а в восьмом ряду 35 мест. Сколько мест в последнем ряду амфитеатра?

Решение:

(35-23):(8-4)=3 - на 3 места больше в каждом следующем ряду
За 8-м рядом еще 8 рядов.
35 + 3 * 8 = 59 мест в последнем ряду
Ответ: 59

3FE074

В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение:

a₁=17, d=2
a_n =a₁ + d(n-1)
a₁₃=17 + 2(13-1)=41
$S_n=\frac{a_1+a_n}2n$
$S_{13}=\frac{17+41}2\ast13=377$

Ответ: 377

4C08B1

В амфитеатре 15 рядов. В первом ряду 20 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=20 и разностью d=2. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a₁₀, имеем:
a₁₀=a₁+d(10-1)=20+2*9=38

Ответ: 38

Другой вариант решения.

Такую задачу можно решить и на пальцах, не зная формулы (на ОГЭ ведь нужен только ответ).
1 ряд - 20, 2 - 22, 3 - 24, 4 - 26, 5 - 28, 6 - 30, 7 - 32, 8 - 34, 9 - 36, 10 - 38

Ответ: 38

94AFB9

В амфитеатре 14 рядов. В первом ряду 16 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=16 и разностью d=2. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a₁₄, имеем:
a₁₄=a₁+d(14-1)=16+2*13=42
$S_n=\frac{a_1+a_n}2n$
$S_{14}=\frac{16+42}2\ast14=406$

Ответ: 406

Другой вариант решения.

Такую задачу можно решить и на пальцах, не зная формулы (на ОГЭ ведь нужен только ответ).
1 ряд - 16, 2 - 18, 3 - 20, 4 - 22, 5 - 24, 6 - 26, 7 - 28, 8 - 30, 9 - 32, 10 - 34, 11 - 36, 12 - 38, 13 - 40, 14 - 42.
Все сложим и получим 406

Ответ: 406

6E4FB2

В амфитеатре 12 рядов. В первом ряду 24 места, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько мест в девятом ряду амфитеатра?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=24 и разностью d=3. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a₉, имеем:
a₉=a₁+d(9-1)=24+3*8=48

Ответ: 48

Другой вариант решения.

Такую задачу можно решить и на пальцах, не зная формулы (на ОГЭ ведь нужен только ответ).
1 ряд - 24, 2 - 27, 3 - 30, 4 - 33, 5 - 36, 6 - 39, 7 - 42, 8 - 45, 9 - 48

Ответ: 48

B1E01A

В амфитеатре 13 рядов. В первом ряду 23 места, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=23 и разностью d=3. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a₁₀, имеем:
a₁₀=a₁+d(10-1)=23 + 3*(10-1)=50

Ответ: 50

DA517E

В амфитеатре 16 рядов. В первом ряду 22 места, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в двенадцатом ряду амфитеатра?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=22 и разностью d=2. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a₁₂, имеем:
a₁₂=a₁+d(12-1)=22 + 2*(12-1)=44

Ответ: 44

171C1C

В амфитеатре 23 ряда, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В седьмом ряду 26 мест, а в одиннадцатом ряду 34 места. Сколько мест в последнем ряду амфитеатра?

Решение:

В седьмом ряду 26 мест, а в одиннадцатом ряду 34 места, тогда 11-7=4 и (34-26):4=2 места прибавляется с каждым рядом), тогда 23-11=12 рядов еще с 11 ряда по 23.

34 + 2*12=58

или можно по формуле (находим 13 элемент с 11 ряда, по 23, так как именно столько элементов если считать включительно находится между 11 и 23 рядом, принимая при этом 11 ряд за 1 элемент, а 23 за 13)

a_n =a₁ + d(n-1)
Необходимо найти a₁₃, имеем:
a₁₃=a₁+d(13-1)=34 + 2*(13-1)=58

Ответ: 58

A2B716

В амфитеатре 11 рядов. В первом ряду 18 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=18 и разностью d=3. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a₁₁, имеем:
a₁₁=a₁+d(11-1)=18 + 3*(11-1)=48

48 мест в 11 ряду, надой найти среднее значение для все х рядов и умножить на количество рядов, тогда (48+18)/2*11=363

Ответ: 363

B2E2D7

В амфитеатре 14 рядов. В первом ряду 18 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в девятом ряду амфитеатра?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=18 и разностью d=2. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a9, имеем:
a9=a₁+d(9-1)=18 + 2*(9-1)=34

Ответ: 34

4A0C5D

В амфитеатре 15 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В третьем ряду 26 мест, а в седьмом ряду 38 мест. Сколько мест в последнем ряду амфитеатра?

Решение:

В третьем ряду 26 мест, а в 7 ряду 38 мест, тогда 7-3=4 и (38-26):4=3 места прибавляется с каждым рядом), тогда 15-3=12 рядов еще с 3 ряда по 15.

26 + 3*12=62

или можно по формуле (находим 13 элемент с 3 ряда, по 15, так как именно столько элементов если считать включительно находится между 3 и 15 рядом, принимая при этом 3 ряд за 1 элемент, а 15 за 13)

a_n =a₁ + d(n-1)
Необходимо найти a₁₃, имеем:
a₁₃=a₁+d(13-1)=26 + 3*(13-1)=62

Ответ: 62

799955

В амфитеатре 12 рядов. В первом ряду 18 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=18 и разностью d=2. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a12, имеем:
a12=a₁+d(12-1)=18 + 2*(12-1)=40 мест в 12 ряду.

В среднем получается (18+40)/2=29 мест в каждом ряду. 29*12=348 мест

Ответ: 348

EDC956

В амфитеатре 13 рядов. В первом ряду 22 места, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько мест в одиннадцатом ряду амфитеатра?

Решение:

Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=22 и разностью d=3. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a9, имеем:
a9=a₁+d(9-1)=22 + 3*(11-1)=52

Ответ: 52

689DAF

В амфитеатре 13 рядов. В первом ряду 18 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение:

Найдем число месте в 13 ряду. Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=18 и разностью d=2. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a13, имеем:
a13=a₁+d(13-1)=18 + 2*(13-1)=42

При этом в среднем (42+18)/2=30 мест в каждом ряду. 30*13=390 мест

Ответ: 390

7E8F96

В амфитеатре 18 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В шестом ряду 26 мест, а в восьмом ряду 30 мест. Сколько мест в последнем ряду амфитеатра?

Решение:

В 6 ряду 26 мест, а в 8 ряду 30 мест, тогда 8-6=2 и (30-26):2=2 места прибавляется с каждым рядом, тогда 18-6=12 рядов еще с 6 ряда по 18.

26 + 2*12=50

или можно по формуле (находим 13 элемент с 3 ряда, по 18, так как именно столько элементов если считать включительно находится между 3 и 18 рядом, принимая при этом 6 ряд за 1 элемент, а 18 за 13)

a_n =a₁ + d(n-1)
Необходимо найти a₁₃, имеем:
a₁₃=a₁+d(13-1)=26 + 2*(13-1)=50

Ответ: 50

E1CD90

В амфитеатре 19 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В третьем ряду 25 мест, а в седьмом ряду 37 мест. Сколько мест в последнем ряду амфитеатра?

Решение:

В 3 ряду 25 мест, а в 7 ряду 37 мест, тогда 7-3=4 и (37-25):4=3 места прибавляется с каждым рядом, тогда 19-3=16 рядов еще с 3 ряда по 19.

25 + 3*16=73

или можно по формуле (находим 17 элемент с 3 ряда, по 19, так как именно столько элементов если считать включительно находится между 3 и 19 рядом, принимая при этом 3 ряд за 1 элемент, а 19 за 17)

a_n =a₁ + d(n-1)
Необходимо найти a₁₇, имеем:
a₁₇=a₁+d(17-1)=25 + 3*(17-1)=73

Ответ: 73

ECE598

В амфитеатре 23 ряда, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду 27 мест, а в седьмом ряду 31 место. Сколько мест в последнем ряду амфитеатра?

Решение:

В 5 ряду 27 мест, а в 7 ряду 31 место, тогда 7-5=2 и (31-27):2=2 места прибавляется с каждым рядом, тогда 23-5=18 рядов еще с 5 ряда по 23.

27 + 2*18=63

или можно по формуле (находим 19 элемент с 5 ряда, по 23, так как именно столько элементов если считать включительно находится между 5 и 23 рядом, принимая при этом 5 ряд за 1 элемент, а 23 за 19)

a_n =a₁ + d(n-1)
Необходимо найти a₁₉, имеем:
a₁₉=a₁+d(19-1)=27 + 2*(19-1)=63

Ответ: 63

28E6E3

В амфитеатре 18 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В третьем ряду 24 места, а в шестом ряду 33 места. Сколько мест в последнем ряду амфитеатра?

Решение:

В 3 ряду 24 места, а в 6 ряду 33 места, тогда 6-3=3 и (33-24):3=3 места прибавляется с каждым рядом, тогда 18-3=16 рядов еще с 3 ряда по 18.

24 + 3*16=72

или можно по формуле (находим 17 элемент с 3 ряда, по 18, так как именно столько элементов если считать включительно находится между 3 и 18 рядом, принимая при этом 3 ряд за 1 элемент, а 18 за 17)

a_n =a₁ + d(n-1)
Необходимо найти a₁₇, имеем:
a₁₇=a₁+d(17-1)=24 + 3*(17-1)=72

Ответ: 72

60D7EA

В амфитеатре 15 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В седьмом ряду 36 мест, а в девятом ряду 42 места. Сколько мест в последнем ряду амфитеатра?

Решение:

В 7 ряду 36 мест, а в 9 ряду 42 места, тогда 9-7=2 и (42-36):2=3 места прибавляется с каждым рядом, тогда 15-7=8 рядов еще с 7 ряда по 15.

36 + 3*8=60

или можно по формуле (находим 9 элемент с 7 ряда, по 15, так как именно столько элементов если считать включительно находится между 7 и 15 ряд, принимая при этом 7 ряд за 1 элемент, а 15 за 9)

a_n =a₁ + d(n-1)
Необходимо найти a9, имеем:
a9=a₁+d(9-1)=36 + 3*(9-1)=60

Ответ: 60

4BCB6B

В амфитеатре 21 ряд, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду 25 мест, а в девятом ряду 33 места. Сколько мест в последнем ряду амфитеатра?

Решение:

В 5 ряду 25 мест, а в 9 ряду 33 места, тогда 9-5=4 и (33-25):4=2 места прибавляется с каждым рядом, тогда 21-5=16 рядов еще с 5 ряда по 21.

25 + 2*16=57

или можно по формуле (находим 17 элемент с 5 ряда, по 21, так как именно столько элементов если считать включительно находится между 5 и 21 рядом, принимая при этом 5 ряд за 1 элемент, а 21 за 17)

a_n =a₁ + d(n-1)
Необходимо найти a17, имеем:
a17=a₁+d(9-1)=25 + 2*(17-1)=57

Ответ: 57

901C60

В амфитеатре 12 рядов. В первом ряду 15 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение:

Найдем число месте в 12 ряду. Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=15 и разностью d=3. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a12, имеем:
a12=a₁+d(12-1)=15 + 3*(12-1)=48

При этом в среднем (48+15)/2=31.5 место в каждом ряду. 31,5*12=378 мест

Ответ: 378

8B9D31

В амфитеатре 12 рядов. В первом ряду 20 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение:

Найдем число месте в 12 ряду. Число мест в ряду представляет собой арифметическую прогрессию с первым членом a₁=20 и разностью d=2. Член арифметической прогрессии с номером n может быть найден по формуле
a_n =a₁ + d(n-1)
Необходимо найти a12, имеем:
a12=a₁+d(12-1)=20 + 2*(12-1)=42

При этом в среднем (42+20)/2=31 место в каждом ряду. 31*12=372 мест

Ответ: 372

EF268C

Распад радиоактивного изотопа

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 7 минут. В начальный момент масса изотопа составляла 640 мг. Найдите массу изотопа через 42 минуты. Ответ дайте в миллиграммах.

Решение:

Через 7 минут масса изотопа станет 640 * ¹/₂,
через 14 минут - 640*(¹/₂)² ,
...,
через 42 минуты масса станет
640*(¹/₂)⁶ = 640/64=10 мг

Ответ: 10

Другой вариант решения.

Заметим, что массы изотопа в заданные моменты времени представляют собой геометрическую прогрессию со знаменателем q=1/2. Масса изотопа в начальный момент времени является первым членом геометрической прогрессии b₁, масса изотопа через 7 минут — вторым членом прогрессии, а масса изотопа через 42 минуты − седьмым членом прогрессии и может быть определена по формуле b₇=b_1*q^7-1 .
b₇=640*(1/2)⁶=640/64=10 мг

Ответ: 10

ACC044

В ходе бета-распада радиоактивного изотопа А каждые 8 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 160 мг. Найдите массу образовавшегося изотопа Б через 40 минут. Ответ дайте в миллиграммах.

Решение:

Масса образовавшегося изотопа Б равна разности массы исходного вещества и массы оставшегося изотопа А. Каждые 8 минут остается половина атомов изотопа А, следовательно, последовательность значений масс изотопа А представляет собой геометрическую прогрессию с первым членом b₁=160 и знаменателем q=¹/₂. Найдем массу изотопа А через 40 минут.
40:8=5, да еще нужно учесть начальное значение, значит n=6

$b_6=b_1\ast{(\frac12)}^{6-1}=160\ast\frac1{32}=5$ мг осталось от изотопа А, а все остальное перешло к изотопу Б.

Тогда масса образовавшегося изотопа Б составит 160 − 5 = 155 мг.

Ответ: 155

Ииии объяснение на пальцах.

Это почему-то самая сложная для понимания задача. Ну да, предметная область выбрана из физики, химии. Но давайте опираться на великий и могучий русский язык. Что-то распадается, но в отличие от других задач с изотопами, атомы не исчезают, а переходят в другое место и там остаются. Без потери массы значит: сколько ушло из А, столько пришло в Б. А слово «стабильный» помогает нам понять, что там они и остаются.

Т.к. атомы уходят каждые 8 минут, то нужно будет делить изотоп А пополам 40 : 8 = 5 раз. Получим:

1. 160 : 2 = 80
2. 80 : 2 = 40
3. 40 : 2 = 20
4. 20 : 2 = 10
5. 10 : 2 = 5

А вот теперь самое главное. Что означают эти числа.

1 способ:

Уменьшая массу изотопа А в два раза, получили, что после 40 минут у него осталось 5 мг атомов. Тогда все остальные «ушли» в Б:

160 – 5 = 155.

2 способ:

Полученные числа также говорят о том, сколько атомов «уходило» в Б каждые 8 минут. В изотопе Б они каждый раз добавлялись к тем, что уже там были, тогда будем складывать эти массы:

80 + 40 + 20 +10 + 5 = 155.

Ответ: 155

E8F846

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 7 минут. В начальный момент масса изотопа составляла 160 мг. Найдите массу изотопа через 28 минут. Ответ дайте в миллиграммах.

Решение:

Геометрическая прогрессия.
b_n=b_1*q^n-1
28:7=4, да + начальная точка, значит n=5
b₅=160*1/2⁴=10

Ответ: 10

Другой вариант решения.

1-160
через 7мин - 80
через 14мин - 40
через 21мин - 20
через 28мин - 10

Ответ: 10

310245

В ходе бета-распада радиоактивного изотопа А каждые 9 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 400 мг. Найдите массу образовавшегося изотопа Б через 36 минут. Ответ дайте в миллиграммах.

Решение:

36:9=4, значит будем делить 4 раза
400/2
200/2
100/2
50/2=25 мг осталось изотопа А, а остальное перешло в Б

400-25=375 мг образовалось изотопа Б

Ответ: 375

Или решайте по формуле n-го члена геометрической прогрессии b_n=b_1*q^n-1 ; b_n- остаток изотопа А, q=1/2 -во сколько раз увеличивается кол-во, n - количество контрольных точек, включая первую, когда изотоп еще не начал делиться.

b₅= 400 * 1/2^(5-1)=25 мг осталось изотопа А, а остальное перешло в Б
400-25=375 мг образовалось изотопа Б

Ответ: 375

1BE872

В ходе бета-распада радиоактивного изотопа А каждые 9 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 640 мг. Найдите массу образовавшегося изотопа Б через 45 минут. Ответ дайте в миллиграммах.

Решение:

Масса образовавшегося изотопа Б равна разности массы исходного вещества и массы оставшегося изотопа А. Каждые 9 минут остается половина атомов изотопа А, следовательно, последовательность значений масс изотопа А представляет собой геометрическую прогрессию с первым членом b₁=640 и знаменателем q=¹/₂. Найдем массу изотопа А через 45 минут.
45:9=5, да еще нужно учесть начальное значение, значит n=6

$b_6=b_1\ast{(\frac12)}^{6-1}=640\ast\frac1{32}=20$ мг осталось от изотопа А, а все остальное перешло к изотопу Б.

Тогда масса образовавшегося изотопа Б составит 640 − 20 = 620 мг.

Ответ: 620

И объяснение на пальцах.

Это почему-то самая сложная для понимания задача. Ну да, предметная область выбрана из физики, химии. Но давайте опираться на великий и могучий русский язык. Что-то распадается, но в отличие от других задач с изотопами, атомы не исчезают, а переходят в другое место и там остаются. Без потери массы значит: сколько ушло из А, столько пришло в Б. А слово «стабильный» помогает нам понять, что там они и остаются.

Т.к. атомы уходят каждые 9 минут, то нужно будет делить изотоп А пополам 45 : 9 = 5 раз. Получим:

1. 640 : 2 = 320
2. 320 : 2 = 160
3. 160 : 2 = 80
4. 80 : 2 = 40
5. 40 : 2 = 20

то есть это и есть остаточная масса изотопа A, само собой при сохранении общей массы остается из нее вычесть остаточную массу изотопа А и получим массу изотопа Б

640-20=620

Ответ: 620

E89579

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 8 минут. В начальный момент масса изотопа составляла 320 мг. Найдите массу изотопа через 40 минут. Ответ дайте в миллиграммах.

Решение:

Геометрическая прогрессия.
b_n=b_1*q^n-1
40:8=5, да + начальная точка, значит n=6
b₆=320*(1/2)⁵=10

Ответ: 10

Проверим.

было - 320 мг
через 8 мин - 320/2
через 16 мин - 160/2
через 24 мин - 80/2
через 32 мин - 40/2
через 40 мин - 20/2=10 мг

Ответ: 10

319371

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 8 минут. В начальный момент масса изотопа составляла 160 мг. Найдите массу изотопа через 40 минут. Ответ дайте в миллиграммах.

Решение:

Геометрическая прогрессия.
b_n=b_1*q^n-1
40:8=5, да + начальное значение, значит n=6
b₆=160*(1/2)⁵=5

Ответ: 5

Проверим.

было - 160 мг
через 8 мин - 160/2
через 16 мин - 80/2
через 24 мин - 40/2
через 32 мин - 20/2
через 40 мин - 10/2

Ответ: 5

8F4FB6

В ходе бета-распада радиоактивного изотопа А каждые 7 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 640 мг. Найдите массу образовавшегося изотопа Б через 42 минуты. Ответ дайте в миллиграммах.

Решение:

Масса образовавшегося изотопа Б равна разности массы исходного вещества и массы оставшегося изотопа А. Каждые 7 минут остается половина атомов изотопа А, следовательно, последовательность значений масс изотопа А представляет собой геометрическую прогрессию с первым членом b₁=640 и знаменателем q=¹/₂. Найдем массу изотопа А через 42 минут.
42:7=6, да еще нужно учесть начальное значение, значит n=7

$b_7=b_1\ast{(\frac12)}^{7-1}=640\ast\frac1{64}=10$ мг осталось от изотопа А, а все остальное перешло к изотопу Б.

Тогда масса образовавшегося изотопа Б составит 640 − 10 = 630 мг.

Ответ: 630

И объяснение на пальцах.

Это почему-то самая сложная для понимания задача. Ну да, предметная область выбрана из физики, химии. Но давайте опираться на великий и могучий русский язык. Что-то распадается, но в отличие от других задач с изотопами, атомы не исчезают, а переходят в другое место и там остаются. Без потери массы значит: сколько ушло из А, столько пришло в Б. А слово «стабильный» помогает нам понять, что там они и остаются.

Т.к. атомы уходят каждые 9 минут, то нужно будет делить изотоп А пополам 45 : 9 = 5 раз. Получим:

1. 640 : 2 = 320
2. 320 : 2 = 160
3. 160 : 2 = 80
4. 80 : 2 = 40
5. 40 : 2 = 20
6. 20 : 2 = 10

то есть это и есть остаточная масса изотопа A, само собой при сохранении общей массы остается из нее вычесть остаточную массу изотопа А и получим массу изотопа Б

640-10=630

Ответ: 630

428917

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 9 минут. В начальный момент масса изотопа составляла 400 мг. Найдите массу изотопа через 36 минут. Ответ дайте в миллиграммах.

Решение:

Геометрическая прогрессия.
b_n=b_1*q^n-1
36:9=4, да + начальная точка, значит n=5
b₅=400*(1/2)⁴=25

Ответ: 25

Проверим.

было - 400 мг
через 9 мин - 400/2
через 18 мин - 200/2
через 27 мин - 100/2
через 36 мин - 50/2=25 мг

Ответ: 25

B0E713

В ходе бета-распада радиоактивного изотопа А каждые 8 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 480 мг. Найдите массу образовавшегося изотопа Б через 32 минут. Ответ дайте в миллиграммах.

Решение:

Масса образовавшегося изотопа Б равна разности массы исходного вещества и массы оставшегося изотопа А. Каждые 8 минут остается половина атомов изотопа А, следовательно, последовательность значений масс изотопа А представляет собой геометрическую прогрессию с первым членом b₁=480 и знаменателем q=¹/₂. Найдем массу изотопа А через 32 минут.
32:8=4, да еще нужно учесть начальное значение, значит n=5

$b_5=b_1\ast{(\frac12)}^{5-1}=480\ast\frac1{16}=30$ мг осталось от изотопа А, а все остальное перешло к изотопу Б.

Тогда масса образовавшегося изотопа Б составит 480 − 30 = 450 мг.

Ответ: 450

И объяснение на пальцах.

Это почему-то самая сложная для понимания задача. Ну да, предметная область выбрана из физики, химии. Но давайте опираться на великий и могучий русский язык. Что-то распадается, но в отличие от других задач с изотопами, атомы не исчезают, а переходят в другое место и там остаются. Без потери массы значит: сколько ушло из А, столько пришло в Б. А слово «стабильный» помогает нам понять, что там они и остаются.

Т.к. атомы уходят каждые 9 минут, то нужно будет делить изотоп А пополам 32 : 8 = 4 раза. Получим:

1. 480 : 2 = 240
2. 240 : 2 = 120
3. 120 : 2 = 60
4. 60 : 2 = 30

то есть это и есть остаточная масса изотопа A, само собой при сохранении общей массы остается из нее вычесть остаточную массу изотопа А и получим массу изотопа Б

480-30=450

Ответ: 450

0881D3

В ходе бета-распада радиоактивного изотопа А каждые 7 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 160 мг. Найдите массу образовавшегося изотопа Б через 28 минут. Ответ дайте в миллиграммах.

Решение:

Масса образовавшегося изотопа Б равна разности массы исходного вещества и массы оставшегося изотопа А. Каждые 7 минут остается половина атомов изотопа А, следовательно, последовательность значений масс изотопа А представляет собой геометрическую прогрессию с первым членом b₁=160 и знаменателем q=¹/₂. Найдем массу изотопа А через 28 минут.
28:7=4, да еще нужно учесть начальное значение, значит n=5

$b_5=b_1\ast{(\frac12)}^{5-1}=160\ast\frac1{16}=10$ мг осталось от изотопа А, а все остальное перешло к изотопу Б.

Тогда масса образовавшегося изотопа Б составит 160 − 10 = 150 мг.

Ответ: 150

И объяснение на пальцах.

Это почему-то самая сложная для понимания задача. Ну да, предметная область выбрана из физики, химии. Но давайте опираться на великий и могучий русский язык. Что-то распадается, но в отличие от других задач с изотопами, атомы не исчезают, а переходят в другое место и там остаются. Без потери массы значит: сколько ушло из А, столько пришло в Б. А слово «стабильный» помогает нам понять, что там они и остаются.

Т.к. атомы уходят каждые 9 минут, то нужно будет делить изотоп А пополам 28 : 7 = 4 раза. Получим:

1. 160 : 2 = 80
2. 80 : 2 = 40
3. 40 : 2 = 20
4. 20 : 2 = 10

то есть это и есть остаточная масса изотопа A, само собой при сохранении общей массы остается из нее вычесть остаточную массу изотопа А и получим массу изотопа Б

160-10=150

Ответ: 150

40495A

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 6 минут. В начальный момент масса изотопа составляла 640 мг. Найдите массу изотопа через 42 минуты. Ответ дайте в миллиграммах.

Решение:

Геометрическая прогрессия.
b_n=b_1*q^n-1
42:6=7 , да+ начальная точка, следовательно n=8
b₈=640*(1/2)⁷=5

Ответ: 5

Проверим.

было - 640 мг
через 6 мин - 640/2
через 12 мин - 320/2
через 18 мин - 160/2
через 24 мин - 80/2
через 30 мин - 40/2
через 36 мин - 20/2
через 42 мин - 10/2=5 мг

Ответ: 5

F1E75D

В ходе бета-распада радиоактивного изотопа А каждые 9 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 320 мг. Найдите массу образовавшегося изотопа Б через 54 минуты. Ответ дайте в миллиграммах.

Решение:

Масса образовавшегося изотопа Б равна разности массы исходного вещества и массы оставшегося изотопа А. Каждые 9 минут остается половина атомов изотопа А, следовательно, последовательность значений масс изотопа А представляет собой геометрическую прогрессию с первым членом b₁=320 и знаменателем q=¹/₂. Найдем массу изотопа А через 54 минут.
54:9=6, да еще нужно учесть начальное значение, значит n=7

$b_7=b_1\ast{(\frac12)}^{7-1}=320\ast\frac1{64}=5$ мг осталось от изотопа А, а все остальное перешло к изотопу Б.

Тогда масса образовавшегося изотопа Б составит 320 − 5 = 315 мг.

Ответ: 315

И объяснение на пальцах.

Это почему-то самая сложная для понимания задача. Ну да, предметная область выбрана из физики, химии. Но давайте опираться на великий и могучий русский язык. Что-то распадается, но в отличие от других задач с изотопами, атомы не исчезают, а переходят в другое место и там остаются. Без потери массы значит: сколько ушло из А, столько пришло в Б. А слово «стабильный» помогает нам понять, что там они и остаются.

Т.к. атомы уходят каждые 9 минут, то нужно будет делить изотоп А пополам 54 : 9 = 6 раз. Получим:

1. 320 : 2 = 160
2. 160 : 2 = 80
3. 80 : 2 = 40
4. 40 : 2 = 20
5. 20 : 2 = 10
6. 10 : 2 = 5

то есть это и есть остаточная масса изотопа A, само собой при сохранении общей массы остается из нее вычесть остаточную массу изотопа А и получим массу изотопа Б

320-5=315

Ответ: 315

BD2D58

В ходе бета-распада радиоактивного изотопа А каждые 7 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 480 мг. Найдите массу образовавшегося изотопа Б через 35 минут. Ответ дайте в миллиграммах.

Решение:

Масса образовавшегося изотопа Б равна разности массы исходного вещества и массы оставшегося изотопа А. Каждые 7 минут остается половина атомов изотопа А, следовательно, последовательность значений масс изотопа А представляет собой геометрическую прогрессию с первым членом b₁=480 и знаменателем q=¹/₂. Найдем массу изотопа А через 35 минут.
35:7=5, да еще нужно учесть начальное значение, значит n=6

$b_6=b_1\ast{(\frac12)}^{6-1}=480\ast\frac1{32}=15$ мг осталось от изотопа А, а все остальное перешло к изотопу Б.

Тогда масса образовавшегося изотопа Б составит 480 − 15 = 465 мг.

Ответ: 465

И объяснение на пальцах.

Это почему-то самая сложная для понимания задача. Ну да, предметная область выбрана из физики, химии. Но давайте опираться на великий и могучий русский язык. Что-то распадается, но в отличие от других задач с изотопами, атомы не исчезают, а переходят в другое место и там остаются. Без потери массы значит: сколько ушло из А, столько пришло в Б. А слово «стабильный» помогает нам понять, что там они и остаются.

Т.к. атомы уходят каждые 7 минут, то нужно будет делить изотоп А пополам 35 : 7 = 5 раз. Получим:

1. 480 : 2 = 240
2. 240 : 2 = 120
3. 120 : 2 = 60
4. 60 : 2 = 30
5. 30 : 2 = 15

то есть это и есть остаточная масса изотопа A, само собой при сохранении общей массы остается из нее вычесть остаточную массу изотопа А и получим массу изотопа Б

480-15=465

Ответ: 465

29C852

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 8 минут. В начальный момент масса изотопа составляла 320 мг. Найдите массу изотопа через 48 минут. Ответ дайте в миллиграммах.

Решение:

Геометрическая прогрессия.
b_n=b_1*q^n-1
48:8=6, да + начальное значение, значит n=7
b₇=320*(1/2)⁶=5

Ответ: 5

Проверим.

было - 320 мг
через 8 мин - 320/2
через 16 мин - 160/2
через 24 мин - 80/2
через 32 мин - 40/2
через 40 мин - 20/2
через 48 мин - 10/2

Ответ: 5

61D051

В ходе бета-распада радиоактивного изотопа А каждые 7 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 640 мг. Найдите массу образовавшегося изотопа Б через 49 минут. Ответ дайте в миллиграммах.

Решение:

Масса образовавшегося изотопа Б равна разности массы исходного вещества и массы оставшегося изотопа А. Каждые 7 минут остается половина атомов изотопа А, следовательно, последовательность значений масс изотопа А представляет собой геометрическую прогрессию с первым членом b₁=640 и знаменателем q=¹/₂. Найдем массу изотопа А через 49 минут.
49:7=7, да еще нужно учесть начальное значение, значит n=8

$b_8=b_1\ast{(\frac12)}^{8-1}=640\ast\frac1{128}=5$ мг осталось от изотопа А, а все остальное перешло к изотопу Б.

Тогда масса образовавшегося изотопа Б составит 640 − 5 = 635 мг.

Ответ: 635

И объяснение на пальцах.

Это почему-то самая сложная для понимания задача. Ну да, предметная область выбрана из физики, химии. Но давайте опираться на великий и могучий русский язык. Что-то распадается, но в отличие от других задач с изотопами, атомы не исчезают, а переходят в другое место и там остаются. Без потери массы значит: сколько ушло из А, столько пришло в Б. А слово «стабильный» помогает нам понять, что там они и остаются.

Т.к. атомы уходят каждые 7 минут, то нужно будет делить изотоп А пополам 49 : 7 = 7 раз. Получим:

1. 640 : 2 = 320
2. 320 : 2 = 160
3. 160 : 2 = 80
4. 80 : 2 = 40
5. 40 : 2 = 20
6. 20 : 2 = 10
7. 10 : 2 = 5

то есть это и есть остаточная масса изотопа A, само собой при сохранении общей массы остается из нее вычесть остаточную массу изотопа А и получим массу изотопа Б

640-5=635

Ответ: 635

0F4A9F

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 9 минут. В начальный момент масса изотопа составляла 640 мг. Найдите массу изотопа через 45 минут. Ответ дайте в миллиграммах.

Решение:

Геометрическая прогрессия.
b_n=b_1*q^n-1
45:9=5, да + начальная точка, значит n=6
b₆=640*(1/2)⁵=20

Ответ: 20

Проверим.

было - 640 мг
через 9 мин - 640/2
через 18 мин - 320/2
через 27 мин - 160/2
через 36 мин - 80/2
через 45 мин - 40/2=20 мг

Ответ: 20

1862E5

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 9 минут. В начальный момент масса изотопа составляла 320 мг. Найдите массу изотопа через 63 минуты. Ответ дайте в миллиграммах.

Решение:

Геометрическая прогрессия.
b_n=b_1*q^n-1
63:9=7, да + начальная точка, значит n=8
b₈=320*(1/2)⁷=2,5

Ответ: 2,5

Проверим.

было - 320 мг
через 9 мин - 320/2
через 18 мин - 160/2
через 27 мин - 80/2
через 36 мин - 40/2
через 45 мин - 20/2
через 54 мин - 10/2
через 63 мин - 5/2=2,5 мг

Ответ: 2,5

5C8260

В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 8 минут. В начальный момент масса изотопа составляла 200 мг. Найдите массу изотопа через 32 минуты. Ответ дайте в миллиграммах.

Решение:

Геометрическая прогрессия.
b_n=b_1*q^n-1
48:8=4, да + начальное значение, значит n=5
b₅=200*(1/2)⁴=12,5

Ответ: 12,5

Проверим.

было - 200 мг
через 8 мин - 200/2
через 16 мин - 100/2
через 24 мин - 50/2
через 32 мин - 25/2=12,5 мг

Ответ: 12,5

F4E63B

В ходе бета-распада радиоактивного изотопа А каждые 8 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 320 мг. Найдите массу образовавшегося изотопа Б через 40 минут. Ответ дайте в миллиграммах.

Решение:

Масса образовавшегося изотопа Б равна разности массы исходного вещества и массы оставшегося изотопа А. Каждые 8 минут остается половина атомов изотопа А, следовательно, последовательность значений масс изотопа А представляет собой геометрическую прогрессию с первым членом b₁=320 и знаменателем q=¹/₂. Найдем массу изотопа А через 40 минут.
40:8=5, да еще нужно учесть начальное значение, значит n=6

$b_6=b_1\ast{(\frac12)}^{6-1}=320\ast\frac1{32}=10$ мг осталось от изотопа А, а все остальное перешло к изотопу Б.

Тогда масса образовавшегося изотопа Б составит 320 − 10 = 310 мг.

Ответ: 310

И объяснение на пальцах.

Это почему-то самая сложная для понимания задача. Ну да, предметная область выбрана из физики, химии. Но давайте опираться на великий и могучий русский язык. Что-то распадается, но в отличие от других задач с изотопами, атомы не исчезают, а переходят в другое место и там остаются. Без потери массы значит: сколько ушло из А, столько пришло в Б. А слово «стабильный» помогает нам понять, что там они и остаются.

Т.к. атомы уходят каждые 7 минут, то нужно будет делить изотоп А пополам 40 : 8 = 5 раз. Получим:

1. 320 : 2 = 160
2. 160 : 2 = 80
3. 80 : 2 = 40
4. 40 : 2 = 20
5. 20 : 2 = 10

то есть это и есть остаточная масса изотопа A, само собой при сохранении общей массы остается из нее вычесть остаточную массу изотопа А и получим массу изотопа Б

320-10=310

Ответ: 310

07233D