ГДЗ по Информатике за 4 класс, автор Рудченко (учебник)

: Категория: Информатика 4 класс

Статья содержит ответы на домашние задания по информатике для 4 класса, автора Рудченко Татьяны Александровны. Это учебник в мягкой обложке издательства Просвещение, по программе Перспектива, выпущенный в 2021 году. В учебнике 128 страниц, более 200 заданий, на которые мы и собрали правильные, верные ответы.
Итак, информатика это не только предмет о управлении электронными машинами, но прежде всего о том как решать поставленные перед вами логические задачи. Именно логическими задачами можно назвать все домашние работы по информатике. И именно эти самые ответы мы вам и представляем.

ГДЗ по Информатике за 4 класс, автор Рудченко (учебник)

Выбирайте интересующее вас задание, кликайте по вкладке и смотрите ответы. Здесь все более чем понятно.

Круговой турнир 1-7

ИГРЫ
Игра. Круговой турнир. Игра крестики-нолики
Номер №1
Устройте соревнование с соседом по парте в крестики−нолики. Сыграйте 5 партий. Поля для игры находятся на вкладыше тетради проектов. Перед каждой партией посчитайтесь (при помощи любой считалки) — кто останется, тот пусть играет крестиками.
Заполни таблицу вашего соревнования. Очки подсчитывай, как в футболе: за победу — 2 очка, за ничью — 1 очко, за поражение — 0 очков.

Ответь на вопросы, напиши ответы в окнах.
В каких партиях ты играл крестиками? _
Сколько партий закончилось победой крестиков? _
Сколько партий закончилось победой ноликов? _
Сколько партий закончилось вничью? _
Кто выиграл в соревновании (или оно закончилось вничью)? _
Это и другие задания из учебника надо выполнять в рабочей тетради.

Партия \ Игрок
1−я партия
2−я партия
3−я партия
4−я партия
5−я партия
ИТОГО:

Решение

Соревнование в крестики−нолики:

Партия \ Игрок	я	сосед
1−я партия	1	1
2−я партия	1	1
3−я партия	2	0
4−я партия	1	1
5−я партия	0	2
ИТОГО:	5	5

Ответы на вопросы:
В каких партиях ты играл крестиками? 2, 3, 4
Сколько партий закончилось победой крестиков? 2
Сколько партий закончилось победой ноликов? 0
Сколько партий закончилось вничью? 3

Кто выиграл в соревновании (или оно закончилось вничью)? Ничья

Номер №2
Проведите круговой турнир по крестикам−ноликам в группах по 3 — 4 человека. Перед каждой партией посчитайтесь (при помощи любой считалки) — кто останется, тот пусть играет крестиками.
Заполни таблицу турнира. Очки подсчитывай, как в футболе: за победу — 2 очка, за ничью — 1 очко, за поражение — 0 очков.

Игрок					Очки	Место
	*
		*
			*
				*

Ответь на вопросы, напиши ответы в окнах:
Сколько партий было проведено в турнире? _
В скольких партиях ты играл крестиками? _
Сколько партий закончилось победой крестиков? _
Сколько партий закончилось победой ноликов? _
Сколько партий закончилось вничью? _

Решение

Круговой турнир по крестикам−ноликам:

Игрок	я	игрок 2	игрок 3	игрок 4	Очки	Место
я	*	2	1	1	4	1
игрок 2	0	*	2	1	3	2
игрок 3	1	0	*	1	2	4
игрок 4	1	1	1	*	3	2

Ответы на вопросы:
Сколько партий было проведено в турнире? 6
В скольких партиях ты играл крестиками? 2
Сколько партий закончилось победой крестиков? 2
Сколько партий закончилось победой ноликов? 0
Сколько партий закончилось вничью? 4

Номер №3
Проведите ещё один круговой турнир по крестикам−ноликам в той же группе, что и при выполнении задачи 2. Теперь в каждой партии пусть играет крестиками тот, чья фамилия идёт раньше по алфавиту.
Заполни таблицу турнира. Очки подсчитывай, как в футболе.
Изменились ли результаты турнира по сравнению с предыдущим турниром (из задачи 2)? Подумай почему.

Решение

Круговой турнир по крестикам−ноликам:

Игрок	Арбузов	Волков	Барбарискина	Гайкина	Очки	Место
я	*	1	0	0	1	4
игрок 2	1	*	1	2	4	1
игрок 3	2	1	*	0	3	3
игрок 4	2	0	2	*	4	1

Результаты турнира изменились по сравнению с предыдущим турниром, потому что теперь право первого хода не зависит от случая. Игрок, который ходит первым, имеет больше инициативы в игре.

Номер №4
Из всех слов мешка S построй в окне цепочку Q так, чтобы слова в цепочке Q стояли в алфавитном порядке.

Решение

Построим цепочку Q:

⇓ Q
ТАБУРЕТ
ТАЗ
ТАЙГА
ТАЙМ
ТАЙНИК
ТАЙНЫЙ
ТАЙФУН
ТАКСИ
ТАКСИСТ
ТАКТ
ТАЛАНТ
ТАМ
ТАНЕЦ
ТАНК
ТАНКЕР
⇓

Номер №5
Дана программа А и поле Робика после выполнения этой программы. Отметь жирной точкой положение Робика до и после выполнения программы А.
Позиция после выполнения программы А:

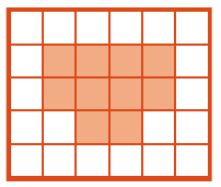
⇓ А
ВЛЕВО
ВНИЗ
ВЛЕВО
ВВЕРХ
ВЛЕВО
ВВЕРХ
ВПРАВО
ВПРАВО
ВПРАВО
⇓

Решение

Красная точка — начальная позиция Робика.
Синяя точка — позиция Робика после выполнения программы А.

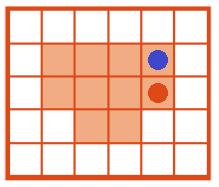
Номер №6
Выполни склеивание мешков, нарисуй мешок Ш ⓧ П.

Решение

Выполним склеивание мешков:

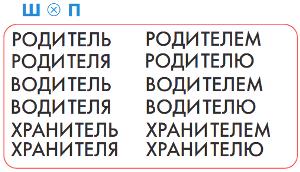
Номер №7
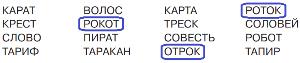
Найди здесь три слова, мешки букв которых одинаковые. Напиши эти три слова в ответе.

КАРАТ
ВОЛОС
КАРТА
РОТОК
КРЕСТ
РОКОТ
ТРЕСК
СОЛОВЕЙ
СЛОВО
ПИРАТ
СОВЕСТЬ
РОБОТ
ТАРИФ
ТАРАКАН
ОТРОК
ТАПИР

Решение

Три слова, мешки букв которых одинаковые:
РОКОТ, ОТРОК, РОТОК.

Цепочка позиций 8-11

Правила игры. Цепочка позиций
Номер №8
Аня и Саша начали играть в крестики−нолики. Аня — Первая, она ставит крестики, а Саша — Вторая. Дострой цепочку Р так, чтобы она стала цепочкой позиций какой−либо партии Ани и Саши. Для этого воспользуйся заготовками с листа вырезания: вырежи, наклей и заполни столько полей, сколько потребуется для завершения партии.

Проверь своё решение:
а) убедись, что последняя бусина цепочки Р — это заключительная позиция игры крестики−нолики;
б) по заключительной позиции сосчитай, сколько всего ходов было сделано в этой партии;
в) теперь сосчитай, сколько бусин получилось в цепочке Р: бусин должно быть на одну больше, чем ходов (почему?).
Чем закончилась партия Р? Поставь галочку в клетке рядом с верным ответом:

Выиграла Аня _
Выиграла Саша _
Ничья _

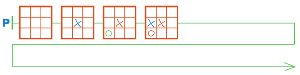
Решение

Достроим цепочку Р:

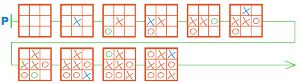
Проверим решение:
а) последняя бусина цепочки Р — это заключительная позиция игры крестики−нолики;
б) в этой партии было сделано 9 ходов;
в) в цепочке Р получилось бусин, потому что цепочка включает начальную позицию игры.

Чем закончилась партия Р?
Выиграла Аня _
Выиграла Саша _
Ничья √

Номер №9
Заполни окна так, чтобы эти равенства были верными.

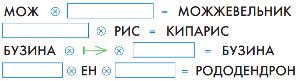
Решение

Заполним окна:

Номер №10
Петя и Толя сыграли партию в крестики−нолики. Петя был Первым, Толя был Вторым. Дострой цепочку Н так, чтобы она стала цепочкой партии Пети и Толи.
Проверь своё решение: по заключительной позиции сосчитай, сколько всего ходов было сделано в этой партии. В цепочке Н бусин должно быть на одну больше, чем ходов.
Чем закончилась партия Н? Поставь галочку в клетке рядом с верным ответом.

Выиграл Петя _
Выиграл Толя _
Ничья _

Решение

Достроим цепочку Н:

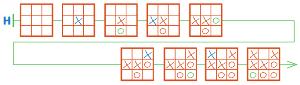
Проверим решение: в этой партии было сделано 8 ходов. В цепочке Н бусин на одну больше, чем ходов.
Чем закончилась партия Н?
Выиграл Петя _
Выиграл Толя √
Ничья _

Номер №11
Построй в окне такое дерево, чтобы для него все следующие утверждения были истинными:
В этом дереве предыдущая бусина перед каждой круглой бусиной — треугольная.
В этом дереве предыдущая бусина перед каждой треугольной бусиной — квадратная.
На каждом уровне этого дерева ровно 2 листа.
Мешок А — это мешок всех бусин этого дерева.

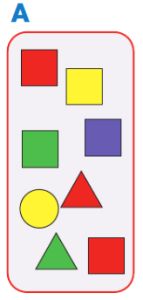
Решение

Игра камешки 12-25

Игра камешки
Номер №12
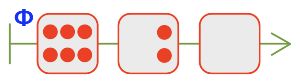
Нарисуй в окне цепочку какой−нибудь партии игры камешки с такими правилами: начальная позиция — 8 камешков, разрешается брать 1 или 2 камешка за ход.

Решение

Нарисуем цепочку партии игры камешки:

Номер №13
Устройте соревнование с соседом по парте в игру камешки с такими правилами: начальная позиция — 7 камешков, можно брать 1 или 2 камешка за ход. Сыграйте 8 партий. Начинайте игру по очереди: пусть один из вас играет Первым в партиях с чётными номерами, а другой — с нечётными. Заполни таблицу соревнования. За каждую победу игрок получает 1 очко, за поражение — 0 очков.

Партия \ Игрок
1−я партия
2−я партия
3−я партия
4−я партия
5−я партия
6−я партия
7−я партия
8−я партия
ИТОГО:

Ответь на вопросы, напиши ответы в окнах.
В каких партиях ты играл Первым? _
Кто выиграл в соревновании (или оно закончилось вничью)? _
Сколько раз ты выиграл в партиях, в которых:

был Первым? _
был Вторым? _

Решение

Проведём соревнование:

Партия \ Игрок	Я	ИГОРК 2
1−я партия	0	1
2−я партия	1	0
3−я партия	1	0
4−я партия	0	1
5−я партия	1	0
6−я партия	0	1
7−я партия	0	1
8−я партия	1	0
ИТОГО:	4	4

Ответим на вопросы:
В каких партиях ты играл Первым? 1, 3, 5, 7
Кто выиграл в соревновании (или оно закончилось вничью)? Соревнование закончилось вничью.
Сколько раз ты выиграл в партиях, в которых:
был Первым? 2
был Вторым? 2

Номер №14
Нарисуй в первом окне цепочку какой−нибудь партии игры камешки, в которой выиграл Первый (начальная позиция — 10 камешков, можно брать 1, 2 или 3 камешка за ход).
Во втором окне нарисуй цепочку такой партии игры камешки (с теми же правилами), в которой выиграл Второй.

Решение

Нарисуем цепочку партии игры камешки, в которой выиграл Первый:

Нарисуем цепочку партии игры камешки, в которой выиграл Второй:

Номер №15
Вот два одинаковых начала партий игры крестики−нолики. Дострой цепочки А и В так, чтобы в партии А выиграл Первый, а в партии В — Второй.

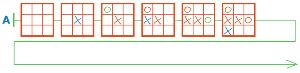
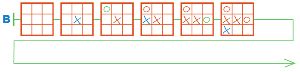
Решение
Достроим цепочки А и В: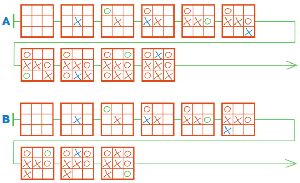

Номер №16
Построй в первом окне цепочку партии игры камешки с такими правилами: начальная позиция — 11 камешков, можно брать только 1 камешек за ход. Назови цепочку именем С.
Чем закончилась партия С? Поставь галочку в клетке рядом с ответом.

Выиграл Первый _
Выиграл Второй _

Подумай, можно ли построить другую цепочку партии по тем же правилам. Поставь галочку в клетке рядом с ответом.

Можно _
Нельзя _

Если ты считаешь, что можно, нарисуй такую цепочку во втором окне.

Решение

Построим цепочку партии игры камешки:

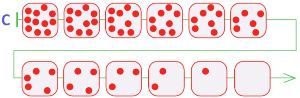
Чем закончилась партия С?
Выиграл Первый √
Выиграл Второй _
Подумай, можно ли построить другую цепочку партии по тем же правилам.
Можно _
Нельзя √
Другую цепочку партии по тем же правилам построить нельзя, потому что каждый игрок по правилам может совершать только 1 вариант хода — брать один камешек.

Номер №17
Вася получил задание заполнить таблицы для нарисованного мешка Ю. Он начал выполнять задание (см. таблицы). Закончи начатую им работу — заполни пустые клетки в таблицах, не видя мешка Ю.

Цвет \ Фигурка	ЯБЛОКИ	ГРУШИ	СЛИВЫ
КРАСНЫЕ	2	5
ЖЁЛТЫЕ			0
СИНИЕ		1

КРАСНЫЕ	ЖЁЛТЫЕ	СИНИЕ
10		3

ЯБЛОКИ	ГРУШИ	СЛИВЫ
6	6	5

Решение

Заполним таблицы:

Цвет \ Фигурка	ЯБЛОКИ	ГРУШИ	СЛИВЫ
КРАСНЫЕ	2	5	3
ЖЁЛТЫЕ	4	0	0
СИНИЕ	0	1	2

КРАСНЫЕ	ЖЁЛТЫЕ	СИНИЕ
10	4	3

ЯБЛОКИ	ГРУШИ	СЛИВЫ
6	6	5

Вычисления:
Посчитаем количество фигурок:
1. Всего в мешке Ю 10 красных фигурок. Известно, что среди них 2 яблока и 5 груш, значит, слив:
10 – 2 – 5 = 3
2. Всего в мешке Ю 5 слив. Известно, что среди них 3 красных и ни одной жёлтой, значит, синих слив:
5 – 3 = 2
3. Всего в мешке Ю 3 синих фигурки. Известно, что среди них 1 груша и 2 сливы, значит, яблок:
3 – 1 – 2 = 0
4. Всего в мешке Ю 6 яблок. Известно, что среди них 2 красных и ни одного синего, значит, жёлтых яблок:
6 – 2 – 0 = 4
5. Всего в мешке Ю 6 груш. Известно, что среди них 5 красных и 1 синяя, значит, жёлтых груш:
6 – 5 – 1 = 0

Номер №18
Дана программа М и начальная позиция Робика. Дорисуй позицию после выполнения программы М. Обрати внимание, что на поле есть стены, через которые Робик проходить не может.
Напиши в окне программу длиной в 7 команд, которую Робик сможет выполнить из этой же начальной позиции и третья команда в которой — вниз. Назови программу именем Р.
Дорисуй теперь позицию Робика после выполнения программы Р.
Начальная позиция:

⇓ M
ВНИЗ
ВНИЗ
ВПРАВО
ВВЕРХ
ВВЕРХ
ВПРАВО
ВПРАВО
ВПРАВО
ВНИЗ
ВПРАВО
ВПРАВО
ВНИЗ
ВНИЗ
ВПРАВО
ВНИЗ
ВЛЕВО
⇓

Решение

Дорисуем позицию после выполнения программы М: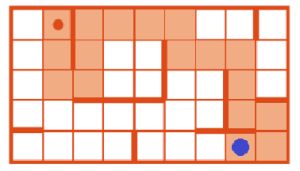

Напишем программу Р:

⇓ Р
ВЛЕВО
ВНИЗ
ВНИЗ
ВПРАВО
ВНИЗ
ВПРАВО
ВПРАВО
⇓

Дорисуем позицию Робика после выполнения программы Р: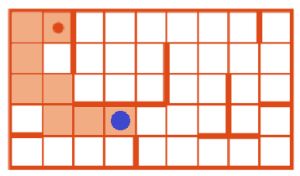

Номер №19
Вспомни: в круговом турнире на первом этапе игроки делятся на пары, которые проводят по одной партии игры между собой. Из каждой пары в следующий этап выходит один игрок — победитель в этой партии.
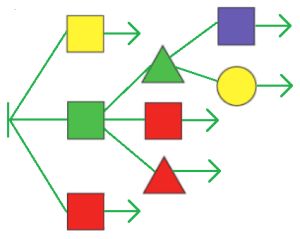
Оля, Лена, Ян и Коля провели кубковый турнир в камешки с начальной позицией 9 камешков (разрешалось брать 1, 2 или 3 камешка за ход). Всего в турнире было сыграно 3 партии: одна партия длиной в 3 хода, другая — в 4 хода, третья — в 5 ходов. Вот дерево этого турнира (в скобках около имени помечено, кто в партии был Первым, а кто — Вторым). Напиши имя победителя в жёлтом окне на первом уровне дерева. Для каждой партии турнира построй какую−нибудь цепочку этой партии и запиши её в окне между именами игроков.

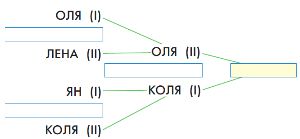
Решение

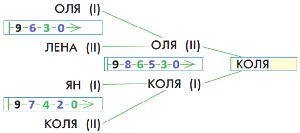
Номер №20
На уроках русского языка ты познакомился с понятиями основы и окончания слова. Представь каждое из данных слов как результат склеивания основы и окончания, заполни окна. Если окончание пустое, рисуй в окне пустую цепочку.

Решение

Заполним окна:

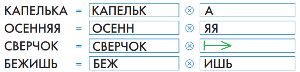
Номер №21
Мешок Y — это мешок всех цепочек из дерева Q. Нарисуй в окне такое дерево Q, чтобы в нём было ровно 23 буквы.

Решение

Нарисуем дерево Q:

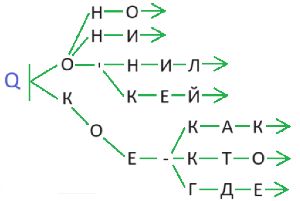
Номер №22
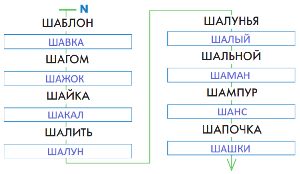
Напиши в каждом окне цепочки N русское слово так, чтобы слова в цепочке N стояли в алфавитном порядке.

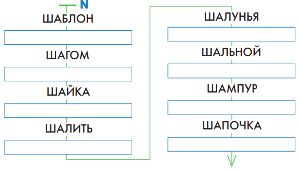
Решение

Заполним окна:

Номер №23
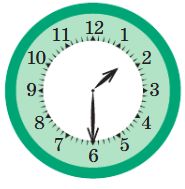
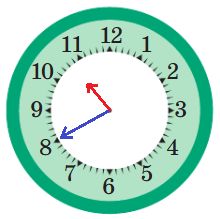
Для каждых часов напиши в окне, сколько времени прошло, пока часовая стрелка прошла ту часть циферблата, которая закрашена красным.

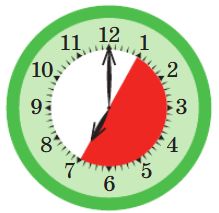
__ ч.

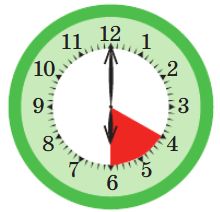
__ ч.

__ ч.

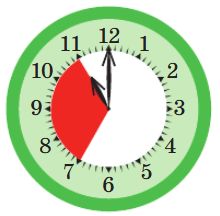
__ ч.

Решение

06 ч.

02 ч.

06 ч.

04 ч.

Номер №24
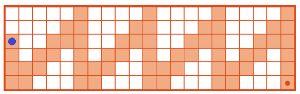
Покажи, как разрезать фигуру М на 3 одинаковые фигуры, — начерти линии разреза.

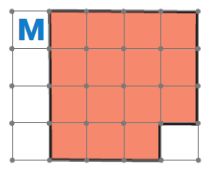
Решение

Начертим линии разреза, чтобы разрезать фигуру М на 3 одинаковые фигуры:

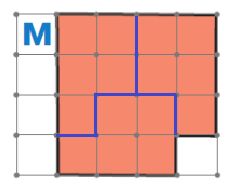
Номер №25
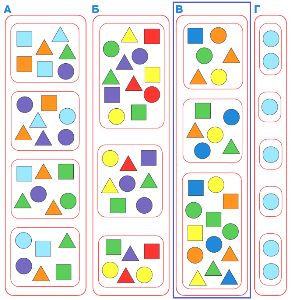
Найди один мешок мешков, в каждом мешке которого есть две одинаковые бусины. Напиши имя этого мешка в окне в ответе.
Ответ: в мешке мешков _ в каждом мешке есть две одинаковые бусины.

Решение

Ответ: в мешке мешков В в каждом мешке есть две одинаковые бусины.

Игра ползунок 26-35

Игра ползунок
Номер №26
Сыграйте круговой турнир в ползунок (в группах по 3—4 человека) на поле размером 3х3 точки. Поля для игры находятся на вкладыше тетради проектов.
Заполни таблицу турнира. За каждую победу игрок получает 1 очко, за поражение — 0 очков.

Решение

Правила игры ползунок:

Игровое поле — это несколько рядов точек, расположенных в прямоугольнике. Например, в этом задании в каждом ряду 3 точки, всего 3 ряда (3х3 точки).
На первом ходу игрок соединяет горизонтальным или вертикальным отрезком две любые соседние точки на поле. На каждом из следующих ходов игроки по очереди проводят горизонтальный или вертикальный отрезок, который соединяет один из концов получившейся до этого ломаной линии с какой−нибудь соседней точкой, через которую эта линия ещё не прошла. Соединять точки по диагонали нельзя.
Игра заканчивается, если очередной ход сделать нельзя. Выигрывает тот игрок, который сделал последний ход.
Таблица турнира:

Партия \ Игрок	Я	Игрок 2	Игрок 3	Игрок 4	Очки	Место
Я	*	1	0	1	2	1
Игрок 2	0	*	1	1	2	1
Игрок 3	1	0	*	0	1	3
Игрок 4	0	0	1	*	1	3

Номер №27
Митя и Катя начали играть в ползунок. Митя — Первый, он рисует красным карандашом, Катя — Вторая, она рисует зелёным карандашом. Дострой цепочку Q так, чтобы она стала цепочкой позиций какой−либо партии Мити и Кати.

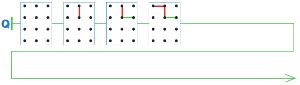
Решение

Достроим цепочку Q:

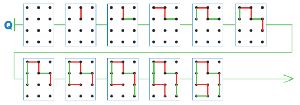
Номер №28
Построй в первом окне цепочку партии игры камешки, в которой выиграл Первый (начальная позиция — 5 камешков, можно брать 1, 3 или 4 камешка за ход).
Во втором окне построй цепочку партии (этой же игры), в которой выиграл Второй.

Решение

Построим цепочку партии, в которой выиграл Первый:

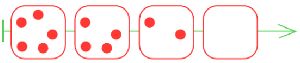
Построим цепочку партии, в которой выиграл Второй:

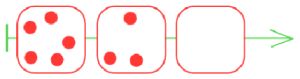
Номер №29
Цепочка V — это цепочка партии игры ползунок, которая закончилась на десятом ходу выигрышем Второго (ходы игроков нарисованы только в заключительной позиции). Первый рисовал красным карандашом, Второй — зелёным. Нарисуй ходы игроков на пустых полях цепочки V (конечно, в начальной позиции надо оставить пустое поле).

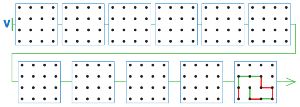
Решение

Нарисуем ходы игроков на полях цепочки V:

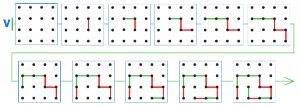
Номер №30
Заполни окна так, чтобы равенство было верным:

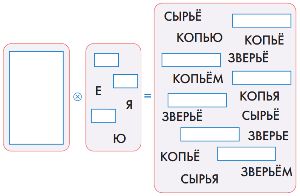
Решение

Заполним окна:

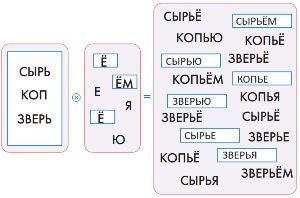
Номер №31
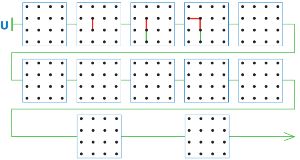
Цепочка U — это цепочка партии в ползунок (в некоторых позициях ходы игроков не нарисованы). Первый рисует красным карандашом, Второй — зелёным. Нарисуй ходы игроков на пустых полях цепочки U так, чтобы в этой партии (на одиннадцатом ходу) выиграл Первый.

Решение

Нарисуем ходы игроков на полях цепочки U (выиграл Первый):

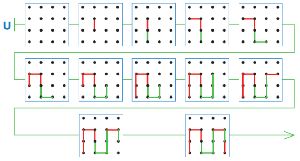
Номер №32
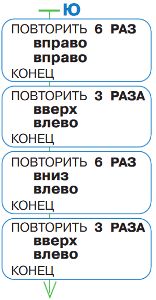
Дана начальная позиция Робика и программа Ю. Дорисуй позицию Робика после выполнения программы Ю.
Начальная позиция:

Решение

Позиция Робика после выполнения программы Ю:

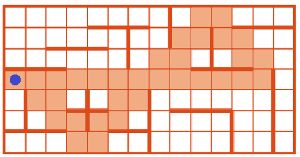
Номер №33
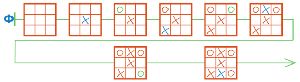
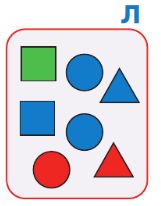
Дорисуй все позиции цепочки Ф так, чтобы получилась цепочка партии игры крестики−нолики, которая закончилась выигрышем Первого.

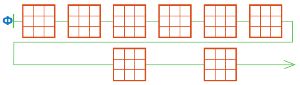
Решение

Дорисуем позиции цепочки Ф:

Номер №34
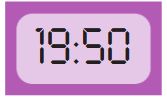
Ответь на вопросы — напиши ответ в окне рядом с каждым вопросом.
Какое время показывают эти часы? _
Какое время будут показывать часы через 2 часа? _
Какое время показывали часы 3 часа назад? _

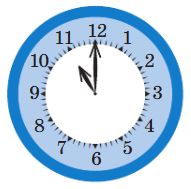
Решение

Какое время показывают эти часы? 11 ч 00 мин / 23 ч 00 мин
Какое время будут показывать часы через 2 часа? 13 ч 00 мин / 01 ч 00 мин
Какое время показывали часы 3 часа назад? 08 ч 00 мин / 20 ч 00 мин

Номер №35
Слова в этом словаре упорядочены по некоторому правилу, которое использует русский алфавитный порядок. Это правило называется правилом обратного словаря. Постарайся описа́ть это правило.

ИЗБА	БРУСНИКА	ЗАГЛАВИЕ
ПАЛУБА	ТУНИКА	БЕСПРАВИЕ
СУДЬБА	ИНФОРМАТИКА	ВОЗДЕЙСТВИЕ
ГОЛОВА	ПОГРЕБ	ВЗАИМОДЕЙСТВИЕ
КРУЖКА	РЫБОЛОВ	СОДЕЙСТВИЕ
СТРУЖКА	БИОЛОГ	СООТВЕТСТВИЕ
ПИЧУЖКА	ВЫВОД	БОБСЛЕЙ
СКАЗКА	ПОЗЖЕ	ВОЛЧОК

Решение

По правилу обратного словаря слова располагаются в алфавитном порядке не начальных, а конечных букв. Если последние буквы у слов одинаковые, то слова располагаются в алфавитном порядке предпоследних букв, и так далее.

Игра сим 36-43

Игра сим
Номер №36
Сыграйте круговой турнир в сим (3—4 человека) на окружности с пятью точками. Поля для игры находятся на вкладыше тетради проектов. Перед каждой партией посчитайтесь (при помощи любой считалки) — кто останется, тот играет Первым.
Заполни таблицу турнира. Очки подсчитывай, как в футболе: за победу — 2 очка, за ничью — 1 очко, за поражение — 0 очков.

Решение

Правила игры сим:
Начальная позиция игры — это окружность, на которой отмечено несколько точек. Например, в этом задании на окружности пять точек.
Игроки по очереди соединяют отрезками своих цветов любые две ещё не соединённые отрезком точки. Игрок, который нарисовал треугольник, проиграл.
Партия заканчивается вничью, если новый отрезок больше провести невозможно, при этом одноцветных треугольников не возникло.
Заполним таблицу турнира:

Игрок \ Партия	Я	Игрок 2	Игрок 3	Игрок 4	Очки	Место
Я	*	2	1	0	3	2
Игрок 2	0	*	1	2	3	2
Игрок 3	1	1	*	0	2	4
Игрок 4	2	0	2	*	4	1

Номер №37
Цепочка Z на следующей странице — это начало партии игры сим на окружности с пятью точками. Первый рисует отрезки синим, а Второй — зелёным. Закончи цепочку Z так, чтобы она стала цепочкой позиций партии в сим.
Убедись, что последняя бусина цепочки Z — это заключительная позиция партии в сим:
а) Есть ли на поле одноцветный треугольник?
б) Если одноцветного треугольника нет, то все ли пары точек соединены?
Чем закончилась партия Z? Поставь галочку в клетке рядом с верным ответом.
Выиграл Первый _
Выиграл Второй _
Ничья _

Решение

Закончим цепочку Z:

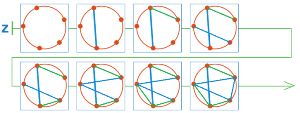
Убедимся, что последняя бусина цепочки Z — это заключительная позиция партии в сим:
а) На поле есть одноцветный треугольник.
б) На поле есть одноцветный треугольник.
Чем закончилась партия Z? Поставь галочку в клетке рядом с верным ответом.
Выиграл Первый _
Выиграл Второй √
Ничья _

Номер №38
Покажи, как разрезать фигуру Y на 3 одинаковые фигуры, — начерти линии разреза.

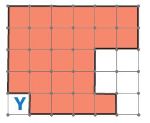
Решение

Фигура Y, разделенная на 3 одинаковые фигуры:

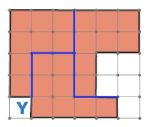
Номер №39
Цепочка W — это цепочка партии игры ползунок (ходы игроков не нарисованы). Первый рисует красным карандашом, Второй — зелёным. Нарисуй ходы игроков на полях цепочки W так, чтобы в этой партии на одиннадцатом ходу выиграл Первый.
Теперь нарисуй ходы игроков на полях цепочки F так, чтобы в этой партии на десятом ходу выиграл Второй.

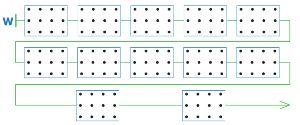
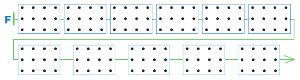
Решение

Нарисуем ходы игроков в цепочке W, чтобы в этой партии на одиннадцатом ходу выиграл Первый:

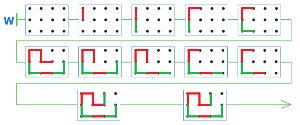
Нарисуем ходы игроков в цепочке F, чтобы в этой партии на десятом ходу выиграл Второй:

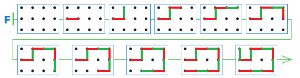
Номер №40
Вот начало некоторой партии игры сим. Дострой цепочку R так, чтобы в этой партии выиграл Второй.
Убедись, что последняя бусина цепочки R является заключительной позицией партии, в которой выиграл Второй: на поле должен быть треугольник из синих отрезков и не должно быть треугольника из зелёных отрезков.

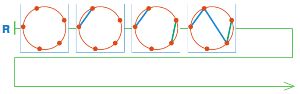
Решение

Достроим цепочку R, чтобы в этой партии выиграл Второй:

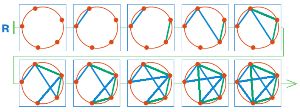
Номер №41
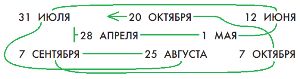
Вот даты одного календарного года. Соедини эти даты в цепочку так, чтобы они шли друг за другом в календарном порядке.

31 ИЮЛЯ
20 ОКТЯБРЯ
12 ИЮНЯ
28 АПРЕЛЯ
1 МАЯ
7 СЕНТЯБРЯ
25 АВГУСТА
7 ОКТЯБРЯ

Решение

Соединим даты в цепочку:

Номер №42
Выполни склеивание мешков G и R — заполни таблицу.

Решение

Мешок G \ Мешок R	КРАСНЫЙ	ОРАНЖЕВЫЙ	СИНИЙ	ЗЕЛЁНЫЙ
СВЕТЛО−	СВЕТЛО−КРАСНЫЙ	СВЕТЛО−ОРАНЖЕВЫЙ	СВЕТЛО−СИНИЙ	СВЕТЛО−ЗЕЛЁНЫЙ
ЯРКО−	ЯРКО−КРАСНЫЙ	ЯРКО−ОРАНЖЕВЫЙ	ЯРКО−СИНИЙ	ЯРКО−ЗЕЛЁНЫЙ
ТЁМНО−	ТЁМНО−КРАСНЫЙ	ТЁМНО−ОРАНЖЕВЫЙ	ТЁМНО−СИНИЙ	ТЁМНО−ЗЕЛЁНЫЙ

Номер №43
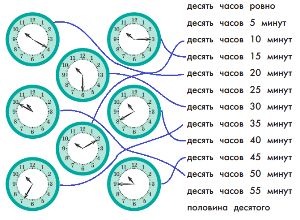
Соедини каждые часы с названием времени, которое они показывают.

↓↑
десять часов ровно
десять часов 5 минут
десять часов 10 минут
десять часов 15 минут
десять часов 20 минут
десять часов 25 минут
десять часов 30 минут
десять часов 35 минут
десять часов 40 минут
десять часов 45 минут
десять часов 50 минут
десять часов 55 минут
половина десятого

Решение

Задачи для самопроверки 44-49

Задачи для самопроверки
Номер №44
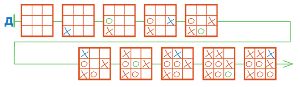
Маша и Сима сыграли партию в крестики−нолики. Маша была Первой, Сима — Второй. Дострой цепочку Д так, чтобы она стала цепочкой партии Маши и Симы.
Чем закончилась партия Д? Поставь галочку в клетке рядом с верным ответом.
Выиграла Маша _
Выиграла Сима _
Ничья _

Решение

Достроим цепочку Д:

Чем закончилась партия Д?
Выиграла Маша √
Выиграла Сима _
Ничья _

Номер №45
Построй в первом окне цепочку партии игры камешки, в которой выиграл Первый (начальная позиция — 6 камешков, можно брать 1, 3 или 4 камешка за ход).
Во втором окне построй цепочку партии (этой же игры), в которой выиграл Второй.

Решение

Построим цепочку партии, в которой выиграл Первый:

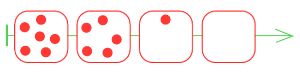
Построим цепочку партии, в которой выиграл Второй:

Номер №46
Дорисуй в первом окне заключительную позицию партии в ползунок на поле 4х3 точки, в которой выиграл Первый.
Дорисуй во втором окне заключительную позицию партии в ползунок на поле 4х3 точки, в которой выиграл Второй.

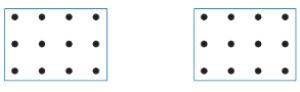
Решение

Дорисуем заключительную позицию партии, в которой выиграл Первый:

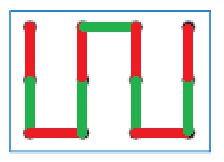
Дорисуем заключительную позицию партии, в которой выиграл Второй:

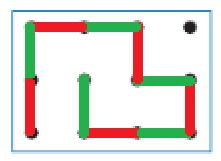
Номер №47
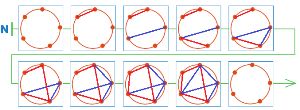
Вот незаполненная цепочка N партии в сим. Дорисуй позиции так, чтобы партия с цепочкой N закончилась выигрышем Первого (Первый рисует красные отрезки, Второй — синие).
Убедись, что в партии с цепочкой N выиграл Первый: на поле должен быть треугольник из синих отрезков и не должно быть треугольника из красных отрезков.

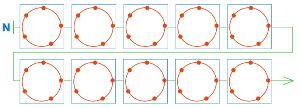
Решение

Дорисуем позиции в цепочке N:

Номер №48
Упорядочи все слова из мешка R по правилу обратного словаря, описанному тобой при решении задачи 35. Построй цепочку слов в окне.

Решение

Построим цепочку слов:

⇓
БУЛКА
СОК
СИРОП
КОМПОТ
ШПРОТЫ
⇓

Номер №49
Раскрась фигурки в мешках так, чтобы эти два мешка стали одинаковыми.

Решение

Одинаковые мешки:

Выигрышная стратегия и позиция 50-58

ВЫИГРЫШНАЯ СТРАТЕГИЯ
Выигрышная стратегия. Выигрышная позиция
Номер №50
Для игры камешки с теми же разрешёнными ходами, что и на листе определений (можно брать 1, 3 или 4 камешка), докрась числовую линейку — раскрась красным или синим позиции с 9−й по 15−ю.
Теперь, пользуясь раскрашенной линейкой, ответь на вопросы.
Какой ход должен сделать игрок (сколько камешков взять) из позиции 8, чтобы противнику досталась проигрышная позиция? _
Какой ход должен сделать игрок (сколько камешков взять) из позиции 11, чтобы противнику досталась проигрышная позиция? _
Какой ход должен сделать игрок (сколько камешков взять) из позиции 15, чтобы противнику досталась проигрышная позиция? _
Нарисуй в окне цепочку такой разумной партии в камешки по этим правилам с начальной позицией 15, в которой выигрывает Первый.

Решение

Числовая линейка с выигрышными позициями:

Ответы на вопросы:
Какой ход должен сделать игрок (сколько камешков взять) из позиции 8, чтобы противнику досталась проигрышная позиция? 1
Какой ход должен сделать игрок (сколько камешков взять) из позиции 11, чтобы противнику досталась проигрышная позиция? 4
Какой ход должен сделать игрок (сколько камешков взять) из позиции 15, чтобы противнику досталась проигрышная позиция? 1
Цепочки партии в камешки с начальной позицией 15, в которой выигрывает Первый:

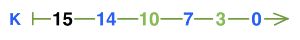
Номер №51
Для игры камешки с начальной позицией 12 камешков, в которой можно брать 1 или 2 камешка за ход, найди выигрышные и проигрышные позиции, раскрась числовую линейку до 12. Пользуясь раскрашенной линейкой, ответь на вопросы на этой и следующей страницах.
Какой ход должен сделать игрок (сколько камешков взять) из позиции 5, чтобы противнику досталась проигрышная
позиция? _
Какой ход должен сделать игрок (сколько камешков взять) из позиции 10, чтобы противнику досталась проигрышная позиция? _
Нарисуй в окне цепочку разумной партии в камешки по этим правилам с начальной позицией 12 камешков, в которой выигрывает Второй.

Решение

Числовая линейка выигрышных и проигрышных позиций:

Ответы на. вопросы:
Какой ход должен сделать игрок (сколько камешков взять) из позиции 5, чтобы противнику досталась проигрышная
позиция? 2
Какой ход должен сделать игрок (сколько камешков взять) из позиции 10, чтобы противнику досталась проигрышная позиция? 1
Цепочки партии в камешки с начальной позицией 12 камешков, в которой выигрывает Второй: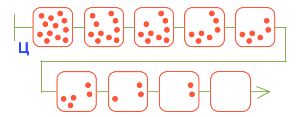

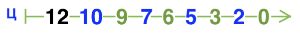
Номер №52
Найди выигрышные и проигрышные позиции для игры камешки с начальной позицией 11 камешков, в которой можно брать 1 или 3 камешка за ход, раскрась числовую линейку до 11. Пользуясь раскрашенной линейкой, ответь на вопрос.
Может ли выиграть Второй в партии с начальной позицией 11 камешков? _

Решение

Выигрышные позиции в игре камешки с начальной позицией 11 камешков, в которой можно брать 1 или 3 камешка за ход всегда имеет Первый игрок.
Числовая линейка выигрышных и проигрышных позиций:

Ответ:
Может ли выиграть Второй в партии с начальной позицией 11 камешков? НЕТ

Номер №53
Вот начала двух партий в ползунок. Дострой цепочки К и Л так, чтобы в партии К выиграл Первый, а в партии Л — Второй.

Решение

Достроим цепочку К (выиграл Первый):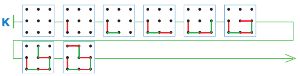

Достроим цепочку Л (выиграл Второй):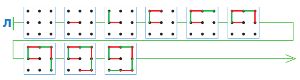

Номер №54
Найди выигрышные и проигрышные позиции для игры камешки с начальной позицией 15 камешков, в которой можно брать 1, 2 или 3 камешка за ход, раскрась числовую линейку до 15. Нарисуй в окне цепочку разумной партии в камешки с такими правилами и начальной позицией 15 камешков.

Решение

Выигрышные позиции для игры камешки с начальной позицией 15 камешков, в которой можно брать 1, 2 или 3 камешка за ход: 1, 2, 3, 5, 6, 7, 9, 10, 11, 13, 14, 15 камешков.
Числовая линейка выигрышных и проигрышных ходов:

Цепочки партии в камешки:

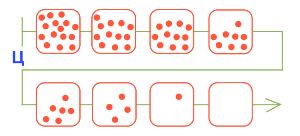
Номер №55
Упорядочи все слова из мешка R по правилу обратного словаря, описанному тобой при решении задачи 35. Построй цепочку слов в окне.

Решение

Построим цепочку слов по правилу обратного словаря:
⇓
ОРАНЖЕВОЕ
ЧЕРНОЕ
СИНИЙ
КРАСНЫЙ
БЕЛЫЙ
ГОЛУБАЯ
ЗЕЛЁНАЯ
ЖЕЛТАЯ
⇓

Номер №56
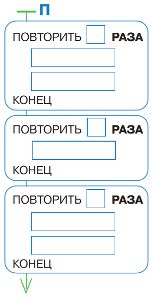
В программе П вместо команд стоят окна, в конструкциях повторения пропущено число повторов. Заполни окна в программе так, чтобы после выполнения программы П из данной начальной позиции получилась указанная позиция.
Начальная позиция:

Позиция после выполнения программы П:

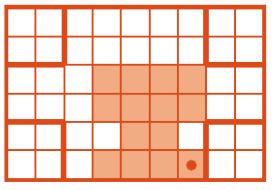
Решение

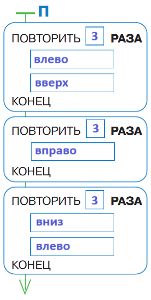
Заполним окна в программе П:

Номер №57
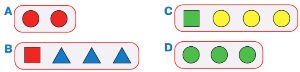
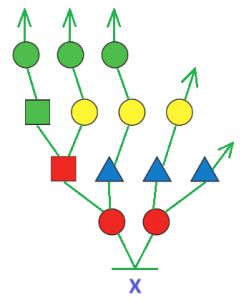
Мешок A — это мешок бусин первого уровня дерева Х. Мешок B — это мешок бусин второго уровня дерева Х. Мешок C — это мешок бусин третьего уровня дерева Х. Мешок D — это мешок бусин четвёртого уровня дерева Х. Нарисуй в окне дерево Х, в котором четыре уровня бусин и для которого истинно утверждение:
В дереве Х нет двух одинаковых цепочек.

Решение

Построим дерево Х:

Номер №58
Напиши в каждом окне одну букву так, чтобы для каждого слова из мешка в словарике было такое же слово. Все слова в словарике — это русские названия птиц.

АИСТ−РАЗИНЯ
ГАГА−ГРЕБЁНУШКА
ГАГАРА
ГУСЬ
ЖУРАВЛЬ
КАНЮК
КОРШУН
ЛЕБЕДЬ−КЛИКУН
ЛЕБЕДЬ−ШИПУН
ОРЁЛ−КАРЛИК
ОРЁЛ−СКОМОРОХ
ТЕТЕРЕВ−МЕЖНЯК
ЧЕГЛОК
ЧИРОК−СВИСТУНОК
ЧИРОК−ТРЕСКУНОК
ЦАПЛЯ−ГОЛИАФ

Решение

Стратегии в игре камешки 59-72

Выигрышные стратегии в игре камешки
Номер №59
Теперь, когда вы знаете о выигрышных стратегиях в игре камешки, устройте соревнование с соседом по парте (можно брать 1 или 2 камешка). Сыграйте четыре партии. Пусть один из вас будет Первым в партиях с чётными номерами, а другой — с нечётными. Начальную позицию в каждой партии выбирает Первый. Для выбора разумного хода пользуйтесь раскрашенным началом числовой линейки для этой игры со с. 41.
Заполни таблицу соревнования (см. на следующей странице). За каждую победу игрок получает 1 очко, за поражение — 0 очков. Определи истинность утверждений.
В каждой партии соревнования выиграл Первый. _
Окончательный счёт соревнования — 2:2. _

Партия \ Игрок
1−я партия
2−я партия
3−я партия
4−я партия
ИТОГО:

Решение

Таблица соревнования:

Партия \ Игрок	Я	СОСЕД
1−я партия	1	0
2−я партия	0	1
3−я партия	1	0
4−я партия	0	1
ИТОГО:	2	2

Истинность утверждений.
В каждой партии соревнования выиграл Первый. И
Окончательный счёт соревнования — 2:2. И

Номер №60
Выясни, у кого из игроков есть выигрышная стратегия в игре камешки с такими правилами начальная позиция — 213 камешков, можно брать 1 или 2 камешка за ход. Можешь воспользоваться началом раскрашенной числовой линейки:
Ответ: выигрышная стратегия есть у _. Он должен на каждом ходу забирать столько камешков, чтобы противнику оставалось _

Решение

Ответ: выигрышная стратегия есть у Второго. Он должен на каждом ходу забирать столько камешков, чтобы противнику оставалось количество камешков, кратное трем.

Номер №61
Выясни, у кого из игроков есть выигрышная стратегия в игре камешки с такими правилами: начальная позиция — 25 камешков, можно брать 1 или 2 камешка за ход. Нарисуй в окне такую цепочку партии этой игры, в которой этот игрок следует своей выигрышной стратегии. Для решения можешь воспользоваться началом раскрашенной числовой линейки из задачи 60.

Решение

Выигрышная стратегия есть у первого игрока, потому что количество камней в начальной позиции не кратно трем.
Цепочка партии: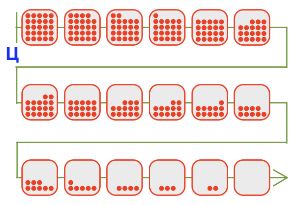

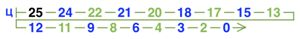
Номер №62
Для игры камешки с теми же ходами, что и на листе определений (можно брать 1, 2 или 3 камешка), продолжи раскрашивание числовой линейки до 18. Ответь на вопросы на следующей странице.
Кто из игроков имеет выигрышную стратегию при игре с такими правилами и начальной позицией 15 камешков? _
Кто из игроков имеет выигрышную стратегию при игре с такими правилами и начальной позицией 16 камешков? _
Нарисуй в первом окне цепочку разумной партии в камешки по этим правилам с начальной позицией 15. Нарисуй во втором окне цепочку разумной партии в камешки по этим правилам с начальной позицией 16.

Решение

Числовая линейка:

Кто из игроков имеет выигрышную стратегию при игре с такими правилами и начальной позицией 15 камешков? Первый
Кто из игроков имеет выигрышную стратегию при игре с такими правилами и начальной позицией 16 камешков? Второй
Цепочки игры в камешки с начальной позицией 15: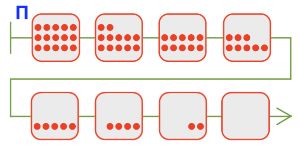

П⇒15-12-10-8-5-4-2-0⇒

Цепочки игры в камешки с начальной позицией 16: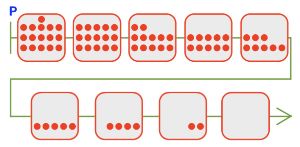

Р⇒16-15-12-10-8-5-4-2-0⇒

Номер №63
Устройте соревнование с соседом по парте в камешки (можно брать 1, 2 или 3 камешка за ход). Сыграйте четыре партии. Пусть один из вас будет Первым в играх с чётными номерами, а другой — с нечётными. Начальную позицию в каждой партии выбирает Первый. Пусть начальная позиция будет больше 20 и меньше 30 камешков. За победу игрок получает 1 очко, за поражение — 0 очков. Старайтесь следовать выигрышной стратегии, если она есть.
Заполни таблицу соревнования, определи истинность утверждений:
Окончательный счёт соревнования — 2:2. _
В каждой партии соревнования выиграл Первый. _

Партия \ Игрок	Я	СОСЕД
1−я партия
2−я партия
3−я партия
4−я партия
ИТОГО:

Решение

Таблица соревнования:

Партия \ Игрок	Я	СОСЕД
1−я партия	0	1
2−я партия	1	0
3−я партия	0	1
4−я партия	1	0
ИТОГО:	2	2

Истинность утверждений.
Окончательный счёт соревнования — 2:2. И
В каждой партии соревнования выиграл Первый. И

Номер №64
Покажи, как разрезать фигуру Y на 3 одинаковые фигуры, — начерти линии разреза.

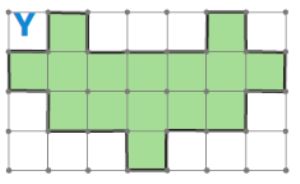
Решение

Линии разреза фигуры Y на 3 одинаковые фигуры:

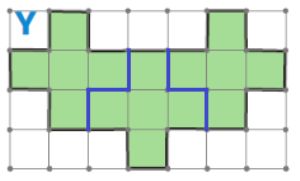
Номер №65
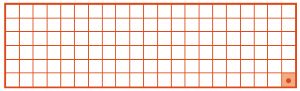
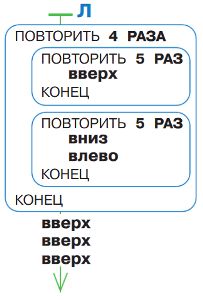
Дорисуй позицию Робика после выполнения программы Л.
Начальная позиция:

Решение

Позиция Робика после выполнения программы Л:

Номер №66
Нарисуй на каждом циферблате стрелки так, чтобы часы показывали то время, какое указано. Следи, чтобы минутная стрелка была длиннее часовой.

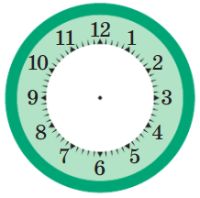
ровно два часа

половина девятого

половина одиннадцатого

половина первого

Решение

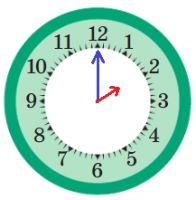
ровно два часа

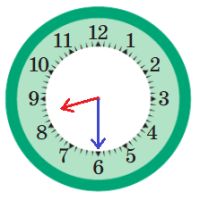
половина девятого

половина одиннадцатого

половина первого

Номер №67
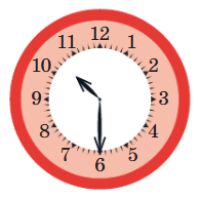
Ответь на вопросы — напиши ответ в окне рядом с каждым вопросом.
Какое время показывали часы 3 часа назад? _
Какое время показывали часы полчаса назад? _
Какое время будут показывать часы через полтора часа? _

Решение

Какое время показывали часы 3 часа назад? Половину восьмого
Какое время показывали часы полчаса назад? Десять часов ровно
Какое время будут показывать часы через полтора часа? Двенадцать часов ровно

Номер №68
Используя числовую линейку, раскрашенную в ходе решения задачи 62, выясни, кто из игроков имеет выигрышную стратегию в такой игре камешки: начальная позиция — 212 камешков, можно брать 1, 2 или 3 камешка за ход. Заполни окна в ответе.
Ответ: выигрышную стратегию имеет _. Он должен на каждом ходу забирать столько камешков, чтобы противнику оставалось _

Решение

Числовая линейка, раскрашенная в задаче 62:

Ответ: выигрышную стратегию имеет второй игрок. Он должен на каждом ходу забирать столько камешков, чтобы противнику оставалось число камешков, кратное четырем.

Номер №69
Маша составила конструкцию из 9 шестерёнок. Красная шестерёнка крутится по часовой стрелке. В какую сторону крутится синяя шестерёнка? Укажи стрелками направление вращения каждой шестерёнки, допиши ответ.
Ответ: синяя шестерёнка крутится _ часовой стрелок_.

Решение

Ответ: синяя шестерёнка крутится по часовой стрелке.

Номер №70
Заполни таблицу так, чтобы получилась таблица склеивания мешков Z и X чисел и чтобы мешок Z ⓧ X был мешком всех трёхзначных чисел, в записи которых участвуют только цифры 1, 2 и 3.

Решение

Мешок Z \ Мешок X	11	12	13	21	22	23	31	32	33
1	111	112	113	121	122	123	131	132	133
2	211	212	213	221	222	223	231	232	233
3	311	312	313	321	322	323	331	332	333

Номер №71
Дана программа Т, в которой пропущены некоторые команды, и позиция Робика после выполнения этой программы (положение Робика не указано). Напиши в окнах программы пропущенные команды — в каждом окне по одной команде. Отметь положение Робика на поле до и после выполнения программы Т.
Начальная позиция:

Позиция после выполнения программы Т: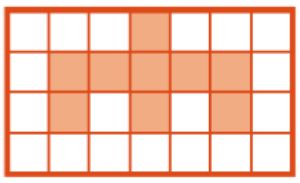

⇓ Т
_____
_____
_____
_____
ВНИЗ
ВВЕРХ
ВВЕРХ
_____
_____
_____
_____
⇓

Решение

Начальная позиция:

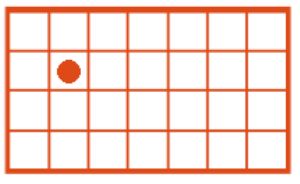
Программа Т:

⇓ Т
ВНИЗ
ВВЕРХ
ВПРАВО
ВПРАВО
ВНИЗ
ВВЕРХ
ВВЕРХ
ВНИЗ
ВПРАВО
ВПРАВО
ВНИЗ
⇓
Позиция после выполнения программы Т: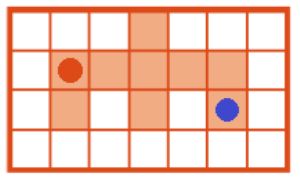

Номер №72
Покажи, как разрезать фигуру R на 3 одинаковые фигуры, — начерти линии разреза.

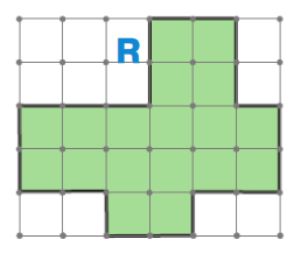
Решение

Линии разреза фигуры R на 3 одинаковые фигуры:

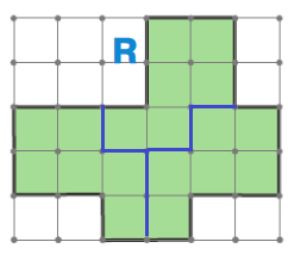
Задачи для самопроверки 73,74

Задачи для самопроверки
Номер №73
Раскрась числовую линейку до 30 для игры камешки, в которой можно брать 1, 2 или 4 камешка. Ответь на вопросы.
Кто из игроков имеет выигрышную стратегию при игре с такими правилами и начальной позицией 19 камешков? _
Кто из игроков имеет выигрышную стратегию при игре с такими правилами и начальной позицией 21 камешек? _
Нарисуй в первом окне цепочку разумной партии в камешки по этим правилам с начальной позицией 19. Нарисуй во втором окне цепочку разумной партии в камешки по этим правилам с начальной позицией 21.

Решение

Числовая линейка до 30 для игры камешки, в которой можно брать 1, 2 или 4 камешка:

Кто из игроков имеет выигрышную стратегию при игре с такими правилами и начальной позицией 19 камешков? Первый игрок
Кто из игроков имеет выигрышную стратегию при игре с такими правилами и начальной позицией 21 камешек? Второй игрок
Цепочка партии в камешки с начальной позицией 19:

Г⇒19-15-11-9-5-3-2-0⇒

Цепочка партии в камешки с начальной позицией 21:

Г⇒21-19-15-11-9-5-3-2-0⇒

Номер №74
Устройте соревнование с соседом по парте в камешки (можно брать 1, 2 или 4 камешка за ход). Сыграйте четыре партии. Пусть один из вас будет Первым в играх с чётными номерами, а другой — с нечётными. Начальную позицию в каждой партии выбирает Первый. Пусть начальная позиция будет больше 20 и меньше 380 камешков. За победу игрок получает 1 очко, за поражение — 0 очков. Старайтесь следовать выигрышной стратегии, если она есть.
Заполни таблицу соревнования, определи истинность утверждений:
Окончательный счёт соревнования — 2:2. _
В каждой партии соревнования выиграл Первый. _

Партия \ Игрок	Я	СОСЕД
1−я партия
2−я партия
3−я партия
4−я партия
ИТОГО:

Решение

Таблица соревнования:

Партия \ Игрок	Я	СОСЕД
1−я партия	1	0
2−я партия	0	1
3−я партия	1	0
4−я партия	0	1
ИТОГО:	2	2

Истинность утверждений:
Окончательный счёт соревнования — 2:2. И
В каждой партии соревнования выиграл Первый. И

Дерево игры 75-82

ДЕРЕВЬЯ
Дерево игры
Номер №75
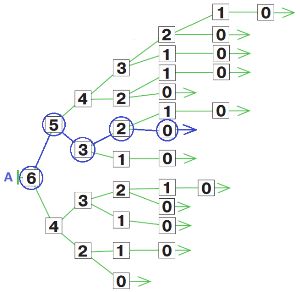
Нарисуй в первом окне дерево игры камешки с такими правилами: начальная позиция — 6 камешков, за ход разрешается брать 1 или 2 камешка. Назови дерево именем А.
Проверь, все ли листья дерева А — заключительные позиции игры камешки (попросту говоря, нули).
Нарисуй во втором окне цепочку какой−нибудь партии в камешки (с теми же правилами), в которой выиграл Первый. Найди и обведи красным цепочку в дереве А, которая соответствует этой партии.
Нарисуй в третьем окне цепочку какой−нибудь партии в камешки (с теми же правилами), в которой выиграл Второй. Найди и обведи синим цепочку в дереве А, которая соответствует этой партии.

Решение

Нарисуем дерево А:

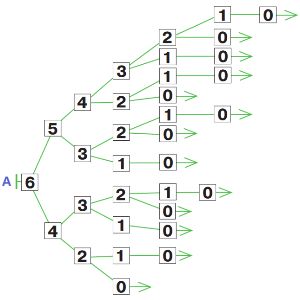
Нарисуем цепочку партии, в которой выиграл Первый:

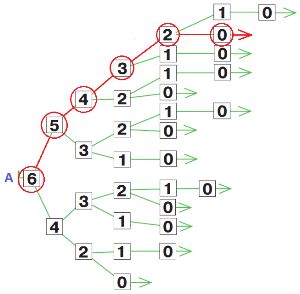
Нарисуем цепочку партии, в которой выиграл Второй:

Номер №76
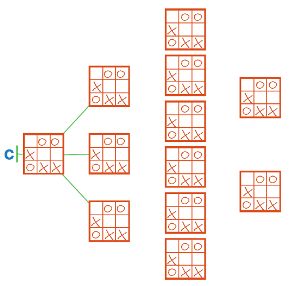
Дерево С (см. на следующей странице) — это ветка дерева игры крестики−нолики. Дорисуй крестики и нолики на позициях второго, третьего и четвёртого уровней дерева С, добавь нужные линии и стрелки.
Проверь своё решение: убедись, что все листья дерева С — заключительные позиции игры крестики−нолики.
Теперь обведи в дереве С заключительные позиции всех партий, в которых выиграл Первый, красным. Сколько получилось таких листьев? _
Обведи в дереве С заключительные позиции всех партий, в которых выиграл Второй, синим. Сколько получилось таких листьев? _
Обведи в дереве С заключительные позиции всех партий, которые закончились вничью, зелёным. Сколько получилось таких листьев? _

Решение

Дорисуем дерево С:

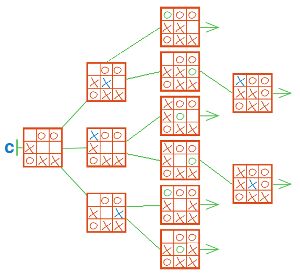
Теперь обведи в дереве С заключительные позиции всех партий, в которых выиграл Первый, красным. Сколько получилось таких листьев? 2

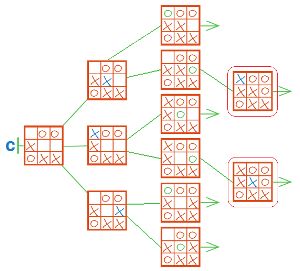
Обведи в дереве С заключительные позиции всех партий, в которых выиграл Второй, синим. Сколько получилось таких листьев? 4

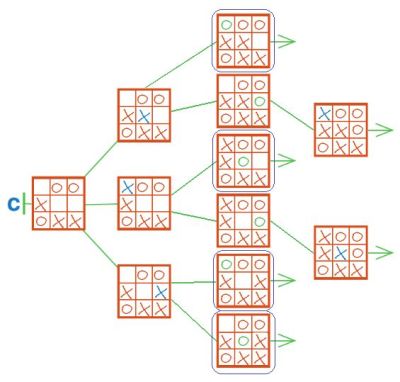
Обведи в дереве С заключительные позиции всех партий, которые закончились вничью, зелёным. Сколько получилось таких листьев? 0

Номер №77
В сутках 24 часа, часовая стрелка за сутки проходит два полных круга на циферблате. Сутки начинаются в полночь, в этот момент часы со стрелками показывают ровно 12 ч, а цифровые часы — ровно 0 ч. В полдень (через 12 ч после полуночи) часы со стрелками показывают снова ровно 12 ч и цифровые часы тоже показывают ровно 12 ч. Через один час после полудня часы со стрелками покажут ровно 1 ч — это 1 час дня. Цифровые часы в этот момент будут показывать ровно 13 ч: (12 + 1) час.
Напиши показания цифровых часов на то время, которое показывают часы со стрелками.
до полудня: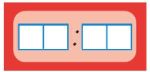

после полудня:

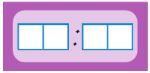
Решение

до полудня:

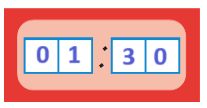
после полудня:

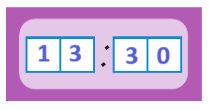
Номер №78
Для каждых часов со стрелками напиши показания цифровых часов в это же время: до полудня и после полудня.

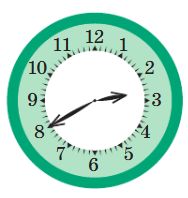
до полудня:

после полудня:

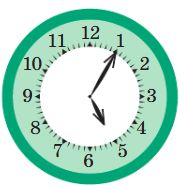
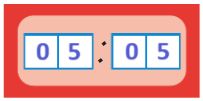
до полудня:

после полудня:

Решение

до полудня: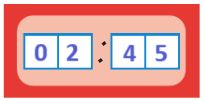

после полудня:

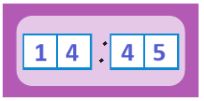
до полудня:

после полудня: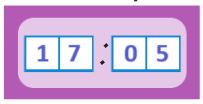

Номер №79
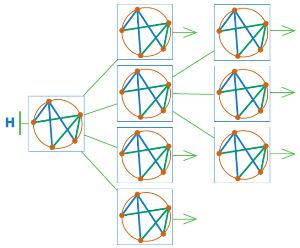
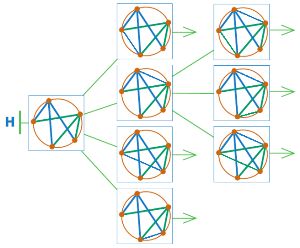
Дорисуй дерево Н — ветку дерева игры сим: позицию первого уровня оставь как есть, в остальных позициях дорисуй ходы. Ход из позиции первого уровня должен сделать Первый игрок, он рисует синим карандашом.
Проверь, все ли листья дерева Н — заключительные позиции игры сим.

Решение

Дорисуем дерево Н:

Номер №80
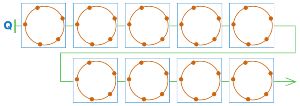
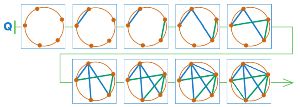
Вот незаполненная цепочка Q партии в сим. Дорисуй позиции так, чтобы окончание этой партии было цепочкой из дерева Н из задачи 79 и партия с цепочкой Q закончилась выигрышем Первого.

Решение

Дорисуем позиции в цепочке Q (выигрыш Первого):

Номер №81
Дана начальная позиция Робика. Напиши в окне программу, после выполнения которой Робик окажется в правом верхнем углу поля. Назови программу именем С. Дорисуй позицию Робика после выполнения программы С.
Начальная позиция:

Решение

Напишем программу С:
⇓ С
ВПРАВО
ВПРАВО
ВВЕРХ
ВЛЕВО
ВВЕРХ
ВПРАВО
ВПРАВО
ВВЕРХ
ВВЕРХ
ВПРАВО
ВВЕРХ
ВПРАВО
ВНИЗ
ВПРАВО
ВВЕРХ
ВПРАВО
ВВЕРХ
ВПРАВО
⇓
Дорисуем позицию Робика после выполнения программы С:

Номер №82
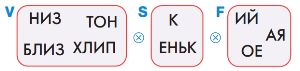
Вспомни: результатом склеивания трёх мешков будет мешок всех таких цепочек, которые получаются при склеивании цепочки из первого мешка, цепочки из второго мешка и цепочки из третьего мешка. Построй мешок V ⓧ S ⓧ F.
Проверь своё решение: для этого сначала вычисли, сколько всего цепочек должно получиться в результате склеивания мешков, в которых 4, 2 и 3 цепочки.

Решение

Вычислим, сколько всего цепочек должно получиться в результате склеивания мешков, в которых 4, 2 и 3 цепочки:
4 * 2 * 3 = 24
Построим мешок V ⓧ S ⓧ F:

Позиции на дереве игры 83-88

Исследуем позиции на дереве игры
Номер №83
Нарисуй в первом окне дерево игры камешки с такими правилами: начальная позиция — 6 камешков, за ход разрешается брать 1 или 3 камешка. Назови дерево именем А.
Рассмотри позиции твоего дерева А: обведи в нём все выигрышные позиции красным, проигрышные — синим. Кто из игроков имеет выигрышную стратегию в этой игре? _
Нарисуй во втором окне цепочку какой−нибудь такой партии игры камешки с этими правилами, в которой этот игрок следует выигрышной стратегии.

Решение

Дерево А игры камешки с начальной позицией 6 камешков:

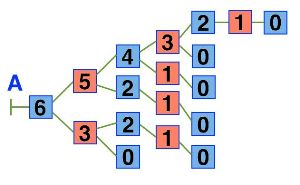
Кто из игроков имеет выигрышную стратегию в этой игре? Второй
Цепочка партии игры камешки, в которой игрок следует выигрышной стратегии:

Номер №84
Дерево L (см. на следующей странице) — это ветка дерева игры ползунок. В каждой позиции отмечены цветом отрезки, появляющиеся на каждом ходу: красным — ходы Первого, зелёным — ходы Второго. Исследуй позиции дерева L: обведи выигрышные позиции красным, проигрышные — синим. Кто из игроков имеет выигрышную стратегию в позиции первого уровня?
Построй в окне какую−нибудь цепочку окончания игры из позиции первого уровня, в которой этот игрок следует выигрышной стратегии. Вырезай игровые поля из вкладыша, наклеивай в окно и рисуй на них ходы игроков.

Решение

Выигрышную стратегию в позиции первого уровня имеет Второй игрок.
Построим цепочку окончания игры из позиции первого уровня:

Номер №85
Мешок М — это мешок целых чисел от 20 до 29. Нарисуй два мешка К и Л, в каждом из которых есть непустая цепочка цифр и таких, что К ⓧ Л = М.

Решение

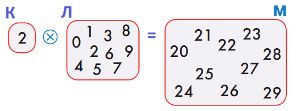
Номер №86
Нарисуй в первом окне дерево игры камешки с такими правилами: начальная позиция — 5 камешков, за ход разрешается брать 1, 3 или 4 камешка. Назови дерево именем D.
Рассмотри позиции твоего дерева D: обведи в нём все выигрышные позиции красным, проигрышные — синим. Кто из игроков имеет выигрышную стратегию в этой игре? _
Нарисуй во втором окне цепочку какой−нибудь такой партии игры камешки с этими правилами, в которой этот игрок следует выигрышной стратегии.

Решение

Дерево игры камешки с начальной позицией 5 камешков, за ход разрешается брать 1, 3 или 4 камешка:

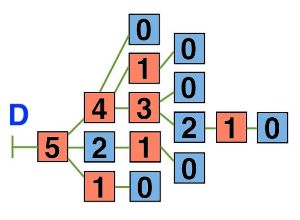
Кто из игроков имеет выигрышную стратегию в этой игре? Первый игрок
Цепочку партии игры камешки, в которой игрок следует выигрышной стратегии:

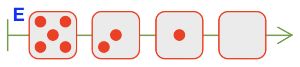
Номер №87
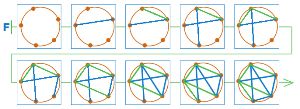
Нарисуй в первом окне цепочку такой партии в сим на окружности с четырьмя точками, которая закончилась ничьей. Воспользуйся заготовками со вкладыша тетради проектов.
Подумай, может ли партия в сим на окружности с тремя точками закончиться иначе, чем вничью. Если да, то нарисуй во втором окне заключительную позицию такой партии.

Решение

Цепочка партии в сим на окружности с четырьмя точками, которая закончилась ничьей:

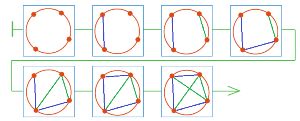
Партия в син на окружности с тремя точками не может закончиться иначе, чем вничью. Потому что если на окружности имеется всего три точки, то и линий, которые их соединяют может быть нарисовано всего три. При этом соединяя точки линиями по очереди, две из них будут нарисованы одним игроком, одна — вторым игроком. Следовательно ни один из игроков не сможет нарисовать три линии, минимальное количество линий, для того, чтобы образовался треугольник.

Номер №88
Правила игры крестики−нолики допускают ничью. Заключительные позиции с ничьей — это ни выигрышные, ни проигрышные позиции. Но в дереве игры крестики−нолики есть такие ветки, которые не содержат листьев с ничейными заключительными позициями. Позиции на такой ветке можно исследовать так же, как позиции игры камешки или ползунок.
Дорисуй дерево Q так, чтобы оно стало веткой дерева игры крестики−нолики. Позицию первого уровня оставь такой, как есть, а в остальных позициях нарисуй следующие ходы игроков и проведи линии между позициями.
Исследуй позиции дерева Q: обведи выигрышные позиции красным, проигрышные позиции — синим (ничейных заключительных позиций в дереве Q нет).
Построй в окне какую−нибудь цепочку из дерева Q длины 5 — окончание партии, которая завершилась выигрышем Первого. Воспользуйся заготовками со вкладыша тетради проектов.

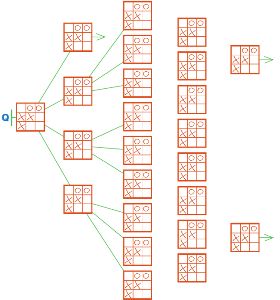
Решение

Дорисуем дерево Q:

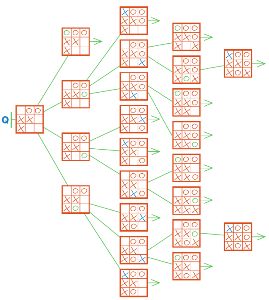
Исследуем позиции дерева Q:

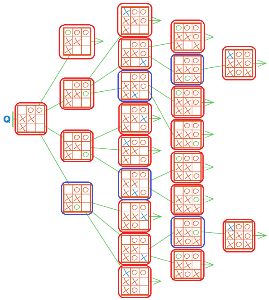
Построим цепочку из дерева Q длины 5 — окончание партии, которая завершилась выигрышем Первого:

Дополнительные задачи 89-106

Дополнительные задачи
Номер №89
Выясни, у кого из игроков есть выигрышная стратегия в игре камешки с такими правилами: начальная позиция — 62 камешка, можно брать 1, 2 или 4 камешка за ход.
Ответ: выигрышная стратегия есть у _.
А у кого есть выигрышная стратегия в такой же игре, но с начальной позицией в 60 камешков?
Ответ: выигрышная стратегия есть у _.

Решение

Для понимания воспользуемся числовой прямой, которую делали для задания 73 для игры в камешки с теми же правилами:

На числовой прямой мы видим, что проигрышные позиции находятся на числах, которые кратны трем. Значит начальная позиция 62 камешка — выигрышная. А начальная позиция 60 — проигрышная.
Выясни, у кого из игроков есть выигрышная стратегия в игре камешки с такими правилами: начальная позиция — 62 камешка, можно брать 1, 2 или 4 камешка за ход.
Ответ: выигрышная стратегия есть у первого игрока.
А у кого есть выигрышная стратегия в такой же игре, но с начальной позицией в 60 камешков?
Ответ: выигрышная стратегия есть у второго игрока.

Номер №90
Нарисуй в первом окне дерево игры камешки с такими правилами: начальная позиция — 6 камешков, за ход разрешается брать 1, 3 или 4 камешка. Назови дерево именем D.
Рассмотри позиции твоего дерева D: обведи в нём все выигрышные позиции красным, проигрышные — синим. Кто из игроков имеет выигрышную стратегию в этой игре? _
Нарисуй во втором окне цепочку какой−нибудь такой партии игры камешки с этими правилами, в которой этот игрок следует выигрышной стратегии.

Решение

Дерево игры камешки D с начальной позицией 6 камешков, за ход разрешается брать 1, 3 или 4 камешка:

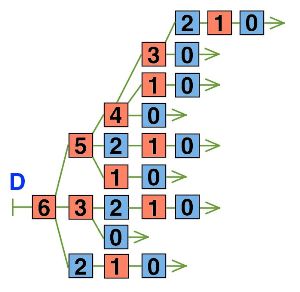
Кто из игроков имеет выигрышную стратегию в этой игре? первый игрок
Цепочка партии игры камешки, в которой первый игрок следует выигрышной стратегии:

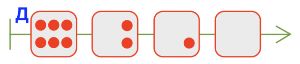
Д⇒6-2-1-0⇒

Номер №91
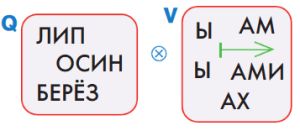
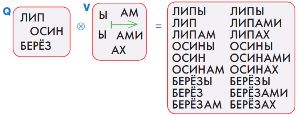
В мешке Q лежат основы русских слов, в мешке V — окончания существительных. При склеивании мешков Q и V получится мешок русских слов, причём каждое из слов — во всех падежах. Выполни склеивание мешков, заполни окно.

Решение

Выполним склеивание мешков:

Номер №92
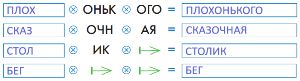
Вот равенства, в которых с корнем слова склеиваются суффикс и окончание. В каждом равенстве придумай и запиши в первое окно корень слова так, чтобы при склеивании его с указанными суффиксом и окончанием получилось русское слово. Заполни окна.

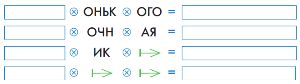
Решение

Номер №93
Нарисуй в первом окне дерево игры камешки с такими правилами: начальная позиция — 6 камешков, за ход разрешается брать 1, 2 или 4 камешка. Назови дерево именем F.
Рассмотри позиции твоего дерева F: обведи в нём все выигрышные позиции красным, проигрышные — синим. Кто из игроков имеет выигрышную стратегию в этой игре? _
Нарисуй во втором окне цепочку какой−нибудь такой партии игры камешки с этими правилами, в которой этот игрок следует выигрышной стратегии.

Решение

Дерево игры камешки с начальной позицией 6 камешков, за ход разрешается брать 1, 2 или 4 камешка:

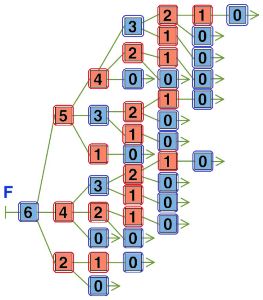
Кто из игроков имеет выигрышную стратегию в этой игре? Второй игрок
Цепочка партии игры камешки, в которой второй игрок следует выигрышной стратегии:

Ф⇒6-2-0⇒

Номер №94
Нарисуй в окне такую цепочку Щ, чтобы все следующие утверждения были истинными:
В цепочке Щ вторая бусина после каждой круглой — синяя.
В цепочке Щ предыдущая бусина перед каждой квадратной — красная.
Мешок Л — это мешок бусин цепочки Щ.

Решение

Номер №95
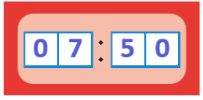
Нарисуй, как расположены стрелки на часах в тот момент, когда цифровые часы показывают данное время после полудня. Для этого сначала напиши в окнах красных цифровых часов, что показывали часы 12 часов назад, до полудня. Не забудь, что минутная стрелка должна быть длиннее часовой.

до полудня:

после полудня:

до полудня:

после полудня:

до полудня:

после полудня:

до полудня:

после полудня: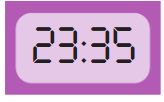

Решение

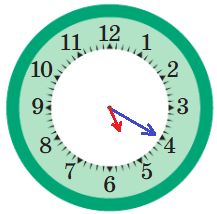
до полудня:

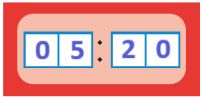
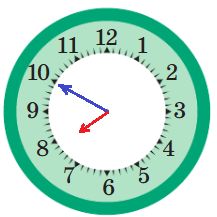
до полудня:

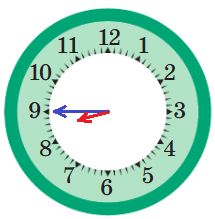
до полудня:

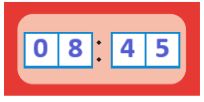
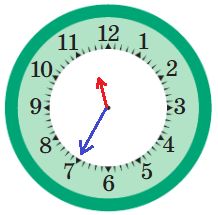
до полудня:

Номер №96
Напротив каждого слова напиши в окне другое русское слово с таким же мешком букв.

ТЯПКА — _
АДРЕС — _
СМОЛА — _

Решение

ТЯПКА — ПЯТКА
АДРЕС — СРЕДА
СМОЛА — МАСЛО

Номер №97
Упорядочи все слова из мешка V по правилу обратного словаря, описанному тобой при решении задачи 35. Построй цепочку слов в окне.

Решение

⇓
ДЯДЕЧКА
ЛЕЕЧКА
КОПЕЕЧКА
ПЕЧКА
БОБ
ГЕРБ
СЕРБ
ДУБ
СРУБ
ГНЕВ
НАГРЕВ
ПРИЛИВ
⇓

Номер №98
В игре Кто первым назовёт число 100 участвуют двое. Первый называет любое число от 1 до 9 включительно. Второй прибавляет к названному числу любое целое число от 1 до 9 и называет новую сумму. И так далее. Выигрывает тот, кто назовёт число 100. У кого из игроков есть выигрышная стратегия? Какая это стратегия?
Эта игра очень похожа на игру камешки, только игроки не забирают камешки, а, наоборот, складывают в кучу, начиная с нуля; в конце должно быть 100 камешков. Для решения задачи, как и раньше, удобно сначала раскрасить часть числовой линейки. Как и в игре камешки, исследовать позиции надо, начиная с заключительной. В этой игре заключительная позиция — 100 камешков.
Ответ: выигрышная стратегия есть у _. На каждом ходу он должен прибавить такое число, чтобы получилось _

Решение

Раскрасим начало числовой прямой, начиная с клетки с цифрой 100, так как это является заключительной позицией:

100

При анализе числовой прямой мы видим, что проигрышные позиции имеют числа, кратные десяти. Так как первый игрок не сможет назвать число 10, значит начальная позиция является проигрышной.
Ответ: выигрышная стратегия есть у второго игрока. На каждом ходу он должен прибавить такое число, чтобы получилось число, кратное десяти.

Номер №99
Мешок П — это мешок целых чисел от 5230 до 5239. Нарисуй два таких мешка Т и Р, в каждом из которых есть непустая цепочка цифр и таких, что Т ⓧ Р = П.

Решение

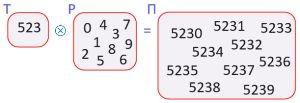
Номер №100
Найди в мешке две цепочки букв, при склеивании которых получится слово русского языка — имя числа. Заполни окна в ответе.

Решение

Имя числа — ДЕВЯНОСТО.

Номер №101
Покажи, как разрезать фигуру S на 4 одинаковые фигуры, — начерти линии разреза.

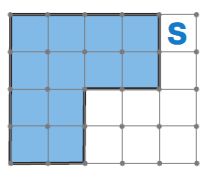
Решение

Линии разреза фигуры S на 4 одинаковые фигуры:

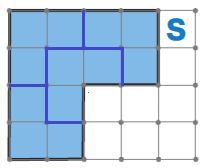
Номер №102
Правила игры сим допускают ничью. Это значит, что в дереве этой игры есть ничейные заключительные позиции, которые не являются ни проигрышными, ни выигрышными.
Дорисуй дерево U (см. на следующей странице). Позицию первого уровня оставь такой, как есть, а в остальных позициях нарисуй следующие ходы игроков. Ход из позиции первого уровня должен сделать Второй, он рисует зелёным карандашом. Проведи линии между позициями так, чтобы получилась ветка дерева игры сим.
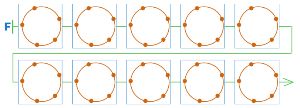
Обведи в дереве U все выигрышные позиции красным, все проигрышные позиции — синим (не забудь, что заключительные позиции с ничьей не являются ни проигрышными, ни выигрышными). После этого в дереве U некоторые позиции останутся непомеченными: пользуясь ими, игрок может свести партию к ничьей. Дорисуй позиции в цепочке F так, чтобы окончание этой партии было цепочкой из дерева U и партия с цепочкой F закончилась выигрышем Второго.

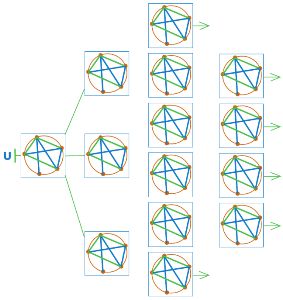
Решение

Дорисуем дерево U:

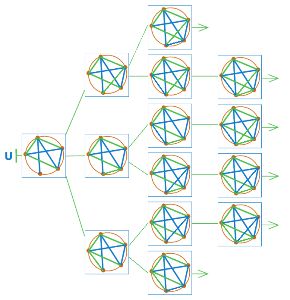
Обведём в дереве U выигрышные (красным) и проигрышные (синим) позиции:

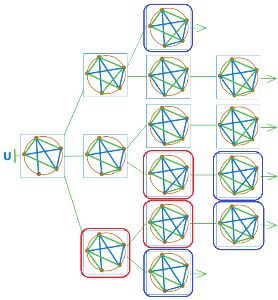
Дорисуем позиции в цепочке F:

Номер №103
Реши задачу:
Четвёртым классам поручили посадить в школьном саду 9 деревьев. Ребята из 4 «А» и из 4 «Б» договорились работать по очереди: в один день после уроков один класс высаживает 1, 2 или 3 дерева, а на следующий день другой класс высаживает 1, 2 или 3 дерева. Было решено назвать победителем ту команду, которая посадит последнее дерево. В первый день выпало работать команде 4 «А». Как команде 4 «А» стать победителем?
Эта задача — пересказ игры камешки. Для её решения удобно сначала раскрасить числовую линейку — пометить на ней выигрышные и проигрышные позиции. Пользуясь раскрашенной числовой линейкой, заполни окна в ответе.

Ответ:
День 1. Сначала 4 «А» должен посадить _ дерево(а), тогда останется _ непосаженных деревьев.
День 2. 4 «Б» может посадить 1, 2 или 3 дерева, тогда останется _‚ _ или _ непосаженных деревьев.
День 3. Теперь 4 «А» должен посадить столько деревьев, чтобы осталось _ непосаженных дерева.
День 4. 4 «Б» может посадить 1, 2 или 3 дерева, тогда останется _, _ или _ непосаженных дерева.
День 5. 4 «А» высаживает все оставшиеся деревья и побеждает.

Решение

Примем за начальную позицию 0 посаженных деревьев, а за конечную позицию 9 посаженных деревьев. Тогда мы можем нарисовать числовую прямую аналогичную игре в камешки:

В первый день команда из 4 «А» имеет выигрышную позицию.
Ответ:
День 1. Сначала 4 «А» должен посадить 1 дерево(а), тогда останется 8 непосаженных деревьев.
День 2. 4 «Б» может посадить 1, 2 или 3 дерева, тогда останется 7‚ 6 или 5 непосаженных деревьев.
День 3. Теперь 4 «А» должен посадить столько деревьев, чтобы осталось 4 непосаженных дерева.
День 4. 4 «Б» может посадить 1, 2 или 3 дерева, тогда останется 3, 2 или 1 непосаженных дерева.
День 5. 4 «А» высаживает все оставшиеся деревья и побеждает.

Номер №104
Обведи красным три слова, мешки букв которых одинаковые.

ПАРАДНЫЙ
ПРИМЕРКА
РАСКЛАДКА
ПАРАШЮТ
ПРОСАДКА
РАСПАДОК
ПАРАДОКС
ПРОКЛАДКА
ПОДКЛАДКА

Решение

Слова, мешки букв которых одинаковые:

Номер №105
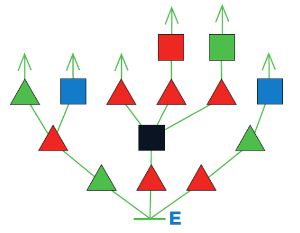
Нарисуй в окне все цепочки из дерева, для которых это утверждение истинно:
В этой цепочке следующая бусина после каждой треугольной красной — квадратная.

Решение

Все цепочки из дерева, в которых следующая бусина после каждой треугольной красной — квадратная:

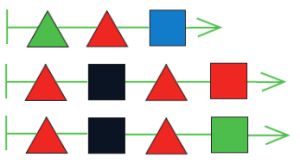
Номер №106
Напиши в каждом окне цепочки Б знак препинания так, чтобы все эти утверждения были истинными:
В цепочке Б многоточие идёт раньше двоеточия.
В цепочке Б открывающая скобка идёт раньше двоеточия.
В цепочке Б тире идёт позже вопросительного знака.
В цепочке Б запятая идёт раньше двоеточия.
В цепочке Б точка идёт раньше закрывающей скобки.
В цепочке Б точка идёт раньше вопросительного знака.
В цепочке Б пятая бусина — вопросительный знак.

Решение

Дерево вычисления 107-119

Дерево вычисления
Номер №107
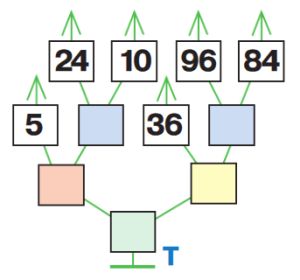
Дано выражение и дерево его вычисления Т. Заполни цветные окна в дереве, напиши в окне значение выражения.
5 * (24 – 10) + 36 : (96 – 84) = _

Решение

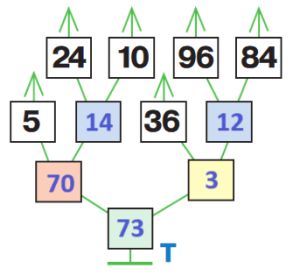
5 * (24 – 10) + 36 : (96 – 84) = 73

Номер №108
Дано выражение и дерево его вычисления S. Заполни цветные окна в дереве, напиши в окне значение выражения.
80 : 16 – 120 : (46 + 14) = _

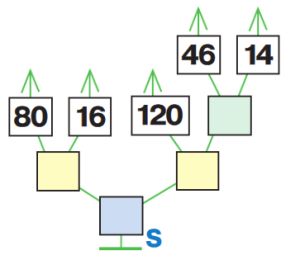
Решение

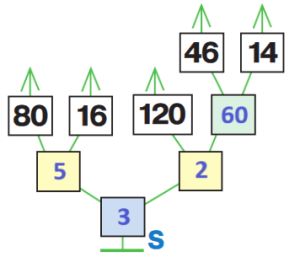
80 : 16 – 120 : (46 + 14) = 3

Номер №109
Дано выражение и дерево его вычисления К. Заполни окна в дереве, напиши в окне значение выражения.
(35 – 15) : (3 + 2) + 3 * (7 + 4) = _

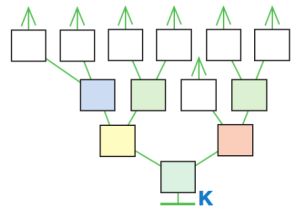
Решение

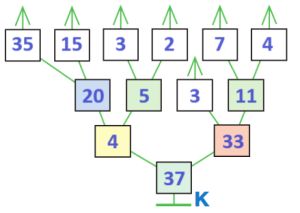
(35 – 15) : (3 + 2) + 3 * (7 + 4) = 37

Номер №110
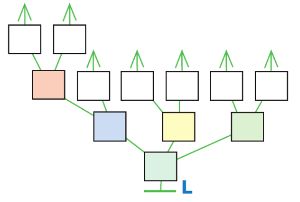
Дано выражение и дерево его вычисления L. Заполни окна в дереве, напиши в окне значение выражения.
(8 * 5 – 10) + 81 : 9 + (8 + 3) = _

Решение

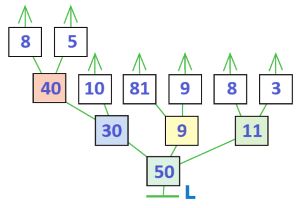
(8 * 5 – 10) + 81 : 9 + (8 + 3) = 50

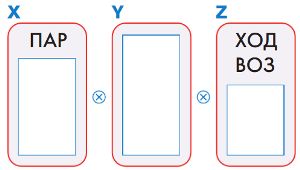
Номер №111
Заполни окна в мешках так, чтобы в мешке X ⓧ Y ⓧ Z было ровно 9 слов и там оказались слова САМОЛЁТ, ПАРОВОЗ и ТЕПЛОХОД.

Решение

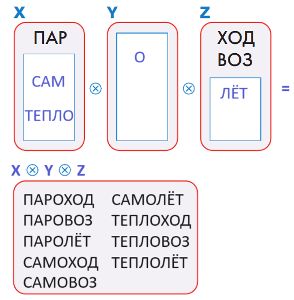
Номер №112
Выясни, у кого из игроков есть выигрышная стратегия в такой игре камешки: начальная позиция — 43 камешка, можно брать 1, 2 или 3 камешка за ход. Заполни окно в ответе. Можешь воспользоваться раскрашенной числовой линейкой из задачи 62.
Ответ: выигрышная стратегия есть у _.

Решение

Числовая линейка из задачи 62:

Проигрышные позиции в данной игре имеются на позициях с числами, кратными четырем. Число 43 не кратно 4, значит первый игрок имеет выигрышную стратегию.
Ответ: выигрышная стратегия есть у первого игрока.

Номер №113
Дано дерево вычисления N. Вычисли значение выражения — заполни цветные окна дерева, затем запиши в окне выражение, значение которого вычислено при помощи этого дерева.

	-умножение
	-деление
	-сложение
	-вычитание

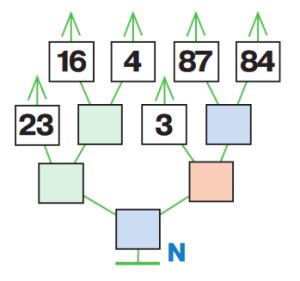
Решение

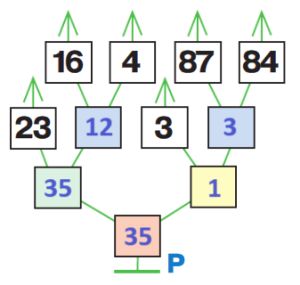
23 + (16 + 4) – 3 * (87 – 84) = 34

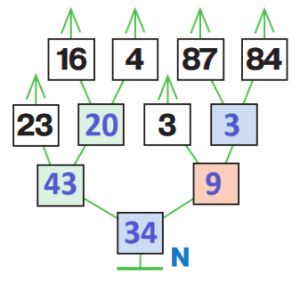
Номер №114
Дано дерево вычисления P. Вычисли значение выражения — заполни цветные окна дерева, затем запиши в окне выражение, значение которого вычислено при помощи этого дерева.

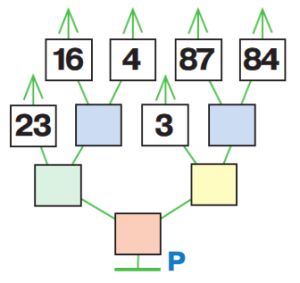
Решение

(23 + (16 – 4)) * (3 : (87 – 84)) = 35

Номер №115
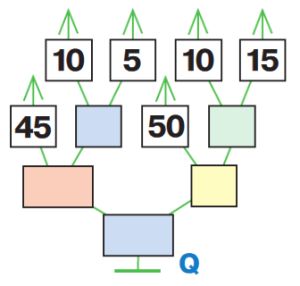
Дано дерево вычисления Q. Расставь скобки в выражении так, чтобы дерево Q стало деревом вычисления значения этого выражения. Заполни цветные окна дерева Q, найди значение выражения.
45 * 10 – 5 – 50 : 10 + 15 = _

Решение

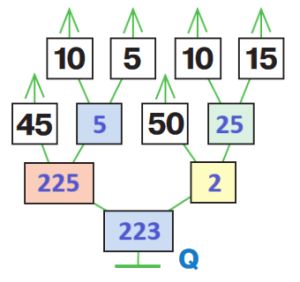
45 * (10 – 5) – 50 : (10 + 15) = 223

Номер №116
Реши задачу, напиши ответ.
Третьим классам поручили посадить 5 деревьев. Ребята из 3 «А» и из 3 «Б» работают по очереди: в один день один класс высаживает 1, 3 или 4 дерева, а на следующий день другой класс высаживает 1, 3 или 4 дерева. Победителем назовут ту команду, которая посадит последнее дерево. Как команде 3 «А» стать победителем, если им выпало работать в первый день?
Для решения задачи построй в первом окне дерево. Затем, пользуясь деревом, опиши во втором окне действия команды 3 «А» (см. образец ответа в задаче 103).

Решение

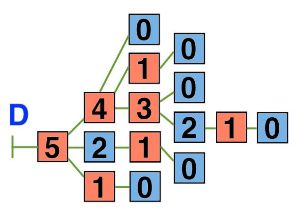
Возьмем за начальную позицию 5 непосаженных деревьев, а за конечную позицию 0 непосаженных деревьев.
Дерево непосаженных деревьев:

Ответ:
Чтобы команде 3 «А» стать победителем, в первый день им нужно посадить 3 дерева. Таким образом останется посадить 2 дерева. Во второй день команде 3 «Б» останется возможность посадить лишь 1 дерево. Останется непосаженным одно дерево. В третий день команда 3 «А» должна посадить 1 последнее дерево, и она станет победителем.

Номер №117
Дана программа R (в которой пропущено несколько команд) и начальная позиция Робика. Напиши в каждом окне команду так, чтобы Робик смог выполнить программу R из данной начальной позиции. Дорисуй позицию Робика после выполнения твоей программы R.
Начальная позиция:

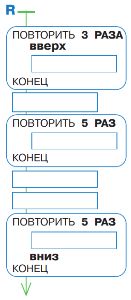
Решение

Напишем программу R:

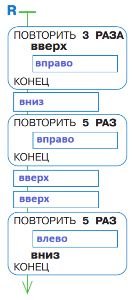
Позиция Робика после выполнения программы R:

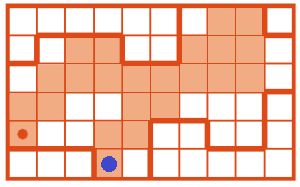
Номер №118
Соедини все фигурки в одну цепочку так, чтобы все эти утверждения были истинными:
В этой цепочке следующая фигурка после каждого страуса — индюк.
В этой цепочке вторая фигурка перед каждым страусом — курица.
В этой цепочке следующая фигурка после каждого гуся — страус.

Решение

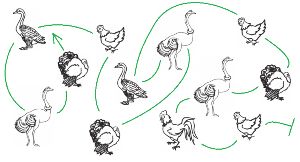
Номер №119
Нарисуй положение стрелок в тот момент, когда цифровые часы показывают данное время.
16:45

18:05

21:20

23:55

Решение

16:45

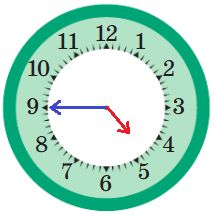
18:05

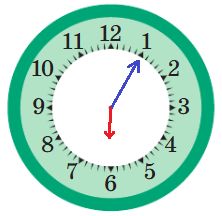
21:20

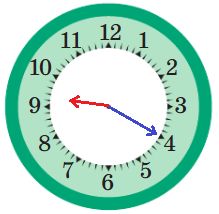
23:55

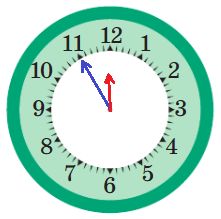
Цепочка выполнения программы 120-130

Робик. Цепочка выполнения программы
Номер №120
Дана начальная позиция Робика и программа H. Дорисуй цепочку Р так, чтобы она стала цепочкой выполнения программы H.
Начальная позиция:

⇓ н
ВНИЗ
ВЛЕВО
ВНИЗ
ВПРАВО
ВНИЗ
⇓

Решение

Дорисуем цепочку Р:

Номер №121
Напиши в окне программу с именем Л так, чтобы цепочка У была цепочкой выполнения программы Л.

Решение

Напишем программу Л:

⇓ Л
ВВЕРХ
ВЛЕВО
ВПРАВО
ВВЕРХ
ВПРАВО
⇓

Номер №122
Даны деревья вычисления Л и М. Для каждого дерева вычисли значение выражения — заполни в дереве цветные окна. Затем запиши выражение для каждого дерева в окне под ним.

	-умножение
	-деление
	-сложение
	-вычитание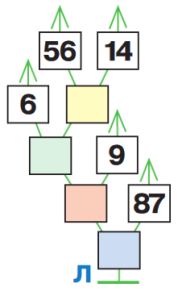

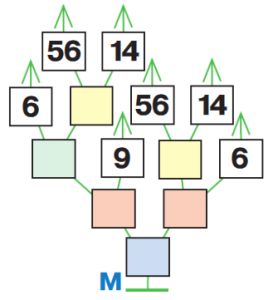
Решение

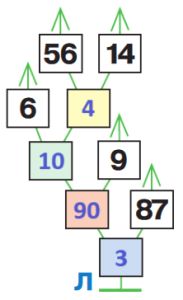
(6 + (56 : 14)) * 9 – 87 = 3

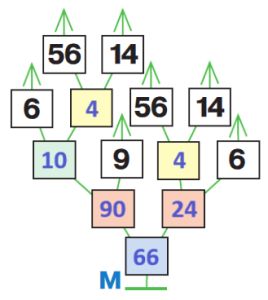
(6 + (56 : 14)) * 9 – ((56 : 14) * 6) = 66

Номер №123
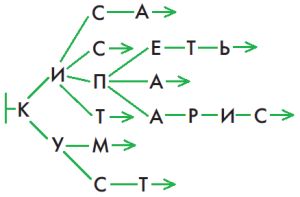
Нарисуй в окне такое дерево букв, чтобы мешок V был мешком всех цепочек из этого дерева и чтобы в дереве было ровно 19 букв.

Решение

Номер №124
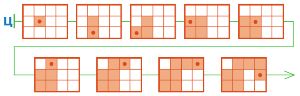
Догадайся, из какого начального положения на поле размером 4х3 Робик сможет выполнить программу Щ — не наткнётся на стену и не сломается. Построй цепочку Ц — цепочку выполнения программы Щ из этого начального положения. Воспользуйся заготовками со вкладыша тетради проектов.
⇓ Щ
ВНИЗ
ВЛЕВО
ВВЕРХ
ВПРАВО
ВВЕРХ
ВПРАВО
ВПРАВО
ВНИЗ
⇓

Решение

Цепочка Ц — цепочка выполнения программы Щ:

Номер №125
Какая стратегия будет выигрышной для Первого в такой игре камешки: начальная позиция — 49 камешков, можно брать 1, 3 или 5 камешков? Для решения можешь раскрасить числовую линейку со вкладыша тетради проектов.
Ответ: Первый должен на каждом ходу забирать столько камешков, чтобы Второму оставалось _.

Решение

Числовая линейка игры камешки с начальной позицией 49 камешков, где можно брать 1, 3 или 5 камешков:

При анализе числовой линейки мы видим, что все клетки с четными числами — проигрышные позиции. Значит, начальная позиция 49 является выигрышной для первого игрока.
Ответ: Первый должен на каждом ходу забирать столько камешков, чтобы Второму оставалось четное количество камешков.

Номер №126
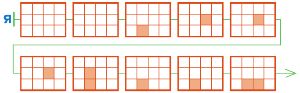
Цепочка Я — это цепочка выполнения программы Ю (позиции в цепочке Я не дорисованы). Догадайся, из какого начального положения Робик выполнил программу Ю, дорисуй позиции цепочки Я.
⇓ Ю
ВПРАВО
ВВЕРХ
ВЛЕВО
ВНИЗ
ВПРАВО
ВВЕРХ
ВНИЗ
ВВЕРХ
ВЛЕВО
⇓

Решение

Цепочка Я — это цепочка выполнения программы Ю: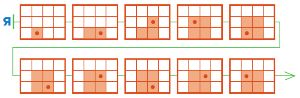

Номер №127
Даны три мешка мешков слов. Найди такой мешок, в каждом мешке которого есть слово, первая и последняя буквы которого одинаковы. Заполни окно в ответе.
Ответ: в каждом мешке мешка _ есть слово, первая и последняя буквы которого одинаковы.

Решение

Ответ: в каждом мешке мешка S есть слово, первая и последняя буквы которого одинаковы.

Номер №128
Заполни таблицу так, чтобы получилась таблица склеивания мешков слов A и B. Затем построй результат склеивания мешков A и B — мешок с английскими числительными.

Мешок A \ Мешок B		TY	TH
	FIFTEEN
SIX				SIXTEENTH
	SEVENTEEN		SEVENTH
		EIGHTY

Решение

Мешок A \ Мешок B	TEEN	TY	TH	TEENTH
FIF	FIFTEEN	FIFTY	FIFTH	FIFTEENTH
SIX	SIXTEEN	SIXTY	SIXTH	SIXTEENTH
SEVEN	SEVENTEEN	SEVENTY	SEVENTH	SEVENTEENTH
EIGH	EIGHTEEN	EIGHTY	EIGHTH	EIGHTEENTH

Номер №129
Соедини все эти армянские буквы в одну цепочку так, чтобы оба утверждения были истинными:
В этой цепочке первая буква после каждой буквы Ջ («дже») — буква Թ («тхо»).
В этой цепочке вторая буква после каждой буквы Վ («вэу») — буква Գ («гим»).

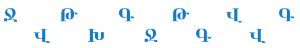
Решение

Номер №130
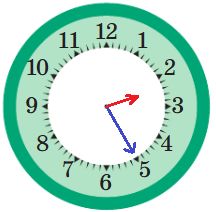
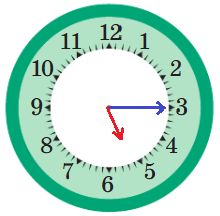
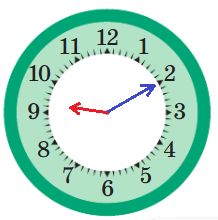
Нарисуй положение стрелок в тот момент, когда цифровые часы показывают данное время.
14:25

17:15

22:40

21:10

Решение

14:25

17:15

22:40

21:10

Дерево выполнения программ 131-139

Дерево выполнения программ
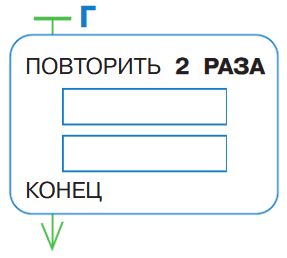
Номер №131
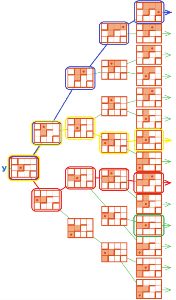
Дерево У на следующей странице — это дерево выполнения программ длиной в 4 команды из данной начальной позиции. Обрати внимание, что на поле есть стены, через которые Робик проходить не может.
Обведи в дереве У цепочку выполнения программы А синим, цепочку выполнения программы Б красным, цепочку выполнения программы В жёлтым.
Напиши команды в окнах программы Г так, чтобы в дереве У нашлась цепочка выполнения программы Г. Обведи лист для этой цепочки зелёным.

⇓ А
ВВЕРХ
ВПРАВО
ВПРАВО
ВНИЗ
⇓

⇓ Б
ВЛЕВО
ВПРАВО
ВВЕРХ
ВПРАВО
⇓

⇓ В
ВВЕРХ
ВНИЗ
ВЛЕВО
ВПРАВО
⇓

Решение

Напишем программу Г:

Номер №132
Нарисуй в окне такую цепочку Ю, чтобы все эти утверждения были истинными:
В цепочке Ю следующая бусина после каждой красной — квадратная.
В цепочке Ю вторая бусина перед каждой треугольной — красная круглая.
В цепочке Ю ровно четыре красные бусины.
В цепочке Ю ровно две круглые бусины.

Решение

Номер №133
Обведи красным два слова, мешки букв которых одинаковые.

ВАЛЕЖНИК
РОМАНТИК
РАЗУМНИК
СТРАЖНИК
НАВОЗНИК
ПЕСЧАНИК
ПАСЕЧНИК
ПИТОМНИК
ПАЛОМНИК

Решение

Слова, мешки букв которых одинаковые:

Номер №134
Построй в окне дереве Ш — дерево выполнения программ длиной в 3 команды из данной начальной позиции. Воспользуйся заготовками со вкладыша тетради проектов.
Начальная позиция:

Решение

Построим дерево Ш: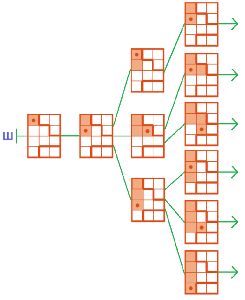

Номер №135
В мешке L лежат грузинские буквы. Раскрась буквы в мешке так, чтобы таблица стала таблицей для мешка L.

Цвет \ БУКВА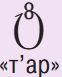
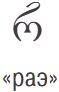
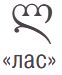
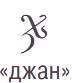
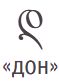
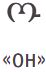
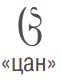
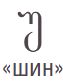
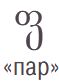
СИНИЙ	0	1	0	0	0	2	0	3	0	0
КРАСНЫЙ	2	0	2	2	2	0	2	2	2	1
ЖЁЛТЫЙ	0	3	0	3	0	4	0	2	0	2
ЗЕЛЁНЫЙ	3	0	0	1	0	1	3	0	0	2

Решение

Номер №136
Дерево Ю — это дерево выполнения программ длиной в 5 команд.
Обведи синим в дереве Ю все цепочки выполнения таких программ, в результате выполнения которых Робик оказывается в нижнем левом углу поля. Построй одну такую программу — напиши её в окне программы А.
Обведи красным в дереве Ю цепочку выполнения программы, в результате выполнения которой на поле останется только одна незакрашенная клетка. Построй эту программу — напиши её в окне программы Б.

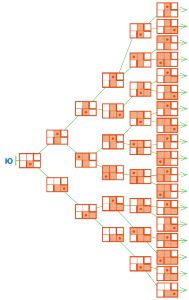
Решение

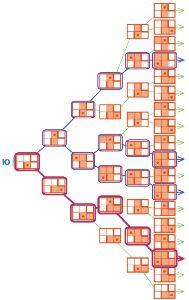
⇓ А
ВВЕРХ
ВЛЕВО
ВНИЗ
ВВЕРХ
ВНИЗ
⇓

⇓ Б
ВПРАВО
ВЛЕВО
ВВЕРХ
ВЛЕВО
ВНИЗ
⇓

Номер №137
Соедини каждое выражение с деревом его вычисления, заполни цветные окна деревьев и найди значение выражений.

↓↑
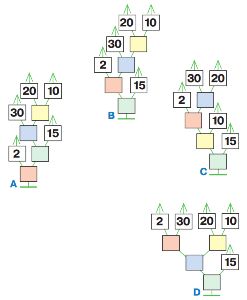
2 * 30 – 20 : 10 + 15 = _
2 * (30 – 20) : 10 + 15 = _
2 * (30 – 20 : 10) + 15 = _
2 * (30 – 20 : 10 + 15) = _

	-умножение
	-деление
	-сложение
	-вычитание

Решение

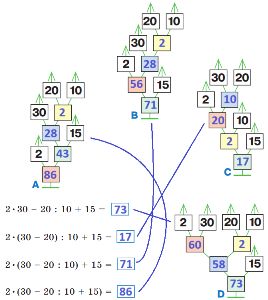
Номер №138
Мешок В — это мешок всех целых двузначных чисел: от 10 до 99. Нарисуй два таких мешка А и Б, в каждом из которых есть непустая цепочка цифр и таких, что А ⓧ Б = В.

Решение

Номер №139
Определи истинность утверждений для дерева С, заполни таблицу. Если утверждение не имеет смысла для дерева С, поставь прочерк.

Утверждение	С
В этом дереве ровно десять цепочек.
Среди цепочек из этого дерева нет цепочек длины 2.
Предыдущая фигурка перед каждым жуком — бабочка.
Среди цепочек из этого дерева есть цепочки длины 5.
Первая фигурка каждой цепочки из этого дерева — жук.
Последняя фигурка каждой цепочки из этого дерева — бабочка.
В этом дереве предыдущая фигурка перед каждой бабочкой — жук.
Четвёртая фигурка каждой цепочки из этого дерева — бабочка.

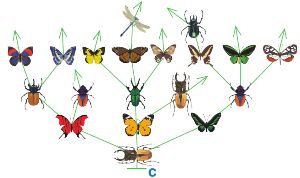
Решение

Утверждение	С
В этом дереве ровно десять цепочек.	И
Среди цепочек из этого дерева нет цепочек длины 2.	И
Предыдущая фигурка перед каждым жуком — бабочка.	-
Среди цепочек из этого дерева есть цепочки длины 5.	И
Первая фигурка каждой цепочки из этого дерева — жук.	И
Последняя фигурка каждой цепочки из этого дерева — бабочка.	Л
В этом дереве предыдущая фигурка перед каждой бабочкой — жук.	И
Третья фигурка каждой цепочки из этого дерева — жук.	И
Предыдущая фигурка перед каждой стрекозой — бабочка.	И
В этом дереве есть цепочка длины 6.	Л
Четвёртая фигурка каждой цепочки из этого дерева — бабочка.	-

Дерево всех вариантов 140-153

Дерево всех вариантов
Номер №140
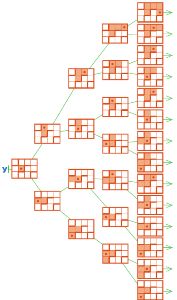
Выясни, сколько можно построить разных цепочек, для которых мешок R — мешок букв этой цепочки. Построй в левом окне дерево перебора вариантов.
Построй в правом окне мешок всех цепочек из твоего дерева, заполни окно в ответе.
Проверь своё решение: все ли слова длины 3 из букв мешка R есть в правом окне? Все ли цепочки из твоего дерева есть в мешке? Сосчитай, сколько листьев в дереве и сколько слов получилось в мешке.
Ответ: можно построить _ разных цепочек.

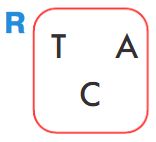
Решение

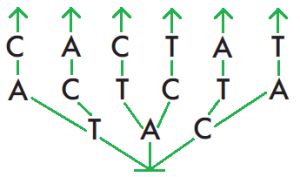
Ответ: можно построить 6 разных цепочек.

Номер №141
Выясни, сколько можно построить разных цепочек, для которых мешок Ф — мешок бусин этой цепочки. Построй в левом окне дерево перебора вариантов. Проверь, что в твоём дереве нет одинаковых цепочек (одинаковых вариантов). Построй в правом окне мешок всех цепочек из твоего дерева.
Сосчитай, сколько цепочек получилось в мешке, заполни окно в ответе.
Ответ: можно построить _ разных цепочек.

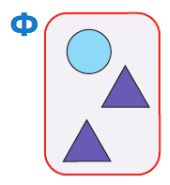
Решение

Ответ: можно построить 3 разных цепочек.

Номер №142
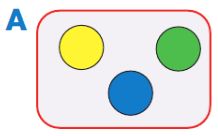
Выясни, сколько можно построить A разных цепочек длины 3, используя только такие бусины, которые есть в мешке A.
Для того чтобы не потерять ни одного возможного решения, построй в окне дерево всех вариантов, используя бусины из мешка A. Обрати внимание, что в цепочках могут быть и две, и три одинаковые бусины. Пользуясь деревом, сосчитай, сколько вариантов решения имеет эта задача, заполни окно в ответе.
Ответ: можно построить _ вариантов таких цепочек.

Решение

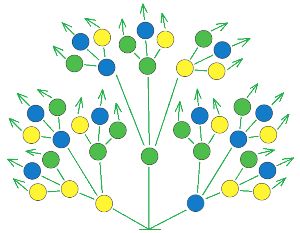
Ответ: можно построить 27 вариантов таких цепочек.

Номер №143
Выясни, сколько вариантов решений имеет эта задача:
Мальчишки соревновались в стрельбе по воздушным шарикам из самодельного лука. Шарики были трёх цветов: зелёные, синие и красные, по 4—5 штук каждого цвета. Петя выстрелил два раза и
оба раза попал: два синих шарика лопнули. В шарики каких цветов он мог бы попасть, сделав два точных выстрела?
Для того чтобы не потерять ни одного возможного решения, построй в окне дерево всех вариантов из бусин нужного цвета. Пользуясь деревом, сосчитай, сколько вариантов решения имеет эта задача, заполни окно в ответе.
Ответ: задача имеет _ вариантов решения.

Решение

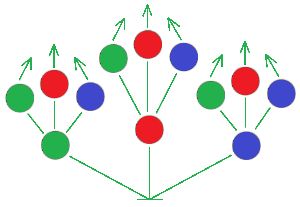
Ответ: задача имеет 9 вариантов решения.

Номер №144
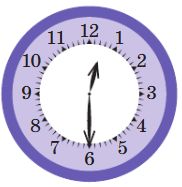
Ответь на вопросы — напиши ответ в окне рядом с каждым вопросом.
Какое время показывают эти часы? _
Какое время будут показывать часы через 3 часа? _
Какое время показывали часы 2 часа назад? _
Какое время будут показывать часы через полчаса? _
Какое время показывали часы полтора часа назад? _

Решение

Какое время показывают эти часы? Половину первого
Какое время будут показывать часы через 3 часа? Половину четвёртого
Какое время показывали часы 2 часа назад? Половину одиннадцатого
Какое время будут показывать часы через полчаса? Один час ровно
Какое время показывали часы полтора часа назад? Одиннадцать часов ровно

Номер №145
Слова в этом словарике упорядочены по правилу обратного словаря. Но одно слово по ошибке стоит не на том месте. Пометь это слово галочкой и покажи стрелкой, в какое место этого словарика его надо переставить.

БОТВИНЬЯ
ДОНЬЯ
ХАВРОНЬЯ
СПРОСОНЬЯ
ГОРБУНЬЯ
ПЕВУНЬЯ
РЕВУНЬЯ
РЕЗВУНЬЯ
БЕГУНЬЯ
ВИЗГУНЬЯ
ЛГУНЬЯ
ПРЫГУНЬЯ
ПОПРЫГУНЬЯ
ШАЛУНЬЯ
КОЛДУНЬЯ
ГЛАЗУНЬЯ
КРИКУНЬЯ
КОПУНЬЯ
ВРУНЬЯ
ИГРУНЬЯ
ГОВОРУНЬЯ
ПЛЯСУНЬЯ
БОЛТУНЬЯ
ХВАСТУНЬЯ

Решение

Номер №146
Реши задачу:
Ваня по утрам часто одевается в темноте, чтобы не разбудить свою маленькую сестрёнку, и поэтому иногда приходит в школу в разных носках. В ящике у него лежат 4 пары носков: красные, чёрные, зелёные и синие. Сосчитай, сколько есть способов надеть 2 носка из этого набора.
Для того чтобы не потерять ни одного возможного варианта, построй в окне дерево всех вариантов из круглых бусин нужного цвета.
Пользуясь деревом, ответь на вопрос задачи, заполни окно в ответе.
Ответ: есть _ вариантов надеть 2 носка из этого набора.

Решение

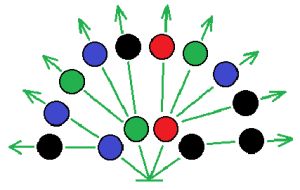
Ответ: есть 10 вариантов надеть 2 носка из этого набора.

Номер №147
Реши задачу:
В харчевне «Три пескаря» на первое предлагали борщ и уху, на второе — стейк из свинины, рыбные котлеты и овощное рагу, на десерт — мороженое. Каждый обед должен состоять из одного первого блюда, одного второго и десерта, при этом в обеде не должно быть больше одного рыбного блюда. Сколько вариантов таких обедов можно получить из этого набора блюд?
Для того чтобы не потерять ни одного возможного варианта, построй в окне дерево всех вариантов из прямоугольников с сокращёнными названиями блюд. На первом уровне дерева помести названия первых блюд, на втором — вторых, на третьем — название десерта.
Пользуясь деревом, ответь на вопрос задачи, заполни окно в ответе.
Ответ: из этого набора блюд можно получить _ вариантов обедов.

Решение

Сократим названия блюд:
Борщ — Б
Уха — У
Стейк из свинины — С
Рыбные котлеты — Р
Овощное рагу — О
Мороженое — М

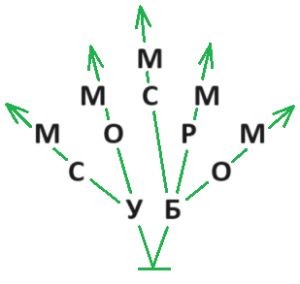
Ответ: из этого набора блюд можно получить 5 вариантов обедов.

Номер №148
На каждых цифровых часах напиши время, которое указано под ними.

2 часа ровно после полудня

половина третьего после полудня

6 часов ровно после полудня

половина девятого до полудня

7 часов ровно после полудня

половина десятого после полудня

Решение

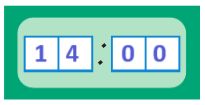
2 часа ровно после полудня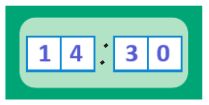

половина третьего после полудня

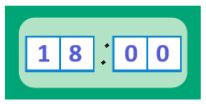
6 часов ровно после полудня

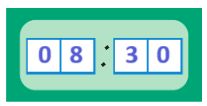
половина девятого до полудня

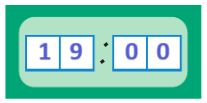
7 часов ровно после полудня

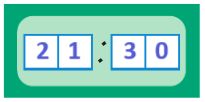
половина десятого после полудня

Номер №149
Нарисуй в окне дерево вычисления для выражения и вычисли его значение:
(24 + 6) : 3 + 72 : 8 = _
Для этого тебе сначала нужно показать, как ты будешь обозначать арифметические действия: раскрась квадратики рядом с названиями действий цветными карандашами:

_ — сложение
_ — вычитание
_ — умножение
_ — деление

Теперь проверь своё решение — заполни цветные окна дерева, запиши ответ в окне в примере и проверь правильность вычисления.

Решение

	-умножение
	-деление
	-сложение
	-вычитание

Нарисуем дерево вычисления:

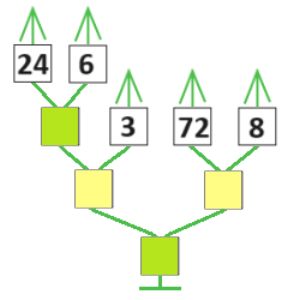
Вычислим значение:
(24 + 6) : 3 + 72 : 8 = 19
Проверим решение:

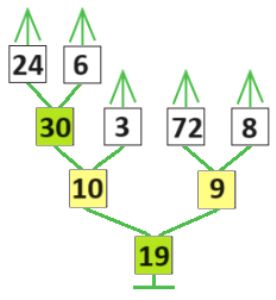
Номер №150
Заполни таблицы так, чтобы сумма мешков А ⓧ Б и В ⓧ Д была мешком русских имён целых сотен: 300, 400, 500, 600, 700, 800, 900. Заполни столько строк каждой таблицы, сколько нужно. Какие имена могли быть у числа 200, если бы оно лежало в мешке А ⓧ Б или мешке В ⓧ Д? Заполни окна в ответе.
Таблица А ⓧ Б

Мешок А \ Мешок Б

Таблица В ⓧ Д

Мешок В \ Мешок Д

Ответ: в мешке А ⓧ Б число 200 имело бы имя _, в мешке В ⓧ Д число 200 имело бы имя _.

Решение

Таблица А ⓧ Б

Мешок А \ Мешок Б	ста
три	триста
четыре	четыреста

Таблица В ⓧ Д

Мешок В \ Мешок Д	сот
пять	пятьсот
шесть	шестьсот
семь	семьсот
восемь	восемьсот
девять	девятьсот

Ответ: в мешке А ⓧ Б число 200 имело бы имя двеста, в мешке В ⓧ Д число 200 имело бы имя двесот.

Номер №151
Найди начальное положение Робика, из которого он сможет выполнить программу Д. Отметь это положение в начальной позиции. Дорисуй теперь позицию Робика после выполнения программы Д.
Начальная позиция:

⇓ Д
ВЛЕВО
ВЛЕВО
ВНИЗ
ВНИЗ
ВПРАВО
ВПРАВО
ВНИЗ
ВНИЗ
ВЛЕВО
ВЛЕВО
ВВЕРХ
⇓

Решение

Начальная позиция:

Позиция Робика после выполнения программы Д:

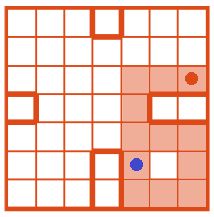
Номер №151
Покажи, как разрезать фигуру N на 4 одинаковые фигуры, — начерти линии разреза.

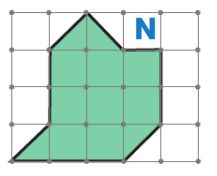
Решение

Линии разреза фигуры N на 4 одинаковые фигуры:

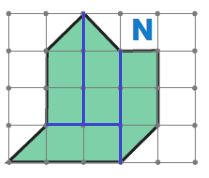
Номер №153
Раскрась синим один квадратик в одной фигурке так, чтобы какие−нибудь две фигурки стали одинаковыми.
Обведи две одинаковые фигурки красным.

Решение

Две одинаковые фигуры:

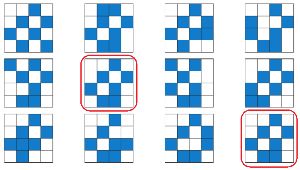
Задачи для самопроверки 154-157

Задачи для самопроверки
Номер №154
Дано дерево вычисления U. Вычисли значение выражения — заполни цветные окна дерева, затем запиши в окне под деревом выражение, значение которого вычислено при помощи этого дерева.

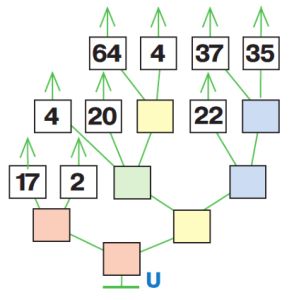
	-умножение
	-деление
	-сложение
	-вычитание

Решение

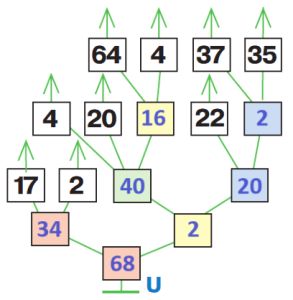
17 * 2 * ((4 + 20 + (64 : 4)) : (22 – (37 – 35))) = 68

Номер №155
Дорисуй дерево R так, чтобы оно стало веткой дерева игры крестики−нолики. Позицию первого уровня оставь такой, как есть, а в остальных позициях нарисуй следующие ходы игроков. Исследуй позиции дерева R: обведи выигрышные позиции красным, проигрышные позиции синим (ничейных позиций в этой ветке нет). Ответь на вопрос.
Выигрышной или проигрышной является позиция первого уровня дерева R? _

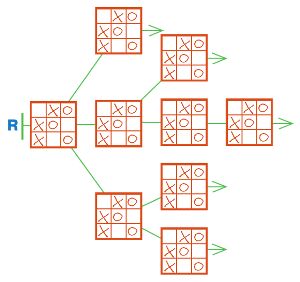
Решение

Дорисуем дерево R:

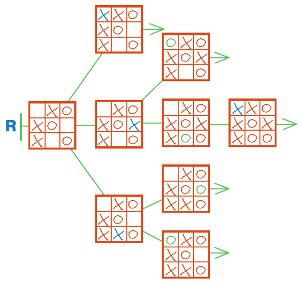
Исследуем позиции дерева R:

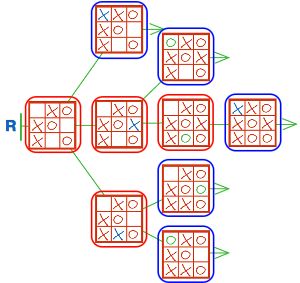
Выигрышной или проигрышной является позиция первого уровня дерева R? Позиция первого уровня дерева R является выигрышной.

Номер №156
Дорисуй позиции так, чтобы дерево С стало деревом выполнения программ из начальной позиции, которая стоит на первом уровне дерева. Обведи в дереве С синим все цепочки выполнения таких программ, в результате выполнения которых Робик оказывается в правом нижнем углу поля.
Построй одну такую программу — напиши её в окне.

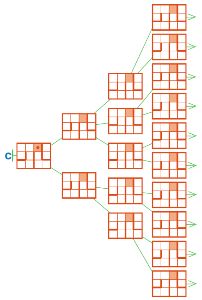
Решение

Дорисуем позиции в дереве:

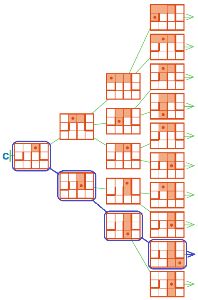
Построим программу:
⇓
ВНИЗ
ВНИЗ
ВПРАВО
⇓

Номер №157
Выпиши в правом окне все цепочки цифр длины 4, составленные только из нулей и единиц. Для этого в левом окне построй дерево всех вариантов.

Решение

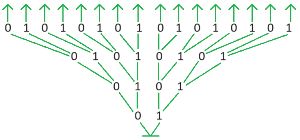
Все цепочки цифр длины 4, составленные только из нулей и единиц:

1. 0000
2. 0001
3. 0010
4. 0011
5. 0100
6. 0101
7. 0110
8. 0111
9. 1000
10. 1001
11. 1010
12. 1011
13. 1100
14. 1101
15. 1110
16. 1111

Лингвистические задачи 158-169

ЛИНГВИСТИЧЕСКИЕ ЗАДАЧИ
Лингвистические задачи
Номер №158
Реши лингвистическую задачу.
Даны русские, английские и греческие слова. В английском языке используется латинский алфавит (латиница), а в греческом — греческий алфавит. Определи язык каждого слова: обведи каждое русское слово синим, каждое английское — красным, каждое греческое — зелёным.

Решение

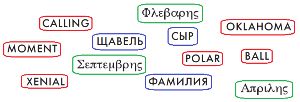
Номер №159
Реши лингвистическую задачу.
Даны голландские и чувашские слова (см. на следующей странице). В чувашском языке, как и в русском, используется кириллица (в чувашском — с дополнительными знаками). В голландском языке используется латиница. Отдели голландские слова от чувашских: обведи каждое чувашское слово красным, каждое голландское — синим.

HUMUS
КАНАШЛА
HEUP
СУНАР
ЧУП
BAKKEN
BOON
МАЙРА
ПИЛЕШ
TON
MOTOR
MAART
ВЫРТ
УЛПУТ

Решение

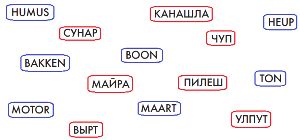
Номер №160
Реши лингвистическую задачу.
Даны русские и чувашские слова. В чувашском языке, как и в русском, используется кириллица (в чувашском — с дополнительными знаками). Найди и обведи здесь все слова, которые точно не могут быть русскими (а значит, они чувашские). Для решения нужно использовать знания, полученные на уроках русского языка.

Решение

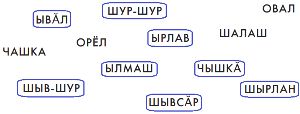
Номер №161
Напиши в правом окне все трёхзначные чётные числа, в записи которых есть только цифры 2, 3, 6, 9 и нет двух одинаковых цифр. Для решения построй в левом окне дерево всех вариантов.

Решение

Напишем все трёхзначные чётные числа, в записи которых есть только цифры 2, 3, 6, 9 и нет двух одинаковых цифр:

1. 236
2. 296
3. 326
4. 362
5. 392
6. 396
7. 632
8. 692
9. 926
10. 932
11. 936
12. 962

Дерево всех вариантов:

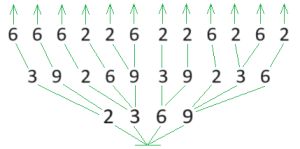
Номер №162
Реши лингвистическую задачу.
Русский, украинский и белорусский языки пользуются похожими алфавитами — все эти алфавиты образовались на основе кириллицы. При этом в украинском алфавите нет буквы ы (а в белорусском она есть), в белорусском алфавите нет буквы и (а в украинском она есть), в русском алфавите нет буквы i (а в украинском и белорусском она есть). В украинском и белорусском алфавитах есть и другие буквы, которых нет в русском, но в каждом из этих алфавитов свои (в одном одни, в другом другие).
Даны русские, украинские и белорусские слова. Обведи синим каждое русское слово, красным — каждое украинское слово, зелёным — каждое белорусское слово. Обведи чёрным каждое слово, язык которого нельзя определить.

Решение

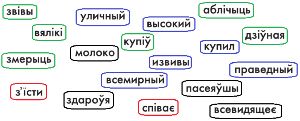
Номер №163
Реши лингвистическую задачу.
Даны фразы, написанные на украинском и белорусском языках (см. на следующей странице). Пользуясь данными, полученными при решении предыдущей задачи, напиши букву Б в окне рядом с каждой белорусской фразой, букву У — рядом с каждой украинской и знак ? — рядом с каждой фразой, язык которой нельзя определить.

_ Прийшов, побачив, переміг.
_ З легендаў і казак былых покаленняў
Ты выткана, дзіўная родная мова.
_ I широкую долину не забуду я.
_ Малы жук, а вялікі гук.
_ Якби ви вчились так, як треба,
То й мудрість би була своя.
_ Дарогі, цёмныя дарогі! Хто вас аблічыць? Хто вас змерыць? Хто вашы звівы ўсе праверыць?
_ Не пасеяўшы, не пажнеш.
_ Реве та стогне Дніпр широкий.
_ По улиці вітер віє
Та сніг замітає.
_ Думи мої, думи мої,
Лихо менi з вами!
_ Огнi горять, музика грає.
_ Спiває, плаче Ярославна,
Як та зозуленька кує.
_ Што хутарок, то гаварок, што сяльцо, то нараўцо.
_ Добрага здароўя!
_ Сонце грiє, вiтер вiє.
_ Можа на двое варожа.

Решение

У Прийшов, побачив, переміг.
Б З легендаў і казак былых покаленняў
Ты выткана, дзіўная родная мова.
У I широкую долину не забуду я.
Б Малы жук, а вялікі гук.
У Якби ви вчились так, як треба,
То й мудрість би була своя.
Б Дарогі, цёмныя дарогі! Хто вас аблічыць? Хто вас змерыць? Хто вашы звівы ўсе праверыць?
Б Не пасеяўшы, не пажнеш.
У Реве та стогне Дніпр широкий.
У По улиці вітер віє
Та сніг замітає.
У Думи мої, думи мої,
Лихо менi з вами!
У Огнi горять, музика грає.
У Спiває, плаче Ярославна,
Як та зозуленька кує.
Б Што хутарок, то гаварок, што сяльцо, то нараўцо.
Б Добрага здароўя!
У Сонце грiє, вiтер вiє.
? Можа на двое варожа.

Номер №164
Покажи, как разрезать фигуру V на 4 одинаковые фигуры, — начерти линии разреза.

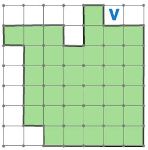
Решение

Линии разреза фигуры V на 4 одинаковые фигуры:

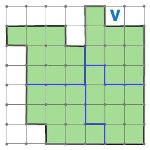
Номер №165
В каждой из этих четырёх конструкций покажи стрелкой, в какую сторону будет вращаться каждая шестерёнка, если красную шестерёнку вращать по часовой стрелке.

Решение

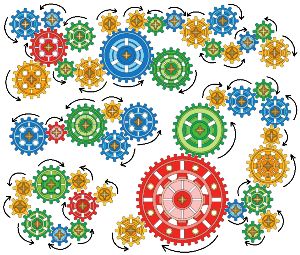
Номер №166
Дострой равенство со склеиванием мешков — заполни окна. В каждом окне можно нарисовать столько цепочек, сколько нужно.

Решение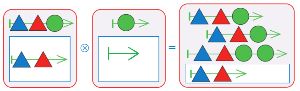

Номер №167
Дан мешок В всех букв дерева G. Построй дерево G так, чтобы все следующие утверждения были истинными:
В дереве G ровно четыре уровня букв.
Каждая буква дерева G, кроме листьев, имеет ровно одну следующую букву.
В каждой цепочке из дерева G следующая буква после каждой непоследней гласной — согласная.
В каждой цепочке из дерева G следующая буква после каждой непоследней согласной — гласная.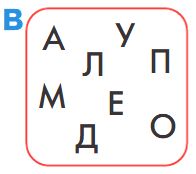

Решение

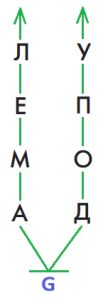
Номер №168
Вот дерево Ф и таблица для мешка всех его бусин. Раскрась бусины дерева Ф по таблице так, чтобы это утверждение было истинным:
В дереве Ф нет двух одинаковых цепочек.

ЖЁЛТЫЕ	5
СИНИЕ	1
КРАСНЫЕ	7
ЗЕЛЁНЫЕ	0
ЧЁРНЫЕ	0

Решение

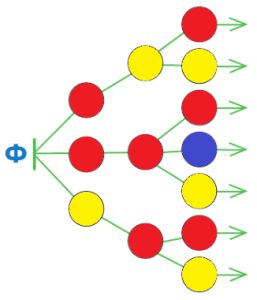
Номер №169
Построй такое равенство со склеиванием цепочек букв, в котором каждая цепочка — это слово русского языка. Напиши слова в окнах.

Решение

МОРЕ

ХОД

МОРЕХОД

Шифрование 170-184

Шифрование
Номер №170
Дана фраза и её шифровка:

МЫ ШИФРУЕМ СЛОВА
ПУ БЁЦТОАП ФНИДЯ

Здесь использован шифр, при котором каждая русская буква заменяется другой русской буквой. Какой именно буквой заменяется каждая буква при шифровании, указывается в таблице шифра. Слова в шифровке разделены пробелами так же, как и слова в исходном тексте. Напиши в таблице шифра 1 все коды букв, которые ты сможешь выяснить, используя эту шифровку.

Таблица шифра 1

Решение
Таблица шифра 1

Номер №171
Мешок S — это мешок шифровок для слов: ПОКА, ПИЩА, НОТА, ЛЬЮ, ЛУГ, ЛУК (был использован тот же шифр, что и в задаче 170). Для каждого слова найди его шифровку, напиши её в окне рядом со словом. Напиши в таблице шифра 1 все новые коды букв, которые ты сможешь выяснить, используя эти шифровки.

ПОКА — _
ПИЩА — _
НОТА — _
ЛЬЮ — _
ЛУГ — _
ЛУК — _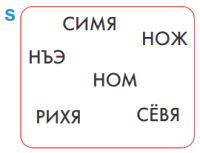

Решение

Таблица шифра 1

ПОКА — СИМЯ
ПИЩА — СЁВЯ
НОТА — РИХЯ
ЛЬЮ — НЪЭ
ЛУГ — НОЖ
ЛУК— НОМ

Номер №172
Мешок F — это мешок шифровок для слов: ЧАЙ, ДАЙ, ЧЬЯ, ЭХО, ЗУБ, ЧИЖ (был использован тот же шифр, что и в задачах 170—171). Для каждого слова найди его шифровку, напиши её в окне рядом со словом. Напиши в таблице шифра 1 все новые коды букв, которые ты сможешь выяснить, используя эти шифровки.

ЧАЙ — _
ДАЙ — _
ЧЬЯ — _
ЭХО — _
ЗУБ — _
ЧИЖ — _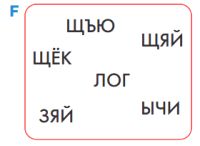

Решение

Таблица шифра 1

ЧАЙ — ЩЯЙ
ДАЙ — ЗЯЙ
ЧЬЯ — ЩЪЮ
ЭХО — ЫЧИ
ЗУБ — ЛОГ
ЧИЖ — ЩЁК

Номер №173
Заполни оставшиеся пустые клетки в таблице шифра 1 на с. 105, учитывая, что в этом шифре гласные зашифрованы только гласными, а согласные — только согласными. Теперь проверь себя — таблица шифра 1 должна быть полностью заполнена.

Решение

Таблица шифра 1

Номер №174
Пользуясь таблицей шифра 1, зашифруй эту фразу, напиши шифровку в окне.
НИКОМУ НЕ ГОВОРИ

Решение

Таблица шифра 1

Зашифруем фразу:

Номер №175
Дана фраза и её шифровка:
ЛИНГВИСТИЧЕСКАЯ ЗАДАЧА
13.10.15.4.3.10.19.20.10.25.6.19.12.1.33 9.1.5.1.25.1
Здесь использован шифр, в котором каждая русская буква заменяется её порядковым номером в алфавите. Между кодами букв ставится точка. Слова в шифровке разделены пробелами так же, как и слова в исходном тексте. Заполни все клетки таблицы шифра 2.
Таблица шифра 2

Решение

Таблица шифра 2

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

Номер №176
Пользуясь таблицей шифра 2, зашифруй фразу и запиши шифровку в окне.
УЧЕБНИК ИНФОРМАТИКИ

Решение

Таблица шифра 2

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

УЧЕБНИК ИНФОРМАТИКИ
21.25.6.2.15.10.12 10.15.22.16.18.14.1.20.10.12.10

Номер №177
Напиши в окна цепочки Z все слова в алфавитном порядке так, чтобы мешок Q был мешком слов цепочки Z.

⇓
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
⇓

Решение

⇓
КАК
КАКОЙ
КАКОЙ-НИБУДЬ
КАКОЙ-ТО
КАК-ТО
КОГДА-ТО
КАП-КАП
КОГДА-НИБУДЬ
КОГДА-НИКОГДА
КОГДА-ТО
КОГОТЬ
⇓

Номер №178
Пользуясь таблицей шифра 2 из задачи 175, расшифруй фразу, запиши её в окне.
19.12.16.18.16
15.1.19.20.21.17.10.20
13.6.20.16

Решение

Таблица шифра 2

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

19.12.16.18.16
СКОРО
15.1.19.20.21.17.10.20
НАСТУПИТ
13.6.20.16
ЛЕТО

Номер №179
Покажи, как разрезать фигуру W на 4 одинаковые фигуры, — начерти линии разреза.

Решение

Линии разреза фигуры W на 4 одинаковые фигуры: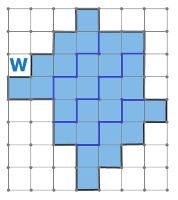

Номер №180
Придумай и напиши в левом окне слово русского языка, для шифровки которого с помощью таблицы шифра 2 из задачи 175 будут использоваться только цифры 1, 2 и точки. Не забудь поставить точки между кодами букв. В правом окне напиши шифровку этого слова.

Решение

Таблица шифра 2

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

Буквы, для шифровки которых используются только цифры 1, 2:
1 — А
2 — Б
11 — Й
12 — К
21 — У
22 — Ф
С их помощью можно составить слово фуфайка.

Слово	Шифровка
ФУФАЙКА	22.21.22.1.11.12.1

Номер №181
Нарисуй в окне дерево вычисления для выражения и вычисли его значение:
(22 – 10) * 4 – 81 : 9 = _
Для этого тебе сначала нужно показать, как ты будешь обозначать арифметические действия: раскрась квадратики рядом с названиями действий цветными карандашами:

_ — сложение
_ — умножение
_ — вычитание
_ — деление

Теперь проверь своё решение — заполни все цветные окна в дереве, напиши ответ в окне в примере и проверь правильность вычисления.

Решение

	-умножение
	-деление
	-сложение
	-вычитание

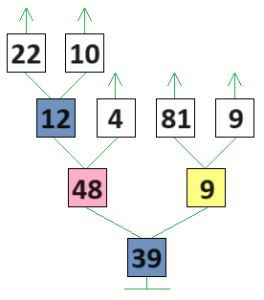
(22 – 10) * 4 – 81 : 9 = 39

Номер №182
Вот русское слово, зашифрованное с помощью шифра из таблицы шифра 2, в этой шифровке между буквами забыли поставить точки.

91320181

Чтобы расшифровать такую неполную шифровку, придётся перебирать все возможные варианты. Для этого удобно построить дерево. На первом уровне такого дерева находятся числа, которые могут быть кодом первой буквы, на втором — числа, которые могут быть кодом второй буквы, и так далее. Красным крестом в дереве перечёркнуты те числа, которые не являются кодами никакой буквы, — их нет в таблице шифра 2.
Дерево G — это дерево расшифровки нашей неполной шифровки. Напиши рядом с каждым (незачёркнутым) числом в дереве С, какую букву шифрует это число. Пользуясь деревом С, напиши в окне все цепочки букв, которые может шифровать данная неполная шифровка. Выбери из них знакомое тебе русское слово, запиши его в окне в ответе.
Ответ: эта запись шифрует слово _

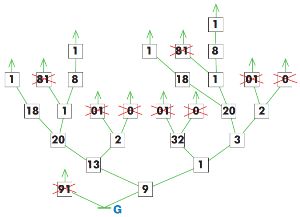
Решение

Таблица шифра 2

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

Все цепочки букв, которые может шифровать данная неполная шифровка:
1. 9.13.20.18.1 — ЗЛТРА
2. 9.13.20.1.8.1 — ЗЛТАЖА
3. 9.1.3.20.18.1 — ЗАВТРА
4. 9.1.3.20.1.8.1 — ЗАВТАЖА
Ответ: эта запись шифрует слово ЗАВТРА

Номер №183
В этой шифровке, полученной при помощи таблицы шифра 2 из задачи 175, забыли поставить точки:

18622119

Узнай, какое русское слово здесь зашифровано. Для этого построй в первом окне дерево вариантов. Зачёркивай красным крестом те числа в дереве, которых нет в таблице шифра 2.
Напиши рядом с каждым незачёркнутым числом твоего дерева букву, которую шифрует это число. Пользуясь деревом вариантов, напиши во втором окне все цепочки букв, которые может шифровать данная неполная шифровка. Выбери из них знакомое тебе русское слово, запиши его в окне в ответе.
Ответ: эта запись шифрует слово _.

Решение

Таблица шифра 2

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

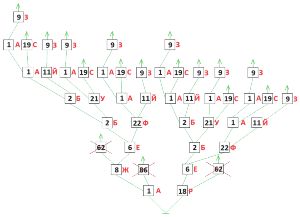
Все цепочки букв, которые может шифровать данная неполная шифровка:

1. АЖЕББААЗ
2. АЖЕББАС
3. АЖЕББЙЗ
4. АЖЕБУАЗ
5. АЖЕБУС
6. АЖЕФААЗ
7. АЖЕФАС
8. АЖЕФЙЗ
9. РЕББААЗ
10. РЕББАС
11. РЕББЙЗ
12. РЕБУАЗ
13. РЕБУС
14. РЕФААЗ
15. РЕФАС
16. РЕФЙЗ

Ответ: эта запись шифрует слово РЕБУС.

Номер №184
В каждой из этих шести конструкций покажи стрелкой, в какую сторону будет вращаться каждая шестерёнка, если красную шестерёнку начать вращать по часовой стрелке. Пометь галочкой те конструкции, в которых шестерёнки вращаться не смогут. Попытайся объяснить почему. Обсуди это с одноклассниками.

Решение

В одной из конструкций связаны друг с другом связаны сразу три шестерёнки, если одна из них вращается по часовой стрелке, то обе остальные должны вращаться против часовой стрелки. Но они не смогут, так как связаны и друг с другом.
В остальных двух конструкциях в кольцо соединено нечетное количество шестерёнок, поэтому в каком−либо месте кольца соединятся шестерёнки, которые вращаются в одном направлении, и не смогут двигаться.

Задачи для самопроверки 185-186

Задачи для самопроверки
Номер №185
Реши лингвистическую задачу.
Вот обозначения некоторых дат на языке суахи́ли и их переводы на русский язык (в перепутанном порядке):

tarehe tano Octoba jumatano	понедельник, 4 апреля
tarehe nne Aprili jumatatu	вторник, 3 декабря
tarehe tatu Disemba jumanne	понедельник, 5 октября
tarehe pili Aprili jumamosi	суббота, 2 апреля
tarehe tano Octoba jumatatu	среда, 5 октября

Напиши на языке на языке суахи́ли следующие даты:
среда, 4 апреля _
суббота, 5 декабря _

Решение

Соединим обозначения дат и их переводы в правильном порядке:
1. Названия месяцев похожи на названия месяцев в английском языке: Octoba — October, октябрь; Aprili — April, апрель; Disemba — December, декабрь.
Соединим обозначение даты со словом Disemba с переводом со словом декабрь.
2. Среди оставшихся обозначений дат есть повтор дня недели — понедельника в октябре и апреле. Сравним обозначения дат, найдём повтор слова. Это слово jumatatu, значит, оно обозначает понедельник.
Также делаем вывод, что обозначения дат на языке суахили строятся в порядке: число — месяц — день недели.
Соединим обозначения дат со словом jumatatu с переводом со словом понедельник, учитывая указанный месяц.
3. Расставим оставшиеся переводы, учитывая указанные месяцы.

tarehe tano Octoba jumatano	среда, 5 октября
tarehe nne Aprili jumatatu	понедельник, 4 апреля
tarehe tatu Disemba jumanne	вторник, 3 декабря
tarehe pili Aprili jumamosi	суббота, 2 апреля
tarehe tano Octoba jumatatu	понедельник, 5 октября

Напишем на языке на языке суахи́ли следующие даты:
среда, 4 апреля tarehe nne Aprili jumatano
суббота, 5 декабря tarehe tano Disemba jumamosi

Номер №186
Построй таблицу шифра по следующим правилам:
1. Код каждой гласной — парная ей гласная.
2. Остальные буквы остаются без изменений — каждая из них кодирует сама себя.
Зашифруй при помощи этого шифра следующую фразу, напиши шифровку в первом окне.
ЧИЖИК−ПЫЖИК ГДЕ ТЫ БЫЛ
Расшифруй следующую шифровку, запиши фразу во втором окне.
НЯДЁ−НЯДЁ ЮМИВЯТЬСА
ПЁ ЮТРЯМ Ы ВЭЧЭРЯМ

Решение

Построим таблицу шифра:

А Б В Г Д Е Ё Ж З И Й К Л М Н О П
Я Б В Г Д Э О Ж З Ы Й К Л М Н Ё П

Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я
Р С Т Ю Ф Х Ц Ч Ш Щ Ъ И Ь Е У А

Зашифруем фразу:
ЧИЖИК−ПЫЖИК ГДЕ ТЫ БЫЛ
ЧЫЖЫК−ПИЖЫК ГДЭ ТИ БИЛ

Расшифруем шифровку:
НЯДЁ−НЯДЁ ЮМИВЯТЬСА
НАДО−НАДО УМЫВАТЬСЯ
ПЁ ЮТРЯМ Ы ВЭЧЭРЯМ
ПО УТРАМ И ВЕЧЕРАМ

Дополнительные задачи 187-212

Дополнительные задачи
Номер №187
Дострой это равенство так, чтобы в каждом мешке была хотя бы одна непустая цепочка. В каждом окне можно нарисовать столько цепочек, сколько нужно.

Решение

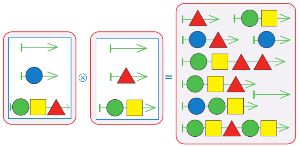
Номер №188
Сима, Даша, Гриша и Яна сыграли круговой турнир по крестикам−ноликам. Даша выиграла у Симы и Яны. Гриша проиграл Симе и выиграл у Даши, а с Яной сыграл вничью. Сима и Яна сыграли вничью. Заполни таблицу этого турнира (за победу 2 очка, за ничью 1 очко, за поражение 0 очков).

Игрок	Сима	Даша	Гриша	Яна	Очки	Место
Сима
Даша
Гриша
Яна

Решение

Игрок	Сима	Даша	Гриша	Яна	Очки	Место
Сима	x	0	2	1	3	2
Даша	2	x	0	2	4	1
Гриша	0	2	х	1	3	2
Яна	1	0	1	х	2	4

Номер №189
Определи истинность утверждений для цепочек К и Л, заполни таблицу. Если окажется, что утверждение не имеет смысла для цепочки, поставь в клетке таблицы прочерк.

Утверждение	К	Л
Следующая бусина после каждой квадратной — голубая круглая.
Следующая бусина после каждой красной — зелёная квадратная.
Следующая бусина после каждой круглой — красная треугольная.
Вторая бусина перед каждой зелёной — голубая.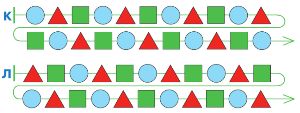

Решение

Утверждение	К	Л
Следующая бусина после каждой квадратной — голубая круглая.	И	И
Следующая бусина после каждой красной — зелёная квадратная.	И	-
Следующая бусина после каждой круглой — красная треугольная.	-	И
Вторая бусина перед каждой зелёной — голубая.	И	-

Номер №190
Дорисуй ходы игроков на позициях в цепочке Z так, чтобы эта цепочка стала цепочкой какой−нибудь партии в ползунок.

Решение

Цепочка партии в ползунок:

Номер №191
Придумай и напиши в левом окне полученную по таблице шифра 2 из задачи 175 шифровку, в которой не поставлены точки и которая шифрует два разных имени девочек: одно из 3 букв, а другое из 4 букв. Напиши в правом окне эти расшифровки.

Решение

Таблица шифра 2

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

Шифровка Имена
311333 Валя (3.1.13.33)
311333 Эля (31.13.33)

Номер №192
Реши лингвистическую задачу.
Вот запись счёта от одного до пяти на аварском, белорусском, болгарском, гавайском, кумыкском, турецком и чешском языках:

1. адзiн, два, тры, чатыры, пяць _
2. бир, эки, уьч, дёрт, беш _
3. едно, две, три, четири, пет _
4. цо, кIиго, лъабго, ункъо, щуго _
5. bir, iki, üç, dört, beş _
6. ekahi, elua, ekolu, eha, elima _
7. jeden, dva, tři, čtyři, pět _

Известно, что белорусский, болгарский и чешский языки родственны между собой, а также родственны русскому (это славянские языки).
Турецкий и кумыкский — родственные между собой тюркские языки.
Аварский и гавайский языки не родственны ни между собой, ни остальным языкам.
Известно также, что гавайский, турецкий и чешский пользуются различными разновидностями латинского алфавита, а остальные языки — кириллицей. В аварском и белорусском используются дополнительные, по сравнению с русским алфавитом, буквы.
Определи, какая запись из какого языка, напиши название языка в окне рядом с каждой строчкой.

Решение

Решим задачу:
1. По ранее изученным заданиям мы можем определить язык первой записи — белорусский.
2. Белорусский, болгарский и чешский языки родственны между собой, а также родственны русскому. Изучим записи, видим, что записи под номерами 3 и 7 по произношению очень напоминают русский и белорусский языки. Значит, под номерами 3 и 7 — записи на болгарском и чешском языках.
Чешский язык используем разновидности латинского алфавита, а болгарский — кириллицу. Значит, под номером 3 мы видим запись на болгарском языке, а под номером 7 — на чешском.
3. В аварском используются дополнительные, по сравнению с русским алфавитом, буквы. Среди оставшихся записей мы видим две с использованием кириллицы, из них одна — с дополнительными символами — под номером 4.
4. Латинским алфавитом пользуются гавайский и турецкий языки, значит, оставшаяся запись кириллицей под номером 2 — на кумыкском языке.
5. Турецкий и кумыкский — родственные между собой тюркские языки. Сравним оставшиеся записи с записью на кумыкском, видим сходство с ней записи под номером 5. Значит, это запись на турецком языке.
6. Осталась одна запись. Так как гавайский язык не родственен остальным представленным языкам, делаем вывод, что запись под номером 6 сделана на нём.

1. адзiн, два, тры, чатыры, пяць белорусский
2. бир, эки, уьч, дёрт, беш кумыкский
3. едно, две, три, четири, пет болгарский
4. цо, кIиго, лъабго, ункъо, щуго аварский
5. bir, iki, üç, dört, beş турецкий
6. ekahi, elua, ekolu, eha, elima гавайский
7. jeden, dva, tři, čtyři, pět чешский

Номер №193
Мешок A — это мешок бусин цепочки B. Цепочка B — это цепочка выполнения программы C для Робика. Вырежи все бусины мешка A из листа вырезания и построй в первом окне цепочку выполнения программы C. Напиши во втором окне программу C.

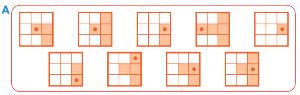
Решение

Построим цепочку выполнения программы C:

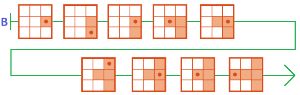
Напишем программу C:
⇓ с
ВНИЗ
ВВЕРХ
ВЛЕВО
ВПРАВО
ВВЕРХ
ВНИЗ
ВЛЕВО
ВЛЕВО
⇓

Номер №194
Дано несколько цепочек партий игры в камешки, в которых на каждом ходу можно брать 1, 2 или 4 камешка. Обведи все цепочки тех партий, в которых игрок, имеющий выигрышную стратегию, следует этой стратегии. Для решения задачи раскрась сначала числовую линейку до 12−й позиции.

Решение

Числовая линейка для игры камешки, в которой можно брать 1, 2 или 4 камешка:

Цепочки тех партий, в которых игрок, имеющий выигрышную стратегию, следует этой стратегии:

Номер №195
Дострой равенство, в котором с корнем слова склеиваются два суффикса и окончание, так, чтобы в результате склеивания получилось русское название ягоды.

*Н*

Решение

ЗЕМЛ

*ЯН*

ИК

ЗЕМЛЯНИКА

В русском языке нет названий ягод, имеющих в составе суффикс −н−.

Номер №196
Дано начало программы S и поле Робика после выполнения этой программы. Допиши программу S (заполнять все строки в окне необязательно). Отметь положение Робика на поле до и после выполнения программы.
Позиция после выполнения программы S:

⇓ S
ВЛЕВО
ВЛЕВО
______
______
______
______
______
⇓

Решение

Отметим положение Робика на поле до выполнения программы красной точкой, после выполнения программы — синей: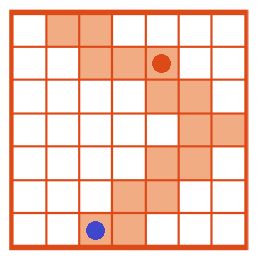

Допишем программу S:
⇓ S
ВЛЕВО
ВЛЕВО
ВВЕРХ
ВЛЕВО
ВПРАВО
ВНИЗ
ВПРАВО
ВПРАВО
ВНИЗ
ВПРАВО
ВНИЗ
ВПРАВО
ВЛЕВО
ВНИЗ
ВЛЕВО
ВНИЗ
ВЛЕВО
ВНИЗ
ВЛЕВО
⇓

Номер №197
Напиши в окне все трёхзначные нечётные числа, делящиеся на 9, в записи которых есть только цифры 0, 1, 4, 5, 8 и нет двух одинаковых цифр. Для решения построй в другом окне дерево всех вариантов.

Решение

Число делится на 9 только тогда, когда делится на 9 сумма его цифр. Построим дерево трёхзначных чисел, в записи которых есть только цифры 0, 1, 4, 5, 8, нет двух одинаковых цифр, а сумма цифр делится на 9:

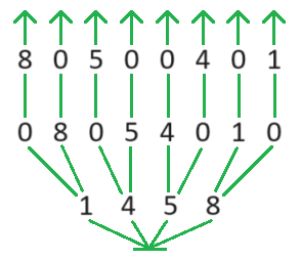
Напишем все нечётные числа из представленных:
1. 405
2. 801

Номер №198
Найди такой мешок мешков (см. на следующей странице), для каждого мешка которого следующее утверждение истинно. Напиши имя этого мешка в окне в ответе.
Таблица А — это таблица этого мешка.

Цвет \ Форма	КВАДРАТНЫЕ	КРУГЛЫЕ	ТРЕУГОЛЬНЫЕ
СИНИЕ	0	1	1
КРАСНЫЕ	1	2	0
ЗЕЛЁНЫЕ	1	0	2
ЖЁЛТЫЕ	0	1	2

Ответ: утверждение истинно для каждого мешка из мешка мешков _.

Решение

Ответ: утверждение истинно для каждого мешка из мешка мешков Л.

Номер №199
Дострой равенство, в котором с приставкой склеивается корень слова, суффикс и окончание так, чтобы в результате склеивания получилось русское слово.

*ХОД*

Решение

ВЫ

*ХОД*

ОЙ

ВЫХОДНОЙ

Номер №200
Соедини все фигурки в одну цепочку так, чтобы все утверждения были истинными.
В этой цепочке следующая фигурка после каждой сумки — башмак.
В этой цепочке следующая фигурка после каждого платья — сумка.
В этой цепочке вторая фигурка после каждой скрипки — сумка.
Задачу будет легче решать, если вырезать такие же фигурки из листа вырезания, сложить нужную цепочку на столе и затем уже соединить фигурки в тетради.

Решение

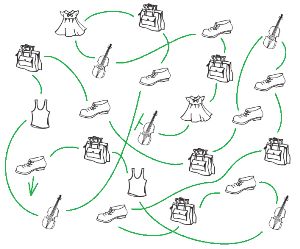
Номер №201
Вот правила игры стрелка. Двое играющих по очереди переводят часовую стрелку на 2 или на 3 часа вперёд. В начальной позиции часовая стрелка указывает на 12. Побеждает тот, кто первым поставит стрелку на 6 (прежде чем остановиться на цифре 6, стрелка может сделать несколько оборотов). У кого из игроков есть выигрышная стратегия?
Для решения задачи, как всегда, нужно рассмотреть все возможные позиции, начиная с заключительной — с 6 часов. Сделать это можно с помощью специальной круглой числовой линейки (см. рисунок справа).
После того как ты обойдёшь круглую линейку один раз (начиная с 6), некоторые позиции останутся незакрашенными. Чтобы раскрасить все позиции, нужно будет обойти линейку несколько раз.
Ответ: выигрышная стратегия есть у _.

Решение

Раскрасим круглую числовую линейку, сделав несколько проходов по кругу:

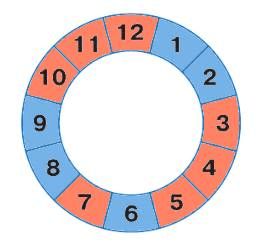
Ответ: выигрышная стратегия есть у первого игрока.

Номер №202
Расставь скобки так, чтобы равенство стало верным:
6 * 8 + 20 : 4 – 2 = 58
Нарисуй в окне дерево вычисления значения этого выражения. Для этого тебе сначала нужно показать, как ты будешь обозначать арифметические действия: раскрась квадратики рядом с названиями действий цветными карандашами:

_ — сложение
_ — вычитание
_ — умножение
_ — деление

Теперь проверь своё решение — заполни цветные окна дерева, проверь, что на первом уровне получилось число 58.

Решение

Расставим скобки:
6 * 8 + 20 : (4 – 2) = 58
Нарисуем дерево вычисления:

	-умножение
	-деление
	-сложение
	-вычитание

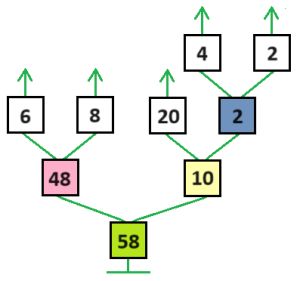
Номер №203
Вот правила игры король. Двое играют на шахматной доске*, передвигая по очереди одного короля. Допускаются ходы на одну клетку влево, на одну клетку вниз или влево−вниз (см. рисунок). Выигрывает тот, кому удастся поставить короля в левый нижний угол поля — на клетку a1.
Сыграйте круговой турнир в короля (3—4 человека). Сначала выберите какую−нибудь клетку поля в качестве начальной позиции. Играть лучше на настоящей шахматной доске королём. Но можно играть и на нарисованной доске (она есть на вкладыше тетради проектов), передвигая маленькую фишку.
Напиши в окне в ответе имя клетки, выбранной для начальной позиции. Заполни таблицу турнира. Очки подсчитывай так: за победу игрок получает 1 очко, за поражение — 0 очков.
Ответ: начальная позиция — клетка _.

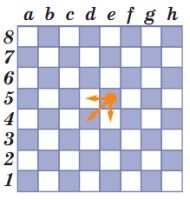
* Шахматная доска — это поле размером 8х8 клеток, раскрашенных в шахматном порядке (см. рисунок справа). Каждая клетка этого поля имеет имя, состоящее из буквы (место клетки по горизонтали) и цифры (место клетки по вертикали). Например, клетка, отмеченная оранжевой точкой, имеет имя d4, а клетка с зелёной точкой — имя g6.

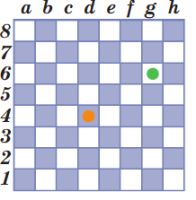
Решение

Ответ: начальная позиция — клетка f6.
Таблица турнира:

Игрок	1 игрок	2 игрок	3 игрок	4 игрок	Очки	Место
1 игрок	Х	1	0	1	2	2
2 игрок	0	Х	0	0	0	4
3 игрок	1	1	Х	1	3	1
4 игрок	0	1	0	Х	1	3

Номер №204
При каких начальных положениях короля в игре король из задачи 203 имеет выигрышную стратегию Первый, а при каких — Второй?
Для решения задачи нужно отметить каждую возможную позицию короля (каждую клетку шахматной доски) как выигрышную или проигрышную (соответственно красным или синим). Например, можно ставить жирную точку красным или синим. Как всегда, начинать надо с заключительной позиции — в данном случае с клетки a1.
Ответь на вопросы — заполни окна:
Кто из игроков имеет выигрышную стратегию в игре король с начальной позицией d4? _
Кто из игроков имеет выигрышную стратегию в игре король с начальной позицией e3? _
Напиши в окне названия трёх каких−нибудь начальных позиций, в которых выигрышную стратегию имеет Первый. _
Напиши в окне названия трёх каких−нибудь начальных позиций, в которых выигрышную стратегию имеет Второй. _

Решение

Шахматная доска со всеми выигрышными и проигрышными позициями для первого игрока (отмечено красным) и для второго игрока (отмечено синим):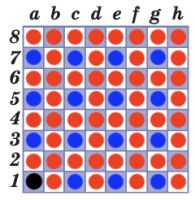

Ответы на вопросы:
Кто из игроков имеет выигрышную стратегию в игре король с начальной позицией d4? Первый игрок
Кто из игроков имеет выигрышную стратегию в игре король с начальной позицией e3? Первый игрок
Напиши в окне названия трёх каких−нибудь начальных позиций, в которых выигрышную стратегию имеет Первый. a8, f3, *g6*
Напиши в окне названия трёх каких−нибудь начальных позиций, в которых выигрышную стратегию имеет Второй. e7, a5, *g3*

Номер №205
Теперь, когда вы знаете о выигрышной стратегии в игре король, устройте соревнование с соседом по парте. Сыграйте четыре партии. Пусть один из вас будет Первым в играх с чётными номерами, а другой — с нечётными. Начальную позицию в каждой партии пусть выбирает Первый. За победу игрок получает 1 очко, за поражение — 0 очков. Заполни таблицу соревнования.

Игрок
1 игрок
2 игрок
3 игрок
4 игрок
ИТОГО

Решение

Я начинал первым и выбирал начальную позицию в 1 и 3 партиях. Мой сосед начинал первым и выбирал начальную позицию во 2 и 4 партиях.
Таблица соревнования:

Игрок	Я	СОСЕД
1 игрок	1	0
2 игрок	0	1
3 игрок	1	0
4 игрок	0	1
ИТОГО	2	2

Номер №206
Напиши в правом окне все цепочки букв длины 2 и 3, которые можно составить, используя буквы О, Н, К (каждую букву можно брать несколько раз). Для этого построй в левом окне дерево всех вариантов. Теперь найди среди этих цепочек 5 русских слов и обведи их красным.

Решение

Построим дерево вариантов:

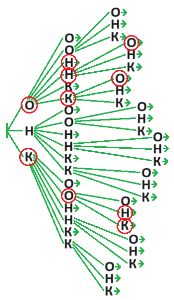
5 русских слов:
1. Он
2. Оно
3. Око
4. Кон
5. Кок
Напишем все цепочки букв длины 2 и 3, которые можно составить, используя буквы О, Н, К:

ОО	НО	КО
ОН	НН	КН
ОК	НК	КК
ООО	НОО	КОО
ООН	НОН	КОН
ООК	НОК	КОК
ОНО	ННО	КНО
ОНН	ННН	КНН
ОНК	ННК	КНК
ОКО	НКО	ККО
ОКН	НКН	ККН
ОКК	НКК	ККК

Номер №207
Вот рисунки птиц и их силуэтов в полёте. Прочитай текст (на этой и следующей страницах) и соедини каждую птицу с её силуэтом.

Птицы в воздухе
«Узнаю́т птицу по полёту», — гласит пословица. И действительно, многих птиц, особенно крупных, легко узнать в воздухе благодаря их характе́рным внешним признакам. Для этого совершенно необязательно видеть детали окраски или строения таких птиц, достаточно только контура, силуэта летящей птицы на фоне неба.
Длинные вытянутые ноги и широкий размах крыльев позволяют легко узнать в воздухе журавлей, аистов и цапель. Журавли и аисты в полёте вытягивают шею, и различить их можно только по характеру самого полёта: у аистов взмахи крыльев сочетаются с частым и длительным парением. Цапли же во время полёта втягивают голову в плечи.
Силуэты уток и гусей в воздухе кажутся короткохво́стыми (лапы не выдаются за пределы туловища), с массивным туловищем, шея вытянута вперёд. Несколько похожи на них и силуэты летящих гага́р, но из−за вытянутых назад сравнительно больших лап их тело кажется более длинным и короткокры́лым.
Хищные птицы (их называют дневными хищными или, более правильно, соколообра́зными) легко узнаются по их силуэту в воздухе. Короткая шея, широкие или, наоборот, узкие крылья и довольно длинный хвост позволяют отличить их от других птиц. Все хищные птицы прекрасно летают. Но в зависимости от того, где обитает и как охотится тот или иной хищник, длина и форма крыльев, а значит, и манера полёта чрезвычайно разнообразны.
Чёрный ко́ршун и каню́к охотятся на открытой местности, в поисках добычи паря на широких и длинных крыльях. Важным признаком для различения этих птиц является силуэт хвоста. У ко́ршуна он имеет вырезку, а у канюка́ хвост очень широкий и закруглённый.
Ястреб−тетеревя́тник охотится в лесной чаще. Широкие и сравнительно короткие крылья, узкий и более длинный, чем у канюка́, хвост помогают ему маневрировать во время охоты среди кустов и деревьев.
У со́колов (например, чеглока́) с их стремительным полётом крылья узкие, заострённые на конце и почти серпови́дной формы.

Каню́к

Серый гусь

Чернозобая гага́ра

Ястреб−тетеревя́тник

Серая цапля

Чёрный ко́ршун

Со́кол чегло́к

Серый журавль
↓↑

Решение

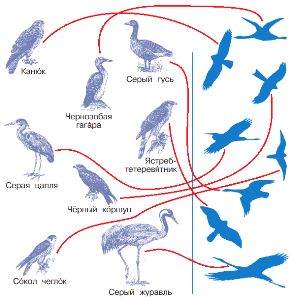
Номер №208
Нарисуй два таких мешка слов, чтобы длина каждого слова в каждом из этих мешков была не меньше 2 и при склеивании этих мешков получился мешок из 5 русских имён месяцев года.

Решение

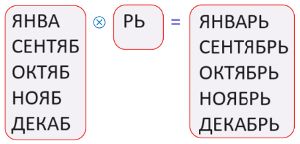
Номер №209
Реши задачу. Построй дерево в окне.
Известно, что К. М. Петров, В. Д. Петров, П. Б. Петров, Н. В. Петров, М. С. Петров, И. В. Петров, А. К. Петров, Д. М. Петров, Р. Б. Петров, Г. Д. Петров, Б. К. Петров являются представителями одного рода. Построй дерево родства Петровых, если известно, что у каждого отца было по два сына, внуков у основателя рода — четыре, а у его сыновей — по два.

Решение

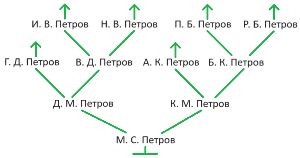
Номер №210
Дано дерево вычислений F. Вычисли значение выражения — заполни цветные окна дерева, затем напиши в окне выражение, значение которого вычислено при помощи этого дерева.

	-умножение
	-деление
	-сложение
	-вычитание

Решение

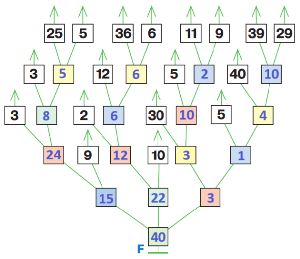
Запишем выражение:
(3 * (3 + (25 : 5))) – 9 + ((2 * (12 – (36 : 6))) + 10) + (30 : (5 * (11 – 9))) * (5 – (40 : (39 – 29))) = 40

Номер №211
Реши задачу, напиши ответ в окне.
Гриша пошёл с папой в тир. Уговор был такой: Гриша делает 5 выстрелов и потом за каждое попадание получает право сделать ещё 2 выстрела. Гриша выстрелил 17 раз. Сколько раз он попал в цель?
Нарисуй в окне дерево выстрелов Гриши: каждая бусина дерева — это выстрел, каждый лист дерева — это промах, за каждой бусиной−попаданием следуют две бусины.
Ответ: Гриша попал в цель _ раз.
Проверь своё решение: сколько всего бусин в дереве? Сколько в дереве бусин, которые не являются листьями?

Решение

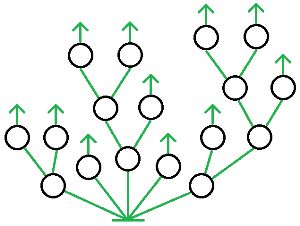
Всего бусин в дереве 17. Бусин, которые не являются листьями, 6.
Ответ: Гриша попал в цель 6 раз.

Номер №212

Вот зашифрованная фраза из известной детской песенки:

ШЫР−ПИР Ю ПЯПЮЖГЫ ЗЭЛЭМЪГЫЙ ГЁСРЫГ,
ФЁД ГЯГ, ФЁД ГЯГ, ЗЭЛЭМЪГЫЙ ГЁСРЫГ.

В этом шифре русские буквы зашифрованы русскими буквами, при этом использованы правила русского языка, которые изучают в первом классе. Запятые, точка и дефис использованы в этой фразе по правилам русского языка — они не зашифрованы. Догадайся, как построен шифр, расшифруй фразу — напиши расшифровку. Заполни таблицу шифра.
Теперь зашифруй с помощью построенного шифра этот стишок Ренаты Мухи:

ВЧЕРА КРОКОДИЛ УЛЫБНУЛСЯ ТАК ЗЛОБНО,
ЧТО МНЕ ДО СИХ ПОР ЗА НЕГО НЕУДОБНО

Решение

В тексте каждая гласная заменена на парную ей. Звонкие согласные заменены на парные им глухие и наоборот. Согласные, не имеющие пары, заменены друг на друга: р // л, м // н, х // ц, ч // щ. Й обозначает саму себя.
Расшифруем фразу:
ШЫР−ПИР Ю ПЯПЮЖГЫ ЗЭЛЭМЪГЫЙ ГЁСРЫГ,
ЖИЛ−БЫЛ У БАБУШКИ СЕРЕНЬКИЙ КОЗЛИК,
ФЁД ГЯГ, ФЁД ГЯГ, ЗЭЛЭМЪГЫЙ ГЁСРЫГ.
ВОТ КАК, ВОТ КАК, СЕРЕНЬКИЙ КОЗЛИК.
Построим таблицу шифра:

Зашифруем стишок:
ВЧЕРА КРОКОДИЛ УЛЫБНУЛСЯ ТАК ЗЛОБНО,
ФЩЭЛЯ ГЛЁГЁТЫР ЮРИПМЮРЗА ДЯГ СРЁПМЁ,
ЧТО МНЕ ДО СИХ ПОР ЗА НЕГО НЕУДОБНО
ЩДЁ НМЭ ТЁ ЗЫЦ БЁЛ СЯ МЭКЁ МЭЮТЁПМЁ

ГДЗ по Информатике за 4 класс, автор Рудченко (учебник)

Круговой турнир 1-7

Цепочка позиций 8-11

Игра камешки 12-25

Игра ползунок 26-35

Игра сим 36-43

Задачи для самопроверки 44-49

Выигрышная стратегия и позиция 50-58

Стратегии в игре камешки 59-72

Задачи для самопроверки 73,74

Дерево игры 75-82

Позиции на дереве игры 83-88

Дополнительные задачи 89-106

Дерево вычисления 107-119

Цепочка выполнения программы 120-130

Дерево выполнения программ 131-139

Дерево всех вариантов 140-153

Задачи для самопроверки 154-157

Лингвистические задачи 158-169

Шифрование 170-184

Задачи для самопроверки 185-186

Дополнительные задачи 187-212

ГДЗ по вашей программе

Все ГДЗ (МОЯ решалка)

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33