Эта страница является продолжением трилогии рабочих тетрадей по математике весьма популярного автора Мерзляк. Так это 3 и заключительная часть математики по рабочим тетрадям в 6 классе. Ну и так как это третья часть, то логично предположить, что ее изучение начинается примерно в феврале и продолжается до конца учебного года. Именно тогда она может оказаться для вас наиболее актуальной.
 Что относительно самого предмета, то о его необходимости, незаменимости и актуальности говорить не приходится. Так ясно, что предмет нужный, интересный и при этом применим практически в нашем мире. Мы же далее расскажем об ответах к этой самой 3 части рабочей тетради по математике за 6 класс.

Сами ответы лучше всего использовать для сверки, а не для списывания. Это логично из смысловых заключений о том, что знания все же должны рождаться в осмыслении полученной информации, а не простом списывании.

ГДЗ ответы для рабочей тетради по математике 6 класс, 3 часть Мерзляк

Кликаем по вкладкам и выбираем интересующие вас задания. Там и можно будет ознакомиться с ответами.

 Эта страница является продолжением трилогии рабочих тетрадей по математике весьма популярного автора Мерзляк. Так это 3 и заключительная часть математики по рабочим тетрадям в 6 классе. Ну и так как это третья часть, то логично предположить, что ее изучение начинается примерно в феврале и продолжается до конца учебного года. Именно тогда она может оказаться для вас наиболее актуальной.
 Что относительно самого предмета, то о его необходимости, незаменимости и актуальности говорить не приходится. Так ясно, что предмет нужный, интересный и при этом применим практически в нашем мире. Мы же далее расскажем об ответах к этой самой 3 части рабочей тетради по математике за 6 класс.

Сами ответы лучше всего использовать для сверки, а не для списывания. Это логично из смысловых заключений о том, что знания все же должны рождаться в осмыслении полученной информации, а не простом списывании.

ГДЗ ответы для рабочей тетради по математике 6 класс, 3 часть Мерзляк

Кликаем по вкладкам и выбираем интересующие вас задания. Там и можно будет ознакомиться с ответами.

№371

Положительные и отрицательные числа. Номер №371

Заполните пропуски.
1) Отрицательные числа записывают с помощью знака _, а _ числа − знака "+".
2) Число _ не относят ни к положительным, ни к отрицательным числам.
3) Если одно число _, а другое число _, то о таких числах говорят, что они имеют разные знаки.
4) Если два числа положительные или отрицательные, то говорят, что эти числа имеют _ знаки.

Решение

1) Отрицательные числа записывают с помощью знака −, а положительные числа − знака "+".
2) Число 0 не относят ни к положительным, ни к отрицательным числам.
3) Если одно число положительное, а другое число отрицательное, то о таких числах говорят, что они имеют разные знаки.
4) Если два числа положительные или отрицательные, то говорят, что эти числа имеют одинаковые знаки.

№372

Номер №372

Из чисел 3; −7; 0; −8; −1,4; 16 положительными являются числа: _, а отрицательными: _

Решение

Из чисел 3; −7; 0; −8; −1,4; 16 положительными являются числа: 3 и 16, а отрицательными: −7; −8; −1,4.

№373

Номер №373

Запишите пять отрицательных дробей со знаменателем 4.

Решение

$-\frac{1}{4}, -\frac{3}{4}, -\frac{5}{4}, -\frac{7}{4}, -\frac{9}{4}.$

№374

Номер №374

Подчеркните одной чертой пары чисел, имеющих разные знаки, и двумя чертами пары чисел, имеющих одинаковые знаки:
1) −7 и 9;
2) −8 и −10;
3) 14 и 19;
4) 5 и −3.

Решение

1) -7 и 9;
2) -8 и -10;
3) 14 и 19;
4) 5 и -3.

№375

Номер №375

Заполните таблицу.

Дата	Температура воздуха в 7 ч	Изменение температуры за последующие 5 ч	Температура воздуха за 12 ч
01.10	5°C	Повысилась на 9°C
15.10		Понизилась на 2°C	12°C
01.11	−2°C	Повысилась на 7°C
15.11	3°C	Понизилась на 4°C
01.12	−4°C	Понизилась на 5°C
15.12		Повысилась на 6°C	−14°C

Решение

Дата	Температура воздуха в 7 ч	Изменение температуры за последующие 5 ч	Температура воздуха за 12 ч
01.10	5°C	Повысилась на 9°C	14°C
15.10		Понизилась на 2°C	12°C
01.11	−2°C	Повысилась на 7°C	5°C
15.11	3°C	Понизилась на 4°C	−1°C
01.12	−4°C	Понизилась на 5°C	−9°C
15.12		Повысилась на 6°C	−14°C

 

№376

Номер №376

После четырех одинаковых стирок от куска мыла осталась его третья часть. На сколько таких же стирок хватит оставшейся части мыла?

Решение

Все мыло примем за единицу, тогда:
1) $1 - \frac{1}{3} = \frac{2}{3}$ (мыла) − израсходовали за 4 стирки;
2) $\frac{2}{3} : 4 = \frac{2}{3} * \frac{1}{4} = \frac{1}{3} * \frac{1}{2} = \frac{1}{6}$ (мыла) − расходуется за одну стирку;
3) $\frac{1}{3} : \frac{1}{6} = \frac{1}{3} * 6 = 2$ (стирки) − можно сделать оставшейся частью мыла.
Ответ: 2 стирки

№377

Номер №377

Заполните пропуски.
1) Прямую, на которой выбрали _, называют координатной прямой.
2) Все положительные числа и нуль называют _ числами.
3) Все _ числа _ называют неположительными числами.

Решение

Заполните пропуски.
1) Прямую, на которой выбрали начало отсчета, единичный отрезок и направление, называют координатной прямой.
2) Все положительные числа и нуль называют неотрицательными числами.
3) Все отрицательные числа нуль называют неположительными числами.

№378

Номер №378

Запишите координаты точек A, B, C, D, E, F, K, M, изображенных на рисунке.
1)
2)

Решение 1
K(−9), M(−6), F(−3), E(−2), A(2), B(5), C(9), D(11).

Решение 2
M(−5,5), C(−4), K(−2,5), B(−1), E(0,5), A(2), D(5), F(6,5).

№379

Номер №379

Начертите координатную прямую и отметьте на ней числа 0; 1; 3; −2; −6; 3,5; −4,5; 5; −1,5.

Решение

№380

Номер №380

Подчеркните среди данных чисел те, которые расположены на координатной прямой правее числа −0,4.
0; −4; 0,2; −0,3; 2; −0,45; −1,3; −0,7; −0,1.

Решение

0; −4; 0,2; -0,3; 2; −0,45; −1,3; −0,7; -0,1.

№381

Номер №381

На координатной прямой отметили числа a, b и c.
Укажите, верно ли утверждение.

Утверждение Да/Нет
Число a − отрицательное
Число c − положительное
Числа b и c имеют одинаковые знаки
Числа a и b имеют разные знаки
Числа a и c имеют разные знаки

Решение

Утверждение Да/Нет
Число a − отрицательное Да
Число c − положительное Да
Числа b и c имеют одинаковые знаки Нет
Числа a и b имеют разные знаки Нет
Числа a и c имеют разные знаки Да

№382

Номер №382

На координатной прямой отметили точки, соответствующие числам −6; 1; 3,4; −1,5; 0. Напишите под каждой точкой соответствующее число.

Решение

№383

Номер №383

Начертите координатную прямую, взяв за единичный отрезок, длина которого в 6 раз больше стороны клетки. Отметьте точки P(1), $Q(\frac{1}{6})$, $R(\frac{1}{3})$, $S(-1\frac{1}{6})$, $T(1\frac{2}{3})$, $X(-2\frac{1}{2})$, $Y(-\frac{5}{6})$, $Z(-\frac{2}{3})$.

Решение

$R(\frac{1}{3} = \frac{2}{6})$
$T(1\frac{2}{3} = 1\frac{4}{6})$
$X(-2\frac{1}{2} = -2\frac{3}{6})$
$Z(-\frac{2}{3} = -\frac{4}{6})$

№384

Номер №384

Отметьте на координатной прямой точки, удаленную от точки A(−2):
1) в положительном направлении на 6 единиц;
2) в отрицательном направлении на 4 единицы;
3) на 7 единиц.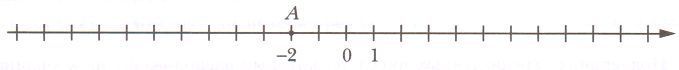

Решение

1)
2)
3)

№385

Номер №385

Числами, удаленными от числа 4 на 8 единиц, являются числа _

Решение

Числами, удаленными от числа 4 на 8 единиц, являются числа −4 и 12.

№386

Номер №386

На координатной прямой отметили числа −9 и 6. Какая из точек A, B, C или D является началом отсчета?

Решение

Между точками −9 и 6 на координатной прямой 15 единиц и 5 одинаковых отрезков, тогда:
1) 15 : 5 = 3 (единицы) − приходится на 1 отрезок;
2) 6 : 3 = 2 (отрезка) − будет между началом отсчета и точкой 6, значит точка C является началом отсчета.
Ответ: точка C

№387

Номер №387

Стоя неподвижно на ступеньке эскалатора метро, Вася поднимается вверх за 1 мин. Поднимаясь по ступенькам неподвижного эскалатора, он делает это за 40 с. За какое время Вася поднимается вверх, если будет идти по ступенькам движущегося эскалатора?

Решение

1 мин = 60 с
Пусть длина эскалатора равна x метров, тогда:
1) $\frac{x}{60}$ (м/с) − скорость эскалатора;
2) $\frac{x}{40}$ (м/с) − скорость Васи;
3) $\frac{x}{60} + \frac{x}{40} = \frac{2x + 3x}{120} = \frac{5x}{120} = \frac{x}{24}$ (м/с) − суммарная скорость Васи и эскалатора;
4) $x : \frac{x}{24} = x * \frac{24}{x} = 24$ (с) − будет подниматься Вася вверх, если будет идти по ступенькам движущегося эскалатора.
Ответ: 24 секунды

№388

Номер №388

Заполните пропуски.
1) Числом, противоположным самому себе, считают число _
2) Выражение −a означает, что записано число, противоположное числу _
3) Если число положительное, то противоположное ему число является _; если число отрицательное, то противоположное ему число является _
4) Целыми числами называют _ числа, _ числа и число _
5) Целыми положительными числами называют _ числа.
6) _ числа вместе образуют рациональные числа.

Решение

1) Числом, противоположным самому себе, считают число 0.
2) Выражение −a означает, что записано число, противоположное числу a.
3) Если число положительное, то противоположное ему число является отрицательным; если число отрицательное, то противоположное ему число является положительным.
4) Целыми числами называют натуральные числа, противоположные им числа и число 0.
5) Целыми положительными числами называют натуральные числа.
6) Целые и дробные числа вместе образуют рациональные числа.

№389

Номер №389

Заполните таблицу.

Число	2	−0,4	0,6	0	−100	1234	−18,6	$4\frac{1}{3}$	−5000
Противоположное число

Решение

Число	2	−0,4	0,6	0	−100	1234	−18,6	$4\frac{1}{3}$	−5000
Противоположное число	−2	0,4	−0,6	0	100	−1234	18,6	$-4\frac{1}{3}$	5000

 

№390

Номер №390

Заполните таблицу.

a	5	−6				−425
−a			−1,2	7	-9		-216	$8\frac{2}{7}$

 

Решение

a	5	−6	1,2	-7	9	−425	216	$-8\frac{2}{7}$
−a	-5	6	−1,2	7	-9	425	-216	$8\frac{2}{7}$

 

№391

Номер №391

Укажите, верно ли утверждение.

Утверждение Да/Нет
$\frac{3}{7}$ − положительное число
$\frac{3}{7}$ − рациональное число
$\frac{3}{7}$ − неотрицательное число
$\frac{3}{7}$ − неположительное число
−8 − отрицательное число
−8 − неположительное число
−8 − натуральное число
−8 − неотрицательное число
−8 − целое число
−8 − рациональное число
−8 − целое отрицательное число
−8 − неположительное число
Любое натуральное число является рациональным числом
Любое целое число является рациональным числом
Любое целое неотрицательное число является натуральным числом
Если рациональное число не является целым, то оно является дробным числом
Если рациональное число не является дробным, то оно является натуральным числом
Если число a целое, то число −a также целое

Решение

Утверждение Да/Нет
$\frac{3}{7}$ − положительное число Да
$\frac{3}{7}$ − рациональное число Да
$\frac{3}{7}$ − неотрицательное число Да
$\frac{3}{7}$ − неположительное число Нет
−8 − отрицательное число Да
−8 − неположительное число Да
−8 − натуральное число Нет
−8 − неотрицательное число Нет
−8 − целое число Да
−8 − рациональное число Да
−8 − целое отрицательное число Да
−8 − неположительное число Да
Любое натуральное число является рациональным числом Да
Любое целое число является рациональным числом Да
Любое целое неотрицательное число является натуральным числом Нет
Если рациональное число не является целым, то оно является дробным числом Да
Если рациональное число не является дробным, то оно является натуральным числом Нет
Если число a целое, то число −a также целое Да

№392

Номер №392

Решите уравнение.
1) −y = 13
2) −y = −18
3) −y = −(−7)

Решение 1
−y = 13
y = −13
Ответ: y = −13

Решение 2
−y = −18
y = 18
Ответ: y = 18

Решение 3
−y = −(−7)
−y = 7
y = −7
Ответ: y = −7

№393

Номер №393

Отметьте на координатной прямой точки с координатами 5; −7; 2,5; −4,5 и точки, координаты которых противоположны этим числам.

Решение

Числу 5 противоположно число −5.
Числу −7 противоположно число 7.
Числу 2,5 противоположно число −2,5.
Числу −4,5 противоположно число 4,5.

№394

Номер №394

Запишите все целые числа, расположенные на координатной прямой между числами:
1) −9 и −5;
2) −5 и 3;
3) −2,1 и $\frac{2}{3}$.

Решение 1
−9 < x < −5, где x − целое число:
x = {−8, −7, −6.}
Ответ: −8, −7, −6.

Решение 2
−5 < x < 3, где x − целое число:
x = {−4, −3, −2, −1, 0, 1, 2.}
Ответ: −4, −3, −2, −1, 0, 1, 2.

Решение 3
$-2,1 < x < \frac{2}{3}$, где x − целое число:
x = {−2, −1, 0.}
Ответ: −2, −1, 0.

№395

Номер №395

Между числами −50 и 30 на координатной прямой расположено _ целых чисел.

Решение
От −50 до 0 расположено 49 целых чисел.
Само число 0.
От 0 до 30 расположено 29 целых чисел.
Тогда:
49 + 1 + 29 = 50 + 29 = 79 целых чисел расположено между числами −50 и 30.
Ответ: Между числами −50 и 30 на координатной прямой расположено 79 целых чисел.

№396

Номер №396

В коробке лежат 20 карандашей − красные, синие и зеленые. Красных карандашей в 9 раз больше, чем синих. Сколько в коробке зеленых карандашей?

Решение

Пусть x синих карандашей лежало в коробке, тогда:
9x (красных) − карандашей лежало в коробке;
20 − (x + 9x) = 20 − 10x (зеленых) − карандашей лежало в коробке, следовательно x = 1, так как при x = 2 выражение 20 − 10x не имеет смысла.
Тогда:
20 − 10x = 20 − 10 * 1 = 20 − 10 = 10 (зеленых) − карандашей лежало в коробке.
Ответ: 10 зеленых карандашей

№397

Номер №397

Заполните пропуски.
1) Модулем числа a называют _ до точки, изображающей _
2) Модуль числа принимает только _ значения.
3) Модуль неотрицательного числа равен _
4) Модуль отрицательного числа равен числу, _
5) Модули _ чисел равны.

Решение

1) Модулем числа a называют расстояние от начала отсчета до точки, изображающей это число на координатной прямой.
2) Модуль числа принимает только неотрицательные значения.
3) Модуль неотрицательного числа равен этому числу.
4) Модуль отрицательного числа равен числу, противоположному данному.
5) Модули противоположных чисел равны.

№398

Номер №398

Найдите модуль.
1) |−8| =
2) |17| =
3) |$-14\frac{2}{9}$| =
4) |−256| =
5) |378| =
6) |−0,3| =

Решение 1
|−8| = 8

Решение 2
|17| = 17

Решение 3
$|-14\frac{2}{9}| = 14\frac{2}{9}$

Решение 4
|−256| = 256

Решение 5
|378| = 378

Решение 6
|−0,3| = 0,3

№399

Номер №399

Найдите значение выражения.
1) |−11| + |−19| =
2) |12| + |−12| =
3) |−18| : |2| − |1,5| * |−6| =

Решение 1
|−11| + |−19| = 11 + 19 = 30

Решение 2
|12| + |−12| = 12 + 12 = 24

Решение 3
|−18| : |2| − |1,5| * |−6| = 18 : 2 − 1,5 * 6 = 9 − 9 = 0

№400

Номер №400

Решите уравнение.
1) |x| = 15;
x =
или
x =
2) |x| = −9
3) |−x| = 3,6

Решение 1
|x| = 15
x = 15
или
x = −15
Ответ: x = ±15

Решение 2
|x| = −9
нет решений, так как |x| ≥ 0
Ответ: нет корней

Решение 3
|−x| = 3,6
−x = 3,6
x = −3,6
или
−x = −3,6
x = 3,6
Ответ: x = ±3,6

№401

Номер №401

Запишите числа 3,5; −6; 6,3; −0,6; 8,1; −9,4; 0 в порядке убывания их модулей.

Решение

|3,5| = 3,5
|−6| = 6
|6,3| = 6,3
|−0,6| = 0,6
|8,1| = 8,1
|−9,4| = 9,4
|0| = 0
9,4 > 8,1 > 6,3 > 6 > 3,5 > 0,6 > 0, тогда числа в порядке убывания их модулей:
−9,4; 8,1; 6,3; −6; 3,5; −0,6; 0.

№402

Номер №402

Отметьте на координатной прямой целые значения x, при которых верно неравенство.
1) |x| < 3,4
2) 2 < |x| < 4,5

Решение 1
|x| < 3,4
неравенство верно при x = −3; −2; −1; 0; 1; 2; 3.
Ответ:

Решение 2
2 < |x| < 4,5
неравенство верно при x = −4; −3; 3; 4.
Ответ:

№403

Номер №403

Укажите, верно ли утверждение.

Утверждение Да/нет
Если два числа равны, то их модули также равны
Если модули двух чисел равны, то эти числа равны
Если модули двух чисел равны, то эти числа равны или противоположны
Модуль целого числа всегда является натуральным числом

Решение

Утверждение	Да/нет
Если два числа равны, то их модули также равны	Да
Если модули двух чисел равны, то эти числа равны	Нет
Если модули двух чисел равны, то эти числа равны или противоположны	Да
Модуль целого числа всегда является натуральным числом	Нет

 

№404

Номер №404

Расставьте в пустых кружках натуральные числа от 1 до 6 так, чтобы сумма чисел, расположенных на одном диаметре, была равна 21.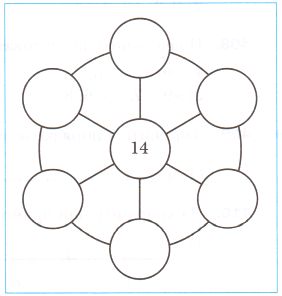

Решение

21 − 14 = 7 − поэтому для того, чтобы сумма чисел, расположенных на одном диаметре, была равна 21, необходимо на каждый диаметр добавить пару чисел, сумма которых равна 7.
Возможны следующие пары:
1 и 6 (1 + 6 = 7)
2 и 5 (2 + 5 = 7)
3 и 4 (3 + 4 = 7)
Ответ: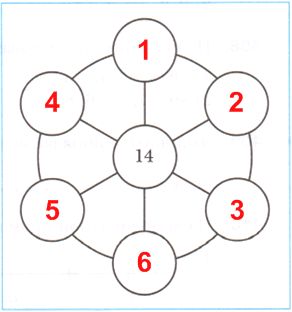

№405

Номер №405

Заполните пропуски.
1) На координатной прямой из двух чисел _ число расположено правее _
2) Любое _ число больше любого _ числа.
3) Из двух отрицательных чисел _ то, модуль которого больше.
4) Любое _ число меньше нуля, любое _ число больше нуля.
5) Если a − положительное число, то пишут a _ 0.
6) Если a − _ число, то пишут a < 0.
7) Если a − _ число, то пишут a ≥ 0.
8) Если a − _ число, то пишут a ≤ 0.

Решение

1) На координатной прямой из двух чисел большее число расположено правее меньшего.
2) Любое положительное число больше любого отрицательного числа.
3) Из двух отрицательных чисел меньше то, модуль которого больше.
4) Любое отрицательное число меньше нуля, любое положительное число больше нуля.
5) Если a − положительное число, то пишут a > 0.
6) Если a − отрицательное число, то пишут a < 0.
7) Если a − неотрицательное число, то пишут a ≥ 0.
8) Если a − неположительное число, то пишут a ≤ 0.

№406

Номер №406

Сравните числа.
1) 74 ☐ −75
2) −38 ☐ 0
3) −2,6 ☐ −2,8
4) −0,3001 ☐ −0,3
5) $-\frac{6}{11}$ ☐ $-\frac{6}{13}$
6) $-\frac{3}{7}$ ☐ $-\frac{9}{14}$

Решение 1
74 > −75

Решение 2
−38 < 0

Решение 3
−2,6 > −2,8

Решение 4
−0,3001 < −0,3

Решение 5
$-\frac{6}{11} < -\frac{6}{13}$

Решение 6
$-\frac{3}{7} = -\frac{6}{14}$
$-\frac{6}{14} > -\frac{9}{14}$, значит:
$-\frac{3}{7} > -\frac{9}{14}$

№407

Номер №407

Подчеркните последовательность чисел, расположенных в порядке возрастания.
1) 1, 0, −2, 3, −4
2) 0, 1, −2, 3, −4
3) 3, 1, 0, −2, −4
4) −4, −2, 0, 1, 3

Решение

1) 1, 0, −2, 3, −4
2) 0, 1, −2, 3, −4
3) 3, 1, 0, −2, −4
4) -4, -2, 0, 1, 3

№408

Номер №408

Подчеркните последовательность чисел, расположенных в порядке убывания.
1) −9, 8, −7, 6, −5
2) −9, −7, −5, 6, 8
3) 8, 6, −5, −7, −9
4) −5, −7, 6, 8, −9

Решение

1) −9, 8, −7, 6, −5
2) −9, −7, −5, 6, 8
3) 8, 6, -5, -7, -9
4) −5, −7, 6, 8, −9

№409

Номер №409

Запишите в порядке возрастания числа: −7; 4,3; 0,4; −6,9; 0; −12; 3,5.

Решение

−12 < −7 < −6,9 < 0 < 0,4 < 3,5 < 4,3

№410

Номер №410

На координатной прямой отметили числа a и b. Сравните эти числа и их модули.
1)
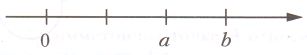a ☐ b
|a| ☐ |b|
2)
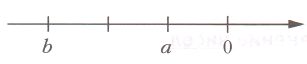a ☐ b
|a| ☐ |b|
3)
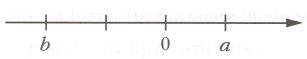a ☐ b
|a| ☐ |b|

Решение 1
a < b
|a| < |b|

Решение 2
a > b
|a| < |b|

Решение 3
a > b
|a| < |b|

№411

Номер №411

Запишите все целые значения x, при которых верно неравенство −4,62 < x < 3.

Решение

−4,62 < x < 3, где x − целые числа
x = {−4; −3; −2; −1; 0; 1; 2}
Ответ: −4; −3; −2; −1; 0; 1; 2.

№412

Номер №412

Укажите наименьшее целое число, при котором верно неравенство x ≥ −8.

Решение

x ≥ −8, x − наименьшее целое число
x = −8
Ответ: −8

№413

Номер №413

Укажите наибольшее целое число, при котором верно неравенство x ≤ −12,4.

Решение

x ≤ −12,4, x − наибольшее целое число
x = −13
Ответ: −13

№414

Номер №414

При каких целых значениях y верно неравенство:
1) |y| ≤ 3;
2) |y| < 4,2;
3) |y| ≤ 0?

Решение 1
|y| ≤ 3, y − целое число
y = {−3; −2; −1; 0; 1; 2; 3}
Ответ: −3; −2; −1; 0; 1; 2; 3.

Решение 2
|y| < 4,2, y − целое число
y = {−4; −3; −2; −1; 0; 1; 2; 3; 4}
Ответ: −4; −3; −2; −1; 0; 1; 2; 3; 4.

Решение 3
|y| ≤ 0, y − целое число
y = {0}
Ответ: 0

№415

Номер №415

На координатной прямой отметили числа a, b, c, d.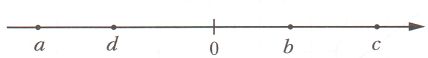
Сравните числа.
1) a ☐ d
2) d ☐ c
3) 0 ☐ d
4) −a ☐ d
5) −b ☐ 0
6) −b ☐ −d

Решение
1) a < d
2) d < c
3) 0 > d
4) −a > d
5) −b < 0
6) −b < −d

№416

Номер №416

Запишите, какую цифру можно поставить вместо звездочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи).
1) −4,07 < −4,*2;
*\ = _
2) −5,4*8 < −5,478;
*\ = _
3) −35,6 > −35,*;
*\ = _
4) −2,71 > −2,*9;
*\ = _

Решение 1
−4,07 < −4,*2
* = 0
−4,07 < −4,02
Ответ: 0

Решение 2
−5,4*8 < −5,478
* = 8
−5,488 < −5,478
* = 9
−5,498 < −5,478
Ответ: 8; 9.

Решение 3
−35,6 > −35,*
* = 7
−35,6 > −35,7
* = 8
−35,6 > −35,8
* = 9
−35,6 > −35,9
Ответ: 7; 8; 9.

Решение 4
−2,71 > −2,*9
* = 7
−2,71 > −2,79
* = 8
−2,71 > −2,89
* = 9
−2,71 > −2,99
Ответ: 7; 8; 9.

№417

Номер №417

Поставьте в квадрате после утверждения знак "+", если оно верно, или знак "−", если оно неверно.
1) Если a > 2, то a − положительное число. ☐
2) Если a < 0,1, то a − отрицательное число. ☐
3) Если a > −1, то a − положительное число. ☐
4) Если a < −0,4, то a − отрицательное число. ☐

Решение

1) Если a > 2, то a − положительное число. +
2) Если a < 0,1, то a - отрицательное число. -
3) Если a > −1, то a − положительное число. -
4) Если a < -0,4, то a - отрицательное число. +

№418

Номер №418

Запишите все целые значения x, при которых будут верными одновременно два двойных неравенства:
−4 ≤ x ≤ 3 и −3,7 ≤ x < 5.

Решение

−4 ≤ x ≤ 3, x − целое число
x = {−4; −3; −2; −1; 0; 1; 2; 3}
−3,7 ≤ x < 5, x − целое число
x = {−3; −2; −1; 0; 1; 2; 3; 4}
тогда верными одновременно два двойных неравенства при x = {3; −2; −1; 0; 1; 2; 3}
Ответ: 3; −2; −1; 0; 1; 2; 3.

№419

Номер №419

Числа a и b − положительные, |a| > |b|. Подчеркните верное неравенство.
1) a > b
2) a < b

Решение

1) a > b
2) a < b

№420

Номер №420

Числа a и b − отрицательные, a < b. Подчеркните верное неравенство.
1) |a| < |b|
2) |a| > |b|

Решение

1) |a| < |b|

2) |a| > |b|

№421

Номер №421

Заполните пропуск.
1) Если a и b − положительные числа и a < b, то −a ☐ −b.
2) Если a и b − отрицательные числа и a > b, то −a ☐ −b.

Решение 1
Если a и b − положительные числа и a < b, то −a > −b.

Решение 2
Если a и b − отрицательные числа и a > b, то −a < −b.

№422

Номер №422

Найдите два числа, каждое из которых больше $-\frac{8}{15}$, но меньше $-\frac{7}{15}$.

Решение

$-\frac{8}{15} = -\frac{24}{45}$
$-\frac{7}{15} = -\frac{21}{45}$
$-\frac{24}{45} < -\frac{23}{45} < -\frac{21}{45}$
$-\frac{24}{45} < -\frac{22}{45} < -\frac{21}{45}$
Ответ: $-\frac{23}{45}, -\frac{22}{45}$.

№423

Номер №423

Существуют ли натуральные числа m, n, k, при которых выполняется равенство $\frac{1}{m} + \frac{1}{n} + \frac{1}{k} = \frac{1}{m + n + k}$?

Решение

Если числа m, n, k − натуральные, то:
$\frac{1}{m} > \frac{1}{m + n + k}$
$\frac{1}{n} > \frac{1}{m + n + k}$
$\frac{1}{k} > \frac{1}{m + n + k}$
следовательно:
$\frac{1}{m} + \frac{1}{n} + \frac{1}{k} > \frac{1}{m + n + k}$, поэтому ни при каких натуральных числах m, n, k не будет выполняться равенство:
$\frac{1}{m} + \frac{1}{n} + \frac{1}{k} = \frac{1}{m + n + k}$
Ответ: не существует

№424

Номер №424

Заполните пропуски.
1) Чтобы сложить два числа с разными знаками, надо:
а) найти _ слагаемых;
б) из _ модуля вычесть _;
в) перед полученным числом поставить знак _;
2) Чтобы сложить два отрицательных числа, надо:
а) найти _;
б) сложить _;
в) перед полученным числом поставить _
3) Сумма двух _ чисел равна нулю.
4) Если одно из двух слагаемых равно 0, то сумма равна _

Решение

1) Чтобы сложить два числа с разными знаками, надо:
а) найти модули слагаемых;
б) из большего модуля вычесть меньший модуль;
в) перед полученным числом поставить знак слагаемого с большим модулем;
2) Чтобы сложить два отрицательных числа, надо:
а) найти модули слагаемых;
б) сложить модули слагаемых;
в) перед полученным числом поставить знак "−".
3) Сумма двух противоположных чисел равна нулю.
4) Если одно из двух слагаемых равно 0, то сумма равна самому числу.

№425

Номер №425

Заполните таблицу.

a	−5	−6	−0,2	13	−4	−9	7	10	0
b	−3	−7	−0,8	−8	12	6	−15	−10	−4
a + b

Решение

1) −5 + (−3) = −(5 + 3) = −8
2) −6 + (−7) = −(6 + 7) = −13
3) −0,2 + (−0,8) = −(0,2 + 0,8) = −1
4) 13 + (−8) = 13 − 8 = 5
5) −4 + 12 = 12 − 4 = 8
6) −9 + 6 = −(9 − 6) = −3
7) 7 + (−15) = −(15 − 7) = −8
8) 10 + (−10) = 10 − 10 = 0
9) 0 + (−4) = −4

Ответ:

a	−5	−6	−0,2	13	−4	−9	7	10	0
b	−3	−7	−0,8	−8	12	6	−15	−10	−4
a + b	−8	−13	−1	5	8	−3	-8	0	4

 

№426

Номер №426

Выполните сложение.
1) −0,7 + 1,2 =
2) −6 + (−1,8) =
3) 1,8 + (−4,2) =
4) 4 + (−1,6) =
5) −1 + 0,8 =
6) −2,3 + (−1,1) =
7) −5,2 + 9 =
8) 7 + (−10,4) =

Решение 1
−0,7 + 1,2 = 1,2 − 0,7 = 0,5

Решение 2
−6 + (−1,8) = −(6 + 1,8) = −7,8

Решение 3
1,8 + (−4,2) = −(4,2 − 1,8) = −2,4

Решение 4
4 + (−1,6) = 4 − 1,6 = 2,4

Решение 5
−1 + 0,8 = −(1 − 0,8) = −0,2

Решение 6
−2,3 + (−1,1) = −(2,3 + 1,1) = −3,4

Решение 7
−5,2 + 9 = 9 − 5,2 = 3,8

Решение 8
7 + (−10,4) = −(10,4 − 7) = −3,4

№427

Номер №427

Расшифруйте название прибора, применяемого для измерения углов.

О	$-\frac{1}{6} + (-\frac{3}{5})$
Р	$-\frac{7}{8} + \frac{2}{9}$
А	$\frac{1}{4} + (-\frac{11}{12})$
Т	$-\frac{17}{27} + (-\frac{1}{3})$
И	$-\frac{5}{14} + \frac{3}{4}$
С	$-\frac{5}{6} + (-\frac{2}{9})$
Б	$-\frac{13}{24} + \frac{5}{16}$
Я	$\frac{7}{8} + (-\frac{3}{10})$
Л	$\frac{2}{7} + (-\frac{5}{14})$

 

$-\frac{2}{3}$	$-1\frac{1}{18}$	$-\frac{26}{27}$	$-\frac{47}{72}$	$-\frac{23}{30}$	$-\frac{1}{14}$	$\frac{23}{40}$	$-\frac{11}{48}$	$\frac{11}{28}$	$\frac{23}{40}$

Решение

О = $-\frac{1}{6} + (-\frac{3}{5}) = -(\frac{5}{30} + \frac{18}{30}) = -\frac{23}{30}$
Р = $-\frac{7}{8} + \frac{2}{9} = -\frac{63}{72} + \frac{16}{72} = -(\frac{63}{72} - \frac{16}{72}) = -\frac{47}{72}$
А = $\frac{1}{4} + (-\frac{11}{12}) = \frac{3}{12} + (-\frac{11}{12}) = -(\frac{11}{12} - \frac{3}{12}) = -\frac{8}{12} = -\frac{2}{3}$
Т = $-\frac{17}{27} + (-\frac{1}{3}) = -(\frac{17}{27} + \frac{9}{27}) = -\frac{26}{27}$
И = $-\frac{5}{14} + \frac{3}{4} = -\frac{10}{28} + \frac{21}{28} = \frac{21}{28} - \frac{10}{28} = \frac{11}{28}$
С = $-\frac{5}{6} + (-\frac{2}{9}) = -(\frac{15}{18} + \frac{4}{18}) = -\frac{19}{18} = -1\frac{1}{18}$
Б = $-\frac{13}{24} + \frac{5}{16} = -\frac{26}{48} + \frac{15}{48} = -(\frac{26}{48} - \frac{15}{48}) = -\frac{11}{48}$
Я = $\frac{7}{8} + (-\frac{3}{10}) = \frac{35}{40} + (-\frac{12}{40}) = \frac{35}{40} - \frac{12}{40} = \frac{23}{40}$
Л = $\frac{2}{7} + (-\frac{5}{14}) = \frac{4}{14} + (-\frac{5}{14}) = -(\frac{5}{14} - \frac{4}{14}) = -\frac{1}{14}$

 

$-\frac{2}{3}$	$-1\frac{1}{18}$	$-\frac{26}{27}$	$-\frac{47}{72}$	$-\frac{23}{30}$	$-\frac{1}{14}$	$\frac{23}{40}$	$-\frac{11}{48}$	$\frac{11}{28}$	$\frac{23}{40}$
А	С	Т	Р	О	Л	Я	Б	И	Я

Ответ: АСТРОЛЯБИЯ

№428

Номер №428

Найдите значение выражения.
1) $-3\frac{7}{16} + (-2\frac{5}{32})$
2) $-4\frac{2}{9} + (-1\frac{17}{36})$
3) $-7 + 1\frac{13}{16}$
4) $-1\frac{1}{12} + 3\frac{4}{9}$
5) $-5\frac{16}{21} + 2\frac{5}{9}$
6) $4\frac{9}{16} + (-9\frac{5}{6})$
7) $3\frac{5}{17} + (-5\frac{8}{51})$
8) $-2\frac{6}{7} + 6\frac{2}{3}$

Решение 1
$-3\frac{7}{16} + (-2\frac{5}{32}) = -(3\frac{14}{32} + 2\frac{5}{32}) = -5\frac{19}{32}$

Решение 2
$-4\frac{2}{9} + (-1\frac{17}{36}) = -(4\frac{8}{36} + 1\frac{17}{36}) = -5\frac{25}{36}$

Решение 3
$-7 + 1\frac{13}{16} = -(7 - 1\frac{13}{16}) = -(6\frac{16}{16} - 1\frac{13}{16}) = -5\frac{3}{16}$

Решение 4
$-1\frac{1}{12} + 3\frac{4}{9} = 3\frac{16}{36} - 1\frac{3}{36} = 2\frac{13}{36}$

Решение 5
$-5\frac{16}{21} + 2\frac{5}{9} = -(5\frac{48}{63} - 2\frac{35}{63}) = -3\frac{13}{63}$

Решение 6
$4\frac{9}{16} + (-9\frac{5}{6}) = -(9\frac{40}{48} - 4\frac{27}{48}) = -5\frac{13}{48}$

Решение 7
$3\frac{5}{17} + (-5\frac{8}{51}) = -(5\frac{8}{51} - 3\frac{15}{51}) = -(4\frac{59}{51} - 3\frac{15}{51}) = -1\frac{44}{51}$

Решение 8
$-2\frac{6}{7} + 6\frac{2}{3} = 6\frac{14}{21} - 2\frac{18}{21} = 5\frac{35}{21} - 2\frac{18}{21} = 3\frac{17}{21}$

№429

Номер №429

Впишите в пустую клетку такое число, чтобы получилось верное равенство.
1) −8 + ☐ = −5
2) −8 + ☐ = −14
3) 8 + ☐ = −3
4) ☐ + (−9) = −16
5) ☐ + (−12) = −19
6) 15 + ☐ = 0

Решение 1
−8 + ☐ = −5
☐ = −5 − (−8)
☐ = −5 + 8
☐ = 8 − 5
☐ = 3
Ответ: −8 + 3 = −5

Решение 2
−8 + ☐ = −14
☐ = −14 − (−8)
☐ = −14 + 8
☐ = −(14 − 8)
☐ = −6
Ответ: −8 + (−6) = −14

Решение 3
8 + ☐ = −3
☐ = −3 − 8
☐ = −(3 + 8)
☐ = −11
Ответ: 8 + (−11) = −3

Решение 4
☐ + (−9) = −16
☐ = −16 − (−9)
☐ = −16 + 9
☐ = −(16 − 9)
☐ = −7
Ответ: −7 + (−9) = −16

Решение 5
☐ + (−12) = −19
☐ = −19 − (−12)
☐ = −19 + 12
☐ = −(19 − 12)
☐ = −7
Ответ: −7 + (−12) = −19

Решение 6
15 + ☐ = 0
☐ = 0 − 15
☐ = −15
Ответ: 15 + (−15) = 0

№430

Номер №430

Запишите три числа, сумма которых равна нулю и каждое последующее из них на 6 больше предыдущего.

Решение

Так как сумма трех числе равна нулю, то одно из чисел равно нулю, а два других числа являются противоположными числами.
По условию каждое последующее из чисел на 6 больше предыдущего, значит:
первое число −6;
второе число 0;
третье число 6.
Проверим:
−6 + 0 + 6 = 0
Ответ: −6; 0; 6.

№431

Номер №431

Составьте числовое выражение и вычислите его значение:
1) к сумме чисел −7 и −20 прибавить число 16;
2) к числу −6,3 прибавить сумму чисел −2,8 и 1,4;
3) к сумме чисел −1,3 и −1,9 прибавить сумму чисел −4,2 и 5,1.

Решение 1
(−7 + (−20)) + 16 = −(7 + 20) + 16 = −27 + 16 = −(27 − 16) = −11

Решение 2
−6,3 + (−2,8 + 1,4) = −6,3 − (2,8 − 1,4) = −6,3 − 1,4 = −(6,3 + 1,4) = −7,7

Решение 3
(−1,3 + (−1,9)) + (−4,2 + 5,1) = −(1,3 + 1,9) + (5,1 − 4,2) = −3,2 + 0,9 = −(3,2 − 0,9) = −2,3

№432

Номер №432

Закончите предложение.
1) Сумма двух чисел больше каждого слагаемого, если эти числа _
2) Сумма двух чисел меньше каждого слагаемого, если эти числа _
3) Сумма двух чисел меньше одного слагаемого и больше другого, если эти числа _

Решение

1) Сумма двух чисел больше каждого слагаемого, если эти числа положительные.
2) Сумма двух чисел меньше каждого слагаемого, если эти числа отрицательные.
3) Сумма двух чисел меньше одного слагаемого и больше другого, если эти числа разных знаков.

№433

Номер №433

Запишите в строку пять таких чисел, чтобы сумма любых двух соседних чисел была положительной, а сумма всех пяти чисел − отрицательной.

Решение

Пусть искомые пять чисел равны:
−3; 5; −4; 6; −5, тогда:
сумма соседних чисел будет равна:
−3 + 5 = 5 − 3 = 2
5 + (−4) = 5 − 4 = 1
−4 + 6 = 6 − 4 = 2
6 + (−5) = 6 − 5 = 1
сумма всех чисел будет равна:
−3 + 5 + (−4) + 6 + (−5) = −3 + 5 − 4 + 6 − 5 = (5 + 6) − (3 + 4 + 5) = 11 − 12 = −(12 − 11) = −1
Ответ: −3; 5; −4; 6; −5.

№434

Номер №434

Можно ли записать в строку шесть таких чисел, чтобы сумма любых двух соседних чисел была положительной, а сумма всех шести чисел − отрицательной?

Решение

Сумма двух соседних чисел будет положительной в двух случаях:
1) оба числа положительные;
2) соседние числа с разными знаками, но модуль положительного числа больше, чем модуль отрицательного.
Представим, что их шести чисел 3 положительных и 3 отрицательных. Тогда в каждой из пар чисел (положительное + отрицательное) модуль положительного числа будет больше модуля отрицательного. Следовательно модуль суммы трех положительных чисел будет больше модуля суммы трех отрицательных чисел, а значит сумма всех шести чисел будет числом положительным. Получается нельзя записать в строку шесть таких чисел, чтобы сумма любых двух соседних чисел была положительной, а сумма всех шести чисел − отрицательной.
Ответ: нет, нельзя.

№435

Номер №435

Можно ли записать в строку девять таких чисел, чтобы сумма любых трех соседних чисел была положительной, а сумма всех девяти чисел − отрицательной?

Решение

Так как сумма любых трех соседних чисел положительна, то сумма всех девяти чисел будет также положительной, следовательно, нельзя записать девять таких чисел, чтобы сумма любых трех соседних чисел была положительной, а сумма всех девяти чисел − отрицательной.
Ответ: нет, нельзя

№436

Номер №436

Заполните пропуски.
1) Для любых рациональных чисел a и b справедливо равенство a + b = _. Это утверждение называют _ свойством сложения.
2) Для любых рациональных чисел a, b и c справедливо равенство (a + b) + c = _. Это утверждение называют _ свойством сложения.

Решение

1) Для любых рациональных чисел a и b справедливо равенство a + b = b + a. Это утверждение называют переместительным свойством сложения.
2) Для любых рациональных чисел a, b и c справедливо равенство (a + b) + c = a + (b + c). Это утверждение называют сочетательным свойством сложения.

№437

Номер №437

Выполните сложение, выбирая удобный порядок вычислений.
1) −14 + 9 + 14 + (−9)
2) −19 + 18,74 + (−18,7)
3) 42 + (−50) + 13 + (−5)
4) −1,7 + (−3,3) + 5
5) −8 + 4,2 + (−9) + 5,8
6) −2,72 + 3,48 + 1,72 + (−7,48)
7) −1,3 + 2,19 + 0,4 + (−2,19)
8) $-4\frac{9}{16} + 5\frac{7}{18} + 4\frac{7}{16} + (-5\frac{13}{18})$

Решение 1
−14 + 9 + 14 + (−9) = (−14 + 14) + (9 + (−9)) = 0 + 0 = 0

Решение 2
−19 + 18,74 + (−18,7) = −19 + (18,74 + (−18,7)) = −19 + 0,04 = −18,96

Решение 3
42 + (−50) + 13 + (−5) = (42 + 13) + (−50 + (−5)) = 55 + (−55) = 0

Решение 4
−1,7 + (−3,3) + 5 = (−1,7 + (−3,3)) + 5 = −5 + 5 = 0

Решение 5
−8 + 4,2 + (−9) + 5,8 = (−8 + (−9)) + (4,2 + 5,8) = −17 + 10 = −7

Решение 6
−2,72 + 3,48 + 1,72 + (−7,48) = (3,48 + (−7,48)) + (−2,72 + 1,72) = −4 + (−1) = −5

Решение 7
−1,3 + 2,19 + 0,4 + (−2,19) = (2,19 + (−2,19)) + (−1,3 + 0,4) = 0 + (−0,9) = −0,9

Решение 8
$-4\frac{9}{16} + 5\frac{7}{18} + 4\frac{7}{16} + (-5\frac{13}{18}) = (-4\frac{9}{16} + 4\frac{7}{16}) + (5\frac{7}{18} + (-5\frac{13}{18})) = -\frac{2}{16} + (-\frac{6}{18}) = -\frac{1}{8} + (-\frac{1}{3}) = -\frac{3}{24} + (-\frac{8}{24}) = -\frac{11}{24}$

№438

Номер №438

Найдите сумму всех целых чисел, расположенных на координатной прямой между числами −7 и 12.

Решение

−6 + (−5) + (−4) + (−3) + (−2) + (−1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (−6 + 6) + (−5 + 5) + (−4 + 4) + (−3 + 3) + (−2 + 2) + (−1 + 1) + 0 + 7 + 8 + 9 + 10 + 11 = 7 + 8 + 9 + 10 + 11 = 15 + 19 + 11 = 15 + 30 = 45
Ответ: 45

№439

Номер №439

Чему равна сумма всех целых чисел, которые больше −8, но меньше 6?

Решение

−7 + (−6) + (−5) + (−4) + (−3) + (−2) + (−1) + 0 + 1 + 2 + 3 + 4 + 5 = −7 + (−6) = −13
Ответ: −13

№440

Номер №440

Найдите сумму всех целых чисел, удовлетворяющих неравенству $-12\frac{1}{3} < x ≤ 9,6$.

Решение

−12 + (−11) + (−10) + (−9) + (−8) + (−7) + (−6) + (−5) + (−4) + (−3) + (−2) + (−1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = −12 + (−11) + (−10) = −23 + (−10) = −33
Ответ: −33

№441

Номер №441

Упростите выражение −3,8 + m + 6,36 + (−6,2) + n + (−8,36) и найдите его значение при m = −14, n = 52.

Решение

−3,8 + m + 6,36 + (−6,2) + n + (−8,36) = (−3,8 + (−6,2)) + (6,36 + (−8,36)) + m + n = −10 + (−2) + m + n = −12 + m + n
при m = −14, n = 52:
−12 + (−14) + 52 = −14 + (−12 + 52) = −14 + 40 = 26
Ответ: 26

№442

Номер №442

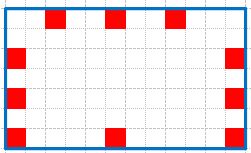
Расставьте вдоль стен четырехугольной комнаты 10 стульев так, чтобы возле каждой стены было поровну стульев.

Решение

№443

Номер №443

Заполните пропуски.
1) Разностью рациональных чисел a и b называют такое рациональное число x, которое в сумме с числом _ дает число _
2) Чтобы найти разность двух чисел. можно к _ прибавить число, _
3) Если разность a − b _, то a < b.
4) Если разность a − b _, то a > b.
5) Чтобы из числа 8 вычесть число −10, надо к числу 8 прибавить число _
6) Чтобы из числа − 6 вычесть число 7, надо к числу _ прибавить число _

Решение

1) Разностью рациональных чисел a и b называют такое рациональное число x, которое в сумме с числом b дает число a.
2) Чтобы найти разность двух чисел. можно к уменьшаемому прибавить число, противоположное вычитаемому.
3) Если разность a − b отрицательна, то a < b.
4) Если разность a − b положительна, то a > b.
5) Чтобы из числа 8 вычесть число −10, надо к числу 8 прибавить число 10.
6) Чтобы из числа − 6 вычесть число 7, надо к числу (−6) прибавить число (−7).

№444

Номер №444

Выполните вычитание.
1) 3 − 8
2) −4 − 9
3) 9 − (−5)
4) −7 − (−6)
5) 0 − 16
6) 0 − (−19)

Решение 1
3 − 8 = 3 + (−8) = −5

Решение 2
−4 − 9 = −4 + (−9) = −13

Решение 3
9 − (−5) = 9 + 5 = 14

Решение 4
−7 − (−6) = −7 + 6 = −1

Решение 5
0 − 16 = 0 + (−16) = −16

Решение 6
0 + 19 = 19

№445

Номер №445

Заполните пропуски в цепочке вычислений.

Решение
1) 9 − 12 = 9 + (−12) = −3
2) −3 − 5 = −3 + (−5) = −8
3) −8 + 6 = −2
4) −2 − (−2) = −2 + 2 = 0
Ответ:

№446

Номер №446

Заполните таблицу.

a	12	6	0	−5	−10	−8	2	0
b	18	15	4	3	12	-6	-1	-5
a − b
b − a

Полученные результаты показывают, что при одних и тех же значениях a и b выражения a − b и b − a принимают _ значения.

Решение
1)
12 − 18 = 12 + (−18) = −6
18 − 12 = 6
2)
6 − 15 = 6 + (−15) = −9
15 − 6 = 9
3)
0 − 4 = 0 + (−4) = −4
4 − 0 = 4
4)
−5 − 3 = −5 + (−3) = −8
3 − (−5) = 3 + 5 = 8
5)
−10 − 12 = −10 + (−12) = −22
12 − (−10) = 12 + 10 = 22
6)
−8 − (−6) = −8 + 6 = −2
−6 − (−8) = −6 + 8 = 2
7)
2 − (−1) = 2 + 1 = 3
−1 − 2 = −1 + (−2) = −3
8)
0 − (−5) = 0 + 5 = 5
−5 − 0 = −5

a	12	6	0	−5	−10	−8	2	0
b	18	15	4	3	12	-6	-1	-5
a − b	-6	-9	-4	-8	-22	-2	3	5
b − a	6	9	4	8	22	2	-3	-5

Полученные результаты показывают, что при одних и тех же значениях a и b выражения a − b и b − a принимают противоположные значения.

№447

Номер №447

Найдите разность.
1) $\frac{4}{9} - (-\frac{1}{6}) = \frac{4}{9} + \frac{}{}$
2) $-\frac{5}{8} - (-\frac{7}{10}) = -\frac{5}{8} + \frac{}{}$
3) $\frac{7}{12} - \frac{17}{18}$
4) $-\frac{9}{20} - \frac{4}{15}$
5) $\frac{3}{10} - \frac{8}{15}$
6) $-\frac{11}{25} - (-\frac{3}{10})$

Решение 1
$\frac{4}{9} - (-\frac{1}{6}) = \frac{4}{9} + \frac{1}{6} = \frac{8}{18} + \frac{3}{18} = \frac{11}{18}$

Решение 2
$-\frac{5}{8} - (-\frac{7}{10}) = -\frac{5}{8} + \frac{7}{10} = -\frac{25}{40} + \frac{28}{40} = \frac{3}{40}$

Решение 3
$\frac{7}{12} - \frac{17}{18} = \frac{7}{12} + (-\frac{17}{18}) = \frac{21}{36} + (-\frac{34}{36}) = -\frac{13}{36}$

Решение 4
$-\frac{9}{20} - \frac{4}{15} = -\frac{9}{20} + (-\frac{4}{15}) = -\frac{27}{60} + (-\frac{16}{60}) = -\frac{43}{60}$

Решение 5
$\frac{3}{10} - \frac{8}{15} = \frac{3}{10} + (-\frac{8}{15}) = \frac{9}{30} + (-\frac{16}{30}) = -\frac{7}{30}$

Решение 6
$-\frac{11}{25} - (-\frac{3}{10}) = -\frac{11}{25} + \frac{3}{10} = -\frac{22}{50} + \frac{15}{50} = -\frac{7}{50}$

№448

Номер №448

Выполните вычитание.
1) $-3\frac{1}{6} - (-2\frac{3}{8}) = -3\frac{1}{6} + $
2) $-5\frac{7}{20} - 2\frac{9}{25}$
3) $-4\frac{4}{15} - (-6\frac{5}{9})$
4) $1\frac{5}{7} - (-2\frac{3}{5})$

Решение 1
$-3\frac{1}{6} - (-2\frac{3}{8}) = -3\frac{1}{6} + 2\frac{3}{8} = -3\frac{4}{24} + 2\frac{9}{24} = -2\frac{28}{24} + 2\frac{9}{24} = -\frac{19}{24}$

Решение 2
$-5\frac{7}{20} - 2\frac{9}{25} = -5\frac{7}{20} + (-2\frac{9}{25}) = -5\frac{35}{100} + (-2\frac{36}{100}) = -7\frac{71}{100}$

Решение 3
$-4\frac{4}{15} - (-6\frac{5}{9}) = -4\frac{4}{15} + 6\frac{5}{9} = -4\frac{12}{45} + 6\frac{25}{45} = 2\frac{13}{45}$

Решение 4
$1\frac{5}{7} - (-2\frac{3}{5}) = 1\frac{5}{7} + 2\frac{3}{5} = 1\frac{25}{35} + 2\frac{21}{35} = 3\frac{46}{35} = 4\frac{11}{35}$

№449

Номер №449

Решите уравнение.
1) x + 9 = 3
x = 3 − 9
x =
2) 12 − x = 17
x = 12 − 17
x = −5
3) x + 20 = −14
4) −1,5 − x = 4
5) x − 0,8 = −1,2
6) 10 − x = −2

Решение 1
x + 9 = 3
x = 3 − 9
x = −6
Ответ: x = −6

Решение 2
12 − x = 17
x = 12 − 17
x = −5
Ответ: x = −5

Решение 3
x + 20 = −14
x = −14 − 20
x = −34
Ответ: x = −34

Решение 4
−1,5 − x = 4
−x = −1,5 − 4
x = −5,5
Ответ: x = −5,5

Решение 5
x − 0,8 = −1,2
x = −1,2 + 0,8
x= −0,4
Ответ: −0,4

Решение 6
10 − x = −2
x = 10 − (−2)
x = 10 + 2
x = 12
Ответ: x = 12

№450

Номер №450

Найдите числа, которых не хватает в цепочке вычислений.

Решение

Первый квадрат:
1,4 − x = −2,4
x = 1,4 − (−2,4)
x = 1,4 + 2,4
x = 3,8
Средний кружок:
x + 1,5 = −2,5
x = −2,5 − 1,5
x = −4
Второй квадрат:
−2,4 − x = −4
−x = −2,4 − (−4)
−x = −2,4 + 4
−x = 1,6
x = −1,6
Последний квадрат:
−2,5 − (−1,4) = −2,5 + 1,4 = −1,1
Ответ:

№451

Номер №451

Не выполняя вычислений, поставьте знак "=" или знак "≠", чтобы образовалось верное утверждение.
1) −6 − 7 ☐ −6 + (−7)
2) −5 − 9 ☐ − 5 − (−9)
3) 0 − (−4) ☐ 0 + 4
4) −8 − (−3) ☐ −8 + (−3)

Решение 1
−6 − 7 = −6 + (−7)

Решение 2
−5 − 9 ≠ − 5 − (−9)

Решение 3
0 − (−4) = 0 + 4

Решение 4
−8 − (−3) ≠ −8 + (−3)

№452

Номер №452

Впишите в пустую клетку такое число, чтобы получилось верное равенство.
1) 0 − ☐ = −5
2) 2 − ☐ = −4
3) ☐ − 3 = −7
4) ☐ − 9 = −8

Решение 1
0 − ☐ = −5
☐ = 0 − (−5)
☐ = 0 + 5
☐ = 5
Ответ: 0 − 5 = −5

Решение 2
2 − ☐ = −4
☐ = 2 − (−4)
☐ = 2 + 4
☐ = 6
Ответ: 2 − 6 = −4

Решение 3
☐ − 3 = −7
☐ = −7 + 3
☐ = −4
Ответ: −4 − 3 = −7

Решение 4
☐ − 9 = −8
☐ = −8 + 9
☐ = 1
Ответ: 1 − 9 = −8

№453

Номер №453

Найдите значение выражения.
1) −26 + 17 − 32 + 20
2) 1,8 − 3,6 − 2,6 + 5,2
3) −0,6 − (−0,8) + (−1,7) + 6,1

Решение 1
−26 + 17 − 32 + 20 = (−26 + (−32)) + (17 + 20) = −58 + 37 = −21

Решение 2
1,8 − 3,6 − 2,6 + 5,2 = (−3,6 − (2,6)) + (1,8 + 5,2) = −6,2 + 7 = 0,8

Решение 3
−0,6 − (−0,8) + (−1,7) + 6,1 = −0,6 + 0,8 + (−1,7) + 6,1 = (−0,6 + (−1,7)) + (0,8 + 6,1) = −2,3 + 6,9 = 4,6

№454

Номер №454

Составьте числовое выражение и вычислите его значение:
1) из числа 6,4 вычесть сумму чисел −15,2 и 4,7;
2) к числу −1,2 прибавить разность чисел 2,2 и 3,8;
3) к разности чисел −1,4 и −2,9 прибавить сумму чисел 3,9 и −8;
4) из суммы чисел −5,2 и 9 вычесть разность чисел 0,6 и −4,8.

Решение 1
6,4 − (−15,2 + 4,7) = 6,4 − (−10,5) = 6,4 + 10,5 = 16,9

Решение 2
−1,2 + (2,2 − 3,8) = −1,2 + (−1,6) = −2,8

Решение 3
(−1,4 − (−2,9)) + (3,9 + (−8)) = (−1,4 + 2,9) + (−4,1) = 1,5 + (−4,1) = −2,6

Решение 4
(−5,2 + 9) − (0,6 − (−4,8)) = 3,8 − (0,6 + 4,8) = 3,8 − 5,4 = −1,6

№455

Номер №455

Решите уравнение.
1) |x| + 4 = 10
|x| =
|x| =
x =
или
x =
2) |x| − 12 = 3
3) |x| + 1,4 = 0,8
4) 17 − |x| = −7
5) |x + 5| = 2
x + 5 = 2
или
x + 5 = −2
6) |x − 3,7| = 3,7

Решение 1
|x| + 4 = 10
|x| = 10 − 4
|x| = 6
x = 6
или
x = −6
Ответ: x = ±6

Решение 2
|x| − 12 = 3
|x| = 3 + 12
|x| = 15
x = 15
или
x = −15
Ответ: x = ±15

Решение 3
|x| + 1,4 = 0,8
|x| = 0,8 − 1,4
|x| = −0,6 − нет корней
Ответ: нет корней

Решение 4
17 − |x| = −7
|x| = 17 − (−7)
|x| = 17 + 7
|x| = 24
x = 24
или
x = −24
Ответ: x = ±24

Решение 5
|x + 5| = 2
x + 5 = 2
x = 2 − 5
x = −3
или
x + 5 = −2
x = −2 − 5
x = −7
Ответ: x = −7 и x = −3

Решение 6
|x − 3,7| = 3,7
x − 3,7 = 3,7
x = 3,7 + 3,7
x = 7,4
или
x − 3,7 = −3,7
x = −3,7 + 3,7
x = 0
Ответ: x = 0 и x = 7,4

№456

Номер №456

Концами отрезка CD являются точки координатной прямой. Найдите координату точки D, если:
1) C(7); CD = 12;
2) C(−4,5); CD = 7,2.

Решение 1
C(7); CD = 12.
Пусть точка D имеет координату x. Рассмотрим два случая.
а) Точка D расположена справа от точки C. Тогда
x = 7 + 12
x = 19
б) Точка D расположена слева от точки C. Тогда
x = 7 − 12
x = −5
Ответ: D(−5) или D(19)

Решение 2
C(−4,5); CD = 7,2.
Пусть точка D имеет координату x. Рассмотрим два случая.
а) Точка D расположена справа от точки C. Тогда
x = −4,5 + 7,2
x = 2,7
б) Точка D расположена слева от точки C. Тогда
x = −4,5 − 7,2
x = −11,7
Ответ: D(−11,7) или D(2,7)

№457

Номер №457

Решите уравнение.
1) ||x| + 3| = 4
|x| + 3 = 4
или
|x| + 3 = −4
2) ||x| − 6| = 5

Решение 1
||x| + 3| = 4
|x| + 3 = 4
|x| = 4 − 3
|x| = 1
x = 1
или
x = −1
или
|x| + 3 = −4
|x| = −4 − 3
|x| = −7 − нет корней
Ответ: x = ±1

Решение 2
||x| − 6| = 5
|x| − 6 = 5
|x| = 5 + 6
|x| = 11
x = 11
или
x = −11
или
|x| − 6 = −5
|x| = −5 + 6
|x| = 1
x = 1
или
x = −1
Ответ: x = ±11; x = ±1.

№458

Номер №458

Работник Балда нанялся к Попу на работу с условием получить в конце года одежду и 10 рублей. Но через 7 месяцев он уволился и получил одежду и 2 рубля. Сколько стоила одежда?

Решение

1) 12 − 7 = 5 (месяцев) − недоработал Балда;
2) 10 − 2 = 8 (рублей) − недополучил Балда;
3) 8 : 5 = 1,6 (рубля) − в месяц составляла заработная плата Балды;
4) 1,6 * 7 = 11,2 (рубля) − заработал Балда за 7 месяцев;
5) 11,2 − 2 = 9,2 (рубля) − стоила одежда.
Ответ: 9,2 рубля

№459

Номер №459

Заполните пропуски.
1) Чтобы умножить два числа с разными знаками, надо _ и перед полученным произведение поставить _
2) Чтобы умножить два отрицательных числа, надо _
3) При умножении числа на _ получаем число, противоположное данному.
4) Если числа a и b имеют _ знаки, то произведение ab положительно.
5) Если произведение ab положительно, то числа a и b имеют _ знаки.
6) Если числа a и b имеют _ знаки, то произведение ab отрицательно.
7) Если произведение ab отрицательно, то числа a и b имеют _ знаки.
8) Если хотя бы одно из чисел a или b равно нулю, то произведение ab равно _
9) Если произведение ab равно нулю, то _ равно _
10) При _ значениях x выражение $x^2$ принимает только _ значения.

Решение

1) Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведение поставить знак "−".
2) Чтобы умножить два отрицательных числа, надо умножить их модули.
3) При умножении числа на (−1) получаем число, противоположное данному.
4) Если числа a и b имеют одинаковые знаки, то произведение ab положительно.
5) Если произведение ab положительно, то числа a и b имеют одинаковые знаки.
6) Если числа a и b имеют разные знаки, то произведение ab отрицательно.
7) Если произведение ab отрицательно, то числа a и b имеют разные знаки.
8) Если хотя бы одно из чисел a или b равно нулю, то произведение ab равно нулю.
9) Если произведение ab равно нулю, то хотя бы одно из чисел a или b равно нулю.
10) При любых значениях x выражение $x^2$ принимает только неотрицательные значения.

№460

Номер №460

Заполните таблицу.

Число a Число b Произведение ab
положительное положительное
положительное отрицательное
положительное отрицательное
отрицательное положительное

Решение

Число a	Число b	Произведение ab
положительное	положительное	положительное
положительное	отрицательное	отрицательное
отрицательное	положительное	отрицательное
отрицательное	отрицательное	положительное

 

№461

Номер №461

Заполните таблицу.

a	−12	9	−6	0	−0,4	−0,7	$-\frac{1}{3}$	$-\frac{2}{9}$
b	2	−9	−8	−1,8	0,5	−4	3	$-\frac{9}{16}$
ab

 

Решение

1) −12 * 2 = −24
2) 9 * (−9) = −81
3) −6 * (−8) = 48
4) 0 * (−1,8) = 0
5) −0,4 * 0,5 = −0,2
6) −0,7 * (−4) = 2,8
7) $-\frac{1}{3} * 3 = -1$
8) $-\frac{2}{9} * (-\frac{9}{16}) = \frac{1}{1} * \frac{1}{8} = \frac{1}{8}$
Ответ:

a	−12	9	−6	0	−0,4	−0,7	$-\frac{1}{3}$	$-\frac{2}{9}$
b	2	−9	−8	−1,8	0,5	−4	3	$-\frac{9}{16}$
ab	-24	-81	48	0	-0.2	2?8	-1	$\frac{1}{8}$

 

№462

Номер №462

Выполните умножение.
1) $-\frac{3}{8} * \frac{5}{6}$
2) $-\frac{14}{15} * (-\frac{3}{7})$
3) $\frac{18}{55} * (-\frac{11}{18})$
4) $-\frac{21}{32} * (-\frac{12}{35})$
5) $\frac{17}{40} * (-\frac{8}{51})$
6) $-\frac{15}{22} * \frac{4}{27}$

Решение 1
$-\frac{3}{8} * \frac{5}{6} = -\frac{1}{8} * \frac{5}{2} = -\frac{5}{16}$

Решение 2
$-\frac{14}{15} * (-\frac{3}{7}) = \frac{2}{5} * \frac{1}{1} = \frac{2}{5}$

Решение 3
$\frac{18}{55} * (-\frac{11}{18}) = \frac{1}{5} * (-\frac{1}{1}) = -\frac{1}{5}$

Решение 4
$-\frac{21}{32} * (-\frac{12}{35}) = \frac{3}{8} * \frac{3}{5} = \frac{9}{40}$

Решение 5
$\frac{17}{40} * (-\frac{8}{51}) = \frac{1}{5} * (-\frac{1}{3}) = -\frac{1}{15}$

Решение 6
$-\frac{15}{22} * \frac{4}{27} = -\frac{5}{11} * \frac{2}{9} = -\frac{10}{99}$

№463

Номер №463

Найдите произведение.
1) $-3 * \frac{5}{16}$
2) $\frac{7}{24} * (-8)$
3) $-\frac{13}{15} * (-30)$
4) $18 * (-\frac{7}{12})$
5) $-2\frac{6}{7} * (-\frac{12}{35})$
6) $-2\frac{3}{8} * 1\frac{13}{19}$
7) $-5\frac{1}{16} * (-1\frac{11}{45})$
8) $-2\frac{1}{3} * (-1\frac{3}{14})$

Решение 1
$-3 * \frac{5}{16} = -\frac{15}{16}$

Решение 2
$\frac{7}{24} * (-8) = \frac{7}{3} * (-1) = -\frac{7}{3} = -2\frac{1}{3}$

Решение 3
$-\frac{13}{15} * (-30) = \frac{13}{1} * 2 = 26$

Решение 4
$18 * (-\frac{7}{12}) = 3 * (-\frac{7}{2}) = -\frac{21}{2} = -10\frac{1}{2}$

Решение 5
$-2\frac{6}{7} * (-\frac{12}{35}) = \frac{20}{7} * \frac{12}{35} = \frac{4}{7} * \frac{12}{7} = \frac{48}{49}$

Решение 6
$-2\frac{3}{8} * 1\frac{13}{19} = -\frac{19}{8} * \frac{32}{19} = -\frac{1}{1} * \frac{4}{1} = -4$

Решение 7
$-5\frac{1}{16} * (-1\frac{11}{45}) = \frac{81}{16} * \frac{56}{45} = \frac{9}{2} * \frac{7}{5} = \frac{63}{10} = 6\frac{3}{10}$

Решение 8
$-2\frac{1}{3} * (-1\frac{3}{14}) = \frac{7}{3} * \frac{17}{14} = \frac{1}{3} * \frac{17}{2} = \frac{17}{6} = 2\frac{5}{6}$

№464

Номер №464

Вычислите.
1) $(-2)^2$
2) $(-3)^3$
3) $(-\frac{2}{7})^2$
4) $(-0,3)^3$
5) $(-1)^2$
6) $(-1)^3$

Решение 1
$(-2)^2 = -2 * (-2) = 4$

Решение 2
$(-3)^3 = -3 * (-3) * (-3) = -27$

Решение 3
$(-\frac{2}{7})^2 = -\frac{2}{7} * (-\frac{2}{7}) = \frac{4}{49}$

Решение 4
$(-0,3)^3 = -0,3 * (-0,3) * (-0,3) = -0,027$

Решение 5
$(-1)^2 = -1 * (-1) = 1$

Решение 6
$(-1)^3 = -1 * (-1) * (-1) = -1$

№465

Номер №465

Заполните цепочку вычислений.

Решение

1) 0,4 * (−9) = −3,6
2) −3,6 − 1,8 = −5,4
3) −5,4 + 1,4 = −4
4) −4 * (−5) = 20
Ответ:

№466

Номер №466

Выполните действия.
1) −3,6 * 0,3 + 2,8 * (−0,5)
а) −3,6 * 0,3
б) 2,8 * (−0,5)
2) 5,4 * (−0,7) − (−2,5) * (−2,8)
3) −6,6 * 0,8 − 3,2 * (−1,6)
4) $-1\frac{3}{5} * 3\frac{1}{3} - (1 - \frac{3}{8}) * (\frac{1}{3} - 1)$
а) $-1\frac{3}{5} * 3\frac{1}{3}$
б) $1 - \frac{3}{8}$
в) $\frac{1}{3} - 1$
5) $(-6 - 2\frac{2}{7} * (-1\frac{5}{44})) * (-2\frac{17}{19})$

Решение 1
−3,6 * 0,3 + 2,8 * (−0,5) = −2,48
а) −3,6 * 0,3 = −1,08
б) 2,8 * (−0,5) = −1,4
в) −1,08 + (−1,4) = −2,48

Решение 2
5,4 * (−0,7) − (−2,5) * (−2,8) = −10,78
а) 5,4 * (−0,7) = −3,78
б) −2,5 * (−2,8) = 7
в) −3,78 − 7 = −10,78

Решение 3
−6,6 * 0,8 − 3,2 * (−1,6) = −0,16
а) −6,6 * 0,8 = −5,28
б) 3,2 * (−1,6) = −5,12
в) −5,28 − (−5,12) = −5,28 + 5,12 = −0,16

Решение 4
$-1\frac{3}{5} * 3\frac{1}{3} - (1 - \frac{3}{8}) * (\frac{1}{3} - 1) = -5\frac{3}{4} = -4\frac{11}{12}$
а) $-1\frac{3}{5} * 3\frac{1}{3} = -\frac{8}{5} * \frac{10}{3} = -\frac{8}{1} * \frac{2}{3} = -\frac{16}{3} = -5\frac{1}{3}$
б) $1 - \frac{3}{8} = \frac{8}{8} - \frac{3}{8} = \frac{5}{8}$
в) $\frac{1}{3} - 1 = \frac{1}{3} - \frac{3}{3} = -\frac{2}{3}$
г) $\frac{5}{8} * (-\frac{2}{3}) = \frac{5}{4} * (-\frac{1}{3}) = -\frac{5}{12}$
д) $-5\frac{1}{3} - (-\frac{5}{12}) = -5\frac{4}{12} + \frac{5}{12} = -4\frac{16}{12} + \frac{5}{12} = -4\frac{11}{12}$

Решение 5
$(-6 - 2\frac{2}{7} * (-1\frac{5}{44})) * (-2\frac{17}{19}) = 10$
а) $2\frac{2}{7} * (-1\frac{5}{44}) = \frac{16}{7} * (-\frac{49}{44}) = \frac{4}{1} * (-\frac{7}{11}) = -\frac{28}{11} = -2\frac{6}{11}$
б) $-6 - (-2\frac{6}{11}) = -6 + 2\frac{6}{11} = -5\frac{11}{11} + 2\frac{6}{11} = -3\frac{5}{11}$
в) $-3\frac{5}{11} * (-2\frac{17}{19}) = \frac{38}{11} * \frac{55}{19} = \frac{2}{1} * \frac{5}{1} = 10$

№467

Номер №467

Не выполняя вычислений, сравните $(-19)^3$ и $(-0,2)^2$.

Решение

$(-19)^3 < 0, (-0,2)^2 > 0$, следовательно, $(-19)^3 < (-0,2)^2$.

№468

Номер №468

Сравните, не выполняя вычислений.
1) 17 * 17 * 17 ☐ (−17) * (−17) * (−17)
2) −48 * 48 ☐ −48 * (−48)
3) −125 * 125 * 125 * 125 ☐ −125 * (−125) * (−125) * (−125)
4) 193 * (−612) * 0 * 851 ☐ 153 * (−476) * (−7326)

Решение 1
17 * 17 * 17 > 0, (−17) * (−17) * (−17) < 0, следовательно:
17 * 17 * 17 > (−17) * (−17) * (−17)

Решение 2
−48 * 48 < 0, −48 * (−48) > 0, следовательно:
−48 * 48 < −48 * (−48)

Решение 3
−125 * 125 * 125 * 125 < 0, −125 * (−125) * (−125) * (−125) > 0, следовательно:
−125 * 125 * 125 * 125 < −125 * (−125) * (−125) * (−125)

Решение 4
193 * (−612) * 0 * 851 = 0, 153 * (−476) * (−7326) > 0, следовательно:
193 * (−612) * 0 * 851 < 153 * (−476) * (−7326)

№469

Номер №469

Найдите значение выражения.
$-1\frac{3}{16} * (-8) + 2\frac{1}{42} * (-2\frac{6}{17}) - (-1\frac{11}{28}) * (-1\frac{3}{13})$
а) $-1\frac{3}{16} * (-8)$
б) $2\frac{1}{42} * (-2\frac{6}{17})$

Решение

$-1\frac{3}{16} * (-8) + 2\frac{1}{42} * (-2\frac{6}{17}) - (-1\frac{11}{28}) * (-1\frac{3}{13}) = 3\frac{1}{42}$
а) $-1\frac{3}{16} * (-8) = \frac{19}{16} * 8 = \frac{19}{2} * 1 = 9\frac{1}{2}$
б) $2\frac{1}{42} * (-2\frac{6}{17}) = \frac{85}{42} * (-\frac{40}{17}) = \frac{5}{21} * (-\frac{20}{1}) = -\frac{100}{21} = -4\frac{16}{21}$
в) $(-1\frac{11}{28}) * (-1\frac{3}{13}) = \frac{39}{28} * \frac{16}{13} = \frac{3}{7} * \frac{4}{1} = \frac{12}{7} = 1\frac{5}{7}$
г) $9\frac{1}{2} + (-4\frac{16}{21}) = 9\frac{21}{42} - 4\frac{32}{42} = 8\frac{63}{42} - 4\frac{32}{42} = 4\frac{31}{42}$
д) $4\frac{31}{42} - 1\frac{5}{7} = 4\frac{31}{42} - 1\frac{30}{42} = 3\frac{1}{42}$

№470

Номер №470

Составьте числовое выражение и найдите его значение:
1) разность произведений чисел −1,5 и −0,6 и чисел −2,1 и −0,9;
2) произведение суммы чисел 1,8 и −4,3 и разности чисел −1,6 и −0,4.

Решение 1
(−1,5 * (−0,6)) − (−2,1 * (−0,9)) = −0,99
а) −1,5 * (−0,6) = 0,9
б) −2,1 * (−0,9) = −1,89
в) 0,9 − 1,89 = −0,99

Решение 2
(1,8 + (−4,3)) * (−1,6 − (−0,4)) = 30
а) 1,8 + (−4,3) = −2,5
б) −1,6 − (−0,4) = −1,6 + 0,4 = −1,2
в) −2,5 * (−1,2) = 3

№471

Номер №471

Решите уравнение.
1) (x + 1,6)(x + 0,2)(x − 9) = 0
Так как произведение равно нулю, то хотя бы один из множителей равен нулю, т.е.
x + 1,6 = 0
x = −1,6
или
x + 0,2 = 0
или
2) (x − 7)(x + 3)(x − 4) = 0

Решение 1
(x + 1,6)(x + 0,2)(x − 9) = 0
Так как произведение равно нулю, то хотя бы один из множителей равен нулю, т.е.
x + 1,6 = 0
x = −1,6
или
x + 0,2 = 0
x = −0,2
или
x − 9 = 0
x = 9
Ответ: x = −1.6; x = −0,2; x = 9.

Решение 2
(x − 7)(x + 3)(x − 4) = 0
Так как произведение равно нулю, то хотя бы один из множителей равен нулю, т.е.
x − 7 = 0
x = 7
или
x + 3 = 0
x = −3
или
x − 4 = 0
x = 4
Ответ: x = −3; x = 4; x = 7.

№472

Номер №472

Каким числом, положительным или отрицательным, являются значение выражения mn + 6p, если m и n − отрицательные числа, p − положительное?

Решение

m и n − отрицательные числа, тогда mn > 0.
6 и p − положительные числа, тогда 6p > 0.
Следовательно, mn + 6p − сумма двух положительных чисел. Тогда значение выражения mn + 6p − положительное число.
Ответ: положительным

№473

Номер №473

Каким числом, положительным или отрицательным, является значение выражения 4a − bc, если a, b и c − отрицательные числа?

Решение

4 − положительное число, a − отрицательное число, тогда 4a < 0.
b и c − отрицательные числа, тогда bc > 0.
4a − bc = 4a + (−bc)
bc > 0, значит −bc < 0
Следовательно 4a − bc = 4a + (−bc) − сумма двух отрицательных чисел. Тогда значение выражения 4a − bc − отрицательное число.
Ответ: отрицательным

№474

Номер №474

Двенадцать человек несут 12 буханок хлеба, каждый мужчина несет 2 буханки, каждая женщина − полбуханки, а ребенок − четверть буханки. Сколько мужчин несут хлеб? Женщин? Детей?

Решение

Пусть было:
x (мужчин);
y (женщин).
Тогда:
12 − (x + y) = 12 − x − y (детей) − было;
2x (буханок) − несли мужчины;
$\frac{1}{2}y$ (буханок) − несли женщины;
$\frac{1}{4}(12 - x - y)$ (буханок) − несли дети.
Так как, всего несли 12 буханок, можно составить уравнение:
$2x + \frac{1}{2}y + \frac{1}{4}(12 - x - y) = 12$ |*4
8x + 4y + 12 − x − y = 48
7x + 3y = 48 − 12
7x + 3y = 36
y = 36 − 7x
пусть x = 1:
y = 36 − 7 * 1 = 36 − 7 = 29;
12 − 1 − 29 = 11 − 29 = −18 < 0, что невозможно, так как детей не может быть меньше 0;
пусть x = 2:
y = 36 − 7 * 2 = 36 − 14 = 22;
12 − 2 − 22 = 10 − 22 = −12 < 0, что невозможно, так как детей не может быть меньше 0;
пусть x = 3:
y = 36 − 7 * 3 = 36 − 21 = 15;
12 − 3 − 15 = 9 − 15 = −6 < 0, что невозможно, так как детей не может быть меньше 0;
пусть x = 4:
y = 36 − 7 * 4 = 36 − 28 = 8;
12 − 4 − 8 = 8 − 8 = 0, что невозможно, так как детей не может быть равно 0;
пусть x = 5:
y = 36 − 7 * 5 = 36 − 35 = 1;
12 − 1 − 5 = 11 − 5 = 6 > 0 − подходит.
Проверка:
2x = 2 * 5 = 10 (буханок) − несли мужчины;
$\frac{1}{2}y = \frac{1}{2} * 1 = \frac{1}{2}$ (буханки) − несли женщины;
$\frac{1}{4}(12 - 5 - 1) = \frac{1}{4} * 6 = \frac{1}{2} * 3 = \frac{3}{2} = 1\frac{1}{2}$ (буханок) − несли дети.
$10 + \frac{1}{2} + 1\frac{1}{2} = 10 + 2 = 12$ (буханок) − несли всего, что соответствует условию задачи.
Ответ: 5 мужчин, 1 женщина и 6 детей.

№475

Номер №475

Заполните пропуски.
1) Для любых рациональных чисел a и b выполняется равенство ab =_. Это утверждение называют _ свойством умножения.
2) Для любых рациональных чисел a, b и c выполняется равенство (ab)c = _. Это утверждение называют _ свойством умножения.

Решение

1) Для любых рациональных чисел a и b выполняется равенство ab =ba. Это утверждение называют переместительным свойством умножения.
2) Для любых рациональных чисел a, b и c выполняется равенство (ab)c = a(bc). Это утверждение называют сочетательным свойством умножения.

№476

Номер №476

Упростите выражение и запишите его коэффициент в пустую клетку.
1) 3a * (−1,5) = −4,5a; -4,5
2) −4x * 0,8;
3) −6a * 7b;
4) −5a * 8b * (−2c);
5) $-\frac{3}{7}x * (-\frac{7}{3})y$;
6) 0,4m * (−2,5n).

Решение 1
3a * (−1,5) = −4,5a -4,5

Решение 2
−4x * 0,8 = −3,2x -3,2

Решение 3
−6a * 7b = −42ab -42

Решение 4
−5a * 8b * (−2c) = 80abc 80

Решение 5
$-\frac{3}{7}x * (-\frac{7}{3})y = xy$ 1

Решение 6
0,4m * (−2,5n) = −mn -1

№477

Номер №477

Вычислите наиболее удобным способом.
1) −0,5 * 27 * 4 = (−0,5 * 4) * 27;
2) −12,5 * (−4,83) * (−8);
3) $\frac{7}{19} * (-0,25) * (-2\frac{5}{7}) * (-0,4)$.

Решение 1
−0,5 * 27 * 4 = (−0,5 * 4) * 27 = −2 * 27 = −54

Решение 2
−12,5 * (−4,83) * (−8) = (−12,5 * (−8)) * (−4,83) = 100 * (−4,83) = −483

Решение 3
$\frac{7}{19} * (-0,25) * (-2\frac{5}{7}) * (-0,4) = (\frac{7}{19} * (-\frac{19}{7})) * (-0,25 * (-0,4)) = -1 * 0,1 = -0,1$

№478

Номер №478

Укажите, положительным, отрицательным или нулем является произведение трех чисел, если:
1) два числа положительные, одно − отрицательное;
2) два числа отрицательные, одно − положительное;
3) одно число положительное, одно − отрицательное, а одно − нуль;
4) три числа отрицательные.

Решение

1) два числа положительные, одно − отрицательное:
(+) * (+) * (−) = (−) − отрицательное
2) два числа отрицательные, одно − положительное:
(−) * (−) * (+) = (+) − положительное
3) одно число положительное, одно − отрицательное, а одно − нуль;
(+) + (−) * 0 = 0
4) три числа отрицательные.
(−) * (−) * (−) = (−) − отрицательные

№479

Номер №479

Какое количество отрицательных множителей должно содержать произведение, чтобы оно было:
1) положительным;
2) отрицательным?

Решение

1) Чтобы произведение было положительным, оно должно содержать четное количество отрицательных множителей.
2) Чтобы произведение было отрицательным, оно должно содержать нечетное количество отрицательных множителей.

№480

Номер №480

Упростите выражение и найдите его значение.
1) $-\frac{9}{16}a * 5\frac{1}{3}b$, если $a = -\frac{1}{2}, b = \frac{1}{12}$;
$-\frac{9}{16}a * 5\frac{1}{3}b = (-\frac{9}{16} * 5\frac{1}{3})ab =$
2) $-\frac{1}{7}m * 2,8n * (-1\frac{1}{12}p)$, если $m = 2\frac{1}{13}, n = -\frac{5}{9}, p = 20$;

Решение 1
$-\frac{9}{16}a * 5\frac{1}{3}b$, если $a = -\frac{1}{2}, b = \frac{1}{12}$
$-\frac{9}{16}a * 5\frac{1}{3}b = (-\frac{9}{16} * 5\frac{1}{3})ab = (-\frac{9}{16} * \frac{16}{3})ab = (-\frac{3}{1} * \frac{1}{1})ab = -3ab$
если $a = -\frac{1}{2}, b = \frac{1}{12}$:
$-3 * (-\frac{1}{2}) * \frac{1}{12} = -1 * (-\frac{1}{2}) * \frac{1}{4} = \frac{1}{8}$

Решение 2
$-\frac{1}{7}m * 2,8n * (-1\frac{1}{12}p)$, если $m = 2\frac{1}{13}, n = -\frac{5}{9}, p = 20$
$-\frac{1}{7}m * 2,8n * (-1\frac{1}{12}p) = -\frac{1}{7}m * \frac{28}{10}n * (-\frac{13}{12}p) = -\frac{1}{7}m * \frac{14}{5}n * (-\frac{13}{12}p) = -\frac{1}{1}m * \frac{2}{5}n * (-\frac{13}{12}p) = \frac{26}{60}mnp = \frac{13}{30}mnp$
если $m = 2\frac{1}{13}, n = -\frac{5}{9}, p = 20$:
$\frac{13}{30}mnp = \frac{13}{30} * 2\frac{1}{13} * (-\frac{5}{9}) * 20 = \frac{13}{30} * \frac{27}{13} * (-\frac{5}{9}) * 20 = \frac{1}{1} * \frac{1}{1} * (-\frac{1}{1}) * 10 = -10$

№481

Номер №481

За 1 ч бригада маляров покрасила половину стены. Оставшуюся часть стены покрасил один маляр за 4 ч. Сколько маляров было в бригаде, если производительность труда у всех маляров бригады одинакова?

Решение

Примем всю стену за единицу, тогда:
1) $\frac{1}{2}$ (стены) − покрасила бригада маляров за 1 час;
2) $1 - \frac{1}{2} = \frac{1}{2}$ (стены) − осталось покрасить одному маляру;
3) $\frac{1}{2} : 4 = \frac{1}{2} * \frac{1}{4} = \frac{1}{8}$ (стены в час) − производительность каждого маляра;
4) $\frac{1}{2} : \frac{1}{8} = \frac{1}{2} * 8 = 4$ (маляра) − было в бригаде.
Ответ: 4 маляра

№482

Номер №482

Заполните пропуски.
1) Для любых рациональных чисел a, b и c справедливо равенство a(b + c) = _. Это утверждение называют _ свойством умножения относительно _
2) Преобразование выражения, содержащего скобки, в результате которого получают выражение, не содержащее скобок, называют _
3) Если перед скобками стоит знак "−", то при раскрытии скобок надо _ этот знак, а все знаки, стоящие перед слагаемыми внутри скобок, _
4) Если перед скобками стоит знак "+", то при раскрытии скобок надо _ этот знак, а все знаки, стоящие перед слагаемыми внутри скобок _.
5) Замену выражения ab + ac на выражение a(b + c) называют _
6) Слагаемые, имеющие одинаковую буквенную часть, называют _
7) Чтобы привести подобные слагаемые, надо сложить их _ и полученный результат _

Решение

1) Для любых рациональных чисел a, b и c справедливо равенство a(b + c) = ab + ac. Это утверждение называют распределительным свойством умножения относительно сложения.
2) Преобразование выражения, содержащего скобки, в результате которого получают выражение, не содержащее скобок, называют раскрытием скобок.
3) Если перед скобками стоит знак "−", то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми внутри скобок, изменить на противоположное.
4) Если перед скобками стоит знак "+", то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми внутри скобок, оставить без изменений.
5) Замену выражения ab + ac на выражение a(b + c) называют вынесением общего множителя за скобки.
6) Слагаемые, имеющие одинаковую буквенную часть, называют подобными.
7) Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.

№483

Номер №483

Раскройте скобки.
1) 3(a − 2b);
2) −2(3m − 5n + 4p);
3) (x − 7y − 3z) * (−0,4);
4) −0,6d(−6a − 8b + 9c);
5) $-18(\frac{1}{6}m - \frac{5}{9}n + \frac{2}{3}p)$;
6) $\frac{2}{3}a(9b - 12c - 6d)$.

Решение 1
3(a − 2b) = 3 * a − 3 * 2b = 3a − 6b

Решение 2
−2(3m − 5n + 4p) = −2 * 3m − (−2) * 5n + (−2) * 4p = −6m + 10n − 8p

Решение 3
(x − 7y − 3z) * (−0,4) = x * (−0,4) − 7y * (−0,4) − 3z * (−0,4) = −0,4x + 2,8y + 1,2z

Решение 4
−0,6d(−6a − 8b + 9c) = −0,6d * (−6a) − (−0,6d) * 8b + (−0,6d) * 9c = 3,6ad + 4,8bd − 5,4cd

Решение 5
$-18(\frac{1}{6}m - \frac{5}{9}n + \frac{2}{3}p) = -18 * \frac{1}{6}m - (-18) * \frac{5}{9}n + (-18) * \frac{2}{3}p = -3 * \frac{1}{1}m - (-2) * \frac{5}{1}n + (-6) * \frac{2}{1}p = -3m + 10n - 12p$

Решение 6
$\frac{2}{3}a(9b - 12c - 6d) = \frac{2}{3}a * 9b - \frac{2}{3}a * 12c - \frac{2}{3}a * 6d = \frac{2}{1}a * 3b - \frac{2}{1}a * 4c - \frac{2}{1}a * 2d = 6ab - 8ac - 4ad$

№484

Номер №484

Раскройте скобки и упростите выражение.
1) a − (b + a);
2) −(m − n) − n;
3) c + (−c + d);
4) (a + 1,6) − (a + 2,4);
5) −(3,4 − x) + (−x + 1,6);
6) −(x − 2,7 + y) − (6,5 − x).

Решение 1
a − (b + a) = a − b − a = −b

Решение 2
−(m − n) − n = −m + n − n = −m

Решение 3
c + (−c + d) = c − c + d = d

Решение 4
(a + 1,6) − (a + 2,4) = a + 1,6 − a − 2,4 = −0,8

Решение 5
−(3,4 − x) + (−x + 1,6) = −3,4 + x − x + 1,6 = −1,8

Решение 6
−(x − 2,7 + y) − (6,5 − x) = −x + 2,7 − y − 6,5 + x = −y − 3,8

№485

Номер №485

Запишите сумму двух выражений и упростите ее.
1) −6 − a и a + 17;
2) a − b + c и −a + b + c;
3) 7,3 − 4,6 + 5,8 и −10,4 + 4,6 − 5,8.

Решение 1
(−6 − a) + (a + 17) = −6 − a + a + 17 = 11

Решение 2
(a − b + c) + (−a + b + c) = a − b + c − a + b + c = 2c

Решение 3
(7,3 − 4,6 + 5,8) + (−10,4 + 4,6 − 5,8) = 7,3 − 4,6 + 5,8 − 10,4 + 4,6 − 5,8 = 7,3 − 10,4 = −3,1

№486

Номер №486

Запишите разность двух выражений и упростите ее:
1) −5,6 + m и m + 3,8;
2) a − b и −b + a − c;
3) −5,3 + 1,8 − x и 1,8 − x − 1,4.

Решение 1
(−5,6 + m) − (m + 3,8) = −5,6 + m − m − 3,8 = −9,4

Решение 2
(a − b) − (−b + a − c) = a − b + b − a + c = c

Решение 3
(−5,3 + 1,8 − x) − (1,8 − x − 1,4) = −5,3 + 1,8 − x − 1,8 + x + 1,4 = −3,9

№487

Номер №487

Приведите подобные слагаемые.
1) 6a − 17a + 19a − 8a;
2) −4x + 5x + 13x − 15x;
3) 2a − 3b + 4a − 2b;
4) −7x + 5y + 3x − 10y.

Решение 1
6a − 17a + 19a − 8a = (6 − 17 + 19 − 8)a = 0a = 0

Решение 2
−4x + 5x + 13x − 15x = (−4 + 5 + 13 − 15)x = −1x = −x

Решение 3
2a − 3b + 4a − 2b = (2a + 4a) + (−3b − 2b) = (2 + 4)a +(−3 − 2)b = 6a + (−5b) = 6a − 5b

Решение 4
−7x + 5y + 3x − 10y = (−7x + 3x) + (5y − 10y) = (−7 + 3)x + (5 − 10)y = −4x + (−5y) = −4x − 5y

№488

Номер №488

Раскройте скобки и приведите подобные слагаемые.
1) 2(7a − 6) − 9a = 14a − 12 − 9a;
2) −5x − 4(8 − 3x);
3) −3(2m − 5) − 8(1 − 6m);
4) −7(3a − 2b) + 2(5a + 2b).

Решение 1
2(7a − 6) − 9a = 14a − 12 − 9a = 5a − 12

Решение 2
−5x − 4(8 − 3x) = -5x − 32 + 12x = 7x − 32

Решение 3
−3(2m − 5) − 8(1 − 6m) = -6m + 15 − 8 + 48m = 42m + 7

Решение 4
−7(3a − 2b) + 2(5a + 2b) = -21a + 14b + 10a + 4b = −11a + 18b

№489

Номер №489

Вынесите за скобки общий множитель.
1) am + bm;
2) 3x − 6y + 9z;
3) 5m + 5n − 5.

Решение 1
am + bm = a * m + b * m = m(a + b)

Решение 2
3x − 6y + 9z = 3 * x − 3 * 2y + 3 * 3z = 3(x − 2y + 3z)

Решение 3
5m + 5n − 5 = 5 * m + 5 * n − 5 * 1 = 5(m + n − 1)

№490

Номер №490

Вычислите значение выражения наиболее удобным способом.
1) 74 * 128 − 74 * 228 = 74 * (128 − 228);
2) 43 * 15 − 55 * 15 + 7 * 15;
3) $-23,4 * 6\frac{7}{15} + 3\frac{8}{15} * (-23,4)$;
4) $-3,2 * 2\frac{11}{18} + 3,2 * 3\frac{13}{18} - 3,2 * \frac{7}{18}$.

Решение 1
74 * 128 − 74 * 228 = 74 * (128 − 228) = 74 * (−100) = −7400

Решение 2
43 * 15 − 55 * 15 + 7 * 15 = 15 * (43 − 55 + 7) = 15 * (50 − 55) = 15 * (−5) = −75

Решение 3
$-23,4 * 6\frac{7}{15} + 3\frac{8}{15} * (-23,4) = -23,4 * (6\frac{7}{15} + 3\frac{8}{15}) = -23,4 * 10 = -234$

Решение 4
$-3,2 * 2\frac{11}{18} + 3,2 * 3\frac{13}{18} - 3,2 * \frac{7}{18} = 3,2 * (-2\frac{11}{18} + 3\frac{13}{18} - \frac{7}{18}) = 3,2 * (3\frac{13}{18} - 3) = 3\frac{1}{5} * \frac{13}{18} = \frac{16}{5} * \frac{13}{18} = \frac{8}{5} * \frac{13}{9} = \frac{104}{45} = 2\frac{14}{45}$

№491

Номер №491

Упростите выражение и найдите его значение.
1) −7(3m − 8) + 5(6m − 7) при m = 3;
−7(3m − 8) + 5(6m − 7) = −21m + 56 +
2) −1,2(2a − 3) − (4 − 5a) − 0,6(1 − a) при a = −2,5;
3) $\frac{5}{12}(4,8x - 1\frac{1}{5}y) - 5,4(\frac{4}{9}x + 1,5y)$ при x = 4, $y = -1\frac{2}{43}$.

Решение 1
−7(3m − 8) + 5(6m − 7) при m = 3
−7(3m − 8) + 5(6m − 7) = −21m + 56 + 30m − 35 = 9m + 21
при m = 3:
9m + 21 = 9 * 3 + 21 = 27 + 21 = 48

Решение 2
−1,2(2a − 3) − (4 − 5a) − 0,6(1 − a) при a = −2,5
−1,2(2a − 3) − (4 − 5a) − 0,6(1 − a) = −2,4a + 3,6 − 4 + 5a − 0,6 + 0,6a = 3,2a − 1
при a = −2,5:
3,2 * (−2,5) − 1 = −8 − 1 = −9

Решение 3
$\frac{5}{12}(4,8x - 1\frac{1}{5}y) - 5,4(\frac{4}{9}x + 1,5y)$ при x = 4, $y = -1\frac{2}{43}$
$\frac{5}{12}(4,8x - 1\frac{1}{5}y) - 5,4(\frac{4}{9}x + 1,5y) = \frac{5}{12}(\frac{48}{10}x - \frac{6}{5}y) - \frac{54}{10}(\frac{4}{9}x + \frac{15}{10}y) = \frac{5}{12}(\frac{24}{5}x - \frac{6}{5}y) - \frac{27}{5}(\frac{4}{9}x + \frac{3}{2}y) = \frac{5}{12} * \frac{24}{5}x - \frac{5}{12} * \frac{6}{5}y - \frac{27}{5} * \frac{4}{9}x - \frac{27}{5} * \frac{3}{2}y = \frac{1}{1} * \frac{2}{1}x - \frac{1}{2} * \frac{1}{1}y - \frac{3}{5} * \frac{4}{1}x - \frac{81}{10}y = 2x - \frac{1}{2}y - \frac{12}{5}x - 8,1y = 2x - 0,5y - 2,4x - 8,1y = -0,4x - 8,6y$
при x = 4, $y = -1\frac{2}{43}$:
$-0,4 * 4 - 8,6 * (-1\frac{2}{43}) = -1,6 - \frac{86}{10} * (-\frac{45}{43}) = -1,6 - \frac{43}{5} * (-\frac{45}{43}) = -1,6 - \frac{1}{1} * (-\frac{9}{1}) = -1,6 + 9 = 7,4$

№492

Номер №492

Вынесите за скобки общий множитель.
1) 8am − 16an + 12a;
2) −35mp + 21mn − 14mk;
3) 0,2abc + 0,6abd − 1,2abm.

Решение 1
8am − 16an + 12a = 4a * 2m − 4a * 4n + 4a * 3 = 4a(2m − 4n + 3)

Решение 2
−35mp + 21mn − 14mk = −7m * 5p − 7m * (−3n) − 7m * 2k = −7m(5p − 3n + 2k)

Решение 3
0,2abc + 0,6abd − 1,2abm = 0,2ab * c + 0,2ab * 3d − 0,2ab * 6m = 0,2ab(c + 3d − 6m)

№493

Номер №493

Докажите, что значение выражения (2n − 9) * 0,9 − 0,6(8n − 5) − (−2,1 − 3n) не зависит от значения переменной.

Решение

Доказательство.
(2n − 9) * 0,9 − 0,6(8n − 5) − (−2,1 − 3n) = 1,8n − 8,1 − 4,8n + 3 + 2,1 + 3n = −3, следовательно значение выражения не зависит от значения переменной. Что и требовалось доказать.

№494

Номер №494

Найдите значение выражения.
1) 3a − (a + 2b), если a − b = 0,3;
3a − (a + 2b) = 3a − a − 2b = 2a − 2b = 2(a − b) =
2) 4(3x − 5y) − 2(x − y), если 9y − 5x = −0,7;
3) $6a(3b + 2c) - 9a(b - \frac{1}{3}c)$, если $a = -2\frac{1}{3}, 3b + 5c = 1\frac{1}{14}$.

Решение 1
3a − (a + 2b), если a − b = 0,3:
3a − (a + 2b) = 3a − a − 2b = 2a − 2b = 2(a − b) = 2 * 0,3 = 0,6

Решение 2
4(3x − 5y) − 2(x − y), если 9y − 5x = −0,7:
4(3x − 5y) − 2(x − y) = 12x − 20y − 2x + 2y = 10x − 18y = −2(9y − 5x) = −2 * (−0,7) = 1,4

Решение 3
$6a(3b + 2c) - 9a(b - \frac{1}{3}c)$, если $a = -2\frac{1}{3}, 3b + 5c = 1\frac{1}{14}$:
$6a(3b + 2c) - 9a(b - \frac{1}{3}c) = 18ab + 12ac - 9ab + 3ac = 9ab + 15ac = 3a(3b + 5c) = 3 * (-2\frac{1}{3}) * 1\frac{1}{14} = 3 * (-\frac{7}{3}) * \frac{15}{14} = 1 * (-\frac{1}{1}) * \frac{15}{2} = -7\frac{1}{2}$

№495

Номер №495

Старший брат идет от дома до школы 30 мин, а младший − 40 мин. Через сколько минут старший брат догонит младшего, если тот вышел из дома на 5 мин раньше?

Решение

Примем весь путь от дома до школы за единицу, тогда:
1) $\frac{1}{30}$ (пути в минуту) − скорость старшего брата;
2) $\frac{1}{40}$ (пути в минуту) − скорость младшего брата;
3) $\frac{1}{40} * 5 = \frac{1}{8}$ (пути) − прошел младший брат до выхода старшего;
4) $\frac{1}{30} - \frac{1}{40} = \frac{4 - 3}{120} = \frac{1}{120}$ (пути в минуту) − скорость сближения братьев;
5) $\frac{1}{8} : \frac{1}{120} = \frac{1}{8} * 120 = 15$ (мин) − потребуется старшему брату, чтобы догнать младшего.
Ответ: через 15 минут

№496

Номер №496

Заполните пропуски.
1) Частным рациональных чисел a и b (b ≠ _) называют такое рациональное число x, _ которого с числом _ равно числу _
2) Чтобы найти частное двух чисел с разными знаками, надо разделить _ и поставить перед полученным числом _
3) Чтобы найти частное двух отрицательных чисел, надо разделить _
4) Частное любого рационального числа a и числа _ равно числу a .
5) Если a ≠ 0, то _ : _ = 1.
6) Если a ≠ _, то _ : a = 0.
7) На _ делить нельзя.

Решение

1) Частным рациональных чисел a и b (b ≠ 0) называют такое рациональное число x, произведение которого с числом b равно числу a.
2) Чтобы найти частное двух чисел с разными знаками, надо разделить модуль делимого на модуль делителя и поставить перед полученным числом знак "−".
3) Чтобы найти частное двух отрицательных чисел, надо разделить модуль делимого на модуль делителя.
4) Частное любого рационального числа a и числа 1 равно числу a .
5) Если a ≠ 0, то a : a = 1.
6) Если a ≠ 0, то 0 : a = 0.
7) На нуль делить нельзя.

№497

Номер №497

Заполните таблицу.

Число a Число b Частное a : b
положительное положительное
отрицательное отрицательное
положительное отрицательное
отрицательное отрицательное

Решение

Число a	Число b	Частное a : b
положительное	положительное	положительное
положительное	отрицательное	отрицательное
отрицательное	положительное	отрицательное
отрицательное	отрицательное	положительное

 

№498

Номер №498

Заполните таблицу.

a	36	−28	−48	−18	−15	−20	0
b	−4	−7	6	−1	15	−20	−42
a : b

Решение

1) 36 : (−4) = −(36 : 4) = −9
2) −28 : (−7) = 28 : 7 = 4
3) −48 : 6 = −(48 : 6) = −8
4) −18 : (−1) = 18 : 1 = 18
5) −15 : 15 = −(15 : 15) = −1
6) −20 : (−20) = 20 : 20 = 1
7) 0 : (−42) = 0
Ответ:

a	36	−28	−48	−18	−15	−20	0
b	−4	−7	6	−1	15	−20	−42
a : b	-9	4	-8	18	-1	1	0

№499

Номер №499

Заполните таблицу.

a	b	a + b	a − b	ab	a : b
-18	-6
-12	3
15	-5
-8	16
-4	-4
9	-9

Решение

a + b
1) −18 + (−6) = −24
2) −12 + 3 = −9
3) 15 + (−5) = 15 − 5 = 10
4) −8 + 16 = 8
5) −4 + (−4) = −8
6) 9 + (−9) = 9 − 9 = 0
a − b
1) −18 − (−6) = −18 + 6 = −12
2) −12 − 3 = −15
3) 15 − (−5) = 15 + 5 = 20
4) −8 − 16 = −24
5) −4 − (−4) = −4 + 4 = 0
6) 9 − (−9) = 9 + 9 = 18
ab
1) −18 * (−6) = 18 * 6 = 108
2) −12 * 3 = −(12 * 3) = −36
3) 15 * (−5) = −(15 * 5) = −75
4) −8 * 16 = −(8 * 16) = −128
5) −4 * (−4) = 4 * 4 = 16
6) 9 * (−9) = −(9 * 9) = −81
a : b
1) −18 : (−6) = 18 : 6 = 3
2) −12 : 3 = −(12 : 3) = −4
3) 15 : (−5) = −(15 : 5) = −3
4) −8 : 16 = −(8 : 16) = −0,5
5) −4 : (−4) = 4 : 4 = 1
6) 9 : (−9) = −(9 : 9) = −1
Ответ:

a	b	a + b	a − b	ab	a : b
-18	-6	-24	-12	108	3
-12	3	-9	-15	-36	-4
15	-5	10	20	-75	-3
-8	16	8	-24	-128	-0.5
-4	-4	-8	0	16	1
9	-9	0	18	-81	-1

 

№500

Номер №500

Выполните деление.
1) $\frac{8}{13} : (-\frac{4}{5})$;
2) $-\frac{5}{14} : (-\frac{15}{28})$;
3) $-\frac{12}{13} : \frac{4}{39}$;
4) $12 : (-\frac{4}{5})$;
5) $\frac{12}{19} : (-6)$;
6) $-1\frac{5}{7} : (-3\frac{3}{4})$.

Решение 1
$\frac{8}{13} : (-\frac{4}{5}) = -(\frac{8}{13} * \frac{5}{4}) = -(\frac{2}{13} * \frac{5}{1}) = -\frac{10}{13}$

Решение 2
$-\frac{5}{14} : (-\frac{15}{28}) = \frac{5}{14} * \frac{28}{15} = \frac{1}{1} * \frac{2}{3} = \frac{2}{3}$

Решение 3
$-\frac{12}{13} : \frac{4}{39} = -(\frac{12}{13} * \frac{39}{4}) = -(\frac{3}{1} * \frac{3}{1}) = -9$

Решение 4
$12 : (-\frac{4}{5}) = -(12 * \frac{5}{4}) = -(3 * \frac{5}{1}) = -15$

Решение 5
$\frac{12}{19} : (-6) = -(\frac{12}{19} * \frac{1}{6}) = -(\frac{2}{19} * \frac{1}{1}) = -\frac{2}{19}$

Решение 6
$-1\frac{5}{7} : (-3\frac{3}{4}) = \frac{12}{7} : \frac{15}{4} = \frac{12}{7} * \frac{4}{15} = \frac{4}{7} * \frac{4}{5} = \frac{16}{35}$

№501

Номер №501

Решите уравнение.
1) −5x = 25;
2) 7x = −6;
3) $-\frac{3}{11}x = -9$;
4) −4,5 : x = −0,9;
5) $1\frac{8}{27} : x = -1\frac{5}{9}$;
6) $-2\frac{5}{8} : x = 1\frac{19}{20}$.

Решение 1
−5x = 25
x = 25 : (−5)
x = −5
Ответ: x = −5

Решение 2
7x = −6
x = −6 : 7
$x = -\frac{6}{7}$
Ответ: $x = -\frac{6}{7}$

Решение 3
$-\frac{3}{11}x = -9$
$x = -9 : -\frac{3}{11}$
$x = 9 * \frac{11}{3}$
$x = 3 * \frac{11}{1}$
x = 33
Ответ: x = 33

Решение 4
−4,5 : x = −0,9
x = −4,5 : (−0,9)
x = 5
Ответ: x = 5

Решение 5
$1\frac{8}{27} : x = -1\frac{5}{9}$
$x = 1\frac{8}{27} : (-1\frac{5}{9})$
$x = \frac{35}{27} : (-\frac{14}{9})$
$x = \frac{35}{27} * (-\frac{9}{14})$
$x = \frac{5}{3} * (-\frac{1}{2})$
$x = -\frac{5}{6}$
Ответ: $x = -\frac{5}{6}$

Решение 6
$-2\frac{5}{8} : x = 1\frac{19}{20}$
$x = -2\frac{5}{8} : 1\frac{19}{20}$
$x = -\frac{21}{8} : \frac{39}{20}$
$x = -\frac{21}{8} * \frac{20}{39}$
$x = -\frac{7}{2} * \frac{5}{13}$
$x = -\frac{35}{26}$
$x = -1\frac{9}{26}$
Ответ: $x = -1\frac{9}{26}$

№502

Номер №502

Заполните цепочку вычислений.

Решение

1) −6,3 : 0,9 = −63 : 9 = −7
2) −7 + 1,4 = −5,6
3) −5,6 : (−7) = 5,6 : 7 = 0,8
4) 0,8 * (−0,15) = −0,12
Ответ:

№503

Номер №503

Выполните действия.
1) 4,8 : (−8) + (−3,6) : (−0,9);
2) −2,5 * 6 − 5,4 : (−0,6);
3) $-16 : 1\frac{11}{13} + 1\frac{1}{4} : (-\frac{15}{38})$;
4) $(-8 - 1\frac{3}{13} : (-1\frac{17}{39})) : (-5\frac{5}{14})$.

Решение 1
4,8 : (−8) + (−3,6) : (−0,9) = 3,4
а) 4,8 : (−8) = −0,6
б) (−3,6) : (−0,9) = 36 : 9 = 4
в) −0,6 + 4 = 3,4

Решение 2
−2,5 * 6 − 5,4 : (−0,6) = −6
а) −2,5 * 6 = −15
б) 5,4 : (−0,6) = 54 : (−6) = −9
в) −15 − (−9) = −15 + 9 = −6

Решение 3
$-16 : 1\frac{11}{13} + 1\frac{1}{4} : (-\frac{15}{38}) = -11\frac{5}{6}$
а) $-16 : 1\frac{11}{13} = -16 : \frac{24}{13} = -16 * \frac{13}{24} = -2 * \frac{13}{3} = -\frac{26}{3} = -8\frac{2}{3}$
б) $1\frac{1}{4} : (-\frac{15}{38}) = \frac{5}{4} * (-\frac{38}{15}) = \frac{1}{2} * (-\frac{19}{3}) = -\frac{19}{6} = -3\frac{1}{6}$
в) $-8\frac{2}{3} + (-3\frac{1}{6}) = -8\frac{4}{6} + (-3\frac{1}{6}) = -11\frac{5}{6}$

Решение 4
$(-8 - 1\frac{3}{13} : (-1\frac{17}{39})) : (-5\frac{5}{14}) = 1\frac{1}{3}$
а) $1\frac{3}{13} : (-1\frac{17}{39}) = \frac{16}{13} : (-\frac{56}{39}) = \frac{16}{13} * (-\frac{39}{56}) = \frac{2}{1} * (-\frac{3}{7}) = -\frac{6}{7}$
б) $-8 - (-\frac{6}{7}) = -8 + \frac{6}{7} = -7\frac{1}{7}$
в) $-7\frac{1}{7} : (-5\frac{5}{14}) = \frac{50}{7} : \frac{75}{14} = \frac{50}{7} * \frac{14}{75} = \frac{2}{1} * \frac{2}{3} = \frac{4}{3} = 1\frac{1}{3}$

№504

Номер №504

Найдите числа, которых не хватает в цепочке вычислений.
1)
2)

Решение 1
Первый прямоугольник
x : (−1,2) = −5
x = −5 * (−1,2)
x = 6
Второй кружок
x = −5 + 4,6
x = −0,4
Второй прямоугольник
−0,4 * x = −32
x = −32 : (−0,4)
x = 80
Третий прямоугольник
−32 : x = 40
$x = -\frac{32}{40}$
$x = -\frac{8}{10}$
x = −0,8
Ответ:

Решение 2
Второй прямоугольник
0,7 * x = −1,47
x = −1,47 : 0,7
$x = -\frac{147}{70}$
$x = -\frac{21}{10}$
x = −2,1
Второй кружок
x = −1,47 − 0,13
x = −1,6
Третий кружок
x * (−0,03) = −0,96
x = −0,96 : (−0,03)
x = 96 : 3
x = 32
Второй прямоугольник
−1,6 * x = 32
x = 32 : (−1,6)
x = 320 : (−16)
x = −20
Ответ:

№505

Номер №505

Решите уравнение.
1) $-\frac{1}{3}x - \frac{1}{4}x + \frac{1}{5}x = 1\frac{8}{15}$;
2) $2\frac{5}{6}x - 3\frac{3}{4}x - 1\frac{5}{12}x = -1\frac{5}{9}$.

Решение 1
$-\frac{1}{3}x - \frac{1}{4}x + \frac{1}{5}x = 1\frac{8}{15}$
$-\frac{20}{60}x - \frac{15}{60}x + \frac{12}{60}x = \frac{23}{15}$
$-\frac{35}{60}x + \frac{12}{60}x = \frac{23}{15}$
$-\frac{23}{60}x = \frac{23}{15}$
$x = \frac{23}{15} : (-\frac{23}{60})$
$x = \frac{23}{15} * (-\frac{60}{23})$
$x = \frac{1}{1} * (-\frac{4}{1})$
x = −4
Ответ: −4

Решение 2
$2\frac{5}{6}x - 3\frac{3}{4}x - 1\frac{5}{12}x = -1\frac{5}{9}$
$2\frac{10}{12}x - 3\frac{9}{12}x - 1\frac{5}{12}x = -1\frac{5}{9}$
$2\frac{10}{12}x - 4\frac{14}{12}x = -1\frac{5}{9}$
$-2\frac{4}{12}x = -1\frac{5}{9}$
$-2\frac{1}{3}x = -1\frac{5}{9}$
$x = -1\frac{5}{9} : (-2\frac{1}{3})$
$x = \frac{14}{9} : \frac{7}{3}$
$x = \frac{14}{9} * \frac{3}{7}$
$x = \frac{2}{3} * \frac{1}{1}$
$x = \frac{2}{3}$
Ответ: $x = \frac{2}{3}$

№506

Номер №506

Найдите числа, которых не хватает в цепочке вычислений.

Решение

Первый верхний прямоугольник
−0,7 * x = −0,84
x = −0,84 : (−0,7)
x = 1,2
Второй верхний кружок
x : (−0,06) = 20
x = 20 * (−0,06)
x = −1,2
Второй верхний прямоугольник
−0,84 + x = −1,2
x = −1,2 − (−0,84)
x = −1,2 + 0,84
x = −0,36
Нижний кружок
x = −0,7 : 0,02
x = −70 : 2
x = −35
Нижний прямоугольник
−35 * x = 20
x = 20 : (−35)
$x = -\frac{20}{35}$
$x = -\frac{4}{7}$
Ответ:

№507

Номер №507

Найдите числа, которых не хватает в цепочке вычислений.
1)
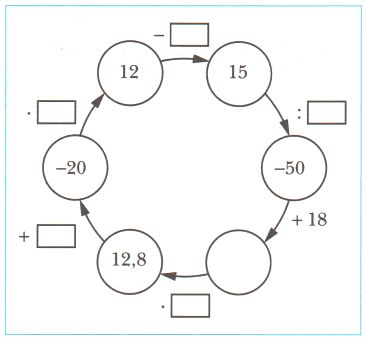2)

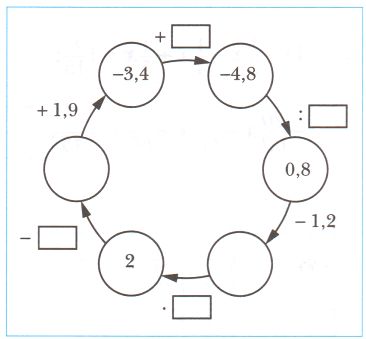
Решение 1
1)
12 − x = 15
x = 12 − 15
x = −3
2)
15 : x = −50
x = 15 : (−50)
x = −0,3
3)
x = −50 + 18
x = −32
4)
−32 * x = 12,8
x = 12,8 : (−32)
x = −0,4
5)
12,8 + x = −20
x = −20 − 12,8
x = −32,8
6)
−20 * x = 12
x = 12 : (−20)
x = −0,6
Ответ: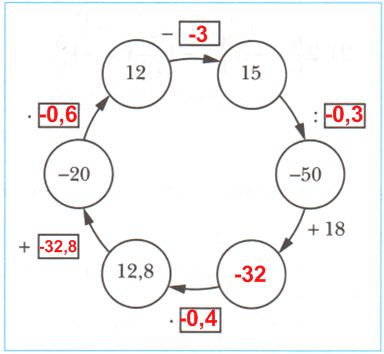

Решение 2
1)
−3,4 + x = −4,8
x = −4,8 − (−3,4)
x = −4,8 + 3,4
x = −1,4
2)
−4,8 : x = 0,8
x = −4,8 : 0,8
x = −6
3)
x = 0,8 − 1,2
x = −0,4
4)
−0,4 * x = 2
x = 2 : (−0,4)
x = −5
5)
x + 1,9 = −3,4
x = −3,4 − 1,9
x = −5,3
6)
2 − x = −5,3
x = 2 − (−5,3)
x = 2 + 5,3
x = 7,3
Ответ: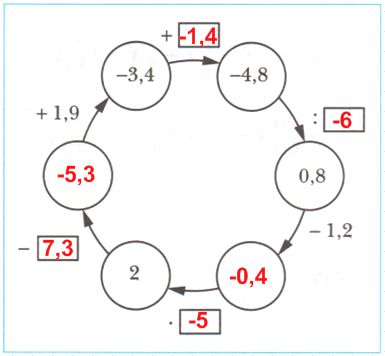

№508

Номер №508

Найдите значение выражения.
1) 7,2 : (8 − 10) − 4,9 : (−1,4 + 0,7);
2) $(1\frac{16}{21} - 3\frac{4}{9}) : (-1\frac{11}{42}) + 1\frac{5}{7} : (-4)$.

Решение 1
7,2 : (8 − 10) − 4,9 : (−1,4 + 0,7) = 3,4
а) 8 − 10 = −2
б) −1,4 + 0,7 = −0,7
в) 7,2 : (−2) = −3,6
г) 4,9 : (−0,7) = −7
д) −3,6 − (−7) = −3,6 + 7 = 3,4

Решение 2
$(1\frac{16}{21} - 3\frac{4}{9}) : (-1\frac{11}{42}) + 1\frac{5}{7} : (-4) = \frac{19}{21}$
а) $1\frac{16}{21} - 3\frac{4}{9} = 1\frac{48}{63} - 3\frac{28}{63} = 1\frac{48}{63} - 2\frac{91}{63} = -1\frac{43}{63}$
б) $-1\frac{43}{63} : (-1\frac{11}{42}) = \frac{106}{63} : \frac{53}{42} = \frac{106}{63} * \frac{42}{53} = \frac{2}{3} * \frac{2}{1} = \frac{4}{3} = 1\frac{1}{3}$
в) $1\frac{5}{7} : (-4) = \frac{12}{7} * (-\frac{1}{4}) = \frac{3}{7} * (-\frac{1}{1}) = -\frac{3}{7}$
г) $1\frac{1}{3} + (-\frac{3}{7}) = 1\frac{7}{21} - \frac{9}{21} = \frac{28}{21} - \frac{9}{21} = \frac{19}{21}$

№509

Номер №509

Заполните пропуски в цепочке вычислений, если:
1) x = 12;
2) x = 6.
1)
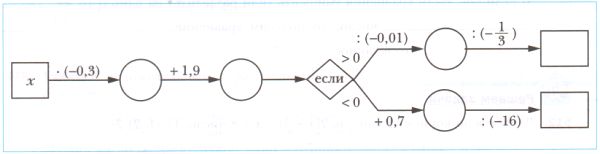2)Решение 1

при x = 12:
1) 12 * (−0,3) = −3,6
2) −3,6 + 1,9 = −1,7 < 0, тогда:
3) −1,7 + 0,7 = −1
4) $-1 : (-16) = \frac{1}{16}$
Ответ:

Решение 2
при x = 6:
1) 6 * (−0,3) = −1,8
2) −1,8 + 1,9 = 0,1 > 0, тогда:
3) 0,1 : (−0,01) = −10
4) $-10 : (-\frac{1}{3}) = 10 * 3 = 30$
Ответ:

№510

Номер №510

Масса арбуза была 10 кг и в нем содержалось 99% воды. Через несколько дней содержание воды в нем уменьшилось до 98%. Какова стала масса арбуза?

Решение

1) 100% − 99% = 1% − сухого вещества было в арбузе;
2) 10 * 0,01 = 0,1 (кг) − сухого вещества было в арбузе;
3) 100% − 98% = 2% − сухого вещества стало в арбузе;
4) 0,1 : 0,02 = 10 : 2 = 5 (кг) − стала масса арбуза.
Ответ: 5 кг

№511

Номер №511

Заполните пропуски.
1) Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) _, то получится уравнение, имеющее те же корни, что и данное.
2) Если какое−нибудь слагаемое перенести из одной части уравнения в другую, _, то получим уравнение, имеющее те же корни, что и данное.
3) Если обе части уравнения умножить (или разделить) на одно и то же _ число, то получим уравнение, _ что и данное.

Решение

1) Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и тоже число, то получится уравнение, имеющее те же корни, что и данное.
2) Если какое−нибудь слагаемое перенести из одной части уравнения в другую, изменить при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.
3) Если обе части уравнения умножить (или разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни что и данное.

№512

Номер №512

Является ли корнем уравнения 2(x + 3) = x + 8 число:
1) −1;
2) 2?

Решение 1
2(x + 3) = x + 8
при x = −1:
2 * (−1 + 3) = −1 + 8
−2 + 6 = 7
4 ≠ 7
Ответ: число −1 не является корнем уравнения

Решение 2
2(x + 3) = x + 8
при x = 2
2 * (2 + 3) = 2 + 8
2 * 5 = 10
10 = 10
Ответ: число 2 является корнем уравнения

№513

Номер №513

Решите уравнение.
1) 5x = 32 + x;
2) 4x + 16 = 28 − 2x;
3) −3(x − 1) = 24 − 10x;
4) 2(4x + 5) − 3(x + 6) = 9x + 8.

Решение 1
5x = 32 + x
5x − x = 32
4x = 32
x = 32 : 4
x = 8
Ответ: x = 8

Решение 2
4x + 16 = 28 − 2x
4x + 2x = 28 − 16
6x = 12
x = 12 : 6
x = 2
Ответ: x = 2

Решение 3
−3(x − 1) = 24 − 10x
−3x + 3 = 24 − 10x
−3x + 10x = 24 − 3
7x = 21
x = 21 : 7
x = 3
Ответ: x = 3

Решение 4
2(4x + 5) − 3(x + 6) = 9x + 8
8x + 10 − 3x − 18 = 9x + 8
8x − 3x − 9x = 8 − 10 + 18
−4x = 16
x = 16 : (−4)
x = −4
Ответ: x = −4

№514

Номер №514

Решите уравнение.
1) $\frac{5}{6}x + 8 = \frac{1}{4}x - 6$;
2) 1,5(2x + 5) + x = 3(0,5x − 7) + 3,5;
3) $\frac{11}{18}x - \frac{2}{9} = \frac{5}{12}x + 1\frac{1}{3}$;
4) $\frac{2}{3}(4\frac{1}{2}x - \frac{3}{5}) - \frac{5}{7}(\frac{7}{15}x - \frac{7}{9}) = -1\frac{32}{45}$.

Решение 1
$\frac{5}{6}x + 8 = \frac{1}{4}x - 6$
$\frac{5}{6}x - \frac{1}{4}x = -6 - 8$
$\frac{10}{12}x - \frac{3}{12}x = -14$
$\frac{7}{12}x = -14$
$x = -14 : \frac{7}{12}$
$x = -14 * \frac{12}{7}$
$x = -2 * \frac{12}{1}$
x = −24
Ответ: x = −24

Решение 2
1,5(2x + 5) + x = 3(0,5x − 7) + 3,5
3x + 7,5 + x = 1,5x − 21 + 3,5
4x − 1,5x = −17,5 − 7,5
2,5x = −25
x = −25 : 2,5
x = −10
Ответ: x = −10

Решение 3
$\frac{11}{18}x - \frac{2}{9} = \frac{5}{12}x + 1\frac{1}{3}$
$\frac{11}{18}x - \frac{5}{12}x = 1\frac{1}{3} + \frac{2}{9}$
$\frac{22}{36}x - \frac{15}{36}x = 1\frac{3}{9} + \frac{2}{9}$
$\frac{7}{36}x = 1\frac{5}{9}$
$x = \frac{14}{9} : \frac{7}{36}$
$x = \frac{14}{9} * \frac{36}{7}$
$x = \frac{2}{1} * \frac{4}{1}$
x = 8
Ответ: x = 8

Решение 4
$\frac{2}{3}(4\frac{1}{2}x - \frac{3}{5}) - \frac{5}{7}(\frac{7}{15}x - \frac{7}{9}) = -1\frac{32}{45}$
$\frac{2}{3} * \frac{9}{2}x - \frac{2}{3} * \frac{3}{5} - (\frac{5}{7} * \frac{7}{15}x - \frac{5}{7} * \frac{7}{9}) = -1\frac{32}{45}$
$\frac{1}{1} * \frac{3}{1}x - \frac{2}{1} * \frac{1}{5} - (\frac{1}{1} * \frac{1}{3}x - \frac{5}{1} * \frac{1}{9}) = -1\frac{32}{45}$
$3x - \frac{2}{5} - (\frac{1}{3}x - \frac{5}{9}) = -1\frac{32}{45}$
$3x - \frac{2}{5} - \frac{1}{3}x + \frac{5}{9} = -1\frac{32}{45}$
$2\frac{2}{3}x = -1\frac{32}{45} + \frac{2}{5} - \frac{5}{9}$
$\frac{8}{3}x = -1\frac{32}{45} + \frac{18}{45} - \frac{25}{45}$
$\frac{8}{3}x = -1\frac{14}{45} - \frac{25}{45}$
$\frac{8}{3}x = -1\frac{39}{45}$
$\frac{8}{3}x = -1\frac{13}{15}$
$\frac{8}{3}x = -\frac{28}{15}$
$x = -\frac{28}{15} : \frac{8}{3}$
$x = -\frac{28}{15} * \frac{3}{8}$
$x = -\frac{7}{5} * \frac{1}{2}$
$x = -\frac{7}{10}$
Ответ: $x = -\frac{7}{10}$

№515

Номер №515

Найдите корень уравнения.
1) $\frac{x - 6}{x + 9} = \frac{7}{4}$;
2) $\frac{x - 2,4}{6} = \frac{x + 0,6}{11}$.

Решение 1
$\frac{x - 6}{x + 9} = \frac{7}{4}$
4(x − 6) = 7(x + 9)
4x − 24 = 7x + 63
4x − 7x = 63 + 24
−3x = 87
x = 87 : (−3)
x = −29
Ответ: x = −29

Решение 2
$\frac{x - 2,4}{6} = \frac{x + 0,6}{11}$
11(x − 2,4) = 6(x + 0,6)
11x − 26,4 = 6x + 3,6
11x − 6x = 3,6 + 26,4
5x = 30
x = 30 : 5
x = 6
Ответ: x = 6

№516

Номер №516

Найдите корень уравнения.
1) $\frac{x}{8} - \frac{x}{12} = -\frac{1}{3}$;
2) $\frac{5x}{14} + \frac{3x}{4} = 4\frac{3}{7}$.

Решение 1
$\frac{x}{8} - \frac{x}{12} = -\frac{1}{3}$
НОК (8; 12; 3) = 24. Умножим обе части данного уравнения на 24:
$(\frac{x}{8} - \frac{x}{12}) * 24 = -\frac{1}{3} * 24$
$\frac{x}{8} * 24 - \frac{x}{12} * 24 = -\frac{1}{3} * 24$
$\frac{x}{1} * 3 - \frac{x}{1} * 2 = -\frac{1}{1} * 8$
3x − 2x = −8
x = −8
Ответ: −8

Решение 2
$\frac{5x}{14} + \frac{3x}{4} = 4\frac{3}{7}$
НОК (4; 7; 14) = 28. Умножим обе части данного уравнения на 28:
$(\frac{5x}{14} + \frac{3x}{4}) * 28 = 4\frac{3}{7} * 28$
$\frac{5x}{14} * 28 + \frac{3x}{4} * 28 = \frac{31}{7} * 28$
$\frac{5x}{1} * 2 + \frac{3x}{1} * 7 = \frac{31}{1} * 4$
10x + 21x = 124
31x = 124
x = 124 : 31
x = 4
Ответ: 4

№517

Номер №517

При каком значении a уравнение (a − 5)x = 3 + 4a имеет корень, равный числу −2?

Решение

Поскольку число −2 является корнем данного уравнения, то:
x = −2, значит:
(a − 5)x = 3 + 4a
(a − 5) * (−2) = 3 + 4a
−2a + 10 = 3 + 4a
−2a − 4a = 3 − 10
−6a = −7
a = −7 : (−6)
$a = \frac{7}{6} = 1\frac{1}{6}$
Ответ: при $a = 1\frac{1}{6}$

№518

Номер №518

Решите уравнение.
1) 5x + 8 = 3(3x − 4) − 4x;
2) 12 − 7x = 4(3 + 2x) − 15x.

Решение 1
5x + 8 = 3(3x − 4) − 4x
5x + 8 = 9x − 12 − 4x
5x − 9x + 4x = −12 − 8
0x = −20
0 ≠ −20 − нет решений
Ответ: нет решений

Решение 2
12 − 7x = 4(3 + 2x) − 15x
12 − 7x = 12 + 8x − 15x
−7x − 8x + 15x = 12 − 12
0x = 0
0 = 0
x − любое число
Ответ: x − любое число

№519

Номер №519

Мальчики составляют 45% всех учащихся школы. Известно, что 20% всех мальчиков и 30% всех девочек учатся на отлично. Какой процент всех учащихся школы составляют отличники?

Решение

45% = 0,45;
20% = 0,2;
30% = 0,3.
Пусть x учащихся всего в школе, тогда:
1) 0,45x (мальчиков) − в школе;
2) x − 0,45x = 0,55x (девочек) − всего в школе;
3) 0,45x * 0,2 = 0,09x (учащихся) − отличники−мальчики;
4) 0,55x * 0,3 = 0,165x (учащихся) − отличники−девочки;
5) 0,09x + 0,165x = 0,255x (учащихся) − отличники;
6) $\frac{0,255x}{x} * 100$% = 0,255 * 100% = 25,5% − всех учащихся школы составляют отличники.
Ответ: 25,5%

№520

Номер №520

За коробку конфет и торт Вася заплатил 240 р., причем торт стоит в 3 раза больше, чем конфеты. Сколько рублей заплатил Вася за коробку конфет?

Решение

Пусть коробка конфет стоит x р., тогда торт − 3x р.
Поскольку вся покупка стоит 240 р., то x + 3x = 240 р.
Тогда:
4x = 240
x = 240 : 4
x = 60
Следовательно, коробка конфет стоит 60 р.
Ответ: 60 рублей

№521

Номер №521

Владимир и Борис решили вместе 73 уравнения, причем Владимир решил на 9 уравнений больше, чем Борис. Сколько уравнений решил каждый из них?

Решение

Пусть Борис решил x уравнений, тогда Владимир решил x + 9 уравнений.
Так как, Владимир и Борис решили вместе 73 уравнения, можно составить уравнение:
x + (x + 9) = 73
x + x + 9 = 73
2x = 73 − 9
2x = 64
x = 64 : 2
x = 32 (уравнения) − решил Борис, значит:
x + 9 = 32 + 9 = 41 (уравнение) − решил Владимир.
Ответ: 32 уравнения − Борис, 41 уравнение − Владимир.

№522

Номер №522

На первом озере было в 4 раза больше уток, чем на втором. Когда с первого озера улетели 3 утки, а на второе прилетели 12 уток, то на озерах стало уток поровну. Сколько уток было на каждом озере сначала?

Решение

Пусть на втором озере было сначала x уток, тогда на первом было 4x уток. Потом на втором озере стало (x + 12) уток, а на первом − (4x − 3) уток. Поскольку уток на озерах стало поровну, то получаем уравнение:
x + 12 = 4x − 3
Отсюда:
x − 4x = −3 − 12
−3x = −15
x = −15 : (−3)
x = 5
Следовательно, на втором озере было 5 уток, а на первом − 4 * 5 = 20 уток.
Ответ: 20 и 5 уток

№523

Номер №523

Одна сторона треугольника в 2,5 раза меньше второй и на 16 см меньше третьей. Найдите стороны треугольника, если его периметр равен 52 см.

Решение

Пусть x (см) − длина первой стороны треугольника, тогда:
2,5x (см) − длина второй стороны треугольника;
x + 16 (см) − длина третьей стороны треугольника.
Так как, периметр треугольника равен 52 см, можно составить уравнение:
x + 2,5x + (x + 16) = 52
3,5x + x + 16 = 52
4,5x = 52 − 16
4,5x = 36
x = 36 : 4,5
x = 8 (см) − длина первой стороны треугольника, тогда:
2,5x = 2,5 * 8 = 20 (см) − длина второй стороны треугольника;
x + 16 = 8 + 16 = 24 (см) − длина третьей стороны треугольника.
Ответ: 8 см, 20 см и 24 см.

№524

Номер №524

Килограмм печенья дешевле килограмма конфет на 60 р. За 5 кг печенья заплатили столько, сколько за 3 кг конфет. Сколько стоит 1 кг печенья? 1 кг конфет?

Решение

Пусть 1 кг печенья стоит x р., тогда 1 кг конфет − (x + 60) р.
За 5 кг печенья заплатили 5x р., а за 3 кг конфет − 3(x + 60) р.
Получаем уравнение:
5x = 3(x + 60)
5x = 3x + 180
5x − 3x = 180
2x = 180
x = 180 : 2
x = 90
Отсюда:
90 р. − стоит 1 кг печенья;
90 + 60 = 150 р. − стоит 1 кг конфет.
Ответ: 90 рублей − 1 кг печенья, 150 рублей − 1 кг конфет.

№525

Номер №525

Велосипедист преодолевает расстояние между селом и станцией за 2 ч, а пешеход − за 5 ч. Найдите скорости велосипедиста и пешехода, если скорость пешехода на 6 км/ч меньше скорости велосипедиста.

Решение

Пусть x (км/ч) − скорость пешехода, тогда:
x + 6 (км/ч) − скорость велосипедиста;
5x (км) − преодолевает за 5 часов пешеход;
2(x + 6) (км) − преодолевает за 2 часа велосипедист.
Так как, пешеход и велосипедист преодолевают одинаковое расстояние, равное расстоянию между селом и станцией, можно составить уравнение:
5x = 2(x + 6)
5x = 2x + 12
5x − 2x = 12
3x = 12
x = 12 : 3
x = 4 (км/ч) − скорость пешехода, тогда:
x + 6 = 4 + 6 = 10 (км/ч) − скорость велосипедиста.
Ответ: 4 км/ч − скорость пешехода, 10 км/ч − скорость велосипедиста.

№526

Номер №526

Вера и Катя купили одинаковое количество конфет. Когда Вера съела 4 конфеты, а Катя − 12 конфет, то у Веры осталось в 2 раза больше конфет, чем у Кати. Сколько конфет было у каждой из них сначала?

Решение

Пусть девочки купили по x конфет. Потом у Веры стало (x − 4) конфеты, а у Кати − (x − 12) конфет. Поскольку по условию значение выражения (x − 4) в 2 раза больше значения выражения (x − 12). то получаем уравнение:
x − 4 = 2(x − 12)
Отсюда:
x − 4 = 2x − 24
x − 2x = −24 + 4
−x = −20
x = 20
Значит по 20 конфет было у каждой девочки сначала.
Ответ: по 20 конфет

№527

Номер №527

Купили 16 тетрадей по 35 р. и по 60 р., заплатив за всю покупку 810 р. Сколько купили тетрадей каждого вида?

Решение

Пусть купили x тетрадей по 35 р. Тогда по 60 р. купили (16 − x) тетрадей. За тетради первого вида (по 35 р.) заплатили 35x р., а за тетради второго вида − 60(16 − x) р. Поскольку за все тетради заплатили 810 р., то получаем уравнение:
35x + 60(16 − x) = 810
Отсюда:
35x + 960 − 60x = 810
−25x = 810 − 960
−25x = −150
x = −150 : (−25)
x = 6
Следовательно, купили 6 тетрадей по 35 рублей, значит:
16 − x = 16 − 6 = 10 (тетрадей) − купили по 60 рублей.
Ответ: 6 тетрадей по 35 рублей, 10 тетрадей по 60 рублей.

№528

Номер №528

В первой цистерне было 690 л воды, а во второй − 540 л. Цистерны одновременно открыли. Каждую минуту из первой цистерны вытекает 25 л воды, а из второй − 30 л. Через сколько минут во второй цистерне воды останется в 1,5 раза меньше, чем в первой?

Решение

Пусть через x (минут) − во второй цистерне воды останется в 1,5 раза меньше, чем в первой, тогда:
25x (л) − воды вытечет из первой цистерны;
30x (л) − воды вытечет из второй цистерны;
690 − 25x (л) − воды останется в первой цистерне;
540 − 30x (л) − воды останется во второй цистерне.
Так как, во второй цистерне воды останется в 1,5 раза меньше, чем в первой, можно составить уравнение:
690 − 25x = 1,5(540 − 30x)
690 − 25x = 810 − 45x
−25x + 45x = 810 − 690
20x = 120
x = 120 : 20
x = 6 (мин) − потребуется, чтобы во второй цистерне воды осталось в 1,5 раза меньше, чем в первой.
Ответ: через 6 минут

№529

Номер №529

Емкость имеет форму цилиндра. Как, не имея никаких других емкостей и не выполняя никаких измерений, наполнить водой половину этой емкости?

Решение

Нужно наклонить цилиндр таким образом, как показано на рисунке и налить воду до указанного уровня.

№530

Номер №530

Заполните пропуски.
1) Две прямые, при пересечении которых образовались четыре прямых угла, называют _
2) Перпендикулярность прямых обозначают символом "_".
3) Перпендикулярным называют отрезки, лежащие на _

Решение

1) Две прямые, при пересечении которых образовались четыре прямых угла, называют перпендикулярными.
2) Перпендикулярность прямых обозначают символом "⊥".
3) Перпендикулярным называют отрезки, лежащие на перпендикулярных прямых.

№531

Номер №531

Проведите через точку M прямую c, перпендикулярную прямой a.
1)
2)
3)

Решение 1

Решение 2

Решение 3

№532

Номер №532

На рисунке изображен прямоугольник ABCD. Заполните пропуски.
AB ⊥ _
AB ⊥ _
BC ⊥ _
BC ⊥ _

Решение

AB ⊥ BC
AB ⊥ AD
BC ⊥ AB
BC ⊥ CD

№533

Номер №533

Какие из изображенных прямых перпендикулярны прямой CD?

Решение

Продлим прямые до пересечения с прямой CD.
CD⊥MN
CD⊥EF

№534

Номер №534

Найдите на рисунке пары перпендикулярных прямых.

Решение

Продлим прямые до их пересечения.
AB⊥PR
MK⊥CD

№535

Номер №535

Проведите через точку K прямые, перпендикулярные прямым AB и BD.
1)
2)

Решение 1
a⊥BD
b⊥AB

Решение 2
a⊥BD
b⊥AB

№536

Номер №536

Проведите через каждую вершину треугольника прямую, перпендикулярную противоположной стороне.
1)
2)
3)

Решение 1

Решение 2

Решение 3

№537

Номер №537

Начертите окружность с центром в точке O, радиус которой равен 1,5 см, и проведите два перпендикулярных диаметра.

Решение

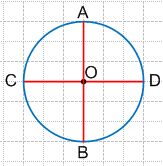AB⊥CD

№538

Номер №538

Некоторый вид бактерий размножается со скоростью две бактерии в минуту (каждую минуту из одной бактерии образуются две). Если поместить в колбу одну бактерию, то колба заполнится бактериями за 1 ч. За какое время заполнится эта колба, если поместить в нее две бактерии?

Решение

Если поместить в колбу одну бактерию, то через одну минуту их будет две, что удовлетворяет условию, когда помещают сразу две бактерии. Следовательно, если поместить в колбу сразу две бактерии, то колба заполнится на одну минуту быстрее.
Изобразим схематично:

	1 мин	1 мин	1 мин	1 мин	1 мин	...
Первый случай	1 б.	2 б.	4 б.	8 б.	16 б.	...
Второй случай		2 б.	4 б.	8 б.	16 б.	...

Значит, если в первом случае колба заполняется за 1 час, то во втором случае колба заполняется за:
1 ч − 1 мин = 60 мин − 1 мин = 59 (мин)
Ответ: за 59 минут

№539

Номер №539

Заполните пропуски.
1) Точки M и N называют симметричными относительно прямой l, если прямая l _ отрезку MN и _
2) Любые _, симметричные относительно прямой, _
3) Точки A и $A_1$ называют симметричными относительно точки O, если точка O является _
4) Любые _, симметричные относительно некоторой точки, _

Решение

1) Точки M и N называют симметричными относительно прямой l, если прямая l перпендикулярна отрезку MN и делит его пополам.
2) Любые две фигуры, симметричные относительно прямой, равны.
3) Точки A и $A_1$ называют симметричными относительно точки O, если точка O является серединой отрезка $AA_1$.
4) Любые две фигуры, симметричные относительно некоторой точки, равны.

№540

Номер №540

Постройте отрезок, симметричный отрезку AB относительно прямой m.
1)
2)
3)

Решение 1

Решение 2

Решение 3

№541

Номер №541

Подчеркните номера рисунков, на которых изображены фигуры, симметричные относительно прямой a.
1)
2)
3)
4)
5)

Решение

1) не симметричны
2) симметричны
3) не симметричны
4) симметричны
5) не симметричны
Ответ: 2, 4.

№542

Номер №542

Постройте отрезок, симметричный отрезку AB относительно точки M.
1)
2)

Решение 1

Решение 2

№543

Номер №543

Подчеркните номера рисунков, на которых изображены фигуры, симметричные относительно точки A.
1)
2)
3)
4)
5)

Решение

1) не симметричны
2) не симметричны
3) симметричны
4) симметричны
5) симметричны
Ответ: 3, 4, 5.

№544

Номер №544

Постройте окружность, симметричную окружности с центром O относительно прямой l.

Решение

№545

Номер №545

Постройте треугольник, симметричный треугольнику ABC относительно прямой n.

Решение

№546

Номер №546

1) Проведите оси симметрии шестиугольника ABCDEF, обозначьте проведенные оси. Запишите сторону шестиугольника, симметричную стороне BC относительно каждой его оси симметрии.
_ симметрична BC относительно оси _
_ симметрична BC относительно оси _
2) Найдите центр симметрии шестиугольника ABCDEF, обозначьте его буквой O. Вершина _ симметрична вершине F относительно центра O.

Решение
1)
FE симметрична BC относительно оси b.
CB симметрична BC относительно оси a.
2)
Вершина C симметрична вершине F относительно центра O.

№547

Номер №547

Дорисуйте фигуру, изображенную на рисунке, так, чтобы прямая m была осью симметрии полученной фигуры.

Решение

№548

Номер №548

На рисунке изображены некоторые стороны многоугольника, осью симметрии которого является прямая m. Постройте этот многоугольник.

Решение

№549

Номер №549

Постройте окружность, симметричную окружности с центром O относительно точки A.
1)
2)

Решение 1

Решение 2

№550

Номер №550

1) Постройте треугольник, симметричный треугольнику ABC относительно точки C.
2) Постройте треугольник, симметричный треугольнику DEF относительно точки M.

Решение 1

Решение 2

№551

Номер №551

На рисунке изображены стороны AB, BC и CD и центр симметрии O восьмиугольника ABCDEFKM. Постройте этот восьмиугольник.

Решение

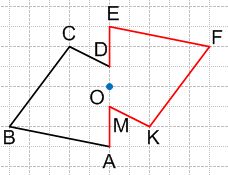
№552

Номер №552

Какой из отрезков, изображенных на рисунке, симметричен сам себе относительно:
1) оси l;
2) оси m;
3) точки O.

Решение

1) Относительно оси l отрезок AD симметричен сам себе.
2) Относительно оси m отрезок AD симметричен сам себе.
3) Относительно точки O отрезки AD, BE и FC симметричны сами себе.
Ответ:
1) AD;
2) AD;
3) AD, BE, FC.

№553

Номер №553

Окружности с центрами $O_1$ и $O_2$ симметричны относительно прямой a. Постройте прямую a.

Решение

1) Проведем отрезок $O_1O_2$
2) Через середину отрезка $O_1O_2$ проведем прямую перпендикулярную отрезку $O_1O_2$. Данная прямая и будет прямой a.

№554

Номер №554

Треугольники ABC и $A_1B_1C_1$ симметричны относительно прямой b (точки A1, B1, C_1 симметричны соответственно точкам A, B, C). Постройте прямую b.

Решение

1) Соединим симметричные точки отрезками.
2) Проведем прямую, перпендикулярную данным отрезкам. Данная прямая и будет прямой b.

№555

Номер №555

Постройте фигуру $F_1$, симметричную фигуре F относительно прямой a, а затем фигуру $F_2$, симметричную фигуре $F_1$ относительно прямой b.
Также фигуру $F_2$ можно было получить из фигуры F с помощью:
1) осевой симметрии относительно прямой _, а затем осевой симметрии относительно прямой _;
2) центральной симметрии относительно _

Решение

Также фигуру $F_2$ можно было получить из фигуры F с помощью:
1) осевой симметрии относительно прямой b, а затем осевой симметрии относительно прямой a;
2) центральной симметрии относительно точки O.

№556

Номер №556

Несколько учащихся ушли из школы, а несколько пришли. В результате этого количество учащихся уменьшилось на 10%, а процент мальчиков среди учащихся увеличился с 50% до 55%. Увеличилось или уменьшилось количество мальчиков?

Решение

100% = 1
10% = 0,1
50% = 0,5
55% = 0,55
Пусть в школе было x учащихся, тогда:
1) 0,5x (мальчиков) − было в школе;
2) x * (1 − 0,1) = 0,9x (учащихся) − стало в школе;
3) 0,9x * 0,55 = 0,495x (мальчиков) − стало в школе;
4) 0,5x > 0,495x, значит количество мальчиков в школе уменьшилось.
Ответ: уменьшилось

№557

Номер №557

Заполните пропуски.
1) Две прямые на плоскости, которые _ называют параллельными.
2) Параллельность прямых обозначают символом "_".
3) Отрезки, лежащие на _, называют параллельными.
4) Если две прямые, лежащие в одной плоскости, перпендикулярны третьей прямой, то _

Решение

1) Две прямые на плоскости, которые не пересекаются называют параллельными.
2) Параллельность прямых обозначают символом "∥".
3) Отрезки, лежащие на параллельных прямых, называют параллельными.
4) Если две прямые, лежащие в одной плоскости, перпендикулярны третьей прямой, то они параллельны.

№558

Номер №558

Проведите через каждую из точек C и D прямую, параллельную прямой a.
1)
2)
3)

Решение 1

Решение 2

Решение 3

№559

Номер №559

Найдите на рисунке пары параллельных прямых.

Решение

AB∥FE
CD∥KM

№560

Номер №560

Проведите через точку K прямые, параллельные сторонам угла MON.
1)
2)

Решение 1

Решение 2

№561

Номер №561

Проведите через каждую вершину треугольника ABC прямую, параллельную противоположной стороне.

Решение

№562

Номер №562

Можно ли считать два луча параллельными, если они лежат в одной плоскости и не имеют общих точек? Ответ обоснуйте.

Решение

Нет, нельзя считать два луча параллельными, если они лежат в одной плоскости и не имеют общих точек, так как они могут лежать например следующим образом:

№563

Номер №563

На рисунке изображен прямоугольный параллелепипед ABCDMNKE. Запишите ребра:
1) параллельные ребру MN;
2) параллельные ребру BC;
3) скрещивающиеся с ребром AM.

Решение

1) ребру MN параллельны ребра: EK, AB, CD.
2) ребру BC параллельны ребра: AD, NK, ME.
3) с ребром AM скрещиваются ребра: NK, BC, CD, EK.

№564

Номер №564

Какой процент воды содержится в 0,5 л лимонада, если в 1 л лимонада содержится 80% воды?

Решение

Процент содержания воды не меняется от количества лимонада. Поэтому в 0,5 литрах лимонада, либо в другом его количестве, содержание воды всегда составит 80%.
Ответ: 80%

№565

Номер №565

Заполните пропуски.
1) Две перпендикулярные координатные прямые, начала отсчета которых совпадают, называют _, а точку их пересечения − _
2) Горизонтальную ось координат называют осью _ и обозначают буквой _, а вертикальную ось координат называют осью _ и обозначают буквой _
3) Вместе оси координат образуют _
4) Плоскость, на которой задана прямоугольная система координат, называют _
5) Координатные оси разбивают плоскость на _ части, которые называют _
6) Положение точки на координатной плоскости _ определяется парой чисел (x; y) которые называют _ этой точки.
7) Записывая координаты точки, на первое место всегда ставят _, а на второе − _
8) Начало координат имеет координаты _
9) Если точка лежит на оси _, то ее ордината равна нулю.
10) Если точка лежит на оси _, то ее абсцисса равна нулю.
11) Две точки с _ симметричны относительно начала координат.
12) Две точки с равными _ и противоположными _ симметричны относительно оси ординат.
13) Две точки с равными _ и противоположными _ симметричны относительно оси абсцисс.

Решение

1) Две перпендикулярные координатные прямые, начала отсчета которых совпадают, называют осями координат, а точку их пересечения − началом координат.
2) Горизонтальную ось координат называют осью абсцисс и обозначают буквой x, а вертикальную ось координат называют осью ординат и обозначают буквой y.
3) Вместе оси координат образуют прямоугольную систему координат.
4) Плоскость, на которой задана прямоугольная система координат, называют координатной плоскостью.
5) Координатные оси разбивают плоскость на четыре части, которые называют координатными четвертями.
6) Положение точки на координатной плоскости однозначно определяется парой чисел (x; y) которые называют координатами этой точки.
7) Записывая координаты точки, на первое место всегда ставят абсциссу, а на второе − ординату.
8) Начало координат имеет координаты (0;0).
9) Если точка лежит на оси абсцисс, то ее ордината равна нулю.
10) Если точка лежит на оси ординат, то ее абсцисса равна нулю.
11) Две точки с противоположными абсциссами и ординатами симметричны относительно начала координат.
12) Две точки с равными ординатами и противоположными абсциссами симметричны относительно оси ординат.
13) Две точки с равными абсциссами и противоположными ординатами симметричны относительно оси абсцисс.

№566

Номер №566

Пронумеруйте координатные четверти.

Решение

№567

Номер №567

Найдите координаты точек, изображенные на рисунке.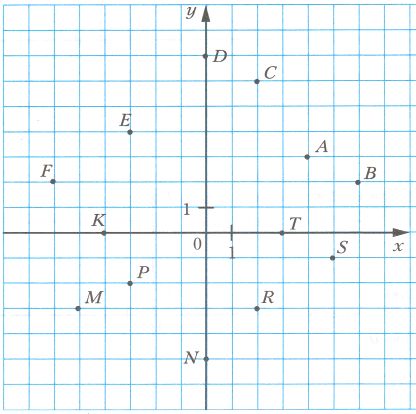

Решение

A(4;3), B(6;2), C(2;6), D(0;7), E(−3;4), F(−6;2), K(−4; 0), M(−5;−3), N(0;−5), P(−3;−2), R(2;−3), S(5;−1), T(3;0).

№568

Номер №568

Отметьте на координатной плоскости точки:
A(1; 3),
B(4; −2),
C(−3; 6),
D(−4; 4),
F(−2; −4),
K(−1; −1),
M(0; 3),
N(−5; 0),
P(2; −5).

Решение

№569

Номер №569

Постройте отрезки AB и СD и найдите координаты точки K пересечения этих отрезков, если A(−1; 3), B(5; 0), C(4; 4), D(2; −2).

Решение

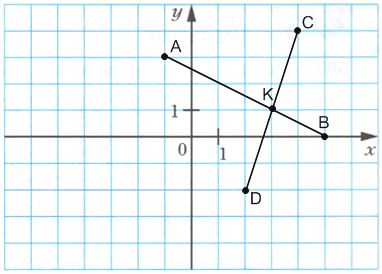Ответ: K(3;1)

№570

Номер №570

Начертите на координатной плоскости треугольник MNK, если M(−3; 1), N(2; −4), K(3;3).
1) Найдите координаты точки A − точки пересечения стороны MN с осью x.
2) Найдите координаты точки B − точки пересечения стороны MK с осью y.

Решение

Ответ:
1) A(−2;0);
2) B(0;2).

№571

Номер №571

Точка $A_1$ симметрична точке A относительно начала координат, точка $A_2$ − относительно оси x, точка $A_3$ − относительно оси y. Заполните таблицу.

Точка	A	$A_1$	$A_2$	$A_3$
Координаты точки	(−2; 5)

Решение

Точки, симметричные начала координат, имеют координаты (x; y) и (−x; −y), тогда:
$A_1(-(-2); -5) = A_1(2; -5)$
Точки, симметричные оси x, имеют координаты (x; y) и (x; −y), тогда:
$A_2(-2; -5)$
Точки, симметричные оси y, имеют координаты (x; y) и (−x; y), тогда:
$A_3(-(-2); 5) = A_3(2; 5)$
Ответ:

Точка	A	$A_1$	$A_2$	$A_3$
Координаты точки	(−2; 5)	(2; 5)	(−2; −5)	(2; 5)

 

№572

Номер №572

Даны координаты трех вершин прямоугольника ABCD: A(−4; −1), C(2; 3) и D(2; −1).
1) Начертите этот прямоугольник.
2) Найдите координаты вершины B.
3) Найдите координаты точки E − точки пересечения диагоналей прямоугольника.
4) Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
2) B( ; )
3) E( ; )
4) AD = см.
AB = см.
S =
P =

Решение

1)
2) B(−4; 3)
3) E(−1; 1)
4) AD = 6 см.
AB = 4 см.
S = AD * AB = 4 * 6 = 24 $см^2$
P = 2(AD + AB) = 2(4 + 6) = 2 * 10 = 20 см

№573

Номер №573

Постройте на координатой плоскости отрезок AB, где A(−1; −1), B(2; 2). Постройте отрезок, симметричный отрезку AB относительно:
1) начала координат;
2) оси x;
3) оси y.

Решение 1
Точка $A_1$, симметричная точке A относительно начала координат будет иметь координаты:
$A_1(-(-1); -(-1)) = A_1(1; 1)$
Точка $B_1$, симметричная точке B относительно начала координат будет иметь координаты:
$B_1(-2; -2)$
Построим отрезок $A_1B_1$, симметричный отрезку AB относительно начала координат:

Решение 2
Точка $A_1$, симметричная точке A относительно оси x будет иметь координаты:
$A_1(-1; -(-1)) = A_1(-1; 1)$
Точка $B_1$, симметричная точке B относительно оси x будет иметь координаты:
$B_1(2; -2)$
Построим отрезок $A_1B_1$, симметричный отрезку AB относительно оси x:


Решение 3
Точка $A_1$, симметричная точке A относительно оси y будет иметь координаты:
$A_1(-(-1); -1) = A_1(1; -1)$
Точка $B_1$, симметричная точке B относительно оси y будет иметь координаты:
$B_1(-2; 2)$
Построим отрезок $A_1B_1$, симметричный отрезку AB относительно оси y:

№574

Номер №574

Изобразите на координатной плоскости все точки (x; y) такие, что:
1) x = 3, y − произвольное число;
2) y = −2, x − произвольное число.
1)
2)

Решение 1
x = 3, y − произвольное число.

Решение 2
y = −2, x − произвольное число.

№575

Номер №575

Изобразите на координатной плоскости все точки (x; y) такие, что:
1) −2 ≤ x ≤ 2, y − произвольное число;
2) −3 < y < 3, x − произвольное число;
3) |x| ≤ 4, |y| ≤ 4;
4) |x| > 1, y > 2.
1)
Задание рисунок 1
2)
Задание рисунок 2
3)
Задание рисунок 3
4)
Задание рисунок 4

Решение 1
−2 ≤ x ≤ 2, y − произвольное число.

Решение 2
−3 < y < 3, x − произвольное число

Решение 3
|x| ≤ 4, |y| ≤ 4

Решение 4
|x| > 1, y > 2

№576

Номер №576

Начертите на координатной плоскости:
1) ломаную с вершинами в точках (0; −6); (1; −4); (1; −1); (0,5; 1); (0; 2); (1; 3); (0; 4);
2) ломаную с вершинами в точках (0,5; 1); (3; 4); (7; 6); (10; 5); (11; 2); (9; 1); (11; −1); (9; −5); (5; −7); (0,5; −5);
3) отрезок с концами в точках (0; 4) и (2; 7).
Постройте фигуру, симметричную полученной относительно оси y.
Раскрасьте образовавшуюся "бабочку".

Решение

№577

Номер №577

У Вани столько же братьев, сколько и сестер, а у каждой его сестры в два раза меньше сестер, чем братьев. Сколько всего детей в этой семье?

Решение

Пусть было x сестер было всего, тогда:
x + 1 (братьев) − было всего, включая самого Ваню;
x − 1 (сестер) − было у каждой сестры.
Так как, у каждой сестры в два раза меньше сестер, чем братьев, можно составить уравнение:
2(x − 1) = x + 1
2x − 2 = x + 1
2x − x = 1 + 2
x = 3 (сестры) − было всего, тогда:
x + 1 = 3 + 1 = 4 (брата) − было всего;
3 + 4 = 7 (детей) − было всего в семье.
Ответ: 7 детей

№578

Номер №578

На рисунке изображен график изменения температуры воздуха на протяжении суток.
Заполните пропуски.
1) Температура воздуха в 4 ч была _ °C, в 10 ч − _ °C, в 14 ч − _, в 16 ч − _.
2) Температура воздуха была равна 2°C в _; равна 4°C в _; −1°C в _; 5°C в _.
3) Самая низкая температура была _ °C в _ ч.
4) Самая высокая температура была _ °C в _ ч.
5) Нулевой температура была в _
6) Температура воздуха была ниже 0°C с _ ч до _ ч, а выше 0°C с _ ч до _ ч и с _ ч до _ ч.
7) Температура повышалась с _ ч до _ ч, а понижалась с _ ч до _ ч и с _ ч до _ ч.

Решение

1) Температура воздуха в 4 ч была −1 °C, в 10 ч − 0 °C, в 14 ч − 3 °C, в 16 ч − 5 °C.
2) Температура воздуха была равна 2°C в 12 ч и в 22 ч; равна 4°C в 15 ч и в 20 ч; −1°C в 4 ч и в 9 ч; 5°C в 16 ч и в 19 ч.
3) Самая низкая температура была −3 °C в 7 ч.
4) Самая высокая температура была 6 °C в 17 ч.
5) Нулевой температура была в 3 ч, 10 ч и 24 ч
6) Температура воздуха была ниже 0°C с 3 ч до 10 ч, а выше 0°C с 0 ч до 3 ч и с 10 ч до 24 ч.
7) Температура повышалась с 7 ч до 17 ч, а понижалась с 0 ч до 7 ч и с 17 ч до 24 ч.

№579

Номер №579

На рисунке изображен график изменения температуры раствора во время химического опыта.
Заполните пропуски.
1) Начальная температура раствора была _
2) Температура раствора была 30°C через _ мин после начала опыта.
3) Через 1 ч после начала опыта температура раствора была _°C.
4) Температура раствора понизилась с 15°C до 10°C за _ мин.

Решение

1) Начальная температура раствора была 15°C.
2) Температура раствора была 30°C через 50 мин после начала опыта.
3) Через 1 ч после начала опыта температура раствора была 35°C.
4)
а) Температура раствора понизилась с 15°C до 10°C за 100 мин. (если брать во внимание, что в начале опыта температура раствора была 15°C, а через 100 мин температура раствора составила 10°C)
б) Температура раствора понизилась с 15°C до 10°C за 20 мин. (если брать во внимание, что через 80 мин температура раствора была 15°C и потом только понижалась и через 20 мин составила 10°C)

№580

Номер №580

На рисунке изображен график зависимости объема воды в цистерне от времени наполнения.
Заполните пропуски.
1) Объем цистерны равен _ $м^3$.
2) Цистерна наполнилась водой за _ ч.

Решение

1) Объем цистерны равен 40 $м^3$.
2) Цистерна наполнилась водой за 100 мин = $\frac{100}{60} = 1\frac{40}{60} = 1\frac{2}{3}$ ч.

№581

Номер №581

На рисунке изображен график движения мотоциклиста.
Заполните пропуски.
1) За первый час движения мотоциклист проехал _ км.
2) Первая остановка мотоциклиста длилась _ мин, а вторая − _ мин.
3) Через 2 ч после начала движения мотоциклист был на расстоянии _ км от дома.
4) Мотоциклист повернул обратно, когда был на расстоянии _ км от дома.
5) На обратном пути мотоциклист двигался со скоростью _ км/ч.

Решение

1) За первый час движения мотоциклист проехал 60 км.
2) Первая остановка мотоциклиста длилась 30 мин, а вторая − 60 мин.
3) Через 2 ч после начала движения мотоциклист был на расстоянии 90 км от дома.
4) Мотоциклист повернул обратно, когда был на расстоянии 120 км от дома.
5) На обратном пути мотоциклист двигался со скоростью 60 км/ч, так как за 2 часа (с 4 ч до 6 ч) мотоциклист проехал 120 км, следовательно 120 : 2 = 60.

№582

Номер №582

На рисунке изображены графики движения велосипедиста (отрезок OA) и пешехода (отрезок OB).
Заполните пропуски.
1) Скорость движения пешехода равна _ км/ч, а велосипедиста − _ км/ч.
2) За 2 ч велосипедист проехал путь в _ раза больший чем прошел пешеход за то же время.

Решение

1) Скорость движения пешехода равна 5 км/ч, а велосипедиста − 15 км/ч.
2) За 2 ч велосипедист проехал путь в 3 раза больший чем прошел пешеход за то же время, так как за 2 часа:
30 (км) − проехал велосипедист;
10 (км) − прошел пешеход;
30 : 10 = 3.

№583

Номер №583

В таблице приведены данные измерения температуры воздуха на протяжении суток через каждый час. Используя эти данные, постройте график изменения температуры.

Время суток, ч	0	1	2	3	4	5	6
Температура, °C	1	0	-1	-3	-6	-8	-9

Время суток, ч 0 1 2 3 4 5 6
Температура, °C 1 0 −1 −3 −6 −8 −9

Время суток, ч	7	8	9	10	11	12
Температура, °C	-10	-9	-8	-6	-2	0

Время суток, ч 7 8 9 10 11 12
Температура, °C −10 −9 −8 −6 −2 0

Время суток, ч	13	14	15	16	17	18
Температура, °C	1	3	5	8	9	6

Время суток, ч 13 14 15 16 17 18
Температура, °C 1 3 5 8 9 6

Время суток, ч	19	20	21	22	23	24
Температура, °C	5	3	2	0	-1	-3

Время суток, ч 19 20 21 22 23 24
Температура, °C 5 3 2 0 −1 −3

Решение

№584

Номер №584

На улице, встав в кружок, разговаривали четыре девочки: Катя, Маша, Оля и Света. Девочка в зеленом платье (это была не Катя и не Маша) стояла между девочкой в голубом платье и Светой. Девочка в белом платье стояла между девочкой в розовом платье и Машей. Какого цвета платье было у каждой девочки?

Решение

Так как девочка в белом платье стояла между девочкой в розовом платье и Машей и девочка в зеленом платье (это была не Катя и не Маша), то Маша точно в голубом платье.
Значит девочка в зеленом платье стояла между Машей и Светой. Значит девочка в зеленом платье Оля.
Девочка в белом платье стояла между девочкой в розовом платье и Машей.
Значит девочки стояли так:
Следовательно Катя в белом платье, а в розовом платье Света.
Ответ: в зеленом − Оля; в розовом − Света; в белом − Катя; в голубом − Маша.