В этой статье речь пойдет об ответах по математике за 6 класс 2 части из 3 весьма популярного учебного издания, - рабочей тетради автора Мерзляк. Математика весьма нужный и полезный школьный предмет. Это быстро понимаешь, когда идешь в магазина за покупками или занимаешься строительными работами. Здесь что не случай, то нужны математические знания. Это мы не упоминаем про более сложные варианты, когда речь идет о высокотехнологичных разработках, будь то конструкции связанные с робототехникой на производстве с транспортными системами... Там конечно уровень математики совсем другой, но основами этих знаний являются самые простые основы заложенные именно в начальной и общей программе.
 Что же, о практичности предмета поговорили, теперь можно перейти и к непосредственны ответам на домашние задания по нашему учебнику.

Ответы это прежде всего возможность свериться с вашими решениями, а не возможность списать все с интернета и тем самым "срезать" себе путь поступив полегче, потеряв при этом на собственных знаниях:)

ГДЗ ответы для рабочей тетради №2 по математике 6 класс Мерзляк

Кликаем по вкладкам и смотрим ответы

 В этой статье речь пойдет об ответах по математике за 6 класс 2 части из 3 весьма популярного учебного издания, - рабочей тетради автора Мерзляк. Математика весьма нужный и полезный школьный предмет. Это быстро понимаешь, когда идешь в магазина за покупками или занимаешься строительными работами. Здесь что не случай, то нужны математические знания. Это мы не упоминаем про более сложные варианты, когда речь идет о высокотехнологичных разработках, будь то конструкции связанные с робототехникой на производстве с транспортными системами... Там конечно уровень математики совсем другой, но основами этих знаний являются самые простые основы заложенные именно в начальной и общей программе.
 Что же, о практичности предмета поговорили, теперь можно перейти и к непосредственны ответам на домашние задания по нашему учебнику.

Ответы это прежде всего возможность свериться с вашими решениями, а не возможность списать все с интернета и тем самым "срезать" себе путь поступив полегче, потеряв при этом на собственных знаниях:)

ГДЗ ответы для рабочей тетради №2 по математике 6 класс Мерзляк

Кликаем по вкладкам и смотрим ответы

Номер 243

§19. Отношения. Номер №243

Заполните пропуски.
1) _ двух чисел a и b, отличны от _, называют отношением чисел a и b, или _ числа _ к числу _
2) В отношении числа a к числу b числа a и b называют _, число a − _ членом отношения, а число b − _
3) Отношение чисел a и b можно записывать _ способами: _ или _
4) Отношение _, если его члены умножить или _ на одно и то же число, не равное _
5) Отношение чисел a и b показывает, во сколько раз _, или какую часть _ составляет от _

Решение

1) Частное двух чисел a и b, отличны от нуля, называют отношением чисел a и b, или отношением числа a к числу b.
2) В отношении числа a к числу b числа a и b называют членами отношения, число a − предыдущим членом отношения, а число b − последующим.
3) Отношение чисел a и b можно записывать двумя способами: $\frac{a}{b}$ или a : b.
4) Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
5) Отношение чисел a и b показывает, во сколько раз число a больше числа b, или какую часть число a составляет от числа b.

№244

Номер №244

Заполните таблицу.

Отношение	3 : 7	$\frac{11}{18}$
Предыдущий член			20	$1\frac{1}{3}$
Последующий член			0,3	6

Решение

Отношение	3 : 7	$\frac{11}{18}$	20 : 0,3	$1\frac{1}{3} : 6$
Предыдущий член	3	11	20	$1\frac{1}{3}$
Последующий член	7	18	0,3	6

№245

Номер №245

Найдите отношение.
1) 1,8 : 7,2 =
2) 2,8 : 0,07 =
3) 4 дм : 8 см = 40 см : 8 см =
4) 10 м : 1 км =
5) 36 кг : 240 г =
6) 42 мин : 2 ч =

Решение 1

$1,8 : 7,2 = \frac{1,8}{7,2} = \frac{18}{72} = \frac{1}{4} = 0,25$

Решение 2
$2,8 : 0,07 = \frac{2,8}{0,07} = \frac{280}{7} = 40$

Решение 3
4 дм : 8 см = 40 см : 8 см = 5

Решение 4
10 м : 1 км = 10 м : 1000 м = $\frac{10}{1000} = \frac{1}{100} = 0,01$

Решение 5
36 кг : 240 г = 36000 г : 240 г = $\frac{36000}{240} = \frac{3600}{24} = 150$

Решение 6
42 мин : 2 ч = 42 мин : 120 мин = $\frac{42}{120} = \frac{7}{20} = 0,35$

№246

Номер №246

Заполните пропуски.
1) Масштаб карты 1 : 5000 означает, что все расстояния на карте в _, чем на местности.
2) Масштаб чертежа механизма 1 : 40 означает, что все размеры механизма в _, чем на чертеже.
3) Если на карте задан масштаб 1 : 200000, то это означает, что 1 см на _ соответствует _ на местности.

Решение

1) Масштаб карты 1 : 5000 означает, что все расстояния на карте в 5000 раз меньше, чем на местности.
2) Масштаб чертежа механизма 1 : 40 означает, что все размеры механизма в 40 раз больше, чем на чертеже.
3) Если на карте задан масштаб 1 : 200000, то это означает, что 1 см на карте соответствует 200000 см или 2 км на местности.

№247

Номер №247

Расстояние между двумя городами на карте, масштаб которой 1 : 500000, равно 4,6 см. Вычислите расстояние между этими городами на местности.

Решение

4,6 * 500000 = 2300000 (см) = 23 (км) − расстояние на местности.
Ответ: 23 км

№248

Номер №248

Расстояние между селами Вишневое и Яблоневое равно 180 км. Каким будет расстояние между этими селами на карте с масштабом 1 : 600000?

Решение

180 км = 18000000 см
18000000 : 600000 = 180 : 6 = 30 (см) − расстояние между селами на карте.
Ответ: 30 см

№249

Номер №249

Замените отношение дробных чисел отношением натуральных чисел.
1) $2 : \frac{3}{7} = (2 * 7) : (\frac{3}{7} * 7) =$
2) $\frac{4}{11} : \frac{9}{11} =$
3) $\frac{2}{9} : \frac{5}{12} = (\frac{2}{9} * ) : (\frac{5}{12} * ) =$
4) 0,6 : 0,07 =
5) $2\frac{3}{8} : 1\frac{1}{6} =$
6) $\frac{5}{14} : \frac{13}{21} =$

Решение 1
$2 : \frac{3}{7} = (2 * 7) : (\frac{3}{7} * 7) = 14 : 3$

Решение 2
$\frac{4}{11} : \frac{9}{11} = (\frac{4}{11} * 11) : (\frac{9}{11} * 11) = 4 : 9$

Решение 3
$\frac{2}{9} : \frac{5}{12} = (\frac{2}{9} * 36) : (\frac{5}{12} * 36) = (2 * 4) : (5 * 3) = 8 : 15$

Решение 4
0,6 : 0,07 = (0,6 * 100) : (0,07 * 100) = 60 : 7

Решение 5
$2\frac{3}{8} : 1\frac{1}{6} = \frac{19}{8} : \frac{7}{6} = (\frac{19}{8} * 24) : (\frac{7}{6} * 24) = (19 * 3) : (7 * 4) = 57 : 28$

Решение 6
$\frac{5}{14} : \frac{13}{21} = (\frac{5}{14} * 42) : (\frac{13}{21} * 42) = (5 * 3) : (13 * 2) = 15 : 26$

№250

Номер №250

Как изменится отношение в результате следующих действий? Заполните таблицу.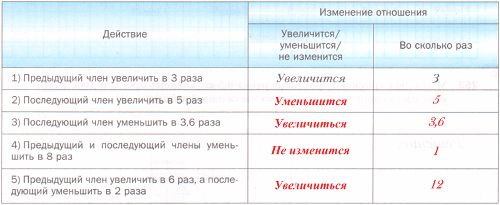

Решение

Пусть:
a − предыдущий член;
b − последующий член;
$a : b = \frac{a}{b}$ − их отношение.
Тогда:
1) если предыдущий член увеличить в 3 раза, то:
$3a : b = \frac{3a}{b} = 3\frac{a}{b}$ − начальное отношение увеличилось в 3 раза;
2) если последующий член увеличить в 5 раз, то:
$a : 5b = \frac{a}{5b} = \frac{1}{5} * \frac{a}{b}$ − начальное отношение уменьшилось в 5 раз;
3) если последующий член уменьшить в 3,6 раза, то:
$a : \frac{b}{3,6} = a * \frac{3,6}{b} = \frac{3,6a}{b} = 3,6\frac{a}{b}$ − начальное отношение увеличилось в 3,6 раза;
4) если предыдущий и последующий члены уменьшить в 8 раз, то:
$\frac{a}{8} : \frac{b}{8} = \frac{a}{8} * \frac{8}{b} = \frac{a}{b}$ − начальное отношение не изменилось;
5) если предыдущий член увеличить в 6 раз, а последующий уменьшить в 2 раза, то:
$6a : \frac{b}{2} = 6a * \frac{2}{b} = \frac{12a}{b} = 12\frac{a}{b}$ − начальное отношение увеличилось в 12 раз.
Ответ:

№251

Номер №251

Расстояние между двумя городами на местности равно 315 км, а на карте − 10,5 см. Найдите масштаб карты.
Решение.
315 км = см
Ответ:

Решение

315 км = 31500000 см
10,5 см : 31500000 см = 105 : 315000000 = 1 : 3000000 − масштаб карты.
Ответ: 1 : 3000000

№252

Номер №252

Размеры участка прямоугольной формы составляют 81 м и 27 м. Начертите план этого участка в масштабе 1 : 900.

Решение

81 м = 8100 см, 27 м = 2700 см.
1) 8100 : 900 = 81 : 9 = 9 (см) − длина участка на плане;
2) 2700 : 900 = 27 : 9 = 3 (см) − ширина участка на плане.
Ответ: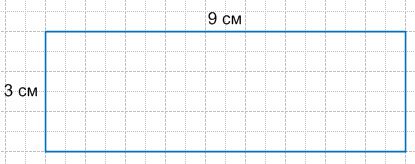

№253

Номер №253

Масса двух арбузов и трех дынь равна 8,5 кг, а одного арбуза и двух дынь − 5 кг. Какова масса одного арбуза и какова масса одной дыни?

Решение

Обозначим:
А − арбуз;
Д − дыня.
Тогда можно составить 2 уравнения:
2А + 3Д = 8,5 и А + 2Д = 5
Найдем разницу полученных уравнений:
2А + 3Д − (А + 2Д) = 8,5 − 5
2А + 3Д − А − 2Д = 3,5
А + Д = 3,5
А = 3,5 − Д
Подставим полученное значение А во второе уравнение
3,5 − Д + 2Д = 5
Д = 5 − 3,5
Д = 1,5 (кг) − масса одной дыни, тогда:
А + Д = 3,5
А + 1,5 = 3,5
А = 3,5 − 1,5
А = 2 (кг) − масса одного арбуза.
Ответ: 2 кг масса арбуза, 1,5 кг масса дыни.

№254

Номер №254

Заполните пропуски.
1) Равенство _ называют пропорцией.
2) В пропорции a : b = c : d (или _) числа a и d называют _ членами пропорции, а числа b и c − _
3) Запись a : b = c : d читают так: a относится к b, как _ или отношение a к b равно _
4) Произведение _ членов пропорции равно _. Это утверждение называют _
5) Если $\frac{a}{b} = \frac{c}{d}$, то a _ = _
6) Если a, b, c и d − числа, отличные от _, и ad = bc, то отношения _ и _ равны и могут образовать пропорцию _

Решение

1) Равенство двух отношений называют пропорцией.
2) В пропорции a : b = c : d (или $\frac{a}{b} = \frac{c}{d}$) числа a и d называют крайними членами пропорции, а числа b и c − средними членами пропорции.
3) Запись a : b = c : d читают так: a относится к b, как c относится к d или отношение a к b равно отношению c к d.
4) Произведение крайних членов пропорции равно произведению ее средних членов. Это утверждение называют основным свойством пропорции.
5) Если $\frac{a}{b} = \frac{c}{d}$, то ad = bc.
6) Если a, b, c и d − числа, отличные от нуля, и ad = bc, то отношения a : b и c : d равны и могут образовать пропорцию $\frac{a}{b} = \frac{c}{d}$.

№255

Номер №255

Заполните таблицу.

Пропорция	2,7 : 9 = 3,6 : 12	$\frac{20}{75} = \frac{12}{45}$
Крайние члены пропорции			10; 24	0,5; 120
Средние члены пропорции			40; 6	30; 2

Решение

Пропорция	2,7 : 9 = 3,6 : 12	$\frac{20}{75} = \frac{12}{45}$	$\frac{10}{40} = \frac{6}{24}$	0,5 : 30 = 2 : 120
Крайние члены пропорции	2,7; 12	20; 45	10; 24	0,5; 120
Средние члены пропорции	9; 3,6	75; 12	40; 6	30; 2

 

№256

Номер №256

Запишите в виде пропорции утверждение.
1) 2 относится к 3, как 12 относится к 18: _
2) $\frac{1}{4}$ относится к 10, как 1 относится к 40: _
3) x относится к 2,4, как 6 относится к 2,7: _

Решение 1

2 относится к 3, как 12 относится к 18: 2 : 3 = 12 : 18

Решение 2
$\frac{1}{4}$ относится к 10, как 1 относится к 40: $\frac{1}{4} : 10 = 1 : 40$

Решение 3
x относится к 2,4, как 6 относится к 2,7: x : 2,4 = 6 : 2,7

№257

Номер №257

Впишите в пустую клетку такое число, чтобы образовалась пропорция.
1) 48 : 6 = 32 : ☐;
2) 72 : 12 = ☐ : 5;
3) ☐ : 12 = 7 : 21.

Решение 1

48 : 6 = 32 : ☐
48 : 6 = 8, тогда:
32 : ☐ = 8
☐ = 32 : 8
☐ = 4
Ответ: 48 : 6 = 32 : 4

Решение 2
72 : 12 = ☐ : 5
72 : 12 = 6, тогда:
☐ : 5 = 6
☐ = 6 * 5
☐ = 30
Ответ: 72 : 12 = 30 : 5

Решение 3
☐ : 12 = 7 : 21
$7 : 21 = \frac{7}{21} = \frac{1}{3}$, тогда:
$☐ : 12 = \frac{1}{3}$
$☐ = \frac{1}{3} * 12$
☐ = 4
Ответ: 4 : 12 = 7 : 21

№258

Номер №258

Вычислив данные отношения, установите, можно ли из них составить пропорцию. В случае утвердительного ответа запишите эту пропорцию.
1) 3,2 : 0,8 и 76 : 19;
2) $\frac{5}{18} : \frac{7}{36}$ и $\frac{2}{7} : \frac{16}{35}$.

Решение 1
3,2 : 0,8 = 32 : 8 = 4
76 : 19 = 4
4 = 4, данные отношения равны, значит можно составить пропорцию:
3,2 : 0,8 = 76 : 19

Решение 2
$\frac{5}{18} : \frac{7}{36} = \frac{5}{18} * \frac{36}{7} = \frac{5}{1} * \frac{2}{7} = \frac{10}{7} = 1\frac{3}{7}$
$\frac{2}{7} : \frac{16}{35} = \frac{2}{7} * \frac{35}{16} = \frac{1}{1} * \frac{5}{8} = \frac{5}{8}$
$1\frac{3}{7} ≠ \frac{5}{8}$ − значит пропорцию составить нельзя.

№259

Номер №259

Не вычисляя данные отношения, установите, можно ли из них составить пропорцию. В случае утвердительного ответа запишите эту пропорцию.
1) 6 : 5 и 0,3 : 0,2;
2) $13\frac{8}{9} : 8\frac{1}{3}$ и $7\frac{1}{2} : 4\frac{1}{2}$.

Решение 1
6 : 5 и 0,3 : 0,2
воспользуемся основным свойством пропорции по которому произведение крайних членов должно быть равно произведению средних членов:
6 * 0,2 = 1,2
5 * 0,3 = 1,5
1,2 ≠ 1,5 − значит пропорцию составить нельзя.

Решение 2
$13\frac{8}{9} : 8\frac{1}{3}$ и $7\frac{1}{2} : 4\frac{1}{2}$
$13\frac{8}{9} * 4\frac{1}{2} = \frac{125}{9} * \frac{9}{2} = \frac{125}{2} = 62\frac{1}{2}$
$8\frac{1}{3} * 7\frac{1}{2} = \frac{25}{3} * \frac{15}{2} = \frac{25}{1} * \frac{5}{2} = \frac{125}{2} = 62\frac{1}{2}$
$62\frac{1}{2} = 62\frac{1}{2}$ − значит пропорцию составить можно.
$13\frac{8}{9} : 8\frac{1}{3} = 7\frac{1}{2} : 4\frac{1}{2}$

№260

Номер №260

Образуйте новую пропорцию из пропорции:
1) $\frac{25}{9} = \frac{50}{18}$, поменяв местами крайние члены;
2) 24 : 10 = 36 : 15, поменяв местами средние члены.

Решение 1

$\frac{25}{9} = \frac{50}{18}$
25 и 18 − крайние члены.
Поменяв их местами, получим:
$\frac{18}{9} = \frac{50}{25}$

Решение 2
24 : 10 = 36 : 15
10 и 36 − средние члены.
Поменяв их местами, получим:
24 : 36 = 10 : 15

№261

Номер №261

Решите уравнение.
1) x : 12 = 7 : 10
10 * x = 12 * 7
$x = \frac{12 * 7}{10} =$
x =
2) $\frac{2}{x} = \frac{8}{5}$
x * =
$x = \frac{}{}$
x =
3) 4,8 : 5,1 = x : 34
4) $\frac{x}{117} = \frac{5}{72}$

Решение 1
x : 12 = 7 : 10
10 * x = 12 * 7
$x = \frac{12 * 7}{10} = \frac{84}{10}$
x = 8,4
Ответ: x = 8,4

Решение 2
$\frac{2}{x} = \frac{8}{5}$
x * 8 = 2 * 5
$x = \frac{2 * 5}{8} = \frac{1 * 5}{4} = \frac{5}{4}$
$x = 1\frac{1}{4}$
Ответ: $x = 1\frac{1}{4}$

Решение 3
4,8 : 5,1 = x : 34
x * 5,1 = 4,8 * 34
$x = \frac{4,8 * 34}{5,1} = \frac{48 * 34}{51} = \frac{16 * 34}{17} = \frac{16 * 2}{1}$
x = 32
Ответ: x = 32

Решение 4
$\frac{x}{117} = \frac{5}{72}$
x * 72 = 117 * 5
$x = \frac{117 * 5}{72} = \frac{13 * 5}{8} = \frac{65}{8}$
$x = 8\frac{1}{8}$
Ответ: $x = 8\frac{1}{8}$

№262

Номер №262

На пошив 18 одинаковых костюмов израсходовали 61,2 м ткани. Сколько требуется ткани, чтобы сшить 23 таких костюма?

Решение

Пусть требуется x м ткани.
Запишем кратко условие задачи:
18 костюмов − 61,2 м
23 костюма − x м
Отношения $\frac{61,2}{18}$ и $\frac{x}{23}$ равны, поскольку каждое из них показывает, сколько метров ткани расходуют на один костюм.
Составим пропорцию:
$\frac{61,2}{18} = \frac{x}{23}$
18 * x = 61,2 * 23
$x = \frac{61,2 * 23}{18} = \frac{612 * 23}{180} = \frac{34 * 23}{10} = \frac{782}{10}$
x = 78,2 (м) − ткани требуется, чтобы сшить 23 таких костюма.
Ответ: 78,2 м

№263

Номер №263

Из 250 кг свежего винограда получают 75 кг изюма. Сколько килограммов изюма получат из 80 кг свежего винограда?

Решение

Пусть получат x кг изюма получат из 80 кг свежего винограда.
Запишем кратко условие задачи:
250 кг винограда − 75 кг изюма
80 кг винограда − x кг изюма
Отношения $\frac{75}{250}$ и $\frac{x}{80}$ равны, поскольку каждое из них показывает, сколько изюма получается из 1 кг винограда.
Составим пропорцию:
250 * x = 75 * 80
$x = \frac{75 * 80}{250} = \frac{75 * 8}{25} = 3 * 8$
x = 24 (кг) − изюма получат из 80 кг свежего винограда.
Ответ: 24 кг

№264

Номер №264

Токарь до обеденного перерыва выточил 36 деталей, что составляет 60% дневной нормы. Сколько деталей должен выточить токарь за рабочий день?

Решение
Пусть токарю надо выточить x деталей. Примем количество всех деталей, которые надо выточить, за 100%. Запишем кратко условие задачи:
36 деталей − 60%
x деталей − 100%
Отношения $\frac{60}{36}$ и $\frac{100}{x}$ равны, поскольку каждое из них показывает, сколько процентов составляет 1 деталь.
Составим пропорцию:
$\frac{60}{36} = \frac{100}{x}$
60 * x = 36 * 100
$x = \frac{36 * 100}{60} = \frac{36 * 10}{6} = 6 * 10$
x = 60 (деталей) − надо выточить токарю за рабочий день.
Ответ: 60 деталей

№265

Номер №265

Сплав содержит 14% цинка. Сколько килограммов сплава надо взять, чтобы он содержал 3,5 кг цинка?

Решение

Пусть надо взять x кг сплава, чтобы он содержал 3,5 кг цинка. Примем весь сплав за 100%. Запишем кратко условие задачи:
3,5 кг − 14%
x кг − 100%
Отношения $\frac{14}{3,5}$ и $\frac{100}{x}$ равны, поскольку каждое из них показывает, сколько процентов составляет 1 кг сплава.
Составим пропорцию:
$\frac{14}{3,5} = \frac{100}{x}$
14 * x = 100 * 3,5
$x = \frac{100 * 3,5}{14} = \frac{50 * 3,5}{7} = \frac{50 * 35}{70} = \frac{5 * 35}{7} = 5 * 5$
x = 25 (кг) − сплава надо взять, чтобы он содержал 3,5 кг цинка.
Ответ: 25 кг

№266

Номер №266

Расстояние между городами A и B на местности равно 228 км, а на карте − 3,8 см. Каково расстояние на местности между городами C и D, если расстояние между ними на этой карте равно 2,4 см?

Решение

Пусть x (км) − расстояние между городами C и D.
Запишем кратко условие задачи:
228 км − 3,8 см
x км − 2,4 см
Отношения $\frac{3,8}{228}$ и $\frac{2,4}{x}$ равны, поскольку каждое из них показывает масштаб карты.
Составим пропорцию:
$\frac{3,8}{228} = \frac{2,4}{x}$
3,8 * x = 2,4 * 228
$x = \frac{2,4 * 228}{3,8} = \frac{24 * 228}{38} = \frac{24 * 6}{1} = 144$ (км) − расстояние между городами C и D.
Ответ: 144 км

№267

Номер №267

Найдите отношение a к b, если:
1) $\frac{b}{a} = \frac{2}{11}$
2) $\frac{a}{16} = \frac{b}{19}$
3) $\frac{10}{b} = \frac{3}{a}$

Решение 1
$\frac{b}{a} = \frac{2}{11}$
$\frac{a}{b} = \frac{11}{2} = 5\frac{1}{2}$

Решение 2
$\frac{a}{16} = \frac{b}{19}$
поменяем местами средние члены отношений:
$\frac{a}{b} = \frac{16}{19}$

Решение 3
$\frac{10}{b} = \frac{3}{a}$
поменяем местами крайние члены отношений:
$\frac{a}{b} = \frac{3}{10}$

№268

Номер №268

Решите уравнение.
1) $\frac{6}{11} : \frac{3}{22} = \frac{12}{17} : x$
2) $\frac{21}{x + 3} = \frac{7}{4}$
7(x + 3) =
3) $\frac{12}{13} = \frac{7,4 - x}{2,6}$
4) $48 : 35 = \frac{1}{14}x : \frac{1}{16}$

Решение 1
$\frac{6}{11} : \frac{3}{22} = \frac{12}{17} : x$
$\frac{6}{11}x = \frac{3}{22} * \frac{12}{17}$
$\frac{6}{11}x = \frac{3}{11} * \frac{6}{17}$
$x = \frac{3 * 6}{11 * 17} : \frac{6}{11}$
$x = \frac{3 * 6}{11 * 17} * \frac{11}{6}$
$x = \frac{3 * 1}{1 * 17} * \frac{1}{1}$
$x = \frac{3}{17}$
Ответ: $x = \frac{3}{17}$

Решение 2
$\frac{21}{x + 3} = \frac{7}{4}$
7(x + 3) = 21 * 4
$x + 3 = \frac{21 * 4}{7}$
x + 3 = 3 * 4
x + 3 = 12
x = 12 − 3
x = 9
Ответ: x = 9

Решение 3
$\frac{12}{13} = \frac{7,4 - x}{2,6}$
13(7,4 − x) = 12 * 2,6
$7,4 - x = \frac{12 * 2,6}{13}$
$7,4 - x = \frac{1,2 * 26}{13}$
7,4 − x = 1,2 * 2
7,4 − x = 2,4
x = 7,4 − 2,4
x = 5
Ответ: x = 5

Решение 4
$48 : 35 = \frac{1}{14}x : \frac{1}{16}$
$35 * \frac{1}{14}x = 48 * \frac{1}{16}$
$5 * \frac{1}{2}x = 3 * \frac{1}{1}$
$\frac{5}{2}x = 3$
$x = 3 : \frac{5}{2}$
$x = 3 * \frac{2}{5}$
$x = \frac{6}{5} = 1\frac{1}{5}$
Ответ: $x = 1\frac{1}{5}$

№269

Номер №269

Составьте все возможные пропорции, которые следуют из равенства 16 * 3 = 6 * 8.

Решение

16 * 3 = 6 * 8
1) $\frac{16}{8} = \frac{6}{3}$;
2) $\frac{16}{6} = \frac{8}{3}$;
3) $\frac{8}{16} = \frac{3}{6}$;
4) $\frac{6}{16} = \frac{3}{8}$.

№270

Номер №270

Докажите, что если $\frac{a}{b} = \frac{c}{d}$, то $\frac{a + c}{b + d} = \frac{c}{d}$.

Решение

Доказательство.
Поскольку $\frac{a}{b} = \frac{c}{d}$, то ad = bc
(a + c)d = ad + cd
(b + d)c = bc + cd
ad + cd = bc + cd
(ad + cd) − cd = (bc + cd) − cd
ad + cd − cd = bc + cd − cd
ad = bc
Следовательно, если $\frac{a}{b} = \frac{c}{d}$, то $\frac{a + c}{b + d} = \frac{c}{d}$.

№271

Номер №271

Заполните пропуски.
1) Процентное отношение двух чисел − это _
2) Процентное отношение двух чисел показывает, сколько _
3) Чтобы найти процентное отношение двух чисел, надо их отношение _ и к результату _

Решение

1) Процентное отношение двух чисел − это их отношение выраженное в процентах.
2) Процентное отношение двух чисел показывает, сколько процентов одно число составляет от другого.
3) Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.

№272

Номер №272

Сколько процентов составляет число 80 от числа:
1) 100;
2) 320;
3) 240;
4) 60?

Решение 1
$\frac{80}{100} * 100$% = 80%

Решение 2
$\frac{80}{320} * 100$% = $\frac{1}{4} * 100$% = 25%

Решение 3
$\frac{80}{240} * 100$% = $\frac{1}{3} * 100$% = $\frac{100}{3}$% = $33\frac{1}{3}$%

Решение 4
$\frac{80}{60} * 100$% = $\frac{4}{3} * 100$% = $\frac{400}{3}$% = $133\frac{1}{3}$%

№273

Номер №273

Алена прочитала 112 страниц книги, в которой всего было 280 страниц. Сколько процентов страниц книги прочитала Алена?

Решение

$\frac{112}{280} * 100$% = $\frac{2}{5} * 100$% = 2 * 20% = 40 (%) страниц книги прочитала Алена.
Ответ: 40%

№274

Номер №274

У Васи было 500 р. Он купил новую ручку за 35 р. Сколько процентов денег Вася потратил на покупку ручки?

Решение

$\frac{35}{500} * 100$% = $\frac{7}{100} * 100$% = 7 (%) денег Вася потратил на покупку ручки.
Ответ: 7%

№275

Номер №275

Найдите процент содержания железа в руде, если 90 т этой руды содержат 6,48 т железа.

Решение

$\frac{6,48}{90} * 100$% = $\frac{648}{90}$% = $\frac{72}{10}$% = 7,2 (%) − процент содержания железа в руде.
Ответ: 7,2%

№276

Номер №276

В первый день туристы прошли 9 км, а во второй − 18 км. Сколько процентов составляет путь, пройденный во второй день, от пути, пройденного в первый день?

Решение

$\frac{18}{9} * 100$% = 2 * 100% = 200 (%) − составляет путь, пройденный во второй день, от пути, пройденного в первый день.
Ответ: 200%

№277

Номер №277

Заполните таблицу.

Начальное значение величины	Конечное значение величины	Изменение величины	Изменение величины в процентах
10 м	12 м	2 м	$\frac{2}{10} * 100 = $ (%)
25 кг	19 кг
6 ц	18 ц
48 мин	30 мин
16 кг	26 кг

Решение

Начальное значение величины	Конечное значение величины	Изменение величины	Изменение величины в процентах
10 м	12 м	2 м	$\frac{2}{10} * 100 = $ (%)
25 кг	19 кг	6 кг	$\frac{6}{25} * 100 = 6 * 4 = 24$ (%)
6 ц	18 ц	12 ц	$\frac{12}{6} * 100 = 2 * 100 = 200$ (%)
48 мин	30 мин	18 мин	$\frac{18}{48} * 100 = \frac{3}{8} * 100 = \frac{3}{2} * 25 = \frac{75}{2} = 37,5$ (%)
16 кг	26 кг	10 кг	$\frac{10}{16} * 100 = \frac{5}{8} * 100 = \frac{5}{2} * 25 = \frac{125}{2} = 62,5$ (%)

 

№278

Номер №278

Цена некоторого товара возросла со 128 р. до 160 р. На сколько процентов повысилась цена товара?

Решение

1/) 160 − 128 = 32 (р.) − на столько повысилась цена товара;
2) $\frac{32}{128} * 100 = \frac{1}{4} * 100 = 25$ (%) − размер повышения цены товара.
Ответ: на 25%

№279

Номер №279

Цена некоторого товара снизилась со 160 р. до 128 р. На сколько процентов снизилась цена товара?

Решение

1) 160 − 128 = 32 (р.) − на столько снизилась цена товара;
2) $\frac{32}{160} * 100 = \frac{1}{5} * 100 = 20$ (%) − на столько снизилась цена товара.
Ответ: на 20%

№280

Номер №280

На рисунке четырехугольники ABCD и OPCN − квадраты, а четырехугольники MBPO и EOND − прямоугольники, AB = 10 см, CP = 2 см. Сколько процентов площади квадрата ABCD составляет площадь:
1) квадрата OPCN;
2) квадрата AMOE;
3) прямоугольника MBPO;
4) прямоугольника AMND?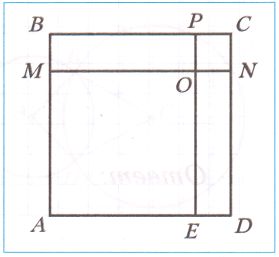

Решение 1
1) 2 * 2 = 4 $(см^2)$ − площадь квадрата OPCN;
2) 10 * 10 = 100 $(см^2)$ − площадь квадрата ABCD;
3) $\frac{4}{100} * 100 = 4$ (%) − площади квадрата ABCD составляет площадь квадрата OPCN.
Ответ: 4%

Решение 2
Так как, ABCD и OPCN − квадраты, то:
AB = BC = CD = AD = 10 (см);
OP = PC = CN = ON = 2 (см);
MO = BC − PC = 10 − 2 = 8 (см), тогда:
1) 8 * 8 = 64 $(см^2)$ − площадь квадрата AMOE;
2) 10 * 10 = 100 $(см^2)$ − площадь квадрата ABCD;
3) $\frac{64}{100} * 100 = 64$ (%) − площади квадрата ABCD составляет площадь квадрата AMOE.
Ответ: 64%

Решение 3
Так как, ABCD и OPCN − квадраты, то:
AB = BC = CD = AD = 10 (см);
OP = PC = CN = ON = 2 (см);
BP = BC − PC = 10 − 2 = 8 (см), тогда:
1) 8 * 2 = 16 $(см^2)$ − площадь прямоугольника MBPO;
2) 10 * 10 = 100 $(см^2)$ − площадь квадрата ABCD;
3) $\frac{16}{100} * 100 = 16$ (%) − площади квадрата ABCD составляет площадь прямоугольника MBPO.
Ответ: 16%

Решение 4
Так как, ABCD и OPCN − квадраты, то:
AB = BC = CD = AD = 10 (см);
OP = PC = CN = ON = 2 (см);
ND = CD − CN = 10 − 2 = 8 (см), тогда:
1) 8 * 10 = 80 $(см^2)$ − прямоугольника AMND;
2) 10 * 10 = 100 $(см^2)$ − площадь квадрата ABCD;
3) $\frac{80}{100} * 100 = 80$ (%) − площади квадрата ABCD составляет площадь прямоугольника AMND.
Ответ: 80%

№281

Номер №281

Пальто стоило 1400 р. Сначала его цену повысили на 15%, а потом новую цену снизили на 15%. Какой стала цена пальто после этих изменений? На сколько процентов изменилась начальная цена пальто?

Решение

После повышения новая цена пальто составила 115% начальной цены.
После понижения окончательная цена пальто составила 85% цены, образовавшейся после повышения.
115% = 1,15;
85% = 0,85.
1) 1400 * 1,15 = 1610 (р.) − цена пальто после повышения цены;
2) 1610 * 0,85 = 1368,5 (р.) − цена пальто после всех изменений;
3) 1400 − 1368,5 = 31,5 (р.) − на столько изменилась цена пальто после всех изменений;
4) $\frac{31,5}{1400} * 100 = \frac{31,5}{14} = \frac{315}{140} = \frac{9}{4} = 2\frac{1}{4} = 2,25$ (%) − на сколько процентов изменилась начальная цена пальто.
Ответ: 1368,5 рублей; на 2,25%.

№282

Номер №282

К сплаву массой 700 г содержащему 80% олова, добавили 300 г олова. Найдите процентное содержание олова в новом сплаве.

Решение

80% = 0,8
1) 700 + 300 = 1000 (г) − масса нового сплава.
2) 700 * 0,8 = 560 (г) − олова содержится в начальном сплаве;
3) 560 + 300 = 860 (г) − олова содержится в новом сплаве;
4) $\frac{860}{1000} * 100 = \frac{860}{10} = 86$ (%) − процентное содержание олова в новом сплаве.
Ответ: 86%

№283

Номер №283

В растворе, состоящем из соли и воды, масса которого равна 80 кг, содержится 10% соли. Каким станет процентное содержание соли в растворе, если к данному раствору добавить 10 кг воды и 10 кг соли?

Решение

10% = 0,1
1) 80 * 0,1 = 8 (кг) − соли;
2) 80 + 10 + 10 = 100 (кг) − масса нового раствора;
3) 8 + 10 = 18 (кг) − масса соли в новом растворе;
4) $\frac{18}{100} * 100 = 18$ (%) − процентное содержание соли в новом растворе.
Ответ: 18%

№284

Номер №284

Сколько граммов воды надо добавить к 600 г раствора, содержащего 15% соли, чтобы получить новый раствор, который будет содержать 10% соли?

Решение

15% = 0,15; 10% = 0,1.
1) 600 * 0,15 = 90 (г) − соли содержится в каждом из растворов.
2) Пусть надо добавить x г воды. Тогда масса нового раствора равна (600 + x) г, а масса соли в нем составляет 10% массы раствора.
Получаем уравнение.
0,1 * (600 + x) = 90
600 + x = 90 : 0,1
600 + x = 900
x = 900 − 600
x = 300 (г) − воды надо добавить, , чтобы получить новый раствор, который будет содержать 10% соли.
Ответ: 300 г

№285

Номер №285

Первый шкаф на 20% дешевле второго. На сколько процентов второй шкаф дороже первого?

Решение

Пусть первый шкаф стоит a р., а второй − b р. Тогда a = 0,8b, так как 100% − 20% = 80% или 0,8.
Отсюда:
$b = a : 0,8 = a : \frac{8}{10} = a * \frac{10}{8} = \frac{5}{4}a = 1,25a$
1,25 * 100% = 125% − составляет цена второго шкафа от цены первого;
125% − 100% = 25% − на столько процентов второй шкаф дороже первого.
Ответ: на 25%

№286

Номер №286

Число a составляет 1% от числа b. Как надо изменить число b, чтобы число a составило от него 4%?

Решение

1% = 0,01;
4% = 0,04.
По условию a = 0,01b. Необходимо так изменить число b, чтобы число a стало равно $a = 0,04b_1$.
Так как, число a останется неизменным, то можно составить уравнение:
$0,01b = 0,04b_1$
$b_1 = \frac{0,01b}{0,04}$
$b_1 = \frac{1}{4}b$
Следовательно число b нужно уменьшить в 4 раза, чтобы число a составило от него 4%.
Ответ: уменьшить в 4 раза

№287

Номер №287

Цену некоторого товара снизили на 25%. На сколько процентов надо повысить новую цену, чтобы получить начальную цену?

Решение

Начальная цена товара составляет 100%, тогда 100% − 25% = 75% − составляет новая цена товара от начальной цены.
Пусть цена некоторого товара была x, тогда после снижения цена товара стала 0,75x.
Пусть новая цена товара y, тогда y = 0,75x, тогда:
$x = \frac{y}{0,75} = \frac{100y}{75} = \frac{4}{3}y$
$\frac{4}{3} * 100 = \frac{400}{3} = 133\frac{1}{3}$%
Тогда:
$133\frac{1}{3} - 100 = 33\frac{1}{3}$% − на столько процентов надо повысить новую цену, чтобы получить начальную цену.
Ответ: на $33\frac{1}{3}$%

№288

Номер №288

Сторону квадрата увеличили на 30%. На сколько процентов:
1) увеличился его периметр;
2) увеличилась его площадь?

Решение 1

Пусть сторона квадрата равна a, тогда:
100% + 30% = 130% − составляет увеличенная длина стороны квадрата от начальной длины.
130% = 1,3
1) 4a − периметр начального квадрата;
2) 4 * 1,3a = 5,2a − периметр увеличенного квадрата;
3) $\frac{5,2a}{4a} * 100 = \frac{52}{40} * 100 = 13 * 10 = 130$ (%) − составил увеличенный периметр квадрата от начального;
4) 130% − 100% = 30% − на столько увеличился периметр квадрата.
Ответ: на 30%

Решение 2
Пусть сторона квадрата равна a, тогда:
100% + 30% = 130% − составляет увеличенная длина стороны квадрата от начальной длины.
130% = 1,3
1) $a * a = a^2$ − площадь начального квадрата;
2) $1,3a * 1,3a = 1,69a^2$ − периметр увеличенного квадрата;
3) $\frac{1,69a^2}{a^2} * 100 = 1,69 * 100 = 169$ (%) − составила увеличенная площадь квадрата от начальной;
4) 169% − 100% = 69% − на столько увеличилась площадь квадрата.
Ответ: на 69%

№289

Номер №289

Василий Сладкоежкин похудел на 25%, потом прибавил в весе на 20%, снова похудел, но на 10%, снова прибавил в весе на 20%. Похудел он или поправился после этих изменений в весе?

Решение

100% = 1;
25% = 0,25;
20% = 0,2;
10% = 0,1.
Пусть вес Василия был x, тогда:
1) (1 − 0,25)x = 0,75x − составил вес Василия после первого похудения;
0,75x;
2) (1 + 0,2) * 0,75x = 1,2 * 0,75x = 0,9x − составил вес Василия после первой прибавки;
3) (1 − 0,1) * 0,9x = 0,9 * 0,9x = 0,81x − составил вес Василия после первого похудения;
4) (1 + 0,2) * 0,81x = 1,2 * 0,81x = 0,972x − составил вес Василия после второго похудения;
5) 0,972x < x − значит Василий после всех изменений похудел.
Ответ: Василий похудел

№290

Номер №290

Иван Иванович плыл в лодке против течения реки. Из лодки в воду упал спасательный круг, но Иван Иванович заметил это только через 20 мин, развернул лодку и поплыл за кругом, не изменяя собственную скорость лодки. Через сколько минут он догонит круг?

Решение

Пусть:
x (м/мин) − собственная скорость лодки;
y (м/мин) − скорость течения реки;
x + y (м/мин) − скорость лодки по течению;
x − y (м/мин) − скорость лодки против течения;
20y (м) − проплыл спасательный круг за 20 минут;
20(x − y) (м) − прошла лодка за 20 минут;
20y + 20(x − y) = 20y + 20x − 20y = 20x (м) − составило расстояние между спасательным кругом и лодкой через 20 минут;
(x + y) − y = x + y − y = x (м/мин) − скорость сближения спасательного круга и лодки;
$\frac{20x}{x} = 20$ (мин) − потребуется Иван Ивановичу, чтобы догнать спасательный круг.
Ответ: через 20 минут

№291

Номер №291

Заполните пропуски.
1) Две переменные величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая _
2) Если две переменные величины прямо пропорциональны, то _ соответствующих значений этих величин равно _ для данных величин, _
3) Две переменные величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая _
4) Если две переменные величины обратно пропорциональны, то _ соответствующих значений этих величин равно _ для данных величин, _

Решение

1) Две переменные величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшаются) во столько же раз.
2) Если две переменные величины прямо пропорциональны, то отношение соответствующих значений этих величин равно одному и тому же, постоянному для данных величин, числу.
3) Две переменные величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
4) Если две переменные величины обратно пропорциональны, то произведение соответствующих значений этих величин равно одному и тому же для данных величин, числу.

№292

Номер №292

За несколько одинаковых ручек заплатили 240 р. Сколько надо заплатить за такие ручки, если их купить:
1) в 3 раза больше;
2) в 3 раза меньше?

Решение

Количество ручек и их стоимость являются прямо пропорциональными величинами, значит во сколько раз увеличится (уменьшится) количество ручек, во столько же раз увеличится (уменьшится) их стоимость.
Тогда:
1) 240 * 3 = 720 (рублей) − надо заплатить за такие ручки, если их купить в 3 раза больше;
2) 240 : 3 = 80 (рублей) − надо заплатить за такие ручки, если их купить в 3 раза меньше.
Ответ: 1) 720 рублей; 2) 80 рублей.

№293

Номер №293

За несколько одинаковых ручек заплатили 240 р. Сколько надо заплатить за такое же количество ручек, каждая из которых:
1) в 3 раза дороже;
2) в 3 раза дешевле?

Решение

Цена ручек и их стоимость являются прямо пропорциональными величинами, значит во сколько раз увеличится (уменьшится) цена ручек, во столько же раз увеличится (уменьшится) их стоимость.
Тогда:
1) 240 * 3 = 720 (рублей) − надо заплатить за такое же количество ручек, каждая из которых в 3 раза дороже;
2) 240 : 3 = 80 (рублей) − надо заплатить за такое же количество ручек, каждая из которых в 3 раза дешевле.
Ответ: 1) 720 рублей; 2) 80 рублей.

№294

Номер №294

Велосипедист за некоторое время проехал 32 км. За это же время пешеход, скорость которого в 4 раза меньше скорости велосипедиста, пройдет _ км, а мотоциклист, скорость которого в 5 раз больше скорости велосипедиста, проедет _ км.

Решение

Скорость и расстояние являются прямо пропорциональными величинами, поэтому во сколько раз увеличится (уменьшится) скорость, во столько же раз увеличится (уменьшится) пройденное расстояние.
Тогда:
Велосипедист за некоторое время проехал 32 км. За это же время пешеход, скорость которого в 4 раза меньше скорости велосипедиста, пройдет 32 : 4 = 8 км, а мотоциклист, скорость которого в 5 раз больше скорости велосипедиста, проедет 32 * 5 = 160 км.

Номер №295

Номер №295

Площадь прямоугольника равна 80 $см^2$. Какой станет его площадь, если ширина останется без изменений, а длину:
1) увеличить в 6 раз;
2) уменьшить в 10 раз?

Решение

Длина и площадь прямоугольника являются прямо пропорциональными величинами, поэтому во сколько раз увеличится (уменьшится) длина, во столько же раз увеличится (уменьшится) площадь.
Тогда:
1) 80 * 6 = 480 $(см^2)$ − составит площадь прямоугольника, если длину увеличить в 6 раз.
2) 80 : 10 = 8 $(см^2)$ − составит площадь прямоугольника, если длину уменьшить в 10 раз.
Ответ: 1) 480 $см^2$; 8 $см^2$.

№296

Номер №296

Если рабочий будет изготавливать по 10 деталей в день, то он выполнит заказ за 24 дня. За сколько дней он выполнит заказ, если будет изготавливать по 30 деталей в день?

Решение

Производительность и время являются обратно пропорциональными величинами, поэтому во сколько раз увеличится (уменьшится) производительность, во столько же раз уменьшится (увеличится) время.
1) 30 : 10 = 3 − во столько раз больше деталей будет изготавливать рабочий в день;
2) 24 : 3 = 8 (дней) − потребуется рабочему, чтобы выполнить заказ.
Ответ: за 8 дней

№297

Номер №297

Высота прямоугольного параллелепипеда равна 18 см. Какой станет высота, если при неизменном объеме площадь основания параллелепипеда:
1) увеличить в 9 раз;
2) уменьшить в 5 раз?

Решение

Высота и площадь прямоугольного параллелепипеда являются обратно пропорциональными величинами, поэтому во сколько раз увеличится (уменьшится) площадь, во столько же раз уменьшится (увеличится) высота.
Тогда:
1) 18 : 9 = 2 (см) − станет высота прямоугольного параллелепипеда, если его площадь увеличить в 9 раз;
2) 18 * 5 = 90 (см) − станет высота прямоугольного параллелепипеда, если его площадь уменьшить в 5 раз.
Ответ: 1) 2 см; 2) 90 см.

№298

Номер №298

Заполните таблицу, если величина y прямо пропорциональна величине x.

x	0,2	7	2,4
y			7,2	1,8	300

Решение

7,2 : 2,4 = 3, значит:
3x = y;
$x = \frac{y}{3}$.
тогда:
1) при x = 0,2: y = 0,2 * 3 = 0,6;
2) при x = 7: y = 7 * 3 = 21;
3) при y = 1.8: x = 1,8 : 3 = 0,6;
4) при y = 300: x = 300 : 3 = 100.
Ответ:

x	0,2	7	2,4	0,6	100
y	0,6	21	7,2	1,8	300

 

№299

Номер №299

Автомобиль движется со скоростью 80 км/ч. Заполните таблицу, в первой строке которой указано время движения t, а во второй − пройденный путь s.

t (ч)	3	0,5		2,5
s (км)			320		256

Формула, задающая зависимость s от t, имеет вид: s = _

Решение

Время и расстояние являются прямо пропорциональными величинами, поэтому во сколько раз увеличится (уменьшится) время, во столько же раз увеличится (уменьшится) пройденное расстояние, значит:
формула, задающая зависимость s от t, имеет вид:
s = 80t
$t = \frac{s}{80}$
Тогда:
1) при t = 3: s = 3 * 80 = 240 (км);
2) при t = 0,5: s = 0,5 * 80 = 40 (км);
3) при s = 320: t = 320 : 80 = 4 (ч);
4) при t = 2,5: s = 2,5 * 80 = 200 (км);
5) при s = 256: t = 256 : 80 = 3,2 (ч).
Ответ:

t (ч)	3	0,5	4	2,5	3,2
s (км)	240	40	320	200	256

 

№300

Номер №300

За n кг яблок заплатили m р. Пользуясь таблицей, определите цену 1 кг яблок. Заполните таблицу.

n (кг)	5	8		1,6
m (р.)	125		90		225

Цена 1 кг яблок равна _
Формула, задающая зависимость m от n, имеет вид: m = _

Решение

Цена 1 кг яблок равна 125 : 5 = 25 (р.)
Формула, задающая зависимость m от n, имеет вид: m = 25n
$n = \frac{m}{25}$
1) при n = 8: m = 8 * 25 = 200 (р.);
2) при m = 90: n = 90 : 25 = 3,6 (кг);
3) при n = 1.6: m = 1,6 * 25 = 40 (р.);
4) при m = 225: n = 225 : 25 = 9 (кг).
Ответ:

n (кг)	5	8	3,6	1,6	9
m (р.)	125	200	90	40	225

 

№301

Номер №301

Заполните таблицу, если величина y обратно пропорциональна величине x.

x	16	6		20
y	3		12		100

 

Решение

Так как, величина y обратно пропорциональна величине x, то значит во сколько раз увеличивается (уменьшается) x, во столько же раз уменьшается (увеличивается) y:
1) при x = 6: $y = \frac{16}{6} * 3 = \frac{16}{2} * 1 = 8$;
2) при y = 12: $x = \frac{3}{12} * 16 = \frac{1}{4} * 16 = 4$;
3) при x = 20: $y = \frac{16}{20} * 3 = \frac{8}{10} * 3 = 0,8 * 3 = 2,4$;
4) при y = 100: $x = \frac{3}{100} * 16 = \frac{48}{100} = 0,48$.
Ответ:

x	16	6	4	20	0.48
y	3	8	12	2.4	100

 

№302

Номер №302

Для отопления дома заготовили 72 т угля. Заполните таблицу, в первой строке которой указано количество m угля, расходуемого в день; а во второй − количество t дней, на которое хватит заготовленного угля.

m	0.4	1.2
t (дни)			100	80

Формула, задающая зависимость m от t, имеет вид: m = _

Решение

Формула, задающая зависимость m от t, имеет вид: $m = \frac{72}{t}$
$t = \frac{72}{m}$
Тогда:
1) при m = 0,4: $t = \frac{72}{0,4} = \frac{720}{4} = 180$ (дней);
2) при m = 1,2: $t = \frac{72}{1,2} = \frac{720}{12} = 60$ (дней);
3) при t = 100: $m = \frac{72}{100} = 0,72$ (т);
4) при t = 80: $m = \frac{72}{80} = \frac{9}{10} = 0,9$ (т).
Ответ:

m	0.4	1.2	0.72	0.9
t (дни)	180	60	100	80

 

№303

Номер №303

Разделите:
1) число 63 в отношении 3 : 4;
2) число 72 в отношении 2 : 3 : 7;
3) число 126 в отношении 2 : 4 : 6 : 9.

Решение 1
1) 3 + 4 = 7 (частей) − всего;
2) 63 : 7 = 9 − приходится на одну часть;
3) 3 * 9 = 27 − приходится на 3 части;
4) 4 * 9 = 36 − приходится на 4 части.
Ответ: 27 и 36

Решение 2
1) 2 + 3 + 7 = 12 (частей) − всего;
2) 72 : 12 = 6 − приходится на одну часть;
3) 2 * 6 = 12 − приходится на 2 части;
4) 3 * 6 = 18 − приходится на 3 части;
5) 7 * 6 = 42 − приходится на 7 частей.
Ответ: 12, 18 и 42.

Решение 3
1) 2 + 4 + 6 + 9 = 21 (часть) − всего;
2) 126 : 21 = 6 − приходится на одну часть;
3) 2 * 6 = 12 − приходится на 2 части;
4) 4 * 6 = 24 − приходится на 4 части;
5) 6 * 6 = 36 − приходится на 6 частей;
6) 9 * 6 = 54 − приходится на 9 частей.
Ответ: 12, 24, 36 и 54.

№304

Номер №304

Для изготовления сплава из железа и меди взяли 12 частей железа и 5 частей меди (все части имеют одинаковую массу). Сколько килограммов меди взяли, если получили 51 кг сплава?

Решение

Пусть масса одной части сплава равна x кг. Тогда масса железа равна 12x кг, а меди − 5x кг.
Так как получили 51 кг сплава, можно составить уравнение:
12x + 5x = 51
17x = 51
x = 51 : 17
x = 3 (кг) − масса одной части сплава, тогда:
5x = 5 * 3 = 15 (кг) − меди взяли, если получили 51 кг сплава.
Ответ: 15 кг

№305

Номер №305

Периметр треугольника равен 69 см, а длины сторон относятся как 5 : 8 : 10. Найдите стороны треугольника.

Решение

Пусть длина одной стороны треугольника равна 5x см. Тогда длина второй стороны − 8x см, третьей − 10x см.
Так как периметр треугольника равен 69 см, можно составить уравнение:
5x + 8x + 10x = 69
23x = 69
x = 69 : 23
x = 3 (см) − приходится на одну часть, тогда:
5x = 5 * 3 = 15 (см) − длина первой стороны;
8x = 8 * 3 = 24 (см) − длина второй стороны;
10x = 10 * 3 = 30 (см) − длина третьей стороны.
Ответ: 15 см, 24 см, 30 см.

№306

Номер №306

Стороны треугольника относятся как 3 : 4 : 6. Разность наибольшей и наименьшей сторон равна 18 см. Найдите длину средней стороны.

Решение

Пусть длина одной стороны треугольника равна 3x см. Тогда длина второй стороны − 4x см, третьей − 6x см.
Так как разность наибольшей и наименьшей сторон равна 18 см, можно составить уравнение:
6x − 3x = 18
3x = 18
x = 18 : 3
x = 6 (см) − приходится на одну часть, тогда:
4x = 4 * 6 = 24 (см) − длина средней стороны.
Ответ: 24 см

№307

Номер №307

Начертите прямой угол ABC и проведите луч BD так, чтобы градусные меры углов ABD и CBD относились как 7 : 8.

Решение

Пусть ∠ABD = 7x, тогда ∠CBD = 8x
Так как прямой угол равен 90°, имеем:
7x + 8x = 90
15x = 90
x = 90 : 15
x = 6° − приходится на одну часть.
Следовательно:
∠ABD = 7x = 7 * 6 = 42°
∠CBD = 8x = 8 * 6 = 48°
Ответ: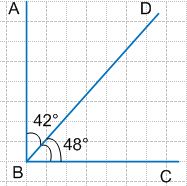

№308

Номер №308

Три бизнесмена создали общество. Первый внес в уставной капитал 150000 р., второй − 120000 р., а третий − 100000 р. Через год они получили 296000 р. прибыли. Как они должны поделить полученную прибыль в соответствии с вложенными средствами?

Решение

150000 : 120000 : 100000 = 15 : 12 : 10
Будем считать, что уставной капитал состоит из
15 + 12 + 10 = 37 (частей), каждая из которых состоит одинаковой суммы денег.
Первый бизнесмен внес 15 частей, второй − 12 частей, третий − 10 частей.
Тогда:
1) 296000 : 37 = 8000 (р.) − приходится на одну часть;
2) 15 * 8000 = 120000 (р.) − должен получить первый бизнесмен;
3) 12 * 8000 = 96000 (р.) − должен получить второй бизнесмен;
4) 10 * 8000 = 80000 (р.) − должен получить третий бизнесмен.
Ответ: 1−ый: 120000 рублей, 2−ой: 96000 рублей, 3−ий: 80000 рублей.

№309

Номер №309

Ремонт школы проводили три бригады. В первой бригаде было 8 человек, работавших 12 дней, во второй − 14 человек, работавших 9 дней, в третьей − 18 человек, работавших 15 дней. За ремонт школы три бригады получили 1230000 р. Сколько рублей получила каждая бригада?

Решение

1) 8 * 12 = 96 (человеко−дней) − наработала первая бригада;
2) 14 * 9 = 126 (человеко−дней) − наработала вторая бригада;
3) 18 * 15 = 270 (человеко−дней) − наработала третья бригада;
4) 96 + 126 + 270 = 492 (человеко−дней) − наработали три бригада всего;
5) 1230000 : 492 = 2500 (р.) − приходится на один человеко−день;
6) 96 * 2500 = 240000 (р.) − получила первая бригада;
7) 126 * 2500 = 315000 (р.) − получила вторая бригада;
8) 270 * 2500 = 675000 (р.) − получила третья бригада.
Ответ: 240000 рублей, 315000 рублей, 675000 рублей.

№310

Номер №310

Найдите такие значения a, b, c и d, чтобы их сумма была равна 250 и a : b = 2 : 3, b : c = 4 : 5, c : d = 6 : 11.

Решение

a : b = 2 : 3 = 8 : 12, b : c = 4 : 5 = 12 : 15, следовательно,
a : b : c = 8 : 12 : 15 = 16 : 24 : 30.
c : d = 6 : 11 = 30 : 55, следовательно, a : b : с : d = 16 : 24 : 30 : 55.
Тогда:
1) 16 + 24 + 30 + 55 = 125 (частей) − всего;
2) 250 : 125 = 2 − приходится на одну часть;
3) a = 16 * 2 = 32;
4) b = 24 * 2 = 48;
5) c = 30 * 2 = 60;
6) d = 55 * 2 = 110.
Ответ: a = 32, b = 48, c = 60; d = 110.

№311

Номер №311

Найдите такие значения x, y и z, чтобы их сумма была равной 505 и x : y = 3 : 5, а $y : z = 2\frac{1}{3} : 3$.

Решение

x : y = 3 : 5 = 21 : 35
$y : z = 2\frac{1}{3} : 3 = \frac{7}{3} : 3 = 35 : 45$, следовательно:
x : y : z = 21 : 35 : 45, тогда:
1) 21 + 35 + 45 = 101 − всего частей;
2) 505 : 101 = 5 − приходится на одну часть;
3) x = 21 * 5 = 105;
4) y = 35 * 5 = 175;
5) z = 45 * 5 = 225.
Ответ: x = 105; y = 175; z = 225.

№312

Номер №312

Заполните пропуски.
1) Окружность легко начертить с помощью _. Для этого надо установить _ на бумагу, тогда другая ножка _ при _ опишет окружность. Точку, в которую упирается _, называют _ окружности.
2) Все точки окружности удалены от ее _ на одинаковое расстояние.
3) Радиусом окружности называют отрезок, соединяющий центр окружности с _
4) _, соединяющий любые две точки окружности, называют _
5) Хорду, проходящую через центр окружности, называют _
6) Диаметр окружности _ больше радиуса окружности.
7) Две точки окружности делят ее на две части, каждую из которых называют _
8) Часть плоскости, ограниченную окружностью, вместе с этой окружностью называют _
9) Если точка удалена от центра круга на расстояние, _ или _, то эта точка принадлежит кругу.
10) Если в круге провести два радиуса, то они разделят круг на две части, каждую из которых называют _
11) Диаметр делит круг на две _ части каждого из которых называют _

Решение

1) Окружность легко начертить с помощью циркуля. Для этого надо установить иглу циркуля на бумагу, тогда другая ножка циркуля при вращении опишет окружность. Точку, в которую упирается острие циркуля, называют центром окружности.
2) Все точки окружности удалены от ее центра на одинаковое расстояние.
3) Радиусом окружности называют отрезок, соединяющий центр окружности с любой ее точкой.
4) Отрезок, соединяющий любые две точки окружности, называют хордой.
5) Хорду, проходящую через центр окружности, называют диаметром.
6) Диаметр окружности в 2 раза больше радиуса окружности.
7) Две точки окружности делят ее на две части, каждую из которых называют дугой окружности.
8) Часть плоскости, ограниченную окружностью, вместе с этой окружностью называют кругом.
9) Если точка удалена от центра круга на расстояние, меньшее радиуса круга или равное ему, то эта точка принадлежит кругу.
10) Если в круге провести два радиуса, то они разделят круг на две части, каждую из которых называют сектором.
11) Диаметр делит круг на две равные части каждого из которых называют полукругом.

№313

Номер №313

На рисунке изображена окружность с центром O. Отрезок OA − _ окружности, отрезок OC − _, отрезок CD − _, отрезок BC − _
Всего на рисунке изображены _ радиуса и _ хорды.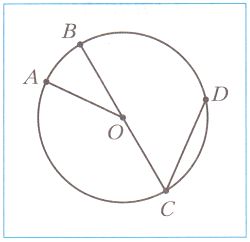

Решение

На рисунке изображена окружность с центром O. Отрезок OA − радиус окружности, отрезок OC − радиус окружности, отрезок CD − хорда окружности, отрезок BC − диаметр окружности.
Всего на рисунке изображены 3 радиуса и 2 хорды.

№314

Номер №314

Начертите окружность с центром A и радиусом 1,5 см.
Диаметр этой окружности равен _ см. Проведите два радиуса этой окружности. Закрасьте образовавшиеся при этом _ разными цветами.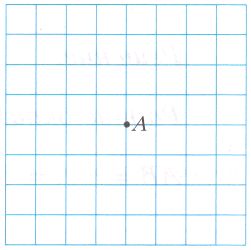

Решение

Диаметр этой окружности равен 2 * 1,5 см. Проведите два радиуса этой окружности. Закрасьте образовавшиеся при этом сектора разными цветами.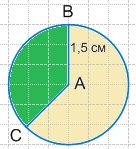

№315

Номер №315

На рисунке изображен круг с центром O.
Из отмеченных точек кругу принадлежат точки _, кругу не принадлежат точки _, окружности, ограничивающей этот круг, принадлежат точки _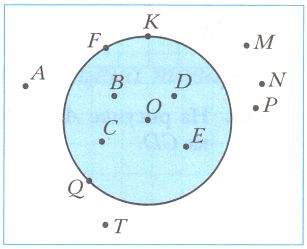

Решение

На рисунке изображен круг с центром O.
Из отмеченных точек кругу принадлежат точки B, D, O, C, E, K, F, Q, кругу не принадлежат точки A, M, N, P, T, окружности, ограничивающей этот круг, принадлежат точки K, F, Q.

№316

Номер №316

Радиус окружности с центром A равен 7 см, а радиус окружности с центром B − 4 см. Расстояние между центрами этих окружностей равно:
1) _ см;
2) _ см.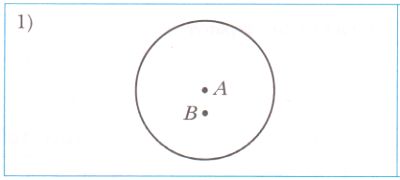

Решение 1
7 − 4 = 3 (см) − расстояние между центрами окружностей A и B.
Ответ: 3 см

Решение 2
7 + 4 = 11 (см) − расстояние между центрами окружностей A и B.
Ответ: 11 см

№317

Номер №317

Радиусы окружностей 5 см и 2 см, расстояние между их центрами − 9 см. Подчеркните номер рисунка, на котором показано расположение этих окружностей.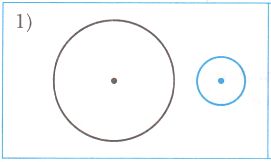

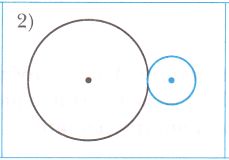
Решение

5 + 2 = 7 (см) < 9 (см), значит между окружностями должно быть расстояние длиной 9 − 7 = 2 (см).
Следовательно на рисунке №1 показано расположение этих окружностей.
Ответ: рисунок №1

№318

Номер №318

Точки A и C − центры окружностей. Найдите периметр четырехугольника ABCD, если длина стороны клетки равна 0,5 см.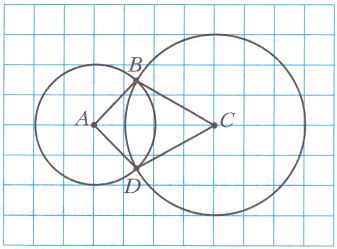


Решение

Радиус окружности с центром A равен 0,5 * 2 = 1 см.
AB = AD = 1 см.
Радиус окружности с центром C равен 0,5 * 3 = 1,5 см.
BC = CD = 1,5 см.
Тогда:
AB + AD + BC + CD = 1 + 1 + 1,5 + 1,5 = 5 (см) − периметр четырехугольника ABCD.
Ответ: 5 см

№319

Номер №319

На рисунке AB = 2 см, BC = 5 см. Найдите длину отрезка CD,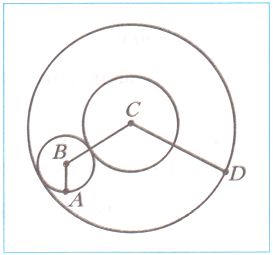

Решение

CD = AB + BC = 2 + 5 = 7 (см)
Ответ: 7 см

№320

Номер №320

Начертите две окружности с центром A так, чтобы данная окружность с центром O лежала внутри одной из них, а другая окружность лежала внутри данной.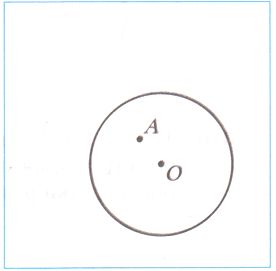

Решение

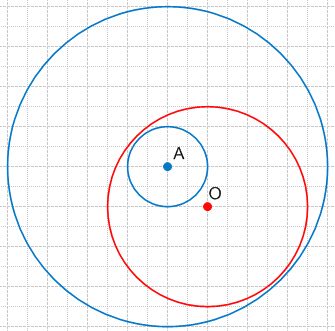
№321

Номер №321

Отметьте на каждой из изображенных окружностей по одной точке так, чтобы эти точки были ближе всего друг к другу, обозначьте их A и B. Измерьте расстояние между ними. Оно равно _ см.
Отметьте на окружностях наиболее удаленные друг от друга точки, обозначьте их C и D. Измерьте расстояние между ними. Оно равно _ см.

Решение

Радиус окружности с центром $O_1$ равен 0,8 см.
Радиус окружности с центром $O_2$ равен 0,5 см.
$O_1O_2 = 4,5$ см.
Тогда:
$AB = O_1O_2 - (O_1A + O_2B) = 4,5 - (0,8 + 0,5) = 4,5 - 1,3 = 3,2$ см;
$CD= O_1O_2 + (O_1C + O_2D) = 4,5 + (0,8 + 0,5) = 4,5 + 1,3 = 5,8$ см.
Ответ:
Отметьте на каждой из изображеных окружностей по одной точке так, чтобы эти точки были ближе всего друг к другу, обозначьте их A и B. Измерьте расстояние между ними. Оно равно 3,2 см.
Отметьте на окружностях наиболее удаленные друг от друга точки, обозначьте их C и D. Измерьте расстояние между ними. Оно равно 5,8 см.

№322

Номер №322

С помощью циркуля постройте треугольник со сторонами 2 см, 3 см и 4 см.

Решение

Построим отрезок AC = 4 см.
Построим окружность с центром A радиусом 2 см.
Построим окружность с центром C радиусом 3 см.
Одну из точек пересечения данных окружностей обозначим точкой B.
Проведем отрезки AB и BC.
Получим треугольник ABC со сторонами 2 см, 3 см и 4 см.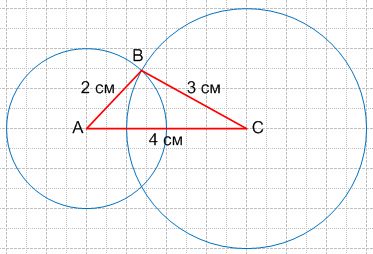

№323

Номер №323

Дима выбрал в библиотеке 5 книг. По правилам библиотеки одновременно можно взять только 2 книги. Сколько у Димы есть вариантов выбора двух книг из пяти?

Решение

Присвоим выбранным книгам номера 1, 2, 3, 4, 5.
Дима может выбрать книги следующими способами:
1) 1 и 2;
2) 1 и 3;
3) 1 и 4;
4) 1 и 5;
5) 2 и 3;
6) 2 и 4;
7) 2 и 5;
8) 3 и 4;
9) 3 и 5;
10) 4 и 5.
Ответ: 10 вариантов выбора двух книг есть у Димы.

№324

Номер №324

Заполните пропуски.
1) Длина окружности _ пропорциональна ее диаметру.
2) Число π равно отношению длины любой окружности к ее _
3) Приближенное значение числа π с точностью до сотых равно _

Решение

1) Длина окружности прямо пропорциональна пропорциональна ее диаметру.
2) Число π равно отношению длины любой окружности к ее диаметру.
3) Приближенное значение числа π с точностью до сотых равно 3,14.

№325

Номер №325

Подчеркните формулу, по которой вычисляют длину l окружности, если известен ее диаметр d:
1) l = 2πd
2) l = πd
3) $l = \frac{πd}{2}$
4) l = 4πd

Решение

Формула длины окружности, если известен ее диаметр:
l = πd
Ответ: 2) l = πd

№326

Номер №326

Подчеркните формулу, по которой вычисляют длину l окружности, если известен ее радиус r:
1) l = πr
2) $l = \frac{πr}{2}$
3) l = 2πr
4) l = 4πr

Решение

Формула длины окружности, если известен ее радиус:
l = 2πr
Ответ: 3) l = 2πr

№327

Номер №327

Подчеркните формулу, по которой вычисляют площадь S круга, если известен его радиус r.
1) $S = πr^2$
2) $S = 2πr^2$
3) $S = \frac{πr^2}{2}$
4) $S = \frac{πr^2}{4}$

Решение

Формула площади круга, если известен его радиус:
$S = πr^2$
Ответ: 1) $S = πr^2$

№328

Номер №328

Подчеркните формулу, по которой вычисляют площадь S круга, если известен его диаметр d:
1) $S = πd^2$
2) $S = 2πd^2$
3) $S = \frac{πd^2}{2}$
4) $S = \frac{πd^2}{4}$

Решение

d = 2r
$r = \frac{d}{2}$
$S = π(\frac{d}{2})^2 = \frac{πd^2}{4}$
Формула площади круга, если известен его диаметр:
$S = \frac{πd^2}{4}$
Ответ: 4) $S = \frac{πd^2}{4}$

№329

Номер №329

Вычислите длину окружности, диаметр которой равен 8 см.

Решение

l = πd = 3,14 * 8 = 25,12 (см) − длина окружности.
Ответ: 25,12 см

№330

Номер №330

Вычислите длину окружности, радиус которой равен 2,25 см.

Решение

l = 2πr = 2 * 3,14 * 2,25 = 6,28 * 2,25 = 14,13 (см) − длина окружности.
Ответ: 14,13 см

№331

Номер №331

Вычислите площадь круга, радиус которого равен 6 см.

Решение

$S = πr^2 = 3,14 * 6^2 = 3,14 * 36 = 113,04 (см^2)$ − площадь круга.
Ответ: 113,04 $см^2$

№332

Номер №332

Вычислите площадь круга, диаметр которого равен 10 см.

Решение

$S = \frac{πd^2}{4} = \frac{3,14 * 10^2}{4} = \frac{3,14 * 100}{4} = 3,14 * 25 = 78,5 (см^2)$ − площадь круга.
Ответ: 78,5 $см^2$

№333

Номер №333

Чему равен радиус окружности, длина которой равна 16π см?

Решение

l = 2πr
по условию:
l = 16π
тогда:
16π = 2πr
$r = \frac{16π}{2π}$
r = 8 (см) − радиус окружности.
Ответ: 8 см

№334

Номер №334

Чему равен радиус круга, площадь которого равна 16π $см^2$?

Решение

$S = πr^2$
по условию:
S = 16π
тогда:
$16π = πr^2$
$r^2 = 16$
$r^2 = 4^2$
r = 4 (см) − радиус круга.
Ответ: 4 см

№335

Номер №335

Точки A, B и C делят окружность на 3 равные дуги. Чему равна длина каждой из этих дуг, если радиус окружности равен 12 см?

Решение

1) l = 2πr = 2 * 3,14 * 12 = 6,28 * 12 = 75,36 (см) − длина окружности;
2) 75,36 : 3 = 25,12 (см) − длина каждой из дуг.
Ответ: 25,12 см

№336

Номер №336

Вычислите площадь круга, если длина окружности, ограничивающей его, равна 21,98 см.

Решение

Если длина окружности равна l, то ее радиус $r = \frac{l}{2π}$, тогда:
1) $r = \frac{21,98}{2 * 3,14} = \frac{7}{2 * 1} = 3,5$ (см) − радиус окружности;
2) $S = πr^2 = 3,14 * 3,5^2 = 3,14 * 12,25 = 38,465 (см^2)$ − площадь круга.
Ответ: 38,465 $см^2$

№337

Номер №337

Как изменится длина окружности, если ее радиус увеличить в 3 раза?

Решение

Длина окружности прямо пропорциональна ее радиусу. Значит, при увеличении радиуса в 3 раза ее длина увеличится в 3 раза.
Ответ: увеличится в 3 раза

№338

Номер №338

Как изменится длина окружности, если ее радиус уменьшить на 2 см?

Решение

Пусть радиус данной окружности равен r см. После изменения радиус окружности стал (r − 2) см.
l = 2πr (см) − начальная длина окружности;
l = 2π(r − 2) = 2πr − 4π (см) − измененная длина окружности;
2πr > 2πr − 4π, значит длина окружности уменьшится;
2πr − (2πr − 4π) = 2πr − 2πr + 4π = 4π (см) − на столько уменьшится длина окружности.
Ответ: уменьшится на 4π см

№339

Номер №339

Пять кругов, имеющих равные радиусы, расположены так, как показано на рисунке. Найдите отношение площади закрашенной фигуры к сумме площадей данных пяти кругов.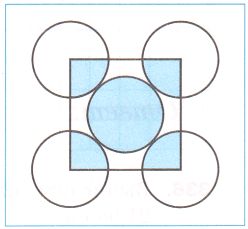

Решение

Площадь одного круга равна $S = πr^2$, тогда:
$S = 5πr^2$ − сумма площадей пяти кругов.
$S = \frac{πr^2}{4}$ − площадь одного закрашенного сектора.
Всего закрашено 4 одинаковых сектора и один круг целиком, значит:
$S = πr^2 + 4\frac{πr^2}{4} = πr^2 + πr^2 = 2πr^2$ − площадь закрашенной фигуры;
$\frac{2πr^2}{5πr^2} = \frac{2}{5} = 0,4$ − отношение площади закрашенной фигуры к сумме площадей данных пяти кругов.
Ответ: 0,4

№340

Номер №340

Вычислите площадь закрашенной фигуры, если длина стороны клетки равна 1 см.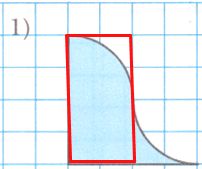

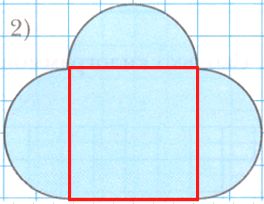
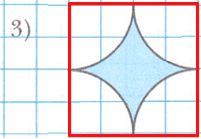
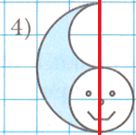
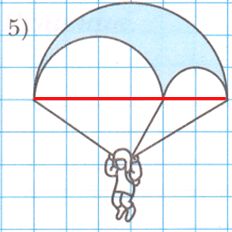
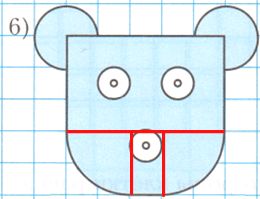
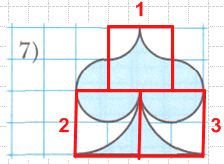
Решение 1


Дорисуем и получим прямоугольник со сторонами 4 см и 2 см. Причем незакрашенная часть прямоугольника, равна закрашенной части за прямоугольником.
Тогда:
4 * 2 = 8 $(см^2)$ − площадь закрашенной фигуры.
Ответ: 8 $см^2$

Решение 2

Дорисуем и получим квадрат со стороной 4 см и 3 одинаковых полукруга с радиусом 2 см.
Тогда:
1) $S = a^2 = 4^2 = 16 (см^2)$ − площадь квадрата;
2) $S = \frac{πr^2}{2} = \frac{3,14 * 2^2}{2} = 3,14 * 2 = 6,28 (см)^2$ − площадь каждого полукруга;
3) $3 * 6,28 = 18,84 (см)^2$ − сумма площадей трех полукругов;
4) $16 + 18,84 = 34,84 (см)^2$ − площадь закрашенной фигуры.
Ответ: 34,84 $см^2$

Решение 3

Дорисуем и получим квадрат со стороной 4 см и 4 одинаковых не закрашенных четверти круга с радиусом 2 см.
Тогда:
1) $S = a^2 = 4^2 = 16 (см^2)$ − площадь квадрата;
2) $S = \frac{πr^2}{4} = \frac{3,14 * 2^2}{4} = \frac{3,14 * 4}{4} = 3,14 (см)^2$ − площадь каждой четверти круга;
3) $3,14 * 4 = 12,56 (см^2)$ − сумма площадей четырех четвертей круга;
4) $16 - 12,56 = 3,44 (см^2)$ − площадь закрашенной фигуры.
Ответ: 3,44 $см^2$

Решение 4

Дорисуем и увидим, что из большого полукруга с радиусом 2 см, вырезали 2 полукруга с радиусом 1 см.
Тогда:
1) $S = \frac{πr^2}{2} = \frac{3,14 * 2^2}{2} = 3,14 * 2 = 6,28 (см)^2$ − площадь большого полукруга;
2) $S = \frac{πr^2}{2} = \frac{3,14 * 1^2}{2} = \frac{3,14}{2} = 1,57 (см)^2$ − площадь каждого из маленьких полукругов;
3) $1,57 * 2 = 3,14 (см^2)$ − сумма площадей двух маленьких полукругов;
4) $6,28 - 3,14 = 3,14 (см^2)$ − площадь закрашенной фигуры.
Ответ: 3,14 $см^2$

Решение 5

Дорисуем и увидим, что из большого полукруга с радиусом 3 см, вырезали 2 полукруга с радиусом 2 см и 1 см.
Тогда:
1) $S = \frac{πr^2}{2} = \frac{3,14 * 3^2}{2} = \frac{3,14 * 9}{2} = 1,57 * 9 = 14,13 (см)^2$ − площадь полукруга с радиусом 3 см;
2) $S = \frac{πr^2}{2} = \frac{3,14 * 2^2}{2} = 3,14 * 2 = 6,28 (см)^2$ − площадь полукруга с радиусом 2 см;
3) $S = \frac{πr^2}{2} = \frac{3,14 * 1^2}{2} = \frac{3,14}{2} = 1,57 (см)^2$ − площадь полукруга с радиусом 1 см;
4) $14,13 - (6,28 + 1,57) = 6,28 (см^2)$ − площадь закрашенной фигуры.
Ответ: 6,28 $см^2$

Решение 6

Дорисуем и получим:
1) прямоугольник со сторонами 5 см и 3 см;
2) прямоугольник со сторонами 2 см и 1 см;
3) два сектора по $\frac{3}{4}$ круга с радиусом 1 см;
4) две четверти круга с радиусом 2 см;
5) три не закрашенных круга с радиусом 0,5 см.
Тогда:
1) 5 * 3 = 15 $(см^2)$ − площадь прямоугольника со сторонами 5 см и 3 см;
2) 2 * 1 = 2 $(см^2)$ − площадь прямоугольника со сторонами 2 см и 1 см;
3) $S = 2 * \frac{3}{4}πr^2 = \frac{3 * 3,14 * 1^2}{2} = 1,5 * 3,14 = 4,71 (см^2)$ − сумма площадей двух секторов по $\frac{3}{4}$ круга с радиусом 1 см;
4) $S = 2 * \frac{πr^2}{4} = \frac{3,14 * 2^2}{2} = 3,14 * 2 = 6,28 (см^2)$ − сумма площадей двух четвертей круга с радиусом 2 см;
5) $S = 3πr^2 = 3 * 3,14 * 0,5^2 = 9,42 * 0,25 = 2,355 (см^2)$ − сумма площадей трех не закрашенных кругов с радиусом 0,5 см;
6) (15 + 2 + 4,71 + 6,28) − 2,355 = 27,99 − 2,355 = 25,635 $(см^2)$ − площадь закрашенной фигуры.
Ответ: 25,635 $см^2$

Решение 7

Дорисуем и получим:
1) три одинаковых квадрата со стороной 2 см;
2) две четверти круга с радиусом 1 см.
Тогда:
$S = a^2 = 2^2 = 4 (см)^2$ − площадь каждого из квадратов;
$S = 2 * \frac{πr^2}{4} = \frac{3,14 * 1^2}{2} = 3,14 * 2 = 1,57 (см^2)$ − сумма площадей двух четвертей круга с радиусом 1 см;
Найдем площадь закрашенной части в первом квадрате:
$4 - 1,57 = 2,43 (см^2)$
Найдем площадь закрашенной части во втором и в третьем квадрате. Для этого нужно из площади каждого из квадратов вычесть площадь четверти круга с радиусом 2 см и прибавить площадь полукруга с радиусом 1 см.
$4 - \frac{3,14 * 2^2}{4} + \frac{3,14 * 1^2}{2} = 4 - 3,14 + 1,57 = 0,86 + 1,57 = 2,43 (см^2)$ − площадь закрашенной части и во втором и в третьем квадрате.
$2,43 * 2 = 4,86 (см^2)$ − сумма площадей закрашенных частей во втором и в третьем квадратах.
Найдем площадь закрашенной фигуры:
$1,57 + 2,43 + 4,86 = 4 + 4,86 = 8,86 (см^2)$ − площадь закрашенной фигуры.
Ответ: 8,86 $см^2$

№341

Номер №341

Известно, что 100 синиц за 100 дней съели 100 кг зерна. Сколько килограммов зерна съедят 10 синиц за 10 дней?

Решение

1/) 100 : 100 = 1 (кг) − зерна съедают 100 синиц за 1 день;
2) 100 : 10 = 10 (раз) − во столько раз стало меньше синиц;
3) 1 : 10 = 0,1 (кг) − зерна съедают 10 синиц за 1 день;
4) 0,1 * 10 = 1 (кг) − зерна съедают 10 синиц за 10 дней.
Ответ: 1 кг

№342

Номер №342

Заполните пропуски.
1) Цилиндр можно получить в результате вращения _ вокруг одной из его _
2) Основания цилиндра являются _
3) Развертка цилиндра состоит из _

Решение

1) Цилиндр можно получить в результате вращения прямоугольника вокруг одной из его сторон.
2) Основания цилиндра являются два равных круга.
3) Развертка цилиндра состоит из прямоугольника и двух равных кругов.

№343

Номер №343

На рисунке изображен цилиндр. Отрезок MK − _ цилиндра, отрезок OM − радиус нижнего _, отрезок $O_1K$ − _. Длину отрезка $OO_1$ называют _ цилиндра.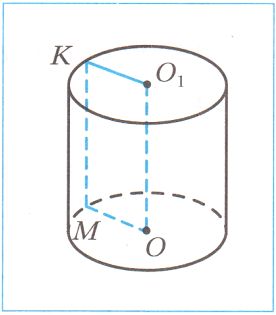

Решение

На рисунке изображен цилиндр. Отрезок MK − образующая цилиндра, отрезок OM − радиус нижнего основания, отрезок $O_1K$ − радиус верхнего основания. Длину отрезка $OO_1$ называют высотой цилиндра.

№344

Номер №344

Подчеркните формулу, по которой вычисляют площадь $S_{бок}$ боковой поверхности цилиндра, если известны радиус r основания и высота h цилиндра:
1) $S_{бок} = πrh$
2) $S_{бок} = πr^2h$
3) $S_{бок} = 2πrh$
4) $S_{бок} = 2πr^2h$

Решение

Формула площади боковой поверхности цилиндра, если известны радиус его основания и высота цилиндра: $S_{бок} = 2πrh$
Ответ: 3) $S_{бок} = 2πrh$

№345

Номер №345

Заполните таблицу, где r − радиус основания цилиндра, h − высота цилиндра, а $S_{бок}$ − площадь его боковой поверхности.

r, см	4	8,5	1,2
h, см	3	2		8
$S_{бок}, см^2$			10π	56π

Решение

$S_{бок} = 2πrh$, тогда:
$h = \frac{S_{бок}}{2πr}$
$r = \frac{S_{бок}}{2πh}$
при r = 4 см, h = 3 см:
$S_{бок} = 2π * 4 * 3 = 2π * 12 = 24π (см^2)$
при r = 8,5 см, h = 2 см:
$S_{бок} = 2π * 8,5 * 2 = 2π * 17 = 34π (см^2)$
при r = 1,2 см, $S_{бок} = 10π (см^2)$:
$h = \frac{10π}{2π * 1,2} = \frac{100π}{2π * 12} = \frac{100}{24} = \frac{25}{6} = 4\frac{1}{6} (см)$
при h = 8 см, $S_{бок} = 56π (см^2)$:
$r = \frac{56π}{2π * 8} = \frac{7π}{2π} = 3,5 (см)$
Ответ:

r, см	4	8,5	1,2	3,5
h, см	3	2	$4\frac{1}{6}$	8
$S_{бок}, см^2$	24π	34π	10π	56π

 

№346

Номер №346

Найдите площадь боковой поверхности цилиндра, развертка которого изображена на рисунке (длины отрезков даны в сантиметрах).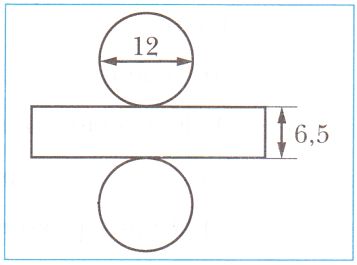

Решение

$S_{бок} = 2πrh = π * 2r * h = πdh = 3,14 * 12 * 6,5 = 3,14 * 78 = 244,92 (см^2)$ − площадь боковой поверхности цилиндра.
Ответ: 244,92 $см^2$

№347

Номер №347

Заполните пропуски.
1) Конус можно получить в результате вращения _ вокруг одной из его сторон, прилежащих к _
2) Развертка конуса состоит из _

Решение

1) Конус можно получить в результате вращения прямоугольного треугольника вокруг одной из его сторон, прилежащих к прямому углу.
2) Развертка конуса состоит из сектора и круга.

№348

Номер №348

На рисунке изображен конус.
Точка _ − вершина.
Отрезок CD − _ конуса.
Отрезок CE − _ конуса.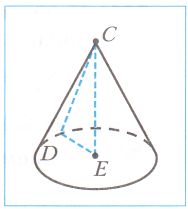

Решение

Точка C − вершина.
Отрезок CD − образующая конуса.
Отрезок CE − высота конуса.

№349

Номер №349

Заполните пропуски.
1) Шар можно получить в результате вращения _ вокруг его _
2) Сферу можно получить в результате вращения _ вокруг ее _
3) Сечением (_) шара плоскостью всегда является _
4) Если плоскость сечения шара проходит через центр шара, то в сечении образуется _, радиус которого равен _
5) Цилиндр, конус и шар − примеры тел _

Решение

1) Шар можно получить в результате вращения полукруга вокруг его диаметра.
2) Сферу можно получить в результате вращения полуокружности вокруг ее диаметра.
3) Сечением (разрезом) шара плоскостью всегда является круг.
4) Если плоскость сечения шара проходит через центр шара, то в сечении образуется круг, радиус которого равен радиусу шара.
5) Цилиндр, конус и шар − примеры тел вращения.

№350

Номер №350

Площадь сечения шара плоскостью, проходящей через центр шара, равна 100π $см^2$. Чему равен радиус шара?

Решение

Если плоскость сечения шара проходит через центр шара, то в сечении образуется круг, радиус которого равен радиусу шара.
Площадь круга находится по формуле:
$S = πr^2$
Тогда по условию:
$πr^2 = 100π$
$r^2 = \frac{100π}{π}$
$r^2 = 100$
$r^2 = 10^2$
r = 10 (см) − радиус шара.
Ответ: 10 см

№351

Номер №351

Запишите числа 1, 1, 2, 2, 3, 3, 4 и 4 в таком порядке, чтобы между единицами стояло одно число, между двойками − два числа, между тройками − три, а между четверками − четыре.

Решение

4, 1, 3, 1, 2, 4, 3, 2.

№352

Номер №352

В школе измерили рост шестиклассников. Результаты измерений представили в виде столбчатой диаграммы.
Всего измерили рост _ шестиклассников. Наибольший рост, равный _ см, имеют _ шестиклассников, наименьший рост, равный _ см, имеют _ шестиклассников. Больше всего учащихся, чей рост равен _ см, их _ человек, что на _ учащихся _, чем имеющих рост 125 см.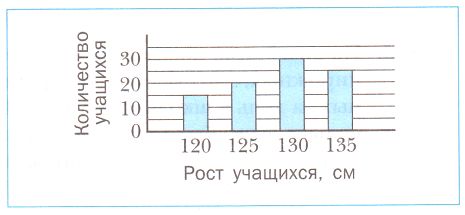

Решение

Всего измерили рост 15 + 20 + 30 + 25 = 90 шестиклассников. Наибольший рост, равный 135 см, имеют 25 шестиклассников, наименьший рост, равный 120 см, имеют 15 шестиклассников. Больше всего учащихся, чей рост равен 130 см, их 30 человек, что на 10 учащихся больше, чем имеющих рост 125 см.

№353

Номер №353

На диаграмме изображены объемы продаж тетрадей в отделе канцтоваров в течение одной недели.
Одинаковое количество тетрадей было продано в _ и _ − по _ тетрадей, наибольшее количество − в _ (_ тетрадей), наименьшее − в _ (_ тетрадей). В среднем за один день продавали (105 + _ + _) : _ = _ (театр.).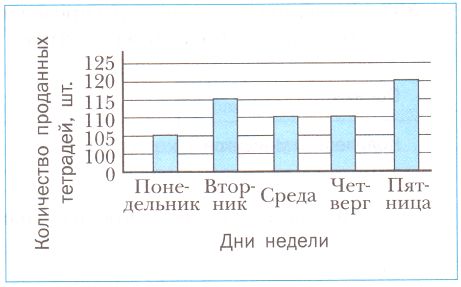

Решение

Одинаковое количество тетрадей было продано в среду и четверг − по 110 тетрадей, наибольшее количество − в пятницу (120 тетрадей), наименьшее − в понедельник (105 тетрадей). В среднем за один день продавали (105 + 115 + 110 + 110 + 120) : 5 = 560 : 5 = 112 (театр.).

№354

Номер №354

На диаграмме показано распределение фруктовых деревьев, растущих в саду. Подчеркните номер верного утверждения.
1) Яблонь в саду растет больше, чем вишен.
2) Вишни составляют более 50% всех деревьев сада.
3) Черешен и слив растет больше, чем яблонь.
4) Яблони составляют более 25% всех деревьев сада.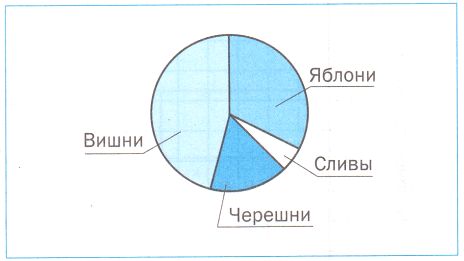

Решение

1) Яблонь в саду растет больше, чем вишен.
2) Вишни составляют более 50% всех деревьев сада.
3) Черешен и слив растет больше, чем яблонь.
4) Яблони составляют более 25% всех деревьев сада.

№355

Номер №355

На круговой диаграмме приведено распределение площади поля под посев различных культур.
Пшеницей засеяли _% площади поля. Горохом засеяли площадь в _ раза _, чем пшеницей. _ засеяли на 10% больше площади всего поля, чем _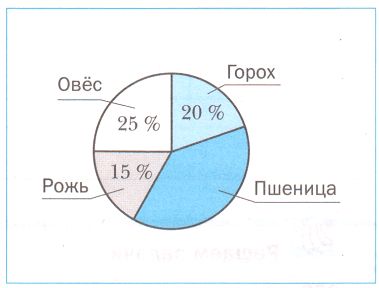

Решение

Пшеницей засеяли 100 − (15 + 25 + 20) = 100 − 60 = 40% площади поля. Горохом засеяли площадь в 40 : 20 = 2 раза меньше, чем пшеницей. Овсом засеяли на 10% больше площади всего поля, чем рожью.

№356

Номер №356

На диаграмме показано количество пирожков, пирожных, ватрушек и бутербродов. Известно, что больше всего было продано пирожков, меньше всего − бутербродов, а пирожных − больше, чем ватрушек.
В школьном буфете было продано _ пирожков, _ ватрушек, а пирожков на _ больше, чем бутербродов.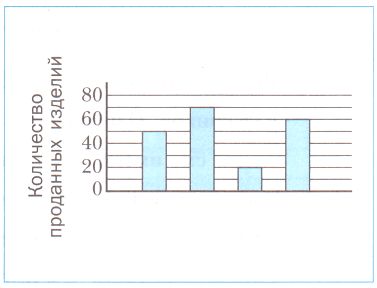

Решение

В школьном буфете было продано 70 пирожков, 50 ватрушек, а пирожков на 70 − 20 = 50 больше, чем бутербродов.

№357

Номер №357

В таблице приведено распределение оценок, полученных учащимися 6 класса за контрольную работу по математике.

Оценка	2	3	4	5
Количество учащихся	2	9	10	4

Постройте соответствующую диаграмму.

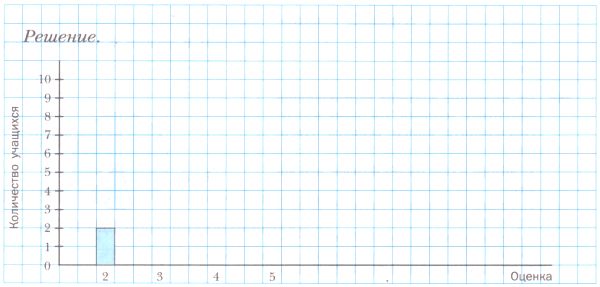
Решение

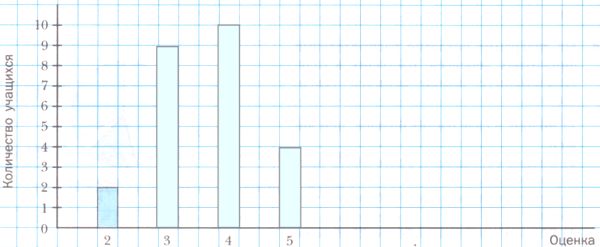
№358

Номер №358

В городе работает 5 радиостанций. В таблице приведены результаты опроса граждан, у которых спрашивали, какую радиостанцию они предпочитают слушать.

Радиостанция	Радио 1	Радио 2	Радио 3	Радио 4	Радио 5
Процент опрошенных, предпочитающих эту радиостанцию	32%	14%	26%	10%	18%

Представьте приведенные данные в виде столбчатой диаграммы, взяв для изображения одного процента столбик высотой 2 мм.

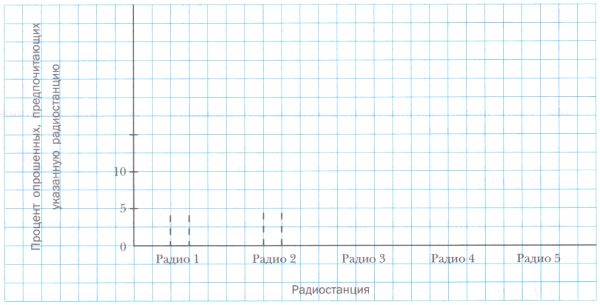
Решение

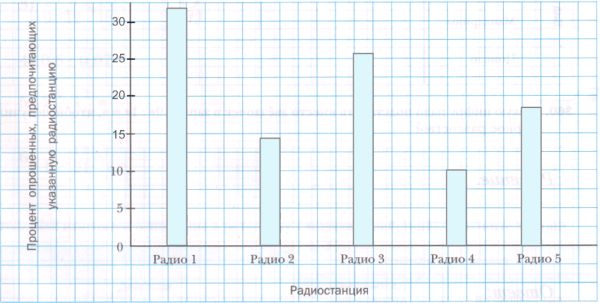
№359

Номер №359

Оптовая фирма поставляет в магазины цитрусовые: апельсины, грейпфруты, лимоны, мандарины и помело. На диаграмме показано, сколько фруктов было поставлено фирмой в магазины за месяц.
Больше всего поставлено _, что составляет _% всех цитрусовых, меньше всего поставлено − _, что составляет _% всех цитрусовых.
Приведенные сведения можно представить в виде столбчатой диаграммы.

Решение

1) 18 + 6 + 2 + 4,5 + 9,5 = 26 + 14 = 40 (т) − цитрусовых поставлено всего;
2) $\frac{18}{40} * 100 = \frac{18}{2} * 5 = 9 * 5 = 45$ (%) − было поставлено мандаринов;
3) $\frac{2}{40} * 100 = \frac{1}{20} * 100 = 5$ (%) − было поставлено помело.
Ответ:
Больше всего поставлено мандаринов, что составляет 45% всех цитрусовых, меньше всего поставлено − помело, что составляет 5% всех цитрусовых.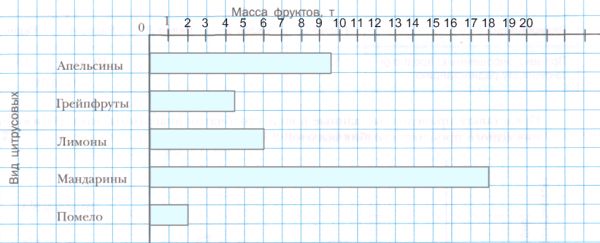

№360

Номер №360

Какую цифру надо подставить вместо звездочек в запись 9* : 1* = *, чтобы получилось верное равенство?

Решение

Пусть * = 1, тогда:
$91 : 11 = 8\frac{3}{11}$ − не подходит;
пусть * = 2, тогда:
$92 : 12 = 7\frac{8}{12} = 7\frac{2}{3}$ − не подходит;
пусть * = 3, тогда:
$93 : 13 = 7\frac{2}{13}$ − не подходит;
пусть * = 4, тогда:
$94 : 14 = 6\frac{10}{14} = 6\frac{5}{7}$ − не подходит;
пусть * = 5, тогда:
$95 : 15 = 6\frac{5}{15} = 6\frac{1}{3}$ − не подходит;
пусть * = 6, тогда:
$96 : 16 = 6$ − подходит;
пусть * = 7, тогда:
$97 : 17 = 5\frac{12}{17}$ − не подходит;
пусть * = 8, тогда:
$98 : 18 = 5\frac{8}{18} = 5\frac{4}{9}$ − не подходит;
пусть * = 9, тогда:
$99 : 19 = 5\frac{4}{19}$ − не подходит.
Ответ: * = 6

№361

Номер №361

Заполните пропуски.
1) Событие, которое в одних и тех же условиях может произойти, а может и не произойти, называют _
2) Наука, которая занимается оценками _, называется теорией вероятностей.
3) Вероятность _ события равна 1.
4) Вероятность _ события равна 0.
5) Если эксперимент заканчивается одним из n _ исходов, из которых m являются _ для наступления данного события, то вероятность этого события равна _

Решение

1) Событие, которое в одних и тех же условиях может произойти, а может и не произойти, называют случайным.
2) Наука, которая занимается оценками вероятностей случайных событий, называется теорией вероятностей.
3) Вероятность достоверного события равна 1.
4) Вероятность невозможного события равна 0.
5) Если эксперимент заканчивается одним из n равновозможных исходов, из которых m являются благоприятными для наступления данного события, то вероятность этого события равна $\frac{m}{n}$.

№362

Номер №362

Одну грань кубика покрасили в белый цвет, две грани − в красный, а остальные грани − в синий. Вероятность того, что при бросании кубика выпадет белая грань, равна _, красная − _, синяя − _

Решение

Всего у кубика 6 граней, значит при бросании кубика существует 6 равновозможных исходов (n = 6).
1) существует один благоприятный исход для выпадении белой грани (m = 1), тогда:
$\frac{m}{n} = \frac{1}{6}$ − вероятность того, что при бросании кубика выпадет белая грань;
2) существует два благоприятных исхода для выпадении красной грани (m = 2), тогда:
$\frac{m}{n} = \frac{2}{6} = \frac{1}{3}$ − вероятность того, что при бросании кубика выпадет красная грань;
3) существует три благоприятных исхода для выпадении синей грани (m = 3), тогда:
$\frac{m}{n} = \frac{3}{6} = \frac{1}{2}$ − вероятность того, что при бросании кубика выпадет синяя грань.
Ответ:
Одну грань кубика покрасили в белый цвет, две грани − в красный, а остальные грани − в синий. Вероятность того, что при бросании кубика выпадет белая грань, равна $\frac{1}{6}$, красная − $\frac{1}{3}$, синяя − $\frac{1}{2}$.

№363

Номер №363

В коробке лежат 14 красных и 21 синий карандашей. Вероятность того, что наугад выбранный карандаш окажется красным, равна _, а синим − _

Решение

1) 14 + 21 = 35 (карандашей) − всего лежит в коробке;
2) $\frac{14}{35} = \frac{2}{5}$ − вероятность того, что наугад выбранный карандаш окажется красным;
3) $\frac{21}{35} = \frac{3}{5}$ − вероятность того, что наугад выбранный карандаш окажется синим.
Ответ: Вероятность того, что наугад выбранный карандаш окажется красным, равна $\frac{2}{5}$, а синим − $\frac{3}{5}$.

№364

Номер №364

В вазе стоят 5 белых, 4 красных и 6 желтых роз. Вероятность того, что наугад взятый цветок будет розой, равна _, красной розой − _, бордовой розой − _

Решение

1) 5 + 4 + 6 = 15 (роз) − было всего в вазе;
2) $\frac{15}{15} = 1$ − вероятность того, что наугад взятый цветок будет розой;
3) $\frac{4}{15}$ − вероятность того, что наугад взятый цветок будет красной розой;
4) $\frac{0}{15} = 0$ − вероятность того, что наугад взятый цветок будет бордовой розой.
Ответ: Вероятность того, что наугад взятый цветок будет розой, равна 1, красной розой − $\frac{4}{15}$, бордовой розой − 0.

№365

Номер №365

В лотерею разыгрывали 3 телевизора, 4 фотоаппарата, 8 мобильных телефонов. Было выпущено 100 лотерейных билетов. Вероятность выиграть телевизор равна _, фотоаппарат − _, мобильный телефон − _, остаться без выигрыша − _

Решение

1) 3 + 4 + 8 = 15 (предметов) − всего разыгрывалось в лотерею, то есть всего было 15 выигрышных билетов;
2) 100 − 15 = 85 (билетов) − было без выигрыша;
3) $\frac{3}{100} = 0,03$ − вероятность выигрыша телевизора;
4) $\frac{4}{100} = 0,04$ − вероятность выигрыша фотоаппарата;
5) $\frac{8}{100} = 0,08$ − вероятность выигрыша мобильного телефона;
6) $\frac{85}{100} = 0,85$ − вероятность остаться без выигрыша.
Ответ: Вероятность выиграть телевизор равна 0,03, фотоаппарат − 0,04, мобильный телефон − 0,08, остаться без выигрыша − 0,85.

№366

Номер №366

В коробке лежат 15 карточек, пронумерованных числами от 1 до 15. Из коробки наугад взяли одну карточку. Какова вероятность того, что на ней записано число:
1) нечетное;
2) простое;
3) двузначное;
4) не кратное 3;
5) в записи которого есть цифра 4?

Решение

При взятии карточки может произойти 15 равновозможных исходов.
1) Среди чисел от 1 до 15 содержится 8 нечетных чисел. Следовательно, при взятии карточки благоприятных исходов будет 8. Тогда искомая вероятность равна $\frac{8}{15}$.
2) Среди чисел от 1 до 15 содержится 6 простых чисел. Следовательно, при взятии карточки благоприятных исходов будет 6. Тогда искомая вероятность равна $\frac{6}{15} = \frac{2}{5}$.
3) Среди чисел от 1 до 15 содержится 6 двузначных чисел. Следовательно, при взятии карточки благоприятных исходов будет 6. Тогда искомая вероятность равна $\frac{6}{15} = \frac{2}{5}$.
4) Среди чисел от 1 до 15 содержится 10 чисел, не кратных 3. Следовательно, при взятии карточки благоприятных исходов будет 10. Тогда искомая вероятность равна $\frac{10}{15} = \frac{2}{3}$.
5) Среди чисел от 1 до 15 содержится 2 числа, в записи которых есть цифра 4. Следовательно, при взятии карточки благоприятных исходов будет 2. Тогда искомая вероятность равна $\frac{2}{15}$.

№367

Номер №367

В коробке лежат 10 белых и несколько синих шаров. Сколько синих шаров лежит в коробке, если вероятность того, что наугад выбранный шар окажется белым, равна $\frac{5}{6}$?

Решение

Пусть в коробке лежат x синих шаров. Тогда при вынимании шара может произойти (10 + x) равновозможных исходов.
Так как, вероятность того, что наугад выбранный шар окажется белым, равна $\frac{5}{6}$, можно составить уравнение:
$\frac{10}{10 + x} = \frac{5}{6}$
5(10 + x) = 6 * 10
50 + 5x = 60
5x = 60 − 50
5x = 10
x = 2 (синих) − шара лежит в коробке.
Ответ: 2 синих шара

№368

Номер №368

На четырех карточках записаны числа 3, 4, 5 и 6. Какова вероятность того, что произведение чисел, записанных на двух наугад выбранных карточках, будет кратным числу 10?

Решение

В данном опыте существует 6 равновозможных исходов:
1) 3 и 4;
2) 3 и 5;
3) 3 и 6;
4) 4 и 5;
5) 4 и 6;
6) 5 и 6.
Из данных исходов, только в двух произведение чисел будет кратным числу 10: 4 и 5; 5 и 6. Значит существует только 2 благоприятных исхода, тогда:
$\frac{2}{6} = \frac{1}{3}$ − вероятность того, что произведение чисел, записанных на двух наугад выбранных карточках, будет кратным числу 10.
Ответ: $\frac{1}{3}$

№369

Номер №369

На четырех карточках записаны числа 1, 2, 3 и 4. Какова вероятность того, что сумма чисел, записанных на двух наугад выбранных карточках, будет нечетным числом?

Решение

В данном опыте существует 6 равновозможных исходов:
1) 1 и 2;
2) 1 и 3;
3) 1 и 4;
4) 2 и 3;
5) 2 и 4;
6) 3 и 4.
Из данных исходов в четырех случаях сумма чисел, записанных на двух наугад выбранных карточках, будет нечетным числом: 1 и 2; 1 и 4; 2 и 3; 3 и 4.
Значит существует только 4 благоприятных исхода, тогда:
$\frac{4}{6} = \frac{2}{3}$ − вероятность того, что сумма чисел, записанных на двух наугад выбранных карточках, будет нечетным числом.
Ответ: $\frac{2}{3}$

№370

Номер №370

Разделите изображенную на рисунке фигуру на 9 равных фигур, состоящих из квадратов.

Решение