В этой статье будут приведены задания, который вам вполне могут встретиться при сдаче ОГЭ по геометрии (математики). Задачи взяты из открытого банка заданий ФИПИ. То есть они вполне реальные как по возможности своего появления на экзамене, так и по сложности, что вам может попасться.
В этой статье будут приведены задания, который вам вполне могут встретиться при сдаче ОГЭ по геометрии (математики). Задачи взяты из открытого банка заданий ФИПИ. То есть они вполне реальные как по возможности своего появления на экзамене, так и по сложности, что вам может попасться.
Далее приведем примеры этих заданий и само собой и ответы для них. Но прежде буквально пару слов теории, о том что такое трапеция и как вычисляется ее площадь. Трапе́ция (от др.-греч. τραπέζιον — «столик» от τράπεζα — «стол») — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту.
$S=\frac{a+b}2\ast h$
Конечно можно вычислить площадь и по гибридному пути, то есть разбить трапецию на пару треугольников и прямоугольник, но это уже дело вашего удобства и понимания.
Реальные задания по геометрии из банка ФИПИ
Основания трапеции равны 4 и 10, а высота равна 5. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{4+10}2\ast5=35$
Ответ: 35
3E05A1

Основания трапеции равны 3 и 5, а высота равна 9. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{3+5}2\ast9=36$
Ответ: 36
FB21B9

Основания трапеции равны 4 и 12, а высота равна 6. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{4+12}2\ast6=48$
Ответ: 48
DC3C24

Основания трапеции равны 7 и 11, а высота равна 7. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{7+11}2\ast7=63$
Ответ: 63
A3751A

Основания трапеции равны 2 и 4, а высота равна 11. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{2+4}2\ast11=33$
Ответ: 33
6839CB

Основания трапеции равны 6 и 14, а высота равна 8. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{6+14}2\ast8=80$
Ответ: 80
822BB2

Основания трапеции равны 7 и 19, а высота равна 6. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{7+19}2\ast6=78$
Ответ: 78
F70300

Основания трапеции равны 8 и 14, а высота равна 5. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{8+14}2\ast5=55$
Ответ: 55
444775

Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{5+13}2\ast9=81$
Ответ: 81
39FB77

Основания трапеции равны 13 и 23, а высота равна 5. Найдите площадь этой трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
$S=\frac{13+23}2\ast5=90$
Ответ: 90
FEC9A6
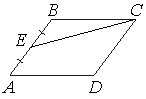
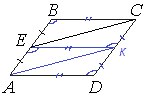
Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Решение 2-мя способами:
1 способ
Так как ABCD - параллелограмм, то AВ = CD.
Пусть точка К - середина стороны CD.
Так как по условию точка Е - середина стороны АВ, то
AE = BE = DK = KC .
ВС = АD = ЕК (средняя линия)
∠В = ∠АЕК - соответственные углы
∠В = ∠D - противолежащие углы параллелограмма
∠D = ∠ЕКС - соответственные ⇒
отрезки AK, KE и EC разбивают параллелограмм на 4 равновеликих треугольника (по двум сторонам и углу между ними) ⇒
SDAK = SАКЕ = SКЕС = SВСЕ = 180 / 4 = 45
Площадь трапеции состоит из трёх равновеликих треугольников ⇒
SDAEC = 45 * 3 = 135 кв.ед.
Ответ: 135
Лайфхак для быстрого решения: площадь параллелограмма разделим на 4 и умножим на 3
Sтрапеции = Sпаралл. : 4 * 3
2 способ
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 180 / 2 = 90.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 90 / 2 = 45. Следовательно,
SAECD = SABCD - SCDE = 180 - 45 = 135.
Ответ: 135
40519C

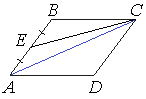
Площадь параллелограмма ABCD равна 60. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 60 / 2 = 30.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 30 / 2 = 15. Следовательно,
SAECD = SABCD - SCDE = 60 - 15 = 45.
Ответ: 45
41DF2E

Площадь параллелограмма ABCD равна 32. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 32 / 2 = 16.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 16 / 2 = 8. Следовательно,
SAECD = SABCD - SCDE = 32 - 8 = 24.
Ответ: 24
FD1877

Площадь параллелограмма ABCD равна 76. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 76 / 2 = 38.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 38 / 2 = 19. Следовательно,
SAECD = SABCD - SCDE = 76 - 19 = 57.
Ответ: 57
87D35B

Площадь параллелограмма ABCD равна 96. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 96 / 2 = 48.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 48 / 2 = 24. Следовательно,
SAECD = SABCD - SCDE = 96 - 24 = 72.
Ответ: 72
EFCEB8

Площадь параллелограмма ABCD равна 104. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 104 / 2 = 52.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 52 / 2 = 26. Следовательно,
SAECD = SABCD - SCDE = 104 - 26 = 78.
Ответ: 78
5A41E8

Площадь параллелограмма ABCD равна 92. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 92 / 2 = 46.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 46 / 2 = 23. Следовательно,
SAECD = SABCD - SCDE = 92 - 23 = 69.
Ответ: 69
CE80A9

Площадь параллелограмма ABCD равна 132. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 132 / 2 = 66.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 66 / 2 = 33. Следовательно,
SAECD = SABCD - SCDE = 132 - 33 = 99.
Ответ: 99
0D5AAC

Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 28 / 2 = 14.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 14 / 2 = 7. Следовательно,
SAECD = SABCD - SCDE = 28 - 7 = 21.
Ответ: 21
9CE80E

Площадь параллелограмма ABCD равна 128. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 128 / 2 = 64.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 64 / 2 = 32. Следовательно,
SAECD = SABCD - SCDE = 128 - 32 = 96.
Ответ: 96
18E5DD
С подобным рисунком есть задачи и на нахождение площади второй части параллелограмма - треугольника. Их решение можно посмотреть в статье "Найдите площадь треугольника", но на эту страничку тоже продублируем:

Площадь параллелограмма ABCD равна 132. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 132 / 2 = 66.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 66 / 2 = 33
Ответ: 33
9A5992

Площадь параллелограмма ABCD равна 68. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 68 / 2 = 34.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 34 / 2 = 17
Ответ: 17
795F61

Площадь параллелограмма ABCD равна 44. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 44 / 2 = 22.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 22 / 2 = 11
Ответ: 11
1ABE2A

Площадь параллелограмма ABCD равна 84. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 84 / 2 = 42.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 42 / 2 = 21
Ответ: 21
A6BEE2

Площадь параллелограмма ABCD равна 196. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 196 / 2 = 98.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 98 / 2 = 49
Ответ: 49
ADA977

Площадь параллелограмма ABCD равна 112. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 112 / 2 = 56.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 56 / 2 = 28
Ответ: 28
4DB6C1

Площадь параллелограмма ABCD равна 104. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 104 / 2 = 52.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 52 / 2 = 26
Ответ: 26
CDB192

Площадь параллелограмма ABCD равна 148. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 148 / 2 = 74.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 74 / 2 = 37
Ответ: 37
E2BFC0

Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 140 / 2 = 70.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 70 / 2 = 35
Ответ: 35
20E710

Площадь параллелограмма ABCD равна 136. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Решение:
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SACВ= 136 / 2 = 68.
Медиана треугольника делит его на два равновеликих треугольника, поэтому
SCВE = 1/2 SACВ = 68 / 2 = 34
Ответ: 34
2373D8
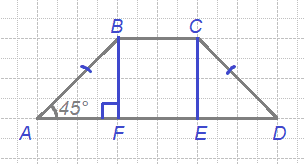
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.
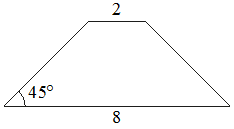
Решение:
Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.
Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (8 - 2) / 2 = 3
Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 3
$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
SАВСD = (2 + 8) : 2 * 3 = 15
Ответ: 15
AC6781
В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.
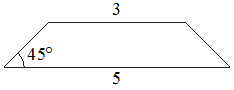
Решение:
Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.
Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (5 - 3) / 2 = 1
Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 1
$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
SАВСD = (3 + 5) : 2 * 1 = 4
Ответ: 4
A002C2
В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.
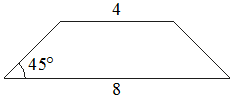
Решение:
Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.
Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (8 - 4) / 2 = 2
Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 2
$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
SАВСD = (4 + 8) : 2 * 2 = 12
Ответ: 12
03F9DB
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.
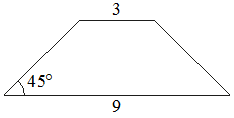
Решение:
Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.
Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (9 - 3) / 2 = 3
Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 3
$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
SАВСD = (3 + 9) : 2 * 3 = 18
Ответ: 18
D2652B
В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.
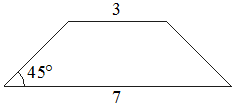
Решение:
Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.
Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (7 - 3) / 2 = 2
Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 2
$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
SАВСD = (3 + 7) : 2 * 2 = 10
Ответ: 10
1CEEC4
В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.
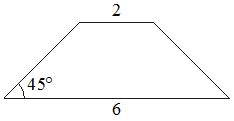
Решение:
Введём обозначения, как показано на рисунке. Опустим к большему основанию 2 перпендикуляра - высоты.
Так как трапеция равнобедренная,
АF = DЕ = (АD - ВС) / 2 = (6 - 2) / 2 = 2
Треугольник АВF - прямоугольный. Сумма углов треугольника равна 180°.
∠АВF = 180° - 90° - 45° = 45°, а раз углы при основании получились равны, значит треугольник АВF равнобедренный и
ВF = АF = 2
$S_{АВСD}=\frac{ВС+АD}2\ast h=\frac{ВС+АD}2\ast ВF$
SАВСD = (2 + 6) : 2 * 2 = 8
Ответ: 8
24CEEC
Задания второй части ОГЭ с расширенным решением
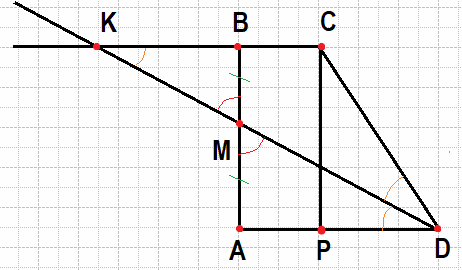
Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение:
Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD — равнобедренный: KC=CD=41. Найдём BK (BK=AD), вычитая известное основание из известной стороны по условиям задачи:
BK=AD=41-16=25.
Углы KMB и AMD равны как вертикальные, при пересечении двух прямых. Рассмотрим треугольники KMB и AMD. Эти треугольники равны по стороне, так как BA делится по условиям задачи пополам и двум углам KBM = MAD и BKM = MDA.
Проведем отрезок CP от одного основания к другому при этом параллельно BA. То есть у нас получится, что BC = AP, из этого мы сможем найти отрезок PD.
PD=AD-BC=25-16=9
Теперь если бы наш треугольник CPD был бы прямоугольным, то было бы верно утверждение CP2=PD2+CD2
Это исходя из теоремы Пифагора. Подставим известные нам значения для PD и СD. Получаем:
CP2=412-92
CP=√(1681-81)=√1600=40
Мы видим, что получившееся значение CP равно BA, CP=BA=40, то есть CP является высотой, так как для треугольника CPD действует теорема Пифагора и он прямоугольный. В итоге нам известны основания 25, 16 и высота 40. Можем найти площадь трапеции.
$\;S_{BCAD}=\frac{25+16}2\ast40=\frac{41}2\ast40=20.5\ast20=820$
Ответ: 820
0A23B5
Боковые стороны AB и CD трапеции ABCD равны соответственно 24 и 25, а основание BC равно 9. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение:
Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD — равнобедренный: KC=CD=25. Найдём BK (BK=AD), вычитая известное основание из известной стороны по условиям задачи:
BK=AD=25-9=16.
Углы KMB и AMD равны как вертикальные, при пересечении двух прямых. Рассмотрим треугольники KMB и AMD. Эти треугольники равны по стороне, так как BA делится по условиям задачи пополам и двум углам KBM = MAD и BKM = MDA.
Проведем отрезок CP от одного основания к другому при этом параллельно BA. То есть у нас получится, что BC = AP, из этого мы сможем найти отрезок PD.
PD=AD-BC=16-9=7
Теперь если бы наш треугольник CPD был бы прямоугольным, то было бы верно утверждение CP2=PD2+CD2
Это исходя из теоремы Пифагора. Подставим известные нам значения для PD и СD. Получаем:
CP2=252-72
CP=√(625-49)=√576=24
Мы видим, что получившееся значение CP равно BA, CP=BA=24, то есть CP является высотой, так как для треугольника CPD действует теорема Пифагора и он прямоугольный. В итоге нам известны основания 9, 16 и высота 24. Можем найти площадь трапеции.
$\;S_{BCAD}=\frac{9+16}2\ast24=\frac{25}2\ast24=12.5\ast24=300$
Ответ: 300
954230
Боковые стороны AB и CD трапеции ABCD равны соответственно 10 и 26, а основание BC равно 1. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение:
Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD — равнобедренный: KC=CD=26. Найдём BK (BK=AD), вычитая известное основание из известной стороны по условиям задачи:
BK=AD=KC-BC=26-1=25
Углы KMB и AMD равны как вертикальные, при пересечении двух прямых. Рассмотрим треугольники KMB и AMD. Эти треугольники равны по стороне, так как BA делится по условиям задачи пополам и двум углам KBM = MAD и BKM = MDA.
Проведем отрезок CP от одного основания к другому при этом параллельно BA. То есть у нас получится, что BC = AP, из этого мы сможем найти отрезок PD.
PD=AD-BC=25-1=24
Теперь если бы наш треугольник CPD был бы прямоугольным, то было бы верно утверждение CP2=PD2+CD2
Это исходя из теоремы Пифагора. Подставим известные нам значения для PD и СD. Получаем:
CP2=262-242
CP=√(676-576)=√100=10
Мы видим, что получившееся значение CP равно BA, CP=BA=10, то есть CP является высотой, так как для треугольника CPD действует теорема Пифагора и он прямоугольный. В итоге нам известны основания 1, 25 и высота 10. Можем найти площадь трапеции.
$\;S_{BCAD}=\frac{1+25}2\ast10=\frac{26}2\ast10=13\ast10=130$
Ответ: 130
096495
Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 29, а основание BC равно 4. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение:
Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD — равнобедренный: KC=CD=29. Найдём BK (BK=AD), вычитая известное основание из известной стороны по условиям задачи:
BK=AD=KC-BC=29-4=25
Углы KMB и AMD равны как вертикальные, при пересечении двух прямых. Рассмотрим треугольники KMB и AMD. Эти треугольники равны по стороне, так как BA делится по условиям задачи пополам и двум углам KBM = MAD и BKM = MDA.
Проведем отрезок CP от одного основания к другому при этом параллельно BA. То есть у нас получится, что BC = AP, из этого мы сможем найти отрезок PD.
PD=AD-BC=25-4=21
Теперь если бы наш треугольник CPD был бы прямоугольным, то было бы верно утверждение CP2=PD2+CD2
Это исходя из теоремы Пифагора. Подставим известные нам значения для PD и СD. Получаем:
CP2=292-212
CP=√(841-576)=√400=20
Мы видим, что получившееся значение CP равно BA, CP=BA=20, то есть CP является высотой, так как для треугольника CPD действует теорема Пифагора и он прямоугольный. В итоге нам известны основания 4, 25 и высота 20. Можем найти площадь трапеции.
$\;S_{BCAD}=\frac{4+25}2\ast20=\frac{29}2\ast20=14.5\ast20=290$
Ответ: 290
5AF0E1
Боковые стороны AB и CD трапеции ABCD равны соответственно 6 и 10, а основание BC равно 1. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение:
Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD — равнобедренный: KC=CD=10. Найдём BK (BK=AD), вычитая известное основание из известной стороны по условиям задачи:
BK=AD=KC-BC=10-1=9
Углы KMB и AMD равны как вертикальные, при пересечении двух прямых. Рассмотрим треугольники KMB и AMD. Эти треугольники равны по стороне, так как BA делится по условиям задачи пополам и двум углам KBM = MAD и BKM = MDA.
Проведем отрезок CP от одного основания к другому при этом параллельно BA. То есть у нас получится, что BC = AP, из этого мы сможем найти отрезок PD.
PD=AD-BC=9-1=8
Теперь если бы наш треугольник CPD был бы прямоугольным, то было бы верно утверждение CP2=PD2+CD2
Это исходя из теоремы Пифагора. Подставим известные нам значения для PD и СD. Получаем:
CP2=102-82
CP=√(100-64)=√36=6
Мы видим, что получившееся значение CP равно BA, CP=BA=6, то есть CP является высотой, так как для треугольника CPD действует теорема Пифагора и он прямоугольный. В итоге нам известны основания 1, 8 и высота 6. Можем найти площадь трапеции.
$\;S_{BCAD}=\frac{1+8}2\ast6=\frac{9}2\ast6=4.5\ast6=27$
Ответ: 27
7E8F98
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 13, а основание BC равно 4. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение:
Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD — равнобедренный: KC=CD=13. Найдём BK (BK=AD), вычитая известное основание из известной стороны по условиям задачи:
BK=AD=KC-BC=13-4=9
Углы KMB и AMD равны как вертикальные, при пересечении двух прямых. Рассмотрим треугольники KMB и AMD. Эти треугольники равны по стороне, так как BA делится по условиям задачи пополам и двум углам KBM = MAD и BKM = MDA.
Проведем отрезок CP от одного основания к другому при этом параллельно BA. То есть у нас получится, что BC = AP, из этого мы сможем найти отрезок PD.
PD=AD-BC=9-4=5
Теперь если бы наш треугольник CPD был бы прямоугольным, то было бы верно утверждение CP2=PD2+CD2
Это исходя из теоремы Пифагора. Подставим известные нам значения для PD и СD. Получаем:
CP2=132-52
CP=√(169-25)=√144=12
Мы видим, что получившееся значение CP равно BA, CP=BA=12, то есть CP является высотой, так как для треугольника CPD действует теорема Пифагора и он прямоугольный. В итоге нам известны основания 4, 9 и высота 12. Можем найти площадь трапеции.
$\;S_{BCAD}=\frac{4+9}2\ast12=\frac{13}2\ast12=6.5\ast12=78$
Ответ: 78
D9CD8D
Боковые стороны AB и CD трапеции ABCD равны соответственно 16 и 34, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение:
Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD — равнобедренный: KC=CD=34. Найдём BK (BK=AD), вычитая известное основание из известной стороны по условиям задачи:
BK=AD=KC-BC=34-2=32
Углы KMB и AMD равны как вертикальные, при пересечении двух прямых. Рассмотрим треугольники KMB и AMD. Эти треугольники равны по стороне, так как BA делится по условиям задачи пополам и двум углам KBM = MAD и BKM = MDA.
Проведем отрезок CP от одного основания к другому при этом параллельно BA. То есть у нас получится, что BC = AP, из этого мы сможем найти отрезок PD.
PD=AD-BC=32-2=30
Теперь если бы наш треугольник CPD был бы прямоугольным, то было бы верно утверждение CP2=PD2+CD2
Это исходя из теоремы Пифагора. Подставим известные нам значения для PD и СD. Получаем:
CP2=342-302
CP=√(1156-900)=√256=16
Мы видим, что получившееся значение CP равно BA, CP=BA=12, то есть CP является высотой, так как для треугольника CPD действует теорема Пифагора и он прямоугольный. В итоге нам известны основания 4, 9 и высота 12. Можем найти площадь трапеции.
$\;S_{BCAD}=\frac{2+32}2\ast16=\frac{34}2\ast16=17\ast16=272$
Ответ: 272
3FECDD
Боковые стороны AB и CD трапеции ABCD равны соответственно 4 и 5, а основание BC равно 1. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение:
Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD — равнобедренный: KC=CD=5. Найдём BK (BK=AD), вычитая известное основание из известной стороны по условиям задачи:
BK=AD=KC-BC=5-1=4
Углы KMB и AMD равны как вертикальные, при пересечении двух прямых. Рассмотрим треугольники KMB и AMD. Эти треугольники равны по стороне, так как BA делится по условиям задачи пополам и двум углам KBM = MAD и BKM = MDA.
Проведем отрезок CP от одного основания к другому при этом параллельно BA. То есть у нас получится, что BC = AP, из этого мы сможем найти отрезок PD.
PD=AD-BC=4-1=3
Теперь если бы наш треугольник CPD был бы прямоугольным, то было бы верно утверждение CP2=PD2+CD2
Это исходя из теоремы Пифагора. Подставим известные нам значения для PD и СD. Получаем:
CP2=52-32
CP=√(25-9)=√16=4
Мы видим, что получившееся значение CP равно BA, CP=BA=4, то есть CP является высотой, так как для треугольника CPD действует теорема Пифагора и он прямоугольный. В итоге нам известны основания 1, 3 и высота 4. Можем найти площадь трапеции.
$\;S_{BCAD}=\frac{1+3}2\ast4=\frac{4}2\ast4=2\ast4=8$
Ответ: 8
F8F38E
Боковые стороны AB и CD трапеции ABCD равны соответственно 28 и 35, а основание BC равно 7. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение:
Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD — равнобедренный: KC=CD=35. Найдём BK (BK=AD), вычитая известное основание из известной стороны по условиям задачи:
BK=AD=KC-BC=35-7=28
Углы KMB и AMD равны как вертикальные, при пересечении двух прямых. Рассмотрим треугольники KMB и AMD. Эти треугольники равны по стороне, так как BA делится по условиям задачи пополам и двум углам KBM = MAD и BKM = MDA.
Проведем отрезок CP от одного основания к другому при этом параллельно BA. То есть у нас получится, что BC = AP, из этого мы сможем найти отрезок PD.
PD=AD-BC=28-7=21
Теперь если бы наш треугольник CPD был бы прямоугольным, то было бы верно утверждение CP2=PD2+CD2
Это исходя из теоремы Пифагора. Подставим известные нам значения для PD и СD. Получаем:
CP2=352-212
CP=√(1225-441)=√784=28
Мы видим, что получившееся значение CP равно BA, CP=BA=4, то есть CP является высотой, так как для треугольника CPD действует теорема Пифагора и он прямоугольный. В итоге нам известны основания 28, 7 и высота 28. Можем найти площадь трапеции.
$\;S_{BCAD}=\frac{7+28}2\ast28=\frac{35}2\ast28=17.5\ast28=490$
Ответ: 490
9CA354
Боковые стороны AB и CD трапеции ABCD равны соответственно 8 и 10, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение:
Введём обозначения, как показано на рисунке. Продолжим биссектрису и отрезок BC до пересечения в точке K. При этом углы CKD и ADK (BKM = MDA) будут равны, как накрест лежащие при параллельных прямых (основания трапеции). Из равенства этих углов следует, что треугольник треугольник CKD — равнобедренный: KC=CD=10. Найдём BK (BK=AD), вычитая известное основание из известной стороны по условиям задачи:
BK=AD=KC-BC=10-2=8
Углы KMB и AMD равны как вертикальные, при пересечении двух прямых. Рассмотрим треугольники KMB и AMD. Эти треугольники равны по стороне, так как BA делится по условиям задачи пополам и двум углам KBM = MAD и BKM = MDA.
Проведем отрезок CP от одного основания к другому при этом параллельно BA. То есть у нас получится, что BC = AP, из этого мы сможем найти отрезок PD.
PD=AD-BC=8-2=6
Теперь если бы наш треугольник CPD был бы прямоугольным, то было бы верно утверждение CP2=PD2+CD2
Это исходя из теоремы Пифагора. Подставим известные нам значения для PD и СD. Получаем:
CP2=102-62
CP=√(100-36)=√64=8
Мы видим, что получившееся значение CP равно BA, CP=BA=4, то есть CP является высотой, так как для треугольника CPD действует теорема Пифагора и он прямоугольный. В итоге нам известны основания 8, 2 и высота 8. Можем найти площадь трапеции.
$\;S_{BCAD}=\frac{2+8}2\ast8=\frac{10}2\ast8=5\ast8=40$
Ответ: 40
8D9E03