Задания по ОГЭ математика на вычисление площади параллелограмма. Ряд задач при сдаче ОГЭ будет связан с вычислением площади параллелограмма. Некоторые из задач прям нам кажутся простыми и очевидными, но есть и посложнее, которые требуют определенных знаний не связанных с обычными формулами вычисления площади. как основание умноженное на высоту. Ведь площадь придется вычислять по косвенным признакам, извлекая из них уже факты.
Задания по ОГЭ математика на вычисление площади параллелограмма. Ряд задач при сдаче ОГЭ будет связан с вычислением площади параллелограмма. Некоторые из задач прям нам кажутся простыми и очевидными, но есть и посложнее, которые требуют определенных знаний не связанных с обычными формулами вычисления площади. как основание умноженное на высоту. Ведь площадь придется вычислять по косвенным признакам, извлекая из них уже факты.
Ну что уж поделаешь, такой уровень задач по геометрии и такие порой высокие требования предъявляют для сдачи экзамена ОГЭ по геометрии. Все что остается тем, кто готовится к этому экзамену, так это решать и пополнять свой багаж знаний не только формулами, но и опытом решения. Ведь порой опыт имеет куда более значимый фактор при решении, так как здесь можно идти уже не по логике решения, которая порой не дается так быстро как хотелось бы, а именно по памяти как надо сделать, чтобы получить правильный ответ.
Среди задач на вычисление площади параллелограмма из открытого банка ФИПИ есть и е, на которые достаточно краткого ответа, и с развернутым ответом. И те, и другие, перед вами. Любое из них может вам попасться на экзамене в этом году.
Задания по ОГЭ математика на вычисление площади параллелограмма
Вспоминаем, что площадь параллелограмма равна произведению длины основания на высоту:
S = ah
Реальные задания по геометрии из банка ФИПИ
Найдите площадь параллелограмма, изображённого на рисунке.

Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+7) * 4 = 40
Значение длины второй стороны параллелограмма - лишние данные, они не используются в решении.
Ответ: 40
E8FC9F
Найдите площадь параллелограмма, изображённого на рисунке.
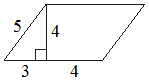
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+4) * 4 = 28
Значение длины второй стороны параллелограмма - лишние данные, они не используются в решении.
Ответ: 28
5AEBBA
Найдите площадь параллелограмма, изображённого на рисунке.
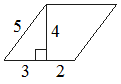
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+2) * 4 = 20
Значение длины второй стороны параллелограмма - лишние данные, они не используются в решении.
Ответ: 20
460490
Найдите площадь параллелограмма, изображённого на рисунке.

Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+8) * 4 = 44
Значение длины второй стороны параллелограмма - лишние данные, они не используются в решении.
Ответ: 44
29D63A
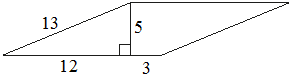
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (12+3) * 5 = 75
Значение длины второй стороны параллелограмма - лишние данные, они не используются в решении.
Ответ: 75
D97D85
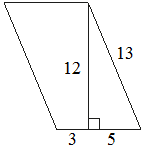
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (3+5) * 12 = 96
Значение длины второй стороны параллелограмма - лишние данные, они не используются в решении.
Ответ: 96
B08979
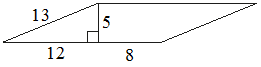
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (12+8) * 5 = 100
Значение длины второй стороны параллелограмма - лишние данные, они не используются в решении.
Ответ: 100
956EDE
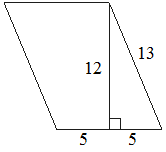
Найдите площадь параллелограмма, изображённого на рисунке.
Решение:
Площадь параллелограмма равна произведению длины основания на высоту:
S = ah
S = (5+5) * 12 = 120
Значение длины второй стороны параллелограмма - лишние данные, они не используются в решении.
Ответ: 120
66228A
Задания второй части ОГЭ с расширенным решением
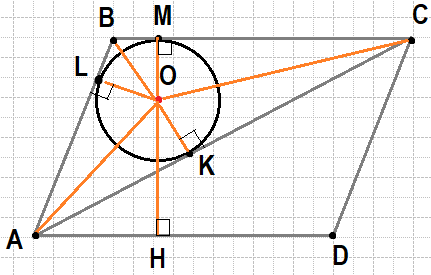
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{25-9}$ = 4
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству о касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 4.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{4+4+2BM+2MC}2\ast3=3\ast(4+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(3+4)\ast(BM+MC)=7\ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$\frac{7\ast(BM+MC)}2=3\;\ast\;(\;4\;+\;B\;M\;+\;M\;C)\\7\ast(BM+MC)\;=\;6\;\ast\;(\;4\;+\;B\;M\;+\;M\;C)\\7\ast(BM+MC)\;=\;24\;+\;6\;\ast\;(B\;M\;+\;M\;C)\\7\ast(BM+MC)\;-\;6\;\ast\;(B\;M\;+\;M\;C)\;=\;24\\B\;M\;+\;M\;C\;=\;24\\\\\\$
То есть основание BC = 24.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(3+4)*24=168
Ответ: 168
701E1F
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 6 и 5. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{169-25}$ = 12
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству о касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{12+12+2BM+2MC}2\ast5=5\ast(12+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(6+5)\ast(BM+MC)=11\ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$\frac{11\ast(BM+MC)}2=5\ast(12+BM+MC)\\11\ast(BM+MC)\;=\;10\ast(12+BM+MC)\\11\ast(BM+MC)\;=\;120\;+\;10\ast(BM+MC)\\11\ast(BM+MC)\;-\;10\;(BM+MC)\;=\;120\\B\;M+M\;C\;=\;120\\\\\\$
То есть основание BC = 120.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+6)*120=1320
Ответ: 1320
B520E8
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 7 и 5. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{169-25}$ = 12
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству о касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{12+12+2BM+2MC}2\ast5=5\ast(12+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(7+5)\ast(BM+MC)=12\ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$\frac{12\ast(BM+MC)}2=5\ast(12+BM+MC)\\12\ast(BM+MC)\;=\;10\ast(12+BM+MC)\\12\ast(BM+MC)\;=\;120\;+\;10\ast(BM+MC)\\12\ast(BM+MC)\;-\;10\;(BM+MC)\;=\;120\\2\ast(BM+MC)\;=\;120\\BM+MC\;=\;60\\\\\\\\$
То есть основание BC = 60.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(7+5)*60=720
Ответ: 720
7AFAA8
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 8 и 5. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{169-25}$ = 12
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству о касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{12+12+2BM+2MC}2\ast5=5\ast(12+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(8+5)\ast(BM+MC)=13\ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$\frac{13\ast(BM+MC)}2=5\ast(12+BM+MC)\\13\ast(BM+MC)\;=\;10\ast(12+BM+MC)\\13\ast(BM+MC)\;=\;120\;+\;10\ast(BM+MC)\\13\ast(BM+MC)\;-\;10\;(BM+MC)\;=\;120\\3\ast(BM+MC)\;=\;120\\BM+MC\;=\;40\\\\\\\\$
То есть основание BC = 40.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+8)*40=520
Ответ: 520
15838B
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{169-25}$ = 12
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству о касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 12.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{12+12+2BM+2MC}2\ast5=5\ast(12+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(9+5)\ast(BM+MC)=14\ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$\frac{14\ast(BM+MC)}2=5\ast(12+BM+MC)\\14\ast(BM+MC)\;=\;10\ast(12+BM+MC)\\14\ast(BM+MC)\;=\;120\;+\;10\ast(BM+MC)\\14\ast(BM+MC)\;-\;10\;(BM+MC)\;=\;120\\4\ast(BM+MC)\;=\;120\\BM+MC\;=\;30\\\\\\\\$
То есть основание BC = 30.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(5+9)*30=420
Ответ: 420
221DAD
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 13 и 7. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{625-49}$ = 24
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству о касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{24+24+2BM+2MC}2\ast7=7\ast(24+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(13+7)\ast(BM+MC)=20\ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$\frac{20\ast(BM+MC)}2=7\ast(24+BM+MC)\\20\ast(BM+MC)\;=\;14\ast(24+BM+MC)\\20\ast(BM+MC)\;=\;336\;+\;14\ast(BM+MC)\\20\ast(BM+MC)\;-\;14\;(BM+MC)\;=\;336\\6\ast(BM+MC)\;=\;336\\BM+MC\;=\;56\\\\\\\\$
То есть основание BC = 56.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(13+7)*56=1120
Ответ: 1120
716CE8
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 14 и 7. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{625-49}$ = 24
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству о касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{24+24+2BM+2MC}2\ast7=7\ast(24+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(14+7)\ast(BM+MC)=21\ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$\frac{21\ast(BM+MC)}2=7\ast(24+BM+MC)\\21\ast(BM+MC)\;=\;14\ast(24+BM+MC)\\21\ast(BM+MC)\;=\;336\;+\;14\ast(BM+MC)\\21\ast(BM+MC)\;-\;14\;(BM+MC)\;=\;336\\7\ast(BM+MC)\;=\;336\\BM+MC\;=\;48\\\\\\\\$
То есть основание BC = 48.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(14+7)*48=1008
Ответ: 1008
A4192E
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 15 и 7. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{625-49}$ = 24
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству о касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{24+24+2BM+2MC}2\ast7=7\ast(24+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(15+7)\ast(BM+MC)=22\ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$\frac{22\ast(BM+MC)}2=7\ast(24+BM+MC)\\22\ast(BM+MC)\;=\;14\ast(24+BM+MC)\\22\ast(BM+MC)\;=\;336\;+\;14\ast(BM+MC)\\22\ast(BM+MC)\;-\;14\;(BM+MC)\;=\;336\\8\ast(BM+MC)\;=\;336\\BM+MC\;=\;42\\\\\\\\$
То есть основание BC = 42.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(15+7)*42=924
Ответ: 924
2E555E
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 17 и 7. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{625-49}$ = 24
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству о касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{24+24+2BM+2MC}2\ast7=7\ast(24+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(17+7)\ast(BM+MC)=24\ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$\frac{24\ast(BM+MC)}2=7\ast(24+BM+MC)\\24\ast(BM+MC)\;=\;14\ast(24+BM+MC)\\24\ast(BM+MC)\;=\;336\;+\;14\ast(BM+MC)\\24\ast(BM+MC)\;-\;14\;(BM+MC)\;=\;336\\10\ast(BM+MC)\;=\;336\\BM+MC\;=\;33,6\\\\\\\\$
То есть основание BC = 33,6.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(17+7)*33,6=806,4
Ответ: 806,4
DFC86B
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 19 и 7. Найдите площадь параллелограмма ABCD.
Решение:
Сделаем построения и введём обозначения, как показано на рисунке. O — центр окружности, вписанной в треугольник ABC. Центр вписанной окружности — это точка пересечения биссектрис, поэтому AO,BO,CO — биссектрисы. Из прямоугольного треугольника AOK по теореме Пифагора найдём AK:
AK=$\sqrt{AO^2+ОК^2}=\;\sqrt{625-49}$ = 24
Рассмотрим треугольники ALO и AOK, они прямоугольные, так как радиусы перпендикулярны касательным сторонам по свойству о касательных, а углы LAO и OAK равны, так как АО биссектриса. AO — общая сторона, а следовательно, треугольники равны, откуда AL=AK= 24.
Аналогично из равенства треугольников COM и COK (общая сторона, и два угла) получаем MC = CK
Аналогично из равенства треугольников BOL и BOM — BL=BM.
Площадь треугольника ABC можно найти как произведение радиуса вписанной окружности на полупериметр:
$Sabc=\frac{AB+BC+CA}2\ast OK=\frac{AL+LB+BM+MC+CK+KA}2\ast OK=\frac{24+24+2BM+2MC}2\ast7=7\ast(24+BM+MC)$
* из этой площади нам неизвестно BM и MC, которые составляют основание. При этом площадь параллелограмма равна произведению высоты на основание:
$Sabcd=MH\ast BC=(MO+OH)\ast(BM+MC)=(19+7)\ast(BM+MC)=26\ast(BM+MC)$
Мы знаем, что диагональ в параллелограмме делит его на два равных треугольника (равны две стороны и угол между ними). В итоге получается, что площадь любого из этих треугольников равна половине площади самого параллелограмма. То есть получаем уравнение:
$\frac{26\ast(BM+MC)}2=7\ast(24+BM+MC)\\26\ast(BM+MC)\;=\;14\ast(24+BM+MC)\\26\ast(BM+MC)\;=\;336\;+\;14\ast(BM+MC)\\26\ast(BM+MC)\;-\;14\;(BM+MC)\;=\;336\\12\ast(BM+MC)\;=\;336\\BM+MC\;=28\\\\\\\\$
То есть основание BC = 28.
Площадь параллелограмма после принятия к вычислению всех известных величин равна:
Sabcd= MH * BC =(19+7)*28=728
Ответ: 728
1D6569
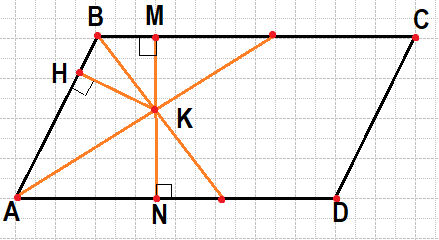
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=7.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=7.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.
Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =19*(7+7)=19*14=266.
Ответ: 266
97C87B
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=3.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=3.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.
Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =11*(3+3)=11*6=66.
Ответ: 66
F8A0E6
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=9.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=9.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.
Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =12*(9+9)=12*18=216.
Ответ: 216
67503F
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 10.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=10.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=10.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.
Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =19*(10+10)=19*20=380.
Ответ: 380
D60F99
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=17, а расстояние от точки K до стороны AB равно 10.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=10.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=10.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.
Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =17*(10+10)=17*20=340.
Ответ: 340.
B435D4
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=18, а расстояние от точки K до стороны AB равно 1.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=1.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=1.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.
Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =18*(1+1)=18*2=36.
Ответ: 36
E097F7
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=7, а расстояние от точки K до стороны AB равно 4.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=4.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=4.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.
Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =7*(4+4)=7*8=56.
Ответ: 56
80A169
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 8.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=8.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=8.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.
Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =2*(8+8)=2*16=32.
Ответ: 32
569075
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=6, а расстояние от точки K до стороны AB равно 6.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=6.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=6.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.
Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =6*(6+6)=6*12=72.
Ответ: 72
FD6657
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 1.
Решение:
Введём обозначения, как показано на рисунке. Пусть К — точка пересечения биссектрис, КН — высота треугольника АКВ, MN — высота параллелограмма, проходящая через точку К.
Рассмотрим треугольники AHK и AKN. Они одинаковые, так как: во-первых, они прямоугольные, углы HAK и KAN равны, так как АК — биссектриса угла А. Во-вторых, сторона AK — общая. Тогда KN=KH=1.
Тоже само можно сказать и о треугольниках BKH и BKM (по общей стороне и двум углам). Значит MK=KH=1.
Получается что H, то есть высота параллелограмма равна H = MK+KH. Теперь зная высоту и основание из условия, можно найти площадь.
Итак, площадь параллелограмма это произведение высоты на основание:
S=AD*MN=AD*(MK + KN) =2*(1+1)=2*2=4.
Ответ: 4
A7594E