В этих задачах из открытого банка ФИПИ мы представим вашему вниманию задачи по нахождению номинала основания трапеции. Трапеция это геометрическая фигура четырехугольник, где две стороны параллельны, но не равны, - это основания и две стороны трапеции идут между оснований. Если одна из сторон расположена перпендикулярно основанию, то это прямоугольная трапеция, если две..., то это уже прямоугольник или даже квадрат;) Поэтому частный случай, как правило, является метаморфозой приводящей к другой геометрической фигуре.
В этих задачах из открытого банка ФИПИ мы представим вашему вниманию задачи по нахождению номинала основания трапеции. Трапеция это геометрическая фигура четырехугольник, где две стороны параллельны, но не равны, - это основания и две стороны трапеции идут между оснований. Если одна из сторон расположена перпендикулярно основанию, то это прямоугольная трапеция, если две..., то это уже прямоугольник или даже квадрат;) Поэтому частный случай, как правило, является метаморфозой приводящей к другой геометрической фигуре.
Однако мы не будем о исключениях, а поговорим о наших правилах, о вполне реальных и возможных задачах по ОГЭ, для нахождения основания трапеции.
В следующих заданиях нужно найти основание трапеции, где-то большее, где-то меньшее, а в заданиях части 2 ОГЭ - оба. Вот что предлагает открытый банк заданий ФИПИ по этой теме.
Реальные задания по геометрии из банка ФИПИ
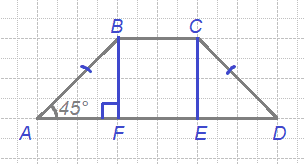
В равнобедренной трапеции известны высота, меньшее основание и угол при основании (см. рисунок). Найдите большее основание.

Решение:
Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ = 6
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
АD = АF + ЕD + FЕ = 2АF + FЕ = 2 * 5 + 6 = 16
Ответ: 16
D5D947
В равнобедренной трапеции известна высота, большее основание и угол при основании (см. рисунок). Найдите меньшее основание.

Решение:
Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
ВС = FЕ = АD - (АF + ЕD) = АD - 2АF = 15 - 2 * 5 = 5
Ответ: 5
EFBE26
В равнобедренной трапеции известна высота, меньшее основание и угол при основании (см. рисунок). Найдите большее основание.

Решение:
Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ = 7
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
АD = АF + ЕD + FЕ = 2АF + FЕ = 2 * 5 + 7 = 17
Ответ: 17
33462D
В равнобедренной трапеции известна высота, большее основание и угол при основании (см. рисунок). Найдите меньшее основание.

Решение:
Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
ВС = FЕ = АD - (АF + ЕD) = АD - 2АF = 14 - 2 * 5 = 4
Ответ: 4
C56952
В равнобедренной трапеции известна высота, меньшее основание и угол при основании (см. рисунок). Найдите большее основание.

Решение:
Введем обозначения, как показано на рисунке.
Треугольник АВF - прямоугольный. Сумма углов любого треугольника равна 180°, значит
∠АВF = 180° - 90° - 45° = 45°,
∠АВF = ∠ВАF , следовательно, треугольник АВF равнобедренный и
АF = ВF = 5
Проведем высоту СЕ из угла С.
В четырехугольнике ВСЕF противолежащие стороны параллельны, а углы F и Е прямые, значит это прямоугольник. В прямоугольнике противолежащие стороны равны, значит
ВF = СЕ = 5, ВС = FЕ = 3
Так как трапеция равнобедренная, то углы при основании равны, то есть
∠ВАF = ∠CDE = 45°, ∠ECD = 180° - 90° - 45° = 45°, отсюда треугольник АВF = СDЕ по двум сторонам и углу между ними. Значит
АF = ЕD = 5
АD = АF + ЕD + FЕ = 2АF + FЕ = 2 * 5 + 3 = 13
Ответ: 13
99B09B
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 8 и 15. Найдите длину основания BC.

Решение:
Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 8.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 15 - 8 = 7
Ответ: 7
267796
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 11. Найдите длину основания BC.

Решение:
Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 1.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 11 - 1 = 10
Ответ: 10
7FE0DC
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 10 и 11. Найдите длину основания BC.

Решение:
Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 10.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 11 - 10 = 1
Ответ: 1
DF571C
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 3 и 11. Найдите длину основания BC.

Решение:
Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 3.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 11 - 3 = 8
Ответ: 8
1F937D
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 8 и 17. Найдите длину основания BC.

Решение:
Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 8.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 17 - 8 = 9
Ответ: 9
54505A
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 17 и 19. Найдите длину основания BC.

Решение:
Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 17.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 19 - 17 = 2
Ответ: 2
4FA4EB
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 16 и 17. Найдите длину основания BC.

Решение:
Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 16.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 17 - 16 = 1
Ответ: 1
0A07C8
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 8 и 18. Найдите длину основания BC.

Решение:
Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 8.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 18 - 8 = 10
Ответ: 10
A6EA51
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 11 и 14. Найдите длину основания BC.

Решение:
Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 11.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 14 - 11 = 3
Ответ: 3
51BD7F
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 14 и 19. Найдите длину основания BC.

Решение:
Проведём вторую высоту и введём обозначения, как показано на рисунке.
Рассмотрим треугольники ABF и ЕCD, они прямоугольные,
AB = CD, BF = CЕ, ∠А = ∠D (так как трапеция равнобедренная) следовательно ∠ЕСD = ∠АВF, а значит эти треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Отсюда
AF = ЕD = 14.
Высоты BF и CЕ перпендикулярны AD, значит, они параллельны, BF равно CЕ, следовательно, ВСЕF — прямоугольник, значит
BC = FЕ = AЕ - AF = 19 - 14 = 5
Ответ: 5
0BC157
Задания ОГЭ с развернутым ответом
Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.
Решение:
Продлим стороны AB и CD до пересечения в точке O В треугольнике AKD сумма углов KAD и KDA равна 90°, следовательно, величина
∠AOD=180-(∠OAD-∠ODA)=90º
Значит, треугольник AOD — прямоугольный. Рассмотрим треугольник AOD, при этом проведем медиану OF. Примечательно, что данная медиана будет делить любой из отрезков пополам, который параллельный отрезку AD и находящийся между сторонами АO и OD. Все дело в том, что любой из треугольников с той же вершиной O, что и треугольник AOD и с основанием находящимся между сторонам АO и OD при этом параллельным AD будет подобен самому треугольнику AOD. (по трем углам). Из свойства о медиане в прямоугольном треугольнике мы знаем, что медиана, проведенная к гипотенузе, равна половине гипотенузы.
$OM=\frac{BC}2$
а для MN будет справедливо следующее утверждение:
$\frac{BC}2+MN=\frac{AD}2\\MN\;=\frac{AD}2-\frac{BC}2\\MN\;=\frac{AD-BC}2$
При этом есть и KL, она является средней линией трапеции, которая обладает следующим свойством. Средняя линия трапеции параллельна основаниям и равна их полусумме. Значит:
$KL\;=\;\frac{AD+BC}2\\\\\\$
При этом из условия задачи мы знаем, что соединяющие середины противоположных сторон трапеции, равны 11 и 10. То есть разница между KL и МН это разница между этими значениями, при этом KL=11 больше МН=10, исходя их равенств выше, то есть.
KL-МН=11-10=1
Выражая тоже самое исходя из равенств выше получаем.
$\;\frac{AD+BC}2-\frac{AD-BC}2=1\\\frac{AD+BC-(AD-BC)}2=1\\\frac{AD+BC-AD+BC}2=1\\\frac{2BC}2=1\\BC=1\\\\\\\\$
Теперь подставляем значение BC=1 в выше полученное равенство, при условии KL=11:
$\;KL=\frac{AD+BC}2^{}\\11=\frac{AD+1}2\\AD+1=22\\AD=22-1\\AD=21\\\\\\\\\\\\\\$
Ответ: 1, 21
62EB73
Углы при одном из оснований трапеции равны 47° и 43°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 16 и 14. Найдите основания трапеции.
Решение:
Продлим стороны AB и CD до пересечения в точке O В треугольнике AKD сумма углов KAD и KDA равна 90°, следовательно, величина
∠AOD=180-(∠OAD-∠ODA)=90º
Значит, треугольник AOD — прямоугольный. Рассмотрим треугольник AOD, при этом проведем медиану OF. Примечательно, что данная медиана будет делить любой из отрезков пополам, который параллельный отрезку AD и находящийся между сторонами АO и OD. Все дело в том, что любой из треугольников с той же вершиной O, что и треугольник AOD и с основанием находящимся между сторонам АO и OD при этом параллельным AD будет подобен самому треугольнику AOD. (по трем углам). Из свойства о медиане в прямоугольном треугольнике мы знаем, что медиана, проведенная к гипотенузе, равна половине гипотенузы.
$OM=\frac{BC}2$
а для MN будет справедливо следующее утверждение:
$\frac{BC}2+MN=\frac{AD}2\\MN\;=\frac{AD}2-\frac{BC}2\\MN\;=\frac{AD-BC}2$
При этом есть и KL, она является средней линией трапеции, которая обладает следующим свойством. Средняя линия трапеции параллельна основаниям и равна их полусумме. Значит:
$KL\;=\;\frac{AD+BC}2\\\\\\$
При этом из условия задачи мы знаем, что соединяющие середины противоположных сторон трапеции, равны 16 и 14. То есть разница между KL и МН это разница между этими значениями, при этом KL=16 больше МН=14, исходя их равенств выше, то есть.
KL-МН=16-14=2
Выражая тоже самое исходя из равенств выше получаем.
$\;\frac{AD+BC}2-\frac{AD-BC}2=2\\\frac{AD+BC-(AD-BC)}2=2\\\frac{AD+BC-AD+BC}2=2\\\frac{2BC}2=2\\BC=2\\\\\\\\$
Теперь подставляем значение BC=2 в выше полученное равенство, при условии KL=16:
$\;KL=\frac{AD+BC}2^{}\\16=\frac{AD+2}2\\AD+2=32\\AD=32-2\\AD=30\\\\\\\\\\\\\\$
Ответ: 2, 30
9B51F6
Углы при одном из оснований трапеции равны 39° и 51°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 19 и 3. Найдите основания трапеции.
Решение:
Продлим стороны AB и CD до пересечения в точке O В треугольнике AKD сумма углов KAD и KDA равна 90°, следовательно, величина
∠AOD=180-(∠OAD-∠ODA)=90º
Значит, треугольник AOD — прямоугольный. Рассмотрим треугольник AOD, при этом проведем медиану OF. Примечательно, что данная медиана будет делить любой из отрезков пополам, который параллельный отрезку AD и находящийся между сторонами АO и OD. Все дело в том, что любой из треугольников с той же вершиной O, что и треугольник AOD и с основанием находящимся между сторонам АO и OD при этом параллельным AD будет подобен самому треугольнику AOD. (по трем углам). Из свойства о медиане в прямоугольном треугольнике мы знаем, что медиана, проведенная к гипотенузе, равна половине гипотенузы.
$OM=\frac{BC}2$
а для MN будет справедливо следующее утверждение:
$\frac{BC}2+MN=\frac{AD}2\\MN\;=\frac{AD}2-\frac{BC}2\\MN\;=\frac{AD-BC}2$
При этом есть и KL, она является средней линией трапеции, которая обладает следующим свойством. Средняя линия трапеции параллельна основаниям и равна их полусумме. Значит:
$KL\;=\;\frac{AD+BC}2\\\\\\$
При этом из условия задачи мы знаем, что соединяющие середины противоположных сторон трапеции, равны 19 и 3. То есть разница между KL и МН это разница между этими значениями, при этом KL=19 больше МН=3, исходя их равенств выше, то есть.
KL-МН=19-3=16
Выражая тоже самое исходя из равенств выше получаем.
$\;\frac{AD+BC}2-\frac{AD-BC}2=16\\\frac{AD+BC-(AD-BC)}2=16\\\frac{AD+BC-AD+BC}2=16\\\frac{2BC}2=16\\BC=16\\\\\\\\$
Теперь подставляем значение BC=16 в выше полученное равенство, при условии KL=19:
$\;KL=\frac{AD+BC}2^{}\\19=\frac{AD+16}2\\AD+16=38\\AD=38-16\\AD=22\\\\\\\\\\\\\\$
Ответ: 16, 22
7673A9
Углы при одном из оснований трапеции равны 50° и 40°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 13. Найдите основания трапеции.
Решение:
Продлим стороны AB и CD до пересечения в точке O В треугольнике AKD сумма углов KAD и KDA равна 90°, следовательно, величина
∠AOD=180-(∠OAD-∠ODA)=90º
Значит, треугольник AOD — прямоугольный. Рассмотрим треугольник AOD, при этом проведем медиану OF. Примечательно, что данная медиана будет делить любой из отрезков пополам, который параллельный отрезку AD и находящийся между сторонами АO и OD. Все дело в том, что любой из треугольников с той же вершиной O, что и треугольник AOD и с основанием находящимся между сторонам АO и OD при этом параллельным AD будет подобен самому треугольнику AOD. (по трем углам). Из свойства о медиане в прямоугольном треугольнике мы знаем, что медиана, проведенная к гипотенузе, равна половине гипотенузы.
$OM=\frac{BC}2$
а для MN будет справедливо следующее утверждение:
$\frac{BC}2+MN=\frac{AD}2\\MN\;=\frac{AD}2-\frac{BC}2\\MN\;=\frac{AD-BC}2$
При этом есть и KL, она является средней линией трапеции, которая обладает следующим свойством. Средняя линия трапеции параллельна основаниям и равна их полусумме. Значит:
$KL\;=\;\frac{AD+BC}2\\\\\\$
При этом из условия задачи мы знаем, что соединяющие середины противоположных сторон трапеции, равны 15 и 13. То есть разница между KL и МН это разница между этими значениями, при этом KL=15 больше МН=13, исходя их равенств выше, то есть.
KL-МН=15-13=3
Выражая тоже самое исходя из равенств выше получаем.
$\;\frac{AD+BC}2-\frac{AD-BC}2=3\\\frac{AD+BC-(AD-BC)}2=3\\\frac{AD+BC-AD+BC}2=3\\\frac{2BC}2=3\\BC=3\\\\\\\\$
Теперь подставляем значение BC=3 в выше полученное равенство, при условии KL=15:
$\;KL=\frac{AD+BC}2^{}\\15=\frac{AD+3}2\\AD+3=30\\AD=30-3\\AD=27\\\\\\\\\\\\\\$
Ответ: 3, 27
AE4891
Углы при одном из оснований трапеции равны 53° и 37°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 6 и 2. Найдите основания трапеции.
Решение:
Продлим стороны AB и CD до пересечения в точке O В треугольнике AKD сумма углов KAD и KDA равна 90°, следовательно, величина
∠AOD=180-(∠OAD-∠ODA)=90º
Значит, треугольник AOD — прямоугольный. Рассмотрим треугольник AOD, при этом проведем медиану OF. Примечательно, что данная медиана будет делить любой из отрезков пополам, который параллельный отрезку AD и находящийся между сторонами АO и OD. Все дело в том, что любой из треугольников с той же вершиной O, что и треугольник AOD и с основанием находящимся между сторонам АO и OD при этом параллельным AD будет подобен самому треугольнику AOD. (по трем углам). Из свойства о медиане в прямоугольном треугольнике мы знаем, что медиана, проведенная к гипотенузе, равна половине гипотенузы.
$OM=\frac{BC}2$
а для MN будет справедливо следующее утверждение:
$\frac{BC}2+MN=\frac{AD}2\\MN\;=\frac{AD}2-\frac{BC}2\\MN\;=\frac{AD-BC}2$
При этом есть и KL, она является средней линией трапеции, которая обладает следующим свойством. Средняя линия трапеции параллельна основаниям и равна их полусумме. Значит:
$KL\;=\;\frac{AD+BC}2\\\\\\$
При этом из условия задачи мы знаем, что соединяющие середины противоположных сторон трапеции, равны 6 и 2. То есть разница между KL и МН это разница между этими значениями, при этом KL=6 больше МН=2, исходя их равенств выше, то есть.
KL-МН=6-2=4
Выражая тоже самое исходя из равенств выше получаем.
$\;\frac{AD+BC}2-\frac{AD-BC}2=4\\\frac{AD+BC-(AD-BC)}2=4\\\frac{AD+BC-AD+BC}2=4\\\frac{2BC}2=4\\BC=4\\\\\\\\$
Теперь подставляем значение BC=4 в выше полученное равенство, при условии KL=6:
$\;KL=\frac{AD+BC}2^{}\\6=\frac{AD+4}2\\AD+4=12\\AD=12-4\\AD=8\\\\\\\\\\\\\\$
Ответ: 4, 8
B9101E
Углы при одном из оснований трапеции равны 86° и 4°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 4 и 1. Найдите основания трапеции.
Решение:
Продлим стороны AB и CD до пересечения в точке O В треугольнике AKD сумма углов KAD и KDA равна 90°, следовательно, величина
∠AOD=180-(∠OAD-∠ODA)=90º
Значит, треугольник AOD — прямоугольный. Рассмотрим треугольник AOD, при этом проведем медиану OF. Примечательно, что данная медиана будет делить любой из отрезков пополам, который параллельный отрезку AD и находящийся между сторонами АO и OD. Все дело в том, что любой из треугольников с той же вершиной O, что и треугольник AOD и с основанием находящимся между сторонам АO и OD при этом параллельным AD будет подобен самому треугольнику AOD. (по трем углам). Из свойства о медиане в прямоугольном треугольнике мы знаем, что медиана, проведенная к гипотенузе, равна половине гипотенузы.
$OM=\frac{BC}2$
а для MN будет справедливо следующее утверждение:
$\frac{BC}2+MN=\frac{AD}2\\MN\;=\frac{AD}2-\frac{BC}2\\MN\;=\frac{AD-BC}2$
При этом есть и KL, она является средней линией трапеции, которая обладает следующим свойством. Средняя линия трапеции параллельна основаниям и равна их полусумме. Значит:
$KL\;=\;\frac{AD+BC}2\\\\\\$
При этом из условия задачи мы знаем, что соединяющие середины противоположных сторон трапеции, равны 4 и 1. То есть разница между KL и МН это разница между этими значениями, при этом KL=4 больше МН=1, исходя их равенств выше, то есть.
KL-МН=4-1=3
Выражая тоже самое исходя из равенств выше получаем.
$\;\frac{AD+BC}2-\frac{AD-BC}2=3\\\frac{AD+BC-(AD-BC)}2=3\\\frac{AD+BC-AD+BC}2=3\\\frac{2BC}2=3\\BC=3\\\\\\\\$
Теперь подставляем значение BC=3 в выше полученное равенство, при условии KL=4:
$\;KL=\frac{AD+BC}2^{}\\4=\frac{AD+3}2\\AD+3=8\\AD=8-3\\AD=5\\\\\\\\\\\\\\$
Ответ: 3, 5
BA70C1
Углы при одном из оснований трапеции равны 18° и 72°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 4. Найдите основания трапеции.
Решение:
Продлим стороны AB и CD до пересечения в точке O В треугольнике AKD сумма углов KAD и KDA равна 90°, следовательно, величина
∠AOD=180-(∠OAD-∠ODA)=90º
Значит, треугольник AOD — прямоугольный. Рассмотрим треугольник AOD, при этом проведем медиану OF. Примечательно, что данная медиана будет делить любой из отрезков пополам, который параллельный отрезку AD и находящийся между сторонами АO и OD. Все дело в том, что любой из треугольников с той же вершиной O, что и треугольник AOD и с основанием находящимся между сторонам АO и OD при этом параллельным AD будет подобен самому треугольнику AOD. (по трем углам). Из свойства о медиане в прямоугольном треугольнике мы знаем, что медиана, проведенная к гипотенузе, равна половине гипотенузы.
$OM=\frac{BC}2$
а для MN будет справедливо следующее утверждение:
$\frac{BC}2+MN=\frac{AD}2\\MN\;=\frac{AD}2-\frac{BC}2\\MN\;=\frac{AD-BC}2$
При этом есть и KL, она является средней линией трапеции, которая обладает следующим свойством. Средняя линия трапеции параллельна основаниям и равна их полусумме. Значит:
$KL\;=\;\frac{AD+BC}2\\\\\\$
При этом из условия задачи мы знаем, что соединяющие середины противоположных сторон трапеции, равны 15 и 4. То есть разница между KL и МН это разница между этими значениями, при этом KL=15 больше МН=4, исходя их равенств выше, то есть.
KL-МН=15-4=11
Выражая тоже самое исходя из равенств выше получаем.
$\;\frac{AD+BC}2-\frac{AD-BC}2=11\\\frac{AD+BC-(AD-BC)}2=11\\\frac{AD+BC-AD+BC}2=11\\\frac{2BC}2=11\\BC=11\\\\\\\\$
Теперь подставляем значение BC=11 в выше полученное равенство, при условии KL=15:
$\;KL=\frac{AD+BC}2^{}\\15=\frac{AD+11}2\\AD+11=30\\AD=30-11\\AD=19\\\\\\\\\\\\\\$
Ответ: 11, 19
ECF283
Углы при одном из оснований трапеции равны 80° и 10°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 20 и 17. Найдите основания трапеции.
Решение:
Продлим стороны AB и CD до пересечения в точке O В треугольнике AKD сумма углов KAD и KDA равна 90°, следовательно, величина
∠AOD=180-(∠OAD-∠ODA)=90º
Значит, треугольник AOD — прямоугольный. Рассмотрим треугольник AOD, при этом проведем медиану OF. Примечательно, что данная медиана будет делить любой из отрезков пополам, который параллельный отрезку AD и находящийся между сторонами АO и OD. Все дело в том, что любой из треугольников с той же вершиной O, что и треугольник AOD и с основанием находящимся между сторонам АO и OD при этом параллельным AD будет подобен самому треугольнику AOD. (по трем углам). Из свойства о медиане в прямоугольном треугольнике мы знаем, что медиана, проведенная к гипотенузе, равна половине гипотенузы.
$OM=\frac{BC}2$
а для MN будет справедливо следующее утверждение:
$\frac{BC}2+MN=\frac{AD}2\\MN\;=\frac{AD}2-\frac{BC}2\\MN\;=\frac{AD-BC}2$
При этом есть и KL, она является средней линией трапеции, которая обладает следующим свойством. Средняя линия трапеции параллельна основаниям и равна их полусумме. Значит:
$KL\;=\;\frac{AD+BC}2\\\\\\$
При этом из условия задачи мы знаем, что соединяющие середины противоположных сторон трапеции, равны 20 и 17. То есть разница между KL и МН это разница между этими значениями, при этом KL=20 больше МН=17, исходя их равенств выше, то есть.
KL-МН=20-17=3
Выражая тоже самое исходя из равенств выше получаем.
$\;\frac{AD+BC}2-\frac{AD-BC}2=3\\\frac{AD+BC-(AD-BC)}2=3\\\frac{AD+BC-AD+BC}2=3\\\frac{2BC}2=3\\BC=3\\\\\\\\$
Теперь подставляем значение BC=3 в выше полученное равенство, при условии KL=20:
$\;KL=\frac{AD+BC}2^{}\\20=\frac{AD+3}2\\AD+3=40\\AD=40-3\\AD=37\\\\\\\\\\\\\\$
Ответ: 3, 37
7B2FE8
Углы при одном из оснований трапеции равны 39° и 51°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 19 и 17. Найдите основания трапеции.
Решение:
Продлим стороны AB и CD до пересечения в точке O В треугольнике AKD сумма углов KAD и KDA равна 90°, следовательно, величина
∠AOD=180-(∠OAD-∠ODA)=90º
Значит, треугольник AOD — прямоугольный. Рассмотрим треугольник AOD, при этом проведем медиану OF. Примечательно, что данная медиана будет делить любой из отрезков пополам, который параллельный отрезку AD и находящийся между сторонами АO и OD. Все дело в том, что любой из треугольников с той же вершиной O, что и треугольник AOD и с основанием находящимся между сторонам АO и OD при этом параллельным AD будет подобен самому треугольнику AOD. (по трем углам). Из свойства о медиане в прямоугольном треугольнике мы знаем, что медиана, проведенная к гипотенузе, равна половине гипотенузы.
$OM=\frac{BC}2$
а для MN будет справедливо следующее утверждение:
$\frac{BC}2+MN=\frac{AD}2\\MN\;=\frac{AD}2-\frac{BC}2\\MN\;=\frac{AD-BC}2$
При этом есть и KL, она является средней линией трапеции, которая обладает следующим свойством. Средняя линия трапеции параллельна основаниям и равна их полусумме. Значит:
$KL\;=\;\frac{AD+BC}2\\\\\\$
При этом из условия задачи мы знаем, что соединяющие середины противоположных сторон трапеции, равны 19 и 17. То есть разница между KL и МН это разница между этими значениями, при этом KL=19 больше МН=17, исходя их равенств выше, то есть.
KL-МН=19-17=2
Выражая тоже самое исходя из равенств выше получаем.
$\;\frac{AD+BC}2-\frac{AD-BC}2=2\\\frac{AD+BC-(AD-BC)}2=2\\\frac{AD+BC-AD+BC}2=2\\\frac{2BC}2=2\\BC=2\\\\\\\\$
Теперь подставляем значение BC=2 в выше полученное равенство, при условии KL=19:
$\;KL=\frac{AD+BC}2^{}\\19=\frac{AD+2}2\\AD+2=38\\AD=38-2\\AD=36\\\\\\\\\\\\\\$
Ответ: 2, 36
84CE9A
Углы при одном из оснований трапеции равны 7° и 83°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 14 и 11. Найдите основания трапеции.
Решение:
Продлим стороны AB и CD до пересечения в точке O В треугольнике AKD сумма углов KAD и KDA равна 90°, следовательно, величина
∠AOD=180-(∠OAD-∠ODA)=90º
Значит, треугольник AOD — прямоугольный. Рассмотрим треугольник AOD, при этом проведем медиану OF. Примечательно, что данная медиана будет делить любой из отрезков пополам, который параллельный отрезку AD и находящийся между сторонами АO и OD. Все дело в том, что любой из треугольников с той же вершиной O, что и треугольник AOD и с основанием находящимся между сторонам АO и OD при этом параллельным AD будет подобен самому треугольнику AOD. (по трем углам). Из свойства о медиане в прямоугольном треугольнике мы знаем, что медиана, проведенная к гипотенузе, равна половине гипотенузы.
$OM=\frac{BC}2$
а для MN будет справедливо следующее утверждение:
$\frac{BC}2+MN=\frac{AD}2\\MN\;=\frac{AD}2-\frac{BC}2\\MN\;=\frac{AD-BC}2$
При этом есть и KL, она является средней линией трапеции, которая обладает следующим свойством. Средняя линия трапеции параллельна основаниям и равна их полусумме. Значит:
$KL\;=\;\frac{AD+BC}2\\\\\\$
При этом из условия задачи мы знаем, что соединяющие середины противоположных сторон трапеции, равны 14 и 11. То есть разница между KL и МН это разница между этими значениями, при этом KL=14 больше МН=11, исходя их равенств выше, то есть.
KL-МН=14-11=3
Выражая тоже самое исходя из равенств выше получаем.
$\;\frac{AD+BC}2-\frac{AD-BC}2=3\\\frac{AD+BC-(AD-BC)}2=3\\\frac{AD+BC-AD+BC}2=3\\\frac{2BC}2=3\\BC=3\\\\\\\\$
Теперь подставляем значение BC=3 в выше полученное равенство, при условии KL=14:
$\;KL=\frac{AD+BC}2^{}\\14=\frac{AD+3}2\\AD+3=28\\AD=28-3\\AD=25\\\\\\\\\\\\\\$
Ответ: 3, 25
C5871A