Весьма интересная тема возведения числа в степень. Причем в ней есть не только праздный интерес эксперимента с цифрами, но и вполне прагматичная практика, применяемая каждодневно, которую быть может мы упускаем из виду, но которая как раз подразумевает возведения числа в степень. Это измерения площади, объема, переход от одного разряда к другому...
 Итак, возведение в степень, степень числа, - что это такое, как высчитывается, как это понимать? Именно об этом и будет моя статья, которая поможет вам в очередной раз окунуться в практический эксперимент с цифрами, узнать о новой главе в математике! Начнем!

Как записывается степень числа и что она означает

 Начну с простого и общепринятого. Степень числа это уже полученный и определенный результат, который находится из вычисления типа - aⁿ. Как это записывается теперь нам понятно, что это значит? Здесь же приведу выражение такого вида.

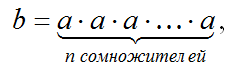
Такое выражение более предметно для нашей темы, так как по факту b и есть степень числа, которая находится путем умножения числа а самого на себя n раз. Это можно записать так. b = aⁿ. А если тоже самое выразить в цифрах, а не условных буквенных символах, то получается так.

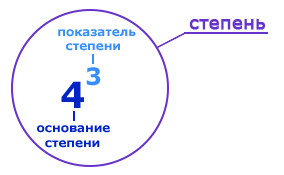
И тут пришло самое время для определения, что же такое степень числа.

Степень числа - это результат вычисления, при умножении числа на само себя такое количество раз, какое указано в показателе степени числа. 

Весьма просто и понятно, если вдуматься и перечитать еще раз, взглянув на все то, о чем я уже говорил. Самое время переходить к частным случаям, которые как всегда начинают проявляться при попытке применять для вычислений крайние и критические значения. Давайте о них.

Свойства степени числа (особенности)

Далее в виде таблички приведу эти самые критические показатели, для вычисления степени числа.

Резюмирую:

1) Если любое число взять в показатели степени 1, то получится тоже самое число!
2) Если любое число взять в показатели степени 0, то получится 1! Заметьте, что не 0, так как в противном случае последующие свойства при этом потеряют свой смысл вычисления.
3) При умножении/делении одинаковых чисел показатели степени складываются при умножении и вычитаются при делении.
4) При возведении числа в степени в степень, степени перемножаются между собой.
5) При умножении/делении разных чисел при одинаковом показателе степени, числа можно вначале умножить/разделить, а потом результат взять в том самом одинаковом показателе степени.

Что же, это весьма кратко, на само деле не плохо бы потренировать ваше сознание на возможное применение этих свойств на практике, что я сейчас и сделаю. 

Пример возведения числа в степень

Давайте еще раз о том же выражении, что уже приводил.

То есть согласно определения получается так.

4³=4*4*4=16*4=64

 В общем то для этого простого примера все понятно. Да и все остальные случаи с конкретными примерами вполне под силу, если обращаться к табличке выше, а потом основные правила и свойства запомнятся и вы будете обходиться вовсе без подсказок.

Онлайн калькулятор возведения числа в степень

Ну и оставить вас без какого-либо тематического развлечения я просто не мог. Оно в очередной раз вам позволит осознать как же происходят вычисления, какие цифры получаются при возведении в степень... А да, заметьте, что я еще на сказал, что показатель степени числа может быть не только целым числом. Что при этом получится, вы можете сами проверить на онлайн калькуляторе.

Побалуемся с возведением в степень!?

Проверим теперь ваши знания с помощью теста - онлайн