Задания и тренажеры по математике

Математика - наука точная. И, как в любой науке, в ней важна практика. 45 минут в день в школе  - это капля в море математической науки. За это время учитель может лишь успеть объяснить новый материал, объяснить, как решать то или иное задание. Но наработка навыков счета, навыков решения задач приходит только с практикой. Практика очень важна в изучении математики. Без практики не получится быстро считать в уме или при помощи письменных приемов. Математика помогает поддерживать ум и мыслительные способности в тонусе. Она вокруг нас. Каждый день, сами того не подозревая, мы выполняем какие-то математические задачи. А если жизнь не подкидывает вам нужное их количество, мы поможем. Вот вам дополнительные задания по математике в виде тренажеров и заданий на лето, на каникулы, чтобы поддерживать мозг в тонусе.

Категория: Задания и тренажеры по математике

Контрольная поделена на 2 части. Первая часть - арифметический диктант. Диктует учитель. Вторая часть на карточках по вариантам, раздается ученикам. Задания соответствуют пройденному на уроке математики материалу по соответствующим УМК.

Категория: Задания и тренажеры по математике

Задачи про весыХотя и не увидишь сейчас везде чашечных весов, поскольку их везде заменили электронные, но все же тема взвешивания на них не должна пройти мимо учеников. Именно поэтому задачи про весы и взвешивание предметов и даже животных были и будут в учебниках и рабочих тетрадях по математике. Давайте рассмотим некоторые из них, порешаем вместе. Мы вам с удовольствием объясним, как решаются такие задачи.

Категория: Задания и тренажеры по математике

Калькулятор столбиком Ингода нашим школьникам задают примеры для решения которых необходимо записывать все столбиком. В итоге, когда ученики осваивают такие вычисления, то приходится все равно выполнять эту рутинную работу, то есть писать все поэтапно и по строкам. Так вот, чтобы хоть как-то и немного облегчить им труд, в том числе и для сверки таких предметов, мы предлагаем воспользоваться нашим калькулятором. В него можно внести, вбить цифры и выбрать действие. В итоге он все посчитает и перед вами появиться пример столбиком в таком виде, в котором его сразу можно будет записать в тетрадь. Все это очень удобно и здорово!

Категория: Задания и тренажеры по математике

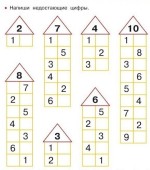Задания с домиками на состав числаЗнание "на зубок" состава числа очень поможет ребенку преуспеть в математике, поскольку большинство математических действий потребуют знать состав числа до десяти. Можно, конечно, считать, загибая пальцы, но это долго и в некоторых случаях не уместно. Когда нужно начинать это учить? Можно непосредственно при подготовке к школе, а в первом классе уже не только можно, но и нужно. А поскольку составу числа в школе уделяется не много времени, мы подготовили для вас некоторые задания, которые помогут на практике закрепить знание состава чисел до 10.

Категория: Задания и тренажеры по математике

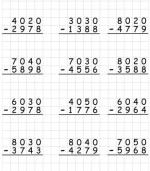Умение считать в уме, конечно же, дело большое и нужное. Но что же делать с трех, четырех, пятизначными числами? В уме их так просто не сосчитаешь и хочется взять листочек бумаги и произвести сложение или вычитание в столбик. При определенной практике счет в столбик не составит труда. Но только если была эта самая практика. Очень важно научиться быстро складывать и вычитать столбиком большие числа, если сложно это сделать в уме. Для этих целей и предназначен наш тренажер по математике на этой страничке. Это умение пригодится на всех самостоятельных работах даже в старших классах и выручит на ЕГЭ. Ведь всем известно, что основная ошибка экзамена - это ошибка в вычислених. Чтобы потренироваться, нужно скачать и распечатать нужный лист с заданием.

Категория: Задания и тренажеры по математике

Тренажер на сложение и вычитание с переходом через десятокНавыки счета очень важны не только для успешной учебы, но и пригодятся в жизни человеку до самой старости. Именно поэтому их нужно отработать и закрепить еще в начальных классах. На уроках, к сожалению, не столь много времени, чтобы успеть поупражняться на тренажерах, поэтому такие занятия стоит проводить с ребенком дома. Учитель не в праве давать ребенку задания на дом сверх программы, потому отработка навыков счета полностью лежит на совести родителей. Нельзя, чтобы ребенок пользовался при выполнении домашнего задания калькулятором. Да, сейчас ему будет проще, но как он будет складывать и вычитать на самостоятельной и контрольной работе без калькулятора? Сложение и вычитание с переходом через десяток стоит особняком среди других. Для того, чтобы правильно выполнять такие действия, нужно хорошо знать состав числа, поэтому для начала закрепите с ребенком тему на состав числа, а потом приступайте непосредственно к решению уравнений.

Категория: Задания и тренажеры по математике
Онлайн калькулятор на сложение
Слагаемое 1
Слагаемое 2

Категория: Задания и тренажеры по математике

Тренажер на сложение и вычитание в пределах 100 В нашу жизнь прочно вошло такое приспособление для счета как калькулятор, но в школьной программе учителя требуют, чтобы ученики обходились без него, чтобы считали в уме или на черновике с помощью письменных приемов. Но считать в уме в пределах сотни не так уж просто. Для этого нужна практика и еще раз практика. Нужно решать уравнения каждый день. Решать в уме и столбиком, складывать и вычитать. Для этого и пригодятся наши тренажеры по математике. Для разминки, начать лучше с простых примеров и постепенно переходить к более сложным. Собственно, в таком порядке уравнения и расположены в первом тренажере. Второй тренажер поможет закрепить всю тему, в нем собраны все примеры на сложение и вычитание в пределах сотни вразброс. Оставлены окошечки под ответы.

Категория: Задания и тренажеры по математике

 Если вы начали читать эту статью с желанием разобраться как же все-таки найти эти непонятные проценты из какого-либо числа, то уж не останавливайтесь, ведь на то есть две причины! Первая, вам это явно пойдет на пользу, ведь любой мало-мальски грамотный человек должен знать, как же посчитать проценты от любого числа. Второе, я думаю, мое объяснение будет весьма импозантным и доходчивым, чтобы хмурое небо разошлось в вашем сознании, и вы ясно увидели, как же это все логично и просто на самом деле!

Категория: Числа в математике

 В одной из статей я уже рассказывал о простых числах... Повторюсь, что это натуральные числа, который делятся лишь сами на себя и на 1. Так вот, такие простые числа имеют и свою определенную практичную ценность!
 Все дело в том, что когда мы имеет дело с дробями и находим наименьший общий знаменатель, то именно для его нахождения у двух дробей и используются эти самые простые числа, когда они являются массивом, то есть "набором" множителей, выражающих какое-то другое число. 
 И как вы уже начали догадываться, именно о разложение числа на простые множители и пойдет речь в моей статье.

Категория: Числа в математике

 Не буду ходить вокруг да около, а начну сразу с определения. Именно оно расставит все точки над "И". Итак, просто́е число́ — это натуральное (целое положительное) число, имеющее только два возможных натуральных делителя — единицу и самого себя.

   Другими словами, число является простым, если оно больше 1 и при этом делится без остатка только на 1 и на само себя. Все вот так просто о простых числах. Дальше расскажу уже необязательную но интересную программу об этих числах.

Категория: Числа в математике

 Весьма интересен путь человечества в совершенствовании исчисления, расчетов, подсчетов и записи натуральных чисел. Да, действительно, было неминуемо и кроме того, неотвратима необходимость сохранения всяческих данных в числовом формате. Это относилось и к простому учету зерна у крестьянина и к необходимости знать сколько же золотых монет у императора, царя, фараона, правителя...
 В целом числовые форматы со времен своего появления и до нашего времени нисколько не утратили актуальности своего значения, разве что постепенно трансформировались в истории человечества. Не трудно предположить, что первые цифры были черточки и более ничего... Но сами понимаете, если особо считать нечего, то одной, двух, ну 10 черточек достаточно. А вот когда счет идет на десятки, сотни и тем более уж десятки тысяч, то без условностей не обойтись. Со временем часть единиц, то есть этих самых черточек стала превращаться в новые символы, так и появились разряды и классы.

Категория: Числа в математике

 В этой статье, как вы уже догадались по заголовку, я расскажу вам про среднее арифметическое число. Расскажу о том, что это такое, как его находить и для того, чтобы у вас была возможность "побаловаться", приведу еще и онлайн калькулятор по нахождению среднего арифметического. Итак, давайте вначале с того, что же такое среднее арифметическое число. 
 Пусть не каждый, но многие из вас учатся в средних образовательных школах (СОШ), одна получше, другая похуже, но в целом каждый из вас учится в средненькой такой школе! Этот пример хотя и можно отнести к иронии, но как говорится в каждой шутке есть доля правды. Ведь среднее арифметическое как раз и отображает обобщенный показатель из выбранного множества. Среднее арифметическое отображает "нейтралитет" среди критических значений, при этом, чем более критично учитываемое значение, тем большее влияние оно оказывает на наше среднее арифметическое. И с точностью наоборот, если все числа из выборки равны, как говорят "под одну гребенку", то и среднее будет равно любому из равных. 

Категория: Числа в математике

 Если вы читали нашу статью о возведении в степень или что-то аналогичное, то наверное уже усвоили одну из особенностей, можно сказать свойств возведения в степень. Любое из чисел в 0 степени равно 1.  С первого взгляда может показаться, что число в 0 степени равно 0, но это не так. Почему? Сейчас объясним!
 Лучше всего объяснять не на пальцах, а на конкретных примерах. Поэтому перейдем сразу к ним. Именно используя вычисления и логику, мы и будем постепенно двигаться к нашему умозаключению!

Категория: Числа в математике

 Весьма интересная тема возведения числа в степень. Причем в ней есть не только праздный интерес эксперимента с цифрами, но и вполне прагматичная практика, применяемая каждодневно, которую быть может мы упускаем из виду, но которая как раз подразумевает возведения числа в степень. Это измерения площади, объема, переход от одного разряда к другому...
 Итак, возведение в степень, степень числа, - что это такое, как высчитывается, как это понимать? Именно об этом и будет моя статья, которая поможет вам в очередной раз окунуться в практический эксперимент с цифрами, узнать о новой главе в математике! Начнем!

Категория: Числа в математике

 Не знаю как вы, но я порой нет нет да и задаюсь вопросом, -  что такое частное чисел? ...вот в голове очень хорошо уложилось что такое сумма (произведение), разность (вычитание), произведение (умножение), а вот деление никак не ассоциируется со словом частное! Ведь подобное слово в нашей жизни в большинстве случаев применяется для определения какой-либо особенности, то есть скажем частного из общего, но никак не в качестве слова поделить что-то на что-то.
 Ну да ладно, на вопрос о том, что такое частное можно сказать я уже ответил в своих рассуждениях! Сейчас осталось рассказать о частном из всех возможных простых математических операций, то есть о делении, однако уже в ключе математического мышления, с определением что такое частное и примерами деления для разных чисел.

Категория: Числа в математике

 Одна из важных математических операций это произведение чисел. Что же скрыто за этими словами как произведение, умножение...? Именно об этом в нашей статье.
 Давайте наверное начнем с банальных вещей. Когда у нас появляется много чего-то, то довольно сложно это хранить даже в виде информации. Нам каким-то образом это приходится компактно сокращать. Вот скажем у нас появилось более чем две пары носков в шкафу, а точнее пусть их будет 15... Как нам из записать на бумаге. Да, конечно, мы можем взять и записать 2+2+2... и так далее, пока не перечислим цифру два, с которой ассоциируется одна из пар носков на их количество, то есть на 15. Но это ведь право не удобно, особенно если представить, что речь идет не только о наших носках в шкафу, но и о случае их хранения в магазине! И здесь проще записать словами так. У нас две пары носков взято какое-то количество раз! 

Категория: Числа в математике

 Еще одно простое математическое действие, как называют его операция, - разность чисел. В этой статье как раз поговорим об этой самой разности. На самом деле разность это лишь результат вычисления, а получается он когда из уменьшаемого вычитают вычитаемое.
 Ну давайте не буде торопиться, сейчас мы все разберем более подробно с примерами и объяснениями.

Категория: Числа в математике

 В то время когда мы с вами не задумываясь манипулируем операциями над числами, нам совсем невдомек, как же легко и подсознательно нам даются эти самые простые математические вычисления.
 Однако для тех, кто только всего лишь учится, делает свои первые шаги в логике складывания, в голове порой происходит непонятная каша... Конечно, со времени все встанет на свои места, "каша сварится" и будет вполне себе! Однако чтобы это произошло быстрее, необходимо направить обучающихся, подсказать и рассказать им о процессах сложения, суммирования чисел.

Категория: Числа в математике

 Вроде как весьма простое и постоянно применяемое в нашей жизни понятие числа становится весьма неопределенным и размытым, когда вопрос ставится в лоб! А что такое число и какими они бывают? Здесь надо бы выдержать паузу, дабы подумать с чего начать и ограничить себя в неуместной информации для большинства.
 Действительно, раз уж наш сайт ориентирован прежде всего для школьников, то и рассказывать о числах мы будем не то что поверхностно, а просто умолчим о тех из них, которые не применяются в школьной программе. Начнем!

Числа в математике

Геометрия